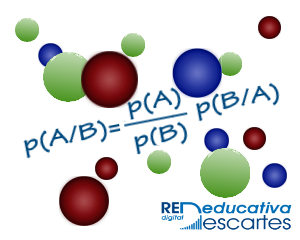Mostrando artículos por etiqueta: probabilidad
Título: Ejercicios de probabilidad a posteriori. Teorema de Bayes
Sección: Miscelánea
Bloque: Estadística y probabilidad
Unidad: Probabilidad elemental
Nivel/Edad: 4º ESO E. Académicas (15 o más años)
Idioma: Castellano
Autoría: Ildefonso Fernández Trujillo
Haz clic en la imagen para abrir el recurso
Descargar recurso Código para embeber como iframe |
Código para abrir en ventana emergente |
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Ejercicios de probabilidad total
Sección: Miscelánea
Bloque: Estadística y probabilidad
Unidad: Probabilidad elemental
Nivel/Edad: 4º ESO E. Académicas (15 o más años)
Idioma: Castellano
Autoría: Ildefonso Fernández Trujillo
Haz clic en la imagen para abrir el recurso
| Código para embeber como iframe |
Código para abrir en ventana emergente |
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Misceláneas. La probabilidad total.
A las cuentas del estado tradicionalmente se les ha llamado estadísticas y habitualmente estas cuentas se han dado a conocer por parte de los sucesivos gobiernos de forma periódica. En la actualidad el diccionario define la estadística como: Ciencia que utiliza conjuntos de datos numéricos para obtener, a partir de ellos, inferencias basadas en el cálculo de probabilidades. En la wikipedia encontramos: "La estadística (la forma femenina del término alemán Statistik, derivado a su vez del italiano statista, "hombre de Estado") es una rama de las matemáticas y una herramienta que estudia usos y análisis provenientes de una muestra representativa de datos, que busca explicar las correlaciones y dependencias de un fenómeno físico o natural, de ocurrencia en forma aleatoria o condicional...."
Dentro de la particularidad que nos ocupa: la probabilidad total, también hemos de tener en cuenta el juego ya que diferentes artistas y científicos interesados en el azar lo han tomado como referencia para elaborar obras y contenidos de indudable valor. En este sentido mostramos a continuación la imagen de una ruleta donde se recomienda el estudio de la situación de los números en la misma.
Ruleta francesa
La imagen anterior enlaza con uno de los blogs del escritor, bloguero y divulgador "freelance" (por libre) Alfred López sobre curiosidades generales, donde muestra una breve pero selecta información relacionada con el tema de la probabilidad y la ruleta. (En este enlace se expone la procedencia de las imágenes que se usan)
En la imagen siguiente puede verse el mantel (que incorpora el cero) de la mesa de juego de la ruleta, lo que nos permite seguir la exposición enlazada anteriormente.
Tapete de ruleta francesa
En la Wikipedia podemos documentarnos, de manera concisa y precisa, sobre el azar
Enlazamos, a continuación con el esmerado trabajo JUGANDO CON LA PROBABILIDAD, elaborado por un grupo de profesores de la Universidad de Granada.
dados
Lo dicho anteriormente y la propia experiencia nos lleva al objetivo principal de esta entrada, un intento de análisis del alma del azar, la incertidumbre. Cuando, a relativamente temprana edad, nos enfrentamos formalmente con la resolución de situaciones donde interviene el azar, ya llevamos un bagaje de conocimientos adquiridos naturalmente a través de los juegos en familia o con las amistades, es decir, ya conocemos la incertidumbre. Pero este conocimiento, lejos de ayudar, en principio parece ser perjudicial, ya que automáticamente la intuición prevé que la solución de una situación donde interviene el azar es inútil ya que fácticamente y de forma inmediata no tiene ningún sentido tangible, es imposible de constatar fácticamente. Más adelante cuando aceptamos la utilidad del conocimiento de la tendencia de un suceso y es más, cuando la realidad nos muestra como una probabilidad se convierte en un hecho fáctico previsto gracias a un buen estudio previo basado en el azar es cuando percibimos la importancia fundamental del conocimiento de las herramientas estadísticas y su utilización. Como introducción a ese estudio y suponiendo que la persona que accede a este artículo ya posee una base elemental de los fundamentos estadísticos y de probabilidad, hemos elaborado la siguiente utilidad donde se analizan y resuelven situaciones relacionadas con la probabilidad total de un suceso.
Probabilidad
En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra, en francés, la introducción al teorema de Bayes.
Animamos a colaborar elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo. 2018
Título: Probabilidade
Sección: EDAD
Bloque: Estadística y probabilidad
Unidad: Probabilidad elemental
Nivel/Edad: 4º ESO-E. Aplicadas (15 a 16 años)
Idioma: Gallego
Autoría: Mª José García Cebrian
Haz clic en la imagen para abrir el recurso
| Código para embeber como iframe |
Código para abrir en ventana emergente |
Puedes encontrar todos los materiales del Proyecto EDAD en https://proyectodescartes.org/EDAD/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Probabilidade
Sección: EDAD
Bloque: Estadística y probabilidad
Unidad: Probabilidad elemental
Nivel/Edad: 4º ESO-E. Académicas (15 a 16 años)
Idioma: Gallego
Autoría: José Ireno Fernández Rubio, Emilio Pazo Núñez
Haz clic en la imagen para abrir el recurso
| Código para embeber como iframe |
Código para abrir en ventana emergente |
Puedes encontrar todos los materiales del Proyecto EDAD en https://proyectodescartes.org/EDAD/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Probabilitat
Sección: EDAD
Bloque: Estadística y probabilidad
Unidad: Probabilidad elemental
Nivel/Edad: 4º ESO-E. Aplicadas (15 a 16 años)
Idioma: Catalán
Autoría: MªJosé García Cebrian
Haz clic en la imagen para abrir el recurso
| Código para embeber como iframe |
Código para abrir en ventana emergente |
Puedes encontrar todos los materiales del Proyecto EDAD en https://proyectodescartes.org/EDAD/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Probabilitat
Sección: EDAD
Bloque: Estadística y probabilidad
Unidad: Probabilidad elemental
Nivel/Edad: 4º ESO-E. Académicas (15 a 16 años)
Idioma: Catalán
Autoría: José Ireno Fernández Rubio, Emilio Pazo Núñez
Haz clic en la imagen para abrir el recurso
| Código para embeber como iframe |
Código para abrir en ventana emergente |
Puedes encontrar todos los materiales del Proyecto EDAD en https://proyectodescartes.org/EDAD/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Probabilidad
Sección: EDAD
Bloque: Estadística y probabilidad
Unidad: Probabilidad elemental
Nivel/Edad: 4º ESO-E. Aplicadas (15 a 16 años)
Idioma: Castellano
Autoría: MªJosé García Cebrian, José Ireno Fernández Rubio
Haz clic en la imagen para abrir el recurso
| Código para embeber como iframe |
Código para abrir en ventana emergente |
Puedes encontrar todos los materiales del Proyecto EDAD en https://proyectodescartes.org/EDAD/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Probabilidad
Sección: EDAD
Bloque: Estadística y probabilidad
Unidad: Probabilidad elemental
Nivel/Edad: 4º ESO-E. Académicas (15 a 16 años)
Idioma: Castellano
Autoría: José Ireno Fernández Rubio, Emilio Pazo Núñez
Haz clic en la imagen para abrir el recurso
| Código para embeber como iframe |
Código para abrir en ventana emergente |
Puedes encontrar todos los materiales del Proyecto EDAD en https://proyectodescartes.org/EDAD/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
En este artículo se pone de manifiesto la conveniencia y utilidad de contar con una herramienta, la calculadora de la Normal, que nos permita dar respuesta de manera cómoda y rápida a múltiples y rutinarios problemas de probabilidad que surgen en estudios con poblaciones que se ajustan a cualquier distribución normal. Se evita el paso de tipificación a la N(0, 1) y se mejora la precisión usual obtenida.
LA DISTRIBUCIÓN NORMAL
Pensemos en voz alta:
- ¿Me gustan los problemas de probabilidad?
- ¿Es difícil plantear y resolver situaciones en las que se requiere contar y recontar casos utilizando técnicas de combinatoria?
- ¿Se parecen mucho algunos problemas de probabilidad a otros?
- ¿Puede pensarse que resolver muchos problemas de probabilidad consiste en realidad en medir de forma aproximada áreas de un aspecto muy determinado?
- Cuando resuelvo un problema de probabilidad siempre tiendo a "dudar" de mi respuesta… y es que siempre he tenido mala "pata" con eso de la suerte.
La estructuración, orden, entendimiento y control en ese escurridizo e inestable mundo, parece llegar en el momento que las Matemáticas clásicas intervienen en el azar con toda su “potencia de fuego” y cuando también, por qué no, se adentran en él con todo su rigor. La introducción del concepto de variable aleatoria —que no es más que el de función— y su ubicación en este contexto con un carácter protagonista supone un primer paso básico y fundamental que conviene tener presente.
Variable aleatoria, funciones de probabilidad y de distribución
El concepto de variable aleatoria como función numérica y su aplicación en la Estadística y la Probabilidad supone un extraordinario avance en estas dos disciplinas. Muchos problemas y situaciones prácticas procedentes de experimentos aparentemente muy diferentes se pueden modelar en un mismo marco teórico mediante variables aleatorias con sus respectivas funciones de probabilidad y de distribución.
- En los casos en que la variable aleatoria sea discreta ―valores aislados―, existen modelos teóricos como la distribución Binomial, la distribución Hipergeométrica, la distribución Geométrica, la Binomial Negativa , la Multinomial,… que permiten la adaptación y estudio de muchos problemas relacionados con experimentos aleatorios procedentes de situaciones muy distintas.
- En los casos en los que la variable aleatoria sea continua ―que pueda tomar, al menos teóricamente, cualquier valor de un intervalo―, sin duda es el modelo de la distribución Normal el que se adapta a un mayor número de situaciones. Caracteres morfológicos como peso, estatura, diámetros, perímetros de la mayoría de especies tanto animales como plantas, errores cometidos en la medición de la mayoría de las magnitudes, caracteres fisiológicos, psicológicos o aquellos que se obtengan en general como suma de otros factores, se distribuyen siguiendo un modelo cuya función de densidad adopta una particular forma y que se conoce como modelo de la distribución Normal.
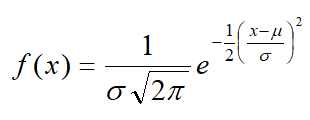
Función de densidad de la distribución normal de media µ y desviación típica σ
Cada modelo de distribución normal va a depender numéricamente de dos parámetros fundamentales que son la media aritmética μ y la desviación típica σ. Es decir, hay una infinidad de distribuciones normales. Por ejemplo:
- Se dice que el cociente intelectual de las personas sigue una distribución normal de media 100 y desviación típica 15. ¿Cuál sería la probabilidad de que una persona tenga un cociente entre…?
- La estatura de los varones de entre 35 y 55 años en España sigue una distribución normal de media 172,9 cm y desviación típica 3,55 cm. ¿Cuál sería la probabilidad de que un varón…?
- La distribución de las notas de selectividad en la asignatura de matemáticas sigue una distribución normal de media 5,85 y desviación típica 2,25. ¿Cuál sería la probabilidad de que un alumno…?
- La distribución de pesos de una ganadería sigue una distribución normal de media 540 kg y desviación típica 15 kg. ¿Cuál sería la probabilidad de que en un grupo de 20 reses al menos la mitad…?
Por otro lado, en Estadística Inferencial el modelo de distribución normal aparece en resultados tan importantes como el Teorema Central del Límite, en las distribuciones en el muestreo de algunos parámetros como las medias muestrales o las proporciones muestrales, así como en aproximaciones de otros modelos teóricos como la distribución binomial o la de Poisson.
Así pues, con la distribución Normal, estamos ante un tema estratégico clave sobre el que se fundamentan y desarrollan otros muchos y que, por tanto, conviene cuanto menos familiarizar a cualquier persona que se "asome" al mundo de la estadística y probabilidad y, por supuesto, que han de conocer y entender todos aquellos que intenten profundizar en él en un futuro.
La distribución normal N(0, 1)
Aunque hay una infinidad de distribuciones normales, tantas como valores toman los dos parámetros anteriores, µ y σ, obviamente todas se corresponden a un único tipo de función o familia de funciones con propiedades comunes en las que µ genera una traslación y σ un cambio de escala. Por ello, dentro de todas las posibles distribuciones normales se considera la que tiene por media cero y desviación típica uno, que usualmente se denota como N(0, 1), y que se establece como referente para hacer manejable este tipo de distribución. Todas las demás podrán relacionarse con la N(0, 1) y, por tanto, basta centrarse en el análisis de ésta y posteriormente trasladar su conocimiento al resto.
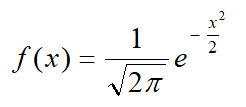
Función de densidad de la distribución normal de media 0 y desviación típica 1, la N(0, 1)
Por tanto, es la N(0, 1) es objeto de minucioso y pormenorizado estudio cuando se busca investigar las diferentes probabilidades que toma su función de distribución.
Probabilidad para valores menores o iguales que zα
La integral anterior no es elemental, es decir no existe una primitiva que pueda expresarse como un conjunto finito de operaciones de funciones elementales y consecuentemente no puede calcularse mediante la aplicación de la regla de Barrow. Por ello, usualmente lo que se aborda es la construcción de una tabla de valores aproximados ―la tabla de la normal cero uno― en la que se refleja el valor de p(z ≤ zα ) para un conjunto de valores de zα.
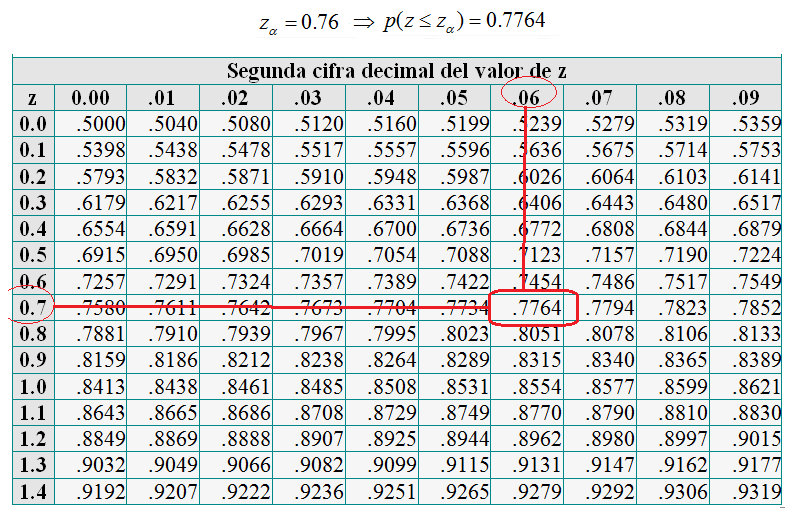Fragmento de la Tabla de la N(0, 1)
En la primera columna de la tabla se refleja el valor de desde 0 a 3,9 con incrementos de una décima (el extremo superior depende de la precisión empleada en el cálculo de valor de p(z ≤ zα )), y en la primera fila se consideran diez columnas etiquetadas desde 0,00 hasta 0,09, de manera que si zα = 0,76 entonces la p(z ≤ zα ) queda reflejada en la fila de etiquetada como 0,7 y en la columna 0,06 (0,76=0,7+0,06). Generalmente el valor de esta probabilidad se refleja con cuatro cifras decimales y cuando éstas no son suficientes hay tablas en la que se consideran cinco decimales. Indiquemos, de nuevo, que el cálculo de esa integral definida no es inmediato y, por ello, la precisión del valor reflejado en la tabla será dependiente del método de cálculo aproximado usado. Para valores de zα del orden de las milésimas o inferior puede considerarse una interpolación, por ejemplo si zα = 0,752 se realizaría una interpolación entre los valores correspondientes a zα = 0,75 y zα = 0,76, es decir, una interpolación posiblemente lineal (aunque no sería la más ajustada) entre los correspondientes valores que son 0,7734 y 0,7764.
Construida la tabla, también es posible plantearse el problema inverso, es decir, dada una probabilidad identificar el valor de zα correspondiente. Para ello se localiza el valor de dicha probabilidad en la tabla, y una vez encontrado entonces la fila y columna donde se ubica nos aporta dicho zα = fila+columna, pudiéndose abordar también una interpolación en caso de que la probabilidad dada no se localice exactamente en la tabla, sino que se encuentre entre dos elementos de la misma.
Para valores negativos de zα, para probabilidades asimilables a barridos a la derecha p(z > zα ) o franjas de probabilidad determinadas entre dos valores p(z-α ≤ z ≤ zα ), se recurre a ciertas estrategias sencillas basadas en razonamientos más o menos directos que utilizan como elementos fundamentales la simetría de la curva y el valor unitario del área global bajo la misma.
Tipificación
Lo obtenido para esa distribución normal particular, la N(0, 1), es muy significativo y extrapolable a cualquier otra distribución normal, pues mediante una fácil transformación en la variable aleatoria ―Tipificación― convertiremos cualquier pregunta directa o inversa sobre una normal cualquiera en una cuestión planteada sobre la N(0, 1) con su correspondiente respuesta rápida.
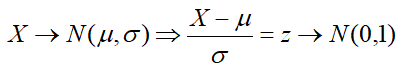Tipificación de una variable aleatoria
Consecuentemente la importancia de la N(0,1), de la tabla de valores asociada y de la tipificación es evidente. Las técnicas y estrategias que permiten la localización de cualquier valor de probabilidad de manera directa o las que se utilizan para la localización de valores críticos que dejan una determinada probabilidad a la izquierda, a la derecha o en una franja central ―manejo inverso―, deben ser comprendidas y utilizadas perfectamente por los alumnos de bachillerato o de primeros cursos de estudios universitarios. Pero, esto no es óbice para preguntarse: ¿la vigencia de la tabla de la N(0,1) es incuestionable?
Preguntémenos y respondamos:
- ¿Cántas veces realizamos el mismo tipo de razonamiento y estrategia en problemas de distribuciones normales?
- ¿Cuántas veces repetiremos el procedimiento hasta automatizarlo?
- ¿Cuántas veces llegaremos a cansarnos de tipificar y consultar la tabla, e interpolar valores?
La respuesta puede ser variable dependiendo de las circunstancias, del número de problemas y de preguntas que desee o necesite responder, pero estamos seguros de que si trabaja o estudia en este contexto la cuantificación será elevada. Por tanto, ¿no estima necesario y conveniente evitar este proceso? y simplemente ¿no desea proceder a realizar una consulta rápida y automática? Posiblemente esté pensando o diciendo ¡Sí! y aquí trataremos de dar satisfacción a su deseo con "La calculadora de la Normal". Quienes ya tengan cierta edad, recordarán lo imprescindibles que también eran las tablas de logaritmos o las tablas trigonométricas hace no mucho tiempo y quienes tengan menos edad podrán indagar por su cuenta y riesgo o en el enlace anterior.
La calculadora de la Normal
La calculadora de la Normal es una escena desarrollada con DescartesJS y lo que pretendemos es que cualquiera con conocimientos teóricos básicos, disponga de una herramienta fácil, directa y rápida que le permita abordar y resolver problemas relacionados con la distribución normal.
Somos conscientes que las calculadoras de gama alta con cierto nivel científico disponen de la posibilidad de cálculo de valores de probabilidad de cualquier distribución normal e incluso en algunos casos de cálculo de valores críticos, (z-valores). Sin embargo el interfaz o la secuencia de cálculo no suelen ser naturales y a menudo muy diferentes de unos modelos a otros. A nuestro entender no se produce esa estrecha comunión entre el modelo teórico que proporcionan el profesor o el libro y el escueto y solitario número con que responde la calculadora. Es por esto, entre otras cosas, por lo que decidimos emprender el desarrollo de una escena sencilla y útil, rápida y con aspectos muy elementales, tanto gráficos como algebraicos que mantengan al menos una mínima conexión ―necesaria en nuestra opinión― con el desarrollo teórico clásico. Y aquí la tienen a su disposición:
El manejo es intuitivo y sencillo, no obstante puede consultar las indicaciones.
Finalmente, sólo nos queda indicaros que esperamos que la utilización de esta escena, de esta calculadora de la Normal, os resulte interesante desde el punto de vista didáctico y útil desde el punto de vista técnico y, en particular, para nuestros colegas docentes que les ayude a implementar el aprendizaje significativo de este tema que consideramos estratégico en Estadística y Probabilidad.
Nota bene técnica
Para aquellos interesados en las consideraciones y criterios matemáticos adoptados en el desarrollo de esta herramienta ―y sólo para ellos por ser cuestiones que, posiblemente, no interesen al usuario habitual― indiquemos algunos detalles técnicos:
- El usuario establece la media y desviación típica y la calculadora realiza la tipificación a la N(0, 1) o viceversa. Aunque no sería necesario mostrar esta tipificación, se refleja por cuestión metodológica en entornos de aprendizaje donde conviene que ésta quede explicitada. Es una calculadora para cualquier media y desviación típica, por lo que representa una mejora respecto a lo habitual.
- Internamente se contruye una tabla para la N(0,1) en la que se ha considerado como intervalo significativo [-4, 4], es decir, p(z<=-4)=0 y p(z<=4)=1.
- En el intervalo [-4, 4] se considera un partición regular de paso una diezmilésima, es decir los valores zα aportados por el usuario o determinados por la calculadora tienen una precisión de cuatro cifras decimales. Esto representa una mejora respecto a la tabla usual que suele estar restringida a dos decimales. Puede ampliarse a más cifras, pero en esta versión se ha ajustado a esta precisión buscando que la necesidad computacional no ralentice el tiempo de respuesta y sea adecuado para la mayoría de dispositivos actuales.
- El cálculo de p(z ≤ zα ), para los valores de zα de esa partición comprendidos en [-4, 0], se realiza calculando la integral definida correspondiente mediante integración numérica aplicando la regla de Simpson compuesta que en este caso tiene una cota de error inferior a 1·10-19. En las escena se reflejan sólo 9 cifras decimales, pero podrían incluirse más (al menos hasta doce correspondientes a la precisión de cálculo interna de Descartes). Esto representa una mejora respecto a lo usual en las tablas que son cuatro o cinco cifras decimales.
- El cálculo de p(z ≤ zα ), para los valores de zα de esa partición comprendidos en (0, 4] se determinan por simetría con los del intervalo [-4, 0] como 1-p(z ≤ -zα ).
- En Inferencia Estadística, por ejemplo en intervalos de confianza o en contraste de hipótesis, es fundamental el manejo inverso de la tabla de la normal. En esta escena se ofrece la posibilidad de localización directa de valores que determinan ciertas probabilidades, tanto franjas de áreas entre dos valores (zα/2) como barridos a la izquierda o a la derecha (zα). La precisión es de cuatro cifras decimales, lo que representa una mejora respecto a lo usual.
