Mostrando artículos por etiqueta: puzles
La semana pasada en Radio Descartes, en el espacio “¿Quién es el personaje misterioso?”, entrevistamos a una matemática excepcional que vivió desde 1850 a 1891. Considerada como la más grande anterior al siglo XX, destacó por dos ideas fundamentalmente, como nos dijo la profesora de la universidad de Estrasburgo Michèle Audin (nacida en 1954): Su famoso teorema, asociado al nombre de Cauchy, que asombró a su maestro Weierstrass, prueba que no siempre una ecuación en derivadas parciales con coeficientes analíticos y condiciones iniciales analíticas tiene solución analítica y el estudio dificilísimo del movimiento de rotación de un cuerpo sólido alrededor de un punto fijo, cuya modelización matemática conduce a un sistema de ecuaciones diferenciales y por el que le concedieron en 1888 el Premio Bordin de la Academia de las Ciencias de París.
Hoy, trascurrida una semana, corresponde desvelar su identidad, como sigue siendo habitual, a través de una escena de DescartesJS que presenta tres imágenes que se pueden ir seleccionando sucesivamente a través de un control de botón. Cada imagen ha sido recortada en 24 cuadrados que pueden girar 90 grados alrededor de su centro cada vez que se hace clic con el ratón sobre cada uno de ellos hasta completar una vuelta completa. Esto es lo que conocemos como puzle giratorio. Un contador indica el número de piezas que están correctamente rotadas con lo que se puede saber si el puzle ha sido armado y en su caso cuantas piezas nos faltan por obtener la imagen definitiva.
La primera imagen representa el DOODLE que GOOGLE-RUSSIA dedicó el día 15 de enero de 2014 a nuestra matemática rusa en el 164 aniversario de su nacimiento.
La segunda imagen es una composición de una fotografía de nuestra matemática muy joven, quizá recién casada, poco antes de salir de su Rusia natal en 1869 para estudiar en Heidelberg y un retrato de su maestro Carl Weierstrass con quien estudió posteriormente en Berlín.
La tercera imagen representa las portadas de tres libros que tratan de nuestra matemática. Uno de ellos se menciona al final de la entrevista que la hicimos, el titulado “Demasiada felicidad” de Alice Munro, Premio Nobel de Literatura en 2013. Los otros libros son “Recordando a…” de Michèle Audin, a la que ya hemos mencionado anteriormente y “Love and Mathematics” de Pelageya Polubarinova-Kochina (1899-1999), jefa del departamento de mecánica teórica de la Universidad de Novosibirsk.
El autor de este artículo, la edición de las imágenes y la programación del puzle es Ángel Cabezudo Bueno y tiene licencia CC BY-NC-SA 3.0.
El puzle giratorio básico tiene su origen en una documentación aportada por Juan Guillermo Rivera Berrío.
Gracias por la atención que ha recibido este sexto personaje matemático y no os perdáis el septimo podcast que emitiremos el próximo día 3 de noviembre en este blog de difusión.
La semana pasada en Radio Descartes, en el espacio “¿Quién es el personaje misterioso?” entrevistamos a un matemático, astrónomo y físico alemán que vivió desde 1777 a 1855. Contribuyó significativamente en muchos campos, incluida la teoría de números, el análisis matemático, la geometría diferencial, la geodesia, el magnetismo y la óptica. Denominado como "el príncipe de los matemáticos" es considerado uno de los científicos que más influencia ha tenido en la historia.
Hoy, trascurrida una semana, corresponde desvelar su identidad, como sigue siendo habitual, a través de una escena de DescartesJS que presenta tres imágenes que se pueden ir seleccionando sucesivamente a través de un control de botón. Cada imagen ha sido recortada en 24 cuadrados que pueden girar 90 grados alrededor de su centro cada vez que se hace clic con el ratón sobre cada uno de ellos hasta completar una vuelta completa. Esto es lo que conocemos como puzle giratorio. Un contador indica el número de piezas que están correctamente rotadas con lo que se puede saber si el puzle ha sido armado y en su caso cuantas piezas nos faltan por obtener la imagen definitiva.
La primera imagen representa una composición alegórica que incluye la efigie de nuestro personaje inmerso en el espacio astronómico que tanto estudió y en donde se observan diferentes elementos matemáticos vinculados a su obra científica. También podemos reconocer su firma autógrafa.
La segunda imagen es un dibujo que recrea la historia de nuestro personaje a los 10 años, en el aula donde es instruido en aritmética, sentado en su pupitre con sus compañeros y donde su profesor les plantea en la pizarra el problema de sumar todos los números del 1 al 100.
La tercera imagen representa la parte ilustrada en el anverso de un billete de 10 marcos emitido por el Deutsche Bundesbank (Banco Federal Alemán) y que utiliza como motivo la figura de nuestro personaje y su famosa gráfica de Distribución Normal de probabilidad.
El autor de este artículo, la edición de las imágenes y la programación del puzle es Ángel Cabezudo Bueno y tiene licencia CC BY-NC-SA 3.0.
El puzle giratorio básico tiene su origen en una documentación aportada por Juan Guillermo Rivera Berrío.
Gracias por la atención que ha recibido este quinto personaje matemático y no os perdáis el sexto podcast que emitiremos el próximo día 20 de octubre en este blog de difusión.
La semana pasada en Radio Descartes, en el espacio “¿Quién es el personaje misterioso?” entrevistamos a un filósofo y matemático francés, una de las personalidades más destacadas de su tiempo y que más ha influido en el modo de adquirir el conocimiento y en el desarrollo de la ciencia. Su obra ha sido tan seguida y estudiada que no habrá sido muy difícil dar con el personaje pues en la entrevista se daban al menos dos pistas claves:
- A los ejes donde representamos las curvas les llamamos ejes “cartesianos” en su honor.
- Escribió un libro sobre el “Método” para demostrar la verdad.
Hoy, trascurrida una semana, corresponde desvelar su identidad, como sigue siendo habitual, a través de una escena de DescartesJS que presenta tres imágenes que se pueden ir seleccionando sucesivamente a través de un control de botón. Cada imagen ha sido recortada en 24 cuadrados que pueden girar 90 grados alrededor de su centro cada vez que se hace clic con el ratón sobre cada uno de ellos hasta completar una vuelta completa. Esto es lo que conocemos como puzle giratorio. Un contador indica el número de piezas que están correctamente rotadas con lo que se puede saber si el puzle ha sido armado y en su caso cuantas piezas nos faltan por obtener la imagen definitiva.
La primera imagen representa el busto del personaje obtenido de un recorte del retrato pintado por Frans Hals y que se encuentra en el Museo del Louvre, París. Me he permitido incluir en el ángulo inferior derecho la firma autógrafa de nuestro insigne matemático, pues creo que puede tener cierto interés para nuestros lectores.
La segunda imagen es una composición de dos partes, a la izquierda un ex libris editado en París en 1668 del “Discurso del Método. Para conducir bien la razón y buscar la verdad en las ciencias. Más La Dióptrica y los Meteoros” y a la derecha un fragmento traducido al español de las cuatro reglas o preceptos que aparecen en la segunda parte del discurso y que le permitió alcanzar el conocimiento empezando por desprenderse, dudando, de todas las nociones adquiridas en los libros: 1. Regla de la evidencia, 2. Regla del análisis, 3. Regla de la síntesis y 4. Regla de la enumeración. En la cuarta parte del discurso, se encuentra la conocida frase “Je pense, donc je suis” (Cogito, ergo sum/Pienso, luego existo) que nuestro personaje consideró tan firme y segura para tomarla como principio de la filosofía que buscaba. He grabado esta frase y se puede escuchar cuando cualquiera de las tres imágenes del puzle se arma completamente con sus 24 piezas.
La tercera imagen es un cuadro de Pierre Louis Dumesnil, que se encuentra en el Museo Nacional de Versalles. Representa a nuestro personaje en la Corte de la reina Cristina de Suecia con la que se carteaba desde 1646. La amistad y admiración que le profesaba la reina era extraordinaria. Nuestro personaje aceptó su invitación y llegó a Estocolmo en 1649 siendo recibido con grandes honores. Toda la corte se reunía en la biblioteca del palacio para escuchar sus lecciones de filosofía, física y matemáticas. En febrero del año siguiente moría allí de neumonía, según la versión oficial, como consecuencia del frío de la capital sueca, las pocas condiciones para vencerlo y su precaria salud que le acompañó desde niño, aunque un investigación más reciente habla de conspiración y envenenamiento como consecuencia de los odios y persecuciones que desataron sus teorías filosóficas en algunos círculos de influencia de su época.
El autor de este artículo, la edición de las imágenes y la programación del puzle es Ángel Cabezudo Bueno y tiene licencia CC BY-NC-SA 3.0
El puzle giratorio básico tiene su origen en una documentación aportada por Juan Guillermo Rivera Berrío.
Gracias por la atención que ha recibido este cuarto personaje y no os perdáis el quinto podcast que emitiremos el próximo día 29 de septiembre en este blog de difusión.
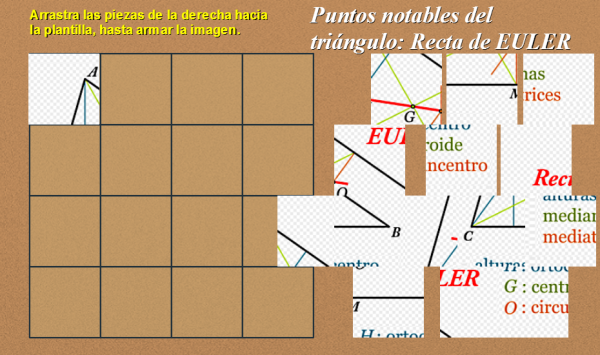
Una vez publicados los artículos de esta serie de puntos notables del triángulo (Ortocentro, Baricentro, Circuncentro e Incentro) concluimos en éste con una propiedad interesante: Se trata de la Recta de Euler, donde se sitúan curiosamente el ortocentro, el baricentro ó centroide y el circuncentro que es motivo para nuevas reflexiones sobre la geometría del triángulo.
Utilizamos como recurso didáctico, al igual que en los anteriores casos, un puzle de arrastre que cuando se arma se muestran algunas observaciones y se enumeran algunas propiedades que invitan a la reflexión y a visitar dos materiales de consulta donde se puede encontrar respuesta a distintas cuestiones a través de la interacción con las escenas de DescartesJS y el visionado de un vídeo.
La siguiente imagen lleva un enlace al puzle que se abrirá en una nueva ventana.
Una vez completada la publicación de la serie de puntos notables del triángulo, todos estos materiales se integrarán en una unidad que llevará por título “Puzles geométricos: Puntos notables del triángulo” y formará parte de la Miscelánea en la sección de Materiales de esta Web.
La semana pasada en Radio Descartes, en el espacio “¿Quién es el personaje misterioso?” hacíamos una entrevista a un célebre matemático, astrónomo, geógrafo, filósofo, filólogo y poeta de la antigüedad griega y evitábamos dar su nombre con el objetivo de que fueran los escuchantes los que con los datos aportados pudieran averiguarlo.
Hoy, trascurrida una semana tal como anunciábamos, vamos a descubrir al personaje a través de una escena de DescartesJS que presenta tres imágenes seleccionadas a través de un control de botón. Cada imagen ha sido recortada en 24 cuadrados que pueden girar 90 grados alrededor de su centro cada vez que se hace clic con el ratón sobre cada uno de ellos hasta completar una vuelta completa. Esto es lo que conocemos como puzle giratorio. Un contador indica el número de piezas que están correctamente rotadas con lo que se puede saber si el puzle ha sido armado y en su caso cuantas piezas nos faltan por obtener la imagen definitiva.
La primera imagen es una composición que muestra un grabado con la efigie que se atribuye al personaje y un esquema que refiere los datos que utilizó para medir el radio de la Tierra.
La segunda imagen es un dibujo que representa un mesolabio, ingenio que se atribuye a nuestro personaje, que sirvió para determinar mecánicamente la medida de dos segmentos medios proporcionales entre otros dos y permitía a los constructores de cubos encontrar la arista del cubo de volumen doble a otro dado.
La tercera imagen es una copia del siglo I del mapamundi atribuido a nuestro personaje. Las tierras y océanos quedan situados geográficamente mediante una red de meridianos de longitud y paralelos de latitud tal como se identificaban en aquellos tiempos.
El autor de este artículo, la edición de las imágenes y la programación del puzle es Ángel Cabezudo Bueno es y tiene licencia CC BY-NC-SA 3.0
El puzle giratorio básico tiene su origen en una documentación aportada por Juan Guillermo Rivera Berrío.
Gracias por la atención que ha recibido este tercer personaje y no os perdáis el podcast del próximo que emitiremos el día 8 de septiembre en este blog de difusión.
En los tres artículos publicados anteriormente de esta misma serie hemos tratado y por este orden el Ortocentro, el Baricentro y el Circuncentro.
Con el Incentro, que hoy es el motivo de este artículo, terminamos la serie de puntos notables que estaba prevista.
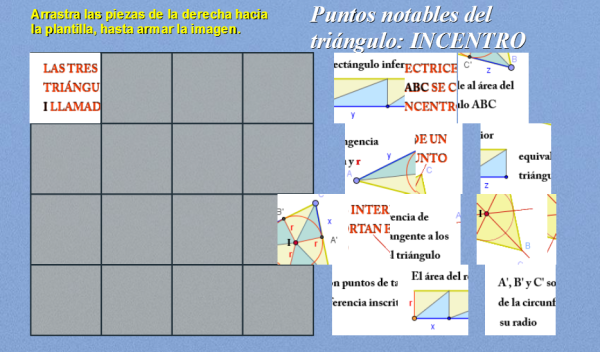
Utilizamos como recurso didáctico, al igual que en los anteriores casos, un puzle de arrastre que una vez armado muestra una imagen donde intervienen como elementos de la composición las bisectrices interiores a un triángulo, el incentro, la circunferencia inscrita y texto. Además cuando se completa el puzle se repasa la definición de bisectriz y se enumeran algunas propiedades que invitan a la reflexión y a visitar dos materiales de consulta donde se puede encontrar respuesta a distintas cuestiones a través de la interacción con las escenas de DescartesJS y de Geogebra y con las explicaciones que allí se recogen.
La siguiente imagen lleva un enlace al puzle que se abrirá en una nueva ventana.
Una vez completada la publicación de la serie de puntos notables del triángulo, se integrarán todos estos materiales en una unidad que llevará por título “Puzles geométricos: Puntos notables del triángulo” y donde además se pondrá como reto armar un nuevo puzle para obtener la Recta de Euler, donde se sitúan curiosamente el ortocentro, el baricentro y el circuncentro que será motivo para nuevas reflexiones sobre la geometría del triángulo.
La semana pasada en Radio Descartes, en el espacio “¿Quién es el personaje misterioso?” hacíamos una entrevista a una célebre matemática de época pasada y evitábamos dar su nombre con el objetivo de que fueran los escuchantes los que con los datos aportados pudieran averiguarlo.
Nos comprometíamos descubrir al personaje al cabo de una semana a través de una escena de DescartesJS que presenta tres imágenes seleccionadas a través de un control de botón. Cada imagen ha sido recortada en 24 cuadrados que pueden girar 90 grados alrededor de su centro cada vez que se hace clic con el ratón sobre cada uno de ellos hasta completar una vuelta completa. Esto es lo que conocemos como puzle giratorio. Un contador indica el número de piezas que están correctamente rotadas con lo que se puede saber si el puzle ha sido armado y en su caso cuantas piezas nos faltan por obtener la imagen definitiva.
La primera imagen es una bonita composición en la que aparece nuestra misteriosa matemática y astrónoma observando las estrellas en un precioso cielo nocturno.
La segunda imagen es un fotograma de la película ÁGORA que recrea la vida de esta matemática y sobre la que pudo dar su opinión en la misma entrevista. Aparece de pie delante de sus alumnos sentados en sus gradas en una de sus habituales clases de astronomía; en ésta les explica la caída vertical y rectilínea de los cuerpos sobre la Tierra.
La tercera imagen es otro fotograma de la película ÁGORA. Aparece nuestra protagonista junto a su padre trabajando sobre una mesa delante de unos manuscritos.
El autor de este artículo, la edición de las imágenes y la programación del puzle es Ángel Cabezudo Bueno y tiene licencia CC BY-NC-SA 3.0
El puzle giratorio básico tiene su origen en una documentación aportada por Juan Guillermo Rivera Berrío.
Gracias por la atención que ha recibido este segundo personaje y no os perdáis el podcast del próximo que emitiremos el día 11 de agosto en este blog de difusión.
En los dos artículos publicados anteriormente de esta misma serie hemos tratado y por este orden el Ortocentro y el Baricentro.
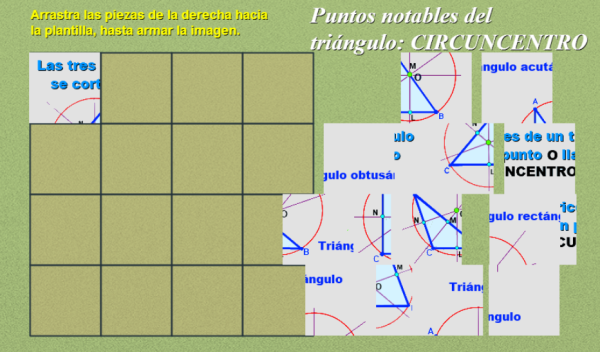
Como continuación, hoy le toca el turno al Circuncentro. Utilizamos como recurso didáctico un puzle de arrastre que una vez armado muestra una imagen de su representación gráfica en tres casos según que el triángulo donde se construye sea acutángulo, rectángulo u obtusángulo. Además cuando se completa el puzle se repasa la definición de mediatriz y se enumeran algunas propiedades que invitan a la reflexión y a visitar dos materiales de consulta donde se puede dar respuesta a distintas cuestiones a través de la interacción con las escenas de DescartesJS y las explicaciones más detalladas que allí se recogen.
La siguiente imagen lleva un enlace al puzle que se abrirá en una nueva ventana.
Una vez completada la publicación de la serie de puntos notables del triángulo, se integrarán todos estos materiales en una unidad que llevará por título “Puzles geométricos: Puntos notables del triángulo” y donde además se pondrá como reto armar un nuevo puzle para obtener la Recta de Euler, donde se sitúan curiosamente el ortocentro, el baricentro y el circuncentro que será motivo para nuevas reflexiones sobre la geometría del triángulo.
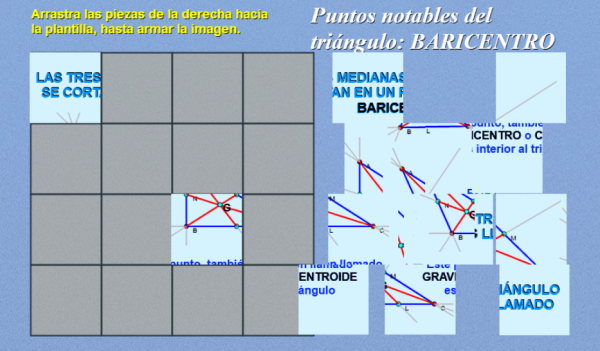
Continuamos en este artículo con la serie de puntos notables del triángulo tal como anunciábamos la semana anterior cuando presentábamos el Ortocentro. Hoy hemos elegido el Baricentro que también suele denominarse Gravicentro y Centroide según diferentes textos donde se consulte.
Se utiliza el puzle como recurso didáctico construido con DescartesJS. Cuando el puzle queda armado se observa una imagen de la posición que ocupa el baricentro en cada uno de los tres tipos de triángulo -rectángulo, acutángulo y obtusángulo- donde se dibujan las tres medianas, indicándose que en los tres casos el punto de corte, el baricentro, es interior. En este momento se repasa el concepto de mediana como recta y como segmento, se enumeran algunas propiedades que invitan a la reflexión y se proporcionan los enlaces a los materiales de consulta donde se puede dar respuesta a distintas cuestiones a través de la interacción con las escenas y las explicaciones más detalladas que allí se recogen.
La siguiente imagen lleva un enlace al puzle que se abrirá en una nueva ventana.
Una vez completada la publicación de la serie de puntos notables del triángulo, integraremos todos estos materiales en un único cuerpo didáctico que llevará por título “Puzles geométricos: Puntos notables del triángulo”.
Este trabajo es el primero de una serie que se irá publicando sucesivamente. Se pretende hacer una revisión de los puntos notables de un triángulo: ortocentro, baricentro, incentro y circuncentro.
Se utilizará el puzle como recurso didáctico construido con DescartesJS y que una vez armado producirá una serie de consultas a materiales didácticos procedentes de diferentes subproyectos: Miscelánea, Unidades Didácticas, Un_100…
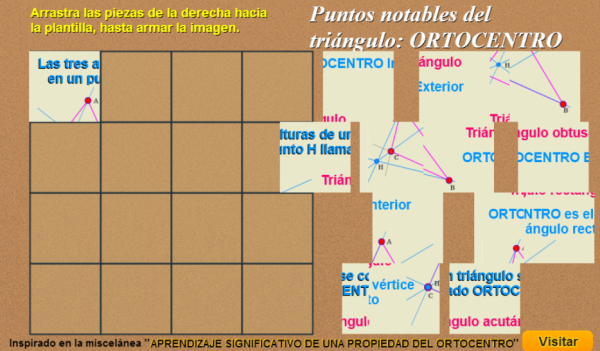
En el caso que nos ocupa ahora, cuando el puzle queda armado se observa una imagen de la posición que ocupa el ortocentro según que el triángulo donde se dibujan las alturas sea acutángulo, rectángulo u obtusángulo. En este momento se repasa el concepto de altura como recta y como segmento, se enumeran algunas propiedades que invitan a la reflexión y se proporcionan los enlaces a los materiales de consulta donde se puede dar respuesta a distintas cuestiones a través de la interacción con las escenas y las explicaciones más detalladas que allí se recogen.
La siguiente imagen lleva un enlace al puzle que se abrirá en una nueva ventana.
Una vez completada la publicación de la serie de puntos notables del triángulo, podremos pensar en integrar todos estos materiales en un solo cuerpo didáctico que llevará por título “Puzles geométricos: Puntos notables del triángulo”.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri)


 CONTACTO
CONTACTO
