La partición de un cubo en pirámides triangulares tiene su cardinal mínimo en cinco pirámides, pero hay una única forma de realizar esta partición. La descomposición en seis pirámides triangulares amplía el número de formas de realizarla y da lugar a particiones que podemos encuadrar en dos bloques: no prismáticas o prismáticas. En estas últimas todas las pirámides son equivalentes (igual volumen) o incluso congruentes. En este artículo nos centraremos en la partición prismática de un cubo en pirámides triangulares equivalentes. Análisis previos que nos conducen a esta situación fueron detallados en el artículo "Partición del cubo en pirámides (parte II)".
Particiones de un cubo en pirámides triangulares equivalentes
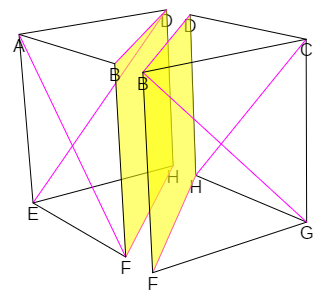
El plano determinado por dos diagonales con igual dirección en dos caras opuestas de un cubo interseca a éste dividiéndolo en dos prismas triangulares cuyas bases son triángulos rectángulos isósceles. Consecuentemente, la descomposición de un cubo en pirámides triangulares puede abordarse analizando la partición de un prisma recto de base un triángulo isósceles rectángulo. Este procedimiento es el que denominaremos partición prismática del cubo. Sin pérdida de generalidad consideraremos que el lado del cubo es la unidad.
Escena 1. División del cubo en dos prismas triangulares
1. Descomposición de un prisma triangular en pirámides triangulares
Consideremos el prisma recto de vértices {A, B, C, E, F, G}, donde la base superior se corresponde con los tres primeros vértices y la inferior con los tres últimos (ver escena 1). Queremos descomponerla en pirámides de base triangular y para ello hemos de tene en cuenta que:
- El menor número de pirámides se obtendrá cuando se consideren sólo los seis vértices del prisma como posibles vértices de las pirámides de la partición.
- Los elementos primarios mínimos para abordar la partición son ocho triángulos (las dos bases del prisma y seis más resultantes de dividir las tres caras laterales en triángulos) y 12 segmentos (las nueve aristas y las tres diagonales de las caras laterales). Y dado que dos pirámides de la partición han de tener tres caras diferentes como mínimo, entonces también son como mínimo tres las pirámides que formarán la partición (ocho caras entre tres nos da un valor mayor que dos).
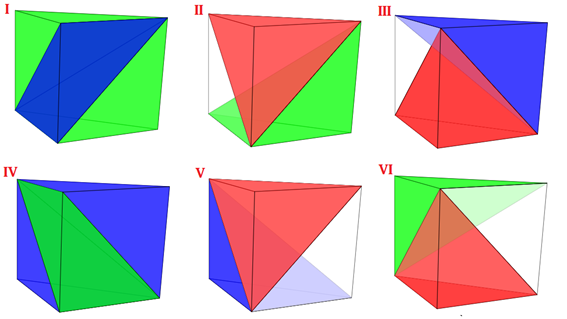
Basándonos en que una pirámide triangular queda determinada sin más que elegir dos segmentos con distinta dirección no coplanarios, una forma de abordar la partición del prisma de vértices {A, B, C, E, F, G} en tres pirámides triangulares se logra considerando dos aristas no coplanarias, una de la base ABC y otra de la EFG (Ver escena 2). Los cuatro vértices de esas dos aristas determinan una pirámide triangular que parte al prisma en tres bloques (se puede simular la situación en dicha escena 2) quedando fijadas, junto a ésta, las otras dos pirámides buscadas. Hay sólo seis posibilidades que vamos a denotar como partición I, II, III, IV, V y VI.
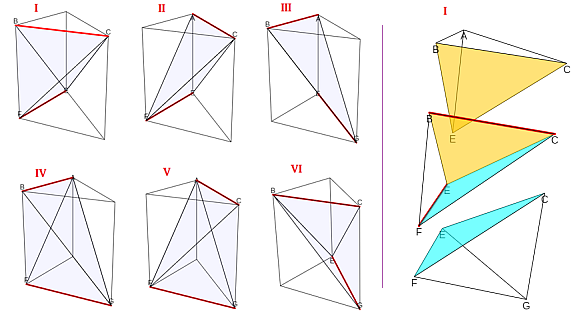
Escena 2. Particiones del prisma en tres pirámides triangulares (I, II, III, IV, V y VI) y detalle de la partición tipo I
- BC con EF que conduce a la pirámide BCEF y determina a ABCE y CEFG
- AC con EF que conduce a ACEF y determina a ABCF y CEFG
- AB con EG que conduce a ABEG y determina a ABCG y BEFG
- AB con FG que conduce a ABFG y determina a ABCG y AEFG
- AC con FG que conduce a ACFG y determina a ABCF y AEFG
- BC con EG que conduce a BCEG y determina a ABCE y BEFG
Distinguiendo los vértices por su nombre, en esas seis particiones aparecen doce pirámides diferentes, lo cual obviamente se corresponde con las combinaciones que se pueden obtener a partir de los seis vértices {A, B, C, E, F, G} agrupándolos de cuatro en cuatro, que son los vértices de una pirámide, y quitando aquellas agrupaciones en las que los cuatro vértices son coplanarios. Así pues, son C6, 4 = 15 combinaciones diferentes {ABCE, ABCF, ABEF, ABEG, ABFG, ACEF, ACEG, ACFG, AEFG, BCEF, BCEG, BCFG, BEFG, CEFG} y se excluyen los tres casos que hemos tachado por ser cuatro vértices coplanarios. Este podría ser también otro procedimiento alternativo al anterior para analizar las diferentes particiones del prisma.
En esas doce pirámides intervienen 15 aristas posibles, pues son combinaciones de seis vértices tomados de dos en dos, C6, 2 = 15. Son las reflejadas en la tabla 1, donde se indica su medida respectiva.
| AB=1 | ||||
| AC=√2 | BC=1 | |||
| AE=1 | BE=√2 | CE=√3 | ||
| AF=√2 | BF=1 | CF=√2 | EF=1 | |
| AG=√3 | BG=√2 | CG=1 | EG=√2 | FG=1 |
Tabla 1. Aristas de las pirámides y longitud de las mismas
En la tabla 2 podemos agrupar toda la información anterior y comparar las pirámides de esas particiones buscando detectar cuales son iguales o del mismo tipo. FIjándonos en la medida de las aristas que las componen se observa que hay tres tipos de pirámides que hemos etiquetado como X, Y, Z y, como detallaremos a continuación, en el tipo X se distinguen dos modalidades que etiquetamos como 1 y 2. También se refleja si la partición está constituida por pirámides congruentes entre sí (y por tanto también equivalentes) o si son sólo equivalentes.
| Partición | Pirámide | Aristas | Tipo | Modalidad | Congruencia y Equivalencia |
| I | ABCE | 1, 1, 1, √2, √2, √3 | X | 2 | Congruencia |
| BCEF | 1, 1, 1, √2, √2, √3 | X | 1 | ||
| CEFG | 1, 1, 1, √2, √2, √3 | X | 2 | ||
| II | ABCF | 1, 1, 1, √2, √2, √2 | Y | Equivalencia | |
| ACEF | 1, 1, √2, √2, √2, √3 | Z | |||
| CEFG | 1, 1, 1, √2, √2, √3 | X | 2 | ||
| III | ABCG | 1, 1, 1, √2, √2, √3 | X | 1 | Equivalencia |
| ABEG | 1, 1, √2, √2, √2, √3 | Z | |||
| BEFG | 1, 1, 1, √2, √2, √2 | Y | |||
| IV | ABCG | 1, 1, 1, √2, √2, √3 | X | 1 | Equivalencia |
| ABFG | 1, 1, 1, √2, √2, √3 | X | 2 | ||
| AEFG | 1, 1, 1, √2, √2, √3 | X | 1 | ||
| V | ABCF | 1, 1, 1, √2, √2, √2 | Y | Equivalencia | |
| ACFG | 1, 1, √2, √2, √2, √3 | Z | |||
| AEFG | 1, 1, 1, √2, √2, √3 | X | 1 | ||
| VI | ABCE | 1, 1, 1, √2, √2, √3 | X | 2 | Equivalencia |
| BCEG | 1, 1, √2, √2, √2, √3 | Z | |||
| BEFG | 1, 1, 1, √2, √2, √3 | Y |
Tabla 2. Desglose de particiones, pirámides que lo conforman, longitud de las aristas que lo componen, tipo de pirámide y modalidad, y congruencia y/o equivalencia
Cada partición del prisma la vamos a distinguir con el número romano que le hemos asignado o sin más que nombrar los tipos de pirámide que la forman para lo que convendremos hacerlo de arriba hacia abajo de acuerdo a la ubicación inicial de la pirámide en la que la base superior tiene de vértices ABC y la inferior EFG. Así la partición II viene dada por {Y, Z, X2}.
Procedamos a analizar cada uno de los tipos de pirámides que aparecen en dichas particiones.
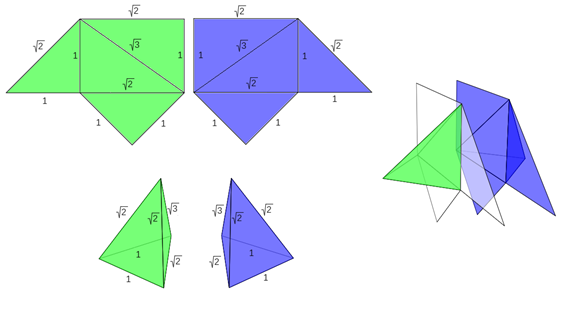
1.1 Pirámide tipo Y
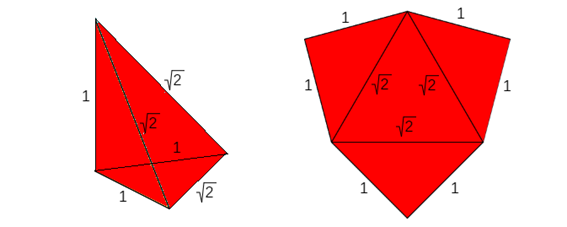
Atendiendo sólo a la forma, es decir, considerando que todas las caras son de igual color y no etiquetando los vértices, sólo es posible una pirámide triangular cuyas aristas midan 1, 1, 1, √2 , √2, √2 (escena 3). Su desarrollo plano está compuesto por un triángulo equilátero de lado 2 y tres triángulos rectángulos isósceles de catetos 1 y de hipotenusa2. El desarrollo, como se ha representado en la figura, tiene simetría axial con eje de simetría cualquiera de las alturas del triángulo equilátero y por tanto, independientemente de la orientación con la que se realiza el plegado (hacia dentro o hacia fuera) se obtiene la misma pirámide. El volumen de esta pirámide es 1/6 u3.
Escena 2. Pirámide triangular tipo Y (trirrectángula)
1.2 Pirámide tipo Z
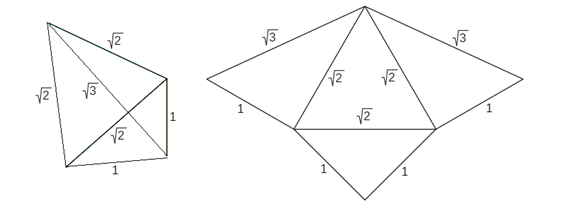
De manera análoga al caso anterior, si atendemos sólo a la forma, sólo es posible una pirámide triangular cuyas aristas midan 1, 1, √2, √2, √2, √3 (escena 3). Su desarrollo plano está compuesto por un triángulo equilátero de lado √2, un rectángulo isósceles de catetos 1 e hipotenusa √2 y dos triángulos rectángulos de catetos 1 y √2 e hipotenusa √3. Este desarrollo, como está representado en la figura, tiene simetría axial con eje de simetría la altura del triángulo equilátero que es altura a la vez del triángulo rectángulo isósceles. Así pues, independientemente de la orientación con la que se realiza el plegado (hacia dentro o hacia fuera) se obtiene la misma pirámide. El volumen de esta pirámide es también 1/6 u3, por tanto, equivalente a la pirámide tipo Y.
Escena 3. Pirámide triangular tipo Z
1.3 Pirámide tipo X
Con las aristas de medidas 1, 1, 1, √2, √2, √3 se pueden construir dos pirámides triangulares siendo una simétrica de la otra (escena 4). Los desarrollos planos son simétricos entre sí. Eligiendo uno de ellos, si se pliega hacia dentro se obtiene una de las pirámides y al plegarlo hacia fuera se obtiene la otra. Ambas tienen volumen 1/6 u3, es decir, son equivalentes entre sí y a las pirámides Y y Z.
También en la parte inferior de dicha figura puede observarse cómo ambas pirámides son simétricas, una respecto a la otra, en el sentido de que si hacen coincidir dos caras que sean iguales el plano que separa a ambas pirámides es un plano de simetría de las mismas. X1 y X2 son, por tanto, congruentes entre sí.
Escena 4. Pirámides triangulares tipo X —X1 en color azul y X2 en color verde—, desarrollo plano de las mismas y simetría de una respecto a la otra
1.4 Particiones del prisma triangular
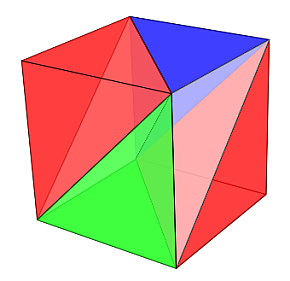
Las seis particiones del prisma reflejadas en la tabla 2 están representadas en la escena 5, donde se han mantenido los colores usados anteriormente en cada tipo de pirámide para así poder distinguir a simple vista cuál es la pirámide utilizada: rojo para tipo Y, blanco para tipo Z, azul para X1 y verde para X2.
Escena 5. Particiones del prisma triangular
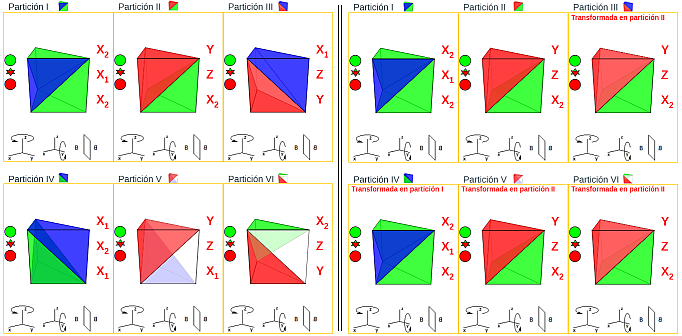
No obstante, de esas seis hay solamente dos que no son congruentes entre sí, pues tenemos que se cumplen las siguientes relaciones:
- Las particiones II, III, V y VI son congruentes entre sí:
- La partición tipo V —compuesta por las pirámides Y, Z, X1— es congruente con la III —compuesta por las pirámides X1, Z, Y—, basta realizar un giro de 180⁰.
- La partición VI —compuesta por las pirámides X2, Z, Y— es congruente con la II —compuesta por las pirámides Y, Z, X2— mediante un giro.
- La partición tipo V —compuesta por las pirámides Y, Z, X1— es congruente con la II —compuesta por las pirámides Y, Z, X2— mediante una simetría (según lo indicado con anterioridad Y es simétrica de sí misma, Z también, y X1 es simétrica de X2.
- Las particiones I y IV son congruentes entre sí:
- La partición IV —compuesta por las pirámides X1, X2, X1— es simétrica de la I —compuesta por las pirámides X2, X1, X2—.
Escena 6. Congruencias en las particiones del prisma triangular
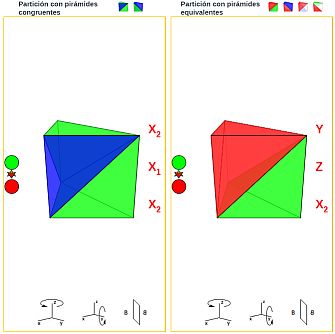
Si nuestro objetivo final es exclusivamente la partición de dicho prisma en pirámides triangulares tendríamos que indicar que, salvo isometrías, sólamente hay dos particiones posibles y, por tanto, bastaría considerar, por ejemplo, la partición I y la II. En ellas, a su vez, en la partición I las pirámides son congruentes entre sí (y consecuentemente equivalentes) y en la II son sólo equivalentes.
Escena 7. Partición del prisma con pirámides congruentes y con pirámides equivalentes
Todo lo analizado en este punto está englobado en el siguiente objeto interactivo: 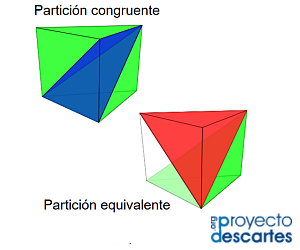
Escena 8. Partición de un prisma triangular en pirámides triangulares equivalentes
2. Partición prismática de un cubo en pirámides triangulares equivalentes
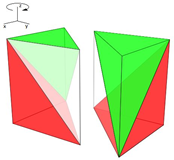
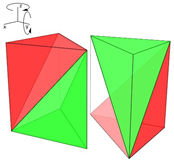
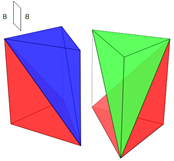
Para abordar la partición prismática del cubo, es decir, su descomposición mediante la unión de dos prismas es necesario tener en cuenta que la orientación de uno de ellos respecto al otro es significativa y consecuentemente hemos de considerar como diferentes las seis particiones del prisma triangular obtenidas en la sección anterior, dado que ellas son el fruto de hacer una distinción entre la cara inferior y la superior del prisma. O bien podemos hacer la lectura de que partiendo de las dos únicas particiones I y II del prisma al aplicarles isometrías tendríamos que son seis las particiones posibles en un prisma al distinguir la cara inferior de la superior.
Seleccionada una de las seis particiones posibles del prisma triangular, al aplicarle isometrías obtendremos otro prisma y los dos juntos conformarán una partición prismática del cubo en seis pirámides triangulares equivalentes. En la tabla 3 se reflejan las posibles transformaciones isométricas a realizar.
 |
 |
 |
 |
 |
 |
| Giro alrededor del eje Oz | Giro alrededor del eje Oz y del eje Oy | Simetría respecto a un plano |
Tabla 3. Isometrías para obtener un cubo a partir de un prisma triangular
En la tabla 4 se reflejan estas transformaciones aplicadas a cada una de las seis particiones:
| Partición | Giro Oz | Giro Oz, Oy | Simetría |
| I = X2, X1, X2 | X2, X1, X2 = I | X2, X1, X2 = I | X1, X2, X1 = IV |
| II = Y, Z, X2 | Y, Z, X2 = II | X2, Z, Y = VI | Y, Z, X1 = V |
| III = X1, Z, Y | X1, Z, Y = III | Y, Z, X1 = V | X2, Z, Y= VI |
| IV = X1, X2, X1 |
X1, X2, X1 = IV | X1, X2, X1 = IV | X2, X1, X2 = I |
| V = Y, Z, X1 |
Y, Z, X1 = V | X1, Z, Y = III | Y, Z, X2 = II |
| VI = X2, Z, Y | X2, Z, Y = VI | Y, Z, X2 = II | X1, Z, Y = III |
Tabla 4. Isometrías para obtener un cubo a partir de un prisma triangular
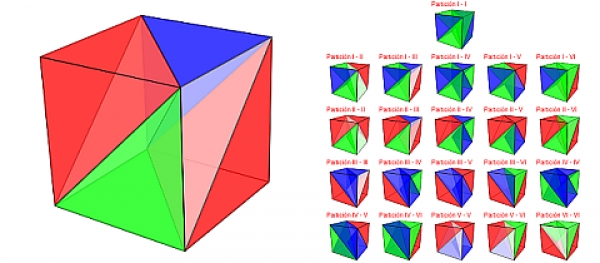
Por tanto, las diferentes particiones del cubo en seis pirámides equivalentes se obtienen sin más que hallar las variaciones con repetición de 6 elementos (las seis diferentes particiones del prisma) tomados de dos en dos, es decir, un total de VR6,2=62=36 posibilidades.
Escena 8. Partición prismática del cubo en pirámides triangulares equivalentes
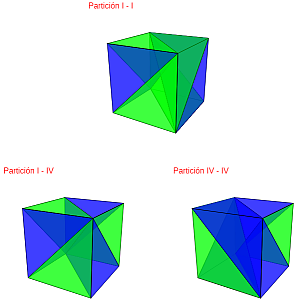
De partida, al comparar esas 36 posibilidades, se observa que la partición P2-P1 es congruente con la P1-P2 sin más que realizar un giro de 180º alrededor de la vertical (eje Oz) y, por tanto, quedan reducidas a 21 las posibles particiones (combinaciones con repetición CR6,2). Éstan son : {I-I, I-II, I-III, I-IV, I-V, I-VI, II-II, II-III, II-IV, II-V, II-VI, III-III, III-IV, III-V, III-VI, IV-IV, IV-V, IV-VI, V-V, V-VI, VI-VI}. Y en particular, entre ellas, hay tres casos en los que todas las pirámides son congruentes: {I-I, I-IV, IV-IV}.
En la siguiente escena se muestran todas esas particiones:
Escena 9. Partición del cubo con pirámides triangulares equivalentes
Y en ésta los tres casos en los que hay congruencia entre todas las pirámides.
Escena 10. Partición del cubo con pirámides triangulares congruentes
Pero para finalizar, en lugar de cerrar el tema, quizás sea mejor dejar una pregunta abierta: "Si comparamos las anteriores veintiuna particiones del cubo ¿cuántas son congruentes a su vez entre sí?, es decir, ¿cuántas son diferentes salvo isometrías?"...



 CONTACTO
CONTACTO


