Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.

Tabla de contenido

Prefacio

Desde el origen de la humanidad, hemos observado con atención el entorno que nos rodea. La naturaleza se convirtió en nuestra primera fuente de inspiración y aprendizaje. Observando los patrones en las hojas, las simetrías en las flores o las formas de los panales de abeja, comenzamos a comprender que existían formas y estructuras que podían ser replicadas. Obsérvalo en el video.

Este hábito de imitar la naturaleza no solo nos permitió resolver problemas prácticos, como construir refugios o crear herramientas, sino que también sentó las bases para el desarrollo de conceptos más abstractos.

Así surgió la geometría, una disciplina que encuentra sus raíces en la necesidad de medir y entender el espacio.

⇐ Imagen: Euclid, in ancient greece. Lexica Aperture v5

"Geometría Plana: Lo que debes saber" nace con un objetivo claro: poner al alcance de todos este conocimiento geométrico mediante un enfoque práctico, interactivo y visualmente claro.

Esta obra ofrece una exploración fundamental de los conceptos de la geometría plana, accesible para estudiantes de diversos niveles y contextos educativos.

Contenido y estructura
El recorrido del libro comienza con los orígenes históricos de la geometría en civilizaciones antiguas como Egipto y Grecia, sin olvidar la cultura maya o azteca, contextualizando así la relevancia de esta disciplina a lo largo de la historia humana. Desde allí, avanzamos sistemáticamente por los elementos fundamentales. La organización del contenido permite una progresión natural desde conceptos sencillos hasta ideas más complejas, siempre manteniendo un enfoque didáctico y accesible.

Relación con National Reporting System (NRS)
El libro no está estructurado específicamente en torno a los niveles del National Reporting System (NRS)[11] para la educación matemática de adultos, pero los utiliza haciendo que sus contenidos sean relevantes para estudiantes en diversos niveles de este sistema1.

NRS Niveles 1-2
La introducción a formas geométricas básicas (triángulos, cuadrados, círculos) y sus propiedades métricas (perímetro, área) resulta fundamental para estos niveles iniciales. Las actividades prácticas e interactivas del libro son especialmente beneficiosas para desarrollar una comprensión intuitiva de estas figuras

NRS Nivel 3
El estudio de ángulos y sus clasificaciones (agudos, rectos, obtusos), así como las relaciones entre ángulos formados por paralelas y una secante, constituyen una base crucial para la comprensión de formas y la resolución de problemas geométricos más complejos.

NRS Niveles 3-5
El tratamiento de polígonos regulares e irregulares y sus propiedades métricas permite profundizar en la clasificación y análisis de figuras bidimensionales, desarrollando habilidades analíticas progresivamente más sofisticadas.

NRS Niveles 4-6
El sistema de coordenadas cartesianas y conceptos como la distancia entre dos puntos y el punto medio proporcionan herramientas matemáticas avanzadas para representar y analizar figuras en el plano, conectando la geometría con el álgebra

Un enfoque pedagógico integrador
La perspectiva histórica que ofrece contextualiza el aprendizaje para estudiantes de todos los niveles, mostrando la relevancia de la geometría a través del tiempo y en diversas culturas, lo que ayuda a motivar el aprendizaje y a conectar los conceptos abstractos con aplicaciones del mundo real.

El carácter práctico y visualmente claro de la obra, con sus elementos interactivos, crea un entorno de aprendizaje enriquecido para desarrollar y aplicar conceptos matemáticos.

La exploración interactiva facilita la comprensión y retención de ideas para estudiantes en diferentes etapas de su formación.

Es importante destacar que todos los ejercicios y pruebas incluidos en este libro están diseñados como herramientas de aprendizaje, no como instrumentos de evaluación. Su propósito fundamental es reforzar la comprensión de los conceptos, estimular el razonamiento geométrico y proporcionar oportunidades para la práctica significativa. Invitamos a los lectores a abordarlos con curiosidad y sin presiones, como un camino para profundizar en su entendimiento de la geometría plana.

Para educadores
Los docentes encontrarán un recurso valioso para complementar la enseñanza de los estándares de contenido matemático. Aunque no sigue la estructura específica de los niveles NRS, pueden utilizarlo de manera selectiva, alineando los capítulos y temas con los estándares definidos para cada nivel, pudiendo auxiliarse de las explicaciones a los NRS Nivel 1 , NRS Nivel 2 y NRS Nivel 3 que se muestran en las referencias.

La claridad en la presentación de los conceptos y el uso de elementos interactivos resultarán particularmente útiles para involucrar a los estudiantes en el aprendizaje de la geometría plana, independientemente de su nivel específico

Vivimos tiempos donde la tecnología redefine constantemente nuestras formas de crear y aprender. En sintonía con esta realidad, la preparación de "Geometría Plana: Lo que debes saber" ha incorporado el uso de inteligencia artificial como una herramienta complementaria. Su rol ha sido el de un asistente versátil, contribuyendo en aspectos como la generación de código o la búsqueda de patrones en la exposición de temas complejos. Sin embargo, el corazón de este libro, su estructura, su enfoque didáctico, la pasión por la geometría y la garantía de su rigor, sigue siendo profundamente humano y es responsabilidad íntegra del autor.

Sobre los editores

Este libro, "Geometría Plana: Lo que debes saber", se publica de forma gratuita como parte del compromiso de poner al alcance de todos el conocimiento matemático y la educación abierta.

La obra es una publicación del Fondo Editorial RED Descartes de la Red Educativa Digital Descartes, con sede en Córdoba (España), como contribución al Proyecto iCartesiLibri.

Esta edición ha sido posible gracias a la colaboración entre la Red Educativa Digital Descartes y la Institución Universitaria Pascual Bravo (IUPB) en Medellín, Colombia, una institución de educación superior enfocada en la formación tecnológica.

A través de esta colaboración interinstitucional e internacional, se busca poner al alcance de estudiantes, docentes y público en general un recurso educativo de calidad que contribuya a la formación matemática, eliminando las barreras económicas de acceso al conocimiento.

Todas las obras se distribuyen bajo licencia Creative Commons 4.0 Internacional: Reconocimiento-No Comercial-Compartir Igual (CC BY-NC-SA 4.0), lo que permite a cualquier persona descargar, compartir y adaptar el contenido siempre que se reconozca la autoría original, no se utilice con fines comerciales y se comparta bajo la misma licencia cualquier material derivado.

Sobre el autor

José M. Fernández (Zhema) es docente del Departamento de Educación de Adultos del Harry S Truman College de Chicago, Illinois, EE.UU. Fernández ha escrito varios libros para el Proyecto iCartesiLibri. que abarcan gráficos, ecosistemas, mapas y otros valiosos recursos didácticos dirigidos a estudiantes adultos.

Su objetivo está alineado con el de los editores: democratizar el conocimiento con un enfoque práctico, interactivo y visualmente claro.

Los libros incluyen elementos interactivos y están diseñados para desarrollar el pensamiento crítico y la capacidad analítica. Todos han estádo publicándose por el Fondo Editorial RED Descartes bajo una licencia Creative Commons.

El presente trabajo es el proyecto especial del ABE/ASE Master Teacher 2025 del profesor Fernández, consistente en "presentar un contenido original en una conferencia o capacitación".

La credencial de ABE/ASE Master Teacher es el último paso en la Trayectoria Profesional del Personal Docente ABE/ASE de Illinois, establecida por la Junta de Colegios Comunitarios de Illinois.

⇐ Imagen: Professor Fernandez teaching Chat GPT Plus

Introducción

1.1 Los orígenes de la Geometría

Desde tiempos inmemoriales, la geometría ha sido una herramienta fundamental para el desarrollo de la civilización humana. Las antiguas culturas egipcia, mesopotámica, griega, china, india, maya, azteca e inca, entre otras, desarrollaron conocimientos geométricos que les permitieron construir monumentos impresionantes, diseñar ciudades, medir tierras, navegar por los mares y comprender los movimientos de los astros.

Estas civilizaciones antiguas, a través de la observación, la experimentación y el razonamiento, sentaron las bases de la geometría que conocemos y utilizamos hoy en día. Sus descubrimientos y métodos, aunque a menudo empíricos El método empírico es un modelo de investigación que se basa en la observación de la realidad para obtener el conocimiento basándose en la experiencia y en la evidencia que se puede observar con los sentidos. El término empírico proviene del griego empeirikos, que significa "experimentado". y prácticos, fueron fundamentales para el avance de esta disciplina y su aplicación en diversos campos.

Nuestro conocimiento es el resultado de un largo proceso de desarrollo.

Antes de iniciar los estudios, haremos un recorrido por la geometría de las antiguas civilizaciones, explorando cómo cada cultura abordó esta disciplina de manera única, adaptándola a sus necesidades y creencias. Cómo aplicaron la geometría en la construcción de pirámides y en la medición de tierras, o cómo desarrollaron un sistema numérico avanzado y transformaron la geometría en un sistema axiomáticoUn sistema axiomático puede verse como un conjunto de reglas y verdades básicas que se usan como punto de partida para construir estructuras matemáticas más grandes y complejas. y deductivo.

Muchas otras culturas, como la sumeria,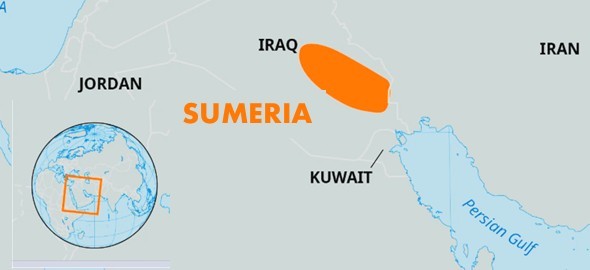Sumeria fue una civilización antigua que floreció en el sur de Mesopotamia (el actual Irak) aproximadamente entre el 4500 y el 1900 a.C. Los sumerios son conocidos por inventos como la escritura cuneiforme, la rueda y los primeros sistemas de irrigación. La cultura babilonia heredó y desarrolló muchos de los logros de la civilización sumeria también desarrollaron conocimientos geométricos originales que aplicaron en la construcción, la astronomía y la planificación urbana.

⇐ Imagen: Beham, (Hans) Sebald (1500-1550): Geometria (B.126, P.128), from The Seven Liberal Arts, P., Holl. 123-129. First state of two. Wikimedia Commons

1.1.1 Egipto

Los egipcios
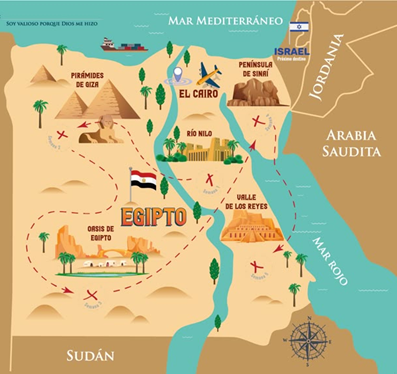
Egipto desarrollaron la geometría de forma práctica para resolver problemas cotidianos relacionados con la agricultura, la construcción y la administración de sus recursos. Su enfoque era principalmente empírico, es decir, basado en la experiencia y la observación, más que en la deducción teórica.

Dos papiros El papiro es un soporte de escritura que se elaboraba a partir de la planta del mismo nombre. Se considera el antecesor del papel moderno. Son documentos históricos y culturales de gran valor. Los nombres con que se conocen están asociados generalmente al descubridor o al lugar donde se encuentran. son fuentes importantes de nuestro conocimiento sobre la geometría egipcia.

• El Papiro de Rhind (1650 a.C.) contiene problemas geométricos prácticos que los egipcios sabían resolver, como el cálculo de áreas de triángulos y rectángulos, así como el volumen de cilindros.
• El Papiro de Moscú (1850 a.C.) incluye fórmulas para calcular el área de una esfera truncada y los volúmenes de pirámides y prismas.

La geometría en el Antiguo Egipto surgió de las necesidades prácticas a través de la observación y la experimentación.

Los egipcios aplicaron principios básicos del teorema de Pitágoras Este teorema establece la relación entre los lados de un triángulo rectángulo.
Será estudiado en el capítulo 6.3.
Los babilonios y egipcios conocían la relación entre los lados de un triángulo rectángulo mucho antes de Pitágoras, pero él recibió el crédito por demostrarlo y establecerlo como un teorema matemático formal. para construir ángulos rectos, una técnica fundamental en la construcción de sus monumentales edificaciones. También lograron desarrollar una fórmula para calcular el área del círculo
Un círculo es una figura plana delimitada por una línea curva cerrada cuyos puntos están a la misma distancia del centro. Lo estudiaremos en el capítulo 8. que, aunque era una aproximación, sentó las bases para el cálculo preciso en el futuro.

La geometría egipcia tuvo un impacto significativo en la civilización griega, cuyos matemáticos se inspiraron en las técnicas prácticas de los egipcios para desarrollar aún más esta disciplina. Aunque no se conocen figuras individuales destacadas en la geometría egipcia, el conocimiento fue transmitido por escribas Un escriba en el Antiguo Egipto era una persona altamente educada y especializada en la escritura y la lectura. Los escribas desempeñaban un papel fundamental en la administración, la religión y la sociedad egipcia, ya que eran los responsables de registrar y conservar información importante. que preservaron y aplicaron estas técnicas matemáticas.

⇐ Imagen Problema 34 del Papiro de Rhind: "10 panes se reparten entre 3 hombres de manera que el segundo recibe la mitad que el primero y el tercero la cuarta parte que el primero. ¿Cuánto recibe cada uno?" circa 1650 a.C. Matemáticas del reparto

1.1.2 Babilonia

Los babilonios
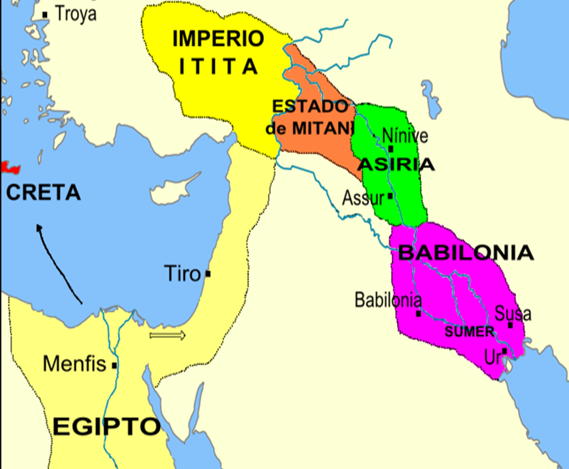
Babilonia desarrollaron una geometría más abstracta en comparación con los egipcios, y para ello se valieron de tablas matemáticas y un sistema numérico avanzado, el sistema sexagesimal El sistema sexagesimal es un sistema de conjuntos de numeración posicional que emplea como base el número 60. Tuvo su origen en la antigua Mesopotamia, en la civilización Sumeria. El sistema sexagesimal se usa actualmente para medir tiempos (horas, minutos y segundos) y ángulos (grados) principalmente. El número 60 tiene la ventaja de tener muchos divisores: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 y 60, con lo que se facilita el cálculo con fracciones. . Este sistema les permitía realizar cálculos más complejos y precisos.

El desarrollo de conceptos relacionados con triángulos rectángulos, influyeron en el desarrollo posterior de la geometría en otras culturas, como la griega.

Las tablas babilónicas, que datan de entre 1800 y 1600 a.C., son documentos antiguos que contienen problemas geométricos relacionados con el cálculo de áreas y volúmenes. Una de las tablas más conocidas es la Plimpton 322, que contiene una lista de ternas pitagóricas Una terna pitagórica es un conjunto ordenado de tres números enteros positivos a, b, c. Son solución de la ecuación ${\displaystyle a^{2}+b^{2}=c^{2}}$ que resuelve el Teorema de Pitágoras, el cual estudiaremos en el capítulo 6.3. , lo que sugiere que los babilonios tenían conocimiento sobre las relaciones entre los lados de los triángulos rectángulos.

Los babilonios hicieron uso de aproximaciones matemáticas avanzadas para llevar a cabo cálculos de áreas y volúmenes. Esto demuestra un alto nivel de análisis en su enfoque de la geometría. Además, desarrollaron conceptos relacionados con los triángulos rectángulos, lo que más tarde influiría en el desarrollo de la trigonometría. La influencia de la geometría mesopotámica se extendió hasta los griegos, quienes adoptaron algunos de sus enfoques conduciéndolos hacia la geometría abstracta.

Aunque no se conocen figuras individuales destacadas en el campo de las matemáticas en Mesopotamia, al igual que en Egipto, el conocimiento era transmitido y desarrollado por los escribas, quienes desempeñaban un papel fundamental en la preservación y avance de las técnicas matemáticas.

⇐ Imagen:Tablilla de arcilla, teoría de triángulos rectángulos, similar a la geometría euclidiana. De Tell Harmal (antiguo Shaduppum), Irak. 2003-1595 a.C. Museo de Irak en Bagdad, Irak. Tomada por Osama Shukir Muhammed Amin FRCP(Glasg) Cerebro Digital

1.1.3 Grecia

Los griegos
Antigua Grecia transformaron la geometría práctica utilizada por egipcios y babilonios en un sistema axiomático y lógico. En lugar de centrarse en problemas específicos, los griegos se enfocaron en deducciones abstractas y en la búsqueda de verdades universales que pudieran ser demostradas a través de la razón.

La geometría en la antigua Grecia pasó de ser una herramienta práctica a un sistema axiomático y lógico.

Uno de los documentos más influyentes en la historia de la geometría es "Elementos" de Euclides
Euclides (325 - 265 a.C.), escrito alrededor del 300 a.C. Esta obra maestra establece axiomasUn axioma es una proposición tan clara y evidente que se admite sin demostración. Por ejemplo: si a una bolsa con 10 bolas le añades 1, ahora la bolsa tiene más bolas que antes. Esta afirmación es intuitiva y evidente, no necesita demostrarse. y teoremasUn teorema es una afirmación o una idea que se puede demostrar que es verdadera usando razonamiento lógico y otros conocimientos o reglas que ya sabemos que son ciertas (como axiomas o postulados). que siguen siendo la base de la geometría moderna. Euclides no solo recopiló el conocimiento geométrico existente, sino que también lo organizó de manera lógica y rigurosa, sentando las bases para la geometría deductiva.

El desarrollo del método axiómatico permitió a los griegos desarrollar una geometría basada en la razón y la lógica, en lugar de la experiencia y la observación.

El Teorema de PitágorasEl teorema de Pitágoras, que estudiaremos en el capítulo 6.3, establece que en todo triángulo rectángulo, la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa. ${\displaystyle a^{2}+b^{2}=c^{2}}$, que relaciona los lados de un triángulo rectángulo, ya era conocido por los babilonios y fue formalizado y demostrado matemáticamentelos por los griegos. La influencia de la geometría griega ha sido enorme y perdura hasta nuestros días. Los griegos establecieron una base teórica que influyó en todo el desarrollo posterior de la geometría.

Grandes matemáticos griegos como Euclides, considerado el "Padre de la Geometría", Pitágoras
Pitágoras (570-490 a.C.), famoso por su teorema, y Arquímedes
Arquímides (287-212 a.C.), cuyos avances en la geometría del círculo y el cálculo de áreas fueron notables, contribuyeron de manera significativa al desarrollo de esta disciplina.

⇐ Imagen: Manuscrito griego de los siglos XI-XII donde podemos admirar el famoso pentagrama místico de los pitagóricos por su relación con la razón áurea. EL LEGADO DE LAS MATEMÁTICAS

1.1.4 China

La geometría en la China
China - Imperio Antiguo se desarrolló con un enfoque principal en aplicaciones prácticas, como la construcción, la agrimensura y la astronomía.

Los chinos se centraron en resolver los problemas relacionados con la vida cotidiana y las necesidades prácticas.

Uno de los documentos más antiguos que nos da información sobre la geometría china es "Los nueve capítulos sobre el arte matemático", que data del 200 a.C. Este libro contiene problemas prácticos relacionados con áreas, volúmenes y proporciones, y muestra un enfoque utilitario de la geometría.

Los chinos hicieron un uso práctico de razones y proporciones en sus cálculos geométricos. También desarrollaron aproximaciones para el cálculo de π (pi)
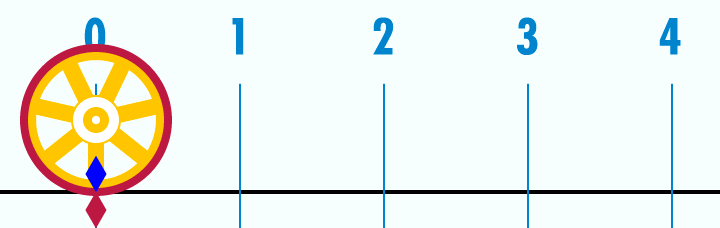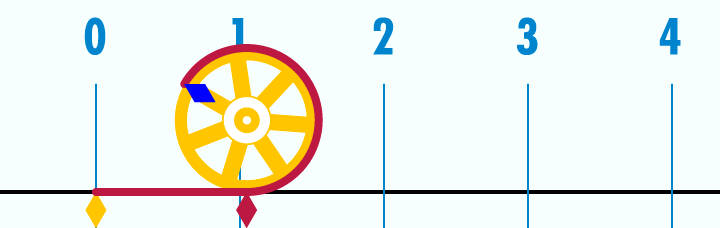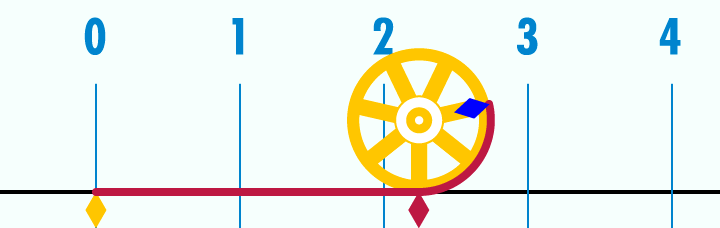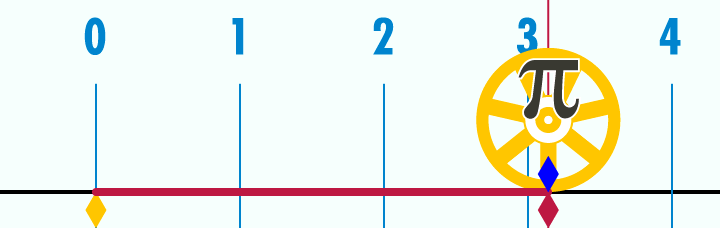
El número π (pi) es una de las constantes matemáticas más importantes e indica la relación entre el perímetro y el diámetro de un círculo. Un círculo es una figura geométrica que tiene un centro desde el cual la distancia cualquier punto del borde es la misma. Lo estudiaremos en el capítulo 8.

La geometría china, aunque menos conocida en Occidente en comparación con la griega, tuvo una influencia significativa en el desarrollo de las matemáticas en Asia. Sus métodos y técnicas se difundieron por toda la región y contribuyeron al avance de esta disciplina en diferentes culturas.

Grandes matemáticos chinos como Liu Hui
Liu Hui (220-280 d. C.), quien comentó y mejoró "Los nueve capítulos", y Zu Chongzhi
Zu Chongzhi (429-500 d. C.), quien calculó el valor de π con una precisión notable para su época, dejaron un legado importante en el campo de la geometría y las matemáticas en general.

⇐ Imagen: Versión publicada en el año 1820, de "Los nueve capítulos sobre el arte matemático" en China.. Wiki Arquelogía

1.1.5 India

En la antigua India
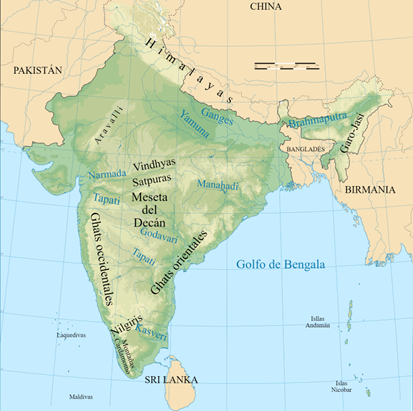
India , la geometría se desarrolló en estrecha relación con los rituales religiosos y la astronomía. Los Sulba SutrasUn texto védico es un escrito sagrado que forma parte de los Vedas, los textos más antiguos y fundamentales de la tradición religiosa y filosófica de la India, asociados con el hinduismo. Los Sulba Sutras son textos védicos que datan de entre el 800 y el 500 a.C. son las fuentes más antiguas que documentan los conocimientos geométricos de esta civilización. Los matemáticos indios, particularmente Brahmagupta
Brahmagupta (circa 598-670 d. C.) en el siglo VII d.C., fueron los primeros en tratar el cero como un número y definir sus propiedades matemáticas, incluyendo las operaciones con él. La palabra "cero" proviene del sánscrito "shunya", que significa vacío..

Los indios conocían el teorema de Pitágoras mucho antes que los griegos, lo que demuestra un desarrollo temprano de conceptos geométricos fundamentales. Además, trabajaron con ideas avanzadas sobre raíces cuadradas y proporciones, que eran esenciales para sus cálculos y construcciones.

La geometría hindú, nacida de su interacción con la religión y la astronomía, dejó un profundo legadoa en la historia de las matemáticas. Trascendió al mundo islámico y, posteriormente, a Europa.

La influencia de la geometría india trascendió sus fronteras. A través de la Edad de Oro del IslamLa Edad de Oro del Islam es un período histórico que tuvo lugar entre los siglos VIII y XIII. Durante esta época, el mundo islámico experimentó un extraordinario desarrollo en los campos de la ciencia, la filosofía, la medicina, la literatura, las matemáticas, la astronomía, la arquitectura y otras disciplinas culturales y académicas., sus conocimientos se difundieron por el mundo islámico y, eventualmente, llegaron a Europa, donde impactaron el desarrollo de la geometría y las matemáticas en general.

Grandes matemáticos indios como Aryabhata
Aryabhata (476-550 d. C.) y Brahmagupta jugaron un papel crucial en este legado. Aryabhata desarrolló fórmulas geométricas relacionadas con esferas y círculos, mientras que Brahmagupta realizó importantes aportaciones en geometría cíclica, rama de la geometría euclidiana que se centra en el estudio de las propiedades de las figuras inscritas en circunferencias.

⇐ Imagen: Two 1st century indian mathematicians developing a geometric theorem in the hall of a marble palace Lexica Aperture v5

1.1.6 Mayas

Los mayas
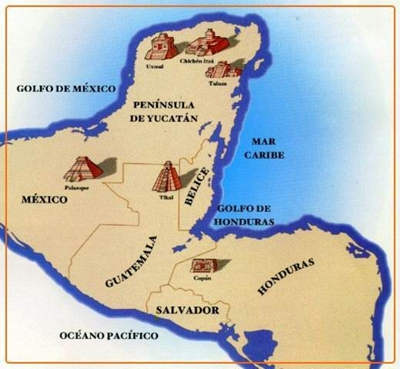
Civilización Maya. Mesoamérica fueron una civilización mesoamericana que desarrolló la geometría con un enfoque principal en la construcción, la astronomía y la elaboración de calendarios. Su conocimiento geométrico era esencial para la creación de sus impresionantes ciudades, la alineación precisa de sus edificios con eventos astronómicos y la creación de calendarios complejos que regían su vida ritual y agrícola.

Aunque no se conservan muchos documentos escritos de los mayas, los códices Los códices son documentos manuscritos realizados en hojas plegadas, usualmente de papel amate o pergamino, que forman un libro. Históricamente, se les asocia principalmente con las culturas mesoamericanas, como la maya, azteca y mixteca, aunque también existieron códices en otras partes del mundo. Al igual que los papiros, reciben el nombre del lugar donde se encuentran o del descubridor. que han sobrevivido, como el Códice de Dresde, nos dan información valiosa sobre sus conocimientos geométricos. Si bien estos códices se centran principalmente en la astronomía, también contienen cálculos geométricos que eran fundamentales para lograr alineaciones arquitectónicas precisas con los cuerpos celestes.

Los mayas hicieron un uso sofisticado de la geometría en sus construcciones. La famosa pirámide de Chichén Itzá
Pirámide de Chichen_itza
(600-1200 d. C.), está construida con una precisión geométrica notable. Utilizaron principios geométricos para asegurar que sus templos estuvieran alineados con los solsticios
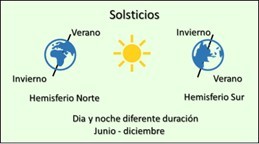
Uaxactún (Guatemala). Pirámide con tres templos más pequeños encima. Se podía observar en el amanecer el solsticio de verano sobre el templo norte y el solsticio de invierno sobre el templo sur. Durante los solsticios, un hemisferio recibe más luz solar que el otro.
y los equinoccios

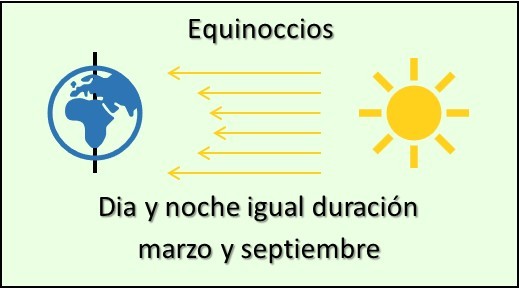
En la piámide de Kukulkán, en Chichén Itzá, la luz del sol proyecta sombras en la escalinata norte de la pirámide, creando la ilusión de una serpiente emplumada descendiendo. . Los mayas llegaron a sus conocimientos geométricos a través de la observación y la experimentación, en lugar de basarse en teorías y conceptos desarrollados en otras culturas.

⇐ Imagen: A mayan building the solar calendar on top of a temple. Lexica Aperture v5

1.1.7 Aztecas

Los aztecas,
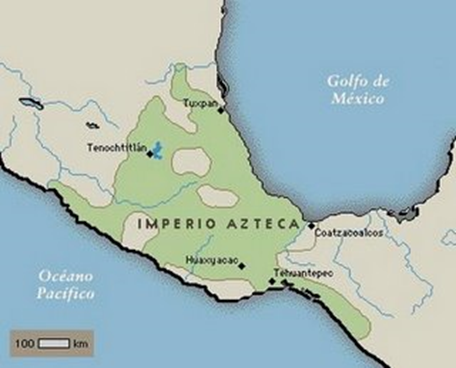
Imperio Azteca una civilización mesoamericana que floreció en el valle de México, desarrollaron conocimientos geométricos que aplicaron en la construcción de sus impresionantes templos
Reproducción del Templo Mayor. Tenochtitlán. México y en la planificación urbana de sus ciudades.

La geometría era una herramienta fundamental para los aztecas, ya que les permitía diseñar y construir estructuras monumentales con precisión y simetría.

Aunque no se conservan muchos documentos escritos de los aztecas que se centren específicamente en la geometría, los códices que han sobrevivido, como el Códice Borbónico, contienen información valiosa sobre sus conocimientos geométricos. Estos códices muestran que los aztecas tenían un conocimiento práctico de proporciones y medidas, que utilizaban en la arquitectura y otras áreas.

A la derecha se muestra una imagen del Códice Borbónico. Es un "libro" de origen azteca, confeccionado en una tira de papel hecho con fibras vegetales. De las 40 páginas originales, solo tiene actualmente 36.

Los aztecas hicieron un uso extensivo de la simetría y las proporciones en su arquitectura. Sus templos, como la Pirámide del Sol
La Pirámide del Sol, construida entre los siglos I y VII d. C. en Teotihuacan
(600-1200 d. C.), están diseñados con una simetría y proporciones armoniosas. La geometría también era fundamental en la planificación urbana, se caracterizaban por su diseño cuadriculado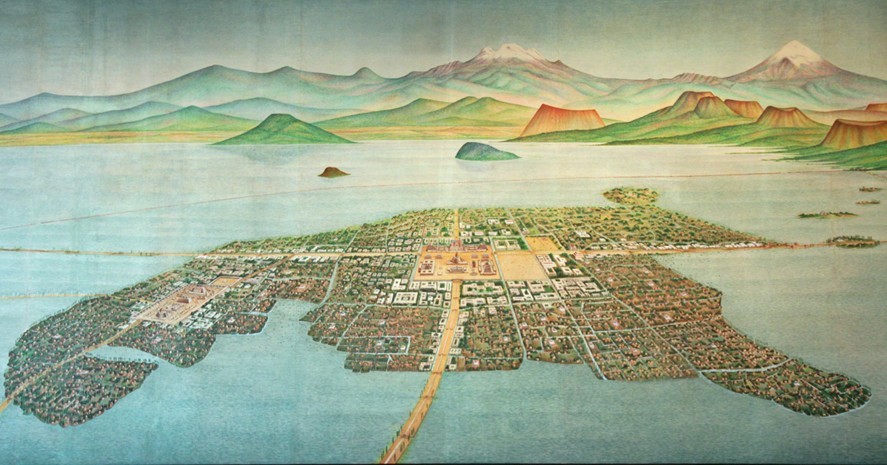
Tenochtitlán y el lago Texcoco en 1519 bien planificadas. y su organización espacial.

Su legado arquitectónico y urbanístico es un testimonio de su habilidad para aplicar principios geométricos en la creación de estructuras impresionantes yciudades.

⇐ Imagen: Aztec calendar on top of an aztec temple Lexica Aperture v5

1.1.8 Incas

Los incas,
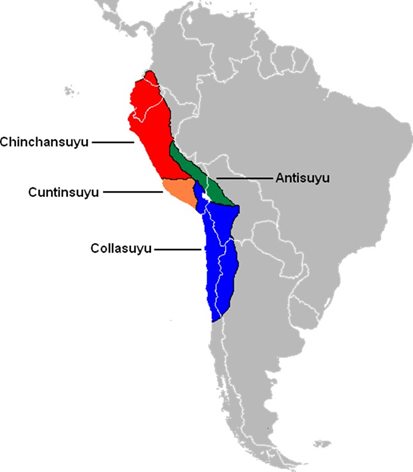
Imperio Inca fueron una civilización andina que floreció en América del Sur. Utilizaron la geometría de manera práctica para la construcción de su impresionante infraestructura, que incluía caminos, terrazas agrícolas, ciudades y complejos ceremoniales. Su dominio de la geometría fue esencial para superar los desafíos del terreno montañoso y construir estructuras duraderas que siguen en pie hasta nuestros días. Aunque no se conservan documentos escritos de los incas que se centren específicamente en la geometría, se cree que los quipus
Los quipus eran un sistemas de cuerdas anudadas que utilizaban los incas para registrar información. podrían haber contenido datos matemáticos relevantes. Sin embargo, la interpretación de los quipus sigue siendo un tema de investigación y debate.

Sus terrazas agrícolas fueron diseñadas para maximizar el uso del suelo y evitar la erosión

Los incas hicieron un uso práctico de la geometría para resolver problemas de construcción en terrenos montañosos. Sus terrazas agrícolas
Los amplios escalones construidos en las laderas de las montañas, le permitió a los Incas ganar tierras para desarrollar la agricultura y adaptarse al paisaje., por ejemplo, fueron diseñadas con precisión geométrica para maximizar el uso del suelo y evitar la erosión. También construyeron caminos y puentes
Puente Inca Q'eswachaka, en Perú, es el único puente colgante inca que aún se mantiene en pie. Se reconstruye cada año por comunidades quechuas que requerían un conocimiento profundo de la geometría para superar obstáculos naturales y conectar diferentes partes de su vasto imperio.

Su conocimiento geométrico les permitió superar los desafíos del terreno montañoso y construir estructuras duraderas que siguen en pie hasta nuestros días. Aunque no se conocen figuras individuales destacadas, su legado arquitectónico
Las ventanas trapezoidales incas se encuentran en edificios como el Templo de las Tres Ventanas en Machu Picchu y en el Coricancha en Cuzco es un testimonio de su habilidad para aplicar principios geométricos en la creación de obras maestras de la ingeniería.

⇐ Imagen:Incas building Machu Picchu with the terraces and the temple of the sun. Lexica Aperture v5

1.1.9 El Papiro de Rhind

El Papiro de Rhind fue descubierto en 1858 en Tebas, Egipto, y fue adquirido por el egiptólogo escocés Alexander Henry Rhind
Alexander Henry Rhind
(1833-1863), de ahí su nombre. Actualmente, el papiro se encuentra en el Museo Británico de Londres, donde se conserva y se estudia para seguir revelando los secretos de las matemáticas egipcias.

Es un documento de carácter didáctico² que contiene problemas geométricos y aritméticos que abarcan desde operaciones básicas con números enteros y fracciones hasta problemas de proporciones y ecuaciones lineales. También incluye tablas de fracciones y métodos para realizar cálculos con fracciones, lo que demuestra un conocimiento avanzado de este tema por los egipcios. La imagen de la derecha muestra una parte del Papiro de Rhind que contiene la solución de un problema geométrico a través de ecuaciones de primer grado. Las incógnita se denomina AHA ³ (que significa montón)

Fue escrito por el escriba Ahmes Ahmes es el primer matemático cuyo nombre se conoce. El escriba Ahmes (o Ahmose) vivió y copió el famoso Papiro Matemático Rhind durante el reinado del faraón Apofis. El propio papiro Rhind menciona que fue copiado por Ahmes en el año 33 del reinado de Apofis (aproximadamente a mediados del siglo XVI a.C.), a partir de un documento más antiguo que databa del reinado de Amenemhat III, Dinastía XII.
a mediados del siglo XVI a. C., a partir de textos que, según él mismo refiere, tenían trescientos años de antigüedad en ese momento. El Papiro de Rhind revela que los egipcios tenían un conocimiento empírico de conceptos geométricos que más tarde serían formalizados y desarrollados por los griegos, como el teorema de Pitágoras. Este papiro nos recuerda que las matemáticas han sido una herramienta esencial para el desarrollo de las civilizaciones y que su estudio nos permite apreciar la inteligencia y la capacidad de resolución de problemas de nuestros antepasados.

⇐ Imagen: Beham, (Hans) Sebald (1500-1550): Geometria (B.126, P.128), from The Seven Liberal Arts, P., Holl. 123-129. First state of two. Wikimedia Commons

1.1.10 Solución de un problema geométrico egipcio

Los egipcios, a pesar de que no tenían el concepto de π como una constante matemática, desarrollaron un método que les permitía obtener resultados útiles para sus necesidades en la construcción y la agrimensura. Su influencia en la geometría griega es innegable, ya que los griegos, como Heródoto
Heródoto de Halicarnaso
(484 - 425 a. C.)
Fue un historiador y geógrafo griego, considerado como el padre de la historia en el mundo occidental. documentó en sus escritos, aprendieron de los egipcios durante sus viajes.

El problema 50 del Papiro de Rhind

Calcular el área de un campo Como la mayoría de los problemas matemáticos egipcios, este está directamente relacionado con situaciones del mundo real: la medición de la tierra para fines agrícolas. circular
cuyo diámetro tiene 9 khet El khet era una unidad de longitud utilizada en el Antiguo Egipto que equivalía a 100 codos reales, aproximadamente 52,5 metros. Era utilizada principalmente para medir tierras y campos de cultivo..

Los egipcios aproximaban el área del círculo dividiéndolo en cuadrados, utilizando un octágono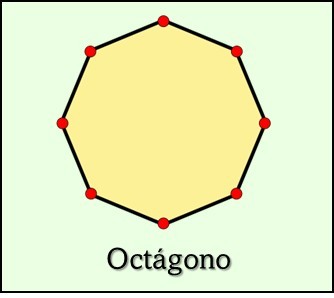
El octágono es un polígono regular de ocho lados. Visualmente se "parece" a una circunferencia. para representarlo. Ahmes calcula el área del círculo considerándolo igual a la de un cuadrado de lado 9.

Dice: "resta al diámetro $\frac{1}{9}$ del mismo, que es 1. La diferencia es 8. Ahora multiplica 8 veces 8, que da 64. Este es el área El escriba está empleando la siguiente fórmula $$A = \left(d - \frac{1}{9}d\right)^2$$ El método de Ahmes proporciona una aproximación del área del círculo. del círculo"

La solución En el interactivo se puede apreciar mejor. El círculo rojo exterior es el círculo original, el círculo punteado azul es el círculo "reducido" después de restar $\frac{1}{9}$. El cuadrado gris tiene como lado exactamente el diámetro de este círculo reducido.
En términos modernos, Ahmes logró una aproximación de
$π ≈ \frac{256}{81}≈ 3.1605$.
Compare con $3.1416$ que usamos tres mil años después usando computadoras. que se propone en el papiro es la siguiente:

• Se toma el diámetro del círculo, que es 9 khet.
• Se resta un noveno del diámetro, lo que nos da 8 khet.
• Se eleva al cuadrado el resultado, 8 khet, obteniendo 64 khet cuadrados.

Por lo tanto, el área del círculo es de 64 khet cuadrados.

1.2 El puente entre lo antiguo y la moderno

Gran parte del conocimiento de los antiguos griegos, romanos, persas, indios y chinos llegó a Europa a través de las traducciones realizadas durante la Edad de Oro del islam. Este fue un período de florecimiento cultural, científico, económico y político en el mundo islámico que abarcó aproximadamente desde el siglo VIII hasta el siglo XIII.

Los musulmanes La palabra musulmán deriva del árabe muslim que significa literalmente "aquel que se somete" o "aquel que se entrega". Por lo tanto, un musulmán es, etimológicamente y según la propia fe islámica, una persona que acepta y se somete voluntariamente a la voluntad de Dios (Alá). tradujeron, preservaron y expandieron el conocimiento de civilizaciones antiguas y se destacaron en áreas como matemáticas, astronomía, medicina, química, filosofía, y geografía. Matemáticos como Al-Juarismi introdujeron el álgebra El término "álgebra" proviene de la obra de Al-Juarismi "Al-Kitab al-Mukhtasar fi Hisab al-Jabr wal-Muqabala" Médicos como Avicena (Ibn Sina) escribieron obras fundamentales como el Canon de MedicinaEl Canon de medicina es una enciclopedia médica de 5 volúmenes escrita por el científico y médico musulmán persa Ibn Sina (Avicena) alrededor del año 1025. El libro se basaba en una combinación de su propia experiencia personal, del conocimiento médico del mundo islámico medieval, influenciado por la medicina griega y romana y las medicinas persa, china y de la India. , que se usó en Europa durante siglos.

En la Casa de la Sabiduría de Bagdad, se tradujeron al árabe obras de autores clásicos como Aristóteles, Platón, Euclides, Hipócrates, Ptolomeo y Galeno. Estas traducciones no se limitaron a copiar el original; los eruditos musulmanes escribieron comentarios y análisis críticos que expandieron las ideas de los antiguos

Este conocimiento llega a Europa a través la península ibérica (actual España). Entre los siglos XII y XIII, en Al-Andalus, la Escuela de Traductores de Toledo Los textos traducidos por la Escuela de Traductores de Toledo proporcionaron a Europa conocimientos esenciales en áreas como lógica, matemáticas, astronomía, medicina y filosofía. Por ejemplo: El sistema numérico decimal y el uso del "cero", que se originó en la India, llegó a Europa a través de las traducciones árabes. Los textos médicos de Avicena y Al-Razi (Rhazes) se convirtieron en pilares de la enseñanza médica en las universidades europeas se convirtió en un punto clave para la transferencia de conocimiento. Los textos árabes fueron traducidos al latín por eruditos hispanos y judíos que trabajaban en colaboración con académicos musulmanes.

Europa occidental había perdido gran parte del acceso directo al conocimiento de la antigüedad clásica tras la caída del . Imperio Romano A partir de la caída del Imperio Romano de Occidente se desmantelaron las redes administrativas, educativas y culturales que sostenían el conocimiento a gran escala. Las bibliotecas fueron saqueadas, quemadas o simplemente abandonadas. Los materiales (papiro, pergamino) eran frágiles. Sin instituciones estables que promovieran y financiaran la labor de traducción y con la destrucción física causada por guerras e incendios, una gran cantidad de obras desapareció. Muchas de las obras originales en griego se habían perdido o eran inaccesibles. Sin embargo, los musulmanes preservaron y enriquecieron ese legado. Así, cuando Europa comenzó a salir de la "Edad Oscura" y entró en el Renacimiento del siglo XII, los textos árabes sirvieron como puente entre la antigüedad clásica y la modernidad.

Elementos Geométricos

2.1 Las 3 dimensiones espaciales

Cuando nos movemos, podemos hacerlo en tres direcciones diferentes: hacia adelante o hacia atrás, hacia un lado o hacia el otro, hacia arriba o hacia abajo. Esas direcciones son dimensiones ⁴ que están relacionadas con el espacio físico que podemos percibir y representar mediante trazos y coordenadas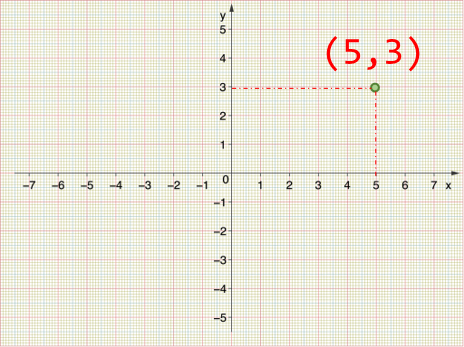 Las coordenadas (5,3) son una forma de describir dónde está algo usando números, basándonos en un sistema de referencia. Este sistema se usa en mapas, gráficos, planos y hasta en el espacio tridimensional. ¡Es como un GPS para señalar ubicaciones exactas! Lo estudiaremos en el capítulo 7. .

1. Primera dimensión (1D):
• Representa un espacio lineal.
• Se describe mediante una sola coordenada (longitud).



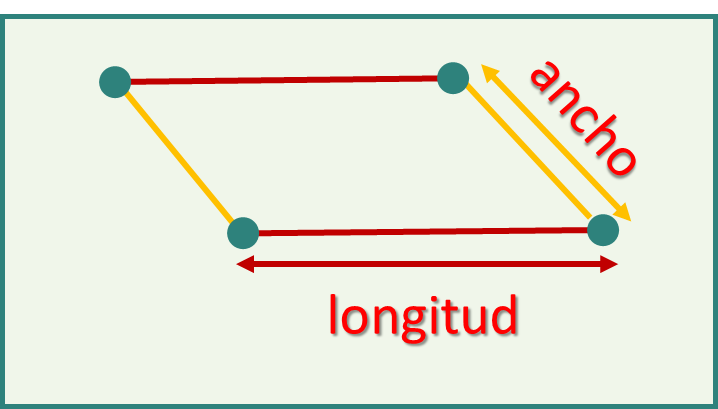2. Segunda dimensión (2D):
• Representa un espacio plano.
• Se describe con dos coordenadas (longitud y ancho).



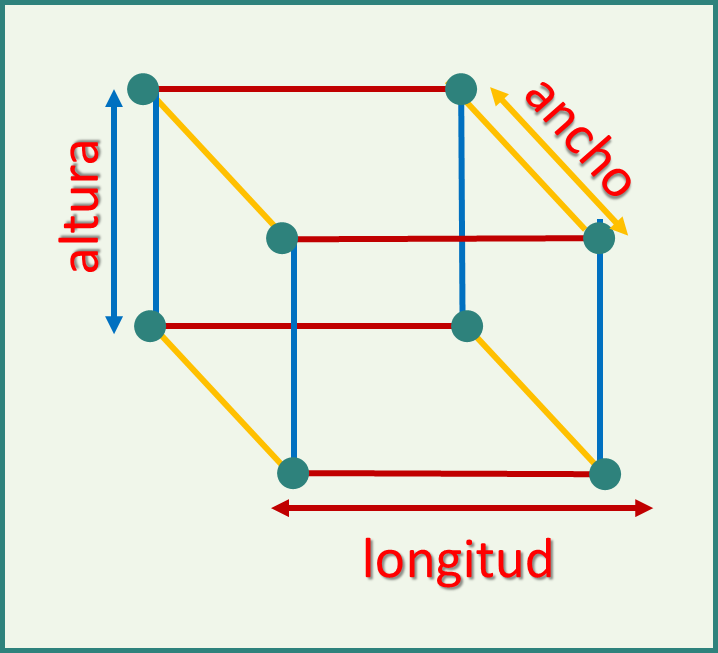3. Tercera dimensión (3D):
• Representa un espacio volumétrico.
• Se describe con tres coordenadas (longitud, ancho y altura).

⇐ Imagen: A house showing three clearly defined dimensions... Lexica Aperture v3.5

Experimentamos las tres dimensiones espaciales en nuestro diario vivir:

• Un tren se mueve en línea recta. Se mueve en una sola dirección: Largo
• Un auto se mueve en línea recta, pero también puede girar a la derecha o a la izquierda. Puede moverse en dos direcciones: Largo y ancho
• Un avión se mueve en línea recta, también puede girar a la derecha o a la izquierda y, además, puede moverse hacia arriba o hacia abajo. Puede moverse en tres direcciones: Largo, ancho y altura

Estas tres dimensiones son utilizadas en geometría para clasificar y describir objetos, estudiando las propiedades y relaciones de estas figuras en diferentes dimensiones.

2.2 Interactivo - Explorando dimensiones

2.3 Elementos básicos de la Geometría

Las letras no son palabras, pero sin ellas no podemos formar palabras. Las letras son esenciales para construirlas.

De manera similar, en geometría necesitamos elementos básicos, como las letras en el lenguaje, para construir las figuras.

Estos elementos son los fundamentos que no requieren demostración; están ahí, simplemente debemos utilizarlos. Sin estos elementos, no podríamos definir ninguna figura geométrica. Son los ladrillos con los que se construye todo el edificio de la geometría.

Este conjunto de conceptos en los que se basa la Geometría son los axiomasLos axiomas son verdades evidentes o principios fundamentales que se consideran universalmente ciertos, no solo en un campo específico de las matemáticas, sino en la lógica general. Son afirmaciones que se aceptan sin necesidad de demostración porque se consideran intrínsecamente verdaderas. y postuladosLos postulados son afirmaciones fundamentales que son específicas de un campo particular de las matemáticas, especialmente la geometría. Son las bases sobre las cuales se construye un sistema geométrico específico, como la geometría euclidiana., que son verdades fundamentales que se aceptan sin demostración. Muchos de estos axiomas y postulados se refieren a puntos, líneas y planos.

Todas las figuras geométricas, por complejas que sean, se pueden construir a partir de
puntos, líneas y planos.

De la geometría elemental estudiaremos la Geometría plana que contempla el estudio de las figuras que tienen únicamente dos dimensiones: largo y ancho. La Geometría del espacio, que estudia los cuerpos geométricos provistos de largo, ancho y altura, no serán objeto de estudio en este libro.

2.4 El punto

El punto es el elemento más básico de la geometría y no tiene dimensiones. No tiene ni longitud, ni anchura, ni altura.

• Se representa con un pequeño círculo relleno o una cruz.
• Se denotan con una letra mayúscula: A, B, P, M, etc.
• En ocasiones, pueden representarse varios puntos con la misma letra, diferenciadas con un subíndice numérico o literal: P₁,P₂, P₃, P_a,P_b, P_c,etc.

Los puntos se utilizan para marcar posiciones en el espacio, como la intersección de dos líneas o el centro de un círculo.

2.5 La línea

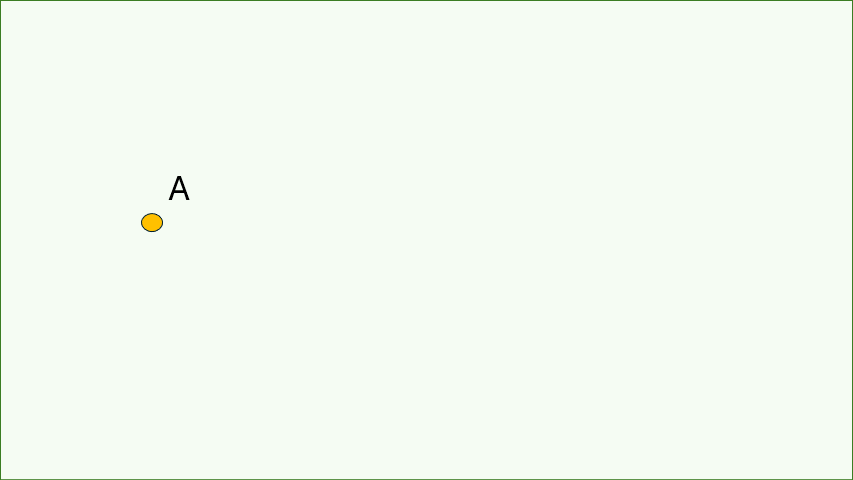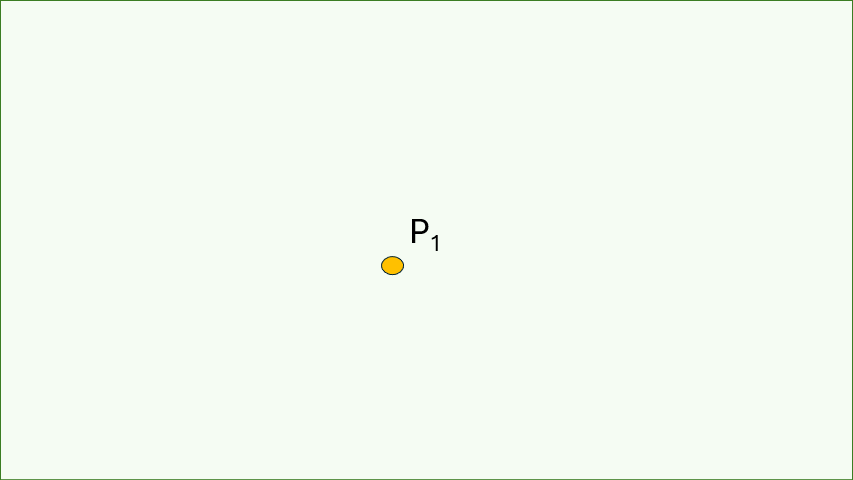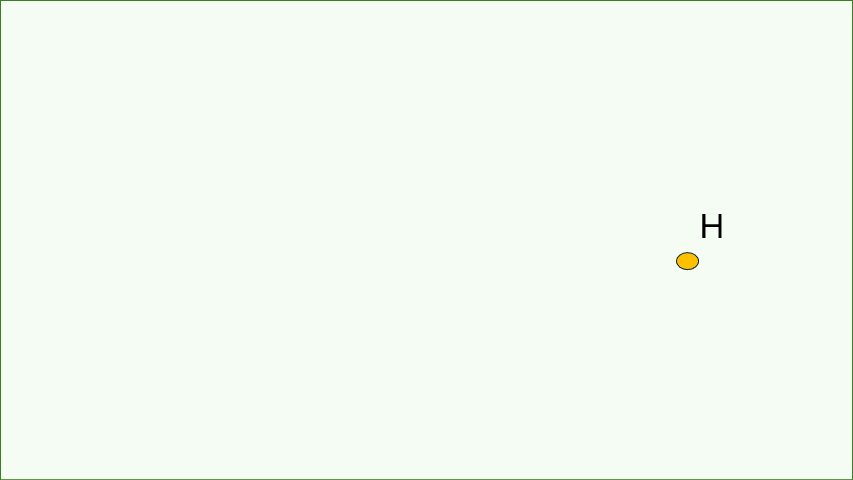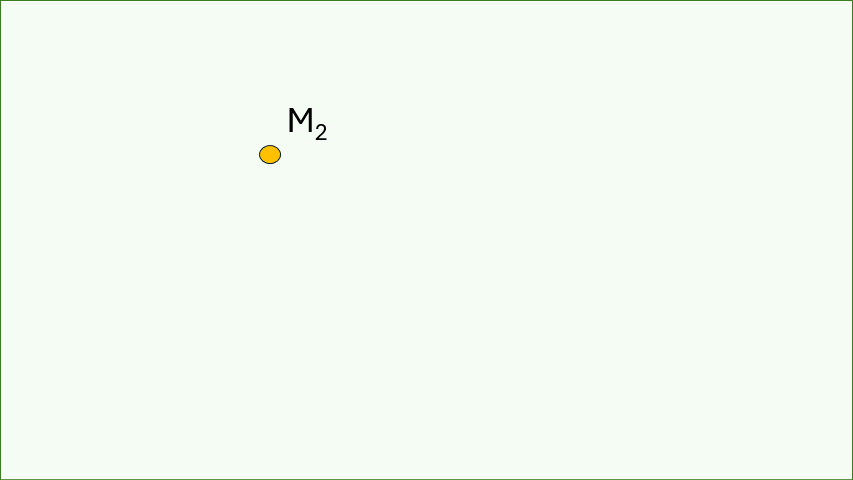
La línea tiene una sola dimensión: la longitud.

• Se extiende infinitamente en dos direcciones opuestas.
• Se representa con una línea recta con flechas en ambos extremos para indicar su extensión infinita.

Las líneas pueden ser rectas (como una regla) o curvas (como un círculo).

Las líneas se utilizan para conectar puntos, definir bordes de figuras y representar trayectorias.

2.5.1 Postulados fundamentales de la línea

Los postulados de la línea son principios básicos de la geometría que describen las propiedades fundamentales de ellas. Estos postulados provienen de los fundamentos de la geometría euclidiana, ⁵ establecidos por Euclides en su obra Elementos La obra Elementos de Euclides es uno de los textos más importantes de la historia de las matemáticas. En esta obra, Euclides estableció los fundamentos de la geometría y otros principios matemáticos, organizados de manera lógica y sistemática. Su enfoque consistió en partir de conceptos básicos (definiciones, axiomas y postulados) para desarrollar teoremas más complejos a través de demostraciones . Estos son los postulados más relevantes relacionados con la línea

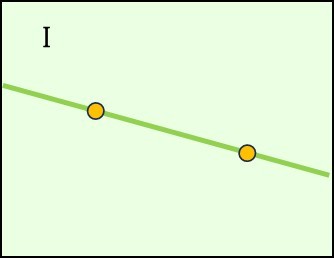
• Postulado de existencia de la línea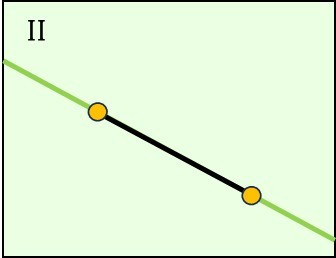
  Por dos puntos distintos siempre pasa una y solo una línea recta. Esto significa que dos puntos determinan una línea única.



• Postulado de continuidad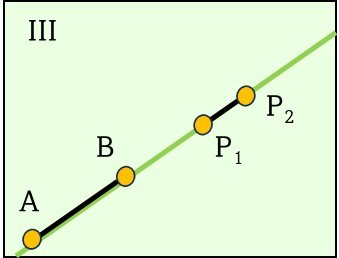
  Una línea recta es infinita en ambas direcciones. Aunque en un dibujo representemos solo un segmento de línea, matemáticamente continúa sin fin.


• Postulado de divisibilidad
  Una línea recta puede dividirse en segmentos más pequeños. Esto implica que podemos seleccionar cualquier punto en una línea y dividirla en partes.


• Postulado de intersección
  Si dos líneas rectas se cruzan, lo hacen en un solo punto. Las líneas no pueden cruzarse en más de un punto en la geometría euclidiana.

2.5.2 Conceptos básicos sobre la línea

En geometría, los conceptos de línea, recta y segmento son fundamentales para describir formas y estructuras.

• Línea
  Una línea es una figura geométrica que consiste en una sucesión continua e infinita de puntos. No tiene grosor, solo longitud.
• Recta
  La recta es una línea que no tiene curvaturas ni cambios de dirección a lo largo de su trayectoria. No tiene principio ni tiene fin.
  Se denota con dos letras mayúsculas que representan dos puntos en la recta y se escribe el símbolo de recta encima de las letras. $\overleftrightarrow {AB}$
• Semirrecta
  La semirrecta es una línea que tiene principio pero no tiene fin
  Se denota con dos letras mayúsculas que representan dos puntos en la semirrecta y se escribe el símbolo de semirrecta encima de las letras. $\overrightarrow {AB}$
• Segmento
  El segmento es una porción finita de una recta que está delimitada por dos puntos, llamados extremos.
  Se denota con dos letras mayúsculas que representan los extremos del segmento, y se coloca una línea sin flechas encima de las letras. $\overline {AB}$

Compruebe en el interactivo de la siguiente página, estos conceptos básicos sobre la línea.

2.5.3 Interactivo - Líneas rectas

2.5.4 Relación entre dos rectas

En geometría, las líneas pueden interactuar de diversas maneras dependiendo de su posición y relación en el espacio. Estas interacciones son fundamentales para entender cómo se forman las figuras en geometría y cómo se describen sus propiedades. Estas relaciones son esenciales en el cálculo de áreas y volúmenes, y la resolución de problemas.

• Líneas Paralelas
  Son dos o más líneas que nunca se intersectan Significa que no se cruzan, cortan o confluyen en ningún punto. Es decir, no tienen ningún punto en común. y siempre mantienen la misma distancia entre ellas y tienen la misma dirección. Se denotan $AB||CD$.
  Ejemplo: Los rieles de un tren.


• Líneas Secantes
  Son dos líneas que se cruzan en un único punto. Pueden formar aberturas estrechas o anchas en el punto de intersección. Se denota $AB \sec CD$ o $AB \bigcap CD$
  Ejemplo: Dos carreteras que se cruzan en una intersección.


• Líneas Perpendiculares
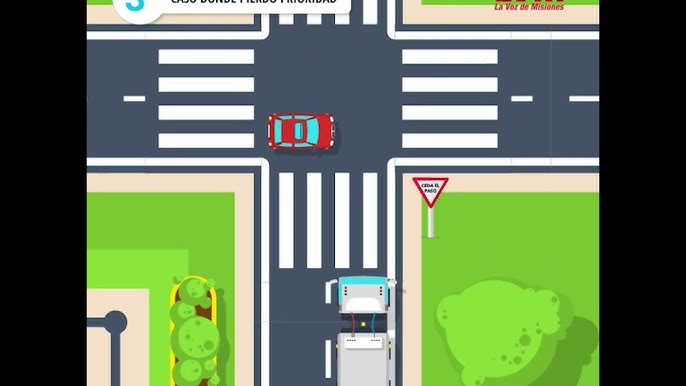  Son dos líneas secantes que se intersectan formando un ángulo recto. ⁶. Pueden ser rectas, segmentos o semirrectas. Se denotan $AB \perp CD$
  Ejemplo: El cruce de dos calles.

Cuando dos líneas comparten todos sus puntos, es decir, son exactamente la misma línea, se denominan Líneas Coincidentes.

2.5.5 Interactivo - Relaciones entre rectas

Las líneas paralelas, perpendiculares y secantes son fundamentales en nuestra vida diaria, a menudo sin que nos demos cuenta.

Las vemos en paredes, pisos y techos para crear estructuras estables y estéticamente agradables. Son parte de nuestro diario vivir.

2.5.6 Comprobación rápida - Elementos básicos

2.6 El plano

• El plano tiene dos dimensiones: longitud y ancho.
• Se extiende infinitamente en todas las direcciones dentro de esas dos dimensiones.
• Se representa con una figura plana de cuatro lados, aunque en realidad se extiende infinitamente.
• Los planos se utilizan para representar superficies planas, como el suelo, una pared o la página de un libro.

Si tienes tres puntos que no están alineados en una sola línea recta, puedes formar un plano único que los contenga.

2.7 Interactivo - Práctica de conceptos básicos

⇐ Imagen: From a point comes a single straight line that reaches a square ... Lexica Aperture v5

2.8 Comprobación - Elementos básicos

⇐ Imagen: A collage of images of Egyptian, Babylonian, Indian, Mayan, Chinese constructions. Lexica Aperture v5

Ángulos

3.1 Definición de ángulo

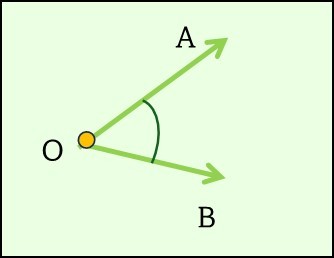Un ángulo es la abertura que se forma cuando dos líneas rectas (o segmentos de línea) se encuentran en un punto común llamado vértice. En la figura, los segmentos $\overline {AO}$ y $\overline {BO}$ se encuentran en el punto $O$, que es el vértice del ángulo formado: $\angle AOB$.

3.1.1 Grados y radianes

Los ángulos se miden en grados El grado se representa generalmente con el símbolo ° en la parte superior derecha del valor del mismo, por ejemplo 60°. o radianes y representan la medida de la abertura o separación entre las dos líneas.

Grados sexagesimales
Los heredamos de los babilonios, quienes dividieron el círculo
Mapa babilónico del mundo conocido como Imago Mundi. Esta tablilla de arcilla data 700-500 a.C. y puede apreciarse prefectamente la repesentación de un círculo. en 360 partes. El número 360 es un mútiplo de 60, que es un número altamente divisible 12 números lo dividen exactamente.
1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 y 60.
La factorización de 60 es 2² × 3 × 5. Está compuesto por la multiplicación de los tres primeros números primos (2, 3 y 5) elevados a ciertas potencias , lo que facilitaba sus cálculos. Los babilonios observaron que las constelaciones parecían regresar a su posición inicial después de aproximadamente 360 días. Por lo tanto, dividieron el camino que recorre el sol en 360 partes iguales, y así un círculo completo paso a contener 360 grados. astronómicos.

Radianes
Mientras que los grados son una división arbitraria, Se dice arbitraria porque se deriva fundamentalmente de la práctica, los grados son una convención adoptada y transmitida a lo largo de la historia. el radián El nombre "radián" fue adoptado porque la medida de este ángulo, depende directamente de la medida del radio de la circunferencia. es una unidad de medida "natural" basada en la relación entre el radio y la circunferencia de un círculo.
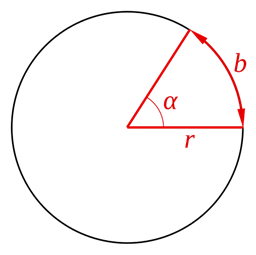
Un radián es el ángulo que se forma cuando la longitud del arco de un círculo es igual a la longitud del radio de ese círculo.
Una circunferencia completa tiene 2π radianes, que equivalen a 360 grados.

En 1714, Roger Cotes
Roger Cotes (1682-1716) vio que los radianes eran una manera natural de medir ángulos, simplificando muchas fórmulas y cálculos, sobre todo los relacionados con funciones trigonométricas y movimientos circulares.

Trabajaremos fundamentalmente con grados sexagesimales, no obstante, ejercitaremos también los radianes.

⇐ Imagen: From a point comes a single straight line that reaches a square on a gradient background in green tones... Lexica Aperture v5

Hemos mencionado a la constante pi ($\pi$) varias veces. En este video verán el por qué esta constante matemática es crucial para el desarrollo de las matemáticas, la ingeniería, la arquitectura, la física, la biología y la astronomía.

Al $\pi$ representar la relación que existe entre la circunferencia de un círculo y su diámetro, resulta esencial para cálculos geométricos relacionados con círculos y esferas, lo que a su vez tiene implicaciones en todas las áreas mencionadas, aparececiendo en numerosas ecuaciones fundamentales que describen el universo que nos rodea.

3.1.2 Elementos de un Ángulo

Los ángulos están formados por dos lados que se encuentran en un punto llamado vértice.

• Lados del ángulo:
  Son las dos líneas o segmentos que se encuentran en el vértice y forman el ángulo. Normalmente, se les llama lado inicial y lado terminal.
• Vértice:
  Es el punto donde los lados del ángulo se intersectan.
• Medida del ángulo:
  Es el tamaño de la abertura entre los lados del ángulo y se mide en grados (°) o radianes (rad).

Una vuelta completa tiene 360° grados
equivalentes a 2π radianes.

Los ángulos son esenciales en la vida diaria, tanto en el diseño de estructuras como en disciplinas como la navegación, astronomía, y tecnología. Por ejemplo, los ingenieros calculan ángulos para construir puentes, los arquitectos los utilizan para diseñar estructuras sólidas, y los navegantes los usan para trazar rutas en el mar utilizando mapas y brújulas.

Puertas:
Cuando abrimos una puerta, el ángulo que forma con el marco varía en dependencia de la abertura que se le haya dado. La abertura de un ángulo puede ir desde 0° hasta 360°.

Tijeras:
Cuando usamos unas tijeras, los filos forman un ángulo. Dependiendo de qué tan abierta esté, esta puede ser muy abierta, muy estrecha o cerrada.

Fútbol:
Los campos de fútbol tienen cuatro esquinas, cada esquina forma un ángulo recto (90°).

Si observas a tu alrededor, verás que practicamente todas las cosas que veas tienen ángulos y, como veremos más adelante, las curvas también tienen ángulos.

3.2 Clasificación de ángulos

Las semirrectas forman diferentes aberturas al formar un ángulo. Esto permite su clasificación. La clasificación de los ángulos es fundamental en geometría y tiene diversas aplicaciones prácticas.

1. Facilitar la comprensión y el estudio de la geometría:


• Organización del conocimiento: La clasificación permite agrupar los ángulos según sus características (medida, posición, etc.), lo que facilita su estudio y comprensión.
• Identificación de propiedades: Cada tipo de ángulo tiene propiedades específicas que son útiles para resolver problemas geométricos.
• Desarrollo de habilidades: La clasificación de ángulos ayuda a desarrollar habilidades de razonamiento lógico y espacial.


2. Aplicaciones prácticas en diversos campos:


• Arquitectura e ingeniería: La construcción de edificios, puentes y otras estructuras requiere el uso preciso de ángulos.
• Navegación: La orientación y el cálculo de rutas se basan en la medición y clasificación de ángulos.
• Diseño: El diseño de objetos, desde muebles hasta automóviles, implica el uso de ángulos precisos.
• Informática y videojuegos: Los gráficos por computadora y los videojuegos utilizan ángulos para crear imágenes y animaciones realistas.

3.2.1 Clasificación de ángulos según su medida

Tipo de ángulo	Descripción	Imagen
Ángulo agudo	Un ángulo agudo es aquel cuya medida es menor de 90°. En otras palabras, es un ángulo "pequeño" que se encuentra entre 0° y 90°.
Ángulo recto	Un ángulo recto mide exactamente 90°. Se reconoce fácilmente por su forma de "L" perfecta. Las líneas que forman un ángulo recto son perpendiculares entre sí.
Ángulo obtuso	Un ángulo obtuso mide más de 90° pero menos de 180°. Es un ángulo "grande" que se encuentra entre 90° y 180°.
Ángulo llano	Un ángulo llano mide exactamente 180°. Forma una línea recta.
Ángulo cóncavo	Un ángulo cóncavo mide más de 180° pero menos de 360°.
Ángulo completo	Un ángulo completo mide 360°. Representa una vuelta completa.

Observa, en el siguiente interactivo, la abertura que forma el lado con el punto rojo al moverse. Este parará antes de llegar a los ángulos con valor de 90° (recto), 180° (llano) y 360° (completo).

La clasificación de ángulos por medidas, y como veremos más adelante, posición y suma, brinda una estructura organizada para el estudio de la geometría. Cada clasificación resalta diferentes propiedades y relaciones entre los ángulos, lo que a su vez facilita la resolución de problemas y la comprensión de conceptos más avanzados.

3.2.2 Clasificación de ángulos según su posición

Tipo de ángulo	Descripción	Imagen
Ángulos consecutivos	Son aquellos que tienen el mismo vértice y un lado en común..
Ángulos Adyacentes	Son ángulos consecutivos cuyos lados no comunes son semirrectas opuestas.
Ángulos opuestos por el vértice	on los ángulos que tienen el mismo vértice y sus lados son semirrectas opuestas. Estos ángulos miden lo mismo.

Los ángulos consecutivos, adyacentes y opuestos por el vértice son importantes en geometría porque permiten identificar y relacionar ángulos que comparten un vértice o un lado.

Son relaiones cruciales para resolver problemas geométricos relacionados con líneas rectas, polígonos y otras figuras, ya que sus propiedades permiten calcular medidas de ángulos desconocidos basándose en la relación que tienen con otros ángulos conocidos.

Analizaremos mucho más de estas relaciones cuando estudiemos en el siguiente capítulo las propiedades de los ángulos que se forman cuando una recta secante corta a dos rectas paralelas.

3.2.3 Clasificación de ángulos según su suma

Tipo de ángulo	Descripción	Imagen
Ángulos Complementarios	Son aquellos cuya suma de sus medidas es igual a 90°.
Ángulos Suplementarios	Son aquellos cuya suma de sus medidas es igual a 180°.

Los ángulos complementarios y suplementarios tienen una importancia fundamental en diversos campos, tanto teóricos como prácticos.

• Permiten construir ángulos específicos y figuras geométricas con precisión. Por ejemplo, los ángulos complementarios son esenciales en la creación de ángulos rectos.
• Son la base para comprender y demostrar teoremas geométricos más complejos.
• Ayudan a establecer relaciones entre ángulos en diferentes contextos, como en triángulos, polígonos y figuras formadas por líneas paralelas y secantes.
• Facilitan el cálculo de medidas de ángulos desconocidos.

Son fundamentales en el diseño y construcción de edificios, en la navegación marítima y aérea, y en la creación de gráficos y animaciones, así como en el desarrollo de videojuegos.

3.3 Ángulos formados entre paralelas y secante

En el capítulo Relación entre dos rectas vimos las líneas paralelas y secantes, las cuales juegan un papel fundamental en la Geometría. Estas propiedades son conocidas desde la antigüedad. Según cuenta la leyenda, el filósofo Tales de Mileto Según la leyenda, Tales clavó un bastón vertical en el suelo y midió la longitud de su sombra.
Simultáneamente, midió la longitud de la sombra proyectada por la pirámide.
Basándose en el principio de que "la relación entre la altura de un objeto y la longitud de su sombra es constante a una hora determinada del día", estableció una proporción.
La clave es que en el mismo instante en el que la sombra del bastón y su altura fueran iguales, la sombra de la pirámide y su altura también lo serían.

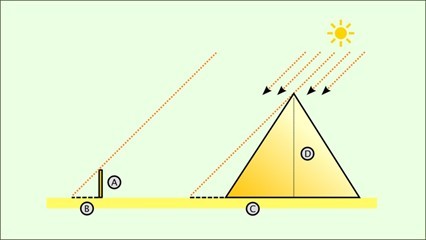Con este método, Tales pudo calcular la altura de la pirámide sin necesidad de medirla directamente. utilizó estas propiedades para medir la altura de las pirámides de Guiza, alrededor del año 500 a. C.

3.3.1 Interactivo - Ángulos

3.3.2 Clasificación ángulos entre paralelas y secante

3.3.3 Interactivo - Angulos entre paralelas

3.4 Comprobación - Ángulos

Polígonos
Regulares

4.1 Introducción a los polígonos

Las figuras planas son formas geométricas bidimensionales que se encuentran en un plano. Se caracterizan por tener longitud y anchura, pero no profundidad.

Entre las más comunes se encuentran los polígonos, La palabra polígono está formada por dos voces de origen griego: "polys": muchos y "gonía": ángulos; por lo tanto, es una figura con muchos ángulos. Aunque el nombre se centra en los ángulos, las propiedades de un polígono dependen tanto de sus lados como de sus ángulos. La longitud de los lados y la medida de los ángulos determinan la forma y el tamaño del polígono. que son formas cerradas formadas por segmentos de línea recta. Pueden ser regulares o irregulares.

Los polígonos regulares son los que tienen lados y ángulos internos de la misma medida, son figuras simétricas. Los irregulares son los que tienen los lados y ángulos internos distintos entre sí, con medidas diferentes.

⇐ Imagen: A 3d house made with pentagons and hexagons, next to a forest made with triangle... Lexica Aperture v3.5

4.2 Polígonos regulares

Un polígono regular es una figura geométrica plana cerrada que tiene todos sus lados y ángulos iguales. Están formados por segmentos de recta que se unen en sus extremos. Todos sus vértices están a la misma distancia del centro. Los polígonos regulares son figuras simétricas. La simetría se refiere a una propiedad que describe la correspondencia exacta entre dos partes de un objeto o figura cuando se las compara a través de un punto, una línea o un plano.

La mariposa es simétrica con relación a la línea vertical que la cruza

4.2.1 Circunferencia inscrita y circunscrita

Vimos en el capítulo Solución de un problema geométrico egipcio , que ellos aproximaban el área del círculo utilizando un octágono para representarlo.

Esta particularidad se debe a que un polígono regular puede estar inscrito Un polígono está inscrito en una circunferencia cuando todos sus vértices están sobre la circunferencia. En la imagen 4.2, la figura (un hexágono) tiene sus vértice sobre la circunferencia de color rojo. en una circunferencia, teniendo todos sus vértices exactamente sobre la circunferencia. El radio del polígono coincide con el radio El radio es la distancia del centro de la circunferencia a cuaquier punto del borde. En el capítulo 8 estudiaremos detenidamente el círculo y la circunferencia. de la circunferencia.

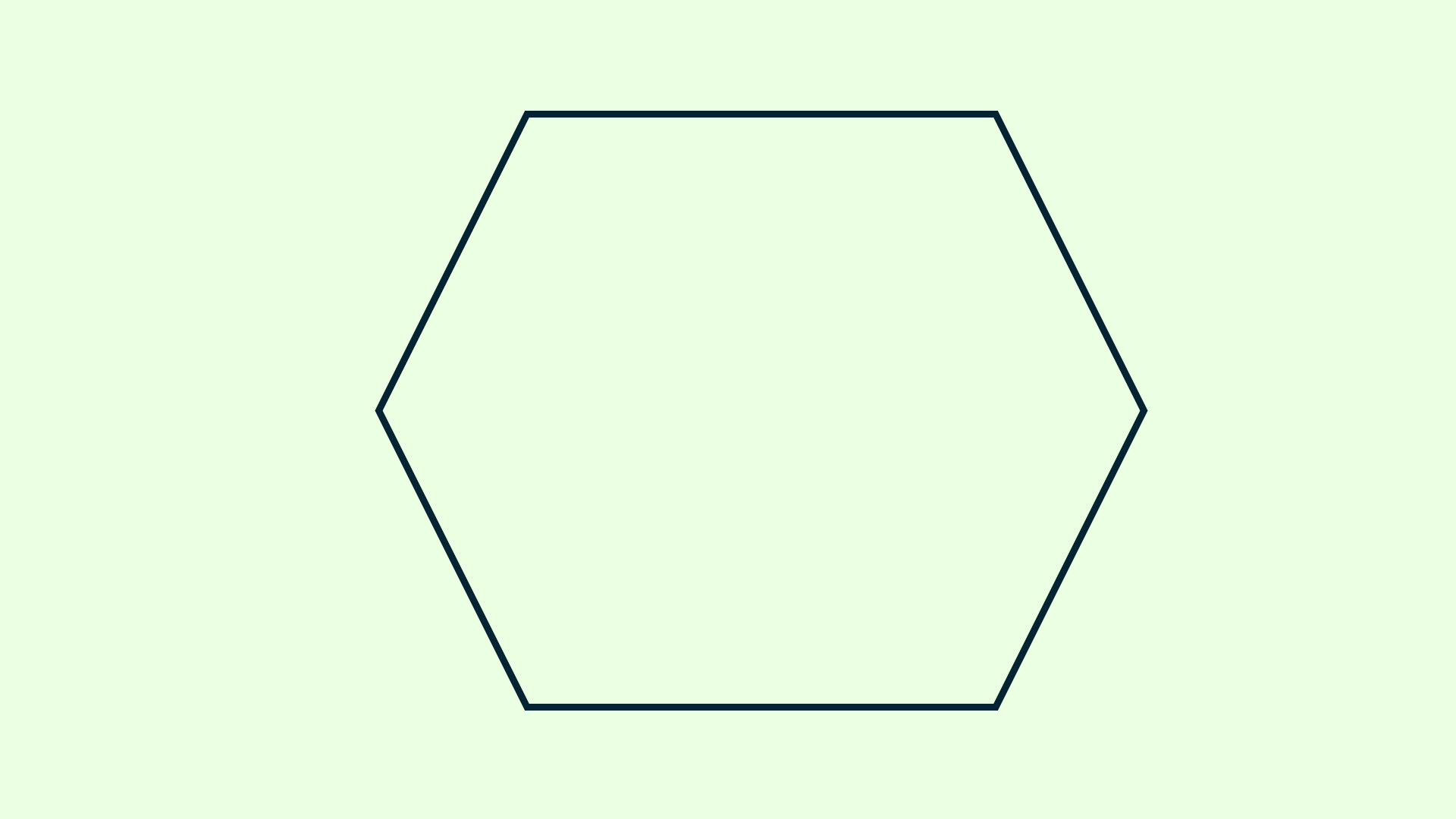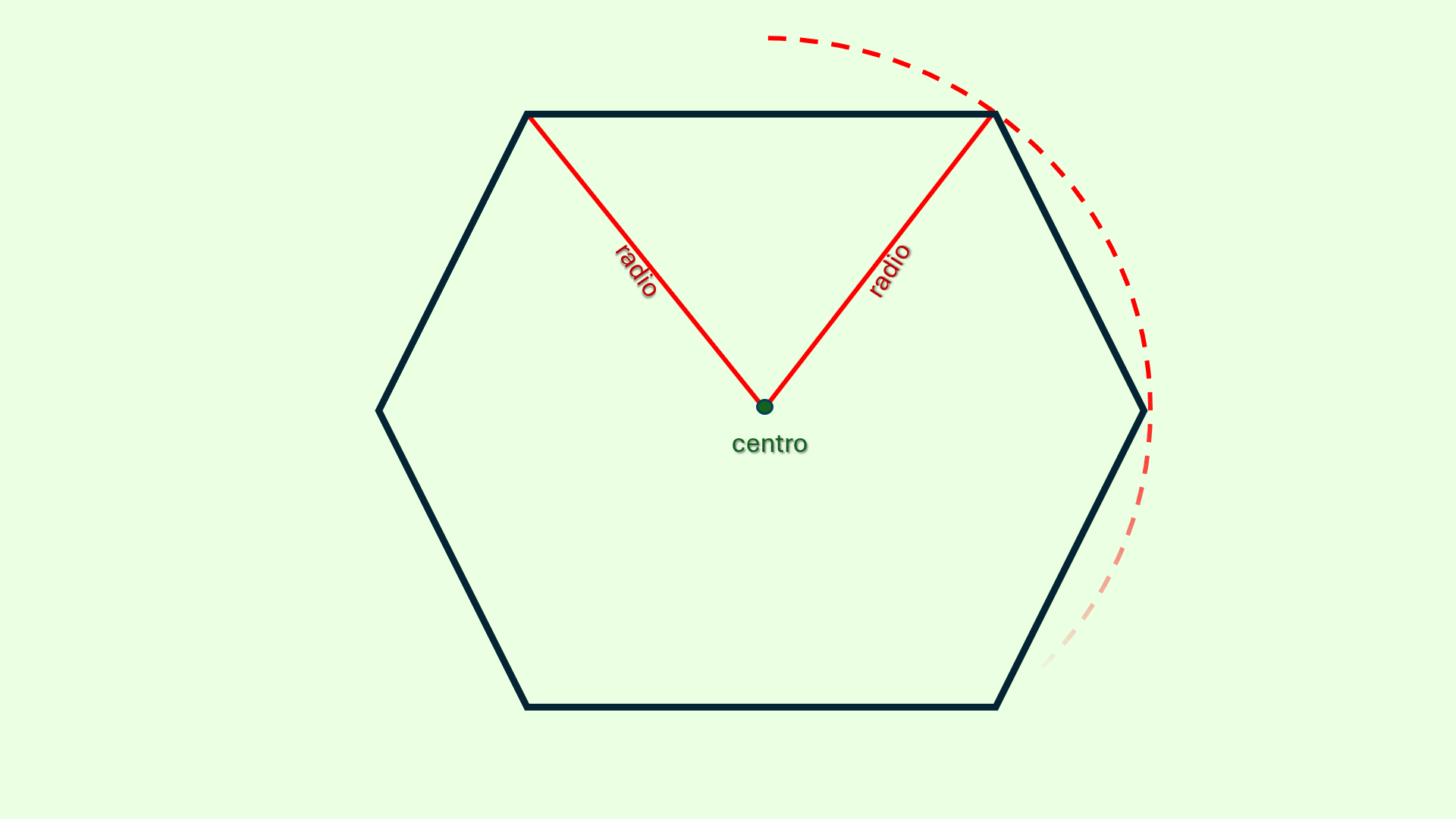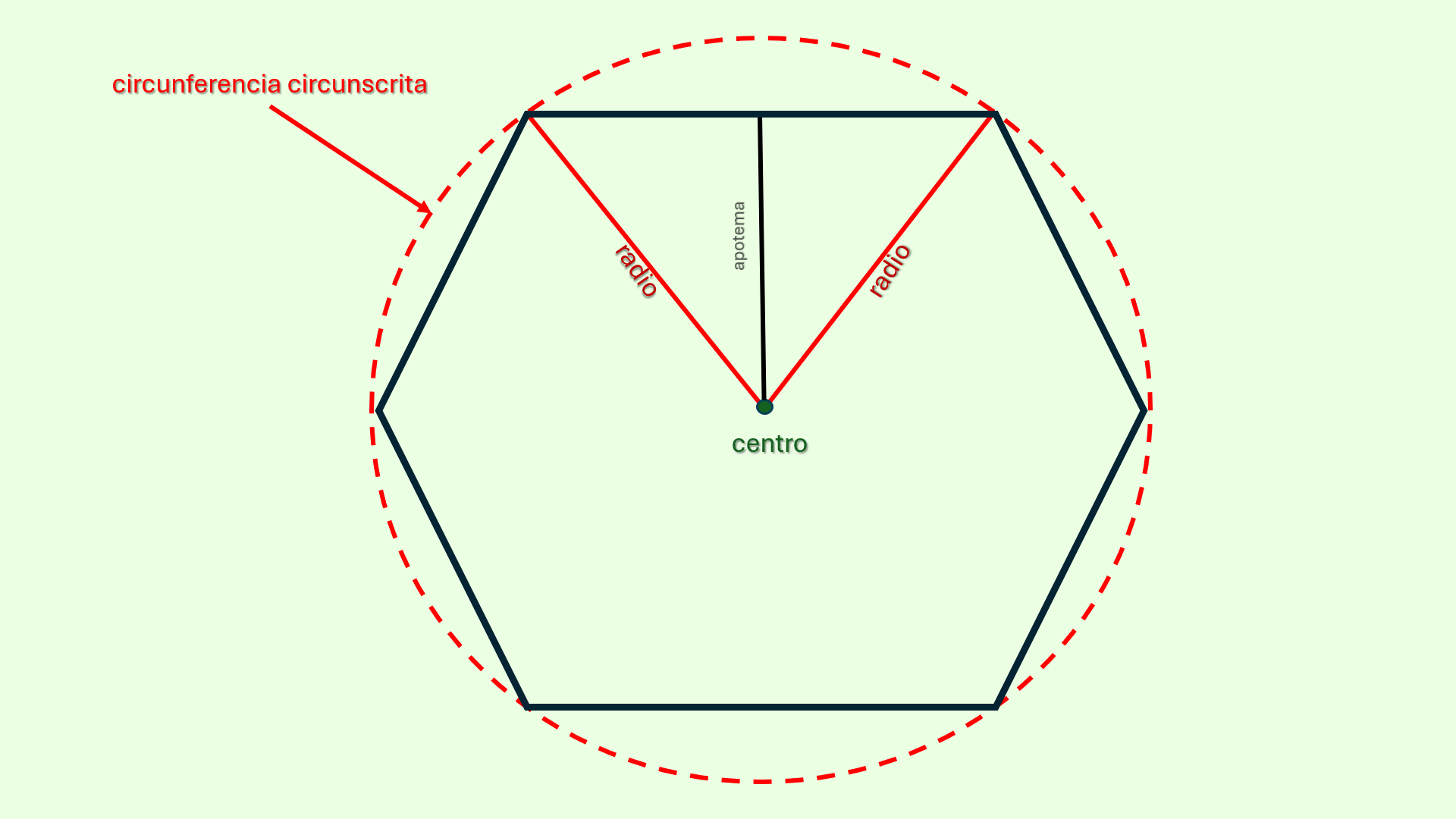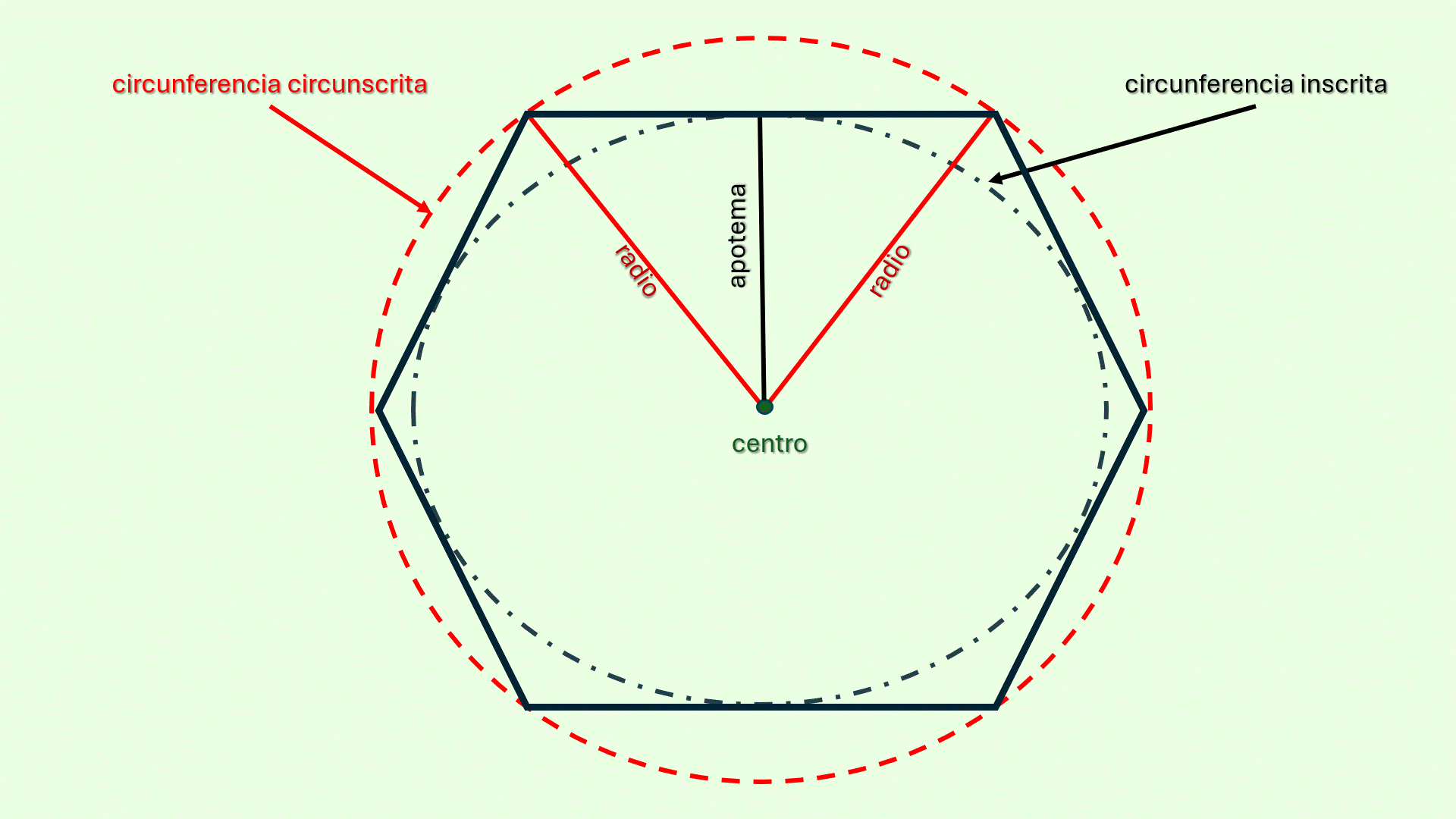
De igual manera, puede estar circunscrito Un polígono está circunscrito a una circunferencia cuando todos sus lados son tangentes a la circunferencia interna. En la imagen 4.2 la figura (un hexágono) tiene todos sus lados tocando en un punto la circunferencia de color azul. en una circunferencia. En este caso cada uno de los lados del polígono toca la circunferencia en un punto. La apotema
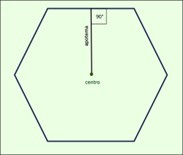
La apotema​ de un polígono regular es la menor distancia entre el centro y cualquiera de sus lados, siendo sus extremos el centro del polígono y el punto medio de cualquiera de sus lados.
Siempre es perpendicular a dicho lado. del polígono coincide con el radio de la circunferencia inscrita.

⇐ Imagen: Light texture with color. Lexica Aperture v3.5

4.2.2 Elementos de los polígonos regulares

El conocimiento de los elementos de un polígono regular (lados, vértices, ángulos, apotema, etc.) es esencial para comprender conceptos geométricos más avanzados. Esto sienta las bases para la comprensión de otras figuras geométricas y sus propiedades. Trabajar con polígonos ayuda a desarrollar la capacidad de visualizar y analizar formas en el espacio. Mejora la habilidad para resolver problemas geométricos

• Los segmentos que delimitan y forman el polígono se denominan lados.
• La cantidad de lados determina el nombre del polígono regular.
• El punto común de dos lados consecutivos se denomina vértice.
• Los lados que forman el vértice también forman, hacia la parte interior, el ángulo interior.

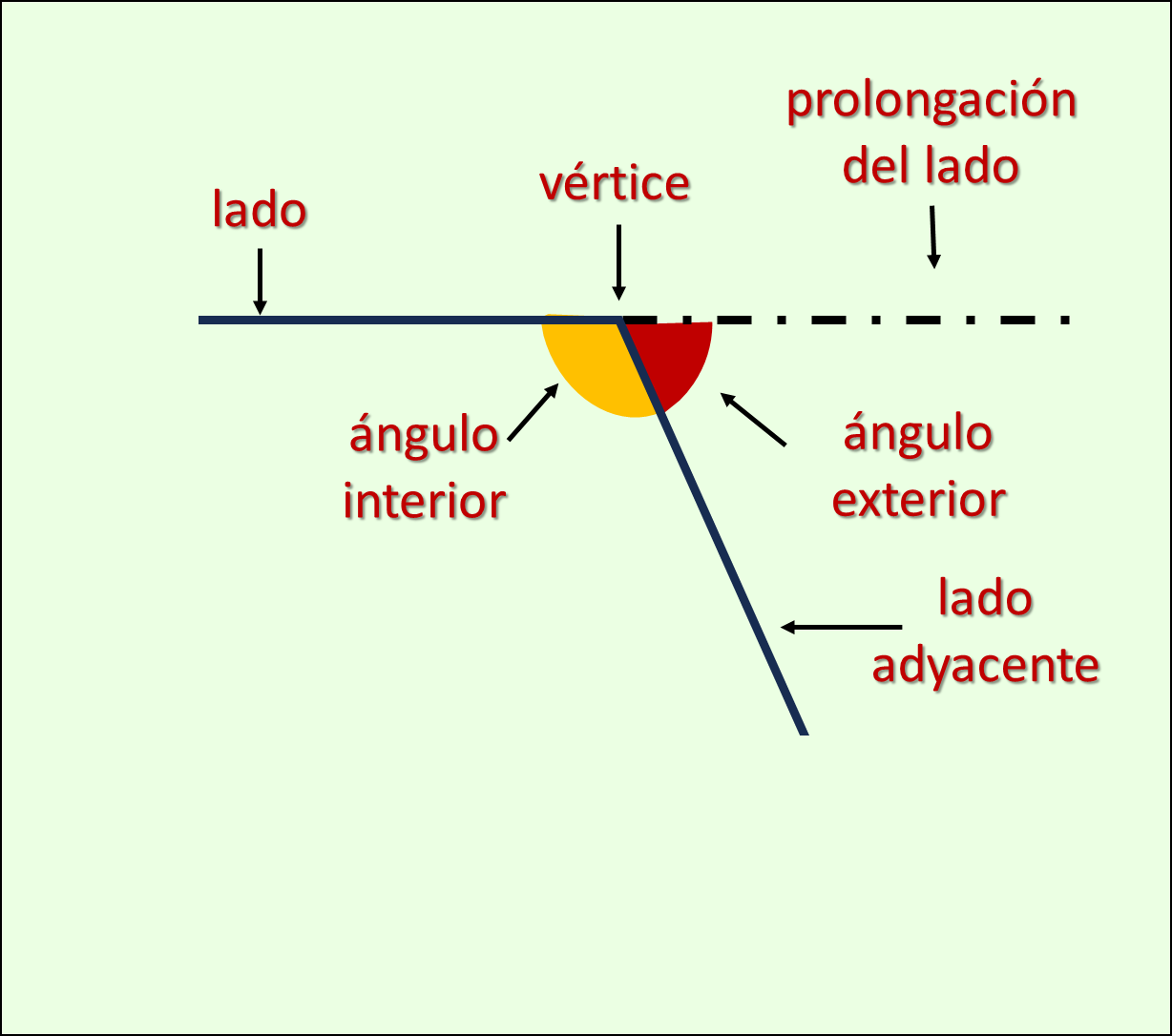
• El punto interior equidistante de todos los vértices y lados se denomina centro
• Los segmento que une el centro del polígono con uno de sus vértices se denomina radio.
• Los ángulos exteriores se forman entre un lado del polígono y la prolongación del lado adyacente.
• Los ángulos centrales se forman entre dos radios consecutivos que van a los vértices del polígono.
• La línea perpendicular que une el centro con uno de sus lados es la apotema

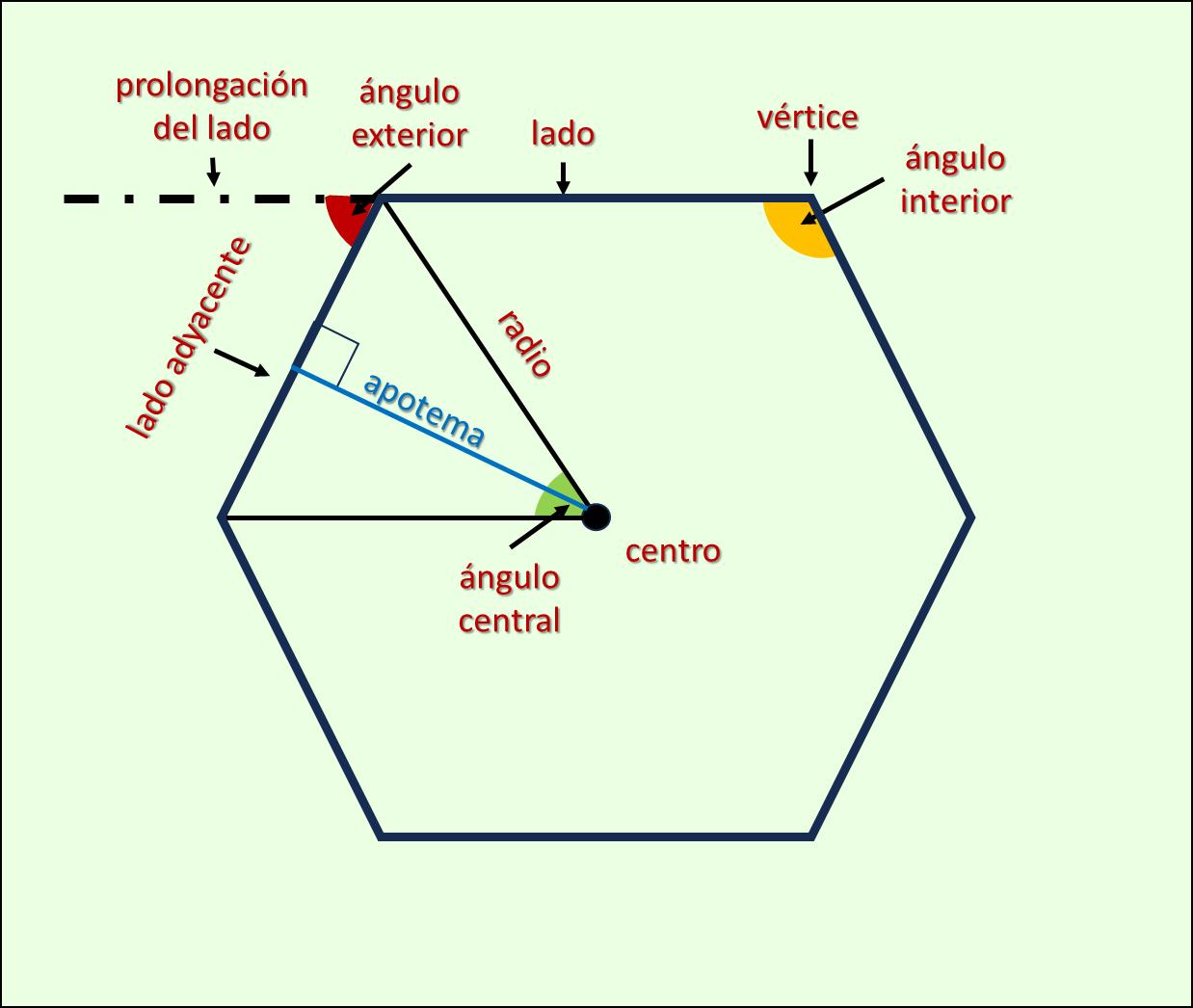
Nomenclatura de los polígonos regulares

Para nombrar los polígonos regulares se utiliza un prefijo numérico que indica el número de lados. Por ejemplo, hepta significa siete, así el polígono regular de siete lados se llama heptágono.

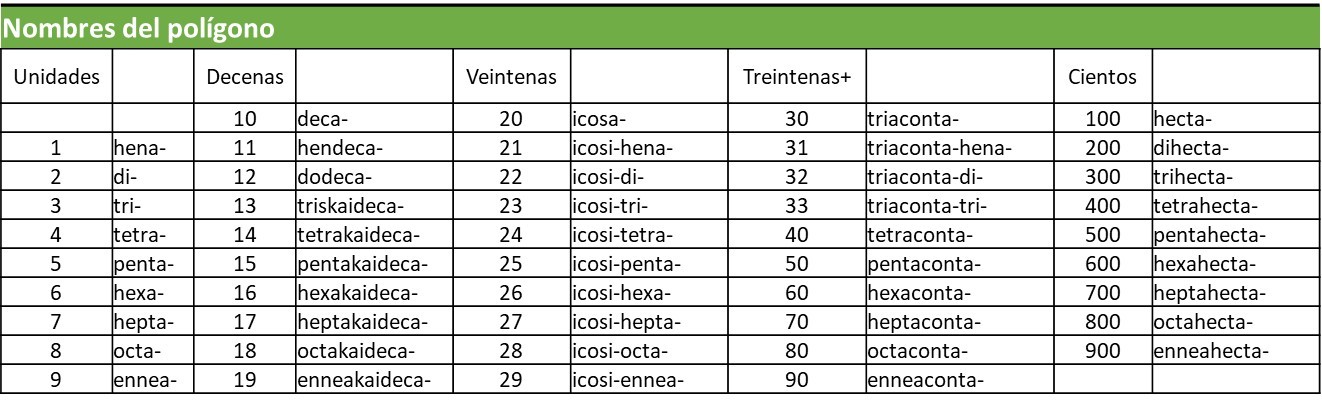
Características de los polígonos regulares

Los polígonos regulares se caracterizan porque sus lados, sus ángulos interiores y sus ángulos centrales son iguales. Además, sus ángulos exteriores son iguales y siempre suman 360 grados. Otra característica muy importante es que el centro geométrico
El centroide es el punto que representa el centro geométrico de una figura. Es como el "punto de equilibrio" de una figura plana o tridimensional. En un polígono regular, el centroide coincide con el centro de su circunferencia inscrita y circunscrita. siempre coincide con el centro del polígono.

La suma de los ángulos interiores de un polígono depende del número de lados que el mismo tenga. Se calcula por la fórmula siguiente donde $n$ es el número de lados del polígono.

$(n - 2) \times 180^{\circ}$

Para conocer el valor de un ángulo interior, dividimos la suma total de los ángulos interiores entre el número de lados. Para conocer el valor de un ángulo exterior, dividimos 360 entre el número de lados.

Ejemplo: Calcule el valor de un ángulo interior y uno exterior de un dodecágono.
El dodecágono tiene 12 lados, la suma total de sus ángulos internos es: $$(12 - 2) \times 180 = 10 \times 180 = 1800$$ Dividiendo el resultado entre la cantidad de lados del dodecágono (12) obtenemos el valor de un ángulo interno: $\frac{1800 }{12} = 150$
Para calcular el valor de un ángulo externo, dividimos 360 entre 12. $\frac{360}{12}= 30$

4.2.3 Interactivo - Ángulos de polígonos regulares

4.2.4 Perímetro de polígonos regulares

El perímetro es una propiedad métrica que consiste en la medida de la distancia total alrededor del borde de una figura plana. Es la longitud del contorno de una forma.

Las unidades de medida del perímetro son unidades lineales: centímetros (cm), metros (m), pulgadass (in), etc.

El perímetro ($P$) de los polígonos regulares, dado que todos los lados tienen la misma longitud, se cálcula como: $$P = n \times l$$ Donde:
$n$ representa la cantidad de lados.
$l$ representa la medida de un lado.

4.2.5 Interactivo - Perímetro polígonos regulares

4.2.6 Área de polígonos regulares

El área es otra propiedad métrica que consiste en la medida de la superficie dentro de los límites de una figura bidimensional. Es la cantidad de espacio que ocupa una figura.

Las unidades de medida del área son unidades cuadradas: centímetros cuadrados (cm²), metros cuadrados (m²), pulgadas cuadradas (in²), etc.

El área ($A$) de todos los polígonos⁷ regulares se calcula mediante la fórmula: $$A = \frac{P \times a}{2}$$ Donde:
$P$ representa el perímetro.
$a$ representa la apotema.

4.2.7 Interactivo - Área de polígonos regulares

4.3 Triángulo equilátero

Un triángulo⁸. es un polígono de tres lados Dentro de los triángulos tenemos el triángulo equilátero, que es el polígono regular más simple que existe. El triángulo equilátero (a veces llamado equiángulo) tiene todos sus lados y ángulos internos iguales. Debido a esta igualdad, posee una alta simetría.

Características Principales:

• Lados:
  Los tres lados del triángulo equilátero tienen la misma longitud.
• Ángulos:
  Los tres ángulos internos del triángulo equilátero miden 60 grados cada uno.
• Altura:
  La altura de un triángulo equilátero divide la base en dos partes iguales, y también es la mediana y la bisectriz del ángulo opuesto.
• Simetría:
  Posee tres ejes de simetría.

Propiedades métricas del triángulo equilátero

Perímetro
El perímetro de un triángulo equilátero es igual a la suma de sus tres lados. $$P = 3 l$$ donde: $l$ es la longitud de uno de sus lados.⁹

Área
Si conoces la longitud de un lado ($l$), la fórmula más utilizada para el cálculo del área es: $$A = \frac{\sqrt{3}}{4} \times l^2$$

Altura
La altura¹⁰ ($h$) de un triángulo equilátero se puede calcular con la siguiente fórmula: $$h = \frac{\sqrt{3}}{2} \times l$$

Líneas notables del triángulo equilátero

En los triángulos hay líneas que tienen propiedades especiales que generan puntos significativos dentro de la figura. Estas líneas reciben el nombre de líneas notables.

• Mediana:
  Es el segmento que une un vértice con el punto medio del lado opuesto.
  El punto de intersección de las tres medianas se llama baricentro, que es el centro de gravedad del triángulo.


• Altura:
  Es el segmento perpendicular trazado desde un vértice hasta el lado opuesto (o su prolongación).
  El punto de intersección de las tres alturas se llama ortocentro.


• Bisectriz:
  Es el segmento que divide un ángulo interno del triángulo en dos ángulos iguales.
  El punto de intersección de las tres bisectrices se llama incentro, que es el centro de la circunferencia inscrita en el triángulo.


• Mediatriz:
  Es la linea perpendicular a un lado del triángulo que pasa por su punto medio.
  El punto donde se intersecan las 3 mediatrices se le llama circuncentro y es el centro de una circunferencia que pasa por los tres vértices del triángulo.

En un triángulo equilátero, la mediana, la altura, la bisectriz y la mediatriz trazadas desde el mismo vértice coinciden en una sola línea.

Cada una de estas líneas
cumple todas las funciones a la vez.

El baricentro, circuncentro, ortocentro e incentro coinciden en el triángulo equilátero

4.4 Cuadrado

Un cuadrado es un polígonos regular de cuatro¹¹ lados iguales y cuatro ángulos iguales. Sus lados son perpendiculares entre sí.

Características principales

• Lados
  Todos los lados de un cuadrado tienen la misma longitud y sus lados opuestos son paralelos.¹²
• Ángulos
  La suma de sus ángulos internos es de $(4-2)\times 180=360°$, por lo tanto cada ángulo interior mide $\frac {360}{4}= 90°$.
• Diagonales
  Son segmentos que unen dos vértices no consecutivos. Las diagonales del cuadrado tienen la misma longitud y forman ángulos rectos en el punto de instersección y son bisectrices de los ángulos de los vértices.
• Centro
  El centro (punto medio) del cuadrado es el punto donde se intersectan las diagonales del cuadrado y los segmentos que unen los puntos medios de los lados opuestos.

Propiedades métricas del cuadrado

Perímetro
Al tener cuatro lados, el cálculo del perímetro se calcula multiplicando la longitud de un lado por cuatro:¹³ $$P= 4l$$ Área
El área del cuadrado, cómo polígono regular, se puede calcular mediante la fórmula $$A = \frac{P \times a}{2}$$

No obstante, la fórmula propia del cuadrado para el cálculo de su área se expresa como¹⁴: $$A = l^2$$

4.5 Pentágono regular

Un pentágono La palabra pentágono proviene del griego: "penta" que significa cinco y "gonia" que significa ángulo. regular es un polígono de cinco lados iguales. Sus características más importantes son:

• Lados:
  Un pentágono regular tiene cinco lados iguales.
• Vértices:
  Tiene cinco vértices, que son los puntos donde se unen los lados.
• Ángulos
  La suma de los ángulos interiores del pentágono $(n=5)$ es :
  

  $(5-2) \times 180 = 540$

  Cada ángulo interior tiene un valor de:

  $\frac{540}{5} = 108$

• Diagonales
  Un pentágono regular tiene cinco diagonales.
• Centro
  Es el punto equidistante de todos los vértices y de todos los lados.
• Apotema
  Es el segmento que une el centro del pentágono con el punto medio de cualquiera de sus lados. Es el radio de la circunferencia inscrita.
• Radio
  Es el segmento que une su centro con cualquier vértice. Es el radio de la circunferencia circunscrita.
• Ángulos centrales
  El ángulo central es el ángulo formado por dos radios consecutivos que unen el centro del polígono con dos vértices adyacentes. Cada uno de estos ángulos miden $\frac {360}{5}= 72°$.

Relación del pentágono con el número áureo
El pentágono regular tiene una relación intrínseca con el número áureo.

El cociente entre la diagonal y el lado de un pentágono regular es constante e igual al número áureo ($φ$).

El número áureo¹⁵, es un número irracional (1.6180339887...) que se representa con la letra griega phi (φ). Aparece en numerosas construcciones
La relación entre la altura y el tamaño de la base de la pirámide de Guiza, en Egipto, responde a la proporción áurea. geométricas, en obras de arte
Leonardo da Vinci utilizó la proporción áurea en sus obras para crear armonía y equilibrio visual. y en la naturaleza. La secuencia de Fibonacci
En la secuencia de Fibonacci cada término es la suma de los dos anteriores. Si tomas dos números consecutivos y divides el mayor por el menor, el resultado se acerca al número áureo. se observa en patrones de crecimiento de plantas
Trazas de la espiral áurea en las semillas de girasol. y la espiral de las conchas marinas
Nautilus donde la espiral áurea está perfectamente visible. . También se encuentra en la estructura de algunos animales y en la proporción de partes del cuerpo humano
El hombre de Vitruvio.
Leonardo da Vinci

Propiedades métricas del pentágono regular

Perímetro
Al tener cinco lados, el cálculo del perímetro se calcula multiplicando la longitud de un lado por cinco: $P= 5l$

Área
El área del pentágono, cómo polígono regular, se calcula mediante la fórmula $$A = \frac{P \times a}{2}$$ Donde:
$A$ representa el área.
$P$ representa el perímetro.
$a$ representa la apotema.

Existen otras formas de cálculo del área del pentágono regular, pero involucran conocimientos trigonométricos que están fuera del alcance de este libro.

4.6 Hexágono regular

Un hexágono La palabra hexágono proviene del griego: "hexa" que significa seis y "gonia" que significa ángulo. regular es un polígono de seis lados iguales con las siguientes particularidades.

• Lados:
  Un pentágono regular tiene seis lados iguales.
• Vértices:
  Tiene seis vértices, que son los puntos donde se unen los lados.
• Ángulos
  La suma de los ángulos interiores del pentágono $(n=6)$ es :
  

  $(6-2) \times 180 = 720$

  Cada ángulo interior tiene un valor de:

  $\frac{720}{5} = 120$

• Diagonales
  Tiene nueve diagonales.
• Centro
  Es el punto interior que está a la misma distancia de todos los vértices y de todos los lados.
• Apotema
  Es el segmento que une el centro del hexágono con el punto medio de cualquiera de sus lados. Es el radio de la circunferencia inscrita.
• Radio
  Es el segmento que une el centro del hexágono con cualquiera de sus vértices.Es el radio de la circunferencia circunscrita y tiene la misma longitud que los lados.
• Angulos centrales
  Cada uno de los ángulos centrales mide 60 grados, por eso, un hexágono regular puede dividirse en seis triángulos equiláteros idénticos.
  Formación de seis triángulos equiláteros idénticos en un hexágono regular.

Medidas del hexágono regular

Perímetro
Al tener seis lados, el cálculo del perímetro se calcula multiplicando la longitud de un lado por seis: $P= 6l$

Área por la fórmula general
El área del pentágono, cómo polígono regular, se calcula mediante la fórmula $$A = \frac{P \times a}{2}$$ Donde: $A$ representa el área, $P$ representa el perímetro y $a$ representa la apotema.

La capacidad de descomponer el hexágono en triángulos equiláteros permite fórmulas específicas de cálculo del área más allá de la fórmula general de los polígonos regulares

Área conociendo el valor del lado ($l$)
$$\text{Área} = \frac{3\sqrt{3}}{2} l^2$$ Donde $l$ es la longitud de un lado del hexágono.

Área conociendo el valor de la apotema ($a$):
$$\text{Área} = 2\sqrt{3} \times a^2$$ Donde $a$ el el valor de la apotema.

Elegir la fórmula adecuada dependerá de qué datos se tengan disponibles (longitud del lado, apotema, etc.).

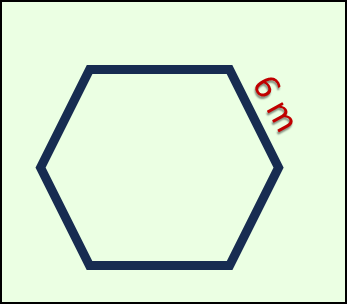
Ejemplo:
Calcule el área del hexágono regular que se muestra en la imagen. Redondee el resultado a la décima más cercana

Nos dan como dato que el hexágono tiene $6 m$ de lado. Eso nos permite utilizar la fórmula del área en función del lado $\text{A} = \frac{3\sqrt{3}}{2} l^2$

Sustituyendo los valores tenemos: $\text{A} = \frac{3\sqrt{3}}{2} \times 6^2$. Calculando
$\text{A} = \frac{3\sqrt{3}\times 36}{2} = 93.5$

El área del hexágono regular de lado $6 m$ es de $93.5 m^2$

4.7 Otros polígonos regulares

Estudiamos el triángulo equilátero, el cuadrado, el pentágono y el hexágono, los cuales son polígonos regulares muy conocidos y utilizados, pero existen muchísimos más. Veamos algunos.

Heptágono
Tienen 7 lados. Menos común en la vida cotidiana que el hexágono.
Aparece en algunas monedas.
Ha tenido connotaciones místicas y simbólicas en algunas culturas

Decágono
Tienen 10 lados.
Aparece en monedas y algunos diseños arquitectónicos y decorativos.
Tiene relación con el número aureo.

Octadecágono
Tienen 18 lados.
Presente en diseños decorativos y en los mandalas¹⁶.
Es muy útil cuando se busca crear figuras que sean lo más parecidas a una circunferencia.

Imagen: From a point comes a single straight line that reaches a square on a gradient⇒
background in green tones... Lexica Aperture v3.5

4.8 Comprobación - Ángulos de Polígonos

Cuadriláteros

5.1 Características de los cuadriláteros

Los cuadriláteros son figuras geométricas planas que tienen cuatro lados, cuatro vértices y cuatro ángulos interiores que suman 360°. Son un caso especial de los polígonos, y su estudio es fundamental en geometría debido a su amplia aplicación en matemáticas, ingeniería, diseño y arquitectura.

Clasificación de los cuadriláteros¹⁷

1. Cuadriláteros simples:
   No tienen lados que se crucen. Se subdividen en:
   • Convexos:
     todos los ángulos interiores miden menos de 180°. Ambas diagonales de un cuadrilátero convexo se encuentran completamente dentro de la figura. Ejemplo: los paralelogramos
   • Cóncavos:
     tiene al menos un ángulo interior que mide más de 180°, y al menos una de sus diagonales se encuentra parcialmente fuera de la figura. Ejemplo: el dardo.
2. Cuadriláteros complejos:
   Tienen lados que se cruzan, formando una figura como un lazo. Ejemplo: los cuadriláteros cruzados.

5.2 Paralelogramos

El paralelogramo es una figura geométrica común en matemáticas y aparece en muchos contextos prácticos, como diseño arquitectónico, ingeniería y arte.

Un paralelogramo es un cuadrilátero en el que los lados opuestos son paralelos y de igual longitud. Esta simple característica da lugar a una serie de propiedades importantes.

• Los lados opuestos son paralelos entre sí, es decir, nunca se cruzan.
• Los pares de lados opuestos tienen la misma medida.
• La suma de los ángulos consecutivos (que comparten un lado) es siempre 180°.
• Las diagonales se bisecan: La palabra "bisecan" se refiere a la acción de dividir algo en dos partes iguales. "las diagonales se bisecan" significa que se cortan entre sí, dividiéndose en dos segmentos de la misma longitud. cortándose en el punto medio.
• Tiene un eje de simetría en el punto de intersección de las diagonales.

Perímetro:
El perímetro es el contorno de la figura, es la suma de todos los lados. Los paralelogramos tienen sus lados opuestos iguales, por lo que, si llamamos a un lado ($a$) y al otro ($b$) tendríamos:

$$P = 2a + 2b = 2 (a+b)$$

Área:
El área es la superficie que encierra el perímetro. La altura ($h$) de un paralelogramo es el segmento de recta que va perpendicularmente desde un vértice al lado opuesto, llamado base ($b$), formando un ángulo de 90°.

El área se calcula mediante la fórmula
$$A = b × h$$

Dentro del conjunto de paralelogramos, encontramos subtipos específicos que tienen características adicionales y que estudiarenos a continación:

• Rectángulo:
• Rombo:
• Cuadrado: Ya estudiado en el capítulo 4
• Romboide:

5.2.1 Ejercicios - Área del paralelogramo

5.2.2 Rectángulos

Un rectángulo es un paralelogramo que tiene cuatro ángulos rectos (90°).

Características principales:

• La característica más distintiva del rectángulo es que todos sus ángulos interiores miden exactamente 90°.
• Los lados opuestos del rectángulo son paralelos entre sí y tienen la misma longitud.
• Las diagonales de un rectángulo tienen la misma longitud
• Como todo cuadrilátero, la suma de los ángulos interiores es 360°.
• Tiene dos ejes de simetría (vertical y horizontal). También es simétrico con respecto al punto donde se cruzan las diagonales (su centro).

Un cuadrado es un caso especial de rectángulo en el que todos los lados son iguales. Por lo tanto, todos los cuadrados son rectángulos, pero no todos los rectángulos son cuadrados.

Perímetro:
Es la suma de todos los lados. El rectánglo tienes sus lados opuestos iguales. Asumiendo que un lado es ($a$) y el otro ($b$), su perímetro se calcula por la fórmula ¹⁸ :

$$P = 2a + 2b = 2(a+b)$$

Área:
El área es la superficie que encierra el perímetro. Se calcula multiplicando mediante la fórmula:

$$A = b × h$$

5.2.3 Ejercicios - Área del rectángulo

El cálculo del área del rectángulo es muy utilizada en la vida real, por ejemplo:

• Para saber cuántos azulejos, baldosas, pintura o madera se necesita para cubrir una pared o un piso.
• Para diseñar habitaciones, oficinas o edificios
• El área de una imagen o pantalla rectangular se usa para determinar su tamaño y resolución.

5.2.4 Romboide

Un romboide es un cuadrilátero que pertenece a la familia de los paralelogramos. En esta figura, los lados opuestos son paralelos y de longitud igual, pero los ángulos no son rectos (es decir, no miden 90°). Parece un rectángulo que lo han "empujado" quedando inclinado.

Características principales:

• Los lados opuestos son paralelos y tienen la misma longitud. Los lados adyacentes pueden ser de longitudes diferentes.
• Los ángulos opuestos son iguales. Los ángulos consecutivos (adyacentes) son suplementarios, es decir, la suma de dos ángulos consecutivos es 180°
• Las diagonales del romboide no son perpendiculares entre sí. Las diagonales no se bisecan mutuamente en partes iguales (a menos que el romboide sea un rombo).
• El romboide no tiene ejes de simetría,

Perímetro:
Es la suma de todos los lados. El romboide tiene sus lados opuestos iguales. Siendo un lado ($a$) y el otro la altura ($b$), su perímetro se calcula por la fórmula

$$P = 2a + 2b = 2(a+b)$$

Área:
El área es la superficie que encierra el perímetro. Se calcula multiplicando mediante la fórmula:

$$A = b × h$$

5.2.5 Ejercicios - Área del romboide

Como has apreciado, el romboide es un paralelogramo con lados opuestos paralelos e iguales, pero sin ángulos rectos. Aunque comparte propiedades con el rectángulo y como veremos a continuación, con el rombo, su falta de perpendicularidad en las diagonales y la ausencia de ángulos rectos lo distinguen.

Es una figura útil en geometría y diseño para representar formas inclinadas y equilibradas.

5.2.6 Rombo

El rombo¹⁹ es un cuadrilátero paralelogramo de lados iguales. Algunos cortes de diamantes tienen una forma alargada o facetados que recuerdan a la geometría de un rombo.

Características principales:

• Todos los lados de un rombo tienen la misma longitud y los lados opuestos paralelos.
• Los ángulos opuestos de un rombo tienen la misma medida. A diferencia del cuadrado, sus ángulos no son rectos.
• Las diagonales de un rombo se cortan formando ángulos rectos. Las diagonales bisecan sus ángulos.
• Posee dos ejes de simetría.

El perímetro de un rombo se calcula multiplicando la longitud de un lado por cuatro: $$P = 4l$$

El área de un rombo se puede calcular multiplicando la longitud de las diagonales mayor ($D$) y menor ($d$) y dividiendo el resultado por dos: $$Área = \frac{(D × d)}{2}$$

5.3 Deltoide

Un deltoide es un cuadrilátero que tiene la forma de un cometa. Es un cuadrilátero convexo (es decir, sus ángulos interiores son menores de 180°) y se caracteriza por tener dos pares de lados adyacentes congruentes (iguales en longitud), pero los lados opuestos no son necesariamente iguales ni paralelos.

Características principales

• Tiene dos pares de lados adyacentes iguales Si los lados consecutivos son a,a,b,b, entonces a y b son de diferentes longitudes.
• Las diagonales son perpendiculares entre sí (forman un ángulo de 90°). Una de las diagonales (la diagonal mayor) biseca a la otra (la corta en dos partes iguales).
• Tiene un par de ángulos opuestos iguales (los que están entre los lados desiguales). Los otros dos ángulos son diferentes.
• Posee un eje de simetría, que es la diagonal mayor. Este eje divide al deltoide en dos partes iguales.

El perímetro de un rombo se calcula multiplicando la longitud de un lado por cuatro: $$P = 4l$$

El área del deltoide se calcula igual que la del rombo, multiplicando la longitud de las diagonales mayor ($D$) y menor ($d$) y dividiendo el resultado por dos: $$Área = \frac{(D × d)}{2}$$

5.3.1 Tabla de diferencias entre rombo y deltoide

Tanto el rombo como el deltoides tienen la misma fórmula para calcular el área. Esto se debe a que ambas figuras pueden dividirse en cuatro triángulos al trazar sus diagonales, y estas diagonales se cruzan formado ángulos rectos. La fórmula del área se deriva de la suma de los cuatro triángulos formados por las diagonales.

Aunque la fórmula es la misma, es importante notar que la geometría interna de cada figura es diferente, especialmente en la relación entre las diagonales. Analiza la siguiente tabla para que lo compruebes.

5.3.2 Ejercicios - Área del rombo y deltoide

5.4 Trapecios

Un trapecio es un cuadrilátero. Su característica principal es que tiene al menos un par de lados opuestos que son paralelos En Estados Unidos un trapecio, es un cuadrilátero que tiene al menos un par de lados paralelos, mientras que un trapezoide, es un cuadrilátero que no tiene lados paralelos.
En otros sistemas educativos, los términos son diferentes. El trapecio es un cuadrilátero sin lados paralelos (lo que los estadounidenses llaman "trapezoid") y trapezoide es un cuadrilátero con al menos un par de lados paralelos (lo que los estadounidenses llaman "trapezium"). . Estos lados paralelos reciben el nombre de bases, y los otros dos lados se llaman lados no paralelos o lados oblicuos.

Características del trapecio

• Dos de sus lados son paralelos y se denominan bases.
• La suma de los cuatro ángulos interiores siempre es igual a 360°.
• La altura es la distancia perpendicular entre las bases paralelas.
• La línea media es el segmento que une los puntos medios de los lados no paralelos. Es paralela a las bases y su longitud es igual al promedio de las longitudes de las bases.

Tipos de trapecios

Los trapecios se clasifican en función de sus ángulos y lados, pudiendo ser trapecios rectángulos, trapecios isósceles y trapecios escalenos.

Trapecio rectángulo	Trapecio isósceles	Trapecio escaleno
Tiene dos ángulos rectos (90°). Uno de los lados oblicuos es perpendicular a las bases.	Los lados no paralelos son de igual longitud. Los ángulos adyacentes a cada base son iguales. Tiene simetría con respecto a una línea perpendicular a las bases.	No tiene lados iguales, excepto las bases paralelas. No tiene simetría.

Trapezoides

Un trapezoide, en Estados Unidos de América, es un cuadrilátero que no tiene ningún par de lados opuestos paralelos, a diferencia de un trapecio que sí tiene un par de lados paralelos. No es objeto de estudio en este libro.

5.4.1 Propiedades métricas del trapecio

Perímetro:
El perímetro de un trapecio se calcula sumando la longitud de cada lado: $$P = a+b+B+c$$

Área:
El área del trapecio se calcula a partir de la media de sus bases $\frac{(B + b)}{2}$ multiplicada por la altura ($h$) $$A = \frac{(B+b)}{2} \times h$$

5.4.2 Ejercicios - Área del trapecio

En la vida diaria, el trapecio se utiliza en puentes, estructuras arquitectónicas, bases de presas o represas, etc.

Por ejemplo, en las presas la forma trapezoidal de la base permite una distribución más uniforme de la presión del agua sobre el terreno. La base más ancha aumenta el área de contacto, lo que reduce la presión por unidad de área y evita el hundimiento. La base ancha también aumenta la resistencia al deslizamiento de la presa sobre el terreno.

5.5 Comprobación - Cuadriláteros

⇐ Imagen: A collage of images of Egyptian, Babylonian, Indian, Mayan, Chinese constructions. Lexica Aperture v5

Triángulos

6.1 Los triángulos

En el Capítulo 4 estudiamos que el triángulo es un polígono de tres lados y tres ángulos, siendo la figura geométrica plana más simple que se puede construir con líneas rectas y que permite analizar y comprender propiedades fundamentales, como ángulos, congruencia y semejanza.

Los triángulos son omnipresentes y tienen una importancia enorme en diversos campos:

• Matemáticas:
  Son la base de la trigonometría, una rama fundamental de las matemáticas que se utiliza para calcular distancias y ángulos.
• Física e ingeniería:
  La forma triangular proporciona una gran estabilidad estructural, por lo que se utiliza en la construcción de puentes, edificios y otras estructuras. La triangulación es una técnica utilizada en topografía y navegación para determinar posiciones y distancias.
• Diseño y arquitectura:
  Los triángulos se utilizan en diseños arquitectónicos y artísticos por su atractivo estético y su capacidad para crear dinamismo y equilibrio.

Los triángulos tienen clasificaciones en función de la medida de sus lados y la medida de sus ángulos, así como líneas notables, que son segmentos especiales que ayudan a estudiar sus propiedades geométricas y resolver problemas relacionados con ellos.

Los triánguos también tienen propiedades métricas, como el perímetro y el área, que son fundamentales para entender su tamaño, forma y proporciones

⇐ Imagen: Stylish sophistication chic background abstract luxury triangles. Lexica Aperture v3.5

6.1.1 Clasificación los triángulos

Nombre del Triángulo	Clasificación	Descripción	Imagen
Clasificación por la medida de sus lados
Equilátero	Lados	Tres lados iguales
Isósceles	Lados	Dos lados iguales
Escaleno	Lados	Tres lados desiguales
Clasificación por la medida de sus ángulos
Acutángulo	Ángulos	Tres ángulos agudos (menores de 90°)
Rectángulo	Ángulos	Un ángulo recto (90°)
Obtusángulo	Ángulos	Un ángulo obtuso (mayor de 90°)

6.1.2 Líneas notables del triángulo:

Cuando estudiamos el polígono regular triángulo equilátero en el Capítulo 4, vimos que los triángulos tienen líneas con propiedades especiales que generan puntos importantes dentro de la figura denominadas líneas líneas notables.

Estas líneas notables son la altura, la bisectriz, la mediana, y la mediatriz

A diferencia del triángulo equilátero, donde todas coinciden, estas líneas se ubican de manera diferente en cada tipo de triángulo. Estudiemos cada una de ellas, analizando su comportamiento según el tipo de triángulo.

Altura

La altura de un triángulo es un concepto fundamental que define la distancia perpendicular desde un vértice hasta el lado opuesto, conocido como base.

• La altura se traza desde un vértice del triángulo hasta el lado opuesto (o su prolongación) formando un ángulo de 90 grados, es decir: es perpendicular a la base.
• Cada triángulo tiene tres alturas, una por cada uno de sus vértices y lados opuestos.
• Las tres alturas de un triángulo siempre se intersectan en un punto llamado ortocentro. La ubicación del ortocentro varía según el tipo de triángulo.
• La altura es esencial para calcular el área de un triángulo.

La posición de la altura varía en dependencia del tipo de triángulo

Altura en el triángulo acutángulo

Todas las alturas se encuentran dentro del triángulo.

El ortocentro se localiza dentro del triángulo.

Altura en el triángulo rectángulo:

Dos de las alturas coinciden con los catetos del triángulo.

El ortocentro se encuentra en el vértice del ángulo recto.

Altura en el triángulo obtusángulo

Dos de las alturas se encuentran fuera del triángulo.

El ortocentro se localiza fuera del triángulo.

Bisectriz

La bisectriz es el segmento que divide un ángulo interno del triángulo en dos ángulos iguales. El punto de intersección de las tres bisectrices se llama incentro, que es el centro de la circunferencia inscrita en el triángulo. Es el lugar geométrico de los puntos que equidistan de los lados del ángulo.

El incentro siempre se encuentra dentro del triángulo, independientemente de si el triángulo es acutángulo, rectángulo u obtusángulo.

Mediana

La mediana es el segmento que une un vértice con el punto medio del lado opuesto. El punto de intersección de las tres medianas se llama baricentro

El baricentro siempre se encuentra dentro del triángulo, sin importar el tipo de triángulo. El baricentro también es conocido como el centro de gravedad del triángulo.

No debe confundirse la bisectriz con la mediana. La bisectriz se relaciona con la división de ángulos, mientras que la mediana se relaciona con la división de lados. Ambas son líneas notables en un triángulo, pero tienen propiedades y aplicaciones distintas.

Mediatriz

La mediatriz es la línea perpendicular a un lado del triángulo que pasa por su punto medio.

El punto donde se intersecan las 3 mediatrices se le llama circuncentro y es el centro de la circunferencia circunscrita al triángulo.

La ubicación del circuncentro varía según el tipo de triángulo

Mediatriz en el triángulo acutángulo:

En un triángulo acutángulo, el circuncentro está dentro del triángulo.

Mediatriz en el triángulo recto:

En un triángulo rectángulo, el circuncentro se encuentra en el punto medio de la hipotenusa.

Mediatriz en el triángulo obtusángulo:

En un triángulo obtusángulo, el circuncentro está fuera del triángulo.

6.1.3 Propiedades métricas de los triángulos

Las propiedades métricas de los triángulos relacionadas con el perímetro y el área son fundamentales para entender su tamaño, forma y proporciones. A continuación detallamos cada concepto:

Perímetro

El perímetro de un triángulo es la suma de las longitudes de sus tres lados y se expresa en las mismas unidades que los lados. Si los lados del triángulo son a, b y c, el perímetro se calcula como:²⁰ $$P = a + b + c$$

Área

El área de un triángulo es la medida de la superficie encerrada por sus lados. y se expresa en unidades cuadradas.

Fórmula básica
Cuando se conoce la longitud de la base (b) y la altura (h) correspondiente, el área se calcula como: $$A= \frac {b \times h} {2}$$

Fórmula de Herón
Cuando se conocen los tres lados y no se conoce la altura, se puede calcular el semiperímetro ($s$) y aplicar la fórmula de Herón. $$A= \sqrt{[s \times(s-a) \times(s-b) \times(s-c)]}$$

6.1.4 Ejercicios - Área del triángulos

6.2 Triángulos rectángulos

Dentro de los triángulos, el triángulo rectángulo se caracteriza por tener un ángulo de 90°. El lado mayor del triángulo rectángulo se denomina hipotenusa, El vocablo hipotenusa viene del griego antiguo y significa "tender por debajo". Esto se refiere a la idea de que la hipotenusa está tendida o estirada, desde un extremo del ángulo recto, hasta el otro. y es el lado que se opone al ángulo recto. Los otros dos lados reciben el nombre de catetos. El vocablo cateto viene del griego antiguo y significa "perpendicular". Los catetos son los lados "perpendiculares" que convergen en el ángulo de 90° del triángulo rectángulo

Ese ángulo recto es lo que hace único al triángulo rectángulo, el cual lo define y permite establecer una estructura fundamental en geometría, permitiendo la entrada a conceptos matemáticos esenciales.

Uno de ellos es el Teorema de Pitágoras, que establece una relación precisa entre los lados de un triángulo rectángulo. Esta relación no solo es clave para resolver problemas geométricos, sino que también tiene aplicaciones prácticas en arquitectura, ingeniería y física.

Además, los triángulos rectángulos son el fundamento de las relaciones trigonométricas: seno, coseno y tangente, que conectan los ángulos agudos de un triángulo rectángulo con las proporciones entre sus lados, las cuales se utilizando para resolver triángulos y modelar fenómenos en disciplinas como astronomía, navegación y análisis de señales.

Los triángulos rectángulos tiene una peculiaridad, sus ángulos agudos son complementarios, la suma de estos dos ángulos es siempre 90°. Esto implica que, al conocer uno de los ángulos agudos, el otro puede determinarse directamente, una propiedad que simplifica cálculos y análisis.

6.2.1 Clasificación de los triángulos rectángulos

Los triángulos rectángulos se clasifican principalmente según la longitud de sus lados. Dentro de esta clasificación, encontramos dos tipos principales:

• Triángulo rectángulo isósceles:
  Este tipo de triángulo rectángulo tiene dos catetos de igual longitud. Como consecuencia, los dos ángulos agudos miden 45 grados cada uno.
  


• Triángulo rectángulo escaleno:
  En este caso, todos los lados del triángulo rectángulo tienen longitudes diferentes.
  Como consecuencia, los dos angulos agudos tendrán diferentes medidas.

6.2.2 Líneas y puntos notables en los triángulos rectángulos

• Altura:
  Es la distancia perpendicular desde un vértice hasta el lado opuesto. En un triángulo rectángulo, dos de las alturas coinciden con los catetos.
  El ortocentro, punto donde se cruzan las alturas, en el triángulo rectángulo coincide con el vértice del ángulo recto.
• Mediana:
  Es el segmento que une un vértice con el punto medio del lado opuesto. La mediana trazada desde el vértice del ángulo recto tiene una longitud que es la mitad de la longitud de la hipotenusa.
  El baricentro, punto donde se cruzan las medianas, siempre se encuentra dentro del triángulo, como en cualquier otro triángulo.
• Mediatriz
  Es la línea perpendicular a un lado del triángulo que pasa por su punto medio.
  El circuncentro, es el punto de intersección de las mediatrices y se encuentra en el punto medio de la hipotenusa.


• Bisectriz:
  Es el segmento que divide un ángulo interno del triángulo en dos ángulos iguales.
  El incentro es el punto donde se cruzan las bisectrices y siempre se encuentra dentro del triángulo.

6.3 Teorema de Pitágoras

El Teorema de Pitágoras es uno de los principios matemáticos más famosos y fundamentales. Evidencias históricas indican que las relaciones entre los lados de un triángulo rectángulo ya eran conocidas en civilizaciones anteriores a Pitágoras, como la babilónica y la egipcia. Por ejemplo, la tablilla babilónica Plimpton 322, La tablilla de barro Plimpton 322 muestra 60 números en 15 filas y 4 columnas. Se sabe que es un trozo de una tablilla más grande que tenía 38 filas y 8 columnas. La hipótesis más sólida es que era una tablilla escolar. datada alrededor del 1800 a.C., muestra conocimientos de ternas pitagóricas Se denominan ternas pitagóricas al conjuntos de tres números enteros que cumplen la relación del teorema:
$a^2+b^2=c^2$.

Pitágoras y su escuela²¹ demostraron formalmente el teorema, otorgándole un lugar central en la matemática griega, por eso se conoce el teorema con su nombre. El teorema es esencial para la geometría euclidiana, permitiendo calcular distancias y relaciones entre lados de triángulos rectángulos.

Tiene innumerables aplicaciones. En la construcción y arquitectura para calcular distancias, ángulos y dimensiones; en la navegación y topografía para determinar posiciones y distancias en mapas y terrenos. Se utiliza en física e ingeniería para cálculos de vectores, fuerzas y movimientos.

TEOREMA
En todo triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos

El Teorema de Pitágoras es notable no solo por su importancia, sino también por la gran variedad de formas en que se puede demostrar. No existe un número definitivo de demostraciones, pero se estima que hay cientos. En los siguientes tres animados, se puede apreciar el teorema en tres diferentes formas de demostración gráfica.

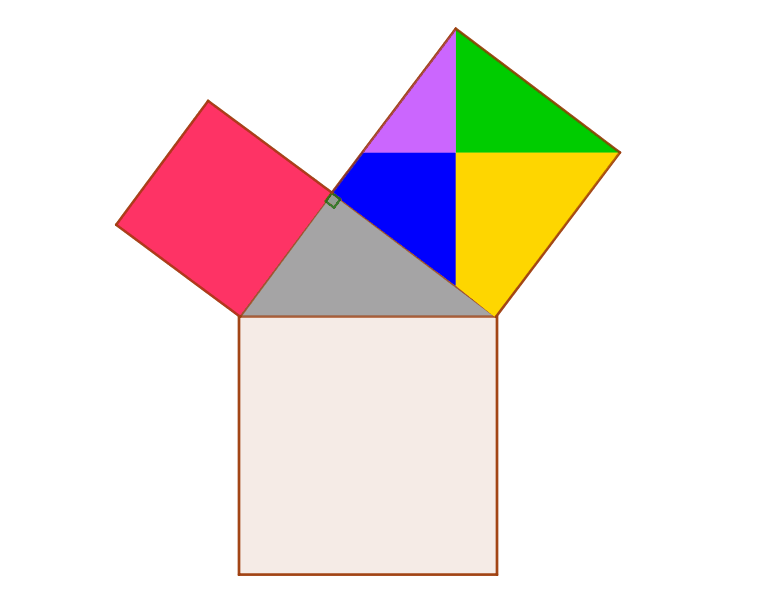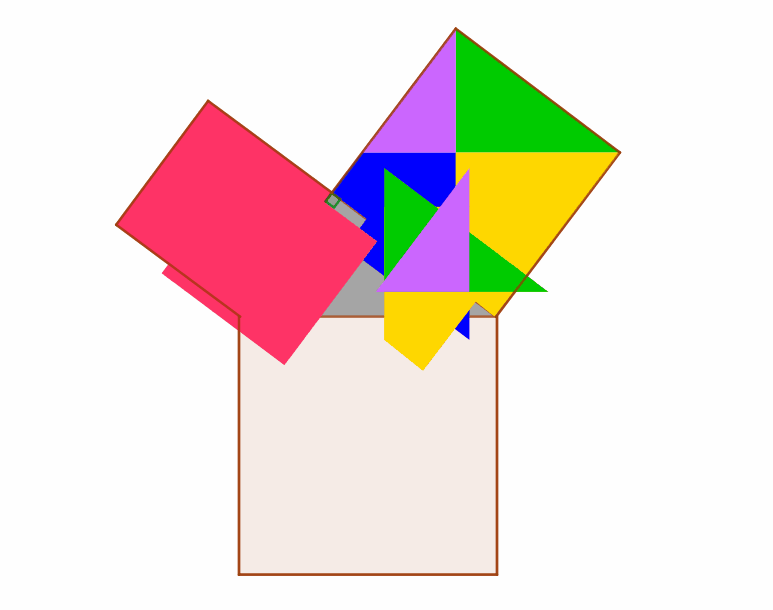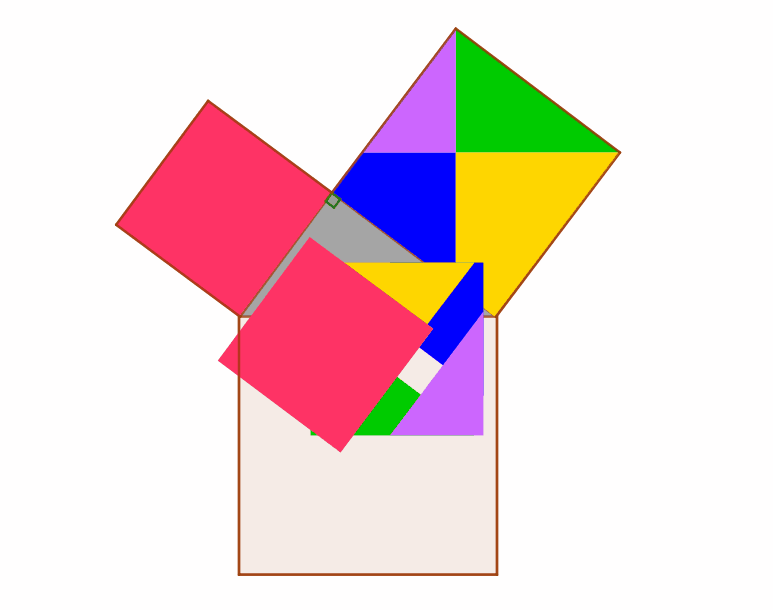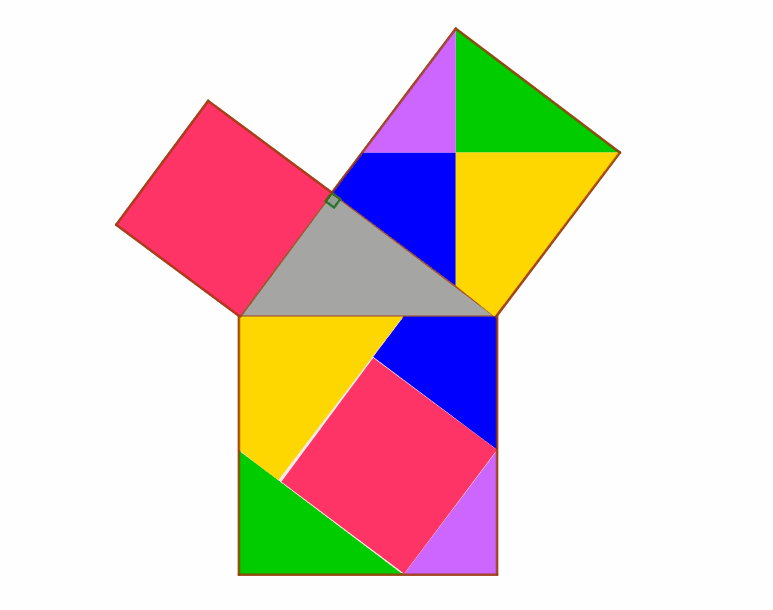
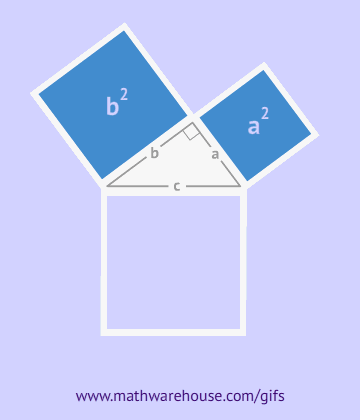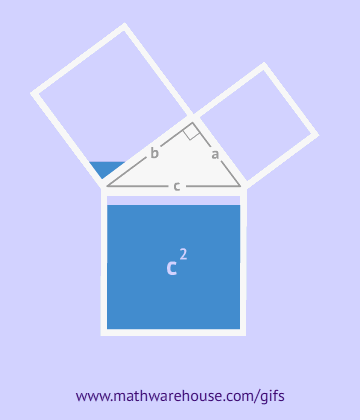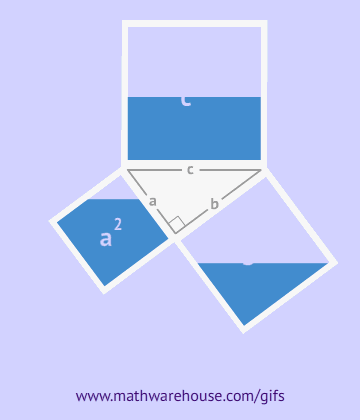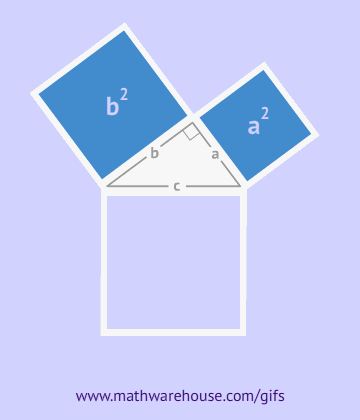
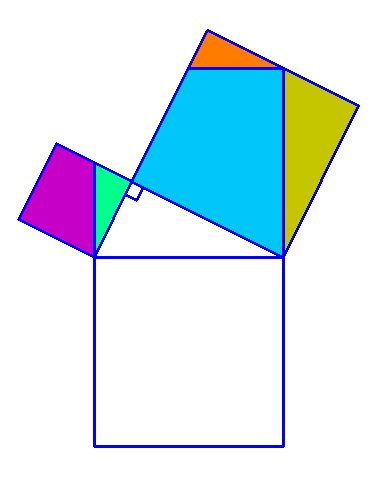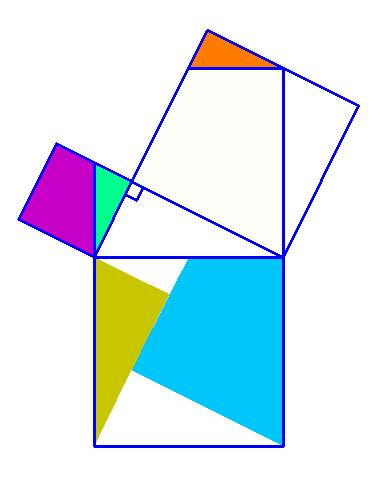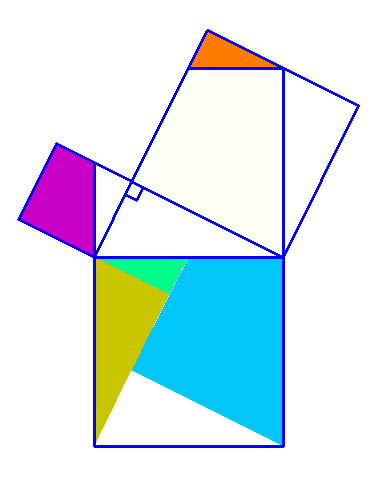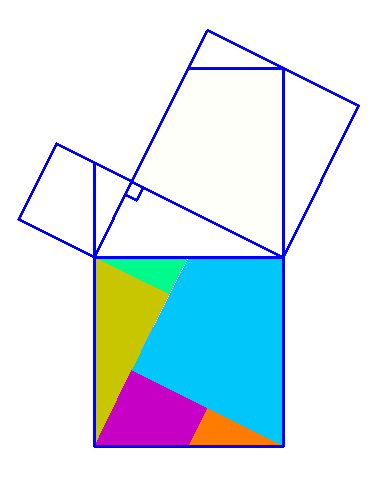
El cuadrado de la hipotenusa	Wikimedia	Matemáticas Cercanas

6.3.4 Un presidente y el teorema de Pitágoras

Posiblemente lo que menos imaginas es que un presidente de los Estados Unidos de América contribuyera a las Matemáticas con una ingeniosa demostración de uno de los teoremas más conocidos a través de la historia. Este es el caso de James A. GarfieldJames A. Garfield
(11/19/1831 - 09/19/1881).
Fue asesinado en julio de 1881. vigésimo presidente de los Estados Unidos y su demostración del teorema de Pitágoras²³.

En la figura, $ABC$ es un triángulo rectángulo con un ángulo recto en $C$. Las longitudes de los lados del triángulo son $a, b$ y $c$. El teorema de Pitágoras afirma que $c^{2}=a^{2}+b^{2}$

Para demostrar el teorema, Garfield dibujó una línea perpendicular, a través de $B$, a $AB$ y en esta línea eligió un punto $D$ tal que $BD=BA$. Entonces, desde $D$ trazó otra perpendicular $DE$ sobre la línea extendida $CB$. En la figura se puede ver fácilmente que los triángulos $ABC$ y $BDE$ son congruentes, ya que tanto $AC$ como $DE$ son perpendiculares a $CE$, los cuales son, además, paralelos y por lo que el cuadrilátero $ACED$ es un trapecio. El teorema se demuestra calculando el área de este trapecio de dos maneras diferentes.

(I)  A_ACED $= \frac{(AC+DE)}{2} \times CE = \frac{(a+b)}{2} \times (a+b)$

(II)  A_ACED$= A △ACB + A  △ABD + A △BDE$ $= \frac{(a \times b)}{2} + \frac{(c \times c)}{2} + \frac{(a \times b)}{2}$

De lo que se obtiene: $= (a+b) \times \frac{(a + b)}{2} = \frac{(a \times b)}{2} + \frac{(c \times c)}{2} + \frac{(a \times b)}{2}$
Al simplificar la expresión resulta: $c^{2}=a^{2}+b^{2}$

6.3.5 Ejercicios de aplicación - Teorema de Pitágoras

6.4 Comprobación - Teorema de Pitágoras

Sistema de
Coordenadas

7.1 Sistema de Coordenadas Cartesianas

Un sistema de coordenadas cartesianas es un método utilizado en matemáticas para representar puntos en un plano mediante dos ejes perpendiculares. Fue ideado por René Descartes
Rene Descartes
Marzo 31,1596 - febrero 11, 1650. y se emplea ampliamente en geometría, álgebra y otras áreas de las matemáticas y la ciencia.

Este sistema sirve para localizar puntos en un espacio bidimensional (en el plano) o tridimensional (en el espacio), describiendo su posición mediante un conjunto de números denominados coordenadas. Esto permite representar gráficamente relaciones matemáticas y analizar propiedades geométricas.

Es importante destacar que el sistema cartesiano como lo conocemos hoy en día es una síntesis de ideas desarrolladas a lo largo de siglos. René Descartes, con su obra "La Geometría" (1637), formalizó el sistema que utilizamos actualmente.

Elementos del sistema

El sistema consta de dos ejes perpendiculares que se cruzan en un punto denominado origen.

• Eje $x$: Es el eje horizontal y se llama el eje de las abscisas.
• Eje $y$: Es el eje vertical y se llama el eje de las ordenadas.
• El punto donde ambos ejes se intersectan es el origen, y su coordenada es el par ordenado $(0,0)$.

División del plano en cuadrantes

Los ejes dividen el plano en cuatro cuadrantes, que son las regiones delimitadas por los ejes. Se numeran en sentido antihorario comenzando desde la región superior derecha:

• Primer cuadrante (I):
  Los puntos en esta región tienen coordenadas positivas:
  $x > 0, y>0$


• Segundo cuadrante (II):
  Los puntos tienen abscisa negativa y ordenada positiva:
  $x<0, y>0$

• Tercer cuadrante (III):
  Los puntos tienen ambas coordenadas negativas:
  $x<0, y < 0$



• Cuarto cuadrante (IV):
  Los puntos tienen abscisa positiva y ordenada negativa:
  $x>0, y<0$

7.2 Representación de puntos en el plano

En el sistema de coordenadas cartesianas, cada punto del plano se identifica mediante un par ordenado $(x,y)$, donde:

En el siguiente interactivo puede practicar lo aprendido.

7.2.1 Interactivo - Plano cartesiano

7.3 Sistema de coordenadas en un mapa

El sistema de coordenadas en un mapa, como el que utiliza la CTA (Chicago Transit Authority) en sus mapas de transporte, es una adaptación práctica del sistema de coordenadas cartesianas, pero con algunas diferencias clave que lo hacen más útil para la navegación y ubicación en mapas.

En este enfoque, se utilizan dos tipos de marcadores para las coordenadas:

• Eje horizontal:
  Representado con letras (por ejemplo, A, B, C, etc.).
• Eje vertical:
  Representado con números (por ejemplo, 1, 2, 3, etc.).

En lugar de puntos en un plano cartesiano que usan pares ordenados $(x,y)$, los puntos en el mapa se identifican mediante una combinación de letra y número, como $B3$ o $D7$.

El objetivo principal de este sistema es permitir que las personas encuentren ubicaciones específicas en un mapa de manera intuitiva y rápida. Es particularmente útil en mapas grandes, como los que representan sistemas de transporte público (por ejemplo, estaciones de tren, puntos de interés, etc.), donde cada sección del mapa puede ser referenciada mediante una cuadrícula.

7.3.1 Interactivo - Coordenadas en un mapa

En el interactivo de la derecha puedes practicarlo. Si buscas la estación en la intersección de la letra H y el número 2, verás que coincide con la estación Polk de la línea rosada (Pink Line).

Este sistema reduce la complejidad de navegar grandes áreas, como la ciudad de Chicago, Nueva York, Londres,Madrid, etc.

7.4 Distancia entre dos puntos:

La distancia entre dos puntos es la recta imaginaria que los une en el espacio, marcando el menor trayecto entre ambos. Por ejemplo, si usas una regla para encontrar la distancia entre dos puntos, la distancia será el valor absoluto El valor absoluto o módulo de un número real $x$, denotado como $|x|$, es el valor de $x$ sin considerar el signo, sea este positivo o negativo.
|-5|=5      |5|=5 de la diferencia entre ambos números mostrados en la regla.