DescartesJS
Nivel II
INTERACTIVO
Juan Guillermo Rivera Berrío
Institución Universitaria Pascual Bravo
Joel Espinosa Longi
Alejandro Radillo Díaz
Universidad Nacional Autónoma de México
Título de la obra:
DescartesJS - Nivel II
Autores:
Juan Guillermo Rivera Berrío
Joel Espinosa Longi
Alejandro Radillo Díaz
2ª edición – 2019
Diseño del libro: Juan Guillermo Rivera Berrío
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Núcleo del libro interactivo: julio 2022
Fondo Editorial Pascual Bravo
Calle 73 73A-226
PBX: (574) 4480520
Apartado 6564
Medellín, Colombia
www.pascualbravo.edu.co
ISBN: 978-958-56858-6-4
Este libro digital interactivo se ha diseñado con fundamento en la filosofía del Proyecto DescartesJS: "Trabajando altruistamente por la comunidad educativa de la aldea global", que sólo busca desarrollar contenidos educativos para el provecho de la comunidad académica, esperando únicamente como retribución el uso y difusión de estos contenidos. El contenido del libro, al igual que los objetos interactivos se han diseñado de tal forma que se puedan leer en ordenadores y dispositivos móviles sin necesidad de instalar ningún programa o plugin. El libro se puede descargar para su uso en local sin dependencia con la red, a excepción de algunos vídeos incluidos en el texto. Todos los objetos interactivos se han diseñado con el Editor DescartesJS.
Véase https://proyectodescartes.org/iCartesiLibri/descripcion.htm.
El contenido de este libro se basa en un curso de capacitación del editor DescartesJS para docentes que, por la dificultad de concertar un horario presencial, permite una opción autodidacta acompañada de material interactivo para una mayor comprensión de los temas tratados.
Retomando la introducción a la documentación de DescartesJS de Radillo, Abreu y Espinosa, podríamos coincidir en que este libro está destinado tanto a personas que no han usado DescartesJS como a personas que tienen cierta experiencia y desean mejorarla. En cada apartado del libro se proponen ejercicios y se incluyen ejemplos para que el lector pueda comprender paso a paso la funcionalidad de DescartesJS y su enorme potencial para crear objetos interactivos de aprendizaje. Esta segunda parte contempla temas de animación, elementos de programación, vectores y matrices, interfaces con otros interactivos, diseño 3D, entre otros temas, que permitan generar escenas de mayor complejidad a las presentadas en el primer nivel. Es importante precisar que en este libro se incluye documentación tomada del texto de Radillo et al.
Presentamos dos ejemplos, que sirvan de motivación a los lectores. El primer ejemplo es una superficie paramétrica (puedes rotarla con clic sostenido).
El segundo ejemplo es una escena interactiva diseñada para el libro digital interactivo de Percepción visual, en la que se genera la ilusión de caras distorsionadas (véase http://illusionoftheyear.co).
Esta ilusión fue diseñada por Jason Tangen, Sean Murphy y Matthew Thompson de la Universidad de Queensland, Australia. Ocupó el segundo puesto en los premios a la mejor ilusión de 2012.
Como en el Nivel I, es importante tener a la mano el editor de DescartesJS (DescartesJS.exe en Windows, DescartesJS.app en macOS o DescartesJS.bin en Linux), el instalador puede descargarse desde: http://descartes.matem.unam.mx/, que se encuentra en constante mantenimiento incluyendo nuevas mejoras, de tal forma que es siempre una buena práctica reinstalarlo con cierta frecuencia. El programa del editor es una interfaz gráfica para el usuario mediante la cual podrá guardar archivos html con diversos tipos de interactivos. En la se muestra la ventana inicial del editor, el cual se puede buscar dentro de los programas en el ordenador, una vez que se haya instalado.
Al terminar este capítulo, habrás diseñado algunos objetos interactivos con el editor DescartesJS, dos de ellos los presentamos a continuación:
La anterior escena usa vectores para almacenar los países y las coordenadas de las capitales, un vector por cada categoría que para el ejemplo serían tres: países, abscisas y ordenadas. Las dos últimas indican la posición en el mapa de cada ciudad capital.
El segundo objeto interactivo es una suma de matrices, cuyos elementos son colores:
Tal como lo explicamos en el nivel I, una forma de evitar el ingreso o lectura de muchas variables es el uso de vectores. Inicialmente, presentamos la descripción básica de este elemento del selector Definiciones:
Iniciamos nuestro estudio de vectores con una primera actividad, cuyo propósito es generar un sistema de preguntas tipo selección múltiple. Un primer modelo podría ser el siguiente (descárgalo aquí):
en el cual usamos el control tipo casilla de verificación; sin embargo, para nuestro propósito, no es funcional cuando las respuestas son extensas. Así que, a partir de este modelo (que ya descargaste), hemos realizado los siguientes cambios:
Seguramente, ya habrás dado un vistazo a la configuración del objeto interactivo y te habrán surgido varias inquietudes. No te preocupes, que daremos una explicación del contenido del interactivo y las modificaciones que aún faltan; por ahora, haz los cambios sugeridos en el vídeo y verifica que si funcionen bien las nuevas casillas de verificación.
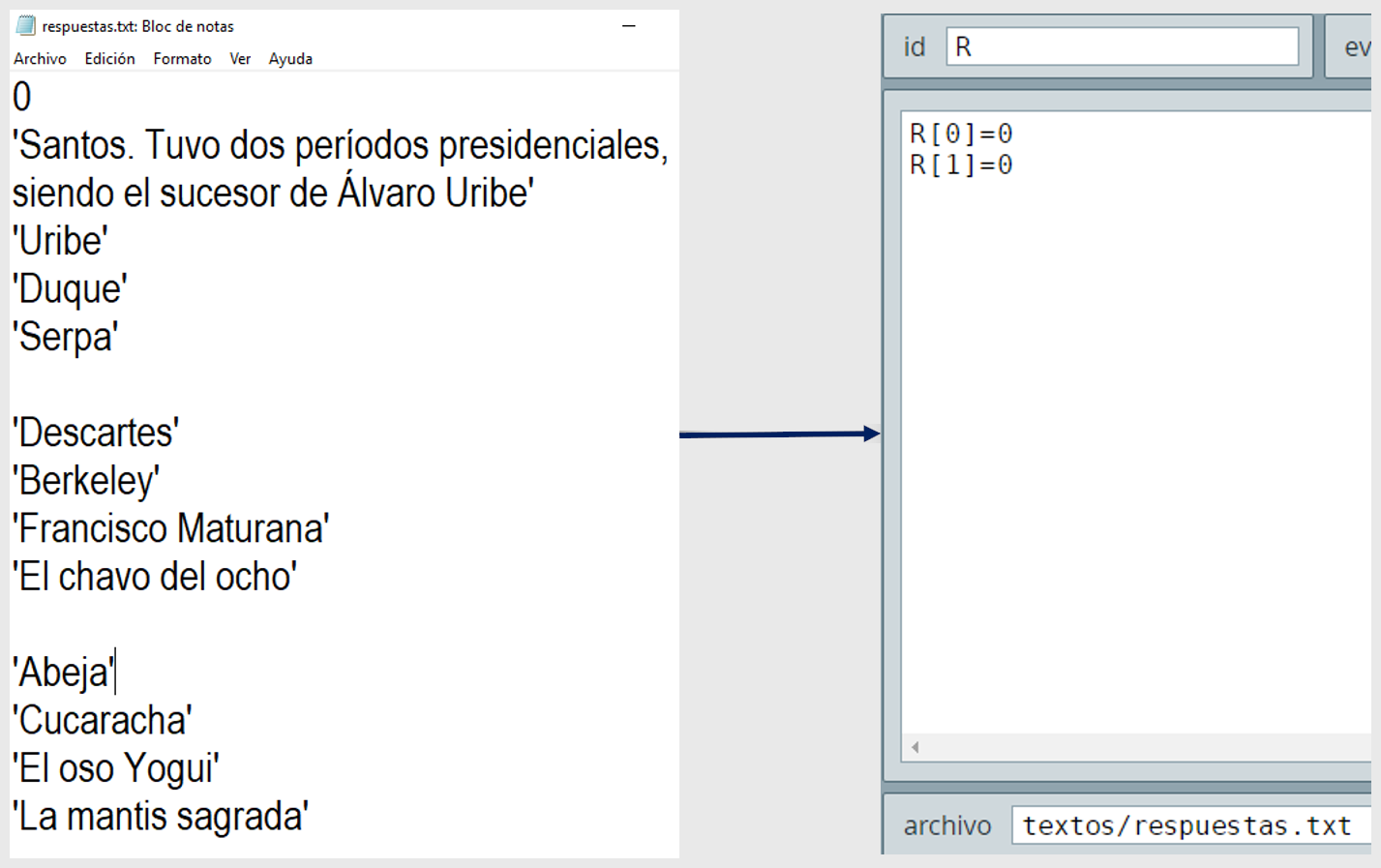
En el selector Definiciones hemos definido dos vectores, uno para las preguntas y otro para las respuestas. Para el ejemplo hemos creado sólo tres preguntas:

Descartes crea por defecto un vector de tamaño 3, donde el primer elemento es R[0]. Este primer elemento, en la mayoría de los casos, no lo tendremos en cuenta. Como hemos diseñado el ejemplo para tres preguntas P[1], P[2] y P[3], el tamaño del vector sería 4.
Para cada pregunta tendremos cuatro respuestas (selección múltiple), lo que requiere un vector de tamaño 13 (12 respuestas más el vector R[0]).
Si observas el vector R, notarás que hemos cometido un error, pues el tamaño lo hemos dejado en 3 pero... ¡aún así funciona el iterativo! Esto es cierto, pues Descartes, por ahora, es tolerante con este error; sin embargo, procurando una buena disciplina de programaciónEn la mayoría de lenguajes de programación, el mal dimensionamiento de un vector genera errores, impidiendo la ejecución del programa., el vector R debe quedar dimensionado como lo muestra la .
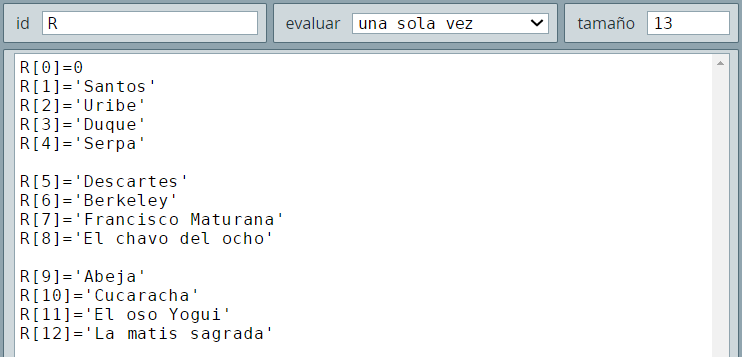
R de dimensión 13.Observa que en el algoritmo INICIO, hemos declarado dos variables (total_preguntas y pregunta), las cuales nos servirán para entender la configuración de los dos controles tipo botón.
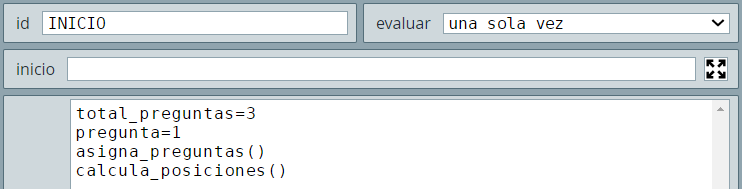
INICIO del interactivo "Selección múltiple"Pero no sólo basta con estas variables, también hay que comprender cómo funcionan las siguientes variables.
Habrás notado que los dos botones se encuentran centrados horizontalmente y a unos 10 pixeles del borde inferior. Esto se logra usando las variables de espacio, así:
x del botón: x = (E1._w-120)/2y = E1._h-40Para el botón verificar de dimensiones $120 \times 30$ pixeles, la configuración usada es:

El uso de estas variables permitió que no se afectara la configuración cuando cambiamos las dimensiones de la escena. Este botón sólo se muestra cuando la variable ver es cero (0), a la cual se le asigna uno (1), al hacer clic sobre el botón.
Su configuración es similar al anterior botón, pero con un ancho de botón de 160 pixeles. Se muestra cuando la variable ver es uno (1) y, además, cuando la variable pregunta no ha superado el total de preguntas, es decir:

Al hacer clic sobre este último botón, se ejecutan las siguientes acciones:
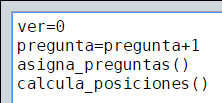
una de ellas es la variable pregunta que se incrementa en uno (1), permitiendo mostrar (ver=0) la siguiente pregunta. Las dos funciones invocadas, al igual que lo hace el algoritmo INICIO, las explicamos a continuación.
asigna_preguntas()Podríamos haber usado vectores para asignar las respuestas a cada pregunta, pero para facilitar su comprensión hemos usado cuatro variables r1, r2, r3 y r4. Observa con cuidado las expresiones asignadas con respecto al vector R que almacena el total de respuestas:
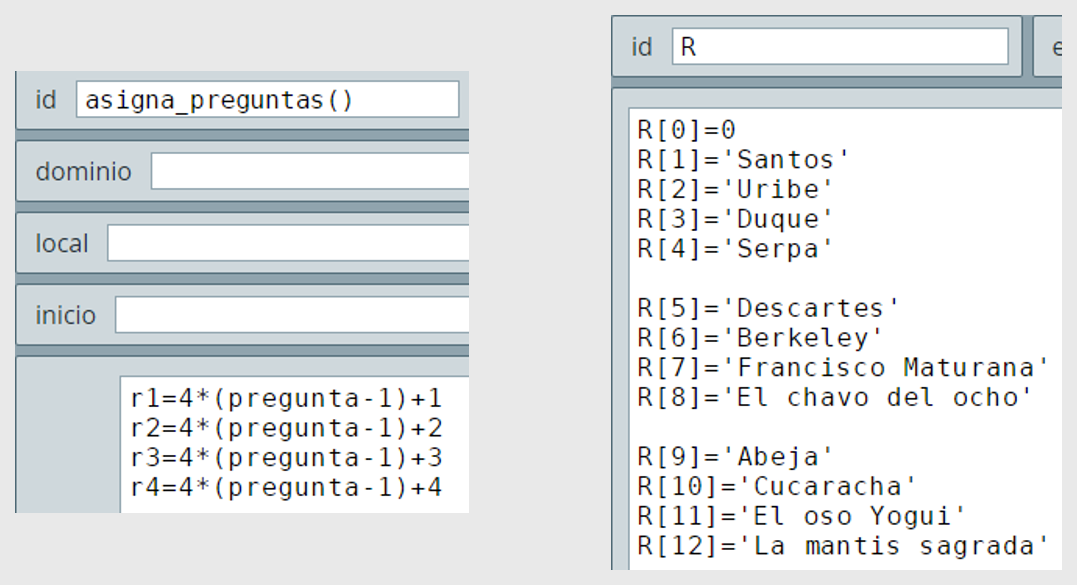
Por ejemplo, si la pregunta es la segunda (pregunta = 2), los valores de r1, r2, r3 y r4 serían 5, 6, 7 y 8 que corresponden al segundo bloque de respuestas del vector R.
calcula_posiciones()Las expresiones asociadas a esta función, fueron diseñadas para el modelo con casillas de verificación, las cuales se posicionaban verticalmente en forma aleatoria:
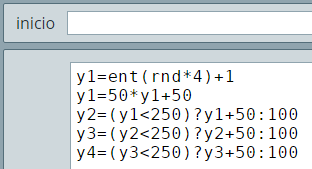
En este segundo modelo vamos a usar las coordenadas del espacio para ubicar la respuestas, por lo que debemos cambiar las expresiones por:
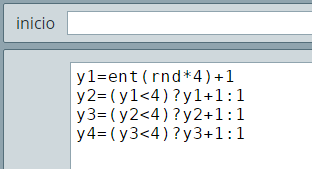
La verdadera aleatoriedad la tiene r1, que corresponde a la respuesta verdadera. Observa en el siguiente vídeo cómo vamos a posicionar las respuestas, de acuerdo a los valores de y1, y2, y3 y y4.
Pudiste observar que ya podemos usar respuestas largas, para ello, hemos puesto un ancho de 500 pixeles. Las demás acciones realizadas ya las hemos explicado en el nivel I. Las expresiones para ubicar las respuestas verticalmente debes analizarlas y deducir su funcionalidad.
Ahora sólo nos falta identificar cuando una selección es correcta o no y, además, explicar las condiciones para mostrar el arco relleno. Para esto, es necesario que indagues sobre las variables del ratón en el siguiente texto.
Ahora entenderás por qué en el círculo relleno usamos la siguiente condición:
(abs(s-E1.mouse_y)<0.5) & (abs(-7-E1.mouse_x)<0.5) & (E1.mouse_clicked=1)
La familia de círculos con centro en (-7, s), con s variando de -2 a 4 y con pasos 3, son círculos con centros en (-7, -2), (-7, 0), (-7, 2) y (-7, 4). Cuando s es igual a 2 y hacemos clic cerca del centro (-7, 2), significa que se cumplen las tres condiciones y se activa el círculo. Estas mismas condiciones las hemos usado en el algoritmo CALCULOS para calcular una variable llamada selecciona, la cual es igual a uno (1) si se ha activado algún círculo:
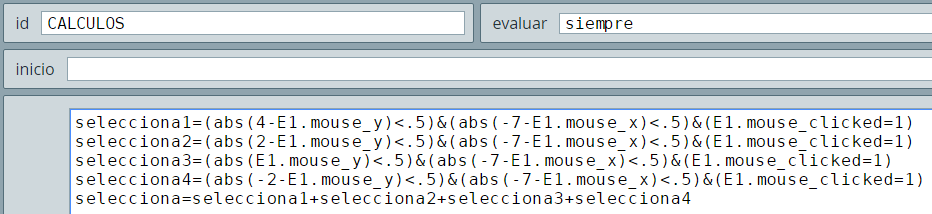
Corregimos los textos para acierto y desacierto:
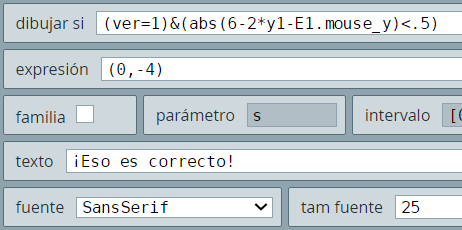
Para evitar que se vuelva a hacer clic en otra respuesta, agregamos un espacio igual a E1, pero con transparencia, el cual lo hemos llamado mascara:
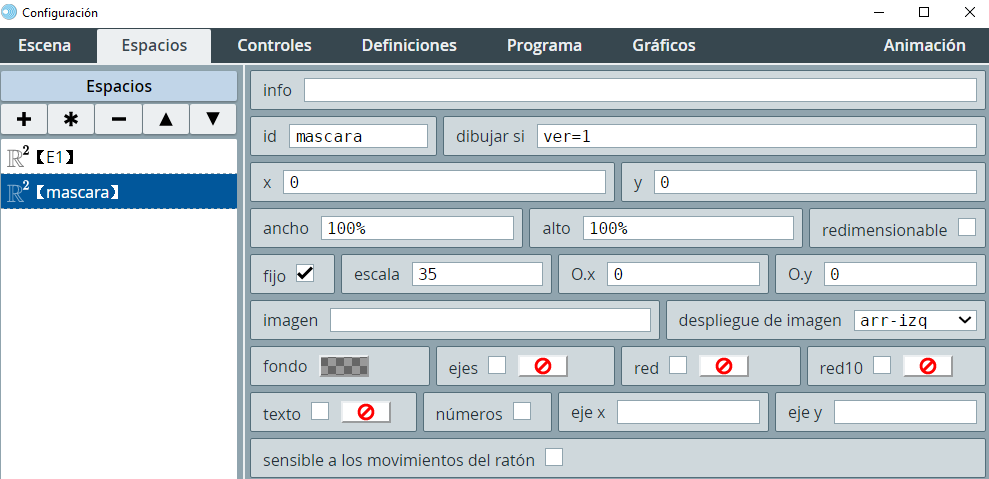
Modificamos la condición del control Verificar, así:

Obviamente, debemos tener la posibilidad de hacer clic en el botón Otra pregunta, por ello, cambiamos el espacio donde debe aparecer este botón:

Finalmente, el objeto interactivo quedaría así:
La imagen de fondo y las de los botones quedan a tu gusto... ya sabes cómo hacerlo.
Tu tarea es ampliar el sistema de preguntas a 10. Si pusiste atención a las explicaciones, podrás concluir que las modificaciones son pocas, excepto por las preguntas y respuestas. Es importante que no olvides que la respuesta correcta siempre debe ir al inicio.
Si has terminado la tarea anterior, observaste que es algo engorroso digitar las 40 respuestas correspondientes a las 10 preguntas. Existe una opción, la cual consiste en digitar el contenido de los vectores en archivos de texto (bloc de notas en Windows); por ejemplo, preguntas.txt y respuestas.txt.
Cuando creas un vector, observarás que al final hay una casilla para incluir la dirección a un archivo, en este campo de texto se introduce la ruta relativa a un archivo del cual se obtendrá la información para llenar las entradas del vector.
En la puedes observar la creación de un archivo de texto con el nombre respuestas.txt. En este archivo hemos digitado el contenido de las respuestas, encerradas en comillas simples. Los espacios entre bloques de respuestas es por facilidad de lectura, los cuales no son tenidos en cuenta al asignar los valores de los elementos del vector. Por otra parte, en el editor de DescartesJS, para el vector R, hemos incluido la ruta relativa al archivos respuestas.txt.
Puedes practicar con el objeto interactivo que hemos diseñado, para verificar el funcionamiento de esta alternativa, seguramente es más cómodo, pues sólo debes digitar los contenidos entre comillas simples.
Puedes hacerlo con sólo tres preguntas y verificar en varios navegadores... Te recomendamos que lo hagas.
Si verificaste la lectura de archivos y en Chrome no te ha funcionado, es porque tienes una versión del editor DescartesJS anterior a la 1.024
En este navegador existe una directiva de seguridad que impide la lectura externa de archivos de texto. Por ello, a partir de la versión 1.024 el contenido de los archivos se guardan al final del archivo html.
La alternativa, anterior a esta versión, consistía en copiar los datos de los archivos de texto al final del archivo html, que puedes abrir y modificar con el bloc de notas. Aprenderás cómo hacerlo en la siguiente actividad.
Continuamos nuestro estudio de vectores con el diseño de una actividad interactiva que consiste en identificar la ciudad capital de países europeos. Inicialmente, descarga el objeto interactivo aquí y, luego, analiza las explicaciones de cómo se ha diseñado.
La escena tiene una tamaño de $600 \times 550$ pixeles. En el espacio E1 hemos agregado una imagen con el mapa de Europa:
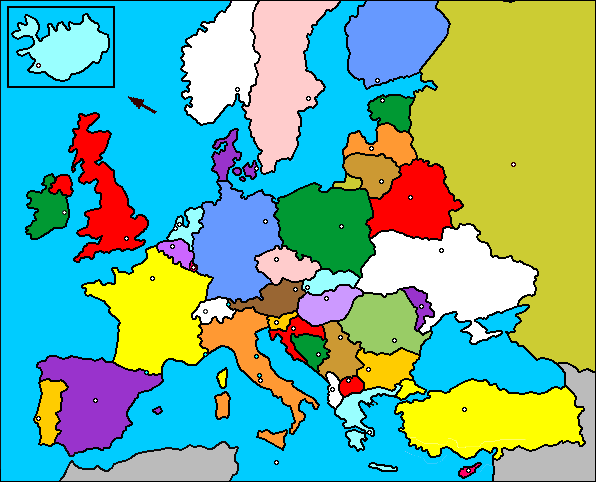
De este mapa seleccionamos 10 países e identificamos sus coordenadas, tal como se muestra en el siguiente vídeo:
Obviamente, el color del texto habría que cambiarlo en colores claros. Una vez identificadas las coordenadas, creamos tres archivos de texto: paises.txt, abscisas.txt y ordenadas.txt y los guardamos en una carpeta de nombre Ficheros.
Observa la que describe cómo se asignan los datos a los vectores P, X e Y.
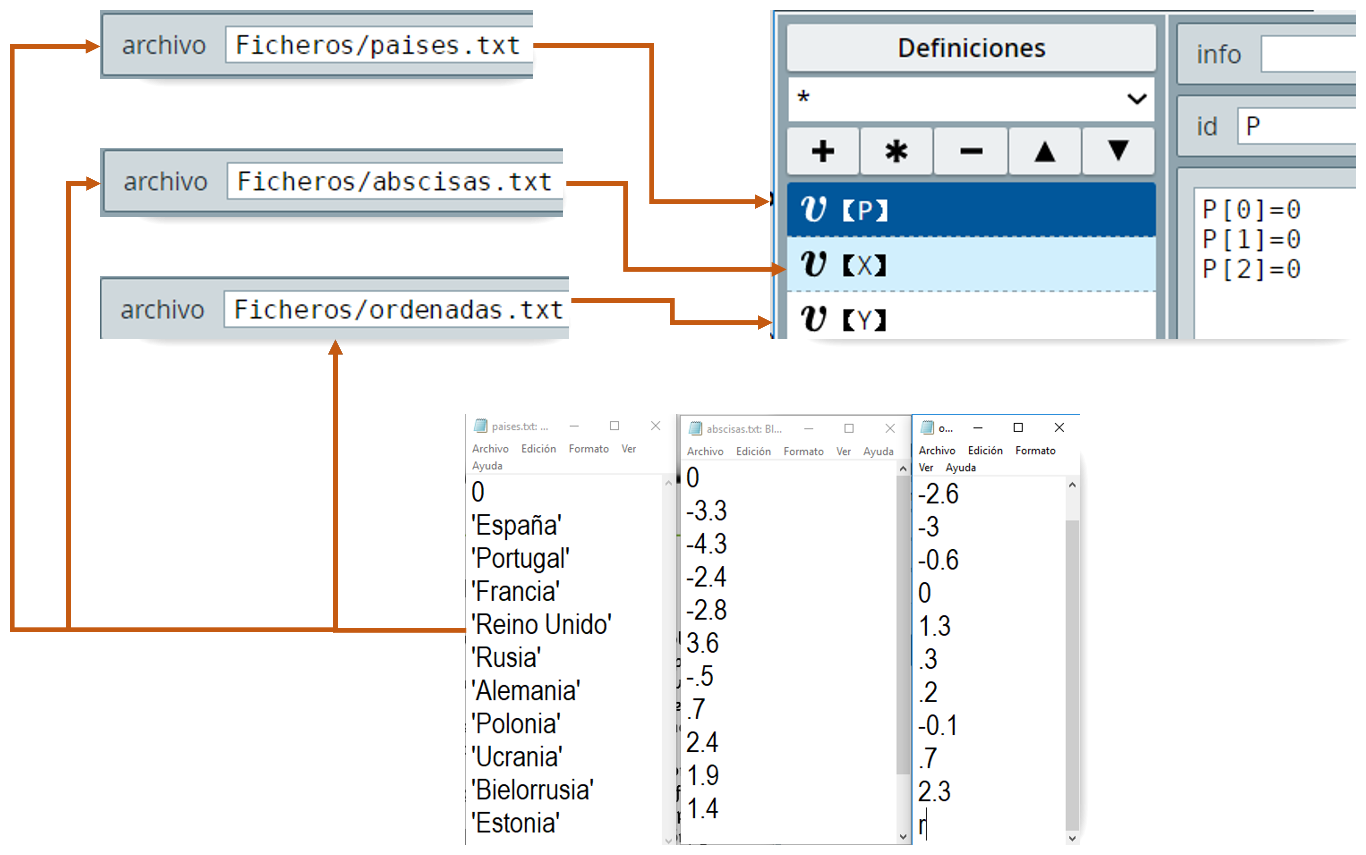
P, X e Y.No explicamos los demás elementos que constituyen el objeto interactivo, pues ya estás en capacidad de analizarlos y comprenderlos. Observa que para cada pregunta aleatoria (p = ent(rnd*10)+1) se han usado variables del ratón para detectar sí se ha hecho clic en la capital correcta.
Como lo dijimos antes, el interactivo así diseñado funciona bien en la mayoría de los navegadores, excepto en Chrome si tienes una versión anterior a la 1.024, situación que se corrige si los datos externos (países, abscisas y ordenadas), se escriben dentro del archivo index.html, tal como lo vamos a explicar a continuación en la siguiente presentación.
Para observar las diapositivas debes hacer clic sobre la imagen, luego usar la flecha del teclado para avanzar. Debes tener el sonido activado, pues cada diapositiva tiene una explicación en archivo de audio.
Con esta alternativa no necesitamos los archivos txt, y es funcional en Chrome.
Amplía el número de países a 20. Una ayuda: debes cambiar p=ent(rnd*10)+1 por p=ent(rnd*20)+1 y no olvidar redimensionar los vectores.
Otra forma de almacenar información es a través de tablas, tal como lo hacemos en una hoja de cálculo. Si bien las matrices han sido más un tema de álgebra lineal, ello no significa que no podamos definir nuestros arreglos (matrices) para procesar información. Veamos, inicialmente, cómo se procesa esta información en álgebra lineal:
Una de las primeras aplicaciones de las matrices, que nos muestra el vídeo de Bill Shillito, es la solución de ecuaciones de un sistema de fuerzas, las cuales se organizan en matrices y vectores, tal como lo muestra la siguiente escena interactiva:
Una matriz, entonces, es una tabla rectangular de datos ordenados en filas y columnas. Si una matriz tiene $m$ filas y $n$ columnas, decimos que la matriz es de orden $m \times n$. Todos los elementos de las matrices se denotan con subíndices $a_{ij}$, el valor de $i$ representa la fila y el valor de $j$ la columna. Los valores de $i$ van de $1$ a $m$ y los valores de $j$ van de $1$ a $n$; $a_{ij}$ es el elemento de la fila $i$ y la columna $j$.
No es nuestro propósito desarrollar un curso de álgebra matricial, sólo es una muestra de cómo se puede usar este tipo de arreglos de información. En el vídeo de Shillito se explican algunas operaciones con matrices, de las cuales hemos seleccionado la más simple... la suma de matrices:
La herramienta de autor DescartesJS presenta su modelo de matriz de la siguiente forma:
Si prestaste atención, habrás notado dos diferencias significativas con respecto a las matrices que hemos definido previamente. La primera es el orden de los elementos, pues DescartesJS usa $columnas \times filas$ y no $filas \times columnas$ como tradicionalmente se hace en álgebra lineal. La segunda es que todas las matrices tendrán por defecto una fila y una columna de subíndice cero (0). No obstante estas diferencias, la posibilidad de almacenar datos en arreglos bidimensionales se constituye en una herramienta muy valiosa para el diseño de algunos objetos interactivos, no necesariamente de álgebra linealUtilizando matrices de DescartesJS, se diseñaron algunas unidades interactivas de álgebra lineal en el proyecto Un_100, las cuales se pueden consultar en http://proyectodescartes.org/Un_100/Algebra_lineal.htm. En otro capítulo abordaremos la interface con la herramienta GeoGebra, la cual posee una utilidad de Cálculo Simbólico CAS (Computer Algebra System), más apropiada para cálculos matriciales inmediatos.. Por ejemplo, la siguiente actividad almacena códigos de colores para sumar matrices cuyos elementos corresponden a un color (recuerda que la suma se realiza entre elementos de la misma fila y la misma columna).
Esta actividad consiste en sumar matrices a través de colores, es decir, la suma de A y B da como resultado otra matriz de colores. Recuerda que dos colores iguales dan el mismo color. Para colores diferentes, ten en cuenta:
El diseño del objeto interactivo lo vamos a explicar a través de la siguiente presentación. Recuerda que para observar las diapositivas debes hacer clic sobre la imagen y luego usar la flecha del teclado para avanzar. Debes tener el sonido activado, pues cada diapositiva tiene una explicación en archivo de audio. Abre el editor de DescartesJS para que vayas construyendo el objeto interactivo.
Presentamos, de nuevo, el objeto interactivo para que te sirva de orientación.
En la presentación anterior se indican seis familias de polígonos para dibujar las tres matrices color. Es decir, por cada matriz de $3 \times 2$ (3 filas, 3 columnas) se usaron dos familias de polígonos (dos filas de polígonos). Hasta este punto, la escena que hemos diseñado, tendría la siguiente forma:
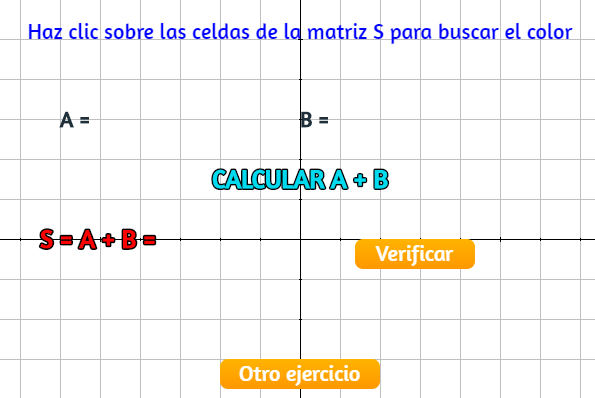
Hemos dejado visible la red cartesiana para una mejor ilustración.
Observa que están dispuestos los seis cajones para las tres matrices de nuestro interés (A,B yS). Para la matrizA, los polígonos los podemos dibujar con las siguientes familias:

y

El funcionamiento de cada fila es simple:
s = -5, se dibuja el polígono (-5,4)(-5,3)(-4,3)(-4,4)(-5,4), que corresponde a la esquina superior izquierda de la matriz de polígonos de A.s = -4 (paso 1): (-4,4)(-4,3)(-3,3)(-3,4)(-4,4)s = -3 (paso 2): (-3,4)(-3,3)(-2,3)(-2,4)(-3,4)Lo cual, nos dibujaría la primera fila deA:

El ancho que hemos usado para la línea de los polígonos es 2. Este procedimiento se repite para las cinco líneas restantes.
Sin embargo, hay una forma de dibujar la matriz de polígonos completa, que vamos a explicar a continuación:
Usaremos una familia de polígonos con la siguiente expresión:

Haz clic sobre la imagen para ver mejor la expresión.
No nos extrañaría que decidieras dibujar los polígonos con el procedimiento anterior, pero te sugerimos prestar atención a la explicación de cómo surge esta expresión y su utilidad para familias más extensas, ¿qué tal una matriz de $10 \times 10$?, ¡sería mejor una familia en lugar de 10!
En primer lugar, es necesario explicar qué significa el operador módulo %. Este operador devuelve el residuo de una división. Por ejemplo, a = 23%7 asignará el valor de 2 a la variable a, ya que 7 cabe 3 veces en 23 y sobra un residuo de 2. Ahora, observemos la matriz A de polígonos, en la cual hemos puesto los valores de las abscisas en rojo y la ordenadas en azul.
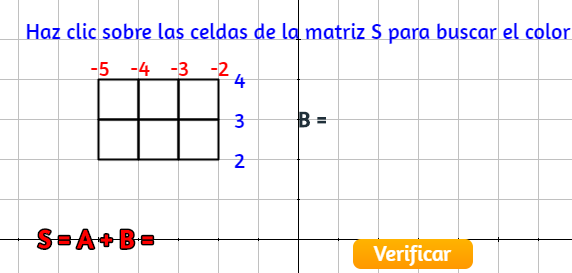
Sabemos que cada cuadrado se dibuja con cinco puntos, donde el primero y el último son iguales. La expresión dibuja cada cuadrado iniciando con el punto superior izquierdo, que para los seis cuadrados serían los puntos (-5,4), (-4,4), (-3,4), (-5,3), (-4,3) y (-3,3), verifiquemos que dichos puntos son generados por la expresión (s%3-5,4-ent(s/3)) con s=0 hasta s=5, que es el primer punto de la familia:
s = 0: (0-5,4-0) → (-5,4)s = 1 (paso 1): (1-5,4-0) → (-4,4)s = 2 (paso 2): (2-5,4-0) → (-3,4)Recuerda que la función ent devuelve la parte entera de la división, que para los puntos anteriores es cero.
s = 3 (paso 3): (0-5,4-1) → (-5,3)s = 4 (paso 4): (1-5,4-1) → (-4,3)s = 5 (paso 5): (2-5,4-1) → (-3,3)Puedes verificar otros puntos de la familia de polígonos. Termina de dibujar las demás familias de polígonos con las siguientes expresiones:


Hecho esto, nuestra escena tendría la siguiente forma:
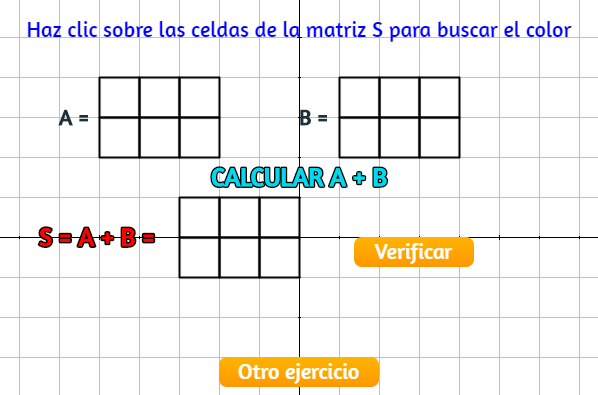
Sólo nos faltan los colores.
Los colores en DescartesJS se asignan a través de una ventana como la que se presenta a continuación (versión anterior de DescartesJS), con la cual puedes interactuar:
Lee el siguiente texto que describe el funcionamiento del panel de colores y cómo se puede usar tanto el sistema sexagesimal como el decimal en una escala de 0 a 1:
Hemos usado los siguientes colores en nuestro objeto interactivo:
| Número | Color | Valor hexadecimal | Valor decimal | Intervalo [0,1] |
| 1 | Amarillo | ffff00 | 255 255 0 | 1 1 0 |
| 2 | Azul | 0000ff | 0 0 255 | 0 0 1 |
| 3 | Rojo | ff0000 | 255 0 0 | 1 0 0 |
| 4 | Blanco | ffffff | 255 255 255 | 1 1 1 |
| 5 | Verde | 00ff00 | 0 255 0 | 0 1 0 |
| 6 | Naranja | ffc800 | 255 200 0 | 1 0.78 0 |
| 7 | Rosa | ffafaf | 255 175 175 | 1 0.7 0.7 |
| 8 | Gris claro | c0c0c0 | 192 192 192 | 0.75 0.75 0.75 |
| 9 | Turquesa | 00ffff | 0 255 255 | 0 1 1 |
| 10 | Magenta | ff00ff | 255 0 255 | 1 0 1 |
| 11 | Amarillo claro | ffffc8 | 255 255 200 | 1 1 0.78 |
Observa que los cuatro primeros colores generan los demás colores (excepto el gris claro que no hace parte de la escena), por ello, los elementos de las matrices A y B son números entre 1 y 4: ent(rnd*4)+1, es decir, sus contenidos son colores amarillo, azul, rojo o blanco. Por otra parte, la matriz S tiene elementos cuyo contenido son colores resultantes de sumar los elementos de A y B, recuerda que los almacenamos en las variables r1, r2, r3, r4, r5 y r6 con valores que van de 1 a 11 (excepto el 8 que corresponde al gris claro).
Los valores decimales que generan estos colores se encuentran en los vectores f1, f2 y f3; por ejemplo, el color turquesa (9) se obtiene con f1[9] = 0, f2[9] = 1 y f3[9] = 1, verifica en el selector Definiciones para otros colores.
Con lo anteriormente explicado, procedemos a asignar los colores a nuestras familias matriciales de polígonos, es decir, "las matrices de colores".
En forma similar al análisis que hicimos de los polígonos lo haremos con el panel de colores, es decir, para el Rojo (Red), Verde (Green) y Azul (Blue), conocidos como colores RGB. Para ello, analicemos la matriz A, con el siguiente supuesto:

Es decir, A[0,0]=4 (blanco), A[1,0]=3 (rojo), A[2,0]=2 (azul), A[0,1]=2 (azul), A[1,1] = A[2,1] = 1 (amarillo). Revisa la matriz en Definiciones.
Así las cosas, el color del primer polígono de la fila 0 es blanco, del segundo de la fila 0 es rojo, del tercero de la fila 0 es azul, del primero de la fila 1 es azul,...
Para asignar el color blanco, se logra con f1[4], f2[4] y f3[4] en el panel de colores, lo mismo que f1[A[0,0]], f2[A[0,0]] y f3[A[0,0]].
Dado lo anterior, el panel de colores para la matriz A, se debe configurar, así:
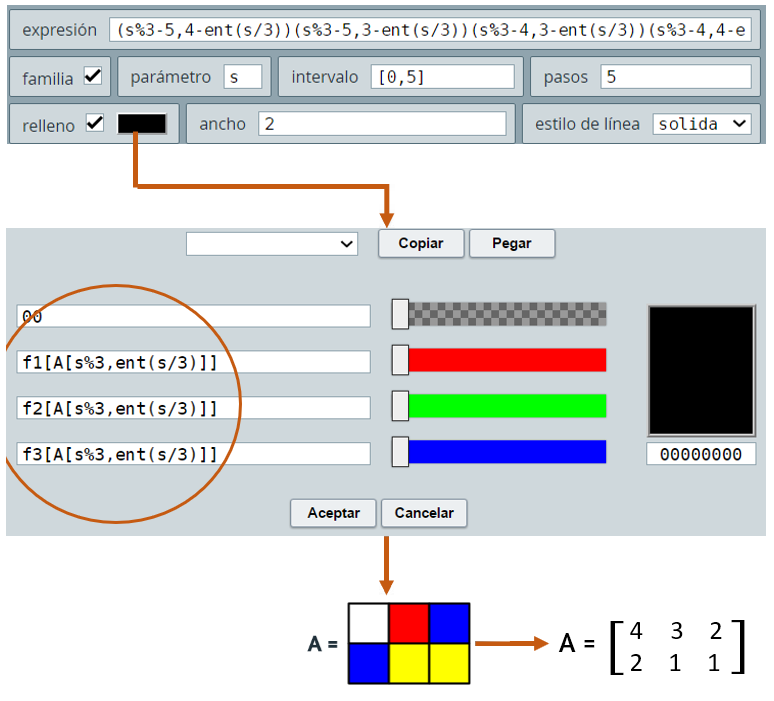
Sólo para verificar, veamos qué ocurre con s = 4 → A[s%3, ent(s/3)] = A[4%3, ent(4/3)] = A[1,1], que sabemos que es igual a 1 (color amarillo); por lo tanto, se asignarían los colores RGB f1[1], f2[1], f3[1], que corresponden respectivamente a 1, 1, 0 (ver los vectores en Definiciones), es decir, el amarillo.
En forma similar se asignan los colores de las matrices B y A:

Termina, entonces, el objeto interactivo. Si es necesario, regresa a los apartados anteriores y analiza con cuidado el procedimiento de diseño realizado.
¡Eso es todo!
Al terminar este capítulo, habrás diseñado objetos interactivos como:
Este objeto incluye generación de cubos en forma matricial y aleatoria, colores aleatorios, variables de espacio y el parámetro posini.
Este objeto interactivo incluye espacios HTMLIframe y, obviamente, superficies paramétricas. Se hará énfasis en parámetros como el despliegue del espacio, el modelo de la superficie y en los valores de Nu y Nv en las superficies.
El diseño 3D que abordamos en este capítulo requiere de un nuevo espacio que, inicialmente, no aparece en el editor de configuraciones. Desde el selector Espacios puedes agregar un espacio 3D, el cual tiene las siguientes características:
Para iniciar nuestra primera actividad, agrega un espacio R3. Notarás que el color por defecto es negro, el cual es necesario modificar de acuerdo al diseño de la escena que pretendemos obtener.
Para el diseño de escenas tridimensionales, es importante comprender el sistema de coordenadas de los espacios 3D, por ello, hemos programado la siguiente actividad:
Diseñaremos, paso a paso, un plano cartesiano 3D similar al de la
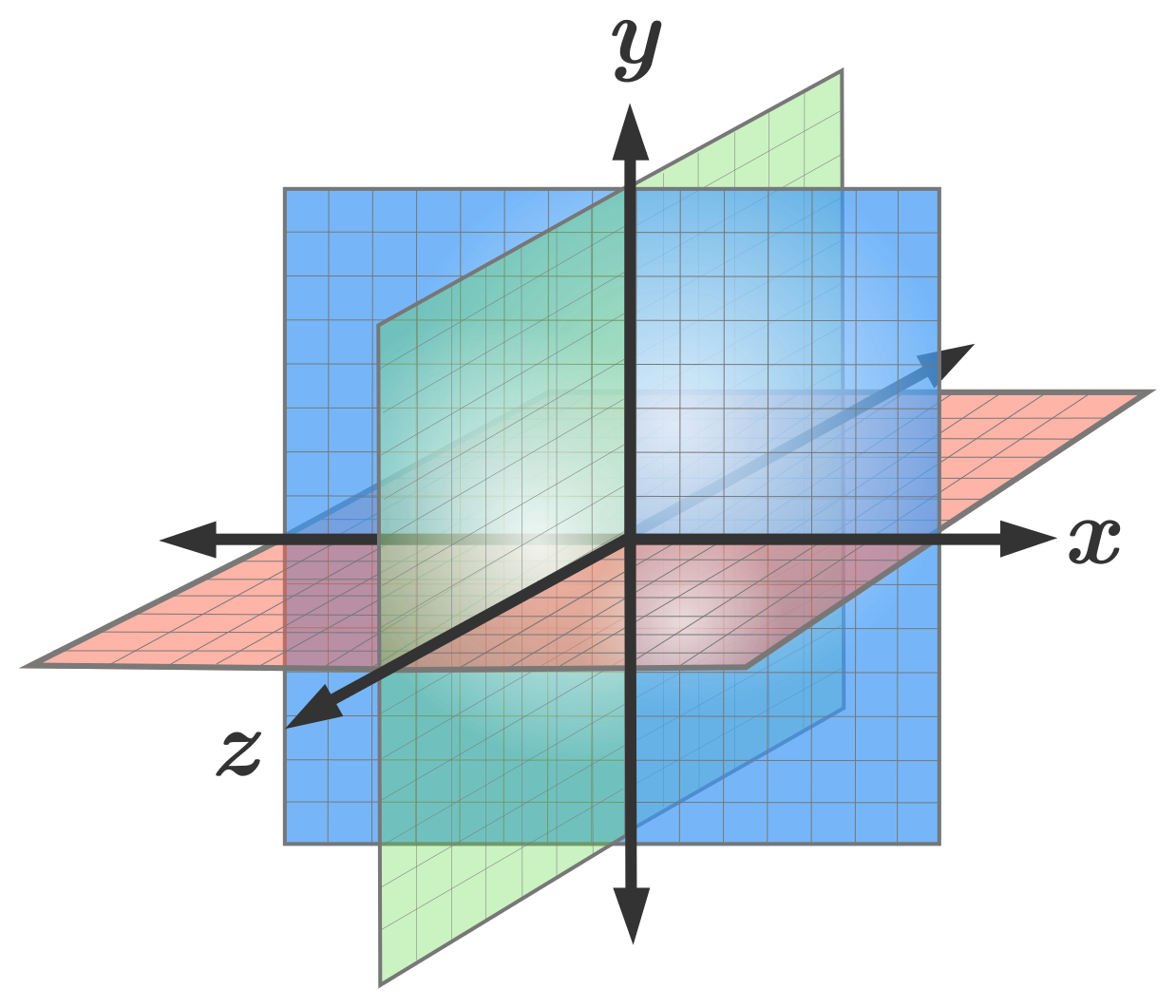
R3 de $600 \times 550$ pixeles, escala 40, despliegue pintor y cambia el color del fondo a blanco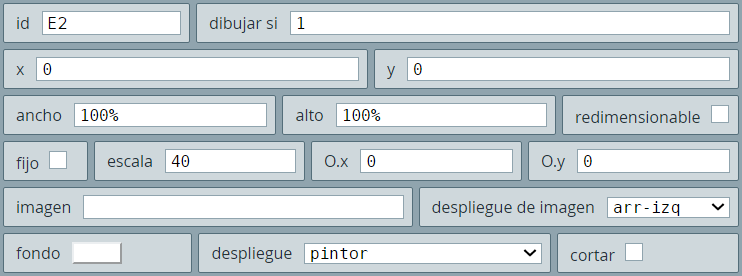
DescartesJS asume por defecto el sistema dextrógiroUn sistema dextrógiro es aquel donde un observador situado en el semieje $0Z$ ve al semieje $0Y$ coincidir con el semieje $0X$, cuando el semieje $0Y$ gira $90°$ en sentido antihorario. Por otra parte, el sistema levógiro es aquel en el que el semieje $0X$ coincide con el semieje $0Y$ a través de un giro de $90°$ en sentido horario. El sistema de la es dextrógiro., con el semieje $0Z$ vertical, el semieje $0Y$ horizontal y el $0X$ perpendicular a la pantalla.
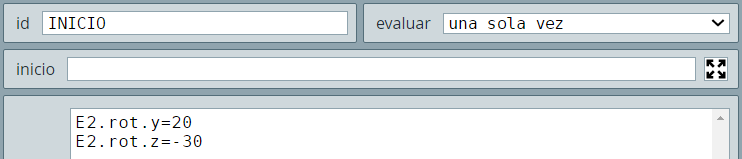
(-5,0,0)(5,0,0), ancho = 1, Nu = 1 y color negro. El segundo es el eje $Y$ en las coordenadas (0,-5,0)(0,5,0), ancho = 1, Nu = 1 y color rojo. El tercero es el eje $Z$ en las coordenadas (0,0,-4)(0,0,4), ancho = 1, Nu = 1 y color azul.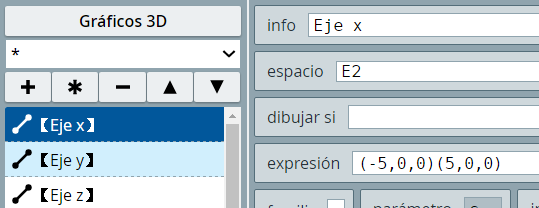
(5,0,0), (0,5,0) y (0,0,4.5) con los textos X, Y y Z respectivamente (pon algunos espacios en el texto para que no se monten en el eje). Hasta aquí, tu escena debe estar así: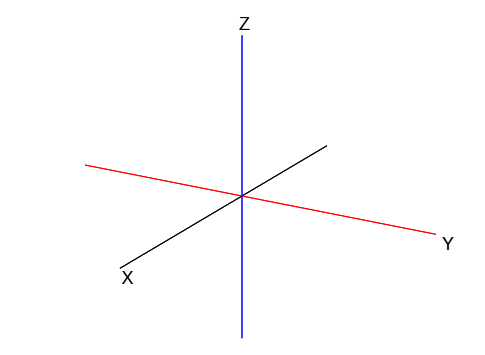
cono, así (para el semieje $0Y$):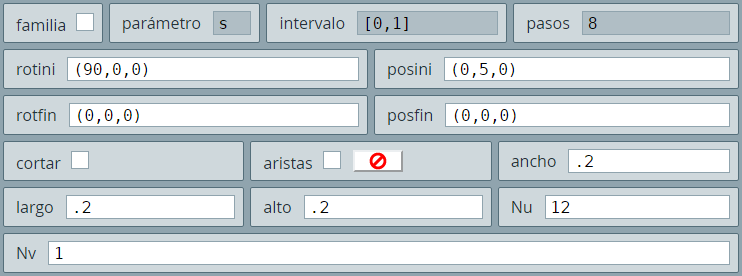
El color debe ser igual al del eje, en este caso rojo. Para el semieje $-0Y$, basta cambiar el ángulo a -90°.
En la siguiente página puedes consultar los parámetros comunes a los gráficos 3D, entre ellos el posini y el rotini.
Dado que el cono, por defecto, es dibujado con el vértice hacia abajo (semieje = $-0Z$) y teniendo en cuenta el sistema dextrógiro, lo hemos rotado 90° alrededor del eje $X$. No olvides cambiar los valores del ancho, el largo y el alto de los conos por 0.2.
para el semieje $0X$ el posini es (5,0,0), el rotini (0,-90,0) (sentido horario) y color negro, para el semieje $-0X$ sólo cambia el signo del ángulo. Para el semieje $0Z$... ¡te lo dejamos a ti!
DescartesJS, por defecto, crea una superficie paramétrica con las siguientes ecuaciones x=2*u-1 y=2*v-1 z=x^2-y^2, conocida como la "silla de montar". Agrega esta superficie, a la cual le haremos los siguientes cambios: i) hacemos z=0, lo cual nos convierte la superficie en un plano en $XY$ de ancho y largo igual a 2 pixeles, con el eje $Z$ pasando por su centro. Los parámetros u y v son vectores unitarios en $X$ y $Y$ respectivamente, si las expresiones fueran x=2*u y=2*v, el plano se dibujaría en el primer cuadrante del plano $XY$, para centrarlo es que se debe restar un (1) pixel; ii) Como hemos dibujado ejes $X$ e $Y$ de cinco (5) pixeles, cambiamos las expresiones a x=10*u-5 y=10*v-5. Hazlo y observa el resultado.
Para mejorar el diseño, usa un color naranja, con transparencia de y modelo luz, este mismo color úsalo en el reverso. Este sería el resultado:
Observa que Nu y Nv los hemos cambiado a 10, pues ese es el número de divisiones que necesitamos en las direcciones u y v. Para el plano $YZ$ usamos las ecuaciones y=10*v-5 z=8*u-4 x=0, color azul, transparencia de y divisiones Nu=Nv=10. Finalmente, para el plano $ZX$ las ecuaciones paramétricas son z=8*u-4 x=10*v-5 y=0, color verde, transparencia de y Nu=Nv=10.
La escena final es esta:
Guarda esta escena con el nombre plano3D, porque la vamos a necesitar en el capítulo IV.
Habrás notado que redujimos los planos en medio pixel ¿cómo lo hicimos?... es tarea tuya rediseñarlo.
Rediseña la actividad anterior de tal forma que: i) los planos $YZ$ y $ZX$ estén inclinados 45° con respecto al plano $XY$. En un sistema dextrógiro, el ángulo es positivo en el sentido antihorario, por ejemplo, en el plano $YZ$ es positivo desde el semieje $0Y$ al semieje $0Z$; ii) las cuadrículas de los planos deben tener seis divisiones. La tarea debe quedar así:
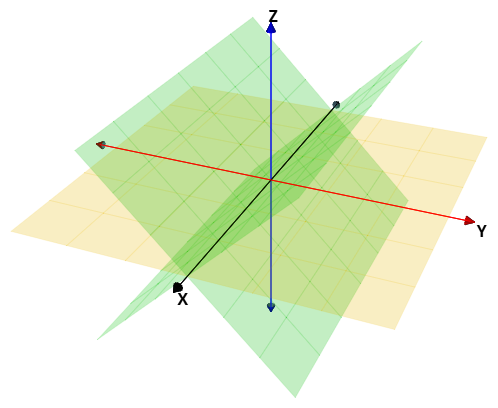
Las habilidades matemáticas comienzan con la observación y representación del mundo real. Cuando percibimos un objeto realizamos varias operaciones mentales. En estas operaciones intervienen los conceptos previos que tenemos del mundo y nuestras habilidades para realizar relaciones entre lo percibido y nuestra forma de percibir. Lo cierto es que existen diferentes formas de percibir, unas más lentas y otras más rápidas. Igualmente, podemos realizar relaciones mentales diferentes; también podemos utilizar en forma distinta nuestros conceptos para resolver problemas, como los que plantearemos en este apartado; es decir, unos contarán, otros calcularán, dependiendo del nivel de formación.
En este apartado diseñaremos algunos objetos interactivos relacionados con conceptos como: volumen, cantidad y ubicación espacial. Un ejemplo de ello se observa en la anterior escena.
Diseñar un objeto interactivo que genere bloques (cubos) al azar distribuidos en un volumen de largo, ancho y alto no mayor que cuatro (4). Dadas estas condiciones, lo que buscamos es una pila máxima de 64 cubos ($4 \times 4 \times 4$).
Para comprender como generar estos cubos en un espacio 3D, partimos de la escena diseñada en la actividad anterior.
cubo, es que el ancho corresponde a la diagonal del cubo, por ello, es importante calcular su lado, el cual se consigue agregando las siguientes expresiones en el algoritmo INICIO: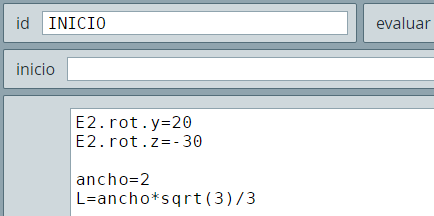
De acuerdo a lo anterior, agrega un cubo con dicho ancho, es decir, en el campo de texto ancho escribes ancho (ver ).
Observarás que el cubo queda con su centro de gravedad en el origen de coordenadas:
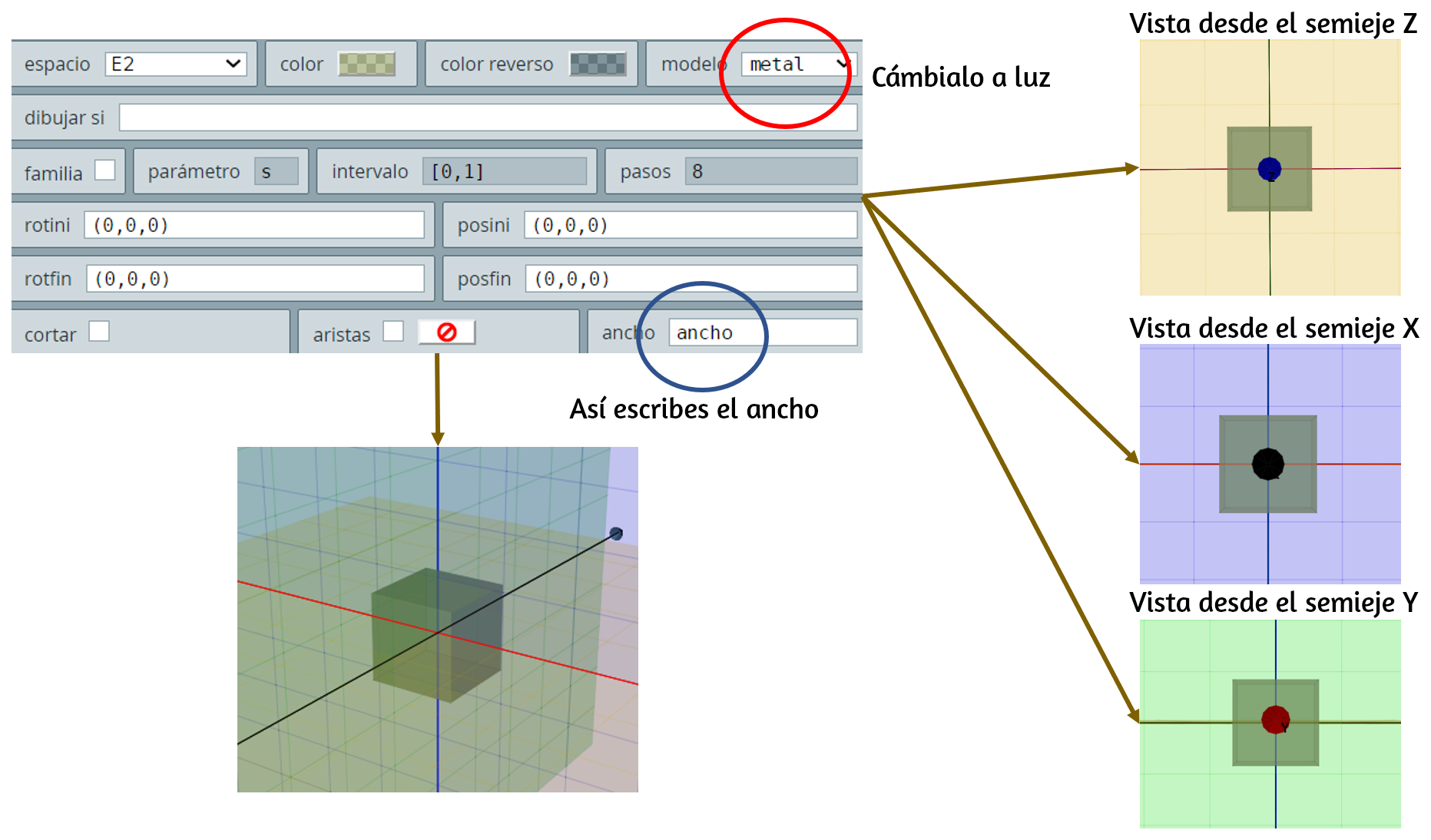
Nu=Nv=1. Para correr el cubo al primer octante, cambiamos el posini por (L/2,L/2,L/2) que es lo mismo que desplazar el cubo medio lado en todas las direcciones positivas $X$, $Y$ y $Z$.Cambia el color del cubo por verde y el modelo a luz.
Con estos cambios, hemos avanzado así:
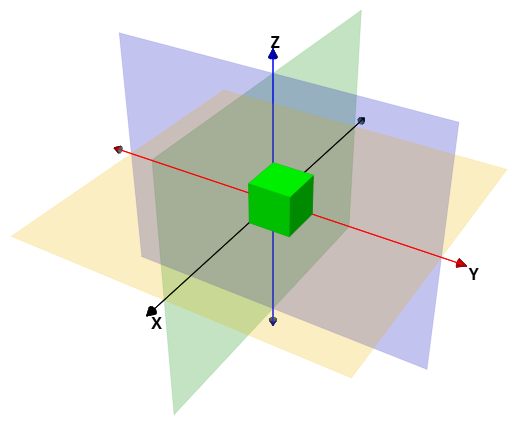

Pero, sólo obtenemos una fila de cubos. Veamos cómo logramos llevarlo a una parrilla o matriz de cubos en el plano $XY$.

Obteniendo:
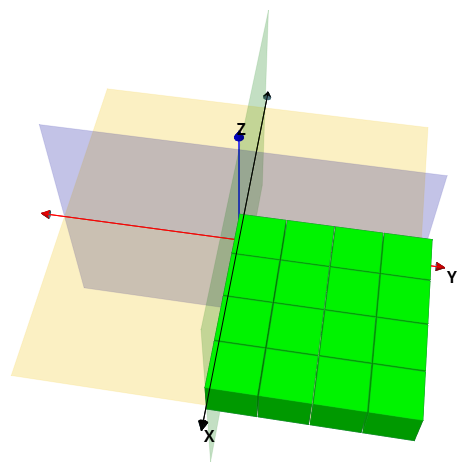
(z=-L/2); para ello, agrega una familia de cubos, color naranja, modelo luz y esta familia:
La escena obtenida es esta:
En la escena anterior, hemos eliminado los planos cartesianos, situación que también haremos con los ejes, pues ya han prestado la ayuda que necesitábamos para comprender cómo se generan los cubos.
E2), color negro, escala 40 y despliegue pintor.INICIO escribe las siguientes expresiones:
L/2 a la izquierda y hacia el fondo, pues ya no tenemos el sistema de ejes cartesianos, las expresiones se simplifican significativamente. Agrega un cubo de color verde, modelo luz y con esta familia:
Agregaremos tres familias de cubos iguales a la anterior con alturas (z=L, 2L y 3L) y colores amarillo, rojo y turquesa. En la siguiente página te mostramos la segunda.

Hasta aquí, hemos obtenido:

INICIO incluimos las siguientes expresiones: v=ent(rnd*7)+10, a=v-ent(rnd*5), r=a-ent(rnd*4) y t=r-ent(rnd*3). La primera nos genera números entre 10 y 16, los cuales definen la cantidad de cubos verdes, las demás expresiones son fáciles de interpretar.
En los campos de texto dibujar si, escribimos s<v para los cubos verdes, s<a para los amarillos, s<r para los rojos y s<t para los turquesas. Así las cosas, nuestro objeto ha cumplido con lo solicitado en la actividad:
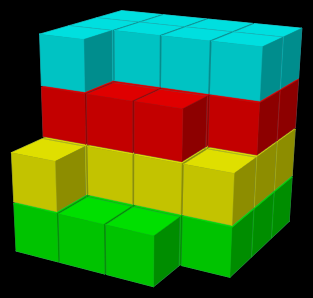
En la actividad anterior, el número total de cubos se obtiene sumando v+a+r+t. Incluye los controles y textos necesarios para que la actividad tenga el siguiente diseño:
Es posible utilizar una sola familia de cubos para la actividad anterior. Observa la expresión que podemos usar, de tal forma que se generen todos los cubos de la actividad:

El número de cubos lo calculamos con la expresión cubos=17+ent(rnd*48), por lo que en la casilla dibujar si pusimos la expresión booleana s<cubos. También, creamos tres vectores de colores, de tal forma que los colores de los cubos cambien de acuerdo a:

Hemos incluido, también, una imagen de fondo de la Mezquita de Córdoba. El resultado lo puedes observar en la página siguiente.
Puedes observar que la configuración aleatoria es diferente a la que realizamos en la actividad anterior, pues es posible que aparezcan cubos en uno, dos, tres o en los cuatro niveles, mientras que en la actividad parecen en todos los niveles.
Comprender este apartado, nos permite crear otros objetos interactivos que respondan a otras áreas del conocimiento. Por ejemplo, en la siguiente escena hemos diseñado una losa de hormigón con el propósito de calcular las cargas sobre ella.
En este caso se usaron superficies y paralelepípedos. El objeto recrea un sistema constructivo con sus pisos y particiones, que permite al estudiante de un curso de hormigón armado acercarse a la realidad de los objetos representados.
Terminamos este capítulo con el diseño de algunas superficies paramétricas.
En el apartado anterior diseñamos varios planos con ecuaciones paramétricas, de este diseño explicamos como configurar los parámetros u y v, de tal forma que el plano estuviese en los planos $XY$, $ZY$ y $ZX$; por ejemplo, para un plano de 10 divisiones en $X$ y $Y$, empleamos las ecuaciones paramétricas: x=10u-5, y=10v-5 y z=0. Estas ecuaciones se pueden escribir, también, así:
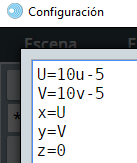
La comprensión de cómo dimensionar u y v, además de la simplificación anterior de las ecuaciones paramétricas, permite un diseño correcto de las superficies paramétricas.
No nos detendremos a explicar cómo surgen estas superficies y, menos aún, cómo se obtienen sus ecuaciones; nuestro propósito es explicar el procedimiento para dibujarlas en DescartesJS. Tampoco haremos una extensa presentación de superficies, para ello, recomendamos el libro digital interactivo "Curvas y superficies paramétricas" y las unidades didácticas Superficies curiosas I y Superficies curiosas II, diseñadas por Josep Mª Navarro Canut.
Iniciamos con una superficie sencilla cuyas ecuaciones son x = ucos(v), y = usen(v) y z = u, con u en el intervalo [-1, 1] y v en [0, 2π]. Esta información la podemos escribir así:
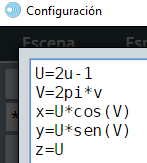
Observa que el intervalo [-1, 1] nos indica que la dimensión de u es 2 o, como lo hicimos con los planos, son dos las divisiones, por ello hicimos U=2u-1. Así las cosas, iniciemos con el diseño de esta primera superficie:
E2), despliegue pintor y color de fondo 001e51 (obviamente, puedes escoger los colores a tu gusto). .
.INICIO, incluye E2.rot.y=-30.
le asignaremos un valor de 90, con un mínimo de 60, un máximo de 100 e incrementos de 2.
El segundo control, también pulsador, es para asignar transparencia al color de la superficie:

el valor será cero, con un mínimo de cero (0), un máximo de uno (1) e incrementos de 0.05.
verde y un reverso naranja. Es importante, luego de asignar el color, incluir la transparencia, tal como aparece en esta imagen: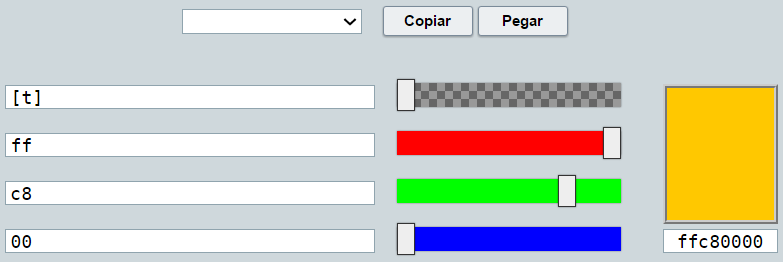
Ahora, podemos observar cómo ha quedado diseñada esta superficie. Obsérvala en la siguiente página e interactúa con ella.
Esta superficie se genera con las siguientes ecuaciones paramétricas: x = 2cosh(v/2)*cos(u), y = 2cosh(v/2)*sin(u) y z = v, con u y v en el intervalo $[-\pi, \pi]$, es decir, con divisiones para u y v de $2\pi$. Habrás notado que para simplificar las ecuaciones usando la forma U = au + b, el coeficiente a corresponde a la dimensión de u y el coeficiente b al punto de inicio en el eje $X$, que para el caso de nuestra catenoide sería: $U = 2\pi u - \pi$. La ecuaciones, entonces, en una forma simplificada serían:
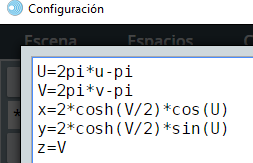
Sigue el procedimiento anterior para el diseño de esta superficie paramétrica, teniendo en cuenta los siguientes cambios:
25, mínimo 10 y máximo 30.E2.rot.y = 30.Nu = 30 y Nv = 30Hemos explicado que en la expresión U = av + b el valor de a determina la dimensión que, para la catenoide, se refiere al ángulo, o sea $2\pi$. Modifica la expresión para U, de tal forma que el ángulo varíe entre $0$ y $2\pi;$ además, usa una familia para generar tres catenoides. La escena sería esta:
Esta superficie se define por las ecuaciones x=(|u|-1)2cos(v), y = (|u|-1)2sen(v) y z = u con u en $[-1, 1]$ y v en $[0, 2\pi]$. Con la misma configuración anterior, excepto por la escala que cambiamos a 110, hemos diseñado dos trompos intercambiando las expresiones de x e y, y separando los trompos con el posini:
Aquí U = 2u -1 y V = 2pi*v, los posinis empleados fueron (0,-1,0) y (0,1,0), por ello es que quedan tangentes los trompos. Para incluir el control a, hicimos V = a*v, además de reducir Nu y Nv a 20.
Esta superficie super-toroide, llamada "toto lapa", hace parte de la familia de primitivas basadas en el toro, tanto u como v están en el intervalo $[-\pi, \pi]$, lo que significa que las dimensiones (los ángulos) son $2π$, iniciando en $-π$.
Las ecuaciones que definen esta superficie son:
x = cos(u)/(sqrt(2)+sin(v)),
y = sin(u)/(sqrt(2)+sin(v)) y
z = 1/(sqrt(2)+cos(v)).
Haremos un ejercicio interesante para saber cómo funcionan los ángulos en esta superficie. Para ello, sigue el procedimiento anterior, con una escala de 50 e incluyendo un control tipo pulsador k, con valor 0.8, mínimo 0.5 y máximo 2. Además, debes tener el control a, que permite variar el ángulo en las expresiones U = au y V = av. El ejercicio consiste en dibujar dos toroides, uno de ellos rotado 180° con respecto al eje $Y$ (rotini). Las ecuaciones quedarían así:
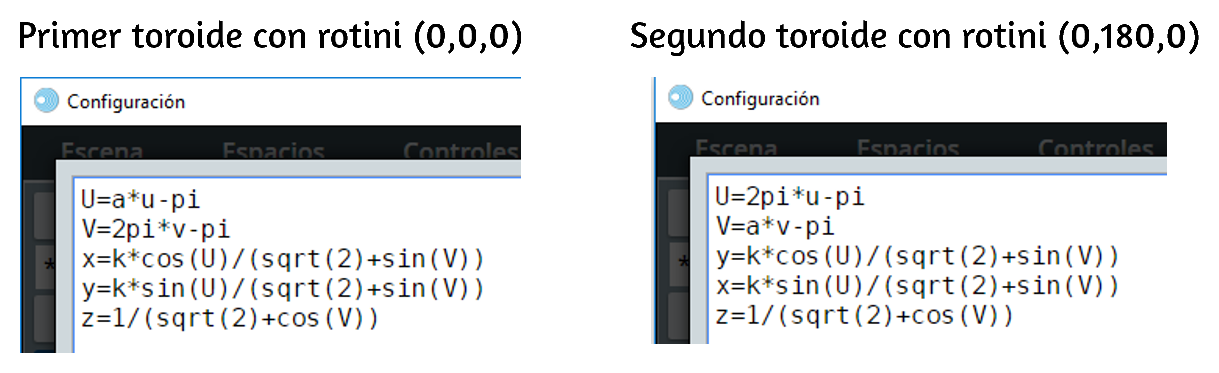
Observa que hemos intercambiado las expresiones en x e y en el segundo toroide.
Las superficies, Nu = Nv = 25, que se obtienen son las siguientes:
Usa el control a ¿con respecto a qué eje cambia el ángulo en el segundo toroide?
¿Qué efecto tiene el control k?
Esta superficie curiosa con ecuaciones x = 2*u/(u*u+v*v+1), y = (u*u+v*v-1)/(u*u+v*v+1) y z = 2*v/(u*u+v*v+1), con u y v en $[-1.5, π]$, la hemos diseñado en una escala de 120. Observa la escena interactiva y constrúyela teniendo en cuenta que el control k sólo afecta a x e y
¿dónde pondrías los controles a1 y a2?
Son muchas las superficies paramétricas que podríamos explorar, por ello, te recomendamos la unidad didáctica de Josep Ma Navarro para que practiques modificando sus atributos.
Un último ejemplo es esta hermosa caracola, usa el control a y la transparencia para que observes cómo se enrolla.
Los desarrollos que presentamos en este capítulo se hicieron gracias a la propuesta presentada por la profesora de la Universidad de Cantabria, Elena Álvarez Sáiz. En este capítulo nuestro objetivo es diseñar objetos interactivos de aprendizaje en los que intervienen dos herramientas de autor: DescartesJS y GeoGebra. Pero no se trata de presentaciones aisladas de una u otra herramienta, la importancia de este capítulo radica en que comunicaremos las dos herramientas, de tal forma que cada una envíe información a la otra. Esta comunicación permite que tengamos, en una sola escena, las fortalezas de DescartesJS, que estamos aprendiendo, y las de GeoGebra, que según la información de su página es:
Quizá faltó, en esta presentación de la herramienta, precisar el poder de su cálculo simbólico (CAS), el cual nos será de utilidad para diseñar escenas que incluyan desarrollos algebraicos que no son posibles con DescartesJS.
Una primera muestra de escenas de GeoGebra, se muestran en el siguiente objeto interactivo. Las tres últimas escenas también las hemos diseñado en DescartesJS. En la segunda escena se hace manifiesto el cálculo simbólico de GeoGebra.
Dado que el procesador geométrico es más robusto que DescartesJS, tendrás que esperar un poco más a que se muestren las escenas, pero la espera vale la pena, cuando se trata de diseños especiales y de una intencionalidad didáctica.
Pero, lo que más nos interesa es la comunicación entre las dos herramientas, situación que puedes apreciar en la siguiente escena interactiva, en la cual hacemos uso del
cálculo simbólico de GeoGebra, en especial para el cálculo de derivadas, integrales y raíces de una ecuación.
La comunicación se realiza cuando seleccionamos una opción e introducimos una función, datos que DescartesJS envía a GeoGebra y ésta retorna la solución.
Este tipo de escenas las aprenderemos a diseñar en los siguientes apartados. Diseñaremos, también, algunos tutoriales para aprender GeoGebra desde DescartesJS.
Es preciso advertir que no profundizaremos en aspectos que son propios de un curso de GeoGebra, para lo cual recomendamos leer los manuales existentes en la red. Si bien trabajaremos con el entorno gráfico de esta herramienta, es más para comprender con qué nos comunicaremos desde DescartesJS. Por otra parte, si no es de interés del lector de este libro el uso de GeoGebra, puede continuar con el próximo capítulo, lo cual no interfiere con los objetivos de este nivel.
Otro problema, que ya hemos detectado, es el enlace al procesador geométrico vía página GeoGebra pues, como ocurrió con la versión 4.4, éste puede cambiar. Es por ello que hemos preparado una versión liviana para uso en línea o en local y para el logro de nuestros propósitos, la cual puedes obtener de la carpeta descargas de este libro, si prefieres, puedes descargarla aquí. En ella no encontrarás un ejecutable de GeoGebra, pues sólo contiene los elementos mínimos requeridos para este capítulo.
Si has trabajado con GeoGebra, puedes practicar con la escena interactiva y verificar algunos comandos en la barra de entrada, por ejemplo, escribe Derivada[x^2] y presiona la tecla intro, observarás que se obtiene la función derivada f(x)=2x.
Volviendo a nuestro archivo de interface (interfaz o protocolo), te sugerimos abrir una carpeta con el nombre GeoGebra, en ella guardarás la carpeta GeoGebra5 y el archivo interfaz. Una vez hecho lo anterior, puedes ejecutar el archivo interface_inicial.html y practicar con GeoGebra o, si no lo conoces, practicar con esta herramienta; no obstante, recuerda que el propósito no es aprender GeoGebra.
O, en algunos casos, un editor como el bloc de notas. En este capítulo usaremos el editor Notepad++.
Iniciemos, entonces, explorando el archivo que nos permitirá realizar la comunicación entre las dos herramientas de autor. Para ello, ejecuta el editor HTML y abre el archivo interface_inicial.html.
Las primeras líneas que observarás son las siguientes:
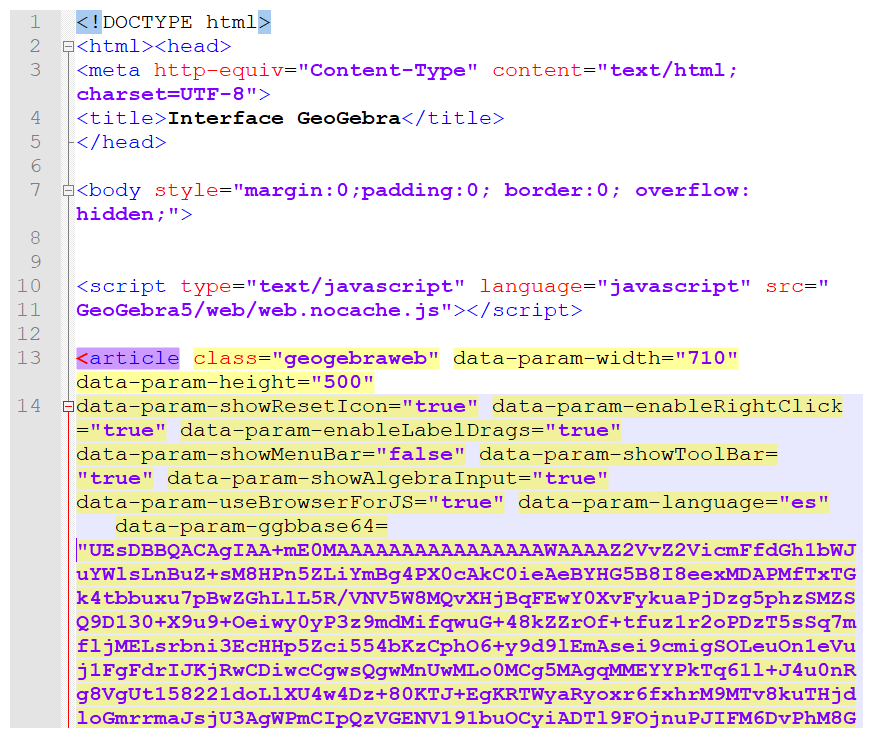
De estas líneas, por ahora, nos interesan los bloques <script> y <article>. En el primero se invoca un archivo JavaScript de nombre web.nocache.js que ejecuta GeoGebraWebA partir de GeoGebra 4.2 se introdujeron genuinos documentos HTML5 GeoGebra por lo que los applets dan inicio con mayor rapidez. Además, en tanto Java ya no es un requisito previo en esta tecnología, se abre la disponibilidad de GeoGebra para los dispositivos móviles del estilo de los smartphones. GeoGebra detecta automáticamente el navegador web en uso y decide si está ejecutándose en una tablet y trata el documento en formato HTML5 (https://wiki.GeoGebra.org/)., el cual está compuesto de un conjunto de archivos JS y HTML, que permiten la publicación de objetos interactivos en la red, este archivo se encuentra en la carpeta GeoGebra5.
Es importante, entonces, que el archivo lo tengas guardado en la carpeta que hemos sugerido con el nombre GeoGebra que contiene, además, la subcarpeta GeoGebra5.
El segundo bloque (<article>) contiene la configuración de la escena y el archivo de GeoGebra (ggb) que se constituye en la escena misma. Para la configuración se usa la expresión data-param-comando, donde comando es un elemento de configuración; por ejemplo, data-param-width="710" indica que la escena tendrá un ancho de 710 pixeles. Por otra parte, el contenido de la escena (archivo ggb) se guarda codificado en base 64 con el parámetro data-param-ggbbase64, que generalmente es extenso, luego nos ocupamos de cómo obtener esta codificación de una escena GeoGebra.
Con respecto a los comandos de configuración, es necesario que le des una lectura a la lista de comandos que aparece en la siguiente página.
De acuerdo a esta información y la configuración dada en la escena anterior, concluimos que es una escena de $710 \times 500$ pixeles, con el botón reset, el menú de herramientas, clic derecho, etiquetas y cuadro de entradas habilitados, además de configurar el idioma a español.
Uno de los comandos que usaremos para el diseño de las actividades de este capítulo es customToolBar, el cual nos permite definir cuáles herramientas deben aparecer en el menú; por ejemplo, queremos mostrar una escena de GeoGebra de $600 \times 400$ pixeles que sólo muestre las herramientas: elige y mueve, punto, segmento, polígono y elimina objeto.
Debemos, entonces, identificar la cadena de valores correspondiente a esas herramientas, para ello, puedes consultar el siguiente texto:
Bastaría con agregar el parámetro: data-param-customToolBar="0|1|15|16|6" en la etiqueta <article>, así:
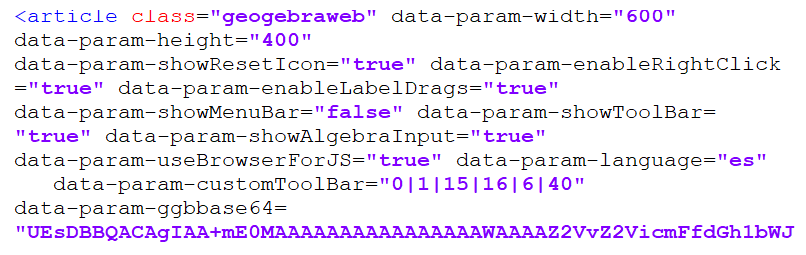
Observa que hemos incluido seis herramientas cuyos valores no necesariamente tienen que ir en un orden ascendente. Hemos agregado, además, la herramienta de desplazamiento gráfico cuyo valor es 40.
En la siguiente página puedes observar y escuchar una explicación más amplia sobre la configuración de la escena. Al final de la presentación, te daremos una clave para capturar el archivo ggb, codificado en Base64, de cualquier escena de GeoGebra, tanto las que diseñemos con la herramienta, como las que se publican en la red, en especial del portal de GeoGebra.
La presentación sigue el mismo formato de las anteriores que hemos presentado, para ello, recuerda que para observar las diapositivas debes hacer clic sobre la imagen y luego usar la flecha del teclado para avanzar. Debes tener el sonido activado, pues cada diapositiva tiene una explicación en archivo de audio.
Ya es momento de avanzar con el proceso de comunicación entre las dos herramientas, así que presta atención al procedimiento que seguiremos a continuación, en el cual estaremos configurando tanto el editor de DescartesJS, como el archivo que hemos denominado interface_inicial.html... manos a la obra.
Iniciamos con la siguiente actividad (espera a que cargue GeoGebra):
Diseñar una escena interactiva, usando DescartesJS y GeoGebra, cuyo propósito es enviar órdenes (comandos) desde DescartesJS a GeoGebra, cuyos resultados se muestren en la escena. Al final se obtendrá una circunferencia circunscrita de un triángulo.
La comunicación de DescartesJS con GeoGebra ha sido posible gracias al trabajo de nuestra colega Elena Álvarez publicado como Aplicaciones de la comunicación para integrar cálculo simbólico en Descartes, en el cual explica:
Lo explicado por Elena tiene que ver con el "cómo funciona la escena"; sin embargo, es necesario que expliquemos el "cómo funciona calculos.html", que es nuestro archivo de comunicación. Nuestro propósito no es ahondar en los métodos y eventos de JavaScript, pues no está en el alcance de este libro, pero si podemos estudiar los bloques principales de este archivo de interface, para poder intervenirlos de tal forma que responda a nuestras necesidades de diseño de otras escenas interactivas.
Para iniciar, partamos de lo explicado por Elena en su escena de comunicación con GeoGebra, para lo cual descarga este archivo: calculos1.zip, lo descomprimes y guardas en la carpeta que hemos llamado GeoGebra. Al ejecutar el archivo, observarás la siguiente escena interactiva:
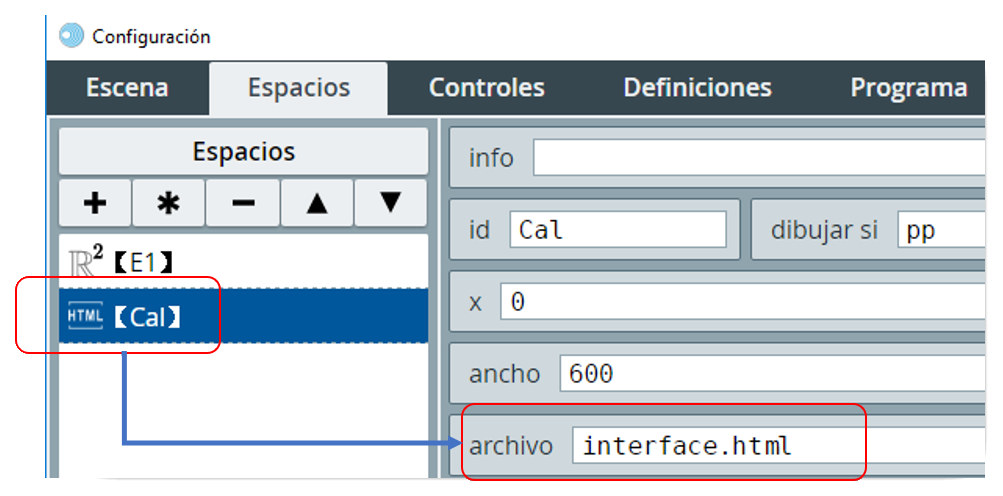
El diseño de la escena es sencillo. Para analizarla abre (con DescartesJS) el archivo index.html. Observarás que se trata de una escena de $600 \times 350$ pixeles, en la que hay dos espacios. El primero, es un espacio R2 con nombre E1; el segundo es un espacio HTMLIFrame que, como Elena, hemos llamado Cal. En este segundo espacio, el archivo html que es invocado es interface.html (Elena lo llama calculos.html), hemos dejado en dibujar si la expresión pp, la cual es falsa (pues pp=0), de tal forma que no se muestre este espacio (la escena de GeoGebra), pues sólo nos interesa darle órdenes y recibir respuestas.
En el selector Controles, hemos diseñado un control tipo campo de texto y dos botones. Sólo explicamos el primero, pues ya estás en capacidad de comprender los otros dos.
Este control llamado orden envía el mensaje de tipo set, de nombre evalua y cuyo valor es el mismo de la variable orden. El mensaje es enviado a la página cargada en el HTMLIFrame Cal (en nuestra escena, a la página interface.html).
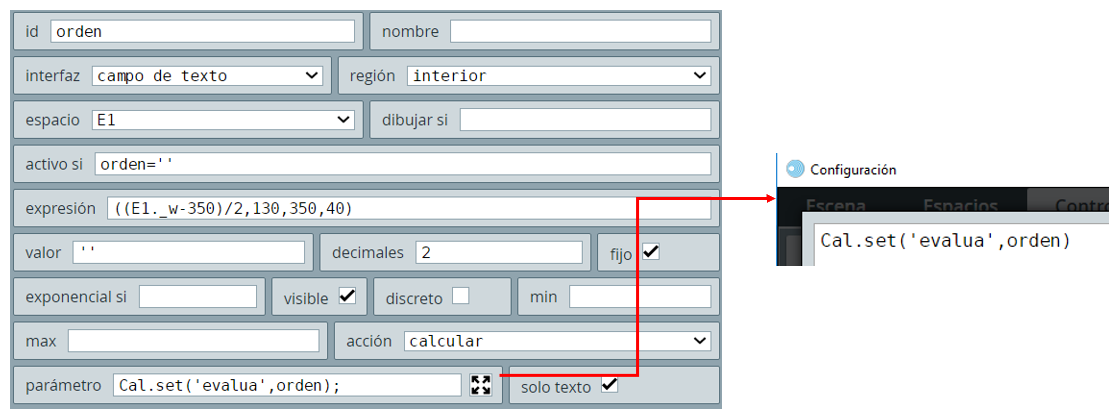
El archivo de comunicación (interface.html) ejecuta la orden dada (comando GeoGebra), comunicando a DescartesJS el resultado, a través de una variable con nombre vCalculado, que incluimos en el texto diseñado en el selector Gráficos.
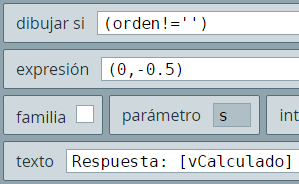
Es importante que conozcas algunos comandos de GeoGebra, pues sin ello la escena anterior no es de tu utilidad. Si no eres un usuario de GeoGebra, te mostramos cinco comandos que puedes introducir en la escena anterior:
Derivada[5x^6-4x^2,2]. Calcula la segunda derivada de la función $5x^6 - 4x^2$.Derivada[6x^3*y^2-sen(x*y),y,1]. Calcula la derivada parcial de la expresión $6x^3 y^2 - sen(xy)$.Factoriza[x^2-x-6]. Factoriza el polinomio $x^2 - x - 6$.Desarrolla[(3x-5)(2x+4)]. Desarrolla el producto $(3x - 5)(2x + 4)$.Integral[6x^2+2x-20,0,3]. Calcula la integral entre $0$ y $3$ de la función $6x^2 + 2x - 20$.Es importante que no olvides la mayúscula inicial, de lo contrario GeoGebra desconocerá el comando enviado y el archivo interface nos retornará el mensaje: "No está disponible de momento".
Hasta aquí, hemos explicado el funcionamiento de la escena. Ahora, nos adentramos en el archivo de comunicación.
Abre el archivo interface.html con un editor html (Notepad++, por ejemplo). Los primeros bloques ya los conoces, en especial los bloques <script>type="text/javascript" language="javascript" src="../GeoGebra5/web/web.nocache.js"></script> y el bloque <article>, donde el segundo nos permitió configurar el entorno de una escena de GeoGebra. Como la escena GeoGebra la hemos dejado oculta en nuestro diseño, sólo nos queda explicar el último <script>.
Una primera exploración hazla en la línea 92, a partir de esta línea podrás observar 467 comandos de GeoGebra almacenados en dos matrices: vComandosD y vComandosG.
En la primera matriz se almacenan los comandos en español y en la segunda en inglés. Esta es una buena estrategia de Elena, pues GeoGebra finalmente ejecuta los comandos en inglés.
A continuación, puedes explorar los primeros 100 comandos:
La otra parte de la interface de comunicación, es la siguiente:
Observa que la hemos dividido en cinco bloques, para su explicación.
Bloque líneas 21-35. Hasta la línea 30, aparecen elementos de JavaScript que no modificaremos en el resto de este capítulo. Las dos primeras expresiones crean las dos matrices antes descritas. A continuación aparece un método y una función JavaScript, necesarios para la comunicación. Como dijimos antes, su explicación está por fuera del alcance de este libro, basta saber que las debes dejar tal cual. La expresión nombre=data.name; asigna el nombre de la variable enviada desde DescartesJS a la variable nombre, que para nuestra escena es evalua (recuerda que la enviamos con la expresión Cal.set('evalua',orden)). Este mismo nombre se asigna a la variable aux, si no se envía evalua, aux será cero.
Bloque líneas 37-45. Mensaje con el comando enviado desde DescartesJS o, de otra forma, el valor de la variable evalua que es el mismo introducido en el control orden. Este valor recibido (data.value) se asigna a dComando, con el que se invoca la función calculosCAS(dComando) para ejecutar el comando enviado. Una vez evaluado, el resultado se asigna a la variable rComando, cuyo valor es retornado a DescartesJS en la variable vCalculado.
Bloque líneas 51-63. Útil para las siguientes escenas.
Bloque líneas 66-83. Es el bloque con la función calculosCAS(dComando). Lo que se realiza es una partición (split) en dos del comando enviado, separando la palabra que está antes del corchete de apertura (str[0]) de la expresión que está después de él (str[1]); por ejemplo, la orden Derivada[x^4], se divide en str[0]='Derivada' y str[1]='x^4]'. Con la primera palabra, cadena o string, se busca en la matriz de comandos en español el índice del elemento que la contiene esta palabra vComandosD.indexOf(com), donde com es la primera cadena (Derivada), que para el ejemplo es 95 (según la tabla de comandos anterior). Recuerda que esto es necesario, pues el comando a ejecutar en GeoGebra debe estar en español.
Finalmente, se realiza la ejecución del comando con las siguientes expresiones:
cEjecuta=vComandosG[pos]; (Derivative para nuestro ejemplo)
comando='f:'+cEjecuta+'['+str2; (Derivative[x^4], para el ejemplo)
calculo=document.ggbApplet.evalCommandCAS(comando);
el resultado se asigna a la variable calculo cuyo valor es retornado al bloque que invocó la función y se asigna a la variable vCalculado.
Quizá te hayas perdido en alguna parte de la explicación, así que vamos a hacer una trazabilidad del algoritmo con un ejemplo (prueba de escritorio).
'Factoriza[x^2-9]'. Eso quiere decir que orden='Factoriza(x^2-9)'.Cal.set('evalua',orden);. Eso quiere decir que DescartesJS envía la variable evalua con el contenido de orden (que es 'Factoriza[x^2-9]').nombre la expresión 'evalua' (ver primer bloque).dComando='Factoriza[x^2-9]' (data.value), rComando=calculoCAS(dComando), es decir, debemos ir al cuarto bloque.com=str1=str[0]='Factoriza'str2=str[1]='x^2-9]' pos=195 (ver tabla de comandos en interface.html) cEjecuta='Factor' (ver tabla de comandos en interface.html) comando='f:'+cEjecuta+'['+str2;='f:Factor[x^2-9]' (orden en inglés) calculo=document.ggbApplet.evalCommandCAS(comando); (GeoGebra ejecuta la orden y el resultado se asigna a calculo)return calculo (se envía el resultado al bloque 2)rComando.window.parent.postMessage({ type: "set", name: "vCalculado", value: rComando }, '*'); (Se envía este resultado (rComando) a DescartesJS guardado en la variable vCalculado).El quinto bloque garantiza la existencia de una escena de GeoGebra (ggbOninit), sin ésta no sería posible la comunicación.
Ya nos vamos acercando a solucionar la actividad planteada en este apartado, pero debemos aprender cómo enviar dos comandos simultáneos. Para ello, modificaremos la escena anterior, para lograr la siguiente:
Los cambios en la escena son pocos, obviamente tendrás que cambiar el título de la escena. El primer cambio es el nombre del espacio HTMLIframe, que será calculadora:
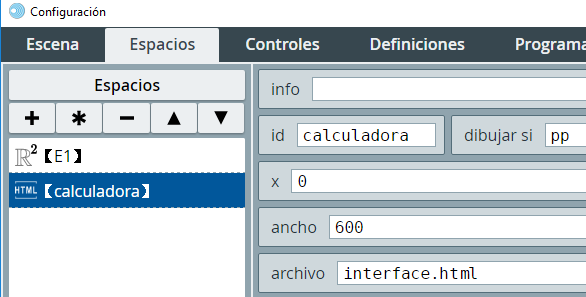
El segundo cambio lo realizamos en el control campo de texto, en el que agregamos un segundo mensaje, así:
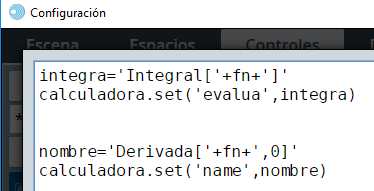
Observa que en el control campo de texto ya no se espera un comando de GeoGebra, se debe ingresar una función en x. Por ello, hay que construir el comando.
Supongamos que la función ingresada es 'x^3-2x', entonces la variable integra sería igual a 'Integral[x^3-2x]', comando que se envía al archivo de comunicación con la instrucción calculadora.set('evalua',integra), situación que funciona igual a la escena anterior, es decir, el archivo interface.html nos retornará el resultado de la integral en la variable vCalculado.
En este control vamos a introducir una segunda orden a ejecutar por GeoGebra, para ello asignamos a la variable nombre el comando 'Derivada['+fn+',0]', que para el ejemplo sería 'Derivada[x^3-2x,0]', el número cero es un truco que usamos, pues la derivada cero es la misma función. Luego enviamos el mensaje con la instrucción calculadora.set('name',nombre). Seguro te preguntarás para qué esta orden, la idea es que GeoGebra nos retorna la función en el formato $x^3 - 2x$.
Por otra parte, debemos incluir un bloque adicional en interface.html que pueda leer el mensaje name:
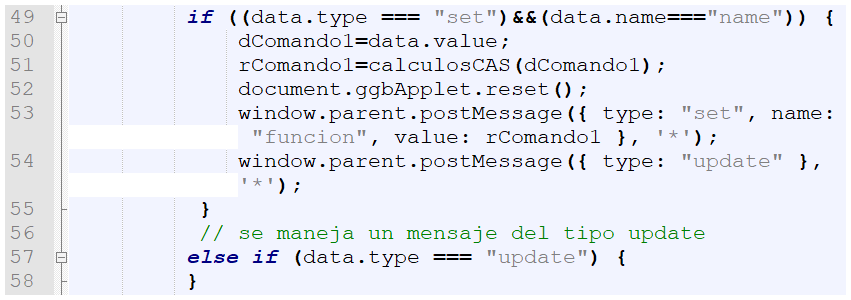
Analiza bien este bloque y compáralo con el bloque evalua. Observa que uno de los cambios es la variable retornada a DescartesJS que ahora es funcion.
Otro cambio está en la ejecución de la variable dComando (dComando1 en el nuevo bloque), pues obliga a crear la función:
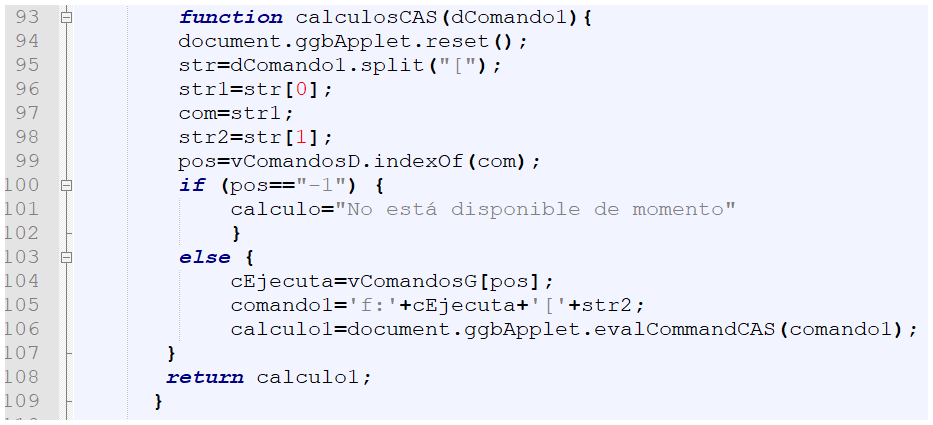
¿Lo anterior quiere decir que para n comandos necesitamos n bloques y n funciones en la interface.html?, la respuesta es sí y no. Es cierto para algunos casos especiales, como los objetos geométricos en los que debemos realizar otras acciones, y es "no" para el caso de la ejecución de comandos como los de esta escena, los cuales se pueden ejecutar con el bloque 3 que no hemos explicado aún (¿recuerdas el Bloque líneas 51-63?).
Finalmente, sólo nos resta diseñar cómo se escribirá el resultado, lo cual lo podemos hacer con un gráfico tipo texto enriquecido o, si lo prefieres, con gráfico tipo texto simple. El primer tipo lo profundizaremos en otro capítulo de este libro, sin embargo, en la siguiente imagen se describe cómo usarlo para esta escena:
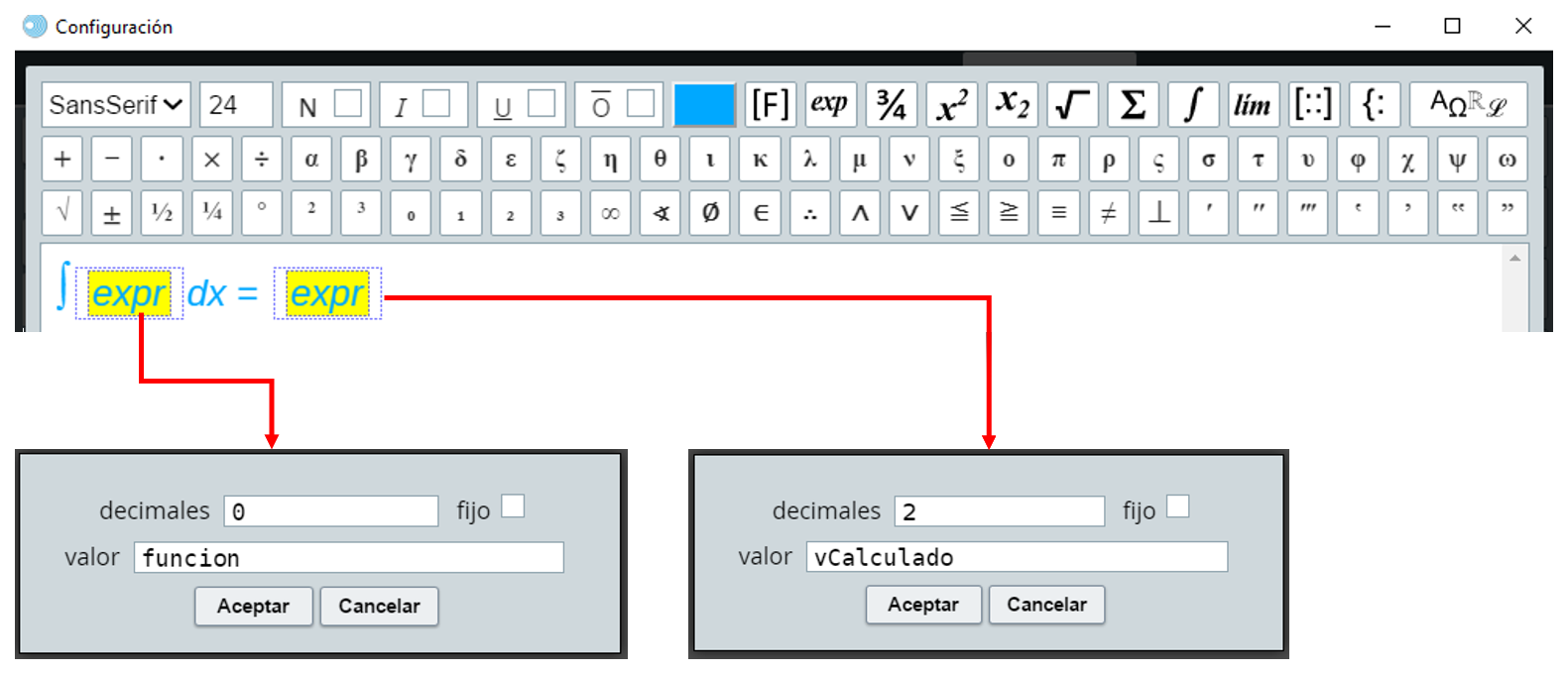
Con texto simple sería así:

Realiza los siguientes cambios en la escena anterior:
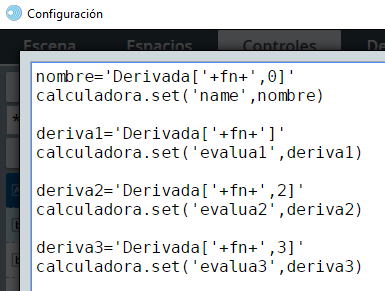
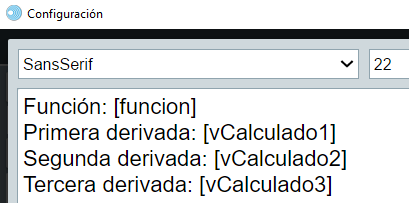
Observa que hemos usado las variables evalua1, evalua2 y evalua3 para enviar los mensajes, y esperamos recibir los resultados en las variables vCalculado1, vCalculado2 y vCalculado3.
Por ahora, ejecuta la escena interactiva y observarás algo así como esto:
Podrás notar, si sabes de cálculo diferencial, que la escena funciona bien, sin la necesidad de saber qué está ocurriendo en el archivo de comunicación.
Pero, como la idea es que sepas qué ocurre, hacemos una descripción detallada del Bloque líneas 51-63 que habíamos dejado pendiente, el cual se ha convertido en el Bloque líneas 60-72, pues recuerda que incluimos el bloque para la variable name que genera la expresión de la función.
Observa, entonces, el bloque que procesa las tres derivadas:
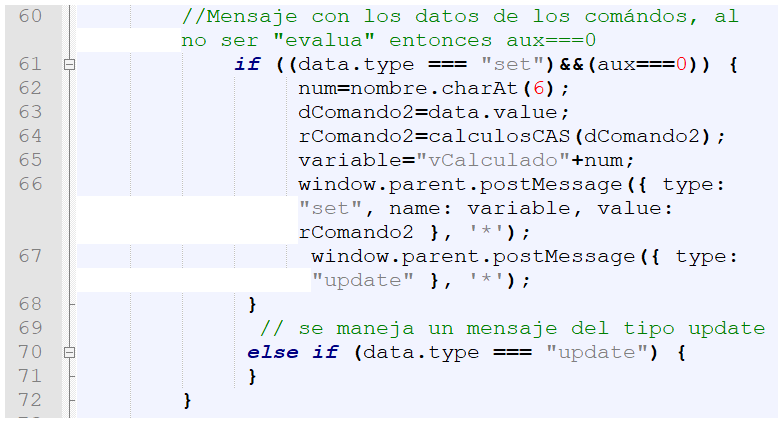
Su funcionamiento es el siguiente:
evalua1, evalua2 y evalua3, la variable aux es igual a cero (aux===0), por ello se ejecuta este bloque.num captura el sexto carácter (charAt) del nombre de estas variables, es decir, 1, 2 y 3.dComando2 toma el valor de estas variables (uno a la vez).rComando2 se le asigna el resultado obtenido de la función calculosCAS(), es decir, la primera, segunda y tercera derivada.variable los nombres vCalculado1, vCalculado2 y vCalculado3.Ahora ya podemos diseñar la actividad 6, de tal forma que los resultados se muestren en el entorno de GeoGebra, ello porque se trata de una construcción geométrica. Sigue, entonces, los siguientes pasos:
escalar.ejemplo0.interface.html que tienes en la carpeta calculos1 (descargado en el apartado 3.2.1).E1, en formato decimal, será 00, 30, 81, por ello debes diseñar este color para E1, así:
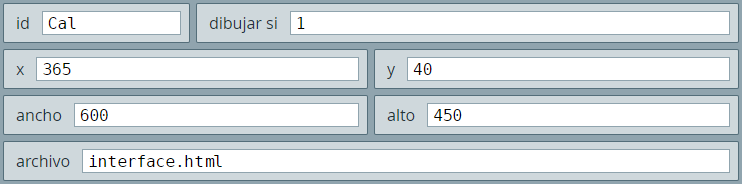
interface.html y cambia sus dimensiones a $595 \times 450$, es decir, data-param-width="595" data-param-height="450".Si has seguido bien los pasos anteriores, debes tener tu escena así:

Observa que el entorno GeoGebra de nuestra interface tiene tres características que debemos cambiar. La primera es que muestra la ventana de entrada, que eliminamos con este comando: data-param-showAlgebraInput="false". La segunda y tercera tienen que ver con el plano cartesiano que está ausente y el color del fondo del entorno de GeoGebra.
Tienes dos alternativas para cambiar el entorno. Una de ellas, si eres usuario de GeoGebra, es abrir la herramienta GeoGebra, configurar el color y copiar en el portapapeles el archivo codificado ggb64 (CTRL+SHIFT+B) y luego reemplazarlo en el archivo interface.html, tal como lo hemos explicado antes (apartado 3.1).
Otra alternativa, para los no usuarios de GeoGebra, es copiar una de las siguientes plantillas:
Nota que la plantilla 2 tiene el mismo color de fondo del espacio E1. Recomendamos seleccionar esta plantilla, pues el resultado final permite obtener una escena que se vuelve trasparente para el usuario, es decir, no distinguirá entre DescartesJS y GeoGebra.
Si presentas problemas para copiar la plantilla, puedes descargarlas desde el siguiente enlace: Plantillas, abres la plantilla que te gusta con el editor HTML y haces la copia del ggb64.
Continuamos con nuestro diseño de la actividad.
Practicando GeoGebra con DescartesJS (usa coordenadas relativas (0, 4.8) y 26 de tamaño de fuente).Para no extendernos en explicaciones que ya no necesitas, continúa el paso a paso para la configuración de escena en DescartesJS, en la presentación de la siguiente página. Al final, debes tener una escena como lo muestra esta imagen:

La siguiente presentación fue diseñada con el presentador HTML Reveal.js, creada por Hakim El Hattab. Te sugerimos observarla en pantalla ampliada para que puedas analizar la configuración de la escena. Para pasar de una diapositiva a otra, haz clic en las flechas que aparecen en la parte inferior derecha de la presentación.
Pudiste observar que el diseño consta de tres controles, dos algoritmos y 15 gráficos tipo texto. En estos últimos se centra el esfuerzo en el diseño de la escena, pues es la construcción del guion de la escena interactiva.
Es importante agregar un tercer espacio, que garantice la no intervención en el entorno GeoGebra en el primer paso de la construcción, pues de no hacerlo el usuario podría desplazarlo y dar al traste con el propósito de la escena: "construir la circunferencia circunscrita a un triángulo". Este es el espacio a agregar:
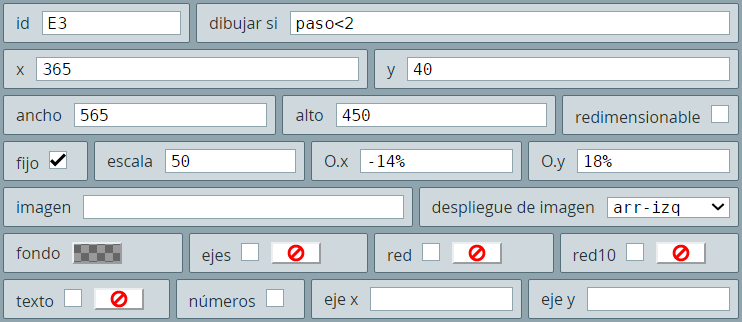
Como se indicó en la presentación, sólo necesitamos dos bloques para ejecutar los comandos requeridos de GeoGebra, los cuales pasamos a explicar a continuación.
El primer bloque no lo intervenimos, recuerda que es el que define la variables vComandosD, vComandosG, data, nombre y aux.
Después del primer bloque, vas a agregar lo siguiente y lee la explicación a continuación:
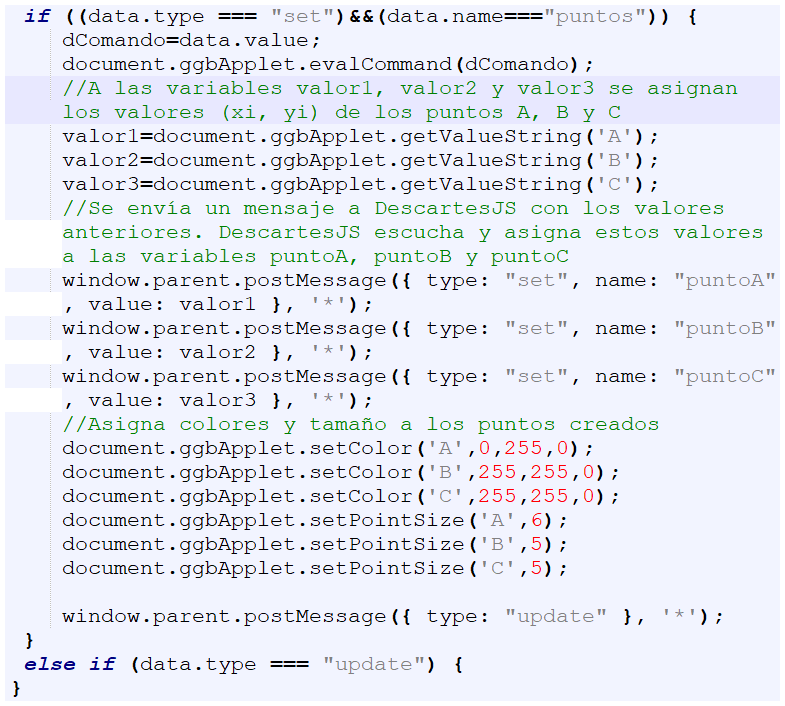
Este nuevo bloque se ejecuta cuando ingresamos el punto en el primer paso de la escena (paso=1), revisa el parámetro en el control tipo texto (mensaje=(paso=1)?Cal.set('puntos',entrada1):mensaje), cuyo mensaje es puntos con su correspondiente entrada o, si se prefiere, data.value. Adicionalmente, desde el evento del selector Programa, se enviaron dos puntos adicionales.
GeoGebra, por defecto, asigna las letras A, B, C, D,... a los puntos que se generan, por lo tanto, los tres puntos enviados serían A, B y C.
Siguiendo con la interface, se asignan a las variables valor1, valor2 y valor3 los puntos creados, a través de comandos como: valor1=document.ggbApplet.getValueString('A');.
A continuación, se envían tres mensajes a DescartesJS con los valores de estas variables, que DescartesJS recibe como puntoA, puntoB y puntoC, algo innecesario, pues DescartesJS ya los conoce; no obstante, lo hacemos sólo con fines didácticos, además de haberlos incluido en uno de los textos.
En el bloque hemos agregado dos atributos para los puntos: document.ggbApplet.setColor y document.ggbApplet.setPointSize, que permiten asignar color y tamaño a los puntos.
A continuación, hacemos algunos cambios al bloque de la variable aux que ya habíamos explicado cómo funciona. Observa los cambios:
aux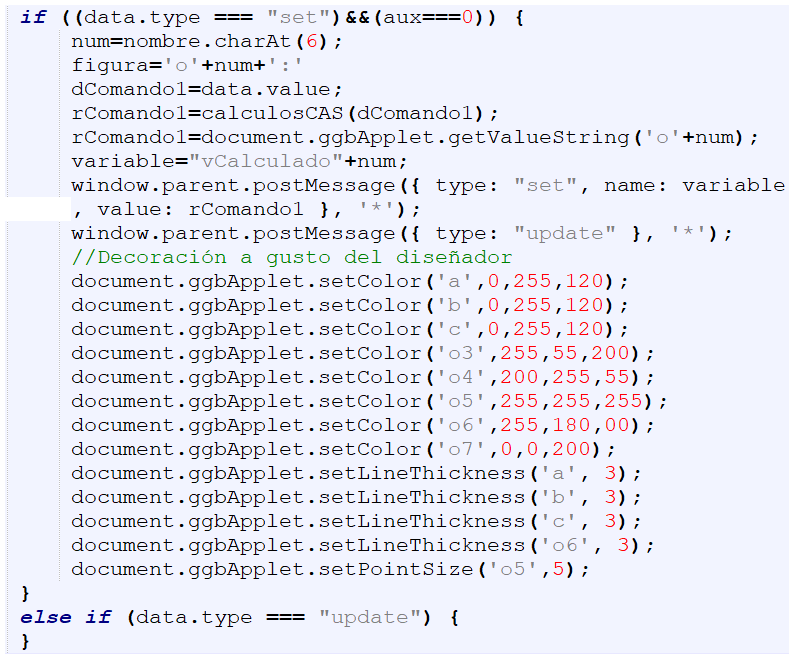
Observa que hemos agregado la variable figura cuyos contenidos son o1, o2, o3,... según el sexto carácter de evalua1, evalua2, evalua3, evalua4,...
GeoGebra asigna las letras a, b, c, d,... a los segmentos, rectas y curvas que vamos creando, como el segundo paso fue crear el triángulo, automáticamente los lados serían a, b y c. Por otra parte, el triángulo recibe el nombre o2, pues fue ordenado por el mensaje evalua2, las dos mediatrices son o3, y o4 ordenados por evalua3 y evalua4, el punto de intersección es o5, y la circunferencia o6.
Las líneas finales del bloque son de decoración (color, espesor de línea y tamaño de puntos). La escena final, entonces, sería:
Otra forma de establecer una comunicación entre las dos herramientas de autor, es "escuchar" lo que se hace en el entorno gráfico (vista gráfica) de GeoGebra, que permita controlar las acciones del usuario o, como lo haremos en este último apartado, conducir esas acciones para el logro de un resultado de aprendizaje. Es una forma sencilla de contribuir a manuales o tutoriales interactivos de GeoGebra.
Dado el avance que hemos logrado hasta este momento, en cada uno de los ejemplos que presentamos a continuación, sólo haremos una descripción de algunos aspectos a tener en cuenta en el diseño de las escenas interactivas. Queda como tu tarea el explorar estos ejemplos, tanto desde el editor DescartesJS como en el archivo interface.html, e identificar y comprender la lógica de programación empleada.
Vamos a realizar la misma construcción anterior pero desde el entorno gráfico de GeoGebra. El diseño, como lo dijimos antes, se constituye en un tutorial para que un usuario, que ingresa por primera vez a GeoGebra, conozca algunas de sus herramientas y construya un objeto geométrico. Esta primera escena interactiva la puedes explorar en la carpeta ejemplo1, la cual se encuentra en la subcarpeta GeoGebra en interactivos, para ello, es necesario que descargues el libro.
El entorno gráfico incluye siete herramientas que usaremos en la escena:

En la página de la derecha puedes observar la escena interactiva, la cual sugerimos abrir en la ventana emergente (Ampliar) para comprender los aspectos que resaltaremos de la misma.
Un primer aspecto a observar es la presencia de cinco espacios que hemos denominado "mascara", los cuales tienen por objetivo bloquear algunas herramientas que no son necesarias para la construcción en un paso determinado. En el diseño de una escena tipo tutorial, se debe considerar las acciones inesperadas del usuario, tales como activar herramientas así sólo sea por curiosidad, lo que llevaría al fracaso de la construcción, paso a paso, del objeto geométrico. Estos espacios "mascara" son transparentes y se ubican sobre las herramientas que deseemos bloquear.
control4='(140,0)'; Cal.set('evalua',control4), el cual envía la orden de construir el punto (140,0). Este punto se dibujará en el entorno gráfico, pero dado que la abscisa es bastante lejana, será transparente para el usuario. En conclusión, los mensajes enviados no interfieren la construcción geométrica, su propósito es establecer la comunicación.
Si observas el archivo interface.html, notarás que sólo usamos dos bloques (evalua y puntos), los cuales ya hemos explicado anteriormente. Su función es comunicar información sobre los elementos gráficos (puntos y rectas) creados en el entorno gráfico, además de atributos como el color.
Finalmente, el esfuerzo en DescartesJS se centra en el selector Gráficos, desde el cual se muestran mensajes al usuario para que, paso a paso, realice la construcción del objeto geométrico.
Este segundo ejemplo (carpeta ejemplo2), lo hemos incluido porque usamos otras estrategias para comunicarnos con la interface.
Una primera estrategia es enviar mensajes a través de un evento (selector Programa), herramienta de DescartesJS que explicamos en el nivel I; sin embargo, te recordamos cómo funciona:
El evento que usamos hace uso de variables del ratón, de tal forma que cuando hacemos clic sobre la ventana gráfica de GeoGebra (E3.mouse_pressed), se ejecutan las acciones escritas en parámetro:
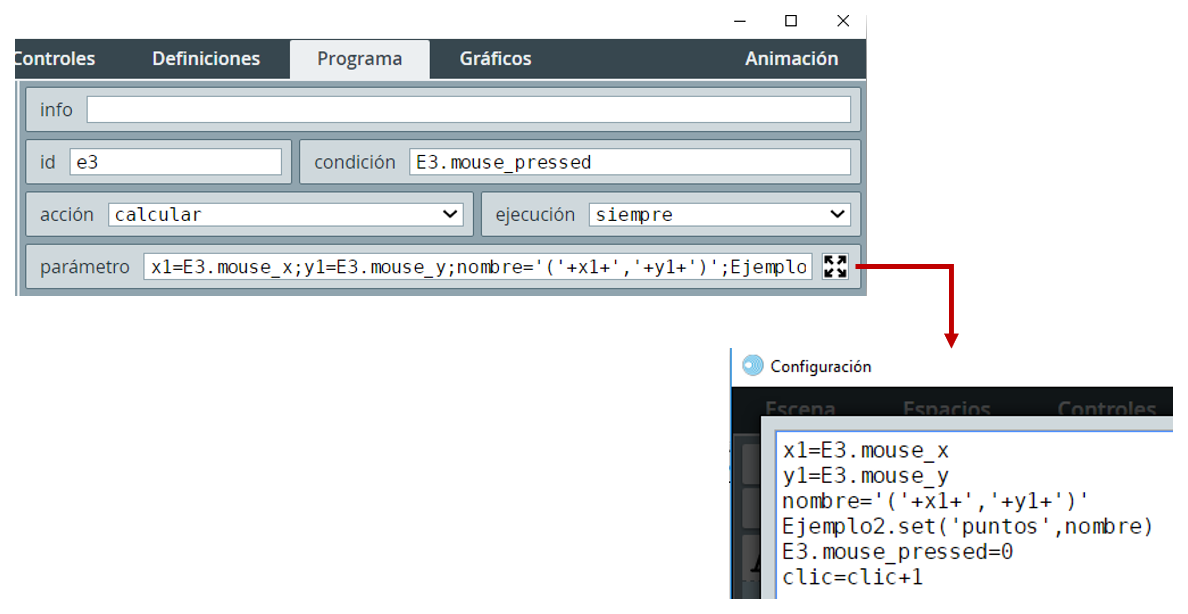
Observa que las dos primeras acciones se encargan de identificar las coordenadas del punto sobre el cual se hizo clic (x1=E3.mouse_x y y1=E3.mouse_y). Con esos datos se asigna a la variable nombre el punto seleccionado; por ejemplo, si hacemos clic en (3,4), entonces nombre='('+3+','+4+')'='(3,4)'. Luego se envía el mensaje a la interface de comunicación con la instrucción Ejemplo2.set('puntos',nombre) (para este ejemplo, el nombre del espacio HTMLIframe lo hemos llamado Ejemplo2).
Terminamos con las instrucciones E3.mouse_pressed=0 y clic=clic+1, la primera para que el evento quede nuevamente funcional y la segunda para contar cuántos clic hemos hecho, y controlar que no se hagan más de tres.
Una segunda estrategia es haber usado un espacio transparente R2, tipo mascara, que cubre la ventana gráfica de GeoGebra, diseñado de tal forma que los ejes y escala coincidan. Este espacio sólo aparece mientras se marcan los puntos.
Por otra parte, el archivo interface usa tres bloques, dos de ellos ya explicados (puntos y aux). El tercer bloque es reset, que se ejecuta para reiniciar la escena, su funcionamiento es sencillo, pues sólo ejecuta el comando: document.ggbApplet.reset(), es decir, reinicio. A continuación, presentamos la escena:
Algo que se nos pasó por alto, en el primer ejemplo, que quizá te haya sorprendido, es el uso de funciones de cadena, las cuales es conveniente que leas en el siguiente texto (otras funciones fueron presentadas en el Nivel I).
Este último ejemplo tiene como característica a destacar la actualización permanente de las bisectrices del triángulo, lo cual se logra enviando un mensaje (siempre) que se origina en el algoritmo CALCULOS.
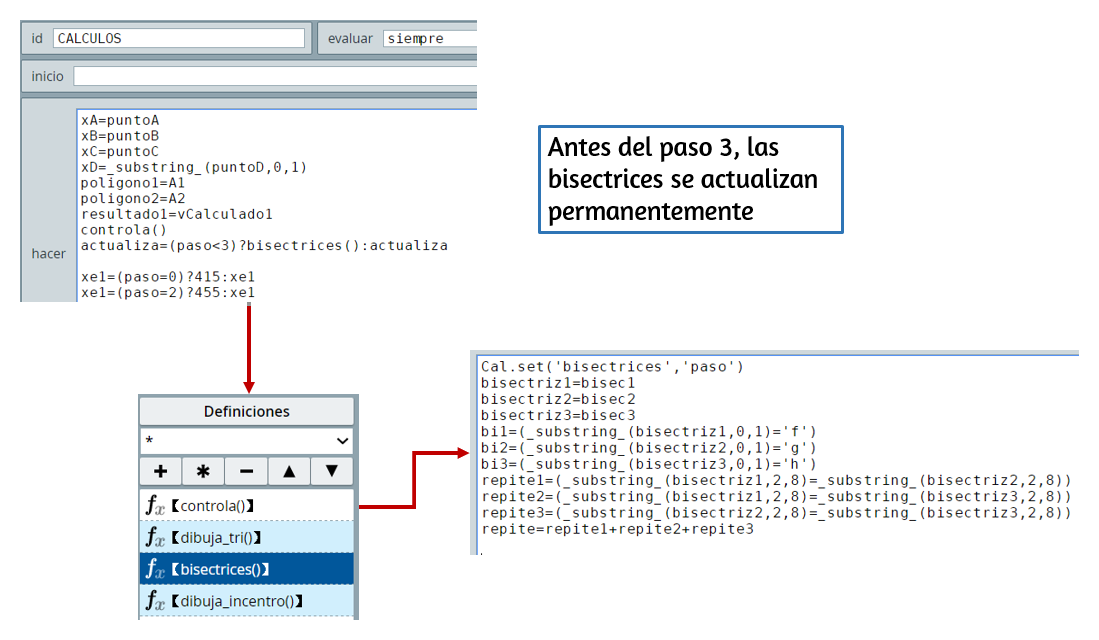
Esta comunicación permanente permite que interactuemos con la ventana gráfica y obtener inmediatamente las ecuaciones de las bisectrices. En la siguiente página puedes observar el ejemplo.
En este ejemplo hemos usado mas ventanas tipo mascara, de tal forma que el usuario sólo pueda usar las herramientas requeridas para la construcción que se pretende lograr. Otra característica es que no usamos plantilla en el diseño.
Como tarea final, diseña una propuesta similar a los ejemplos presentados, que tenga como objetivo la construcción de algún objeto geométrico (mediatriz de un segmento, tangente a una circunferencia, tangentes comunes a dos circunferencias, construcción de un triángulo equilátero, entre otras).
Al terminar este capítulo, habrás diseñado plantillas como:
Una plantilla es un diseño o esquema predefinido, que podemos reusar en cualquier otra actividad u objeto interactivo. Su uso permite ahorrar esfuerzos en nuestros diseños; por ejemplo, sí estamos diseñando objetos 3D que deben incluir los ejes coordenados y los planos cartesianos, una buena idea es tener una plantilla con estos elementos. Esta plantilla es, entonces, todas las instrucciones para dibujar los ejes $X$, $Y$ y $Z$, además de las puntas de los ejes (conos), y los planos $XY$, $XZ$ y $YZ$:
Este grupo de instrucciones se denomina "macro-instrucciones" o, para simplificar, Macros.
Antes de realizar las actividades que incluyen macros, te recomendamos leer el siguiente texto:
En el texto anterior, pudiste observar un ejemplo de un circuito eléctrico que incorpora una macro correspondiente al gráfico de una bombilla, la cual se invoca dos veces para diseñar el circuito. A continuación, diseñaremos una plantilla cuyo objetivo es obtener un gráfico que se dibuje en dos esquinas de la plantilla, es decir, diseñar adornos gráficos para la plantilla. La macro debe permitir su reconfiguración desde la escena que la invoca, tal como se muestra en la siguiente imagen:
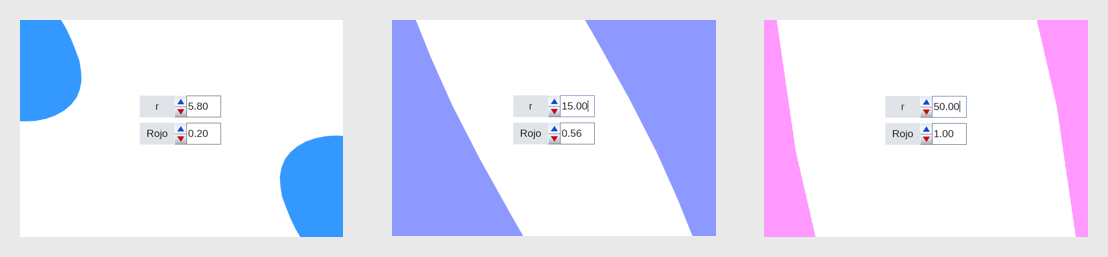
Diseño de la macro. Creamos una nueva escena de $600 \times 400$ pixeles. El adorno que usaremos es la curva paramétrica llamada "gota de agua"Véase el libro Curvas y superficies paramétricas (página 53). con algunas variaciones que permitan dibujarla en dos extremos de la escena.
Las curvas paramétricas que definen la gota de agua son: $x = r^2 (cos b)^3 sen(b)$, $y = r^2 (cos b)^2$, con $b$ en el intervalo $[0, π]$. Las variaciones que hemos realizado son dos; la primera es multiplicar estas ecuaciones por 0.2, de tal forma que se reduzca el tamaño de la gota y, la segunda, sumar o restar valores a x e y, para ubicar dos gotas en los extremos.
Agregamos, entonces, el gráfico tipo ecuación tal como se muestra en la siguiente imagen:
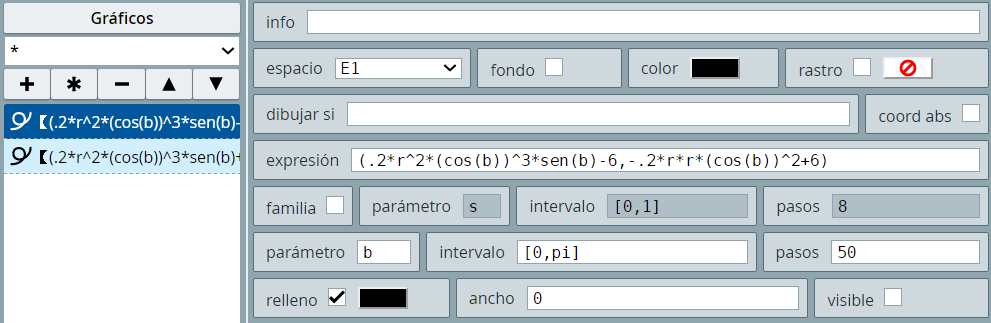
Observa que restamos 6 a la abscisa y sumamos 6 a la ordenada, de tal forma que la gota se ubique en el extremo superior izquierdo. Luego copiamos esta curva cambiando de signos los valores sumados a x e y, dibujar una segunda gota en el extremo inferior derecho. Por otra parte, tanto el color de la gota como su relleno los configuramos así:

En el algoritmo INICIO definimos las cinco variables que permitirán reconfigurar la macro que guardaremos a continuación.
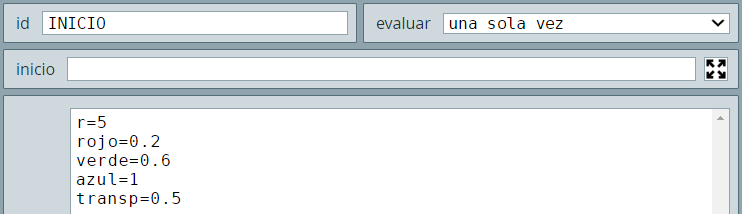
La escena que obtenemos es esta:
Puedes desplazar los gráficos con clic sostenido para que observes las gotas.
Finalmente, guardamos la escena como gota.html y creamos la macro exportándola así:
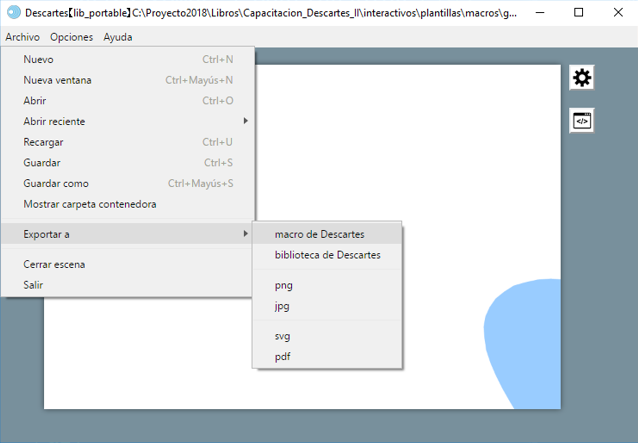
Una vez creada la macro, podemos invocarla desde una escena nueva:
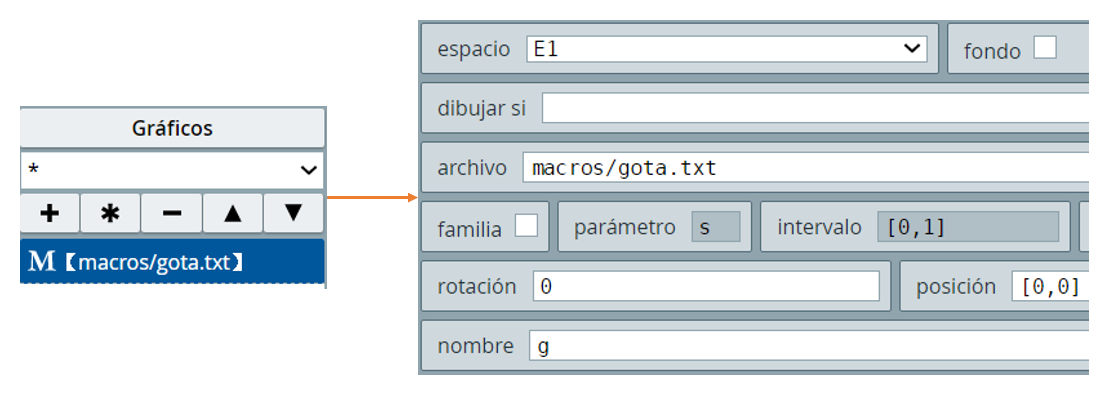
Tal como lo dice el texto sobre macros, podemos intervenir las variables de la macro (r, rojo, verde, azul, transp), anteponiendo el nombre de la macro a dichas variables (g según la imagen anterior); por ejemplo, g.azul=0.5 cambia el valor del componente azul del color y relleno de la gota.
Como ejemplo, hemos agregado dos controles que permitan reconfigurar la macro. El primero de ellos cambia la variable r de la curva:
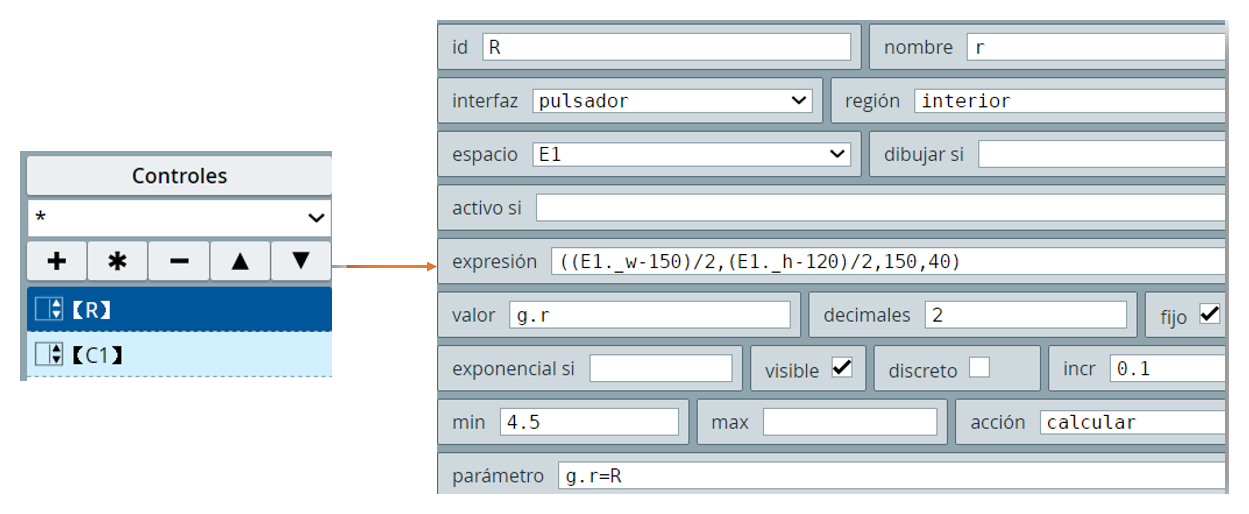
El segundo control te queda como tarea.
Es importante, para esta macro, que uses escenas del mismo tamaño ($600 \times 400$) y, para todas las macros, que el nombre del espacio sea el mismo del que generó la macro, que para el ejemplo es E1.
A continuación, puedes interactuar con la escena obtenida. Usa valores de r para 15 y 50 y, además, aumenta la tonalidad del rojo.
Existen varias macros que algunos diseñadores cartesianos han desarrollado en diferentes proyectos. Dos de ellas, por su utilidad, las vamos a explicar detalladamente en este apartado. Para ello, descarga esta carpeta, luego la descomprimes en el lugar donde vas a diseñar las actividades de este capítulo.
Esta macro fue diseñada para el proyecto Telesecundaria. La barra aparece inicialmente en un avance del 50%, que irá creciendo hasta el extremo verde o decreciendo hasta el extremo rojo, según la configuración que se dé en la escena que la incorpora. Observa un ejemplo:
Como no se trata de diseñar la macro, sólo nos detenemos a describir su configuración.
Abre, con el editor DescartesJS, la macro Barra_Jinich.html, en la que observarás: En el algoritmo INICIO se definen las siguientes variables: B=0.50; L=600; H=20, donde B corresponde al avance de la barra (50%), L y H son la longitud y la altura de la barra en pixeles. Sólo se usan tres gráficos:
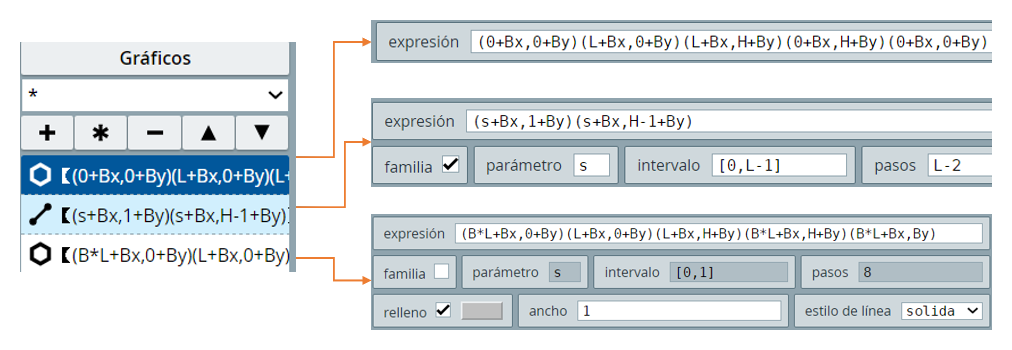
Si observas el color del gráfico segmento, notarás que se define con tres funciones:

Estas funciones usan como variables la longitud de la barra (L) y, obviamente, la variable s de la familia de segmentos; por ejemplo: Rojo(s) = (s<L/2)+(s>=L/2)*(1-(s-L/2)/(L/2)), expresión que garantiza el cambio de tonalidad del rojo. Estas funciones se constituyen en la novedad de esta macro.
En el ejemplo de aplicación que mostramos anteriormente, invocamos la macro Jinich.txt con el nombre barra, así:
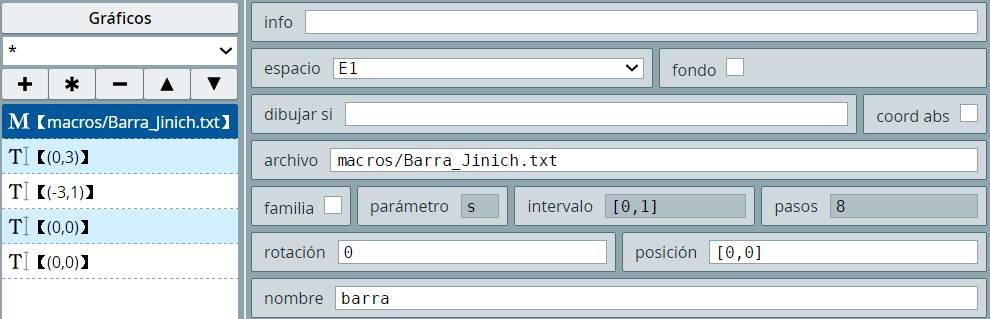
La reconfiguramos en el algoritmo INICIO:
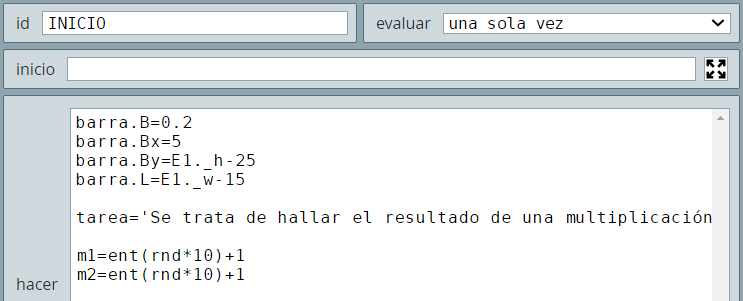
Como la variable barra.B es la que hace crecer o decrecer la barra, basta con aumentarla en 0.1 por cada acierto o reducirla en 0.1 en caso contrario. El resto del ejemplo es fácil de diseñar.
La barra Jinich la hemos usado en el proyecto "Plantillas". Observa dos ejemplos (haz clic sobre cada imagen):
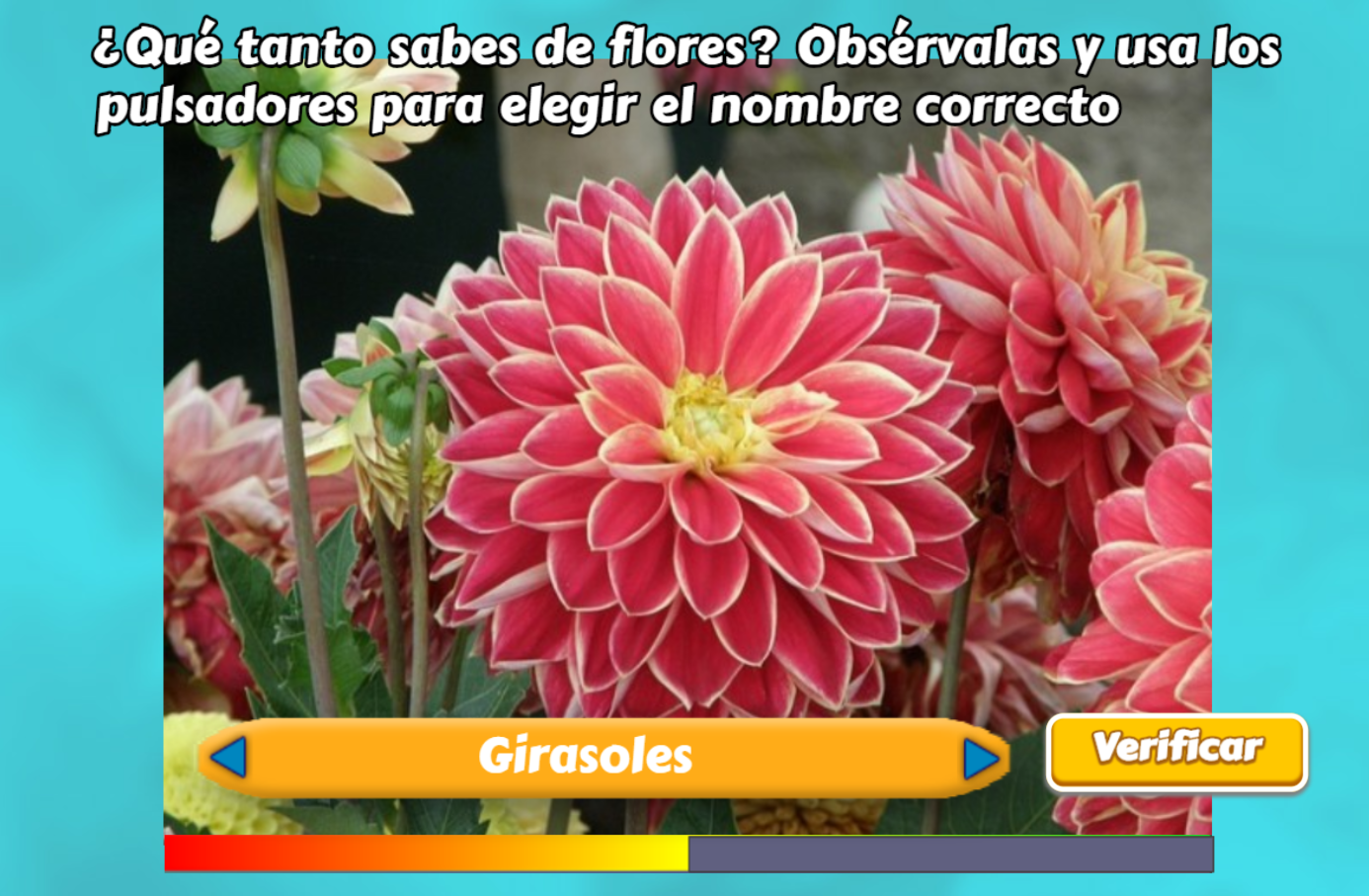

En muchos diseños necesitamos que un grupo de objetos aparezcan en un orden aleatorio. Por ejemplo, en las dos actividades del capítulo las respuestas no aparecen en el orden que las escribimos en el archivo de texto, pues al estar la respuesta correcta en el primer lugar, sería demasiado obvio el resto de la actividad. Por ello, optamos por recurrir a una posición aleatoria para que aparezcan las respuestas.
Otra situación puede ser que necesitemos seleccionar n datos de un repositorio que contiene m datos, donde n es menor que m. Para actividades repetitivas, tampoco es conveniente que se seleccionen siempre los primeros n datos; por ello, sería necesario que se escojan aleatoriamente del universo de datos.
Las plantillas ejemplo de la página anterior usan, también, la posición aleatoria. En la primera, los datos son imágenes que no siempre aparecen en el mismo orden. En la segunda, los datos son las coordenadas en el que aparecen las piezas del puzle, que siempre tendrán una posición aleatoria.
A continuación, diseñaremos una escena que usa la macro random.txt, la cual se encuentra en la carpeta que previamente descargaste. En esta carpeta hemos dejado tanto la macro como la escena que le dio origen, así que puedes abrir random.html con el editor DescartesJS y explorar cómo fue diseñada. Para su uso, sólo nos interesa la variable n_numeros (cantidad de números a aleatorizar) y la función creaAleatorios():

Iniciemos, pues, con el diseño de la escena, la cual es de $600 \times 250$ pixeles (en este caso no necesitamos que el tamaño sea igual al de la escena random.html, pero si es necesario que se conserve el nombre del espacio, E1).
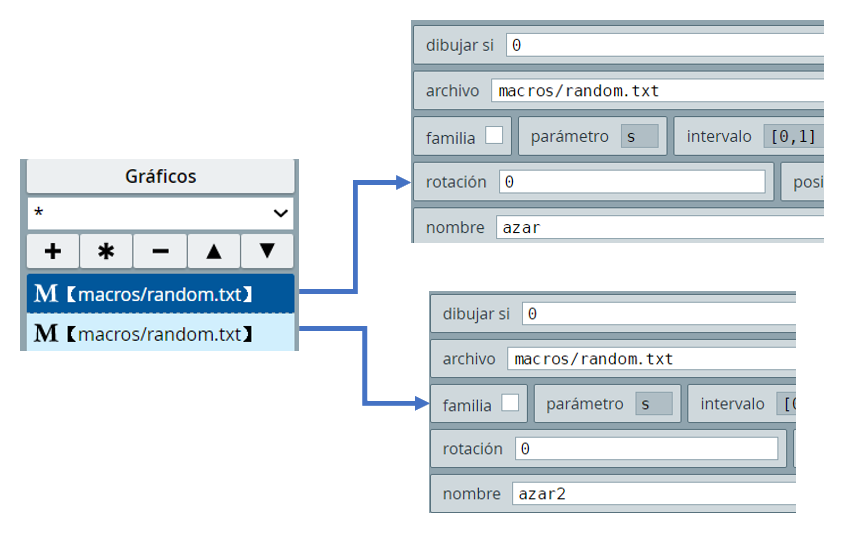
En dibujar si hemos puesto cero (0), con el fin de evitar que aparezcan los seis números en posiciones aleatorias que trae por defecto la macro. Hemos invocado dos veces la macro random.txt porque vamos a generar dos grupos de números. La primera macro la hemos llamado azar y la segunda azar2.
El propósito de la escena es que muestre, en primer lugar, cinco números del 1 al 5 en posición aleatoria (5 de 5) y, en segundo lugar, cinco números seleccionados aleatoriamente de los números del 1 al 20 (5 de 20).
La macro random, entonces, genera números enteros del 1 a n_numeros, que luego los posiciona aleatoriamente. Para el primer grupo de cinco números, usamos las siguientes instrucciones: azar.n_numeros=5; azar.creaAleatorios() (observa que debemos anteponer el nombre de la macro). Para el segundo grupo: azar2.n_numeros=20; azar2.creaAleatorios(). En los resultados a mostrar, debemos usar los vectores azar.resultadoVec[] y azar2.resultadoVec[], obteniendo:
El control tipo botón debe ejecutar las instrucciones anteriores, de tal forma que se generen nuevos grupos de números en posición aleatoria.
Vamos a diseñar la primera actividad propuesta al inicio del capítulo, usando dos macros.
Diseñar una plantilla para realizar evaluaciones tipo selección múltiple de única respuesta. La respuesta se debe seleccionar de un grupo de cuatro posibles. Para el diseño se debe usar las macro sombras.txt y random.txt, esta última para presentar las posibles respuestas en posiciones aleatorias. Tanto las preguntas como las respuestas se deben almacenar en archivos tipo txt, para ello puedes usar los datos de la Tarea 1.
Iniciemos la actividad abriendo la Tarea 1 con el editor DescartesJS (Si no hiciste la Tarea 1, puedes usar la escena interactivo3.html que se encuentra en la carpeta interactivos de este libro).
A este escena la haremos los siguientes cambios:
E1, hacemos este cambio:
Estos dos primeros cambios obedecen a que debemos ajustar la escena para un nuevo entorno gráfico, como lo veremos a continuación.
expresion y el ancho del texto: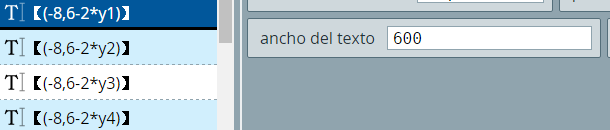
Observa que sólo es cambiar -6 por -8 y ajustar el texto a 600 pixeles.
-7 a -9. Lo que obliga a cambiar la condición de la tercera curva por (abs(s-E1.mouse_y)<.5)&(abs(-9-E1.mouse_x)<.5)&(E1.mouse_clicked=1), en coherencia con la nueva abscisa.
(0,6.5) por (0,6.8) y cambiamos el tamaño de la letra a 20 (igual para las respuestas)Hasta aquí hemos hecho cambios a los objetos gráficos existentes en la Tarea 1. Ahora, vamos a incorporar tres macros, tres rectángulos y cinco textos nuevos.
Esta macro fue diseñada para el proyecto "Pizarra Interactiva", la cual tiene una función similar a la que vimos en la macro gota: es decir, un adorno en las esquinas de la escena.
sombras.txt, así: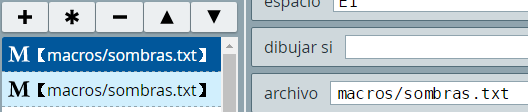
La primera la llamamos adorno en la posición [0,0], la segunda tiene el nombre adorno2 en la posición [710,500]. Estas posiciones corresponden a las esquinas donde se ubican estas macros gráficas, lo que significa que puedes ajustarlas a tu gusto (obviamente, debes haber copiado las macros en una carpeta donde tienes la Tarea 1).
random.txt, asegurándote de asignar cero (0) en la casilla de texto dibujar si.Cada rectángulo tiene radio del borde de 20, que puedes cambiar.
El segundo rectángulo es una familia de cuatro, que se convierten en los contenedores de las respuestas.
El tercer rectángulo colorea de verde la respuesta correcta, una vez se haya seleccionado la respuesta y cliclado en el botón verificar.
Se indican los colores de relleno de los rectángulo, sugerimos un color un poco más obscuro para los bordes.
Es importante que los rectángulos estén al inicio, para evitar que se superpongan a los textos.
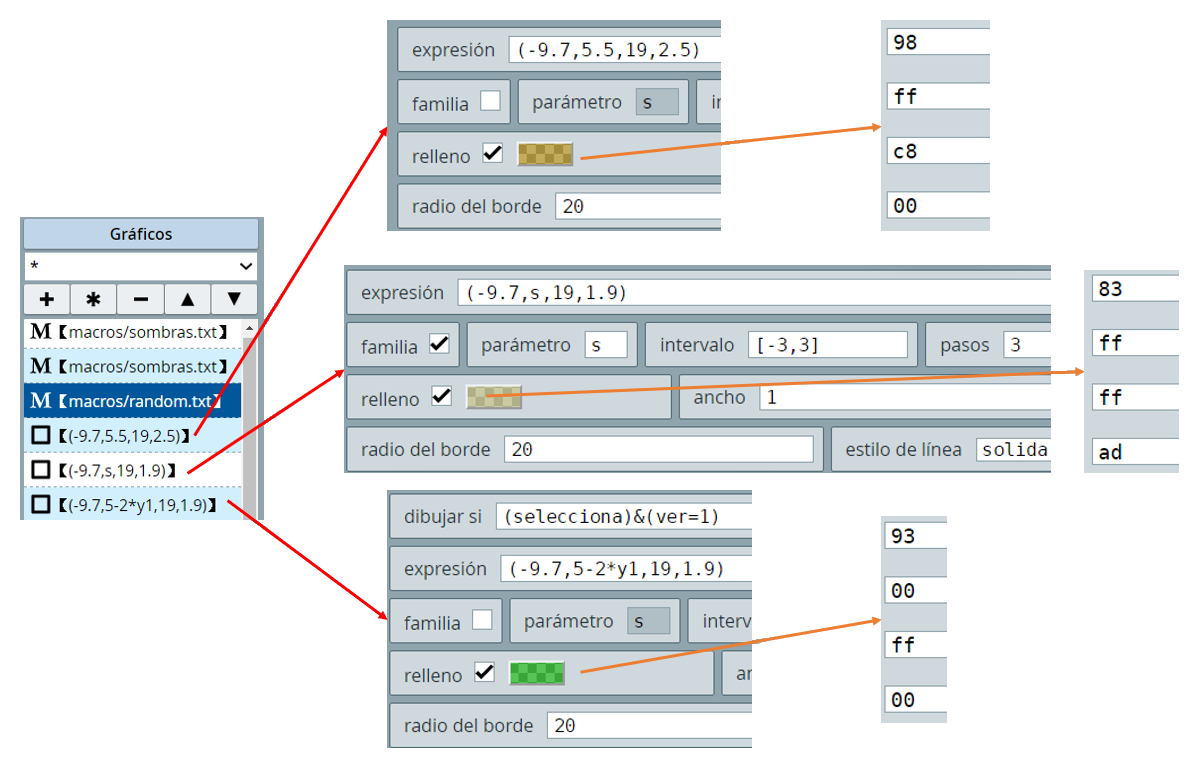
Luego retornamos al selector Gráficos para agregar los cinco textos nuevos.
botón, el cual permitirá mostrar los resultados de la evaluación. Este botón tendrá la siguiente configuración: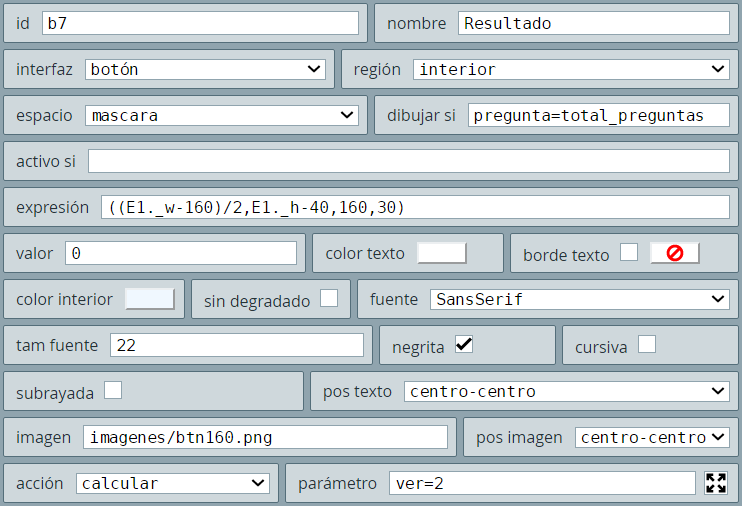
calcula_posiciones() por: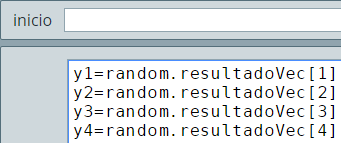
En este caso hemos usado los resultados de la macro random, la cual posiciona las respuestas aleatoriamente.
En el algoritmo INICIO haremos cambios significativos. En primer lugar, modificamos los colores de los adornos de las esquinas, de tal forma que tenga tonalidades similares a las dadas a los rectángulos.
En segundo lugar, hemos definido el número de preguntas como el primer elemento del vector NP[], que luego definiremos.
Por último, calculamos las posiciones aleatorias de las preguntas, antes de invocar la función calcula_posiciones()
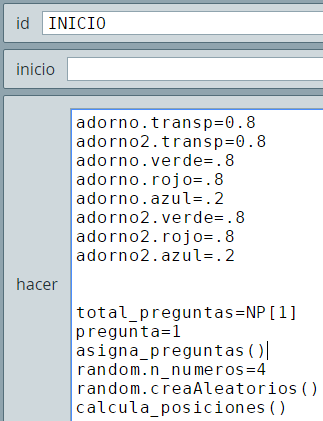
CALCULOS sólo tenemos que cambiar la abscisa -7 por -9:
Ahora sólo nos falta configurar los vectores con las preguntas y respuestas, para retornar al selector Gráficos y agregar los últimos cincos textos.
La creación de vectores con datos externos la explicamos en la siguiente presentación:
La expresión "Hemos creado una plantilla" es una afirmación, que se justifica porque la escena obtenida permite, con un editor HTML, modificar los <script> sin necesidad de intervenir con el editor DescartesJS, es decir, podemos cambiar el número de preguntas, las preguntas y respuestas y obtener una nueva escena.
También pudiste observar que en la escena final ya aparecen los cinco textos que nos falta diseñar.
Todos estos textos los ubicaremos en las coordenada relativas (0,-4.5) y con punto de anclaje centro-centro:
Haz clic en el círculo de la respuesta correcta, el cual se mostrará si (ver=0)&(pregunta=1)&(E1.mouse_clicked=0), su tamaño es 23 y color azul.Ninguna respuesta correcta... ¡Muy lamentable!, el cual se mostrará si (ver=2)&(buenas=0), su tamaño es 25 y color rojo.Sólo una respuesta correcta... ¡Lamentable!, el cual se mostrará si (ver=2)&(buenas=1), su tamaño es 25 y color naranja.Respondiste [buenas] respuestas correctas de [total_preguntas] preguntas, el cual se mostrará si (ver=2)&(buenas>1)&(buenas<total_preguntas), su tamaño es 25 y color brown.¡Excelente! Todas las respuestas correctas, el cual se mostrará si (ver=2)&(buenas=total_preguntas), su tamaño es 25 y color verde.Modifica la escena de tal manera que se obtenga una plantilla de selección múltiple de única respuesta con cinco opciones de respuesta, tal como lo mostramos en la segunda escena al inicio del capítulo, la cual puedes abrir aquí.
En el proyecto "Plantillas" puedes encontrar varios ejemplos que incorporan los elementos que hemos usado en la última actividad. Presentamos dos de esas plantillas:
En este plantilla se han usado las macros sombras y random
En esta otra plantilla, también de selección múltiple de única respuesta, se han usado las instrucciones de la macro random incorporadas en la escena. Igual se hace con la barra Jinich, que sólo avanza (no retrocede) con las preguntas realizadas, por ello su color único.
Una variante interesante es que las preguntas aparecen, también, en posiciones aleatorias. Puedes verificarlo observado el número de la pregunta.
Bueno... ¡Eso es todo!
Este capítulo complementa lo explicado en el nivel I. La actividad final consiste en usar textos simples y enriquecidos, usando diferentes fuentes, tal como se muestra en la siguiente imagen:

En el nivel I y en lo trabajado en este nivel, hemos usado con frecuencia el texto simple, pues no hemos tenido necesidad de diseñar textos con expresiones matemáticas complejas. DescartesJS presenta dos opciones para el diseño de texto, el simple y el enriquecido. Antes de explorar el segundo, veamos algunas herramientas que nos permiten "diseños menos simples en el texto simple".
La herramienta de introducción de textos se encuentra disponible para una variedad de gráficos tales como punto, texto, etcétera, así como para textos relacionados a otros elementos del interactivo más allá de los gráficos. No obstante, su funcionamiento es el mismo en todos los casos.
Normalmente introducimos el texto en el campo de texto; sin embargo, para expresiones cortas que se deben enriquecer, presionamos el botón T que hay después del campo de texto y aplicamos las herramientas anteriores.
Comprobemos que tanto le prestaste atención al texto anterior. En la siguiente escena interactiva, ingresa en el cuadro de texto la expresión que permite generar el texto en color azul.
Obviamente, las expresiones matemáticas complejas hacen complejo el diseño con texto simple; por ello, es importante que usemos el texto enriquecido:
Una forma sencilla de entender cómo funciona la ventana del texto enriquecido es a través de dos vídeos, que presentamos a continuación.
El primer vídeo hace uso de seis botones de la ventana: color, [F], fracción, potencia, raiz y tabla. Obsérvalo:
Observa que hemos usado coordenadas relativas y centrado de texto, opciones que no estaban disponibles en las versiones de DescartesJS anteriores.
En el segundo vídeo usamos una integral y un sumatorio. Observa que el color del texto lo podemos definir desde el selector Gráficos.
En los dos ejemplos recurrimos a la caja de fórmulas ([F]) para ingresar las expresiones matemáticas.
A continuación, veremos cómo cambiar las fuentes (fonts) del texto.
En el apartado 7.9 del Nivel I explicamos cómo descargar y cambiar las fuentes para nuestros textos, suministrando 16 fuentes diferentes. Estas fuentes fueron descargadas de https://www.fontsquirrel.comFont Squirrel es una página web que recopila una amplia variedad de tipografías gratuitas y libres para uso comercial. Cada una de las fuentes tipográficas de la web incorpora una ficha en la que se especifica cómo es la fuente y sus características principales, así como la explicación del proceso de creación. Esta ficha contiene también el tipo de licencia que ofrece cada una de las fuentes y, según esta licencia, sus usos permitidos (https://graffica.info). y, posteriormente, generábamos el código Base64 desde https://www.fontsquirrel.com/tools/webfont-generator.
En este libro, retomamos el cambio de fuentes pero utilizando otras colecciones, entre ellas google fonts (https://www.cufonfonts.com)Nuestra serie de colecciones temáticas lo ayuda a descubrir nuevas fuentes que han sido examinadas y organizadas por nuestro equipo de diseñadores, ingenieros y colaboradores, y nuestra clasificación predeterminada organiza las fuentes según su popularidad, tendencias y su ubicación geográfica (https://fonts.google.com/about)., Digital Fonts, Brand Fonts, Old School Fonts, etcétera.
En el siguiente vídeo te explicamos cómo descargar la fuente, generar el código Base64 e incorporar esta fuente en una escena interactiva a través del archivo HTML generado por DescartesJS. Una vez comprendas cómo cambiar las fuentes, puedes diseñar la actividad propuesta al inicio de este capítulo.
En la generación del código Base64, es importante que tengas en cuenta que ya no se trata de una fuente Squirrel:

Desarrolla una escena que muestre los textos indicados en la Actividad del capítulo. Para ello, debes usar textos simples, textos enriquecidos y cambios de fuentes.
Para terminar este capítulo, conoce un poco de nuestro sufrido país hermano... Venezuela.
Te sugerimos ampliar la escena interactiva.
En el nivel I diseñamos escenas de vídeos interactivos, las cuales usaban las funciones intrínsecas de DescartesJS. En este capítulo emplearemos otras funciones que son propias del vídeo, sea este en local (etiqueta <video>) o reproducido en YouTube; por ejemplo, control de volumen, control de tiempo, (avance o retroceso), autoreproducción (autoplay), entre otros.
Es importante recordar que el objetivo del vídeo interactivo es permitir al usuario interactuar con la escena, en la cual el objeto principal es el vídeo. La interacción se realiza a través de preguntas o de la selección de opciones presentadas como botones o puntos gráficos dibujados sobre el vídeo. Esta interacción se logra si sólo se habilitan los controles de vídeo antes mencionados, que sólo permitan al usuario interferir en la reproducción de acuerdo a una intencionalidad didáctica. La comunicación bidireccional escena – HTML posibilita una gran variedad de alternativas o modelos de vídeos interactivos.
En este capítulo presentamos algunas de estas alternativas. Se hará una descripción técnica de los comandos JavaScript relacionados con la reproducción del vídeo y, por otra parte, se explicará cómo modificar la escena para incorporar otros vídeos y las interacciones correspondientes.
Presentamos, por una parte, modelos que incorporan vídeos almacenados en una carpeta de cada modelo; es decir, modelos para ejecución en local. Si bien es posible reproducirlos en línea en ordenadores y algunos dispositivos móviles, su propósito principal es poderlos descargar e instalar en ordenadores que presentan baja conectividad; por otra parte, presentamos modelos que incluyen enlaces a vídeos de YouTube que, obviamente, requieren conexión a Internet, si bien es posible usar cualquier vídeo entre la gran abundancia que presenta este popular repositorio, recomendamos diseñar tus propios vídeos y luego subirlos a YouTube.
Cada sección guarda estrecha similitud en sus aspectos técnicos y de programación, que se diferencia por ligeros cambios en las palabras reservadas o comandos utilizados por el API de YouTube.
Dedicaremos este apartado a los vídeos que tendremos guardados en una carpeta, es decir, que no dependen de conectividad con la red (recuerda que pueden estar en formato mp4, webm u ogg). Presentaremos seis modelos con un mayor detalle en el primero, pues muchos de los aspectos técnicos y de programación son repetitivos.
Este primer modelo es muy simple en su interacción, pues sólo realiza preguntas abiertas durante la reproducción del vídeo. Hemos usado algunos elementos trabajados en este libro, tales como la macro sombras.txt y el uso de la fuente Amaranth. Por otra parte, hemos utilizado la opción de proyecto, para tener un sólo intérprete en los seis vídeos interactivos.
El vídeo diseñado es el siguiente:
Para la comprensión del diseño de este objeto interactivo, es importante que abras el archivo index.html que se encuentra en la carpeta video_interactivo_modelo1_local, siguiendo la ruta interactivos/videos_interactivos_local.
Algunas características del diseño son las siguientes:
A continuación se describen las carpetas y archivos necesarios para este objeto interactivo, localizados en la carpeta denominada video_interactivo_modelo1_Local, en la que se encuentran:
videolocal.js, librería que permite la comunicación con la escena DescartesJS.index.html. Es la escena DescartesJS.ivideo.html. Es el HTML que se embebe en la escena, permitiendo mostrar el vídeo.Además de estos elementos, hay otros en el directorio de archivos previo que son comunes a los seis modelos: intérprete (carpeta lib), macros y fuentes. En la siguiente imagen se muestran estos elementos:
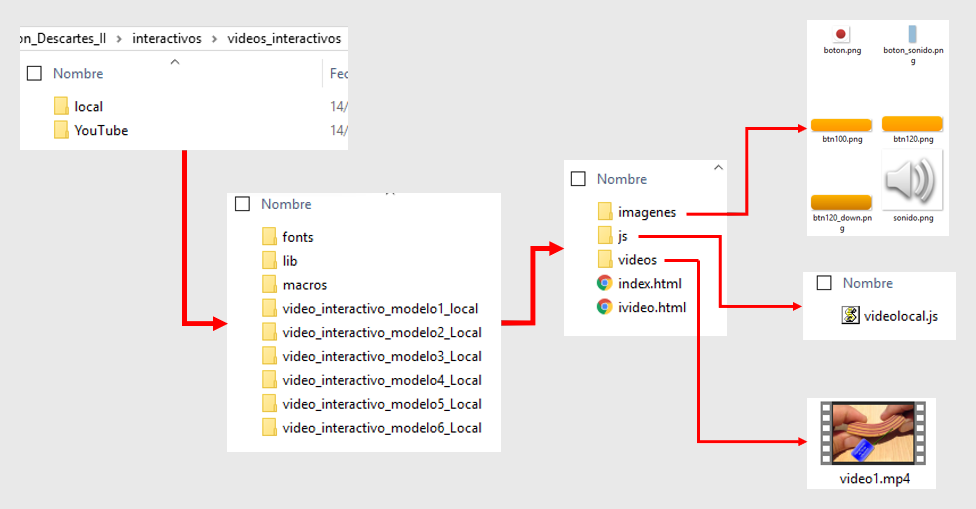
La mayoría de elementos de la escena estás en capacidad de comprenderlos, motivo por el cual sólo nos concentraremos en aquellos que establecen la comunicación con el vídeo.
Preguntas y respuestas. La escena está diseñada preguntas con respuesta escrita. La primera pregunta tiene los siguientes elementos:
P[1]='¿Qué material es el que se está flexionando?'
R[1]='Goma'
R2[1]='goma'
tiempo[1]=10
Hemos incluido dos respuestas, previendo que el usuario responda con la primera letra en mayúscula, pese a la advertencia de usar minúsculas. Se incluye, además, el tiempo desde el inicio del vídeo en el cual se hará la pregunta. En forma similar se hacen las demás preguntas; por ejemplo, la pregunta dos:
P[2]='La fisura se debe a la...'
R[2]='Flexión'
R2[2]='flexión'
tiempo[2]=18

Variables de comunicación. En el código de esta escena se incluyen instrucciones que permiten comunicarla con el archivo ivideo.html, que se incluye en el espacio HTMLIframe, que es el que gestiona el vídeo en sí:
play_pause. Variable que permite enviar órdenes al archivo HTML para que detenga o reanude la reproducción del vídeo. Si deseamos enviar el valor 'seguir' a la variable play_pause, podemos hacerlo con la función continuar() con estas instrucciones: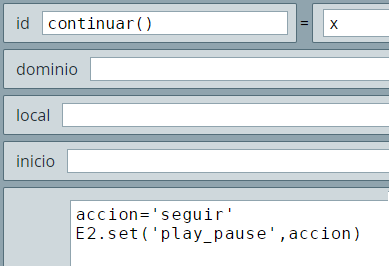
Observa que usamos la función E2.set('play_pause',accion), la cual función se usa para el espacio HTMLIFrame subordinado, e indica que el espacio principal que lo contiene recibirá en la variable play_pause el valor que el espacio subordinado tiene en su variable accion.
E2 es el espacio HTMLIframe subordinado. Observa la función parada(), en la escena, que se ejecuta a través de un evento que controla el tiempo de reproducción para cada pregunta. La acción, entonces, sería parar o detener el vídeo para responder a la pregunta.
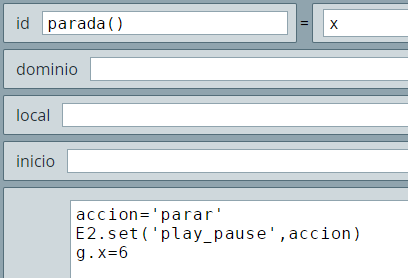
actualizar_tiempo. Variable que reasigna el tiempo en segundos a partir del cual se debe reanudar la reproducción del vídeo. En este modelo se controla con un control gráfico (g):
La orden para actualizar el tiempo de reproducción es:
E2.set('actualizar_tiempo',g.x*avanzado/6)
avanzado. Es el tiempo transcurrido en el momento que se detiene la reproducción. El tiempo del vídeo se actualiza con valores entre 0 y el tiempo transcurrido (avanzado).El cálculo de esta variable se realiza a partir de la variable t, cuyo valor es enviado por el archivo de comunicación videolocal.js. En la siguiente imagen se describe cómo se realiza el cálculo:
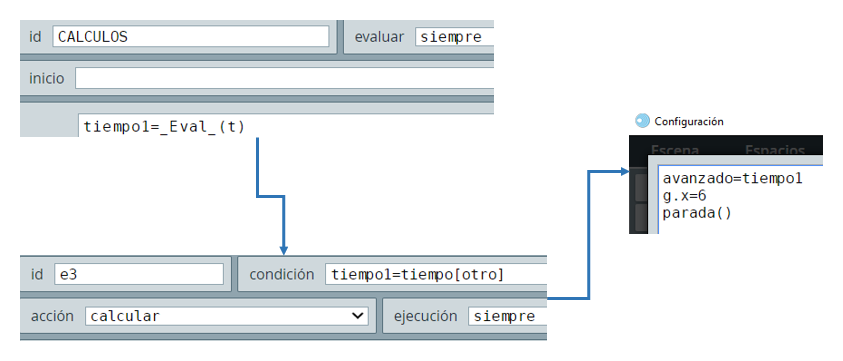
cambia_volumen. Variable que modifica el valor del volumen entre un valor mínimo (0) y un valor máximo (100). Al igual que la variable anterior, se controla con un control gráfico (sonido):
La orden para modificar el volumen es:
E2.set('cambia_volumen',(sonido.x)*20)
Una función interesante es el cambio de formato del tiempo de reproducción recibido de videolocal.js, que permite escribir el tiempo en el formato horas:minutos:segundos:. En la siguiente imagen se muestra cómo se obtiene este formato.
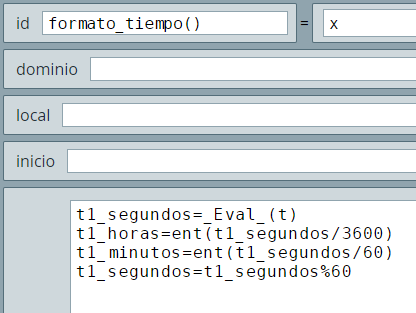
videolocal.jsEste archivo permite la comunicación con la escena, es decir, es la interface de comunicación.
Mensajes hacia la escena. Para la manipulación del vídeo desde la escena, se requiere conocer el tiempo reproducido del vídeo (variable t) y la duración del vídeo (variable t2). La captura de estas dos variables se logra a través de los comandos:
seg = Math.round(myVid.currentTime);
duracion = Math.round(myVid.duration);
Donde myVid es la variable que contiene el nombre del video, la cual se declara con el comando:
myVid = document.getElementById("video1");
Para el caso de la primera variable a enviar (t) a la escena, se usan los siguientes comandos:
Contador.innerHTML = seg;
document.getElementById("texto_a_enviar").value = seg;
document.getElementById("texto_a_enviar").click();
En los cuales, la variable texto_a_enviar se maneja a través de un input creado en el archivo ivideo.html, que explicamos más adelante. La variable contenido envía a la escena el texto_a_enviar (seg) con el nombre (t), a través del siguiente bloque de comandos:
En forma similar se envía la variable t2.
Mensajes desde la escena. Desde la escena se maneja un mensaje del tipo set que puede ser asociado a alguna de las siguientes variables: play_pause, retrocede, actualizar_tiempo, o cambia_volumen (en la descripción de la escena se explicita cómo se envían estos mensajes).
play_pause. Se esperan dos posibles valores: parar o seguir lo que permite parar o reanudar el vídeo, así:
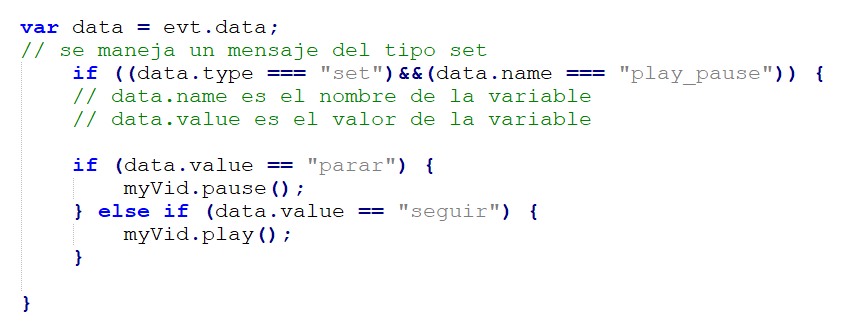
Variables de avance y retroceso (retrocede, actualiza_tiempo). Permiten modificar el tiempo de reproducción del vídeo:

Variable de control de volumen (cambia_volumen). Asigna valores entre 0 (mínimo) y 1 (máximo) al volumen del vídeo.
ivideo.htmlEs el HTML que se embebe en la escena, para la modificación de la escena no hay necesidad de intervenirla. Algunos bloques de diseño importantes son:
<script src="js/videolocal.js"></script>. Invoca la interface de comunicación.
<input id="texto_a_enviar" type="text" style="VISIBILITY:hidden;display:none"/>. Comando de entrada al que se le asigna el valor de la variable texto_a_enviar. Para nuestro caso es la variable t, la propiedad VISIBILITY permite ocultar el cuadro de texto que genera este comando. En la librería videolocal.js se simula la tecla intro (enter) para enviar automáticamente este mensaje a la escena, con el comando: document.getElementById("texto_a_enviar").click();
Vídeo. La reproducción del vídeo se realiza con la etiqueta HTML5 <video>, la cual permite que el vídeo se adapte al tamaño del espacio HTMLIframe de la escena. El bloque es el siguiente:
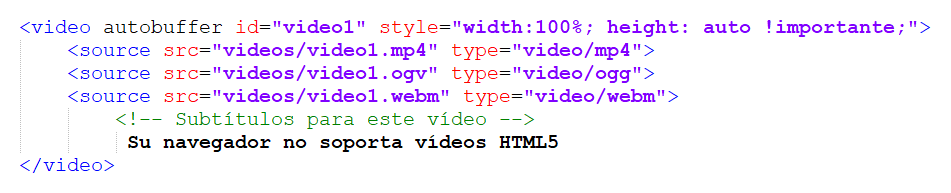
Es una versión modificada del modelo anterior, donde los cambios más significativos son:
60% de la escena.E4) se sobrepone al vídeo para presentar las preguntas. Se le da una transparencia para que el usuario pueda observar las imágenes del vídeo.E1) se ha modificado el color de la macro sombras.txt (sombra.rojo=0.5). Esta macro también se ha puesto en el espacio E4 (máscara) en el que se hacen las preguntas.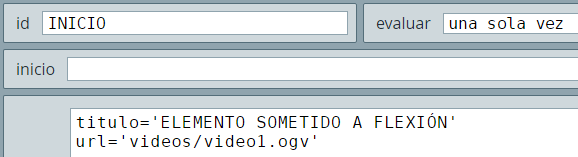
Estos cambios los puedes explorar en el archivo index.html localizado en la carpeta denominada video_interactivo_modelo2_Local.
El diseño es sólo ilustrativo, pues estás en capacidad de hacer los cambios que permitan ajustar la escena a tu gusto. En la siguiente página presentamos el vídeo interactivo.
Este modelo es bastante simple, pues sólo consiste en enviar un mensaje al archivo videolocal.js parta que reproduzca el vídeo en un tiempo t, según la opción seleccionada.
Este mensaje se configura mediante el siguiente comando en el archivo indexb.html:
E2.set('actualizar_tiempo',ti)
donde ti es el tiempo en segundos en el que se actualiza el tiempo en el vídeo. En realidad, la interacción en este modelo es mínima, pues sólo se trata de hacer clic en los botones.
Este modelo presenta dos novedades con respecto a los anteriores. La primera es que se realiza una comunicación adicional con otra escena interactiva diseñada con DescartesJS, se trata de la Actividad 7 (selección múltiple con cuatro respuestas), la cual hemos intervenido para un poco en sus dimensiones, para que se ajuste al vídeo interactivo, además de cambiar las preguntas:

La escena envía datos al modelo, tales como: número de preguntas, respuestas acertadas y orden de continuar el vídeo una vez se ha respondido la pregunta.
En las siguientes imágenes se describen las instrucciones incorporadas en la actividad para que se logre la comunicación.

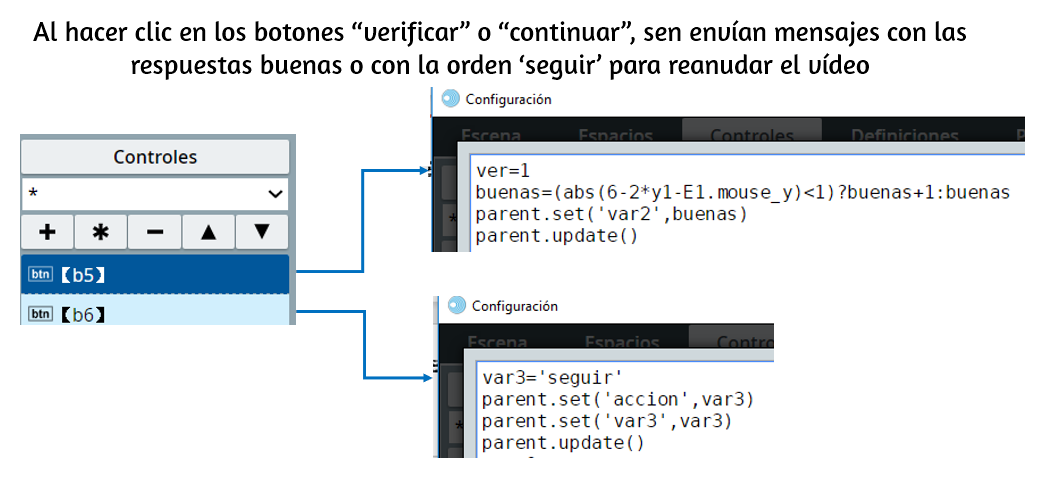
Puedes observar el uso de la expresión parent.set, la cual detallamos a continuación.
La segunda novedad es la inclusión de marcas de tiempo, las cuales indican en qué momento se harán las preguntas:

En el algoritmo INICIO del espacio principal (indexb.html) se definen los tiempos de parada del vídeo para realizar las preguntas, es decir, para invocar la escena subordinada (index2.html):
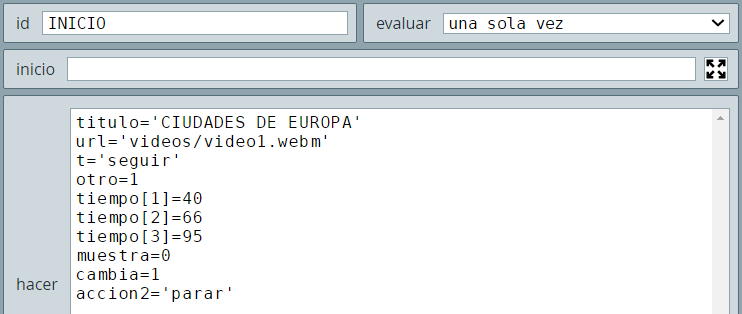
La barra de tiempo es un segmento entre los puntos (-6,-3.7) y (6,-3.7), es decir, de longitud 12; por ello, las marcas de tiempo se calculan así:

donde xr es la abscisa que varía de acuerdo al tiempo de reproducción y x1, x2 y x3 las abscisas donde se dibujan las marcas de tiempo (segmentos color naranja).
Hemos agregado un evento que hace la funciones del botón continuar vídeo en los modelos anteriores. El evento se ejecuta cuando la actividad (index2.html) envía el mensaje 'seguir' en la variable var3, permitiendo a la escena principal enviar ese mensaje al vídeo (videolocal.js)... he ahí la doble comunicación:
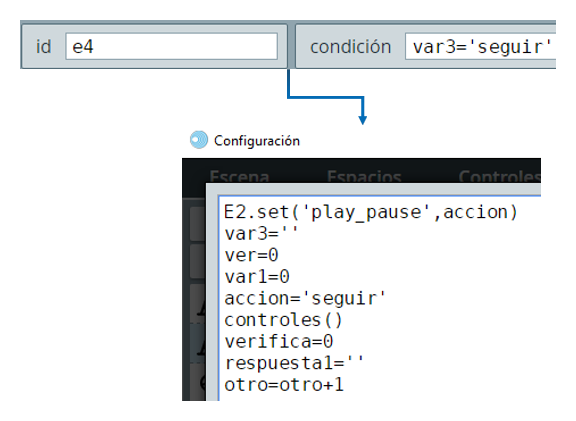
Y he aquí el cuarto modelo de vídeo interactivo:
En este modelo incluimos marcas en la línea de tiempo del vídeo para diferentes actividades. El modelo está diseñado de tal forma que permite una edición sencilla desde el editor de Descartes, con la posibilidad de incluir tres tipos de actividades: imágenes con información complementaria, preguntas de selección múltiple y escenas interactivas.
Para modificar el vídeo interactivo, nos centramos únicamente en las tres actividades que interactúan con el vídeo.
Actividad “Para saber más”. Se presentan en la línea de tiempo marcadas con color azul. Su objetivo es presentar una imagen con información complementaria. Esta actividad detiene la reproducción del vídeo, muestra la imagen y un botón de cierre que permite la reanudación del vídeo. Para su modificación se requiere:
i1.jpg, i2.jpg, ... con un tamaño sugerido de $600 \times 400$ píxeles. Si no se desea este tipo de actividad en el vídeo, se recomienda dejar, al menos, la imagen i1.jpg para evitar lentitud en el editor de Descartes, pues por su diseño trata de leer al menos esta primera imagen.INICIO, podemos modificar los valores del vector t_info. Estos valores son los segundos transcurridos en el vídeo para presentar las imágenes. Si se desean más de cuatro imágenes, basta copiar las líneas adicionales; por ejemplo, para una quinta imagen a los dos minutos: t_info[5]=120. Si no se desea incluir imágenes, asignamos un tiempo de 1000 segundos o más. En la siguiente imagen, se observa que aparecerán cuatro actividades "Para saber más", dos preguntas y cinco actividades de DescartesJS (aunque podrían ser de otra herramienta).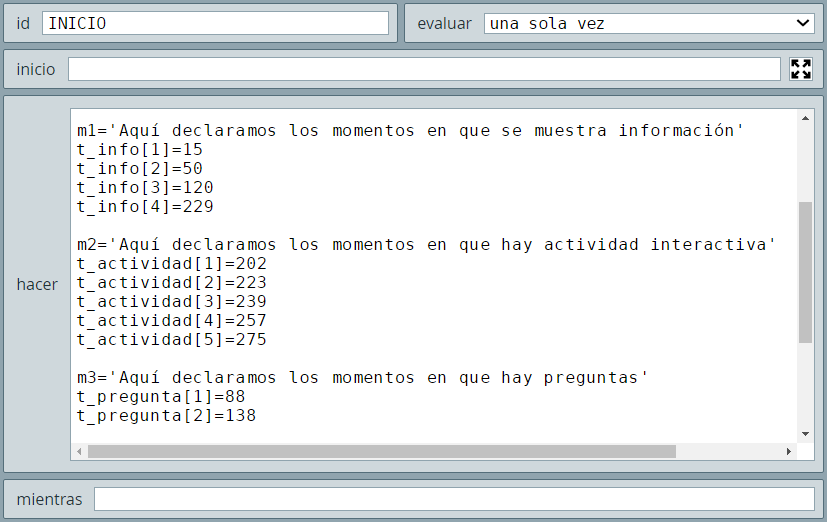
Actividad “Preguntas”. Se presentan en la línea de tiempo marcadas con color naranja. Son preguntas de selección múltiple, que reanudan el vídeo una vez se seleccione una respuesta.
Para este modelo, el diseño de las preguntas está incorporado en la escena principal. Se podría modificar el modelo incluyendo preguntas a través de una segunda comunicación, tal como se hizo en el modelo anterior. En la siguiente imagen, se muestra cómo es el diseño de las preguntas.
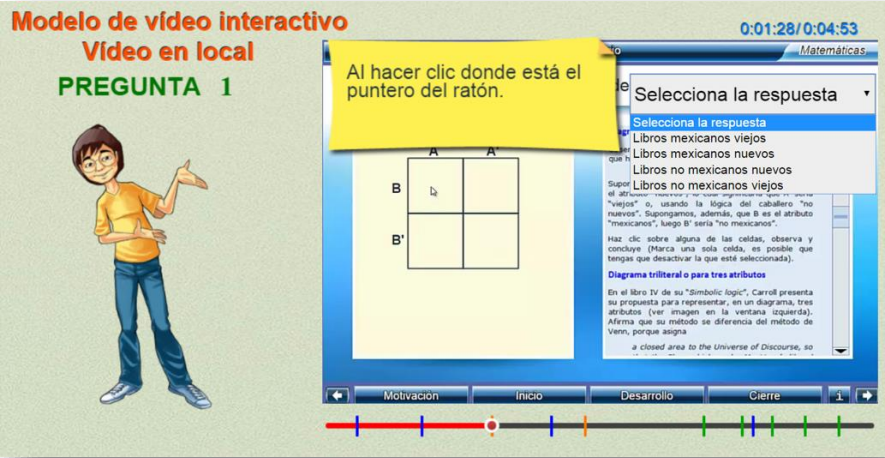
Para su modificación se requiere:
INICIO, podemos modificar los valores del vector t_pregunta. Estos valores son los segundos transcurridos en el vídeo para presentar la pregunta. Si se desean más preguntas, basta copiar las líneas adicionales; por ejemplo, para una tercera pregunta a los dos minutos: t_pregunta[3]=120. Si no se desea incluir preguntas, asignamos un tiempo de 1000 segundos o más (explora la configuración para saber el por qué).P. Como se observa en la imagen anterior, el enunciado de la pregunta puede tener más de una línea (para el modelo máximo tres), que se separan por comas. En nuestro ejemplo, se tienen formuladas dos preguntas P[1] y P[2]. Por otra parte, en el vector R, se asignan las posiciones en la que se encuentran las respuestas correctas (ver siguiente apartado). En la siguiente imagen, se observa que aparecerán sólo dos preguntas en el vídeo interactivo.
Una función interesante es organiza_preguntas(), la cual se encarga de distribuir el texto de la pregunta en un máximo de tres líneas. Este recurso se utilizó porque el modelo original fue diseñado en 2015, año en el cual el editor DescartesJS no contaba con las opciones actuales punto de anclaje y ancho del texto. Lo hemos dejado sólo para que explores cómo se usan las funciones de cadena para organizar el texto de la pregunta. Obviamente, puedes rediseñar la escena de tal forma que no se tengan que usar estas funciones.
'Libros mexicanos nuevos', que corresponde a la posición dos; es decir, R[1] = 2.Este menú se modifica en los controles tipo menú que aparecen en el apartado Controles del editor de DescartesJS, basta cambiar el contenido de la casilla opciones. Cada repuesta se separa con coma. La primera opción 'Selecciona respuesta' no se modifica. El modelo está diseñado para un máximo de cinco preguntas. Si no se desean hacer preguntas, es suficiente con modificar los tiempos del vector t_pregunta; es decir, no es necesario eliminar los cinco controles de preguntas.
Actividad "Escena DescartesJS". Se presentan en la línea de tiempo marcadas con color verde. Para el modelo son escenas de DescarteJS, pero igual podemos incluir otro tipo de escenas que estén adaptadas a HTML5, GeoGebra por ejemplo (ver varios ejemplos al final de este apartado).
INICIO, podemos modificar los valores del vector t_actividad. Estos valores son los segundos transcurridos en el vídeo para presentar una de las escenas interactivas. Si se desean más actividades, basta copiar las líneas adicionales; por ejemplo, para una sexta actividad a los cinco minutos: t_actividad[6]=300. Al igual que en los caso anteriores, basta con asignar un tiempo grande (1000, por ejemplo) para no incluir este tipo de actividades.practica1.html, practica2.html,..., con los correspondientes archivos y carpetas de soporte.El modelo permite la inclusión de escenas con las siguientes dimensiones: $970 \times 550$ para vídeos en local y $790 \times 520$ para vídeos de YouTube, cada una de ellas tienen un tratamiento de diseño adaptable para ajustarlas a la escena principal.
A continuación puedes interactuar con este quinto modelo de vídeo interactivo. Te recomendamos hacerlo en una ventana ampliada.
Es el mismo modelo anterior con dos novedades de animación. La primera es una animación usando https://www.moovly.com/El creador de videos Moovly hace que sea simple e intuitivo crear videos atractivos que cautiven a su audiencia. No necesita habilidades de edición o un gran presupuesto para hacer un video o editarlo fácilmente en nuestro editor de video en línea. (https://www.moovly.com/). y, la segunda, una animación DescartesJS. Pero... explora el vídeo en la siguiente página.
Para terminar este apartado, presentamos algunos ejemplos de vídeos interactivos con GeoGebra.
Este ejemplo corresponde a un vídeo de 3 minutos y 46 segundos, en el que se hacen cuatro preguntas de respuesta escrita. Al final aparece la escena de GeoGebra construida en el vídeo. En este caso la comunicación es sólo entre DescartesJS y el vídeo, puesto que la escena de GeoGebra es simplemente un HTMLIframe embebido en
Este es el vídeo interactivo:
En este ejemplo hay doble comunicación, tanto con el vídeo como con la escena de GeoGebra. Es un forma de explicar una construcción geométrica con el concurso del usuario.
La interacción del usuario con GeoGebra se realiza construyendo los tres arcos finales que conforman el huevo. Esto se logra a través de las funciones dibuja_arco2(), dibuja_arco3() y controla(), donde la última verifica que el usuario haya dibujado correctamente los arcos.

La verificación se hace a través de funciones de cadena. Por ejemplo, para el primer arco:
arco1a=_substring_(A1,4,_length_(A1))
arco1b=_substring_(A2,4,_length_(A2))
verifica1a=(_Eval_(arco1b)>0)
verifica1b=(arco1a = arco1b)
arco_correcto1=(verifica1a)&(verifica1b)
Este es el vídeo interactivo:
En este ejemplo hay comunicación con dos escenas de GeoGebra, pero sólo se limita a enviar dos mensajes con los colores de los ángulos.
Se realizan dos construcciones geométricas. La primera es un polígono inscrito en una circunferencia, el cual tiene como propiedad que los ángulos opuestos suman 180°.
La segunda, es un ángulo inscrito en una circunferencia, que se compara con el ángulo central correspondiente.
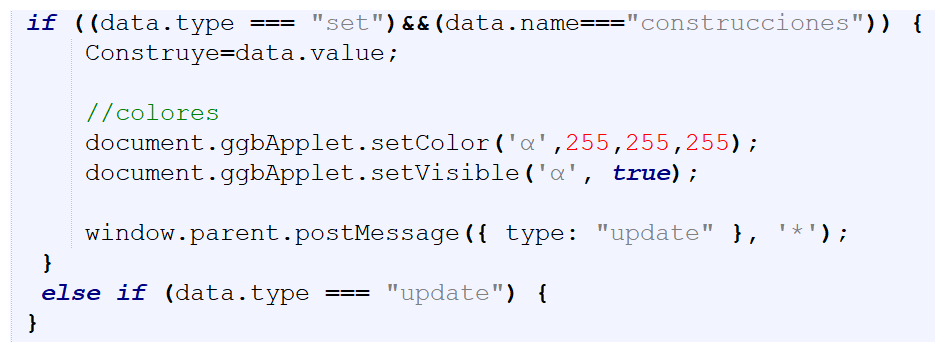
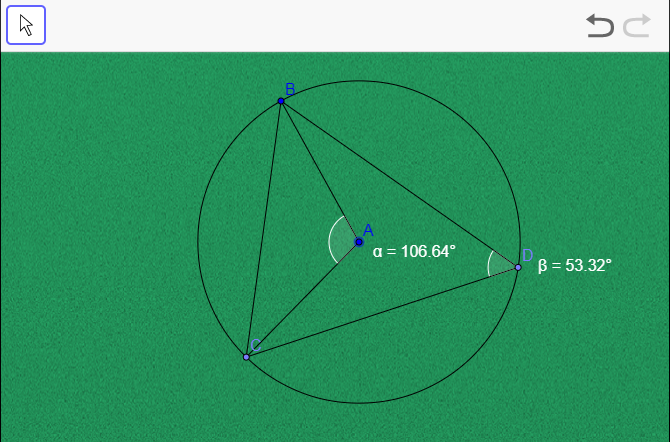
Este es el vídeo interactivo:
Terminamos con dos ejemplo más, que puedes abrir e interactuar con ellos haciendo clic en las siguientes imágenes:
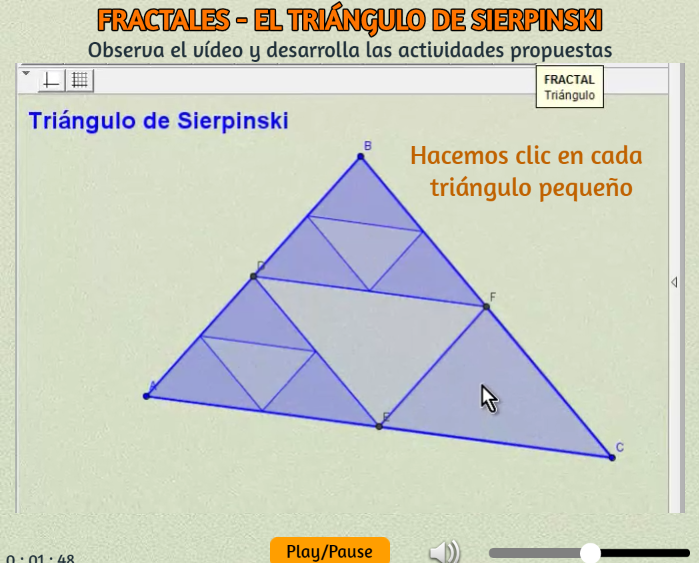
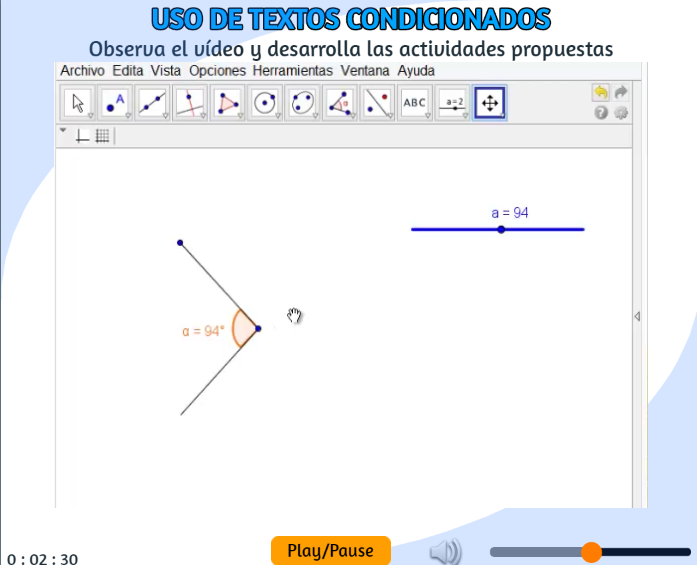
Si deseas diseñar un vídeo interactivo como los anteriores en una forma más rápida, puedes recurrir a una plantilla de las que hemos dispuesto en https://proyectodescartes.org/plantillas/. No obstante, lo explicado anteriormente es de utilidad para que diseñes tus propios modelos, basta que te esfuerces un poco para programar, tanto el código DescartesJS como la interface videolocal.js
A continuación, te presentamos un vídeo que explica cómo se modifican las plantillas para modelos en local:
Google, en general, y YouTube, en particular, suministran rutinas JavaScript de programación, más conocidas como JavaScript API, las cuales permiten incrustar una aplicación Google (YouTube, Google Maps,...) en un sitio web y controlarla mediante JavaScript. Estas APIs, que hemos llamado interface o interfaz, anteriormente eran una especie de plug-in que hoy en día se han estandarizado en JavaScript, buscando una mayor compatibilidad con los sistemas operativos y navegadores.
En este último apartado, veremos cómo aprovechar la API de YouTube para reproducir los vídeos, pausar o detener esos videos, ajustar el volumen, o recuperar información sobre el video como su duración.
No obstante, siempre recomendamos diseñar vídeos interactivos con los modelos en local, pues no tienen dependencia externa que puedan frustrar uno de los atributos que esperamos de nuestros objetos interactivos... la perdurabilidad. Esta frustración puede presentarse por dos razones; la primera es la eliminación del vídeo por el autor, incluso en nuestro propio canal (una demanda, por ejemplo); la segunda, porque Google cambie políticas o modificaciones en los atributos de sus aplicaciones que hagan inservible la interface (algo similar se ha presentado con la API de Google Maps, al modificar la llamada API key).
Pese a estos posibles inconvenientes la actual API de YouTube funciona muy bien, así que presentamos cinco modelos de comunicación DescartesJS - YouTube y varios ejemplos de aplicación. Sólo en el primer modelo haremos una explicación más detallada de los elementos que intervienen en la comunicación, excepto por aquellos de uso frecuente en el editor de DescartesJS o que ya han sido ampliamente trabajados en este libro o en el nivel anterior.
Presentamos, a continuación, un vídeo introductorio a este apartado, en el que puedes observar dos tipos de interacciones, la típica de YouTube (clic en una parte del vídeo, para este ejemplo en el botón más información) y, al final, la interacción que más nos interesa en las aplicaciones de Descartes:
Los comandos de comunicación entre DescartesJS y el vídeo de YouTube los explicamos en los siguientes apartados.
Este modelo es igual al presentado en el modelo 1 de los vídeos en local, sólo se diferencia por el contenido del vídeo y porque hemos incorporado la macro Barra Jinich, tal como se muestra en la siguiente imagen:
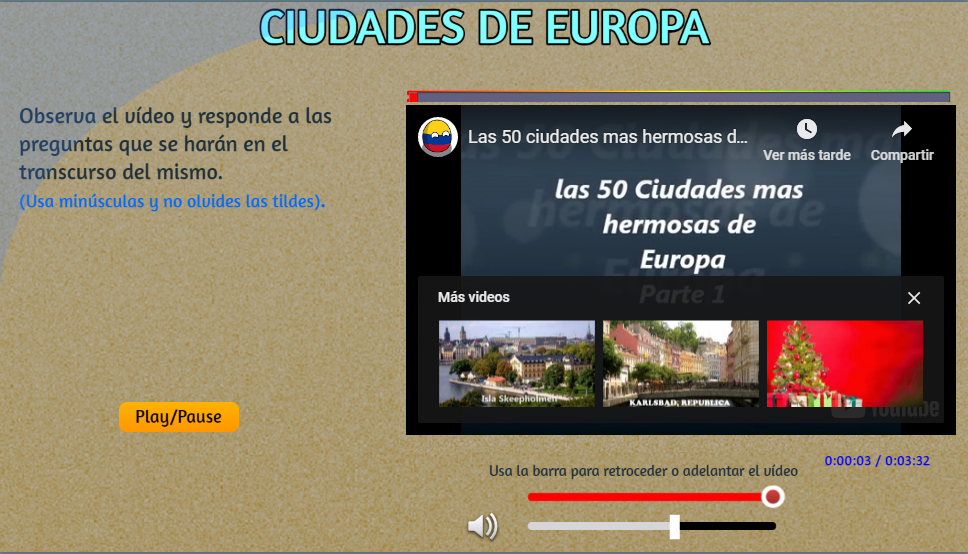
La imagen fue capturada en una pausa del vídeo. Se puede observar la presencia de vídeos relacionados en la parte inferior, pese a que se dio lo orden de no hacerlo (rel=0). Al indagar en Google, obtuvimos la siguiente información:
1, que es el valor predeterminado, el reproductor muestra videos relacionados. Si el valor del parámetro se establece en 0, el reproductor no muestra videos relacionados. Después del cambio, no podrá desactivar los videos relacionados. En cambio, si el parámetro rel se establece en 0, los videos relacionados provendrán del mismo canal que el video que se acaba de reproducir (https://developers.google.com).
¡He ahí un cambio de política de Google!
La programación del vídeo interactivo en DescartesJS es similar al modelo en local (ver archivo indexb.html), de la cual destacamos:
Identificación del vídeo (id). El id de los vídeos en YouTube se presenta luego de la expresión watch?v=; por ejemplo, el vídeo del canal de YouTube "las 50 ciudades más hermosas de Europa" tiene este enlace:
https://www.YouTube.com/watch?v=V6CQjkm_qcY
El id del vídeo, entonces, es V6CQjkm_qcY.
Si queremos otro vídeo, una vez lo tengamos identificado, vamos al algoritmo INICIO y modificamos la expresión url='V6CQjkm_qcY'.
Vídeo introductorio con el logo. Al inicio de cada vídeo aparece el logo de la Institución Universitaria Pascual Bravo. Tienes tres opciones: i) Conservar este logo, ii) crear tu logo y subirlo a YouTube, luego incorporas el id obtenido (ver apartado sobre el archivo ivideo.html) o, iii) eliminar el logo. Si la decisión es la última opción, basta cambiar la dirección YouTube en ivideo.html y cambiar la condición en el evento e4 por tiempo1>3000 (¿por qué?).
Instrucciones de comunicación. En el código de esta escena se incluyen instrucciones que permiten comunicarla con el archivo ivideo.html, el cual se incluye en un espacio HTMLIframe. A continuación describimos los elementos de la escena que permiten gestionar el vídeo:
play_pause. Variable que permite enviar órdenes al archivo HTML para que detenga o reanude la reproducción del vídeo. Si deseamos enviar el valor seguir a la variable play_pause, podemos hacerlo con instrucciones como:accion='seguir'; E2.set('play_pause',accion)
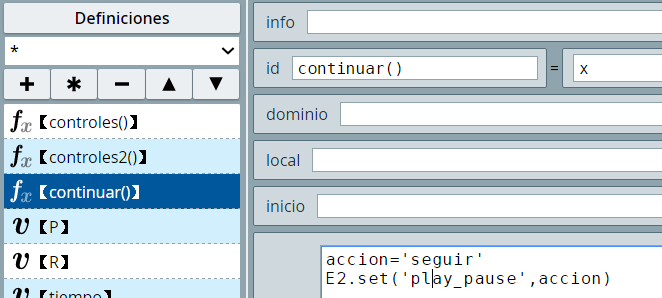
E2 es el espacio HTMLIframe. Observa la función parada(), en la escena, que se ejecuta a través de un evento que controla el tiempo de reproducción para cada pregunta. La acción, entonces, sería parar o detener el vídeo para responder a la pregunta.
actualizar_tiempo. Variable que reasigna el tiempo en segundos a partir del cual se debe reanudar la reproducción del vídeo. En este modelo se controla con un control gráfico (g):
La orden para actualizar el tiempo de reproducción es:
E2.set('actualizar_tiempo', g.x*avanzado/6)
Donde la variable avanzado es el tiempo transcurrido en el momento que se detiene la reproducción, que se calcula a través del evento e3. El tiempo del vídeo se actualiza con valores entre 0 y el tiempo transcurrido (avanzado).

cambia_volumen. Variable que modifica el valor del volumen entre un valor mínimo (0) y un valor máximo (100). Al igual que la variable anterior, se controla con un control gráfico (sonido):
La orden para modificar el volumen es:
E2.set('cambia_volumen', (sonido.x-1)*20)
cambia_video. Como lo indicamos antes, la identificación de nuestro vídeo la asignamos a la variable url del vídeo. La orden para modificar el enlace de YouTube del vídeo es:E2.set('cambia_idYouTube', url)
Finalmente, desde el archivo HTML se capturan los valores del tiempo de reproducción (t) y de la duración total del vídeo (t2), a través de las siguientes instrucciones:
tiempo1=_Eval_(t)
tiempo_reproduccion=_Eval_(t2)
Esta captura permite controlar los tiempos para realizar las preguntas, además de presentar el tiempo de reproducción en la escena y su duración:
YouTube.jsEste archivo de comunicación lo puedes encontrar en la carpeta js, del cual destacamos:
t) y la duración del vídeo (variable t2). La captura de estas dos variables se logra a través de los comandos:seg = Math.round(player.getCurrentTime());
duracion = Math.round(player.getDuration());
Donde player es la variable que contiene el nombre del video, la cual se declara con el comando:
player = document.getElementById("video1");
Para el caso de la primera variable a enviar (t) a la escena, se usan los siguientes comandos:
Contador.innerHTML = seg;
document.getElementById("texto_a_enviar").value = seg;
document.getElementById("texto_a_enviar").click();
En los cuales, la variable texto_a_enviar se maneja a través de un input creado en el archivo ivideo.html, que explicamos más adelante. La variable contenido envía a la escena el texto a enviar (seg) con el nombre (t), a través del siguiente bloque de comandos:

En forma similar se envía la variable t2.
play_pause, retrocede, actualizar_tiempo, o cambia_volumen (en la descripción de la escena se explicita cómo se envían estos mensajes).play_pause. Se esperan dos posibles valores: 'parar' o 'seguir', lo que permite parar o reanudar el vídeo, así:

Variables de avance y retroceso del vídeo (retrocede, actualiza_tiempo). Permiten modificar el tiempo de reproducción del vídeo:

Variable de control de volumen (cambia_volumen). Asigna valores entre 0 (mínimo) y 100 (máximo) al volumen del vídeo:

Variable que cambia la url del vídeo. Asigna el valor de la url definida por la escena:
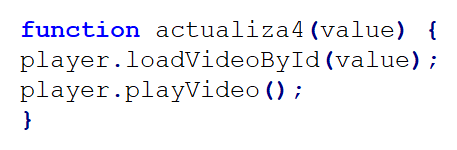
ivideo.htmlEs el HTML que se embebe en la escena, para la modificación de la escena no hay necesidad de intervenirla. Algunos bloques de diseño importantes son:
<script src="js/YouTube.js"></script>. Invoca la librería descrita en el apartado anterior.
<input id="texto_a_enviar" type="text" style="VISIBILITY:hidden;display:none"/>. Comando de entrada al que se le asigna el valor de la variable texto_a_enviar. Para nuestro caso es la variable t, la propiedad VISIBILITY permite ocultar el cuadro de texto que genera este comando. En la librería YouTube.js se simula la tecla intro (enter) para enviar automáticamente este mensaje a la escena, con el comando:
document.getElementById("texto_a_enviar").click();
<iframe>. La reproducción del vídeo se realiza con la etiqueta HTML5 <video>, la cual permite que el vídeo se adapte al tamaño del espacio HTMLIframe de la escena. El bloque es el siguiente:

Aquí es importante describir varios aspectos:
src) aparece el id j8SdsVIBbZQ, que corresponde al vídeo logo explicado en el apartado de modificación de la escena.enablejsapi=1 es un comando para que se habilite la API de YouTube, que es lo que permite que podamos intervenir el vídeo.autoplay=0).controls=0)Finalmente, el vídeo interactivo es el siguiente:
En este vídeo hemos incorporado la línea de tiempo y las marcas donde se van a realizar las preguntas. Nos detendremos únicamente en explicar cómo se diseñaron.
gris claro con las siguiente configuración: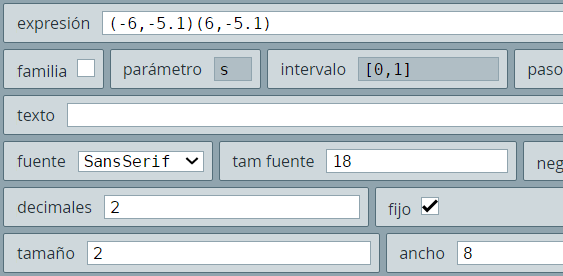
Es decir, el segmento es de una longitud de 12 pixeles que va desde -6 a 6:

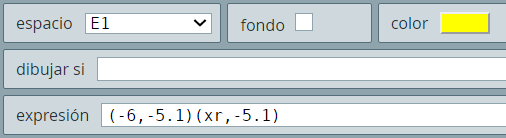
La longitud variables está dada por xr, que se calcula en el algoritmo CALCULOS, así:
xr=-6+tiempo1*12/tiempo2
La fórmula es una relación simple entre la longitud máxima (12 pixeles) asociada al tiempo total (tiempo2) y la longitud (xr) asociada al tiempo transcurrido (tiempo1).
En forma similar se calculan las abscisas de las marcas de tiempo:
x1=-6+tiempo[1]*12/tiempo2
x2=-6+tiempo[2]*12/tiempo2
3=-6+tiempo[3]*12/tiempo2
Estas marcas son segmentos verticales de ancho 6 que se dibujan en las abscisas x1, x2 y x3. Para la primera, la configuración sería:
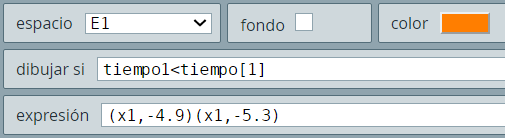
El vídeo es el siguiente:
El funcionamiento de este vídeo es similar al mostrado en el modelo en local. En este modelo de YouTube hemos escogido un vídeo de nuestra colega cartesiana Eva Perdiguero Garzo, publicado en el canal de la Red Educativa Digital Descartes, lo cual nos garantiza un mayor nivel de perdurabilidad.

Se trata de un vídeo relacionado con una unidad didáctica del Proyecto Pizarra Interactiva, llamada "Medición de ángulos". Es en este proyecto donde se usa, por primera vez, la macro sombras.
Las actividades que vamos a incluir son seis (6), dos de información complementaria "para saber más", dos actividades evaluativas y dos escenas interactivas tomadas de la unidad didáctica.
En tanto que ya estás en capacidad de explorar y comprender la escena DescartesJS y los archivos de comunicación ivideo.html y YouTube.js, sólo nos resta presentar el vídeo:
Si deseas explorar o modificar las escenas interactivas incorporadas en la carpeta practicas, debes hacerlo con los archivos actividad1.html y actividad2.html. Observarás que no hemos intervenido estas escenas, las cuales fueron diseñadas en 2015.
El vídeo utilizado en este modelo corresponde al cálculo de la matriz adjunta, el cual ha generado cierta discusión en el canal de YouTube, pues en otras latitudes, España por ejemplo, la matriz adjunta se define de otra manera; sin embargo, sea cual fuere el nombre que le demos, finalmente es útil para comprender cómo calcular la matriz inversa y, en consecuencia la matriz o vector solución de un sistema de ecuaciones. Este vídeo hace parte de una unidad didáctica interactiva del Proyecto (Un_100).
El vídeo interactivo cuenta con dos actividades "para saber más", una evaluativa y, al final, una actividad interactiva de la unidad didáctica.
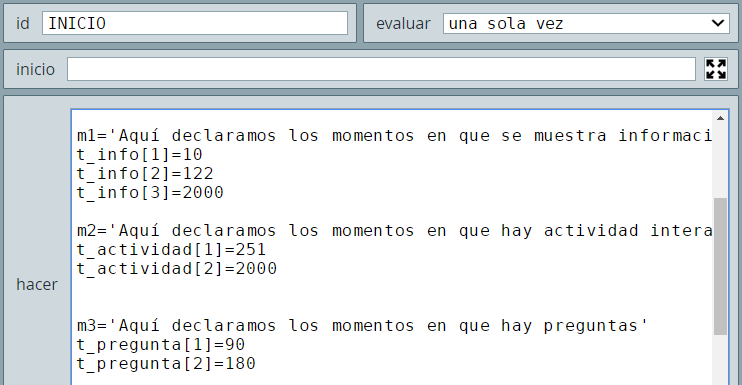
He aquí el vídeo interactivo (ponle volumen al audio, pues presenta un nivel bajo el vídeo original).
Finalmente, presentamos algunos ejemplos de aplicación, entre ellos algunos con la herramienta GeoGebra.
En los ejemplos de GeoGebra se presentan suspensiones del vídeo, para que practiques con la herramienta lo explicado en el vídeo. En el segundo ejemplo (Euler's Line), podrás observar el efecto "no deseado" de una de las nuevas políticas de Google.
Este es un vídeo interactivo publicado en el foro de GeoGebra, versión lengua inglesa. El vídeo original de YouTube se encuentra publicado en https://www.YouTube.com/watch?v=pUcBaVVjZ8s. Hemos incorporado música de fondo, descargada de https://www.bensound.com.
Haz clic sobre la imagen para ver el vídeo:
Este es otro ejemplo que hace uso de la herramienta GeoGebra, se diseñó empleando el vídeo publicado en https://www.YouTube.com/watch?v=Bn1T1olLbUU
En este ejemplo se evidencia el impacto negativo de la afectación realizada al comando rel, pues en el momento de enviar un mensaje con el comando pause, aparecen los vídeos relacionados, dificultando identificar la imagen pausada para dar respuesta a las preguntas:
Una solución posible sería recurrir al modelo de vídeos interactivos en local; sin embargo, aún no renunciaremos a interactuar con YouTube, tal como lo veremos en siguiente ejemplo.
Como en el vídeo anterior, tuvimos que recurrir a un audio de fondo pues el vídeo original carece de audio.
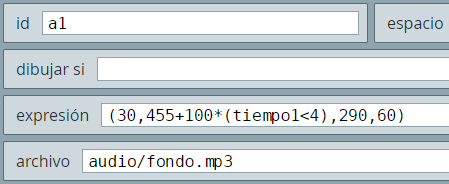
Dado que el control de audio que hemos venido utilizando es para comunicarnos con el vídeo, ya no tiene sentido en este y el anterior modelo; por ello, lo hemos eliminado y dejado visible en control a1

Para este modelo, hemos evitado que el audio se siga escuchando cuando pausamos el vídeo, a través de instrucciones como:
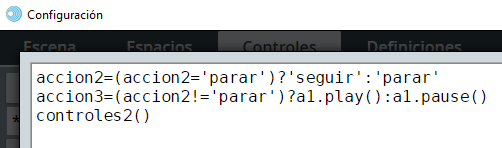
El vídeo es el siguiente:
Habíamos advertido que una posible solución a los molestos vídeos relacionados, era recurrir a un modelo en local; no obstante, podemos recurrir a no usar el espacio mascara y dejar que el vídeo se reproduzca sin restringir la opción de pausarlo o reproducirlo haciendo clic sobre él.
Esto permite que sólo se muestran los vídeos relacionados la primera vez que hacemos clic sobre el vídeo, pues tenemos la posibilidad de cerrar la ventana. El presente modelo muestra tres escenas interactivas de GeoGebra, luego de ciertas explicaciones.
Este tipo de modelo permite que el usuario se convierta en un actor más del vídeo... compruébalo:
Para terminar este apartado, te invitamos a que explores la bella Andalucía.
En este vídeo recorrerás la comunidad autónoma de Andalucía, al final aparecerá un mapa interactivo diseñado en DescartesJS, por cada pregunta acertada se mostrará un pequeño clip de la provincia señalada.
Si deseas diseñar un vídeo interactivo como los anteriores en una forma más rápida, puedes recurrir a una plantilla de las que hemos dispuesto en https://proyectodescartes.org/plantillas/. No obstante, lo explicado anteriormente es de utilidad para que diseñes tus propios modelos, basta que te esfuerces un poco para programar, tanto el código DescartesJS como la interface YouTube.js
A continuación, te presentamos un vídeo que explica cómo se modifican las plantillas para modelos con vídeos YouTube:
Diseña tu vídeo interactivo. Puedes hacerlo con un vídeo en local o de YouTube. Usa alguno de los modelos anteriores, ¡No uses modelos de las plantillas!
La evaluación final consta de seis pruebas. Haz clic sobre cada imagen para realizar la prueba.
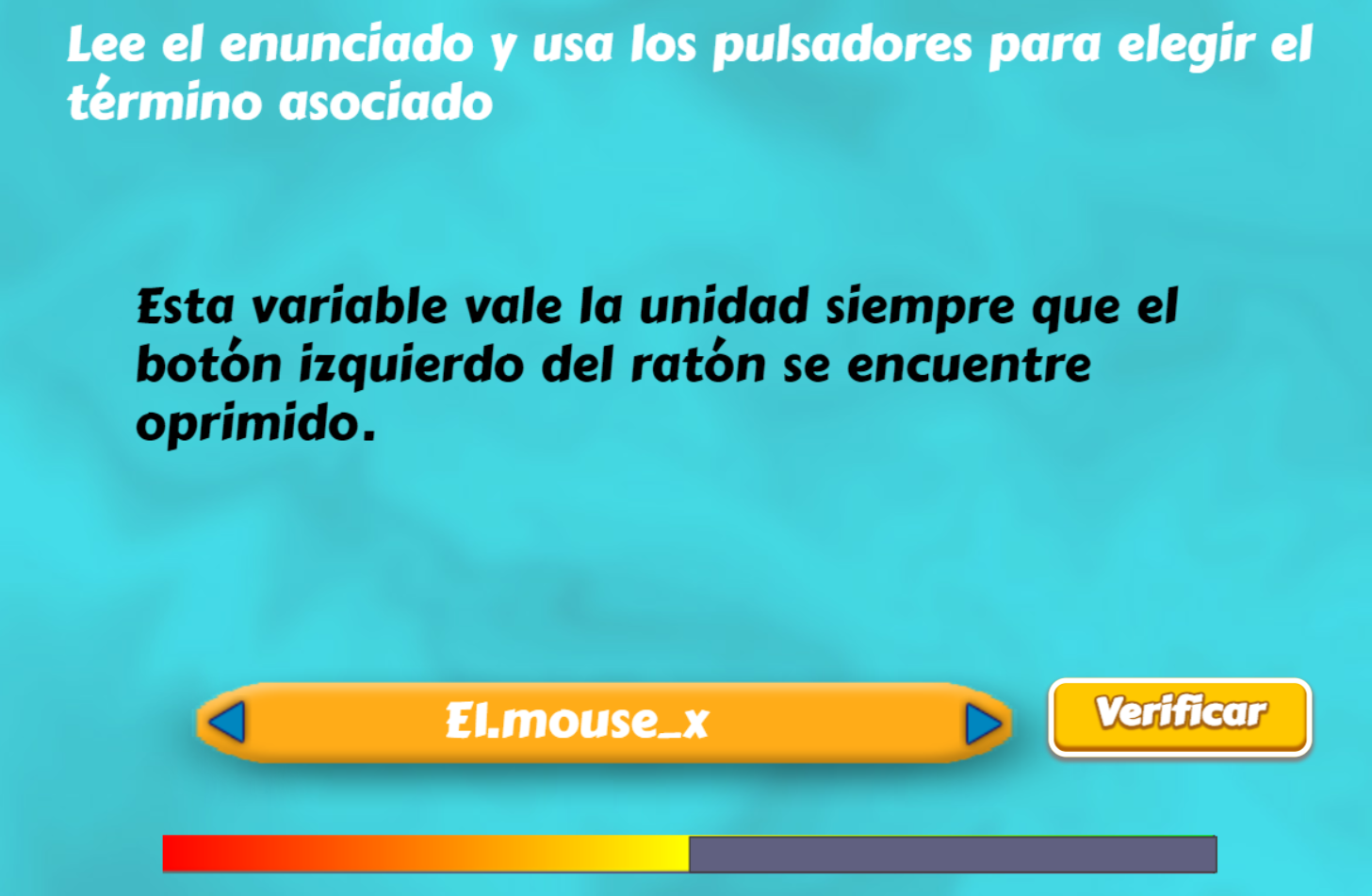

En esta prueba se presentan 15 preguntas de un banco de 32, por lo que sería una buena idea repetir la prueba para mejorar tu nota.


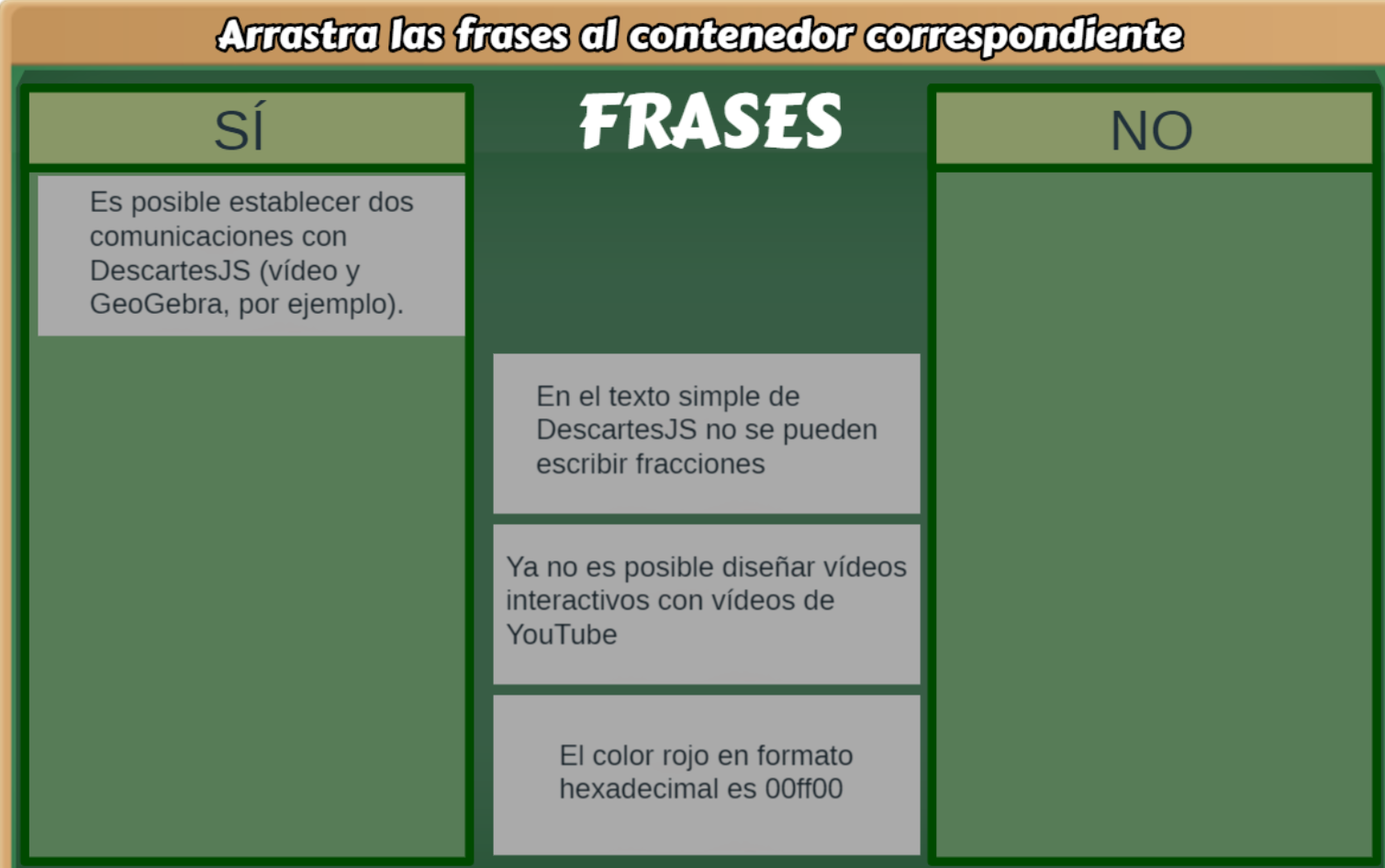

Ahora que has concluido la capacitación en DescartesJS, te dejamos dos juegos clásicos de los 80 para que te relajes. El primero es Lode Runner adaptado a HTML5 por Antoine Brassard Lahey y Simon Boyer. El segundo es el clásico juego de autos de la Commodore 64 Out Run, adaptado para HTML5 por Jake Gordon.