Química
Volumen I
Interactivo
Primera parte
Jorge Wilson Ocampo Vásquez
José Gregorio Doria Andrade
Juan Guillermo Rivera Berrío
Institución Universitaria Pascual Bravo
Obra derivada de Chemistry 2e
Paul Flowers
University of North Carolina at Pembroke
Klaus Theopold (University of Delaware)
Richard Langley and Stephen F. Austin (State University)
William R. Robinson, PhD
Fondo Editorial Pascual Bravo
Medellín
Título de la obra: Química - Volumen I
Interactivo
Autores:
Jorge Wilson Ocampo Vásquez
José Gregorio Doria Andrade
Juan Guillermo Rivera Berrío
Revisoras
Elena Esperanza Alvarez Saiz
María José García Cebrian
Diseño del libro: Juan Guillermo Rivera Berrío
Código JavaScript para el libro: Joel Espinosa Longi
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Fondo Editorial Pascual Bravo
Calle 73 73A-226
PBX: (574) 4480520
Apartado 6564
Medellín, Colombia
www.pascualbravo.edu.co
ISBN:
978-958-56858-9-5
LICENCIA
Para generar esta obra derivada se ha tomado como referencia OpenStax - Chemistry 2e, OpenStax CNX. 14 feb. 2019 Textbook is licensed under a Creative Commons Attribution License 4.0 license.
Este libro digital interactivo se ha diseñado con fundamento en la filosofía del Proyecto Descartes: "Trabajando altruistamente por la comunidad educativa de la aldea global", que sólo busca desarrollar contenidos educativos para el provecho de la comunidad académica, esperando únicamente como retribución el uso y difusión de estos contenidos. El contenido del libro, al igual que los objetos interactivos se han diseñado de tal forma que se puedan leer en ordenadores y dispositivos móviles sin necesidad de instalar ningún programa o plugin. El libro se puede descargar para su uso en local sin dependencia con la red, a excepción de los ocho vídeos incluidos en el texto. Algunos de los objetos interactivos se han diseñado con el Editor DescartesJS.
Este primer volumen del libro de texto de Química se adhiere al alcance y la secuencia de los cursos de química universitaria.
El libro de texto brinda una oportunidad importante para que los estudiantes aprendan los conceptos básicos de la química y comprendan cómo esos conceptos se aplican a sus vidas y al mundo que los rodea. El libro también incluye una serie de características innovadoras, que incluyen ejercicios interactivos y aplicaciones del mundo real, diseñadas para mejorar el aprendizaje de los estudiantes. La segunda edición se ha revisado para incorporar explicaciones más claras, más actuales y más dinámicas, mientras se mantiene la misma organización que la primera edición. Se han realizado mejoras sustanciales en las figuras, ilustraciones y ejercicios de ejemplo que apoyan la narrativa del texto.
Este libro de texto de Química se adhiere al alcance y la secuencia de la mayoría de los cursos de química general. El contenido de este libro de texto ha sido desarrollado y organizado para proporcionar una progresión lógica de los conceptos fundamentales a los más avanzados de la ciencia química. Los temas se introducen en el contexto de experiencias familiares siempre que sea posible, se tratan con el rigor adecuado para satisfacer el intelecto del alumno y se refuerzan en las discusiones posteriores del contenido relacionado. La organización y las características pedagógicas fueron desarrolladas y examinadas con comentarios de educadores de química dedicados al proyecto.
El texto original, desarrollado por Flowers P., Theopold K., Langley R. y Robinson W.R., ha sido publicado en versiones html y pdf. Esta obra derivada, en español y como libro interactivo, creada por Ocampo JW, Doria J. & Rivera J.G., presenta las siguientes aportaciones: traducción al español, diseño en formato libro tipo eBook, incorporación de 56 objetos interactivos de aprendizaje, 36 de ellos diseñados con el editor DescartesJS, y ocho vídeos.
Para evitar, al máximo, la dependencia con la conectividad en la red, las expresiones matemáticas se han construido recurriendo a las librerías de $KaTeX$ y al complemento mhchem.min.js y, en algunos casos, al editor DescartesJS.
Se ha conservado la propuesta pedagógica en los ejemplos presentados en cada uno de los capítulos y, en la mayoría de los ejemplos, un problema propuesto, denominado "Comprueba tu aprendizaje". Al final de cada capítulo se han incluido tanto los problemas propuestos como las respuestas.
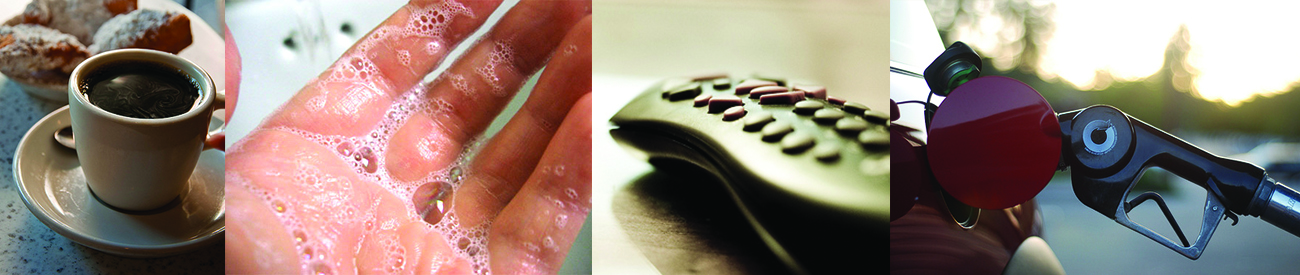
Figura 1.1. Las sustancias y procesos químicos son esenciales para nuestra existencia, nos brindan sustento, nos mantienen limpios y saludables, fabrican dispositivos electrónicos, permiten el transporte y mucho más (crédito "izquierda": modificación del trabajo por "vxla"/Flickr; crédito "izquierdo medio"”: modificación del trabajo por "la voz italiana"/Flickr; crédito "derecho medio": modificación del trabajo por Jason Trim; crédito "derecho": Modificación del trabajo de "gosheshe "/Flickr).
Tu alarma se apaga y, después de presionar "snooze" una o dos veces, te levantas de la cama. Haces una taza de café para ayudarte a ponerse en pie, y luego te bañas, te vistes, desayunas y revisas tu teléfono en busca de mensajes. De camino a la universidad, te detienes para llenar el tanque de gasolina de tu auto, casi llegando tarde al primer día de la clase de química. Cuando encuentras un asiento en el aula, lees la pregunta proyectada en la pantalla: “¡Bienvenido a clase! ¿Por qué deberíamos estudiar química?
¿Tienes una respuesta? Puede que estés estudiando química porque cumples con un requisito académico, pero si consideras tus actividades diarias, podrías encontrar la química interesante por otras razones. Casi todo lo que haces y te encuentras durante el día tiene que ver con la química. Hacer café, cocinar huevos y tostar el pan implica química. Los productos que usas, como jabón y champú, las telas que usas, los productos electrónicos que te mantienen conectado a tu mundo, la gasolina que impulsa tu automóvil, todo esto y más involucran sustancias y procesos químicos. Ya sea que lo sepas o no, la química es parte de tu mundo cotidiano.
En este curso, aprenderás muchos de los principios esenciales que subyacen en la química de la vida moderna.
A lo largo de la historia humana, las personas han tratado de convertir la materia en formas más útiles. Nuestros antepasados de la Edad de Piedra convirtieron trozos de pedernal en herramientas útiles y madera tallada en estatuas y juguetes. Estos esfuerzos implicaron cambiar la forma de una sustancia sin cambiar la sustancia en sí. Pero a medida que aumentaba nuestro conocimiento, los humanos también empezaron a cambiar la composición de las sustancias: la arcilla se convertía en cerámica, las pieles se curaban para hacer prendas de vestir, los minerales de cobre se convertían en herramientas y armas de cobre, y el grano se convertía en pan.
Los humanos comenzaron a practicar la química cuando aprendieron a controlar el fuego y a usarlo para cocinar, hacer cerámica y fundir metales. Posteriormente, comenzaron a separar y utilizar componentes específicos de la materia. Una variedad de fármacos como el aloe, la mirra y el opio se aislaron de las plantas. Los tintes, como el índigo y el púrpura tirio, se extrajeron de la materia vegetal y animal. Los metales se combinaron para formar aleaciones (por ejemplo, el cobre y el estaño se mezclaron para hacer bronce) y las técnicas de fundición más elaboradas produjeron hierro. Los álcalis se extrajeron de las cenizas y los jabones se prepararon combinando estos álcalis con grasas. El alcohol se produjo por fermentación y se purificó por destilación.
Los intentos por comprender el comportamiento de la materia se remontan a más de 2500 años. Ya en el siglo VI a. C. los filósofos griegos discutían un sistema en el que el agua era la base de todas las cosas.
Es posible que hayas escuchado del postulado griego que la materia consta de cuatro elementos: tierra, aire, fuego y agua. Posteriormente, los alquimistas difundieron una fusión de tecnologías químicas y especulaciones filosóficas desde Egipto, China y el Mediterráneo oriental, que intentaron transformar "metales básicos" como el plomo en "metales nobles" como el oro, y crear elixires para curar enfermedades y prolongar la vida (Figura 1.2).
Figura 1.2. Esta representación muestra el taller de un alquimista alrededor de 1580. Aunque la alquimia hizo algunas contribuciones útiles sobre cómo manipular la materia, no era científica según los estándares modernos (crédito: Chemical Heritage Foundation).
De la alquimia vinieron las progresiones históricas que llevaron a la química moderna: el aislamiento de las drogas de las fuentes naturales, la metalurgia y la industria de los tintes.
Hoy en día, la química continúa profundizando nuestra comprensión y mejorando nuestra capacidad para aprovechar y controlar el comportamiento de la materia.
La química se conoce a veces como "la ciencia central" debido a su interconexión con una amplia gama de otras disciplinas STEM (STEM significa áreas de estudio en los campos de la ciencia, la tecnología, la ingeniería y las matemáticas). La química y el lenguaje de los químicos juegan un papel vital en la biología, la medicina, la ciencia de los materiales, la ciencia forense, la ciencia ambiental y muchos otros campos (Figura 1.3). Los principios básicos de la física son esenciales para comprender muchos aspectos de la química, y existe una amplia superposición entre muchas subdisciplinas dentro de los dos campos, como la físico-química y la química nuclear. Las matemáticas, las ciencias computacionales y la teoría de la información proporcionan herramientas importantes que nos ayudan a calcular, interpretar, describir y, en general, dar sentido al mundo químico. La biología y la química convergen en la bioquímica, que es crucial para comprender los muchos factores y procesos complejos que mantienen vivos a los organismos vivos (como nosotros). La ingeniería química, la ingeniería de materiales y la nanotecnología combinan principios químicos y hallazgos empíricos para producir sustancias útiles, desde la gasolina hasta los tejidos y la electrónica. La agricultura, la ingeniería de alimentos, la ciencia veterinaria, la elaboración de cerveza y la elaboración de vinos ayudan a proporcionar sustento en forma de alimentos y bebidas a la población mundial. La medicina, la farmacología, la biotecnología y la botánica identifican y producen sustancias que nos ayudan a mantenernos saludables.
La ciencia ambiental, la geología, la oceanografía y la ciencia atmosférica incorporan muchas ideas químicas para ayudarnos a comprender y proteger mejor nuestro mundo físico. Las ideas químicas se utilizan para ayudar a entender el universo en astronomía y cosmología.
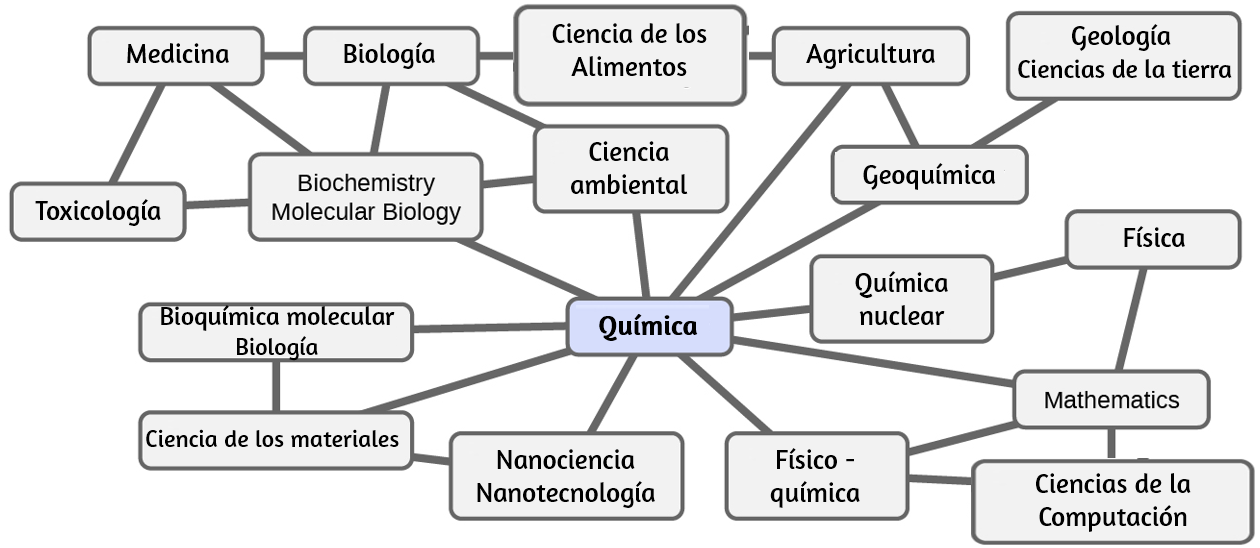
Figura 1.3. El conocimiento de la química es fundamental para comprender una amplia gama de disciplinas científicas. Este diagrama muestra solo algunas de las interrelaciones entre la química y otros campos.
¿Cuáles son algunos cambios en la materia que son esenciales para la vida diaria? Digerir y asimilar alimentos, sintetizar polímeros que se usan para hacer ropa, recipientes, utensilios de cocina y tarjetas de crédito, y refinar el petróleo crudo en gasolina y otros productos son solo algunos ejemplos. A medida que avanzas en este curso, descubrirás muchos ejemplos diferentes de cambios en la composición y estructura de la materia, cómo clasificar estos cambios y cómo ocurrieron, sus causas, los cambios en la energía que los acompañan y los principios y leyes involucrados. A medida que aprendas sobre estas cosas, aprenderás química, el estudio de la composición, las propiedades y las interacciones de la materia.
La práctica de la química no se limita a los libros o laboratorios de química: sucede cuando alguien está involucrado en cambios en la materia o en condiciones que pueden llevar a tales cambios.
La química es una ciencia basada en la observación y la experimentación. Hacer química implica intentar responder preguntas y explicar observaciones en términos de las leyes y teorías de la química, utilizando procedimientos aceptados por la comunidad científica. No hay una sola ruta para responder una pregunta o explicar una observación, pero hay un aspecto común en cada enfoque: cada uno utiliza el conocimiento basado en experimentos que pueden reproducirse para verificar los resultados. Algunas rutas implican una hipótesis, una explicación tentativa de las observaciones que actúa como una guía para recopilar y verificar información. Una hipótesis se prueba mediante experimentación, cálculo y/o comparación con los experimentos de otros y luego se refina según sea necesario.
Algunas hipótesis son intentos de explicar el comportamiento que se resume en las leyes. Las leyes de la ciencia resumen una gran cantidad de observaciones experimentales, y describen o predicen alguna faceta del mundo natural. Si tal hipótesis resulta ser capaz de explicar una gran cantidad de datos experimentales, puede alcanzar el estado de una teoría. Las teorías científicas son explicaciones bien fundamentadas, exhaustivas y comprobables de aspectos particulares de la naturaleza. Se aceptan las teorías porque proporcionan explicaciones satisfactorias. El camino del descubrimiento que conduce de la pregunta y la observación a la ley o de la hipótesis a la teoría, combinado con la verificación experimental de la hipótesis y cualquier modificación necesaria de la teoría, se denomina método científico (Figura 1.4).
Figura 1.4. El método científico sigue un proceso similar al que se muestra en este diagrama. Se muestran todos los componentes clave, aproximadamente en el orden correcto. El progreso científico rara vez es limpio y ordenado: requiere una investigación abierta y la reelaboración de preguntas e ideas en respuesta a los hallazgos.
Los químicos estudian y describen el comportamiento de la materia y la energía en tres dominios diferentes: macroscópico, microscópico y simbólico. Estos dominios proporcionan diferentes formas de considerar y describir el comportamiento químico.
Macro es una palabra griega que significa "grande". El dominio macroscópico nos es familiar: es el reino de las cosas cotidianas que son lo suficientemente grandes como para ser percibidas directamente por la vista o el tacto humano.
En la vida diaria, esto incluye los alimentos que comes y la brisa que sientes en tu cara. El dominio macroscópico incluye la química diaria y de laboratorio, donde observamos y medimos las propiedades físicas y químicas, como la densidad, la solubilidad y la inflamabilidad.
Micro proviene del griego y significa "pequeño". El dominio microscópico de la química a menudo se visita en la imaginación. Algunos aspectos del dominio microscópico son visibles a través de microscopios ópticos estándar, por ejemplo, muchas células biológicas. Los instrumentos más sofisticados son capaces de generar imágenes de entidades incluso más pequeñas, como moléculas y átomos (consulta la Figura 1.5 (b)).
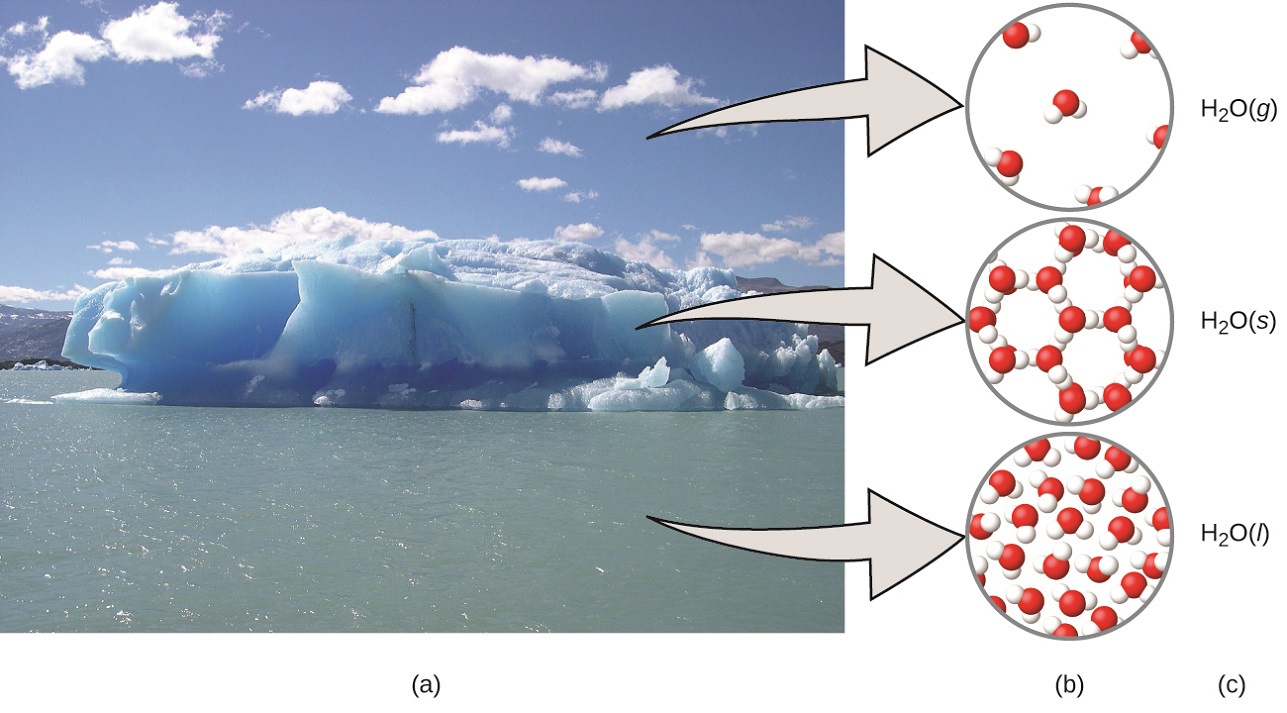
Figura 1.5. (a) La humedad en el aire, los icebergs y el océano representan agua en el dominio macroscópico. (b) A nivel molecular (dominio microscópico), las moléculas de gas están muy separadas y desorganizadas, las moléculas de agua sólida están muy juntas y organizadas, y las moléculas de líquido están muy juntas y desorganizadas. (c) La fórmula H2O simboliza el agua, y (g), (s) y (l) simbolizan sus fases. Ten en cuenta que las nubes en realidad comprenden gotas de agua líquida muy pequeñas o cristales de agua sólida. El agua gaseosa en nuestra atmósfera no es visible a simple vista, aunque puede ser percibida como humedad (crédito a: modificación del trabajo de "Gorkaazk"/Wikimedia Commons).
Sin embargo, la mayoría de los sujetos en el dominio microscópico de la química son demasiado pequeños para ser vistos incluso con los microscopios más avanzados y solo se pueden representar en la mente. Otros componentes del dominio microscópico incluyen iones y electrones, protones y neutrones, y enlaces químicos, cada uno de los cuales es demasiado pequeño para ver.
El dominio simbólico contiene el lenguaje especializado utilizado para representar componentes de los dominios macroscópicos y microscópicos. Los símbolos químicos (como los que se usan en la tabla periódica), las fórmulas químicas y las ecuaciones químicas forman parte del dominio simbólico, al igual que los gráficos, dibujos y cálculos. Estos símbolos juegan un papel importante en la química porque ayudan a interpretar el comportamiento del dominio macroscópico en términos de los componentes del dominio microscópico.
Uno de los desafíos para los estudiantes que aprenden química es reconocer que los mismos símbolos pueden representar diferentes cosas en los dominios macroscópicos y microscópicos, y una de las características que hace que la química sea fascinante es el uso de un dominio que debe imaginarse para explicar el comportamiento en un dominio que se puede observar.
Una forma útil de entender los tres dominios es a través de la sustancia esencial y ubicua del agua. El agua es un líquido a temperaturas moderadas, se congelará para formar un sólido a temperaturas más bajas y hervirá para formar un gas a temperaturas más altas (Figura 1.5), estas son observaciones macroscópicas.
Pero algunas propiedades del agua caen en el dominio microscópico, lo que no se puede observar a simple vista.
La descripción de que el agua comprende dos átomos de hidrógeno y un átomo de oxígeno, y la explicación de la congelación y la ebullición en términos de atracciones entre estas moléculas, se encuentra dentro del ámbito microscópico. La fórmula H2O, que puede describir el agua a nivel macroscópico o microscópico, es un ejemplo del dominio simbólico. Las abreviaturas (g) para gas, (s) para sólido y (l) para líquido también son simbólicas.
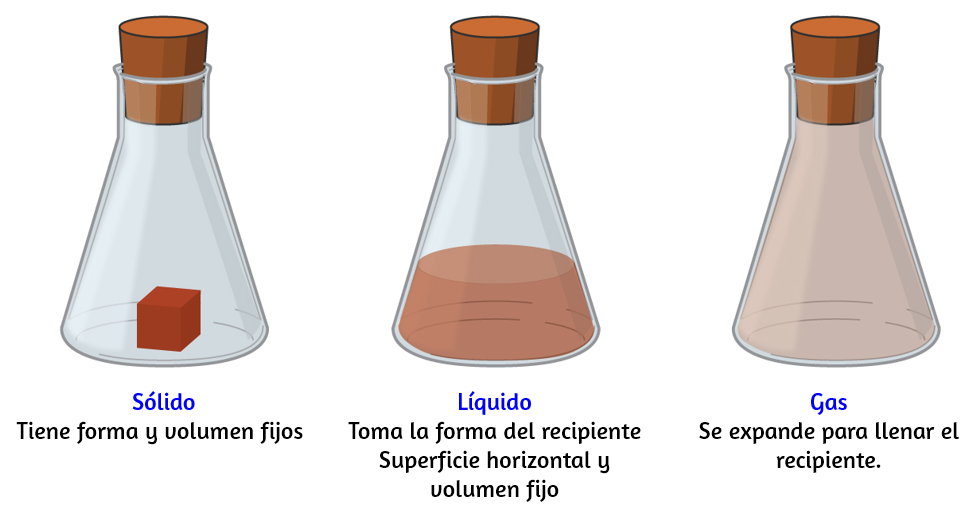
Figura 1.6. Los tres estados o fases más comunes de la materia son sólidos, líquidos y gases.
La materia se define como cualquier cosa que ocupa espacio y tiene masa, y está a nuestro alrededor. Los sólidos y los líquidos son más obvios: podemos ver que ocupan espacio y su peso nos dice que tienen masa. Los gases también son materia; Si los gases no ocuparan espacio, un globo no se inflaría (aumentaría su volumen) cuando se llenara con gas.
Los sólidos, los líquidos y los gases son los tres estados de la materia que se encuentran comúnmente en la tierra (Figura 1.6). Un sólido es rígido y posee una forma definida. Un líquido fluye y toma la forma de su recipiente, excepto que forma una superficie superior plana o ligeramente curvada cuando se actúa por gravedad (en gravedad cero, los líquidos adoptan una forma esférica). Tanto las muestras líquidas como las sólidas tienen volúmenes que son casi independientes de la presión. Un gas toma tanto la forma como el volumen de su recipiente.
En la siguiente página, presentamos nuestra primera escena interactiva, tomada de las simulaciones Phet, puedes calentar, enfriar o comprimir los átomos y moléculas y observar cómo cambian entre sólido, líquido y fases gaseosas. Con esta escena se espera que logres los siguientes resultados de aprendizaje:
Un cuarto estado de la materia, el plasma, ocurre naturalmente en los interiores de las estrellas. Un plasma es un estado gaseoso de la materia que contiene cantidades apreciables de partículas cargadas eléctricamente (Figura 1.7).
La presencia de estas partículas cargadas imparte propiedades únicas a los plasmas que justifican su clasificación como un estado de materia distinto de los gases. Además de las estrellas, los plasmas se encuentran en otros entornos de alta temperatura (tanto naturales
como artificiales), como rayos, ciertas pantallas de televisión e instrumentos analíticos especializados que se utilizan para detectar trazas de metales.
Algunas muestras de materia parecen tener propiedades de sólidos, líquidos y/o gases al mismo tiempo. Esto puede ocurrir cuando la muestra está compuesta de muchas piezas pequeñas.
Por ejemplo, podemos verter arena como si fuera un líquido porque está compuesta de muchos granos pequeños de arena sólida. La materia también puede tener propiedades de más de un estado cuando se trata de una mezcla, como con las nubes. Las nubes parecen comportarse de manera similar a los gases, pero en realidad son mezclas de aire (gas) y pequeñas partículas de agua (líquida o sólida).
Figura 1.7. Se puede usar una antorcha de plasma para cortar metal (crédito: "Hypertherm"/Wikimedia Commons).
La masa de un objeto es una medida de la cantidad de materia que contiene. Una forma de medir la masa de un objeto es medir la fuerza que se necesita para acelerar el objeto. Se necesita mucha más fuerza para acelerar un automóvil que una bicicleta porque el automóvil tiene mucha más masa. Una forma más común de determinar la masa de un objeto es usar un equilibrio para comparar su masa con una masa estándar.
Aunque el peso está relacionado con la masa, no es lo mismo. Peso se refiere a la fuerza que la gravedad ejerce sobre un objeto. Esta fuerza es directamente proporcional a la masa del objeto. El peso de un objeto cambia a medida que cambia la fuerza de la gravedad, pero su masa no. La masa de un astronauta no cambia solo porque va a la luna. Pero su peso en la luna es solo una sexta parte de su peso ligado a la Tierra porque la gravedad de la luna es solo una sexta parte de la de la Tierra. Puedes sentirte "sin peso" durante su viaje cuando experimentas fuerzas externas insignificantes (gravitacionales o de cualquier otro tipo), aunque, por supuesto, nunca estás "sin masa".
La ley de conservación de la materia resume muchas observaciones científicas sobre la materia: establece que no hay cambios detectables en la cantidad total de materia presente cuando se convierte de un tipo a otro (un cambio químico) o cambios entre sólidos, líquidos o gaseosos. La elaboración de la cerveza y el funcionamiento de las baterías dan ejemplos de la conservación de la materia (Figura 1.8).
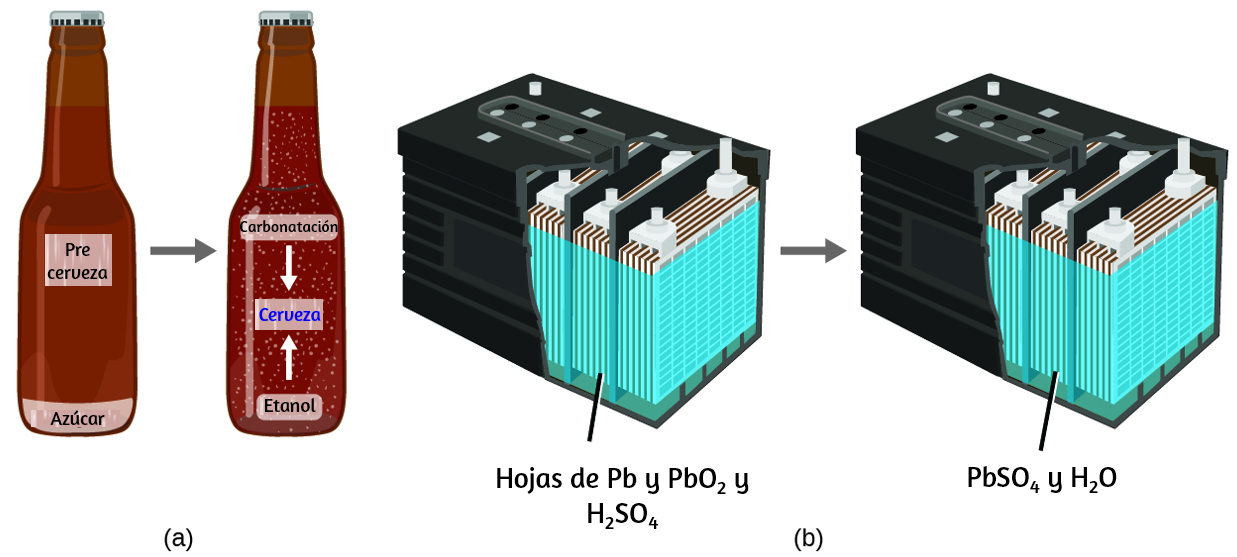
Figura 1.8. (a) La masa de los materiales precursores de la cerveza es la misma que la de la cerveza producida: el azúcar se ha convertido en alcohol y dióxido de carbono. (b) La masa de plomo, óxido de plomo y ácido sulfúrico consumida por la producción de electricidad es exactamente igual a la del sulfato de plomo y el agua que se forma.
Durante la elaboración de la cerveza, los ingredientes (agua, levadura, granos, malta, lúpulo y azúcar) se convierten en cerveza (agua, alcohol, carbonatación y sustancias aromatizantes) sin pérdida real de sustancia. Esto se ve más claramente durante el proceso de embotellado, cuando la glucosa se convierte en etanol y dióxido de carbono, y la masa total de las sustancias no cambia. Esto también se puede ver en una batería de plomo con ácido: las sustancias originales (plomo, óxido de plomo y ácido sulfúrico), que son capaces de producir electricidad, se convierten en otras sustancias (sulfato de plomo y agua) que no producen electricidad, sin cambio en la cantidad real de materia.
Si bien esta ley de conservación es válida para todas las conversiones de materia, los ejemplos convincentes son pocos y están muy lejos porque, fuera de las condiciones controladas en un laboratorio, rara vez recopilamos todo el material que se produce
durante una conversión en particular. Por ejemplo, cuando comes, digieres y asimilas alimentos, toda la materia del alimento original se conserva. Pero debido a que parte de la materia está incorporada en tu cuerpo, y mucho se excreta como varios tipos de desechos, es difícil de verificar mediante la medición.
La materia puede ser clasificada en varias categorías. Dos amplias categorías son las mezclas y las sustancias puras. Una sustancia pura tiene una composición constante. Todas las muestras de una sustancia pura tienen exactamente la misma composición y propiedades.
Cualquier muestra de sacarosa (azúcar de mesa) consiste en un 42,1% de carbono, un 6,5% de hidrógeno y un 51,4% de oxígeno en masa. Cualquier muestra de sacarosa también tiene las mismas propiedades físicas, como el punto de fusión, el color y el dulzor, independientemente de la fuente de la que se aísla. Las sustancias puras se pueden dividir en dos clases: elementos y compuestos. Las sustancias puras que no pueden descomponerse en sustancias más simples mediante cambios químicos se denominan elementos. El hierro, la plata, el oro, el aluminio, el azufre, el oxígeno y el cobre son ejemplos familiares de los más de 100 elementos conocidos, de los cuales alrededor de 90 están presentes de forma natural en la Tierra, y aproximadamente dos docenas se han creado en laboratorios.
Las sustancias puras que pueden descomponerse por cambios químicos se llaman compuestos. Este desglose puede producir elementos u otros compuestos, o ambos. El óxido de mercurio (II), una naranja, un sólido cristalino, se pueden descomponer por calor en los elementos mercurio y oxígeno (Figura 1.9). Cuando se calienta en ausencia de aire, el compuesto de sacarosa se descompone en el elemento carbono y el compuesto agua (la etapa inicial de este proceso, cuando el azúcar se está volviendo marrón, se conoce como caramelización, que es lo que imparte el característico sabor dulce y de nuez a las manzanas de caramelo, las cebollas caramelizadas y el caramelo). El cloruro de plata (I) es un sólido blanco que puede descomponerse en sus elementos, plata y cloro, por absorción de la luz. Esta propiedad es la base para el uso de este compuesto en películas fotográficas y gafas fotocrómicas (aquellas con lentes que se oscurecen cuando se exponen a la luz).
Las propiedades de los elementos combinados son diferentes de aquellas en el estado libre o no combinado.
Por ejemplo, el azúcar blanco cristalino (sacarosa) es un compuesto resultante de la combinación química del elemento carbono, que es un sólido negro en una de sus formas no combinadas, y los dos elementos hidrógeno y oxígeno, que son gases incoloros cuando no están combinados.
El sodio libre, un elemento que es un sólido metálico brillante y brillante, y el cloro libre, un elemento que es un gas amarillo verdoso, se combinan para formar cloruro de sodio (sal de mesa), un compuesto que es un sólido blanco y cristalino. Muchos compuestos se descomponen cuando se calientan. En el vídeo de la siguiente página, se muestra la descomposición del óxido de mercurio, $HgO$.
Figura 1.9. (a) El óxido de mercurio compuesto (II), (b) cuando se calienta, (c) se descompone en gotitas plateadas de mercurio líquido y gas de oxígeno invisible (crédito: modificación de la obra de Paul Flowers).
Una mezcla se compone de dos o más tipos de materia que pueden estar presentes en cantidades variables y pueden estar separadas por cambios físicos, como la evaporación (aprenderás más sobre esto más adelante). Una mezcla con una composición que varía de un punto a otro se llama una mezcla heterogénea. El aderezo italiano es un ejemplo de una mezcla heterogénea (Figura 1.10). Su composición puede variar porque puede prepararse a partir de cantidades variables de aceite, vinagre y hierbas.
No es lo mismo de un punto a otro a lo largo de la mezcla: una gota puede ser principalmente vinagre, mientras que una gota diferente puede ser principalmente aceite o hierbas porque el aceite y el vinagre se separan y las hierbas se asientan. Otros ejemplos de mezclas heterogéneas son las galletas con chispas de chocolate (podemos ver los trozos separados de chocolate, nueces y masa para galletas) y el granito (podemos ver el cuarzo, la mica, el feldespato y más).
Vídeo 1. Este vídeo muestra la reacción de descomposición del HgO y el oxígeno. Este trabajo fue creado por la Escuela de Ciencias y Matemáticas de Carolina del Norte (licenciado bajo Creative Commons CC-BY 3.0).
Una mezcla homogénea, también llamada solución, exhibe una composición uniforme y aparece visualmente de la misma forma. Un ejemplo de una solución es una bebida deportiva, que consiste en agua, azúcar, colorantes, saborizantes y electrolitos mezclados uniformemente (Figura 1.10). Cada gota de una bebida deportiva sabe igual porque cada gota contiene las mismas cantidades de agua, azúcar y otros componentes.
Figura 1.10. (a) El aderezo para ensaladas de aceite y vinagre es una mezcla heterogénea porque su composición no es uniforme en todo. (b) Una bebida deportiva comercial es una mezcla homogénea porque su composición es uniforme en todo (crédito "izquierda": modificación del trabajo por John Mayer; crédito "derecha": modificación del trabajo por Umberto Salvagnin; crédito b "izquierda": modificación del trabajo por Jeff Bedford).
Ten en cuenta que la composición de una bebida deportiva puede variar: se puede hacer con algo más o menos azúcar, saborizantes u otros componentes, y aún así ser una bebida deportiva. Otros ejemplos de mezclas homogéneas incluyen aire, jarabe de arce, gasolina y una solución de sal en agua. Aunque hay poco más de 100 elementos, decenas de millones de compuestos químicos resultan de diferentes combinaciones de estos elementos. Cada compuesto tiene una composición específica y posee propiedades físicas y químicas definidas que lo distinguen de todos los demás compuestos. Y, por supuesto, hay innumerables formas de combinar elementos y compuestos para formar diferentes mezclas. En la figura 1.11 se muestra un resumen de cómo distinguir entre las diversas clasificaciones principales de la materia.
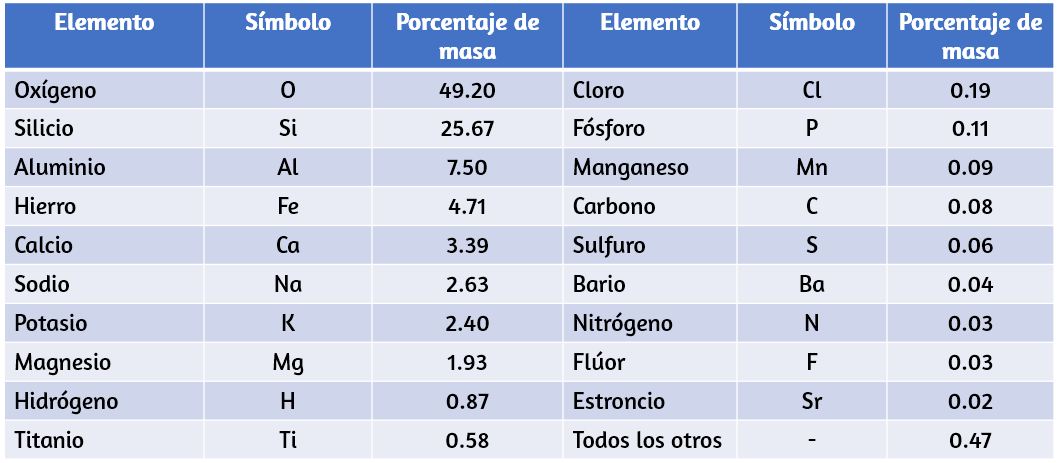
Once elementos constituyen aproximadamente el 99% de la corteza y la atmósfera de la tierra (Tabla 1.1). El oxígeno constituye casi la mitad y el silicio aproximadamente la cuarta parte de la cantidad total de estos elementos. La mayoría de los elementos en la tierra se encuentran en combinaciones químicas con otros elementos; aproximadamente una cuarta parte de los elementos también se encuentran en el estado libre.
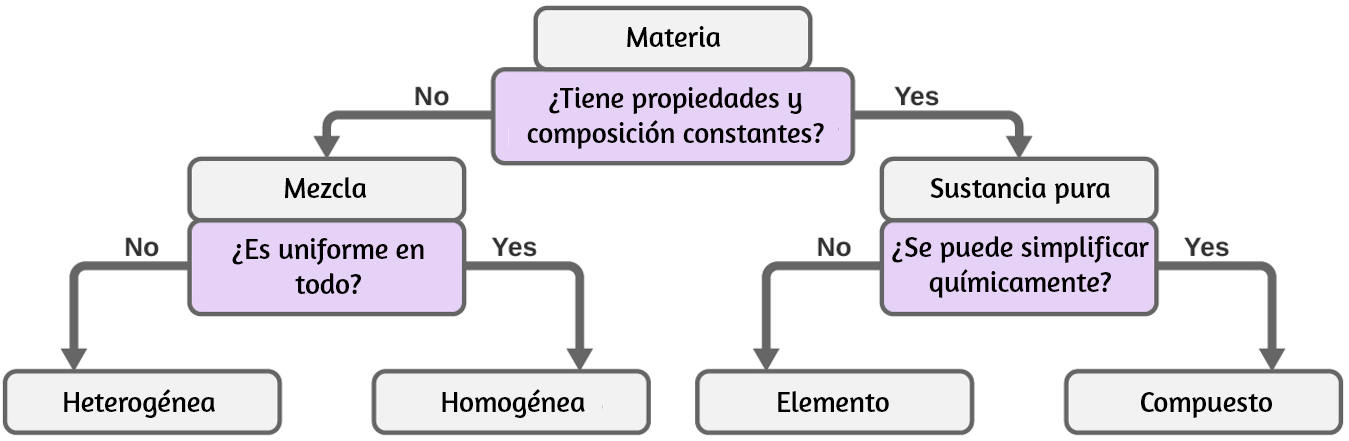
Figura 1.11. Dependiendo de sus propiedades, una sustancia dada puede clasificarse como una mezcla homogénea, una mezcla heterogénea, un compuesto o un elemento.
Tabla 1.1. Composición elemental de la tierra.
Un átomo es la partícula más pequeña de un elemento que tiene las propiedades de ese elemento y puede entrar en una combinación química.
Consideremos el elemento oro, por ejemplo. Imagina cortar una pepita de oro por la mitad, luego cortar una de las mitades por la mitad y repetir este proceso hasta que quede una pieza de oro que sea tan pequeña que no se pueda cortar por la mitad (independientemente de lo pequeño que pueda ser tu cuchillo). Esta pieza de oro de tamaño mínimo es un átomo (del atomo griego, que significa "indivisible") (Figura 1.12). Este átomo ya no sería oro si se siguiera dividiendo.
Figura 1.12. (a) Esta fotografía muestra una pepita de oro. (b) Un microscopio de exploración de túneles (STM) puede generar vistas de las superficies de los sólidos, como esta imagen de un cristal de oro. Cada esfera representa un átomo de oro (crédito a: modificación del trabajo por el Servicio Geológico de los Estados Unidos; crédito b: modificación del trabajo por "Erwinrossen"/Wikimedia Commons).
La primera sugerencia de que la materia está compuesta de átomos se atribuye a los filósofos griegos Leucipo y Demócrito, quienes desarrollaron sus ideas en el siglo V a. C. Sin embargo, no fue hasta principios del siglo XIX que John Dalton (1766–1844), un maestro de escuela británico con un gran interés en la ciencia, apoyó esta hipótesis con medidas cuantitativas.
Desde entonces, los experimentos repetidos han confirmado muchos aspectos de esta hipótesis, y se ha convertido en una de las teorías centrales de la química. Se siguen utilizando otros aspectos de la teoría atómica de Dalton, pero con revisiones menores.
Un átomo es tan pequeño que su tamaño es difícil de imaginar. Una de las cosas más pequeñas que podemos ver a simple vista es un solo hilo de una tela de araña: estas hebras tienen aproximadamente 1/10,000 de un centímetro (0.0001 cm) de diámetro. Aunque la sección transversal de una hebra es casi imposible de ver sin un microscopio, es enorme en una escala atómica. Un solo átomo de carbono en la hebra tiene un diámetro de aproximadamente 0.000000015 centímetros, y tomaría aproximadamente 7000 átomos de carbono para abarcar el diámetro de la hebra. Para poner esto en perspectiva, si un átomo de carbono fuera del tamaño de una moneda de diez centavos, la sección transversal de una hebra sería más grande que un campo de fútbol, lo que requeriría unos 150 millones de átomos de carbono para cubrirlo. La figura 1.13 muestra vistas microscópicas y atómicas cada vez más cercanas del algodón ordinario.
Figura 1.13. Estas imágenes proporcionan una visión cada vez más cercana: (a) una cápsula de algodón, (b) una sola fibra de algodón vista bajo un microscopio óptico (ampliada 40 veces), (c) una imagen de una fibra de algodón obtenida con un microscopio electrónico (ampliación mucho mayor que con el microscopio óptico); y (d y e) modelos a nivel atómico de la fibra (esferas de diferentes colores representan átomos de diferentes elementos). (crédito c: modificación del trabajo de "Featheredtar"/Wikimedia Commons).
Un átomo es tan ligero que su masa también es difícil de imaginar. Un billón de átomos de plomo ($1,000,000,000$ de átomos) pesan alrededor de $3 \times 10^{-13}\; gramos$, una masa que es demasiado liviana para pesarla incluso en las balanzas más sensibles del mundo. Requeriría pesar más de $300,000,000,000,000$ de átomos de plomo ($300\space trillones$, o $\space\space 3 \times 10^{14}$), y pesarían solo $0.0000001\; gramos$.
Es raro encontrar colecciones de átomos individuales. Solo unos pocos elementos, como los gases helio, neón y argón, consisten en una colección de átomos individuales que se mueven de forma independiente unos de otros. Otros elementos, como los gases hidrógeno, nitrógeno, oxígeno y cloro, están compuestos por unidades que consisten en pares de átomos (Figura 1.14). Una forma del elemento fósforo consiste en unidades compuestas de cuatro átomos de fósforo. El elemento azufre existe en varias formas, una de las cuales consiste en unidades compuestas de ocho átomos de azufre. Estas unidades se llaman moléculas. Una molécula consiste en dos o más átomos unidos por fuerzas fuertes llamadas enlaces químicos.
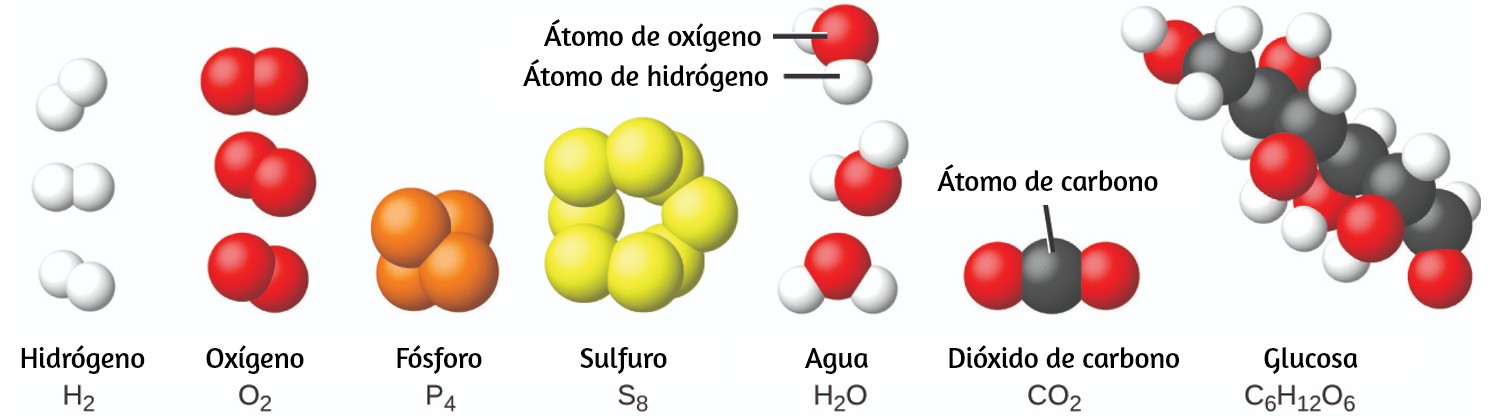
Figura 1.14. Los elementos hidrógeno, oxígeno, fósforo y azufre forman moléculas que consisten en dos o más átomos del mismo elemento. Los compuestos agua, dióxido de carbono y glucosa consisten en combinaciones de átomos de diferentes elementos.
Los átomos en una molécula se mueven como una unidad, al igual que las latas de refresco en un paquete de seis o un montón de llaves unidas en un solo llavero. Una molécula puede consistir en dos o más átomos idénticos, como en las moléculas que se encuentran en los elementos de hidrógeno, oxígeno y azufre, o puede consistir en dos o más átomos diferentes, como en las moléculas que se encuentran en el agua. Cada molécula de agua es una unidad que contiene dos átomos de hidrógeno y un átomo de oxígeno. Cada molécula de glucosa es una unidad que contiene 6 átomos de carbono, 12 átomos de hidrógeno y 6 átomos de oxígeno. Al igual que los átomos, las moléculas son increíblemente pequeñas y ligeras. Si un vaso de agua ordinario se ampliara al tamaño de la tierra, las moléculas de agua en su interior serían aproximadamente del tamaño de pelotas de golf.
Química en la vida cotidiana
El agua se compone de los elementos hidrógeno y oxígeno combinados en una proporción de 2 a 1. El agua se puede descomponer en hidrógeno y gases de oxígeno mediante la adición de energía. Una forma de hacerlo es con una batería o una fuente de alimentación, como se muestra en (Figura 1.15).
La descomposición del agua implica una reorganización de los átomos en moléculas de agua en moléculas diferentes, cada una compuesta de dos átomos de hidrógeno y dos átomos de oxígeno, respectivamente. Dos moléculas de agua forman una molécula de oxígeno y dos moléculas de hidrógeno. La representación de lo que ocurre, $\ce{2H2O(l) -> 2H2(g) + O2(g)}$, se explorará con mayor profundidad en los capítulos posteriores.
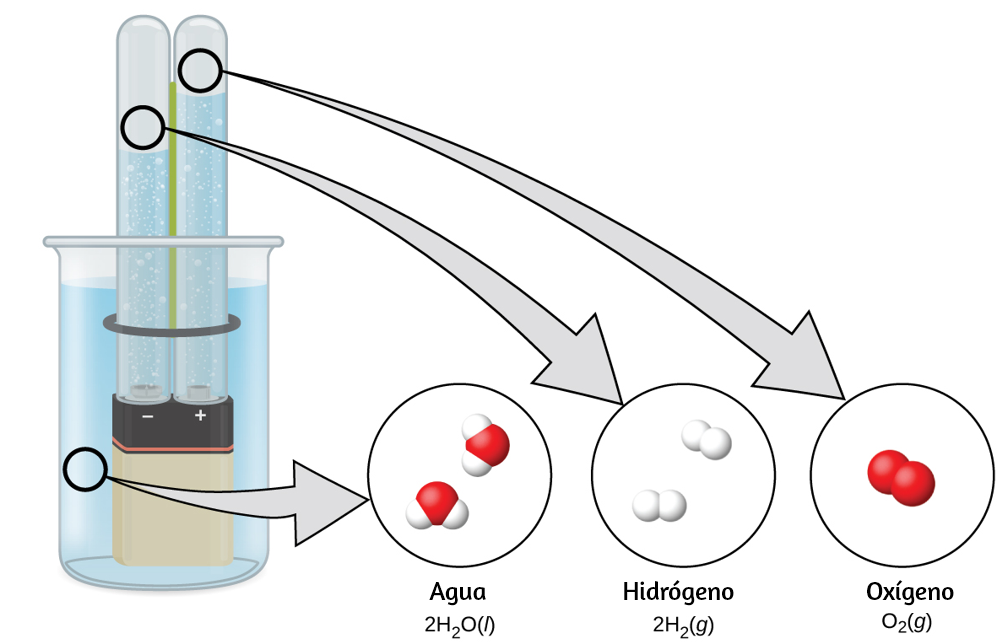
Figura 1.15. La descomposición del agua se muestra en los niveles macroscópico, microscópico y simbólico. La batería proporciona una corriente eléctrica (microscópica) que descompone el agua. A nivel macroscópico, el líquido se separa en los gases hidrógeno (a la izquierda) y oxígeno (a la derecha). Simbólicamente, este cambio se presenta al mostrar cómo el $H_2O$ líquido se separa en los gases $H_2$ y $O_2$.
Los dos gases producidos tienen propiedades claramente diferentes. El oxígeno no es inflamable, pero se requiere para la combustión de un combustible, y el hidrógeno es altamente inflamable y una potente fuente de energía. ¿Cómo se puede aplicar este conocimiento en nuestro mundo? Una aplicación involucra la investigación de un transporte más eficiente en el uso de combustible. Los vehículos de celda de combustible (FCV) funcionan con hidrógeno en lugar de gasolina (Figura 1.16). Son más eficientes que los vehículos con motores de combustión interna, no son contaminantes y reducen las emisiones de gases de efecto invernadero, lo que nos hace menos dependientes de los combustibles fósiles. Sin embargo, los FCV aún no son económicamente viables y la producción actual de hidrógeno depende del gas natural.
Si podemos desarrollar un proceso para descomponer económicamente el agua, o producir hidrógeno de otra manera ambientalmente racional, los FCV pueden ser el camino del futuro.
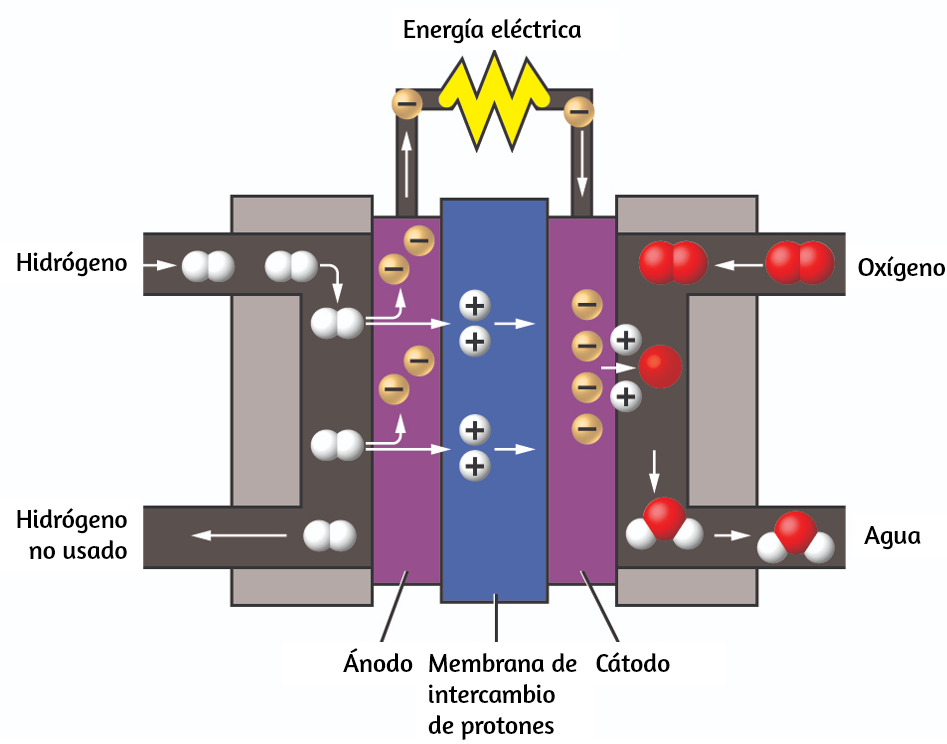
Figura 1.16. Una celda de combustible genera energía eléctrica a partir de hidrógeno y oxígeno a través de un proceso electroquímico y produce solo agua como producto de desecho.
Química en la vida cotidiana
Imagina cuán diferente sería tu vida sin teléfonos celulares (Figura 1.17) y otros dispositivos inteligentes. Los teléfonos celulares están hechos de numerosas sustancias químicas, que se extraen, refinan, purifican y ensamblan utilizando una comprensión extensa y profunda de los principios químicos.
Alrededor del 30% de los elementos que se encuentran en la naturaleza se encuentran dentro de un teléfono inteligente típico. El estuche/cuerpo/armazón consiste en una combinación de polímeros resistentes y duraderos compuestos principalmente de carbono, hidrógeno, oxígeno y nitrógeno [acrilonitrilo butadieno estireno (ABS) y termoplásticos de policarbonato], y metales estructurales livianos y fuertes, como el aluminio, magnesio y hierro. La pantalla de visualización está hecha de un vidrio especialmente templado (vidrio de sílice reforzado por la adición de aluminio, sodio y potasio) y recubierto con un material para hacerlo conductor (como el óxido de indio y estaño). La placa de circuito usa un material semiconductor (generalmente silicio); Metales comúnmente usados como cobre, estaño, plata y oro; y elementos más desconocidos como itrio, praseodimio y gadolinio. La batería se basa en iones de litio y en una variedad de otros materiales, como hierro, cobalto, cobre, óxido de polietileno y poliacrilonitrilo.
Figura 1.17. Casi un tercio de los elementos naturales se utilizan para hacer un teléfono celular (crédito: modificación de obra por John Taylor).
Las características que distinguen una sustancia de otra se llaman propiedades. Una propiedad física es una característica de la materia que no está asociada con un cambio en su composición química. Los ejemplos de propiedades físicas incluyen densidad, color, dureza, puntos de fusión y ebullición, y conductividad eléctrica. Algunas propiedades físicas, como la densidad y el color, pueden observarse sin cambiar el estado físico de la materia. Otras propiedades físicas, como la temperatura de fusión del hierro o la temperatura de congelación del agua, solo se pueden observar cuando la materia experimenta un cambio físico, el cual es un cambio en el estado o las propiedades de la materia sin ningún cambio acompañante en las identidades químicas de las sustancias contenidas en la materia. Se observan cambios físicos cuando la cera se derrite, cuando el azúcar se disuelve en el café y cuando el vapor se condensa en agua líquida (Figura 1.18).
Figura 1.18. (a) La cera sufre un cambio físico cuando la cera sólida se calienta y forma cera líquida. (b) La condensación de vapor dentro de una olla es un cambio físico, ya que el vapor de agua se transforma en agua líquida (crédito a: modificación del trabajo por "95jb14"/Wikimedia Commons; crédito b: modificación del trabajo por "mjneuby"/Flickr).
El cambio de un tipo de materia en otro tipo (o la incapacidad de cambiar) es una propiedad química. Los ejemplos de propiedades químicas incluyen inflamabilidad, toxicidad, acidez y muchos otros tipos de reactividad. El hierro, por ejemplo, se combina con el oxígeno en presencia de agua para formar óxido; El cromo no se oxida (Figura 1.19). La nitroglicerina es muy peligrosa porque explota fácilmente.
Otros ejemplos de cambios físicos incluyen la magnetización y desmagnetización de metales (como se hace con las etiquetas de seguridad antirrobo comunes) y la molienda de sólidos en polvos (que a veces pueden producir cambios notables en el color). En cada uno de estos ejemplos, hay un cambio en el estado físico, la forma o las propiedades de la sustancia, pero ningún cambio en su composición química. El neón casi no representa peligro porque es muy poco reactivo.
Figura 1.19. (a) Una de las propiedades químicas del hierro es que se oxida; (b) una de las propiedades químicas del cromo es que no lo hace (crédito a: modificación del trabajo de Tony Hisgett; crédito b: modificación del trabajo de "Atoma"/Wikimedia Commons).
Un cambio químico siempre produce uno o más tipos de materia que difieren de la materia presente antes del cambio. La formación de óxido es un cambio químico porque el óxido es un tipo diferente de materia que el hierro, el oxígeno y el agua presentes antes de que se formara el óxido.
Figura 1.20. (a) El cobre y el ácido nítrico experimentan un cambio químico para formar nitrato de cobre y dióxido de nitrógeno gaseoso marrón. (b) Durante la combustión deln fósforo, la celulosa en el fósforo y el oxígeno del aire experimentan un cambio químico para formar dióxido de carbono y vapor de agua. (c) Cocinar la carne roja provoca una serie de cambios químicos, incluida la oxidación del hierro en la mioglobina, que provoca el cambio familiar del color rojo al marrón. (d) Un plátano que se vuelve marrón es un cambio químico a medida que se forman nuevas sustancias más oscuras (y menos sabrosas). (Crédito b: modificación del trabajo de Jeff Turner; crédito c: modificación del trabajo de Gloria Cabada-Leman; crédito d: modificación del trabajo de Roberto Verzo).
Las propiedades de la materia caen en una de dos categorías. Si la propiedad depende de la cantidad de materia presente, es una propiedad extensa. La masa y el volumen de una sustancia son ejemplos de propiedades extensivas; por ejemplo, un galón de leche tiene una masa más grande que una taza de leche. El valor de una propiedad extensa es directamente proporcional a la cantidad de materia en cuestión. Si la propiedad de una muestra de materia no depende de la cantidad de materia presente, es una propiedad intensiva (la temperatura, por un ejemplo). Si el galón y la taza de leche están a 20 °C (temperatura ambiente), cuando se combinan, la temperatura se mantiene en 20 °C. Otro ejemplo son las propiedades distintas pero relacionadas del calor y la temperatura. Una gota de aceite de cocina caliente salpicado en tu brazo causa una pequeña molestia, mientras que una olla de aceite caliente produce quemaduras graves. Tanto la gota como la olla de aceite están a la misma temperatura (una propiedad intensiva), pero la olla claramente contiene mucho más calor (propiedad extensiva).
Química en la vida cotidiana
Es posible que hayas visto el símbolo que se muestra en la figura 1.21 en contenedores de productos químicos en un laboratorio o lugar de trabajo.
A veces llamado "diamante de fuego" o "diamante de peligro", este diamante de riesgo químico proporciona información valiosa que resume brevemente los diversos peligros de los que debes estar atento al trabajar con una sustancia en particular.
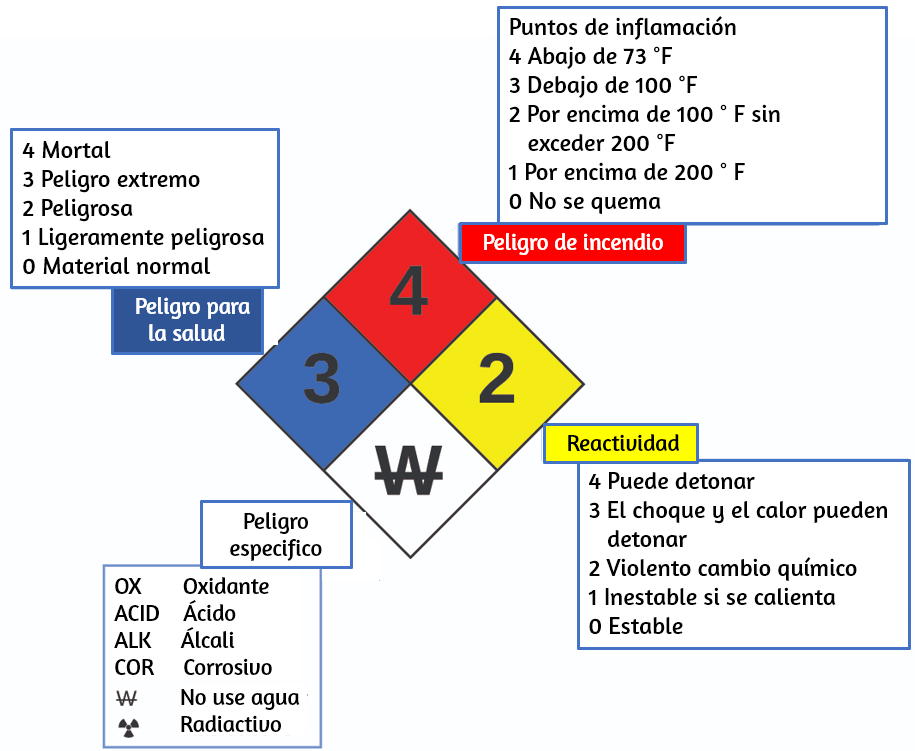
Figura 1.21. El diamante de peligro de la Agencia Nacional de Protección contra Incendios (NFPA, por sus siglas en inglés) resume los principales peligros de una sustancia química.
El Sistema de Identificación de Peligros 704 de la Agencia Nacional de Protección contra Incendios (NFPA) fue desarrollado por NFPA para proporcionar información de seguridad sobre ciertas sustancias.
El sistema detalla la inflamabilidad, la reactividad, la salud y otros peligros. Dentro del símbolo de diamante general, el diamante superior (rojo) especifica el nivel de riesgo de incendio (rango de temperatura para el punto de inflamación). El diamante azul (izquierdo) indica el nivel de peligro para la salud. El diamante amarillo (a la derecha) describe los peligros de reactividad, como la facilidad con que la sustancia se detonará o un cambio químico violento. El diamante blanco (abajo) señala peligros especiales, como si se trata de un oxidante (que permite que la sustancia se queme en ausencia de aire/oxígeno), sufre una reacción inusual o peligrosa con el agua, es corrosivo, ácido, alcalino, Un peligro biológico, radioactivo, etc. Cada peligro se clasifica en una escala de 0 a 4, donde 0 no es peligroso y 4 es extremadamente peligroso.
Si bien muchos elementos difieren dramáticamente en sus propiedades químicas y físicas, algunos elementos tienen propiedades similares. Por ejemplo, muchos elementos conducen bien el calor y la electricidad, mientras que otros son malos conductores. Estas propiedades se pueden usar para clasificar los elementos en tres clases: metales (elementos que conducen bien), no metales (elementos que conducen mal) y metaloides (elementos que tienen conductividades intermedias).
La tabla periódica es una tabla de elementos que coloca elementos con propiedades similares muy cerca (Figura 1.22). Aprenderás más sobre la tabla periódica a medida que continúes tu estudio de química.
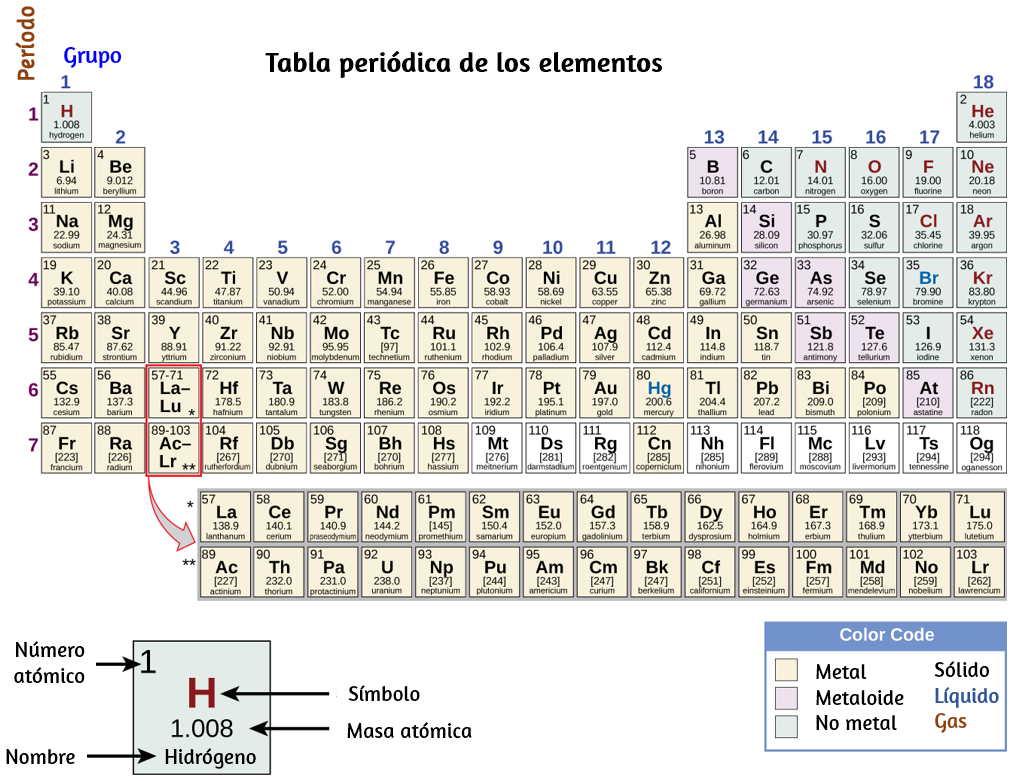
Figura 1.22. La tabla periódica muestra cómo se pueden agrupar los elementos de acuerdo con ciertas propiedades similares. Observa que el color de fondo indica si un elemento es un metal, metaloide o no metal, mientras que el color del símbolo del elemento indica si es un sólido, líquido o gas.
Presentamos, también, una tabla periódica interactiva diseñada por Juan Guillermo Rivera Berrío, en la cual puedes seleccionar un elemento químico y conocer algunas características adicionales, que se explicarán con más detalle en capítulos posteriores.
En este interactivo, pasa el puntero del ratón sobre un elemento para leer algunas de sus características. También puedes identificar los tipos de elementos metales y no metales. El color del elemento define si se trata de un elemento sólido, líquidos, gaseoso o desconocido.
Las mediciones proporcionan gran parte de la información que dan las hipótesis, teorías y leyes que describen el comportamiento de la materia y la energía tanto en el dominio macroscópico como en el microscópico de la química. Cada medición proporciona tres tipos de información: el tamaño o la magnitud de la medición (un número); un estándar de comparación para la medida (una unidad); y una indicación de la incertidumbre de la medida. Mientras que el número y la unidad se representan explícitamente cuando se escribe una cantidad, la incertidumbre es un aspecto del resultado de la medición que se representa de manera más implícita y se explicará más adelante.
El número en la medición se puede representar de diferentes maneras, incluida la forma decimal y la notación científica (la notación científica también se conoce como notación exponencial). Por ejemplo, el peso máximo de despegue de un avión Boeing 777-200ER es de 298,000 kilogramos, que también puede escribirse como 2.98 × 105 kg. La masa del mosquito promedio es de aproximadamente 0.0000025 kilogramos, que puede escribirse como 2.5 × 10−6 kg.
Las unidades, como litros, libras y centímetros, son estándares de comparación para las mediciones. Una botella de 2 litros de un refresco contiene un volumen de bebida que es el doble del volumen aceptado de 1 litro. La carne utilizada para preparar una hamburguesa de 0.25 libras pesa un cuarto del peso aceptado de 1 libra. Sin unidades, un número puede ser sin sentido, confuso o posiblemente mortal. Supongamos que un médico prescribe fenobarbital para controlar las convulsiones de un paciente y establece una dosis de "100" sin especificar unidades. Esto no solo será confuso para el profesional médico que administra la dosis, sino que las consecuencias pueden ser terribles: 100 mg administrados tres veces al día pueden ser eficaces como anticonvulsivos, pero una dosis única de 100 g es más de 10 veces la cantidad letal.
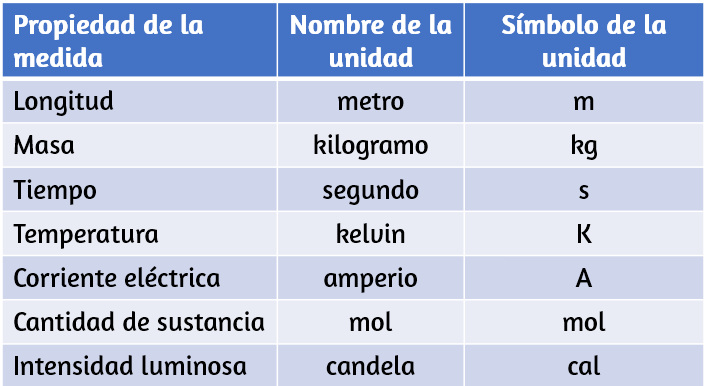
Las unidades de medida para siete propiedades fundamentales ("unidades base") se enumeran en la tabla 1.2. Los estándares para estas unidades están fijados por acuerdo internacional, y se denominan Sistema Internacional de Unidades o Unidades SI (del francés, Système International d’Unités). Las unidades SI han sido utilizadas por el Instituto Nacional de Estándares y Tecnología (NIST) de los Estados Unidos desde 1964. Las unidades para otras propiedades pueden derivarse de estas siete unidades base.
Tabla 1.2. Unidades base del sistema SI.
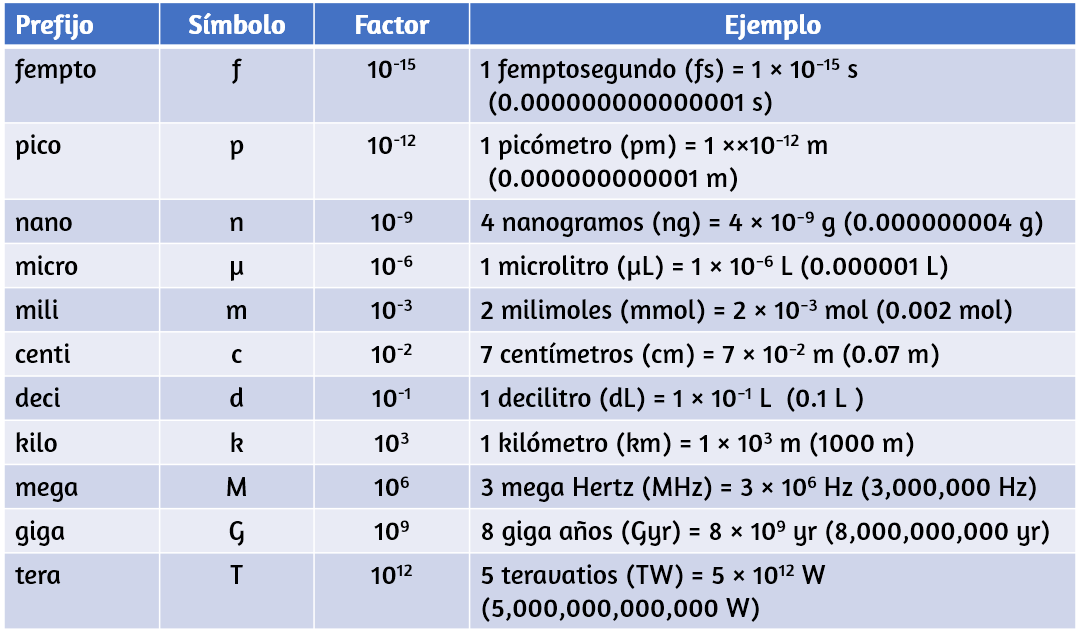
Las unidades de medición diarias a menudo se definen como fracciones o múltiplos de otras unidades. La leche se envasa comúnmente en envases de 1 galón (4 cuartos de galón), 1 cuarto de galón (0.25 galones) y una pinta (0.5 cuarto de galón). Este mismo enfoque se usa con unidades SI, pero estas fracciones o múltiplos son siempre potencias de 10. Las unidades SI fraccionales o múltiples se nombran usando un prefijo y el nombre de la unidad base. Por ejemplo, una longitud de 1000 metros también se denomina kilómetro porque el prefijo kilo significa "mil", que en notación científica es 103 (1 kilómetro = 1000 m = 103 m). Los prefijos utilizados y las potencias a las que se elevan el 10 se enumeran en la Tabla 1.3.
Es importante que sepas identificar la notación científica en una calculadora. En la siguiente página te presentamos una calculadora, diseñada por Peter Dematté, en la cual vas realizar el siguiente cálculo: 20! (digitas 20 y lueho haces clic en x!). El número que te aparece es 2.43290200811766e+18, que es lo mismo que 2.43x1018.
Tabla 1.3. Prefijos de unidades comunes
Las unidades iniciales del sistema métrico, que eventualmente evolucionaron hacia el sistema SI, se establecieron en Francia durante la Revolución Francesa. Los estándares originales para el metro y el kilogramo fueron adoptados allí en 1799 y eventualmente por otros países. Esta sección presenta cuatro de las unidades base del SI que se usan comúnmente en química. Otras unidades del SI se introducirán en capítulos posteriores de este libro.
La unidad estándar de longitud tanto en el SI como en los sistemas métricos originales es el metro (m). Un metro se especificó originalmente como 1/10,000,000 de la distancia desde el Polo Norte hasta el ecuador.
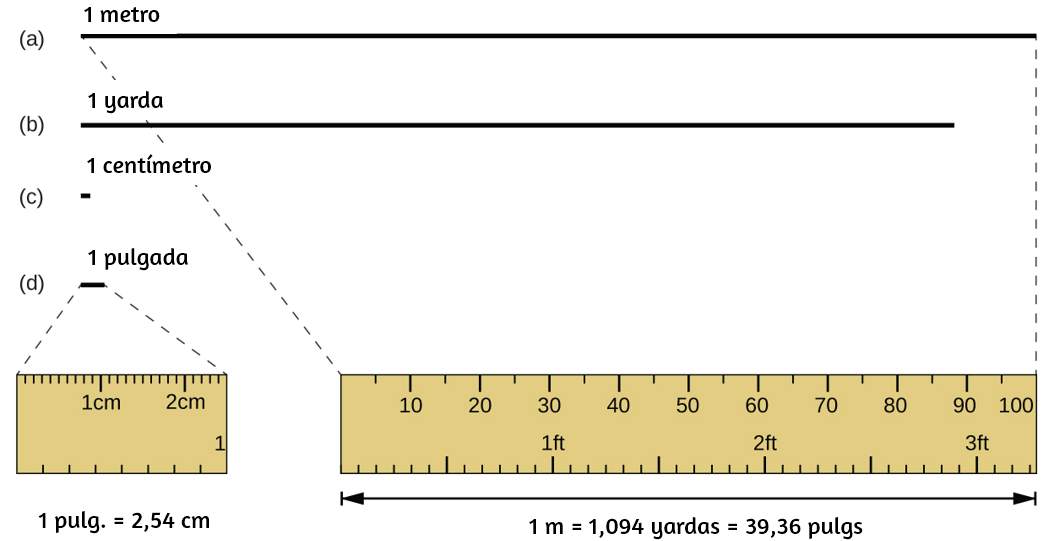
Figura 1.23. Se muestran las longitudes relativas de 1 m, 1 yd, 1 cm y 1 pulg (no del tamaño real), así como comparaciones de 2.54 cm y 1 pulg., y de 1 m y 1.094 yd.
Ahora se define como la distancia que la luz en el vacío viaja en 1/299,792,458 de segundo. Un metro es aproximadamente 3 pulgadas más largo que una yarda (Figura 1.23); Un metro mide aproximadamente 39.37 pulgadas o 1.094 yardas. Las distancias más largas a menudo se dan en kilómetros $(1 \;km = 1000 m = 10^3\; m)$, mientras que las distancias más cortas se pueden dan en centímetros $(1\; cm = 0.01\; m = 10^{-2}\; m)$ o milímetros $(1\; mm = 0.001\; m = 10^{−3} \;metro)$.
La unidad estándar de masa en el sistema SI es el kilogramo (kg). Un kilogramo se definió originalmente como la masa de un litro de agua (un cubo de agua con una longitud de borde de exactamente 0.1 metros). Ahora está definido por un cierto cilindro de aleación de platino-iridio, que se mantiene en Francia (Figura 1.24). Cualquier objeto con la misma masa que este cilindro se dice que tiene una masa de 1 kilogramo. Un kilogramo es de aproximadamente 2.2 libras. El gramo (g) es exactamente igual a 1/1000 de la masa del kilogramo (10−3 kg).
La temperatura es una propiedad intensiva. La unidad de temperatura SI es el kelvin (K). La convención IUPAC es usar kelvin (todo en minúsculas) para la palabra, K (mayúscula) para el símbolo de la unidad, y sin la palabra "grado" ni el símbolo de grado (°). El grado Celsius (°C) también se permite en el sistema SI, con la palabra "grado" y el símbolo de grado utilizado para las mediciones de Celsius. Los grados Celsius son de la misma magnitud que los de kelvin, pero las dos escalas colocan sus ceros en diferentes lugares.
Figura 1.24. Esta réplica de un prototipo de kilogramo se encuentra en el Instituto Nacional de Estándares y Tecnología (NIST) en Maryland (crédito: Institutos Nacionales de Estándares y Tecnología).
El agua se congela a 273.15 K (0 °C) y hierve a 373.15 K (100 °C) por definición, y la temperatura normal del cuerpo humano es de aproximadamente 310 K (37 °C).
La unidad de tiempo base del SI es el segundo (s). Los intervalos de tiempo pequeños y grandes se pueden expresar con los prefijos apropiados; por ejemplo, 3 microsegundos = 0.000003 s = 3 × 10−6 y 5 megasegundos = 5,000,000 s = 5 × 106s. Alternativamente, se pueden usar horas, días y años.
Podemos derivar muchas unidades de las siete unidades base SI. Por ejemplo, podemos usar la unidad base de longitud para definir una unidad de volumen, y las unidades base de masa y longitud para definir una unidad de densidad.
El volumen es la medida de la cantidad de espacio ocupado por un objeto. La unidad de volumen SI estándar se define por la unidad base de longitud (Figura 1.25).
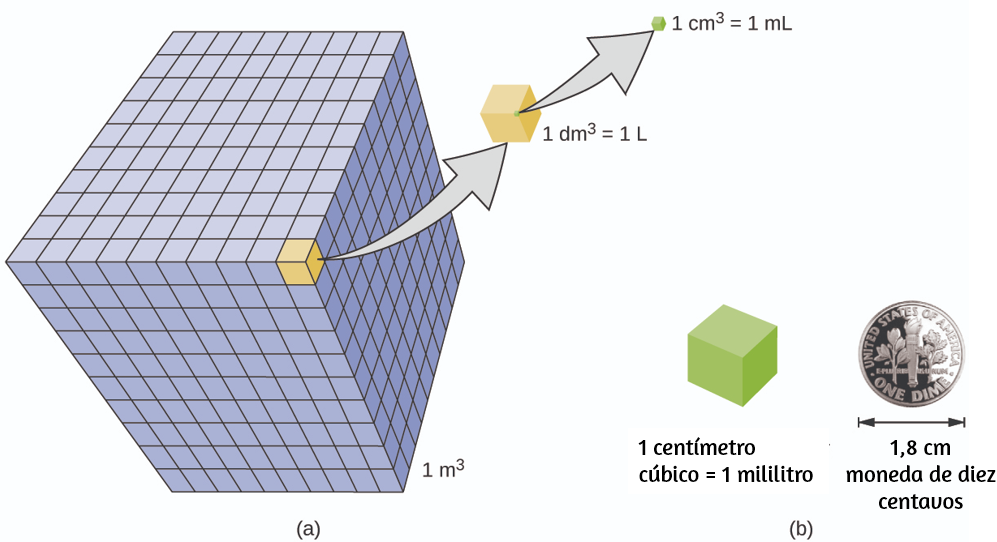
Figura 1.25. (a) Los volúmenes relativos se muestran para cubos de 1 m3, 1 dm3 (1 l) y 1 cm3 (1 ml) (no a escala). (b) El diámetro de una moneda de diez centavos se compara con respecto a la longitud del borde de un cubo de 1 cm3 (1 ml).
El volumen estándar es un metro cúbico (m3), un cubo con una longitud de borde de exactamente un metro. Para dispensar un metro cúbico de agua, podríamos construir una caja cúbica con longitudes de borde de exactamente un metro. Esta caja podría contener un metro cúbico de agua o cualquier otra sustancia.
Una unidad de volumen más utilizada se deriva del decímetro (0.1 m, o 10 cm).
Un cubo con longitudes de borde de exactamente un decímetro contiene un volumen de un decímetro cúbico (dm3). Un litro (L) es el nombre más común para el decímetro cúbico. Un litro es alrededor de 1.06 cuartos de galón.
Un centímetro cúbico (cm3) es el volumen de un cubo con una longitud de borde de exactamente un centímetro. La abreviatura cc (por centímetro cúbico) a menudo es utilizada por profesionales de la salud. Un centímetro cúbico es equivalente a un mililitro (mL) y es 1/1000 de un litro.
Utilizamos la masa y el volumen de una sustancia para determinar su densidad. Así, las unidades de densidad están definidas por las unidades básicas de masa y longitud.
La densidad de una sustancia es la relación entre la masa de una muestra de la sustancia y su volumen. La unidad SI para densidad es el kilogramo por metro cúbico (kg/m3). Sin embargo, para muchas situaciones, esto es una unidad inconveniente, y con frecuencia usamos gramos por centímetro cúbico (g/cm3) para las densidades de sólidos y líquidos, y gramos por litro (g/l) para gases.
Aunque hay excepciones, la mayoría de los líquidos y sólidos tienen densidades que van desde aproximadamente 0.7 g/cm3 (la densidad de la gasolina) hasta 19 g/cm3 (la densidad del oro). La densidad del aire es de aproximadamente 1.2 g/l. La tabla 1.4 muestra las densidades de algunas sustancias comunes.
Si bien hay muchas maneras de determinar la densidad de un objeto, tal vez el método más directo consiste en encontrar por separado la masa y el volumen del objeto, y luego dividir la masa de la muestra por su volumen. En el siguiente ejemplo, la masa se encuentra directamente al pesar, pero el volumen se encuentra indirectamente a través de mediciones de longitud.
$$densidad = \cfrac{masa}{volumen}$$Tabla 1.4. Densidades de sustancias comunes
Ejemplo 1.1
Cálculo de la densidad
El oro, en lingotes, barras y monedas, ha sido una forma de moneda durante siglos. Con el fin de estafar a la gente para que pague por un lingote de oro sin invertir realmente en un lingote de oro, la gente ha considerado llenar los centros huecos de los lingotes con plomo para engañar a los compradores para que piensen que todo el ladrillo es oro. No funciona: el plomo es una sustancia densa, pero su densidad no es tan grande como la del oro, 19.3 g/cm3. ¿Cuál es la densidad del plomo si un cubo de plomo tiene una longitud de borde de 2.00 cm y una masa de 90.7 g?
Solución
La densidad de una sustancia se puede calcular dividiendo su masa por su volumen. El volumen de un cubo se calcula al cubicar la longitud del borde.
$$volumen = 2.00 \;cm \times 2.00\; cm \times 2.00\; cm = 8.00\; cm^3$$ $$densidad = \cfrac{masa}{volumen} = \cfrac{90.7\;g}{8.00\;cm^3} = \cfrac{11.3\;g}{1.00\;cm^3} = 11.3\; g/cm^3$$(Discutiremos la razón para redondear al primer decimal en la siguiente sección).
Comprueba tu aprendizaje
En esta unidad interactiva del Proyecto @prende.mx, puedes comprender la importancia de la densidad en otros fenómenos como la flotabilidad de un objeto en diferentes líquidos.
Ejemplo 1.2
Uso del desplazamiento del agua para determinar la densidad
La simulación de PhET ilustra otra forma de determinar la densidad, utilizando el desplazamiento del agua. Dado que la simulación está diseñada en flash (no compatible con dispositivos móviles), hemos realizado un vídeo corto, para que lo observes y determines la densidad de los bloques rojo y amarillo.
Solución
En la simulación de densidad al seleccionar Misma masa, puedes elegir entre varios bloques de colores de 5.00 kg que puedes colocar en un tanque que contiene 100.00 L de agua.
El bloque amarillo flota (es menos denso que el agua), y el nivel del agua sube a 105.00 L. Mientras flota, el bloque amarillo desplaza a 5.00 L de agua, una cantidad igual al peso del bloque. El bloque rojo se hunde (es más denso que el agua, que tiene una densidad = 1.00 kg/L), y el nivel del agua aumenta a 101.25 L.
Por lo tanto, el bloque rojo desplaza 1.25 L de agua, una cantidad igual al volumen del bloque. La densidad del bloque rojo es:
$$densidad = \cfrac{masa}{volumen} = \cfrac{5.00 \;kg}{1.25\; L} = 4.00 \;kg/L$$Observa que dado que el bloque amarillo no está completamente sumergido, no puedes determinar su densidad a partir de esta información. Pero si puedes inferir qué ocurriría si se sumerge totalmente en la parte inferior del tanque (la mitad sumergida sube el nivel a 105.00 L), el nivel del agua aumentaría a 110.00 L, lo que significa que ahora desplaza a 10.00 L de agua, y se puede encontrar su densidad:
$$densidad = \cfrac{masa}{volumen} = \cfrac{5.00 \;kg}{10.00 \;L} = 0.500 \;kg/L$$
El conteo es el único tipo de medición que está libre de incertidumbre, siempre que la cantidad de objetos que se cuentan no cambie mientras el proceso de conteo está en curso. El resultado de tal medición de conteo es un ejemplo de un número exacto. Al contar los huevos en una caja, se puede determinar exactamente cuántos huevos contiene la caja. Los números de cantidades definidas también son exactos. Por definición, 1 pie es exactamente 12 pulgadas, 1 pulgada es exactamente 2.54 centímetros y 1 gramo es exactamente 0.001 kilogramo. Sin embargo, las cantidades derivadas de mediciones distintas del conteo son inciertas en diferentes grados debido a las limitaciones prácticas del proceso de medición utilizado.
Los números de cantidades medidas, a diferencia de cantidades definidas o contadas directamente, no son exactos. Para medir el volumen del líquido en un cilindro graduado, debes hacer una lectura en la parte inferior del menisco, el punto más bajo en la superficie curva del líquido.
Consulta la ilustración en la figura 1.26. La parte inferior del menisco en este caso se encuentra claramente entre las marcas 21 y 22, lo que significa que el volumen del líquido es ciertamente mayor que 21 ml pero menor que 22 ml. El menisco parece estar un poco más cerca de la marca de 22 ml que de la marca de 21 ml, por lo que una estimación razonable del volumen del líquido sería de 21.6 ml. En el número 21.6, entonces, los dígitos 2 y 1 son ciertos, pero el 6 es una estimación.
Algunas personas pueden estimar que la posición del menisco está a una distancia igual de cada una de las marcas y estimar el dígito de la décima como 5, mientras que otras pueden pensar que está aún más cerca de la marca de 22 ml y estimar que este dígito es 7.
Nota que sería inútil intentar estimar un dígito para el lugar de la centésima, dado que el dígito de al décima es incierto. En general, las escalas numéricas como la de este cilindro graduado permitirán realizar mediciones a una décima parte de la división de escala más pequeña. La escala en este caso tiene divisiones de 1 ml, por lo que los volúmenes se pueden medir con una precisión de 0.1 ml.
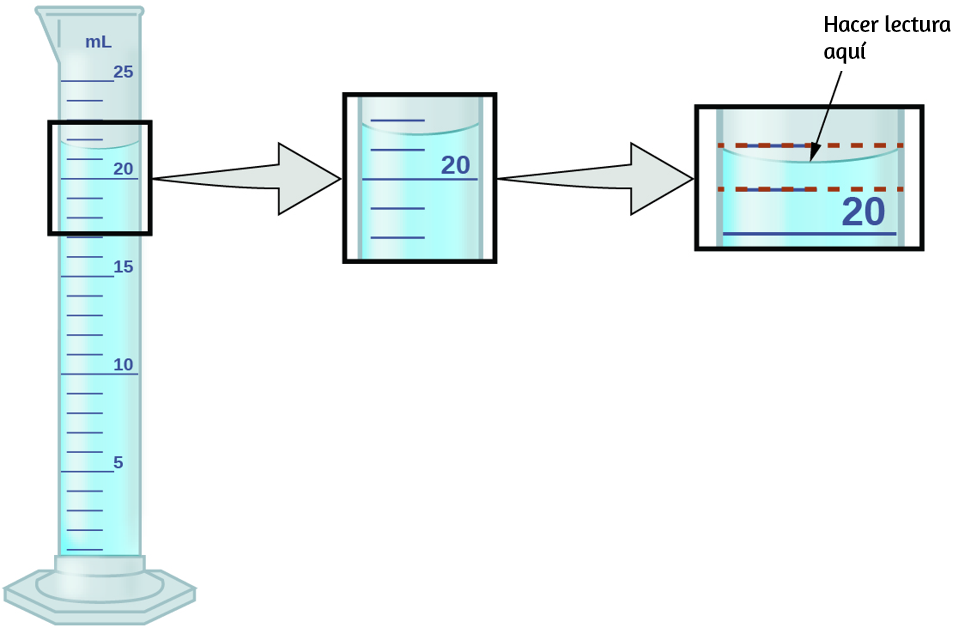
Figura 1.26. Para medir el volumen de líquido en este cilindro graduado, debes subdividir mentalmente la distancia entre las marcas de 21 y 22 ml en décimas de mililitro y luego hacer una lectura (estimación) en la parte inferior del menisco.
Este concepto es válido para todas las mediciones, incluso si no realizas una estimación activa.
Si colocas un cuarto (moneda de 25 centavos de Estados Unidos ) en una balanza electrónica estándar, puedes obtener una lectura de 6.72 g. Los dígitos 6 y 7 son ciertos, y el 2 indica que la masa del cuarto es probable entre 6.71 y 6.73 gramos. El cuarto pesa alrededor de 6.72 gramos, con una incertidumbre nominal en la medida de ± 0.01 gramos. Si la moneda se pesa en un abalanza más sensible, la masa podría ser 6.723 g. Esto significa que su masa se encuentra entre 6.722 y 6.724 gramos, una incertidumbre de 0.001 gramos. Cada medida tiene cierta incertidumbre, que depende del dispositivo utilizado (y la capacidad del usuario). Todos los dígitos de una medición, incluido el último dígito incierto, se llaman cifras significativas o dígitos significativos. Ten en cuenta que el cero puede ser un valor medido; por ejemplo, si se encuentra en una escala que muestra el peso a la libra más cercana y muestra "120", entonces 1 (cientos), 2 (decenas) y 0 (unidades) son todos valores significativos (medidos).
Un resultado de medición se informa correctamente cuando sus dígitos significativos representan con precisión la certeza del proceso de medición. Pero, ¿qué pasaría si estuvieras analizando un valor reportado y tratando de determinar qué es significativo y qué no? Bueno, para empezar, todos los dígitos distintos de cero son significativos, y solo los ceros requieren cierta reflexión. Usaremos los términos “principal o inicial”, “arrastre” y “cautivo” para los ceros y consideraremos cómo tratarlos.
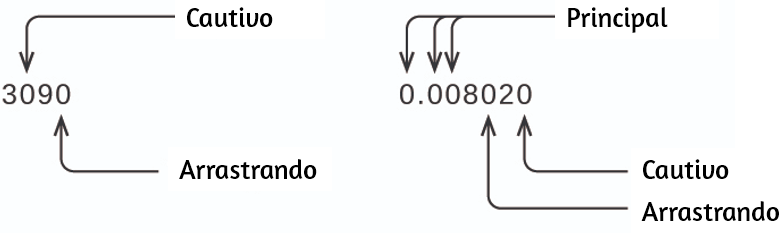
Comenzando con el primer dígito distinto de cero a la izquierda, cuenta este dígito y todos los dígitos restantes a la derecha. Este es el número de cifras significativas en la medición, a menos que el último dígito sea un cero al final del punto decimal.
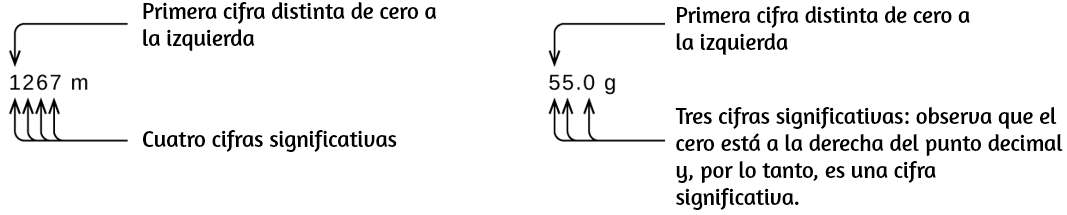
Los ceros cautivos resultan de la medición y por lo tanto son siempre significativos. Sin embargo, los ceros iniciales nunca son significativos, simplemente nos dicen dónde se encuentra el punto decimal.
Los ceros (iniciales) a la izquierda en este ejemplo no son significativos. Podríamos usar la notación exponencial y expresar el número como $8.32407 \times 10^{−3}$ entonces el número $8.32407$ contiene todas las cifras significativas, y 10−3 localiza el punto decimal.
El número de cifras significativas es incierto en un número que termina con un cero a la izquierda de la ubicación del punto decimal. Los ceros en la medida de 1.300 gramos podrían ser significativos o simplemente podrían indicar dónde se encuentra el punto decimal.
La ambigüedad se puede resolver con el uso de la notación exponencial: $1.3 × 10^{3}$ (dos cifras significativas), $1.30 \times 10^{3}$ (tres cifras significativas, si se midió el lugar de las decenas), o $1.300 \times 10^3$, etcétera. En los casos en que solo esté disponible el número con formato decimal, es prudente suponer que todos los ceros finales no son significativos.
Al determinar cifras significativas, asegúrate de prestar atención a los valores informados y piense en la medición y las cifras significativas en términos de lo que es razonable o probable al evaluar si el valor tiene sentido. Por ejemplo, el censo oficial de enero de 2014 informó que la población residente de los EE. UU. Era de $317,297,725$. ¿Crees que la población de EE. UU. Estaba determinada correctamente a las nueve cifras significativas informadas, es decir, al número exacto de personas? La gente nace, muere o se muda constantemente, y se asume que se tiene en cuenta la gran cantidad de personas que en realidad no se cuentan. Debido a estas incertidumbres, podría ser más razonable esperar que sepamos que la población se encuentra dentro de aproximadamente un millón o así, en cuyo caso, la población debe reportarse como $3.17 \times 10^8$ personas.
Un segundo principio importante de incertidumbre es que los resultados calculados a partir de una medición son al menos tan inciertos como la medición en sí misma.
Ten en cuenta la incertidumbre en las mediciones para evitar una tergiversación de la incertidumbre en los resultados calculados. Una forma de hacer esto es informar el resultado de un cálculo con el número correcto de cifras significativas, que se determina mediante las siguientes tres reglas para redondear números:
Los siguientes ejemplos ilustran la aplicación de esta regla al redondear algunos números diferentes a tres cifras significativas:
Vamos a trabajar a través de estas reglas con algunos ejemplos.
Ejemplo 1.3
Redondear numeros
Redondea al número de cifras significativas indicado:
(a) $31.57$ (a dos cifras significativas)
(b) $8.1649$ (a tres cifras significativas)
(c) $0.051065$ (a cuatro cifras significativas)
(d) $0.90275$ (a cuatro cifras significativas)
Solución
(a) $31.57$ se redondea a $32$ (el dígito eliminado es 5, y el dígito retenido es par)
(b) $8.1649$ se redondea "abajo" a $8.16$ (el dígito eliminado, 4, es menor que 5)
(c) $0.051065$ se redondea "hacia abajo" a $0.05106$ (el dígito eliminado es 5, y el dígito retenido es par)
(d) $0.90275$ se redondea a $0.9028$ (el dígito eliminado es 5, y el dígito que es retenido es número par).
Comprueba tu aprendizaje
Ejemplo 1.4
Suma y resta con cifras significativas
Regla: cuando sumes o restes números, redondea el resultado al mismo número de cifras decimales que el número con el menor número de cifras decimales (es decir, el valor menos seguro en términos de suma y resta).
(a) Suma $1.0023\; g$ y $4.383\; g$.
(b) Resta $421.23 \;g$ de $486\; g$.
Solución
a)
$1.0023\; g$
$+4.383\; g$
──────
$5.3853 \;g$
La respuesta es $5.385\; g$ (redondeando al lugar de las milésimas; tres decimales)
b)
$486\; g$
$-421.23\; g$
──────
$64.77\; g$
La respuesta es $65 \;g$ (redondeando a las unidades; no hay decimales)
Comprueba tu aprendizaje
Ejemplo 1.5
Multiplicación y división con cifras significativas
Regla: al multiplicar o dividir números, redondea el resultado al mismo número de dígitos que el número con la menor cantidad de cifras significativas (el valor menos seguro en términos de multiplicación y división).
(a) Multiplica $0.6238\; cm$ por $6.6\; cm$.
(b) Divide $421.23\; g$ por $486\; ml$.
Solución
a) $0.6238 \;cm \times 6.6\; cm = 4.11708\; cm^2 \rarr $ el resultado es $4.1\; cm^2$ (redondeado a dos cifras significativas)
cuatro cifras significativas × dos cifras significativas → dos cifras significativas en la respuesta
b) $\cfrac{421.23\; g}{486 \;mL} = 0.86728 ... \;g/ml$ → el resultado es $0.867\; g/ml$ (redondeando a tres cifras significativas)
$\cfrac{5\; cifras\; significativas}{3\; cifras\; significativas} \rarr {3\; cifras \;significativas}$.
Comprueba tu aprendizaje
En medio de todos estos aspectos técnicos, es importante tener en cuenta la razón de estas reglas sobre cifras y redondeos significativos: representar correctamente la certeza de los valores informados y garantizar que un resultado calculado no se represente como más seguro que el valor menos seguro utilizado en el cálculo.
Ejemplo 1.6
Cálculo con cifras significativas
Una bañera común tiene $13.44 \;dm$ de largo, $5.920 \;dm$ de ancho y $2.54\; dm$ de profundidad. Supón que la bañera es rectangular y calcula su volumen aproximado en litros.
Solución
$$\begin{aligned} V &= 13.44\; dm \times 5.920 \;dm \times 2.54\; dm \\ &= 02.09459 ... \;dm^3\; (valor\; de\; la\; calculadora) \\ &= 202\; dm^3 \;o \;202\; L \end{aligned}$$(respuesta redondeada a tres cifras significativas)
Comprueba tu aprendizaje
Ejemplo 1.7
Determinación experimental de la densidad utilizando el desplazamiento de agua
Una pieza de barra de refuerzo se pesa y luego se sumerge en un cilindro graduado parcialmente lleno de agua, con los resultados como se muestran en la siguiente figura.
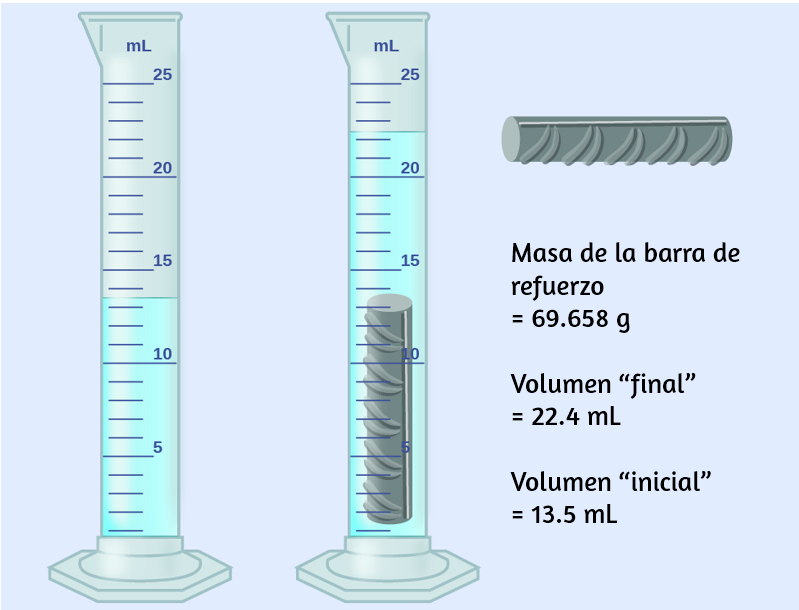
(a) Usa estos valores para determinar la densidad de esta pieza de barra de refuerzo.
(b) La barra de refuerzo es principalmente de hierro. ¿Tu resultado en (a) apoya esta afirmación? ¿Cómo?
Solución
a) El volumen de la barra de refuerzo es igual al volumen del agua desplazada:
$$volumen = 22.4\; ml − 13.5 \;ml = 8.9 \;ml = 8.9\; cm^3$$(redondeado al 0.1 mL más cercano, según la regla para la suma y la resta).
La densidad es la relación masa-volumen:
$$densidad = \cfrac{masa}{volumen} = \cfrac{69.658\; g}{8.9 \;cm^3} = 7.8\; cm^3$$b) De la tabla 1.4, la densidad del hierro es de $7.9 \;g/cm^3$, muy cercana a la de la barra de refuerzo, lo que apoya la afirmación
Comprueba tu aprendizaje
Los científicos suelen realizar mediciones repetidas de una cantidad para garantizar la calidad de sus hallazgos y evaluar tanto la precisión como la exactitud de sus resultados. Se dice que las mediciones son precisas si producen resultados muy similares cuando se repiten de la misma manera. Una medición se considera exacta si produce un resultado muy cercano al valor verdadero o aceptado. Los valores precisos concuerdan entre sí; Los valores exactos concuerdan con un valor verdadero. Estas caracterizaciones pueden extenderse a otros contextos, como los resultados de una competencia de tiro con arco (Figura 1.27).
Supongamos que un químico de control de calidad en una compañía farmacéutica tiene la tarea de verificar la exactitud y la precisión de tres máquinas diferentes que están destinadas a dispensar 10 onzas (296 ml) de jarabe para la tos en botellas de almacenamiento. Ella procede a usar cada máquina para llenar cinco botellas y luego determina cuidadosamente el volumen real dispensado, obteniendo los resultados tabulados en la Tabla 1.5.
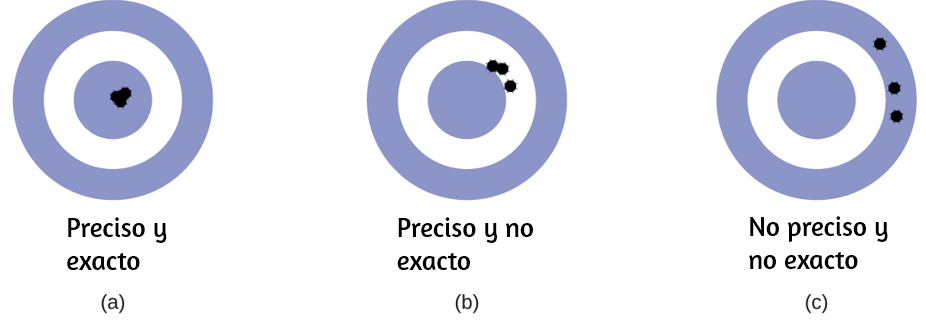
Figura 1.27. (a) Estas flechas están cerca tanto de la diana, por lo que son exactas y precisas. (b) Estas flechas están cerca una de la otra pero no en el objetivo, por lo que son precisas pero no exactas. (c) Estas flechas no están en el objetivo ni cerca unas de otras, por lo que no son ni precisas ni exactas.
Tabla 1.5. Volumen (ml) de medicamentos para la tos administrados por dispensadores de 10 onzas (296 ml)
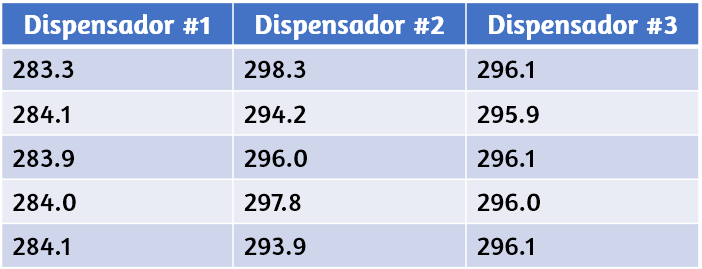
Teniendo en cuenta estos resultados, informarás que el dispensador # 1 es preciso (todos los valores están cerca uno del otro, dentro de unas pocas décimas de mililitro) pero no es exacto (ninguno de los valores está cerca del valor objetivo de 296 ml, cada uno más de 10 ml demasiado bajo).
Los resultados para el dispensador # 2 representan una precisión mejorada (cada volumen está a menos de 3 ml de los 296 ml) pero la exactitud es peor (los volúmenes varían en más de 4 ml). Finalmente, puedes informar que el dispensador # 3 está funcionando bien, dispensando jarabe para la tos con exactitud (todos los volúmenes dentro de 0,1 ml del volumen objetivo) y con precisión (volúmenes que difieren entre sí en no más de 0,2 ml).
A menudo ocurre que una cantidad de interés puede no ser fácil (o incluso posible) medir directamente, sino que debe calcularse a partir de otras propiedades medidas directamente y relaciones matemáticas apropiadas. Por ejemplo, considera medir la velocidad promedio de un atleta que corre a esprint. Esto se logra típicamente midiendo el tiempo requerido para que el atleta corra desde la línea de inicio hasta la línea de meta, y la distancia entre estas dos líneas, y luego calcula la velocidad de la ecuación que relaciona estas tres propiedades:
$$velocidad = \cfrac{distancia}{tiempo}$$Un velocista de calidad olímpica puede correr 100 m en aproximadamente 10 s, lo que corresponde a una velocidad media de
$$\cfrac{100 \;m}{10\; s} = 10\; m/s$$Observa que esta aritmética simple implica dividir los números de cada cantidad medida para obtener el número de la cantidad calculada (100/10 = 10) y, de la misma manera, dividir las unidades de cada cantidad medida para obtener la unidad de la cantidad calculada (m/s = m/s). Ahora, considera usar esta misma relación para predecir
el tiempo requerido para que una persona que corre a esta velocidad recorra una distancia de 25 m. Se utiliza la misma relación entre las tres propiedades, pero en este caso, las dos cantidades proporcionadas son una velocidad (10 m/s) y una distancia (25 m). Para obtener la propiedad buscada, el tiempo, la ecuación se debe reorganizar adecuadamente:
$$tiempo = \cfrac{distancia}{velocidad}$$Así las cosas:
$$\cfrac{25\; m}{10\; m/s} = 2.5\; s$$Nuevamente, la aritmética en los números (25/10 = 2.5) estuvo acompañada por la misma aritmética en las unidades (m/(m/s) = s) para obtener el número y la unidad del resultado, 2.5 s. Ten en cuenta que, al igual que para los números, cuando una unidad se divide por una unidad idéntica (en este caso, m/m), el resultado es "1", o, como se dice comúnmente, las unidades se "cancelan".
Estos cálculos son ejemplos de un enfoque matemático versátil conocido como análisis dimensional (o el método de etiquetado de factores). El análisis dimensional se basa en esta premisa: las unidades deben someterse a las mismas operaciones matemáticas que sus números asociados.
Este método se puede aplicar a cálculos que van desde simples conversiones de unidades hasta cálculos más complejos de varios pasos que involucran varias cantidades diferentes.
Se puede usar una relación de dos cantidades equivalentes expresadas con diferentes unidades de medida como un factor de conversión de unidades. Por ejemplo, las longitudes de 2,54 cm y 1 pulgada son equivalentes (por definición), por lo que se puede derivar un factor de conversión unitario de la relación,
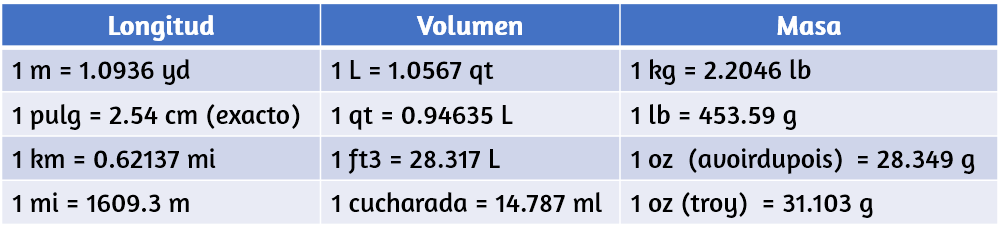
$$\cfrac{2.54 \;cm}{1\; pulg}\; o\; 2.54 \cfrac{cm}{pulg}$$Otros factores de conversión, comúnmente usados, se dan en la tabla 1.6.
Tabla 1.6. Factores comunes de conversión
Cuando una cantidad (como la distancia en pulgadas) se multiplica por un factor de conversión de unidad apropiado, la cantidad se convierte a un valor equivalente con diferentes unidades (como la distancia en centímetros). Por ejemplo, el salto vertical de un jugador de baloncesto de 34 pulgadas se puede convertir a centímetros así:
Como esta simple aritmética involucra cantidades, la premisa del análisis dimensional requiere que multipliquemos tanto los números como las unidades. Los números de estas dos cantidades se multiplican para obtener el número de la cantidad del producto, 86, mientras que las unidades se multiplican para dar un resultado $\cfrac{pulg \times cm}{pulg}$. Al igual que para los números, una proporción de unidades idénticas también es numéricamente igual a uno, en $\frac{pulg}{pulg} = 1$, y el producto unitario se simplifica así a cm (cuando las unidades idénticas se dividen para obtener un factor de 1, se dice que se "cancelan"). El análisis dimensional se puede usar para confirmar la aplicación correcta de los factores de conversión de unidades como se muestra en el siguiente ejemplo.
Ejemplo 1.8
Usando un factor de conversión de unidades
La masa de un frisbee de competición es de $125 \;g$. Convierte su masa a onzas usando el factor de conversión unitario derivado de la relación $1 \;oz = 28.349\; g$ (tabla 1.6).
Solución
Dado el factor de conversión, la masa en onzas se puede deducir usando una ecuación similar a la que se usa para convertir la longitud de pulgadas a centímetros.
$x \;oz = 125 \;g \times factor\; de\; \text{conversión}\; unitario$
El factor de conversión de unidades se puede representar como:
$$\cfrac{1 \;oz}{28.349\; g}\; y \;\cfrac{28.349\; g}{1\; oz}$$El factor de conversión de unidades correcto es la proporción que cancela las unidades de gramos y deja onzas.
$$x \;oz = 125\; \bcancel{g} \times \cfrac{1 \;oz}{28.349\; \bcancel{g} } = \cfrac{125}{28.349}\; oz$$ $$x \;oz = 4.41\; oz\; (con \;tres \;cifras\; significativas)$$Comprueba tu aprendizaje
Más allá de las conversiones de unidades simples, el método de la etiqueta del factor puede usarse para resolver problemas más complejos que involucran cálculos. Independientemente de los detalles, el enfoque básico es el mismo: todos los factores involucrados en el cálculo deben estar orientados de manera apropiada para garantizar que sus etiquetas (unidades) se cancelen y/o combinen de manera apropiada para obtener la unidad deseada en el resultado.
Ejemplo 1.9
Cálculo de cantidades a partir de resultados de medición y relaciones matemáticas conocidas
¿Cuál es la densidad del anticongelante común en unidades de g/ml? Una muestra de 4.00 qt del anticongelante pesa 9.26 lb.
Solución
Como $densidad = \frac{masa}{volumen}$, necesitamos dividir la masa en gramos por el volumen en mililitros. En general: el número de unidades de B = el número de unidades de A x factor de conversión de unidades. Los factores de conversión necesarios se dan en la tabla 1.6:
$1 \;lb = 453.59\; g; \;1 L = 1.0567 \;qt; 1 \;l = 1,000 \;ml$. La masa se puede convertir de libras a gramos de la siguiente manera:
El volumen se puede convertir de cuartos de galón (qt de quarter en inglés) a milímetros a través de dos pasos:
Paso 1. Convertir cuartos de galón a litros.
$$4.00 \;\bcancel{qt} = \frac{1 \;lb}{1.0567 \;\bcancel{qt}} = 3.78\; L$$Paso 2. Convertir litros en mililitros.
$$3.78 \;\bcancel{L} \times \frac{1000 \;mL}{1\; \bcancel{L}} = 3.78 \times 10^3\; mL$$entonces,
$$densidad = \cfrac{4.20 \times 10^3\; g}{3.78 \times 10^3\; mL} = 1.11 g/mL$$alternativamente, el cálculo podría configurarse de manera que uses tres factores de conversión de unidades de forma secuencial de la siguiente manera:
$$\frac{9.26 \;\bcancel{lb}}{4.00\; \bcancel{qt}} \times \frac{453.59 \;g}{1 lb\bcancel{lb}} \times \frac{1.0567\; \bcancel{qt}}{1 \;\bcancel{L}} \times \frac{1 \;L\bcancel{L}}{1000 \;mL} = 1.11 g/mL$$Comprueba tu aprendizaje
Ejemplo 1.10
Cálculo de cantidades a partir de resultados de medición y relaciones matemáticas conocidas
Mientras conducía de Filadelfia a Atlanta, a una distancia de aproximadamente 1250 km, un Lamborghini Aventador Roadster 2014 usa 213 l de gasolina.
(a) ¿Qué ahorro de combustible (promedio), en millas por galón, obtuvo el Roadster durante este viaje?
(b) Si la gasolina cuesta $ \$ $ 3.80 por galón, ¿cuál fue el costo del combustible para este viaje?
Solución
(a) Primero convierte la distancia de kilómetros a millas:
$$1250\; \bcancel{km} \times \frac{0.62137 \;mi}{1 \;\bcancel{km}} = 777\; mi$$y luego convertir el volumen de litros a galones:
$$213 \;\bcancel{L} \times \frac{1.0567 \;\bcancel{qt}}{1 \;\bcancel{L}} \times \frac{1 gal}{4 \;\bcancel{qt}} = 53.6 \;gal$$finalmente, el kilometraje promedio sería:
$$\frac{777 \;mi}{56.3 \;gal} = 13.8 \;millas/\text{galón} = 13.8\; mpg$$(b) Al usar el volumen previamente calculado en galones, encontramos:
$$56.3\;\bcancel{gal} \times \frac{\$ 3.80}{1\; \bcancel{gal}} = \$ 214$$Comprueba tu aprendizaje
Usamos la palabra temperatura para referirnos al calor o al frío de una sustancia. Una forma en que medimos un cambio en la temperatura es usar el hecho de que la mayoría de las sustancias se expanden cuando su temperatura aumenta y se contraen cuando su temperatura disminuye. El mercurio o el alcohol en un termómetro de vidrio común cambia su volumen a medida que cambia la temperatura, y la posición del líquido atrapado a lo largo de una escala impresa puede usarse como una medida de la temperatura.
Las escalas de temperatura se definen en relación con las temperaturas de referencia seleccionadas: dos de las más utilizadas son las temperaturas de congelación y ebullición del agua a una presión atmosférica específica.
En la escala Celsius, 0 °C se define como la temperatura de congelación del agua y 100 °C como la temperatura de ebullición del agua. El espacio entre las dos temperaturas se divide en 100 intervalos iguales, lo que llamamos grados. En la escala Fahrenheit, el punto de congelación del agua se define como 32 °F y la temperatura de ebullición es 212 °F. El espacio entre estos dos puntos en un termómetro Fahrenheit se divide en 180 partes iguales (grados).
La definición de las escalas de temperatura Celsius y Fahrenheit como se describe en el párrafo anterior da como resultado una relación un poco más compleja entre los valores de temperatura en estas dos escalas que para diferentes unidades de medida para otras propiedades. La mayoría de las unidades de medida para una propiedad dada son directamente proporcionales entre sí (y = mx). Usando unidades de longitud familiares como un ejemplo:
$$longitud \;en \;pies = \cfrac{1 \;pie}{12 \;pulg} \times longitud\; en \;pulgadas$$donde y = longitud en pies, x = longitud en pulgadas y la constante de proporcionalidad, m, es el factor de conversión. Sin embargo, las escalas de temperatura Celsius y Fahrenheit no comparten un punto cero común, por lo que la relación entre estas dos escalas es lineal en lugar de proporcional (y = mx + b). En consecuencia, convertir una temperatura de una de estas escalas en la otra requiere más que una simple multiplicación por un factor de conversión, m, también debes tener en cuenta las diferencias en los puntos cero (b) de las escalas.
La ecuación lineal que relaciona las temperaturas en grados Celsius y Fahrenheit se deriva fácilmente de las dos temperaturas utilizadas para definir cada escala. Al representar la temperatura en grados Celsius como x y la temperatura en grados Fahrenheit como y, la pendiente, m, se calcula como:
La intersección en y de la ecuación, b, se calcula luego utilizando cualquiera de los pares de temperatura equivalentes, $(100 °C, 212 °F)$ o $(0 °C, 32 °F)$, como:
$$b = y − mx = 32 °F − \cfrac{9 °F}{5 °C} \times 0 °C = 32 °F$$La ecuación que relaciona las escalas de temperatura (T) es entonces:
$$T_{°F} = \cfrac{9 °F}{5 °C} \times T{°} + 32 °C$$Una forma abreviada de esta ecuación que omite las unidades de medida es:
$$T_{°F} = \cfrac95 \times T_{°C} + 32$$El reordenamiento de esta ecuación produce la forma útil para convertir de Fahrenheit a Celsius:
$$T_{°C} = \cfrac95(T{\degree F} - 32)$$Como se mencionó anteriormente en este capítulo, la unidad de temperatura SI es el kelvin (K). A diferencia de las escalas Celsius y Fahrenheit, la escala de kelvin es una escala de temperatura absoluta en la que 0 (cero) K corresponde a la temperatura más baja que se puede alcanzar teóricamente.
Dado que la escala de temperatura de kelvin es absoluta, no se incluye un símbolo de grado en la abreviatura de la unidad, K. El descubrimiento a principios del siglo XIX de la relación entre el volumen y la temperatura de un gas sugería que el volumen de un gas sería cero a −273.15 °C. En 1848, el físico británico William Thompson, quien más tarde adoptó el título de Lord Kelvin, propuso una escala de temperatura absoluta basada en este concepto (en el capítulo sobre gases de este texto se proporciona más información sobre este tema).
La temperatura de congelación del agua en esta escala es de 273.15 K y su temperatura de ebullición es de 373.15 K. Observa que la diferencia numérica en estas dos temperaturas de referencia es 100, la misma que para la escala Celsius, por lo que la relación lineal entre estas dos escalas de temperatura Exhiben una pendiente de 1 $\cfrac{K}{\;\degree C}$. Siguiendo el mismo enfoque, las ecuaciones para la conversión entre las escalas de temperatura kelvin y Celsius serían:
$$T_K = T_{\;\degree C} + 273.15$$ $$T_{\;\degree C} = T_K − 273.15$$El $273.15$ en estas ecuaciones se ha determinado experimentalmente, por lo que no es exacto. La figura 1.28 muestra la relación entre las tres escalas de temperatura.
Aunque la escala de temperatura kelvin (absoluta) es la escala de temperatura oficial del SI, Celsius se usa comúnmente en muchos contextos científicos y es la escala de elección para contextos no científicos en casi todas las áreas del mundo. Muy pocos países (los EE. UU. y sus territorios, las Bahamas, Belice, las Islas Caimán y Palau) todavía usan Fahrenheit para el clima, la medicina y la cocina.
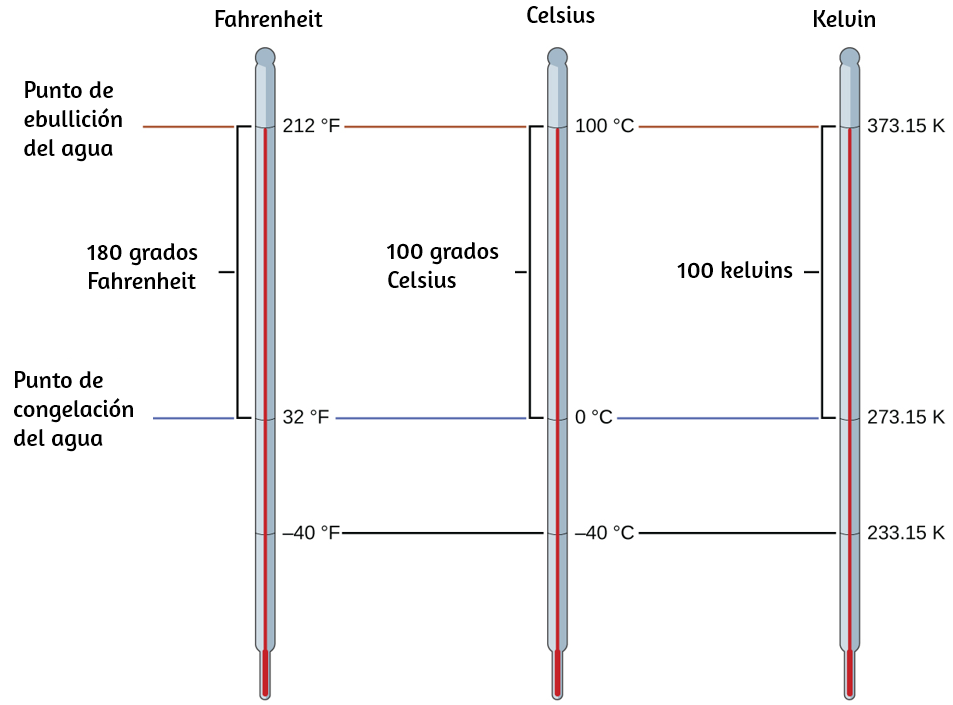
Figura 1.28. Se comparan las escalas de temperatura Fahrenheit, Celsius y kelvin.
Ejemplo 1.11
Conversión de Celsius
La temperatura corporal normal se ha aceptado comúnmente como 37.0 °C (aunque varía según la hora del día y el método de medición, así como entre individuos). ¿Cuál es esta temperatura en la escala de kelvin y en la escala de Fahrenheit?
Solución
$$K = °C + 273.15 = 37.0 + 273.2 = 310.2 K$$Comprueba tu aprendizaje
Ejemplo 1.12
Conversión de Fahrenheit
Hornear una pizza preparada requiere una temperatura del horno de 450 °F. Si estás en Europa y el termómetro de tu horno usa la escala Celsius, ¿cuál es el ajuste? ¿Cuál es la temperatura kelvin?
Solución
$$°C = \cfrac59(°F − 32) = \cfrac59(450 − 32) = \cfrac59 \times 418 = 232 °C$$→ configurar el horno a 230 °C (tres cifras significativas)
$$K = °C + 273.15 = 230 + 273 = 503 K \rarr 5.0 \times 10^2 K \\ (dos \;cifras\; significativas)$$Comprueba tu aprendizaje
Existen otras escalas. En la siguiente escena interactiva, diseñada por José Luis San Emeterio Peña, vemos la equivalencia entre la escala Celsius y las escalas Fahrenheit (de uso extendido en los países anglosajones) y Réaumur (casi en desuso).
Te dejamos dos escenas interactivas. La primera, diseñada por Juan Guillermo Rivera Berrío, permite practicar con los diferentes prefijos, tomando como referente de medida el gramo. La segunda, es un aplicativo gratuito para realizar diferentes conversiones, el cual hemos modificado para este texto(véase Js Measurements Converters).
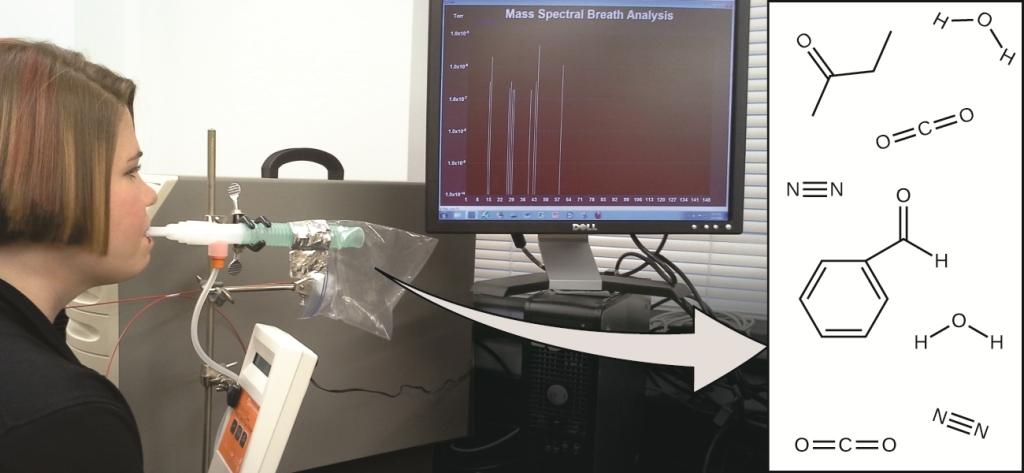
Figura 2.1. El análisis de las moléculas en una respiración exhalada puede proporcionar información valiosa, lo que lleva a un diagnóstico temprano de enfermedades o la detección de la exposición ambiental a sustancias nocivas (crédito: modificación de la obra de Paul Flowers).
Tu estado de salud general y tu susceptibilidad a las enfermedades dependen de la compleja interacción entre tu composición genética y la exposición ambiental, con un resultado difícil de predecir. La detección temprana de biomarcadores, sustancias que indican la enfermedad o el estado fisiológico de un organismo, podría permitir el diagnóstico y el tratamiento antes de que una afección se vuelva grave o irreversible. Estudios recientes han demostrado que tu aliento exhalado puede contener moléculas que pueden ser biomarcadores para la exposición reciente a contaminantes ambientales o para condiciones patológicas que van desde el asma hasta el cáncer de pulmón. Los científicos están trabajando para desarrollar "huellas digitales" de biomarcadores que podrían usarse para diagnosticar una enfermedad específica según las cantidades e identidades de ciertas moléculas en el aliento exhalado de un paciente.
Un concepto esencial que subyace a este objetivo es el de la identidad de una molécula, que está determinada por los números y tipos de átomos que contiene, y cómo están unidos entre sí. Este capítulo describirá algunos de los principios químicos fundamentales relacionados con la composición de la materia, incluidos los fundamentales para el concepto de identidad molecular.
La primera discusión registrada sobre la estructura básica de la materia proviene de los antiguos filósofos griegos, los científicos de su época. En el siglo quinto antes de Cristo, Leucipo y Demócrito argumentaron que toda la materia estaba compuesta de pequeñas partículas finitas que llamaban atomos, un término derivado de la palabra griega que significa "indivisible". Pensaban que los átomos eran partículas en movimiento que diferían en forma y tamaño, y que podrían unirse. Más tarde, Aristóteles y otros llegaron a la conclusión de que la materia consistía en varias combinaciones de los cuatro "elementos" (fuego, tierra, aire y agua) y podía dividirse infinitamente. Curiosamente, estos filósofos pensaron en los átomos y los "elementos" como conceptos filosóficos, pero aparentemente nunca consideraron realizar experimentos para probar sus ideas.
La visión aristotélica de la composición de la materia prevaleció durante más de dos mil años, hasta que el maestro de escuela inglés John Dalton ayudó a revolucionar la química con su hipótesis de que el comportamiento de la materia podría explicarse utilizando una teoría atómica. Publicada por primera vez en 1807, muchas de las hipótesis de Dalton sobre las características microscópicas de la materia siguen siendo válidas en la teoría atómica moderna. Aquí están los postulados de la teoría atómica de Dalton.
Figura 2.2. Un centavo de cobre anterior a 1982 (izquierda) contiene aproximadamente 3 × 1022 átomos de cobre (varias docenas se representan como esferas marrones a la derecha), cada una de las cuales tiene las mismas propiedades químicas (crédito: modificación del trabajo por "slgckgc"/Flickr).
Figura 2.3. El óxido de cobre (II), un compuesto negro en polvo, resulta de la combinación de dos tipos de átomos: cobre (esferas marrones) y oxígeno (esferas rojas), en una proporción de 1: 1 (crédito: modificación del trabajo de "Chemicalinterest"/Wikimedia Commons).
La teoría atómica de Dalton proporciona una explicación microscópica de las muchas propiedades macroscópicas de la materia que has aprendido. Por ejemplo, si un elemento como el cobre consta de un solo tipo de átomo, entonces no puede descomponerse en sustancias más simples, es decir, en sustancias compuestas por menos tipos de átomos. Y si los átomos no se crean ni se destruyen durante un cambio químico, entonces la masa total de materia presente cuando la materia cambia de un tipo a otro permanecerá constante (la ley de conservación de la materia).
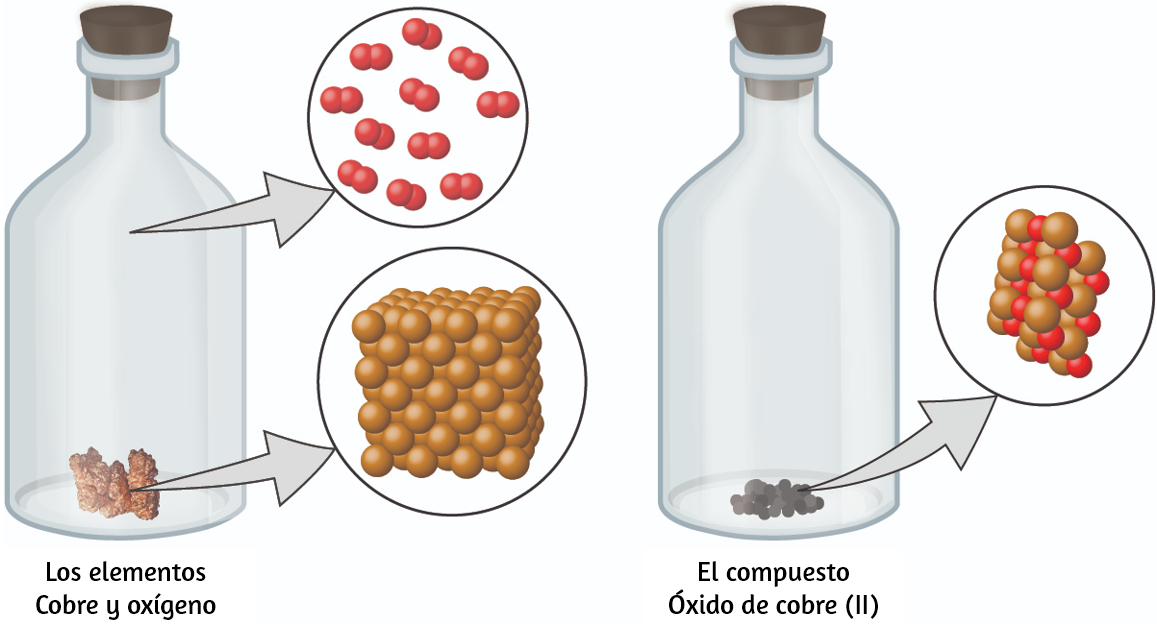
Figura 2.4. Cuando los elementos cobre (un sólido de color marrón rojizo brillante, mostrado aquí como esferas marrones) y oxígeno (un gas claro e incoloro, mostrado aquí como esferas rojas) reaccionan, sus átomos se reorganizan para formar un compuesto que contiene cobre y oxígeno (un polvo sólido negro). (crédito cobre: modificación del trabajo por http://images-of-elements.com/copper.php).
En la siguiente escena interactiva, diseñada por Claudio Francisco Nebbia Rubio, podrás observar diferentes modelos sobre el átomo. Esta escena hace parte del proyecto Telesecundaria, publicado por la Red Descartes.
El interactivo permite que tengas una visión histórica del desarrollo del concepto de átomo con el fin de que puedas explorar cada modelo atómico, sus propiedades y características principales.
Ejemplo 2.1
Probando la teoría atómica de Dalton
En el siguiente dibujo, las esferas verdes representan átomos de un elemento determinado.
Las esferas moradas representan átomos de otro elemento. Si las esferas se tocan, son parte de una sola unidad de un compuesto. ¿El siguiente cambio químico representado por estos símbolos viola alguna de las ideas de la teoría atómica de Dalton? ¿Si es así, Cuál?
Solución
Los materiales de partida consisten en dos esferas verdes y dos esferas de color púrpura. Los productos consisten en una sola esfera verde y una esfera púrpura.
Esto viola el postulado de Dalton de que los átomos no se crean ni se destruyen durante un cambio químico, sino que simplemente se redistribuyen (en este caso, los átomos parecen haber sido destruidos).
Comprueba tu aprendizaje
Dalton conoció los experimentos del químico francés Joseph Proust, quien demostró que todas las muestras de un compuesto puro contienen los mismos elementos en masa en la misma proporción. Esta declaración se conoce como la ley de proporciones definidas o la ley de composición constante. La sugerencia de que los números de átomos de los elementos en un compuesto dado siempre existen en la misma proporción es consistente con estas observaciones.
Por ejemplo, cuando se analizan diferentes muestras de isooctano (un componente de la gasolina y uno de los estándares utilizados en el sistema de clasificación de octano), se encuentra que tienen una relación de masa de carbono a hidrógeno de 5.33: 1, como se muestra en la tabla 2.1.
Vale la pena señalar que aunque todas las muestras de un compuesto particular tienen la misma proporción de masa, lo contrario no es cierto en general. Es decir, las muestras que tienen la misma relación de masa no son necesariamente la misma sustancia. Por ejemplo, hay muchos otros compuestos además del isooctano que también tienen una relación de masa de carbono a hidrógeno de 5.33: 1.00.
Tabla 2.1. Composición constante de isooctano
Dalton también usó datos de Proust, así como los resultados de sus propios experimentos, para formular otra ley interesante. La ley de proporciones múltiples establece que cuando dos elementos reaccionan para formar más de un compuesto, una masa fija de un elemento reaccionará con masas del otro elemento en una proporción de números enteros pequeños. Por ejemplo, el cobre y el cloro pueden formar un sólido verde cristalino con una relación de masa de 0.558 g de cloro por 1 g de cobre, así como un sólido marrón cristalino con una relación de masa de 1.116 g de cloro por 1 g de cobre.
Estas relaciones por sí mismas pueden no parecer particularmente interesantes o informativas; sin embargo, si tomamos una proporción de estas relaciones, obtenemos un resultado útil y posiblemente sorprendente: una proporción pequeña de números enteros.
$$\cfrac{\frac{1.116\; g \;Cl}{1\; g \;Cu}}{\frac{0.558 \;g \;Cl}{1\; g \;Cu}} = \frac21$$Esta relación de 2 a 1 significa que el compuesto marrón tiene el doble de cloro por cantidad de cobre que el compuesto verde.
Esto puede explicarse por la teoría atómica si la proporción de cobre a cloro en el compuesto marrón es de 1 átomo de cobre a 2 átomos de cloro, y la relación en el compuesto verde es de 1 átomo de cobre a 1 átomo de cloro. La proporción de átomos de cloro (la proporción de sus masas) es, por lo tanto, de 2 a 1 (Figura 2.5).
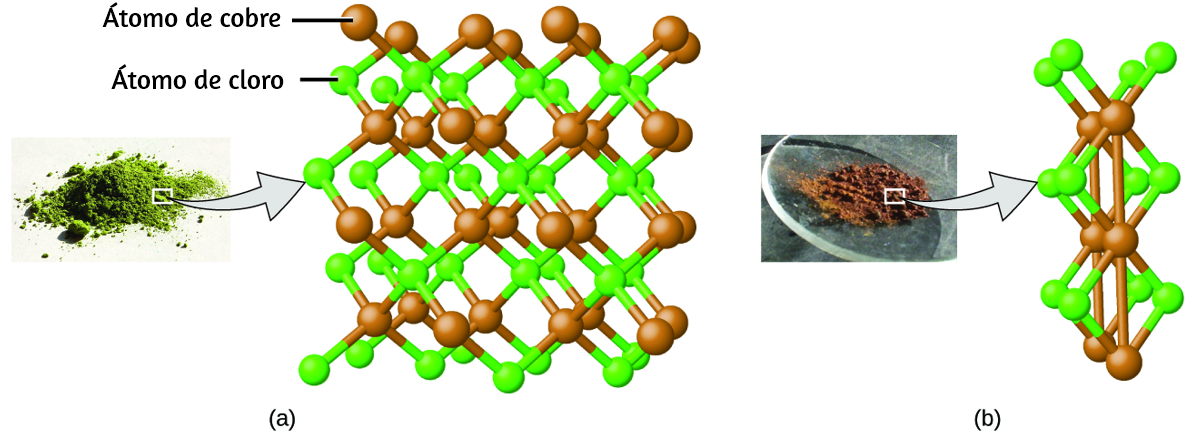
Figura 2.5. En comparación con el compuesto de cloro de cobre en (a), donde el cobre está representado por esferas marrones y el cloro por esferas verdes, el compuesto de cloro de cobre en (b) tiene el doble de átomos de cloro por átomo de cobre (crédito a: modificación del trabajo por "Benjah-bmm27"/Wikimedia Commons; Crédito b: modificación del trabajo por "Walkerma"/Wikimedia Commons).
Ejemplo 2.2
Leyes de proporciones definidas y múltiples
Se analiza una muestra del compuesto A (un gas transparente e incoloro) que contiene 4.27 g de carbono y 5.69 g de oxígeno. Se analiza una muestra de compuesto B (también un gas transparente e incoloro) que contiene 5.19 g de carbono y 13.84 g de oxígeno. ¿Son estos datos un ejemplo de la ley de proporciones definidas, la ley de proporciones múltiples, o ninguna? ¿Qué te dicen estos datos sobre las sustancias A y B?
Solución
En el compuesto A, la relación de masa de carbono a oxígeno es
$$\cfrac{1.33\; g\; O}{1\; g\; C}$$En el compuesto B, la relación de masa de carbono a oxígeno es
$$\cfrac{2.67 \;g \;O}{1\; g\; C}$$La razón entre estas dos proporciones, es:
$$\cfrac{\cfrac{1.33\; g\; O}{1 \;g\; C}}{\cfrac{2.67\; g\;O}{1\; g \;C}}$$Esto apoya la ley de proporciones múltiples. Esto significa que A y B son compuestos diferentes, con A que tiene la mitad de oxígeno por cantidad de carbono (o el doble de carbono por cantidad de oxígeno) que B. Un posible par de compuestos que encajarían en esta relación sería A = CO y B = CO2.
Comprueba tu aprendizaje
Si la materia está compuesta de átomos, ¿de qué están compuestos los átomos? ¿Son las partículas más pequeñas, o hay algo más pequeño? A fines del siglo XIX, varios científicos interesados en preguntas como estas investigaron las descargas eléctricas que podrían producirse en gases de baja presión, y el descubrimiento más importante realizado por el físico inglés J. J. Thomson utilizando un tubo de rayos catódicos. Este aparato consistía en un tubo de vidrio sellado del que se había eliminado casi todo el aire; El tubo contenía dos electrodos metálicos. Cuando se aplicó alto voltaje a través de los electrodos, apareció un haz visible llamado rayo catódico entre ellos. Este haz se desvió hacia la carga positiva y se alejó de la carga negativa, y se produjo de la misma manera con propiedades idénticas cuando se utilizaron diferentes metales para los electrodos. En experimentos similares, el rayo se desvió simultáneamente por un campo magnético aplicado, y las mediciones de la extensión de la desviación y la intensidad del campo magnético le permitieron a Thomson calcular la relación carga-masa de las partículas de rayo catódico. Los resultados de estas mediciones indicaron que estas partículas eran mucho más ligeras que los átomos (Figura 2.6).
Según sus observaciones, Thomson propuso: las partículas son atraídas por las cargas positivas (+) y repelidas por las cargas negativas (-), por lo que deben cargarse negativamente (las cargas iguales y las cargas diferentes se atraen); son menos masivos que los átomos e indistinguibles, independientemente del material de origen, por lo que deben ser constituyentes fundamentales y subatómicos de todos los átomos. Aunque controvertida en ese momento, la idea de Thomson fue aceptada gradualmente, y su partícula de rayos catódicos es lo que ahora llamamos un electrón, una partícula subatómica cargada negativamente con una masa más de mil veces menos que la de un átomo.
El término "electrón" fue acuñado en 1891 por el físico irlandés George Stoney, de "ión eléctrico".
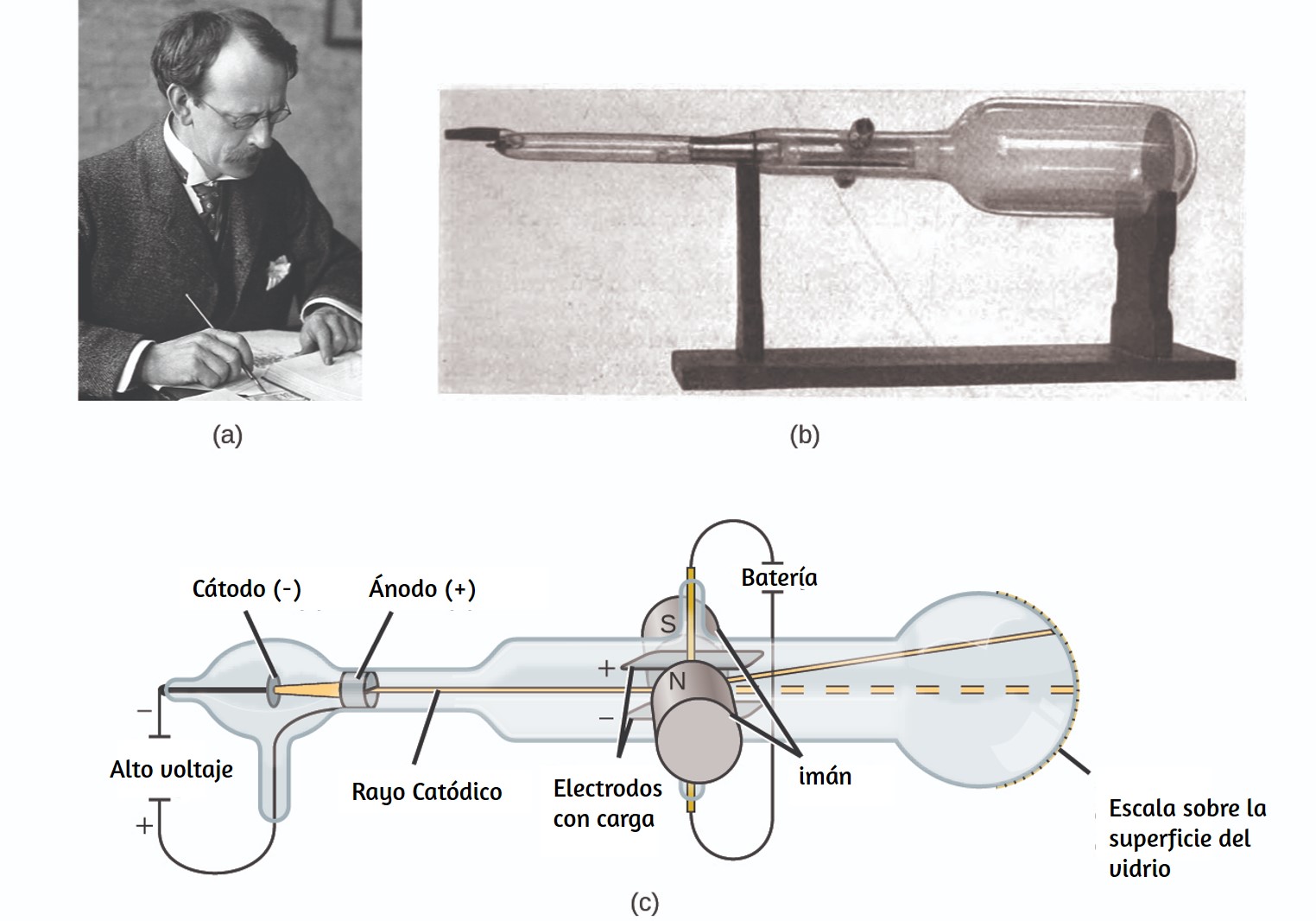
Figura 2.6. (a) J. J. Thomson produjo un haz visible en un tubo de rayos catódicos. (b) Este es un primer tubo de rayos catódicos, inventado en 1897 por Ferdinand Braun. (c) En el rayo catódico, el haz (mostrado en amarillo) proviene del cátodo y se acelera más allá del ánodo hacia una escala fluorescente en el extremo del tubo. Las desviaciones simultáneas por campos eléctricos y magnéticos aplicados permitieron a Thomson calcular la relación masa-carga de las partículas que componen el rayo catódico (crédito a: modificación del trabajo de la Fundación Nobel; crédito b: modificación del trabajo de Eugen Nesper; crédito c: modificación del trabajo de "Kurzon"/Wikimedia Commons).
Basándose en sus observaciones, Thomson propuso: que las partículas eran atraídas por el positivo (+) y repelidos por cargas negativas (-), por lo que deben ser cargadas negativamente.
Como las cargas iguales se repelen y a diferencia, las cargas son menos masivas que los átomos e indistinguibles, independientemente del material de origen, de modo que deben ser constituyentes fundamentales de todos los átomos. Aunque controvertida en ese momento, la idea de Thomson fue gradualmente aceptada, y su partícula de rayos catódicos es lo que ahora llamamos un electrón, una carga negativa, subatómica, con una masa más de mil veces menor que la de un átomo. El término "electrón" fue itroducido en 1891 por el físico irlandés George Stoney.
En 1909, el físico estadounidense Robert A. Millikan descubrió más información sobre el electrón a través de su experimentos "gota de aceite". Millikan creó gotitas de aceite microscópicas, que podrían cargarse eléctricamente por fricción a medida que formado o utilizando rayos X. Estas gotitas cayeron inicialmente debido a la gravedad, pero su progreso hacia abajo podría ser frenado o incluso revertido por un campo eléctrico más bajo en el aparato. Al ajustar la intensidad del campo eléctrico y realizar mediciones cuidadosamente y cálculos apropiados, Millikan pudo determinar la carga en caídas individuales (Figura 2.7).
Al observar los datos de carga que Millikan recopiló, es posible que haya reconocido que la carga de una gota de aceite es siempre un múltiplo de una carga específica, $1,6 \times 10^{−19}\; C$. Millikan concluyó que, por lo tanto, este valor debe ser una carga fundamental: la carga de un solo electrón: con sus cargas medidas debido a un exceso de un electrón $(1\; vez\; 1.6 \times 10^{−19}\; C)$, dos electrones $(2 \;veces \;1.6 \times 10^{−19}\; C)$, para tres $(3 \;veces\; 1.6 \times 10^{−19} \;C)$, y así sucesivamente, en una gota de aceite dada. Dado que la carga de un electrón ahora se conocía debido a la investigación de Millikan, y la relación carga-masa ya se conocía debido a la investigación de Thomson (1.759 × 1011 C / kg).
Figura 2.7 . El experimento de Millikan midió la carga de las gotas de aceite individuales. Los datos tabulados son ejemplos de algunos valores posibles.
Solo se requería un cálculo simple para determinar la masa de electron tambien
$$\begin{aligned} Masa \; del \; \text{electrón} &= 1.6 \times 10^{−19} \; C \times \cfrac{1\;kg}{1.759 \times 10^{11}\; C} \\ &= 9.107 \times 10^{-31} \; kg \end{aligned}$$Los científicos habían establecido que el átomo no era indivisible como Dalton había creído, y debido al trabajo de Thomson, Millikan y otros, se conocía la carga y la masa de las partículas subatómicas negativas (los electrones). Sin embargo, la parte cargada positivamente de un átomo aún no se entendía bien. En 1904, Thomson propuso el modelo de átomos de "pudín de ciruela", que describía una masa cargada positivamente con una cantidad igual de carga negativa en forma de electrones incrustados en ella, ya que todos los átomos son eléctricamente neutros.
Un modelo competitivo fue propuesto en 1903 por Hantaro Nagaoka, quien postuló un átomo similar a Saturno, que consiste en una esfera cargada positivamente rodeada por un halo de electrones (Figura 2.8).
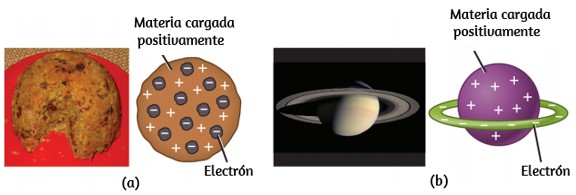
Figura 2.8 . (a) Thomson sugirió que los átomos se parecían al pudín de ciruela, un postre inglés que consiste en una torta húmeda con pasas incrustadas ("ciruelas"). (b) Nagaoka propuso que los átomos se parecían al planeta Saturno, con un anillo de electrones que rodean un "planeta" positivo. Modificación del trabajo de "Man vyi" / Wikimedia Commons; crédito b: Modificación de obra de “NASA” / Wikimedia Commons)
El siguiente gran avance en la comprensión del átomo provino de Ernest Rutherford, un físico de Nueva Zelanda que pasó su carrera científica en Canadá e Inglaterra. Realizó una serie de experimentos con un haz de partículas alfa de alta velocidad y carga positiva (partículas α) que se produjeron por la descomposición radioactiva del radio; Las partículas α constan de dos protones y dos neutrones. Rutherford y sus colegas Hans Geiger (más tarde famoso por el contador Geiger) y Ernest Marsden apuntaron un haz de partículas α, cuya fuente estaba incrustada en un bloque de plomo para absorber la mayor parte de la radiación, en una pieza muy delgada de lámina de oro y examinó la dispersión resultante de las partículas α utilizando una pantalla luminiscente que brillaba brevemente al ser golpeada por una partícula α. ¿Qué descubrieron?
La mayoría de las partículas pasaron a través de la lámina sin ser desviadas en absoluto. Sin embargo, algunos se desviaron ligeramente y un número muy pequeño se desvió casi directamente hacia la fuente (Figura 2.9). Rutherford describió el hallazgo de estos resultados: “Fue el evento más increíble que me ha sucedido en mi vida. Fue casi tan increíble como si dispararas un proyectil de 15 pulgadas a un pedazo de papel de seda y volviera y te golpeara.
Figura 2.9. Geiger y Rutherford dispararon partículas α en un pedazo de lámina de oro y detectaron dónde iban esas partículas, como se muestra en este diagrama esquemático de su experimento. La mayoría de las partículas pasaron directamente a través de la lámina, pero algunas se desviaron ligeramente y un número muy pequeño se desvió significativamente.
Esto es lo que Rutherford dedujo: debido a que la mayoría de las partículas α en movimiento rápido pasaron a través de los átomos de oro sin desviarse, deben haber viajado a través del espacio esencialmente vacío dentro del átomo. Las partículas alfa están cargadas positivamente, por lo que surgieron desviaciones cuando se encontraron con otra carga positiva (como las cargas se repelen entre sí). Dado que las cargas iguales se repelen entre sí, las pocas partículas α con carga positiva que cambiaron de manera abrupta deben haber golpeado otro cuerpo que también tenía una carga positiva altamente concentrada.
Como las desviaciones ocurrieron una pequeña fracción del tiempo, esta carga solo ocupó una pequeña cantidad de espacio en la lámina de oro. Analizando en detalle una serie de experimentos, Rutherford sacó dos conclusiones:
Este análisis llevó a Rutherford a proponer un modelo en el que un átomo consiste en un núcleo muy pequeño, cargado positivamente, en el cual la mayor parte de la masa del átomo se concentra, rodeada por electrones cargados negativamente, de modo que el átomo es eléctricamente neutral (Figura 2.10).
Figura 2.10. Las partículas α se desvían solo cuando chocan o pasan cerca del núcleo de oro cargado positivamente, mucho más pesado. Debido a que el núcleo es muy pequeño en comparación con el tamaño de un átomo, se desvían muy pocas partículas α. La mayoría pasa a través de la región relativamente grande ocupada por electrones, que son demasiado ligeros para desviar las partículas que se mueven rápidamente
Después de muchos más experimentos, Rutherford también descubrió que los núcleos de otros elementos contienen el núcleo de hidrógeno como un "bloque de construcción", y llamó a esta partícula más fundamental como El protón, la partícula subatómica cargada positivamente que se encuentra en el núcleo. Con una adición, que aprenderás a continuación, este modelo nuclear del átomo, propuesto hace más de un siglo, todavía se usa hoy.
La siguiente escena interactiva de Phet de Colorado simula el famoso experimento en el que se refutó el modelo de Pudín de Ciruela del átomo mediante la observación de las partículas alfa rebotando en los átomos y se determinó que debía tener un pequeño núcleo.
Otro hallazgo importante fue el descubrimiento de isótopos. A principios del siglo XX, los científicos identificaron varias sustancias que parecían ser elementos nuevos, aislándolas de los minerales radiactivos.
Por ejemplo, un "nuevo elemento" producido por la desintegración radiactiva del torio recibió inicialmente el nombre de mesotorio. Sin embargo, un análisis más detallado mostró que era químicamente idéntico al radio, a pesar de tener una masa atómica diferente. Este resultado llevó al químico inglés Frederick Soddy a darse cuenta de que un elemento podría tener tipos de átomos con diferentes masas que eran químicamente indistinguibles. Estos diferentes tipos se llaman isótopos: átomos del mismo elemento que difieren en masa. Soddy recibió el Premio Nobel de Química en 1921 por este descubrimiento.
Quedaba un enigma: se sabía que el núcleo contenía casi toda la masa de un átomo, y el número de protones solo proporcionaba la mitad, o menos, de esa masa. Se hicieron propuestas para explicar qué constituía la masa restante, incluida la existencia de partículas neutras en el núcleo. Como era de esperar, la detección de partículas no cargadas es muy difícil, y no fue hasta 1932 que James Chadwick encontró evidencia de neutrones, partículas subatómicas no cargadas con una masa aproximadamente igual a la de los protones. La existencia del neutrón también explicaba los isótopos: difieren en masa porque tienen diferentes números de neutrones, pero son químicamente idénticos porque tienen el mismo número de protones.
El desarrollo de la teoría atómica moderna reveló mucho sobre la estructura interna de los átomos. Se sabe que un átomo contiene un núcleo muy pequeño compuesto de protones cargados positivamente y neutrones (sin carga eléctrica), rodeado por un volumen mucho mayor de espacio que contiene electrones cargados negativamente.
El núcleo contiene la mayoría de la masa de un átomo porque los protones y los neutrones son mucho más pesados que los electrones, mientras que los electrones ocupan casi todo el volumen de un átomo. El diámetro de un átomo es del orden de $10^{-10} \; m$, mientras que el diámetro del núcleo es aproximadamente de $10^{-15}\; m$, aproximadamente $100.000$ veces más pequeño. Para una perspectiva sobre sus tamaños relativos, considera esto: si el núcleo fuera del tamaño de un arándano, el átomo sería aproximadamente del tamaño de un estadio de fútbol (Figura 2.11)
Figura 2.11. Si un átomo pudiera expandirse al tamaño de un estadio de fútbol, el núcleo sería el tamaño de un solo arándano (Crédito medio: modificación del trabajo por "babyknight"/Wikimedia Commons; crédito derecho: modificación del trabajo por Paxson Woelber).
Los átomos, los protones, neutrones y electrones son extremadamente pequeños. Por ejemplo, un átomo de carbono pesa menos de $2 \times 10^{-23}\; g$, y un electrón tiene una carga de menos de $2 \times 10^{-19}\;C$ (Coulomb). Al describir las propiedades de objetos diminutos como los átomos, usamos unidades de medida apropiadamente pequeñas, como la unidad de masa atómica (uma) y la unidad fundamental de carga (e). La uma se definió originalmente en base al hidrógeno, el elemento más liviano, y más tarde en términos de oxígeno.
Desde 1961, se ha definido con respecto al isótopo más abundante de carbono, a los cuales se les asignan masas de exactamente $12 \;uma$ (este isótopo se conoce como "carbono-12"). Por lo tanto, una uma es exactamente $\frac12$ de la masa de un átomo de carbono-12: $1\; uma = 1.6605 \times 10^{-24}\; g$ (el Dalton (Da) y la unidad de masa atómica unificada (u) son unidades alternativas que son equivalentes a la uma). La unidad fundamental de carga (también llamada carga elemental) es igual a la magnitud de la carga de un electrón (e) con $e = 1.602 \times 10^{-19}\; C$.
Un protón tiene una masa de 1.0073 uma y una carga de 1+. Un neutrón es una partícula ligeramente más pesada con una masa de 1.0087 uma y una carga de cero; como su nombre lo indica, es neutral. El electrón tiene una carga de 1− y es una partícula mucho más liviana con una masa de aproximadamente 0,00055 uma (se necesitarían aproximadamente 1800 electrones para igualar la masa de un protón). Las propiedades de estas partículas fundamentales se resumen en la tabla 2.2. (Un estudiante observador podría notar que la suma de las partículas subatómicas de un átomo no es igual a la masa real del átomo: la masa total de seis protones, seis neutrones y seis electrones es 12.0993 uma, ligeramente mayor que 12.00 uma. Esta masa "faltante" es conocida como el defecto de masa).
Tabla 2.2. Propiedades de las partículas subatómicas
El número de protones en el núcleo de un átomo es su número atómico (Z). Este es el rasgo definitorio de un elemento: su valor determina la identidad del átomo. Por ejemplo, cualquier átomo que contenga seis protones es el elemento carbono y tiene el número atómico 6, independientemente de cuántos neutrones o electrones pueda tener. Un átomo neutro debe contener el mismo número de cargas positivas y negativas, por lo que el número de protones es igual al número de electrones. Por lo tanto, el número atómico también indica el número de electrones en un átomo. El número total de protones y neutrones en un átomo se llama su número de masa (A).
El número de neutrones es, por lo tanto, la diferencia entre el número de masa y el número atómico: A - Z = número de neutrones.
Número atómico (Z) = número de protones número de masa
(A) = número de protones + número de neutrones
A - Z = número de neutrones
Los átomos son eléctricamente neutros si contienen la misma cantidad de protones cargados positivamente y electrones cargados negativamente. Cuando los números de estas partículas subatómicas no son iguales, el átomo está cargado eléctricamente y se llama ión. La carga de un átomo se define de la siguiente manera:
Carga atómica = número de protones - número de electrones
Como se explicará en detalle más adelante en este capítulo, los átomos (y las moléculas) generalmente adquieren carga al ganar o perder electrones. Un átomo que gana uno o más electrones exhibirá una carga negativa y se llama anión. Los átomos cargados positivamente, llamados cationes, se forman cuando un átomo pierde uno o más electrones.
Por ejemplo, un átomo de sodio neutro (Z = 11) tiene 11 electrones. Si este átomo pierde un electrón, se convertirá en un catión con una carga 1+ (11 - 10 = 1+). Un átomo de oxígeno neutro (Z = 8) tiene ocho electrones, y si gana dos electrones se convertirá en un anión con una carga 2- (8 - 10 = 2 -).
Ejemplo 2.3
Composición de un átomo
El yodo es un oligoelemento esencial en nuestra dieta; se necesita para producir hormona tiroidea. La falta de yodo en la dieta puede llevar al desarrollo de un bocio, un agrandamiento de la glándula tiroides (Figura 2.12).
Figura 2.12. (a) La falta de yodo en la dieta puede causar un agrandamiento de la glándula tiroides llamado bocio. (b) La adición de pequeñas cantidades de yodo a la sal, que previene la formación de bocios, ha ayudado a eliminar esta preocupación en los EE. UU., donde el consumo de sal es alto (crédito a: modificación del trabajo por "Almazi"/Wikimedia Commons; crédito b: modificación del trabajo por Mike Mozart).
La adición de pequeñas cantidades de yodo a la sal de mesa (sal yodada) esencialmente ha eliminado este problema de salud en los Estados Unidos, pero hasta el 40% de la población mundial todavía está en riesgo de deficiencia de yodo.
Los átomos de yodo se agregan como aniones, y cada uno tiene una carga 1 y una masa de 127. Determina el número de protones, neutrones y electrones en uno de estos aniones de yodo.
Solución
El número atómico del yodo (53) nos dice que un átomo de yodo neutro contiene 53 protones en su núcleo y 53 electrones fuera de su núcleo.
Debido a que la suma de los números de protones y neutrones es igual al número de masa, 127, el número de neutrones es 74 (127 - 53 = 74). Dado que el yodo se agrega como un anión 1−, el número de electrones es 54 [53 - (1–) = 54].
Comprueba tu aprendizaje
Un símbolo químico es una abreviatura que usamos para indicar un elemento o un átomo de un elemento. Por ejemplo, el símbolo para el mercurio es Hg (Figura 2.13).
Utilizamos el mismo símbolo para indicar un átomo de mercurio (dominio microscópico) o para etiquetar un contenedor de muchos átomos del elemento mercurio (dominio macroscópico).
Figura 2.13. El símbolo Hg representa el elemento mercurio independientemente de la cantidad; podría representar un átomo de mercurio o una gran cantidad de mercurio.
Los símbolos de varios elementos comunes y sus átomos se enumeran en la tabla 2.3.. Algunos símbolos se derivan del nombre común del elemento; otras son abreviaturas del nombre en otro idioma. La mayoría de los símbolos tienen una o dos letras, pero se han usado símbolos de tres letras para describir algunos elementos que tienen números atómicos mayores que 112. Para evitar confusiones con otras notaciones, solo la primera letra de un símbolo está en mayúscula. Por ejemplo, Co es el símbolo del elemento cobalto, pero CO es la notación del compuesto monóxido de carbono, que contiene átomos de los elementos carbono (C) y oxígeno (O).
Todos los elementos conocidos y sus símbolos se encuentran en la tabla periódica en la (figura 2.26). Tradicionalmente, el descubridor (o descubridores) de un nuevo elemento nombra el elemento.
Tabla 2.3. Elementos y Símbolos
Sin embargo, hasta que el nombre sea reconocido por la Unión Internacional de Química Pura y Aplicada (IUPAC), el nombre recomendado del nuevo elemento se basa en la(s) palabra(s) latina(s) para su número atómico. Por ejemplo, el elemento 106 fue llamado unnilhexium (Unh), el elemento 107 fue llamado unnilseptium (Uns), y el elemento 108 fue llamado unniloctium (Uno) por varios años.
Estos elementos ahora llevan el nombre de científicos (u ocasionalmente ubicaciones); por ejemplo, el elemento 106 ahora se conoce como seaborgium (Sg) en honor de Glenn Seaborg, un ganador del Premio Nobel que participó activamente en el descubrimiento de varios elementos pesados.
El símbolo para un isótopo específico de cualquier elemento se escribe colocando el número de masa como un superíndice a la izquierda del símbolo del elemento (Figura 2.14). El número atómico a veces se escribe como un subíndice que precede al símbolo, pero como este número define la identidad del elemento, al igual que su símbolo, a menudo se omite. Por ejemplo, el magnesio existe como una mezcla de tres isótopos, cada uno con un número atómico de 12 y con números de masa de 24, 25 y 26, respectivamente. Estos isótopos se pueden identificar como $^{24}Mg, ^{25}Mg \;y\;^{26}Mg$. Estos símbolos de isótopos se leen como "elemento, número de masa" y se pueden simbolizar de manera consistente con esta lectura.
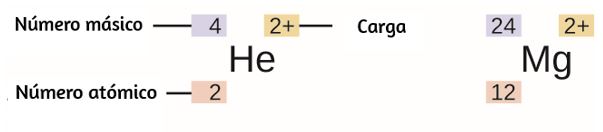
Figura 2.14. El símbolo para un átomo indica el elemento a través de su símbolo usual de dos letras, el número de masa como un superíndice izquierdo, el número atómico como un subíndice izquierdo (a veces se omite) y la carga como un superíndice derecho.
Por ejemplo, $^{24}Mg$ se lee como "magnesio 24" y puede escribirse como "magnesium-24" o "Mg-24". $^{25}Mg$ se lee como "magnesio 25" y se puede escribir como "magnesium-25" o " Mg-25. Todos los átomos de magnesio tienen 12 protones en su núcleo. Difieren solo porque un átomo de $^{24}Mg$ tiene 12 neutrones en su núcleo, un átomo de $^{25}Mg$ tiene 13 neutrones, y un $^{26}Mg$ tiene 14 neutrones.
La información sobre los isótopos naturales de los elementos con números atómicos del 1 al 10 se proporciona en la tabla 2.4.
Tabla 2.4. Composiciones nucleares de átomos de elementos muy ligeros
En la siguiente tabla interactiva, diseñada por Peter Mahaffy, Brian Martin, Tyler deBoon, Mckenzie Oliver, Ashley Ritter, Marc-Olivier Lajeunesse, Rachel Hislop-Hook, y Shawn Ritter, puedes explorar y descubrir algunas de las muchas formas en las que el conocimiento de los isótopos es importante. Estos recursos revisados por pares se han desarrollado como parte de un proyecto IUPAC para aumentar la comprensión de la ciencia de los isótopos, así como algunas de las muchas aplicaciones de este campo de estudio.
Ten en cuenta que, además de los nombres y símbolos estándar, a menudo se hace referencia a los isótopos del hidrógeno utilizando nombres comunes y símbolos que los acompañan.
El hidrógeno-2, simbolizado en $^2H$, también se denomina deuterio y, a veces, simbolizado por D. El hidrógeno-3, simbolizado en $^3H$, también se denomina tritio y en ocasiones, simbolizado por T.
Debido a que cada protón y cada neutrón contribuyen aproximadamente una uma a la masa de un átomo, y cada electrón contribuye mucho menos, la masa atómica de un solo átomo es aproximadamente igual a su número de masa (un número entero). Sin embargo, las masas promedio de los átomos de la mayoría de los elementos no son números enteros porque la mayoría de los elementos existen naturalmente como mezclas de dos o más isótopos. La masa de un elemento que se muestra en una tabla periódica o que aparece en una tabla de masas atómicas es una masa promedio ponderada de todos los isótopos presentes en una muestra natural de ese elemento. Esto es igual a la suma de la masa de cada isótopo individual multiplicada por su abundancia fraccional.
$$ masa\; media = \sum_i\; (abundancia\; fraccional \times masa\; \text{isotópica})$$Por ejemplo, el elemento boro se compone de dos isótopos: aproximadamente el 19.9% de todos los átomos de boro son $^{10}B$ con una masa de 10.0129 uma, y el 80.1% restante son $^{11}B$ con una masa de 11.0093 uma. La masa atómica media para el boro se calcula que es:
Es importante entender que ningún átomo de boro pesa exactamente 10.8 uma; 10.8 uma es la masa promedio de todos los átomos de boro, y los átomos de boro individuales pesan aproximadamente 10 uma o 11 uma.
Ejemplo 2.4
Cálculo de la masa atómica media
Un meteorito encontrado en el centro de Indiana contiene rastros del gas noble neón recogido del viento solar durante el viaje del meteorito a través del sistema solar. El análisis de una muestra del gas mostró que consistía en 91.84% $^{20}Ne$ (masa 19.9924 amu), 0.47% $^{21}Ne$ (masa 20.9940 uma) y 7.69% $^{22}Ne$ (masa 21.9914 uma). ¿Cuál es la masa media del neón en el viento solar?
Solución
$masa\; media = (0.9184 \times 19.924\; uma) + (0.0047 \times 20.9940\; uma)+ (0.0769 \times 21.9914\; uma) = (18.36 + 0.099 + 1.69)\; uma = 20.15\; uma$La masa promedio de un átomo de neón en el viento solar es de 20.15 uma (la masa promedio de un átomo de neón terrestre es 20.1796 uma. Este resultado demuestra que podemos encontrar pequeñas diferencias en la abundancia natural de isótopos, dependiendo de su origen).
Enlace a aprendizaje
Use el siguiente simulador para construir átomos de los primeros 10 elementos, mira qué isótopos existen, comprobar la estabilidad nuclear y adquiere experiencia con los símbolos isotópicosLa escena interactiva fue descargada de Phet de Colorado, en la cual puedes construir un átomo con protones, neutrones y electrones, y observar cómo cambia el elemento, la carga y la masa. Además, también puedes probar tus ideas... ¡jugando!.
Comprueba tu aprendizaje
También podemos hacer variaciones de este tipo de cálculo, como se muestra en el siguiente ejemplo.
Ejemplo 2.5
Cálculo del porcentaje de abundancia
El cloro natural consiste en $^{35}Cl$ (masa 34.96885 uma) y $^{37}Cl$ (masa 36.96590 uma), con una masa promedio de 35.453 uma. ¿Cuál es el porcentaje de composición de Cl en términos de estos dos isótopos?
Solución
La masa promedio de cloro es la fracción que es $^{35}Cl$ por la masa de $^{35}Cl$ más la fracción que es $^{37}Cl$ por la masa de $^{37}Cl$.
masa media = (fracción de $^{35}Cl$ \times masa de $^{35}Cl$) + (fracción de $^{37}Cl \times$ masa de $^{37}Cl$)
Si dejamos que x represente la fracción que es $^{35}Cl$, entonces la fracción que es $^{37}Cl$ está representada por 1.00 - x. (La fracción que es $^{35}Cl$ + la fracción que es $^{37}Cl$ debe sumar hasta 1, por lo que la fracción de $^{37}Cl$ debe ser igual a 1.00 menos la fracción de $^{35}Cl$).
Sustituyendo esto en la ecuación de masa promedio o media, tenemos:
35.453 uma = (x × 34.96885 uma) + [(1.00 − x) × 36.96590 uma]
35.453 = 34.96885x + 36.96590 − 36.96590x
1.99705x = 1.513
x = $\cfrac{1.513}{1.99705} = 0.7576$
Entonces, la solución para x es, x = 0.7576, lo que significa que 1.00 - 0.7576 = 0.2424. Por lo tanto, el cloro consiste en 75.76% de $^{35}Cl$ y 24.24% de $^{37}Cl$.
Comprueba tu aprendizaje
La presencia y abundancia natural de los isótopos puede determinarse experimentalmente usando un instrumento llamado un espectrómetro de masas. En el espectrómetro de masas (Figura 2.15), la muestra se vaporiza y se expone a un haz de electrones de alta energía que hace que los átomos (o moléculas) de la muestra se carguen eléctricamente, generalmente al perder uno o más electrones. Luego, estos cationes pasan a través de un campo eléctrico o magnético (variable) que desvía la trayectoria de cada catión en una medida que depende de su masa y carga (similar a la forma en que se realiza la trayectoria de un gran rodamiento de bolas de acero que pasa por un imán) desviada en menor medida que la de un pequeño acero BB).
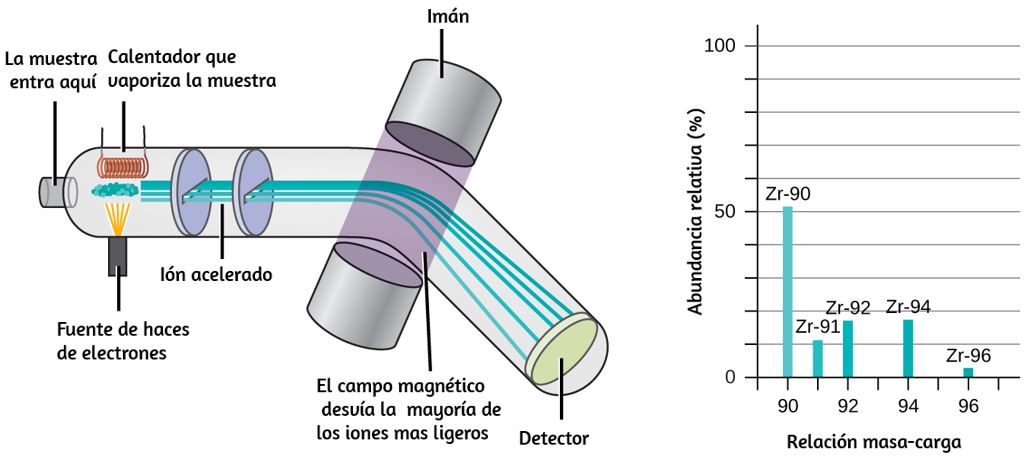
Figura 2.15. El análisis del circonio en un espectrómetro de masas produce un espectro de masas con picos que muestran los diferentes isótopos de Zr.
Los iones se detectan y se crea un gráfico del número relativo de iones generados en comparación con sus relaciones masa-carga (un espectro de masas). La altura vertical característica de cada pico en un espectro de masas es proporcional a la fracción de cationes con la relación de masa a carga especificada.
Desde su uso inicial durante el desarrollo de la teoría atómica moderna, MS (espectrómetro de masas) ha evolucionado para convertirse en una herramienta poderosa para el análisis químico en una amplia gama de aplicaciones.
En el siguiente interactivo diseñado por Wolfgang Christian y Francisco Esquembre puedes ver el funcionamiento del espectromerto de masa, haciendo clic en la tabla para seleccionar la masa de una molécula y su velocidad.
El espectrómetro de masas que Bainbridge elaboró en 1933 permite medir la masa de iones de una misma carga. Cuando los iones salen de un colimador, que no está representado aquí, éstos son seleccionados según su velocidad $v = \frac{E}{B}$ y diferenciados por su masa. Este dispositivo permite también separar los isótopos de un mismo átomo.
Una fórmula molecular es una representación de una molécula que usa símbolos químicos para indicar los tipos de átomos seguidos de subíndices para mostrar el número de átomos de cada tipo en la molécula (un subíndice se usa solo cuando está presente más de un átomo de un tipo dado). Las fórmulas moleculares también se usan como abreviaturas para los nombres de los compuestos.
La fórmula estructural para un compuesto proporciona la misma información que su fórmula molecular (los tipos y números de átomos en la molécula), pero también muestra cómo los átomos están conectados en la molécula. La fórmula estructural para el metano contiene símbolos para un átomo de C y cuatro átomos de H, que indican el número de átomos en la molécula (Figura 2.16).
Figura 2.16. Una molécula de metano se puede representar como (a) una fórmula molecular, (b) una fórmula estructural, (c) un modelo de bolas y palos (con clic sostenido puedes mover la molécula), y (d) un modelo de espacio relleno. Los átomos de carbono e hidrógeno están representados por esferas blancas y grises o, respectivamente. Al hacer clic en la parte superior derecha, se amplia la imagen y puedes apreciar mejor el interactivo haciendo clic sostenido para rotar la imagen o girando la rueda para hacerla mas grande o mas chica.
Las líneas representan enlaces que mantienen unidos los átomos (un enlace químico es una atracción entre átomos o iones que los mantienen unidos en una molécula o en un cristal). Discutiremos los enlaces químicos y veremos cómo predecir la disposición de los átomos en una molécula más adelante. Por ahora, simplemente debes saber que las líneas son una indicación de cómo los átomos están conectados en una molécula. Un modelo de bola y palo muestra la disposición geométrica de los átomos con tamaños atómicos no a escala, y un modelo de relleno de espacio muestra los tamaños relativos de los átomos.
Aunque muchos elementos están formados por átomos individuales y discretos, algunos existen como moléculas formadas por dos o más átomos del elemento unidos químicamente entre sí. Por ejemplo, la mayoría de las muestras de los elementos de hidrógeno, oxígeno y nitrógeno están compuestas por moléculas que contienen dos átomos cada una (llamadas moléculas diatómicas) y, por lo tanto, tienen las fórmulas moleculares $H_2,\quad O_2\quad y\quad N_2$, respectivamente. Otros elementos que se encuentran comúnmente como moléculas diatómicas son el flúor $(F_2)$, el cloro ($Cl_2$), el bromo ($Br_2$) y el yodo ($I_2$). La forma más común del elemento azufre está compuesta por moléculas que constan de ocho átomos de azufre; Su fórmula molecular es $S_8$ Figura 2.17.Hemos incluido dos tipos de interactivos. El primero aparece cuando haces clic en la expresión "Figura xxx", que es un modelo 3D diseñado en la aplicación Kekule, diseñado por Chen Jiang. El segundo interactivo es el que aparece en la página, diseñado en el aplicativo http://web.chemdoodle.com producido por http://www.ichemlabs.com.
Es importante tener en cuenta que un subíndice que sigue a un símbolo y un número delante de un símbolo no representan lo mismo; por ejemplo, $H_2$ y 2H representan especies claramente diferentes.
Figura 2.17. Una molécula de azufre se compone de ocho átomos de azufre y, por lo tanto, se escribe como S8. Puede representarse como (a) una fórmula estructural, (b) En el interactivo puedes seleccionar entre un modelo de bolas y palos, y un modelo de espacio relleno. Los átomos de azufre están representados por esferas amarillas.
$H_2$ es una fórmula molecular; representa una molécula diatómica de hidrógeno, que consiste en dos átomos del elemento que están unidos químicamente entre sí. La expresión 2H, por otro lado, indica dos átomos de hidrógeno separados que no se combinan como una unidad. La expresión $2H_2$ representa dos moléculas de hidrógeno diatómico (Figura 2.18) .
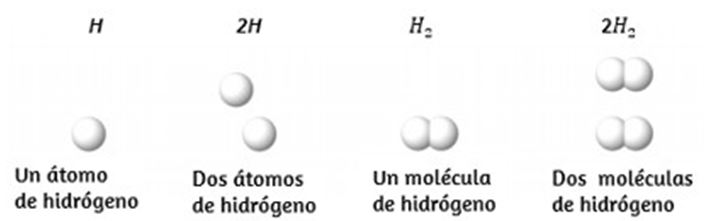
Figura 2.18. Los símbolos H, 2H, H2 y 2H2 representan entidades muy diferentes.
Los compuestos se forman cuando dos o más elementos se combinan químicamente, lo que resulta en la formación de enlaces. Por ejemplo, el hidrógeno y el oxígeno pueden reaccionar para formar agua, y el sodio y el cloro pueden reaccionar para formar sal de mesa. Algunas veces describimos la composición de estos compuestos con una fórmula empírica, que indica los tipos de átomos presentes y la proporción de números enteros más simple del número de átomos (o iones) en el compuesto. Por ejemplo, el dióxido de titanio (usado como pigmento en la pintura blanca y en el tipo de protector solar de color blanco y grueso) tiene una fórmula empírica de $TiO_2$. Esto identifica los elementos titanio (Ti) y oxígeno (O) como los constituyentes del dióxido de titanio e indica la presencia de dos veces más átomos del elemento oxígeno que átomos del elemento titanio (Figura 2.19).
Figura 2.19 (a) El compuesto blanco de dióxido de titanio proporciona una protección eficaz contra el sol. (b) Un cristal de dióxido de titanio, $TiO_2$, contiene titanio y oxígeno en una proporción de 1 a 2. Los átomos de titanio son grises y los átomos de oxígeno son rojos (crédito a: modificación del trabajo por “osseous”/ Flickr).
Como se discutió anteriormente, podemos describir un compuesto con una fórmula molecular, en la que los subíndices indican el número real de átomos de cada elemento en una molécula del compuesto.
En muchos casos, la fórmula molecular de una sustancia se deriva de la determinación experimental de su fórmula empírica y su masa molecular (la suma de las masas atómicas para todos los átomos que componen la molécula).
Por ejemplo, se puede determinar experimentalmente que el benceno contiene dos elementos, carbono (C) e hidrógeno (H), y que por cada átomo de carbono en el benceno, hay un átomo de hidrógeno. Así, la fórmula empírica es CH. Una determinación experimental de la masa molecular revela que una molécula de benceno contiene seis átomos de carbono y seis átomos de hidrógeno, por lo que la fórmula molecular para el benceno es $C_6H_6$ (Figura 2.20).
Figura 2.20. El benceno, $C_6H_6$, se produce durante la refinación del petróleo y tiene muchos usos industriales. Una molécula de benceno se puede representar como (a) una fórmula estructural, (b) y (c) el interactivo que puedes rotar con clic sostenido o cambiar su tamñao con la bola del ratón. (d) El benceno es un líquido claro.
Si conocemos la fórmula de un compuesto, podemos determinar fácilmente la fórmula empírica (esto es algo así como un ejercicio académico; la cronología inversa generalmente se sigue en la práctica real). Por ejemplo, la fórmula molecular para el ácido acético, el componente que le da al vinagre su sabor intenso, es $C_2H_4O_2$.
Esta fórmula indica que una molécula de ácido acético (Figura 2.21) contiene dos átomos de carbono, cuatro átomos de hidrógeno y dos átomos de oxígeno. La proporción de átomos es 2: 4: 2. Dividir por el mínimo común denominador (2) da la relación más simple de números enteros de átomos, 1: 2: 1, por lo que la fórmula empírica es $CH_2O$. Ten en cuenta que una fórmula molecular es siempre un múltiplo entero de una fórmula empírica.
Figura 2.21. a) El vinagre contiene ácido acético, $C_2H_4O_2$, que tiene una fórmula empírica de $CH_2O$. Puede representarse como (b) y (c) como un modelo de bola y pal. (crédito a: modificación del trabajo por "HomeSpot HQ"/Flickr)
Ejemplo 2.6
Momento de inercia de un sistema de partículas
Las moléculas de glucosa (azúcar en la sangre) contienen 6 átomos de carbono, 12 átomos de hidrógeno y 6 átomos de oxígeno. ¿Cuáles son las fórmulas moleculares y empíricas de la glucosa?
Solución
La fórmula molecular es $C_6H_{12}O_6$ porque una molécula en realidad contiene 6 átomos de carbono, 12 H y 6 O. La proporción más simple de números enteros de C a H a O en la glucosa es 1: 2: 1, por lo que la fórmula empírica es $CH_2O$.
Comprueba tu aprendizaje
Es importante tener en cuenta que puede ser posible que los mismos átomos se dispongan de diferentes maneras: los compuestos con la misma fórmula molecular pueden tener diferentes enlaces de átomo a átomo y, por lo tanto, estructuras diferentes. Por ejemplo, ¿podría haber otro compuesto con la misma fórmula que el ácido acético, $C_2H_4O_2$? Y si es así, ¿cuál sería la estructura de sus moléculas?.
Si predices que podría existir otro compuesto con la fórmula $C_2H_4O_2$, entonces demuestras una buena comprensión química y es correcto. También se pueden organizar dos átomos de C, cuatro átomos de H y dos átomos de O para formar un formiato de metilo,
que se utiliza en la fabricación, como insecticida y para acabados de secado rápido. Las moléculas de formiato de metilo tienen uno de los átomos de oxígeno entre los dos átomos de carbono, que difieren de la disposición en las moléculas de ácido acético.
¿Qué es lo que hacen los químicos? Según Lee Cronin (Figura 2.22), los químicos producen moléculas muy complicadas al "cortar" moléculas pequeñas e "ingeniería inversa". Se pregunta si podríamos "hacer un conjunto de química universal realmente genial" por lo que él llama química de "aplicación". ¿Podríamos "aplicar" la química? En una charla de TED de 2012, Lee describe una posibilidad fascinante: combinar una colección de "tintas" químicas con una impresora 3D capaz de fabricar un aparato de reacción (diminutos tubos de ensayo, cubiletes y similares) para crear un "conjunto de herramientas universales de química". "Este kit de herramientas podría usarse para crear medicamentos personalizados para combatir una nueva especie" o para imprimir "medicamentos configurados personalmente para su composición genética, en torno a una situación de salud. Dice Cronin: "Lo que Apple hizo por la música, me gustaría hacer por el descubrimiento y distribución de medicamentos recetados". Observa su charla completa en el sitio web
El ácido acético y el formiato de metilo son ejemplos de compuestos isómeros con la misma fórmula química pero diferentes estructuras moleculares Figura 2.23. Ten en cuenta que esta pequeña diferencia en la disposición de los átomos tiene un efecto importante en sus respectivas propiedades químicas. Seguramente no querrás usar una solución de formiato de metilo como sustituto de una solución de ácido acético (vinagre) cuando prepares el aderezo para ensaladas.
Figura 2.23 . Las moléculas de (a y b) ácido acético y formiato de metilo (c y d) son isómeros estructurales; tienen la misma fórmula ($C_2H_4O_2$) pero diferentes estructuras (y por lo tanto diferentes propiedades químicas).
Existen muchos tipos de isómeros (Figura 2.24). El ácido acético y el formiato de metilo son isómeros estructurales, compuestos en los que las moléculas difieren en la forma en que los átomos están conectados entre sí. También hay varios tipos de isómeros espaciales, en los cuales las orientaciones relativas de los átomos en el espacio pueden ser diferentes. Por ejemplo, la carvona compuesta (que se encuentra en las semillas de alcaravea, la menta verde y las cáscaras de mandarina) consiste en dos isómeros que son imágenes especulares entre sí. S - (+) - la carvona huele a alcaravea, y R - (-) - la carvona huele a menta verde.
Figura 2.24. Las moléculas de carvona son isómeros espaciales; sólo difieren en las orientaciones relativas de los átomos en el espacio (parte inferior izquierda del crédito: modificación del trabajo por "Miansari66"/ Wikimedia Commons; parte inferior derecha del crédito: modificación del trabajo por Forest & Kim Starr).
Cuando los primeros químicos trabajaron para purificar minerales y descubrieron más elementos, se dieron cuenta de que varios elementos podían agruparse por sus comportamientos químicos similares. Uno de estos grupos incluye el litio (Li), el sodio (Na) y el potasio (K): todos estos elementos son brillantes, conducen bien el calor y la electricidad, y tienen propiedades químicas similares. Un segundo grupo incluye el calcio (Ca), el estroncio (Sr) y el bario (Ba), que también son brillantes, buenos conductores del calor y la electricidad, y tienen propiedades químicas en común. Sin embargo, las propiedades específicas de estos dos grupos son notablemente diferentes entre sí. Por ejemplo: Li, Na y K son mucho más reactivos que Ca, Sr y Ba; Li, Na y K forman compuestos con oxígeno en una relación de dos de sus átomos a un átomo de oxígeno, mientras que Ca, Sr y Ba forman compuestos con uno de sus átomos a un átomo de oxígeno. El flúor (F), el cloro (Cl), el bromo (Br) y el yodo (I) también exhiben propiedades similares entre sí, pero estas propiedades son
drásticamente diferentes de las de cualquiera de los elementos anteriores.
Dimitri Mendeleev en Rusia (1869) y Lothar Meyer en Alemania (1870) reconocieron independientemente que existía una relación periódica entre las propiedades de los elementos conocidos en ese momento. Ambas tablas publicadas con los elementos dispuestos de acuerdo con el aumento de la masa atómica. Pero Mendeleev fue un paso más allá que Meyer: usó su tabla para predecir la existencia de elementos que tendrían las propiedades similares al aluminio y al silicio, pero que aún no se conocían. Los descubrimientos del galio (1875) y el germanio (1886) brindaron un gran apoyo al trabajo de Mendeleev. Aunque Mendeleev y Meyer tuvieron una larga disputa sobre la prioridad, las contribuciones de Mendeleev al desarrollo de la tabla periódica ahora son más ampliamente reconocidas (Figura 2.25).
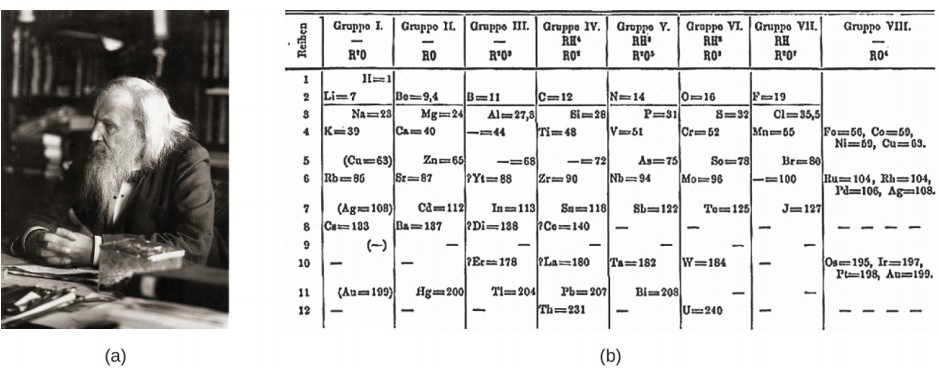
Figura 2.25. (a) A Dimitri Mendeleev se le atribuye la creación de (b) la primera tabla periódica de los elementos (crédito a: modificación de la obra de Serge Lachinov; Crédito b: modificación de la obra de "Den fjättrade ankan"/Wikimedia Commons)
En el siglo XX, se hizo evidente que la relación periódica involucraba números atómicos en lugar de masas atómicas. La declaración moderna de esta relación, la ley periódica, es la siguiente: las propiedades de los elementos son funciones periódicas de sus números atómicos. Una tabla periódica moderna organiza los elementos en orden creciente de sus números atómicos y agrupa los átomos con propiedades similares en la misma columna vertical (Figura 2.26). Cada caja representa un elemento y contiene su número atómico, símbolo, masa atómica promedio y (a veces) nombre. Los elementos están organizados en siete filas horizontales, llamadas períodos o series, y 18 columnas verticales, llamadas grupos o familias. Los grupos están etiquetados en la parte superior de cada columna. En los Estados Unidos, las etiquetas tradicionalmente eran números con letras mayúsculas. Sin embargo, la IUPAC recomienda que se utilicen los números del 1 al 18, y estas etiquetas son más comunes. Para que la tabla se ajuste a una sola página, las partes de dos de las filas, un total de 14 columnas, generalmente se escriben debajo del cuerpo principal de la tabla.
Muchos elementos difieren dramáticamente en sus propiedades químicas y físicas, pero algunos elementos son similares en sus comportamientos. Por ejemplo, muchos elementos aparecen brillantes, son maleables (se pueden deformar sin romperse), dúctiles y conducen bien el calor y la electricidad. Otros elementos no son brillantes, maleables o dúctiles, y son malos conductores del calor y la electricidad. Podemos clasificar los elementos en grandes clases con propiedades comunes: metales (elementos brillantes, maleables, buenos conductores de calor y electricidad, de color amarillo sombreado); no metales (elementos que parecen opacos, malos conductores de calor y electricidad, verde sombreado); y metaloides (elementos que conducen el calor y la electricidad moderadamente bien, y poseen algunas propiedades de los metales y algunas propiedades de los no metales: púrpura sombreada).
Figura 2.26 Los elementos en la tabla periódica están organizados de acuerdo a sus propiedades
Los elementos también pueden clasificarse en los elementos del grupo principal (o elementos representativos) en las columnas etiquetadas 1, 2 y 13–18; los metales de transición en las columnas etiquetadas 3–12Según la definición de la IUPAC, los elementos del grupo 12 no son metales de transición, aunque a menudo se los denomina como tales. Se proporcionan detalles adicionales sobre los elementos de este grupo en un capítulo sobre metales de transición y química de coordinación.; y metales de transición interna en las dos filas en la parte inferior de la tabla (Figura 2.27). Los elementos de la fila superior se denominan lantánidos y los elementos de la fila inferior son actínidos.
Los elementos pueden subdividirse aún más por propiedades más específicas, como la composición de los compuestos que forman. Por ejemplo, los elementos del grupo 1 (la primera columna) forman compuestos que consisten en un átomo del elemento y un átomo de hidrógeno. Estos elementos (excepto el hidrógeno) se conocen como metales alcalinos, y todos tienen propiedades químicas similares. Los elementos del grupo 2 (la segunda columna) forman compuestos que consisten en un átomo del elemento y dos átomos de hidrógeno: estos se llaman metales alcalinotérreos, con propiedades similares entre los miembros de ese grupo. Otros grupos con nombres específicos son los pnictógenos o nitrogenoideos o nitrogenoides (grupo 15), los calcógenos o anfígenos (grupo 16), los halógenos (grupo 17) y los gases nobles (grupo 18), también conocidos como gases inertes). El primer elemento del grupo también puede hacer referencia a los grupos: por ejemplo, los calcógenos pueden denominarse grupo de oxígeno o familia de oxígeno. El hidrógeno es un elemento único, no metálico, con propiedades similares a los elementos del grupo 1 y del grupo 17. Por esa razón, el hidrógeno se puede mostrar en la parte superior de ambos grupos, o por sí solo.
Al estudiar la tabla periódica, es posible que hayas notado algo sobre las masas atómicas de algunos de los elementos. El elemento 43 (tecnecio), el elemento 61 (prometio) y la mayoría de los elementos con número atómico 84 (polonio) y más tienen su masa atómica dada entre corchetes. Esto se hace para los elementos que consisten completamente en isótopos radiactivos inestables. No se puede determinar un peso atómico promedio para estos elementos porque sus radioisótopos pueden variar significativamente en abundancia relativa, dependiendo de la fuente, o incluso pueden no existir en la naturaleza. El número entre corchetes es el número de masa atómica (una masa atómica aproximada) del isótopo más estable de ese elemento.
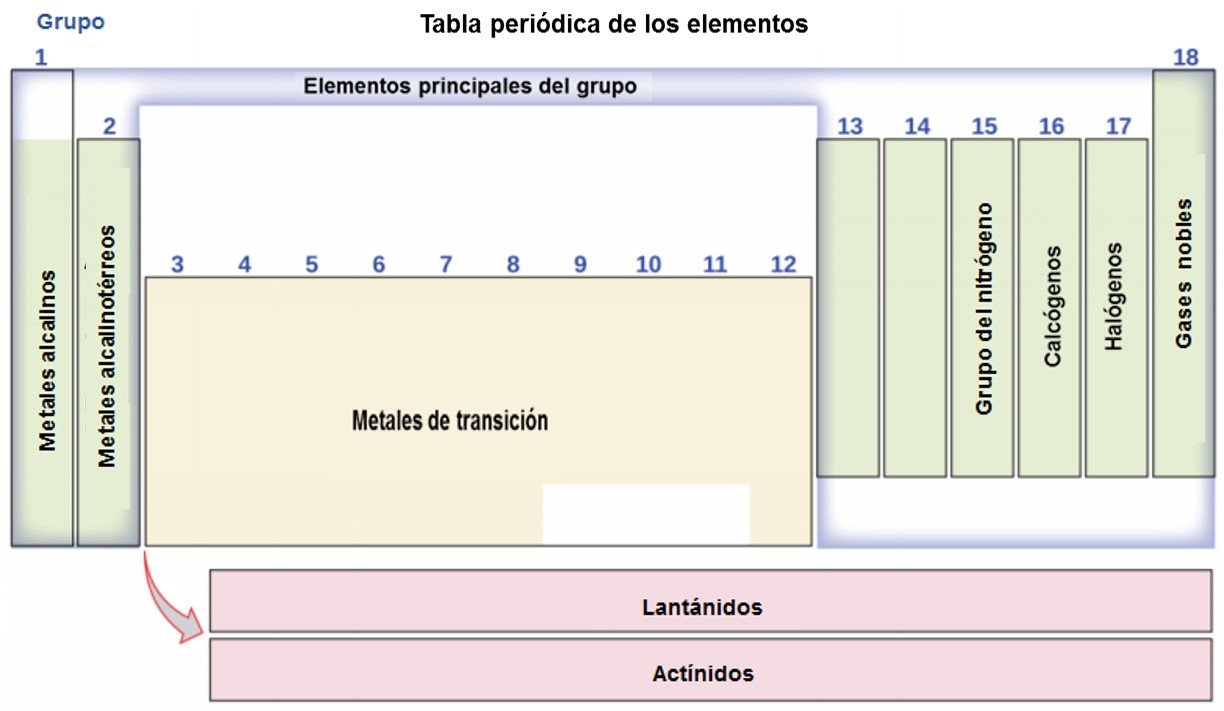
Figura 2.27. La tabla periódica organiza elementos con propiedades similares en grupos.
Ejemplo 2.7
Nombramiento de grupos de elementos
Los átomos de cada uno de los siguientes elementos son esenciales para la vida. Da el nombre del grupo para lo siguiente elementos:
Solución
Los nombres de la familia son los siguientes:
Comprueba tu aprendizaje
A continuación, presentamos una interesante tabla periódica que hace parte del proyecto three.js, creado por Mr. Doob, que tiene como propósito "crear una biblioteca 3D fácil de usar y liviana con un renderizador WebGL predeterminado".
En reacciones químicas ordinarias, el núcleo de cada átomo (y por lo tanto la identidad del elemento) permanece sin cambios. Sin embargo, los electrones se pueden agregar a los átomos por transferencia de otros átomos, perdidos por transferencia a otros átomos o compartidos con otros átomos. La transferencia y el intercambio de electrones entre los átomos gobiernan la química de los elementos. Durante la formación de algunos compuestos, los átomos ganan o pierden electrones, y forman partículas cargadas eléctricamente llamadas iones (Figura 2.28).
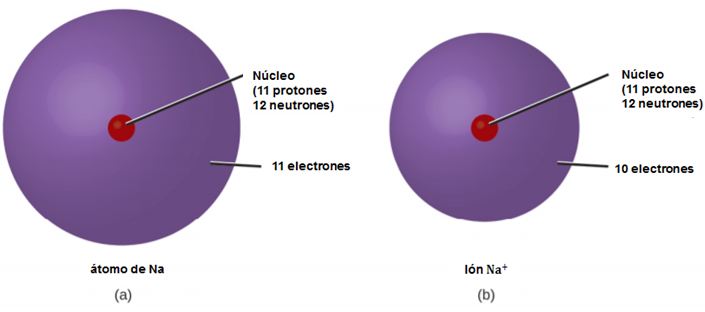
Figura 2.28. (a) Un átomo de sodio (Na) tiene igual número de protones y electrones (11) y no está cargado. (b) Un catión de sodio (Na+) ha perdido un electrón, por lo que tiene un protón más (11) que los electrones (10), lo que le da una carga positiva global, significada por un signo + superpuesto.
Puedes usar la tabla periódica para predecir si un átomo formará un anión o un catión, y con frecuencia puedes predecir la carga del ion resultante. Los átomos de muchos metales del grupo principal pierden suficientes electrones para dejarlos con la misma cantidad de electrones que un átomo del gas noble precedente.
Para ilustrar, un átomo de un metal alcalino (grupo 1) pierde un electrón y forma un catión con una carga de 1+; un metal alcalinotérreo (grupo 2) pierde dos electrones y forma un catión con una carga 2+, y así sucesivamente. Por ejemplo, un átomo de calcio neutro, con 20 protones y 20 electrones, pierde fácilmente dos electrones. Esto da como resultado un catión con 20 protones, 18 electrones y una carga 2+. Tiene el mismo número de electrones que los átomos del gas noble anterior, argón, y está simbolizado como Ca2+. El nombre de un ión metálico es el mismo que el nombre del átomo metálico a partir del cual se forma, por lo que el Ca2+ se denomina ión calcio.
Cuando los átomos de elementos no metálicos forman iones, generalmente obtienen suficientes electrones para darles el mismo número de electrones que un átomo del próximo gas noble en la tabla periódica. Los átomos del grupo 17 ganan un electrón y forman aniones con una carga 1; los átomos del grupo 16 ganan dos electrones y forman iones con una carga 2, y así sucesivamente. Por ejemplo, el átomo de bromo neutro, con 35 protones y 35 electrones, puede ganar un electrón para proporcionarle 36 electrones. Esto da como resultado un anión con 35 protones, 36 electrones y una carga 1. Tiene el mismo número de electrones que los átomos del siguiente gas noble, el criptón, y se simboliza $Br^{−}$ (en un capítulo posterior se proporciona una discusión de la teoría que respalda el estado favorecido de los números de electrones de gases nobles reflejados en estas reglas predictivas para la formación de iones).
La tabla periódica permite predecir la posible formación y carga de iones (Figura 2.29). Moviéndose desde el extremo izquierdo hacia la derecha en la tabla periódica, los elementos del grupo principal tienden a formar cationes con una carga igual al número del grupo. Es decir, los elementos del grupo 1 forman iones 1+; Los elementos del grupo 2 forman 2+ iones, y así sucesivamente.
viéndose desde el extremo derecho hacia la izquierda en la tabla periódica, los elementos a menudo forman aniones con una carga negativa igual al número de grupos movidos a la izquierda desde los gases nobles. Por ejemplo, los elementos del grupo 17 (un grupo a la izquierda de los gases nobles) forman 1− iones; los elementos del grupo 16 (dos grupos a la izquierda) forman 2− iones, y así sucesivamente. Esta tendencia se puede usar como guía en muchos casos, pero su valor predictivo disminuye al moverse hacia el centro de la tabla periódica. De hecho, los metales de transición y algunos otros metales a menudo exhiben cargas variables que no son predecibles por su ubicación en la tabla. Por ejemplo, el cobre puede formar iones con una carga de 1+ o 2+, y el hierro puede formar iones con una carga de 2+ o 3+.
Figura 2.29. Algunos elementos exhiben un patrón regular de carga iónica cuando forman iones.
Ejemplo 2.8
Composición de Iones
Un ion encontrado en algunos compuestos utilizados como antitranspirantes contiene 13 protones y 10 electrones. ¿Cuál es su símbolo?
Solución
Debido a que el número de protones permanece sin cambios cuando un átomo forma un ion, el número atómico del elemento debe ser 13. Sabiendo que esto nos permite usar la tabla periódica para identificar el elemento como Al (aluminio). El átomo de Al ha perdido tres electrones y, por lo tanto, tiene tres cargas positivas más (13) que electrones (10). Este es el catión de aluminio, $Al^{3+}$.
Comprueba tu aprendizaje
Ejemplo 2.9
Formación de Iones
El magnesio y el nitrógeno reaccionan para formar un compuesto iónico.
Di qué forma un anión, que forma un catión, y las cargas de cada ion. Escribe el símbolo para cada ión y nómbralos
Solución
La posición del magnesio en la tabla periódica (grupo 2) nos dice que es un metal. Los metales forman iones positivos (cationes). Un átomo de magnesio debe perder dos electrones para tener el mismo número de electrones que un átomo del gas noble anterior, el neón. Por lo tanto, un átomo de magnesio formará un catión con dos electrones menos que protones y una carga de 2+. El símbolo para el ión es $Mg^{2+}$, y se llama ión de magnesio. La posición del nitrógeno en la tabla periódica (grupo 15) revela que es un no metal. Los no metales forman iones negativos (aniones). Un átomo de nitrógeno debe ganar tres electrones para tener el mismo número de electrones que un átomo del siguiente gas noble, neón. Por lo tanto, un átomo de nitrógeno formará un anión con tres electrones más que protones y una carga de 3−. El símbolo para el ion es $N^{3-}$, y se llama ion nitruro.
Comprueba tu aprendizaje
Los iones que hemos analizado hasta ahora se llaman iones monoatómicos, es decir, son iones formados a partir de un solo átomo. También encontramos muchos iones poliatómicos. Estos iones, que actúan como unidades discretas, son moléculas cargadas eléctricamente (un grupo de átomos unidos con una carga total). Algunos de los iones poliatómicos más importantes se enumeran en la Tabla 2.5. Los oxianiones son iones poliatómicos que contienen uno o más átomos de oxígeno. En este punto de tu estudio de química, debes memorizar los nombres, fórmulas y cargas de los iones poliatómicos más comunes. Debido a que los usarás repetidamente, pronto te serán familiares.
Tabla 2.5. Iones poliatómicos comunes
Observa que existe un sistema para nombrar algunos iones poliatómicos; -ato y -ito son sufijos que designan iones poliatómicos que contienen más o menos átomos de oxígeno. Per- (abreviatura de "hiper") e hipo (que significa "debajo de") son prefijos que significan más átomos de oxígeno que -ato y menos átomos de oxígeno que -ito, respectivamente. Por ejemplo, el perclorato es $ClO_4^{-}$, el clorato es $ClO_3^{-}$, el clorito es $ClO_2^{-}$ y el hipoclorito es $ClO^{-}$. Desafortunadamente, el número de átomos de oxígeno correspondientes a un sufijo o prefijo dado no es consistente; por ejemplo, el nitrato es $NO_3^{-}$, mientras que el sulfato es $SO_4^{2-}$.
La naturaleza de las fuerzas atractivas que mantienen unidos a los átomos o iones dentro de un compuesto es la base para clasificar el enlace químico. Cuando se transfieren electrones y se forman iones, se producen enlaces iónicos. Los enlaces iónicos son fuerzas electrostáticas de atracción, es decir, las fuerzas atractivas experimentadas entre objetos de carga eléctrica opuesta (en este caso, cationes y aniones). Cuando los electrones se "comparten" y se forman moléculas, se producen enlaces covalentes. Los enlaces covalentes son las fuerzas atractivas entre los núcleos cargados positivamente de los átomos unidos y uno o más pares de electrones que se encuentran entre los átomos. Los compuestos se clasifican como iónicos o moleculares (covalentes) sobre la base de los enlaces presentes en ellos.
Cuando un elemento compuesto de átomos que fácilmente pierde electrones (un metal) reacciona con un elemento compuesto de átomos que gana fácilmente electrones (un no metal), generalmente ocurre una transferencia de electrones, que produce iones.
Por ejemplo, el compuesto formado por esta transferencia se estabiliza por las atracciones electrostáticas (enlaces iónicos) entre los iones de carga opuesta presentes en el compuesto. Por ejemplo, cuando cadacada átomo de sodio en una muestra de metal de sodio (grupo 1) entrega un electrón para formar un catión de sodio, $Na^{+}$, y cada átomo de cloro en una muestra de gas de cloro (grupo 17) acepta un electrón para formar un cloruro. El anión, $Cl^{-}$, el compuesto resultante, NaCl, está compuesto de iones de sodio e iones de cloruro en la relación de un ion de $Na^{+}$ para cada ion de $Cl^{-}$. De manera similar, cada átomo de calcio (grupo 2) puede renunciar a dos electrones y transferir uno a cada uno de los dos átomos de cloro para formar $CaCl_2$, que está compuesto de iones $Ca^{2+}$ y $Cl^{-}$ en la relación de un ion $Ca^{2+}$ a dos iones $Cl^{-}$.
Un compuesto que contiene iones y se mantiene unido por enlaces iónicos se llama un compuesto iónico. La tabla periódica puede ayudarnos a reconocer muchos de los compuestos que son iónicos: cuando un metal se combina con uno o más no metales, el compuesto suele ser iónico. Esta guía funciona bien para predecir la formación de compuestos iónicos para la mayoría de los compuestos que se encuentran típicamente en un curso de química introductoria. Sin embargo, no siempre es cierto (por ejemplo, el cloruro de aluminio, $AlCl_3$, no es iónico). A menudo se pueden reconocer compuestos iónicos debido a sus propiedades. Los compuestos iónicos son sólidos que normalmente se funden a altas temperaturas y hierven a temperaturas aún más altas. Por ejemplo, el cloruro de sodio se funde a 801° C y hierve a 1413° C (en comparación, el agua del compuesto molecular se funde a 0° C y hierve a 100° C). En forma sólida, un compuesto iónico no es eléctricamente conductor porque sus iones no pueden fluir ("electricidad" es el flujo de partículas cargadas ).
Sin embargo, cuando está fundido, puede conducir electricidad porque sus iones son capaces de moverse libremente a través del líquido (Figura 2.30).
En cada compuesto iónico, el número total de cargas positivas de los cationes es igual al número total de cargas negativas de los aniones. Por lo tanto, los compuestos iónicos son eléctricamente neutros en general, a pesar de que contienen iones positivos y negativos. Podemos usar esta observación para ayudarnos a escribir la fórmula de un compuesto iónico. La fórmula de un compuesto iónico debe tener una proporción de iones de tal manera que los números de cargas positivas y negativas sean iguales.
Figura 2.30 . El cloruro de sodio se funde a 801°C y conduce la electricidad cuando se funde. (Crédito: modificación del trabajo de Mark Blaser y Matt Evans)
Ejemplo 2.10
Predecir la fórmula de un compuesto iónico
La piedra preciosa zafiro (Figura 2.31) es principalmente un compuesto de aluminio y oxígeno que contiene cationes de aluminio, $Al^{3+}$,y aniones de oxígeno, $O^{2-}$. ¿Cuál es la fórmula de este compuesto?
Figura 2.31. Aunque el óxido de aluminio puro es incoloro, trazas de hierro y titanio le dan a su color característico el zafiro azul (crédito: modificación del trabajo de Stanislav Doronenko)
Solución
Debido a que el compuesto iónico debe ser eléctricamente neutro, debe tener el mismo número de cargas positivas y negativas. Dos iones de aluminio, cada uno con una carga de 3+, nos darían seis cargas positivas, y tres iones de óxido, cada uno con una carga de 2¯, nos darían seis cargas negativas. La fórmula sería $Al_2O_3$.
Comprueba tu aprendizaje
Muchos compuestos iónicos contienen iones poliatómicos (Tabla 2.5) como el catión, el anión o ambos. Al igual que con los compuestos iónicos simples, estos compuestos también deben ser eléctricamente neutros, por lo que sus fórmulas se pueden predecir tratando los iones poliatómicos como unidades discretas. Usamos paréntesis en una fórmula para indicar un grupo de átomos que se comportan como una unidad. Por ejemplo, la fórmula para el fosfato de calcio, uno de los minerales en nuestros huesos, es $Ca_3(PO_4)_2$. Esta fórmula indica que hay tres iones de calcio ($Ca^{2+}$) por cada dos grupos de fosfato ($PO_4^{3-}$). Los grupos $PO_4^{3-}$ son unidades discretas, cada una de las cuales consta de un átomo de fósforo y cuatro átomos de oxígeno, y tiene una carga total de 3−. El compuesto es eléctricamente neutro y su fórmula muestra un recuento total de tres átomos de Ca, dos P y ocho O.
Ejemplo 2.11
Predicción de la fórmula de un compuesto con un anión poliatómico
El polvo para hornear contiene dihidrógeno fosfato de calcio, un compuesto iónico compuesto por los iones $Ca^{2+}$ y $H_2PO_4^{-}$. ¿Cuál es la fórmula de este compuesto?
Solución
Las cargas positivas y negativas deben equilibrarse, y este compuesto iónico debe ser eléctricamente neutro. Por lo tanto, debemos tener dos cargas negativas para equilibrar la carga 2+ del ion calcio. Esto requiere una relación de un ion $Ca^{2+}$ a dos iones $H_2PO_4^{-}$. Designamos esto encerrando la fórmula para el ion fosfato de dihidrógeno entre paréntesis y agregando un subíndice 2. La fórmula es $Ca(H_2PO_4)_2$.
Comprueba tu aprendizaje
Debido a que un compuesto iónico no está formado por moléculas individuales y discretas, es posible que no se simbolice correctamente usando una fórmula molecular. En su lugar, los compuestos iónicos deben estar simbolizados por una fórmula que indique los números relativos de sus iones constituyentes. Para compuestos que contienen solo iones monoatómicos (como NaCl) y para muchos compuestos que contienen iones poliatómicos (como CaSO4), estas fórmulas son solo las fórmulas empíricas introducidas anteriormente en este capítulo. Sin embargo, las fórmulas para algunos compuestos iónicos que contienen iones poliatómicos no son fórmulas empíricas. Por ejemplo, el compuesto iónico de oxalato de sodio se compone de iones $Na^{+}$ y $C_2O_4^{2-}$ combinados en una proporción de 2:1, y su fórmula se escribe como $Na_2C_2O_4$. Los subíndices de esta fórmula no son los números enteros más pequeños posibles, ya que cada uno puede dividirse por 2 para obtener la fórmula empírica, $NaCO_2$. Sin embargo, esta no es la fórmula aceptada para el oxalato de sodio, ya que no representa con precisión el anión poliatómico del compuesto, $C_2O_4^{2-}$.
Muchos compuestos no contienen iones, sino que consisten únicamente en moléculas discretas y neutrales. Estos compuestos moleculares (compuestos covalentes) se producen cuando los átomos comparten, en lugar de transferir (ganan o pierden), electrones. La unión covalente es un concepto importante y extenso en química, y se tratará con gran detalle en un capítulo posterior de este texto. A menudo podemos identificar compuestos moleculares sobre la base de sus propiedades físicas. En condiciones normales, los compuestos moleculares a menudo existen como gases, líquidos de bajo punto de ebullición y sólidos de bajo punto de fusión, aunque existen muchas excepciones importantes. Mientras que los compuestos iónicos generalmente se forman cuando un metal y un no metal se combinan, los compuestos covalentes se forman generalmente por una combinación de no metales. Por lo tanto, la tabla periódica puede ayudarnos a reconocer muchos de los compuestos que son covalentes. Si bien podemos usar las posiciones de los elementos de un compuesto en la tabla periódica para predecir si es iónico o covalente en este punto de nuestro estudio de química, debes tener en cuenta que este es un enfoque muy simplista que no tiene en cuenta una serie de excepciones interesantes.
Ejemplo 2.12
Predecir el tipo de unión en los siguientes compuestos
Predecir si los siguientes compuestos son iónicos o moleculares:
Solución
Comprueba tu aprendizaje
La nomenclatura, una colección de reglas para nombrar cosas, es importante en la ciencia y en muchas otras situaciones. Este módulo describe un enfoque que se utiliza para nombrar compuestos iónicos y moleculares simples, como $NaCl$, $CaCO_3$ y $N_2O_4$. Los más simples son los compuestos binarios, aquellos que contienen solo dos elementos, pero también consideraremos cómo nombrar compuestos iónicos que contienen iones poliatómicos, y una clase específica de compuestos muy importante conocidos como ácidos. Aquí limitaremos nuestra atención a los compuestos inorgánicos, compuestos que se componen principalmente de elementos distintos del carbono, y seguiremos las pautas de nomenclatura propuestas por IUPAC.
Para nombrar un compuesto inorgánico, debemos considerar las respuestas a varias preguntas. Primero, ¿es el compuesto iónico o molecular? Si el compuesto es iónico, ¿el metal forma iones de un solo tipo (carga fija) o más de un tipo (carga variable)? ¿Son los iones mono o poliatómicos? Si el compuesto es molecular, ¿contiene hidrógeno? Si es así, ¿también contiene oxígeno? De las respuestas que obtenemos, colocamos el compuesto en una categoría apropiada y luego lo nombramos como corresponde.
El nombre de un compuesto binario que contiene iones monatómicos consiste en el nombre del anión (el nombre del elemento no metálico con su final reemplazado por el sufijo –uro) seguido del nombre del catión (el nombre del metal). Algunos ejemplos se dan en la (Tabla 2.6).
Tabla 2.6. Nombres de algunos compuestos ionicos
Los compuestos que contienen iones poliatómicos se denominan de manera similar a los que contienen solo iones monoatómicos, es decir, nombrando primero el anión y luego el catión. Los ejemplos se muestran en la Tabla 2.7.
Tabla 2.7. Nombres de algunos compuestos ionicos poliatómicos
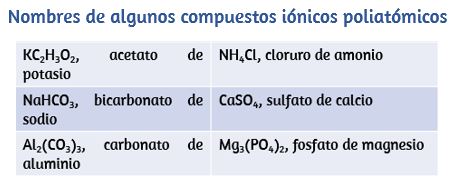
La mayoría de los metales de transición y algunos metales del grupo principal pueden formar dos o más cationes con diferentes cargas. Los compuestos de estos metales con no metales se nombran con el mismo método que los compuestos de la primera categoría, excepto que la carga del ion metálico se especifica con un número romano entre paréntesis después del nombre del metal. La carga del ion metálico se determina a partir de la fórmula del compuesto y la carga del anión. Por ejemplo, considera los compuestos iónicos binarios de hierro y cloro. El hierro normalmente muestra una carga de 2+ o 3+ (ver Figura 2.29), y las dos fórmulas de compuestos correspondientes son $FeCl_2$ y $FeCl_3$. El nombre más simple, "cloruro de hierro", será, en este caso, ambiguo, ya que no distingue entre estos dos compuestos. En casos como este, la carga del ion metálico se incluye como un número romano entre paréntesis inmediatamente después del nombre del metal. Estos dos compuestos se denominan luego de forma inequívoca cloruro de hierro (II) y cloruro de hierro (III), respectivamente. Otros ejemplos se proporcionan en la Tabla 2.8.
Tabla 2.8. Algunos compuestos iónicos con iones metálicos de carga variable
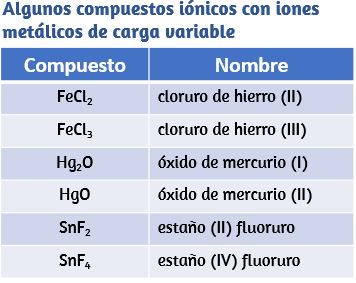
La química en la vida cotidiana
Todos los días te encuentras y usas una gran cantidad de compuestos iónicos. Algunos de estos compuestos, donde se encuentran y para qué se usan, se enumeran en la (Tabla 2.9). Mira la etiqueta o la lista de ingredientes en los diversos productos que usas durante los próximos días, y observa si encuentras alguno de estos en esta tabla, o busca otros compuestos iónicos que ahora puedas nombrar o escribir como una fórmula.
Tabla 2.9. Algunos compuestos iónicos con iones metálicos de carga variable
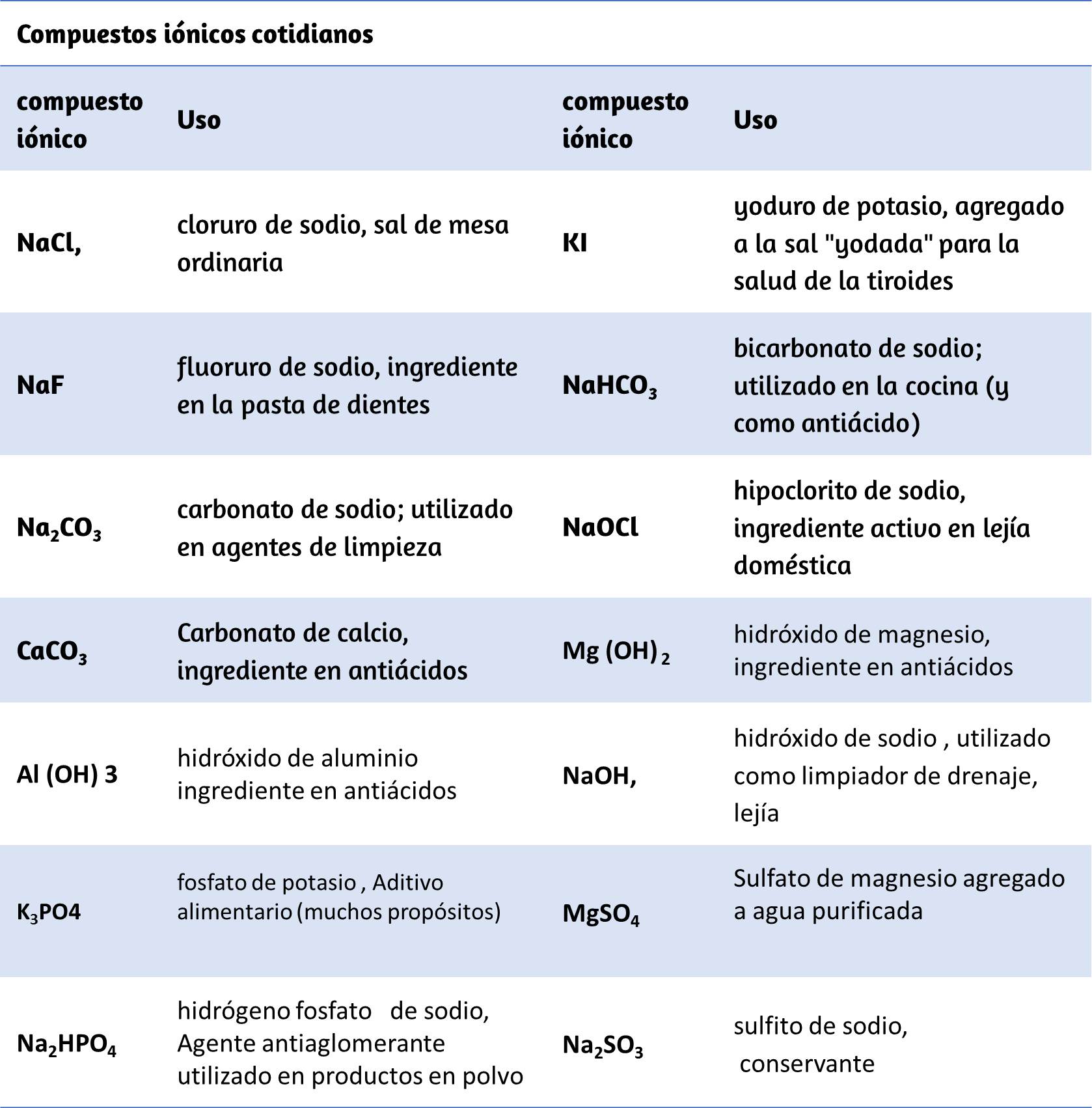
La nomenclatura obsoleta usó los sufijos –ico y –oso para designar metales con cargas más altas y más bajas, respectivamente: el cloruro de hierro (III), $FeCl_3$, antes se llamaba cloruro férrico, y el cloruro de hierro (II), $FeCl_2$, era conocido como el cloruro ferroso.
Aunque esta convención de nombres ha sido abandonada en gran medida por la comunidad científica, se mantiene en uso por algunos segmentos de la industria. Por ejemplo, puedes ver las palabras fluoruro de estaño en un tubo de pasta de dientes. Esto representa la fórmula $SnF_2$, que se denomina mejor como fluoruro de estaño (II). El otro fluoruro de estaño es $SnF_4$, que anteriormente se llamaba fluoruro de estaño, pero ahora se llama fluoruro de estaño (IV).
Los compuestos iónicos que contienen moléculas de agua como componentes integrales de sus cristales se llaman hidratos. El nombre de un hidrato iónico se deriva al agregar un término al nombre del compuesto anhidro (que significa "no hidratado"), eso indica el número de moléculas de agua asociadas con cada unidad de fórmula del compuesto. La palabra añadida comienza con un prefijo griego que indica el número de moléculas de agua (consulta la Tabla 2.10 ) y termina con "hidratar". Por ejemplo, el compuesto anhidro de sulfato de cobre (II) también existe como un hidrato que contiene cinco moléculas de agua. y llamado sulfato de cobre (II) pentahidratado. La soda de lavado es el nombre común para un hidrato de carbonato de sodio que contiene 10 moléculas de agua; El nombre sistemático es carbonato de sodio decahidrato.
Las fórmulas para los hidratos iónicos se escriben agregando un punto centrado verticalmente, un coeficiente que representa el número de moléculas de agua y la fórmula para el agua. Los dos ejemplos mencionados en el párrafo anterior están representados por las fórmulas
Sulfato de cobre (II) pentahidrato: $CuSO_4 \cdot 5H_2O$
Carbonato de sodio decahidrato: $Na_2CO_3 \cdot 10H_2O$
Tabla 2.10. Prefijos en nomenclatura
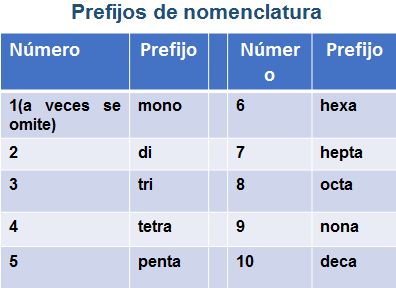
Ejemplo 2.13
Nombrando Compuestos iónicos
Nombra los siguientes compuestos iónicos
Solución
Los aniones en estos compuestos tienen una carga negativa fija ($S^{2−}$, $Se^{2−}$, $N^{3−}$, $Cl^{−}$ y $SO_4^{2-}$), y los compuestos deben ser neutros.
Debido a que el número total de cargas positivas en cada compuesto debe ser igual al número total de cargas negativas, los iones positivos deben ser $Fe^{3+}$, $Cu^{2+}$, $Ga^{3+}$, $Cr^{3+}$ y $Ti^{3+}$. Estos cargos se utilizan en los nombres de los iones metálicos.
Comprueba tu aprendizaje
La química en la vida cotidiana
A principios de la década de 1990, Erin Brockovich (Figura 2.32) descubrió una alta tasa de enfermedades graves en la pequeña ciudad de Hinckley, California. Su investigación finalmente vinculó las enfermedades con el agua subterránea contaminada por Cr (VI) utilizada por Pacific Gas & Electric (PG&E) para combatir la corrosión en una tubería cercana de gas natural. Según lo dramatizado en la película, Erin Brokovich (por la cual Julia Roberts ganó un Oscar), Erin y el abogado Edward Masry demandaron a PG&E por contaminar el agua cerca de Hinckley en 1993. El acuerdo que ganaron en 1996 ($ 333 millones) fue el monto más grande otorgado jamás una demanda directa en los Estados Unidos hasta el momento.
Figura 2.32. (a) Erin Brockovich descubrió que el Cr (VI), utilizado por PG&E, había contaminado el suministro de agua de Hinckley, California. (b) El ion Cr (VI) a menudo está presente en el agua como el cromato de iones poliatómicos, $CrO_4^{2-}$ (izquierda) y dicromato, $Cr_2O_7^{2-}$ (derecha)
Los compuestos de cromo se usan ampliamente en la industria, como el cromado, la fabricación de tinte, como conservantes y para prevenir la corrosión en el agua de la torre de enfriamiento, como ocurrió cerca de Hinckley. En el medio ambiente, el cromo existe principalmente en las formas Cr (III) o Cr (VI). Cr (III), un ingrediente de muchas vitaminas y suplementos nutricionales, forma compuestos que no son muy solubles en agua y tiene una baja toxicidad. Pero el Cr (VI) es mucho más tóxico y forma compuestos que son razonablemente solubles en agua. La exposición a pequeñas cantidades de Cr (VI) puede provocar daños en los sistemas respiratorio, gastrointestinal e inmunitario, así como en los riñones, el hígado, la sangre y la piel. A pesar de los esfuerzos de limpieza, la contaminación del agua subterránea con Cr (VI) sigue siendo un problema en Hinckley y otros lugares a traves del globo. Un estudio realizado en 2010 por el Environmental Working Group encontró que de las 35 ciudades evaluadas en los EE.UU., 31 tenían niveles más altos de Cr (VI) en el agua del grifo que la meta de salud pública de 0.02 partes por billón establecida por la Agencia de Protección Ambiental de California.
Las características de enlace de los compuestos moleculares inorgánicos son diferentes de los compuestos iónicos, y también se nombran utilizando un sistema diferente. Las cargas de cationes y aniones dictan sus proporciones en compuestos iónicos, por lo que especificar los nombres de los iones proporciona información suficiente para determinar las fórmulas químicas. Sin embargo, debido a que el enlace covalente permite una variación significativa en las relaciones de combinación de los átomos en una molécula, los nombres de los compuestos moleculares deben identificar explícitamente estas relaciones.
Cuando dos elementos no metálicos forman un compuesto molecular, a menudo son posibles varias relaciones de combinación. Por ejemplo, el carbono y el oxígeno pueden formar los compuestos $CO$ y $CO_2$. Ya que estas son sustancias diferentes con propiedades diferentes, no pueden tener el mismo nombre (no pueden llamarse óxido de carbono). Para hacer frente a esta situación, utilizamos un método de denominación que es algo similar al utilizado para los compuestos iónicos, pero con prefijos agregados para especificar los números de átomos de cada elemento. El nombre del elemento más metálico (el que está más a la izquierda y/o la parte inferior de la tabla periódica) es el primero, seguido del nombre del elemento más no metálico (el que está más a la derecha y/o arriba) con su final cambiado al sufijo –ido. Los números de los átomos de cada elemento están designados por los prefijos griegos que se muestran en la Tabla 2.10 .
Cuando solo está presente un átomo del primer elemento, el prefijo mono- generalmente se elimina de esa parte. Así, el $CO$ se llama monóxido de carbono y el $CO_2$ se llama dióxido de carbono. Cuando dos vocales son adyacentes, la a en el prefijo griego generalmente se elimina. Algunos otros ejemplos se muestran en la Tabla 2.11 .
Hay algunos nombres comunes que encontrarás al continuar tu estudio de química. Por ejemplo, aunque el $NO$ a menudo se llama óxido nítrico, su nombre propio es monóxido de nitrógeno. De manera similar, el $N_2O$ se conoce como óxido nitroso, aunque nuestras reglas especificarían el nombre de monóxido de dinitrógeno ( el $H_2O$ se suele llamar agua, no monóxido de dihidrógeno.) Debes comprometerte en recordar los nombres comunes de los compuestos a medida que los encuentres.
Tabla 2.11. Compuestos moleculares de dos elementos
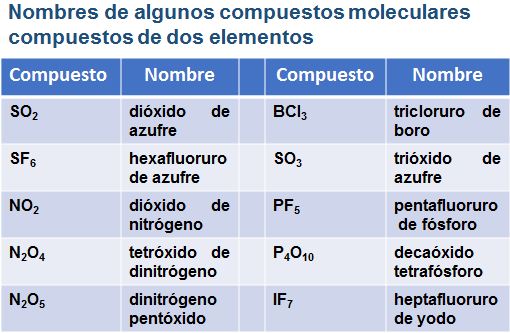
Ejemplo 2.14
Nombrar compuestos covalentes
Nombra los siguientes compuestos covalentes:
Solución
Debido a que estos compuestos consisten únicamente de no metales, usamos prefijos para designar el número de átomos de cada elemento:
Comprueba tu aprendizaje
Escribe las fórmulas para los siguientes compuestos:
Algunos compuestos que contienen hidrógeno son miembros de una importante clase de sustancias conocidas como ácidos. La química de estos compuestos se explora con más detalle en los capítulos posteriores de este texto, pero por ahora, será suficiente observar que muchos ácidos liberan iones de hidrógeno, $H^{+}$, cuando se disuelven en agua.
Para denotar esta propiedad química distinta, una mezcla de agua con un ácido recibe un nombre derivado del nombre del compuesto. Si el compuesto es un ácido binario (compuesto de hidrógeno y otro elemento no metálico):
Tabla 2.11. Nombres de algunos ácidos simples
Por ejemplo, cuando el gas $HCl$ (cloruro de hidrógeno) se disuelve en agua, la solución se llama ácido clorhídrico. Varios otros ejemplos de esta nomenclatura se muestran en la Tabla 2.12 .
Muchos compuestos que contienen tres o más elementos (como compuestos orgánicos o compuestos de coordinación) están sujetos a reglas de nomenclatura especializadas que aprenderás más adelante. Sin embargo, discutiremos brevemente los compuestos importantes conocidos como oxiácidos, compuestos que contienen hidrógeno, oxígeno y al menos otro elemento, y están unidos de forma tal que imparten propiedades ácidas al compuesto (aprenderás los detalles de este en un capitulo posterior). Los oxiácidos típicos consisten en hidrógeno combinado con un ion poliatómico que contiene oxígeno. Para nombrar los oxiácidos:
Por ejemplo, considera el $H_2CO_3$ (que podría estar tentado a llamar "carbonato de hidrógeno"). Para nombrar esto correctamente, se omite "hidrógeno"; la de carbonato se reemplaza por –ic; y se agrega ácido, por lo que su nombre es ácido carbónico. Otros ejemplos se dan en la Tabla 2.13 . Hay algunas excepciones al método de denominación general (por ejemplo, $H_2SO_4$ es se llama ácido sulfúrico, no ácido sulfico, y el $H_2SO_3$ es ácido sulfúroso, no sulfoso).
Tabla 2.13. Nombres de oxiácidos comunes
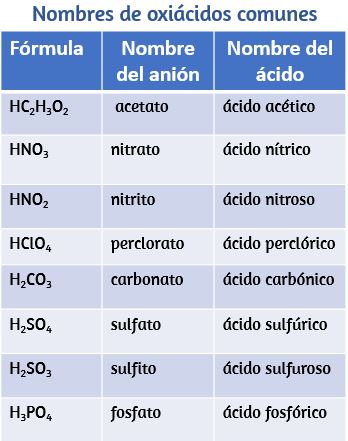
Figura 3.1. El agua en una piscina es una mezcla compleja de sustancias cuyas cantidades relativas deben mantenerse cuidadosamente para garantizar la salud y la comodidad de las personas que usan la piscina. (Crédito: modificación de obra de Vic Brincat)
Las piscinas han sido durante mucho tiempo un medio popular de recreación, ejercicio y terapia física. Dado que no es práctico llenar piscinas grandes con agua dulce de manera frecuente, el agua de la piscina se trata regularmente con productos químicos para prevenir el crecimiento de bacterias y algas dañinas. El mantenimiento adecuado de la piscina requiere adiciones regulares de varios compuestos químicos en [cantidades cuidadosamente medidas. Por ejemplo, la cantidad relativa de ión calcio, $Ca^{2+}$, en el agua debe mantenerse dentro de ciertos límites para evitar la irritación de los ojos y evitar daños en el lecho de la piscina y en las tuberías. Para mantener los niveles adecuados de calcio, los cationes de calcio se agregan al agua en forma de un compuesto iónico que también contiene aniones; por lo tanto, es necesario conocer tanto la cantidad relativa de $Ca^{2+}$ en el compuesto como el volumen de agua en la piscina para alcanzar el nivel de calcio adecuado. Los aspectos cuantitativos de la composición de las sustancias (como el compuesto que contiene calcio) y las mezclas (como el agua de la piscina) son el tema de este capítulo.
Muchos sostienen que la ciencia química moderna comenzó cuando los científicos comenzaron a explorar los aspectos cuantitativos y cualitativos de la química. Por ejemplo, la teoría atómica de Dalton fue un intento de explicar los resultados de las mediciones que le permitieron calcular las masas relativas de elementos combinados en varios compuestos. Comprender la relación entre las masas de los átomos y las fórmulas químicas de los compuestos nos permite describir cuantitativamente la composición de las sustancias.
Un el capítulo ii de este texto se describió el desarrollo de la unidad de masa atómica, el concepto de masas atómicas promedio y el uso de fórmulas químicas para representar la composición elemental de las sustancias. Estas ideas pueden extenderse para calcular el peso fórmula de una sustancia sumando las masas atómicas promedio de todos los átomos representados en la fórmula de la sustancia.
Para sustancias covalentes, la fórmula representa los números y tipos de átomos que componen una sola molécula de la sustancia; por lo tanto, el peso fórmula puede ser referida correctamente como una masa molecular. Considera el cloroformo ($CHCl_3$), un compuesto covalente que se utilizó una vez como anestésico quirúrgico y ahora se usa principalmente en la producción de tetrafluoroetileno, el componente básico del polímero "antiadherente", el teflón.
La fórmula molecular del cloroformo indica que una sola molécula contiene un átomo de carbono, un átomo de hidrógeno y tres átomos de cloro. La masa molecular media de una molécula de cloroformo es, por lo tanto, igual a la suma de las masas atómicas promedio de estos átomos. La Figura 3.2 describe los cálculos utilizados para calcular la masa molecular del cloroformo, que es de $119.37 \;uma$.
 |
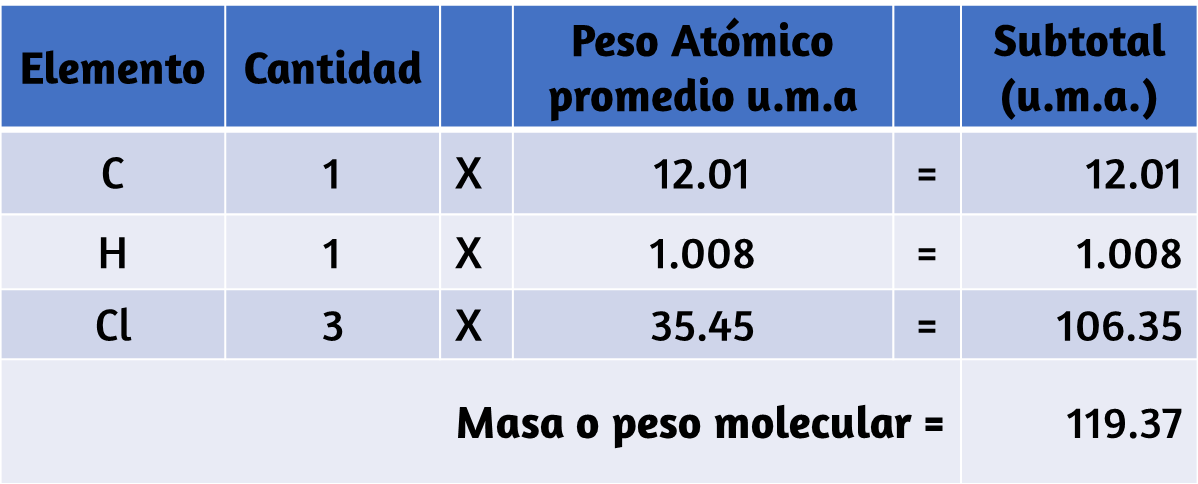Figura 3.2. La masa promedio de una molécula de cloroformo, $CHCl_3$, es $119.37 \;uma$., que es la suma de las masas atómicas promedio de cada uno de sus átomos constituyentes. El modelo muestra la estructura molecular del cloroformo.
Interactua con la molécula, diseñada en Kekule (debes ampliarla con la rueda del ratón, o haces clic sostenido sobre la molecula para rotarla). Puedes, también, hacer clic sobre la tabla para ampliar la figura.
Del mismo modo, la masa molecular de una molécula de aspirina, $C_9H_8O_4$, es la suma de las masas atómicas de nueve átomos de carbono, ocho átomos de hidrógeno y cuatro átomos de oxígeno, lo que equivale a $180.15 \;uma$ Figura 3.3.
 |
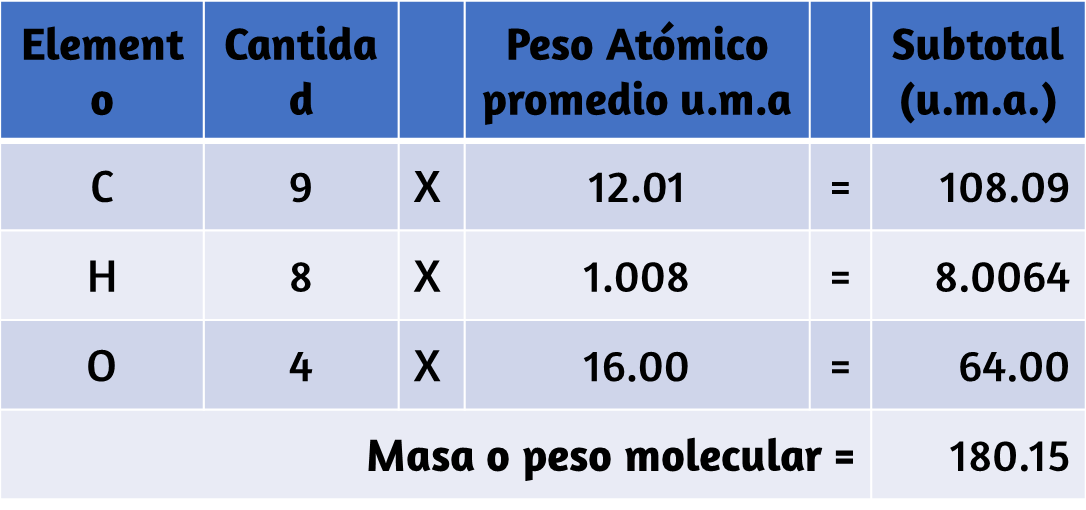Figura 3.3. La masa promedio de una molécula de aspirina es $180.15 \;uma$ El modelo muestra la estructura molecular de la aspirina, $C_9H_8O_4$.
Ejemplo 3.1
Cálculo de la masa molecular para un compuesto covalente
El Ibuprofeno, $C_{13}H_{18}O_2$, es un compuesto covalente y el ingrediente activo en varios medicamentos populares contra el dolor. ¿Cuál es la masa molecular (uma) de este compuesto?
Solución
Las moléculas de este compuesto están compuestas por 13 átomos de C, 18 átomos de H y 2 átomos de O. Siguiendo el enfoque descrito anteriormente, la masa molecular es:
 |
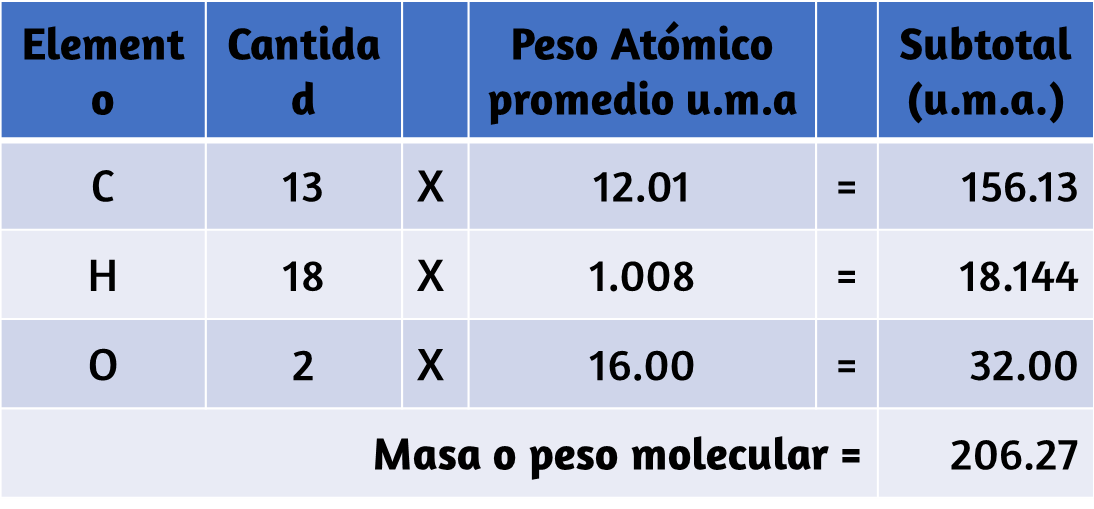Comprueba tu aprendizaje
Los compuestos iónicos están compuestos por cationes discretos y aniones combinados en proporciones para producir materia en masa eléctricamente neutra. El peso formula para un compuesto iónico se calcula de la misma manera que la masa molecular para compuestos covalentes: sumando las masas atómicas promedio de todos los átomos en la fórmula del compuesto.
Sin embargo, ten en cuenta que la fórmula para un compuesto iónico no representa la composición de una molécula discreta, por lo que puede que no se haga referencia correctamente como la "masa molecular". Como ejemplo, considera el cloruro de sodio, NaCl, el nombre químico de la sal de mesa común. El cloruro de sodio es un compuesto iónico compuesto por cationes de sodio, $Na^{+}$ y aniones de cloruro, $Cl^{-}$, combinados en una proporción de 1:1. el peso fórmula para este compuesto se calcula como $58.44 \;uma$. (consulta la Figura 3.4).
 |
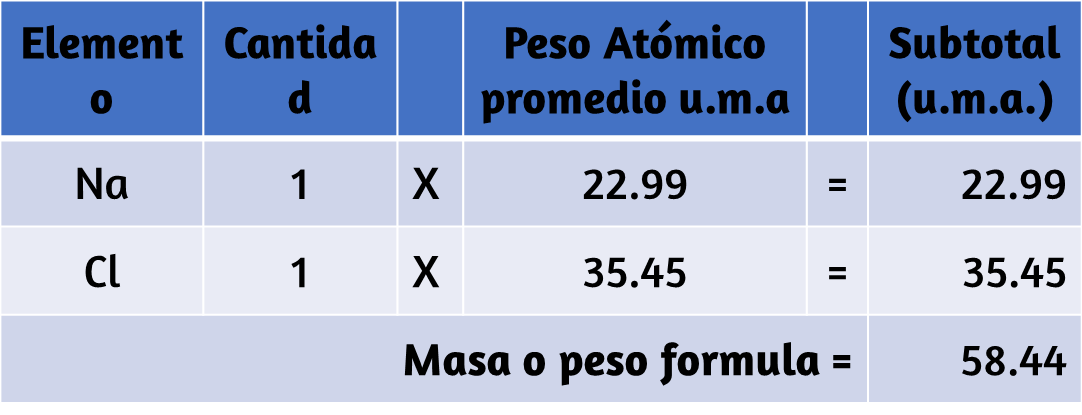Figura 3.4. La sal de mesa, NaCl, contiene una serie de iones de sodio y cloruro combinados en una proporción de 1:1. Su fórmula de masa es de $58.44 \;uma$.
Ten en cuenta que las masas promedio de sodio neutro y átomos de cloro se usaron en este cálculo, en lugar de las masas para cationes de sodio y aniones de cloro. Este enfoque es perfectamente aceptable cuando se calcula el peso fórmula de un compuesto iónico. Aunque un catión de sodio tiene una masa ligeramente más pequeña que un átomo de sodio (ya que le falta un electrón), esta diferencia se compensará por el hecho de que un anión de cloro es ligeramente más masivo que un átomo de cloro (debido al electrón extra). Además, la masa de un electrón es despreciablemente pequeña con respecto a la masa de un átomo típico.
Incluso cuando se calcula la masa de un ion aislado, los electrones faltantes o adicionales generalmente se pueden ignorar, ya que su contribución a la masa total es insignificante, reflejada solo en los dígitos no significativos. Las pocas excepciones a esta guía son los iones muy ligeros derivados de elementos con masas atómicas conocidas con precisión.
Ejemplo 3.2
Cálculo del peso fórmula para un compuesto iónico
El sulfato de aluminio, $Al_2(SO_4)_3$, es un compuesto iónico que se utiliza en la fabricación de papel y en varios procesos de purificación de agua. ¿Cuál es el peso fórmula (uma) de este compuesto?
Solución
 |
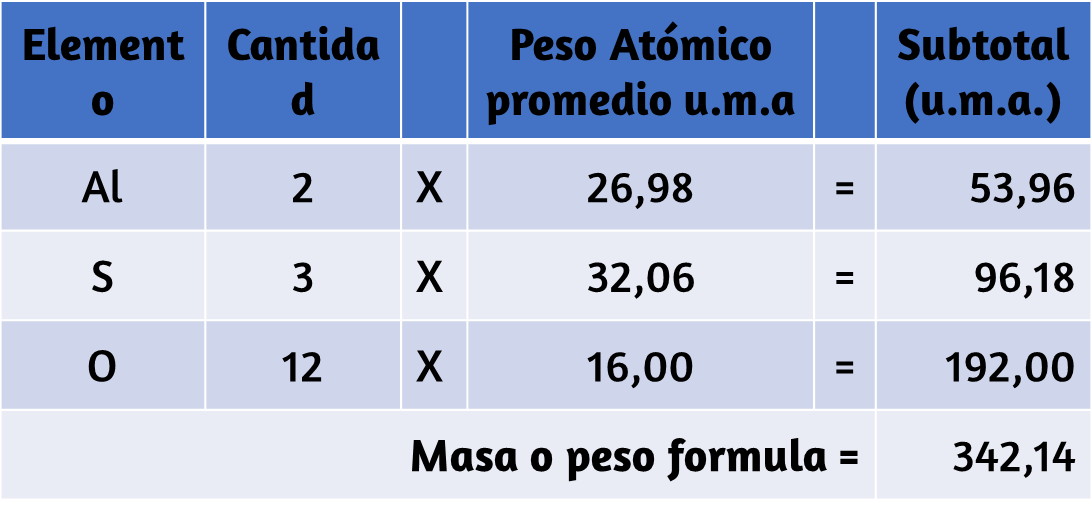Comprueba tu aprendizaje
La identidad de una sustancia se define no solo por los tipos de átomos o iones que contiene, sino también por la cantidad de cada tipo de átomo o ion. Por ejemplo, el agua, el $H_2O$ y el peróxido de hidrógeno, $H_2O_2$, son iguales en que sus respectivas moléculas están compuestas de átomos de hidrógeno y oxígeno. Sin embargo, debido a que una molécula de peróxido de hidrógeno contiene dos átomos de oxígeno, a diferencia de la molécula de agua, que tiene solo uno, las dos sustancias exhiben propiedades muy diferentes. Hoy en día, los instrumentos sofisticados permiten la medición directa de estos rasgos microscópicos que los definen; sin embargo, los mismos rasgos se derivaron originalmente de la medición de las propiedades macroscópicas (las masas y los volúmenes de grandes cantidades de materia) utilizando herramientas relativamente simples (balanzas y material de vidrio volumétrico). Este enfoque experimental requirió la introducción de una nueva unidad para la cantidad de sustancias, la mol o mole, que sigue siendo indispensable en la ciencia química moderna.
La mol es una unidad de cantidad similar a las unidades familiares como par, docena, etc. Proporciona una medida específica del número de átomos o moléculas en una muestra masiva de materia. Una mol se define como la cantidad de sustancia que contiene el mismo número de entidades discretas (como átomos, moléculas e iones) que el número de átomos en una muestra de $^{12}C$ puro que pesa exactamente 12 g. Una connotación latina para la palabra "mole" es "gran masa" o "granel", que es coherente con su uso como el nombre de esta unidad.
La mol proporciona un vínculo entre una propiedad macroscópica, una masa aparente y una propiedad fundamental extremadamente importante, el número de átomos, moléculas, etc., de fácil medición. Se ha determinado experimentalmente que la cantidad de entidades que componen una mol es $6.02214179 \times 10^{23}$, una constante fundamental denominada número de Avogadro ($N_A$) o la constante de Avogadro en honor del científico italiano Amedeo Avogadro. Esta constante se informa correctamente con una unidad explícita de "por mol", una versión convenientemente redondeada que es $6.022 \times 10^{23}\;/ mol$.
De acuerdo con su definición como unidad de cantidad, 1 mol de cualquier elemento contiene el mismo número de átomos que 1 mol de cualquier otro elemento. Las masas de 1 mol de diferentes elementos, sin embargo, son diferentes, ya que las masas de los átomos individuales son drásticamente diferentes. La masa molar o peso formula de un elemento (o compuesto) es la masa en gramos de 1 mol de esa sustancia, una propiedad expresada en unidades de gramos por mol (g/mol) (consulta la Figura 3.5).
Figura 3.5. Cada muestra contiene $6.022 \times 10^{23}$ átomos = 1.00 mol de átomos. De izquierda a derecha (fila superior): $65.4 \;g$ de Zinc, $12.0 \;g$ de Carbono, $24.3 \; g$ de Magnesio y $63.5 \;g$ de Cobre. De izquierda a derecha (fila inferior): $32.1 \;g$ de Azufre, $28.1 \;g$ de Silicio, $207 \;g$ de Plomo y $118.7 \;g$ de Estaño (Crédito: modificación de obra por Mark Ott).
Debido a que las definiciones tanto de la mol como de la unidad de masa atómica se basan en la misma sustancia de referencia, $ ^{12}C$, la masa molar de cualquier sustancia es numéricamente equivalente a su peso atómico o fórmula en uma. Según la definición de uma, un solo átomo $ ^{12}C$ pesa 12 uma (su masa atómica es 12 uma). Según la definición del mol, 12 g de $ ^{12}C$ contienen 1 mol de átomos (su masa molar es 12 g/mol). Esta relación es válida para todos los elementos, ya que sus masas atómicas se miden en relación con la de la sustancia de referencia uma, $ ^{12}C$. Al extender este principio, la masa molar de un compuesto en gramos también es numéricamente equivalente a su masa de fórmula en uma (Figura 3.6).
Figura 3.6. Cada muestra contiene $6,02 \times 10^{23}$ moléculas o unidades de fórmula: 1,00 moles del compuesto o elemento. En sentido horario desde la parte superior izquierda: $130.2 \;g$ de $C_8H_{17}OH$ (1-octanol, peso fórmula $130.2 \;uma$), $454.4 \;g$ de $HgI_2$ (yoduro de mercurio (II), peso fórmula $454.4 \;uma$), $32.0 \;g$ de $CH_3OH$ (metanol, peso fórmula $32.0 \;uma$) y $256.5 \;g$ de $S_8$ (azufre, peso fórmula $256.5 \;uma$). (Crédito: Sahar Atwa)
Tabla 3.1. Relación peso atómico, peso molar y átomos por mol de algunas sustancias.
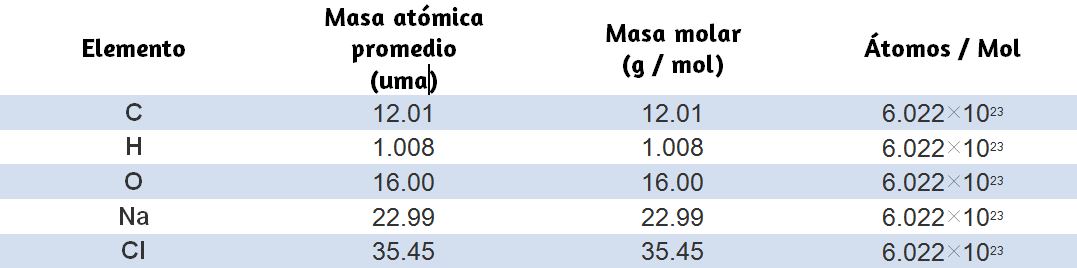
Si bien la masa atómica y la masa molar son numéricamente equivalentes, ten en cuenta que son muy diferentes en términos de escala, como lo representa la gran diferencia en las magnitudes de sus unidades respectivas (uma frente a g/mol).
Figura 3.7. El número de moléculas en una sola gota de agua es aproximadamente 100 mil millones de veces mayor que el número de personas en la tierra (Crédito: "tanakawho"/Wikimedia commons).
Para apreciar la enormidad de la mol, considere una pequeña gota de agua que pese alrededor de $0.03 \; g$ (ver Figura 3.7). Aunque esto representa solo una pequeña fracción de 1 mol de agua (~ $18 \; g$), contiene más moléculas de agua de lo que se puede imaginar claramente. Si las moléculas se distribuyeran equitativamente entre los aproximadamente siete mil millones de personas en la tierra, cada persona recibiría más de 100 mil millones de moléculas.
Enlace a aprendizaje
Las relaciones entre peso formula, la mol y el número de Avogadro se pueden aplicar para calcular varias cantidades que describen la composición de sustancias y compuestos, como se demuestra en los siguientes ejemplos de problemas.
Ejemplo 3.3
Obtener moles desde gramos para un elemento
De acuerdo con las pautas nutricionales del Departamento de Agricultura de los EE.UU. El requisito promedio estimado para el potasio en la dieta es de $4.7 \; g$.
¿Cuál es el requerimiento promedio estimado de potasio en moles?
Solución
Se proporciona la masa de K y se solicita la cantidad correspondiente de K en moles. En referencia a la tabla periódica, la masa atómica de K es de $39.10 \; uma$, por lo que su masa molar es de $39.10 \;g/mol$. La masa dada de K ($4.7 \; g$) es un poco más de una décima parte de la masa molar ($39.10 \;g$), por lo que una estimación razonable de la cantidad de moles sería un poco mayor que $0.1 \;mol$.
El método de factor de conversión es compatible con este enfoque matemático, ya que la unidad "g" se cancela y la respuesta tiene unidades de "mol:"
$$4.7\;\bcancel{g\;K} \times \cfrac{1\;mol\;K}{39.10\;\bcancel{g\;K}} = 0.12\;mol\;K$$La magnitud calculada ($0.12 \; mol\;K$) es consistente con nuestra expectativa de campo de juego, ya que es un poco mayor que $0.1\;mol$.
Comprueba tu aprendizaje
Ejemplo 3.4
Obtener gramos desde moles para un elemento
Un litro de aire contiene $9.2 \times 10^{−4}$ mol de argón. ¿Cuál es la masa de Ar en un litro de aire?
Solución
La cantidad molar de Ar se proporciona y debe utilizarse para obtener la masa correspondiente en gramos. Dado que la cantidad de Ar es menor que 1 mol, la masa será menor que la masa de 1 mol de Ar, aproximadamente $40\;g$. La cantidad molar en cuestión es aproximadamente una milésima parte (~$ 10^{−3}$) de un mol, por lo que la masa correspondiente debe ser aproximadamente una milésima parte de la masa molar (~$ 0.04\;g$):
En este caso, la lógica dicta (y el método de factor de conversión es compatible) multiplicar la cantidad proporcionada (mol) por la masa molar (g/mol):
$$9.2 \times 10^{−4}\;\bcancel{mol\;Ar} \times \cfrac{39.85\;g\;Ar}{1 \;\bcancel{mol\;Ar}} = 0.037\;g\;Ar$$El resultado está de acuerdo con nuestras expectativas, alrededor de $0.04\;g\;Ar$.
Comprueba tu aprendizaje
Ejemplo 3.5
Calcular el número de átomos de la masa para un elemento
El cobre se usa comúnmente para fabricar cables eléctricos (Figura 3.8). ¿Cuántos átomos de cobre hay en $5.00\;g$ de cable de cobre?
Solución
El número de átomos de Cu en el cable se puede calcular convenientemente de su masa mediante un cálculo de dos pasos: primero, calcular la cantidad molar de Cu y luego utilizar el número de Avogadro ($N_A$) para convertir esta cantidad molar en número de átomos de Cu:
Figura 3.8. El alambre de cobre está compuesto de muchos, muchos átomos de Cu. (Crédito: Emilian Robert Vicol)
Teniendo en cuenta que la masa de la muestra proporcionada ($5.00\; g$) es un poco menos de una décima parte de la masa de 1 mol de Cu (~ $64\; g$), una estimación razonable para el número de átomos en la muestra sería del orden de un décimo del $N_A$, o aproximadamente $10^{22}$ átomos de Cu. Realizando los cálculos de dos pasos:
$$5.00\;\cancel{g\;Cu} \times \cfrac{1 \;\bcancel{mol\;Cu}}{63.55\; \cancel{g\;Cu}} \times \cfrac{6.02 \times 10^{23}\; \text{Átomos}\; Cu}{1 \;\bcancel{mol\;Cu}} =$$ $$= 4.74 \times 10^{22}\; \text{Átomos}\; Cu$$El método de factor de conversión produce la cancelación deseada de unidades, y el resultado calculado es del orden de $ 10^{22}$ como se esperaba.
Comprueba tu aprendizaje
Ejemplo 3.6
Calcular las moles desde gramos para un compuesto
Nuestros cuerpos sintetizan proteínas a partir de aminoácidos.
Uno de estos aminoácidos es la glicina, que tiene la fórmula molecular $C_2H_5O_2N$. ¿Cuántos moles de moléculas de glicina hay en $28.35\; g$ de glicina?
Solución
Calcular el número de moles de un compuesto de su masa siguiendo el mismo procedimiento utilizado para un elemento en el ejemplo 3.3:
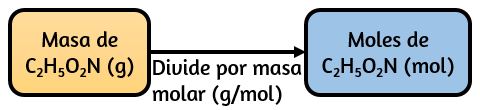
La masa molar de la glicina se requiere para este cálculo, y se calcula de la misma manera que su masa molecular. Una mol de glicina, $C_2H_5O_2N$, contiene 2 moles de C, 5 moles de H, 2 moles de O y 1 mol de N:
 |
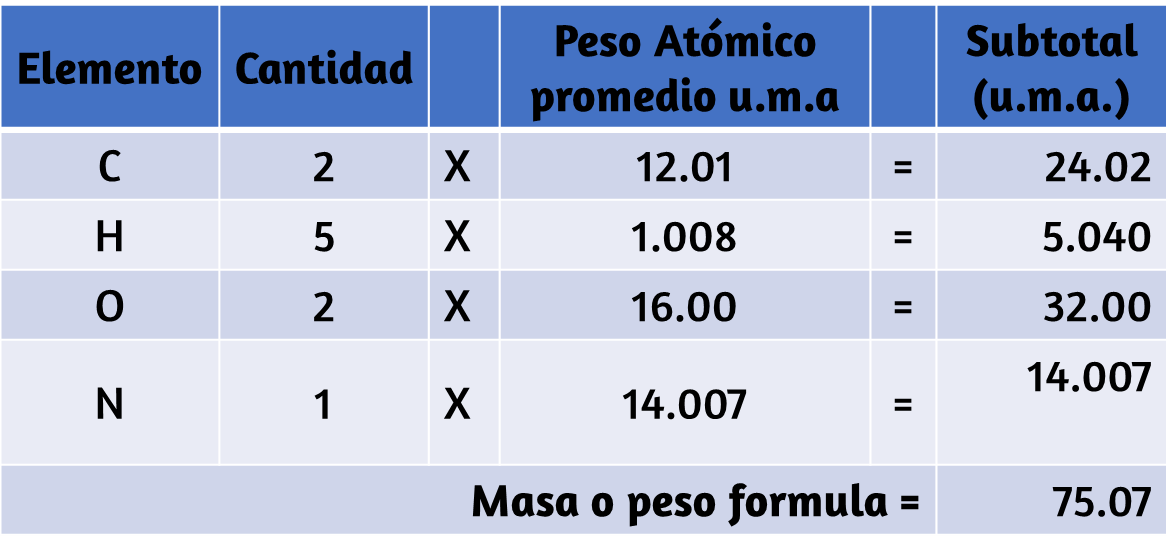La masa de glicina proporcionada (~$28\; g$) es un poco más de un tercio de la masa molar (~ $75\;g/mol$), por lo que se espera que el resultado calculado sea un poco mayor que un tercio de una mol (~$0,33\; mol$). Dividiendo la masa del compuesto por sus rendimientos:
$$28.35\; \bcancel{g\;glicina} \times \cfrac{1 \;{mol\;glicina}}{75.07\; \bcancel{g\;glicina}} = 0.378\; mol\;glicina$$Este resultado es consistente con la estimación aproximada.
Comprueba tu aprendizaje
Ejemplo 3.7
Calcular gramos desde moles para un compuesto
La vitamina C es un compuesto covalente con la fórmula molecular $C_6H_8O_6$. La cantidad diaria recomendada de vitamina C para niños de 4 a 8 años es de $1.42 \times 10^{−4}\; mol$. ¿Cuál es la masa de esta asignación en gramos?
Solución
En cuanto a los elementos, la masa de un compuesto puede obtenerse de su cantidad molar como se muestra:
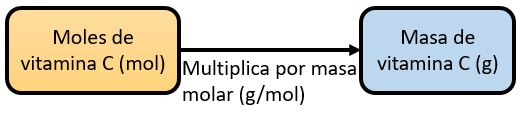
La masa molar para este compuesto se calcula como $176.124\;g/mol$. El número dado de moles es una fracción muy pequeña de una mol (~$ 10^{−4}$ o una diez milésima); por lo tanto, se espera que la masa correspondiente sea aproximadamente una diez milésima parte de la masa molar (~$ 0.02\; g$). Realizando los cálculos de rendimientos:
$$1.42 \times 10^{−4}\; \bcancel{mol\;C_6H_8O_6} \times \cfrac{176.124 \;{g\;C_6H_8O_6}}{1\; \bcancel{mol\;C_6H_8O_6}} = 0.0250\; g\;C_6H_8O_6$$
Esto es consistente con el resultado esperado.
Comprueba tu aprendizaje
Ejemplo 3.8
Calcular el número de átomos y masa molecular de un compuesto
Un paquete de un edulcorante artificial contiene $40.0\; mg$ de sacarina ($C_7H_5NO_3S$), que tiene la fórmula estructural:
Dado que la sacarina tiene una masa molar de $183.18\; g/mol$, ¿cuántas moléculas de sacarina hay en una muestra de $40.0\; mg$ ($0.0400\;g$)? ¿Cuántos átomos de carbono hay en la misma muestra?
Solución
El número de moléculas en una masa dada de compuesto se calcula al hallar primero el número de moles, como se muestra en el (ejemplo 3.6), y luego se multiplica por el número de Avogadro:
Usando la masa proporcionada y la masa molar para los rendimientos de sacarina:
$0.0400\; \cancel{g_{C_7H_5NO_3S}} \times \cfrac{1 \;\bcancel{mol_{C_7H_5NO_3S}}}{183.18\; \cancel{g_{C_7H_5NO_3S}}} \times \cfrac{6.02 \times 10^{23}\; \text{Moléculas}_{C_7H_5NO_3S}}{1 \;\bcancel{mol_{C_7H_5NO_3S}}}$
$$ = 1.31 \times 10^{20}\; \text{Moléculas}\;C_7H_5NO_3S$$La fórmula del compuesto muestra que cada molécula contiene siete átomos de carbono, por lo que el número de átomos de C en la muestra proporcionada es:
$$1.31 \times 10^{20}\; \bcancel{\text{Molécula}_{C_7H_5NO_3S}} \times \cfrac{7 \;\text{Átomos}_C}{1\; \bcancel{\text{Molécula}_{C_7H_5NO_3S}}}$$ $$= 9.17 \times 10^{20}\; \text{Átomos}\;C$$Comprueba tu aprendizaje
La química en la vida cotidiana
El cerebro es el centro de control del sistema nervioso central (Figura 3.9). Envía y recibe señales hacia y desde los músculos y otros órganos internos para monitorear y controlar sus funciones; procesa los estímulos detectados por los órganos sensoriales para guiar las interacciones con el mundo externo; y alberga los complejos procesos fisiológicos que dan origen a nuestro intelecto y emociones. El amplio campo de la neurociencia abarca todos los aspectos de la estructura y función del sistema nervioso central, incluida la investigación sobre la anatomía y fisiología del cerebro. Se han logrado grandes avances en la investigación del cerebro en las últimas décadas, y la iniciativa BRAIN, (más detalles disponibles en www.obamawhitehouse.gov/share/brain-initiative).
Las células especializadas llamadas neuronas transmiten información entre diferentes partes del sistema nervioso central a través de señales eléctricas y químicas. La señalización química ocurre en la interfaz entre diferentes neuronas cuando una de las células libera moléculas (llamadas neurotransmisores) que se difunden a través de la pequeña brecha entre las células (llamada sinapsis) y se unen a la superficie de la otra célula.
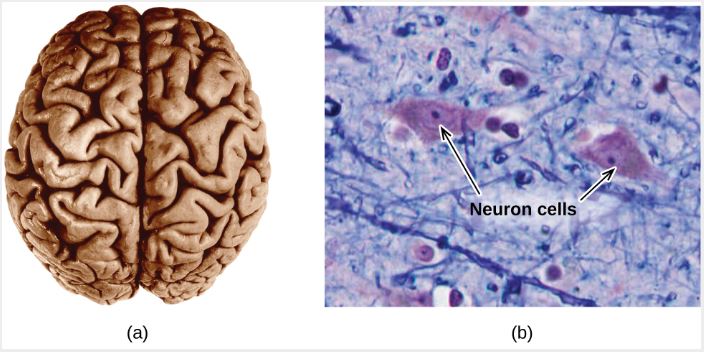
Figura 3.9. (a) Un cerebro humano típico pesa alrededor de $1.5\;kg$ y ocupa un volumen de aproximadamente $1.1\;L$. (b) La información se transmite en el tejido cerebral y en todo el sistema nervioso central mediante células especializadas llamadas neuronas (la micrografía muestra células con un aumento de 1600X).
Estas moléculas de neurotransmisores se almacenan en pequeñas estructuras intracelulares llamadas vesículas que se fusionan con la pared celular y luego se abren para liberar su contenido cuando la neurona se estimula de manera adecuada. Este proceso se llama exocitosis (ver Figura 3.10). Un neurotransmisor que ha sido muy estudiado es la dopamina, $C_8H_{11}NO_2$. La dopamina está involucrada en varios procesos neurológicos que afectan una amplia variedad de comportamientos humanos. Las disfunciones en los sistemas de dopamina del cerebro subyacen a enfermedades neurológicas graves, como el Parkinson y la esquizofrenia.
Un aspecto importante de los procesos complejos relacionados con la señalización de la dopamina es el número de moléculas neurotransmisor liberadas durante la exocitosis. Dado que este número es un factor central para determinar la respuesta neurológica (el pensamiento y la acción posterior), es importante saber cómo este número cambia con ciertas estimulaciones controladas, como la administración de fármacos.
 |
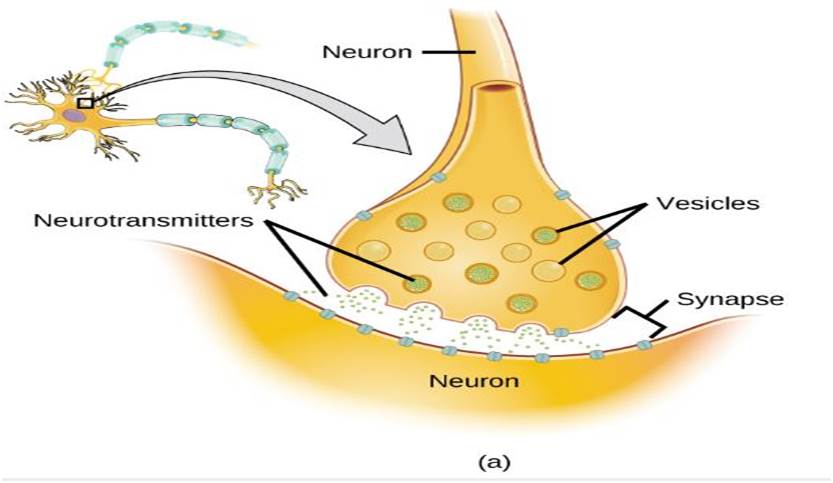Figura 3.10. (a) Las señales químicas se transmiten de las neuronas a otras células mediante la liberación de moléculas de neurotransmisores en los pequeños huecos (sinapsis) entre las células. (b) La dopamina, $C_8H_{11}NO_2$, es un neurotransmisor involucrado en varios procesos neurológicos.
También es importante comprender el mecanismo responsable de cualquier cambio en el número de moléculas de neurotransmisores liberadas, por ejemplo, alguna disfunción en la exocitosis, un cambio en el número de vesículas en la neurona o un cambio en el número de moléculas de neurotransmisores en cada vesícula.
Recientemente se ha logrado un progreso significativo en la medición directa del número de moléculas de dopamina almacenadas en vesículas individuales y la cantidad realmente liberada cuando la vesícula se somete a exocitosis. Usando sondas miniaturizadas, los científicos han determinado que las vesículas de un determinado tipo de neurona cerebral de ratón contienen un promedio de $30,000$ moléculas de dopamina por vesícula (aproximadamente $5 \times 10^{−20}$ mol o 50 Zmol). El análisis de estas neuronas de ratones sometidos a varias terapias con medicamentos muestra cambios significativos en el número promedio de moléculas de dopamina contenidas en vesículas individuales, que aumentan o disminuyen hasta tres veces, según el medicamento específico utilizado.
Estos estudios también indican que no toda la dopamina en una vesícula dada se libera durante la exocitosis, lo que sugiere que puede ser posible regular la fracción liberada mediante terapias farmacéuticasOmiatek, Donna M., Amanda J. Bressler, Ann-Sofie Cans, Anne M. Andrews, Michael L. Heien, and Andrew G. Ewing. “The Real Catecholamine Content of Secretory Vesicles in the CNS Revealed by Electrochemical Cytometry.” Scientific Report 3 (2013): 1447, accessed January 14, 2015, doi:10.1038/srep01447.
En la sección anterior se discutió la relación entre la masa de una sustancia y el número de átomos o moléculas que contiene (moles). Dada la fórmula química de la sustancia, uno puede determinar la cantidad de la sustancia (moles) a partir de su masa, y viceversa. ¿Pero qué pasa si la fórmula química de una sustancia es desconocida? En esta sección, estos mismos principios se aplicarán para calcular las fórmulas químicas de sustancias desconocidas a partir de mediciones de masa experimentales.
La composición elemental de un compuesto define su identidad química, y las fórmulas químicas son la forma más sucinta de representar esta composición elemental.Cuando se desconoce la fórmula de un compuesto, la medición de la masa de cada uno de sus elementos constitutivos es a menudo el primer paso en el proceso de determinación experimental de la fórmula. Los resultados de estas mediciones permiten el cálculo de la composición porcentual del compuesto, definida como el porcentaje en masa de cada elemento en el compuesto.
Por ejemplo, considere un compuesto gaseoso formado únicamente de carbono e hidrógeno. El porcentaje de composición de este compuesto se podría representar de la siguiente manera:
$$\%\;H = \cfrac{masa\;de\;H}{masa\;del\;compuesto} \times 100\%$$ $$\%\;C = \cfrac{masa\;de\;C}{masa\;del\;compuesto} \times 100\%$$Si el análisis de una muestra de $10,0\;g$ de este gas indicara que contiene $2.5\;g\;de\;H$ y $7.5\;g\;de\;C$, el porcentaje de composición se calcularía en un $25\%\;de\;H$ y un $75\%\;de\;C$:
$$\%\;H = \cfrac{2.5\;g\;de\;H}{10.0\;g\;del\;compuesto} \times 100\%=25\%$$ $$\%\;C = \cfrac{7.5\;g\;de\;C}{10.0\;g\;del\;compuesto} \times 100\%=75\%$$Ejemplo 3.9
Cálculo de la composición porcentual
El análisis de una muestra de $12.04$ g de un compuesto líquido compuesto de carbono, hidrógeno y nitrógeno mostró que contenía $7.34$ g C, $1.85$ g H y $2.85$ g N.
¿Cuál es el porcentaje de composición de este compuesto?
Solución
Para calcular la composición porcentual, divida la masa medida experimentalmente de cada elemento por la masa total del compuesto y luego conviértala a un porcentaje:
$$\%\;C = \cfrac{7.34\;g\;de\;C}{12.04\;g\;del\;compuesto} \times 100\%=61.0\%\;de\;C$$ $$\%\;H = \cfrac{1.85\;g\;de\;H}{12.04\;g\;del\;compuesto} \times 100\%=15.4\%\;de\;H$$ $$\%\;N = \cfrac{2.85\;g\;de\;N}{12.04\;g\;del\;compuesto} \times 100\%=23.7\%\;de\;N$$Los resultados del análisis indican que el compuesto es $61.0\%\;C$, $15.4\%\;H$ y $23.7\%\;N$ en masa.
Comprueba tu aprendizaje
El porcentaje de composición también es útil para evaluar la abundancia relativa de un elemento dado en diferentes compuestos de fórmulas conocidas. Como ejemplo, considere los fertilizantes comunes que contienen nitrógeno amoníaco ($NH_3$), nitrato de amonio ($NH_4NO_3$) y urea ($CH_4N_2O$). El elemento nitrógeno es el ingrediente activo para fines agrícolas, por lo que el porcentaje de masa de nitrógeno en el compuesto es una preocupación práctica y económica para los consumidores que eligen entre estos fertilizantes. Para este tipo de aplicaciones, el porcentaje de composición de un compuesto se calcula fácilmente de su peso formula y las masas atómicas de sus elementos constituyentes. Una molécula de $NH_3$ contiene un átomo de N que pesa $14.01\;uma$ y tres átomos de H que pesan un total de ($3 \times 1.008\;uma$) = $3.024\;uma$. Por lo tanto, la fórmula de amoníaco es ($14.01\;uma + 3.024\;uma$) = $17.03\;uma$, y su composición porcentual es:
$$\%\;N = \cfrac{14.01\;g\;de\;N}{17.03\;g\;del\;compuesto} \times 100\%=82.27\%\;de\;N$$ $$\%\;H = \cfrac{3.024\;g\;de\;H}{17.03\;g\;del\;compuesto} \times 100\%=17.76\%\;de\;H$$Este mismo enfoque puede tomarse considerando un par de moléculas, una docena de moléculas o una mol de moléculas, etc. La última cantidad es más conveniente y simplemente involucraría el uso de masas molares en lugar de masas atómicas y de fórmula, como se demuestra en el Ejemplo 3.10.
Mientras se conozca la fórmula molecular o empírica del compuesto en cuestión, el porcentaje de composición puede derivarse de las masas atómicas o molares de los elementos del compuesto.
EJEMPLO 3.10
Determinación de la composición porcentual a partir de una fórmula molecular
La aspirina es un compuesto con la fórmula molecular $C_9H_8O_4$. ¿Cuál es su composición porcentual?
Solución
Para calcular el porcentaje de composición, se necesitan las masas de C, H y O en una masa conocida de $C_9H_8O_4$. Es conveniente considerar 1 mol de $C_9H_8O_4$ y usar su masa molar ($180.159$ g/mol, determinada a partir de la fórmula química) para calcular los porcentajes de cada uno de sus elementos:
$$\%\;C = \cfrac{9\;mol\;de\;C \times masa\;molar\;de\;C}{masa\;molar\;de\;C_9H_8O_4} \times 100\%$$ $$\%\;C = \cfrac{9\;\cancel{mol\;de\;C} \times \cfrac{12.01\;g\;de\;C}{1\cancel{mol\;de\;C}}}{\cfrac{180.159\;g\;de\;C_9H_8O_4}{1\;mol\;de\;C_9H_8O_4}} \times 100\%=60.0\%\;de\;C$$ $$\%\;H = \cfrac{8\;mol\;de\;H \times masa\;molar\;de\;H}{masa\;molar\;de\;C_9H_8O_4} \times 100\%$$Tenga en cuenta que estos porcentajes suman el $100.00\%$ cuando se redondean de manera apropiada.
Comprueba tu aprendizaje
Como se mencionó anteriormente, el enfoque más común para determinar la fórmula química de un compuesto es medir primero las masas de sus elementos constituyentes.
Sin embargo, ten en cuenta que las fórmulas químicas representan los números relativos, no las masas, de los átomos en la sustancia. Por lo tanto, cualquier dato derivado experimentalmente de masa debe usarse para derivar los números correspondientes de átomos en el compuesto. Esto se logra utilizando masas molares para convertir la masa de cada elemento en un número de moles. Estas cantidades molares se utilizan para calcular las relaciones de números enteros que se pueden usar para obtener la fórmula empírica de la sustancia. Considera una muestra de compuesto determinado que contiene $1.71$ g C y $0.287$ g H. Los números correspondientes de átomos (en moles) son:
$$1.17\;\cancel{g\;de\;C} \times \cfrac{1\;mol\;de\;C}{12.01\;\cancel{g\;de\;C}}=0.142\;mol\;de\;C$$ $$0.287\;\cancel{g\;de\;H} \times \cfrac{1\;mol\;de\;H}{1.008\;\cancel{g\;de\;H}}=0.284\;mol\;de\;H$$Por lo tanto, este compuesto puede representarse por la fórmula $C_{0.142}H_{0.248}$. Por convención, las fórmulas contienen subíndices de números enteros, que se pueden lograr dividiendo cada subíndice por el subíndice más pequeño:
$C_{(\frac{0.142}{0.142})} H_{(\frac{0.248}{0.142})}=CH_2$
(Recuerda que los subíndices "1" no se escriben, sino que se asumen si no hay otro número presente).
La fórmula empírica para este compuesto es así $CH_2$. Esta puede o no ser la fórmula molecular del compuesto también; sin embargo, se necesita información adicional para tomar esa determinación.
Considera como otro ejemplo una muestra de compuesto, se determina que contiene $5.31$ g Cl y $8.40$ g O. Siguiendo el mismo enfoque se obtiene una fórmula empírica tentativa de:
$Cl_{0.150}O_{0.525}= Cl_{(\frac{0.150}{0.150})} O_{(\frac{0.525}{0.150})}=ClO_{3.5}$
En este caso, dividir por el subíndice más pequeño todavía nos deja con un subíndice decimal en la fórmula empírica. Para convertir esto en un número entero, multiplique cada uno de los subíndices por dos, reteniendo la misma proporción de átomos y obteniendo $Cl_2O_7$ como la fórmula empírica final.
La Figura 3.11 describe este procedimiento en forma de diagrama de flujo para una sustancia que contiene los elementos A y X.
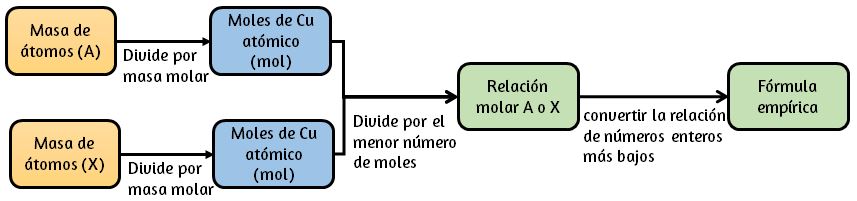
Figura 3.11. La fórmula empírica de un compuesto puede derivarse de las masas de todos los elementos en la muestra.
En resumen, las fórmulas empíricas se obtienen de masas de elementos medidas experimentalmente mediante:
Ejemplo 3.11
Determinación de la fórmula empírica de un compuesto a partir de las masas de sus elementos
Una muestra de la Hematita mineral negra (Figura 3.12), un óxido de hierro que se encuentra en muchos minerales de hierro, contiene $34.97$ g de hierro y $15.03$ g de oxígeno. ¿Cuál es la fórmula empírica de la Hematita?
Figura 3.12. La Hematita es un óxido de hierro que se usa en joyería. (crédito: Mauro Cateb)
Solución
Este problema proporciona la masa en gramos de cada elemento. Comienza por encontrar las moles de cada uno:
A continuación, obtén la relación molar de hierro a oxígeno dividiendo por el número menor de moles:
$$(\frac{0.6261}{0.6261})=1\;mol\;de\;Fe \qquad (\frac{0.9394}{0.6261})=1.5\;mol\;de\;O$$La relación es de $1.000$ moles de hierro a $1.500$ de oxígeno ($Fe_1O_{1.5}$). Finalmente, multiplica la proporción por dos para obtener los subíndices de números enteros más pequeños posibles mientras mantienes la proporción correcta de hierro y oxígeno:
$$2(Fe_1O_{1.5})=Fe_2O_3$$La fórmula empírica es $Fe_2O_3$.
Comprueba tu aprendizaje
Enlace a aprendizaje
Finalmente, con respecto a la obtención de fórmulas empíricas, considere los casos en los que está disponible la composición porcentual de un compuesto en lugar de las masas absolutas de los elementos constituyentes del compuesto. En tales casos, el porcentaje de composición se puede usar para calcular las masas de elementos presentes en cualquier masa de compuesto; estas masas se pueden usar para derivar la fórmula empírica de la manera habitual.
Ejemplo 3.12
Determinación de una fórmula empírica a partir de la composición porcentual
La fermentación bacteriana del grano para producir etanol forma un gas con una composición porcentual de $27.29\%$ C y $72.71\%$ O (Figura 3.13). ¿Cuál es la fórmula empírica de este gas?
Solución
Como la escala para porcentajes es $100$, es más conveniente calcular la masa de los elementos presentes en una muestra que pesa $100$ g.
Figura 3.13. Un óxido de carbono se elimina de estos tanques de fermentación a través de los grandes tubos de cobre en la parte superior.(credit: “Dual Freq”/Wikimedia Commons)
El cálculo es "más conveniente" porque, según la definición de composición porcentual, la masa de un elemento dado en gramos es numéricamente equivalente al porcentaje de masa del elemento. Esta equivalencia numérica resulta de la definición de la unidad de "porcentaje", cuyo nombre se deriva de la frase en latín por centum que significa "por cien". Teniendo en cuenta esta definición, los porcentajes de masa proporcionados pueden expresarse más convenientemente como fracciones:
$$27.29\%\;de\;C = \frac{27.29\;g\;de\;C}{100\;g\;de\:compuesto}$$ $$72.71\%\;de\;O = \frac{72.71\;g\;de\;O}{100\;g\;de\:compuesto}$$Las cantidades molares de carbono e hidrógeno en una muestra de $100$ g se calculan dividiendo la masa de cada elemento por su masa molar:
$$27.29\;\cancel{g\;de\;C} \times \cfrac{1\;mol\;de\;C}{12.01\;\cancel{g\;de\;C}}=2.272\;mol\;de\;C$$ $$72.71\;\cancel{g\;de\;O} \times \cfrac{1\;mol\;de\;O}{16.00\;\cancel{g\;de\;O}}=4.544\;mol\;de\;O$$Los coeficientes para la fórmula empírica tentativa se derivan al dividir cada cantidad molar por la menor de las dos:
$$\cfrac{2.272\;mol\;de\;C}{2.272}=1$$ $$\cfrac{4.544\;mol\;de\;O}{2.272}=2$$Dado que la relación resultante es de un carbono a dos átomos de oxígeno, la fórmula empírica es $CO_2$.
Comprueba tu aprendizaje
Recuerde que las fórmulas empíricas son símbolos que representan los números relativos de los elementos de un compuesto. La determinación de los números absolutos de átomos que componen una sola molécula de un compuesto covalente requiere el conocimiento tanto de su fórmula empírica como de su masa molecular o masa molar. Estas cantidades pueden determinarse experimentalmente mediante diversas técnicas de medición. La masa molecular, por ejemplo, a menudo se deriva del espectro de masas del compuesto (consulte la discusión de esta técnica en el capítulo anterior sobre átomos y moléculas). La masa molar se puede medir mediante varios métodos experimentales, muchos de los cuales se introducirán en capítulos posteriores de este texto.
Las fórmulas moleculares se obtienen comparando la masa molecular o molar del compuesto con su masa de fórmula empírica. Como su nombre indica, una masa de fórmula empírica es la suma de las masas atómicas promedio de todos los átomos representados en una fórmula empírica. Si se conoce la masa molecular (o molar) de la sustancia, se puede dividir por la masa de fórmula empírica para obtener el número de unidades de fórmula empírica por molécula (n):
$$\cfrac{masa\;molecular\;o\;molar\;{\bigg(}uma\;o\;\cfrac {g}{mol}{\bigg)}}{masa\;de\;la\;formula\;\text{empírica}\;{\bigg(}uma\;o\;\cfrac{g}{mol}{\bigg)}}$$ $$=n{\bigg(}\cfrac {unidades\;de\;\text{fórmula}}{\text{molécula}}{\bigg)}$$La fórmula molecular se obtiene multiplicando cada subíndice en la fórmula empírica por n, como lo muestra la fórmula empírica genérica $A_xB_y$:
$$(A_xB_y)_n=A_{nx}B_{ny}$$Por ejemplo, considere un compuesto covalente cuya fórmula empírica se determina como $CH_2O$. La masa de fórmula empírica para este compuesto es de aproximadamente $30$ uma (la suma de $12$ uma para un átomo de C, 2 uma para dos átomos de H y 16 uma para un átomo de O). Si se determina que la masa molecular del compuesto es de $180$ uma, esto indica que las moléculas de este compuesto contienen seis veces el número de átomos representados en la fórmula empírica:
$$\dfrac {180\dfrac {uma}{\text{molécula}}}{30\dfrac{uma}{unidades\;de\;formula}}=6\dfrac{unidades\;de\;formula}{\text{molécula}}$$Las moléculas de este compuesto están representadas por fórmulas moleculares cuyos subíndices son seis veces mayores que los de la fórmula empírica:
$$\left( CH_{2}O\right) _{6}=C_{6}H_{12}O_{6}$$Tenga en cuenta que este mismo enfoque puede usarse cuando se usa la masa molar (g/mol) en lugar de la masa molecular (uma). En este caso, se considera un mol de unidades de fórmula empírica y moléculas, a diferencia de unidades y moléculas individuales.
Ejemplo 3.13
Determinación de la fórmula molecular para la nicotina
La nicotina, un alcaloide en la familia de las plantas de la hierba mora que es principalmente responsable de la naturaleza adictiva de los cigarrillos, contiene $74.02\%$ C, $8.710\%$ H y $17.27\%$ N. Si $40.57$ g de nicotina contiene $0.2500$ mol de nicotina, ¿cuál es la fórmula molecular?
Solución
La determinación de la fórmula molecular a partir de los datos proporcionados requerirá la comparación de la masa de la fórmula empírica del compuesto con su masa molar. Como primer paso, usa la composición porcentual para deducir la fórmula empírica del compuesto. Suponiendo que sea conveniente, una muestra de nicotina de $100$ g produce las siguientes cantidades molares de sus elementos:
$$74.02\;\cancel{g\;de\;C} \times \cfrac{1\;mol\;de\;C}{12.01\;\cancel{g\;de\;C}}=6.163\;mol\;de\;C$$ $$8.710\;\cancel{g\;de\;H} \times \cfrac{1\;mol\;de\;H}{1.008\;\cancel{g\;de\;H}}=8.624\;mol\;de\;H$$ $$17.27\;\cancel{g\;de\;N} \times \cfrac{1\;mol\;de\;N}{14.01\;\cancel{g\;de\;N}}=1.233\;mol\;de\;N$$A continuación, calcule las relaciones molares de estos elementos en relación con el elemento menos abundante, N.
Las relaciones molares de C a N y de H a N son adecuadamente cercanas a números enteros, por lo que la fórmula empírica es $C_5H_7N$. La masa de fórmula empírica para este compuesto es, por lo tanto, $81.13$ uma/unidad de fórmula, o $81.13$ g/mol de unidad de fórmula.
Calcule la masa molar para la nicotina a partir de la masa dada y la cantidad molar de compuesto:
$$\dfrac {40.57\;g\;nicotina}{0.2500\;mol\;nicotina}=162.3\dfrac {g}{mol}$$La comparación de la masa molar y la masa de la fórmula empírica indica que cada molécula de nicotina contiene dos unidades de fórmula:
$$\dfrac{162.3{\dfrac{gr}{moL}}}{81.3{\dfrac{gr}{unidades\;de\;\text{fórmula}}}}=2{\dfrac{unidades\;de\;formula}{\text{molécula}}}$$Finalmente, deriva la fórmula molecular para la nicotina de la fórmula empírica multiplicando cada subíndice por dos:
$$\left( C_5H_7N\right)_{2}=C_{10}H_{14}O_{2}$$Comprueba tu aprendizaje
Las secciones anteriores de este capítulo se centraron en la composición de sustancias: muestras de materia que contienen solo un tipo de elemento o compuesto. Sin embargo, las mezclas, muestras de materia que contienen dos o más sustancias combinadas físicamente, se encuentran más comúnmente en la naturaleza que las sustancias puras. Similar a una sustancia pura, la composición relativa de una mezcla juega un papel importante en la determinación de sus propiedades. La cantidad relativa de oxígeno en la atmósfera de un planeta determina su capacidad para mantener la vida aeróbica. Las cantidades relativas de hierro, carbono, níquel y otros elementos en el acero (una mezcla conocida como "aleación") determinan su resistencia física y resistencia a la corrosión. La cantidad relativa del ingrediente activo en un medicamento determina su efectividad para lograr el efecto farmacológico deseado. La cantidad relativa de azúcar en una bebida determina su dulzura (ver Figura 3.14). Esta sección describirá una de las formas más comunes en que se pueden cuantificar las composiciones relativas de las mezclas.
Figura 3.14. El azúcar es uno de los muchos componentes de la mezcla compleja conocida como café. La cantidad de azúcar en una cantidad dada de café es un determinante importante de la dulzura de la bebida. (Crédito: Jane Whitney)
Las soluciones se han definido previamente como mezclas homogéneas, lo que significa que la composición de la mezcla (y, por lo tanto, sus propiedades) es uniforme en todo su volumen. Las soluciones ocurren con frecuencia en la naturaleza y también se han implementado en muchas formas de tecnología artificial. En el capítulo sobre soluciones y coloides se proporciona un tratamiento más exhaustivo de las propiedades de la solución, pero aquí se proporciona una introducción a algunas de las propiedades básicas de las soluciones.
La cantidad relativa de un componente de solución dada se conoce como su concentración. A menudo, aunque no siempre, una solución contiene un componente con una concentración que es significativamente mayor que la de todos los demás componentes.
Este componente se llama el solvente y puede verse como el medio en el que los otros componentes se dispersan o disuelven. Las soluciones en las que el agua es el solvente son, por supuesto, muy comunes en nuestro planeta. Una solución en la cual el solvente es el agua se llama una solución acuosa.
Un soluto es un componente de una solución que normalmente está presente en una concentración mucho menor que el solvente. Las concentraciones de solutos a menudo se describen con términos cualitativos, como diluido (de concentración relativamente baja) y concentrado (de concentración relativamente alta).
Las concentraciones pueden evaluarse cuantitativamente utilizando una amplia variedad de unidades de medición, cada una conveniente para aplicaciones particulares. La molaridad (M) es una unidad de concentración útil para muchas aplicaciones en química. La molaridad se define como el número de moles de soluto en exactamente 1 litro (1 L) de la solución:
$$M=\dfrac {mol\;soluto}{L\;\text{solución}}$$Ejemplo 3.14
Cálculo de concentraciones molares
Una muestra de refresco de $355$ ml contiene $0.133$ mol de sacarosa (azúcar de mesa). ¿Cuál es la concentración molar de sacarosa en la bebida?
Solución
Dado que la cantidad molar de soluto y el volumen de solución están dados, la molaridad se puede calcular utilizando la definición de molaridad. Según esta definición, el volumen de la solución debe convertirse de mL a L:
$$M\;=\dfrac {mol_{(soluto)}}{L_{(\text{solución})}}=\dfrac {0.133\;mol}{355\;{\cancel{mL}} \times \dfrac {1\;L}{1000\;{\cancel{mL}}}}=0.375\;M$$Comprueba tu aprendizaje
Ejemplo 3.15
Calcular moles y volúmenes a partir de concentraciones molares
¿Cuánta azúcar (mol) está contenida en un sorbo modesto (~$10$ ml) del refresco del Ejemplo 3.14?
Solución
Reorganiza la definición de molaridad para aislar la cantidad buscada, moles de azúcar, luego sustituye el valor de molaridad derivado en el Ejemplo 3.14, $0.375$ M:
$$M=\frac{mol_{(soluto)}}{L_{(\text{solución})}}\quad; despejando;\quad mol_{(soluto)} = M \times L_{(\text{solución})}$$$mol_{(soluto)} = \frac{0.375\;mol\;\text{azúcar}}{\cancel L} {\bigg(}10\;{\bcancel mL} \times \dfrac{1\;{\cancel L}}{1000\;{\bcancel mL}}{\bigg)} = 0.004\;mol\;\text{azúcar}$
Comprueba tu aprendizaje
Ejemplo 3.16
Cálculo de las concentraciones molares de la masa de soluto
El vinagre blanco destilado (Figura 3.15) es una solución de ácido acético, $CH_3CO_2H$, en agua. Una solución de vinagre de $0.500$ L contiene $25.2$ g de ácido acético. ¿Cuál es la concentración de la solución de ácido acético en unidades de molaridad?
Solución
Como en los ejemplos anteriores, la definición de molaridad es la ecuación primaria utilizada para calcular la cantidad buscada. Dado que se proporciona la masa de soluto en lugar de su cantidad molar, usa la masa molar del soluto para obtener la cantidad de soluto en moles:
$M=\frac {mol_{(soluto)}}{L_{(\text{solución})}}=\frac {{25.2\;{\cancel{g_{CH_3CO_2H}}}} \times \frac {1\;mol_{CH_3CO_2H}}{60.052\;{\cancel{g_{CH_3CO_2H}}}}}{0.500\;L_{(\text{solución})}}=0.839\;M$
$$M=\frac {mol_{(soluto)}}{L_{(\text{solución})}}=\dfrac {0.839\;mol_{(soluto)}}{1\;L_{(\text{solución})}}=0.839\;M$$Comprueba tu aprendizaje
Ejemplo 3.17
Determinación de la masa de soluto en un volumen dado de solución
¿Cuántos gramos de NaCl hay en $0.250$ L de una solución de $5.30$ M?
Figura 3.15. El vinagre blanco destilado es una solución de ácido acético en agua.
Solución
El volumen y la molaridad de la solución se especifican, por lo que la cantidad (mol) de soluto se calcula fácilmente como se muestra en el Ejemplo 3.15:
$$M=\dfrac{mol_{(soluto)}}{L_{(\text{solución})}}\quad; despejando;\quad mol_{(soluto)} = M \times L_{(\text{solución})}$$ $$mol_{(soluto)} = \dfrac{5.30\;mol\;NaCl}{\cancel L} \times 0.250\;{\cancel L} = 1.325\;mol\;NaCl$$Finalmente, esta cantidad molar se utiliza para obtener la masa de NaCl:
$$1.325\;\cancel {mol\;NaCl} \times \dfrac{58.44\;g\;NaCl}{1\;\cancel {mol\;NaCl}} = 77.4\;g\;NaCl$$Comprueba tu aprendizaje
Al realizar los cálculos paso a paso, como en el Ejemplo 3.17, es !importante¡ abstenerse de redondear los resultados de los cálculos intermedios, lo que puede generar errores de redondeo en el resultado final. En el Ejemplo 3.17, la cantidad molar de $NaCl$ calculada en el primer paso, $1.325$ moles, se redondearía adecuadamente a $1.32$ moles si se informara; sin embargo, aunque el último dígito ($5$) no es significativo, debe conservarse como un dígito de guarda en el cálculo intermedio. Si el dígito de guarda no se hubiera retenido, el cálculo final para la masa de $NaCl$ habría sido $77.1$ g, una diferencia de $0.3$ g.
Además de retener un dígito de guarda para los cálculos intermedios, los errores de redondeo también se pueden evitar al realizar cálculos en un solo paso (ver Ejemplo 3.18). Esto elimina los pasos intermedios y solo se redondea el resultado final.
Ejemplo 3.18
Determinación del volumen de solución que contiene una masa dada de soluto
En el Ejemplo 3.16, se determinó que la concentración de ácido acético en vinagre blanco era de $0,839$ M. ¿Qué volumen de vinagre contiene $75,6$ g de ácido acético?
Solución
Primero, use la masa molar para calcular los moles de ácido acético de la masa dada:
$$\cancel{g_{(soluto)}} \times \dfrac {mol_{(soluto)}}{\cancel{g_{(soluto)}}} = mol_{(soluto)}$$Luego, use la molaridad de la solución para calcular el volumen de solución que contiene esta cantidad molar de soluto:
$$\cancel{mol_{(soluto)}} \times \dfrac {L_{(\text{solución})}}{\cancel{mol_{(soluto)}}} = L_{(\text{solución})}$$Combinando estos dos pasos en un solo procedimiento:
$$\cancel{g_{(soluto)}} \times \dfrac {\bcancel{mol_{(soluto)}}}{\cancel{g_{(soluto)}}} \times \dfrac {L_{(\text{solución})}}{\bcancel{mol_{(soluto)}}} = L_{(\text{solución})}$$$75.6\;{\cancel{g_{CH_3CO_2H}}} \times \dfrac {1\;\bcancel{mol_{CH_3CO_2H}}}{60.05\;{\cancel{g_{CH_3CO_2H}}}} \times \dfrac {L_{(\text{solución})}}{0.839\;{\bcancel {mol_{(CH_3CO_2H)}}}}=1.50\;L_{(\text{solución})}$
Comprueba tu aprendizaje
La dilución es el proceso mediante el cual la concentración de una solución se reduce mediante la adición de disolvente. Por ejemplo, un vaso de té helado se diluye cada vez más a medida que el hielo se derrite. El agua del hielo derretido aumenta el volumen del solvente (agua) y el volumen total de la solución (té helado), reduciendo así las concentraciones relativas de los solutos que dan sabor a la bebida (Figura 3.16).
Figura 3.16. Ambas soluciones contienen la misma masa de nitrato de cobre. La solución de la derecha está más diluida porque el nitrato de cobre se disuelve en más solvente. (Crédito: Mark Ott)
La dilución también es un medio común para preparar soluciones de una concentración deseada. Al agregar solvente a una porción medida de una solución madre más concentrada, se puede preparar una solución de menor concentración. Por ejemplo, los pesticidas comerciales se venden típicamente como soluciones en las que los ingredientes activos están mucho más concentrados de lo que es apropiado para su aplicación. Antes de que puedan ser utilizados en cultivos, los pesticidas deben ser diluidos.
Esta es también una práctica muy común para la preparación de varios reactivos de laboratorio comunes.
Se puede usar una relación matemática simple para relacionar los volúmenes y concentraciones de una solución antes y después del proceso de dilución. Según la definición de molaridad, la cantidad molar de soluto en una solución (n) es igual al producto de la molaridad de la solución (M) y su volumen en litros (L):
$$n=M\times L$$Expresiones como estas pueden escribirse para una solución antes y después de que se diluya:
$$n_1=M_1\times L_1$$ $$n_2=M_2\times L_2$$Donde los subíndices "1" y "2" se refieren a la solución antes y después de la dilución, respectivamente. Dado que el proceso de dilución no cambia la cantidad de soluto en la solución, $n_1 = n_2$. Por lo tanto, estas dos ecuaciones se pueden establecer iguales entre sí:
$$M_1\times L_1 = M_2\times L_2$$Esta relación se conoce comúnmente como la ecuación de dilución. Aunque esta ecuación usa la molaridad como unidad de concentración y los litros como unidad de volumen, se pueden usar otras unidades de concentración y volumen siempre que las unidades se cancelen adecuadamente según el método de la etiqueta del factor.
Reflejando esta versatilidad, la ecuación de dilución a menudo se escribe en la forma más general:
Donde C y V son concentración y volumen, respectivamente.
Enlace a aprendizaje
Ejemplo 3.19
Determinación de la concentración de una solución diluida
Si $0,850$ L de una solución de nitrato de cobre $5,00$ M, $Cu(NO_3)_2$, se diluye a un volumen de $1,80$ L mediante la adición de agua, ¿cuál es la molaridad de la solución diluida?
Solución
La concentración de stock, $C_1$, y el volumen, $V_1$, se proporcionan, así como el volumen de la solución diluida, $V_2$. Reorganiza la ecuación de dilución para aislar la propiedad desconocida, la concentración de la solución diluida, $C_2$:
$$C_1\times V_1 = C_2\times V_2; \quad Despejando; \quad C_2 = \dfrac {C_1\times V_1}{V_2} $$Como la solución de inicial se diluye más de dos veces (el volumen aumenta de $0,85$ L a $1,80$ L), se espera que la concentración de la solución diluida sea inferior a la mitad de $5$ M. Esta estimación aproximada se comparará con el resultado calculado para verificar errores significativos en el cálculo (por ejemplo, como una sustitución inadecuada de las cantidades dadas). Sustituyendo los valores dados por los términos en el lado derecho de esta ecuación se obtiene:
$$C_2 = \dfrac {C_1\times V_1}{V_2} = \dfrac {0.850\;L \times {\dfrac {5\;mol}{1\;L}}}{1.8\;L} = 2.36\;M$$Este resultado se compara bien con nuestra estimación aproximada (es un poco menos de la mitad de la concentración de stock, $5$ M).
Comprueba tu aprendizaje
Ejemplo 3.20
Volumen de una solución diluida
¿Qué volumen de $0,12$ M HBr se puede preparar a partir de $11$ ml ($0,011$ L) de $0,45$ M HBr?
Solución
Se proporcionan el volumen y la concentración de una solución madre, $V_1$ y $C_1$, y la concentración de la solución diluida resultante, $C_2$. Encuentre el volumen de la solución diluida, $V_2$, reorganizando la ecuación de dilución para aislar $V_2$:
$$C_1\times V_1 = C_2\times V_2; \quad Despejando; \quad V_2 = \dfrac {C_1\times V_1}{C_2} $$Dado que la concentración diluida ($0,12$ M) es un poco más de un cuarto de la concentración original ($0,45$ M), se espera que el volumen de la solución diluida sea aproximadamente cuatro veces el volumen original, o alrededor de $44$mL. Sustituyendo los valores dados y resolviendo los rendimientos de volúmenes desconocidos:
$$V_2 = \dfrac {C_1\times V_1}{C_2} = \dfrac {0.45\;M\times 0.011\;L}{0.12\;M} = 0.041\;L$$El volumen de la solución $0.12$ M es $0.041$ L ($41$ mL). El resultado es razonable y se compara bien con la estimación aproximada.
Comprueba tu aprendizaje
Ejemplo 3.21
Volumen de una solución concentrada necesaria para la dilución
¿Qué volumen de $1.59$ M KOH se requiere para preparar $5.00$ L de 0.100 M KOH?
Solución
Se dan la concentración de una solución madre, $C_1$, y el volumen y la concentración de la solución diluida resultante, $V_2$ y $C_2$. Encuentre el volumen de la solución madre, $V_1$ reorganizando la ecuación de dilución para aislar $V_1$:
$$C_1\times V_1 = C_2\times V_2; \quad Despejando; \quad V_1 = \dfrac {C_2\times V_2}{C_1} $$Dado que la concentración de la solución diluida $0.100$ M es aproximadamente una décima sexta parte de la solución de reserva ($1.59$ M), se espera que el volumen de la solución de reserva sea aproximadamente una décimo sexta parte de la solución diluida, o alrededor de $0.3$ litros. Sustituyendo los valores dados y resolviendo los rendimientos de volúmenes desconocidos:
$$ V_1 = \dfrac {C_2\times V_2}{C_1} = \dfrac {0.100\;M \times 5.00\;L}{1.59\;M} = 0.314\;L$$Por lo tanto, se necesitan $0.314$ L de la solución $1.59$ M para preparar la solución deseada.
Comprueba tu aprendizaje
La sección anterior introdujo la molaridad, una unidad de medida muy útil para evaluar la concentración de soluciones. Sin embargo, la molaridad es solo una medida de concentración. Esta sección describirá algunas otras unidades de concentración que se usan comúnmente en varias aplicaciones, ya sea por conveniencia o por convención.
Anteriormente en este capítulo, el porcentaje de composición se introdujo como una medida de la cantidad relativa de un elemento dado en un compuesto. Los porcentajes también se usan comúnmente para expresar la composición de mezclas, incluidas las soluciones. El porcentaje de masa de un componente de la solución se define como la relación de la masa del componente a la masa de la solución, expresada como un porcentaje:
El porcentaje de masa también se conoce con nombres similares, como porcentaje de masa, porcentaje de peso - peso / porcentaje de peso y otras variaciones sobre este tema. El símbolo más común para el porcentaje de masa es simplemente el signo de porcentaje, $\%$, aunque a menudo se usan símbolos más detallados, incluyendo $\%$ masa, $\%$ peso y (w/w)$\%$. El uso de estos símbolos más detallados puede evitar la confusión de los porcentajes en masa con otros tipos de porcentajes, como los porcentajes en volumen (que se analizarán más adelante en esta sección).
Los porcentajes en masa son unidades de concentración populares para productos de consumo. La etiqueta de una típica botella de lejía líquida (Figura 3.17) indica que la concentración de su ingrediente activo, hipoclorito de sodio (NaOCl), es del $7.4\%$. Por lo tanto, una muestra de $100.0$ g de lejía contendría $7.4$ g de $NaOCl$.
Ejemplo 3.22
Cálculo del porcentaje por masa
Una muestra de $5.0$ g de líquido cefalorraquídeo contiene $3.75$ mg ($0.00375$ g) de glucosa. ¿Cuál es el porcentaje en masa de glucosa en el fluido cefalorraquídeo?
Solución
La muestra de líquido cefalorraquídeo contiene aproximadamente $4$ mg de glucosa en $5000$ mg de líquido, por lo que la fracción de masa de glucosa debe ser un poco menor que una parte en $1000$, o aproximadamente el $0,1\%$.
Sustituyendo las masas dadas en la ecuación que define los rendimientos porcentuales de masa:
$$\%\; glucosa = \dfrac {3.75\;mg\;de\;glucosa \times {\dfrac{1\;g}{1000\;mg}}}{5.0\;g\;de\;fluido\;espinal} \times 100\% = 0.075\%$$El porcentaje de masa calculado está de acuerdo con nuestra estimación aproximada (es un poco menos del 0,1%).
Figura 3.17. El blanqueador líquido es una solución acuosa de hipoclorito de sodio (NaOCl). Esta marca tiene una concentración del $7,4\%$ de NaOCl en masa.
Ten en cuenta que si bien se puede usar cualquier unidad de masa para calcular un porcentaje de masa (mg, g, kg, oz, etc.), se debe usar la misma unidad tanto para el soluto como para la solución, de modo que las unidades de masa se cancelen, lo que produce una relación adimensional. En este caso, la unidad de masa de soluto en el numerador se convirtió de mg a g para que coincida con las unidades en el denominador. Alternativamente, la unidad de masa del fluido cefaloraquideo en el denominador podría haberse convertido de g a mg en su lugar.
Mientras se utilicen unidades de masa idénticas tanto para el soluto como para la solución, el porcentaje de masa calculado será correcto.
Comprueba tu aprendizaje
Ejemplo 3.23
Cálculos utilizando el porcentaje de masa
El ácido clorhídrico "concentrado" es una solución acuosa de HCl al $37.2\%$ que se usa comúnmente como reactivo de laboratorio. La densidad de esta solución es de $1.19$ g/mL. ¿Qué masa de HCl está contenida en $0.500$ L de esta solución?
Solución
La concentración de HCl es cercana al $40\%$, por lo que una porción de $100$ g de esta solución contendría aproximadamente $40$ g de HCl. Como la densidad de la solución no es muy diferente de la del agua ($1$ g/ml), una estimación razonable de la masa de HCl en $500$ g ($0.5$ L) de la solución es aproximadamente cinco veces mayor que en una porción de $100$ g. o $5 \times 40 = 200$ g.
Para poder derivar la masa de soluto en una solución de su porcentaje de masa, la masa de la solución debe ser conocida. Usando la densidad de solución dada, convierta el volumen de la solución a masa, y luego use el porcentaje de masa dado para calcular la masa de soluto. Este enfoque matemático se describe en este diagrama de flujo:
Para una correcta cancelación de la unidad, el volumen de $0.500$ L se convierte en $500$ ml, y el porcentaje de masa se expresa como una proporción, $37.2$ g de solución de HCl /g:
$$500\;{\cancel{mL_{\text{solución}}}} \times \dfrac {1.19\;\bcancel{g_{\text{solución}}}}{1\;{\cancel{mL_{\text{solución}}}}} \times \dfrac {37.2\;g_{HCl}}{100\;{\bcancel {g_{\text{solución}}}}}=221\;g_{HCl}$$Esta masa de HCl es consistente con nuestra estimación aproximada de aproximadamente $200$ g.
Comprueba tu aprendizaje
Los volúmenes de líquidos en un amplio rango de magnitudes se miden convenientemente utilizando equipos de laboratorio comunes y relativamente económicos. La concentración de una solución formada al disolver un soluto líquido en un solvente líquido se expresa a menudo como un porcentaje en volumen, $\% vol$ o $\%(v/v)$:
$$ Porcentaje \; en \; Volumen = \dfrac {Volumen \; de \; componente}{\text{volumen de solución}} \times 100\%$$Ejemplo 3.24
Cálculos usando el porcentaje de volumen
El alcohol para frotar (isopropanol) se vende generalmente como una solución acuosa al $70\%$ vol. Si la densidad del alcohol isopropílico es de $0.785$ g/ml, ¿cuántos gramos de alcohol isopropílico están presentes en una botella de $355$ ml de alcohol?
Solución
Según la definición de porcentaje de volumen, el volumen de isopropanol es el $70\%$ del volumen total de la solución. Al multiplicar el volumen de isopropanol por su densidad, se obtiene la masa solicitada:
$$355\;{\cancel{mL_{\text{solución}}}} \times \frac {70\;\bcancel{mL_{isopropanol}}}{100\;{\cancel{mL_{\text{solución}}}}} \times \frac {0.785\;g_{isopropanol}}{1\;{\bcancel {mL_{isopropanol}}}}=195\;g_{isopropanol}$$
Comprueba tu aprendizaje
Las unidades porcentuales "mixtas", derivadas de la masa de soluto y el volumen de solución, son populares para ciertas aplicaciones bioquímicas y médicas. Un porcentaje de masa-volumen es una relación de la masa de un soluto al volumen de la solución expresada como un porcentaje. Las unidades específicas utilizadas para la masa de soluto y el volumen de la solución pueden variar, dependiendo de la solución.
Por ejemplo, la solución salina fisiológica, utilizada para preparar líquidos intravenosos, tiene una concentración de $0.9\%$ de masa/volumen (m/v), lo que indica que la composición es de $0.9$ g de soluto por $100$ ml de solución. La concentración de glucosa en sangre (comúnmente conocida como "azúcar en la sangre") también se expresa típicamente en términos de una relación masa-volumen. Aunque no se expresa explícitamente como un porcentaje, su concentración se suele dar en miligramos de glucosa por decilitro ($100$ ml) de sangre (Figura 3.18).
Figura 3.18. El blanqueador líquido es una solución acuosa de hipoclorito de sodio (NaOCl). Esta marca tiene una concentración del $7,4\%$ de NaOCl en masa.
Las concentraciones de soluto muy bajas a menudo se expresan utilizando unidades apropiadamente pequeñas, como partes por millón (ppm) o partes por billón (ppb). Al igual que las unidades de porcentaje ("parte por cien"), ppm y ppb se pueden definir en términos de masas, volúmenes o unidades de volumen de masas mixtas.
También hay unidades de ppm y ppb definidas con respecto a la cantidad de átomos y moléculas.
Las definiciones basadas en masa de ppm y ppb se dan aquí:
$$ ppm = \dfrac {masa \; de \; soluto}{masa \; de \; \text{solución}} \times 10^6 \; ppm$$ $$ ppb = \dfrac {masa \; de \; soluto}{masa \; de \; \text{solución}} \times 10^9 \; ppb$$Tanto ppm como ppb son unidades convenientes para informar las concentraciones de contaminantes y otros contaminantes traza en el agua. Las concentraciones de estos contaminantes suelen ser muy bajas en aguas tratadas y naturales, y sus niveles no pueden superar los umbrales de concentración relativamente bajos sin causar efectos adversos en la salud y la vida silvestre. Por ejemplo, la EPA ha identificado que el nivel máximo seguro de ión fluoruro en el agua del grifo es de $4$ ppm. Los filtros de agua en línea están diseñados para reducir la concentración de fluoruro y varios otros contaminantes a nivel de trazas en el agua del grifo (Figura 3.19).
Figura 3.19 (a) En algunas áreas, las concentraciones de contaminantes a nivel de trazas pueden hacer que el agua del grifo sin filtrar sea insegura para beber y cocinar. (b) Los filtros de agua en línea reducen la concentración de solutos en el agua del grifo. (Crédito a: modificación del trabajo por Jenn Durfey; crédito b: modificación del trabajo por "vastateparkstaff" / Wikimedia commons)
Ejemplo 3.25
Cálculo de partes por millón y partes por billón de concentraciones
Según la EPA, cuando la concentración de plomo en el agua del grifo alcanza las $15$ ppb, se deben tomar ciertas medidas correctivas. ¿Cuál es esta concentración en ppm? A esta concentración, ¿qué masa de plomo ($\mu$g) estaría contenida en un vaso de agua típico ($300$ mL)?
Solución
Las definiciones de las unidades de ppm y ppb se pueden usar para convertir la concentración dada de ppb a ppm. La comparación de estas dos definiciones de unidades muestra que ppm es $1000$ veces mayor que ppb ($1\;ppm = 10^3\;ppb$). Así:
$$ 15\;ppb \times \dfrac {1 \; ppm }{10^3 \; ppb } = 0.015 \; ppm$$La definición de la unidad de ppb se puede usar para calcular la masa solicitada si se proporciona la masa de la solución. Dado que se da el volumen de solución ($300$ mL), su densidad debe usarse para derivar la masa correspondiente. Supón que la densidad del agua del grifo es aproximadamente la misma que la del agua pura (~$1.00$ g/mL), ya que las concentraciones de cualquier sustancia disuelta no deben ser muy grandes. Reorganizando la ecuación definiendo la unidad de ppb y sustituyendo los rendimientos de las cantidades dadas:
$$ masa \; de \; soluto = \dfrac {ppb \times {masa \; de \; \text{solución}}}{10^9 \; ppb}$$Finalmente, convierta esta masa a la unidad de microgramos solicitada:
$$ 4.5 \times 10^6 \;\mu g \times \dfrac {1 \; \mu g }{10^{-6} \; g } = 4.5 \; \mu g$$Comprueba tu aprendizaje
Con esta simulación tomada de "https://phet.colorado.edu/es/simulation/molarity" puedes prácticar desplazando el boton de volumen o el boton de cantidad de soluto, incluso puedes verificar el resultado de lamolaridad o las moles o el volumen usando la ecuacion que se estudia en este capitulo, al activar la casilla de mostrar valores.
Figura 4.1. Muchos combustibles modernos para cohetes son mezclas sólidas de sustancias combinadas en cantidades cuidadosamente medidas y encendidas para producir una reacción química generadora de empuje (crédito: modificación de obra por la NASA).
Los cohetes de combustible sólido son una característica central en los programas de exploración espacial del mundo, incluido el nuevo Sistema de Lanzamiento Espacial que está desarrollando la Administración Nacional de Aeronáutica y del Espacio (NASA) para reemplazar la flota retirada del Transbordador Espacial (Figura 4.1). Los motores de estos cohetes se basan en mezclas sólidas de productos químicos cuidadosamente preparadas, combinadas en cantidades medidas con precisión. Encender la mezcla inicia una reacción química vigorosa que genera rápidamente grandes cantidades de productos gaseosos. Estos gases son expulsados del motor del cohete a través de su boquilla, proporcionando el empuje necesario para impulsar cargas pesadas al espacio. Tanto la naturaleza de esta reacción química como las relaciones entre las cantidades de sustancias consumidas y producidas por la reacción son consideraciones de importancia crítica que determinan el éxito de la tecnología.
Este capítulo describirá cómo simbolizar reacciones químicas usando ecuaciones químicas, cómo clasificar algunas reacciones químicas comunes mediante la identificación de patrones de reactividad y cómo determinar las relaciones cuantitativas entre las cantidades de sustancias involucradas en las reacciones químicas, es decir, la reacción de la estequiometría.
Un capítulo anterior de este texto introdujo el uso de símbolos de elementos para representar átomos individuales. Cuando los átomos ganan o pierden electrones para producir iones, o se combinan con otros átomos para formar moléculas, sus símbolos se modifican o combinan para generar fórmulas químicas que representan adecuadamente a estas especies. Extender este simbolismo para representar tanto las identidades como las cantidades relativas de sustancias que experimentan un cambio químico (o físico) implica escribir y equilibrar una ecuación química. Considera como ejemplo la reacción entre una molécula de metano ($CH_4$) y dos moléculas de oxígeno diatómico ($O_2$) para producir una molécula de dióxido de carbono ($CO_2$) y dos moléculas de agua ($H_2O$). La ecuación química que representa este proceso se proporciona en la mitad superior de la Figura 4.2, con modelos moleculares de relleno de espacio que se muestran en la mitad inferior de la figura.
Este ejemplo ilustra los aspectos fundamentales de cualquier ecuación química:
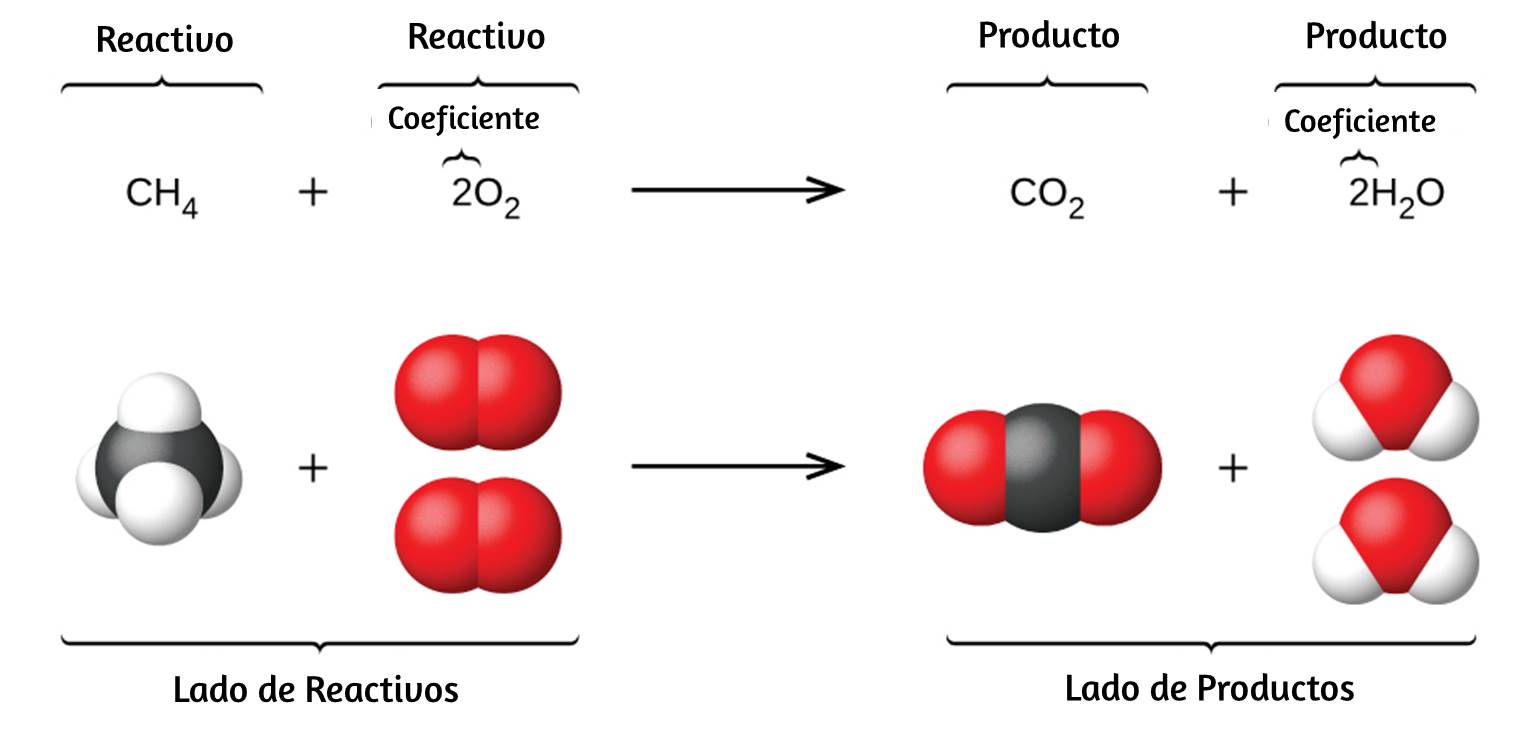
Figura 4.2. La reacción entre metano y oxígeno para producir dióxido de carbono y agua (que se muestra en la parte inferior) puede representarse mediante una ecuación química utilizando fórmulas (parte superior).
Es una práctica sobre común utilizar los coeficientes de números enteros más pequeños posibles en una ecuación química, como se hace en este ejemplo. Tenga en cuenta, sin embargo, que estos coeficientes representan el número relativo de reactivos y productos, y por lo tanto, pueden interpretarse correctamente como razones.
El metano y el oxígeno reaccionan para producir dióxido de carbono y agua en una proporción de 1: 2: 1: 2. Esta relación se satisface si los números de estas moléculas son, respectivamente, 1-2-1-2, o 2-4-2-4, o 3-6-3-6, y así sucesivamente (Figura 4.3).
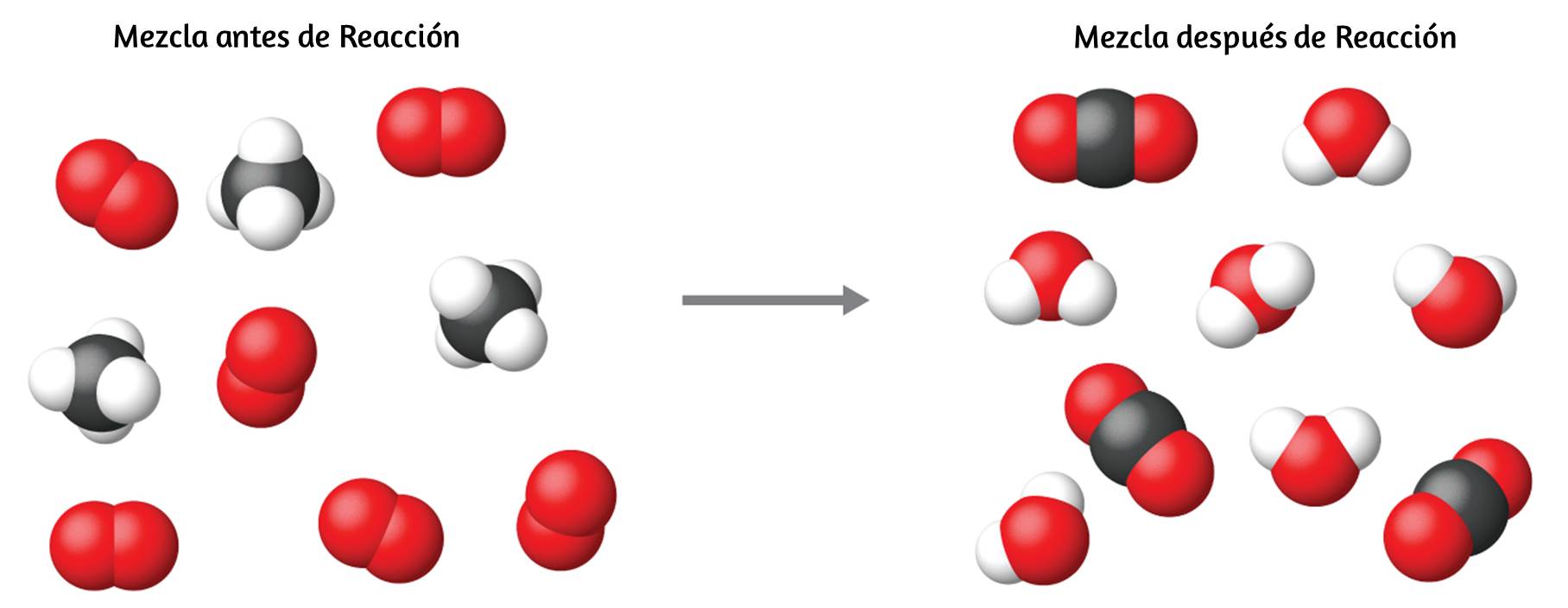
Figura 4.3. Independientemente de los números absolutos de moléculas involucradas, las proporciones entre los números de moléculas de cada especie que reaccionan (los reactivos) y las moléculas de cada especie que se forman (los productos) son las mismas y están dadas por la ecuación de reacción química.
Del mismo modo, estos coeficientes pueden interpretarse con respecto a cualquier cantidad de unidad (número), por lo que esta ecuación puede leerse correctamente de muchas maneras, incluyendo:
La ecuación química descrita en la sección 4.1 esta balanceada, lo que significa que se representan números iguales de átomos para cada elemento involucrado en la reacción en el reactivo y los lados del producto. Este es un requisito que la ecuación debe cumplir para ser consistente con la ley de conservación de la materia. Se puede confirmar simplemente sumando el número de átomos en cada lado de la flecha y comparando estas sumas para asegurarse de que sean iguales. Ten en cuenta que el número de átomos para un elemento dado se calcula multiplicando el coeficiente de cualquier fórmula que contenga ese elemento por el subíndice del elemento en la fórmula. Si un elemento aparece en más de una fórmula en un lado dado de la ecuación, el número de átomos representados en cada uno debe calcularse y luego sumarse. Por ejemplo, ambas especies de productos en la reacción de ejemplo, $CO_2$ y $H_2O$, contienen el elemento oxígeno, por lo que el número de átomos de oxígeno en el lado del producto de la ecuación es
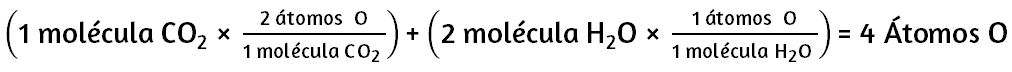
La ecuación de la reacción entre el metano y el oxígeno para producir dióxido de carbono y agua se confirma para ser equilibrada según este enfoque, como se muestra aquí:
$$CH_4+2O_2 \longrightarrow CO_2+2H_2O$$
Una ecuación química equilibrada a menudo se puede derivar de una descripción cualitativa de alguna reacción química mediante un enfoque bastante simple conocido como equilibrio por inspección.
Considera como ejemplo la descomposición del agua para producir hidrógeno molecular y oxígeno. Este proceso está representado cualitativamente por una ecuación química desequilibrada:
$$H_2O \longrightarrow H_2+O_2\qquad(no\;balanceada)$$
La comparación del número de átomos de H y O en cada lado de esta ecuación confirma su desequilibrio:
Los números de átomos de H en el reactivo y los lados del producto de la ecuación son iguales, pero los números de átomos de O no lo son. Para lograr el equilibrio, los coeficientes de la ecuación pueden cambiarse según sea necesario. Por supuesto, ten en cuenta que los subíndices de la fórmula definen, en parte, la identidad de la sustancia, por lo que no se pueden cambiar sin alterar el significado cualitativo de la ecuación.
Por ejemplo, cambiar la fórmula del reactivo de $H_2O$ a $H_2O_2$ daría un equilibrio en el número de átomos, pero al hacerlo también cambia la identidad del reactivo (ahora es peróxido de hidrógeno y no agua). El equilibrio del átomo de O se puede lograr cambiando el coeficiente para $H_2O$ a 2.
$$2H_2O \longrightarrow H_2+O_2\qquad(no\;balanceada)$$
El cambio del átomo de H se vio afectado por este cambio, pero se restablece fácilmente cambiando el coeficiente para el producto $H_2$ a 2.
$$2H_2O \longrightarrow 2H_2+O_2\qquad(balanceada)$$
Estos coeficientes producen números iguales de átomos tanto de H como de O en los lados del reactivo y del producto, y la ecuación balanceada es, por lo tanto:
$$2H_2O \longrightarrow 2H_2+O_2\qquad(balanceada)$$Ejemplo 4.1
Balanceo de ecuaciones químicas
Escribe una ecuación balanceada para la reacción de nitrógeno molecular ($N_2$) y oxígeno ($O_2$) para formar pentóxido de dinitrógeno.
Solución
Primero, escribe la ecuación desequilibrada.
$$N_2+O_2 \longrightarrow N_2O_5\qquad(no\;balanceada)$$Luego, cuenta el número de cada tipo de átomo presente en la ecuación no balanceada.
Aunque el nitrógeno está equilibrado, se necesitan cambios en los coeficientes para equilibrar el número de átomos de oxígeno. Un primer intento razonable sería cambiar los coeficientes para el $O_2$ y el $N_2O_5$ a números enteros que produzcan 10 átomos de O (el mínimo común múltiplo para los subíndices del átomo de O en estas dos fórmulas).
$$N_2+5O_2 \longrightarrow 2N_2O_5\qquad(no\;balanceada)$$
El balance del átomo de N se ha alterado por este cambio; se restaura cambiando el coeficiente para el reactivo $N_2$ a 2
$$2N_2+5O_2 \longrightarrow 2N_2O_5\qquad(balanceada)$$
Los números de átomos de N y O a cada lado de la ecuación son ahora iguales, y por lo tanto la ecuación está balanceada.
Comprueba tu aprendizaje
A veces es conveniente usar fracciones en lugar de números enteros como coeficientes intermedios en el proceso de equilibrar una ecuación química. Cuando se logra el equilibrio, todos los coeficientes de la ecuación se pueden multiplicar por un número entero para convertir los coeficientes fraccionarios en números enteros sin alterar el equilibrio del átomo.
Por ejemplo, considera la reacción del etano ($C_2H_6$) con el oxígeno para producir $H_2O$ y $CO_2$, representados por la ecuación desequilibrada:
$$C_2H_6+O_2 \longrightarrow H_2O + CO_2$$Siguiendo el enfoque de inspección habitual, primero se puede equilibrar los átomos de C y H cambiando los coeficientes para las dos especies de productos, como se muestra:
$$C_2H_6+O_2 \longrightarrow 3H_2O + 2CO_2$$Esto da como resultado siete átomos de O en el lado del producto de la ecuación, un número impar; no se puede usar ningún coeficiente entero con el reactivo $O_2$ para producir un número impar, por lo que un coeficiente fraccional $\frac72$, se utiliza en cambio para producir una ecuación equilibrada provisional:
$$C_2H_6+\frac72O_2 \longrightarrow 3H_2O + 2CO_2$$Una ecuación balanceada convencional con coeficientes de solo enteros se obtiene multiplicando cada coeficiente por 2:
$$2C_2H_6+7O_2 \longrightarrow 6H_2O + 4CO_2$$Finalmente, con respecto a las ecuaciones balanceadas, recuerda que la convención dicta el uso de los coeficientes de números enteros más pequeños. Aunque la ecuación de la reacción entre nitrógeno molecular e hidrógeno molecular para producir amoníaco es, de hecho, equilibrada,
$$3N_2+9H_2 \longrightarrow 6NH_3$$los coeficientes no son los enteros más pequeños posibles que representan los números relativos de moléculas reactantes y de producto. Dividiendo cada coeficiente por el mayor factor común, 3, se obtiene la ecuación preferida:
$$N_2+3H_2 \longrightarrow 2NH_3$$Los estados físicos de los reactivos y productos en las ecuaciones químicas se indican muy a menudo con una abreviatura entre paréntesis que sigue a las fórmulas. Las abreviaturas comunes incluyen s para sólidos, l para líquidos, g para gases y ac para sustancias disueltas en agua (soluciones acuosas, como se presentó en el capítulo anterior). Estas notaciones se ilustran en la ecuación de ejemplo aquí:
$$\ce{2Na(s) + 2H2O(l) \rightarrow 2NaOH(ac) + H2(g)}$$Esta ecuación representa la reacción que tiene lugar cuando el sodio metálico se coloca en el agua. El sodio sólido reacciona con agua líquida para producir gas de hidrógeno molecular y el compuesto iónico hidróxido de sodio (un sólido en forma pura, pero se disuelve fácilmente en agua).
Las condiciones especiales necesarias para una reacción a veces se designan escribiendo una palabra o símbolo encima o debajo de la flecha de la ecuación. Por ejemplo, una reacción llevada a cabo por calentamiento puede estar indicada por la letra griega delta (Δ) sobre la flecha.
$$\ce{CaCO3(s) \xrightarrow[]{\Delta} CaO(s) + CO2(g)}$$Enlace a aprendizaje
Usa la siguiente simulación phet para prácticar el balanceo de ecuaciones químicas.
Aprende en el modo introducción y diviertete en el modo juego.
Otros ejemplos de estas condiciones especiales se encontrarán con mayor profundidad en capítulos posteriores.
Dada la abundancia de agua en la tierra, es lógico que se produzcan muchas reacciones químicas en medios acuosos.
Cuando hay iones involucrados en estas reacciones, las ecuaciones químicas pueden escribirse con varios niveles de detalle apropiados para su uso previsto. Para ilustrar esto, considera una reacción entre compuestos iónicos que tienen lugar en una solución acuosa. Cuando se mezclan soluciones acuosas de $CaCl_2$ y $AgNO_3$, tiene lugar una reacción que produce $Ca(NO_3)_2$ acuoso y $AgCl$ sólido:
$$CaCl_2(ac) + 2AgNO_3(ac) \longrightarrow Ca(NO_3)(ac)+2AgCl(s)$$Esta ecuación balanceada, derivada de la manera habitual, se llama ecuación molecular porque no representa explícitamente las especies iónicas que están presentes en la solución. Cuando los compuestos iónicos se disuelven en agua, pueden disociarse en sus iones constituyentes, que posteriormente se dispersan homogéneamente en toda la solución resultante, en este caso:
$$CaCl_2(ac) \longrightarrow Ca^{2+}(ac)+2Cl^{-}(ac)$$ $$2AgNO_3(ac) \longrightarrow 2Ag^+(ac)+2NO_3(ac)$$ $$Ca(NO_3)_2(ac) \longrightarrow Ca^{2+}(ac)+2NO3^{-}(ac)$$(en el capítulo sobre soluciones se proporciona una discusión detallada de este importante proceso). Los compuestos iónicos disueltos en agua son, por lo tanto, representados de manera más realista como iones disociados.
A diferencia de estos tres compuestos iónicos, el $AgCl$ no se disuelve en agua en un grado significativo, como lo indica su notación de estado físico, s.
La representación explícita de todos los iones disueltos da como resultado una ecuación iónica completa.
En este caso particular, las fórmulas para los compuestos iónicos disueltos se reemplazan por fórmulas para sus iones disociados:
$$Ca^{2+}(ac)+2Cl^{-}(ac)+2Ag^+(ac)+2NO_3(ac) \longrightarrow Ca^{2+}(ac) \\ +2NO_3^{-}(ac)+2AgCl(ac)$$El examen de esta ecuación muestra que dos especies químicas están presentes en forma idéntica en ambos lados de la flecha, $Ca^{2+}(ac)$ y $NO^{3−}(ac)$. Estos iones espectadores, iones cuya presencia se requiere para mantener la neutralidad de la carga, no son modificados química ni físicamente por el proceso, por lo que pueden eliminarse de la ecuación para obtener una representación más concisa llamada ecuación iónica neta:
$$\cancel{Ca^{2+}(ac)}+2Cl^{-}(ac)+2Ag^+(ac)+\cancel{2NO_3(ac)} \longrightarrow \cancel{Ca^{2+}(ac)}+\cancel{2NO_3^{-}(ac)}$$$$+2AgCl(ac)$$ $$2Cl^{-}\;(ac)+2Ag^+\;(ac)\longrightarrow 2AgCl\;(s)$$Siguiendo la convención de usar los enteros más pequeños posibles como coeficientes, esta ecuación se escribe:
$$Cl^{-}(ac)+Ag^+(ac)\longrightarrow AgCl(s)$$Esta ecuación iónica neta indica que el cloruro de plata sólido se puede producir a partir de los iones de cloruro y plata (I) disueltos, independientemente de la fuente de estos iones. Estas ecuaciones iónicas moleculares y completas proporcionan información adicional, a saber, los compuestos iónicos utilizados como fuentes de $Cl^{-}$ y $Ag^{+}$.
Ejemplo 4.2
Ecuaciones Moleculares e Iónicas
Cuando el dióxido de carbono se disuelve en una solución acuosa de hidróxido de sodio, la mezcla reacciona para producir carbonato de sodio acuoso y agua líquida. Escribe ecuaciones balanceadas moleculares, iónicas completas y iónicas netas para este proceso.
Solución
Comienza identificando fórmulas para los reactivos y productos y ordenándolos adecuadamente en forma de ecuaciones químicas:
$$CO_2(ac)+NaOH(ac) \longrightarrow Na_2CO_3(ac)+H_2O(l)\qquad desequilibrada$$El equilibrio se logra fácilmente en este caso al cambiar el coeficiente de $NaOH$ a 2, lo que resulta en la ecuación molecular para esta reacción:
$$CO_2(ac)+2NaOH(ac) \longrightarrow Na_{2}CO_3(ac)+H_{2}O(l)$$Los dos compuestos iónicos disueltos, $NaOH$ y $Na_2CO_3$, se pueden representar como iones disociados para obtener la ecuación iónica completa:
$$CO_2(ac)+2Na^{+}(ac)+2OH^{-}(ac) \longrightarrow 2Na^{+}(ac)+2CO_3^{2-}(ac)+H_2O(l)$$Finalmente, identifica el (los) ion (es) espectador (es), en este caso $Na^+(ac)$, y elimínalo de cada lado de la ecuación para generar la ecuación iónica neta:
$$CO_2(ac) + \cancel{2Na^{+}(ac)}+2OH^{-}(ac) \longrightarrow \cancel{2Na^{+}(ac)}+2CO_3^{2-}(ac)+H_2O(l)$$ $$CO_2(ac)+2OH^{-}(ac) \longrightarrow 2CO_3^{2-}(ac)+H_2O(l)$$Comprueba tu aprendizaje
Los seres humanos interactúan entre sí de diversas maneras y complejas, y clasificamos estas interacciones de acuerdo con patrones comunes de comportamiento. Cuando dos humanos intercambian información, decimos que se están comunicando.
Cuando intercambian golpes con sus puños o pies, decimos que están luchando. Frente a una amplia gama de interacciones variadas entre sustancias químicas, los científicos también han encontrado conveniente (o incluso necesario) clasificar las interacciones químicas mediante la identificación de patrones comunes de reactividad. Este módulo proporcionará una introducción a tres de los tipos más frecuentes de reacciones químicas: precipitación, ácido-base y oxidación-reducción.
Una reacción de precipitación es aquella en la que las sustancias disueltas reaccionan para formar uno (o más) productos sólidos. Muchas reacciones de este tipo implican el intercambio de iones entre compuestos iónicos en solución acuosa y algunas veces se denominan reacciones de doble desplazamiento, reemplazo doble o metátesis. Estas reacciones son comunes en la naturaleza y son responsables de la formación de arrecifes de coral en aguas oceánicas y cálculos renales en animales. Se utilizan ampliamente en la industria para la producción de una serie de productos básicos y productos químicos especializados. Las reacciones de precipitación también desempeñan un papel central en muchas técnicas de análisis químico, incluidas las pruebas puntuales utilizadas para identificar iones metálicos y métodos gravimétricos para determinar la composición de la materia (consulte el último módulo de este capítulo).
El grado en que una sustancia se puede disolver en agua, o cualquier disolvente, se expresa cuantitativamente como su solubilidad, definida como la concentración máxima de una sustancia que se puede lograr en condiciones específicas.
Se dice que las sustancias con solubilidades relativamente grandes son solubles. Una sustancia precipitará cuando las condiciones de la solución sean tales que su concentración supere su solubilidad. Se dice que las sustancias con solubilidades relativamente bajas son insolubles, y estas son las sustancias que precipitan fácilmente de la solución. Se proporciona más información sobre estos conceptos importantes en un capítulo posterior sobre soluciones. Con el fin de predecir las identidades de los sólidos formados por las reacciones de precipitación, uno puede simplemente referirse a los patrones de solubilidad que se han observado para muchos compuestos iónicos (Tabla 4.1).
Tabla 4.1. pautas de solubilidad
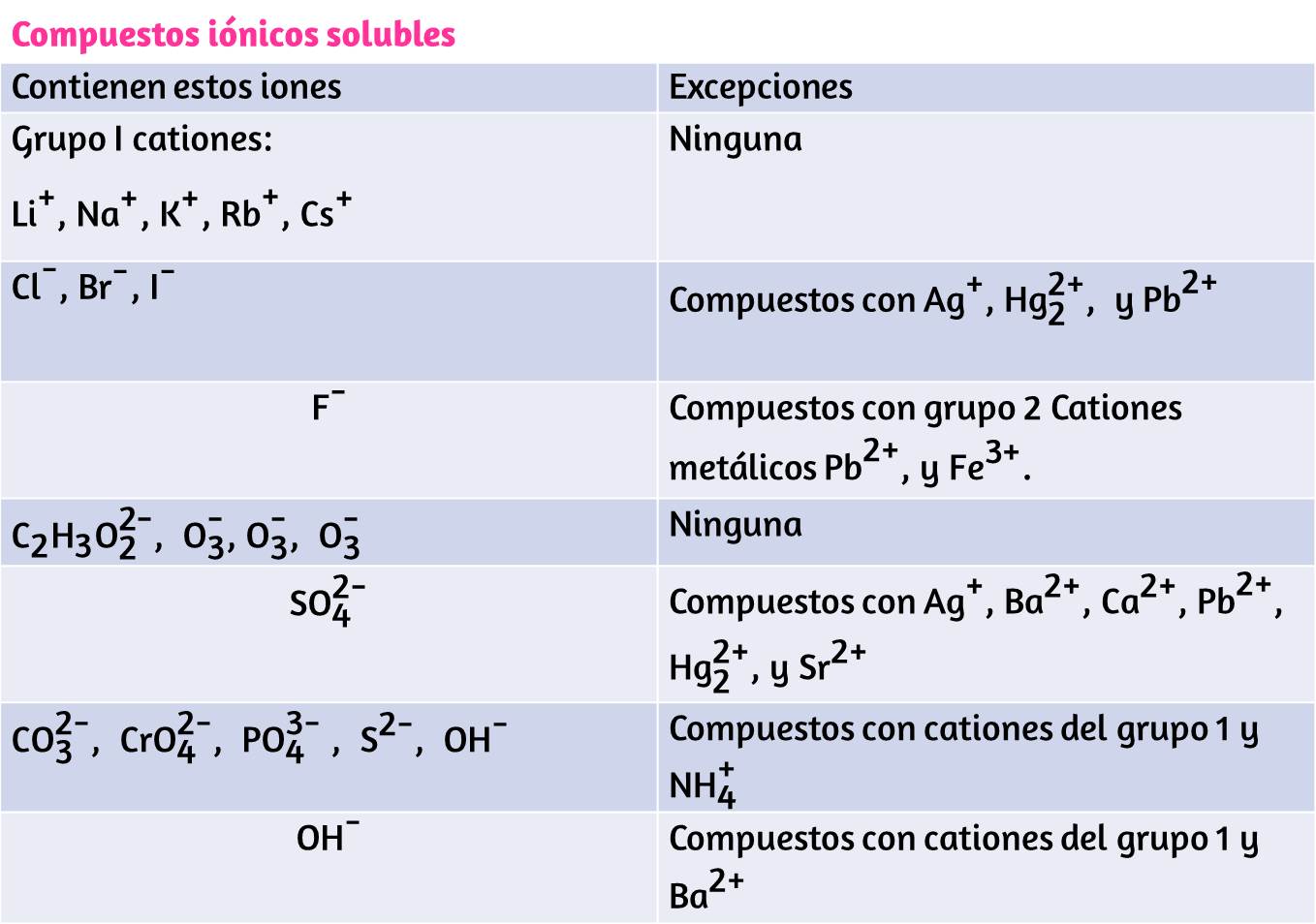
Se observa un ejemplo típico de precipitación cuando se mezclan soluciones de yoduro de potasio y nitrato de plomo, lo que resulta en la formación de yoduro de plomo sólido:
$$2KI(ac)+Pb(NO_3)_2(ac) \longrightarrow PbI_2(s)+2KNO_2(ac)$$Esta observación concuerda con las pautas de solubilidad: el único compuesto insoluble entre todos los involucrados es el yoduro de plomo, una de las excepciones a la solubilidad general de las sales de yoduro.
La ecuación iónica neta que representa esta reacción es:
$$Pb^{2+}(ac)+2I^{-}(ac) \longrightarrow PbI_2(s)$$El yoduro de plomo es un sólido amarillo brillante que anteriormente se usaba como pigmento de un artista conocido como amarillo de yodo (Figura 4.4). Las propiedades de los cristales de $PbI_2$ puros los hacen útiles para la fabricación de detectores de rayos X y rayos gamma.
Las pautas de solubilidad en la Tabla 4.1 se pueden usar para predecir si se producirá una reacción de precipitación cuando se mezclen soluciones de compuestos iónicos solubles. Uno simplemente necesita identificar todos los iones presentes en la solución y luego considerar si es posible el emparejamiento catión/anión podría dar como resultado un compuesto insoluble. Por ejemplo, mezclar soluciones de nitrato de plata y fluoruro de sodio producirá una solución que contiene iones $Ag^+$, $NO_3^{−}$, $Na^+$ y $F^{-}$. Aparte de los dos compuestos iónicos originalmente presentes en las soluciones, $AgNO_3$ y $NaF$, dos compuestos iónicos adicionales pueden derivarse de esta colección de iones: $NaNO_3$ y $AgF$.
Figura 4.4. Se forma un precipitado de $PbI_2$ cuando se mezclan soluciones que contienen $Pb^{2+}$ e $I^{-}$ (crédito: Der Kreole/Wikimedia Commons)
Las pautas de solubilidad indican que todas las sales de nitrato son solubles, pero que $AgF$ es una de las excepciones a la solubilidad general de las sales de fluoruro. Por lo tanto, se predice una reacción de precipitación, como se describe en las siguientes ecuaciones:
$$NaF(ac)+AgNO_3(ac) \longrightarrow AgF(s)+NaNO_3(ac) \qquad (molecular)$$ $$Ag(ac)^+ + F^{-}(ac) \longrightarrow AgF(s) \qquad (\text{iónico}\;neto)$$Ejemplo 4.3
Predicción de reacciones de precipitación
Predice el resultado de mezclar soluciones razonablemente concentradas de los siguientes compuestos iónicos. Si se espera precipitación, escriba una ecuación iónica neta balanceada para la reacción.
Solución
Comprueba tu aprendizaje
Una reacción ácido-base es aquella en la que un ión hidrógeno, $H^+$, se transfiere de una especie química a otra. Tales reacciones son de importancia central para numerosos procesos naturales y tecnológicos, que van desde las transformaciones químicas que tienen lugar dentro de las células y los lagos y océanos, hasta la producción a escala industrial de fertilizantes, productos farmacéuticos y otras sustancias esenciales para la sociedad.
El tema de la química ácido-base, por lo tanto, es digno de una discusión exhaustiva, y un capítulo completo está dedicado a este tema más adelante en el texto.
Para los propósitos de esta breve introducción, consideraremos solo los tipos más comunes de reacciones ácido-base que tienen lugar en soluciones acuosas. En este contexto, un ácido es una sustancia que se disuelve en agua para producir iones hidronio, $H_3O^+$. Como ejemplo, considera la ecuación mostrada aquí:
$$HCl(ac)+H_2O(l) \longrightarrow Cl^{-}(ac)+H_3O^+(ac)$$El proceso representado por esta ecuación confirma que el cloruro de hidrógeno es un ácido. Cuando se disuelven en agua, los iones $H_3O^{+}$ se producen por una reacción química en la que los iones $H^+$ se transfieren de las moléculas de $HCl$ a las moléculas de $H_2O$ (Figura 4.5).
La naturaleza del $HCl$ es tal que su reacción con el agua como se acaba de describir es esencialmente eficiente al 100%: virtualmente cada molécula de $HCl$ que se disuelve en el agua sufrirá esta reacción. Los ácidos que reaccionan completamente de esta manera se llaman ácidos fuertes, y el $HCl$ es uno de los pocos compuestos ácidos comunes clasificados como fuertes (Tabla 4.2). Un número mucho mayor de compuestos se comportan como ácidos débiles y solo reaccionan parcialmente con el agua, dejando una gran mayoría de moléculas disueltas en su forma original y generando una cantidad relativamente pequeña de iones hidronio. Los ácidos débiles se encuentran comúnmente en la naturaleza, siendo las sustancias en parte responsables del sabor ácido de las frutas cítricas, la sensación de picadura de los insectos y los olores desagradables asociados con el olor corporal.
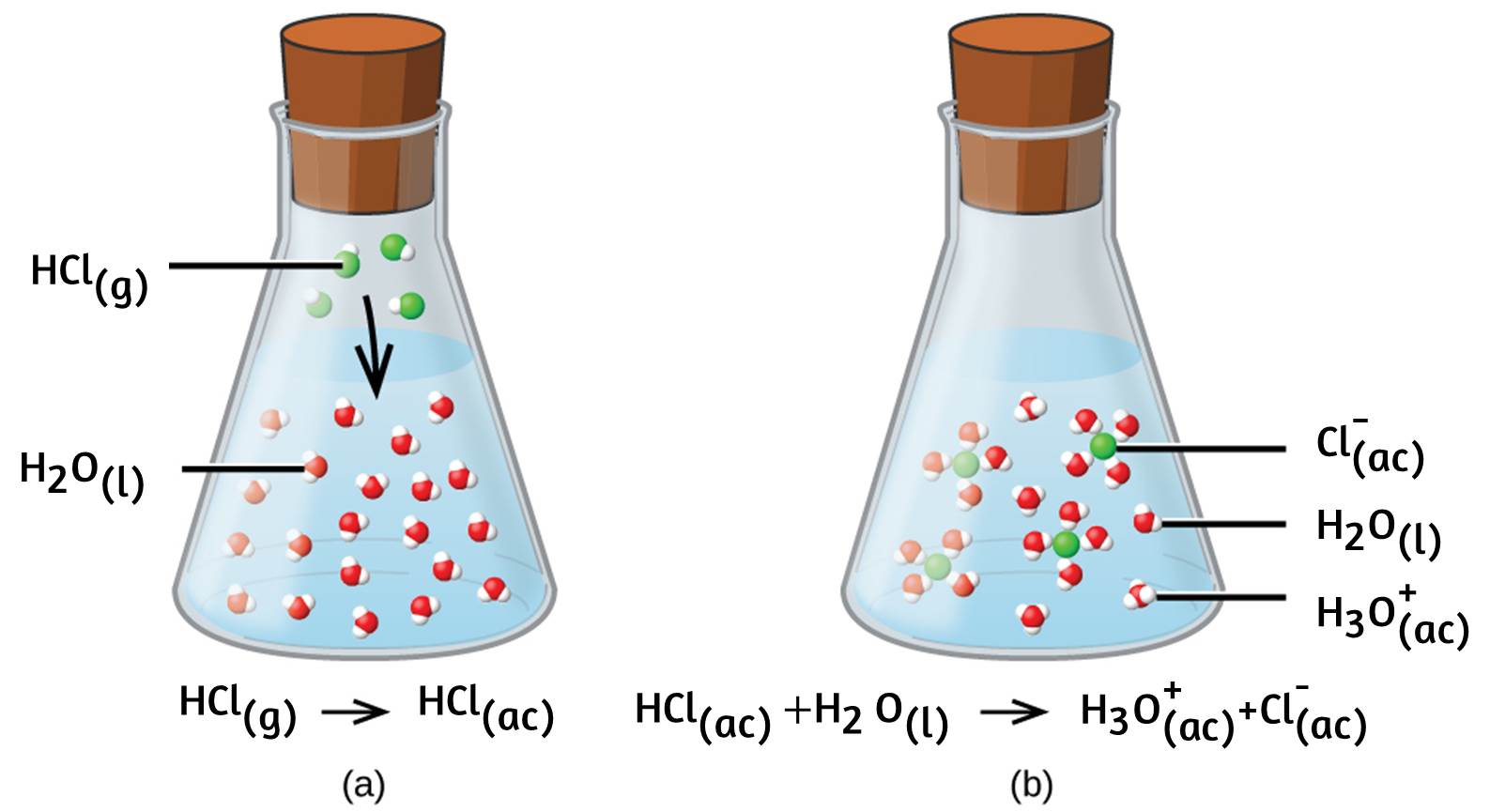
Figura 4.5. Cuando el gas de cloruro de hidrógeno se disuelve en agua, (a) reacciona como un ácido, transfiriendo protones a moléculas de agua para producir (b) iones de hidronio (e iones de cloruro solvatado).
Un ejemplo familiar de un ácido débil es el ácido acético, el ingrediente principal de los vinagres para alimentos:
$$CH_3CO_2H(ac)+H_2O(l) \rightleftharpoons CH_3CO_2^-(ac)+H_3O^+(ac)$$Cuando se disuelven en agua en condiciones típicas, solo alrededor del 1% de las moléculas de ácido acético están presentes en la forma ionizada, $CH_3CO_2^-$ (Figura 4.6) (el uso de una flecha doble en la ecuación anterior denota el aspecto de reacción parcial de este proceso, un concepto que se aborda completamente en los capítulos sobre el equilibrio químico).
Figura 4.6. (a) Las frutas como las naranjas, los limones y las toronjas contienen el ácido cítrico débil, (b) Los vinagres contienen el ácido acético, ácido débil (crédito a: modificación del trabajo de Scott Bauer; Crédito b: modificación del trabajo de Brücke-Osteuropa/Wikimedia Commons)
Una base es una sustancia que se disuelve en agua para producir iones hidróxido, $OH^{-}$. Las bases más comunes son compuestos iónicos compuestos de cationes de metales alcalinos o alcalinotérreos (grupos 1 y 2) combinados con el ion hidróxido, por ejemplo, $NaOH$ y $Ca(OH)_2$. A diferencia de los compuestos ácidos discutidos anteriormente, estos compuestos no reaccionan químicamente con el agua; en su lugar, se disuelven y se disocian, liberando iones de hidróxido directamente en la solución. Por ejemplo, $KOH$ y $Ba(OH)_2$ se disuelven en agua y se disocian completamente para producir cationes ($K^{+}$ y $Ba^{2+}$, respectivamente) e iones hidróxido, $OH^{-}$.
Estas bases, junto con otros hidróxidos que se disocian completamente en el agua, se consideran bases fuertes.
Consideremos como ejemplo la disolución de lejía (hidróxido de sodio) en agua:
$$NaOH(s) \xrightarrow[]{H_2O(l)} Na^+(ac) + OH^{-}(ac)$$Tabla 4.2. Ácidos fuertes comunes.
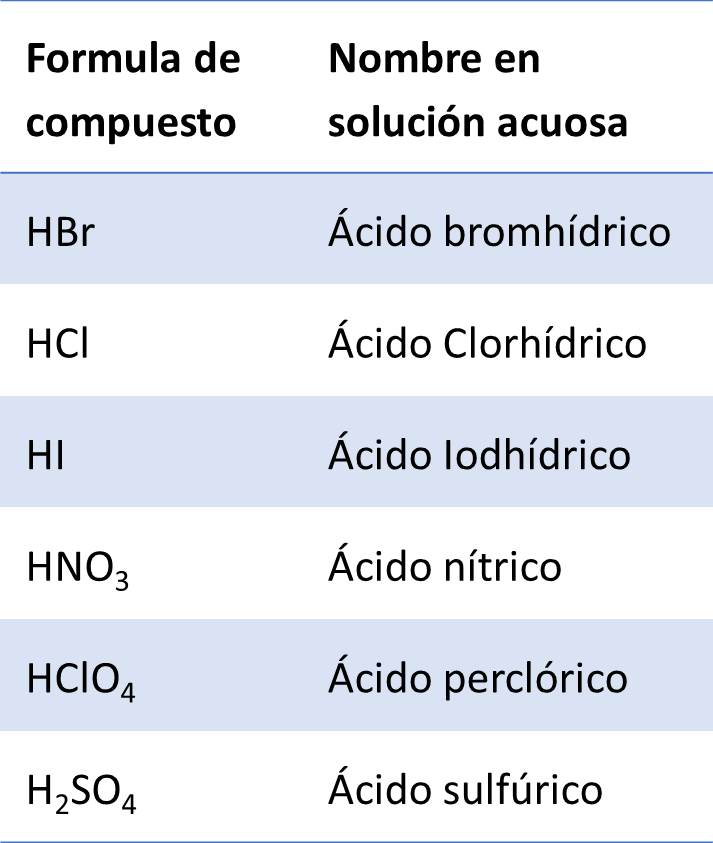
Esta ecuación confirma que el hidróxido de sodio es una base. Cuando se disuelve en agua, el $NaOH$ se disocia para producir iones $Na^+$ y $OH^{-}$. Esto también es cierto para cualquier otro compuesto iónico que contenga iones hidróxido. Dado que el proceso de disociación es esencialmente completo cuando los compuestos iónicos se disuelven en agua en condiciones típicas, el $NaOH$ y otros hidróxidos iónicos se clasifican como bases fuertes.
A diferencia de los hidróxidos iónicos, algunos compuestos producen iones hidróxido cuando se disuelven al reaccionar químicamente con las moléculas de agua. En todos los casos, estos compuestos reaccionan solo parcialmente, por lo que se clasifican como bases débiles. Estos tipos de compuestos también son abundantes en la naturaleza y productos importantes en diversas tecnologías.
Por ejemplo, la producción global de la base débil de amoníaco es generalmente más de 100 toneladas métricas por año, y se usa ampliamente como fertilizante agrícola, una materia prima para la síntesis química de otros compuestos y un ingrediente activo en productos de limpieza para el hogar (Figura 4.7). Cuando se disuelve en agua, el amoníaco reacciona parcialmente para producir iones hidróxido, como se muestra aquí:
$$NH_3(ac)+H_2O(l) \rightleftharpoons NH_4^+(ac)+OH^{-}(ac)$$Esto es, por definición, una reacción ácido-base, en este caso que implica la transferencia de iones $H^+$ de moléculas de agua a moléculas de amoniaco.
Figura 4.7. El amoníaco es una base débil utilizada en una variedad de aplicaciones. (a) El amoníaco puro se aplica comúnmente como fertilizante agrícola. (b) Las soluciones diluidas de amoníaco son limpiadores domésticos eficaces (crédito a: modificación del trabajo por National Resources Conservation Service; crédito b: modificación del trabajo por pat00139)
En condiciones típicas, solo alrededor del 1% del amoniaco disuelto está presente como iones $NH_4^+$.
Una reacción de neutralización es un tipo específico de reacción ácido-base en la que los reactivos son un ácido y una base (pero no agua), y los productos a menudo son una sal y agua.
$$\text{Ácido + Base } \longrightarrow \text{Sal + Agua}$$Para ilustrar una reacción de neutralización, considera qué sucede cuando se ingiere un antiácido típico como la leche de magnesia (una suspensión acuosa de $Mg(OH)_2$ sólido) para aliviar los síntomas asociados con el exceso de ácido estomacal (HCl):
$$Mg(OH)2(s) + 2HCl(ac) \longrightarrow MgCl_2(ac) + 2H_2O(l)$$Ten en cuenta que además del agua, la reacción produce una sal, cloruro de magnesio.
Ejemplo 4.4
Escritura de ecuaciones para reacciones ácido-base
Escribe ecuaciones químicas balanceadas para las reacciones ácido-base descritas aquí:
Solución
Una doble flecha es apropiada en esta ecuación porque indica que el $HOCl$ es un ácido débil que no ha reaccionado completamente.
Comprueba tu aprendizaje
La química en la vida cotidiana
Nuestros estómagos contienen una solución de aproximadamente 0.03 M $HCl$, que nos ayuda a digerir los alimentos que comemos. La sensación de ardor asociada con la acidez estomacal es el resultado del ácido del estómago que se filtra a través de la válvula muscular en la parte superior del estómago hacia la parte inferior del esófago. El revestimiento del esófago no está protegido de los efectos corrosivos del ácido estomacal, como lo está el revestimiento del estómago, y los resultados pueden ser muy dolorosos. Cuando tenemos acidez estomacal, se siente mejor si reducimos el exceso de ácido en el esófago tomando un antiácido. Como habrás adivinado, los antiácidos son bases. Uno de los antiácidos más comunes es el carbonato de calcio, $CaCO_3$.
$$CaCO_3(s)+2HCl(ac) \rightleftharpoons CaCl_2(ac)+H2O(l)+CO_2(g)$$La reacción, No solo neutraliza el ácido estomacal, también produce $CO_2(g)$ lo que puede resultar en un eructo satisfactorio.
La leche de magnesia es una suspensión del hidróxido de magnesio base poco soluble, $Mg(OH)_2$. Funciona de acuerdo a la reacción:
$$Mg(OH)_2(s) \rightleftharpoons Mg^{2+}(ac)+2OH^{-}(ac)$$Los iones hidróxido generados en este equilibrio luego reaccionan con los iones hidronio del ácido del estómago, de modo que:
$$H_3O^{+}(ac) + OH^{-}(ac) \rightleftharpoons 2H_2O(l)$$Esta reacción no produce dióxido de carbono, pero los antiácidos que contienen magnesio pueden tener un efecto laxante. Varios antiácidos tienen hidróxido de aluminio, $Al(OH)_3$, como ingrediente activo. El hidróxido de aluminio tiende a causar estreñimiento, y algunos antiácidos usan hidróxido de aluminio junto con el hidróxido de magnesio para equilibrar los efectos secundarios de las dos sustancias.
Química en la vida cotidiana
Los ejemplos de la química ácido-base son abundantes en el mundo culinario. Un ejemplo es el uso de bicarbonato de sodio en la cocción. $NaHCO_3$ es una base. Cuando reacciona con un ácido como el jugo de limón, el suero de mantequilla o la crema agria en una masa, se forman burbujas de dióxido de carbono a partir de la descomposición del ácido carbónico resultante, y la masa se "eleva". El polvo para hornear es una combinación de bicarbonato de sodio y una o más sales ácidas que reaccionan cuando los dos químicos entran en contacto con el agua en la masa.
A muchas personas les gusta poner jugo de limón o vinagre, que son ácidos, en el pescado cocido (Figura 4.8). Resulta que los peces tienen aminas volátiles (bases) en sus sistemas, que son neutralizadas por los ácidos para producir sales de amonio no volátiles.
Esto reduce el olor de los peces y también agrega un sabor "agrio" que parece que disfrutamos.
Figura 4.8. Se produce una reacción de neutralización entre el ácido cítrico en los limones o el ácido acético en el vinagre y las bases en la carne de pescado.
El decapado es un método utilizado para conservar las verduras en un ambiente ácido producido naturalmente. El vegetal, como un pepino, se coloca en un frasco sellado sumergido en una solución de salmuera. La solución de salmuera favorece el crecimiento de bacterias beneficiosas y suprime el crecimiento de bacterias dañinas. Las bacterias beneficiosas se alimentan de almidones en el pepino y producen ácido láctico como producto de desecho en un proceso llamado fermentación.
El ácido láctico eventualmente aumenta la acidez de la salmuera a un nivel que elimina cualquier bacteria dañina, que requiere un ambiente básico. Sin las bacterias dañinas que consumen los pepinos, pueden durar mucho más tiempo que si estuvieran desprotegidos. Un subproducto del proceso de decapado cambia el sabor de las verduras con el ácido que las hace amargas.
Enlace a aprendizaje
Usa la siguiente simulación Phet. En el item introducción, con ayuda de la lupa, puedes entender mejor la disociación de los ácidos y bases fuertes y con las herramientas el efecto sobre el PH y la conductividad electrica.
Aprende en el modo introducción y diviértete en el modo juego.
La atmósfera de la Tierra contiene aproximadamente un 20% de oxígeno molecular, $O_2$, un gas químicamente reactivo que desempeña un papel esencial en el metabolismo de los organismos aeróbicos y en muchos procesos ambientales que dan forma al mundo. El término oxidación se usó originalmente para describir reacciones químicas que involucran $O_2$, pero su significado ha evolucionado para referirse a una clase de reacción amplia e importante conocida como reacciones de oxidación-reducción (redox). Se utilizarán algunos ejemplos de tales reacciones para desarrollar una imagen clara de esta clasificación.
Algunas reacciones redox implican la transferencia de electrones entre especies reactivas para producir productos iónicos, como la reacción entre sodio y cloro para producir cloruro de sodio:
$$2Na(s)+Cl_2(g) \longrightarrow 2NaCl(s)$$Es útil ver el proceso con respecto a cada reactante individual, es decir, representar el destino de cada reactivo en la forma de una ecuación llamada semi-reacción:
$$2Na(s) \longrightarrow 2Na^+(s) + 2e^{-}$$ $$Cl_2(g)+2e^{-} \longrightarrow 2Cl^{-}(s)$$Estas ecuaciones muestran que los átomos de $Na$ pierden electrones, mientras que los átomos de $Cl$ (en la molécula de $Cl_2$) ganan electrones, los subíndices "s" para los iones resultantes significan que están presentes en forma de un compuesto iónico sólido.
Para reacciones redox de este tipo, la pérdida y ganancia de electrones definen los procesos complementarios que ocurren:
Oxidación = pérdida de electrones
Reducción = ganancia de electrones
En esta reacción, entonces, el sodio se oxida y el cloro sufre una reducción. Visto desde una perspectiva más activa, el sodio funciona como un agente reductor (reductor), ya que proporciona electrones (o reduce) el cloro. Del mismo modo, el cloro funciona como un agente oxidante, ya que elimina (oxida) eficazmente los electrones del sodio.
Agente reductor = especie que se oxida
Agente oxidante = especie que se reduce
Algunos procesos redox, sin embargo, no implican la transferencia de electrones. Considera, por ejemplo, una reacción similar a la que produce $NaCl$:
$$H_2(g)+Cl_2(g) \longrightarrow 2HCl(g)$$El producto de esta reacción es un compuesto covalente, por lo que la transferencia de electrones en el sentido explícito no está involucrada. Para aclarar la similitud de esta reacción con la anterior y permitir una definición inequívoca de las reacciones redox, se ha definido una propiedad llamada número de oxidación. El número de oxidación (o estado de oxidación) de un elemento en un compuesto es la carga que sus átomos tendrían si el compuesto fuera iónico. Las siguientes pautas se utilizan para asignar números de oxidación a cada elemento en una molécula o ion.
Nota: la convención adecuada para informar el cargo es escribir el número primero, seguido del signo (por ejemplo, 2+), mientras que el número de oxidación se escribe con la secuencia inversa, el signo seguido del número (por ejemplo, +2). Esta convención pretende enfatizar la distinción entre estas dos propiedades relacionadas.
Ejemplo 4.5
Asignación de números de oxidación
Sigue las pautas en esta sección del texto para asignar números de oxidación a todos los elementos en las siguientes especies:
Solución
carga en $H_2S = 0 = (2 \times (+1)) + (1 \times x) \\ x = 0 − (2 \times (+1)) = -2$
carga en $SO_3^{2-} = -2 = (3 \times (−2)) + (1 \times x) \\ x = −2 − (3 \times (−2)) = +4$
De acuerdo con la pauta 2, el número de oxidación para el sodio es +1.
Suponiendo el número de oxidación habitual para el oxígeno (−2 según la directriz 3), el número de oxidación para el azufre se calcula según lo indicado en la directriz 4:
carga en $SO_4^{2-} = -2 = (4 \times (−2)) + (1 \times x) \\ x = −2 − (4 \times (−2)) = +6$
Comprueba tu aprendizaje
Usando el concepto de número de oxidación, se ha establecido una definición integral de reacción redox. Las reacciones de oxidación-reducción (redox) son aquellas en las que uno o más elementos involucrados experimentan un cambio en el número de oxidación.
(Si bien la gran mayoría de las reacciones redox involucran cambios en el número de oxidación de dos o más elementos, existen algunas excepciones interesantes a esta regla, Ejemplo 4.6). Las definiciones de los procesos complementarios de esta clase de reacción se revisan correspondientemente como se muestra aquí:
Oxidación = aumento en el número de oxidación
Reducción= disminución en el número de oxidación
Volviendo a las reacciones utilizadas para introducir este tema, ahora ambos pueden identificarse como procesos redox. En la reacción entre sodio y cloro para producir cloruro de sodio, el sodio se oxida (su número de oxidación aumenta de 0 en $Na$ a +1 en $NaCl$) y el cloro se reduce (su número de oxidación disminuye de 0 en $Cl_2$ a -1 en $NaCl$). En la reacción entre el hidrógeno molecular y el cloro, el hidrógeno se oxida (su número de oxidación aumenta de 0 en $H_2$ a +1 en $HCl$) y el cloro se reduce (su número de oxidación disminuye de 0 en $Cl_2$ a -1 en $HCl$).
Se reconocen varias subclases de reacciones redox, incluidas las reacciones de combustión en las que el reductor (también llamado combustible) y el oxidante (a menudo, pero no necesariamente, el oxígeno molecular) reaccionan vigorosamente y producen cantidades significativas de calor, y con frecuencia ligeras, en forma de una llama Las reacciones sólidas de combustible de cohetes, como la que se muestra en la figura 4.1, son procesos de combustión. Una reacción propulsora típica en la que el aluminio sólido se oxida con perclorato de amonio se representa mediante esta ecuación:
$$10Al(s)+6NH_4ClO_4(s) \longrightarrow 4Al_2O_3(s)+2AlCl_3(s)+12H_2O(g)\\+3N_2(g)$$
Enlace a aprendizaje
Las reacciones de un solo desplazamiento (reemplazo) son reacciones redox en las que un ión en solución se desplaza (o reemplaza) a través de la oxidación de un elemento metálico. Un ejemplo común de este tipo de reacción es la oxidación ácida de ciertos metales:
$$Zn(s)+2HCl(ac) \longrightarrow ZnCl_2(ac)+H_2(g)$$Los elementos metálicos también pueden ser oxidados por soluciones de otras sales metálicas; por ejemplo:
$$Cu(s)+2AgNO_3(ac) \longrightarrow Cu(NO_3)_2(ac)+2Ag_2(s)$$Esta reacción se puede observar colocando alambre de cobre en una solución que contiene una sal de plata disuelta. Los iones de plata en solución se reducen a plata elemental en la superficie del alambre de cobre, y los iones $Cu^{2+}$ resultantes se disuelven en la solución para producir un color azul característico (Figura 4.9).
Figura 4.9. (a) Se muestra un cable de cobre junto a una solución que contiene iones de plata (I). (b) El desplazamiento de los iones de plata disueltos por los iones de cobre produce (c) la acumulación de metal plateado de color gris en el cable y el desarrollo de un color azul en la solución, debido a los iones de cobre disueltos (crédito: modificación de obra por Mark Ott).
Ejemplo 4.6
Describiendo reacciones redox
Identifica qué ecuaciones representan reacciones redox, proporcionando un nombre para la reacción, si corresponde. Para aquellas reacciones identificadas como redox, nombre el oxidante y el reductor.
$\qquad(a)\qquad ZnCO_2(s) \longrightarrow ZnO(s)+CO_2(g) $Solución
Las reacciones redox se identifican por definición si uno o más elementos experimentan un cambio en el número de oxidación.
Comprueba tu aprendizaje
Las reacciones redox que tienen lugar en medios acuosos a menudo involucran agua, iones hidronio e iones hidróxido como reactivos o productos. Aunque estas especies no se oxidan ni se reducen, sí participan en el cambio químico de otras maneras (por ejemplo, al proporcionar los elementos necesarios para formar oxianiones). Las ecuaciones que representan estas reacciones a veces son muy difíciles de equilibrar mediante la inspección, por lo que se han desarrollado enfoques sistemáticos para ayudar en el proceso. Un enfoque muy útil es utilizar el método de reacciones medias, que implica los siguientes pasos:
Ejemplo 4.7
Balanceo de reacciones redox en solución ácida
Escriba una ecuación balanceada para la reacción entre el ion dicromato y el hierro (II) para producir hierro (III) y cromo (III) en solución ácida.
$$Cr_2O_7^{2-}+Fe^{2+} \longrightarrow Cr^{3+}+Fe^{3+}$$Solución
Paso 1.
Escribe las dos medias reacciones.
Cada media reacción contendrá un reactivo y un producto con un elemento en común.
$$Fe^{2+} \longrightarrow Fe^{3+}$$ $$Cr_2O_7^{2-} \longrightarrow Cr^{3+}$$Paso 2.
Equilibra todos los elementos excepto el oxígeno y el hidrógeno. La media reacción de hierro ya está balanceada, pero la del cromo muestra dos átomos de $Cr$ a la izquierda y uno de $Cr$ a la derecha. Cambiar el coeficiente en el lado derecho de la ecuación a 2 logra el equilibrio con respecto a los átomos de $Cr$.
$$Fe^{2+} \longrightarrow Fe^{3+}$$ $$Cr_2O_7^{2-} \longrightarrow 2Cr^{3+}$$Paso 3.
Equilibra los átomos de oxígeno mediante la adición de moléculas de $H_2O$. La media reacción del hierro no contiene átomos de $O$. La media reacción del cromo muestra siete átomos de $O$ a la izquierda y ninguno a la derecha, por lo que se agregan siete moléculas de agua en el lado derecho.
$$Fe^{2+} \longrightarrow Fe^{3+}$$ $$Cr_2O_7^{2-} \longrightarrow 2Cr^{3+}+7H_2O$$Paso 4.
Balancea los átomos de hidrógeno agregando iones H+. La media reacción del hierro no contiene átomos de $H$. La media reacción del cromo muestra 14 átomos de $H$ a la derecha y ninguno a la izquierda, por lo que se agregan 14 iones de hidrógeno al lado izquierdo.
$$Fe^{2+} \longrightarrow Fe^{3+}$$ $$Cr_2O_7^{2-}+14H^+ \longrightarrow 2Cr^{3+}+7H_2O$$Paso 5
Equilibra la carga mediante la adición de electrones. La media reacción de hierro muestra una carga total de 2+ en el lado izquierdo (1 ion $Fe^{2+}$) y 3+ en el lado derecho (1 ion $Fe^{3+}$). Al agregar un electrón al lado derecho, la carga total de ese lado se eleva a (3+) + (1−) = 2+, y se logra un balance de carga.
La media reacción del cromo muestra una carga total de (1 × 2−) + (14 × 1+) = 12+ en el lado izquierdo (1 ión $Cr_2O_7^{2−}$ y 14 iones $H^+$). La carga total en el lado derecho es (2 × 3+) = 6 + (2 iones $Cr^{3+}$). Agregar seis electrones al lado izquierdo hará que la carga total de ese lado sea (12+ + 6−) = 6+, y se logre el equilibrio de carga.
$$Fe^{2+} \longrightarrow Fe^{3+}+e^-$$ $$Cr_2O_7^{2-}+14H^++6e^{-} \longrightarrow 2Cr^{3+}+7H_2O$$Paso 6
Multiplica las dos medias reacciones, de modo que el número de electrones en una reacción sea igual al número de electrones en la otra reacción. Para ser coherente con la conservación de masa, y la idea de que las reacciones redox implican la transferencia (no creación o destrucción) de electrones, el coeficiente de la media reacción de hierro debe multiplicarse por 6.
$$6Fe^{2+} \longrightarrow 6Fe^{3+}+6e^{-}$$ $$Cr_2O_7^{2-}+14H^++6e^{-} \longrightarrow 2Cr^{3+}+7H_2O$$Paso 7
Agrega las medias reacciones balanceadas y cancele las especies que aparecen en ambos lados de la ecuación.
$$6Fe^{2+}+Cr_2O_7^{2-}+14H^++6e^{-} \longrightarrow 6Fe^{3+}+6e^{-} + 2Cr^{3+}+7H_2O$$Solo los seis electrones son especies redundantes.
Al eliminarlos de cada lado de la ecuación se obtiene la ecuación simplificada y equilibrada aquí:
$$6Fe^{2+}+Cr_2O_7^{2-}+14H^+ \longrightarrow 6Fe^{3+}+ 2Cr^{3+}+7H_2O$$Una verificación final del átomo y el balance de carga confirma que la ecuación está balanceada.
Tabla 4.3. Verificación balanceo oxidoreducción ejemplo 4.7.
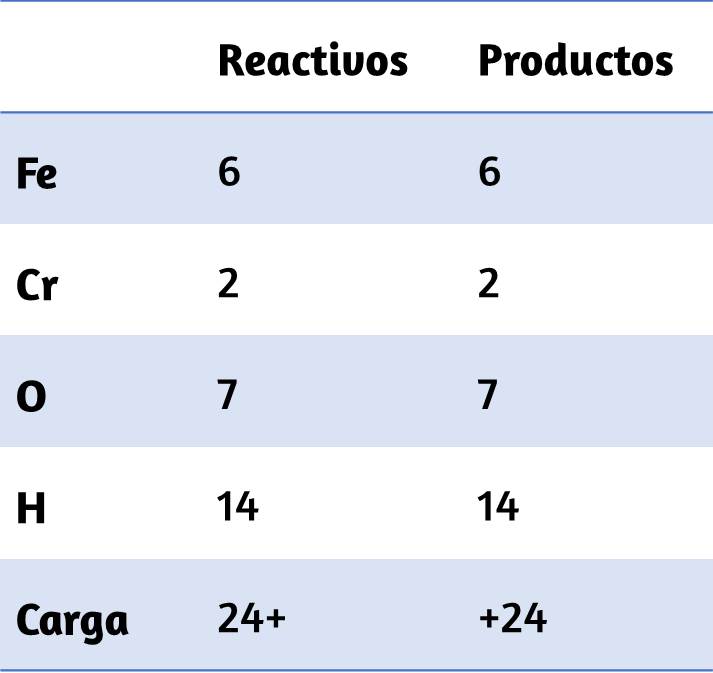
Comprueba tu aprendizaje
Una ecuación química balanceada proporciona una gran cantidad de información en un formato muy breve. Las fórmulas químicas proporcionan las identidades de los reactivos y productos involucrados en el cambio químico, lo que permite la clasificación de la reacción. Los coeficientes proporcionan los números relativos de estas especies químicas, lo que permite una evaluación cuantitativa de las relaciones entre las cantidades de sustancias consumidas y producidas por la reacción. Estas relaciones cuantitativas se conocen como la estequiometría de la reacción, un término derivado de las palabras griegas stoicheion (que significa "elemento") y metron (que significa "medida"). En este módulo, se explora el uso de ecuaciones químicas balanceadas para varias aplicaciones estequiométricas. El enfoque general para usar relaciones estequiométricas es similar en concepto a la forma en que las personas realizan muchas actividades comunes. La preparación de alimentos, por ejemplo, ofrece una comparación apropiada. Una receta para hacer ocho panqueques requiere 1 taza de mezcla para panqueques, 34 taza de leche y un huevo. La "ecuación" que representa la preparación de panqueques según esta receta es
1 taza de mezcla + $\frac34$ taza de leche + 1 huevo $\longrightarrow$ 8 panqueques
Si se necesitan dos docenas de panqueques para un gran desayuno familiar, las cantidades de ingredientes deben aumentarse proporcionalmente de acuerdo con las cantidades que figuran en la receta.
Por ejemplo, el número de huevos necesarios para hacer 24 panqueques es
$$24\: \cancel{panqueques} \times \cfrac{1\:huevo}{8\:\cancel{panqueques}} = 3 \:huevos$$Las ecuaciones químicas balanceadas se usan de manera muy similar para determinar la cantidad de un reactivo requerido para reaccionar con una cantidad dada de otro reactivo, o para producir una cantidad dada de producto, y así sucesivamente. Los coeficientes en la ecuación balanceada se utilizan para obtener factores estequiométricos que permiten el cálculo de la cantidad deseada. Para ilustrar esta idea, considera la producción de amoníaco por reacción de hidrógeno y nitrógeno:
$$N_2(g)+3H_2(g) \longrightarrow 2NH_3(g)$$Esta ecuación muestra que las moléculas de amoníaco se producen a partir de moléculas de hidrógeno en una proporción de 2: 3, y los factores estequiométricos se pueden derivar utilizando cualquier unidad de cantidad (número):
$$\cfrac{2\:\text{moléculas}\:NH_3}{3\;\text{moléculas}\:H_2} \qquad o \qquad \cfrac{2\:moles\:NH_3}{3\:moles\:H_2}$$Estos factores estequiométricos pueden usarse para calcular el número de moléculas de amoníaco producidas a partir de un número dado de moléculas de hidrógeno, o el número de moléculas de hidrógeno requeridas para producir un número dado de moléculas de amoníaco. Se pueden derivar factores similares para cualquier par de sustancias en cualquier ecuación química.
Ejemplo 4.8
Moles de reactivo requeridos en una reacción
¿Cuántos moles de $I_2$ se requieren para reaccionar con 0.429 moles de Al de acuerdo con la siguiente ecuación (observa la Figura 4.10)?
$$2Al+3I_2 \longrightarrow 2AlI_3$$
Figura 4.10. El aluminio y el yodo reaccionan para producir yoduro de aluminio. El calor de la reacción vaporiza parte del yodo sólido como vapor púrpura (crédito: modificación de obra por Mark Ott).
Solución
Refiriéndose a la ecuación química equilibrada, el factor estequiométrico que relaciona las dos sustancias de interés es $\frac{3\;mol\:I_2}{2\:mol\:Al}$. La cantidad molar de yodo se obtiene al multiplicar la cantidad molar de aluminio proporcionada por este factor:
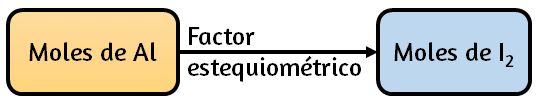$$mol\:I_2=0.429\:mol\:Al\times\cfrac{3\:mol\:I_2}{2\:mol\:Al}=0.644\:mol\:I_2$$
Comprueba tu aprendizaje
Ejemplo 4.9
Número de moléculas de producto generadas por una reacción
¿Cuántas moléculas de dióxido de carbono se producen cuando se queman 0,75 moles de propano de acuerdo con esta ecuación?
$$C_3H_8+5O_2 \longrightarrow 3CO_2+4H_2O$$Solución
El enfoque aquí es el mismo que para el Ejemplo 4.8, aunque se solicita el número absoluto de moléculas, no el número de moles de moléculas. Esto simplemente requerirá el uso del factor de conversión de moles a números, el número de Avogadro. La ecuación equilibrada muestra que el dióxido de carbono se produce a partir del propano en una proporción de 3 a 1:
$$0.75\:\cancel{mol\:C_3H_8}\:\times\cfrac{3\:\bcancel{mol\:CO_2}}{1\:\cancel{mol\:C_3H_8}}\times\cfrac{6.022\times\:10^{23}\:moléculas\:CO_2}{1\:\bcancel{mol\:CO_2}}=1.4\times\:10^{24}\:moléculas\:CO_2$$
Comprueba tu aprendizaje
Estos ejemplos ilustran la facilidad con que pueden relacionarse las cantidades de sustancias involucradas en una reacción química de estequiometría conocida. Sin embargo, la medición directa de números de átomos y moléculas no es una tarea fácil, y la aplicación práctica de la estequiometría requiere que utilicemos la propiedad de la masa que se mide con mayor facilidad.
Ejemplo 4.10
Relacion de masa entre reactivos y productos
¿Qué masa de hidróxido de sodio, $NaOH$, se requeriría para producir 16 g de la leche antiácida de magnesia [hidróxido de magnesio, $Mg(OH)_2$] por la siguiente reacción?
$$MgCl_2(ac)+2NaOH(ac) \longrightarrow Mg(OH)_2(s)+2NaCl(ac)$$Solución
El enfoque utilizado anteriormente en el Ejemplo 4.8 y el Ejemplo 4.9 también se utiliza aquí; es decir, debemos obtener un factor estequiométrico apropiado de la ecuación química equilibrada y usarlo para relacionar las cantidades de las dos sustancias de interés. En este caso, sin embargo, se proporcionan y solicitan masas (no cantidades molares), por lo que se requieren pasos adicionales del tipo aprendido en el capítulo anterior. Los cálculos requeridos se resumen en este diagrama de flujo:
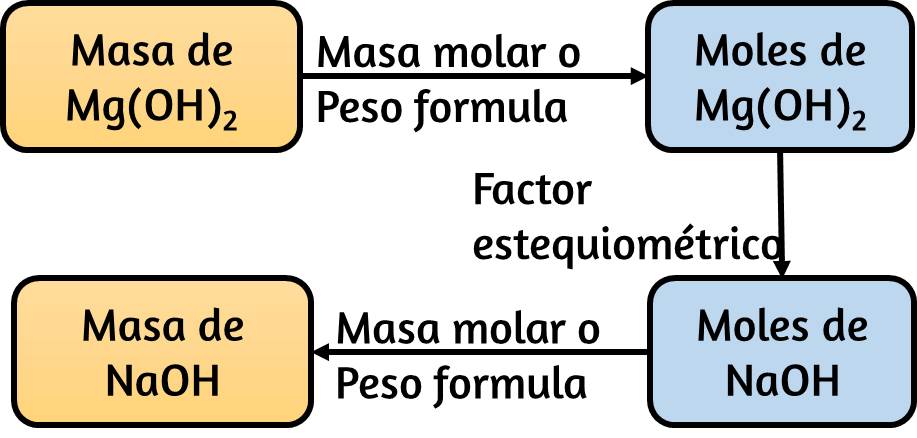$$16\:\cancel{g\:Mg(OH)_2}\:\times\cfrac{1\:\bcancel{mol\:Mg(OH)_2}}{58.3\:\cancel{g\:Mg(OH)_2}}\times\cfrac{2\:\sout{mol\:NaOH}}{1\:\bcancel{mol\:Mg(OH)_2}}\:\times\:\cfrac{40.0\:g\:NaOH}{1\:\sout{mol\:NaOH}}=22\:g\:NaOH$$
Comprueba tu aprendizaje
Ejemplo 4.11
Masas Relacionadas De Reactivos
¿Qué masa de oxígeno gaseoso, $O_2$, del aire se consume en la combustión de 702 g de octano, $C_8H_{18}$, uno de los componentes principales de la gasolina?El octano (o n-octano) es un hidrocarburo alcano lineal de 8 átomos de carbono, de fórmula $C_8H_{18}$, y tiene varios isómeros que en ocasiones son llamados de la misma forma. Es una molécula orgánica. El isómero de más importancia es el 2,2,4-Trimetilpentano (isooctano) porque fue seleccionado como punto de referencia 100 para la escala del octanaje, en la que el heptano tiene el punto de referencia 0 (wikipedia).
En la siguiente página puedes interactuar con la molécula, diseñada en ChemDoodle (recuerda que con la bola del ratón, puedes ampliar la molécula).
Solución
El enfoque requerido aquí es el mismo que para el Ejemplo 4.10, diferenciándose solo en que las masas proporcionadas y solicitadas son para especies reactivas.
$$702\:\cancel{g\:C_8H_{18}}\:\times\cfrac{1\:\bcancel{mol\:C_8H_{18}}}{114.23\:\cancel{g\:C_8H_{18}}}\times\cfrac{25\:\sout{mol\:O_2}}{2\:\bcancel{mol\:C_8H_{18}}}\:\times\:\cfrac{32.0\:g\:O_2}{1\:\sout{mol\:O_2}}=2.46\times\:10^3\:g\:O_2$$Comprueba tu aprendizaje
Estos ejemplos ilustran solo unos pocos casos de cálculos de estequiometría de reacción. Son posibles numerosas variaciones en los pasos computacionales de inicio y finalización dependiendo de qué cantidades particulares se proporcionan y se buscan (volúmenes, concentraciones de solución, etc.).
Figura 4.11. El diagrama de flujo muestra los diversos pasos computacionales involucrados en la mayoría de los cálculos de estequiometría de reacción.
Independientemente de los detalles, todos estos cálculos comparten un componente esencial común: el uso de factores estequiométricos derivados de ecuaciones químicas balanceadas. La Figura 4.11 proporciona un resumen general de los diversos pasos computacionales asociados con muchos cálculos de estequiometría de reacción.
Química en la vida cotidiana
Las bolsas de aire (Figura 4.12) son una característica de seguridad que se ofrece en la mayoría de los automóviles desde la década de 1990.
Figura 4.12. Las bolsas de aire se despliegan al impactar para minimizar las lesiones graves a los pasajeros. (Crédito: Jon Seidman)
La operación efectiva de una bolsa de aire requiere que se infle rápidamente con una cantidad apropiada (volumen) de gas cuando el vehículo está involucrado en una colisión. Este requisito se cumple en muchos sistemas de bolsas de aire para automóviles mediante el uso de reacciones químicas explosivas, una opción común es la descomposición de la azida de sodio, $NaN_3$. Cuando los sensores en el vehículo detectan una colisión, una corriente eléctrica pasa a través de una cantidad cuidadosamente medida de $NaN_3$ para iniciar su descomposición:
Esta reacción es muy rápida y genera nitrógeno gaseoso que puede desplegarse e inflar completamente una bolsa de aire típica en una fracción de segundo (~ 0.03–0.1 s). Entre las muchas consideraciones de ingeniería, la cantidad de azida sódica utilizada debe ser adecuada para generar suficiente nitrógeno para inflar completamente la bolsa de aire y garantizar su correcto funcionamiento.
Por ejemplo, una pequeña masa (~ 100 g) de $NaN_3$ generará aproximadamente 50 L de $N_2$.
Las cantidades relativas de reactivos y productos representados en una ecuación química balanceada se denominan a menudo cantidades estequiométricas. Todos los ejercicios del módulo anterior incluían cantidades estequiométricas de reactivos.
Por ejemplo, al calcular la cantidad de producto generado a partir de una cantidad dada de reactivo, se asumió que cualquier otro reactivo requerido estaba disponible en cantidades estequiométricas (o mayores). En este módulo, se consideran situaciones más realistas, en las que los reactivos no están presentes en cantidades estequiométricas.
Considera otra analogía con los alimentos, haciendo sándwiches de queso a la parrilla (Figura 4.13):
1 rebanada de queso + 2 rebanadas de pan $\longrightarrow$ 1 sándwich
Las cantidades estequiométricas de ingredientes de sándwich para esta receta son rebanadas de pan y queso en una proporción de 2 a 1. Con 28 rebanadas de pan y 11 rebanadas de queso, uno puede preparar 11 sándwiches según la receta provista, utilizando todo el queso provisto y quedando seis rebanadas de pan. En este escenario, el número de sándwiches preparados ha sido limitado por el número de rebanadas de queso, y las rebanadas de pan se han proporcionado en exceso.
Considera este concepto ahora con respecto a un proceso químico, la reacción del hidrógeno con el cloro para producir cloruro de hidrógeno:
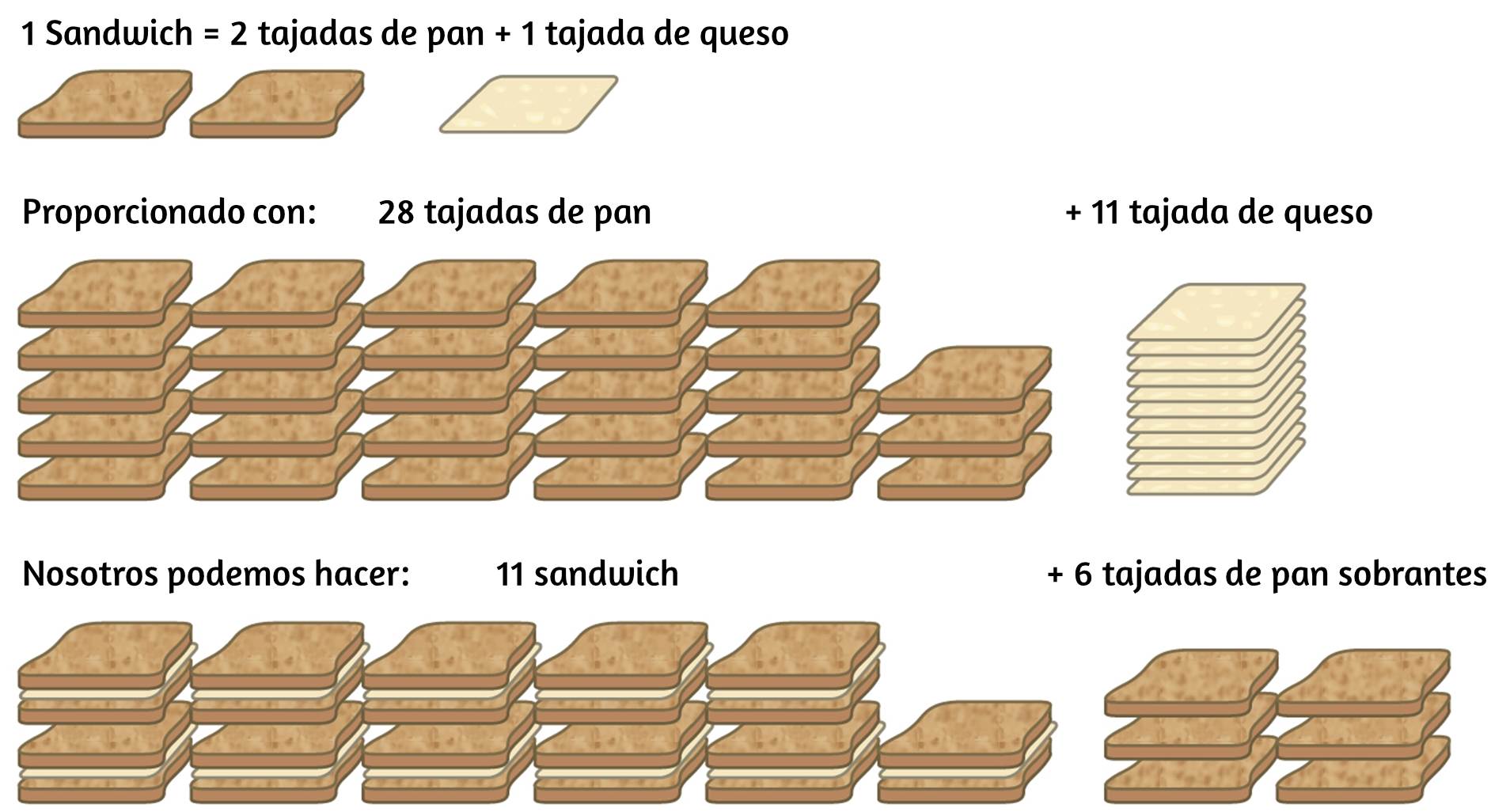
Figura 4.13. La fabricación de emparedados puede ilustrar los conceptos de reactivos limitantes y en exceso.
$$H_2(g)+Cl_2(g) \longrightarrow 2HCl(g)$$La ecuación balanceada muestra que el hidrógeno y el cloro reaccionan en una relación estequiométrica de 1 a 1.
Si estos reactivos se suministran en otras cantidades, uno de los reactivos casi siempre se consumirá por completo, lo que limita la cantidad de producto que se puede generar. Esta sustancia es el reactivo limitante, y la otra sustancia es el reactivo en exceso. La identificación de los reactivos limitantes y en exceso para una situación dada requiere calcular las cantidades molares de cada reactivo proporcionado y compararlas con las cantidades estequiométricas representadas en la ecuación química equilibrada. Por ejemplo, imagina que combinas 3 moles de $H_2$ y 2 moles de $Cl_2$. Esto representa una relación 3 a 2 (o 1.5 a 1) de hidrógeno a cloro presente para la reacción, que es mayor que la relación estequiométrica de 1 a 1. El hidrógeno, por lo tanto, está presente en exceso, y el cloro es el reactivo limitante. La reacción de todo el cloro provisto (2 mol) consumirá 2 mol de los 3 mol de hidrógeno provisto, dejando 1 mol de hidrógeno sin reaccionar.
Un enfoque alternativo para identificar el reactivo limitante implica comparar la cantidad de producto esperada para la reacción completa de cada reactivo. Cada cantidad de reactivo se usa para calcular por separado la cantidad de producto que se formaría según la estequiometría de la reacción. El reactivo que produce la menor cantidad de producto es el reactivo limitante. Para el ejemplo del párrafo anterior, la reacción completa del hidrógeno produciría
mol de $HCl$ producidas = 3 mol $H_2 \times\cfrac{2\:mol\:HCl}{1\:mol\:H_2} = 6\:mol\:HCl$
La reacción completa del cloro proporcionado produciría
mol de $HCl$ producidas = 2 mol $Cl_2 \times \cfrac{2\:mol\:HCl}{1\:mol\:Cl_2} = 4\:mol\:HCl$
El cloro se consumirá completamente una vez que se hayan producido 4 moles de $HCl$. Dado que se proporcionó suficiente hidrógeno para producir 6 moles de $HCl$, quedará hidrógeno sin reaccionar una vez que se complete esta reacción. El cloro, por lo tanto, es el reactivo limitante y el hidrógeno es el reactivo en exceso (Figura 4.14).
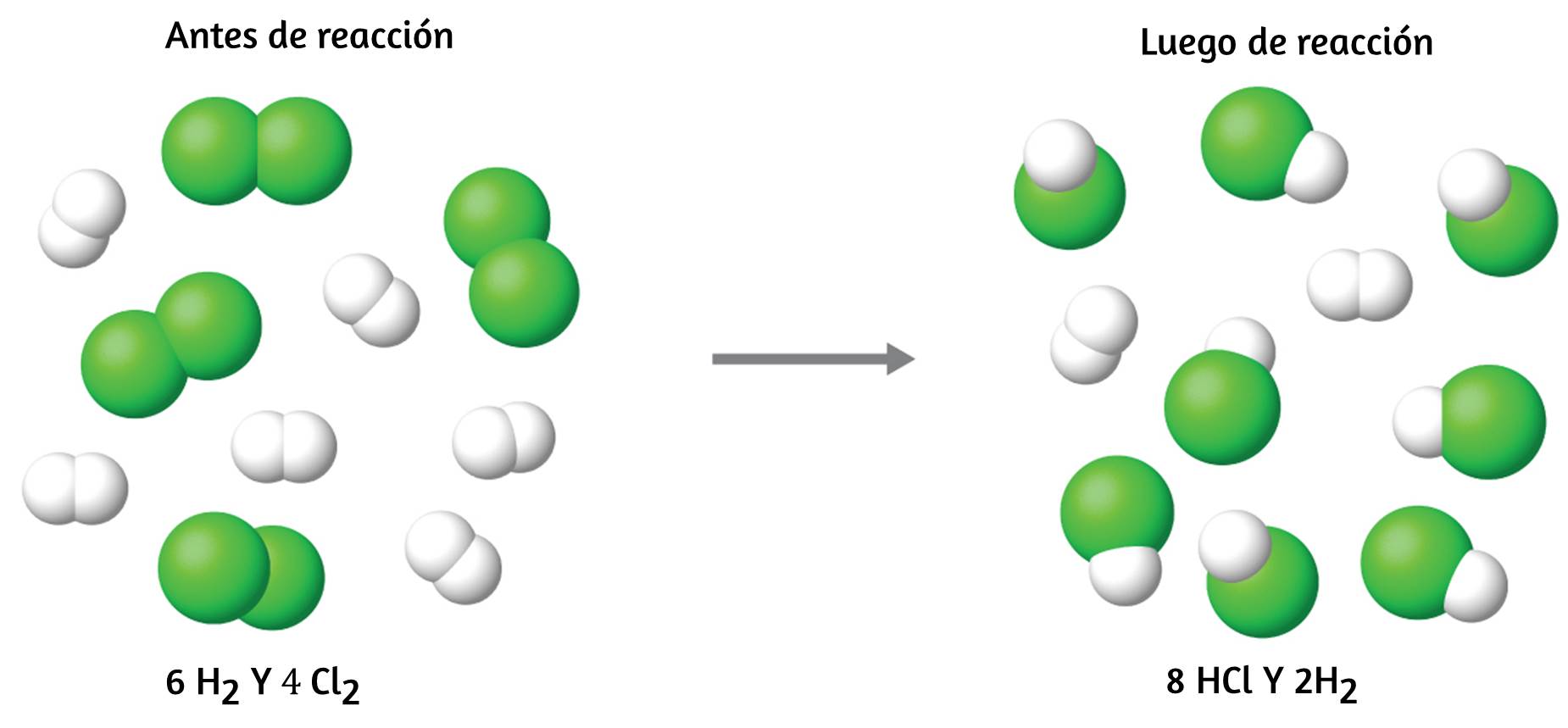
Figura 4.14. Cuando el $H_2$ y el $Cl_2$ se combinan en cantidades no estequiométricas, uno de estos reactivos limitará la cantidad de $HCl$ que se puede producir. Esta ilustración muestra una reacción en la que el hidrógeno está presente en exceso y el cloro es el reactivo limitante.
Enlace a aprendizaje
Ejemplo 4.12
Identificación del reactivo limitante
El nitruro de silicio es una cerámica muy dura, resistente a altas temperaturas, utilizada como componente de álabes de turbina en motores de jet.
El nitruro de silicio se prepara de acuerdo con la siguiente ecuación:
$$3Si(s)+2N_2(g) \longrightarrow Si_3N_4(s)$$¿Cuál es el reactivo limitante cuando reaccionan 2.00 g de $Si$ y 1.50 g de $N_2$?
Molécula de nitruro de silicio, puedes interactuar con ella usando el ratón.
Solución
Calcula las cantidades molares proporcionadas de reactivos y luego compara estas cantidades con la ecuación balanceada para identificar el reactivo limitante.
$$mol\:Si = 2.00\:g\:Si \times \cfrac{1\:mol\:Si}{28.09\:g\:Si}=0.0712\:mol\:Si$$ $$mol\:N_2 = 1.50\:g\:N_2 \times \cfrac{1\:mol\:N_2}{28.02\:g\:N_2}=0.0535\:mol\:N_2$$La relación molar $Si: N_2$ proporcionada es:
$$\cfrac{3\:mol\:Si}{2\:mol\:N_2}=\cfrac{1.5\:mol\:Si}{1\:mol\:N_2}$$La comparación de estas relaciones muestra que el $Si$ se proporciona en una cantidad menor que la estequiométrica, y también lo es el reactivo limitante.
Alternativamente, calcula la cantidad de producto que se espera para la reacción completa de cada uno de los reactivos proporcionados. Los 0.0712 moles de silicio producirían
mol $Si_3N_4$ producidas = $0.0712\:mol\:Si\times \cfrac{1\:mol\:Si_3N_4}{3\:mol\:Si} \\ =0.0237\:mol\:Si_3N_4$
Mientras que los 0.0535 moles de nitrógeno producirían.
mol $Si_3N_4$ producidas = $0.0535\:mol\:N_2 \times \cfrac{1\:mol\:Si_3N_4}{2\:mol\:N_2} \\ =0.0268\:mol\:Si_3N_4$
Dado que el silicio produce la menor cantidad de producto, es el reactivo limitante.
Comprueba tu aprendizaje
La cantidad de producto que puede producirse por una reacción en condiciones específicas, calculada según la estequiometría de una ecuación química balanceada apropiada, se denomina rendimiento teórico de la reacción. En la práctica, la cantidad de producto obtenido se denomina rendimiento real y, a menudo, es menor que el rendimiento teórico por varias razones. Algunas reacciones son inherentemente ineficientes, y están acompañadas de reacciones secundarias que generan otros productos. Otros están, por naturaleza, incompletos (considera las reacciones parciales de ácidos y bases débiles que se analizaron anteriormente en este capítulo). Algunos productos son difíciles de recolectar sin alguna pérdida, por lo que una recuperación menos que perfecta reducirá el rendimiento real. La medida en que se alcanza el rendimiento teórico de una reacción se expresa comúnmente como su rendimiento porcentual:
$$Porcentaje\:\:de\:\:rendimiento = \cfrac{Rendimiento\:\:real}{rendimiento\:\:\text{teórico}} \times 100\%$$Los rendimientos reales y teóricos pueden expresarse como masas o cantidades molares (o cualquier otra propiedad apropiada; por ejemplo, volumen, si el producto es un gas). Siempre que ambos rendimientos se expresen utilizando las mismas unidades, estas unidades se cancelarán cuando se calcule el porcentaje de rendimiento.
Ejemplo 4.13
Cálculo del porcentaje de rendimiento
Tras la reacción de 1.274 g de sulfato de cobre con exceso de metal de zinc, se obtuvieron 0.392 g de metal de cobre de acuerdo con la ecuación:
$$CuSO_{4}\:(ac)+Zn\:(s) \longrightarrow Cu\:(s)+ZnSO_4\:(ac)$$¿Cuál es el porcentaje de rendimiento?
Solución
La información proporcionada identifica al sulfato de cobre como el reactivo limitante, por lo que el rendimiento teórico se encuentra en el enfoque ilustrado en el módulo anterior, como se muestra aquí:
$$1.274\:\cancel{g\:CuSO_4} \times \frac{\cancel{1\:mol\:CuSO_4}}{159.62\:\cancel{g\:CuSO_4}} \times \frac{\cancel{1\:mol\:Cu}}{\cancel{1\:mol\:CuSO_4}} \times \frac{63.55\:g\:Cu}{\cancel{1\:mol\:Cu}}$$ $$=0.5072\:g\:Cu$$
Utilizando este rendimiento teórico y el valor proporcionado para el rendimiento real, se calcula que el rendimiento porcentual es
$$Porcentaje\:\:de\:\:rendimiento = \frac{Rendimiento\:\:real}{rendimiento\:\:\text{teórico}} \times 100\%$$ $$Porcentaje\:\:de\:\:rendimiento = \frac{0.392\:g\:Cu}{0.5072\:g\:Cu} \times 100\% = 77.3\%$$Comprueba tu aprendizaje
La química en la vida cotidiana
El diseño intencional de productos químicos y procesos que minimizan el uso de sustancias peligrosas para el medio ambiente y la generación de desechos se conoce como química verde. La química verde es un enfoque filosófico que se está aplicando a muchas áreas de la ciencia y la tecnología, y su práctica se resume en las pautas conocidas como los "Doce principios de la química verde" (consulta los detalles en este sitio web https://www.epa.gov/greenchemistry). Uno de los 12 principios está dirigido específicamente a maximizar la eficiencia de los procesos para sintetizar productos químicos. La economía atómica de un proceso es una medida de esta eficiencia, definida como el porcentaje en masa del producto final de una síntesis en relación con las masas de todos los reactivos utilizados:
Aunque la definición de economía atómica a primera vista parece muy similar a la del porcentaje de rendimiento, ten en cuenta que esta propiedad representa una diferencia en las eficiencias teóricas de diferentes procesos químicos. El porcentaje de rendimiento de un proceso químico dado, por otro lado, evalúa la eficiencia de un proceso comparando el rendimiento del producto realmente obtenido con el rendimiento máximo predicho por la estequiometría.
La síntesis de la medicación común contra el dolor sin receta, el ibuprofeno, ilustra muy bien el éxito de un enfoque de química verde (Figura 4.15). El ibuprofeno se comercializó por primera vez a principios de la década de 1960, utilizando una síntesis de seis pasos que requirió 514 g de reactivos para generar cada mol (206 g) de ibuprofeno, una economía atómica del 40%. En la década de 1990, la Compañía BHC (ahora BASF Corporation) desarrolló un proceso alternativo que requiere solo tres pasos y tiene una economía atómica de aproximadamente el 80%, casi el doble que el proceso original. El proceso de BHC genera significativamente menos residuos químicos; utiliza materiales menos peligrosos y reciclables; y proporciona importantes ahorros de costos para el fabricante (y, posteriormente, para el consumidor). En reconocimiento del impacto ambiental positivo del proceso de BHC, la compañía recibió el Premio a las vías sintéticas más ecológicas de la Agencia de protección ambiental en 1997.
Figura 4.15. (a) El ibuprofeno es un popular medicamento para el dolor sin receta que se vende comúnmente como tabletas de 200 mg. (b) El proceso BHC para sintetizar ibuprofeno requiere solo tres pasos y muestra una impresionante economía atómica. (crédito a: modificación del trabajo por Derrick Coetzee).
En el siglo XVIII, la concentración de las muestras de vinagre se determinó observando la cantidad de carbonato de potasio, $K_2CO_3$, que debía agregarse, poco a poco, antes de que cesara el burbujeo. Cuanto mayor sea el peso de carbonato de potasio agregado para alcanzar el punto donde terminó el burbujeo, más concentrado estará el vinagre.
Ahora sabemos que la efervescencia que se produjo durante este proceso se debió a la reacción con ácido acético, $CH_3CO_2H$, el compuesto principal responsable del olor y sabor del vinagre. El ácido acético reacciona con el carbonato de potasio de acuerdo con la siguiente ecuación:
$$2CH_3CO_2H(ac)+K_2CO_3(s) \longrightarrow 2CH_3CO_2K(ac) + CO_2(g)\\ + H_2O(l)$$El burbujeo se debió a la producción de $CO_2$. La prueba del vinagre con carbonato de potasio es un tipo de análisis cuantitativo: la determinación de la cantidad o concentración de una sustancia en una muestra. En el análisis del vinagre, la concentración del soluto (ácido acético) se determinó a partir de la cantidad de reactivo que se combinó con el soluto presente en un volumen conocido de la solución. En otros tipos de análisis químicos, la cantidad de una sustancia presente en una muestra se determina midiendo la cantidad de producto que resulta.
El enfoque descrito para medir la concentración de vinagre fue una versión temprana de la técnica analítica conocida como titulación. Una titulación típica implica el uso de una bureta (Figura 4.16) para realizar adiciones incrementales de una solución que contiene una concentración conocida de alguna sustancia (el valorante) a una solución de muestra que contiene la sustancia cuya concentración se va a medir (el analito). El valorante y el analito experimentan una reacción química de estequiometría conocida y, por lo tanto, la medición del volumen de solución de valoración requerido para completar la reacción con el analito (el punto de equivalencia de la titulación) permite el cálculo de la concentración del analito.
El punto de equivalencia de una titulación puede detectarse visualmente si un cambio distinto en el aspecto de la solución de muestra acompaña a la finalización de la reacción.
Figura 4.16. (a) Un estudiante llena una bureta en preparación para un análisis de titulación. (b) Una bureta típica permite mediciones de volumen al 0.01 mL más cercano (crédito a: modificación del trabajo de Mark Blaser y Matt Evans; crédito b: modificación del trabajo de Mark Blaser y Matt Evans).
La detención de la formación de burbujas en el análisis de vinagre clásico es un ejemplo, aunque, más comúnmente, se agregan tintes especiales llamados indicadores a las soluciones de muestra para impartir un cambio de color en o muy cerca del punto de equivalencia de la titulación. Los puntos de equivalencia también pueden detectarse midiendo alguna propiedad de la solución que cambia de manera predecible durante el curso de la titulación.
Independientemente del enfoque adoptado para detectar el punto de equivalencia de una titulación, el volumen de titulación realmente medido se denomina punto final. Los métodos de titulación diseñados adecuadamente aseguran que la diferencia entre la equivalencia y los puntos finales sea insignificante. Aunque cualquier tipo de reacción química puede servir como base para un análisis de titulación, los tres descritos en este capítulo (precipitación, ácido-base y redox) son los más comunes. En el capítulo sobre equilibrios ácido-base se proporcionan detalles adicionales sobre el análisis de titulación.
Ejemplo 4.14
Análisis de titulación
El punto final en una titulación de una muestra de 50,00 ml de $HCl$ acuoso se alcanzó mediante la adición de 35,23 ml de un valorante de $NaOH$ 0,250 M. La reacción de titulación es:
$$HCl(ac)+NaOH(ac) \longrightarrow NaCl(ac)+H_2O(l)$$¿Cuál es la molaridad del $HCl$?
Solución
En cuanto a todos los cálculos de estequiometría de reacción, la cuestión clave es la relación entre las cantidades molares de las especies químicas de interés como se muestra en la ecuación química balanceada. Se sigue el enfoque descrito en los módulos anteriores de este capítulo, con consideraciones adicionales requeridas, ya que las cantidades de reactivos proporcionados y solicitados se expresan como concentraciones de solución.
Para este ejercicio, el cálculo seguirá los siguientes pasos descritos:
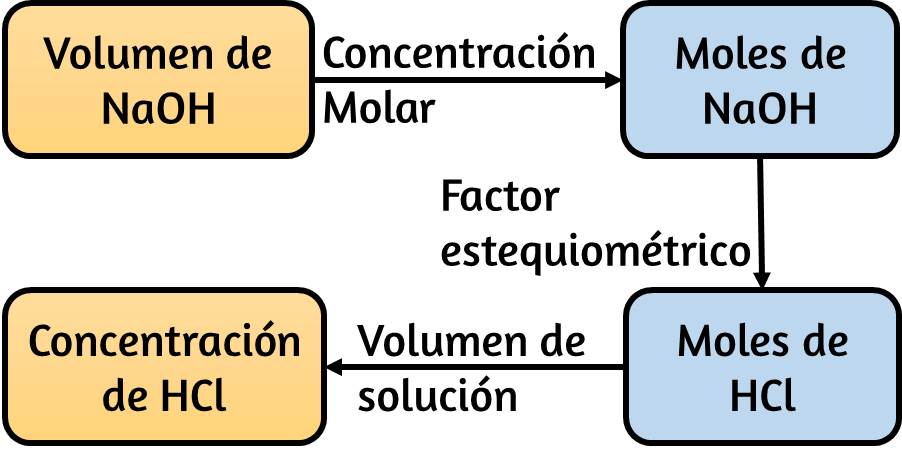
La cantidad molar de HCl se calcula para ser
$$35.23\:\cancel{mL\:NaOH} \times\cfrac{1\:\cancel{L}}{1000\:\cancel{mL}} \times \cfrac{0.250\:\cancel{mol\:NaOH}}{1\:\cancel{L}} \times \cfrac{1\:mol\:HCl}{1\:\cancel{mol\:NaOH}}$$ $$=8.81\times 10^{-3}\:mol\:HCl$$Utilizando el volumen proporcionado de solución de HCl y la definición de molaridad, la concentración de HCl es:
$$\begin{aligned} M &= \cfrac{mol\:HCl}{L\:\text{solución}} \\ &= \cfrac{8.81\times10^{-3}\:mol\:HCl}{50.00\:mL \times \cfrac{1\:L}{1000\:mL}} \\ &= 0.17 \end{aligned}$$Nota: Para estos tipos de cálculos de titulación, es conveniente reconocer que la molaridad de la solución también es igual al número de milimoles de soluto por mililitro de solución:
$M=\cfrac{mol\:soluto}{L\:\text{solución}} \times \cfrac{\cfrac{10^3\:mmol}{1\:mol}}{\cfrac{10^3\:ml}{L}}$
El uso de esta versión de la unidad de molaridad acortará el cálculo al eliminar dos factores de conversión:
$\cfrac{35.23\;mL\;NaOH\times \cfrac{0.250\;mmol\;NaOH}{1\;mL\;NaOH} \times \cfrac{1\;mmol\;HCl}{1\;mmol\;NaOH}}{50.00\;mL\;\text{solución}}$
$$=0.176\:M\:HCl$$Comprueba tu aprendizaje
Un análisis gravimétrico es aquel en el que una muestra se somete a algún tratamiento que provoca un cambio en el estado físico del analito que permite su separación de los otros componentes.
Las mediciones de masa de la muestra, el analito aislado, o algún otro componente del sistema de análisis, usado junto con la estequiometría conocida de los compuestos involucrados, permiten el cálculo de la concentración del analito. Los métodos gravimétricos fueron las primeras técnicas utilizadas para el análisis químico cuantitativo, y siguen siendo herramientas importantes en el laboratorio de química moderna.
El cambio de estado requerido en un análisis gravimétrico puede lograrse mediante diversos procesos físicos y químicos. Por ejemplo, el contenido de humedad (agua) de una muestra se determina de forma rutinaria midiendo la masa de una muestra antes y después de someterla a un proceso de calentamiento controlado que evapora el agua. También son comunes las técnicas gravimétricas en las que el analito se somete a una reacción de precipitación del tipo descrito anteriormente en este capítulo. El precipitado se aísla típicamente de la mezcla de reacción por filtración, se seca cuidadosamente y luego se pesa (Figura 4.17). La masa del precipitado se puede usar, junto con las relaciones estequiométricas relevantes, para calcular la concentración de analito.
Ejemplo 4.15
Análisis gravimétrico
Una mezcla sólida de 0.4550 g que contiene $MgSO_4$ se disuelve en agua y se trata con un exceso de $Ba(NO_3)_2$, dando como resultado la precipitación de 0.6168 g de $BaSO_4$.
$$MgSO_4(ac) + Ba(NO_3)_2(ac) \longrightarrow BaSO_4(s) + Mg(NO_3)_2(ac)$$
Figura 4.17. El precipitado se puede eliminar de una mezcla de reacción por filtración.
¿Cuál es la concentración (porcentaje en masa) de $MgSO_4$ en la mezcla?
Solución
El plan para este cálculo es similar a otros utilizados en los cálculos estequiométricos, siendo el paso central la conexión entre los moles de $BaSO_4$ y $MgSO_4$ a través de su factor estequiométrico.
Una vez que se calcula la masa de $MgSO_4$, se puede utilizar junto con la masa de la mezcla de muestra para calcular el porcentaje de concentración solicitado.
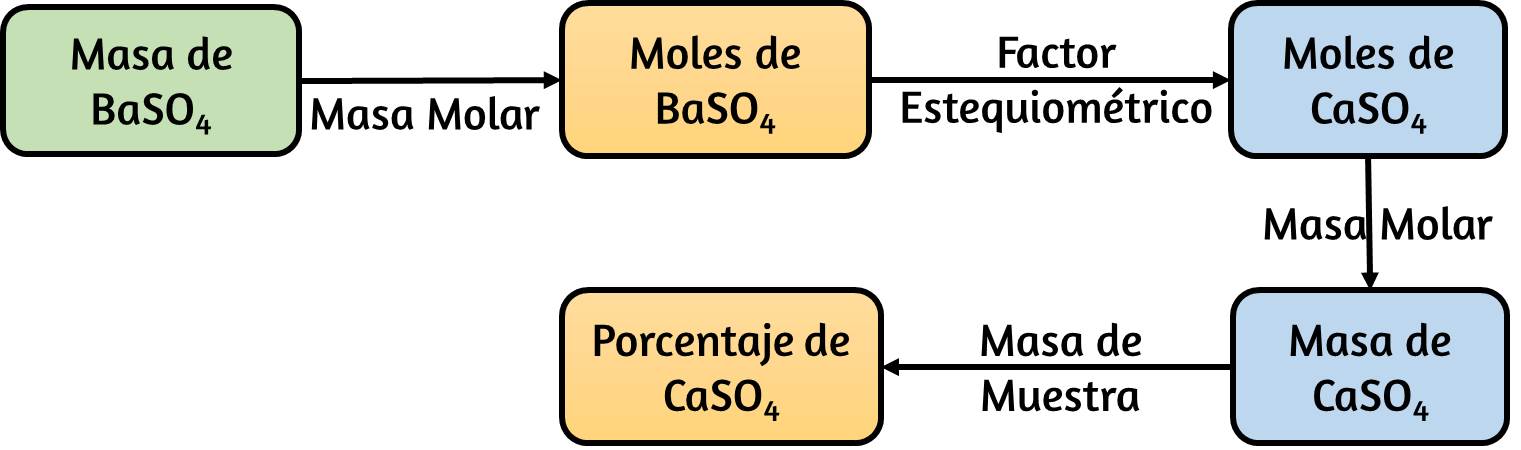
La masa de $MgSO_4$ que produciría la masa precipitada proporcionada es
$0.6168\:\cancel{g\:BaSO_4} \times\cfrac{1\;\cancel{mol\;BaSO_4}}{233.43\;\cancel{g\;BaSO_4}} \times \cfrac{1\;\cancel{mol\;MgSO_4}}{1\;\cancel{mol\;BaSO_4}} \times \cfrac{120.37\;g\;MgSO_4}{1\;\cancel{mol\;MgSO_4}}$
$= 0.3181\;g\;MgSO_4$
La concentración de MgSO4 en la mezcla de muestra se calcula entonces para ser
$Porcentaje \;\; MgSO_4 = \cfrac{masa\;\;de\;\;MgSO_4}{masa\;\;de\;\;la\;\;muestra} \times 100\% = \cfrac{0.3181\:g}{0.455\;g}\times 100 = 69.91\%$
La composición elemental de hidrocarburos y compuestos relacionados puede determinarse mediante un método gravimétrico conocido como análisis de combustión. En un análisis de combustión, una muestra pesada del compuesto se calienta a una temperatura alta bajo una corriente de gas de oxígeno, lo que resulta en su combustión completa para producir productos gaseosos de identidades conocidas.
La combustión completa de hidrocarburos, por ejemplo, producirá dióxido de carbono y agua como los únicos productos. Los productos de combustión gaseosos se barren a través de dispositivos de recolección separados, previamente pesados, que contienen compuestos que absorben selectivamente cada producto (Figura 4.18). El aumento de masa de cada dispositivo corresponde a la masa del producto absorbido y se puede usar en un cálculo estequiométrico apropiado para derivar la masa del elemento relevante.
Figura 4.18. Este diagrama esquemático ilustra los componentes básicos de un dispositivo de análisis de combustión para determinar el contenido de carbono e hidrógeno de una muestra.
Comprueba tu aprendizaje
Ejemplo 4.16
Análisis de combustión
El polietileno es un polímero de hidrocarburo usado para producir bolsas de almacenamiento de alimentos y muchos otros artículos de plástico flexible. Un análisis de combustión de una muestra de 0,00126 g de polietileno produce 0,00394 g de $CO_2$ y 0,00161 g de $H_2O$. ¿Cuál es la fórmula empírica del polietileno?
Solución
El supuesto principal en este ejercicio es que todo el carbono en la muestra quemada se convierte en dióxido de carbono, y todo el hidrógeno en la muestra se convierte en agua:
$$C_xH_y(s) + exceso\;\;O_2(g) \longrightarrow xCO_2(g) + \frac{y}{2} H_2O(g)$$Ten en cuenta que una ecuación equilibrada no es necesaria para la tarea en cuestión. Para derivar la fórmula empírica del compuesto, solo se necesitan los subíndices x e y.
Primero, calcula las cantidades molares de carbono e hidrógeno en la muestra, utilizando las masas proporcionadas de dióxido de carbono y agua, respectivamente. Con estas cantidades molares, la fórmula empírica para el compuesto se puede escribir como se describe en el capítulo anterior de este texto. Un resumen de este enfoque se da en el siguiente diagrama de flujo:
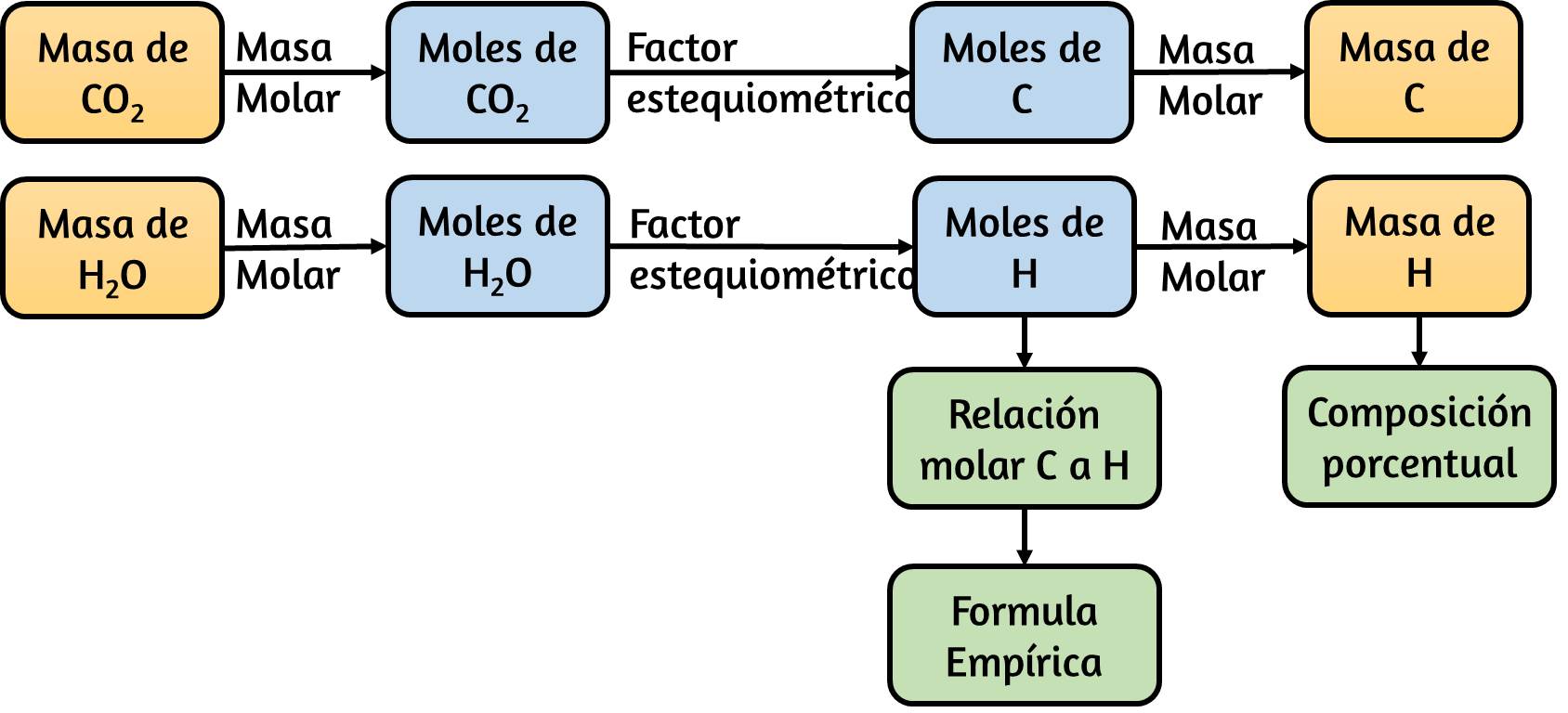$$mol\;C = 0.00394\;g\;CO_2 \times \cfrac{1\;mol\;CO_2}{44.01\;g\;CO_2} \times \cfrac{1\;mol\;C}{1\;mol\;CO_2}$$
$$ = 8.95\times 10^{-5}\;mol\;C$$
$$mol\;H = 0.00161\;g\;H_2O \times \cfrac{1\;mol\;H_2O}{18.02\;g\;H_2O} \times \cfrac{1\;mol\;H}{1\;mol\;H_2O}$$
$$ = 1.79\times 10^{-4}\;mol\;H$$
La fórmula empírica para el compuesto se deriva luego identificando los múltiplos de números enteros más pequeños para estas cantidades molares. La relación molar de H a C es
$$\cfrac{H}{C} = \cfrac{1.79\times 10^{-4}\;mol\;H}{8.95\times 10^{-5}\;mol\;C} = \cfrac{2\;mol\;H}{1\;mol\;C}$$y la fórmula empírica para el polietileno es $CH_2$.
Comprueba tu aprendizaje
El etileno o eteno es un compuesto químico orgánico formado por dos átomos de carbono enlazados mediante un doble enlace. Es uno de los productos químicos más importantes de la industria química, siendo el compuesto orgánico más utilizado en todo el mundo. Casi el 60% de su producción industrial se utiliza para obtener polietileno (wikipedia).
Figura 5.1. . Deslizar una cabeza de fósforo a lo largo de una superficie rugosa inicia una reacción de combustión que produce energía en el Forma de calor y luz (crédito: modificación de obra de Laszlo Ilyes).
Las reacciones químicas, como las que ocurren cuando enciendes una cerilla, involucran cambios en la energía y en la materia. Las sociedades en todos los niveles de desarrollo no podrían funcionar sin la energía liberada por las reacciones químicas. En 2012, aproximadamente el $85\%$ del consumo de energía en los EE. UU. Provino de la combustión de productos derivados del petróleo, carbón, madera y basura. Utilizamos esta energía para producir electricidad ($38\%$); para el transporte de alimentos, materias primas, productos manufacturados y personas ($27\%$); para la producción industrial ($21\%$); y para calentar y alimentar nuestros hogares y empresas ($10\%$).Administración de Información de Energía de EE. UU., Consumo de Energía Primaria por Fuente y Sector, 2012, http://www.eia.gov/. Datos derivados de US Energy Information Administration, Monthly Energy Review (enero de 2014).
Si bien estas reacciones de combustión nos ayudan a satisfacer nuestras necesidades energéticas esenciales, también son reconocidas por la mayoría de la comunidad científica como una contribución importante al cambio climático global.
Las formas útiles de energía también están disponibles a partir de una variedad de reacciones químicas distintas de la combustión. Por ejemplo, la energía producida por las baterías en un teléfono celular, automóvil o linterna es el resultado de reacciones químicas. Este capítulo presenta muchas de las ideas básicas necesarias para explorar las relaciones entre los cambios químicos y la energía, con un enfoque en la energía térmica.
Los cambios químicos y los cambios en la energía que los acompañan son partes importantes de nuestro mundo cotidiano (Figura 5.2). Los macronutrientes en los alimentos (proteínas, grasas y carbohidratos) experimentan reacciones metabólicas que proporcionan la energía para mantener nuestros cuerpos funcionando. Quemamos una variedad de combustibles (gasolina, gas natural, carbón) para producir energía. Para el transporte, la calefacción, y la generación de electricidad. Las reacciones químicas industriales utilizan enormes cantidades de energía para producir materias primas (como hierro y aluminio). La energía se utiliza para fabricar esas materias primas en productos útiles, como automóviles, rascacielos y puentes.
Más del $90\%$ de la energía que utilizamos proviene originalmente del sol. Todos los días, el sol proporciona a la Tierra casi $10,000$ veces la cantidad de energía necesaria para satisfacer todas las necesidades energéticas del mundo para ese día.
Nuestro desafío es encontrar maneras de convertir y almacenar la energía solar entrante para que pueda usarse en reacciones o procesos químicos que son tanto conveniente y no contaminante.
Las plantas y muchas bacterias capturan la energía solar a través de la fotosíntesis. Nosotros liberamos de la energía almacenada en las plantas cuando quemamos madera o productos vegetales como el etanol. También utilizamos esta energía para alimentar nuestros cuerpos al comer alimentos que provienen directamente de las plantas o de animales que obtienen su energía al comer plantas. El carbón y el petróleo también liberan energía solar almacenada: estos combustibles son materia vegetal y animal fosilizada.
Figura 5.2. La energía involucrada en los cambios químicos es importante para nuestra vida diaria: (a) Una hamburguesa con queso para el almuerzo proporciona la energía que necesita para pasar el resto del día; (b) la combustión de la gasolina proporciona la energía que mueve tu automóvil entre el hogar, el trabajo y la escuela; y (c) el coque, una forma procesada de carbón, proporciona la energía necesaria para convertir el mineral de hierro en hierro, que es esencial para hacer muchos de los productos que utilizamos a diario. (Crédito a: modificación del trabajo por "Pink Sherbet Photography" / Flickr; crédito b: modificación del trabajo por Jeffery Turner)
Este capítulo presentará las ideas básicas de un área importante de la ciencia relacionada con la cantidad de calor absorbido o liberado durante los cambios químicos y físicos, un área llamada termoquímica. Los conceptos introducidos en este capítulo son ampliamente utilizados en casi todos los campos científicos y técnicos.
Los científicos de los alimentos los utilizan para determinar el contenido de energía de los alimentos. Los biólogos estudian la energética de los organismos vivos, como la combustión metabólica del azúcar en dióxido de carbono y agua.
Las industrias de petróleo, gas y transporte, proveedores de energía renovable y muchos otros se esfuerzan por encontrar mejores métodos para producir energía para nuestras necesidades comerciales y personales. Los ingenieros se esfuerzan por mejorar la eficiencia energética, encontrar mejores formas de calentar y enfriar nuestros hogares, refrigerar nuestros alimentos y bebidas, y satisfacer las necesidades de energía y refrigeración de las computadoras y los productos electrónicos, entre otras aplicaciones. Comprender los principios termoquímicos es esencial para químicos, físicos, biólogos, geólogos, todo tipo de ingenieros y casi cualquier persona que estudie o haga ciencia de cualquier tipo.
La energía puede definirse como la capacidad de suministrar calor o de trabajo. Un tipo de trabajo (w) es el proceso de hacer que la materia se mueva contra una fuerza opuesta. Por ejemplo, trabajamos cuando inflamos un neumático de bicicleta: movemos la materia (el aire en la bomba) contra la fuerza opuesta del aire que ya está en el neumático.
Como la materia, la energía viene en diferentes tipos. Un esquema clasifica la energía en dos tipos: energía potencial, la energía que tiene un objeto debido a su posición relativa, composición o condición, y energía cinética, la energía que posee un objeto debido a su movimiento.
El agua en la parte superior de una cascada o presa tiene energía potencial debido a su posición; cuando fluye hacia abajo a través de los generadores, tiene energía cinética que se puede utilizar para trabajar y producir electricidad en una planta hidroeléctrica (Figura 5.3). Una batería tiene energía potencial porque los productos químicos que contiene pueden producir electricidad que puede funcionar.
Figura 5.3.(a) El agua en una elevación más alta, por ejemplo, en la parte superior de las Cataratas Victoria, tiene una energía potencial más alta que el agua en una elevación más baja. A medida que el agua cae, parte de su energía potencial se convierte en energía cinética. (b) Si el agua fluye a través de generadores en el fondo de una presa, como la Presa Hoover que se muestra aquí, su energía cinética se convierte en energía eléctrica. (Crédito a: modificación del trabajo por Steve Jurvetson; Crédito b: modificación del trabajo por “Curimedia” / Wikimedia commons)
La energía se puede convertir de una forma a otra, pero toda la energía presente antes de que ocurra un cambio siempre existe de alguna forma una vez que se completa el cambio. Esta observación se expresa en la ley de conservación de la energía: durante un cambio químico o físico, la energía no se puede crear ni destruir, aunque se puede cambiar de forma.
Cuando una sustancia se convierte en otra, siempre hay una conversión asociada de una forma de energía en otra. El calor generalmente se libera o se absorbe, pero a veces la conversión involucra luz, energía eléctrica o alguna otra forma de energía. Por ejemplo, la energía química (un tipo de energía potencial) se almacena en las moléculas que componen la gasolina. Cuando la gasolina se quema dentro de los cilindros del motor de un automóvil, los productos gaseosos de esta reacción química que se expanden rápidamente generan energía mecánica (un tipo de energía cinética) cuando mueven los pistones de los cilindros.
De acuerdo con la ley de conservación de la materia, no hay un cambio detectable en la cantidad total de materia durante un cambio químico. Cuando ocurren reacciones químicas, los cambios de energía son relativamente modestos y los cambios de masa son demasiado pequeños para medirlos, por lo que las leyes de conservación de la materia y la energía se mantienen bien. Sin embargo, en las reacciones nucleares, los cambios de energía son mucho más grandes (por un millón de factores aproximadamente), los cambios de masa son medibles y las conversiones de materia-energía son significativas.
La energía térmica es la energía cinética asociada con el movimiento aleatorio de átomos y moléculas. La temperatura es una medida cuantitativa de "caliente" o "frío". Cuando los átomos y las moléculas de un objeto se mueven o vibran rápidamente, tienen una energía cinética ($K_E$) promedio más alta y decimos que el objeto está "caliente". Cuando los átomos y las moléculas se mueven lentamente, tienen un $K_E$ promedio más bajo y decimos que el objeto está "frío" (Figura 5.4).
Suponiendo que no se produzca una reacción química o un cambio de fase (como la fusión o la vaporización), aumentar la cantidad de energía térmica en una muestra de materia hará que aumente su temperatura. Y, suponiendo que no se produzca una reacción química o un cambio de fase (como la condensación o la congelación), disminuir la cantidad de energía térmica en una muestra de materia hará que su temperatura disminuya.
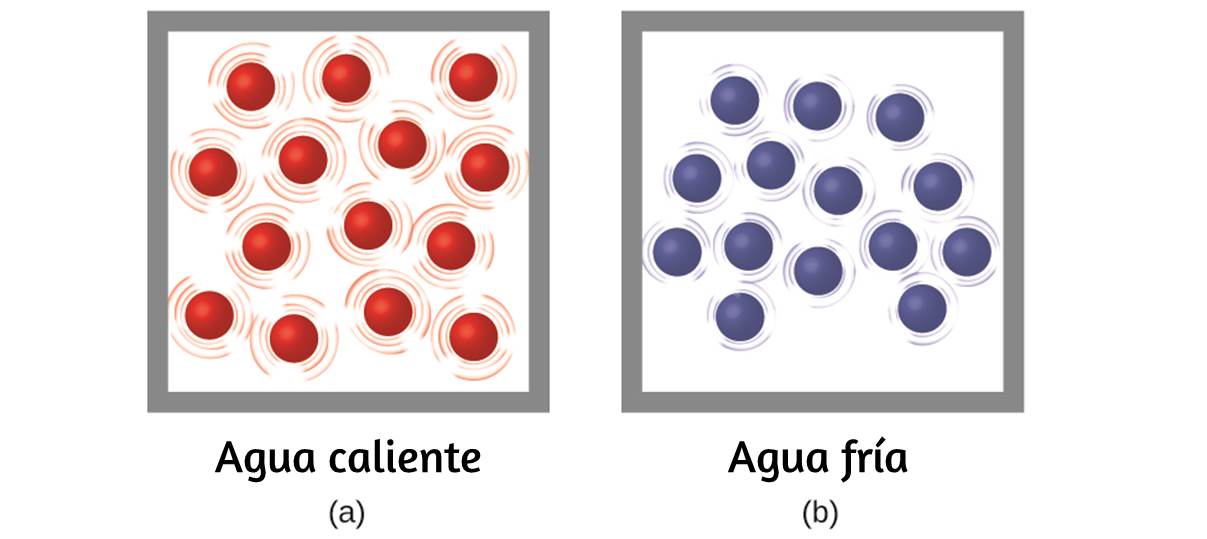
Figura 5.4.(a) Las moléculas en una muestra de agua caliente se mueven más rápidamente que (b) las de una muestra de agua fría.
La mayoría de las sustancias se expanden a medida que aumenta su temperatura y se contraen a medida que disminuye su temperatura. Esta propiedad se puede usar para medir los cambios de temperatura, como se muestra en la Figura 5.5. El funcionamiento de muchos termómetros depende de la expansión y contracción de las sustancias en respuesta a los cambios de temperatura.
El calor (q) es la transferencia de energía térmica entre dos cuerpos a diferentes temperaturas. El flujo de calor (un término redundante, pero uno comúnmente usado) aumenta la energía térmica de un cuerpo y disminuye la energía térmica del otro. Supongamos que inicialmente tenemos una sustancia de alta temperatura (y alta energía térmica) (H) y una sustancia de baja temperatura (y baja energía térmica) (L).
Enlace a aprendizaje
Los átomos y las moléculas en H tienen un $K_E$ promedio más alto que los de L. Si ponemos la sustancia H en contacto con la sustancia L, la energía térmica fluirá espontáneamente de la sustancia H a la sustancia L.
Figura 5.5. (a) En un termómetro de alcohol o mercurio, el líquido (teñido de rojo para visibilidad) se expande cuando se calienta y se contrae cuando se enfría, mucho más que el tubo de vidrio que contiene el líquido. (b) En un termómetro bimetálico, dos metales diferentes (como el latón y el acero) forman una tira de dos capas. Cuando se calienta o se enfría, uno de los metales (latón) se expande o contrae más que el otro metal (acero), lo que hace que la tira se enrolle o desenrolle. Ambos tipos de termómetros tienen una escala calibrada que indica la temperatura. (crédito a: modificación del trabajo por "dwstucke" / Flickr)
La temperatura de la sustancia H disminuirá, al igual que el $K_E$ promedio de sus moléculas; la temperatura de la sustancia L aumentará, junto con el $K_E$ promedio de sus moléculas. El flujo de calor continuará hasta que las dos sustancias estén a la misma temperatura (Figura 5.6).
La materia que experimenta reacciones químicas y cambios físicos puede liberar o absorber calor. Un cambio que libera calor se llama proceso exotérmico. Por ejemplo, la reacción de combustión que se produce cuando se usa un soplete de oxiacetileno es un proceso exotérmico, este proceso también libera energía en forma de luz como lo demuestra la llama del soplete (Figura 5.7).
Enlace a aprendizaje
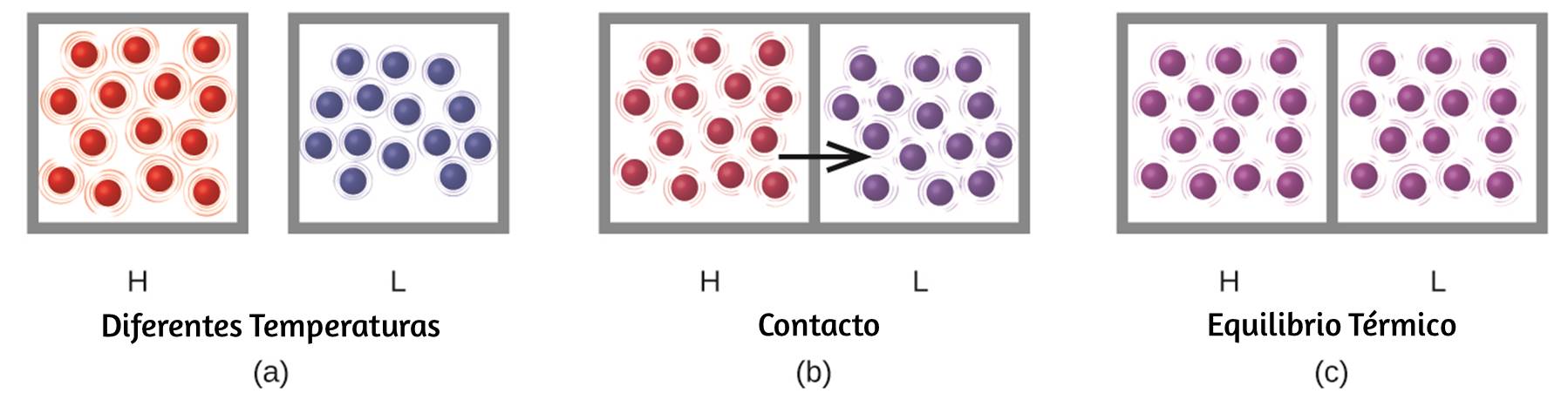
Figura 5.6. (a) Las sustancias H y L están inicialmente a diferentes temperaturas, y sus átomos tienen diferentes energías cinéticas promedio. (b) Cuando se contactan entre sí, las colisiones entre las moléculas dan como resultado la transferencia de energía cinética (térmica) de la materia más caliente a la más fría. (c) Los dos objetos alcanzan el "equilibrio térmico" cuando ambas sustancias están a la misma temperatura y sus moléculas tienen la misma energía cinética promedio.
Enlace a aprendizaje
Una reacción o cambio que absorbe calor es un proceso endotérmico. Una compresa fría utilizada para tratar las distensiones musculares proporciona un ejemplo de un proceso endotérmico. Cuando las sustancias en la compresa fría (agua y una sal como el nitrato de amonio) se juntan, el proceso resultante absorbe el calor, lo que provoca la sensación de frío.
Figura 5.7. (a) Un soplete de oxiacetileno produce calor por la combustión de acetileno en oxígeno. La energía liberada por esta reacción exotérmica se calienta y luego derrite el metal que se está cortando. Las chispas son pequeños trozos de metal fundido que se alejan volando. (b) Una compresa fría utiliza un proceso endotérmico para crear la sensación de frío. (crédito a: modificación del trabajo de "Skatebiker" / Wikimedia commons)
Históricamente, la energía se medía en unidades de calorías (cal). Una caloría es la cantidad de energía requerida para elevar un gramo de agua en $1$ grado C ($1\;kelvin$). Sin embargo, esta cantidad depende de la presión atmosférica y la temperatura de inicio del agua. La facilidad de medición de los cambios de energía en las calorías ha significado que las calorías todavía se usan con frecuencia. La caloría (con una C mayúscula), o una gran cantidad de calorías, comúnmente utilizada para cuantificar el contenido de energía de los alimentos, es una kilocaloría. La unidad SI de calor, trabajo y energía es el joule. Un joule (J) se define como la cantidad de energía utilizada cuando una fuerza de $1$ newton mueve un objeto $1$ metro.
Se nombra en honor del físico inglés James Prescott Joule. Un joule es equivalente a $1\;\cfrac{kg \times m^2}{s^2}$, que también se llama 1 newton-metro. Un $kilojoule\;(kJ)$ es $1000\; julios$. Para estandarizar su definición, $1\;\text{caloría}$ se ajustó a $4.184\;julios$.
Ahora presentamos dos conceptos útiles para describir el flujo de calor y el cambio de temperatura. La capacidad térmica (C) de un cuerpo de materia es la cantidad de calor (q) que absorbe o libera cuando experimenta un cambio de temperatura (ΔT) de 1 grado Celsius (o equivalente, 1 kelvin):
$$C = \cfrac {q}{\Delta T}$$La capacidad de calor está determinada por el tipo y la cantidad de sustancia que absorbe o libera calor. Por lo tanto, es una propiedad extensiva, su valor es proporcional a la cantidad de la sustancia.
Por ejemplo, considera las capacidades de calor de dos sartenes de hierro fundido. La capacidad de calor de la sartén grande es cinco veces mayor que la de la sartén pequeña porque, aunque ambos están hechos del mismo material, la masa de la sartén grande es cinco veces mayor que la masa de la sartén pequeña. Más masa significa que hay más átomos presentes en el recipiente más grande, por lo que se necesita más energía para que todos esos átomos vibren más rápido. La capacidad térmica de la pequeña sartén de hierro fundido se encuentra al observar que se necesitan $18,150\;J$ de energía para elevar la temperatura de la sartén en $50.0^{\degree}C$:
$$C_{\text{sartéen}\;\text{pequeña}} = \cfrac{18,140\;J}{50.0^{\degree}C} = 363 \cfrac{J}{{\degree}C}$$La sartén de hierro fundido más grande, aunque está hecha de la misma sustancia, requiere $90,700\;J$ de energía para elevar su temperatura en $50.0\;{\degree}C$. El recipiente más grande tiene una capacidad de calor (proporcionalmente) mayor porque la mayor cantidad de material requiere una mayor cantidad de energía para producir el mismo cambio de temperatura:
$$C_{sarten\;grande} = \cfrac{90,700\;J}{50.0\;{\degree}C} = 1814 \cfrac{J}{{\degree}C}$$La capacidad calorífica específica (c) de una sustancia, comúnmente llamada su "calor específico", es la cantidad de calor requerida para elevar la temperatura de $1$ gramo de una sustancia en $1$ grado Celsius (o $1$ kelvin):
$$C = \cfrac {q}{m \times \Delta T}$$La capacidad de calor específica depende solo del tipo de sustancia que absorbe o libera calor. Es una propiedad intensiva: lo que importa es el tipo, pero no la cantidad, de la sustancia. Por ejemplo, la pequeña sartén de hierro fundido tiene una masa de $808\;g$. El calor específico del hierro (el material utilizado para hacer la sartén) es por lo tanto:
$$C_{Hierro} = \cfrac{18,140\;J}{808\;g \times 50.0\;{\degree}C} = 0.449 \cfrac{J}{{\degree}C}$$La sartén grande tiene una masa de $4040\;g$. Usando los datos para esta cacerola, también podemos calcular el calor específico del hierro:
Aunque la sartén grande posee más masa que la sartén pequeña, ya que ambas están hechas del mismo material, ambas producen el mismo valor para el calor específico (para el material de construcción, el hierro). Tenga en cuenta que el calor específico se mide en unidades de energía por temperatura por masa y es una propiedad intensiva, que se deriva de una relación de dos propiedades extensivas (calor y masa). La capacidad calorífica molar, también una propiedad intensiva, es la capacidad calorífica por mol de una sustancia en particular y tiene unidades de J/mol °C (Figura 5.8).
Figura 5.8. Debido a su masa más grande, una sartén grande tiene una capacidad de calor más grande que una sartén pequeña. Debido a que están hechos del mismo material, ambas sartenes tienen el mismo calor específico. (Crédito: Mark Blaser)
El agua tiene un calor específico relativamente alto (aproximadamente $4,2\; \cfrac{J}{g \times {\degree}C}$ para el líquido y $2,09\; \cfrac {J}{g \times {\degree}C}$ para el sólido); la mayoría de los metales tienen calores específicos mucho más bajos (generalmente menos de $1\; \cfrac{J}{g \times\; \degree C}$).
El calor específico de una sustancia varía algo con la temperatura. Sin embargo, esta variación suele ser lo suficientemente pequeña como para tratar el calor específico como constante en el rango de temperaturas que se considerará en este capítulo. Los calores específicos de algunas sustancias comunes se enumeran en la Tabla 5.1.
Tabla 5.1 Composición elemental de la tierra
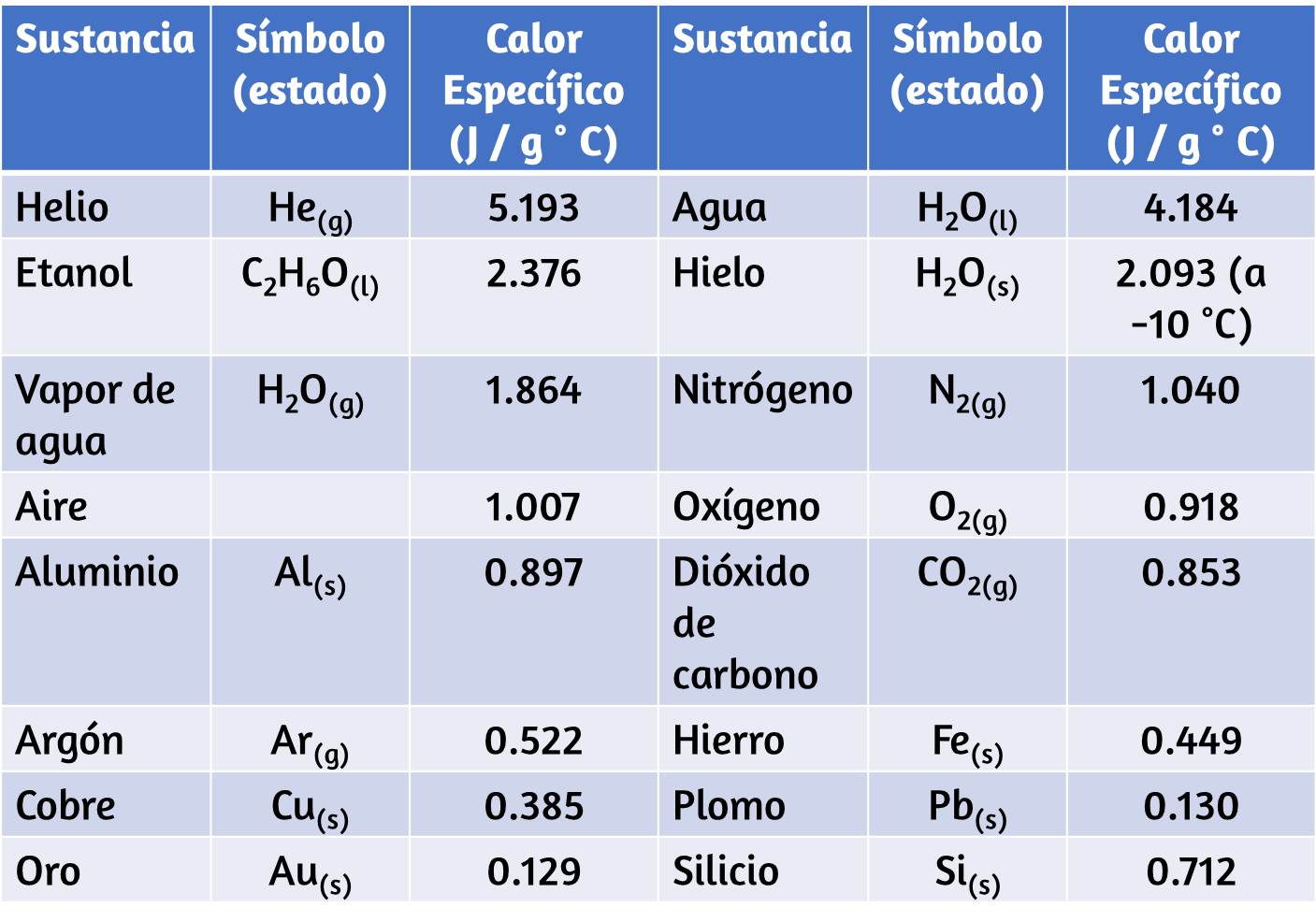
Si conocemos la masa de una sustancia y su calor específico, podemos determinar la cantidad de calor, q, entrando o saliendo de la sustancia midiendo el cambio de temperatura antes y después de que el calor se gane o se pierda:
$q = calor\;\text{específico} \times masa\;de\;la\;sustancia \times cambio\;de\;temperatura $
En esta ecuación, c es el calor específico de la sustancia, m es su masa y ΔT (que se lee "delta T") es el cambio de temperatura, $T_{final} - T_{inicial}$. Si una sustancia gana energía térmica, su temperatura aumenta, su temperatura final es más alta que su temperatura inicial, $T_{final} - T_{inicial}$ tiene un valor positivo y el valor de q es positivo. Si una sustancia pierde energía térmica, su temperatura disminuye, la temperatura final es más baja que la temperatura inicial, $T_{final} - T_{inicial}$ tiene un valor negativo y el valor de q es negativo.
Ejemplo 5.1
Medición de calor
Se calienta un matraz que contiene $8.0 \times 10^2\;g$ de agua, y la temperatura del agua aumenta de $21\;\degree C$ a $85\;\degree C$. ¿Cuánto calor absorbió el agua?
Solución
Para responder a esta pregunta, considere estos factores:
El calor específico del agua es $4.184\; \cfrac{J}{g \times \degree C}$, por lo que para calentar $1\;g$ de agua a $1\; \degree C$ se requieren $4.184\;J$. Observamos que ya que se requiere $4.184\;J$ para calentar $1\;g$ de agua a $1\; \degree C$, necesitaremos $800$ veces más para calentar $8.0 \times 10^2\;g$ de agua en $1\; \degree C$. Finalmente, observamos que como se requieren $4.184\;J$ para calentar $1\;g$ de agua a $1\; \degree C$, necesitaremos $64$ veces más para calentarlo a $64\; \degree C$ (es decir, de $21\; \degree C$ a $85\; \degree C$). Esto se puede resumir usando la ecuación:
$$q = C \times m \times {\Delta T} = C \times m \times (T _{final} - T _{inicial})$$ $$q = 4.184\; \cfrac{J}{g \times \degree C} \times ({8.0\times10^2\;g}) \times {(85 - 21) \degree C}$$ $$q = 4.184\; \cfrac{J}{g \times \degree C} \times ({8.0\times10^2\;g}) \times {64\; \degree C}$$ $$q = 214,220.8\;J = 2.14 \times 10^5\;kJ$$Debido a que la temperatura aumentó, el agua absorbió calor y q es positiva.
Comprueba tu aprendizaje
Tenga en cuenta que la relación entre calor, calor específico, masa y cambio de temperatura se puede usar para determinar cualquiera de estas cantidades (no solo el calor) si los otros tres son conocidos o pueden deducirse.
Ejemplo 5.2
Determinar otras cantidades
Una pieza de metal desconocido pesa $348\;g$. Cuando la pieza de metal absorbe $6.64\;kJ$ de calor, su temperatura aumenta de $22.4\; \degree C$ a $43.6\; \degree C$. Determine el calor específico de este metal (que podría proporcionar una pista de su identidad).
Solución
Dado que los cambios de masa, calor y temperatura son conocidos para este metal, podemos determinar su calor específico usando la relación:
$$q = C \times m \times {\Delta T} = C \times m \times (T _{final} - T _{inicial})$$Sustituyendo los valores conocidos:
$$6,640\;J = C \times {348\;g} \times (43.6-22.4) \degree C$$Resolviendo
Comparando este valor con los valores de la Table 5.1, este valor coincide con el calor específico del aluminio, lo que sugiere que el metal desconocido puede ser el aluminio.
Comprueba tu aprendizaje
Química en la vida cotidiana
La luz solar que llega a la Tierra contiene miles de veces más energía de la que capturamos actualmente. Los sistemas térmicos solares proporcionan una posible solución al problema de convertir la energía del sol en energía que podemos utilizar. Las plantas termosolares a gran escala tienen diferentes especificaciones de diseño, pero todas concentran la luz solar para calentar alguna sustancia; El calor "almacenado" en esa sustancia se convierte en electricidad.
La estación generadora de Solana en el desierto de Sonora en Arizona produce $280$ megavatios de energía eléctrica. Utiliza espejos parabólicos que enfocan la luz solar en tuberías llenas con un fluido de transferencia de calor (HTF) (Figura 5.9). El HTF hace dos cosas: convierte el agua en vapor, que hace girar las turbinas, que a su vez produce electricidad, y funde y calienta una mezcla de sales, que funciona como un sistema de almacenamiento de energía térmica. Después de que el sol se pone, la mezcla de sal fundida puede liberar suficiente calor almacenado para producir vapor y hacer funcionar las turbinas durante $6$ horas. Las sales fundidas se usan porque poseen una serie de propiedades beneficiosas, que incluyen altas capacidades de calor y conductividad térmica.
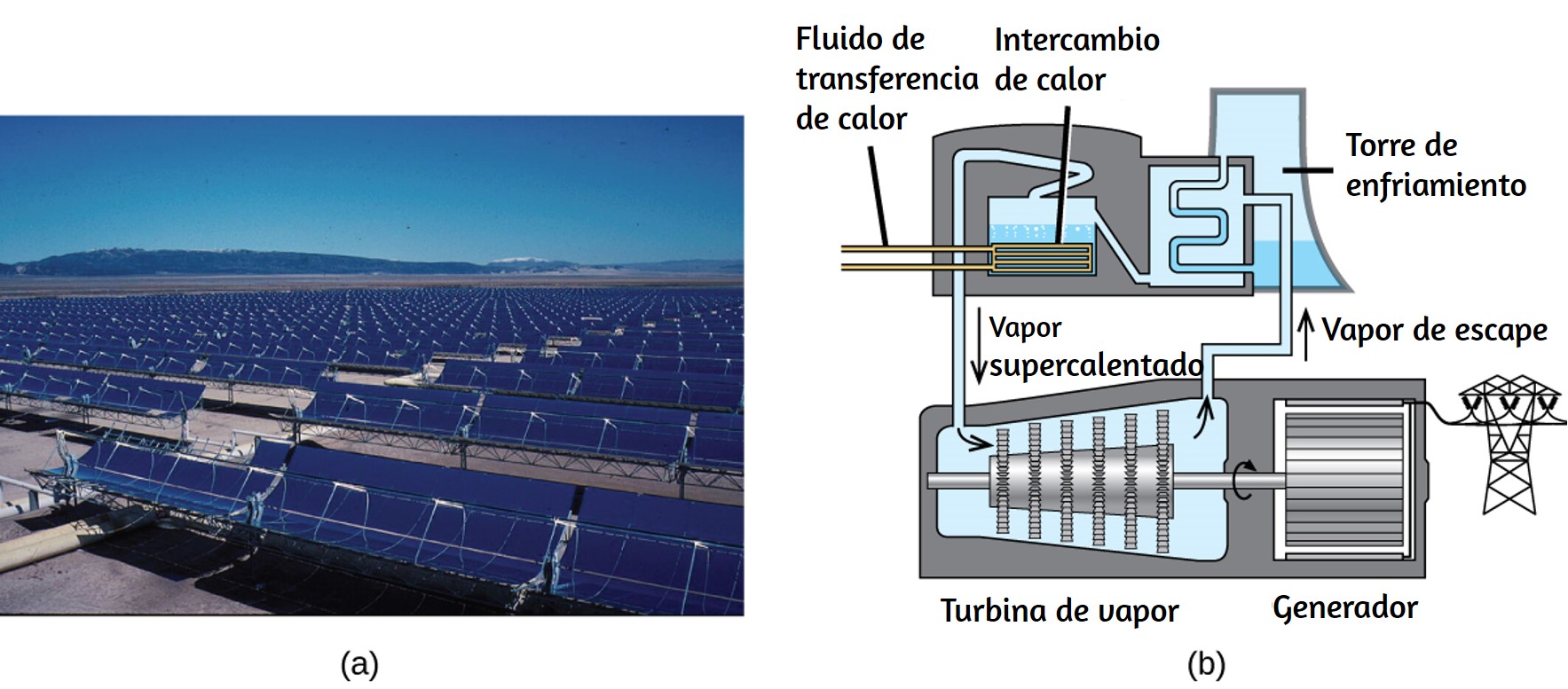
Figura 5.9. Esta planta termosolar utiliza espejos de canalización parabólica para concentrar la luz solar. (crédito a: modificación del trabajo por la Oficina de Administración de Tierras)
El sistema de generación solar Ivanpah de $377$ megavatios, ubicado en el desierto de Mojave en California, es la planta de energía solar térmica más grande del mundo (Figura 5.10). Sus $170,000$ espejos enfocan grandes cantidades de luz solar en tres torres llenas de agua, produciendo vapor a más de $538\; \degree C$ que impulsa turbinas que producen electricidad. Produce suficiente energía para alimentar $140,000$ hogares.
El agua se utiliza como fluido de trabajo debido a su gran capacidad de calor y al calor de vaporización.
Figura 5.10. (a) La planta termosolar de Ivanpah usa $170,000$ espejos para concentrar la luz solar en torres llenas de agua. (b) Cubre $4000$ acres de terreno público cerca del desierto de Mojave y la frontera de California y Nevada. (Crédito a: modificación del trabajo por Craig Dietrich; crédito b: modificación del trabajo por “USFWS Pacific Southwest Region” / Flickr)
Una técnica que podemos usar para medir la cantidad de calor involucrada en un proceso químico o físico es la calorimetría. La calorimetría se usa para medir las cantidades de calor transferidas hacia o desde una sustancia. Para ello, el calor se intercambia con un objeto calibrado (calorímetro). El cambio de temperatura medido por el calorímetro se usa para derivar la cantidad de calor transferido por el proceso en estudio. La medición de la transferencia de calor utilizando este enfoque requiere la definición de un sistema (la sustancia o sustancias que sufren el cambio químico o físico) y sus alrededores (todas las demás materias, incluidos los componentes del aparato de medición, que sirven para proporcionar calor al sistema). o absorber el calor del sistema).
Un calorímetro es un dispositivo que se usa para medir la cantidad de calor involucrado en un proceso químico o físico. Por ejemplo, cuando ocurre una reacción exotérmica en solución en un calorímetro, el calor producido por la reacción es absorbido por la solución, lo que aumenta su temperatura. Cuando ocurre una reacción endotérmica, el calor requerido es absorbido por la energía térmica de la solución, lo que disminuye su temperatura (Figura 5.11). El cambio de temperatura, junto con el calor y la masa específicos de la solución, se pueden utilizar para calcular la cantidad de calor involucrada en cada caso.
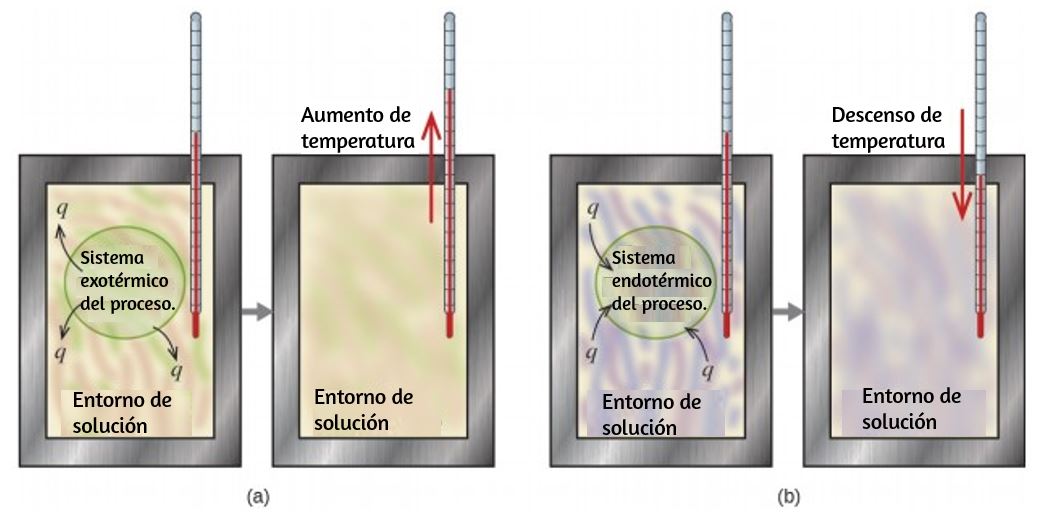
Figura 5.11. En una determinación calorimétrica, (a) ocurre un proceso exotérmico y el calor, q, es negativo, lo que indica que la energía térmica se transfiere desde el sistema a su entorno, o (b) ocurre un proceso endotérmico y el calor, q, es positivo, lo que indica que la energía térmica se transfiere del entorno al sistema.
Los científicos utilizan calorímetros bien aislados que casi evitan la transferencia de calor entre el calorímetro y su entorno, lo que efectivamente limita el "entorno" a los componentes que no son del sistema con el calorímetro (y el propio calorímetro). Esto permite la determinación precisa del calor involucrado en los procesos químicos, el contenido de energía de los alimentos, etc.
Los estudiantes de química general a menudo usan calorímetros simples construidos a partir de tazas de poliestireno (Figura 5.1). Estos calorímetros de “taza de café”, fáciles de usar, permiten un mayor intercambio de calor con el ambiente exterior y, por lo tanto, producen valores de energía menos precisos.
Figura 5.12 Se puede construir un calorímetro simple a partir de dos tazas de poliestireno. Un termómetro y un agitador se extienden a través de la cubierta hasta la mezcla de reacción.
Solución de calorímetros comerciales también están disponibles. Los calorímetros relativamente económicos suelen consistir en dos vasos de pared delgada que se anidan de manera que minimizan el contacto térmico durante el uso, junto con una cubierta aislada, un agitador manual y un termómetro simple.
Los calorímetros más caros utilizados para la industria y la investigación suelen tener un recipiente de reacción completamente cerrado y bien aislado, un mecanismo de agitación motorizado y un sensor de temperatura más preciso (Figura 5.13).
Figura 5.13. Los calorímetros de solución comercial varían desde (a) modelos simples y económicos para uso de los estudiantes hasta (b) modelos costosos y más precisos para la industria y la investigación.
Antes de discutir la calorimetría de las reacciones químicas, considere un ejemplo más simple que ilustra la idea central detrás de la calorimetría. Supongamos que inicialmente tenemos una sustancia de alta temperatura, como una pieza caliente de metal (M), y una sustancia de baja temperatura, como agua fría (W). Si colocamos el metal en el agua, el calor fluirá de M a W. La temperatura de M disminuirá y la temperatura de W aumentará, hasta que las dos sustancias tengan la misma temperatura, es decir, cuando alcancen el equilibrio térmico ( Figura 5.14). Si esto ocurre en un calorímetro, idealmente toda esta transferencia de calor ocurre entre las dos sustancias, sin que el ambiente externo gane o pierda calor.
En estas circunstancias ideales, el cambio de calor neto es cero:
$$q_{sustancia\;M} + q_{sustancia\;W} = 0$$
Figura 5.14. En un proceso simple de calorimetría, (a) el calor, q, se transfiere del metal caliente, M, al agua fría, W, hasta que (b) ambos están a la misma temperatura.
Esta relación se puede reorganizar para mostrar que el calor ganado por la sustancia M es igual al calor perdido por la sustancia W:
$$q_{sustancia\;M} = -q_{sustancia\;W}$$La magnitud del calor (cambio) es, por lo tanto, la misma para ambas sustancias, y el signo negativo simplemente muestra que la sustancia M y la sustancia W son opuestas en la dirección del flujo de calor (ganancia o pérdida), pero no indica el signo aritmético de q valor (que se determina según si la materia en cuestión gana o pierde calor, según la definición).
En la situación específica descrita, la sustancia M es un valor negativo y la sustancia W es positiva, ya que el calor se transfiere de M a W.
Ejemplo 5.3
Transferencia de calor entre sustancias a diferentes temperaturas
Una pieza de varilla de refuerzo de $360.0\;g$ (una varilla de acero utilizada para hormigón armado) se deja caer en $425\;mL$ de agua a $24.0\; \degree C$. La temperatura final del agua se midió como $42.0\; \degree C$. Calcule la temperatura inicial de la pieza de refuerzo. Supón que el calor específico del acero es aproximadamente el mismo que para el hierro (Tabla 5.1), y que toda la transferencia de calor ocurre entre la barra de refuerzo y el agua (no hay intercambio de calor con el entorno).
Solución
La temperatura del agua aumenta de $24.0\; \degree C$ a $42.7\;\degree C$, por lo que el agua absorbe calor. Ese calor vino de la barra de refuerzo, que inicialmente estaba a una temperatura más alta. Suponiendo que toda la transferencia de calor fue entre la barra de refuerzo y el agua, sin que el calor se "pierda" en el ambiente exterior, entonces el calor emitido por la barra de refuerzo = - calor absorbido por el agua, o:
$$q_{\text{Barra de refuerzo}} = -q_{Agua}$$Puesto que sabemos cómo el calor se relaciona con otras magnitudes medibles, tenemos:
$$ (C \times m \times {\Delta T})_{Barra\;de\;refuerzo} = -(C \times m \times {\Delta T})_{Agua}$$Dejando f = final e i = inicial, y rebar = Barra de refuerzo; en forma expandida, esto se convierte en:
$$ C_{rebar} \times m_{rebar} \times (T_{f} - T_{i})_{rebar} = -C_{Agua} \times m_{Agua} \times (T_{f} - T_{i})_{Agua}$$La densidad del agua es $1.0\; \cfrac{g}{mL}$, entonces $425\;mL$ de agua = $425\;g$. Observando que la temperatura final de la barra de refuerzo y del agua es de $42.7\;\degree C$, sustituyendo los valores conocidos se obtiene:
$ (0.449 \cfrac{J}{g\;\degree C})({360\;g})(42.7\;\degree C - T_{i\;rebar}) = (-4.184 \cfrac{J}{g\;\degree C})({425.0\;g})(42.7\;\degree C - 24.0\;\degree C)$
$$T _{i\;rebar} = \cfrac{-4.184 \cfrac{J}{g\;\degree C} \times {425.0\;g} \times (42.7\;\degree C - 24.0\;\degree C)}{0.449 \cfrac{J}{g\;\degree C} \times {360\;g}} + 42.7\;\degree C$$Resolver esto da $T_i$, barra de refuerzo = $248\; \degree C$, por lo que la temperatura inicial de la barra de refuerzo fue de $248\; \degree C$.
Comprueba tu aprendizaje
Comprueba tu aprendizaje
Este método también se puede utilizar para determinar otras cantidades, como el calor específico de un metal desconocido.
Ejemplo 5.4
Identificación de un metal midiendo calor específico
Una pieza de metal de $59.7\;g$ que se había sumergido en agua hirviendo se transfirió rápidamente a $60.0\;mL$ de agua inicialmente a $22.0\;\degree C$. La temperatura final es de $28.5\;\degree C$. Use estos datos para determinar el calor específico del metal. Use este resultado para identificar el metal.
Solución
Suponiendo una transferencia de calor perfecta, el calor emitido por el metal = − calor absorbido por el agua, o:
$$q_{metal} = -q_{Agua}; \quad lease; \quad q_{m} = -q_{a} $$En forma expandida, esto es:
$(C_{m})(m_{m})(T_f - T_i)_{m} =\; \; -(C_{a})(m_{a})(T_f - T_i)_{a}$
Observando que, dado que el metal estaba sumergido en agua hirviendo, su temperatura inicial era de $100.0\;\degree C$; y que, para el agua, $60.0\;mL$ = $60.0\;g$; tenemos:
$(C_{m})(59.7\;g)(28.5\;\degree C - 100.0\;\degree C) = -(4.184 \cfrac{J}{g\;\degree C})(60.0\;g)(28.5\;\degree C - 22.0\;\degree C)$
Resolviendo esto:
$$C_{m} = \cfrac {(4.184 \cfrac{J}{g\;\degree C})(60.0\;g)(6.5\;\degree C)}{(59.7\;g)(-71.5\;\degree C)} = 0.38 \cfrac{J}{g\;\degree C}$$Comparando esto con los valores de la Tabla 5.1, nuestro calor específico experimental es el más cercano al valor del cobre $(0.39 \cfrac{J}{g\;\degree C})$, por lo que identificamos el metal como cobre.
Cuando usamos calorimetría para determinar el calor involucrado en una reacción química, se aplican los mismos principios que hemos estado discutiendo.
Comprueba tu aprendizaje
La cantidad de calor absorbida por el calorímetro a menudo es lo suficientemente pequeña como para que podamos descuidarla (aunque no para mediciones muy precisas, como se discutirá más adelante), y el calorímetro minimiza el intercambio de energía con el ambiente exterior. Debido a que la energía no se crea ni se destruye durante una reacción química, el calor producido o consumido en la reacción (el "sistema"), $q_{\text{reacción}}$, más el calor absorbido o perdido por la solución (el "entorno"), $q_{\text{solución}}$, debe sumar a cero:
Esto significa que la cantidad de calor producido o consumido en la reacción es igual a la cantidad de calor absorbido o perdido por la solución:
$$q_{\text{reacción}} = - q_{\text{solución}} $$Este concepto se encuentra en el corazón de todos los problemas y cálculos de calorimetría.
Ejemplo 5.5
Calor producido por una reacción exotérmica
Cuando se agregan $50,0\;mL$ de HCl $1.00\;M_{(ac)}$ Y $50.0\;mL$ de NaOH $1.00\;M_{(ac)}$, Ambos a $22,0\;\degree C$, a un calorímetro de taza de café, la temperatura de la mezcla alcanza un máximo de $28,9\;\degree C$. ¿Cuál es la cantidad aproximada de calor producido por esta reacción?
$$HCl_{(ac)} + NaOH_{(ac)} \longrightarrow NaCl_{(ac)} + H_2O_{(l)}$$Solución
Para visualizar lo que está sucediendo, imagine que podría combinar las dos soluciones tan rápido que no hubo reacción mientras se mezclaban; luego, después de mezclar, tuvo lugar la reacción. En el instante de la mezcla, tiene $100.0\;mL$ de una mezcla de HCl y NaOH a $22.0\;\degree C$. El HCl y el NaOH reaccionan hasta que la temperatura de la solución alcanza los $28.9\;\degree C$.
El calor emitido por la reacción es igual al absorbido por la solución. Por lo tanto:
$$q_{\text{reacción}} = - q_{\text{solución}} $$(Es importante recordar que esta relación solo se mantiene si el calorímetro no absorbe el calor de la reacción, y no hay intercambio de calor entre el calorímetro y el ambiente exterior).
A continuación, sabemos que el calor absorbido por la solución depende de su cambio específico de calor, masa y temperatura:
$$ q_{\text{solución}} = -(C \times m \times {\Delta T})_{\text{solución}}$$Para proceder con este cálculo, necesitamos hacer algunas suposiciones o aproximaciones más razonables. Como la solución es acuosa, podemos proceder como si fuera agua en términos de sus valores específicos de calor y masa. La densidad del agua es de aproximadamente $1.0\; \cfrac{g}{mL}$, por lo que $100.0\;mL$ tiene una masa de aproximadamente $1.0 \times 10^2\;g$ (dos cifras significativas). El calor específico del agua es de aproximadamente $4.184\; \cfrac{J}{g \times \degree C}$, por lo que lo usamos para el calor específico de la solución. Sustituyendo estos valores se obtiene:
$$q_{\text{solución}} = (4.184 \cfrac{J}{g\; \degree C})(100.0g )(28.9\degree C - 22.0\degree C ) = 2.9 \times 10^3J$$Finalmente, ya que estamos tratando de encontrar el calor de la reacción, tenemos:
El signo negativo indica que la reacción es exotérmica. Produce $2.9\;kJ$ de calor.
Comprueba tu aprendizaje
Química en la vida cotidiana
Cuando trabaje o juegue al aire libre en un día frío, puede usar un calentador de manos para calentar las manos (Figura 5.15).
Un calentador de manos reutilizable común contiene una solución sobresaturada de $\ce{NaC2H3O2}$ (acetato de sodio) y un disco de metal. Doblar el disco crea sitios de nucleación alrededor de los cuales el $\ce{NaC2H3O2}$ metaestable cristaliza rápidamente (un capítulo posterior sobre soluciones investigará la saturación y la supersaturación con más detalle).
Figura 5.15. Los calentadores químicos para manos producen calor que calienta la mano en un día frío. En este, puede ver el disco de metal que inicia la reacción de precipitación exotérmica. (crédito: modificación del trabajo de Science Buddies TV / YouTube)
El proceso $\ce{NaC2H3O2_{(aq)} -> NaC2H3O2_{(s)}}$ es exotérmico, y el calor producido por este proceso es absorbido por sus manos, calentándolas (al menos por un tiempo). Si el calentador de manos se recalienta, el $\ce{NaC2H3O2}$ se vuelve a disolver y puede reutilizarse.
Otro calentador de manos común produce calor cuando se abre, exponiendo el hierro y el agua del calentador de manos al oxígeno del aire. Una versión simplificada de esta reacción exotérmica es $\ce{2Fe^3_{(s)} + 3/2 O2_{(g)} -> Fe2O3_{(s)}}$. La sal en el calentador de manos cataliza la reacción, por lo que produce calor más rápidamente; La celulosa, la vermiculita y el carbón activado ayudan a distribuir el calor de manera uniforme. Otros tipos de calentadores de manos usan fluido más ligero (un catalizador de platino ayuda a que el fluido más ligero se oxida exotérmicamente), carbón (el carbón se oxida en un caso especial) o unidades eléctricas que producen calor al pasar una corriente eléctrica de una batería a través de cables resistivos.
Enlace a aprendizaje
Ejemplo 5.6
Flujo de calor en una bolsa de hielo instantánea
Cuando el nitrato de amonio sólido se disuelve en agua, la solución se enfría. Esta es la base para una "bolsa de hielo instantánea" (Figura 5.16). Cuando $3.21\;g$ de $\ce{NH4NO3}$ sólido se disuelve en $50.0\;g$ de agua a $24.9\;\degree C$ en un calorímetro, la temperatura disminuye a $20.3\;\degree C$.
Calcule el valor de q para esta reacción y explique el significado de su signo aritmético.
Indique cualquier suposición que haya hecho.
Solución
Suponemos que el calorímetro evita la transferencia de calor entre la solución y su entorno externo (incluido el calorímetro en sí), en cuyo caso:
$$q_{rxn} = -q_{sln}$$
Figura 5.16. Una compresa fría instantánea consiste en una bolsa que contiene nitrato de amonio sólido y una segunda bolsa de agua. Cuando la bolsa de agua se rompe, el paquete se enfría porque la disolución del nitrato de amonio es un proceso endotérmico que elimina la energía térmica del agua. La compresa fría luego elimina la energía térmica de su cuerpo.
Suponiendo también que el calor específico de la solución es el mismo que el del agua, tenemos:
$$q_{rxn} = - q_{sln} = - (C\times m\times \Delta T)_{sln}$$con "rxn" y "sln" utilizados como abreviatura de "reacción" y "solución", respectivamente.
$$q_{rxn} = (4.184\; \cfrac{J}{g\;\degree C})(53.2\;g)(20.3\;\degree C - 24.9\;\degree C)$$El signo positivo para q indica que la disolución es un proceso endotérmico.
Comprueba tu aprendizaje
Si la cantidad de calor absorbido por un calorímetro es demasiado grande para descuidarla o si necesitamos resultados más precisos, entonces debemos tener en cuenta el calor absorbido tanto por la solución como por el calorímetro.
Los calorímetros descritos están diseñados para operar a presión constante (atmosférica) y son convenientes para medir el flujo de calor que acompaña los procesos que ocurren en la solución. Se utiliza un tipo diferente de calorímetro que funciona a volumen constante, conocido coloquialmente como un calorímetro de bomba o bomba calorimétrica, para medir la energía producida por las reacciones que producen grandes cantidades de calor y productos gaseosos, como las reacciones de combustión. (El término "bomba" proviene de la observación de que estas reacciones pueden ser lo suficientemente vigorosas como para parecerse a explosiones que dañarían otros calorímetros.) Este tipo de calorímetro consiste en un contenedor de acero robusto (la "bomba") que contiene los reactivos y es en sí mismo sumergido en agua (Figura 5.17). La muestra se coloca en la bomba, que luego se llena con oxígeno a alta presión. Se utiliza una pequeña chispa eléctrica para encender la muestra.
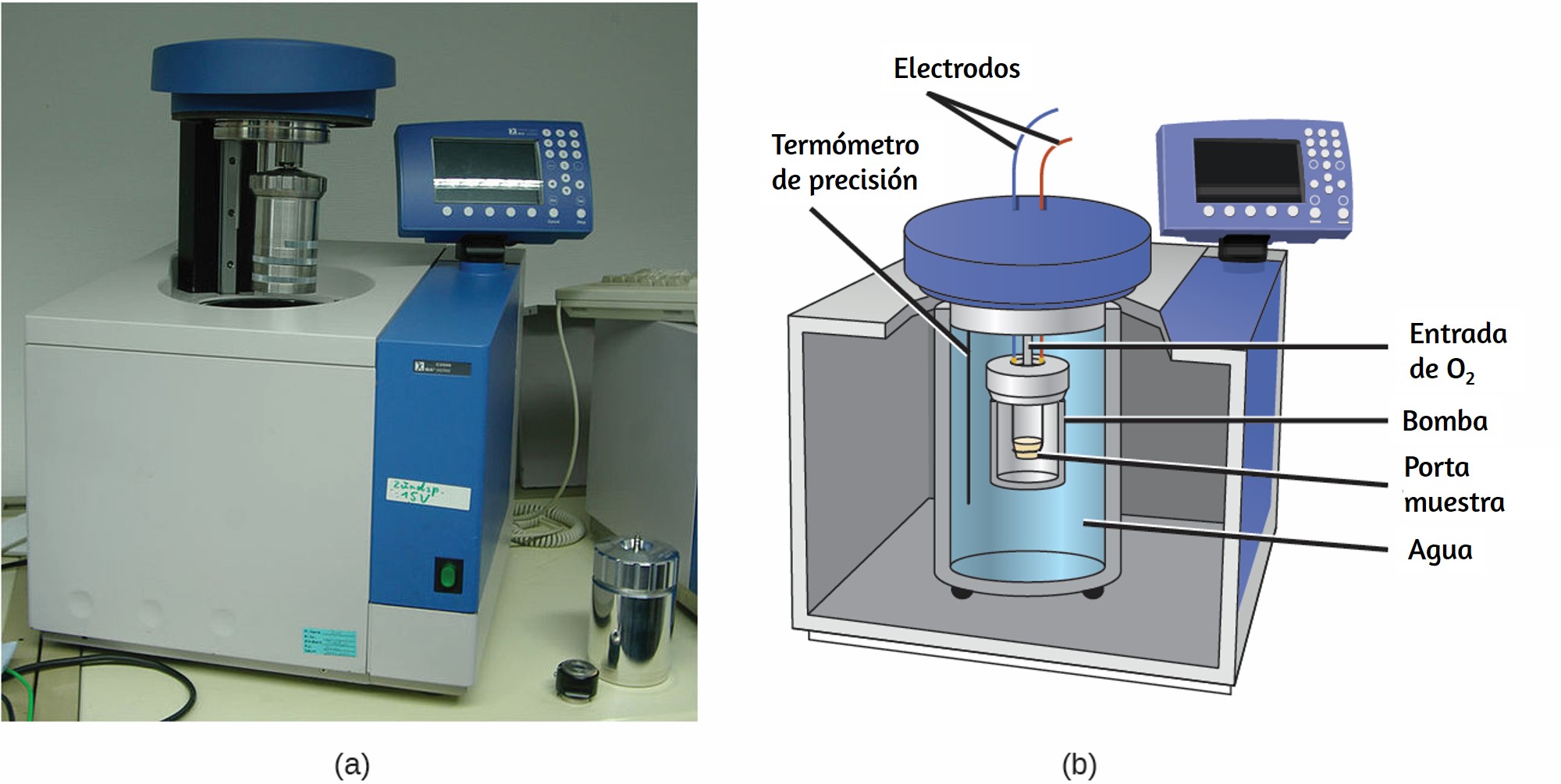
Figura 5.17. (a) Se utiliza un calorímetro de bomba para medir el calor producido por reacciones que involucran reactivos o productos gaseosos, como la combustión. (b) Los reactivos están contenidos en la "bomba" hermética a los gases, que está sumergida en agua y rodeada de materiales aislantes. (crédito a: modificación del trabajo de "Harbor1" / Wikimedia commons)
La energía producida por la reacción es absorbida por la bomba de acero y el agua circundante. Se mide el aumento de temperatura y, junto con la capacidad de calor conocida del calorímetro, se usa para calcular la energía producida por la reacción. Los calorímetros de bomba requieren calibración para determinar la capacidad calorífica del calorímetro y garantizar resultados precisos. La calibración se lleva a cabo utilizando una reacción con un q conocido, como una cantidad medida de ácido benzoico encendido por una chispa de un cable de fusible de níquel que se pesa antes y después de la reacción. El cambio de temperatura producido por la reacción conocida se usa para determinar la capacidad calorífica del calorímetro. La calibración generalmente se realiza cada vez antes de usar el calorímetro para recopilar datos de investigación.
Enlace a aprendizaje
Ejemplo 5.7
Calorimetría de bomba
Cuando se queman $3.12\;g$ de glucosa, $\ce{C6H12O6}$, en una bomba calorimétrica, la temperatura del calorímetro aumenta de $23.8\;\degree C$ a $35.6\;\degree C$.
El calorímetro contiene $775\;g$ de agua, y la bomba tiene una capacidad calorífica de $893\;\cfrac{J}{\degree C}$. ¿Cuánto calor produjo la combustión de la muestra de glucosa?
Solución
La combustión produce calor que es absorbido principalmente por el agua y la bomba. (Las cantidades de calor absorbidas por los productos de reacción y el exceso de oxígeno sin reaccionar son relativamente pequeñas y su tratamiento está más allá del alcance de este texto. Los omitiremos en nuestros cálculos).
El calor producido por la reacción es absorbido por el agua y la bomba:
$$q_{rxn} = (q_{agua} + q_{bomba})$$$q_{rxn} = [(4.184 \cfrac{J}{g\;\degree C})(775\;g)(35.6\;\degree C - 23.8\;\degree C)]\;+[(893\cfrac{J}{\degree C})(35.6\;\degree C - 23.8\;\degree C)]$
$$q_{rxn} = -(38,300\;J + 10,500\;J)$$ $$q_{rxn} = -48,800\;J = -48.8\;kJ$$Esta reacción liberó $48.8\;kJ$ de calor cuando se quemaron $3.12\;g$ de glucosa.
Comprueba tu aprendizaje
Desde que se construyó el primero en $1899$, se han construido $35$ calorímetros para medir el calor producido por una persona viva.Francis D. Reardon y col. "El calorímetro humano Snellen revisado, rediseñado y actualizado: características de diseño y rendimiento". Ingeniería y computación médica y biológica 8 (2006) 721–28,http://link.springer.com/article/10.1007/s11517-006-0086-5. Estos calorímetros de cuerpo entero son lo suficientemente grandes como para contener a un ser humano. Más recientemente, los calorímetros de toda la sala permiten realizar actividades relativamente normales, y generan datos que reflejan más de cerca el mundo real. Estos calorímetros se usan para medir el metabolismo de las personas en diferentes condiciones ambientales, diferentes regímenes dietéticos y con diferentes condiciones de salud, como la diabetes. En los humanos, el metabolismo generalmente se mide en calorías por día. Una caloría nutricional (Caloría) es la unidad de energía utilizada para cuantificar la cantidad de energía derivada del metabolismo de los alimentos, que equivale a 1000 calorías (1 kcal), la cantidad de energía necesaria para calentar $1\;kg$ de agua a $1\;\degree C$.
Química en la vida cotidiana
En su vida cotidiana, es posible que esté más familiarizado con la energía que se da en Calorías, o calorías nutricionales, que se utilizan para cuantificar la cantidad de energía en los alimentos. Una caloría (cal) = exactamente $4.184\;julios$, y una Caloría (tenga en cuenta el uso de mayúsculas) = $1000\;cal$, o $1\;kcal$. (Esta es aproximadamente la cantidad de energía necesaria para calentar $1\;kg$ de agua a $1\;\degree C$).
Los macronutrientes en los alimentos son proteínas, carbohidratos y grasas o aceites. Las proteínas proporcionan alrededor de $4$ calorías por gramo, los carbohidratos también proporcionan alrededor de $4$ calorías por gramo, y las grasas y aceites aportan alrededor de $9$ calorías por g. Las etiquetas nutricionales en los paquetes de alimentos muestran el contenido calórico de una porción de los alimentos, así como el desglose en calorías de cada uno de los tres macronutrientes (Figura 5.18).
Por lo tanto, puede usar las etiquetas de los alimentos para contar sus calorías. ¿Pero de dónde vienen los valores? ¿Y cuán precisos son? El contenido calórico de los alimentos se puede determinar mediante el uso de calorimetría de bomba; es decir, quemando la comida y midiendo la energía que contiene. Se pesa una muestra de comida, se mezcla en una licuadora, se liofiliza, se muele en polvo y se forma un gránulo. El pellet se quema dentro de un calorímetro de bomba, y el cambio de temperatura medido se convierte en energía por gramo de alimento.
Figura 5.18. (a) Los macarrones con queso contienen energía en forma de macronutrientes en los alimentos. (b) La información nutricional de los alimentos se muestra en la etiqueta del paquete. En los Estados Unidos, el contenido de energía se da en calorías (por porción); el resto del mundo usualmente usa kilojulios. (crédito a: modificación del trabajo de "Rex Roof" / Flickr)
Para el ejemplo que se muestra en (b), la energía total por porción de $228\;g$ se calcula mediante:
$$(5\;\cancel {g_{prot}} \times 4 \cfrac{cal}{\cancel {g}}) + (31\;\cancel{g_{car}} \times 4\cfrac{cal}{\cancel{g}}) + (12\;\cancel{g_{gras}} \times 9 \cfrac{cal}{\cancel{g}}) = 252\;cal$$En esta ecuación se usa “prot” por proteína, “cal” por caloría, “car” por carbohidrato, “gras” por grasa
Hoy, el contenido calórico en las etiquetas de los alimentos se deriva utilizando un método llamado sistema Atwater que utiliza el contenido calórico promedio de los diferentes componentes químicos de los alimentos, proteínas, carbohidratos y grasas. Las cantidades promedio son las que figuran en la ecuación y se derivan de los diversos resultados obtenidos por la calorimetría de bomba de alimentos integrales.
La cantidad de carbohidratos se descuenta una cierta cantidad para el contenido de fibra, que es carbohidrato no digerible. Para determinar el contenido energético de un alimento, las cantidades de carbohidratos, proteínas y grasas se multiplican por las calorías promedio por gramo de cada uno y los productos sumados para obtener la energía total.
Enlace a aprendizaje
La termoquímica es una rama de la termodinámica química, la ciencia que se ocupa de las relaciones entre el calor, el trabajo y otras formas de energía en el contexto de los procesos químicos y físicos. A medida que nos concentramos en la termoquímica en este capítulo, debemos considerar algunos conceptos de termodinámica ampliamente utilizados.
Las sustancias actúan como depósitos de energía, lo que significa que se les puede agregar o quitarles energía. La energía se almacena en una sustancia cuando se eleva la energía cinética de sus átomos o moléculas. La mayor energía cinética puede estar en forma de mayores traducciones (movimientos de desplazamiento o de línea recta), vibraciones o rotaciones de los átomos o moléculas.
Cuando se pierde energía térmica, las intensidades de estos movimientos disminuyen y la energía cinética cae. El total de todos los tipos posibles de energía presente en una sustancia se llama energía interna (U), a veces simbolizada como E.
A medida que un sistema sufre un cambio, su energía interna puede cambiar, y la energía puede transferirse del sistema a los alrededores, o de los alrededores al sistema. La energía se transfiere a un sistema cuando absorbe calor (q) del entorno o cuando el entorno funciona (w) en el sistema. Por ejemplo, la energía se transfiere al cable de metal a temperatura ambiente si se sumerge en agua caliente (el cable absorbe el calor del agua), o si dobla el cable rápidamente hacia adelante y hacia atrás (el cable se calienta debido al trabajo realizado en eso). Ambos procesos aumentan la energía interna del cable, que se refleja en un aumento de la temperatura del cable. Por el contrario, la energía se transfiere fuera de un sistema cuando el sistema pierde calor o cuando el sistema funciona en los alrededores. La relación entre energía interna, calor y trabajo puede representarse mediante la ecuación:
$$\Delta U = q + w$$La termoquímica es una rama de la termodinámica química, la ciencia que se ocupa de las relaciones entre el calor, el trabajo y otras formas de energía en el contexto químico y físico, como se muestra en la Figura 5.19. Esta es una versión de la primera ley de la termodinámica, y muestra que la energía interna de un sistema cambia a través del flujo de calor dentro o fuera del sistema ($q$positivo es flujo de calor; $q$ negativo es flujo de calor) o trabajo realizado en o por el sistema. El trabajo, $w$, es positivo si se realiza en el sistema y negativo si lo hace el sistema.
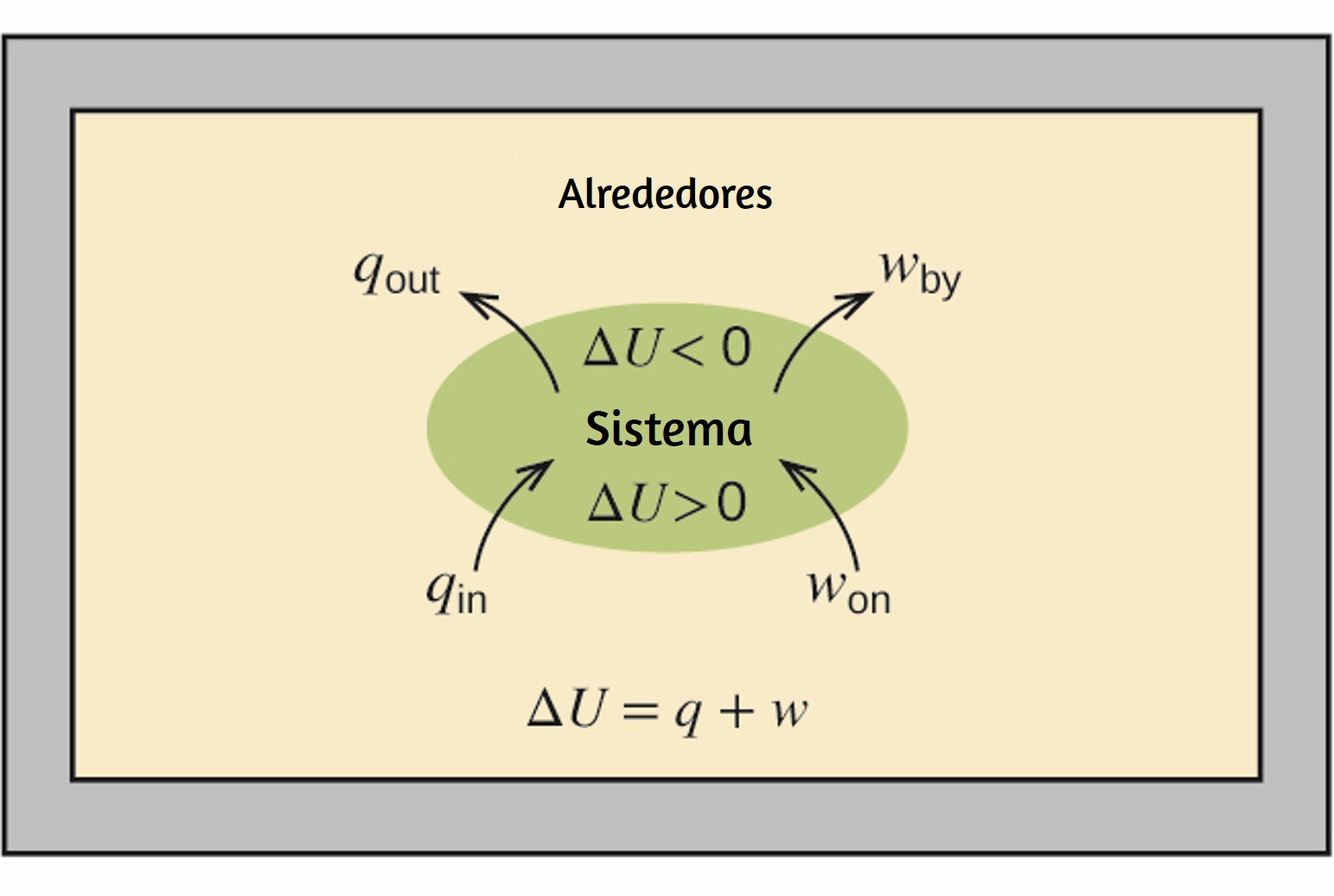
Figura 5.19. La energía interna, $U$, de un sistema puede modificarse mediante el flujo de calor y el trabajo. Si el calor fluye hacia el sistema, $q_{in}$, o el trabajo se realiza en el sistema, ganó, su energía interna aumenta, $\Delta U > 0$. Si el calor fluye fuera del sistema, $q_{out}$ o el trabajo lo realiza el sistema, $w_{by}$, su energía interna la energía disminuye, $\Delta U < 0$.
Un tipo de trabajo llamado trabajo de expansión (o trabajo de presión-volumen) ocurre cuando un sistema empuja los alrededores contra una presión de restricción, o cuando los alrededores comprimen el sistema. Un ejemplo de esto ocurre durante la operación de un motor de combustión interna. La reacción de la gasolina y el oxígeno es exotérmica. Parte de esta energía se emite en forma de calor, y parte funciona empujando el pistón en el cilindro. Las sustancias involucradas en la reacción son el sistema, y el motor y el resto del universo son los alrededores. El sistema pierde energía al calentar y al trabajar en los alrededores, y su energía interna disminuye. (El motor puede mantener el automóvil en movimiento porque este proceso se repite muchas veces por segundo mientras el motor está funcionando).
Consideraremos cómo determinar la cantidad de trabajo involucrado en un cambio químico o físico en el capítulo sobre termodinámica.
Enlace a aprendizaje
Como se discutió, la relación entre la energía interna, el calor y el trabajo se puede representar como $\Delta U = q + w$. La energía interna es un ejemplo de una función de estado (o variable de estado), mientras que el calor y el trabajo no son funciones de estado. El valor de una función de estado depende solo del estado en el que se encuentra un sistema y no de cómo se alcanza ese estado. Si una cantidad no es una función de estado, entonces su valor depende de cómo se alcanza el estado. Un ejemplo de una función de estado es altitud o elevación. Si te paras en la cumbre del monte. Kilimanjaro, estás a una altitud de $5895\;m$, y no importa si caminaste allí o saltaste en paracaídas. Sin embargo, la distancia que recorrió hasta la cima del Kilimanjaro no es una función de estado. Puede subir a la cumbre por una ruta directa o por un camino indirecto más tortuoso (Figura 5.20). Las distancias recorridas serían diferentes (la distancia no es una función de estado) pero la elevación alcanzada sería la misma (la altitud es una función de estado).
Los químicos generalmente usan una propiedad conocida como entalpía (H) para describir la termodinámica de los procesos químicos y físicos.
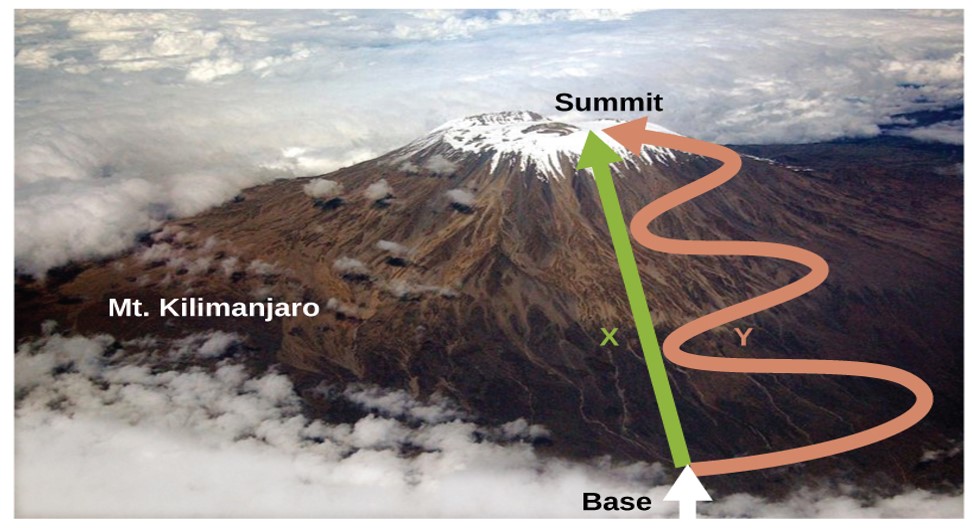
Figura 5.20. Las rutas X e Y representan dos rutas diferentes a la cumbre del monte. Kilimanjaro Ambos tienen el mismo cambio en la elevación (la altitud o la elevación en una montaña es una función de estado; no depende de la ruta), pero tienen distancias CON recorridos muy diferentes (la distancia recorrida no es una función de estado; depende de la ruta). (crédito: modificación del trabajo de Paul Shaffner)
La entalpía se define como la suma de la energía interna $(U)$ de un sistema y el producto matemático de su presión $(P)$ y volumen $(V)$:
$$H = U + PV $$La entalpía también es una función de estado. Los valores de entalpía para sustancias específicas no pueden medirse directamente; solo se pueden determinar los cambios de entalpía para procesos químicos o físicos. Para los procesos que tienen lugar a presión constante (una condición común para muchos cambios químicos y físicos), el cambio de entalpía (\Delta H) es:
$$\Delta H=\Delta U+P\Delta V$$El producto matemático $P\Delta V$ representa el trabajo $(w)$, es decir, el trabajo de expansión o presión-volumen como se indicó.
Por sus definiciones, los signos aritméticos de $\Delta V$ y $w$ siempre serán opuestos:
$$P\Delta V=−w$$Sustituyendo esta ecuación y la definición de energía interna en la ecuación de cambio de entalpía se obtiene:
$$\Delta H=\Delta U+P\Delta \quad V=q_p+w−w=q_p$$Donde $q_p$ es el calor de reacción en condiciones de presión constante.
Y así, si un proceso químico o físico se lleva a cabo a presión constante con el único trabajo realizado por expansión o contracción, entonces el flujo de calor $(q_p)$ y el cambio de entalpía $(\Delta H)$ para el proceso son iguales.
El calor emitido cuando opera un quemador Bunsen es igual al cambio de entalpía de la reacción de combustión de metano que tiene lugar, ya que ocurre a la presión esencialmente constante de la atmósfera. Por otro lado, el calor producido por una reacción medida en un calorímetro de bomba (Figura 5.17) no es igual a $\Delta H$ porque el recipiente de metal cerrado de volumen constante evita que la presión permanezca constante (puede aumentar o disminuir si la reacción produce cantidades aumentadas o disminuidas de especies gaseosas). Los químicos generalmente realizan experimentos en condiciones atmosféricas normales, a presión externa constante con $q = \Delta H$, lo que hace que la entalpía sea la opción más conveniente para determinar los cambios de calor para las reacciones químicas.
Las siguientes convenciones se aplican cuando se usa $\Delta H$:
Esta ecuación indica que cuando $1\;mol$ de hidrógeno gaseoso y $\ce{1/2mol}$ de oxígeno gaseoso a cierta temperatura y presión cambian a $1\;mol$ de agua líquida a la misma temperatura y presión, se liberan $286\;kJ$ de calor a los alrededores. Si los coeficientes de la ecuación química se multiplican por algún factor, el cambio de entalpía debe multiplicarse por ese mismo factor ($\Delta H$ es una propiedad extensiva):
(aumento de dos veces en las cantidades)
$$\ce{2H2 _{(g)} + O2 _{(g)} -> 2H2O _{(l)}};\quad \Delta H=2 \times (-286\;kJ)=-572\;kJ$$(disminución de dos veces en las cantidades)
$$\ce{1/2H2 _{(g)} + 1/4O2 _{(g)} -> 1/2H2O _{(l)}};\quad \Delta H=\cfrac{1}{2} \times (-286\;kJ)=-143\;kJ$$Ejemplo 5.8
Escribir ecuaciones termoquímicas
Cuando $0.0500\;mol$ de $\ce{HCl_{(ac)}}$ reacciona con $0.0500\;mol$ de $\ce{NaOH_{(ac)}}$ para formar $0.0500\;mol$ de $\ce{NaCl_{(ac)}}$, se producen $2.9\;kJ$ de calor. Escriba una ecuación termoquímica equilibrada para la reacción de un mol de HCl.
$$\ce{HCl _{(ac)} + NaOH _{(ac)} -> NaCl _{(ac)} + H2O _{(l)}}$$Solución
Para la reacción de $0.0500\;mol$ de ácido (HCl), $q = −2.9\;kJ$. Los reactivos se proporcionan en cantidades estequiométricas (la misma relación molar que en la ecuación equilibrada), por lo que la cantidad de ácido puede usarse para calcular un cambio de entalpía molar. Como $\Delta H$ es una propiedad extensiva, es proporcional a la cantidad de ácido neutralizado:
$$\Delta H= 1 \cancel{\;mol\;HCl} \times \cfrac{-2.9\;kJ}{0.0500 \cancel{\;mol\;HCl}}=-58\;kJ$$La ecuación termoquímica es entonces
$$\ce{HCl _{(ac)} + NaOH _{(ac)} -> NaCl _{(ac)} + H2O _{(l)}}; \quad \Delta H=-58\;kJ$$Comprueba tu aprendizaje
Asegúrese de tener en cuenta tanto la estequiometría como los reactivos limitantes al determinar el $\Delta H$ para una reacción química.
Ejemplo 5.9
Escribir ecuaciones termoquímicas
Un oso gomoso contiene $2,67\;g$ de sacarosa, $\ce{C12H22O11}$. Cuando reacciona con $7.19\;g$ de clorato de potasio, $\ce{KClO3}$, se producen $43.7\;kJ$ de calor. Escriba una ecuación termoquímica para la reacción de un mol de sacarosa:
$$\ce{C12H22O11 _{(ac)} + 8KClO3 _{(ac)} -> 12CO2 _{(g)} + 11H2O _{(l)} + 8KCl _{(ac)}}$$Solución
A diferencia del ejercicio de ejemplo anterior, este no implica la reacción de cantidades estequiométricas de reactivos, por lo que debe identificarse el reactivo limitante (limita el rendimiento de la reacción y la cantidad de energía térmica producida o consumida).
Las cantidades proporcionadas de los dos reactivos son
$$2.67\; \cancel{g} \times \frac{1\;mol}{342.3\; \cancel{g}}= 0.00780\;mol\; \ce{C12H22O11}$$ $$7.19\; \cancel{g} \times \frac{1\;mol}{122.5\; \cancel{g}}= 0.0587\;mol\; \ce{KClO3}$$La relación molar proporcionada de perclorato a sacarosa es entonces
La ecuación balanceada indica que se requieren $8$ mol de $\ce{KClO3}$ para la reacción con $1$ mol de $\ce{C12H22O11}$. Dado que la cantidad proporcionada de $\ce{KClO3}$ es menor que la cantidad estequiométrica, es el reactivo limitante y puede usarse para calcular el cambio de entalpía:
$$\Delta H=- \frac{4.7 kJ}{0.0587\;mol\; \ce{KClO3}}=744 \frac{kJ}{mol\; \ce{KClO3}}$$Como la ecuación, como está escrita, representa la reacción de $8$ mol de $\ce{KClO3}$, el cambio de entalpía es
$$ \frac {744\;kJ}{\cancel {mol\; \ce{KClO3}}} \times 8\;mol \cancel {mol\; \ce{KClO3}}=5.960\;kJ$$El cambio de entalpía para esta reacción es $−5,960\;kJ$, y la ecuación termoquímica es:
$\ce{C12H22O11 _{(ac)} + 8KClO3 _{(ac)} -> 12CO2 _{(g)} + 11H2O _{(l)} + 8KCl _{(ac)}}; $
ΔH=-5,960\;kJ
Comprueba tu aprendizaje
Los cambios de entalpía generalmente se tabulan para reacciones en las que tanto los reactivos como los productos se encuentran en las mismas condiciones. Un estado estándar es un conjunto de condiciones comúnmente aceptado que se utiliza como punto de referencia para la determinación de propiedades en otras condiciones diferentes. Para los químicos, el estado estándar de IUPAC se refiere a materiales bajo una presión de $1\;bar$ y soluciones a $1\;M$, y no especifica una temperatura. Muchas tablas termoquímicas enumeran valores con un estado estándar de $1\;atm$. Debido a que el $\Delta H$ de una reacción cambia muy poco con cambios tan pequeños en la presión $(1\;bar = 0.987\;atm)$, los valores de $\Delta H$ (excepto los valores medidos con mayor precisión) son esencialmente los mismos en ambos conjuntos de condiciones estándar. Incluiremos una "o" en superíndice en el símbolo de cambio de entalpía para designar el estado estándar. Como la temperatura habitual (pero no técnicamente estándar) es de $298,15\;K$, esta temperatura se supondrá a menos que se especifique alguna otra temperatura. Por lo tanto, el símbolo $(\Delta H \degree )$ se utiliza para indicar un cambio de entalpía para un proceso que se produce en estas condiciones. (El símbolo $\Delta H$ se usa para indicar un cambio de entalpía para una reacción que ocurre en condiciones no estándar).
Los cambios de entalpía para muchos tipos de procesos químicos y físicos están disponibles en la literatura de referencia, incluidos los de reacciones de combustión, transiciones de fase y reacciones de formación. Mientras discutimos estas cantidades, es importante prestar atención a la naturaleza extenssiva de la entalpía y los cambios de entalpía.
Dado que el cambio de entalpía para una reacción dada es proporcional a las cantidades de sustancias involucradas, puede informarse sobre esa base (es decir, como el $\Delta H$ para cantidades específicas de reactivos). Sin embargo, a menudo nos resulta más útil dividir una propiedad extensa $(\Delta H)$ por otra (cantidad de sustancia), e informar un valor intensivo por cantidad de $\Delta H$, a menudo "normalizado" por mol. (Tenga en cuenta que esto es similar a determinar el calor específico de la propiedad intensiva a partir de la capacidad de calor de la propiedad extensiva, como se vio anteriormente).
Entalpía estándar de combustión $(\ce{\Delta H^{\degree}_C})$ es el cambio de entalpía cuando se quema 1 mol de una sustancia (se combina vigorosamente con oxígeno) en condiciones de estado estándar; a veces se le llama "calor de combustión". Por ejemplo, la entalpía de combustión de etanol, $-1,366.8\; \frac{kJ}{mol}$, es la cantidad de calor producida cuando un mol de etanol experimenta una combustión completa a $25\;\degree C$ y $1$ presión atmosférica, produciendo productos también a $25\;\degree C$ y $1\;atm$.
$$\ce{C2H5OH _{(l)}+3O2 _{(g)} -> 2CO2 _{(g)}+3H2O _{(l)} ; \Delta H\degree =−1366.8\;kJ}$$Se han medido entalpías de combustión para muchas sustancias; Algunos de estos se enumeran en la Table 5.2. Muchas sustancias fácilmente disponibles con grandes entalpías de combustión se utilizan como combustibles, incluidos el hidrógeno, el carbono (como el hulla o el carbón vegetal) y los hidrocarburos (compuestos que contienen solo hidrógeno y carbono), como el metano, el propano y los componentes principales de la gasolina.
Tabla 5.2 Entalpias Molares Estándar de Combustión
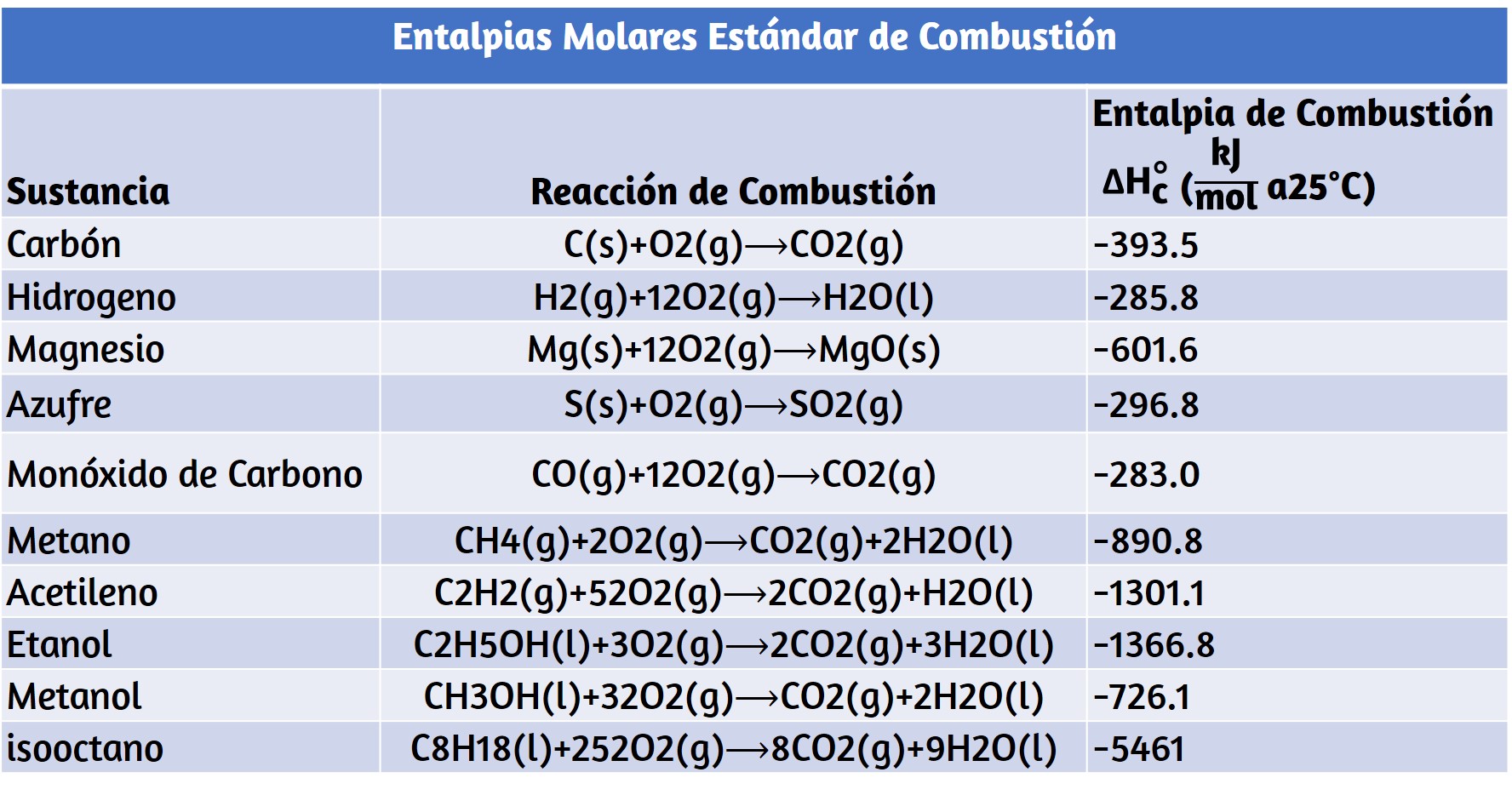
Ejemplo 5.10
Usando la entalpía de la combustión
Como sugiere la Figura 5.21, la combustión de gasolina es un proceso altamente exotérmico. Determinemos la cantidad aproximada de calor producido al quemar $1.00\;L$ de gasolina, suponiendo que la entalpía de la combustión de la gasolina es la misma que la del isooctano, un componente común de la gasolina. La densidad del isooctano es $0.692\; \frac{g}{mL}$.
Solución
Comenzando con una cantidad conocida ($1.00\;L$ de isooctano), podemos realizar conversiones entre unidades hasta llegar a la cantidad deseada de calor o energía.
Figura 5.21. La combustión de la gasolina es muy exotérmica. (crédito: modificación del trabajo de "AlexEagle" / Flickr)
La entalpía de combustión del isooctano proporciona una de las conversiones necesarias. La Tabla 5.2 da este valor como $−5,460\;kJ$ por $1\;mol$ de isooctano $\ce{C8H18}$.
Usando estos datos,
$1.00L\; \ce{C8H18} \times \frac{1000\;mL \ce{C8H18}}{1\;L\; \ce{C8H18}} \times \frac{0.692\;g\; \ce{C8H18}}{1\;mL\; \ce{C8H18}} \times \frac{1\;mol\; \ce{C8H18}}{114\;g\; \ce{C8H18}} \times \frac {-5,460\;kJ}{1\;mol\;\ce{C8H18}}$
$$=-3.31 \times 10^4\;kJ$$La combustión de $1.00\;L$ de isooctano produce $33,100\;kJ$ de calor. (Esta cantidad de energía es suficiente para derretir $99,2\;kg$, o aproximadamente $218\;libras$ de hielo).
Nota: Si realiza este cálculo paso a paso, encontrará:
$$1.00\;L \; \ce{C8H18 ->} \; 1.00\times10^3\;mL\:\ce{C8H18}$$Comprueba tu aprendizaje
Química en la vida cotidiana
A medida que las reservas de combustibles fósiles disminuyen y se vuelven más costosas de extraer, se está buscando fuentes de combustible de reemplazo para el futuro. Entre los biocombustibles más prometedores se encuentran los derivados de las algas (Figura 5.22). Las especies de algas utilizadas no son tóxicas, son biodegradables y se encuentran entre los organismos de más rápido crecimiento del mundo. Alrededor del $50\%$ del peso de las algas es aceite, que se puede convertir fácilmente en combustible como el biodiesel.
Las algas pueden producir $26,000\;galones$ de biocombustible por hectárea, mucha más energía por acre que otros cultivos. Algunas cepas de algas pueden florecer en agua salobre que no se puede usar para cultivar otros cultivos. Las algas pueden producir biodiesel, biogasolina, etanol, butanol, metano e incluso combustible para aviones.
Figura 5.22. (a) Se pueden cultivar pequeños organismos de algas (b) en grandes cantidades y eventualmente (c) convertirse en un combustible útil como el biodiesel. (crédito a: modificación del trabajo de Micah Sittig; crédito b: modificación del trabajo de Robert Kerton; crédito c: modificación del trabajo de John F. Williams)
Según el Departamento de Energía de los EE. UU., Solo $39,000$ kilómetros cuadrados (aproximadamente el $0.4\%$ de la masa de tierra de los EE. UU. O menos de $\frac{1}{7}$ del área utilizada para cultivar maíz) pueden producir suficiente combustible de algas para reemplazar todo el combustible a base de petróleo utilizado en los Estados Unidos. El costo de los combustibles de algas se está volviendo más competitivo, por ejemplo, la Fuerza Aérea de los Estados Unidos está produciendo combustible para aviones a partir de algas a un costo total de menos de $\$5$ por galón For more on algal fuel, see http://www.theguardian.com/.
El proceso utilizado para producir combustible de algas es el siguiente: cultivar algas utilizar la luz solar como fuente de energía y el $\ce{CO2}$ como materia prima); cosechar las algas; extraer los compuestos de combustible (o compuestos precursores); procesar según sea necesario (por ejemplo, realizar una reacción de transesterificación para hacer biodiesel); purificar; y distribuir (Figura 5.23).
Figura 5.23. Las algas convierten la luz solar y el dióxido de carbono en aceite que se cosecha, extrae, purifica y transforma en una variedad de combustibles renovables.
Enlace a aprendizaje
Una entalpía estándar de formación $\Delta H^o_f$ es un cambio de entalpía para una reacción en la que exactamente $1\;mol$ de una sustancia pura se forma a partir de elementos libres en sus estados más estables en condiciones de estado estándar. Estos valores son especialmente útiles para calcular o predecir cambios de entalpía para reacciones químicas que no son prácticas o peligrosas de llevar a cabo, o para procesos para los que es difícil realizar mediciones. Si tenemos valores para las entalpías de formación estándar apropiadas, podemos determinar el cambio de entalpía para cualquier reacción, que practicaremos en la siguiente sección sobre la ley de Hess.
La entalpía estándar de formación de $\ce{CO2 _{(g)}}$ es $−393.5\; \frac {kJ}{mol}$. Este es el cambio de entalpía para la reacción exotérmica:
$$\ce{C _{(s)}+O2 _{(g)} -> CO2 _{(g)};\;\Delta H^{\degree}_f=\Delta H\degree =−393.5\;kJ}$$Comenzando con los reactivos a una presión de $1\;atm$ y $25\; \degree C$ (con el carbono presente como grafito, la forma más estable de carbono en estas condiciones) y terminando con un mol de $\ce{CO2}$, también a $1\;atm$ y $25\; \degree C$. Para dióxido de nitrógeno, $\ce{NO2 _{(g)}}$, $\Delta H^{\degree}_{f}$ es $33.2\; \frac{kJ}{mol}$. Este es el cambio de entalpía para la reacción:
$$\ce{1/2N2 _{(g)}+O2 _{(g)} -> NO2 _{(g)}; \Delta H^{\degree}_f=\Delta H^{\degree}=+33.2\;kJ}$$Una ecuación de reacción con $12\;moles$ de $\ce{N2}$ y $1\;mol$ de $\ce{O2}$ es correcta en este caso porque la entalpía estándar de formación siempre se refiere a $1\;mol$ de producto, $\ce{NO2 _{(g)}}$.
Encontrará una tabla de entalpías estándar de formación de muchas sustancias comunes en el Apéndice G. Estos valores indican que las reacciones de formación varían desde muy exotérmicas (como $-2984\; \frac{kJ}{mol}$ para la formación de $\ce{P4O10}$) hasta fuertemente endotérmicas (como $+226.7\; \frac{kJ}{mol}$ para la formación de acetileno, $\ce{C2H2}$). Por definición, la entalpía estándar de formación de un elemento en su forma más estable es igual a cero en condiciones estándar, que es $1\;atm$ para gases y $1\;M$ para soluciones.
Ejemplo 5.11
Evaluar una entalpía de formación
El ozono, $\ce{O3 _{(g)}}$, se forma a partir del oxígeno, $\ce{O2 _{(g)}}$, mediante un proceso endotérmico. La radiación ultravioleta es la fuente de energía que impulsa esta reacción en la atmósfera superior. Suponiendo que tanto los reactivos como los productos de la reacción están en sus estados estándar, determine la entalpía estándar de formación, $\Delta H^{\degree}_f$ de ozono a partir de la siguiente información:
$$\ce{3O2_{(g)} -> 2O3_{(g)};\Delta H^{\degree}=+286\;kJ}$$Solución
$\Delta H^{\degree}_f$ es el cambio de entalpía para la formación de un mol de una sustancia en su estado estándar a partir de los elementos en sus estados estándar. Por lo tanto, $\Delta H^{\degree}_f$ para $\ce{O3 _{(g)}}$ es el cambio de entalpía para la reacción:
$$\ce{3/2O2_{(g)} -> O3_{(g)}}$$Para la formación de $2\;mol$ de $\ce{O3_{(g)}}$, $\Delta H^{\degree} = + 286\;kJ$. Esta relación, ($ \frac{286\;kJ}{2\;mol} \ce{O3}$), puede usarse como factor de conversión para encontrar el calor producido cuando se forma $1\;mol$ de $\ce{O3_{(g)}}$, que es la entalpía de formación de $\ce{O3 _{(g)}}$:
$$\Delta H^{\degree} \text{ para 1 mol de } \ce{O3_{(g)}}= 1\;\cancel{mol\; \ce{O3}} \times \frac {286\;kJ}{ 2\cancel{\;mol \; \ce{O3}}} = 143\;kJ$$Por lo tanto, $\Delta H^{\degree}_f\; [\ce{O3_{(g)}}] = + 143\; \frac{kJ}{mol}$.
Comprueba tu aprendizaje
Ejemplo 5.12
Escribir ecuaciones de reacción para $\Delta H^{\degree}_f$ Escriba las ecuaciones de reacción de calor de formación para:
Solución
Recordando que las ecuaciones de reacción $\Delta H^{\degree}_f$ son para formar $1\;mol$ del compuesto a partir de sus elementos constituyentes en condiciones estándar, tenemos:
(a) $\ce{2C_{(s,graphite)} + 3H2 _{(g)} + 12O2 _{(g)} -> C2H5OH _{(l)}}$
(b) $\ce{3Ca _{(s)} + 12P4 _{(s)} + 4O2 _{(g)} -> Ca3(PO4)2 _{(s)}}$
Nota: El estado estándar del carbono es el grafito, y el fósforo existe como $\ce{P4}$.
Comprueba tu aprendizaje
Hay dos formas de determinar la cantidad de calor involucrado en un cambio químico: medirlo experimentalmente o calcularlo a partir de otros cambios de entalpía determinados experimentalmente. Algunas reacciones son difíciles, si no imposibles, de investigar y realizar mediciones precisas para experimentación. E incluso cuando una reacción no es difícil de realizar o medir, es conveniente poder determinar el calor involucrado en una reacción sin tener que realizar un experimento.
Este tipo de cálculo generalmente implica el uso de la ley de Hess, que establece: Si un proceso puede escribirse como la suma de varios procesos escalonados, el cambio de entalpía del proceso total es igual a la suma de los cambios de entalpía de los distintos pasos. La ley de Hess es válida porque la entalpía es una función de estado: los cambios de entalpía dependen solo de dónde comienza y termina un proceso químico, pero no del camino que toma de principio a fin. Por ejemplo, podemos pensar que la reacción del carbono con el oxígeno para formar dióxido de carbono ocurre directamente o mediante un proceso de dos pasos. El proceso directo está escrito:
En el proceso de dos pasos, se forma el primer monóxido de carbono:
$$\ce{C _{(s)} + 1/2O2 _{(g)} -> CO_{(g)}\;\Delta H \degree =−111\;kJ}$$Luego, el monóxido de carbono reacciona aún más para formar dióxido de carbono:
$$\ce{CO _{(g)} + 1/2O2 _{(g)} -> CO2_{(g)}\;\Delta H \degree =−283\;kJ}$$La ecuación que describe la reacción general es la suma de estos dos cambios químicos:
$$\text{paso 1: } \ce{C_{(s)} + 1/2O2 _{(g)} -> CO_{(g)}}$$ $$\text{paso 2: } \ce{CO_{(g)} + 1/2O2_{(g)} -> CO2_{(g)}}$$¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
$$\text{suma: } \ce{C_{(s)} + O2_{(g)} + CO_{(g)} + 1/2O2_{(g)} -> CO_{(g)} + CO2_{(g)}}$$Debido a que el $CO$ producido en el Paso 1 se consume en el Paso 2, el cambio neto es:
$$\ce{C_{(s)}+O2_{(g)} -> CO2_{(g)}}$$Según la ley de Hess, el cambio de entalpía de la reacción será igual a la suma de los cambios de entalpía de los pasos.
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
$$\text{suma: } \ce{C _{(s)} + O2 _{(g)} -> CO2 _{(g)}\;\Delta H \degree =−394\;kJ}$$El resultado se muestra en la Figura 5.24. Vemos que $\Delta H$ de la reacción general es la misma, ya sea que ocurra en uno o dos pasos. Este hallazgo ($\Delta H$ general para la reacción = suma de los valores de $\Delta H$ para los "pasos" de la reacción en la reacción general) en general es cierto para los procesos químicos y físicos.
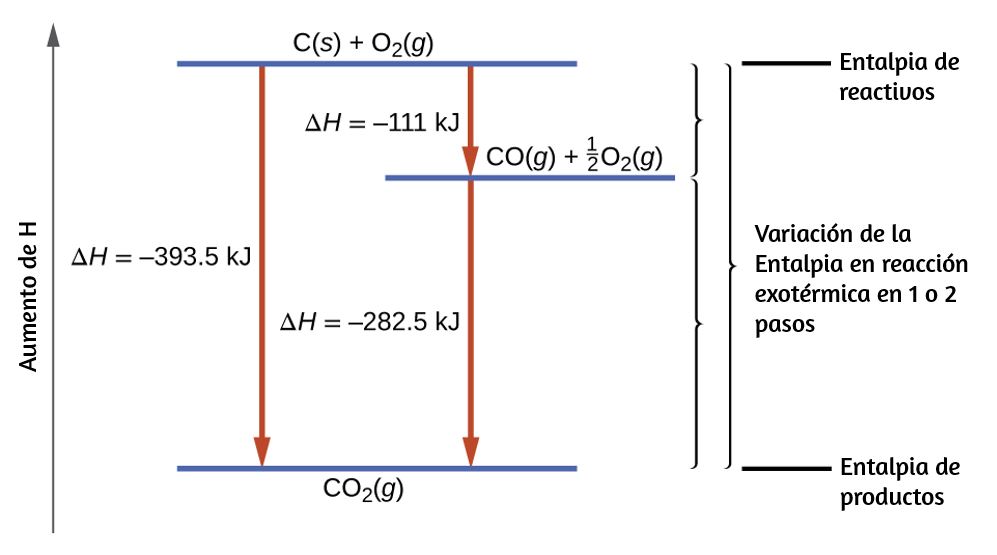
Figura 5.24. Se puede pensar que la formación de $\ce{CO2 _{(g)}}$ a partir de sus elementos ocurre en dos pasos, que suman la reacción general, como lo describe la ley de Hess. Las líneas azules horizontales representan entalpías. Para un proceso exotérmico, los productos tienen una entalpía más baja que los reactivos.
Antes de seguir practicando el uso de la ley de Hess, recordemos dos características importantes de $\Delta H$.
Cuando se forman $2$ moles de $\ce{NO2}$ (el doble), el $\Delta H$ será dos veces mayor:
$$\ce{1N2 _{(g)} + 2O2 _{(g)} -> 2NO2 _{(g)}; \quad \Delta H=+66.4\;kJ}$$En general, si multiplicamos o dividimos una ecuación por un número, entonces el cambio de entalpía también debe multiplicarse o dividirse por el mismo número.
Luego, para la reacción "inversa", el cambio de entalpía también se "invierte":
$$\ce{2HCl _{(g)} -> H2 _{(g)} + Cl2 _{(g)}; \quad \Delta H=+184.6\;kJ}$$Ejemplo 5.13
Cálculo paso a paso de $\Delta H \degree _f$ utilizando la ley de Hess
Determine la entalpía de formación, $\Delta H^{\degree}_f$, de $\ce{FeCl3 _{(s)}}$ a partir de los cambios de entalpía del siguiente proceso de dos pasos que ocurre en condiciones de estado estándar:
$$\ce{Fe _{(s)} + Cl2 _{(g)} -> FeCl2 _{(s)}; \quad \Delta H \degree =−341.8\;kJ}$$ $$\ce{FeCl2 _{(s)} + 1/2Cl2 _{(g)} -> FeCl3 _{(s)}; \quad \Delta H \degree =−57.7\;kJ}$$Solución
Estamos tratando de encontrar la entalpía estándar de formación de $\ce{FeCl3 _{(s)}}$, que es igual a $\Delta H^{\degree}$ para la reacción:
$$\ce{Fe _{(s)} + 3/2Cl2 _{(g)} -> FeCl3 _{(s)}; \quad \Delta H^{\degree}_f=?}$$Al observar las reacciones, vemos que la reacción para la que queremos encontrar $\Delta H^{\degree}$ es la suma de las dos reacciones con valores de $\Delta H$ conocidos, por lo que debemos sumar sus $\Delta H_s$:
$$\text{Ecuación 1: } \ce{Fe _{(s)} + Cl2 _{(g)} -> FeCl2 _{(s)}; \quad \Delta H^{\degree}=−341.8\;kJ}$$ $$\text{Ecuación 2: } \ce{FeCl2 _{(s)} + 1/2Cl2 _{(g)} -> FeCl3 _{(s)}; \quad \Delta H^{\degree}=−57.7\;kJ}$$___________________________________________________________________
$$\text{Suma: }\ce{Fe _{(s)} + 3/2Cl2 _{(g)} -> FeCl3 _{(s)}; \quad \Delta H^{\degree}=-399.5\;kJ}$$La entalpía de formación, $\Delta H^{\degree}_f$, de $\ce{FeCl3 _{(s)}}$ es $−399.5 \frac{kJ}{mol}$.
Comprueba tu aprendizaje
Aquí hay un ejemplo menos directo que ilustra el proceso de pensamiento involucrado en la resolución de muchos problemas legales de Hess. Muestra cómo podemos encontrar muchas entalpías estándar de formación (y otros valores de $\Delta H$) si son difíciles de determinar experimentalmente.
Ejemplo 5.14
Un problema más desafiante con la ley de Hess
El monofluoruro de cloro puede reaccionar con el flúor para formar trifluoruro de cloro:
(i) $\ce{ClF _{(g)} + F2 _{(g)} -> ClF3 _{(g)}; \; \Delta H^{\degree}=?}$
Use las reacciones aquí para determinar el $\Delta H^{\degree}$ para la reacción (i):
(ii) $\ce{2OF2 _{(g)} -> O2 _{(g)} + 2F2 _{(g)}; \; \Delta H^{\degree}_{(ii)}=−49.4\;kJ}$
(iii) $\ce{2ClF _{(g)} + O2 _{(g)} -> Cl2O _{(g)} + OF2 _{(g)}; \; \Delta H^{\degree}_{(iii)}=+205.6\;kJ}$
(iv) $\ce{ClF3 _{(g)} + O2 _{(g)} -> 1/2Cl2O _{(g)} + 3/2OF2 _{(g)}; \; \Delta H^{\degree}_{(iv)}=+266.7\;kJ}$
Solución
Nuestro objetivo es manipular y combinar las reacciones (ii), (iii) y (iv) de modo que se sumen a la reacción (i). Yendo de izquierda a derecha en (i), primero vemos que se necesita $\ce{ClF _{(g)}}$ como reactivo. Esto se puede obtener multiplicando la reacción (iii) por $\frac{1}{2}$, lo que significa que el cambio de $\Delta H^{\degree}$ también se multiplica por $\frac{1}{2}$:
$\ce{ClF _{(g)} + 1/2O2 _{(g)} -> 1/2Cl2O _{(g)} + OF2 _{(g)}};$
$ \ce{\Delta H^{\degree}_{(iii)}=1/2 \times +205.6\;kJ=+102.8\;kJ}$
A continuación, vemos que $\ce{F2}$ también se necesita como reactivo. Para obtener esto, invierta y reduzca a la mitad la reacción (ii), lo que significa que el $\Delta H^{\degree}$ cambia de signo y se reduce a la mitad:
$\ce{F2 _{(g)} + 1/2O2 _{(g)} -> OF2 _{(g)}; \Delta H^{\degree}_{(ii)}=(1/2);\times 49.4\;kJ=24.7\;kJ}$
Para obtener $\ce{ClF3}$ como producto, invierta (iv), cambiando el signo de $\Delta H^{\degree}$:
$\ce{1/2Cl2O _{(g)} + 3/2OF2 _{(g)} -> ClF3 _{(g)} + O2 _{(g)}; \quad \Delta H^{\degree}_{(iv)}=-266.7\;kJ}$
Ahora verifique para asegurarse de que estas reacciones se sumen a la reacción que queremos:
$$\ce{ClF _{(g)} + 1/2O2 _{(g)} -> 1/2Cl2O _{(g)} + 1/2OF2 _{(g)}; \Delta H^{\degree}=+102.8\;kJ}$$ $$\ce{1/2O2 _{(g)} + F2 _{(g)} -> OF2 _{(g)}; \Delta H \degree =+24.7\;kJ}$$ $$\ce{1/2Cl2O _{(g)} + 3/2OF2 _{(g)} -> ClF3 _{(g)} + O2 _{(g)}; \Delta H \degree =−266.7\;kJ}$$___________________________________________________________________
$$\ce{ClF _{(g)} + F2_{(g)} -> ClF3 _{(g)}; \Delta H \degree =−139.2\;kJ}$$Los reactivos $\ce{1/2O2}$ y $\ce{1/2O2}$ cancelan el producto $\ce{O2}$; el producto $\ce{1/2Cl2O}$ cancela el reactivo $\ce{1/2Cl2O}$; y el reactivo $\ce{3/2OF2}$ es cancelado por los productos $\ce{1/2OF2}$ y $\ce{OF2}$. Esto deja solo reactivos $\ce{ClF _{(g)}}$ y $\ce{F2 _{(g)}}$ y el producto $\ce{ClF3 _{(g)}}$, que es lo que queremos. Dado que la suma de estas tres reacciones modificadas produce la reacción de interés, la suma de los tres valores de $\Delta H^{\degree}$ modificados dará el $\Delta H^{\degree}$ deseado:
$$\Delta H^{\degree}=(+102.8\;kJ)+(24.7\;kJ)+(−266.7\;kJ)=−139.2\;kJ$$También podemos usar la ley de Hess para determinar el cambio de entalpía de cualquier reacción si las entalpías correspondientes de formación de los reactivos y productos están disponibles.
Comprueba tu aprendizaje
Las reacciones escalonadas que consideramos son: (i) descomposiciones de los reactivos en sus elementos componentes (para los cuales los cambios de entalpía son proporcionales al negativo de las entalpías de formación de los reactivos), seguidos por (ii) las combinaciones de los elementos dara los productos (con la entalpía cambios proporcionales a las entalpías de formación de los productos). El cambio de entalpía estándar de la reacción global es, por lo tanto, igual a: (ii) la suma de las entalpías estándar de formación de todos los productos más (i) la suma de los negativos de las entalpías estándar de formación de los reactivos.
Esto generalmente se reorganiza ligeramente para escribirse de la siguiente manera, con $\sum$ representando "la suma de" y "n" representando los coeficientes estequiométricos:
$$\Delta H^{\degree}_{rxn} = \sum n \times \Delta H^{\degree}_f (productos) − \sum n \times \Delta H^{\degree}_f (reactivos)$$El siguiente ejemplo muestra en detalle por qué esta ecuación es válida y cómo usarla para calcular el cambio de entalpía para una reacción de interés.
Ejemplo 5.15
Usando la Ley de Hess
¿Cuál es el cambio de entalpía estándar para la reacción?
$$\ce{3NO2 _{(g)} + H2O _{(l)} -> 2HNO3 _{(aq)} + NO _{(g)}; \Delta H^{\degree} =?}$$Solución: usando la ecuación
Use la forma especial de la ley de Hess dada anteriormente, y los valores del Apéndice G:
$\Delta H^{\degree}_{rxn} = \sum n \times \Delta H^{\degree}_f (productos) − \sum n \times \Delta H^{\degree}_f (reactivos)$
$$\Delta H^{\degree}_{rxn} =$$ $$ \ce{\bigg[2\cancel{mol\;HNO3 _{(aq)}} \times \frac{−207.4\;kJ}{\cancel{mol\;HNO3 _{(aq)}}} + 1\;\bcancel{mol NO _{(g)}} \times \frac{+90.2\;kJ}{\bcancel{mol NO _{(g)}}}\bigg]}$$ $$ - \ce{\bigg[3 \cancel{molNO2 _{(g)}} \times \frac{+33.2\;kJ}{\cancel{molNO2 _{(g)}}} + 1\; \bcancel{mol\;H2O _{(l)}} \times \frac{−285.8\;kJ}{\bcancel{mol\;H2O _{(l)}}}\bigg]}$$$=2(−207.4\;kJ)+1(+90.2\;kJ)−3(+33.2\;kJ)−1(−285.8\;kJ)$
$ = - 138.4\;kJ$
Solución: respaldar por qué la ecuación general es válida
Alternativamente, podemos escribir esta reacción como la suma de las descomposiciones de $\ce{3NO2 _{(g)}}$ y $\ce{1H2O _{(l)}}$ en sus elementos constituyentes, y la formación de $\ce{2HNO3 _{(aq)}}$ y $\ce{1NO _{(g)}}$ a partir de sus elementos constituyentes. Al escribir estas reacciones y observar sus relaciones con los valores de $\Delta H^{\degree}_f$ para estos compuestos (del Apéndice G), tenemos:
$$\ce{3NO2 _{(g)} -> 3/2N2 _{(g)} + 3O2 _{(g)}}$$ $$\Delta H^{\degree}_1 = −99.6\;kJ$$ $$\ce{H2O _{(l)} -> H2 _{(g)} + 12O2 _{(g)}}$$ $$\Delta H^{\degree}_2 = + 285.8\;kJ\;[−1 \times \Delta H^{\degree}_f (H2O)]$$ $$\ce{H2 _{(g)} + N2 _{(g)} + 3O2 _{(g)} -> 2HNO3 _{(aq)}}$$ $$\Delta H^{\degree}_3 = −414.8\;kJ\; [2 \times \Delta H^{\degree}_f\;(HNO3)]$$ $$\ce{12N2 _{(g)} + 12O2 _{(g)} -> NO _{(g)}}$$ $$\Delta H^{\degree}_4 = + 90.2\; kJ\; [1 \times \Delta H^{\degree}_f\;(NO)]$$Sumar estas ecuaciones de reacción da la reacción que nos interesa:
$$\ce{3NO2 _{(g)} + H2O _{(l)} -> 2HNO3 _{(aq)} + NO _{(g)}}$$Sumar sus cambios de entalpía da el valor que queremos determinar:
$$\ce{\Delta H^{\degree}_{rxn} = \Delta H^{\degree}_1 + \Delta H^{\degree}_2 + \Delta H^{\degree}_3 + \Delta H^{\degree}_4}$$ $$\Delta H^{\degree}_{rxn} = (- 99.6\;kJ) + (+ 285.8\;kJ) + (- 414.8\;kJ) + (+ 90.2\;kJ)$$ $$\Delta H^{\degree}_{rxn} = - 138.4\;kJ$$Entonces, el cambio de entalpía estándar para esta reacción es $\Delta H^{\degree} = −138.4\;kJ$.
Tenga en cuenta que este resultado se obtuvo (1) multiplicando el $\Delta H^{\degree}_f$ de cada producto por su coeficiente estequiométrico y sumando esos valores, (2) multiplicando el $\Delta H^{\degree}_f$ de cada reactivo por su coeficiente estequiométrico y sumando esos valores, y luego Para más información sobre el combustible de algas, consulte http://www.theguardian.com/. restando el resultado encontrado en (2) del resultado encontrado en (1). Este es también el procedimiento para usar la ecuación general, como se muestra.
Comprueba tu aprendizaje
