SUMAR

ARIO

Red Descartes 2025/Año 5, núm. 9

Diseño de portadas

La portada es la imagen de presentación de la actividad gamificada; constituye el primer contacto y la referencia inicial que los participantes tendrán de la experiencia. Que sea atractiva y motivadora puede marcar una diferencia significativa, contribuyendo a que el proceso comience con un impacto positivo y genere un interés inmediato.

Red Descartes 2025/Año 5, núm. 9

La imagen de portada que proponemos incorpora el título de la actividad, personajes emblemáticos y un diseño visualmente atractivo que fomenta la inmersión en la experiencia. Además, la portada es ilustrativa y refleja de manera clara y coherente la esencia y el propósito de la actividad.

Mejora en la narrativa

La trama de la actividad gamificada sitúa a los protagonistas como una patrulla intertemporal, un grupo de viajeros del tiempo con una misión crucial: viajar a un pasado histórico para evitar que un grupo de individuos, que también poseen la capacidad de manipular el tiempo, alteren los acontecimientos y provoquen daños irreparables en el continuo espacio-tiempo.

Solicitamos a una inteligencia artificial que elaborara la introducción de una narrativa basada en la idea previamente expuesta, obteniendo como resultado lo siguiente:

Red Descartes 2025/Año 5, núm. 9

Sonido y música

La incorporación de efectos sonoros, himnos, sintonías o canciones puede convertirse en un elemento clave para acompañar y potenciar la acción, añadiendo profundidad emocional y dinamismo a cualquier proyecto. Estos elementos no solo enriquecen la experiencia auditiva, sino que también refuerzan el mensaje, crean atmósferas únicas y guían las emociones del público.

La Inteligencia Artificial (IA) permite adaptar y personalizar efectos sonoros y musicales con precisión, ofreciendo herramientas para crear experiencias auditivas únicas que potencian emociones y refuerzan narrativas. A continuación, presentamos ejemplos de integración musical, como canciones con voz, piezas instrumentales y efectos sonoros, todos incluidos en un reproductor interactivo que permite aplicar y modificar efectos en tiempo real, brindando una experiencia sonora personalizada y envolvente.

Red Descartes 2025/Año 5, núm. 9

Red Descartes 2025/Año 5, núm. 9

Introducción de imágenes

Las imágenes desempeñan un papel fundamental en las actividades gamificadas. En este apartado, no solo nos referimos a su diseño y creación, sino también a su edición y adaptación mediante el uso de inteligencia artificial. Las posibilidades en este ámbito son prácticamente ilimitadas, por lo que nos centraremos en exponer, comentar y analizar algunos ejemplos concretos que ilustran estas aplicaciones.

Para comenzar, crearemos una imagen con inteligencia artificial generativa que capture la esencia de un viaje en el tiempo protagonizado por una patrulla temporal, ambientado en los albores del siglo XX.

A continuación, reemplazaremos el rostro del personaje en primer plano por el del reconocido científico alemán Albert Einstein. El resto de la imagen no será modificada.

Red Descartes 2025/Año 5, núm. 9

Procedemos a ajustar la expresión facial de Einstein, añadiendo una sonrisa a su rostro, manteniendo intactos todos los demás elementos de la escena.

Red Descartes 2025/Año 5, núm. 9

Ahora vamos a enfocarnos en un primer plano del rostro de Einstein, pero queremos que aparezca con un aspecto más envejecido.

Finalmente, dado que estamos ante una ficción que gira en torno a los viajes en el tiempo, hemos decidido incorporar un elemento clave para que nuestro protagonista pueda moverse con fluidez entre distintas épocas históricas. Para lograrlo, lo dotaremos de la capacidad de cambiar su vestimenta, adaptándola a los estilos propios de cada período. De esta manera, no solo podrá integrarse de manera natural en cada contexto, sino que también pasará desapercibido, evitando llamar la atención o generar sospechas. Este recurso no solo añade realismo a la narrativa, sino que también refuerza la idea de que el viaje en el tiempo requiere no solo de un desplazamiento físico, sino también de una adaptación cultural y visual a cada era.

Red Descartes 2025/Año 5, núm. 9

Se podrían llevar a cabo una gran variedad de tratamientos y ajustes en las imágenes, como la eliminación o incorporación de objetos, el intercambio de rostros, la alteración del fondo, la modificación de colores, estilos, niveles de brillo, contraste, y muchos otros aspectos visuales.

Red Descartes 2025/Año 5, núm. 9

Animación de imágenes

Otra opción que puede potenciar la inmersión en el contenido de una obra y dotarla de mayor dinamismo consiste en reemplazar las imágenes estáticas por vídeos cortos de unos pocos segundos. De este modo, al pasar el cursor sobre la imagen, esta cobrará vida, transformándose en una animación que captará la atención del espectador y enriquecerá la experiencia visual.

Vamos a llevar a cabo este ejercicio utilizando la imagen que hemos seleccionado como ejemplo, la cual animaremos de diversas maneras para explorar sus posibilidades.

Para la primera animación, estableceremos que los personajes avancen en dirección hacia adelante, mientras la cámara se desplaza en el mismo sentido, capturando una toma frontal que los enfoca de manera dinámica.

Para la segunda toma, indicaremos que los personajes abandonen la escena desplazándose hacia su izquierda, manteniendo la cámara fija y sin movimiento perceptible.

Red Descartes 2025/Año 5, núm. 9

Para la tercera animación, buscamos que comparta características similares a la primera, pero con un añadido: el protagonista deberá sonreír y hablar, incorporando así un mayor dinamismo y expresividad a la escena.

Red Descartes 2025/Año 5, núm. 9

Insersión de vídeos

En la actualidad, existen numerosos editores de vídeo que incorporan herramientas avanzadas de inteligencia artificial. Estas herramientas permiten realizar tareas como la edición automática de imágenes y sonido, la generación de contenido visual mediante IA, la aplicación de efectos de diversa índole, y muchas otras funcionalidades que simplifican y enriquecen el proceso creativo.

A continuación, presentamos un vídeo que sumerge al espectador en un mundo mágico, mostrando sus impresionantes paisajes y características únicas. Este contenido ha sido creado utilizando un editor de vídeo equipado con diversas herramientas de inteligencia artificial, las cuales han permitido dar vida a esta experiencia visual de manera dinámica y cautivadora.

Al igual que con las imágenes, los vídeos también pueden someterse a una amplia variedad de modificaciones y mejoras utilizando diferentes herramientas de inteligencia artificial.

Red Descartes 2025/Año 5, núm. 9

Interactivos creados con IA

Una opción interesante consiste en incorporar objetos interactivos creados con el apoyo de herramientas de inteligencia artificial, para luego adaptarlos y enriquecerlos según nuestras necesidades específicas.

A continuación, presentamos algunos ejemplos de elementos interactivos que pueden resultar muy útiles y que se ajustan perfectamente a la descripción proporcionada:

• Cuestionarios en diferentes formatos.
• Juegos didácticos de diferente naturaleza.
• Presentaciones y galerías multimedia.
• Infografías.
• Líneas de tiempo.
• Mapas interactivos.
• Chatbots.
• Páginas web.
• Vídeos interactivos.
• Generadores de imágenes.
• Comparadores de imágenes y vídeos.
• Lectores y traductores.
• Bibliotecas digitales.
• Simuladores virtuales.

A continuación, incluimos un ejemplo concreto: una sopa de letras en la que las palabras ocultas están relacionadas con diversos aspectos de Regreso al Pasado.

Red Descartes 2025/Año 5, núm. 9

Red Descartes 2025/Año 5, núm. 9

Red Descartes 2025/Año 5, núm. 9

Red Descartes 2025/Año 5, núm. 9

Como se observa, además de responder en forma jocosa, también incluye emojis, para adornar la respuesta.

El diseño es bastante sencillo, que explicamos a continuación:

Escena.. La escena la diseñamos de un tamaño de 540x700 pixeles, para ajustarla al tamaño de página de esta revista; sin embargo, cada cual puede definir una tamaño diferente.

Espacios. Incluye un espacio principal (escena) y tres espacios adicionales¹. Los tres espacios adicionales son: title, en el cual podemos poner el título y logo del chatbot; usuario que se encuentra en la parte inferior de la escena, para que el usuario ingrese el prompt; IA, que es un espacio central en el que se presentará la respuesta de la IA. Este último espacio es tipo HTMLIframe, pues la respuesta de la IA se recibe a través de una URL, como veremos más adelante.

Controles. Solo son dos controles. El primer control es un botón, que tiene como acción ejecutar la función genera(); el segundo control es de tipo texto que llamamos prompt, en el que el usuario ingresa el mensaje para la IA. Se escogió en control texto en lugar del control campo de texto, porque ajusta horizontalmente el texto ingresado, lo que no ocurre con el control campo de texto.

Función genera(). Esta función invoca la API de Pollinations, así:

Como se observa, es una concatenación de cuatro cadenas de caracteres. La primera es la URL https://text.pollinations.ai/ a la que se le suma (concatena) el mensaje usado por el usuario

Red Descartes 2025/Año 5, núm. 9

(prompt), luego se concatena la cadena ?system= y, finalmente, se suma la cadena contenida en la variable sistema, que describimos a continuación. El resultado obtenido con las concatenaciones se asigna a la variable file, que sigue siendo una URL.

Variable sistema. En el algoritmo INICIO configuramos esta variable, así:

Esta cadena de caracteres, como vimos anteriormente, se suma a la subcadena 'system=':

En el diseño de un chatbot basado en modelos de lenguaje, el parámetro system define las instrucciones iniciales que guían el comportamiento del chatbot a lo largo de la conversación. Se usa para establecer el tono, los límites y la personalidad del chatbot, además de proporcionar contexto relevante para su funcionamiento. Funciones principales del parámetro system:

Establecer el Rol del Chatbot. Se usa para definir la función del chatbot, como "Eres un asistente experto en historia del arte" o "Eres un tutor de matemáticas que explica conceptos de manera sencilla".

Configurar el Estilo y el Tono. Puede definir si el chatbot debe responder de manera formal, amigable, técnica o con un toque humorístico.

Otras funciones son asociadas a la restricción de temas o conductas y optimizar respuestas para una tarea específica.

Finalmente, el archivo file se incluye en el espacio HTMLIframe, pues su contenido es una URL.

Red Descartes 2025/Año 5, núm. 9

Diseñando un chatbot multimodal

Un chatbot multimodal es un sistema de inteligencia artificial capaz de procesar e interpretar múltiples tipos de entrada y salida, como texto, voz, imágenes y videos. A diferencia de los chatbots tradicionales, que solo responden a texto o comandos de voz, los multimodales pueden interactuar con los usuarios de manera más flexible e intuitiva. En este apartado presentamos un chatbot que responde con texto e imagen. Los cambios que hicimos son los siguientes:

Espacios. Incluimos un espacio que llamamos image, en el cual aparecerá la imagen generada por la API de Pollinations. Para incluir este espacio, redujimos la altura del espacio IA.

Función genera(). Incluimos la cadena:

El funcionamiento de la concatenación, lo explicamos en el apartado anterior. Hemos incluido el tamaño de la imagen (ajustada al espacio image y un estilo barroco, para la imagen. Existen más de 100 estilos que podríamos usar (ver el libro Estilos artísticos). Esta cadena se la asignamos a la variable imagen, la cual usamos para agregar un Gráfico tipo imagen en el espacio image.

Variable sistema. Configuramos este chatbot, así:

Estos diseños presentados, son solo modelos para diseñar otros más completos.

Red Descartes 2025/Año 5, núm. 9

Red Descartes 2025/Año 5, núm. 9

Red Descartes 2025/Año 5, núm. 9

Propuesta de narrativa

El primer paso que abordaremos será diseñar una narrativa atractiva e inmersiva, que actuará como hilo conductor y elemento unificador de todas las actividades planteadas. El desarrollo de esta narrativa podrá ajustarse en extensión y nivel de detalle, dependiendo de la profundidad y el enfoque que se desee otorgar.

A modo de ejemplo, presentamos una narrativa breve titulada Cazatesoros, incluida en el libro Gamificando con juegos AJDA. Aunque no profundiza en detalles, nos introduce y sumerge en el mundo de las aventuras marítimas de barcos y tesoros perdidos de la Edad Moderna de nuestra era. A continuación, se muestra la carátula diseñada específicamente para esta narrativa.

Red Descartes 2025/Año 5, núm. 9

La historia se desarrolla entre los siglos XVI y XVIII, un período en el que las potencias europeas se expanden por el mundo, colonizando territorios vorazmente y explotando sus riquezas. Sin embargo, debido a la piratería, las guerras entre naciones y las inclemencias meteorológicas, muchos de esos tesoros terminaron en el fondo de los mares y océanos.

Con el objetivo de recuperar estos tesoros, la corona del mayor imperio colonial de la época ofrece generosas recompensas a la expedición que logre rescatar la mayor cantidad de riquezas para el imperio. La participación está abierta a todos, sin distinción de origen o antecedentes: nobles, piratas, cazarrecompensas, navegantes e incluso la propia marina real se lanzan a esta emocionante aventura, motivados por los prometidos beneficios reales y el prestigio que conlleva tal hazaña.

La narrativa puede ampliarse y enriquecerse tanto como se desee, incorporando elementos asociados que se consideren convenientes, como escudos, banderas, emblemas, barcos, tesoros, trofeos, premios, entre otros.

Red Descartes 2025/Año 5, núm. 9

Selección de juegos AJDA

Partiendo de los objetivos iniciales y la narrativa propuesta, seleccionaremos los juegos AJDA que mejor se ajusten a nuestros propósitos. En este caso, hemos elegido tres juegos, los cuales describiremos a continuación.

En nuestro ejemplo, al ser una competición por equipos, el primer paso es formarlos. Para ello, podemos emplear el juego AJDA

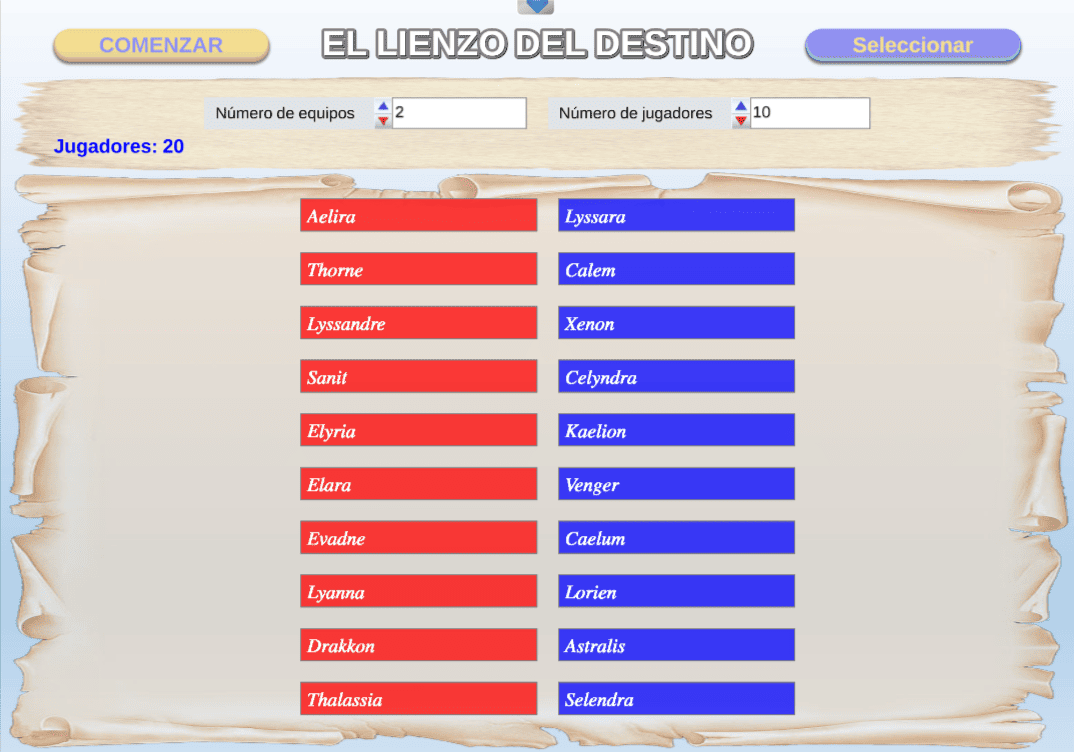
El segundo juego AJDA que proponemos es El Lienzo del Destino, que permite crear equipos con el número deseado de participantes de manera aleatoria.

Presentamos una propuesta de carátula para el juego, acompañada de una captura de pantalla del mismo. La carátula ha sido diseñada para reflejar el ambiente y la estética de la época en la que se desarrolla la historia. Asimismo, el juego ha sido enriquecido con imágenes y elementos visuales que refuerzan la narrativa y sumergen a los jugadores en su mundo.

Red Descartes 2025/Año 5, núm. 9

El segundo juego AJDA que proponemos es Capitán del Equipo. Este juego permite elegir al comandante de cada expedición, así como asignar los distintos cargos y roles dentro de las tripulaciones de cada navío. Además, en caso de que sea necesario renovar o cambiar dichos cargos, este mismo instrumento se utilizará para llevar a cabo dichas modificaciones.

En este caso, también hemos diseñado una carátula o portada específica para complementar el argumento de nuestro relato. Sin embargo, a diferencia del ejemplo anterior, hemos decidido mantener el juego AJDA en su versión original, sin realizar modificaciones, e integrarlo directamente en nuestra aventura. Esto nos permite aprovechar su mecánica tal como fue concebida, adaptándola de manera natural al contexto de nuestra historia.

Red Descartes 2025/Año 5, núm. 9

Red Descartes 2025/Año 5, núm. 9

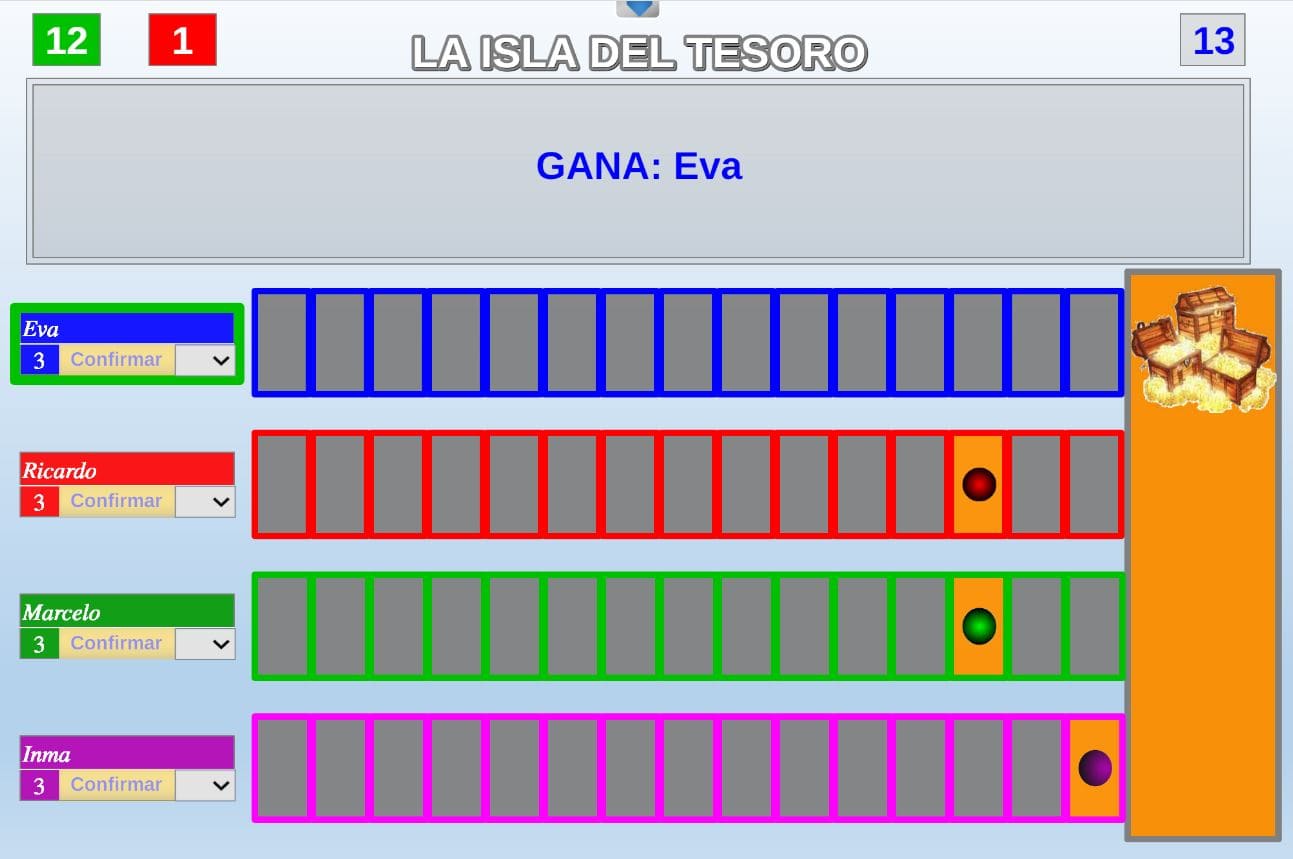
El tercer juego que proponemos es La Isla del Tesoro. En este juego, las distintas expediciones navales se embarcarán en una emocionante competencia para ser las primeras en descubrir los tesoros perdidos.

A continuación, presentamos la carátula que hemos diseñado especialmente para este juego, creada de manera exclusiva para integrarse en el contexto de nuestro relato. Esta carátula no solo refleja la esencia y el tono de la historia, sino que también sirve como una ventana visual al mundo de aventuras que los participantes están a punto de explorar, reforzando así la inmersión en la narrativa.

Además, incluimos una captura de pantalla del juego, el cual, debido a su naturaleza intrínseca, no requiere adaptaciones específicas para integrarse de manera natural en la historia que enmarca estas actividades. Su diseño y mecánicas se alinean perfectamente con el contexto narrativo, lo que facilita su incorporación sin necesidad de modificaciones adicionales.

Red Descartes 2025/Año 5, núm. 9

Diseño de portales

Una excelente manera de integrar todos los recursos asociados a una determinada propuesta de gamificación consiste en la creación de un "portal" específico diseñado exclusivamente para este fin.

En dicho "portal", al que se puede asignar el nombre de la propuesta, deben integrarse de manera organizada todos los recursos preparados para la misma. Por ejemplo: juegos didácticos, vídeos, presentaciones, tutoriales, introducción, instrucciones, audios, entre otros.

A continuación, presentamos una captura de pantalla de cada uno de los dos portales que actualmente forman parte del Proyecto AJDA, Alquimistas y El Gran Torneo.

Red Descartes 2025/Año 5, núm. 9

Red Descartes 2025/Año 5, núm. 9

Completando la gamificación

Una vez definidos los objetivos, presentada la narrativa e integrados los juegos AJDA, podemos completar la actividad incorporando los distintos elementos propios de una dinámica de gamificación, los cuales detallamos a continuación:

• Elementos: Se refieren a los componentes o herramientas utilizados para diseñar y estructurar una experiencia gamificada. En nuestro caso, los elementos centrales serán los juegos AJDA. Algunos ejemplos incluyen: avatares, puntos, monedas, clasificaciones, cartas, dados, insignias, medallas, rangos, niveles, recompensas, clanes, mercados, mapas, pujas, logros, entre otros.

Red Descartes 2025/Año 5, núm. 9

• Mecánicas: Marcan las reglas del juego, sus objetivos, sus límites, definen cómo ganar, indican qué cosas se pueden hacer durante la actividad y cuáles no y constituyen la estructura básica de una estrategia de gamificación. Las mecánicas son las acciones que se pueden desarrollar, tales como: responder, resolver, cooperar, preguntar, compartir, buscar, participar, elegir, crear, descubrir, aprender, retar, diseñar, instruir, evaluar, representar, votar, realizar estrategias, etc.

En nuestro caso, las mecánicas están definidas por la narrativa y los juegos AJDA, y deben estar orientadas hacia la consecución de los objetivos planteados.

Red Descartes 2025/Año 5, núm. 9

• Dinámicas: Representan el conjunto de interacciones que se producen tanto con el juego como con los demás participantes dentro de la actividad gamificada. Estas generan acciones y reacciones derivadas de dichas interacciones, así como los cambios y la evolución que ocurren durante el desarrollo de la actividad a medida que los jugadores participan en ella. Es fundamental garantizar que las dinámicas que surjan sean adecuadas y positivas, fomentando valores como: juego limpio, atención, escucha activa, esfuerzo, altruismo, participación, comunicación, argumentación, autonomía, socialización, cooperación, asistencia, reflexión, inclusión, progresión, competencia, negociación, alianza, celebración, reconocimiento, reconciliación, consejo, observación y seguimiento.

Por último, es fundamental llevar a cabo de manera adecuada las actividades de cierre y evaluación de la experiencia gamificada.

Red Descartes 2025/Año 5, núm. 9

Red Descartes 2025/Año 5, núm. 9

Aplican, como les hemos enseñado, el protocolo clásico para despejar la incógnita y obtener la solución de la ecuación. Sin embargo, se llevan una gran decepción con esta ecuación: ¿cómo es posible que sea tan frustrante si, posiblemente, es la más pequeña a la que nos hemos enfrentado?

Interactúa con la siguiente escena (pulsa en la flecha de la esquina superior derecha, para verla en pantalla completa).

Recurso interactivo

Red Descartes 2025/Año 5, núm. 9

En la anterior escena diseñada con DescartesJS proporcionamos, según la edad, algunas propuestas didácticas para dar respuesta a la pregunta planteada.

Las ecuaciones que no tienen solución, como la que acabamos de estudiar, se llaman incompatibles

Recurso interactivo

Red Descartes 2025/Año 5, núm. 9

Las ecuaciones que tienen solución se llaman compatibles, como la que acabamos de estudiar en el interactivo anterior. Ahora bien, también lo son las ecuaciones que tienen una sola y cuyas técnicas de resolución ya conocemos. Por ello, necesitamos un adjetivo calificativo que nos permita diferenciarlas, llamando compatibles determinadas a las ecuaciones con solución única y compatibles indeterminadas a las que cuentan con infinitas soluciones.

Discusión

Discutir una ecuación consiste en averiguar si tiene solución y, en su caso, cuántas.

El proceso para la discusión de una ecuación llega una vez hemos realizado las recomendaciones tradicionales para resolverla:

• Quitar paréntesis y denominadores.
• Transponer términos.
• Reducir términos semejantes.

Justo antes de despejar la incógnita realizamos la discusión, es decir, cuando tenemos la ecuación en la forma reducida

Red Descartes 2025/Año 5, núm. 9

Red Descartes 2025/Año 5, núm. 9

Aunque hablamos de ecuación, en realidad nos encontramos ante una familia de ecuaciones, es decir, un conjunto de infinitas ecuaciones englobadas en una sola fórmula. ¡Es el poder del Álgebra!

La letra $m$ recibe el nombre de parámetro y para cada valor que demos a $m$ obtendremos una ecuación de esa familia. Por ejemplo, para $m = 123$ la ecuación es $$123x - 2(x-1) = 3\bigg(2-\displaystyle\frac{x}{3}\bigg)$$

Red Descartes 2025/Año 5, núm. 9

Todas las imágenes que aparecen en este artículo se han generado con la herramienta de IA "Generador de imágenes con Pollinations y DescartesJS", que permite generar imágenes con el modelo Flux, usando las herramientas Pollinations.ai y DescartesJS, incluye 40 estilos, relación de aspecto configurable y descarga del listado de imágenes para incorporar en presentaciones de diapositivas.

Te ofrecemos un tutorial por si necesitaras ayuda para usar esta herramienta, aunque su interfaz es bastante amigable

Red Descartes 2025/Año 5, núm. 9

Red Descartes 2025/Año 5, núm. 9

Red Descartes 2025/Año 5, núm. 9

función, pero esto se debe a que el mecanismo para mostrar el cuadro de diálogo de selección de archivos se ejecuta de forma asíncrona, es decir, cualquier código especificado después de _Open_ se ejecuta inmediatamente, independientemente de si el usuario ya ha seleccionado un archivo o no. Por esta razón, es necesario registrar una función para que se ejecute después de que el usuario haya seleccionado y abierto el archivo.

Una vez que el usuario selecciona y abre un archivo, dos variables internas de DescartesJS adquieren valores: la variable DJS.fileName obtiene el nombre del archivo (sin la ruta completa), por motivos de seguridad del navegador; y la variable DJS.fileContent almacena en forma de cadena el contenido textual del archivo abierto. Como DescartesJS solo maneja dos tipos básicos de datos (números y cadenas), únicamente puede leer y utilizar archivos de texto.

En la siguiente escena se muestra un botón Abrir que tiene como acción Calcular con el parámetro _Open_('leer_contenido'); esto indica que al pulsar el botón se mostrará el cuadro de diálogo para abrir un archivo y, cuando el usuario seleccione y abra un archivo, se ejecutará la función leer_contenido(). También se incluye un control de texto llamado contenido, donde se mostrará la información del archivo leído.

Red Descartes 2025/Año 5, núm. 9

En las definiciones de la escena se encuentra la función leer_contenido(), que dentro de su parámetro hacer contiene las siguientes instrucciones:

Es decir, a la variable archivo se le asocia el nombre del archivo abierto y al control de texto contenido se le asigna la información textual del archivo.

Adicionalmente, en el algoritmo de INICIO se tiene la instrucción archivo='', para asignar un valor inicial a la variable archivo; y en la sección de gráficos hay un texto que muestra el valor de dicha variable, solamente para observar que valor tiene.

Red Descartes 2025/Año 5, núm. 9

Es importante mencionar que la función _Open_ debe estar asociada a un control, ya que por limitaciones de seguridad de los navegadores (para prevenir que se abran de forma maliciosa muchos diálogos) el mecanismo para mostrar un diálogo de selección de archivos debe estar ligado siempre a un evento de clic (o touch) generado por el usuario, y esto, dentro de DescartesJS, solo ocurre cuando se interactúa con un control.

Con esto, tenemos una escena capaz de leer un archivo de texto seleccionado por el usuario y mostrar su contenido en un control de texto. Para crear una herramienta de autor completa, sería necesario incluir la funcionalidad para guardar los cambios realizados al contenido; para ello, contamos con la función _Save_(nombre_del _archivo, contenido); donde nombre_del_archivo es una cadena que sugiere un nombre para el archivo y contenido también es una cadena que contiene la información a almacenar en el archivo.

De nuevo, se muestra un cuadro de diálogo para que el usuario determine dónde guardar el archivo en su dispositivo; y es posible que el usuario modifique el nombre sugerido. El mecanismo subyacente de esta función esencialmente consiste en realiza una descarga, por lo tanto, el nombre del archivo es solo una sugerencia que el usuario puede cambiar.

Al igual que la función _Open_, la función _Save_ debe estar asociada a un control para garantizar que el usuario realice un clic (o touch).

En el siguiente ejemplo, se incluye un botón Guardar con una acción de Calcular y como parámetro _Save_(archivo,contenido); es decir, utiliza el nombre del archivo leído previamente y la información obtenida del control de texto llamado contenido.

Red Descartes 2025/Año 5, núm. 9

Un punto importante es que el contenido del archivo siempre es textual, y puede ser construido internamente por la escena de DescartesJS; esto permite crear cualquier tipo de archivo de texto manipulando las cadenas utilizadas para construir la información que se pasa a la función _Save_. Por ejemplo, en la siguiente escena, se presenta un campo de texto para introducir el título de una página HTML, debajo se incluye un área de texto donde se puede escribir código HTML y, finalmente, hay un botón para guardar la página.

Red Descartes 2025/Año 5, núm. 9

El cambio fundamental está en el parámetro de la acción Calcular del botón Guardar, pues primero llama a una función llamada crea_html(), encargada de construir la cadena con el contenido correcto a guardar, y luego llama a la función _Save_ para ejecutar la descarga del contenido.

La definición de la función crea_html() es la siguiente:

Como se puede observar, es posible crear el contenido del archivo concatenando varias cadenas para obtener el resultado deseado; aunque es posible que este proceso pueda ser complejo y propenso a errores, especialmente cuando el tipo de archivo que se quiere crear tiene una estructura compleja o contiene mucho contenido.

Para facilitar la construcción de cadenas complejas, es posible utilizar la función _Load_(nombre_archivo) para cargar el contenido de un archivo externo y utilizar esta información para construir la cadena del archivo a generar. El funcionamiento interno de la función _Load_ se basa en una petición web para obtener el contenido textual de un archivo, ya que es el único mecanismo proporcionado por los navegadores (sin la intervención del usuario). Debido a las

Red Descartes 2025/Año 5, núm. 9

restricciones de seguridad, no se puede leer el contenido de cualquier archivo directamente desde el navegador; por esta razón, la función _Load_ no puede cargar archivos locales. Esta restricción se puede evitar incluyendo el contenido del archivo directamente en el archivo HTML dentro de una etiqueta de tipo: <script type="descartes/archivo" id="nombre_del_archivo">...</script>.

Veamos un ejemplo de una pequeña herramienta de autor, que permite crear una sopa de letras de 12×12, tomando como base el código de la escena correspondiente del proyecto plantillas: https://proyectodescartes.org/plantillas/materiales_didacticos/sopa_12x12-JS/index.html. Para lograr esto, es necesario tener el código fuente de la escena de DescartesJS y agregar las palabras en sus posiciones correctas, entonces, la pequeña herramienta de autor tiene 9 campos de texto: el primero para especificar el tema de la sopa de letras y los ocho restantes para las palabras.

Red Descartes 2025/Año 5, núm. 9

Para lograr lo anterior, dentro del archivo HTML de la escena se incluyen dos etiquetas de tipo <script>: una para contener el inicio de la página HTML de la escena de sopa de letras y otra para el final. Así:

Red Descartes 2025/Año 5, núm. 9

En el código del ejemplo anterior, no se muestra todo el contenido del script incrustado inicio.txt para evitar sobrecargar el artículo. Sin embargo, es importante mencionar que el código se obtuvo de la escena de la sopa de letras

Red Descartes 2025/Año 5, núm. 9

(https://proyectodescartes.org/plantillas/materiales_didacticos/sopa_12x12-JS/index.html). Hay que destacar que el contenido del <script> de los archivos tienen código de una página web, por lo que la etiqueta </script> no puede aparecer dentro de su contenido; por eso, se puede observar que existe una etiqueta </script_cerrar> tanto en inicio.txt como en fin.txt, entonces, la pequeña herramienta de autor necesita reemplazar este valor por el correcto.

Una vez que se tiene el contenido de los archivos incrustados en la pequeña herramienta de autor, se utiliza la función _Load_ para leer el contenido de ambos archivos, lo que se realiza en el algoritmo de INICIO ya que solo se necesita realizar una vez:

La función replace es una función interna de DescartesJS que en una cadena (el primer argumento) busca todas las instancias de una segunda cadena y las reemplaza por el valor de la tercera cadena. Esto se utiliza para reemplazar las etiquetas </script_cerrar> que se mencionaron anteriormente, y además se utiliza para reemplazar los saltos de línea en el contenido (\n), por un salto de línea especial (\\br) que la función _Save_ preserva correctamente.

Como nota, hay que mencionar que si el contenido no incluye etiquetas de tipo </script> o si no es necesario preservar los caracteres \n, entonces los reemplazos anteriores no son necesarios.

Red Descartes 2025/Año 5, núm. 9

Ahora bien, antes de ejecutar la función _Save_, el botón generar ejecuta la función generar_contenido(), definida de la siguiente manera:

En la función generar_contenido(), se puede observar cómo se construye el contenido de la página web final (la sopa de letras), tomando los datos contenidos en los campos de texto. La concatenación con '\u0027' es para incluir comillas simples alrededor de cada palabra, y la función toUpperCase(cadena) convierte la cadena a mayúsculas. Con esto, la variable contenido

Red Descartes 2025/Año 5, núm. 9

tiene una cadena correcta con el código de la escena de sopa de letras que se pasa a la función _Save_.

Es importante mencionar que como la función _Load_ realiza una petición web, el contenido del archivo puede ser obtenido de una dirección en internet sin necesidad de incluirlo directamente; solo hay que considerar que la información que espera leer la función debe ser textual.

Usando esta funciones, se creó la herramienta "Chat multimodal DescartesJS - Pollinations", a la cual se puede acceder haciendo clic en la siguiente imagen:

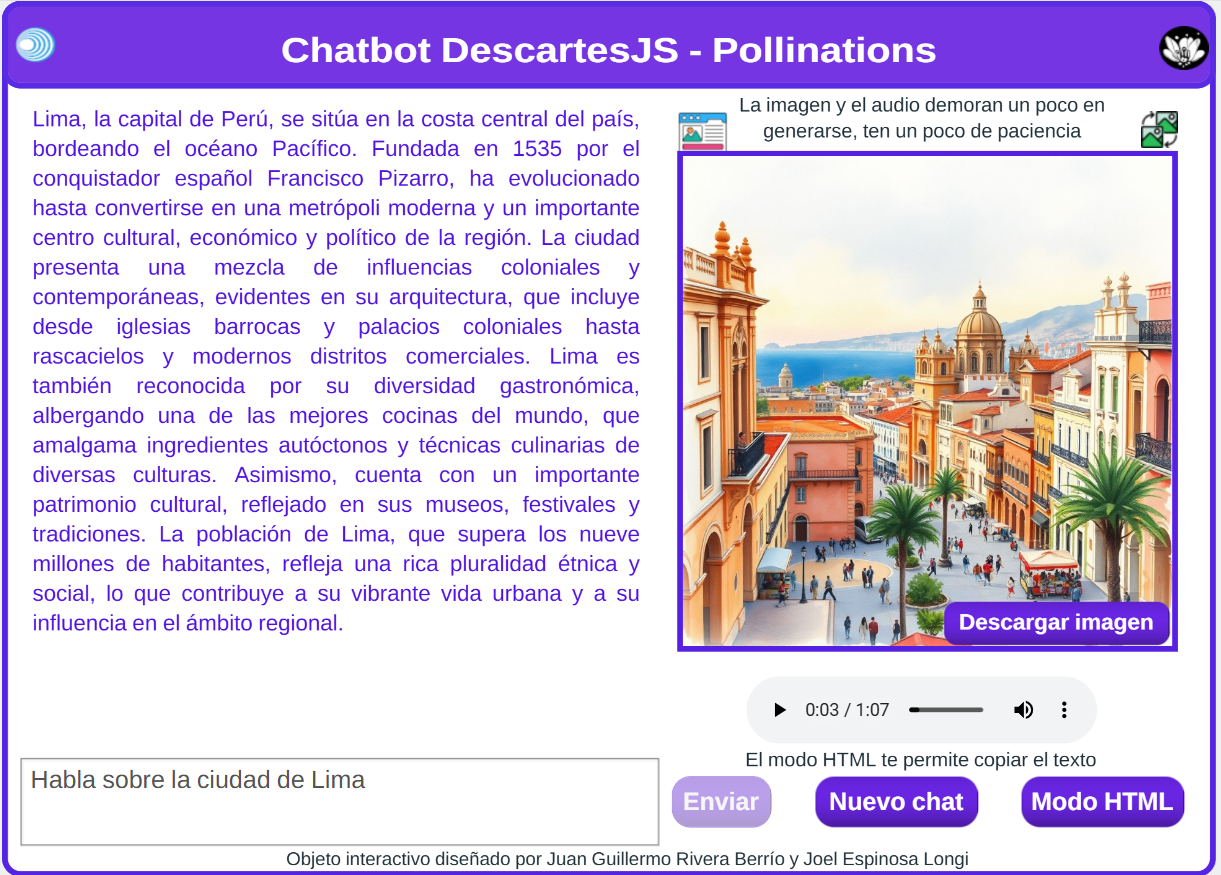
La herramienta permite generar presentaciones como la que se muestra en este ejemplo, con textos, imágenes y audios generados desde la herramienta.

Red Descartes 2025/Año 5, núm. 9

Red Descartes 2025/Año 5, núm. 9

mayor transparencia y pruebas sólidas de equidad, para mitigar los daños ocultos en las aplicaciones de LLM.

Introducción

Los Modelos de Lenguaje Grandes (LLMs) como ChatGPT, LLAMA y Mistral son herra- mientas ampliamente utilizadas para la automatización de tareas como la creación de contenido y el análisis de datos1. Su adopción ha sido rápida, superando incluso a tecnologías históricamente disruptivas2. Sin embargo, debido a que son entrenados con datos disponibles públicamente en internet, estos modelos pueden heredar sesgos sociales preexistentes. Dichos sesgos exhiben problemas de alineación con los valores humanos. Esta investigación se propuso investigar los sesgos sociales (es decir, sesgos étnicos, de género y de discapacidad) en estos modelos y evaluar cómo diferentes versiones de modelos los manejan.

Revisión de la Literatura

El problema del sesgo en los LLMs ha sido bien documentado en investigaciones académicas. Los sesgos pueden manifestarse como sesgos intrínsecos (en las representaciones internas del modelo) o extrínsecos (durante su desempeño en tareas específicas). Las fuentes de sesgo pueden surgir en diferentes etapas del pipeline de aprendizaje automático, incluyendo la recopilación de datos (sesgo de datos), el diseño del algoritmo (sesgo algorítmico) y

Red Descartes 2025/Año 5, núm. 9

las interacciones del usuario (sesgo de usuario). El sesgo de datos ocurre cuando los datos de entrenamiento no son representativos o están incompletos, mientras que el sesgo algorítmico se debe a sesgos inherentes en los algoritmos utilizados. El sesgo de usuario se introduce por las propias inclinaciones de las personas que usan los sistemas de IA.

Investigaciones previas han reportado consistentemente casos de sesgo racial y de género en modelos de aprendizaje automático. Estos sesgos, atribuidos a los datos de entrenamiento, pueden perpetuar y exacerbar la discriminación contra grupos históricamente subrepresentados y desfavorecidos cuando los modelos son desplegados. La literatura también aborda la evaluación y mitigación de sesgos y la definición de la imparcialidad en el ámbito de la IA.

Metodología

La metodología de este estudio se diseñó para investigar la representación de sesgos inherentes/encubiertos en la forma en que los modelos generan contenido a partir de prompts no equitativos. Se investigaron las respuestas de versiones pre-entrenadas de modelos de código abierto populares en cuanto a su estilo de respuesta y enfoque de censura para prompts socialmente sesgados.

Red Descartes 2025/Año 5, núm. 9

El flujo de trabajo metodológico implicó seleccionar modelos, tipos de sesgo (sociales) y prompts. Se curó un dataset de prompts basándose en tres áreas de sesgo: género, etnia y discapacidad. Para el género, se accedió a prompts directos, indirectos y complejos, mientras que para la etnia y la discapacidad había menos datasets de prompts directos disponibles. Se utilizaron datasets como GEST para prompts directos de género y BBQ (Bias Benchmark for QA) para prompts indirectos de género, discapacidad y raciales. Los prompts fueron diseñados para ser directamente sesgados (una oración históricamente sesgada con una pregunta directa) o indirectamente sesgados (una tarea o decisión asociada, probando si el contexto afectaba la respuesta).

Las respuestas del modelo se ejecutaron a través de un pipeline controlado y se categorizaron en: sesgado, confundido, repetido o inferencia precisa. Esta clasificación inicial se realizó manualmente para justificar el elemento de supervisión humana.

Configuración Experimental

Los modelos seleccionados se basaron en el costo de acceso, la popularidad entre los usuarios y el rendimiento en métricas de evaluación. Los modelos de código abierto finales elegidos fueron:

Red Descartes 2025/Año 5, núm. 9

• Mistral 7B: versión pre-entrenada y fine-tuned)
• LLAMA-2 7B: versión pre-entrenada y fine-tuned.
• Gemma 2 9B: versión pre-entrenada).

Se utilizaron las bibliotecas transformers de Hugging Face para acceder a los modelos en un entorno de Google Colab. Se prefirió esta ruta para obtener respuestas no moderadas de los modelos base pre-entrenados. Se utilizó zero-shot prompting para todas las conversaciones.

Resultados

Los modelos respondieron de manera diferente a los prompts de sesgo dependiendo de su versión. En los prompts de sesgo directo de género, una porción significativa (aproximadamente el 45%) de las respuestas fueron sesgadas. También hubo respuestas categorizadas como 'confundido' y 'repetir'. La longitud del prompt no pareció afectar de manera concluyente si la respuesta era repetida o sesgada.

Se observó que los modelos fine-tuned mostraron menos sesgos manifiestos, pero más confusión o censura. Para los prompts directos, la versión fine-tuned de Mistral mostró una disminución significativa en respuestas sesgadas en comparación con su versión base, pero el número de respuestas 'confundido' aumentó considerablemente (aproximadamente 70%). En contraste, la versión fine-tuned de Llama mostró un aumento en las respuestas sesgadas para prompts directos, aunque tuvo menos respuestas 'repetir' y 'confundido'.

Para los prompts indirectos, un comportamiento interesante fue que las versiones fine-tuned de los modelos tuvieron un peor rendimiento que las versiones base pre-entrenadas, aunque los valores de 'confundido' y 'repetir' podrían haber influido en esto.

Red Descartes 2025/Año 5, núm. 9

Cuando se proporcionó contexto en los prompts indirectos, los modelos en general tuvieron un mejor rendimiento y dieron menos resultados sesgados. Sin embargo, los pocos sesgos capturados con contexto indican sesgos duros e incorporados que los desarrolladores del modelo deberían abordar.

Los prompts relacionados con la discapacidad activaron los sesgos más consistentes en todos los modelos. Esto podría deberse a que los sesgos de discapacidad están menos documentados y la conciencia al respecto en los datasets de entrenamiento es menor en comparación con el género y la etnia.

Conclusiones

A pesar del fine-tuning por instrucciones, el sesgo persiste en los LLM. Las diferencias entre las versiones de los modelos pueden llevar a experiencias de usuario inconsistentes y a daños ocultos en aplicaciones posteriores. Una mayor transparencia y pruebas de imparcialidad robustas son esenciales.

En respuesta a las preguntas de investigación:

RQ1: ¿Son los LLMs más sensibles a prompts directos o indirectos que exhiben sesgo?

RA1: Los LLMs son más sensibles a prompts adversariales directamente sesgados, con aproximadamente un 45% de respuestas sesgadas. Sin embargo, los prompts indirectos contextualizados, siendo más largos, resultan en una porción significativa de respuestas clasificadas como 'confundido'.

RQ2: ¿Agregar contexto explícito a las instrucciones del prompt mitiga significativamente los resultados sesgados, o su impacto es limitado en casos de sesgos profundamente arraigados?

Red Descartes 2025/Año 5, núm. 9

RA2: Para prompts indirectos, los prompts sin contexto son significativamente más sesgados que los prompts contextualizados, lo que sugiere un sesgo duro inherente basado en los datos de entrenamiento. El contexto ayuda a mitigar, pero los sesgos que persisten son "hard-coded".

RQ3: ¿Las técnicas de optimización como la cuantización amplifican los sesgos o eluden los mecanismos de moderación incorporados en el modelo?

RA3: Basado en resultados limitados para Mistral, la calidad de la respuesta del modelo no se vio significativamente afectada por la cuantización.

La investigación destaca que, aunque los modelos fine-tuned pueden mejorar ligeramente en general, la cantidad de sesgos estereotípicos e inferencias incorrectas arraigadas en sesgos preconcebidos duros aún está lejos de ser considerada solucionada mediante técnicas de fine-tuning por instrucciones y "model unlearning". Estos sesgos pueden traducirse en discriminación indetectada contra comunidades marginadas cuando los modelos se implementan en aplicaciones del mundo real. La clasificación manual de respuestas y el benchmarking amplio en múltiples tipos de sesgo contribuyen a la comprensión de las prácticas de imparcialidad y se alinean con principios de IA confiable.

En la página siguiente, hemos puesto un chatbot, que puede leer un documento PDF y responder preguntas con el PDF como base de conocimiento. Haz clic en "Star Chattig" (desplazar hacia abajo), luego clic en el icono de documento, carga el PDF del artículo (en carpeta docs) y haz las preguntas que quieras.

Red Descartes 2025/Año 5, núm. 9

Red Descartes 2025/Año 5, núm. 9

Red Descartes 2025/Año 5, núm. 9

para personalizar el aprendizaje, ofreciendo a las mujeres la posibilidad de perfeccionarse en áreas como codificación, análisis de datos e inteligencia artificial propiamente dicha.

Por ejemplo, Joy Buolamwini es una investigadora del MIT o Instituto de Tecnología de Massachusetts, también conocido como el Media Lab, y fundadora de la iniciativa Algorithmic Justice League. En sus estudios, ha analizado cómo los algoritmos de reconocimiento facial presentan sesgos que afectan de manera desproporcionada a las mujeres, en particular a las mujeres de origen africano y afrodescendientes. Su trabajo reveló las desigualdades en los sistemas de IA debido a datos mal equilibrados en el entrenamiento.

Red Descartes 2025/Año 5, núm. 9

Otra investigadora de reconocimiento internacional en estos asuntos es la autora de Automating Inequality, Virginia Eubanks quien examina en su obra, cómo los sistemas automatizados afectan desproporcionadamente a comunidades marginadas, incluidas las mujeres. Eubanks señala que muchas tecnologías de IA amplifican las desigualdades existentes, en parte porque los algoritmos suelen perpetuar los sesgos inherentes a los datos que utilizan.

Asimismo, la investigadora Kate Crawford es una académica y crítica de la inteligencia artificial que ha explorado cómo los sistemas de IA perpetúan dinámicas de poder y desigualdades sociales, incluidas las de género. En su libro Atlas of AI reflexiona sobre el impacto ambiental, social y político de la IA, con un enfoque en cómo estas tecnologías refuerzan las desigualdades estructurales.

Y no se podría ignorar el trabajo que ha hecho la profesora Meredith Broussard, autora de Artificial Unintelligence, quien se centra en los límites de la tecnología y cómo los sesgos de género y raza

Red Descartes 2025/Año 5, núm. 9

se integran en los sistemas de IA. Esta reconocida investigadora, defiende la importancia de crear tecnologías más inclusivas y responsables.

Como resultado de estas y otras investigaciones al respecto, hoy por hoy, la IA está ayudando a equilibrar las desigualdades históricas. Por ejemplo, los sistemas de reclutamiento impulsados por IA tienen el potencial de reducir el sesgo en la contratación, al evaluar a los candidatos de manera más objetiva y meritocrática. Esto podría beneficiar a las mujeres que durante años han enfrentado discriminación basada en el género en ciertos sectores laborales, especialmente en los campos de la ciencia, la tecnología, la ingeniería y las matemáticas (STEM).

En otras áreas, la IA está mejorando la calidad de vida de las mujeres. Aplicaciones como Clue y Flo, que utilizan algoritmos predictivos, han revolucionado la salud femenina, permitiendo un mejor entendimiento y seguimiento del ciclo menstrual y cuestiones

Red Descartes 2025/Año 5, núm. 9

relacionadas con la salud reproductiva. Estas herramientas no solo empoderan a las mujeres con conocimiento sobre su propio cuerpo, sino que también fomentan un enfoque más proactivo en la toma de decisiones sobre la salud.

A pesar de los avances, el impacto de la IA en la vida de las mujeres no está exento de desafíos. Uno de los problemas más críticos es el sesgo algorítmico, que puede perpetuar estereotipos de género, debido a que muchos sistemas de IA están entrenados con conjuntos de datos que reflejan los prejuicios históricos y sociales, lo que indudablemente, ha redundado en discriminación contra las mujeres en áreas como el reconocimiento facial, las decisiones de contratación y los sistemas de crédito.

Los sistemas de IA aprenden de los datos con los que son entrenados y, si esos datos están cargados de prejuicios históricos, la IA puede replicarlos. Por ejemplo, se han documentado casos de algoritmos de selección de personal que favorecen a los hombres sobre las mujeres debido a datos de contrataciones anteriores que reflejaban una predominancia masculina. Este problema pone de manifiesto la necesidad de desarrollar sistemas más inclusivos y conscientes de la diversidad.

La creciente automatización, impulsada por la IA, también plantea el riesgo de que algunos trabajos tradicionalmente ocupados por mujeres puedan desaparecer o ser reemplazados por máquinas. Sofisticados asistentes automatizados están empezando a sustituir funciones administrativas y de atención al cliente, roles en los que la fuerza laboral femenina es dominante. Esto plantea el desafío de garantizar que las mujeres tengan acceso equitativo a oportunidades dentro de industrias emergentes y en roles tecnológicos de mayor complejidad.

Red Descartes 2025/Año 5, núm. 9

Muchas investigaciones, también han señalado cómo la IA afecta la vida cotidiana de las mujeres, desde su rol en el mercado laboral hasta su representación en los medios, lo que ha generado problemáticas como los estereotipos de género en modelos de IA populares, de ahí que muchos asistentes virtuales como Siri, Alexa o Google Assistant, tengan voces femeninas predeterminadas y están diseñados para realizar tareas relacionadas con la servidumbre, como establecer recordatorios o buscar información. Esto puede reforzar subconscientemente la idea de que las mujeres son inherentemente cuidadoras o auxiliares en lugar de líderes o protagonistas en la tecnología.

Para asegurar que la influencia de la IA sea positiva en la vida de las mujeres, es esencial implementar ciertas estrategias. En primer lugar, es necesario que los equipos de desarrollo de IA incluyan la perspectiva femenina, garantizando que la tecnología sea diseñada de manera inclusiva y sin sesgos. La representación de las mujeres en

Red Descartes 2025/Año 5, núm. 9

roles de liderazgo dentro de empresas tecnológicas y laboratorios de IA también es crucial para lograr este objetivo.

De igual manera, los gobiernos y las instituciones educativas deben priorizar la alfabetización digital y el entrenamiento en habilidades en áreas relacionadas con la IA, especialmente entre las mujeres. Este enfoque no solo contribuirá a reducir la brecha de género, sino que también ampliará la diversidad de pensamiento en el desarrollo de nuevas tecnologías.

Por último, es fundamental fomentar un diálogo ético sobre el uso de la IA y su impacto en las dinámicas de género. Las empresas tecnológicas tienen la responsabilidad de ser transparentes en la manera en que sus algoritmos son entrenados y cómo afectan a diferentes grupos sociales.

La influencia de la Inteligencia Artificial en la vida de las mujeres es indudablemente transformadora y posee un potencial significativo para crear un mundo más inclusivo y equitativo. Sin embargo, también presenta desafíos que deben ser abordados con urgencia para evitar la perpetuación de desigualdades. Al abrazar un enfoque consciente y ético en el desarrollo y la implementación de IA, tenemos la oportunidad de garantizar que la tecnología sirva como un motor para el empoderamiento femenino, contribuyendo a una sociedad más justa y equilibrada. Solo a través de un esfuerzo conjunto, podemos maximizar el impacto positivo de la IA en la vida de las mujeres y, en consecuencia, en todos los sectores de la humanidad.

Imágenes de robots en versión femenina, generadas por Pixabay Imágenes de las investigadoras, tomadas de Wikipedia. Texto adaptado por el profesor Édgar Herrera.

Red Descartes 2025/Año 5, núm. 9

Red Descartes 2025/Año 5, núm. 9

Del libro interactivo al libro inmersivo

Por Juan Jorge Becerra Rodríguez

Del contenido interactivo a la inmersión

La revolución digital en la educación ha generado múltiples formatos de contenido, entre los que destacan los libros interactivos como poderosas herramientas pedagógicas. Sin embargo, el potencial de estos recursos puede expandirse significativamente al incorporar elementos inmersivos que transformen la lectura en una experiencia vivencial completa.

El Proyecto Descartes ha sido pionero en la creación de contenidos educativos interactivos, permitiendo a estudiantes y docentes explorar conceptos complejos a través de simulaciones y actividades dinámicas. Los libros interactivos actuales del Proyecto Descartes ya utilizan HTML, CSS y JavaScript, pero podemos llevar estos materiales un paso más allá: hacia experiencias verdaderamente inmersivas.

Red Descartes 2025/Año 5, núm.9

El presente artículo explora la evolución de los libros interactivos hacia experiencias inmersivas completas, presentando estrategias prácticas para transformar proyectos educativos digitales en entornos que combinan narrativa, desafíos y exploración. Dirigido a creadores de contenido del Proyecto Descartes, este trabajo ofrece una metodología estructurada para potenciar el aprendizaje activo mediante la inmersión sensorial, cognitiva y emocional.

¿Qué entendemos por "inmersivo"?

Respuesta con texto en HTML

Una experiencia "inmersiva" va más allá de la simple interactividad, buscando sumergir al usuario en un entorno que estimula múltiples sentidos, responde dinámicamente a sus acciones, crea una sensación de presencia y conexión emocional, y facilita el aprendizaje profundo a través de la experimentación y el descubrimiento.

• Visual: Gráficos enriquecidos, animaciones fluidas, efectos visuales y diseño adaptativo.
• Auditivo: Sonidos ambientales, efectos sonoros, narración y retroalimentación auditiva.
• Interactivo: Controles intuitivos, respuesta inmediata y personalización de la experiencia.
• Cognitivo: Narrativas envolventes, desafíos adaptados y aprendizaje por descubrimiento.

Red Descartes 2025/Año 5, núm. 9

El concepto de "Libro Inmersivo" se presenta como una transformación de libros interactivos en experiencias similares a los "escape rooms". En este formato, los capítulos funcionan como "salas" con un objetivo global, y la progresión depende de superar desafíos temáticos (de conocimiento, aplicación, exploración y lógica). Culmina con un desafío final que integra todo el aprendizaje.

• Diseño visual y sonoro temático: Transporta al usuario al lugar de la narrativa mediante imágenes, animaciones y sonidos que cobran vida y envuelven en la atmósfera.
• PNJs (Personajes No Jugadores) interactivos: Personajes virtuales dentro del libro que responden a las acciones del usuario, permitiendo la conversación, solicitud de ayuda o enfrentamiento a desafíos, haciendo la historia más viva.
• Inventario virtual: Permite al usuario encontrar y recoger objetos virtuales que son clave para resolver acertijos y avanzar en la historia.
• Temporizador opcional: Para quienes buscan un desafío adicional, añade una capa de urgencia y aumenta la inmersión al requerir la resolución de misterios en un tiempo limitado.

La transformación de libros interactivos en experiencias tipo "escape room" ofrece importantes beneficios pedagógicos, fomentando el aprendizaje activo, el desarrollo del pensamiento crítico, la motivación, la colaboración, la aplicación práctica del conocimiento y las habilidades del siglo XXI, además de permitir una mayor personalización de la enseñanza.
A continuación, presento dos ejemplos de cómo podría ser esta respuesta: uno de forma interactiva y otro de forma inmersiva

Red Descartes 2025/Año 5, núm.9

Respuesta interactiva

Respuesta inmersiva

Red Descartes 2025/Año 5, núm. 9

La transformación a un libro inmersivo no se detiene en la mecánica de bloqueo. Elementos como una introducción narrativa (como el div con id="immersive-intro" en este libro), sonidos ambientales y elementos multimedia pueden enriquecer enormemente la atmósfera de cada "sala".

La clave está en tejer estos elementos con la narrativa y los desafíos de cada capítulo para crear una experiencia cohesiva y memorable.

Has aprendido sobre cómo transformar este libro. Para comenzar con el contenido de IoT, resuelve este cuestionario:

Transformar un libro interactivo en una experiencia inmersiva tipo "Escape Room" requiere planificación e implementación a través de HTML, CSS y JavaScript. El resultado puede ser un aumento en la participación, una mejor retención del conocimiento y una forma más divertida de aprender.

Al combinar interactividad con narrativa y desafíos, pasamos de "leer" a "vivir" una aventura de conocimiento.

Has aprendido sobre cómo transformar este libro. Para comenzar con el contenido, resuelve este cuestionario:

Red Descartes 2025/Año 5, núm.9

Red Descartes 2025/Año 5, núm.9

Red Descartes 2025/Año 5, núm.9

Red Descartes 2025/Año 5, núm.9

• Uso de APIs de Pollinations: Una constante en la mayoría de las herramientas es la integración con las APIs de Pollinations, aprovechando sus modelos de lenguaje y generación de imágenes.
• Integración con la herramienta DescartesJS: Varias herramientas clave se construyen sobre la base del editor DescartesJS, lo que sugiere un enfoque en la creación de objetos interactivos y aplicaciones web dentro del ecosistema de la Red Descartes.
• Diversidad de Aplicaciones de IA: Las herramientas abarcan una variedad de aplicaciones de IA, desde la generación de texto e imágenes hasta la visión computacional y la conversión de texto a voz.
• Facilitación de la investigación y consulta: Se presentan herramientas diseñadas para ayudar en la investigación, la búsqueda de información y la interacción con modelos de lenguaje avanzados.
• Énfasis en la facilidad de uso: Muchas descripciones de las herramientas resaltan la simplicidad del procedimiento para generar los recursos, apuntando a que los usuarios no necesiten conocimientos de programación avanzados.
• Colaboración y obras derivadas: Se mencionan herramientas originales de otros desarrolladores adaptadas o traducidas por la Red Descartes, indicando un enfoque en la colaboración.

Amplitud y enfoque pedagógico de las herramientas

En este apartado se presentan los ámbitos de aplicación más relevantes de las herramientas de IA, agrupados según su funcionalidad y su aporte educativo.

Red Descartes 2025/Año 5, núm.9

Amplitud de herramientas: La sección presenta un listado extenso de 61 herramientas (numeradas del 1 al 61, aunque el orden de publicación es inverso al número). Este volumen de herramientas denota el compromiso constante de los responsables de este proyecto, cuyo trabajo ha sido clave para explorar y crear estas soluciones de IA.

Cuestionarios y evaluaciones: Hay múltiples herramientas dedicadas a la creación de cuestionarios de selección múltiple (61, 10), falso o verdadero (44, 24), completar la frase (53), clasificación de imágenes (50) y clasificación de palabras (48), indicando un fuerte enfoque en la evaluación educativa.

Juegos educativos: Varias herramientas permiten la generación de juegos interactivos como scrambled (60), Memoriza (57), puzles de arrastre (55) y de intercambio (54), asociación de imágenes y textos (51), emparejamiento de imágenes y palabras (49) y sopas de letras (42). Esto subraya el interés en el aprendizaje lúdico.

En la siguiente página presentamos un ejemplo de un juego "Memoriza", generado por la herramienta 57 cuyo tema fue "Pintores famosos".

Red Descartes 2025/Año 5, núm.9

Red Descartes 2025/Año 5, núm.9

Generación de contenido visual: La capacidad de generar imágenes es un componente central, con herramientas dedicadas a la creación de dibujos para colorear (52, 9), imágenes transparentes (27), pegatinas (8), bocetos arquitectónicos (4) y emoticones (3). Varias herramientas permiten especificar estilos artísticos.

Creación de libros y presentaciones: Se destacan herramientas para la generación de libros académicos (38), libros de cuentos (17, 36), libros para colorear (35) y presentaciones de diapositivas (22, 16, 15), mostrando la aplicación de la IA en la creación de materiales didácticos estructurados.

Chatbots y asistentes virtuales: Se presentan diversas implementaciones de chatbots, desde diálogos inteligentes generales (59) hasta chatbots personalizados por área de conocimiento (47) y chatbots con personalidad (34). La integración multimodal (37, 6, 2) que incluye texto, audio e imagen es un avance notable. La capacidad de hablar con un asistente virtual (40) añade otra dimensión a la interacción.

Herramientas de investigación: La herramienta 45 ("Investigación profunda") y la 33 ("Investigando con DescartesJS y Pollinations") demuestran un uso de la IA para asistir en la investigación académica, con énfasis en la consulta de fuentes confiables y la verificación de información.

Red Descartes 2025/Año 5, núm.9

Red Descartes 2025/Año 5, núm.9

Creación de páginas web y código: La herramienta 46 permite la creación rápida de páginas web sin necesidad de programación, y la herramienta 39 genera código, mostrando la aplicación de la IA en el desarrollo web.

Uso de múltiples modelos de lenguaje: Varias herramientas (59, 44, 24, 23, 5) mencionan el uso de múltiples modelos de lenguaje (LLM) como Gemini, GPT, Mistral, DeepSeek y Llama, ofreciendo flexibilidad y alternativas a los usuarios.

Funcionalidad multimodal: La integración de texto, audio e imagen en una sola herramienta (como en el chatbot multimodal 37 y la herramienta 2) es un avance significativo, permitiendo una experiencia de usuario más rica y diversas aplicaciones, especialmente en la generación de contenido digital.

Enfoque en Pollinations: La API de Pollinations es la tecnología subyacente más mencionada, lo que sugiere una colaboración o dependencia importante con esta plataforma para la funcionalidad de muchas de las herramientas.

Licencia Creative Commons: La Red Educativa Digital Descartes opera bajo una licencia Creative Commons (BY-NC-SA 4.0), lo que permite la distribución y adaptación no comercial de sus obras, lo cual es coherente con la mención de obras derivadas.

Red Descartes 2025/Año 5, núm.9

Citas relevantes

Sobre el generador de cuestionarios de selección múltiple con Pollinations (61): "Este nuevo modelo permite intervenir el diseño, incluyendo MathJax para expresiones matemáticas, regenerar imágenes y límites más amplios del número de preguntas."

Sobre el diálogo inteligente de IA con Pollinations (59): "Esta herramienta es un poderoso asistente de chat con inteligencia artificial que puede responder preguntas, brindar sugerencias creativas, escribir textos e incluso ayudarlo a resolver problemas complejos."

Sobre el generador de tutoriales interactivos (58): "¿Quieres diseñar tutoriales llamativos e interactivos para tus estudiantes? Esta herramienta te los diseña con unos cuantos clics..."

Sobre la herramienta "Investigación profunda con Pollinations" (45): "Usando GPT-4o, a partir de un tema o pregunta de investigación, ingresado por el usuario, esta herramienta presenta buenos resultados obtenidos en su búsqueda en la web. Se ha configurado para que, por defecto, entregue las fuentes consultadas y los enlaces correspondientes."

Red Descartes 2025/Año 5, núm.9

Sobre el chatbot multimodal DescartesJS - Pollinations (37): "Esta herramienta permite obtener respuestas del chatbot en tres formatos: texto, audio e imagen. El audio y la imagen se generan a partir del texto obtenido con GPT-4o."

Sobre el creador de cuentos infantiles con Pollinations (17): "Generador de cuentos infantiles completo con generación de texto coherente usando la API de Pollinations.ai, imágenes en estilo Pixar que complementan cada acto del cuento, títulos variados y creativos para cada acto, haciendo que cada cuento sea único..."

Sobre la herramienta de IA multimodal con DescartesJS y Pollinations (2): "En resumen, esta herramienta multimodal combina texto, voz e imágenes para ofrecer una experiencia de usuario más completa y enriquecedora, siendo útil en educación, consultas informativas y generación de contenido visual."

Conclusiones

La sección "Herramientas IA" demuestra un compromiso activo en la exploración y aplicación de la inteligencia artificial para fines educativos y de creación de contenido. La dependencia de las API de Pollinations es un factor clave, permitiendo la integración de capacidades avanzadas de generación de texto e imagen en herramientas accesibles a los usuarios. La integración con DescartesJS fortalece el ecosistema existente de la Red Descartes, ofreciendo nuevas posibilidades para la creación de recursos interactivos. La diversidad de herramientas presentadas abarca desde la evaluación y el juego hasta la investigación y la generación de contenido multimodal, reflejando un enfoque amplio en el potencial de la IA para transformar la educación y la creación digital. El énfasis en la facilidad de uso y la provisión de tutoriales y ejemplos sugiere un esfuerzo por democratizar el acceso a estas tecnologías.

Red Descartes 2025/Año 5, núm.9

Red Descartes 2025/Año 5, núm.9

Red Descartes 2025/Año 5, núm.9

El nombre de «Parábola», el cual significa equiparación,⁴ fue asignado a esta curva por Apolonio de Perga (262-190 a. C.) en el desarrollo de su trabajo sobre Las Cónicas, y demostró que, para su obtención, el cono no necesita ser recto, ni de ángulo recto en el vértice⁵.

Apolonio, a diferencia de sus predecesores, prescinde del cono para abordar el estudio de las curvas cónicas por métodos exclusivamente planimétricos [2] y definiéndolas como lugares geométricos [1].

Carrillo de Albornoz, A. y De León, M. [1] resaltan que en Las Cónicas de Apolonio, «En el libro VI, dedicado fundamentalmente a la igualdad y semejanza de cónicas, aparece el siguiente interesante problema: dada la cónica y dado un cono circular recto, hallar una sección del cono que sea igual a la cónica dada⁶», si bien, Gonzalez [5] plantea que sobresale en este Libro la proposición 28, donde se resuelve el problema con relación a la parábola⁷.

En el presente trabajo se aborda la determinación de la ecuación de la parábola para valores variables tanto del ángulo del cono como de la distancia entre el vértice del cono y de la sección parabólica, lo cual permite dar respuesta al problema propuesto, desde una perspectiva trigonométrica.

Red Descartes 2025/Año 5, núm.9

Definiciones básicas

En un cono circular recto, a cualquier semirrecta sobre la superficie, que parte desde el vértice, se le denomina generatriz y al triángulo formado por un diámetro del círculo de la base y dos generatrices se le denomina triángulo axial, el cual contiene al eje axial del cono⁸. El ángulo del cono corresponde al ángulo del triángulo axial, el cual se denotará por $α$ en el presente artículo (Figura 5).

Al cortar un cono de base circular con un plano transversal que pasa por un punto diferente al vértice del cono, de modo tal que este sea paralelo a una generatriz, se obtiene una sección cónica denominada sección parabólica. A la curva plana que limita a la sección parabólica, y que está sobre la superficie del cono, se le denomina parábola, la cual, tiene un eje axial paralelo a la generatriz del cono (Figura 6).

Red Descartes 2025/Año 5, núm.9

En el blog Gaussianos puede observarse una representación dinámica de la parábola en un cono inclinado de base circular

Caracterización de la parábola

El trabajo pionero de Menecmo, quien logró traducir en expresiones geométricas básicas algunas de las propiedades de las secciones cónicas⁹, proporcionó las bases para el desarrollo posterior de sus variadas propiedades, «que serían plasmadas por Apolonio en los primeros libros de Las Cónicas» [5]. Apolonio «dedujo una propiedad plana fundamental o ''síntoma'' de la sección (del cono), dando una condición necesaria y suficiente para que un punto esté sobre la curva.»[2], para lo cual, compara elementos de las secciones con los elementos del círculo base[6], consiguiendo así prescindir del cono, al intuir que la parábola admite una caracterización particular que la identifica como lugar plano totalmente, esto es, «pensaba las cónicas como el lugar geométrico determinado por una colección de puntos». [4]

Para la representación plana de la sección parabólica, se partirá de la consideración de que, en correspondencia con la Proposición I.7 de Apolonio «todo segmento que biseca una serie de cuerdas paralelas de una sección de un cono se denomina diámetro» (en [6]). Así, si un cono es cortado por un plano transversal, que no contiene el vértice, en dirección perpendicular a la base de un triángulo axial, «la intersección del plano de corte y el plano del triángulo axial será un diámetro de la sección resultante del cono» (en [6]), el cual corresponde a un eje axial de dicha sección cónica. Para un cono de base circular, la sección cónica transversal que no contiene el vértice, y cuyo eje axial es paralelo a una generatriz, se extiende a cualquier círculo formado por

Red Descartes 2025/Año 5, núm.9

un plano de corte paralelo a la base del triángulo axial, en cualquier punto sobre el eje.

En correspondencia con lo expuesto en la Proposición I.8 de Apolonio, si el diámetro de la sección cónica es paralelo a la generatriz del cono, esto es, la sección cónica es parabólica, esta «se extiende hasta el infinito»[6]. De acuerdo con lo anterior, en un triángulo axial un segmento paralelo a la base corresponde al diámetro de un círculo, y un segmento paralelo a uno de los lados diferentes a la base es un diámetro extendido hasta el infinito, o eje axial, de una parábola (Figura 7).

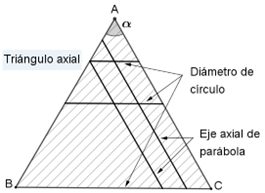
Para la caracterización de la parábola se considerará un cono circular recto de vértice $A$, donde $\overline{AB}$ y $\overline{AC}$ son generatrices, $\overline{BC}$ es un diámetro de la base circular con centro $M$, $\overline{AM}$ es el eje axial, $α$ es el ángulo del cono, y en el cual, el $∆ABC$ es el triángulo axial (Figura 8).

Red Descartes 2025/Año 5, núm.9

Sea $\overline{GH}$ una cuerda del círculo de la base del cono, la cual corta perpendicularmente al diámetro $\overline{BC}$ en el punto $I$ y considérese un plano que pasa por $\overline{GH}$ paralelo a $\overline{AC}$, el cual corta a $\overline{AB}$ en el punto $D$.

El plano, así establecido, genera la sección parabólica $GDH$, y correspondientemente la curva sobre el cono, esto es la parábola $GDH$, de vértice $D$ y eje axial $\overline{DI}$ paralelo a $\overline{AC}$.

Sea $J$ el punto de corte del eje axial del cono con $\overline{DI}$, y trácese por él una paralela al diámetro $\overline{BC}$, la cual cortará a $\overline{AB}$ en $E$ y a $\overline{AC}$ en $F$, con lo cual, $J$ es el centro de $\overline{EF}$. Adicionalmente, trácese por el punto $J$ una paralela a $\overline{GH}$, la cual pertenecerá a la sección parabólica y cortará a la parábola en $K$ y en $L$. La sección $EKFL$ es paralela a la base del cono $BGCH$, por lo tanto, también corresponde a un círculo, para el cual $\overline{EF}$ y $\overline{LK}$ son diámetros (Figura 9).

Red Descartes 2025/Año 5, núm.9

1. Representación planimétrica conjunta de una sección parabólica y un triángulo axial de un cono

Para la representación planimétrica de una sección parabólica, se establecerá un triángulo axial, como sección principal¹⁰, con lo cual, tanto la gráfica de la sección parabólica como la del triángulo axial se incluirán en un mismo plano.

Sea el triángulo axial $ABC$ y los segmentos $\overline{EF}$, diámetro de la sección cónica circular $EKFL$ cuyo centro es $J$, y $\overline{DI}$ el eje axial de la sección parabólica $GDH$, cuyo vértice es $D$, el cual pasa por $J$ (ver Figura 9 y Applet 1). Trácese la circunferencia $C_{1}$, con centro en $J$ y radio igual a $d(J,F)$, y la recta perpendicular a $\overline{DI}$ que pasa por el punto $J$, la cual corta a $C_{1}$ en $L'$ y en $K'$ (representaciones de $L$ y $K$ en el plano $ABC$). Adicionalmente, trácese la circunferencia $C_{2}$, con centro en $M$ y radio igual a $d(M,C)$, y la recta perpendicular a $\overline{BC}$ que pasa por el punto $I$, la cual corta a $C_{2}$ en $H'$ y en $G'$, siendo $\overline{H'G'}$ una cuerda de $C_{2}$ (representación de $\overline{HG}$ en el plano $ABC$).

Trácese la circunferenca $C_{3}$, con centro en $I$ y radio igual a $d(I,H')$, y la recta perpendicular a $DI$ que pasa por $I$, la cual corta a $C_{3}$ en $H''$ y en $G''$ (representaciones de $H$ y $G$ en el plano $ABC$), donde, $IH'=IH''$.

Así, de acuerdo con la construcción realizada los puntos $L'$, $K'$, $H''$ y $G''$ hacen parte de la parábola $G''DH''$, de vértice $D$ y eje axial $\overline{DI}$, pudiendo determinarse infinitos puntos sobre ella, de forma similar.

Red Descartes 2025/Año 5, núm.9

La parábola $G''DH''$ es la representación de la parábola $GDH$ del cono de ángulo $α$, en el plano del triángulo axial $ABC$.

En el Applet 1 puede verse que al variar el ángulo del cono ($α$) o la distancia entre els vértice del cono y de la sección parabólica ($AD$), en una representación planimétrica, se obtendrán parábolas de distinta ampliación.

Red Descartes 2025/Año 5, núm.9

2. Distancias y áreas características en una sección parabólica.

Sea $ABC$ un triángulo axial de un cono de ángulo $α$, con $E$ y $D$ sobre $\overline{AB}$, $F$ sobre $\overline{AC}$ e $I$ sobre $\overline{BC}$, donde $\overline{EF}$||$\overline{BC}$ y $\overline{DI}$||$\overline{AC}$, así, se tiene que $∆ABC$~$∆DBI$, con lo cual, $\dfrac{BC}{BA}=\dfrac{IC}{DA}$   (1). Por otro lado, $\dfrac{BC}{CA}=\dfrac{BI}{ID}$   (2), de donde, multiplicando miembro a miembro (1) y (2), se tiene que $\dfrac{(BC)^2}{{BA}\cdot{AC}}=\dfrac{{BI}\cdot{IC}}{{ID}\cdot{DA}}$   (3).

Al ser $H'$ el punto de intersección de las circunferencias $C_{2}$, con centro en $M$, y $C_{3}$, con centro en $I$, al unir $H'$ con $B$ y con $C$ se forma el triángulo rectángulo $BH'C$, de altura $IH'$ (Figura 10), donde, $(IH')^2={BI}\cdot{IC}$ (teorema de segmentos proporcionales en un triángulo rectángulo). Como $IH'=IH''$, por ser radios de la circunferencia $C_{3}$, entonces $(IH'')^2={BI}\cdot{IC}$   (4).

Sea $V$ el punto de corte de la circunferencia $C_{3}$ con la recta $DI$, con lo cual, $IV=IH''$. Al trazar una perpendicular a $\overline{DV}$ por el punto $V$ y una paralela a $\overline{DV}$ por $H''$, estas se intersecan en el punto $T$, formándose el cuadrado de área $A_{1}={IV}\cdot{IH''}=(IH'')^2$   (5).

Trácese el segmento $DH''$ y la perpendicular a este por el punto $H''$, la cual corta a la recta $DI$ en $W$ (Figura 11), formándose el triángulo rectángulo $DH''W$, de altura $IH''$. donde, $(IH'')^2={DI}\cdot{IW}$ (teorema de segmentos proporcionales en un triángulo rectángulo). Así, de (5), $A_{1}=(IH'')^2={DI}\cdot{IW}$   (6).

Red Descartes 2025/Año 5, núm.9

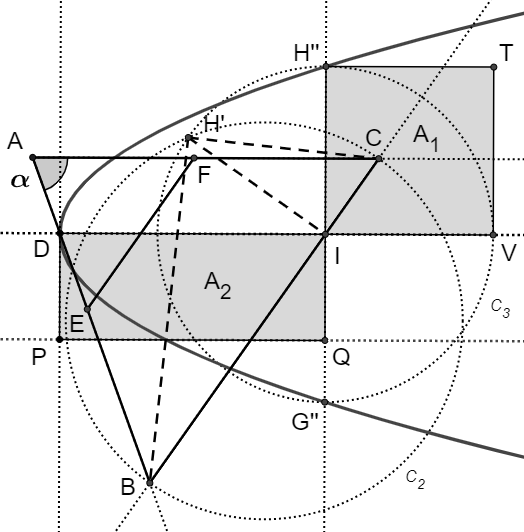
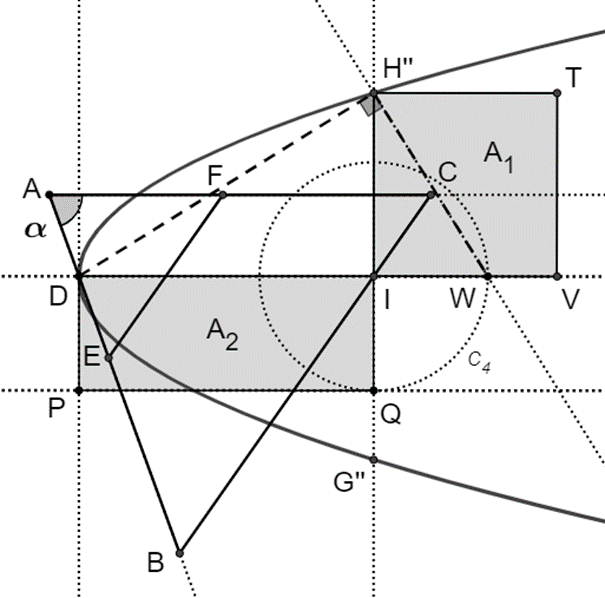
Red Descartes 2025/Año 5, núm.9

Trácese la circunferencia $C_{4}$, con centro en $I$ y radio igual a $d(I,W)$, la cual corta a la recta $IH''$ en $Q$, de donde, $IW=IQ$. Adicionalmente, trácese la perpendicular a $DI$ por el punto $D$ y la paralela a $DI$ por el punto $Q$, las cuales se cortan en el punto $P$, con lo cual, se forma el rectángulo $IDPQ$, donde $IQ=DP$. Sea $A_{2}$ el área de $IDPQ$, donde $A_{2}={DI}\cdot{DP}$   (7).

Como $IW=IQ=DP$, entonces, de (6) se puede establecer que $A_{1}=(IH'')^2={DI}\cdot{DP}$, con lo cual, $A_{2}=A_{1}$, así, $\dfrac{A_{1}}{A_{2}}=1$   (8).

Sea $s=\dfrac{DP}{DA}$, con lo cual, $DP={s}\cdot{DA}$   (9), luego, reemplazando (9) en (3), y de acuerdo con (4) , (6), (7) y (8), se obtiene,

$\dfrac{(BC)^2}{{BA}\cdot{AC}}={s}\dfrac{{BI}\cdot{IC}}{{ID}\cdot{DP}}={s}\dfrac{A_{1}}{A_{2}}=s$   (10).

Como $(IH'')^2={DP}\cdot{ID}$, para cualquier valor del ángulo $α$, $(IH'')^2$ es directamente proporcional a $ID$ [$(IH'')^2 ∝ ID$], cuya constante de proporcionalidad es $p=DP$, así,

En la parábola al segmento $p=DP$, se le denomina lado recto

Red Descartes 2025/Año 5, núm.9

3. La parábola en función de $α$ y de $r$.

Sea $X×Y=\{(x,y)∈R/x∈X ∧ y∈Y\}$ un sistema cartesiano, si $x=IH''$ y $y=DI$, entonces, de (11) se tiene que $x^2=py$. Haciendo $r=DA$ en (9), se tiene que $p=sr$, con lo cual, para cualquier ángulo $α$, $x^2=sry$, de donde, $y=\dfrac{1}{p}x^2=\dfrac{1}{sr}x^2$   (12).

Al hacer un análisis de la relación $s=\dfrac{DP}{DA}=\dfrac{(BC)^2}{{BA}\cdot{AC}}$, mediante el uso del software de geometría dinámica GeoGebra, se logra determinar que, para un valor constante de $r=DA$, al variar el ángulo del cono ($α$), también lo hace $p=DP$, esto es, $s$ varía y, con ello, la sección parabólica correspondiente, como se puede observar en el Applet 2.

En la Tabla 1 se muestran los valores de $s$ para distintos valores de $α$, y al graficar los diferentes pares ordenados ($α,s$) (Figura 8), se encuentra que estos presentan una disposición senoidal, lográndose determinar que corresponden a puntos de la función

Así, de (12) y (13) se tiene que, para cualquier valor de $α$,

Red Descartes 2025/Año 5, núm.9

Igualmente, mediante el software de geometría dinámica se logra determinar que, para un valor constante del ángulo $α$, el valor de $s$ también es constante, de modo que, al variar la distancia $r=DA$, también lo hace proporcionalmente la distancia $p=DP$ y, con ello, varía la sección parabólica correspondiente.

Red Descartes 2025/Año 5, núm.9

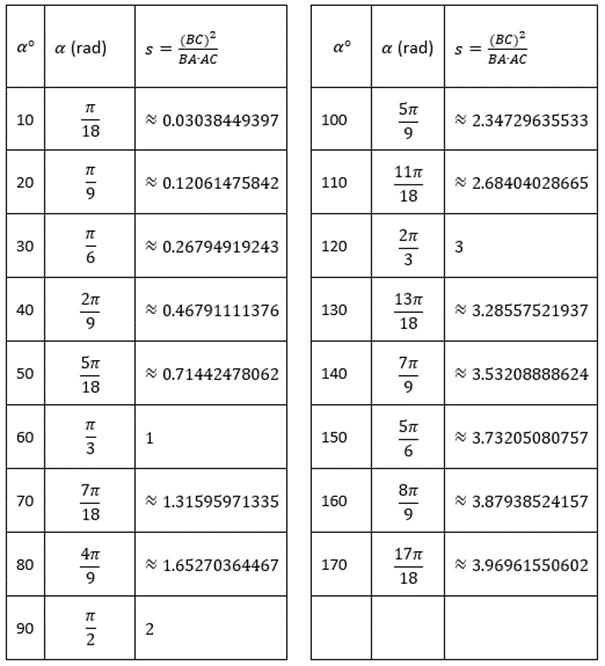
Red Descartes 2025/Año 5, núm.9

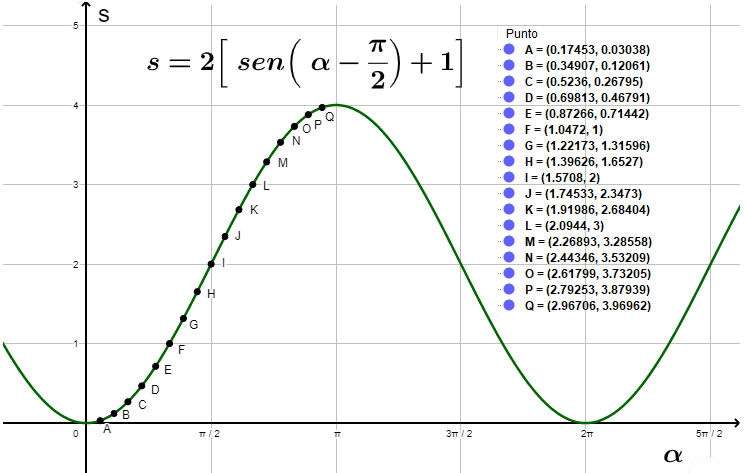
4. Obtención de parábolas $y=kx^2$, a partir de conos de ángulo variable ($0<α<π$)

Comúnmente, la ecuación y la gráfica de $y=x^2$ han servido de referencia en el tratamiento de la parábola como función cuadrática, a partir de la cual, se lleva a cabo la transformación $y=kx^2$, donde la gráfica de la parábola se cierra (contrae) si $|k|>1$ o se abre (extiende) si $0<|k|<1$.

Red Descartes 2025/Año 5, núm.9

A partir de (12) y (14) se concluye que $y=kx^2=\dfrac{1}{sr}x^2$, si y solo si, $r=\dfrac{1}{ks}$, esto es,

función mediante la cual, para un valor constante de $k$, es posible determinar el valor de $r$, requerido para que una sección parabólica sea coincidente con la parábola $y=kx^2$, en un cono de ángulo $α$ (con $0<α<π$) (Figura 9).

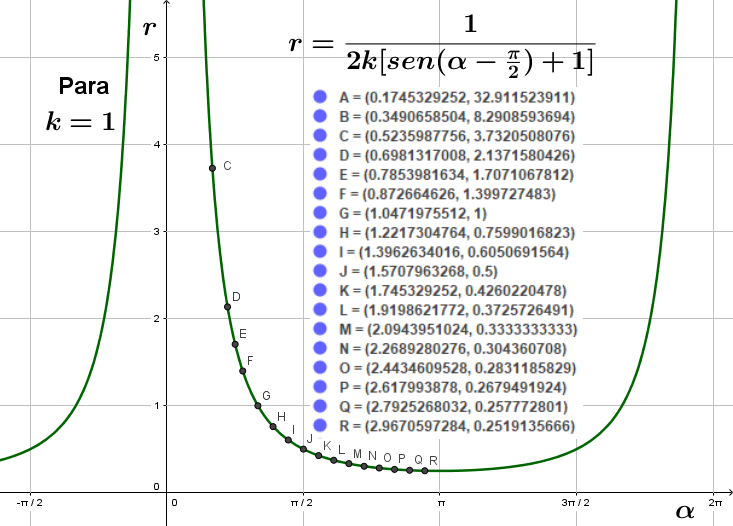
Red Descartes 2025/Año 5, núm.9

En la Tabla 2 puede verse los valores que deben tener $r$ y $s$ para obtener secciones cónicas coincidentes con la parábola $y=kx^2$, en conos de diferente ángulo $α$. y para diferentes valores de $k$

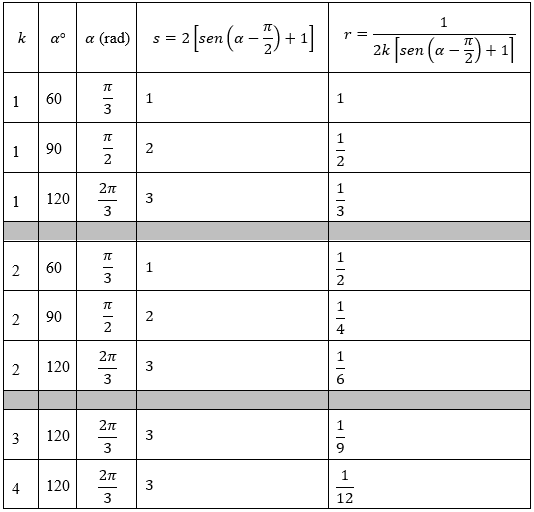
Red Descartes 2025/Año 5, núm.9

Igualmente, a partir de (15) se obtiene la función

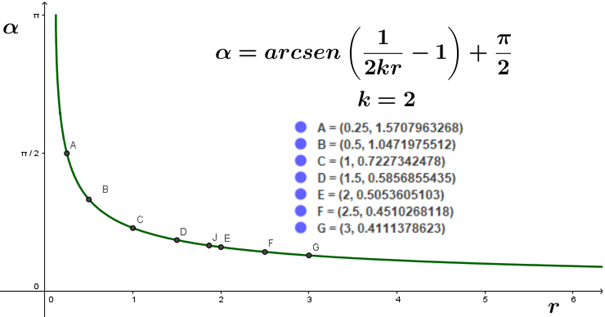
Red Descartes 2025/Año 5, núm.9

En la Tabla 3 puede verse los valores que debe tener el ángulo $α$, para obtener secciones parabólicas coincidentes con la parábola $y=kx^2$, para diferentes valores de $r$.

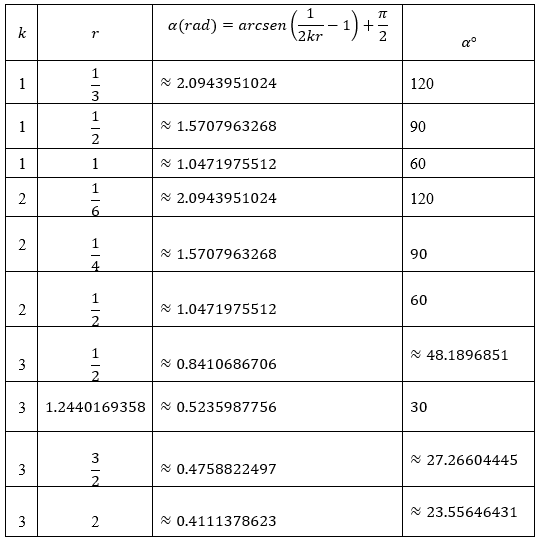
Red Descartes 2025/Año 5, núm.9

5. Ejemplo interactivo

En el Applet 3 puede asignarse valores para el ángulo del cono ($α$) y el coeficiente $k$ de la parábola, cuya función es $y=kx^2$, y para dichos valores encontrar la distancia $r=DA$, a la cual se encuentra el vértice de la sección parabólica que es coincidente con la gráfica de la función, en una representación planimétrica.

Red Descartes 2025/Año 5, núm.9

Referencias bibliográficas

Red Descartes 2025/Año 5, núm.9

Red Descartes 2025/Año 5, núm. 9

Red Descartes 2025/Año 5, núm.9

Un itinerario formativo es un conjunto de actividades interactivas que se presentan al estudiante de manera adaptativa, según las respuestas que vaya ofreciendo en cada etapa. Dentro de este recorrido, ciertas tareas se identifican como hitos fundamentales. Para alcanzarlos, si un alumno no responde correctamente, se activan caminos alternativos que ofrecen recursos y ejercicios de refuerzo, con el fin de consolidar los conceptos clave antes de avanzar al siguiente nivel.

Definición de nodos y rutas

• Cuestionario (Quiz): el estudiante debe elegir la respuesta correcta entre un conjunto de opciones (normalmente cuatro).
• Respuesta abierta: se le solicita al alumno que formule su propia respuesta, sin opciones prefijadas.
• Repaso: se propone revisar contenido y realizar cálculos o ejercicios prácticos, cuyo resultado no se comprueba de forma automática.
• Ejercicios por pasos (Steps): se trabajan ejercicios complejos mediante una secuencia paso a paso, donde cada paso puede ser de tipo quiz, respuesta abierta o repaso

Cada actividad incluye retroalimentación detallada tanto cuando el estudiante acierta como cuando comete errores, pudiendo incorporar desde explicaciones paso a paso hasta herramientas interactivas (por ejemplo, laboratorios interactivos de visualización de conceptos) y breves vídeos demostrativos que refuerzan el aprendizaje.

Red Descartes 2025/Año 5, núm. 9

La estructura organizativa se articula en torno a secciones temáticas: cada tema se subdivide en apartados que agrupan contenidos relacionados y, a su vez, en cada apartado se ofrecen varios itinerarios, concebidos para abordar objetivos de aprendizaje muy concretos. Esta organización modular permite una navegación flexible.

En la Figura 2 se ilustra uno de estos itinerarios: los hitos clave —puntos en los que se verifica el dominio de un concepto— aparecen marcados en rojo, y los posibles caminos que llevan a su consecución, incluidos los de refuerzo en caso de respuestas incorrectas, se representan en azul.

Según el tipo de nodo y la navegación establecida, la herramienta conduce al estudiante por el camino definido según se vayan acertando o no las actividades que se plantean. Si un alumno resuelve correctamente un reto en un nodo, avanza hacia contenidos más complejos; de lo contrario, se le redirige a recursos de apoyo.

Red Descartes 2025/Año 5, núm. 9

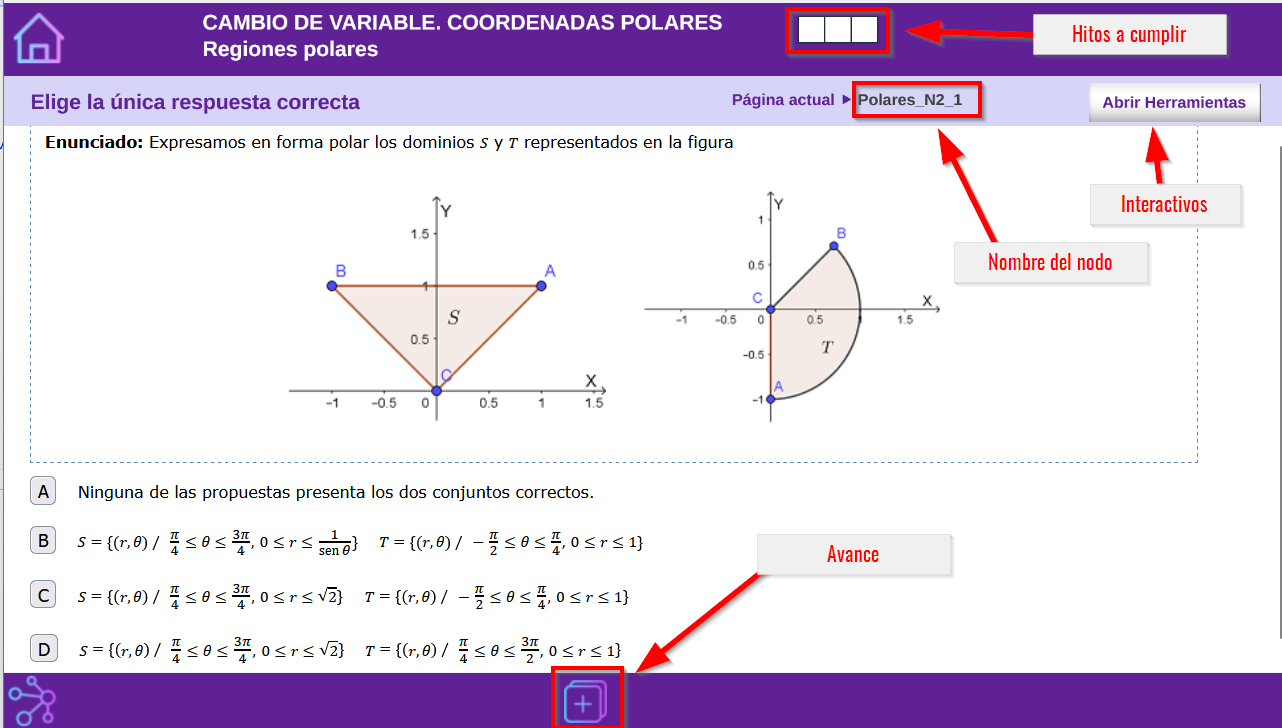
Red Descartes 2025/Año 5, núm. 9

Funcionamiento interno

La base del sistema se ha construido con la herramienta DescartesJS, que permite crear recursos didácticos interactivos integrables en páginas HTML Asimismo, se ha establecido un mecanismo de comunicación bidireccional entre la herramienta y dichas páginas HTML para gestionar la navegación y recopilar datos de avance de los alumnos.

La estructura del itinerario se describe en ficheros de texto plano, donde se especifican:

• Nombre y tipo de cada nodo.
• Nodos sucesores según respuestas correctas o erróneas.
• Puntos de control (hitos) que marcan el progreso.

Los itinerarios se configuran por tanto sin ningún conocimiento de DescartesJS. En el caso del itinerario de la figura 2 la información para definir la navegación debe almacenarse en un fichero de texto con la estructura que se muestra a continuación.

Red Descartes 2025/Año 5, núm. 9

El primer valor es el nombre del nodo, el segundo el tipo y los dos siguientes son el nodo al que acceder si la respuesta es o no correcta. El último valor es 1 si el nodo es un hito a cumplir y -1 si es un nodo secundario.

Registro de navegación

Gracias a la comunicación entre DescartesJS y el servidor (vía AJAX/PHP), cada paso del estudiante se almacena en una base de datos: nodos visitados, intentos realizados y tiempo invertido. Esto permite:

• Monitorizar en tiempo real el progreso.
• Detectar puntos de bloqueo y ajustar el itinerario.
• Generar informes automatizados de uso

Además, gracias a la comunicación entre DescartesJS y las páginas html, la acción que se realice sobre la página web vinculada al nodo se remite a la herramienta y se puede establecer la navegación.

Experimentación en el aula

Durante los últimos dos años, hemos utilizado estos recursos en la Universidad de Cantabria desplegándolos en la asignatura de Cálculo II de primer curso en primer lugar, dirigidas a los estudiantes de los

Red Descartes 2025/Año 5, núm. 9

grados de Ingeniería Mecánica, Industrial y Química. En este tiempo se han diseñado más de setenta itinerarios formativos, distribuidos en ocho bloques temáticos que cubren gran parte de los contenidos de esta asignatura.

En la página siguiente aparece el listado de todos los itinerarios creados con los enlaces a los mismos. Para consultarlos es necesario identificarse con un nombre de usuario y especificar la asignatura correspondiente. No obstante, dado que este proceso de registro está pensado para recopilar información sobre asignaturas regladas, se puede utilizar el valor PRUEBA tanto en el campo de usuario como en el de asignatura. De este modo se puede explorar y verificar los itinerarios sin que esas entradas de prueba influyan en los datos reales ni alteren el análisis posterior.

Actualmente contamos con un histórico de más de 3.000 itinerarios completados y evaluados por los estudiantes, quienes han valorado aspectos como la satisfacción global, la utilidad y calidad del contenido, la facilidad de uso, la adecuación del nivel de las actividades, la claridad de la retroalimentación y el tiempo requerido.

La valoración de los itinerarios ha sido muy positiva, reflejando altos niveles de satisfacción y consenso en la calidad y utilidad de los contenidos.

Conclusión

La experiencia ha demostrado que una estructura de aprendizaje flexible mejora tanto la motivación como el rendimiento académico. Actualmente, se trabaja en ampliar los tipos de actividades, incorporar informes más complejos e incorporar nuevas herramientas como puede ser los asistentes soportados por inteligencia artificial.

Red Descartes 2025/Año 5, núm. 9

Referencia

Red Descartes 2025/Año 5, núm. 9

Red Descartes 2025/Año 5, núm. 9

Red Descartes 2025/Año 5, núm. 9

Normas de publicación

Características de los artículos

• El autor puede presentar el artículo en un documento de texto con un máximo de ocho páginas en Arial tamaño 12.
• Si el autor tiene competencias en el diseño HTML y CSS, puede usar la plantilla de la revista, con un máximo de 10 páginas.
• El título será menor a 150 caracteres.
• Las imágenes, figuras, tablas, videos y objetos interactivos se deben enviar en un archivo zip aparte.
• Idioma. La revista acepta artículos en español, inglés y portugués.
• Los artículos, preferiblemente, se relacionarán con aspectos educativos y el uso de las tecnologías en los procesos de enseñanza-aprendizaje. No obstante, se aceptan artículos de otras áreas del conocimiento, siempre que estos incorporen contenidos digitales diseñados con el editor DescartesJS.
• Presentar los permisos para el uso de contenido sujeto a derechos de autor, incluyendo los que provienen de Internet.

Red Descartes 2025/Año 5, núm. 9

El artículo y los anexos deben enviarse en una archivo zip, a través de un enlace (vía hosting o Google Drive, por ejemplo).

Los artículos deben abordar temas como:

• Difusión relacionada con la Red Educativa Digital Descartes
• Reseñas de libros interactivos
• Aplicaciones con DescartesJS
• Novedades DescartesJS
• Experiencias en el aula
• Investigaciones que incluyan el uso de contenidos digitales interactivos diseñados con DescartesJS

Evaluación de los artículos

El o los autores podrán sugerir revisores, indicando los datos de contacto (nombre y dirección de correo).

Los editores del Consejo Editorial, en primera instancia, valorarán los artículos para verificar que cumplen con los objetivos de publicación de la revista, si el concepto es positivo se asignarán mínimo dos revisores quienes evaluarán el artículo y harán las recomendaciones pertinentes, entre ellas la aceptación o no de su publicación.

Red Descartes 2025/Año 5, núm. 9