Número 4
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Revista Digital Red Descartes
https://proyectodescartes.org/revista/index.html
ISSN: 2792-4483

Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
La “Revista Digital Red Descartes” tiene como objetivo principal la difusión de todo lo concerniente al proyecto Descartes ―proyecto educativo de ámbito global que persigue la mejora de la educación apoyándose en las tecnologías de la información y de la comunicación (TIC) y en las del aprendizaje y el conocimiento (TAC)―, pero con visión abierta a acoger todo aquello que signifique un gran avance en el ámbito educativo con herramientas y recursos similares.
Nuestra revista se caracteriza y distingue por ser una publicación interactiva, es decir, aporta como elemento identificador el que dentro de su contenido aparecen elementos que dan respuesta adecuada, contextualizada, a las acciones que sobre ellos realice el lector/actor. Esa interactividad es identificadora del aporte que suministran los recursos desarrollados con nuestra herramienta Descartes, pero sin exclusividad a ellos. Nuestra línea de trabajo está abierta a cualquier recurso promotor del aprendizaje y del conocimiento, aunque tengamos obviamente nuestra predilección personal básica por lo que promovemos, desarrollamos y difundimos ¡desde casi un cuarto de siglo de existencia!
Así pues, abrimos una nueva línea de trabajo, inmersa en nuestro sello editorial y servicio altruista, con vocación de seguir transmitiéndoles interés por la educación y, en particular, con la utilización de los recursos educativos interactivos de nuestro proyecto Descartes, desarrollados con la herramienta homónima: Descartes, y en una revista con soporte en los “Libros interactivos de RED Descartes”. Confiamos poder rebatir a Quintiliano cuando afirmaba: “Facilius est multa facere quam diu” ―Es más fácil hacer muchas cosas que hacer una durante mucho tiempo―.
Consejo Editorial
Presidente
Ángel Cabezudo Bueno
Coordinación editorial
Juan Guillermo Rivera Berrío
Editores
Mª José García Cebrian
Yecid E. Gaviria Restrepo
José Román Galo Sánchez
José Antonio Salgueiro
Administración web
Francisco Rodríguez Villanego
Josep Mª Navarro Canut
Código JavaScript
Joel Espinosa Longi
Colaboradores
Elena Álvarez Saiz
Carlos A. Rojas Hincapié
Edison Arbey Escobar
Ramiro A. Lopera Sánchez
Manuel Muñoz Cañadas
Diseño de portada
Julieth A. Gómez Hernández
Viñetas: klipartz.com/
Recursos interactivos:
DescartesJS
Fuentes: Lato y UbuntuMono
ISSN: 2792-4483
EDITORIAL
La producción de contenidos digitales de la Red Educativa Digital Descartes no para en el segundo semestre de 2022, tampoco lo hace las continuas mejoras del editor DescartesJS. Nuestra biblioteca de libros interactivos se ha enriquecido con obras como: "Telescopio espacial James Webb - El comienzo", "Cuarta Revolución Industrial - Fundamentos", "Compostaje y lombricultivo ", "Matemáticas para las Ciencias 3" y "Mucho teatro (De y para instituto)".
En este número de la "Revista Digital Red Descartes" presentamos nueve artículos. De nuevo Joel nos sorprende con un artículo que da cuenta de la mejora en el editor DescartesJS, al incorporar gradientes y patrones al editor de colores. Las extraordinarias imágenes del telescopio espacial James Webb no han sido ajenas para nuestra Red, en dos artículos se describen las primeras imágenes capturadas por el Webb y algunos métodos de visualización, tanto en animación como en objetos interactivos. José Galo contribuye con un artículo sobre las superficies regladas desarrollables con todo el rigor matemático que ello conlleva, además de aportar escenas interactivas, desarrolladas con DescartesJS. Jorge Andrés Rodríguez presenta una reflexión sobre la enseñanza del diseño, en la que, según el autor, hay dos elementos fundamentales, el saber práctico que sugiere una acción y el teórico que sienta las bases para el contexto.
En la práctica docente, el uso de herramientas -digitales o no- se presentan experiencias especiales que ameritan sistematizarlas; en ese sentido, Manuel Muñoz nos expone experiencias del alumnado de Educación Primaria, empleando plantillas con un círculo fraccionado en diversos sectores o fracciones iguales de diferentes valores. Por su parte, José Antonio Salgueiro, nos presenta un artículo que describe cómo usar el editor DescartesJS, para crear contenidos digitales.
SUMAR
| 06 |  |
Las imágenes del telescopio James Webb en Descartes JS Juan Guillermo Rivera Berrío |
| 20 |  |
Reflexiones sobre el conocimiento práctico y teórico y la enseñanza significativa en el diseño Jorge Andrés Rodríguez Acevedo |
| 32 |  |
Animaciones del Webb con DescartesJS Juan Guillermo Rivera Berrío |
| 42 |  |
El tuit destacado Roberto Rohde |
| 46 |  |
Superficies regladas desarrollables, diseño y construcción con DescartesJS José Román Galo Sánchez |
ARIO
| Formación en DescartesJS José Antonio Salgueiro González |
 |
58 |
| Recurso para multiplicar Manuel Muñoz Cañadas |
 |
66 |
| Colores, gradientes y patrones Joel Espinosa Longi |
78 |
| Proyecto Descartes: cognición y didáctica en la creación de contenido digital David Oswaldo Zapata Tamayo |
 |
88 |
| Publicaciones iCartesiLibri 2021 - 2022 |
 |
94 |
DescartesJS
Las imágenes del telescopio
James Webb en Descartes JS
Juan Guillermo Rivera Berrío
mundo las primeras imágenes del Telescopio Espacial James Webb, imágenes que presentan resoluciones que van desde los 4k hasta los 16k. El programa internacional Webb es liderado por la NASA con sus socios, la ESA (Agencia Espacial Europea) y la Agencia Espacial Canadiense.
proyecto iCartesiLibri el libro "Telescopio espacial James Webb - El comienzo", en el cual diseñamos algunas escenas interactivas, que vamos a describir en este artículo.

- El comienzo".
Red Descartes 2022/Año 2, núm. 4
Comparando las imágenes del Webb
Un mes después de publicarse las primeras imágenes del Webb, pudimos registrar las siguientes imágenes en el libro, algunas de ellas procesadas por astrónomos aficionados:
Red Descartes 2022/Año 2, núm. 4
 Una vez publicadas las primeras imágenes del Webb, científicos y astrónomos aficionados analizaron cada uno de los nuevos objetos astronómicos nunca antes observados. Otros, hicieron comparaciones con las imágenes obtenidas antes del Webb, tal como lo hizo el físico y desarrollador de software John Christensen, partiendo de la pregunta ¿Cuánto más poderoso es el telescopio espacial James Webb en comparación con el Hubble? Para dar respuesta a esta pregunta, Christensen desarrolló la aplicación WebbCompare, la cual permite comparar las imágenes del Webb con las obtenidas por el Hubble.
Una vez publicadas las primeras imágenes del Webb, científicos y astrónomos aficionados analizaron cada uno de los nuevos objetos astronómicos nunca antes observados. Otros, hicieron comparaciones con las imágenes obtenidas antes del Webb, tal como lo hizo el físico y desarrollador de software John Christensen, partiendo de la pregunta ¿Cuánto más poderoso es el telescopio espacial James Webb en comparación con el Hubble? Para dar respuesta a esta pregunta, Christensen desarrolló la aplicación WebbCompare, la cual permite comparar las imágenes del Webb con las obtenidas por el Hubble.
Una vez pongas el puntero del ratón sobre la imagen, aparece un menú en la esquina superior izquierda de la imagen, la cuarta opción te permite ampliar la imagen en pantalla completa.
Red Descartes 2022/Año 2, núm. 4
En la siguiente escena, presentamos la galaxia Cartwheel usando la aplicación de Christensen. Puedes desplazar el botón central para comparar la imagen obtenida por el Webb con la del Hubble. Si lo deseas, puedes activar el "Zoom" de la librería OpenSeadragon, haciendo clic en el cuadro señalado. En el modo Zoom, además de ampliar la imagen, puedes desplazarla con clic izquierdo sostenido.
Red Descartes 2022/Año 2, núm. 4
En esta otra escena, diseñada con DescartesJS, hemos puesto tres imágenes más del Webb, usando la aplicación de Christensen sin la opción del Zoom.
Red Descartes 2022/Año 2, núm. 4
Es cierto que es posible intervenir la aplicación de Christensen para comparar nuevas imágenes; sin embargo, decidimos diseñar la aplicación en DescartesJS, que explicamos a continuación.
Tomemos una de las imágenes publicadas por Judy SchmidtSchmidt es una procesadora de imágenes espaciales aficionada. Su trabajo se puede ver en su página de Flickr o siguiéndola en Twitter. Schmidt lleva años estudiando datos espaciales sin procesar para obtener imágenes impresionantes., la Galaxia espiral IC 5332, cuyas imágenes para los dos telescopios son:

Uno de los problemas presentados para intervenir la aplicación de Christensen es el tamaño de las imágenes, que para los ejemplos anteriores eran iguales, otro problema es cuando las imágenes tienen diferencias en su ángulo de rotación. Ambos problemas son sencillos de solucionar con DescartesJS.
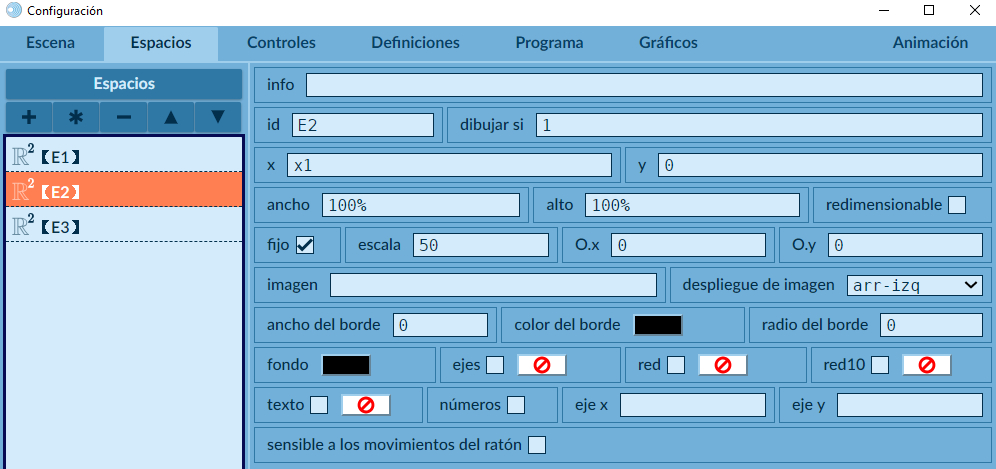
Para este ejemplo, las imágenes tienen un tamaño de 800x657 pixeles y con el mismo ángulo de rotación. Creamos, entonces una escena de ese tamaño y en ella tres espacios 2D, cada uno con escala igual a 50, los dos primeros con fondo negro y el tercero con fondo transparente.
Red Descartes 2022/Año 2, núm. 4
En los tres desactivamos los ejes y las redes y, además, los fijamos. La "x" del espacio E2 es variable (x1), es el espacio que vamos a desplazar horizontalmente.
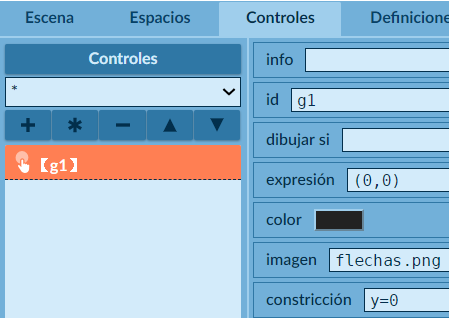 Agregamos un control gráfico en el centro de la escena (0,0), con restricción al movimiento vertical (y=0). La imagen del control es un par de flechas de 50x50 pixeles, tal como las usa Christensen.
Agregamos un control gráfico en el centro de la escena (0,0), con restricción al movimiento vertical (y=0). La imagen del control es un par de flechas de 50x50 pixeles, tal como las usa Christensen.
Red Descartes 2022/Año 2, núm. 4
En el selector "Programa", realizamos los siguientes cálculos:
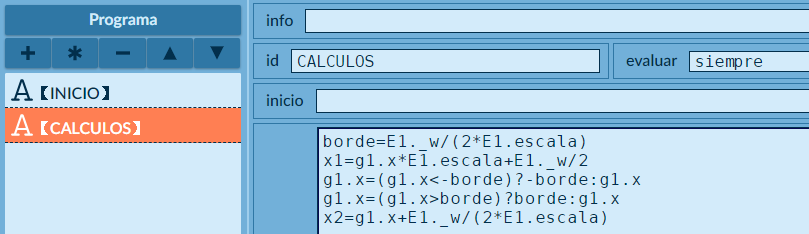
borde, x1 y x2.La variable borde determina la abscisa máxima a la que debemos desplazar el control gráfico, como el ancho es 800 y la escala es 50, obtendríamos un valor de 8 para borde. Los dos condicionales evitan que "desbordemos" el control gráfico.
La variable x1 inicialmente sería 400, pues g1.x lo definimos en cero. Esta variable determina el valor "x" del espacio E2.

El valor de la variable x2 evita que E2 se desplace, tal como veremos a continuación.
Red Descartes 2022/Año 2, núm. 4
Ahora, sólo nos falta explicar lo que hemos puesto en el selector "Gráficos"
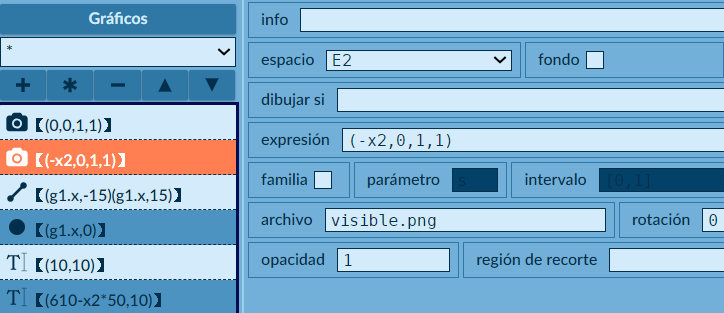
Hemos agregado las dos imágenes de la galaxia IC 5332. Observa que en el espacio E2 pusimos la del Hubble, variando su abscisa con
-x2, lo que evita que la imagen se desplace y permita la comparación con la imagen del Webb, puesta en E1. Observa, también, que la escala de la imagen es del 100% (los dos últimos valores en "expresión"), que podemos modificar para ajustar imágenes de diferente tamaño, así como la rotación que ahora es cero.
Hemos puesto un segmento vertical de color blanco y ancho 3, que se desplaza con g1.x, al igual que un punto de color semitransparente y tamaño 30. Finalmente, están los textos correspondientes a cada telescopio, dejando la abscisa del texto para el Hubble estática con x2.
En la siguiente escena puedes ver el resultado. Sugerimos ampliarla para una mejor observación de los detalles.
Red Descartes 2022/Año 2, núm. 4
Otra comparación, no realizada por Christensen, la hicimos con la nebulosa Anillo del sur, capturada con el instrumento de infrarrojo medio (MIRI, por sus siglas en inglés), que muestra las dos estrellas del centro unidas en una estrecha órbita, revelando, por primera vez, que la segunda estrella está rodeada de polvo. La escena la presentamos en la siguiente página. Para este ejercicio, rotamos la imagen del Webb $15\degree$ y redujimos la escala de la imagen del Hubble al 43%.
Red Descartes 2022/Año 2, núm. 4
Observa que en la imagen derecha, se alcanza a apreciar la rotación de la imagen.
Estas intervenciones con DescartesJS no son sencillas de realizar con la aplicación de Christensen. A continuación, presentamos un ejemplo que evidencia los desfases generados por la diferencia de tamaños; para ello, hemos usado la Galaxia fantasma Messier 74.
Red Descartes 2022/Año 2, núm. 4
La galaxia con tonos violeta fue procesada por Gabriel Brammer, la segunda fue procesada por Schmidt usando colores de diversos filtros, que muestran todo el polvo brillante en el centro de la NGC 628 o Messier 74.
La escena inicial fue diseñada con DescartesJS, corrigiendo los desfases por la diferencias de tamaño y escala en las imágenes. Hemos incorporado un botón "Zoom", que presenta una segunda escena usando la aplicación de Christensen, en la que son evidentes los desfases entre las dos imágenes.
El atractivo de esta segunda escena, como vimos anteriormente, es la posibilidad de ampliar las imágenes; sin embargo, con DescartesJS podemos hacer algo similar, para comprobarlo hemos diseñado un último modelo, que incluye un control para ampliar las imágenes y dos más para desplazarlas. Observála en la página siguiente.
Red Descartes 2022/Año 2, núm. 4
Usamos la galaxia espiral NGC 74968 de la constelación de Grus o Grulla, procesada por Schmidt. La imagen de la derecha es una combinación de filtros NIRCam y MIRI para mostrar el polvo continuo y de línea de emisión en NGC7496, mientras que la de la izquierda es una combinación de datos del Hubble y el Webb.
En conclusión, en este artículo, además de contribuir a la divulgación del telescopio espacial James Webb, demostramos que el editor DescartesJS es una potente herramienta para diseñar, en forma sencilla, aplicaciones en el campo de la astronomía.
Red Descartes 2022/Año 2, núm. 4
Constelación Andrómeda (wikimedia.org)
Red Descartes 2022/Año 2, núm. 4
Diseño y
Educación
Reflexiones sobre el conocimiento práctico y teórico y la enseñanza significativa en el diseño
Jorge Andrés Rodríguez Acevedo
su vida profesional al aplicar lo aprendido donde, en ocasiones, no hay una relación entre lo teórico y práctico y estos distan de su finalidad.
Red Descartes 2022/Año 2, núm. 4
Enseñar siempre ha sido una labor ardua y compleja, no por mucho el modelo enseñanza aprendizaje no ha variado considerablemente en las últimas décadas, Paiget & Vigotsky
La enseñanza y el aprendizaje es una interacción entre dos o más personas, en el ámbito del diseño esto implica diferenciar la enseñanza tradicional de la enseñanza significativa.
La enseñanza significativa se rige por la relación no arbitraria y sustantiva de ideas compartidas con algún aspecto relevante de la estructura del conocimiento de la persona, lo que implica un cierto grado de discernimiento del tema que se quiere aprender; por lo tanto, la enseñanza debe ser necesariamente conducida. Por dicha razón, el conocimiento significativo debe estar activo en el desarrollo continuo de la persona
Este artículo pretende gestionar un resumen autorreflexivo para el desarrollo de cuestionamientos sobre la enseñanza significativa del diseño y sus dos aristas fundamentales, el conocimiento teórico y el práctico, y tratar de entender, en algún grado, la enseñanza proyectual como raíz epistemológica del a hacer del diseño.
Reflexión conocimiento teórico práctico
En la enseñanza del diseño siempre hay dos aristas fundamentales, el saber práctico que sugiere una acción y el teórico que sienta las bases para el contexto, y ejecutar el primero. Ambos saberes buscan una transmutación de la realidad para convertirla en proyección.
Red Descartes 2022/Año 2, núm. 4
 Aristóteles en ética a Nicómaco
Aristóteles en ética a Nicómaco
Para Aristóteles, la sabiduría práctica estaría vinculada a la sabiduría política, es decir, al saber, capaz de justificar las normas y valores para lograr una convivencia ordenada y sin conflictos, por consiguiente justa, en la cual sea posible realizar una vida feliz digna de los humanos y por lo tanto buena.
En el diseño ocurre una transformación diferente, respecto a cómo se enseña y se aprende este tipo de conocimiento.
El conocimiento proyectual forma parte de un grupo de disciplinas que sólo pueden aprenderse en la práctica, aunque parezca paradójico a diseñar se aprende diseñando. Es por eso que los trabajos realizados en los talleres de Diseño, tienen un rol vertebrador en las carreras de diseño y demandan al alumno la integración de diversos campos epistemológicos (
Entonces parece extraño que el saber práctico ocupase mas relevancia en las disciplinas proyectuales. No necesariamente, hace falta una actitud mas comprometida frente a los profesionales que enseñan en el diseño, como también a los estudiantes que se forman.
Red Descartes 2022/Año 2, núm. 4
El vínculo entre ambos saberes es irrefutable, puesto que la vida práctica requiere del elemento contemplativo o reflexivo (lo teórico).
Quien se halle provisto tan sólo de la técnica de su profesión se encontrará, por muy bien que la posea, en la situación de un trabajador que durante toda su vida se ocupa en un sólo punto de esa gran máquina, desconociendo las fuerzas que la ponen en movimiento y sin tener idea de las otras partes del ingenio y de su cooperación en el fin total, será un servicial instrumento de la sociedad pero no un órgano que la plasme conscientemente (
Doberti
Bajo este enfoque es importante analizar que hay una cuestión más profunda que requiere cierto grado de discernimiento entre la enseñanza del diseño y su aplicación práctica en contextos determinados, y su comprensión teórica. Esto requiere un planteamiento superior ya que estamos hablando de un saber que tiene sus fundamentos en distintas áreas del conocimiento y por tanto tributa a todos. Lo que requiere una resignificación de su valor teórico y práctico, por que ambos son válidos y aplicables.
La ciencia, las metodologías y los procesos constantemente están sujetos al riesgo conceptual, y este riesgo consiste en ser progresivo o regresivo, lo que permite diagnosticar su estado de hipótesis, además lleva a replantear nuevas soluciones o reflexiones desde una postura creativa (filosófica). Lo que no permite falsar con exactitud ni corroborar con exactitud
Red Descartes 2022/Año 2, núm. 4
La afirmación de Kuhn expone la posibilidad de que los procesos integrales del conocimiento, por lo menos en ciertos periodos de tiempo, están en constante cambio, lo que implica a su vez que en el diseño debe existir una mejora sistemática en la educación.
La formación docente en diseño viene con la relación de la formación profesional del diseñador, donde se incorporan algunas dinámicas pedagógicas de sus propios docentes, esta conjunción es lo que soporta la base de la propuesta de enseñanza, de igual manera, de esta serie de crónicas y experimentos prácticos se van conformando la enseñanza proyectual
Por otra parte, es importante enumerar hasta que punto se tiene un conocimiento teórico desarrollado por la lectura y la práctica docente, y por otra, donde esta la continua evolución de docente proyectista, que a su vez esté inmerso en la práctica comercial del hacer continuo del diseño, lo que lo lleva a estar actualizado desde todas las aristas posibles.
En la variopinta topografía de la práctica profesional existen unas tierras altas y firmes desde las que se divisa un pantano. En las tierras altas, los problemas fáciles de controlar se solucionan por medio de la aplicación de la teoría y la técnica con base en la investigación. En las tierras bajas del pantano, los problemas confusos y poco claros se resisten a una solución técnica. Lo paradójico de esta situación es que los problemas de las tierras altas tienden a ser de relativa importancia para los individuos o para la sociedad en su conjunto, aún a pesar de lo relevante que puede resultar su interés técnico, mientras que en el pantano residen aquellos otros problemas de mayor preocupación humana. El práctico debe elegir ¿Tendrá que quedarse en las tierras altas donde le es posible resolver problemas de relativa importancia según los estándares de rigor predominantes, o descenderá al pantano de los problemas relevantes y de la investigación carente de rigor? (
Red Descartes 2022/Año 2, núm. 4
Debido a la naturaleza del diseño y puesto que los diseñadores resuelven dificultades, es importante reflexionar sobre la realidad teórica versus la necesidad práctica, los problemas planteados en la realidad a menudo nunca se presentan como esquemas delimitados o con pasos secuenciales a resolver. De hecho, esta naturaleza es tan común que la mayoría de problemas a resolver siempre distan de una naturaleza de diseño y vienen disfrazados de distintos aparejos. Otro rasgo implica pensar teniendo en consideración que los aprendizajes no son iguales para todos.
La enseñanza significativa
Según Freire
Por tratarse de una disciplina como el diseño que integra tantas áreas de acción, hace falta considerar un campo humano y ético que soporte elementos frente al quehacer disciplinar, esto se logar con docentes más articulados con las temáticas prácticas desde lo práctico y fundamentados en lo teórico, donde la enseñanza presenta un reto.
En diseño y en educación siempre se presentan situaciones que conllevan a establecer diferentes mecanismos pedagógicos y didácticos, pero son los procesos educativos con una visión más holística los que podrían dotar de habilidades al estudiantado para su vida profesional.
Red Descartes 2022/Año 2, núm. 4
Para Bustingorry & Mora
Una construcción de conocimiento significativo se justifica en que los alumnos aprendan lo mejor posible, donde hay una construcción desde la episteme y la praxis, de allí que tengan estrategias de evolución del aprendizaje y de la enseñanza, y su pilar fundamental sea el aspecto ético
Entonces, cuando se habla de conocimiento significativo en diseño podría decirse que son todos aquellos fundamentos teórico prácticos que involucran una reorganización cognitiva constante, apoyada en la resiliencia y en la creatividad donde se halle un profesional más humano.
“Este aprendizaje subyace a la integración constructiva de pensamientos, sentimientos y acciones, que a su vez conducen al engrandecimiento humano, generando una sensación buena, agradable y aumentando la disposición para la adquisición de nuevos conocimientos”
Si bien la propuesta apunta a una mejora sistemática en la educación mediada por recursos prácticos, teóricos o digitales, no olvidemos que los recursos no significan mejor educación. Hace falta una mejor preparación frente a la didáctica de la enseñanza y la motivación.
Red Descartes 2022/Año 2, núm. 4
Por otro lado, se presenta el estudiante con todas sus dinámicas sociales, psicológicas y personales donde la academia lo centra como el recurso más valioso. A si mismo también, llenos de atadijos, complicaciones y tal vez por condición generacional de un desánimo perturbador, teniendo en consideración que los aprendizajes no seducen por igual a todos.
Lo adquirido versus lo requerido: La mayor deficiencia detectada es el desconocimiento de la realidad laboral, indica que en el periodo de formación nos vemos empapados de la parte positiva, por decirlo así del diseño, la problemática radica desde las aulas de clase, pues la mayoría de los profesores no laboran en algo directamente relacionado con la actividad del diseño ni aplicación del conocimiento del campo (
Los anteriores párrafos ejemplifican una realidad condensada donde se establece el factor estudiantil con sus condiciones sociológicas y el factor pedagógico con la experiencia respectiva del docente, elementos a tener en cuenta, ambos en pro del bienestar del alumno en el campo profesional.
Por otro lado, Vigotsky
Red Descartes 2022/Año 2, núm. 4
Esto supone el surgimiento de profesionales mejor preparados y jerárquicamente definidos, donde los campos de acción estén debidamente delimitados por el conocimiento teórico y práctico en sus áreas respectivas. La necesidad parece indicar que se deben formar diseñadores en tres direcciones, el diseño como arte se relaciona con la capacidad expresiva, el diseño como ciencia se vincula a la presentación sistemática y objetiva de información, y el diseño como comunicación, esto mediado con la interpretación de la audiencia
A modo de cierre se puede exponer la demarcación de la disciplina que construye el diseño. Esta se provee de dos componentes trasversales, lo teórico y lo práctico. Es parte de la profesión del diseño dar un buen manejo de la justificación del conocimiento, los lenguajes técnicos y la construcción conceptual que da sustento comunicacional al proyecto en sí. Esto legitima al diseñador como profesional holístico, pero a su vez lo desafía a legitimar esa teoría utilizada por medio de los conocimientos necesarios para resolver determinado problema que tiene asidero en la vida práctica.
Así mismo, el docente posee una acción transformadora, ya que en el recae el modelo ético de un profesional íntegro, el cual lo lleva por distintos parajes de la enseñanza práctica y teórica en busca de la solución de problemas que nos atraviesan para la técnica cultural y la metodología de diseño como pensamiento sistemático.
Falta reflexión teórica que sistematice estas experiencias y trascienda el anecdotario de mero interés testimonial sobre procesos de trabajo específicos. Lo que se encuentra publicado en general tiende a mostrar, no a sistematizar el conocimiento ni a plantear problemas conceptuales (
Red Descartes 2022/Año 2, núm. 4
El grado de ambigüedad en lo que se considera como conocimiento teórico y práctico a menudo se ejemplifica como la dialéctica del profesor que defiende su saber como una postura firme de lo que prima en sus clases. Es aquí donde se necesita un puente entre lo pertinente y su cimiento conceptual, lo que involucra la participación de diferentes actores que trabajen con algún grado de sinergia.
Es imperativo que la academia, el estado y la empresa conversen en función de la producción de sociedad con la labor del diseño como agente conciliador del origen práctico y también teórico de sus saberes, ya que, a su vez, debido al crecimiento de la disciplina y su participación en múltiples aspectos de la vida en sociedad, exige una incorporación cada vez más sólida de la teoría en la formación del profesional del diseño.
Por último, no se entiende una institución de educación superior ajena a las demandas sociales, esto es, no se justifica una universidad inútil o disfuncional, pues ella tiene un papel relevante en la sociedad. Por eso, ante una sociedad como la actual, también necesitamos renovar los cimientos de la universidad que le permita a la revolucionaria sociedad del conocimiento, reformas orientadas en múltiples direcciones: en las metodologías docentes y los procesos formativos de los estudiantes
Evaluación
En la siguiente escena interactiva se presentan algunas afirmaciones ¿falsas?, ¿verdaderas?
Si has leído el artículo, sabrás cuáles son ciertas y cuáles son falsas.
Red Descartes 2022/Año 2, núm. 4
Red Descartes 2022/Año 2, núm. 4
Red Descartes 2022/Año 2, núm. 4
probando
DescartesJS
Animaciones del Webb con DescartesJS
Juan Guillermo Rivera Berrío
La incorporación de animaciones en una página con texto, puede resultar contraproducente para la lectura
Por ello, hemos recomendado usar animaciones en páginas con poca cantidad de texto o, como mejor opción, una imagen estática que enlace con la imagen animada; por ejemplo, haz clic en la siguiente imagen:

Fuente: Eos: Science News by AGU
Red Descartes 2022/Año 2, núm. 4
Un ejemplo de esta alternativa, es la imagen que aparece al lado derecho de este texto. Usando el editor DescartesJS, hemos puesto tres botones en la parte inferior de la imagen, para que el usuario active la animación y, si lo desea, amplíe o reduzca su tamaño (zoom).
A continuación, explicamos cómo se diseñó esta imagen. Presentaremos varios ejemplos usando imágenes del telescopio espacial James Webb, elección que justificará el uso de esta alternativa.
Red Descartes 2022/Año 2, núm. 4
¿Por qué usar animaciones?
El auge de las animaciones en la web inicia con la creación del Formato de Intercambio de Gráficos o más conocido como GIF (Graphics Interchange Format, por sus siglas en inglés), creado por CompuServe en 1987. En 1996 con el lanzamiento de Macromedia Flash las animaciones se hicieron más populares. Desde esa década de los 90, los banner, imágenes y textos animados inundaron la Red, buscando destacarse en su diseño más no en su contenido. Algunos, equivocadamente, usan las animaciones sólo con el propósito de decorar una página web con un efecto que puede ser negativo, en tanto que distrae al lector o, peor aún, al estudiante cuando se trata de una página educativa.
Un uso adecuado de las animaciones puede lograr que la página sea atractiva para el lector, sin incomodarlo. Por ejemplo, en el diseño de menús o de botones como en el siguiente ejemplo:
El uso de animaciones como fondo de una página de un libro digital puede ser atractivo, siempre que sea concordante con el tema tratado y con un mínimo de texto, algunas páginas suelen usar la técnica del parallax que da un efecto de profundidad.
Existen animaciones que son muy útiles para conocer el estado de un proceso:

Red Descartes 2022/Año 2, núm. 4
Otro tipo de animaciones son las usadas en galerías de imágenes, que en una sola ventana muestra mucha información al usuario:
Con el lanzamiento de las primeras imágenes del telescopio espacial James Webb, han surgido animaciones con el propósito de comparar las imágenes del Webb con las obtenidas por otros telescopios. Un tipo de animación, que ha resultado muy útil, es la diseñada para desplazamiento horizontal, pues una imagen de alta resolución como las entregadas por el Webb, no es posible mostrarlas en una página sin reducir su tamaño. A continuación, explicamos cómo hacerlo con el editor DescartesJS.
Red Descartes 2022/Año 2, núm. 4
Diseño de una animación de desplazamiento lateral con DescartesJS
Este ejercicio de diseño lo haremos con la imagen obtenida del Webb de la galaxia espiral barrada NGC1365, procesada por Judy Schmidt y publicada el 15 de agosto de 2022.
La animación a obtener es la que se muestra en la imagen de la izquierda, en la que hemos incorporado botones para activar o parar la animación, lo que le da un valor agregado con respecto a las animaciones en formato GIF.
La imagen de la NGC1365, descargada de Flickr, tiene un tamaño de $1426\times 1238$ pixeles. Dado que una escena DescartesJS de este tamaño resulta incómodo de trabajar, hemos escalado la escena al 50%; es decir, $713\times 619$ pixeles. Esta asignación de escala la haremos en el editor. Este tamaño no es el mismo que usaremos para la escena, pues nuestro propósito es que una franja horizontal de
Red Descartes 2022/Año 2, núm. 4
la imagen quede oculta; es decir, el ancho de la escena debe ser inferior al ancho de la imagen. Para el ejercicio, hemos escogido un tamaño de escena de $400\times 619$ pixeles, que ocultaría $313$ pixeles de ancho de la imagen ($713 - 400$). Con estas dimensiones en mente, iniciamos el diseño:
- Espacio de trabajo. Creamos el espacio
E1, con una escala de $1$, fijo, con fondo negro, ejes y red desactivados. - Controles. Agregamos dos controles, así: el primero es un botón de reproducción de la animación de tamaño 40x40, que pondremos en la posición (180, 560); es decir, centrado verticalmente y a $59$ pixeles del borde inferior. Este botón se dibuja sólo si la variable
pausaes cero. Usamos una imagen de tamaño $40\times 40$ pixeles para el botón, similar a esta:

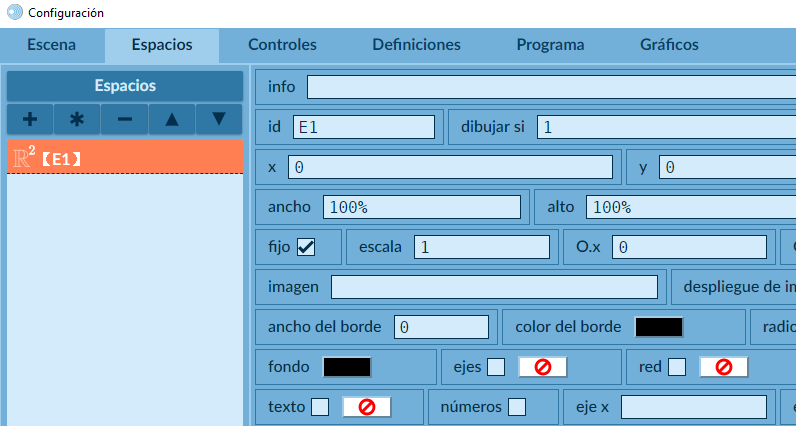
Red Descartes 2022/Año 2, núm. 4
Seleccionamos la acción calcular, con estos parámetros: pausa=1 y play=0, que permite que se deje de mostrar el botón de reproducir y aparezca el boton para pausar la animación.
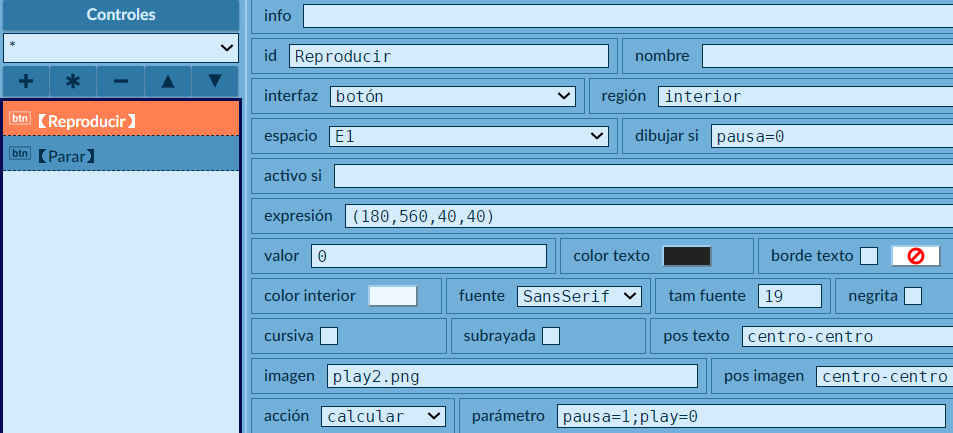
El segundo botón es para pausar la animación, su configuración es similar, basta con cambiar los valores de las variables.
- Selector Programa. Agregamos dos eventos, donde ambos tienen como acción "animar" con una ejecución alternada. El primero se ejecuta si
pausa = 1y el segundo si se cumpleplay = 1.

- Gráficos. Agregamos un sólo gráfico... la galaxia NGC1365, así:
Red Descartes 2022/Año 2, núm. 4
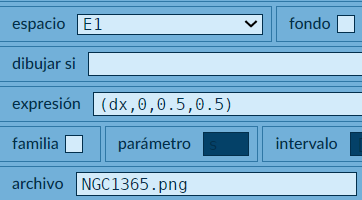
En la abscisa hemos puesto la variable dx, la cual permite el desplazamiento horizontal de la imagen, que hemos escalado al 50%.
- Animación. La animación se ejecuta cuando se cumple alguno de los eventos anteriores. Hemos puesto un incremento (
paso) de $3$, el cual puede ser cambiado para aumentar o disminuir la velocidad de la animación. Los límites derecho e izquierdo, en los dos condicionales, se obtuvieron dividiendo por $2$ la franja no visible; es decir $313/2 \approx 157$.

¡Eso es todo! A continuación, presentamos dos ejemplos adicionales, diseñados siguiendo la explicación anterior.
Red Descartes 2022/Año 2, núm. 4
Nebulosa de Carina (imagen compuesta de NIRCam y MIRI)
La imagen, obtenida de webbtelescope.org, tiene un tamaño de $2000\times 693$ pixeles. Hemos usado una escena de $640\times 693$, con la imagen sin escalar, obteniendo:
Red Descartes 2022/Año 2, núm. 4
Nebulosa de Carina (imagen NIRCam)
La imagen. obtenida de webbtelescope.org, tiene un tamaño de $2000\times 1158$ pixeles. Hemos usado una escena de $640\times 653$, con la imagen escalada al 65%. Incluimos el archivo de audio Planetary Paths de Joel Cummins y Andy Farag, obteniendo:
Red Descartes 2022/Año 2, núm. 4
El tuit destacado
Roberto Rohde
@RARohde
Hace 110 años, un periódico de Nueva Zelanda advirtió que la quema de carbón podría eventualmente cambiar el clima. Esto se basó en el trabajo de Svante Arrhenius, quien 16 años antes había medido el efecto de calentamiento del dióxido de carbono en la atmósfera. No digas que no te lo advertimos.

Hablar del cambio climático no es una novedad, saber que hace 110 años se hizo una advertencia al respecto, quizá tampoco impacte. Sin embargo, la discusión en torno al tuit de Roberto Rohde
Red Descartes 2022/Año 2, núm. 4
publicado el 14 de agosto de 2022 cuando "arde Europa, afectada por olas de calor, incendios y sequías (https://www.telam.com.ar/)" y sus ríos se están secando (https://www.dw.com/), hace destacable el tuit.
Rohde es un científico, PhD en física, estudioso del cambio climático y los combustibles fósiles. Su tuit rápidamente se volvió viral, lo que generó respuestas a favor y en contra.
Parte de la discusión, la transcribimos a continuación:
. Smith Eso fue totalmente desacreditado por experimentos de diseño similar realizados por Angstrom. Si Arrhenius estaba en lo cierto, la troposfera debería haberse calentado, especialmente en los trópicos. Sin embargo, 5 décadas de datos satelitales no muestran esencialmente ningún calentamiento en la troposfera.
Rohde. No me parece "esencialmente sin calentamiento".
Maher ¡El Dr. Michael Mann dice que solo toma unos pocos años y los océanos y los árboles eliminan el CO2 de la atmósfera! ¡¡El alarmismo es una enfermedad!!
Rohde. Unos años "después del cero neto".
Wisdom. Eres Chicken Little. Todos los días afirmas que el mundo se acabará a menos que abracemos la pobreza y la muerte. Sigue sin suceder, pero nunca dejas de predecirlo.
Rohde. ¿Es ese insulto, caracterización errónea e ignorancia deliberada lo que pasa como sabiduría en estos días?
Klages. El término smog fue acuñado en un Congreso de Salud de Londres a fines de 1905 como un acrónimo compuesto por las palabras inglesas smoke y fog.
Red Descartes 2022/Año 2, núm. 4
Rohde. Si bien al Dr. Des Voeux se le atribuyó en ese momento haber acuñado la palabra "smog" en un documento presentado en el Congreso de Salud Pública de 1905, no es el primer uso. Una columna en el Santa Cruz Sentinel de 1880 es el primer uso registrado de "smog", que también se refiere a la niebla humeante en Gran Bretaña.
Manuel. Ya se están produciendo cambios significativos.
Wirbelwind. Podríamos haber evitado esto. Prevengamos al menos un mundo inhabita
Moene. Tenga en cuenta que la física detrás de la absorción de radiación por CO2 (sobre la cual construyó el conocimiento Arrhenius) fue descubierta por Eunice Newton Foote en 1856.
Paige. Georges-Louis Leclerc escribió sobre la geoingeniería antropogénica ya en 1778... Nada de lo que estamos presenciando hoy debería ser una sorpresa.
Mike. Un photoshop mal creado de un artículo inexistente sin referencias. El miedo vende, nos da miles de millones y billones y seamos felices. Cambiaremos el clima.....
Rohde. Siéntase libre de leer más sobre la historia de ese --> artículo muy real de 1912.
Smith. Sus cálculos estaban equivocados en ~40% (quemar 1 tonelada de carbón produce ~4.2klbs de CO2, no 7k lbs), y eres demasiado parcial para darte cuenta ¡¡¡Pero mi conclusión sigue siendo cierta!!!, nunca sabe de qué cojones está hablando.
Rohde. Oh wow, todo el castillo de naipes se derrumba porque alguien hace 110 años estaba un poco equivocado en sus matemáticas. Por cierto, si va a criticar la propaganda de las noticias,
Red Descartes 2022/Año 2, núm. 4
la crítica aún mejor es que el consumo de carbón en 1912 en realidad estaba más cerca de los 1.000 millones de toneladas que de los 2.000 millones de toneladas.
Algunas imágenes aportadas en la discusión:
Red Descartes 2022/Año 2, núm. 4
Matemáticas
Superficies regladas desarrollables, diseño y construcción con DescartesJS
José Román Galo Sánchez
En este artículo se describen y clasifican las superficies regladas desarrollables poniendo de manifiesto que estas son cilindros, conos y superficies tangenciales. Mediante el uso de escenas interactivas, desarrolladas con DescartesJS, se permite al usuario diseñar y abordar la construcción virtual de "sus" cilindros, conos y superficie tangenciales personalizadas, pero también se le da la posibilidad de convertirlos en objetos tridimensionales tangibles sin más que proceder a la obtención automática de sus desarrollos planos y, mediante su impresión en papel, proceder a su construcción.
Red Descartes 2022/Año 2, núm. 4
Superficies regladas desarrollables
Una superficie es reglada si está constituida por una familia de rectas. Todas estas superficies se pueden parametrizar como:
$$\vec{r} : D \subset \Reals^2 \to \Reals^3\\ (\textcolor{red}{u}, \textcolor{DeepSkyBlue}{v}) \to \vec{r}(\textcolor{red}{u}, \textcolor{DeepSkyBlue}{v}) = \vec{c}(\textcolor{red}{u}) + \textcolor{DeepSkyBlue}{v}\vec{d}(\textcolor{red}{u})\tag{1}$$donde $\vec{c}(\textcolor{red}{u})$ y $\vec{d}(\textcolor{red}{u})$ son curvas en el espacio tridimensional. La primera es la curva base o curva directriz y la segunda es el vector director de cada una de las rectas denominado generatriz. Efectivamente, fijado un valor del parámetro $\textcolor{red}{u}$ puede observarse que la expresión obtenida es la ecuacion de una recta y variando $\textcolor{red}{u}$ geométricamente lo que se puede interpretar es que se va recorriendo cada punto de la curva base $\vec{c}(\textcolor{red}{u})$ y por él pasa una recta cuya dirección viene dada por $\vec{d}(\textcolor{red}{u})$.
También puede expresarse de manera equivalente como:
$$\begin{split} \vec{r}(\textcolor{red}{u}, \textcolor{DeepSkyBlue}{v}) &= \vec{c}(\textcolor{red}{u}) + \textcolor{DeepSkyBlue}{v}\vec{d}(\textcolor{red}{u})\\ &= (1-\textcolor{DeepSkyBlue}{v})\vec{c}(\textcolor{red}{u}) + \textcolor{DeepSkyBlue}{v} \Big(\vec{d}(\textcolor{red}{u}) + \vec{c}(\textcolor{red}{u} )\Big)\\ &= (1-\textcolor{DeepSkyBlue}{v}) \vec{c_1}(\textcolor{red}{u}) + \textcolor{DeepSkyBlue}{v} \vec{c_2}(\textcolor{red}{u})\tag{2}\\ \end{split}$$que algebraicamente representa, para cada valor de $\textcolor{red}{u}$, a una recta (o un segmento si consideramos $0 \le \textcolor{DeepSkyBlue}{v} \le 1)$, pero en este caso lo que se pone de manifiesto es que esa recta se apoya en un punto de la curva $\vec{c_1}(\textcolor{red}{u})$ y en otro de la curva $\vec{c_2}(\textcolor{red}{u})$.
El ejemplo más simple de superficie reglada es un plano, pero entre
Red Descartes 2022/Año 2, núm. 4
otras, también lo son los cilindros, los conos, la banda de Moebius y el hiperboloide.
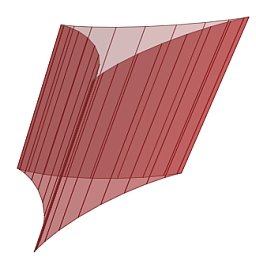 |
 |
| Cilindro generalizado | Cono generalizado |
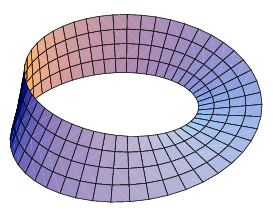 |
 |
| Banda de Möbius | Hiperboloide |
Una herramienta matemática que permite caracterizar la curvatura de cualquier superficie regular es la denominada curvatura de Gauss y se verifica que dicha curvatura es invariante por isometrías. Todas las superficies regladas cumplen que su curvatura de Gauss es menor
Red Descartes 2022/Año 2, núm. 4
o igual que cero y, en particular, que la curvatura de Gauss de un plano es identicamente nula. En base a lo anterior, todas las superficies regladas que tienen curvatura cero son isométricas con el plano y son denominadas como superficies desarrollables ya que, consecuentemente, pueden construirse a partir de su desarrollo plano.
En la parametrización (1) la condición de curvatura nula equivale a que el denominado parámetro de distribución sea nulo, y éste viene dado por:
$$p(\textcolor{red}{u}) = \vec{d'}(\textcolor{red}{u})\cdot \Big(\vec{c'}(\textcolor{red}{u})\times \vec{d'}(\textcolor{red}{u})\Big) \tag{3}$$o en el caso de la parametrización (2) como:
$$p(\textcolor{red}{u}) = \vec{c'}_2(\textcolor{red}{u})\cdot \big(\vec{c'_1}(\textcolor{red}{u}) \times \big(\vec{c_2}(\textcolor{red}{u}) - \vec{c_1}(\textcolor{red}{u})\big)\big). \tag{4}$$De (4) se observa que para que la superficie reglada sea desarrollable tiene que ocurrir que para todo $\textcolor{red}{u}$ el vector tangente a la curva $\vec{c_1}(\textcolor{red}{u})$, el vector tangente a $\vec{c_2}(\textcolor{red}{u})$ y el vector director de la recta que une a ambas curvas sean coplanarios al ser el producto mixto de los tres cero, o dicho de otra forma que el plano tangente es constante a lo largo de cada recta generatriz.
Pero un análisis más detenido de cuándo es identicamente nulo el parámetro de distribución nos puede permitir clasificar a las superficies desarrollables. Así en la expresión (3):
- Si $\vec{d'}(\textcolor{red}{u})$ es identicamente nulo, entonces $\vec{d}(\textcolor{red}{u})$ es un vector constante, es decir que todas las rectas tienen la misma dirección y la superficie es un cilindro generalizado de ecuación $\vec{r}(\textcolor{red}{u}, \textcolor{DeepSkyBlue}{v}) = \vec{c}(\textcolor{red}{u}) + \textcolor{DeepSkyBlue}{v} \vec{d}$.
Red Descartes 2022/Año 2, núm. 4
- Si $\vec{c'}(\textcolor{red}{u})$ es idénticamente nulo, entonces $\vec{c}(\textcolor{red}{u})$ es el vector de posición de un punto $V$ y la superficie desarrollable es un cono generalizado de vértice $V$, cuya ecuación sería:
$$\vec{r}(\textcolor{red}{u}, \textcolor{DeepSkyBlue}{v}) = \overrightarrow{OV} + \textcolor{DeepSkyBlue}{v} \vec{d} (\textcolor{red}{u}).$$ También puede expresarse en función de una curva base como $\vec{r}(\textcolor{red}{u}, \textcolor{DeepSkyBlue}{v}) = \overrightarrow{OV} + \textcolor{DeepSkyBlue}{v} \big( \vec{c_b}(\textcolor{red}{u})-\overrightarrow{OV}\big)$. - En cualquier otro caso se demuestra que es una superficie tangencial, la cual mediante un cambio de parámetro se puede expresar como $\vec{r}(\textcolor{red}{u}, \textcolor{DeepSkyBlue}{v}) = \vec{\alpha}(\textcolor{red}{u}) + {\textcolor{DeepSkyBlue}{v}} \vec{\alpha}'(\textcolor{red}{u})$.
Superficies desarrollables con Descartes
Con Descartes podemos desarrollar escenas interactivas que nos permitan modelar y diseñar, a discreción y según el deseo de cada cual, superficies desarrollables y no solamente visualizarlas virtualmente sino también obtener su desarrollo plano y a partir de él, imprimiéndolo, poder construir de manera real y tangible el modelo tridimensional diseñado, si bien hemos de indicar que no siempre será fácil lograr esa construcción, especialmente cuando la curva directriz no es plana.
En la siguiente imagen animada, como adelanto, podemos observar la definición y obtención de un cilindro cuya curva directriz es la curva plana denominada bifolium y la generatriz es una recta inclinada respecto al plano que contiene a la curva directriz. También se refleja la obtención de manera automatizada del desarrollo de ese cilindro y la posibilidad de proceder a su impresión.
Red Descartes 2022/Año 2, núm. 4
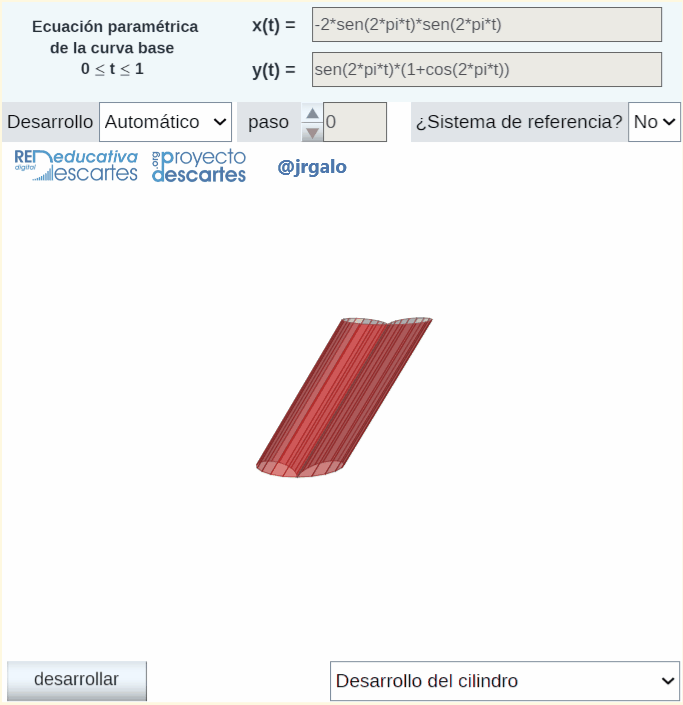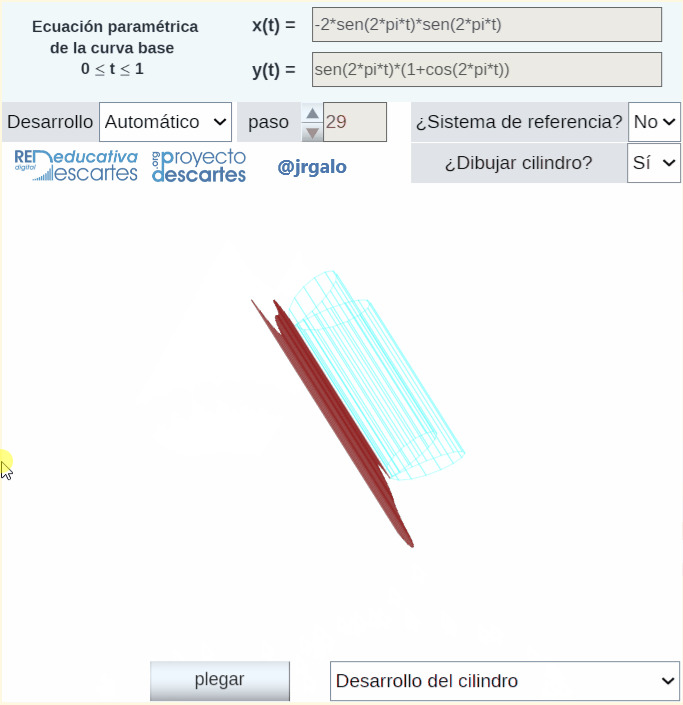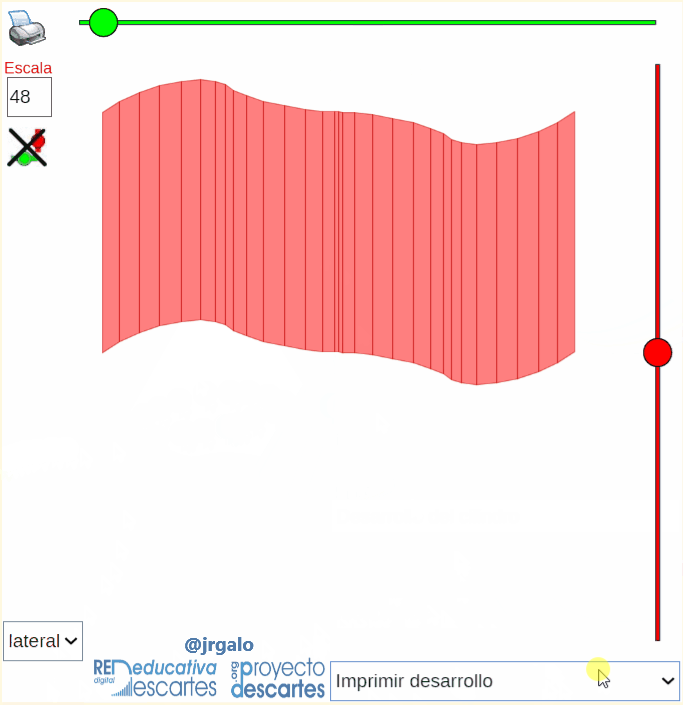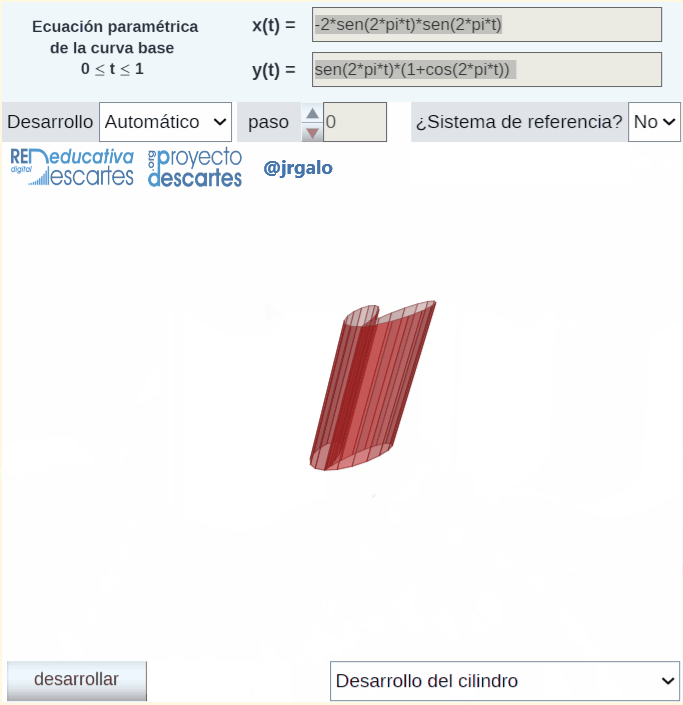
He de reseñar que para la obtención automática y animada del desarrollo plano se aplica la rotación de Rodrigues descrita en un artículo anterior de esta revista
Red Descartes 2022/Año 2, núm. 4
Cilindros generalizados
En la miscelánea interactiva "Construyo mis cilindros generalizados con curva base 3D" se abordan las superficies que pueden parametrizarse como $\vec{r} (\textcolor{red}{u}, \textcolor{DeepSkyBlue}{v}) = \vec{c}(\textcolor{red}{u}) + \textcolor{DeepSkyBlue}{v} \vec{d}$.
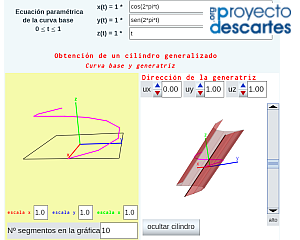
Pulsa sobre la imagen para acceder a la escena interactiva
El usuario define su curva directriz tridimensional $\vec{c} (\textcolor{red}{u})$ (que en particular puede ser plana) y la dirección de la generatriz que en este caso es constante y, seleccionando la opción de menú correspondiente, puede simular la generación de su cilindro, obtener su desarrollo plano e imprimirlo si lo desea.
En el caso en el que la curva directriz es plana, imprimiendo la base, se tiene una guía sobre la que proceder a la reproducción física del cilindro a partir del desarrollo impreso, pero en el caso de curva tridimensional no siempre será fácil esa construcción ya que no dispone de la reproducción física tridimensional de la curva directriz en la que poder apoyarse para poder plegar el desarrollo.
Red Descartes 2022/Año 2, núm. 4
Se requeriría abordar una impresión 3D de la directriz o bien construir la superficie lateral de un prisma cuya base inferior fuera plana y la superior siguiera el perfil de la curva directriz que serviría como soporte sobre el que apoyar y construir el cilindro. Ambas opciones pueden programarse, pero no se contemplan en este recurso interactivo.
Conos generalizados
Con idéntica funcionalidad tenemos la miscelánea "Construyo mis conos generalizados con curva base 3D" correspondiente a la parametrización $\vec{r} (\textcolor{red}{u}, \textcolor{DeepSkyBlue}{v}) = \overrightarrow{OV} + \textcolor{DeepSkyBlue}{v} \big( \vec{c_b} (\textcolor{red}{u}) - \overrightarrow{OV} \big)$. En ella, definiendo la curva directriz tridimensional y el vértice se procede a generar el cono y a obtener su desarrollo plano. En este caso la reproducción material del cono, gracias a la referencia del vértice, puede ser más sencilla.
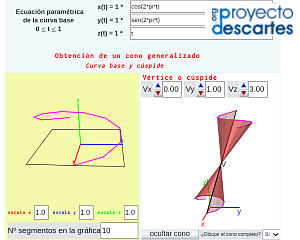
Pulsa sobre la imagen para acceder a la escena interactiva
Red Descartes 2022/Año 2, núm. 4
Superficies tangenciales
Finalmente tenemos la miscelánea "Construyo mis superficies tangenciales" asociada a las parametrizaciones del tipo
$$\vec{r} (\textcolor{red}{u}, \textcolor{DeepSkyBlue}{v}) = \vec{\alpha}(\textcolor{red}{u}) + \textcolor{DeepSkyBlue}{v} \vec{\alpha'}(\textcolor{red}{u})$$
y en las que en cada punto de la curva directriz la generatriz sigue la dirección de la recta tangente a dicha directriz. He aquí la escena interactiva:
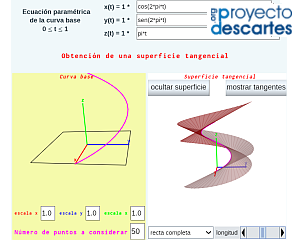
Pulsa sobre la imagen para acceder a la escena interactiva
En ella hay que detallar y aclarar algunas cuestiones:
- El usuario define la curva directriz y esta, teóricamente, ha de ser diferenciable para que en todo punto esté definida la recta tangente que es la generatriz de la superficie.
- A nivel interno en la escena interactiva se trabaja de manera discreta, pues esa es la realidad computacional y de ella podemos obtener provecho. Por tanto, realmente, lo que se tiene es que la curva directriz es una poligonal y para segmentos de longitud pequeña la dirección de estos
Red Descartes 2022/Año 2, núm. 4
son buenas aproximaciones de la recta tangente. Consecuentemente en cada nodo de esa poligonal (punto de la curva directriz) se puede optar por considerar la dirección de la tangente bien por la del segmento anterior a ese nodo (que se corresponde con diferencias finitas regresivas) o la del segmento posterior (diferencias progresivas) o la media aritmética de ellas (diferencias centradas). En la escena se ha optado por considerar la tangente asociada a las diferencias regresivas.
- En toda superficie tangencial los puntos singulares son los puntos de la curva directriz (arista de retroceso), los cuales se corresponden con el valor del parámetro $\textcolor{DeepSkyBlue}{v = 0}$, y la superficie está formada por dos hojas $(\textcolor{DeepSkyBlue}{v} \lt 0\text{ y } \textcolor{DeepSkyBlue}{v}\gt 0)$ —en la escena se ha indicado como semirrecta negativa y semirrecta positiva—.
- Para aproximar cada una de las hojas de la superficie, entre cada dos tangentes consecutivas de la poligonal aproximante citada se considera el ángulo plano que forman ambas (en la escena un triángulo). Obviamente a medida que se considera más número de segmentos la aproximación es mejor. Ver las siguientes imágenes:
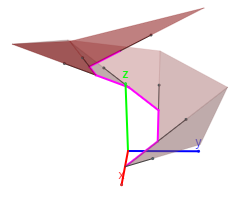 |
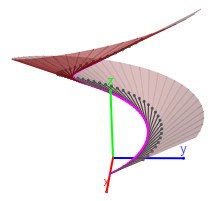 |
| Aproximación con seis segmentos | Aproximación con cincuenta segmentos |
Red Descartes 2022/Año 2, núm. 4
- La aproximación es similar a la ya señalada en el caso de los cilindros que se aproximan por prismas y la de los conos aproximados por pirámides. Y a partir de esta, la obtención dinámica del desarrollo plano y este en sí es algo inmediato con la parafernalia técnica que habitualmente empleo usando la citada rotación de Rodrigues.
En la animación siguiente se refleja parte de lo que puedes abordar y obtener con esta escena interactiva.
Red Descartes 2022/Año 2, núm. 4
Nota bene final: ¡Os invito a construir vuestras superficies regladas desarrollables! tanto de manera virtual como real. Y también, usando el editor de DescartesJS, a indagar en el código de la escena interactiva para ver "cómo lo hice", pero en este caso he de advertir que el buen consejo dado por Fernández-Mesa
Bibliografía
Red Descartes 2022/Año 2, núm. 4
Educación
Abierta
Formación en DescartesJS
José Antonio Salgueiro González
Competencia Digital Docente (MRCDD) se recogen las competencias digitales que debe adquirir cualquier docente del siglo XXI a lo largo de su desarrollo profesional, independientemente de la materia, etapa o tipo de enseñanza que imparta.
- Área 1: Compromiso profesional.
- Área 2: Contenidos digitales.
- Área 3: Enseñanza y aprendizaje.
- Área 4: Evaluación y retroalimentación.
- Área 5: Empoderamiento del alumnado.
- Área 6: Desarrollo de la competencia digital del alumnado.
instrumentos que permitan abordar
ciertos aspectos del área dedicada a los
contenidos digitales. Y, más concretamente,
aquellos que permiten al profesorado crear los
contenidos digitales a medida, para
su práctica docente.
Red Descartes 2022/Año 2, núm. 4
En el MRCDD, se establecen, además para el área que estamos tratando, varios aspectos específicos, como el que literalmente contempla la:
Utilización de herramientas de autor para la modificación, diseño y creación de contenidos educativos digitales nuevos o derivados de otros contenidos con niveles de agregación crecientes Marco de Referencia de la Competencia Digital Docente. Página 53 ..
En este sentido, Descartes, con una trayectoria de 25 años, código abierto y gratuito, es una potente herramienta de autor multipropósito que permite desarrollar objetos educativos interactivos en cualquier área de conocimiento. Además, DescartesJS es un intérprete de Descartes que es compatible con HTML5, consecuentemente las escenas interactivas desarrolladas con Descartes funcionan en cualquier dispositivo tipo ordenador, tableta o smartphone independientemente del sistema operativo que porte.

Red Descartes 2022/Año 2, núm. 4
Qué podemos crear con DescartesJS
En base a las necesidades de nuestro alumnado y según nuestra formación, imaginación y creatividad, con DescartesJS podemos generar contenidos digitales e interactivos para:
- Situaciones de aprendizaje para retos concretos y específicos, como el problema de la naranjada para 4º de Primaria (9-10 años)
- Ejercicios aleatorios ilimitados de autocorrección, como el interactivo diseñado para practicar la división como reparto mediante plantillas circulares, y que podemos manipular en la página siguiente.
Red Descartes 2022/Año 2, núm. 4
- Rúbricas interactivas de evaluación, como la diseñada para evaluar una entrevista radiofónica y que se encuentra en la página 35 del libro "La radio ficción en el aula. Uso educativo del pódcast", aunque para comodidad de nuestros lectores incluimos también en la página siguiente de esta revista.
- Exponer estrategias de resolución de ejercicios en etapas superiores, como la escena que podemos encontrar en la página 187 del libro titulado "Ejercicios de Trigonometría. Procesos, métodos y actitudes", para la materia de matemáticas en 1º de Bachillerato (16-17 años), y que también insertamos en la página siguiente. Por cierto, además de la exposición, el alumnado debe superar algunos retos para avanzar en la misma interactuando.
Red Descartes 2022/Año 2, núm. 4
Red Descartes 2022/Año 2, núm. 4
Cómo podemos formarnos en la herramienta de autor DescartesJS
El programa de Educación Abierta de RED Descartes ha celebrado varias ediciones de la acción formativa titulada "Edición de objetos interactivos con DescartesJS" donde, con una metodología basada en la denominada clase invertida, cada participante recibe con antelación los contenidos a tratar en cada sesión, para que pueda tomar contacto con los mismos, familiarizarse con el editor de escenas, realizar sencillas prácticas y terminar aclarando y consultando dudas durante el desarrollo de la sesión por videoconferencia, que será grabada y divulgada posteriormente en el portal de RED Descartes.

Quien suscribe este artículo participó en la primera edición del curso, y puede asegurar que con la segunda sesión ya podemos crear nuestro primer recurso interactivo, sin más que seguir las indicaciones del vídeo embebido a continuación.
Red Descartes 2022/Año 2, núm. 4
Además del vídeo, puede ser de gran utilidad el material de referencia ofrecido previamente y correspondiente a la segunda sesión del "Curso DescartesJS".
Con este material es más que suficiente para iniciarnos en DescartesJS y crear nuestro primer recurso interactivo con esta potente herramienta de autor. No obstante, si avanzamos en su manejo y deseamos dar un paso más, podemos consultar:
Red Descartes 2022/Año 2, núm. 4
Cómo podemos conseguir el editor DescartesJS
DescartesJS es un programa de código abierto y gratuito soportado por el Instituto de Matemáticas de la Universidad Nacional Autónoma de México, cuya descarga para Windows, macOS o Linux podemos realizar desde la dirección
https://descartes.matem.unam.mx/

Red Descartes 2022/Año 2, núm. 4
Matemática
para la
diversidad
Recurso para multiplicar
Manuel Muñoz Cañadas
Aún siendo una premisa básica, no por ello se hace. Así que entiendo, que nuestro objetivo como docentes será la búsqueda incansable de ambos.
Daremos el verdadero sentido a la matemática como ciencia experimental, cuando seamos fieles a esos elementos de la enseñanza aprendizaje que nos mantendrán a discente y docente en una actitud de progreso, y nos permitirá acercar el conocimiento matemático basado en la experiencia a la diversidad del alumnado.
En esta ocasión, aprovecho estas páginas para exponer experiencias del alumnado de Educación Primaria, empleando plantillas con un círculo fraccionado en diversos sectores o fracciones iguales de diferentes valores. Podemos plastificarlas para mejorar sus prestaciones.
Por ahora, abordamos resolución de problemas a través de la multiplicación con el material didáctico que se indicará a continuación, pero esto representa solo un capítulo de un libro interactivo en fase de publicación.
Red Descartes 2022/Año 2, núm. 4
Presentación de las plantillas
Estas son las plantillas que utilizamos, con opción de poder descargarlas en el enlace indicado.
Plantillas circulares pdf (clic icono).
Recortar las fracciones pdf (clic icono).
Red Descartes 2022/Año 2, núm. 4
Junto a las plantillas empleamos regletas, policubos, dinero didáctico, fracciones...
Red Descartes 2022/Año 2, núm. 4
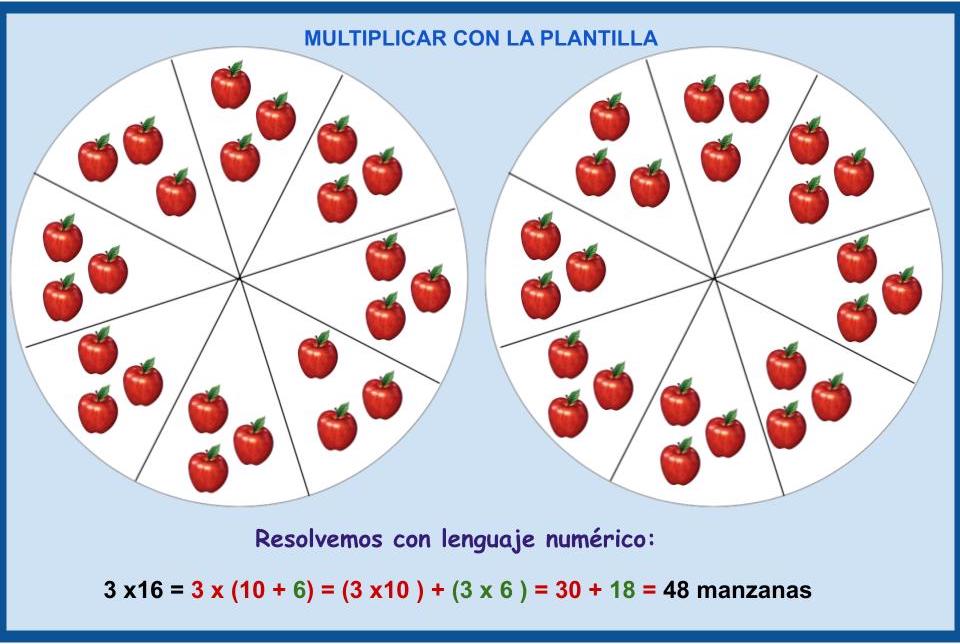
Representamos los datos con cromos, policubos, frutas didácticas... En el siguiente problema emplearemos la propiedad distributiva .
Problema: En cada una de las dos cajas metemos ocho bolsas, con tres manzanas en cada bolsa. ¿Cuántas manzanas tenemos en total?
Red Descartes 2022/Año 2, núm. 4
Problemas con plantillas y regletas
Se colocan los datos propuestos en el problema, actuando de forma manipulativa primero y de forma digital después. Hemos trabajado con Descartes y plantillas para conseguir las escenas adecuadas.
Problema: Dos maestras y un maestro de mi colegio tienen la misma edad, veintiocho años. Calcula los años que tienen entre los tres.
Las regletas o números de colores, nos van a ayudar a la comprensión y solución de problemas. Las vamos a utilizar junto a las plantillas. Si quieres más información sobre ellas haz clic en la imagen que aparece en la página siguiente.
Red Descartes 2022/Año 2, núm. 4
Construcción de tablas de multiplicar
La alumna manipula, comprende, deduce, aprende y representa en lenguaje matemático la experiencia, que podrá memorizar con la práctica.
Red Descartes 2022/Año 2, núm. 4
Descarga las tablas para completarlas de forma escrita.
Tablas de multiplicar en PDF (clic en icono).
Practica las tablas. Mueve la barra a izquierda o derecha según te interese.
Problemas con plantillas y dinero
El dinero didáctico es un excelente complemento para las plantillas. Ayuda fácilmente a resolver cálculos de forma comprensible, tanto con número naturales como decimales. Esta experiencia se ha confirmado en la práctica con la diversidad del alumnado. A continuación, se incorporan actividades interactivas programadas en Descartes.
Red Descartes 2022/Año 2, núm. 4
Resuelvo los problemas
Si expresamos en lenguaje matemático:
- En la primera actividad:
17x4= (10x4)+(5x4)+(2x4)= 40+20+8= 68€ - En la tercera actividad:
117x4= (100x4)+(10x4)+(5x4)+(2x4)=400+40+20+8= 468€ -
En actividades de producto con un número decimal:
151'90x7= (100x7)+(50x7)+(1x7)+(0'90x7)= 700+350+7+6'30= 700+300+50+13'30= 1063'30€
Red Descartes 2022/Año 2, núm. 4
Visualiza las fichas sobre actividades que se realizan por escrito. Puedes descargalas en sus enlaces.
Multiplicar un número entero por un decimal.Clic en icono.
Red Descartes 2022/Año 2, núm. 4
Construye tablas de multiplicar.Clic en icono de la impresora.
PDF convertido a HTML5 por IDR Solutions
Red Descartes 2022/Año 2, núm. 4
Más multiplicación con plantillas de Descartes
- Escribimos con lenguaje matemático algunos de los problemas del interactivo:
0'20 x 4 = 0'20+0'20+0'20+0'20= 0'80€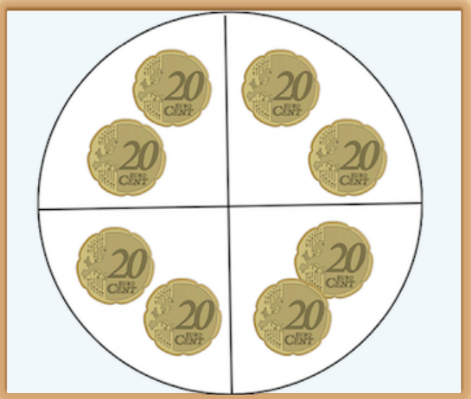
Red Descartes 2022/Año 2, núm. 4
250 x 6 = (200x6)+(50x6)= 1200+300 = 1500€

Red Descartes 2022/Año 2, núm. 4
DescartesJS
Colores, gradientes
y patrones
Joel Espinosa Longi
().
Red Descartes 2022/Año 2, núm. 4
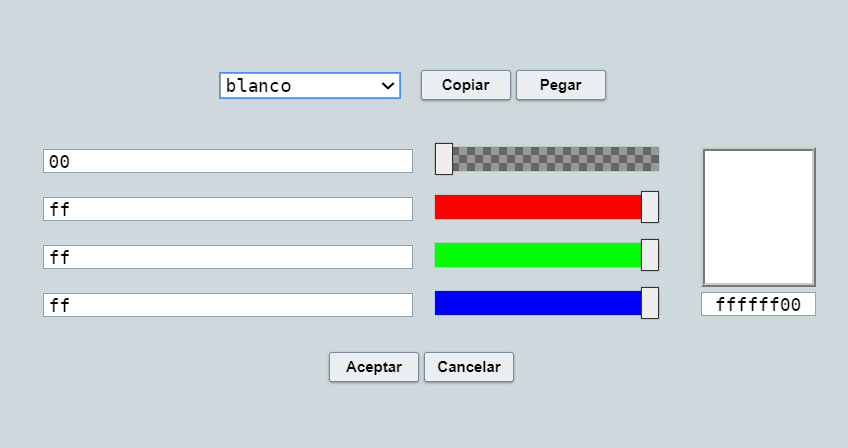
Aprovechando las funcionalidades que proporciona el elemento canvas de HTML, sobre el cual se basa el dibujado de la mayoría de los elementos presentados por DescartesJS, a partir de la versión 1.2 del editor de DescartesJS y la versión del 20 de noviembre de 2022 del intérprete de DescartesJS () se incorpora un nuevo editor de colores (), el cual permite, al igual que el original, editar colores en formato RGB pero, además, incluye la capacidad de utilizar gradientes e imágenes para rellenar el dibujo de espacios, controles y gráficos.

Red Descartes 2022/Año 2, núm. 4
En el nuevo editor de colores se presenta, en la parte superior, tres pestañas para seleccionar el tipo de relleno que se utilizará para colorear algún elemento. La primera pestaña, RGB (), preserva el funcionamiento original, donde se pueden especificar colores a partir de sus componentes de color rojo, verde y azul, así como su transparencia.
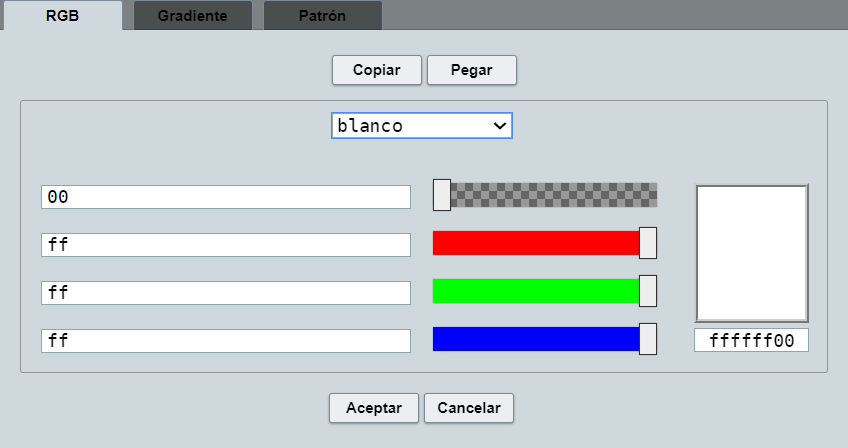
En la pestaña Gradiente (), se presenta una barra debajo de los botones Copiar y Pegar, donde se muestra una vista previa del gradiente.
Después se encuentran cuatro campos de texto que especifican las coordenadas de dos puntos que definen un segmento de recta que determina la posición y dirección del gradiente.
Red Descartes 2022/Año 2, núm. 4
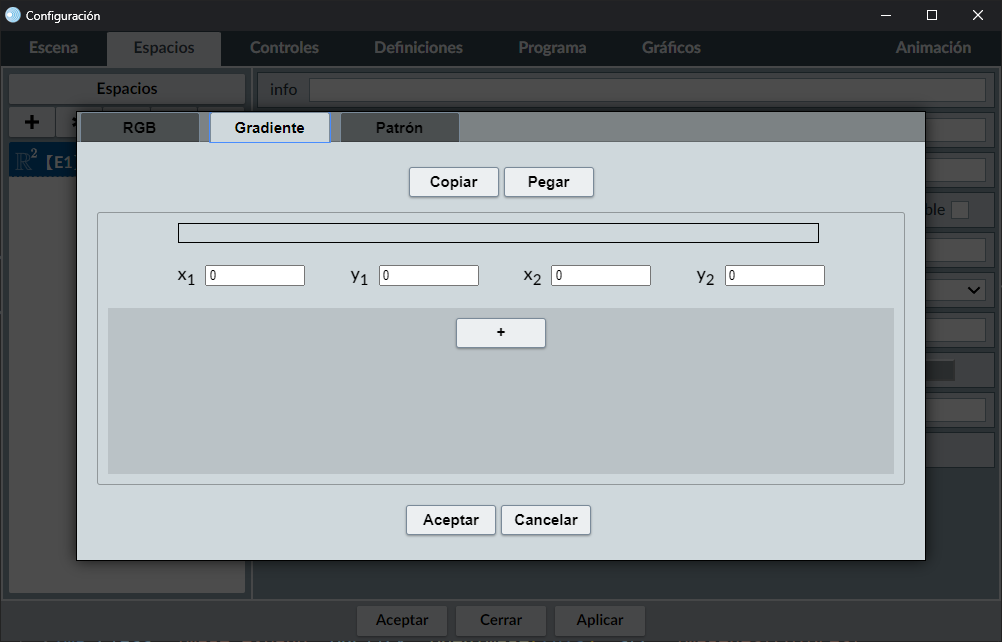
La razón de utilizar las coordenadas de dos puntos (x1, y1) y (x2, y2) viene de la especificación del elemento canvas para crear gradientes, https://developer.mozilla.org/en-US/docs/Web/API/CanvasRenderingContext2D/createLinearGradient, donde se utiliza un segmento que determina la posición y dirección en la que se crea el gradiente.
Estas coordenadas se establecen de forma absoluta respecto al canvas donde se dibuja, en el siguiente interactivo () modifica las coordenadas (x1, y1) y (x2, y2) y observa cómo cambia la dirección del gradiente utilizado como color de fondo del espacio.
Red Descartes 2022/Año 2, núm. 4
Para los gráficos contenidos en un espacio las coordenadas de (x1, y1) y (x2, y2), siempre son absolutas respecto al espacio que contiene el gráfico.
En el siguiente ejemplo () las coordenadas del segmento son iguales a las del gradiente, por lo que parece que el gradiente se mueve junto con el segmento al cambiar las coordenadas.
Red Descartes 2022/Año 2, núm. 4
Hay que mencionar que DescartesJS utiliza un canvas para dibujar cada espacio, así como los elementos gráficos que viven en él, mientras que cada control utiliza su propio canvas para dibujarse.
Al utilizar un gradiente como el color de un control, las coordenadas se refieren al área de dibujo del propio control y son independientes del espacio donde vive, en el siguiente ejemplo () se observa el uso de un gradiente como el color de fondo de un botón. En controles los gradientes se pueden utilizar para colorear las etiquetas o texto de los mismos.
Red Descartes 2022/Año 2, núm. 4
canvas donde se dibuja.Por último, debajo de los campos de texto para especificar las coordenadas (x1, y1) y (x2, y2), aparece un botón de “+” (más) que permite agregar una parada de color en el gradiente.
Al presionar al botón “+” aparece un conjunto de controles para especificar las características de la parada (), en primer lugar aparece un campo de texto donde se especifica un porcentaje (en decimal) que corresponde a la posición dentro del segmento (especificado por (x1, y1) y (x2, y2)) donde se coloca el color indicado, a continuación se presenta un botón que permite seleccionar un color (el cual utiliza un mecanismo proporcionado por el propio sistema
Red Descartes 2022/Año 2, núm. 4
operativo), y por último se muestra un botón “-” (menos) con el que se puede eliminar la parada correspondiente.

Es indispensable que la especificación de un gradiente cuente con al menos dos paradas para que funcione. Los porcentajes de cada parada deben especificarse como un valor, es decir, no se aceptan expresiones para su definición y en caso de salirse del rango [0, 1], los valores se truncan para quedar dentro de dicho rango.
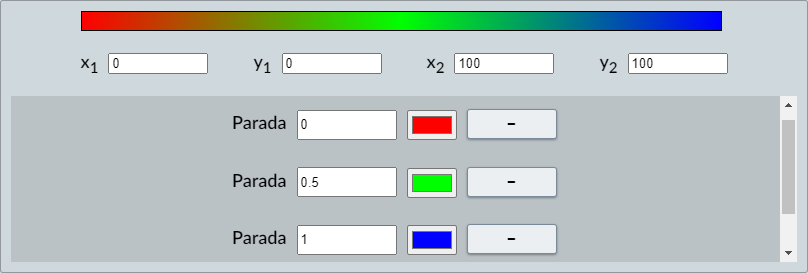
La última pestaña, Patrón, permite especificar una imagen para rellenar el color de un elemento gráfico (), siguiendo la especificación del elemento canvas, https://developer.mozilla.org/en-US/docs/Web/API/CanvasRenderingContext2D/createPattern. En esta pestaña solo se incluye un campo de texto donde se especifica la dirección de la imagen que se utilizará para rellenar el elemento gráfico, ya sea un espacio, un gráfico, o un control. Debajo del campo
Red Descartes 2022/Año 2, núm. 4
de texto aparece una vista previa de la imagen, en caso de que la imagen exista y su dirección se escriba directamente; en caso de que no exista la imagen o que se especifique como una variable (por ejemplo, [nombre_imagen]) se mostrará una cruz roja en la vista previa.
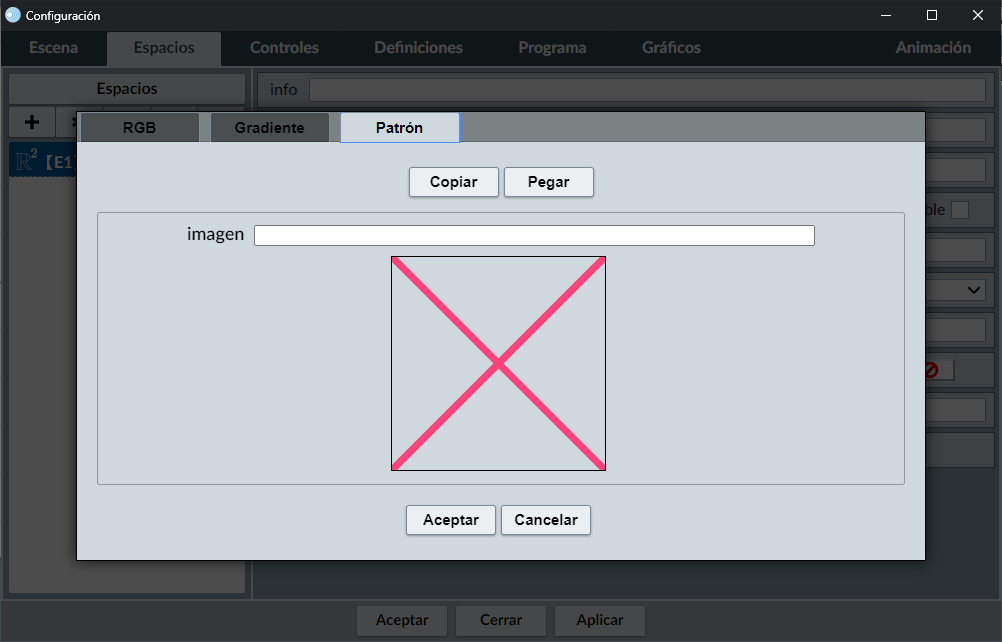
Las imágenes del patrón siempre se comienzan a dibujar desde la esquina superior izquierda del canvas donde se dibuja el elemento gráfico.
En la siguiente escena interactiva se muestra un octágono construido por medio de un gráfico de tipo curva, que utiliza un relleno de tipo patrón. El espacio donde se dibuja la curva no se encuentra fijo, por lo que al mover el espacio se puede observar como la imagen se comienza a dibujar desde la esquina superior izquierda del espacio (el origen del canvas que contiene el gráfico); esto debido a la especificación dada directamente por el API de programación del canvas.
Red Descartes 2022/Año 2, núm. 4
Al igual que los gradientes, las imágenes como patrón se pueden utilizar para espacios, elementos gráficos y controles. Con las mismas consideraciones del elemento canvas que contiene el elemento a dibujarse.
Red Descartes 2022/Año 2, núm. 4
Pedagogía
Proyecto Descartes: cognición y didáctica en la creación de contenido digital
David Oswaldo Zapata Tamayo
Red Descartes 2022/Año 2, núm. 4
La discusión avanzó de tal manera que en el Renacimiento, en pleno auge del antropocentrismo, la razón y la lógica, la reflexión se engolfó en dos posibilidades: nacíamos con ideas prefijadas que íbamos recordando poco a poco, cuando el sujeto entra en relación con lo que es conocido (el racionalismo de René Descartes) o simplemente nacíamos como un tablero en blanco (tabula rasa) que iba siendo escrito por el sujeto en la medida que captaba información y fuera asumida como propia (el empirismo de John Locke).
En la historia más reciente de la educación, aparecen unos primeros atisbos disruptivos de las formas de enseñanza, partiendo de la propuesta de un “anarquista pedagógico”, el escritor ruso León Tolstoi, que en 1959 abre su casa de campo para enseñar desde la libertad del aprendizaje a un grupo de jóvenes, por fuera de los procedimientos instruccionales de su época, pues argumentaba que desde la libertad del niño se podía construir aprendizaje
No fue sino hasta el surgimiento de la pedagogía (aproximadamente en el siglo XIX) y de los aportes de la psicología enfocada en el aprendizaje y las teorías cognitivas, que comienzan a aparecer propuestas para analizar, validar y establecer paradigmas que aportaran al aprendizaje, tal es el caso del modelo desarrollista o cognitivo, que buscaba que el estudiante accediera, progresiva y secuencialmente, a la información o a las temáticas de estudio. Este escenario de aprendizaje estaba enmarcado en la autogestión, la autodisciplina y el deseo de sentirse autónomo en la construcción del saber. En consecuencia, aparecieron propuestas divergentes, como lo es la reconocida “Escuela Nueva”, dentro de la que figuran grandes pedagogos como María Montessori, John Dewey y Ovidio Decroly, y las propuestas cognitivas, con los aportes de Jean Piaget, David Ausubel e incluso Donal Novak. De estas vertientes han surgido otras importantes aportaciones a los procesos cognitivos, como el realizado por Howard Gardner (1983) con su teoría de las
Red Descartes 2022/Año 2, núm. 4
inteligencias múltiples, Daniel Goleman (1995) con la inteligencia emocional o incluso los actuales aportes del aprendizaje invisible de Cristóbal Cobo.
En concordancia con lo anterior, las mediaciones pedagógicas reclaman una importancia absoluta a la hora de intencionar el aprendizaje, pues no sólo se responde a unas expectativas de
Red Descartes 2022/Año 2, núm. 4
aprendizaje, sino que se busca que el estudiante logre un aprendizaje desde el contexto: geográfico, sociocultural, cognitivo, saberes previos, etc. De esta manera, los escenarios de aprendizaje de la era digital, en pleno desarrollo del siglo XXI, deben indudablemente aportar al éxito del conocimiento en las nuevas generaciones, como es la propuesta del modelo tecnológico educativo o tecnocrático, que de entrada puede presentar un sinnúmero de objeciones o inconformidades al asumir que dicho modelo no da cumplimiento u oportunidad al aprendizaje que se adquiere por la interacción kinestésica. Lo cierto del caso es que este modelo permite potenciar la interacción visual y auditiva, genera recordación, motiva al estudiante a resolver las dificultades, genera un resultado que va más allá de la puntuación y, en el caso de la gamificación, reta al estudiante ganarle a una máquina que lo pone a prueba.
Imaginemos, por ejemplo, qué hubiese sido del sistema educativo mundial si en la pandemia del COVID-19 el modelo tecnocrático no viniera estableciendo la vinculación de las nuevas tecnologías de la información y la comunicación con los procesos de mediación pedagógica. En el contexto de América Latina y el Caribe, se estima que:
En el 2020, a medida que la pandemia de la COVID se propagaba por todo el planeta, la mayor parte de los países anunciaron el cierre temporal de escuelas, lo que afectó a más del 91% de los estudiantes en todo el mundo. En abril de 2020, cerca de 1.600.000 niños y jóvenes estaban fuera de la escuela
El impacto que fue soportado por cientos de estrategias pedagógicas digitales de libre acceso de innumerables plataformas educativas, ya en marcha o emergentes, como respuesta a la eventualidad, hicieron posible el fortalecimiento de las didácticas y metodologías propias de los escenarios digitales, al punto de que muchas instituciones educativas hoy están buscando la forma de consolidar estrategias y
Red Descartes 2022/Año 2, núm. 4
didácticas de la bimodalidad y robustecer así el acto educativo pospandemia.
Con todo lo anterior, es importante enfocar la atención en la simbiosis que se configura en la red educativa digital Descartes: aprendizaje interactivo, democratización educativa, construcción del saber de interés, conservación y divulgación del conocimiento, un verdadero escenario de las propuestas STEM (Science, Technology, Engineering and Mathematics), que amplía el espectro educativo a los idiomas y a los juegos como estrategia de aprendizaje (gamificación curricular); en resumen, un verdadero escenario de I+D+i (Investigación, Desarrollo e Innovación). Sin embargo, queda claro que “la tecnología no es trascendente si no es considerada como una herramienta para conformar el aprendizaje social y la inteligencia colectiva, pues el conocer implica generar. La educación formal supone incidir en la colectividad del aprendizaje”
Por tal razón, bien se puede reconocer los aportes que hace la RED Descartes al fortalecimiento de los currículos, ya que posibilita los contenidos de forma libre y autogestionables, que sirven no sólo como un soporte para la planificación y desarrollo curricular, sino que también son un escenario donde se puede aportar y actualizar contenido mientras se procura vincular a los estudiantes a través de la interacción con elementos didácticos que fomentan el aprendizaje, desde la motivación que generan las actividades hasta los ejemplos gráficos y el aprender “haciendo”. El docente o profesional que tiene injerencia en el saber específico ofrecido por la RED Descartes puede crear contenido ayudado por las guías técnicas y requisitos tecnológicos, revalidando que los escenarios digitales aportan a “desarrollar procesos en el estudiante que lo llevarán a hacer un uso más inteligente, estratégico y social […]; lo valioso no es acceder a la información, sino la creación social, la capacidad de atención que esta generará”
Red Descartes 2022/Año 2, núm. 4
Así las cosas, el reconocimiento de los ambientes digitales interactivos, contar con docentes que sean creadores de contenidos de forma creativa e innovadora y la participación de estudiantes en escenarios académicos abiertos, dinámicos y científicos, contribuirá sin duda al fortalecimiento de las formas y los modos de conservar, divulgar y generar conocimiento, siendo esto un aporte seguro al logro del cuarto objetivo de desarrollo sostenible (2030): “garantizar una educación de calidad inclusiva y equitativa, y promover las oportunidades de aprendizaje permanente para todos”
Bibliografía
Red Descartes 2022/Año 2, núm. 4
Publicaciones iCartesiLibri
2021 - 2022
42 libros publicados desde 2021 a la fecha de publicación de este número de la Revista Digital Red Descartes.
Nuevos libros en los apartados de Formación, Ciencias sociales y humanas, Ciencias agroindustriales, Ciencias computacionales, Matemáticas, Física, Química, Ingeniería, Lengua inglesa y Literatura.
En la siguiente página presentamos las portadas, autores y enlaces a los libros.
Red Descartes 2022/Año 2, núm. 4
Red Descartes 2022/Año 2, núm. 4
Normas de publicación
Características de los artículos
- El autor puede presentar el artículo en un documento de texto con un máximo de ocho páginas en Arial tamaño 12.
- Si el autor tiene competencias en el diseño HTML y CSS, puede usar la plantilla de la revista, con un máximo de 10 páginas.
- El título será menor a 150 caracteres.
- Las imágenes, figuras, tablas, videos y objetos interactivos se deben enviar en un archivo zip aparte.
- Idioma. La revista acepta artículos en español, inglés y portugués.
- Los artículos, preferiblemente, se relacionarán con aspectos educativos y el uso de las tecnologías en los procesos de enseñanza-aprendizaje. No obstante, se aceptan artículos de otras áreas del conocimiento, siempre que estos incorporen contenidos digitales diseñados con el editor DescartesJS.
- Presentar los permisos para el uso de contenido sujeto a derechos de autor, incluyendo los que provienen de Internet.
Red Descartes 2022/Año 2, núm. 4
El artículo y los anexos deben enviarse en una archivo zip, a través de un enlace (vía hosting o Google Drive, por ejemplo).
Los artículos deben abordar temas como:
- Difusión relacionada con la Red Educativa Digital Descartes
- Reseñas de libros interactivos
- Aplicaciones con DescartesJS
- Novedades DescartesJS
- Experiencias en el aula
- Investigaciones que incluyan el uso de contenidos digitales interactivos diseñados con DescartesJS
Evaluación de los artículos
El o los autores podrán sugerir revisores, indicando los datos de contacto (nombre y dirección de correo).
Los editores del Consejo Editorial, en primera instancia, valorarán los artículos para verificar que cumplen con los objetivos de publicación de la revista, si el concepto es positivo se asignarán mínimo dos revisores quienes evaluarán el artículo y harán las recomendaciones pertinentes, entre ellas la aceptación o no de su publicación.
Red Descartes 2022/Año 2, núm. 4