Título de la obra:
Notas para un curso de Matemáticas Discretas
Autor:
Guillermo Carvajal Rincón
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN: 978-84-18834-95-0

Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
El presente libro interactivo de Matemáticas Discretas recopila cinco temas para cumplir con el programa de la asignatura: matemáticas discretas de la Institución Universitaria Pascual Bravo de la ciudad de Medellín, correspondiente al plan de estudio del primer semestre de los estudiantes de tecnología e ingeniería en desarrollo de software, temario que servirá de soporte para futuras asignaturas comprendidas en su malla curricular.
Los temas impartidos son: sistemas de numeración, lógica proposicional, teoría de conjuntos, relaciones y grafos.
En el texto se han incluido vínculos a artículos relacionados con el tema tratado, videos explicativos de YouTube, donde expositores comparten el o los temas vistos en el respectivo apartado, objetos interactivos que recrean los conceptos explicados, al final de cada capítulo se propone una serie de ejercicios para que el estudiante refuerce su aprendizaje.
Un reconocimiento especial para el profesor Juan Guillermo Rivera Berrío, que con su paciencia y dedicación a mis constantes requerimientos, me ha permitido terminar esta obra que ahora presento a mis lectores.
El libro también incorpora elementos adicionales para potenciar su presentación. Este ejemplo presenta el uso de la biblioteca $\KaTeX$ para el uso de fórmulas matemáticas.
Un sistema de (numeración) es un conjunto de símbolos y reglas de generación que permiten construir todos los números válidos. Estas reglas son diferentes para cada sistema de numeración considerado, pero una regla común a todos es que para construir números válidos en un sistema de numeración determinado, solo se pueden utilizar los símbolosLos símbolos son aquellos caracteres que no se repiten en un sistema de numeración permitidos en ese sistema.
Para indicar en qué sistema de numeración se representa una cantidad se añade como subíndiceO se expresa claramente el sistema, por ejemplo: octal, hexadecimal a la derecha el número de símbolos que se pueden representar en dicho sistema. Los sistemas de numeración pueden clasificarse en dos grandes grupos: posicionales y no-posicionales.
Así, en la vida diaria, los sistemas de numeración sirven fundamentalmente para contar. En nuestra civilización, usamos habitualmente el sistema decimal (indo arábigo) para dicho propósito, que es un sistema posicional, cuyo probable origen fue una herramienta inmediata y disponible para todos: los 10 dedos de ambas manos.
En consecuencia, cualquier sistema consta fundamentalmente de una serie de elementos que lo conforman, una serie de reglas que permite establecer operaciones y relaciones entre tales elementos. Por ello, puede decirse que un sistema de numeración es el conjunto de elementos (símbolos o números), operaciones y relaciones que por intermedio de reglas propias permite establecer el papel de tales relaciones y operaciones.
A continuación, se examinarán los sistemas numéricos posicionales, no considerando aquellos sistemas que no permiten una notación
posicional como es el sistema numérico romano.
Ejemplo:
El sistema decimal (base 10) debe su nombre, ya que usa 10 símbolos:
(0, 1, 2, 3, 4, 5, 6, 7, 8 y 9).
El sistema octal (base 8) utiliza 8 símbolos:
(0, 1, 2, 3, 4, 5, 6 y 7).
El sistema hexadecimal (base 16) utiliza 16 símbolos:
(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E y F).
El sistema binario (base 2) utiliza 2 símbolos:
(0 y 1).
La referencia a sistemas numéricos posicionales se hace incluyendo la designación del sistema en el cual se expresa dicho sistema, ejemplo: binario, octal, decimal, hexadecimal, o colocando el número entre paréntesis y escribir un subíndice después del paréntesis derecho, el cual hace referencia al sistema en cuestión. Así: (65421)8, número en base octal. O (D0CE)16, número en base hexadecimal.
| Nombre | Decimal | Binario | Octal | Hexadecimal |
|---|---|---|---|---|
| Base | 10 | 2 | 8 | 16 |
| Dígitos | 0,1, ... 9 | 0, 1 | 0,1,... 7 | 0,1, ... F |
| 0 | 0000 | 0 | 0 | |
| 1 | 0001 | 1 | 1 | |
| 2 | 0010 | 2 | 2 | |
| 3 | 0011 | 3 | 3 | |
| 4 | 0100 | 4 | 4 | |
| 5 | 0101 | 5 | 5 | |
| 6 | 0110 | 6 | 6 | |
| 7 | 0111 | 7 | 7 | |
| 8 | 1000 | 10 | 8 | |
| 9 | 1001 | 11 | 9 | |
| 10 | 1010 | 12 | A | |
| 11 | 1011 | 13 | B | |
| 12 | 1100 | 14 | C | |
| 13 | 1101 | 15 | D | |
| 14 | 1110 | 16 | E | |
| 15 | 1111 | 17 | F | |
| 16 | 10000 | 20 | 10 | |
| 17 | 10001 | 21 | 11 | |
| 18 | 10010 | 22 | 12 | |
| 19 | 10011 | 23 | 13 | |
| 20 | 10100 | 24 | 14 |
Todos estamos familiarizados con el sistema de numeración decimal porque utilizamos los números decimales todos los días. Aunque los números decimales son triviales, a menudo, su estructura de pesos no se comprende. El "peso" es el valor de la base numérica del sistema, elevada a un exponente un número menor de su posición, contada ésta de izquierda a derecha del guarismo. Vamos a repasar la estructura de los números decimales. Este repaso nos ayudará a entender más fácilmente la estructura del sistema de numeración binario, que es tan importante en las computadoras y en la electrónica digital.
En el sistema de numeración decimal cada uno de los diez dígitos, de 0 a 9, representa una determinada cantidad. Como ya sabe, los diez símbolos (dígitos) no se limitan a expresar solamente diez cantidades diferentes, ya que usamos varios dígitos en las posiciones adecuadas dentro de un número para indicar la magnitud de la cantidad. La siguiente imagen ilustra lo antes dicho
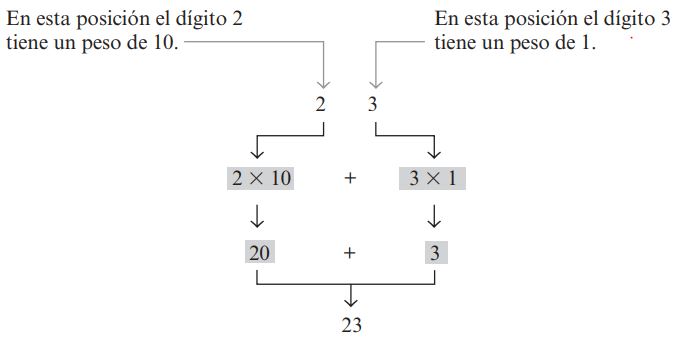
Es posible determinar cantidades hasta nueve antes de quedarse sin dígitos; si se desea especificar una cantidad mayor que nueve, se emplean dos o más dígitos y la posición de cada dígito dentro del número indica la magnitud que representa. Por ejemplo, si deseamos expresar la cantidad veintitrés, usaremos (en sus respectivas posiciones dentro del número) el dígito 2 para representar la cantidad de veinte y el dígito 3 para representar la cantidad de 3, como se ilustra en la figura 1.1
En esta posición el dígito 2 tiene un peso de $10^1$ y el dígito 3 tiene un peso de $10^0$ o sea: 2 x $10^1$ + 3 x $10^0$Toda cantidad elevada a la cero tiene un valor de 1 = 20 + 3 = 23
La posición de cada dígito en un número decimal indica la magnitud de la cantidad representada y se le puede asignar un peso. Los pesos para los números enteros son las potencias positivas de diez, que aumentan de derecha a izquierda, comenzado por $10^0$ = 1.
. . . $ 10^5 $ $ 10^4 $ $ 10^3 $ $ 10^2 $ $ 10^1 $ $ 10^0 $
Para números fraccionarios, los pesos son las potencias negativas de diez que decrecen de izquierda a derecha comenzando por $10^{-1}$, después de la coma decimal
$ 10^3 $ $ 10^2 $ $ 10;^1 $ $ 10^0 $,$ 10^{-1} $ $ 10^{-2} $ $ 10^{-3} $ $ 10^{-4} $ $ 10^{-5} $ . . .
Ejercicio
Expresar el número decimal 874 como una suma de valores de cada digito
Para obtener la solución, cada digito decimal se multiplica por la base, elevada a un exponente, el cual expresa su peso, así:
874 = 8 x $10^2$ + 7 x $10^1$ + 4 x $10^0$
= 8 x 100 + 7 x 10 + 4 x 1
= 800 + 70 + 4 = 874
El sistema de numeración binario es simplemente otra forma de representar magnitudes. Es menos complicado que el sistema decimal porque sólo emplea dos dígitos. El sistema decimal con sus diez dígitos es un sistema en base diez; el sistema binario con sus dos dígitos es un sistema en base dos. Los dos dígitos binarios (bits) son 1 y 0. La posición de un 1 o un 0 en un número binario indica su peso; o valor dentro del número, del mismo modo que la posición de un dígito decimal determina el valor de ese dígito. Los pesos de un número binario se basan en las potencias de dos. Tabla 1.3
Para aprender a contar en el sistema binario, en primer lugar es preciso observar cómo se cuenta en el sistema decimal. Comenzamos
en cero y continuamos hasta el nueve antes de quedarnos sin dígitos. Luego, comenzamos con otra posición de dígito (a la izquierda) y continuamos contando desde 10 hasta 99. En este punto, se terminan todas las combinaciones con dos dígitos, por lo que es necesaria una tercera posición de dígito para poder contar desde 100 hasta 999.
Cuando contamos en binario se produce un situación similar excepto en que sólo disponemos de dos dígitos, denominados bitsUn conjunto ordenado de 8 bits conforman un byte. El byte es la unidad de información estándar utilizada en informática y en telecomuicaciones.
Empezamos a contar: 0, 1. En este punto, ya hemos utilizado los dos dígitos, por lo que incluimos otra posición de dígito y continuamos: 10, 11. Ahora, hemos agotado todas las combinaciones de dos dígitos, por lo que es necesaria una tercera posición. Con tres posiciones de dígito continuamos contando: 100, 101, 110 y 111. Necesitamos una cuarta posición de dígito para continuar, y así sucesivamente. En la siguiente tabla (1.2) se muestra cómo se cuenta desde cero hasta veinte. Observe en cada columna la alternancia de 1s y 0s.
Aprender a contar en binario le ayudará a entender básicamente cómo pueden utilizarse los circuitos digitales para contar sucesos. Puede tratarse de cualquier cosa, desde elementos que contar en una línea de montaje hasta operaciones de recuento en una computadora.
| Decimal | Número binario |
|---|---|
| 0 | 0 0 0 0 |
| 1 | 0 0 0 1 |
| 2 | 0 0 1 0 |
| 3 | 0 0 1 1 |
| 4 | 0 1 0 0 |
| 5 | 0 1 0 1 |
| 6 | 0 1 1 0 |
| 7 | 0 1 1 1 |
| 8 | 1 0 0 0 |
| 9 | 1 0 0 1 |
| 10 | 1 0 1 0 |
| 11 | 1 0 1 1 |
| 12 | 1 1 0 0 |
| 13 | 1 1 0 1 |
| 14 | 1 1 1 0 |
| 15 | 1 1 1 1 |
| 16 | 1 0 0 0 0 |
| 17 | 1 0 0 0 1 |
| 18 | 1 0 0 1 0 |
| 19 | 1 0 0 1 1 |
| 20 | 1 0 1 0 0 |
La estructura de pesos de los números binarios
Un número binario es un número con peso. El bit más a la derecha es el LSB (Least Significant Bit, bit menos significativo) en un número binario entero y tiene un peso de $2^{0}$ = 1. El bit más a la izquierda es el MSB (Most Significant Bit, bit más significativo); su peso depende del tamaño del número binario.
Los números fraccionarios también pueden representarse en el sistema binario colocando bits a la derecha de la coma binaria, del mismo modo que los números decimales fraccionarios se colocan a la derecha de la coma decimal. En un número binario con parte fraccionaria, el bit más a la izquierda es el MSB y tiene un peso de $2^{-1}$ = 0,5, (Tabla 1.3, parte derecha). Los pesos fraccionarios de los respectivos bits decrecen de izquierda a derecha según las potencias negativas de dos para cada bit.
La estructura de pesos de un número binario es:
$ 2^{n-1} $...$ 2^{3} $ $ 2^{2} $ $ 2^{1} $ $ 2^{0} $,$ 2^{-1} $ $ 2^{-2} $ $ 2^{-3} $ ... $ 2^{-n} $
donde n es el número de bits a partir de la coma binaria. Por tanto, todos los bits a la izquierda de la coma binaria tienen pesos que son potencias positivas de dos, como previamente se ha visto para los números enteros. Todos los bits situados a la derecha de la coma binaria tienen pesos que son potencias negativas de dos, o pesos fraccionales.

El valor decimal de cualquier número binario puede hallarse sumando los pesos de todos los bits que están a 1 y descartando los pesos de todos los bits que son 0.
Conversión de número binario a decimal
Ejemplo:
Convertir el número entero binario 1101101 a decimal.
Solución:
Se determina el peso de cada bit que está a 1, y luego se obtiene la suma de los pesos para obtener el número decimal.
Peso: $2^{6}$ $2^{5}$ $2^{4}$ $2^{3}$ $2^{2}$ $2^{1}$ $2^{0}$
Número binario 1 1 0 1 1 0 1
1101101 = $2^{6}$ $2^{5}$ $2^{3}$ $2^{2}$ $2^{0}$
= 64 + 32 + 8 + 4 + 1 = 109
Conversión de decimal binario a decimal:
Ejemplo:
Convertir el número binario fraccionario 0,1011 a decimal.
Solución:
Se determina el peso de cada bit que está a 1, luego se obtiene la suma de los pesos para obtener el número decimal.
Peso: $2^{-1}$ $2^{-2}$ $2^{-3}$ $2^{-4}$
Número binario 0, 1 0 1 1
0,1011 = $2^{-1}$ + $2^{-3}$ + $2^{-4}$
= 0,5 + 0,125 + 0,0625 = 0,6875
Conversión decimal a binario:
Método de la suma de pesos
Una forma de hallar el número binario equivalente a un número decimal determinado consiste en encontrar el conjunto de pesos binarios cuya suma es igual al número decimal. Una forma fácil de recordar los pesos binarios es que el peso más bajo es 1, es decir $2^{0}$, y que duplicando cualquier peso, se obtiene el siguiente peso superior; por tanto, la lista de los siete primeros pesos binarios será: 1, 2, 4, 8, 16, 32, 64.
Por ejemplo, el número decimal 9 puede expresarse como la suma de pesos binarios siguiente:
9 = 8 + 1 ó 9 = $2^{3}$ + $2^{0}$
Colocando los 1s en las posiciones de pesos apropiadas, $2^{3}$ y $2^{0}$, y los 0s en las posiciones $2^{2}$ y $2^{1}$ se determina el número binario correspondiente al decimal 9.
$2^{3}$ $2^{2}$ $2^{1}$ $2^{0}$
1 0 0 1 Número binario para el decimal 9.
Método de la división sucesiva por dos
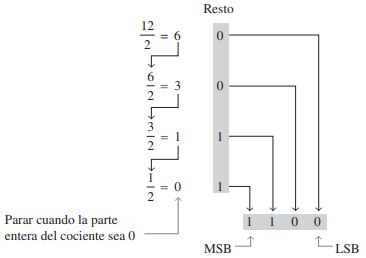
Un método sistemático para convertir a binario números enteros decimales es el proceso de la división sucesiva por dos. Por ejemplo, para convertir el número decimal 12 a binario, comenzamos dividiendo 12 entre 2. A continuación, cada cociente resultante se divide entre dos hasta obtener un cociente cuya parte entera sea igual a 0. Los restos generados en cada división forman el número binario. El primer resto es el bit menos significativo (LSB) del número binario y el último resto es el bit más significativo (MSB).
Este procedimiento se muestra en los pasos siguientes para la conversión a binario del número decimal 12.
Conversión de fracciones decimales a binario
Una forma fácil de recordar los pesos binarios fraccionarios es que el peso más significativo es 0,5, es decir $2^{-1}$, y que dividiendo entre dos cualquier peso se obtiene el siguiente peso menor; luego una lista de los cuatro primeros pesos binarios fraccionarios sería: 0,5; 0,25; 0,125; 0,0625.
Suma de pesos. El método de la suma de pesos se puede aplicar a los números decimales fraccionarios, por ejemplo:
0,625 = 0,5 + 0,125 = $2^{-1}$ + $2^{-3}$ = 0,101
Lo que indica que hay un 1 en la posición $2^{-1}$, un 0 en la posición $2^{-2}$ y un 1 en la posición $2^{-3}$
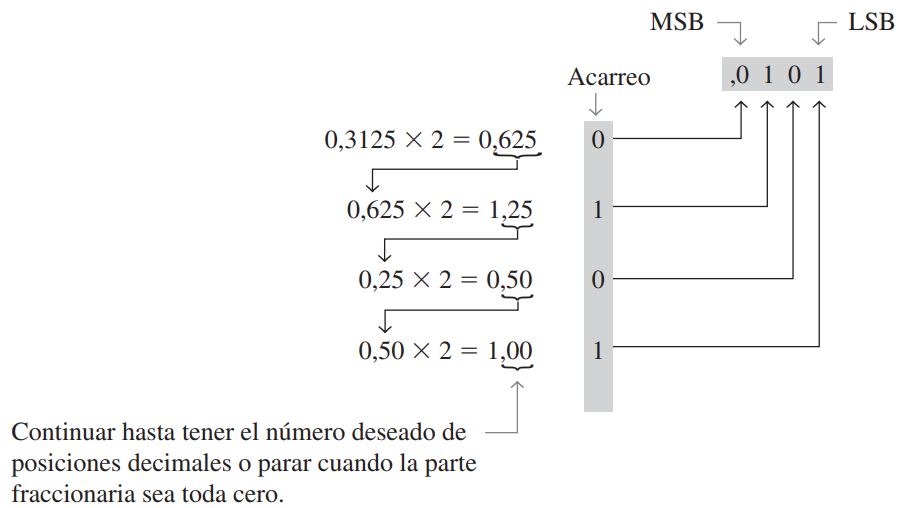
Multiplicación sucesiva por 2. Como hemos visto, los números decimales enteros pueden convertirse a binario dividiendo sucesivamente entre dos. Los números decimales fraccionarios pueden convertirse en números binarios multiplicando sucesivamente por 2. Por ejemplo, para convertir a binario el número decimal fraccionario 0,3125, comenzamos multiplicando 0,3125 por 2 y después se multiplica cada parte fraccional resultante del producto por 2 hasta que el producto fraccionario sea cero o hasta que se alcance el número deseado de posiciones decimales.
Los dígitos acarreados o, acarreos, generados por las multiplicaciones dan lugar al número binario. El primer acarreo que se obtiene es el MSB y el último acarreo es el LSB. Ejemplo:
La aritmética binaria es esencial en todas las computadoras digitales y en muchos otros tipos de sistemas digitales. Para entender los sistemas digitales, es necesario conocer los fundamentos de la suma, resta, multiplicación y la división binaria. He aqui los algoritmos de estas operaciones.
| 1er término | Operador | 2do término | Resultado | Acarreo | |
|---|---|---|---|---|---|
| 0 | + | 0 | = | 0 | 0 |
| 0 | + | 1 | = | 1 | 0 |
| 1 | + | 0 | = | 1 | 0 |
| 1 | + | 1 | = | 0 | 1 |
| 1 | + | 1 | + | 1 | =1, acarrea 1 |
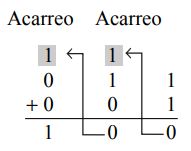
Apliquemos la anterior tabla al siguiente ejemplo:
Sumar los números binario 11 y 1.
| 1er término | Operador | 2do término | Resultado | Acarreo | |
|---|---|---|---|---|---|
| 0 | - | 0 | = | 0 | 0 |
| 1 | - | 0 | = | 1 | 0 |
| 1 | - | 1 | = | 0 | 0 |
| 0 | - | 1 | = | 1 | Presto 1 de la columna anterior |
Ilustremos con un ejemplo la anterior tabla; restar del binario 101 el binario 011.
Cuando se restan números, algunas veces se genera un acarreo negativo que pasa a la siguiente columna de la izquierda.
En binario, sólo se produce un acarreo negativo cuando se intenta restar 1 de 0. En este caso, cuando se acarrea un 1 a la siguiente columna de la izquierda, en la columna que se está restando se genera un 10, y entonces debe aplicarse la última de las cuatro reglas enumeradas.
| Multiplicando | Operador | Multiplicador | Resultado | |
|---|---|---|---|---|
| 0 | x | 0 | = | 0 |
| 0 | x | 1 | = | 0 |
| 1 | x | 0 | = | 0 |
| 1 | x | 1 | = | 1 |
La multiplicación con números binarios se realiza de la misma forma que con números decimales. Se realizan los productos parciales, desplazando cada producto parcial sucesivo una posición hacia la izquierda, y sumando luego todos los productos parciales.
Ejemplo: Multiplicar los siguientes números binarios: 11 x 11 y 111 x 101

| Dividendo | Operador | Divisor | Resultado | |
|---|---|---|---|---|
| 0 | $\div$ | 0 | = | 0 |
| 0 | $\div$ | 1 | = | 0 |
| 1 | $\div$ | 0 | = | 0 |
| 1 | $\div$ | 1 | = | 1 |
Ejercicios propuestos
Convertir el siguiente número: (65)16 a decimal
Esta unidad tiene como propósito que el estudiante vincule las proposiciones simples y compuestas mediante los conectivos lógicos para lograr la integración de las diferentes proposiciones y realizar las operaciones entre ellas a través de sus tablas de verdad.
Las (reglas de la lógica) le dan un significado preciso a los enunciados o sentencias matemáticas. Estas reglas se usan para distinguir entre argumentos válidos y no válidos. Por ejemplo, estas reglas nos ayudan a entender y razonar enunciados como “Existe un entero que no es la suma de dos cuadrados” o “Para todo entero positivo n, la suma de enteros positivos que no sobrepasan n, es n (n + 1)/2”. La lógica es la base de todo razonamiento matemático.
Además de su importancia en el razonamiento matemático, la lógica tiene numerosas aplicaciones en ciencias de la computación. Las reglas de la lógica se usan en el diseño de circuitos de computadores, la construcción de programas informáticos, la verificación de que un programa esté bien construido, la programación computacional y en muchas otras aplicaciones.
Empezamos nuestro estudio con una introducción a la construcción de los bloques básicoso tablas de verdad de la lógica: las proposiciones. Una proposición es una oración declarativa que es correcta o falsa, pero no ambas cosas a la vez.
Las siguientes oraciones declarativas son proposiciones:
Las proposiciones 1 y 3 son correctas, mientras que la 2 y 4 son falsas.
En el siguiente ejemplo se dan algunas oraciones que no son proposiciones. Consideremos las siguientes oraciones:
Las frases 1 y 2 no son proposiciones porque no son declarativas. Las frases 3 y 4 no son proposiciones porque no son ni verdaderas ni falsas, ya que no se les han asignado valores a las variables.
Para denotar proposiciones usamos letraso llamadas también: variables proposicionales., igual que usamos letras para denotar variables. Por convenio, las letras que se utilizan para denotar proposiciones son p, q, r, s, ... El valor de verdad de una proposición es verdadero, y se denota por V, si es una proposición verdadera, o falso, denotado por F, si es una proposición falsa.
El área de la lógica que trata de proposiciones se llama cálculo proposicional o lógica proposicional
Fue desarrollada sistemáticamente por primera vez por el filósofo griego Aristóteles Aristóteles, cuyo nombre en griego antiguo es Ἀριστοτέλης, nació en Estagira (384 a.C.) y falleció en Calcis (322 a.C.). Fue un filósofo, polímata y científico griego. A continuación, te presento un resumen de su vida y obra:
Formación y Academia de Platón: Aristóteles fue hijo del médico real de Macedonia. Durante veinte años, estudió en la Academia de Platón, primero como discípulo y luego como investigador y tutor. Aunque se consideró como candidato para suceder a Platón, finalmente no fue elegido y se marchó a Assos, donde escribió su diálogo “Sobre la filosofía” y fundó un centro de estudio.
Tutor de Alejandro Magno: Aceptó el cargo de preceptor de Alejandro Magno, quien siempre le tuvo gran respeto. Aristóteles fundó el Liceo en Atenas, donde enseñaba mientras paseaba (de ahí el nombre de escuela “peripatética”). Durante este tiempo, realizó investigaciones en diversos campos, como arte dramático, constituciones políticas, deportes olímpicos y zoología.
Obras y Legado: Aristóteles escribió numerosas obras, abarcando temas como lógica, ética, política, naturaleza, física y metafísica.
Sobre el alma: Exploración de la naturaleza del alma y la mente.
Ética a Eudemo y Ética a Nicómaco: Reflexiones sobre la moral y la virtud.
Política y Constitución de Atenas: Análisis político y constitucional.
Aristóteles dejó un legado duradero en la filosofía y la ciencia occidental.

Muchos enunciados matemáticos se construyen combinando una o más proposiciones. Las nuevas proposiciones, llamadas fórmulas o proposiciones compuestas, se forman a partir de las existentes usando operadores lógicos
Procedimiento gráfico que permite determinar los posibles valores de verdad de una proposición compuesta, a partir de las combinaciones de los valores de verdad de las proposiciones simples que las componen.
Una tabla de verdadUna tabla de verdad, o tabla de valores de verdades, es una tabla que muestra el valor de verdad de una proposición compuesta, para cada combinación de verdad que se pueda asignar.Fue desarrollada por Charles Sanders Peirce por los años 1880, pero el formato más popular es el que introdujo Ludwig Wittgenstein en su Tractatus logico-philosophicus, publicado en 1921. Wikipedia muestra las relaciones entre los valores de verdad de proposiciones.
Para denotar proposiciones usamos letras, al igual que usamos letras para denotar variables, estas son: p, q, r, s, …
El valor de verdad de una proposición es verdadero, y se denota por V, si es una proposición verdadera, o falso, denotado por F, si es una proposición falsa
área de la lógica que trata de proposiciones.
se construyen combinando una o más proposiciones, se forman a partir de las existentes usando operadores lógicosLos operadores lógicos se denominan también operadores Booleanos, se usan para combinar dos valores Booleanos y devolver un resultado verdadero o falso
Definición:
Sea p una proposición.
El enunciado: “No se cumple p”, es otra proposición, la negación de p. La negación de p se denota mediante ¬ p. La proposición ¬ p se lee “no p”
Ejemplo: La negación del enunciado: “Hoy es viernes”, es “No se cumple que hoy es viernes” u, “Hoy no es viernes” o, “No es viernes hoy”.
La negación de una proposición se puede considerar como el resultado de aplicar el operador negación sobre una proposición.
| Tabla de verdad para la negación de una proposición | |
|---|---|
| p | ¬ p |
| V | F |
| F | V |
Definición:
Operadores lógicos que se usan para formar nuevas proposiciones a partir de dos o más proposiciones ya creadas.
Definición:
Sean p y q proposiciones. La proposición “p y q”, denotada por p Λ q, es la proposición que es verdadera cuando tanto p como q son verdaderas y falsa en cualquier otro caso. La proposición p y q se llama conjunción de p y q.
| Tabla de verdad de la conjunción de dos proposiciones | ||
|---|---|---|
| p | q | p Λ q |
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | F |
Ejemplo: Hallar la conjunción de las proposiciones p y q en el caso de que p es el enunciado “Hoy es viernes” y q es: “Hoy llueve”.
Solución: La conjunción de estas proposiciones, p Λ q, es el enunciado: “Hoy es viernes y hoy llueve”. La proposición es verdadera los viernes con lluvia y es falsa cualquier día que no sea viernes y los viernes que no llueva.
Definición:
Sean p y q proposiciones. La proposición “p o q”, denotada por p v q, es la proposición que es falsa cuando tanto p como q son falsas y verdadera en cualquier otro caso. La proposición p v q se llama disyunción de p y q.
| Tabla de verdad de la disyunción de dos proposiciones | ||
|---|---|---|
| p | q | p v q |
| V | V | V |
| V | F | V |
| F | V | V |
| F | F | F |
El uso del conectivo lógico “o” en una disyunción se asocia al significado en sentido inclusivo de la palabra “o”.
Ejemplo: “Los estudiantes que hayan cursado cálculo o ciencias de la computación pueden matricularse en esta clase”.
Usamos el o exclusivo cuando decimos:
“Los estudiantes que hayan cursado cálculo o ciencias de la computación, pero no ambas, pueden matricularse en esta clase”.
Uso exclusivo no inclusivo de la disyunción o:
“Se sirve sopa o ensalada como entrada”
Ejemplo: Hallar la disyunción de las proposiciones p y q en el caso de que p es el enunciado “Hoy es viernes” y q es: “Hoy llueve”.
Solución: La disyunción de p y q, p v q, es el enunciado:
“Hoy es viernes u hoy llueve”
Esta proposición es verdadera cualquier día que sea viernes o llueva (incluidos los viernes que llueve). Es solo falsa los días que ni son viernes ni llueve.
Cuando se usa el “o” en sentido exclusivo para conectar dos proposiciones p y q, obtenemos la proposición “p o q (pero no ambas)”. Esta proposición es verdadera cuando p es verdadera y q falsa y cuando p es falsa y q verdadera. Es falsa cuando tanto p como q son falsas y cuando ambas son verdaderas.
Definición:
Sean p y q proposiciones. El conectivo o exclusivo de p y q denotado por p ⊕ q, es la proposición que es verdadera cuando exactamente una de las proposiciones P y q es verdadera y es falsa en cualquier otro caso.
| Tabla de verdad para el o exclusivo de dos proposiciones | ||
|---|---|---|
| p | q | p ⊕ q |
| V | V | F |
| V | F | V |
| F | V | V |
| F | F | F |
Definición:
Sean p y q proposiciones. La implicación p → q es la proposición que es falsa cuando p es verdadera y q es falsa y verdadera en cualquier otro caso. En esta implicación p se llama hipótesis (o antecedente o premisa) y q se llama tesis o conclusión (o consecuencia).
Tabla de verdad para la implicación de dos proposiciones
| Tabla de verdad para la implicación | ||
|---|---|---|
| p | q | p → q |
| V | V | V |
| V | F | F |
| F | V | V |
| F | F | V |
La implicación a veces se denomina declaración condicional
Debido a que las implicaciones desempeñan un papel esencial en el razonamiento matemático, existen muchas formas de expresar p → q
“Si p, entonces q” “si p, q” “p es suficiente para q” “q si p” “q cuando p” “una condición necesaria para p es q” “p implica q” “P si solo q” “una condición suficiente para q es p” “q siempre que p” “q es necesario para p” “q se deduce de p”
Ejemplo: “Si hoy hace sol, entonces iremos a la playa”. “Si hoy es viernes, entonces 2 + 3 = 5, es verdadera por la definición de implicación, ya que la conclusión es verdadera (el valor de verdad de la hipótesis no importa)
Ejemplo:
“Si hoy es viernes, entonces 2 + 3 = 6, es verdadera para todos los días excepto los viernes, incluso aunque 2 + 3 = 6 sea falsa.
En los razonamientos matemáticos consideramos la implicación de una forma más general que en lenguaje natural. El concepto matemático de implicación es independiente de la relación causa – efecto entre hipótesis y conclusión. La definición de implicación específica los valores de verdad; no se basa en el uso del lenguaje.
Hay algunas implicaciones relacionadas con p → q que pueden formarse a partir de ella. La proposición q → p se llama reciproca de p → q. La contrarrecíproca de p → q es ¬ q → ¬ p. La proposición ¬ p → ¬ q es la inversa
La contrarrecíproca ¬ q → ¬ p de una implicación p → q tiene la misma tabla de verdad que p → q. Para verlo, tener en cuenta que la contrarrecíproca es falsa solo cuando ¬ p es falsa y ¬ q es verdadera, esto es, sólo cuando p es verdadera y q falsa. Por otra parte, ni la recíproca, q → p, ni la inversa ¬ p → ¬ q, tienen los mismos valores de verdad que p → q para todos los posibles valores de p y q. Para ver esto, observa que cuando p es verdadera y q falsa, la implicación
original (directa) es falsa, pero la reciproca y la inversa son ambas verdaderas. Cuando dos fórmulas tienen siempre los mismos valores de verdad las llamamos equivalentes, de tal forma que una implicación y su contrarrecíproca son equivalentes. La reciproca y la inversa de una implicación también son equivalentes.
Ejemplo:
¿Cuáles son las contrarrecíproca, recíproca e inversa de la implicación: “El equipo local gana siempre que llueve”?
Solución:
Como “q siempre que p” es una forma de expresar la implicación p → q, la afirmación original se puede expresar como:
“Si llueve, entonces el equipo local gana”.
La contrarrecíproca de esta implicación es: “Si el equipo local no gana, no llueve”
La recíproca es: “Si el equipo local gana, entonces llueve”.
La inversa es: “Si no llueve, entonces el equipo local no gana”. Sólo el contrarrecíproco es equivalente a la afirmación original.
Definición:
Sean p y q proposiciones. La bicondicional, o doble implicación, p ↔ q es la proposición que es verdadera cuando p y q tienen los mismos valores de verdad y falsa en los otros casos.
| Tabla de verdad para la bicondicional p ↔ q | ||
|---|---|---|
| p | q | p → q |
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | V |
La terminología “p si, y solo si, q”, se usa para esta bicondicional. Hay otras formas en la que comúnmente se expresa p ↔ q:
“p es necesario y suficiente para q”
“si p, entonces q” y recíprocamente: “p sii q”
Observe que p ↔ q tiene exactamente los mismos valores de verdad que (p → q) Λ (q → p).
Ejemplo:
Sea p la afirmación “puedes tomar el vuelo” y sea q la afirmación “compras un tiquete”. Entonces, p ↔ q es el enunciado:
“Puedes tomar el vuelo si, y solo si, compras el tiquete”.
Esta afirmación es verdadera si p y q son ambas verdaderas o ambas falsas, esto es, si compras un tiquete y puedes tomar el vuelo o si no compras el tiquete y no puedes tomar el vuelo. Es falsa cuando p y q tienen valores de verdad opuestos.
Las bicondicionales se expresan a menudo usando las construcciones “si, entonces” o “solo si”. La otra parte del “sí, y solo si” es implícita.
Por ejemplo: “si acabas tu comida, puedes tomar postre” (lenguaje natural); matemática y lógicamente: “Puedes tomar postre si, y solo si, acabas tu comida” ó: “Si acabas tu comida, entonces puedes tomar postre”, ó “Puedes tomar postre sólo si acabas tu comida”
Precedencia de operadores lógicos
Generalmente, se utilizan paréntesis para específicar el orden en el que se deben aplicar los operadores lógicos en una fórmula.
El operador conjunción precede siempre al operador disyunción.
Los operadores condicional y bicondicional tienen precedencia inferior que los operadores conjunción y disyunción.
| Precedencia de operadores lógicos | |
|---|---|
| Operador | Precedencia |
| $\neg$ | 1 |
| $\bigwedge$ | 2 |
| $\bigvee$ | 3 |
| $\to$ | 4 |
| $\gets$ | 5 |
Definición
El paso del lenguaje natural al lenguaje formal.
Hay muchas razones para traducir frases del lenguaje natural a expresiones con variables proposicionales y conectivos lógicos, esto evita ambigüedades.
Una vez que hemos traducido frases del lenguaje natural a expresiones lógicas, podemos analizar estas expresiones lógicas para determinar sus valores de verdad, las podemos manipular y podemos usar las reglas de inferencia.
Ejemplo 1:
¿Cuál es la formalización de la siguiente frase?:
“Puedes acceder a internet desde el campus sólo si estudias ciencias de la computación o no eres alumno de primero”.
Utilizaremos variables proposicionales para representar cada parte de la oración y determinar los conectivos lógicos apropiados entre ellas. Representaremos las frases: “Puedes acceder a internet desde el campus”, “estudias ciencias de la computación” y “eres alumno de primero” por p, q y r, respectivamente. Considerando que “solo si” es una forma de expresar una implicación, la frase puede representarse como: p → (q v ¬r).
Ejemplo 2:
¿Cuál es la formalización de la siguiente frase?:
“No puedes montar en la montaña rusa si mides menos de 1,20 metros, a no ser que seas mayor de dieciséis años”.
Utilizaremos variables proposicionales para representar cada parte de la oración y determinar los conectivos lógicos apropiados entre ellas.
Representaremos las frases: “Puedes montar en la montaña rusa”, “mides menos de 1,20 metros” y “eres mayor de dieciséis años” por q, r y s, respectivamente. La frase puede representarse como: ( r Λ ¬s) → ¬q.
Los conectivos lógicos tienen un amplio campo de aplicación en las búsquedas de grandes colecciones de información como, los índices de páginas web.
En las búsquedas booleanas se usa la conexión AND para emparejar datos almacenados que contengan los dos términos de búsqueda, la conexión OR se usa para emparejar uno o ambos términos de la búsqueda y la conexión NOT (a veces escrita AND NOT) se usa para excluir un término particular de la búsqueda.
Aquellos juegos que se pueden resolver usando el razonamiento lógico se conocen como juegos lógicos.
Resolver juegos lógicos es una excelente forma de practicar con las reglas de la lógica.
Hay programas de computador diseñados para desarrollar razonamiento lógico que a menudo utilizan juegos de lógica para ilustrar sus capacidades.
Los ordenadores representan la información usando bits. Un bit tiene dos valores posibles 0 (cero) y 1 (uno).
El significado de la palabra bit viene de la expresión inglesa binary digit, ya que ceros y unos son los dígitos usados en las representaciones binarias de los números.
Un bit se puede utilizar para representar un valor de verdad, ya que dos son los valores de verdad: verdadero y falso.
Usaremos el bit 1 para representar el valor verdadero y 0 para el falso.
Una variable se llama variable booleana si su valor es verdadero o falso. Por consiguiente, una variable booleana se puede representar usando un bit.
Las operaciones con bit en el ordenador se corresponden con los conectivos lógicos. Reemplazando el valor verdadero por 1 y el valor falso por 0 en las tablas de verdad de los operadores Λ, v, ⊕, se obtiene la siguiente tabla:
| Tabla de verdad para los operadores de bit OR, AND y XOR | ||||
|---|---|---|---|---|
| x | y | x v y | X Λ y | X ⊕ y |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 |
Utilizaremos las expresiones OR, AND, XOR para los operadores: v, Λ, ⊕ respectivamente.
Una cadena de bits es una sucesión de cero o más bits.
Un tipo importante de paso utilizado en argumentos matemáticos es la sustitución de una sentencia por otra de igual valor de verdad.
Definición: Una fórmula que es siempre verdadera, no importa los valores de verdad de las proposiciones que la componen, se denomina tautología. Una fórmula que es siempre falsa se denomina contradicción. Finalmente, una proposición que no es ni una tautología ni una contradicción se denomina contingencia
Ejemplo de una tautología y una contradicción
| Ejemplo de una tautología y una contradicción | |||
|---|---|---|---|
| p | ¬ p | p v ¬ p | p Λ ¬ p |
| V | F | V | F |
| F | V | V | F |
Las fórmulas que tienen los mismos valores de verdad en todos los casos posibles se llaman lógicamente equivalentes.Esta equivalencia lógica se demuestra mediante la elaboración de tablas de verdad de las proposiciones
Definición: Se dice que las proposiciones p y q son lógicamente equivalentes si p ↔ q es una tautología.
La notación p ≡ q denota que p y q son lógicamente equivalentes. Una forma de determinar si dos proposiciones son equivalentes es utilizar una tabla de verdad.
Ejemplo
| Tabla de verdad para ¬(p v q) y ¬p Λ ¬q equivalentes lógicos | ||||||
|---|---|---|---|---|---|---|
| p | q | p v q | ¬(p v q) | ¬p | ¬q | ¬p Λ ¬q |
| V | V | V | F | F | F | F |
| V | F | V | F | F | V | F |
| F | V | V | F | V | F | F |
| F | F | F | V | V | V | V |
Sea p: “Hace frio” y sea q: “Está lloviendo”, traduzca a lenguaje formal (formalización):
a. No hace frío b. Hace frío y está lloviendo
Sea p: “Hace frio” y sea q: “Está lloviendo” traduzca a lenguaje natural:
a. - p Λ - q b. - (- q)
Sea p: “Es alto” y sea q: “Es apuesto” traduzca a lenguaje formal (formalización):
a. Es alto y apuesto b. Es falso que es bajo o apuesto. c. No es alto ni apuesto.
Sea p: “Es alto” y sea q: “Es apuesto” traduzca a lenguaje formal (formalización):
a. Es alto, o es bajo y apuesto b. No es cierto que es bajo o no es apuesto
Sean p: “Enrique lee Newsweek” y q: “Enrique lee The New Yorker” y sea r: “Enrique lee Time”, escriba c/u de las siguientes sentencias en lenguaje formal:
a. Enrique lee Newsweek y The New Yorker, o no lee Newsweek y Time.
b. No es verdad que Enrique lee Newsweek, pero no Time
c. No es verdad que Enrique lee Time o The New Yorker, pero no Newsweek
Halle el valor de verdad de los enunciados:
(a) París está en Francia.
(b) Es falso que París esté en Francia.
(c) París no está en Francia.
Halle el valor de verdad de los enunciados:
(a) 3 + 3 = 7.
(b) Es falso que 3 + 3 = 7.
(c) 3 + 3 ≠ 7
Halle el valor de verdad de los enunciados:
Es falso que 2 + 2 = 4 o Londres está en Francia.
Es la proposición: ¿p v – (p ʌ q) una tautología?
Verifique que la proposición: (p ʌ q) ʌ - (p v q) es una contradicción.
Demuestre que las proposiciones: – (p ʌ q) y - p v – q son equivalentes lógicos.
Construya la tabla de verdad de: (p → q) → (p ʌ q)
Demuestre que las proposiciones: p ↔ q y (p → q) Λ (q → p) son equivalentes lógicos.
Es una tautología: ((p v q) Λ ┐p ) → q?. Demuestre.
Qué tipo de fórmula es: (p v q) Λ ┐ p Λ ┐ q. Demuestre
Considere las afirmaciones:
- El programa está bien escrito y bien documentado
- El programa está bien documentado y bien escrito
¿Son lógicamente equivalentes? (Demostrar)
Considere las afirmaciones:
- Él o no está informado o él no es honesto
- No es verdadero que él esté informado y sea honesto
¿Son lógicamente equivalentes? (Demostrar)
Los conjuntos, idea esbozada inicialmente por CantorGeorg Cantor, cuyo nombre completo era Georg Ferdinand Ludwig Philipp Cantor, fue un matemático nacido en San Petersburgo, Rusia, el 3 de marzo de 1845, y fallecido en Halle, Alemania, el 6 de enero de 1918. Su legado es fundamental en las matemáticas modernas, y su trabajo revolucionó la teoría de conjuntos.
Durante su educación, Cantor demostró un gran talento en matemáticas y se graduó con excelentes informes.
Cantor es conocido por ser el inventor, junto con Dedekind, de la teoría de conjuntos, que se ha convertido en la base de las matemáticas modernas.
Gracias a sus audaces investigaciones sobre conjuntos infinitos, Cantor fue el primero en formalizar la noción de infinito mediante los números transfinitos (cardinales y ordinales).
Aunque no pudo demostrar la hipótesis del continuo, su trabajo en este campo fue influyente y sigue siendo objeto de estudio en matemáticas y filosofía.
En resumen, Georg Cantor fue un visionario matemático cuyas ideas siguen influyendo en la teoría de conjuntos y la comprensión del infinito en las matemáticas modernas. Su legado perdura y su nombre está grabado en la historia de las matemáticas. , se utilizan para agrupar objetos.

Generalmente los objetos de un conjunto tienen propiedades similares.
Definición:
Definición: Los objetos de un conjunto se llaman también elementos o miembros del conjunto. Se dice que un conjunto contiene a sus miembros.
Formas de describir un conjunto:
Notación de Lista (extensión)
Enumerar todos los miembros del conjunto cuando esto sea posible, se enumeran entre llaves. {a, b, c, d}.
Conjunto de las vocales del alfabeto: V = {a, e, i, o, u}.
Un conjunto puede contener elementos no relacionados. {a, 2, Alfredo, Sevilla}.
A veces la notación con { } se utiliza para describir un conjunto sin enumerar todos sus miembros. Solo enumeramos algunos de ellos y utilizamos tres puntos suspensivos para indicar la secuencia de formación de los elementos que conforman el conjunto.
Conjunto de enteros positivos menores que 100: {1, 2, 3, …, 99}.
Conjuntos que desempeñan un valor importante en matemáticas discretas:
N = {0, 1, 2, 3,…} conjunto de números naturales.
Z = {…, -2, -1, 0, 1, 2, 3,…} conjunto de los enteros.
Z+ = {1, 2, 3,…} conjunto de enteros positivos.
Q = {p/q | p ∈ Z, q ∈ Z, q ≠ 0} conjunto de los números racionales.
R = conjunto de los números reales.
Definición: Dos conjuntos son iguales si; y solo si, tienen los mismos elementos.
{1, 3, 5} = {3, 5, 1} = {1, 3, 3, 3, 5, 5}, no importa el orden y cantidad de los elementos.
Otra forma de describir conjuntos es usando la notación construcción de conjuntos. (comprensión).
Caracterizamos todos los elementos del conjunto declarando la propiedad o propiedades que deben tener sus miembros.
O = {x | x es un entero positivo menor que 10}
R = {x | x es un número real}
Un conjunto queda descrito completamente por sus elementos. De hecho, dos conjuntos son iguales si tienen los mismos elementos, y son diferentes si un solo elemento de un conjunto no es también elemento del otro conjunto.
Axioma de extensionalidad:
Sean A y B dos conjuntos. Entonces A y B son iguales si y solo si tienen los mismos miembros. Si A y B son iguales, escribimos A = B.
Entonces:
O también:
Si P es una cierta propiedad, entonces todos los elementos de un universo que satisfacen P forman un conjunto.
Representación Gráfica
Conjunto universal U: Contiene todos los elementos bajo consideración, este conjunto se representa por: ${\square}$
Círculos, representan conjuntos: $\bigcirc$
Notación
Notación de pertenencia:
a ∈ A, a es un elemento del conjunto A
a ∉ A, a no es un elemento del conjunto A
Generalmente se utilizan letras minúsculas para denotar elementos de conjuntos.
Conjunto vacío o conjunto nulo: Ø ó { }. (no tiene elementos).
Ejemplo: Conjunto de todos los elementos positivos que son mayores que sus cuadrados: es el conjunto vacío.
{Ø}: conjunto unitario.
Definición: Un conjunto A se dice que es subconjunto de B si, y solo si, todo elemento de A es también un elemento de B.
La notación A ⊆ B, indica que A es un subconjunto de B.
A ⊆ B, si y solo si, la cuantificación: ∀x (x ∈ A $\to$ x ∈ B) es verdadera.
Definición: A es un subconjunto propio de B si A es subconjunto de B, pero A no es igual a B. Si A es un subconjunto propio de B, escribimos A ⊂ B.
Un subconjunto propio es, esencialmente, solo una parte de un conjunto. Por ejemplo, la mayoría de los subcomités son subconjuntos propios de los comités, porque no todos los miembros de un comité forman parte de un subcomité. Todas las tautologías son expresiones lógicas, pero hay expresiones que no son tautologías.
Definición: A es un superconjunto de B si B es subconjunto de A. La proposición de que A es un superconjunto de B se expresa como A ⊃ B. Además, A es un superconjunto propio de B si A es un superconjunto de B que es diferente de B. En este caso escribimos A ⊃ B.
Definición: Sean A y B conjuntos. (La unión) de los conjuntos A y B, denotada por A ∪ B, es el conjunto que contiene aquellos elementos que están bien en A o bien en B, o en ambos.
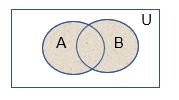
Un elemento x pertenece a la unión de los conjuntos A y B, si, y solo si pertenece a A ó x pertenece a B. Esto nos dice que:
Ejemplo: La unión de los conjuntos {1, 3, 5} y {1, 2, 3} es el conjunto {1, 2, 3, 5}; esto es {1, 3, 5} ∪ {1, 2, 3} = {1, 2, 3, 5}.
Definición: Sean A y B conjuntos. La intersección de los conjuntos A y B, denotada por A ∩ B, es el conjunto que contiene aquellos elementos que están tanto en A como en B. (comunes a ambos).
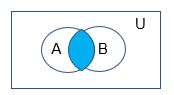
Un elemento x pertenece a la intersección de los conjuntos A y B si, y solo si, x pertenece a A y x pertenece a B. Esto nos dice que:
Ejemplo: La intersección de los conjuntos {1, 3, 5} y {1, 2, 3} es el conjunto {1, 3}; esto es {1, 3, 5} ∩ {1, 2, 3} = {1, 3}.
Definición: Se dice que dos conjuntos son disjuntos si su intersección es el conjunto vacío.
Ejemplo: Sea A = {1, 3, 5, 7, 9} y B = {2, 4, 6, 8, 10}. Como A ∩ B = Φ, A y B son disjuntos.
Definición: Sean A y B conjuntos. La diferencia de los conjuntos A y B, denotada por A – B, es el conjunto que contiene aquellos elementos que están en A, pero no en B. La diferencia de A y B se llama también el complementario de B con respecto a A.
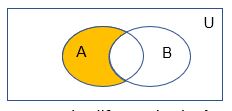
Un elemento x pertenece a la diferencia de A y B si, y solo si, x ∈ A y x ∉ B. Esto nos dice que:
Ejemplo: La diferencia de {1, 3, 5} y {1, 2, 3} es el conjunto { 5 }; esto es {1, 3, 5} - {1, 2, 3} = { 5 }. Esto es distinto de la diferencia de {1, 2, 3} y {1, 3, 5}, que es el conjunto { 2 }.
Definición: Sea U el conjunto universal. El conjunto complementario de A, denotado por Ā, es el complementario de A con respecto a U. En otras palabras, el complementario de conjunto A es: U – A.
Un elemento pertenece a Ā si, y solo si, x ∉ A. Esto nos dice que:
Ejemplo: Sea A = {a, e, i, o, u} (donde el conjunto universal es el abecedario). Entonces Ā = {b, c, d, ...}.

El principio de inclusión – exclusión es una técnica muy importante utilizada en los problemas de recuento.
A veces estamos interesados en encontrar el cardinal El cardinal de un conjunto hace referencia a la cantidad de elemntos de ese conjunto de la unión de conjuntos. Para encontrar el número de elementos de la unión de dos conjuntos finitos A y B tener en cuenta que | A | + | B | cuenta exactamente una vez cada elemento que está en A, pero no en B, o que está en B. pero no en A, y exactamente dos veces cada elemento que está tanto en A como en B. Por tanto, si el número de elementos que está tanto en A como en B se sustrae de | A | + | B |, contaremos los elementos de A ∩ B sólo una vez. Por tanto:
| A U B | = | A | + | B | - | A ∩ B |
Para tres conjuntos se tendrá:
| A U B U C | = | A | + | B | + | C | - | A ∩ B | - | A ∩ C | - | B ∩ C | + | A ∩ B ∩ C |
La interpretación gráfica de esta fórmula se muestra en la Figura 3.6
| A U B U C | = | A | + | B | + | C | - | A ∩ B | - | A ∩ C | - | B ∩ C | + | A ∩ B ∩ C |
Reescriba las siguientes declaraciones usando la notación de conjuntos:
a. El elemento 1 no es miembro de A.
b. A es un subconjunto de C.
c. F contiene todos los elementos de G.
Considere las siguientes premisas:
S1: Algunos estudiantes son perezosos.
S2: Todos los hombres son perezosos.
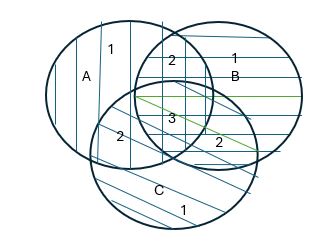
Use un diagrama de Venn para determinar la validez de la siguiente conclusión, explique la deducción:
- Algunos estudiantes son hombres.
Reescriba las siguientes declaraciones usando la notación de conjuntos:
a. El elemento 5 es un miembro de B.
b. A no es un subconjunto de D.
c. F contiene todos los elementos de G.
Traduce estas cuantificaciones a lenguaje natural y determina su valor de verdad.
a. ∀ x ∈ Z ($x^2$ > 0)
b. ∃ x ∈ R ($x^2$ = x)
Determine si cada una de estas sentencias es verdadera o falsa
a. x ∈ {x}
b. {x} ⊆ {x}
c. {x} ∈ {x}
Enumere los elementos de los siguientes conjuntos; aquí N = {1,2, 3…}
a. A = {x | x ∈ N, 3 < x < 12}
b. B = {x | x ∈ N, x es par, x < 15}
c. C = {x | x ∈ N, 4 + x = 3}
¿Cuál es el conjunto de las partes (subconjuntos) del conjunto vacío?
¿Cuál es el conjunto de las partes de {Ø}?
Considere las siguientes premisas:
S1: Todos los diccionarios son útiles.
S2: María sólo tiene novelas rosas.
S3: Ninguna novela rosa es útil.
Use un diagrama de Venn para determinar la validez de la siguiente conclusión, explique su conclusión:
- Las novelas rosas no son diccionarios
Describa con palabras como podría probar lo siguiente, (en teoría de conjuntos):
a. A es igual a B.
b. A es un subconjunto propio de B.
Dados los conjuntos: C = {1, 5, 9}; D = {1, 2, 3, 4, 5}; E = {1, 3, 5, 7, 9}. Inserte el símbolo correcto: ⊆, ⊈; entre:
(a). C, D; (b) C, E.
Dado el conjunto: X = {x | x2 = 9, 2x = 4}, ¿Es X el conjunto vacío?
Enumere los miembros de estos conjuntos
a. {x|x es un número entero positivo menor que 12}
b. {x|x es el cuadrado de un entero y x < 100}
Traduce estas cuantificaciones a lenguaje natural y determina su valor de verdad.
a. ∀ x ∈ R ($x^2$ ≠ -1)
b. ∃ x ∈ Z ($x^2$ = 2)
Hallar la unión, la intersección y el conjunto diferencia de A y B, donde A = {1, 3, 4, 5} y B = {3, 5, 7, 8}.
Definición: Las relaciones binarias (entre elementos de conjuntos) son conjuntos de pares, se representan mediante una estructura llamada Relación.
“El predicado” es el enlace de los componentes de una relación.
Definición formal: Sean A y B dos conjuntos. Una relación de A en B es cualquier conjunto de pares (x, y), x ∈ A e y ∈ B. Si (x, y) ∈ R, diremos que x es R-relacionado con y. Para expresar que R es una relación de A en B, escribimos:
R : A ⇔ B.
El producto cartesiano: A x B, se define como el conjunto de todos los pares (x, y), x ∈ A, y ∈ B. Por consiguiente una relación.
R: A ⇔ B es siempre un subconjunto de A x B.
Una relación en un conjunto A es una relación de A en A.
De hecho A x B es en sí misma una relación, la relación universal. La relación universal contiene todos los pares posibles. El opuesto de la relación universal es la relación vacía, que no contiene ningún par.Las relaciones binarias representan relaciones entre los elementos de dos conjuntos.
Definición: Todo “predicado” define una relación. Recíprocamente, toda relación R define un predicado. Específicamente, si (x, y) es un par, se puede definir un predicado PR para cada relación R que es verdadera si (x, y) ∈ R y falsa en caso contrario. Este predicado suele expresarse como xRy:
xRy ≡ (x, y) ∈ R
Definición: Sea R una relación de X a Y. El dominio de R, abreviado por dom R, es el conjunto de todos los elementos x ∈ X que aparecen en, al menos, un par (x, y) ∈ R. Esto puede expresarse como:
dom R = {x | ∃y((x, y) ∈ R)}
Definición: El rango de R, que se abrevia como ran R, es el conjunto de todos los elementos y ∈ Y que aparecen en, al menos, un par (x, y) ∈ R. Esto puede expresarse como:
ran R = {y | ∃x((x, y) ∈ R)}
El dominio consta de todos los orígenes y el rango de todos los destinos, en una representación de grafo de una relación.
Definición: Sea A un conjunto y sea R una relación de A en A. Entonces R se dice que es una relación sobre A.
Definición: Si R: X ⇔ Y es una relación, entonces la relación inversa R~: Y ⇔ X se define como {(y, x) | (x, y) ∈ R}. Por consiguiente xRy ≡ y R~x.
Todas las operaciones de conjuntos pueden aplicarse a las relaciones. Los conjuntos resultantes contienen pares ordenados y son, por tanto, relaciones.
Cualquier incremento en el espacio de dominio o en el espacio de rango se denomina una extensión.
Cualquier reducción del espacio de dominio y el espacio de rango se denomina una restricción.
Definición: Una relación binaria R sobre X es reflexiva si, para cada x ∈ X, el par (x, x) está en la (relación.) Por consiguiente,
R es reflexiva ≡ ∀x (xRx)
Definición: Una relación R sobre X es no reflexiva si, para cada x ∈ X, el par (x, x) ∉ R. En otras palabras, no existe x ∈ X, tal que xRx.
Definición: Una relación R sobre un conjunto X es simétrica si, para todo x e y perteneciente a X, xRy implica yRx. Por consiguiente,
R es simétrica ≡ ∀x ∀y (xRy ⇒ yRx)
Definición: Una relación R sobre X es antisimétrica si, para todo y ≠ x, xRy excluye a yRx. En otras palabras, si se alcanzan xRy e yRx, entonces x = y. Por consiguiente,
R es antisimétrica ≡ ∀x ∀y (xRy ˄ yRx ⇒ x = y)
Definición: Una relación R sobre X es transitiva si, para todo x, y, z en X, siempre que xRy e yRz, entonces xRz. Esto es,
R es transitiva ≡ ∀x ∀y ∀z (xRy ˄ yRz ⇒ xRz)
Definición: Una relación R es una relación de equivalencia si y solo si es reflexiva, simétrica y transitiva.
Definición:
Sean
R: X ⇔ Y y
S: Y ⇔ Z dos relaciones.
La composición de R y S, que se denota R o S, contiene los pares (x, z) si y solo si existe un objeto intermedio y tal que (x, y) está en R y (y, z) está en S. Por consiguiente,
x(R o S)z = ∃y((xRy ˄ yRz)
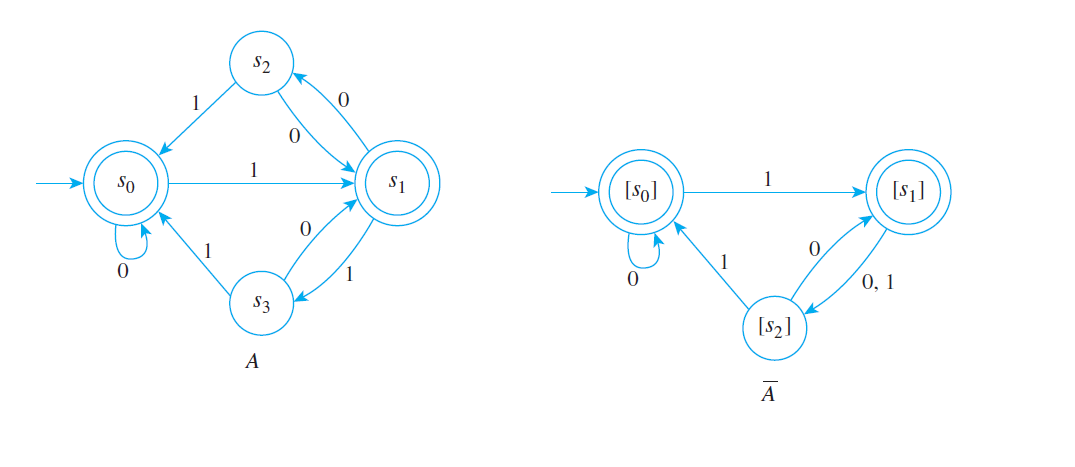
El concepto de Relación de Equivalencia tiene gran importancia en las matemáticas. Por ejemplo, se usa para definir nuevos conceptos en términos de conceptos conocidosEste apartado es tomado de la Unidad Interactiva "Relaciones de Equivalencia" del proyecto Prometeo (Julio Arnoldo Prado Saavedra y Víctor Manuel Amezcua Y Raz):
También se usa para calcular en términos de operaciones básicas, o para simplificar entidades en términos de entidades equivalentes más sencillas:
Definición:
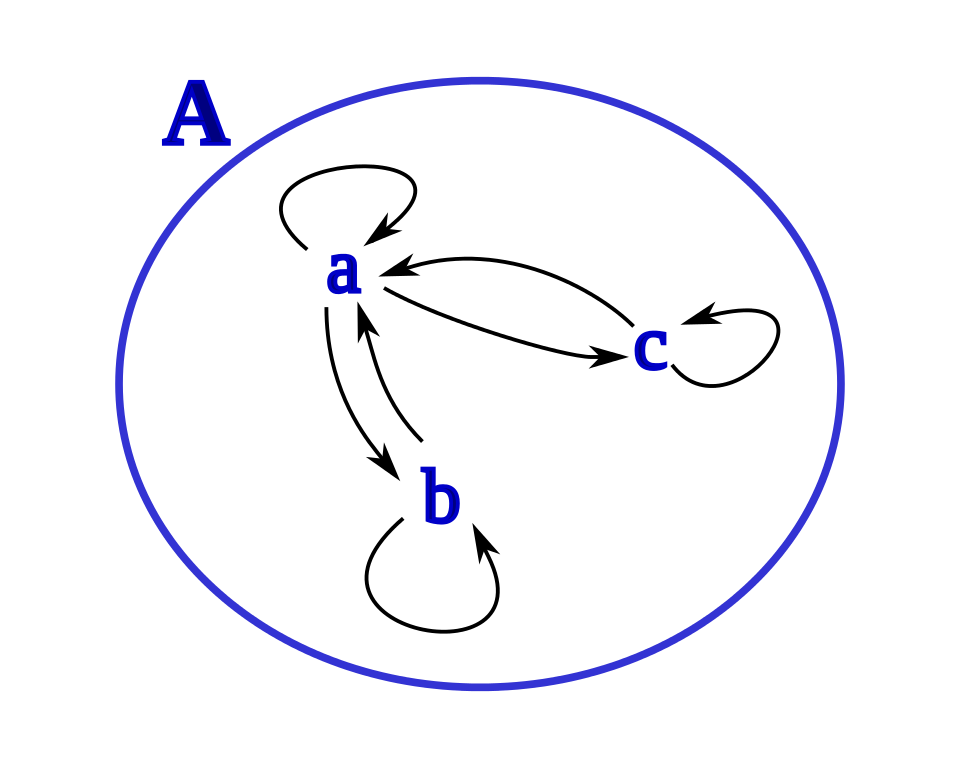
Un grafo dirigido, o dígrafo, consta de un conjunto V de vértices (o nodos) junto con un conjunto E de pares ordenados de elementos de V llamados aristas (o arcos). Al vértice a se le llama vértice inicial de la arista (a, b), y al vértice b se le llama vértice final de esta arista.
Una arista de la forma (a, a) se representa usando un arco que conecta el vértice a consigo mismo. Una arista de esta forma se llama bucle.o también llamado: loop o lazo
Definición:
Una relación es reflexiva si, y sólo si, hay un bucle en cada vértice del grafo dirigido, de modo que todos los pares ordenados de la forma (x, x) pertenecen a la relación.
Una relación es simétrica si, y sólo si, para cada arista entre vértices distintos de su dígrafo existe una arista en sentido opuesto, de modo que (y, x) está en la relación siempre que (x, y) lo está. Análogamente, una relación es antisimétrica si, y sólo si, no hay ninguna pareja de aristas con sentidos opuestos uniendo dos vértices distintos.
Definición:
Finalmente, una relación es transitiva si, y sólo si, siempre que hay una arista uniendo un vértice x con un vértice y y una arista uniendo el vértice y con un vértice z hay una tercera arista que une x con z (completando un triángulo en el que cada lado es una arista orientada en la dirección correcta).
Sea P = {(1,2), (2,4), (3,3)} y Q = {(1,3), (2,4), (4,2)}
Calcular:
P U Q, P ∩ Q; dom (P); dom (Q); dom (P U Q); ran (P); ran (Q); ran(P ∩ Q).
Para la siguiente relación, indique si es: reflexiva, no reflexiva, simétrica o transitiva:
Sean (x) e (y) niños, y sea xRy verdadera si (x) es un hermano de (y) o si (x) = (y).
¿Cuáles son los rangos de las relaciones: S = {(x, x2) | x ∈ N} y T = {(x, 2x) | x ∈ N} donde: N = {0,1, 2, …}?
L representa la relación “menor o igual que” y D representa la relación “divide”, donde xDy significa “x divide a y”. Tanto L como D están definidas sobre el conjunto {1,2,3,6}. Escribir L y D como conjuntos, y calcular L ∩ D.
Para la siguiente relación, indique si es: reflexiva, no reflexiva, simétrica o transitiva:
Sean (x) e (y) seres humanos, y sea xRy verdadera si (x) e (y) pertenecen a la misma familia.
¿Qué clase de relación tienen los aeropuertos de las ciudades costeras colombianas de la costa atlántica?
La relación antecesora, ¿qué tipo de propiedad(es) tiene?
Que valor de verdad tiene la relación binaria R sobre X: R es reflexiva = ∀ x (xRx).
¿Es la relación subconjuntos sobre conjuntos transitiva?, por qué?, explique
Qué tipo de propiedad tiene la relación R sobre X si, ∀ x ∈ X, el par (x, x) ∉ R.
¿Es la relación: <, transitiva?, por qué?, explique
Sean A y B el conjunto de todos los estudiantes y el conjunto de todas las asignaturas que se imparten en una escuela, respectivamente. Supongamos que R1 consta de todos los pares ordenados (a, b) en los que el estudiante a ha cursado la asignatura b y que R2 consta de todos los pares ordenados (a, b) en los que a es un estudiante que necesita aprobar la asignatura b para graduarse.
¿Cuáles son las relaciones R1 ∪ R2 R1 ∩ R2 R1 - R2 R2 - R1 R1 ⊕ R2?
Sea R1 la relación “menor que” en el conjunto de los números reales y sea R2 la relación” mayor que” en el conjunto de los números reales, esto es, R1 = {(x, y) | x < y} y R2 = {(x, y) | x > y}. Hallar R1 ∪ R2 R1 ∩ R2 R1 - R2 R2 - R1 R1 ⊕ R2?
¿Puede una relación en un conjunto no ser ni reflexiva ni irreflexiva?, explique.
Da un ejemplo de relación irreflexiva en el conjunto de todas las personas.
Usa cuantificadores para expresar lo que significa que una relación sea asimétrica.

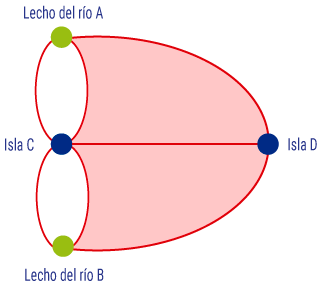
El matemático suizo Leonard Euler se interesó en el problema de los puentes de Königsberg, y en 1736 presentó un trabajo en la Academia de Ciencias de San Petersburgo en el que daba una solución. Para resolver el problema Euler utilizó un esquema con puntos y líneas. Usó puntos para representar los lechos del río y las islas, marcados con las letras A, B, C y D; los siete puentes los representó mediante líneas (Leticia Montserrat).
La obra de Euler es considerada como el comienzo de la teoría de gráficas, que forma parte de la topología. El esquema anterior es llamado gráfica (o grafo), los puntos se llaman vértices (o nodos) y las líneas se llaman aristas (o lados).
Los grafos se utilizan en la solución de:
Definición: Los (grafos) son estructuras discretas que constan de vértices y aristas que conectan entre si esos vértices.
Hay diferentes tipos de grafos, se diferencian entre sí por el tipo y número de aristas que puedan conectar c/par de vértices.
Ejemplos de utilización:
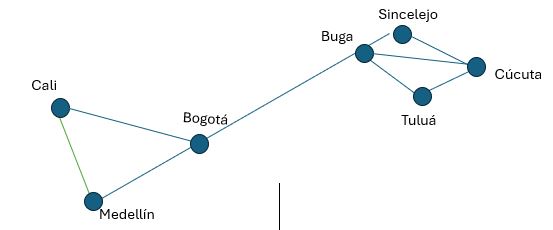
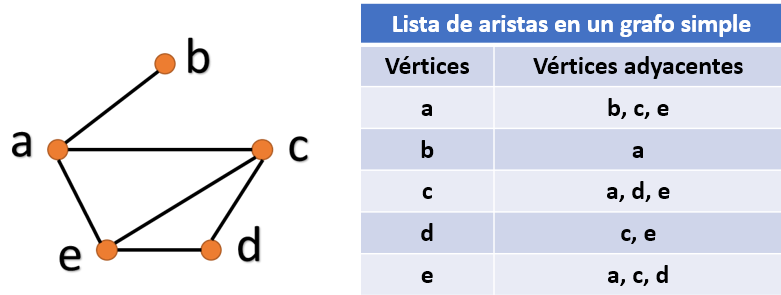
Grafo simple: consta de vértices y aristas no dirigidas. Cada arista conecta dos vértices distintos y no hay dos aristas que conecten un mismo par de vértices
Definición formal: Un grafo simple G = (V, E) consta de V, un conjunto no vacío de vértices, y de E, un conjunto de pares ordenados de elementos distintos de V. A estos pares se les llama aristas.
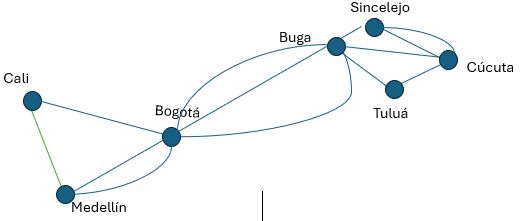
Multígrafo: consta de vértices y aristas no dirigidas entre esos vértices, pero admitiendo la existencia de aristas múltiples entre pares de vértices. Todo grafo simple es multígrafo. Sin embargo, no todos los multígrafos son grafos simples, puesto que en un multígrafo puede haber dos o más aristas conectando un mismo par de vértices.
Definición formal: Un multígrafo G = (V, E) consta de un conjunto V de vértices, un conjunto E de aristas, y una función f de E en {{u, v} | u, v ∈ V, u ≠ v}. Se dice que las aristas e1 y e2 son aristas múltiples o paralelas si f(e1) = f(e2).
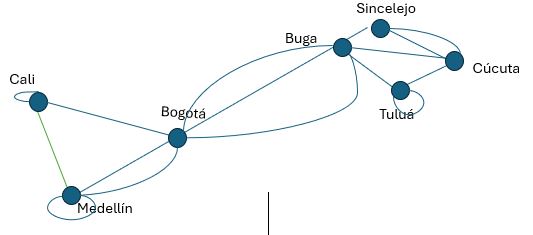
Pseudografo: Son más generales que los multígrafos, ya que una arista de un Pseudografo puede conectar un vértice consigo mismo.
Definición formal: Un pseudografo G = (V, E) consta de un conjunto V de vértices, un conjunto E de aristas, y una función f de E en {{u, v} | u, v ∈ V}. Una arista e es un bucle, o lazo, si f(e) = {u, v} = {u} para algún u ∈ V.
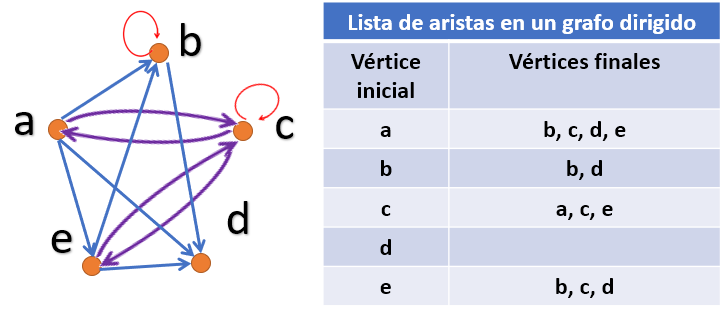
Grafo dirigido: Las aristas de un grafo dirigido son pares ordenados. Se admiten bucles, pares ordenados con sus dos elementos iguales,
pero no se admiten aristas múltiples en la misma dirección entre dos vértices.
Definición formal: Un grafo dirigido G = (V, E) consta de un conjunto V de vértices, y de un conjunto E de aristas, que son pares ordenados de elementos de V. Utilizamos una flecha apuntando desde u hacia v para indicar la dirección de la arista (u, v).
Multígrafos dirigidos: pueden tener aristas dirigidas múltiples desde un vértice a un segundo vértice (que, eventualmente, puede coincidir con el primero), para representar este tipo de redes.
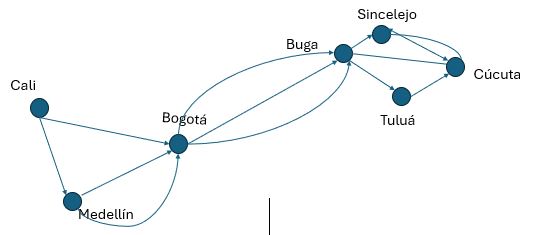
Definición formal: Un multígrafo dirigido G = (V, E) consta de un conjunto V de vértices, un conjunto E de aristas, y una función f de E en {{u, v} | u, v ∈ V}. Se dice que las aristas e1 y e2 son aristas múltiples si f(e1) = f(e2).
Gafos de solapamiento de nichos en ecología: Se emplean en muchos modelos que tienen que ver con las interacciones entre especies animales distintas.
Grafos de conocidos: se utilizan para representar relaciones entre personas.
Gafos de influencias: Para observar en un grupo de personas, quienes pueden influir en la forma como piensan otras.
Grafos de llamadas: se pueden utilizan para representar las llamadas telefónicas en una red.
Definición: Se dice que dos vértices u y v de un grafo no dirigido G son adyacentes (o vecinos) en G si e = {u, v}, se dice que la arista e es incidente con los vértices u y v. También se dice que la arista e conecta u y v. Se dice que los vértices u y v son extremos de la arista e.
Para seguirle la pista a cuantas aristas son incidentes con un vértice, definimos:
Definición: El grado de un vértice de un grafo no dirigido es el número de aristas incidentes con él, exceptuando los bucles, cada uno de los cuales contribuye con dos unidades al grado del vértice. El grado del vértice v se denota por δ(v).
A los vértices de grado cero se les llama aislados. Claramente, un vértice aislado no es adyacente a ningún vértice. Se dice que un vértice es colgante, o que es una hoja, si y solo si, tiene grado uno.
Teorema 1: La suma de los grados de los vértices de un grafo no dirigido es un número par.
Teorema 2: Todo grafo no dirigido tiene un número par de vértices de grado impar.
Definición: Si (u, v) es una arista del grafo dirigido G, se dice que u es adyacente a v y que v es adyacente desde u. Al vértice u se le llama vértice inicial de (u, v) y a v se le llama vértice final o terminal de (u, v). Los vértices inicial y final de un bucle coinciden.
Definición: En un grafo dirigido, el grado de entrada de un vértice v, denotado por δ - (v), es el número de aristas que tienen a v como vértice final. El grado de salida de un vértice v, denotado por δ +(v), es el número de aristas que tienen a v como vértice inicial (nótese que un bucle contribuye con una unidad tanto al grado de entrada como al grado de salida del vértice correspondiente).
Matriz de adyacencia
Basada en la adyacenciao cercanía de los vértices unidos por la misma arista de vértices, en grafos sin aristas múltiples, específica los vértices que son adyacentes a cada uno de los vértices del grafo
Los habitantes de Königsberg (hoy Kaliningrado) solían dar largos paseos por la ciudad los domingos. Hubo quien se preguntó si sería posible comenzar el paseo en algún sitio de la ciudad, atravesar todos los puentes sin cruzar ninguno dos veces y regresar al punto de partida.
El matemático suizo Leonhard Euler resolvió este problema. Su solución, publicada en 1736, es posiblemente la primera ocasión en que se utilizó la teoría de grafos. Euler estudió el problema usando el multígrafo que se obtiene si se representan las cuatro regiones mediante vértices y los siete puentes mediante aristas
A continuación, se transcribe la unidad didáctica Los puentes de Königsberg, diseñada por Leticia Montserrat en el proyecto Los puentes de Königsberg.
Planteamiento del problema: Los puentes de Königsberg
Königsberg era el nombre de una ciudad atravesada por el río Preger.
En el siglo XVIII era una ciudad alemana, pero ahora pertenece a Rusia y su nombre es Kaliningrado. Dentro de la ciudad hay dos islas fluviales que están conectadas a los lechos del río por puentes. En el siglo XVIII eran siete y estaban dispuestos como se muestra a continuación.
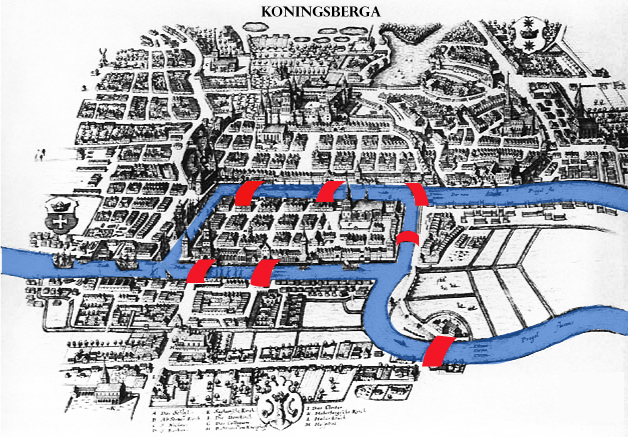
Se convirtió en tradición que los habitantes de Königsberg pasaran sus domingos por la tarde paseando por la ciudad. Se cree que intentaban cruzar cada uno de los siete puentes que unen el norte y el sur del río a las dos islas, pero sólo una vez y sin volver sobre sus pasos. ¿Es posible hacerlo?
Esto es equivalente a preguntarse si es posible caminar por la ciudad de tal manera que se cruce una sola vez cada puente.
Problema
Queremos encontrar un camino a través de la ciudad de tal manera que no se cruce cada uno de los siete puentes más de una vez.
¿Es posible resolver este problema?
Si no es posible, ¿puedes explicar por qué?
Si se puede resolver, explica cómo puedes saber que tienes todas las soluciones.
Exploración inicial del problema
En el siguiente espacio interactivo podrás elegir partir de cualquiera de los lechos del río o de las islas. Elige un punto de partida y pulsa el botón "Iniciar" para hacer un recorrido por los siete puentes.
En el siguiente espacio interactivo podrás elegir partir de cualquiera de los lechos del río o de las islas y el número de puentes.
Elige un punto de partida y un número de puentes. Pulsa sobre el botón "Iniciar" para hacer un recorrido por los puentes. Para cambiar de posición inicial pulsa sobre "Cambiar posición" y luego sobre "Iniciar". Pulsa sobre el botón "Limpiar" para borrar los caminos que hayas trazado si así lo requieres.
¿Lograste trazar un recorrido pasando sólo una vez por cada puente en todos los casos?
Si no lo lograste en todos los casos, ¿en qué casos lo lograste y en qué casos no lo lograste?, ¿Cuál crees que es el motivo?
Formalización del problema - La teoría de grafos
Euler, como se dijo antes, usó puntos para representar los lechos del río y las islas, marcados con las letras A, B, C y D; los siete puentes los representó mediante líneas.

Ahora, ya puedes resolver el problema, usando el grafo anterior.
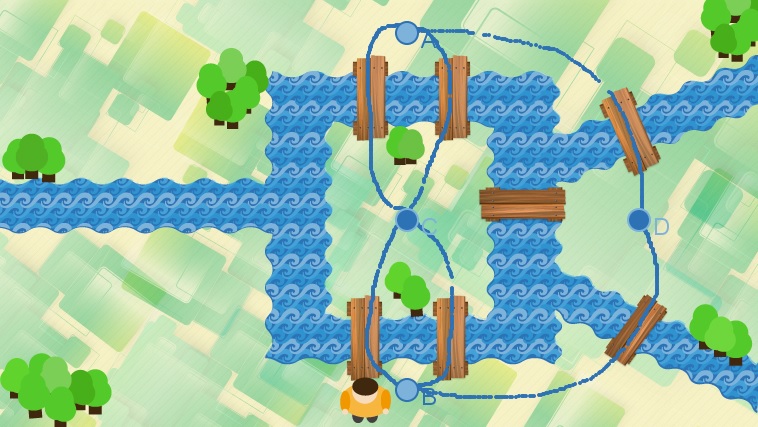
El problema de los puentes de Königsberg se reduce a dibujar la gráfica que usó Euler partiendo de un punto con un único trazo, es decir, sin despegar el lápiz del papel (o, en este caso, sin dejar de pulsar sobre el cursor), y sin recorrer la misma línea dos veces.
A un recorrido con estas características se le llama camino euleriano. Cuando el punto de inicio y el punto final coinciden, el recorrido es un circuito euleriano.
Vértices pares
Al inicio planteamos el siguiente problema: ¿es posible recorrer los siete puentes sobre el río Preger sin pasar por ninguno más de una vez? En la sección anterior vimos que este problema equivale a trazar una gráfica con cuatro vértices (los lechos del río y las islas) y siete aristas (los puentes) sin despegar el lápiz del papel y sin recorrer la misma arista más de una vez. Ahora, veremos qué relación hay entre el número de vértices, el número de aristas que hay en cada vértice y el tipo de recorridos que se pueden hacer sobre una gráfica.
En el siguiente espacio interactivo traza un recorrido en cada gráfica, tomando en cuenta las siguientes preguntas.
Preguntas
¿Es posible trazar un camino euleriano de cada una de las gráficas?
¿Y un ciclo o circuito euleriano?
Coloca el control gráfico (verde) en uno de los puntos de alguna de las gráficas y pulsa el botón "Iniciar". Para cambiar el punto de inicio pulsa el botón "Cambiar posición" y luego pulsa "Iniciar". Pulsa el botón "Limpiar" para borrar los caminos que hayas trazado si así lo requieres.
Vértices pares e impares
En el siguiente espacio interactivo traza un recorrido en cada gráfica. Nuevamente averigua: ¿Es posible trazar un camino euleriano de cada una de las gráficas? ¿Y un ciclo euleriano?
Coloca el control gráfico verde en uno de los puntos de alguna de las gráficas y pulsa el botón "Iniciar". Para cambiar el punto de
inicio pulsa el botón "Cambiar posición" y luego pulsa "Iniciar". Pulsa sobre el botón "Limpiar" para borrar los caminos que hayas trazado si así lo requieres.
En resumen
Podemos concluir que:
Cuando una gráfica tiene sólo vértices pares (vértices con un número par de aristas), el recorrido es un ciclo euleriano, pues sin importar en qué vértice se inicie el recorrido, al hacerlo sin levantar el lápiz del papel y pasando sólo una vez por cada vértice, regresamos al vértice del que partimos.
Cuando la gráfica tiene dos vértices impares (vértices con un número impar de aristas), el recorrido no es un ciclo euleriano, sino un camino euleriano, pues los puntos de partida y de terminación son distintos.
Y finalmente, en una gráfica con dos vértices impares, no se puede obtener un camino euleriano si se parte de un vértice par.
A continuación se te ofrecen 5 preguntas de opción múltiple para que te autoevalúes.
Definición formal: Un circuito euleriano de un grafo G es un circuito simple que contiene a todas las aristas de G.
Circuito Hamiltoniano: Responde a la pregunta: ¿Podemos desplazarnos por las aristas de un grafo comenzando en un vértice y volviendo a él después de haber visitado cada vértice del grafo exactamente una vez?
Definición formal: Un circuito hamiltoniano es un camino simple que contiene a todas las aristas de G.
Condición necesaria y suficiente para la existencia de circuitos y caminos euleriano:
Si todos los vértices de un multígrafo conexo tienen grado par, entonces el grafo contiene un circuito euleriano.
Un circuito euleriano empieza en un vértice y termina en el mismo vértice.
Teorema: Un multígrafo conexo contiene un circuito euleriano si, y solo si, cada uno de sus vértices tienen grado par.
Teorema: Un multígrafo conexo contiene un camino euleriano, pero no un circuito euleriano, si, y solo si, tiene exactamente dos vértices de grado impar.
Definición: Se dice que un camino xo, x1, …, xn-1, xn del grafo G = (V, E) es un camino hamiltoniano si V = {xo, x1, …, xn-1, xn} y xi ≠ xj para 0 ≤ i < j ≤ n. Se dice que un circuito xo, x1, …, xn-1, xn (con n > 1) del grafo G = (V, E) es un circuito hamiltoniano si xo, x1, …, xn-1, xn es un camino hamiltoniano.
Teorema de Dirac: Sea G un grafo simple con n vértices para n ≥ 3 tal que todos los vértices de G tienen grado mayor o igual que n/2. Entonces, G contiene un circuito hamiltoniano.
Teorema de Ore: Sea G un grafo simple con n vértices para n ≥ 3 tal que δ(u) + δ (v) ≥ n para cada par de vértices no adyacentes u y v de G. Entonces, G contiene un circuito hamiltoniano.
¿Cuándo se podrán pintar las líneas que separan los carriles de las calles de una ciudad sin pasar más de una vez por cada calle? (suponga que todas las calles son de doble sentido).
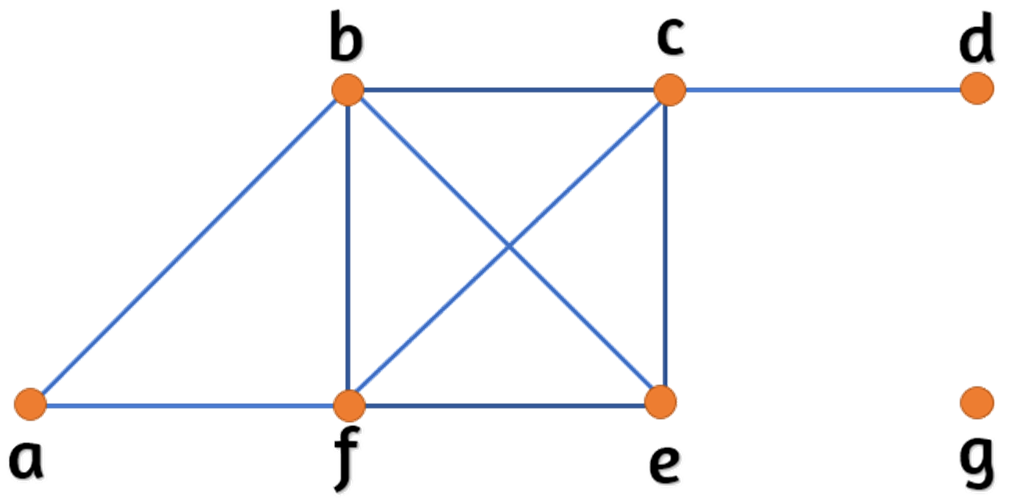
Halle el número de vértices, el número de aristas y el grado de cada vértice del grafo no dirigido
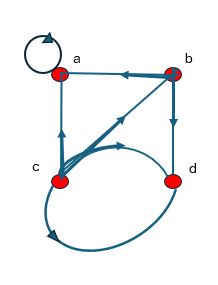
Determina el número de vértices y de aristas y halla los grados de entrada y de salida de c/u de los vértices del multígrafo dirigido
¿Qué representa el grado de un vértice en un grafo de colaboración?
¿Qué representan el grado de entrada y el grado de salida de un vértice en un grafo dirigido que represente un torneo de todos contra todos?
Determinar si el grafo contiene o no un circuito euleriano (¿cuál?). Si no existe ningún circuito euleriano, determinar si el grafo contiene o no un camino euleriano. (¿cuál?).
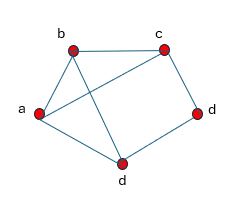
Determinar si se puede o no trazar el dibujo correspondiente con un lápiz de manera continua sin levantar el lápiz del papel y sin repetir ningún trazo.

Construir un grafo de orden 5 cuyos vértices tengan grados 1, 2, 2, 3, 4. ¿Cuántas aristas tiene el grafo? Explicar
En un grupo de 15 personas, ¿es posible que cada persona tenga exactamente 3 amigos? Explique. (Suponga que la amistad es una relación simétrica: si x es amigo de y, entonces y es amigo de x).