Estadística, probabilidad e inferencia
INTERACTIVO
Juan Jesús Cañas Escamilla
José Román Galo Sánchez
Red Educativa Digital Descartes
Fondo Editorial RED Descartes

Córdoba (España)
2022
Título de la obra:
Estadística, probabilidad e inferencia
Interactivo
Autores:
Juan Jesús Cañas Escamilla
José Román Galo Sánchez
Editor técnico:
Juan Guillermo Rivera Berrío
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Núcleo del libro interactivo: julio 2022.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN: 978-84-18834-44-8

Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
Pierre-Simon Laplace (Normandía, Francia, 23 de marzo de 17491 - París, 5 de marzo de 1827) fue un astrónomo, físico y matemático francés, como estadístico sentó las bases de la teoría analítica de la probabilidad (Crédito: Jean-Baptiste Paulin Guérin - http://www.photo.rmn.fr/, Dominio público, https://es.wikipedia.org/)
Este libro digital interactivo se ha diseñado utilizando el editor de DescartesJS, de tal forma que se pueda leer en ordenadores y dispositivos móviles sin necesidad de instalar ningún programa o plugin.
El libro es una tercera versión del publicado por los mismos autores en el proyecto iCartesiLibri (Estadistica Probabilidad e Inferencia).

Juan Jesús Cañas Escamilla
José R. Galo Sánchez
Francis Galton (Birmingham, 16 de febrero de 1822 - Haslemere, Surrey, 17 de enero de 1911) fue un polímata, antropólogo, geógrafo, explorador, inventor, meteorólogo, estadístico, psicólogo y eugenista británico, creó el concepto estadístico de correlación y regresión hacia la media (Crédito: Eveleen Myers - http://www.npg.org.uk/collections/, Dominio público, https://es.wikipedia.org/).
Vivimos en un mundo que cambia de forma acelerada. Todos formamos parte de una monumental gran base de datos a la que continuamente acceden y utilizan desde los estados y grandes multinacionales hasta el negocio más pequeño o el individuo más alejado de la última aldea de cualquier país. Ya nada es ajeno a nadie. Lo que ocurre en cualquier lugar del mundo es presentado por los medios de comunicación prácticamente en directo en los salones de las casas o en los teléfonos inteligentes de cada individuo, estableciéndose así multitud de interrelaciones que avivan la interdependencia de todos y todo termina por influir de un modo u otro en el resto. Esta nueva situación de aldea global proporciona a la estadística un nuevo y mayor protagonismo en prácticamente todos los aspectos de la vida.
Todas las ciencias, animadas por las nuevas posibilidades que permiten el manejo y la rápida transmisión de imponentes bases de datos utilizan a la estadística como herramienta básica de su espectacular desarrollo.
Este nuevo contexto nos sitúa en un punto de partida inicial motivante para iniciar nuestro curso.
Como ya se ha mencionado, el primer contacto que se suele tener con la Estadística suele ser a través de los medios de comunicación. La lectura rápida de cualquier periódico enfoca nuestra atención en los titulares y en la imagen de portada. Es aquí donde se suelen presentar las tablas y gráficos estadísticos que tienen la gran virtud de actuar como elemento acaparador de atención, aunando tanto una capacidad importante de información como una gran facilidad y sencillez a la hora del descifrado de la misma.
Esta primera idea que todos tenemos puede suponer un aceptable punto de partida inicial para comenzar nuestro curso.
La palabra Estadística etimológicamente deriva de la palabra "status", que significa estado o situación.
Vamos a reflejar algunas pinceladas rápidas sobre la aparición de la Estadística, o algo parecido a ella, en algunos momentos históricos.
Seguramente para encontrar pistas sobre el origen de la estadística, tendríamos que remontarnos a antes del comienzo mismo de la propia Historia. Restos arqueológicos y monumentos prehistóricos contienen signos y muescas que pueden interpretarse como referencias a posibles anotaciones sobre cantidades, probablemente de ganado y caza que pueden indicarnos un rudimentario sistema de control sobre determinados datos.
 |
 |
En muchos monumentos egipcios se encontraron interesantes estelas, jeroglíficos, en una palabra, "documentos" en los que se puede interpretar una gran organización y administración estatal en lo que se refiere a contabilización de riqueza agrícola, ganadera e industrial, así como a movimientos poblacionales, censos, etc.
 |
 |
En la cultura asiria o mesopotámica se conservan tablillas con inscripciones cuneiformes sobre importantes datos estadísticos referentes a producciones agrícolas, ganaderas, así como también datos sobre contabilidad, medicina, astronomía, etc.
 |
 |
En la Biblia también podemos encontrar referencias estadísticas. Así por ejemplo, en uno de los libros del Pentateuco, bajo el nombre de Números, puede leerse lo que podría interpretarse como el censo que realizó Moisés después de la salida de Egipto.
“Haz un censo general de toda la asamblea de los hijos de Israel, por familias y por linajes, describiendo por cabezas los nombres de todos los varones aptos para el servicio de armas en Israel”.
 |
 |
En China aparecen innumerables documentos con referencias a poblaciones, censos, recuentos bienes agrícolas, ganaderos, de origen militar. Por ejemplo, en uno de sus clásicos "Shu-King" escrito hacia el año 550 a.C., Cunfucio nos narra cómo el Rey Yao en el año 2238 mandó hacer una estadística agrícola, industrial y comercial en todos sus dominios.
 |
 |
Grecia, la cuna del pensamiento occidental, también tuvo importantes observaciones estadísticas en lo que refiere a distribución de terreno, servicio militar, etc.
Es en Roma donde puede decirse que la Estadística adquiere un gran desarrollo. La burocracia romana utiliza la Estadística como instrumento de apoyo a la gran capacidad organizativa política, jurídica y administrativa del imperio. Una muestra es el Census que se realizaba cada 5 años y que tenía por objeto no sólo saber el número de habitantes, sino también su cantidad de bienes. El propio origen de la cultura cristiana está ligado a uno de los censos romanos
 |
 |
La Iglesia, después del Concilio de Trento estableció la obligación de la inscripción de nacimientos, matrimonio y defunciones de la población cristiana, con lo que se erige como creadora y también custodia de una impresionante base de datos de los cuales se han servido posteriormente las ciencias sociales para la elaboración de multitud de estudios.
 |
 |
En la edad moderna se produce un gran desarrollo científico- matemático que enriquece mucho a la Estadística. Científicos importantes de esta época como Copérnico, Galileo, Bacon, Descartes…, contribuyen al desarrollo de lo que se conoce como el método científico donde la estadística tiene un papel fundamental.
Blaise Pascal y Christiaan Huygens, en el siglo XVII, realizan trabajos con bases de datos relativas a nacimientos y defunciones y la influencia de causas naturales y sociales en estas variables.
 |
 |
En el siglo XIX la estadística entra en una nueva fase de su desarrollo con el auge y generalización del método científico en todas las ciencias, tanto naturales como sociales. Figuras muy relevantes de esta época serían Francis Galton (1822 - 1911) y Karl Pearson (1857 – 1936), verdaderos pioneros de la estadística moderna.
 |
 |
Siguiendo los pasos de Galton, Ronald Fisher (1890 – 1962), en su publicación Métodos estadísticos para investigadores establece los fundamentos de la metodología estadística actual.
Con la aparición de los ordenadores, en la segunda mitad del siglo XX, la estadística entra en una nueva era en la que metodología gira hacia técnicas de computación rápidas e iterativas que permiten actuar sobre grandes bases de datos en muy poco tiempo. Los paquetes estadísticos se popularizan y su aplicación en las distintas ciencias también.
 |
 |
Así pues, la estadística aparece a lo largo de la historia como un poderoso instrumento utilizado por gobiernos e instituciones así como tambien elemento auxiliar de las distintas ciencias, ayudando a estas a desentrañar las grandes preguntas que la curiosidad del ser humano siempre ha perseguido; es decir: qué variables intervienen en un fenómeno, que leyes permiten el comportamiento de las mismas y qué relación de dependencia hay entre ellas.
Video
En el siguiente vídeo, elaborado por la UNED, podemos ver una historia de la Estadística.
La estadística, en general, es la ciencia que trata de la recopilación, organización presentación, análisis e interpretación de datos que intervienen en un fenómeno, con el fin de realizar una perfecta descripción y en gran parte inferir resultados o tomar decisiones.
Dentro de la estadística se distinguen dos ramas fundamentales,
En la anterior escena interactiva tienes una introducción a la Estadística.
A continuación recordamos algunos de los conceptos generales relacionados con la estadística.
Es obvio que todo estudio estadístico ha de estar referido a un conjunto o colección de objetos. Este conjunto de personas o cosas es lo que denominaremos población.
Cada uno de estos objetos que forman parte de la población se denominan elemento o individuo. En sentido estadístico un individuo puede ser algo con existencia real, como un automóvil o una casa, o algo mucho más abstracto como la temperatura, una opinión, un voto, un sentimiento o un intervalo de tiempo.
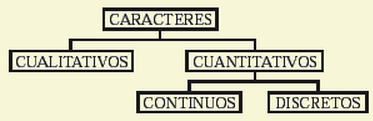
A su vez, cada elemento de la población tiene una serie de características que pueden ser objeto del estudio estadístico (carácter). Así, por ejemplo, si consideramos como elemento a una persona, podemos distinguir en ella multitud de caracteres como el sexo, la edad, estatura, peso, color de pelo, nivel de estudios, etc.
Normalmente en un estudio estadístico hay muchos condicionantes y de distinta naturaleza que impiden trabajar con todos los elementos de la población, por tanto, se suele recurrir a un subconjunto de la misma.
Una muestra es cualquier subconjunto de una población. Cuando los elementos que componen la muestra están escogidos aleatoriamente y todos los elementos tienen la misma probabilidad de ser elegidos diremos que la muestra es aleatoria simple.
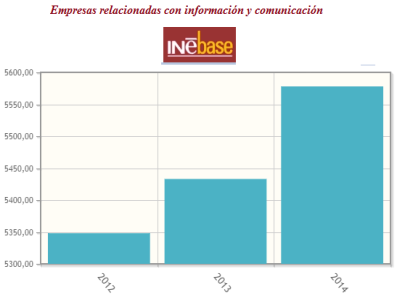 |
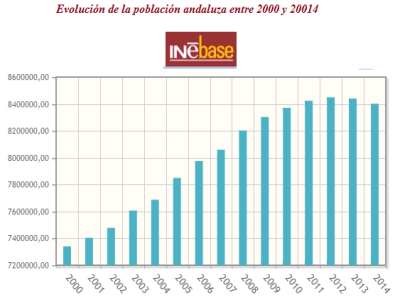 |
En las siguientes escenas del subproyecto ED@D (Educación Digital con Descartes) de la RED Descartes podrás practicar un poco con los conceptos anteriores.
El paso siguiente a la recogida de datos en un trabajo de campo es una primera presentación de los mismos de manera que dicha representación sea fácil de visualizar, sencilla de interpretar y directa. Estas cualidades se reflejan bastante bien en las tablas estadísticas. Las listas, boletines y actas de notas, clasificación de equipos con puntuaciones, detalles de los goles, todo son en realidad tabulaciones de datos.
Con bastante frecuencia y como complemento a las tablas se recurre a los gráficos estadísticos. La mayor parte de la información que recibimos hoy en día proviene fundamentalmente de los medios de comunicación de masas.
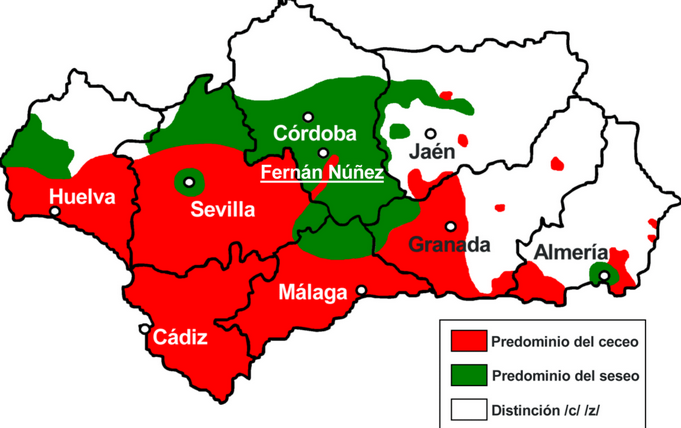
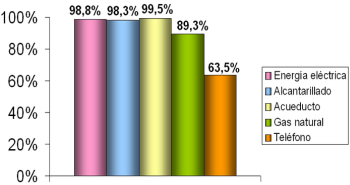
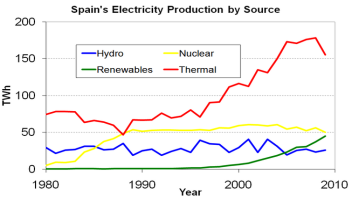
En prensa, internet y televisión fundamentalmente, y también en las ciencias sociales, se recurre de manera muy habitual a los gráficos estadísticos (pictogramas, climogramas, pirámides de población, diagramas de barras, de sectores) como elementos aglutinadores de la información a la par que fáciles de descifrar. Los gráficos estadísticos por tanto, constituyen también una herramienta fundamental en lo que se refiere a una primera información sencilla y rápida de las características más elementales de una distribución estadística.
 |
 |
 |
 |
 |
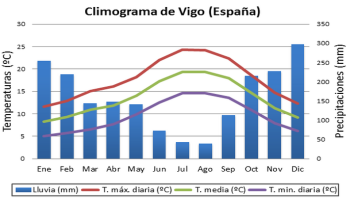 |
Cualquier estudio estadístico comienza con la recogida de datos. Esta recogida puede ser física y directa o virtual mediante la importación de ficheros procedentes de distintas instituciones u organismos.
El segundo paso es la presentación de estos datos de forma sencilla, coherente y a ser posible atractiva para el lector. En este sentido, la estadística dispone los datos generalmente en tablas y se ayuda, a su vez, en muchas ocasiones de gráficos que resumen o aclaran aspectos reseñables de la distribución.
La forma más sencilla de tabular una variable estadística es mediante columnas. En la primera se proponen los distintos valores, generalmente ordenados, de la variable estadística o del correspondiente atributo. En la segunda, la cuantificación de esos valores en nuestro estudio, esto es las frecuencias absolutas. De esta forma efectuamos una tabulación mínima.
Desde el punto de vista didáctico, la tabulación se completa con varias columnas más en las que se anotan también las frecuencias relativas, y las acumuladas, tanto absolutas como relativas.
Generalmente las tablas que nos encontraremos reunirán la información mínima necesaria para la representación gráfica y el cálculo de parámetros estadísticos fundamentales en una distribución.
Para el caso de un carácter cualitativo:
Observa lo anterior en la siguiente imagen:

Y ahora realiza algunos ejercicios de tabulación en la siguiente escena interactiva.
Para el caso de una variable discreta
Observa una tabulación mínima en la siguiente imagen:
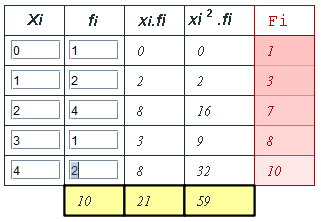
Y ahora realiza algunos ejercicios de tabulación en la escena interactiva presentada en la siguiente página.
Para el caso de una variable continua:
Observa una tabulación mínima en la siguiente imagen:
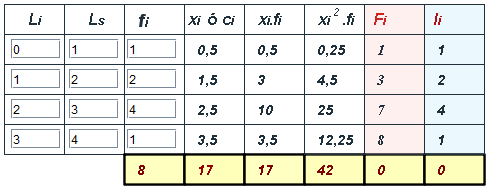
Y ahora realiza algunos ejercicios de tabulación en la siguiente escena interactiva.
Diagramas de barras
El diagrama de barras es, junto al de sectores, el gráfico más utilizado para variable cualitativa y cuantitativa discreta. Se utiliza como complemento a la tabla de frecuencias o incluso en algunos casos como sustitución de ésta.
En el eje de abscisas se sitúan a igual distancia los distintos atributos o bien los valores discretos de la variable y posteriormente a partir de cada atributo o valor discretos se levantan barras de igual grosor y cuya altura sea la de la correspondiente frecuencia absoluta observada.
En la siguiente escena puedes observar como se construyen diagramas de barras y practicar realizando algunos ejemplos.
Y ahora practica en la escena interactiva de la siguiente página, realizando tú los gráficos.
Diagrama de sectores
Tiene la misma filosofía de construcción que el diagrama de barras pero la representación en sectores circulares, figuradamente trozos de tarta. Requiere previamente que mediante proporcionalidaad directa asignemos a cada fecuencia absoluta un determinado ángulo.
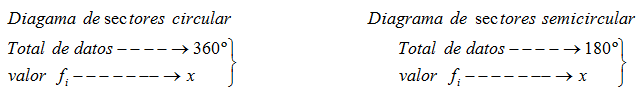
En las siguientes escenas puedes observar como se construyen diagramas de sectores (pasa el ratón por los recuadros de colores).
Y ahora practica realizando tú los gráficos.
Histograma
Este tipo de gráfico es el que se utiliza con más frecuencia en el caso de variables cuantitativas continuas. Los datos se representan mediante rectángulos de base igual a la amplitud del intervalo y altura igual a la frecuencia absoluta si todos los intervalos tienen la misma amplitud.
Si no se cumple esta premisa de igualdad de amplitud, las alturas de los rectángulos serán calculadas de tal manera
que el área total de cada rectángulo
represente o sea proporcional a la
correspondiente frecuencia absoluta,
esto habitualmente se conoce con el
nombre de normalidar las frecuencias,
(dividir cada frecuencia entre la amplitud
del intervalo).
Si se unen los centros de los segmentos
superiores de cada rectángulo, se obtiene
una figura poligonal conocida como Polígono de frecuencias.
Cuando realizamos los gráficos anteriores utilizando
las frecuencias acumuladas obtenemos el denominado histograma de frecuencias acumuladas y el polígono de fecuencias acumuladas.
En la escena de la siguiente página, puedes generar
datos, hacer el recuento y ver el histograma
correspondiente.
También se traza el histograma de las frecuencias acumuladas, en cada dato se acumula la frecuencia de los datos anteriores.
Todos sabemos lo que significa la nota media de los exámenes de un curso, o el hermano mediano en una familia o seguir la moda en cuanto a determinada tendencia. En estadística vamos a estudiar ciertos valores que resuman la tendencia habitual o central de los datos de una distribución. A los parámetros o medidas estadísticas que informan sobre la tendencia habitual o central de los datos de una distribución se les denomina en estadística medidas de tendencia central. Las más utilizadas son la media aritmética, la mediana y la moda.
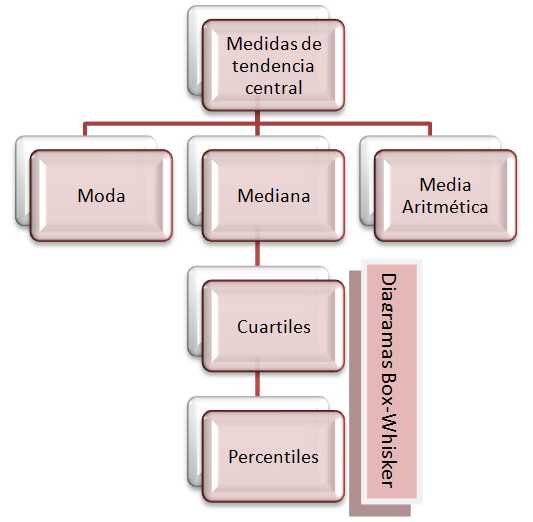
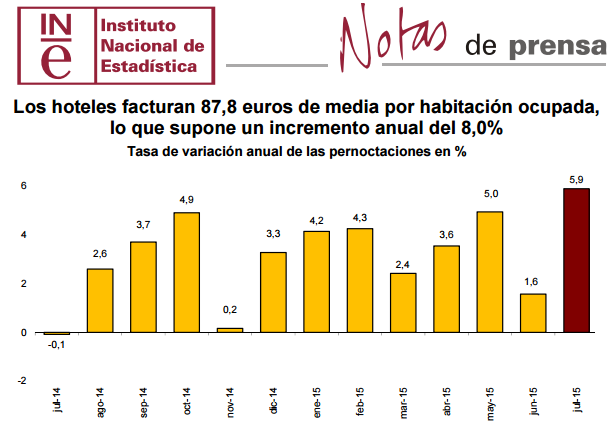
La palabra media, se ha incorporado al diccionario de cualquier persona. Continuamente nos estamos refiriendo a ella desde todos los órdenaes de la vida. hablamos de gasto medio, de sueldo medio, consumo eléctrico medio, notas medias, estar por encima de la media en consumo de tal cosa, inflacción media etc... En estadística la definición de media aritmética es muy sencilla. La media aritmética se define como la suma de todos los datos dividida entre el número total de los mismos. A veces no dispondremos de los valores concretos de los datos sino de una agrupación de los mismos en intervalos. En estos casos tendremos que elegir un valor de cada intervalo y que intervendrá en representación del mismo en el cálculo de la media. Como habitualmente dispondremos de una tabla de datos con sus correspondientes frecuencias absolutas, aplicaremos la siguiente fórmula:
Abreviadamente:
De la propia definición de media aritmética se desprenden algunas características y comentarios acerca de este parámetro, como por ejemplo:
| Para el caso de variable continua, sola- mente tenemos que sustituir $x_i$ por $c_i$, siendo ésta última la marca de clase de cada intervalo; es decir, el punto medio o valor central de cada intervalo. Por abuso de lenguaje se suele utilizar indistintamente también para variables continuas el símbolo $x_i$ para las marcas de clase | $$\={X} = \frac{\sum_{i=1}^n c_i\cdot f_i}{N}$$ |
Practica con el cálculo de la media para variable discreta.
Observa ejemplos para el cálculo de la media para variable discreta y continua.
En esta otra escena puedes ver más ejemplos.
Para completar el estudio sobre la media también puedes consultar más información sobre la Media ponderada pulsando sobre la imagen siguiente:
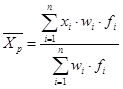
y sobre la Media geométrica y la Media armónica pulsando sobre esta otra imagen:
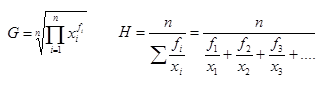
Todo el mundo entiende cuál es el hijo mediano de un matrimonio o lo que significa tener una altura mediana.
Estamos ante un parámetro que prioriza más la posición que ocupa el dato en cuestión que el propio valor en sí mismo.
Supongamos tres hermanos de $2, 7$ y $10$ años respectivamente. La mediana en este caso es $7$. Si otra familia también tiene tres hijos de $6, 7$ y $15$ años, la mediana también es $7$. Hemos cambiado los datos extremos y sin embargo la mediana no ha variado. Se define la mediana como aquel valor de la variable estadística que deja el $50\%$ de observaciones inferiores a él; así pues, la mediana divide en dos partes iguales a la distribución estadística. A partir de la definición se pueden extraer unas primeras propiedades de la mediana:
En el caso continuo se puede razonar exactamente igual identificando en este caso el intervalo mediana.
Si queremos asociar a la mediana un valor representativo del intervalo, muchos autores señalan simplemente la marca de clase de dicho intervalo y otros están de acuerdo en utilizar una fórmula que interpola linealmente el valor en el intervalo en el que se encuentre la mediana.
$$\begin{split} L_{i-1} &= \text{Límite inferior del intervalo mediana}\\ a &= \text{Amplitud del intervalo mediana}\\ F_{i-1} &= \text{Frecuencia acumulada anterior al intervalo mediana}\\ f_i &= \text{Frecuencia absoluta del intervalo mediana}\\ N &= \text{Total de datos} \end{split}$$
| En la siguiente escena puedes practicar con el cálculo de la mediana en casos muy sencillos, (pocos datos) y en otros en los que es necesaria la tabulación de los datos. Puedes también observar el polígono de frecuencias acumuladas y la interpretación gráfica de la mediana que se hace sobre este polígono en caso de variable discreta. |
|
En la siguiente escena puedes realizar ejercicios de cálculo de la mediana para caso discreto y del intervalo mediana para el caso continuo.
Nota: Para realizar ejercicios con la calculadora pasa al apartado número 6 de este tema.
Cuando alguien nos dice que determinada cosa está de moda, por ejemplo un equipo de fútbol, una canción, una prenda de vestir, un oficio, una tendencia u opinión política, etc., entendemos que ese algo es muy frecuente en nuestro entorno y que por tanto nos lo vamos a encontrar con mucha frecuencia.
Se define la moda como el valor de la variable estadística que tiene la frecuencia absoluta más alta. Si existen varios valores con esta característica, entonces se dice que la distribución tiene varias modas (distribución plurimodal).

Esta medida de centralización se puede calcular también en el caso de un carácter cualitativo y es sin duda la de más fácil cálculo. Se suele utilizar como complemento a la media aritmética y mediana ya que por sí sola no aporta una información determinante de la distribución.
Como principales características de la moda se pueden mencionar:
En el caso de variable continua se puede hablar de intervalo modal. Si queremos asociar un valor concreto del intervalo, algunos autores acuerdan utilizar la marca de clase y otros, cuando la amplitud de los intervalos es la misma, una fórmula que interpola linealmente el valor en el intervalo a partir de los intervalos anterior y posterior.
$$\begin{split} L_{i-1} &= \text{Límite inferior del intervalo modal}\\ a &= \text{Amplitud de los intervalos}\\ D_1 &= \text{Diferencia de la frecuencia absoluta entre el intervalo modal}\\ & \;\;\;\;\;\;\;\text{y el anterior}\\ D_2 &= \text{Diferencia de la frecuencia absoluta entre el intervalo modal}\\ & \;\;\;\;\;\;\;\text{y el siguiente} \end{split}$$
En la siguiente escena puedes practicar con el cálculo de la moda para variable discreta. También puedes relacionar el valor modal con el diagrama de barras en cada ejercicio que realices.
En la siguiente escena puedes practicar con el cálculo del intervalo modal para variable continua en el caso en que los intervalos tengan la misma amplitud. También en la escena puedes relacionar el valor modal con el histograma de frecuencias absolutas.
¿Cómo proceder cuando en una variable continua los intervalos de agrupación de los datos no son todos de la misma amplitud? Pulsa sobre la siguiente imagen y podrás verlo:
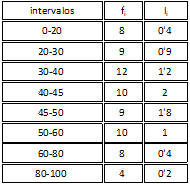
En las siguientes escenas puedes practicar con el cálculo de la moda y resto de parámetros para variables discretas, continuas y también continuas con intervalos de diferente amplitud. Es conveniente que realices algunos ejercicios de forma manual y que compruebes los resultados con los que se obtienen en la escena.
Variable discreta
Variable continua
Nota: Para realizar ejercicios con la calculadora pasa al apartado número 6 de este capítulo.
Hay ciertos valores en una distribución estadística que si se sobrepasan por exceso o por defecto pueden ser signo de alguna disfunción. Pensemos en el caso de los controles de crecimiento del feto en el embarazo o en los valores de seguridad de azúcar o colesterol en sangre.
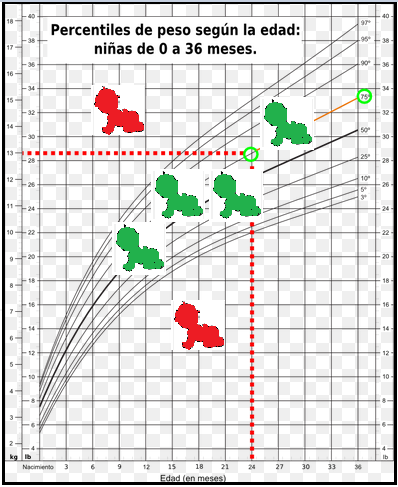
Estos valores en estadística están relacionados con los parámetros de posición.
Los cuartiles constituyen las más populares de las medidas de localización. Se utilizan continuamente en multitud de disciplinas y representan valores estratégicos en cualquier distribución estadística ya que siguiendo el mismo patrón que la mediana, dividen a dicha distribución de tal forma que:
Para la variable continua, se puede razonar exactamente de la misma forma, identificando en este caso el intervalo cuartil primero o tercero. Si queremos asociar valores representativos del intervalo a los cuartiles, muchos autores señalan simplemente la marca de clase de dichos intervalos y otros están de acuerdo en utilizar una fórmula que interpola linealmente los valores en los correspondientes intervalos.
$$\begin{split} L_{i-1} &= \text{Límite inferior del intervalo } Q_1\\ a &= \text{Amplitud del intervalo } Q_1\\ F_{i-1} &= \text{Frecuencia acumulada anterior a } Q_1\\ f_i &= \text{Frecuencia absoluta del intervalo } Q_1\\ N &= \text{Total de datos} \end{split}$$
$$\begin{split} L_{i-1} &= \text{Límite inferior del intervalo } Q_3\\ a &= \text{Amplitud del intervalo } Q_3\\ F_{i-1} &= \text{Frecuencia acumulada anterior a } Q_3\\ f_i &= \text{Frecuencia absoluta del intervalo } Q_3\\ N &= \text{Total de datos} \end{split}$$
En las escenas de cálculo de la moda, para variables discreta o continua, del apartado anterior, puedes introducir datos y calcular, además de los cuartiles y percentiles, los demás parámetros estadísticos.
En la siguiente escena puedes practicar con el cálculo de cuartiles para variable discreta y continua.
Ahora puedes experimentar cómo los valores atípicos influyen sensiblemente en la media y en los cuartiles, y esa influencia es menor para la mediana.
Este tipo de diagramas lo han popularizado mucho los distintos paquetes estadísticos que circulan por el universo informático y algunas calculadoras científicas, que en su modo de estadística, son capaces de generarlos. Se trata de un dibujo muy sencillo que refleja también de forma muy simple muchas de las características de la distribución.
Se construyen fundamentalmente a partir de la información que ofrecen la mediana y los cuartiles primero y tercero. Son los denominados diagramas de caja y bigotes. Para la construcción del rectángulo, la caja, solamente necesitamos las cotas que serán los valores de $Q_1$ y $Q_3$ y para la longitud de los bigotes los valores mínimo y máximo de la distribución. Los segmentos se dibujaran de forma continua o no dependiendo de la presencia de lo que se denominarán valores atípicos.
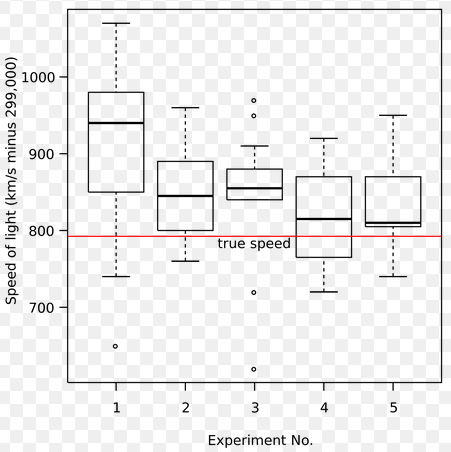
Para empezar, en la escena de la siguiente página puedes construir el diagrama con unos pocos datos.
En la siguiente escena podemos ver con más detalle cómo
se construye este tipo de diagramas.
Ahora puedes practicar y comprobar si has comprendido el significado y los elementos de los diagramas de cajas y bigotes.
Valores atípicos
La representación gráfica de los datos de una distribución estadística mediante los box-whisker se ha popularizado mucho y ofrece una primera visión gráfica muy acertada de las características principales de los elementos de la distribución.
El diagrama de cajas y bigotes nos proporciona información de cómo se encuentran concentrados los datos.
Sin embargo para saber si hay algún valor más alejado o atípico que pueda influir distorsionando el estudio de los diferentes parámetros estadísticos, algunos autores consideran el siguiente criterio para distinguir y localizar a dichos posibles valores atípicos
Cuando existen estos valores, el convenio que existe es dibujarlos en el box-whisker como puntos aislados en lugar de unirlos de forma continua mediante un segmento.
En la animación de la siguiente página puedes observar cómo se detectan los valores atípicos aplicando el criterio anterior.
Veamos otro ejemplo:
Supongamos que en una clase se pregunta por el número de hermanos que tienen los alumnos y se distribuyen los datos en la siguiente tabla. Nos preguntamos si alguno de los datos de la tabla puede considerarse atípico o aislado.
| No de hermanos | Frecuencia | Frecuencia acumulada |
|---|---|---|
| 0 | 2 | 2 |
| 1 | 8 | 10 |
| 2 | 15 | 25 |
| 3 | 6 | 31 |
| 7 | 1 | 32 |
| 9 | 1 | 33 |
Valores aislados por la izquierda
$\displaystyle x\lt Q_1 -1,5\cdot(Q_3-Q_1) \implies x\lt 1-1,5\cdot (2-1) \implies x \lt -0,5$
No hay valores aislados por la izquierda
Valores aislados por la derecha
$\displaystyle x\gt Q_1 +1,5\cdot(Q_3-Q_1) \implies x\gt 2+1,5\cdot (2-1) \implies x \gt 3,5$
$x=7$ y $x=9$ serían valores aislados por la derecha.
Un alumno tiene tres exámenes con notas $6, 5$ y $4$ y otro alumno con notas $1, 5$ y $9$. Las notas medias de ambos es $5$ y la mediana también $5$, sin embargo estos parámetros no describen las características de ambas distribuciones puesto que se observa claramente que las notas del primer alumno son más homogéneas que las del segundo.
Por lo general, las medidas de centralización no detectan ciertas circunstancias de la distribución que son muy importantes y que deben tenerse en cuenta en lo que respecta a la descripción de dicha distribución. Las medidas de dispersión indican si los datos están más o menos agrupados respecto de las medidas de centralización. Fundamentalmente respecto a la media aritmética.
En muchos procesos de fabricación se requiere mucha precisión en las medidas de determinadas piezas. Es extremadamente difícil conseguir medidas exactas puesto que toda máquina construida por el hombre es susceptible del error, no existe la máquina de precisión perfecta. Sin embargo, a pesar de estas mínimas diferencias, hay algunas piezas que deben rechazarse puesto que no cumplen con los criterios de medición que establecen. ¿Hasta qué punto las diferencias observadas son admisibles, pues no ocasionan ningún tipo de problema en el engranaje de dichas piezas? En estos criterios aparecen involucradas las medidas de dispersión, y entre ellas el rango y la desviación media.

Llamamos rango o recorrido, a la diferencia entre el mayor y el menor valor de la variable, indica la longitud del intervalo en el que se hallan todos los datos de la distribución. El rango es una medida de dispersión importante aunque insuficiente para valorar convenientemente la homogeneidad de los datos, de ahí que deba complementarse con otras medidas.
En este sentido encontramos la variación media que nos sirve para calcular cuánto se desvían en promedio los datos de la media aritmética. Se define como la media de los valores absolutos de las diferencias entre la media aritmética y los diferentes datos. No es una de las medidas de dispersión más usuales.
En la siguiente escena puedes practicar con el cálculo del rango y la desviación media de variable tanto discreta como continua.
La medida de dispersión más popularizada es sin duda la varianza. La filosofía de esta medida es la misma que la de la desviación media; esto es, detectar las variaciones de cada valor respecto a la media aritmética. Sin embargo para ello en lugar de utilizar el valor absoluto, eleva esas diferencias al cuadrado, con ello evita posibles compensaciones, dado que todos los términos son positivos, y además al elevarlas al cuadrado amplifica estas diferencias si son mayores a uno en valor absoluto y las minora en caso de ser menores de uno (también en valor absoluto). Por último, considera el promedio de dichas diferencias al que denomina varianza.
Del mismo modo que ocurre para la media, la varianza es un parámetro muy sensible a las puntuaciones extremas. Ademas, las unidades en que se mide no son las mismas que las de los datos de la distribución.
Comparando con el mismo tipo de datos, una varianza elevada significa que los datos están más dispersos. Mientras que un valor de la varianza bajo indica que los valores están por lo general más próximos a la media.
Un valor de la varianza igual a cero implicaría que todos los valores son iguales, y por lo tanto también coinciden con la media aritmética.
Algunas propiedades de la varianza:
A partir de la definición de la varianza, si se desarrolla la expresión y simplificando los resultados se obtiene otra expresión para la misma que permite un cálculo más directo y sencillo.
Suele recordarse diciendo:
"La varianza es igual a la media de los cuadrados menos el cuadrado de la media"
El principal inconveniente que presenta la varianza es que las unidades no son las mismas que las de los datos de la distribución (se ha elevado al cuadrado). Esto se solventa con la definición de un nuevo parámetro que se calculará a partir del anterior que es la desviación típica y que definimos en el siguiente apartado.
La estadística ha irrumpido en todas las facetas de la vida. En el mundo del deporte también desde hace tiempo. Los ojeadores y cazatalentos americanos fundamentalmente de baloncesto o de beisbol utilizan las estadísticas de los jugadores como elementos clave a la hora de negociar traspasos o contratos. Dentro de los parámetros que se estudian en cada jugador, la desviación típica en alguna de las facetas del juego pueden ser un magnífico elemento que defina un jugador como muy seguro o como irregular.
El término desviación típica fue incorporado a la estadística por Karl Pearson en 1894. La principal ventaja que representa la desviación típica respecto a la varianza es que su unidad de medida es la misma que la de los datos. Esto hace mucho más sencilla la posible interpretación.
La desviación típica es una medida del grado de dispersión de las observaciones alrededor de su valor medio, se define como la raíz cuadrada positiva de la varianza. Tiene el mismo cometido que ésta y además la ventaja de que las unidades en las que se mide son las mismas que las de los datos de la distribución. Puede considerarse la medida de dispersión por excelencia y aparece como tecla o función directa en cualquier calculadora o programa estadístico.
Si partimos de la definición de varianza, la fórmula para el cálculo de la desviación típica sería:
De la misma forma que en el apartado anterior, si desarrollamos y simplificamos la expresión anterior se llega a otra mucho más simple que es la que se utiliza en la práctica y cuya expresión es:
Obviamente, cuanto mayor sea la desviación típica, mayor será la dispersión de los valores de la distribución respecto a la media aritmética y, por tanto, bajará el nivel de representatividad de ésta con respecto a las observaciones.
Algunas propiedades de la desviación típica son las siguientes:
En la página siguiente presentamos dos escenas interactivas. En la primera, además de la desviación típica, puedes practicar calculando la varianza de distintas series de datos, tanto para variable discreta como continua. En la segunda escena puedes practicar con el cálculo de la desviación típica de variables discretas y continuas.
Recuerda que puedes ampliar las escenas, para interactuar con ellas en una ventana aparte.
Puedes practicar con el cálculo de parámetros de dispersión en ejercicios que tú mismo puedes plantear en el apartado sexto: "6. Manejo de Calculadora".
Qué es más homogénea, una población de perros con desviación típica $2 Kg$ u otra de vacas de desviación típica $5 Kg$?
 |
 |
Si se realiza un estudio estadístico en dos poblaciones diferentes, y queremos comparar resultados, no se puede acudir simplemente al valor de la desviación típica para ver la mayor o menor homogeneidad de los datos, es decir, el valor numérico por sí solo no nos indicará que distribución de datos está más o menos dispersa.
Recurrimos para ello a otro parámetro, llamado coeficiente de variación y que se define como el cociente entre la desviación típica y la media de una población. Es un coeficiente carente de unidades y sirve para comparar la dispersión de dos poblaciones distintas, correspondiendo a la población más homogénea un coeficiente de variación menor y a la menos homogénea un coeficiente de variación mayor.
Practica con el cálculo del coeficiente de variación, en la siguiente escena.
Puntuaciones típicas o normalizadas
Antonio obtuvo una nota en Matemáticas de $6,75$ en una clase en la que la media del examen fué $7,25$ y la desviación típica $1,75$. Alberto en cambio obtuvo una nota de $5,75$ en una clase en la que la media fue de $4,75$ y la desviación típica de $2$. Si suponemos que el profesor era el mismo, podríamos pensar comparativamente con su clase que nota es mejor, la de Antonio o la de Alberto. En este sentido, las puntuaciones típicas sirven para comparar datos correspondientes de distintas poblaciones.
Estas puntuaciones típicas son valores que resultan de dividir la diferencia de cada valor menos la media entre la desviación típica de la población. A este proceso también se le suele denominar tipificación. Una vez efectuada la tipificación obtendremos una variable estadística cuya media aritmética es cero y cuya desviación típica es uno.
Las puntuaciones típicas son el resultado de dividir las puntuaciones diferenciales entre la desviación típica. Este proceso se llama tipificación.
En la escena anterior, puedes observar, mediante la normalización de datos, la comparación de las notas dadas a $100$ alumnos por dos profesores. Se presentan cuatro situaciones.
¿Quieres efectuar la comparación de las notas de dos profesores tuyos? Puedes hacerlo en la siguiente escena, la cual también puedes utilizar como simulador de situaciones.
La utilización de calculadoras en ejercicios de estadística es obviamente fundamental, tanto si se hacen manualmente (utilización de la calculadora para largas operaciones elementales habituales en este tipo de ejercicios), o si se quieren aprovechar otras ventajas directas del modo estadístico. Cualquier calculadora científica ofrece de forma directa el cálculo de los parámetros estadísticos más usuales.
Dependiendo del modelo, debes consultar el manual de uso para aprender a disponer la calculadora en modo ESTADISTICA UNIDIMENSIONAL y la forma en la que han de introducirse los datos. Este proceso de introducción de datos es el que suele variar de un modelo a otro, aunque en la mayoría el procedimiento es sencillo.
La calculadora de la RED DESCARTES, no tiene un condicionante material físico como las habituales del mercado, tiene un funcionamiento muy sencillo y alguna ventaja adicional con los modelos más simples que normalmente son de las que dispone el alumnado. Comentamos un poco la forma de trabajar con esta calculadora.


En la pantalla de resultados observarás:
En las siguientes escenas, diseñadas por Juan Jesús Cañas Escamilla, puedes plantear los ejercicios de variable discreta y continua con los datos que prefieras, inventados o procedentes de algún problema concreto. Las escenas admiten tabulaciones de hasta $36$ filas.
Una vez introducidos los datos al pulsar el control "Actualizar", se completa toda la tabla con todos los valores necesarios para el cálculo de los parámetros estadísticos. Si pulsas el control "Ver parámetros" puedes acceder al valor de dichos parámetros; media, mediana, moda, percentiles, desviación típica además de los diagramas de barras e histogramas de frecuencias relativas y relativas acumuladas.
Variable discreta
Variable continua
A continuación tienes el enunciado de diferentes problemas. Trabájalos y una vez los hayas resuelto puedes hacer clic sobre el botón para ver la solución.
Juan Jesús Cañas Escamilla
José R. Galo Sánchez
Karl Pearson (Londres, 27 de marzo de 1857, 27 de abril de 1936) fue un prominente científico, matemático y pensador socialista británico, que estableció la disciplina de la estadística matemática. Fue el fundador de la bioestadística, https://es.wikipedia.org/).
En definitiva, el hombre siempre ha intentado buscar relaciones entre magnitudes de manera que conocida una de ellas, generalmente la menos “costosa”, le permita inferir lo más acertadamente posible los valores de la otra magnitud.
En este sentido la Estadística también ofrece su ayuda y aborda con bastante éxito esta empresa.
Así pues, en muchas ocasiones un trabajo estadístico necesita estudiar sobre cada individuo varias variables con el objeto de encontrar una posible relación entre las mismas.
Cuando sobre una población estudiamos simultáneamente dos variables estadísticas, al conjunto de los pares de valores correspondientes a cada individuo se denomina distribución bidimensional.
 |
 |
 |
 |
EJEMPLO 1
Las notas de $10$ alumnos en Matemáticas y en Lengua vienen dadas en la siguiente tabla:
| MATEMÁTICAS | 2 | 4 | 5 | 5 | 6 | 6 | 7 | 7 | 8 | 9 |
| LENGUA | 2 | 2 | 5 | 6 | 5 | 7 | 5 | 8 | 7 | 10 |
Los pares de valores {(2,2), (4,2), (5,5), ..., (8,7), (9,10)}, forman la distribución bidimensional.
EJEMPLO 2
Vamos a estudiar en los últimos doce años las precipitaciones medias en nuestro país, en litros por metro cuadrado y la producción de aceite en miles de toneladas métricas. Los datos aparecen reflejados en la siguiente tabla:

EJEMPLO 3
En una clase de $30$ alumnos y alumnas se ha realizado un estudio sobre el número de horas diarias de estudio X y el número de asignaturas suspensas al final de curso Se obtuvieron los siguientes datos:
$(2,0) , (2,2) , (0,5) , (2,1) , (1,2) , (2,1) , (3,1) , (4,0) ,(0,4) ,(2,2) ,\\ (2,1) , (2,1) , (4,0) , (3,1) , (2,4), (2,1) , (1,2) , (2,1) , (2,0) , (3,0) ,\\ (3,1) , (2,2) , (2,2) ,(2,1) ,(0,5) , (1,3) , (2,2) , (2,1) , (1,3) , (1,4)$Una vez que hemos recogido todos los datos, la mejor forma de estudiarlos es disponerlos en una tabla estadística. Existen fundamentalmente dos tipos de tabulación para variables bidimensionales.
Tabla bidimensional simple. Está formada por tres filas o columnas en las que se representan ordenadamente los valores de las variables y sus frecuencias. La tabulación suele hacerse ordenando los datos de menor a mayor respecto a una de las variables. En caso de que todas las frecuencias sean iguales a uno, se puede omitir la fila o columna correspondiente a las mismas.
| $X_1$ | $Y_1$ | $f_1$ |
| $X_2$ | $Y_2$ | $f_2$ |
| $\cdots$ | $\cdots$ | $\cdots$ |
| $\cdots$ | $\cdots$ | $\cdots$ |
| $X_m$ | $Y_m$ | $f_m$ |
Tabla de doble entrada. Está formada por tantas filas y columnas como valores tengamos de cada una de las variables, añadiendo una fila y una columna más para representar los totales. Está indicada para casos con bastantes datos, en los que para cada valor de una variable, existen varios valores de la otra.
Escogiendo la primera y la última fila, tenemos la tabla estadística correspondiente a la primera variable unidimensional. Con la primera y última columnas construimos la tabla correspondiente a la segunda variable unidimensional.
Estas dos distribuciones reciben el nombre de distribuciones marginales. En la última celda aparecerá el total de la última fila y de la última columna, es decir, el número total de elementos estudiados
($N$).
Además, en esta tabla puede resultar de interés estudiar distribuciones unidimensionales correspondientes a un valor determinado de alguna de las variables, llamadas distribuciones condicionadas.
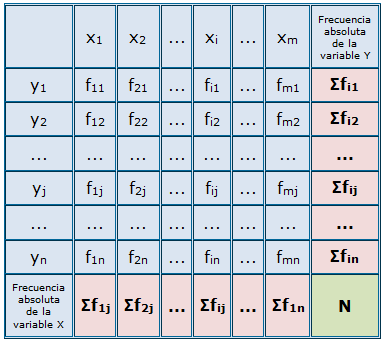
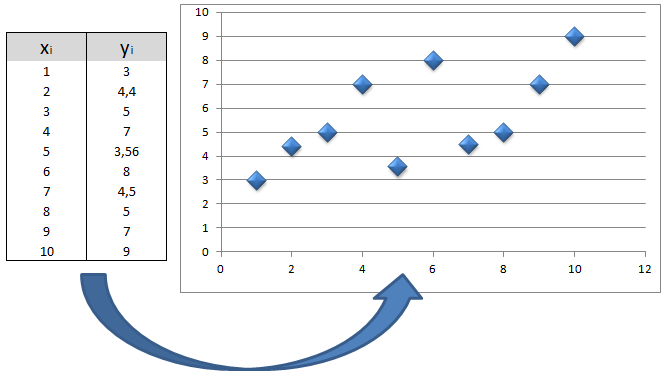
En el caso en el que todas las frecuencias absolutas de cada valor $(x_i , y_i)$ sean unitarias, un diagrama de dispersión consiste en hacer corresponder de forma cartesiana los valores de la variable bidimensional con los puntos del plano. Para representar el dato correspondiente al par $(x_i, y_i)$, colocaremos un punto en esas mismas coordenadas.
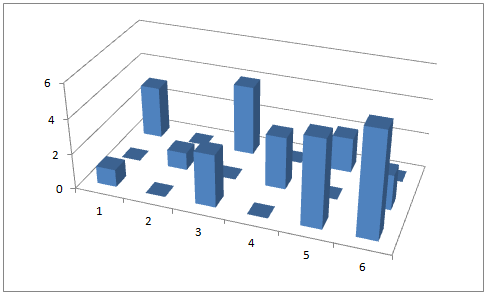
En el caso en el que existan frecuencias absolutas distintas de uno. Se puede utilizar el denominado prismograma. Es similar a un diagrama de barras o de rectángulos, pero intentando darle un aspecto tridimensional.
Representamos tres ejes (igual que representamos los ejes $x, y, z$). En el eje vertical representamos las frecuencias y en los otros los valores de las variables $X$ e $Y$. Para cada par de valores $(x_i, y_j)$, representamos un prisma o una barra vertical de altura igual a su frecuencia. Este gráfico no se utiliza apenas porque su interpretación suele ser complicada.
Nota: Como alternativa al prismograma, se puede utilizar un diagrama de puntos en los que de forma “artesanal” se disponga en las coordenadas de cada valor, tantos puntos como indique su frecuencia absoluta.
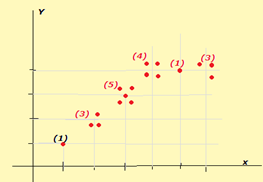
O también un diagrama de puntos de mayor o menor grosor según sea la frecuencia absoluta.
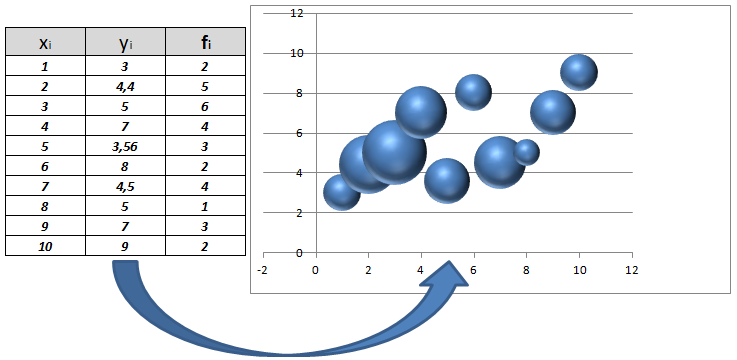
El objetivo de cualquier estudio bidimensional es observar si existe algún tipo de relación entre las dos variables estudiadas. La relación entre las dos variables cuantitativas queda reflejada mediante la función a la que parece acercarse la nube de puntos representada en el diagrama de dispersión. Prestaremos una especial atención a relación lineal aunque puedan existir otras interesantes como la cuadrática, exponencial, etc.

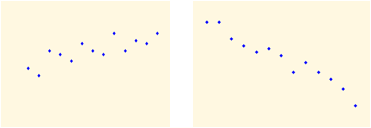
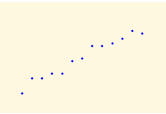
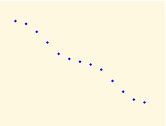

Los principales componentes elementales de una línea de ajuste y, por lo tanto, de una correlación, son la forma, la fuerza y el sentido.
Video
A continuación tenemos un vídeo que nos introduce en la idea general de relación entre variables o correlación.
Hasta ahora hemos hablado de correlación entre variables y del caso particular que nos ocuparemos en este tema como es el de la correlación lineal en un sentido global y difuso. Hemos mencionado en algún momento que la correlación puede ser fuerte o débil, positiva o negativa, sin embargo ¿qué entenderemos por fuerte o débil?, ¿cómo mediremos esta correlación? Nos hace falta un indicador o medidor que nos permita condensar en un parámetro todas estas facetas de la correlación. En este sentido vamos a estudiar un parámetro que será crucial en la cuantificación de la correlación lineal. A este nuevo parámetro lo denominamos covarianza y se define como:
La fórmula anterior es de difícil cálculo. Como ocurría en el caso de la varianza, desarrollando y simplificando la expresión anterior se llega a otra mucho más sencilla en lo que respecta al cálculo práctico y que es la que se utiliza normalmente en cualquier tipo de problema.
A pesar de disponer de las fórmulas anteriores, es muy importante que aprendas a utilizar tu calculadora para la realización de los problemas prácticos.
Lo más importante para la utilización de las calculadoras es la introducción de datos en el modo estadística, que todos los modelos de calculadora científica tienen.
En el caso de la calculadora Descartes, la introducción de datos es muy simple:
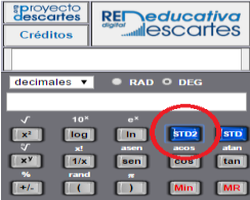 |
 |
Puedes practicar con la calculadora de Descartes (haz clic en el icono de herramientas), aplicándola a ejemplos concretos.
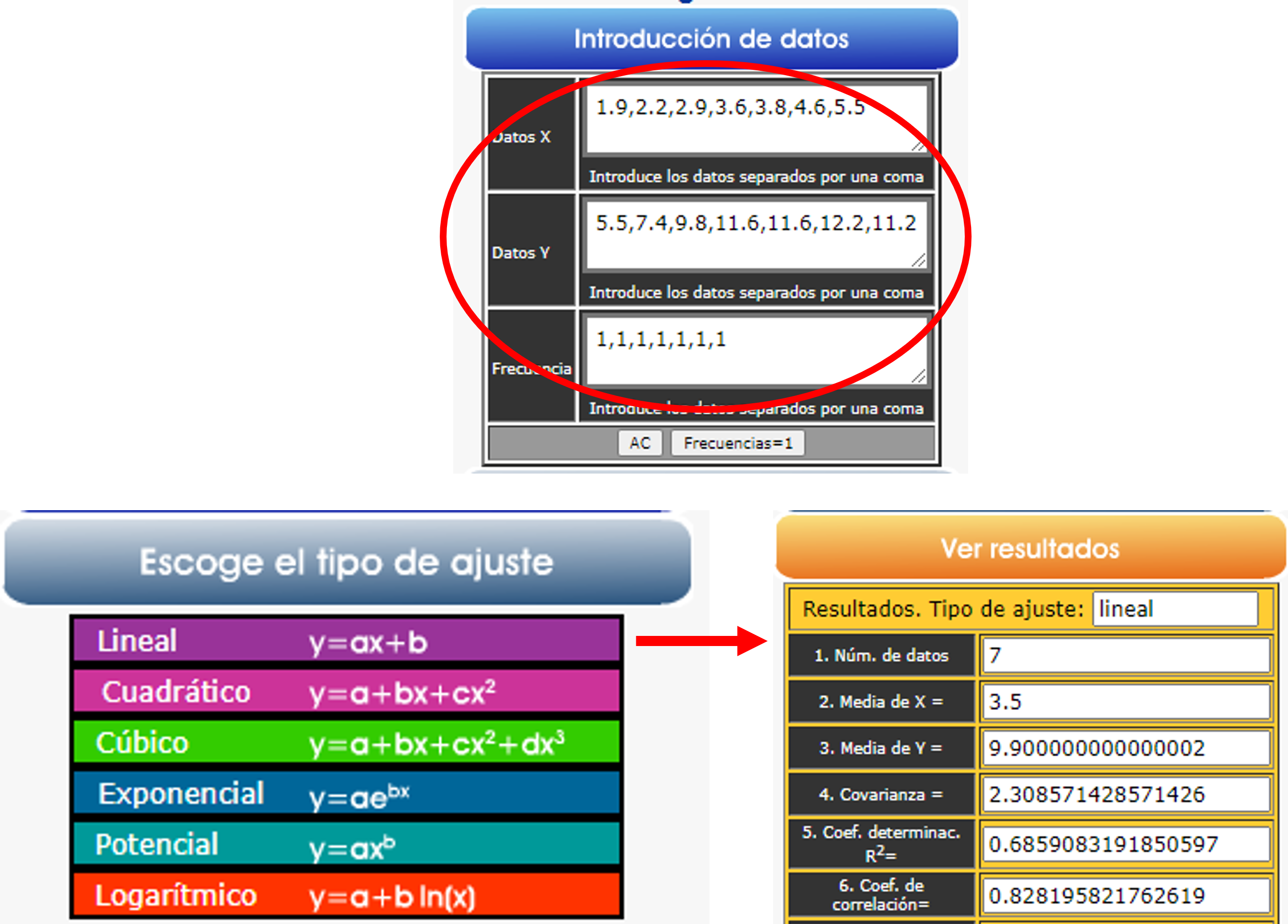
Se define este coeficiente como el cociente entre la covarianza y el producto de las desviaciones típicas de ambas variables, es decir:
| $$r=\frac{\sigma_{xy}}{\sigma_x \cdot \sigma_y}$$ |  Karl Pearson
Karl Pearson
|
Este coeficiente tomará siempre valores comprendidos entre -1 y 1 y según sean estos, podremos deducir que:
En la siguiente escena puedes observar y relacionar una nube de puntos con su correspondiente coeficiente de correlación lineal. La escena te permite tanto elegir el número de puntos con el que quieres trabajar como la modificación de la posición de dichos puntos ya que se trata de controles gráficos que se pueden mover simplemente pulsando y arrastrando. Puedes comprobar que determinadas formas curvilíneas (dependencia casi funcional), sin embargo toman como coeficiente de correlación lineal números próximos a cero. Es interesante que manipules la escena y observes qué ocurre con el coeficiente de correlación lineal. Extrae tus propias conclusiones.
A continuación de la escena, tenemos en un vídeo una clase de la Universidad de Salamanca sobre la correlación lineal.
Nube de puntos y valores del coeficiente de correlación lineal
Video
Podemos decir que la regresión lineal es una técnica estadística que trata de estudiar la relación entre varias variables estadísticas. Cuando solamente tenemos dos variables diremos que estamos en regresión lineal simple. En investigación, el análisis de regresión se utiliza para predecir una de las variables a partir de la otra u otras.
Cuando la nube de puntos de un diagrama de dispersión nos informe de una posible correlación lineal, el análisis de regresión tendrá como gran objetivo la predicción de valores para la variable dependiente ($Y$) a partir de los valores de la variable independiente ($X$) utilizando para ello una función (una recta) que aproximará lo mejor posible a la nube de puntos.
El método que se utiliza para la localización de esta recta es el llamado de los mínimos cuadrados.
Para el caso anterior, el método consiste en considerar la función que determinaría la suma de todas las distancias verticales (coordenada $y_i$), elevadas al cuadrado para evitar que las positivas y negativas se contrarresten, entre cada punto y su proyección vertical sobre la hipotética recta. A esta función posteriormente se le calcula dónde alcanzaría el mínimo.
El método de mínimos cuadrados
El día de Año Nuevo de 1801, el astrónomo italiano Giuseppe Piazzi descubrió el planeta enano Ceres. Fue capaz de seguir su órbita durante $40$ días.
Durante el curso de ese año muchos científicos intentaron estimar su trayectoria con base en las observaciones de Piazzi, pero resolver las ecuaciones no lineales de Kepler de movimiento es muy difícil.
La mayoría de las evaluaciones fueron inútiles y el único cálculo suficientemente preciso que permitió a Franz Xaver von Zach, astrónomo alemán, reencontrar al final de ese año a Ceres fue el de Carl Friedrich Gauss. Gauss por entonces era un joven de 24 años, pero los fundamentos de su enfoque ya los había planteado en 1795, cuando tenía 18 años. Sin embargo, su método de mínimos cuadrados no se publicó sino hasta 1809 en el segundo volumen de su trabajo sobre mecánica celeste, "Theoria Motus Corporum Coelestium in sectionibus conicis solem ambientium"".
El francés Adrien-Marie Legendre desarrolló el mismo método de forma independiente en 1805.
 |
|
Como se ha mencionado anteriormente, en los casos en los que se observe cierto grado de correlación lineal, intentaremos aproximar la nube de puntos mediante una recta. A estas líneas se les llaman rectas de regresión. Dependiendo del procedimiento de minimización de distancias que se emplee, bien sean verticales u horizontales, y utilizando el procedimiento de mínimos cuadrados obtendremos dos tipos de recta:
Como puedes observar, se trata de las clásica expresión de una recta en su forma punto pendiente.
La obtención de las expresiones de las rectas anteriores no es sencilla. Como características fáciles de descubrir podemos señalar que el signo de la pendiente depende únicamente de la covarianza en ambas expresiones y que ambas pasan por el punto común:
$$\big(\={X}, \={Y}\Big)$$
En la siguiente escena puedes practicar con el cálculo de todos los parámetros relacionados con la regresión en variables bidimensionales. Puedes introducir los datos que desees seleccionando previamente las filas que necesites (máximo de $36$). Sigue las instrucciones y podrás comprobar el valor de todos los parámetros y la representación gráfica de la nube de puntos y de las dos rectas de regresión.
Es importante que practiques y construyas tablas tú mismo y que la escena te sirva de apoyo y comprobación de resultados. También convendría que supieras utilizar tu calculadora y usarla en los problemas prácticos. En este sentido, ten en cuenta que lo que puede variar en cada calculadora es la introducción de los datos.
Una vez que conozcas este procedimiento, el resto suele ser muy parecido. Como ejemplo, recordar el caso de la calculadora DESCARTES (ver el apartado 2.4.1). Realiza algún ejercicio de regresión utilizando la calculadora para variable bidimensional de DESCARTES.
Video
En el siguiente video puedes asistir a una clase sobre regresión lineal
En la siguiente escena puedes manipular la nube de puntos y observar como varía el ajuste por mínimos cuadrados y como cambian las rectas de regresión.
Una de las primeras acciones que se realizan en cualquier estudio estadístico es la depuración de los datos, localizando y decidiendo si los elementos anómalos que se denominan en la literatura científica como "outliers" o valores atípicos, deben tenerse en cuenta en la realización del estudio o no.
La siguiente escena sirve para analizar la influencia que puede tener la variación de un solo dato en un análisis estadístico, en concreto en la regresión lineal.
En la escena aparece una nube de puntos, el número de ellos se puede elegir mediante el control "número de puntos". A veces la nube aparece muy dispersa y aunque es posible realizar un ajuste lineal las conclusiones estadísticas serían muy poco o nada fiables, pero puede cambiarse sin más que pulsar el botón "Inicio". Uno de los puntos es un control gráfico que puede moverse y desplazarse a voluntad utilizando los dos controles situados abajo o directamente pulsando y arrastrando. Con el botón "ver rectas" se observa la solución global del problema. Mediante el botón "ver tabla" se pueden observar los datos reales del problema.
Con el botón "ver parámetros" puedes identificar todos los parámetros calculados y necesarios para el modelo de regresión. También se dispone de un botón para ver cómo varía el ángulo de las dos rectas y otro para un gráfico que relaciona el coeficiente de correlación y el ángulo al desplazar el punto variable. Haz clic en la imagen para abrir la escena.
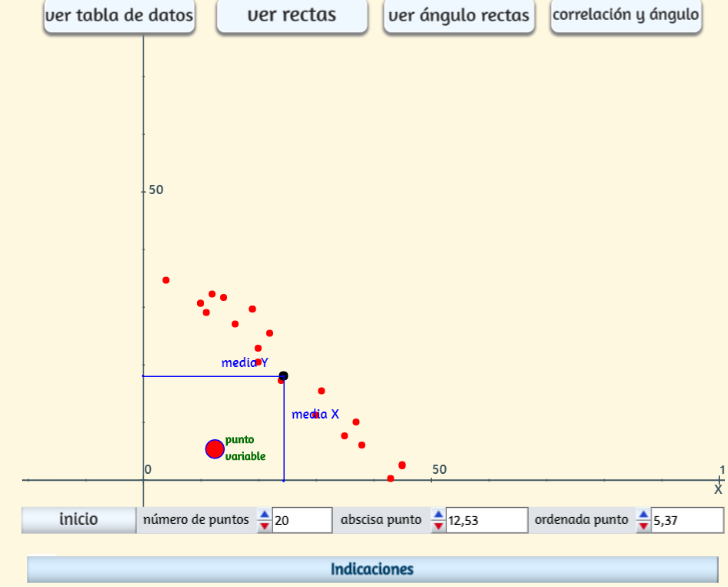
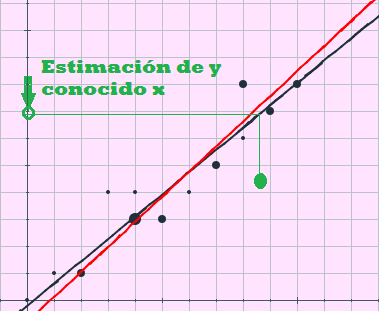
Una vez que conocemos la mayor o menor relación entre las variables mediante el coeficiente de correlación lineal y que hemos calculado las rectas de regresión, podemos utilizarlas para predecir el valor de una de las variables a partir de la otra. La fiabilidad de la estimación depende fundamentalmente de dos consideraciones:
 |
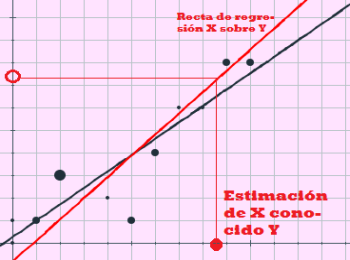 |
En la siguiente escena puedes realizar estimaciones para ejercicios concretos. Puedes introducir los valores de $X$, de $Y$ y las frecuencias que desees. Una vez introducidos los datos sólo tienes que seguir las indicaciones que se dan en la escena y realizar las estimaciones que quieras, tanto para la variable $X$ como para la variable $Y$.
A continuación tienes el enunciado de diferentes problemas. Trabájalos y una vez los hayas resuelto puedes hacer clic sobre el botón para ver la solución.
Juan Jesús Cañas Escamilla
José R. Galo Sánchez
Percy Alexander MacMahon (26 de septiembre de 1854 - 25 de diciembre de 1929) fue un matemático que se destacó especialmente en el campo de las particiones de números y la combinatoria enumerativa, https://es.wikipedia.org/).
En muchas ocasiones, en la vida real nos vemos en la necesidad de contar. Esta acción aparentemente sencilla puede llegar a ser muy complicada. El hecho de contar objetos presentes y observables directamente es muy simple, pero pensemos en situaciones donde la mera observación no basta. Imagina como contar todas las matrículas de automovil que pueden construirse con tres letras y cuatro números, imagina que necesitas conocer todos los signos de 5 elementos que se pueden formar con un punto y una raya, o todas las posibles banderas de tres franjas horizontales de distintos colores, ...
Como ves las situaciones son incontables y como ves también la expresión que continuamente aparece en este tipo de contexto es ¿CUÁNTOS...?
La parte de las matemáticas que se dedica al estudio de este tipo de situaciones es la Combinatoria. Esta teoría nos proporcionará las técnicas y fórmulas que permitan encontrar respuestas a muchos problemas como los anteriores. En combinatoria las cuestiones planteadas se analizan fundamentalmente atendiendo a las siguientes preguntas:
Es evidente también que con un manejo aceptable de las técnicas de recuento que analizaremos en esta unidad; se pueden abordar de una forma más interesante problemas de probabilidad en los que el único enfoque posible sea el concepto de probabilidad en el sentido clásico de Laplace y nos veamos obligados a contar casos posibles y favorables.
A continuación tenemos tres vídeos que nos pueden ayudar a introducirnos en la combinatoria y su aplicación en la probabilidad.
Video
Videos
A continuación veamos una curiosidad que relaciona la combinatoria con la filosofía. Imaginemos que el libro definitivo, el que explica las verdades universales existe y que tiene por ejemplo 100 páginas. Con este simple supuesto, la combinatoria nos dice que dicho libro, en realidad es el fruto de una variación con repetición de 30 elementos ($26$ letras, el espacio entre palabras, el punto, la coma y los dos puntos) tomados de n en n (donde n es el total de signos que se podrían introducir en 100 páginas). En realidad las posibles agrupaciones son inimaginables , pero eso sí finitas.
Bueno ¡pues a trabajar! Pongamos a escribir a $1000, 10000, 1000000$ monos y tarde o temprano alguno de los monos será el autor de la obra definitiva. Será cuestion de descubrir la variación con repetición "ganadora". Esta anécdota es conocida como el teorema de los mil o de los infinitos monos y relaciona a estos monos con las obras de Shakespeare. Observa el siguiente vídeo:
Las estafas piramidales, la extensión de rumores, las visitas a una página web,..., a menudo manejan o conducen a números escandalosamente grandes. Las circunstancias anteriores y muchas otras tienen como motor de transmisión algo tan simple como el "boca a boca", de manera que números pequeños conducen al final a situaciones inabarcables como resultado del principio general de recuento. También la base sobre la que se apoya el edificio de la teoría combinatoria es el principio general de recuento que a su vez es el mismo principio de cardinalidad del producto cartesiano en la teoría de conjuntos.
Si un experimento puede realizarse de $n$ formas diferentes y un segundo experimento puede hacerlo de $m$ formas diferentes; entonces los dos experimentos juntos se pueden realizar de $n\times m$ formas diferentes.
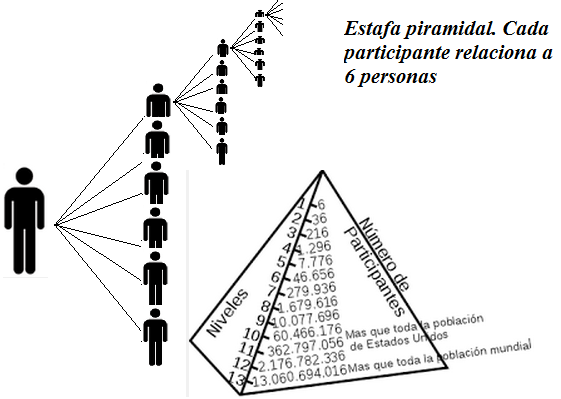
En el lenguaje de teoría de conjuntos se expresa como: $$\begin{rcases} Card(A) &= n \\ Card(B9 &= m \end{rcases}\implies Card(A\times B) = n\cdot m$$
Veamos un par de ejemplos:
Video
Observa el siguiente vídeo sobre el principio general de recuento:
Supongamos que a un concurso literario en el que se conceden tres premios distintos, se presentan ocho escritores. Nos preguntamos por las distintas formas en las que se pueden conceder estos premios.
Este problema sin duda se puede resolver sin necesidad de conocimientos previos sobre combinatoria.
Pensemos que disponemos de tres puestos. Para el primero se puede elegir a cualquiera de los ocho participantes. Para el segundo, no puedo elegir al que ya está elegido para el primero, por tanto solamente podremos elegirlo entre los siete restantes. Para el tercero, siguiendo el mismo razonamiento nos quedarán seis participantes. Ahora aplicando el principio general de recuento al conjunto $(P1 \times P2 \times P3)$, el total de resultados posibles para el reparto de los tres premio sería: $8 \times 7 \times 6 = 336$.
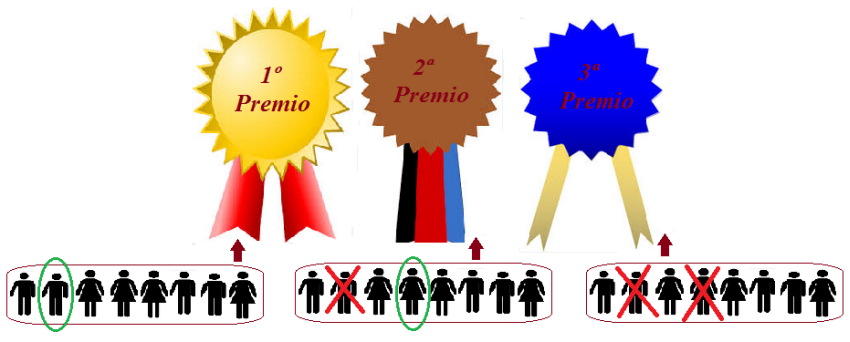
En combinatoria, denominamos variaciones ordinarias o sin repetición de $n$ elementos tomados de $m$ en $m$ (siendo $m$ menor o igual que $n$) a cada uno de los distintos grupos de $m$ elementos escogidos de entre los $n$, de manera que:
El número de variaciones ordinarias lo representamos $V_{n,m}$ y se calcula:
En la siguiente escena puedes practicar con la formación de algunas variaciones sin repetición. A medida que practicas irás descubriendo como se van construyendo, sus características y la idea que permite calcular el número total de variaciones sin repetición.
Dentro de los juegos de apuestas más populares en España se encuentra sin duda la quiniela de fútbol. ¿Cuántos resultados posibles pueden darse en catorce encuentros entre equipos de primera y segunda división?. Este problema puede resolverse también sin conocimientos previos de combinatoria.
Imaginamos que cada resultado es un grupo de $14$ símbolos y que dichos símbolos solamente pueden ser $1, X$ o $2$. Así para el primer signo que pongamos tendremos $3$ posibilidades, para el segundo también otras $3$ y así sucesivamente hasta llegar al símbolo $14$. Ahora no tenemos más que aplicar otra vez el principio general de recuento al conjunto $(P_1\times P_2\times \cdots \times P_{14})$.
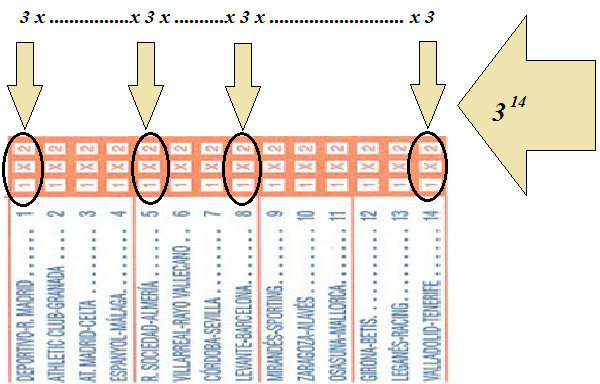
Piensa también por ejemplo en:
En combinatoria denominamos variaciones con repetición de $n$ elementos tomados de $m$ en $m$, (obsérvese que no hay restricción alguna en cuanto a los valores de $n$ y $m$), a los distintos grupos de $m$ elementos, repetidos o no, que se pueden formar. Considerando:
Al número de variaciones con repetición lo denotaremos, $VR_{n,m}$ y se calcula:
En la siguiente escena puedes practicar con la formación de algunas variaciones con repetición. A medida que practicas irás descubriendo cómo se van construyendo, sus características y la idea que permite calcular el número total de variaciones con repetición.
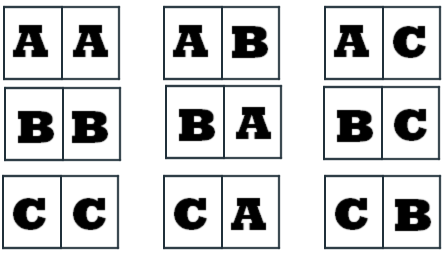
Observa que para $3$ elementos, tomados de $2$ en $2$, el número de variaciones es $3^2$:
Imaginemos cuatro amigos que deciden fotografiarse juntos en una fiesta para conservar el momento. Si deciden que la fotografía sea de los cuatros en línea. ¿De cuántas formas diferentes podrán realizar la fotografía?.
 Un primer análisis de la situación nos sitúa el problema al mismo nivel del que se resolvió en el epígrafe correspondiente a las variaciones sin repetición. En realidad se trata del mismo razonamiento. La primera posición la pueden ocupar cualquiera de los cuatro amigos. La segunda la pueden ocupar cualquiera menos el que ocupó la primera, es decir tres posibilidades , y así seguiremos hasta la cuarta posición que podrá ser ocupada por una persona. Aplicando ahora el principio general de recuento al conjunto $(B_1\times B_2\times B_3\times B_4)$, el número de posibles agrupaciones sería $4 \times 3 \times 2 \times 1 = 24$ resultados distintos.
Un primer análisis de la situación nos sitúa el problema al mismo nivel del que se resolvió en el epígrafe correspondiente a las variaciones sin repetición. En realidad se trata del mismo razonamiento. La primera posición la pueden ocupar cualquiera de los cuatro amigos. La segunda la pueden ocupar cualquiera menos el que ocupó la primera, es decir tres posibilidades , y así seguiremos hasta la cuarta posición que podrá ser ocupada por una persona. Aplicando ahora el principio general de recuento al conjunto $(B_1\times B_2\times B_3\times B_4)$, el número de posibles agrupaciones sería $4 \times 3 \times 2 \times 1 = 24$ resultados distintos.
Existen muchas situaciones en las que se puede aplicar el mismo razonamiento.
Video
Denominamos permutaciones ordinarias o sin repetición de $n$ elementos, a cada uno de los distintos grupos que pueden formarse de manera que:
Al número de permutaciones ordinarias de $n$ elementos lo representaremos por $P_n$ y se calcula:
a este número se le denomina factorial de $n$ y se representa como $n!$ Se utiliza tanto, que aparece como tecla directa en todas las calculadoras científicas.
En la siguiente escena puedes practicar con la formación de algunas permutaciones sin repetición. A medida que practicas irás descubriendo como se van construyendo, sus características y la idea que permite calcular el número total de permutaciones sin repetición.
Supongamos que disponemos de $3$ vasos azules iguales, $2$ vasos iguales amarillos y $1$ naranja. Si quisiéramos ponerlos en línea recta en una estantería. ¿De cuántas formas distintas lo podríamos hacer?
Para ayudar a contar todos los casos y ayudándonos de que conocemos las permutaciones sin repetición, vamos a pegar en la parte opuesta, la que vemos, etiquetas que identifiquen y distingan como distintos a todos los vasos. De esta forma disponemos de $6$ vasos distintos que se pueden ordenar de $6!$ formas distintas.
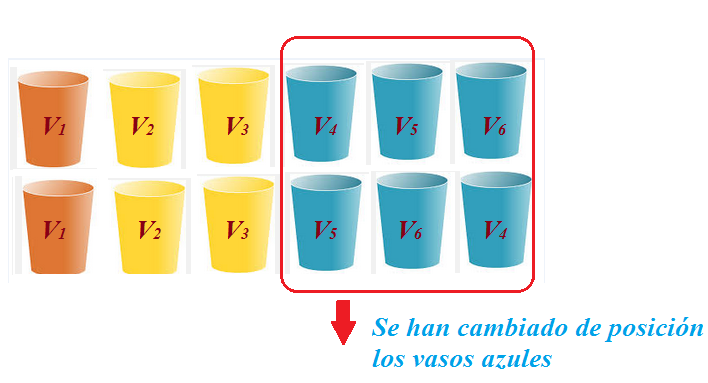
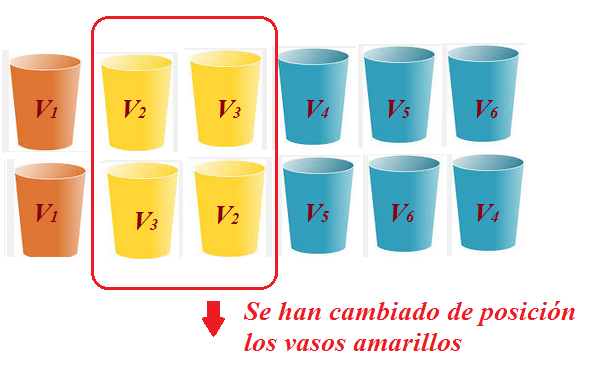
Es decir, que si giramos los vasos para que se vean las etiquetas distinquiríamos todas las permutaciones, pero si no vemos las etiquetas, ordenaciones que antes eran distintas las veríamos iguales.
Las permutaciones anteriores serían identificadas como:

La idea, por tanto, para contar las permutaciones con repetición es identificar como una sola agrupación las, en nuestro caso, $2!$ y $3!$ reordenaciones que no distinguiríamos. No se distinguirían por tanto $(2! \times 3! \times 1!)$ permutaciones
A continuación puedes observar como se irían confeccionando algunas de las permutaciones con repetición de 6 elementos de los que uno se repite tres veces, otro dos veces y otro una vez:

Denominamos permutaciones con repetición de $n$ elementos en los que uno de ellos se repite $a$ veces, otro $b$ veces y así hasta el último que se repite $k$ veces, donde $(a+b+c+\cdot k = n)$ a todas las ordenaciones posibles de estos $n$ elementos.
Consideramos dos ordenaciones distintas si difieren en el orden de colocación de algún elemento (distinguible).
Denotaremos a este tipo de permutación como: $$\LARGE P_n^{a,b,c, \cdot k}$$ y se calcula como:
En la siguiente escena puedes practicar con ejemplos de formación de algunas permutaciones con repetición.
Existen muchas situaciones en las que el orden deja de ser determinante. Pensemos en un pintor que dispone de cinco colores, rojo, azul, verde, negro y blanco. Desea conseguir nuevos colores mezclando cantidades iguales de tres colores diferentes de los cinco que dispone en su paleta. El orden en que mezcle los colores seleccionados no es significativo, es decir, el resultado de mezclar rojo, blanco y verde es exactamente el mismo que el de mezclar verde, blanco y rojo.
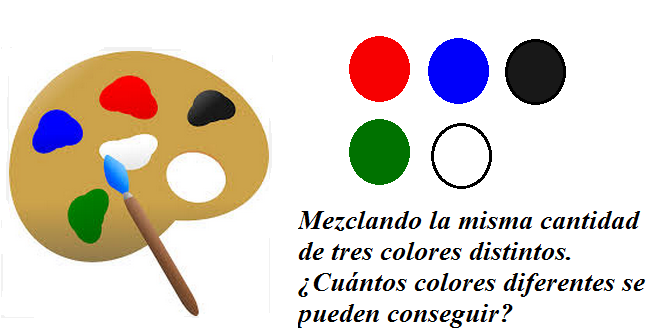
Así pues, todas las permutaciones de estos tres colores se deberían analizar como una sola agrupación. Por tanto, para localizar todos los posibles colores resultantes de la mezcla de tres de los cinco de que disponemos, $V_{5,3}$ entre las $P_3$.
A este tipo de agrupación la denominaremos Combinación sin repetición
Existen otras muchas situaciones parecidas en las que necesitamos conocer el número de agrupaciones en las que NO IMPORTA EL ORDEN. Por ejemplo:
entre otras muchas más.
Denominamos combinaciones ordinarias o sin repetición de $n$ elementos tomados de $m$ en $m$, (siendo $m$ menor o igual que $n$) a las distintas agrupaciones de $m$ elementos de manera que:
Se puede observar fácilmente que: las combinaciones sin repetición de $n$ elementos tomados de $m$ en $m$, podrían formarse a partir de considerar las variaciones sin repetición de $n$ elementos tomados de $m$ en $m$ y posteriormente identificar las posibles reordenaciones de una agrupación, (permutaciones de $m$ elementos), como una única ya que el orden no interviene en la agrupación que estamos considerando; esto es:
Video
En el siguiente video podemos observar el planteamiento de un problema que requiere de la combinatoria y su solución.
En la siguiente escena puedes practicar con ejemplos de formación de algunas combinaciones sin repetición.
Propiedades de los números combinatorios
Los números combinatorios aparecen muy frecuentemente en multitud de situaciones en Matemáticas, Física, Biología, etc...Figuran como tecla directa en cualquier calculadora científica. Como propiedades más interesantes merecen destacarse:
$1. \dbinom{n}{0} = 1\\ 2. \dbinom{n}{n} = 1$
$3. \dbinom{n}{1} = n\\ 4. \dbinom{n}{m} = \dbinom{n}{n-m}\\ 5. \dbinom{n}{m} + \dbinom{n}{m+1} = \dbinom{n+1}{m+1}$
Cuando no existían calculadoras científicas, el cálculo de números combinatorios requería de un trabajo complicado. El triángulo de Pascal permitía de una forma recurrente y muy fácil calcular cualquier número combinatorio, aunque es verdad que para cantidades elevadas también era bastante engorroso.
En la siguiente escena puedes ver muchas líneas del triángulo de Pascal y unas propiedades curiosas.
Binomio de Newton
Una de las aplicaciones más interesantes desde el punto de vista algebraico para los matemáticos, constituye el desarrollo de las distintas potencias de un binomio. Conocido como binomio de Newton, utiliza los números combinatorios y sus propiedades para desarrollar de forma fácil y directa la potencia natural de cualquier expresión del tipo:
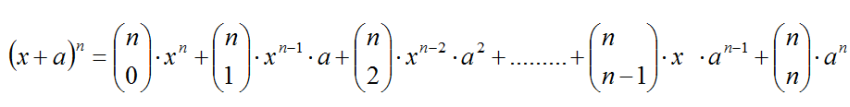
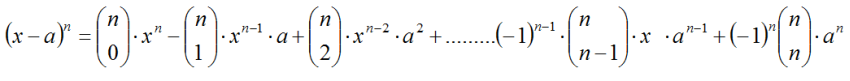
Supongamos que un amigo nos invita a merendar a su casa. Como a las seis personas que estaremos en la merienda nos gustan los pasteles, quiero llevar media docena que compraré en la pastelería de la esquina. Al entrar en el establecimiento, la oferta es impresionante. Hay mucha variedad, piononos de Rute, piononos de Santa fé, milhojas, brazo de gitano, bizcotelas, borrachos, etc. En total la oferta es de $20$ variedades de pasteles diferentes. ¿De cuántas formas puedo hacer mi compra?
Analizando un poco el problema, en realidad no importa el orden en que aparezcan los pastelitos en mi bandeja. Observamos también que pueden repetirse pasteles, incluso se podría comprar una bandeja de seis dulces iguales.
Estamos por tanto ante una combinación (no importa el orden), y con posibilidad de repetición. Estamos ante una combinación con repetición de $20$ elementos tomados de $6$ en $6$: $CR_{20,6}$.

Denominamos combinaciones con repetición de $n$ elementos tomados de $m$ en $m$ (ninguna limitación con respecto a $n$ y $m$), a las distintas agrupaciones de $m$ elementos elegidos de entre los $n$ de manera que:
El número de combinaciones ordinarias de $n$ elementos tomados de $m$ en $m$, lo denotaremos $CR_{n,m}$ y se calcula:
Para explicar la fórmula anterior vamos a desarrollar un método de codificación que nos ayude sobre un ejemplo concreto y que sea un poco más fácil que el del principio. Supongamos que en un restaurante se ofrecen cuatro posibilidades de menús; digamos $A, B, C$ y $D$. Si un grupo de $6$ amigos decide hacer un pedido, calculemos todos los casos distintos que podrían realizarse. Desde el punto de vista combinatorio, estamos ante combinaciones con repetición de cuatro elementos tomados de seis en seis.
En primer lugar utilizamos tres líneas (rayas) para separar las cuatro posibles opciones de los distintos menús. También utilizaremos el símbolo($\LARGE .$) (punto) para significar el pedido de cada persona. De esta forma, el pedido de por ejemplo cuatro menús $A$ y dos menús $B$ lo codificaríamos:
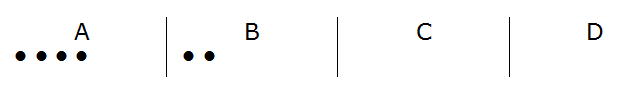
Es decir, el código del pedido sería:

Si por ejemplo quisiéramos expresar el pedido de seis menús $D$ su codificación sería la siguiente:
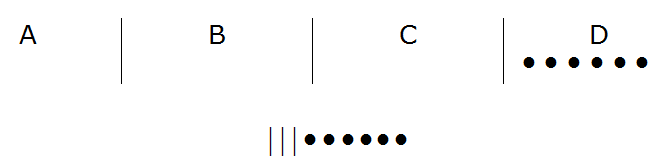
La posición inversa también se manifiesta asequible, es decir, descifrar cualquier código que se confeccione con tres rayas y seis puntos como un determinado y único pedido también sería sencillo. Por ejemplo si queremos descifrar el código $\LARGE ..|..||..$, lo podríamos interpretar como dos menús $A$, dos menús $B$, ningún menú $C$ y dos menús $D$.
Veamos algún ejemplo más de codificación:

Se ha establecido por tanto una correspondencia biunívoca entre las combinaciones con repetición de cuatro elementos tomados de seis en seis y las distintas agrupaciones de seis puntos y tres rayas; esto es, las permutaciones con repetición de 9 elementos donde uno se repite tres veces y otro seis. A su vez, este tipo de agrupación, podría ser considerada como una combinación de 9 elementos tomados de 6 en 6.
$$\large CR_{4,6} = PR_9^{6,3} = \frac{9!}{6!\cdot 3!} = \dbinom{9}{6} = \dbinom{4+6-1}{6}$$En la siguiente escena puedes practicar con ejemplos de formación de algunas combinaciones con repetición.
En el siguiente video puedes observar de forma resumida todos los casos de agrupaciones enumerados en este tema.
Desde el punto de vista práctico, es muy importante tener las ideas muy claras sobre el tipo de conjunto al que nos estemos refiriendo en cualquier problema de combinatoria.
Video
También conviene saber que a menudo los problemas de este tipo no son puros, es decir no se trata de combinaciones puras o variaciones puras,sino que tendremos que aplicar las técnicas de recuento y también la lógica y la particular creatividad que requiera la situación. En este sentido la siguiente escena te ayudará a manejar estos contextos en los que está involucrada la combinatoria.
El siguiente cuadro resumen con ejemplos también puede servirte de ayuda (haz clic en la imagen).

Video
Para empezar a hacer problemas, puedes ver el siguiente vídeo:
A continuación tienes el enunciado de diferentes problemas. Trabájalos y una vez los hayas resuelto puedes hacer clic sobre el botón para ver la solución.
Juan Jesús Cañas Escamilla
José R. Galo Sánchez
Christiaan Huygens (La Haya, 14 de abril de 1629 - ibídem, 8 de julio de 1695) fue un astrónomo, físico, matemático e inventor neerlandés. Hizo aportes importantes en la teoría de la probabilidad, fue miembro de la Royal Society (https://es.wikipedia.org/). Crédito imagen: Caspar Netscher , Dominio Púublico.
La innata curiosidad del ser humano, ha hecho que desde siempre el hombre se haya interesado tanto por el motivo por el que ocurren los fenómenos como por adivinar lo que deparará el futuro. Para ello ha recurrido a todo, astrólogos, profetas, adivinadores, brujos…, utilizando los métodos más inverosímiles; desde la superstición, la observación e interpretación de los vuelos de aves, la lectura de vísceras de animales sacrificados, la magia y rituales sacerdotales hasta las más sofisticadas formulaciones en las teorías más recientes.
| En muchas ocasiones el éxito ha sido completo de manera que ante unas determinadas condiciones iniciales se pueden concluir unos resultados determinados completos y precisos. Sin embargo existen experiencias que escapan al determinismo, es como si no se pudieran someter a las leyes que el hombre ha descubierto y que por tanto imposibilitan ante una determinada situación o experiencia concluir un resultado determinado. Estamos en un contexto tan difícil y extraño en el que las reglas dependen de tantos parámetros que hacen inviable la predicción o quizás ni siquiera existan estas reglas. Estamos en el territorio del azar Se dice que el origen de la probabilidad es un tanto accidental y fruto de las disquisiciones sobre una determinada jugada de dados que obsesionaba a un antiguo escritor y jugador francés del siglo XVII, Antoine Gombaud, conocido por Chevalier de Mère, amigo del matemático también francés Blaise Pascal al cuál pedía consejo respecto a las garantías de éxito que ofrecía dicha jugada. |
 Chevalier de Mère
Chevalier de Mère Blaise Pascal
Blaise Pascal |
Video
En el siguiente vídeo se plantea el denominado problema del caballero de Mére. Se inicia en el instante que comienza a plantearse el mismo, pero si quieres puedes verlo desde su inicio.
El problema de Mére
La historia se pone de acuerdo en que el cruce de correspondencia respecto a dicho problema que establecen Pascal y el genial abogado y matemático también francés Pierre de Fermat, puede considerarse como origen de esta teoría.
Posteriormente es el matemático Christian Huygens quien publica en 1656 el primer libro impreso sobre probabilidad, De ratiociniis in ludo aleae. Es sobre todo en el siglo siguiente cuando el matemático francés Abraham de Moivre profundiza e impulsa de forma más intensa el estudio de la probabilidad con la introducción de importantes conceptos como el de la normal.
Video
En el siguiente vídeo podemos ver una visión de la probabilidad en el programa REDES
Existen experimentos en los que conocidas las condiciones iniciales se pueden predecir los resultados finales. Por ejemplo:
Sin embargo, existen experiencias en las que no ocurre esto o por lo menos así lo parece:
A todos estos experimentos se les denomina aleatorios. ¿Y quién se atreve a estudiar concienzudamente este tipo de experimentos cuyos resultados parecen escapar de todo control y lógica? La respuesta la encontramos, evidentemente, en las Matemáticas y sobre todo y especialmente en algunos matemáticos. Es fundamentalmente a partir del siglo XVIII cuando se estructuran, proponen y desarrollan los conceptos relacionados con la probabilidad hasta cotas realmente prodigiosas.
En este tema vamos a utilizar un vocabulario bastante específico con
algunos conceptos que seguramente ya conoces de cursos anteriores pero que conviene recordar.
En el siguiente enlace puedes informarte sobre alguno de los más importantes matemáticos que trabajaron sobre el tema así como de sus contribuciones (haz clic sobre la imagen).

En cualquier experimento aleatorio la primera cosa que nos preguntamos es sobre lo que puede pasar. ¿Qué resultados puede ofrecer y cuáles no? Sería muy interesante disponer de todo el abanico de posibles resultados. En este sentido, al conjunto formado por todos los posibles resultados elementales de un experimento aleatorio se le denomina espacio muestral de dicho experimento. Dependiendo de como sea este conjunto, los espacios muestrales pueden ser:
Consideremos por ejemplo:
Los ejemplos que podrían exponerse son innumerables y seguro que ya estás pensando en diversas situaciones. No obstante, de partida, queremos que te fijes y pienses en lo que te vamos a exponer. Observa el ejemplo (1) y el (4), el espacio muestral es el mismo, pero ¿puede considerarse el mismo?, esto es, los sucesos que aparecen sí son los mismos pero la ocurrencia de cada suceso en el experimento (1) no tiene el mismo comportamiento que la ocurrencia de cada suceso en el experimento (4) ¿No te parece?
En la siguiente escena puedes observar algunos ejemplos de experimentos aleatorios, sus espacios muestrales y cómo construirlos.
En el contexto probabilístico, denominamos suceso a cualquier subconjunto de un espacio muestral; esto es, a cualquier posible resultado de un experimento aleatorio.
Entre los diferentes sucesos destacaremos los siguientes:
En la escena siguiente puedes observar algunos ejemplos de un suceso y del suceso contrario o complementario.
Desde el punto de vista matemático es importantísimo definir en este conjunto de todos los sucesos asociados a un experimento aleatorio, operaciones matemáticas que permitan la manipulación e interacción entre ellos.
Así se pueden definir en el conjunto de todos los sucesos asociados a cualquier espacio muestral, fundamentalmente dos operaciones que dotarán a dicho conjunto de una sólida estructura matemática importante conocida con el nombre de Álgebra de Boole.
Unión de sucesos
Imaginemos que María y Luis celebran su cumpleaños el mismo día. María ha decidido invitar a sus amigos y Luis a los suyos. Cotejando las respectivas listas de invitados observaron que alguno de ellos estaba invitado a ambas fiestas. ¿A cuál de ellas asistirían?. Este problema puede resultar embarazoso hasta que a ambos cumpleañeros se les ocurre la solución mágica. ¿Y si UNIMOS ambas fiestas y la celebramos juntos. El suceso unión de $A$ y $B$ es el suceso que ocurre cuando ocurre $A,$ ocurre $B$ u ocurren ambos. Está formado por todos los elementos de $A$ y todos los de $B$. Lo indicamos así:
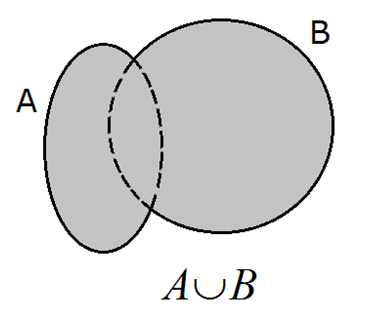
Intersección de sucesos
A Juan le gusta el fútbol, el baloncesto, las películas de aventuras, la música clásica y los documentales de viajes. A su amiga Irene le van las películas románticas, el tenis, la música disco y los documentales de viajes. ¡Qué pocas cosas tenemos en común! exclamó Irene. Sin embargo podríamos quedar para ver algún documental de viajes. Efectivamente es algo que ambos adoramos. Es nuestra INTERSECCIÓN agregó Juan.
El suceso intersección de $A$ y $B$, es el suceso que ocurre cuando ocurre $A$ y ocurre $B$. Está formado por los resultados comunes a los sucesos $A$ y $B$. Lo indicamos así:
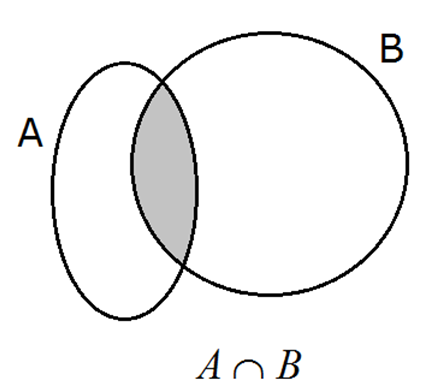
Resta de sucesos
El lunes Manuel salió con sus amigos Miguel, Pablo, María , Laura y Sofía y se le ocurrió contar una ocurrencia muy graciosa que le paso en su último viaje. Fue muy divertido y a todos les entusiasmó.
El jueves siguiente Manuel volvió a salir con otro grupo de amigos entre los que también estaban Laura y Sofía. Manuel volvió a contar la misma anécdota pero antes se disculpó con Laura y Sofía diciéndoles que por favor no contaran el final. Por supuesto que al RESTO de el grupo les resutó igual de divertida.
En realidad no se trata de una nueva operación ya que se define a partir de las dos operaciones anteriores. Sin embargo dada la gran asiduidad y el carácter fundamentalmente práctico con el que aparece en muchas situaciones, merece la pena que hablemos de ella en un apartado propio.
La diferencia de dos sucesos($A-B$) es el suceso que ocurre cuando ocurren los elementos de $A$ que no están en $B$.
Representamos la resta de sucesos como:
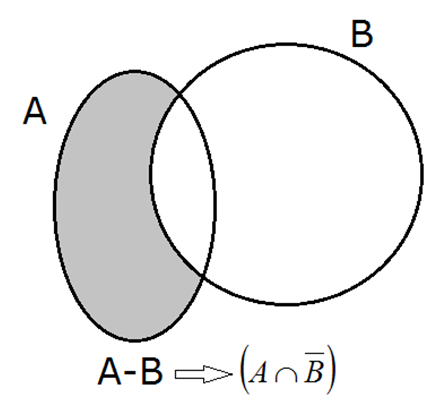
En relación con las operaciones unión e intersección surgen también dos importantes tipos de sucesos.
Consideremos un experimento aleatorio. Dicho experimento tendrá asociado un espacio muestral ($E$). Consideremos también en dicho espacio muestral el conjunto de todos los sucesos posibles de dicho experimento al que normalmente se le nota con la letra griega omega.
$$\Large \Omega$$El conjunto de todos los sucesos de un espacio muestral, junto con las operaciones unión e intersección definidas anteriormente, cumple una serie de propiedades que lo dotan de una estructura matemática conocida como álgebra de Boole.
$$\large (\Omega, \cup, \cap)\;\;\text{ tiene estructura de álgebra de Boole}$$En el siguiente cuadro se resumen las propiedades y consecuencias directas más importantes que se desprenden de dicha estructura.

Dos consecuencias que se derivan de estas propiedades, son:
$$A \cup \empty = A\;\;\text{ y }\;\; A\cap \empty = \empty\\ A \cup E = E\;\;\text{ y }\;\; A\cap E =A$$Una tercera consecuencia son las leyes de De Morgan, que son muy útiles en la práctica, ya que en muchas situaciones se podrán calcular probabilidades de un suceso a partir de las probabilidades de otros más fáciles o bien que se den como datos. Recuerda por tanto:
En muchas ocasiones es muy útil considerar en el espacio muestral asociado a un experimento aleatorio una determinada partición de dicho conjunto que permita una mayor facilidad a la hora de abordar la probabilidad de cualquier suceso a partir de las probabilidades de sucesos más pequeños considerados a partir de dicha partición. En este sentido:
Se dice que los sucesos $A_1, A_2, A_3. \cdots, A_n$, constituyen un sistema completo de sucesos para un determinado experimento cuando se cumplen:
Así por ejemplo en el experimento aleatorio del lanzamiento de un dado pueden considerarse muchas situaciones que constituyan espacios completos de sucesos y que sean interesantes de tener en cuenta de acuerdo al problema en concreto que se nos presente.
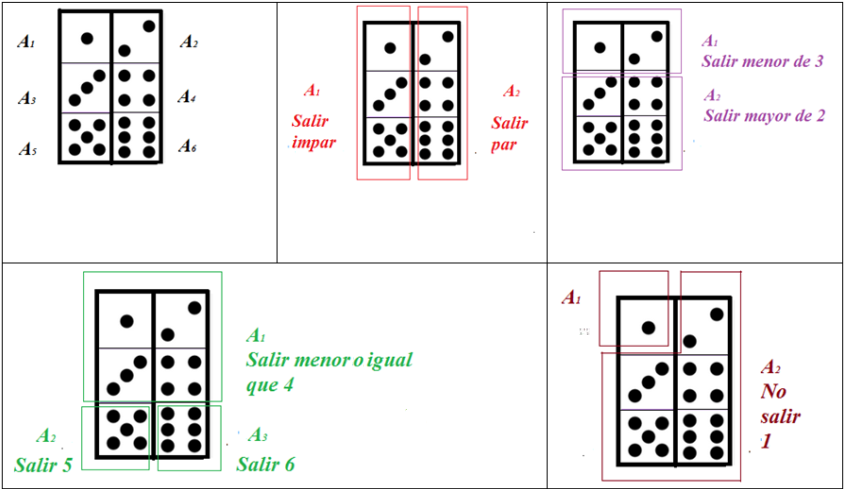
La idea de probabilidad es uno de esos conceptos que cualquier ser humano tiene preaprendido. Todos tenemos conocimiento intuitivo de lo que supone que una cosa sea muy difícil que ocurra (acertar en la lotería) o de algo que sea más fácil que ocurra (lanzar una moneda y que salga cara). Otra cosa es la definición matemática. Desde el punto de vista formal, el concepto de probabilidad se puede abordar desde tres puntos de vista diferentes.
La probabilidad de un suceso $A$ de un experimento aleatorio se puede definir como el número al que se aproximan las frecuencias relativas de dicho suceso cuando el experimento se repite un número indefinido de veces.
 |
$$\LARGE p(A) = \lim\limits_{n \to \infin} \frac{n_A}{n}$$ |
Si un espacio muestral consta de un número finito de sucesos simples y todos ellos tienen la misma posibilidad de suceder (equiprobables). Se define la probabilidad de cualquier suceso $A$ como:
 |
$$\large p(A) = \frac{\text{Número de casos favorables}}{\text{Número de casos posibles}}$$ |
Si un espacio muestral consta de un número finito de sucesos simples y todos ellos tienen la misma posibilidad de suceder (equiprobables). Se define la probabilidad de cualquier suceso $A$ como:
 |
$\large 1) \;\;p(A) \ge 0\\ 2)\;\; p(E) = 1\\ 3)\;\; p(A\cup B) = p(A) + P(B),\\ \text{siendo}\;\;A \text{ y } B\;\;\;\text{incompatible}$ |
Como primeras consecuencias y propiedades de la definición axiomática tenemos:
Video
En el siguiente vídeo puedes recabar algunas ideas sobre la probabilidad.
En la siguiente escena puedes comprobar la probabilidad teórica con la experiencia práctica. La idea es ver como la repetición del juego se aproxima a la idealización teórica.
- Entonces, ¿estas seguro de que vendrás?
- Te digo que sí, llueva o no llueva allí estaré.
Este final de conversación entre dos amigos nos indica que la cita se va a producir INDEPENDIENTEMENTE de lo que ocurra con las posibles inclemencias del tiempo. Sin embargo, existen muchas situaciones en las que la ocurrencia de un suceso influye en la ocurrencia o no de otro.
Así por ejemplo en medicina, el hecho de que una mujer sea portadora de cierta enfermedad influye en que el próximo hijo que tenga adquiera dicha enfermedad, o por ejemplo si una persona es fumadora el riesgo de padecer hipertensión es mucho mayor que en un no fumador.
En el siguiente esquema se ofrece una idea intuitiva del concepto de probabilidad condicionada
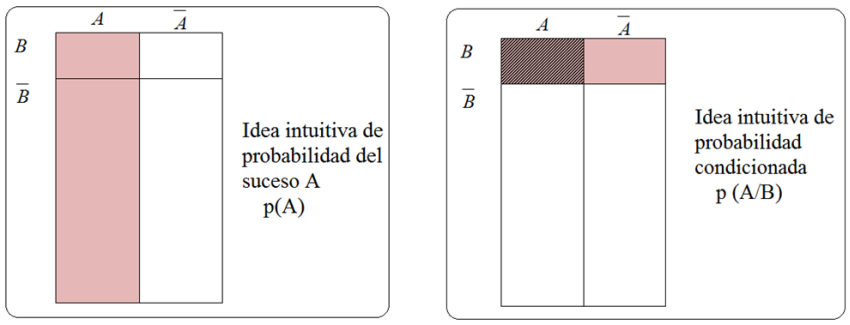
Y en la siguiente escena podrás experimentarla. En ella se juega con el juego de abrir y ganar o de Monty HallEl problema de Monty Hall o paradoja de Monty Hall es un problema matemático de probabilidad basado en el concurso televisivo estadounidense Trato hecho (Let's Make a Deal). El problema fue planteado y resuelto por el matématico Steve Selvin en la revista American Statistician en 1975 y posteriormente popularizado por Marilyn vos Savant en Parade Magazine en 1990. El problema fue bautizado con el nombre del presentador de dicho concurso, Monty Hall (https://es.wikipedia.org/).:
El concepto de probabilidad condicionada va ligado siempre a sucesos compuestos, en el sentido de que la ocurrencia o no de uno de ellos influya o no en la ocurrencia o no del otro. Imagina que sabemos que en una urna hay sobres blancos y azules. Los sobres blancos, casi todos tienen premio. Los sobres azules casi ninguno tiene premio. Evidentemente si me dicen que el sobre que he elegido es blanco, eso aumentará mis expectativas de haber conseguido premio. Por el contrario si me dicen que el sobre elegido es azul, mis expectativas de premio serán mucho peores.
Siempre que tenga sentido, se denomina probabilidad condicionada del suceso $A$ respecto del suceso $B$, (probabilidad de $A$ condicionado a $B$) y se representa $p(A/B)$ al cociente:
De la misma forma se puede definir la probabilidad del suceso $B$ condicionado al suceso $A$ como:
De las definiciones anteriores se obtiene la fórmula general para la probabilidad de la intersección de sucesos. En realidad se trata de la formulación general para la probabilidad de la intersección de sucesos.
En la siguiente escena podrás ver el cáculo de la probabilidad de sucesos compuestos:
La fórmula anterior se puede generalizar para cualquier número de sucesos:
$p(A_1\cap A_2\cap A_3\cdots \cap A_n)\\ = p(A_1)\cdot p(A_2/A_1)\cdot p(A_3/A_1\cap A_2)\cdots p(A_n/A_1\cap\cdots\cap A_{n-1})$Imagina que vamos a sacar dos cartas de una baraja. Realizamos el experimento sacando en primer lugar una de las cartas, anotamos su valor, la devolvemos a la baraja, mezclamos bien y extraemos la segunda carta. ¿Influye lo que ocurrió en la primera extracción en lo que ocurirá en la segunda?
En muchas situaciones en la que la probabilidad aparece ligada a sucesos compuestos, la ocurrencia de un suceso no influye en nada en la ocurrencia o no del otro. Por así decirlo, no existe nada adicional que modifique las posibilidades de ocurrencia del segundo suceso cuando se sabe que ha ocurrido el primero; esto es, si el primero no hubiera ocurrido, las posibilidades del segundo seguirían siendo exactamente las mismas. En estos casos, se habla de Independencia de los sucesos.
Cuando se cumpla que $p(B/A)$ coincida con $p(B)$ se dice que los sucesos $A$ y $B$ son independientes. En este caso la probabilidad de la intersección obtenida en el epígrafe anterior quedaría simplemente como el producto de las probabilidades de cada suceso.
La fórmula anterior se conoce con el nombre de criterio de independencia y es lo que en la práctica nos lleva a calificar sucesos como independientes.
En el siguiente vídeo puedes recabar algunas ideas sobre sucesos independientes y dependientes.
Videos

Y otro vídeo en el que se trata el tema de las predicciones.

Mediante este resultado, se hace presente la clásica afirmación "divide y vencerás". Nos preguntamos globalmente por la probabilidad de que ocurra un suceso y contestamos a partir del conocimiento que tenemos de las distintas probabilidades de que ocurra dicho suceso cuando han ocurrido otros que en realidad completan todo el espacio muestral.
Formalmente; supongamos que $A_1, A_2, A_3, \cdots A_n$, constituyen un sistema completo de sucesos para el espacio muestral $E$ asociado al experimento aleatorio considerado. Supongamos también que $B$ es un suceso cualquiera del espacio $E$, para el cuál se conocen las probabilidades $p(B/A_i)$.
En estas condiciones podemos deducir que:
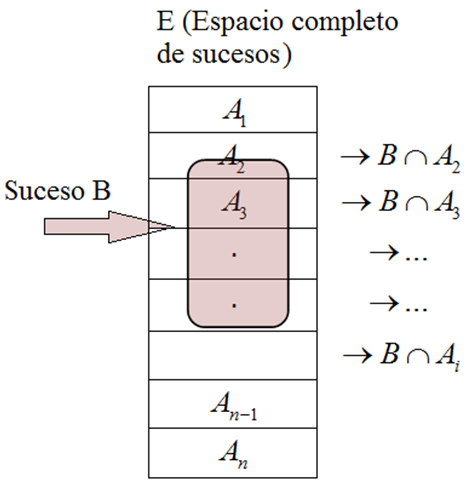
Demostración
$B=(B\cap A_i)\cup (B\cap A_2)\cup\cdots \cup (b\cap A_n)\;\;\text{unión disjunta}\;\;\\
\implies (B\cap A_i)\cap (B\cap A_i) = \empty$
En consecuencia
$p(B) = p(B\cap A_1) + p(B\cap A_2)+\cdots + p(B\cap A_n)\\
\implies p(B)= p(A_1)\cdot p(B/A_1) + p(B)= p(A_2)\cdot p(B/A_2) +\cdots + p(B)= p(A_n)\cdot p(B/A_n)\\
\implies \sum_{i=1}^n p(A_i)\cdot p(B/A_i)$
| Por ejemplo, la clásica situación que se presenta en los centros de secundaria. Imagina un IES que dispone de tres modalidades mutuamente excluyentes de bachillerato y de dos idiomas, inglés y francés. La modalidad $A$ la cursa el $50\%$ de los alumnos, la $B$ el $35\%$ y la $C$ el $15\%$. Se sabe también que eligen francés el $60\%$ de los de la modalidad $A$, el $90\%$ de los de $B$ y el $70\%$ de los de $C$. ¿Cuál será la probabilidad de que elegido un alumno al azar estudie inglés. | 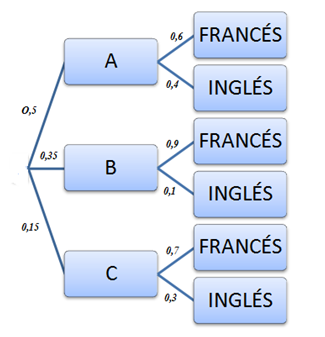 |
En la siguiente escena puedes practicar con la probabilidad condicionada y aplicar el Teorema de la probabilidad total.
¡Ha ocurrido el suceso $B$!, nos preguntamos cuál sería la probabilidad de que ocurra $A_i$ sabiendo de antemano que ha ocurrido $B$. Si nos fijamos lo directo es conocer lo contrario, es decir, las probabilidades de $B$ condicionadas a los diferentes $A_i$. Por ejemplo:
Situaciones como las anteriores son las que se van a resolver con este segundo gran resultado relativo a la probabilidad condicionada. Formalmente; supongamos que $A_1, A_2, A_3, \cdots A_n$, constituyen un sistema completo de sucesos para el espacio muestral $E$ asociado al experimento aleatorio considerado. Supongamos también que $B$ es un suceso cualquiera del espacio $E$, para el cuál se conocen las probabilidades $p(B/A_i)$.
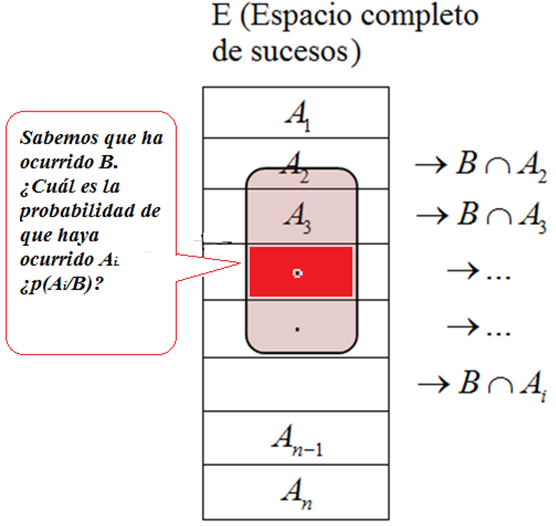
En estas condiciones podemos deducir que:
$$p(A_i/B) = \frac{p(A_i) p(B/A_i)}{p(A_1) p(B/A_1) + p(A_2) p(B/A_2)+\cdots +p(A_n) p(B/A_n)}$$
También puede expresarse:
Video
En el siguiente vídeo puedes recabar algunas ideas sobre el Teorema de Bayes.
Una situación clásica de aplicación del teorema de Bayes es la siguiente:
En un taller se produce la pieza $X$ de recambio para cierto producto. En dicho taller hay tres máquinas, $A, B$ y $C$ que producen el $45\%, 30\%$ y $25\%$, respectivamente, del total de las piezas producidas en él. Los porcentajes de producción defectuosa de estas máquinas son del $3\%, 4\%$ y $5\%$.
Seleccionamos una pieza al azar; calcula:
a) Probabilidad de que sea defectuosa.
b)Tomamos, al azar, una pieza y resulta ser defectuosa; calcula la probabilidad de haber sido producida por la máquina $B$.
c) ¿Qué máquina tiene la mayor probabilidad de haber producido la citada pieza defectuosa?
a) $p(Def) = p(A)\cdot p(Def/A) + p(B)\cdot p(Def/B) + p(C)\cdot p(Def/C) = 0,45\cdot 0,03 + 0,3\cdot 0,04 + 0,25\cdot 0,05 = 0,038$
b) $p(B/Def) = \frac{p(B)\cdot p(Def/B)}{p(Def)} = \frac{0,3\cdot 0,04}{0,45\cdot 0,03+0,3\cdot 0,04+ 0,25\cdot 0,05} = 0,3158$
c) $p(A/Def) = \frac{p(A)\cdot p(Def/A)}{p(Def)} = \frac{0,45\cdot 0,03}{0,45\cdot 0,03+0,3\cdot 0,04+ 0,25\cdot 0,05} = 0,3553$
d) $p(C/Def) = \frac{p(C)\cdot p(Def/C)}{p(Def)} = \frac{0,25\cdot 0,05}{0,45\cdot 0,03+0,3\cdot 0,04+ 0,25\cdot 0,05} = 0,32894$
En la siguiente escena interactiva puedes prácticar con el Teorema de Bayes.
A continuación tienes el enunciado de diferentes problemas. Trabájalos y una vez los hayas resuelto puedes hacer clic sobre el botón para ver la solución.
Juan Jesús Cañas Escamilla
José R. Galo Sánchez
Jacob Bernoulli (Basilea, 27 de diciembre de 1654 - ibíd. 16 de agosto de 1705), también conocido como Jacob, Jacques o James Bernoulli, fue un destacado matemático y científico suizo; hermano mayor de Johann Bernoulli (miembro de la familia Bernoulli).Sus contribuciones a la geometría analítica, a la teoría de probabilidades y al cálculo de variaciones fueron de extraordinaria importancia. (https://es.wikipedia.org/). Crédito imagen: Niklaus Bernoulli (1662-1716) , Dominio Público.
Concepto de variable aleatoria.
El concepto de variable aleatoria viene a dotar de una mayor potencia matemática y de un mejor manejo y utilización del heterodoxo mundo de los espacios muestrales ya que traslada el experimento a función y la ocurrencia o no de un suceso con la posibilidad de que la función tome o no unos determinados valores numéricos.
Como veremos más adelante existirán también modelos de variables aleatorias teóricos que podrán adaptarse perfectamente a multitud de problemas prácticos y que simplificarán mucho el tratamiento y solución de dichas situaciones. En este sentido veremos la importancia sobre todo de la distribución binomial.
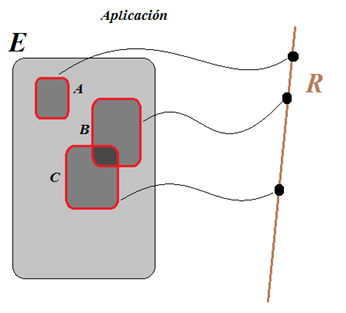
Supongamos que lanzamos dos dados cúbicos. El espacio muestral formado por los posibles resultados estaría compuesto por:
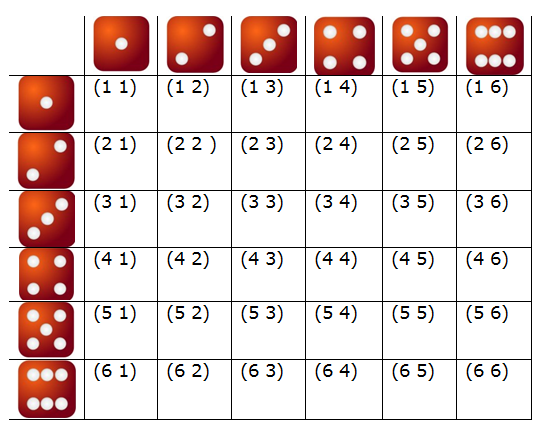
Si consideramos una función que asocie a cada resultado posible del experimento la suma de los resultados de las caras superiores obtenidas; esta función podría tomar los valores desde $2$ hasta $12$.
$$\large \Omega \to \Reals\\ (1,1)\to 2\\ (1,2)\to 3\\ (2,1)\to 3\\ \cdots\\ \cdots$$Además se puede asociar a cada valor de la variable la probabilidad de que tome dicho valor;
$p(X=2) =\frac{1}{36}, p(X=3) =\frac{2}{36}, p(X=4) =\frac{3}{36},\\ p(X=5)=\frac{4}{36}, p(X=6) =\frac{5}{36} p(X=7) =\frac{6}{36},\\ p(X=8) =\frac{5}{36}, p(X=9)=\frac{4}{36}, p(X=10) =\frac{3}{36},\\ p(X=11) =\frac{2}{36}, p(X=12) =\frac{1}{36}$Se define una variable aleatoria como una función que asocia a cada suceso de un espacio muestral un número real.
$$\begin{split}
\Large X & : \Omega \to R\\
& \; A \to X(A)
\end{split}$$
Según sean los valores del recorrido de esta función, ($X(A)$), podemos clasificar las variables aleatorias en:
Una variable aleatoria continua es aquella que toma valores en un conjunto continuo (en toda la recta real, en un intervalo o en una unión de intervalos)
Si dado un gran número de observaciones se construye un histograma con intervalos de clase de longitud pequeña, se obtiene una gráfica que intuitivamente tiende a una curva cada vez que aumenta el número de observaciones, reduciendo la longitud de las clases del histograma.
En cualquier variable aleatoria discreta se puede definir una función particular denominada función de probabilidad que asocia a cada valor de la variable la probabilidad de que dicha variable tome ese valor.
De la propia definición se desprende que para que una función sea función de probabilidad se debe cumplir que:
A partir de la función de probabilidad se puede definir la denominada función de distribución como:
PARÁMETROS ASOCIADOS
Para el cálculo práctico de la varianza en problemas concretos se suele recurrir a esta otra fórmula a la que se llega desarrollando el cuadrado de la anterior y que resulta mucho más sencilla para el cálculo directo.
$$\large \sigma^2 = \sum_{i=1}^n x_i^2 \cdot p_i - \mu^2$$A partir de la fórmula de la varianza y para solventar el problema de que el parámetro venga dado en las mismas unidades de medida que los datos de la variable se define la desviación típica como:
De la misma forma que antes, para el cálculo práctico directo se suele utilizar:
$$\large \sigma = \sqrt{\sum_{i=1}^n x_i^2\cdot p_i - \mu^2}$$PROPIEDADES
Las propiedades más interesantes de la media o esperanza matemática y de la varianza son las que tienen relación con el comportamiento de estos parámetros con respecto a la suma y producto por un escalar de variables aleatorias.
EJEMPLO 1
Consideramos el experimento consistente en lanzar dos dados y observar las caras superiores. En este experimento la variable aleatoria que definimos sería la que asigna a cada suceso la suma de las puntuaciones de las caras superiores.
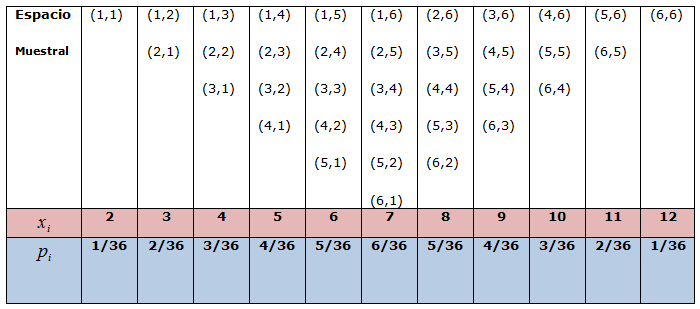
$$\overline{X} = \mu = \sum_{i=1}^n x_i\cdot p_i = 2\cdot \frac{1}{36} + 3\cdot \frac{2}{36}+ \cdots + 11\cdot \frac{2}{36} + 12\cdot \frac{1}{36} = 7$$
$$\sigma = \sqrt{\sum_{i=1}^n x_i^2\cdot p_i - \mu^2} = \sqrt{\sum_{i=1}^n x_i^2\cdot p_i - \mu^2}\implies$$ $$\sigma = \sqrt{2^2 \cdot \frac{1}{36} + 3^2\cdot \frac{2}{36}+ \cdots + 11^2 \cdot \frac{2}{36} + 12^2\cdot \frac{1}{36} - 7^2}=2,42$$
EJEMPLO 2
Consideramos el experimento consistente en el lanzamiento de tres monedas y la variable que asocia a cada suceso el número de cruces obtenidas.
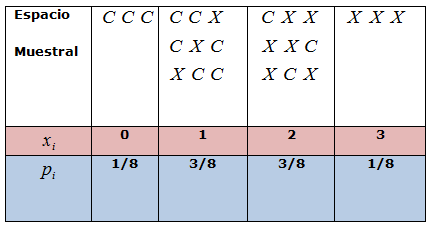
$$\overline{X} = \mu = \sum_{i=1}^n x_i\cdot p_i = 0\cdot \frac{1}{8} + 1\cdot \frac{3}{8}+ 2\cdot \frac{3}{8} + 3\cdot \frac{1}{8} = 1,5$$
$$\sigma = \sqrt{\sum_{i=1}^n x_i^2\cdot p_i - \mu^2} = \sqrt{\sum_{i=1}^n x_i^2\cdot p_i - \mu^2}\implies$$ $$\sigma = \sqrt{0^2\cdot \frac{1}{8} + 1^2\cdot \frac{3}{8}+ 2^2\cdot \frac{3}{8} + 3^2\cdot \frac{1}{8} - 1,5^2}=0,8666$$
EJEMPLO 3
Consideramos el experimento consistente en lanzar dos dados y la variable que asigna a cada suceso la mayor de las puntuaciones obtenidas.
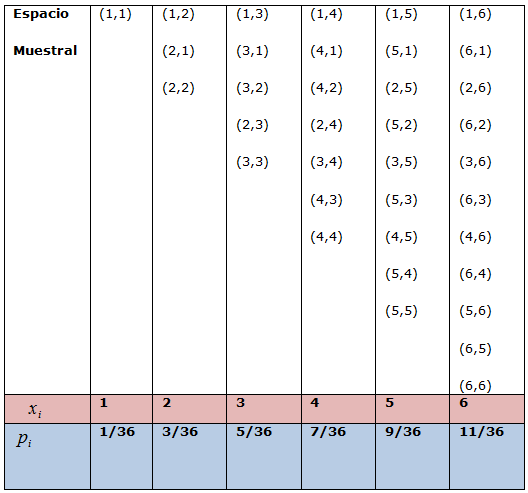
$$ \begin{split} \overline{X} &= \mu = \sum_{i=1}^n x_i\cdot p_i\\ &= 1\cdot \frac{1}{36} + 2\cdot \frac{3}{36}+ 3\cdot \frac{5}{36} + 4\cdot \frac{7}{36} + 5\cdot \frac{9}{36} + 6\cdot \frac{11}{36} = 4,47 \end{split}$$
$$\sigma = \sqrt{\sum_{i=1}^n x_i^2\cdot p_i - \mu^2} = \sqrt{\sum_{i=1}^n x_i^2\cdot p_i - \mu^2}\implies$$ $$\sigma = \sqrt{1^2\cdot \frac{1}{36} + 2^2\cdot \frac{3}{36}+ \cdots 5^2\cdot \frac{9}{36} + 6^2\cdot \frac{11}{36} - 4,47^2}=1,41$$
EJEMPLO 4
Extracción de tres bolas de una urna que contiene $6$ bolas blancas y $4$ negras. Si consideramos la variable aleatoria número de bolas negras extraídas.
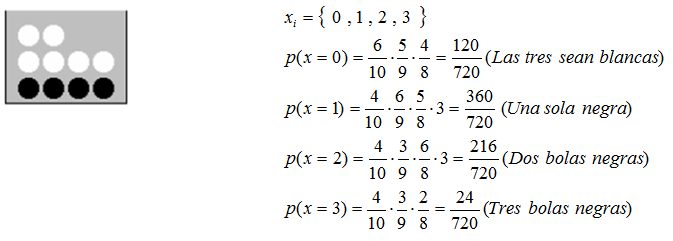
$$ \overline{X} = \mu = \sum_{i=1}^n x_i\cdot p_i = 0\cdot \frac{12}{72} + 1\cdot \frac{36}{72}+ 2\cdot \frac{216}{720} + 3\cdot \frac{24}{720} = \frac{6}{5} = 1,2$$
$$\sigma = \sqrt{\sum_{i=1}^n x_i^2\cdot p_i - \mu^2} = \sqrt{\sum_{i=1}^n x_i^2\cdot p_i - \mu^2}\implies$$ $$\sigma = \sqrt{0^2\cdot \frac{12}{72} + 1^2\cdot \frac{36}{72}+ 2^2\cdot \frac{216}{720} + 3^2\cdot \frac{24}{720} - 1,2^2}=0,7483$$
En la siguiente escena aparecen el diagrama de barras para frecuencias relativas del lanzamiento de dos dados un total de veces que puedes modificar mediante el control "nº de veces".
Puedes manipular dicho control y observar qué ocurre cuando se aumenta o disminuye, además puedes hacer la comparación con el modelo teórico de su función de probabilidad, representada de forma gráfica. Intenta extraer tus propias conclusiones.
| Un experimento aleatorio se conoce como de Bernoulli cuando solamente da lugar a dos resultados posibles complementarios entre sí: Éxito y fracaso. |  |
Las características que debe reunir un experimento para considerarse una distribución binomial son:
Si consideramos la variable $X$ que representa el número de éxitos obtenidos en n pruebas realizadas, se dice que esta variable sigue una distribución binomial de parámetros $n$ y $p$
$$\large (B(n,p))$$
Para la simulación de modelos de probabilidad como por ejemplo el modelo de una distribución binomial existe un artefacto muy simple y con bastantes aplicaciones didácticas como es el aparato de Galton.
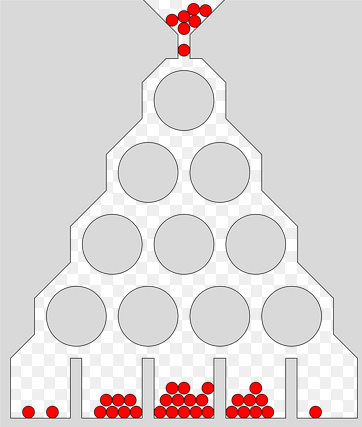
Un aparato de Galton está constituido por un conjunto variable de pisos huecos con topes. En el primer piso hay un sólo tope, en el segundo dos, en el tercero tres y así sucesivamente. Si dejamos que una bola caiga desde el primer piso, al chocar con cada tope puede ir a la derecha o a la izquierda. En principio si no se hace nada especial en el tope, la probabilidad de ir a la izquierda es la misma que la de ir a la derecha.
Video
Observa el siguiente vídeo.
En la simulación del aparato de Galton que aparece en la escena de la siguiente página, vemos que estas probabilidades las podemos cambiar con lo que en realidad en dicha escena simulamos toda una familia de aparatos de Galton (ventajas del mundo virtual). Al final de los pisos, cuyo número también es variable en la escena, aparecen una especie de canales contenedores para recoger las bolitas.
Mediante este sencillo aparato, Galton simulaba de forma práctica modelos teóricos de probabilidad. Si observamos el recorrido de una bola en el aparato de Galton.
En cada bifurcación la bola puede ir a la izquierda con probabilidad $p$ o a la derecha con probabilidad "$q=1-p$". La variable aleatoria que toma valor $0$ si cae a la izquierda o $1$ si cae a la derecha se llama de Bernoulli y la variable $X$ que da el número de unos al finalizar el experimento (lugares a la derecha) se denomina binomial.
Manipula la siguiente escena cambiando los controles, conjeturando y comprobando sobre los canales de más o menos probabilidad. Cambia también el control que en principio aparece con valor por defecto de $1/2$.
Podrías simular modelos para el lanzamiento de dados, cartas, o cualquier otra experiencia en la que aparezcan solamente dos resultados posibles: éxito (bola que va a la derecha) y fracaso (bola que va a la izquierda).
Otra escena interactiva la hemos obtenido del proyecto Phet de la Universidad de ColoradoEscena descargada de Phet interactive solutions.. Ambas escenas, dan cuenta del concepto de distribución binomial, simulando el conocido aparato de Galton. En la versión original de Galton, la probabilidad de ir a la izquierda o la derecha en cada camino es $0.5$. En esta escena podemos elegir cualquier valor $p$ para la probabilidad de ir a la derecha:
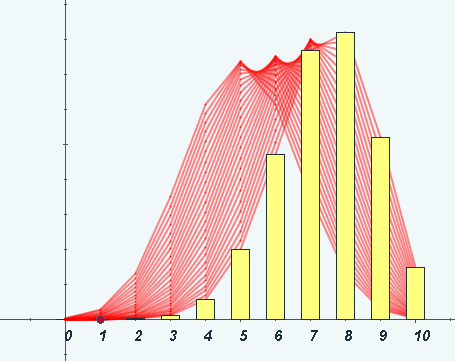
La distribución binomial constituye un modelo de probabilidad teórico al que se adaptan multitud de situaciones y problemas de la vida real. Conviene por tanto profundizar en este modelo teórico para así poder transferir los resultados a las distintas situaciones concretas.
En este sentido se puede deducir la función de probabilidad asociada a una distribución binomial. Si consideramos una distribución $\large B(n,p)$. En la que denominamos:
$$A = \text{Éxito}$$ $$\overline{A} = \text{Fracaso}$$Uno de los casos en los que se obtienen "$r$" éxitos sería:
$$A\; A\; A\; A\; A \cdots \overline{A}\; \overline{A}\; \overline{A}\; \overline{A}$$Es decir primero "$r$" éxitos y después "$n-r$" fracasos.
Particularizando a $4$ éxitos y $3$ fracasos, para ayudarnos en la deducción, existirían muchas situaciones en las que podría presentarse el suceso cuatro éxitos y tres fracasos, por ejemplo:
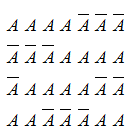
En realidad en las agrupaciones anteriores vemos dos elementos distintos, uno se repite $4$ veces y otro $3$. Esta situación es una vieja conocida en combinatoria. Hablamos de las agrupaciones de $7$ elemenos en los que uno se repite $4$ veces y otro $3$, esto es: Permutaciones con repetición de $7$ elementos en los que uno se repite $4$ veces y otro $3$. El número de permutaciones de este tipo vendría dado por:
$$P_7^{4,3} = \frac{7!}{4!\cdot 3!} = \frac{7!}{4!\cdot (7-4)!} = \dbinom{7}{4} = C_{7,4}$$Es decir que todos los casos posibles en los que se presentan cuatro éxitos y tres fracasos sería el número combinatorio:
$$\dbinom{7}{4}$$En general, la expresión para todos los casos en los que se pueden presentar "$r$" éxitos y "$n-r$" fracasos sería:
$$\large P_n^{r, n-r} = \frac{n!}{r!(n-r)!} = \dbinom{n}{r} = C_{n,r}$$Teniendo en cuenta que la probabilidad de éxito es "$p$" y la de fracaso "$(1-p)$" y la independencia de cada prueba, deducimos que la función que nos permite calcular la probabilidad de que la variable aleatoria $X$ (número de éxitos obtenidos en $n$ pruebas), sería:
$$\large p(X=r) = \dbinom{n}{r}p^r(1-p)^{n-r}$$En la siguiente escena puedes observar las representaciones gráficas de distintas distribuciones binomiales. Puedes cambiar los valores de la binomial que coinciden con los controles "$n$" y "$p$".
Observa cómo cambia la forma de la gráfica y extrae tus propias conclusiones.
Esperanza matemática, varianza y desviación típica de la binomial
Consideramos la variable aleatoria $X$ que sigue una binomial $B(n,p).$ Recordamos que la variable aleatoria $X$ expresa el número de éxitos que se obtienen al realizar "n" pruebas o ensayos independientes de Bernoulli con probabilidad "$p$" de éxito y "$(1-p)$" de fracaso. Esta variable puede interpretarse perfectamente como suma de "n" variables de Bernoulli, una por cada uno de los ensayos realizados. En consecuencia, para deducir la esperanza matemática y la varianza de la binomial $B(n,p)$ podemos calcular la esperanza matemática y varianza de la variable correspondiente a un ensayo y después aplicar las propiedades generales de dichos parámetros con respecto a la suma de variables independientes. Para un ensayo:
$E[X] = 1\cdot p + 0\cdot (1-p) = p\\ var[X] = 1^2\cdot p + 0^2\cdot (1-p) - p^2 = p-p^2= p\cdot (1-p) = p\cdot q$ $$\Downarrow$$ $E[X + X + \cdots + X] = E[n\cdot X] = n\cdot E[X] 0 n\cdot p\\ var[X + X + \cdots + X] = \textcolor{brown}{var[X] + var[X] + \cdots + var[X] = n\cdot var[X] = n\cdot p\cdot q}\\ \text{al ser independientes los ensayos}$
Por tanto:
Media: $\mu = n\cdot p$
Varianza: $\sigma^2 = n\cdot p\cdot q$ siendo $q = 1-p$
Desviación típica: $\sigma = \sqrt{n\cdot p\cdot q}$
Tabulación de la binomial
Aunque las calculadoras científicas realizan sin ningún tipo de problema los cálculos que se derivan de la función de probabilidad de cualquier distribución binomial, hasta hace relativamente poco tiempo dichos cálculos resultaban muy largos y engorrosos, por este motivo se realizaron tabulaciones para las distribuciones binomiales más habituales y a ellas se recurría para determinar de la forma más aproximada posible los valores concretos del problema particular.
En dichas tablas se podía localizar la probabilidad de "$r$" éxitos de una varriable aleatoria $B(n,p)$, sin más que encuadrar la columna de la probabilidad y la fila relativa al número de pruebas.
Por ejemplo si quiero calcular para la $B(5,0.3)$ La probabilidad de $4$ éxitos. Miraré la tabla como se indica en la figura de la siguiente página:
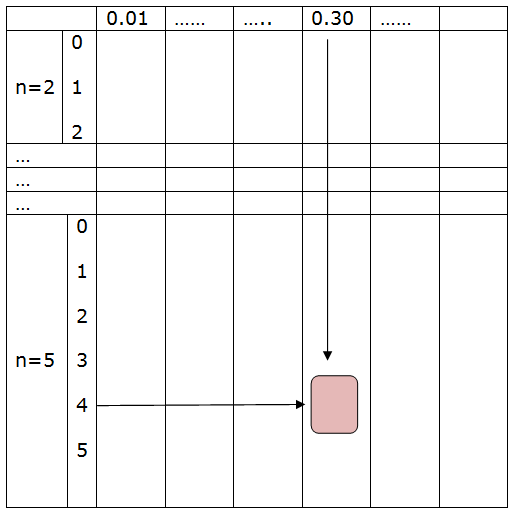
Existen tablas muy extensas para las binomiales. La más popular era la que condensaba en una página todas las binomiales de hasta $n=10$ y distintas probabilidades comprendidas entre un valor mínimo $0,01$ y un máximo de 0,5 con paso de $0,05$.
A continuación puedes ver dicha tabla.
EJEMPLO:
Vamos a utilizar la tabla para resolver una situación sencilla.
Supongamos que Ramona realiza un examen tipo test de $10$ preguntas con cuatro opciones cada una de las que sólo una es correcta. Si responde de forma aleatoria a todas las preguntas. Calcula:
a) Probabilidad de contestar $5$ preguntas bien.
b) Probabilidad de contestar bien al menos $3$ preguntas.
El problema evidentemente se puede enmarcar en una binomial de parámetros $n=10$ y $p=0,25$
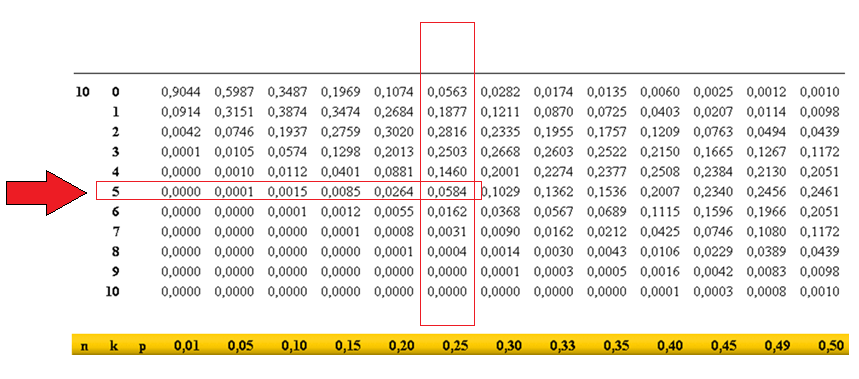
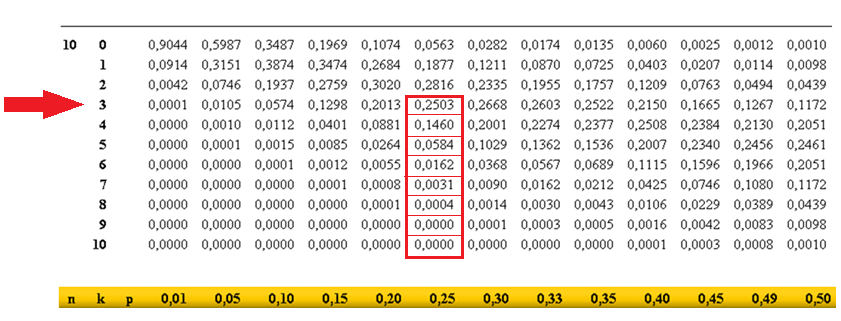
a) $p(x=5) = 0,0584$
b) $p(x\ge 3) = p(x=3)+p(x=4)+\cdots + p(x=10)\\
0,2503+0,1460+0,0584+,0,0162+ 0,0031+0,0004+0,0+0,0 0 0 = 4744$
o también:
$p(x\ge 3) = 1 - p(\lt 3) = 1- [p(x=0) + p(x=1) +px(x=2)]\\ = 1 - (0,0563+0,1877+0,2816) = 0,4744$
Video
En el siguiente vídeo podemos asistir a una clase sobre la distribución binomial:
La distribución binomial es una distribución teórica que permite resolver de forma muy directa multitud de problemas prácticos. Algunas veces también es muy interesante observar si una serie de datos que provienen de alguna situación, en la que no es posible una intervención matemática deductiva concreta, son parecidos a los que se obtendrían de forma teórica mediante una binomial de ciertos parámetros. Si se comprueba que los valores teóricos y los reales son aceptablemente parecidos, no en una ocasión sino en varias, entonces parece plausible pensar que la experiencia que da lugar a los datos pueda imaginarse teóricamente como una binomial. Esto puede permitir inferir resultados de forma previa.
Por ejemplo:
 |
 |
 |
 |
En la siguiente escena puedes comprobar si una serie de datos se parece a los obtenidos en una binomial y como se calcularían los parámetros de esa binomial.
Puedes cambiar los valores del control "$n$" de la binomial hasta un máximo de $8$. En la escena puedes comprobar la diferencia entre los valores esperados y los reales de forma numérica y gráfica en los respectivos diagramas de barras.
La distribución binomial es sin duda la más importante de las distribuciones de probabilidad discretas. Sin embargo existen situaciones que no pueden ser interpretadas mediante está distribución. Imagina por ejemplo una población de 100 personas en las que hay por ejemplo 5 con cierta característica especial. Si se van escogiendo personas una tras otra sin reemplazamiento, considerando éxito si la persona tiene dicha característica y fracaso el que no la tenga. Esta experiencia no se ajusta a una binomial ya que la probabilidad de éxito no se mantiene constante en cada extracción.
| Existen bastantes situaciones interesantes que no se pueden enfocar bajo la óptica directa de la binomial. En los siguientes epígrafes se estudiarán algunas distribuciones teóricas discretas clásicas con las que se pueden abordar un gran número de problemas concretos. | |
 | Familia uniforme |
 | Familia hipergeométrica |
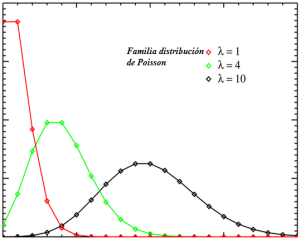 | Familia de Poisson |
Hasta ahora hemos analizado distribuciones que modelaban situaciones en las que se realizaban pruebas que entrañaban una dicotomía (proceso de Bernoulli) de manera que, en cada experiencia, la probabilidad de obtener cada uno de los dos posibles resultados se mantenía constante.
Si el proceso consistía en una serie de extracciones o selecciones ello implicaba la reposición de cada extracción o selección, o bien la consideración de una población muy grande (cartas en un casino). Sin embargo, si la población es pequeña y las extracciones no se remplazan, las probabilidades no se mantendrán constantes. La distribución hipergeométrica viene a cubrir esta necesidad de modelar procesos de Bernoulli con probabilidades no constantes (sin reemplazamiento).
La distribución hipergeométrica es especialmente útil en todos aquellos casos en los que se extraigan muestras o se realicen experiencias repetidas sin devolución del elemento extraído o sin retornar a la situación experimental inicial.
Es una distribución fundamental en el estudio de muestras pequeñas de poblaciones pequeñas y en el cálculo de probabilidades de juegos de azar.
Tiene grandes aplicaciones en el control de calidad para procesos experimentales en los que no es posible retornar a la situación de partida.
Las consideraciones a tener en cuenta en una distribución hipergeométrica:
En estas condiciones, se define la variable aleatoria X = “nº de éxitos obtenidos”. La función de probabilidad de esta variable sería:
| $$\large p(X=x) = \frac{\dbinom{k}{x}\cdot \dbinom{N-k}{n-x}}{\dbinom{N}{n}}$$ | $N = \text{ tamaño de la población}\\ k = \text{Número de individuos que...}\\ n = \text{ tamaño de la muestra}\\ x = \text{ valor que toma la variable}$ |
La media, varianza y desviación típica de esta distribución vienen dadas por:
EJEMPLO 1:
Supongamos la extracción aleatoria de $8$ elementos de un conjunto formado por $40$ elementos totales (cartas baraja española) de los cuales $10$ son del tipo $A$ (salir oro) y $30$ son del tipo complementario (no salir oro).
Si realizamos las extracciones sin devolver los elementos extraídos y llamamos X al número de elementos del tipo $A$ (oros obtenidos) que extraemos en las $8$ cartas; $X$ seguirá una distribución hipergeométrica de parámetros $40 , 8 , 10/40$. $H(40,8,0,25)$.
Para calcular la probabilidad de obtener $4$ oros:
EJEMPLO 2:
De cada $20$ piezas fabricadas por una máquina, hay $2$ que son defectuosas.
Para realizar un control de calidad, se observan $15$ elementos y se rechaza el lote si hay alguna que sea defectuoso. Vamos a calcular la probabilidad de que el lote sea rechazado.
$N=20\\ n=15\\ X = \text{ número de piezas defectuosas de las 15 escogidas}\\ p(X\ge 1) = 1-p(X\lt 1= = 1- p(X=0)$
$$1 - \frac{\dbinom{2}{0}\cdot \dbinom{20-2}{15}}{\dbinom{20}{15}} = 1 - \frac{816}{15504} = \frac{18}{19} = 0,947$$Cuando $N$ es muy grande, como criterio se suele considerar $N \gt 10n$, la distribución hipergeométrica se puede aproximar por la binomial $\bold{B( n, p )}$ con $\bold{p = k/N}$.
En la siguiente escena puedes observar la función de probabilidad de la distribución hipergeométrica. Puedes cambiar los diferentes parámetros que configuran dicha distribución y observar como cambia esta función a medida que se varía alguno de ellos.
Extrae tus propias conclusiones. Así mismo, puedes utilizar también la escena como calculadora directa que permite resolver situaciones concretas que se puedan plantear en problemas específicos.
Lógicamente hay un límite para los valores de la población de manera que la escena funcione con fluidez (valores menores de $200$).
 |
Hay ocasiones en las que un proceso que podría encuadrarse dentro de lo que conocemos como distribución binomial, ofrece dificultades que en ocasiones incluso hacen inviable la resolución de un problema. |
En este sentido, pensemos el caso en que la constante “$p$”, probabilidad de éxito de un experimento de Bernoulli sea muy pequeña; (lo que habitualmente se denominan casos muy raros), o
bien el caso en que los cálculos que se derivan de la fórmula de la binomial sean tan farragosos que saquen de rango nuestra calculadora. Sería importante disponer de otra alternativa más interesante.
Por otro lado, pensemos también en situaciones en las que los elementos de la población pueden considerarse extraordinariamente numerosos, (coches que pasan durante un tiempo por una autopista, metros de tela de una producción en una fábrica, individuos de un país susceptibles de padecer cierta enfermedad, entre otros ejemplos posibles. Un proceso de Poisson se presenta en relación con un acontecimiento (éxito) durante un periodo de tiempo o espacio. Se conoce que el número de éxitos en la unidad de estudio, instante temporal o espacial determinado es
$$\Large \lambda$$y a su vez este es independiente del número de éxitos en otro instante o espacio.
Si llamamos $X = \text{ nº de éxitos obtenidos en un determinado periodo}$. Diremos que $X$ sigue una distribución de Poisson.
La función de probabilidad de esta variable viene determinada por la fórmula:
Los parámetros media, varianza y desviación típica de esta distribución vienen dados por
$$\large \mu = \lambda\\ \sigma^2 = \lambda\\ \sigma = \sqrt{\lambda}$$EJEMPLO 1:
Cierta enfermedad tiene probabilidad de ocurrir $p=1/100000$, lo que en Medicina se denomina prevalencia. Calcula la probabilidad de que en una ciudad de $500000$ habitantes haya más de $3$ personas con dicha enfermedad. ¿Cuál sería en dicha ciudad el número de enfermos esperado?
Solución:
El problema se podría abordar mediante una $B( 500000, 0,00001 )$
En este caso aproximaremos por un modelo de Poisson de parámetro
EJEMPLO 2:
En una carretera se producen un promedio de $2$ accidentes anuales. Calcula la probabilidad de que este año se produzcan más de $3$ accidentes.
$$\text{Poisson de parámetro }\; \lambda = 2\\ p(X\gt 3) = 1 - p(X\le 3)\\ 1 - [p(X=0) + p(X=1) + p(X=2) + p(X=3)]\\ 1 - \frac{e^{-2}\cdot 2^0}{0!} + \frac{e^{-2}\cdot 2^1}{1!} + \frac{e^{-2}\cdot 2^2}{2!} + \frac{e^{-2}\cdot 2^3}{3!} = 0,143$$
Video
En el siguiente vídeo podemos asistir a una clase sobre la distribución de Poisson:
En la siguiente escena puedes observar la función de probabilidad de la distribución de Poisson. Puedes cambiar los diferentes parámetros que configuran dicha distribución y observar como cambia esta función a medida que se varía alguno de ellos.
Extrae tus propias consecuencias. Así mismo puedes utilizar también la escena como calculadora directa que permite resolver situaciones particulares que se puedan plantear en problemas concretos.
| Consideramos una sucesión de variables aleatorias independientes de Bernoulli. Es decir una sucesión de pruebas independientes con dos posibles resultados y con probabilidad de éxito constante e idéntica en cada prueba. $X_1, X_2, \cdots, Xi$, ... donde $X_i \to$ Bernoulli de probabilidad ($p$) Esta sucesión como tal, al menos teóricamente, puede ser infinita. |
 |
Si consideramos la variable aleatoria $X = \text{nº de experiencias realizadas hasta obtener el primer éxito}$, diremos que sigue una distribución geométrica.
De acuerdo con la definición anterior, la variable $X$ puede tomar valores desde uno en adelante. De este modo tenemos que la función de probabilidad para X, que es fácil de deducir puesto que los primeros $k-1$ son fracasos y el $k$-ésimo éxito, sería:
$$f(k) = p(X= k) = (1-p)^{k-1}\cdot p$$En algunos textos se considera la variable nº de fracasos obtenidos hasta el primer éxito. En este caso el valor más pequeño que puede tomar la variable es cero y la formulación cambia un poco.
Los parámetros media, varianza y desviación típica de esta distribución vienen dados por:
$$\large \mu = \frac{1}{p}; \;\;\; \sigma^2 = \frac{1-p}{p^2}\;\;\text{ y } \;\;\sigma = \sqrt{\frac{1-p}{p^2}}$$EJEMPLO 1:
Supongamos que queremos hacer un estudio sobre la variable aleatoria referente al número de veces que un jugador necesita para poder efectuar la salida en el juego del parchís. Hay que recordar que, en este juego, un jugador no comienza el mismo hasta obtener un $5$ al lanzar el dado.
Podría ocurrir que solamente necesitara:
La variable puede seguir tomando valores indefinidamente puesto que es posible encontrar a un jugador cuya “mala suerte“ haga que NUNCA obtenga el dichoso $5$. Estaríamos ante el caso de una distribución geométrica de parámetro $1/6$.
EJEMPLO 2:
Un matrimonio quiere tener una hija, y por ello deciden tener hijos hasta el nacimiento de la esperada hija.
Calcular el número esperado de hijos (entre varones y hembras) que tendrá el matrimonio.
Calcular la probabilidad de que la pareja acabe teniendo tres hijos o más.
$\large \mu = \frac{1}{0,5}=2$
$$\large \begin{split}
p(X\ge 3) &= 1-p(X\lt 3)\\
&= 1 - [p(X=1) + p(X=2)]\\
&= 1- [0,5 + 0,5^2] = 1-(0,75)\\
&= 0,25
\end{split}$$
En la siguiente escena puedes observar la función de probabilidad de la distribución Geométrica.
Puedes cambiar los diferentes parámetros que configuran dicha distribución y observar como cambia esta función a medida que se varía alguno de ellos.
Extrae tus propias consecuencias. Así mismo puedes utilizar también la escena como calculadora directa que permite resolver situaciones particulares que se puedan plantear en problemas concretos.
 Imagina una persona que está jugando al baloncesto con sus amigos y que al finalizar el partido comienza a lanzar tiros libres.
Imagina una persona que está jugando al baloncesto con sus amigos y que al finalizar el partido comienza a lanzar tiros libres.
A uno de ellos, especialmente desacertado, se le ocurre comentar: ¡No pienso irme de aquí hasta conseguir anotar cinco canastas!
Esta situación puede ilustrar bastante bien el problema que resuelve la distribución binomial negativa. Una distribución binomial negativa de parámetros "$r$" y "$p$" surge como una secuencia infinita de intentos de tipo Bernoulli en los que:
Si llamamos $X =$ número de experimentos realizados hasta obtener el r-ésimo éxito, diremos que la variable $X$ sigue una distribución binomial negativa de parámetros $r, p$.
Es fácil deducir que la función de probabilidad de esta variable será:
$$f(k) = p(X=k) = \dbinom{k-1}{r-1}p^r\cdot (1-p)^{k-r}$$La fórmula anterior no es difícil de deducir. Piensa que para esta situación estamos seguros de que el $k$-ésimo intento es un éxito y que en los $k-1$ intentos anteriores se deben redistribuir los anteriores $r-1$ éxitos. La distribución geométrica sería un caso particular de binomial negativa cuando $r = 1$. Los parámetros media, varianza y desviación típica asociados a esta distribución serían:
$$\large \mu = r\cdot\frac{1}{p}; \;\;\; \sigma^2 = r\cdot\frac{1-p}{p^2}\;\;\text{ y } \;\;\sigma = \sqrt{r\cdot\frac{1-p}{p^2}}$$EJEMPLO 1:
Para tratar a un paciente de una afección de pulmón, han de ser operados en operaciones independientes sus $5$ lóbulos pulmonares. La técnica a utilizar es tal que si todo va bien, lo que ocurre con probabilidad de $7/11$, el lóbulo queda definitivamente sano, pero si no es así se deberá esperar el tiempo suficiente para intentarlo posteriormente de nuevo. Se practicará la cirugía hasta que $4$ de sus $5$ lóbulos funcionen correctamente. ¿Cuál es el valor de intervenciones que se espera que deba padecer el paciente? ¿Cuál es la probabilidad de que se necesiten $10$ intervenciones?
Este es un ejemplo claro de experimento aleatorio regido por una ley binomial negativa, ya que se realizan intervenciones hasta que se obtengan $4$ lóbulos sanos, y éste es el criterio que se utiliza para detener el proceso. Identificando los parámetros se tiene que si $X$ es Número de operaciones hasta obtener $r=4$ con resultado positivo,
EJEMPLO 2:
Se sabe que la probabilidad de que un niño expuesto a una enfermedad contagiosa la contraiga es de $0,4$. Calcula la probabilidad de que el décimo niño estudiado sea el tercero en contraer la enfermedad.
Podemos enfocar el problema como una binomial negativa de parámetros $X = 10, k=3$ y $p=0,4$
$$p(X=10) = \dbinom{9}{2}\cdot 0,4^3\cdot 0,6^7 = 0,0645$$En la siguiente escena puedes observar la función de probabilidad de la distribución Binomial negativa. Puedes cambiar los diferentes parámetros que configuran dicha distribución y observar como cambia esta función a medida que se varía alguno de ellos. Extrae tus propias conclusiones. Así mismo, puedes utilizar también la escena como calculadora directa que permite resolver situaciones particulares que se puedan plantear en problemas concretos.
| Supongamos un experimento aleatorio en el que los resultados posibles pueden tomar un conjunto de “$n$” valores discretos y donde cualquiera de estos valores puede obtenerse con igual probabilidad. |  |
Es una distribución muy sencilla que asigna probabilidades iguales a un conjunto finito de puntos del espacio. Modeliza fenómenos en los que tenemos un conjunto de n sucesos posibles, cada uno de los cuales con la misma probabilidad de ocurrir.
Si consideramos la variable aleatoria que hace corresponder cada uno de esos sucesos a un número natural desde $1$ a “$n$”, obtenemos lo que se denomina una distribución uniforme. El único parámetro de la distribución es “$n$” de ahí que se suela representar por:$$\large X \to U(n)$$
Por ejemplo el lanzamiento de un dado correspondería a una distribución uniforme con $n=6$. La función de probabilidad de una distribución uniforme viene dada por:
$$P(x) = \frac1n\;\;\;\text{para}\;\;\; x = \lbrace 1,2, 3 , \cdots, n\rbrace$$Los parámetros media, varianza y desviación típica de una distribución uniforme no son difíciles de obtener:
$\mu = \displaystyle\sum_{i=1}^n i\cdot \frac1n = \frac1n \cdot(1+2+3+\cdots + n) = \frac1n \cdot (\frac{1+n}{2})\cdot n = \frac{1+n}{2}$
$\sigma^2 = \displaystyle\sum_{i=1}^n i^2\cdot \frac1n - \mu^2 = \frac1n\cdot (1^2+ 2^2+3^2+ \cdots + n^2) - \big(\frac{1+n}{2}\big)^2 = \frac{n^2-1}{12}$
$\displaystyle\sigma = \sqrt{\frac{n^2-1}{12}}$
En la siguiente escena puedes observar la función de probabilidad de la distribución Uniforme. Puedes cambiar los diferentes parámetros que configuran dicha distribución y observar como cambia esta función a medida que se varía alguno de ellos.
A continuación tienes el enunciado de diferentes problemas. Trabájalos y una vez los hayas resuelto puedes hacer clic sobre el botón para ver la solución.
Juan Jesús Cañas Escamilla
José R. Galo Sánchez
Johann Carl Friedrich Gauss (Braunschweig, 30 de abril de 1777-Gotinga, 23 de febrero de 1855) fue un matemático, astrónomo y físico alemán que contribuyó significativamente en muchos ámbitos, incluida la estadística. (https://es.wikipedia.org/). Crédito imagen: C. A. Jensen , Dominio Público.
Las distribuciones de probabilidad de una variable aleatoria continua pueden imaginarse como idealizaciones del polígono de frecuencias, asociado al histograma de frecuencias relativas, cuando se aumenta indefinidamente el número de datos y se disminuye paulatinamente la amplitud de los intervalos. Este proceso “límite” proporciona una primera idea de función asociada a dicha variable continua.
Las distribuciones de probabilidad de una variable continua se definen a partir de una función particular a la que llamaremos función de densidad. Consideremos inicialmente un ejemplo:
En un instituto se decide estudiar el tiempo, llamémosle $X$, que emplean los alumnos en desplazarse desde su casa hasta el citado centro. Se trata de una variable estadística que al menos teóricamente puede tomar cualquier valor dentro de un determinado intervalo (entre $0$ y $20$ minutos por ejemplo).
Este tipo de variable se suele representar gráficamente mediante un histograma que consiste en levantar un rectángulo sobre cada uno de los intervalos (clases) donde toma sus valores. La base del rectángulo es la amplitud del intervalo. Si variamos las bases de los intervalos, evidentemente cambia la forma del histograma.
Si el número de alumnos a los que controlamos el tiempo fuese suficientemente grande y vamos aumentando el número de intervalos (o lo que es lo mismo, consideramos clases cada vez más pequeñas), la línea poligonal que forman los puntos medios de los lados superiores de los rectángulos, llamada poligonal de frecuencias. tiende a una curva que recibe el nombre de Función de Densidad de la variable $X$.
En la siguiente escena puedes observar el proceso límite que vislumbra la idea de función de densidad. Por motivos de agilidad en cuanto al funcionamiento de la escena se ha limitado los valores máximos para el control correspondiente al tamaño de la población y el de partición (límite de intervalos que se consideran).
En la siguiente imagen puedes observar el resultado que ofrece la escena anterior para el caso de una población de $50000$ elementos y una partición de $1000$ intervalos
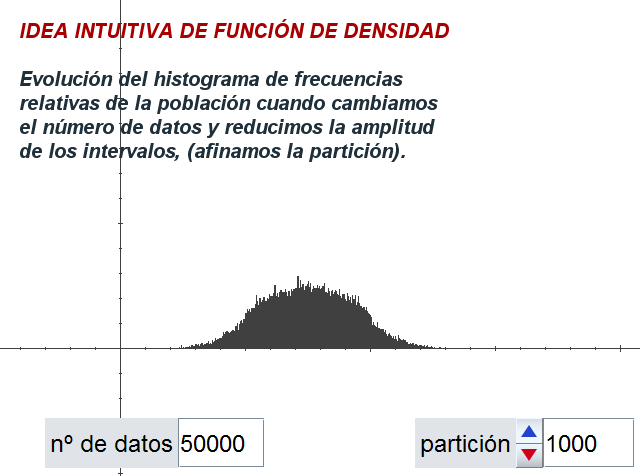
Una función $f(x)$ se admite como función de densidad de una variable aleatoria continua $X$ si verifica:
Algunos ejemplos de función de densidad
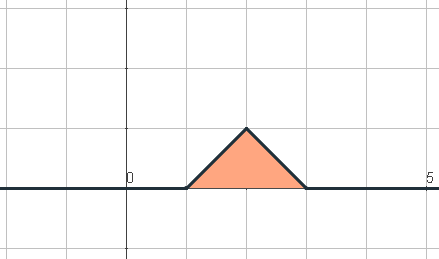 |
$$f(x) = \begin{cases} 0 &\text{si } x\lt 1 \\ x-1 &\text{si } 1\le x\le 2\\ -x+3 &\text{si } 2\le x\le 3\\ 0 &\text{si } x\gt 3 \end{cases}$$ |
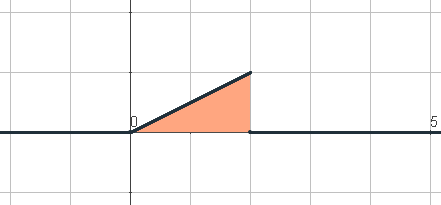 |
$$g(x) = \begin{cases} 0 &\text{si } x\lt 0 \\ \frac12 x &\text{si } 0\le x\le 2\\ 0 &\text{si } x\gt 2 \end{cases}$$ |
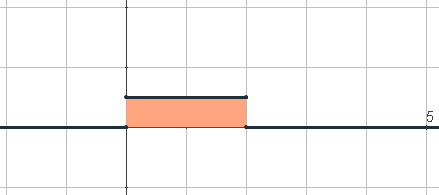 |
$$h(x) = \begin{cases} 0 &\text{si } x\lt 0 \\ \frac12 &\text{si } 0\le x\le 2\\ 0 &\text{si } x\gt 2 \end{cases}$$ |
Nota: En variable continua no tiene sentido el estudio de la probabilidad en un valor aislado (siempre sería cero), pero sí lo tiene el de considerar la probabilidad de que la variable tome valores comprendidos dentro de un intervalo.
Asociaremos la probabilidad de que una variable continua tome valores entre los puntos del intervalo $[a , b]$ como el área comprendida entre la curva, el eje $OX$ y las rectas $x = a$ y $x = b$.
La media o esperanza matemática es el valor más representativo de todos los que toma la variable continua $X$, puede imaginarse como el punto sobre el eje de abscisas en el cuál la superficie generada por la función y el eje permanecerían en equilibrio. El cálculo matemático se haría:
La desviación típica se define como una medida de la dispersión de los valores de la variable $X$ con respecto a la media. Mientras más pequeña sea la desviación más estrecha será la gráfica de $f(x)$ respecto a la media. Su cálculo se haría:
La distribución normal es sin duda la más importante de las distribuciones continuas tanto en la teoría como en la práctica estadística. Puede decirse que en este universo, la mayoría de los fenómenos naturales se comportan básicamente de forma normal o “gaussiana”. En estadística inferencial, el teorema central del límite y las pruebas de normalidad sobre una serie de datos, van a ser básicas en el desarrollo moderno de la estadística.
Aunque fue reconocida por primera vez por el francés Abraham de Moivre (1667-1754), posteriormente, Carl Friedrich Gauss (1777-1855) elaboró desarrollos más profundos y formuló la ecuación de la curva. Se suele conocer popularmente como la "campana de Gauss".
La distribución de una variable normal está completamente determinada por el conocimiento de dos parámetros:
$$\text{Media }\mu\\ \text{Desviación típica }\sigma$$La notación que emplearemos será:
Que llamaremos normal de media $\mu$ y desviación típica $\sigma$
La expresión de la función de densidad para la distribución normal viene dada por:
Las principales características (propiedades) de esta función son:
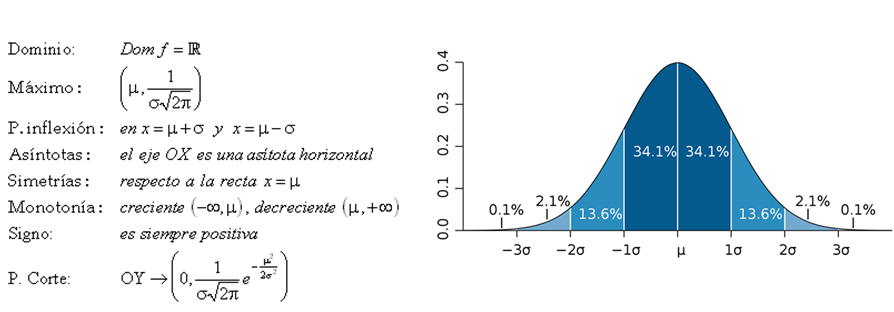
En la siguiente escena puedes manipular los controles para observar el comportamiento de la gráfica de la distribución normal cuando cambias la media y la desviación típica de la misma.
Videos
Puedes observar dos clases sobre la distribución normal correspondientes a la Universidad Politécnica de Valencia.
Entre la familia de las distribuciones normales, la que tiene por media cero y por desviación típica uno es sin duda la más importante de todas. Esta distribución aparece totalmente tabulada y como veremos más adelante permitirá el cálculo de cualquier tipo de probabilidad en cualquier tipo de distribución normal.
La notación que emplearemos para referirnos a esta normal será $N(0,1)$.
Su función de densidad viene dada por la fórmula:
Como ya se ha mencionado al principio del tema, el cálculo de probabilidades en variable continua se asocia al cálculo de áreas. En el caso particular de la distribución $N(0,1)$
Si queremos calcular el valor de que la variable tome un valor menor o menor o igual que "$z$", tendríamos que calcular un área mediante el proceso de integración indefinida, con la dificultad añadida de que la función a integrar no admite una primitiva en términos de función elemental.
Afortunadamente no tendremos que realizar este tipo de ejercicio cada vez que queramos calcular una probabilidad ya que disponemos de una tabulación que permite calcular con bastante precisión el valor de que la variable tome valores menores o menores o iguales que cualquier valor "$z$" comprendido entre $0$ y $4$ con incrementos de una céntésima.
Esto será suficiente para localizar cualquier tipo de probabilidad como veremos más adelante.
En la siguiente imagen podemos ver la representación gráfica de la $N(0, 1)$
Detalle de la tabulación de la $N(0,1)$. Ejemplo de cálculo de una probabilidad (aréa correspondiente al barrido a la izquierda de la función):
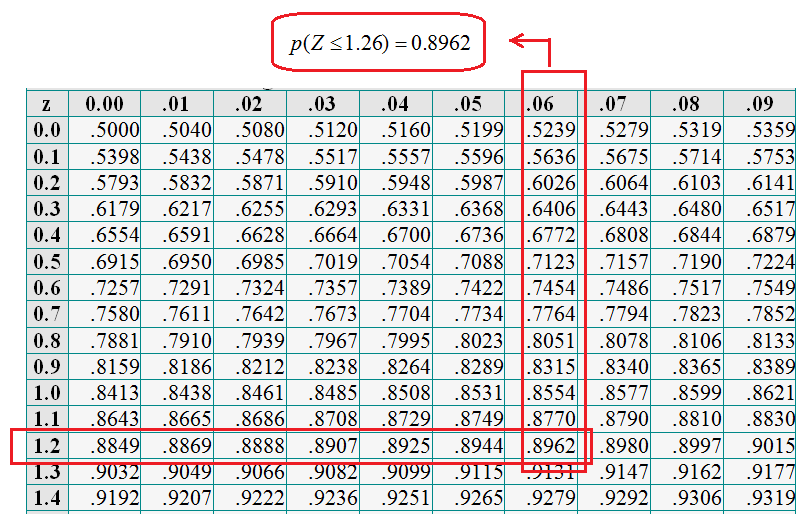
La tipificación es el procedimiento que permite pasar de cualquier distribución normal a la distribución $N(0,1)$. En una distribución continua, si efectuamos el cambio de variable:
Siendo $\mu =$ media y $\sigma =$ desviación típica.
En la siguiente escena puedes comprobar como la gráfica de la función de densidad de cualquier distribución normal, mediante ese cambio de variable, se transforma en la gráfica de la función de densidad de la N(0,1). Para ello basta con que cambies los controles media y desviación típica de la escena.
En las siguientes escenas puedes observar lo que ocurre al tipificar una variable. Puedes calcular probabilidades de distribuciones normales distintas a la N(0,1), además puedes elegir entre cálculo de probabilidades a la izquierda, (barrido izquierda), cálculo de probabilidades a la derecha, (barrido derecha) o cálculo de probabilidades entre dos valores, (barrido de una franja).
Cálculo de probabilidades a la izquierda mediante tipificación
Cálculo de probabilidades a la derecha mediante tipificación
Los valores más importantes en cuanto al cálculo de probabilidades de la distribución normal $N(0, 1)$ aparecen tabulados en una tabla muy sencilla, que presenta una disposición en filas y columnas permitiendo una rápida localización del valor cuya área a la izquierda se asocia con $p(Z \lt z)$.
En la primera columnna aparece la parte entera y el primer decimal del valor desde el $0,0$ al $4.0$ (en algunas tablas no llega hasta el $4$ y suele terminar en $3,5$ ).
En la primera fila aparece la segunda cifra decimal, desde el $0,00$ al $0,09$. Para calcular la probabilidad de que la variable sea menor o menor o igual que, por ejemplo el valor $z = 1,23$, miramos la primera columna y nos situamos en $1,2$, (parte entera y primera cifra decimal). Después en la primera fila elegimos el valor $0,03$, (segunda cifra decimal). El valor que buscamos es la intersección de la fila en la que está situado el valor $1,2$ y la columna correspondiente a $0,03$.
Esta tabulación es muy simple. Ocupa apenas una página y se ha popularizado mucho. No obstante, es muy concisa y contiene la información mínima que se necesita para la localización de cualquier tipo de probabilidad. Para determinar probabilidades que no aparecen directas en la tabla se emplearán tácticas muy simples que abordaremos en los siguientes epígrafes.
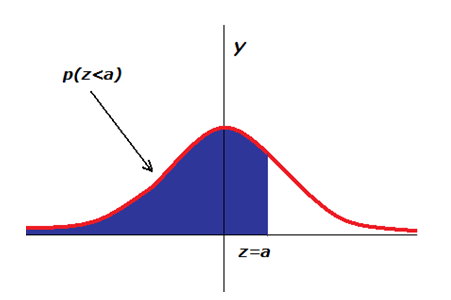
Ejemplo de tabulación de la $N(0,1)$
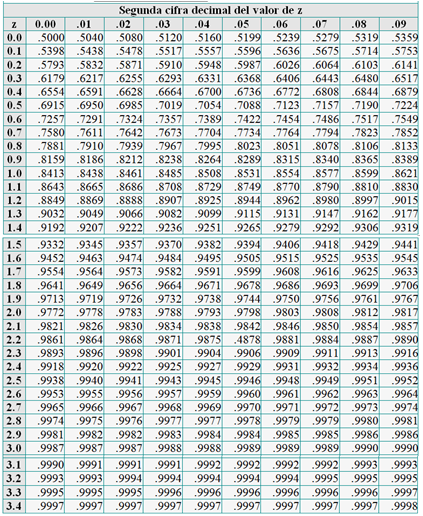
Como ya se ha dicho anteriormente, los valores de la tabla de la $N(0,1)$ se corresponden directamente a barridos a la izquierda. En consecuencia, si el valor en cuestión es uno de los que aparece deirectamente en la tabla, bastará proceder como se indicó en el epígrafe anterior.
Por el contrario, si el valor no es de los que aparece en la tabla ya que es negativo.
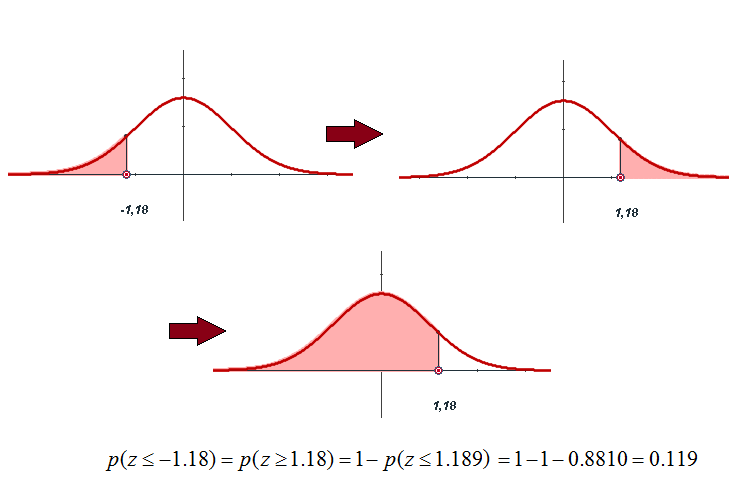
Como ya se ha dicho anteriormente los valores de la tabla de la $N(0,1)$ corresponden directamente a barridos a la izquierda. En consecuencia, no existen de forma directa valores que correspondan a barridos a la derecha. Vamos a distinguir entre valores positivos y negativos.
- Para el caso $p ( z \gt a )$ siendo "$a$" un valor positivo.
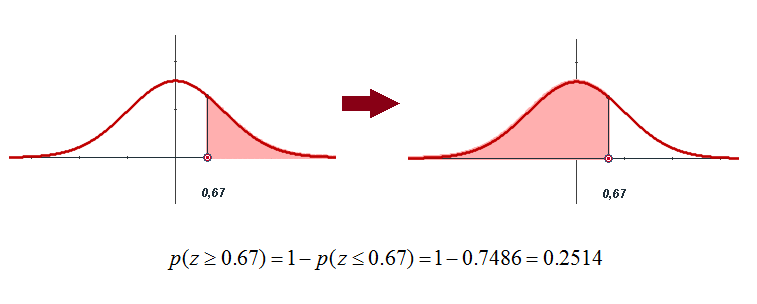
- Para el caso $p ( z \gt -a )$ siendo "$-a$" un valor negativo.
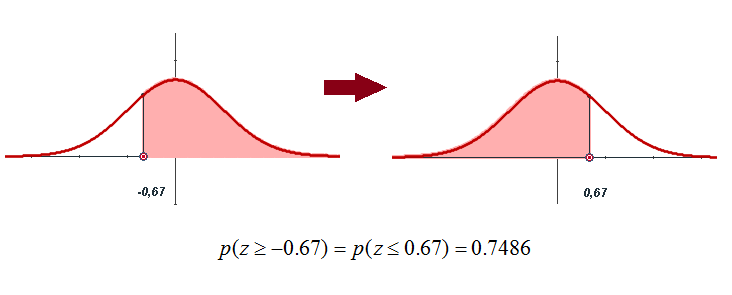
Como ya se ha dicho anteriormente los valores de la tabla de la $N(0,1)$ corresponden directamente a barridos a la izquierda. En consecuencia, no existen de forma directa valores que correspondan a la franja del área o barrido correspondiente a dos valores. Vamos a distinguir tres casos:
- Para el caso $p ( a \lt z \lt b )$, siendo "$a$" y "$b$" valores positivos.
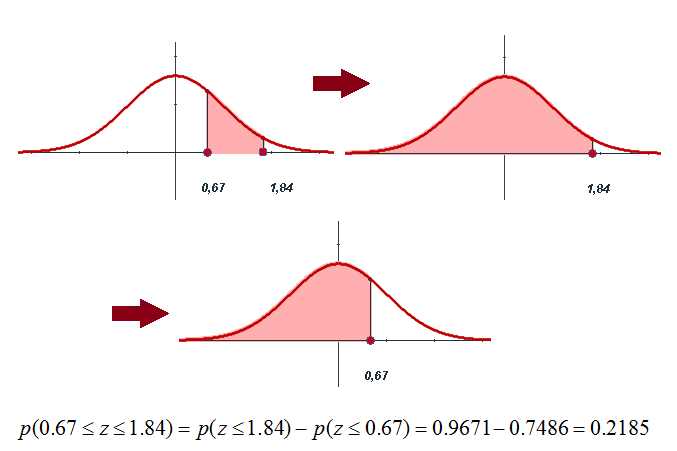
- Para el caso $p (- a \lt z \lt - b )$, siendo "$-a$" y "$-b$" valores negativos.
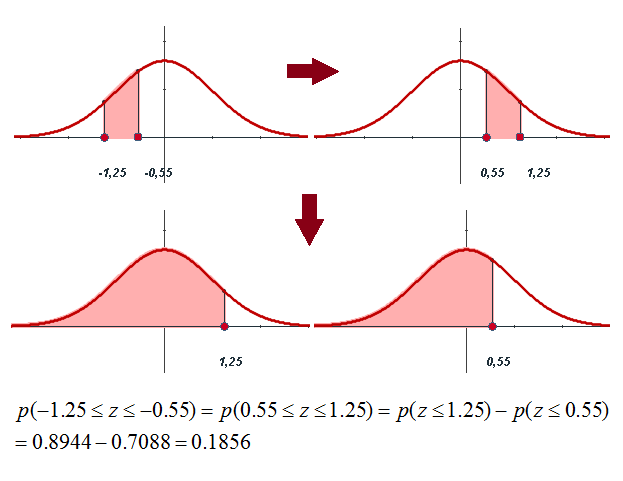
- Para el caso $p (- a \lt z \lt b )$, siendo "$-a$" negativo y "$b$" positivo.
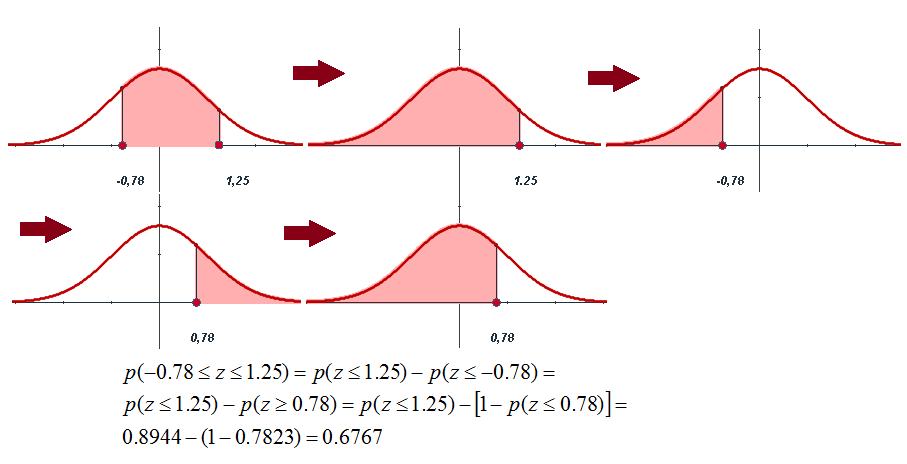
En la siguiente escena puedes practicar con el cálculo de probabilidades a la derecha (barrido a la derecha). Puedes elegir, en el primer control de menú, la opción $\lt\lt \text{mayor}\gt\gt$ y, en el segundo control, $\lt\lt \text{valor de z}\gt\gt$ puedes cambiarlo directamente. La escena resuelve directamente sin necesidad de realizar ninguna táctica. No obstante, es conveniente que practiques con la tabla y que compruebes tus resultados con los que se reflejan en la escena de forma directa.
Existen muchas ocasiones en las que nos interesa saber cuál es el valor de una determinada distribución que deja a su izquierda o derecha una probabilidad determinada. Pensemos por ejemplo en una nota de corte para acceso a una determinada titulación, o en los valores de perímetro craneal que determinan que un feto se encuentre entre los percentiles $25$ y $75$. También se verá en temas posteriores la importancia del cálculo de los denominados "zeta sub alfa medios y zeta sub alfa", tan importantes en intervalos de confianza y contraste de hipótesis. En definitiva, conviene tener cierta habilidad en la utilización de la tabla de la $N(0,1)$ en el sentido expuesto anteriormente. Recordemos también la propia limitación de la tabla en cuanto a que presenta únicamente valores entre $0$ y como mucho $4$ y, además, que las probabilidades correspondientes son únicamente de lo que denominamos barridos a la izquierda.
En la siguiente imagen se muestra la localización del valor de la variable en la $N(0,1)$ que deja a la izquierda una probabilidad de $0.776$ (haz clic sobre la imagen para ampliarla).
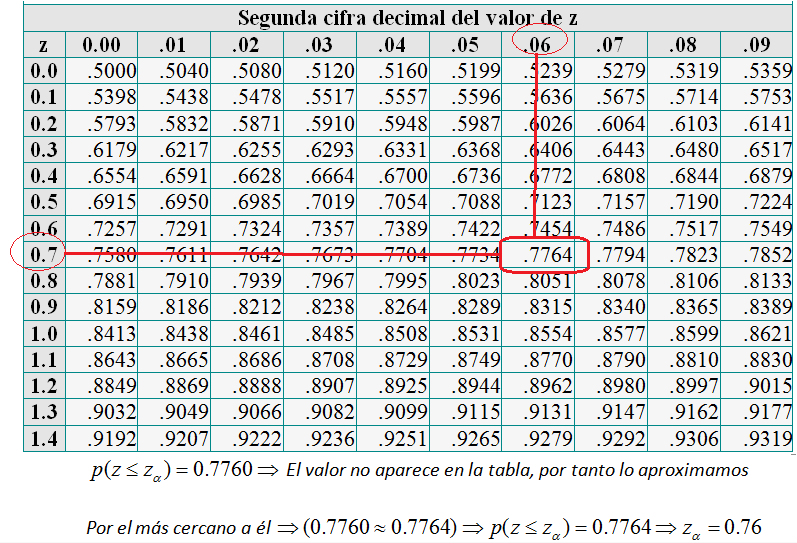
Se trata de calcular el valor de la distribución $N(0,1)$ que llamaremos $z_a$ y que proporciona un barrido a la izquierda de valor "$k$", es decir, tal que $p( z \lt z_a) = k$.
Normalmente el valor de "$k$" no coincidirá exactamente con uno de los que aparece en la tabla, por tanto debemos considerar el más proximo. En el caso en el que haya dos o más que estén a la misma distancia de "$k$", lo habitual es considerar como valor de $z_a$ la media aritmética de los calculados.
Por ejemplo, supongamos que nos interesa conocer el valor de la distribución $N(0,1)$ que determine su percentil $70$; es decir, el valor $z_a$ tal que $p( z \lt z_a)= 0.7$.
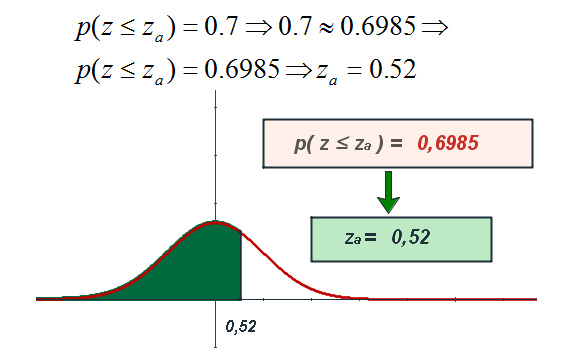
En la siguiente escena puedes calcular directamente, y sin necesidad de utilizar ninguna tabla, los valores que dejan una probabilidad a la izquierda de lo que quieras. Basta con que introduzcas el valor deseado en el control <<probabilidad>>. No obstante, puedes practicar el cálculo de este tipo de valores con la tabla de la $N(0,1)$. También, puedes utilizar la escena para comprobar el error que se comete al realizar los cálculos de forma manual (con la tabla), o de forma directa en la escena.
Se trata de calcular el valor de la distribución $N(0,1)$ que llamaremos $z_a$ y que proporciona una probabilidad a la derecha o barrido a la derecha de valor "$k$", es decir, tal que $p( z \gt z_a )= k$. Teniendo en cuenta que en la tabla de la $N(0,1)$, los valores que aparecen corresponden a barridos a la izquierda, debemos realizar una táctica sencilla que permita localizar el valor $z_a$.
Por ejemplo, supongamos que nos interesa conocer el valor de la distribución $N(0,1)$, tal que la probabilidad a la derecha de ese valor sea de $0.2$, es decir, el valor $z_a$ tal que $p( z \gt z_a) = 0.2$.
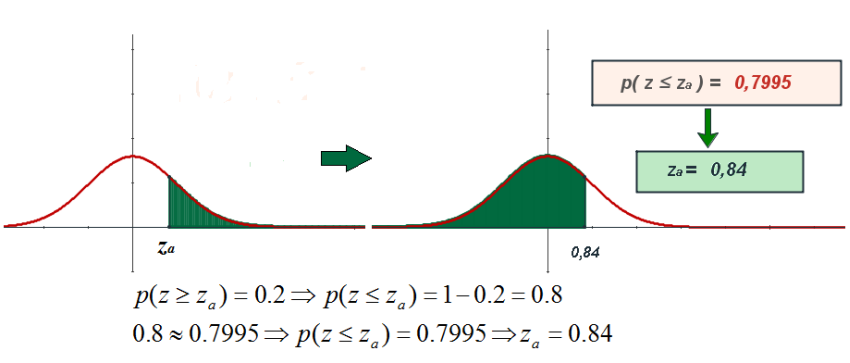
En la siguiente escena puedes calcular directamente y sin necesidad de utilizar ninguna tabla los valores que dejan una probabilidad a la derecha de lo que quieras. Basta con que introduzcas el valor deseado en el control <<probabilidad>>.
No obstante, puedes practicar el cálculo de este tipo de valores con la tabla de la $N(0,1)$. También puedes utilizar la escena para comprobar el error que se comete al realizar los cálculos de forma manual, (con la tabla) o de forma directa en la escena.
Se trata de calcular el valor de la distribución $N(0,1)$que llamaremos $z_a$ y que proporciona una probabilidad central de valor "$k$", es decir, tal que $p(-z_a \lt z \lt z_a)= k$.
En este caso, teniendo en cuenta que los valores de la tabla de la Normal $N(0,1)$ corresponden únicamente a barridos de probabilidad a la izquierda, debemos razonar un poco más.
Por ejemplo, supongamos que nos interesa conocer los valores de la distribución $N(0,1)$ que encierren una probabilidad central del $0.9$; es decir, los valores $z_a$ y $-z_a$ tal que $p(-z_a \lt z \lt z_a )= 0.9$
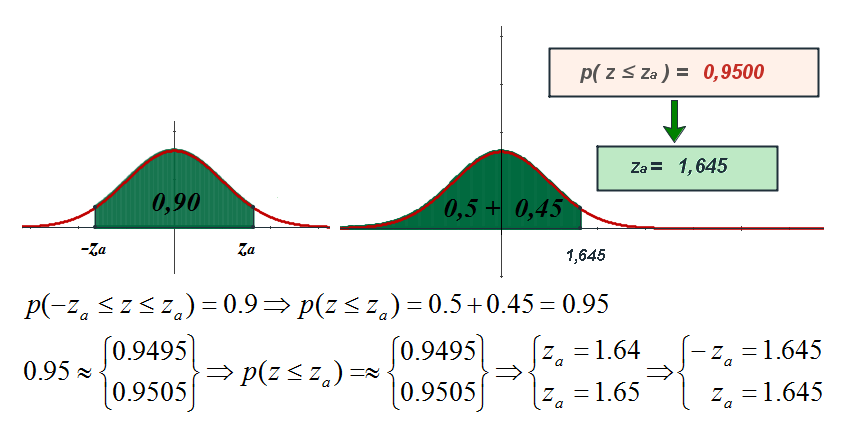
En la siguiente escena puedes calcular directamente y sin necesidad de utilizar ninguna tabla los valores que dejan una probabilidad central de lo que quieras. Basta con que introduzcas el valor deseado en el control <<probabilidad>>.
No obstante, puedes practicar el cálculo de este tipo de valores con la tabla de la $N(0,1)$. También puedes utilizar la escena para comprobar el error que se comete al realizar los cálculos de forma manual(con la tabla), o de forma directa en la escena.
Partimos de un ejemplo:
Se sabe que la probabilidad de padecer cierta infección hospitalaria es de $0.005$. Sobre una población de $1000$ pacientes nos interesaría estudiar la probabilidad de que haya por ejemplo más de $10$ infecciones, o $10$ o menos de $10$.
Según los datos que se desprenden del problema, estamos ante una distribución binomial de parámetros $B(1000 , 0.005)$. Para responder a las preguntas que se plantearon anteriormente, nos podemos encontrar con algunos serios incovenientes, pues la calculadora científica clásica, evidentemente, no puede con la carga operacional y se sale de rango. En estos casos es muy útil el resultado que se estudiará en el siguiente epígrafe y que proporciona las condiciones en las que una distribución binomial puede aproximarse por una distribución normal transformando las situaciones anteriores en preguntas que se contestan muy fácilmente en el nuevo ambiente de la distribución normal. El planteamiento del problema si lo abordamos mediante una binomial sería:
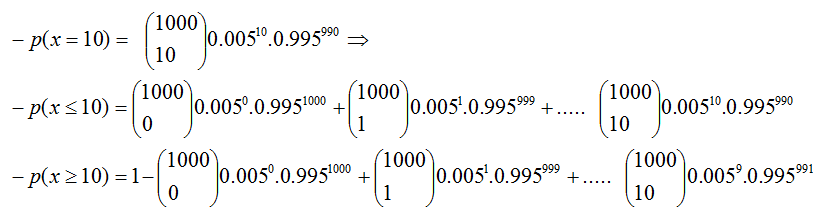
Teorema de Moivre
 Este resultado establece las condiciones en las que una distribución discreta como la binomial puede aproximarse por una distribución normal, proporcionando además los parámetros media o esperanza y desviación típica de dicha distribución normal.
Este resultado establece las condiciones en las que una distribución discreta como la binomial puede aproximarse por una distribución normal, proporcionando además los parámetros media o esperanza y desviación típica de dicha distribución normal.
La sencillez de las condiciones que establece el teorema, el ahorro operacional que proporciona y la calidad de la aproximación hace que sea uno de los resultados más utilizados en estadística.
Supongamos una distribución binomial $B( n , p )$ en la que se cumplan simultáneamente las condiciones:
$$n\cdot p \ge 5\;\;\;\;\; n\cdot (1-p)\ge 5$$Entonces
$$B(n, p) \to N(n\cdot p, \sqrt{n\cdot p\cdot q})$$En la siguiente escena puedes practicar un poco con las condiciones y tesis del teorema de Moivre. Si pulsas el botón de dibujar la normal, observarás la poca diferencia que ofrece la aproximación.
CORRECCIÓN POR CONTINUIDAD (Corrección de Yates)
La distribución binomial es una variable discreta y por tanto tiene sentido el preguntarnos tanto por probabilidades puntuales, como por probabilidades en las que sí tenga importancia saber si el primer o último valor entra o no entra en las posibilidades del problema. Sin embargo, cuando efectuamos la aproximación por una distribución normal, por tanto continua, las consideraciones anteriores dejan de ser determinantes, ya que la primera no tendría sentido y la segunda no ofrecería diferencia alguna.
Para aclarar y diferenciar este tipo de situaciones se ha adoptado, como norma general, realizar correcciones que vienen a solucionar ese matiz diferenciador en las distribuciones discretas, que se “difumina” en la aproximación mediante una distribución continua. En este sentido, convenimos efectuar las siguientes"correcciones" sobre los valores, conocida popularmente como correcciones de Yates
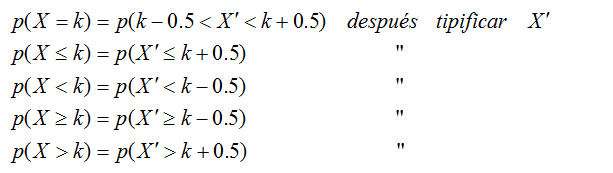
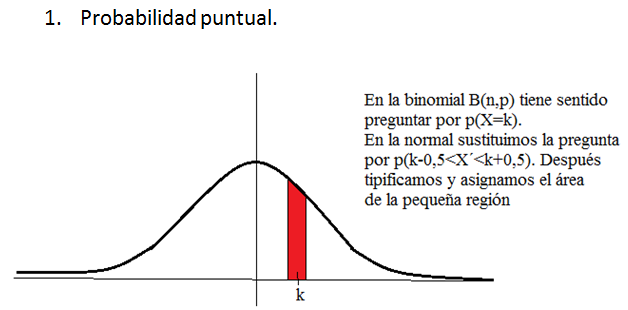
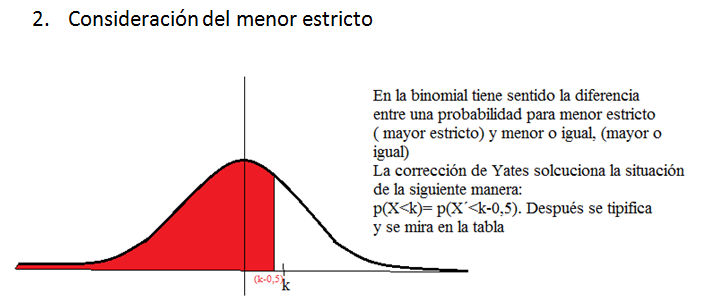
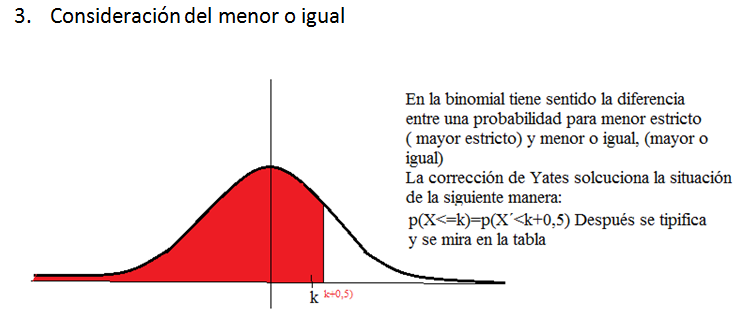
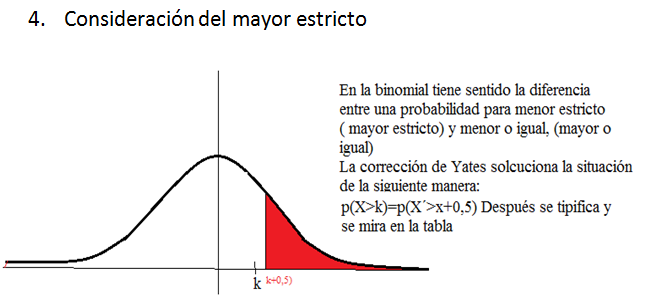
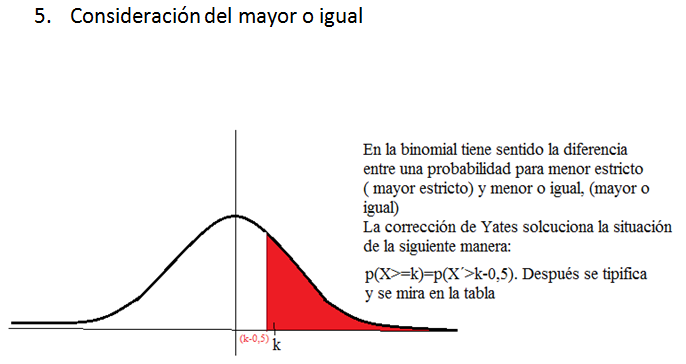
Veamos un ejemplo muy sencillo de aplicación del teorema de Moivre con la corrección de Yates. Supongamos que el $90\%$ de los miembros de un club pasan sus vacaciones en la playa. Calcula una aproximación, obtenida utilizando tablas de la normal, de la probabilidad de que, en un grupo de $6000$ miembros del club, $5450$ o menos vayan a ir a la playa a pasar sus vacaciones.

A continuación tienes el enunciado de diferentes problemas. Trabájalos y una vez los hayas resuelto puedes hacer clic sobre el botón para ver la solución.
Juan Jesús Cañas Escamilla
José R. Galo Sánchez
Abraham de Moivre (26 de mayo de 1667, Champagne - 27 de noviembre de 1754, Londres) fue un matemático francés, conocido por su fórmula epónima, por sus aportaciones a la teoría de la probabilidad y porque predijo la fecha de su muerte a través de un cálculo estadístico (https://es.wikipedia.org/).
Hasta ahora, con la estadística descriptiva, se han ido estudiando las características de una población a partir de ciertos parámetros obtenidos de la misma, realizando una labor primoldialmente descriptiva de los aspectos principales de dicha población.
Diremos que se ha realizado un estudio exhaustivo o censo, cuando lo hayamos realizado sobre todos los elementos de una población. En el caso en el que la investigación se haga sobre una muestra, diremos que se ha realizado un estudio por muestreo.
A diferencia de la estadística descriptiva, la estadística inferencial tiene otros objetivos:
La Inferencia estadística persigue la obtención de conclusiones sobre distintos aspectos de una población, a partir de los datos obtenidos en una muestra de dicha población. También intenta medir su significación, es decir, la confianza que nos merecen dichas conclusiones.
Por ejemplo:
Llamaremos parámetro a cualquier valor representativo de una población; media, mediana, moda varianza…
Llamaremos estadístico a cualquiera de los valores representativos obtenidos en las diferentes muestras de la población; media muestral, varianza muestral, desviación típica muestral…
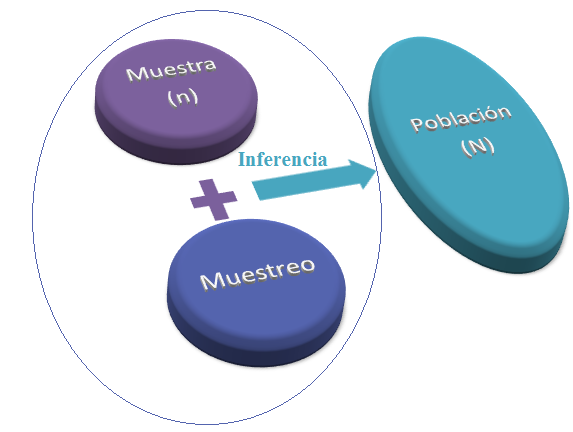
El estudio de determinadas características de una población se efectúa a través de las diversas muestras que pueden extraerse de ella.
Los métodos de muestreo probabilístico son aquellos que se basan fundamentalmente en el principio de equiprobabilidad; es decir: aquellos en los que todos los individuos tienen la misma probabilidad de ser elegidos para formar parte de una muestra. Este aspecto es crucial con respecto a la representatividad de dichas muestras y debe tratarse con mucho cuidado ya que procedimientos que en principio parecen aleatorios muchas veces no lo son. Pensemos en una macroencuesta a nivel mudial. Imaginemos que deseamos realizar un estudio sobre hábitos alimenticios y para ello elegimos de forma aleatoria números de teléfono en los distintos países y realizamos llamadas para contactar con los individuos de nuestra muestra. ¿Estamos seguros de que todos los individuos de la población han tenido la misma probabilidad de ser elegidos? En principio el procedimiento es aleatorio pero todavía en algunos países el teléfono es un artículo de lujo al que una gran parte de la población aún no tiene acceso. En consecuencia esos individuos no tendrían ninguna posibilidad de ser elegidos con nuestro procedimiento.
Representatividad de las muestras - Muestreo aleatorio
La característica más importante de una muestra es su representatividad respecto al estudio estadístico que se esté haciendo. Si la muestra no es representativa diremos que está sesgada.
El proceso mediante el cual se elige una muestra se llama muestreo, y para que nos proporcione una muestra representativa debe ser aleatorio. Un muestreo es aleatorio cuando los individuos de la muestra se eligen al azar, de forma que todos tienen la misma probabilidad de ser elegidos.
Observa la siguiente escena interactiva:
En la escena cada uno de los $625$ cuadraditos representa un alumno de un instituto ficticio, se quiere estudiar el "número de hermanos", puedes animar una elección totalmente aleatoria o realizar tú el muestreo, simulando encuestas, haciendo clic.
Hazlo así: Decide primero el tamaño de la muestra, por ejemplo $62$ alumnos, sitúa el ratón sobre el recuadro y con los ojos cerrados selecciona un cuadrito (alumno), a partir de este cuenta y haz clic cada 10 cuadritos ($625/62\approx 10$), cuando llegues al final de la lista (cuadrado) sigue desde el principio. Este tipo de muestreo aleatorio se llama sistemático.
Dentro de los métodos de muestreo probabilísticos pueden destacarse los siguientes:
Para la realización de este tipo de muestreo, se asigna un número a cada individuo de la población y a través de algún procedimiento aleatorio, con reemplazamiento, como sorteo, tabla de números aleatorios, función ran# de la calculadora, etc., y se eligen tantos sujetos como sea necesario para completar el tamaño de muestra.
 |
 |
 |
Este tipo de procedimiento exige, como el anterior, numerar todos los elementos de la población, pero en lugar de extraer “n” números aleatorios sólo se extrae uno. Se parte de ese número aleatorio y a partir de él se seleccionan los lugares múltiplos de un número “$k$” obtenido previamente. Por ejemplo supongamos un control de tráfico en el que se decide parar a partir de un momento dado a los vehículos que ocupen el lugar $20, 40, 60,\cdots$.


EJEMPLO: Una ganadería tiene $3000$ vacas. Se quiere extraer una muestra de $120$. Explica cómo se debería obtener la muestra:
a) Mediante muestreo aleatorio simple
b) Mediante muestreo sistemático.
Solución:
a) En primer lugar se asignaría un número a cada vaca desde el $1$ al $3000$. Posteriormente se sortean $120$ números entre $1$ y $3000$ (se puede utilizar la función “ran” $\cdot 3000$.
b) En primer lugar el coeficiente de elevación $3000/120$ es decir $25$.
En segundo lugar sortear un número entre el $1$ y el $25$;“ran” $\cdot 25$, supongamos que se obtiene el nº $3$. Las vacas seleccionadas serán: $3, 28, 53,\cdots 2978$.
Consiste en considerar categorías típicas diferentes entre sí (estratos) que poseen gran homogeneidad respecto a alguna modalidad. Se puede estratificar, por ejemplo, según la profesión, el municipio de residencia, el sexo, el estado civil, etc. Lo que se pretende con este tipo de muestreo es asegurarse de que todos los estratos de interés estén representados adecuadamente en la muestra.
La distribución de la muestra en función de los diferentes estratos se denomina afijación, y puede ser de diferentes tipos:

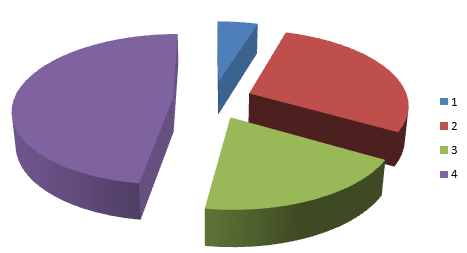 |
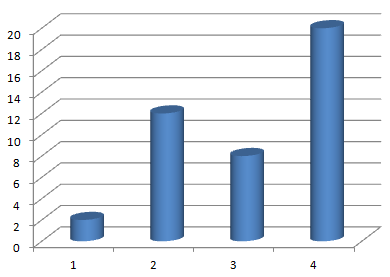 |
EJEMPLO: Supongamos que nos interesa estudiar el grado de aceptación que la implantación de la nueva ley educativa ha tenido entre los padres de alumnos de una provincia. Seleccionamos 600 individuos. Se conoce que los 10000 niños escolarizados se distribuyen: $6000$ en colegios públicos, $3000$ en colegios concertados y $1000$ en privados no concertados.
Queremos que los tres estratos estén representados de acuerdo a:
a) Afijación simple.
b) Afijación proporcional.
Solución:
a) Los tres estratos tendrán el mismo número de elementos ( en este caso $200$ )
b) Para realizar la afijación proporcional:
Para conocer el tamaño de cada estrato en la muestra no tenemos más que multiplicar esa proporción por el tamaño muestral.
Representatividad de las muestras - Muestreo estratificado
En ocasiones cuando la población objeto de estudio, pertenece a distintos grupos o estratos conviene elegir la muestra de forma que todos ellos queden representados.
Este tipo de muestreo, escogiendo un reparto proporcional a los estratos, se llama estratificado.
En este caso la variable a estudiar es el color preferido, y se ha decidido hacerlo por niveles: 1º-2º ESO, 3º-4º ESO y Bachillerato.
Practica en la siguiente escena:
En el muestreo por conglomerados, la muestra seleccionada es todo un grupo de elementos de la población que forman en sí una unidad compacta, a esta unidad es a la que llamamos conglomerado. Este tipo de muestreo consiste en seleccionar aleatoriamente un cierto número de conglomerados y en investigar después todos los elementos de los mismos. Las unidades hospitalarias, los departamentos universitarios, una caja de determinado producto, etc., son conglomerados naturales. En otras ocasiones se pueden utilizar conglomerados no naturales como, por ejemplo, las urnas electorales. Cuando los conglomerados son áreas geográficas suele hablarse de "muestreo por áreas".

 |
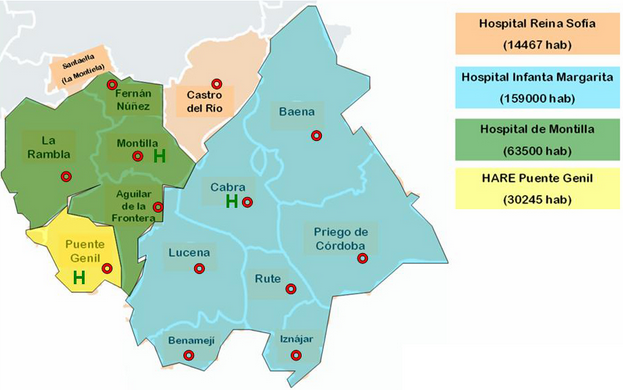 |
EJEMPLO: Supongamos que interesara estudiar algún aspecto concerniente a los políticos que componen las corporaciones locales de municipios de aproximadamente 15000 habitantes. Sabemos que por término medio una corporación local en estos casos suele estar compuesta por 12 políticos de los distintos partidos. ¿Cómo realizar el muestreo si necesitáramos una muestra de tamaño 600?
Solución: En primer lugar elegiríamos aleatoriamente $50$ pueblos de alrededor de $15000$ habitantes. Una vez elegidos estudiamos a todos los elementos de estas corporaciones.
En la siguiente escena puedes trabajar con la idea fundamental del muestreo probabilístico:
En ocasiones la naturaleza del estudio, las necesidades económicas, las características de una determinada población u otra razón, obligan a recurrir a métodos de obtención de muestras que no son aleatorias. Este tipo de muestreo tienen como principal inconveniente su dificultad de representatividad respecto de la población de partida. Se pueden mencionar como algunos de los métodos de muestreo no aleatorio más utilizados:
finalmente, puedes profundizar un poco más con algunos vídeos, a los que puedes acceder haciendo clic en las imágenes de la siguiente página.



Supongamos una población de la que conocemos la proporción “p” de individuos que cumple cierta característica. Si de esta población extraemos muestras de tamaño “$n$”, y en cada muestra a su vez estudiamos la proporción de individuos que cumple la característica estudiada, obtendremos diferentes proporciones muestrales:
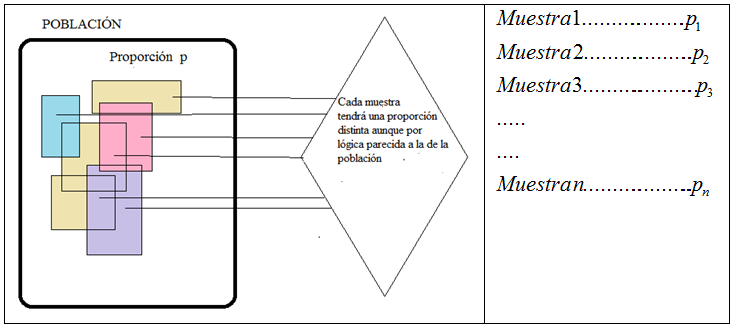
De manera que si llamamos
$$\^P$$a la variable aleatoria formada por los distintos valores que toman las proporciones muestrales.
Esta variable aleatoria como tal tiene las siguientes características:
Además, a medida que crece el tamaño $n$, la distribución de las proporciones muestrales se aproxima cada vez más a la DISTRIBUCIÓN NORMAL (siempre que "$p$" no esté muy próxima a $0$ ni a $1$)
$$\text{Para } n \text{ suficientemente grande } \implies \^p \to N\Big(p, \sqrt{\frac{p(1-p)}{n}}\Big)$$EJEMPLO: En una población se conoce que un $2\%$ de la misma es favorable a la construcción de un centro de rehabilitación para toxicómanos. Si suponemos que en un barrio de la misma viven 500 personas. Calcula la probabilidad de encontrar en dicho barrio más de $9$ personas favorables a la construcción de dicho centro.

En la siguiente escena puedes observar el comportamiento de la distribución de las proporciones muestrales cuando cambias el tamaño de la población.
También puedes cambiar la proporción poblacional y el tamaño de la misma, observando la aproximación de la binomial a la normal cuando se cumplen las condiciones del teorema de Moivre.
Supongamos que tenemos una población de la que se conoce la media y la desviación típica, llamémoslas:
$$\large \text{Media } = \mu$$ $$\large \text{Desviación típica } = \sigma$$Supongamos también que extraemos muestras de tamaño “$n$” de dicha población. Cada muestra proporcionará una determinada media (media muestral).
Si consideramos cada una de estas medias como valores de una variable aleatoria podemos estudiar su distribución, a lo que llamaremos distribución muestral de medias o distribución en el muestreo de las medias muestrales.
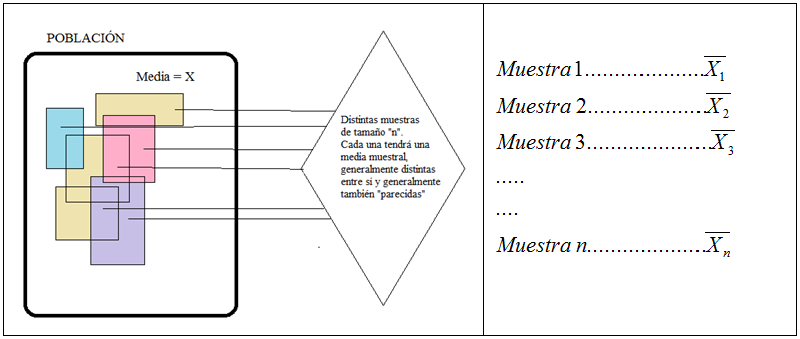
Llamamos a la variable aleatoria que toma los distintos valores de las medias muestrales de tamaño "$n$"
$$\large \^X$$Las características principales de esta variable aleatoria son:
Además, a medida que el tamaño de la muestra crece, la distribución de la variable medias muestrales de tamaño n, se aproxima cada vez más a la distribución normal, esto es:
$$\text{Para } n \text{ suficientemente grande } \implies \^X \to N\Big(\mu, \frac{\sigma}{\sqrt{n}}\Big)$$En el siguiente vídeo podemos observar los conceptos generales de distribuciones en el muestreo.
Video
EJEMPLO : Las puntuaciones de un test de inteligencia para adultos siguen una distribución Normal de media $100$ y desviación típica $16$. Si extraemos una muestra aleatoria simple de 25 individuos:
a) Calcula la probabilidad de que la media muestral sea inferior a $95$
b) Probabilidad de que esté comprendida entre $98$ y $102$
Solución: Se dan las características en la población para poder asegurar que las medias muestrales siguen:
a) $(\^X \to N\big(100, \frac{16}{\sqrt{25}}\big) \implies \^X \to N(100, 3,2)\\ p\big(\^X \le 95\big) = p\big(z \le \frac{95-100}{3,2}\big) = p(z\le -1,56\big) = 0,0594$
b) $p\Big(98 \le \^X \le 102\Big) = p \Big( \frac{98-100}{3,2}\le z \le \frac{102-100}{3,2}\Big)\\ = 0(-0,62\le z \le 0,62)\\ p(z\le 0,62) - p(z\le -0,62) = 0,4648$
En la siguiente escena puedes observar como se distribuyen las medias muestrales. Puedes manipular el control <<Tamaño muestral>> y observar como influye en el reagrupamiento o dispersión de datos en la distribución normal. Para el caso en que la población de partida no sea normal, puedes observar las escenas finales del siguiente epígrafe, (Teorema central del límite).
El teorema central del límite es sin duda el resultado más importante relacionado con el muestreo y las distribuciones en el muestreo de las medias muestrales y de las proporciones muestrales. Este resultado tiene muchas versiones. Una de las más simples es la que sigue:
Si $X$ es una variable aleatoria de una población con media y desviación típica
$$\text{Media } = \mu\\
\text{Desviación típica } = \sigma$$
Entonces se verifica:
a) La distribución de las medias muestrales de tamaño “$n$” tiene:
y por desviación típica
b) Además la distribución de las medias muestrales se aproxima cada vez más a la distribución normal.
Entendiendo por aproximarse a la normal que:
1) Si se sabe que la población de partida es normal entonces sea cual sea el tamaño de las muestras, la distribución de las medias muestrales será una distribución normal.
2) Si la población de partida no es normal, la distribución de las medias podrá aproximarse a la normal con ciertasgarantías para un tamaño muestral mayor o igual que $30$.
Video
En el siguiente vídeo podemos observar Una clase sobre teorema central del límite.
En las siguientes escenas puedes comprobar la tesis del teorema central del límite en tres casos de distribuciónes de partida. El primer caso sobre una población de partida normal, el segundo con una distribución de partida no normal sesgada a la derecha y en el tercer caso partiendo de una distribución uniforme.
Comprueba como a medida que se aumenta el control tamaño muestral y se afina la partición, la tendencia hacia la normalidad de la distribución de las medias muestrales.
Teorema central del límite para una población normal
Teorema central del límite en una distribución de partida no normal, sesgada a la derecha
Teorema central del límite en una distribución de partida uniforme
A continuación tienes el enunciado de diferentes problemas. Trabájalos y una vez los hayas resuelto puedes hacer clic sobre el botón para ver la solución.
Juan Jesús Cañas Escamilla
José R. Galo Sánchez
William Sealy Gosset (Canterbury 11 de junio de 1876 – 16 de octubre de 1937) fue un estadístico, conocido por su sobrenombre literario Student, contribuyó a crear un campo fundamental que hoy se conoce como “diseño de experimentos”, clave para la industria farmacéutica (https://es.wikipedia.org/). Crédito imagen: User Wujaszek, Dominio público.
En la unidad anterior,(teoría del muestreo), se obtenía información de los estadísticos, (fundamentalmente media, proporcion y desviación típica), obtenidos en las muestras extraídas al azar de poblaciones cuyos parámetros eran conocidos considerando a equellos como variables aleatorias. En este sentido eran estudiadas las distribuciones en el muestreo de las medias muestrales o las proporciones muestrales a partir de la media poblacional y la proporción poblacional.
Sin embargo, lo realmente interesante es el proceso contrario; esto es, pretender conocer información, en la medida de lo posible, de ciertos parámetros de la población (desconocidos) a partir de la información que proporcionan los estadísticos de muestras extraídas de forma aleatoria.
Por ejemplo: deseamos conocer la proporción de personas de la ciudad de Barcelona ($6$ millones de habitantes) que utilizan habitualmente internet. Para ello realizamos una encuesta sobre $1200$ habitantes elegidos aleatoriamente en los que resultó que el $75\%$ de ellos sí usaban con frecuencia internet.
Podríamos inferir por tanto como una primera aproximación del parámetro poblacional buscado, el valor del estadístico que se ha obtenido en la muestra. Por tanto podemos decir que hemos estimado el parámetro proporción poblacional de manera puntual por el valor del estadístico proporción obtenido en la muestra.
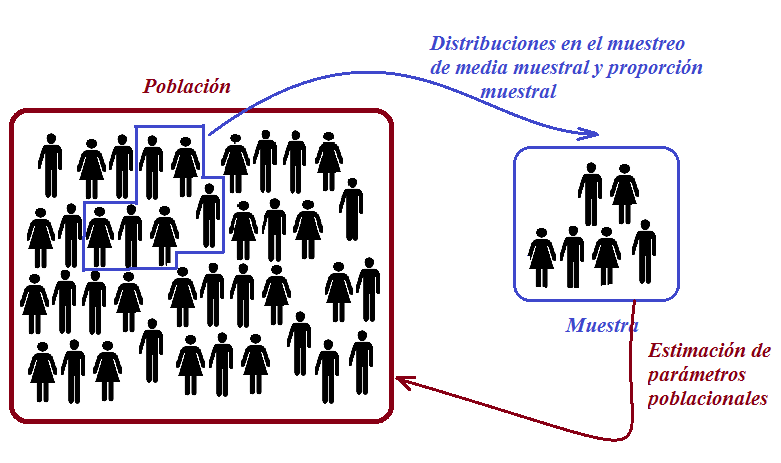
Al proceso mediante el cuál inferimos valores de parámetros poblacionales a partir de los resultados obtenidos en una muestra extraida aleatoriamente se denomina estimación.
Si realizamos dicha estimación asignando un valor muestral concreto al parámetro poblacional que se desea estimar, estaremos ante una estimación puntual. En general, se verifica que cualquier parámetro poblacional que se quiera estimar tiene siempre en la muestra su estadístico paralelo:
Media poblacional... Media muestral
Varianza poblacional... Varianza muestral
En los estudios estadísticos se pueden utilizar diferentes estimadores para un mismo parámetro. Dos de las características principales que poseen los estimadores son el sesgo y la eficiencia.
Por ejemplo, para estimar una media poblacional se pueden elegir entre los estadísticos: media aritmética muestral, mediana muestral o moda muestral. La pregunta que nos haríamos es cuál de ellos sería el “mejor”. Tanto la media muestral como la mediana muestral son estimadores insesgados, sin embargo, la varianza de la media muestral es menor que la de la mediana muestral. Los estimadores centrados o insesgados más precisos son aquellos que tienen menor desviación típica.
Existe toda una teoría en estadística que aborda el tema de la estimación puntual y que excede los objetivos de este estudio. Nuestro principal trabajo se centra en otro tipo de estimación. La estimación por intervalos.
Supongamos que para realizar una estimación de un parámetro poblacional, un profesor encarga la tarea a un grupo de diez alumnos. Estos a su vez seleccionan diez muestras aleatorias sobre las que calculan los correspondientes estadísticos muestrales. Evidentemente estos estadísticos no tienen por qué coincidir. Nuestro problema consiste ahora en elegir de entre los diez el que “creamos” mejor como estimador del parámetro poblacional. ¿Cómo actuamos?¿Cuál elegimos?
La estimación puntual es poco útil como aproximación del parámetro poblacional que se desea estimar ya que solamente proporciona un valor concreto, el cual además varía con cada elección de la muestra. Desde el punto de vista estadístico, es mucho más interesante no concretar un valor sino obtener un intervalo dentro del cuál se tiene cierta confianza de que se encuentre el parámetro poblacional desconocido y objeto principal de nuestra estimación.
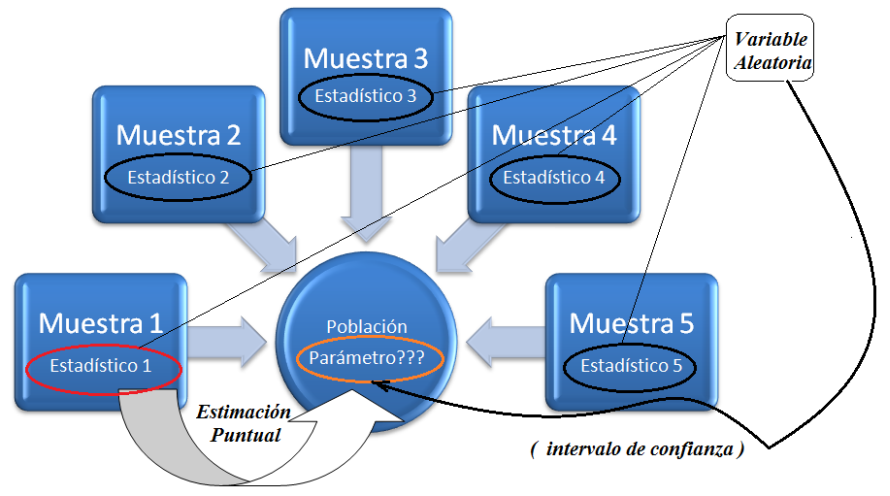
En este sentido, definimos los siguientes conceptos:
La idea global de la estimación mediante un intervalo de confianza es la siguiente. Supongamos que quiero estimar un parámetro poblacional, generalmente la media poblacional o la proporción poblacional desconocidos ambos. La población global es inabordable por diversos motivos logísticos, por ejemplo puede ser muy numerosa o que económicamente el proceso sea muy caro. Consideramos por tanto la extracción de una muestra aleatoria, por ahora que creamos lo suficientemente grande como para que los parámetros obtenidos en dicha muestra sean parecidos a lo que debería ocurrir en la población. Un intervalo de confianza es considerar dos valores de manera que se tenga cierto nivel de certeza (confianza) de que el verdadero valor del parámetro poblacional se encuentre entre los que determinan nuestro intervalo.
Por ejemplo, cuando decimos que en un estudio hecho por una empresa se estimó que la estatura media de los jóvenes españoles oscila entre $172$ cm y $178$ cm, y que el trabajo se realizó con un nivel de confianza del $95\%$, entendemos que la verdadera estatura media poblacional será seguramente un valor comprendico entre los dos anteriores y que la probabilidad de que el intervalo $[172, 178]$ realmente cubra a la verdadera estatura media es de $0,95$. Entendiendo esto último como que si realizamos la estimación por ejemplo $100$ veces, con la elección de $100$ muestras aleatorias distintas, aproximadamente $95$ de nuestras respuestas en forma de intervalos de confianza cubriran al verdadero valor del parámetro estatura media poblacional. ¿Será nuestra respuesta $[172, 178]$ uno de estos intervalos, digamos buenos? Hay un $95\%$ de posibilidades de que sí.
Supongamos una población en la que queremos estimar la proporción “$p$” desconocida (por ejemplo la proporción de personas que van al cine habitualmente en una determinada ciudad).
Supongamos también que extraemos una muestra aleatoria simple de tamaño “$n$” en la que obtenemos un valor concreto para la proporción, llamémosle
$$\large \^p$$Sabemos que la distribución en el muestreo de las proporciones muestrales, sigue una normal de parámetros
$$\large N\bigg(p, \sqrt{\frac{p(1-p)}{n}}\bigg)$$en los casos en que se cumplan las hipótesis sobre normalidad que estipula el teorema de Moivre. Esto quiere decir que si tipificamos
$$\large \frac{\^{\^p}-p}{\sqrt{\frac{p(1-p)}{n}}} =z \;\text{ seguirá una }\;N(0,1)$$Si queremos calcular los valores
$$\Large \pm x_{\frac{\alpha}{2}}$$tales que dejan una probabilidad central de
$$\large (1-\alpha)$$bastaría con ir a la tabla de la normal y localizar el valor que deja un barrido a su izquierda de $$\large 1 -\frac{\alpha}{2}$$
De lo anterior, la notación empleada. Por ejemplo, para calcular los valores críticos asociados a un nivel de confianza del $95\%$ se razonaría:
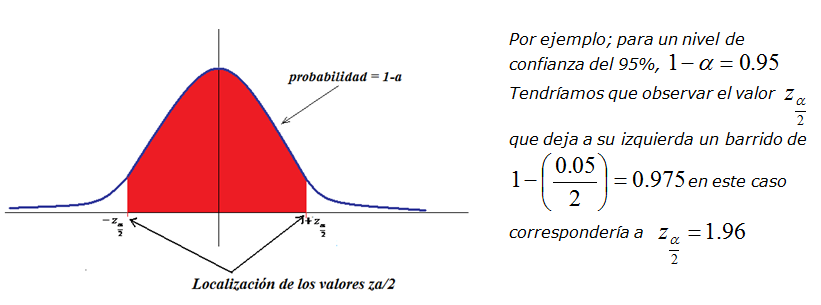
De forma más o menos intuitiva podemos decir que:

EJEMPLO: En una muestra de $100$ personas extraida de una población, $20$ de ellas son portadoras de cierta enfermedad. Estima un intervalo de confianza a un nivel del $95\%$ para la proporción de personas portadoras de la enfermedad.
$\large \^p = \frac{20} {100} = 0,2\\ \text{Para }\; 1 - \alpha = 0,95 \implies z_{\frac{\alpha}{2}} = 1,96\\ 0,2 - 1,96\cdot \sqrt{\frac{0,2\cdot 0,8}{100}} = 0,2-0,0784 = 0,1216\\ 0,2 + 1,96\cdot \sqrt{\frac{0,2\cdot 0,8}{100}} = 0,2+0,0784 = 0,2784\\ \text{Intervalo de confianza }\; \implies (0,1216, 0,2784)$En la siguiente escena puedes observar como los intervalos de confianza que se calculan, van cubriendo o no a la verdadera proporción poblacional.
Puedes cambiar el tamaño de la muestra y el nivel de confianza modificando los respectivos controles.
Observa como al modificar estos controles, cambia la longitud del intervalo y el número de estos que cubren al parámetro poblacional. La escena tiene un límite de $100$ intervalos de confianza.
La escena permite también realizar todos los intervalos de forma continua si pulsas el control de <<animar>>
Intervalos de confianza, estimación de una proporción poblacional
Supongamos una población en la que queremos estimar la media poblacional desconocida que denominaremos
$$\mu$$por ejemplo la estatura media de los alumnos de primaria de una ciudad. Supongamos también que extraemos una muestra aleatoria simple de tamaño “$n$” en la que obtenemos un valor concreto para la media muestral. Sabemos que si la población de partida es normal o el tamaño de la muestra es mayor de $30$, la distribución en el muestreo de las medias muestrales sigue una normal de parámetros:
$$\^X \to N\Big(\mu, \frac{\sigma}{\sqrt{n}}\Big) \implies \text{Tipificando}\\ \implies \frac{\^X-\mu}{\frac{\sigma}{\sqrt{n}}}\;\;\text{sigue una }\;N(0,1)$$En esta distribución pueden calcularse los valores, que encierran una probabilidad de
$$\large (1-\alpha)$$Simplemente mirando y deduciendo en la tabla de la normal $N(0,1)$
$$\large p\Big(-z_{\frac{\alpha}{2}}\le z\le z_{\frac{\alpha}{2}}\Big)$$ $$\large = 1-\alpha \implies \begin{cases} \frac{\^X - \mu}{\frac{\sigma}{\sqrt{n}}} = -z_{\frac{\alpha}{2}} \implies \^X = \mu -z_{\frac{\alpha}{2}}\cdot \frac{\sigma}{\sqrt{n}}\\ \frac{\^X - \mu}{\frac{\sigma}{\sqrt{n}}} = +z_{\frac{\alpha}{2}} \implies \^X = \mu +z_{\frac{\alpha}{2}}\cdot \frac{\sigma}{\sqrt{n}} \end{cases}$$Es decir que el intervalo cuya probabilidad de contener a la media poblacional es $(1-\alpha)$ sería: $\large \^X = \mu \pm z_{\frac{\alpha}{2}}\cdot \frac{\sigma}{\sqrt{n}}$. Teniendo en cuenta que no se conoce la media poblacional $\mu$; la sustituimos por la media muestral obtenida $\overline{X}$, llegando así a la siguiente expresión para determinar el intervalo de confianza:
EJEMPLO RESUELTO: En una muestra de $400$ bolsas de frutos secos de los que habitualmente se venden en el mercado, se obtuvo que el peso medio de las mismas fue de $102$ gramos.
Se sabe de otros estudios que la desviación típica poblacional del peso de este tipo de artículo es de 2 gramos.
Estima un intervalo de confianza a un nivel del $90\%$ para la media poblacional del peso de la bolsa de frutos secos.
$\text{La media muestral }\; \overline{X} = 102\\ \text{Para }\; 1- \alpha = 0,90 \implies z_{\frac{\alpha}{2}} = 1,64$
Aplicando la fórmula:
$102-1,64\cdot \frac{2}{\sqrt{400}} = 102-1,64\cdot\frac{2}{20} = 102 -0,164 = 101,836\\
102+1,64\cdot \frac{2}{\sqrt{400}} = 102+1,64\cdot\frac{2}{20} = 102 +0,164 = 102,164$
$$\large \text{Intervalo de confianza }\; \implies (101,836,\hspace{5pt} 102,164)$$
En el siguiente vídeo podemos ver una clase sobre el intervalo de confianza para la media con desviación típica poblacional conocida.
Video
En la siguiente escena puedes observar cómo los intervalos de confianza que se calculan van cubriendo o no a la verdadera media poblacional.
Puedes cambiar el tamaño de la muestra y el nivel de confianza modificando los respectivos controles.
Intervalos de confianza, estimación de media poblacional
Supongamos una población en la que queremos estimar la media poblacional desconocida que denominaremos
$$\large \mu$$Consideremos también que extraemos una muestra aleatoria simple de tamaño “$n$” en la que obtenemos un valor concreto para la media muestral. Sabemos que si la población de partida es normal o el tamaño de la muestra es mayor de $30$, la distribución en el muestreo de las medias muestrales sigue una normal de parámetros:
$$\large \^X \to N\Big(\mu, \frac{\sigma}{\sqrt{n}}\Big)\\ \implies \text{Tipificando }\\ \implies \frac{\^X-\mu}{\frac{\sigma}{\sqrt{n}}}\;\text{ sigue una }\;N(0,1)$$Pero nos encontramos con el problema de que la desviación típica de la población también es desconocida. Algunos autores optan directamente por considerar como sustituto de la desviación típica de la población, la desviación típica muestral.
Nosotros optamos en este caso por otro procedimiento como es sustituir la desviación típica poblacional desconocida por la
Otros autores optan por procedimientos más depurados y complicados como el que puedes ver en el siguiente vídeo.
Video
Razonando de la misma forma que en el caso anterior, una vez hecha la sustitución de:
$\text{Desviación típica poblaicional }\; = \sigma$
$\sigma \to \^S$
$\text{Cuasidesviación típica }\; \^S$
En esta distribución pueden calcularse los valores que encierran una probabilidad de
$$\large (1-\alpha)$$Simplemente mirando y deduciendo en la tabla de la normal $N(0,1)$
$$\large p\Big(-z_{\frac{\alpha}{2}}\le z\le z_{\frac{\alpha}{2}}\Big)$$ $$\large = 1-\alpha \implies \begin{cases} \frac{\^X - \mu}{\frac{\^S}{\sqrt{n}}} = -z_{\frac{\alpha}{2}} \implies \^X = \mu -z_{\frac{\alpha}{2}}\cdot \frac{\^S}{\sqrt{n}}\\ \frac{\^X - \mu}{\frac{\^S}{\sqrt{n}}} = +z_{\frac{\alpha}{2}} \implies \^X = \mu +z_{\frac{\alpha}{2}}\cdot \frac{\^S}{\sqrt{n}} \end{cases}$$Es decir que el intervalo cuya probabilidad de contener a la media poblacional es $(1-\alpha)$ sería: $\large \^X = \mu \pm z_{\frac{\alpha}{2}}\cdot \frac{\^S}{\sqrt{n}}$. Teniendo en cuenta que no se conoce la media poblacional $\mu$; la sustituimos por la media muestral obtenida $\overline{X}$, llegando así a la siguiente expresión para determinar el intervalo de confianza:
$$\large \overline{X} \pm z_{\alpha/2}\cdot \frac{\^S}{\sqrt{n}}$$El cálculo de la cuasivarianza y cuasidesviación típica aparece como tecla directa en cualquier calculadora científica. La definición de estas medidas y su relación con la varianza y desviación típica habituales se especifican en el siguiente desarrollo:
$$\large \^S^2 = \sum_{i=1}^n \frac{(x_i - \mu)^2\cdot f_i}{n-1}$$En consecuencia:
En la siguiente escena al pulsar <<genera muestra>> se selecciona una muestra aleatoria de la población tomando como parámetros el tamaño y nivel de confianza indicados en los campos de texto así etiquetados y se dibuja el intervalo de confianza indicando sus extremos. Si se cambia el tamaño de la muestra, ésta es completamente nueva y consecuentemente se observa como el intervalo cambia significativamente. Si lo que cambiamos es el nivel de confianza la muestra no varía y lo que acontece es una ligera variación en la longitud del intervalo, los cambios son menos significativos.
Intervalo de confianza para la media poblacional Desconocida la desviación típica de la población
Vamos a imaginarnos un juego. Supongamos que hay situada una linea en el suelo que se encuentra a cierta distancia de nosotros. El juego consiste en lanzar un palo que puede ser de disitintas longitudes y tratar de que alguna de las partes de nuestro palito toque a la línea dibujada en el suelo.
Por lógica mientras más pequeño sea el palo que lanzamos más difícil será tocar la línea y al contrario, con uno más largo la dificultad será menor. Evidentemente los jugadores mejores en este juego necesitarán un longitud de palo más pequeño que los peores. Las reglas del juego deben fijar por tanto una longitud máxima para los palitos, algo parecido a lo que en intervalos de confianza llamaremos error máximo admisible.
Un intervalo de confianza es siempre un entorno centrado en la media muestral y con un radio que depende fundamentalmente del nivel de confianza que se considere y también del tamaño de la muestra elegida.
Atendiendo a cómo calculamos los valores de dicho intervalo, nos podemos dar cuenta de que la amplitud de dicho intervalo depende fundamentalmente de dos elementos:
El intervalo de confianza para el caso de la estimación de una proporción poblacional es un entorno centrado en la proporción muestral y cuyo radio depende fundamentalmente de el valor crítico asociado al nivel de confianza y del tamaño de la muestra considerada.
Se denomina error máximo admisible al valor de este radio; esto es:
De la expresión anterior se deduce fácilmente que al aumentar el nivel de confianza, aumentan también los valores críticos asociados y por tanto el radio del intervalo. Por tanto puede decirse que perdemos precisión en la estimación cuando intentamos aumentar la fiabilidad.
Para el caso del tamaño muestral, al estar en un denominador, cuando aumenta disminuye el radio del intervalo. por tanto ganamos precisión.
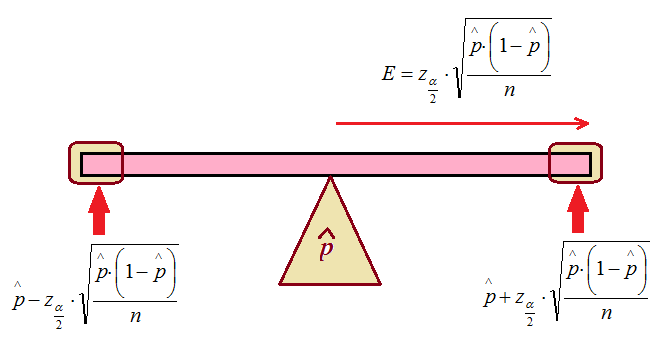
En la siguiente escena puedes observar como varía el error máximo admisible, es decir el radio del intervalo y por tanto la longitud del mismo cuando cambiamos los controles correspondientes al nivel de confianza y al tamaño de las muestras consideradas. Puedes plantearte varias situaciones y extraer tus propias conclusiones.
Intervalo de confianza para estimar una proporción poblacional desconocida
El intervalo de confianza para el caso de la estimación de una media poblacional es un entorno centrado en la media muestral y cuyo radio depende fundamentalmente del valor crítico asociado al nivel de confianza y del tamaño de la muestra considerada.
Se denomina error máximo admisible al valor de este radio; esto es:
De la expresión anterior se deduce fácilmente que al aumentar el nivel de confianza, aumentan también los valores críticos asociados y por tanto el radio del intervalo. Por tanto puede decirse que perdemos precisión en la estimación cuando intentamos aumentar la fiabilidad.
Para el caso del tamaño muestral, al estar en un denominador, cuando aumenta disminuye el radio del intervalo. Por tanto ganamos precisión.
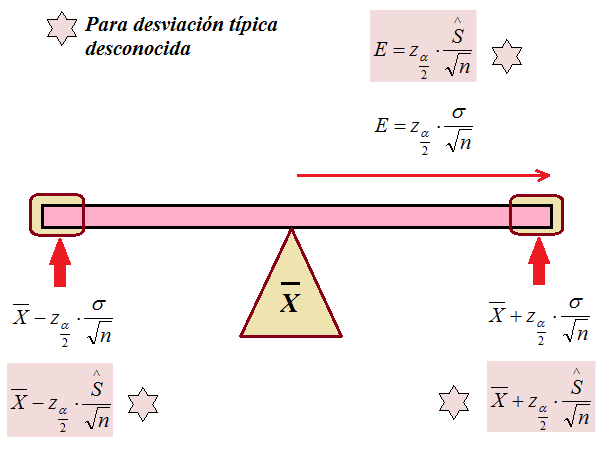
En las siguiente escena puedes observar cómo varía el error máximo admisible, es decir, el radio del intervalo y por tanto la longitud del mismo cuando cambiamos los controles correspondientes al nivel de confianza y al tamaño de las muestras consideradas.
Puedes plantearte varias situaciones y extraer tus propias conclusiones.
Intervalo de confianza para la media poblacional Conocida la desviación típica de la población
Todos los trabajos realizados en estadística van acompañados de un documento anexo muy importante que se denomina ficha técnica. En este documento se especifican algunas de las características más relevantes del trabajo realizado. Entre ellas, siempre nos vamos a encontrar con el método mediante el cuál se ha elegido la muestra y el número de elementos del que consta dicha muestra.
Este número debe cumplir cierto valor mínimo para que se garanticen premisas básicas exigibles al intervalo como el nivel de confianza o el margen de error de dicho intervalo.
Partiendo de las fórmulas que determinan el error máximo admisible de un intervalo de confianza para la proporción poblacional o para la media poblacional, y mediante procedimientos púramente algebraicos, se van a poder deducir fórmulas para la localización de tamaños muestrales mínimos.

Como ya se ha mencionado antes, una pregunta interesante de investigar sería cuál tiene que ser el tamaño de la muestra que se debería considerar para que el intervalo de confianza de una proporción cumpliera determinadas condiciones de amplitud.
Por ejemplo:
Existen otras muchas situaciones en las que es importante la localización de un tamaño muestral mínimo a partir del cual se cumplan determinadas condiciones en nuestra estimación.
De la propia formulación del intervalo se observa que el tamaño que debe exigirse para una muestra depende fundamentalmente del nivel de confianza que se desee para los resultados y de la amplitud del intervalo de confianza, (error máximo), que se esté dispuesto a admitir.
Fijados estos, y simplemente despejando algebraicamente en las fórmulas, podemos calcular el tamaño mínimo de la muestra que debe utilizarse para cumplir con las premisas estipuladas.
Para un nivel de confianza:
$$\large (1-\alpha)$$Deduciendo de la fórmula correspondiente al error máximo admisible en el caso de la proporción:
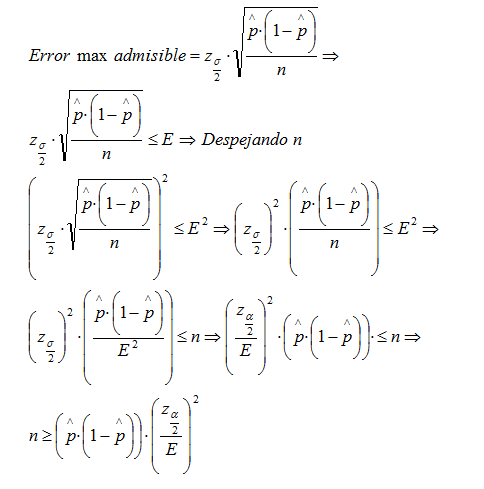
Llegamos a la siguiente expresión para el tamaño mínimo de muestra en el caso de estimación de una proporción
Por ejemplo, los dos ejemplos planteados al inicio de esta sección se resolverían directamente aplicando la fórmula anterior:
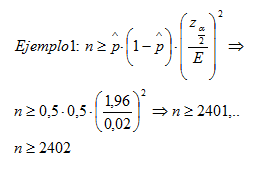 |
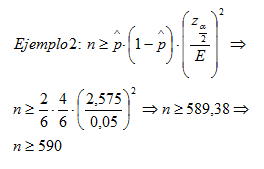 |
En la siguiente escena puedes calcular diversos tamaños muestrales variando los controles correspondientes al nivel de confianza, al error máximo admisible y se puede utilizar también en posibles ejercicios prácticos, para distintas proporciones.
La escena también dispone de la posibilidad de ver el cálculo de los valores críticos asociados al nivel de confianza y también del cálculo práctico de distintos casos de intervalos de confianza para que observes como en la práctica se cumple la acotación del error máximo admisible.
Consideremos dos nuevas situaciones:
Estas situaciones y otras muchas que se podrían plantear conducen al cálculo de un tamaño mínimo de muestra a partir del cual se cumplan determinadas condiciones en nuestra estimación de un parámetro poblacional como la media.
De la propia formulación del intervalo se observa que el tamaño que debe exigirse para una muestra depende fundamentalmente del nivel de confianza que se desee para los resultados, de la amplitud del intervalo de confianza o error máximo que se esté dispuesto a admitir y de la desviación típica poblacional o de la cuasi-desviación típica de la muestra en caso de que no se conozca aquella.
Fijados estos, simplemente despejando algebraicamente en las fórmulas, podemos calcular el tamaño mínimo de la muestra que debe utilizarse para cumplir con las premisas estipuladas.
Así pues para un nivel de confianza
$$\large (1-\alpha)$$Deduciendo de la fórmula correspondiente al error máximo admisible en el caso de la estimación de media poblacional con deviación típica conocida:
Llegamos a la siguiente expresión para el tamaño mínimo de muestra en el caso de estimación de una media poblacional con desviación típìca poblacional conocida
Deduciendo de la fórmula correspondiente al error máximo admisible en el caso de la estimación de media poblacional con deviación típica poblacional desconocida:
Llegamos a la siguiente expresión para el tamaño mínimo de muestra en el caso de estimación de una media poblacional con desviación típica poblacional desconocida
La solución a cada uno de los dos ejemplos planteados al inicio de esta sección sería:
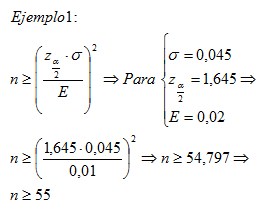 |
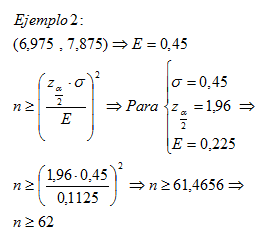 |
En la siguiente escena puedes calcular diversos tamaños muestrales variando los controles correspondientes al nivel de confianza y al error máximo admisible.
La escena también dispone de la posibilidad de ver el cálculo de los valores críticos asociados al nivel de confianza y también del cálculo práctico de distintos casos de intervalos de confianza para estimación de la media poblacional en los que puedes observar como se cumple en la práctica la acotación del error máximo admisible.
De la misma manera, puedes practicar en la siguiente escena en la que la desviación típica poblacional se sustituye por las cuasi-desviaciones típicas muestrales.
El tema de la estimación mediante intervalos de confianza tiene un recorrido práctico muy diverso. Fundamentalmente se trata de ejercicios de carácter muy técnico y que en la mayoría de los casos pasa por la utilización de una fórmula concreta y directa.
Es bueno disponer por tanto de un formulario resumen y sencillo al que acudir cuando se tiene alguna duda en cuanto a la fórmula a utilizar o en la expresión de la misma.
El siguiente cuadro resume todo el tema. Se han sombreado en color rosa las dos fórmulas fundamentales y en verde las que se deducen de las fundamentales.

A continuación tienes el enunciado de diferentes problemas. Trabájalos y una vez los hayas resuelto puedes hacer clic sobre el botón para ver la solución.
Juan Jesús Cañas Escamilla
José R. Galo Sánchez
Ronald Aylmer Fisher (Londres, Reino Unido, 17 de febrero de 1890 – Adelaida, Australia, 29 de julio de 1962) fue un estadístico y biólogo, responsable de la prueba exacta de Fisher y de la hipótesis nula presentado en su libro The Design of Experiments (1935) (https://es.wikipedia.org/). Crédito imagen: Desconocido, Dominio público.
Para decidir si cierta información relativa a un parámetro poblacional se puede considerar como cierta, en estadística se suelen utilizar los contrastes de hipótesis. Un contraste de hipótesis proporcionará unos criterios universales para valorar si la hipótesis que planteamos es cierta.
IDEA SOBRE UNA REGLA DE DECISIÓN
Cualquier persona a lo largo de su vida utiliza reglas de decisión ante situaciones concretas. Incluso esas reglas a veces son irracionales e incluso disparatadas.
 |
 |
 |
 |
Otras veces también se recurre a procedimientos mucho más lógicos y científicos.
En estadística para decidir sobre dos situaciones competitivas, complementarias y excluyentes recurriremos al procedimiento conocido por el nombre de Contraste de Hipótesis.
Un ejemplo sencillo. Pensemos en una moneda de la que sospechamos sobre su autenticidad. A simple vista no se diferencia en nada de una auténtica. Podríamos realizar la experiencia de lanzar al aire dicha moneda y contabilizar el número de caras o cruces que se obtienen. Nuestra experiencia nos dice que la probabilidad de obtener cara en una moneda normal es $0,5$, pero, ¿y si sospechamos que no es así? Evidentemente en este caso la probabilidad de que salga cara deberá de ser muy diferente a 0,5. Al primer planteamiento, suponer que la probabilidad de que salga cara es $0,5$ , le llamamos hipótesis nula ($H_0$) y al segundo planteamiento, hipótesis alternativa ($H_1$).
Para aceptar o rechazar una de las hipótesis, necesitamos realizar un experimento y establecer unas reglas que nos ayuden a decidir si se acepta (H0 ) o no. En el ejemplo de la moneda, el experimento podría ser lanzar la moneda 15 veces y observar los resultados. Las reglas tendrán en cuenta el posible error asociado a cada decisión y dependerán de los riesgos que estemos dispuestos a asumir. Un ejemplo de regla de decisión conservadora:
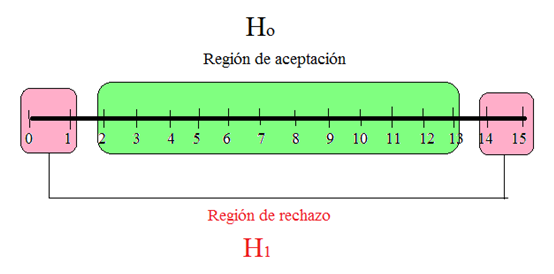
Es decir, lanzamos una moneda al aire $15$ veces y aceptamos la hipótesis nula (la moneda no está trucada) si el número de caras obtenidas está entre 2 y 13. Si ($H_0$) es cierta y el resultado de nuestro experimento es $0$ o $1$ caras, o bien $14$ o $15$ caras, evidentemente nos equivocamos al rechazar la hipótesis nula. En estos casos decimos que cometemos un error de tipo I o error $\alpha$. Por el contrario, si el resultado obtenido está entre $2$ y $13$ caras y sin embargo, es cierta ($H_1$), también nos equivocamos y decimos que cometemos un error de tipo II o error $\beta$.
Una hipótesis estadística es una afirmación o proposición respecto a alguna característica de una población, generalmente fundamentada sobre un parámetro de la misma. Contrastar una hipótesis es comparar las predicciones con la realidad que observamos ocurrida en una muestra. Si dentro del margen de error que estamos dispuestos a admitir, hay coincidencia, aceptaremos la hipótesis y en caso contrario la rechazaremos.
Hipótesis nula. Lo de “nula” viene de que partimos del supuesto de que las diferencias entre el valor verdadero del parámetro y su valor hipotético, en realidad no son tales sino debidas al azar, es decir no hay diferencia o dicho de otra forma la diferencia es nula. Hipótesis alternativa (en algunos textos también aparece la notación $H_a$.Por ejemplo:
Normalmente cuando queremos plantear las hipótesis de una determinada situación debemos tener en cuenta que aquello que queramos demostrar irá siempre a la hipótesis alternativa ya que el error que cometemos cuando rechazamos $H_0$ lo podemos medir (está fijado de antemano por el nivel de significación).
Piensa en los ambientes judiciales. La labor del fiscal pasa por demostrar que alguien ha cometido un delito. Es decir que trabajaría como hipótesis alternativa.
 Por el contrario, el abogado defensor no tiene que demostrar, su labor es más defensiva ya que si el fiscal no demuestra su acusación entonces el reo será declarado (no culpable), es decir, inocente. Evidentemente esto es un planteamiento muy simple de la situación ya que a menudo los abogados defensores van más allá de la pura estrategia defensiva y tratan de demostrar la inocencia, aunque siempre subyace el lema in dubio pro reo, (en caso de duda, a favor del reo) al que todos estamos acostumbrados o el de es preferible no condenar a $10$ culpables que condenar a un solo inocente.
Por el contrario, el abogado defensor no tiene que demostrar, su labor es más defensiva ya que si el fiscal no demuestra su acusación entonces el reo será declarado (no culpable), es decir, inocente. Evidentemente esto es un planteamiento muy simple de la situación ya que a menudo los abogados defensores van más allá de la pura estrategia defensiva y tratan de demostrar la inocencia, aunque siempre subyace el lema in dubio pro reo, (en caso de duda, a favor del reo) al que todos estamos acostumbrados o el de es preferible no condenar a $10$ culpables que condenar a un solo inocente.
bilateral a aquél en el que la hipótesis nula se formula en términos de igual y la alternativa en términos de distinto. En estos casos la región de aceptación sería el área central determinada por los valores críticos que previamente son determinados por el nivel de significación.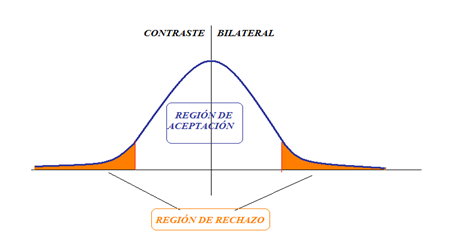
unilateral derecho a aquél en el que la hipótesis nula se formula en términos de menor o igual y la alternativa en términos de mayor. En estos casos la región de aceptación sería el área que deja a su izquierda el valor crítico que previamente determina el nivel de significación.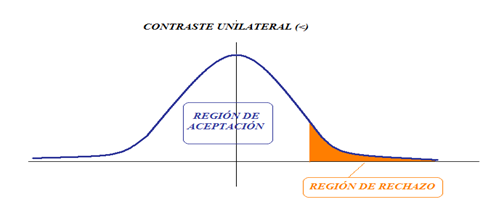
unilateral izquierdo a aquél en el que la hipótesis nula se formula en términos de mayor o igual y la alternativa en términos de menor. En estos casos la región de aceptación sería el área que deja a su derecha el valor crítico que previamente determina el nivel de significación.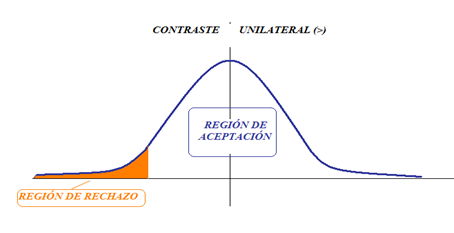
En los ejemplos planteados al principio, el primero sería un contraste bilateral, el segundo y tercero unilaterales izquierdos.
El planteamiento general de cualquier problema en el que se quiera contrastar una determinada hipótesis debe reunir siempre los siguientes puntos:
hipótesis alternativa.

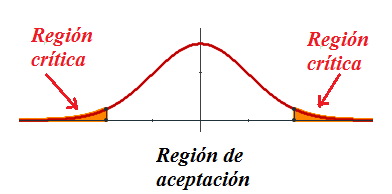
En la siguiente escena puedes practicar con la localización de la región crítica en contrastes bilaterales.
La escena te lo proporciona directamente aunque te recomendamos que utilices la tabla de la normal y después compares tus resultados con los que ofrece la escena.
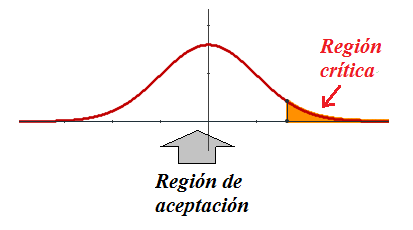
En la siguiente escena puedes practicar con la localización de la región crítica en contrastes bilaterales.
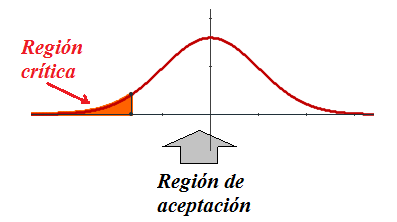
En la siguiente escena puedes practicar con la localización de la región crítica en contrastes bilaterales.
La escena te lo proporciona directamente aunque te recomendamos que utilices la tabla de la normal y después compares tus resultados con los que ofrece la escena.
El valor en este caso del estadístico de contraste sería:
$$\text{Cuasi } \^S =\sqrt{\frac{40}{39}}\cdot 5,345 \implies \^S = 5,413 \implies \frac{103,25 -100}{\frac{5,413}{\sqrt{4}}} = 3,797$$
Resumimos todo en el siguiente ejemplo:
Un informe de la Asociación de Compañías Aéreas (ACA) indica que el precio medio del billete de avión desde la ciudad A a la ciudad B es de $120$ euros. Para contrastar esta información se considera una muestra aleatoria de $100$ viajeros entre estas dos ciudades que volaron en distintas compañías, en la que se observó que la media del billete era de $128$ euros y una desviación típica de $40$ €.
¿Se puede considerar con un nivel de significación del $1\%$ que la información de la ACA es correcta?
El estadístico de contraste en este caso es la media muestral que tipificada quedaría:
$$Z= \frac{\overline{X}-\mu_0}{\frac{\^S}{\sqrt{n}}}$$La región de aceptación es:
$$1-\alpha = 0,99 \implies \begin{cases} -Z_{\alpha /2} &= -2,575\\ Z_{\alpha /2} &= 2,575 \end{cases}$$$\text{Valor particular de } S_0 = 40 \implies \^S = \sqrt{\frac{100}{99}} \cdot 40 = 1,005\cdot 40 = 40,2015$
$$Z = \frac{128-120}{40,2015/10} = 1,9899$$El valor estadístico de contraste cae dentro de la región de aceptación $1,9899 \in (-2,575, 2,575)$, se acepta por tanto la hipótesis nula.
También podría razonarse teniendo en cuenta la región de aceptación como el intervalo de confianza para la media:
$$\Big(120-2,575\cdot \frac{40,2015}{10}, 120+2,575\cdot \frac{40,2015}{10}\Big)$$ $$= (109,648, 130,252)$$El valor de la media muestral $128$ sí está dentro del intervalo (región de aceptación)
El aceptar la hipótesis nula significa que puede aceptarse que el precio medio de los billetes es de 120 euros. No hay indicios suficientes para decir que no sea cierto que la media de los billetes sea de $120$ euros y que las diferencias obtenidas con nuestra muestra pueden considerarse debidas al azar.
Para terminar este epígrafe, observa los siguientes vídeos.
Videos
En el primer vídeo puedes ver una clase resumen de planteamiento general de un problema de contraste de hipótesis. Y en el segundo otra clase de introducción al contraste de hipótesis.
Vamos a partir de un ejemplo: Se conoce que el $75\%$ de los alumnos de un centro de enseñanza realizan correctamente un test psicotécnico que lleva utilizándose mucho tiempo. Para tratar de mejorar este resultado, se modificó la redacción del test, y se propuso para realizar el experimento a un grupo de $120$ alumnos de ese centro, elegidos al azar. De los $120$ alumnos a los que se le pasó el nuevo test, lo realizaron correctamente $107$. ¿Podemos afirmar que la nueva redacción del test ha aumentado la proporción de respuestas correctas, a un nivel de significación = $0,025$?
La pregunta que se hace en el problema anterior, está formulada en términos de se puede "afirmar o demostrar", por tanto esto lo llevaremos a la hipótesis alternativa. es decir el planteamiento de contraste que consideramos idóneo para esta situación sería:
 $$\begin{rcases}
H_0 & : p\le 0,75 \\
H_1 & : p\gt 0,75
\end{rcases} \text{Ya que pretendemos demostrar que la}\\\text{proporción ha mejorado}$$
$$\begin{rcases}
H_0 & : p\le 0,75 \\
H_1 & : p\gt 0,75
\end{rcases} \text{Ya que pretendemos demostrar que la}\\\text{proporción ha mejorado}$$
El valor de la proporción muestral $p_0 = \frac{107}{120} = 0,89166$. Al ser un constraste unilateral derecho. Determinamos la región de aceptación y rechazo para un nivel de significación de $\alpha = 0,025$.
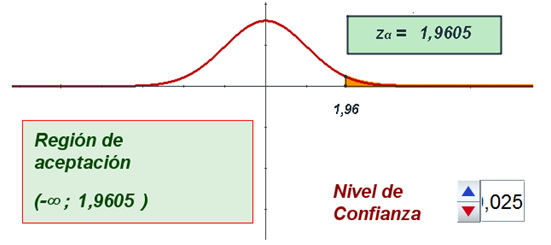
Calculamos ahora el estadístico de contraste:
$$Z = \frac{0,891666-0,75}{\sqrt{\frac{0,75\cdot (1-0,75)}{120}}} = \frac{0,141666}{0,03952847} = 3,5839$$ $$3,5839 \notin (-\infin, 1,96) \implies \text{ Rechazamos } H_0$$Conclusión:
A partir de los datos estadísticos obtenidos en la muestra, podemos concluir que existen evidencias estadísticamente significativas
$(\alpha = 0,025)$, que permiten demostrar que la nueva redacción aumenta el porcentaje de alumnos que realizan correctamente el test.
En la siguiente tabla se resumen de forma muy concisa toda la formulación necesaria para la realización de un problema de contraste para una proporción.

En las siguientes escenas se ofrece una esquematización de los pasos a dar en un contraste de hipótesis para una proporción para los casos de contraste bilateral, unilateral derecho o unilateral izquierdo.
En dichas escenas se pueden variar si se quiere manualmente los controles correspondientes a la proporción y al nivel de significación.
Puedes practicar tanto como desees. Es recomendable observar lo que ocurre con un contraste de una proporción para distintos niveles de significación.
Contraste de hipótesis bilateral para una proporción
Contraste de hipótesis unilateral derecho para una proporción
Contraste de hipótesis unilateral izquierdo para una proporción
Existen muchas situaciones en las que se pretende dilucidar si el parámetro media poblacional ha cambiado por algún motivo ocasional o inducido.
En estadística inferencial el barómetro universal que cuantifica si el cambio observado es fruto de las fluctuaciones propias del azar o bien se trata de un cambio mucho más importante o significativo es el contraste de hipótesis para la media. Partamos de un ejemplo:
 Con el fín de aumentar el consumo medio de los clientes, unos grandes almacenes deciden realizar una campaña de publicidad. La campaña consistirá en anuncios diarios en el periódico local y en la emisión de varias cuñas radiofónicas. Antes de la campaña, los datos de la gerencia del centro comercial reflejaban un consumo medio por cliente y día de $23,75$ euros con una desviación típica poblacional de $4,875$ euros. Después de la campaña se escogió una muestra aleatoria de $121$ clientes obteniéndose una media muestral de $25,34$ euros.
Con el fín de aumentar el consumo medio de los clientes, unos grandes almacenes deciden realizar una campaña de publicidad. La campaña consistirá en anuncios diarios en el periódico local y en la emisión de varias cuñas radiofónicas. Antes de la campaña, los datos de la gerencia del centro comercial reflejaban un consumo medio por cliente y día de $23,75$ euros con una desviación típica poblacional de $4,875$ euros. Después de la campaña se escogió una muestra aleatoria de $121$ clientes obteniéndose una media muestral de $25,34$ euros.
¿Puede afirmarse con un nivel de significación del $4,5\%$ que la campaña ha sido efectiva y que el consumo medio efectivamente ha aumentado?
De nuevo en la pregunta que se hace se menciona la palabra "afirmar o demostrar", por tanto, aquello que queremos demostrar lo llevamos a la hipótesis alternativa.
En este caso el planteamiento del contraste quedaría como sigue:
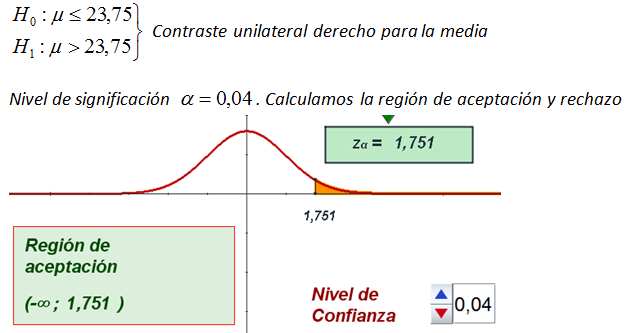
Cálculo estadístico de contraste:
$$\begin{rcases} \mu_0 &= 23,75\\ \sigma &= 4,875\\ n &= 121\\ \overline{X} &= 25,34 \end{rcases} \implies z=\frac{25,34-23,75}{\Big(\frac{4,875}{\sqrt{121}} \Big)} = 3,58769$$ $$3,58769 \notin (-\infin, 1,751) \implies \text{Rechazamos } H_0$$Conclusión:
A partir de los datos ofrecidos por la muestra, existen evidencias estadísticamente significativas (nivel de significación $0,04$) de que la media del consumo cliente/día es mayor de $23,75$ euros. Por tanto la campaña ha sido efectiva.
En la siguiente tabla se resumen de forma muy concisa toda la formulación necesaria para la realización de un problema de cualquier tipo de contraste para una media.
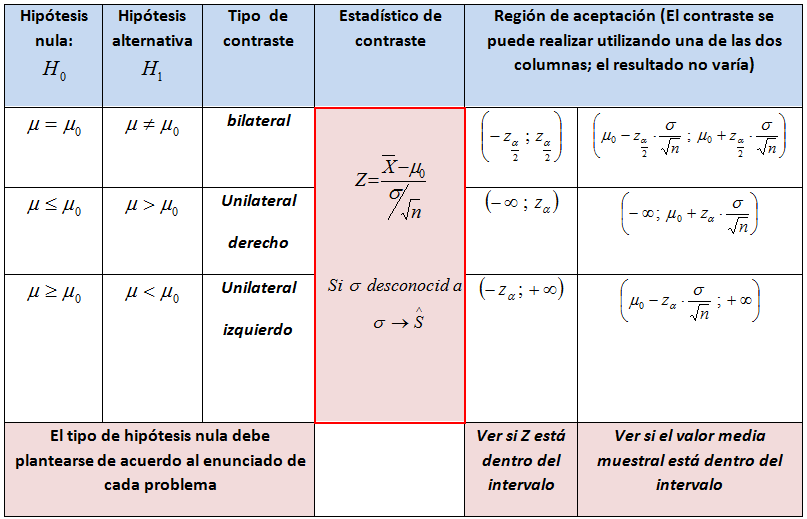
En las siguientes escenas se ofrece una esquematización de los pasos a dar en un contraste de hipótesis para una media en los casos de contraste bilateral, unilateral derecho o unilateral izquierdo.
En dichas escenas se pueden variar si se quiere manualmente los controles correspondientes a la media, al nivel de significación y también se puede elegir en el menú de opciones los casos de desviación típica poblacional conocida o desconocida.
Puedes practicar tanto como desees. Es recomendable observar lo que ocurre con un contraste de una media para distintos niveles de significación y también si varía mucho o poco la opción de desviación típica poblacional conocida o desconocida.
Contraste de hipótesis bilateral para la media
Contraste de hipótesis unilateral derecho para la media
Contraste de hipótesis unilateral izquierdo para la media
Todo lo que tiene relación con la Estadística Inferencial está acompañado de forma natural por el error. En los contrastes de hipótesis esto se pone mucho más de manifiesto ya que debemos elegir entre dos proposiciones antagónicas a partir de los datos que se reflejan en una determinada muestra aleatoria.
Asumiendo que la elección está en gran parte supeditada a estos valores concretos escogidos de una muestra específica, el error se antoja como algo natural y por tanto consustancial al propio proceso del contraste de hipótesis. Puesto que el error es protagonista irrenunciable, aprendamos a convivir con él, estudiarlo, acotarlo y por supuesto utilizarlo.
Lo primero de lo que podemos darnos cuenta es que existen dos tipos de errores que pueden ocurrir en el contraste y que uno de ellos es más fácil de manejar que el otro. Pensemos en el ejemplo de la moneda que no sabemos si está cargada o no. Si la prueba que realizamos para comprobar si esta moneda es buena o no es realizar por ejemplo $10$ lanzamientos y nuestra regla de decisión es que si salen entre 1 y 9 caras la consideramos buena y si por el contrario salen $0$ caras o $10$ caras la consideramos cargada. pensemos en lo que puede ocurrir.
Ahora bien, la probabilidad de que una moneda cargada se lance $10$ veces y obtengamos entre $1$ y $9$ caras no puedo calcularla ya que no sé qué probabilidad de salir cara tienen las monedas cargadas. El error por tanto no puedo controlarlo como antes, no tiene la misma naturaleza que el primero.
Este ejemplo puede ilustrar los dos tipos de errores que se pueden cometer al realizar un contraste de hipótesis.

Cuando se efectúa pues un contraste de hipótesis pueden ocurrir varias situaciones que conllevan a los denominados errores:
En la siguiente tabla se resumen todas las situaciones y errores posibles al realizar una prueba de contraste de hipótesis.
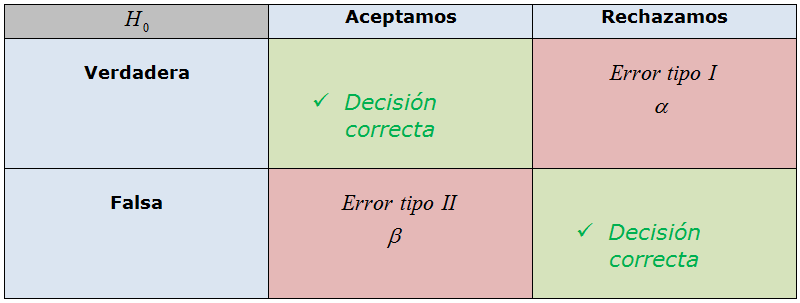
Como ya se ha mencionado, el error tipo I se comete cuando rechazamos la hipótesis nula pero en realidad no tendríamos que haberlo hecho puesto que era cierta. La probabilidad de que esto ocurra es el nivel de significación, valor que podemos controlar de antemano puesto que aparece en las premisas del contraste. Es interesante que sea un valor pequeño y a su vez lleve a un equilibrio de todo el proceso, puesto que un valor exageradamente pequeño de este nivel de significación conducirá prácticamente siempre al mismo resultado de aceptación de hipótesis nula del contraste.
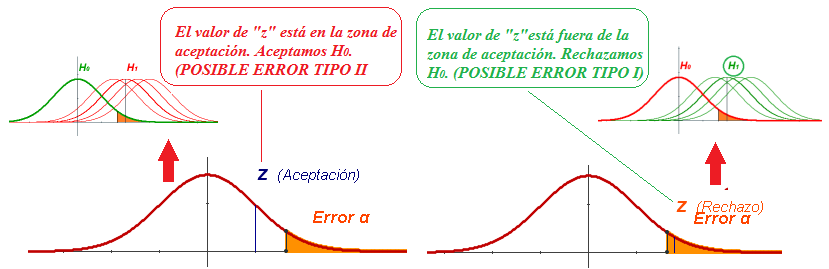
Los valores más usados para el nivel de significación en los trabajos de inferencia suelen ser.
$$\alpha = 0,05\\ \alpha = 0,01\\ \alpha = 0,1$$El hecho de que el error tipo I se pueda controlar da pie a que en muchos casos en los que no se observa bien lo que debe considerarse como hipótesis nula, incluso existen problemas en editoriales diferentes con el mismo enunciado y con dos versiones distintas.
En este sentido se pueden dar las siguientes sugerencias para el planteamiento adecuado de un contraste:
En las siguientes escenas puedes aclararte un poco con el concepto de error tipo I.
Hay una escena por cada tipo de contraste, bilateral, unilateral izquierdo y unilateral derecho.
Puedes cambiar los controles con los valores que desees. Trata de interpretar las distintas situaciones que van apareciendo. Quizás el control más determinante sea el de las "medias muestrales".
A medida que este control aumenta o disminuye, el valor del estadístico "$z$" sale o entra en la región crítica.
Observa también que la imagen que aparece pequeña en la parte superior derecha de la escena, cambia en el momento en el que "$z$" sale o entra en la región crítica. Intenta dar una explicación a dicho cambio.
Situación general de error tipo I en contraste bilateral
Situación general de error tipo I en contraste unilateral izquierdo
Situación general de error tipo I en contraste unilateral derecho
Cuando no se rechaza $H_0$, siendo falsa, se puede cometer el error denominado error tipo II. (también denominado error beta).
Pero ¿cuál es beta? De hecho, sería una información ciertamente relevante poder comunicar en un estudio de contraste el valor de este tipo de error. En los paquetes estadísticos no se da información de este error ya que sería necesario concretar el valor de $H_1$. Sin embargo si que se puede especular un poco con el error tipo II haciendo alguna suposición más o menos dirigida.
Supongamos que queremos demostrar que la edad media de los asistentes a cierto concierto es más de $18$ años con un nivel de significación del $4,5\%$.
Se sabe que la desviación típica poblacional es $3,6$ años. Para ello se consideró una muestra de $36$ individuos para la que se obtuvo una media de $19$.
Planteando el problema, se tendrá:
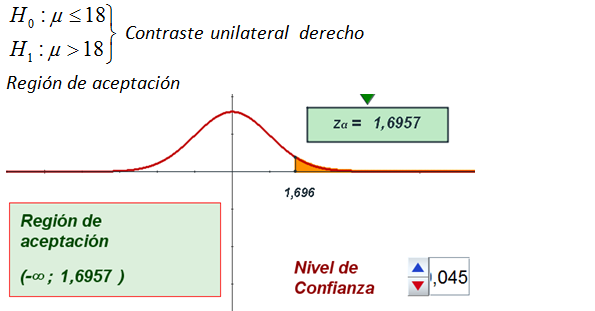
Estadístico de contraste:
$$z = \frac{19-18}{\Big(\frac{3,6}{\sqrt{36}}\Big)} = 1,666$$ $$1,666 \in (-\infin, 1,6957)$$Aceptamos por tanto la hipótesis nula. La hubiéramos aceptado siempre que:
$$z = \frac{\overline{X} - 18}{\Big(\frac{3,6}{\sqrt{36}}\Big)} \lt 1,6957 \implies \overline{X} -18 \lt 1,01742\\ \implies \overline{X} \lt 19,01742$$Es decir, hubiéramos aceptado la hipótesis nula para cualquier media muestral menor de $19,01742$.
Ahora y haciendo una suposición no estadística de que en realidad la media de edad de los asistentes era mayor de $18$ (nos quedamos con un valor cercano y redondo por ejemplo de $20$) ¿Cuál sería la probabilidad de que en la distribución de las medias muestrales de tamaño $36$ de una población en la que $\mu =20$ nos encontremos medias de menos de $19,01742$
$$\overline{X} \to N\Bigg(20, \frac{3,6}{\sqrt{26}}\Bigg) \implies p(\overline{X}\le 19,01742)\\ = \Bigg(z \le \frac{19,01742-20}{\frac{3,6}{\sqrt{26}}}\Bigg) = p(z \le -1,64) = 0,0505$$
La siguiente imagen ilustra la situación típica para el error de tipo II
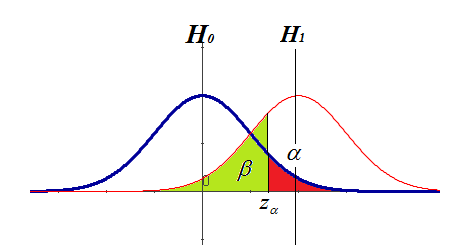
En las siguientes escenas se plantean las situaciones habituales de error tipo II para contraste unilateral izquierdo y unilateral derecho. En la escena se ha propuesto de antemano una $H_1$ más o menos alejada de la $H_0$ sin ningún criterio estadístico claro, salvo quizás el de que se aprecie claramente la situación que se produce en tanto al error tipo II.
En las escenas debes observar los controles y como influyen en el resultado del contraste. También es importante que aprecies que en el momento en que se acepta la hipótesis nula por estar el valor del estadístico "$z$" dentro de la zona de aceptación, en la parte inferior aparece el cálculo del posible error tipo II. Importante también es entender que en el momento en que se rechaza la hipótesis nula, desaparece la posibilidad de calibrar el error tipo II.
Situación general de error tipo II en contraste unilateral izquierdo
Situación general de error tipo II en contraste unilateral derecho
A continuación tienes el enunciado de diferentes problemas. Trabájalos y una vez los hayas resuelto puedes hacer clic sobre el botón para ver la solución.
Barnett, V. & Lewis, T. (1994). Outliers in statistical data. Ed. Wiley.
Calot, G. (1974). Curso de Estadística Descriptiva. Madrid: Ed. Paraninfo.
García Pérez A. (1992). Estadística Aplicada: conceptos básicos. Madrid: Ed. Universidad Nacional de Educación a Distancia.
García Pérez A. (2000). Métodos avanzados de Estadística Aplicada. Madrid: Ed. Universidad Nacional de Educación a Distancia.
Quesada V., Isidro A. & López L.A. (1992). Curso y ejercicios de Estadística. Ciudad de Mexico: Ed. Alhambra Universidad.
Taylor, S.J. & Bogdan, R. (1987) Introducción a los métodos cualitativos de investigación. Barcelona: Ed. Paidós, SAICF.
Tucker, H. (1966) Introducción a la teoría matemática de las probabilidades y a la estadística. Ed. Vicens Vives.