ELECTRÓNICA DIGITAL
Conceptos y Métodos Básicos
Oscar Ignacio Botero Henao
Institución Universitaria Pascual Bravo
Córdoba (España)
2022
Título de la obra:
ELECTRÓNICA DIGITAL
Conceptos y Métodos Básicos
Autor:
Oscar Ignacio Botero Henao
Revisión:
Juan Guillermo Rivera Berrío
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN: 978-84-18834-46-2

Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
Tabla de contenido
Agradecimientos
Ofrezco mis más sinceros agradecimientos a las siguientes personas, debido a su apoyo y colaboración en la elaboración de este Libro Interactivo de Aprendizaje (LIA).
- Doctor Juan Guillermo Rivera Berrio
- Magister y Profesor Ramiro Antonio Lopera Sánchez
- Magister y Profesor Sergio Hernando Ruiz Obando
- Profesor José María Fernández
- Profesional Gustavo Adolfo Tobón Pereira
- Mónica María Díaz Moreno (esposa)
Prefacio
DATOS DEL AUTOR: OSCAR IGNACIO BOTERO HENAO
-
► Magister en Gestión de la Tecnología Educativa (UdeS)
-
► Especialista en Administración de la Informática Educativa (UdeS)
-
► Ingeniero de Sistemas (FUMC)
-
► Especialista Tecnológico en Sistemas Automáticos de Control (En otra hora se llamaba Tecnológico Pascual Bravo)
-
► Tecnólogo Electrónico (En otra hora se llamaba Tecnológico Pascual Bravo)
El contenido de este Libro Interactivo de Aprendizaje - LIA, con licencia Creative Commons, es de uso libre enfocado básicamente a la academia, con el fin de ofrecer una herramienta de consulta y aprendizaje en el área de la Electrónica Digital; igualmente, para los hobbistas de esta área.
Se abordan tópicos como:
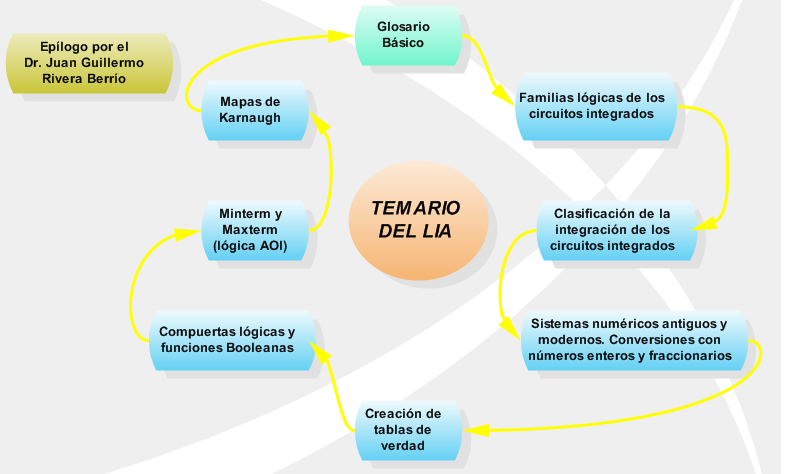
Se incluyen biografías simples de personajes fundamentales para esta área, notas informativas, fórmulas, ejemplos, ejercicios propuestos con respuesta y objetos interactivos de aprendizaje (OIA); que sirven de apoyo al aprendizaje del área de Electrónica Digital.
ESTILOS PARA PERSONAJES:

Nombre (Fechas de vida) Profesión y Nacionalidad. Biografía simple.
NOTAS COMPLEMENTARIAS:
NOTA: Información complementaria.
FÓRMULAS:
$$ 2n= No. de combinaciones posibles para un sistema digital $$
ETIQUETAS PARA LOS EJEMPLOS:
► Ejemplo: La etiqueta en color purpura indica que es uno o varios ejemplos solucionados como demostración.ETIQUETAS PARA LOS EJERCICIOS:
► Ejercicio: La etiqueta en color verde indica ejercicios con respuestas para que resuelva y autoevalúe el aprendizaje adquirido.OBJETOS INTERACTIVOS DE APRENDIZAJE - OIA:
Dando clic en la esquina superior derecha se expande el OIA.
Este Libro Interactivo de Aprendizaje (LIA) titulado "ELECTRÓNICA DIGITAL, Conceptos Básicos" contiene figuras a las cuales usted como usuario, le puede dar "CLIC" para que ejecute un "zoom" (ampliación de la imagen), con el objetivo de visualizarla en una ventana emergente de forma expandida y poder visualizarla plenamente. En las figuras expandibles observará el siguiente ícono dentro de ella.

!Ensaya! Dando clic sobre la imagen, observa si la figura es expandible.
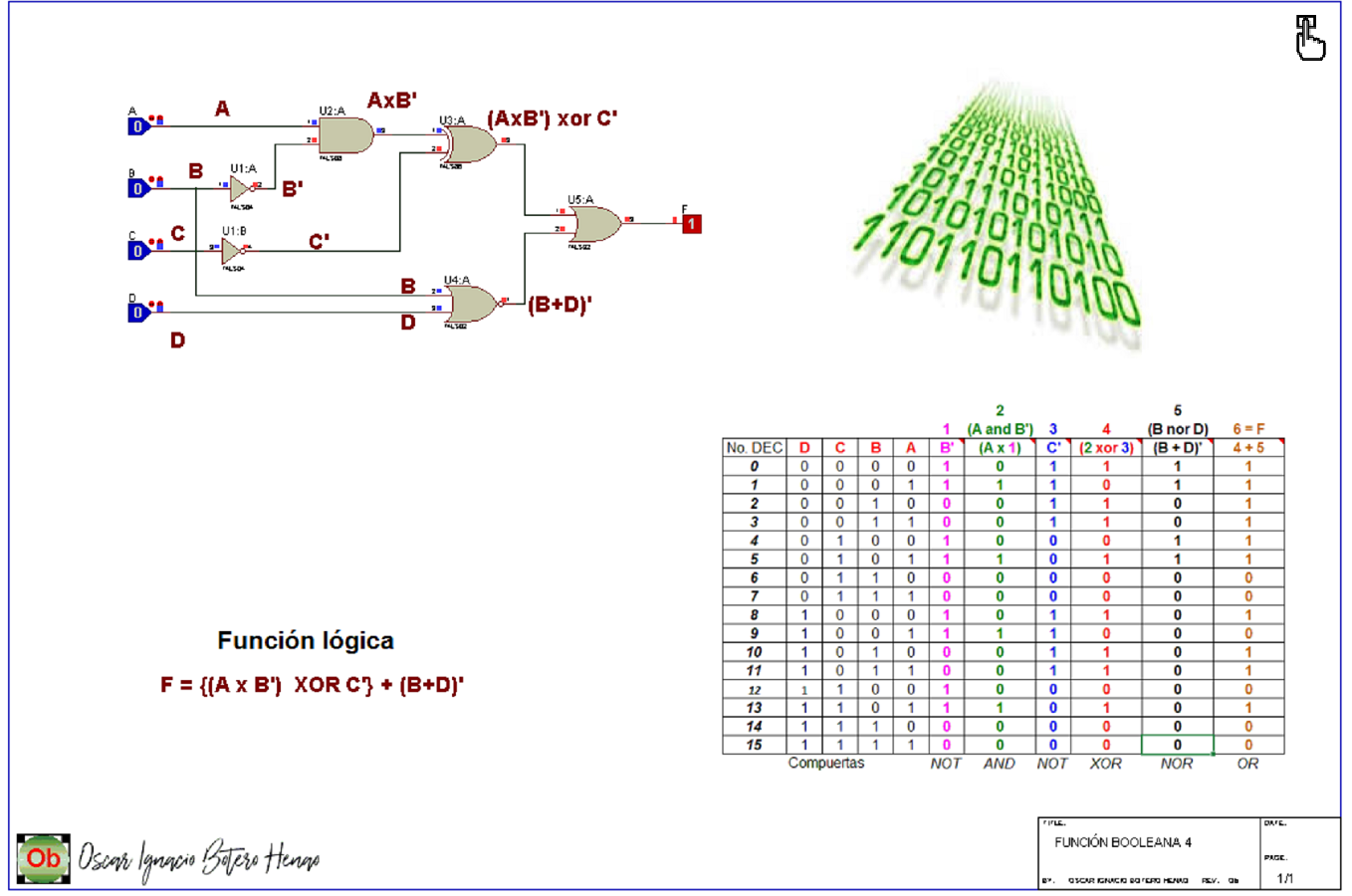
Haz clic sobre la imágen... y verás el resultado.
GLOSARIO
Glosario Básico
A continuación se muestra la definición de la terminología básica a nivel del área de la Electrónica Digital, el cual se trabajará en este capítulo del libro.
► BIT: es la mínima unidad de almacenamiento y se representa por un "0" o un "1" lógico.

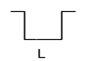
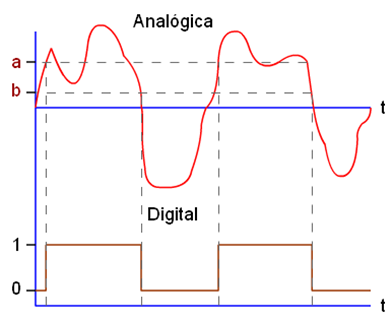
En el ejemplo de la figura 8, la señal digital toma el valor "1" cuando supera al valor a, y toma valor "0" cuando desciende por debajo del valor b. Cuando la señal permanece entre los valores a y b, se mantiene con el valor anterior.
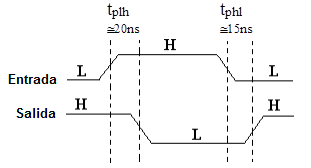
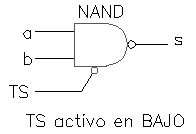
La compuerta se habilita cuando TS está en un nivel bajo "0", observar que la entrada TS tiene un círculo, el resto del comportamiento cuando está habilitada es el de una compuerta NAND común.
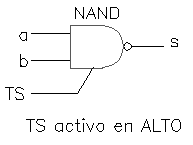
La compuerta se habilita cuando TS está en un nivel alto "1", observar que la entrada TS no tiene el círculo, el resto del comportamiento cuando está habilitada es el de una compuerta NAND común.
Objeto Interactivo de Aprendizaje - OIA
En el siguiente Objeto Interactivo de Aprendizaje ("OIA"), podrá autoevaluar el aprendizaje adquirido con respecto al glosario básico del área de la Electrónica Digital.
!Animate! a participar en esta actividad de refuerzo formativo.
El objetivo de esta actividad, es encontrar 10 palabras pertenecientes al glosario básico del área de la Electrónica Digital.
!Vamos!
Dando clic en la esquina superior derecha se expande el OIA.
FAMILIAS LÓGICAS DE CIRCUITOS INTEGRADOS
Familias Lógicas
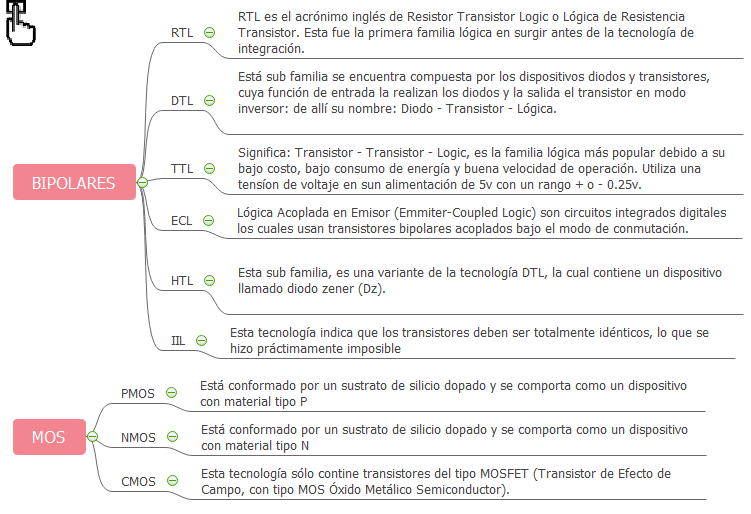
Familias lógicas TTL y CMOS
En la siguiente figura se procede a realizar una comparación de las características principales entre las dos familias lógicas más importantes, ellas son: TTL y CMOS:
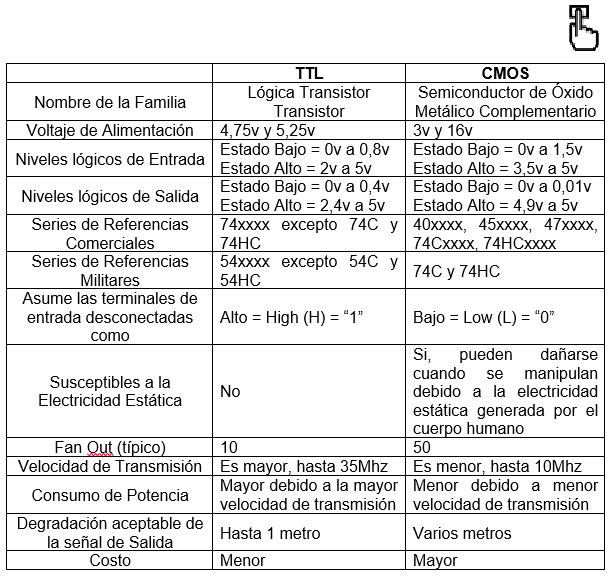
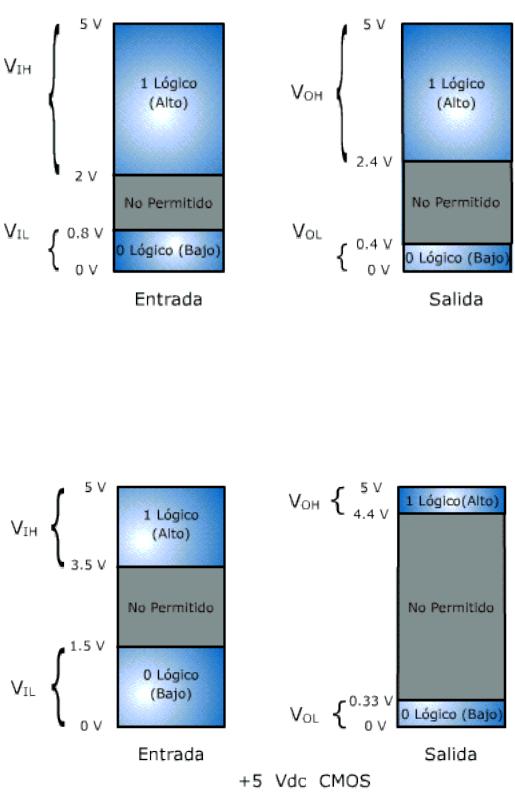
Comparación de los estados o niveles entre estas dos familias operando con 5v de alimentación, la zona blanca que se observa en la parte media, se le llama zona de incertidumbre, debido a que el diapositivo no detecta si es un "1" o un "0" lógico.
El siguiente video publicado en TikTok, en el canal CURSOS.GANT, se describen familias de circuitos digitales:
Vídeo:
En la siguiente página, hay otro video publicado en TikTok, en el canal LoFi(860862) - skollbeats que, también, describe familias de circuitos digitales.
CLASIFICACIÓN DE LA INTEGRACIÓN DE LOS CIRCUITOS INTEGRADOS
Clasificación
La clasificación del nivel de integración de los circuitos integrados depende de la cantidad de compuertas lógicas que contenga.
► SSI (SMALL SCALE INTEGRATION, INTEGRACIÓN A PEQUEÑA ESCALA): contiene hasta 10 compuertas lógicas. ► SMSI (MEDIUM SCALE INTEGRATION, INTEGRACIÓN A MEDIANA ESCALA): contiene entre 10 y 100 compuertas lógicas. ► LSI (LARGE SCALE INTEGRATION, INTEGRACIÓN A GRAN ESCALA): contiene entre 100 y 10.000 compuertas lógicas. ► VLSI (VERY LARGE SCALE INTEGRATION, INTEGRACIÓN A MUY ALTA ESCALA): contiene 10.000 y 100.000 compuertas lógicas. ► UVLSI (ULTRA VERY LARGE SCALE INTEGRATION, ULTRA ALTA ESCALA DE INTEGRACIÓN): contiene más de 100.000 compuertas lógicas.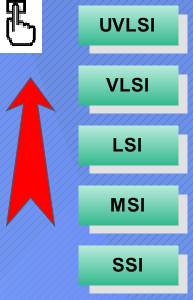
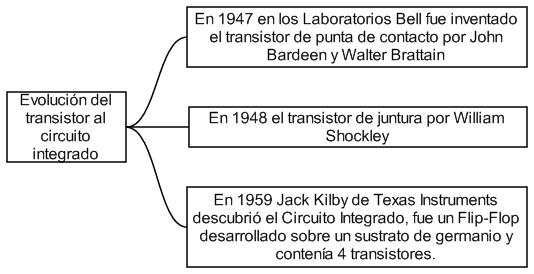
Personajes Históricos en la Electrónica

John Bardeen (1908-1991) Ingeniero Eléctrico y Físico estadounidense. Licenciado en física y matemáticas. En 1945 empezó a trabajar en los Laboratorios Bell de Nueva Jersey realizando investigaciones científicas alrededor de los semiconductores. En 1956 fue galardonado con el Premio Nobel de Física por su investigación en semiconductores y por el descubrimiento del efecto transistor. La primera aplicación se realizó en los audífonos.

Walter Houser Brettain (1902-1987) Físico chino. Terminada la guerra volvió a los laboratorios Bell y, trabajando en colaboración con otros eminentes físicos, prosiguió investigando en la línea anterior, centrando principalmente su estudio en el silicio y el germanio. En 1956 compartió el Premio Nobel de Física con los también físicos norteamericanos John Bardeen y William Shockley por el diseño del transistor de germanio, ingenio cuyo posterior desarrollo sería la base de los modernos microprocesadores y del formidable despegue de la informática. Autor de numerosos artículos sobre física del estado sólido, Walter Houser Brattain registró diversas patentes a lo largo de su vida.

William Bradford Schockley (1910-1989) Físico norteamericano. Doctorado por la Universidad de California, en 1953 fue nombrado director del departamento de transistores de la empresa Bell Telephone Company. Shockley colaboró con John Bardeen y Walter Houser Brattain en la construcción de dispositivos semiconductores que reemplazarán a los tubos de vacío.
En la figura a continuación se encuentran ubicados de izquierda a derecha los siguientes personajes: John Bardeen, William Bradford Shockley y Walter Houser Brattain.

NOTAS COMPLEMENTARIAS:
El transistor fue inventado en los Laboratorios Bell de Estados Unidos el 16 diciembre de 1947 por John Bardeen, Walter Houser Brattain y William Bradford Shockley, recibiendo el nobel de física en 1956 por esta investigación..

Jack St. Clair Kilby (1923-2005) ingeniero eléctrico y físico estadounidense. Inventor del circuito integrado. En su carrera, patentó más de 60 inventos. A partir de 1958 fue empleado de la compañía de semiconductores estadounidense Texas Instruments, donde desarrolló el microchip en este mismo año. En el 2000 recibió el Premio Nobel de Física.

Objeto Interactivo de Aprendizaje - OIA
En este objeto interactivo de aprendizaje debe depositar en cada contenedor el personaje correspondiente.
Dando clic en la esquina superior derecha se expande el OIA.
SISTEMAS NUMÉRICOS ANTIGUOS Y MODERNOS. Conversiones con números enteros y fraccionarios
Sistemas de Numeración
A lo largo de la historia de la humanidad, el ser humano ha buscado diferentes maneras de representar cantidades. Si nos remontamos hacia más de dos mil años, los pueblos de aquella época no utilizaban números para contar objetos, sino que hacían uso de cualquier elemento que pudiera servirles para contar, ya sea utilizando sus propios dedos, dibujando símbolos, marcando bastones (ramas) o haciendo nudos en una cuerda, entre otros.
Ahora bien, el primer uso que se le dio a los números, se relaciona con la necesidad de ordenar elementos y no con la de contar o medir objetos.
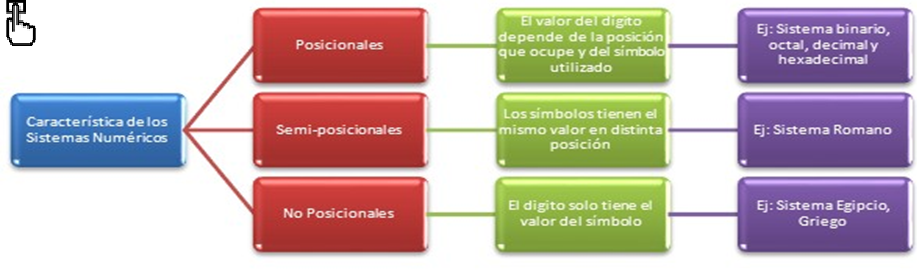
A continuación, la explicación de los 6 sistemas de numeración más característicos de la historia, reconociendo sus elementos principales y los símbolos que utilizaron para representar las cantidades establecidas.
Sistemas Numéricos Antiguos

- El sistema de numeración Egipcio
Los Egipcios han dejado un gran legado cultural, por sus monumentales construcciones, conocimientos y descubrimientos en agricultura, arte y matemáticas.
• El sistema numérico es no posicional. • Utilizado en medición de construcciones. • Contaban de 10 en 10. • No tenían representación para el número cero (0). • Utilizaban jeroglíficos para agrupar las unidades.

- El sistema de numeración Chino
La cultura china es una de las más completas y antiguas de la humanidad. Su legado perdura hasta la actualidad, ya que han sido gestores de grandes descubrimientos, realizando aportes importantes para la humanidad.
• El sistema numérico es posicional. • Utiliza 9 símbolos y las potencias de 10. • No tenían representación para el número cero (0).

- Los sistemas de numeraciones Griegos (Ático y Jónico)

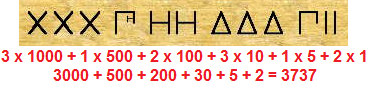
Este sistema utilizaba las 24 letras del alfabeto griego, junto con algunos otros símbolos, tal como muestra la siguiente figura:

- El sistema de numeración Romano
Es el sistema de numeración que ha perdurado en el tiempo. Actualmente se utiliza para numerar capítulos o escenas de una obra de teatro, para designar el nombre de algunas autoridades (como emperadores, reyes y papas), para ordenar los contenidos de un índice y los tomos de una enciclopedia, entre otros.
• El sistema numérico es semiposicional. • Se utilizan letras mayúsculas y reglas.
► Ejemplos:
- El sistema de numeración Maya
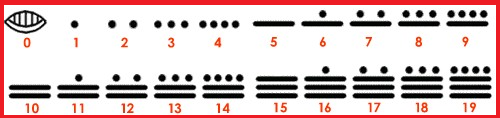
Analizando los símbolos que se presentan, se puede observar que el número 14 está formado por 2 rayas y 4 puntos. Como las rayas representan al 5 y los puntos al 1, se multiplica 2×5 y 4×1, obteniendo un total de 10 + 4 = 14.
► Ejemplo:Para escribir números iguales o superiores al número 20, las cifras adquirían un valor que dependía de la posición en donde se encontraban, disponiéndose en columnas y asignándole un valor de abajo hacia arriba, en el que hay que multiplicar el valor de cada cifra por 1, 20, 20×20, 20x20x20… según el lugar que ocupe, como se observa a continuación:
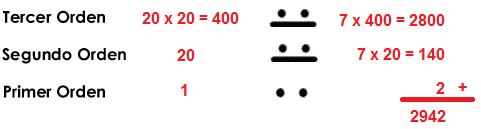
- El sistema de numeración Inca


Objetos Interactivos de Aprendizaje - OIA
En este OIA, arrastre cada Sistema Numérico Antiguo al contenedor correspondiente.
Dando clic en la esquina superior derecha se expande el OIA.
En la siguiente página, se presenta una unidad interactiva del proyecto @prende.mxEl proyecto @prende.mx es una iniciativa de la Secretaría de Educación Pública del gobierno mejicano a través de la cual busca la introducción de las TIC en la Educación., en la cual se puede explorar y aprender sobre las similitudes y diferencias entre el sistema decimal de numeración y el sistema maya.
Sistemas Numéricos Modernos en la Informática
Un sistema numérico es un conjunto de símbolos y reglas que se utilizan para representar cantidades.
Un número está constituido por una sucesión de dígitos situados ordenadamente a izquierda y a derecha de un punto de referencia (en los países anglosajones se utiliza un punto, mientras que en los latinos se utiliza una coma).
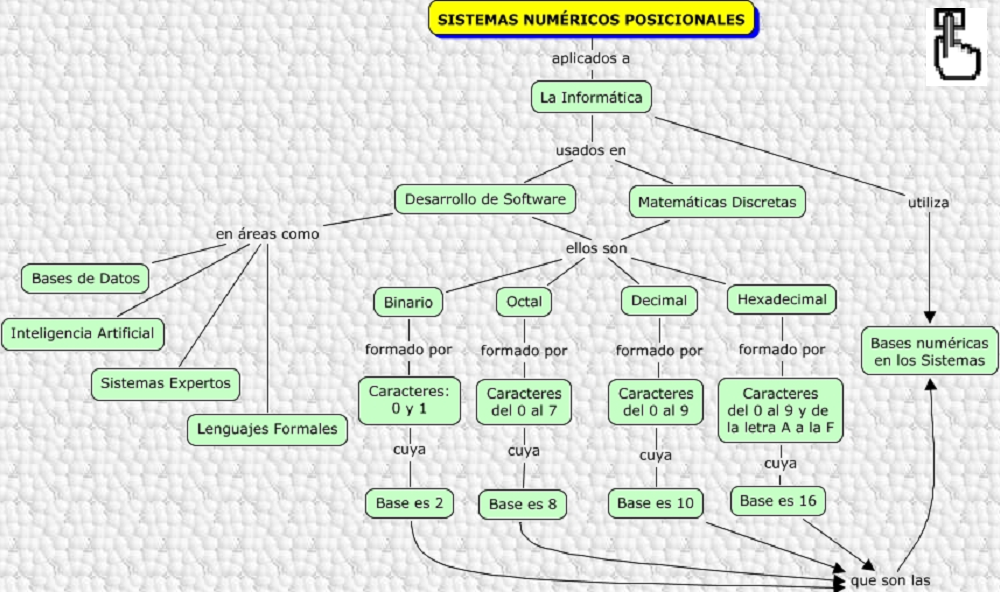
Los sistemas numéricos más utilizados son: decimal, octal y hexadecimal y la principal característica de estos sistemas es que utilizan una base de dígitos, es decir un sistema básico. Así:
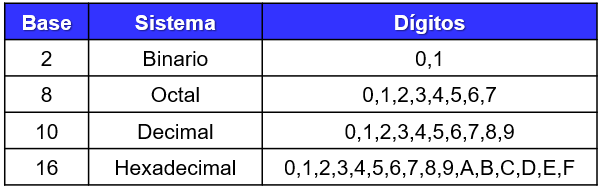
Para definir los números y sus bases, se escribirá el numero y se pondrá la base como subíndice.
• 11012 = 1101b = 1101 base binaria. • 678 = 67o = 67 base octal. • 4210 = 42d = 42 base decimal. • 5FA16 = 5FAh = 5FA base hexadecimal.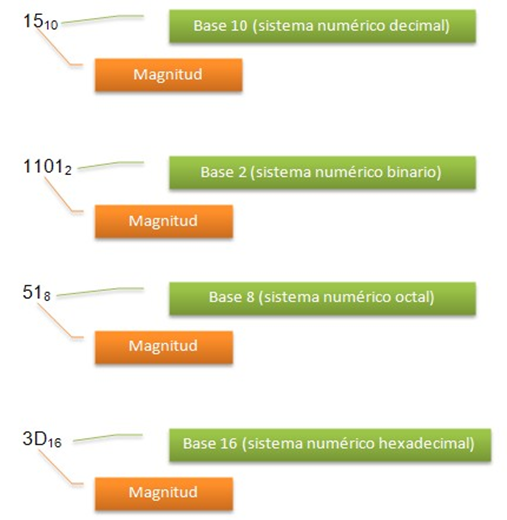
Al hablar de sistemas numéricos es necesario tratar el tema de las conversiones existentes entre unos y otros sistemas de numeración, dichos procesos son necesarios en las aplicaciones tecnológicas de electrónica y computación. La equivalencia entre un sistema y otro se logra realizando operaciones aritméticas básicas.
Conversiones entre Sistemas Numéricos
Conversión de Decimal a Binario
Para la conversión de la parte entera, se va dividiendo la cantidad decimal por 8 (divisiones sucesivas), tantas veces como sea posible, hasta que llegue a un cociente de 1. Luego, se toma el último "Cociente" y todos los "Residuos" comenzando con el último (bit más significativo - MSB) hasta llegar al primero (bit menos significativo - LSB).
► Ejemplo: • 27,375d a binario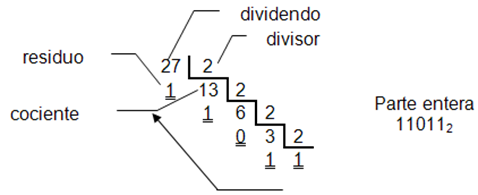
O también, así:
27 ÷ 2 = 13 y sobra 1
13 ÷ 2 = 6 y sobra 1
6 ÷ 2 = 3 y sobra 0
3 ÷ 2 = 1 y sobra 1
1
Parte entera = 11011
Para la conversión de la parte fraccionaria se multiplica por la base (2) sucesivamente hasta la cantidad de digitos que se requieran, se toman para la respuesta los números enteros de cada producto y lo que sobra lo sigue multiplicando por 2.
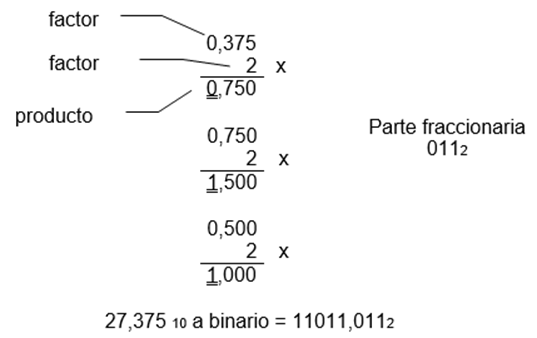
0,375 x 2 = 0 y sobra 0,75
0,75 x 2 = 1 y sobra 0,5
0,5 x 2 = 1 y sobra 0
Parte fraccionaria = 011
R/. 27,375d = 11011,011b
Los ejercicios con respuesta tiene como finalidad practicar la conversión de Decimal a Binario.
• 91,12d a binario = R/. 1011011,000111b • 146,56d a binario = R/. 10010010,10001111bEl siguiente video complementa su proceso de formación:
Vídeo:
Video realizado por Rafael Nuila, titulado "Convertir decimal a binario", licencia de atribución de Creative Commons.
En el siguiente Objeto Interactivo se aprecia el procedimiento de conversión de decimal a binario:
Conversión de Decimal a Octal
Para la conversión de la parte entera, se va dividiendo la cantidad decimal por 8 (divisiones sucesivas), tantas veces como sea posible, hasta que llegue a un cociente menor de 8. Luego, se toma el último "Cociente" y todos los "Residuos" comenzando con el último hasta llegar al primero.
► Ejemplo: • 310,625d a octal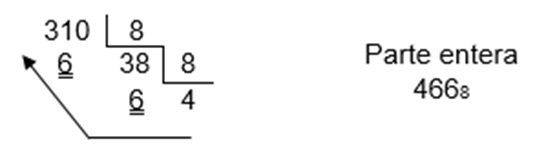
O también, así:
310 ÷ 8 = 38 y sobra 6
38 ÷ 8 = 4 y sobra 6
4
Parte entera = 466
Para la conversión de la parte fraccionaria se multiplica por la base (8) sucesivamente hasta la cantidad de digitos que se requieran, se toman para la respuesta los números enteros de cada producto y lo que sobra lo sigue multiplicando por 8.

0,625 x 8 = 5 y sobra 0
0
Parte fraccionaria = 5
R/. 310,625d = 466,5o
Los ejercicios con respuesta tiene como finalidad practicar la conversión de Decimal a Binario.
• 84,15d a octal = R/. 124,114o
• 125,3d a octal = R/. 175,231463o
Vídeo:
Video realizado por Rafael Nuila, titulado "Convertir decimal a octal", licencia de atribución de Creative Commons.
Conversión de Decimal a Hexadecimal
Se denomina Hexadecimal, porque "Hexa" hace alusión a las 6 letras que utiliza este sistema numérico y "Decimal" porque usa los caracteres del 0 al 9 (base decimal).
Para la conversión de la parte entera, se va dividiendo la cantidad decimal por 16 (divisiones sucesivas), tantas veces como sea posible, hasta que llegue a un cociente menor de 16. Luego, se toma el último "Cociente" y todos los "Residuos" comenzando con el último hasta llegar al primero.
► Ejemplo: • 158,25d a hexadecimal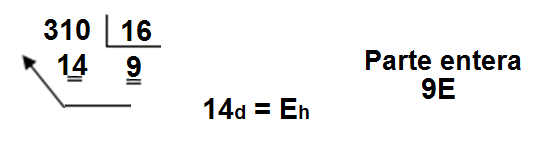
También se puede colocar de la siguiente forma:
158 ÷ 16 = 9 y sobra 14d = Eh
9
Parte entera = 9E
Para la conversión de la parte fraccionaria se multiplica por la base (16) sucesivamente hasta la cantidad de digitos que se requieran, se toman para la respuesta los números enteros de cada producto y lo que sobra lo sigue multiplicando por 16.
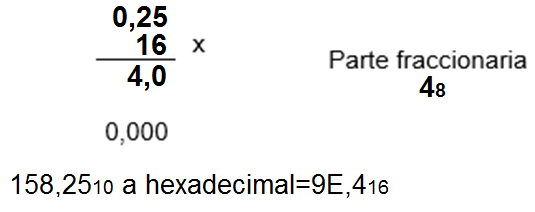
0,25 x 16 = 4 y sobra 0
0
Parte fraccionaria = 4
R/. 158,25d = 9E,4h
► Ejercicios:Los ejercicios con respuesta tiene como finalidad practicar la conversión de Decimal a Hexadecimal.
• 92,15d a hexadecimal = R/. 5C,266h
• 101,8d a hexadecimal = R/. 65,CCCh
Vídeo:
Conversión de Binario a Decimal
Para las conversiones de Binario, Octal y Hexadecimal al sistema numérico Decimal, se utilizará el "método de la suma de pesos".
Para realizar la conversión de binario a decimal, tome los dígitos de la parte entera desde el lado derecho y multiplique cada bit por 2 elevado a la potencia consecutiva (comenzando con 20), a esto se le denomina técnicamente "ponderar"; después de ello realice la suma de todos los resultados y el número resultante será el equivalente al sistema decimal.
Para la parte fraccionaria, tome los dígitos de izquierda a derecha con exponentes negativos comenzando con 2-1 y multiplique por cada bit que está en esa posición y finalmente sume los resultados de la parte fraccionaria.
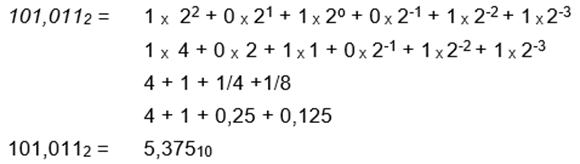
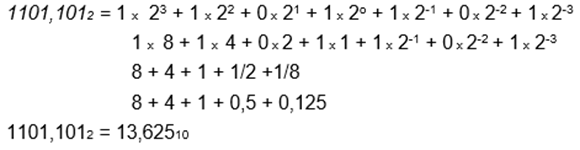
Observe el siguiente video para que complemente su proceso de formación:
Vídeo:
Conversión de Octal a Decimal
El sistema octal recibe ese nombre porque trabaja en base 8 y tiene un total de ocho símbolos que van desde el 0 hasta el 7.
Para convertir de octal a decimal simplemente tienes que coger el número en octal de derecha a izquierda y asignar a cada uno la potencia en base ocho que le corresponde, siendo la primera de todas 80 = 1.
► Ejemplos: • 374,25o a decimalParte entera: 374o = 3×82+7×81+4×80 = 192+56+4 = 252d
Parte fraccionaria: 0,25o = 2×8-1+5×8-2 = 0,25+0,078125 = 0,328125d
R/. 374,25o = 252,328125d
• 406,57o a decimalParte entera: 406o = 4×82+0×81+6×80 = 256+0+6 = 262d
Parte fraccionaria: 0,57o = 5×8-1+7×8-2 = 0,625+0,109375 = 0,734375d
R/. 406,57o = 262,734375d
Vídeo:
Conversión de Hexadecimal a Decimal
Multiplicamos el valor de posición de cada digito por el hexadecimal correspondiente.
El resultado del número decimal equivalente se obtiene, sumando todos los productos obtenidos en el paso anterior.
► Ejemplos: • 3AF,Dh a decimalParte entera: 3AFh = 3×162+A×161+F×160 = 768+160+15 = 943d
Parte fraccionaria: 0,Dh = D×16-1 = 0,8125d
R/. 3AF,DBh = 943,8125d
Parte entera: ABCh = A×162+Bx161+C×160 = 2560+176+12 = 2748d
Parte fraccionaria: 0,37h = 3x16-1+7×16-2 = 0,1875+0,02734375= 0,21484375d
R/: 406,57h = 262,734375d
Vídeo:
Conversión de Binario a Octal
Este método consiste en agrupar de a tres (3) bits. Para la parte entera se comienza de derecha a izquierda, o sea del bit menos significativo (LSB) hasta el más significativo (MSB), para la parte fraccionaria se procede a agrupar al contrario, o sea de izquierda a derecha. Cuando las cifras no estan completas, o sea de a tres (3) bits se completan con ceros (0) a la izquierda para la parte entera y con ceros a la derecha para la parte fraccionaria.
Hay que recordar que el sistema numérico octal va desde el número 0 hasta el número 7, lo que abarca un total de 8 caracteres.
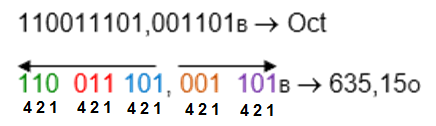
Parte entera: 001 001 011 011b, agrupados de a 3 bits = 1 1 3 3o
Parte fraccionaria: 101 000b, agrupados de a 3 bits = 5 0o
R/: 1001011011,1010b = 1133,50o
• 111010011,101011b a Octal
Parte entera: 111 010 011b, agrupados de a 3 bits = 7 2 3o
Parte fraccionaria: 101 011b, agrupados de a 3 bits = 5 3o
R/: 111010011,101011b = 723,53o
Conversión de Octal a Binario
Cada caracter octal se representa en 3 bits, tanto para la parte entera como la fraccionaria.
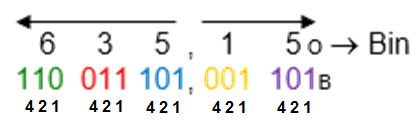
Parte entera: 3 7o, representados en 3 bits cada caracter = 011 111b
Parte fraccionaria: 6 1o, representados en 3 bits cada caracter = 110 001b
R/: 37,61o = 011111,110001b
• 152,731o a Binario
Parte entera: 1 5 2o, representados en 3 bits cada caracter = 001 101 010b
Parte fraccionaria: 7 3 1o, representados en 3 bits cada caracter = 111 011 001b
R/: 152,731o = 001101010,111011001b
Conversión de Binario a Hexadecimal
Este método es similar a la conversión de Binario a Octal, pero agrupando de a cuatro (4) bits. Para la parte entera se comienza de derecha a izquierda, o sea del bit menos significativo (LSB) hasta el más significativo (MSB), para la parte fraccionaria se procede a agrupar al contrario, o sea de izquierda a derecha. Cuando las cifras no estan completas, o sea de a cuatro (4) bits se completan con ceros (0) a la izquierda para la parte entera y con ceros a la derecha para la parte fraccionaria.
Hay que recordar que el sistema numérico hexadecimal consta de los números decimales del cero al nueve (0-9) hexa porque tiene 6 letras (A-F), lo que abarca un total de 16 caracteres.
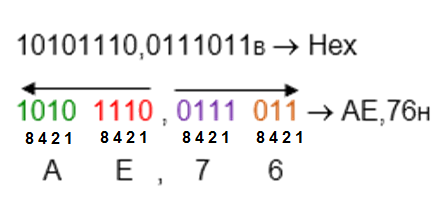
Parte entera: 0011 0110 1111b, agrupados de a 4 bits = 3 6 Fh
Parte fraccionaria: 1010 1100b, agrupados de a 4 bits = A Ch
R/: 1011011011,101011b = 36F,AC h
Parte entera: 0001 1110 1011b, agrupados de a 4 bits = 1 E Bh
Parte fraccionaria: 1000 1010b, agrupados de a 4 bits = 8 Ah
R/: 111101011,1000101b = 1EB,8Ah
Conversión de Hexadecimal a Binario
Cada caracter hexadecimal se representa en 4 bits, tanto para la parte entera como la fraccionaria; similar a la conversión de octal a binario.
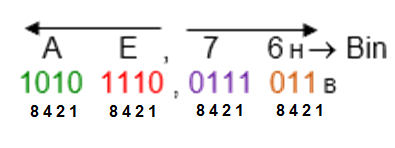
Parte entera: F 4 Ah, representados en 4 bits cada caracter = 1111 0100 1010b
Parte fraccionaria: 1 Bh, representados en 4 bits cada caracter = 0001 1011b
R/: F4A,1Bh = 111101001010,00011011b
Parte entera: 1 5 Bh, representados en 4 bits cada caracter = 0001 0101 1011b
Parte fraccionaria: 7 3 1h, representados en 4 bits cada caracter = 0111 0011 0001b
R/: 15B,731h = 000101011011,011100110001b
► Ejercicios propuestos con respuestas para practicar las diferentes conversiones y así verificar el nivel de aprendizaje::
• ¿111111111,10001b = hexadecimal? ➤ R/. 1FF,88h
• ¿1010111,11101b = octal? ➤ R/. 127,72o
• ¿142,75d = octal ➤ R/. 216, 6o
• ¿109,Eh = decimal? ➤R/. 265,875d
• ¿375,25o = hexadecimal? ➤ R/. FD,54h
• ¿357,15o = binario? ➤ R/. 11101111,001101b
• ¿A35,B7h = binario? ➤ R/. 101000110101,10110111b
• ¿197,8125d = hexadecimal? ➤ R/. C5,Dh
• ¿381,0Ah = octal? ➤ R/. 1601,024o
• ¿11010011,01101b = decimal? ➤ R/. 211,40625d
• ¿301,75d = binario? ➤ R/. 100101101,11b
• ¿164,15o = decimal? ➤ R/. 116,203125d
En el siguiente OIA, diseñado por Alfredo Sierra, puede convertir números de un sistema a otro.
Ingrese, en primer lugar, el número a convertir. Luego haga clic sobre uno de los seis botones de conversión. Los números hexadecimales se deben escribir en mayúscula.
CREACIÓN DE TABLAS DE VERDAD
Variables y Combinaciones para crear una tabla de verdad
Para crear una tabla de verdad se utiliza el sistema numérico binario, se le asigna a cada variable de la función una columna y por medio de la siguiente fórmula se obtiene el número de combinaciones que tendrá la tabla.
FÓRMULAS:
$$ 2n = Número de combinaciones posibles $$
$$ n = Cantidad de variables de la función $$
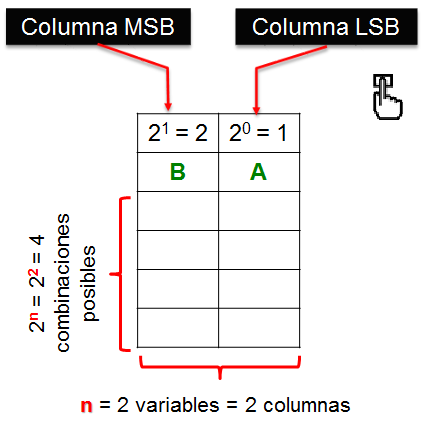
Las variables se asignan en orden de derecha a izquierda o sea del bit menos significativo (LSB) hacia el más significativo (MSB) y se hace en sistema numérico binario.
Tabla con una variable
La columna A tiene una ponderación de 1, lo que quiere decir que en esa columna se colocarán ꞌ0ꞌ y ꞌ1ꞌ alternados de a uno, comenzando con el ꞌ0ꞌ.
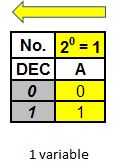
Tabla con dos variables
La columna A tiene una ponderación de 1, lo que quiere decir que en esa columna se colocarán ꞌ0ꞌ y ꞌ1ꞌ alternados de a uno, comenzando con ꞌ0ꞌ.
La columna B tiene una ponderación de 2, lo que quiere decir que en esa columna se colocarán ꞌ0ꞌ y ꞌ1ꞌ alternados de a dos, comenzando con ꞌ0ꞌ.
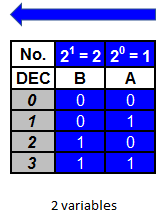
Tabla con tres variables
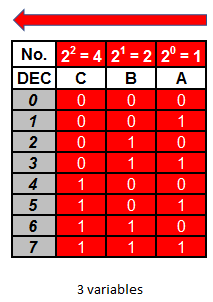
La columna A tiene una ponderación de 1, lo que quiere decir que en esa columna se colocarán ꞌ0ꞌ y ꞌ1ꞌ alternados de a uno, comenzando con ꞌ0ꞌ.
La columna B tiene una ponderación de 2, lo que quiere decir que en esa columna se colocarán ꞌ0ꞌ y ꞌ1ꞌ alternados de a dos, comenzando con ꞌ0ꞌ.
La columna C tiene una ponderación de 4, lo que quiere decir que en esa columna se colocarán ꞌ0ꞌ y ꞌ1ꞌ alternados de a cuatro, comenzando con ꞌ0ꞌ.
Tabla con cuatro variables
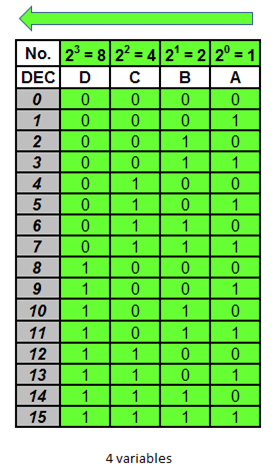
La columna A tiene una ponderación de 1, lo que quiere decir que en esa columna se colocarán ꞌ0ꞌ y ꞌ1ꞌ alternados de a uno, comenzando con ꞌ0ꞌ.
La columna B tiene una ponderación de 2, lo que quiere decir que en esa columna se colocarán ꞌ0ꞌ y ꞌ1ꞌ alternados de a dos, comenzando con ꞌ0ꞌ.
La columna C tiene una ponderación de 4, lo que quiere decir que en esa columna se colocarán ꞌ0ꞌ y ꞌ1ꞌ alternados de a cuatro, comenzando con ꞌ0ꞌ.
La columna D tiene una ponderación de 8, lo que quiere decir que en esa columna se colocarán ꞌ0ꞌ y ꞌ1ꞌ alternados de a ocho, comenzando con ꞌ0ꞌ. Y así sucesivamente, hasta completar todas las variables del sistema.
COMPUERTAS LÓGICAS Y FUNCIONES BOOLEANAS
George Boole

George Boole (1815-1864) Matemático Británico. Es el inventor del álgebra de Boole, que marca los fundamentos de la aritmética computacional moderna; en este sistema, las proposiciones se reducen a símbolos que se operan matemáticamente, lo que llevó a un avance fundamental de la lógica. A los 16 años enseñaba matemáticas en un colegio privado y más tarde fundó uno propio. En 1849 fue nombrado profesor de matemáticas del Queen's College, en Cork, donde permaneció el resto de su vida. Se destaca su obra Análisis Matemático de la Lógica (1847), donde plasmó sus primeras observaciones sobre los vínculos entre la lógica y las matemáticas que dio pie al nacimiento de la lógica matemática.
Compuertas Lógicas
Una compuerta lógica es un dispositivo electrónico con una función booleana propia, que realizan operaciones lógicas como: suma, multiplicación, niegan, afirman, incluyen o excluyen.
Las compuerta lógicas trabajan con niveles lógicos y no con los flancos de la señal.
El sistema numérico binario es el que se utiliza para los datos de entrada a la compuerta lógica, igualmente el que entrega en su salida.
Cada compuerta lógica tiene su complemento y son 8 en total.
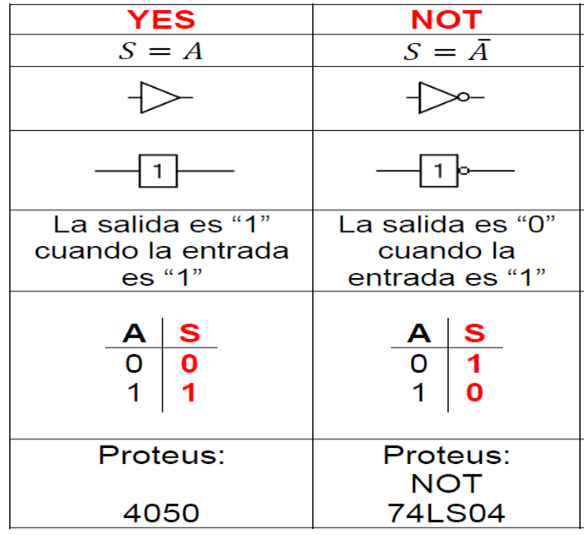
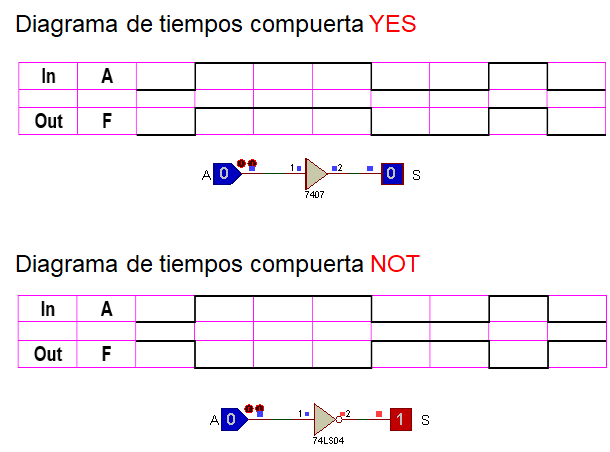
Compuertas YES y su complemento NOT
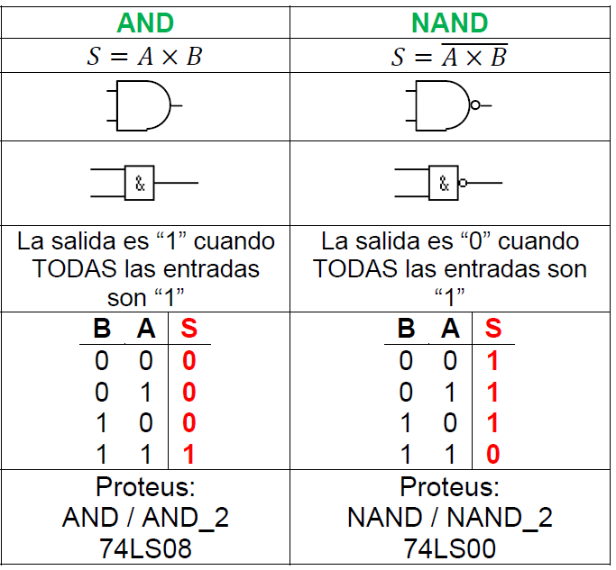
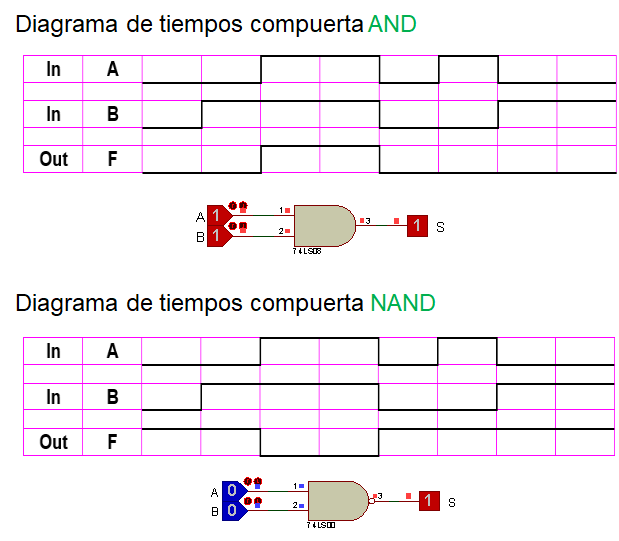
Compuertas AND y su complemento NAND
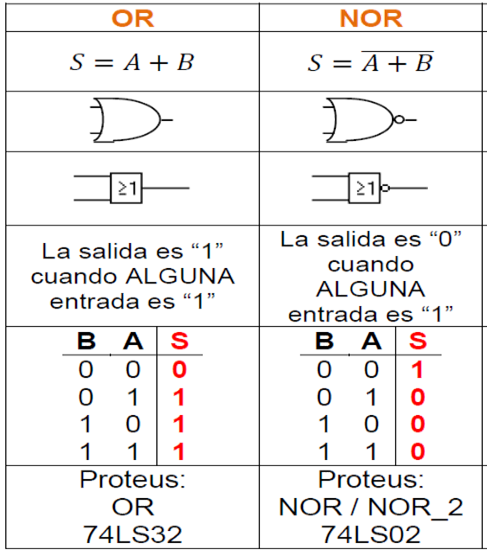
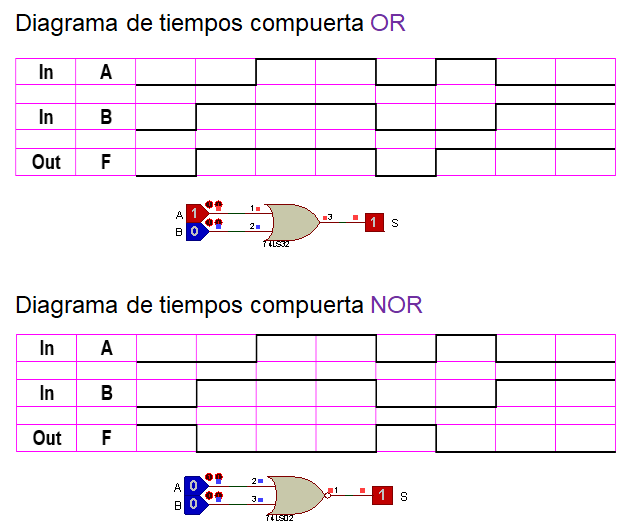
Compuertas OR y su complemento NOR
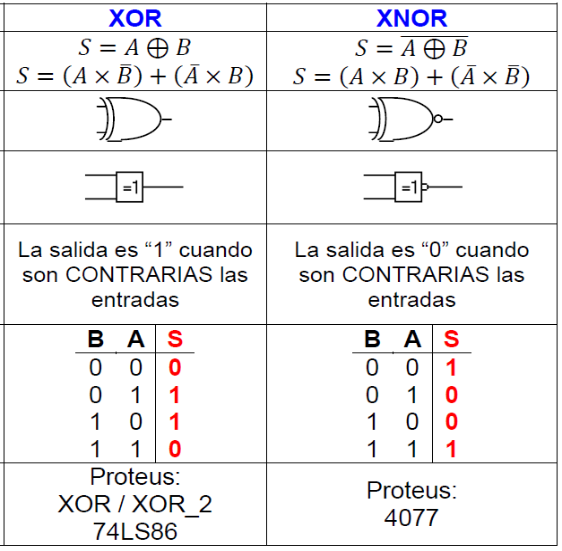
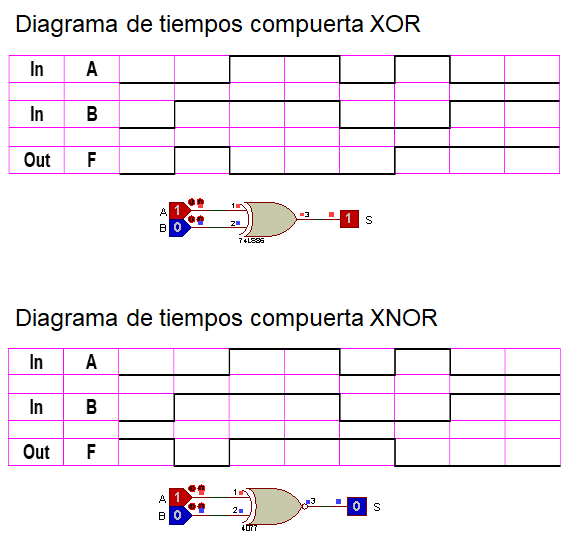
Compuertas XOR y su complemento XNOR
En el siguiente objeto interactivo de aprendizaje, diseñado por Juan Guillermo Rivera BerríoEl OIA se diseñó tomando como referencia la escena de MushroomFX, se describen las compuertas lógicas y su funcionamiento.
Referencias Comerciales de las Compuertas Lógicas

Estructura interna de las compuertas lógicas básicas
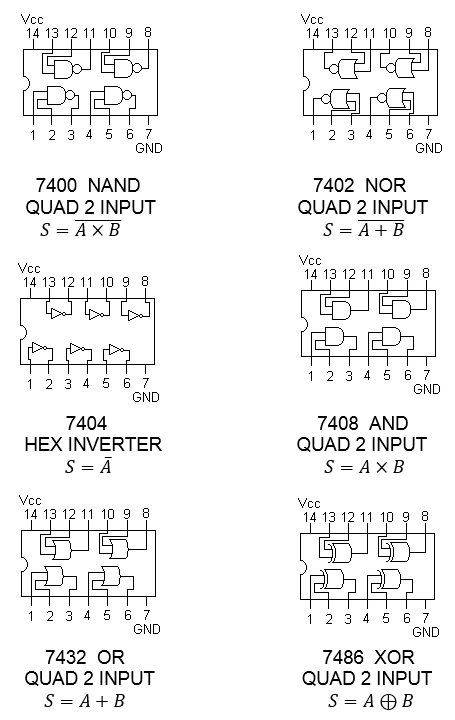
Estructura interna de las compuertas lógicas básicas en la familia TTL
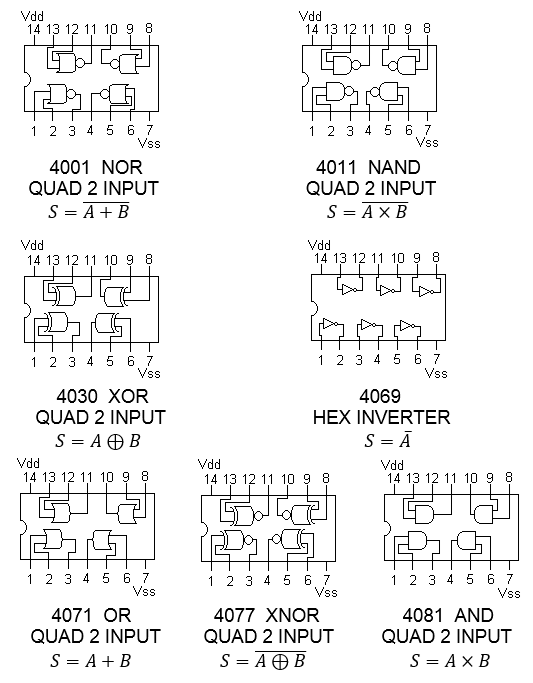
Estructura interna de las compuertas lógicas básicas en la familia CMOS (1 y 2 entradas)
Funciones Booleanas
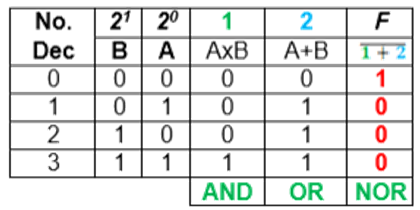
► Ejemplos: • Halle la tabla de verdad paso a paso y dibuje el circuito (plano esquemático - SCH), para la siguiente función Booleana: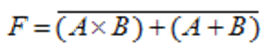
n = 2 variables (A y B)
2n = 22 = 4 combinaciones posibles
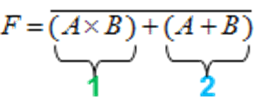
Vídeo:
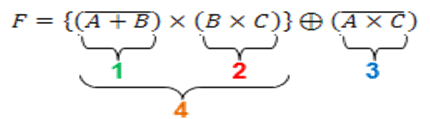
• Halle la tabla de verdad paso a paso y dibuje el circuito (plano esquemático - SCH), para la siguiente función Booleana:
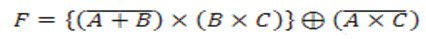
n = 3 variables (A, B y C)
2n = 23 = 8 combinaciones posibles
Vídeo:
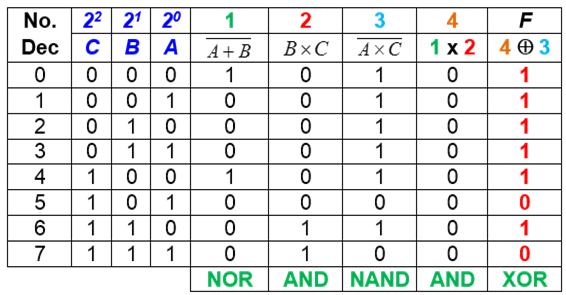
• Halle la tabla de verdad paso a paso y su función lógica, con base en siguiente circuito (pano SCH):
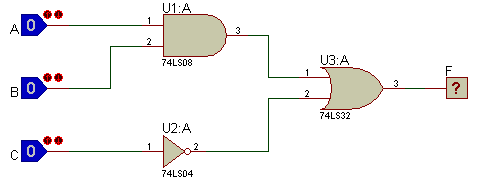
Se procede a estiquetar cada alambre comenzando por las entradas hasta llegar a la salida y así hallar la Función Booleana de la respuesta.
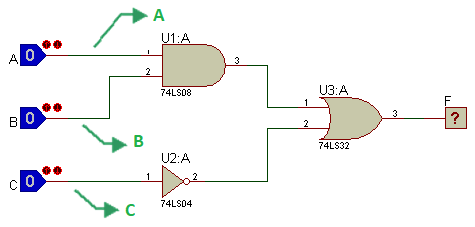
Ahora, se estiquetan los alambres de las salidas de las compuertas AND y NOT.
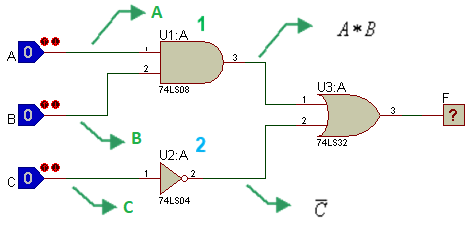
Finalmente, se estiqueta el alambre de la salida de la compuerta OR, que es la función Booleana final.
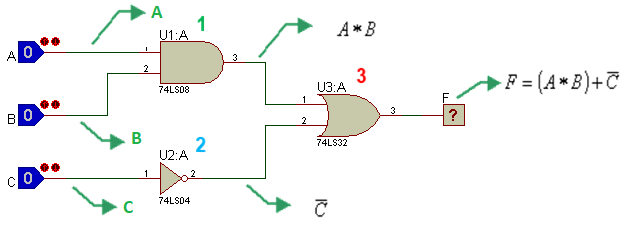
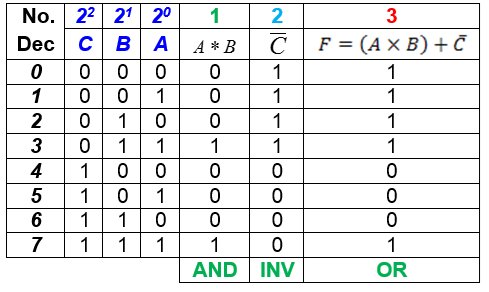
Se observa en la función Booleana obtenida en la salida que contiene 3 variables (A, B y C), lo que conlleva a una tabla de verdad de 8 combinaciones y se procede a elaborarla paso a paso
n = 3 variables (A, B y C)
2n = 23 = 8 combinaciones posibles
Vídeo:
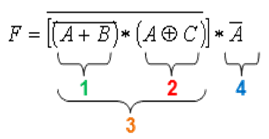
• Halle la tabla de verdad paso a paso y dibuje el circuito (plano esquemático - SCH), para la siguiente función Booleana:
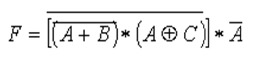
n = 3 variables (A, B y C)
2n = 23 = 8 combinaciones posibles
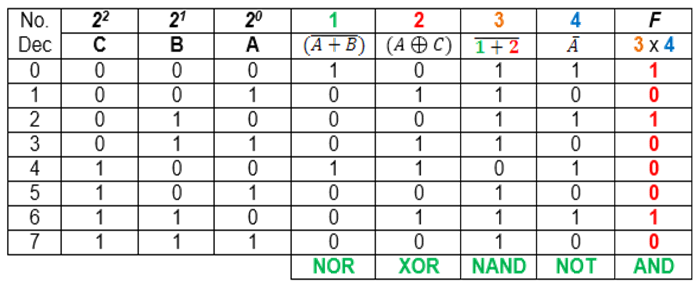
Vídeo:
► Ejercicios propuestos con respuestas para practicar Funciones Booleanas, con el fin de verificar el aprendizaje:
➤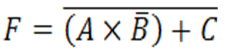
R/. en orden descendente en la tabla 1-0-1-1-0-0-0-0
➤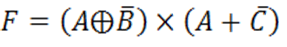
R/. en orden descendente en la tabla 1-0-0-1-0-0-0-1
➤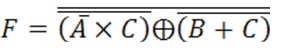
R/. en orden descendente en la tabla 1-1-0-0-1-0-1-0
➤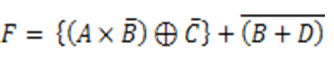
R/. en orden descendente en la tabla 1-1-1-1-1-1-0-0-1-0-1-1-0-1-0-0
Objeto Interactivo de compuertas lógicas
Una opción a Proteus, es usar el objeto interactivo diseñado por Buys de Barbanson, que se incluye en la barra de herramientas de este libro con el icono:
En el siguiente video se muestra cómo se puede simular el Ejemplo 1.
Vídeo:
MINTERM Y MAXTERM (Lógica AOI)
Introducción
En muchas ocasiones este método simplifica las funciones lógicas, pero su objetivo no es ese, es convertir una función lógica booleana con múltiples de tipos de compuertas lógicas, en sólo tres (3) tipos de compuertas (AND – OR – INV), por ello ha este sistema se le llama “Lógica AOI”, debido a las iniciales de las compuertas lógicas.
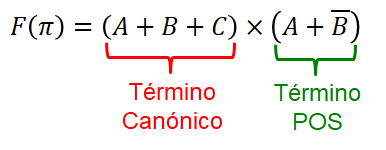
Término Canónico: es un término producto o suma en el cual aparecen declaradas todas las variables de la función lógica (negadas o no negadas).
Término Canónico Producto:
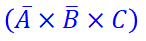
Término Canónico Suma:
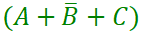
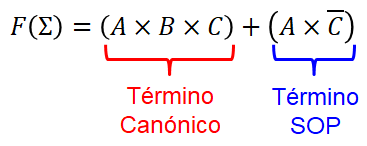
Formatos POS o SOP: es un término en una función donde NO se presentan todas las variables de la función.
Minterm o Minitérminos (∑)
Toda tabla de verdad tiene una función lógica y ésta se puede expresar como una SUMA DE PRODUCTOS CANÓNICOS, donde cada término PRODUCTO será un MINTERM. Cada MINTERM se asocia con una combinación de entradas que producirá un ꞌ1ꞌ en la función de salida.
Si una variable vale ꞌ0ꞌ se niega y si vale ꞌ1ꞌ no se niega.
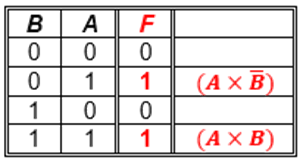
► Ejemplo: • Se tiene la siguiente tabla de verdad y se requiere hallar la función por Minterm e implementar el circuito: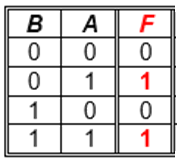
Como es por Minterm, se tiene en cuenta solo las salidas que valen '1'
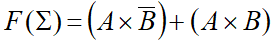
Maxterm o Maxitérminos (∏)
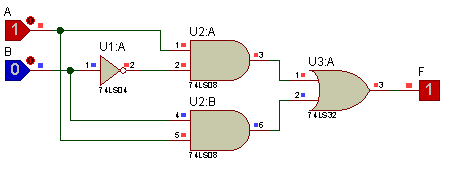
Toda tabla de verdad tiene una función lógica y ésta se puede expresar como una PRODUCTOS DE SUMAS CANÓNICAS, donde cada término SUMA será un MAXTERM. Cada MAXTERM se asocia con una combinación de entradas que producirá un ꞌ0ꞌ en la función de salida.
Si una variable vale ꞌ0ꞌ no se niega y si vale ꞌ1ꞌ se niega.
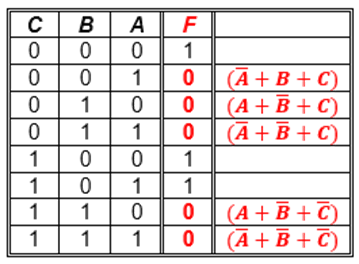
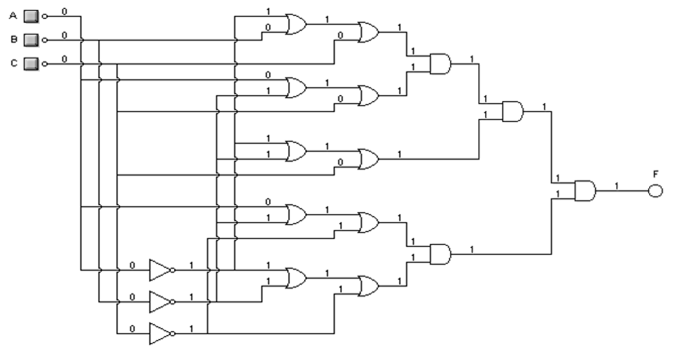
► Ejemplo: • Se tiene la siguiente tabla de verdad y se requiere hallar la función por Minterm e implementar el circuito: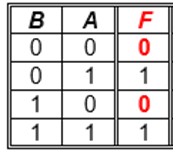
Como es por Maxterm, se tiene en cuenta solo las salidas que valen '0'
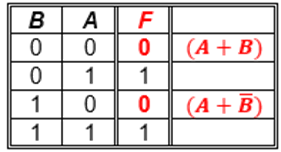
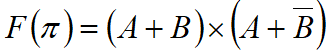
Ejemplos de Minterm y Maxterm
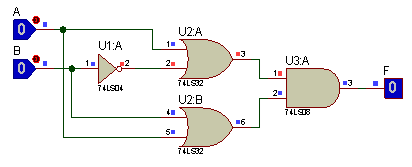
► Ejemplos: • Se tiene la siguiente función booleana, donde se involucran términos canónicos y un formato SOP (Suma de Productos):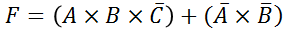
Nótese que el primer término es canónico y el segundo término es formato SOP (Suma de Productos) ya que le falta la variables C o C’.
Para la solución se debe convertir en término canónico; para ello se debe completar el término SOP teniendo en cuenta las dos (2) posibles opciones de la variable C.
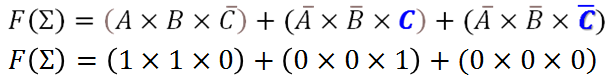
Como es por Minterm, se tiene en cuenta solo las salidas que valen '1'
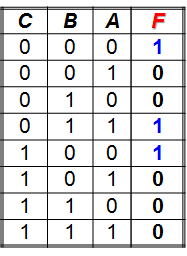
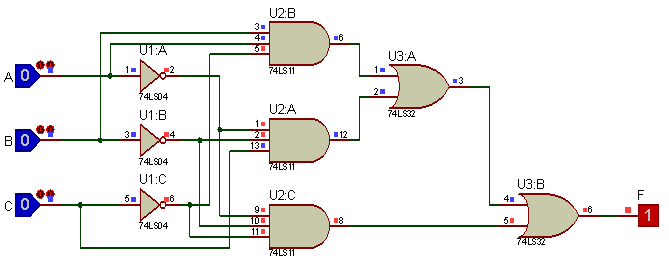
1 - La variable C no esté en ꞌ0ꞌ, la variable B esté en ꞌ0ꞌ.
2 - Las tres variables no estén en ꞌ1ꞌ.
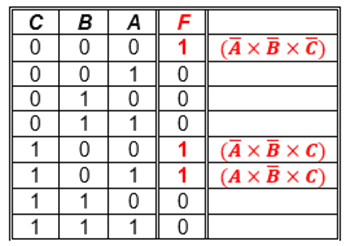
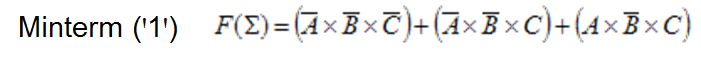
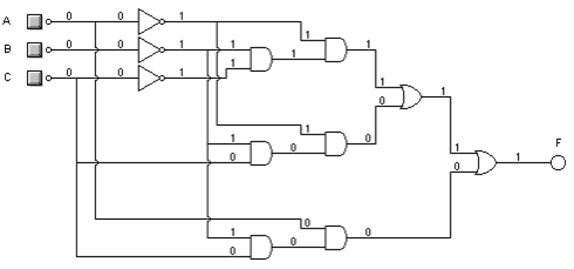
1 - La variable C no esté en ꞌ0ꞌ, la variable B esté en ꞌ0ꞌ.
2 - Las tres variables no estén en ꞌ1ꞌ.
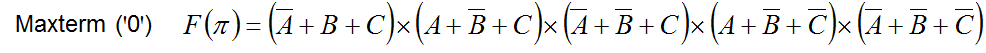
► Ejercicios propuestos con respuestas para practicar Lógica AOI, con el fin de verificar lo aprendido:
➤ ¿La siguiente función está expresada de forma Minterm o Maxterm? y halle la tabla de la función:
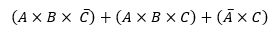
R/. La función está expresada de forma Minterm con dos términos canónicos y uno en formato SOP (suma de productos) y la tabla en orden descendente es: 0-0-0-1-1-0-1-1
➤ Se tiene la respuesta de una tabla de verdad en el siguiente orden descendente: 1-0-1-0-1-1-1-0 y se requiere hallar la función por Maxterm.
La función expresada por Maxterm es:
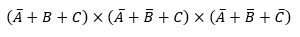
A continuación, un curioso video sobre cómo explicar las compuertas lógicas:
Video publicado en TikTok, en el canal @wiltonpalma_9425
MAPAS DE KARNAUGH
Maurice Karnaugh y John Venn

Maurice Karnaugh (1924- ) Matemático y Físico Norte Americano. Estudió matemáticas y física en el City College de Nueva York (1944-1948), luego en la Universidad de Yale donde hizo su licenciatura (1949), M.Sc. (1950) y Ph.D. en Física con una tesis sobre la teoría de la resonancia magnética y grecas duplicación de Óxido Nítrico (1952). Trabajo como: Investigador en los Laboratorios Bell desde 1952 hasta 1966. En el centro de investigación de IBM de 1966 a 1993. Profesor de informática en el Politécnico de Nueva York de 1980 a 1999. Miembro del IEEE desde 1975 (Instituto de Ingenieros Eléctricos y Electrónicos – Institute of Electrical and Electronics Engineers). Actualmente gobernador emérito del ICCC (Consejo Internacional para las Comunicaciones Computacionales – International Council for Computer Communication). En 1950 creó el método llamado mapa de Karnaugh, cuya función es minimizar o simplificar las funciones algebraicas booleanas.

John Venn (1834-1923). Matemático y Lógico Británico. Se conoce por su método de representar de forma gráfica 1880 las proposiciones, teniendo en cuenta sus características de cualidad y cantidad; además, de silogismos que posteriormente fueron utilizados en la teoría de conjuntos.
Un mapa de Karnaugh consiste de una serie de cuadrados y cada uno de ellos representa una línea o combinación de la tabla de verdad. Cada cuadrado del mapa alberga un ꞌ0ꞌ, un ꞌ1ꞌ o una ꞌXꞌ (no importa, don't care); depende si la solución es por minterm (Σ) o por maxterm (∏).
Recuerden que la siguiente fórmula es para saber cuantas combinaciones va a tener la tabla.
$$\displaystyle n = No.\quad de \quad variables\;\; $$ $$\displaystyle 2^n = No.\quad de \quad combinaciones\;\; $$
Los mapas de Karnaugh se utilizan en funciones hasta de 8 variables.
Procedimiento
Los pasos a seguir son:
• Obtener una expresión booleana en forma de minterm o maxterm (lógica AOI). • Colocar ꞌ1ꞌ o ꞌ0ꞌ en el mapa de Karnaugh de acuerdo a la expresión. • Se agrupan conjuntos adyacentes de 2, 4, 8, 16, 32 o 64, unos o ceros. • Si un ꞌ1ꞌ o ꞌ0ꞌ no tiene datos adyacentes, es una isla y no tiene simplificación. • Los conjuntos solo se conforman de forma horizontal y vertical, nunca en diagonal.Distribución de las celdas
Las variables de la expresión son ordenadas en del código Gray, nombrado así en honor del investigador Frank Gray, es un sistema de numeración binario en el que dos números consecutivos difieren solamente en uno de sus dígitos.

Frank Gray (1887-1969). Físico Norteamericano. Fue un investigador que trabajo en los laboratorios Bell. Realizó muchas innovaciones tanto mecánicas como electrónicas para la televisión. Diseñó el código Gray que es un sistema binario en el que dos números consecutivos difieren solamente en uno de sus dígitos.
Mapa de Karnaugh de dos (2) variables
$$\displaystyle 2 = variables\;\; $$ $$\displaystyle 2^2 = tabla\quad con\quad 4\quad combinaciones\;\; $$
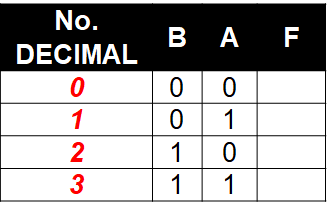
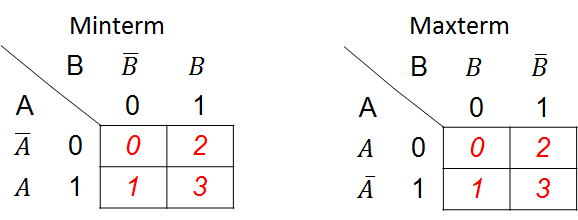
Mapa de Karnaugh de tres (3) variables
$$\displaystyle 3 = variables\;\; $$ $$\displaystyle 2^3 = tabla\quad con\quad 8\quad combinaciones\;\; $$
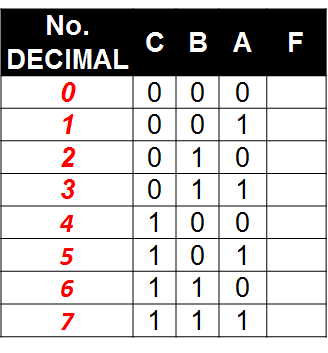
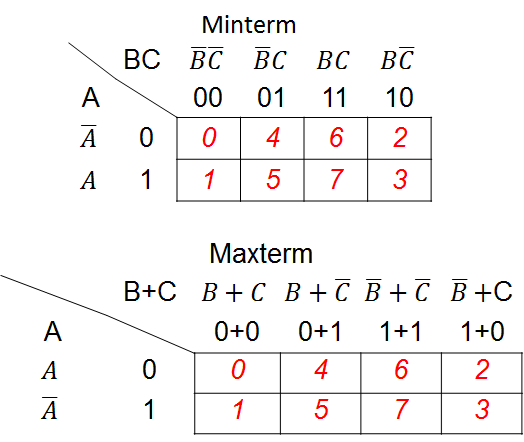
Mapa de Karnaugh de cuatro (4) variables
$$ 4 = variables\;\; $$ $$ 2^4 = tabla\quad con\quad 16\quad combinaciones\quad binarias\;\; $$
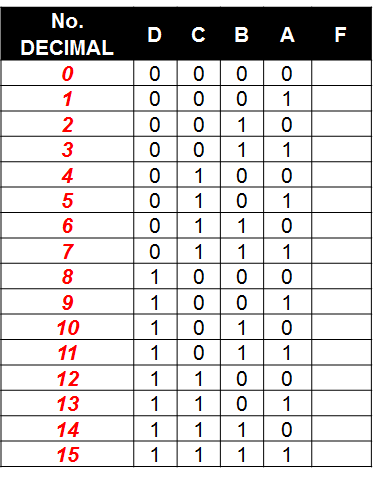
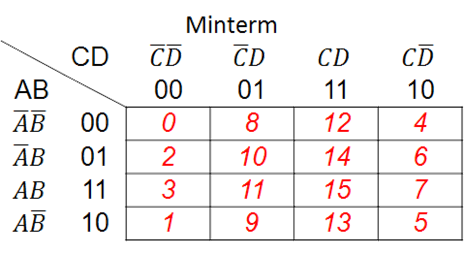
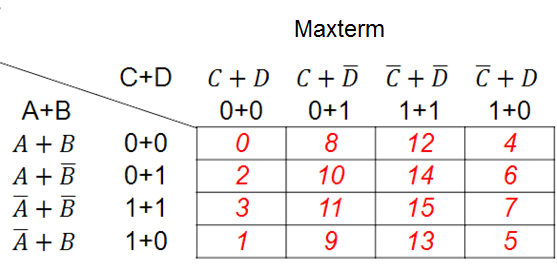
Objeto interactivo de aprendizaje (OIA)
En el siguiente OIA, se explican las relaciones existentes entre las tablas de verdad y los mapas de Karnaugh:
Ejercicios con Mapas de Karnaugh
Agrupación de datos adyacentes
Los mapas de Karnaugh de 3 variables se pueden doblar horizontalmente, uniéndose el extremo izquierdo con el derecho, para formar ya sea una pareja o un cuarteto, como se observa en la siguiente figura.
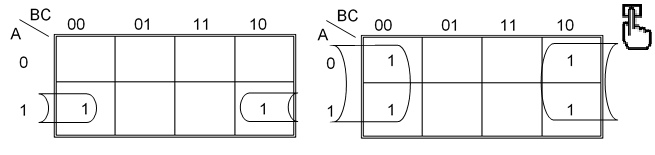
Recuerde, que se tienen en cuenta las variables que NO cambian.
Siempre se lee filas y columnas. Para el mapa del lado izquierdo, observe que los dos (2) '1' se encuentran localizados en la fila 'A=1', lo cual no cambia de estado y con especto a las dos columnas que ocupan no cambia la variable 'C=0'. El mapa está desarrollado por minterm ya que los datos que descargó al mapa son '1'.
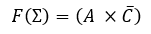
Para el mapa del lado derecho, observe que los cuatro (4) '1' cambian de fila y con especto a las dos columnas que ocupan no cambia la variable 'C=0'. El mapa está desarrollado por minterm ya que los datos que descargó al mapa son '1'.
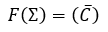
Los mapas de Karnaugh de 4 variables se pueden doblar horizontal, vertical o en ambos sentidos simultáneamente, uniéndose el extremo izquierdo con el derecho, el superior con el inferior o las cuatro esquinas, para formar ya sea una pareja, cuarteto u octeto, como se observa en la siguiente figura.
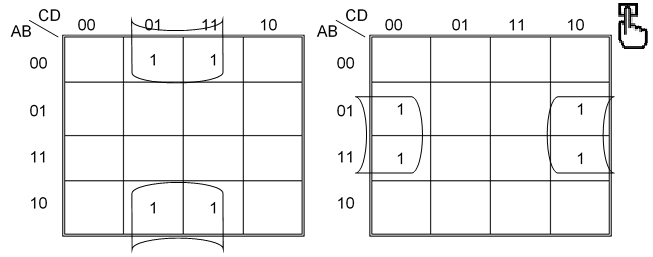
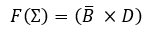
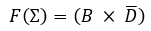
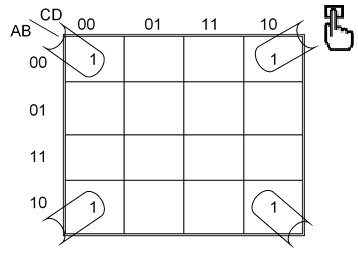
Implementación por medio de maxterm con tres variables.
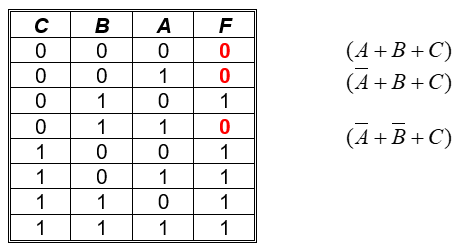
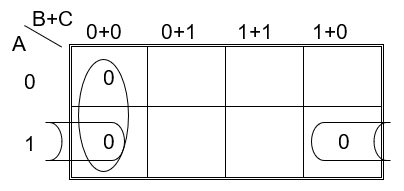
Función simplificada: $\bold{F(\pi) = (B+C)\times (\overline{A} +C)}$
Implementación por medio de maxterm con tres variables:
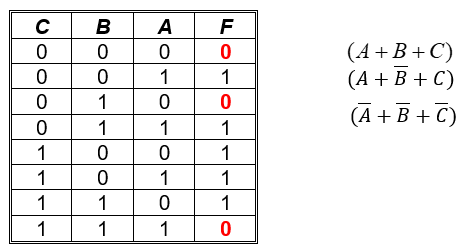
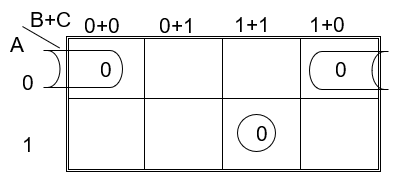
Función simplificada: $\bold{F(\pi) = (A+C)\times (\overline{A} + \overline{B}+ \overline{C})}$
Implementación por medio de maxterm con cuatro variables:
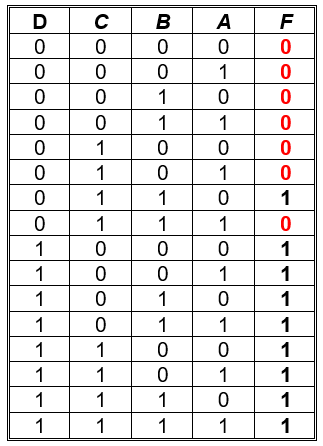
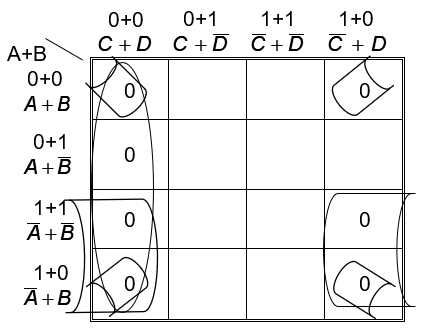
Implementación por medio de maxterm con cuatro variables:
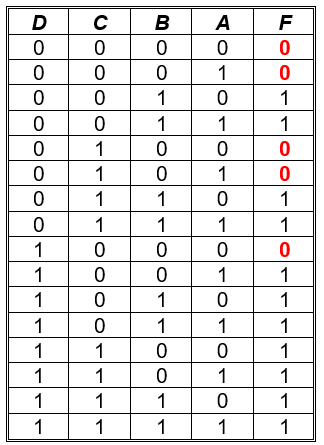
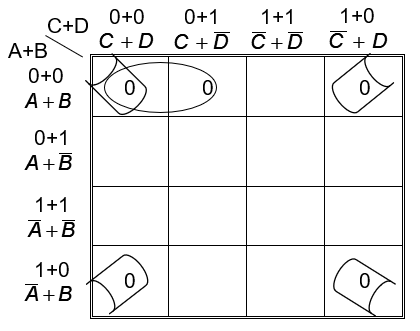
► Ejercicios propuestos con respuestas para practicar Mapas de Karnaugh, con el fin de verificar lo aprendido:
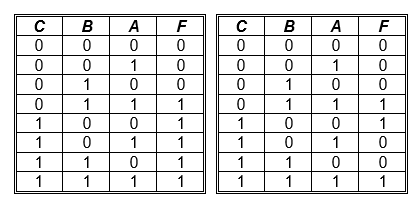
➤ Para la tabla de la izquierda utilizar mapas K por maxterm y para la de la derecha utilizar mapas K por minterm. Baje los datos de la tabla al mapa y luego simplifique, para hallar la nueva función booleana:
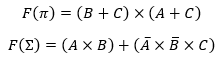
Objetos Interactivos de Aprendizaje (OIA)
Dando clic en la esquina superior derecha se expande el OIA.
Para este OIA, arrastra cada "Interrogante" al contenedor correspondiente.
Los siguientes OIA fueron diseñados por Juan Guillermo Rivera Berrío y Hernán Dario Ortíz.
EPÍLOGO
En la mayoría de sistemas digitales, el número de estados discretos es tan solo de dos y se les denomina niveles lógicos. Estos niveles se representan por un par de valores de voltaje, uno cercano al valor de referencia del circuito (normalmente 0 voltios, tierra o "GND"), y otro cercano al valor dado por la fuente de alimentación del circuito. Estos dos estados discretos reciben muchas parejas de nombres en libros de electrónica y otros textos especializados, siendo los más comunes "0" y "1", "false" y "true", "off" y "on" o "bajo" y "alto" entre otros. Tener solo estos dos valores nos permite usar el álgebra booleana y códigos binarios, los que nos proporciona herramientas muy potentes para realizar cálculo sobre las señales de entrada.
Los más complejos sistemas digitales, aplicados y útiles hoy en día son posibles gracias a la integración de los componentes, herramientas, equipos y subsistemas electrónicos, informáticos y mecánicos. En tiempos modernos es tan fácil tocar una pantalla con nuestras manos (pantalla táctil), ejecutar un comando de voz y cambiar un canal o abrir una ventana, apagar y encender una bombilla; todo gracias a la electrónica digital. Como su nombre lo indica ella se sustenta en su propio lenguaje, el lenguaje de código binario "1" y "0", se crean ciclos de palabras, password, secuencias de bit y byte y se hace realidad lo que nunca se pensó poder monitorear en tiempo real un proceso a miles de kilómetros de distancia. Todas las demás ciencias hoy en día se deben a la invención de los sistemas digitales, es difícil pensar en cocinar algo, llamar a un pariente lejano o ir al cine sin dejar a un lado la electrónica digital (https://es.wikipedia.org/).
Este libro es un pequeño aporte a esos sistemas digitales, con el propósito de acercar al estudiante al lenguaje digital. Para ello, se presentaron conceptos básicos como las tablas de verdad, la lógica booleana, las compuertas lógicas y, finalmente, los mapas de Karnaugh.
Como cierre final, se presentan tres objetos interactivos de aprendizaje, que resumen, en parte, los temas tratados en este libro.
SOPA DE LETRAS
Dando clic en la esquina superior derecha se expande el OIA.
Este OIA consta de una sopa de letras con términos tratados en este LIA (Libro Interactivo de Aprendizaje).
PREGUNTAS SÍ/NO
Dando clic en la esquina superior derecha se expande el OIA.
En este OIA, responde SÍ o NO a cada "Interrogante" que se realiza.
PUZLE GIRATORIO
Dando clic en la esquina superior derecha se expande el OIA.
Actividad lúdica, que permite usar imágenes enlazadas a Flickr.

