Tabla de contenido

Actividad del capítulo

Al terminar este capítulo, habrás diseñado los siguientes objetos interactivos:

Marcos y fondos

En este objeto interactivo incorporamos imágenes en el selector Espacios y en el control tipo botón. Por primera vez, haremos uso del condicional dibujar si, algunas expresiones simples con variables matemáticas y la escritura de textos simples.

Animación 3D

En este objeto interactivo incorporamos una animación. Es una primera incursión al uso de algoritmos, que permitan realizar actividades iterativas.

Formatos de imágenes

Es común que el primer objeto multimedia que se nos ocurre incorporar a un diseño con destino a la web sea una imagen. Las imágenes que usamos son fotografías, diseños, gráficos, fondos y, en ocasiones, imágenes animadas.

Dada esta tendencia de diseño, es importante conocer los diferentes formatos que podemos usar en el editor DescartesJS y algunas recomendaciones para evitar la carga de imágenes de gran peso o de pobre resolución que, en términos técnicos, se refiere a los niveles de compresión (tamaño) y al tratamiento de color (calidad).

Actualmente, los formatos de imagen se agrupan en dos. La primera agrupación son las imágenes pixeladas o de mapa de bits, en la que un pixel o punto es un color; por ejemplo, si la imagen es de $8$ bits, significa que cada pixel puede tener hasta $256$ colores, una de $16$ bits puede lograr hasta $65,536$ colores por pixel. Obviamente, el segundo ejemplo es de mayor calidad y, en consecuencia, de mayor peso. Las diferencias de calidad la podemos observar entre los videojuegos de $8$ bits (Nintendo, por ejemplo) y los de $16$ bits (Super Nintendo, por ejemplo), tal como se aprecia en la Figura 1.1.

Los formatos de imagen en esta primera agrupación que se pueden usar en el editor DescartesJS son: jpg, gif y png.

El segundo grupo corresponde a las imágenes vectoriales, que se construyen con elementos geométricos, como círculos, polígonos, muros, arcos, entre otros.

La ventaja de una imagen vectorial es que no pierde calidad al aumentar su tamaño, por contraste a las imágenes pixeladas que sí pierden calidad. En la Figura 1.2, se puede apreciar esta gran diferencia.

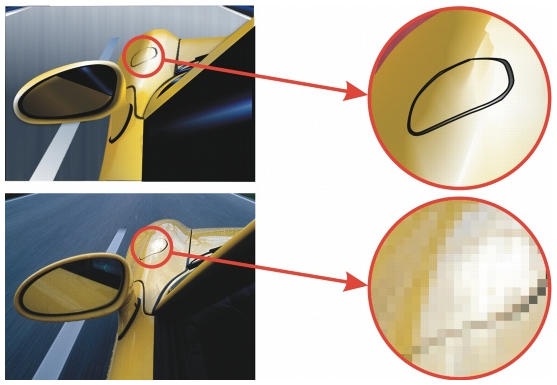
El formato svg es el recomendado por el consorcio internacional de estándares para la web (W3C)El World Wide Web Consortium (W3C) es una comunidad internacional que desarrolla estándares que aseguran el crecimiento de la Web a largo plazo. Fue fundado en $1994$ para dirigir a la Web hacia su pleno potencial mediante el desarrollo de protocolos comunes que promuevan su evolución y aseguren su interoperabilidad. (crédito: https://www.masadelante.com/faqs/w3c)., formato que es ampliamente compatible con la web y en particular con el editor DescartesJS.

En la siguiente página, presentamos cuatro formatos de imágenes vectoriales.

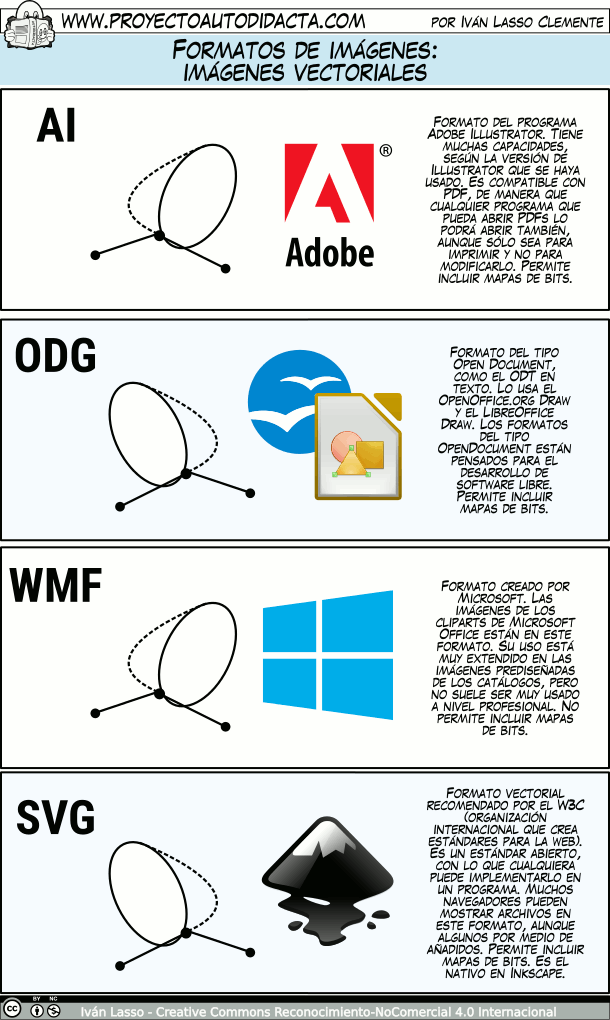
A continuación, describimos los formatos de imágenes pixeladas que podemos usar con nuestro editor.

Formato GIF (Graphic Interchange Format)

Las imágenes en este formato pueden contener entre $2$ y $256$ colores, es un formato muy popular en imágenes animadas. Dado este número de colores tan limitado, las imágenes que se obtienen son muy pequeñas y por tanto de bajo peso. En nuestros ejercicios, usaremos este formato para los botones (controles) e imágenes animadas.

Formato JPG o JPEG (Joint Photographic Experts Group).

Este formato soporta $16.7$ millones de colores ($24$ bits) y es el más empleado para las fotografíasLa sigla JPEG (Joint Photographic Expert Group) surge de la reunión que tuvo lugar en $1982$ entre un grupo de expertos en fotografía, que trabajaban principalmente en las formas de transmitir información (imágenes fijas o animadas). En $1986$, el ITU-T desarrolló métodos de compresión destinados al envío de faxes. Estos dos grupos se unieron para crear el Grupo Conjunto de Expertos en Fotografía (JPEG) (crédito: https://es.ccm.net).. El nivel de pérdidas en calidad depende del nivel de compresión. Es un formato muy usado en los diseños de la web.

Formato PNG (Portable Network Graphics).

Este formato utiliza una compresión sin pérdidas, permitiendo imágenes con color verdadero, escala de grises y paleta de $8$ bits, fue desarrollado en $1995$ como una alternativa gratuita al formato GIF, cuyos derechos pertenecen a Unisys (propietario del algoritmo de compresión LZW).

Es a Unisys que los editores de software deben pagar regalías por usar este formato. PNG es un acrónimo recursivo de "Png No es Gif" (crédito: https://es.ccm.net). Este formato goza de popularidad por permitir transparencias en sus imágenes, lo cual significa un mayor peso, tal como se muestra en la Figura 1.4.

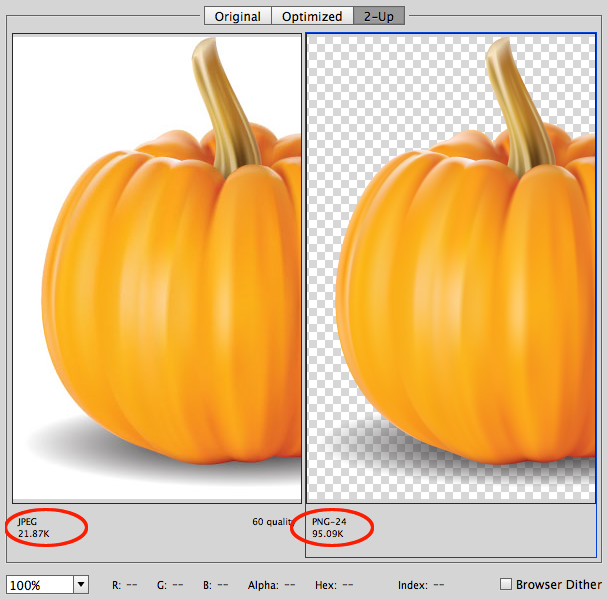
¡Advertencia! En el editor DescartesJS, es importante que hagas coincidir mayúsculas y minúsculas, tanto del nombre de la imagen como de su extensión. Es común que al descargar una imagen de la web, la extensión se escriba en mayúscula. Si no atiendes esta advertencia, al publicar tu objeto interactivo, las imágenes no se visualizarán.

Botones y fondos

Para lograr el diseño de los objetos interactivos en la actividad propuesta en este capítulo, te hemos compartido un grupo de imágenes en diferentes formatos (png, gif, jpg) y para diferentes propósitos (fondos, botones, marcos e imágenes animadas). Estas imágenes las puedes descargar en este enlace: imágenes

Para el primer objeto usaremos dos espacios, uno para los marcos (bordes) del espacio, y otro para los fondos. Recurriremos a la propiedad de transparencia del color del fondo, de tal forma que sólo sean visibles los marcos. Por ejemplo, uno de los marcos es una pantalla de televisión (17.png en la carpeta marcos), al usar transparencias, podemos lograr algo como esto (has clic en el botón inferior, para reproducir el vídeo):

En el ejemplo anterior, lo que hicimos fue crear dos espacios. El primero, es un espacio que incluye un control tipo video. En el segundo espacio se encuentra lo novedoso de la escena, pues se trata de un espacio $\Reals^2$ sobrepuesto al primero, en el que hemos puesto una transparencia total al color de fondo, además de una imagen de borde en formato png (permite la transparencia). La imagen seleccionada (carpeta marcos), presenta una imagen de un televisor antiguo, con transparencia en la zona correspondiente a la pantalla, de tal forma que se logra un efecto bastante realista. Algo similar haremos en nuestro primer objeto interactivo.

¡Sugerencia! El esfuerzo realizado para crear un objeto interactivo, se puede ver frustrado al usar contenidos multimedia externos que, en el futuro, presentan enlaces rotos o cambios en los protocolos de acceso. Esta situación es común en los vídeos de servicios como YouTube o Vimeo. Sugerimos, entonces, usar vídeos en local o de tu propio canal de YouTube.

Por otra parte, en el caso de las imágenes, es importante evitar cualquier violación de derechos de autor. Trata de diseñar tus propias imágenes o, al menos, usar repositorios de dominio público. Las imágenes que hemos compartido, provienen de los siguientes repositorios:

• Fondos: https://www.freepik.com/
• Marcos: https://www.klipartz.com/es/search?q=marcos
• Botones: http://www.freebuttons.com/index.php
• Patrones: http://www.bettertextures.com/ (véase, también, este enlace).

Puedes consultar estos repositorios y elegir otras imágenes para la tarea final de este capítulo. Igualmente, puedes investigar qué otros repositorios de imágenes de dominio público o gratuitos hay en la red.

Fondos

Nuestra primera tarea es diseñar el espacio que va a contener los fondos de pantalla. En realidad, tendremos que usar varios espacios $ℝ^2$ para mostrar varios fondos. Por ahora, nos preocuparemos por el primer espacio, para ello, observa la Figura 1.5.

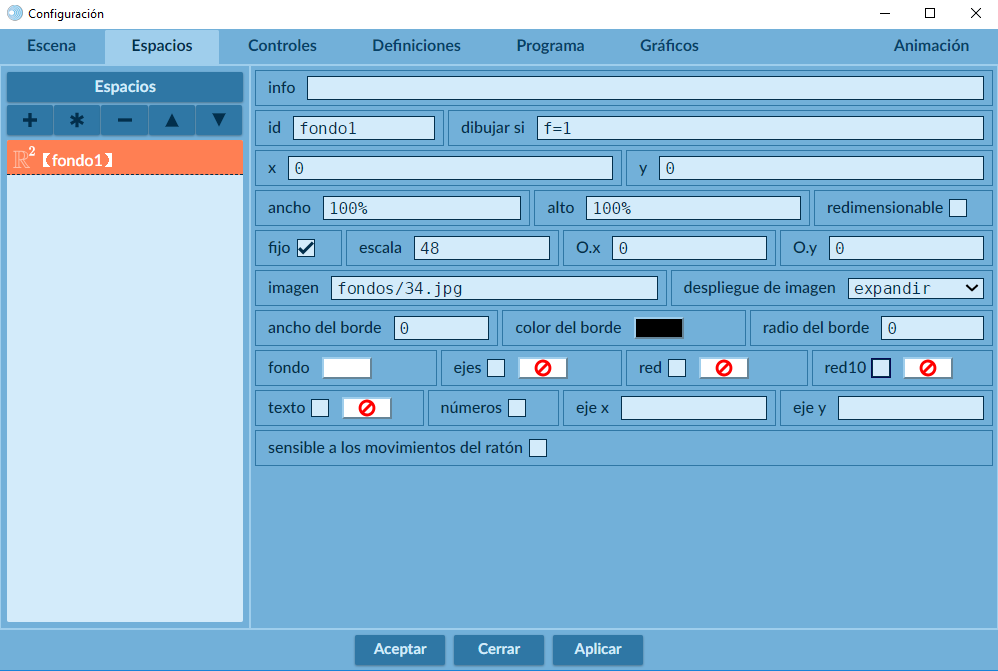
Si observas con detalle, notarás la siguiente configuración de este primer espacio, que puedes lograr con estos pasos:

• Desactivamos la malla del espacio cartesiano (ejes, red y red10) y hacemos clic en el botón aplicar.
• Siguiendo el procedimiento del capítulo anterior, guardamos la actividad como actividad2.html, debes hacerlo antes de continuar la configuración del espacio, pues así es que te aparecerá la imagen de fondo.
• Como fondo hemos incorporado la imagen 34.jpg de la carpeta fondos. Es importante que se escriba correctamente la ruta relativa; para el ejemplo, la imagen se encuentra en la carpeta fondos, la cual debe estar en el mismo directorio del archivo html.
• Para que la imagen cubra todo el espacio, debes seleccionar en despliegue de imagen la opción expandir.

Ahora, resumimos lo anterior y te explicamos cómo usar una variable de control, en el siguiente vídeo:

Observa que hemos vinculado una variable f con valor de 1 en el selector Programa. Continuemos, entonces, con el diseño de nuestra actividad.

• En la casilla dibujar si, escribimos f=1. Estro significa que el espacio se dibujará siempre que está igualdad sea verdadera. Como en el selector Programa asignamos 1 a esta variable, la condición dibujar si es verdadera. En el vídeo cambiamos la condición a f=2, lo cual es falso, por ello, no se dibujó el espacio.
• Como se trata de mostrar varios fondos, procedemos a copiar más espacios. Para este ejercicio, lo haremos con tres espacios, usando una de las utilidades del panel del selector Espacios, pero... mejor observa el vídeo:

Es posible que el vídeo te haya dejado anonadado 😊. Algo normal, pues hemos usado varias de las utilidades de la herramienta DescartesJS, como son las variables (selector Programa) y los botones (selector Controles). Pero, no te preocupes, pues todo es muy sencillo y sólo necesitas un mínimo de lógica, que explicamos a continuación.

Continuemos, entonces, con los pasos de nuestra actividad.

• Creamos dos nuevos espacios $\Reals^2$. Para ello, recurrimos al selector Espacios y con el botón * clonamos los dos espacios. En cada espacio cambiamos su identificador (id) por E2 y E3, las imágenes del fondo a utilizar, para el ejemplo, son fondos/35.jpg y fondos/36.jpg (no olvides la dirección relativa de las imágenes) respectivamente. Además, cambiamos el condicional dibujar si por f=2 y f=3.

Botones

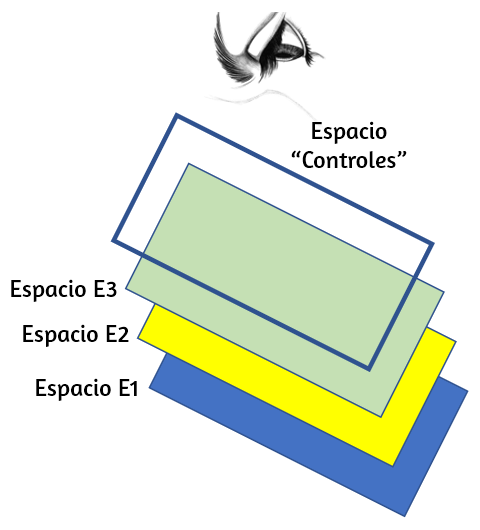
Como la idea es incluir unos botones para controlar la actividad, éstos no pueden estar sobre uno de los tres espacios que hemos creado, pues al cambiar a otro desparecerían. Por ello, creamos un cuarto espacio que llamaremos controles, el cual estaría por encima de los tres anteriores. Este último espacio es el que se observaría al hacer clic en el botón aplicar, lo cual nos obligó a asignarle transparencia total al fondo (observa el vídeo), de tal forma que se puedan ver los espacios E1, E2 o E3, según se seleccione. Observa la Figura 1.6 que te da una idea de esta situación.

• Nuestro siguiente paso es la creación de los botones que permitirán cambiar el valor de la variable f, de tal forma que podamos observar los espacios E1, E2 y E3 de acuerdo al valor de esta variable. Estos botones los creamos en el selector Controles.

Con el botón + creamos el primer control, seleccionando la opción botón, es decir, cuando aparece el cuadro de diálogo, cambiamos el tipo del control de pulsador a botón.

• A continuación, debemos configurar nuestro botón. En primer lugar debemos cambiar la región donde se va mostrar este control que, para nuestro ejercicio, será al interior de la escena, las otras opciones las explicaremos más adelante. Por omisión, los botones se asignan al primer espacio (en este ejemplo, E1) que, como ya explicamos, debemos cambiar al espacio controles. Podríamos dejar el control con el diseño original; sin embargo, le vamos a asignar la imagen de la carpeta botones/, llamada der6.gif. Esta imagen tiene un tamaño de $37\times 37$ pixeles que es importante para la siguiente configuración.

Si observas el contenido de la carpeta botones, notarás que la imagen der6.gif está acompañada de otra imagen llamada der6_over.gif. Cuando estas imágenes están presentes, significa que al pasar el ratón sobre (over) el botón, presentará un cambio de imagen.

La siguiente configuración debemos hacerla en el parámetro expresión, la cual cuenta con cuatro valores. Los dos últimos corresponden al ancho y alto de la imagen, es decir, $37\times 37$. Los dos primeros números definen la posición de la imagen dentro del espacio controles (recuerda que la $x$ crece de izquierda a derecha y la $y$ de arriba a abajo) ; por ejemplo, si la escena es de un tamaño de $970\times 550$ pixeles, una posición de x=953 y y=513 dibujaría el botón en la esquina inferior derecha del espacio ¿por qué? Prueba varias posiciones, antes de continuar con la actividad.

Para nuestra actividad (observa el vídeo), el valor de la expresión es: (180,80,37,37).

• Nuestro último paso, para este botón, fue definir una acción para cuando hagamos clic sobre él. Esa acción es calcular, pero ¿calcular qué? Nuestro propósito es que haya un cambio de fondo o, si se prefiere, de espacio. Como los espacios se muestran de acuerdo al valor de la variable f, necesitamos que la acción incremente el valor de f, que inicialmente es 1. En el cuadro de diálogo parámetro, definimos esta acción con la expresión f = f+1 ¿muy extraño? Seguramente que sí para el matemático, pues f no puede ser igual a f+1 ¡es un absurdo! He aquí un primer concepto de programación que debes entender.

La expresión f = f+1 no es una igualdad ¡es una asignación!, que significa lo siguiente: al valor de la variable f le sumamos 1 y el resultado de está operación se lo asignamos, de nuevo, a la variable f, es decir, la asignación funciona de derecha a izquierda. La confusión generada por esta expresión, motivó a que en algunos lenguajes de programación se utilicen expresiones como f:=f+1, para no confundirla con una igualdad. Poco a poco te acostumbrarás a estas asignaciones.

Así las cosas, cuando hagas clic en aplicar aparecerá nuestro botón con la acción configurada, de tal forma que al hacer clic en el botón por primera vez, el valor de f será 1+1, el siguiente clic cambia el valor de f a 3, y así sucesivamente. Recuerda que el espacio E2 se dibuja si, f=2 y E3 si f=3. Pero como sólo tenemos tres espacios, no podemos permitir que el botón siga sumando uno a la variable, por ello, en el cuadro de diálogo dibujar si, escribimos la expresión f<3, que significa que si f ya tomó el valor de 3, el botón no se dibuja.

• El último paso es crear el botón que permita mostrar los fondos anteriores, es decir, si f=3 estará mostrando el espacio E3. Necesitamos otro botón para que reduzca el valor de f y muestre los espacios E2 y E1. Para ello, clonamos el primer botón y hacemos los siguientes cambios: la imagen por izq6.gif, la posición por (60,80,37,37) que lo ubica a la izquierda del primer botón, la acción por f=f-1 (reduce el valor de f) y el condicional por f>1, es decir, se dibuja cuando aparezca el espacio E1.

Tarea 2

Amplía la actividad $2$ a cinco fondos y la guardas con el nombre tarea2.html. Recuerda que el espacio controles debe ir al final, para ello, usa las flechas del panel del selector de Espacios. Si quieres conocer más sobre la configuración de los botones, lee el siguiente texto:

Botones y marcos

Dado que el procedimiento es similar, es suficiente que observes el siguiente vídeo:

Algunos aspectos del vídeo a tener en cuenta:

• No olvidar que el último espacio debe ser el de controles, por ello, lo hemos desplazado usando el panel del selector Espacios.
• Si queremos que se observe tanto la imagen del fondo como la del marco, es necesario usar transparencia en el color de los marcos.
• Hicimos una primera incursión al objeto gráfico texto, que profundizaremos más adelante.

Tarea 2 (continuación)

Amplía la tarea 2, incluyendo cinco marcos.

Imágenes animadas y animaciones

La historia de la animación es rica en descubrimientos y en invenciones. Uno de los primeros descubrimientos fue "la persistencia de la visión o retiniana", descubierto por Peter Mark Roget y estudiada por Joseph-Antoine Ferdinand Plateau, que inventa el FenaquistoscopioPlateau definió el principio de la persistencia de los estímulos luminosos en la retina (Persistencia de la visión) y determinó que su duración es de una décima de segundo. Este tiempo no es constante, sino que aumenta cuando el ojo está adaptado a la oscuridad; ese es el mecanismo por el cual, a partir de imágenes fijas, percibimos la sensación de movimiento durante la proyección de una película.

En $1832$, Plateau inventó un primitivo dispositivo estroboscópico, el fenaquistiscopio, el primer dispositivo capaz de proporcionar la ilusión de una imagen en movimiento a partir de una secuencia de imágenes fijas. Compuesto de dos discos coaxiales, uno con pequeñas aberturas radiales y equidistantes, a través de las cuales el espectador puede mirar y otro disco conteniendo una secuencia de imágenes fijas impresa. Cuando los dos discos rotan a la velocidad adecuada, la sincronía entre las aberturas y las imágenes crea una ilusión de animación de las imágenes. La proyección de fotografías estroboscópicas, creando la ilusión de movimiento, daría lugar, eventualmente, a la invención del cinematógrafo de los hermanos Lumière (https://es.wikipedia.org/wiki/Joseph-Antoine_Ferdinand_Plateau)..

Nuestro propósito, en esta sesión, no es hacer un discurso sobre la historia de la animación; sin embargo, el dispositivo de Plateau llama la atención, en tanto que el éxito de las primeras animaciones se debió a la comprensión de cómo percibimos las imágenes, en especial aquellas que se presentan en una sucesión de secuencias, las cuales entremezclan lo percibido con lo recién percibido (una décima de segundo antes), pero, que sea el dispositivo de Plateau (simulado con DescartesJS) el que hable por sí sólo:

Tampoco es nuestro propósito realizar un curso de animación. Lo que vamos a presentar es cómo podemos incorporar algunas animaciones en nuestros objetos interactivos y, así, desarrollar la segunda actividad planteada al inicio del capítulo.

Imágenes animadas

Una primera opción es incorporar animaciones prediseñadas en nuestro objeto interactivo, como la que se muestra a continuación, diseñada por Matt Boldt:

Otra opción es incorporar un objeto flash (no recomendado en la actualidad) o un gif animado, como el de la Figura 1.7:

Esta última opción fue muy popular en la animación para las páginas web, especialmente para íconos, botones, menús y banners.

Patrones

Iniciamos nuestra última actividad, de este capítulo, diseñando el fondo de nuestro espacio de trabajo.

• Creamos un nuevo objeto interactivo (Archivo → Nuevo).
• Desactivamos los checkbox ejes, red y red10, y activamos el checkbox fijo, este último para evitar el desplazamiento de las imágenes que vamos a incorporar.
• Diseñamos el fondo usando una imagen de la carpeta patrones/ (la imagen 15.jpg). Si observas el tamaño de esta imagen, notarás que es de $96\times 96$ pixeles, muy pequeña para cubrir nuestro espacio de trabajo (observa la Figura 1.8). DescartesJS cuenta con una opción que permite replicar la imagen sobre todo el espacio, para ello, selecciona la opción mosaico del menú despliegue de imagen.

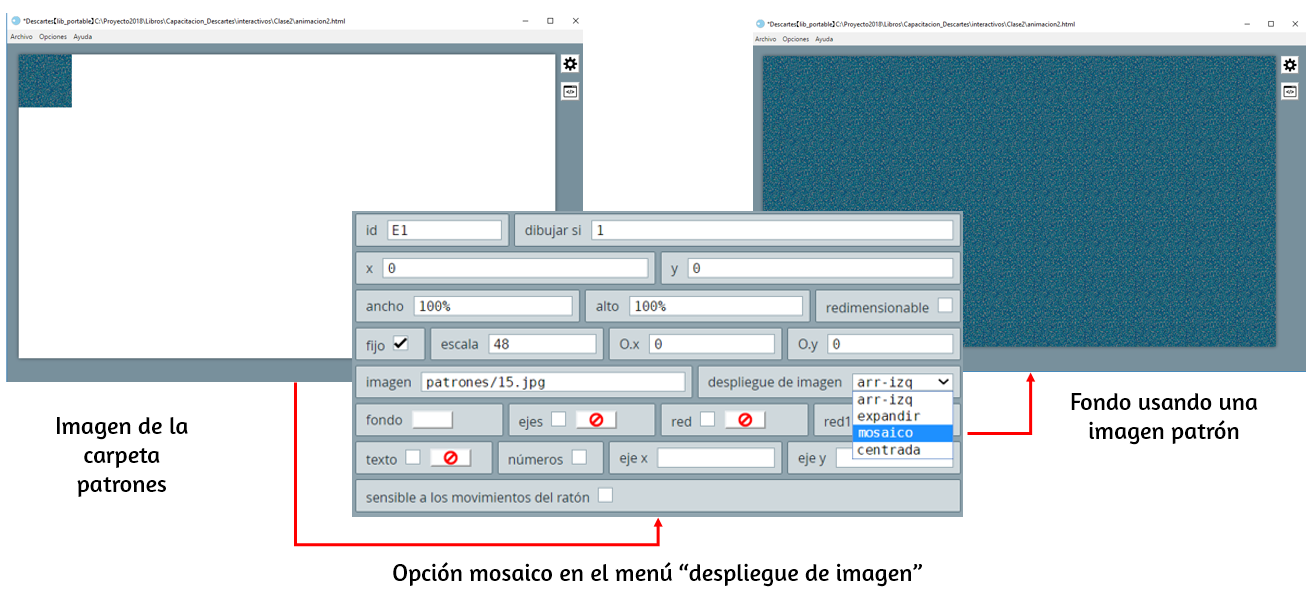
Para que entiendas cómo se logra obtener el fondo anterior, debes saber que los patrones o mosaicos más conocidos son las teselaciones, que se basan en la repetición.

Una única plantilla, azulejo o célula, se combina mediante duplicados sin cambios o modificaciones [...] Otros patrones, como la teselación de Penrose y los patrones indios Pongal o Kolam, usan simetría, que es una forma de repetición finita, en lugar de una traslación, que puede repetirse hasta el infinito. Los patrones fractales también utilizan aumentos o escalas que producen un efecto conocido como autosimilaridad o invariancia de escala. Algunas plantas, como los helechos, incluso generan un patrón usando una transformación afín que combina la traslación, con el escalado, la rotación y la reflexión.https://es.wikipedia.org/wiki/Patrón_(estructura)

Una teselación que solemos usar es la cenefa, tal como lo puedes observar en la siguiente escena interactiva del Proyecto Canals:

Continuemos con el diseño de nuestra actividad en la que tenemos, hasta el momento, el fondo de nuestro espacio de trabajo.

• Agregamos un espacio $\Reals^3$ con fondo transparente. Ya habrás notado que sólo cuando agregamos este tipo de espacio es que aparece el selector Gráficos 3D.
• En este selector agregamos (con el botón +) un dodecaedro cuyo color (el que desees) tendrá una ligera transparencia (observa la Figura 1.9) y activamos el checkbox aristas.



• Seguramente, no te gustará el tamaño de este sólido platónico. No te preocupes, en el selector Espacios puedes cambiar la escala del espacio tridimensional, te sugerimos una escala de 140, aunque podrás tener otro gusto con el cual no vamos a discutir... por ahora.

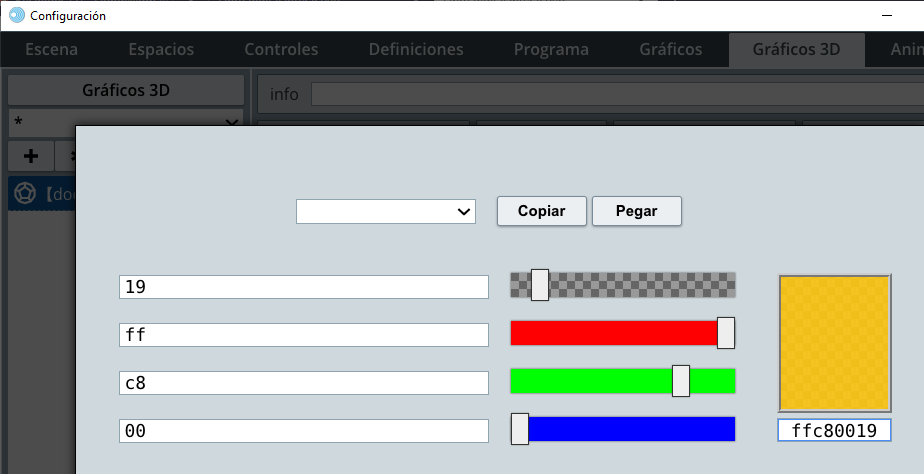
Hasta este momento de diseño de la actividad, debes tener algo así como lo que muestra esta imagen:

• Si observas la actividad al inicio del capítulo, tenemos una imagen de una gallina con sus pollitos. Obviamente, como en nuestro dodecaedro, esta imagen debe tener transparencia, pues una imagen sin ella se vería bastante fea en nuestra actividad. Un formato de imagen con estas características es del tipo png o svg. En nuestra actividad, hemos usado una de formato svg, que puedes descargar aquí (si te aparece la imagen, con clic derecho la puedes guardar en tu carpeta de imágenes con el nombre que quieras).

Nosotros la tenemos con el nombre gallina (recurrimos a nuestra creatividad para asignar nombres). Muy bien, ahora la vamos a agregar desde el selector Gráficos, con la ruta imagenes/gallina.svg en el campo de texto archivo y en la posición dada por la expresión (6,3.5,.6,.6).

Imágenes en espacios bidimensionales

La expresión anterior, merece este apartado antes de continuar con nuestra actividad, pues a diferencia de los botones, la posición de las imágenes si obedecen a las coordenadas cartesianas.

Este gráfico consiste en una imagen tipo jpg, png, svg o gif que puede insertarse en nuestro objeto interactivo. La imagen debe estar en la misma carpeta que el interactivo o en una subcarpeta. La expresión es un campo de texto en el que se introducen las coordenadas (cartesianas) donde habrá de mostrarse la imagen en el interactivo. Por defecto son dos coordenadas y corresponden a dónde estará situada la esquina superior izquierda de la imagen. No obstante, se pueden introducir cuatro entradas en los paréntesis, en donde la tercera y cuarta entradas corresponden al factor de escala del ancho y alto de la imagen. En caso de definir las cuatro entradas, las dos primeras ya no marcan la esquina superior izquierda de la imagen, sino su centro. La tercera y cuarta entradas (las escalas horizontal y vertical) pueden adoptar valores negativos, en cuyo caso la imagen se invertirá horizontal y/o verticalmente.

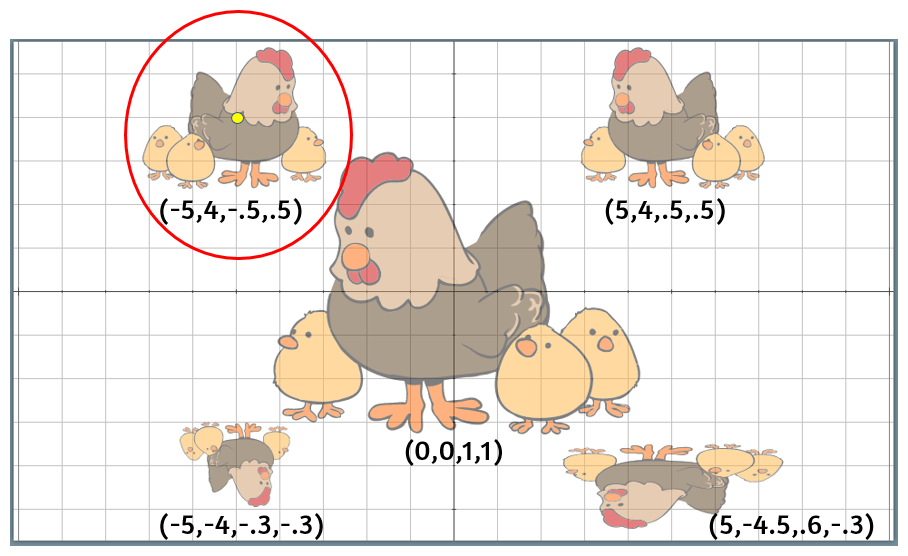
De acuerdo a lo anterior, analiza las siguientes imágenes en las que hemos puesto la expresión (debajo de ella) que ha permitido dibujarlas tal como se muestra en la Figura 1.10.

La imagen del centro está en las coordenadas (0,0) del plano cartesiano, por ello se ve en el centro de la escena, y su escala (1,1) indica que es el tamaño real de la imagen. Por otra parte, la imagen que está encerrada en el círculo, se encuentra en la coordenadas (-5,4) (ver el punto amarillo) y reducida a la mitad de su tamaño (-.5,.5). El signo menos del primer número indica que se invierte horizontalmente.

Observa la imagen inferior derecha, la cual tiene una desproporción. Ello obedece a que le dimos una escala horizontal del doble de la vertical, (.6,-.3).

¿Complejo de entender? Quizá, pero no tanto. Te sugerimos practicar con varias posiciones y escalas y así, seguramente, lo comprenderás mejor.

• Retornando a nuestra actividad, la expresión que hemos usado para nuestra gallina y sus pollitos es (6,3.5,.6,.6) que, seguramente, ya estarás en capacidad de comprender su significado, tanto de la posición de la imagen en el plano cartesiano como la escala utilizada.

Hay otras opciones para configurar la imagen que dejamos para tu consulta, en el texto de la página siguiente.

Si quieres conocer más sobre la configuración del gráfico imagen, lee el siguiente texto y continúa practicando:

Nuestra actividad está a punto de terminar, sólo nos falta animar el dodecaedro, pero antes queremos destacar el diseño obtenido, pues el objeto 3D sobre un plano 2D lo hemos usado en una escena diseñada por Josep Mª Navarro Canut, que trata sobre superficies paramétricas. Disfruta de ella, seleccionando e interactuando con cualquiera de las superficies dispuestas en el menú.

Animaciones en DescartesJS

El editor de configuraciones de DescartesJS cuenta con un selector de Animación que, inicialmente, puedes consultar en el siguiente texto:

Más adelante profundizaremos en los algoritmos de DescartesJS, mientras tanto vamos a explicar cómo logramos animar nuestro dodecaedro.

• En la Figura 1.11 se muestra el Selector Animación, configurado para hacer rotar indefinidamente el dodecaedro.



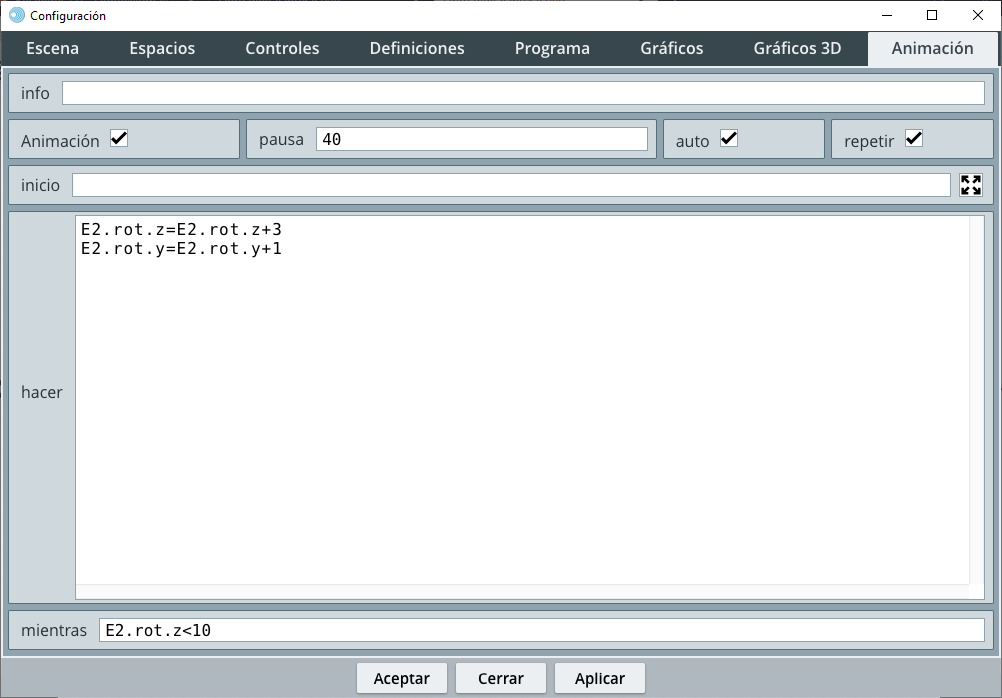
De acuerdo al texto anterior, hemos activado los checkbox Animación, auto (inicia la animación al ejecutar la escena) y repetir (ejecuta la animación indefinidamente).

• Lo que queremos que se repita son las siguientes asignaciones (recuerda que una asignación se ejecuta de derecha a izquierda de la igualdad):
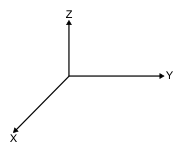
• E2.rot.z = E2.rot.z + 3, en el espacio 3D de DescartesJS, los ejes cartesianos tienen la siguiente configuración:

• El término E2.rot.z significa la rotación del espacio E2 (así tenemos identificado nuestro espacio tridimensional, dale una mirada al selector Espacios) alrededor del eje $z$. La asignación repetitiva E2.rot.z = E2.rot.z + 3, significa que sumaremos 3 a dicha rotación.
• E2.rot.y = E2.rot.y + 1, en este caso, la asignación indica que sumamos 1 a la rotación del espacio E2 alrededor del eje $y$.

Por defecto las rotaciones alrededor de $z$ y $y$ son cero, lo que significa que las asignaciones anteriores se ejecutarán mientras, E2.rot.z<10 (observa la imagen anterior), es decir, tomará valores de $3$, $6$ y $9$ y allí termina; sin embargo, como activamos el checkbox repetir, el proceso vuelve y se repite indefinidamente.

• Sigue las instrucciones anteriores y haz clic en el botón Aceptar y obtendrás la animación.

Comprendemos que puede ser un poco complejo si no tienes conocimientos básicos de programación, pero no te preocupes que en el próximo capítulo haremos una explicación detallada de tres estructuras básicas de programación: asignación, condicional simple y bucles o ciclos "hacer-mientras".

• Finalmente, vamos a incluir un botón que permita parar o reanudar la animación. Agrega, entonces, un botón en el selector Controles, con nombre Animar, imagen botones/1.gif y expresión (0,0,150,40). Luego, en el menú acción seleccionas animar

¡Eso es todo! Ya tienes la segunda actividad diseñada.

Gifs animados en DescartesJS

Suponemos que te has sorprendido con el objeto interactivo anterior, pues apareció otra animación no mostrada en la actividad inicial ¡Fue adrede!, sólo para explicar cómo incluir gifs animados en una escena de DescartesJS.

Ya habíamos dicho que DescartesJS admite imágenes en formato svg, jpg, png y gif; sin embargo, un gif animado aparecerá estático. Pero, hay un pequeño truco que podemos usar, consiste en agregar un espacio HTMLIFrame e incluir el gif animado.

Haz lo siguiente:

• Agrega el espacio, con ancho 323 y alto 350 (las dimensiones del gif).

• Posiciona el espacio en x = 10 y en y = 40.
• En archivo escribes gifs/5.gif y, ahora sí, ¡Eso es todo!

Aplicaciones con gifs animados

Juego Memoriza

A propósito de gifs animados, ¿qué tal este puzle "Memoriza"?:

Puzle animado

Actividad para hallar una imagen animada que se ha cortado en 15 piezas, también animadas.

Imágen animada de portada de https://gifer.com/es/ y las de pie de página desde https://www.klipartz.com/

¡Hasta la próxima sesión!