FUNÇÃO LINEAR E
FUNÇÃO QUADRÁTICA

Carlos Alberto Rojas Hincapié
Red Educativa Digital Descartes, Colômbia
Tradução: Lindberg Barbosa Lira de Almeida
Córdoba (Espanha)
2021
Título da obra:
FUNÇÃO LINEAR E FUNÇÃO QUADRÁTICA
Autor:
Carlos Alberto Rojas Hincapié.
Tradução:
Lindberg Barbosa Lira de Almeida
Design do modelo do livro: Juan Guillermo Rivera Berrío
Código JavaScript para o livro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interativos: DescartesJS
Fontes: Lato e UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Red Educativa Digital Descartes
Córdoba (Espanha)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN: 978-84-18834-67-7

Este trabalho está licenciado sob uma licença Creative Commons 4.0 Internacional: Atribuição-NãoComercial-Compartilhamento Igual.
Conhecendo a estrutura do livro interativo
No início de cada capítulo, concentramo-nos em:
Sabemos ou queremos aprender
 Competências e habilidades que desenvolvemos e que se concentram em distinguir, formular e representar situações por meio do conceito de uma função.
Competências e habilidades que desenvolvemos e que se concentram em distinguir, formular e representar situações por meio do conceito de uma função.
Para complementar os momentos de aprendizagem, encontraremos:

Exploração.
Cenas de exploração que auxiliam na compreensão do conteúdo que será abordado na seção a ser estudada.

Cena interativa.
Cenário interativo que auxilia na compreensão dos conteúdos e na resolução das atividades propostas.

São questões de análise que surgem a partir dos conceitos apresentados em cada seção.

Questões que permitem avaliar a aprendizagem, de acordo com as competências estudadas em cada secção.
 Lembrar, este ícone que está localizado na parte superior esquerda do livro, leva você a qualquer momento para o sumário, a partir dele você pode ir para qualquer seção.
Lembrar, este ícone que está localizado na parte superior esquerda do livro, leva você a qualquer momento para o sumário, a partir dele você pode ir para qualquer seção.
 Clique no ícone, use a calculadora onde quer que a encontre, se necessário.
Clique no ícone, use a calculadora onde quer que a encontre, se necessário.
Este livro digital interativo foi concebido com base na filosofia de Proyecto DescartesJS: "Trabalhando de forma altruísta para a comunidade educacional da aldeia global", que visa apenas desenvolver conteúdos educacionais em benefício da comunidade acadêmica, esperando apenas a utilização e divulgação desse conteúdo como contrapartida. O conteúdo do livro, assim como os objetos interativos, foram pensados de forma que possam ser lidos em computadores e dispositivos móveis sem a necessidade de instalação de nenhum programa ou plugin. O livro pode ser baixado para uso local sem depender de conexão com a internet, com exceção de alguns vídeos incluídos no texto. Todos os objetos interativos foram desenhados com o Editor DescartesJS.
Ver https://proyectodescartes.org/iCartesiLibri/descripcion.htm.
O conteúdo deste livro é baseado na função linear e quadrática para professores e alunos que, devido à dificuldade de organizar um horário presencial, permite uma opção autodidata acompanhada de material interativo para uma melhor compreensão dos tópicos abordados.
Voltando à introdução de Documentação DescartesJS de Radillo, Abreu e Espinosa, podemos concordar que este livro se destina tanto a pessoas que ainda não utilizaram DescartesJS quanto a pessoas que possuem alguma experiência e desejam aprimorá-la. Em cada seção do livro são propostos exercícios e incluídos exemplos para que o leitor possa entender passo a passo a funcionalidade do DescartesJS e seu enorme potencial para criar objetos interativos de aprendizagem.
Alguns objetos interativos foram desenhados pelas seguintes pessoas: Alexandra Guzmán Velásquez, Carlos Alberto Jaime Vergara, Carlos Alberto Rojas Hincapié, Carlos Alberto Serrato Hernández, Carlos Mario Restrepo Restrepo, Claudio Francisco Nebbia Rubio, Erika Paulina Tovilla Rubio, José Luis Abreu León, José R. Galo Sánchez, Juan Guillermo Rivera Berrio, Julio Arnoldo Pardo Saavedra, Julio Cesar Domínguez Tovar, Héctor Javier Herrera Mejía, María Lourdes Velasco Arregui, Marta Olivero Serrat, Miguel Ángel Cabezón Ochoa, Oscar Escamilla González, Valentina Muñoz Porras, entre outros.
Esses objetos interativos foram adaptados e modificados ao Plugin DescartesJS para as plataformas atuais e podem ser utilizados no livro por professores e alunos de acordo com as atividades exigidas em cada seção. Todas as modificações dos objetos interativos foram realizadas pelo atual autor do livro interativo, além da elaboração de outros objetos interativos.
 Exploração.
Assista às seguintes cenas interativas como uma introdução aos conceitos de função linear.
Exploração.
Assista às seguintes cenas interativas como uma introdução aos conceitos de função linear.
 Cena interativa.
Cena interativa.
Vamos explorar o plano cartesiano.
Mova o ponto vermelho e observe que cada ponto tem um valor no plano de coordenadas.
 Escena interactiva.
Escena interactiva.
Vamos explorar as partes do plano cartesiano.
Escreva, em cada uma das caixas, os nomes correspondentes, iniciando sempre com letra maiúscula. (Escreva em palavras).
Verifique suas respostas

 Cena interativa.
Cena interativa.
Gráfico de um movimento.
Modifique os valores da função, aperte o botão start e observe a movimentação dos atletas e o gráfico de suas trajetórias.
Cena interativa adaptada pelo autorVer. Proyecto Descartes.org, Telesecundaria.
 Identificar, com o auxílio de objetos interativos de aprendizagem, as características e elementos da função linear e afim, seu domínio, amplitude, se é crescente ou decrescente, interseção com os eixos e aplicações na solução
de situações do cotidiano que modelam esses conceitos matemáticos.
Identificar, com o auxílio de objetos interativos de aprendizagem, as características e elementos da função linear e afim, seu domínio, amplitude, se é crescente ou decrescente, interseção com os eixos e aplicações na solução
de situações do cotidiano que modelam esses conceitos matemáticos.
Aprenderás a:
Conseguirás:
Introdução
Você já deve estar familiarizado com coordenadas cartesianas e saber representar pontos. Esta unidade didática destina-se a introduzir o conceito de função e ter noções básicas para cursos posteriores.
Através de exemplos e exercícios, consolidam-se os conceitos marcados como objetivos para este capítulo.
O que é uma função?
Uma função é uma relação entre duas grandezas que podem variar, de forma que cada valor da primeira corresponde a um único valor da segunda chamada imagem.
A variável que consideramos primeiro, $ x $, é chamada de variável independente, a outra variável, $y$, é chamada de variável dependente porque seu valor depende do valor que assumi a primeira.
Uma função $f(x)$ com variáveis $x$ e $y$ expressa-se da forma:$$\color{Red}y = f(x)$$
Neste caso, $f ( x )$ é a imagen de $x $, ou seja, o valor que corresponde a $y$ pela função ou relação.
 Cena interativa.
Cena interativa.
Representação de uma função por meio de um diagrama.
Domínio de uma função. É o conjunto $X$ de todos os números reis para os quais a função $f$ existe ou é definida.
Imagem de uma função É o conjunto de todos os valores que satisfazem $y=f(x)$, ou seja é o valor da função $f$ em $x$.
Gráfico de uma função
É a representação no plano cartesiano de todos os pares $(x,y)$; onde $x$ é o valor da variável independente, enquanto $y$ é a imagem da função no ponto $x$.
Exemplo. Representação gráfica da função com fórmula $\color{red} p(a) = 4a$ levando em conta que $p$ é o perímetro de um quadrado de lado $a$.
Dando valores a variável $a = 1, 2, 3, 4$ (valores positivos pois trata-se de comprimentos).
Calculamos a imagem de cada valor de $a$ para obter $p$:
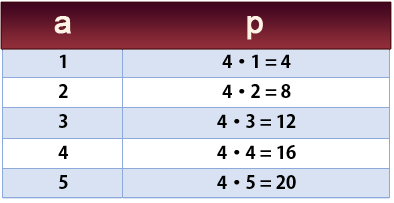
Agora representamos os pares de pontos $(a, p)$ no plano de coordenadas, perímetro x lado do quadrado.
 Cena interativa.
Cena interativa.
Observe o gráfico obtido, com o clique esquerdo sustentado, você pode mover a imagem ou controlar o zoom.
Gráfico: Perímetro x lado do quadrado, $\quad \color{Red} p(a) = 4a$
A representação gráfica de uma função linear é uma função de proporcionalidade direta, uma reta que passa pela origem das coordenadas, sua expressão algébrica é da forma: $$\color{Red}y = mx $$ onde $m$ é a inclinação da reta (ou ainda $m$ é a constante de proporcionalidade).
 Cena interativa.
Cena interativa.
Mova o controle deslizante m e observe a mudança na inclinação.
Com a ajuda da cena interativa, responda às perguntas da próxima página.

 Cena interativa.
Cena interativa.
Observe e analise esta outra forma da função $\color{Red}y = mx + b$
Mova os controles m, x, b e observe a mudança na função.

Os gráficos da equação $y = mx + b$ são retas paralelas à função $y = mx$, que cruzam o eixo de ordenadas $y$ a uma altura $b$.
Essas funções são chamadas de funções afins.
Consequentemente, apenas alguns valores são necessários para obter seu respectivo gráfico, desde que o domínio da função que pode ser abreviado Dom f = Df e sua imagem que pode ser escrita imagem de f = imf ou intervalo da função sejam os números reais.
A representação gráfica de uma função afim é uma reta que não passa pela origem das coordenadas, onde $b$ é a ordenada de $x = 0$ (seu gráfico é uma reta).

Com a cena interativa mostrada abaixo, responda:
 Cena interativa.
Cena interativa.
Observe e analise esta outra forma da função.
Mova o controle m e b, observe a função afim $\color{Red}y = mx + b$.

Elementos da função afim, y = mx + b
A função afim $f(x) = mx + b$ é uma função de primeiro grau (ou seja, um polinômio em $x$ de grau menor ou igual a 1), onde $m$ é conhecido como inclinação, ou coeficiente angular da reta e $b$ é a interseção com o eixo $y$ ou ainda coeficiente linear da reta , cujo corte no eixo $y$ é o ponto $(0 ,b)$
Uma das maneiras de encontrar a inclinação m de uma reta é tomar dois pontos na reta, sejam os pontos $\begin{aligned} P_1 (x_1, y_1) \end{aligned}$ e $\begin{aligned} P_2 (x_2, y_2) \end{aligned}$, então a inclinação é dada pela expressão: $$\color{Red} m = \frac{y_2 - y_1}{x_2 - x_1} $$
 Cena interativa.
Cena interativa.
Observe a inclinação $m$ da reta.
 Deslize o ponto vermelho ou azul, ou digite os valores de cada um e aperte "enter <┘", observe o resultado na inclinação.
Deslize o ponto vermelho ou azul, ou digite os valores de cada um e aperte "enter <┘", observe o resultado na inclinação.
O que pode ser concluído se $m > 0$, se $m < 0$, ou se $m = 0$?
Se você tem dois pontos pertencentes a uma reta, pode encontrar a função afim (equação da reta) que passa por esses pontos aplicando o método conhecido como ponto- inclinação
Primeiro encontramos a inclinação e depois aplicamos a expressão: $$\color{Red} y - y_1 = m (x - x_1)$$
 Cena interativa.
Cena interativa.
Observe e analise outro procedimento para encontrar a equação da função afim.
 Escreva os valores e pressione "enter <┘". Podes conferir as respostas utilizando a calculadora.
Escreva os valores e pressione "enter <┘". Podes conferir as respostas utilizando a calculadora.
A representação gráfica de uma função constante é uma reta paralela a $eixo\space x$, cuja expressão algébrica é da forma: $$y = k$$ donde $k$ é uma constante, e seu valor é um número real.
 Cena interativa.
Cena interativa.
Observe e analise o gráfica da função constante.
Modifique o valor de $k$, observe a função $\space\space y = k$
Responda as perguntas que encontrarás na página seguinte.

| a) $y = -2x + 1\space\space$ | b) $y = 0.5x - 1\space\space$ | c) $y = -x\space\space$ | d) $y = -1.5$ |
| a) $y = -2x + 3\space\space$ | b) $y = 3x\space\space$ | c) $y = 3x + 5$ |
Verifique as respostas na cena seguinte.
Vamos começar recordando da equação geral da reta, a função afim.Véase Libro electrónico: Función lineal, cuadrática y volúmenes
A equação $Ax + By + C = 0$ onde $A,B$ e $C$ são números reais e $A,B$ não são simultaneamente nulos, é conhecida como a equação geral do primeiro grau nas variáveis $x$ e $y$.
A equação explícita da reta quando dois pontos são conhecidos exclui as retas paralelas ao eixo y, cujas equações são da forma $x = constante$, mas todas as retas do plano, sem exceção, estão incluídas na equação $Ax + By + C = 0$ que é conhecida como equação geral da reta.
Tendo em mente a expressão anterior, temos que:
O coeficiente de $x$ é a inclinação$ m = \frac{-A}{B}$ e a ordenada ou interseção com o $eixo\space y$ é $b = \frac{-C}{B} $
O termo independente b é chamado de ordenada na origem de uma reta, onde (0, b) é o ponto de interseção com o eixo das ordenadas.
 Cena interativa.
Cena interativa.
Seja uma função afim na forma geral, encontre o valor da inclinação.
Escreva nas caixas o valor que corresponde à inclinação da função dada e pressione"enter <┘"


Posições relativas entre retas planas
Retas paralelas. Sejam $ m_1$ e $m_2 $ inclinações de duas retas respectivamente, então as retas são paralelas se suas inclinações são iguais, $ m_1 = m_2 $. Observe um exemplo no gráfico seguinte.
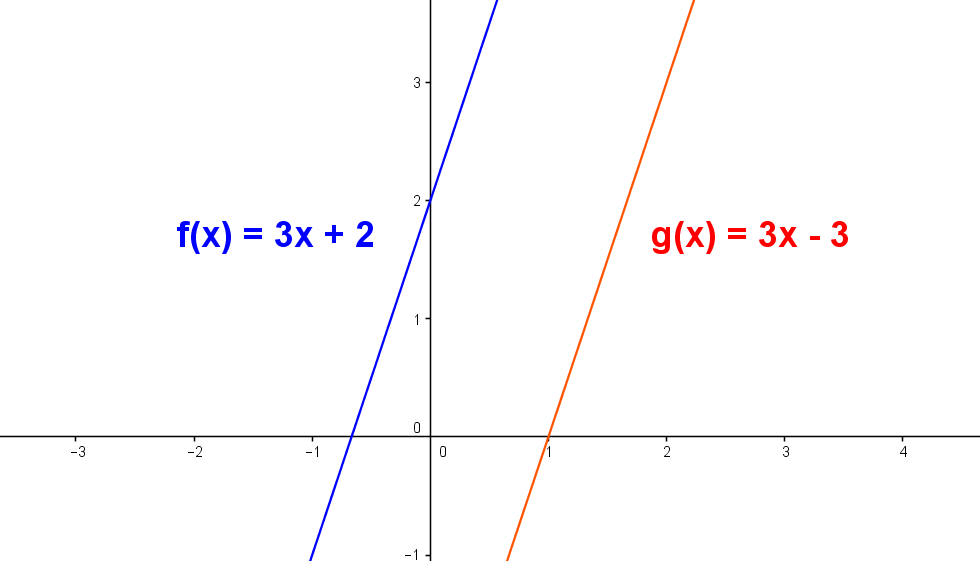
Retas perpendiculares. Duas retas no plano são perpendiculares se o produto de suas inclinações $ m_1 $ e $ m_2 $ satisfazem: $ m_1 . m_2 = -1 $.
Por exemplo, a inclinação de uma reta é $ m_1 = 3 $. E a inclinação de outra reta é $ m_2= \frac{-1}{3} $. Logo, $ m_1 . m_2 = \frac{-1}{3} . 3 = \frac{-3}{3} = -1 $, portanto, a perpendicularidade é verificada, observe no gráfico a seguir.
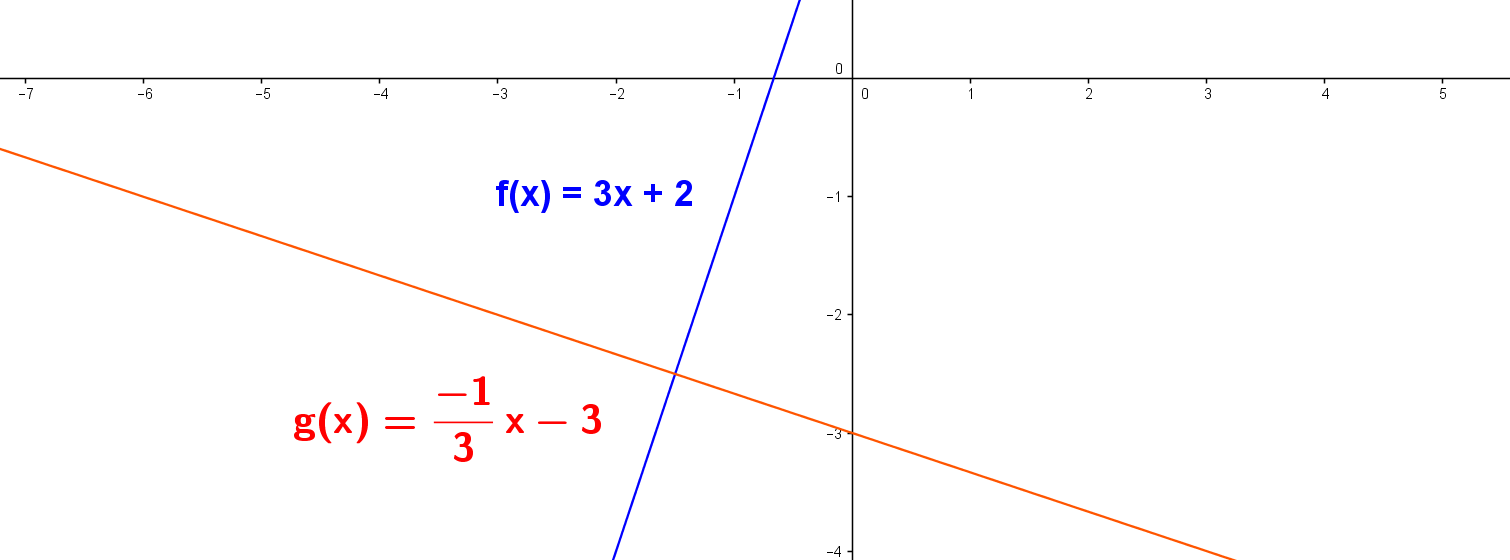
Retas secantes: Interceptam-se em um ponto comum, portanto suas inclinações são diferentes.
Retas coincidentes: Têm os mesmos coeficientes. Retas coincidentes são duas retas que estão localizadas no mesmo plano, têm todos os seus pontos em comum, ou seja, estão localizadas uma acima da outra.
Agora, verifique a posição relativa das retas abaixo com a cena interativa.
 Cena interativa.
Cena interativa.
Insira os coeficientes de cada reta e pressione "enter <┘". Para ver o gráfico das retas, pressione o botão solução.
Uma equação linear é uma igualdade matemática entre duas expressões algébricas, chamadas membros, nas quais aparecem elementos conhecidos e desconhecidos.
 Cena interativa.
Cena interativa.
Resolver equações de primeiro grau (linear).

 Cena interativa.
Cena interativa.
Formulação de problemas com equações lineares.
Instruções
Observe a formulação dos seguintes problemas.
 Pressione o botão mais exemplos para ver outros problemas e o botão dados diferentes para mudar os dados do problema.
Pressione o botão mais exemplos para ver outros problemas e o botão dados diferentes para mudar os dados do problema.
Um sistema de equações é formado por duas ou mais equações com duas incógnitas nas quais queremos encontrar uma solução comum, que corresponde a um ponto $(x,y)$ que satisfaz todas as equações ao mesmo tempo.
Seja a equação linear, expressa na forma: $$\color{red} ax + by = c$$
donde $a, b$ y $c$ são números reais e as variáveis $x$, $y$ as incógnitas.
Os sistemas de equações, também conhecidos como:
O sistema 2 x 2 é formado por duas equações expressas assim:
$$\color{red} ax + by = c \qquad (1)$$ $$\color{red} dx + ey = f \qquad (2)$$Métodos de solução.
1. Método da Adição.
O método consiste em multiplicar uma ou ambas as equações por algum número para obtermos um sistema no qual os coeficientes de $x$ e de $y$ são iguais e de sinais opostos, para eliminar a incógnita ao somar as duas equações.
2. Método da Substituição.
O Método consiste em isolar uma das incógnitas de uma das equações e substituir esse valor na outra equação, desta forma, chegamos a uma equação de primeiro grau com uma incógnita.
3. Método da Comparação.
O método consiste em uma pequena variante do da substituição. Para resolver um sistema de equações, uma incógnita deve ser isolada nas duas equações e em seguida igualar o resultado de ambas, daí obtém-se uma equação de primeiro grau com uma incógnita.
4. Método Gráfico.
Vamos agora ao método gráfico para resolver um sistema de duas equações lineares com duas incógnitas.
As variáveis $x$ e $y$ são as incógnitas, que nos dará como solução o ponto comum $(x, y)$ interseção das retas do gráfico. Lembre-se que:
$$\color{red} ax + by = c \qquad (1) \\ dx + ey = f \qquad (2)$$
Veja exemplos da solução gráfica de um sistema de equações 2 x 2 na seguinte cena interativa.
 Cena interativa.
Cena interativa.
Solução método gráfico de um sistema de equações lineares.
Podem ocorrer os seguintes casos:
 Veja exemplos do uso dos métodos da adição, substituição e comparação. Cenas interativas adaptadas pelo autor.
Ver. Proyecto Descartes.org, ed@d, matemáticas.
Veja exemplos do uso dos métodos da adição, substituição e comparação. Cenas interativas adaptadas pelo autor.
Ver. Proyecto Descartes.org, ed@d, matemáticas.

Resolva o seguinte sistema de equações lineares.
 Verifique a solução utilizando o método gráfico. Insira os coeficientes $a, b, c, e, d$ e $f$ respectivamente no sistema
Verifique a solução utilizando o método gráfico. Insira os coeficientes $a, b, c, e, d$ e $f$ respectivamente no sistema
e pressione o botão solução para ver a solução gráfica.
 Identificar e resolver problemas que se ajustam a funções quadráticas mediante soluções gráficas e analíticas
que estabelecem relações entre variáveis.
Identificar e resolver problemas que se ajustam a funções quadráticas mediante soluções gráficas e analíticas
que estabelecem relações entre variáveis.
Aprenderás a:
 Cena interativa.
Cena interativa.
Analise a seguinte cena interativa da função $y = x^2$.
Analisar as duas cenas interativas apresentadas a seguir, e responder a perguntas na página seguinte.
 Cena interativa.
Cena interativa.
Mova o ponto azul e aumente ou diminua o número de decimais com a ajuda do controle da cena.

 Cena interativa.
Cena interativa.
Move o ponto azul e aumente ou diminua o número de decimais com ajuda do controle da Cena.

1. Qual dos dois gráficos corresponde a uma função? Porque?
2. Qual é a imagem de $x=2$ em cada um dos gráficos?
A parábola é o gráfico da função quadrática, um polinômio de segundo grau, cuja equação geral é: $$\color{red} y = ax^2 + bx + c $$
donde a, b e c são números reais.
Aparece em numerosos fenômenos naturais ou, em outros menos freqüentes, em nossas cidades: o esguinchar de uma fonte, a trajetória descrita por uma bola de futebol em um chute forte, o movimento de um projétil disparado por um canhão,...
Parábolas são comumente conhecidas como gráficos de funções quadráticas. Definição geométrica da parábola:
A parábola é o conjunto de pontos do plano que estão à mesma distância de um ponto fixo chamado Foco (F) e de uma reta chamada diretriz (d)
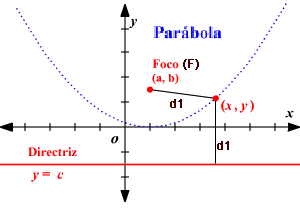
O eixo focal é o eixo perpendicular a diretriz(d) que passa pelo foco(F). O ponto da parábola que pertence ao eixo focal chama-se vértice.
A diretriz (d), é a reta perpendicular ao eixo focal que se encontra a uma distância $c$ do vértice e fora da parábola (Figura 1.3).
 Cena interativa.
Cena interativa.
Representação gráfica da parábola $\color{red} y = x^2$.
Com o mouse, você pode mover o ponto P ao longo da parábola e verificar que a distância de P ao foco F e a reta d é sempre a mesma.
No gráfico você representou a parábola cuja diretriz é a reta $y = -\frac14$ e cujo foco é o ponto $F(0,\frac14)$.
Dizemos que a equação desta parábola está incompleta, porque os termos $b$ e $c$ não aparecem, isto é, $b = c = 0$.
 Cena interativa.
Cena interativa.
Observemos o gráfico da parábola $\quad \color{red}y = ax^2$
Mova o controle a, Observe o que acontece com o gráfico da parábola.
Responda às perguntas abaixo com a ajuda da cena interativa.

Observe que se $x = 0$ então $y = 0$. Mostre que todas essas parábolas sempre se interceptam em um único ponto, no eixo $x$; esse ponto é a origem do sistema.

A reta pela qual, dobrando o papel, permitiria sobrepor as duas metades ou ramos da parábola, chama-se eixo de simetria.
A parábola $y=ax^2$ é uma curva simétrica em relação a $x=0$, de modo que desenhando um dos ramos até o vértice, podemos obter o outro ramo como se fosse um espelho. Você também pode verificar analiticamente.
 Cena interativa.
Cena interativa.
Observemos o gráfico da parábola $\quad \color{red}y = ax^2$.
 Mova o controle a, observe e responda as perguntas da página seguinte.
Mova o controle a, observe e responda as perguntas da página seguinte.
Observe que tomamos valores de x que são simétricos em relação à origem, que é o vértice, ou seja: $$x = 1,\quad x = -1 $$ $$x = 2,\quad x = -2$$

Além disso, mova o ponto $P$ e verifique se os pontos na tabela estão no gráfico e se são realmente simétricos.
 Escreva um valor para $a$ e complete a tabela a seguir, você pode conferir na cena interativa anterior:
Escreva um valor para $a$ e complete a tabela a seguir, você pode conferir na cena interativa anterior:
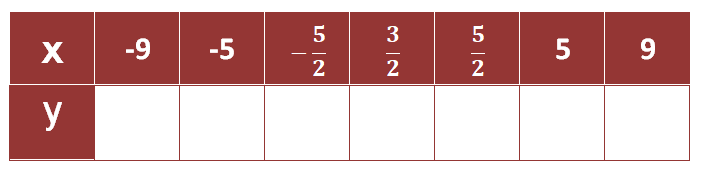

A equação desta parábola também está incompleta com $a=\not 0$, mas agora só falta o termo $bx$, isto é, $b = 0$.
 Cena interativa.
Cena interativa.
Observemos o gráfico da parábola $\quad \color{red}y = ax^2 + c$.
Mova os controles a e c, observe e responda as perguntas.
Como antes, consideramos valores de $x$ simétricos em relação ao vértice. Com o ponteiro do mouse, você pode verificar a simetria que também pode ser vista na tabela de valores.
Na cena interativa, altere os valores de $a$ e $c$ para ver as simetrias.
Tal como no caso anterior, analise e responda às questões e à experimentação proposta.

 Escreva um valor para $a$, $c$ e complete a tabela a seguir, você pode conferir na cena interativa anterior:
Escreva um valor para $a$, $c$ e complete a tabela a seguir, você pode conferir na cena interativa anterior:

Novamente, a equação desta parábola também está incompleta com $a=\not 0$. Agora falta o termo $c$; então teremos $c = 0$.
 Cena interativa.
Cena interativa.
Vamos ver o gráfico da parábola $\quad \color{red}y = ax^2 + bx$.
Mova os controles a e b, observe e responda as perguntas.
Tal como no caso anterior, analise e responda às questões e à experimentação proposta.

 Veja agora a seguinte análise:
Veja agora a seguinte análise:
Se os pontos de corte com o eixo $x$, estão no dito eixo, devem ter sua coordenada $y = 0$; ou seja, será verificado que:
então, se resolvermos esta equação, obteremos os valores de $x$ aos quais corresponde $y = 0$.
Vamos proceder assim, tiramos o fator comum $x$ e teremos:
$$( a x + b ) x = 0$$ $$então,\space ( a x + b ) = 0 \quad e \quad x = 0$$portanto, uma das soluções é $x = 0$, com a qual um dos pontos de interseção é a origem do sistema $(0,0)$.
A outra solução será obtida de, $$a x + b = 0$$ $$a x = -b$$ $$x = \frac {-b}{a}$$ portanto, o outro ponto de interseção terá coordenadas $( -\frac {b}{a}, 0 )$.

 Escreva um valor para $a$, $b$ e complete a tabela a seguir, você pode conferir na cena interativa anterior:
Escreva um valor para $a$, $b$ e complete a tabela a seguir, você pode conferir na cena interativa anterior:
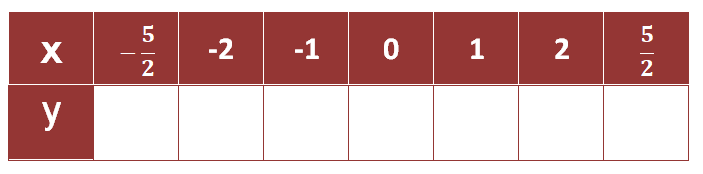

Recordemos!
Primeiro faça os cálculos e depois verifique os resultados com a ajuda das cenas interativas.
 Cena interactiva.
Cena interactiva.
Observemos o gráfico da parábola $\quad \color{red}y = ax^2 + bx$.
Mova os controles a e b, observe e responda as perguntas.
Você consegue identificar o eixo de simetria?
Linha imaginária que divide a parábola em duas partes iguais.
Finalmente veremos a função quadrática completa, ou seja, a função onde os coeficientes $a, b$ e $c$ são números reais diferentes de zero.
 Cena interativa.
Cena interativa.
Observemos o gráfico da parábola $\quad \color{red}y = ax^2 + bx + c$.
Mova os controles a, b e c, observe as mudanças no gráfico.
Responda às perguntas abaixo com a ajuda da cena interativa.

 Sugestão. Use a cena interativa na página anterior.
Sugestão. Use a cena interativa na página anterior.
Para as questões 5, 6 e 7, resolva as equações das parábolas obtidas e encontre o número de soluções.
Quantas soluções você obtém em cada caso?
O vértice da parábola
Já vimos que o vértice da parábola está sempre localizado no eixo de simetria da parábola e, além disso, depois de responder a questão 8, verifica-se que o referido vértice tem a abcissa $x=-\frac {b}{2a}$, portanto a ordenada do vértice é obtida substituindo o valor $x$ na equação da parábola.
O vértice $(x,y)$ da parábola será representado pelo ponto $v(h,k)$.

 Cena interativa.
Cena interativa.
Observemos os principais dados de uma parábola da forma: $\color{red}y = ax^2 + bx + c$.
Mova os controles a, b e c, observe e responda as perguntas.

Você pode utilizar todos os conceitos já vistos (simetria, vértice, corte com os eixos,...) para representar o gráfico de qualquer parábola de forma simples e eficiente.

Com efeito, basta seguir os passos abaixo:
Acabamos de estudar a parábola da forma $y = a x^2 + b x + c $ em detalhes passo a passo, então devemos saber muito bem como encontrar todos os seus dados.
Agora vamos praticar o que aprendemos nesta seção com a seguinte atividade.

 Cena interativa.
Cena interativa.
Verifique sua resposta na cena interativa que aparece quando você pressiona o botão Resposta.

Você pode fazer o exercício quantas vezes quiser, primeiro faça os cálculos e depois verifique os resultados com a ajuda da cena interativa.
Foram trabalhados os principais conceitos, relações e gráficos de
$$\color{red}y = ax^2 + bx + c$$Agora, vamos focar no vértice e ver outra expressão que relaciona o vértice com a equação da parábola, essa expressão é:
$$\color{red}y = a(x - h)^2 + k$$ onde $h$ e $k$ correspondem respectivamente ao ponto no eixo $x$ e ao ponto no eixo $y$ do vértice, ou seja, o vértice tem coordenadas $(h, k)$. O ponto $a$ indica a abertura ascendente ou descendente da parábola e quanto mais seu valor se afasta de zero, menor será a abertura da curva. Mas vamos ver de onde vem essa expressão, seja:
Mas vamos ver de onde vem essa expressão, seja:
$$\color{red}ax^2 + bx + c = 0$$ Agrupando os termos com variável $x$ e evidenciando um fator comum,
Na fórmula $\quad \displaystyle (ax^2 + bx) + c = a(x^2 + \frac{b}{a}x) + c = 0 $
completamos o quadrado perfeito, lembra como?, ou seja, somamos e subtraímos a mesma expressão para não alterar a equação, neste caso é $(\frac{b}{2a})^2$, lembre-se que você tem que multiplicar por $a$, o termo fora do trinômio. $$ a \bigg(x^2 + \frac{b}{a}x + (\frac{b}{2a})^2 \bigg) + c - a \bigg(\frac{b}{2a}\bigg)^2 = 0 $$
Agora, fatoramos o trinômio quadrado $(x^2 + \frac{b}{a}x + (\frac{b}{2a})^2)$, que corresponde a um trinômio quadrado perfeito: $$ a \bigg(x + \frac{b}{2a} \bigg)^2 + c - a \bigg(\frac{b}{2a} \bigg)^2 = 0 $$ portanto, temos que $\quad h = -\frac{b}{2a} \quad y \quad k = c - a (\frac{b}{2a} )^2$
Então, obtemos a expresão em termos do vértice $(h,k)$ $$\color{red}y = a(x - h)^2 + k$$

 Cena interativa.
Cena interativa.
Verifique sua resposta na cena interativa que aparece quando você pressiona o botão Resposta.

Seções cônicas
Uma seção cônica é a curva resultante das diferentes interseções entre um cone e um plano; se o referido plano não passa pelo vértice,
Elas são classificadas em quatro tipos de cônicas: elipse, parábola, hipérbole e circunferência, veja o gráfico abaixo:
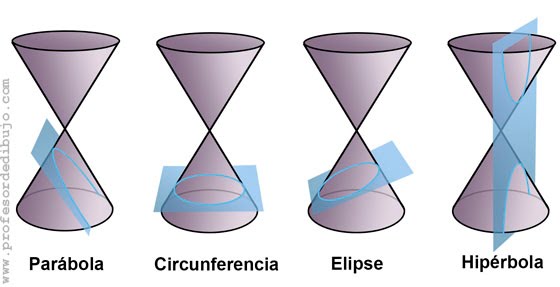
As cônicas são representadas por equações quadráticas com duas incógnitas.
A equação geral que representa uma seção cônica é uma equação quadrática com variáveis $x$ e $y$ da forma:
$$\color{red}Ax^2 + By^2 + Cx + Dy + E + Fxy= 0$$ em que $A$ e $B$ não podem ser zero ao mesmo tempo, trabalharemos com o coeficiente de $xy=0$ para simplificar.Agora vamos focar na expressão que gera uma parábola, e que representa uma função, neste caso a análise será feita para quando for $A =\not 0$, $D =\not 0$ e $B = 0$. O que ocorre quando acontece o contrário, $A = 0$ e $B =\not 0$.
Para o caso quando $B = 0$, temos que a expressão é:
$$\color{red}Ax^2 + Cx + Dy + E = 0$$ que corresponde a uma parábola vertical com abertura para cima ou para baixo, que determina uma função ( Ver 3D).Completando o trinômio quadrado perfeito para a variável $x$ na equação $Ax^2 + Cx + Dy + E = 0$, obtém-se a chamada equação canônica de uma parábola vertical, com a forma:
$$\color{red}(x - h)^2 = 4p(y - k)$$ onde o ponto v(h,k) corresponde ao vértice da parábola e p a distância do vértice ao foco ou do vértice a diretriz.
Analise o processo que foi realizado para obter a equação canônica.
 Lembre-se!
Lembre-se!
Uma parábola tem os seguintes elementos:
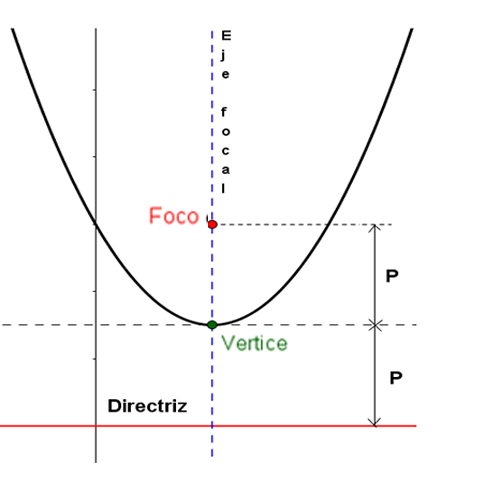
Exemplo.
Observe o procedimento para passar para a equação canônica:

Dada a equação geral $\color{red}Ax^2 + Cx + Dy + E = 0$, encontre sua equação canônica, gráfico e os elementos da parábola.
 Cena interativa.
Cena interativa.
Realize todos os cálculos antes e confira sua resposta na cena interativa.
Se conheces o vértice $v(-2,-4)$ e o foco $F(-2,-7)$, podes encontrar a equação geral?
A função quadrática é também conhecida como equação de segundo grau, onde $\color{red}y = f(x)$, pode ser expressa da forma:
$$\color{red}f(x) = a x^2 + bx + c$$ A equação quadrática é a equação: $f(x)=0$ que pode ter uma solução real dupla, ou dois números reais ou dois números complexos.
A equação quadrática é a equação: $f(x)=0$ que pode ter uma solução real dupla, ou dois números reais ou dois números complexos.
Para resolver ou encontrar as soluções da equação quadrática
$$\color{red}a x^2 + bx + c = 0$$ podemos:Então, temos os seguintes casos, se:
 Recordemos!
Recordemos!
A equação quadrática apresenta as possíveis soluções:
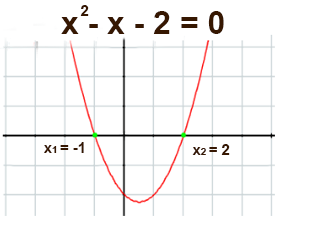
A figura mostra a solução gráfica da equação $f(x) = x^2 - x - 2$, que tem duas soluções reais diferentes
$x_1 = -1$ e $x_2 = 2$, que corresponde as ordenadas dos pontos de interseção com o eixo $x$.
 Escena interactiva.
Escena interactiva.
Observemos a solução da equação $\quad \color{red}ax^2 + bx + c = 0$.


Cena interativa.
 Usando as instruções dadas, encontre a solução da equação quadrática aplicando um dos métodos.
Usando as instruções dadas, encontre a solução da equação quadrática aplicando um dos métodos.
Confira a solução na cena interativa.
Como uma bola deve ser lançada verticalmente para atingir a distância horizontal máxima? Como se chama essa trajetória? Matemáticamente, como esse movimento pode ser interpretado?
Vejamos algumas aplicações na física.

Situação Problema 1.
Observe na cena a seguir a curva descrita, quando uma bola é lançada verticalmente com certa velocidade.
 Cena interativa.
Cena interativa.
Modifique o controle da velocidade e pressione o botão animar

Situação Problema 2.
 Modifique o controle da velocidade e pressione animar para ver a trajetória da bola.
Modifique o controle da velocidade e pressione animar para ver a trajetória da bola.
 Cena interativa.
Cena interativa.
Insira os valores de Y max e t vertice, pressione "enter <┘" para ver os resultados e verifique na Cena interativa.


Situação Problema 3.
 Uma cerca deve ser feita para uma área retangular, expressa por uma função quadrática.
Uma cerca deve ser feita para uma área retangular, expressa por uma função quadrática.
Pressione o botão animar, realize os cálculos e verifique na cena interativa as respostas.
 Cena interativa.
Cena interativa.
Digite os resultados da medição dos lados e o total da Área encontrada, pressione "enter <┘" para ver os resultados.
Rojas, C., Restrepo, C., Herrera, H., Córdoba, F., Cardeño, J. (2013).Objetos virtuales de aprendizaje –OVA–. 1° Versión. Fondo Editorial ITM. Medellín
Rojas, C., Restrepo, C., Correa, D., Castrillón, E., Ortiz, H., Herrera, H., Córdoba, F., Cardeño, J. (2012). Función lineal, cuadrática y volúmenes. Guía para docentes. Fondo Editorial ITM. Medellín
Ruiz, C. (2014). Proyectodescartes.org-EDAD. Obtenido de: http://proyectodescartes.org/EDAD/materiales_didacticos
Abreu L., José y Muñoz P., (2004). Proyectodescartes.org-Telesecundaria. Obtenido de: http://proyectodescartes.org/Telesecundaria/materiales_didacticos
Barbero, E. (2004). ProyectoDescartes.org. Obtenido de: http://proyectodescartes.org/uudd/materiales_didacticos
Ramírez, M. (2011). Álgebra y Trigonometría. Caldas(Ant.) Corporación Universitaria Lasallista. 315 pag.