|
SUMANDO BITS |
|
|
Lógica Digital |
|
|
|
|
|
1. LA SUMA BINARIA |
|
|
Uno de los requisitos claves en los ordenadores digitales es el usar funciones lógicas para poder llevar a cabo operaciones aritméticas. La operación básica es la suma, como cabría imaginar. Si podemos efectuar sumas, será fácil también restar y poder implementar multiplicaciones y divisiones. Recordemos como funciona la suma binaria. Para ello observa la pequeña escena que sigue (recordemos que sólo disponemos de dos dígitos: el 0 y el 1). Si observáis atentamente la escena, veréis que en la cuarta fila aparecen dos dígitos para la suma de dos bits. Este hecho nos obliga a considerar en un posible circuito con dos entradas (los dos bits a sumar) y dos salidas (la suma y el llamado acarreo). |
|
|
|
|
|
|
|
|
2. SEMISUMADOR BINARIO |
|
|
El circuito que se representa a continuación, permite la suma de dos bits. Nos devuelve el resultado de dicha suma y el valor del acarreo que se pueda generar. |
|
|
|
1.- Dibuja en tu cuaderno el circuito que aparece en la escena. Representa su tabla de verdad (recuerda que tenemos dos salidas). 2.- ¿Qué función lógica efectúa la suma? ¿Qué función lógica nos da el acarreo de la suma de dos bits? |
|
Ahora bien, la realidad es que un ordenador no suele sumar números de un solo bite, lo que suele hacer es trabajar con tiras de varios bits cada una. Por tanto necesitaremos de varios circuitos trabajando conjuntamente. Pero hay un problema con el circuito anterior. 3.- Efectúa, en tu cuaderno, las siguientes sumas usando el circuito anterior: 10001 + 1011, 1010 + 101. ¿Qué problema aparece? Como habréis podido ver, las sumas anteriores no pueden efectuarse adecuadamente con el circuito representado, ya que nos encontramos con el problema de arrastrar el acarreo cuando dicho acarreo es 1. Por este motivo al circuito anterior se le conoce cómo semisumador y no es apto para implementar otros circuitos, efectivos, para los ordenadores, pero nos da pistas de cómo hacerlo. |
|
|
3. SUMADOR BINARIO |
|
|
Bien, el problema aparecido
con el semisumador
queda resuelto con el circuito representado en la escena de la derecha.
Evidentemente es algo más complejo, pero resuelve de forma adecuada la suma
de dos bits. A
dicho circuito se le conoce cómo sumador. |
|
|
|
4.- Copia el circuito representado, en tu cuaderno. Construye la tabla de verdad asociada. 5.- Intenta hallar las expresiones booleanas para la suma y para el acarreo de salida. 6.- Efectúa las sumas de la actividad 3 ayudándote del sumador. Observa que ahora no aparece el error anterior.
|
|
7 (actividad voluntaria).- Intenta diseñar un circuito que reste dos bits. Debes considerar el problema que nos aparece al intentar restar a un 0 un 1, así cómo el posible acarreo. Para ello es aconsejable que primero construyas una tabla de verdad adecuada. [nota: un poco de consulta bibliográfica no os vendrá nada mal. Esta actividad no es sencilla, es todo un reto.] |
|
|
4. UNA CUESTIÓN PRÁCTICA |
|
|
|
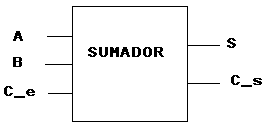
En la práctica, a la hora de representar circuitos reales, para no complicarlos excesivamente, el sumador suele representarse mediante una caja negra con tres entradas y dos salidas como se puede ver en la siguiente figura: |
||
|
|
8.- Usando la figura anterior dibuja un circuito que pueda sumar dos números de cinco bits. |
|
|
|
||
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Josep Mª Navarro Canut |
|
|
|
|
Proyecto Descartes.org. Año 2013 |
|
|
|
|
|