| |
9.
Rectángulo asociado a un polígono regular |
Definición:
"Un
polígono se dice que es regular si tiene todos sus lados
y ángulos iguales".
Observación
1: Todo
polígono regular puede inscribirse en una
circunferencia.
Observación
2: A cada
polígono regular podemos asignarle un rectángulo cuyos
lados son el radio de la circunferencia circunscrita y el
lado del polígono.
|
| |
9.1 Razón de los rectángulos asociados a
polígonos
- Varía
el parámetro N,
correspondiente al número de lados de un
polígono regular y anota la razón del
rectángulo asociado.
- ¿Por
qué inicialmente decrece la razón y es
creciente posteriormente?
- ¿Cómo
se denomina el rectángulo correspondiente al
cuadrado (N=4)?
- ¿Cómo
se denomina el rectángulo correspondiente al
hexágono (N=6)?
- ¿Cómo
se denomina el rectángulo correspondiente al
octógono (N=8)?
- ¿Cómo
se denomina el rectángulo correspondiente al
decágono (N=10)?
|
| |
|
|
| |
9.2 ¿Está asociado "tu
rectángulo" a algún polígono?
|
|
| |
9.3 Determinación analítica de
proporciones.
Determina
analíticamente, para un número arbitrario de
lados, la longitud del lado de un polígono
regular en función del radio de la
circunferencia circunscrita a él.
A
partir de la expresión anterior halla la razón
entre el radio y el lado del decágono regular o
proporción áurea.
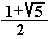
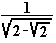
|
|
| |
10.
Rectángulos semejantes recíprocos |
Definición:
"Dado
un rectángulo diremos que un rectángulo semejante a él
es su recíproco si el lado menor
del primero es el lado mayor del segundo o
viceversa"
|
| |
10.1 Recíproco de un
rectángulo.
- Fija
una razón o proporción y desplaza el punto P
hasta que obtengas otro rectángulo con igual
razón.
| Ayúdate
con los pulsadores inferiores para
ajustar la posición de dicho punto y
alcanzar la razón buscada |
- ¿Cuántos
rectángulos son recíprocos de uno dado?
|
| |
|
| |
10.2 Ángulo entre la diagonal de un
rectángulo y la de su recíproco
¿Qué
ángulo forma la diagonal de un rectángulo y la
de su recíproco?
¿Cual
es el procedimiento para dibujar el recíproco de
un rectángulo?
¿Dibuja
los rectángulos asociados a los polígonos de 4,
6, 8 y 10 lados y determina sus recíprocos?
|
| |
Teoría
del gnomon
|
|
| |
Observación
1: La
teoría del gnomon o de la expansión gnómica tiene su
base en la frase de Aristóteles: "Hay ciertas cosas
que no sufren alteración salvo en magnitud, cuando
crecen ..."

Observación
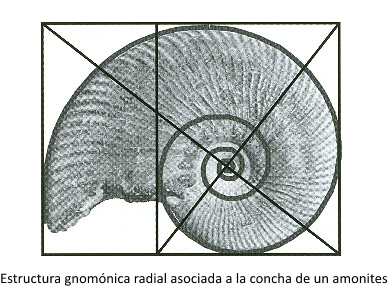
2: El
crecimiento gnómico se manifiesta en los tejidos más
consistentes de los animales como los huesos, dientes
cuernos o conchas. El crecimiento es acumulativo
manteniendo la forma (semejanza) frente a los tejidos
blandos que son desechados y reemplazados.
|
|
| |
|
Definición:
"El
gnomon de un rectángulo es otro que añadido al primero
genera otro rectángulo semejante al inicial".
Observación
3: El gnomon
de un rectángulo es el rectángulo necesario para
obtener su recíproco
|
|
| |
|
|
| |
10.3 Gnomon de un rectángulo
|
|
| |
|
11.2
Identificación de rectángulos áureos
- Observa
la pintura de Dalí que se adjunta e identifica
los rectángulos áureos.
- Mira
bien el anexo a la taza de cinco metros de
longitud que, en el título de la obra, el autor
denomina ¿inexplicable ?
¿Consideras que es inexplicable? o como
buen crítico matemático eres capaz de
darle una razonada explicación.
- ¿Todavía
no te has construido un cartabón áureo y otro
cartabón cordobés? Recuerda que con ellos
podrás identificar rápidamente los rectángulos
áureo y cordobés. Ahora es el momento oportuno
para dar explicaciones.
|
|
Construcción gnómica con el
rectángulo áureo
|
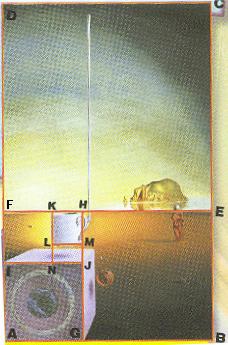
Dalí
"Semitaza
gigante volando con anexo
inexplicable
de cinco metros de longitud"
|
| En
la figura adjunta sobre la pintura original se han
superpuesto los rectángulos (cuyos lados son de color
rojo) y que están identificados por las letras desde la
A a la N. Podemos
observar como el genio de Dalí usa la construcción
gnómica del rectángulo áureo buscando obtener la
proporción divina, la belleza autogenerando belleza.
Los
rectángulos áureos son: ABCD, ABEF, AGHF, IJKF, JHKN,
MJNL
|
 |
| |
|
|
11.3
Identificación de rectángulos cordobeses
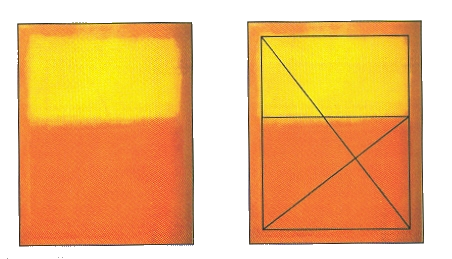
- Observa
la pintura de Rothko que se adjunta e identifica
los rectángulos cordobeses.
- Compruébalo
con tu cartabón cordobés
|
|
Construcción gnómica con el
rectángulo cordobés
|
Mark
Rothko, 1956. Naranja y amarillo
|
|
¿Qué
indujo al pintor a utilizar esa proporción y no la
áurea?
¿Divino
versus humano?
|
 |
|