
 |
FUNCIONES: Funciones de proporcionalidad inversa. |
| Análisis. | |
| Funciones de proporcionalidad inversa. | |
|
Este tipo de funciones relacionan las variables x e y a través de expresiones del tipo
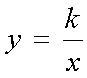 siendo k un número real cualquiera distinto de cero. La gráfica de este tipo de funciones es una curva denominada hipérbola equilátera. |
|
|
En la imagen adjunta puedes ver distintos tipos de funciones de proporcionalidad inversa sin más que variar el valor de k. Contesta a las preguntas que se te plantean al margen referentes a sus propiedades. | |
|
|
1.- Modifica los valores de k e intenta encontrarle un significado gráfico a este parámetro. |
|
2.- Determina el dominio y el recorrido de cualquier función de este tipo. | |
|
3.- Estudia sus intervalos de monotonía y sus extremos relativos. ¿Qué pasa si k es negativo? | |
|
4.- Estudia sus posibles simetrías. ¿Son funciones pares, impares o ninguna de ambas cosas? | |
|
5.- ¿Son funciones acotadas? Si la respuesta es afirmativa, ¿superior, inferiormente o ambas cosas a la vez? Determina sus extremos absolutos (si los tiene). | |
| 6.- Una vez analizado el aspecto y las propiedades de estas funciones, ¿podrías explicar por qué se les da el nombre de funciones de proporcionalidad inversa? | |
| EJERCICIO. | |
|
Al igual que hemos hecho en los casos anteriores vamos a ver una aplicación práctica. Un grifo con un caudal de 15 litros por minuto ha empleado 16 horas en llenar un depósito. Se trata de averiguar cuánto hubiera tardado si el caudal hubiera sido otro distinto (mayor o menor). Al plantear este problema, vemos que evidentemente cuanto mayor sea el caudal menos tiempo se tardará en llenar el depósito y cuanto menor sea el caudal más tiempo tardará. Los datos del problema nos permiten calcular con facilidad el volumen del depósito: 16 horas = 16 x 60 = 960 minutos; luego el volumen es de 15 x 960 = 14.400 litros. Como el volumen del depósito es constante, si duplico el caudal, el tiempo de llenado se reduce a la mitad y lo mismo sucede con cualquier variación que se me ocurra. En otras palabras, las magnitudes caudal del grifo y tiempo de llenado son inversamente proporcionales. Además, si llamamos "x" a la primera e "y" a la segunda, se cumple xy = 14400, o también
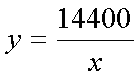 Ahora podemos averiguar cuánto tiempo tarda en llenarse el depósito con cualquier caudal que se nos ocurra. En concreto, averigua cuánto tiempo tardaría en llenarse el depósito con caudales de 10, 20, 25 o 30 litros por minuto usando la imagen adjunta: | |
|
|
| José Luis Alonso Borrego Adaptación a DescartesJS: Joan Carles Fiol Colomar |
||
 |
||
| ProyectoDescartes.org Año 2015 | ||

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.