
 |
FUNCIONES: Interpolación. |
| Análisis. | |
| Interpolación. | |||||||||
|
En todo este tema has visto distintas maneras de expresar una función. Has visto, por ejemplo, que en numerosas ocasiones las funciones se expresan mediante tablas de valores obtenidos de la observación o de la experimentación. También has visto que cuando la función puede ser expresada mediante una relación matemática (en especial una relación matemática sencilla) es muy fácil obtener información de la misma. Por lo tanto, un problema con el que nos tendremos que enfrentar con frecuencia es cómo obtener una expresión matemática que represente la función que estamos estudiando cuando los datos los hemos obtenido experimentalmente o mediante observación de algún fenómeno. En la mayoría de los casos este problema es demasiado complejo para resolverlo, por lo que nos conformaremos con una aproximación. El proceso por el que a una tabla de valores se le asocia una expresión matemática que la represente se denomina Interpolación. La función obtenida debe representar de forma exacta los valores de la tabla, pero no proporciona más que una estimación de los valores que no aparezcan en la tabla. Una vez que hemos aceptado que no vamos a dar con una expresión exacta sino aproximada, surge otro problema. ¿De qué tipo es la función con la que vamos a realizar la aproximación? o dicho de una manera más rigurosa ¿qué tipo de interpolación vamos a hacer?. La representación gráfica de los puntos de la tabla nos puede dar una idea, pues los puntos que se representen pueden mostrar una tendencia. Por ejemplo, si resulta que los puntos parecen estar alineados debemos buscar una función lineal para representarlos. Diremos en ese caso que realizamos una interpolación lineal. Si la apariencia de los puntos se asemeja a una parábola realizaríamos una interpolación cuadrática. Y así con cualquier tipo de función cuyo aspecto conociéramos previamente. En la práctica puede suceder que no dispongamos de puntos suficientes para adivinar la tendencia, o que aún teniendo puntos suficientes, la gráfica no se parezca a nada conocido. Existen procedimientos bastante complejos para interpolar ese tipo de funciones, pero que no están a nuestro alcance. En una situación de este tipo nosotros nos conformaremos con una interpolación lineal entre cada pareja de puntos, obteniendo una función definida a trozos y cada trozo definido por una función lineal. |
|||||||||
|
Para comprender todo esto mejor haremos uso del siguiente ejemplo: A lo largo del día se han recogido los siguientes datos de temperaturas:
Haz una estimación de la temperatura que ha hecho a las 11h, a las 12h, a las 14h, a las 15h y a las 16h. | |||||||||
|
|
Para resolver este problema representaremos gráficamente los puntos de la tabla A(10,7), B(13,18) y C(17,11). Después calcularemos la ecuación de la recta que pasa por A y por B y la que pasa por B y por C. Recuerda que para ello debes hacer uso de la fórmula que nos da la ecuación de la recta conocidos dos de sus puntos: 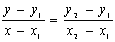 | ||||||||
| |||||||||
|
Naturalmente los valores obtenidos son simples estimaciones en las que se supone que la temperatura ha ido cambiando de forma lineal y esto puede no ser cierto. Cuanto mayor sea el número de puntos de los que se parte y más próximos estén entre sí mejor será la estimación. | |||||||||
| José Luis Alonso Borrego Adaptación a DescartesJS: Joan Carles Fiol Colomar |
||
 |
||
| ProyectoDescartes.org Año 2015 | ||

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.