- Iniciamos la construcción eligiendo tres puntos A, B y C no alineados, que serán los vértices del triángulo de partida.
Identificamos las coordenadas de cada punto. En nuestro ejemplo A(-3, -5), B(4, -3) y C(1, 4).
- Hallamos las coordenadas de los vectores determinados por A y B (lado c del triángulo), por B y C (lado a) y por A y C (lado b). Resultando, en nuestro ejemplo inicial, (7, 2) para el lado c, (-3, 7) para el lado a y (4, 9) para el lado b, ya que:
-
Para saber la medida de los ángulos que forman los lados del triángulo, calculamos los productos escalares de los vectores, con origen común, que determinan.
Por comodidad llamamos a las componentes de estos vectores (cx, cy), a las del lado c y (bx, by) y (ax, ay), a las de los lados b y a respectivamente. El ángulo, por ejemplo, que determinan los lados b y c, vértice A, es:
- Análogamente se determinan los ángulos en los vértices B y C.
- Antes de continuar con la construcción del triángulo de Morley se deben calcular los ángulos
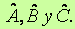 Una vez calculados estos ángulos, se puede pulsar el botón adelante (haciendo clic en la flechita azul), de siguiente escena, valor 1, para comprobar si los cálculos son correctos. Una vez calculados estos ángulos, se puede pulsar el botón adelante (haciendo clic en la flechita azul), de siguiente escena, valor 1, para comprobar si los cálculos son correctos.
- Si hemos realizado la propuesta de trabajo de la página anterior, ya tenemos la ecuación de las rectas que contienen a los lados del triángulo ABC. En caso contrario debemos hallar esas ecuaciones y comprobar que coinciden con las que nos muestra la escena al pulsar el botón adelante, para que tome el valor 2.
- Ahora es el momento, si aún no lo hemos hecho, de hallar las ecuaciones de las trisectrices de cada ángulo. Estas ecuaciones pueden deducirse de varias formas diferentes. Una de ellas es, por ejemplo, considerando el punto por el que tienen que pasar y la pendiente que debe tener cada trisectriz, que podemos calcular a partir de las pendientes, ya conocidas, de las rectas que definen al vértice considerado, ya que sumándole, o restándole, un tercio del ángulo del vertice correspondiente, al ángulo que la recta forma con la horizontal, que lo conocemos aplicando la función arco tangente a la pendiente de la recta que contiene al lado, obtendremos, mediante la función tangente, la pendiente de la trisectriz correspondiente. En el caso de que ya hayamos calculado las ecuaciones de las trisectrices, podemos pulsar el botón adelante para comprobar que coinciden con las que muestra la escena cuando dicho botón toma el valor 3.
- Haciendo la intersección de cada par de trisectrices adyacentes encotraremos las coordenadas de los puntos M, N y P. Cuando tengamos esas coordenadas pulsamos sobre el botón adelante, hasta que este muestre el valor 4, para comprobar que coinciden con las que muestra la escena.
- Ahora, aplicando la fórmula de la distancia entre dos puntos, o calculando los módulos de los vectores que los puntos M, N y P determinan, encontramos que el triángulo que forman es equilátero, salvo error en los decimales por redondeo. La comprobación la verificamos pulsando el botón adelante para que este tome el valor 5. Con esta última verificación hemos construido el triángulo descubierto por F. Morley y comprobado el teorema que lleva su nombre.
|


