 |
¡ FELIZ 2026 ! |
NÚMEROS |
|
¡ FELIZ 2026 !
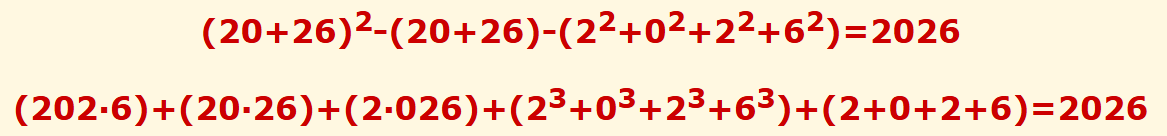
Despedimos el año 2025, un año muy interesante desde el punto de vista matemático, con algunas propiedades numéricas muy curiosas que no se volverán a repetir en muchos años. Entre ellas, la de ser un cuadrado perfecto. Se pueden recordar las propiedades de este año que termina en el documento ¡Feliz 2025!.
Como cada año que finaliza, lo despedimos el 31 de diciembre, día número 365 de cualquier año no bisiesto. Antes de empezar con las propiedades del número 2026, vamos a ver una propiedad muy interesante también del número 365.
• El número 365 se puede expresar como la suma de los cuadrados de tres números naturales consecutivos:
102 + 112 + 122 = 100 + 121 + 144 = 365
• El número 365 también se puede expresar como la suma de los cuadrados de los dos números naturales consecutivos a los anteriores:
132 + 142 = 169 + 196 = 365
Y a continuación pasamos a estudiar las propiedades del número 2026.
PROPIEDADES DEL NÚMERO 2026
• Descomposición factorial. 2026 es un número biprimo o semiprimo porque es el producto de dos números primos.
2026 = 2 · 1013
• Número de divisores: (1+1)·(1+1)=4
1 , 2 , 1013 y 2026
• Suma de sus cifras:
2 + 0 + 2 + 6 = 10
• Suma de los cuadrados de sus cifras:
22 + 02 + 22 + 62 = 4 + 0 + 4 + 36 = 44
• Suma de los productos de cada dos cifras consecutivas:
2 · 0 + 0 · 2 + 2 · 6 = 0 + 0 + 12 = 12
• El número 2026 se obtiene como resultado de las siguientes operaciones utilizando solamente sus cifras en el mismo orden:
(20+26)2 - (20+26) - (22+02+22+62) = 2026
(202·6) + (20·26) + (2·026) + (23+03+23+63) + (2+0+2+6) = 2026
ACTIVIDADES CON EL NÚMERO 2026
Las siguientes actividades se proponen para números desde una hasta cuatro cifras. Como ayuda para resolverlas, si el número tiene menos de cuatro cifras se puede completar añadiendo ceros a la izquierda.
1. El número 2026 no tiene ninguna cifra impar.
¿Cuál fue el año anterior con todas las cifras impares? ¿Cuántos años tenías?
¿Cuál será el año siguiente con todas sus cifras impares? ¿Cuántos años tendrás?
2. El número 2026 se escribe uniendo dos números que se diferencian en 6 unidades, 20 y 26.
¿Cuáles fueron los cinco años anteriores con esta propiedad?
¿Cuáles serán los cinco años siguientes?
¿Cada cuántos años sucede esto? ¿Por qué?
3. La suma de las cifras del número 2026 es 10.
¿Cuáles fueron los cinco años anteriores con esta propiedad?
¿Cuáles serán los cinco años siguientes?
4. La suma de los cuadrados de las cifras del número 2026 es 44.
¿Cuáles fueron los cinco años anteriores con esta propiedad?
¿Cuáles serán los cinco años siguientes?
5. La suma de los productos de cada dos cifras consecutivas del número 2026 es 12.
¿Cuáles fueron los cinco años anteriores con esta propiedad?
¿Cuáles serán los cinco años siguientes?
6. Escribimos la fecha de un día cualquiera del año con el formato dd/mm/aa, es decir, dos cifras para el día del mes, dos cifras para el mes y dos cifras para el año.
¿Qué días del año verifican dd + mm = aa?
¿Qué días del año verifican dd · mm = aa?
¿Qué días del año verifican dd · mm · aa = 2026?
7. Escribimos la hora, minutos y segundos de un instante de cualquier día del año con el formato hh:mm:ss, es decir, dos cifras para la hora, dos cifras para los minutos y dos cifras para los segundos. ¿Qué instantes de cada día verifican hh · mm · ss = 26?
8. El año 2026 comienza y termina en jueves.
¿Cuál fue el año anterior que empezó y terminó en jueves?
¿Cuál será el año siguiente?
En el siguiente enlace se pueden encontrar las soluciones a estas actividades.
OTRAS PROPIEDADES DEL NÚMERO 2026
Según los conjuntos numéricos que se estudian en la enseñanza de las Matemáticas, el número 2026 es un número natural, entero, racional y real. También se puede decir que es par o múltiplo de 2. En Matemáticas Recreativas aparecen otros tipos de números que verifican algunas propiedades curiosas y que reciben distintas denominaciones.
Según algunas de estas propiedades se puede decir que el número 2026:
• Es un número deficiente porque la suma de sus divisores, excepto él mismo, es menor que 2026.
1 + 2 + 1013 = 1016 < 2026.
• Es un número feliz porque se obtiene 1 al final de la siguiente secuencia de operaciones:
2026 → 22+02+22+62=44 → 42+42=32 → 32+22=13 → 12+32=10 → 12+02=1
En algunos formatos de fechas se utilizan solamente dos cifras para escribir el año. Así 2026 se escribe como 26, que indica el año número 26 del siglo XXI. El número 26 es el único número que está comprendido entre un cuadrado perfecto y un cubo perfecto:
52 = 25 < 26 < 27 = 33
CUADRADO MÁGICO ADITIVO CON CONSTANTE MÁGICA 2026
Utilizando todos los números naturales comprendidos entre 499 y 514, ambos incluidos, se puede construir un cuadrado mágico aditivo, de orden cuatro, con constante mágica 2026. Este cuadrado mágico, que figura a continuación, tiene las mismas propiedades que el cuadrado mágico aditivo conocido como Chautisa Yantra.
Propiedades de este cuadrado mágico:
• La suma de los números de cada una de las cuatro filas es igual a 2026.
• La suma de los números de cada una de las cuatro columnas es igual a 2026.
• La suma de los números de cada una de las diagonales es igual a 2026.
• Es un cuadrado mágico pandiagonal, la suma de los números situados en las diagonales secundarias es igual a 2026.
• La suma de los números situados en las cuatro esquinas es 2026.
• La suma de los números situados en el cuadrado central es 2026.
• Si se divide el cuadrado en cuatro cuadrados de 2×2, la suma de los números situados en cada uno de ellos es 2026.
• La suma de los números situados en cualquier otro cuadrado de 2×2 también es 2026.
• La suma de los números situados en las esquinas de los cuadrados de 3×3 es igual a 2026.
• Existen más grupos de cuatro números cuya suma es 2026.
• Si se permutan cíclicamente las filas o las columnas del cuadrado mágico inicial, se obtiene otro cuadrado mágico con las mismas características.
Si a cada uno de los números de este cuadrado mágico se le resta 500, se obtiene otro cuadrado mágico aditivo con números más pequeños, con las mismas propiedades que el cuadrado mágico anterior y con constante mágica 26, número con el que se representa de forma reducida el año.
Aplicando la última propiedad de estos cuadrados mágicos y reordenando filas y columnas mediante permutaciones cíclicas, se obtiene el siguiente cuadrado mágico aditivo de constante mágica 26. Los números de las tres primeras casillas corresponden al orden que ocupan en el abecedario las iniciales del autor de este documento.
Pero independientemente de lo que digan las Matemáticas de este número,
¡ FELIZ 2026 !
| Autor: Luis Barrios Calmaestra | ||
 |
Proyecto Descartes. Año 2026 | |

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.