HORMIGÓN ARMADO - HIPÓTESIS ACI-318
Ingeniería Civil
 
Revisión de momento resistente en una sección rectangular con la hipótesis ACI-318
Este método se fundamenta en las siguientes hipótesis:
a) Se admite que las secciones planas normales al eje de flexión permanecen planas luego de la flexión, es decir, las deformaciones son proporcionales a su distancia al eje neutro. Esta hipótesis se ha verificado experimentalmente y es correcta, excepto para mediciones muy pequeñas y en la rama descendente del diagrama esfuerzo-deformación.

b) El diagrama de tensiones de compresión no es rectilíneo y debe ajustarse a los resultados experimentales sobre cilindros. El ACI-318-02 Sec. 10.2.6 acepta, para el bloque de compresiones, cualquier curva siempre que sus predicciones de la última resistencia estén en concordancia razonable con los resultados experimentales. En otros términos, no se acepta la proporcionalidad entre las tensiones y las deformaciones.

c) Se admite adherencia perfecta entre el hormigón y el acero. Para el hormigón reforzado con varillas corrugadas esta hipótesis es realista.

d) El trabajo del hormigón a tracción se desprecia, que no influye apreciablemente en los resultados.

e) Resultados experimentales demuestran que la deformación del hormigón en el instante de la falla o rotura,  varía entre 0.0032 y 0.0037. Para hormigones de 140 a 350 kgf /cm2, estando del lado de la seguridad, se asume que la falla es inminente cuando euc alcanza el valor de 0.003.

En la siguiente figura se ilustran las condiciones de deformación específica supuestas para la resistencia última de una sección rectangular y una sección circular. Tanto la deformación en el acero como la deformación en el hormigón son directamente proporcionales a la distancia desde el eje neutro. Este hipótesis es válida para todo el rango de cargas, desde carga nula hasta la carga última.

Hipotesis ACI-318

Esta hipótesis  puede considerarse satisfecha para una distribución rectangular de esfuerzos, tal como se ilustra en la siguiente figura. Charles S. Whitney propuso este método considerando una distribución uniforme de los esfuerzos de compresión de intensidad 0.85 f'c actuando sobre un área rectangular limitada por los bordes de la sección y una recta paralela el eje neutro, localizada a una distancia A de la fibra de máxima deformación en compresión.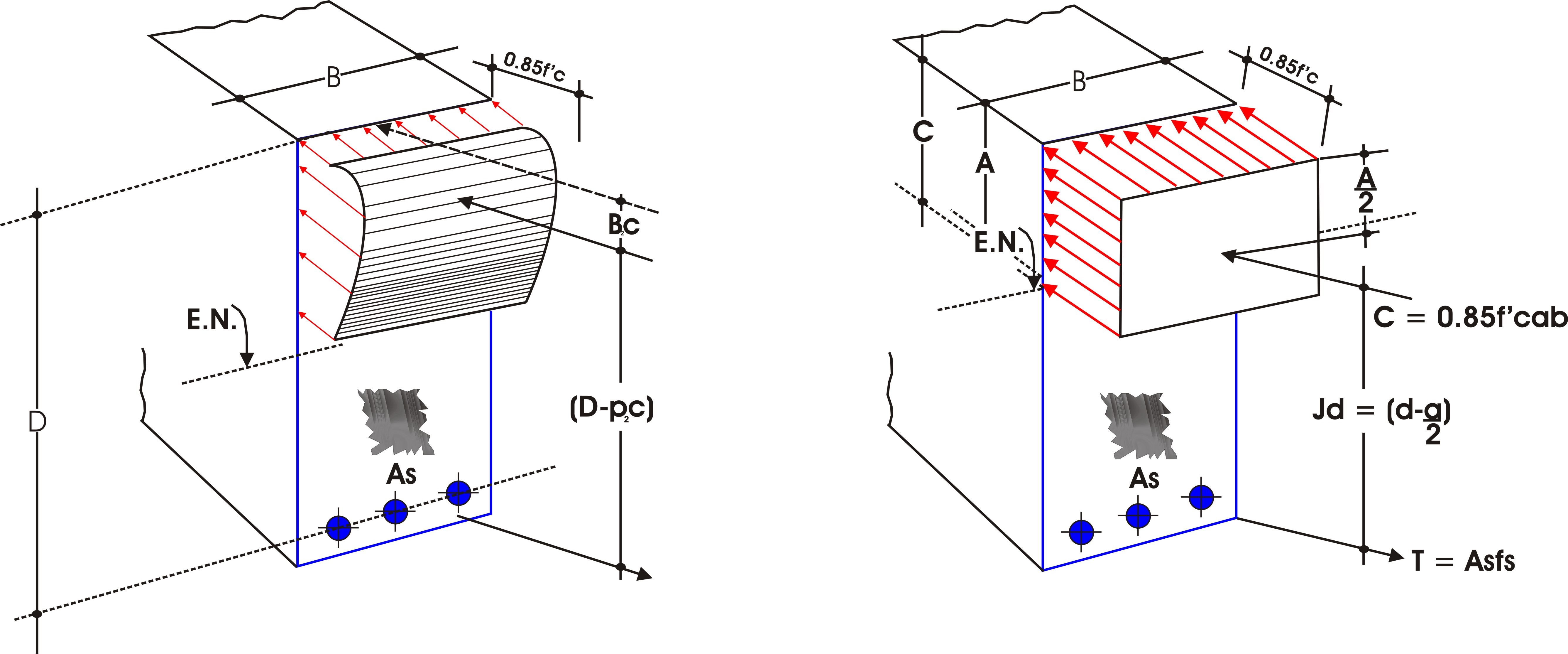

Whitney
En la siguiente escena interactiva puedes practicar este método con algunas secciones.
Actividad. Calcular el momento resistente en una sección rectangular.
En la escena se presentan diferentes secciones rectangulares de vigas de hormigón, además de la posibilidad de cambiar tamaños y números de barras de acero y las propiedades mecánicas de los elementos.

Se propone calcular el momento resistente, utilizando la hipótesis de la ACI o por tanteo.

Realiza varios ejercicios hasta que estés seguro de haber comprendido cómo se calcula el momento resistente con la hipótesis ACI 318.
     
 
Juan Guillermo Rivera Berrio
 
ProyectoDescartes.org. Año 2014
 
 
 

Licencia de Creative Commons
Los contenidos de este recurso didáctico están bajo una licencia de Creative Commons si no se indica lo contrario.