circulares para
Educación Primaria
Plantillas de fracciones circulares para Educación Primaria
J. Manuel Muñoz Cañadas
Miembro de la RED Descartes, España
Maestro de Educación Primaria
Imparte cursos para la formación
del profesorado de Educación Primaria
Asesor y participante en proyectos del
CEIP José Cortines Pacheco
Córdoba (España)
2024
Plantillas de fracciones circulares para Educación Primaria
Autor:
J. Manuel Muñoz Cañadas
Colaborador interactivos DescartesJS:
José Antonio Salgueiro González
Diseño del libro: Juan Guillermo Rivera Berrío
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN: 978-84-10368-03-3
LICENCIA
Introducción
Con el contenido de este libro se pretende abarcar el currículo de matemáticas desde los cinco a los doce años, presentando modelos de actuación con plantillas que contienen círculos fraccionados o sectores circulares. Siempre tendremos en cuenta que las actividades digitales interactivas constituyen un refuerzo y no sustituyen a la imprescindible experiencia, que aporta la manipulacion del material didáctico.
Indicadores para entender la estructura del libro.
Presentación de las plantillas con fracciones circulares
Presentación de las plantillas con fracciones circulares.
Al construir los círculos fraccionados se pueden colorear o (clic video) emplear cartulina de diferentes colores para cada fracción. Se pueden plastificar. También hay multiples opciones en el mercado. Excelente el uso de Mathigon-polypad como recurso digital.
Plantillas circulares pdf (clic icono).
Recortar las fracciones pdf (clic icono).
Representación y concepto de fracción
Representación y concepto de una fracción.
Una fracción representa el número de partes que cogemos de una unidad que está dividida en partes iguales , como un círculo en nuestro caso. En el lenguaje hacemos continuas referencias a distancias, tiempo, superficies, capacidades, personas, objetos...en las que se emplean fracciones.
Escribo fracciones con letra
Puedes copiar el nombre de cada fracción que está escrito en la escena.
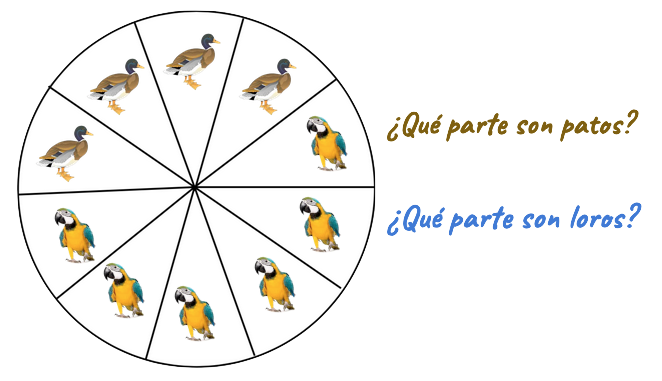
- Se ha cogido la plantilla de los doceavos porque es el número total de animales que hay.
- Se coloca un animal en el espacio de cada fracción o sector circular.
- Dos sectores o fracciones del círculo para las gallinas, otras dos para las vacas, tres para los caballos y cinco para las ovejas.
- Representación numérica:
$$\color{RoyalBlue}\ vacas\displaystyle\frac{2}{12}\quad caballos\displaystyle\frac{3}{12}\quad ovejas\displaystyle\frac{5}{12}\quad gallinas\displaystyle\frac{2}{12}$$
Escribo fracciones con letra
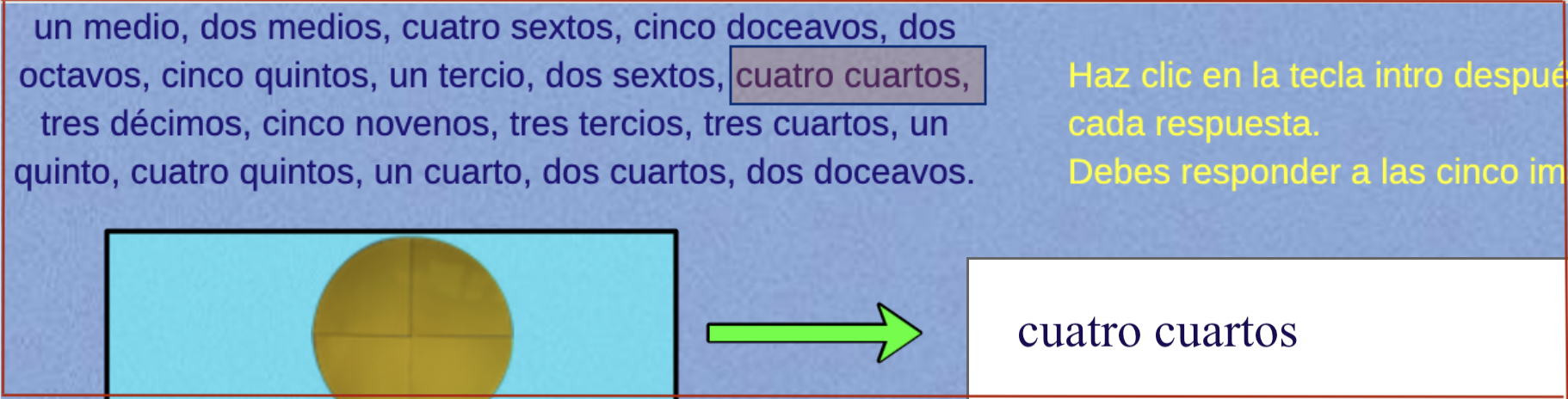
Practica con el siguiente juego la escritura con letra de una fracción. Obsevarás en la escena la escritura de cada fracción para que tengas una referencia y poder escribirla sin errores.
Forma fracciones pdf (clic icono).
Escena diseñada por Eduardo Barbero Corral para la unidad Ejercicio de fracciones.
Comparación de fracciones
Comparación de fracciones
 Ordenamos las diferentes fracciones para establecer relación entre ellas y descubrir sus valores, para ello, colocamos una fracción sobre otra considerando el tamaño.
Ordenamos las diferentes fracciones para establecer relación entre ellas y descubrir sus valores, para ello, colocamos una fracción sobre otra considerando el tamaño.
 Se utiliza el signo matemático adecuado
Se utiliza el signo matemático adecuado < o > , que indica el orden de mayor o menor. Hacemos una observación, si todos los numeradores son 1, ¿es mayor la fracción que tenga el denominador 5, o la que tiene 9? ¿Por qué es eso así?
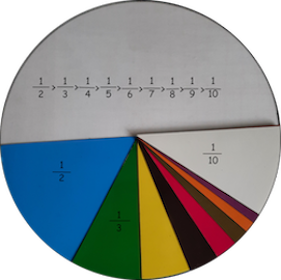 De forma intuitiva se han colocado las diferentes fracciones una sobre otra para poder comparar su tamaño y valor.
Enseguida se entiende, que la que tiene mayor superficie vale más y por tanto hay menos partes. También se puede saber el valor de cada fracción colocándola sobre su círculo fraccionado en el que encaje la fracción. Hay que utilizar los signos indicados
De forma intuitiva se han colocado las diferentes fracciones una sobre otra para poder comparar su tamaño y valor.
Enseguida se entiende, que la que tiene mayor superficie vale más y por tanto hay menos partes. También se puede saber el valor de cada fracción colocándola sobre su círculo fraccionado en el que encaje la fracción. Hay que utilizar los signos indicados < y > , para expresar la comparación entre las fracciones.
Forma los modelos $\, \displaystyle\frac{4}{6}, \, \displaystyle\frac{3}{8}, \, \displaystyle\frac{3}{4} \,$, y ordena de mayor a menor.

 Podríamos utilizar otro recurso exclusivamente con números dependiendo del nivel del alumnado, calculando el valor del cociente de cada fracción, para lo cual, recurrimos
a los valores que indicamos en la tabla. Los resultados de las fracciones se presentan en la tabla del capítulo "Representación decimal de una fracción".
Podríamos utilizar otro recurso exclusivamente con números dependiendo del nivel del alumnado, calculando el valor del cociente de cada fracción, para lo cual, recurrimos
a los valores que indicamos en la tabla. Los resultados de las fracciones se presentan en la tabla del capítulo "Representación decimal de una fracción".
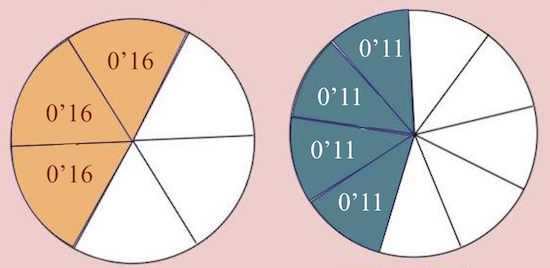
- Juega a rellenar con fracciones los diferentes círculos fraccionados.
- Observa si entre el tamaño de la fracción y la cantidad de fracciones que necesitamos para completar un círculo, hay una relación inversa.
- Si el tamaño de la fracción es más grande, se ponen menos fracciones.
- Si el tamaño de la fracción es menos grande, se ponen más fracciones.
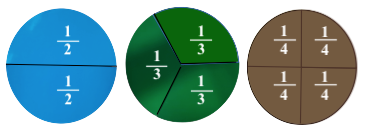
Lo demostramos con números. Si las fracciones son más grandes, entonces hay menos fracciones.
$$\color{RoyalBlue}\displaystyle\frac{1}{2} + \displaystyle\frac{1}{2} = \displaystyle\frac{2}{2}= 1,\space dos\space fracciones\space de \space\displaystyle\frac{1}{2} $$
$$\color{DarkGreen}\displaystyle\frac{1}{3} + \displaystyle\frac{1}{3} +\displaystyle\frac{1}{3}= \displaystyle\frac{3}{3}= 1,\space tres\space fracciones \space de \space\displaystyle\frac{1}{3}$$
$$\color{Brown}\displaystyle\frac{1}{4} + \displaystyle\frac{1}{4} +\displaystyle\frac{1}{4} +\displaystyle\frac{1}{4}= \displaystyle\frac{4}{4}= 1,\space cuatro\space fracciones\space de\space \displaystyle\frac{1}{4}$$
Queremos ordenar fracciones. Emplea material manipulativo.
- Podemos formar todas las fracciones que se muestran en el interactivo.
- Comparamos los tamaños de las diferentes superficies que ocupan en el círculo.
- Escribimos con lenguaje matemático, < o > , el orden que queremos expresar.
Ordena cinco fracciones de mayor a menor valor según el espacio que ocupan en el círculo y completa con su número correcto.
Actividades para mejorar la comprensión respecto al valor de una fracción y la comparación con otras .En el botón introducción de la barra del interactivo, se pueden formar múltiples fracciones para favorecer la comprensión de este concepto.
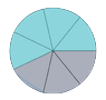 Con el pulsador de exploración, podrás superponer las representaciones circulares y comparar sus valores. Cuando pases a la parte de ejercicios, observa el botón de "Ver círculos" y lo presionas para que aparezcan las fracciones representadas
y puedas entender la comparación entre ellas.Proyecto Pizarra Digital Proyecto Pi.
Con el pulsador de exploración, podrás superponer las representaciones circulares y comparar sus valores. Cuando pases a la parte de ejercicios, observa el botón de "Ver círculos" y lo presionas para que aparezcan las fracciones representadas
y puedas entender la comparación entre ellas.Proyecto Pizarra Digital Proyecto Pi.
 En la primera jarra se han echado dos partes de agua y una de zumo de naranja.
En la primera jarra se han echado dos partes de agua y una de zumo de naranja.
 En la segunda jarra se han echado dos partes de agua y otras dos de zumo de naranja.
En la segunda jarra se han echado dos partes de agua y otras dos de zumo de naranja.
 En la tercera jarra se han echado tres partes de zumo de naranja y cinco partes de agua.
En la tercera jarra se han echado tres partes de zumo de naranja y cinco partes de agua.
¿En cuál de las jarras habrá más zumo de naranja?
Fracciones equivalentes
Fracciones equivalentes.
¿Cómo conseguimos equivalencias a un medio?
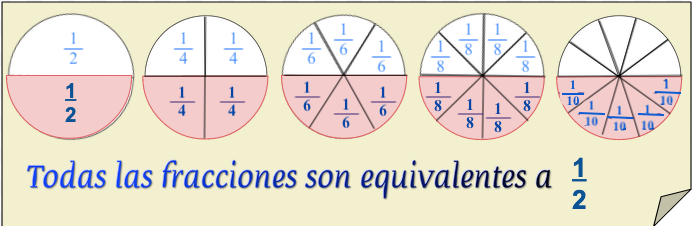
Y las podemos representar así:
$$\fcolorbox{837D3C}{FFF8DC}{$\displaystyle\frac{1}{2} = \displaystyle\frac{2}{4} = \displaystyle\frac{3}{6} = \displaystyle\frac{4}{8} = \displaystyle\frac{5}{10} = ...son\ equivalentes $}$$Equivalencias a un medio.
Ampliamos nuestro sentido numérico. Sumar cuatro veces la misma fracción es igual que multiplicar la fracción por cuatro. Comprueba.
Siempre nos resultará el valor de un medio:
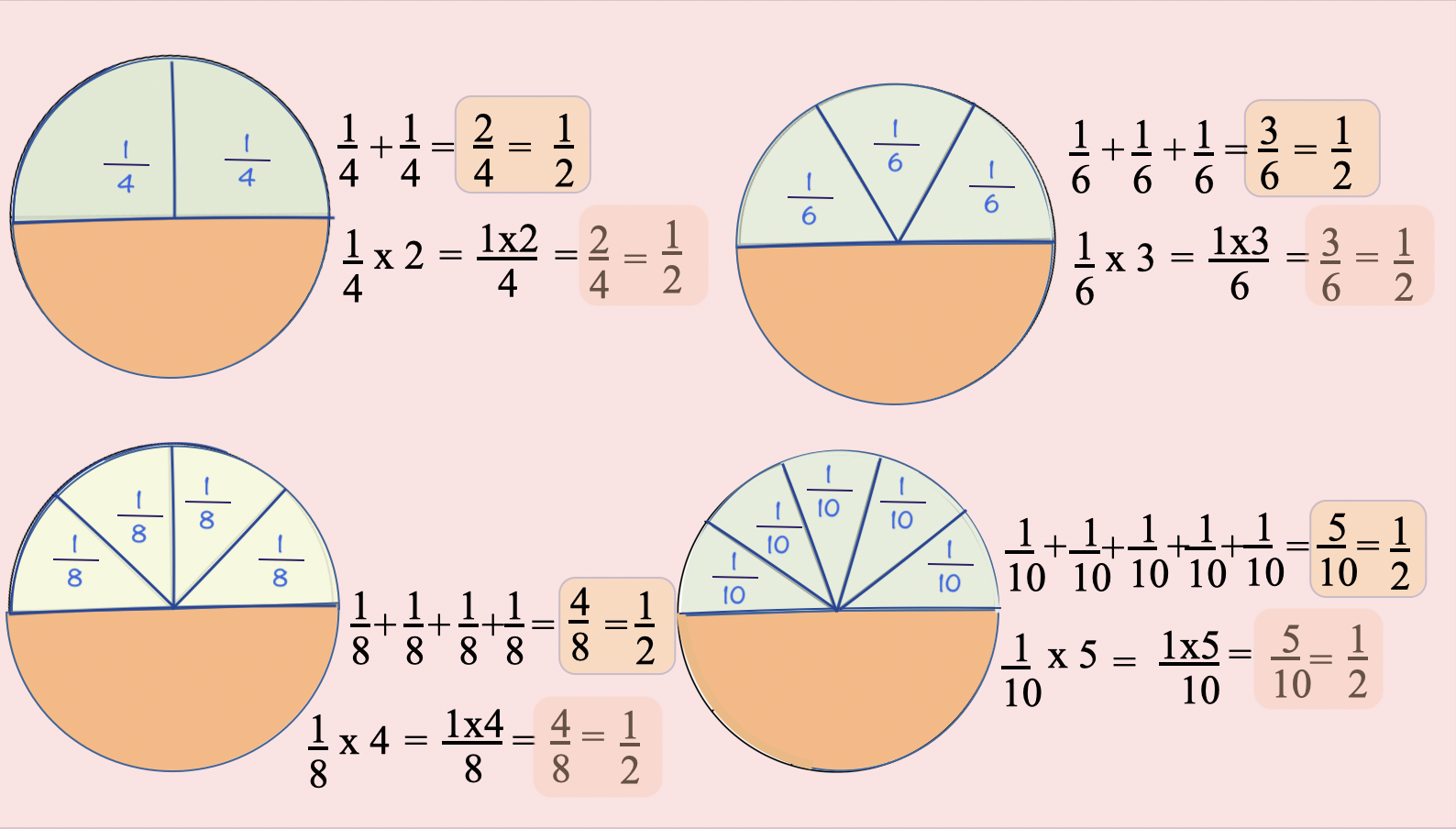
Seguimos con las equivalencias.
Equivalencias a un tercio.
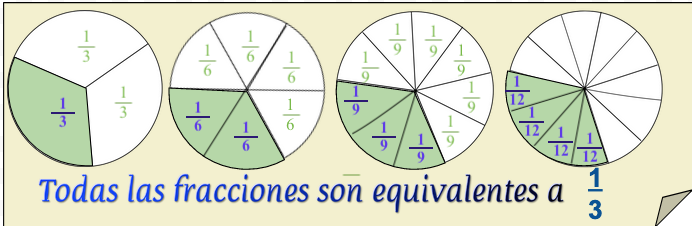
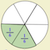 La dividida en sextos se pueden hacer tercios y en cada uno caben dos sextos. Por eso un tercio equivale a dos sextos (mismo valor).
La dividida en sextos se pueden hacer tercios y en cada uno caben dos sextos. Por eso un tercio equivale a dos sextos (mismo valor).
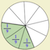 Después encontramos otra, que también permite formar tercios y en un tercio caben tres novenos .
Después encontramos otra, que también permite formar tercios y en un tercio caben tres novenos .
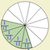 ¿Y si queremos dividir el tercio en cuatro partes? Dividimos en cuatro partes iguales y resultan ser cuatro doceavos.
¿Y si queremos dividir el tercio en cuatro partes? Dividimos en cuatro partes iguales y resultan ser cuatro doceavos.
Y se representan así:
$$\fcolorbox{837D3C}{FFF8DC}{$\displaystyle\frac{1}{3} = \displaystyle\frac{2}{6} = \displaystyle\frac{3}{9} = \displaystyle\frac{4}{12} = \displaystyle\frac{5}{15} = ...son\ equivalentes $}$$Ahora veamos en el siguiente interactivo la formación de fracciones equivalentes obtenidas al dividir de forma sucesiva a :
Equivalencias a un cuarto.
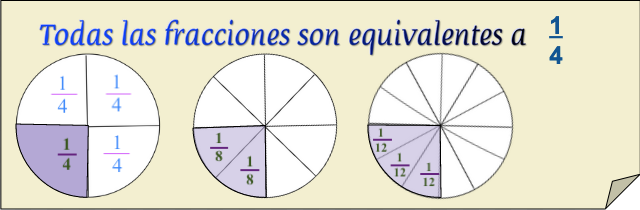
Las fracciones equivalentes a un cuarto se representan así:
$$\fcolorbox{837D3C}{FFF8DC}{$\displaystyle\frac{1}{4} = \displaystyle\frac{2}{8} = \displaystyle\frac{3}{12} = \displaystyle\frac{4}{16} = \displaystyle\frac{5}{20} = ... son\ equivalentes $}$$Utilizando fracciones equivalentes podemos resolver facilmente suma y resta de fracciones con diferentes denominadores cambiando las fracciones iniciales por otras equivalentes a ellas, que tengan un denominador común. Lo veremos en suma y resta de fracciones.
Escena diseñada por Diego Luis Feria Gómez para Proyecto Canals.Fracción de una cantidad
Fracción de una cantidad
 Si le doy a mis hermanas cuatro sextos de los dieciocho caramelos que me han regalado en mi cumpleaños.
Si le doy a mis hermanas cuatro sextos de los dieciocho caramelos que me han regalado en mi cumpleaños.
- ¿Cuántos son los caramelos que han quedado para mí?
- ¿Cuántos son los caramelos que se han quedado mis hermanas?
En la escena anterior, resolveremos el problema con elementos que tengamos, como policubos, regletas, figuras y la plantilla adecuada.
 Cogemos la plantilla de los tercios porque se dice que un tercio son naranjas.
Cogemos la plantilla de los tercios porque se dice que un tercio son naranjas.
 Se reparte la fruta en tres partes colocando cuatro piezas de fruta en cada parte.
Se reparte la fruta en tres partes colocando cuatro piezas de fruta en cada parte.
 Se ve que en un tercio caben cuatro naranjas, y está resuelto el problema.
Se ve que en un tercio caben cuatro naranjas, y está resuelto el problema.
 Antonia ha gastado los dos quintos del dinero que tenía ahorrado en comprar un libro, y todavía le han sobrado cuarenta y cinco euros de los ahorros. ¿Cuánto le ha costado el libro?
Antonia ha gastado los dos quintos del dinero que tenía ahorrado en comprar un libro, y todavía le han sobrado cuarenta y cinco euros de los ahorros. ¿Cuánto le ha costado el libro?
Fracción decimal
La fracción decimal
Denominador diez

$$ porque\displaystyle\frac{1}{10} = 0,1$$
El sentido numérico
"Greeno (1991) indicó que un buen sentido numérico se manifiesta cuando se tiene un cálculo mental flexible, se realizan buenas estimaciones numéricas y se hacen inferencias adecuadas sobre las cantidades. Para activar estas habilidades es necesario desarrollar una «intuición cuantitativa», un sentido de lo que significan las cantidades que representan los números (Wagner y Davis, 2010). Sowder(1992) define sentido numérico como una red conceptual, bien organizada, que permite relacionar los números y las operaciones, sus propiedades y resolver los problemas de una forma creativa y flexible."Una fracción decimal tiene un denominador formado por la unidad seguida de ceros : 10, 100, 1000...
| $$ \displaystyle\frac{1}{10} = 0'1 $$ | $$ \displaystyle\frac{11}{10} = 1'1 $$ | $$ \displaystyle\frac{11}{100} = 0'11 $$ | $$ \displaystyle\frac{25}{100} = 0'25 $$ | $$ \displaystyle\frac{4}{1000} = 0'004 $$ | $$ \displaystyle\frac{37}{1000} = 0'037 $$ |
|---|
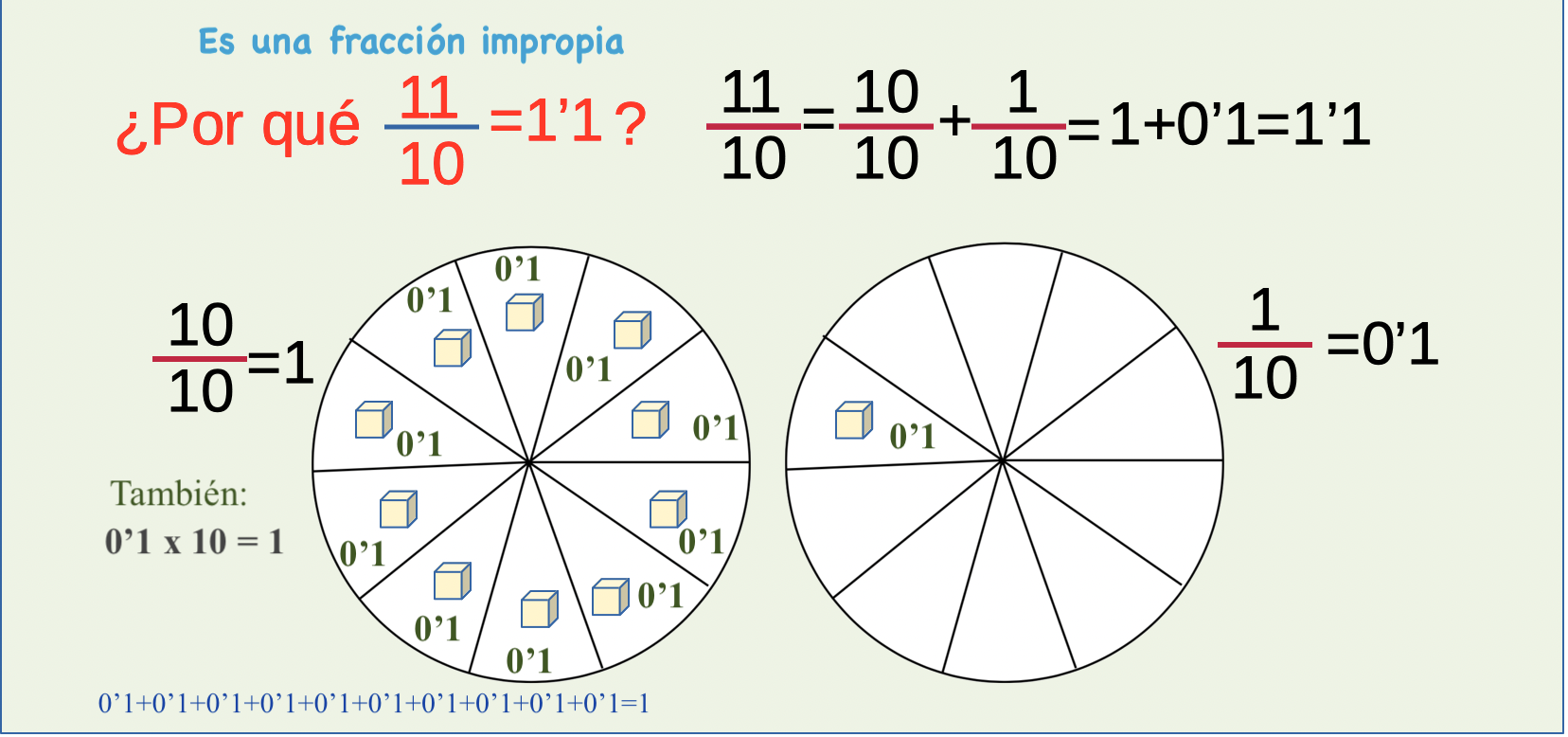
¿Por qué la fracción decimal 11/10 equivale a 1'1?
Denominador cien
Tengo 0'53 euros que equivalen a 53 partes de 100, ¿ qué fracción faltaría para juntar 100 céntimos de euro ? La fracción con denominador 100 la leeremos ... centésimas.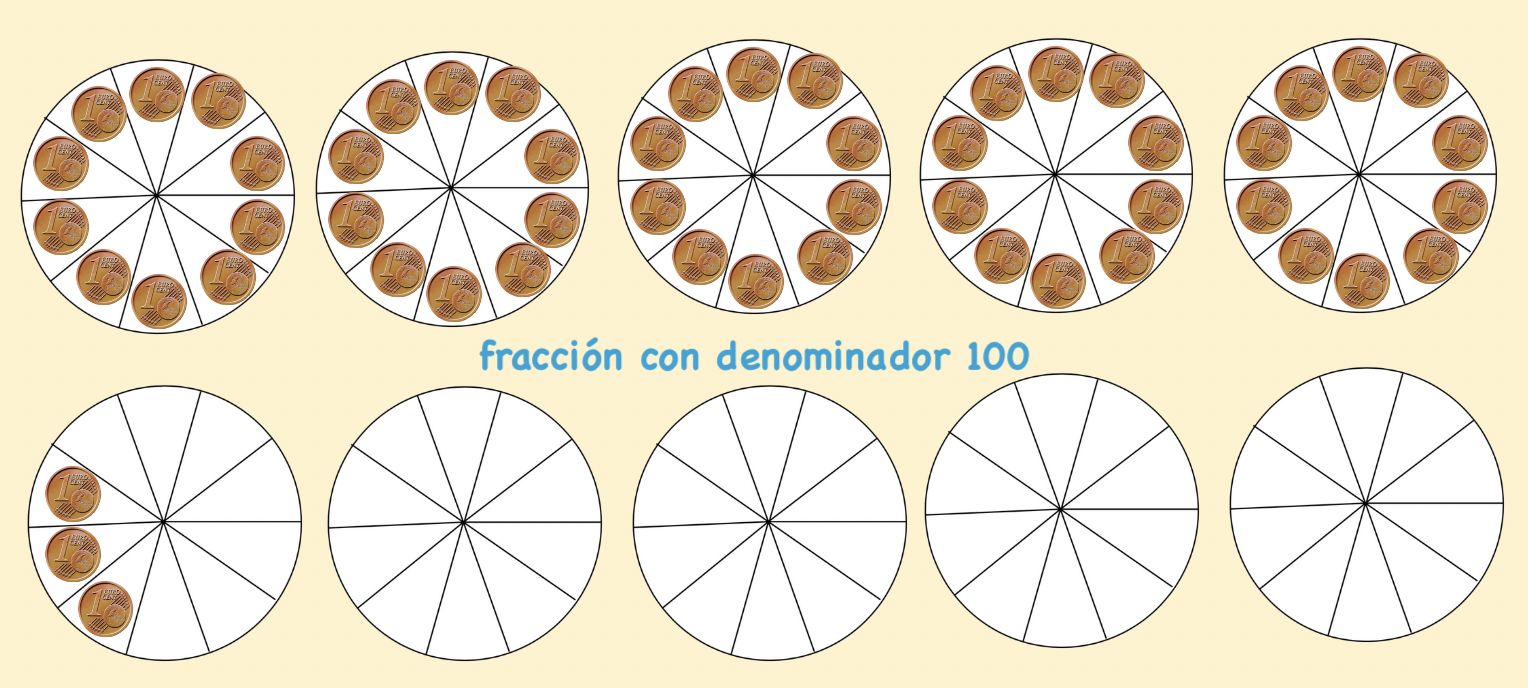
 Hemos representado en la imagen diez círculos divididos en décimos. Cada círculo representa diez céntimos,
porque en cada sector o fracción del círculo podemos colocar 1 céntimo y si hay diez plantillas en total, el valor será 10 céntimos x 10 plantillas = 100 céntimos .
Hemos representado en la imagen diez círculos divididos en décimos. Cada círculo representa diez céntimos,
porque en cada sector o fracción del círculo podemos colocar 1 céntimo y si hay diez plantillas en total, el valor será 10 céntimos x 10 plantillas = 100 céntimos .
 Tenemos 53 céntimos de los 100 céntimos representados por la fracción 53 de 100, y su representación decimal es 0'53 .
Tenemos que entender, que el 0 representa que no hay una parte entera, que equivaldría a 1 euro, y _'53 es una parte de cien y se expresa después de una coma.
Tenemos 53 céntimos de los 100 céntimos representados por la fracción 53 de 100, y su representación decimal es 0'53 .
Tenemos que entender, que el 0 representa que no hay una parte entera, que equivaldría a 1 euro, y _'53 es una parte de cien y se expresa después de una coma.
- Para calcular la cantidad que nos falta, podemos restar:
$$\color{navy}100 \space céntimos - 53 \space céntimos = \fcolorbox{837D3C}{FFF8DC}{$47 \space céntimos$}$$ - Otra opción partiendo del círculo completo:
$$ \color{navy}Como \space 1 = \displaystyle\frac{100}{100} $$ $$ \color{navy}1 - \displaystyle\frac{53}{100}= \displaystyle\frac{100}{100} - \displaystyle\frac{53}{100}=\displaystyle\frac{47}{100}=\fcolorbox{837D3C}{FFF8DC}{$0'47 \space \text{€}$}\;$$
Algoritmo de una suma con fracciones
Algoritmo de una suma con fracciones
La suma de fracciones puede tener dos casos.
 Que las fracciones tengan igual denominador.
Que las fracciones tengan igual denominador.
 Que las fracciones tengan distinto denominador.
Que las fracciones tengan distinto denominador.
Suma de fracciones con igual denominador
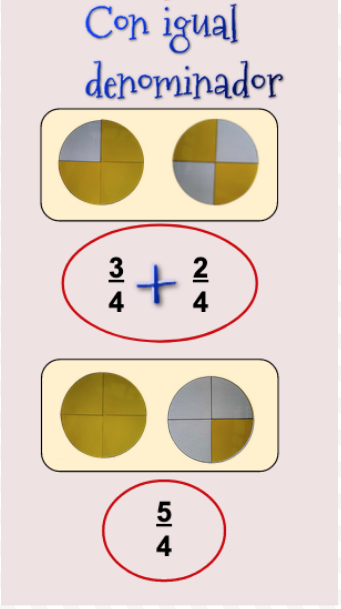
Suma de fracciones con igual denominador
- Hay un primer caso para elegir fracciones manteniendo la igualdad:
$$Suman\quad\displaystyle\frac{5}{3}\quad\fcolorbox{837D3C}{FFF8DC}{$\displaystyle\frac{3}{3} + \displaystyle\frac{2}{3}$} = \fcolorbox{837D3C}{B9F3E7}{$\displaystyle\frac{1}{3} + \displaystyle\frac{1}{3} + \displaystyle\frac{3}{3}$}$$ - En el segundo caso la igualdad se consigue:
$$ Suman\quad\displaystyle\frac{6}{4}\quad\fcolorbox{837D3C}{FFF8DC}{$\displaystyle\frac{3}{4} + \displaystyle\frac{3}{4} $}= \fcolorbox{837D3C}{B9F3E7}{$\displaystyle\frac{1}{4} + \displaystyle\frac{1}{4} + \displaystyle\frac{4}{4}$}$$ - En el tercer caso la igualdad la conseguimos:
$$ Suman\quad\displaystyle\frac{8}{5}\quad\fcolorbox{837D3C}{FFF8DC}{$\displaystyle\frac{2}{5} + \displaystyle\frac{2}{5} + \displaystyle\frac{4}{5}$} = \fcolorbox{837D3C}{B9F3E7}{$\displaystyle\frac{5}{5} + \displaystyle\frac{3}{5}$}$$
Suma de fracciones con distinto denominador
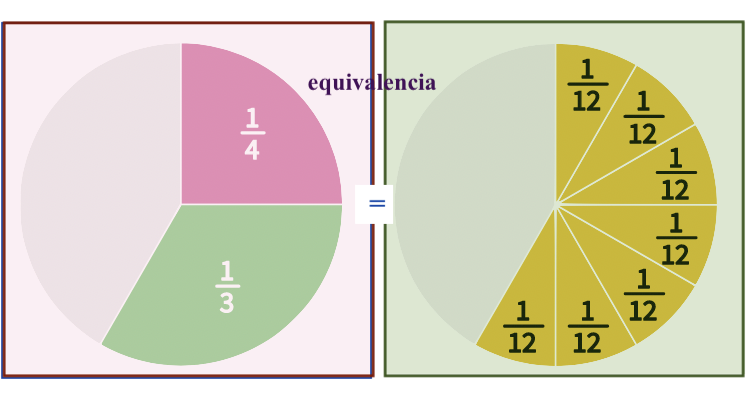
En los dos gráficos observamos cuando se pueden sumar las fracciones. Solo las sumaremos cuando con sus equivalencias conseguimos otras fracciones que tienen un denominador igual.
Buscar un denominador común
Conseguimos fracciones equivalentes a las dadas
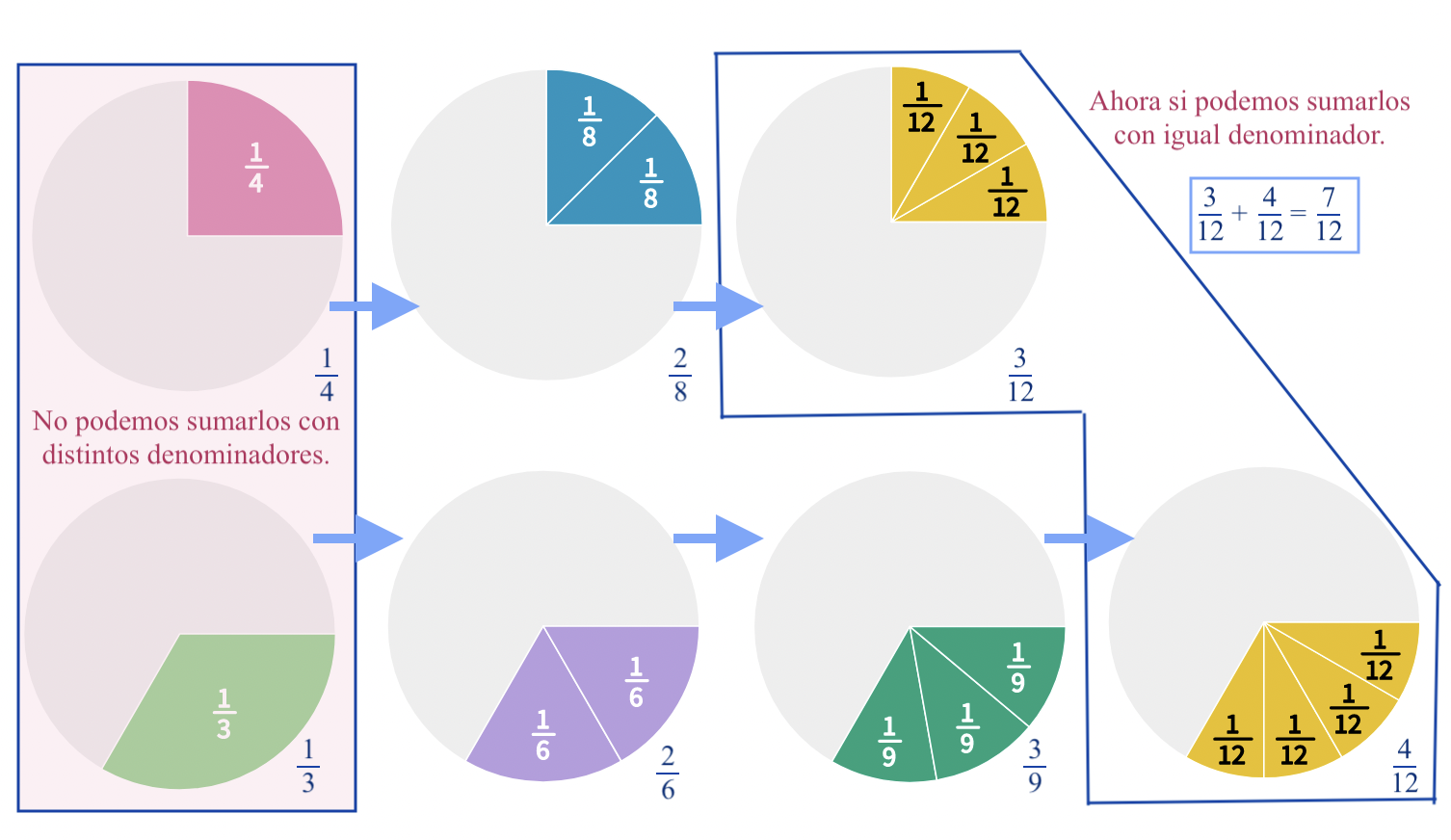
 Para sumar las fracciones con diferente denominador tenemos que conseguir que tengan un denominador común
a las dos fracciones, y en este caso, buscaremos la plantilla de círculos que nos interesa.
Para sumar las fracciones con diferente denominador tenemos que conseguir que tengan un denominador común
a las dos fracciones, y en este caso, buscaremos la plantilla de círculos que nos interesa. $$\color{navy}\displaystyle\frac{1}{3} + \displaystyle\frac{4}{6} = \displaystyle\frac{2}{6} + \displaystyle\frac{4}{6} = \fcolorbox{837D3C}{FFF8DC}{$\displaystyle\frac{6}{6}$} \quad porque\space\displaystyle\frac{1}{3}=\displaystyle\frac{2}{6}$$
Fraccciones equivalentes. Hacer partes del mismo valor
Mostramos otro modelo interactivo para comprender las fracciones equivalentes al hacer partes del mismo valor en cada fracción, tratando de conseguir que tengan un denominador igual a ambas fracciones.
$$ medios:\space\displaystyle\frac{1}{2}=\displaystyle\frac{2}{4}=\fcolorbox{837D3C}{B9F3E7}{$\displaystyle\frac{3}{6}$} \quad y\space tercios:\space\displaystyle\frac{1}{3}=\fcolorbox{837D3C}{B9F3E7}{$\displaystyle\frac{2}{6}$}$$ $$\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}=\displaystyle\frac{3}{6}+\displaystyle\frac{2}{6}=\fcolorbox{837D3C}{B9F3E7}{$\displaystyle\frac{5}{6}$}$$
Algoritmo de una resta de fracciones
Algoritmo de una resta de fracciones
Resta con igual denominador
De una botella de zumo de naranja de tres cuartos de litro, me tomo dos vasos de un cuarto cada uno. ¿Qué cantidad de zumo quedaría para otro vaso?.
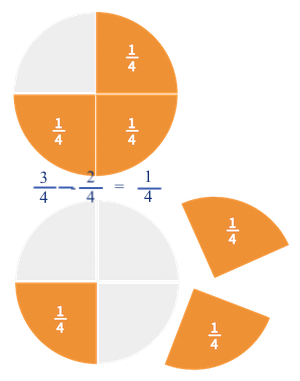 Emplearemos el círculo dividido en cuartos y las fracciones correspondientes para repre-sentar gráficamente los datos del problema y
así podremos descubrir la solución, que es-cribiremos con lenguaje nu-mérico.
Emplearemos el círculo dividido en cuartos y las fracciones correspondientes para repre-sentar gráficamente los datos del problema y
así podremos descubrir la solución, que es-cribiremos con lenguaje nu-mérico.
Tenemos que recordar los cocientes de cada fracción:
$$\displaystyle\frac{3}{4} = 0'75\space litros$$
$$\displaystyle\frac{1}{4} = 0'25\space litros$$

Encontrar la fracción que falta para completar todo el círculo, después colocarla correctamente en cada contenedor. Estamos en un caso de resta de fracciones de igual denominador.
Resta con diferente denominador
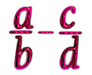 Representación gráfica que explica la resta de fracciones de distinto denominador.
Buscamos una plantilla común a las dos fracciones, que permita formar medios y tercios como ocurre con la plantilla dividida en sextos .
Conseguiremos fracciones equivalentes a un medio y a un tercio y se podrán restar.
Representación gráfica que explica la resta de fracciones de distinto denominador.
Buscamos una plantilla común a las dos fracciones, que permita formar medios y tercios como ocurre con la plantilla dividida en sextos .
Conseguiremos fracciones equivalentes a un medio y a un tercio y se podrán restar.
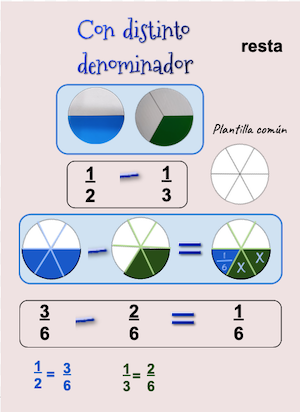
Con números decimales:
Los utilizamos como recurso y sería:$$\color{navy}\displaystyle\frac{1}{2}-\displaystyle\frac{1}{3} = 0,50-0,33 = 0,17\quad \thickapprox\quad\displaystyle\frac{1}{6}$$
 De una botella de un litro de naranjada, Juan se bebió dos quintos y Julia se bebió un medio. ¿Qué fracción de naranjada queda en la botella?
De una botella de un litro de naranjada, Juan se bebió dos quintos y Julia se bebió un medio. ¿Qué fracción de naranjada queda en la botella?
¡Observa una solución gráfica del problema !
Buscamos denominador común con fracciones equivalentes
$$\color{navy}\displaystyle\frac{1}{2} = \displaystyle\frac{5}{10} \quad y \quad\displaystyle\frac{2}{5} = \displaystyle\frac{4}{10};\space entonces\space sumamos\displaystyle\frac{5}{10}+\displaystyle\frac{4}{10}=\displaystyle\frac{9}{10}$$
¿Qué fracción queda en la botella?:$$\color{navy}\displaystyle\frac{10}{10} - \displaystyle\frac{9}{10} = \fcolorbox{837D3C}{FFF8DC}{$\displaystyle\frac{1}{10}\space queda\space en\space la\space botella$}$$
Resolvemos el problema con números decimales:
$$\color{navy}\displaystyle\frac{1}{2}-\displaystyle\frac{2}{5} = 0,50-(2·0,20)=0,50-0,40= 0,10=\displaystyle\frac{1}{10} $$
Algoritmo de una división
Algoritmo de una división

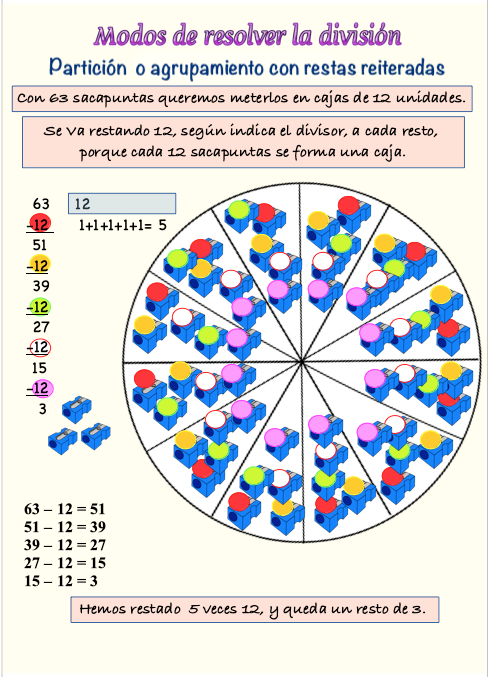
Es hacer partes iguales en el dividendo

En la siguiente actividad tienes que leer muy bien cada texto y elegir si es cierto o falso el contenido que expresa. Son textos matemáticos para comprender y resolver situaciones utilizando la división por partición. Recuerda que en este modo de resolver la división, el divisor indica de cuánto tienen que hacerse las partes en el dividendo, y la cantidad de esas partes que se puedan hacer expresará el cociente.
Tablas de dividir con las plantillas
Descarga en pdf algunas tablas de dividir para realizarlas de forma manipulativa y escrita.
Tablas de dividir :10, :12, :20, :32 en pdf (clic icono).
Cogemos partes de cuatro y las repartimos...
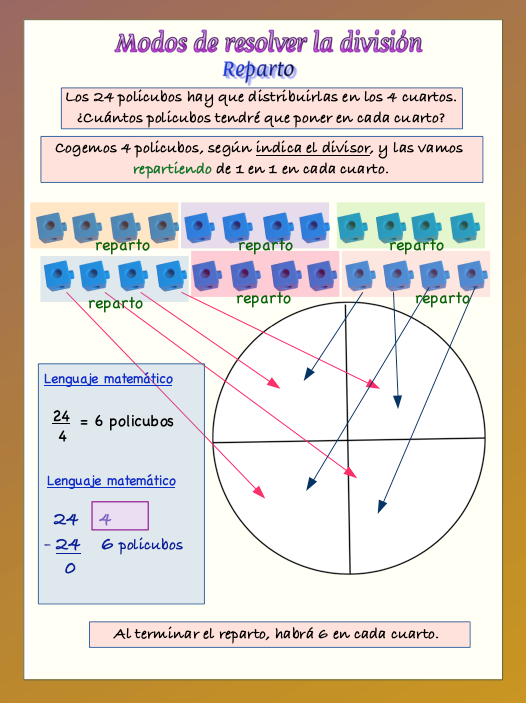
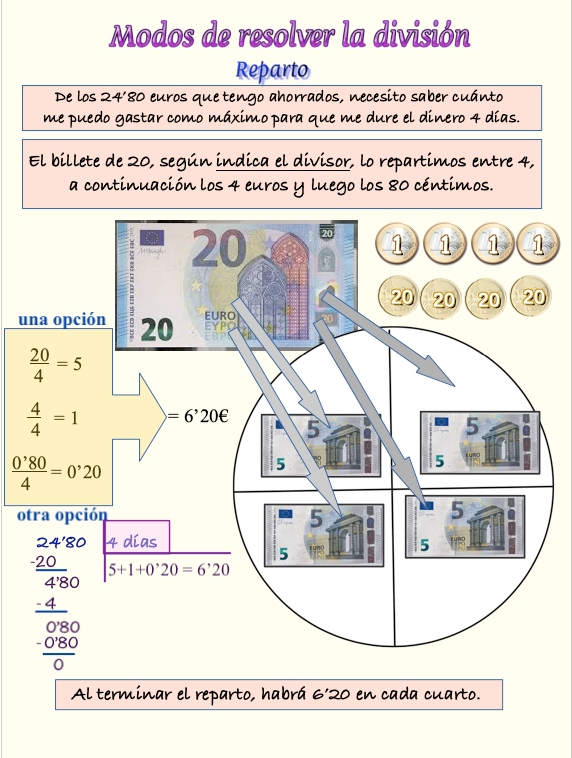
Conviene realizar la manipulación con dinero y plantillas, así como hacer diferentes cambios equivalentes de billetes o monedas según interesen para asegurarse mayor eficacia en la comprensión. La opción digital también la emplearemos, como complemento, para reforzar la comprensión y solucionar los problemas.
A continuación escribimos en lenguaje matemático algunos de los problemas planteados.
Algoritmo 1153:3= (150:3)+ (3:3) = 50 + 1= 51 euros.
Utilizamos nuestro sentido numérico, y por ello, no descomponemos 150 en 100 + 50 porque ni 100 ni 50 son divisibles por 3, pero 150 sí. Si hubiese cumplido esa condición de divisibilidad lo hubiésemos descompuesto.
Algoritmo 2 con fracciones
$$\displaystyle\frac{153}{3}=\displaystyle\frac{150}{3}+\displaystyle\frac{3}{3}= 50 + 1 = 51$$Algoritmo 1 2132:4= (2000:4)+ (100:4) +(32:4)= 500 + 25 + 8 = 532 euros
En este caso no hemos realizado una descomposición en decenas y unidades, 30 + 2, porque ni 30 ni 2 son divibles por 4, pero 32 sí lo es.
Algoritmo 2 con fracciones
$$\displaystyle\frac{2132}{4}=\displaystyle\frac{2000}{4}+\displaystyle\frac{100}{4}+\displaystyle\frac{32}{4}= 500 + 25 + 8 = 533 $$Algoritmo 1
$$ \begin{aligned} \displaystyle\frac{212,34}{3} & = \displaystyle\frac{21234}{100} : 3 = \displaystyle\frac{21234}{300}\\ & =\displaystyle\frac{21000}{300}+\displaystyle\frac{234}{300}= \displaystyle\frac{21000}{300}+\displaystyle\frac{210}{300} +\displaystyle\frac{24}{300}\\ & = \displaystyle\frac{7000}{100}+\displaystyle\frac{7}{10} +\displaystyle\frac{8}{100}=70+0'7 +0'08 = 70'78 \end{aligned}$$En la primera línea expresamos la cantidad 212'34 en forma de fracción decimal y luego dividimos la fracción por 3. Esta operación se especificará en otro capítulo. En la segunda línea se descompone el numerador de la fracción, en cantidades divisibles por 3. En la tercera línea resultan fracciones decimales que son equivalentes y resolveremos con números decimales.
- Recuerda hacer primero una estimación de las veces que cabe el divisor en el dividendo y colocar ese número estimado en el cociente.
- Puedo empezar a dar a cada una
500€, que pasaría a formar parte del cociente, porque 4 x500= 2000€. - No puedo repartir otros 500€, entonces reparto
200€, teniendo otro nuevo cociente parcial, porque 4 x200= 800€.
Algoritmo de una multiplicación
Algoritmo de la multiplicación
 En cada una de las dieciséis cajas representadas por cada fracción del círculo, se han metido tres manzanas y queremos calcular la cantidad de manzanas que hay entre todas las cajas.
En cada una de las dieciséis cajas representadas por cada fracción del círculo, se han metido tres manzanas y queremos calcular la cantidad de manzanas que hay entre todas las cajas.
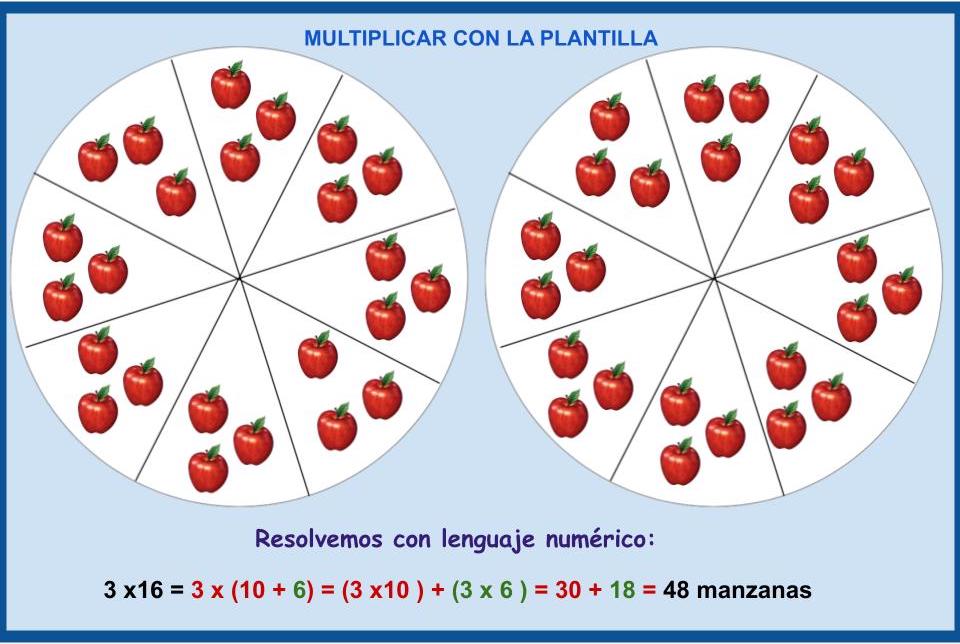
Hemos resuelto un problema fácilmente con ayuda de la plantilla. Después se ha resuelto con lenguaje numérico aplicando la propiedad distributiva para la mejor comprensión del cálculo.
3x16= 3x(10+6)= (3x10)+(3x6)= 30+18= 48 manzanas
Tablas de multiplicar en PDF (clic en icono).
 VIDEO. Construcción, comprensión y memorización de tablas de multiplicar.
VIDEO. Construcción, comprensión y memorización de tablas de multiplicar.
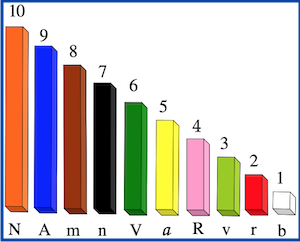 Las regletas o números de colores, nos van a ayudar a la compren-sión y solución de problemas con multi-plicación y las vamos a utilizar junto a las plan-tillas.
Si quieres más información sobre ellas haz clic en la imagen.
Las regletas o números de colores, nos van a ayudar a la compren-sión y solución de problemas con multi-plicación y las vamos a utilizar junto a las plan-tillas.
Si quieres más información sobre ellas haz clic en la imagen.
Situación con una expresión algebraica.
Archivo descargable con problemas que emplean como recurso el dinero didáctico y círculos fraccionados. Empleamos números decimales.
Multiplicar un número entero positivo por un decimal.Clic en icono.
Si expresamos en lenguaje matemático:
- En la primera actividad:
17x4= (10x4)+(5x4)+(2x4)= 40+20+8= 68€ - En la tercera actividad:
117x4= (100x4)+(10x4)+(5x4)+(2x4)=400+40+20+8= 468€ -
En actividades de producto con un número decimal:
151'90x7= (100x7)+(50x7)+(1x7)+(0'90x7)=
700+350+7+6'30=
700+300+50+13'30=
1063'30€
Suma y resta de número natural y fracción
Suma y resta de número natural y fracción.
 En el cumpleaños de Amalia,
cuatro amigas se comen un tercio cada una de los bombones que le habían regalado a Amalia.
En el cumpleaños de Amalia,
cuatro amigas se comen un tercio cada una de los bombones que le habían regalado a Amalia.
- ¿Cuántos tercios han comido entre todas las amigas?
- ¿Cuantas cajas de bombones había?
- ¿Sabes los tercios que han quedado por comer?
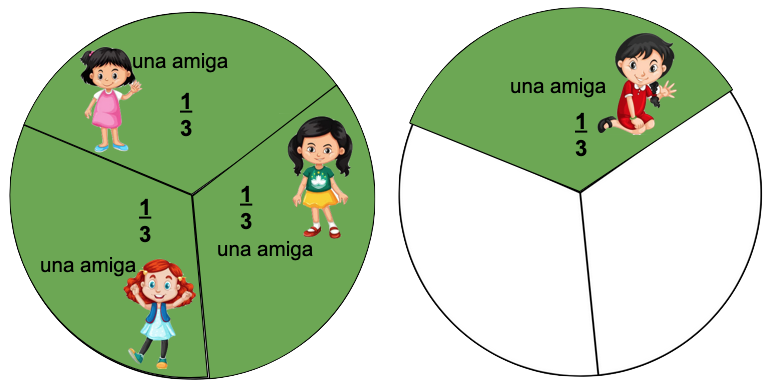
- La expresión de una caja completa más un tercio, lo representamos:
$$\color{navy}1 + \displaystyle\frac{1}{3}$$ - El 1, representa una caja, porque: $\color{navy}\quad \displaystyle\frac{3}{3} = 1$, entonces:
$$\color{navy}1 + \displaystyle\frac{1}{3} = \displaystyle\frac{3}{3} + \displaystyle\frac{1}{3} =\fcolorbox{837D3C}{FFF8DC}{$\displaystyle\frac{4}{3}$}$$ - También como son 4 y cada una toma $\color{navy}\displaystyle\frac{1}{3}$ se expresa:
$$\color{navy}4 \cdot \displaystyle\frac{1}{3} = \fcolorbox{837D3C}{FFF8DC}{$\displaystyle\frac{4}{3}$} \; \text{entre todas}$$ - Si las dos cajas completas se representan:
$$\color{navy}\displaystyle\frac{3}{3}+\displaystyle\frac{3}{3}=\displaystyle\frac{6}{3}$$ - En una caja quedan dos tercios por comer y se resuelve:
$$\color{navy}\displaystyle\frac{6}{3} - \displaystyle\frac{4}{3} = \displaystyle\frac{2}{3} \; \text{ por comer.}$$ - Lo que toma cada una, en forma de suma se puede escribir:
$$\color{navy}\displaystyle\frac{1}{3} + \displaystyle\frac{1}{3}+ \displaystyle\frac{1}{3}+ \displaystyle\frac{1}{3}=\fcolorbox{837D3C}{FFF8DC}{$\displaystyle\frac{4}{3}$}$$
 Mamá ha comprado dos litros y tres cuartos de zumo de zanahoria.
¿Cuántos cuartos hay entre las tres botellas de zumo que ha comprado?
Mamá ha comprado dos litros y tres cuartos de zumo de zanahoria.
¿Cuántos cuartos hay entre las tres botellas de zumo que ha comprado?
 VIDEO. En la siguiente presentación podemos resolver el problema planteado anteriormente.
Calculamos el resultado de la fracción y a continuación realizamos la suma de una cantidad entera con una fracción.
VIDEO. En la siguiente presentación podemos resolver el problema planteado anteriormente.
Calculamos el resultado de la fracción y a continuación realizamos la suma de una cantidad entera con una fracción.
Fracción propia y fracción impropia
Las fracciones impropias tienen el numerador mayor o igual que el denominador y representa una unidad o varias, que se suma con otra fracción propia. Construye fracciones con Phet.
$$\fcolorbox{837D3C}{da8ca6}{$\displaystyle\frac{6}{4}$} =\displaystyle\frac{4}{4}+\displaystyle\frac{2}{4}=1+\displaystyle\frac{2}{4}$$
Escena diseñada por Diego Luis Feria Gómez para Proyecto Canals. La fracción impropia siempre se forma con un círculo completo o varios, más la suma de otro círculo incompleto.
La fracción impropia siempre se forma con un círculo completo o varios, más la suma de otro círculo incompleto.
 Sabemos que los círculos completos están divididos en partes del mismo valor que el círculo incompleto.
Sabemos que los círculos completos están divididos en partes del mismo valor que el círculo incompleto.
 Reconocer las fracciones representadas de forma gráfica y escribirlas con lenguaje matemático.
Reconocer las fracciones representadas de forma gráfica y escribirlas con lenguaje matemático.
 Después, escribir con letra si se trata de fracción propia o impropia.
Después, escribir con letra si se trata de fracción propia o impropia.
 Por último, completar el texto matemático con las palabras "denominador" y "numerador".
Por último, completar el texto matemático con las palabras "denominador" y "numerador".
La fracción impropia y el llamado número mixto.
Escena diseñada para Proyecto Pizarra Interactiva.- Un número mixto es una forma numérica de representar una fracción mayor que la unidad, también llamada fracción impropia. $$\fcolorbox{837D3C}{FFF8DC}{$2 \displaystyle\frac{2}{6}$} = 2 + \displaystyle\frac{2}{6} = \displaystyle\frac{12}{6} + \displaystyle\frac{2}{6} = \fcolorbox{837D3C}{FFF8DC}{$\displaystyle\frac{14}{6}$} \; \text{ en fracción impropia.}$$
Producto de una fracción por un entero positivo
Producto de una fracción por un número entero positivo.
He pintado las seis cajas con cuatro colores diferentes, pero no todas las cajas tienen los cuatro colores. Construye las imágenes con el material o dibuja los círculos y colorea. ¿Podrías realizar otras situaciones?
- ¿Cuántos cuartos de color naranja hay?
- ¿Cuántos cuartos de color azul hay?
- ¿Cuántos cuartos de color rosa hay?
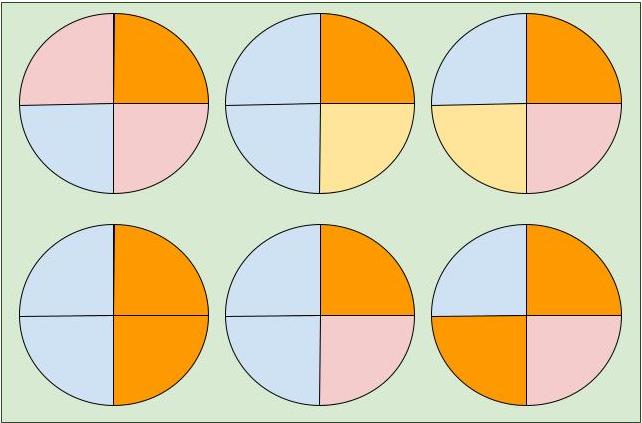
$$\color{indianred}\text{En forma de suma}\space\displaystyle\frac{1}{4} + \displaystyle\frac{1}{4} + \displaystyle\frac{1}{4} + \displaystyle\frac{1}{4} + \displaystyle\frac{1}{4} + \displaystyle\frac{1}{4} + \displaystyle\frac{1}{4} + \displaystyle\frac{1}{4} = \fcolorbox{837D3C}{FFF8DC}{$\displaystyle\frac{8}{4}$}$$ $$\color{indianred}\text{En forma de producto}\space\displaystyle\frac{1}{4} \cdot 8 = \fcolorbox{837D3C}{FFF8DC}{$\displaystyle\frac{8}{4}$}\; \text{son de color naranja.}$$
Suma de entero y fracción o producto de una fracción por un número entero positivo, utilizamos dos algoritmos que dan el mismo resultado. Realiza otros casos. Comprobemos con un ejemplo del interactivo.
- Primer algoritmo, suma de entero y fracción,$$\color{crimson}2 + \displaystyle\frac{4}{3} = \displaystyle\frac{6}{3}+\displaystyle\frac{4}{3}=\fcolorbox{837D3C}{FFF8DC}{$\displaystyle\frac{10}{3}$} \quad porque \space sustituimos\space 2=\displaystyle\frac{6}{3}=\displaystyle\frac{3}{3}+\displaystyle\frac{3}{3}$$
- Segundo algoritmo, producto de una fracción por un número entero positivo $$\color{crimson}\displaystyle\frac{1}{3}\cdot10 = \fcolorbox{837D3C}{FFF8DC}{$\displaystyle\frac{10}{3}$}$$
Producto de fracciones
 De los 12 alumnas y alumnos de la clase, un tercio de la mitad lleva gafas.¿Qué fracción del alumnado lleva gafas?
De los 12 alumnas y alumnos de la clase, un tercio de la mitad lleva gafas.¿Qué fracción del alumnado lleva gafas?
$$\color{Crimson} \displaystyle\frac{1}{3}\cdot \space\displaystyle\frac{1}{2}=\displaystyle\frac{1}{6}\space\space lleva\space gafas$$
Video didáctico que justifica la forma de realizar el problema.
Producto de dos fracciones.
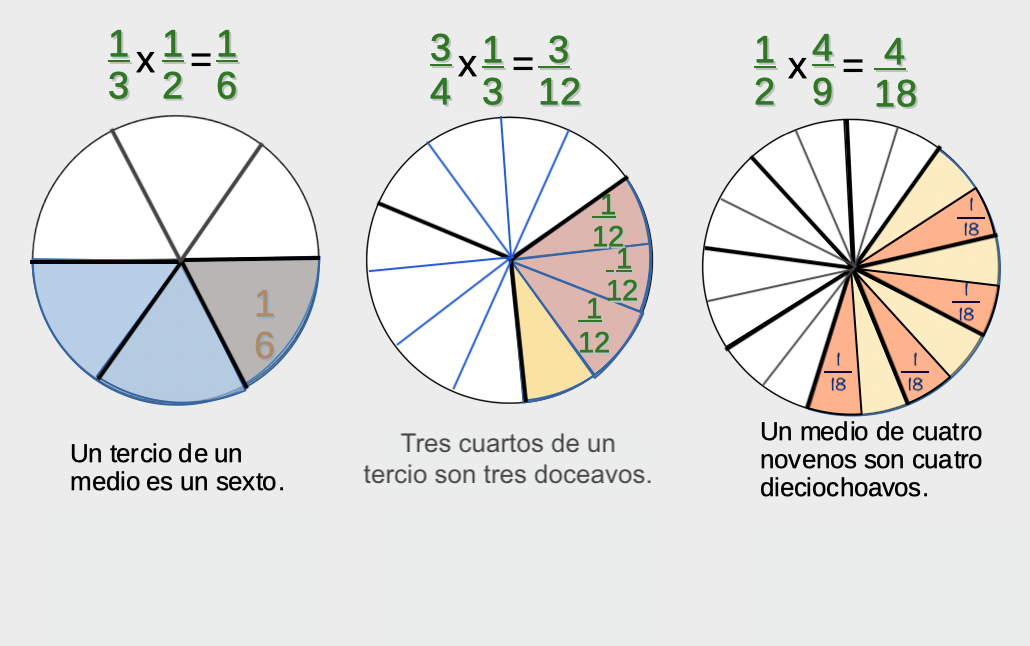
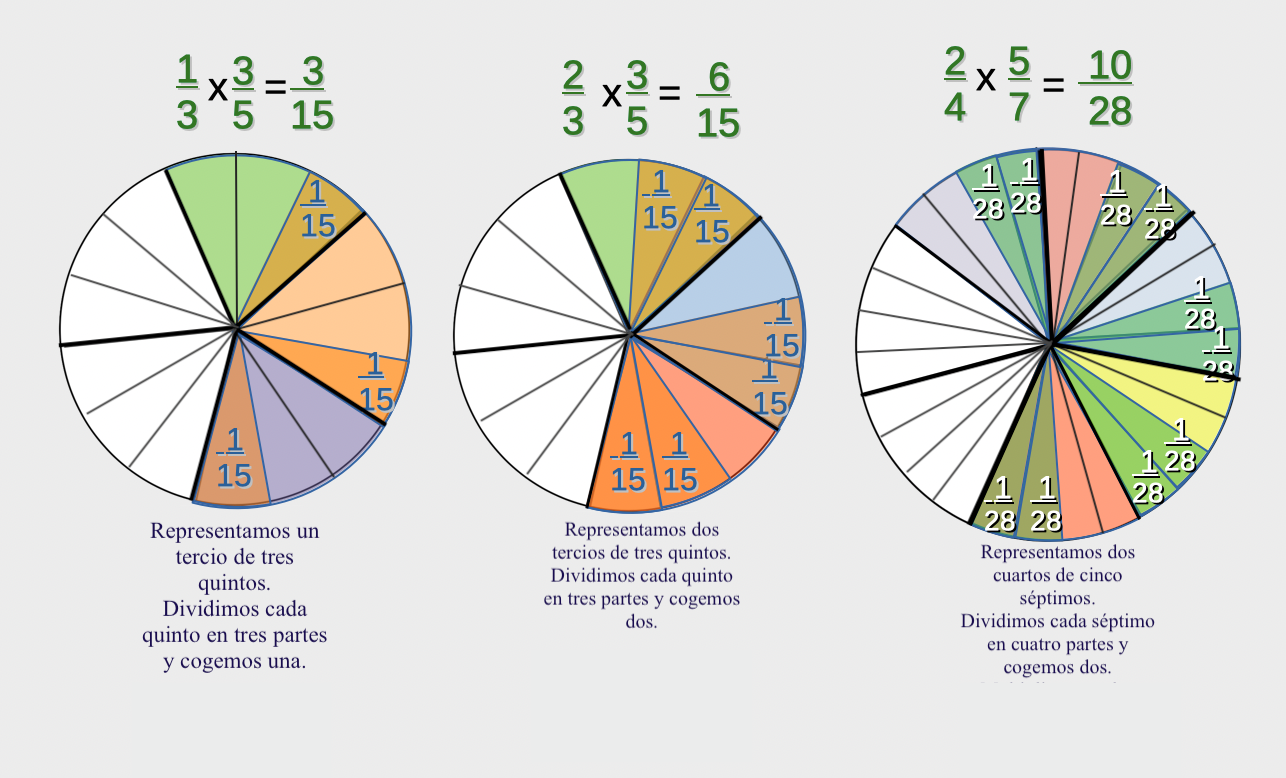
Ampliamos el sentido numérico.
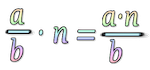 Si multiplicamos una fracción por un número natural se hace mayor la fracción:
Si multiplicamos una fracción por un número natural se hace mayor la fracción:
$$ \displaystyle\frac{1}{3} \cdot 2= \displaystyle\frac{1}{3}+\displaystyle\frac{1}{3}=\displaystyle\frac{2}{3}\qquad\displaystyle\frac{1}{3}\cdot 3=\displaystyle\frac{1}{3}+\displaystyle\frac{1}{3}+\displaystyle\frac{1}{3}=\displaystyle\frac{3}{3}$$
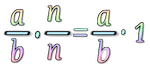 Si multiplicamos una fracción por otra que equivale a 1:$$\displaystyle\frac{1}{7} \cdot \displaystyle\frac{7}{7}=\displaystyle\frac{1}{7}\cdot 1 = \displaystyle\frac{1}{7}$$ resulta la misma fracción porque la fracción está una sola vez.
Si multiplicamos una fracción por otra que equivale a 1:$$\displaystyle\frac{1}{7} \cdot \displaystyle\frac{7}{7}=\displaystyle\frac{1}{7}\cdot 1 = \displaystyle\frac{1}{7}$$ resulta la misma fracción porque la fracción está una sola vez.
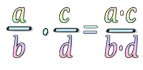 Pero cuando multiplicamos dos fracciones propias, el valor del resultado se hace menor. Observa los ejemplos a continuación:
Pero cuando multiplicamos dos fracciones propias, el valor del resultado se hace menor. Observa los ejemplos a continuación:
$$ \displaystyle\frac{1}{8} \cdot \displaystyle\frac{1}{4}=\displaystyle\frac{1}{32}\qquad \displaystyle\frac{1}{3} \cdot \displaystyle\frac{1}{5}=\displaystyle\frac{1}{15}\qquad \displaystyle\frac{1}{3} \cdot \displaystyle\frac{3}{5}=\displaystyle\frac{3}{15}$$
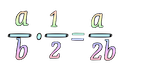 Observamos en la tabla, que siempre que multiplicamos una fracción por un medio o por un tercio $$ \displaystyle\frac{1}{4}\cdot \displaystyle\frac{1}{2} = \displaystyle\frac{1}{8}\qquad \displaystyle\frac{1}{4}\cdot\displaystyle\frac{1}{3}=\displaystyle\frac{1}{12}$$ nos resulta otra fracción que vale la mitad o la tercera parte
Observamos en la tabla, que siempre que multiplicamos una fracción por un medio o por un tercio $$ \displaystyle\frac{1}{4}\cdot \displaystyle\frac{1}{2} = \displaystyle\frac{1}{8}\qquad \displaystyle\frac{1}{4}\cdot\displaystyle\frac{1}{3}=\displaystyle\frac{1}{12}$$ nos resulta otra fracción que vale la mitad o la tercera parte
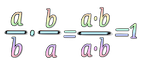 Si multiplicamos una fracción por su inversa:
Si multiplicamos una fracción por su inversa:
$$ \displaystyle\frac{3}{2}\cdot \displaystyle\frac{2}{3} = \displaystyle\frac{6}{6}= 1$$ nos resultará siempre 1.
| $$ \displaystyle\frac{1}{3} \cdot \displaystyle\frac{1}{2}= \displaystyle\frac{1}{6}$$ | $$ \displaystyle\frac{1}{4} \cdot \displaystyle\frac{1}{2}= \displaystyle\frac{1}{8} $$ | $$ \displaystyle\frac{1}{5} \cdot \displaystyle\frac{1}{2}= \displaystyle\frac{1}{10} $$ |
|---|---|---|
| $$ \displaystyle\frac{1}{3} \cdot \displaystyle\frac{1}{3}= \displaystyle\frac{1}{9}$$ | $$ \displaystyle\frac{1}{4} \cdot \displaystyle\frac{1}{3}= \displaystyle\frac{1}{12} $$ | $$ \displaystyle\frac{1}{5} \cdot \displaystyle\frac{1}{3}= \displaystyle\frac{1}{15} $$ |
| $$ \displaystyle\frac{1}{4} \cdot \displaystyle\frac{1}{4}= \displaystyle\frac{1}{16}$$ | $$ \displaystyle\frac{1}{4} \cdot \displaystyle\frac{1}{5}= \displaystyle\frac{1}{20} $$ | $$ \displaystyle\frac{1}{4} \cdot \displaystyle\frac{1}{6}= \displaystyle\frac{1}{24} $$ |
Relación entre porcentaje y fracción del círculo
La fracción ocupa un tanto por ciento del círculo.
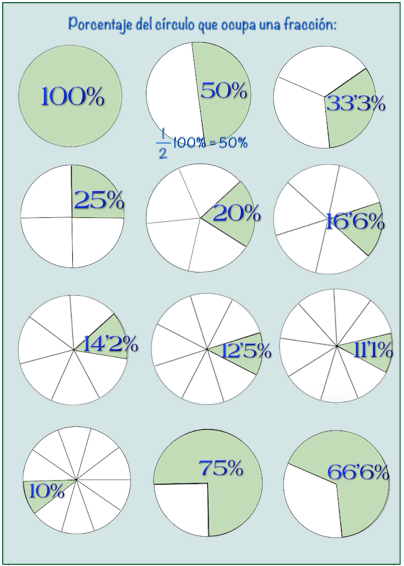
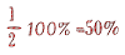 Queremos aprender y memorizar la relación entre cada fracción y el porcentaje que ocupa en el círculo. Podemos utilizar la calculadora para comprobar si los porcentajes son correctos.
Con la imagen de la tabla de la página anterior nos aprenderemos las relaciones. Algoritmos para resolver el %.
Queremos aprender y memorizar la relación entre cada fracción y el porcentaje que ocupa en el círculo. Podemos utilizar la calculadora para comprobar si los porcentajes son correctos.
Con la imagen de la tabla de la página anterior nos aprenderemos las relaciones. Algoritmos para resolver el %. Establece relación entre fracción y tanto por ciento, para ello, señala la imagen que corresponda con el porcentaje que se indica.
Puedes comprobar los cálculos de la actividad anterior.
Si damos al círculo completo el valor de 100%, al dividirlo en medios, tercios, cuartos, quintos... ¿cuál será el tanto por ciento que corresponderá a cada una de esas partes en que ha sido fraccionado? Ahora ponemos en práctica las relaciones aprendidas.
Representación decimal de una fracción
Representación decimal de una fracción.
Primero, a todo el círculo le asignamos el valor de un euro o simplemente el valor uno. Después vamos dividiendo dicho valor en diferentes partes, de dos, de tres, de cuatro, de cinco... y así obtenemos la representación decimal de cada fracción.
Comprueba los valores que necesites con la calculadora modelo de Splinterbl(clic icono).
- ¿Qué número decimal le corresponde a cada fracción? Practica y memoriza las equivalencias entre ambos, con la ayuda de las representaciones gráficas.
- Puedes realizar el cálculo con la calculadora para comprobar los valores.
![]() Establece la equivalencia entre fracción y número decimal. Identifica en las imágenes los valores que te van indicando los textos
Establece la equivalencia entre fracción y número decimal. Identifica en las imágenes los valores que te van indicando los textos
Comprueba los valores que necesites con la calculadora modelo de Splinterbl(clic icono).

Tabla con la representación decimal de una fracción.
El signo indica que el valor es aproximado.
| $$ \displaystyle\frac{1}{2} = 0'50 $$ | $$ \displaystyle\frac{1}{3}\thickapprox 0'33 $$ | $$ \displaystyle\frac{1}{4} = 0'25 $$ | $$ \displaystyle\frac{1}{5} = 0'20 $$ | $$ \displaystyle\frac{1}{6}\thickapprox 0'16 $$ | $$ \displaystyle\frac{1}{7}\thickapprox 0'14 $$ | $$ \displaystyle\frac{1}{8} = 0'125 $$ |
|---|---|---|---|---|---|---|
| $$ \displaystyle\frac{1}{9}\thickapprox 0'11 $$ | $$ \displaystyle\frac{1}{10} = 0'10 $$ | $$ \displaystyle\frac{2}{3}\thickapprox 0'66 $$ | $$ \displaystyle\frac{2}{4} = 0'50 $$ | $$ \displaystyle\frac{3}{4} = 0'75 $$ | $$ \displaystyle\frac{2}{5} = 0'40 $$ | $$ \displaystyle\frac{3}{5} = 0'60 $$ |
División de dos fracciones y de fracción con número natural
División de dos fracciones y fracción con número natural.
Pincha en cada punto de la lista.
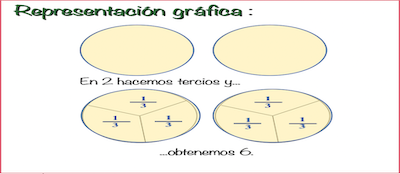
Problemas resueltos de forma gráfica y numérica
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 | 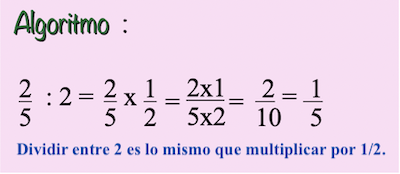 |  |
Utilizamos la equivalencia entre fracción y número decimal
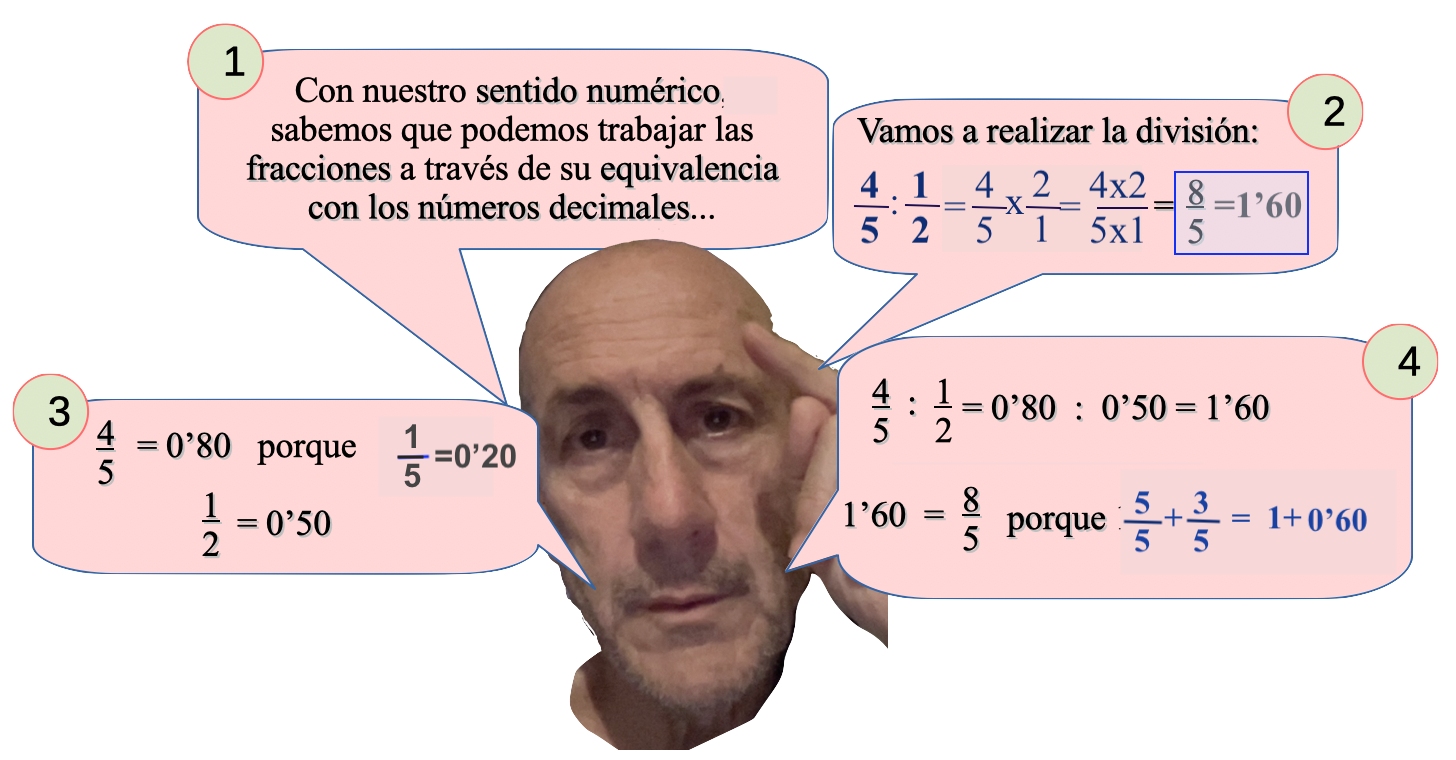
Ampliamos el sentido numérico.
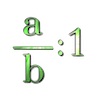 Dividir una fracción entre 1 es hacer una sola parte en la fracción y por lo tanto el resultado es la misma fracción. Por eso dividir cualquier cantidad entre 1, resulta la misma cantidad.
Dividir una fracción entre 1 es hacer una sola parte en la fracción y por lo tanto el resultado es la misma fracción. Por eso dividir cualquier cantidad entre 1, resulta la misma cantidad.
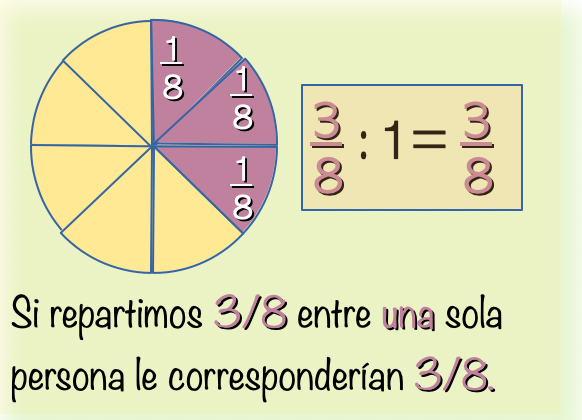 $$\color{indianred}\text{comprobamos con los equivalentes números decimales:}$$
$$\color{navy}\displaystyle\frac{3}{8}=0,375\quad\text{lo dividimos }\quad 0,375 : 1= 0,375$$
$$\color{indianred}\text{comprobamos con los equivalentes números decimales:}$$
$$\color{navy}\displaystyle\frac{3}{8}=0,375\quad\text{lo dividimos }\quad 0,375 : 1= 0,375$$
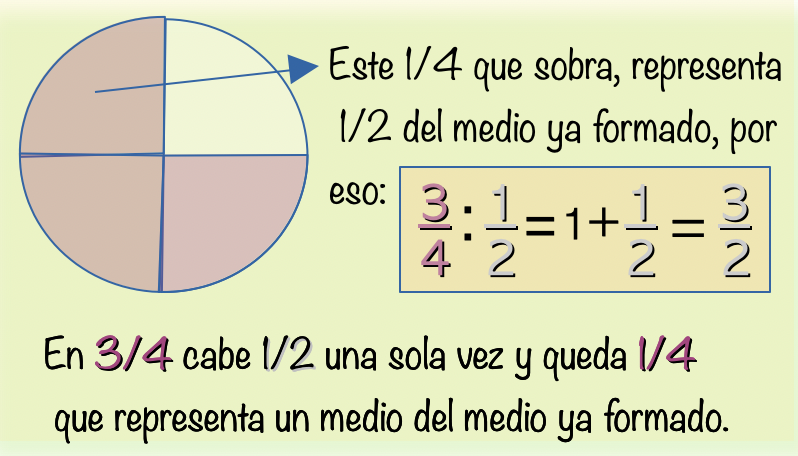
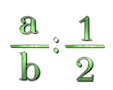 Dividir una fracción entre $\displaystyle\frac{1}{2}$ significa aumentar el doble el valor de la fracción, por eso es igual dividir entre un medio que multiplicar por su número inverso que es 2.
Dividir una fracción entre $\displaystyle\frac{1}{2}$ significa aumentar el doble el valor de la fracción, por eso es igual dividir entre un medio que multiplicar por su número inverso que es 2.
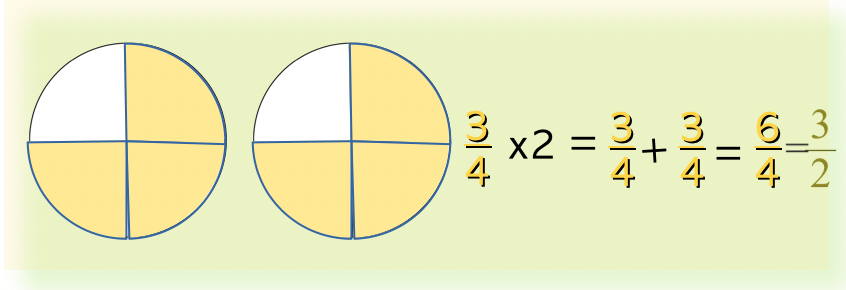
 $$\color{indianred}\text{ empleamos el algoritmo de la multiplicación:}$$
$$\color{navy}\displaystyle\frac{3}{4}\cdot2=\displaystyle\frac{6}{4}\quad o\quad\displaystyle\frac{5}{6}\cdot2=\displaystyle\frac{10}{6}$$
$$\color{indianred}\text{ empleamos el algoritmo de la multiplicación:}$$
$$\color{navy}\displaystyle\frac{3}{4}\cdot2=\displaystyle\frac{6}{4}\quad o\quad\displaystyle\frac{5}{6}\cdot2=\displaystyle\frac{10}{6}$$
 $$\color{indianred}\text{comprobamos con los equivalentes números decimales:}$$
$$\color{navy}\displaystyle\frac{3}{4}:\displaystyle\frac{1}{2}=\displaystyle\frac{6}{4}= 1,50 \quad y\quad\displaystyle\frac{3}{4}\cdot2=0'75\cdot2=1'50$$
$$\color{indianred}\text{comprobamos con los equivalentes números decimales:}$$
$$\color{navy}\displaystyle\frac{3}{4}:\displaystyle\frac{1}{2}=\displaystyle\frac{6}{4}= 1,50 \quad y\quad\displaystyle\frac{3}{4}\cdot2=0'75\cdot2=1'50$$
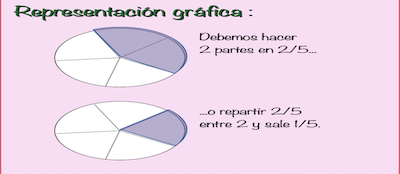
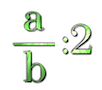 Dividir una fracción entre 2 sería reducir a la mitad el valor de la fracción . Ahora entenderemos que dividir entre 2 es lo mismo que multiplicar por su número inverso que es $\displaystyle\frac{1}{2}$ .
Dividir una fracción entre 2 sería reducir a la mitad el valor de la fracción . Ahora entenderemos que dividir entre 2 es lo mismo que multiplicar por su número inverso que es $\displaystyle\frac{1}{2}$ .
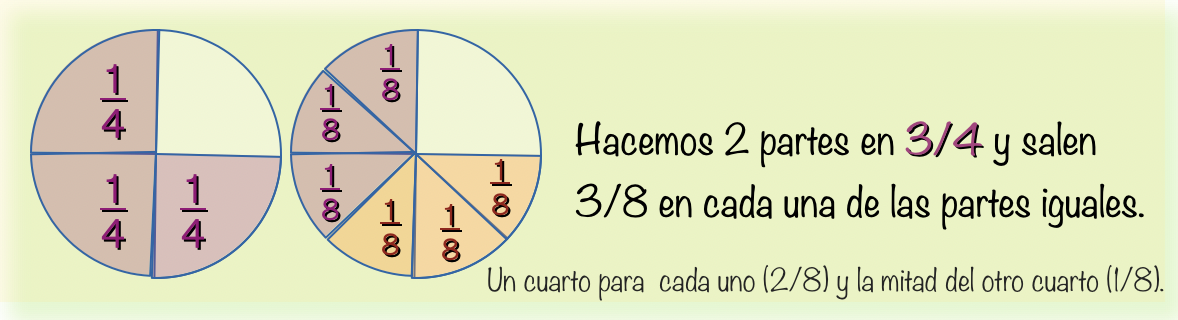 $$\color{indianred}\text{empleamos el algoritmo de la multiplicación:} $$
$$\color{navy}\displaystyle\frac{3}{4}\cdot\displaystyle\frac{1}{2}=\displaystyle\frac{3}{8}\quad o\quad\displaystyle\frac{5}{7}\cdot\displaystyle\frac{1}{2}=\displaystyle\frac{5}{14}$$
$$\color{indianred}\text{comprobamos con los equivalentes números decimales:}$$
$$\color{navy} \displaystyle\frac{3}{4}=0'75 \quad \ 0'75:2 = 0'375\space\text{es igual que}\space\displaystyle\frac{3}{4}\cdot\displaystyle\frac{1}{2}= 0´75\cdot\ 0'50 = 0'375$$
$$\color{indianred}\text{empleamos el algoritmo de la multiplicación:} $$
$$\color{navy}\displaystyle\frac{3}{4}\cdot\displaystyle\frac{1}{2}=\displaystyle\frac{3}{8}\quad o\quad\displaystyle\frac{5}{7}\cdot\displaystyle\frac{1}{2}=\displaystyle\frac{5}{14}$$
$$\color{indianred}\text{comprobamos con los equivalentes números decimales:}$$
$$\color{navy} \displaystyle\frac{3}{4}=0'75 \quad \ 0'75:2 = 0'375\space\text{es igual que}\space\displaystyle\frac{3}{4}\cdot\displaystyle\frac{1}{2}= 0´75\cdot\ 0'50 = 0'375$$
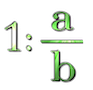 Observa que al dividir 1 entre una fracción, resulta la fracción inversa. Si multiplicar y dividir son operaciones inversas, tiene que cumplirse que:
Observa que al dividir 1 entre una fracción, resulta la fracción inversa. Si multiplicar y dividir son operaciones inversas, tiene que cumplirse que:
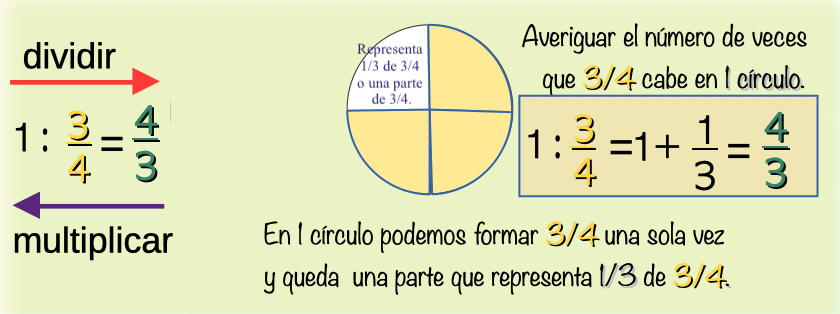
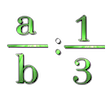 Dividir una fracción entre $\displaystyle\frac{1}{3}$ es obtener una fracción que resulta valer el triple, por eso dividir entre $\displaystyle\frac{1}{3}$ es igual que multiplicar por 3.
Dividir una fracción entre $\displaystyle\frac{1}{3}$ es obtener una fracción que resulta valer el triple, por eso dividir entre $\displaystyle\frac{1}{3}$ es igual que multiplicar por 3.
 $$\color{indianred}\text{empleamos el algoritmo de la multiplicación:} $$
$$\color{navy}\displaystyle\frac{3}{4}\cdot3=\displaystyle\frac{3}{4}+\displaystyle\frac{3}{4}+\displaystyle\frac{3}{4}=\displaystyle\frac{9}{4}$$
$$\color{indianred}\text{comprobamos con los equivalentes números decimales:}$$
$$\color{navy}\displaystyle\frac{3}{4}\cdot3=\displaystyle\frac{9}{4}= 2'25\quad\text{pero también}\quad 0'75\cdot 3=2'25$$
$$\color{navy}\text{Recuerda que}\space\displaystyle\frac{3}{4}=0'75\space porque\space\displaystyle\frac{1}{4}=0'25$$
$$\color{indianred}\text{empleamos el algoritmo de la multiplicación:} $$
$$\color{navy}\displaystyle\frac{3}{4}\cdot3=\displaystyle\frac{3}{4}+\displaystyle\frac{3}{4}+\displaystyle\frac{3}{4}=\displaystyle\frac{9}{4}$$
$$\color{indianred}\text{comprobamos con los equivalentes números decimales:}$$
$$\color{navy}\displaystyle\frac{3}{4}\cdot3=\displaystyle\frac{9}{4}= 2'25\quad\text{pero también}\quad 0'75\cdot 3=2'25$$
$$\color{navy}\text{Recuerda que}\space\displaystyle\frac{3}{4}=0'75\space porque\space\displaystyle\frac{1}{4}=0'25$$
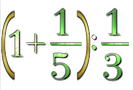 En el caso de dividir un número mixto entre otra fracción, cambiamos el número mixto a fracción impropia
y luego se calcula la operación como hemos indicado multiplicando y sustituyendo el divisor por su inverso.
Pincha para ver otro ejemplo.
En el caso de dividir un número mixto entre otra fracción, cambiamos el número mixto a fracción impropia
y luego se calcula la operación como hemos indicado multiplicando y sustituyendo el divisor por su inverso.
Pincha para ver otro ejemplo.
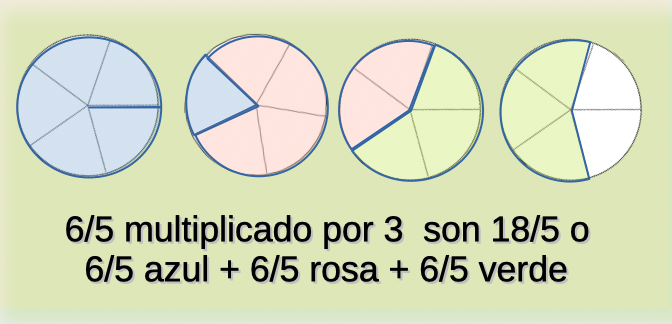 $$\color{indianred}\text{comprobamos con los equivalentes números decimales:}$$
$$\color{navy}\displaystyle\frac{18}{5}=\displaystyle\frac{5}{5}+\displaystyle\frac{5}{5}+\displaystyle\frac{5}{5}+\displaystyle\frac{3}{5}= 1+1+1+0'60= 3'60$$
$$\color{navy}\text{Pero también}\quad\ (1+0'20): 0'33= 1'20:0'33\thickapprox 3'6$$
$$\color{indianred}\text{comprobamos con los equivalentes números decimales:}$$
$$\color{navy}\displaystyle\frac{18}{5}=\displaystyle\frac{5}{5}+\displaystyle\frac{5}{5}+\displaystyle\frac{5}{5}+\displaystyle\frac{3}{5}= 1+1+1+0'60= 3'60$$
$$\color{navy}\text{Pero también}\quad\ (1+0'20): 0'33= 1'20:0'33\thickapprox 3'6$$
 Si se dividen los dos términos de una fracción por el mismo número , se obtiene una fracción equivalente o la misma fracción.
También le llamamos simplificar la fracción.
Si se dividen los dos términos de una fracción por el mismo número , se obtiene una fracción equivalente o la misma fracción.
También le llamamos simplificar la fracción.
$$\color{navy}\displaystyle\frac{6:2}{8:2}=\displaystyle\frac{3}{4} $$
$$\color{indianred}\text{comprobamos con los equivalentes números decimales:}$$
$$\color{navy}\displaystyle\frac{6}{8}= 6\cdot 0'125= 0'75\quad y \quad\ 0'75:\displaystyle\frac{2}{2} =0'75\quad también\space\displaystyle\frac{3}{4}=0'75$$
$$\color{navy}\text{Recuerda que}\space\displaystyle\frac{3}{4}=0'75\space porque\space\displaystyle\frac{1}{4}=0'25$$
Quedan libres cuatro quintos del armario para que tres amigas guarden su ropa deportiva y sus accesorios. Tienen que averiguar la parte que les correspodería a cada una.
 $$\color{navy}\text{A cada niña le corresponde}\quad\displaystyle\frac{1}{5}+\displaystyle\frac{1}{15}$$
$$\color{navy}\ y\space como\displaystyle\frac{1}{5}=\displaystyle\frac{3}{15}\space entonces\displaystyle\frac{3}{15}+\displaystyle\frac{1}{15}=\displaystyle\frac{4}{15}$$
$$\color{navy}\text{A cada niña le corresponde}\quad\displaystyle\frac{1}{5}+\displaystyle\frac{1}{15}$$
$$\color{navy}\ y\space como\displaystyle\frac{1}{5}=\displaystyle\frac{3}{15}\space entonces\displaystyle\frac{3}{15}+\displaystyle\frac{1}{15}=\displaystyle\frac{4}{15}$$
Proponemos priorizar esta estrategia de obtener las fracciones equivalentes de las fracciones dadas, cuando vamos a dividir.
Haciendo clic sobre mi imagen, tienes posibilidad de ver algún ejemplo más sobre la división de fracciones y el desarrollo de su algoritmo. Representaremos un modelo gráfico que nos ayude a comprender el resultado numérico.
Realiza las actividades del interactivo haciendo clic en la imagen.
Valores de los ángulos centrales que forman las fracciones
Valor de ángulos centrales que forman las fracciones en el círculo.
Utilizamos el medidor o transportador de ángulos
Comprueba los valores que necesites con la calculadora modelo de Splinterbl(clic icono).
Emplea el medidor de ángulos colocándolo sobre el ángulo que se propone medir. Escribe en la casilla correspondiente el valor ángulo que hayas medido.
¿Cuántos grados mide cada fracción del círculo?
| $$ 1\space círculo = 360º $$ | $$ \displaystyle\frac{1}{2}\space 360º = 180º $$ | $$ \displaystyle\frac{1}{3}\space 360º = 120º$$ | $$ \displaystyle\frac{1}{4}\space 360º = 90º $$ |
|---|---|---|---|
| $$ \displaystyle\frac{1}{5}\space 360º = 72º $$ | $$ \displaystyle\frac{1}{6}\space 360º = 60º $$ | $$ \displaystyle\frac{1}{8}\space 360º = 45º $$ | $$ \displaystyle\frac{1}{10}\space 360º = 36º $$ |
| $$ \displaystyle\frac{1}{7}\space 360º\thickapprox 51,4º $$ | $$ \displaystyle\frac{1}{9}\space 360º = 40º $$ | $$ \displaystyle\frac{2}{3}\space 360º = 240º $$ | $$ \displaystyle\frac{3}{4}\space 360º = 270º $$ |
- Se reparte fotocopia que lleva los circulos divididos en medios, cuartos, tercios, quintos, sextos, séptimos, octavos, novenos, décimos.
- Se recortan los diferentes sectores.
- Se colorea de diferente color cada sector.
- Se investiga el valor del ángulo central que tiene cada sector.
- Para calcular el valor del ángulo, dibujamos la fracción o sector las veces que sean precisas para completar un círculo; si con seis formamos el círculo, el ángulo del sector vale 60º.


Construcción de polígonos regulares inscritos en la circunferencia
Construcción de polígonos con los sectores o fracciones del círculo
Utilizaremos una regla y un rotulador para ir construyendo los diferentes polígonos, uniendo los extremos de los lados de los ángulos centrales que forman cada sector o fracción del círculo.
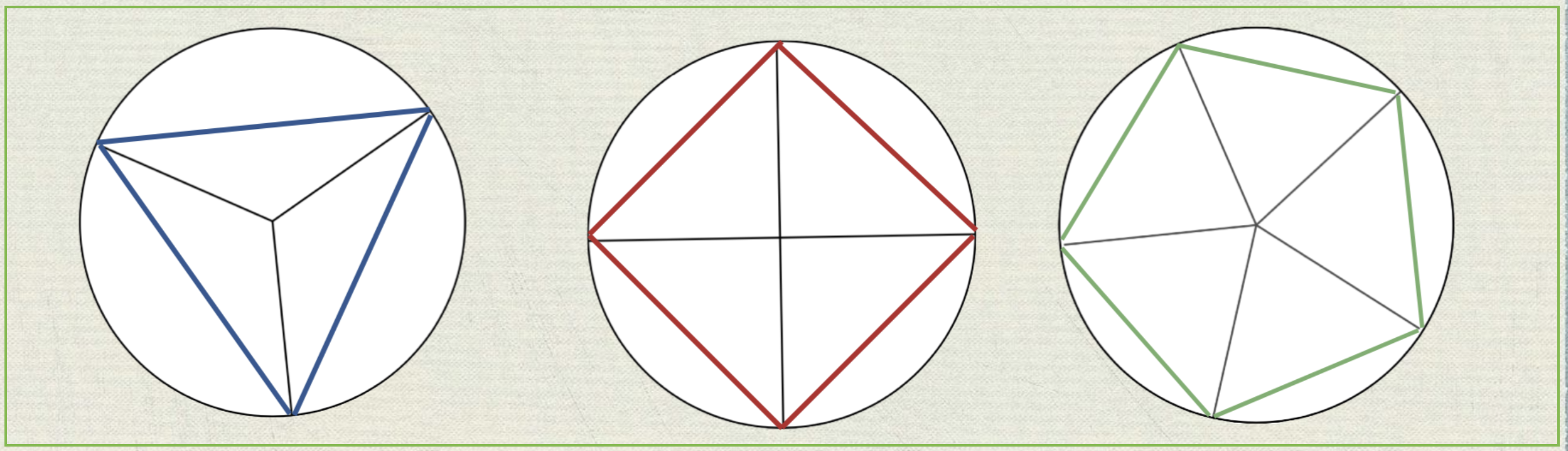
Actividades escritas para mejorar el conocimiento de los polígonos regulares, los triángulos que los forman y el valor de los ángulos de esos triángulos. Archivo pdf descargable en el icono de descarga.
Construcción de polígonos.
El alumnado construirá polígonos, visualizará su construcción, aprenderá sus nombres, jugará a su identificación, practicará el cálculo de sus perímetros. Se hace una referencia a Arquímides como persona importante con su gran aportación matemática.
Este recurso se ha diseñado específicamente para reforzar, afianzar y consolidar lo aprendido con el empleo del material, y amplia la posibilidad, por ejemplo, de construir y visualizar polígonos regulares inscritos con un gran número de lados.
Relacionamos vaso de capacidad con fracción de un círculo
 Mostramos relaciones que podemos establecer entre los vasos medidores de capacidades y las fracciones o sectores circulares. Es conveniente que se emplee un material igual o semejante que permita la experiencia.
Mostramos relaciones que podemos establecer entre los vasos medidores de capacidades y las fracciones o sectores circulares. Es conveniente que se emplee un material igual o semejante que permita la experiencia.
Tabla de relaciones entre la fracción del círculo, el vaso de capacidad y las equivalencias entre diferentes unidades.
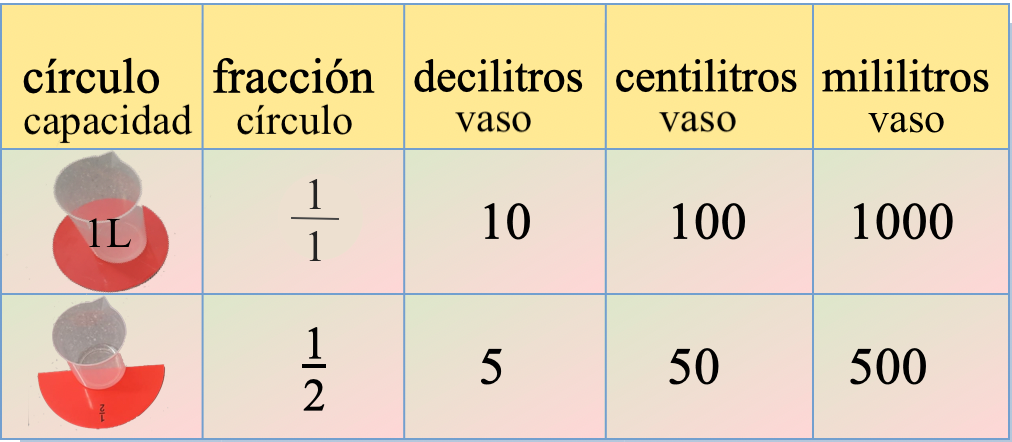
Situaciones con problemas sobre unidades de capacidad. Uso con PDI.
Tabla de relaciones entre la fracción del círculo, el vaso de capacidad y las equivalencias entre diferentes unidades.
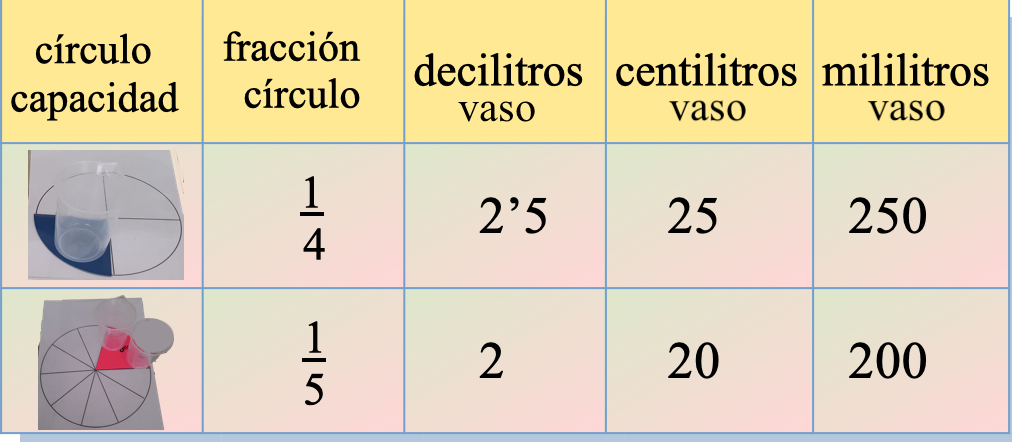
Elige en la barra naranja para elegir la respuesta.
Fracción del círculo, capacidades y equivalencia entre unidades.
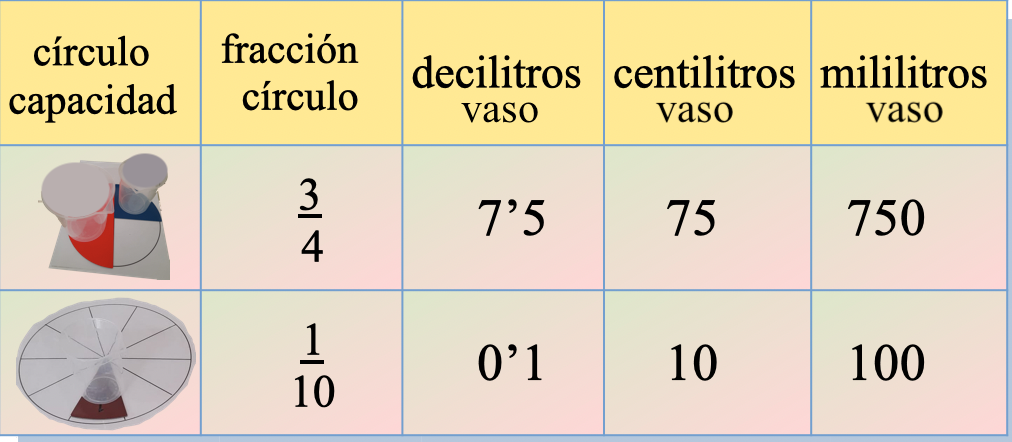
Resuelve los problemas
Con los materiales mencionados, mejoramos la comprensión de las equivalencias entre distintas unidades. Otras posibilidades, también se ofrecen, con los bloques multibase, cuyo planteamiento didáctico esperamos ofrecer en próximos capítulos de otro libro.
Créditos de imágenes
Presentamos a continuación, los créditos referentes a las imágenes y aplicaciónes que han contribuido a la construcción del presente libro:
- Videos páginas 5, 16, 59 : (https://es.vidnoz.com/).
- Dibujos paginas 10, 11, 33, 37...(Clip art gratis)
- Biblioteca de manipulativos Polypad en páginas 12, 13... fondo como pág 60, presentaciones pág 58, 59, elaboración de imágenes pág 50...Mathigon-polypad
- https://free-images.com/display/grass_flower_on_white.html
- Generador de logos y gráficos
- Freepik
- Construye fracciones con Phet.
- Canva




