Vectores y rectas en el plano
(Libro de ejercicios)
Miguel Angel Cabezón Ochoa
Red Educativa Digital Descartes
Córdoba (España)
2022
VECTORES Y RECTAS EN EL PLANO (Libro de ejercicios)
Autor: MIGUEL ANGEL CABEZÓN OCHOA
Diseño del libro: Juan Guillermo Rivera Berrío
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Núcleo del libro interactivo: julio 2022
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN: 978-84-18834-26-4

Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
Este libro de ejercicios nace dentro del curso de "Edición de libros interactivos" de RED Descartes. Son escenas de Descartes colocadas en este modelo de libro.
El tema vectores y rectas es el inicio de los alumnos en la geometría analítica. Se verán los vectores de forma intuitiva, obteniendo la base para poder estudiarlos más profundamente en cursos venideros. Se verán las distintas formas de la recta y el paso de una a otra.
Un vector es un segmento orientado determinado por dos puntos $A$ y $B$ y el orden de estos. El primero de los puntos se llama origen y el segundo extremo, se escribe $\ \overrightarrow{AB}$.
Pulsa los botones de la siguiente escena para ver los elementos anteriores
Las coordenadas de un vector $\overrightarrow{AB}$: son las coordenadas del extremo $B(b_1,b_2)$ menos las coordenadas del origen $A(a_1,a_2)$. $$\overrightarrow{AB}=(b_1,b_2)-(a_1,a_2)=(b_1-a_1,b_2-a_2) $$
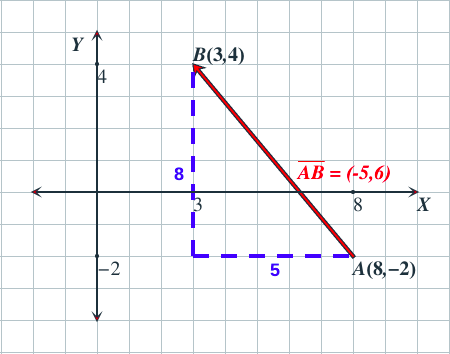
En la siguiente escena puedes realizar ejercicios similares a los del ejemplo. Pulsa el botón Solución para ver la solución y el botón Ejercicio para generar uno nuevo.
El módulo de un vector es la distancia entre los puntos A y B.
Si las coordenadas de un vector $\vec{v}$ son $(v_1,v_2)$, entonces el módulo de $\vec{v}$ es: $$\quad |\vec{v}|=\sqrt{v_1^2+v_2^2}$$
$|\vec{v}|=\sqrt{(8)^2+6^2}=\sqrt{100}=10$
Primero buscamos las coordenadas del vector $ \overrightarrow{AB}$: $\\ \overrightarrow{AB}=(-5,9)-(7,4)=(-12,5)\\ $ El módulo del vector $\overrightarrow{AB}$ es: $\\ |\overrightarrow{AB}|=\sqrt{(-12)^2+5^2}=\sqrt{169}=13$
En la siguiente escena puedes realizar ejercicios similares a los del ejemplo. Pulsa el botón Solución para ver la solución y el botón Ejercicio para generar uno nuevo.
Los vectores $\vec{u}=(u_1,u_2)$ y $\vec{v}=(v_1,v_2)$ son paralelos (tienen la misma dirección), cuando sus coordenadas son proporcionales $$\frac{u_1}{v_1}=\frac{u_2}{v_2}$$
Si $\ \rightarrow\color{blue}\ \ \displaystyle \frac{6}{3}=\frac{14}{7}$
No $\ \rightarrow \color{blue}\ \ \displaystyle \frac{6}{2}\not =\frac{14}{5}$
Un vector paralelo a $\vec{u}$ es $\vec{v}=k\cdot\vec{u}=(3k,4k) \\ |\vec{v}|=\sqrt{9k^2+16k^2}=\sqrt{25k^2}=5k=15 \rightarrow k=3 \\ \vec{v}=3·(3,4)=(9,12)$. Para k=-3 se obtiene otro vector paralelo a $\vec{u} \rightarrow \vec{v}=-3·(3,4)=(-9,-12)$
En la siguiente escena puedes realizar ejercicios similares a los del ejemplo. Pulsa el botón Solución para ver la solución y el botón Ejercicio para generar uno nuevo.
Los vectores $\vec{u}=(u_1,u_2)$ y $\vec{v}=(v_1,v_2)$ son perpendiculares (sus direcciones se cortan formando ángulo recto), cuando sus coordenadas cumplen: $ \ u_1 \cdot v_1+ u_2\cdot v_2=0$
Si $\ \rightarrow\ \color{blue}6\cdot(-2)+3\cdot 4=0$
No $\ \rightarrow \color{blue} 6\cdot 2+4\cdot 1=12+4=16\not= 0 $
Un vector perpendicular a $\vec{u}$ es $\vec{v}=(-4k,3k) \\ |\vec{v}|=\sqrt{16k^2+9k^2}=\sqrt{25k^2}=5k=15 \rightarrow k=3 \\ \vec{v}=3·(-4,3)=(-12,9)$. Para k=-3 se obtiene otro vector paralelo a $\vec{u} \rightarrow \vec{v}=-3·(-4,3)=(12,-9)$
En la siguiente escena puedes realizar ejercicios similares a los del ejemplo. Pulsa el botón Solución para ver la solución y el botón Ejercicio para generar uno nuevo.
Para sumar dos vectores $\vec {u}$ y $\vec {v}$ gráficamente se dibujan de forma que el extremo de $\vec{u}$ coincida con el origen de $\vec{v}$. El vector $\vec{u}+\vec{v}$ es el vector que resulta al unir el origen de $\vec {u}$ con el extremo de $\vec {v}$
Haz coincidir el origen de un vector con el extremo de otro para obtener su suma
Dados los vectores $\vec {u}(u_1,u_2)$ y $\vec {v}=(v_1,v_2)$. El vector suma es; $$\vec{u}+\vec{v}=(u_1,u_2)+(v_1,v_2)=(u_1+v_1,u_2+v_2)$$
$\ \color{blue} \vec{u} + \vec{v}=(7,8)+(-2,3)=(7-2,8+3)=(5,11)$
$\ \color{blue} \vec{u} + \vec{v}+ \vec{w}=(3,5)+(-6,7)+(9,-1)=$
$=(3-6+9,5+7-1)=(6,11)$
Para restar dos vectores $\vec {u}$ y $\vec {v}$ gráficamente se dibujan de forma que sus orígenes coincidan. El vector $\vec{u}-\vec{v}$ es el vector que resulta al unir el extremo de $\vec {v}$ con el extremo de $\vec {u}$
Haz coincidir los orígenes y luego une el extremo del vector $\vec{u}$ con el extremo del vector $\vec{v}$ para obtener $\vec{u}-\vec{v}$
Dados los vectores $\vec {u}(u_1,u_2)$ y $\vec {v}=(v_1,v_2)$. El vector resta es; $$\vec{u}-\vec{v}=(u_1,u_2)-(v_1,v_2)=(u_1-v_1,u_2-v_2)$$
$\ \color{blue} \vec{u}-\vec{v}=(7,8)-(-2,3)=(7+2,8-3)=(9,5)$
$\ \color{blue} \vec{u}-\vec{v}-\vec{w} =(1,8)-(-2,7)-(-2,-3)=$
$=(1+2+2,8-7+3)=(5,4)$
$\ \color{blue} \vec{u}+\vec{v}-\vec{w} =(4,5)+(-2,1)-(-5,-3)=$
$=(4-2+5,5+1+3)=(7,9)$
El resultado de la multiplicación de un número real k por un vector $\vec {u}$, es otro vector cuyo módulo es el producto de k por el módulo del vector y su sentido es el mismo si k positivo y contrario si k es negativo.
Cambia el valor de $k$ para ver el producto $k\cdot\vec{v}$
Dado el vector $\vec {u}(u_1,u_2)$ y el número $k$. El producto $ k·\vec {u}$ es; $$k·\vec{u} = k·(u_1,u_2)=(k·u_1,k·u_2)$$
$\ \color{blue} 7·\vec{u}=7·(3,-9)=(21,-63)$
$\ \color{blue} 7·\vec{u} + 2·\vec{v}=7·(1,4)+2·(3,-9)=\\ (7,28)+(6,-18)= (13,-10)$
El vector opuesto de $\vec{u}$ es: $ \\ -\vec{u} = -(10,-4)=(-10,4)$
En la siguiente escena puedes realizar ejercicios similares a los del ejemplo. Pulsa el botón Solución para ver la solución y el botón Ejercicio para generar uno nuevo.
Una recta queda determinada conocido un punto y un vector de dirección de la misma.
Si $A$ es un punto de la recta , $\vec {v}$ su vector de dirección y $P$ un punto cualquiera . Se verifica: $$\vec{OP}=\vec{OA}+\vec{AP}=\vec{AP}+t·\vec{v}$$
La ecuación vectorial de la recta que pasa por el punto $A=(a_1,a_2)$ y tiene de vector de dirección $\ \vec {v}=(v_1,v_2) $ es: $$ (x,y)=(a_1,a_2)+t\cdot(v_1,v_2)$$
$(x,y)=(3,5)+t·(7,8)$
Un punto de la recta es $(3,-8)$,para obtener más puntos basta dar valores a t: $\\ si \ t=1\ (x,y)=(5,-2) \\ si\ t=2\ (x,y)=(5,-2)$
$\\ (5,-4)=(-7,2)+t\cdot(6,-3)= (-7+6t,2-3t) \Rightarrow $ $\begin{cases} 5=-7+6t & \rightarrow \ t=2 \\ -4=2-3t & \rightarrow \ t=2 \end{cases} \Rightarrow $ la solución es $t=2$ , $\Rightarrow A$ pertenece a la recta.
$\\ (5,-7)=(-7,2)+t\cdot(6,-3)= (-7+6t,2-3t) \Rightarrow $ $\begin{cases} 5=-7+6t & \rightarrow \ t=2 \\ -7=2-3t & \rightarrow \ t=-3 \end{cases}$ como $2\neq -3 $ no hay solución $\Rightarrow B$ no pertenece a la recta.
En la siguiente escena puedes realizar ejercicios similares a los del ejemplo. Pulsa el botón Solución para ver la solución y el botón Ejercicio para generar uno nuevo.
Si en la ecuación vectorial $(x,y)=(a_1,a_2)+t\cdot(v_1,v_2)$ igualamos las coordenadas obtenemos las ecuaciones paramétricas de la recta:
Las ecuaciones paramétricas de la recta que pasa por el punto $A(a_1,a_2)$ y tiene de vector de dirección $\vec{v}=(v_1,v_2)$ son:
$$\begin{cases} x= & a_1+t\cdot v_1\\ y= & a_2+ t\cdot v_2 \end{cases}$$ Un vector de dirección de la recta es:
$\vec{AB}=(9,8)-(5,6)=(4,2)$. Las ecuaciones paramétricas son: $$\begin{cases}
x= & 5+4t\\
y= & 6+ 2t
\end{cases}$$
En la siguiente escena puedes realizar ejercicios similares a los del ejemplo. Pulsa el botón Solución para ver la solución y el botón Ejercicio para generar uno nuevo.
Si en las ecuaciones paramétricas de la recta $\begin{cases} x= &a_1+t\cdot v_1\\ y= &a_2+ t\cdot v_2 \end{cases}$ despejamos $\ t$ $\rightarrow \begin{cases} t= &\displaystyle \frac{x-a_1}{v_1}\\ t= & \displaystyle\frac{y-a_2}{v_2} \end{cases}$ e igualamos obtenemos la ecuación continua.
Ecuación continua de la recta que pasa por $A(a_1,a_2)$ y tiene por vector de dirección $\vec{v}=(v_1,v_2)$ $$\displaystyle \frac{x-a_1}{v_1}=\frac{y-a_2}{v_2}$$
Un vector de dirección de la recta es: $\vec{AB}$ $\\ \vec{AB}=(2,9)-(3,7)=(-1,2)\\$ La ecuación continua es:$\ \displaystyle \frac{x-3}{-1}=\frac{y-7}{2}$
En la siguiente escena puedes realizar ejercicios similares a los del ejemplo. Pulsa el botón Solución para ver la solución y el botón Ejercicio para generar uno nuevo.
Si en la ecuación continua de la recta despejamos $\ y-a_2$
$$ \frac{x-a_1}{v_1}=\frac{y-a_2}{v_2} \rightarrow y-a_2=\frac{v_2}{v_1}\cdot(x-a_1) $$$\displaystyle \frac{v_2}{v_1}$ es la pendiente y se representa con la letra m
La ecuación punto pendiente de la recta que pasa por el punto $A(a_1,a_2)$ y tiene de pendiente $m$ es:
$$ y-a_2=m\cdot(x-a_1)$$Un vector de dirección de la recta es $\vec{AB}$ $\\ \vec{AB}=(3,1)-(5,8)=(-2,7) \rightarrow m=\displaystyle -\frac{7}{2}\\$ La ecuación punto pendiente de la recta es: $$y-8= -\frac{7}{2}\cdot(x-5)$$
En la siguiente escena puedes realizar ejercicios similares a los del ejemplo. Pulsa el botón Solución para ver la solución y el botón Ejercicio para generar uno nuevo.
Si en la ecuación punto pendiente de la recta despejamos $y$ obtenemos la ecuación explícita de la recta.
$y=m\cdot(x-a_1)+a_2 \rightarrow y=mx-ma_1+a_2 =mx+n$ donde $\ n=-ma_1+a_2$
La ecuación explícita de la recta es de la forma: $$y=mx+n$$ Donde $m$ es la pendiente y $n$ la ordenada en el origen.
La pendiente es $m=\displaystyle\frac{10}{5}=2$
La ecuación que buscamos es $\ y=2x+n$
Para encontrar el valor de $n$ utilizamos la condición de que la recta pasa por el punto $(3,4) \\$
$4=2\cdot 3+n \rightarrow n=-2 \\$La ecuación explícita buscada es $y=2x-2$
En la siguiente escena puedes realizar ejercicios similares a los del ejemplo. Pulsa el botón Solución para ver la solución y el botón Ejercicio para generar uno nuevo.
Si en la ecuación continua quitamos denominadores y agrupamos todo en un mismo lado de la igualdad obtenemos la ecuación general.
$\displaystyle \frac{x-a_1}{v_1}=\frac{y-a_2}{v_2} \rightarrow v_2\cdot (x-a_1)=v_1\cdot(y-a_2) \rightarrow \\
v_2\cdot x-v_1\cdot y-a_1\cdot v_2+a_2\cdot v_1=0 \rightarrow Ax+By+C =0 $
La ecuación general o implícita de la recta es de la forma: $$Ax+By+C=0$$ Donde $(-B,A)$ es un vector de dirección de la recta.
Un vector de dirección de la recta $Ax+By+C=0$ es $(-B,A)\ $ luego $(-B,A)=(7,2) \rightarrow A=2 \ B=-7 \\$ por tanto la ecuación que buscamos es $\ 2x-7y+C=0.\\$La recta pasa por el punto $\ C= (3,7)\\$ $2\cdot 3-7\cdot 10+C=0 \rightarrow 6-70+C=0 \rightarrow C=64\\$ La ecuación general buscada es $2x-7y+64=0$
En la siguiente escena puedes realizar ejercicios similares a los del ejemplo. Pulsa el botón Solución para ver la solución y el botón Ejercicio para generar uno nuevo.
Apoya el ratón en el punto blanco para mover la recta , observa su ecuación
Apoya el ratón en el punto blanco para mover la recta , observa su ecuación
Apoya el ratón en el punto blanco para ver el punto de corte o para mover la recta roja hasta que sea paralela o coincidente con la recta azul.
Sea la recta $\vec{r}$ de vector director $(u_1,u_2)$ y la recta $\vec{s}$ de vector director $(v_1,v_2)$
| Paralelas | $$\displaystyle \frac{u_2}{u_1}=\frac{v_2}{v_1}$$ | $\ \ \ \ Si \ P \in \vec{r} \Rightarrow P \notin \vec{s}$ |
| Coincidentes | $$\displaystyle \frac{u_2}{u_1}=\frac{v_2}{v_1}$$ | $\ \ \ \ Si \ P \in \vec{r} \Rightarrow P \in \vec{s}$ |
| Secantes | $$\displaystyle \frac{u_2}{u_1}\neq \frac{v_2}{v_1}$$ |
$\\[-0.2cm] \vec{v_r}=(2,3)\ , \ \vec{v_s}=(4,9) \rightarrow \displaystyle \frac{4}{2}=\frac{6}{3} \rightarrow \vec{v_r} \parallel \vec{r_s} \\[0.2cm] $ $P=(2,5) \in \vec{r} \rightarrow \displaystyle \frac{2+6}{4}=\frac{5+7}{6} \rightarrow P\in \vec{s} \\[0.1cm] $ Las rectas $\vec{r}$ y $\vec{s}$ son coincidentes.
En la siguiente escena puedes realizar ejercicios similares a los del ejemplo. Pulsa el botón Solución para ver la solución y el botón Ejercicio para generar uno nuevo.
Sea la recta $\vec{r}$ de pendiente $m_1$ y la recta $\vec{s}$ de pendiente $m_2$
| Paralelas | $m_1=m_2$ | $\ \ \ \ Si \ P \in \vec{r} \Rightarrow P \notin \vec{s}$ |
| Coincidentes | $m_1=m_2$ | $\ \ \ \ Si \ P \in \vec{r} \Rightarrow P \in \vec{s}$ |
| Secantes | $m_1\neq m_2$ |
$\\[-0.3cm] m_r=3 \ , \ m_s=3 \rightarrow m_r=m_s $
$P=(0,4) \in \vec{r}$. Para ver si $P\in \vec{s}$ sustituimos las coordenadas de $P$ en $\vec{s}$ y comprobamos si verifica la ecuación.
$3\cdot 0+8=3 \neq 4 \rightarrow P\notin \vec{s} \\[0.1cm] $
Las rectas $\vec{r}$ y $\vec{s}$ son paralelas.
$\\[-0.5cm] m_r=2 \ , \ m_s=\displaystyle \frac{6}{2}=3 \rightarrow m_r\neq m_s $
Las rectas $\vec{r}$ y $\vec{s}$ son secantes.
En la siguiente escena puedes realizar ejercicios similares a los del ejemplo. Pulsa el botón Solución para ver la solución y el botón Ejercicio para generar uno nuevo.
Sean las rectas: $$\vec{r}\equiv Ax+By+c=0 \ y \ \vec{s} \equiv A^\prime x+B^\prime y+C^\prime=0$$
| Paralelas | $$ \frac{A}{A^\prime}=\frac{B}{B^\prime}\neq\frac{C}{C^\prime}$$ |
| Coincidentes | $$ \frac{A}{A^\prime}=\frac{B}{B^\prime}=\frac{C}{C^\prime}$$ |
| Secantes | $$ \frac{A}{A^\prime}\neq\frac{B}{B^\prime}$$ |
$ \displaystyle \frac{6}{3}=\frac{4}{2}=\frac{8}{4} \rightarrow $ Las rectas $\vec{r}$ y $\vec{s}$ son coincidentes.
En la siguiente escena puedes realizar ejercicios similares a los del ejemplo. Pulsa el botón Solución para ver la solución y el botón Ejercicio para generar uno nuevo.