JOSÉ BENJAMÍN GALLEGO ALZATE
Instituto Tecnológico Metropolitano
Córdoba (España)
2023
Título de la obra:
VALOR DEL DINERO EN EL TIEMPO. Modelos y Aplicaciones
Autor:
JOSÉ BENJAMÍN GALLEGO ALZATE
Edición del libro:John Jairo García Mora. Grupo GNOMON, ITM
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN: 978-84-18834-78-3
Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
El libro VALOR DEL DINERO EN EL TIEMPO: Modelos y Aplicaciones, es fruto de varios años de trabajo del autor como profesor de economía, ingeniería económica y matemáticas financieras en el Instituto Tecnológico Metropolitano (ITM) de la ciudad de Medellín (Colombia). En los últimos años mi plan de trabajo ha contado con el tiempo para su escritura, situación que motiva expresar mi gratitud con el ITM.
Varias características permiten identificar la naturaleza de este libro. En primer lugar, los conceptos básicos de valor económico, dinero, interés, tasa de interés y equivalencia, entre otros, se presentan contextualizados desde diferentes teorías económicas. Con ello se pretende que el estudiante pueda ampliar el ámbito de significación e interpretación de dichos términos .
La segunda característica consiste en presentar, los más explicito posible, el desarrollo matemático requerido para deducir las diferentes fórmulas que son utilizadas como modelos matemáticos para el cálculo de los resultados económicos de las diferentes operaciones financieras. La intencionalidad pedagógica de esta característica consiste en que el estudiante, desde el manejo de las matemáticas operativas y del cálculo de funciones, comprendan los procesos lógicos-matemáticos que fundamentan a los diferentes modelos de valoración financiera tratados en este libro, y así avance en la adquisición de capacidades y habilidades para comprender, razonar, plantear y resolver situaciones financieras en diferentes contextos.
Finalmente, en los capítulos hallaran aplicaciones utilizando las herramientas y funciones predefinidas de Excel en la solución de diferentes problemas; se ofrece además algunos videos para reforzar los conceptos, como algunos cuestionarios interactivos.
Se pretende que el estudiante aprenda algunas herramientas y funciones que el programa Excel ofrece sobre el tema tratado en este libro, pero no de forma mecánica, sino mediada por la comprensión previa del proceso lógico-matemático de cada función.
Al tener presente el contexto de los conceptos básicos, sumado a la comprensión del proceso lógico-matemático de cada una de las fórmulas tratadas en este libro en la valoración del dinero en el tiempo, y si además se utilizan las herramientas de Excel para el cálculo ágil y oportuno de dicha valoración, el estudiante pasará al análisis e interpretación de los resultados obtenidos para tomar decisiones sobre el manejo del dinero.
Fundamentados en la naturaleza determinada por las tres características enunciadas, y aunado al propósito pedagógico que las inspiran, esperamos que el libro constituya un aporte significativo a la docencia en este campo, en el Instituto Tecnológico Metropolitano. Así mismo, y en general, que sea significativo para todos aquellos estudiantes y profesionales en sus procesos de aprendizaje y formación.
Por diversas motivaciones, hemos optado por escribir y publicar el libro en dos volúmenes, siendo este el primero constituido por cuatro capítulos. El capítulo uno se dedica a los conceptos básicos, tales como valor económico, valoración, dinero, valor del dinero en el tiempo, interés, tasa de interés, equivalencia, conceptos que constituyen los rudimentos de los temas tratados a lo largo del libro.
El capítulo dos se dedica a la valoración de operaciones financieras bajo su forma simple y a algunas aplicaciones que se presentan en la práctica cotidiana.
El capítulo tres se ocupa de la valoración compuesta e incluye las modalidades de capitalización vencida, anticipada y continua.
En este capítulo tres se extienden los modelos de valoración compuesta a los casos de operaciones con divisas, en Unidades de Valor Real (UVRs), y al caso de las captaciones de recursos por entidades financieras bajo títulos denominados Certificado de Depósito a Término, CDT.
Finalmente, el capítulo cuatro versa sobre las tasas de interés efectivas y equivalentes, en diferente contextos de aplicación, no sólo en los casos de las divisas, de los créditos indexados, sino también en la obtención de indicadores de rentabilidad como son la tasa de interés neta, la tasa de interés real y la tasa de interés neta-real.
El próximo volumen dos se centrará en el manejo del valor del dinero en el tiempo bajo las formas de series de ingresos y/o egresos, y a la evaluación de alternativas de inversión. Se estudia las series uniformes o anualidades así como las series que crecen o decrecen de manera uniforme en modo de gradientes aritmético, geométrico o escalonado. Se incluye además aplicaciones en los sistemas de amortización y en métodos de evaluación de opciones de inversión.
Expresamos muestra gratitud con los profesores Luis Lorenzo Torres Herrera y Victoria Peñalver por la autorización para incluir sus videos en este libro. Así mismo, a los autores de los demas videos utilizados disponibles con licencia Creative Commons. A todos ellos les reconocemos sus derechos y les ofrecemos sus respectivos créditos.
Nuestro agradecimiento con el profesor Luis Ceferino Franco A., del Departamento de Finanzas de la Facultad de Ciencias Económicas y Administrativas del ITM, por la revisión del capítulo uno de este libro. Sus sugerencias llevaron a cualificar el texto.
Especial gratitud tenemos con el profesor John Jairo García Mora por todo el trabajo editorial de este libro y por sus enseñanzas en la edición de textos virtuales e interactivos.
Muchas gracias al Instituto Tecnológico Metropolitano.
En este libro las imágenes que se muestran en la ubicación de cada video fueron creadas con la AI (Artificial Intelligence) del explorador Microsoft Edge empleando como palabras clave el titulo del respectivo video. Así mismo, las tablas y figuras incluidas en los diferentes capítulos que no presentan sus respectivas fuentes, son elaboraciones del autor.
IN MEMORIAM
Dedicado a la memoria de los profesores
FRED RESTREPO GIRALDO
Profesor de tiempo completo del Instituto Tecnológico Metropolitano. Departamento de Finanzas.

RUBÉN DARÍO GUERRA TAMAYO
Profesor Asistente del Instituto Tecnológico Metropolitano. Departamenteo de Ciencias Básicas.

Este capítulo tiene como propósito presentar y discutir algunos conceptos básicos empleados en este libro, abordados desde diferentes enfoques y disciplinas de la ciencia económica. Se trabajan conceptos como valor económico, valoración, dinero, valor del dinero en el tiempo, interés, tasa de interés, y equivalencia.
Los bienes económicos son objetos o cosas útiles que el hombre dispone para la satisfacción de sus necesidades o deseos. En la explicación del valor de los bienes económicos, la historia del pensamiento económico permite identificar dos perspectivas o enfoques en el significado de la expresión valor económico.
Un primer enfoque identifica el valor de los bienes económicos con la utilidad, la importancia o la significación (lo estimable) que se le da a una cosa. Esta identificación implica la existencia de una relación entre un sujeto que valora, que asigna importancia o significación, y la cosa valorada.
Desde el ámbito de la economía, esa conexión se halla en la satisfacción de las necesidades que al individuo le proporciona la cosa. Las cosas que presentan esa relación directa con la satisfacción de las necesidades humanas y se tiene el poder de utilizarlas con ese propósito, son identificadas como bienes económicos, por Carl Menger (2017).
El valor es, para el mismo autor, la significación que unos concretos bienes o cantidades parciales de bienes adquieren para nosotros, cuando somos conscientes de que dependemos de ellos para la satisfacción de nuestras necesidades. El valor como significación se constituye en un juicio sobre el bien en relación con la satisfacción de necesidades, y es por lo tanto un valor subjetivo.
En la tradición subjetiva del valor, el filósofo griego Aristóteles (384 AC-322 AC), al reflexionar sobre la naturaleza de los bienes, distinguía entre el valor de uso y el valor de cambio de éstos, y afirmaba que el segundo fenómeno se deriva del primero (Schumpeter, 1994), indicando con ello que el aspecto fundamental para la asignación de valor a los bienes económicos es el juicio subjetivo, es la valoración subjetiva, vinculado éste con la utilidad que ofrece el bien en la satisfacción de las necesidades humanas.
De esta manera, cada bien es poseedor de un valor y, si son objeto de intercambio, se presenta entre ellos una relación de valores; empero Aristóteles no hace indicación de cuál es la medida de esos valores que permita determinar su magnitud y expresar, por ejemplo, la razón de intercambio entre bienes, los valores relativos.
Esta misma posición está presente en los Escolásticos (Siglo IX – Siglo XIV), dado que para ellos el valor se basaba en la satisfacción de necesidades, llegando incluso al desarrollo de una teoría utilitarista del valor de cambio.
Para los Escolásticos, el costo de un bien (que podemos entender como el esfuerzo humano materializado en la producción), aunque es un factor determinante del valor de cambio, no es
la fuente lógica o causa de éste, sino que es, al contrario, causado por la utilidad del bien; el valor de cambio es el reflejo de los usos que las personas se proponen hacer de los bienes y de la importancia que se les dé a éstos (Schumpeter, 1994).
La posición subjetivista del valor se enfrentó al problema que se ha identificado en la literatura económica como la paradoja del valor. La paradoja consiste en la pregunta del por qué muchos bienes que presentan alta utilidad para la especie humana, como son por ejemplo el agua y el aire, tienen poco o nulo valor de cambio, y otros bienes que son mucho menos útiles, como algunas piedras preciosas (diamantes, rubíes, por ejemplo), tienen un alto valor de cambio o precio. La paradoja es la situación consistente en que cosas claramente muy útiles y necesarias gozan de un bajo precio, mientras otras cosas menos útiles tienen un valor de cambio alto.
Ferdinando Galiani (1728-1782), aunque no fue el primero en ofrecerla, elabora explicación al problema a partir del concepto de escasez. Para Galiani, el valor se explica no solo por la utilidad sino también por la escasez de los bienes; aquellos bienes que ante una necesidad tiene una disposición en gran cantidad (hay abundancia), a pesar de ser muy útiles, el valor es bajo; al contrario, con disposición pequeña (hay escasez), el valor es alto.
Ahora bien, en cuanto al concepto de valor, este economista italiano lo define como la significación de la relación de equivalencia entre una mercancía y una cantidad de otra; el valor de una mercancía tiene sentido en relación con una cantidad de otra (Schumpeter, 1994), no por sus condiciones intrínsecas.
Así mismo se manifiesta Jacob Bernoulli (1700-1782):
El valor no es una propiedad intrínseca de las cosas, sostiene Bernoulli, sino una relación, que Carl Menger denominara causal, entre una persona que valora o estima y el bien u objeto que es valorado o estimado.
La valoración está en relación con la importancia que tiene un bien en la satisfacción de las necesidades; es más, indica que la importancia o utilidad de un bien adicional está en relación inversamente proporcional con la cantidad de bienes que ya se poseen para satisfacer dichas necesidades.
Así entonces, la significación, importancia o utilidad en la satisfacción de las necesidades que ofrece un bien disminuye con la cantidad de bienes que se posean para ello, hay una utilidad o satisfacción decreciente, y la utilidad ofrecida por la última unidad adicional de un bien es lo que conocemos hoy en día como utilidad marginal (Schumpeter, 1994).
Un último autor que deseamos reseñar en esta corriente del valor subjetivo es Étienne Bonnot de Condillac (1714-1780).
Para este autor el valor de los bienes tiene su fuente en la utilidad, entendida no desde las cualidades físicas de éstos, sino en el sentido de la importancia que un individuo le otorga al bien en cuanto es capaz de satisfacer necesidades, es decir, y de nuevo, desde la utilidad que se da por la relación entre un sujeto que valora y la cosa valorada, valoración que aumenta o disminuye (fluctúa) de acuerdo con las cantidades disponibles, por la escasez o la abundancia, respectivamente (Roll, 1975).
En el segundo enfoque del valor económico de los bienes, se hace alusión al valor en relación con la cristalización del esfuerzo humano que configura o produce el bien económico. Darle configuración a un bien económico destinado a satisfacer necesidades humanas exige de esfuerzo humano en la elaboración de dicho bien, requiere de la aplicación de conocimientos técnicos y tecnológicos, y la utilización de diferentes recursos como materias primas, herramientas y equipos.
En este contexto, el valor del bien económico se determina por la valoración del esfuerzo humano cristalizado en su elaboración, en la producción. Estamos entonces ante la presencia de un valor objetivo; el valor es determinado por la magnitud del esfuerzo humano cristalizado al producirse el bien.
Un representante de la tradición objetiva del valor es el economista Alemán Karl Marx (1818-1883). K. Marx reconoce en las mercancías, en los productos reproducibles y destinados al intercambio, el doble carácter de valor de uso y valor de cambio. El valor de uso indica que el bien es útil en la satisfacción de las necesidades, es además soporte material del valor de cambio.
Para Marx, el valor de uso constituye una relación entre el consumidor y el objeto consumido y, por ello, de poca importancia en la explicación u obtención de las leyes que rigen el sistema de producción capitalista, objeto de estudio en su teoría económica.

Karl Marx
Al contrario, Marx encuentra en el valor de cambio, entendido como relación cuantitativa de mercancías, la expresión o forma exterior de un proceso social (Marx, 1975). Así entonces, en la construcción teórica de la economía política Marx le otorga relevancia al valor de uso o utilidad de la mercancía en cuanto éste encierra un valor que es la materialización del trabajo humano.
Marx sostiene que el valor de cambio en cuanto relación cuantitativa entre diferentes mercancías, en cuanto proporción en la que los diferentes valores de uso se intercambian, es la forma de expresarse, de manifestarse, algo que todas las mercancías tienen en común y de igual magnitud en todas estas relaciones de intercambio: la de ser productos del trabajo. La unidad de medida del valor es el trabajo abstracto (no el trabajo concreto o particular de un carpintero, panadero o médico) y su magnitud la cantidad de trabajo socialmente necesario para la producción de las mercancías (Marx, 1975). El valor de una mercancía es la cantidad de trabajo socialmente necesario, necesario según las condiciones sociales existentes, cristalizado o incorporado en ella.
La mercancía es a la vez un objeto de utilidad y un valor, y la sustancia del valor es el trabajo.
El tiempo de trabajo socialmente necesario consiste en dos elementos. En primer lugar, el empresario capitalista adelanta capital para la adquisición de medios de producción representados en maquinaria, equipos, instalaciones, materias primas, siendo en general medios materiales para la producción que Marx denomina capital constante adelantado (C) que, al ser resultado de un proceso de producción anterior, los identifica como trabajo indirecto, como trabajo muerto.
El capital constante es importante en la determinación de la capacidad de producción de una empresa y, en general, de un país al concretar condiciones técnicas de producción, por la incor- poración de progreso tecnológico, determinación de la escala y la organización del proceso de producción.
En el proceso de producción de las mercancías, no todo el capital constante adelantado es utilizado, por lo que en la determinación del valor sólo se incorpora aquella parte que corresponde, para el caso de activos fijos, al desgaste por el uso de los medios de trabajo.
Tomando en consideración esta salvedad obtenemos el capital constante utilizado $(C_u\ )$ constituido por el costo de las materias primas y el desgaste que se deriva de la utilización de los equipos y la maquinaria en el proceso de producción.
El empresario capitalista también dispone, en segundo lugar, de capital para la adquisición de trabajo vivo o directo, al contratar trabajadores y pagarles por la fuerza de trabajo el salario que les permita vivir, desembolso denominado por Marx capital variable (V) (Marx, 1975); el nivel de cualificación del trabajo es igualmente un determinante de la capacidad productiva del trabajo que, integrado con el capital constante, afectan el tiempo de trabajo socialmente necesario para producir una mercancía.
Sin embargo, estas diferencias en cualificación son conceptualmente tratadas desde la categoría de trabajo abstracto, de trabajo en general. Es entonces el tiempo de trabajo socialmente necesario la base sobre la que gira el valor de cada mercancía, determinante a su vez de la relación cuantitativa de cambio, denominada valor de cambio.
Ahora bien, según Marx lo que paga el capitalista por la fuerza de trabajo es un menor valor con respecto al valor creado por el trabajador al usar su fuerza de trabajo en el proceso de producción, diferencia que es la fuente del excedente identificado como plusvalía (P), excedente apropiado por el dueño de los medios de producción. El trabajo vivo es el único generador de nuevo valor.
La plusvalía es producto del trabajo no remunerado, excedente que, expresado en términos relativos respecto al capital variable, constituye la cuota de plusvalía $(\rho)$, o sea $\rho=\frac{P}{V}$.
Así mismo, y aunque la ganancia del capitalista (G) es igual a la plusvalía, es decir $P=G$, en el cálculo de la cuota de ganancia Marx toma en consideración todo el capital adelantado en la producción de las mercancías, debido a que, en la transformación de la plusvalía en ganancia, entra todo el capital. La tasa o cuota de ganancia es por lo tanto $g=\frac{P}{C+V}=\frac{G}{C+V}$ . Por la forma de establecerse estas relaciones, obtenemos que la cuota de plusvalía es mayor a la cuota de ganancia, $\rho>g$.
Al capital constante utilizado más el capital variable empleado en la producción de las mercancías Marx lo denomina precio de costo (Marx, 1977), precio que permite resarcir la inversión de capital al transferir una parte del valor del capital adelantado que va a reaparecer en el producto.
El valor de una mercancía $\left(V_m\right)$, para el productor individual, es por lo tanto la suma del capital constante utilizado en su producción (representado por los materiales utilizados y el desgate de los medios de trabajo por su uso, $C_u$), el capital variable (V) que es el pago al trabajador por la fuerza de trabajo empleada en forma de salarios, y la plusvalía que genera éstos (P). De esta manera, el valor de la mercancía es estimado como $V_m=C_u+V+P$, siendo $C_u+V$ lo que constituye para Marx el precio de costo ($PC=C_u+V$), o costos de producción de la mercancía para el capitalista, por lo que el valor de la mercancía también se puede expresar como $V_m=PC+P$. La magnitud del valor contenido en la mercancía, es decir la cantidad de trabajo abstracto contenido, de trabajo vivo y trabajo indirecto, es el socialmente necesario; magnitud que a su vez es el soporte o la base sobre la que giran los valores de cambio de las mercancías.
Se comprenderá entonces que, si el capitalista individual vende en el mercado la mercancía por su valor, es decir si el precio del mercado es igual al valor, realiza una ganancia equivalente al 100% de la plusvalía. En cambio, si vende la mercancía por un precio de venta igual al precio de costos (a los costos de producción del capitalista), la ganancia es cero; sin embargo en esta situación recupera el capital utilizado en la producción de la mercancía. Por lo tanto, siempre que el precio de venta de la mercancía en el mercado sea mayor al precio de costo y menor al valor de ésta, existe ganancia para el capitalista, por lo que el nivel de la plusvalía $P$ deja margen para la competencia entre capitalistas.
En la actualidad, el análisis teórico del valor ha desembocado en el planteamiento de dos teorías de los precios, la teoría de los precios desde el enfoque del equilibrio general y la teoría de los precios de producción (Klimovsky, 2000). La primera es la teoría neoclásica de los precios que surgen del equilibrio general de la economía, enfoque basado en la valoración subjetiva que realizan los agentes de los bienes económicos y en el comportamiento racional de éstos. El comportamiento racional indica que el accionar, la toma de decisiones, de los agentes económicos está orientada por el propósito de obtener el máximo beneficio posible en la asignación de sus recursos escasos o limitados. En esta teoría, el consumidor como agente económico racional orienta su accionar al objetivo de maximizar la utilidad (maximiza una función de utilidad) o satisfacción al asignar sus recursos escasos (el consumidor está sujeto a la restricción del nivel de recursos poseídos, a la restricción presupuestal) en la adquisición (selección) de una canasta de bienes. Así mismo el productor, como agente racional, se orienta por el objetivo de obtener la máxima ganancia posible en la asignación de sus recursos escasos; el productor racional elige la combinación de factores de producción que le posibilite el nivel de producción más alto y de esta manera, el máximo beneficio.
Es la interacción entre las decisiones de los consumidores y los productores, la fuerza económica que determinan la demanda y la oferta de mercado, respectivamente, así como el mecanismo o condición para la determinación de los precios de equilibrio, con igualdad entre las cantidades de bienes ofrecidas y demandadas.
La segunda perspectiva es la teoría de los precios de producción que, soportada desde la visión del valor como cristalización del trabajo humano abstracto, plantea un mecanismo de funcionamiento de la economía de un país a partir del ajuste de las tasas de ganancias de las empresas a una tasa de ganancia media o general de la economía. Con base en los precios de producción determinados por el mecanismo de tasa media de ganancia, la economía logra su equilibrio.
¿En qué consisten estos precios de producción y cómo desde los valores de las mercancías se llega a estos precios? Permítanos de nuevo recurrir ampliamente a Karl Marx para ilustrar el asunto.
El análisis de la transformación de los valores en precios de producción de Marx, pasa por la formación de la cuota general o media de ganancias. Para ello, partamos de una economía formada por cinco ramas de la producción, cada una dotada con un capital total de 2,000 unidades monetarias (um), con diferentes composiciones de capital constante y capital variable, pero al interior de cada rama la composición orgánica del capital es la misma. En la columna (e) de la Figura 1.1, observamos que la rama de producción 1 es la más intensiva en capital (la composición orgánica es de 19, el capital constante adelantado es 19 veces el capital variable utilizado, es decir que, en otro sentido, el capital constante adelantado es el 95% del capital total de la rama) mientras que la rama 5 tiene la menor composición orgánica (de 1.5). Las diferentes composiciones orgánicas del capital indican que las ramas tienen diferencias en cuanto a la capacidad de producción, en términos de capital constante.
Estas diferencias inciden en la magnitud del tiempo de trabajo abstracto que cada rama emplea en la producción de las mercancías.
La cuota de plusvalía se asume igual al 100% en todas las ramas, significando esto que el nivel de la plusvalía es exactamente igual al monto invertido en cada rama de la producción en forma de capital variable (ver Figura 1.1 columnas (c) y (d)); por ello, en todas ellas se presenta el mismo grado de explotación del trabajo.
Se supone además que entre las ramas de producción no hay diferencia en rotación del capital, así como la implementación de una misma jornada laboral.
Existe una relación entre la tasa de ganancia, la tasa de plusvalía y la composición orgánica del capital. Si como ya dijimos, $g=\frac{P}{C+V}$ es la tasa de ganancia del capitalista, $\rho=\frac{P}{V}$ es la tasa de plusvalía y $\left(\frac{C}{C+V}\right)$ es la composición orgánica del capital, y si despejamos $P$ de la cuota de plusvalía, o sea $P=\rho\ast V$ , y la reemplazamos en la fórmula de tasa de ganancia, es decir, $g=\frac{\rho\ast V}{C+V}$ obtenemos que $g=\rho\ast\frac{V}{C+V}$.
La tasa de ganancia tiene relación directa con la tasa de plusvalía o grado de explotación del trabajo e indirecta con la inversa de la composición orgánica del capital; esto último parece contradictorio con la realidad capitalista, asunto que abordaremos más adelante.
En la Figura 1.1, el valor de la producción de cada rama se calcula en la columna (g) y es conformado por el capital constante usado más el capital variable pagado por la fuerza de trabajo y la plusvalía obtenida con la tasa del 100% sobre el capital variable; este valor también se obtiene como la suma del precio de costo de la columna (f) con la plusvalía. Globalmente, la economía produce el valor de 8,440 um.
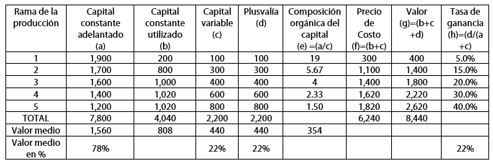
Desde la noción del valor de las mercancías ya desarrollado, la existencia de diferentes composiciones orgánicas del capital entre ramas de la producción ocasiona la presencia de diferentes tasas de ganancia entre ellas, siendo la más baja en aquella con mayor composición orgánica del capital, en la rama 1 donde mayor es la capacidad productiva en términos de capital constante, y la mayor tasa de ganancia se presenta en sectores con menor composición orgánica, en la rama cinco con menor capacidad productiva en términos de capital constante; ver Figura 1.1 columnas (e) y (h).
La tasa de ganancia más alta es del 40% perteneciente a la rama de la producción cinco, caracterizada ésta por tener la menor composición orgánica del capital, al utilizar más capital variable que constante, y esto ocurre porque para Marx el trabajo vivo es el único generador de plusvalía y, por ello, de ganancia.
Se observa además como en la rama 1 de la producción con mayor relación entre el capital constante y el capital variable (de 19), es decir, en aquellas más mecanizadas, tecnificadas, o incluso automatizada, la tasa de ganancia es la menor de todas (5%).
Las ramas intensivas en trabajo presentan las ganancias más altas en comparación con las ramas intensivas en capital constante. Esta situación es la misma a la ya comentada más arriba respecto a la relación de la tasa de ganancia con la tasa de plusvalía y la inversa de la composición orgánica del capital.
Realmente la situación anterior es contradictoria con la realidad económica y, de darse, sería insostenible para el sistema de producción; el sistema económico no sería estable. A pesar que en el planteamiento teórico de Marx las ramas más atrasadas en la incorporación de capital fijo, de medios de producción, son las que mayor ganancia genera, como acabamos de ver de la Figura 1.1, en la realidad económica se observa el desarrollo de inversiones cada vez más amplias en los sectores de alta composición orgánica del capital, utilizando técnicas de producción modernas que incorporan progreso tecnológico, de innovaciones en productos, proceso y en diseño organizacional, del desarrollo de fuerzas productivas; y estas mejoras en la capacidad productiva unidas a la cualificación de los trabajadores harían que el tiempo de trabajo socialmente se reduzca por cada mercancía elaborada, resultando contradictorio que se premie socialmente con mayor ganancia a las producciones ineficientes. Adicionalmente, la situación de mayor ganancia en la rama 1 conduce a pensar que la competencia haría mover a los capitales en busca de tasas de ganancias más altas, a dicha ramas, que son incluso más atrasadas. La realidad económica no muestra evidencia de movilidad de capital de sectores intensivos en capital constante a sectores intensivos en trabajo, en verdad la tendencia es la contraria.
Al parecer la teoría del valor trabajo de K. Marx entra en contradicción con la tendencia observada en el sistema de producción que pretendía explicar.
En la solución de la anterior inquietud, Marx desarrolla la forma transfigurada del valor en precios de producción (Marx, 1977).
En la economía en su conjunto, el tiempo de trabajo socialmente necesario que actúa como el centro de balance es el tiempo socialmente necesario medio, es decir según las condiciones imperantes socialmente en la economía. No es por lo tanto el tiempo socialmente necesario de cada rama en particular, sino el tiempo socialmente necesario en el conjunto de la economía; es el valor medio el que reconoce el mercado (Salama y Valier, 1984). Por ello, la movilidad de capital no se da de las ramas intensivas en capital constante hacia aquellas más trazadas, no, la tendencia es la contraria.
Con la transformación de los valores a precios de producción realizada por Marx, las ramas atrasadas son penalizadas con transferencia de plusvalía hacia los sectores más avanzados, que se ven beneficiados, situación que ocasiona nivelación de la tasa de ganancia al umbral medio de la economía; así mismo, esto genera movilidad de capitales de ramas atrasadas hacia las más avanzadas superando de esta forma la contradicción inicial.
Veamos el procedimiento de ajuste de la economía por medio de los precios de producción. La economía en su conjunto, representada por las cinco ramas de la producción, invierte en capital constante la suma de 7,800 um de las cuales en la producción se utilizan 4,040 um; así mismo en capital variable se invierte y utiliza en total el monto de 2,200 um; ver columnas (a), (b) y (c) de Figura 1.1.
El capital total invertido por la economía en su conjunto es por ello 10,000 um. Adicionalmente, la plusvalía generada por la economía en su conjunto es de 2,200 um. Dicho valor representa en relación con el capital variable una cuota global de plusvalía del 100%, y una cuota general de ganancia del 22% respecto al capital total invertido en la economía. Es esta última la ganancia media de la economía en su conjunto formada por las cinco ramas. Ver Figura 1.1 final de columnas (d y h).
Esta cuota general de ganancia del sistema económico, o ganancia media, es también denominada por Marx ganancia social.
Desde cada rama de producción, en términos de valor medio, el capital constante es de 1,560 um y el capital variable medio de 440 um para un capital total medio de 2,000 um.
El valor medio del capital total se traduce en términos porcentuales en una composición orgánica de 78% de capital constante y 22% de capital variable por rama. Bajo el supuesto de 100% de cuota de plusvalía, se alcanza como ganancia media por rama de producción el mismo 22% (que es el valor medio de la economía en su conjunto por este concepto).
Una vez determinada la ganancia media de la economía en su conjunto, la estabilidad del sistema de producción se da por medio del precio de producción.
Este concepto lo define Marx como la suma del precio de costo más la ganancia media. Así, para la rama 1 de la Figura 1.2, el precio de producción es de 740, resultado de sumar el precio de costo de 300 con la ganancia media de 440. En cambio, el valor en esta misma rama es de solo 400, determinado por 300 de precio de costo y 100 de cuota de plusvalía. Al comparar el precio de producción con el valor de las mercancías producidas en esta rama, se observa que ha recibido por transferencia de ganancia un monto de 340, equivalente a un aumento en la ganancia de 17% (valor que se obtiene de dividir la ganancia incrementada sobre el capital total de la rama, $340/2,000=0.17$). Por lo tanto, en esta rama con alta composición orgánica del capital, el precio de producción es mayor al valor de las mercancías producidas.
La situación anterior también se puede observar al comparar la tasa de ganancias de la rama 1 con la tasa de ganancia media. Mientras ella tiene una ganancia del 5% sobre el capital invertido, por medio del ajuste de la ganancia media obtiene ganancia de 22%, superando el valor inicial en un 17%. (22%-5%=17%).
La rama 1 intensiva en capital constante se ve favorecida con la determinación del precio de producción y el ajuste por la ganancia media de la economía.
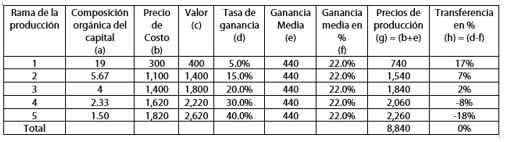
La situación para la rama 5 es totalmente la contraria. Esta rama de la producción tiene la más baja composición orgánica del capital (de 1.5) indicando menor tecnificación, pero intensiva en la utilización de fuerza de trabajo. Como es el trabajo la fuente de la plusvalía, según Marx, es la rama con la mayor tasa de ganancia (del 40%). Con el ajuste vía ganancia media, el valor de las mercancías producidas es mayor al valor en términos de precio de producción de la misma rama (de 2,620 um se pasa a 2,260 um, respectivamente), ajuste que significa salida o transferencia de ganancia de 360 um que en términos relativos respecto al capital de la rama representa una caída de 18% en su tasa de ganancia. En términos de los precios de producción, la ganancia medio del 22% representa para la rama cinco una transferencia hacia otras ramas del 18% de su ganancia inicial (pasa de 40% a tener por ajuste 22%, siendo la diferencia 18%). Esta rama se ve penalizada con transferencia de plusvalía o valor por medio de los precios de producción, y es ocasionada porque el tiempo de trabajo socialmente necesario en la rama es mayor al tiempo de trabajo socialmente necesario medio, que es el reconocido por el mercado, situación que se traduce en desperdicio de tiempo de trabajo o ineficiencia.
En general, se observa en la última columna de la Figura 1.2 que las tres primera ramas de las producción, caracterizadas por alta composición orgánica del capital, la rentabilidad media de ganancia del 22% representa transferencia positiva, es decir hacia estas ramas, de plusvalía provenientes de otras ramas; en cambio las ramas cuatro y cinco de la producción, caracterizadas por baja composición orgánica del capital y por ello intensivas en trabajo, el ajuste general por la tasa de ganancia media les significa transferir hacia otras ramas de la economía parte de su ganancia. Las ramas cuatro y cinco transfieren a la economía un porcentaje total de 26% a favor de las otras tres ramas; de este monto, la rama uno recibe un 17%, la rama 2 un 7% y la rama 3 un 2%. Esto último haría que la movilidad de capitales, la competencia, se dirija hacia estas ramas de la producción y la tasa de ganancia de cada una de ellas, tiendan a igualarse al valor medio social.
Al ocurrir este ajuste en la tasa de ganancias, el sistema se estabiliza con una cuota de plusvalía del 100% y una tasa de ganancia media del 22%, no generando incentivos para la movilidad de capitales en busca de mejores tasas de ganancia. El sistema se ajusta a favor de los sectores tecnificados, a los sectores intensivos en capital constante. El ajuste vía precios de producción significa que el sistema económico se halla en equilibrio, se restablecen las condiciones de producción y la distribución del excedente se realiza con base en la tasa media de ganancia, igual para todas las ramas de la producción (Klimovsky, 2000).
El mecanismo de ajuste es propiciado por la competencia entre capitalistas. Marx sostiene que las distintas tasas de ganancia son compensadas entre sí por la concurrencia (Marx, 1977), por las condiciones sociales de producción de la economía en conjunto, para así llegar a la tasa media de ganancia, que es el reparto equitativo de la ganancia total.
Con la transformación de los valores en precios de producción y la perecuación de la ganancia, las ramas más atrasadas son penalizadas con transferencia de plusvalía, mientras que las ramas con mayor composición orgánica del capital, es decir más mecanizadas, son beneficiadas al recibir transferencia de plusvalía, ocasionando que la movilidad de capitales se dirija hacia estas últimas (Salama y Valier, 1984).
Empero, es necesario expresar que a pesar de la transformación de los valores en precios de producción, para Marx sigue siendo el trabajo abstracto la medida del valor y su magnitud el tiempo de trabajo socialmente necesario, es decir, el tiempo medio según las condiciones imperantes en la economía en su conjunto; esto es, el tiempo de trabajo socialmente necesario sigue actuando como centro de gravedad sobre el que gira el valor de cambio de las mercancías (Boundi, 2018)
Esta solución de Marx no estuvo exenta de críticas. Para este hecho, son interesantes las observaciones realizadas por Paul M. Sweezy (1979) y su solución alternativa. Así mismo, independientemente de los intereses prácticos (políticos) de la explicación de Marx sobre el origen de la plusvalía y del valor de las mercancías, el valor en el sentido de precios de producción está determinado por el capital constante utilizado, el capital variable aplicado y la ganancia media; al precio de costo y la ganancia media.
Esta consideración ha permitido pensar el valor en términos de una teoría de los costos de producción y de la distribución. El pago por el trabajo representa el costo por remuneración al factor trabajo; existe además costo por el desgaste de los equipos y por la recuperación de todos los materiales utilizados en la producción de la mercancía; y la ganancia media es un excedente que se distribuye en ganancia del capitalista y como renta de la tierra.
Mientras el enfoque de Marx se desarrolla desde la producción, esto es, desde la oferta, el enfoque de la teoría del valor subjetivo es desde el agente consumidor, esto es desde la demanda. En el desarrollo posterior de la teoría del valor, en particular desde Alfred Marshall, se integra tanto la demanda y la oferta dando lugar a la teoría moderna de los precios del equilibrio general. Es desde este enfoque que consideramos en adelante el problema del valor y la acción de asignar valor.
Cuando el valor de un bien se expresa en términos de dinero, tenemos la forma precio del valor. Pero este valor así expresado no es el precio de mercado del bien. El consumidor valora subjetivamente los bienes, y su acción es la fuerza que determina la demanda, pero este valor puede ser diferente al precio que finalmente se determine en el mercado, por la interacción con la oferta del bien. Es posible incluso que la valoración subjetiva de un bien por parte del consumidor individual implique que lo que está dispuesto a pagar por él sea mayor al precio del mercado, a lo que efectivamente paga por el bien.
Así mismo, y desde el enfoque de valor objetivo, los valores de las mercancías de las diferentes ramas de la producción no son los precios de mercado de éstas. Con los precios de producción, a partir del ajuste vía la tasa media de ganancia, el sistema económico alcanza su equilibrio por medio de la competencia entre ramas de la producción en el mercado; empero en el proceso de ajuste, los valores son diferentes a los precio del mercado que se van generando. Una vez cumplido el ajuste, los precios de producción son precios de equilibrio y teóricamente los precios del mercado para la economía en su conjunto.
De estos dos enfoques teóricos del valor, es la teoría neoclásica de los precios (y del valor subjetivo) la base de la economía financiera, de la teoría financiera. El fundamento teórico de la teoría financiera es la microeconomía que versa sobre cómo los agentes económicos disponen y asignan recursos escasos en el tiempo en condiciones de incertidumbre o riesgos, orientado por el principio de racionalidad económica. El modelo microeconómico de comportamiento racional de los agentes económicos es extendido a la toma de decisiones financieras de estos agentes.
Dicho enfoque teórico es soporte de la teoría de la utilidad esperada, del estudio del riesgo y de la teoría de portafolio, como de los mercados eficientes. Es además aplicada en el desarrollo de modelos de valoración, de asignación o determinación del valor, de activos sujetos a condiciones de incertidumbre y de riesgo, situación que surge del desconocimiento de los agentes económicos sobre lo que ocurrirá en el futuro .
Desarrollemos entonces, el modelo microeconómico básico de conducta de un agente económico en un instante en el tiempo. Para el caso del agente económico denominado consumidor individual, el valor subjetivo sobre la relación de utilidad de un bien respecto a la satisfacción de las necesidades humanas, se traduce en la capacidad que tiene el consumidor individual para establecer el orden de significancia de los bienes en términos de preferencias.
El juicio subjetivo consiste en establecer un orden de preferencias. Para establecer dicho orden, el consumidor debe conocer las opciones de bienes que están disponibles y tener la capacidad de establecer la jerarquía ordinal de estos bienes con base en sus preferencias; la utilidad del bien se establece de manera ordinal, no cardinal.
Para ilustrar esta situación supongamos que el consumidor tiene opciones sobre dos bienes, o también puede ser dos canastas de bienes, tales como $x_1$ y $x_2$. Se supone que el consumidor está en capacidad de establecer si $x_1$ es estrictamente preferida a $x_2$, ($x_1> x_2$); si $x_2$ es estrictamente preferida a $x_1$, ($x_1\lt x_2$); si $x_1$ es al menos tan preferida como $x_2$, ($x_1≥ x_2$); o si le son indiferentes, ($x_{1\sim }x_{2}$). En general, se trata de establecer la capacidad del consumidor de ordenar completamente los bienes de acuerdo con sus preferencias y no exista indecisión en la elección del bien o canasta bienes a adquirir.
Las preferencias son transitivas, esto es: si el bien $x_1> x_2$ y el bien $x_2> x_3$, por lo tanto el bien $x_1> x_3$.
Con el fin de establecer una formulación matemática de las preferencias, por medio de una función de utilidad, se suponen además que éstas son continuas, no se presenta saciabilidad del consumidor (éste prefiere más a menos), y el conjunto de bienes al menos tan preferibles como otro dado, es un conjunto convexo. Para simplificar y continuando con dos bienes, la notación funcional de la utilidad puede ser:
$$ U={f(x}_1\ast x_2)\tag{1.1}$$Si se fija la utilidad en un nivel arbitrario, el consumidor puede obtener ese nivel de utilidad con diferentes combinaciones de cantidades de bien $x_1$ y bien $x_2$. Para el nivel particular de utilidad (utilidad constante) $U_0$, la función anterior se convierte en:
$$ U_0={f(x}_1\ast x_2) \tag{1.1.1}$$Y se le denomina ecuación de la curva de indiferencia.
La curva de indiferencia consiste en distintas combinaciones de cantidades de bienes (de $x_1$ y $x_2$) que ofrecen al consumidor el mismo grado de satisfacción o utilidad. La pendiente de la curva de indiferencia nos da la tasa a la que el consumidor estaría dispuesto a cambiar, por ejemplo unidades del bien $x_2$, por unidades adicionales del bien $x_1$; es una tasa de sustitución entre bienes y se le conoce como relación marginal de sustitución, RMS.
Aunque el consumidor esté en capacidad de ordenar sus preferencias, esto no indica que tenga capacidad de adquisición. La posibilidad de adquirir un bien o una cesta de bienes está determinada por la renta de que disponga y los precios de mercado de los distintos bienes o cestas de bienes. Esta renta disponible es limitada, por lo que el comportamiento racional del consumidor es lograr la máxima utilidad posible al realizar la elección de consumo con sus recursos limitados, escasos.
La renta disponible para adquirir bienes limita entonces el conjunto de bienes que se puede adquirir, es por ello una restricción de presupuesto.
Si identificamos como:
Renta disponible: $R_d$
Precio del bien $x_1:p_1$
Precio del bien $x_2: p_2$
La restricción presupuestaria del consumidor estará dada por la ecuación siguiente:
$$R_d=p_1x_1+p_2x_2 \tag{1.2} $$En esta ecuación (1.2), si despejamos $x_2$ , es equivalente a:
Si en (1.3) el consumo del bien $x_1$ es cero, la cantidad máxima posible de adquirir del bien 2 con la renta disponible es $x_2=\frac{R_d}{p_2}$. Y viceversa, para el bien uno, la cantidad máxima posible a adquirir con consumo cero del bien dos es de $x_1=\frac{R_d}{p_1}$.
La derivada de la ecuación (1.3) con respecto a $x_1$ es la pendiente de la restricción presupuestal. Ver (1.4)
$$\frac{\partial x_2}{\partial x_1}=-\frac{p_1}{p_2} \tag{1.4}$$Dicha pendiente tiene la interpretación de costos de oportunidad, en este caso de una unidad del bien $x_1$ en términos del bien $x_2$. Por ejemplo, si el consumidor decide aumentar el consumo del bien $x_1$ en una unidad se reduce el consumo del bien $x_2$ en una razón de $\frac{p_1}{p_2}$; o también, el costo de decidir adquirir una unidad adicional del bien $x_1$ está representado en el sacrificio de reducir el consumo del bien $x_2$ en una cantidad equivalente a la relación de los precios. El costo de oportunidad es el valor de la opción dejada al decidir hacer el uso alternativo de la renta disponible; en este caso es el costo que representa dejar de consumir cantidad del bien $x_2$.
Con base en la ecuación (1.4), la reducción en el consumo de $x_2$ es de:
$$\partial x_2=-\frac{p_1}{p_2}\partial x_1 \tag{1.5} $$Hasta aquí el consumidor ha logrado establecer su orden de preferencias así como las posibilidades de consumo desde su restricción presupuestaria.
Preguntemos ahora ¿cómo realiza la elección de las cantidades de los bienes a consumir? Para ello, dada la situación de recursos escasos representada en la renta disponible limitada para satisfacer sus necesidades, se postula, como agente racional, que la asignación de los recursos en la adquisición de los bienes de consumo es aquella que ofrezca la máxima utilidad. La decisión de consumo es por lo tanto óptima.
El problema del consumidor es, en consecuencia, el de maximizar la utilidad condicionada a la renta disponible, a la restricción presupuestal, que representamos de la siguiente manera:
$$Maximizar\ U={(x}_1\ast x_2)\ \ $$ $$Sujeto\ a\ R_d=p_1x_1+p_2x_2$$ $$x1≥0; x2≥0$$Para la solución aplicamos el método del multiplicador de Lagrange. El procedimiento es el siguiente:
Paso 1. Construir la función lagrangiana. Ésta es:
$$L\left(x_1,x_2,\ \lambda\right)={(x}_1\ast x_2)\ +\ \lambda(R_d-p_1x_1-p_2x_2) (1.6) $$Paso 2. Tomar las derivadas parciales de $L$ con respecto a $x_1$, $x_2$, $\ \lambda$, e igualarlas a cero. Ellas son:
$$\frac{\partial L}{\partial x_1}=\frac{\partial(x_1\ast x_2)}{\partial x_1}-\frac{\ \partial\lambda(R_d-p_1x_1-p_2x_2)}{\partial x_1} $$ $$\frac{\partial L}{\partial x_1}=x_2-\lambda p_1=0 \tag{1.7} $$Las ecuaciones (1.7) a (1.9) son las condiciones de primer orden para el máximo de la función de utilidad. Dividiendo (1.7) entre (1.8), tenemos:
$$\frac{\frac{\partial(x_1\ast x_2)}{\partial x_1}}{\frac{\partial(x_1\ast x_2)}{\partial x_2}}=\frac{x_2}{x_1}=\frac{\lambda p_1}{\lambda p_2} $$En la ecuación anterior, a la expresión total de la izquierda se le denomina relación marginal de sustitución (RMS) que simplificada queda como:
$$\frac{{\partial x}_2}{\partial x_1}=\frac{\lambda p_1}{\lambda p_2}=\frac{p_1}{p_2}$$Esto es:
$$RMS=\frac{{\partial x}_2}{\partial x_1}=\frac{p_1}{p_2} \tag{1.10}$$Por lo tanto, son dos condiciones de primer orden para el máximo. Primera condición, que la relación marginal de sustitución sea igual a la relación de los precios, esto es, que la pendiente de la curva de indiferencia sea igual a la pendiente de la restricción presupuestal, al costo de oportunidad (ecuación 1.10). La segunda condición es que la combinación de bienes elegida como óptima pertenezca a la restricción presupuestal (ecuación 1.9).
Paso 3. Hallar las demandas de bienes. Resolviendo el sistema de tres ecuaciones, de (1.7) a (1.9), obtenemos las funciones de demandas de los bienes $x_1$ y $x_2$.
De (1.10), tenemos:
$$x_2=\frac{p_1}{p_2}x_1 \tag{1.11} $$Reemplazando (1.11) en (1.9), tenemos:
$$R_d-p_1x_1-p_2\frac{p_1}{p_2}x_1=0 $$ $$R_d-p_1x_1-p_1x_1=0 $$Si identificamos la cantidad óptima del bien uno como $x_1^\ast$, entonces la función de demanda ordinaria del consumidor para el bien $x_1^\ast\ $ está dada por:
$$x_1^\ast=\frac{R_d}{2p_1} \tag{1.12} $$Con el mismo procedimiento, la función de demanda para el bien dos, $x_2^\ast$ ,es:
Estas funciones de demanda, conocidas frecuentemente como demandas marshallianas, surgen del supuesto de comportamiento racional del consumidor. Esta conducta enfrenta en el consumidor su orden de preferencias, que se basa en la valoración subjetiva, en su juicio sobre la relación del bien con la satisfacción de sus necesidades, y los recursos escasos para adquirirlas, disponibilidad de recursos representada por la restricción de presupuesto. El resultado es adquirir el conjunto de bienes que ofrezca la mayor satisfacción posible. Así entonces, el punto óptimo de consumo, en función de la renta $R_d$ y de los precios vigentes $p_1$, $p_2$, es ($x_1^\ast,x_2^\ast$).
Veamos un ejemplo numérico. Supongamos que $R_d=1,000$ , $p_1=4$ y $p_2=10$. Las demandas de bienes son:
$$x_1^\ast=\frac{1,000}{2\ast4}=125$$ $$x_2^\ast=\frac{1,000}{2\ast10}=50$$Observemos si la combinación de consumo elegida pertenece a la restricción presupuestal (segunda condición para un máximo).
$$R_d-p_1x_1-p_2x_2=0$$ $$1,000-4\ast125-10\ast50=0$$Con el consumo de ambos bienes se agota el presupuesto. El punto óptimo pertenece a la línea de presupuesto. En esta condición, el costo de oportunidad, ver ecuación (1.4), es la relación de los precios dada por:
Significa que el precio del bien uno es el 40% del bien dos. Igualmente, si se desea adquirir una unidad adicional del bien uno, debemos sacrificar el consumo de 0.4 unidades del bien dos. O viceversa, si se desea consumir una unidad adicional del bien 2, debemos sacrificar el consumo de 2.5 unidades del bien uno. Es esta la relación que los economistas denominan el costo de oportunidad, en esta ocasión identificado como el sacrificio que se hace en el consumo de un bien para adquirir una unidad adicional del otro bien. Este concepto es utilizado además en la toma de decisiones financieras, como veremos más adelante en este capítulo.
La utilidad ordinal es, por lo tanto:
$$\ U=x_1\ast x_2\ \ $$ $$\ U=125\ast50\ \ $$ $$U=6,250\ \ $$Si hacemos que el nivel ordinal de utilidad sea fijo, y despejamos, por ejemplo $x_2$, tenemos la ecuación de una curva de indiferencia, así:
$$x_2=\frac{6,250}{x_1}$$Tomando la derivada de $x_2$ respecto a $x_1$, esta queda como:
$$\frac{\partial x_2}{\partial x_1}=-\frac{6,250}{x_1^2}$$Esta ecuación es la pendiente negativa de la curva de indiferencia y nos da la relación de sustitución entre los dos bienes; determina en cuánto cambia $x_2$ si cambia $x_1$ infinitesimal (por ejemplo, en una unidad). Esto es:
$$\partial x_2=-\frac{6,250}{x_1^2}\partial x_1$$Desde el equilibrio, con $x_1=125$, si la cantidad adquirida de este bien cambia a 126, es decir se incrementa la adquisición en una unidad ($\partial x_1=1$), el cambio en $x_2$ es de: $$\partial x_2=-\frac{6,250}{{125}^2}\ast1=-0.4$$
Se cumple entonces la primera condición necesaria para un máximo restringido en la que la relación de sustitución es igual a la relación de los precios, en el ejercicio de -0.40.
En términos técnicos, esta condición plantea que la pendiente de la curva de indiferencia es igual a la pendiente de la línea de restricción presupuestal.
Este modelo básico de conducta se extiende al estudio del comportamiento del productor o empresario (a la empresa o la organización), cuyo accionar racional (maximiza el beneficio), determina la función de oferta del mercado.
Es la interacción entre la oferta y la demanda, esto es, las acciones recíprocas del productor y el consumidor (y en estas acciones están implícitas sus perspectivas de valor) lo que determina el precio de equilibrio de mercado (precio que es diferente al concepto de valor), con el que éste se vacía.
El modelo se extiende además a representaciones de decisiones intertemporales en las que intervienen el consumo y el ahorro (la inversión), es además base en el desarrollo de modelos de optimización bajo condiciones de incertidumbre y de riesgo (como en el caso de la maximización de la utilidad esperada en inversiones), así como en la valoración de activos financieros, todos modelos propios de la economía financiera (Marín & Rubio, 2011), como ya se ha indicado.
En el desarrollo actual de la economía financiera, dado el progreso de la disciplina, el modelo descrito ha evolucionado hacia matizaciones del supuesto de racionalidad, en el que las emociones, el comportamiento respecto al miedo, la aversión al riesgo, juegan un papel básico en la asignación de recursos escasos, en la toma de decisiones de los agentes económicos. Son modelos que, desarrollados desde la economía experimental, la psicología económica, o las finanzas conductuales, han dado lugar a propuestas teóricas alternativas de toma de decisiones en condiciones no racionales. Un ejemplo es el desarrollo de la hipótesis de mercados adaptativos, por Andrew W. Lo (2018), como opción a la teoría de los mercados eficientes, así como la teoría de la racionalidad limitada ( o acotada) que hace presencia en los agentes económicos (limitaciones cognitivas de la mente humana).
En síntesis, la valorización es la acción y el efecto de valorar, de asignar valor. La acción la ejecuta un tasador, por ejemplo, un agente económico que estima sobre la base de sus preferencias, de los recursos disponibles y del conocimiento del mercado, entre otras variables a considerar en el proceso, el valor de un activo. El efecto es la estimación y la asignación de valor a un bien o activo. Por ejemplo, se asigna valor cuando se responde a la pregunta sobre el valor de una casa, de un terreno, de un producto; dicho valor es expresado en términos de alguna unidad monetaria, como en dólares o pesos, por ejemplo.
En la valoración se consideran múltiples criterios, de naturaleza subjetiva y objetiva, entre ellos los precios, los recursos disponibles, así como la incertidumbre y el riesgo. Sin embargo la valoración que realiza el agente económico (el tasador) de un activo no es el precio del mercado. Para la determinación del precio de mercado, deben confluir los agentes económicos que desde su accionar e interés individual crean la oferta y la demanda, es decir, un comprador y un vendedor, cada uno con su propia tasación. Es la interacción de la oferta y la demanda, la acción recíproca de estas dos fuerzas, la que determina el precio de mercado.
Empero, ambas cotizaciones, el valor y el precio de mercado, se expresan en una cierta cantidad de unidades monetarias específicas.
El dinero es aquel bien, cosa o convención social que facilita la realización del intercambio de bienes y servicios. Para J.K. Galbraith (1983), el dinero es lo que se da o se recibe generalmente por la compra o la venta de artículos, servicios u otras cosas. Para Carl Menger, el dinero es el producto natural, de las distintas situaciones económicas de los pueblos, o, dentro de unos mismos pueblos, de distintos períodos de su historia (Menger, 2017).
La definición de Menger es clara dentro de su concepción del dinero como resultado orgánico del desarrollo de los pueblos. El surgimiento del dinero se da ante las dificultades e ineficiencia que implicaba el intercambio por medio del trueque, en un estadio social en la que hace presencia la propiedad privada de los medios y del resultado de la producción de mercancías, con una mayor división del trabajo y la más amplia diversidad de bienes producidos. Estos avances en la civilización, posibilitaron que por la costumbre diferentes mercancías fueran asumiendo el papel de un medio que facilitaba el intercambio.
En la historia de la humanidad son diferentes las mercancías que han asumido el papel de dinero, entre ellas, el ganado (vacuno, caballar), el cobre, la plata, el oro. Dadas las cambiantes condiciones sociales, en un momento posterior nace la acuñación de monedas de metales nobles, se desarrolla posteriormente el papel moneda respaldado en oro, llegando en la actualidad al dinero fiduciario, que es moneda de curso legal emitido por el estado pero sin respaldo en plata u oro. Ya en el siglo XXI hace presencia el fenómeno de las criptomonedas como posible forma futura que adopte el dinero, siendo creada la primera entre los años 2008-2009 bajo la denominación de Bitcoin. Para que sea dinero, cualquiera sea la forma que adopte éste, debe contar con el uso general, ser aceptado por todos, y mediar en todas las transacciones de todos los bienes (Menger, 2013).
Modernamente se ha definido al dinero como un activo, o bien económico, que cumple tres funciones básicas en la economía: las de medio de pago, unidad de cuenta y reserva de valor.
En su función de medio de pago, el dinero es un instrumento general de pago, que facilita de manera ágil y eficiente la realización de las transacciones comerciales, dada la aceptación general y la confianza del público en él. Como medio general de pago, el dinero resuelve las dificultades del trueque y se constituye en un medio cómodo para realizar las compras y las ventas de bienes y servicios.
En su función de unidad de cuenta, el dinero es una unidad de medida del valor, esto es, unidad empleada en la expresión de los valores, y los precios, de los diferentes bienes y servicios. En unidades de dinero expresamos los costos de producción y el precio de venta de todos los diferentes bienes y servicios, se realizan las cotizaciones de las diferentes monedas extranjeras, se expresan además los salarios de empleados públicos y privados, los rendimientos de una inversión, el valor de un activo financiero y su precio de mercado, etc.
Como unidad de cuenta, el dinero es por lo tanto un patrón común, con aceptación general, con el que se miden los valores o precios de los bienes y servicios en una economía
Como reserva de valor, el dinero es un depósito de valor, conserva valor que se puede utilizar para realizar futuras transacciones comerciales y financieras (como el pago de deudas, recibir rendimientos financieros de inversiones, entre otros); dicho valor se expresa en su poder adquisitivo o de compra. Sin embargo, la reserva de valor cambia con la modificación de los precios o valores de los bienes y servicios; el valor del dinero, representado en su poder adquisitivo, cambia de forma inversa con respecto a los precios de los bienes y servicios. Si el precio de una mercancía sube, una misma unidad monetaria comprará una cantidad menor de ésta, implicando un deterioro del poder adquisitivo.
Desde el punto de vista empírico, existen varias definiciones de los activos que harían parte de la definición de dinero. Por ejemplo, se considera dinero al efectivo en manos del público en forma de monedas y billetes (dicho agregado se identifica con la letra E), y los depósitos a la vista que son las cuentas corrientes o cuentas manejadas por medio de cheques, así como las cuentas manejadas por medio de tarjeta débito (el agregado se representa por la letra D); la suma de estos dos agregados monetarios es la oferta monetaria señalada como $M_1$. En consecuencia, bajo esta aproximación, la oferta monetaria es:
$$M_1=E+D \tag{1.14}$$Este agregado cubre aquellos activos con naturaleza líquida (billetes y monedas) y aquellos con mayor grado de liquidez (cheques y cuenta débito).
Desde aproximadamente los años sesenta del siglo pasado, se observa un progresivo aumento de la actividad financiera, de los flujos financieros, y el dinero cediendo el papel de medio de intercambio para intercambiarse el mismo por medio de diferentes formas de dinero con el fin de obtener ganancias, en su uso especulativo.
Al fenómeno de crecimiento de la actividad financiera a nivel nacional e internacional, profundizada especialmente desde los años setenta y ochenta del siglo pasado, proceso que ha dado lugar al crecimiento acelerado de los productos y mercados financieros, a la circulación de nuevas formas de dinero como títulos (acciones, obligaciones), divisas, entre otros, con un arsenal de posibilidades de inversiones financieras dadas por el poder del dinero de financiación, se le conoce como financierización (Torres López, 2002).
Según Torres López, este fenómeno se caracteriza por el gigantesco y desproporcionado desarrollo de los flujos financieros, la creación de espacio privilegiado para el beneficio en la circulación monetaria, y un nuevo poder monetario fuera del poder del Estado (2002).
La financierización, es la generalización del dinero creando dinero, desde el poder de financiación de éste, en la realización de una amplia posibilidad de inversiones financieras, con fines especulativos y de obtención de ganancias, actividad profundizada por el desarrollo tecnológico (inteligencia artificial, tecnologías de la cuarta revolución industrial); fenómeno en el que la circulación monetaria por estos motivos ha superado con creces la circulación monetaria por motivo de transacciones, producto de las necesidades de la economía real, del dinero como instrumento que facilita los intercambios.
Ya hemos indicado que el dinero como reserva de valor, es poseedor de valor en cuanto representa un poder de compra. Este poder adquisitivo del dinero no es constante en las economías de los diferentes países, sino cambiante con el tiempo debido a las variaciones de los precios de los bienes y servicios, a los cuales les sirve como unidad de cuenta.
Si una mercancía cualquiera tiene como precio el equivalente a 100 pesos, significa lo anterior que un peso tiene la capacidad de compra de 0.01 partes de esa mercancía; ahora bien, si por alguna circunstancia el precio de la mercancía cambia a 200 pesos, en este caso un peso solo adquiere 0.005 partes de dicho bien y ha visto deteriorado su poder de compra en un 50%.
En caso contrario, si el precio disminuye, por ejemplo a 50, el dinero ve aumentado su poder adquisitivo a 0.02. Lo más típico o frecuente en las economías nacionales es el aumento del nivel general de los precios en el tiempo, implicando deterioro de poder de compra del dinero, del valor del dinero. El aumento en el nivel general de los precios de los bienes y servicios provoca cambio en el valor de la moneda, en su capacidad de compra.
Es posible pensar que este cambio en el valor de la moneda sea la razón para que un agente económico prefiera una suma de dinero hoy, por ejemplo 500,000 pesos, a recibir esa misma cantidad en una fecha futura, por ejemplo dentro de un año. Ante la posibilidad de ocurrencia de un aumento de los precios.
La reflexión del agente económico lo llevaría a identificar el posible deterioro del poder de compra del dinero y, en consecuencia, al establecer en el ordenamiento de sus preferencias, ubicar en primer lugar disponer de la cantidad de dinero hoy y no dentro de un año.
Sin embargo ¿qué ocurre con este orden de preferencia si la posibilidad de inflación es cero?, es decir, si no hay deterioro de la capacidad de compra del dinero, la reserva de valor mantiene el poder adquisitivo constante dada la variación cero en el nivel general de los precios.
Esta pregunta nos conduce al sentido en que la teoría financiera utiliza la expresión valor del dinero en el tiempo. Bajo la premisa de mantenerse constante el poder adquisitivo del dinero, en el orden de preferencias de cualquier agente económico seguirá en primer lugar
el disponer de los 500,000 pesos hoy y no dentro de un año. La razón está en la posibilidad de invertir esos recursos hoy para dentro de un año tener una cantidad mayor al monto inicialmente invertido, representado por los rendimientos de la inversión.
Por lo tanto, aún con inflación cero, es decir con el dinero manteniendo su poder adquisitivo constante, las personas prefieren una suma de dinero hoy a tener esa misma cantidad en el futuro, debido a que hoy tiene un mayor valor porque se puede invertir y ganar intereses, logrando así en el futuro una cantidad de dinero mayor a la inicial.
Es por estas razones que dos sumas iguales de dinero, ubicadas en distintos instantes en el tiempo, no representan igual valor económico; no son equivalentes en el orden de preferencias de los agentes económicos. No son equivalentes por el cambio en el valor de la moneda debido al deterioro del poder adquisitivo y porque el agente económico tiene la preferencia por el dinero hoy ante la posibilidad de inversión.
El concepto de valor del dinero en el tiempo utilizado en la teoría financiera se fundamenta en este orden de preferencias, en la de preferir invertir y obtener intereses.
La decisión de inversión es una acción que se ejecuta en el tiempo, y su propósito es obtener rendimientos, ganancias o , en general, intereses. Si hoy invertimos una suma de dinero, suma que podemos llamar capital financiero, es por la expectativa de tener más dinero en el futuro.
Es esa suma adicional de dinero que se obtiene de las inversiones, lo que se denomina valor del dinero en el tiempo en la teoría financiera; es la variación en la cantidad de dinero que ocurre en un período de tiempo dado.
Si se hace hoy una inversión de 1,000,000 de pesos y al cabo de un año se recibe la suma de 1,080,000, la variación en la cantidad de dinero en este tiempo específico es de 80,000 pesos y es el valor del dinero en el tiempo de esta inversión.
¿Por qué la inversión requiere de esa suma adicional de dinero? ¿Qué justifica el valor del dinero en el tiempo? Son varias las razones que justifican la existencia de esa suma de dinero adicional en un período de tiempo dado, razones que pasamos a considerar.
En primer lugar, la suma de dinero que se destina a la inversión, denominado capital financiero, en el tiempo ve afectado su poder adquisitivo ante la presencia de la inflación, que no es más que el aumento general y sostenido en el nivel de los precios. Al realizarse una inversión, el agente económico procura que la suma adicional obtenida en el tiempo de la inversión esté por encima de la inflación.
Es decir, un elemento que guía su acción es que, con la inversión, el valor del dinero en el tiempo no sólo cubra la pérdida del poder adquisitivo derivada de la inflación, sino que rinda un valor adicional, por encima de ésta.
Veamos el asunto con un ejemplo. Supongamos que contamos con 10,000,000 de pesos y podemos comparar al inicio del año una motocicleta que tiene ese valor. Resulta que decidimos destinar esos recursos a una inversión, que al cabo de un año se liquidó en la suma de 11,000,000.
En este caso, la variación de la cantidad de dinero en el plazo de un año es de 1,000,000 y es el monto del valor del dinero en el tiempo que podemos denominar rendimientos de la inversión. Una vez liquidada la inversión, supongamos que nos dirigimos al concesionario para comprar la moto, planteando tres escenarios.Dado que el dinero pierde poder adquisitivo en presencia de la inflación, en las inversiones se busca que sus resultados compensen por encima a ésta y genere un crecimiento real del capital y, en general, de la riqueza.
Como guía del agente inversor, es el propósito de alcanzar que el porcentaje representante del valor del dinero en el tiempo sea mayor al porcentaje de la inflación.
En nuestro país, es el Departamento Administrativo Nacional de Estadísticas (DANE), el responsable de realizar la medición de la inflación mensual y acumulada anual.
Para ello utiliza una metodología de índices de precios y calcula, por ejemplo, el Índice de Precios al Consumidor (IPC). Si la inflación la representamos por $\pi$, esta se calcula como:
$$\pi=\frac{{IPC}_n-{IPC}_{n-1}}{{IPC}_{n-1}}>0 \tag{1.15}$$ $$ \pi=\frac{{IPC}_n}{{IPC}_{n-1}}-1>0$$Por lo tanto:
$$ \frac{{IPC}_n}{{IPC}_{n-1}}=(\pi+1) \tag{1.16}$$Veamos un ejemplo. En el mes de agosto de 2022 el IPC se determinó en 121.50, ya para septiembre del mismo año, éste se ubicó en 122.63, según datos reportados por el DANE. Con estos datos la variación porcentual del IPC de septiembre de 2022 fue de:
$$\pi=\frac{122.63}{121.5}-1=0.0093>0$$En términos porcentuales, en septiembre de 2022 la inflación de Colombia medida por el Índice de Precios al Consumidor fue de 0.93%.
Para que las inversiones aporten crecimiento real del capital, la variación porcentual de la cantidad dinero (var), debe ser mayor a la inflación, es decir: $var>\pi$. En caso de $var=\pi$, los resultados de la inversión mantienen el poder adquisitivo del dinero constante, el capital es constante en términos de poder de compra; y si el resultado es $var<\pi$ la inversión no ha compensado la pérdida de poder adquisitivo del dinero debido a la inflación, ocasionando un deterioro real del capital.
Una segunda variable por considerar en la justificación del monto por valor del dinero en el tiempo, es el costo de oportunidad.
Ya hemos indicado su definición en términos de la restricción presupuestal del agente económico que maximiza la utilidad en la decisión de consumo. Este modelo lo podemos extender a la decisión de asignación óptima de los recursos escasos entre gasto en consumo presente o ahorro (inversión).
En este contexto teórico, el ahorro significa sacrificio de consumo presente, con la esperanza de un consumo mayor en el futuro derivado del valor del dinero en el tiempo que logre como compensación al esfuerzo de ahorrar, por hacer el sacrificio de menor gasto en consumo.
El dejar de consumir bienes implica al agente consumidor un costo representado en el valor de la satisfacción (utilidad) que dejada de percibir, valor que constituye su costo de oportunidad, y es lo que por lo menos debe compensarse para que se justifique realizar el esfuerzo del ahorro.
En otros términos, el agente económico espera que la inversión de los ahorros como mínimo genere un valor del dinero en el tiempo (rendimientos) igual al valor del sacrificio por no usar el dinero en las asignaciones alternativas; el monto del valor del dinero en el tiempo debe ser suficientemente atractivo en términos financieros para que los recursos escasos se faciliten a la inversión.
Supongamos que el poseedor de un capital de 10,000,000 de pesos tiene un costo de oportunidad (CO) del 10% anual. Recibe tres propuestas con el fin de que lo ceda en préstamo.
Una primera propuesta es pagarle un 8.5% anual por el capital, la segunda del 10% anual y la última del 12%. El análisis es comparar estas ofertas con el respectivo costo de oportunidad.
La primera oferta la rechaza porque ésta al menos no es igual a sus costos de oportunidad y prefiere mantener el capital en su uso alternativo, la segunda oferta le es indiferente dado que ofrece el mismo nivel de valor que el costo de oportunidad, la tercera opción es preferible porque la oferta de compensación es mayor al costo de oportunidad. El agente racional toma como decisión destinar los recursos de capital a la tercera oferta, cederlo en préstamo.La razón de la decisión es que el valor del dinero en el tiempo ofrecido es mayor a su costo de oportunidad, esto es: $var>CO$.
Una tercera variable por considerar es la incertidumbre y el riesgo (IR). No está en las capacidades y habilidades humanas conocer con certeza qué va a suceder el día de mañana, de tener conocimiento preciso sobre las condiciones económicas y sociales futuras en un país y región. Sobre el futuro sabemos que es incierto.
Existe diferencia entre tomar decisiones en condiciones de incertidumbre y tomar decisiones en condiciones de riesgo.
La diferencia está en poder conocer o determinar la probabilidad de ocurrencia de un evento, de conocer su distribución de probabilidades. Según Sullivan, Wicks y Luxhoj (2004), las decisiones bajo riesgo son aquellas en la que se modela la toma de decisiones en
términos de escenarios posibles que se aceptan y la probabilidad de ocurrencia puede calcularse; en cambio la toma de decisiones bajo incertidumbre se da bajo varios futuros desconocidos para los cuales no puede calcularse la probabilidad de ocurrencia. Para el análisis y de toma de decisiones en condiciones de incertidumbre, existe técnicas no probabilísticas
Un riesgo muy común es el crediticio. Suponga que usted le presta una determinada cantidad de dinero a un amigo ¿Qué seguridad tiene en el reintegro del dinero con su respectivo incremento? ¿hay posibilidad de que no le pague?
En realidad, se presenta una probabilidad de pérdida en la inversión debido al incumplimiento en el pago, hay por lo tanto un riesgo.
Existen agentes económicos conservadores con respecto al riesgo y prefieren las inversiones más seguras, en condiciones de certeza.
En cambio, hay otros agentes con mayor preferencia al riesgo, con carácter osado o amantes del azar como son los especuladores, y ello se explica por el mayor valor del dinero en el tiempo que pueden obtener en las inversiones. Lo anterior porque existe una relación positiva entre riesgo y rendimiento de la inversión: a mayor riesgo mayor es la rentabilidad esperada de la inversión (así también el fracaso ante la no ocurrencia de lo esperado).
Así entonces, por la capacidad de asumir riesgos, los agentes económicos requieren de una compensación (una prima de riesgo), una suma de dinero adicional al inicialmente invertido, compensación que es mayor mientras mayor es el riesgo asumido. El riesgo hace parte de la justificación de la existencia del valor del dinero en el tiempo.
Por último, debemos considerar que el dinero es un activo, es un bien económico (BE). Ceder en calidad de préstamo una determinada suma de dinero, es igual a desprenderse de un activo (un apartamento, un carro, una finca) y permitir el disfrute de éste por otra persona, de acceder a los beneficios que su utilización genera. Es por las posibilidades que genera el activo en préstamo lo que motiva el cobro de un valor adicional. En el caso de un apartamento se cobra un arriendo; por el dinero se cobra una suma adicional en el tiempo en que se ha facilitado.
¿Qué posibilidades genera el dinero? En general todas aquellas derivadas de su capacidad de financiación. Los agentes económicos buscan acceder al dinero para financiar gastos en consumo e inversión. Y por ello pagan un precio, un alquiler, que denominamos valor del dinero en el tiempo.
En el caso de consumo, se accede a financiación de corto plazo vía tarjetas de crédito, por ejemplo.
En el caso de la inversión, se accede a financiación para la ejecución de proyectos productivos, obras civiles e incluso, para la actividad especulativa con activos financieros, inversiones éstas que a su vez se dirigen a generar rendimientos. Se accede por diferentes vías y diferentes activos (como son los créditos bancarios, los bonos, las acciones, los aportes de socios, etc.). Estos recursos no son gratuitos sino que tienen un costo para el que los recibe en calidad de préstamo; por ello hay que pagar un precio llamado valor del dinero en el tiempo.
Por lo tanto, el valor del dinero en el tiempo (VDT), es una suma adicional de dinero que se genera como contraprestaciones derivadas de la inflación, el costo de oportunidad, el riesgo y la incertidumbre, y por el dinero ser un activo o bien económico.
En términos de notación tenemos que:
$$VDT=f(\pi,\ CO,IR,BE) $$La expresión cuantitativa del valor del dinero en el tiempo se denomina, en general, intereses ($I$), y a su expresión porcentual respecto a un monto de dinero inicial, tasa de interés ($i$).
Si se toma en préstamo un capital ($P$) de 10,000,000 de pesos y genera el pago al final de un año un monto total ($F$) de 11,000,000 de pesos, los intereses equivalen a 1,000,000 de pesos y son la expresión cuantitativa del valor del dinero en el tiempo. Es decir:
$$I=F-P$$ $$I=11,000,000-10,000,000=1,000,000$$A la razón matemática de los intereses con respecto al capital inicial, se le conoce como tasa de interés. Dicha razón puede expresarse en decimales o en porcentaje. Esto es:
$$i=\frac{1,000,000}{10,000,000}=0.10$$$i$%=$0.10\ast100$%=$10$%
La tasa de interés es el cociente o resultado que se obtiene al dividir los intereses con respecto al capital inicial. Es lo que hemos denominado más arriba variación porcentual de la cantidad de dinero (var% ).
En el caso de hacer una inversión, para la expresión cuantitativa del valor del dinero en el tiempo se utiliza la palabra rendimiento que, en término porcentual, se le denomina tasa de rendimiento.
En este libro nos referiremos en general a intereses.
Para efectos de cuantificar los resultados de las inversiones y los créditos, y desarrollar modelos básicos de la valoración del dinero en el tiempo, definimos los siguientes símbolos:
$P$: Representa a una suma de dinero que denominamos capital inicial, principal, valor actual o valor presente.
$I$: Es un monto de dinero que expresa el valor del dinero en el tiempo; son los intereses de un préstamo o los rendimientos de una inversión.
$F$: Es una suma de dinero al final de un plazo, es un monto único, o valor futuro. Este es igual al capital más los intereses, esto es: $F=P+I$.
$n$: Es el tiempo o plazo en el que se realiza la operación financiera, generalmente dado en años.
$i$%: Es la tasa de interés que siempre está acompañada de una unidad de tiempo, como el mes, el semestre, el año, unidad que recibe el nombre de período de interés.
Con el desarrollo de los próximos capítulos iremos agregando nuevas representaciones de variables y su significado.
En términos de poder adquisitivo, el valor del dinero cambia a través del tiempo, siendo típico el deterioro motivado por la inflación.
En la época actual es fácil captar este fenómeno sólo observando los altos precios de los alimentos, los combustibles y las divisas como el dólar, por citar sólo unos casos, que vive las economías nacionales y la economía mundial en condiciones de postpandemia.
Esta situación se resume en la expresión de que un millón de pesos colombiano de hoy no tiene el mismo valor de un millón de pesos dentro de un año. Por esta razón se prefiere esa suma de dinero hoy que dentro de un año.
Como ya hemos indicado, existen otras razones para la justificación de una compensación como valor del dinero en el tiempo, expresados en una suma adicional de dinero denominado en general intereses y expresado porcentualmente como tasa de interés.
La pregunta ahora es ¿de cuánto es esa suma adicional de dinero?, esto es, ¿de cuánto es la compensación?
En la práctica de las operaciones financieras de inversión y financiación, los agentes involucrados se ponen de acuerdo sobre el plazo (el tiempo) y la tasa de rendimiento o de interés que se espera como compensación por los recursos implicados en la operación. La compensación se acuerda en términos porcentuales al concretarse o pactarse la tasa de interés.
Son el tiempo o plazo de la operación financiera y la tasa de interés acordada en ésta como compensación, las variables que determinan el concepto de equivalencia financiera, un acuerdo que es relativo a las partes involucradas.
En este libro equivalencia económica (financiera) significa que dos cantidades distintas de dinero en distintos momentos en el tiempo, representan para las partes igual valor económico. Esta igualdad de valor surge del acuerdo sobre el monto de la compensación del valor del dinero en un determinado plazo.
Veamos un caso sencillo:
Si las partes en la contratación de un crédito por 5,000,000 de pesos acuerdan como plazo un año y liquidarlo con una tasa de interés del 12% anual, se acuerda implícitamente como compensación la suma de 600,000 pesos ($I=5,000,000*0.12$). Al final del año se hace un pago con valor de 5,600,000 pesos.
Para las partes involucradas significa que los 5,000,000 de pesos iniciales equivalen a 5,600,000 pesos dentro de un año, si la tasa de interés es del 12% anual. Estas dos cantidades distintas de dinero, ubicadas en distintos momentos en el tiempo, tienen igual valor económico para las partes. Desde el punto de vista de las preferencias, estas dos sumas de dinero son equivalentes porque a las partes les resulta indiferente los 5,000,000 de pesos hoy o recibir 5,600,000 dentro de un año.
Los modelos o fórmulas que vamos a estudiar desde el próximo capítulo de este libro, consideran el valor del dinero en el tiempo y permiten calcular valores equivalentes para las partes involucradas en la transacción financiera. Son fórmulas de equivalencia del valor del dinero en el tiempo; son modelos de valoración de un capital en los que, además de su monto inicial, intervienen como variables la tasa de interés y el tiempo.
Estos son representaciones gráficas de las transacciones financieras, que resultan de gran utilidad para plantear y resolver las diferentes situaciones de análisis y solución de problemas. Consiste en una recta horizontal que representa el tiempo, segmentada en unidades de medida de éste, como el mes, el trimestre, el semestre, el año. En el instante cero se representa el presente, y con un desplazamiento hacia la derecha en la línea de tiempo, un momento futuro. Con flechas hacia arriba se va a indicar la ocurrencia de un movimiento de efectivo en calidad de ingreso o entrada de efectivo.

Así mismo, con una flecha hacia abajo se representa movimiento de efectivo en calidad de egreso o de salida de efectivo. El diagrama se completa con el dato de la tasa de interés y la incógnita o valor a determinar. Ver Figura 1.3 para el ejemplo anterior.
1.1. ¿Qué significa los términos valor económico, valoración y valor del dinero en el tiempo?
1.2. ¿Qué son valor subjetivo y valor objetivo de los bienes económicos?
1.3. ¿Qué es y cómo se mide la inflación, los intereses y la tasa de interés?
1.4. ¿Qué es el dinero y qué funciones cumple en la economía de un país?
1.5. ¿Cuál es el significado de la expresión poder adquisitivo del dinero?
1.6. ¿Qué significa el término equivalencia? Dar un ejemplo que ilustre el concepto.
1.7. Si el costo de oportunidad de un inversionista especulador es el 5% anual y un amigo le ofrece por un préstamo el 5.5% al año ¿el inversionista es indiferente a esta propuesta? Justifique la respuesta.
1.8. Si la inflación anual de un país es de 10.5% y un inversionista obtiene como rendimiento el 12.95% en sus inversiones ¿Qué le ha sucedido al capital de esta persona? Argumente su respuesta.
1.9. Si un capital de 530,200 pesos genera rendimientos de 110,480 pesos en un año ¿Qué tasa de rendimiento se obtuvo? R. 20.84%.
1.10. Construya con sus propios términos lingüísticos el concepto de valor del dinero en el tiempo e indique la manera como la inflación, el costo de oportunidad, el riesgo y el dinero como activo, inciden en su magnitud.
1.11. Con 5,000 pesos se compraba hace un mes una docena de fresas. Hoy esa misma docena tiene un precio de 6,000 pesos ¿De cuánto es la inflación en las fresas?¿con los 5,000 pesos iniciales qué proporción de la docena de fresas puede adquirirse al nuevo precio? ¿de cuánto ha sido el deterioro del poder adquisitivo de los 5,000 pesos iniciales en términos de fresas? R. 20%; 83.33%; 16.67%, respectivamente.
1.12. En la siguiente tabla se presenta el IPC de la economía colombiana en diferentes meses del 2022, calculados por el DANE. Hallar la inflación o variación porcentual ocurrida en cada mes.
| Mes | IPC | Inflación |
|---|---|---|
| Abril | 117.71 | |
| Mayo | 118.70 | |
| Junio | 119.31 | |
| Julio | 120.27 | |
| Agostoo | 121.50 | |
| Septiembre | 122.63 |
Introducción
La ciencia económica realiza la distinción entre gasto en consumo y gasto en inversión.
El gasto en consumo hace referencia a la destinación de una suma de dinero para la adquisición, por parte de un individuo, de bienes y servicios dirigidos a la satisfacción de sus necesidades, sean estas de carácter alimenticias, de abrigo, de salud, de recreación o incluso generadas por condiciones culturales o sociales. En cambio, el gasto en inversión, que igualmente implica destinación de recursos monetarios para la adquisición de bienes, servicios o valores, por parte de un agente económico, tiene como propósito la recuperación aumentada de esos recursos monetarios empleados, recursos que podemos identificar como capital en forma de dinero o financiero; en el caso de la inversión, el fin es obtener un monto mayor al inicialmente invertido, incrementado por la generación de excedente que denominados rendimientos (ganancias, beneficios).
El propósito de toda inversión es la obtención de rendimientos.
En términos generales, las inversiones son de dos tipos. Una primera dimensión es la inversión productiva o real, entendida como aquella que se realiza en bienes y servicios de producción, como los edificios, la maquinaria, los equipos, las herramientas, las materias primas, los
vehículos, inventarios, terrenos, propiedad industrial, outsourcing, etc.; al realizarse la inversión productiva de los recursos monetarios, éstos se transforman en capital productivo (en capital físico y en intangibles), con el fin de generar alguna actividad económica que posibilite el retorno de la inversión.
La segunda dimensión es la inversión financiera, comprendida por aquellas que se realiza en activos financieros, de las que son ejemplos el depósito a término fijo, las acciones, los bonos de deuda pública y de deuda privada, los swaps, los contratos de futuros, los contratos a plazo, los contratos de opciones, los activos digitales (Bitcoin, por ejemplo), etc.; en este caso el capital en forma de dinero se transforma en un documento, en una promesa futura de pago, o en una cuenta virtual, que representa un valor.
En general, al realizar la inversión el capital en forma de dinero se transforma en capital productivo o en valores, con el propósito de obtener excedentes una vez retorne a su calidad de dinero al cabo de un tiempo.
Así entonces, el capital financiero es la suma de dinero que el actor económico no destina al consumo, sino que lo dirige a la inversión productiva y/o financiera con el propósito de generar rendimientos, esto es, obtener un monto final que permita recuperar el capital inicialmente invertido además de un excedente sobre este último.
La diferencia entre el monto final recuperado y la cantidad inicial dedicada a la inversión es la valoración que ha obtenido el capital, esto es, el excedente que identificamos como rendimiento o intereses (el valor del dinero en el tiempo).
Los recursos monetarios que constituyen el capital financiero pueden tener varios orígenes.
Ellos pueden estar constituidos por recursos internos, que son el capital propio del agente inversionista, por los recursos externos obtenidos de un prestamista y que constituyen el capital de deuda, o por una combinación de los dos anteriores.
Cuando el agente económico acude a la consecución de recursos externos para destinarlos a la inversión, decimos que ha realizado la operación de financiación denominada endeudamiento o crédito, obteniendo de esa manera un capital de deuda y debe cancelar al prestamista intereses sobre el monto tomado en préstamo en el tiempo pactado.
Una transacción u operación financiera se realiza bajo modalidad de interés simple cuando los rendimientos liquidados o computados en un periodo no se capitalizan (no se cargan o suman el capital) para el siguiente período de interés, por lo que estos rendimientos ya causados no generan nuevos intereses en el periodo siguiente.
Es decir, los intereses que se liquidan en períodos previos no entran en el cálculo de los intereses en períodos posteriores, por lo que el cálculo de éstos se realiza siempre sobre el capital financiero inicial, sobre el principal, implicando que no exista intereses sobre los intereses.
Una operación financiera a interés simple es la siguiente. Supongo que se toma un préstamo de $\$ 8,000,000$ al $12\%$ anual con un plazo de $6$ años a interés simple ¿Cuánto se debe al final de dicho plazo? Utilicemos este ejercicio para aplicar los símbolos, hacer el diagrama económico (o flujo de caja), deducir la fórmula de interés simple e identificar diferentes tipos de problemas.
Los símbolos involucrados son:
$P = 8,000,000$. Es el principal o monto tomado en préstamo.
$I$ = Representa el monto de los intereses o rendimientos de la operación financiera.
$i$%=$12$% anual, es la tasa de interés; el periodo de interés es el año.
$n = 6$ años. Es el tiempo o plazo de la operación financiera.
$F = ?$ Es el valor futuro o deuda acumulada al fin del plazo, constituido por el capital inicial y los intereses, esto es, $F=P+I$
En este ejemplo la tasa de interés $i$% y el plazo $n$, están dados en la misma unidad de tiempo, en este caso el año. Para el diagrama de caja, obsérvese la siguiente Figura 2.1. En la deducción de la fórmula de interés simple, recurrimos a la operación aritmética del tanto por ciento, que a su vez es una aplicación de la regla de tres simple directa, o proporción directa como recordará el lector. Veamos:
Si $\$8,000,000$ son el $100\%$, ¿Cuánto será el $12\%$? En este caso, al resolver la pregunta obtenemos los intereses del primer año, $I_1$.
$$\tag{2.1} \frac {\$ 8,000,000}{100\%} = \frac {I_1}{12\%} \space \space \space \Leftrightarrow \space \space \space \frac {100\%}{\$ 8,000,000} = \frac {12\%}{I_1} $$
Aplicando la propiedad de la proporción geométrica, tenemos:
$$I_1*100\% = \$8,000,000*12\%$$ $$I_1 = \$8,000,000*(12\%)/(100\%)$$ $$I_1= \$8,000,000*0.12 = \$960.000.00$$y son los intereses del primer año
Al cabo del primer año, el valor de la deuda $F = P + I$, corresponde a $F_1 = \$ 8,000,000 + \$ 960,000 = \$ 8,960,000.$
Para calcular los intereses del segundo año y el respectivo valor de la deuda, realizamos el mismo procedimiento.
$$ \frac {\$ 8,000,000}{100\%} = \frac {I_2}{12\%} \space \space \space \Leftrightarrow \space \space \space \frac {100\%}{\$ 8,000,000} = \frac {12\%}{I_2} $$La deuda al final del año dos es: $$F_2 = \$8,960,000 +\$960,000 = \$9,920,000$$
El proceso se repite para los demás años, de la siguiente manera:
Observamos entonces que los intereses totales, en los seis años, son iguales a:
$$I = \$960,000*6 = \$5.760.000$$El valor futuro de deuda al final del plazo de es:
$$F = P + I = \$8,000,000 + \$5,760,000 = \$13,760,000$$En la Figura 2.2. podemos observar la evaluación del valor futuro en el plazo $n=1, 2, …,6$.
La fórmula para el cálculo del valor futuro simple la podemos obtener generalizando los resultados de los cálculos anteriores, así:
Los intereses en el plazo de los seis años son: $$I = \$960,000*6 = \$5,760,000$$
Lo anterior es igual a: $I = \$8,000,000*0.12*6 = \$5,760,000$
Por ello, y en general, tenemos:
$$\tag{2.2} I = P i n$$El interés total se calcula multiplicando al capital inicial por la tasa de interés (en forma decimal) y el plazo.
Este resultado nos facilita obtener la fórmula para el cálculo del valor futuro en su modalidad simple. Ya sabemos que el valor futuro de un capital es $F = P + I$. También sabemos que $I = Pin$, reemplazamos esta expresión en la primera ecuación obtenemos: $F = P + Pin$, que al tomar factor común $P$ llegamos a la expresión: $$\tag{2.3}F=P(1+in)$$
La tabla que se observa en la figura 2.2 mustra la evolución en el plazo del valor futuro simple
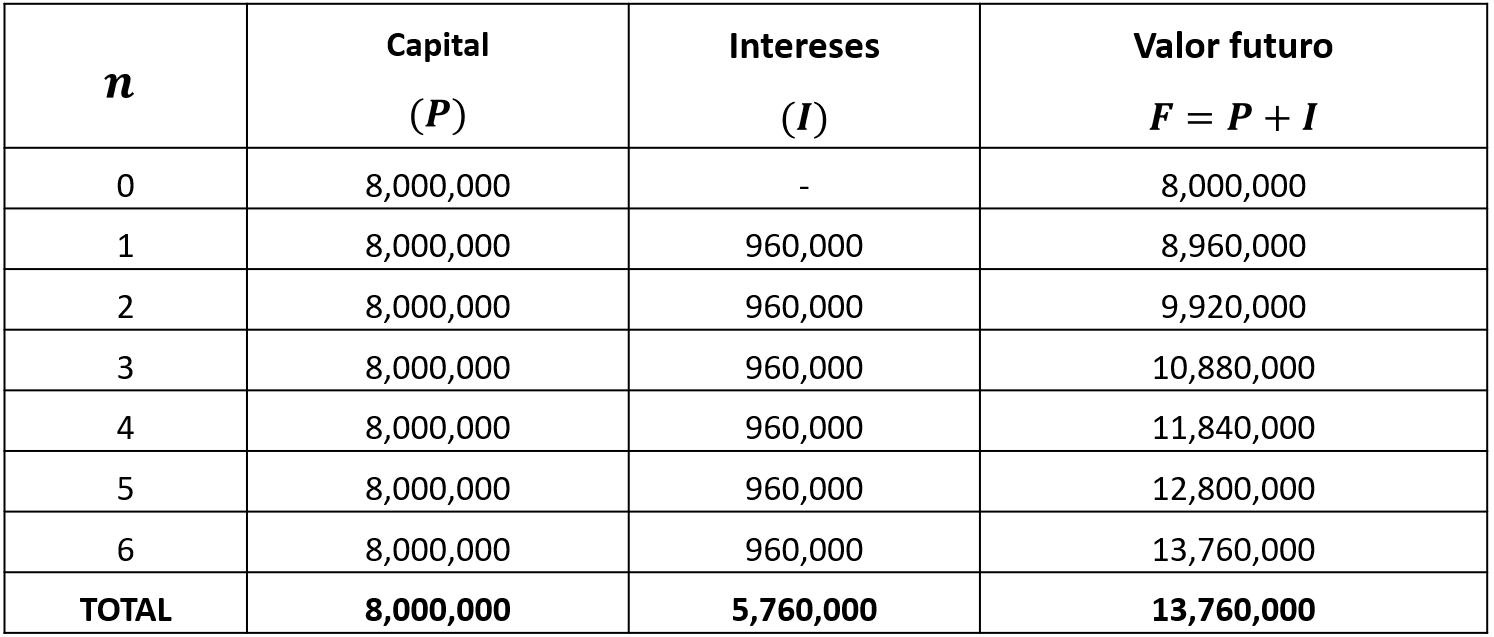
La deuda total acumulada o valor futuro bajo la modalidad de interés simple, se calcula multiplicando el capital por el factor interés simple $(1+in)$ ; veámoslo:
$$F = \$8,000,000(1+0.12*6) = \$13,760,000 $$De lo desarrollado hasta el momento es pertinente observar:
En el interés simple, al no existir capitalización de los intereses causados, el capital no cambia entre periodos de interés, es una cantidad fija.
Esto significa que la liquidación de intereses se realiza con exclusividad sobre el principal o monto inicial de la operación financiera.
Dado que el capital es una cantidad fija en el plazo de la operación financiera, el interés en cada período es así mismo una cantidad constante. Por ello, los intereses totales se obtienen multiplicando al interés periódico por el número de períodos de interés que conforma el plazo total de la operación.
El valor futuro al final de plazo (el monto final) es igual al principal o monto inicial más los intereses totales.
En la última columna de la Figura 2.2, se presenta la evolución de la deuda en el tiempo o plazo dado. Allí podemos identificar la particularidad de que cualquier valor, excepto el primer dato que es el capital inicial del ejemplo que traemos, es igual al valor anterior más una cantidad fija llamada diferencia común, que en este caso son los intereses anuales; es decir, la particularidad es que el futuro bajo la forma simple se comporta como una progresión aritmética a medida que $n$ aumenta, forma una serie finita en progresión aritmética.
Otra manera de indicar lo mismo es señalar que el valor futuro es una función lineal del plazo o tiempo $n$.
Veamos el asunto de la progresión aritmética para la comprensión lógica y matemática del asunto.
El último término de una progresión aritmética se calcula como: $a_m = a_1 + (m-1)d$, ver anexo A. Como el futuro simple se comporta en el tiempo como progresión aritmética, significa que el valor de $F$ en cualquier momento $n$ lo podemos calcular con la fórmula de $a_m$.
Veamos este caso en el que calculamos $F$ para $m = 7$ (en la última columna de la Figura 2.2 se tiene una serie de siete términos).
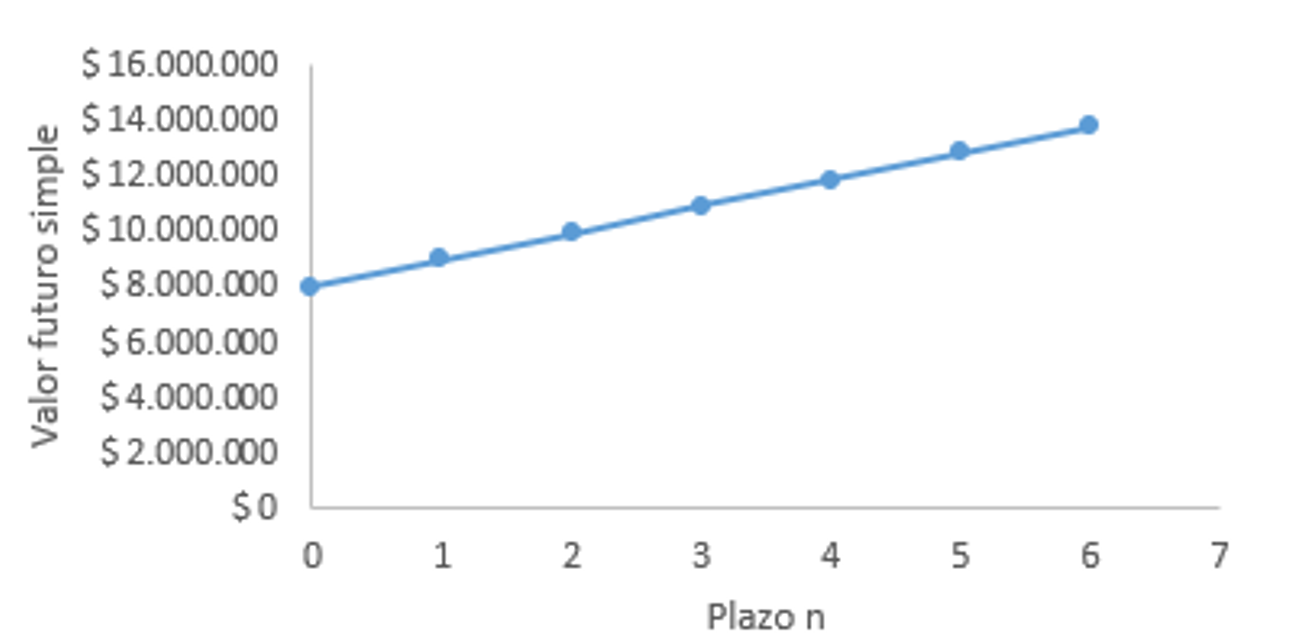
Si definimos $a_1 = \$8,000,000$, y $d = \$960,000$. Entonces el resultado de $a_m = a_1 + (m-1)d$ es:
Obteniendo el valor futuro ya calculado.
Por lo tanto: hallar el valor $a_m$ de una progresión aritmética, es hallar el valor futuro de un capital bajo la modalidad de interés simple.
Una última observación. Al no capitalizar los intereses, la modalidad de interés simple desconoce el valor del dinero en el tiempo en éstos. Con el tiempo los intereses se ven afectado en su poder adquisitivo por las consecuencias de la inflación, ocasionando una pérdida de valor; se incurre además en la pérdida del costo de oportunidad, dejando de percibir los intereses que generaría su reinversión.
De la fórmula $F=P(1+in)$, se desprenden tres tipos de problemas; ellos son:
De la fórmula $I = Pin$, podemos plantearnos además las siguientes preguntas o problemas adicionales:

Ejemplo 2.1_ Cálculo del valor futuro. Un padre de familia deja hoy como herencia a su hijo la suma de $\$38,000,000$ que sólo podrá disfrutar dentro de año y medio apenas cumpla la mayoría de edad. Por medio de un administrador, los recursos se invierten al $8.5\%$ anual simple en una entidad financiera de la ciudad. Si la herencia permanece invertida todo el tiempo que al heredero le falta para cumplir su mayoría de edad ¿Con cuánto podrá disponer éste al cabo de dicho período?
$P = \$38,000,000$
$i\% = 8.5\%$ anual
$n= 1.5$ años
$F=?$
En este caso la tasa de interés y el plazo están expresados en la misma unidad de tiempo, el año.
Podrá disfrutar de $\$42,845,000$ de los cuales $\$4,845,000$ son de intereses.
En Figura 2.4. se ofrece la representación gráfica del problema.
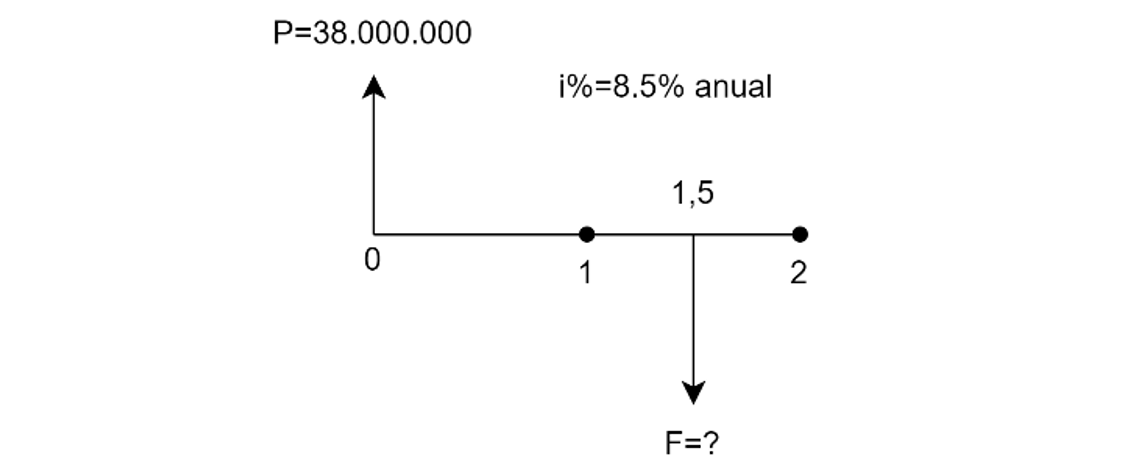

Ejemplo 2.2_ Cálculo del valor futuro. ¿Qué sucede con el valor futuro del ejercicio anterior si se resuelve usando distintos períodos de interés (unidad de tiempo de la tasa de interés) como el semestre, el trimestre, el mes y los demás datos de las variables iniciales, capital, plazo y tasa de interés anual, permanecen constantes?
Lo primero que debemos realizar es convertir las variables que tienen asociado tiempo, como es la tasa de interés y el plazo en años, a la nueva unidad de tiempo indicada en el ejercicio (período de interés). Veamos:
$P = \$38,000,000$
$i\%= 4,25\%$ semestral (se divide por 2 la tasa original ya que en el año hay dos semestres)
$n = 3$ semestres (plazo n convertido a períodos semestrales, mismo período de la tasa de interés)
$F = ?$
$F = \$38,000,000(1+0.0425*3)$
$F = \$38,000,000(1+0.1275)$
$F = \$38.000.000(1.1275)= \$42,845,000$
$P = \$38,000,000$
$i\% = 2.125\%$ trimestral (la tasa de interés original se divide por 4)
$n= 6$ trimestres (plazo $n$ convertido a trimestres)
$F = ?$
$F = \$38,000,000(1+0.02125*6)$
$F = \$38,000,000(1+0.1275)$
$F = \$38.000.000(1.1275)= \$42,845,000$
$P = \$38,000,000$
$i\% = 0.70833\%$ mensual (la tasa original se divide por 12 meses del año)
$n = 18$ meses
$F = ?$
$F = \$38,000,000(1+0.0070833*18)$
$F = \$38,000,000(1+0.1275)$
$F = \$38,000,000(1.1275)= \$42,845,000$
En todos los casos, el capital de $38,000,000$ de pesos resulta multiplicado por el mismo factor $(1.1275)$, por lo que obtenemos el mismo valor futuro.
Por lo tanto, al no existir capitalización en el interés simple, podemos hacer los cálculos adoptando libremente el período de interés, dado que el resultado no cambia.
Pero la unidad de tiempo adoptada en la tasa de interés, $i$%, debe ser la misma en el plazo, $n$.

Ejemplo 2.3_ Cálculo del capital inicial.. En la vida económica cotidiana es frecuente que las diferentes empresas recurran a la financiación por préstamos en el desarrollo de su objeto social. Así, una compañía manufacturera pagó en el día de hoy la suma de $\$150,000,000$ por un préstamo que tomó hace cinco años al $8\%$ anual simple. ¿A cuánto ascendió el monto inicial tomado en préstamo?
$F = \$150,000,000$
$n = 5 \space años$
$i\% = 8\% \space anual$
$P = ?$
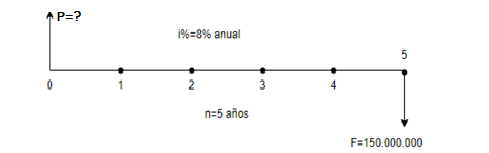
Con la fórmula (2.3) tenemos:
$P = \$150,000,000/((1+0.08*5) )= \$107,142,857$

Ejemplo 2.4_ Cálculo de la tasa de interés. Un microempresario destinó $\$3,850,000$ de su capital para la compra en efectivo de mercancías para su negocio comercial. Al cabo de cinco meses había logrado vender el inventario comprado por un valor de $\$5,398,200$ ¿Qué tasa de rentabilidad simple obtuvo en la actividad comercial?
$F = \$5,398,200$
$P = \$3,850,000$
$n = 5 \space meses$
$i\% = ?$
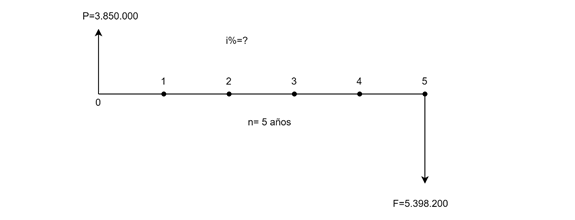
Con la fórmula (2.4) tenemos:
$i\% = \frac{\$5,398,200 - \$3,850,000}{\$3,850,000*5}=0.08.$ En porcentaje, la tasa de interés es de $8\%$ mensual.

Ejemplo 2.5_ Cálculo de la tasa de interés. El señor Pérez deposita hoy $\$251,885.78$ para disponer de $\$300.000$ dentro de $6$ meses y así hacer el pago de la matrícula de su hijo. ¿Qué tasa de interés le cancelaron? Vamos a resolver con (2.2), dado que en el camino nos queda $i$ como incógnita.
$F = \$300,000$
$P = \$251,885.78$
$n = 6 \space meses$
$i\% = ?$
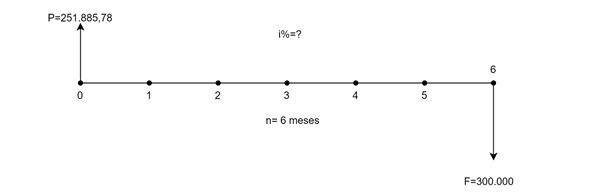
$F = P(1+i*n)$ (2.2). Reemplazando los valores:
$\$300,000 = \$251,885.78(1+i*6)$
$\frac{300,000}{251,885.78}=(1+i*6)$
$1.19102-1 = i*6$
$0,19102 = i*6$
$i = \frac{0.19102}{6}= 0.031836 = 3.184\% \space mensual$

Ejemplo 2.6_ Cálculo del plazo. ¿En cuánto tiempo se triplica un capital en un Banco Comercial que reconoce una tasa de interés del $3\%$ mensual?
$P =$ Capital
$F =3P$. F es tres veces el capital
$i\% = 3\%$ mes
$n = ?$
Podemos resolver desde (2.2)
$F = P(1+i*n)$
$3 P = P(1+0.03*n)$
$\frac{3P}{P}= 1+0.03*n$
$3-1 = 0.03*n$
$n = \frac{2}{0.03} = 66.67 \space meses$

Ejemplo 2.7_ Cálculo del plazo. Un certificado de depósito a término genera una tasa de interés simple de $0.50\%$ mensual. Si un vecino de la ciudad invierte $\$10,000,000$ y al cabo del plazo de la operación obtiene un valor final de $\$10,450,000$. ¿Por cuánto tiempo estuvo invertido el principal?
$F = \$10,450,000$
$P = \$10,000,000$
$i\% = 0.50\%$ mensual
$n = ?$
Desarrollamos con (2.6).
$$n = \frac{\$10,450,000 - \$10,000,000}{\$10,000,000*0,.05}= 9 \space meses$$
Las anualidades son series uniformes, esto es, series de valores iguales que se presentan en tiempos iguales y son manejadas a valor equivalente por medio de una misma tasa de interés, en este caso, de manera simple. Las anualidades las representamos por medio de la letra A.
En este punto, las analudades las estudiamos bajo la forma de cuota fija vencida. Para ello, obtendremos las fórmulas que permiten calcular el valor futuro y el valor presente en modalidad simple.
En el segundo volúmen de este libro, estudiaremos las anualidades bajo la forma compuesta.
La figura 2.10 es la representación general de una anualidad vencida, cuya primera A se halla en $n = 1$ y la última en $n$, mismo lugar donde hacemos el cálculo del valor futuro.
En el cálculo de $F$, procedemos asumiendo que cada A es un valor presente que debemos trasladar al futuro aplicando la fórmula (2.2). Obsérvese que para trasladar la primera A de su posición en período 1 al período n donde se ubica F, debemos realizar un recorrido de $(n-1)$ períodos, así el valor futuro de esta primera A, es:
$$\tag{2.10}F=A[1+(n-1)i]$$Así mismo, para trasladar la segunda A de su posición en período 2 al período $n$, debemos hacer un recorrido de $(n-2)$ períodos.
El futuro en este caso es: $F = A[1+(n-2)i]$.
Y así sucesivamente hasta llegar a la última A ubicada en $n$ en la que $F = A[1+(n-n)i]$, resultando en este caso que $F=A$.
Una vez todos los valores uniformes A fueron trasladados al instante $n$ podemos hallar el valor futuro como su suma, dado que son valores equivalentes. Es decir, el valor futuro de la serie uniforme consiste en la suma de cada uno de estos valores una vez ubicados todos en la misma posición de F, o sea, en $n$ (algunos autores llaman estas posiciones en el tiempo como fecha focal, ff).
Esta suma se expresa en general de la siguiente manera:
$$ F = A[1+(n-1)i]+A[1+(n-2)i]+A[1+(n-3)i]+\\A[1+(n-4)i]+...+A[1+(n-n)i] $$El último elemento de la suma anterior, como $n-n$ es igual a cero, como ya se indicó, es igual a A; la suma queda de la siguiente forma:
$$F=A[1+(n-1)i]+A[1+(n-2)i]+A[1+(n-3)i]+\\A[1+(n-4)i]+...+A$$Esta última expresión la escribimos en orden inverso, del siguiente modo:
$$F=A+A[1+i]+A[1+2i]+A[1+3i]+A[1+4i]+...+\\A[1+(n-2)i]+A[1+(n-1)i] $$Procedemos a tomar factor común A:
En esta última ecuación observamos $n$ veces el número 1, y su suma es $n*1=n$, por ello la ecuación nos queda como:
$$F = A[n*1+i++2i++3i++4i+...+\\(n-2)i+(n-1)i]$$Es decir:
$$F = A[n+i++2i++3i++4i+...+\\(n-2)i+(n-1)i]$$Ahora podemos tomar como factor común a la tasa de interés $i$, en la expresión anterior, resultando:
$$F = A[n+i{(1+2+3+4+...+\\(n-2)+(n-1))}]$$En esta última expresión algebraica, $i$ está multiplicando a la suma finita de términos en progresión aritmética, suma que se resuelve como (ver anexo A):
${\rm Suma}_m=\frac{m}{2}\left[a_1+a_m\right]$, pero en esta ocasión estamos sumando $(n-1)$ datos (es decir $m=(n-1)$ datos).Por lo tanto, si definimos que $a_1=1$ y $a_m=(n-1)$, la suma de los términos de la progresión aritmética indicada es:
$${\rm Suma}_m=\frac{(n-1)}{2}\left[1+(n-1)\right]=\frac{(n-1)n}{2}$$Llevando este resulado a la ecuación de $F$, obtenemos la fórmula para el cálculo del valor futuro de una anualidad bajo la modalidad simple. Esto es:
$$F = A[n+i(1+2+3+4+...+(n-2)+(n-1))]$$Entonces:
$$F = A\Big[n+i\Big[\frac{(n-1)n}{2}\Big]\Big]$$Es decir: $$\tag{2.11}F = A\Big[\frac{2n+(n-1)ni}{2}\Big]$$

Ejemplo 2.8_ Valor futuro de una anualidad. Un padre de familia está en la disponibilidad de ahorrar durante seis meses la suma de $\$200,000$ mensuales en una cuenta de ahorros que le reconoce una tasa de interés del $18\%$ anual. Hallar el valor acumulado al final de los seis meses por estos ahorros.
En este problema, la unidad de tiempo que acompaña la tasa de interés es el año, mientras que el plazo $n$ está expresado en meses. Como los ahorros son mensuales, debemos trabajar con tasa de interés mensual.
$A = \$200,000$
$n = 6 \space meses$
$i\% = 1.5\% \space mensual$, se obtiene dividiendo la tasa del $18\%$ anual por $12$ meses del año.
$F = ?$
$$F=A \Bigg[\frac{2n+(n-1)ni}{2}\Bigg]$$
$$F = \$200,000 \Bigg[\frac{2*6+(6-1)6*0.015}{2}\Bigg]$$
$F = \$1,245,000$
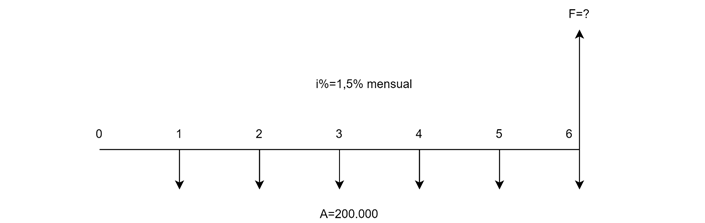
De la fórmula del valor futuro de una anualidad que acabamos de emplear podemos despejar A y obtener la manera de calcular la serie de pagos fija bajo la forma simple.
Esta es:
$$\tag{2.12} A = F \Bigg[\frac{2}{n+(n-1)ni}\Bigg]$$
Ejemplo 2.9_ La anualidad desde un valor futuro.. Una pareja de novios está planeando la compra de una vivienda, siendo la primera meta tener ahorrados en tres años la suma de $\$50,000,000$ para la cuota inicial de ésta.
Una entidad financiera de la ciudad donde viven les ofrece una tasa del $13,8\%$ anual por sus ahorros. Si los dos piensan aportar en partes iguales al valor mensual ahorrado ¿A cuánto asciende el valor del ahorro mensual?
Dado que se proponen realizar un ahorro fijo mensual durante el plazo de la meta, trabajamos con datos mensuales.
$F = \$50,000,000$
$n = 3 \space años$, equivale a $36$ meses
$i\% =$ la tasa del $13,8\%$ anual equivale a $1.15\%$ mensual
$A = ?$
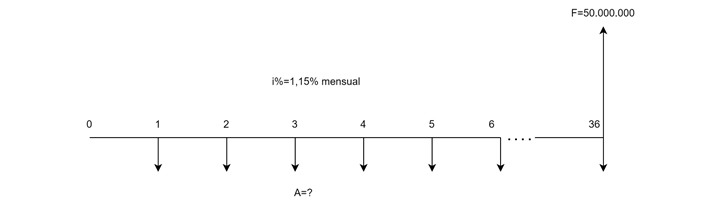
$$A = F \Bigg[ \frac{2}{2n+(n-1)ni}\Bigg]$$
$$A = \$50,000,000\Bigg[\frac{2}{2*36+(36-1)36*0.0115}\Bigg]= \$1,156,203$$
$A = \$1,156,203$
La fórmula para el cálculo del valor presente de una serie uniforme bajo modalidad simple, la deducimos utilizando resultados ya obtenidos. Sabemos que:
$$F = A \Bigg[\frac{2n+(n-1)ni}{2}\Bigg]$$
También sabemos que:
$$P = \frac{F}{1+ni}; \space P = F \bigg[\frac{1}{1+ni}\Bigg]$$
Reemplazando F de la primera ecuación por su equivalente en la segunda, tenemos que:
$$P = A \Bigg[\frac{(2n+(n-1)ni)}{2}\Bigg]*\Bigg[\frac{1}{(1+ni)}\Bigg]$$
Multiplicando términos, la fórmula queda como:
$$\tag{2.13} P = A \Bigg[\frac{(2n+(n-1)ni)}{2(1+ni)}\Bigg]$$
Ejemplo 2.10_ El valor presente de una serie uniforme simple. Por la compra de una hectárea de tierra ubicada en un municipio del Nordeste Antioqueño, un citadino se comprometió a cancelar diez cuotas semestrales de $9,500,000 con una tasa de interés del 8,5% anual simple. ¿Cuál sería el valor del terreno si la compra se hubiese realizado de contado?
$A = \$9,500,000$
$n = 10 \space semestre$
$i\% =$ la tasa del $8.5\%$ anual equivale a $4.25\%$ semestral
$P = ?$
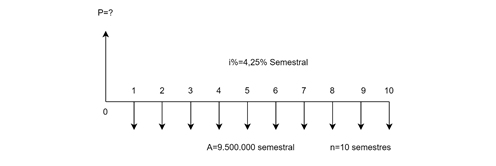
$$P = A \Bigg[\frac{(2n+(n-1)ni)}{(2(1+ni))}\Bigg]$$
$$P = \$9,500,000 \Bigg[\frac{(2*10+(10-1)10*0.0425)}{(2(1+10*0.0425))}\Bigg]= \$79,416,667$$
Si de la fórmula (2.13) se despeja A, se tiene la fórmula para estimar el valor de la anualidad a partir del valor presente o capital inicial. La ecuación es:
$$\tag{2.14}A=P \Bigg[\frac{(2(1+ni))}{(2n+(n-1)ni)}\Bigg]$$

Ejemplo 2.11_ Cálculo de la cuota fija simple desde un valor presente. Un teléfono celular de generación 4G tiene un valor de contado de $\$5,136,950$ y se espera adquirír por medio de un crédito cancelando $24$ cuotas mensuales iguales, con una tasa de interés del $1.5\%$ mensual. Hallar el valor de la cuota.
$P = \$ \space 5,136,950$
$n = 24$ meses
$i\%= $1.5% mensual
$A=?$ $$P = \$ 5,136,950\Bigg[\frac{2(1+24*0.015)}{2*24+(24-1)24*0.015} \Bigg]=\$ 248,267.66$$
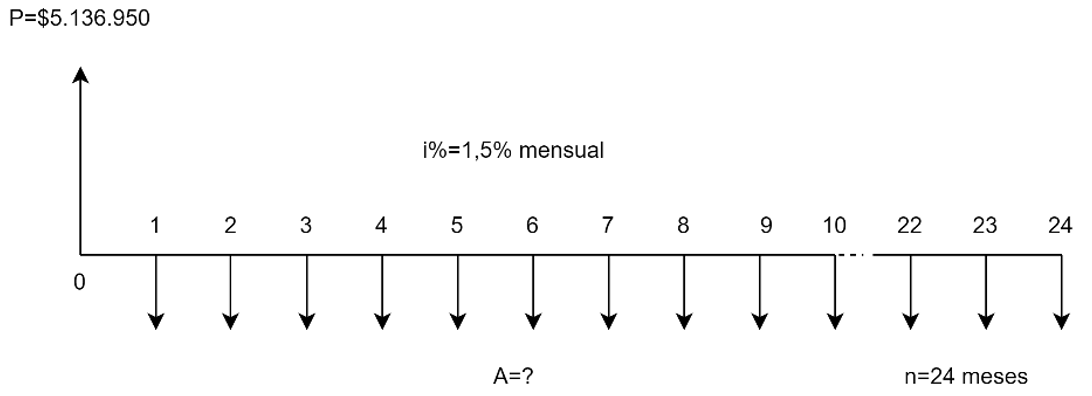
La diferencia básica de esta modalidad anticipada con respecto a la vencida consiste en que la primera anualidad se presenta en el instante cero o presente ( en fecha focal cero, $ff=0$) y la última se ubica en el instante $(n-1)$ como en la figura 2.15. En cuanto al valor futuro, el cálculo se mantiene en el mismo instante $n$.
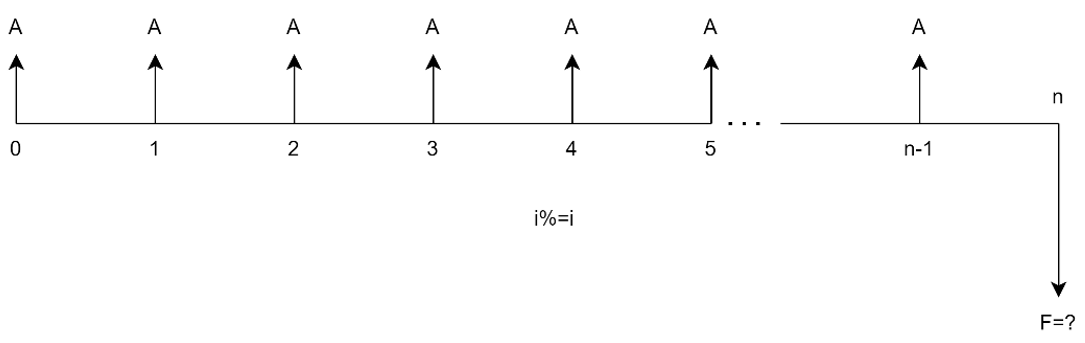
Para hallar el valor futuro de esta serie anticipada, todas las $A$ debemos trasladarlas al mismo instante $n$, donde se ubica $F$ y allí realizar la suma.
Para la $A$ ubicada en instante cero, el valor futuro es $F = A[1+ni]$, trasladada $n$ lugares; para la $A$ ubicada en instante 1, el futuro es $F = A[1+(n-1)i]$, y así sucesivamente.
En general el valor futuro de la serie representada en la figura 2.15 es:
$$ F = A[1+ni]+A[1+(n-1)i]+A[1+(n-2)i]+\\A[1+(n-3)i]+ \ldots +A[1+i] $$Escribiendo esta expresión algebraica en orden invertido, tenemos: $$F = A[1+i]+A[1+2i]+A[1+3i]+A[1+4i]+⋯+\\A[1+(n-1)i]+A[1+ni]$$
Podemos tomar factor común A y sumar n veces el 1 de la ecuación anterior. Entonces:
$$F=A[n+i+2i+3i+4i+⋯+(n-1)i+ni]$$Tomando como factor común la tasa de interés $i$, obtenemos: $$F=A[n+i{(1+2+3+4+(n-1)+n)}]$$
De nuevo, se observa que $i$ multiplica a la suma de $n$ términos de una progresión aritmética. Si identificamos $a_1 = 1$ y $a_m = n$, además tenemos la suma de $m=n$ términos, la suma es:
${\rm Suma}_m=\frac{n}{2}\left[1+n\right]=\frac{(n+1)n}{2}$.
Esta expresión la reemplazamos en la fórmula de futuro y obtenemos:
$$\tag {2.15}F=A\left[\frac{2n+(n+1)ni}{2}\right]$$

Ejemplo 2.12_ Valor futuro simple de una anualidad anticipada.
Al momento del nacimiento de Carlos, su padre se propuso depositar la suma de $5,800,000 anuales y por un periodo de dieciocho años, con el fin de contar con los ahorros suficientes para cubrir los estudios universitarios de su hijo. Si una entidad financiera local le ofrece el pago de 6.5% anual, y el padre de familia hace el primer depósito al momento del nacimiento de Carlos.
¿Cuánto logró ahorrar el padre de Carlos al ejecutar su plan?
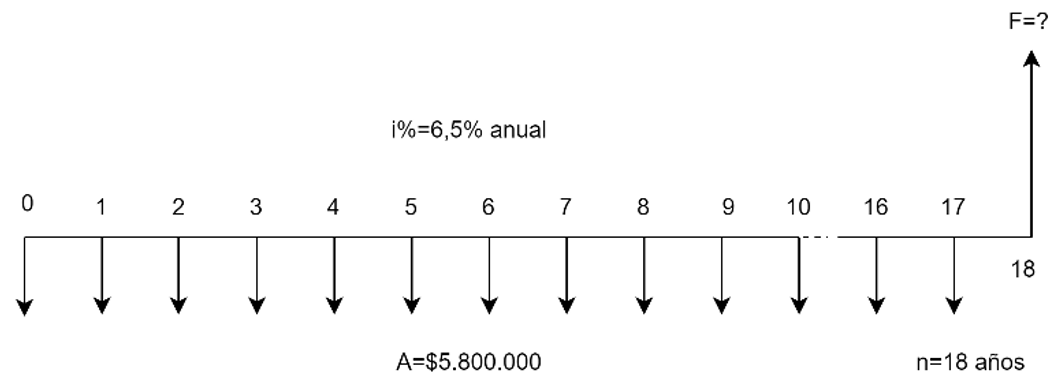
$A = \$ 5,800,000$
$n = 18$ años
$i\% = $6.5% anual
$F = ?$ $$F = A \Bigg[\frac{(2n+(n+1)ni)}{2}\Bigg]$$ $$F = \$5,800,000 \Bigg[\frac{2*18+(18+1)18*0.065}{2}\Bigg]= \$64,467.000$$
De la ecuación 2.15 despejamos $A$ y obtenemos la forma de hallar el valor de la anualidad cuando conocemos el valor futuro. $$\tag{2.16}A = F \Bigg[\frac{2}{(2n+(n+1)ni)}\Bigg] $$

Ejemplo 2.13_ Cálculo de la serie uniforme anticipada de un valor futuro. Una mediana empresa de asesorías contables e inversiones financieras está pensando reemplazar el mobiliario dentro de dos años con un costo de $16,000,000. Con el fin de financiar el cambio con recursos propios, la empresa piensa desarrollar un esquema de ahorro por medio de cuotas fijas bimestrales anticipadas en una entidad financiera que le reconoce una tasa de interés del 9.0% anual simple.
¿De cuánto debe ser la cuota ahorrada para lograr el propósito?
$F = \$16,000,000$
$n= 2$ años y son equivalentes a 12 bimestres
$i\%= $9.0% anual y es equivalente a 1.5% bimestre
$A=?$
$$A=F \Bigg[\frac {2}{(2n+(n+1)ni)}\Bigg]$$
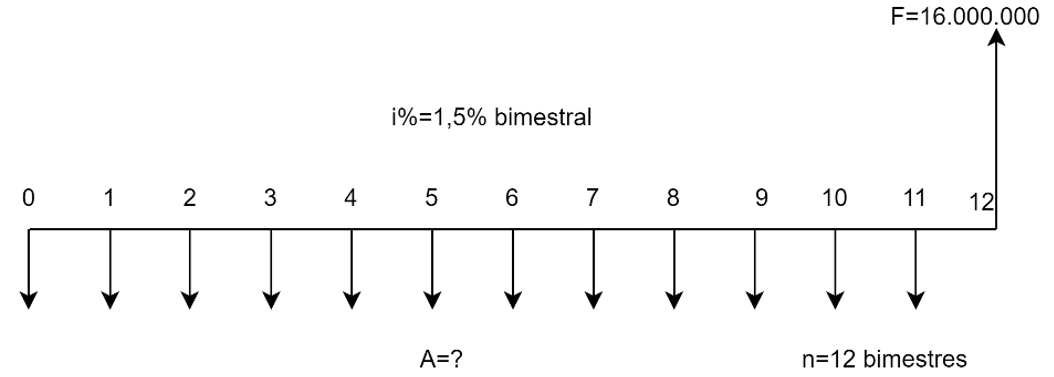
En la determinación de la fórmula para el cálculo del valor presente de una serie uniforme anticipada simple, procedemos del mismo modo como en caso vencido. Es decir, sabemos que: $$P = \frac {F}{(1+ni)} = F*\frac{1}{(1+ni)}$$
Además, que: $$F = A \Bigg[\frac{(2n+(n+1)ni)}{2} \Bigg]$$
Entonces: $$P=A[\frac{(2n+(n+1)ni)}{2}]*\frac{1}{(1+ni)}$$
Multiplicando numeradores y denominadores entre sí, obtenemos la fórmula para convertir una anualidad anticipada en valor presente, como: $$\tag {2.17}P = A \Bigg[\frac{2n+(n+1)ni}{2(1+ni)}\Bigg] $$

Ejemplo 2.14_ Valor presente de una anualidad anticipada. Una empresa de turismo ha tomado en arriendo un local en la zona norte del país por el plazo de un año, inicialmente. El canon de arrendamiento anticipado se acordó en $2,000,000 mensuales. Si el costo de oportunidad del arrendador es del 1.3% mensual ¿cuánto tendría que pagar el arrendatario hoy para cubrir el canon de arrendamiento de todo el año en un solo desembolso?
$A = \$2,000,000$
$n = 1$ año e igual a 12 meses
$i\% =$ 1.3% mensual
$P = ?$
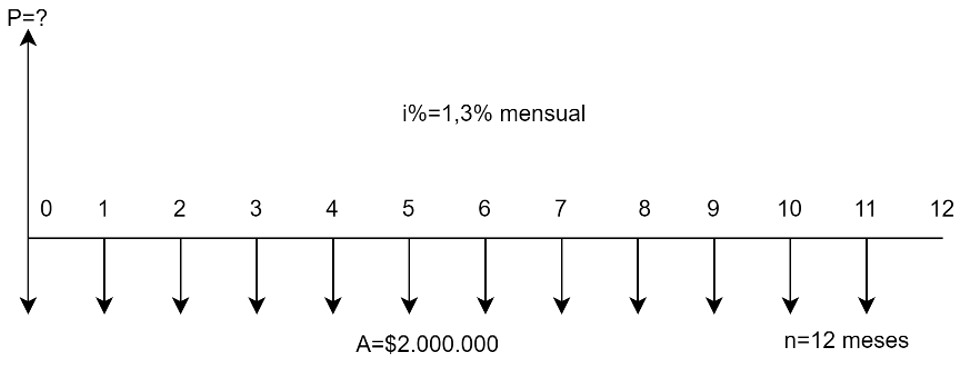
En el cálculo de la anualidad anticipada de un valor presente, podemos expresar $A$ en términos de $P$, de la anterior ecuación, obtenido: $$\tag{2.18} A = P \Bigg[\frac{2(1+ni)}{2n+(n+1)ni} \Bigg] $$

Ejemplo 2.15_ Cálculo de la serie uniforme anticipada desde un valor presente. La compañía Electric-Hogar desea reemplazar la actual maquinaria y los equipos, con el fin de mejorar la productividad y eficiencia en el proceso de producción y comercialización de sus productos, mejorando asi la calidad de éstos, reduciendo además los productos defectuosos y los desechos.
Para el efecto recurre a financiación externa a la empresa por valor de $500,000,000 y con un costo anual del 12% simple. Si el esquema de pago es por medio de una cuota fija trimestral anticipada ¿a cuánto asciende ésta?
$P = 500,000,000$
$n = 10$ años, equivalen a 40 trimestres
$i\% =$ 12% anual, equivale a 3.0% trimestral
$A = ?$ $$A = P \Bigg[\frac{2(1+ni)}{2n+(n+1)ni}\Bigg]$$ $$A=\$500,000,000\Bigg[\frac{2(1+40*0.03)}{(2*40+(40+1)40*0.03)}\Bigg]=\$17,027,864$$
La traslación de la tierra alrededor del sol describe una órbita elíptica que se completa cada 365 días, 5 horas y 49 minutos, como se encuentra en los libros de textos sobre este tema, tiempo al que el hombre ha denominado año. Con fines prácticos, el año exacto ha sido definido en 365 días y cada cuatro años se forma el año bisiesto constituido por 366 días. En la práctica comercial y en el mundo de las finanzas, también es común observar que al año lo hacen equivalente a 360 días, dividido en 12 meses de 30 días cada uno.
La utilización de una u otra medida del año en las prácticas comerciales y financieras, dará lugar a valoraciones diferentes de los activos, capitales y de los rendimientos, por ejemplo. En el caso de los rendimientos, si en la práctica del interés simple se recurre al año constituido por 360 días, nos referimos al interés comercial, al contrario, si se recurre al año constituido por 365 o 366 días, estamos ante la presencia del interés exacto.

Ejemplo 2.16_ Cálculo de valor futuro simple con interés comercial y exacto. Se abre un CDT por valor de $20,000,000 el primero de marzo de 2022 al 5.3% anual simple y vencimiento el 31 de agosto. Determinar el valor a redimir en dicha fecha y el monto de los intereses, por los métodos de interés comercial e interés exacto.
Por interés comercial. Año de 360 días
$P = \$20,000,000$
$i\%=$5.3% anual, al dividir por 360 días resulta la tasa de interés diaria
$n = 180$ días
$F = ?$
$F = P(1+i*n)$
$F = 20,000,000(1+0.(053/360)*180)=20,530,000$
$I = P*i*n$
$I = 20,000,000*(0.053/360)*180=530,000$
Por interés exacto. Año de 365 días
$i\%=$5.3% anual, se divide por 365 días para la tasa de interés diaria
$n = 183$ días exactos entre fechas de la operación.
En los mercados financieros es frecuente observar que poseedores de títulos valores, como el pagaré, la letra de cambio, o el certificado de depósito a término, decidan negociarlos antes de la fecha de su vencimiento, motivados por alguna eventualidad que les exige disponer de efectivo o por especulación en la búsqueda de mayores rendimientos.
También es normal encontrar personas o inversores interesados en dichos documentos, motivados por las ganancias que pueden lograr en la transacción.
El valor del título al vencimiento se denomina valor nominal (Vn) y se determina como el valor futuro de un capital inicial. Sobre el valor nominal se realiza el descuento (D), que es una rebaja o disminución de intereses al negociarse el activo financiero antes de la fecha de su vencimiento, por adelantar su vencimiento; el descuento es una cantidad de dinero sustraída del valor nominal.
Entre ambas partes, el oferente y el demandante, se llega a un acuerdo sobre el valor del documento objeto de transacción, acuerdo que concreta el otorgamiento de un descuento sobre el valor estipulado en el propio título.
El precio al que se vende el título una vez aplicado el descuento, se denomina valor efectivo (Ve) y es igual al valor nominal menos el descuento acordado, generalmente expresado en una tasa.
De lo expresado se desprende que el valor efectivo se resuelve con la fórmula $Ve=Vn-D$; y por lo tanto, es cierto que $D=Vn-Ve$.
Por último, la tasa de interés utilizada en la operación se denomina tasa de descuento.
En el caso del interés simple, presentamos dos tipos de descuentos. El primero es el descuento comercial o bancario, y es aquel que se aplica sobre el valor nominal del título en transacción. En cambio, el segundo tipo realiza el descuento sobre el valor efectivo del título y se denomina descuento racional.
Con el siguiente ejercicio ilustramos el proceso de los descuentos, comenzando con la constitución de un título valor, por ejemplo, un pagaré, que luego se vende con un descuento.

Ejemplo 2.17_ Descuento comercial y valor efectivo.Pedro Arango de la vereda la María presta a un familiar la suma de $\$15,000,000$ con plazo de 15 meses y tasa de interés de 2.5% mensual, respaldado en un pagaré.
Luego de 8 meses, Pedro se ve en la necesidad de negociar el pagaré y está dispuesto a otorgar descuento del 2.0% mensual comercial. Hallemos el valor del descuento comercial $(D_C)$ y el valor efectivo o precio de venta del pagaré.
El primer paso es determinar el valor del pagaré al vencimiento, para ello se calcula el valor nominal del pagaré por medio del valor futuro del capital prestado.
Los datos iniciales son:
$P = 15,000,000$
$n = 15$ meses
$i\%=$2.5% mensual
El valor nominal del pagaré es el valor futuro del capital, en este sentido el cálculo es:
$$V_n = F = P(1+i*n)$$ $$V_n = \$15,000,000(1+0.025*15)= \$20,625,000$$En segundo lugar, calculamos el descuento comercial, que es una rebaja de intereses sobre el valor nominal del título valor. Al pagaré le faltan 7 meses para su vencimiento, y el descuento acordado es del 2,0% mensual. El cálculo del monto descontado es una aplicación de la fórmula de interés simple (2.1.), veamos:
$F = 20,625,000$
$n = 7$ meses (tiempo faltante para el vencimiento del título)
$i\%=$2.0% mensual
En el descuento comercial debemos considerar que este se aplica sobre el valor nominal, no sobre el capital inicial. Por ello: $D_c=V_n*i*n$. El monto del descuento comercial ($D_c$ ), es:
$D_c=20,625,000*0.02*7=2,887,500$
En tercer lugar, procedemos a calcular el precio de venta del pagaré o valor efectivo. Como ya se indicó su cálculo es por medio de $V_e = V_n - D_c.$ $$V_e = \$20,625,000 - \$2,887,500 = \$17,737,500$$
El procedimiento hasta aquí desarrollado permite generalizar y deducir la fórmula para calcular el valor efectivo del pagaré.
El valor efectivo del título es igual a $V_e = V_n - D_c$. El descuento comercial es $D_c = V_n*i*n$.
Así entonces, reemplazando esta segunda ecuación en la primera resulta que $V_e=V_n-V_n*i*n$, y al tomar factor común $Vn$ obtenemos la fórmula buscada. Es decir: $$V_e = V_n (1-i*n) (2.17)$$
La anterior fórmula (2.17) es el modelo para calcular el precio de venta del pagaré sin necesidad de calcular previamente el descuento comercial. Veamos:
$V_e = \$20,625,000(1-0.02*7)$
$V_e = \$20,625,000(1-0.14)$
$V_e = \$20,625,000(0.86)= \$17,737,500.$ Valor a vender el pagaré.
Ahora, si $V_e=V_n-D_c$ es claro entonces que $D_c=V_n-V_e$. Veamos:
$D_c = \$20,625,000 - \$17,737,500 = \$2,887,500$.
Y es el descuento de intereses ya calculado.
En conclusión, Pedro Arango vende el título en $\$17,737,500$ otorgando descuento de intereses de $\$2,885,500$ que son los rendimientos que se ganará el nuevo poseedor del documento. Al vender el título en el mes ocho, Pedro obtiene de forma anticipada, antes del vencimiento acordado en la transacción original, intereses por $\$2,737,500$, además recupera su capital inicial de $\$15,000,000$.
El nuevo poseedor, debe esperar que se cumpla el plazo del vencimiento, dentro de 7 meses, para redimir el capital y cobrar los intereses; en total recibirá $\$20,625,000$ de los cuales $\$17,737,500$ es el capital por él invertido.

Ejemplo 2.18_ Descuento racional. Pensemos ahora que la decisión de Pedro es negociar el pagaré utilizando el método del descuento racional, pero con la misma condición de tasa de descuento y plazo para el vencimiento del título. En este caso el descuento racional ($D_r$) se realiza sobre el valor efectivo, esto es, $D_r=V_e*i*n.$
Desde la definición de valor efectivo, éste queda determinado por la expresión $V_e = V_n-D_r$, y es igual a $V_e = V_n - V_e*i*n$, esto es, $V_e+V_e*i*n=V_n$. Ahora bien, tomando factor común $V_e$ al lado izquierdo de la igualdad, tenemos $V_e (1+i*n)=V_n$ ecuación que es igual a: $$\tag{2.18} V_e = \frac {V_n}{1+i*n} $$
Es claro que la ecuación (2.18) tiene la misma estructura que la ecuación (2.2), pero la aplicación es en otro contexto. De allí que a este método se le denomine también descuento justo, dado que el descuento es en sentido inverso al de la valorización simple o de estimación del valor nominal.
El valor efectivo del título y el descuento racional, son:
$$V_e = \frac {\$20,625,000}{1+0.02*7}= \$18,092,105.26$$Resultado que también se obtiene al restar del valor nominal el valor efectivo $(\$20,6250,000- \$18,092,105.26)$.
Es posible desarrollar una fórmula para el cálculo del descuento racional sin pasar previamente por el cálculo del valor efectivo. Veamos:
$D_r = V_n-V_e.$ Es decir,
$D_r=V_n-\frac{V_n}{(1+i*n)}$ , tomando factor común $V_n$,
$D_r = V_n \Bigg[1-\frac{1}{(1+i*n)}\Bigg]$, realizando la resta al interior del corchete,
$D_r = V_n \Bigg[\frac{(1+i*n-1)}{(1+i*n)}\Bigg]$, cancelando los unos
$$ \tag{2.19} D_r = V_n \Bigg[\frac{i*n}{1+i*n}\Bigg] (2.19)$$
Así entonces, $D_r = \$20,625,000 \Bigg[\frac{0.02*7}{1+0.02*7}\Bigg]= \$2,532,894.74$, igual al valor ya determinado.
La operación de venta del pagaré le significa a Pedro acceder a intereses anticipados, pues con la venta obtiene intereses antes del vencimiento del título. Como el descuento comercial es mayor que el descuento racional, a Pedro le es más conveniente vender el título por medio del descuento racional.
En este caso el comprador seguro plantearía como método de compra el descuento comercial.
Ahora bien, si como en este caso el $D_c > D_r$ ¿es posible estimar una tasa de descuento que posibilite la indiferencia por el método para calcular el valor efectivo de un título objeto de oferta antes de su vencimiento? La respuesta es sí, debiéndose cumplir la condición de igualdad de descuentos, o de valores efectivos; el problema planteado consiste en hallar la tasa de descuento equivalente.
Identificando $i_c$ como la tasa de descuento comercial e $i_r$ como la tasa de descuento racional, la deducción desde la igualdad de los descuentos es como sigue:
Punto de partida: $D_c = D_r$. Ahora bien, como el $D_c = V_n*i_c*n$ y el $D_r=V_n \Bigg[\frac{ i_r*n}{(1+i_r*n)}\Bigg]$, procedemos a igualar estas dos ecuaciones:
$V_n*i_c*n=V_n \Bigg[\frac{(i_r*n)}{(1+i_r*n)}\Bigg]$, cancelando $V_n$,
$i_c*n = \frac{(i_r*n)}{(1+i_r*n)}$, despejando $i_c$
$$\tag{2.20}i_c= \frac{i_r}{(1+i_r*n)} $$
Esta fórmula (2.20), en la que $n$ es el tiempo que falta para el vencimiento del título en negociación, permite hallar la tasa de descuento comercial equivalente, es decir que al aplicarla daría el mismo monto del descuento o el mismo valor efectivo, a una tasa de descuento racional.
De esta ecuación (2.20), al despejar $i_r$ tenemos la forma de calcular exactamente lo contrario, es decir la tasa de descuento racional equivalente a una tasa de descuento comercial. La fórmula es:
$i_c = \frac{i_r}{(1+i_r*n)}$
$i_c (1+i_r*n)=i_r$
$i_c +i_c*i_r*n = i_r$
$i_r-i_c*i_r*n=i_c$
$i_r (1-i_c*n)=i_c$ $$\tag{2.21} i_r =\frac{i_c}{(1-i_c*n)}$$

Ejemplo 2.19_ Equivalencia entre tasas de descuento racional y comercial. En la negociación de un título con valor nominal de $ 18,350,350 y vencimiento en 4 meses, el poseedor está dispuesto a otorgar un descuento racional de 2.8% mensual.
Sin embargo, ante la posibilidad que el comprador le plantee realizar la operación por descuento comercial, el propietario está interesado en conocer previamente la tasa de descuento comercial equivalente a la que está interesado otorgar por el título.
Para ello procede a calcular la tasa de descuento comercial que es equivalente al 2.8% mensual racional y a constatar que los descuentos comercial y racional arrojan igual valor.
Procedamos a obtener la tasa de descuento comercial equivalente aplicando (2.20).
$i_c = \frac{i_r}{(1+i_r*n)}$
$i_c = \frac{0.028}{(1+0.028*4)}=0.02518 = 2.518%$
Significa entonces que una tasa de descuento racional de 2.8% mensual equivale a una tasa de descuento 2.518% mensual comercial.
Para constatarlo, calculamos los descuentos por ambos métodos.
Descuento racional
$D_r = V_n \Bigg[\frac{(i_r*n)}{(1+i_r*n)}\Bigg]$
$$D_r = \$18,350,350 \Bigg[\frac{(0.028*4)}{(1+0.028*4)}\Bigg]=\$1,848,237$$
Descuento comercial
$D_c=V_n*i_c*n $
$$D_c = \$18,350,350*0,02518*4 = \$1,848,237 $$
Los descuentos son iguales, lo que significa que el valor efectivo debe ser de $\$16,502,113$ al aplicar ambos métodos de descuento.

Ejemplo 2.20_ Descuento con años comercial y exacto. El primero de julio de 2021, Adíela Agudelo le prestó a un amigo la suma de 15 millones de pesos al 24% anual con el compromiso recibir un pago único el 31 de enero de 2022, y liquidación de intereses con base en año exacto (con 365 días). Para la operación se firma una letra de cambio.
Este acto hace necesario hallar el valor nominal del documento.
Sin embargo, Adíela se vio en la necesidad de negociar la letra de cambio debido a una eventualidad que le hizo requerir del efectivo. Logra negociar con su hermana María el título valor para el 31 de octubre de 2021 con una tasa de descuento del 18% anual, pero en esta ocasión sobre la base del año comercial (asumiendo el año de 360 días).
En este ejemplo calcular: El valor nominal del documento, el descuento al negociar Adiela el documento, el valor efectivo del documento o precio que debe cancelar María. Hallar además el descuento racional con año comercial.
Valor nominal del título con año exacto
$P = \$15,000,000$
$i\%= 0.24/365=0.0006575$ (tasa de interés diaria con año exacto)
$n= 214$ días (exactos de la inversión)
$Vn=P(1+i*n) $
$Vn = F = \$15,000,000(1+0.00065753*214) = \$17,110,685$
Descuento comercial o bancario con año comercial otorgado a María. El descuento se realiza sobre el valor nominal del título.
$D_c=Vn*i*n $, siendo $n=90$ días
$$D_c = \$17,110,685*\Bigg[\frac{0.18}{360*90} \Bigg]= \$769,981 $$
Valor efectivo o precio de venta del título con descuento comercial, precio a pagar por María
$Ve = Vn-D_c $
$Ve = Vn(1-i*n)$
$Ve = \$17,110,685 - \$769,981 = \$16,340,704$
$$Ve = \$17,110,685 \Bigg[\frac{1-0.18}{360*90}\Bigg]= \$16,340,704$$
Descuento racional con año comercial
$$D_r=V_n \Bigg[\frac{i*n}{1+i*n}\Bigg]$$
$$D_r = \$17,110,685 \Bigg[\frac{0.0005*90}{1+0.0005*90}\Bigg] = \$736,824$$
$$Ve= \frac{Vn}{1+ i*n}$$
$$Ve = \frac{\$17,110,685}{1+ 0.0005*90} = \$16,373,861$$
Este valor igualmente se obtiene si restamos $\$17,110,685 - \$736,824$
En los contratos o documentos con los que se formaliza el otorgamiento de créditos o préstamos de dinero, se suele especificar el monto del capital, la tasa de interés, el plazo, la forma y fecha de redimir la obligación.
Con el término vencimiento se hace referencia al momento concreto (días, mes, año) en el que se debe cancelar una obligación financiera, al instante en particular en que un prestatario se obliga a devolver al prestamista el monto tomado en préstamo y sus rendimientos.
El vencimiento simple es un procedimiento matemático que permite calcular un nuevo vencimiento para cancelar varias obligaciones, con vencimientos diferentes, en un monto único y equivalente.
Es decir, esta operación permite sustituir varias deudas por un solo pago que las suple, en un nuevo instante denominado vencimiento. Presentamos dos maneras de cálculo: vencimiento medio y vencimiento común, procediendo con descuento comercial o descuento racional.
Vencimiento medio.La característica básica de este método consiste en afirmar que el monto único o valor nominal $V_N$ del nuevo documento que suple las obligaciones, es igual a la suma de los valores nominales de éstas. En decir: $V_N = V_{n1} + V_{n2} + ⋯ + V_{nn}$. Como consecuencia de esta determinación del valor nominal único, se debe cumplir también la igualdad en términos de valor efectivo, o sea: $V_E = V_{e1} + V_{e2}+⋯+V_{en}$.
El problema del vencimiento medio consiste en hallar el nuevo instante $n$ en el que vence el pago único, en condiciones de equivalencia con los valores iniciales que sustituye. Es decir, se trata de determinar la $n$ que hace equivalente, igual, el $V_N$ con el $V_E$.

Ejemplo 2.21_ Vencimiento medio. Se tiene tres deudas respaldadas con letras de cambio con valores de $\$2,300,400$; $\$5,432,320$ y $\$350,000$ con vencimientos en 5, 3 y 4 meses, respectivamente, otorgadas al 2.5% mensual simple.
Si se desea sustituir este acuerdo inicial de pagos por un solo pago bajo vencimiento medio ¿cuál es el vencimiento de éste? Resolver por descuento comercial.
Cálculo del valor único a pagar.
$V_N = V_{n1} + V_{n2} + ⋯ + V_{nn}$
$V_N = \$2,300,400 + \$5,432,320 + \$350,000 = \$8,082,720$. Y es el valor nominal de la nueva letra.
Cálculo del valor efectivo con descuento comercial
$V_E = V_{e1} + V_{e2} + ⋯ + V_{en}$
$V_E = \$2,300,400(1-0.025*5)+ \$5,432,320(1-0.025*3)+\$350,000(1-0.025*4)$
$V_E = \$7,352,746 $. Con esta operación matemática, observe que el valor nominal de cada letra es descontado al instante cero $(n=0)$, y así obtener el respectivo valor efectivo.
Cálculo del vencimiento ($n$).
La condición es la igualdad $V_E = V_N (1-i*n)$.
En esta igualdad la pregunta es por el nuevo plazo $n$: su ecuación es: $$\tag{2.22} n = \frac{\bigg(1-\frac{V_E}{V_N}\bigg)}{i} = \frac{V_N - V_E}{V_N*i} $$
$$n =\bigg(\frac {\$8,082,720-\$7,307,746}{\$8,082,720*0.025}\bigg)=3.6 \space meses$$
Es decir, tres meses y 18 días. Significa entonces que un capital de $\$7,352,746$ equivale en 3 meses y 18 días a $\$8,082,720$ con una tasa de interés de 2.5% mensual con descuento comercial.

Ejemplo 2.22_ Resolver el ejercicio anterior con descuento racional.
Cálculo del valor efectivo.
$V_E =V_{e1}+V_{e2} + ⋯ + V_{en}$
$$V_E = \frac{\$2,300,400}{(1+0.025*5) }+\frac{\$5,432,320}{(1+0.025*3)}+ \frac{\$350,000}{(1+0.025*4)}\\$$
$$=\$7,416,303$$
Cálculo de $n$
La condición es la igualdad: $$V_E = \frac{V_N}{(1+i*n)}$$
La ecuación para $n$ es: $$n =\frac{V_N - V_E}{V_E*i}$$ $$n =\frac{\$8,082,720 - \$7,416,303}{\$8,082,720*0.025}=3.3 \space meses$$
Es decir, tres meses y 9 días. Por lo tanto, un capital de $\$7,416,303$ equivale en 3 meses y 9 días a $\$8,082,720 $ con una tasa de interés de $2.5\%$ mensual y descuento racional.
Vencimiento común. En este tipo de vencimiento, el valor nominal del nuevo documento, ($V_N$), no es igual a la suma de los valores nominales de las obligaciones individuales, es decir: $V_N ≠ V_{n1}+ V_{n2}+⋯+V_{nn}$.
Esta condición implica un acuerdo previo sobre el valor nominal o monto único que reemplaza las obligaciones.

Ejemplo 2.23_ Vencimiento común con descuento comercial. Se tienen dos deudas de $\$850,000$ y $\$498,900$ al 36% anual simple y vencimiento en 7 y 9 meses, respectivamente.
Las partes acuerdan reemplazar estas obligaciones por un solo pago de $\$1,500,000$. Hallar el instante en que vence la nueva obligación por el método del descuento comercial.
$ V_N = \$1,500,000$
$$ V_E = \$850,000(1-0.03*7)+ \$498,900(1-0.03*9)$$ $$= \$1,035,697$$
$$n = \frac {\$1,500,000 - \$1,035,697}{1,500,000*0.03} = 10.32 \space meses$$
Con vencimiento común, las partes en la negociación pueden acordar, en vez del valor nominal común, el momento común de vencimiento de las obligaciones.
En este caso se procede a determinar el valor nominal del pago que reemplaza el acuerdo inicial. Veamos el asunto con un ejemplo.

Ejemplo 2.24_ Vencimiento común con acuerdo de n . Con los datos del problema anterior y resolviendo por el método de descuento racional, hallar el valor del pago único si las partes acuerdan cancelar las obligaciones en el mes 12.
Debemos despejar $V_N$ de la ecuación de equivalencia, así: $$V_E = \frac{V_N}{(1+i*n)}$$ $$V_E*(1+i*n) = V_N$$ $$V_N = V_E (1+i*n) = \$1,098,314(1+0.03*12)=\$1,498,627$$
En 12 meses las deudas inicialmente contraídas en los meses 7 y 9, quedan canceladas con el pago de $\$1,498,627$.
Cuando la persona que ha tomado en préstamo un capital no cumple con los pagos en las fechas que se ha comprometido al aceptar las condiciones de financiación, incurre en el pago de uno interés sancionatorio denominado interés moratorio o de mora.
Las entidades financieras están autorizadas a aplicar como tasa de mora el 1.5 veces la tasa de interés pactada en sus créditos, sin que la tasa resultante supere la tasa máxima que es autorizada cobrar en el sistema financiero del país.
La tasa de sura, determinada por la Superintendencia Financiera de Colombia, es la tasa de interés que pone límite a los cobros por modalidad de crédito; cobrar por encima de la tasa autorizada es caer en usura y objeto de sanción.
Para la modalidad de interés simple, dado que no existen intereses sobre los intereses, el interés moratorio se determina con base en el capital inicial o principal.
El cálculo del monto de intereses moratorio lo ejemplificamos utilizando el año exacto y el año comercial.

Ejemplo 2.25_ Interés moratorio. Un préstamo de consumo otorgado el 15 de marzo del año en curso por $\$3,500,000$, se acuerda cancelarse el 15 de diciembre del mismo año en un pago único a interés simple del $15\%$ anual. Resulta que el deudor no pagó el día acordado, realizándolo el 25 de enero del año siguiente.
Calcular el valor de la deuda al vencimiento, los intereses de mora y el valor a cancelar incluida la mora, aplicando el año exacto y el comercial.
Año exacto.
Valor futuro del crédito: $F = P(1 + i * n)$
$F = \$3,000,000 \bigg(1+\frac{0.15}{365}*275\bigg)= \$3,339,041$
Interés de mora, $I=P*i*n$. La tasa de interés de mora es 1.5 veces la tasa pactada en el crédito, es decir $i\%$ de mora es igual a $15\%*1.5 = 22.5\%$. Además, la mora exacta es de 41 días calendario.
$Imora = \$3,000,000*\bigg(\frac{0.225}{365}\bigg)*41= \$75,822$
La deuda con interés de mora es: $\$3,339,041 + \$75.822 = \$3,414,863$
Año comercial
$F =3,000,000 \bigg(1+\frac{0.15}{360}*270 \bigg)=\$3.337.500$
$Imora=\$3,000,000*\frac{0.225}{360}*40=\$75.000$
La deuda con mora es: $\$3,337,500 + \$75,000 = \$3,412,500$
Los esquemas de amortización son acuerdos entre las partes sobre el método como un prestatario realizará la devolución del capital tomado en préstamo.
Estos acuerdos, que incluyen la forma de calcular y pagar los intereses, son por lo tanto procedimientos para liquidar o "matar" una deuda.
Existen diferentes formas como un agente económico puede devolver el dinero tomado en crédito, tal como realizar un pago único al final del plazo otorga en el que se incluye el capital más los intereses causados, así mismo, por medio de pagos o abonos periódicos, fijos o variables, que incluyen la amortización al capital y los intereses.
En esta parte estudiaremos los esquemas de amortización a interés simple, incluido el caso del interés global.
El pago periódico, que también llamamos abono o cuota y que representamos por la letra mayúscula A, está compuesto por dos elementos. El primero es el interés periódico representado por I, el segundo es la amortización que representamos por la letra mayúscula R. La amortización, es la parte del pago que va directamente a reducir la deuda, a "matar" el préstamo, reduciendo el saldo insoluto hasta hacerlo igual a cero.
Por lo tanto, podemos expresar la siguiente igualdad: A = I + R, y de aquí es claro que R = A - I, la amortización como un remanente de pago. El saldo insoluto es el monto de la deuda pendiente de pago, es el monto de capital tomado en préstamo que aún se debe.
Sistema de amortización por intereses global. En este modelo de amortización, los intereses son globales porque se calculan sobre el capital inicial para todo el plazo otorgado en la financiación, y es distribuido por el total de pagos o cuotas.
Es decir, en el cálculo del pago periódico sólo se suma como intereses una parte alícuota y constante del interés global.
El procedimiento de cálculo del interés global y de los intereses de cada pago, es de la siguiente manera:
Interés global = $P*i*n $ , con $n$ como plazo y cantidad de pagos. Sin embargo, como el pago periódico es $A = I + R$, la parte de los intereses que entra hacer parte del abono es:
$I =\frac{P*i*n}{n}=P*i$
Desde esta manera del cálculo, los intereses de cada pago son una cantidad fija en cada período.
De igual forma, la amortización $R$ también es una cantidad contante y se calcula como:
$$R = \frac{P}{n}$$Los pagos periódicos son, consecuentemente, también fijos, y se calcula como la suma de los dos elementos anteriores descritos, es decir, como $A = I + R $, por tanto: $$\tag{2.23} A = P*i+\frac{P}{n} = P\bigg(i+\frac{1}{n}\bigg) $$

Ejemplo 2.26_ Esquema de amortización con interés global. Suponga que por una financiación de $15,250,850 se cancelan 14 cuotas mensuales al 1.8% por mes. Hallar el pago mensual y hacer el esquema de amortización.
El interés global. $$P*i*n = \$15,250,850*0.018*14 = \$3,843,214.20$$
El interés de cada cuota:
$I=P*i=\$15,250,850*0.018 = \$274,515.30$, suma fija en cada pago.
Amortización fija: $$R=\frac{P}{n} = \frac{\$15,250,850}{14} = \$1,089,346.43$$
Con estos valores, la cuota fija o el pago mensual queda estimado como:
$A =I + R = \$274,515.30 + \$1,089,346.43$
$A = \$1,363,861.73$
Este valor es el mismo si procedemos directamtente con la fórmula (2.23). Veamos: $$A = \$15,250,850\bigg(0.018+\frac{1}{14}\bigg)= \$1,363,861.73$$
Cada mes, y durante 14 meses, se cancela este valor fijo y se aplica en interés y amortización conforme a los cálculos ya obtenidos. Con cada amortización al capital, el valor de la deuda viva, también conocido como saldo insoluto, disminuye hasta hacerse cero con el pago de la cuota 14.
Para calcular el saldo insoluto, procedemos de la siguiente manera:
$S_t =$ Saldo de la deuda una vez realizado el pago o abono $t$
$S_0 $= Saldo inicial de la deuda, valor del préstamo o monto del capital inicial, $P$
$t$=Período específico en el que se hace el abono o se cancela la cuota y es un valor ente 1 y $n$
El saldo insoluto se calcula restando al saldo inicial las amortizaciones realizadas, es decir: $$\tag{2.24} S_t = S_0-t*R, \space o \space también \space S_t = S_0 - t* \frac{P}{n}$$
Por ejemplo, el saldo insoluto de este crédito una vez realizado el pago 10, $(t=10)$, es de: $$S_{10} = \$15,250,850-10*\$1,089,346.43 = \$4,357,385.71$$
En la Tabla 2.1 se presenta el cuadro de amortización de este caso. En la intercepción de la fila 10 con la columna del saldo insoluto, se encuentra el valor calculado como $S_{10}$.
Permítanos realizar dos observaciones a esta tabla 2.1. En primer lugar, se observa que la columna de saldo insoluto se comporta como una serie en progresión aritmética, a medida que $n$ avanza desde 0 hasta 14, y en la que la diferencia común es precisamente la amortización fija. Por ello, si hacemos que $a_1=\$15,250,580$, el último término de la serie $a_{15}=0.0$, la cantidad de datos $n=15$, y la diferencia común $d = -\$1,089,346.43$; el saldo insoluto se puede calcular con la fórmula para hallar en último término de una progresión aritmética, $a_m=a_1+(m-1)d$.
Tabla 2.1 . Esquema de amortización de crédito con interés global
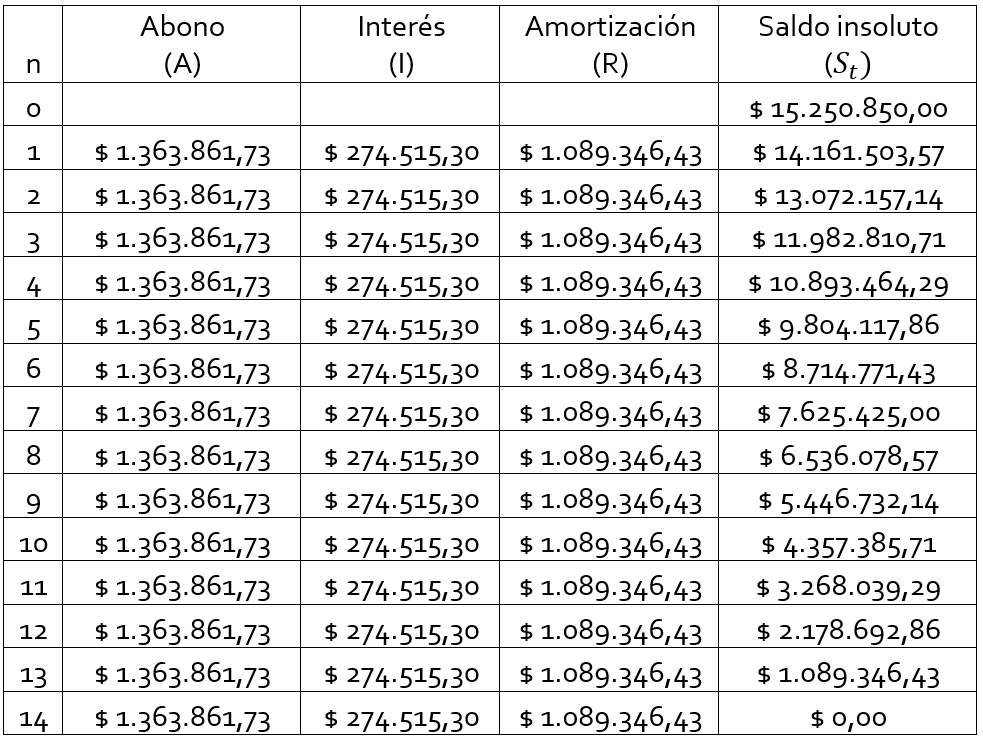
El cálculo para el pago 10, es: $$a_{11}= \$15,250,850+(11-1)*(-\$1,089,346.43)$$ $$a_{11}= \$15,250,850- \$10,893,464.29 = \$ 4,357,385.71.$$
La segunda observación es indicar que este sistema de amortización por interés global implica sobrecostos, y por ello el cobro de una tasa de interés mayor a la originalmente pactado, al cancelar intereses que no corresponden con el saldo de la deuda. Por ejemplo, al cancelarse la cuota 14, se paga por intereses los mismos $\$274,515.30$ aunque el saldo de la deuda es solamente de $\$1,089,346.43$. Este saldo al $1.8\%$ mensual implica intereses de $\$16,608.24$ por lo que el sobrecosto de intereses es de $\$254,907.06$.
El interés fijo global desconoce, al liquidar intereses, el hecho que la deuda se reduce; no cobra interés sobre el saldo o sobre la deuda vida, y ello ocasiona el sobrecosto en esta modalidad de financiación.
Amortización con intereses sobre el saldo. En este sistema de cancelación de deuda, los intereses se calculan sobre el saldo insoluto, y por esta razón, no son fijos sino, al contario, una cantidad que disminuye al ritmo de la amortización. Si es constante, en cambio, la amortización, que se calcula con el mismo método que en el caso del interés global.
Al sumar estos dos componentes para determinar el valor del pago, éste será una cantidad variable y en descenso como consecuencia de la disminución de los intereses liquidados periódicamente.
Para ilustrar este esquema de amortización, utilicemos los datos del ejercicio a interés global, hecho que nos permite realizar comparación entre estos dos sistemas de cancelación de deudas.
Cálculo del primer pago.
Amortización: $$R=\frac{P}{n} = \frac{\$15,250,850}{14}= \$1,089,346.43$$
Es la amortización fija durante el plazo
Interés sobre saldo insoluto: $$I_1 =S _0 *i=\$15,250,850*0.018 = \$274,515.3$$
Monto de la cuota, como: $$A_1 = I_1 + R = \$274,515.30 + \$1,089,346.43 = \$1,363,861.73$$
Saldo insoluto: $$S_1 =S _0 - 1*R = \$15,250,850 - \$1,089,346.43 $$ $$= \$14,161,503.57$$
Cálculo del segundo pago.
Amortización: $R = \$1,089,346.43$
Interés sobre saldo insoluto: $$I_2 =S _1 *i = \$14,161,503.57*0.018$$ $$= \$254,907,06$$
Monto de la cuota: $$A_2 = I_2 + R = \$254,907.06 + \$1,089,346.43 = \$1,353,253.49$$
Saldo insoluto: $$S_2 = S_0 - 2 * R = \$15,250,850 - 2 * \$1,089,346.43$$ $$= \$13,072,157.14$$
Cálculo del tercer pago.
Amortización: $$ R = \$1,089,346.43$$
Interés sobre saldo insoluto: $$I_3 =S _2*i = \$13,072,157.14*0.018 = \$235,298.83 $$
Monto de la cuota: $$A_3 = I_3 + R = \$235,298.83 + \$1,089,346.43 = \$1,324,645.26$$
Saldo insoluto: $$S_3 = S_0 - 3*R= \$15,250,850-3*\$1,089,346.43$$ $$= \$11,982,810.71$$
Los cálculos proceden de la misma forma hasta llegar al pago 14 con el que se salda la deuda. Para el pago decimocuarto, los cálculos son:
Amortización, $R=\$1,089,346.43$
Interés sobre saldo insoluto, $$I_{14}=S_{13}*i = \$1,098,346.43*0.018 = \$19,608.24 $$
Monto de la cuota, como: $$A_{14}=I_{14}+R = \$19,608.24 + \$1,089,346.43$$ $$ = \$1,108,954.66$$
Saldo insoluto, $$S_{14} =S_0-14 * R = \$15,250,850 - 14* \$1,089,346.43=0,0$$
En la siguiente tabla 2.2 observamos el cuadro de amortización de esta alternativa de liquidación de deuda.
Antes de continuar con las observaciones debemos preguntarnos:¿este esquema es en verdad a interés simple? la inquietud se deja para la reflexión.
Algunas observaciones son las siguientes:
Tabla 2.2. Cuadro de amortización fija con intereses sobre saldo
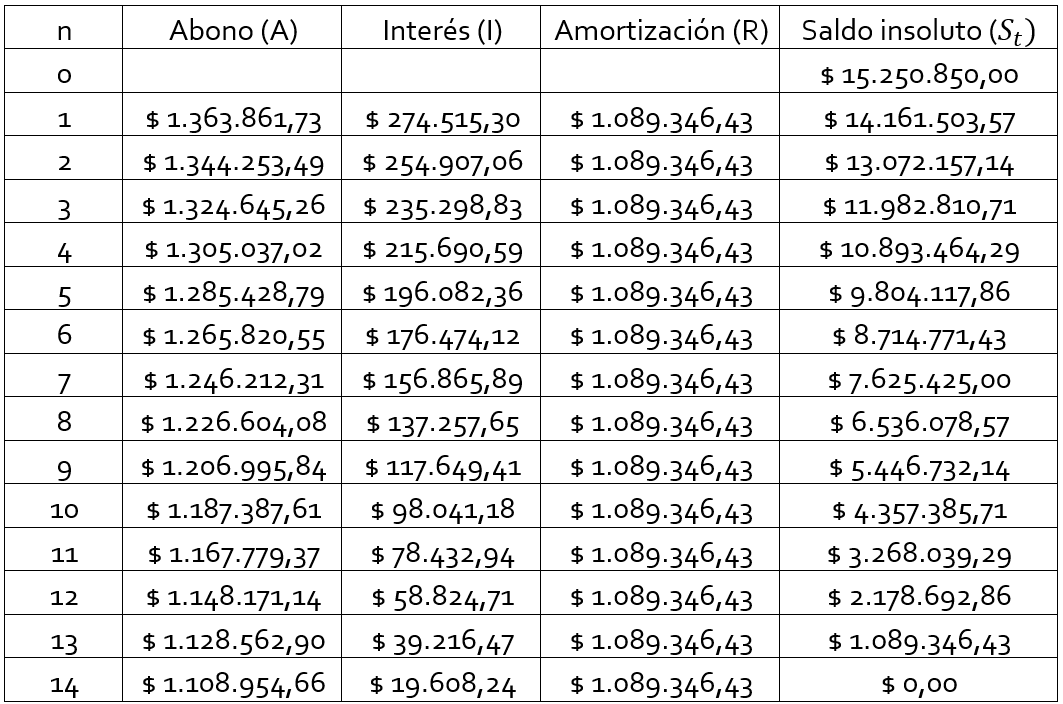
Bajo el esquema de amortización con interés global, los intereses totales alcanzan la suma de $\$3,843,214.20$ mientras que, con el sistema de intereses sobre el saldo insoluto, estos son de $\$2,058,864.75$, significando el primero un sobrecosto representado en la suma de $\$1,784,349.45$
En el sistema de interés sobre el saldo, y por obvia razón, al dividir los intereses de una cuota por el respectivo saldo insoluto, obtenemos siempre la misma tasa de interés del $1.8\%$ mensual, que es la pactada en el crédito; por ejemplo, si tomamos los intereses de la cuota 14, de $\$19,608.24$ y los dividimos por el saldo respectivo de $\$1,089,346.43$ el resultado es $1.8\%$.
En cambio, esto no ocurre en el esquema por interés global; por ejemplo, si relacionamos los valores de la cuota catorce, interés fijo de $\$274,515.30$ sobre el mismo saldo, tenemos una tasa del $25\%$ mensual, representando en este mes un sobrecosto exagerado.
Del procedimiento utilizado para el cálculo de la cuota de cada mes considerando intereses sobre el saldo, extraemos un método general para este modelo de amortización. El cálculo de cualquier cuota t es: $$ \tag{2.25} A_t=\big(S_0-(t-1)R\big)*i+R $$
Recordando que $S_0$ es el capital inicial $P$, y $t=1,2,3...n$.
El cálculo de la primera cuota es:
$A_1=[S_0-(1-1)R]*i+R$
$A_1=[S_0-(0)R]*i+R$
$A_1=S_0*i+R $. Y es la misma fórmula usada en el cálculo de la cuota por interés global: $$A_1 = \$15,250,850*0.018 + \$1,089,346.43 = \$1,346,861.73$$
El cálculo de la décima cuota es:
$A_{10}=[S_0-(10-1)R]*i+R$
$A_{10}=[S_0-(9)R]*i+R$ $$A_{10}=(\$15,250,850 - 9*\$1,089,346.43)*0.018 + \$1,089,346.43$$ $$A_{10}=\$1,187,387.61$$
Valor que se puede constatar en la tabla 2.2
Una última observación consiste en transformar este sistema de cuota variable con interés sobre saldo, a un sistema de cuota fija, aprovechando algunas particularidades que se observan en la tabla 2.2, concretamente en la columna de los intereses, dado que ésta se comporta como una progresión aritmética con diferencia común igual a $\$-19,608.24$.
Empero hay algo más, obsérvese que esta diferencia común es exactamente, pero con signo contrario, a los intereses de la última cuota, que se obtienen de multiplicar el saldo anterior, que es igual a la amortización de la última cuota, por la tasa de interés $(\$1,089,346.43*0.018 = \$19,608.24)$. Ahora bien, si invertimos el orden de la columna de los intereses, es decir escribiendo la serie de menor a mayor, la diferencia común de los datos sigue siendo el mismo valor, aunque ahora positiva.
Este evento nos permite identificar como primer valor de la serie, $a_1 = \$19,608.24$ , además de expresar a la diferencia común como: $d=R*i$. De esta manera podemos concluir que $a_1=d=R*i$.
Sabemos que la suma de $m$ términos en progresión aritmética, haciendo en esta ocación $m=n$, está dada por:
$$S_n = \frac{n}{2} \bigg[2a_1+(n-1)d\bigg]$$
Y si aplicamos las conclusión anterior:
$$S_n = \frac{n}{2} \bigg[2R*i+(n-1)R*i\bigg]$$La fórmula para la suma de los intereses pagados en total por el sistema de interés sobre el saldo es: $$S_n=\frac{n}{2} \bigg[R*i(n+1)\bigg]$$
En el ejercicio que traemos, la suma de dichos intereses son en total de: $$S_{14} = \frac{14}{2} \bigg[\$1,098,346.43*0.018(14+1)\bigg]= \$2,058,864.75$$
Recordemos que $R=P/n$. Aplicando esta expresión en la fórmula anterior de suma, tenemos: $$S_n=\frac{n}{2} \bigg[\frac{P}{n}*i(n+1)\bigg]$$ $$S_n = P\bigg[\frac{(n+1)i}{2} \bigg]$$ $$S_{14}= \$15,250,850 \bigg[\frac{(14+1)*0.018}{2}\bigg] = \$2,058,864.75$$
Ambos modelos nos arrojan igual valor de intereses.
Ahora bien, si dividimos este monto de intereses por n=14 tendríamos un valor igual para cada cuota de intereses como parte alícuota del total y, a su vez, si a este último valor le sumamos la amortización constante, nos da como resultado la cuota fija buscada.
Es decir, y en general: $$A=\frac{S_n}{n}+R$$ $$A=\frac{S_n}{n}+\frac{P}{n}$$ $$A=\frac{[P(n+1)i]}{2n}+\frac{P}{n}$$ $$A=\frac{P(n+1)i+2P}{2n}$$ $$\tag{2.26} A=P \bigg[\frac{(n+1)i+2}{2n} \bigg]$$
Con esta última fórmula, el valor de la cuota fija es: $$A = \$15,250,850 \bigg[ \frac{(14+1)*0.018+2}{2*14}\bigg]= \$1,236,408.20$$
O también, como $R=\frac{P}{n}$, entonces: $$\tag{2.27} A = R \bigg[\frac{(n+1)i+2}{2}\bigg]$$ $$A = \$1,089,346.43 \bigg[\frac{(14+1)*0.018+2}{2}\bigg]= \$1,236,408.20$$
De esta cuota, son por intereses la suma de: $$I=\frac{\$2,058,864.75}{14}=\$147.061,77$$
Amortización: $R = A-I$ $$R = \$1,236,408.20 - \$147,408.77 = \$1,089,346.43$$
El esquema de amortización se presenta en la siguiente tabla 2.3.
Tabla 2.3. Sistema de amortización cuota fija
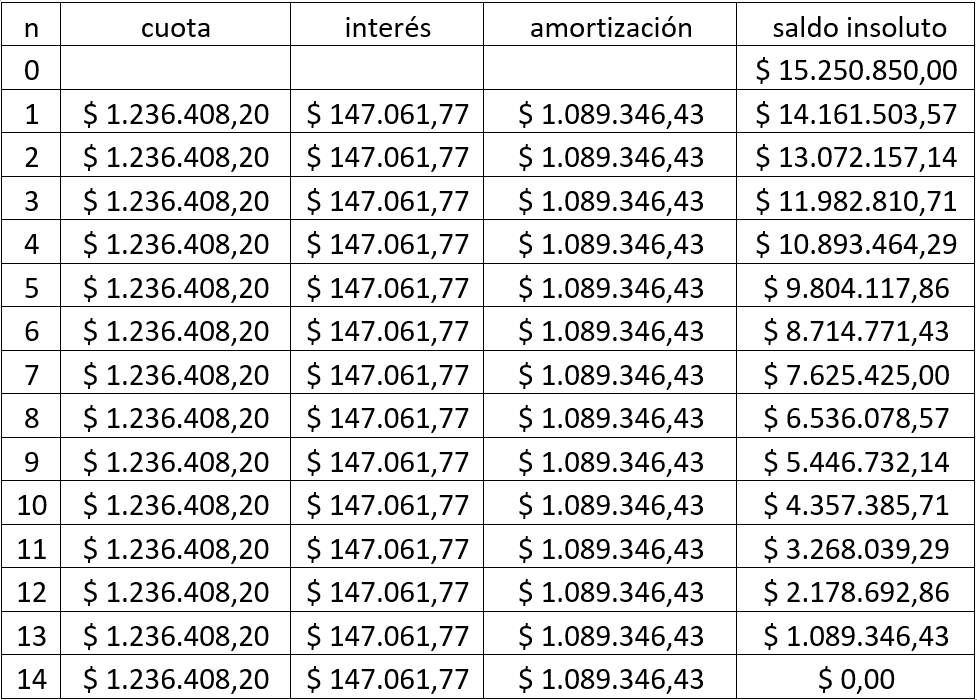
Una operación de inversión o crédito se realiza bajo la modalidad de interés compuesto cuando los rendimientos (o intereses) computados en un período se cargan al capital y generan rendimientos (intereses) en el período inmediatamente siguiente.
Esta operación, de sumar rendimientos al capital, se denomina capitalización, y no es más que la reinversión de los rendimientos. Lo particular de la capitalización compuesta consiste en que, en este caso, no solo el capital inicial genera rendimientos, sino también los rendimientos acumulados de períodos anteriores.
Así entonces, con la reinversión de los rendimientos (intereses), estos son convertidos a capital y generan así rendimientos; en interés compuesto existen rendimientos (intereses) sobre los rendimientos (intereses).
En la conversión de los rendimientos o intereses a capital es necesario indicar, no solo el momento preciso en el que se hace el cálculo y se cargan los intereses al capital (el período de capitalización), sino también la tasa de interés y la modalidad de capitalización. En cuanto a la modalidad, ésta es vencida si la capitalización ocurre al final del período de capitalización, es de forma anticipada si se da al inicio del período de capitalización, o es continua si ésta sucede en cada instante en el tiempo comprendido por el plazo de la operación.
Las formas de capitalización vencida y anticipada se comportan de manera discreta, la última se desenvuelve a tiempo continuo.
En este capítulo estudiaremos estas tres modalidades de capitalización en el marco del análisis del valor del dinero en el tiempo a través del valor futuro de un capital financiero, valor este realizado con un pago único al vencimiento o al final del plazo acordado.
En el cálculo del valor futuro pagó único de un capital financiero con capitalización vencida, la liquidación y suma del interés al capital ocurre al final del período de capitalización. Veamos el siguiente ejemplo.
A un amigo le facilitamos en préstamo la suma de 8,000,000 de pesos al 12% anual vencido con plazo de 6 años. ¿Cuánto debe cancelar en total y en intereses nuestro amigo al final de dicho plazo?
Desarrollamos el caso desde el punto de vista de nuestro amigo, por lo que hablaremos de intereses, no de rendimientos. Los datos y las incógnitas son los siguientes:
$P=8,000,000$
$i=12$% anual
$n=6$ años
capitalización año vencido
$F=?$
$I=?$
En el enunciado del ejercicio el período de capitalización es el año y la modalidad vencida, información resumida en la tasa de interés. Esta información nos dice que al final de cada uno de los seis años, se va a liquidar y capitalizar intereses, al 12% por año. El diagrama de caja del ejercicio lo podemos observar en la siguiente figura 3.1, en el que cada asterisco indica el momento de capitalización al final de cada año.
El cálculo de intereses y del valor futuro lo desarrollamos paso a paso en los primeros tres años para luego generalizar y obtener el modelo que posibilite hallar el valor buscado al vencimiento.
Los intereses y el valor futuro al final del año uno, son:
$I_{1}=P*i$
$I_{1}=8,000,000*0.12$
$I_{1}=960,000$
$F_{1}=P+I$
$F_{1}=8,000,000+960,000$
$F_{1}=8,960,000$
Los intereses del primer año son de 960,000 pesos, y el monto de la deuda de nuestro amigo, el valor futuro al final de año uno, es de 8,960,000 pesos.
El valor futuro acumula los intereses, pero este hecho ocurre al vencerse el período de capitalización; el resultado es la formación de un nuevo capital que, comparado con el caso de interés simple, hasta este momento no hay diferencia entre ambas formas de valoración.
Montos del segundo año.
$I_{2}=P*i$
$I_{2}=8,960,000*0.12$
$I_{2}=1,075,200$
$F_{2}=P+I$
$F_{2}=8,960,000+1,075,200$
$F_{2}=10,035,200$
Hemos utilizado la misma fórmula para calcular los intereses y es correcto porque el capital ha cambiado, se ha formado un nuevo capital. Para este año dos, el capital inicial tiene acumulado los intereses del año uno, es decir, tenemos un nuevo monto de capital. Los intereses para el año dos no se calculan sobre el principal o capital inicial, sino incluyendo los intereses del año anterior.
En el segundo año se liquidan y capitalizan intereses por 1,075,200 pesos y de éstos 960,000 pesos son del capital inicial y el resto, 115,200 pesos son los intereses de los intereses capitalizados el primer año, es decir el 12% de 960,000. Es a partir del segundo año cuando los intereses vencidos generan intereses y el valor futuro compuesto se diferencia del valor futuro simple. La deuda al final del segundo año asciende a 10,035,200 pesos, de cuyo monto 2,035,200 pesos son de intereses acumulados en dos años, y de este último valor,como ya sabemos, 115,200 son intereses de los intereses.
Montos del tercer año
$I_{3}=10,035,200*0.12$
$I_{3}=1,204,224$
$F_{3}=10,035,200+1,204,224$
$F_{3}=11,239,424$
De igual manera, los intereses del año tres son de 1,204,224, y de estos 960,000 corresponden a intereses del capital inicial y el excedente, de 244,224, representan el 12% de los intereses capitalizados en los dos años anteriores(es decir, 2,035,200*0.12).
Así mismo, en el año tres el saldo la deuda de nuestro amigo es de 11,239,424 y de ellos $3,239,424 son intereses acumulados.
De este último valor, los intereses del capital inicial son de 2,880,000 y 359,424 son intereses generados por los intereses capitalizados a la misma tasa de interés.
Como la diferencia del valor futuro en un instante $F_n$ con respecto al valor futuro inmediatamente anterior $F_{(n-1)}$ son los intereses acumulados por el primero, esta situación posibilita un método adicional para determinar los intereses computados y cargados al capital en cada período n en específico. Por ejemplo, si en este ejercicio restamos al valor futuro del año tres el valor futuro del año dos, obtenemos los intereses que fueron capitalizados en el año tres, esto es:
$$I_{3}=F_{3}-F_{2}$$ $I_{3}=11,239,424-10,035,200$Generalizando esta última observación, de la que más adelante deducimos una fórmula para hallar los intereses computados y cargados en un instante n, tenemos que:
$$I_{n}=F_{n}-F_{(n-1)}$$El proceso de cálculo se desarrolla de igual manera hasta el año seis concluyendo con la estimación del valor futuro buscado. En la Tabla 3.1 se presentan los cálculos para el plazo completo, de ella extraemos las siguientes conclusiones:
A partir de su valor inicial, conforme se avanza en el plazo n, el capital es un monto variable y creciente; este comportamiento es resultado de la acumulación de los intereses, que ocurre al final de cada año por su naturaleza vencida.
De igual manera, los intereses son variables y crecientes; como éstos son el 12% de un capital creciente, su monto presenta una tendencia a aumentar conforme al capital.
| n | Capital | Interés | Futuro |
|---|---|---|---|
| 0 | $8,000,000 | $0.00 | $8,000,000 |
| 1 | $8,000,000 | $960,000 | $8,960,000 |
| 2 | $8,960,000 | $1,075,200 | $10,035,200 |
| 3 | $10,075,200 | $1,204,224 | $11,239,424 |
| 4 | $11,239,424 | $1,348,731 | $12,588,155 |
| 5 | $12,588,155 | $1,510,579 | $14,098,733 |
| 6 | $14,098,733 | $1,691,484 | $15,790,581 |
En estos cálculos se supone entonces que la capitalización es inmediata y a la misma tasa. El supuesto de reinversión a la misma tasa está implícito en estos cálculos
El valor futuro es la suma de 15,790,581 de pesos de los cuales 7,790,581 de pesos corresponden a los intereses acumulados en el plazo. Este valor de los intereses acumulados se obtiene al restar del valor futuro final el capital inicial, esto es: $I=F-P$
Al capitalizar los intereses o rendimiento de las inversiones, esta práctica asegura el reconocimiento del valor del dinero en el tiempo en los intereses y la pérdida de poder adquisitivo, hecho que no ocurre en el interés simple.
Para deducir la fórmula general aplicada en el cálculo del valor futuro pago único al final del plazo, detengámonos en la última columna de la tabla 3.1.
Del comportamiento del valor futuro a medida que se avanza discretamente desde el instante cero al año seis, se observa que este
se comporta en el tiempo n como una serie en progresión geométrica (Ver en anexo A progresión geométrica).
En este caso identificamos una razón común de 1.12, que podemos escribir como $(1+0.12)$ siendo el 0.12 la tasa de interés, por lo tanto, la razón en general es $(1+i)$ , de uno más la tasa de interés. Bajo este patrón o característica de razón común, se afirma en consecuencias que cualquier valor de la columna indicada, excepto el primero, es igual al valor anterior multiplicado por 1.12. De este hecho, e identificando $a_{1}=8,000,000$, y a la cantidad de datos $m=7$, el valor futuro lo podemos calcular con la fórmula que permite hallar el término m de una progresión geométrica, es decir con:
$$a_{m}=a_{1}*r^{m-1}$$Veamos:
$a_{7}=8,000,000*(1+0.12)^{7-1}$Por lo tanto:
$$a_{m}=F$$ $$a_{1}*r^{m-1}=P*(1+i)^{n}$$Debe comprenderse que la variable n de la fórmula de futuro es el plazo dado de 6 años, exponente que en el proceso de deducción resulta de restarle uno a la cantidad de datos de la serie, esto es, $n=m-1$, con los valores concretos, 6=7-1.
El futuro compuesto vencido, fórmula que se deduce bajo el concepto de reinversión de intereses, se calcula por lo tanto por:
$$F=P(1+i)^{n}(3.1)$$Ecuación en la que el capital crece de forma exponencial con base $(1+i)$ y exponente $n$, contrario al valor futuro simple cuya ecuación genera una línea recta indicando crecimiento lineal o en progresión aritmética.
De la ecuación (3.1) y un poco de matemáticas operativas, se deducen las siguientes fórmulas que dan lugar a problemas nuevos.
Cálculo del valor presente o el capital inicial, conocido el valor futuro. A la operación de trasladar un valor futuro al presente, también se le denomina actualizar o descontar.
$$P=\frac{F}{(1+i)^{n}}(3.2)$$ $$P=F(1+i)^{-n}$$Cálculo de la tasa de interés que hace equivalentes el valor presente de un capital con su valor futuro, siendo el período de interés el indicado por la unidad de tiempo del plazo $n$.
$$i=\sqrt[n]{\frac{F}{P}}-1(3.3)$$Cálculo del plazo acordado en la operación financiera. El resultado es expresado en la unidad de tiempo que acompaña a la tasa de interés (el período de interés).
Cálculo de los intereses acumulados al final del plazo. Si $I=F-P$, y reemplazamos $F$ por su equivalente de (3.1) nos da que los intereses se pueden calcular como:
$$I=P(1+i)^{n}-P$$Al tomar factor común P, dicha expresión algebraica queda como:
$$I=P\left [ (1+i)^{n}-1 \right ](3.5)$$Cálculo de los intereses a capitalizar en un instante n en específico. Anteriormente indicamos que:
$$I_{n}=F_{n}-F_{n-1}$$Esta expresión es equivalente a:
$$I_{n}=P(1+i)^{n}-P(1+i)^{n-1}$$Tomando factor común $P(1+i)^n$ y simplificando:
$$I_{n}=P(1+i)^{n}\left [ 1-(1+i)^{-1} \right ]$$ $$I_{n}=P(1+i)^{n}\left [ 1-\frac{1}{(1+i)} \right ]$$Dado que el interés a capitalizar en un período $n$ se obtienen como la diferencia entre el valor futuro $n$ y el valor futuro inmediatamente anterior $(n-1)$, esto es, como el margen entre estos dos valores futuros, a los intereses calculados por la ecuación (3.5.1), también se le denomina interés marginal (Plaza Vidaurre, 2012) .

Ejemplo 3.1_ Cálculo del valor futuro y de los intereses acumulados. Un empleado de la empresa Logística a su Servicios S.A. logró un préstamo de 1,500,000 pesos para ser cancelado exactamente dos años después al 7.5% anual vencido con un pago único al final del plazo. Hallar el monto total a cancelar, el valor de los intereses acumulados al cabo del plazo, y los intereses computados y cargados al capital en el año dos.
En la figura 3.2 tenemos el capital en el instante cero y debemos hallar su valor equivalente en dos años al 7.5% anual, por medio del cálculo del valor futuro.
Con la fórmula (3.1)
$F=P\left ( 1+i \right )^{n}$Significa que con el acuerdo entre las partes sobre el plazo y la compensación por valor del dinero en el tiempo, representada por la tasa de interés, el capital inicial de 1,500,000 pesos es equivalente en dos años a 1,733,437.50 pesos.
En cuanto a los intereses acumulados al final del plazo , con la ecuación (3.5):
$$I=P\left [ \left ( 1+i \right )^{n}-1 \right ]$$Estos son de:
A igual resultado se llega si el procedimiento adoptado para el cálculo es restar al monto final el capital inicial.
Los intereses correspondientes y capitalizados en el año dos son:
$$I_{n}=P\left ( 1+i \right )^{n-1}*i$$ $I_{2}=1,500,000\left ( 1+0.075 \right )^{2-1}*0.075$
Ejemplo 3.2_ Cálculo del valor presente o capital inicial. La vecina de la vereda La María, Adíela Agudelo, le comenta a una compañera de trabajo que por un crédito en efectivo pagó al cabo de tres años la suma de 9,840,142.70 de pesos pues había acordado cubrir una tasa de interés del 5.5% anual vencida. Su amiga le pregunta ¿Y de cuánto fue el préstamo?
$F=9,840,142.70$
$n=3$ años
$i$%=$5.5$% anual
$P=?$
Para la solución, reemplazamos los valores conocidos en ecuación (3.2).Ver la figura 3.3

Ejemplo 3.3_ Cálculo de la tasa de interés. Un inversionista de bolsa destina 150,000,000 de pesos para la compra de acciones de una sociedad anónima y al cabo de cuatro años y medio las vende en la suma de 200,500,000 pesos. ¿Qué tasa de rentabilidad anual obtuvo?, suponga el no pago de comisiones y otros gastos.
$F=200,500,000$
$P=150,000,000$
$n= 4.5$ años
$i$%=?
La unidad de tiempo de la tasa de interés, el período de interés, es la misma del plazo n, el año.
Para resolver el problema recurrimos a la ecuación (3.3). Esto es:
$i=\sqrt[n]{\frac{F}{P}}-1$
La tasa de interés del 6.66% anual hace equivalente a 150,000,000 de pesos de hoy con 200,500,000 pesos de dentro de 4.5 años. Significa entonces que dichos valores en pesos representan para las partes involucradas en la operación de compra-venta igual valor económico.

Ejemplo 3.4_ Cálculo del plazo en la operación financiera. La compañía de servicios ambientales “Ciudades sostenibles” destina un capital P para la adquisición de activos fijos y en capital de trabajo. La meta de rentabilidad anual es de 12% sobre la inversión total, recursos que destina a la reinversión en la compañía.
De cumplirse esta expectativa, ¿en cuánto tiempo el capital acumulado en ella es igual a cinco veces el capital inicial?
$P=$ Es el capital inicial invertido, que no especifica un monto.
$F=5P$. El capital acumulado es el valor futuro del capital inicial y alcanza un valor de 5 veces el principal.
$i$%=12% anual.
$n=?$ La unidad de tiempo del plazo es el año, correspondiente al de la tasa de interés.

Para resolver la pregunta recurrimos a la ecuación (3.4)
$$n=\frac{ln\left ( \frac{F}{P} \right )}{ln(1+i)}$$ $$n=\frac{ln\left ( \frac{5P}{P} \right )}{ln(1+0.12)} =14.2 \space años$$
Ejemplo 3.5_ Cálculo del monto de intereses. El emprendimiento en spin-off de una institución universitaria de la ciudad determina la inversión total en un monto de $50,000,000 con la expectativa de generar rendimientos del 20% promedio anual sobre dicha inversión. ¿A cuánto asciende los rendimientos acumulados en los primeros cinco años al mantener sin cambios el capital inicial invertido? ¿de cuánto fueron los rendimientos en el año cinco?
Las preguntas en este problema son por los rendimientos (intereses), por ello utilizamos las ecuaciones (3.5) y (3.5.1).
$P=50,000,000$
$i$%=$20$% anual
$n=5$ años
$I=?$
Rendimiento total
$$I=P\left [ \left ( 1+i \right )^{n}-1 \right ]$$$I=50,000,000\left [ \left ( 1+0.20 \right )^{5}-1 \right ]$
$I=74,416,000$
Rendimientos del año cinco.
$$I_{n}=P\left [ \left ( 1+i \right )^{n-1}*i \right ]$$
$I_{5}=50,000,000\left [ \left ( 1+0.20 \right )^{5-1}*0.20\right ]$
$I_{5}=20,736,000$
En todos los ejercicios desarrollados hasta el momento hemos utilizado una ecuación directa para su solución.
Otra característica ha sido que en los enunciados de los problemas, la capitalización de intereses ha sido año vencido, y tanto el plazo y la tasa de interés son expresados en esa misma unidad de tiempo. Sin embargo esto no siempre es así, al contrario, es más frecuente que la capitalización adopte períodos que son fracciones de año, por ejemplo, mes vencido, trimestre vencido, semestre vencido, etc.
La capitalización de rendimientos con períodos que son fracción de años nos implica nuevas condiciones que entramos a estudiar desde este momento, continuando con la capitalización vencida.
Partamos de la situación en la que una Cooperativa de ahorros ofrece la posibilidad de realizar un depósito de 830,500 de pesos con término fijo de cinco años, operación a la que se cancela una tasa de interés del 8.5% anual semestre vencido. Hallar el valor futuro de esta operación.
En este problema observamos que el plazo y la tasa de interés están expresados en año, en cambio la capitalización es semestre vencido. Esta condición financiera del problema nos indica que en cada año del plazo, se liquida y carga intereses al capital dos veces, una vez por semestre. Observamos además que al enunciarse la tasa de interés inmediatamente se identifica el período y la modalidad de capitalización.
Estos elementos los debemos considerar en la solución del problema, evento que implica la definición de nuevos términos y símbolos.
Los nuevos términos y símbolos son:
Por ejemplo, el semestre está dos veces en el año.
Esta tasa es igual a la división de la tasa nominal anual por la frecuencia de capitalización, esto es $iv=J/k$. En el problema que traemos la tasa de interés del semestre (periódica) es $iv=0.085/2$=$0.0425$=$4.25$%. De lo anterior, es obvio además que $J=k*iv$
Por último, debemos transformar el plazo enunciado en años y expresarlo también en la misma unidad de tiempo del período de capitalización.
Si identificamos al plazo en años con $n$, para convertir a períodos de capitalización sólo basta con multiplicarlo por la frecuencia de capitalización, es decir $n*k$.En este ejercicio el plazo convertido a semestres es por lo tanto: 5 años * 2 semestre/año=10 semestres.
De lo descrito concluimos que aquellas variables que tiene asociada en su expresión una unidad de tiempo, como son el plazo y la tasa de interés, se deben ajustar al período de tiempo que indique la capitalización, si ellas no están expresadas en términos de esta última.
$P=830,500$
$J=8.5$% s.v.
$n=10$ años
$F=?$
Capitalización semestre vencido (c.s.v.)
Frecuencia de capitalización $k=2$
Se liquidan intereses y se suman al capital dos veces al año. Por ello debemos modificar las variables tasa de interés y plazo como ya se indicó, es decir:
$iv=0.085/2$=$0.0425$=4.25% semestre
Plazo: $n*k=5*2$=$10$ semestres
Al tener las variables expresadas en semestres procedemos a realizar el cálculo solicitado. El valor futuro es:
$F=830,500( 1+0.045)^{10}$Si deseamos hacer el ajuste de las variables indicadas directamente en (3.1), la fórmula inicial se transforma en:
$$F=P(1+\frac{J}{k} )^{n*k}$$Esta no es una fórmula nueva, simplemente especifica que debemos realizar el ajuste en las variables indicadas en conformidad con la unidad de tiempo de la capitalización.
Utilizando los datos iniciales del problema, preguntemos ahora ¿qué le sucede al valor futuro de esta operación financiera si la frecuencia de capitalización es trimestral, mensual?, es decir, ¿qué tendencia muestra el valor futuro, y con él los intereses, cuando crecemos la frecuencia de capitalización y las demás variables permanecen constantes?
Resolvamos asumiendo capitalización trimestre vencido (c.t.v.), con $k=4$
$F=830,500(1+\frac{0.085}{4} )^{5*4}$Resolvamos ahora para capitalización mes vencido (c.m.v.), con $k=12$
$F=830,500\left ( 1+\frac{0.085}{12} \right )^{5*12}$En este escenario, son constantes el capital, la tasa nominal anual y el plazo en años.
Sólo hemos cambiado la frecuencia de capitalización; bajo este marco estamos seguros de que los cambios en el valor futuro al final del plazo se deben exclusivamente a los cambios en la frecuencia de capitalización.
El valor futuro describe una tendencia creciente cuando la frecuencia de capitalización crece, y las demás variables permanecen constantes (los economistas identifican este tipo de análisis con la expresión “ceteris paribus”), por lo tanto, existe una relación directa entre $F$ y $k$
En la Tabla 3.2 se presentan los resultados para el futuro y los intereses con diferentes frecuencias de capitalización, usando los mismos datos.
| Capitalización | k | Futuro | Interés |
|---|---|---|---|
| Anual | 1 | $1,248,786.88 | $418,286.88 |
| Semestral | 2 | $1,259,216.12 | $428,716.12 |
| Cuatrimestral | 3 | $1,262,480.03 | $432,340.03 |
| Trimestral | 4 | $1,264,681.10 | $434,181.10 |
| Mensual | 12 | $1,268,423.15 | $437,923.15 |
| Quincenal | 24 | $1,269,371.40 | $438,871.40 |
| Semanal | 50 | $1,269,866.54 | $439,233.54 |
En la siguiente Figura 3.7 se presenta la gráfica de la relación entre el valor futuro vencido y la frecuencia de capitalización, en la que la pendiente de la curva positiva es expresión de dicha relación directa:
Ello implica que si k crece el valor futuro vencido crece, y si k disminuye el valor futuro disminuye.
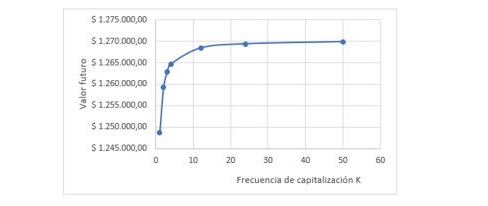
En los rendimientos de una inversión, o en los costos de un crédito, el ascenso de la frecuencia de capitalización tiene un efecto positivo sobre los resultados de estas dos operaciones financieras.
Con valoración anticipada queremos indicar que los rendimientos de una inversión o los intereses de un préstamo se liquidan y se suman al capital al inicio del período de capitalización.
El valor futuro sigue siendo un pago único que ocurre al final del plazo otorgado. En esta situación, el proceso de generación de intereses sobre intereses si inicia más prontamente que en el vencido, generando diferencia en el monto final de los intereses acumulados al final de un plazo.
En la figura 3.8 presentamos la situación del valor futuro bajo la modalidad anticipada del mismo problema de la figura 3.1.
Al comparar ambas figuras observamos que con la capitalización anticipada la primera ocurre en el instante cero.

El algoritmo de solución de este caso pasa por hallar inicialmente una tasa de interés vencida equivalente a la tasa de interés anticipada y con ésta calculamos el valor futuro pago único al final del plazo.
Este procedimiento luego nos permite generalizar el resultado obtenido y así deducir la fórmula que directamente facilite la determinación del valor futuro anticipado, esto es, sin hallar tasa vencida equivalente sino utilizando la tasa de interés anticipada explícitamente.
Más adelante, en este mismo capítulo, establecemos una relación entre este tema de capitalización anticipada y el descuento compuesto.
Permítanos entonces, antes de entrar a resolver el problema de la figura 3.8 y obtener las fórmulas para el cálculo directo del valor futuro y de los intereses anticipados, partir de la siguiente situación.
Supongamos que nos facilitan 1,000,000 de pesos para cancelarlo dentro de seis meses al 8.5% semestre anticipado; supongamos además que los intereses los pagamos, es decir, prescindimos por el momento del supuesto de pago único al final del plazo. Ver la Figura 3.9 en la que la tasa de interés periódica anticipada (la del semestre) se representa por $ia$.
Si se recibe un capital inicial 1,000,000 de pesos en préstamo y pagamos anticipadamente 8.5% de intereses en el semestre, equivalente a 85,000 pesos, se nos presenta la siguiente situación. En primer lugar, al final del plazo sólo debemos de cancelar el capital inicial de 1,000,000 de pesos.
En segundo lugar, y dado el supuesto de cancelar los intereses anticipados, en el mismo momento de realizar la operación financiera ocurre simultáneamente una entrada de dinero, el préstamo recibido, y una salida de dinero, por el pago de los intereses anticipados.

Este evento, de una entrada y simultáneamente darse una salida, permite que nos refiramos a la noción de valor efectivo (VE), dado que los intereses anticipados pagados actúan como un descuento (recordemos las nociones de descuento y valor efectivo.
Dichas nociones ya fueron estudiadas en el capítulo anterior en el caso simple.
En la fecha focal cero, la situación es la de recibir en términos efectivos la suma de 915,000 pesos para cancelar al final del plazo de seis meses, el monto de un millón de pesos.
Con un valor inicial o valor presente efectivo de 915,000 pesos y un valor final a pagar de 1,000,000 de pesos en un semestre hagámonos la siguiente pregunta ¿qué tasas de interés hace equivalente a estos dos valores en un semestre?
Nótese que el procedimento ejecutado hasta el momento, así como en el planteamiento de la pregunta, nos han conducido a un esquema en modalidad vencida, por lo que en esta solución inicial aplicamos la ecuación (3.1.).
Esto es:
$$F=P\left ( 1+iv \right )^{n}$$Resolviendo:
$1,000,000=915,000\left ( 1+iv \right )^{1}$Bajo las condiciones descritas, la tasa de interés periódica del 9.2896% semestral vencida es equivalente a la tasa periódica del 8.5% semestral anticipada.
Esto es, al utilizar la una o la otra en el cálculo del valor futuro al final de plazo, ambas arrojan el mismo valor, como se constata más adelante.
Otra manera de resolver la pregunta anterior es la siguiente:
Si por el préstamo en valor efectivo de 915,000 pesos pagamos 1,000,000 de pesos al final del plazo, de los cuales 85,000 pesos son intereses, la tasa de interés vencida semestral que hace equivalente estos valores, expresada como la relación de los intereses sobre el valor efectivo, es $iv=85,000/915,000$ e igual a $0.092896$, esto es el 9.2896%. Obtenemos la misma tasa periódica vencida.
Dado que ya contamos con esta tasa de interés vencida equivalente pasemos a restituir el supuesto de no pago de los intereses, indicando que son cargados al capital, para calcular el valor futuro pago único al final de plazo en los términos ya estudiados, con el capital original y el mismo plazo.
El valor futuro es:
$$F=P\left ( 1+iv \right )^{n}$$ $F=1,000,000\left ( 1+0.092896 \right )^{1}$Este es el valor futuro con capitalización anticipada que se debe cancelar al final del plazo de un semestre, y es así porque en la tasa de interés periódica semestral, hemos utilizado una tasa vencida equivalente a la anticipada.
¿Cómo se calcula la tasa periódica vencida a partir de una tasa de interés periódica anticipada? Para responder esta cuestión partamos del resultado ya conocido:
$$iv=\frac{85,000}{915,000}=0.092896$$Explicitando la forma de cálculo de los intereses, esta expresión es equivalente a:
$$iv=\frac{1,000,000*0.085}{1,000,000-1,000,000*0.085}=0.092896$$ $$iv=\frac{1,000,000*0.085}{1,000,000(1-0.085)}=0.092896$$ $$iv=\frac{0.085}{(1-0.085)}=0.092896$$Como desde el enunciado del problema que traemos $ia=0.085$, por lo tanto: $$iv=\frac{ia}{(1-ia)}(3.5.2)$$
La ecuación (3.5.2) permite calcular la tasa de interés periódica vencida equivalente a una tasa periódica anticipada.
Un resultado adicional es despejar $ia$ de (3.5.2), para obtener:
$$ia=\frac{iv}{(1+iv)}(3.5.3)$$Esta ecuación es la recíproca a la anterior, es decir, permite hallar la tasa periódica anticipada que es equivalente a una tasa periódica vencida. Ambas ecuaciones nos serán muy útiles en el próximo capítulo.
Pues bien, con estos hallazgos procedemos a concluir con la fórmula que directamente calcula el futuro anticipado.
Hemos obtenido el siguiente resultado:
Fórmula que en general es la ya conocida ecuación (3.1)
$$F=P\left ( 1+iv \right )^{n}$$Ahora bien, como:
$$iv=\frac{ia}{1-ia}$$Por este motivo, (3.1.) es equivalente a:
$$F=P\left ( 1+\frac{ia}{1-ia} \right )^{n}$$Realizando la suma
$$F=P\left ( \frac{1-ia+ia}{1-ia} \right )^{n}$$Concluimos con:
$$F=P\left ( \frac{1}{1-ia} \right )^{n}(3.6)$$ $$F=P(1-ia)^{-n}(3.6.1)$$La ecuación (3.6.) es el resultado pretendido. En esta ecuación ya utilizamos directamente la tasa de interés periódica anticipada. El valor futuro es:
$F=1,000,000(\frac{1}{1-0.085})^{1}$Es decir, el mismo valor ya antes calculado.
Con la ecuación (3.6.1), resolvamos ahora el problema planteado en la figura 3.8. Los datos son:
$P=8,000,000$
i%=12% anual
$n=6$ años
capitalización año anticipado
$F=?$
Como la capitalización es año anticipada, ia=12%, entonces:
$F=8,000,000\left ( 1-0.12 \right )^{-6}=17,226,377.26.$De este valor, son intereses $9,226,377.26 acumulados en seis años.
Con el fin de realizar comparación de resultados con el caso vencido, trabajamos el mismo ejercicio del depósito en la Cooperativa.
Se tiene un capital de 830,500 pesos invertido a cinco años de plazo, y tasa de interés del 8.5% anual. Iniciemos con capitalización semestral anticipada.
Así los datos y sus transformaciones son:
$P=830,500$
$n= 5$ años
$J=8.5$% s.a.
Capitalización semestre anticipado (c.s.a.)
Definimos entonces:
$k=2$ semestres año
$ia=J/k$=$4.25$% semestre. Como en el caso vencido, la periódica anticipada se obtiene dividiendo la nominal por la frecuencia de capitalización:
Plazo: $n*k = 5*2 = 10 \space semestres$
El futuro anticipado es:
$F=830,500\left ( \frac{1}{1-0.0425} \right )^{10}=1,282,188.30$Obsérvese que el plazo y la tasa de interés están dados en la misma unidad de tiempo de la capitalización, son semestrales.
También nótese que si:
$$ia=\frac{J}{k}$$Entonces, la fórmula de futuro anticipado también es igual a:
$$F=P\left ( \frac{1}{1-\frac{J}{k}} \right )^{n*k}$$Para el cálculo de los intereses acumulados en un instante $n$, recordemos que $I=F-P$, y de aquí es claro que:
$$I=P\left ( \frac{1}{1-ia} \right )^{n}-P$$ $$I=P\left [ \left ( \frac{1}{1-ia} \right )^{n}-1 \right ](3.7)$$O también:
$$I=P\left [ \left ( \frac{1}{1-\frac{J}{k}} \right )^{n*k}-1 \right ]$$En el ejercicio que traemos, los intereses cargados al capital al final del plazo son de:
$I=830,500\left [ \left ( \frac{1}{1-0.0425}\right )^{10}-1 \right ]=451,688.30$En la Tabla 3.3 se presentan los cálculos del valor futuro anticipado con diferentes frecuencias de capitalización, ceteris paribus. En todos los casos, el valor futuro anticipado es mayor al futuro vencido (ver estos valores en ejercicio anterior).
| Capitalización | k | Futuro | Interés |
|---|---|---|---|
| Anual | 1 | $1,294,893.84 | $464,393.84 |
| Semestral | 2 | $1,282,188.30 | $451,688.30 |
| Cuatrimestral | 3 | $1,278,144.84 | $447,644.84 |
| Trimestral | 4 | $1,276,157.08 | $445,657.08 |
| Mensual | 12 | $1,272,247.48 | $441,747.48 |
| Quincenal | 24 | $1,271,283.52 | $440,783.52 |
| Semanal | 50 | $1,270,784.35 | $440,284.35 |
En la Figura 3.10 la pendiente negativa de la gráfica entre F y k indica la relación inversa entre estas dos variables.
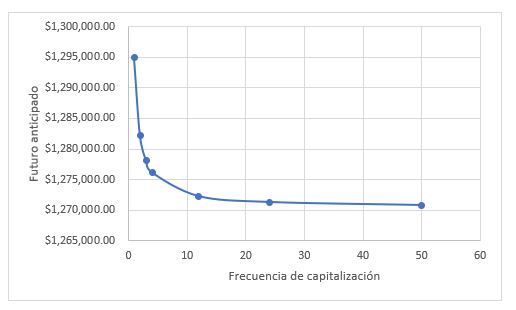
Al crecer la frecuencia de capitalización, hecho que ocurre a medida que pasamos de semestral a cuatrimestral, a trimestral, etc., el valor futuro anticipado se reduce; y viceversa, si disminuye la frecuencia de capitalización, el futuro anticipado crece, ambos ceteris paribus. Esta conclusión es contraria a la del futuro compuesto vencido.
Con la fórmula (3.6) se plantean otros problemas adicionales.
Valor presente de un valor futuro anticipado:
$$P=\frac{F}{\left ( \frac{1}{1-ia} \right )^{n}} (3.8)$$La expresión (3.8) es algebraicamente equivalente a:
$$P=F\left ( 1-ai \right )^{n} (3.8.1)$$Tasa de interés periódica anticipada:
$$ia=1-\frac{1}{\sqrt[n]{\frac{F}{P}}} (3.9)$$O también:
$$ia=\frac{\sqrt[n]{\frac{F}{P}}-1}{\sqrt[n]{\frac{F}{P}}} (3.9.1)$$Cálculo del plazo:
$$n=\frac{ln\left ( \frac{F}{P} \right )}{ln\left ( \frac{1}{1-ia} \right )}=\frac{ln\left ( F \right )-ln\left ( P \right )}{ln\left ( 1 \right )-ln\left ( 1-ia \right )} (3.10)$$Determinación del interés marginal. Si
$$I_{n}=F_{n}-F_{n-1} (3.11)$$Entonces
$$I_{n}=P\left ( \frac{1}{1-ia} \right )^{n}-P\left ( \frac{1}{1-ia} \right )^{n-1}$$En esta ocasión vamos a tomar como factor común el último término del lado derecho de la igualdad.
El lector puede intentar con el mismo método ejecutado en el caso vencido.

Ejemplo 3.6_ Cálculo del valor futuro e intereses. Un ahorrador deposita $10,830,000 en un fondo que reconoce una tasa nominal anual de 5% con capitalización mes anticipado. ¿Cuánto tendrá el ahorrador acumulado en intereses al cabo de dos años y medio?¿a cuánto asciende los intereses cargados al capital en el mes treinta?
$P=10,830,000$
J%=5% m.a.
$n=2.5$ años
I=?
c.m.a.
$k=12$
La solución por medio del valor futuro es:
$F=10,30,000\left ( \frac{1}{1-\frac{0.05}{12}} \right )^{2.5*12}$Por ello los intereses, $I=F-P$, son de $1,445,202.90$ pesos
Resolvamos ahora aplicando una tasa periódica vencida equivalente a la periódica anticipada en la fórmula de valor futuro vencido.
La tasa periódica mes vencido equivalente es:
$$iv=\frac{ia}{1-ia}=\frac{\frac{0.05}{12}}{1-\frac{0.05}{12}}=\frac{0.0041667}{1-.0041667}=0.0041841$$Así $iv$%=$0.41841$% mensual vencido. El futuro es por lo tanto:
$F=10,830,000\left ( 1+0.041841 \right )^{30}=12,275,202.90$Obtenemos igual valor futuro, por lo que los intereses son los mismos de la solución anterior, de $1,445,202.90$ pesos.
Solución del ejercicios por medio de la fórmula para interés acumulado, con ecuación (3.7).
$I=10,830,000\left [ \left ( \frac{1}{1-0.0041667} \right )^{30}-1 \right ]=1,445,202.90$Los intereses computados y cargados en el mes treinta, con (3.12), ascienden a:
$I_{30}=10,830,000\left [ \left ( \frac{1}{1-0.0041667} \right )^{30}*0.0041667 \right ]=51,146.68$
Ejemplo 3.7_ Cálculo del valor presente. Se compra un terreno en el Oriente Antioqueño por un monto de P y se vende al cabo de seis meses por la suma de 1,500,000 de pesos. Si el costo de oportunidad del vendedor del terreno es del 8.5% anual bimestre anticipado ¿en cuánto había comprado éste el terreno?
$F=1,500,000$
$J=8.5$% b.a.
$n=0.5$ años
$P=?$
$ia=2.83$% bimestre anticipado
$plazo=0.5 años*6 bimestres/años=3 bimestres$
Con (3.8), la solución es:
$P=\frac{1,500,000}{\left ( \frac{1}{1-0.0283} \right )^{3}}=1,376,078.38$Con (3.8.1), la solución es:
$P=1,500,000\left ( 1-0.0283 \right )^{3}=1,376,078.38$
Ejemplo 3.8_ Cálculo de la tasa de interés. ¿A qué tasa de interés trimestre anticipado un principal de 15,000,000 de pesos se convierte en 20,000,000 de pesos al cabo de 54 meses?
Con (3.9)
$ia=1-\frac{1}{\sqrt[18]{\frac{20,000,000}{18,000,000}}}$La tasa nominal anual, $J=k*ia$, es de 6.44% t.a.

Ejemplo 3.9_ Cálculo del plazo de la operación financiera. Al vender una casa, la inmobiliaria “El Buen Vecino” recibe un pagaré por la suma de 450,000,000 de pesos para ser cancelado en un plazo $n$ al 6.8% cuatrimestre vencido.
Si el pagaré se liquida por medio de un monto único de 588,873,106 pesos ¿en cuánto tiempo se liquidó éste?
$P=\$450,000,000$
$F=\$588,873,106$
$J=6.8\%\;c.a.$
$ia=2.27\%$ cuatrimestre
$n= \;?$
Con ecuación (3.10):
$n=\frac{ln\left ( 588,873,106 \right )-ln\left ( 400,000,000 \right )}{ln\left ( 1 \right )-ln\left ( 1-0.0226667 \right )}=11.73$ cuatrimestres

Ejemplo 3.10_ Cálculo del plazo. Si un capital financiero de $1$ peso rinde $0.5$ pesos a un costo de oportunidad mensual de 1.2% anticipado ¿En cuánto tiempo se logra dicho rendimiento?
$ia=1.2$% mes
$n=?$
Con (3.7):
$0.5=1\left [ \left ( \frac{1}{1-0.012} \right )^{n}-1 \right ]$
$1.5=\left ( \frac{1}{1-0.012} \right )^{n}$
$1.5=1.01214575^{n}$
$n=\frac{ln\left ( 1.5 \right )}{ln\left ( 1.01214575 \right )}=34$ meses
En esta modalidad los intereses se capitalizan en cada instante durante el tiempo que dura la operación financiera; no es al final ni al inicio de un período de capitalización, sino en cada momento sin interrupción.
Para capturar este fenómeno en la modelación del valor futuro continuo hacemos que la frecuencia de capitalización tienda a infinito ($k→∞$), se incrementa indefinidamente. Si $k$ toma cada vez valores más grandes, los períodos de la capitalización son cada vez más pequeños, siendo casos posibles el día ($k=365$), el minuto ($k=525,600$), el segundo ($k=31,536,000$) o la milésima de segundo. De esta forma el tiempo se hace infinitesimal.
En este apartado trataremos del valor futuro con capitalización continua de una suma de dinero (un stock), sea este un ingreso o un egreso que se comporta de forma discreta y vencida.
Lo que cambia en este caso es la capitalización, que es de naturaleza continua, automática y a la misma tasa de interés.
El valor futuro continuo se realiza con un pago único al final del plazo.La fórmula para el futuro bajo capitalización continua, la obtenemos con el siguiente procedimiento:
Si tenemos la función:
$$f\left ( x \right )=\left ( 1+\frac{1}{x} \right )^{x}$$El límite cuando $x$ tiende a infinito es:
$$\lim_{x\rightarrow \propto }\left ( 1+\frac{1}{x} \right )^{x}=2.7182818=e$$Es decir, el límite de la expresión anterior es el número denominado Euler.
Hemos indicado además que la tasa de interés vencida periódica se calcula como:
$$iv=\frac{J}{k}$$Con esta última expresión, planteamos ahora la siguiente definición: Sea $x$ el inverso de $iv$. Es decir:
$$x=\frac{1}{iv}$$Por lo tanto:
$$x=\frac{1}{\frac{J}{k}}=\frac{k}{J}$$Así mismo tenemos que:
$$k=x*J$$Ahora bien, si $x=\frac{1}{iv}$, entonces $iv=\frac{1}{x}$.
Con esta definición y resultados procedemos a la obtención de lo pretendido, apoyados en la fórmula de compuesto vencido.
$$F=P\left ( 1+iv \right )^{n*k}$$ $$F=P\left ( 1+\frac{1}{x} \right )^{n*k}$$Ecuación que se puede expresar como:
$$F=P\left [ \left ( 1+\frac{1}{x} \right )^{x} \right ]^{n*J}$$Ahora bien, al tomar el límite con $x$ tendiendo a infinito, la función anterior nos queda como:
$$\lim_{x\rightarrow \propto }F=\lim_{x\rightarrow \propto }P\left [ \left ( 1+\frac{1}{x} \right )^{x} \right ]^{n*J}$$Si el límite existe, es la solución para F. Aplicando Euler planteado anteriormente, la función es en consecuencia:
$$F=Pe^{n*J} (3.13)$$Al enunciar que $x$ tiene a infinito, implícitamente estamos indicando que la frecuencia de capitalización $k$ tiende igualmente a infinito, es decir incorporamos en el modelo o ecuación el tiempo continuo, capitalizaciones que son capturadas por Euler ($e=2.7182818$). En la fórmula la tasa de interés pertinente es la nominal.
Con este modelo básico y un poco de matemáticas operativas podemos desarrollar otros problemas.
Cálculo del valor presente:
$$P=\frac{F}{e^{n*J}}=Pe^{-n*J} (3.14)$$Cálculo de la tasa de interés nominal:
$$J=\frac{ln\left ( \frac{F}{P} \right )}{n}=\frac{ln\left ( F \right )-ln\left ( P \right )}{n} (3.15)$$Cálculo del plazo n.
$$n=\frac{ln\left ( \frac{F}{P} \right )}{J}=\frac{ln\left ( F \right )-ln\left ( P \right )}{J} (3.16)$$Cálculo del interés acumulado.
$$I=F-P$$ $$I=Pe^{n*J}-P$$ $$I=P\left [ e^{n*J}-1 \right] (3.17)$$Cálculo del interés marginal. Partiendo de:
$$I_{n}=F_{n}-F_{n-1}$$ $$I_{n}=Pe^{n*J}-Pe^{\left ( n-1 \right )*J}$$Y tomando como factor común a $Pe^{\left ( n-1 \right )*J}$
La ecuación buscada es:
$$I_{n}=Pe^{\left ( n-1 \right )*J}\left ( e^{J}-1 \right ) (3.17.1)$$El lector puede intentar resolver tomando como factor común a $Pe^{n*J}$ y constatar que se llega al mismo resultado.

Ejemplo 3.11_ Cálculo del valor futuro continuo, interés acumulado e interés marginal. Un capitalista ha invertido en capital constante la suma de 45,800,000 pesos y en capital variable la suma de 8,230,548 pesos. Su tasa de ganancias, concepto que en términos modernos sería reemplazado por el de costo de oportunidad, es del 7.2% anual.
Este empresario se pregunta por el valor acumulado en cinco años si capitaliza de forma continua, cuánto interés acumuló en el plazo, y cuánto se liquidó de intereses en el año cinco.
$P=54,030,458$
$J=7.2$% anual
$n=5$ años
$F=?$
Con (3.13):
$F=54,030,548e^{5*0.072}=54,030,548e^{0.36}=77,443,573.73$En la Tabla 3.4 se presenta la evolución del valor futuro continuo en función del plazo y su gráfica en la figura 3.11
Los interés acumulado en los cinco años son:
$I=54,030,548\left ( e^{5*0.072}-1 \right)=23,413,027.73$Intereses liquidados en los 5 años. Con (3.17.):
| n | Capital | Interés | Futuro |
|---|---|---|---|
| 0 | 0 | 0 | $54,030,548 |
| 1 | $54,030,548 | $4,033,669 | $58,064,217 |
| 2 | $58,064,217 | $4,334,804 | $62,399,021 |
| 3 | $62,399,021 | $4,658,420 | $67,057,442 |
| 4 | $67,057,442 | $5,006,196 | $72,063,638 |
| 5 | $72,063,638 | $5,379,936 | $77,443,574 |
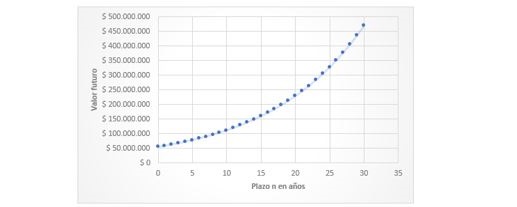

Ejemplo 3.12. Cálculo del valor futuro continuo con datos fracción de año. Resolver el ejercicio anterior suponiendo períodos mensuales. En esta situación debemos expresar el plazo $n$ y la tasa de interés $J$ en equivalentes mensuales.
$iv=\frac{J}{k}=\frac{0.072}{12}=0.006=6.0$% mensual
$Plazo=n*k=5*12=60$ meses
$F=54,030,548e^{60*0.006}=77,443,573.73$Obtenemos el mismo valor
El hecho se explica por lo que ocurre en los elementos que forman el exponente. Obsérvese que al incluir las modificaciones de tasa de interés y plazo en el exponente, la base Euler igualmente queda elevada a 0.36, como en el ejercicio anterior.
Lo que sucede es lo siguiente: Si la tasa de interés periódica mensual se obtiene de $iv=\frac{J}{k}$ (dividimos por $k$), y el plazo transformado a períodos de la tasa de interés es igual a $n*k$ (multiplicamos por $k$), al utilizar estas nuevas variables en la ecuación del valor futuro tenemos que $ F=Pe^{\frac{J}{k}*n*k}$ en la que $k$ divide y luego multiplica, resultando de nuevo $F=Pe^{J*n}$.
Desde el proceso de dedución de (3.13) se comprende que las capitalizaciones están "incluidas" en Euler.
En conclusión, bajo la modalidad continua es posible trabajar los cálculos bajo tasa de interés y plazo expresados en período fracción de año sin alterar el resultado; esto ocurre porque la k que tiende a infinito es capturada en Euler.

Ejemplo 3.13_ Cálculo del valor presente continuo. Para el desarrollo de un proyecto urbanístico, una empresa constructora tiene la opción de adquirir un terreno de 50,000 metros cuadrados dentro de 4 años por un valor de 800,000,000 de pesos. Si en la valoración del terreno se ha tenido en consideración una tasa de 0.5% mensual continua, ¿en cuánto se puede comprar el terreno hoy?
En este ejercicio las unidades de tiempo, el mes para la tasa de interés y el año para el plazo, no coinciden. Bajo la capitalización continua tenemos libre albedrío para determinar en qué unidad de tiempo trabajar, en este caso en meses o en años, dado que el resultado no cambia. Veamos:
Solución en meses
Dada la tasa de interés mensual, convertimos el plazo a meses y obtenemos que es igual a 48. Reemplazando en la fórmula nos da:
$$P=\frac{800,000,000}{e^{0.005*48}}=629,302,289$$Solución en años
Con plazo dado en años, debemos trabajar con la tasa de interés nominal anual, que la calculamos como $J=0.005*12=0.06=6$% anual. Reemplazando de nuevo en la fórmula el resultado es el mismo que en el ejercicio anterior, veamos:
$$P=\frac{800,000,000}{e^{0.06*4}}=629,302,289$$
Ejemplo 3.14_ Tasa de interés nominal. Una persona dispone de un fondo de 5,000,000 de pesos que invierte durante doce meses con el fin de financiar sus vacaciones de fin de año. La inversión realizada bajo capitalización continua liquidó un monto final de 6,200,000 pesos ¿qué tasa de rentabilidad mensual y que tasa nominal anual fue la aplicada en la operación?
$P=5,000,000$
$F=6,200,000$
$n=12$ meses
$i=?$ tasa de interés mensual
$J=?$ tasa nominal anual.
Resolviendo el ejercicio mensualmente con (3.15), la tasa de interés mensual continua es:
$$i=\frac{ln\left ( \frac{6,200,000}{5,000,000} \right )}{12}=0.0179$$Tasa nominal anual continua es:
$J=k*i=12*0.0179=0.2151=21.51$% nominal anual.
Este mismo resultado se logra si en la solución lo hubiéramos trabajado con el año. Veamos:
$$J=\frac{ln\left ( \frac{6,200,000}{5,000,000} \right )}{1}=ln\left ( 1.24 \right )=0.2151$$ $J=21.51$% nominal anual continua.
Ejemplo 3.15_ Hallar el plazo n. En cuánto tiempo un capital equivalente a 5x se triplica si la tasa de interés es del 3.5% semestre continuo.
$P=5X$
$F=3(5X)=15X$
$i=3.5$% semestre continuo
$n=?$
Una tasa de 3.5% semestre equivale a una nominal anual de 7.0%. Podemos trabajar con semestres o años y la respuesta es la misma. Con (3.16):
$$n=\frac{ln\left ( \frac{15x}{5x} \right )}{0.07}=15.69$$En 15.69 años y equivale a 31.39 semestres
Es frecuente observar en la vida cotidiana que diferentes agentes económicos, como comerciantes, empresarios, y el mismo Estado, ante una (o conjunto) obligación o compromiso financiero, se vean en la necesidad de renegociar ésta(s), determinando el nuevo vencimiento, el monto a pagar e incluso hasta nuevas tasas de interés.
La ecuación de valor es una herramienta de las matemáticas financieras que posibilita dar solución a este tipo de situación en términos de valores equivalentes.
Para el manejo a valor equivalentes, los montos se deben trasladar a una misma fecha llamada comúnmente focal, o de valuación (Plaza Vidaurri, 2017).
La ecuación de valor es, como toda ecuación, una igualdad que se establece entre un conjunto de deudas, pagos o, en general, compromisos con vencimiento en ciertas fechas, y un conjunto de nuevas obligaciones equivalentes que las reemplaza con diferentes fechas de vencimiento.

Ejemplo 3.16_ Ecuación de valor. Un comerciante debe pagar dentro de dos meses 580,000 pesos, dentro de nueve meses 950,000 pesos y dentro de catorce meses 1,500,000 pesos, deudas acordadas al 1.8% mensual vencido. Propone a su acreedor realizar dos pagos iguales en los meses diez y dieciocho, sosteniendo la misma tasa de interés del 1.8% mensual vencido. Hallar el monto de los dos nuevos pagos aplicando como fecha focal el presente (ff=0).
La Figura 3.12 presenta gráficamente el problema en el que el acuerdo inicial se identifica con flechas hacia arriba y el acuerdo que lo reemplaza (el nuevo acuerdo) con flechas hacia abajo. Los nuevos pagos están representados por la incógnita $x$.
Como la fecha focal es el presente, todos los valores y las incógnitas los trasladamos a esa fecha, los descontamos, con las respectivas tasas de interés.
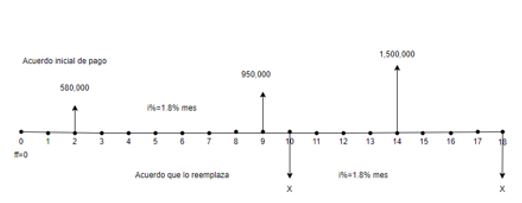
Lo anterior asegura el manejo de valores en términos equivalentes, con igual valor económico para las partes. La igualdad entre los dos esquemas de pago es la siguiente:
$$\frac{580,000}{\left ( 1+0.018 \right )^{2}}+\frac{950,000}{\left ( 1+0.018 \right )^{9}}+\frac{1,500,000}{\left ( 1+0.018 \right )^{14}}$$ $$=\frac{x}{\left ( 1+0.018 \right )^{10}}+\frac{x}{\left ( 1+0.018 \right )^{18}}$$En la primera parte de la igualdad se halla el acuerdo inicial y la suma de sus componentes descontados al 1.8% mensual, es el valor presente de lo adeudado. En la segunda parte está el nuevo acuerdo de pago que reemplaza el anterior, descontados a la fecha focal convenida con el 1.8% mensual.
El problema consiste en hallar x de la ecuación, que corresponde a los nuevos pagos por realizar en los meses 10 y 18 a valor equivalente. El valor de x es:
$$559,671+809,084+1,168,483=0.83661x+0.72534x$$El nuevo acuerdo consiste en cancelar dos cuotas iguales de 1,624,408 de pesos en los meses diez y dieciocho, con la tasa de interés del 1.8% mes vencido.
Para constatar que la deuda se cancela con estos dos pagos, procedemos a realizar la prueba. Inicialmente calculamos el valor futuro de la deuda al instante de realizar el primer pago, es decir con $n=10$, utilizando la tasa de interés del 1.8% mensual. Es decir:
$$F=2,537,237\left ( 1+0.018 \right )^{10}=3,032,765 $$En esa fecha se abona a la deuda la primera cuota de 1,624,408 pesos por lo que el saldo de ésta es de 1,408,357 de pesos.
Calculamos el valor futuro de este nuevo saldo al instante de cancelar la última cuota, con $n=8$, dado que son los meses que faltan para cancelar la última cuota. Al valor obtenido le restamos la cuota de dicho mes 18 y se cancela la deuda. Veamos:
$$F=1,408,537\left ( 1+0.018 \right )^{8}=1,624,408$$Este es el nuevo saldo de la deuda en el mes 18, y es igual a la cuota que se cancela en el mismo mes. El saldo de la deuda es cero con el último pago.

Ejemplo 3.17_ Cambio de fecha focal.. Resolver el ejercicio anterior usando como fecha focal el mes doce (ff=12).
En este caso debemos trasladar todos los valores e incógnitas a la fecha indicada y resolver para $x$. Ver figura 3.13
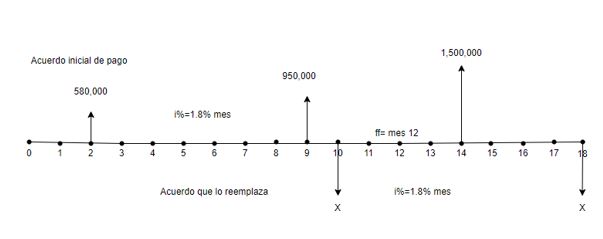
La ecuación de valor es:
$$ 580,000\left ( 1+0.018 \right )^{10}+950,000\left ( 1+0.018 \right )^{3}+\frac{1,500,000}{\left ( 1+0.018 \right )^{2}}$$ $$=x\left ( 1+0.018 \right )^{2}+\frac{x}{\left ( 1+0.018 \right )^{6}}$$Los valores e incógnitas que están ubicados a la izquierda de la fecha focal, los debemos capitalizar; en cambio los valores e incógnitas que están a la derecha de la fecha focal, los debemos descontar.
Los valores de n (el exponente) son los traslados en el tiempo (en meses) que debemos realizar a los datos e incógnitas. Realizando las operaciones matemáticas tenemos:
Con fecha focal doce (ff=12) el resultado es el mismo al alcanzado con fecha focal cero (ff=0). En la aplicación de la ecuación de valor bajo interés compuesto, para hallar los valores a cancelar en el planteamiento de un nuevo acuerdo de pagos, es indiferente la fecha de valuación seleccionada, ceteris paribus.

Ejemplo 3.18_ Ecuación de valor con cambio de tasa de interés. Un grupo inversionista compran una empresa dedicada a la prestación de servicios de consultoría y asesoría en inteligencia de mercado, bajo el siguiente esquema de pagos.
En el día de hoy cancelan de contado 50 millones de pesos, un segundo pago en cuatro meses por 30 millones de pesos y un tercer pago de 45 millones de pesos en doce meses, reconociendo el 1.2% mensual vencido de tasa de interés.
Sin embargo, dadas las expectativas sobre ingresos futuro de la empresa, deciden a última hora un nuevo esquema de pagos conservando el desembolso de contado de 50 millones, y tres pagos adicionales en los meses ocho, diez y doce con la condición de que el pago siguiente sea el doble del pago anterior, asumiendo en esta propuesta como tasa de interés el 1.4% mensual. Encontrar la solución con fecha focal el presente, y posteriormente resolver de nuevo aplicando como fecha focal el mes ocho.
Solución.
Con el cambio de tasa de interés al pasar del primer acuerdo de pago al segundo, nos genera una situación particular en la aplicación de la ecuación de valor. Esta situación es la que se pretende ilustrar con este ejemplo
Realización con ff=0.La ecuación de valor es:
$$50,000,000+\frac{30,000,000}{\left ( 1+0.012 \right )^{4}}+\frac{45,000,000}{\left ( 1+0.012 \right )^{12}}=$$ $$50,000,000+\frac{x}{\left ( 1+0.014 \right )^{8}}+\frac{2x}{\left ( 1+0.014 \right )^{10}}+\frac{4x}{\left ( 1+0.014 \right )^{12}}$$ $$117,600,546=50,000,000+0.8947x+1.74x+3.385x$$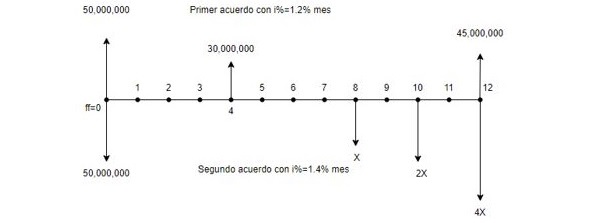
El valor presente del primer acuerdo de pagos, de $117,600,546, se interpreta como el valor de venta de contado de la empresa.
Las nuevas cuotas quedan de la siguiente manera:
Primer pago de 50,000,000 de pesos realizado en momento cero o presente
Segundo pago 11,228,390 de pesos en el mes ocho
Tercer pago 22,456,781 de pesos en el mes diez
Cuarto pago 44,913,562 de pesos en el mes doce
Solución con ff=8
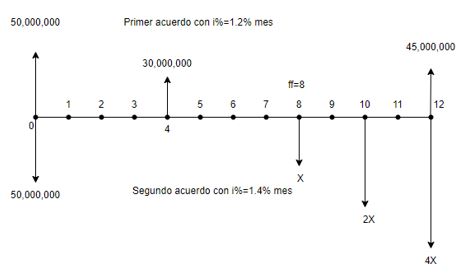
En la Figura 3.15 se representa de nuevo el problema con ff=8. Así mismo, en el ejercicio anterior encontramos que el valor de contado de la empresa es de 117,600,546 de pesos y es equivalente a los pagos del primer acuerdo.
Con este valor establecemos la ecuación de valor (observe la tasa de interés utilizada), así: $$117,600,546\left ( 1+0.014 \right )^{8}=50,000,000\left ( 1+0.014 \right )^{8}+x+$$ $$\frac{2x}{\left ( 1+0.014 \right )^{2}}+\frac{4x}{\left ( 1+0.014 \right )^{4}}$$ $$75,553,371=x+1.9451x+3.7836x$$ $$75,553,371=6.7287817x$$ $$x=11,228,390$$
El valor de x es el mismo hallado anteriormente. Por lo tanto, conservando el abono inicial, los demás pagos son los mismos montos ya calculados ya calculados.
El detalle a resaltar es el siguiente: Con cambio de tasa de interés debemos, como primer paso hallar el valor presente del primer acuerdo con su respectiva tasa de interés y, en segundo paso, utilizar este monto presente para plantear la nueva ecuación de valor, con la nueva tasa de interes.

Ejemplo 3.19_ Cálculo del plazo n. Se firma un contrato de compraventa por una finca cafetera con el compromiso de realizar cuatro pagos siendo el primer de 30,000,000 de pesos dentro de un mes, un segundo pago de 40,000,000 de pesos dentro de seis meses, el tercer abono dentro de doce meses por 60,000,000 de pesos y un último contado de 60,000,000 de pesos para dentro de dieciocho meses, todos estos bajo la tasa de interés del 1.85% mensual.
El comprador se pregunta que si decidiera hacer un sólo pago por valor de 243,107,053 de pesos ¿en qué momento se debería cancelar dicho monto? Utilícese la misma tasa de interés y resolver en fecha focal en cero y luego constatar la respuesta realizado el cálculo en fecha focal quince.
$$\frac{30,000,000}{\left ( 1+0.0185 \right )^{1}}+\frac{40,000,000}{\left ( 1+0.0185 \right )^{6}}+\frac{60,000,000}{\left ( 1+0.0185 \right )^{12}}+\frac{60,000,000}{\left ( 1+0.0185 \right )^{18}}$$ $$=\frac{243,107,053}{\left ( 1+0.0185 \right )^{n}}$$ $$156,578,728=\frac{243,107,054}{\left ( 1+0.0185 \right )^{n}}$$ $$\left ( 1+0.0185 \right )^{n}=\frac{243,107,054}{156,578,728}$$ $$\left ( 1+0.0185 \right )^{n}=1.5526187$$ $$nLn(1.0185)=Ln(1.5526187)$$
$$n=\frac{ln\left ( 1.5526187 \right )}{1.0185}= 24 meses$$
Ahora bien, con ff=15, conservando la misma tasa de interés, los valores del primer acuerdo los trasladamos a la fecha señalada, como se indica al lado izquierdo de la igualdad de la siguiente ecuación.
Obtenemos el mismo resultado de 24 meses

Ejemplo 3.20_ Cálculo de la tasa de interés. Se piensa adquirir un vehículo para el transporte de carga de exportación con el compromiso de cancelar de contado la suma de 80,000,000 de pesos y dos pagos iguales de 120,000,000 de pesos en los meses quince y treinta, con un interés del 1.2% mensual. Si finalmente se pacta realizar dos pagos, el primero es una cuota inicial de 140,000,000 de pesos y en el mes treinta el segundo pago por valor de $ 210,000,000 de pesos ¿Qué tasa de interés permite que estos dos esquemas de financiación sean equivalentes? Resolver en fecha focal cero.
con ff=0. La ecuación de valor es:
$$80,000,000+\frac{120,000,000}{(1+0.012)^{15}}+\frac{120,000,000}{\left ( 1+0.012 \right )^{30}}=140,000,000+$$ $$\frac{200,000,000}{\left ( 1+i \right )^{30}}$$ $$264,240,631=140,000,000+\frac{210,000,000}{\left ( 1+i \right )^{30}}$$ $$124,240,631=\frac{210,000,000}{\left ( 1+i \right )^{30}}$$ $$\left ( 1+i \right )^{30}=\frac{210,000,000}{124,240,631}$$ $$\left ( 1+i \right )^{30}=1.6907$$ $$i=\sqrt[30]{1.6907}-1=0.01765$$La tasa de interés es del 1.77% mensual
Contrario a lo que ocurre al interior de una economía nacional, en la que los intercambios se realizan en la propia unidad monetaria, las transacciones entre naciones se ejecutan en divisas, hecho que implica la necesidad de realizar el cambio de una moneda por otra. Los intercambios entre naciones requieren de un mercado de divisas para convertir una moneda a otra para realizar los pagos.
El precio de una moneda extranjera expresado en términos de una moneda nacional se denomina tipo de cambio nominal ($tc$). El tipo de cambio es la cantidad de moneda nacional dada a cambio por una unidad monetaria extranjera o divisa; también se puede definir como la cantidad de moneda extranjera que pueden comprarse con una unidad de la moneda nacional (Acemoglu, Laibson & List, 2017). Ejemplos son la cantidad de pesos colombianos dados por un dólar de Estados Unidos, o la cantidad de pesos colombianos dados por un Euro.
Como todo precio, el tipo de cambio está sujeto a variaciones que son consecuencia de las condiciones del mercado de divisas, de las circunstancias de la oferta y la demanda de cambio extranjero.
En las transacciones internacionales que realiza un país con el resto del mundo, se demanda divisas cuando nuestros nacionales requieren realizar el pago de las importaciones de bienes y servicios, o ejecutan inversiones en el extranjero; así mismo existe demanda de moneda extranjera por el motivo de pago de intereses y dividendos debido a inversiones que hacen los extranjeros en nuestro país, y por donaciones que hace nuestro país al resto del mundo.
Casos concretos de demanda de moneda extranjera desde el punto de vista financiero, son las demandas de divisas para cumplir con el servicio de la deuda al obtener créditos externos, para la compra de activos financieros extranjeros (como por ejemplo inversiones en bonos y acciones), o para abrir una cuenta bancaria en el exterior.
Además, se requiere divisas por motivo especulación (por ejemplo, porque se desea comprar divisas hoy baratas con la esperanza de venderlas en el futuro a un precio mayor, y así obtener un margen de ganancia o spread al menudeo), y para la cobertura del riesgo vinculado a la variación en la cotización del tipo de cambio.
La oferta de divisas se genera cuando existe pagos hacia nuestro país originado por exportaciones de bienes y servicios, por la entrada al país de la inversión extranjera directa (IED), por las donaciones unilaterales realizadas por el resto del mundo a nuestro país, por los pagos que le hacen a nuestros nacionales de intereses y dividendos originados en inversiones realizadas en el exterior (ingresos recibidos por inversiones en el exterior), ingresos de divisas por pago al trabajo realizado en el exterior.
De acuerdo con las fuerzas que determinan el mecanismo del mercado de divisas, si en un momento y espacio determinados la oferta de moneda extranjera es mayor que su demanda, es decir que existe exceso de divisas, el tipo de cambio nominal de dicha moneda extranjera disminuye en ese mercado en concreto (se reduce su cotización); en cambio cuando la oferta de divisa es menor a la demanda de ésta, o sea hay escasez en el mercado, la cotización de la moneda extranjera sube, el tipo de cambio aumenta.
Si la demanda y la oferta de divisas son las mismas en un determinado momento y espacio, decimos que el tipo de cambio es el de equilibrio y el mercado se vacía.
En general, el mercado de divisa se compone del mercado al contado o corriente, del mercado de forward, los mercados de contratos futuros y de opciones (Appleyard & Field, 2003).
En este capítulo la aplicación se centra en el mercado de contado.
La Tabla 3.5 presenta la cotización del dólar estadounidense respecto al peso colombiano en diferentes fechas, medido por la tasa representativa del mercado (TRM), que es un valor promedio de las operaciones de compra y de venta entre intermediarios.
| Fecha | TMR promedio mes | Var% | Concepto |
|---|---|---|---|
| 2021/01 | 3,494.53 | 0.75% | Depreciación |
| 2021/02 | 3,552.43 | 1.66% | Depreciación |
| 2021/03 | 3,617.00 | 1.82% | Depreciación |
| 2022/01 | 4,000.72 | 0.83% | Depreciación |
| 2022/02 | 3,938.36 | -1.56% | Apreciación |
En promedio, en el mes de enero de 2021 un dólar de los Estados Unidos valía en el mercado al contado 3,494.53 pesos colombianos.
En el mes de febrero del mismo año, el tipo de cambio se ubicó en 3,552.43 pesos colombianos por dólar. Entre estos meses, el dólar subió en promedio 57.9 pesos colombianos equivalente al 1.66% mensual promedio.
Esta variación positiva indica que el peso colombiano se ha depreciado en su valor respecto al dólar o, en sentido contrario, el dólar se ha apreciado respecto al peso colombiano (con un dólar se adquiere más pesos colombianos);la depreciación del tipo de cambio implica dar más pesos colombianos por una misma unidad monetaria extranjera, el dólar como en este ejemplo.
Ahora bien, en el mes de enero de 2022 el dólar valió en el mercado de cambio colombiano 4,000.72 pesos y para el mes siguiente, éste se cotizó en promedio en 3,938.36 pesos, implicando una reducción del precio relativo del dólar de 62.36 pesos y una variación porcentual de -1.56% promedio.
En esta ocasión los colombianos debieron pagar en febrero de 2022 menos pesos por cada dólar que hayan comprado, comparado con el mes anterior, e implica que el peso colombiano ganó valor respecto al dólar, o hubo apreciación del tipo de cambio.
Si definimos:
$tc_{n}=$ Tipo de cambio en instante nLa variación del tipo de cambio se calcula como:
$$var_{n}=\frac{tc_{n}-tc_{n-1}}{tc_{n-1}}$$Y es igual a:
$$var_{n}=\left [ \frac{tc_{n}}{tc_{n-1}}-1 \right ]$$Tomando los valores de la tabla 3.5 para los meses de enero y febrero de los años 2021 y 2022, tenemos los siguientes resultados.
$ var_{02/21}=\frac{3,552.43}{3,494.53}-1=0.0166=1.66$% del mes.Si la variación es positiva se denomina depreciación del tipo de cambio ($Dep$). Es decir, si:
$$var_{n}=\left [ \frac{tc_{n}}{tc_{n-1}}-1 \right ]>0$$Entonces:
$$Dep=\left [ \frac{tc_{n}}{tc_{n-1}}-1 \right ]>0$$Por lo que:
$$\left [ \frac{tc_{n}}{tc_{n-1}} \right ]=(1+Dep)$$Del cálculo anterior tenemos que:
$$\frac{3,552.43}{3,494.53}=(1+0.0166)$$Para el año 2022, la variación del tipo de cambio es.
Si la variación es negativa se denomina apreciación del tipo de cambio ($Apr$). Es decir, si:
$$var_n=\left [ \frac{tc_{n}}{tc_{n-1}}-1 \right ]\lt 0$$Entonces:
$$Apr=\left [ \frac{tc_{n}}{tc_{n-1}}-1 \right ]\lt 0$$Por lo que:
$$\left [ \frac{tc_{n}}{tc_{n-1}} \right ]=(1-Apr)$$Así entonces:
$$\frac{3,938.36}{4,000.70}=(1-0.0156)$$¿Cuál es la importancia para el valor del dinero en el tiempo de estas variaciones en el tipo de cambio? Las operaciones de inversión o créditos se realizan en el tiempo, se crean en un momento presente y se liquidan en un momento futuro, por lo que en ese lapso surge un elemento de riesgo al no contarse con conocimiento cierto sobre el comportamiento de las variables económicas o financieras de interés, en este caso del tipo de cambio. Por ello, cuando se realiza una inversión o se suscribe un préstamo en moneda extranjera estamos sujetos, con el paso del tiempo, al riesgo derivado de las fluctuaciones del tipo de cambio; a un riesgo cambiario.
Procedemos a ilustrar los efectos de las variaciones del tipo de cambio sobre las operaciones de inversión y de créditos que personas naturales y jurídicas del país realizan en el exterior en monedas extranjeras, sin que tomen medidas contra el riesgo derivado de dichas variaciones.
Es decir, trabajamos bajo el escenario de un agente económico nacional que no desarrolla estrategia para cubrirse del riesgo, posición que técnicamente se denomina no cubierta o abierta (accionar común en los especuladores del mercado de cambio).

Ejemplo 3.21_ Efectos de la depreciación del tipo de cambio nominal sobre la inversión. Un empresario colombiano con exceso temporal de liquidez está interesado en realizar una inversión de corto plazo en el exterior en la gestión de sus recursos de efectivo.
Consulta con el JP Morgan Chase Bank de New York la realización de un depósito a término fijo por 90 días, donde le ofrecen una tasa de interés, (tasa externa o prime rate) de 8.52% t.v.
Al momento de realizar la inversión, el tipo de cambio es de 3,900 pesos/dólar; además el empresario colombiano conjetura (tiene la expectativa) de que al momento de liquidar el CDT, la cotización del dólar será de 4,000 pesos/dólar.
Suponiendo que en esta operación financiera no existe costos de transacción, hallar el valor futuro y los intereses en pesos que generaría esta inversión si se cumple la conjetura de este empresario inversor. El capital en pesos colombianos es de 1,000 millones.
$P=1,000$ millones de pesos
$n=90$ días o un trimestre
$J=8.5$%t.v.(tasa externa)
$tc_{n-1}=3,900$ pesos/dólar
$tc_{n}=4,000$ pesos/dólar
$F=?$
$I=?$
Con respecto a la cotización de dólar, en los tres meses de la inversión la conjetura del empresario inversor equivale a:
$$Var_{n}=\frac{4,000}{3,900}-1=0.0256$$Es decir, supone una depreciación del tipo de cambio en el trimestre de 2.56%.
La tasa de interés periódica extranjera es:
$iv=\frac{J}{k}=\frac{0.0852}{4}=0.0213$% por tirmestre
Con esta información procedemos a resolver el ejercicio en tres pasos.
Paso#1. Convertir el capital en pesos a dólares. Para ello dividimos el principal por el tipo de cambio inicial, al momento de hacer la inversión. Esto es:
$P=\frac{1,000,000,000}{3,900}=256,410.26$ dólares
Paso# 2. Hallar el valor futuro del capital en dólares y los intereses. La capitalización es vencida, por ello utilizamos:
$$F=P\left ( 1+i \right )^{n}$$$F=256,410.26\left ( 1+0.0213 \right )^{1}=261,817.80$ dólares
$$I=P\left [ \left ( 1+i \right ) ^{n}-1\right ]$$$I=256,410.26\left [ \left ( 1+0.0213 \right ) ^{1}-1\right ]=5,461.54$ dólares
Paso# 3. Convertir el valor futuro y los intereses a pesos colombianos. En esta ocasión utilizamos la cotización del tipo de cambio al vencimiento de la inversión, y la operación matemática es multiplicar.
$F=261,871.80*4,000=1,047,487,200$ de pesos. De este valor $47,487,200$ de pesos son los intereses en moneda local
En este ejercicio, el capital en dólares sale del país, lo que implica previamente comprar los dólares en nuestro mercado al contado.
Luego, una vez vencida la inversión, se retornan los dólares al país y se hace la venta en el mercado al contado. La compra de dólares en el mercado local es una demanda de esta moneda; la venta es una oferta local de dólares. Como indicamos, todo bajo los supuestos de cero costos de transacción y la posición no cubierta del inversionista.
Generalizando, el valor futuro en pesos colombianos de la inversión en dólares se obtiene como:
$$F=\frac{1,000,000,000}{3,900}*\left ( 1+0.0213 \right )^{1}*4,000$$Nótese que $\frac{4,000}{3,900}=\frac{tc_{n}}{tc_{n-1}}=1+Dep$. Por lo tanto:
$$F=1,000,000,000\left ( 1+0.0123 \right )^{1}*\left ( 1+0.0256 \right )^{1}=1,047,847,200$$Con este último resultado concluimos que en general con depreciación del tipo de cambio, el valor futuro de un capital invertido en modo vencido en el exterior y reintegrado al país es:
$$F=P\left ( 1+i \right )^{n}*\left ( 1+Dep \right )^{n}(3.18)$$Los intereses se determinan como: $$I=P\left [ \left ( 1+i \right )^{n}*\left ( 1+Dep \right )^{n}-1 \right ](3.19)$$
O también, con fracciones de año, las fórmulas son:
$$F=P\left ( 1+iv \right )^{n*k}*\left ( 1+Dep \right )^{n*k}(3.20)$$ $$I=P\left [ \left ( 1+iv \right )^{n*k}*\left ( 1+Dep \right )^{n*k}-1 \right ](3.21)$$En el caso de una apreciación del tipo de cambio, el valor futuro y los rendimientos se calculan como:
$$F=P\left ( 1+i \right )^{n}*\left ( 1-Apr \right )^{n}(3.22)$$ $$F=P\left ( 1+iv \right )^{n*k}*\left ( 1-Apr \right )^{n*k}(3.22.1)$$ $$I=P\left [ \left ( 1+iv \right )^{n*k}*\left ( 1-Apr \right )^{n*k}-1 \right ](3.23)$$
Ejemplo 3.22_ Efectos de la apreciación del tipo de cambio sobre la inversión. Con los datos del ejemplo 3.21, supongamos ahora que en vez de 4,000 pesos/dólar, el inversionista al momento de vender los dólares reintegrados al país se encuentra con un tipo de cambio de 3,850 pesos/dólar, es decir, estamos suponiendo una apreciación del peso colombiano de 1.28% respecto al dólar. Hallar el valor futuro de la inversión en pesos colombiano y los intereses.
Como se presenta una apreciación del tipo de cambio, trabajamos con ecuaciones (3.22) y (3.23).
$$F=1,000,000,000\left ( 1+0.0213 \right )^{1}*\left ( 1-0.0128 \right )^{1}=1,008,206,410$$ $$I=1,000,000,000\left [ \left ( 1+0.0213 \right )^{1}*\left ( 1-0.0128 \right )^{1}-1 \right ]=8,206,410 $$Comparando los rendimientos de este ejemplo con el caso anterior, es significativo los efectos económicos que tiene el comportamiento del tipo de cambio sobre la inversión.
La depreciación del tipo de cambio favoreció la inversión porque al reintegrar los dólares al país se venden por un precio mayor al que se compraron inicialmente, diferencia que constituye una ganancia por cada dólar vendido.
En cambio, con una apreciación del dólar, la rentabilidad de la inversión realizada se ve deteriorada, incluso puede llegar a ser negativa, dado que al vender los dólares en el mercado local su precio es menor que el de compra, diferencia representada en pérdida por cada dólar vendido.
Dado que no tenemos certeza sobre la futura cotización de los precios relativos de las monedas extranjeras, con el paso del tiempo estamos sujetos a un riesgo, en este caso cambiario, sobre el cual en realidad los agentes económicos realizan acciones para cubrirse de él. Estas acciones se denominan estrategias de cobertura de riesgo, tema que no es objeto de este libro.

Ejemplo 3.23_ Efectos de la depreciación y apreciación del tipo de cambio sobre un crédito. Para la puesta en funcionamiento de un trapiche comunitario productor de mieles para la industria licorera del país, el Gobierno Departamental contrató un crédito con la banca inglesa por valor de 2.5 millones de libras esterlinas, para cancelarlo en un pago único dentro de 3 años con una tasa de interés externa (Libor o Sofr) de 3.5% m.v. Al momento de realizar el crédito, en el mercado local una libra esterlina se negocia a 4,000 pesos colombianos. ¿Qué sucede con la deuda en pesos colombianos si al momento de realizar el pago del préstamo el tipo de cambio pesos por libra esterlina es: constante en 4,000 pesos; se deprecia a 4,100 pesos; se aprecia a 3,900 pesos?
$P=2,500,000$ libras
$n=3$ años
$J=3.5$% m.v.(tasa externa Libor o Sofr)
$iv=0.292$% mes
$plazo=n*k=3*12=36$ meses
La deuda el libra esterlina es:
De este valor final la compensación por el valor del dinero en el tiempo suman 276,352.19 libras esterlinas.
Sin embargo, el préstamo debe llegar al país y convertirlo a pesos para financiar las actividades convenidas, es decir se hace una oferta de venta de divisas en el mercado local. Luego, al llegar el momento de pagar el préstamo, se debe hacer la operación de compra de las libras en el mercado local (demanda de divisas).
Estas operaciones, de venta y luego compra de divisas, se dan en diferentes momentos, en los que posiblemente ocurran cambios en la cotización de las monedas, es decir, existe de nuevo un riesgo por tipo de cambio, ya sea por depreciación o apreciación de éste. El riesgo cambiario lo asume quien contrata en moneda diferente a la de su origen.
En el ejercicio se ha supuesto tres escenarios, con tres tipos de cambio, que permiten obtener una síntesis de los efectos que se desean ilustrar.
Ahora bien, en pesos colombianos el monto tomado en préstamo es equivalente a $2,500,000* 4,000$, esto es 10,000 millones de pesos. Bajo el escenario o el supuesto de un tipo de cambio constante, el valor de la deuda en pesos colombianos al final del plazo, es de $2,776,352.19* 4,000$, equivalente a $11,105,407,757$ pesos.
El caso de la depreciación del tipo de cambio.
Bajo este supuesto, la deuda al final del plazo en pesos colombianos es de $2,776,352.19* 4,100$, o sea de $11,383,043,976$ pesos ocasionando un sobrecosto de $277,635,291$ pesos en la deuda.
Dicho sobrecosto de la deuda en moneda nacional equivalente al 2.5% respecto al caso anterior (con tipo de cambio constante), porcentaje que es exactamente igual a la depreciación del tipo de cambio al pasar de $4,000$ pesos a $4,100$ pesos la cotización de la libra esterlina.
El caso de la apreciación del tipo de cambio.
En cambio, con la apreciación interna del tipo de cambio, la deuda en pesos colombianos al final del plazo es de $2,776,352.19* 3,900$, igual a $10,827,773,539$ pesos, significando una reducción en pesos colombianos de $277,635,291$ pesos, respecto al caso de tipo de cambio constante.
Este último valor representa una reducción porcentual de la deuda equivalente a la apreciación del tipo de cambio de 2.5%.
En resumen, la depreciación del tipo de cambio encarece en moneda nacional las deudas contraídas en moneda extranjera; el fenómeno contrario ocurre con la apreciación del tipo de cambio.

Ejemplo 3.24_ El cálculo de la deuda en pesos contraída inicialmente en divisa con variación porcentual del tipo de cambio. Con los datos del ejercicio anterior, supongamos en esta ocasión que el deudor tiene como conjetura la depreciación del tipo de cambio en 0.0686% promedio mensual. En su análisis supone luego el escenario de una apreciación del tipo de cambio en el mismo porcentaje (-0.0686).
Hallar el valor de la deuda en pesos con ambas expectativas.
$P=2,500,000$ libras esterlinas
$n=3$ años
$J=3.5$% m.v.
$iv=0.292$% mes
$plazo=36$ meses
$tc_{n-1}=4,000$ pesos por libra esterlina
$F=?$
Escenario 1: Dep=0.0686% mensual
El valor en pesos del préstamo es de $2,500,000*4,000$ e igual a $10,000,000,000$ pesos. Con depreciación del tipo de cambio, la deuda en pesos colombiano asciende a:
$$F=10,000,000,000\left ( 1+0.029167 \right )^{36}\left ( 1+0.000686 \right )^{36}$$ $$F=11,383,043,976$$Escenario 2: Apr=-0.0686% mensual
$$F=10,000,000,000\left ( 1+0.029167 \right )^{36}\left ( 1-0.000686 \right )^{36}$$ $$F=10,827,773,539$$Obsérvese que son los mismos resultados del ejercicio anterior. Solo que en esta ocasión los datos del problema contemplan las variaciones porcentuales del tipo de cambio y no, como en el ejercicio 3.23, que daba las conjeturas en moneda nacional. Ambos métodos ofrecen el mismo resultado.
Indiquemos de nuevo que las ganancias de una inversionista en activos extranjeros están no sólo en la tasa de interés externa o de rendimiento del activo, sino además en la derivada de la depreciación de nuestra moneda con respecto a la moneda extranjera (o también, por la apreciación de la moneda extranjera frente a la moneda nacional).
De igual manera, el costo de la financiación en moneda extranjera está determinado por la tasa de interés externa a que se contrate los créditos y la variación del tipo de cambio entre las monedas vinculadas en la transacción internacional.
En el año de 1972, el gobierno nacional adoptó el sistema de ahorro y de crédito hipotecario bajo el esquema de la Unidad de Poder Adquisitivo constante (UPAC). El precio inicial de la unidad se determinó en 100 pesos, precio que fue vinculado (indexado) a la inflación medida por el Índice de Precios al Consumidor.
Con esta novedad, se pretendía incentivar el ahorro necesario para la inversión, recursos dirigidos al sector de la construcción de vivienda, con el fin de generar empleo y crecimiento económico del país. Con la UPAC se buscó además que el ahorro y el crédito de largo plazo ajustarán su valor al ritmo de la inflación (fenómeno conocido como corrección monetaria) para mantener el poder adquisitivo del dinero, su reserva de valor, constante en el tiempo (Banco de la República de Colombia, 2002)
En el año de 1994, el sistema UPAC sufre una reforma en su cálculo cuando la corrección monetaria pasa de estar indexada a la inflación a ser vinculada con la tasa de interés representativa de la economía colombiana, la DTF.
Se excluye por lo tanto el ajuste por la inflación. Es esta reforma causa de su crisis y desaparición.
La reforma del sistema es causante de una dificultad que lo llevó a su crisis y posterior liquidación. Mientras la remuneración de los asalariados colombianos mantuvo el ajuste del poder adquisitivo vinculado a la inflación (el incremento salarial se determina por la variación anual del IPC), los créditos hipotecarios en UPAC lo hacían a la tasa de interés DTF.
Bajo esta nuevas condiciones, si el nivel o el crecimiento de la tasa de interés DTF es mayor a la inflación ($i> \pi$ ), la UPC, y con ella las cuotas de los créditos de vivienda contratados en esta unidad, crecen en mayor proporción a ajuste de los salarios, evento que genera un desbalance o brecha entre el crecimiento del valor del crédito y el crecimiento de los salarios, y por ello, de la capacidad de pago de los usuarios del crédito.
Esta brecha lleva a la crisis del sistema UPAC y es reemplazado por la Unidad de Valor Real (UVR).
La ley 546 de 1999 crea el sistema de Unidad de Valor Real, Unidad que entra en funcionamiento en el año 2000 con un valor de 100 pesos la unidad. Su valor se indexa de nuevo a la inflación medida por la variación porcentual del Índice de Precios al Consumidor (IPC), como al inicio del UPAC. Es el sistema vigente actual en la economía colombiana. (Banco de la República de Colombia, 2002 y 2021).
La UVR se define como unidad de cuenta, comparte esta característica con el dinero, pero no es medio de pago.
Como unidad de cuenta expresa el valor o precio del dinero, para medir el aumento o deterioro del poder adquisitivo de éste.
Si una UVR equivale a 100 pesos, podemos decir entonces que 1 peso equivale a 0.01 UVR; así mismo, si una UVR vale 150 pesos es igual decir que 1 peso equivale a 0.009091 UVR.
Con estos valores podemos indicar que el precio del dinero en términos de UVR se ha deteriorado, dado que con un peso compramos menos unidades, su poder adquisitivo ha disminuido; o a la inversa, una UVR con mayor valor está indicando que se debe dar más pesos por la misma unidad hecho que no es más que el deterioro del poder adquisitivo del dinero.
El Banco de la República de Colombia es el responsable del cálculo, aplicando el siguiente modelo (Banco de la República de Colombia, 2021). La fórmula para tal fin es la siguiente:
$$UVR_{t}=UVR_{0}\left ( 1+\pi \right )^{\frac{t}{d}}$$En ella, las variables son:
$UVR_{t}$: Valor de la UVR en día t. Hay un valor de la UVR para cada día t del año, expresado con cuatro cifras decimales.
$UVR_{0}$: Valor de la UVR tomada como base para el cálculo y corresponde al valor de la unidad del día 15 de cada mes.
$\pi$: Es la inflación, en la fórmula original del Banco de la República la representa con la letra i. La inflación se mide como la variación porcentual del índice de precios al consumidor y es calculada por el Departamento Administrativo Nacional de Estadística (DANE).
La inflación del mes n se informa al país a más tardar a los cinco días del mes siguiente (del mes $n+1$).
$d$: Es el período de proyección, esto es, el total de días calendario contados a partir del día 16 de un mes n hasta el día 15 del mes siguiente, $n+1$. Dicho período puede tomar valores de 28, 29, 30 o 31 días dependiendo de los meses involucrados. Es un mes particular, que no comienza en el día uno, sino en el dieciséis, situación explicada por el requerimiento de tiempo para el cálculo de la inflación
$t$: Es el número de días que hay desde el inicio del período de proyección hasta el día específico que se va a proyectar. Cada t se corresponde con una fecha en específico. Con $t=1$ se identifica el día 16 de cada mes, con $t=13 $ se comprende el día 28 de cada mes.

Ejemplo 3.25_ Cálculo de la UVR. El DANE para el mes de abril de 2022 reportó como inflación del mes una variación positiva de 1.25% en el IPC. Adicionalmente, para el 15 de mayo del mismo año la UVR presentó un valor de $304.1363 la unidad.
Hallar el valor de la UVR para los días 16, 25 y 31 de mayo, así como para el 5, 10 y 15 de junio
$UVR_{0}=304.1363$. Es el valor de mayo 15 de 2022
$\pi =1.25$%, es la inflación del mes de abril y con ella se proyecta la UVR desde el día 16 de mayo hasta el día 15 de junio, el mes particular. Nótese además que se trabaja con la inflación rezagada un mes
$d=31$. Es el número total de días que hay entre mayo 16 y junio 15 de 2022.
$t=1$. Corresponde a la proyección de la UVR para el 16 de mayo de 2022.
$t=16$. Corresponde a la proyección de la UVR para el 31 de mayo de 2022
$t=31$. Corresponde a la proyección de la UVR para el 15 de junio de 2022
En la Tabla 3.6 se presentan los cálculos de la UVR para los días indicados.
| Fecha | t | Valor UVR |
|---|---|---|
| 2022/05/16 | 1 | 304.2582 |
| 2022/05/25 | 10 | 305.3575 |
| 2021/05/31 | 16 | 306.0926 |
| 2022/06/05 | 21 | 306.7065 |
| 2022/06/10 | 26 | 307.3216 |
| 2022/06/15 | 31 | 307.9380 |
Calculemos el valor de la UVR para junio 5 de 2022.
$$UVR_{21}=304.1363\left ( 1+0.0125 \right )^{\frac{21}{31}}=306.7064$$Es interesante señalar cómo para el día 15 de junio de 2022, la UVR acumula toda la inflación del mes. Veamos:
Por lo tanto:
$$UVR_{31}=304.1363\left ( 1+0.0125 \right )=307.9380$$De esta observación igualmente se desprende que:
$$\frac{307.9380}{304.1363}=(1+0.0125)$$Y en general:
$$\frac{UVR_{t}}{UVR_{0}}=(1+\pi )$$Esta expresión la utilizaremos en el siguiente ejemplo.
En la economía colombiana es posible invertir y tomar crédito en UVR. Para el primer caso, tenemos la posibilidad de invertir en Títulos de Tesorería TES, que son títulos de deuda pública de la República de Colombia.
Los TES son emitidos por el Ministerio de Hacienda y administrados por el Banco de la República, con denominaciones en pesos, en dólares o UVRs, y colocados a tasas de interés fijas o variables.
Para el caso del crédito, en nuestro país tenemos la opción de acceder a financiación por UVR para la adquisición de vivienda nueva o usada, adquirir locales u oficinas.
Son los conocidos crédito hipotecario en UVR en el que el bien a adquirir, u otro inmueble, es garantía del crédito.

Ejemplo 3.26_ Valor futuro vencido de inversión en UVR. El 15 de mayo de 2019 se realiza una inversión en TES clase B en UVR, títulos que son utilizados por el Gobierno Nacional para obtener recursos destinados a financiar la Nación, por valor de 265,807,400 pesos y plazo de tres años.
Si la tasa de interés es del 3.5% año vencido sobre el capital en UVR, hallar el valor futuro y los intereses generados por la inversión, suponiendo que no se hace pago de intereses año vencido sino un sólo pago al final de plazo.
$P=265,807,400$
$i=0.035$ anual. Es la tasa de interés para el capital en UVR, denominada remunerativa
$n=3$ años
$UVR_{0}=265.8074$, es el valor de la UVR al momento de hacer la transacción financiera
$UVR_{t}=304.1363$, es el valor de la UVR al momento de liquidar el título
Con estos valores de las UVR hallamos la inflación implicita en los datos como:
$$\frac{UVR_{t}}{UVR_{0}}=(1+\pi )$$ $$\frac{UVR_{t}}{UVR_{0}}-1=\pi$$La inflación implícita en los datos de las UVRs es de 14.42% en los tres años de la inversión
.Paso# 1. Convertir el capital en pesos a unidades de valor real.
$$P_{uvr}=\frac{265,807,400}{265.8074}=1,000,000$$Paso# 2. Hallar el valor futuro vencido con capital en UVRs.
$$F_{uvr}=1,000,000\left ( 1+0.035 \right )^{3}=1,108,717.8750$$Paso# 3. Convertir el valor futuro de UVRs a pesos. Liquidar la inversión.
$$F=1,107,717.8750*304.1363=337,201,352.20$$Los intereses de la operación fueron de:
$$I=337,201,352.20-265,807,400=71,393,952$$En resumen, la fórmula para calcular el valor futuro al vencimiento de la deuda es:
$$F=\frac{265,807,400}{265.8074}\left ( 1+0.035 \right )^{3}304.1363$$ $$F=265,807,400(1+.035)^{3}\frac{304.1363}{265.8074}$$Por lo tanto, y en general, la fórmula para el cálculo del valor futuro vencido en pesos de una inversión en UVR, el valor nominal al final del plazo del TES, y los interes que riende el título, son:
$$F=P(1+i)^{n}*\left ( 1+\pi \right )^{n} (3.24)$$ $$I=P\left [ \left ( 1+i \right )^{n}\left ( 1+\pi \right )^{n}-1 \right ](3.25)$$Los rendimientos de la inversión en UVR, así como los intereses a cubrir por acceder a financiación en UVRs, es función de la tasa de interés pactada como remuneración al capital en UVRs y de la variación porcentual de los precios de ésta. Si la variación es positiva, como en este ejercicio, la rentabilidad crece, en cambio, si es negativa, hay deflación, la rentabilidad de la inversión disminuye. En caso de un crédito, el costo aumenta o disminuye, respectivamente.
Existe por lo tanto un riesgo en las inversiones y los créditos en UVR, dada la incertidumbre sobre el comportamiento futuro del nivel de inflación, incluso con el desarrollo de políticas monetaria y fiscal antiinflacionaria, que tengan como propósito la estabilidad del nivel general de los precios.
Los dos temas anteriores los hemos desarrollado bajo capitalización vencida. El lector puede deducir las mismas fórmulas al considerar la capitalización anticipada y la continua, con fines teóricos
Ya hemos indicado que la valorización de un capital por medio de la fórmula de interés compuesto pago único implica el supuesto de reinversión de intereses a la misma tasa de intereses.
Sin embargo, en las operaciones de inversión y crédito, tanto de corto como de largo plazo, es común observar que las partes convengan en sus contratos la liquidación de compromisos financieros a tasas de interés variables o flotantes. Generalmente, el método utilizado para determinar estas tasas variables es especifincado un componente fijo al que se le añade otra parte que cambia. El componente variable es estimado a partir de su vinculación o indexación a una tasa de referencia.
En Colombia es común que el sistema financiero utilice como componente variable (tasa de referencia) a la tasa de interés promedio ponderado de las captaciones a 90 días, conocida como DTF, a la que se le establece un porcentaje por encima, en el otorgamiento de créditos, siendo este último el componente fijo. Por ejemplo, un crédito puede ser concedido a la tasa de interés de DTF+3%; en este caso, la parte flotante es el valor de la DTF. Si al momento de liquidar intereses de un préstamo la DTF es de 5.8%, entonces la tasa de interés del crédito es de 8.8%; en cambio, si la DTF se ubican en 3.9%, la tasa de interés en esta ocasión es de 6.9%. En estas condiciones, la tasa de interés del crédito es variable dada la naturaleza cambiante de la DTF.

Ejemplo 3.27_ Valor futuro vencido con tasa de interés variable. Un Depósito a término fijo se realiza a un año de vencimiento y capitalización de intereses con tasa flotante amarrada exactamente a la DTF, con un principal de $3,500,000. Si las tasas de interés trimestrles son como se indican más adelante, hallar el monto redimido al final del plazo.
$P=3,500,000$
$n=1$ año equivalnete a 4 trimestres
Tasas de interés trimestrales:
$i_{1}=1.5$%
$ i_{2}=1.0$%
$i_{3}=1.2$%
$i_{4}=1.3$%
$F=?$
En cada paso $n$ es igual a un trimestre
$F_{1}=3,500,000\left ( 1+0.015 \right )^{1}=3,552,500$
$F_{2}=3,552,500\left ( 1+0.01 \right )^{1}=3,588,025$
$F_{3}=3,588,025\left ( 1+0.012 \right )^{1}=3,631,081$
$F_{4}=3,631,081\left ( 1+0.013 \right )^{1}=3,678,285$
En el proceso del cálculo, donde el subíndice indica el trimestre, se observa como el valor futuro en el trimestre $n$ se obtiene multiplicando al futuro anterior $(n-1)$ por el factor (1+i). Por ello, en este ejercicio el valor futuro con tasas de interés variables se puede calcular como:
$F=3,500,000\left ( 1+0015 \right )\left ( 1+0.010 \right )\left ( 1+0.012 \right )\left ( 1+0.013 \right )$Por lo tanto, la fórmula general es:
$$F=P\left ( 1+i_{1} \right )\left ( 1+i_{2} \right )\left ( 1+i_{3} \right )...\left ( 1+i_{n} \right )(3.26)$$
Ejemplo 3.28_ Valor futuro con tasas de interés fijas y variables. Si un capital de 3,850,500 pesos se invierte en los tres
primeros años al 3.8% anual anticipado, los dos años siguientes lo hace al 2.95% anual anticipado y los dos últimos años al 4.1% anticipado, ¿cuál es el monto final de dicho capital?
Solución
$P=3,850,500$
$i_{1}=3.8$% año anticipado, con $n=3$ años
$i_{2}=2.59$% año anticipado, con $n=2$ años
$i_{3}=4.1$% año anticipado, con $n=2$ años
$F=4,993,024$ pesos.
En el cálculo, el exponente 3 del primer término después de la igualdad indica que la tasa de interés de 3.8% anual es estable por los tres primeros años; la tasa anual de 2.95% es estable por los dos años siguientes, mientras que la tasa de 4.1% es estable en los dos años restantes. En total, el plazo de la operación es de 7 años y se despliega tres tasas de interés.
Ya hemos indicado que la operación conducente a calcular el valor futuro de un capital la denomínamos capitalización, siendo ésta la suma de los intereses al capital inicial conforme al acuerdo sobre el período y tasa de interés. Así mismo la operación contraria, el tomar un valor futuro para hallar el respectivo valor presente, se denomina descontar o actualizar, siendo éste el proceso de restar intereses. El descuento compuesto es todo lo contrario a la capitalización compuesta.
Si la capitalización vencida se ejecuta con $F=P\left ( 1+i \right )^{n}$, la operación contraria del descuento se realiza con $P=F\left ( 1+i \right )^{-n}.$
Adicionalmente, hemos entendido el descuento como una rebaja de intereses al liquidar o negociar un título valor, un activo financiero, antes de su vencimiento. En este contexto, el descuento significa para el portador del título acceder al cobro de intereses anticipados, antes del vencimiento, y para el comprador la posibilidad de una rentabilidad al redimir el título una vez se cumpla el plazo determinado en su emisión.
Sin embargo, en la jerga de los descuentos, como igualmente indicamos, se recurre a expresiones como valor nominal y valor efectivo de un título. En el contexto de descuento compuesto, el valor nominal también hace referencia al valor futuro del título, es decir al monto capitalizado al final del plazo; y el valor efectivo se refiere al monto actualizado o descontado a partir de un valor nominal. Por lo tanto, las respectivas ecuaciones son las siguientes.
Valor nominal de un título, $V_n=V_e\left(1+i\right)^n$, con $i$ como la tasa de interés y $n$ el plazo al vencimiento
Valor efectivo de un título $V_e=\frac{V_n}{\left(1+i\right)^n}$ con $i$ como la tasa de descuento y $n$ el plazo que falta desde la fecha que el portador lo vende hasta el vencimiento.
Identificando al descuento compuesto con la expresión $DC$, éste se calcula con la siguiente fórmula. $$DC=V_n-V_e$$
Y es igual a: $DC=V_n-\frac{V_n}{\left(1+i\right)^n}$
Es decir:
$$DC=V_n\left[1-\frac{1}{\left(1+i\right)^n}\right](3.27)$$A este método de descuento se le conoce también como descuento racional compuesto.

Ejemplo 3.29_ Descuento racional compuesto. Una letra de cambio es el respaldo de un préstamo de 15,345,200 pesos al 12% m.v. con plazo de ocho meses. El portador decide negociar el documento cinco meses antes de su vencimiento con un descuento de 6% m.v. Hallar el valor nominal del título, el monto del descuento compuesto y el valor efectivo de venta del título.
Hallar el valor nominal del título. Es el valor futuro compuesto vencido
$$V_n=F=P\left(1+i\right)^n$$$P=15,345,200$
$J=12$% m.v.
$iv=1$% mes
$n=8$ meses
El descuento compuesto. Se realiza sobre el valor nominal del título
$V_n=16,613,404$
$J=6$% m.v. Es la tasa anual acordada en la venta como tasa de descuento
$iv=0.5$% mes. Es la tasa de descuento equivalente mensual acordada en la venta del título
$n=5$ meses, tiempo que falta para el vencimiento de la letra de cambio.
$$DC=16,613,404\left[1-\frac{1}{\left(1+0.005\right)^5}\right]=409,177$$Valor efectivo o valor de venta del título. Un primer procedimiento es restarle al valor nominal el descuento compuesto.
$$V_e=V_n-DC$$ $$V_e=16,613,404-409,177=16,204,227$$Un segundo procedimiento para este cálculo es con la fórmula directa del valor efectivo.
$$V_e=\frac{V_n}{\left(1+iv\right)^n}$$ $$V_e=\frac{16,613,404}{\left(1+0.005\right)^5}=16,204,227$$
Ejemplo 3.30_ La rentabilidad con la venta de la letra. En el ejercicio anterior ¿Cuál fue la rentabilidad mensual obtenida por el portador original de la letra en los tres meses de su posesión y su posterior venta? y ¿cuál fue la rentabilidad anual nominal?
$P=15,342,200$
$F=16,204,177$
$n= 3$ meses
$I=?$ Los rendimientos obtenidos en el negocio
$iv=?$La tasa de interés o rentabilidad mensual
$J=?$ m.v., es la tasa nominal anual
El portador original del título, quien destinó a la inversión un capital de 15,342,200 pesos y obtuvo con la venta del título antes del vencimiento un valor efectivo de 16,204,227 pesos, logra como rendimiento en los tres meses de su posesión la suma de:
$$I=16,204,227-15,342,200=862,027$$La rentabilidad mensual es, con:
$$iv=\sqrt[n]{\frac{F}{P}}-1$$$iv=\sqrt[3]{\frac{16,204,177}{15,342,200}}-1=0.0184=1.84$% mensual
La tasa nominal anual es de:
$J=k\ast iv=12\ast0.0184=0.2208=22.1$% m.v.
El vendedor de la letra obtuvo como rentabilidad el 1.84% mensual durante los tres meses que mantuvo en su poder el título. Esta rentabilidad surge, no sólo de la capitalización inicial al calcular el valor nominal del título, sino además del diferencial de la tasa de interés inicial con respecto a la tasa de descuento, siendo ésta última mucho menor que la primera (el título pacta una tasa del 12% nominal y el portador lo negocia con un descuento de 6% nominal)

Ejemplo 3.31_ Relación entre el descuento compuesto y la capitalización anticipada. Un pagaré que se vence en seis meses y con valor nominal de 5,300,000 pesos, se negocia hoy con un descuento de 3.5% semestral. Hallar el valor efectivo o precio de venta del pagaré, el monto del descuento racional realizado y establecer la relación con la capitalización anticipada.
$Vn=5,300,000$
$n=1$ semestre
$iv= 3.5$% semestral
$Ve=?$
$DC=?$
El valor efectivo es:
El monto del descuento es:
$$DC=V_n\left[1-\frac{1}{\left(1+iv\right)^n}\right]$$ $DC=5,300,000\left[1-\frac{1}{\left(1+0.035\right)^1}\right]=179,227$Sobre la relación solicitada, procedemos de la siguiente manera. De este último resultado podemos escribir que:
$$179,227=5,300,000\left[1-\frac{1}{\left(1+0.035\right)^1}\right]$$ $$\frac{179,227}{5,300,000}=\left[1-\frac{1}{(1+0.035)}\right]$$ $$\frac{179,227}{5,300,000}=\left[\frac{1+0.035-1}{1+0.035}\right]$$ $$0.03382=\left[\frac{0.035}{1+0.035}\right]$$En esta última expresión, 0.035 es la tasa de interés periódica vencida, por ello podemos escribir esta última expresión como:
$$0.03382=\left[\frac{iv}{1+iv}\right]$$Ahora bien, la estructura del lado derecho de la última expresión ya sabemos que es equivalente a la tasa de interés periódica anticipada. Por ello (ver ecuación 3.5.3)
$$ia=\frac{iv}{1+iv}$$Por lo tanto, el descuento se puede calcular como $DC=V_n\ast ia$. Este método es conocido como descuento bancario (Plaza Vidaurre, 2012) y el procedimiento consiste en convertir la tasa de descuento vencida, iv, a su equivalente a anticipada, ia, para aplicar al valor nominal del título y obtener el monto del descuento. En este ejercicio el cálculo es:
$$DC=5,300,000\ast0.03382=179,227$$Valor ya cálculado anteriormente. Desde este resultado, es claro que:
$$Ve=Vn-DC$$ $$Ve=Vn-Vn\ast ia$$ $$Ve=Vn(1-ia)$$Y en general:
$$Ve=Vn\left(1-ia\right)^n$$En el ejemplo que traemos, el valor efectivo es por lo tanto:
$$Ve=5,300,000\left(1-0.03382\right)^1=5,120,773$$Es el valor ya calculado.
La fórmula $Ve=Vn\left(1-ia\right)^n$ es equivalente a $P=F\left(1-ia\right)^n$ ecuación 3.8.1 desarrollada con anterioridad. Esta es la relación que habíamos prometido ilustrar. Si es necesario identificar el contexto de aplicación.
En este apartado realizaremos la aplicación del interés compuesto en esquemas de cubrimiento de obligaciones con un pago único al final del plazo, bajo los diferentes esquemas de capitalización de intereses.
Dado que es pago único, no hay amortizaciones ni pagos de intereses; estos últimos se capitalizan. Bajo esta condición, estos esquemas se vuelven muy onerosos para el deudor, dado que el compromiso implica reinversión de intereses a la misma tasa de interés, como ya hemos indicado.
En la práctica, estos esquemas son aconsejables sólo en el corto plazo.

Ejemplo 3.32_ Amortización pago único vencido. Un iPad Pro de 12.9 pulgadas de quinta generación con valor de 5,659,000 pesos fue financiado al 15% m.v. para ser cancelado con un pago al cabo de seis meses. Hallar el valor de la cuota única y calcular el esquema de amortización.
$P= 5,659,000$
$J=15$% m.v
La cuota única es:
$$F=5,659,000{(1+0.0125)}^6=6,096,911.42$$Recordemos que los intereses se calculan sobre el saldo de la deuda. La amortización es el excedente que resulta de restar a la cuota los intereses, y el saldo vigente es igual al saldo anterior menos la amortización. Así, para $n=1$ tenemos.
$$F_1=5,659,000{(1+0.0125)}^1=5,729,737.50$$ $$I_1=P\ast iv=5,659,000\ast0.0125=70,737,50$$ $$R_1=A-I_1=0-70,737.50=-70,737.50$$ $$S_1=S_0-R_1=5,659,000-\left(-70,737.50\right)=5,729,737.50$$Obsérvese como el valor futuro al final de $n=1$ es exactamente el saldo. Este detalle también se ilustra en el siguiente cálculo, para $n=2$.
$$ F_2=5,659,000{(1+0.0125)}^2=5,801,359.22$$ $$I_2=5,729,737.50\ast0.0125=71,621.72$$ $$R_2=0-71,621.72=-71,621.50$$ $$S_2=5,729,737.50-\left(-71,621.72\right)=5,801,359.22$$Los intereses en $n=2$ se han calculado tomando el saldo anterior y aplicando la tasa de interés; empero también se pueden calcular con la fórmula del interés marginal, que se deja como ejercicio para el lector.
El proceso continúa hasta $n=6$. En la tabla 3.7 se presenta el esquema completo. Nótese que la cuota única es el mismo valor ya cálculado con la fórmula de futuro vencido.
Con la cuota única, se cancelan 75,270.51 pesos de intereses sobre el saldo anterior más la amortización de 6,021,640.91 pesos, monto de amortización que cubre al valor exacto del saldo inmediatamente anterior, y así la deuda queda cancelada.

Ejemplo 3.33_ Esquema de amortización con capitalizaciones anticipadas y continuas. Con los datos del ejercicio anterior, calcular la cuota única bajo estas modalidades de capitalización y elaborar las tablas de amortización.
Cuota única anticipada con: $F=P\left(\frac{1}{1-ia}\right)^n$
El valor es:
$F=5,659,000\left(\frac{1}{1-0.0125}\right)^6=6,102,630.40$Para $n=1$
$F_1=5,659,000\left(\frac{1}{1-0.0125}\right)^1=5,730,632.91$Los intereses se calculan con:
$$I=P\left[\left(\frac{1}{1-ia}\right)^n-1\right]$$ $I_1=5,659,000\left[\left(\frac{1}{1-0.0125}\right)^1-1\right]=71,632.91$
| n | Cuota | Interés | Amortización | Saldo |
|---|---|---|---|---|
| 0 | 5,659,000.00 | |||
| 1 | 0.0 | 70,737.50 | -70,737.50 | 5,729,735.50 |
| 2 | 00 | 71,621.72 | -72,621.72 | 5,801,359.22 |
| 3 | 0.0 | 72,516.99 | -72,516.99 | 5,873,876.21 |
| 4 | 0.0 | 73,423.45 | -73,423.45 | 5,947,299.66 |
| 5 | 0.0 | 74,341.25 | -74,341.25 | 6,021,640.91 |
| 6 | 6,096,911.42 | 75,270.51 | 6,021,640.91 | 0.0 |
El lector puede obtener el mismo resultado con la ecuación de interés marginal.
La amortización es:
$$R_1=0-71,632.91=-71,632.91$$ $$S_1=5,659,000-\left(-71,632.91\right)=5,730,632.91$$$$F_2=5,659,000\left(\frac{1}{1-0.0125}\right)^2=5,803,172.57$$ $$I_2=5,730,632.91\left[\left(\frac{1}{1-0.0125}\right)^1-1\right]=72,539.66$$ $$R_2=0-72,539.66=-71,632.91$$ $$S_2=5,730,632.91-\left(-72,539.66\right)=5,803,172.57$$
La capitalización es anticipada, al inicio de cada período, pero los saldos se presentan al final de cada uno de ellos. Así mismo, el pago único es al final del plazo. Nótese que para n=1, los intereses anticipados suman 71,632.91 pesos y son más altos que los vencidos.
Por último, el valor futuro para cada n, como en 1 y 2, son, de nuevo, exactamente igual al saldo en esos mismos instantes.
En la siguiente Tabla 3.8 se presentan los demás cálculos.
Cuota única con capitalización continua.
$$F=Pe^{J\ast n}$$ $$I=P\left(e^{J\ast n}-1\right)$$La cuota única es:
$F=5,659,000e^{0.0125\ast6}=6,099,746.41$
| n | Cuota | Interés | Amortización | Saldo |
|---|---|---|---|---|
| 0 | 5,659,000.00 | |||
| 1 | 0.0 | 71,632.91 | -71,632.91 | 5,730,632.91 |
| 2 | 00 | 72,539.66 | -72,539.66 | 5,803,172.57 |
| 3 | 0.0 | 73,457.88 | -73,457.88 | 5,876,630.45 |
| 4 | 0.0 | 74,387.73 | -74,387.73 | 5,951,018.18 |
| 5 | 0.0 | 75,239.34 | -75,239.34 | 6,026,347.52 |
| 6 | 6,102,630.40 | 76,282.88 | 6,026,347.52 | 0.0 |
Esquema de amortización. Con $n=1$. Debemos trabajar con la tasa de interés mensual. Los valores son:
$F_1=5,659,000e^{0.0125\ast1}=5,730,181.46$
$I_1=5,659,000\left(e^{0.0125\ast1}-1\right)=71,181.46$
$R_1=0-71,181.46=-71,181.46$
$S_1=5,659,000-\left(-71,181.46\right)=5,730,181.46$
Para $n=2$
Los intereses los vamos a calcularlos sobre el saldo anterior, valor este que trae intereses acumulados del período uno. Estos son:
$F_2=5,659,000e^{0.0125\ast2}=5,802,258.27$Ahora bien, con la fórmula (3.17.1), el interés marginal para el año dos es:
$I_2=5,659,000e^{0.0125\ast2}\left(e^{0.0125}-1\right)=72,076.81$. Igual valor
$R_2=0-72,076.82=-72,076.81$
$S_2=5,730,181.46-\left(-71,181.46\right)=5,802,258.27$
En la siguiente Tabla 3.9 se presenta el esquema de amortización de este caso continuo.
| n | Cuota | Interés | Amortización | Saldo |
|---|---|---|---|---|
| 0 | 5,659,000.00 | |||
| 1 | 0.0 | 71,181.46 | -71,181.46 | 5,730,181.46 |
| 2 | 00 | 72,076.81 | -72,076.81 | 5,802,258.27 |
| 3 | 0.0 | 72,983.42 | -72,983.42 | 5,875,241.69 |
| 4 | 0.0 | 73,901.44 | -73,901.44 | 5,949,143.13 |
| 5 | 0.0 | 74,831.01 | -74,831.01 | 6,023,974.14 |
| 6 | 6,099,746.61 | 75,772.27 | 6,023,974.14 | 0.0 |
De los resultados podemos concluir que la cuota única más alta es la de la capitalización anticipada, luego sigue la capitalización continua y por último la vencida, ceteris paribus.
Una hoja de cálculo es una aplicación de software utilizada para organizar, analizar y manipular datos numéricos en forma de tablas con las cuales se pueden realizar cálculos matemáticos. En esta sección nos apoyaremos en la hoja de cálculo Excel para resolver los ejemplos que hemos venido trabajando especialmente de interés compuesto.
Ilustraremos la aplicación de las funciones incorporadas en la hoja de cálculo Excel 2013, así como la herramienta de Buscar Objetivo que es útil en la solución de problemas que se resuelven desde el planteamiento de una ecuación de valor.
En concreto, las funciones y herramientas a estudiar en este apartado se especifican en la siguiente figura 3.16, aclarando que todas ellas son bajo la modalidad vencida.

En el acceso a las funciones que nos ofrece Excel para el propósito plateado, existen varias vías. Una primera opción es, desde el botón $f_x$ (insertar función) de la barra de fórmulas, damos clic y se abre la ventana Insertar función, en ésta seleccionamos la categoría financiera, y nos aparece una lista de funciones ordenadas alfabéticamente, procedemos a seleccionar la función requerida. La segunda posibilidad es, desde la cinta de opciones, dirigirnos a la pestaña Fórmulas, para luego desplegar la opción Financieras del grupo biblioteca de funciones, y de allí seleccionar la función requerida.
Una vez seleccionada la función, se despliega una ventana identificada con el nombre de la fórmula activa y sus argumentos. Para realizar algún cálculo, debemos ingresar datos, ya sea digitándolos directamente en el espacio de cada argumento de la función, o dando clic en dirección de celda, o por medio de una función anidada como argumento; realizado lo anterior hacemos clic en el botón aceptar como orden de ejecución de la función.
En los ejemplos siguientes observaremos estas indicaciones.

Ejemplo 3.34_ Función VF. Un TES de 48,250,000 pesos se hace a 5 años con tasa nominal anual de 5.3% mes vencido. Hallar el valor nominal del título.
En este ejercicio la capitalización es mes vencida, por ello $k=12$. Con este valor debemos ajustar el plazo a períodos de capitalización ($12*5=60$ meses) y aplicar la tasa de interés periódica (mensual) vencida dividiendo la nominal por $k$ ($iv=0.441$% mensual).
Recordemos que el valor nominal de un título es su valor futuro, por ello $Vn=F$. El problema consiste entonces en hallar el valor futuro del TES y para ello utilizamos la función de Excel denominada $VF$. Ver figura 3.17
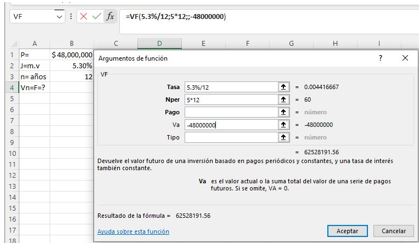
La función fue activada por medio del botón $f_x$ , seleccionamos luego categoría financiera y por último la función $VF$. Al dar clic sobre dicha función se abre la ventana de la figura 3.17 en la que ingresamos los datos directamente en los campos de los argumentos. Nótese que en el argumento tasa se ha planteado la división de la tasa nominal por la frecuencia de capitalización para obtener la tasa periódica mes vencido ($iv=\frac{J}{k}$); así mismo en $Nper$ planteamos la conversión del plazo a períodos de capitalización en meses. En el argumento $VA$ hemos introducido el monto del capital con signo negativo para obtener la respuesta con signo positivo (aunque con la función valor absoluto se puede obviar esta consideración).
Finalmente, al dar clic sobre el botón aceptar obtenemos el valor nominal del título de 62,528,191.56 pesos
De los argumentos de la función $VF$ no hemos activado $PAGO$, por no ser requerido en el cálculo planteado; tampoco hemos asignado valor en $TIPO$, dado que Excel cuando es omitido asume que es cero.
Con cero se indica que el pago es vencido, con uno se indica que es anticipado; pero estos valores aplican cuando en los argumentos utilizamos a $PAGO$ (función que estudiaremos en el volumen dos de este libro).

Ejemplo 3.35_ Función VA de un VF. Un lote de 10,000 metros cuadrados se negoció en el día de hoy por la suma de 150,800,000 de pesos. Si el propietario lo había adquirido hace tres años, y si éste tiene como costo de oportunidad el 3.5% semestral ¿en cuánto había comprado el terreno?
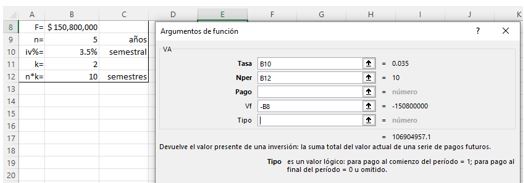
Para resolver este ejemplo, primero realizamos en la hoja de cálculo Excel las conversiones necesarias del plazo y de la tasa de interés coherente con el período de capitalización, el semestre, como se observa en la parte superior izquierda de la figura 3.18.
La introducción de los datos en los argumentos de la función se ha realizado dado clic a cada valor pertinente, por lo que ahora en la ventana de la función, en sus argumentos, aparecen direcciones de celdas (B10, B12, B8).
Los argumentos Pago y Tipo fueron omitidos por las mismas razones del ejercicio anterior. Al dar clic en botón aceptar, la respuesta a la pregunta es $106,904,957.11.

Ejemplo 3.36_ Función NPER. Un bono de deuda pública fue adquirido en 95,000,000 pesos con una tasa de interés de 6.3% anual. Si el valor nominal (futuro) del título es de 128,940.762 pesos ¿Hace cuántos años se emitió este instrumento de deuda?
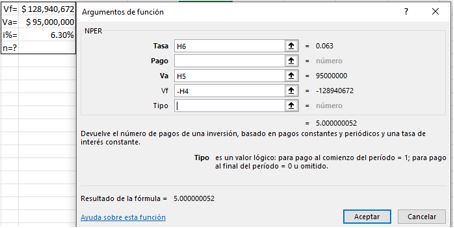
En los argumentos de esta función participan, además de Tasa, el Vf y el Va. En esta ocasión, por requerimiento del algoritmo de Excel para ejecutar la función y realizar el cálculo, es necesario ingresar con signo negativo a uno de estos dos últimos argumentos.
En este ejercicio se ha introducido el Vf como negativo. La respuesta al problema es cinco años. Ver figura 3.19

Ejemplo 3.37_ Función TASA. En el día de hoy se ha vendido un lote de 10 cabezas de ganado vacuno de la raza Gyr en $35,500,000 que se había adquirido en una subasta por valor de 27,350,000 pesos hace 7 meses. ¿Qué tasa de rentabilidad se logró en el negocio?
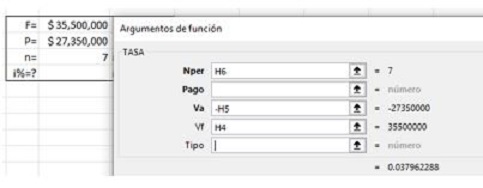
Se logró el 3.8% mensual y es equivalente al 46.6% nominal anual mes vencido.

Ejemplo 3.38_ Función VF. PLAN. El primero de enero de 2017 un empleado público tenía por salario la suma de 5,380,250 pesos. Si este salario se actualizó cada año exactamente al nivel de la inflación anual, que para los fines de año del período 2017-2021 se ubicó respectivamente en: 4.09%, 3.18%, 3.8%, 1.61%, y 5.62%, ¿cuál es el valor del salario para el primero de enero de 2022?
El problema consiste en hallar el valor futuro del salario que identificamos como un VA con tasas múltiples, que en este caso son de inflación. Procedemos con la función VF.PLAN como en la siguiente figura 3.21.
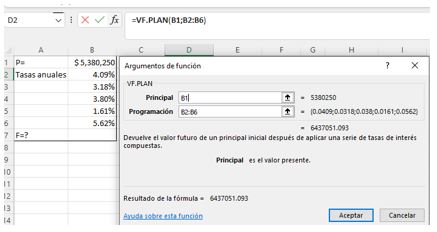
En la parte superior izquierda de la hoja de cálculo tenemos los datos. En el rango B2:B6 se ubican las tasas de inflación desde 2017 hasta 2021, datos a diciembre 31 de cada año, con fuente del DANE.
En los argumentos de la función activa, el principal es un Va, que en este caso es el salario del empleado público; el argumento programación hace referencia a la matriz de las tasas de inflación, en este caso con dimensión de cinco filas y una columna (o vector columna definido por el rango ya indicado). Para ingresar en programación los datos de las tasas, solo basta señalar con clic sostenido la matriz de datos y estos aparecen en forma de rango con dirección de celda. Al dar aceptar, el salario actualizado por la inflación es de 6,437,051 pesos para el primero de enero de 2022, monto que se puede observar en resultado de la fórmula en la parte inferior izquierda de la figura 3.21.

Ejemplo 3.39_ Futuro anticipado en Excel. Un anillo de diamantes adquirido en 300,000 dólares fue subastado a los seis meses en 330,000 dólares. Suponiendo que no hay cobro de comisión en la subasta, ¿qué tasa de rentabilidad mensual anticipada se logró en el negocio? Calcular además la tasa de rentabilidad nominal anual.
Podemos estar pensando que para la solución de este problema con Excel, solo basta con activar la función TASA y en el argumento Tipo digitar 1 para cálculos anticipados. Empero, ese no es el caso. Los valores en Tipo de 0 y 1, funcionan como se ha señalado, para cálculos que involucren el argumento o función PAGO.
Si utilizamos la función TASA obtendremos la rentabilidad mensual vencida. Este valor, lo convertimos luego a mes anticipado, con $ia=\frac{iv}{1+iv}$ y así resolvemos la pregunta por la rentabilidad del mes anticipado.
En la figura 3.22 el resultado de la fórmula es 1.6011863% mes vencido. Con este resultado, la tasa mes anticipada es: $ia=\frac{0.016011868}{1+0.016011868}=0.015759=1.57$% mensual. Así mismo, la tasa de interés nominal anual es de 18.91% m.a.
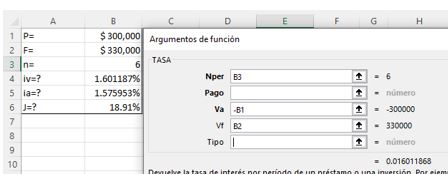
Ahora bien, en el caso que la pregunta sea por el valor futuro, el valor presente, o por el plazo, con capitalización anticipada, procedemos a convertir la tasa periódica anticipada a periódica vencida y así utilizamos las fórmulas de Excel sin ninguna dificultad.
Para lo anterior, recordemos que $iv=\frac{ia}{1-ia}$

Ejemplo 3.40_ Herramienta Buscar Objetivo. Un comerciante de la Central Mayorista de la ciudad de Medellín se ha comprometido en cancelar el inventario de insumos para productos de panadería, por medio de una letra de 3,500,000 pesos en dos meses, una segunda por 4,200,000 pesos en cuatro meses, y una última en siete meses por valor de 3,890,000 pesos, pagos acordados con tasa de interés de 2.5% mes vencido.
Por dificultades de efectivo, el comerciante le propone a su acreedor cancelar su deuda en dos pagos iguales en los meses seis y siete, pero esta vez con un interés mensual de 2.8%. Hallar el valor de los nuevos pagos.
Este es un problema de ecuación de valor con cambio en la tasa de interés al plantearse el nuevo acuerdo de pago. La pregunta objetivo es por los nuevos pagos iguales en los meses seis y siete. Lo resolvemos en dos pasos, siendo el primero determinar el monto presente del primer acuerdo y, en el segundo paso, con el valor anterior hallar los dos nuevos pagos.
En ambos pasos, utilizamos la estructura de un esquema de amortización, como los de las tablas 3.7 a 3.9, recurriendo en esta ocasión al manejo de referencias de celdas relativas y de celdas absolutas (fijadas por medio de la tecla f4 por ser constantes en cada paso del ejercicio).
La ecuación de valor de este problema, con fecha focal cero, es la siguiente:
$$\frac{3,500,000}{\left(1+0.025\right)^2}+\frac{4,200,000}{\left(1+0.025\right)^4}+\frac{3,890,000}{\left(1+0.025\right)^7}=$$ $$\frac{X}{\left(1+0.028\right)^6}+\frac{X}{\left(1+0.028\right)^7}$$El resultado del lado izquierdo de la igualdad en ff=0, es el valor presente (P o Va) de la deuda representada en las tres letras iniciales, y se iguala, como segunda parte, a la pregunta objetivo que son los dos nuevos pagos de igual monto, lado derecho de la ecuación de valor.
La herramienta de Excel para resolver este problema es Buscar objetivo. Esta herramienta permite resolver una ecuación de una variable. En este caso, nos preguntamos por el valor que debe tomar X para que la deuda quede saldada; es decir, y en términos de la ecuación de valor, es la pregunta por la X que hace cero a ésta. Es decir:
$$\frac{3,500,000}{\left(1+0.025\right)^2}+\frac{4,200,000}{\left(1+0.025\right)^4}+\frac{3,890,000}{\left(1+0.025\right)^7}$$ $$-\frac{X}{\left(1+0.028\right)^6}+\frac{X}{\left(1+0.028\right)^7}=0$$El acceso a dicha herramienta es: desde la cinta de opciones, dirigirnos a la pestaña Datos, para luego desplegar la opción Análisis de hipótesis del grupo Previsión, y de allí dar clic en Buscar objetivo. Con ello se abre la ventana de la figura 3.23.
Se resuelve en dos pasos,
Paso#1. Hallar el valor presente de las letras.
En este primer paso el propósito es hallar el valor presente de las tres letras iniciales. Para ello, en la parte superior izquierda de la figura 3.24 tenemos, además de los datos iniciales, en la celda A1 la variable P con interrogación, indicando la pregunta a resolver. En la celda B1 encontramos 500,000 pesos como valor arbitrario de P (un monto supuesto o hipotético).
El monto supuesto aparece además como saldo inicial, de la fila $n=0$, en la tabla de amortización (ver celda h2), ingresado como dirección de celda relativa. Este valor es provisional, y necesario para programar la tabla de amortización como vemos enseguida.
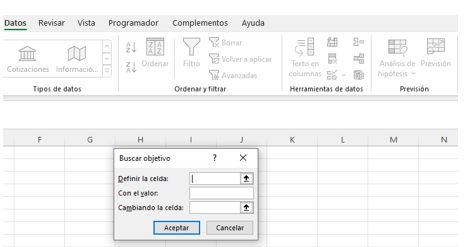
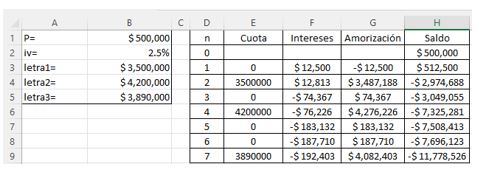
En la tabla de amortización, en la columna cuota aparecen las tres letras en sus respectivos meses de pagos, ingresados en la tabla como dirección de celta.
En aquellos meses donde no existe pago alguno debemos rellenar con ceros, esto es una exigencia de la función.
La programación de las demás columnas es la siguiente:
Los intereses debemos determinarlos sobre el saldo, como ya se ha ilustrado en otros ejercicios, y no con la ecuación de interés marginal debido a que en estos problemas no se da el supuesto de pago único al final del plazo, al contrario, existen varios pagos.
Así entonces, para programar su cálculo, simplemente damos clic, por ejemplo para los intereses n=1, al saldo anterior de 500,000 y lo multiplicamos por la tasa de interés del 2.8%, tasa que fijamos su valor con celda absoluta dado que es la misma para el cálculo de los demás intereses del esquema; es decir, los intereses indicados con dirección de celda $E3$ resultan de la operación $H2*B2$, y es igual a $500,000*0.025=12,500$.
La amortización, como sabemos, se obtiene restando a la cuota los intereses, en cada n en particular. Para n=1, esta es entonces $E3-F3$, ambas direcciones con celda relativa (o sea, $0-12,500=-12,500)$
Para obtener el saldo siguiente, debemos restar al saldo anterior la amortización. Para n=1 tenemos que el nuevo saldo es igual a $H2-G3$. Esto es: $500,000-(-12,500)=512,500$.
Una vez completada la programación de estas tres últimas columnas del esquema de amortización, las señalamos y arrastramos sostenido abarcando el rango $F3:H9$, así se completa los cálculos en las demás celdas faltantes (también puede ser dando doble clic en el vértice inferior derecho de la última celda señalada). Ver de nuevo tabla 3.24.
En este momento procedemos a realizar el cálculo de P activando la función buscar objetivo. Ver la Figura 3.25. La interpretación en este momento es la siguiente, ¿cuál es el valor de P que hace cero al saldo en el esquema de amortización?
Es decir, pretendemos hallar el verdadero valor que debe tomar P, del que provisionalmente hemos asumido 500,000 pesos en n=0 del esquema de amortización, para que el saldo al final del plazo, n=7, sea cero, y no aparezca como saldo -11,778,526 pesos (celda H9).
En los argumentos de la función Buscar objetivo de la Figura 3.25 tenemos en: definir la celda= H9, con el valor de= cero, cambiando la celda= B1.
La pregunta que se responde, de nuevo, es: ¿cuál es el valor de P, ubicado en celda B1 que aplicado al esquema de amortización el saldo al pagar la última cuota, en n=7 y con valor de $3,890,000, sea cero (en H9)? Sólo basta con dar aceptar en la función para la realización del cálculo y obtener el verdadero valor de P, que reemplaza al valor arbitrario inicial, que había sido incorporado provisionalmente en el planteamiento del esquema de amortización de este paso #1.
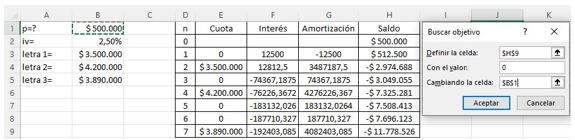
Ver resultado en Figura 3.26. Obsérvese que en las celdas $B1$ y $H2$ ya no aparece el valor arbitrario de P, sino el valor real de este, de 10,408,865 pesos.
Con el pago de las tres letras, el saldo en $H9$ es de cero.
Por lo tanto, las tres letras son equivalentes a un capital de 10,408,865 pesoS en ff=0. Y es la solución del lado izquierdo de la ecuación de valor, esto es:
$$10,408,865=\frac{X}{\left(1+0.028\right)^6}+\frac{X}{\left(1+0.028\right)^7}$$
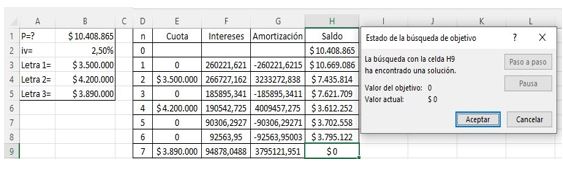
La cuestión ahora es resolver para X, hallar los nuevos pagos.
Paso# 2. Los nuevos pagos
Procedemos igualmente elaborando el esquema de amortización, pero en esta ocasión el saldo inicial de la celda G2 de la figura 3.27, es el valor de P hallado en el paso# 1 (ver celda H2 de la figura 3.26). Debemos además emplear la nueva tasa de interés del 2.8% mensual, dato del problema. Con esta información, la pregunta ahora es por el valor de X (celdas $D8$ y $D9$), a las que provisionalmente asignamos un valor arbitrario de 300,000 pesos.
Programado de igual manera como en paso #1, ejecutamos la herramienta buscar objetivo para el cálculo. Ver Figura 3.27.
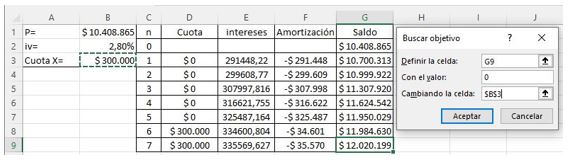
Al dar clic en aceptar, el resultado es pagar en los meses seis y siete la suma de 6,227,120 pesos; con ellos se ha saldado la deuda, como se observa en celda G9 de la figura 3.28.
Así hemos hallado los valores de las dos cuotas que reemplazan al esquema inicial de pago.
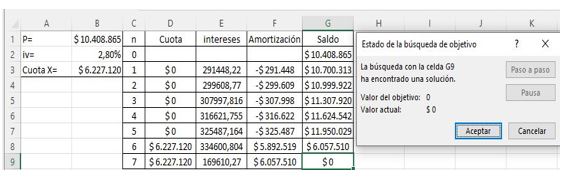

Ejemplo 3.41. Función TASA.INT. El 12 de enero de 2022 se realiza una inversión de renta fija a corto plazo con importe de 589,200 pesos con vencimiento el 30 de junio del mismo año y valor nominal de 601,340 pesos.
Hallar la tasa de rentabilidad simple de esta inversión.
La función TASA.INT permite calcular la tasa de interés o de rendimiento bajo la modalidad simple de una inversión que se liquida con un pago único al final del plazo o vencimiento. Los argumentos de la función son:
Liquidación. Es la fecha en que se hace la inversión.
Vencimiento: Es la fecha en que se redime o liquida la inversión.
Inversión. Es el monto del capital invertido o principal
Amortización. Es el valor nominal o futuro de la inversión
Base. Es un número entre 0 y 4 que especifica la norma para contar los días de la inversión, al considerar cómo se define el mes y el año. Por ejemplo, la base cero indica que el mes es asumido de 30 días y el año de 360 (30/360), convención aplicada en los Estados Unidos; la base 1 indica asumir el mes y el año exactos (mes exacto/año exacto, incluido si es bisiesto) , la base 2 indica el mes asumido exacto y año de por 360 días (mes exacto/360), la base 3 es mes exacto y año de 365 días (mes exacto/365, incluso si es bisiesto); y la base 4 asume mes corriente y año corriente (30 días mes/360), similar a la base cero pero es aplicada en Europa. (Hayat & Millán, 2004)
Los anteriores son nombres particulares dados por el Excel a esas variables, que esperamos no genere confusión.
Para resolver el ejemplo utilizaremos la base 2. Ver la figura 3.29 en la que hemos digitados los valores al extremo superior izquierdo de ésta, y para el cálculo de la tasa de rentabilidad hemos llenado los argumentos de la función con direcciones de celda.
La rentabilidad de la inversión es de 4.39% anual simple. Con base cero el resultado es de 4.42%.
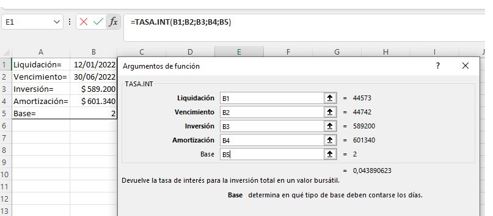

Ejemplo 3.42. tendencias de las modalidades compuesta en relación con la frecuencia de capitalización. Suponga un principal de 10,000,000 de pesos, una tasa de interés nominal anual de 15% y un plazo de cinco años. Realícese el cálculo del valor futuro compuesto bajo los modos vencido, anticipado y continuo, simulando diferentes frecuencias de capitalización, en concreto suponga que k capitaliza anual, semestral, cuatrimestral, trimestral, mensual, semanal, quincenal (k=1,2,3,4,12,24,52).
Disponga los resultados en una tabla y de manera gráfica, analíce los resultados y obtenga algunas conclusiones.
Los resultados se presentan en la siguiente tabla 3.10. La gráfica se muestra en la figura 3.30.
En la tabla 3.10 se observa en el comportamiento de los datos, que el valor futuro anticipado presenta una relación inversa respecto a k, a mayor k es menor el valor futuro, y viceversa; su tendencia es descendente al presentar una pendiente negativa.
En cambio la relación es directa entre el valor futuro vencido y la frecuencia de capitalización, dado que a mayor k mayor es el valor futuro y viceversa.
| k | Vencido | Anticipado | Continuo |
|---|---|---|---|
| 1 | 20,113,572 | 22,537,481 | 21,170,000 |
| 2 | 20,610,326 | 21,806,335 | 21,170,000 |
| 3 | 20,789,282 | 21,584,695 | 21,170,000 |
| 4 | 20,881,520 | 21,447,575 | 21,170,000 |
| 12 | 21,071,813 | 21,270,306 | 21,170,000 |
| 24 | 21,120,646 | 21,219884 | 21,170,000 |
| 52 | 2,147,156 | 21,192,857 | 21,170,000 |
Empero, en el caso del valor futuro continuo, éste no presenta relación con valores discretos de k, esto debido a que en la modelación de esta forma de capitalización, el crecimiento al infinito de la frecuencia de capitalización es capturado por medio de la función que genera el número Euler.
En la figura 3.30 podemos observar dos cosas adicionales. En primer lugar, nótese que en todos los casos cuando k toma un valor en particular (por ejemplo k=24), el valor futuro anticipado es mayor al continuo y este último a su vez es mayor que el futuro vencido. En segundo lugar, obsérvese cómo a medida que k se hace más grande, tanto el valor futuro anticipado como el futuro vencido tienden al valor futuro continuo, convergen al futuro continuo, pero con diferentes pendientes, dadas las relaciones ya indicadas de éstos con la frecuencia de capitalización, K.
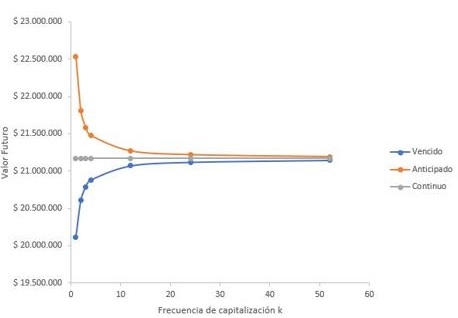
Hallar el valor futuro de la inversión, el interés acumulado y el interés marginal computado en el semestre cuatro, resolviendo el problema en las modalidades de interés compuesto vencido, compuesto continuo y compuesto anticipado.(R. Vencido: 113,535,044; 24,835,044; 4,214,791 respectivamente. Continuo: 114,121,069; 25,421,069; 4,315,649 respectivamente. Anticipado: 114,744,153; 26,044,153; 4,422,938 respectivamente).
Elaborar la tabla de amortización bajo el sistema de cuota única en las modalidades de interés vencido, continuo y anticipado; constatar los resultados presentados en la respuesta del problema anterior. (R. Cuota única vencida 113,535,044; cuota única contínua 114,121,069; cuota única anticipada 114,744,153).
Hacer el diagrama de caja de este problema, plantear la ecuación de valor y hallar el monto de los pagos iguales. (R. Dos pagos iguales de 16,013,203.10 pesos).
¿De cuánto fue el monto inicial prestado por el Banco agrario y con qué tasa de intereses se pacta el nuevo esquema de pago? (R. 104,148,047.04 pesos; 0.86% mensual, respectivamente).
La tasa de interés es una variable clave en la explicación teórica sobre el funcionamiento, la dinámica y el desenvolvimiento de la economía doméstica (nacional) y de la economía mundial. Así mismo, como ya hemos indicado desde la expresión valor del dinero en el tiempo y del concepto de equivalencia, la tasa de interés es un factor de valoración (de determinación del valor) de los diferentes activos financieros.
Para la corriente de la economía neoclásica, perspectiva teórica que supone el pleno empleo de los recursos en su estructura conceptual (no existe desempleo involuntario), la tasa de interés es una recompensa para que los agentes económicos (el consumidor) libere recursos con destino a la inversión en nuevos bienes de capital; la tasa de interés es una retribución por el sacrificio que realiza dicho agente al posponer el consumo. En esta corriente teórica, desde la perspectiva macroeconómica, la tasa de interés es la que iguala el ahorro y la inversión.
En cambio, desde la óptica de la teoría económica de John M. Keynes (1983), la tasa de interés es un fenómeno monetario, al considerarla como el pago que permite el uso del dinero ajeno, y está determinada por la interacción de la oferta y la demanda de dinero; no es por lo tanto, la que iguala el ahorro con la inversión. La tasa de interés es una compensación por renunciar a la preferencia por la liquidez, por renunciar a poseer el dinero en forma líquida, acción que induce a los agentes económicos a tener la riqueza financiera (stock neto de activos financieros) en otras formas distintas al dinero en efectivo (formas como las inversiones en títulos valores, en activos de renta fija y renta variable). Es entonces, una tasa monetaria de interés determinada por la oferta monetaria y la demanda de dinero.
Desde el enfoque de John M. Keynes, el valor del dinero en el tiempo es la compensación por la cesión de la liquidez, recompensa que para el agente económico individual se expresa en la tasa de interés pactada en la operación de cesión del efectivo (en calidad de préstamo, de crédito, o de inversión en activos financieros). En este sentido, John C. Hull (2009) señala que la tasa de interés define la cantidad de dinero que un prestatario se compromete a pagar al prestamista, en un plazo acordado.
Por lo tanto, como compensación al capital financiero, estamos indicando que la tasa de interés es un fenómeno monetario y no hace referencia a la rentabilidad de un capital en forma de bienes de producción (como capital real).
Este capítulo está dedicado al estudio de las tasas de interés nominal, efectiva y equivalente. Para este propósito nos apoyamos en lo estudiado en el capítulo anterior sobre el interés compuesto bajo diferentes modalidades de capitalización.
Estudiaremos además otros indicadores de tasas de interés, como son la tasa efectiva neta, la tasa efectiva real y la tasa efectiva neta real, así como aplicaciones del tema en operaciones financieras realizadas en monedas extranjeras, en Unidades de Valor Real (UVR), e indexadas bajo la tasa de interés de los depósitos a términos fijos, DTF, operaciones propias de la economía colombiana.
La tasa de interés nominal (J), es una tasa de interés de referencia empleada en los acuerdos de operaciones financieras de inversión o crédito. Es de referencia porque no es propiamente la tasa que se aplica en la valoración de las operaciones financieras, pero si suministra información para realizar dicha valoración.
Por ejemplo, si tenemos una tasa de interés nominal anual del 24% mes vencido, expresión que resumimos como $J=24$% m.v., en la valoración futura de un activo se debe utilizar, como ya hemos indicado en el capítulo anterior, la tasa de interés que corresponde al mes y la modalidad de capitalización vencida.
Esto es, debemos trabajar con $iv=\frac{J}{k}=\frac{0.24}{12}=0.02=2.0$%. La información suministrada directa e implícitamente por la tasa de interés nominal son el período de interés, la frecuencia de capitalización, la tasa de interés periódica y la modalidad de capitalización.
Adicionalmente, el término nominal indica, en este contexto, la no consideración de la capitalización de intereses en la tasa de interés. En este sentido, la tasa de interés nominal es como el interés simple, no capitaliza interés, y por ello no representa en la valoración el efecto de los intereses sobre los intereses. Es por esta razón que se puede dividir para obtener una tasa de interés periódica, como $iv$ o $ia$.
Así mismo, si $iv=\frac{J}{k}$ entonces $J=k\ast iv$. De igual manera, si $ia=\frac{J}{k}$ entonces $J=k\ast ia$. La tasa de interés nominal al no capitalizar, permite las operaciones de división y multiplicación.
Es necesario resaltar que las tasas de interés periódica, como $iv$ o $ia$, son tasas que efectivamente se aplican en el período de capitalización, en la valuación de las operaciones financieras cuando existan capitalizaciones que son fracciones de año. Las tasas de interés periódicas son, por lo tanto, tasas efectivas del período de capitalización.
Para el desarrollo de este capítulo, vamos a utilizar con respecto a la tasa nominal anual, los siguientes símbolos y significados.
$J_v$. Es la tasa de interés nominal anual con capitalización vencida ($k_v$)
$J_a$. Tasa de interés nominal anual con capitalización anticipada ($k_a$)
$J_c$. Tasa de interés nominal anual con capitalización continua ($k_c$)
La variable frecuencia de capitalización con subíndice, como en $k_v$, se utiliza con el propósito de diferenciar, igualmente, las modalidades de capitalización.
La tasa de interés efectiva es aquella que surge del proceso de capitalizar intereses. El término efectivo indica capitalización de intereses; esto es, la tasa de interés efectiva es resultado del interés compuesto.
La diferencia que existe entre la tasa de interés nominal y la tasa de interés efectiva, es la misma que media entre el interés simple y el interés compuesto: la capitalización.
La tasa de interés nominal no capitaliza, mientras la tasa efectiva emana de considerar la capitalización. Esto genera una diferencia entre ellas manifestada por los intereses de los intereses; la tasa de interés efectiva, es efectiva porque considera en su cálculo el interés de los intereses.
De esta manera, la tasa de interés nominal evidentemente ignora el valor del dinero en el tiempo, de la misma forma como se observó en el cálculo del interés simple.
Las tasas de interés efectiva y nominal se pueden expresar en cualquier unidad de tiempo. Como máxima unidad, el período de interés es el año; lo anterior como convención social.
Para la tasa efectiva, utilizaremos los siguientes símbolos y significados.
"ie". Significa tasa de interés efectiva, que puede ser en las modalidades vencida, anticipada y continua; es en el contexto específico de un problema donde identificamos a qué modalidad de capitalización se hace referencia. La expresión $ie=8.5$% EA, significa tasa de interés efectiva anual del 8.5%.
"iv". Es la tasa efectiva periódica vencida, tasa de interés periódica vencida"ia". Es la tasa efectiva periódica anticipada, tasa de interés periódica anticipada
Procedamos a determinar la manera de calcular la tasa de interés efectiva, según modalidad de capitalización. Para ello partamos de obtener un crédito de 2,000,000 de pesos al 24% anual y un plazo de un año.
Calcular el valor futuro y los intereses bajo la forma vencida , anticipada, continua, y deducir la fórmula para el cálculo de la tasa efectiva.
En este caso la capitalización es anual. Veamos qué sucede en esta situación utilizando lo aprendido en el capítulo anterior.
Futuro vencido.
$$F=2,000,000\left(1+0.24\right)^1=2,480,000$$ $$I=2,000,000\left[\left(1+0.24\right)^1-1\right]=480,000$$ $$i=\frac{480,000}{2,000,000}=0.24$$Con capitalización año vencido, los intereses que efectivamente se cargan representan el 24% del capital inicial. Decimos por lo tanto que en esta operación financiera, la tasa efectiva de interés es el 24% y corresponde a la misma tasa de interés nominal.
Ahora bien, ¿qué ocurre con esta operación si la capitalización es fracción de año? ¿Por ejemplo, mes vencido (k=12)? Veamos:
Con capitalización fracción de año (el mes), los intereses que efectivamente se cargan al capital inicial representan una tasa de interés efectiva de 26.82% anual y es mayor a la tasa de interés nominal anual. La razón se halla en que la primera tasa surge de considerar la capitalización de intereses. Adicionalmente, se observa que la tasa efectiva vencida tiene una relación directa con la frecuencia de capitalización, esto es, la misma relación del valor futuro vencido con respecto a k ya estudiada en el capítulo anterior.
Por lo tanto, la fórmula para calcular la tasa efectiva anual vencida es:
$$ie=\frac{I}{P}=\frac{P\left[\left(1+\frac{J_v}{k_v}\right)^{k_v\ast n}-1\right]}{P}$$Cancelando P y bajo la convención de expresar la tasa de interés hasta por un año, hacemos por ello n=1, se obtiene en consecuencia que:
$${ie=\left(1+\frac{J_v}{k_v}\right)}^{k_v}-1\tag{4.1}$$E igual a:
$${ie=\left(1+iv\right)}^{k_v}-1\tag{4.1.1}$$Las ecuaciones (4.1) y (4.1.1) calculan la tasa efectiva anual bajo la modalidad vencida, cuando el dato conocido es la tasa nominal anual o la tasa periódica de interés, respectivamente.
Futuro Anticipado
Con capitalización año anticipado, los valores son:
$$F=2,000,000\left(\frac{1}{1-0.24}\right)^1=2,631,579$$ $$I=2,000,000\left[\left(\frac{1}{1-0.24}\right)^1-1\right]=631,579$$ $$i=\frac{631,579}{2,000,000}=0.3158$$La tasa efectiva anual con capitalización año anticipado es de 31.82%.
¿Qué ocurre con la tasa efectiva si la capitalización se realiza mes anticipado?
$$F=2,000,000\left(\frac{1}{1-0.02}\right)^{12}=2,548,690$$ $$I=2,000,000\left[\left(\frac{1}{1-0.02}\right)^{12}-1\right]=548,690$$ $$i=\frac{548,690}{2,000,000}=0.2743$$Con capitalización mes anticipado, la tasa efectiva anual de 27.43% es menor a la tasa efectiva año anticipado, esto es, se observa relación inversa entre la tasa efectiva anual anticipada y la frecuencia de capitalización.
Así mismo, la tasa efectiva anual anticipada es mayor a la tasa efectiva anual vencida.
Por lo tanto, la fórmula para calcular la tasa efectiva anual anticipada es:
$$ie=\frac{I}{P}=\frac{P\left[\left(\frac{1}{1-\frac{J_a}{k_a}}\right)^{k_a\ast n}-1\right]}{P}$$Con n=1, entonces:
$$ie=\left(\frac{1}{1-\frac{J_a}{k_a}}\right)^{k_a}-1\tag{4.2}$$Y es igual a:
$$ie=\left(\frac{k_a}{k_a-J_a}\right)^{k_a}-1\tag{4.2.1}$$Y en términos de tasa periódica, es:
$$ie=\left(\frac{1}{1-ia}\right)^{k_a}-1\tag{4.2.2}$$ $$ie=\left(1-ia\right)^{-k_a}-1$$Futuro continuo
Con capitalización continua, los valores son:
$$F=2,000,000e^{0.24\ast1}=2,542,498$$ $$i=\frac{542,498}{2,000,000}=0.2712$$La tasa efectiva anual continua es de 27.12%. Comparado con los dos casos anteriores, observamos que esta tasa continua es menor a la tasa efectiva anual anticipada pero mayor a la tasa de interés efectiva anual vencida.
¿Qué sucede si trabajamos con datos mensuales u otro período fracción de año? Para el caso mensual la tasa de interés periódica es de 2% y la frecuencia de capitalización es de 12. Por ello:
$$F=2,000,000e^{0.02\ast12}=2,542,498$$ $$I=2,000,000\left[e^{0.24\ast1}-1\right]=542,498$$Obtenemos el mismo resultado en valor futuro y por tanto, en intereses y tasa efectiva anual. Recordemos que las capitalizaciones continuas se capturan por medio de Euler. La tasa efectiva anual continua se calcula, por lo tanto, como:
$$ie=\frac{I}{P}=\frac{P\left[e^{J_c\ast n}-1\right]}{P}$$Con n=1, es:
$$ie=e^{J_c}-1 \tag{4.3}$$En las fórmulas (4.1) a (4.3) intervienen tres variables: la tasa efectiva anual, la tasa nominal anual y la tasa periódica.
En las anteriores ecuaciones, la variable dependiente es la tasa efectiva anual; empero esta relación funcional es posible cambiarla y preguntarnos por la tasa de interés nominal anual o la tasa periódica, esto es, como variables dependientes, conociendo el valor de la tasa efectiva anual.
El resultado es una tasa equivalente a la tasa de interés dada. Esta equivalencia es la que pasamos a estudiar en el siguiente punto.
Ya hemos indicado que equivalencia significa igual valor económico para las partes de una operación financiera.
En cuanto a las tasas de interés, decimos que dos tasas de interés diferentes con distintas frecuencias de capitalización y/o modalidad de capitalización, son equivalentes si arrojan el mismo resultado económico. Esto es, podemos usar la una o la otra en el cálculo de un valor futuro, de un valor presente o de unos intereses, y se obtiene el mismo monto.
En el capítulo anterior mostramos como con la fórmula $iv=\frac{ia}{1-ia}$ hallábamos una tasa de interés periódica vencida a partir de una tasa periódica anticipada dada. Y viceversa, con $ia=\frac{iv}{1+iv}$, se calcula la tasa de interés periódica anticipada a partir de una tasa periódica vencida conocida.
Ahora decimos que se ha hallado una tasa de interés equivalente a otra tasa de interés dada.
Ilustremos el asunto con un ejemplo. Si una entidad de crédito cobra un 1.5% mes anticipado ¿a qué tasa de interés mes vencido es equivalente? Para resolver reemplazamos en la fórmula $iv=\frac{ia}{1-ia}$ y obtenemos que es $iv=\frac{0.015}{1-0.015}$ e igual a 1.523% mes vencido. Decimos por lo tanto que el 1.5% mes anticipado equivale a una tasa mes vencida de 1.52%.
Así mismo, si tenemos $iv = 1.8$% mensual vencido, su equivalente anticipado es $ia=\frac{0.018}{1+0.018}=1.768$% mes anticipado.
Cuando señalamos que un 1.8% mes vencido equivale a 1.768% mes anticipado, quiere decir que si las utilizamos en el cálculo de un valor futuro, de los intereses de una inversión/crédito, o de la tasa de interés efectiva anual, los valores vencidos y anticipados son los mismos.
Procedemos a constatar lo afirmado. Supongamos que nos facilitan $5,000,000 durante tres años para cancelar al final del plazo con pago único, pero nos dan la opción de cancelar con una tasa del 1.8% mes vencido o con 1.768% mes anticipado.
¿Cuál tasa elegimos? Utilicemos la fórmula de futuro vencido y luego la de futuro anticipado para hacer los cálculos y tomar la decisión. Entonces:
Vencido. $F=P\left(1+iv\right)^{n\ast k}$
Es igual a $F=5,000,000\left(1+0.018\right)^{36}= 9,503,640.78$ de pesos.
Anticipado. $F=P\left(\frac{1}{1-ia}\right)^{n\ast k}$
Es igual a $F=5,000,000\left(\frac{1}{1-0.01768}\right)^{36}= 9,503,640.78$ de pesos
Es decir, igual valor económico.
Por lo tanto, bajo los dos diferentes métodos de cálculo de los valores futuros, los intereses ascienden a la suma de $4,503,640.78.
Nótese además que con este ejemplo sencillo hemos pasado de una situación vencida a otra anticipada (pudo haber sido en sentido contrario).
Sin embargo, no hay diferencias entre esas tasas dado que ofrecen el mismo valor económico ya sea medido por el valor futuro o los intereses. Respecto a las tasas existe indiferencia.
Es precisamente este concepto de equivalencia el que está presente en las tasas efectivas. Para constatarlos, calculemos la tasa efectiva anual vencida y la anticipada de este problema.
Tasa efectiva anual vencida. $ie=\left(1+iv\right)^{k_v}-1$,
es decir ${ie}_a=\left(1+0.018\right)^{12}-1=23.87$% efectivo anual (EA)
Tasa efectiva anual anticipada. ${ie}_a=\left(\frac{1}{1-ia}\right)^{k_a}-1$
Es decir $ie=\left(\frac{1}{1-0.01768}\right)^{12}-1=23.87$% EA.
Iguales valores de tasa efectiva anual. En consecuencia, una tasa de 1.8% mensual vencida equivale a una tasa efectiva anual de 23.87%.
Y es igual a expresar que una tasa de 1.768% mes anticipado, equivale a una tasa efectiva anual de 23.87%.
En términos efectivos, no hay diferencia en las opciones, son por lo tanto indiferentes en el orden de preferencia del agente económico.
Con el concepto de equivalencia entre tasas de interés ilustrado, procedamos a ejemplificar el cálculo de tasas de interés equivalentes.

Ejercicio 4.1_ Cálculo de la tasa efectiva anual y nominal de una tasa periódica. En la venta de unas acciones, el poseedor obtuvo en rendimiento el 1.2% mensual.
Hallar la tasa nominal anual vencida y la tasa efectiva anual de este negocio.
Sabemos que $J_v=k_v\ast iv$, por ello $J_v=12\ast0.012=14.4$% m.v.
Para la tasa efectiva anual, $ie=\left(1+iv\right)^{k_v}-1$
Por ello ${ie}_a=\left(1+0.012\right)^{12}-1=15.39$% E.A.
La tasa del 1.2% mensual vencida equivale a una tasa nominal anual del 14.4% m.v., y a una tasa de 15.39% E.A.

Ejercicio 4.2_ Equivalencias entre tasas periódicas. Hallar la tasa periódica anticipada equivalente a una tasa de 1.2% mes vencido. Calcular además las tasas de interés nominal y efectiva anuales.
Sabemos que $ia=\frac{iv}{1+iv}$ , por ello $ia=\frac{0.012}{1+0.012}=1.186$% mes anticipado
Ahora, si $J_a=k_a\ast ia$, por ello $J_a=12\ast0.01186=14.23$% m.a
Para la tasa efectiva anual anticipada, $ie=\left(\frac{1}{1-ia}\right)^{k_a}-1$
Por ello $ie=\left(\frac{1}{1-0.01186}\right)^{12}-1=15.39$% EA.
El 1.2% mes vencido equivale a 1.186% mes anticipado, a un 14.23% nominal anual mes anticipado, y a una tasa efectiva anual de 15.39%. Además, podemos afirmar que la tasa $J_a=14.23$% m.a., es equivalente a $J_v=14.4$% m.v. porque ambas arrojan una misma tasa efectiva de 15.39% EA.

Ejercicio 4.3_ Tasas efectivas inferiores a un año. Un estudiante comentó en clase que realizaba inversiones de todo tipo, utilizando el sistema monetario y de capitales formal del país, así como de manera informal prestándo dinero a familiares y conocidos. Indicó que en las decisiones parte de su costo de oportunidad que, conociendo la situación económica del país, ha estimado en 1.08% mes vencido.
Dado que somos muy curiosos, queremos saber este costo de oportunidad que tasa de interés efectiva representa al trimestre, al semestre y al año.
En este ejercicio podemos notar que la operación matemática para pasar de una tasa de interés efectiva menor a otra tasa efectiva mayor, consiste en hallar la potencia, o sea elevar a la k.
Es necesario comprender el papel que desempeña k como exponente en cada uno de los cálculos; por ejemplo, en el primer cálculo usamos k=3 debido a que en un trimestre, unidad de tiempo en la que es solicitada la tasa, hay tres meses (unidad de tiempo en la que está expresada la tasa de interés dada, el costo de oportunidad del estudiante).

Ejercicio 4.4_ Hallar la tasa efectiva periódica de una efectiva mayor. Visitamos un banco de la ciudad y consultamos la tasa de interés que cobra por los créditos de libre destinación. El funcionario presente informa que es del 13.5% EA. Por curiosidad, nos preguntamos esa tasa a cuánto equivale bimestre vencido y a cuánto bimestre anticipado.
Este ejercicio es contrario al inmediatamente anterior. En esta ocasión el dato dado es una tasa efectiva mayor para calcular otra efectiva de un período menor.
Como tanto $iv$ e $ia$ son tasas efectivas periódicas, el problema consiste en hallar estas tasas.
Caso vencido. Sabemos que $ie=\left(1+iv\right)^{k_v}-1$ , pero la pregunta del ejercicio es por $iv$ mes vencido.
Despejamos $iv$ de la anterior ecuación tenemos que:
$$iv=\sqrt[k_v]{1+ie}-1 \tag{4.4}$$Como: ${ie}_a=13.5$% E.A., y $k_v$=6 , obtenemos la tasa bimestre vencida de:
$iv=\sqrt[6]{1+0.135}-1=2.13$%Para el caso anticipado utilizamos ${ie}_a=\left(\frac{1}{1-ia}\right)^{k_a}-1$, siendo en este caso la incógnita $ia$, la efectiva menor. Despejando $ia$ tenemos:
$$ia=1-\frac{1}{\sqrt[k_a]{1+ie}} \tag{4.5}$$Como: ${ie}_a=13.5$% E.A., y $k_v$=6 , obtenemos la tasa bimestre anticipada de:
$ia=1-\frac{1}{\sqrt[6]{1+0.135}}=2.09$%.Por lo tanto, el 2.09% bimestre anticipado es equivalente a 2.13% bimestre vencido. Para verificarlo hallemos:
$$ia=\frac{iv}{1+iv}$$ $ia=\frac{0.0213}{1+0.0213}=2.09$%En todos los casos, de efectiva mayor a efectiva menor, tenemos que utilizar como operación matemática los radicales (tomar raíz k); no podemos dividir, como en las nominales, porque sería no respetar la capitalización de intereses o el interés compuesto.

Ejercicio 4.5_ Hallar la tasa nominal anual de una tasa efectiva. Determinar la tasa nominal mes vencida de una tasa trimestral vencida de 2.9%, y de una tasa efectiva anual de 28%.
Este ejercicios consiste en pasar de una tasa efectiva (periódica y anual) a su equivalente nominal (pasar de efectiva a nominal anual).
$J_v=?$
$iv=2.9$% trimestre
${ie}_a=28$% EA
En primer lugar debemos hallar la tasa periódica mes vencida a partir de 2.9% trimestral. El asunto es pasar de una tasa efectiva mayor a una tasa efectiva menor.
$iv=\sqrt[3]{1+0.029}-1=0.957$% mensual.Como sabemozs, $J_v=k_v\ast iv$. Por lo tanto $J_v=12\ast0.00957=11.49%$ m.v. Es la respuesta a la primera pregunta.
Para hallar la tasa nominal anual mes vencido ( $J_v=?\ m.v$), de la tasa efectiva del 28%, debemos combinar:
Reemplazando $iv$ en la primera ecuación, tenemos:
$$J_v=k_v\left[\sqrt[k_v]{1+ie}-1\right] \tag{4.6}$$Y es la fórmula para resolver la pregunta. Por lo tanto:
$J_v=12\left[\sqrt[12]{1+0.28}-1\right]=24.94$% m.v.Esta es la respuesta a la segunda pregunta. La fórmula (4.6) permite pasar de una efectiva anual vencida a una tasa nominal anual vencida.

Ejercicio 4.6_ Hallar la tasa nominal anual de una tasa efectiva anticipada. Hallar la tasa nominal anticipada con los datos del ejercicio anterior.
Para hallar la tasa nominal anual mes anticipado, debemos determinar la tasa equivalente a mes anticipado como primer paso, esto es:
$ia=\frac{0.00957}{1+0.00957}=0.948$%.Por lo tanto, como $J_a=k\ast ia$, el resultado es $J_a=12\ast0.00948=11.38$% m.a. Es la respuesta a la primera cuestión.
Para el cálculo de la tasa nominal pedida desde la tasa efectiva anual, combinamos:
$$J_a=k_a\ast ia$$ $$ia=1-\frac{1}{\sqrt[k_a]{1+ie}}$$Al reemplazar la segunda ecuación en la primera, obtenemos:
$$J_a=k_a\left[1-\frac{1}{\sqrt[k_a]{1+ie}}\right] \tag{4.7}$$Así, el valor solicitado es:
$J_a=12\left[1-\frac{1}{\sqrt[12]{1+0.28}}\right]=24.43$% m.aLa ecuación (4.7) es el modelo para calcular una tasa nominal anual con capitalización anticipada de una tasa efectiva anual.

Ejercicios 4.7_ Hallar la tasa nominal anual de una tasa efectiva continua. Si una entidad financiera cobra una tasa de 25% E.A. continua, hallar la tasa nominal anual.
La tasa efectiva continua se calcula como en (4.3). En esta ocasión la
pregunta es por la $J_c$. Esto es, de:
$$ie=e^{J_c}-1 $$Debemos despejar $J_c$, así:
$$ie+1=e^{J_c} $$Tomando logaritmo natural en ambos lados:
$$ln(ie+1)=ln(e^{J_c})$$ $$ln(ie+1)=J_c\ast ln(e)$$Como $ln(e) =1$, entonces:
$$J_c=ln\left(1+ie\right) \tag{4.8}$$La solución al problema es:
$J_c=ln\left(1+0.25\right)=22.31$% nominal anual.La ecuación (4.8) permite obtener de una tasa efectiva continua, la tasa nominal anual equivalente.
Es en el mismo sentido de los dos ejercicios anteriores (pasar de tasa efectiva a tasa nominal), en esta ocasión bajo la modalidad de capitalización continua.

Ejercicios 4.8_ Hallar la tasa efectiva anual de una tasa nominal anual vencida. Si una entidad bancaria de la ciudad le indica que la tasa de interés de captación de ahorro del público es de 5.3% t.v. ¿Qué tasa efectiva anual vencida es equivalente?
Este es un ejercicio que nos ilustra el cálculo de la tasa efectiva anual equivalente tomando como dato la tasa nominal anual dada.
$J_v=\ 5.3$% t.v.
$k_v=4$ trimestres
$ie=$?

Ejercicios 4.9_ Hallar la tasa efectiva anual de una tasa nominal anual anticipada. Con los datos del ejercicio anterior, suponga ahora que la tasa nominal es trimestre anticipado. Hallar la tasa efectiva anual anticipada.
$J_a=\ 5.3$% t.a.
$k_a=4$ trimestresie=?
Resultado de 5.8% EA.

Ejercicios 4.10_ Hallar la tasa efectiva anual de una tasa nominal anual continua. Si un documento de renta fija cancela el 5.9% nominal anual continuo, ¿qué tasa efectiva anual de rentabilidad genera esta inversión?
con $ie=e^{J_c}-1 $, obtenemos $ie=e^{0.059}-1= 6.1$% E.A.
En los siguientes ejercicios procedemos a determinar la equivalencia entre dos tasas de interés nominales, es decir, se calcula una tasa interés nominal equivalente a otra tasa de interés nominal dada. Veamos:

Ejercicios 4.11_ Hallar la tasa nominal anual vencida dada otra nominal vencida. Supongamos que tenemos una tasa nominal anual del 24% trimestre vencido ($J_v=24$%t.v.) y nos piden hallar la tasa nominal equivalente, pero mes vencido (hallar $J_v= m.v.$).
Vamos a proceder en dos pasos.
Paso #1. Calcular la tasa efectiva anual con la tasa nominal anual dada de 24% tv. En el año se capitaliza cuatro veces, una cada trimestre, por lo que $k_v=4$.
$ie=\left(1+\frac{0.24}{4}\right)^4-1= 26.25$% EAPaso #2. Calcular la tasa nominal solicitada utilizando la tasa efectiva anual calculada en el paso anterior. En este segundo paso, la frecuencia de capitalización $k_v=12$, dado que el resultado es pedido mes vencido.
Tenemos:
$$J_v=\ k_v\left(\sqrt[k_v]{1+{ie}_a}-1\right)$$ $J_v=\ 12\left(\sqrt[12]{1+0.2625}-1\right) =23.54$% m.v.Este resultado indica que la tasa nominal anual del 24% trimestre vencido es equivalente a una tasa nominal anual de 23.54% mes vencido.
Se halló inicialmente una tasa efectiva anual equivalente a la tasa nominal anual dada (pasar de nominal a efectiva) y luego, con la efectiva hallada calculamos la tasa nominal equivalente solicitada (pasar de efectiva a nominal).

Ejercicio 4.12_ Hallar la tasa nominal anual anticipada dada otra nominal vencida. Como en el ejercicio anterior, supongamos que tenemos una tasa nominal anual del 24% trimestre vencido ($J_v=24$%t.v.) y nos piden hallar la tasa nominal equivalente, pero esta vez mes anticipado (hallar $J_a= m.a$).
Este ejercicio es similar al anterior, pero combina modalidades de capitalización. Para resolverlo debemos realizar los dos mismos pasos. Sin embargo ya conocemos la tasa efectiva anual vencida de la tasa nominal dada inicialmente, siendo de 26.25% EA., por lo que pasamos a desarrollar el paso dos.
Paso #2. hallar la tasa nominal solicitada, en la que $k_a=12$
$J_a=12\left[1-\frac{1}{\sqrt[12]{1+0.2625}}\right]=23.08$% m.a.¿Es necesario dar siempre estos dos pasos? Mientras el lector adquiere la habilidad es recomendable. Empero, a continuación procedemos a generar una ecuación resumen de los dos pasos dados en este ejercicio, recordando que $k_v$ es la frecuencia de capitalización vencida y $k_a$ es la frecuencia de capitalización anticipada. En este proceso es muy útil los subíndices.
En el paso #1, lo que se hace es hallar una tasa efectiva con base en la tasa nominal dada. Esto es, aplicamos:
$${ie=\left(1+\frac{J_v}{k_v}\right)}^{k_v}-1$$Luego en el paso #2 utilizamos la tasa efectiva del paso anterior para hallar la nominal solicitada, en este caso es anticipada. Es decir, de la siguiente ecuación despejamos $J_a$, dado que el dato conocido es ${ie}_a$, obtenido en el paso anterior.
$$ie=\left(\frac{1}{1-\frac{J_a}{k_a}}\right)^{k_a}-1$$Partamos de la identidad sigueinte:
$$ie=ie$$De esta manera, involucrando las dos modalidades de capitalización, la anterior identidad es equivalente a:
$$\left(\frac{1}{1-\frac{J_a}{k_a}}\right)^{k_a}-1{=\left(1+\frac{J_v}{k_v}\right)}^{k_v}-1$$Cancelando los unos en ambas ecuaciones:
$$\left(\frac{1}{1-\frac{J_a}{k_a}}\right)^{k_a}{=\left(1+\frac{J_v}{k_v}\right)}^{k_v}\tag{4.9}$$Si la pregunta es, como en este caso, por la $J_a$, la ecuación para resolver de forma directa el problema es:
$$J_a=k_a\left[1-\frac{1}{\left(1+\frac{J_v}{k_v}\right)^\frac{k_v}{k_a}}\right] \tag{4.10}$$Y es igual a:
$$J_a=k_a\left[1-\frac{1}{\left(1+iv\right)^\frac{k_v}{k_a}}\right] \tag{4.10.1}$$La tasa nominal mes anticipado es por tanto:
Tenemos el mismo resultado.
Si la pregunta es por la $J_v$ , de la misma igualdad (4.9) tenemos que:
$$\left(\frac{1}{1-\frac{J_a}{k_a}}\right)^{k_a}{=\left(1+\frac{J_v}{k_v}\right)}^{k_v}$$ $$\left(1+\frac{J_v}{k_v}\right)=\left(\frac{1}{1-\frac{J_a}{k_a}}\right)^\frac{k_a}{k_v}$$ $$J_v=k_v\left[\left(\frac{1}{1-\frac{J_a}{k_a}}\right)^\frac{k_a}{k_v}-1\right] \tag{411}$$Y es igual a:
$$J_v=k_v\left[\left(\frac{1}{1-ia}\right)^\frac{k_a}{k_v}-1\right] \tag{4.11.1}$$Veamos el siguiente ejercicio para su aplicación.

Ejercicio 4.13_ Tasa nominal vencida equivalente a una nominal anticipada. Hallar la tasa nominal anual con capitalización semestre vencido equivalente a una tasa nominal anual del 28.9% trimestre anticipado.
$J_v=? s.v$.
$k_v= 2$
$J_a=28.9% t.v.$
$k_a= 4$
En consecuencia, el 28.9% trimestre anticipado equivale a una tasa nominal anual del 32.36% semestre vencido. Si se utiliza la una o la otra en el cálculo de la tasa efectiva anual, con sus propias condiciones de capitalización obviamente, arrojan como resultado el 34.98% EA. Estas dos tasas son equivalentes porque arrojan el mismo resultado de tasa efectiva anual.

Ejercicio 4.14_ Resolver el ejercicio anterior con tasas periódicas. Hallar la tasa nominal anual semestre vencido de una tasa nominal anual del 28.9% trimestre anticipado.
Pretendemos aquí ilustrar otro camino para resolver estos tipos de problemas.
$J_v=? s.v.$
$k_v= 2$
$J_a=28.9% t.v.$
$k_a= 4$
En primer lugar hallamos la tasa periódica anticipada.
$ia=\frac{0.289}{4}=7.23$% t.a.En segundo lugar, debemos hallar la tasa periódica vencida equivalente.
$iv=\frac{0.07225}{1-0.07223}=7.79$% t.v.En tercer lugar, hallamos la tasa periódica semestral (de efectiva menor a efectiva mayor)
$iv=\left(1+0.077876\right)^2-1=16.18% s.v.$En cuarto lugar, hallar la tasa nominal solicitada.
$J_v=2\ast0.161817=32.36\%\; s.v.$Hemos obtenido el mismo resultado. Existe por lo tanto varios caminos para resolver estas conversiones de tasas de interés equivalentes.

Ejercicio 4.15_ Hallar la tasa nominal anual anticipada dada una tasa nominal continua.
Por la venta de sus acciones un inversionista obtuvo una rentabilidad nominal anual de 8.9% continua.
Hallar la tasa nominal anual trimestre anticipado equivalente, constatar además que el resultado es correcto calculando la tasa efectiva anual de cada caso.
La ecuación para este problema es la siguiente. Partimos de la igualdad,
$$\left(\frac{1}{1-\frac{J_a}{k_a}}\right)^{k_a}\ -1=e^{J_C}-1$$ $$\left(\frac{1}{1-\frac{J_a}{k_a}}\right)^{k_a}\ =e^{J_C}$$Despejando $J_a$, tenemos:
$$J_a=k_a\left(1-\frac{1}{\sqrt[k_a]{e^{J_c}}}\right)$$Es decir:
Otambién:
$$J_a=k_a\left(1-e^{-\frac{J_c}{k_a}}\right) \tag{4.12.1}$$El resultado es:
$J_a=4\left(1-e^{-\frac{0.089}{4}}\right)= 8.8$% t.a.En la constatación de este resultado, procedemos a calcular las respectivas tasas efectivas anuales con cada tasa nominal. Se debe verificar igual valor.
Tasa de interés efectiva anual continua: $ie=e^{0089}-1= 9.31$% EA.
Tasa de interés efectiva anual anticipada: $ie=\left(\frac{1}{1-\ \frac{0.088}{4}}\right)^4-1=9.31$% EA.
Se constata igual valor.

4.16_ La tasa nominal continua equivalente a una tasa nominal anticipada. Resulta que Bobby Roger piensa invertir 50,000 dólares en el JP Morgan a una Prime Rate (es la tasa de referencia en los Estados Unidos, como en Colombia es la DTF y en Inglaterra ha sido la Libor y recientemente la SORF) de 7.9% trimestre anticipado, operación ´planeada a largo plazo con un vencimiento en 5.5 años.
B. Roger inicialmente desea saber la tasa efectiva que obtendrá como rentabilidad anual, los intereses que ganaría en la operación y el monto total final que el Banco le debe regresar al vencimiento del plazo. Los datos son:
$P= 50,000$ dólares
$J_a=7.9$% t.a
$n= 5.5$ años
Las preguntas de Roger son:
$ie =?$
$I=?$
$F=?$
Cálculo de la tasa efectiva anticipada:
$ie=\left(\frac{1}{1-\ -\frac{0.079}{4}}\right)^4-1=8.31$% EA.Cálculo de los intereses en el plazo:
$I=50,000\left[\left(\frac{1}{1-\frac{0.079}{4}}\right)^{22}-1\right]=27,546$ dólares.Cálculo del valor futuro o monto final pago único al cabo del plazo:
$ F=50,000\left(\frac{1}{1-\frac{0.079}{4}}\right)^{22}= 77,546$ dólaresSin embargo, Roger pensó: ¿qué tasa de interés nominal anual continua le debería de cancelar el JP Morgan para lograr obtener el mismo rendimiento? Roger se está preguntando por la tasa nominal continua que es equivalente a la nominal anticipada ofrecida por el banco. Para responder partamos de la siguiente igualdad:
$$\left(\frac{1}{1-\frac{J_a}{k_a}}\right)^{k_a}\ =e^{J_C}$$Tomando logaritmos en ambos lados de la igualdad, y recordando que ln(e)=1, tenemos que:
$$J_c=k_aln{\left(\frac{1}{1-\frac{J_a}{k_a}}\right)} \tag{4.13}$$ $$J_c=k_aln{\left(\frac{1}{1-ia}\right)} \tag{4.13.1}$$De esta manera, la tasa consultada por Roger es:
$$J_c=4\ln{\left(\frac{1}{1-\frac{0.079}{4}}\right)}=0.0798$$El banco le debe cancelar una tasa nominal anual continua de 7.98%. La tasa de interés del 7.9% trimestre anticipado equivale a la tasa nominal anual continua de 7.98%. Para constatar vamos a calcular de nuevo la tasa efectiva anual, los intereses y el valor futuro de la inversión de Roger con la tasa nominal continua.
Tasa efectiva anual: $ie=e^{0.0798}-1=8.31$% EA.
Intereses: $I=50,000\left(e^{0.0798\ast5.5}-1\right)=27,546$
Futuro: $F=50,000\left(e^{0.0798\ast5.5}\right)=77,546$
Hemos obtenido iguales valores en tasa efectiva, intereses y valor futuro con lo que se constata la equivalencia entre las dos tasas nominales.
Para disponer de un esquema que posibilite recordar y manejar ágilmente las equivalencias entre tasa de interés, ofrecemos la siguiente estructura de temas:
Tema 1. Hallar la tasa de interés efectiva de otra tasa de interés efectiva. Este caso incluye las situaciones de una tasa efectiva menor a otra tasa efectiva mayor y viceversa, de una efectiva mayor a una efectiva menor.
Tema 2. Hallar la tasa de interés efectiva de una tasa nominal anual
Tema 3. Hallar la tasa nominal anual de una tasa de interés efectiva
Tema 4. Hallar una tasa nominal anual de otra tasa nominal anual.
Estos temas se combinan al cruzar entre ellas las diferentes modalidades de capitalización, en la que es posible emplear las ecuaciones $iv=\frac{ia}{1-ia}$ , así como $ia=\frac{iv}{1-iv}$.
Los intereses o rendimientos que se generan de las inversiones financieras son objetos de retención en la fuente. Según el artículo 395 del Estatuto Tributario colombiano, la retención en la fuente es un procedimiento para adelantar el recaudo de impuestos de los contribuyentes, no es un impuesto adicional.
En los intereses existen diferentes tarifas para la retención. Se aplica la tarifa de 4% cuando se hacen inversiones en instrumentos o títulos de renta fija (como son los Certificados de Depósitos a Término -CDT, los bonos, los títulos de tesorería-TES, las aceptaciones bancarias); la tarifa es de 7% para cuentas de ahorros, cuentas corrientes, y demás
rendimientos financieros. Quiere decir que si hacemos inversiones financieras a los intereses se le retienen el 4% o el 7%, dependiendo del tipo de inversión.
Al liquidar una inversión financiera, se recibe el capital más los intereses netos. Estos intereses netos son el resultado de restar al valor de los intereses el monto por retención en la fuente. Veamos el asunto con el siguiente ejemplo.

Ejercicio 4.17_ Inversión en renta fija. Realizamos la compra de un CDT a 360 días en un banco de la ciudad de Medellín, por 38,500,000 de pesos.
El banco ofrece como tasa de interés (de captación de recursos o tasa de interés pasiva) el J=5.6% t.v. Calcular el valor futuro, los intereses, la tasa de interés efectiva anual, los intereses netos y la tasa de interés efectiva neta.
Valor futuro. $F=38,500,000\left(1+\frac{0.056}{4}\right)^4=40,701,700.$
Intereses $I=38,500,000\left[\left(1+\frac{0.056}{4}\right)^4-1\right]=2,201,700$.
A estos intereses no se les ha deducido la retención en la fuente, no son aún netos.
Tasa efectiva anual $ie=\left(1+\frac{0.056}{4}\right)^4-1=0.057187=5.72$% EA
Vamos ahora a aplicar la retención de la fuente. Definimos intereses netos de retención en la fuente como los intereses totales menos el monto de la retención (se utiliza el subíndice N para indicar neto).
Interés Neto= Intereses- valor de la retención en la fuente. O sea:
$$I_N=I-RF$$EL monto de la retención se calcula como:
$$RF=I\ast rf$$Siendo $rf$% la tasa de retención porcentual o tarifa, del 4% o 7%. El monto de la retención en la fuente de este título en pesos es:
$$RF=2,201,700\ast0.04=88,068$$Hemos utilizado el 4% de retención en la fuente porque la inversión es en instrumento de renta fija. Generalizando lo realizado hasta el momento, tenemos que:
$$I_N=I-RF$$ $$I_N=I-I\ast rf$$Al tomar como factor común intereses, I, tenemos:
$$I_N=I\left(1-rf\right)$$El monto de los intereses netos es:
$$I_N=2,201,700\left(1-0.04\right)$$Observe que, si se resta a los intereses iniciales el interés neto, la diferencia es la retención (2,201,700-2,113,632=88,068).
La fórmula para el cálculo directo de los intereses netos en el caso vencido, es:
$$I_N=P\left[\left(1+\frac{J}{k}\right)^{k\ast n}-1\right]\ast\left(1-rf\right). \tag{4.15}$$La tasa efectiva neta hace referencia a la tasa de interés (o de rentabilidad) obtenida después de haber deducido la retención en la fuente. Esta tasa se calcula como:
$${ie}_N=\frac{I_N}{P}.$$ $${ie}_N=\frac{I_N}{P}=\frac{P\left[\left(1+\frac{J}{k}\right)^{kn}-1\right]\ast\left(1-rf\right)}{P}$$Se cancelan las P y haciendo a n=1, para tasa efectiva anual:
$${ie}_N=\left[\left(1+\frac{J}{k}\right)^k-1\right]\left(1-rf\right).\tag{4.16}$$Así, ya podemos utilizar los valores concretos y obtener:
$${ie}_N=\left[\left(1+\frac{0.056}{4}\right)^4-1\right]\left(1-0.04\right).=0.05489$$Es decir 5.49% EA neta.
Ahora bien, la tasa efectiva anual de la inversión nos dio ${ie}_a=5.72$%. Si a esta tasa la multiplicas por el factor $\left(1-rf\right)=\left(1-0.04\right)$, obtenemos como tasa efectiva neta.
Esto es: ${ie}_N=0.057187\ast(1-0.04)=0.054899533=5.49$% EA, o sea el mismo valor ya calculado. Por lo tanto, la tasa efectiva neta la podemos calcular también desde (4.17):
$${ie}_N=ie\left(1-rf\right) \tag{4.17}$$La ventaja de la fórmula (4.17) consiste en que la variable tasa efectiva anual, $ie$, puede ser en cualquier modalidad de capitalización.
En los análisis de coyuntura económica y en las explicaciones sobre el funcionamiento del sistema económico de largo plazo de una economía doméstica, se recurre al manejo de las variables, y sus indicadores, expresadas en términos reales.
En este contexto, la palabra real significa que a las cifras o valores correspondientes, expresiones de las variables económicas, se le han aislado el efecto de la variación en los precios, de la inflación o deflación.
Una variable económica real es aquella a la que se le ha descontado la variación de los precios, generalmente la inflación dado que es el fenómeno más típico.
El cambio en el tiempo de los valores corrientes de las variables económicas, como son la producción interna de un país, sus exportaciones, la demanda y oferta agregadas, es el resultado combinado de los cambios en los precios y de las cantidades.
Veamos lo anterior con un caso sencillo. Supongamos que una economía doméstica produce solamente un bien en la cantidad de 50 unidades ($Q1$) en el año uno con precio de venta ($P1$) de 80,000 pesos.
El valor de la producción ($V.P.=P1*Q1$) es de $50*80,000=4,000,000$ de pesos; al valor la producción del año uno, valorada por los precios del mismo año, se le denomina valor de la producción corriente o a precios corrientes (a precios del mismo año).
Así mismo, supongamos que para el año dos se produce la misma cantidad de 50 unidades pero el precio es ahora de 100,000 pesos la unidad; en esta ocasión el valor de la producción a precios corrientes (a precios del año dos) es de 5,000,000 de pesos.
Según los datos anteriores, el valor de la producción corriente ha crecido en $1,000,000$ en el año dos respecto al año anterior, equivalente al 25%. Sin embargo, ¿realmente en el año dos se tiene más unidades producidas que el año uno? No. La producción realmente no ha crecido, se produce la misma cantidad de zapatos, de 50 unidades, y la economía doméstica tiene un crecimiento real de cero.
El crecimiento corriente experimentado en la producción del año dos es resultado del aumento del precio del bien, al pasar de $80,000$ a $100,000$ pesos la unidad, aumento igualmente equivalente al 25%. El crecimiento corriente es una ilusión, realmente no se tiene un mayor volumen de producción.
En este sentido, la palabra real hace referencia a la existencia de un mayor volumen de producción de bienes y a una mayor prestación de servicios. Sin embargo, este sentido del término real es diferente al sentido de la palabra efectiva, usada por ejemplo en la tasa de interés efectiva anual, que alude a capitalización de intereses.
¿Qué se debe hacer para medir correctamente el crecimiento? Para que las cifras representen crecimiento real se debe eliminar en las variables económicas, el efecto de la variación de los precios generalmente de inflación.
Es decir, debemos deflactar, operación en la que se acude a los índices de precios, siendo uno de ellos el IPC.
Deflactar, es la operación que convierte cifras económicas- financieras corrientes a cifrar reales, al aislar el efecto en el valor de éstas de las variaciones en los precios. Para ello se divide el valor corriente de cada variable económico por el índice de precios definido, en nuestro caso por $\frac{{IPC}_n}{{IPC}_{n-1}}=\left(1+\pi\right)$. En este libro vamos a utilizar $\left(1+\pi\right)$ como el deflactor.
Para ilustrar la operación anterior, sigamos con el mismo ejemplo sencillo y elaboremos un índice de precios. En la construcción de un índice de precios debemos determinar un año como base de comparación de las cifras.
Digamos que en este caso es el año uno. En segundo lugar, el valor de la producción corriente de cada año se pone en relación (se divide) por el año base, razón que ofrece el índice de precios. Siendo IP el índice de precios, tenemos:
${IP}_1=\frac{4,000,000}{4,000,000}=1$
${IP}_2=\frac{5,000,000}{4,000,000}=1.25$
En el cálculo de estos índices de precios se utiliza el enfoque de índice de precios de Laspeyres dado que, teniendo presente los datos, hemos aplicado:
$${IP}_2=\frac{\sum{P2\ast Q1}}{\sum{P1\ast Q1}}$$Con estos índices, la inflación de la economía doméstica hipotética es:
$\pi=\frac{1.25}{1.0}-1=0.25$ . La inflación es de 25% en el año dos.
Observemos además que ${IP}_2=1.25$, es igual a ${IP}_2=(1+0.25)$, esto es, ${IP}_2=(1+\pi)$
La producción real de esta economía doméstica de un sólo producto la obtenemos deflactando los valores corrientes, es decir dividiendo por el respectivo índice de precios. Los valore reales son:
Producción real año 1=$\ \frac{4,000,000}{1} = 4,000,000$ de pesos. En el año base el valor de la producción corriente y real coinciden.
Producción real año 2 =$\ \frac{5,000,000}{1.25}\ = 4,000,000$ de pesos.
Al descontar la inflación, la producción real del año dos es la misma del año uno, siendo el crecimiento económico real de cero.
Aplicando lo anterior en el contexto del valor del dinero en el tiempo, la lección consiste en la necesidad de analizar en términos reales los rendimientos de las inversiones, como por ejemplo, la rentabilidad expresada por la tasa de interés efectiva. Se trata de determinar si esta tasa ha ocasionado un crecimiento real del capital invertido, si el nuevo capital conformada por el principal más los rendimientos de la inversión ha aumentado realmente, esto es, si se tiene una mayor capacidad de compra. Se debe constar que el dinero adicional logrado, que son los intereses, no sólo logren compensar a la inflación, sino que esté por encima de ésta.
Este es el sentido de la tasa efectiva real que pasamos a estudiar su forma de cálculo.
Lo anterior, nos permitirá además comprender que para lograr rentabilidad real positiva en las inversiones es necesario que la tasa de interés efectiva en sus diferentes modalidades, sea mayor a la inflación. La forma de detectar el cumplimiento de lo anterior, es a través de la tasa de interés efectiva deflactada, esto es, la tasa efectiva real.
El procedimiento para calcular la tasa efectiva real ${(ie}^\pi)$, es deflactando la tasa de interés efectiva. Para deflactar procedemos a dividir la tasa efectiva por el índice de precios, que hemos concluido como $\left(1+\pi\right)$.
En la modalidad vencida, la tasa efectiva anual real es:
$${ie}^\pi=\frac{\left(1+\frac{J}{k}\right)^k}{\left(1+\pi\right)^k}-1$$Expresión que es igual a:
$${ie}^\pi=\frac{\left(1+iv\right)^k}{\left(1+\pi\right)^k}-1$$Ahora bien, si elevamos a la $k$ tanto el numerador como el denominador, obtenemos valores anuales, así:
$${ie}^\pi=\frac{\left(1+\ ie\right)}{\left(1+\pi\right)}-1$$Realizando la resta, nos da que:
$${ie}^\pi=\frac{1+ie\ -1-\ \pi}{1+\pi}$$Siendo igual a:
$${ie}^\pi=\frac{ie\ -\ \pi}{1+\pi} \tag{4.18}$$Con base en la ecuación (4.18), para el cálculo de la tasa efectiva real solo requerimos de la tasa efectiva anual y la inflación anual.
La ventaja de esta ecuación consiste en que $ie$, la tasa efectiva anual, puede ser en cualquier modalidad de capitalización. Con base en (4.18) extraemos las siguientes conclusiones:
Si $ie > \pi$ entonces ${ie}^\pi>0$ . La tasa efectiva real es positiva, significando crecimiento real del capital invertido; se ha generado mayor capacidad de compra, representada en los puntos porcentuales por encima de la inflación.
Si $ie = \pi$ entonces ${ie}^\pi=0$. La tasa efectiva real es cero. Con este resultado, la compensación por valor del dinero en el tiempo al capital cubre exactamente la inflación y el dinero ha conservado el poder adquisitivo constante.
La mayor cantidad de dinero al final del plazo representa igual capacidad de compra que el capital inicial.
Si $ie \lt\pi$ entonces ${ie}^\pi\lt 0$. La tasa efectiva real es negativa. El monto al final del plazo de la inversión representa en términos de capacidad de compra un valor menor al capital inicialmente invertido; se ha presentado un decrecimiento real del capital inicial, a pesar de contarse con una cantidad de dinero mayor (corriente).
El capital inicialmente invertido ha visto deteriorada su capacidad de compra al no ser compensada la inflación por la tasa efectiva de interés.
En conclusión, como guía para las inversiones financieras, la ${ie}^\pi>0$. Sin embargo, recordemos que sobre el futuro sabemos que es incierto y existen riesgos.

Ejercicio 4.18_ Cálculo de la tasa efectiva real. En un pagaré de $150,000,000$ de pesos Kelly Londoño le hizo un préstamo a su vecina con un año de plazo y una tasa de 8.5% t.v.
Si la inflación es de 0.9% promedio mensual, hallar la tasa efectiva, la tasa efectiva real de esta inversión e identificar si ha ocurrido crecimiento real del capital.
Solución.
$J_v=8.5$% t.v.La tasa efectiva anual vencida es:
$ie=\left(1+\frac{0.085}{4}\right)^4-1=8.77$% EATasa efectiva real:
${ie}^\pi=\frac{\left(1+\frac{0.085}{4}\right)^4}{\left(1+0.009\right)^{12}}-1$
${ie}^\pi=\frac{1.087747962}{1.113509675}-1=-2.31$%
En el cálculo de la tasa efectiva real, como la inflación es mensual, se utiliza $k=12$ para lograr la inflación anual; así mismo, la tasa de interés nominal capitaliza cada trimestre por lo que utilizamos en el numerador de la expresión a $k=4$.
La inversión arroja una tasa efectiva real negativa de $2.31$% EA, evento que significa decrecimiento en términos reales del capital.
En este ejercicio, la inflación anual es:
$\pi=\left(1+\frac{0.009}{12}\right)^{12}-1=11.35$% EACon este dato podemos usar (4.18) para hallar la tasa efectiva real, así:
${ie}^\pi=\frac{0.0774\ -\ 0.1135}{1+0.1135}=-2.31$%EAY obtenemos el mismo resultado negativo en la tasa real.
Para constatar la pérdida de poder adquisitivo, vamos a calcular el valor futuro vencido (que podemos llamar ahora corriente) y el valor futuro real.
Futuro corriente:
$$F=150,000,000\left(1+\frac{0.085}{4}\right)^4=163,162,194$$En el año, la inversión le reporta al acreedor intereses por 13,162,194 pesos, equivalente a una tasa efectiva anual vencida de 8.77%, resultado que se puede calificar como positivo, inicialmente. Sin embargo ¿este resultado tiene ese mismo calificativo si lo analizamos en relación con la inflación? Ya sabemos que no.
Para constatar lo dicho hallemos el futuro real, es decir, vamos a deflactar.
$$F=150,000,000\left[\frac{\left(1+\frac{0.085}{4}\right)^4}{\left(1+0.009\right)^{12}}\right]=146,259,660$$Es decir, el valor futuro de 163,162,194 pesos en términos de capacidad de compra equivale o representa un poder adquisitivo de 146,259,660 pesos; es decir, el futuro corriente siendo una cantidad mayor al capital inicial invertido, representa un menor valor en términos reales con respecto al principal invertido. El capital ha perdido valor, ha decrecido su poder de compra.
Si disponer de un capital en forma de dinero es una manera de poseer la riqueza, se puede afirmar en este caso que la acreedora Kelly Londoño ha visto disminuida ésta en 2.31% EA.
No compensar al menos la inflación en las inversiones, es una forma de empobrecerse.
La tasa efectiva neta real es simplemente la tasa efectiva neta deflactada.
Es por lo tanto un indicador de rendimiento de las inversiones financieras más exigente que la real, en cuanto considera la deducción de intereses por retención en la fuente.
Aprovechando la ecuación (4.18) y recordando que la tasa efectiva neta se representa por ${ie}_N$, la tasa efectiva neta real $({ie}_N^\pi)$ es:
$${ie}_N^\pi=\frac{{ie}_N\ -\ \pi}{1+\pi} \tag{4.19}$$
Ejercicio 4.19_ Cálculo de la tasa de interés efectiva neta real. Del ejercicio anterior, supongamos ahora que Kelly Londoño realizó la inversión en una entidad financiera de la ciudad y es objeto de retención en la fuente de 4% sobre los intereses. Hallar la tasa efectiva neta real.
Con (4.17) la tasa efectiva neta anual es:
${ie}_N=0.0877\left(1-0.04\right)=8.42$% EALa tasa efectiva neta real es:
${ie}_N^\pi=\frac{0.0842\ -\ 0.1135}{1+0.1135}=-2.63$%EAEl capital inicial al cabo de un año ha sufrido un deterioro neto real de -2.63%. Con este resultado, como orientación para las inversiones debemos considerar que la expectativa de rentabilidad debe ser ${ie}_N^\pi>0$.
La fórmula (4.19) es la síntesis de la teoría sobre las tasas de interés hasta aquí desarrollada; en este sentido es un concepto complejo, en cuanto a conjunto de relaciones que sintetiza.
Para ilustrar lo anterior vamos a realizar el proceso inverso, de lo general a lo particular, iniciando desde esta ecuación (4.19) para hacer explícito los conceptos y variables relacionadas, bajo el caso vencido.
Iniciando con (4.19)
$${ie}_N^\pi=\frac{{ie}_N\ -\ \pi}{1+\pi}\ \ $$Y teniendo presente que (4.17) es:
$${ie}_N=ie\left(1-rf\right)$$Reemplazando (4.17) en (4.19), tenemos:
$${ie}_N^\pi=\frac{ie\left(1-rf\right)\ -\ \pi}{1+\pi}\ \ $$Ahora bien, como en el caso vencido, la tasa efectiva anual es:
$$ie=\left[\left(1+iv\right)^k-1\right]$$Por lo tanto:
$${ie}_N^\pi=\frac{\left[\left(1+iv\right)^k-1\right]\left(1-rf\right)\ -\ \pi}{1+\pi}$$De igual manera, dado que:
$$iv=\frac{J}{k}$$La anterior ecuación queda como:
Y finalmente, esta última expresión algebraica es igual a:
$${ie}_N^\pi=\frac{1+\left[\left(1+\frac{J}{k}\right)^k-1\right]\left(1-rf\right)\ }{1+\pi}-1 \tag{4.20}$$Esta ecuación (4.20) hace explícito los conceptos de tasa de interés efectiva, tasa de interés efectiva neta, y tasa de interés efectiva neta real, por medio de las variables y operaciones involucradas.
La ecuación (4.19) es la síntesis de la ecuación (4.20); es la síntesis de múltiples determinaciones.
En el capítulo tres de este libro se estudió la forma de determinar el valor futuro y los intereses en moneda local (en pesos colombianos en nuestro caso) de una operación financiera realizada en moneda extranjera. Además del monto del capital invertido, del plazo y la modalidad de capitalización, el resultado económico de la inversión depende también de la tasa de interés externa y las variaciones del precio de la divisa en la que se realizada dicha operación (de la cotizaciones en moneda nacional de la divisa en que se realiza la operación financiera).
Recordemos que si el precio de una moneda extranjera sube con respecto a la moneda nacional (local), a esa variación se le denomina depreciación del tipo de cambio (Dep)
Así mismo, si el tipo de cambio disminuye su cotización, dicha variación es una apreciación de la moneda local respecto a la divisa en cuestión, (Apr).
El impacto de la variación del tipo de cambio sobre el resultado económico de una inversión financiera en divisas se concreta una vez el capital invertido y sus intereses, son convertidos a moneda nacional. En el caso de un crédito tomado con una entidad del exterior, el efecto se puede medir al momento de conseguir las divisas (la compra) para realizar el pago.Vamos a obtener la ecuación para calcular la tasa de interés efectiva de una operación financiera, puede ser de inversión o de crédito, en moneda extranjera.
Denominemos a esta como tasa de interés efectiva con tipo de cambio, representada por ${ie}_{tc}$
En el mismo capítulo tres concluimos que los intereses en moneda local (en nuestro caso el peso colombiano) de una inversión realizada en moneda extranjera bajo la forma de valor futuro pago único en presencia de depreciación del tipo de cambio, se determinan como:
$$I=P\left[\left(1+\frac{J}{k}\right)^{n\ast k}\ast\left(1+Dep\right)^{n\ast k}-1\right]$$En esta ecuación, $I$ son los intereses en pesos colombianos y $J$ es la tasa nominal anual externa.
Si definimos a la tasa efectiva con tipo de cambio como:
Entonces, con n=1, su cálculo es por medio de (4.21):
$${ie}_{tc}=\left(1+\frac{J}{k}\right)^k\ast\left(1+Dep\right)^k-1 \tag{4.21}$$Para el caso de una apreciación del tipo de cambio, la tasa efectiva anual (n=1) se calcula como:
$${ie}_{tc}=\left(1+\frac{J}{k}\right)^k\ast\left(1-Apr\right)^k-1 \tag{4.22}$$
Ejercicio 4.20_ Cálculo de la tasa efectiva con tipo de cambio. Juan José Gallego realiza una inversión en dólares con el JP Morgan de New York que le ofrece una tasa J=4.8%m.v. Su expectativa de depreciación de la divisa es de 0.5% mensual.
Hallar: la tasa efectiva extranjera, la expectativa de devaluación anual, y la tasa efectiva anual con tipo de cambio.
$J=4.8$% m.v.
$Dep=0.5$% mensual
$ei=$?
$Dep=? anual$
${ie}_{tc}=?$
La tasa efectiva por cancelar el JP Morgan es:
$ie=\left(1+\frac{0.048}{12}\right)^{12}-1=4.91$% EALa expectativa de anual de depreciación del tipo de cambio es:
$Dep=\left(1+0.005\right)^{12}-1=6.17$% EALa tasa efectiva con tipo de cambio es:
${ie}_{tc}=\left(1+\frac{0.048}{12}\right)^{12}\ast\left(1+0.005\right)^{12}-1$
${ie}_{tc}=(1+0.0491)\ast(1+0.0617)-1=11.38$%EAObserve el lector que una vez cada paréntesis fue elevado a la $k$, la cifra decimal de cada uno de ellos corresponde, respectivamente, a la tasa de interés efectiva anual externa y a la expectativa de devaluación anual, tasas ya calculadas.
Con estos resultados, y aplicando la propiedad matemática de la distribución, el anterior cálculo es:
${ie}_{tc}=1+0.0491+0.0617+0.0491\ast0.0617-1$
${ie}_{tc}=0.0491+0.0617+0.0491\ast0.0617=11.38%$EAEn general, para el caso de una depreciación del tipo de cambio, el modelo para el cálculo es, por lo tanto:
$${ie}_{tc}=ie+Dep+ie\ast Dep \tag{4.23}$$Para el caso de una apreciación del tipo de cambio, éste es:
$${ie}_{tc}=ie-\ Apr-ie\ast Apr \tag{4.24}$$La rentabilidad en moneda nacional de una inversión en moneda extranjera, así mismo para el costo de un crédito en moneda extranjera, medidos ambos por la tasa efectiva con tipo de cambio, es función de la tasa efectiva de interés externa y de las variaciones en la cotización en moneda nacional de la moneda extranjera.
La rentabilidad de la inversión se favorece si al momento de liquidarla y hacer el cambio de las divisas a moneda nacional, existe depreciación del tipo de cambio; en cambio para un crédito en moneda extranjera con presencia de depreciación del tipo de cambio, el costo en moneda nacional de la deuda se hace mayor.
Es así como, con el comportamiento actual del dólar, aumentando su valor en los mercados regionales, la deuda externa del país se ha visto incrementada en su denominación en moneda nacional.
Las variaciones en la cotización de las divisas constituyen el riesgo cambiario.

Ejercicio 4.21_ Tasa efectiva anual con tipo de cambio bajo capitalización anticipada y apreciación del tipo de cambio. Suponga un crédito en moneda extranjera con $J=7.5$% t.a., y una expectativa de apreciación del tipo de cambio anual de 3.2%.
La tasa efectiva anual externa anticipada es:
$ie=\left(\frac{1}{1-\frac{0.075}{4}}\right)^4-1=7.87$% EACon (4.24):
${ie}_{tc}=0.0787-\ 0.032-0.0787\ast0.032=4.41$% EA
Ejercicio 4.22_ Tasa efectiva anual con tipo de cambio bajo capitalización continua y apreciación del tipo de cambio. Resolver el ejercicio anterior suponiendo ahora que la tasa nominal del 7.5% capitaliza de forma continua.
La tasa efectiva externa anual continua es:
$ie=\left(e\right)^{0.075}-1=7.79$% EALa tasa efectiva con tipo de cambio es:
${ie}_{tc}=0.0779-\ 0.032-0.0779\ast0.032=4.34$% EASon dos factores los que determinan la tasa de interés efectiva de las operaciones financieras (de inversiones o de créditos) en UVRs. Un primer factor es la tasa de interés pactada como remuneración al capital en UVRs, denominada tasa remunerativa.
El segundo factor es la variación en el nivel general de los precios, siendo lo más típico la inflación, que es cancelada por medio de la cotización de la UVR.
Recordemos que la UVR es una unidad de cuenta cuyo valor está indexado a la variación en el IPC. La UVR no es un medio de pago. En esta condición, al momento de liquidarse las operaciones financieras realizadas en UVR, los pagos se deben llevar a cabo en la unidad monetaria del país, el peso colombiano, hecho que implica la liquidación de una tasa de interés efectiva equivalente en pesos, determinada por los dos factores ya reseñados.
Desde la ecuación (3.25) del capítulo anterior, considerando capitalizaciones que son fracción de año, la tasa efectiva de interés en pesos de operaciones financieras en UVR (${ie}_{uvr}$), se calcula por medio de la siguiente ecuación (4.25):
$${ie}_{uvr}=\left(1+\frac{J}{k}\right)^k\left(1+\pi\right)^k-1 \tag{4.25}$$Ecuación igual a:
$${ie}_{uvr}=\left(1+iv\right)^k\left(1+\pi\right)^k-1 \tag{4.25.1}$$En (4.25), el primer elemento después de la igualdad, es el factor $\left(1+\frac{J}{k}\right)^{k\ }$, con $J$ como la tasa remunerativa nominal anual que determina, con su condición de capitalización, la tasa de interés remunerativa efectiva, siendo ésta la tasa de interés sobre el capital en UVRs. El segundo elemento es el factor variación en el IPC, $\left(1+\pi\right)^k$, que surge en la ecuación como consecuencia de la indexación del valor de la UVR a la variación en el nivel general de los precios.
Si un usuario del sistema financiero accede a un crédito en UVRs para la compra de vivienda nueva o usada, debe ser consciente que con los pagos realizados con el medio de pago local, cancela estos dos factores, la tasa remunerativa y la inflación.
De la (4.25.1) y si identificamos a la tasa efectiva remunerativa como ${ie}_r$, al elevar cada componente de la ecuación a la $k$, tenemos datos anuales así:
$${ie}_{uvr}=(1+{ie}_r)(1+\pi)-1$$Aplicando la propiedad distributiva:
$${ie}_{uvr}={ie}_r+\pi+{ie}_r\ast\ \pi (4.26)$$Es común en la economía colombiana expresar la tasa de interés para los créditos de vivienda bajo la forma UVR+%EA. Con UVR se indica que el crédito es en estas unidades y su valor está indexado a las variaciones del IPC; es por lo tanto una manera de indicar el cobro de un porcentaje variable igual a la variación de los precios al consumidor. Con el símbolo %EA se hace referencia a un porcentaje fijo como tasa de interés sobre el capital expresado en UVRs, componente fijo que hemos denominado tasa de interés remunerativa.
Por lo tanto, la tasa efectiva de interés de una operación en UVR, ${ie}_{uvr}$, es una tasa variable debido a la indexación de la UVR a las variaciones en el nivel general de los precios al consumidor.
Además, como los pagos se realizan en moneda local, es también la tasa efectiva de interés equivalente para el capital expresado en la unidad monetaria del país.
En consecuencia, con la expresión UVR+%EA no se indica que la tasa efectiva de un crédito de vivienda realizado en UVR es la suma aritmética de estos dos componentes; no, es como se indica en las ecuaciones (4.25) y (4.26).
En nuestro país existen topes a la tasa remunerativa para los créditos dirigidos a vivienda de interés social (VIS) y para los créditos que no son de interés social (NO VIS), en término efectivo anual. Ejemplos de estas tasas son las siguientes expresiones: UVR%+12.4% EA para NO VIS y UVR%+10.7% EA para VIS.

Ejercicio 4.23_ Tasa efectiva de crédito en UVR. Fátima desea un crédito de $35,280,200$ pesos para mejora de vivienda y por ello acude a un banco de la ciudad en busca de financiación en UVRs. La entidad financiera le informa que la tasa del interés sobre el capital en UVRs es de 0.85% mensual, y se está manejando por inflación el 0.5% mensual.
Bajo estas condiciones iniciales, y si el crédito es en modalidad vencida, calcular la tasa de interés remunerativa anual, la tasa de inflación anual supuesta, la tasa de interés efectiva del crédito, y los intereses en pesos causados en el primer mes.
$iv=0.85$% mensual (tasa remunerativa periódica)
$\pi=0.5$% mensual (inflación mensual, supuesta constante en el plazo)
${ie}_r=?$ Tasa de interés remunerativa EA (es la tasa efectiva sobre el capital en UVRs)
$\pi=?$ Inflación anual EA
${ie}_{uvr}=?$ Tasa de interés EA equivalente en pesos del crédito en UVRs (tasa de interés para realizar los pagos en pesos, dado que la UVR no es medio de pago)
Tasa remunerativa e inflación anuales.
${{ie}_r=\left(1+0.0085\right)}^{12}-1=10.69$% EA. Es la tasa de interés por el monto del capital expresado en UVR. ${{\pi}=\left(1+0.005\right)}^{12}-1=6.17$% EA. Es la inflación anual.Tasa efectiva anual del crédito en UVRs.
${{ie}_{uvr}=\left(1+0.0085\right)}^{12}\ast\left(1+0.005\right)^{12}-1=17.52$% EAEsta tasa representa el costo del capital en moneda local para el deudor. Ésta se ha calculado con la ecuación (4.25) utilizando los datos periódicos, en esta ocasión mensuales.
En el siguiente cálculo, de la misma tasa efectiva anual, se utilizan los valores anuales, obteniendo igual resultado.
${ie}_{uvr}=0.1069+0.0617+0.1068\ast0.0617$
${ie}_{uvr}=0.1069+0.0617+0.0066=17.52$% EAObsérvese que además de la suma de los dos componentes, de tasa remunerativa efectiva e inflación, la tasa efectiva de este ejemplo incluye la suma de un tercer elemento que es el resultado de multiplicar (el producto) los dos primeros factores. La tasa efectiva del crédito es, por lo tanto, más que la suma de UVR%+% EA, esto es, mayor que 6.17% EA+10.69% EA
Los intereses del primer mes en pesos.
$iv=\sqrt[12]{1+0.1752}-1=1.35$%
$I=35,280,200\ast0.0135=477,838$ pesos.La aplicación de este tema se abordará en un próximo capítulo con el estudio de sistemas de amortización de créditos bajo cuotas en UVRs.
En nuestro país un indicador muy utilizado en los acuerdos sobre el valor del dinero en el tiempo, o precio por renunciar a la preferencia por la liquidez, es la tasa de interés de las captaciones de ahorro por medio de los depósitos a término fijo con vencimiento de 90 días, conocida como tasa de interés DTF.
La tasa DTF como indicador representativo en la economía no ha estado exenta de críticas, implicando éstas que para el año 2008 entrara en funcionamiento un nuevo indicador que pretende reflejar el costo del dinero y el nivel de la liquidez, en el mercado monetario. Conocido como Indicador Bancario de Referencia (IBR), refleja el precio al que los bancos están dispuestos a captar o colocar los recursos del mercado monetarios (ASOBANCARIA, 2014).
Dado que la tasa de interés DTF mantiene una alta representatividad en la economía colombiana, estudiamos la metodología del cálculo y la forma como se aplica en los créditos o colocaciones que realizan las entidades financieras.
La DTF nace en el país en 1982, pero es a partir de 1993 cuando se determina como un promedio ponderado de las tasas de interés y de los montos captados a 90 días.
Las entidades financieras que participan en el cálculo de la tasa de interés DTF, son los Bancos Comerciales, las Compañías de Financiamiento Comercial y las Corporaciones Financieras, entidades que reportan a la Superintendencia Bancaria los montos de captaciones diarios y las tasas de interés canceladas.
El cálculo de la DTF lo realiza el Banco de la República con la información recopilada en una semana particular, debido a que inicia un viernes y termina el jueves de la semana siguiente (ver en Figura 4.1 columna fecha de operación). La vigencia es para la semana siguiente, de lunes a viernes (de lunes 7 a viernes 11 de noviembre de 2022, en el caso que traemos).
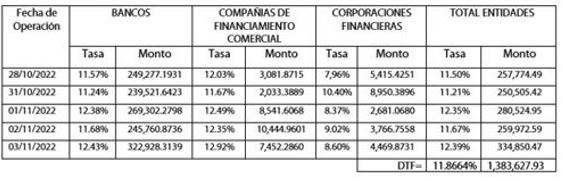
En el día 28 de octubre de 2022, los Bancos Comerciales captan del público la suma de 249,277.1931 millones de pesos colombianos a una tasa 11.57% AE; las Compañías de Financiamiento Comercial captaron la suma de 3,081.8715 millones de pesos a una tasa del 12.03% EA, y las Corporaciones Financieras de 5,415.4251 al 7.96% EA. En total, la captación del día fue de 257,774.49 millones de pesos a una tasa de 11.50% EA, promedio ponderado. A las tasas de interés pagadas por la entidades financieras en estas operaciones, se le denomina tasa de interés de captación o tasa de interés pasiva (dado que estos recursos captados constituyen deudas de éstas con sus clientes).
¿Cómo se obtiene la tasa de interés del 11.50% EA promedio ponderado del día 28 de octubre del 2022? Para responder a esta pregunta definamos las siguientes variables:
$i_{tj}$: Es la tasa de interés de captación en el día t (con t=1,2, …5) de la entidad financiera j (con j=1, 2 o 3). Por ejemplo $i_{12}$, es la tasa de interés captación del 28 de octubre de 2022 de las Compañías de Financiamiento Comercial, con 12.03% EA. Ver figura 4.1.
$w_{tj}$: Es el monto captado en el día t por la entidad financiera j. Para $w_{12}$, el monto es de 3,081.8715 millones de pesos, para las compañías de Financiamiento Comercial. Ver figura 4.1.
$w_t$: Es el monto total captado por las entidades financieras en el día t. Por ejemplo, para el día t=1 (28/10/2022), entre las tres entidades financieras en cuestión captaron recursos del público en una suma de 257,774.49 millones de pesos. Ver figura 4.1.
$\omega_{tj}=\frac{w_{tj}}{w_t}$ . Es la participación relativa de la captación en el día t de la entidad financiera j en el total de captaciones de las entidades financieras en el mismo día. Por ejemplo, para el día t=1 (28/10/2022) la entidad financiera j=2 (Compañía de Financiamiento Comercial) captó del público recursos en una proporción equivalente al 11.96% de las captaciones totales del mismo día. Esta participación relativa en las captaciones en el día t=1, se calcula de la siguiente manera:
$\omega_{12}=\frac{3,081.8715}{257,774.49}=0.1196=11.96$%
Las participaciones relativas de las captaciones de cada entidad financiera en el total de captación en un día específico, son utilizadas como factores de ponderación en el cálculo de la tasa de interés (promedio ponderado) de ese mismo día.
$i_t$: Es la tasa de interés promedio ponderado del día t, y corresponde a la columna tasa, de la columna Total Entidades de tabla 4.1. Por ejemplo, para el día t=1 (28/10/2022) ésta es de 11.50% EA. Esta tasa de interés se calcula de la siguiente manera:
Es decir:
$$i_{t=1}=\sum_{j=1}^{3}{i_{1j}\ast\omega_{1j}} (4. 27.1)$$Para el 28/10/2022, la tasa de interés promedio ponderado es:
$i_{t=1}=0.1157\ast\frac{249,277.19}{257,774.49}+0.1203\ast\frac{3,081.8715}{257,774.49}+0.0796\ast\frac{5,415.43}{257,774.49}$
$i_{t=1}=0.1157\ast0.967035929+0.1203\ast0.01195569+0.0796\ast0.02100838$
$i_{t=1}=0.111886057+0.00143827+0.00167227=0.115=11.5$% EA.
Se pide al lector plantear la ecuación y calcular la misma tasa de interés para los demás días de la semana (para t= 2, …, 5) de la figura 4.1.
Los resultados corresponden a las tasas de interés para cada t de la columna Total Entidades.
Ahora bien, son los datos de tasas de interés y captaciones totales, de la columna Total Entidades, los utilizados en el cálculo de la tasa de interés DTF. Para ello definimos:
$W_{total}=\sum_{t=1}^{5}w_t$. Es la suma total de las captaciones realizadas por las entidades financieras en la semana específica del cálculo. En este caso, para la semana comprendida entre 28/10/20222 a 03/11/2022 se captaron del público la suma total de 1,383,627.93 millones de pesos.
$\varphi_t=\frac{w_t}{W_{total}}$. Es la participación relativa de las captaciones de todas las entidades financieras en el día t sobre el total de captación de la semana. Por ejemplo, para el 28/10/2022 esta participación es de:
$$\varphi_t=\frac{w_t}{W_{total}}= \frac{257,774.49}{1,383,627.93}$$$\varphi_t=18.63$%
Con estas variables e indicadores, la tasa de interés de captaciones de los depósitos a término fijo a 90 días, se determina como:
$$DTF=\sum_{t=1}^{5}{i_t\ast}\varphi_t (4.28).$$Para los datos que traemos en la ejemplificación, la tasa de interés DTF promedio ponderada es:
$DTF=0.115\ast\frac{250,505.42}{1,383,627.93}+0.1121\ast\frac{257,774.49}{1,383,627.93}+0.1235\ast\frac{280,524.95}{1,383,627.93}+0.1167\ast\frac{259,972.59}{1,383,627.93}+0.1239\ast\frac{334,850.47}{1,383,627.93}$Al dividir las expresiones fraccionarias obtenemos cada uno de los factores de ponderación $\varphi_t $ , estos son:
$DTF=0.115\ast0.1863+ +0.1121\ast0.18105+0.1235\ast0.2027+0.1167\ast0.1879+0.1239\ast02420$Un factor de ponderación como 0.1863 significa que la tasa de interés de t=1, esto es 11.5%, participa en la determinación de la tasa DTF con el 18.63%.
Debemos tener presente que la suma de los factores de ponderación es igual a uno o al 100%.
Multipliquemos cada tasa de interés promedio diaria por su factor de ponderación. La suma es:
$DTF= 0.18630333+ 0.1810497+ 0.20274595+ 0.18789198+ 0.24200904=0.118664$Es decir:
$DTF= 11.8664$%EAEn las operaciones financieras de crédito en nuestro país, es frecuente observar que las entidades financieras expresen su tasa de interés de colocación (denominada también tasa de interés activa, dado que los créditos que realizan las entidades financieras a sus clientes son cuentas por cobrar) de la forma DTF+%, o más concreta aún, como DTF+ 7% t.a., por ejemplo.
En dicha expresión, el 7% t.a., es una tasa nominal anual fija durante el plazo del crédito que capitaliza el trimestre anticipado; es además conocida como diferencial o margen (spread).
En cambio la DTF es una tasa efectiva anual y variable durante el plazo del crédito. La tasa de interés de colocación se indexa a la tasa de interés DTF representativa en el mercado de dinero colombiano, constituyendo de esta manera una tasa de interés variable para los créditos.
¿Cuál es el sentido de la expresión en forma de suma? Indiquemos que, contrario o lo que estudiamos con la tasa efectiva de créditos bajo UVR, en esta ocasión si se trata de una suma, pero bajo la salvedad que sólo es posible sumar tasas de interés de igual naturaleza o características.
En este caso, ambas tasas comparten la característica de ser anuales, pero la DTF es efectiva anual y el porcentaje fijo es nominal que capitaliza el trimestre anticipado; por lo tanto, estas tasas no comparten iguales características y por ello no se pueden sumar.
Para poder sumarlas ambas deben tener igual naturaleza, evento que implica realizar el cálculo de tasas equivalentes, por ejemplo, convirtiendo la DTF en nominal trimestre anticipado.
Vamos a realizar un ejemplo que ilustre la aplicación de la operación de sumar ambas tasas, siguiendo la tradición del sistema monetario de nuestro país.

Ejercicio 4.24_ Aplicación de la tasa DTF. Suponga que en la simulación de un crédito la entidad financiera le informa que la tasa de interés es de DTF+5% t.a. Si la tasa DTF al momento de hacer el ejercicio es de 11.87% EA, hallar la tasa de interés mensual vencida equivalente que la simulación implica.
$DTF=11.87$% EA
$J=5$% t.a.
$iv=? m.v.$Bajo el procedimiento del sistema monetario del país, los pasos a seguir son los siguientes:
Paso 1. Convertir la tasa efectiva DTF a una tasa nominal trimestral anticipada. Este primer paso es el caso de pasar de una tasa efectiva a otra nominal anual, bajo modalidad anticipada.
Con la ecuación (4.7), tenemos:
$$J_a=4\left[1-\frac{1}{\sqrt[4]{1+0.1187}}\right]$$$J_a=11.06$% t.a
Paso 2. Sumar las tasa nominal anual halla en el paso 1 con el diferencial. En este paso observamos que ambas tasas comparten igual naturaleza: la de ser nominal anual con capitalización trimestre anticipado, siendo correcto hacer la suma de ambas. Por lo tanto, en términos nominales, el crédito tiene un costo de:
Paso 3. Hallar la tasa efectiva anual con la tasa nominal anual hallada en el paso 2. En este paso se trata de hallar la tasa efectiva anual equivalente a una tasa nominal. Para resolver procedemos como en el ejercicios 4.9.
$$ie=\left(\frac{1}{1-\frac{0.1606}{4}}\right)^4-1=0.1781\ EA$$ Esto es, un 17.81% E.A.Paso 4. Hallar la tasa periódica mes vencido. En este paso, aplicamos el caso de una tasa de interés efectiva mayor a una tasa efectiva menor con modalidad vencida, por lo tanto:
$$iv=\sqrt[12]{1+0.1781}-1=0.0138$$En la simulación, la tasa de interés mes vencido que implica los datos es de 1.38% mensual

Ejercicio 4.25_ Aplicación de la tasa DTF en un crédito. El 15 de septiembre de 2022 se nos concedió un crédito por $12,000,000 pagaderos en cuatro meses por medio de un monto único a la DTF+4.5% t.a. La capitalización de intereses se pactó mes vencido. Hallar el valor cancelado al cabo del plazo.
P=$12,000,000
$n= 4$ meses
P=$12,000,000
$n= 4$ meses
$DTF+4.5$% t.a.
$F=?$
Debido a la capitalización de intereses mensual, se debió utilizar la DTF del respectivo mes. Estas fueron:
15/10/22= 11.05%E.A
15/11/22= 12.71% E.A
15/12/22= 13.09 E.A.
15/01/23=13.73% E.A.
Para liquidar y sumar al capital los intereses vencidos del primer mes (así como en los siguientes) debemos realizar el procedimiento del ejemplo anterior: hallar la tasa periódica mes vencido equivalente.
Para Octubre 15 de 2022, ésta es:
Paso 1.
$J_a=4\left[1-\frac{1}{\sqrt[4]{1+0.1105}}\right]=10.34$%t.a
Paso 2.
$10.34$% t.a.+$4.50$% t.a.=$14.84$% t.a.
Paso 3.
$J_a=4\left[1-\frac{1}{\sqrt[4]{1+0.1105}}\right]=10.34$%t.a
Paso 4.
$iv=\sqrt[12]{1+0.1633}-1=1.27$% mensual
En el primer mes, la capitalización de intereses a la deuda se hace con el 1.27% mensual.
Para los demás meses, realizamos el mismo procedimiento para obtener la tasa de interés mensual equivalente. Esos valores son:
Noviembre 15 de 2022:
$J_a=11.79$% t.a
$11.79$% t.a.+$4.50$% t.a.=$16.29$% t.a.
$ie=18.09$% E.A.
$iv=1.40$% mensual
Diciembre 15 de 2022:
$J_a=12.10$% t.a
$12.10$% t.a.+$4.5$% t.a.=$16.60$%t.a.
$ie=18.47$% E.A.
$iv=1.42$% mensual
Enero 15 de 2023:
$J_a=12.70$% t.a
$ie=19.21$% E.A.
$iv=1.48$% mensual
Se invita al lector a realizar los cálculos y constatar los resultados para los meses de noviembre de 2022 a enero de 2023.
El cálculo del valor futuro es un problema con tasas de interés múltiples (tasa de interés variable), tema estudiado en el capítulo anterior. La solución es:
$$F=12,000,000\left(1+0.0127\right)\left(1+0.014\right)\left(1+0.0142\right)\left(1+0.0148\right)$$ $$F=12,681,474$$Los intereses equivalen a 681,474 pesos en los cuatro meses.
Se invita al lector a resolver el problema aplicando la función VF.PLAN del programa Excel.

Ejercicio 4.26_ Tasa de interés efectiva en Excel. Hallar la tasa efectiva anual de una operación financiera que rinde una tasa J=18.9% t.v.
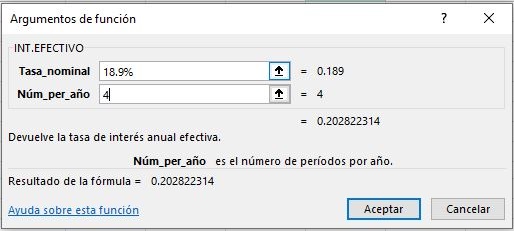
En Excel el cálculo de la tasa efectiva anual vencida es con la función INT.EFECTIVO, que presenta dos argumentos, la tasa nominal y número de períodos años (o frecuencia de capitalización). En la Figura 4.2 se presenta la solución, cuyo resultado es 20.28% E.A

Ejercicio 4.27_ Tasa nominal anual en Excel. Hallar la tasa nominal anual mes vencido a partir de una tasa efectiva anual del 15.76%.
Para resolver este problema, Excel ofrece la función TASA.NOMINAL, con dos argumentos: la tasa de interés efectiva anual y el número de períodos por año (la frecuencia de capitalización).
La respuesta es 14.72% m.v. Ver figura 4.3
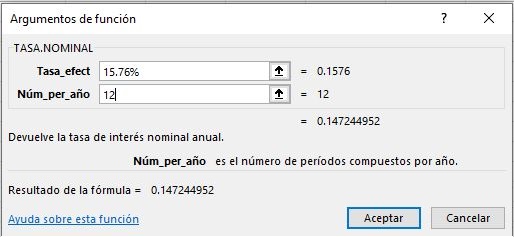
Estas dos funciones de Excel, se aplican para el caso de la capitalización vencida. Los dos últimos ejercicios se elaboraron con datos anuales, pero también es posible utilizar las funciones con datos períodico, incluida la nominal.
Si además se cobró una tasa remunerativa del 11% E.A., ¿qué tasa de interés efectiva anual se cobra por el crédito? (R. 25.58% E.A).
Siendo TEA tasa efectiva anual y TET tasa efectiva trimestral.
Decida dónde realizar la inversión, para ello calcule la tasa efectiva con tipo de cambio de cada alternativa. (R. 16.87% E.A.; 15.90% E.A.; 13.58% E.A.; 13.55% E.A.; respectivamente. El crédito es con el Banco en Japón).
Antes de ofrecer una definición de este concepto, observemos la siguiente situación: Una empresa ganadera tiene seis razas de vacunos, hato constituido por 30 cabezas de ganado Brahman, 35 Gyr, 40 Simmenthal, 45 Guzerat, 50 Angus, y 55 Limousin. Al observar los datos del inventario ganadero, vemos que ellos tienen un patrón o característica particular que los identifica; la existencia de ganado por razas de 30,35,40,45,50 y 55, forma una serie de seis números con la particularidad que cualquier dato, excepto el primero, es igual al anterior más 5. Bajo esta condición, la existencia de ganado constituye una serie en progresión aritmética.
La progresión aritmética, es una sucesión o serie de números en la que cada término, excepto el primero, es igual al término anterior más (o menos) un número fijo llamado diferencia. En toda progresión aritmética intervienen los siguientes elementos.
$a_1$: Es el primer término
$a_m$: Es último término (término en lugar m)
$d$: diferencia común
$m$: cantidad finita de términos
Con la suma de estos términos obtenemos el inventario de ganado, éste es:
$$Suma=30+35+40+45+50+55=255(1)$$.Ahora bien, si cambiamos el orden de los números, de mayor a menor, y volvemos a sumar, el inventario es el mismo, así:
$$Suma=55+50+45+40+35+30=255 (2) $$Ahora bien ¿qué sucede si sumamos (1) + (2)? Ocurre que el resultado es doble, o sea 210. Veamos:
$$Suma=30+35+40+45+50+55=255 (1)$$ $$Suma=55+50+45+40+35+30=255 (2) $$Y es igual a:
$$2Suma=85+85+85+85+85+85=510(3)$$Obsérvese como en el lado derecho de la igualdad (3) tenemos la suma de 6 veces el 85; por ello, abreviadamente la operación es:
$$2Suma=6\ast85=510$$Si de esta última expresión despejamos suma, pasando el número 2 a dividir al otro lado de la igualdad, tenemos que el valor correcto del inventario ganadero.
$$Suma=\frac{6\ast85}{2}=255$$Finalmente, como $85=30+55$, por lo tanto la suma se puede calcular como:
$$ Suma=\frac{6\left(30+55\right)}{2}=255.$$Note en esta última expresión que 6 es la cantidad de datos de la serie, 30 es el primer número de la serie y 55 el último; por ello, y si determinamos a $m=6$, $a_1=30$, $a_m=55$, tenemos que la suma de los m términos de la progresión aritmética es:
$$suma=\frac{m}{2}\left[a_1+a_m\right] (A1)$$Es precisamente este mismo procedimiento el que generalizamos. En términos generales, es decir reemplazando los números concretos por sus equivalentes algebraicos, tenemos la siguiente progresión aritmética:
$a_1$;$(a_1+d)$;$(a_1+2d)$;$(a_1+3d)$;...;($a_1+\left(m-1\right)d)$
Observe como el último término ($a_m$), es igual al primer término más $(m-1)$ veces la diferencia común d.
Es decir:
$$a_m=a_1+\left(m-1\right)d (A2)$$La suma de los m- términos de una progresión aritmética es:
$$Suma=a_1+\left[a_1+d\right]+\left[a_1+2d\right]+\left[a_1+3d\right]+...+\left[a_1+(m-1)d\right]$$Esta suma también se puede escribir de la forma inversa, como sigue:
$$Suma = \left[a_1+(m-1)d\right]+\left[a_1+(m-2)d\right]+...+a_1$$Sumando estas dos ecuaciones, obtenemos:
$$2Suma:\left[2a_1+(m-1)d\right]+\left[2a_1+(m-1)d\right]+...+\left[2a_1+(m-1)d\right]$$El lado derecho de la igualdad es, por lo tanto, la suma de m veces el término $2a1+(m-1)d$, indicada por los puntos suspensivos.
Por lo tanto:
$$2Suma=m\left[2a_1+\left(m-1\right)d\right]$$ $$Suma=\frac{m}{2}\left[2a_1+\left(m-1\right)d\right]$$Sin embargo, sabemos que:
$$a_m=a_1+\left(m-1\right)d$$ Y como: $$2a_1+\left(m-1\right)d=a_1+a_1+\left(m-1\right)d$$Y este último es igual a: $$a_1+a_m$$
En conseceuncia, la ecuación anterior de suma se transforma en:
$$suma=\frac{m}{2}\left[a_1+a_m\right]$$Y es el resultado que inicialmente obtuvimos con el ejemplo numérico.
Vamos a proceder de la misma forma que en las progresiones aritméticas, con el propósito de comprender desde la intuición el problema tratado para pasar luego a su formalización rigurosa.
Un intermediario de papa se propone comprar la producción a cuatro campesinos productores del Municipio de la Unión – Antioquia. Las cantidades en toneladas son: 2, 8, 32, 128 (de nuevo, ¿qué característica o rasgo particular nota en esta serie de datos?). Para saber cuántas toneladas compra en total debemos sumar.
$$ Suma=2+8+32+128=170 (1)$$Tomemos esta suma y multipliquemos por cuatro (¿por qué?), así:
$$ 4Suma=8+32+128+512=680 (2)$$El resultado es cuatro veces mayor al real. Restemos (1) - (2):
$Suma=2+8+32+128=170$ (1) menos
$4Suma=8+32+128+512=680$ (2)
Es igual a: $Suma-4\ suma=2-512$
Factorizando la variable suma, tenemos: $Suma(1-4)=2-512.$
Es decir que $Suma=\frac{2-512}{1-4}=\frac{-510}{-3}=170$, y son las toneladas de papas compradas por el intermediario. Observe como la suma se obtiene restando al primer número de la ecuación (1) el último número de la ecuación (2) y dividiendo por (1-4).
En general, si $a_1=2$, $a_mr=512$, y la razón $r=4$; entonces $Suma=\frac{a_1-a_mr}{1-r}$, con r diferente de 1 (no división por cero)
La progresión geométrica, es una sucesión o serie de números en la que cualquier término, excepto el primero, es igual al anterior multiplicado ( o dividido) por un número fijo llamado razón
En toda progresión geométrica intervienen los siguientes elementos:
$a_1:$ primer número de la serie (término ubicado en el lugar 1)
$a_m:$ último número de la serie (término ubicado en el lugar m)
$r:$ razón común
$m:$ cantidad finita de números o términos de la serie
En general, tenemos la siguiente progresión geométrica:
$$a_1,a_2,a_3,...,a_m$$Serie que expresada en términos del primer valor de la serie y la razón común, queda como:
$$a_1,a_1r, a_1r^2, …a_1r^{m-1}$$Obsérvese como el último término de la progresión geométrica ($a_m$) es igual al primero término ($a_1$) multiplicado por $r^{m-1}$. Esto es:
$$ a_m=a_1\ast r^{m-1}$$La suma de una progresión geométrica con m términos es:
$$Suma=a_1+a_1r+a_1r^2+...+a_1r^{m-2}+a_1r^{m-1} (1)$$Si multiplicamos a la ecuación (1) por $r$ tenemos:
$$rSuma=a_1r+a_1r^2+a_1r^3+...+a_1r^{m-1}+a_1r^m(2)$$Restando (1)-(2), tenemos (los elementos comunes se cancelan):
$${Suma-rSuma=a}_1-a_1r^m$$ $${Suma\left(1-r\right)=a}_1-a_1r^m$$ $$Suma=\frac{{a_1-a}_1r^m}{1-r}$$Esta última expresión algebráica, es la fórmula para hallar la suma de los m - términos de una progresión geométrica, con $r\neq1$. Si a esta fórmula le tomamos factor común $a_1$, nos da:
$$Suma=a_1\left[\frac{1-r^m}{1-r}\right], r\neq1$$Del proceso de deducción de la fórmula obtuvimos:
$a_m=a_1\ast r^{m-1} (1)$
$a_1\ast r^m=a_1r^{m-1}\ast r (2)$
$ suma=\frac{a_1-a_1r^m}{1-r} (3)$
Reemplazando (2) en (3) tenemos:
$$Suma=\frac{a_1-a_1\ast r^{m-1}\ast r}{1-r}$$Sin embargo, como $a_1*r^{m-1}=a_m$ tenemos entonces que:
$$Suma=\frac{a_1-a_m\ast r}{1-r}$$con $r\neq1.$
Página 12. Imagen de Brigitte Werner en Pixabay
Página 15. Imagen de OpenClipart-Vectors en Pixabay