Título de la obra:
Rosetones
Autora:
María José Martínez Debén
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS, GeoGebra
Fuentes: Lato y UbuntuMono
Portada, imágenes y diseño:
María José Martínez Debén
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN: 978-84-18834-85-1

Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
Los temarios de matemáticas en los cursos de secundaria y de bachillerato suelen ser tan extensos que el profesorado, en general, ni se plantea la posibilidad de organizar nada que se salga del currículo. Siempre condicionados por los objetivos marcados en competencia matemática y por unas aulas cada vez más diversas y numerosas, nos olvidamos de que las matemáticas también son un medio para desarrollar otras competencias como la competencia en comunicación lingüística, competencia digital, cultural, artística, …
Creo que es interesante diseñar actividades con las que el alumnado pueda tener otra visión de las matemáticas y de la clase de matemáticas, al mismo tiempo que, desarrollando diferentes destrezas, comprenda la conexión entre las matemáticas y otras áreas de la cultura y la ciencia.
En las siguientes páginas quiero exponer una de esas actividades para trabajar con la sencilla idea de rosetón. Al alumnado se le proponen tareas que tiene que desarrollar utilizando el programa GeoGebra y técnicas de kirigami; centrando el trabajo en copos de nieve y elementos de la arquitectura de poblaciones cercanas, en particular con iglesias del románico y el gótico, con lo que tendrá la oportunidad de conocer un poco más, y desde otra perspectiva, la historia y el arte de su comunidad.
La experiencia nos dice que este tipo de actividades permiten desarrollar habilidades y destrezas importantes y necesarias para todos, al mismo tiempo que dan la oportunidad, a una parte del alumnado que se siente en desventaja en la clase de matemáticas, de sentir lo que vale y puede aportar al resto, también en la clase de matemáticas.
Para entender y clasificar los rosetones se deben considerar dos tipos de isometrías, la rotación y la simetría axial.
Isometría: transformación que conserva distancias y, consecuentemente, ángulos y formas.
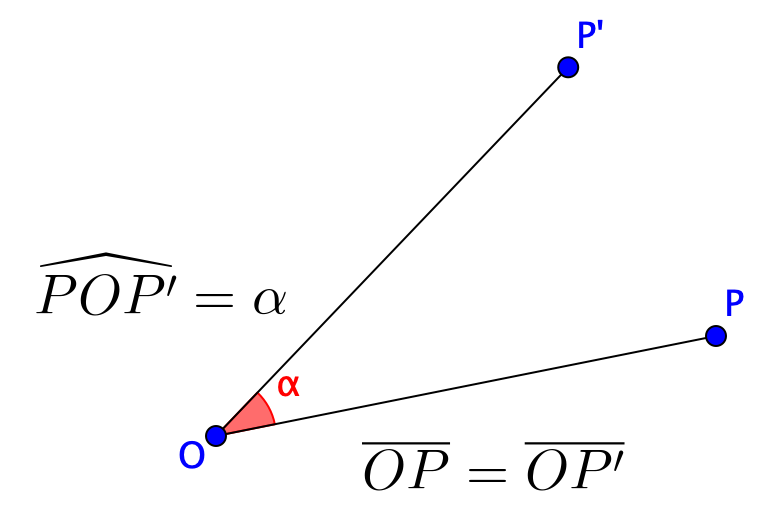
Giro de centro O y ángulo $\alpha$, es un movimiento en el plano que a cada punto P le asocia otro P’, de tal manera que:
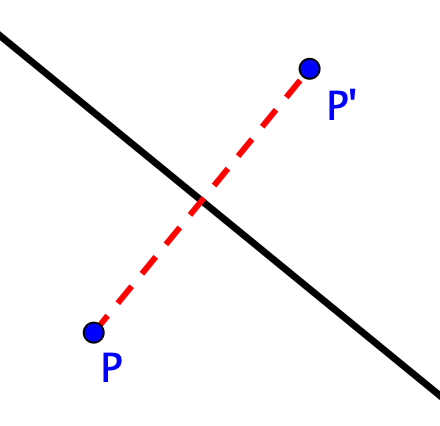
Simetría axial, de eje una recta r, es un movimiento en el plano que asocia cada punto P con su homólogo P’, de tal manera que la recta r es la mediatriz del segmento PP’.
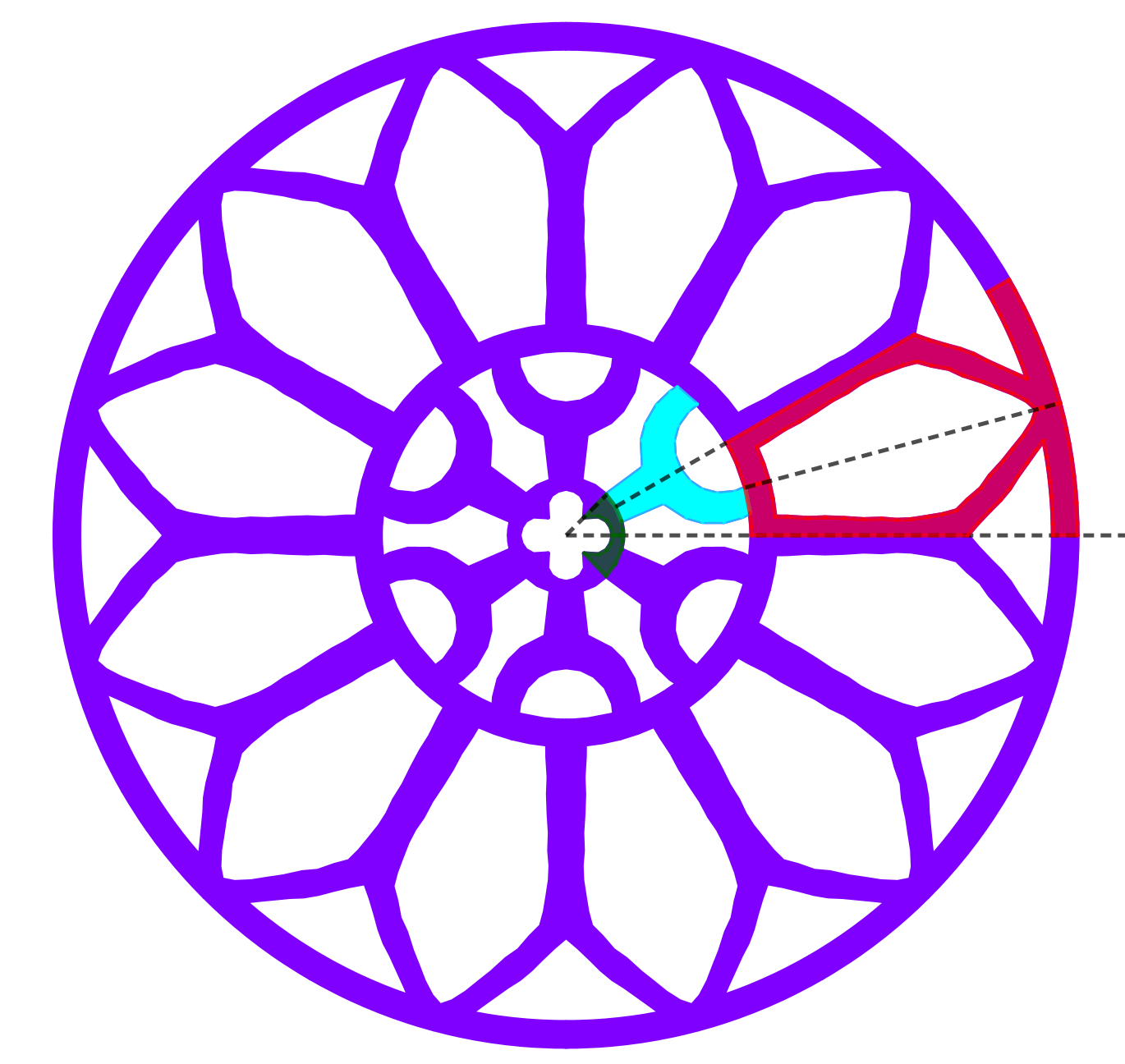
Un rosetón es un objeto que se obtiene al hacer girar un elemento básico alrededor de un punto central. El resultado es una figura en la que ese elemento básico se repite un número n de veces, siendo el ángulo de giro: $\displaystyle\frac{360^\circ}{n}$

Todos los rosetones están dotados de simetría de rotación. El rosetón de la figura es de orden 5, podemos realizar giros de $72^\circ$, $144^\circ$, $216^\circ$, $288^\circ$ o $360^\circ$ alrededor del centro y obtener en cada caso el mismo rosetón, parecería que no lo hubiésemos tocado.
Tipos de rosetones
Ya Leonardo da Vinci (1452-1519) clasificó los rosetones en dos tipos diferentes, rosetones cíclicos y rosetones diédricos. En los segundos aparece una simetría de reflexión y en los primeros no.
Todos los rosetones son de una de estas dos clases.
Rosetones diédricos: El elemento básico, el que rota, tiene un eje de simetría, una mitad es el reflejo de la otra.
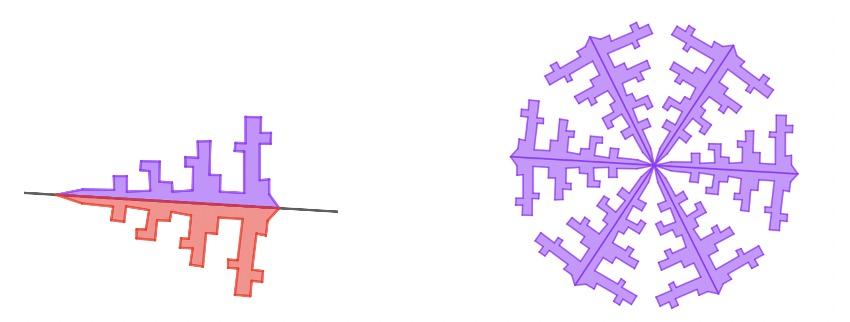
Rosetones cíclicos: En estos no aparece ninguna simetría de reflexión.

El orden de un rosetón nos indica el número de isometrías que tiene ese rosetón.
Si un rosetón cíclico es de orden n podremos realizar giros con n ángulos diferentes y obtener el rosetón inicial.
Si el rosetón es diédrico y de orden n, además de los n giros diferentes podremos realizar simetrías axiales utilizando sus ejes de simetría.
En la siguiente tabla se pueden ver alguna de las características de cada clase de rosetón:
| Clase | Construcción | Orden | Simetría de reflexión |
|---|---|---|---|
| Ciclicos | El elemento básico gira n veces alrededor de un punto, siendo el ángulo de giro $\displaystyle\frac{360^\circ}{n}$ | n | no |
| Diédricos | El elemento básico se construye con una simetría. Después se gira n veces alrededor de un punto, siendo el ángulo de giro $\displaystyle\frac{360^\circ}{n}$ | n | si |

Microfotografía, cortesía de Kenneth Libbrecht. Físico del Instituto de Tecnología de California. En el 2010 obtiene el premio Lennart Nilsson de fotografía científica.
La naturaleza nos proporciona ejemplos de una gran variedad de rosetones y entre ellos, quizás, los copos de nieve sean de los más hermosos.
A lo largo de los siglos, en diferentes civilizaciones, los copos de nieve fueron objeto de estudio aunque, probablemente, el primero en plantearse el porqué de su estructura haya sido Johannes Kepler

…el astrónomo y matemático alemán Johannes Kepler (1571-1630), al que le debemos, entre otras
muchas aportaciones, sus famosas tres leyes del movimiento orbital de los planetas
alrededor del sol. Lo que, seguramente, no sabe, es que Kepler se interesó también por
la causa por la que los cristales de hielo que forman los copos de nieve tienen una
estructura hexagonal, adoptando a veces la forma de una estrella de seis puntas.
Los copos de nieve que forman rosetones siempre tienen un elemento básico se repite seis veces y que tiene un eje de simetría, por lo tanto, rosetones diédricos de orden 6.
Las propiedades, respecto a simetrías y giros, de los copos de nieve nos van a permitir crearlos en nuestros ordenadores con ayuda del programa GeoGebra.
GeoGebra, software libre de matemáticas dinámicas, especialmente indicado para aprender y enseñar.
Al ser software libre se puede descargar e instalar, sin ningún coste, desde la página oficial de GeoGebra. Las indicaciones que aparecen en este libro son para GeoGebra Clásico 5, aunque valen lo mismo para GeoGebra Clásico 6.
La forma desarrollada en este apartado no es la única para obtener un copo con GeoGebra. Con un poco de práctica y conocimiento de algunas herramientas se pueden plantear otras opciones.
Iniciamos abriendo una venta de GeoGebra en la que tengamos la Vista Algebraica, la Vista Gráfica y la Entrada. En la Vista Gráfica no necesitaremos ni los ejes ni la cuadrícula.
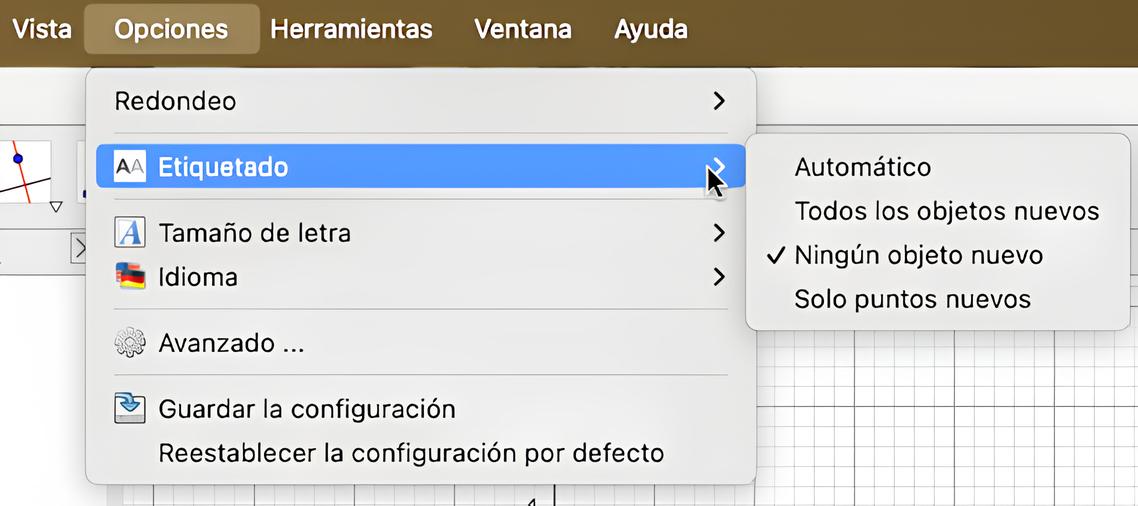
Lo primero, si queremos, en las Opciones, podemos modificar el etiquetado de los objetos para que no nos aparezcan todas las etiquetas en la vista gráfica; en la vista algebraica seguirán apareciendo los objetos con etiqueta.
Pasos para crear el copo de nieve
Dibujamos un hexágono con la herramienta Polígono Regular.
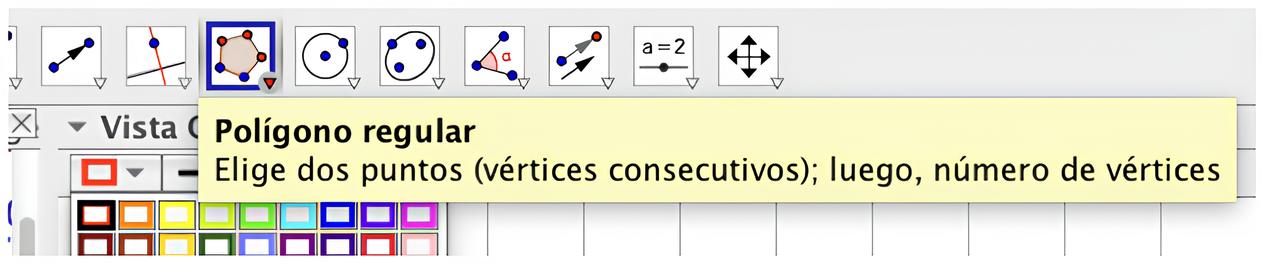
Con la herramienta Punto medio obtenemos el centro del hexágono.
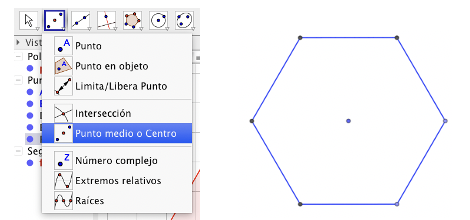
Con la misma herramienta obtenemos el punto medio de un lado del hexágono.
Con la herramienta Recta, uniendo dos puntos, trazamos las dos rectas de la imagen:
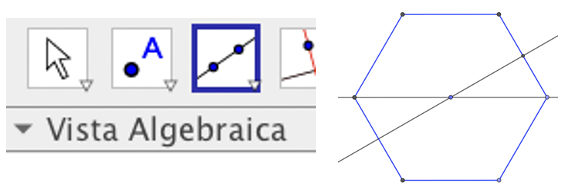
Conviene ampliar la imagen para poder dibujar con más detalle.
Con la herramienta Polígono dibujamos el polígono con la forma que queramos, de manera que un lado del polígono esté sobre la recta que une el centro con un vértice del hexágono.
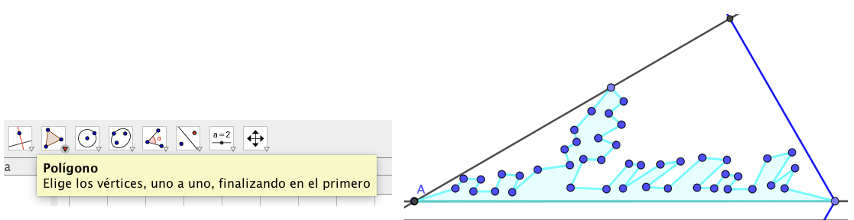
Ocultamos todos los puntos, si no lo hacemos la imagen se nos llenará de un montón de puntos innecesarios. Seleccionándolos todos en la Vista Algebraica, con el ratón derecho, podemos ocultarlos.
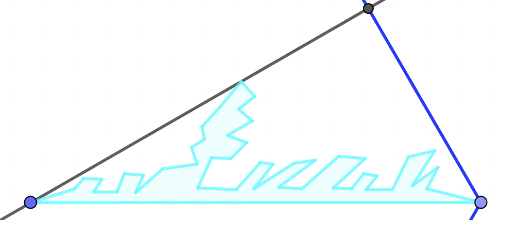
Con la herramienta Simetría Axial reflejamos el polígono creado, polígono2, utilizando como eje de simetría la recta que une el vértice con el centro del hexágono. Obtendremos el polígono polígono2'
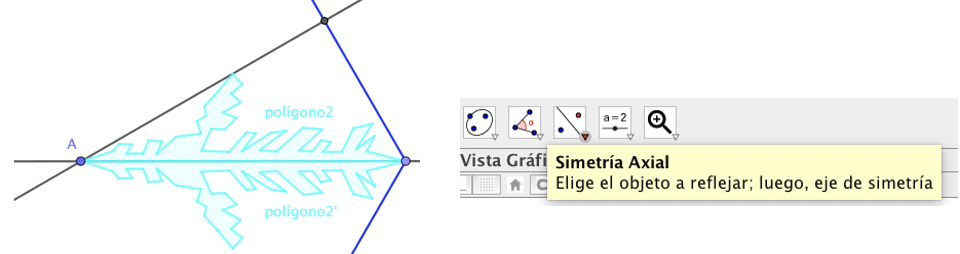
Creamos una listas, Copo={polígono2, polígono2'}.
Para crearla podemos escribir directamente en la Entrada.
De otra manera, marcamos en la vista Algebraica los polígonos polígono2 y polígono2', arrastramos a la Entrada y, si queremos, le ponemos nombre.

Utilizando los comandos Secuencia( < Expresión>, < Variable>, < Valor inicial>, < Valor final> ) y Rota( < Objeto>, <Ángulo>, < Punto> ), tecleamos en Entrada:
Secuencia(Rota(Copo, 60° ·m, A), m, 0, 5)
Creará una lista, lista_1, a la que podremos dar el color que queramos.
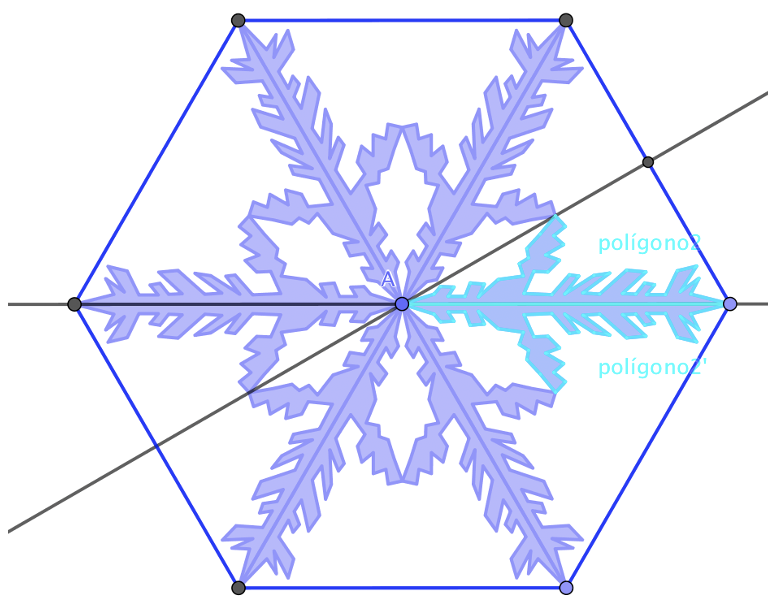
Ocultando todo menos la lista_1 tendremos el copo de nieve.

Al igual que en el apartado anterior, las propiedades, respecto a simetrías y giros, de los copos de nieve nos van a permitir crearlos, de forma sencilla, utilizando técnicas de kirigami.
Kirigami : arte de cortar y doblar papel
El kirigami es arte y la técnica de cortar el papel dibujando con las tijeras... Su término deriva de las palabras japonesas kiri, que significa ‘cortar’, y gami, ‘papel’. El kirigami tiene muchas variantes. El kirigami milenario practicado en oriente desarrolla modelos decorativos y muy artísticos. Hay un kirigami arquitectónico que, usando cuchillas, desarrolla modelos muy elaborados. También existe una variante educativa del kirigami, desarrollada especialmente en Sudamérica, la cual se usa como técnica y material educativo. Para ello se han creado dinámicas, juegos y aplicaciones didácticas del recorte del papel. (Wikipedia)
Dado que el copo es hexagonal, haremos el kirigami sobre un hexágono. Lo primero será obtener un papel hexagonal.
Las indicaciones siguientes muestran el método expuesto en el libro Papiroflexia (Origami) para expertos
Partiendo de un papel cuadrado:
Doblamos por una de las diagonales.
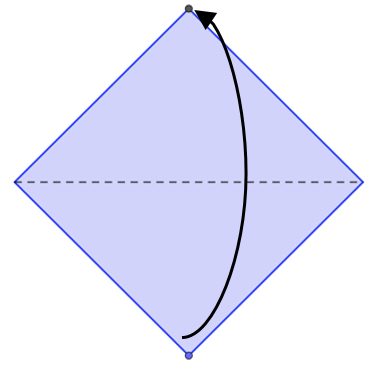
Doblamos y desdoblamos para marcar la mitad de la base del triángulo.
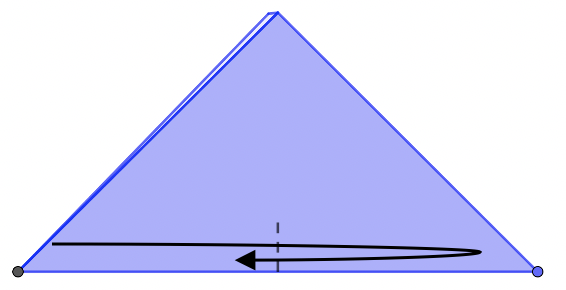
Doblamos y desdoblamos para marcar la mitad del lado indicado.
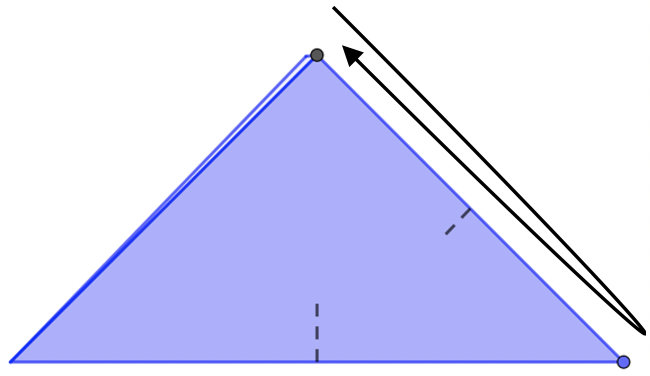
Doblamos y desdoblamos para marcar la mitad de los puntos indicados.
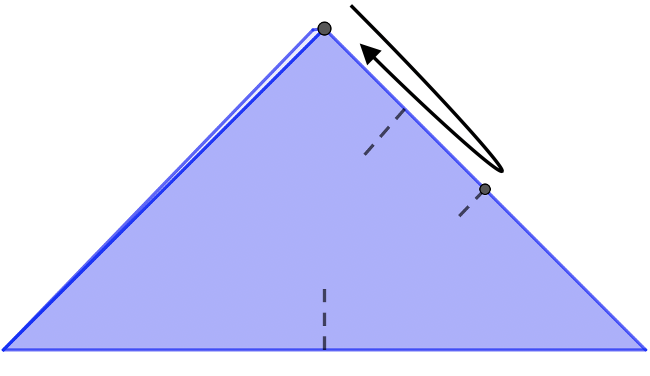
Doblamos por la línea de puntos, uniendo los dos puntos indicados. Quedará como la segunda imagen.
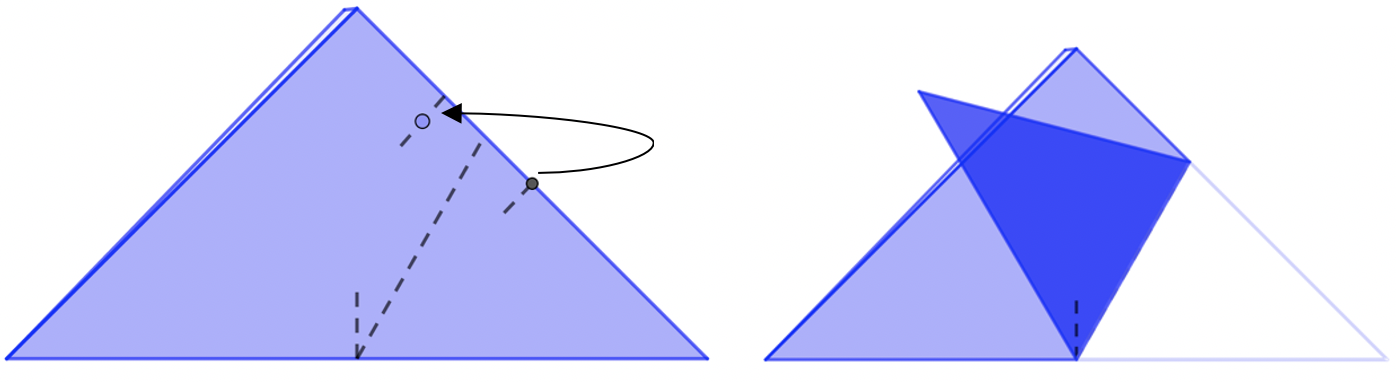
Doblamos ahora por la línea marcada.
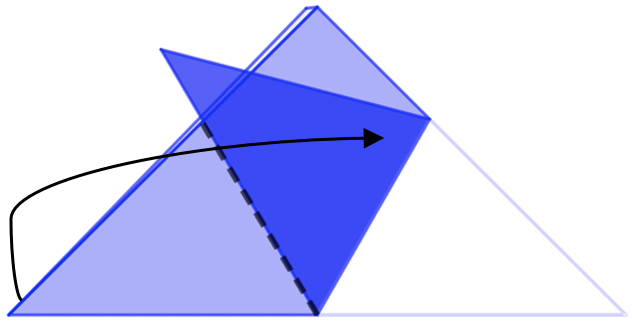
Doblamos cara atrás. Podemos girar primero y después doblar por la mitad.
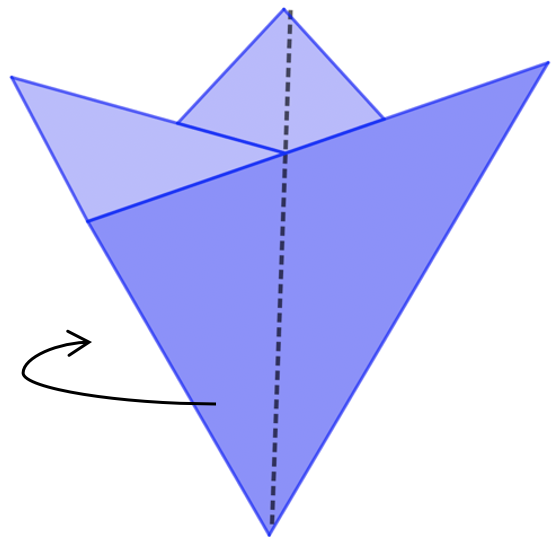
Si recortamos por la línea marcada y desdoblamos tendremos el hexágono.
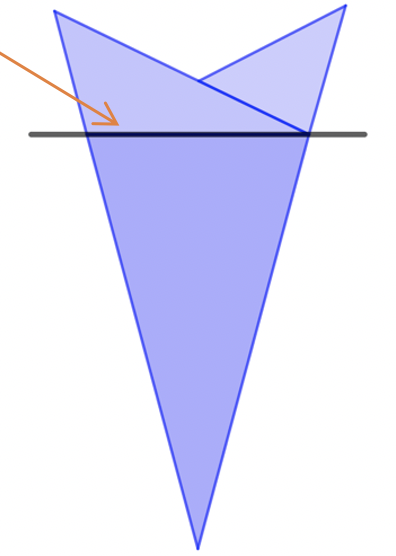
Para obtener el copo de nieve no es necesario recortar el hexágono.
Sin desdoblar, tomamos el lado no abierto como base del polígono. Dibujaremos sobre esa base y después recortaremos.
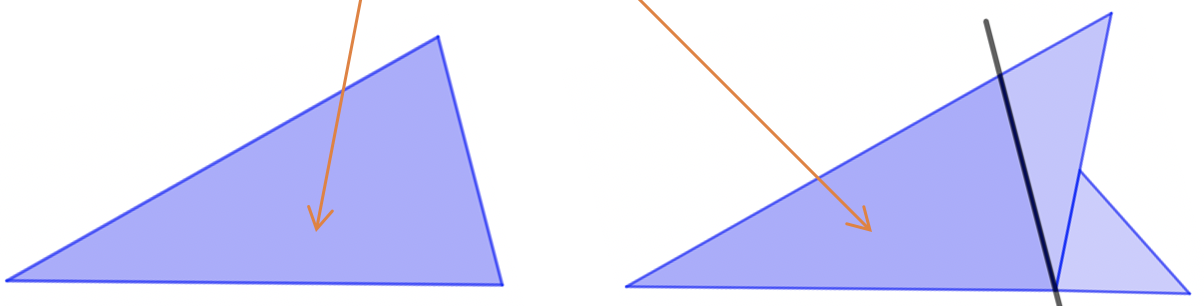
Podríamos recortar si dibujar primero, pero, si queremos un copo en particular, por ejemplo uno similar al que obtuvimos con GeoGebra, quedará mejor si dibujamos primero y después recortamos.
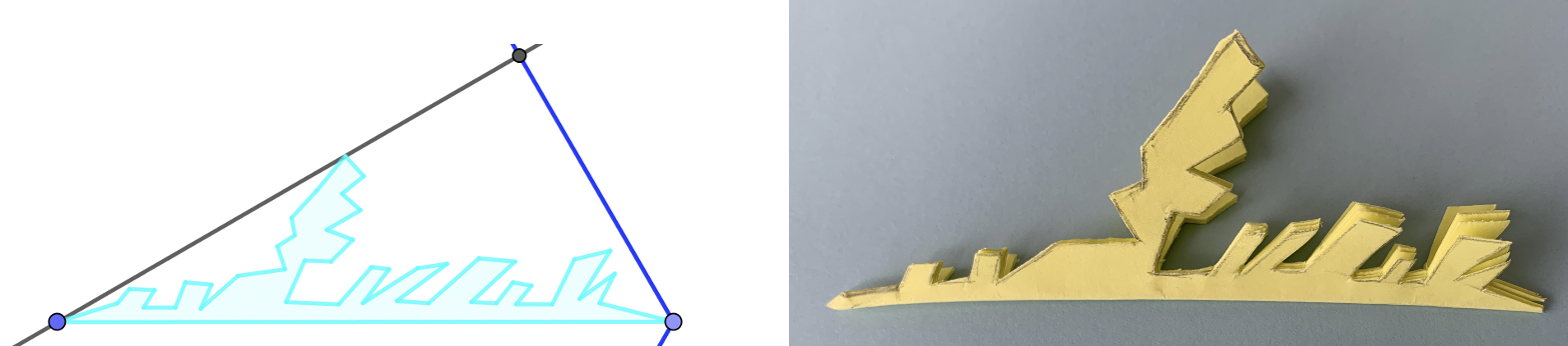
Abriendo el papel tendremos el copo.

Arte Románico
El arte románico es un arte cristiano que se desarrolla en Europa occidental desde finales del siglo X hasta mediados del siglo XII. A partir del siglo XII hablamos de tardorrománico.
Los pueblos europeos, replegados sobre si mismos, viven bajo un régimen feudal, organizados en una sociedad estamental donde cada región vive al margen de las otras. Esta falta de comunicación se refleja en el arte, convirtiéndolo en un estilo falto de unidad.
El aislamiento no es total, sabemos que con los artistas, la mayoría itinerantes buscando trabajo de villa en villa, viajan también las influencias artísticas.
En España este proceso es especialmente activo a través del Camino de Santiago, camino de entrada y de salida de influencias como la islámica o mozárabe, la bizantina ...
Un profundo sentimiento religioso caracteriza la vida en esta época. Cobra auge la vida monástica, los monasterios se convierten no sólo en centros de espiritualidad sino también en focos de actividad intelectual, artística y económica. Alrededor se agrupaban un gran número de campesinos que trabajaban las grandes explotaciones de las abadías y recibían la protección de las mismas. La rápida
expansión de los monasterios y su unidad de formas se debe sobre todo al poder de los monjes benedictinos de Cluny, que imponen sus reglas por todo el occidente europeo.
El arte románico es fundamentalmente un arte rural y monástico, frente al gótico que será urbano.
Impulsada por los abades benedictinos se generalizará la costumbre de hacer peregrinaciones a determinados lugares, para venerar las reliquias allí conservadas. Los principales centros de peregrinación serán Roma, Jerusalén y Santiago de Compostela. A lo largo de estos caminos veremos aparecer numerosas construcciones románicas.
Características generales de la arquitectura románica:
Arte Gótico
El estilo gótico se extiende desde mediados del siglo XII hasta los siglos XV o XVI, según el arraigo del propio gótico en cada región y la facilidad con la que entran las formas renacentistas.
Se inicia un desarrollo económico en los siglos XI, XII, e XIII, que
permite la transformación de la sociedad feudal. El crecimiento de las ciudades propicia la creación de una nueva sociedad de espalda a los estamentos tradicionales y a su forma de vida. La burguesía adquiere cada día un papel más destacado gracias a su actividad económica, comercio e industria, que le permiten alcanzar un poder económico equiparable al de la nobleza y el clero.
En general la situación social del artista no varía mucho respecto del románico. El artista, como cualquier otro artesano, trabaja dentro de un gremio. No se le exige originalidad creativa sino perfección técnica, los eclesiásticos siguen siendo los que conciben la iconografía ya que los artesanos non son intelectuales. Salvo algunas excepciones los artistas son anónimos.
Características generales del Arte Gótico:
El gótico consolidó la relación entre arte y religión que ya había puesto en marcha el Románico, sirviendo tanto para transmitir el mensaje de Dios e infundir el temor del hombre frente al poder divino, como para materializar el poder de la Iglesia.
Rosetones
Un rosetón es una ventana de forma circular que tiene una vidriera calada y adornada con diferentes dibujos y colores.
El rosetón se utilizó en la arquitectura románica y en la gótica, teniendo en esta última un gran desarrollo. Después del siglo XII fueron aumentando tanto en tamaño como en decoración. Los rosetones eran colocados en las fachadas, en cada uno de los frentes del transepto y por encima de las portadas. Los vidrios de los rosetones eran adornados con escenas bíblicas con un gran colorido.
La función de los rosetones es iluminar el interior de los templos y conseguir un ambiente misterioso. Se le ha atribuido un doble simbolismo: uno mariano, por la apariencia que tiene de la estructura de una rosa; otro que sugiere a Cristo, representado en los rayos del sol.

San Miguel de Breamo
En este primer ejemplo veremos dos rosetones sencillos, fáciles de analizar y reproducir.
La iglesia de San Miguel de Breamo está situada en el municipio de Pontedeume, en la comarca del Eume de la provincia de A Coruña. Es el único resto conservado del que fuera el Real Priorato de S. Miguel de Breamo, comunidad monacal de San Agustín, creado, con toda probabilidad, durante el reinado de Fernando II (1157-1188).

San Miguel de Breamo. Fachada norte
La planta es de cruz latina, de una sola nave y tres ábsides. Y la cubierta totalmente abovedada. Estas son dos características no muy abundantes en el románico gallego.
La iglesia sufrió varias reformas a lo largo de su historia, siendo la última de ellas en 1971. Fruto de una de esas reformas, en la primera mitad del siglo XX, es el rosetón de la fachada norte.
Para analizar un rosetón nos fijamos primero en si existe un elemento base que, girando, compone el rosetón completo y, si existe, contamos el número de veces que se repite. Una vez encontrado ese elemento base comprobamos si tiene o no un eje de simetría, determinando así si es cíclico o diédrico.
En el siguiente vídeo se pueden ver los pasos para analizar el rosetón de la fachada norte de Breamo.
Concluimos pues que, es un rosetón diédrico de orden 4.
Sabiendo esto y la forma del elemento básico podremos obtener el rosetón con Kirigami y con Geogebra.
Breamo Norte con Kirigami.
La realización es similar a la de los copos de nieve, la diferencia principal es la forma de doblar el papel, que está determinada por el orden del rosetón.
El papel lo tendremos que doblar tres veces, dos según los dos ejes de simetría que nos marcan los $90^\circ$, y otra por el eje de simetría del elemento básico.
En este caso, podemos empezar por buscar el centro del cuadrado y dibujar una o las dos circunferencias que limitan el elemento básico. Esto nos facilitará el dibujo necesario para después recortar.
Para hacer las dobleces dejamos la circunferencia dibujada hacia afuera, nos interesa, al final, ver los arcos que nos ayuden a dibujar la mitad del elemento básico.
Doblamos de la siguiente forma:
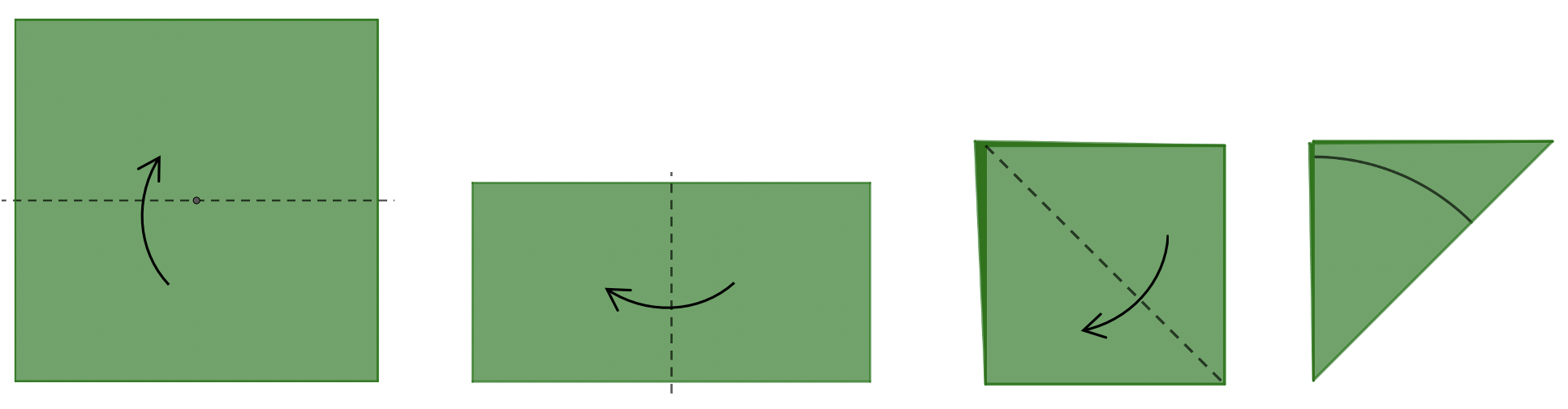
Dibujamos y recortamos:

Abrimos

Breamo Norte con GeoGebra.
Como ya comentamos en el capítulo anterior, antes de comenzar podemos modificar el etiquetado de los objetos para que no nos aparezcan todas las etiquetas en la vista gráfica; en la vista algébrica seguirán apareciendo los objetos con etiqueta. Esto lo podremos hacer en las Opciones.
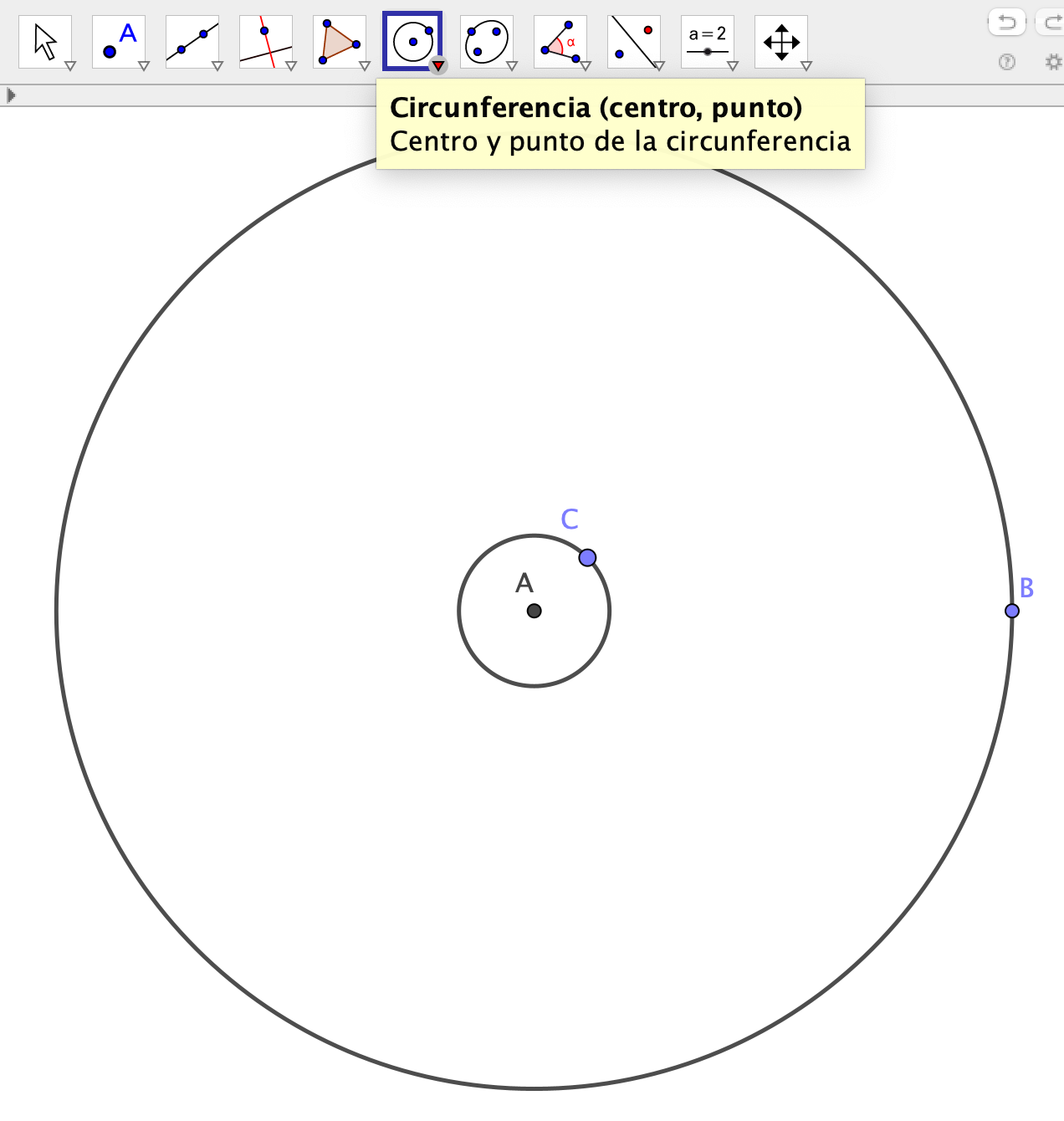
En este caso también tendremos que empezar por obtener el sector en el que dibujar la mitad del elemento básico.
Dibujar dos circunferencias concéntricas.
Dibujar un segmento y rotarlo $45^\circ$ tomando como centro de rotación el centro de las circunferencias.
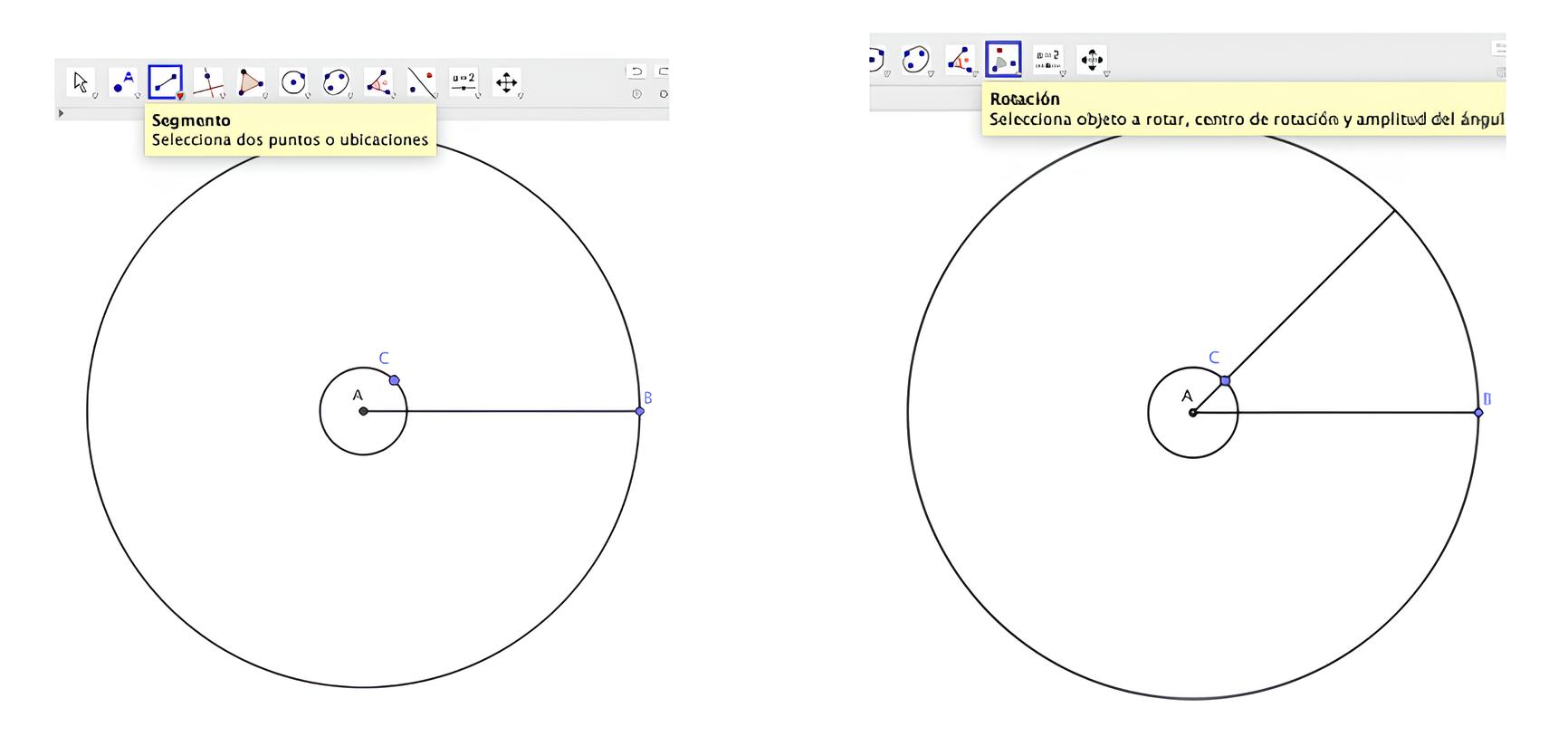
Así tendremos el sector en el que dibujar la mitad del elemento básico del rosetón.
Ampliar la imagen para poder dibujar con más detalle.
Con la herramienta Polígono dibujamos el polígono con la forma de la mitad del elemento base.
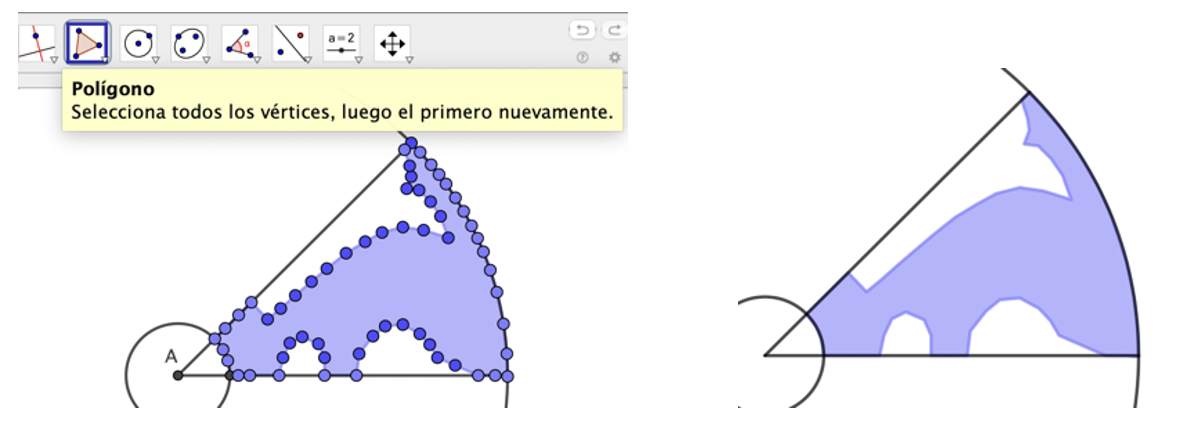
Después, podemos ocultar todos los puntos. Seleccionándolos todos en la Vista Algebraica, con el ratón derecho podemos ocultarlos.
Con la herramienta Simetría Axial reflejamos el polígono creado, polígono1, utilizando como eje de simetría el radio de la circunferencia. Obtendremos el polígono polígono1'
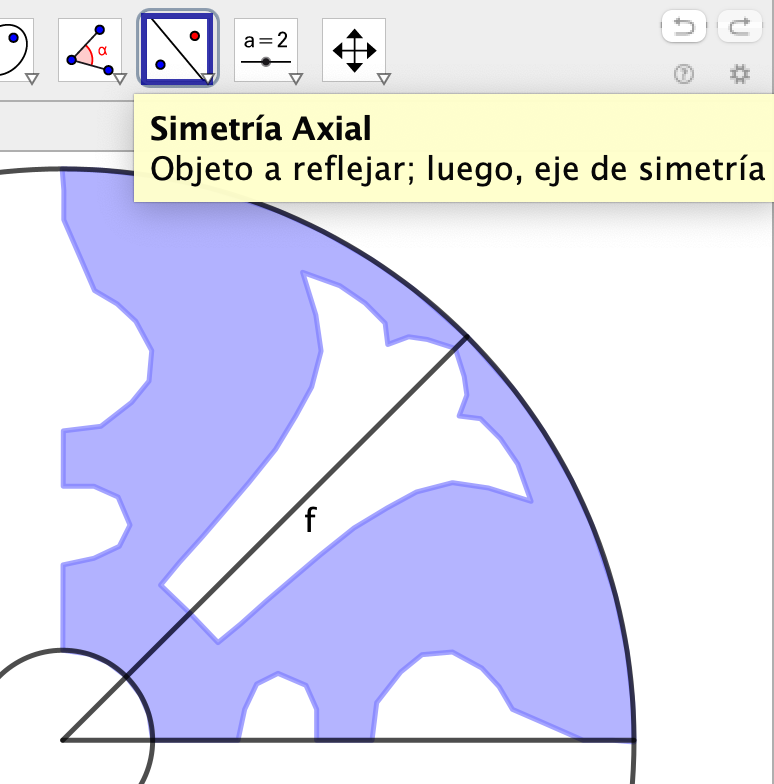
Creamos una lista, Breamo={polígono1, polígono1'}.
Para crearla podemos escribir directamente en la Entrada.
También podemos marcar, en la vista Algebraica, los polígonos polígono1 y polígono1', arrastrar a la Entrada y, si queremos, ponerle nombre.
Utilizando los comandos Secuencia( < Expresión>, < Variable>, < Valor inicial>, < Valor final> ) y Rota( < Objeto>, <Ángulo>, < Punto> ), tecleamos en Entrada:
Secuencia(Rota(Breamo, 90° ·m, A), m, 0, 3)
Creará una lista, lista_1, a la que podremos dar el color que queramos.
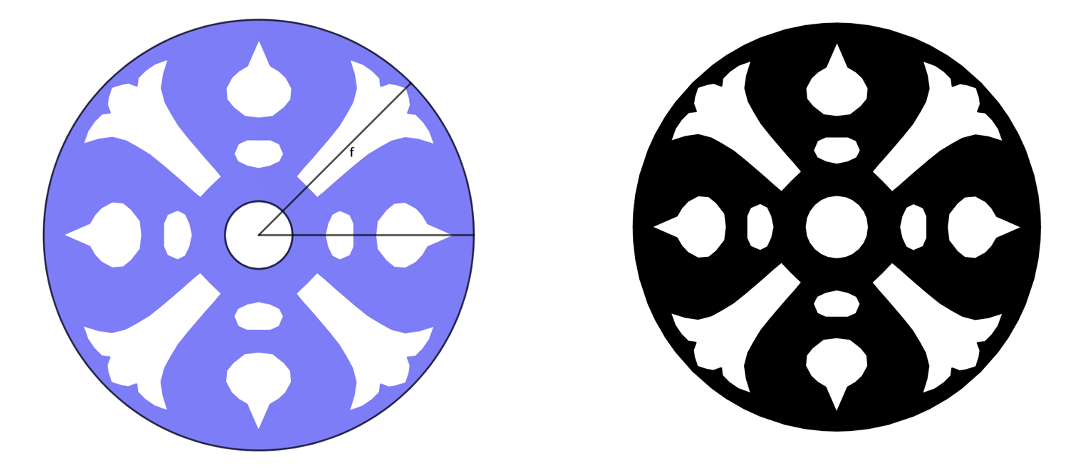
Ocultando todo menos la lista_1 tendremos el rosetón.

San Miguel de Breamo. Fachada principal
La fachada principal de San Miguel de Breamo también tiene rosetón.
En la siguiente escena de GeoGebra podrás buscar los ejes de simetría y el elemento principal para, con ello, determinar el tipo de rosetón y el orden.
El rosetón de la fachada principal es un rosetón diédrico de orden 6, similar a los copos de nieve.
Para dibujarlo con GeoGebra podemos empezar dibujando circunferencias y semicircunferencias.
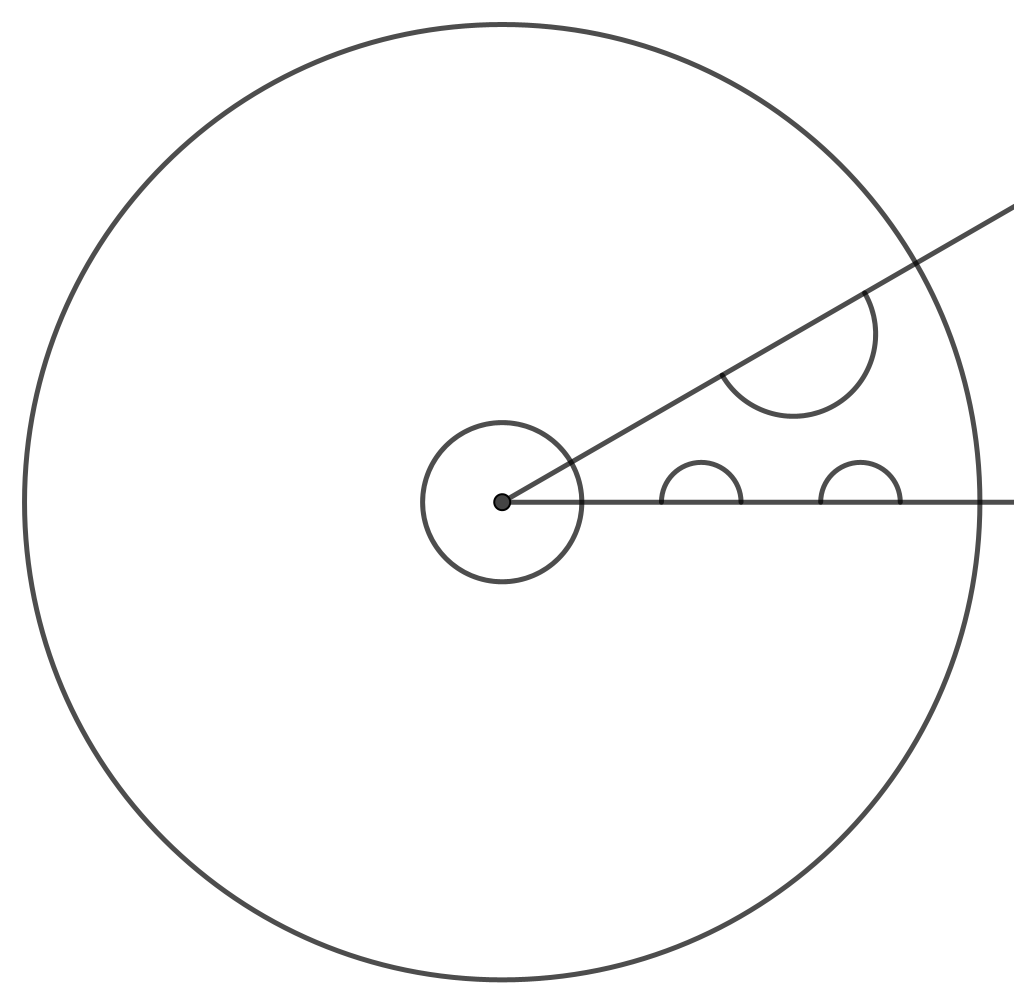
Ya tendríamos la mitad del elemento base y podríamos dibujar el polígono.
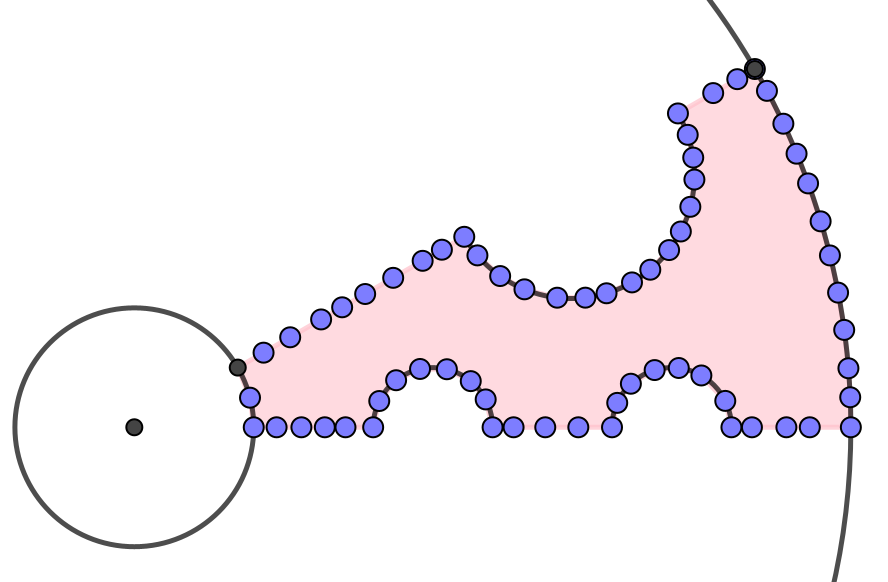
Con una simetría se obtiene el elemento básico y, rotando, el rosetón.
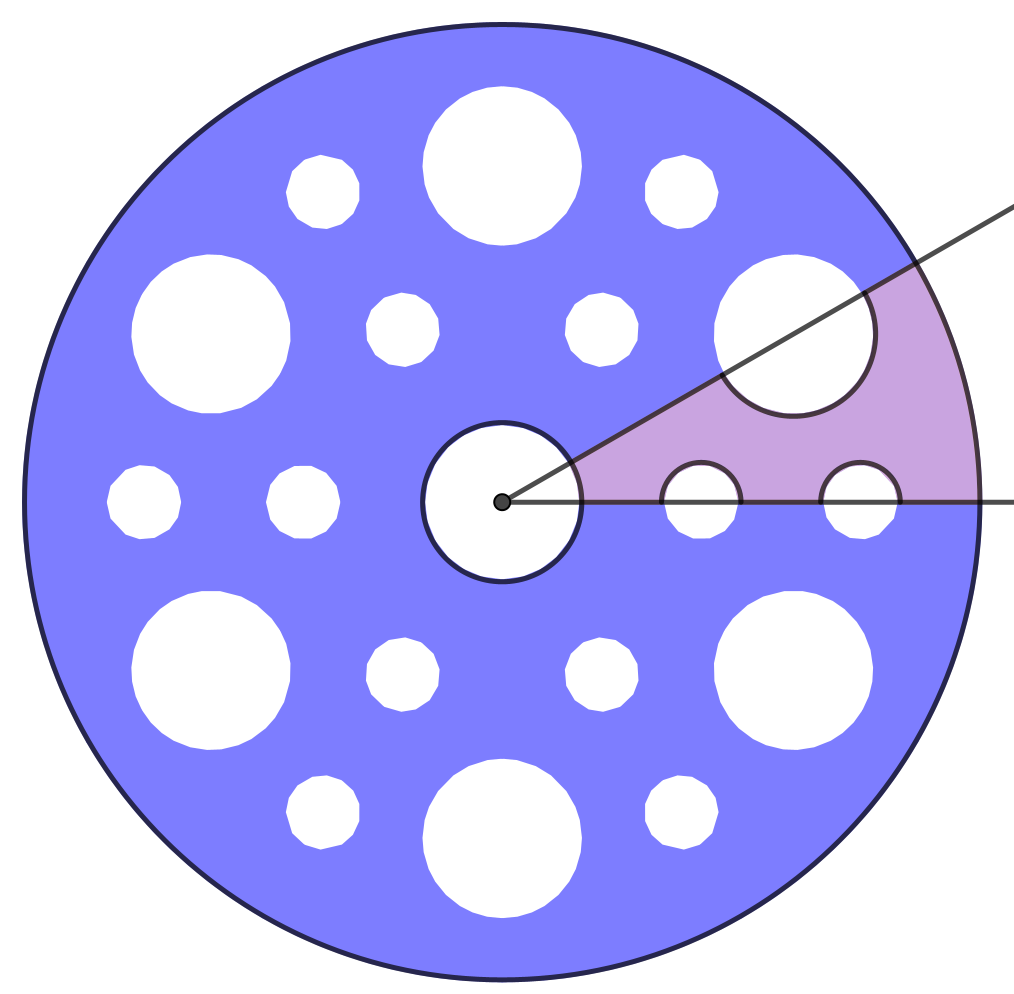
Un pequeño reto sería añadir los triángulos exteriores.

Para obtenerlo con kirigami se debe doblar el papel del mismo modo que para los copos de nieve.


Colegiata de Santa María. A Coruña.
También conocida con el nombre Santa María del Mar, por ser la antigua iglesia del gremio de los mareantes.
Iglesia de estilo románico tardio construida entre los siglos XII al XIV. Se situaba fuera de las antiguas murallas de la ciudad, de ahí proviene su nombre.
Planta basilical de 3 naves y un ábside en la cabecera. Cuenta con tres portadas; la principal tiene gran importancia con un tímpano que data del siglo XII

Ejes de simetría.
Recibe la categoría de colegiata en el siglo XV. Y, en 1931, es declarada Bien de Interés Nacional.
Rosetón diédrico de orden 12.
Ángulo de rotación de $\displaystyle\frac{360^\circ}{12}=30^\circ$.
Es un rosetón más complejo que los de la iglesia de Breamo, el orden del rosetón hace que para obtenerlo por kirigami sea
necesaria un poco más de destreza. Sin embargo, con GeoGebra el orden del rosetón no aumenta la dificultad, trabaja el programa y sólo tendremos que tener claros los ángulos de giro.
La siguiente ventana de GeoGebra te pueden ayudar para crear el rosetón con GeoGebra.
Activa la flecha de la esquina inferior izquierda o mueve el deslizador.
Colegiata de Santa María con Kirigami.
El orden de este rosetón es 12, el doble que un copo de nieve. Esto implica que debemos doblarlo el papel una vez más.
Después, dibujamos la mitad del elemento básico.

Recortar un papel doblado tantas veces no es fácil, conviene utilizar un papel fino, por ejemplo, un papel seda.


Santiago de Betanzos.
Iglesia de estilo gótico del s. XV, situada en el municipio de Betanzos, en la provincia de A Coruña.
La planta basilical distribuye el templo en tres naves, la central más ancha que las laterales, y tres ábsides. La cubierta es a doble vertiente, con un artesonado de madera.
En el siglo XVI se construyó, adosada a la iglesia, la torre municipal o del reloj.

A medida que avanza el gótico los rosetones van ganando en complejidad y tamaño.
En este rosetón, dentro de su sencillez, ya apreciamos más complejidad que en los anteriores. Si queremos clasificarlo e indicar su orden, lo primero que vemos es que tiene tres coronas circulares y en cada una de ellas el orden es diferente. Las coronas son de orden 12, 6 y 4, respectivamente.
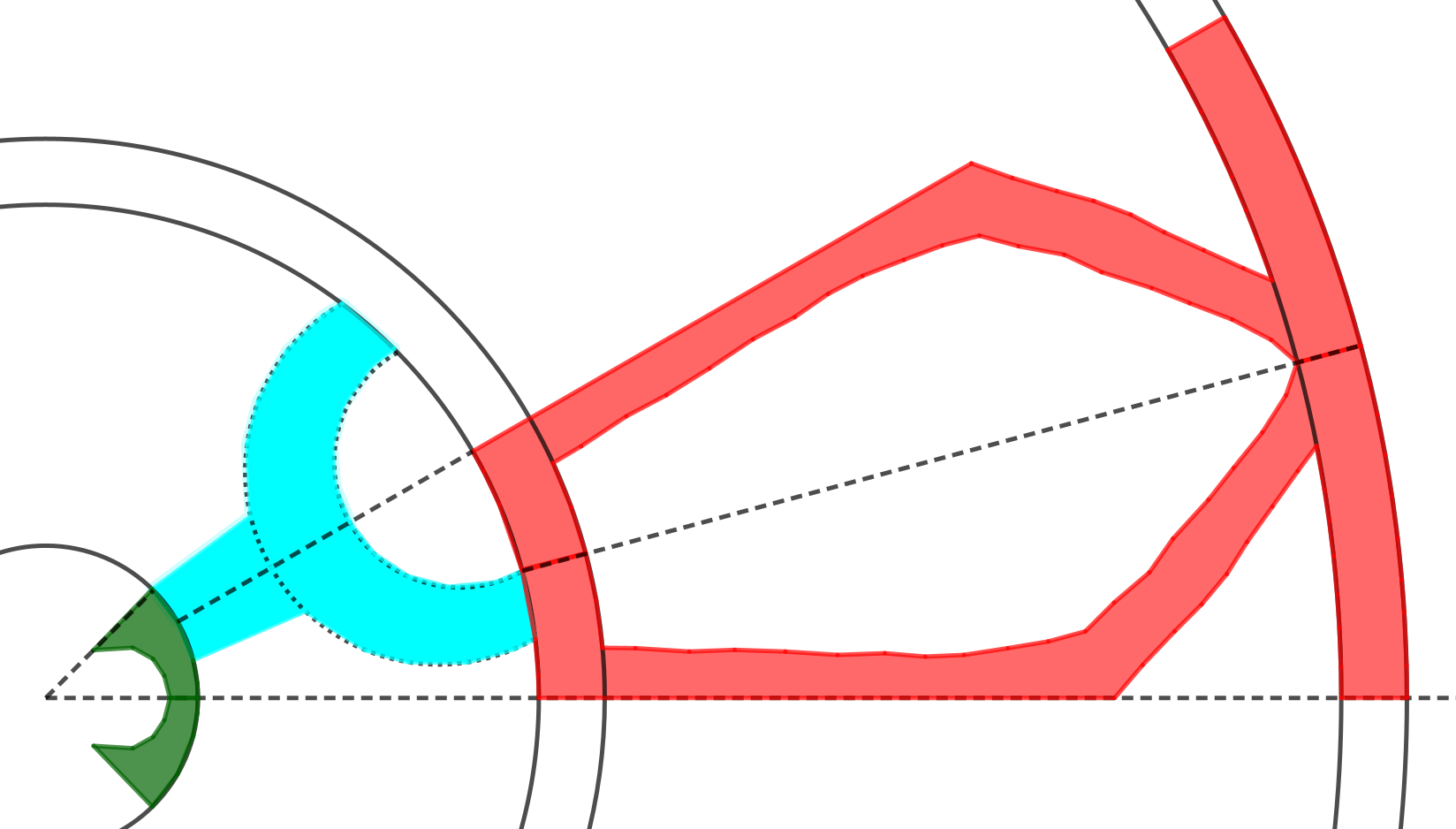
Para trabajar con GeoGebra podemos comenzar por dibujar circunferencias concéntricas que nos delimiten las tres coronas circulares que componen el rosetón.
Trazar rectas o semirrectas girando, según los ángulos necesarios para cada corona, y dibujar los polígonos que forman cada una de las tres mitades de los elementos básicos.
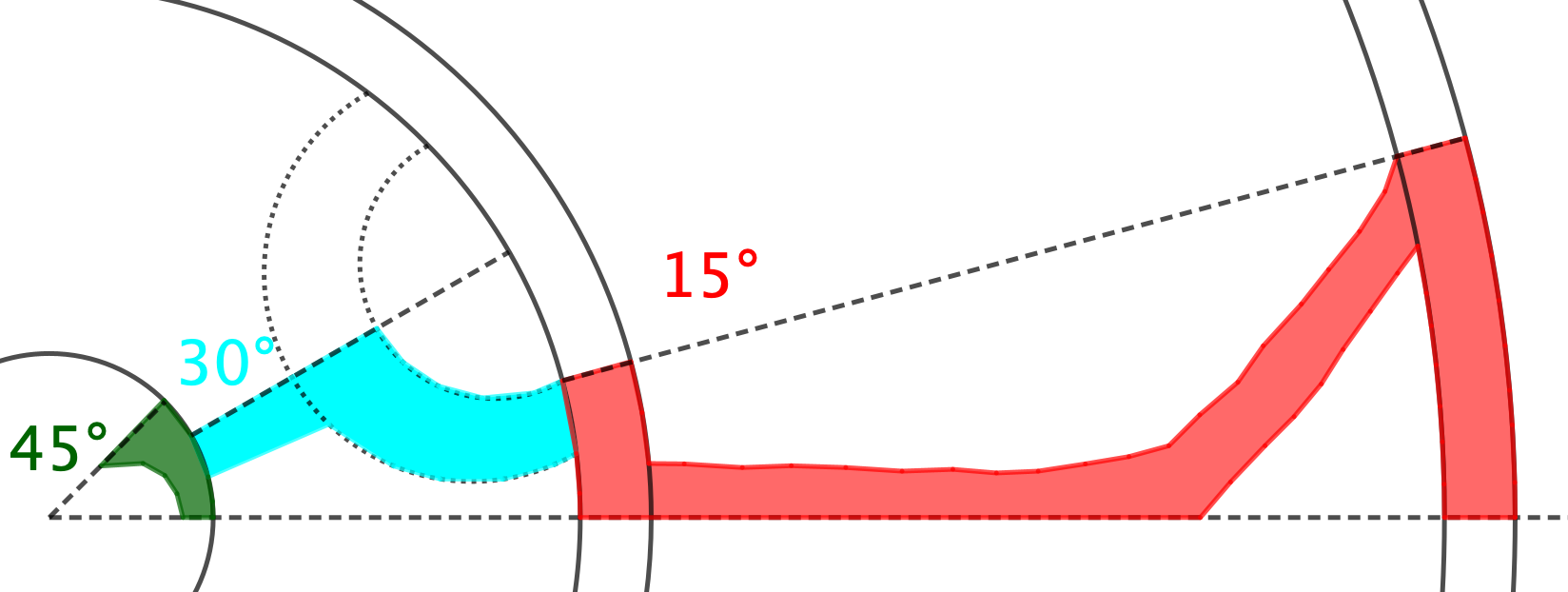
Los respectivos elementos básicos los podremos girar:
Secuencia(Rota(Elemento1, 30° ·m, Punto), m, 1, 12) Secuencia(Rota(Elemento2, 60° ·m, Punto), m, 1, 6) Secuencia(Rota(Elemento3, 90° ·m, Punto), m, 1, 4)
Iglesia de Santiago con Kirigami.
Tendremos que ir dibujando y recortando una a una las tres coronas. Doblando el papel para un hexágono, doblando una vez más y al final, abrir y doblar para la pequeña, tres dobleces.

Por último, unas propuestas más con los resultados de trabajos realizados con GeoGebra y kirigami.

Iglesia de San Francisco, Betanzos

Iglesia de Santa María, Betanzos

Iglesia de Santa María, Betanzos

Iglesia de Santiago, A Coruña

Iglesia de Santiago, A Coruña
Las iglesias que aparecen en todas las imágenes del capítulo anterior están situadas en las comarcas gallegas de A Coruña, Betanzos y Eume, esto es así ya que inicialmente esta actividad fue pensada para trabajar con alumnado de 4º de ESO de un instituto de Cambre, una población cercana a la ciudad de A Coruña.
En el año 2022, entre los dos profesores que impartíamos matemáticas en 4º de ESO llevamos acabo la experiencia, utilizando tres sesiones de nuestras respectivas horas de matemáticas y, después, el trabajo individual del alumnado.
En mayor o menor medida todo el alumnado había tenido algún contacto con el programa GeoGebra, esto permitió que se enfrentasen a esa parte con buena disposición y eficacia. Parte del tiempo lo empleamos en el aula de informática, centrando el trabajo en giros, simetrías y secuencias, totalmente nuevas para ellos.
Coloca el puntero del ratón en la ventana de las diapositivas y desplaza con el teclado o los controles de la esquina inferior izquierda.
Después de las sesiones en el aula organizamos las tareas de la siguiente forma:
Coloca el puntero del ratón en la ventana de las diapositivas y desplaza con el teclado o los controles de la esquina inferior izquierda.