Ángel Cabezudo Bueno
Red Educativa Digital Descartes
Córdoba (España)
2021
Título de la obra:
RELACIONES ENTRE FIGURAS GEOMÉTRICAS EN EL PLANO
Autor:
ÁNGEL CABEZUDO BUENO
Diseño del libro: Juan Guillermo Rivera Berrío
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Núcleo del libro interactivo: julio 2022
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN: 978-84-18834-20-2

Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
El presente material didáctico puede constituir un complemento al correspondiente de Geometría en el nivel educativo de 4º Curso de Educación Secundaria Obligatoria y bien podría ser incluido en una programación de aula para un Taller de Matemáticas.
Se han seleccionado dos partes diferenciadas: Algunas figuras relacionadas con la circunferencia y determinación de lugares geométricos.
El cuadro de Conceptos previos mostrado en la siguiente página es un resumen de figuras geométricas en el plano y algunas propiedades que el alumno debiera conocer antes de consultar esta unidad didáctica, lo que viene a indicar la cantidad de conceptos geométricos, en su mayor parte elementales, que se van a poder relacionar.
Las escenas de geometría construidas con DescartesJS posibilita al alumno observar las propiedades geométricas e interaccionar con los elementos representados lo que le permite reflexionar, analizar y experimentar más fácilmente una serie de cuestiones que se derivan de los siguientes temas:
|
Distancia entre dos puntos.
|
 |
Distancia
de un punto a una recta.
|
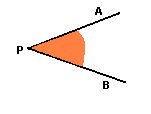 |
Ángulo.
|
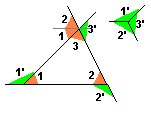 |
Triángulos.
Ángulos interiores y exteriores.
|
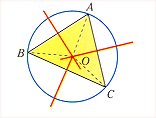 |
Mediatriz de un segmento.
|
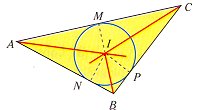 |
Bisectriz de un ángulo.
|
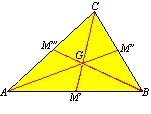 |
Mediana de un triángulo.
|
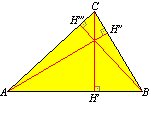 |
Altura de un triángulo..
|
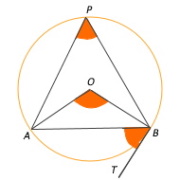 |
Circunferencia.
|
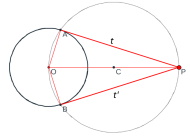 |
Tangente a una circunferencia.
|
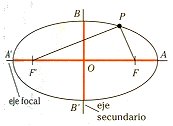 |
Elipse.
|
DEBES DE SABER...
En este apartado vas a aprender a construir la tangente a una circunferencia desde un punto $P$ exterior.
OBSERVA LA SIGUIENTE ESCENA INTERACTIVA...
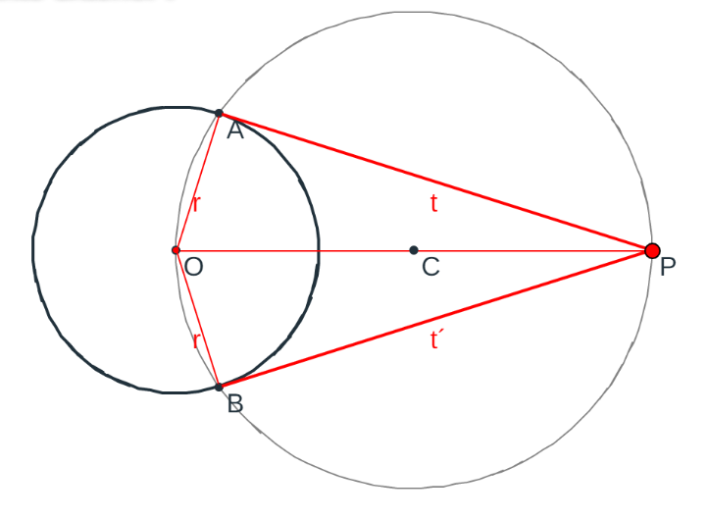
Se trata de dibujar la tangente a la circunferencia de centro $O$ y radio $r=3$ desde el punto $P(10,0)$
Hay dos soluciones: la recta $PA$ y la $PB$ simétricas respecto de la recta que une $P$ con $O$
El punto de contacto $A$ ha de ser el vértice de un ángulo recto cuyos lados, radio y tangente, pasan respectivamente por el centro $O$ y el punto $P$. Este ángulo abarca por tanto el diámetro $OP$ de la circunferencia de centro $C$ (punto medio de $OP$). Lo mismo podemos decir del punto de contacto $B$. Recordar la propiedad de los ángulos inscritos a una circunferencia que abarcan su diámetro (miden $90º$)
Bastará trazar la circunferencia de diámetro $OP$ y unir $P$ con las intersecciones de $A$ y $B$ que produce dicha circunferencia con la circunferencia dada.
EXPERIMENTA:
El punto $P$ es un control que puedes mover arrastrándolo con el ratón. También puedes cambiar su posición introduciendo sus coordenadas $(Px, Py)$ desde la ventana de parámetros.
La circunferencia a la que queremos trazar las tangentes, tiene centro $O(0,0)$ y radio $r$ que podemos cambiar introduciendo su valor desde la ventana de parámetros.
Sitúa el punto $P$ en $(8,-2)$ e introduce el valor del radio $r = 3.5$ de la circunferencia de centro $O(0,0)$. Observa que las tangentes a dicha circunferencia desde $P$ se trazan desde $P$ a los puntos de intersección que produce la circunferencia de diámetro $OP$ sobre la circunferencia dada.
Comprueba este hecho las veces que quieras cambiando el punto $P$ y el radio de la circunferencia de centro $O(0,0)$
OBSERVAR...
EXPERIMENTA CON LA ESCENA INTERACTIVA:
Cambia los puntos A, B y C utilizando los controles (desplazando con el ratón) o introduciendo directamente las coordenadas (Ax, Ay), (Bx, By), (Cx, Cy) en la ventana de parámetros.
Experimenta poniendo A, B y C casi alineados. Utiliza si fuera preciso la escala, disminuyéndola para poder ver la escena. ¿Qué pasa con el centro de la circunferencia? ¿Cómo es la circunferencia? ¿Qué le pasa a las mediatrices m y n?
Mueve el punto C respecto de A y B hasta que queden alineados ¿Qué pasa con el centro de la circunferencia? ¿En qué se ha convertido la circunferencia?
 aparecerá algunas veces al final de un párrafo, al poner el puntero sobre ella se muestra un cuadro de ayuda. Utilízala sólo después de haber reflexionado sobre la cuestión propuesta.
aparecerá algunas veces al final de un párrafo, al poner el puntero sobre ella se muestra un cuadro de ayuda. Utilízala sólo después de haber reflexionado sobre la cuestión propuesta.  - Traza las diagonales. Estas se cortan en el punto medio.
- Traza las diagonales. Estas se cortan en el punto medio. No. Si trazamos las mediatrices de dos lados paralelos (opuestos) estás no se cortan, por tanto no existe centro de la circunferencia que contenga a los cuatro puntos
No. Si trazamos las mediatrices de dos lados paralelos (opuestos) estás no se cortan, por tanto no existe centro de la circunferencia que contenga a los cuatro puntos Trazamos el cuadrilátero y las dos diagonales. Si los cuatro vértices son concíclicos, las dos mediatrices trazadas sobre las diagonales tienen que cortarse en el centro de la circunferencia.
Trazamos el cuadrilátero y las dos diagonales. Si los cuatro vértices son concíclicos, las dos mediatrices trazadas sobre las diagonales tienen que cortarse en el centro de la circunferencia.EXPERIMENTA CON LA ESCENA INTERACTIVA:
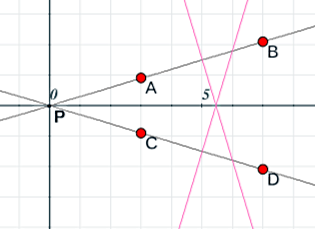
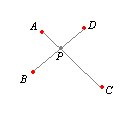
Se consideran cuatro puntos en el plano $A$, $B$, $C$ y $D$.
$A$ y $B$ determinan una recta $m$ con pendiente $p_m$
$C$ y $D$ determinan otra recta $n$ con pendiente $p_n$
En este caso resulta evidente que $PA$x$PB$ = $PC$x$PD$
Cambia la posición del punto $A$, por ejemplo, y advierte que $QA$ = $QB$ ≠ $QC$ = $QD$, por lo que los cuatro puntos no están en la circunferencia de centro $Q$, a la vez que $PA$x$PB$ ≠ $PC$x$PD$
 |
 |
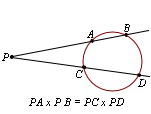
Si el punto es interior las distancias $PA$ y $PB$ son de signos opuestos (pues para ir de $P$ a $A$ se hace en sentido contrario sobre la recta al que se hace para ir de $P$ a $B$. Por tanto si el $P$ punto es exterior a la recta, tiene potencia positiva y si es interior tiene potencia negativa.
Un punto $P$ que esté sobre la circunferencia tendrá potencia 0. ¿Por qué?  Al trazar desde $P$ el segmento que corta a la circunferencia, los puntos de corte son el propio punto $P$ y el punto $B$, extremos de una cuerda.
Al trazar desde $P$ el segmento que corta a la circunferencia, los puntos de corte son el propio punto $P$ y el punto $B$, extremos de una cuerda.
La potencia de $P$ es
$PP$x$PB$=$0$x$PB$=$0$
EXPERIMENTA CON LA SIGUIENTE ESCENA
Observaciones: Se pueden modificar desde la ventana de parámetros, los siguientes:
Estas observaciones te permitirán contestar algunas preguntas.
PIENSA...
Reflexiona sobre las siguientes cuestiones, experimenta en la anterior o en la siguiente escena DESCARTES y trata de dar respuesta.
 Los puntos de corte son $E$ y $F$ diametralmente opuestos. La potencia será $PE$x$PF$.
Los puntos de corte son $E$ y $F$ diametralmente opuestos. La potencia será $PE$x$PF$. Efectivamente se puede comprobar que la potencia de $P$ respecto de la circunferencia de centro $C$ y radio $r$ es el cuadrado de la distancia $PT$. Pues si regresas al concepto de potencia, página 21, la potencia es $PA$x$PB$ donde $A$ y $B$ son los puntos de corte con la circunferencia de la recta secante trazada desde $P$. La tangente a la circunferencia trazada desde $P$ se puede considerar como un caso límite en el que los dos puntos de corte $A$ y $B$ coinciden $PA$=$PB$=$PT$.
Efectivamente se puede comprobar que la potencia de $P$ respecto de la circunferencia de centro $C$ y radio $r$ es el cuadrado de la distancia $PT$. Pues si regresas al concepto de potencia, página 21, la potencia es $PA$x$PB$ donde $A$ y $B$ son los puntos de corte con la circunferencia de la recta secante trazada desde $P$. La tangente a la circunferencia trazada desde $P$ se puede considerar como un caso límite en el que los dos puntos de corte $A$ y $B$ coinciden $PA$=$PB$=$PT$. Dibuja la circunferencia de centro $P$ y radio $PC$ (introduce $lugC$=$PC$). Comprueba que las circunferencias de radio $r$ que tengan su centro sobre aquella cumplen la condición.
Dibuja la circunferencia de centro $P$ y radio $PC$ (introduce $lugC$=$PC$). Comprueba que las circunferencias de radio $r$ que tengan su centro sobre aquella cumplen la condición. Dibuja la circunferencia de radio $PC$ y centro $P$ (introducir $lugC$=$PC$), si mueves el centro de $C$ sobre dicha circunferencia comprobarás que la potencia respecto de $P$ es la misma que antes.
Dibuja la circunferencia de radio $PC$ y centro $P$ (introducir $lugC$=$PC$), si mueves el centro de $C$ sobre dicha circunferencia comprobarás que la potencia respecto de $P$ es la misma que antes. Dibuja la circunferencia de radio $PT$ y centro $P$ (introducir $lugT$=$PT$), cambia el radio $r$ (por ejemplo $r$=$3$), cambia la posición del centro $C$ hasta conseguir que la distancia $PT$ valga lo mismo que valía antes ($lugT$).
Dibuja la circunferencia de radio $PT$ y centro $P$ (introducir $lugT$=$PT$), cambia el radio $r$ (por ejemplo $r$=$3$), cambia la posición del centro $C$ hasta conseguir que la distancia $PT$ valga lo mismo que valía antes ($lugT$). Cambia las posición del centro $C$, modificando sus coordenadas, hasta conseguir que la potencia valga $30$ y lee el valor de la distancia $PC$.
Cambia las posición del centro $C$, modificando sus coordenadas, hasta conseguir que la potencia valga $30$ y lee el valor de la distancia $PC$. Efectivamente, siendo $PE$=$d+r$ y $PF$ = $d-r$, se cumple que la potencia de $P$ respecto de la circunferencia es $PE$x$PF$=$(d+r)(d-r)$=$d^2-r^2$.
Efectivamente, siendo $PE$=$d+r$ y $PF$ = $d-r$, se cumple que la potencia de $P$ respecto de la circunferencia es $PE$x$PF$=$(d+r)(d-r)$=$d^2-r^2$. Dibuja la circunferencia de centro $C$ y radio $PC$ (introduce $lugP$=$PC$). Es evidente que cualquier punto de este lugar dista del centro $C$ lo mismo $PC$=$d$, así pues tendrán la misma potencia respecto de la circunferencia de centro $C$ y radio $r$; es decir el mismo valor de la expresión $(d+r)(d-r)$=$d^2-r^2$
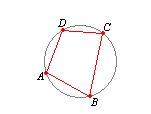
Dibuja la circunferencia de centro $C$ y radio $PC$ (introduce $lugP$=$PC$). Es evidente que cualquier punto de este lugar dista del centro $C$ lo mismo $PC$=$d$, así pues tendrán la misma potencia respecto de la circunferencia de centro $C$ y radio $r$; es decir el mismo valor de la expresión $(d+r)(d-r)$=$d^2-r^2$DEFINICIÓN: Cuadrilátero inscrito en una circunferencia
REFLEXIONA...
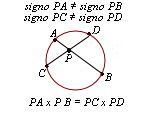
 Si un cuadrilátero es inscriptible sus vértices cumplirán la propiedad de los cuatro puntos concíclicos entonces trazando las diagonales $AC$ y $BD$ estás se cortarán en un punto $P$ interior. Las diagonales representan dos rectas secantes que pasan por $P$ y la potencia de $P$ respecto de la circunferencia es $PA$ x $PC$ = $PB$ x $PD$
Si un cuadrilátero es inscriptible sus vértices cumplirán la propiedad de los cuatro puntos concíclicos entonces trazando las diagonales $AC$ y $BD$ estás se cortarán en un punto $P$ interior. Las diagonales representan dos rectas secantes que pasan por $P$ y la potencia de $P$ respecto de la circunferencia es $PA$ x $PC$ = $PB$ x $PD$
 Se trazan las diagonales y se obtiene el punto de corte $P$. Se calculan los productos $PA$ x $PC$ y $PB$ x $PD$. Si estos productos son iguales, el cuadrilátero es inscriptible.
Se trazan las diagonales y se obtiene el punto de corte $P$. Se calculan los productos $PA$ x $PC$ y $PB$ x $PD$. Si estos productos son iguales, el cuadrilátero es inscriptible. Se trazan las mediatrices de dos lados, p.e. $AB$ y $BC$. El corte equidista de $A$, $B$ y $C$ y es el radio de la circunferencia buscada. El punto $D$ también estará en la circunferencia, pues el cuadrilátero es inscriptible.
Se trazan las mediatrices de dos lados, p.e. $AB$ y $BC$. El corte equidista de $A$, $B$ y $C$ y es el radio de la circunferencia buscada. El punto $D$ también estará en la circunferencia, pues el cuadrilátero es inscriptible.DESCUBRIENDO OTRA PROPIEDAD DEL CUADRILÁTERO INSCRIPTIBLE...
Esta propiedad tiene que ver con la relación existente entre un ángulo inscrito en una circunferencia y el central correspondiente.
 Un ángulo inscrito en una circunferencia mide la mitad del central que abarca el mismo arco.
Un ángulo inscrito en una circunferencia mide la mitad del central que abarca el mismo arco.
EXPERIMENTA CON LA ESCENA SIGUIENTE...
Podrás experimentar que cuando un cuadrilátero es inscriptible los ángulos opuestos son suplementarios.
Los ángulos A y C son opuestos y su suma A + C = 180º. Posiciona los puntos donde quiera que sea, son controles que podrás pinchar y arrastrar con el ratón sobre la circunferencia y comprueba que la relación entre ángulos apuestos es la dicha antes.
¿Tiene esto que ver con el hecho de que el central correspondiente a un ángulo inscrito mide el doble que éste?
Observa la escena en las condiciones iniciales.
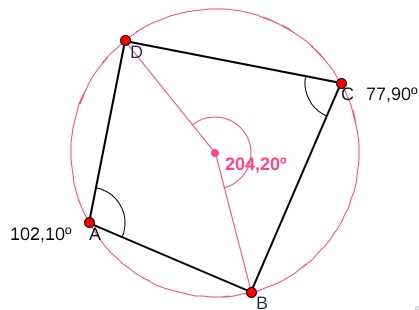
 La recta $BD$ divide al plano en dos semiplanos.
La recta $BD$ divide al plano en dos semiplanos.La suma de los ángulos interiores de un cuadrilátero cualquiera, inscriptible o no, suman $360º$
 Cualquier cuadrilátero se puede dividir en dos triángulos, trazando una diagonal. Como cada triángulo suma $180º$ el cuadrilátero suma $360º$.
Cualquier cuadrilátero se puede dividir en dos triángulos, trazando una diagonal. Como cada triángulo suma $180º$ el cuadrilátero suma $360º$. Inicialmente el cuadrilátero no es inscriptible. Observa que la suma de los ángulos $B+D$ no es $180º$.
Se han trazado las mediatrices a los lados $AB$ y $BC$. Y el corte $O$ de ambas tendrá que ser el centro de la circunferencia. Se cumple que $OA = OB = OC = r$ pero $OD$ no mide los mismo por tanto los cuadro vértices no son concíclicos y el cuadrilátero no queda inscrito.
Si quieres ver la circunferencia donde deben estar situados los cuatro vértices escribe en la ventana de parámetros el valor que debe tener el radio $(r = 4.69)$.
Si desplazas el punto $D$ hasta colocarlo en la circunferencia entonces $B + D = 180º$.
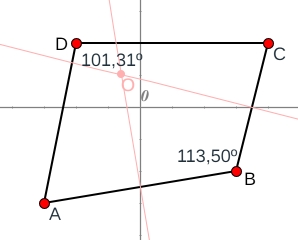
Puedes para ello desplazarlo con el ratón o modificar las coordenadas del punto $(Dx,Dy)$ desde la ventana de parámetros.
Es evidente que la posición del vértice $D$ puede ser cualquiera del arco $AC$.
REFLEXIONA...
Un cuadrilátero rectángulo ¿es siempre inscriptible?
Prueba a formar un rectángulo (cuatro lados paralelos dos a dos), por ejemplo haciendo $AB=CD=6$ y horizontales y $AD=BC=4$ verticales, para facilitar la construcción. ¿Qué pasa con la suma $B+D$? Dibuja otro rectángulo y hazte la misma pregunta.
 Dibuja las diagonales $AC$ y $BD$, estas son iguales y se cortan en el punto medio. Por tanto este punto equidista de los vértices y será el centro de la circunferencia buscada.
Dibuja las diagonales $AC$ y $BD$, estas son iguales y se cortan en el punto medio. Por tanto este punto equidista de los vértices y será el centro de la circunferencia buscada. DEFINICIÓN: Cuadrilátero circunscrito a una circunferencia
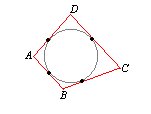
Vamos a descubrir la propiedad que caracteriza a un cuadrilátero circunscribible, pues no todo cuadrilátero lo es.
OBSERVA LA FIGURA ANTERIOR...Ahora hay que fijarse en que los lados $AD$ y $AB$ son tangentes trazadas desde el punto $A$ a la circunferencia y los lados $CB$ y $CD$ son tangentes trazadas desde $C$.
¿Recuerdas qué decíamos en la $página \space 15$ de las rectas tangentes a una circunferencia trazadas desde un punto exterior ella? ¿Cómo son las longitudes de los segmentos limitados entre $A$ y los puntos de tangencia? ¿Y las longitudes de los segmentos limitados entre $C$ y los puntos de tangencia?  Los segmentos limitados entre un punto $P$ exterior a una circunferencia y los puntos de tangencia tienen la misma longitud pues son simétricos respecto de la recta que contiene a $P$ y al centro $O$ de la circunferencia.
Los segmentos limitados entre un punto $P$ exterior a una circunferencia y los puntos de tangencia tienen la misma longitud pues son simétricos respecto de la recta que contiene a $P$ y al centro $O$ de la circunferencia.
EXPERIMENTA CON LA ESCENA SIGUIENTE...
DESCUBRIR LA PROPIEDAD
REFLEXIONA:
Has comprobado que cuando la suma de los lados opuestos vale lo mismo el cuadrilátero se puede circunscribir en una circunferencia.
Cumplida la propiedad, el centro de la circunferencia es la intersección de las bisectrices de los ángulos interiores del cuadrilátero.
 Los puntos de tangencia dividen a cada lado en dos segmentos, siendo iguales aquellos que concurren en un mismo vértice Propiedad de las dos tangentes trazadas desde un punto exterior a una circunferencia.
Los puntos de tangencia dividen a cada lado en dos segmentos, siendo iguales aquellos que concurren en un mismo vértice Propiedad de las dos tangentes trazadas desde un punto exterior a una circunferencia.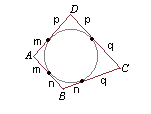
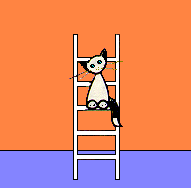 Vamos a presentar una situación real, después hacemos una interpretación geométrica ideal y resolvemos el problema matemáticamente.
Vamos a presentar una situación real, después hacemos una interpretación geométrica ideal y resolvemos el problema matemáticamente.
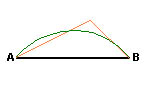
Una escalera está situada sobre el suelo liso y apoyada con un extremo en la pared, se desliza hacia abajo. ¿Por qué línea se mueve el gatito sentado en el centro de la escalera?
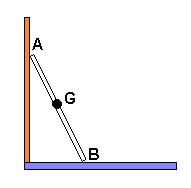 Vista la escena de perfil, un tanto idealizada, tenemos un segmento (la escalera), los apoyos en la pared $A$ y en el suelo $B$ y la situación del gatito $G$.
Vista la escena de perfil, un tanto idealizada, tenemos un segmento (la escalera), los apoyos en la pared $A$ y en el suelo $B$ y la situación del gatito $G$.
Trata de ver la solución e imagina la sucesión de puntos que ocupa $G$ cuando la escalera se desliza (el punto $A$ baja verticalmente y el punto $B$ se desplaza horizontalmente hacia la derecha) ¿Qué trayectoria recorre $G$?
¡A ver si has acertado!
EXPERIMENTA CON LA SIGUIENTE ESCENA
REFLEXIONA...
En condiciones iniciales de la escena, desplaza el control $B$, comprobarás que el lugar del punto $G$ es un cuadrante de circunferencia de radio $OG$.
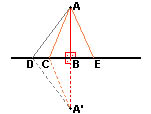
 Para demostrar que el punto $G$ describe un arco de circunferencia basta probar que la distancia de $G$ al origen $O$ es constante (radio de la circunferencia).
Para demostrar que el punto $G$ describe un arco de circunferencia basta probar que la distancia de $G$ al origen $O$ es constante (radio de la circunferencia). El triángulo $OGB$ es isósceles puesto que, por lo visto en el problema anterior, $OG = GB =d/2$. Por tanto la altura $GN$, es también mediana y el punto $N$ es punto medio del segmento $OB$. Queda probado que $x=ON$ es la mitad de $OB$.
El triángulo $OGB$ es isósceles puesto que, por lo visto en el problema anterior, $OG = GB =d/2$. Por tanto la altura $GN$, es también mediana y el punto $N$ es punto medio del segmento $OB$. Queda probado que $x=ON$ es la mitad de $OB$.Modifiquemos las condiciones iniciales del problema de la escalera y supongamos que el gatito no está sentado en medio de la escalera. Desde el punto de vista geométrico diremos que, ahora, la razón $k =\frac{BG}{GA}$ no es 1, por ejemplo que $BG = \frac{GA}{2}$, es decir $k = 0.5$.
ENUNCIADOUn enunciado más general del problema es siguiente:
¡Habrás observado la forma elíptica del lugar de puntos $G$!
Demostremos esta afirmación:
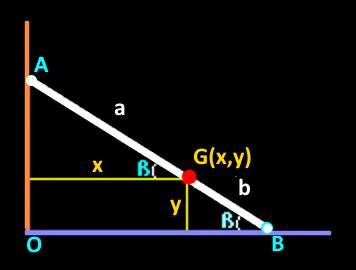 Si el segmento $AB$ está inclinado un ángulo $\beta$ respecto al eje $OB$, entonces $$\tag{1}\displaystyle\frac{y}{b}=sen(\beta)$$ $$\tag{2}\displaystyle\frac{x}{a}=cos(\beta)$$ elevando al cuadrado y sumando miembro a miembro $(1)$ y $(2)$ $$\displaystyle\frac{x^2}{a^2}+\frac{y^2}{b^2}=sen^2(\beta)+cos^2(\beta)$$ y consecuentemente la ecuación de la trayectoria resulta ser la elipse, centrada en el origen, de semiejes $a$ y $b$. $$\displaystyle\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$
Si el segmento $AB$ está inclinado un ángulo $\beta$ respecto al eje $OB$, entonces $$\tag{1}\displaystyle\frac{y}{b}=sen(\beta)$$ $$\tag{2}\displaystyle\frac{x}{a}=cos(\beta)$$ elevando al cuadrado y sumando miembro a miembro $(1)$ y $(2)$ $$\displaystyle\frac{x^2}{a^2}+\frac{y^2}{b^2}=sen^2(\beta)+cos^2(\beta)$$ y consecuentemente la ecuación de la trayectoria resulta ser la elipse, centrada en el origen, de semiejes $a$ y $b$. $$\displaystyle\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$
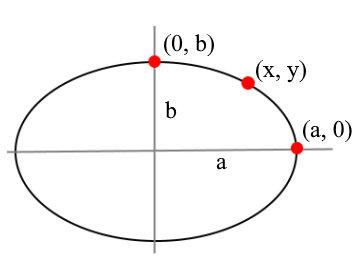 Observa esta circunstancia en la figura adjunta, donde se representa una elipse centrada en el origen de semiejes a y b.
Observa esta circunstancia en la figura adjunta, donde se representa una elipse centrada en el origen de semiejes a y b.
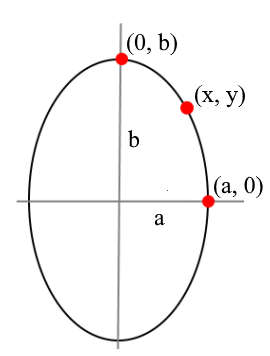 Comprueba que el lugar geométrico es una elipse pero ahora el semieje $a$ es menor que el semieje $b$
Comprueba que el lugar geométrico es una elipse pero ahora el semieje $a$ es menor que el semieje $b$
Se seguirá cumpliendo que $$\displaystyle\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$
Para concluir proponemos las siguientes
CUESTIONES:
 Sustituyendo en la ecuación de la elipse a y b por r se obtiene $$\displaystyle\frac{x^2}{r^2}+\frac{y^2}{r^2}=1$$ $${x^2}+{y^2}={r^2}$$ como queríamos demostrar.
Sustituyendo en la ecuación de la elipse a y b por r se obtiene $$\displaystyle\frac{x^2}{r^2}+\frac{y^2}{r^2}=1$$ $${x^2}+{y^2}={r^2}$$ como queríamos demostrar.
 En la figura adjunta se observa la formación del triángulo rectángulo, de catetos $x$ e $y$ e hipotenusa $r$.
En la figura adjunta se observa la formación del triángulo rectángulo, de catetos $x$ e $y$ e hipotenusa $r$. 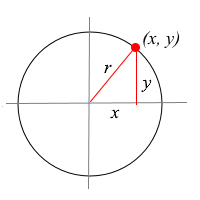
 Utilizando la escena, deslizar el punto $B$ hasta leer el valor $OB = 9$. Pulsar $limpiar$.
Utilizando la escena, deslizar el punto $B$ hasta leer el valor $OB = 9$. Pulsar $limpiar$.
 En la figura vemos a unos futbolistas en posición de lanzar el balón contra la portería. El ángulo de tiro es el formado por el píe del jugador (vértice) y las trayectorias a los postes (lados).
En la figura vemos a unos futbolistas en posición de lanzar el balón contra la portería. El ángulo de tiro es el formado por el píe del jugador (vértice) y las trayectorias a los postes (lados).
¿Qué posiciones deberán ocupar los jugadores para que todos tengan el mismo ángulo de tiro?
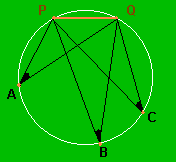 El problema consiste en averiguar el lugar geométrico de los puntos del plano desde los cuales se ve el ancho de la portería con el mismo ángulo.
El problema consiste en averiguar el lugar geométrico de los puntos del plano desde los cuales se ve el ancho de la portería con el mismo ángulo.
RESOLUCIÓN DEL PROBLEMA:
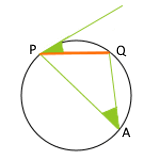 Supongamos que el ángulo de tiro es de $35º$ y que la portería se interpreta como un segmento $PQ$. Vamos a construir el arco de circunferencia.
Supongamos que el ángulo de tiro es de $35º$ y que la portería se interpreta como un segmento $PQ$. Vamos a construir el arco de circunferencia.
OBSERVEMOS LA ESCENA SIGUIENTE:
EXPERIMENTEMOS CON LA ESCENA...
Tener en cuenta esta información para resolver los siguientes
 Se tiene que $$arco = ángulo \space\space central\space\cdotp\space radio$$ $ángulo$ medido en radianes.
Se tiene que $$arco = ángulo \space\space central\space\cdotp\space radio$$ $ángulo$ medido en radianes. La medida del ángulo central que abarca el arco capaz es
$$360º - 2\cdotp50.5º = $$ $$=360º -101º = 259º$$ Pasando a radianes se tiene $$259º \cdotp 3.1416/180º = 4.5204$$ y multiplicando por la medida del radio obtenemos $$3.88\cdotp4.5204 = 17.54$$La diferencia con el resultado de la escena, $17.57$, se debe a que ésta trabaja con más precisión, por ejemplo al tomar el número $pi$ con más decimales.
 Se dibuja el arco capaz desde el cual se ve el segmento $BC$ bajo un ángulo de $45º$.
Se dibuja el arco capaz desde el cual se ve el segmento $BC$ bajo un ángulo de $45º$. El arco capaz resulta muy útil para resolver numerosos problemas de geometría plana. En el siguiente vídeo se define arco capaz, se observa su construcción y se justifica demostrando la relación que existe con el ángulo inscrito y semiinstcrito en una circunferencia.
ARCO CAPAZ MAYOR, IGUAL O MENOR QUE UN SEMICÍRCULO
Consultar la escena de la página siguiente, mostrar $arco=1$, aumentar de escala, si fuera el caso, para ver mejor y verificar que para cualquier segmento $PQ$:
Vamos a enunciar seis problemas que se van a poder resolver aplicando el arco capaz.
Para cada enunciado se podrá ver la solución en su correspondiente vídeo. No obstante sería muy conveniente que el estudiante intentara previamente resolverlo utilizando las herramientas de dibujo necesarias o al menos haciendo un esquema, es decir exponiendo la solución en sus líneas generales con papel y lápiz.
Problema de Pothenot o de los tres puntos:
Consiste en localizar un punto $P$ desde el que se observan otros tres $A$, $B$ y $C$, de posición conocida, bajo los ángulos $\alpha=\angle AB$ y $\beta=\angle BC$.
El $problema \space de \space Pothenot$, de los tres puntos, también se conoce como el $problema \space de \space la \space carta \space marítima$ por su aplicación en náutica. Un enunciado práctico podría ser este:
El patrón de un barco situado en una bahía observa la costa y ve la torre de la iglesia y el cabo con un ángulo de $45º$ y dicha torre y la antena de la emisora con otro de $60º$ El teodolito es un instrumento de medición mecánico-óptico que se utiliza para obtener ángulos verticales y horizontales. Hallar la situación del barco en la bahía.
Una vez resuelto, el patrón del barco podrá situar su barco en la carta náutica y conocer su posición geográfica.
Localizar un punto $P$, interior al triángulo $\triangle ABC$, que equidiste de los lados $AB$ y $BC$ y de forma que el ángulo $\widehat{APB}$ sea $120º$.
Obtener la posición de un jugador de futbol que desde su posición dentro del campo ve un ángulo de $20º$ entre el poste izquierdo ($A$) y el punto de penalti ($B$) y un ángulo de 45º entre el punto de penalti y el banderín de córner ($C$).
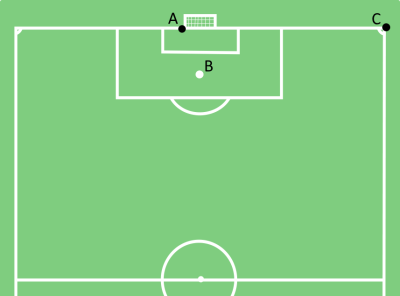
Dada la planta de un cine, en la que se representa la posición de la pantalla $AB$ y de las dos salidas, $S1$ y $S2$, se pide:
| Sitúa el mouse sobre la imagen para ver un esquema de la planta del cine. |  Esquema de la planta del cine
Esquema de la planta del cine 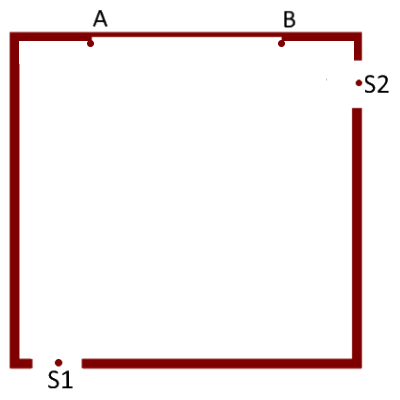
|
Dibujar un triángulo $\triangle ABC$ del que se conocen los ángulos $\angle A=45º$ y $\angle C=60º$ y la longitud del segmento bisectriz, $CM$ de ángulo en $C:$
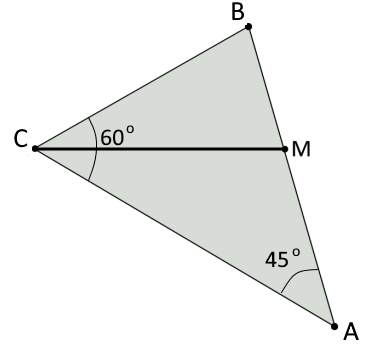
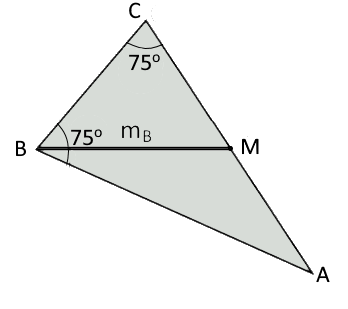
Construir un triángulo isósceles $\triangle ABC$, dada su mediana $m_B$ y el valor de sus ángulos $\angle B=\angle C=75º$.
Justifica razonadamente la construcción empleada.