Frações

     Juan Guillermo Rivera Berrío
     Eduardo Barbero Corral
     José Román Galo Sánchez

Tradução:
Lindberg Barbosa Lira de Almeida

Frações
INTERATIVO

Juan Guillermo Rivera Berrío
Red Educativa Digital Descartes, Colombia

Eduardo Barbero Corral
José Román Galo Sánchez
Red Educativa Digital Descartes, España

Tradução: Lindberg Barbosa Lira de Almeida
Red Educativa Digital Descartes, Brasil

Fondo Editorial RED Descartes

Córdoba (España)
2021

Título da obra
Frações

Juan Guillermo Rivera Berrío
Eduardo Barbero Corral
José Román Galo Sánchez

Tradução: Lindberg Barbosa Lira de Almeida

Design do livro: Juan Guillermo Rivera Berrío
Imagen de capa: foto de Pixelme Stock Photography en Pexels
Livraria turn.js: Emmanuel García
Ferramenta de edição: DescartesJS

Red Educativa Digital Descartes
Córdoba (España) descartes@proyectodescartes.org https://proyectodescartes.org

Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm

ISBN: 978-84-18834-10-3

by-nc-sa/4.0/es by-nc-sa/4.0/pt_BR

Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
Todos los objetos interactivos y los contenidos de esta obra colectiva están protegidos por la Ley de Propiedad Intelectual.

Este obra está licenciado com uma Licença Creative Commons Atribuição-NãoComercial-CompartilhaIgual 4.0 Internacional.

Sumário

Introdução5

Frações: primeira parte8

As Frações no nosso dia a dia10

Uma fração é uma divisão13

Uma fração é parte de um todo14

Uma razão é um fração15

Definição de fração16

Representação de frações19

Leitura de uma fração20

O valor de uma fração24

Ordenando frações26

Frações e números decimais29

Frações equivalentes30

Produtos cruzados32

iii

Encontre o termo que falta35

Simplificação de uma fração36

Frações: segunda parte39

Adição e subtração direta de frações40

Reduzindo frações a um denominador comum43

Adição de frações48

Adição e subtração de frações49

Fração como operador50

Multiplicação gráfica de frações52

Multiplicacão numérica de frações54

Fração inversa de uma fração56

Divisão de frações57

Operações combinadas com frações60

Problemas com frações63

Créditos das imagens65

iv

Introdução

Este livro interativo é direcionado a alunos dos quintos e sextos anos do ensino fundamental. Nas atividades interativas, são gerados números aleatórios, o que permite que a mesma atividade seja utilizada indefinidamente até que o aluno a domine.

A maior parte das páginas está centrada em torno de uma cena interativa, na qual o aluno intervém por meio do mouse ou do teclado, ao realizar a atividade saberá se acertou ou errou.

Créditos imagen: una adaptación de la imagen de School vector creada por brgfx - www.freepik.com

5

Uma história familiar

João está conversando com sua amiga Lúcia:

―Meus avós dizem que os anos voam e meus pais concordam com eles e confirmam que, de fato, estão cada vez mais curtos.
―Como assim ? Disse Lúcia.
―Bem, é o que eu digo, o ano letivo me parece eterno, nunca acaba ...
―Nada disso! Um ano é o que leva para a Terra girar em torno do Sol ”, disse Lúcia com convicção,“ e é igual para todos.
―Lúcia, eu entendo o que você está dizendo. No entanto, o tempo passa rápido quando estou entretido e muito lento quando estou entediado. Isso não acontece com você?
―Sim ”, disse Lúcia, ao mesmo tempo em que balançava a cabeça energicamente para cima e para baixo,“ meu tio me disse que “o tempo é subjetivo”.
―Subje... o quê?
―Que depende de cada pessoa e de cada momento ...
―Não entendo! Disse João timidamente em voz baixa.

Foi o suficiente para Lúcia ver o caminho aberto para expressar seu gosto pela Matemática:

―Bem, matematicamente é possível entender por que um ano é um ano, para todos, e por que é diferente para todos ao mesmo tempo. A matemática serve para explicar nosso mundo.

E diante do rosto espantado de João, sem deixá-lo respirar, Lúcia perguntou:

―Qual a idade do seu avô?
―Oitenta.
―E teu pai?
―Quarenta!
―Não vou perguntar a sua idade porque sei que você tem dez anos, como eu. Então: para seu avô um ano representa uma parte de oitenta, para seu pai uma parte de quarenta e para você é uma parte de dez. Por tanto,…
―Para o meu avô ”, interrompeu João,“ é como quem tem oitenta reais e perde um real, ou seja, dói, mas para ele pouco significa. Para o meu pai dói um pouco mais perder um real, já que tem apenas quarenta reais e eu tenho um calafrio porque perder um real de dez é muito! ...
―Certo! Todo mundo perde um real, mas subjetivamente a perda é menor para uns do que para outros ... ou voltando no tempo: um ano parece pouco para o seu avô, para o seu pai parece algo mais e para nós é muito .
―E isso é matemática? João perguntou.
―Sim! Isso é matemática e pode ser expresso com frações. Escreve-se assim:

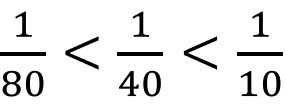
―Bem, vou ter que aprender frações!
―Bem, vamos aprender juntos! Com este livro interativo.

Frações

Primeira parte

As frações no nosso dia a dia

Em nossa linguagem, usamos expressões como estas: "Eu tenho metade", "Falta um quarto de hora", "Eu tenho um décimo de um bilhete de loteria", "Cabe três quartos de um litro", "Está com oitenta e cinco por cento de sua capacidade". Nessas expressões, estamos usando frações. Portanto, o uso de frações é tão antigo quanto a nossa linguagem.

10

Conheça as frações

Na seguinte cena interativa, preencha as caixas de texto com as informações correspondentes:

12

Uma fração é uma divisão

Arraste cada divisão abaixo, e seu resultado, para frente da fração correspondente.

13

Uma fração é parte de um todo

Conte o total de bolas e depois a quantidade de bolas de cada cor. Em cada fração abaixo, coloque o número de bolas dessa cor na parte superior e o número total de bolas na parte inferior. Pressione enter, se estiver ok aparecerá em negrito.

14

Uma razão é uma fração

A cena interativa a seguir nos ajuda a comparar os tamanhos de duas figuras. Meça com a régua, você pode movê-la arrastando suas extremidades. Após digitar os números, pressione Enter. Quando acertar, lhe será dito.

15

Definição de fração

Assim como os números naturais surgem para expressar quantidades que se referem a objetos inteiros, as frações surgem para expressar quantidades de objetos que são divididos em partes iguais, conforme mostrado na imagem a seguir:

Créditos da imagem: uma adaptação da imagem de Food vector creada por brgfx - www.freepik.com

16

Uma fração é o quociente entre dois números. Ou seja, é uma divisão não realizada. Os elementos que compõem a fração são:

O numerador. É o número acima, indica as partes que temos.
O denominador. É o número abaixo, indica o número de partes em que dividimos cada unidade.
O traço de fração. É um traço horizontal que os separa.

Na próxima cena mude os valores dos controles e você verá a representação gráfica da fração.

17

Na cena seguinte, a fração é representada por retângulos. Lembre-se de que o valor da unidade é a área de um quadrado. As frações que excedem um quadrado valem mais do que 1 e as que não o cobrem valem menos do que 1.

18

Representação de frações

Na cena seguinte escreva o numerador e o denominador da fração que representa as partes que aparecem em cada imagem. Tente resolver várias vezes.

19

Leitura de uma fração

O numerador é lido normalmente. Porém, o denominador é lido assim:

o 1 é lido	o 2 é lido	o 3 é lido	o 4 é lido	o 5 é lido
inteiros	meios	terços	quartos	quintos
o 6 é lido	o 7 é lido	o 8 é lido	o 9 é lido	o 10 é lido
sextos	sétimos	oitavos	nonos	décimos

Se o denominador for maior que 10, lê-se o numerador normalmente e o denominador unido a palavra "avos", mas caso ele seja uma potência de 10, o denominador é unido a palavra "ésimos". Exemplo centésimos, milésimos, dez milésimos, ...

20

Inteiros, meios, terços, quartos.

Arraste para cada retângulo as duas palavras, da lista abaixo, que representam as frações a seguir.

21

Como lemos as frações

Conte as partes olhando para as listras. Você pode usar frações equivalentes.

22

Coloque cada fração ao lado de sua representação gráfica

Nesse caso, não não vale por frações equivalentes.

23

O valor de uma fração

Uma vez que uma fração representa uma divisão, para saber qual é o valor de uma fração, devemos realizar essa divisão, porém podemos ter uma idéia desse valor olhando para seu numerador e denominador.

Seu valor será maior quanto maior for o numerador, e será menor quanto maior for o denominador. Se o numerador for menor que o denominador, a fração vale menos que 1. Se o numerador for igual ao denominador, a fração será igual a 1. Se o numerador for maior que o denominador, a fração vale mais do que 1.

24

O valor das frações em relação à unidade

Quando sua resposta estiver correta, você verá as frações representadas graficamente. Verifique se elas valem menos, igual ou mais que a unidade.

Recomendamos que você execute o exercício em uma janela ampliada; para fazer isso, clique no botão"Ampliar".

25

Ordenando frações

Na próxima cena interativa, coloque essas frações em ordem crescente, isto é, da menor para a maior. Quando acertar, lhe será dito.

26

Ordene essas frações da menor "ou igual" para a maior "ou igual"

Pode ser útil saber que essas frações estão representadas acima, mas em uma ordem diferente. Se houver duas frações do mesmo valor, a ordem entre essas duas não importa.

27

Ordene essas frações da maior para a menor

Essas frações são de valores menores ou iguais a 1.

Coloque as frações nos círculos brancos.

28

Frações e números decimais

Para passar uma fração para a forma decimal divide-se o numerador pelo denominador. Existem divisões cujo resultado será um número natural. Outras divisões, seu resultado será um número decimal com algumas casas decimais. Em outras divisões, o resultado será um decimal infinito periódico, que tem um grupo de casas decimais que se repetem e, não importará quantas casas decimais tomarmos, não haverá resto 0. Para passar um número decimal finito à forma de uma fração, é colocado como numerador esse número decimal sem a vírgula e o denominador 1 seguido por tantos zeros quantas forem as casas decimais desse número.

29

Frações equivalentes

Frações equivalentes são aquelas que representam o mesmo valor. Sabemos que existem várias divisões que dão o mesmo resultado. Frações equivalentes têm numeradores e denominadores diferentes, mas valem o mesmo. Cada fração possui infinitas outras frações equivalentes a ela.

30

Exercício de Frações Equivalentes

Nessa cena interativa, quando você resolver corretamente, outras jarras aparecerão com o conteúdo que expressa sua fração. Veja se é equivalente.

Com este exercício, vamos verificar que as frações equivalentes expressam o mesmo valor.

31

Produtos cruzados

Para verificar se duas frações são equivalentes ou não, o método mais fácil são os produtos cruzados. Multiplicamos seus termos em cruz ou cruz de Santo André. O produto do numerador de uma fração pelo denominador da outra deve dar o mesmo em ambos os casos.

Nesta cena interativa uma fração aparece aleatoriamente, coloque outra e depois verifique passo a passo.

32

Coloque todas as frações equivalentes umas às outras no mesmo retângulo

Em frações equivalentes, ao multiplicar seus termos em cruz dá o mesmo produto.

33

Junte as frações equivalentes

Cada fração abaixo é equivalente a outra acima. Coloque-as ao lado. Para fazer isso, você pode encontrar a fração irredutível de cada uma ou verificar os produtos cruzados de ambas.

34

Encontre o termo que falta

Na cena interativa a seguir, usando a propriedade de que seus produtos cruzados são iguais, encontre o termo que falta nessas duas frações equivalentes

35

Simplificando uma fração

Todas as frações equivalentes representam o mesmo número racional. Para expressar o mesmo valor, estamos interessados em usar a fração mais simples, que é aquela com o menor numerador e denominador, chamada de fração irredutível porque não pode mais ser simplificada. Usamos a propriedade fundamental da divisão. Sabemos que se multiplicarmos ou dividirmos o numerador e o denominador pelo mesmo número, obtemos outra fração equivalente.

36

Coloque ao lado de cada fração sua fração irredutível

Na cena interativa a seguir, as seis frações abaixo são as irredutíveis das frações acima, coloque-as juntas.

37

Frações

Segunda parte

Adição e subtração direta de frações

Quando as frações têm o mesmo denominador, podem ser adicionadas e subtraídas diretamente. O numerador é a adição ou subtração dos numeradores.
O denominador é igual ao das frações a serem adicionadas ou subtraídas.

Nas cenas interativas a seguir, pratique adição e subtração.

42

Na cena interativa a seguir, pratique a adição de frações.

Reduzindo frações a um denominador comum

Obervemos o significado das partes de uma fração:

Numerador significa que numera, ou seja, ele nos diz o número de coisas que temos.
Denominador significa que nomeia, ou seja, ele nos diz o tipo de coisa que temos. Não é a mesma coisa ter metade do que ter um terço.

43

Quando adicionamos, fazemos isso com elementos homogêneos, eles têm que ser quantidades da mesma coisa. Portanto, para somar frações é necessário que tenham o mesmo denominador.

Se as frações tiverem denominadores diferentes, são reduzidas a um denominador comum, ou seja, são trocadas por outras equivalentes a elas, mas com o mesmo denominador todas.

Na cena interativa da próxima página, observe graficamente o significado de reduzir frações a um denominador comum. A primeira fração é representada na parte superior, a segunda está na parte inferior.

Ao clicar na ponta da seta, as frações e suas representações gráficas se transformam em outras equivalentes a elas, mas ambas com o mesmo denominador.

44

Antes de ver o procedimento que nos permite reduzir frações heterogêneas (de denominadores diferentes) a um denominador comum, tente realizar duas atividades seguintes do projeto Proyecto Canals, elaboradas por Diego Luis Feria Gómez.

45

Na cena interativa a seguir, duas atividades são apresentadas para determinar o denominador comum como ações antes de adicionar e subtrair frações com um procedimento aritmético.

46

Note que com a ajuda gráfica, você pode determinar o denominador comum sem ter que recorrer a nenhum cálculo aritmético, com a prática você será capaz de identificar mentalmente o denominador comum.

47

Adição de frações

Para somar frações é necessário que todas tenham o mesmo denominador. Se as frações tiverem denominadores diferentes, são reduzidas a um denominador comum, ou seja, são alteradas por outras equivalentes a elas, mas com o mesmo denominador todas. Para fazer isso, siga estas etapas:

48

Adicionando e subtraindo frações

Quando há adições e subtrações, seguimos o mesmo processo como se tivéssemos apenas adições. Na próxima cena interativa, se as frações forem heterogêneas, siga o mesmo processo da cena anterior, começando pelo cálculo do mínimo múltiplo comum dos denominadores.

49

Fração como operador

As frações podem ser usadas como um operador, aplicando-as a um número ou quantidade. Nestes casos, a fração está realizando a operação de multiplicação.

Para multiplicar um número por uma fração, nós o multiplicamos pelo numerador e o dividimos pelo denominador. Se essa divisão não for exata, então podemos deixá-lo como uma fração.

50

Na próxima cena interativa, execute as operações e coloque o resultado arrastando-o da linha abaixo para a bolinha amarela correspondente.

51

Gráfico da multiplicação de frações

Quando uma fração atua como o operador de outra fração, temos um produto de frações.

Na cena interativa a seguir, representamos uma fração no eixo horizontal e a outra fração no eixo vertical.A superfície do retângulo resultante indicará o valor do produto dessas frações.

Conte as partes resultantes, esse número será o numerador do produto.
Conte as peças que formam um quadrado unitário, esse número será o denominador do produto.
Qual é a relação entre o numerador do produto e os numeradores das frações multiplicadas?
Qual é a relação entre o denominador do produto e os denominadores das frações multiplicadas?

Desta forma, podemos deduzir o método que devemos seguir para obter numericamente o produto de duas frações.

Para multiplicar duas frações, multiplicamos seus numeradores e os transformamos no numerador do produto. Multiplicamos seus denominadores e os transformamos no denominador do produto.

52

Você pode colocar outros valores nas frações acima e ver o produto resultante.

53

Multiplicação numérica de frações

Para multiplicar frações, elas não precisam ter o mesmo denominador, eles são multiplicados diretamente.

Multiplicamos seus numeradores e o transformamos em numerador, multiplicamos seus denominadores e o transformamos em denominador.

54

Exercícios de multiplicação de frações

Na cena interativa abaixo, faça várias multiplicações de frações.

55

Fração inversa de uma fração

O inverso de uma fração é outra fração que, quando multiplicada por ela, dá a fração unitária, isto é, 1. A fração que tem o numerador e o denominador trocados em relação a ela é sua fração inversa. Logicamente, se uma fração é inversa de outra, todas as equivalentes a ela também são suas inversas.

A fração de valor 0 é a única que não possui inversa.

56

Divisão de frações

Tanto a multiplicação quanto a divisão de frações são mais fáceis de realizar do que a adição e a subtração.

Dividir uma fração por outra é o mesmo que multiplicar a primeira fração pelo inverso da segunda.

Uma fração pode ser dividida por qualquer outra, exceto para a fração de valor 0.

Divisão de frações

Dividir uma fração por outra é o mesmo que multiplicar a primeira fração pelo inverso da segunda fração.

58

Exercícios de divisão de frações

Na próxima cena interativa, faça várias divisões de frações. Lembre-se do procedimento acima.

59

Operações combinadas com frações

As operações combinadas são expressões compostas de diferentes números agrupados por várias operações, com parênteses, colchetes ou chaves.

Para resolver as operações combinadas, devemos levar em consideração as seguintes indicações:

A missão dos parênteses é unir ou "empacotar" o que está no seu interior.
Os sinais de multiplicação unem mais do que os sinais de adição e subtração, ou seja, quando dois números são unidos pelo sinal de multiplicação formam um bloco inseparável.
Para poder somar ou subtrair dois números, eles devem ser soltos, não podemos somar dois números se um deles estiver ligado do outro lado a outra expressão por meio de um sinal de multiplicação.
As operações combinadas são resolvidas em várias etapas, tudo o que não é resolvido em uma etapa deve ser copiado de volta como estava, sem esquecê-lo ou mudar sua posição.
Como regra geral, é aconselhável começar resolvendo o interior dos parênteses, depois continuar com as multiplicações e terminar somando e subtraindo os restantes.
Antes de começar devemos observar e planejar o processo a seguir, o que vamos fazer antes e depois.

60

Exercícios de operações combinadas

A cena interativa a seguir apresenta exercícios que possuem diferentes operações combinadas.

61

Antes de terminar, pratique com a seguinte atividade de projeto Proyecto Canals, elaborada por Diego Luis Feria Gómez.

Os cartões são arrastados com um clique no canto superior esquerdo.

62

Problemas com frações

Leia o enunciado do problema com atenção e veja o que ele pede para você calcular. Veja os dados que você possui. Faça uma imagem ou esboço do problema. Decida as operações que você deve realizar para chegar ao resultado resolvendo-as na ordem devida.