Juan David Builes Grisales
Institución Universitaria Pascual Bravo
Córdoba (España)
2022.
Título de la obra:
La Magia de la Regla de Tres
Autor:
Juan David Builes Grisales
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Núcleo del libro interactivo: julio 2022
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN: 978-84-18834-47-9
Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
Este libro no es una novela, ni una fábula, ni un cuento, porque todo es real, es la historia de cómo la división entre 2 números, le permitió al hombre solucionar problemas de su entorno, problemas de su cotidianidad, leerlo, es permitirnos identificar uno de los artilugios matemáticos, más transversales, utilizados por el hombre y, después de analizarlo, podrás concluir que prácticamente se aplica en todas las áreas del conocimiento.
Este libro se centrará en los conocimientos, pero no en los contribuidores, es decir, nos centraremos en el concepto, en el conocimiento científico y su aplicación en la solución de problemas reales y dejaremos al margen los autores, como consulta para el lector.
La metodología del libro está enfocado hacia un modelo por competencias, es decir, que el lector identifique, desde la primera página, que es un libro diferente a los que estamos acostumbrados, que el lector tenga una experiencia diferente, innovadora y motivadora y que el mismo libro, lo invite a interactuar con él.
Es muy importante que el lector tenga claro el enfoque metodológico del libro, para que, a través de él, pueda desarrollar sus competencias relacionadas con las reglas de proporcionalidad, aplicados en la solución de problemas reales.
Solucionar problemas cotidianos implica utilizar y relacionar variables de nuestro entorno, pero eso si, con variables que se puedan medir, como la temperatura, el área o el volumen de un cuerpo, o como el tiempo de un evento y seguiría mencionando muchos ejemplos, lo importante es que interpretes que no todo se puede medir, por ejemplo, podemos medir el nivel de colesterol de un ser humano, pero no su sinceridad, en conclusión, sólo podemos medir cantidades físicas.
Las cantidades físicas son variables que podemos medir y relacionar unas con otras, la regla de tres, como se conoce a la regla de proporcionalidad simple directa e inversa, es un artilugio matemático que consiste en construir una proporción de la cuál no conocemos o deseamos conocer un cuarto dato de las variables relacionadas, por eso es llamada regla de tres, por que con 3 datos conocidos puedo encontrar el cuarto.
Las relaciones de proporcionalidad están presentes en la naturaleza sean o no positivas para el hombre, no todas las relaciones de proporcionalidad son negativas, depende de cómo observemos nuestro entorno, por ejemplo, mientras mayor sea el número de árboles que plantemos, mayor será la cantidad de aire limpio que tendremos para respirar, este tipo de relaciones son las que llamamos directamente proporcionales y suceden cuando al aumentar una variable la otra variable también aumenta.
El otro tipo de relaciones son los que se presentan cuando al aumentar una variable la otra disminuye y son las que llamamos inversamente proporcionales, por ejemplo, mientras mayor sea la cantidad de desechos reciclables y reutilizables por el hombre menor será la contaminación que estos producen.
Las proporciones están presentes en nuestra cotidianidad, las encontramos en las estructuras creadas por el hombre en la antigüedad, como el Partenón, en busca de la razón y la proporción perfecta, la que me permito llamar razón de oro, e incluso en el arte, el hombre se ha preocupado por establecer las proporciones perfectas del cuerpo humano, en síntesis, la naturaleza está inmersa en infinitas proporciones y están presentes en toda su existencia.
Para el estudio de las reglas de proporcionalidad en un comienzo se construyó un archivo en excel para que el estudiante pudiera interactuar y editar el documento.
La Secuencia didáctica de proporcionalidad es una tecnología educativa inclusiva, se creó para apoyar el trabajo del estudiante en casa y para acercar el modelo a la inclusión, pero tiene la desventaja que al ser un documento descargable depende siempre del servidor, incluso como es de Microsoft se presenta una dificultad en otras plataformas, por tal motivo, la construcción de este libro permitirá compartir la experiencia para siempre, porque será guardada en una unidad local y no dependerá de un servidor.
Con este libro usted conocerá los modelos matemáticos de las relaciones de proporcionalidad entre cantidades físicas y aprenderá a solucionar situaciones problema aplicando la regla de tres.
Espero que este libro se convierta en una efectiva herramienta para el desarrollo de competencias en la solución de problemas reales.
Este libro hace parte del proyecto VIDEOMÁTICA, una propuesta inclusiva, innovadora y motivadora que implementa el aula invertida y a donde invitamos al lector acceder.
A continuación encontrarás el acceso a la presentación del proyecto Videomática y sus estrategias.
Es innegable la situación crítica del medio ambiente en nuestro planeta y la mayoría nos quedamos con los brazos cruzados.
Mientras mayor sea el número de centros comerciales construidos por el hombre, menores serán los árboles en nuestro entorno y menor será el aire limpio para respirar.
Estamos acabando los recursos de nuestro planeta y nadie hace algo al respecto. ¿Qué pasará cuando se acaben?.
Mientras mayor sea el número de automotores que estén rodando en las calles, mayor será la contaminación producida por ellos.
Es lamentable afirmar, que mientras mayor es el desarrollo humano, menor es el espacio habitable para el hombre, en otras palabras, el progreso humano es inversamente proporcional a un ambiente limpio y saludable y nuestro planeta está cada vez más enfermo.

Está en nuestras manos cambiar esas relaciones de proporcionalidad tan negativas, necesitamos una sociedad en la cual, mientras más progreso más aire limpio y menos contaminación, una sociedad en la cual el progreso sea directamente proporcional a un ambiente limpio y saludable y a un planeta más habitable y sostenible.
Con base en la actividad anterior, plantea 3 acciones que podrías realizar en tu comunidad que mejoren el medio ambiente de ella.
Realizado lo anterior puede continuar con la siguiente actividad denominada, Documento Base, Competencias y Saberes Previos
Esta parte de la actividad sólo la realizan los que dispongan de Internet y Microsoft Excel.
Esta sección busca que el estudiante descargue el documento para que lo pueda editar, en ninguna otra parte del libro se volverá a mencionar. Haga clic en el Objeto Interactivo de Aprendizaje (OIA) Reglas de proporcionalidad, es un archivo de excel descargable y para editarlo debes descargarlo en tu PC, una vez descargado en tu PC ábrelo para que lo puedas editar, recuerda realizar esta rutina cada vez que quieras trabajar con él, lo puedes descargar desde cualquier sitio las veces que lo necesites.
A continuación, encontrarás el acceso directo al documento en Excel, correspondiente a las reglas de proporcionalidad: 
A continuación encontrará las competencias que se desarrollan en este libro:
El tema central que se aborda en este libro son las reglas de proporcionalidad entre variables.
Los pensamientos matemáticos tratados en esta competencia son el pensamiento numérico y el pensamiento variacional.
Los estándares de competencia establecidos por el Magisterio de Educacional Nacional de Colombia para el área de Matemáticas correspondientes a este eje temático son los siguientes:
Identifica y analiza propiedades de covariación directa e inversa entre variables, en contextos numéricos, geométricos y cotidianos y las representa mediante gráficas (cartesianas de puntos, continuas, formadas por segmentos, etc...).
Los indicadores de desempeño correspondientes a estas competencias son los siguientes:
Los siguientes son los saberes previos que se necesitan conocer, los debes recordar e interiorizar:
La proporcionalidad es la relación que existe entre 2 variables, es decir, cómo aumenta o disminuye una variable A respecto a otra variable B. La proporcionalidad establece la relación de cambio de una variable respecto de otra.
Para explicar el concepto de proporcionalidad vamos a contextualizar con una situación exploratoria, vamos a asumir que una empresa, cualquiera, con determinada cantidad de operarios, con determinada cantidad de materia prima y en determinado intervalo de tiempo, produce un número determinado de unidades de un producto; Las variables de la situación exploratoria son, el número de operarios, la cantidad de materia prima, el intervalo de tiempo y las unidades producidas; Podemos relacionar todas las variables entre sí e identificar cuál es la tendencia de las variables relacionadas, por ejemplo, mientras más operarios tenga la empresa, estará en capacidad de producir más unidades del producto, en este caso, las variables son directamente proporcionales y si relacionamos el número de operarios con el intervalo de tiempo, podemos concluir, que mientras más operarios tenga la empresa, menor será el intervalo de tiempo de producción, por lo tanto, estas variables relacionadas son inversamente proporcionales,
y de esta manera podemos relacionar todas las variables y determinar su tendencia.
Una razón es la relación entre 2 cantidades, estas cantidades las llamamos antecedente y consecuente, por ejemplo, tomemos las cantidades a y b, su razón es $\frac{a}{b}$, donde la cantidad a puede ser cualquier variable, por ejemplo, distancia recorrida y la cantidad b puede ser la variable tiempo empleado, entonces la razón de esas cantidades sería:
$$Razón = \frac{Distancia}{Tiempo}$$
Las razones son la base de los números racionales, podemos relacionar un número racional como una razón, a dichas razones las nombramos comúnmente como fracciones, donde al antecedente se le llama numerador y al consecuente se le llama denominador y representan una parte de un todo, podemos sumar, restar, multiplicar o dividir razones y sus aplicaciones cada vez son más numerosas.
Las razones son el artilugio matemático más utilizado por el hombre, para la solución de problemas reales, es una competencia transversal a muchas áreas del conocimiento, y el propósito de este libro, es que conozcas e interiorices el cómo el hombre ha utilizado las razones en la solución de problemas reales.
Si vamos a explicar por importancia, debes tener presente que las operaciones con números racionales suma, resta, multiplicación, división, potenciación y radicación son los más utilizados en la solución de situaciones problema reales y me tomaría todo un libro explicarlo, a lo que nos convoca este libro son las razones y lo importante, en este caso, es que tenga claro que un número racional también es una razón.
Ahora sí, después de aclarar que no vamos a estudiar los números racionales, nos centraremos en las aplicaciones de las razones y encontrará varias escenas de razones para que interactúe con ellas e interiorice el concepto de razón y analice cómo cambian las variables cuando modifico los datos:
En la primera escena puede interactuar con ella, escriba el valor de cada variable y haga clic en hallar razón. Este interactivo le calcula directamente la razón de las cantidades relacionadas, para generar otra situación simplemente haga clic en otro cálculo.
Puede hacer clic con el botón superior derecho, para ver el interactivo en otra ventana.
Una vez interiorizado el concepto de razón como tal, vamos a identificar dónde? y cómo? utilizamos las razones, tenga presente que trabajar por competencias implica una responsabilidad personal, cada lector tiene un ritmo de aprendizaje diferente, se espera que los interactivos le permitan interiorizar el concepto y construir sus competencias y el tiempo de interacción con ellos dependerá de cada lector.
A continuación, encontrará algunas escenas relacionadas con las aplicaciones de las razones en situaciones reales para que interactúes con ellas, en la primera escena trabajaremos el número pi (π), este número surge de la relación de la circunferencia de un círculo respecto a su diámetro, es decir, la razón de la circunferencia respecto al diámetro, este número me establece como cambia la circunferencia de un círculo respecto al cambio del diámetro, como se muestra a continuación:
$$π = \frac{Circunferencia}{Diámetro} = 3.14159...$$
Esta razón le permite calcular circunferencias y áreas de círculos.
Para interactuar con la escena, simplemente haga clic en Generar Círculo, y le mostrará el valor de la circunferencia y del diámetro y su relación llamada pi, después, puede generar otra situación haciendo clic en Otro Círculo. El objetivo es que interiorice el número π como una razón entre la circunferencia y el diámetro de un círculo:
Una vez que haya interiorizado la escena puede continuar con la siguiente.
En la siguiente escena trabajaremos el concepto de razón a través de los lados de figuras geométricas, puede ser cualquier polígono, en este caso utilizaremos pentágonos, para interactuar, con ella y con todas las escenas interactivas que aquí se presenten, debe hacer clic en los botones.
Para comenzar, haga clic en el botón Generar Pentágono y le mostrará, en el plano, un pentágono aleatorio, y en la ventana de la izquierda, las coordenadas de los vértices del pentágono y las dimensiones de sus lados, luego, haga clic en Hallar Razones y le mostrará las razones de los lados del pentágono respecto del lado a y puedes generar otros pentágonos, aleatoriamente, al hacer clic en el botón Otro Pentágono, al hacer clic en el botón superior derecho le accede a la escena en otra ventana con las dimensiones reales, el objetivo es que interiorice las razones entre los lados de los polígonos.
Estas razones son muy útiles porque le permiten establecer cuántas veces están los lados de un polígono respecto a un lado determinado.
Una vez que haya interiorizado la escena puede continuar con la siguiente.
La siguiente escena, es otra aplicación de las razones y se llama comúnmente escala, podemos interpretar una escala como la razón de las dimensiones de los lados de polígonos semejantes y es llamado factor de escala o simplemente escala, si la razón obtenida nos da como resultado un número entre 0 y 1 obtendríamos un polígono más pequeño, dependiendo de la escala, y si la razón obtenida nos da como resultado mayor que 1, obtendríamos un polígono más grande, dependiendo de la escala.
Para comenzar haga clic en Generar Pentágono y le mostrará las coordenadas de los vértices del pentágono y en el plano un pentágono aleatorio, luego, haga clic en Hallar Distancias y le mostrará las dimensiones de los lados del pentágono, luego, debe ingresar el valor de la escala en el teclado numérico de la ventana emergente, una vez ingresada la escala, haga clic en Generar Pentágono y le mostrará en el plano otro pentágono a escala, después, puedes cambiar de escala haciendo clic en Otra Escala o cambiar de pentágono haciendo clic en Otro Pentágono, el objetivo es que interiorice el concepto de escala como una razón:
Una vez que haya interiorizado la escena puede continuar con la siguiente.
En las antiguas construcciones, como por ejemplo el Partenón, entre muchas otras, se evidencia cierta tendencia en sus construcciones y son sus rectángulos, tienen todos una misma razón en sus lados y son proporcionales entre si y su razón es constante y esta constante es llamado Número Áureo y esta sección es llamada sección áurea o rectángulo áureo.
Con la siguiente escena, conocerá la Razón Áurea, yo la llamo la razón dorada y es igual a 1.618, y es simplemente la razón entre los lados de un rectángulo.
Para comenzar haga clic en Generar Rectángulo y le mostrará la razón de los lados y en el plano un rectángulo áureo aleatorio, luego puede generar otro rectángulo haciendo clic en Otro Rectángulo:
Una vez que haya interiorizado la escena puede continuar con la siguiente.
La siguiente escena, estudia los conceptos fundamentales de la Trigonometría y son propiamente dichas las razones entre los lados de un triángulo rectángulo llamadas, valga la redundancia, Razones Trigonométricas, en esta situación debemos escoger un ángulo, por eso en esta situación se escogió el ángulo A del triángulo.
Para comenzar haga clic en Generar Triángulo, y le mostrará las razones seno, coseno y tangente del ángulo A y en el plano el triángulo rectángulo aleatorio con sus dimensiones, después puede generar otro triángulo haciendo clic en Otro Triángulo, el objetivo es que interiorice las razones trigonométricas:
Una vez que haya interiorizado la escena puede continuar con la siguiente.
La siguiente escena estudia la probabilidad de ocurrencia de un evento aleatorio.
La probabilidad de un suceso está determinada por una razón, donde el antecedente es el número de casos posibles y el consecuente es el número de casos totales, es decir, número de veces que se espera ocurra el evento respecto al número de veces posibles, para contextualizar vamos a asumir una situación exploratoria, sean a, b, c y d números enteros. En una caja oscura hay a bolas de color rojo, b bolas blancas, c bolas azules y d bolas amarillas, la razón de cada color de bola es el número de bolas de cada color respecto al número de bolas totales. La siguiente escena te determina la probabilidad al sacar cualquiera de las bolas.
Para interactuar simplemente haga clic en Hallar Probabilidad, y le mostrará las probabilidades de sacar cualquier bola, después, puedes generar otra situación haciendo clic en Otro Ejercicio. El objetivo es que interiorice la probabilidad como una razón:
Una vez que haya interiorizado la escena puede continuar con la siguiente.
La siguiente escena de razones son los porcentajes, los porcentajes se obtienen multiplicando una razón por 100. Para contextualizar el concepto de porcentaje tomemos la situación anterior y determinemos los porcentajes de cada color de las bolas en la caja, sus porcentajes se determinan multiplicando la misma razón por 100, es decir, el número de bolas de cada color respecto al número de bolas totales multiplicado por 100.
Para interactuar simplemente haga clic en Hallar Porcentaje, y le mostrará los porcentajes de cada color de bola, después, puede generar otra situación haciendo clic en Otro Ejercicio.
El objetivo es que interiorice los porcentajes como una razón multiplicada por 100.
Una vez que haya interiorizado la escena puede continuar con la siguiente.
La siguiente, y última escena de razones, estudia los fundamentos del cálculo diferencial y son las razones de cambio o comúnmente llamadas derivadas; la derivada es la razón de cambio de una variable respecto a otra y geométricamente corresponde a la pendiente de la recta tangente de una función.
Para interactuar con ella, haga clic en Graficar Segmento, y le mostrará en el plano un segmento aleatorio con sus puntos y en la ventana superior le muestra la pendiente del segmento, después, puede generar otra situación haciendo clic en Otro Segmento.
El objetivo es que interiorice las derivadas como una razón de cambio.
Una vez que haya interiorizado la escena puede continuar con el siguiente concepto.
Como se mencionó anteriormente, las proporciones están presentes en nuestro entorno y las utilizamos constantemente en situaciones donde se involucren razones, por eso es tan importante, antes de estudiar las proporciones, entienda la importancia de las razones y que conozca donde puedes utilizarlas; Una vez interiorizado el concepto de razón es simple hablar de proporciones, pues simplemente, son igualdades de razones.
Una proporción es una igualdad de razones homogéneas, es decir, ambas razones deben relacionar las mismas variables con las mismas unidades, si tuviéramos la razón $\frac{a}{b}$ y la razón $\frac{c}{d}$ la proporción que formarían sería:
$\frac{a}{b} = \frac{c}{d}$
Los términos a y d son llamados extremos de la proporción y los términos b y c son llamados medios de la proporción. En toda proporción se cumple que el producto de extremos es igual producto de medios, es decir:
$a * d = b * c$
A continuación, encontrará varias escenas interactivas de proporciones, la primera escena son las proporciones que se generan entre los lados de polígonos semejantes, para contextualizar utilizáremos un pentágono, puede ser cualquier polígono.
Para comenzar haga clic en Generar Pentágonos y le mostrará en el plano 2 pentágonos semejantes, o, como se dice comúnmente, a escala, luego haga clic en Establecer Proporciones y le mostrará las proporciones entre los lados de los pentágonos, después, generar otro pentágono haciendo clic en Otro Pentágono.
El objetivo es que interiorice el concepto de proporción como una igualdad de razones e identifique las proporciones presentes en polígonos semejantes:
Una vez que haya interiorizado la escena puede continuar con la siguiente.
En la siguiente escena encontrará otra aplicación de las proporciones, las proporciones en la Ley de Senos, que le permite solucionar triángulos No Rectángulos.
Para comenzar haga clic en Generar Triángulo y le mostrará las proporciones utilizadas en la ley de senos y en el plano un triángulo con sus respectivos lados y dimensiones para que puedas comparar y sacar conclusiones, después, puede generar otro triángulo haciendo clic en Otro Triángulo.
El objetivo es que interiorice las proporciones utilizadas en la Ley de Senos.
Una vez que haya interiorizado la escena puede continuar con la siguiente.
A continuación, encontrará otra escena de aplicación de las proporciones, las proporciones en el Teorema de Thales, el cual me relaciona los segmentos transversales a segmentos paralelos, el objetivo es que interiorices las proporciones utilizadas en el Teorema de Thales:
Para comenzar, haga clic en Generar Construcción y le mostrará las proporciones presentes entre segmentos transversales a segmentos paralelos y en el plano la construcción con sus respectivos lados y dimensiones, para que pueda comparar y sacar conclusiones, después, puede generar otra construcción haciendo clic en Otra Construcción.
El objetivo es que interiorice las proporciones utilizadas en el Teorema de Thales.
Identificar y utilizar las proporciones son una competencia fundamental de las matemáticas operativas y, como puede darse cuenta, la Geometría ha sido una rama donde se utilizan muchos las proporciones, ahora, analizaremos las proporciones en situaciones reales con variables físicas reales, las proporciones que me permitirán contextualizar y generalizar situaciones de la vida real.
La proporcionalidad directa, se presenta cuando al aumentar una de las variables de una razón la otra variable también aumenta, o viceversa, es decir, si una de las variables disminuye, la otra variable también disminuye.
La proporcionalidad inversa, se presenta cuando al aumentar una de las variables de la razón la otra disminuye, o viceversa, es decir, si una de las variables disminuye, la otra variable aumenta.
A continuación, encontrará una escena interactiva de proporcionalidad directa e inversa entre variables, el objetivo es que interactúe e interiorice los conceptos de proporcionalidad directa y proporcionalidad inversa.
Para comenzar, analice la situación y haga clic sostenido sobre una de las expresiones de arriba y desplácelas hacia abajo donde considere que corresponden, una vez que haya desplazado las expresiones, haga clic en verificar. Recuerda que estos interactivos son escalables, quiere decir que, con el botón superior derecho le muestra el interactivo en otra ventana con las dimensiones reales, le recomiendo que lo realice de esa manera.
A continuación, encontrará otra escena interactiva de proporcionalidad directa e inversa entre variables, el objetivo es que interactúe e interiorice los conceptos de proporcionalidad directa y proporcionalidad inversa. Para comenzar, analice la situación y haga clic sobre el botón verdadero, si considera que la expresión es verdadera, sino, haga clic en el botón falso, luego, para avanzar para el siguiente ejercicio, haga clic en el botón inferior derecho:
A continuación, encontrará una escena interactiva correspondiente a las competencias tratadas en el libro y a los saberes previos necesarios para desarrollar esta competencia, para interactuar en ella, haga clic sostenido sobre cualquier punto de color de la columna de la izquierda y trace una línea con la expresión de la columna de la derecha que considere corresponde.
Recuerde que estos interactivos son escalables, quiere decir que, con el botón superior derecho le muestra el interactivo en otra ventana con las dimensiones reales, le recomendamos que éste lo realice así:
La relación simple directa, se presenta cuando se relacionan 2 variables directamente proporcionales.
Para el estudio de esta regla de proporcionalidad se ha creado una actividad exploratoria, la cual busca que interprete e interiorice la regla de proporcionalidad simple directa.
La siguiente tabla, muestra los kilogramos de Dióxido de Carbono producidos por un automóvil convencional, por kilómetros recorridos por el automóvil. Analice la situación y responda en el cuaderno las preguntas desencadenantes.

A continuación, encontrará una serie de preguntas, se espera que las analice y las responda en su cuaderno, antes de la explicación:
| ¿Cómo varían los kilógramos de $\ce{CO2}$ cuando aumentan los kilómetros recorridos por el automóvil? |
| ¿Qué es una variable? |
| ¿Cuáles son las variables de la actividad exploratoria? |
| ¿Qué es una razón? |
| ¿Cuál es la razón de la actividad exploratoria? |
| ¿Qué es proporcionalidad de variables? |
| ¿Cómo es la proporcionalidad entre las variables de la actividad exploratoria? |
| ¿Qué es una proporción? |
| ¿Cuál es el modelo matemático que me determina el valor de la cantidad de kilogramos de Dióxido de Carbono para una cantidad determinada de kilómetros? |
| ¿Qué representa x? |
Una variable, es una cantidad física que puede tomar diferentes valores, en la actividad exploratoria, las variables son los kilómetros recorridos por el automóvil y los kilogramos de Dióxido de Carbono producidos por el mismo y se puede establecer una relación entre ellas, llamada razón.
después de analizar la tabla, podemos concluir que mientras más kilómetros recorra el automóvil, mayor será la cantidad de kilogramos de Dióxido de Carbono que producirá, por lo tanto, estas variables son directamente proporcionales y su gráfica es una recta creciente, como se muestra en la siguiente gráfica:
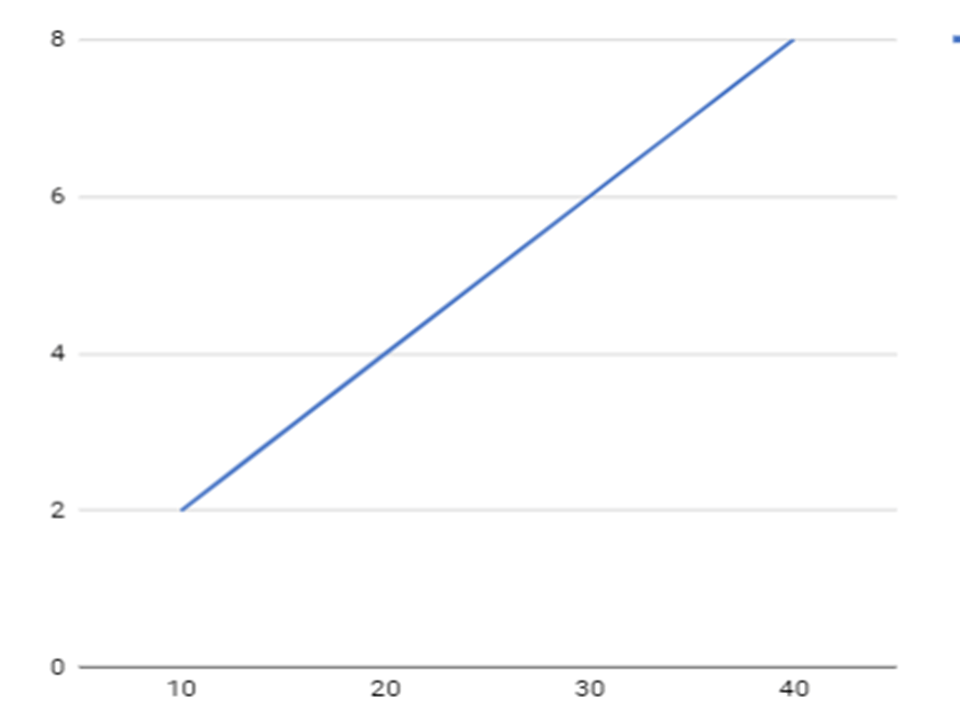
La razón de las variables de la actividad exploratoria, es la relación de la cantidad de kilogramos de Dióxido de Carbono, respecto a los kilómetros recorridos por el automóvil, es decir:
$$Razón = \frac{Kg de \ce{CO2}}{Km}$$
Analicemos la siguiente situación:
Un camión, produce 2 kilogramos de Dióxido de Carbono cada 5 kilómetros de recorrido. ¿Cuál es la cantidad de Dióxido de Carbono producido al recorrer 300 kilómetros?
Con igualdades de razones podemos construir proporciones, el objetivo se convierte, entonces, en encontrar una proporción que me relacione las razones y establecemos una proporción donde la letra x represente el valor desconocido de una de las variables, para ello, se procede de siguiente manera:
Dibuje una tabla de frecuencias con las variables relacionadas, en este caso, es una columna para los kilómetros recorridos por el camión y otra columna para los kilogramos de Dióxido de Carbono, de manera tal que, la primera columna sea la de la variable desconocida, como se muestra en la siguiente tabla:
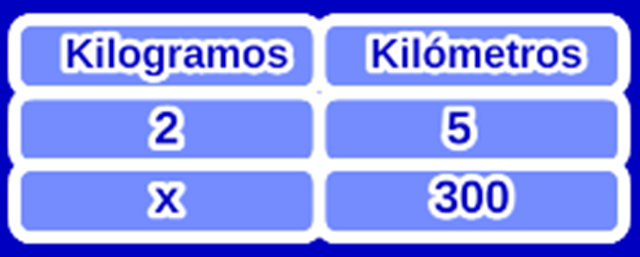
Escriba la proporción, para ello, el primer miembro de la proporción corresponderá a la columna de la variable desconocida y el segundo miembro de la proporción corresponderá a la columna de la variable conocida, en esta situación, con base en la tabla de frecuencias, obtendríamos la siguiente proporción:
$\frac{2}{x}$ = $\frac{5}{300}$
Una vez obtenida la proporción, despeje la variable x, siempre de la siguiente manera, multiplique la diagonal y divida por el otro, es decir, siempre multiplique los extremos de la proporción y divida por el término restante, en este caso:
$x = \frac{2*300}{5} = 120$
120 corresponde a la cantidad de kilogramos de Dióxido de Carbono producidos por el camión, durante los 300 kilómetros recorridos.
A continuación, encontrará un video con la explicación del tema. Estudie el video, para ello, se recomienda que vaya pausando el video a medida que vaya adelantado la explicación y realice un resumen en su cuaderno de notas:
A continuación, encontrará una escena interactiva de la regla de proporcionalidad simple directa, para que interactúe en ella e interiorice sus competencias, esta escena le calcula directamente el valor de la razón, para interactuar en ella, escriba la tabla de valores en las celdas correspondientes y una vez asignados los valores, haga clic en Hallar x, después, puede generar otro cálculo y cambiar los valores haciendo clic en Otro Cálculo.
El objetivo es que interiorice la proporcionalidad simple directa.
A continuación, encontrarás otra escena correspondiente a la proporcionalidad simple directa.
Para comenzar, debe asignarle valores a las variables, una vez que haya asignado los valores de las variables, haga clic en el botón superior izquierdo y le mostrará las variables de la situación planteada, luego, haga clic nuevamente en ese botón y le mostrará la proporción que se genera, luego, vuelva a hacer clic y le mostrará el valor de la incógnita, después, puedes generar otro ejercicio haciendo clic en Otro Ejercicio.
tenga presente que los tiempos de interacción en las escenas depende de cada lector y de su ritmo de aprendizaje, una vez que haya interiorizado la regla de tres simple directa, puede continuar con la siguiente correspondiente a la regla de proporcionalidad simple inversa.
La relación simple inversa, se presenta cuando se relacionan 2 variables inversamente proporcionales.
Para el estudio de esta regla de proporcionalidad, se ha creado una actividad exploratoria, la cual busca que interpretes e interiorices la regla de proporcionalidad simple inversa.
La siguiente tabla, muestra el comportamiento que se presenta entre el número de árboles plantados en Medellín, respecto al número de personas que no tendrían un aire limpio para respirar:
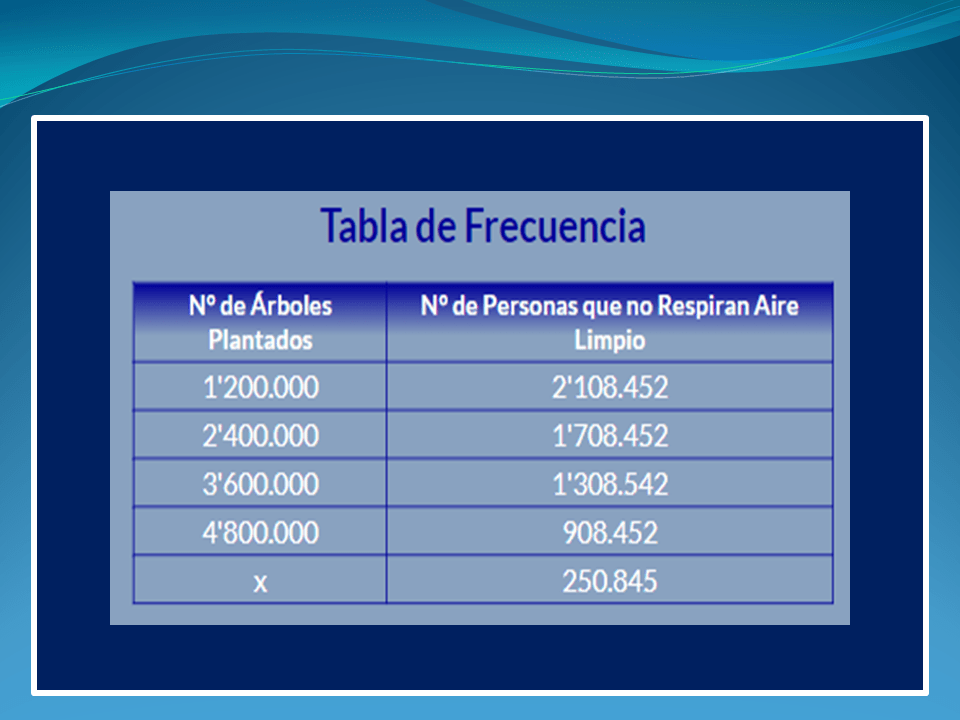
después de analizar la tabla, podemos concluir que, mientras más árboles hayan plantados en Medellín, menor será la cantidad de personas que no respiran un aire limpio, es decir, estas variables son inversamente proporcionales y su gráfica es una recta decreciente, como se muestra en la siguiente gráfica:
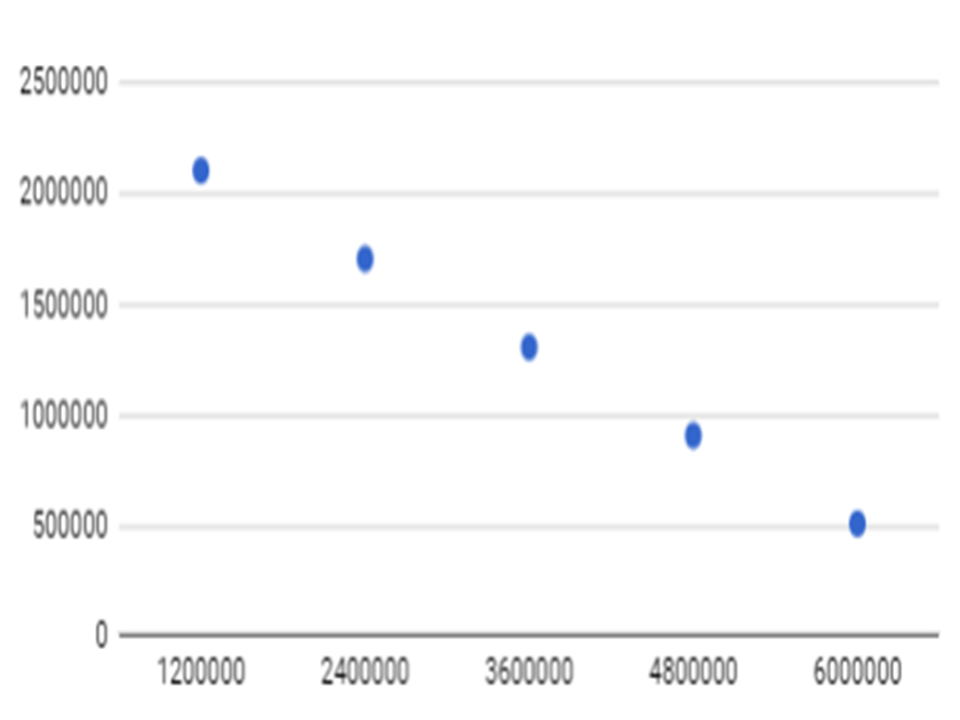
Mientras mayor sea el números de árboles plantados en Medellín, menor será el número de personas que no respiran un aire limpio.
La razón de las variables de la actividad exploratoria es la relación de la cantidad de personas que no respiran un aire limpio, respecto a la cantidad de árboles plantados en Medellín, es decir:
$$Razón = \frac{\text{Número de personas}}{\text{Número de árboles}}$$
Analicemos la siguiente situación:
Para el año 2020, habían sembrados en Medellín 481.154 árboles, para una población de 2'508.452 habitantes. Se necesitan 3 árboles por cada habitante para respirar un aire limpio, por lo tanto, se necesitan 7'525.356 árboles, esto quiere decir que, sólo habría aire libre de contaminación para 160.386 habitantes y el resto de habitantes, que en este caso serían 2'348.066, no tendrían un aire limpio para respirar.
¿Cuál es el números de árboles plantados que se necesitan para que mínimo el 90% de todos los habitantes de Medellín, según los datos obtenidos en el año 2020, puedan respirar un aire limpio?.
Con igualdades de razones podemos construir proporciones, el objetivo se convierte en encontrar una proporción que me relacione las razones, para ello, establecemos una proporción donde la letra x representa el valor desconocido de una de las variables y se procede de siguiente manera:
Dibuje una tabla de frecuencias con las variables relacionadas, en este caso es una columna para el número de personas que no respiran aire limpio y otra columna para la cantidad de árboles plantados, de manera tal que, la primera columna sea siempre la de la variable desconocida, así:

Escriba la proporción, para ello, el primer miembro de la proporción corresponderá a la columna de la variable desconocida y el segundo miembro de la proporción corresponderá a la columna de la variable conocida, pero en este caso, se invierten el orden de los datos de la columna, en esta situación, con base en la tabla de frecuencias, obtendríamos la siguiente proporción:
$$\frac{1200000}{x} = \frac{250845}{2108452}$$
Una vez obtenida la proporción, despeje la variable x, siempre de la siguiente manera, multiplique la diagonal y divida por el otro, es decir, siempre multiplique los extremos de la proporción y divida por el término restante, en este caso:
$$ x = \frac{1200000 * 2108452}{250845} = 10086477$$
10'086.477 corresponde a la cantidad de árboles que se deben plantar para que el 90% de los medellinences respiren un aire limpio.
A continuación, encontrará un video con la explicación del tema. Estudie el video y para ello, se recomienda que vaya pausando el video a medida que vaya adelantado la explicación y realice un resumen en su cuaderno de notas.
A continuación, encontrará una escena interactiva de la regla de proporcionalidad simple inversa, para que interiorice sus competencias, para interactuar en ella, escriba la tabla de datos en las celdas correspondientemente y luego haga clic en Hallar x, después puedes generar otro cálculo haciendo clic en Otro Cálculo. El objetivo es que interiorice la regla de tres simple inversa:
A continuación encontrará otra escena de la regla de tres simple inversa, para comenzar debe asignarle valores a las variables, una vez que haya asignado los valores de las variables haga clic en el botón superior izquierdo y le mostrará las variables de la situación planteada, luego, haga clic nuevamente en ese botón y le mostrará la proporción que se genera, luego, vuelva a hacer clic y le mostrará el valor de la incógnita, después, puedes generar otro ejercicio haciendo clic en Otro Ejercicio:
Una vez que haya interiorizado la regla de tres simple inversa puede continuar con la siguiente, correspondiente a la regla de proporcionalidad compuesta directa directa.
La relación compuesta directa, se presenta cuando se relacionan 2 variables directamente proporcionales a la variable incógnita.
Analicemos la siguiente situación:
En una empresa metalmecánica, 10 operarios de máquina confeccionan 400 unidades de un producto en 4 días. ¿Cuál es el número de unidades producidas por 7 operarios en 6 días? Con igualdades de razones, podemos construir proporciones, el objetivo se convierte en encontrar una proporción que me relacione las razones y establecemos una proporción donde la letra x representa el valor desconocido de una de las variables, para ello, se procede de la siguiente manera:
Dibuje una tabla de frecuencias con las variables relacionadas, en este caso, es una columna para el número de operarios, otra columna para la cantidad de unidades producidas y otra columna para la cantidad de días, tenga en cuenta escribir en la primera columna la variable que deseamos calcular, en este caso, la primera columna debe ser el número de unidades así:

Escriba la proporción, para ello, el primer miembro de la proporción corresponderá a la columna de la variable desconocida y el segundo miembro de la proporción corresponderá a las columnas de las variables conocidas, en esta situación, con base en la tabla de frecuencias, obtendríamos la siguiente proporción:
$$\frac{400}{x} = \frac{10*4}{7*6}$$
Una vez obtenida la proporción, despeje la variable x, de la siguiente manera, multiplique la diagonal y divida por el otro, es decir, multiplique los extremos de la proporción y divida por los términos restantes, en este caso:
$$x = \frac{400 * 7 * 6}{10 *4} = 420$$
420 corresponde a la cantidad de unidades producidas por 7 operarios en 6 días.
A continuación, encontrará un video con la explicación del tema. Estudie el video y para ello se recomienda que vaya pausando el video a medida que vaya adelantado la explicación y realice un resumen en su cuaderno de notas.
A continuación, encontrará una escena interactiva de la regla de proporcionalidad compuesta directa, para que interiorice sus competencias, para interactuar en ella, escriba la tabla de datos en las celdas correspondientemente y haga clic en Hallar x, después, puede generar otro ejercicio haciendo clic en Otro Ejercicio. El objetivo es que interiorice la proporcionalidad compuesta directa directa.
A continuación, encontrará otra escena de la regla de tres compuesta directa. Para comenzar, debe asignarle valores a las variables, una vez que haya asignado los valores de las variables haga clic en el botón superior izquierdo y le mostrará las variables de la situación planteada, luego, haga clic nuevamente en ese botón y le mostrará la proporción que se genera, luego, vuelva a hacer clic y le mostrará el valor de la incógnita, después, puedes generar otro ejercicio haciendo clic en Otro Ejercicio:
Continúa con la proporcionalidad compuesta inversa inversa.
La relación compuesta inversa, se presenta cuando se relacionan 2 variables inversamente proporcionales a la variable incógnita.
Analicemos la siguiente situación:
En una empresa metalmecánica, 10 operarios de máquina confeccionan un lote de producción en 7 días, trabajando en turnos de 8 horas. ¿Cuántos operarios se necesitan para confeccionar el mismo lote en 4 días, trabajando en turnos de 10 horas?.
Con igualdades de razones, podemos construir proporciones, el objetivo se convierte en encontrar una proporción que me relacione las razones y establecemos una proporción donde la letra x representa el valor desconocido de una de las variables, para ello, se procede de la siguiente manera:
Dibuje una tabla de frecuencias con las variables relacionadas, en este caso, es una columna para el número de operarios, otra columna para el número de días trabajados y otra columna para el número de horas trabajadas al día, como se muestra en la siguiente gráfica:

Escriba la proporción, para ello, el primer miembro de la proporción corresponderá a la columna de la variable desconocida y el segundo miembro de la proporción corresponderá a las columnas de las variables conocidas, pero en este caso se invierten el orden de los datos de las columnas, con base en la tabla de frecuencias, se obtiene la siguiente proporción:
$\frac{10}{x} = \frac{4*10}{7*8}$
Una vez obtenida la proporción, despeje la variable x siempre de la siguiente manera, multiplique la diagonal y divida por el otro, es decir, siempre multiplique los extremos de la proporción y divida por los términos restantes, en este caso:
$x = \frac{10*7*8}{4*10} = 14$
14 corresponde a la cantidad de operarios necesarios para realizar el mismo lote en 4 días, trabajando 10 horas diarias.
A continuación, encontrará un video con la explicación del tema. Estudie el video y para ello, se recomienda que vaya pausando el video a medida que vaya adelantado la explicación y realice un resumen en su cuaderno de notas.
A continuación del video, encontrará una escena interactiva de la regla de proporcionalidad compuesta inversa, para que interiorice sus competencias, para interactuar en ella, escriba la tabla de datos en las celdas correspondientemente y haga clic en Hallar x, después, puedes generar otro ejercicio haciendo clic en Otro Cálculo. El objetivo es que interiorice la proporcionalidad compuesta inversa inversa:
A continuación, encontrará otra escena de la regla de tres compuesta inversa. Para comenzar, debe asignarle valores a las variables, una vez que haya asignado los valores de las variables haga clic en el botón superior izquierdo y le mostrará las variables de la situación planteada,
luego haga clic nuevamente en ese botón y le mostrará la proporción que se genera, luego, vuelva a hacer clic y le mostrará el valor de la incógnita, después, puedes generar otro ejercicio haciendo clic en Otro Cálculo:
Continúa con la proporcionalidad compuesta directa inversa.
La relación compuesta directa inversa, se presenta cuando se relacionan una variable directamente proporcional y otra variable inversamente proporcionales, respecto a la variable incógnita.
Analicemos la siguiente situación:
En una empresa, 5 personas construyen 1250 unidades de un producto, en 6 horas. ¿Cuántas personas se necesitan para construir 5000 unidades, en 8 horas?.
Con igualdades de razones podemos construir proporciones, el objetivo se convierte en encontrar una proporción que me relacione las razones y establecemos una proporción donde la letra x representa el valor desconocido de una de las variables para ello se procede de la siguiente manera:
Dibuje una tabla de frecuencias con las variables relacionadas, en este caso, es una columna para el número de personas, otra columna para el número de unidades y otra columna para el número de horas.

Escriba la proporción, para ello, el primer miembro de la proporción corresponderá a la columna de la variable desconocida y el segundo miembro de la proporción corresponderá a las columnas de las variables conocidas, pero en este caso se invierte el orden de los datos de la columna de la variable inversamente proporcional, con base en la tabla de frecuencias, obtendríamos la siguiente proporción:
$$\frac{5}{x} = \frac{1250*8}{5000*6}$$
Una vez obtenida la proporción, despeje la variable x, siempre, de la siguiente manera, multiplique la diagonal y divida por el otro, es decir, siempre multiplique los extremos de la proporción y divida por los términos restantes, en este caso:
$$x = \frac{5*5000*6}{1250*8} = 15$$
15 corresponde a la cantidad de personas necesarias para construir 5000 unidades, en 8 horas.
A continuación, encontrará una escena interactiva de la regla de proporcionalidad compuesta directa inversa, para que interiorice sus competencias, para interactuar en ella, escriba la tabla de datos en las celdas correspondientemente y haga clic en Hallar x, después, puedes generar otro ejercicio haciendo clic en Otro Cálculo.
A continuación, encontrará otra escena de la regla de tres compuesta directa inversa.
Para comenzar, debe asignarle valores a las variables, una vez que haya asignado los valores de las variables, haga clic en el botón superior izquierdo y le mostrará las variables de la situación planteada, luego, haga clic nuevamente en ese botón y le mostrará la proporción que se genera, luego, vuelva a hacer clic y le mostrará el valor de la incógnita, después, puedes generar otro ejercicio haciendo clic en Otro Cálculo:
Una vez interiorizada la regla de proporcionalidad directa inversa, continúa con la proporcionalidad directa-directa-inversa.
La relación compuesta directa e inversa, se presenta cuando se relacionan más de 2 variables directamente e inversamente proporcionales a la vez respecto a la variable incógnita, en este caso, se relacionan 4 variables de las cuales 2 de ellas son directamente proporcionales y 1 inversamente proporcional respecto a la variable incógnita.
Analicemos la siguiente situación:
En una empresa, 12 operarios, con 500 Kilogramos de materia prima, confeccionan 300 unidades de un producto en 8 días. ¿Cuál es el número de operarios necesarios para que se confeccionen 1000 unidades, con 750 Kilogramos de materia prima, en 6 días.
Con igualdades de razones podemos construir proporciones, el objetivo se convierte en encontrar una proporción que me relacione las razones y establecemos una proporción donde la letra x representa el valor desconocido de una de las variables, para ello, se procede de la siguiente manera:
Dibuje una tabla de frecuencias con las variables relacionadas, en este caso, es una columna para el número de operarios, otra columna para el número de Kilogramos de materia prima, otra columna para el número de unidades confeccionadas y otra columna para el número de días trabajados.

Escriba la proporción, para ello, el primer miembro de la proporción corresponderá a la columna de la variable desconocida y el segundo miembro de la proporción corresponderá a las columnas de las variables conocidas, pero en este caso, los datos de las columnas de la variables directas se escriben igual y se invierte el orden de los datos de la columna de la variable inversa, con base en la tabla de frecuencias, obtenemos la siguiente proporción:
$\frac{12}{x} = \frac{500*300*6}{750*1000*8}$
Una vez obtenida la proporción, despeje la variable x de la siguiente manera, multiplique la diagonal y divida por el otro, es decir, multiplique los extremos de la proporción y divida por los términos restantes, en este caso:
$x = \frac{12*750*1000*8}{500*300*6} = 80$
80 corresponde a la cantidad de operarios necesarios para confeccionar 1000 unidades, con 750 Kilogramos de materia prima, en 6 días.
A continuación, encontrará un video con la explicación del tema. Estudie el video y para ello, se recomienda que vaya pausando el video a medida que vaya adelantado la explicación y realice un resumen en su cuaderno de notas.
A continuación, encontrará una escena interactiva de la regla de proporcionalidad compuesta directa directa inversa, para que interiorice sus competencias, para interactuar en ella, escriba la tabla de datos en las celdas correspondientemente y haga clic en Hallar x, después, puede generar otro ejercicio haciendo clic en Otro Cálculo:
A continuación encontrará otra escena de la regla de tres compuesta directa directa inversa. Para comenzar, debe asignarle valores a las variables, una vez que haya asignado los valores de las variables haga clic en el botón superior izquierdo y le mostrará las variables de la situación planteada, luego, haga clic nuevamente en ese botón y le mostrará la proporción que se genera, luego, vuelva a hacer clic y le mostrará el valor de la incógnita, después, puedes generar otro ejercicio haciendo clic en Otro Cálculo:
Continúa con la proporcionalidad compuesta directa-inversa-inversa.
La relación compuesta directa-inversa-inversa, se presenta cuando se relacionan 1 variable directamente proporcional y 2 variables inversamente proporcional respecto a la variable que deseamos calcular.
Analicemos la siguiente situación:
En una empresa metalmecánica, 12 operarios de máquina confeccionan 650 unidades de un producto, en 4 días, trabajando turnos de 6 horas. ¿Cuál es el número de operarios que se necesitan para producir 1083 unidades del mismo producto, en 5 días, trabajando turnos de 8 horas.
Con igualdades de razones podemos construir proporciones, el objetivo se convierte, entonces, en encontrar una proporción que me relacione las razones y establecemos una proporción donde la letra x representa el valor desconocido de una de las variables, para ello, se procede de la siguiente manera:
Dibuje una tabla de frecuencias con las variables relacionadas, en este caso, es una columna para el número de operarios, otra columna para el número de unidades producidas, otra columna para el número de días trabajados y otra columna para el número de horas trabajadas, tenga en cuenta que la primera columna debe ser la variable que deseamos calcular.
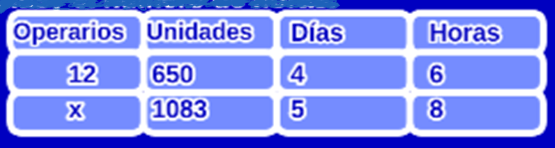
Escriba la proporción, para ello, el primer miembro de la proporción corresponderá a la columna de la variable desconocida y el segundo miembro de la proporción corresponderá a las columnas de las variables conocidas, pero en este caso, los datos de la columna de la variable directa se escribe igual y se invierten el orden de los datos de las columnas de la variables inversas, con base en la tabla de frecuencias, obtenemos la siguiente proporción:
$\frac{12}{x} = \frac{650*5*8}{1083*4*6}$
3. Una vez obtenida la proporción, despeje la variable x, siempre, de la siguiente manera, multiplique la diagonal y divida por el otro, es decir, siempre multiplique los extremos de la proporción y divida por los términos restantes, en este caso:
$x = \frac{12*1083*4*6}{650*5*8} = 12$
12 corresponde al número de operarios necesarios para para producir 1083 unidades, en 5 días de trabajo, trabajando 8 horas diarias.
A continuación, encontrará un video con la explicación del tema. Estudie el video y para ello, se recomienda que vaya pausando el video a medida que vaya adelantado la explicación y realice un resumen en su cuaderno de notas.
A continuación, encontrará una escena interactiva de la regla de proporcionalidad compuesta directa inversa inversa, para que interiorice sus competencias e interactuar en ella, escriba la tabla de datos en las celdas correspondientes y haga clic en Hallar x, después, puedes generar otro ejercicio haciendo clic en Otro Cálculo:
A continuación, encontrará otra escena de la regla de tres compuesta directa inversa inversa. Para comenzar, debe asignarle valores a las variables, una vez que haya asignado los valores de las variables haga clic en el botón superior izquierdo y le mostrará las variables de la situación planteada, luego, haga clic nuevamente en ese botón y le mostrará la proporción que se genera, luego, vuelva a hacer clic y le mostrará el valor de la incógnita, después, puede generar otro ejercicio haciendo clic en Otro Cálculo:
La relación compuesta directa directa directa, se presenta cuando se relacionan más de 2 variables directamente proporcionales, en este caso, son 4 variables de las cuales tres de ellas son directamente proporcionales con la variable que deseamos calcular.
Analicemos la siguiente situación:
En una empresa metalmecánica, 10 operarios de máquina confeccionan 650 unidades de un producto, en 4 días, trabajando turnos de 6 horas. Determine el número de unidades producidas por 7 operarios, en 6 días, trabajando turnos de 8 horas.
Con igualdades de razones podemos construir proporciones, el objetivo se convierte en encontrar una proporción que me relacione las razones y establecemos una proporción, donde la letra x representa el valor desconocido de una de las variables, para ello, se procede de la siguiente manera:
Dibuje una tabla de frecuencias con las variables relacionadas, en este caso, es una columna para el número de operarios, otra columna para el número de unidades producidas, otra columna para el número de días trabajados y otra columna para el número de horas trabajadas, tenga en cuenta que la primera columna debe ser la variable que deseamos calcular.

Escriba la proporción, para ello, el primer miembro de la proporción corresponderá a la columna de la variable desconocida y el segundo miembro de la proporción corresponderá a las columnas de las variables conocidas, con base en la tabla de frecuencias obtenemos la siguiente proporción:
$ \frac{650}{x} = \frac{10*4*6}{7*6*8}$
Una vez obtenida la proporción, despeje la variable x de la siguiente manera, multiplique la diagonal y divida por el otro, es decir, multiplique los extremos de la proporción y divida por los términos restantes, en este caso:
$x = \frac{650*7*6*8}{10*4*6} = 910$
910 corresponde al número de unidades producidas por 7 operarios, en 6 días, trabajando 8 horas diarias.
A continuación, encontrará un video con la explicación del tema. Estudie el video y para ello, se recomienda que vaya pausando el video a medida que vaya adelantado la explicación y realice un resumen en su cuaderno de notas.
A continuación, encontrará una escena interactiva de la regla de proporcionalidad compuesta directa directa directa, para que interiorice sus competencias, para interactuar en ella, escriba la tabla de datos en las celdas correspondientemente y haga clic en Hallar x:
A continuación, encontrará otra escena de la regla de tres compuesta directa directa directa. Para comenzar, debe asignarle valores a las variables, una vez que haya asignado los valores de las variables, haga clic en el botón superior izquierdo y le mostrará las variables de la situación planteada, luego, haga clic nuevamente en ese botón y le mostrará la proporción que se genera, luego, vuelva a hacer clic y le mostrará el valor de la incógnita, después, puedes generar otro ejercicio haciendo clic en Otro Cálculo:
La relación compuesta inversa inversa inversa, se presenta cuando se relacionan más de 2 variables inversamente proporcionales respecto a la variable que deseamos calcular, en este caso, son 4 variables, de las cuales, tres de ellas son inversamente proporcionales respecto a la variable incógnita.
Analicemos la siguiente situación:
Para aumentar la productividad en una empresa metalmecánica, se instalaron líneas alternas de producción automatizadas. Con la instalación de 3 líneas automatizadas alternas y 15 operarios, se realizó un lote de producción en 12 días, trabajando en turnos de 8 horas. ¿Cuántas líneas de producción automatizadas se deben instalar, para que con 6 operarios, se realice la misma producción en 8 días, trabajando turnos de 10 horas?.
Con igualdades de razones podemos construir proporciones, el objetivo se convierte, entonces, en encontrar una proporción que me relacione las razones y establecemos una proporción donde la letra x representa el valor desconocido de una de las variables, para ello, se procede de la siguiente manera:
Dibuje una tabla de frecuencias con las variables relacionadas, en este caso, es una columna para el número de operarios, otra columna para el número de unidades producidas, otra columna para el número de días trabajados y otra columna para el número de horas trabajadas, tenga en cuenta que la primera columna debe ser la variable que deseamos calcular, en este caso, el número de líneas automatizadas, como se muestra en la siguiente tabla.
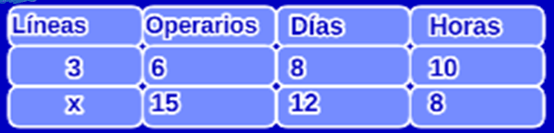
Escriba la proporción, para ello, el primer miembro de la proporción corresponderá a la columna de la variable desconocida y el segundo miembro de la proporción corresponderá a las columnas de las variables conocidas, pero en este caso se invierten el orden de los datos, con base en la tabla de frecuencias obtenemos la siguiente proporción:
$\frac{3}{x} = \frac{15*12*8}{6*8*10}$
Una vez obtenida la proporción, despeje la variable x, siempre, de la siguiente manera, multiplique la diagonal y divida por el otro, es decir, siempre multiplique los extremos de la proporción y divida por los términos restantes, en este caso:
$x = \frac{3*6*8*10}{15*12*8} = 1$
1 corresponde al número de líneas de producción alternas necesarias para producir el mismo lote, con 6 operarios, en 8 días, trabajando 10 horas diarias.
A continuación, encontrará una escena interactiva de la regla de proporcionalidad compuesta inversa inversa inversa, para que interiorice sus competencias, para interactuar en ella, escriba la tabla de datos en las celdas correspondientemente y haga clic en Hallar x:
A continuación encontrará otra escena de la regla de tres compuesta inversa inversa inversa. Para comenzar, debe asignarle valores a las variables, una vez que haya asignado los valores de las variables, haga clic en el botón superior izquierdo y le mostrará las variables de la situación planteada, luego, haga clic nuevamente en ese botón y le mostrará la proporción que se genera, luego, vuelva a hacer clic y le mostrará el valor de la incógnita, después, puede generar otro ejercicio haciendo clic en Otro Cálculo:
Una vez que haya interiorizado la regla de proporcionalidad inversa-inversa-inversa, puedes continuar con la siguiente sección, en esta parte, se mostrarán ejercicios interactivos de cada una de las reglas de proporcionalidad:
A continuación, encontrará aplicaciones de las reglas de proporcionalidad en la solución de situaciones reales:
Recuerda que estos interactivos son escalables, quiere decir que, con el botón superior derecho le muestra el interactivo en otra ventana con las dimensiones reales:
Recuerda que estos interactivos son escalables, quiere decir que, con el botón superior derecho le muestra el interactivo en otra ventana con las dimensiones reales:
Recuerda que estos interactivos son escalables, quiere decir que, con el botón superior derecho le muestra el interactivo en otra ventana con las dimensiones reales:
Recuerda que estos interactivos son escalables, quiere decir que, con el botón superior derecho le muestra el interactivo en otra ventana con las dimensiones reales:
Recuerda que estos interactivos son escalables, quiere decir que, con el botón superior derecho le muestra el interactivo en otra ventana con las dimensiones reales:
Recuerda que estos interactivos son escalables, quiere decir que, con el botón superior derecho le muestra el interactivo en otra ventana con las dimensiones reales:
Recuerda que estos interactivos son escalables, quiere decir que, con el botón superior derecho le muestra el interactivo en otra ventana con las dimensiones reales:
Recuerda que estos interactivos son escalables, quiere decir que, con el botón superior derecho le muestra el interactivo en otra ventana con las dimensiones reales:
A manera de complemento, puede ver más videos de ejercicios resueltos en RAZONES, PROPORCIONES Y PROPORCIONALIDAD.
Recuerda que estos interactivos son escalables, quiere decir que, con el botón superior derecho le muestra el interactivo en otra ventana con las dimensiones reales:
Haga clic en el botón de la esquina superior derecha, para ver el interactivo en una ventana ampliada.
Recuerda que estos interactivos son escalables, quiere decir que, con el botón superior derecho le muestra el interactivo en otra ventana con las dimensiones reales:
Realizado lo anterior puede continuar con la siguiente unidad denominada, Reconociendo Mis Competencias
A continuación, encontrará un Padlet, como un repositorio de objetos interactivos de aprendizaje, para que practique lo aprendido, el objetivo es que realice algunas de las situaciones planteadas en él.
Recuerda que, estos interactivos son escalables, quiere decir que, con el botón superior derecho le muestra el interactivo en otra ventana con las dimensiones reales:
A continuación, encontrará un taller con 9 actividades relacionadas con las reglas de proporcionalidad, para que practique lo aprendido, el objetivo es que realice todas las situaciones planteadas en él.
Haga clic en el botón de la esquina superior derecha, para ver el interactivo en una ventana ampliada.
A continuación, encontrará un taller, tipo cuestionario de selección múltiple única respuesta, para que practique lo aprendido, el objetivo es que realice todas las situaciones planteadas en él, haciendo clic en la respuesta que crea es la correcta, después, haga clic en el botón inferior derecho para avanzar al siguiente punto, al finalizar los 10 puntos, haga clic en verificar.
Recuerda que, estos interactivos son escalables, quiere decir que, con el botón superior derecho le muestra el interactivo en otra ventana con las dimensiones reales:
A continuación encontrará otra escena, tipo selección múltiple única respuesta, seleccione la respuesta que crea es la correcta y haga clic en el botón inferior derecho para avanzar al siguiente punto.
A continuación encontrará una evaluación, la cual le permitirá al lector medir el nivel de apropiación de competencias, el objetivo es que lo realice sin ayuda de los objetos interactivos de aprendizaje y que realice los cálculos con lápiz y papel, con la ayuda de una calculadora.
Recuerda que, estos interactivos son escalables, quiere decir que, con el botón superior derecho se muestra el interactivo en otra ventana con las dimensiones reales, le recomendamos realizarlo de esa manera:
Para comenzar, haga clic en comenzar, seguidamente, seleccione la respuesta que crea es la correcta, una vez seleccionada la respuesta, haga clic en siguiente, al finalizar, haga clic en Resultados y podrás encontrar los resultados obtenidos en la prueba:
La autoevaluación, le permite al lector y al escritor establecer el nivel de satisfacción alcanzado con el libro digital, es muy importante su objetividad en las respuestas, para el mejoramiento continúo de los procesos formativos que cómo educador están a mi cargo y para la actualización del mismo libro. A continuación encontrará la autoevaluación, el objetivo es que la realice concienzudamente:
Recuerda que, estos interactivos son escalables, quiere decir que, con el botón superior derecho le muestra el interactivo en otra ventana con las dimensiones reales:
Eso es todo amigo, espero que haya disfrutado del libro, y lo más importante, que haya aprendido la regla de tres.
Agradecimientos a Juan Guillermo Rivera, por su apoyo tan diligente, gracias a él y sus orientaciones, pude realizar el libro, gracias al Proyecto Educativo Descartes por su altruismo y filantropía que permiten que publiquemos estos libros para la comunidad, estoy muy orgulloso de hacer parte de esta gran familia.