Partición de hexaedros convexos de caras cuadriláteras en pirámides

José R. Galo Sánchez
Interactivo
PARTICIÓN DE HEXAEDROS CONVEXOS DE CARAS CUADRILÁTERAS EN PIRÁMIDES
Libro interactivo
José R. Galo Sánchez
Red Educativa Digital Descartes, España
Córdoba (España)
2021
Título de la obra:
Partición de hexaedros convexos de caras cuadriláteras en pirámides
Autor: José R. Galo Sánchez
Primera edición: Septiembre 2018
Segunda edición: Mayo 2021
Diseño del soporte digital: Juan Guillermo Rivera Berrío
Diseño de cubierta basado en una de Diana María Velásquez García
Librería turn.js: Emmanuel García
Herramienta de edición: DescartesJS
Fuente: Amaranth
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN: 978-84-18834-01-1

Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Sin Obra Derivada.
Todos los objetos interactivos y los contenidos de esta obra colectiva están protegidos por la Ley de Propiedad Intelectual.
Tabla de contenido
PARTE I: Partición de un cubo en pirámides de base cuadrada1
1. Partición de un cubo en pirámides de base cuadrada3
1.1. Cuatro descomposiciones clásicas3
PARTE II: Partición de un cubo en pirámides de base triangular9
1. Partición de un cubo en pirámides de base triangular11
1.1. Partición mediante descomposición de pirámides de base cuadrada11
1.2. Partición mediante construcción específica13
2. Descomposición de un prisma triangular en pirámides triangulares16
2.4. Particiones del prisma triangular en pirámides triangulares equivalentes23
3. Partición prismática de un cubo en pirámides triangulares equivalentes26
1. Partición de un hexaedro convexo {4,4,4,4,4,4} en pirámides de base cuadrilátera37
1.1. Definición de un paralelepípedo38
1.2. Partición del paralelepípedo40
1.3. Definición de un hexaedro convexo {4,4,4,4,4,4}43
1.4. Partición del hexaedro convexo44
iii
PARTE IV: Partición de un hexaedro convexo de caras cuadriláteras en pirámides de base triangular45
1.1. Partición de un paralelepípedo48
1.2. Partición del hexaedro convexo {4,4,4,4,4,4}51
2. Partición de un hexaedro convexo {4,4,4,4,4,4} mediante construcción específica51
2.1. Partición mínima de un paralelepípedo en pirámides triangulares52
2.2. Partición mínima de un hexaedro convexo en pirámides triangulares53
3. Partición prismática de un paralelepípedo en pirámides triangulares55
3.1. Partición de un prisma triangular oblicuo en pirámides triangulares57
Partición de un prisma procedente de un romboiedro59
Partición de un prisma procedente de un romboedro (casos 1 y 2)62
Partición de un prisma procedente de un ortoedro (casos 1, 2 y 3)66
Partición de un prisma procedente de un cubo72
3.2. Partición prismática de los paralelepípedos74
Partición prismática de un cubo74
Partición prismática de un ortoedro (casos 3, 2 y 1)77
Partición prismática de un romboedro (casos 2 y 1)88
Partición prismática de un romboiedro99
Escena general de la partición prismática de un paralelepípedo102
4. Partición hexaédrica y pseudo-prismática de un hexaedro convexo {4,4,4,4,4,4}
4.1. Partición hexaédrica en pirámides triangulares104
4.2. Partición pseudo-prismática en pirámides triangulares108
iv
Introducción
El cubo o hexaedro regular, lo mismo que el resto de los poliedros regulares convexos ―los sólidos platónicos―, tiene un atractivo generalizado tanto para expertos como para profanos. Los primeros, para profundizar en su estudio y análisis, habitualmente suelen proceder a realizar cortes planos con objeto de determinar cuáles son las diferentes secciones poligonales que pueden obtenerse; o bien buscan conocer diferentes descomposiciones o particiones del mismo en otros poliedros. Y algunos de los segundos, y muchos de los primeros, seguro que se han encontrado en algún momento con la actividad lúdica de elaborar puzles o rompecabezas consistentes en montar un cubo a partir de unas piezas dadas; o bien, realizando una lectura recíproca, el diseñador y constructor de estos puzles ha de plantearse cómo partir un cubo en diferentes piezas y sobre ellas puede autoimponerse ciertas restricciones o establecer cierta homogeneidad en la forma, el volumen o cualquier otro atributo o propiedad. En particular se puede establecer, por ejemplo, que las piezas sean de un mismo tipo e incluso iguales. La elegancia alcanzada en la partición obtenida, o la mayor o menor dificultad que involucra el adoptar un criterio u otro, es matizable y opinable y, por tanto, no nos adentraremos en ello. Un planteamiento usual es la partición del cubo1 en pirámides de base cuadrada y en pirámides de base triangular.
En la primera parte se aborda un análisis de la partición del cubo en pirámides de base cuadrada. La partición mínima está compuesta por tres pirámides congruentes y es usual encontrar en la literatura la partición en cuatro (congruentes dos a dos), cinco (cuatro congruentes y una desigual) y seis pirámides congruentes. En este trabajo se engloban todas estas situaciones como casos particulares de una partición genérica basada en la consideración de un punto de la frontera o del interior del cubo que se configura como vértice o cúspide de todas las pirámides constituyentes de la partición. Para cada uno de esos puntos se obtiene una partición y se incluyen recursos interactivos que la muestran virtualmente y, a la vez, aportan los desarrollos planos de las diferentes pirámides permitiendo su impresión y reproducción tangible.
v
En la segunda parte se aborda la partición del cubo en pirámides triangulares. Un detallado análisis conduce, por un lado, a la obtención de la partición mínima que está formada por cinco pirámides (cuatro congruentes y otra desigual) y, por otro, cuando la partición se realiza subdividiendo las particiones en pirámides de base cuadrada obtenidas en la primera parte, la partición mínima del cubo está formada por seis pirámides equivalentes.
Las particiones en seis pirámides equivalentes pueden englobarse, salvo congruencias, en una partición no prismática y en ocho particiones prismáticas. En ellas intervienen pirámides de tres tipos, dos son pirámides autosimétricas y el tercero es una pirámide asimétrica que aparece con sus dos orientaciones posibles.
Entre las ocho particiones prismáticas hay dos de ellas que están formadas exclusivamente por pirámides que no sólo son equivalentes, sino que también son congruentes entre sí.
Pero un cubo no es más que un caso muy particular de Paralelepípedo (poliedro cuyas caras son paralelas dos a dos) y estos lo son respecto a los Hexaedros convexos2 de caras cuadriláteras {4,4,4,4,4,4}. Por tanto, es lógico abordar la generalización del análisis que se ha realizado en las particiones de un cubo a estos casos y es lo que se aborda en la parte tercera y cuarta.
En la tercera parte se realiza la partición de los cuatro tipos de paralelepípedos (cubo, ortoedro, romboedro y romboiedro) en pirámides cuadriláteras. En un recurso interactivo se engloba la definición de cada tipo de paralelepípedo y se realiza su partición pudiendo seleccionar el vértice o cúspide común a todas las pirámides. Dependiendo de esta cúspide el número de pirámides de la partición serán tres, cuatro, cinco o seis, en una situación análoga a la analizada con el cubo. También se obtienen los desarrollos planos de dichas pirámides, pudiéndolos imprimir y así reproducir físicamente la partición y, con ella, construir el paralelepípedo.
En un recurso análogo se aborda el caso genérico del hexaedro {4,4,4,4,4,4}.
La cuarta parte se centra en la partición en pirámides triangulares, donde inicialmente nos centramos en los paralelepípedos y finalmente se muestra la analogía en los hexaedros convexos de caras cuadriláteras.
vi
La división en dos o más pirámides triangulares de cada una de las pirámides cuadriláteras obtenidas en las particiones de los paralelepípedos analizadas en la tercera parte, nos conduce a particiones que tienen un cardinal mínimo de seis pudiendo distinguirse en este caso particiones no prismáticas y prismáticas, compuestas todas por pirámides equivalentes entre sí.
La partición de cardinal mínimo, formada por cinco piramides, requiere una construcción específica que se detalla en cada uno de los cuatro tipos de paralelepípedos y también en el caso general del hexaedro.
A continuación se estudian las particiones prismáticas y para ello primero se analiza la partición de prismas procedentes de la división de cada uno de los diferentes paralelepípedos en dos prismas. En todos los casos siempre son seis las particiones que se obtienen, cada una compuesta por tres pirámides equivalentes entre sí, pero varían las posibles congruencias entre ellas, así como las diferentes pirámides obtenidas en cada caso. En concreto, para un prisma procedente de:
- Un romboiedro son seis particiones no congruentes con doce pirámides diferentes.
- Un romboedro hay que considerar dos casos posibles. En el primero se distinguen tres particiones no congruentes y seis tipos de pirámides, y en el segundo nos encontramos cuatro particiones y también seis tipos.
- Un ortoedro hay que distinguir tres casos, según la regularidad que presente, y cada uno conduce a: tres particiones y seis tipos de pirámides, tres particiones y cinco tipos, y dos particiones y cuatro tipos.
- Un cubo, como ya se vió, son dos las particiones con tres tipos de pirámides.
El análisis anterior nos permite cuantificar y conocer las particiones de cada paralelepípedo y este estudio se presenta siguiendo un esquema general común, yendo desde el caso más regular (el cubo) al menos regular (romboiedro).
- Para un cubo, analizado en la parte primera, se tienen ocho particiones con tres tipos de pirámides. De ellas dos están compuestas sólo por pirámides congruentes entre sí.
- Para un ortoedro los tres casos posibles conducen a: ocho particiones no congruentes con cuatro tipos de pirámides, doce particiones con cinco tipos y doce particiones con seis tipos.
vii
- Para los dos casos posibles del romboedro se obtiene: diez particiones (una de ellas con pirámides todas congruentes) y seis tipos de pirámides, y doce particiones y seis tipos.
- Para el romboiedro tenemos treinta y seis particiones con doce tipos de pirámides. Pero dado que éste puede partirse en dos prismas de seis formas diferentes, en general, se obtienen 216 particiones y 144 pirámides.
Finalmente se aborda la partición de un hexaedro convexo {4,4,4,4,4,4} en particiones pseudo-prismáticas (en base a dos penteaedros {3,4,4,4,3}) análogas a las prismáticas observadas en los paralelepípedos y encontramos una nueva situación que denominamos hexaédrica, pues se obtiene mediante la división previa en dos hexaedros {3,4,4,3,3,3}. Ambas particiones conduce a seis pirámides triangulares, pero en este caso no hay equivalencia entre ellas. Para el caso particular de los paralelepípedos la partición hexaédrica coincide con la prismática.
viii
parte i
Partición de un cubo en pirámides de base cuadrada
1. Partición de un cubo en pirámides de base cuadrada
1.1 Cuatro descomposiciones clásicas
Consideremos un cubo de arista unidad3 y busquemos realizar una partición del mismo en pirámides de base cuadrada atendiendo a que el cardinal de los elementos que componen la partición sea mínimo o que entre sí sean lo más regulares o similares posible. Son cuatro las situaciones que usualmente suelen divulgarse:
-
Descomposición en tres pirámides iguales ―estrictamente deberíamos de decir congruentes4― (interactuar con la escena 1). Al quedar dividido el cubo en tres partes iguales, este caso suele ponerse como un ejemplo visual de por qué el volumen de una pirámide se calcula como:
Vpirámide = (1/3) ÁreaBase · altura
e incluso éste puede ser el primer paso para realizar una demostración de esa igualdad.
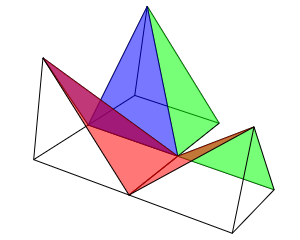
Escena 1. Descomposición de un cubo en tres pirámides cuadradas iguales.
3
- Descomposición en cuatro pirámides, iguales dos a dos (escena 2).
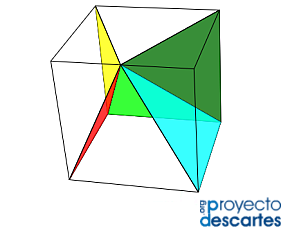
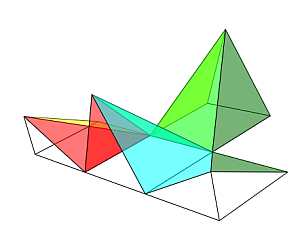
Escena 2. Descomposición de un cubo en cuatro pirámides cuadradas.
- Descomposición en cinco pirámides, cuatro iguales y una desigual, siendo ésta regular (escena 3).
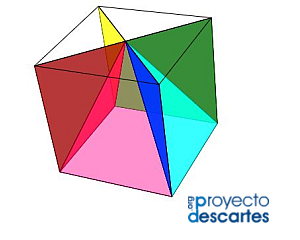
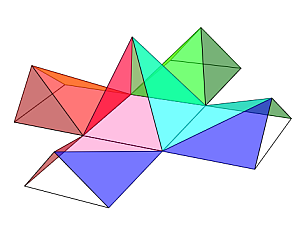
Escena 3. Descomposición de un cubo en cinco pirámides cuadradas.
4
- Descomposición en seis pirámides iguales (escena 4).
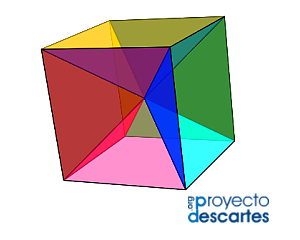
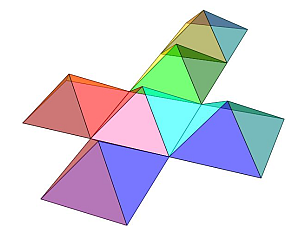
Escena 4. Descomposición de un cubo en seis pirámides cuadradas iguales.
Estas cuatro descomposiciones no son más que situaciones particulares de una partición general del cubo que se realiza en base a los ocho vértices y a un punto adicional del mismo. Veámoslo a continuación.
1.2 Descomposición general
Para construir una partición del cubo en pirámides cuadradas es necesario, obligatorio, utilizar los ocho vértices del cubo y las doce aristas del mismo. Adicionalmente hay que seleccionar o marcar cuál o cuáles serán las cúspides de las pirámides a construir. La introducción de puntos adicionales a los vértices hará que aumente el número de combinaciones de cinco puntos que pueden realizarse y consecuentemente podrá incrementarse el número de pirámides de la partición (no todas las combinaciones posibles de vértices son viables para obtener una partición del cubo). Pasemos analizar diferentes alternativas:
- No incluir ningún punto adicional Esta elección obliga a que la cúspide de cada pirámide sea uno de los vértices del cubo y si además imponemos que todas las pirámides compartan la misma cúspide entonces obviamente obtendremos la partición de cardinal mínimo. Este
5
planteamiento es viable pues basta seleccionar un vértice del cubo y desde él trazar segmentos a cada uno de los otros siete vértices, ello conduce a la partición en tres pirámides que ha sido reflejada en el primer caso descrito antes (escena 1). La partición es única pues, se elija el vértice que se elija, todas las particiones son congruentes mediante giros.
- Añadir un punto adicional. Este punto sería la cúspide común de todas las pirámides a construir para que así el número de éstas sea lo menor posible y constructivamente se procede igual que en el caso anterior trazando segmentos desde la cúspide común a los vértices del cubo. Dicho punto adicional ha de pertenecer al cubo, bien a su interior o a la frontera y por tanto podemos distinguir las siguientes situaciones:
- Punto perteneciente a una arista (ver figura 1). Aquí obtendremos una partición compuesta por cuatro pirámides. En general las cuatro son distintas, pero entre dos de ellas se da siempre una congruencia (una es simétrica de la otra). Y hay un caso particular en el que las pirámides son iguales dos a dos, que es el segundo caso expuesto en la sección anterior, y que acontece cuando el punto adicional considerado es el punto medio de la arista. La arista a la que pertenezca el punto no introduce ninguna variación. Todas serán situaciones congruentes.
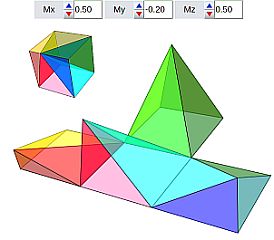
Figura 1. Punto ubicado en una arista, descomposición en cuatro pirámides.
- Punto perteneciente a una cara (ver figura 2). Este caso conduce a la partición en cinco pirámides y de las infinitas posibilidades la situación con más regularidad es
- Punto perteneciente a una arista (ver figura 1). Aquí obtendremos una partición compuesta por cuatro pirámides. En general las cuatro son distintas, pero entre dos de ellas se da siempre una congruencia (una es simétrica de la otra). Y hay un caso particular en el que las pirámides son iguales dos a dos, que es el segundo caso expuesto en la sección anterior, y que acontece cuando el punto adicional considerado es el punto medio de la arista. La arista a la que pertenezca el punto no introduce ninguna variación. Todas serán situaciones congruentes.
6
- cuando el punto elegido es el punto donde se intersecan las diagonales de la cara. Es el tercer caso expuesto con anterioridad. La partición, salvo isometrías, es independiente de la cara seleccionada.
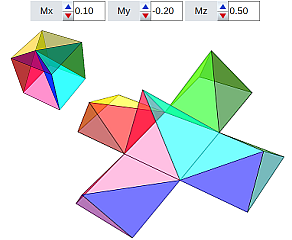
Figura 2. Punto ubicado en una cara, descomposición en cinco pirámides.
- Punto perteneciente al interior del cubo (ver figura 3). Esta situación hace que sean seis pirámides las que forman la partición. De las infinitas particiones posibles, cuando el punto seleccionado es el punto de intersección de las diagonales del cubo se tiene que las seis pirámides son iguales y regulares, éste es el cuarto caso mostrado antes.
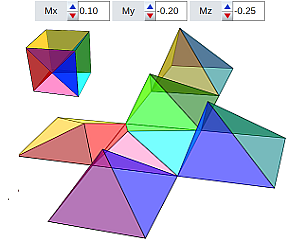
Figura 3. Punto ubicado en el interior del cubo, descomposición en seis pirámides.
7
Todas las situaciones anteriores pueden experimentarse en el recurso interactivo “Partición de un cubo en pirámides de base cuadrada, caso general” con el que se puede interactuar en la escena número 5.
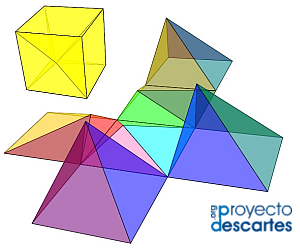
Escena 5. Partición de un cubo en pirámides cuadradas, caso general. |
Hemos de señalar que aunque todas las descomposiciones del cubo cumplen la definición matemática de partición, su reproducción física tiene ciertos matices que hay que reseñar. Por un lado, si disponemos de las pirámides podremos componer el cubo, pero si partimos de un cubo no podrá descomponerse en esas pirámides si esta descomposición se realiza efectuando solamente cortes mediante planos en la que cada uno de ellos fracciona una figura en otras dos independientes o separadas, es decir, lo equivalente a físicamente cortar y dividir en dos partes un objeto con un cuchillo.
8
parte ii
Partición de un cubo en pirámides de base triangular
1. Partición de un cubo en pirámides de base triangular
Podemos plantearnos, al menos, dos procedimientos para descomponer un cubo en pirámides triangulares. Uno, partiendo de las descomposiciones en pirámides de base cuadrada que hemos analizado anteriormente y otro abordando una construcción específica independiente.
1.1 Partición mediante descomposición de pirámides de base cuadrada
Si partimos de las diferentes particiones del cubo en pirámides cuadradas analizadas en la sección anterior, entonces, automáticamente, son conocidas sendas particiones en pirámides triangulares sin más que considerar una de las dos diagonales del cuadrado que constituye la base en cada pirámide. Además las dos subpirámides obtenidas serán equivalentes5, pues la base inicial cuadrada ha quedado dividida en dos partes iguales y la altura es común a ambas y, por tanto, el volumen de cada una de esas pirámides triangulares es la mitad del volumen inicial. En este contexto tendríamos las siguientes situaciones:
- Considerando la partición mínima del cubo en tres pirámides cuadradas obtendríamos una subpartición en seis pirámides triangulares equivalentes. Dado que cada una de las pirámides cuadradas pueden dividirse de dos formas diferentes, según cual sea la diagonal del cuadrado que se considere, tendríamos a su vez varias posibilidades:
- Si la diagonal que se considera conduce a dividir la pirámides cuadradas por su plano de simetría, entonces las seis pirámides son congruentes ya que hay tres coincidentes entre sí mediante traslación y giro (lo que de manera simplificada se suele indicar como iguales) y las otras tres son simétricas de las primeras ―denotaremos a una de las pirámides como tipo X1 y a su simétrica como X2 ―. La partición sería {X1, X2, X1, X2, X1, X2 }. Este caso es el que usualmente puede encontrarse en las fuentes literarias clásicas y en la Web, y que se reproduce de manera interactiva en la escena 6. Veremos que es una situación particular del estudio global que abordaremos en la siguiente sección, correspondiente a lo que denominaremos particiones prismáticas porque agrupando esas pirámides de tres en tres el cubo queda descompuesto en dos prismas triangulares. Este proceso de división podría repetirse considerando la mediana de las nuevas bases y así
11
obtendríamos una partición con doce pirámides equivalentes y dos familias de 6 pirámides congruentes entres sí; y con una nueva división por la mediana serían 24 pirámides equivalentes y 4 familias congruentes y, en general 3•2n pirámides equivalentes y 2n-1 familias de pirámides congruentes entre sí. Un entretenimiento teórico bonito, pero que rápidamente su traslación a un contexto manipulativo no sería físicamente viable.
Escena 6. Partición de un cubo en seis pirámides triangulares congruentes. |
- Si se considera la diagonal perpendicular al plano de simetría, cada pirámide cuadrada queda divida en dos pirámides equivalentes. La partición cuenta con dos tipos de pirámides (interactuar en la escena 7) que denotaremos como tipo Y (la que cuenta con un triedro trirrectángulo) y la otra que nombraremos tipo Z. La partición es {Y, Z, Y, Z, Y, Z }. Esta partición, a diferencia del caso anterior no es prismática.
- Si se combinan las dos posibilidades anteriores se obtienen siempre seis pirámides equivalentes, pero habría dos posibilidades: {X1, X2, X1, X2, Y, Z } o {X1, Y, Z, X2, Y, Z } que también son casos particulares de particiones prismáticas que analizaremos posteriormente.
- Análogamente, en el caso de hacer sólo una subdivisión por cada pirámide cuadrada, la partición en cuatro pirámides cuadradas se convertiría en ocho triangulares, la de cinco en diez y la de seis en doce. En la escena 8 la imagen refleja una partición en doce pirámides triangulares e interactuando con ella pueden reproducirse todas estas situaciones.
12
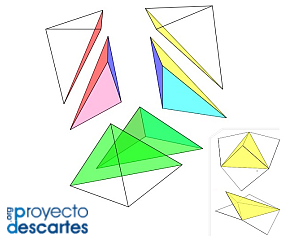
Escena 7. Partición no prismática de un cubo en seis pirámides triangulares equivalentes. |
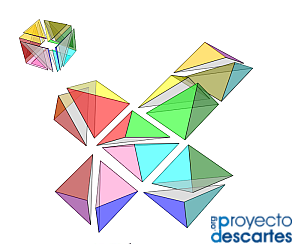
Escena 8. Partición de un cubo en pirámides triangulares por división de pirámides cuadradas, caso general. |
Todas las situaciones anteriores son, o pueden considerarse, interesantes y conducentes a puzles de cierta dificultad tanto en los casos en los que se busca la máxima congruencia o regularidad, como en la posición contraria. Pero ninguna de ellas conduce a la partición con cardinal mínimo, pues el planteamiento realizado viene condicionado por la partición previa en pirámides de base cuadrada. La partición mínima, como veremos en la próxima sección, se corresponde con cinco pirámides y salvo isometrías hay una única posibilidad para su construcción. Por ello, nuestro centro de interés se focalizará posteriormente en la citada descomposición prismática del cubo en seis pirámides triangulares equivalentes, que sin ser el caso único de cardinal mínimo sí que genera una variedad de situaciones que nos proponemos cuantificar y detallar.
1.2 Partición mediante construcción específica
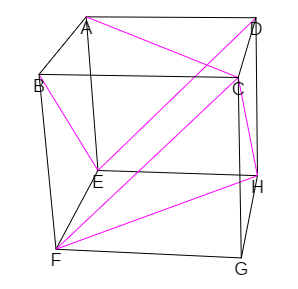
En este apartado partiendo de un cubo de arista la unidad y de vértices {A, B, C, D, E, F, G, H } ―donde los cuatro primeros vértices constituyen la base superior y los otros cuatro la inferior―, nos planteamos realizar una partición del mismo en pirámides triangulares buscando por un lado que la descomposición tenga cardinal mínimo y, por otro, buscando alternativas en las que sin ser de cardinal mínimo se encuentren congruencias o equivalencias.
13
Dado que las pirámides triangulares son poliedros convexos con cuatro caras triangulares (es decir tetraedros) y cuatro vértices, en la planificación de esta partición han de tenerse en consideración las siguientes observaciones:
- Las caras del cubo han de dividirse en triángulos y, por tanto, se parte de un mínimo de 12 triángulos (2 por cada cara del cubo) y 18 segmentos (las doce aristas del cubo, más seis diagonales necesarias para partir cada una de las seis caras del cubo), que junto a los ocho vértices constituyen los elementos primarios a partir de los cuales se han de construir las pirámides de la partición (escena 9).
- El menor número de pirámides se obtiene cuando se consideran exclusivamente los elementos primarios citados. La introducción de cualquier vértice o segmento adicional generará un mayor número de combinaciones posibles, un mayor número de pirámides.
- Dos pirámides de la partición pueden compartir como máximo tres vértices, una cara. O lo que es equivalente han de tener tres caras diferentes.
- Una pirámide triangular de la partición queda determinada sin más que elegir dos segmentos con distinta dirección y que no sean coplanarios (escena 10).
14
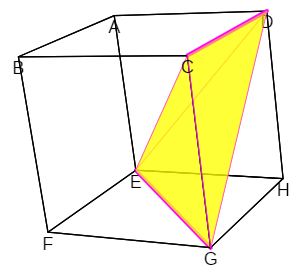
- Cuando todas las diagonales correspondientes a las caras opuestas tienen distinta dirección las particiones en pirámides triangulares tienen más de seis pirámides, salvo:
- Una partición con cinco elementos, que es la de cardenal mínimo, formada por cuatro pirámides trirrectángulas y un tetraedro regular (escena 11).
- Una con seis elementos, que es la indicada en la escena 7, compuesta por las pirámides {Y, Z, Y, Z, Y, Z }.
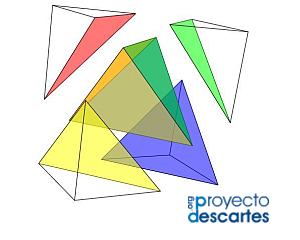
Escena 11. Descomposición de un cubo en cinco pirámides triangulares.
- Cuando al menos un par de las diagonales correspondientes a caras opuestas tienen la misma dirección entonces ese par junto a las dos aristas que son perpendiculares a ellas forman un rectángulo y la partición en pirámides triangulares es posible sólo si se introduce al menos un segmento que bien subdivida ese rectángulo en dos triángulos o bien que lo corte (ver escena 12). Al introducirse en la partición un nuevo elemento primario no puede obtenerse la partición de cardinal mínimo. Ese segmento adicional puede ser:
- Una diagonal del cubo. Aquí la obtención de una partición obliga a incluir más elementos primarios, puntos y segmentos, y consecuentemente se incrementa el número de pirámides obtenidas.
- La diagonal de ese rectángulo. En este caso el cubo queda dividido en dos prismas triangulares rectos con bases que son triángulos rectángulos isósceles ―particiones prismáticas―, situación que detallaremos a continuación y que como veremos conduce a un mínimo de seis pirámides triangulares; y en el caso de ser exactamente seis se cumple que son equivalentes, es decir, que tienen igual volumen.
15
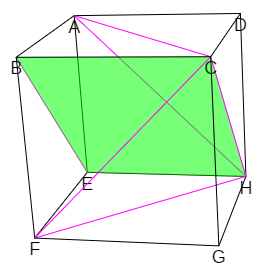
Escena 12. Dos diagonales de caras opuestas que tienen la misma dirección (coplanarias). |
2 Descomposición de un prisma triangular en pirámides triangulares
Con la partición en dos prismas triangulares, indicada en la sección anterior, el problema de partir un cubo queda reducido a la descomposición de un prisma triangular recto, cuyas bases son dos triángulos rectángulos isósceles de catetos 1 y de altura también 1, en pirámides triangulares. Situación que pasamos a analizar en este apartado.
Denotemos los vértices del prisma anterior {A, B, C, E, F, G } donde la base superior se corresponde con los tres primeros vértices y la inferior con los tres últimos (ver la figura 4).
De manera análoga a lo indicado en la sección anterior tenemos:
- El menor número de pirámides se obtendrá cuando se consideren sólo los seis vértices del prisma como posibles vértices de las pirámides de la partición.
- Los elementos primarios mínimos para abordar la partición son ocho triángulos (las dos bases del prisma y seis más resultantes de dividir las tres caras laterales en triángulos) y 12 segmentos (las nueve aristas y las tres diagonales de las caras laterales). Y dado que dos pirámides de la partición han de tener como mínimo tres caras diferentes, entonces también
16
son tres, como mínimo, las pirámides que formarán la partición (ocho caras entre tres nos da un valor mayor que dos).
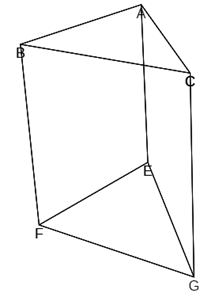
Figura 4. Prisma triangular. |
Basándonos en que una pirámide triangular queda determinada sin más que elegir dos segmentos con distinta dirección no coplanarios, una forma de abordar la partición del prisma {A, B, C, E, F, G } en tres pirámides triangulares se logra considerando dos aristas no coplanarias, una de la base ABC y otra de la EFG (escena 13). Los cuatro vértices de esas dos aristas determinan una pirámide triangular que parte al prisma en tres bloques quedando fijadas así, junto a ésta, las otras dos pirámides buscadas.
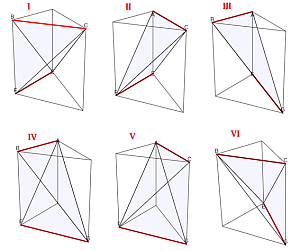
Hay sólo seis posibilidades:
- ― BC con EF que conduce a la pirámide BCEF y determina a ABCE y CEFG
- ― AC con EF que conduce a ACEF y determina a ABCF y CEFG
- ― AB con EG que conduce a ABEG y determina a ABCG y BEFG
- ― AB con FG que conduce a ABFG y determina a ABCG y AEFG
- ― AC con FG que conduce a ACFG y determina a ABCF y AEFG
- ― BC con EG que conduce a BCEG y determina a ABCE y BEFG
17
|
|
Escena 13. Aristas que determinan las seis particiones diferentes. |
|
Distinguiendo los vértices por su nombre, en esas seis particiones aparecen doce pirámides diferentes, lo cual obviamente se corresponde con las combinaciones que se pueden obtener a partir de los seis vértices {A, B, C, E, F, G } agrupándolos de cuatro en cuatro, que son los vértices de una pirámide, y quitando aquellas agrupaciones en las que los cuatro vértices son coplanarios. Así pues, son C6, 4 = 15 combinaciones diferentes {ABCE, ABCF, ABCG, ABEF, ABEG, ABFG, ACEF, ACEG, ACFG, AEFG, BCEF, BCEG, BCFG, BEFG, CEFG} y se excluyen los tres casos que hemos tachado por ser cuatro vértices coplanarios. Éste podría ser también otro procedimiento alternativo al anterior para analizar las diferentes particiones del prisma.
En esas doce pirámides intervienen 15 aristas posibles, pues son combinaciones de seis vértices tomados de dos en dos, C6, 2 = 15. Son las reflejadas en la tabla 1, donde se indica su medida respectiva.
En la tabla 2 podemos agrupar toda la información anterior y comparar las pirámides de esas particiones buscando detectar cuales son iguales o del mismo tipo. Fijándonos en la medida de las aristas que las componen se observa que hay tres tipos de pirámides que hemos etiquetado como X, Y, Z y, como detallaremos a continuación, en el tipo X se distinguen dos modalidades que etiquetamos como 1 y 2. También se refleja si la partición está constituida por pirámides congruentes entre sí (y por tanto también equivalentes) o si son sólo equivalentes.
18
| AB=1 |
||||
| AC=√2 |
BC=1 |
|||
| AE=1 |
BE=√2 |
CE=√3 |
||
| AF=√2 |
BF=1 |
CF=√2 |
EF=1 |
|
| AG=√3 |
BG=√2 |
CG=1 |
EG=√2 |
FG=1 |
Tabla 1. Aristas de las pirámides y longitud de las mismas.
| Partición |
Pirámide |
Aristas |
Tipo |
Modalidad |
Congruencia Equivalencia |
| I |
ABCE |
1, 1, 1, √2, √2, √3 |
X |
2 |
Congruencia |
| BCEF |
1, 1, 1, √2, √2, √3 | X |
1 |
||
| CEFG |
1, 1, 1, √2, √2, √3 | X |
2 |
||
| II |
ABCF |
1, 1, 1, √2, √2, √2 |
Y |
Equivalencia |
|
| ACEF |
1, 1, √2, √2, √2, √3 |
Z |
|||
| CEFG |
1, 1, 1, √2, √2, √3 |
X |
2 |
19
| Partición |
Pirámide |
Aristas |
Tipo |
Modalidad |
Congruencia Equivalencia |
| III |
ABCG |
1, 1, 1, √2, √2, √3 |
X |
1 |
Equivalencia |
| ABEG |
1, 1, √2, √2, √2, √3 | Z |
|
||
| BEFG |
1, 1, 1, √2, √2, √2 | Y |
|
||
| IV |
ABCG |
1, 1, 1, √2, √2, √3 |
X |
1 |
Congruencia |
| ABFG |
1, 1, 1, √2, √2, √3 |
X |
2 |
||
| AEFG |
1, 1, 1, √2, √2, √3 |
X |
1 |
||
| V |
ABCF |
1, 1, 1, √2, √2, √2 |
Y |
Equivalencia |
|
| ACFG |
1, 1, √2, √2, √2, √3 | Z |
|
||
| AEFG |
1, 1, 1, √2, √2, √3 | X |
1 |
||
| VI |
ABCE |
1, 1, 1, √2, √2, √3 |
X |
2 |
Equivalencia |
| BCEG |
1, 1, √2, √2, √2, √3 |
Z |
|||
| BEFG |
1, 1, 1, √2, √2, √2 |
Y |
Tabla 2. Desglose de particiones, pirámides que lo conforman,
longitud de las aristas que lo componen, tipo de pirámide y modalidad, y congruencia y/o equivalencia.
20
Cada partición del prisma la vamos a distinguir con el número romano que le hemos asignado o sin más que nombrar los tipos de pirámide que la forman para lo que convendremos hacerlo de arriba hacia abajo de acuerdo a la ubicación inicial de la pirámide en la que la base superior tiene de vértices ABC y la inferior EFG. Así la partición II viene dada por {Y, Z, X2 }.
Procedamos a analizar cada uno de los tipos de pirámides que aparecen en dichas particiones.
2.1 Pirámide tipo Y
Atendiendo sólo a la forma, es decir, considerando que todas las caras son de igual color y no etiquetando los vértices, sólo es posible una pirámide triangular cuyas aristas midan 1, 1, 1,√2 ,√2,√2 (escena 14). Su desarrollo plano está compuesto por un triángulo equilátero de lado √2 y tres triángulos rectángulos isósceles de catetos 1 y de hipotenusa√2. El desarrollo, como se ha representado en la figura, tiene simetría axial con eje de simetría cualquiera de las alturas del triángulo equilátero y por tanto, independientemente de la orientación con la que se realiza el plegado (hacia dentro o hacia fuera) se obtiene la misma pirámide. El volumen de esta pirámide es 1/6 u3.
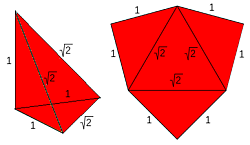
Escena 14. Pirámide triangular tipo Y y desarrollo plano de la misma. |
2.2 Pirámide tipo Z
De manera análoga al caso anterior, si atendemos sólo a la forma, sólo es posible una pirámide triangular cuyas aristas midan 1, 1, √2 ,√2, √2, √3 (escena 15). Su desarrollo plano está compuesto por un triángulo equilátero de lado √2, un rectángulo isósceles de catetos 1 e hipotenusa√2 y dos triángulos rectángulos de catetos 1 y√2e hipotenusa√3. Este desarrollo, como está representado en la figura, tiene simetría axial con eje de simetría la altura del triángulo
21
equilátero que es altura a la vez del triángulo rectángulo isósceles. Así pues, independientemente de la orientación con la que se realiza el plegado (hacia dentro o hacia fuera) se obtiene la misma pirámide. El volumen de esta pirámide es también 1/6 u3, por tanto, equivalente a la pirámide tipo Y.
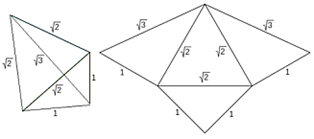
Escena 15. Pirámide triangular tipo Z y desarrollo plano de la misma. |
2.3 Pirámides tipo X
Con las aristas de medidas 1, 1, 1,√2,√2,√3 se pueden construir dos pirámides triangulares siendo una simétrica de la otra (escena 16). Los desarrollos planos son simétricos entre sí. Eligiendo uno de ellos, si se pliega hacia dentro se obtiene una de las pirámides y al plegarlo hacia fuera se obtiene la otra. Ambas tienen de volumen 1/6 u3, es decir, son equivalentes entre sí y a las pirámides Y y Z.
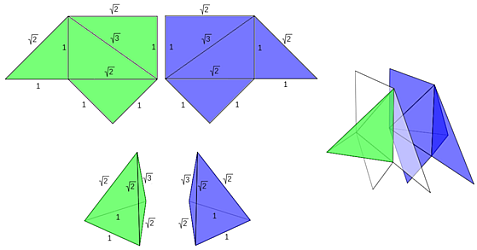
Escena 16. Pirámides triangulares tipo X —X |
22
Ambas pirámides X1 y X2 son simétricas, una respecto a la otra, en el sentido de que si hacen coincidir dos caras que sean iguales el plano que separa a ambas pirámides es un plano de simetría de las mismas. Por tanto, congruentes entre sí.
2.4. Particiones del prisma triangular
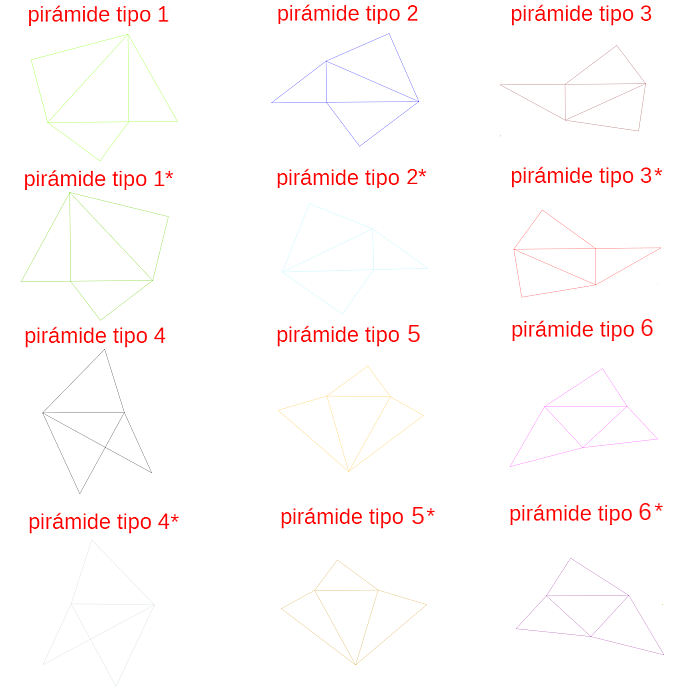
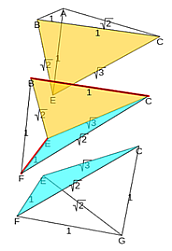
Las seis particiones del prisma reflejadas en la tabla 2 están representadas en la escena 17, donde se han mantenido los colores usados anteriormente en cada tipo de pirámide para así poder distinguir a simple vista cuál es la pirámide utilizada: rojo para tipo Y, blanco para tipo Z, azul para X1 y verde para X2.
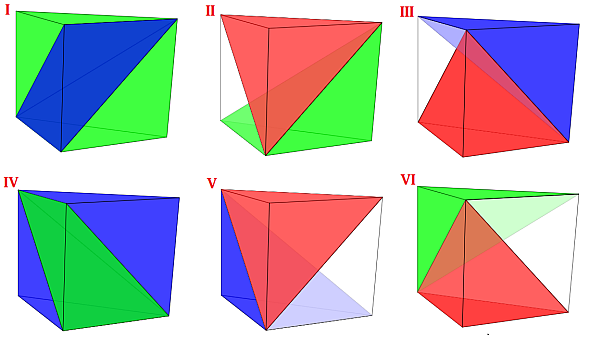
Escena 17. Particiones del prisma triangular. |
Sin embargo, de esas seis particiones hay solamente dos que no son congruentes entre sí, pues tenemos que se cumplen las siguientes relaciones (escena 18):
23
- Las particiones II, III, V y VI son congruentes entre sí:
- La partición tipo V —compuesta por las pirámides Y, Z, X1— es congruente con la III —compuesta por las pirámides X1, Z, Y—, basta realizar un giro de 180º.
- La partición VI —compuesta por las pirámides X2, Z, Y— es congruente con la II —compuesta por las pirámides Y, Z, X2— mediante un giro.
- La partición tipo V —compuesta por las pirámides Y, Z, X1— es congruente con la II —compuesta por las pirámides Y, Z, X2— mediante una simetría (según lo indicado con anterioridad Y es simétrica de sí misma, Z también, y X1 es simétrica de X2).
- Las particiones I y IV son congruentes entre sí:
- La partición IV —compuesta por las pirámides X1, X2, X1— es simétrica de la I —compuesta por las pirámides X2, X1, X2—.
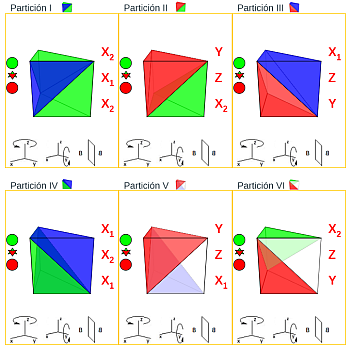
Escena 18. Comparación entre las particiones del prisma triangular. |
24
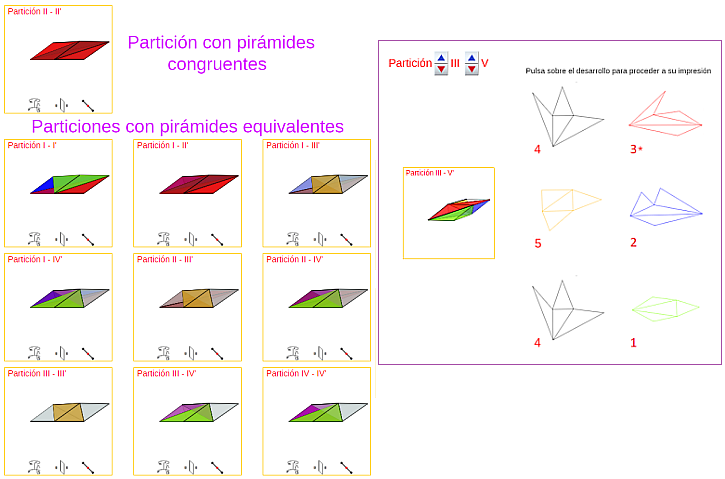
Así pues, salvo isometrías, sólo hay dos particiones diferentes del prisma en pirámides triangulares (escena 19). Basta considerar, por ejemplo, la partición I y la II.
Adicionalmente se verifica que en la partición tipo I las pirámides que la componen son congruentes entre sí (y consecuentemente equivalentes) y en la tipo II son sólo equivalentes.
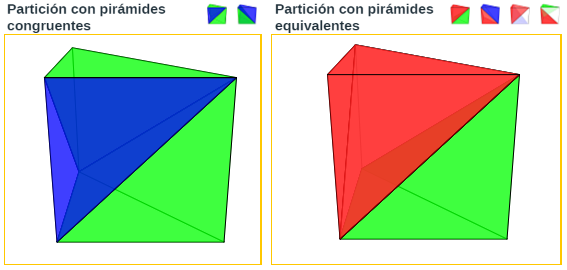
Escena 19. Partición con piramides congruentes y partición con pirámides equivalentes. |
En la escena 20 se refleja un modelo en papel de las particiones obtenidas y de la relación existente entre ellas.

Escena 20. Modelo en papel. |
25
Todas las escenas correspondientes al análisis de la partición de un prisma triangular en pirámides triangulares equivalentes están englobadas en el recurso interactivo incluido en la escena 21.
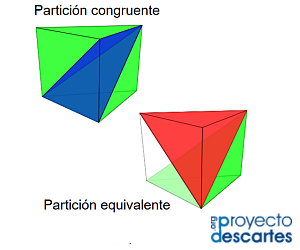
Escena 21. Partición de un prisma triangular en pirámides triangulares equivalentes. |
3. Partición prismática de un cubo en pirámides triangulares equivalentes
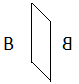
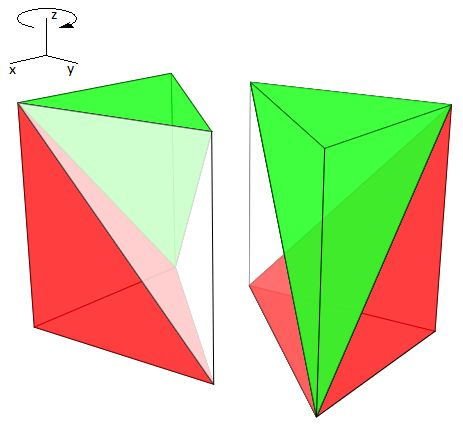
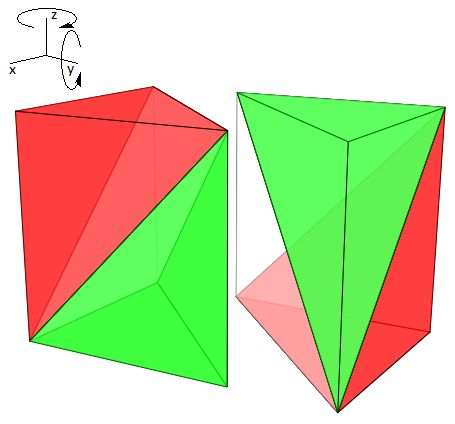
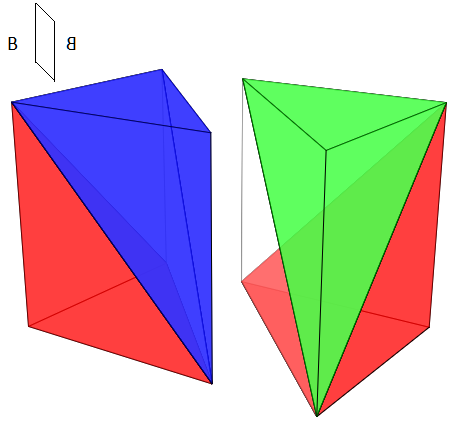
Para construir una partición prismática del cubo basta considerar una de las particiones del prisma triangular obtenidas en el apartado anterior y aplicarle isometrías para transformarlo en otro prisma y al juntar los dos juntos se conforma la partición del cubo buscada. En la tabla 3 se reflejan las posibles transformaciones isométricas a realizar para construir esa partición del cubo.
En esta construcción podemos realizar dos planteamientos. Una primera opción en la que consideramos como distinguibles las seis particiones obtenidas para el prisma y una segunda en la que la construcción la abordamos considerando sólo las dos particiones no congruentes del prisma. La primera opción tiene como ventaja el poder ver todas las particiones posibles, agrupadas por congruencia, y la segunda el ser un análisis más breve.
26
|
|
|
|
|
|
| Giro alrededor del eje Oz | Giros alrededor del eje Oz y del eje Oy | Simetría respecto a un plano |
Tabla 3. Isometrías para obtener un cubo a partir de un prisma triangular.
3.1 Opción A
Consideramos como distinguibles las seis particiones del prisma y procedemos a construir el cubo a partir de ellas. Para ello, en la tabla 4 hemos indicado cómo se transforman esas seis particiones cuando les aplicamos las isometrías indicadas en la tabla 3.
Las seis particiones se transforman en las mismas seis. Consecuentemente, las diferentes particiones del cubo en seis pirámides equivalentes se obtienen sin más que hallar las variaciones con repetición de 6 elementos (las particiones del prisma I, II, III, IV, V y VI) tomados de dos en dos, es decir, un total de VR6,2 = 62 = 36 posibilidades. Pero entre ellas hay congruencias que hemos de detectar.
27
| Partición |
Giro z |
Giro z, y |
Simetría |
| I = X2, X1, X2 |
X2, X1, X2 = I |
X2, X1, X2 = I |
X1, X2, X1 = IV |
| II = Y, Z, X2 |
Y, Z, X2 = II |
X2, Z, Y = VI |
Y, Z, X1 = V |
| III = X1, Z, Y |
X1, Z, Y = III |
Y, Z, X1 = V |
X2, Z, Y = VI |
| IV = X1, X2, X1 |
X1, X2, X1 = IV |
X1, X2, X1 = IV |
X2, X1, X2 = I |
| V = Y, Z, X1 |
Y, Z, X1 = V |
X1, Z, Y = III |
Y, Z, X2 = II |
| VI = X2, Z, Y |
X2, Z, Y = VI |
Y, Z, X2 = II |
X1, Z, Y = III |
Tabla 4. Aplicación de isometrías a las seis particiones de un prisma.
De partida, al comparar esas 36 posibilidades, se observa que un tipo de partición P2-P1 es congruente con la P1-P2 sin más que realizar un giro de 180º alrededor de la vertical (eje Oz) y, por tanto, quedan reducidas a 21 las posibles particiones (combinaciones con repetición CR6,2):
{I-I, I-II, I-III, I-IV, I-V, I-VI, II-II, II-III, II-IV, II-V, II-VI,
III-III, III-IV, III-V, III-VI, IV-IV, IV-V, IV-VI, V-V, V-VI, VI-VI}
Y en particular, entre ellas, hay tres casos en los que todas las pirámides son congruentes entre sí:
{I-I, I-IV, IV-IV}
Puede observarse en la escena 22.
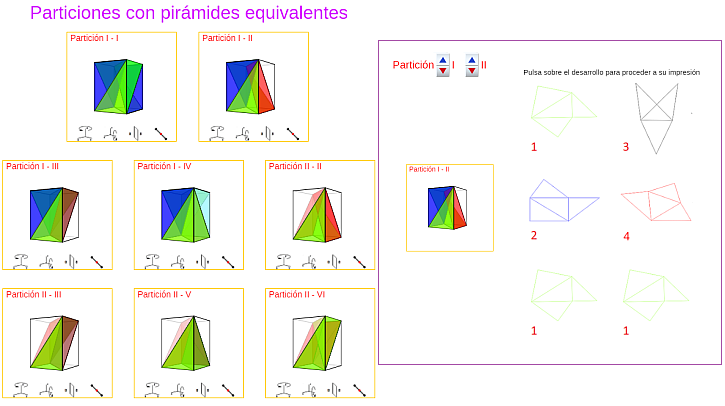
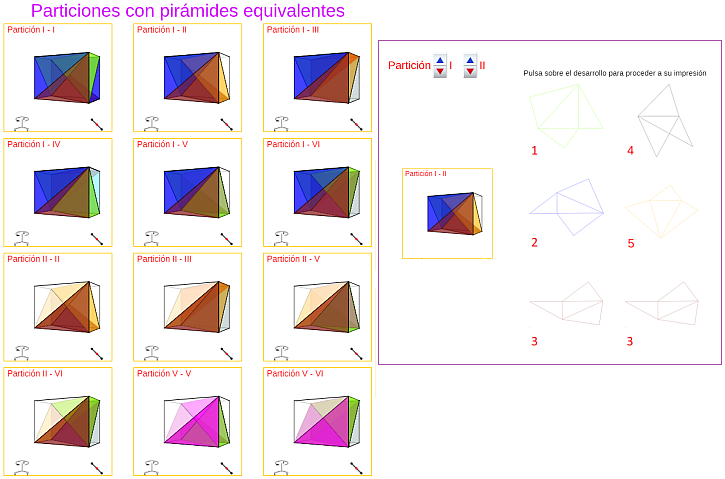
La aplicación de las isometrías, indicadas en la tabla 4, a cada una de las 36 particiones anteriores conduce a las particiones indicadas en la tabla 5, y en la tabla 6 reflejamos las congruencias existentes que reducen a ocho las particiones diferentes del cubo en pirámides equivalentes (escena 23):
{I-I , I-II, I-III, I-IV, II-II, II-III, II-V, II-VI}.
28
Entre ellas hay dos: {I-I, I-IV} que, en particular, están formadas por pirámides congruentes entre sí.

Escena 22. Congruencias mediante giro Oz de 180º. |
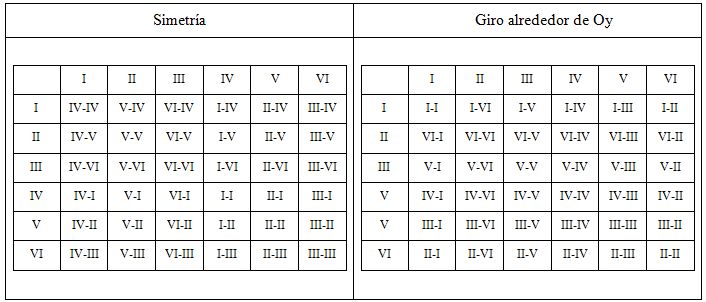
Tabla5. Aplicación de isometrías a las treinta y seis particiones prismáticas del cubo. |
29
Tabla 6. Detección de congruencias entre las diferentes particiones del cubo.
31
3.2 Opción B
En este caso consideramos exclusivamente las dos particiones diferentes del prisma (I y II), junto a sus congruencias respectivas (IV y III, V, VI) y abordemos las combinaciones de las mismas para formar el cubo. Esto nos lleva al detalle reflejado en la tabla 7:
Tabla 7. Las diferentes particiones del cubo, salvo isometrías.
32
3.3 Síntesis
Independientemente de la opción o camino seleccionado del análisis anterior se concluye que, salvo isometrías, hay sólo ocho formas diferentes de descomponer prismáticamente el cubo en seis pirámides equivalentes y entre ellas hay dos en las que todas las pirámides son también congruentes entre sí (todo queda desarrollado y englobado en la escena 24).
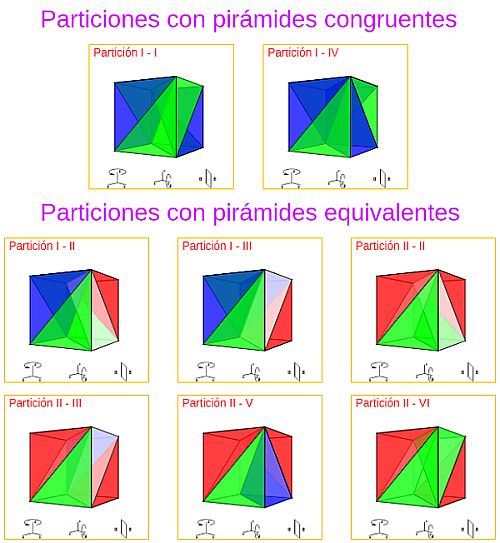
Escena 24. Síntesis de la partición prismática de un cubo en pirámides equivalentes. |
33
parte iii
Partición de un hexaedro convexo de caras cuadriláteras en pirámides de base cuadrilátera
Partición de un hexaedro convexo {4,4,4,4,4,4} en pirámides de base cuadrilátera
Un cubo es un caso particular de paralelepípedo y éste lo es de un hexaedro convexo de caras cuadriláteras, es decir, de un poliedro convexo que cuenta con ocho vértices, doce aristas y seis caras cuadriláteras que podemos representar como {4, 4, 4, 4, 4, 4}. Por la similitud de forma y propiedades entre estos poliedros es lógico plantearse la extensión del análisis realizado en la partición del cubo en pirámides cuadradas a a la partición de estos hexaedros en pirámides de base cuadrilátera y es lo que procederemos a realizar a continuación.
El procedimiento para realizar la partición en pirámides cuadriláteras será el mismo abordado en el caso del cubo, es decir, elegir un punto del interior o de la frontera del poliedro considerado y desde él trazar segmentos que lo unan con los ocho vértices y se reproducirán las situaciones observadas antes:
- Si el punto considerado es un vértice la descomposición estará compuesta por tres pirámides cuadriláteras.
- Si el punto pertenece a una arista serán cuatro las pirámides obtenidas.
- Si el punto es del interior de una cara son cinco las pirámides.
- Si el punto es del interior del hexaedro serán seis las pirámides.
Lo que obviamente cambiará es la regularidad y congruencia entre las pirámides obtenidas ya que ésta depende de la regularidad del poliedro inicial considerado.
Desde el punto de vista teórico la abstracción permite iniciar el planteamiento sin más que marcar “sea un paralelepípedo o sea un hexaedro convexo de caras cuadriláteras”, pero la definición de uno y otro a nivel técnico conlleva el establecimiento de los datos mínimos que determinan dichos poliedros, facilitar la introducción de estos datos al usuario y controlar que efectivamente los datos aportados por el mismo son conducentes a un sólido en la situación aquí considerada y advertir en caso de no serlo. Es un hecho habitual que cuando se desea controlar informáticamente la definición genérica de un objeto matemático su control no sea siempre algo obvio y requiera planteamientos adicionales que sin embargo quedan como evidentes en la
37
formulación académica. Por ejemplo: ¿cómo puede un usuario definir el hexaedro de caras cuadriláteras que desee? y ¿cómo puede controlar el programador que efectivamente sea un hexaedro convexo con esas caras? Son ejemplos, en este contexto, de lo que podemos catalogar como “la obviedad de los problemas académicos que obviamos los matemáticos”. Pero en este caso tendremos que marcar y mostrar el detalle de esa obviedad.
En general todo poliedro convexo queda determinado por un sistema de inecuaciones
Mx ≤ b
donde M es una matriz real de dimensión s×3 y b un vector de s componentes, no obstante estimamos que éste quizás no sea el medio más explícito para la definición interactiva del mismo, por ello vamos a considerar su definición a partir de un número mínimo de vértices y/o direcciones de las aristas. Comenzaremos con un paralelepípedo y después abordaremos el caso más general del hexaedro convexo {4,4,4,4,4,4}.
1.1 Definición de un paralelepípedo
Un paralelepípedo es un hexaedro convexo de caras cuadriláteras en el que las caras opuestas son paralelas. Hay cuatro tipos de paralelepípedos:
- Cubo con seis caras iguales cuadradas y, por tanto, ortogonales entre sí.
- Ortoedro de caras rectangulares ortogonales entre sí
- Romboedro cuyas seis caras son seis rombos iguales.
- Romboiedro en el que las seis caras son romboides.
Una opción para determinar un paralelepípedo es fijar un vértice y los tres adyacentes a él. En la figura 5, correspondiente a la escena interactiva 25 que es donde se aborda la partición del paralelepípedo, se le ofrece al usuario la posibilidad de modificar el vértice etiquetado como A y los tres adyacentes B, D y E y una vez fijados, dibuja el correspondiente poliedro. La escena clasifica el paralelepípedo y controla si degenera en un polígono.
38
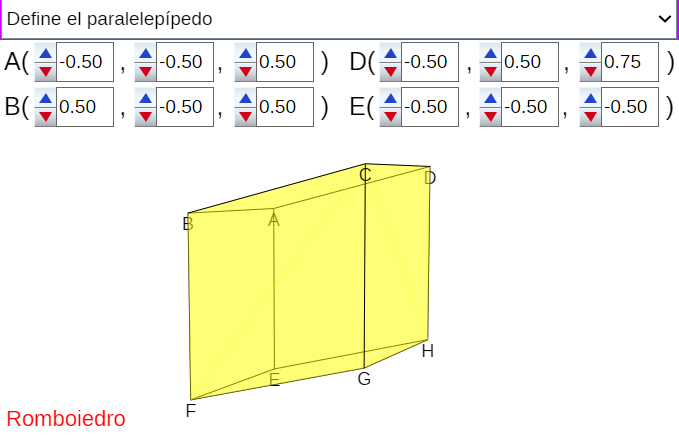
Figura 5. Definición de un paralelepípedo fijando un vértice y otros tres adyacentes a él. |
En dicha escena 25, con objeto de facilitar la reproducción de los diferentes tipos de paralelepípedos y analizar las descomposiciones obtenidas en cada caso particular, se le ofrece al usuario la posibilidad de que seleccione el tipo de paralelepípedo que desea:
- Cubo. Dibuja un cubo de arista unidad, pero la longitud de ésta obviamente no es significativa para la partición. Un mero cambio de escala, una homotecia relaciona a todos los cubos.
- Ortoedro en el que mediante dos controles se permite variar la longitud de las aristas y así poder trabajar con ortoedros que tengan tres o dos dimensiones diferentes e incluso obtener el caso particular del cubo.
- Romboedro en el que basta indicar la amplitud del ángulo agudo, o recto en el caso extremo, que determina el rombo común a todas las caras. Aquí tampoco es significativa la longitud de la arista.
- Romboiedro en general, indicando los cuatro vértices no coplanarios ya señalados.
39
1.2 Partición del paralelepípedo
Definido el paralelepípedo, la partición se aborda seleccionando un punto del interior o de la frontera del mismo. Por defecto se oferta al usuario el punto central o punto medio de una de las cuatro diagonales y se le permite abordar su propia elección. En ésta hay que controlar que el punto sea interior o de la frontera y ello se aborda internamente comprobando que la suma de los volúmenes de las pirámides cuadriláteras construidas con ese punto como cúspide no sea superior al volumen del paralelepípedo original. Interactuar con la escena 25 para experimentar todo lo indicado.
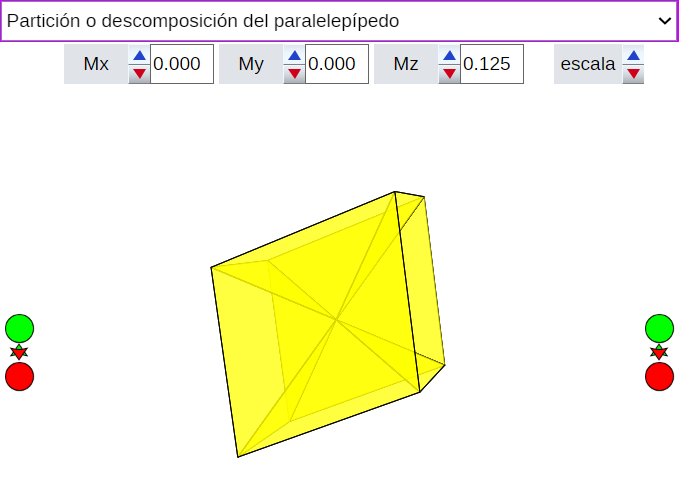
Escena 25. Partición de un paralelpípedo en pirámides de base cuadrilátera. Caso general. |
40
Para cualquier paralelepípedo se verifica que la partición mínima, la de menor número de pirámides, se obtiene cuando el punto común de todas las cúspides de dichas pirámides coincide con un vértice del paralelepípedo. Son tres las pirámides cuadriláteras que componen esa partición y además son equivalentes.
Si bien en la escena 25, sin más que definir adecuadamente los vértices, se puede reproducir la situación antes indicada para cada uno de los tipos de paralelepípedos (cubo, ortoedro, romboedro y romboiedro) en las siguientes escenas se reflejan ejemplos que facilitan la observación de lo señalado en cada situación particular.
Partición de un cubo en tres pirámides cuadriláteras
Este caso ya se ha analizado en detalle en la Parte I, página 3, escena 1.
Partición de un ortoedro en tres pirámides cuadriláteras
En la escena 26 se ha considerado como ejemplo el ortoedro [-0.5, 0]x[-0.5, 1]x[-0.5, 0.5], es decir, con diferentes dimensiones. Como cúspide de las pirámides cuadriláteras se ha tomado el vértice de coordenadas (0, 1, 0.5). Esta escena es la número 25, pero fijando los valores correspondientes a este ejemplo y desactivando los controles que permitirían su modificación.
Escena 26. Un ejemplo de una partición mínima de un ortoedro en pirámides cuadriláteras.
41
Partición de un romboedro en tres pirámides cuadriláteras
La escena 27 refleja un romboedro en el que cada rombo tiene ángulos de 40º y 140º. Como cúspide se ha considerado el vértice etiquetado como C.
Escena 27. Un ejemplo de una partición mínima de un romboedro en pirámides cuadriláteras.
Partición de un romboiedro en tres pirámides cuadriláteras
En la escena 28 puede consultarse un ejemplo de partición de un romboiedro.
Escena 28. Un ejemplo de una partición mínima de un romboiedro en pirámides cuadriláteras.
42
1.3 Definición de un hexaedro convexo {4,4,4,4,4,4}
En este caso una posible alternativa para definir este hexaedro es establecer dos vértices opuestos y para cada uno de ellos marcar la dirección y sentido de las tres aristas que se intersecan en él. Así, para cada vértice se determinan tres planos y si la intersección es adecuada determinan las seis caras cuadriláteras. La escena controla que la intersección de dichos planos sea conducente al deseado hexaedro y aporta detalles de las posibles causas que acontecen cuando el poliedro obtenido no sea del tipo buscado o cuando con los datos aportados no sea posible su construcción. Ver figura 6.
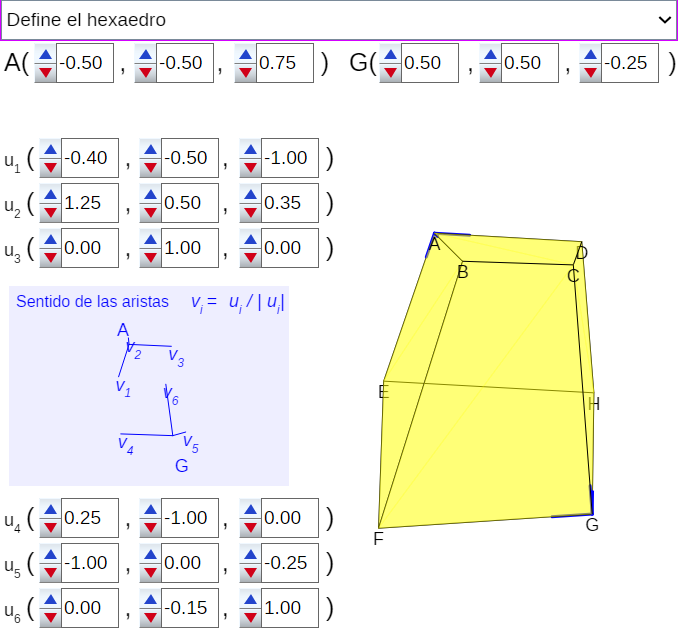
Figura 6. Definición de un hexaedro convexo{4,4,4,4,4,4}. |
43
1.4 Partición del hexaedro convexo
Definido el hexaedro, la partición se realiza seleccionando un punto del interior o de la frontera del mismo. Por defecto se oferta al usuario el punto medio del segmento determinado por los dos vértices que ha fijado el usuario y a partir de él se le permite abordar su propia elección. En ésta hay que controlar que el punto sea interior o de la frontera y ello internamente se aborda comprobando que la suma de los volúmenes de las pirámides cuadriláteras construidas con ese punto como cúspide no sea superior al volumen del hexaedro original.
En la escena 29 se aborda la partición, quedando determinada cada pirámide y se aportan sendos desarrollos planos para que puedan imprimirse y abordar su reproducción física en papel.
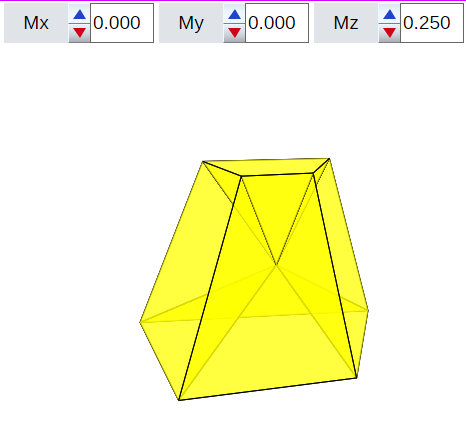
Escena 29. Partición de un hexaedro convexo {4,4,4,4,4,4} en pirámides de base cuadrilátera. Caso general. |
44
parte iv
Partición de un hexaedro convexo de caras cuadriláteras en pirámides de base triangular
Análogamente a lo realizado en el cubo, la partición de un hexaedro convexo de caras cuadriláteras en pirámides de base triangular puede abordarse desde dos perspectivas o procedimientos:
- Descomposición de cada una de las pirámides cuadriláteras obtenidas en la parte III de este artículo en dos triangulares. En este caso, consecuentemente, tendremos que:
- Si el punto considerado es un vértice del hexaedro la descomposición estará compuesta por tres pirámides cuadriláteras que conducen a seis triangulares.
- Si el punto pertenece a una arista serán cuatro las pirámides cuadriláteras obtenidas y ocho las triangulares.
- Si el punto es del interior de una cara son cinco las pirámides cuadriláteras y diez las triangulares.
- Si el punto es del interior del hexaedro serán seis las pirámides cuadriláteras y doce las triangulares.
- Construcción específica.
En el primer caso la partición mínima estará compuesta por seis pirámides triangulares, la correspondiente a la descomposición de la partición en tres pirámides cuadriláteras, pero es imprescindible la segunda perspectiva para poder obtener la partición con menor número de elementos que es la compuesta por cinco pirámides triangulares.
1. Partición de un hexaedro convexo {4,4,4,4,4,4} en pirámides de base triangular por descomposición de pirámides cuadriláteras
Dentro de este apartado analizaremos primero el caso particular del paralelepípedo porque el paralelismo que se exige a sus caras traslada, en determinados casos, algunas de las situaciones observadas en el caso particular del cubo. Por ejemplo, la existencia de particiones prismáticas que para el cubo y el ortoedro son prismas rectos y en el caso del romboedro y romboiedro son prismas inclinados.
47
1.1 Partición de un paralelepípedo mediante división de pirámides cuadriláteras en triangulares
En la escena 30 se puede interactuar para abordar la descomposición de un paralelepídeo en pirámides triangulares mediante la división de las pirámides de base cuadrilátera obtenidas en la parte III (pp. 40-42). La escena permite trabajar con un romboiedro cualquiera o bien seleccionar los casos particulares de romboedro, ortoedro y cubo (este último caso ya se analizó con detalle en la parte I). Seleccionado el paralelepípedo, el usuario fija los elementos que determinan la partición que son: un punto M común a todas las pirámides cuadriláteras de la partición y las diagonales de esas bases cuadriláteras que las dividen en pirámides triangulares.
Escena 30. Partición de un paralelepípedo en pirámides de base triangular
por división de pirámides de base cuadrilátera. Caso general.
La partición mínima de cualquier paralelepípedo mediante este procedimiento conduce a seis pirámides triangulares. Y en este caso podemos observar dos grupos o tipos de particiones:
- No prismáticas. Cuando todas las diagonales consideradas, correspondientes a caras opuestas del paralelepípedo, tienen diferente dirección entre sí.
- Prismáticas. Cuando al menos hay dos caras opuestas en las que las diagonales consideradas son paralelas.
48
En todos los casos las seis pirámides triangulares obtenidas son equivalentes, pues partimos de tres pirámides cuadriláteras ―en concreto las bases son paralelogramos― equivalentes y lo que hacemos es dividir la base cuadrilátera en dos triángulos de igual área y ello es lo que conduce a dos pirámides triangulares cada una con volumen la mitad del volumen de la pirámide cuadrilátera original y, por tanto, equivalentes.
De nuevo, aunque la escena 30 permite reproducir cualquier situación, en las siguientes escenas reflejaremos ejemplos de particiones no prismáticas para cada uno de los tipos particulares de paralelepípedos.
Partición no prismática de un cubo en seis pirámides triangulares
Es el caso particular analizado en la parte II, página 13, escena 7.
Partición no prismática de un ortoedro en seis pirámides triangulares
En la escena 31 se muestra la partición no prismática del ortoedro [-0.5, 0]x[-0.5, 1]x[-0.5, 0.5]. Como cúspide de las pirámides cuadriláteras se ha tomado el vértice de coordenadas (0, 1, 0.5) y para que la partición no sea prismática todas las diagonales que dividen a las caras del ortoedro tienen distinta dirección.
Escena 31. Un ejemplo de una partición no prismática de un ortoedro.
49
En esta partición no prismática y en las análogas que se pueden obtener seleccionando cualquiera de los otros vértices del paralelepípedo se obtienen tres pirámides triangulares trirrectángulas.
Partición no prismática de un romboedro en seis pirámides triangulares
En la escena 32 se muestra la partición no prismática del romboedro construido en base a un rombo de ángulos 40º y 140º y con vértice común el etiquetado como C.
Escena 32. Un ejemplo de una partición no prismática de un romboedro.
Partición no prismática de un romboiedro en seis pirámides triangulares
En la escena 33 puede consultarse un ejemplo de partición de un romboiedro.
Escena 33. Un ejemplo de una partición no prismática de un romboiedro.
50
1.2 Partición de un hexaedro convexo {4,4,4,4,4,4} mediante división de pirámides cuadriláteras en triangulares
La escena 34 permite realizar interactivamente la descomposición de un hexaedro convexo de caras cuadriláteras en pirámides triangulares mediante la división de las pirámides de base cuadrilátera obtenidas en la parte III, p. 44. Como ya se ha indicado, con este procedimiento, la partición mínima está compuesta por seis pirámides triangulares.
Escena 34. Partición de un hexaedro convexo {4,4,4,4,4,4} en seis pirámides triangulares.
Si las diagonales de dos caras opuestas del hexaedro están en un mismo plano, éste divide al hexaedro en dos pentaedros {3,4,4,4,3}, es decir, pentaedros pseudo-prismáticos ―prismas estrictos sólo cuando el hexaedro es un paralelepípedo―. Lo analizaremos posteriormente.
2. Partición de un hexaedro convexo {4,4,4,4,4,4} mediante construcción específica
La determinación de la partición de cardinal mínimo de un hexaedro convexo {4,4,4,4,4,4} en pirámides triangulares requiere abordar una construcción específica y diferente al planteamiento realizado en la sección anterior. Esta construcción sigue un proceso análogo al realizado en la
51
parte II, pp. 13-15, para el caso particular del cubo. Así pues, la partición del hexaedro en pirámides triangulares requiere tener en cuenta las siguientes observaciones:
- El menor número de elementos primarios que tienen que intervenir en la partición son los ocho vértices, las doce aristas y las seis diagonales de las caras. Por tanto, entre las diferentes particiones obtenidas con estos elementos estará la partición mínima buscada (interactuar con la escena 35).
- Una pirámide triangular de la partición queda determinada sin más que elegir dos segmentos con distinta dirección y que no sean coplanarios (escena 36).
2.1 Partición mínima de un paralelepípedo en pirámides triangulares
Según hemos indicado entre los elementos primarios de la partición hemos de considerar seis diagonales, una en cada cara. En particular, en los paralelepípedos sendas diagonales correspondientes a dos caras opuestas o bien son paralelas o bien tienen distinta dirección.
52
Pueden darse, por tanto, las siguientes situaciones:
- Que todas las diagonales tengan distinta dirección, de manera que:
- Si esas seis diagonales no conforman una pirámide única, entonces se obtienen las particiones no prismáticas analizadas en el punto 1.1.
- Si con esas seis diagonales se construye una pirámide triangular, ésta queda ubicada en el interior del paralelepípedo y lo fracciona en cinco pirámides, obteniéndose la partición de cardinal mínimo (escena 37).
Se verifica que las cuatro pirámides exteriores son equivalentes entre sí y el volumen de cada una de ellas es la sexta parte del volumen total y, por tanto, el volumen de la pirámide interior es la tercera parte del total.
Escena 37. Partición de un paralelepído en pirámides triangulares con cardinal mínimo (cinco pirámides).
- Que al menos halla dos diagonales que sean paralelas. En este caso esas dos diagonales determinan un plano que divide al paralelepípedo en dos prismas triangulares, lo cual conduce a particiones prismáticas que analizaremos posteriormente y que contarán como mínimo con seis pirámides triangulares.
2.2 Partición mínima de un hexaedro convexo en pirámides triangulares
Si el hexaedro convexo {4,4,4,4,4,4} no es un paralelepípedo hemos de indicar que la situación análoga a la antes señalada, relativa a diagonales de caras opuestas con diferente dirección, se
53
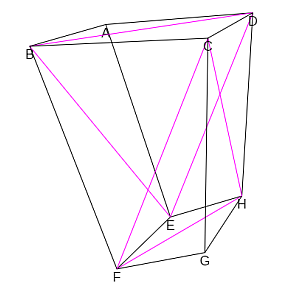
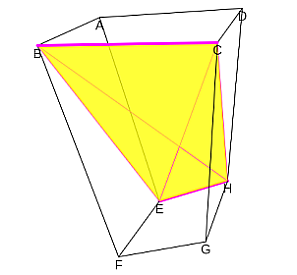
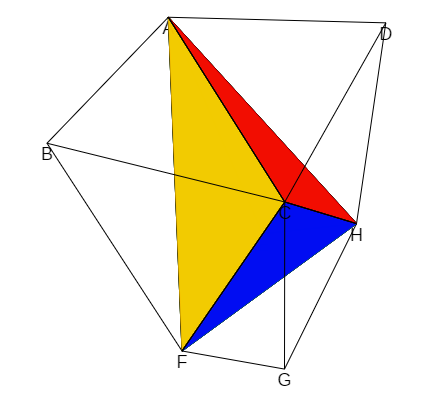
corresponde con diagonales no coplanarias y cuyos vértices no estén conectados mediante alguna arista. Por ejemplo, en la figura 7 podemos observar que la diagonal AC y la FH cumplen ambas condiciones y, sin embargo, AC y EG aunque en general no son coplanarias en este caso están conectadas por las aristas AE y CG.
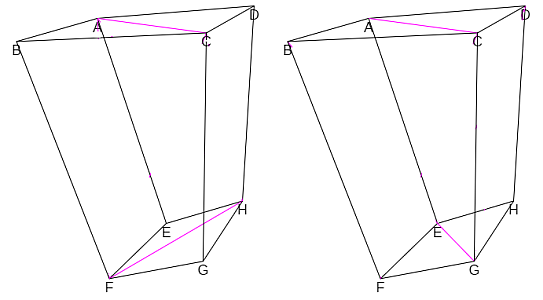
Figura 7. Posición relativa de diagonales de caras opuestas. |
Las posibilidades que pueden acontecer son:
- Que todas las diagonales de caras opuestas verifiquen que no son coplanarias y que no estén conectadas por aristas:
- Si esas seis diagonales no conforman una pirámide única entonces se obtienen particiones no pseudo-prismáticas con un mínimo de seis pirámides (punto 1.2 de esta parte IV).
- Si esas seis diagonales conforman una pirámide única entonces ésta es interior al hexaedro quedando éste descompuesto en cinco pirámides y siendo la partición de cardinal mínimo. Hay dos posibles particiones de cardinal mínimo (ver escena 38).
54
Escena 38. Partición de un hexaedro convexo {4,4,4,4,4,4} en cinco pirámides triangulares.
- Que al menos haya dos diagonales de caras opuestas que no sean coplanarias, pero que estén conectadas por aristas. Por ejemplo, en la imagen derecha de la figura 7 las diagonales AC y EG están en esa situación. Por tanto, la poligonal cerrada ACGE al no ser plana no determina la cara de un poliedro y consecuentemente para abordar la partición es necesario introducir elementos adicionales como podría ser el segmento EC o el AG (el hexaedro inicial queda partido en dos hexaedros {3,4,4,3,3,3}, descomposición que denominaremos hexaédrica) u otros que atraviesen la región espacial enmarcada por dicha poligonal. La necesaria introducción de estos nuevos elementos conduce a que la partición no pueda ser de cardinal mínimo, tendrá un mínimo de seis pirámides.
- Que al menos haya dos diagonales de caras opuestas que sean coplanarias. El hexaedro queda dividido en dos pentaedros {3,4,4,4,3} y la partición decimos que es pseudo-prismática (puede considerarse como un caso particular de la descomposición hexaédrica del apartado anterior). Como mínimo la partición del hexaedro tendrá seis pirámides.
3. Partición prismática de un paralelepípedo en pirámides triangulares
En la sección 2.1 se ha observado que en un paralelepípedo cuando hay al menos dos diagonales de caras opuestas que son coplanarias, entonces puede descomponerse en dos prismas
55
triangulares y, consecuentemente, su partición en pirámides triangulares puede reducirse y realizarse mediante la partición de prismas triangulares en pirámides triangulares. Es lo que hemos denominado partición prismática del paralelepípedo.
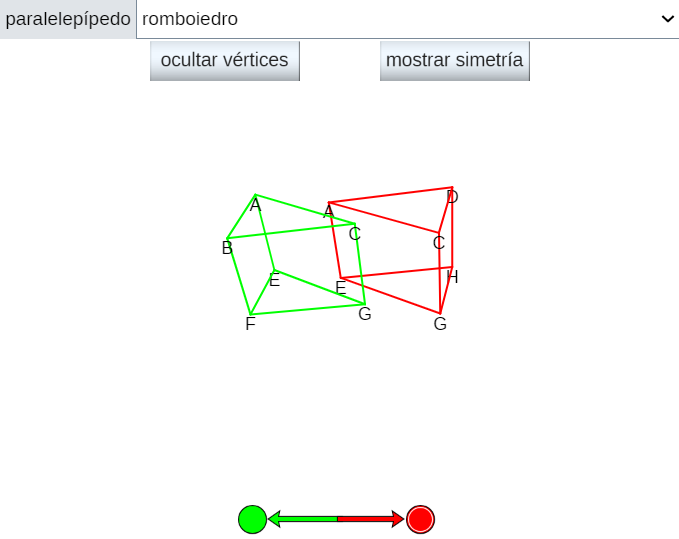
En la escena 39 podemos observar dicha partición seleccionando el tipo de paralelepípedo y pudiendo separar los dos prismas con los controles ubicados en la parte inferior. El botón "mostrar simetría" refleja la simetría central que tiene todo paralelepípedo respecto al punto donde se intersecan sus diagonales y, también, cómo esta simetría se transfiere a los dos prismas de la partición, por ello siempre ambos prismas son congruentes.
Encontramos las siguientes situaciones:
- La partición de un romboiedro conduce a dos prismas oblicuos de base un triángulo escaleno.
- En un romboedro los dos prismas oblicuos tienen por base un triángulo isósceles. En la escena distinguimos dos situaciones:
- En la primera, el corte se efectúa por el plano determinado por dos diagonales menores coplanarias. Este corte determina un rectángulo y, por tanto, las diagonales de esa cara son iguales. Y, adicionalmente, los lados iguales del triángulo isósceles de las bases coinciden en medida con la arista lateral de los prismas. Se obtiene una regularidad que destacamos, pues se transmitirá, según observaremos posteriormente, a la partición en pirámides.
- En la segunda, el corte se efectúa por el plano determinado por dos diagonales mayores coplanarias, que es un plano de simetría del romboedro, y que determina un romboide en el plano de corte. La arista lateral no coincide con los lados de la base y al ser un romboide sus diagonales son distintas, hay menos regularidad en la partición.
- En un ortoedro son dos prismas rectos de base un triángulo rectángulo escaleno. En el caso particular de que el ortoedro tenga algún par de caras cuadradas, la partición realizada sobre éstas conduciría a prismas rectos con bases triángulos rectángulos isósceles
- En un cubo se obtienen dos prismas rectos de base un triángulo rectángulo isósceles y los catetos tienen igual longitud que la arista lateral.
56
Escena 39. Partición de un paralelepípedo en dos prismas triangulares.
3.1 Partición de un prisma triangular oblicuo en pirámides triangulares
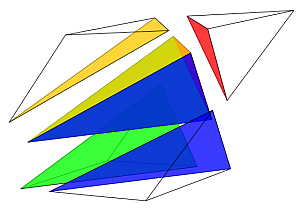
Consideremos inicialmente el caso más genérico, el de un prisma oblicuo de base un triángulo escaleno (ver escena 40), y posteriormente iremos concretando los diferentes casos particulares.
57
Escena 40. Prisma oblicuo de base un triángulo escaleno.
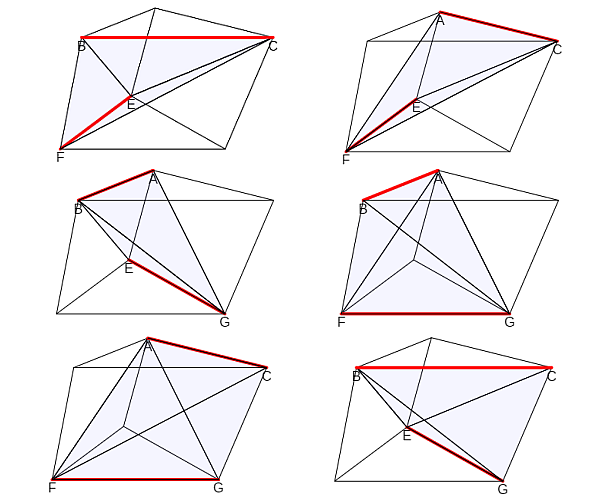
Razonando de manera análoga a la descomposición realizada en las páginas 16 a 18, la partición de un prisma triangular oblicuo en pirámides triangulares con cardinal mínimo se obtiene considerando únicamente como elementos primarios los seis vértices {A, B, C, E, F, G}, las nueve aristas y las diagonales de las caras laterales. Haciendo grupos de cuatro segmentos obtenemos doce pirámides triangulares: {ABCE, ABCF, ABCG, ABEG, ABFG, ACEF, ACFG, AEFG, BCEF, BCEG, BEFG, CEFG}, las cuales determinan seis particiones distintas del prisma. Estas particiones están compuestas cada una por tres pirámides triangulares que son equivalentes entre sí, es decir, el volumen de cada una de ellas es la tercera parte del volumen total del prisma. En la escena 41 se reflejan esas seis particiones.
Para poder comparar esas pirámides y esas particiones denotemos:
- La longitud de las aristas como: a = d(BC) = d(FG), b = d(AC) = d(EG), c = d(AB) = d(EF) y l = d(AE) = d(BF) = d(CG).
- La longitud de las diagonales como: d1 = d(BE), d2 = d(AF), d3 = d(CF), d4 = d(BG), d5 = d(AG) y d6 = d(CE)
58
Escena 41. Partición de un prisma triangular oblicuo en pirámides triangulares.
Partición de un prisma procedente de un romboiedro
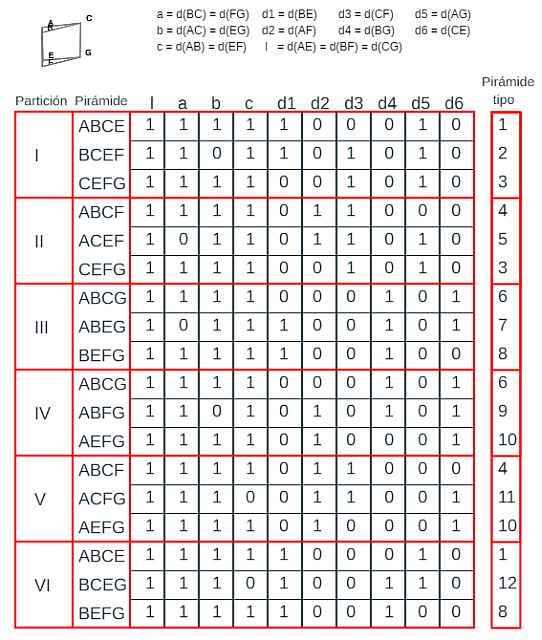
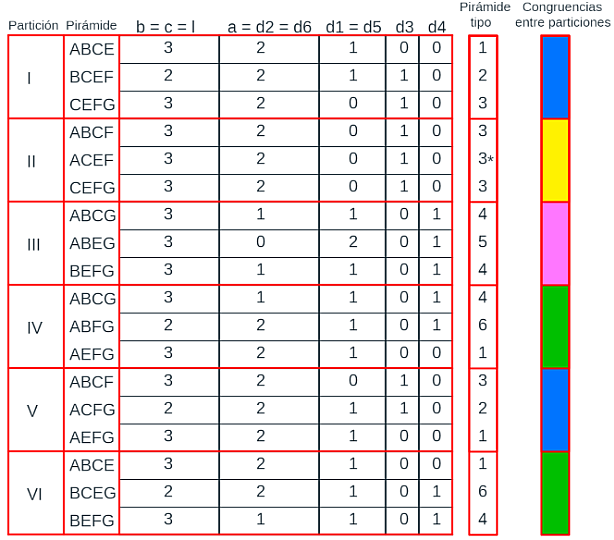
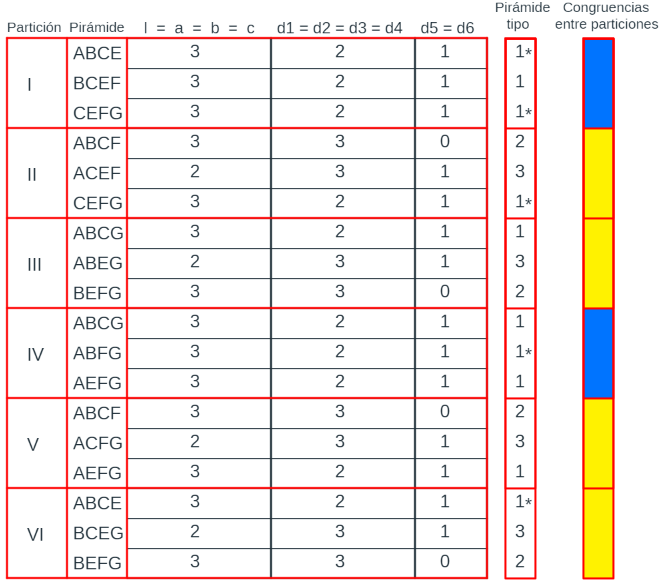
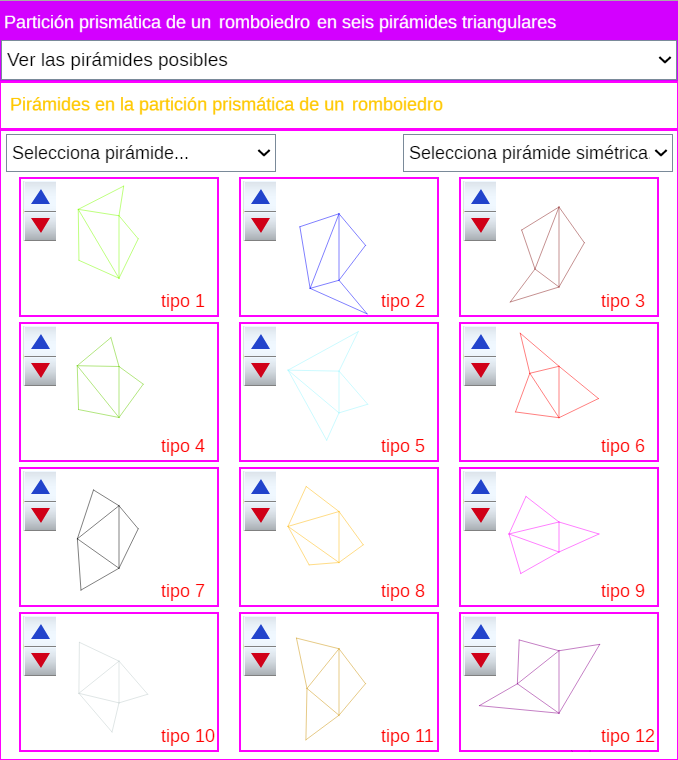
Si consideramos que el prisma triangular procede de la partición de un romboiedro, entonces, en general, las longitudes l, a, b, c, d1, d2, d3, d4, d5, d6 son distintas. En base a ello, en la escena 42 se refleja una tabla donde se detalla cada una de las seis particiones posibles, señalando los vértices de las tres pirámides que conforman cada partición e indicando con un 1 los segmentos que constituyen sus aristas. Esta escena cuenta también con un menú, ubicado en la parte superior, donde se puede seleccionar ver las particiones y observar, si se desea, los segmentos con sendas etiquetas que reflejan su medida.
59
Escena 42. Partición de un prisma triangular oblicuo procedente de un romboiedro en pirámides triangulares.
60
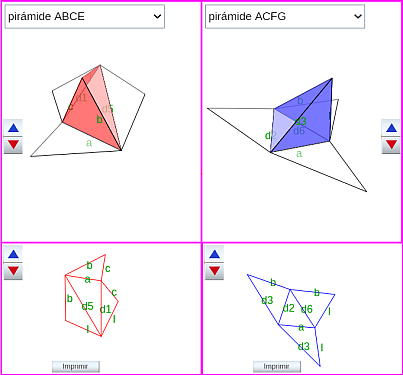
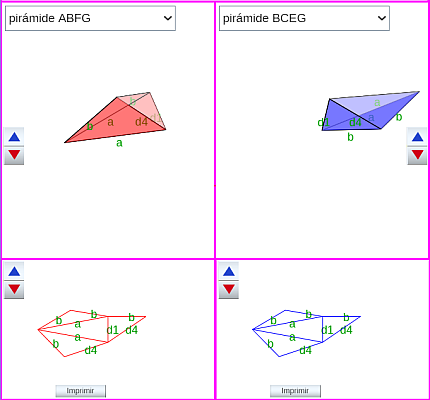
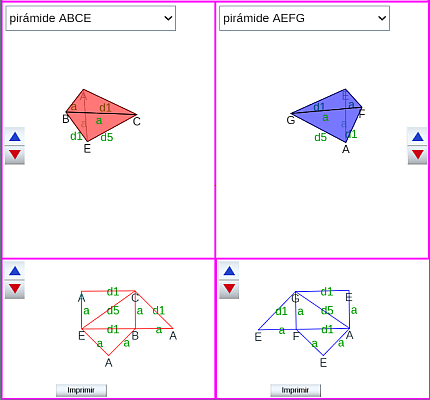
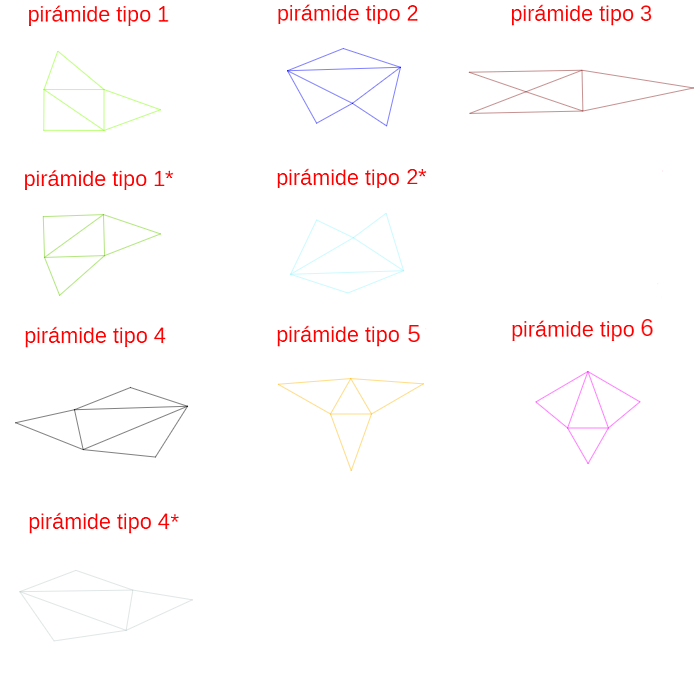
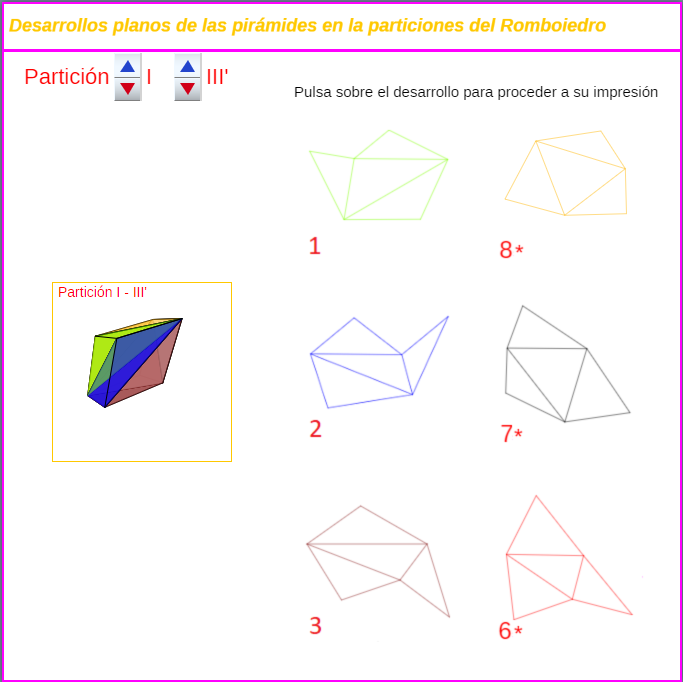
Al tener esos diez segmentos diferente longitud, las doce pirámides son diferentes (en esa tabla en la columna "Pirámide tipo" las hemos numerado del 1 al 12) y en la escena 43 pueden compararse todas ellas, dos a dos. Para cada pirámide se ha coloreado su exterior (en rojo y en azul) y el interior en blanco, pudiendo obtenerse su desarrollo plano mediante una animación, si bien, éste, se muestra directamente en la parte inferior, permitiendo proceder a su impresión y reproducción física si se desea.
Escena 43. Comparación y desarrollos planos de las pirámides triangulares en la partición
de un prisma procedente de un romboiedro.
Ha de tenerse presente que a partir de un desarrollo plano, según se pliegue en un sentido u otro, se obtienen dos pirámides con aristas iguales, pero diferente orientación, es decir, el exterior pasa a ser el interior y viceversa. Ambas son congruentes mediante una simetría central. De esto haremos uso en la partición prismática de cada paralelepípedo.
También, al comparar las seis particiones entre sí se observa que no hay ninguna congruencia entre ellas. Todas están constituidas por grupos de pirámides diferentes.
61
Partición de un prisma procedente de un romboedro (primer caso)
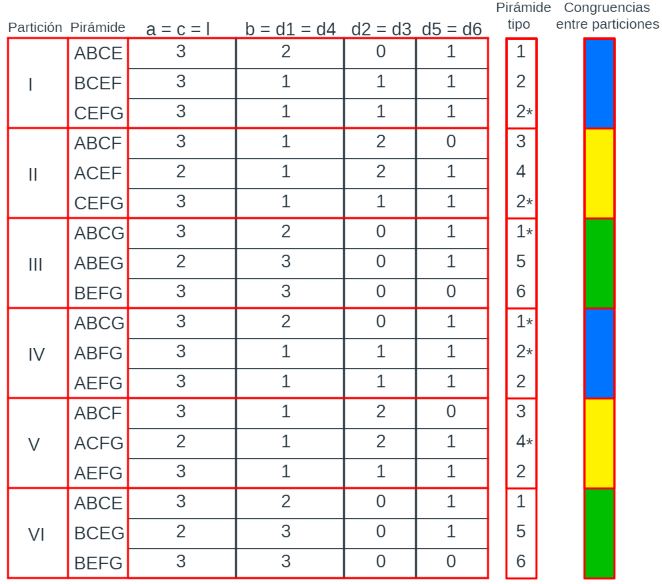
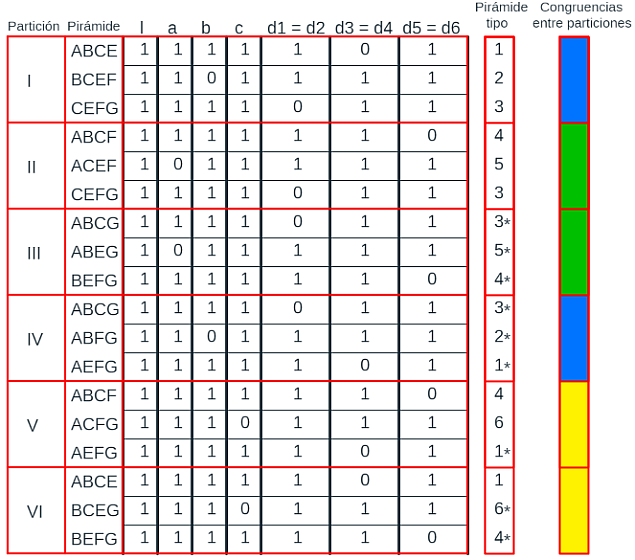
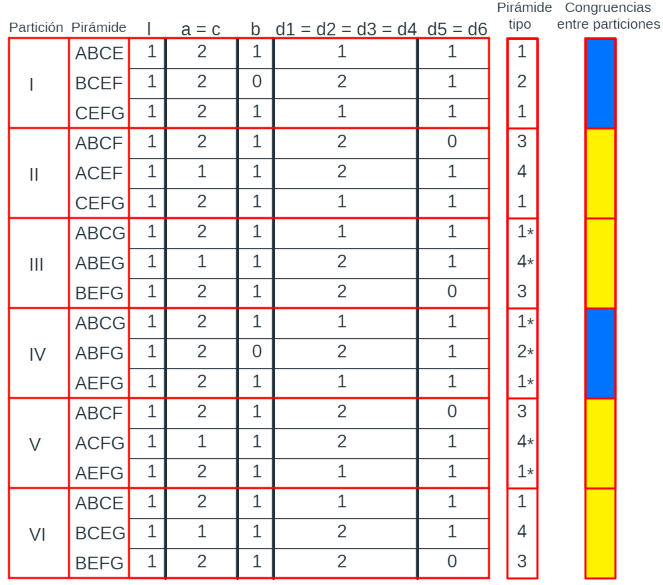
Cuando un romboedro se parte por el plano determinado por dos diagonales menores, la relación que existe entre los segmentos es: a = c = l, b = d1 = d4, d2 = d3 y d5 = d6. En la tabla de la escena 44, se indica cuántas aristas de igual medida intervienen en cada pirámide.
Escena 44. Partición de un prisma triangular oblicuo, procedente de un romboedro, en pirámides triangulares (primer caso).
62
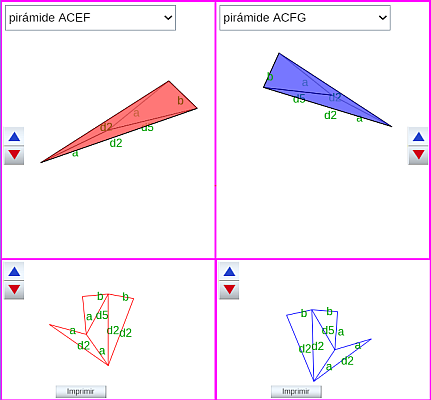
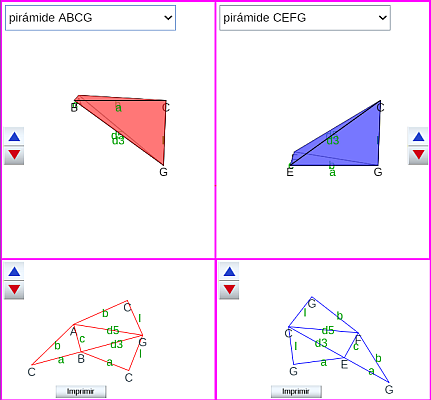
Comparando las doce pirámides entre sí (escena 45), se observa que sólo hay seis tipos diferentes, si bien pueden aparecer con distinta orientación, es decir, que son congruentes mediante una simetría central o especular (según se desee o necesite). En la tabla, esta congruencia se ha indicado incluyendo un asterisco a continuación del tipo. Por ejemplo ACEF y ACFG son ambas de tipo 4, pero tienen distinta orientación, ACFG es la simétrica de ACFG y viceversa. Las pirámides de tipo 3, 5 y 6 son simétricas y, por tanto, 3 = 3*, 5 = 5* y 6 = 6*.
En esta escena pueden imprimirse los desarrollos planos de todas las pirámides y construir las diferentes particiones.
Escena 45. Comparación y desarrollos planos de las pirámides triangulares en la partición
de un prisma procedente de un romboedro (primer caso).
También, al comparar las particiones entre sí, encontramos que son congruentes dos a dos, pues son simétricas por parejas: la I con la IV, II y V, y III y VI (en la tabla se representan con igual color). Así pues, son tres las formas de dividir un prisma de este tipo, salvo congruencias.
63
Partición de un prisma procedente de un romboedro (segundo caso)
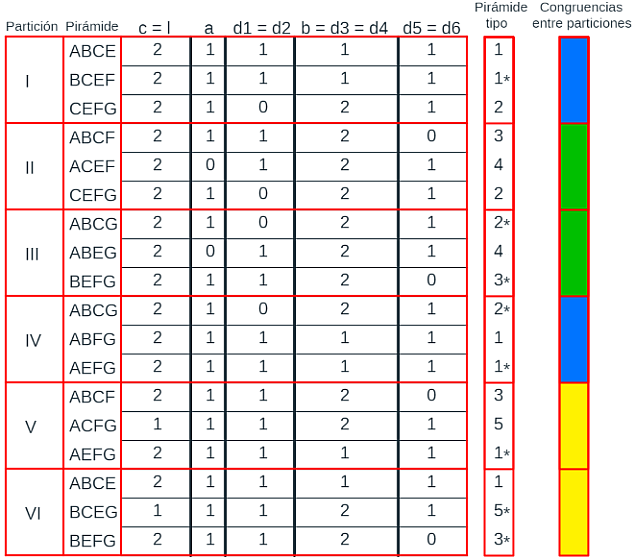
Sin embargo, cuando el romboedro se parte por el plano determinado por dos diagonales mayores, la relación que existe entre los segmentos es: b = c = l, a = d2 = d6, d1 = d5 y d3 y d4 difieren de los anteriores y entre sí. Hay distinta regularidad y en la tabla de la escena 46 se muestra la nueva relación.
Escena 46. Partición de un prisma triangular oblicuo procedente de un romboedro en pirámides triangulares (segundo caso).
64
Comparando las doce pirámides entre sí (escena 47), de nuevo se observa que hay seis tipos diferentes. De ellas la 1 y la 2 son simétricas (1 = 1* y 2 = 2*); la 3 es asimétrica y aparece en las particiones tanto la 3 como la 3*; y las 4, 5 y 6 son asimétricas y no aparecen en las particiones las pirámides 4*, 5*y 6*. Estas observaciones anteriores serán de interés cuando abordemos la contrucción de las particiones prismáticas del romboedro.
Al igual que en los casos anteriores, pueden imprimirse los desarrollos planos de todas las pirámides y construir las diferentes particiones.
Escena 47. Comparación y desarrollos planos de las pirámides triangulares en la partición
de un prisma procedente de un romboedro (segundo caso).
Comparando las particiones encontramos que son cuatro las formas de dividir un prisma de este tipo, salvo congruencias. En este caso I y V son congruentes mediante la composición de un giro alrededor del eje OY y otro alrededor de OZ (según la orientación inicial con la que se representa el prisma en la escena), e igualmente ocurre con IV y VI.
Adicionalmente se da la particularidad que la partición II está formada por pirámides que son sólo de un tipo, es decir, que son congruentes entre sí.
65
Partición de un prisma procedente de un ortoedro (primer caso)
En el caso de que el prisma triangular proceda de un ortoedro cuyas tres dimensiones espaciales sean distintas tenemos que a, c y l tienen longitudes diferentes; pero d1 = d2, d3 = d4 y d5 = d6 porque las caras laterales son rectangulares, y b, en general, será distinto a cualquier valor anterior. En la tabla de la escena 48 se detallan las relaciones existentes.
Escena 48. Partición de un prisma triangular procedente de un ortoedro con las tres dimensiones diferentes.
66
En la escena 49 se pueden comparar las doce pirámides y se puede comprobar que hay seis tipos diferentes, que todas son asimétricas y que en las diferentes particiones aparecen los seis tipos por parejas, es decir, una pirámide y su simétrica. Las doce pirámides son 1, 1*, 2, 2*, 3, 3*, 4, 4*, 5, 5*, 6 y 6*. Pueden imprimirse todos los desarrollos planos de esas pirámides y construir las diferentes particiones.
Escena 49. Comparación y desarrollos planos de las pirámides triangulares en la partición
de un prisma procedente de un ortoedro (primer caso).
Comparando las particiones se obtiene que son tres las formas de dividir un prisma de este tipo, salvo congruencias. I y IV, II y III, V y VI coinciden respectivamente mediante una simetría especular y un giro, o bien de manera equivalente mediante una simetría central.
67
Partición de un prisma procedente de un ortoedro (segundo caso)
Como segundo caso consideremos que dos de las dimensiones del ortoedro coinciden, es decir, un ortoedro que cuente con dos caras cuadradas. Esta situación, a su vez, conduce a dos subcasos según el prisma considerado proceda de la división del ortoedro por dos caras rectangulares o por las dos cuadradas. En la escena 50 reflejamos la primera posibilidad.
Escena 50. Partición de un prisma triangular procedente de un ortoedro con dos dimensiones coincidentes (caso segundo).
68
Aquí, al igual que en el caso general anterior, son tres las particiones obtenidas, pero sólo con cinco tipos de pirámides.
En la escena 51 se pueden observar y comparar esos cinco tipos de pirámides. Las tipo 1, 2, 3 y 5 son asimétricas y aparecen con sus dos orientaciones posibles. Sin embargo la pirámide tipo 4 es simétrica, es decir, 4 = 4*.
Escena 51. Comparación y desarrollos planos de las pirámides triangulares en la partición
de un prisma procedente de un ortoedro (segundo caso).
La partición I y la IV son congruentes mediante una simetría especular y un giro (o bien una simetría central). Y análoga situación acontece con las particiones II y III, y con las V y VI.
La escena permite obtener e imprimir los desarrollos planos de cada una de esas pirámides.
69
Partición de un prisma procedente de un ortoedro (tercer caso)
Si el ortoedro con dos dimensiones iguales lo dividimos a través de las dos caras cuadradas, el prisma obtenido puede partirse en pirámides triangulares de acuerdo a lo reflejado en la escena 52.
Escena 52. Partición de un prisma triangular procedente de un ortoedro con dos dimensiones coincidentes (caso tercero).
70
En este caso sólo tenemos cuatro tipos de pirámides diferentes, apareciendo en las dos orientaciones posibles. Las tipo 1, 2 y 4 son asimétricas y la 3 es simétrica (3 = 3*).
La escena 53 permite comprobar lo indicado.
Escena 53. Comparación y desarrollos planos de las pirámides triangulares en la partición
de un prisma procedente de un ortoedro (tercer caso).
Salvo congruencias solamente tenemos dos formas de partir este prisma. La partición I y la IV son congruentes mediante una simetría especular o bien una simetría central. Las cuatro particiones II, III, V y VI son congruentes entre sí: II y III mediante una simetría central; II y V con una simetría especular y II y VI realizando un giro.
De nuevo la escena permite obtener e imprimir los desarrollos planos de cada una de esas pirámides.
71
Partición de un prisma procedente de un cubo
En el caso de que el prisma triangular proceda de un cubo, ortoedro con las tres dimensiones espaciales iguales, obtenemos que el número de tipos de pirámides son tres y el de particiones dos (ya se detalló en la parte II, sección 2.4 y ahora lo obtenemos como un caso particular de la partición de un ortoedro). En la escena 54 mostramos este resultado siguiendo el esquema
Escena 54. Partición de un prisma triangular procedente de un cubo.
72
general planteado en el análisis de todos los casos anteriores.
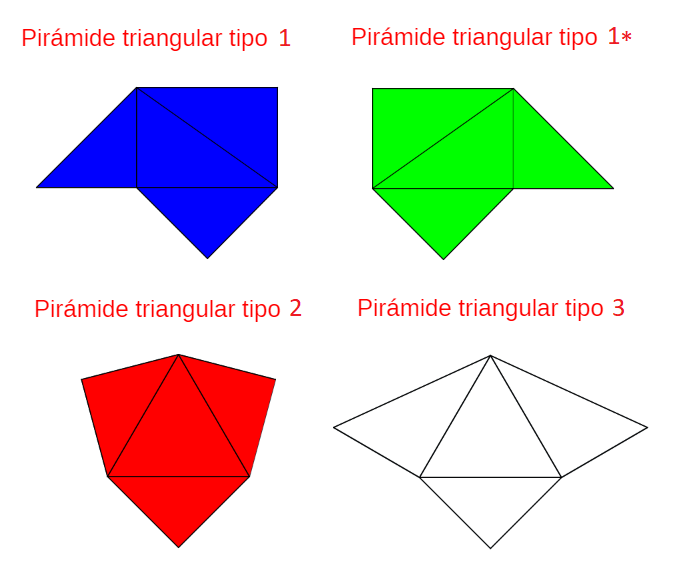
De los tres tipos de pirámides, el 1 es una pirámide asimétrica y aparecen las dos orientaciones posibles: 1 y 1*. Las pirámides tipo 2 y 3 son simétricas. Todo es observable en la escena 55.
Escena 55. Comparación y desarrollos planos de las pirámides triangulares en la partición
de un prisma procedente de un cubo.
La partición I y la IV son congruentes mediante una simetría especular o bien una simetría central. Las cuatro particiones II, III, V y VI son congruentes entre sí: II y III mediante una simetría central; II y V con una simetría especular y II y VI realizando un giro. Así pues, salvo congruencias, solamente tenemos dos formas de partir este prisma, por ejemplo, las particiones I y II. Y, en particular, la I está formada por pirámides que también son congruentes entre sí.
La escena permite obtener e imprimir los desarrollos planos para su construcción en papel.
73
3.2 Partición prismática de los paralelepípedos
Conocidas las diferentes particiones de cada uno de los prismas que se obtienen al dividir un paralelepípedo estamos en condiciones de poder analizar cuáles son las diferentes particiones prismáticas de los paralelepípedos. En este caso, y en orden inverso al considerado en la sección anterior, partiremos del caso más regular ―el cubo―, y avanzaremos hacia el más irregular ―el romboiedro―. Seguiremos un mismo esquema para todos los casos y aunque el cubo ya fue analizado en la parte II, también lo incluiremos aquí.
Partición prismática de un cubo
Todo cubo, salvo congruencias, puede partirse en dos primas triangulares de una única forma. Esos dos prismas tienen simetría especular respecto al plano de corte y simetría central respecto al punto de intersección de las diagonales del cubo.
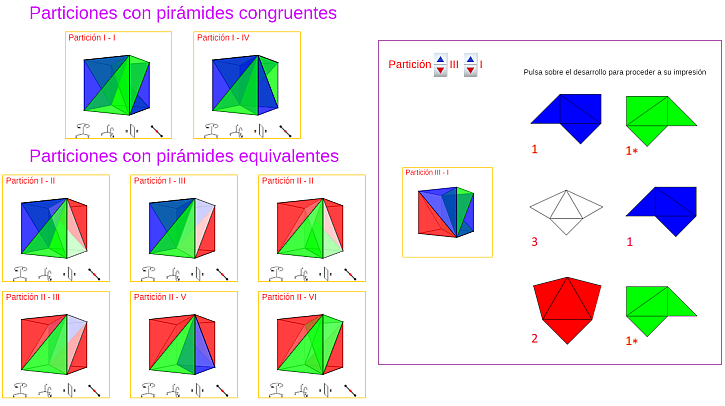
Según lo analizado en la sección anterior, cada uno de esos prismas puede partirse en pirámides triangulares equivalentes de seis formas diferentes (I, II, III, IV, V y VI). Y, en particular, la I y la IV están compuestas por pirámides que no sólo son equivalentes, sino que también son congruentes entre sí.
| I |
1* |
II |
2 |
III |
1 |
IV |
1 |
V |
2 |
VI |
1* |
| 1 |
3 |
3 |
1* |
3 |
3 |
||||||
| 1* |
1* |
2 |
1 |
1 |
2 |
A su vez, cada partición está compuesta por tres pirámides y en ellas aparecen tres tipos que identificamos como 1, 2 y 3.
La pirámide tipo 1 es asimétrica y aparece en sus dos orientaciones posibles que indicamos como 1 y 1*. Ambas están relacionadas bien mediante una simetría central o bien mediante una simetría especular. Sus desarrollos planos son simétricos, pero si se desea puede utilizarse un único desarrollo plano y plegando en un sentido se obtiene una y plegando en el sentido opuesto la otra.
74
La pirámide tipo 2 es simétrica, es decir, 2 = 2*; y también lo es la 3, 3 = 3*.
En la escena 56 se pueden observar las cuatro pirámides (1, 1*, 2 y 3) y sus desarrollos planos.
Escena 56. Pirámides en la partición prismática de un cubo.
Aplicando un giro, una simetría especular y una simetría central se obtienen las siguientes congruencias entre las seis particiones:
|
|
I |
II |
III |
IV |
V |
VI |
 |
I |
VI |
V |
IV |
III |
II |
 |
IV |
V |
VI |
I |
II |
III |
 |
IV |
III |
II |
I |
VI |
V |
75
Es decir, salvo transformaciones isométricas, hay sólo dos particiones diferentes (en las tablas anteriores se han reflejado usando el mismo color para todas particiones congruentes). Así pues, por ejemplo, bastaría considerar la I y la II.
La construcción del cubo se aborda considerando dos de las particiones del prisma anterior y yuxtaponiéndolas. Son 36 la posibilidades, resultado de {I, II, III, IV, V, VI} x {I, II, III, IV, V, VI}. Pero, por las congruencias indicadas, basta considerar las posibles combinaciones de {I, II} con {I, II, III, IV, V, VI}, obteniéndose las siguientes posibilidades:
| I-I |
I-II |
I-III |
I-IV |
I-V |
I-VI |
| II-II |
II-III |
II-IV |
II-V |
II-VI |
Pero entre ellas es necesario buscar posibles congruencias y detectamos que aplicando:
- un giro alrededor de Oy, I-V se transforma en I-III
- un giro alrededor de Oy, I-VI se transforma en I-II
- simetría central, II-IV se transforma en I-III
Por ello, las posibilidades de partir un cubo en pirámides triangulares equivalentes son sólo ocho:
| I-I |
I-II |
I-III |
I-IV |
||
| II-II |
II-III |
II-V |
II-VI |
Y entre ellas I-I y I-IV son particiones formadas por pirámides que no sólo son equivalentes, sino que también son congruentes entre sí.
En la escena 57 pueden observarse las ocho particiones del cubo y obtenerse las que son congruentes con ellas. También pueden imprimirse los desarrollos planos de cada partición y reproducirse un modelo tangible de las mismas.
76
Escena 57. Particiones del cubo en pirámides triangulares.
Desarrollos planos de la partición.
Partición prismática de un ortoedro (tercer caso)
Un ortoedro con dos dimensiones diferentes puede partirse en dos prismas dividiéndolo por las dos caras cuadradas opuestas. Salvo congruencias hay una única forma de hacerlo. Esos dos prismas tienen simetría especular respecto al plano de corte y simetría central respecto al punto de intersección de las diagonales del ortoedro.
Según lo analizado en la sección anterior (3.1), cada uno de esos prismas puede partirse en pirámides triangulares equivalentes de seis formas diferentes (I, II, III, IV, V y VI).
77
| I |
1 |
II |
3 |
III |
1* |
IV |
1* |
V |
3 |
VI |
1 |
| 2 |
4 |
4* |
2* |
4* |
4 |
||||||
| 1 |
1 |
3 |
1* |
1* |
3 |
A su vez, cada partición está compuesta por tres pirámides y en ellas aparecen cuatro tipos que identificamos como 1, 2, 3 y 4.
La pirámide tipo 1 es asimétrica y aparece en sus dos orientaciones posibles que indicamos como 1 y 1*. Ambas están relacionadas bien mediante una simetría central o bien mediante una simetría especular. Sus desarrollos planos son simétricos, pero si se desea puede utilizarse un único desarrollo plano y plegando en un sentido se obtiene una y plegando en el sentido opuesto la otra. También acontece esta situación con las pirámides 2 y 4, y sus repectivas 2* y 4*.Sin embargo la pirámide tipo 3 es simétrica, es decir, 3 = 3*.
En la escena 58 se pueden observar las siete pirámides (1, 1*, 2, 2*, 3, 4 y 4*) y sus desarrollos planos.
Escena 58. Pirámides en la partición prismática de un ortoedro (caso tercero).
78
Aplicando un giro, una simetría especular y una simetría central se obtienen las siguientes congruencias entre las seis particiones:
|
|
I |
II |
III |
IV |
V |
VI |
 |
I |
VI |
V |
IV |
III |
II |
 |
IV |
V |
VI |
I |
II |
III |
 |
IV |
III |
II |
I |
VI |
V |
La situación es similar, casi idéntica, al caso del cubo. Así pues, salvo transformaciones isométricas, hay sólo dos particiones diferentes (en las tablas anteriores se han reflejado usando el mismo color para todas particiones congruentes). Basta considerar, por ejemplo, la I y la II.
La construcción del ortoedro se aborda considerando dos de las particiones del prisma anterior y yuxtaponiéndolas. Son 36 las posibilidades, resultado de {I, II, III, IV, V, VI} x {I, II, III, IV, V, VI}. Pero, por las congruencias indicadas, basta considerar las posibles combinaciones de {I, II} con {I, II, III, IV, V, VI}, obteniéndose las siguientes posibilidades:
| I-I |
I-II |
I-III |
I-IV |
I-V |
I-VI |
| II-II |
II-III |
II-IV |
II-V |
II-VI |
Pero entre ellas es necesario buscar posibles congruencias y detectamos que aplicando:
- un giro alrededor de Oy, I-V se transforma en I-III
- un giro alrededor de Oy, I-VI se transforma en I-II
- simetría central, II-IV se transforma en I-III
79
Por ello, las posibilidades de partir un ortoedro, que cumpla las condiciones especificadas, en pirámides triangulares equivalentes son sólo ocho:
| I-I |
I-II |
I-III |
I-IV |
||
| II-II |
II-III |
II-V |
II-VI |
En la escena 59 pueden observarse estas ocho particiones del ortoedro y obtenerse las que son congruentes con ellas. También pueden imprimirse los desarrollos planos de cada partición y reproducirse un modelo tangible de las mismas.
Escena 59. Particiones del ortoedro en pirámides triangulares (caso tercero).
Desarrollos planos de la partición.
80
Partición prismática de un ortoedro (segundo caso)
Un ortoedro con dos dimensiones diferentes puede partirse en dos prismas si lo dividimos por dos caras rectangulares opuestas. Salvo congruencias hay una única forma de hacerlo. Esos dos prismas tienen simetría central respecto al punto de intersección de las diagonales del ortoedro.
Según lo analizado en la sección anterior (3.1), cada uno de esos prismas puede partirse en pirámides triangulares equivalentes de seis formas diferentes (I, II, III, IV, V y VI).
| I |
1 |
II |
3 |
III |
2* |
IV |
2* |
V |
3 |
VI |
1 |
| 1* |
4 |
4 |
1 |
5 |
5* |
||||||
| 2 |
2 |
3* |
1* |
1* |
3* |
A su vez, cada partición está compuesta por tres pirámides y en ellas aparecen cinco tipos que identificamos como 1, 2, 3, 4 y 5.
La pirámide tipo 1 es asimétrica y aparece en sus dos orientaciones posibles que indicamos como 1 y 1*. Ambas están relacionadas mediante una simetría central. Sus desarrollos planos son simétricos, pero si se desea puede utilizarse un único desarrollo plano y plegando en un sentido se obtiene una y plegando en el sentido opuesto la otra. También acontece esta situación con las pirámides 2, 3 y 5, y sus respectivas 2*, 3* y 5*. Sin embargo, la pirámide tipo 4 es simétrica, es decir, 4 = 4*.
En la escena 60 se pueden observar las nueve pirámides (1, 1*, 2, 2*, 3, 3*, 4, 5 y 5*) y sus desarrollos planos.
Aplicando una simetría central se obtienen las siguientes congruencias entre las seis particiones:
|
|
I |
II |
III |
IV |
V |
VI |
 |
IV |
III |
II |
I |
VI |
V |
81
Así pues, salvo transformaciones isométricas, hay tres particiones diferentes (en las tablas anteriores se han reflejado usando el mismo color para todas particiones congruentes). Basta considerar, por ejemplo, la I, la II y la V.
Escena 60. Pirámides en la partición prismática de un ortoedro (caso segundo).
82
La construcción del ortoedro se aborda considerando dos de las particiones del prisma anterior y yuxtaponiéndolas. Son 36 las posibilidades, resultado de {I, II, III, IV, V, VI} x {I, II, III, IV, V, VI}. Pero, por las congruencias indicadas, basta considerar las posibles combinaciones de {I, II, V} con {I, II, III, IV, V, VI}, obteniéndose las siguientes posibilidades:
| I-I |
I-II |
I-III |
I-IV |
I-V |
I-VI |
| II-II |
II-III |
II-IV |
II-V |
II-VI |
|
| V-III |
V-IV |
V-V |
V-VI |
Pero entre ellas es necesario buscar posibles congruencias y detectamos que aplicando:
- una simetría central, V-IV se transforma en I-VI.
- una simetría central, V-III se transforma en II-VI.
- una simetría central, II-IV se transforma en I-III.
Por ello, las posibilidades de partir un ortoedro, que cumpla las condiciones especificadas, en pirámides triangulares equivalentes son doce:
| I-I |
I-II |
I-III |
I-IV |
I-V |
I-VI |
| II-II |
II-III |
II-V |
II-VI |
||
| V-V |
V-VI |
En la escena 61 pueden observarse estas doce particiones del ortoedro y obtenerse las que son congruentes con ellas. También pueden imprimirse los desarrollos planos de cada partición y reproducirse un modelo tangible de las mismas.
83
Escena 61. Particiones del ortoedro en pirámides triangulares (caso segundo).
Desarrollos planos de la partición.
Partición prismática de un ortoedro (primer caso)
Un ortoedro con sus tres dimensiones diferentes puede partirse en dos prismas usando el plano determinado por dos diagonales paralelas de dos caras rectangulares opuestas. Salvo congruencias, hay tres formas de hacerlo ya que encontramos que hay tres diagonales de longitudes distintas y cada una de éstas conduce a prismas diferentes. Esos dos prismas tienen simetría central respecto al punto de intersección de las diagonales del ortoedro.
84
De las tres posibilidades indicadas mostraremos a continuación una de ellas. Las otras dos son análogas.
Según lo analizado en la sección anterior (3.1), cada uno de esos prismas puede partirse en pirámides triangulares equivalentes de seis formas diferentes (I, II, III, IV, V y VI).
| I |
1 |
II |
4 |
III |
3* |
IV |
3* |
V |
4 |
VI |
1 |
| 2 |
5 |
5* |
2* |
6 |
6* |
||||||
| 3 |
3 |
4* |
1* |
1* |
4* |
A su vez, cada partición está compuesta por tres pirámides y en ellas aparecen seis tipos que identificamos como 1, 2, 3, 4, 5 y 6.
La pirámide tipo 1 es asimétrica y aparece en sus dos orientaciones posibles que indicamos como 1 y 1*. Ambas están relacionadas mediante una simetría central. Sus desarrollos planos son simétricos, pero si se desea puede utilizarse un único desarrollo plano y plegando en un sentido se obtiene una y plegando en el sentido opuesto la otra. También acontece esta situación con las otras cinco pirámides 2, 3, 4, 5 y 6, y sus repectivas 2*, 3*, 4*, 5* y 6*.
En la escena 62 se pueden observar las doce pirámides (1, 1*, 2, 2*, 3, 3*, 4, 4*, 5, 5*, 6 y 6*) y sus desarrollos planos.
Aplicando una simetría central se obtienen las siguientes congruencias entre las seis particiones:
|
|
I |
II |
III |
IV |
V |
VI |
 |
IV |
III |
II |
I |
VI |
V |
Así pues, salvo transformaciones isométricas, hay tres particiones diferentes (en las tablas anteriores se han reflejado usando el mismo color para todas particiones congruentes). Basta considerar, por ejemplo, la I, la II y la V.
85
La construcción del ortoedro se aborda considerando dos de las particiones del prisma anterior y yuxtaponiéndolas. Son 36 las posibilidades, resultado de {I, II, III, IV, V, VI} x {I, II, III, IV, V, VI}. Pero, al igual que en el segundo caso, por las congruencias indicadas basta considerar las posibles combinaciones de {I, II, V} con {I, II, III, IV, V, VI}, obteniéndose las siguientes posibilidades:
| I-I |
I-II |
I-III |
I-IV |
I-V |
I-VI |
| II-II |
II-III |
II-IV |
II-V |
II-VI |
|
| V-III |
V-IV |
V-V |
V-VI |
Pero entre ellas es necesario buscar posibles congruencias y detectamos que aplicando:
- una simetría central, V-IV se transforma en I-VI.
- una simetría central, V-III se transforma en II-VI.
- una simetría central, II-IV se transforma en I-III.
Por ello, las posibilidades de partir un ortoedro, que cumpla las condiciones especificadas, en pirámides triangulares equivalentes son doce:
| I-I |
I-II |
I-III |
I-IV |
I-V |
I-VI |
| II-II |
II-III |
II-V |
II-VI |
||
| V-V |
V-VI |
En la escena 63 pueden observarse estas doce particiones del ortoedro y obtenerse las que son congruentes con ellas. También pueden imprimirse los desarrollos planos de cada partición y reproducirse un modelo tangible de las mismas.
87
Escena 63. Particiones del ortoedro en pirámides triangulares (caso primero).
Desarrollos planos de la partición.
Partición prismática de un romboedro (segundo caso)
Un romboedro puede partirse en dos prismas usando el plano determinado por dos diagonales mayores que sean paralelas. Salvo congruencias, hay una única forma de hacerlo. Esos dos prismas tienen simetría central respecto al punto de intersección de las diagonales del romboedro y también tienen simetría especular respecto al plano de corte. Analizaremos a continuación la partición de ambos prismas.
88
a) Según lo analizado en la sección anterior (3.1), uno de esos prismas puede partirse en pirámides triangulares equivalentes de seis formas diferentes (I, II, III, IV, V y VI).
| I |
1 |
II |
3 |
III |
4 |
IV |
4 |
V |
3 |
VI |
1 |
| 2 |
3* |
5 |
6 |
2 |
6 |
||||||
| 3 |
3 |
4 |
1 |
1 |
4 |
A su vez, cada partición está compuesta por tres pirámides y en ellas aparecen seis tipos que identificamos como 1, 2, 3, 4, 5 y 6.
La pirámide tipo 3 es asimétrica y aparece en sus dos orientaciones posibles que indicamos como 3 y 3*. Ambas están relacionadas mediante una simetría central o una especular. Sus desarrollos planos son simétricos, pero si se desea puede utilizarse un único desarrollo plano y plegando en un sentido se obtiene una y plegando en el sentido opuesto la otra. Las pirámides 4, 5 y 6 también son asimétricas, pero en estas particiones no parecen sus simétricas 4*, 5* y 6*. Las pirámides 1 y 2 son simétricas (1 = 1* y 2 = 2*).
Aplicando un giro alrededor del eje Oz y otro alrededor de Oy, lo que es equivalente a una rotación alrededor de Ox, se obtienen las siguientes congruencias entre las seis particiones:
|
|
I |
IV |
 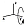 |
V |
VI |
Así pues, salvo transformaciones isométricas, hay cuatro particiones diferentes (en las tablas anteriores se han reflejado usando el mismo color para todas particiones congruentes). Basta considerar, por ejemplo, la I, la II, la III y la IV.
En particular la partición II está formada por pirámides que son congruentes entre sí.
89
b) El otro prisma puede partirse en pirámides triangulares equivalentes de seis formas diferentes (I', II', III', IV', V' y VI').
| I' |
1 |
II' |
3* |
III' |
4* |
IV' |
4* |
V' |
3* |
VI' |
1 |
| 2 |
3 |
5* |
6* |
2 |
6* |
||||||
| 3* |
3* |
4* |
1 |
1 |
4* |
De manera similar, cada partición está compuesta por tres pirámides y en ellas aparecen los seis tipos anteriores 1, 2, 3, 4, 5 y 6. Pero en este caso aparecen 1, 2, 3, 3*, 4*, 5* y 6* y no lo hacen ni 4, ni 5, ni 6.
También aplicando un giro alrededor del eje Oz y otro alrededor de Oy se obtienen las congruencias análogas:
|
|
I' |
IV' |
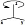 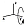 |
V' |
VI' |
Así pues, salvo transformaciones isométricas, hay cuatro particiones diferentes (en las tablas anteriores se han reflejado usando el mismo color para todas particiones congruentes). Basta considerar, por ejemplo, I', II', III' y IV'.
En particular la partición II' está formada por pirámides que son congruentes entre sí.
En la escena 64 se pueden observar las doce pirámides (1, 2, 3, 3*, 4, 4*, 5, 5*, 6 y 6*) y sus desarrollos planos.
90
Escena 64. Pirámides en la partición prismática de un romboedro (caso segundo).
La construcción del ortoedro se aborda considerando una de las particiones del primer prisma analizado y otra del segundo, yuxtaponiéndolas. Son 36 las posibilidades resultado de {I, II, III, IV, V, VI} x {I', II', III', IV', V', VI'}. Pero por las congruencias indicadas basta considerar las resultantes de {I, II, III, IV} x {I', II', III', IV', V', VI'}, obteniéndose las siguientes posibilidades:
91
| I-I' |
I-II' |
I-III' |
I-IV' |
I-V' |
I-VI' |
| II-I' |
II-II' |
II-III' |
II-IV' |
II-V' |
II-VI' |
| III-I' |
III-II' |
III-III' |
III-IV' |
III-V' |
III-VI' |
| IV-I' |
IV-II' |
IV-III' |
IV-IV' |
IV-V' |
IV-VI' |
Aplicando una doble rotación Oz y Oy, o su equivalente alrededor de Ox, se eliminan todas las particiones incluidas en la dos últimas columnas. En la tabla ⍍ representa una partición cualquiera y ⍔ su transformada.
|
|
V-⍍ |
VI-⍍ |
⍍-V' |
⍍-VI' |
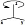  |
I-⍔ |
IV-⍔ |
⍔-I' |
⍔-IV' |
Con una simetría especular respecto al plano de yuxtaposición o una simetría central respecto al punto de intersección de las diagonales del romboedro, tenemos las siguientes transformaciones:
|
|
I |
II |
III |
IV |
V |
VI |
 |
I' |
II' |
III' |
IV' |
V' |
VI' |
 |
V' |
II' |
III' |
VI' |
I' |
IV' |
Que reduce las posibilidades a diez particiones formadas por pirámides triangulares equivalentes y, en particular, la II-II' está formada por pirámides congruentes entre sí.
92
| I-I' |
I-II' |
I-III' |
I-IV' |
| II-II' |
II-III' |
II-IV' |
|
| III-III' |
III-IV' |
||
| IV-IV' |
En la escena 65 pueden observarse estas particiones y las congruentes con ellas. Pueden imprimirse los desarrollos planos de cada partición y reproducirlas de manera tangible.
Escena 65. Particiones de un romboedro en pirámides triangulares (caso segundo). Desarrollos planos de la partición.
93
Partición prismática de un romboedro (primer caso)
Un romboedro puede partirse en dos prismas usando el plano determinado por dos diagonales menores que sean paralelas. Salvo congruencias, hay una única forma de hacerlo. Esos dos prismas tienen simetría central respecto al punto de intersección de las diagonales del romboedro. Analizaremos a continuación la partición de ambos prismas.
a) Según lo analizado en la sección anterior (3.1), uno de esos prismas puede partirse en pirámides triangulares equivalentes de seis formas diferentes (I, II, III, IV, V y VI).
| I |
1 |
II |
3 |
III |
1* |
IV |
1* |
V |
3 |
VI |
1 |
| 2 |
4 |
5 |
2* |
4* |
5 |
||||||
| 2* |
2* |
6 |
2 |
2 |
6 |
A su vez, cada partición está compuesta por tres pirámides y en ellas aparecen seis tipos que identificamos como 1, 2, 3, 4, 5 y 6.
La pirámide tipo 1 es asimétrica y aparece en sus dos orientaciones posibles que indicamos como 1 y 1*. Ambas están relacionadas mediante una simetría central o una especular. Sus desarrollos planos son simétricos, pero si se desea puede utilizarse un único desarrollo plano y plegando en un sentido se obtiene una y plegando en el sentido opuesto la otra. Las pirámides 2 y 4 también son asimétricas, y aparecen ellas y sus simétricas 2* y 4*. Las pirámides 3, 5 y 6 son simétricas (3 = 3*, 5 = 5* y 6 = 6*).
Aplicando una simetría especular respecto al plano que determinan las diagonales mayores que son perpendiculares a las que se han considerado para partir el romboedro, se obtienen las siguientes congruencias entre esas seis particiones:
|
|
I |
II |
III |
IV |
V |
VI |
 |
IV |
V |
VI |
I |
II |
III |
94
Así pues, salvo transformaciones isométricas, hay tres particiones diferentes (en las tablas anteriores se han reflejado usando el mismo color para todas particiones congruentes). Basta considerar, por ejemplo, la I, la II y la III.
b) El otro prisma puede partirse en pirámides triangulares equivalentes de seis formas diferentes (I', II', III', IV', V' y VI').
| I' |
2 |
II' |
2 |
III' |
6 |
IV' |
2* |
V' |
2* |
VI' |
6 |
| 2* |
4* |
5 |
2 |
4 |
5 |
||||||
| 1* |
3 |
1 |
1 |
3 |
1* |
De manera similar, cada partición está compuesta por tres pirámides y en ellas aparecen los seis tipos de pirámides anteriores y sus simétricas.
También aplicando una simetría especular, similar a la anterior, se obtienen las congruencias análogas:
|
|
I' |
II' |
III' |
IV' |
V' |
VI' |
 |
IV' |
V' |
VI' |
I' |
II' |
III' |
Así pues, salvo transformaciones isométricas, hay tres particiones diferentes (en las tablas anteriores se han reflejado usando el mismo color para todas particiones congruentes). Basta considerar, por ejemplo, I', II' y III'.
En la escena 66 se pueden observar las nueve pirámides (1, 1*, 2, 2*, 3, 4, 4*, 5 y 6) y sus desarrollos planos.
95
Escena 66. Pirámides en la partición prismática de un romboedro (caso primero).
96
La construcción del romboedro se aborda considerando una de las particiones del primer prisma analizado y otra del segundo, yuxtaponiéndolas. Son 36 las posibilidades resultado de {I, II, III, IV, V, VI} x {I', II', III', IV', V', VI'}. Pero por las congruencias indicadas basta considerar las resultantes de {I, II, III} x {I', II', III', IV', V', VI'}, obteniéndose las siguientes posibilidades:
| I-I' |
I-II' |
I-III' |
I-IV' |
I-V' |
I-VI' |
| II-I' |
II-II' |
II-III' |
II-IV' |
II-V' |
II-VI' |
| III-I' |
III-II' |
III-III' |
III-IV' |
III-V' |
III-VI' |
Aplicando una doble rotación en Oz y Oy, o su equivalente alredor de Ox, o una simetría central respecto al punto de intersección de las diagonales del romboedro, tenemos las siguientes transformaciones:
|
|
I |
II |
III |
IV |
V |
VI |
 |
IV' |
V' |
VI' |
I' |
II' |
III' |
 |
I' |
II' |
III' |
IV' |
V' |
VI' |
Y sus análogas:
|
|
I' |
II' |
III' |
IV' |
V' |
VI' |
 |
IV |
V |
VI |
I |
II |
III |
 |
I |
II |
III |
IV |
V |
VI |
Lo cual reduce las posibilidades a doce particiones, indicadas en la siguiente tabla:
97
| I-I' |
I-II' |
I-III' |
I-IV' |
I-V' |
I-VI' |
| II-II' |
II-III' |
II-V' |
II-VI' |
||
| III-III' |
III-VI' |
En la escena 67 pueden observarse estas particiones y las congruentes con ellas. Pueden imprimirse los desarrollos planos de cada partición y reproducirlas de manera tangible.
Escena 67. Particiones de un romboedro en pirámides triangulares (primer caso). Desarrollos planos de la partición.
98
Partición prismática de un romboiedro
En la sección 3.1, pp. 59-61, analizamos que un prisma procedente de un romboiedro puede descomponerse en seis particiones en las que intervienen doce pirámides triangulares diferentes y asimétricas. No existe ninguna congruencia entre estas particiones.
| I |
1 |
II |
4 |
III |
6 |
IV |
6 |
V |
4 |
VI |
1 |
| 2 |
5 |
7 |
9 |
11 |
12 |
||||||
| 3 |
3 |
8 |
10 |
10 |
8 |
A partir de ese prisma, la construcción del romboiedro sólo es posible mediante la aplicación de una simetría central. Este prisma simétrico podrá descomponerse a su vez en seis particiones que son simétricas de las anteriores y que estarán compuestas por las respectivas pirámides simétricas (de nuevo denotamos por 1* la pirámide simétrica de la 1, y análogamente el resto).
| I' |
3* |
II' |
3* |
III' |
8* |
IV' |
10* |
V' |
10* |
VI' |
8* |
| 2* |
5* |
7* |
9* |
11* |
12* |
||||||
| 1* |
4* |
6* |
6* |
4* |
1* |
En la escena 68 se reflejan las doce pirámides posibles y sus simétricas, en total veinticuatro pirámides. También puede obtenerse el desarrollo plano de todas ellas.
La yuxtaposición de esos dos prismas da lugar al romboiedro. Y consecuentemente las posibles particiones del mismo son 36, las resultantes del producto {I, II, III, IV, V, VI} x {I', II', III', IV', V', VI'}.
99
En la escena 69 pueden observarse estas trienta y seis particiones. Pueden imprimirse los desarrollos planos de cada partición y reproducirlas de manera tangible.
Escena 69. Particiones de un romboiedro en pirámides triangulares. Desarrollos planos de la partición.
101
Pero para realizar una cuantificación de todas las particiones prismáticas de un romboiedro hemos de tener en consideración que hay seis formas posibles de partirlo en dos prismas. Para cada pareja de caras opuestas hay dos posibilidades correspondientes a las dos diagonales, luego tres parejas por dos diagonales conduce a esas seis formas.
Así pues, en el caso más general, seis posibles particiones prismáticas del romboiedro y para cada una de ellas treinta y seis particiones diferentes en pirámides triangulares, por tanto, un total de 216 particiones. En ellas intervienen 24 x 6 = 144 pirámides (72 pirámides y sus simétricas).
Escena general de la partición prismática de un paralelepípedo
En los apartados anteriores hemos abordado la partición prismática de los diferentes paralelepípedos posibles y hemos contemplando en detalle todos los casos particulares que se pueden encontrar. Para ello, el análisis se ha realizado considerando ejemplos concretos, con datos fijados a priori, y que consecuentemente no pueden ser modificados por el lector (usuario activo) de este artículo. Para dar la posibilidad de que cualquiera pueda seleccionar su paralelepípedo, que elija la partición prismática que desee y que pueda reproducirla en un modelo tangible, aportamos la escena 70, la cual cuenta con un menú con las siguientes opciones:
- Selecciona el paralelepípedo:
- Cubo. La partición en dos prismas es única y la longitud de la arista no es significativa, por tanto, no es necesario introducir ningún dato adicional.
- Ortoedro. Con los dos controles numéricos Bx y Dy puede definirse cualquier ortoedro. La partición en dos prismas se efectúa siempre considerando el plano determinado por la diagonal AC y su paralela EG, por tanto, para obtener cada uno de los tres casos analizados anteriormente es necesario definir adecuadamente dichos controles.
- Romboedro cortando por la diagonal menor. Puede cambiarse el ángulo que define al romboedro y el corte en dos prismas se realiza por el plano ACGE determinado por dos diagonales menores paralelas.
- Romboedro cortando por la diagonal mayor. Puede cambiarse el ángulo y en este caso el corte por el plano ACGE se corresponde con dos diagonales mayores paralelas.
- Romboiedro. Pueden cambiarse las coordenadas de los vértices A, B, D y E y el corte se efectúa, de nuevo, siempre por el plano ACGE.
102
- Ver las pirámides posibles. Opción mediante la que se muestran los desarrollos planos de las diferentes pirámides que pueden aparecer en las particiones. Aquí, en una rápida visión, puede interpretarse que algún desarrollo no coincide con los observados en los casos particulares analizados, pero una atenta observación conducirá a que no es más que un desarrollo equivalente.
- Elegir partición. Puede seleccionarse una de las 36 particiones posibles, ver las pirámides que intervienen en ella e imprimir su desarrollo.
Escena 70. Particiones prismáticas de un paralelepípedo en pirámides triangulares. Caso general.
103
4. Partición hexaédrica y pseudo-prismática de un hexaedro convexo {4,4,4,4,4,4} en pirámides triangulares
En la sección 2.2 de esta cuarta parte (p. 55) observamos que un hexaedro convexo {4,4,4,4,4,4}:
- Cuando dos diagonales de caras opuestas no son coplanarias, pero están conectadas por aristas el hexaedro puede dividirse, considerando un segmento adicional, en otros dos hexaedros {3,4,4,3,3,3} en lo que denominamos partición hexaédrica.
- Cuando hay al menos dos diagonales de caras opuestas que son coplanarias, puede descomponerse en dos pentaedros {3,4,4,4,3} que constituyen lo que denominamos, por analogía con los paralelepípedos, una partición pseudo-prismática.
En la escena 71 pueden observarse dos hexaedros convexos {4,4,4,4,4,4}, uno al que puede realizarse una partición hexaédrica y otro con una partición pseudo-prismática.
Escena 71. Partición hexaédrica y pseudo-prismática de sendos hexaedros convexos {4,4,4,4,4,4}.
Así pues, la partición de un hexaedro {4,4,4,4,4,4} en pirámides triangulares puede realizarse, según los casos, bien mediante la partición de dos hexaedros {3,4,4,3,3,3} o bien de dos pentaedros {3,4,4,4,3}.
104
4.1 Partición hexaédrica en pirámides triangulares
En la escena 72 se muestra la partición hexaédrica de un hexaedro {4,4,4,4,4,4} con vértices {A, B, C, D, E, F, G, H} en el que se han considerado las diagonales AC y EG que no son coplanarias y que están conectadas por las aristas AE y CG. Este hexaedro puede partirse en dos hexaedros {3,4,4,3,3,3} de dos maneras: seleccionando el segmento CE y el AG. Para cada una de estas dos elecciones cada uno de los hexaedros obtenidos pueden partirse en tres pirámides triangulares de tres formas diferentes.
Escena 72. Partición hexaédrica de un hexaedro {4,4,4,4,4,4} en pirámides triangulares.
105
En la tabla siguiente se detallan las diferentes particiones y las pirámides que las componen (son catorce diferentes) cuando el segmento que se considera es el CE.
| Segmento CE | ||||||||||||||||||||||||||
| Hexaedro {3,4,4,3,3,3} primero | Hexaedro {3,4,4,3,3,3} segundo | |||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
Para este caso, eligiendo una partición de cada hexaedro obtenenos que son nueve las particiones obtenidas, es decir, las resultantes de {Ia, IIa, IIIa} x {Ib, IIb, IIIb}.
De manera análoga, eligiendo el segmento AG se obtienen otras nueve particiones: {IVa, Va, VIa} x {IVb, Vb, VIb} con otras catorce pirámides diferentes (cuatro de ellas coincidentes con el caso anterior: ABCF, BEFG, ADCF y DEHG).
| Segmento AG | ||||||||||||||||||||||||||
| Hexaedro {3,4,4,3,3,3} primero | Hexaedro {3,4,4,3,3,3} segundo | |||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
106
Así pues, para una pareja de segmentos no coplanarios conectados por aristas obtenemos dieciocho particiones diferentes en la que intervienen 24 pirámides triangulares.
En la escena 73 se pueden observar todas esas particiones, las pirámides que las forman e imprimir el desarrollo plano de las mismas para reproducir físicamente dicho hexaedro.
Escena 73. Pirámides triangulares que intervienen en la partición hexaédrica de un hexaedro {4,4,4,4,4,4}.
107
4.1 Partición pseudo-prismática en pirámides triangulares
En la escena 74 se muestra la partición pseudo-prismática de un hexaedro {4,4,4,4,4,4} con vértices {A, B, C, D, E, F, G, H} en el que se han considerado las diagonales AC y EG que son coplanarias. En esta situación este hexaedro puede partirse en dos pentaedros {3,4,4,4,3} (pseudo-prismas triangulares). Cada uno de los pseudo-prismas obtenidos pueden partirse en tres pirámides triangulares de seis formas diferentes.
Escena 74. Partición pseudo-prismática de un hexaedro {4,4,4,4,4,4} en pirámides triangulares.
108
En la tabla siguiente se detallan las diferentes particiones y las 24 pirámides que las componen (12 por cada pseudo-prisma).
| Pseudo-prisma {3,4,4,4,3} primero | Pseudo-prisma {3,4,4,4,3} segundo | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Así pues, eligiendo una partición de cada pseudo-prisma obtenenos que el hexaedro {4,4,4,4,4,4} puede partirse de treinta y seis formas, las resultantes de {Ia, IIa, IIIa, IVa, Va, VIa} x {Ib, IIb, IIIb, IVb, Vb, VIb}.
En la escena 75 se pueden observar todas esas particiones, las pirámides que las forman e imprimir el desarrollo plano de las mismas para reproducir físicamente dicho hexaedro.
109
Escena 75. Pirámides triangulares que intervienen en la partición pseudo-prismática de un hexaedro {4,4,4,4,4,4}.
110
Conclusiones
En este artículo se ha abordado la partición de un hexaedro convexo de caras cuadriláteras {4,4,4,4,4,4} en pirámides de caras cuadriláteras y pirámides triangulares. Realizando inicialmente el estudio del caso más regular, un cubo, se han establecido pautas para lograr un análisis más global y, a la vez, detallado para detectar las simplificaciones que introduce cualquier regularidad.
La partición en pirámides de base cuadrilátera presenta un esquema único basado en la consideración de un punto que se ubique bien en la frontera o bien en el interior del poliedro que vamos a partir. Este punto se configura como el vértice o cúspide común de las pirámides que conforman la partición y el hecho de que dicho poliedro sea más o menos regular lo que introduce es una mayor o menor regularidad en las pirámides obtenidas. La partición mímima está formada por tres pirámides y acontece cuando la cúspide seleccionada coincide con un vértice del hexaedro. Si el punto seleccionado se ubica en una arista, en una cara o en el interior se generan sendas particiones formadas por cuatro, cinco y seis pirámides respectivamente. Se aportan las herramientas interactivas suficientes para visualizar de manera digital dichas particiones y también para poder ver e imprimir los desarrollos planos de las pirámides de la partición con los que se puede construir tangiblemente el hexaedro partido.
La partición en pirámides de base triangular se aborda desde dos perspectivas: una basada en la división en dos de cada una de las pirámides cuadriláteras obtenidas en las particiones anteriores y otra mediante una construcción específica. La primera conduce a un mínimo de seis pirámides y la segunda a la partición mínima constituida por cinco pirámides.
- Para cada paralelepípedo hay una única forma de construir la partición mínima en cinco pirámides triangulares. Sin embargo para un hexaedro convexo {4,4,4,4,4,4} genérico se tienen dos formas de obtener esa partición.
- La partición en seis pirámides difiere en el caso de los paralelepípedos y el de un hexaedro genérico:
- Para los paralelepípedos las particiones pueden clasificarse en particiones no prismáticas y particiones prismáticas.
- Para un hexaedro genérico hablaremos de particiones pseudo-prismáticas y no pseudo-prismáticas, pero en este caso y dentro de estas últimas se detectan las que hemos denominado particiones hexaédricas.
113
Para cada tipo de paralelepípedo, según la regularidad que presenta, se han abordado las diferentes formas de partirlo en prismas y en cada caso se han analizado cuántas particiones diferentes, salvo congruencias, pueden obtenerse y los diferentes tipos de pirámides que las componen. En todos los casos se aportan escenas interactivas que permiten definir las dimensiones del paralelepípedo deseado y observar digitalmente las particiones, así como la posibilidad de imprimir los desarrollos planos de las pirámides.
En el caso genérico del hexaedro, el análisis efectuado también cuenta con objetos interactivos que muestran las situaciones posibles, pero en este caso es con ejemplos previamente fijados.
En definitiva un estudio exhaustivo que comprende una amplia casuística y que surgió a raíz de la adaptación a DescartesJS de una escena en la que se observaba una partición prismática de un cubo y en cada uno de los prismas, en los que quedaba dividido, aparecían diferentes tipos de pirámides equivalentes entre sí. Al abordar el análisis de la situación se comprobó que las referencias a las particiones de un cubo en pirámides quedaban planteadas de manera deslavazada o inconexa, mostrando sólo aquellos casos particulares en los que se encuentra mayor regularidad, pero no desde un punto de vista global e integrador. Eso fue el objetivo primario de estudio y lo que ha quedado plasmado en la primera y segunda parte de este artículo. Y una vez realizado este análisis, era de esperar que la inquietud matemática de extender lo aprendido sirviera como catalizador para dar el salto a la generalización del estudio a todos los paralelepípedos, de los que un caso particular es el cubo, y en general al hexaedro convexo de caras cuadriláteras como poliedro no regular que puede considerarse similar al cubo.
114