Física Básica I:
Autores:
Luis M. Castellanos
Roberto E. Lorduy
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS, WebSim y Phet Colorado.
Fuentes: Lato y UbuntuMono
Imagen de portada: ilustración generada por Ideogram AI
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN: 978-84-10368-15-6

Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
La enseñanza de la física ha evolucionado significativamente con la integración de herramientas digitales interactivas, permitiendo una comprensión más profunda y dinámica de los conceptos fundamentales. Este libro, "Física Básica I", está diseñado para proporcionar una introducción clara y estructurada a los principios esenciales de la física, utilizando tanto explicaciones teóricas como recursos interactivos para reforzar el aprendizaje.
El contenido cubre desde los fundamentos del análisis vectorial hasta la cinemática, dinámica, energía y oscilaciones, abordando cada tema con un enfoque didáctico que combina la precisión matemática con ejemplos prácticos. A lo largo del libro, los lectores encontrarán ilustraciones, simulaciones y ejercicios diseñados para fomentar la aplicación del conocimiento en situaciones del mundo real.
Gracias a la colaboración con proyectos educativos como Descartes JS, WebSim y Phet Colorado. La inclusión de código interactivo en JavaScript, desarrollado por Joel Espinosa Longi (IMATE, UNAM), amplía las posibilidades de exploración, brindando a estudiantes y docentes una herramienta versátil y accesible.
Este libro está dirigido a estudiantes de nivel secundario y universitario que inician su camino en la física, así como a cualquier persona interesada en comprender los principios que rigen el universo. Esperamos que esta obra sirva como una guía efectiva en el aprendizaje de la física y motive a los lectores a seguir explorando sus aplicaciones en la ciencia y la tecnología.
Finalmente los autores deseamos expresar nuestra gratitud al profesor Juan Guillermo Rivera por sus invaluables enseñanzas en el área de las inteligencias artificiales sin la cuales no hubiese sido posible la realización de este libro
Luis M. Castellanos
Roberto E. Lorduy

La física es una ciencia natural que proporciona una visión racional del mundo y de los objetos que lo componen, a través de verdades y leyes experimentales que pueden ser expresadas matemáticamente. Se ocupa también de los componentes fundamentales del universo, de las fuerzas que éstos ejercen entre sí y de los efectos de dichas fuerzas. Está estrechamente relacionada con las demás ciencias naturales, y en cierto modo hace parte de todas.
La física contempla la naturaleza desde una perspectiva que permite establecer modelos de la realidad que hagan a ésta más comprensible, por lo cual nuestros antepasados desde sus orígenes intentaron encontrar las causas de los hechos que observaban a su alrededor. En esa búsqueda se propusieron encontrar explicación a aquellos fenómenos cuya regularidad les permitiese establecer modelos inteligibles, haciendo uso de los conocimientos de la época.
La física de hoy continúa su desarrollo, pero con menos especulaciones, más tecnología y flexibilidad, que le permite avanzar en el tiempo. En física, se crean modelos del universo y fenómenos ideales cuyo comportamiento se puede predecir con matemática y comprobar con experimentos. La física que vamos a estudiar intentará establecer modelos obtenidos a partir de la observación de los hechos experimentales, ellos nos permitirán formular las leyes que sirven en la actualidad para explicar algunas interacciones y el comportamiento de la materia en el universo.
En este primer módulo haremos un corto recorrido histórico para revisar algunas ideas que contribuyeron al desarrollo de la física y que nos ubica dentro del contexto filosófico, luego estudiaremos él cálculo vectorial que nos ayuda en el correcto tratamiento de los fenómenos que consideramos adecuados en la física básica contenida en algunos programas de pregrado y secundaria
la luz con la visión y la óptica, el movimiento de los planetas con
las interacciones gravitatorias, la electricidad y el magnetismo con el electromagnetismo
etc. Los alcances logrados en los primeros años del siglo XX permitieron formular
teorías atómicas, y en los últimos años se desarrolla la teoría de la relatividad y se entra en el micro mundo de las partículas elementales.
Los progresos en el desarrollo de las ciencias físicas han sido de tal significado, que la diferencia entre la física y otras ciencias como la química, la biología, la astronomía, etc., da la impresión de no distinguirse. Más aún, otras ciencias tales como la psicología,
la lingüística, etc. parecen adoptar el método científico utilizado por las ciencias exactas. Por esta razón vale la pena mencionar ahora, y con algún detalle en que consiste este método.
Método de estudio sistemático de la naturaleza que incluye las técnicas de observación, reglas para el razonamiento y la predicción, ideas sobre la experimentación planificada y los modos de comunicar los resultados experimentales y teóricos, está compuesto esencialmente de tres etapas retroalimentadas. (Vea la figura 1.1).
La primera etapa consiste en la observación de algún fenómeno que nos interesa estudiar, ella debe ser cuidadosa, exhaustiva y en lo posible exacta.
En esta etapa es importante identificar mediante razonamiento lógico o procedimientos experimentales las variables que puedan influir en el fenómeno que nos concierne.
La segunda etapa debe dar como resultado una hipótesis acerca del tipo de relación matemática que existe entre las variables y la magnitud investigada.
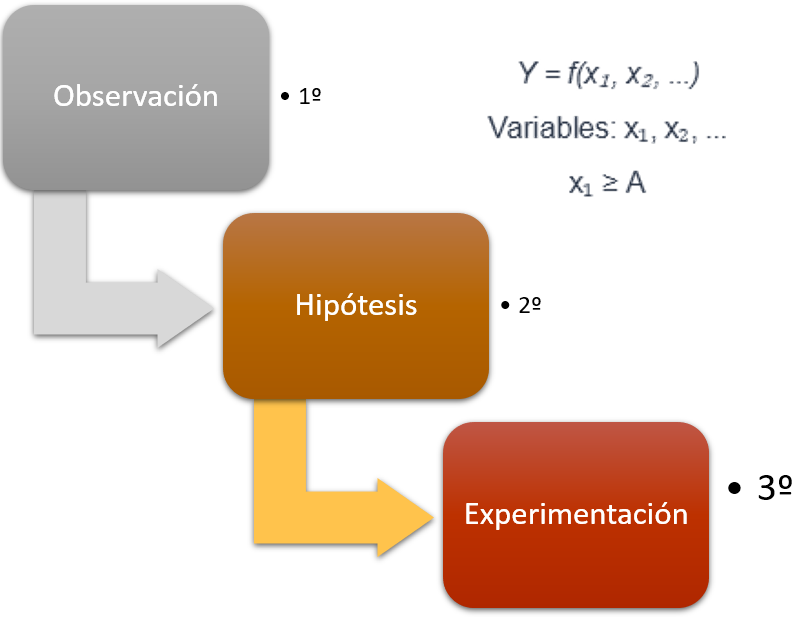
La hipótesis establecida es el resultado de información previamente adquirida y/o genialidad del investigador, se insiste además en que las etapas son retroalimentadas como se dijo inicialmente.
La tercera etapa y quizá la más decisiva, consiste en reproducir el fenómeno observado en forma controlada al antojo del experimentador. El resultado del experimento nos acerca a la certeza o falsedad de las hipótesis emitidas. Esta es una forma de conseguir leyes científicas que a su vez pueden dar lugar a principios generales con los cuales se constituye una teoría. Como resultado del proceso anterior puede decirse que existe una relación especial entre la física, las matemáticas y la experimentación (el laboratorio). Para un buen entendimiento de la mecánica y en general de la física básica,que hacen la esencia de este curso,es necesarios el conocimiento de las siguientes áreas: Aritmética, geometría, trigonometría plana, álgebra vectorial, cálculo diferencial y cálculo integral
En el estudio de cualquier ciencia es imprescindible el uso de vocablos especiales, como lo son en física los conceptos de magnitud, cantidad, medida, etc.
La medida es un procedimiento por el que se obtiene la expresión numérica de la relación que existe entre dos valores de una misma magnitud, uno de los cuales se ha adoptado convencionalmente como unidad. La magnitud es una propiedad de la materia, de un objeto o de un fenómeno físico o químico susceptible de tomar diferentes valores numéricos.
Las leyes de la física se expresan en función de cantidades fundamentales que a su vez pueden describirse en función de otras cantidades básicas. En mecánica, las tres cantidades fundamentales son longitud, masa y tiempo.
Las otras cantidades físicas en la mecánica pueden expresarse en función de esas tres. Por ejemplo, velocidad, volumen, fuerza, aceleración, etc.
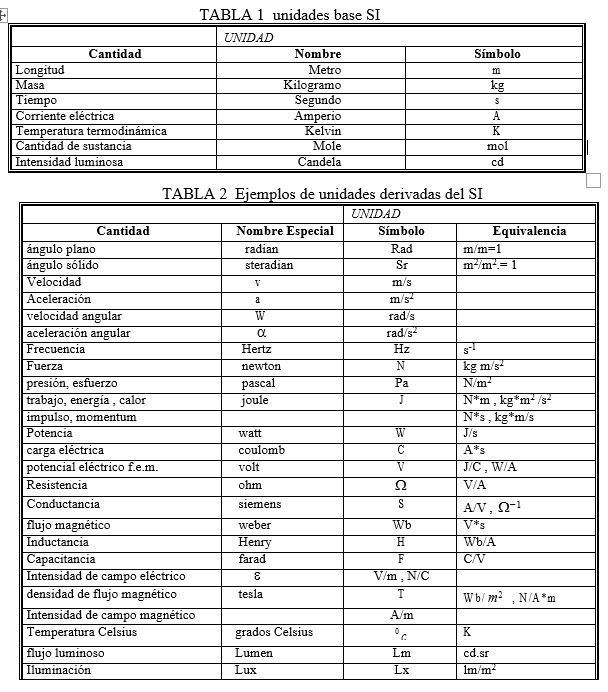
La palabra dimensión suele significar la naturaleza física de una cantidad. Cuando medimos una distancia en unidades como, por ejemplo, pies o metros o millas, se dice que su dimensión es la longitud.
La longitud, la masa y el tiempo son clases distintas de cantidades físicas; a cada una de ellas se le llama dimensión física. Otras dimensiones de las demás cantidades físicas se pueden expresar en términos de estas tres fundamentales.
La dimensión de una cantidad física se representa encerrándola entre paréntesis rectangulares, los símbolos para las dimensiones fundamentales son:
$\lbrack$tiempo$\rbrack$= T; $\lbrack$longitud$\rbrack$= L;$\lbrack$masa$\rbrack$= m;
El análisis dimensional aprovecha el hecho de que las cantidades que tienen la misma dimensión pueden sumarse o restarse en forma algebraica, de modo que los términos en ambos lados de una ecuación deben tener las mismas dimensiones. Uno de los mejores métodos para encontrar errores en un problema es comprobar las dimensiones de la respuesta, por ejemplo, en la ecuación:
$$x= v_o t+ \frac{1}{2}at^2$$
Observamos que la dimensión de $x$ es la longitud L, entonces los términos sumados en el lado derecho de esta ecuación deben tener también dimensiones de longitud en este lado $v_0$ es una velocidad, $t$ es un tiempo y $a$ es una aceleración.
En física, las cantidades pueden variar dentro de márgenes muy grandes o pequeños de magnitud. En un mismo análisis pueden ser de importancia tamaños comparables al radio de un electrón o también grandes como el universo visible. Por ello, las descripciones científicas requieren de un modo cómodo y eficiente para representar esas magnitudes, y efectuar cálculos con las relaciones numéricas que se producen al compararlas.
La notación científica consiste en expresar cualquier número como el producto de una potencia de base diez y un número real mayor o igual a uno, pero menor a diez. Si N es el número que queremos expresar, escribimos:
$\pm{N} $= $\pm{n}$x$10^a$, donde $a$ es un número entero y $1\le n$ $\le 10$.
Ejemplo 1.
Expresar el número 20923.45 en notación científica.
Solución: 20923.45 = 2.092345x$10^4$
Para redondear una respuesta a la cantidad correcta de cifras significativas, se redondea hacia arriba sí la primera cifra no $\lbrack$significativa$\rbrack$Existen Laboratorios donde se desarrollan estos temas es 5 o mayor, y se redondea hacia abajo si es menor, para el caso anterior tenemos:
2.092345x$10^4$ = 2.1x$10^4$.
El resultado obtenido al medir una magnitud física puede variar si se cambia el punto de referencia con respecto al cual se ha efectuado la medida. La posición de la luna el 6 de marzo de 2024 a las 19 horas 15 minutos para un observador situado en Medellín (Colombia), será distinto para otro situado en Greenwich. Ello se debe a la referencia considerada para fijar su situación.
En física es frecuente elegir un sistema de referencia cuando estamos realizando cualquier cálculo donde es necesario comparar nuestras observaciones con hechos o aspectos que consideramos fijos e inmutables.
Los sistemas de coordenadas son de gran utilidad en el manejo matemático de los campos escalares y vectoriales.
Es posible asociar a cada punto del espacio tridimensional un conjunto de tres números que se llaman coordenadas. Éstas pueden verse como un nombre o etiqueta que se utiliza para identificar cada punto. Existen varios sistemas de coordenadas, entre ellos tenemos: Los sistemas de coordenadas cartesianas o rectangulares, cilíndricas, esféricas, coordenadas polares, elípticas, parabólicas, etc.
Los sistemas que se trabajan en este curso y de uso frecuente son el cartesiano, el cilindrico y el polar.
En el sistema cartesiano se identifica un punto cualquiera $P$ en el espacio con las coordenadas $x, y, z$ es decir $P(x,y,z)$
En el sistema de coordenadas cilindricas identificamos el punto mediante las coordenadas $r,\theta\; y \; z$ o sea $P(r,\theta,z)$
Finalmente en sistema de coordenadas esfericas usamos $r,\theta, \phi$ es decir $P(r,\theta, \phi)$
El sistema de coordenadas cartesianas está formado por ejes mutuamente perpendiculares; estos ejes metrizados tienen además instrucciones para localizar puntos y un origen (o). Un punto puede estar localizado sobre un eje (una dimensión), en un plano (dos dimensiones) ó en el espacio (tres dimensiones). La figura 1.2 muestra esta situación.
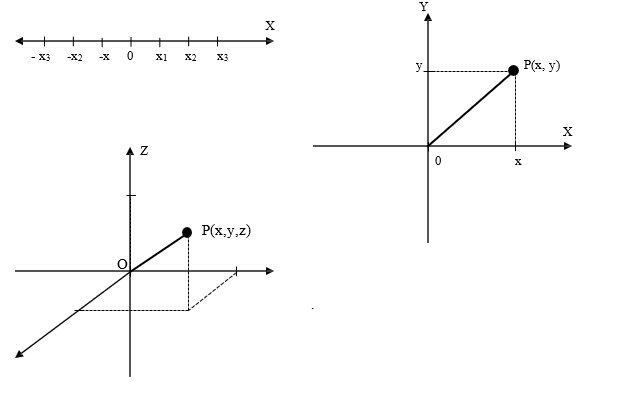
La palabra distancia significa espacio o tiempo entre dos cosas o sucesos. Encontremos la distancia entre dos puntos cualesquiera, en un eje metrizado, en un plano y en el espacio, cada una de estas dimensiones tienen su origen (o).
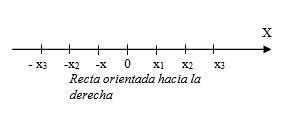
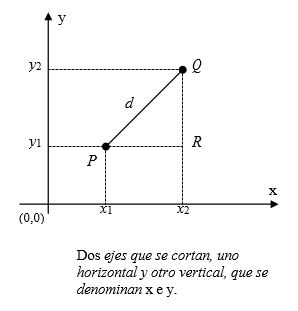
De la misma manera la distancia Entre el punto $Q$ y el punto $R$ es:
$$QR = y_2 - y_1 $$
Aplicando el teorema de Pitágoras al triangulo $PQR$ encontramos que:
$$ d =\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\tag{2} $$
como vemos las coordenadas de un punto en el plano cartesiano son dos ejes que se cortan, uno horizontal y otro vertical, que se denominan x e y.
Si el punto P se localizara en el origen, entonces
$x_1 = 0$
$y_1 = 0$ , de modo que la
distancia d entre un punto Q cualesquiera y el origen (0,0), eliminando los subíndices es:
$$d =\sqrt{x^2+y^2}\tag{3} $$
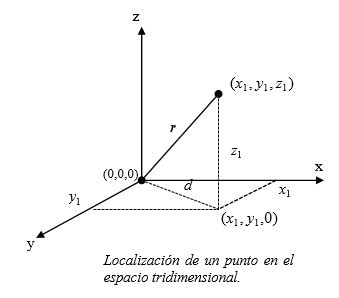
Consideremos un punto cualquiera en el espacio tridimensional cartesiano. Este punto está siempre determinado por tres coordenadas espaciales perpendiculares entre si. En un espacio cartesianos estos ejes son $X,\;Y y\;Z.$ Consideremos la distancia $r$ entre el origen y un punto cualquiera en este sistema. (ver Figura 1.5)
Notemos además que en el triángulo formado por los puntos (0,0,0) , $(x_1 , y_1 ,0) \; y \; (x_1 , y_1 , z_1 )$ podemos determinar la distancia $r$. Entonces $$r^2 = d^2 + z^2$$ $$r =\sqrt{x_1^2+y_1^2+z_1^2}\tag{4}$$
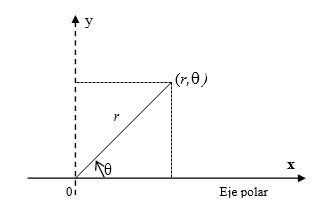
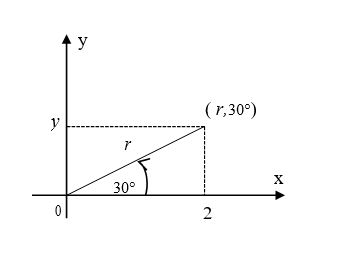
En este sistema a cada punto del plano se le asignan las coordenadas $(r,\theta)$, donde $r$ es la distancia entre el origen llamado polo y el punto; $\theta$ es el ángulo que forma $r$ con el eje fijo x llamado también eje polar. El ángulo es medido generalmente en el sentido contrario a las manecillas del reloj.
De la Figura 1.6 podemos ver:
$$\tan{\theta} =\frac{y}{x},\qquad \theta =\tan^{-1} \frac{y}{x}$$
$$\sin{\theta} =\frac{y}{r},\qquad y =r\sin{\theta}$$
$$\cos{\theta} =\frac{x}{r},\qquad x =r\cos{\theta}$$
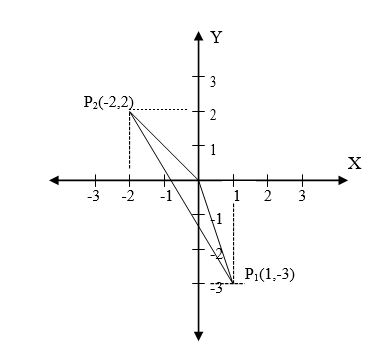
Definimos $(x_1,y_1)$ = (1,-3) como el punto $P_1$ y $(x_2,y_2)$ = (-2,2) como el punto $P_2$. Para encontrar la distancia $d$ entre estos dos puntos, aplicamos la ecuación (2).
Entonces:
$$d =\sqrt{(-2-1)^2+[2-(-3)]^2} $$
$$d =\sqrt{(-3)^2+[5]^2} =\sqrt{34} = 5.83$$
b. Sea $P_1(r_1,\theta_1)$ y $P_2(r_2,\theta_2)$ las coordenadas polares. Donde $r_1$ y $r_2$ son las distancias entre el origen y los puntos respectivos, y $\theta_1$ y $\theta_2$ son los ángulos entre $r_1$ y $r_2$ medidos respecto al eje positivo X.
De la figura
$$r_1 =\sqrt{1^2+(-3)^2} = \sqrt{10}$$
El ángulo entre $r_1$ y el eje X medido por debajo es $\beta_1 = \tan^{-1}(\frac{3}{1})$ = 71.56°,de modo que $\theta_1$ = 360° - 71.56º = 288.4° (ángulo respecto al eje positivo X)
$$\implies P_1(r_1,\theta_1) = (\sqrt{10}, 288.4°)$$
$$r_2 =\sqrt{(-2)^2+(2)^2} =\sqrt{8}$$
El ángulo entre $r_2$ y el eje $Y$ es $\beta_2 = \tan^{-1}(\frac{2}{2}) = 45°$
De modo que $\theta_2 = 45° + 90° = 135°$ (ángulo respecto al eje positivo X).
$$\implies P_2(r_2,\theta_2) = (\sqrt{8}, 135°)$$
De la figura
$$r_1 =\sqrt{1^2+(-3)^2} = \sqrt{10}$$
Son cantidades que están acompañadas de una magnitud numérica y una unidad de medida sin ninguna dirección asociada; sus operaciones se realizan como los números reales. Ejemplos de cantidades escalares: 26s (tiempo), -30 °C (temperatura), 5kg (masa), 6m (distancia), 20J (energía), 10atm (presión), 100watt (potencia), 15Hz (frecuencia), etc.
Son cantidades que van acompañadas de una magnitud numérica, una unidad de medida y además están asociadas con una dirección y sentido al mismo tiempo. Algunos ejemplos de cantidades vectoriales son: velocidad, fuerza, aceleración, torque, momento lineal o cantidad de movimiento, campo eléctrico, campo magnético, campo gravitacional, etc. A continuación, se presentarán algunas definiciones para avanzar en el estudio de los vectores y escalares que permiten más adelante el entendimiento de algunas operaciones y ecuaciones que se presentan en la física.
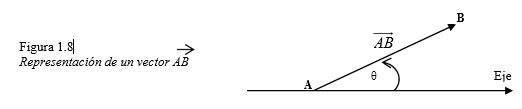
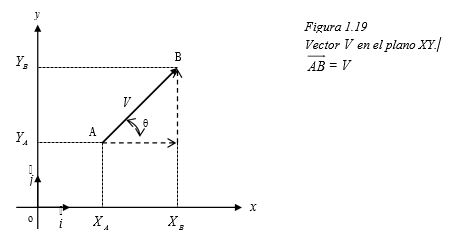
Todo vector está formado por una recta orientada o segmento de recta orientada, que tiene un origen y una cabeza o fin. (Figura 1.8) El punto A en la figura 1.8 es el origen y el punto B es el fin o cabeza del vecto
$\theta$ es la dirección del vector o ángulo que forma con el eje horizontal y se designa de la siguiente manera:
$$dir(\vec{AB})=\theta\qquad\vec{AB}=\vec{V}$$
AB es la magnitud del vector, es decir:
A la pareja $(AB, \theta)$ o $(V, \theta)$ se le llama representación polar del vector, entonces:
$$\vec{AB} = ( \vec{AB}, \theta )\qquad \vec{V} = (\vec{V} , \theta )$$.
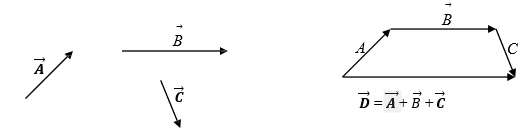
Para sumar vectores se debe tener presente que un vector puede trasladarse a cualquier punto del espacio y no cambia si se le conserva su magnitud y dirección.
Consideremos tres vectores
$\vec{A},\vec{B}, y \; \vec{C} $ orientados tal como se muestran
en la figura 1.10.
En la cabeza del vector $\vec{A}$ se ha colocado el origen del vector $\vec{B}$ y en la cabeza del vector $\vec{B}$ se ha colocado el origen del vector $\vec{C}$ para obtener el vector $\vec{D}$ al cual llamamos suma vectorial o resultante de los vectores $\vec{A}$,$\vec{B}$ y $\vec{C}$.
Esta relación simbólicamente se expresa así:
$$\vec{D} = \vec{A} + \vec{B} + \vec{C}$$
Analíticamente para hallar la resultante de la suma de vectores es necesario recordar los teoremas del $\textit{seno}$ y $\textit{coseno}$ que a continuación describimos para el triángulo de figura dada:
Teorema del Coseno :
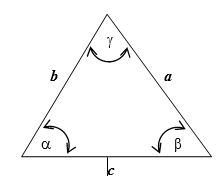
$$a^2 = b^2 + c^2 – 2bc\times\cos\alpha$$
$$b2 = a^2 + c^2 – 2ac\times\cos\beta$$
$$c^2 = a^2 + b^2 – 2ab\times\cos\gamma$$
Teorema del seno:
$$\frac{a}{sin\alpha}=\frac{b}{sin\beta}=\frac{a}{sin\gamma},\qquad$$
Se debe cumplir que
$$\alpha + \beta + \gamma = 180°$$
Ejemplo 7
Sumar los vectores:
$\vec{A} = ( 2 , 60° )\; y \; \vec{B} = ( 3, 0° )$.
Solución
Los vectores $\vec{A}$ $\;$ y $\;$ $\vec{B}$ escritos en forma polar se localizan en el plano de la figura 1.11.
$\vec{A}$ forma un ángulo de 60° con el eje horizontal y $\vec{B}$ se encuentra sobre el eje horizontal.
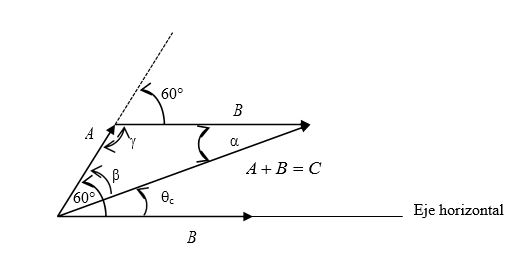
En la figura tenemos que $$\gamma = 180° - 60° = 120°$$ Aplicando el teorema del coseno
$$ C^2 = A^2 + B^2 –2AB\times\cos120°$$
$$ C = 4.36 $$
El ángulo que el vector resultante $\vec{C}$ hace con el eje horizontal es: $\theta_c = 60° - \beta$
. Para encontrar $\beta$ aplicamos el teorema del seno:
$$\frac{B}{\sin\beta}= \frac{C}{\sin120^0}$$
$$\sin\beta=\frac{B.sin120^0}{C}=0.59$$
De modo que $\theta = 60° - 36.2° = 23.8°$
Observe que la magnitud de la suma
$\vec{A}+ \vec{B}$
depende de las magnitudes de $\vec{A}$ y de $\vec{B}$ y
del ángulo entre $\vec{A}$ y $\vec{B}$ . Sólo en el caso especial en que $\vec{A}$ y $\vec{B}$ son paralelos es la magnitud de $\vec{C} =\vec{A} + \vec{B}$ igual a la suma de las magnitudes de $\vec{A}$ y $\vec{B}$ .
Si necesitamos sumar más de dos vectores, podemos sumar primero dos cualquiera de ellos, sumar vectorialmente la resultante al tercero y así sucesivamente.
Ejercicios
Sumar los vectores:
a).
$\vec{A} = ( 4 , 60° )$ y $\vec{B}= ( 2 , 30° )$.
b) Si
$\vec{A} =( 2, 90° )$ ,$\vec{B} =
( 5 , 30° )$ y $\vec{A} = ( 6,0° )$,
cúal es la resultante de sumar analíticamente
$\vec{A}$ + $\vec{B}$ + $\vec{C}$ .
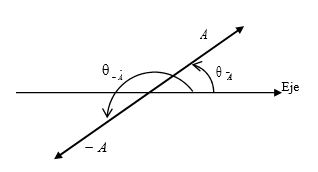
El negativo de un vector cualquiera A se define como otro vector que tiene igual magnitud, pero dirección contraria,(ver figura 1.13) es decir:
$$dir(- \vec{A} ) = dir( \vec{A} ) + 180°.$$
La expresión anterior también se puede escribir de la manera siguiente:
$$\theta_{-A} = \theta_A +180^0$$
Esto es la base para definir la resta de vectores.
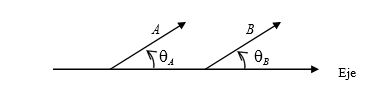
$\vec{A}$ y $\vec{B}$ son iguales si se cumple que $$A = B \quad y \quad \theta_A = \theta_B$$ La figura 1.13 muestra tal situación
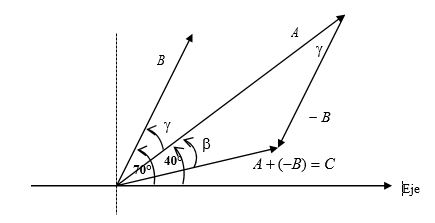
Definimos la diferencia $\vec{A} - \vec{B}$ como la suma de $\vec{A}$ y el opuesto del vector $\vec{B}$:
$$\vec{A} - \vec{B} =\vec{A} + \vec{(-B)}$$Como A= 5 y B =3
$$\implies C =\sqrt{5^2+3^2-2\times5\times3\cos30^0}=2.83$$
El ángulo que forma C con la horizontal lo designamos como $\theta_c$, entonces,
$\theta_c = 40° - \beta$ . En el triángulo que se ve en la figura 1.14 aplicamos el teorema de seno:
$$\frac{B}{\sin\beta}=\frac{C}{\sin30^0}\implies \sin\beta = \frac{B}{C}\times\sin30^0$$
$$\sin\beta=\frac{3}{2.83}\times\sin30^0 = 0.5300 \implies \beta =32^0$$
reemplazando $$\theta_c = 40^0-32^0 = 8^0$$
Ejercicio:si $\vec{A}=(5,90^0)$ y $\vec{B} =(6,20^0) $, hallar $\vec{A}-\vec{B}$
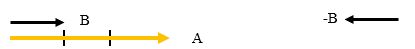
En la figura 1.16 el vector $\vec{A}$ tiene tres unidades de longitud y el vector $\vec{B}$ tiene una unidad de longitud, entonces podemos establecer las siguientes relaciones: $\vec{A}=3\vec{B}$ $\;$ ó $\;$ $\vec{B}=\frac{1}{3}\vec{A}$; en términos del vector opuesto tenemos:$-\vec{B}= \frac{1}{3}\vec{A}$
El vector $\vec{a}$ llamado vector unitario en la dirección de A se define de la siguiente forma: $\hat{a} = \frac{\vec{A}}{A}$; $\hat{a}$ tiene magnitud 1, sin unidades. Su función es describir una dirección. Los vectores unitarios son una notación cómoda para indicar las componentes de los vectores que más adelante estudiaremos. De la definición dada de vector unitario tenemos que: $$\vec{A} = A\hat{a}\tag{5}$$
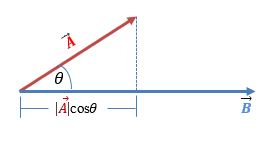
Si $\vec{A}\; y \; \vec{B}$ son dos vectores con sus orígenes en un mismo punto y $\theta$ el ángulo entre ellos, entonces:
$$\vec{A} •\vec{B} = A.B.\cos\theta\tag{6}$$
El ángulo $\theta$ está entre 0° y 180°, es decir, es el ángulo menor entre los vectores (vea la figura 1.17).
En la figura 1.17 el segmento 0A’ es la componente del vector $\vec{A}$ en la dirección del vector $\vec{B}$ , entonces:
$OA´ = \vec{A}.\cos.\theta$ $\;$ o
$$OA´=\frac{\vec{A}•\vec{B}}{B}\tag{7}$$
Propiedades del producto Escalar
1. Conmutativa:
$\vec{A}•\vec{B} =\vec{B}•\vec{A}$ .
2. Distributiva respecto a la suma:
$\vec{A} • (\vec{B} + \vec{C}) = \vec{A} • \vec{B} + \vec{A} • \vec{C}$ .
3. Distributiva respecto al producto por un escalar: $k\vec{A} • \vec{B} =
\vec{A}• (k\vec{B}) =(k\vec{A})•\vec{B}$
4. $\vec{A} •\vec{B}$ = 0 $\implies $
$\vec{A} = 0\quad$ ó $\;$
$\vec{B} = 0\quad$
ó $\;$ $\vec{A}$ es perpendicular a $\vec{B}$
5. $\vec{A}•\vec{A}= A^2$ .
El resultado del producto cruz de dos vectores $\vec{A}$ y $\vec{B}$ es otro vector que tiene las siguientes características:
1.$\;|\vec{A} \times \vec{B}|=AB\sin\theta$, siendo $\theta$ el ángulo menor entre $\vec{A}$ y $\vec{B}$
2.$\;\vec{A}\times \vec{B}$ =$\vec{C}$ , donde $\vec{C}$ es un vector perpendicular al plano formado por $\vec{A}$ y $\vec{B}$ ;
La dirección de $\vec{C}$ se encuentra aplicando la regla de la mano derecha, o también se puede decir que la dirección de $\vec{C}$ es la dirección en que avanza un tornillo de rosca derecha.
1. Anti-conmutatividad: $\vec{A}\times \vec{B} = -\vec{B}\times\vec{A}$
2. Distributiva respecto a la suma:
$\vec{A}\times (\vec{B}+ \vec{C}) =\vec{A}\times \vec{B} + \vec{A}\times \vec{C}$
3. Distributiva respecto al producto por un escalar $k$ : $(k\vec{A}) \times\vec{B} = \vec{A} \times(kB)$ , $k \neq 0 $.
4. $\vec{A}\times\vec{B} = 0 \implies \vec{A} = 0 \quad ó \quad \vec{A} = 0\quadó\quad \vec{A} | |\vec{B} $.
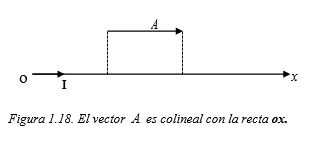
Representación en una dimensión: Consideremos un vector A colineal con una recta orientada, que tiene un origen (o) y un final x como se muestra en la figura 1.18.
En la figura 1.18 $OI = \vec{i}= 1\vec{i}$ es un vector unitario. Como $\vec{A}$ es colineal con la recta Ox, la componente del vector $\vec{A}$ a lo largo del eje x se define así:
$$ A_x =\frac{\vec{A}.\vec{i}}{\vec{|i|}}=A\cos\theta\tag{8} $$
Dado los vectores:
$\vec{A} = ( \vec{A_x} , \vec{A_y} , \vec{A_z})$
$\vec{B} = (\vec{B_x} , \vec{B_y} , \vec{B_z})$
$ \vec{C} = (\vec{C_x} ,\vec{C_y}, \vec{C_z} )$,
Entonces el vector $\vec{C}$ resultante de multiplicar vectorialmente los vectores $\vec{A}\;y \; \vec{B}$ lo podemos escribir:
$$
\vec{C} =\vec{A}\times\vec{B}= \begin{vmatrix}
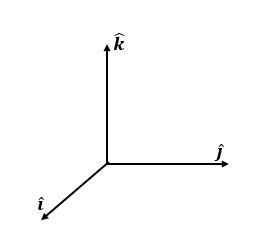
\hat{i} & \hat{j} & \hat{k}\\
A_x & A_y & A_z\\
B_X & B_y & B_z
\end{vmatrix}=\\
\hat{i}(A_yB_z- A_zB_y)- \hat{j}(A_xB_z- A_zB_x)+ \hat{k}(A_xB_y- A_yB_x)$$
Observe que:
$ C_x =(A_yB_z- A_zB_y)$
$C_y =- (A_xB_z- A_zB_x)$
$C_z =(A_xB_y- A_yB_x)$
Si$\vec{A}=(5,60^0)\quad y \quad \vec{B}=(6,335^0)$.
Hallar la magnitud y la dirección de $\vec{A}+\vec{B}$
Solución
Trazamos una línea horizontal que representa el eje X, a continuación se dibujan los vectores $\vec{A} \;y \;\vec{B}$ con sus ángulos medidos respecto al eje positivo de las X como se muestra en la figura 1.22.
De la figura notamos que:
$$\vec{|C|}=\sqrt{5^2+6^2-2\times5\times6\cos95^0}=8.138$$
Finalmente, para encontrar el ángulo $\beta$ aplicamos ahora la ley del seno al triangulo que contiene el ángulo de $95^0$
$$\frac{8.138}{\sin95^0}= \frac{5}{\sin\beta} \implies \beta =37.7^0$$
De la figura
$\beta =\theta_c + 25^0 \implies \theta_c =12.7^0$
por lo tanto, el vector resultante $\vec{C}$, forma un angulo de $12.7^0$ con el eje horizontal

Introducción
En esta segunda unidad se debe entender cómo se describe un movimiento rectilíneo con velocidad constante y a la vez los términos de velocidad media, velocidad instantánea, aceleración media y aceleración instantánea.
Para el análisis de este tipo de movimiento nos basaremos esencialmente en ejercicios de aplicación en determinada temática, sin perder los conceptos básicos de este tipo de movimiento, es decir, el movimiento rectilíneo con velocidad constante y de igual manera el movimiento rectilíneo con aceleración constante.
LA MECÁNICA. El movimiento rectilíneo es una sección de la física dentro de la mecánica, que es el estudio de las relaciones entre fuerza, materia y movimiento, en esta sección estudiaremos la CINEMÁTICA, que es una parte de mecánica que estudia el movimiento de los cuerpos sin tener en cuenta la causa que lo produce, seguidamente estudiaremos la DINÁMICA que también hace parte de la mecánica y estudia el movimiento de los cuerpos teniendo presente la causa que lo produce, es decir, la relación entre el movimiento y sus causas.
Para describir el movimiento de un cuerpo, iniciaremos con los conceptos de velocidad y aceleración. No realizaremos la demostración de las ecuaciones fundamentales de la cinemática, se presentarán y se utilizaran para desarrollar diferentes ejercicios y problemas en las que tienen sus respectivas aplicaciones.
Las posiciones de un cuerpo siempre estarán determinadas por tres coordenadas de posición y un parámetro temporal que especifica el momento en el cual un cuerpo ocupa determinada posición.
Iniciaremos nuestro estudio considerando el movimiento de un cuerpo a lo largo de uno cualquiera de los ejes de nuestro sistema coordenado
La velocidad media
En general depende del intervalo de tiempo elegido, así por ejemplo si en el tiempo $t_1$ una partícula está en el punto $P_1$, con la coordenada $x_1$, y en el tiempo $t_2$ está en el punto $P_2$ con la coordenada $x_2$, el desplazamiento ∆x de la partícula en el intervalo de $t_1\; a\; t_2$ es el cambio de la posición en la coordenada x, o sea que:
$$∆x= x_2- x_1$$
$$∆x= x_{final}- x_{inicial}\tag{2.1}$$
La velocidad media, es la componente x del desplazamiento, ∆x, dividida entre el intervalo de tiempo ∆t que ocurre el desplazamiento.
$$v_{mx}=\frac{(x_2-x_1)}{(t_2-t_1)}= \frac{∆x}{∆t}\tag{2.2}$$ (Velocidad media en el movimiento rectilíneo)
No olvide que tanto ∆x como $v_{mx}$ son cantidades vectoriales que, en este caso particular, solo tienen componente a lo largo del eje x.
Las unidades de la velocidad media se expresan en metros sobre segundos: $\frac{m}{s}$
Se dice que una partícula tiene una velocidad constante si ella no cambia la magnitud de su velocidad ni su dirección, es decir se mueve en línea recta, en un sistema de solo una dimensión. La partícula con movimiento rectilíneo puede localizarse dentro de un sistema de referencia, que a su vez se mueve con velocidad constante.
Podemos afirmar que nuestro Planta Tierra, se mueve con velocidad constante, sin embargo, en su trayectoria alrededor del Sol hay dos puntos donde la velocidad es diferente,
un punto de máxima velocidad (perihelio) y otro de mínima velocidad (afelio), de modo que la velocidad de la Tierra está cambiando, pero estos cambios son tan pequeños que los podemos despreciar y considerar que la Tierra se mueve con velocidad constante. Cuando un cuerpo se mueve con velocidad constante en una dirección, digamos en la dirección del eje X podemos escribir:
$$ v_x =\frac{\Delta x}{\Delta{t}} \quad o \quad v_x = \frac{distancia}{tiempo}\tag{2.3} $$
Para definir la velocidad instantánea nos basaremos en la definición de la velocidad media, moviendo el punto $P_2$ cada vez más cerca al punto $P_1$ en lapsos de tiempo muy cortos, de modo que ∆x y ∆t tienden hacer muy pequeños. La velocidad instantánea en el límite de la velocidad media conforme el intervalo de tiempo se acerca a cero; es igual a la tasa instantánea de cambio de posición con el tiempo.
En el lenguaje del cálculo, esto corresponde a una derivada:
$$v_x=\lim_{\Delta{t\to 0}}\frac{\Delta{x}}{\Delta{t}}= \frac{dx}{dt}\tag{2.4}$$
Siempre que la velocidad de una partícula cambie en magnitud y/o en dirección en un intervalo del tiempo grande o pequeño, decimos que la partícula tiene aceleración. La aceleración al igual que la velocidad es una cantidad vectorial, además la rapidez de la partícula puede aumentar o disminuir, lo cual está ligado a una aceleración o desaceleración. En un movimiento rectilíneo, la única componente distinta de cero está sobre el eje de su movimiento. En lo que sigue definiremos la llamada aceleración media y luego la aceleración instantánea
$\textbf{Aceleración Media}$
Si la componente x de la velocidad cambia en un $∆v_x= v_{2x}- v_{1x}$ en el intervalo de tiempo $∆t= t_2- t_1$, la aceleración media en x es el cociente entre $∆v_x \;y \; ∆t$, de modo que para el movimiento rectilíneo tenemos:
$$a_{mx} = \frac{\Delta{v_x}}{\Delta{t}}\tag{2.5} = \frac{v_{2x}-v_{1x}}{t_2-t_1}$$
Las unidades de la aceleración media en el SI de acuerdo con (2.5) suele escribirse como: $\frac{m}{s^2}$
Aceleración Instantánea
Con el mismo procedimiento como definimos la velocidad instantánea, definimos la aceleración instantánea, es decir en el límite de la aceleración media cuando ∆t→0, la aceleración instantánea es la derivada de la velocidad con respecto al tiempo. Así,:
$$a_x = \lim_{\Delta{t\to 0}}\frac{\Delta{v_x}}{\Delta{t}}\tag{2.6} = \frac{dv_x}{dt}$$
$\textbf{Movimiento Con Aceleración Constante}$
En este particular movimiento la velocidad cambia al mismo ritmo a lo largo del movimiento, por ejemplo, cuando un cuerpo cae libremente, lo hace con aceleración constante. Lo mismo ocurre cuando un cuerpo se desliza sobre un plano inclinado.
Cuando una partícula se mueve con aceleración constante hay que tener presente que: El signo de la aceleración no nos indica si una partícula está acelerando o frenando; se debe comparar los signos algebraicos de la velocidad y la aceleración. Así por ejemplo si la velocidad $v_x$ de la partícula es positiva y está aumentando, la aceleración $a_x$ es positiva y la partícula está acelerada. Si la velocidad es positiva y disminuye, la aceleración es negativa en la dirección +x y la partícula se estaría frenando.
Si la velocidad es negativa y se vuelve menos negativa, la aceleración es positiva, la partícula se mueve en la dirección - x y se frena. Si la velocidad es negativa y se vuelve más negativa, la aceleración es negativa en la dirección - x, la partícula acelera. Estas situaciones se aplicarán en los diferentes ejercicios que estudiaremos más adelante.
Podemos conocer la aceleración de una partícula a partir de una gráfica de su posición contra el tiempo. Matemáticamente como $a_x= dv_x/dt \; y \; v_x= dx/dt$ entonces:
$$a_x =\frac{dv_x}{dt}\tag{2.7}=\frac{d}{dt}(\frac{dx}{dt}) $$
Presentaremos ahora un sistema de ecuaciones para el movimiento rectilíneo con aceleración constante, que no demostraremos, pero que son la base fundamental para la solución de los diferentes ejercicios para la cinemática en línea recta. Luego daremos algunas recomendaciones de la manera como se puede dar solución a problemas y ejercicios en los diferentes temas de la física básica.
Ecuaciones que relacionan la posición x, y la velocidad $v_x$ en cualquier instante t. En $t=0$, la posición inicial es $x_0$ y la velocidad inicial es $v_{ox}$. Las siguientes ecuaciones son válidas solo si la aceleración es constante. $$v_x = v_{0x} + a_xt\tag{2.8}$$ $$x = x_0 + v_{0x}t + \frac{1}{2}a_xt^2\tag{2.9}$$ $$v_x^2 = v^2_{0x} + 2a_x(x-x_0)\tag{2.10}$$
Para cuerpos en caída libre las ecuaciones anteriores tienen la misma forma, la caída libre es un caso especial del movimiento rectilíneo con aceleración constante, donde la aceleración corresponde a la aceleración de la gravedad g y el movimiento se realiza sobre el eje y. El valor aproximado de $g$ cerca de la superficie terrestre es:
$g=9.8m/s^2 = 980cm/s^2 =32pies/s^2$
En ocasiones cuando la aceleración en el movimiento rectilíneo no es constante, pero es una función conocida del tiempo, podemos calcular la velocidad y la posición utilizando las siguientes ecuaciones:
$$v_x =v_{0x} +\int_{x=0}^{t} \!\!\!a_x\cdot dx\tag{2.12}$$
$$x = x_0 +\int_{0}^{t}v_x\cdot dt\tag{2.13}$$
Recomendaciones para la solución de ejercicios
Después de haber leído y entendido la teoría sugerimos los siguientes puntos para que aprendamos a resolver problemas de física:
1.Lea cuidadosamente el problema o ejercicio, entiéndalo perfectamente y trate de situarlo en el tema correspondiente.
2. Identifique las variables conocidas del problema, así como también las variables desconocidas. Debes escribirlas y reconocerlas claramente.
3. En este orden de ideas, busca e identifique cuales ecuaciones están relacionadas con las variables que has identificado.
4. Finalmente aplica las herramientas matemáticas para dar solución al problema.
Nota: Es importante que después de obtener un resultado, las unidades de este deben ser coherentes, es decir, en el proceso de solución las unidades que se van reemplazando deben operarse correctamente, así por ejemplo si la respuesta es una velocidad las unidades al final darán $m/s$, o si la respuesta es una aceleración se debe obtener $m/s^2$.
Observe lo que ocurre al reemplazar las unidades en la ecuación (2.9):
$$x = x_0 + v_{0x}t + \frac{1}{2}a_xt^2$$
$x$ y $x_0$ se dan en $m$ ; $v_0x$ se da en $m/s$ ; $a_x$ está en $m/s^2$ y el tiempo $t$ en segundos $s$.
De modo que al reemplazar en la ecuación (2.9) escribimos:
$$x=( )m+( ) \frac{m}{s}\times s+( )\frac{m}{s^2}\times s^2=( )m$$
Observe que las unidades están acompañadas de ciertos coeficientes o números, lo que está entre paréntesis, como la variable $x$ es una longitud o distancia el resultado da en $m$ (metros).
El movimiento de un proyectil (movimiento parabólico) se realiza en un plano vertical donde se presenta un vector de velocidad inicial $\vec{v_0}$ y un ángulo inicial $\theta_0$ que determina la dirección de la velocidad inicial. El vector $\vec{v_0}$ en el plano vertical tiene inicialmente dos componentes: una componente inicial en la dirección X que hace que el proyectil avance horizontalmente y otra componente inicial en la dirección Y que hace que el proyectil se mueva en la dirección vertical, subiendo o bajando. El movimiento en la dirección X se realiza con velocidad constante, es decir, no cambia durante el movimiento $(a_x=0)$.
El movimiento en la dirección vertical Y, cambia uniformemente hasta alcanzar el punto de máxima altura donde la velocidad $v_y$ es igual a cero y el proyectil empieza el descenso. La aceleración en el movimiento vertical apunta siempre hacia la superficie terrestre y corresponde a la aceleración de la gravedad, es decir, $a_y=-g$ en cualquier instante del tiempo.
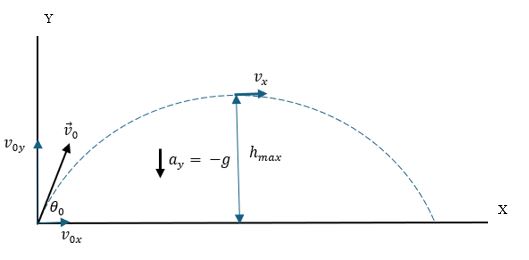
En la figura 2.1 tenemos que: $v_{0x}= v_0 cosθ_0$ ; $v_{0y}= v_0 senθ_0$ ; $\vec{v_0}$ es el vector velocidad inicial; $\theta_0$ es el ángulo inicial del lanzamiento; $h_{max}$ es la altura máxima alcanzada por el proyectil, además, $v_{0x}= v_x$
Para el movimiento en el eje y se utilizan las ecuaciones que corresponden a una caída libre, ósea.
$$v_y= v_{0y}-gt\tag{2.14}$$
$$y- y_0= v_{0y} t- \frac{1}{2} gt^2\tag{2.15}$$
Para el movimiento de un proyectil podemos obtener a partir de las ecuaciones anteriores, otro sistema de ecuaciones que permiten solucionar problemas de este tipo de movimiento. En los ejercicios que desarrollaremos más adelante sobre tiro parabólico, mostraremos la aplicación de estas ecuaciones. Para calcular la posición y la velocidad de un proyectil respecto a un origen localizado en plano vertical, en cualquier instante del tiempo, por ejemplo, la distancia $r$ del proyectil al origen viene dada por:
$$ r =\sqrt{x^2+y^2}\tag{2.16}$$
En esta ecuación (2.16), $r$ es la magnitud del vector posición $\vec{r}$.
La magnitud de la velocidad del proyectil en cualquier instante es:
$$ v =\sqrt{v_x^2+v_y^2}\tag{2.17}$$
Otras ecuaciones que se pueden deducir a partir de la figura 2.1 para el movimiento de un proyectil son el tiempo para alcanzar la altura maxima y la altura maxima (cuando $v_y$=0) :
$$t_{altura\; maxima} = \frac{v_0\sin\theta_0}{g}\tag{2.18}$$
$$h_{max}=\frac{v_0^2}{2g}\sin^2\theta_0\tag{2.19}$$
El alcance horizontal $R$ que corresponde a la distancia entre el origen y el punto donde choca es proyectil es:
$$R =\frac{v_0^2\sin2\theta_0}{g}\tag{2.20}$$
Todas las ecuaciones anteriores para el movimiento parabólico son válidas, cuando la resistencia del aire es muy pequeña,
cuando se considera la resistencia del aire el cálculo de la trayectoria es más complicado, ya que la fricción del proyectil con el aire o cualquier fluido hace que la velocidad cambie y de hecho la aceleración no es constante. La fricción con el aire tiene un efecto acumulativo sobre el movimiento del proyectil. Se recomienda para resolver problemas, definir un sistema de coordenadas y colocar un origen en la posición inicial $(t=0)$ donde el proyectil es lanzado desde esta posición, es decir, $x_0=0$ $\;$ y $\;$ $y_0=0$.
Actividad de simulación
En la siguiente actividad estudiamos la teoría anterior jugando con la simulación Phet de la Universidad de Colorado: haga doble clic en cualquiera de las cuatro ventanas de la imagen a continuación y ábralas. La barra inferior de la simulación es verde y contiene dos iconos: un borrador blanco en un cuadro de fondo amarillo y un cañón de disparo en un cuadro de fondo rojo que pulsamos cada vez que queremos disparar, a la izquierda de estos iconos podemos establecer la velocidad de disparo inicial con valores entre 0 y 30 m/s. Tenga en cuenta que la altura del cañón sobre la superficie se puede variar presionando el símbolo + y arrastrando el cañón verticalmente.
Actividades
1. Incline el cañón en un ángulo de 37° y utilice una velocidad inicial de $v_0 =15 m/s$. Encuentre la distancia (alcance) a la que cae la bala, para ello deslice el objetivo en movimiento, verifique este valor experimental usando los mismos parámetros de la ecuación (2.20)
2. Utilice una regla o cualquier otro instrumento para medir la altura máxima con los mismos datos de ángulo y velocidad y verifique nuevamente la ecuación (2.19)
Si una partícula se mueve en una trayectoria curva, la dirección de su velocidad cambia.
En esta sección trataremos un caso especial en el cual la partícula se mueve en un círculo de radio R con rapidez constante, este movimiento se conoce como movimiento circular uniforme. En este caso solo hay una componente de la aceleración dirigida hacia el centro del círculo y conocida como aceleración radial o centrípeta $a_{rad}$.
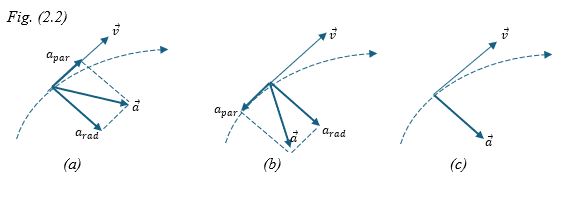
Cuando una partícula en movimiento circular aumenta o disminuye su rapidez el vector aceleración $\vec{a}$ presenta dos componentes: una componente paralela a la velocidad y otra perpendicular a la velocidad que corresponde a la aceleración radial o centrípeta.
En la figura (2.2) se representan las tres situaciones. (cuando se aumenta y se disminuye velocidad y cuando la velocidad es constante).
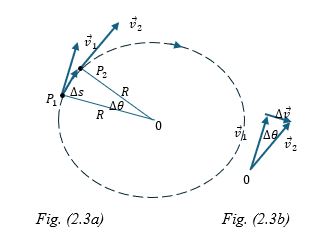
$$ a= (\lim_{\Delta{t\to 0}}\frac{\Delta{S}}{\Delta{t}})\frac{v_1}{R}$$
En el punto $P_1$
$$\lim_{\Delta{t\to 0}}\frac{\Delta{S}}{\Delta{t}} = v_1$$
Además, el punto $P_1$ puede ser cualquier punto de la trayectoria, recordando que se trata de un movimiento circular uniforme, podemos omitir el subíndice y representar con $v$ la rapidez en cualquier punto. Luego:
$$a_{rad}=\frac{v^2}{R}\tag{2.21}$$
Otra relación que podemos encontrar por tratarse de un movimiento circular uniforme es el periodo T, es decir el tiempo que tarda la partícula en dar una vuelta completa siempre es el mismo, entonces:
$$v=\frac{2πR}{T}\tag{2.22} $$
Al reemplazar (2.22) en (2.21) encontramos otra forma de la aceleración radial:
$$ a_{rad}= \frac{4\pi^2R}{T^2}\tag{2.23}$$
Cuando el movimiento circular no es uniforme, significa que la rapidez varía durante el movimiento y el valor de la aceleración radial no es constante, pero tiene la misma forma que presenta la ecuación (2.21) y es perpendicular a la velocidad instantánea y dirigida hacia el centro del círculo.
En Resumen
1. La cinemática describe el movimiento de los objetos en tres dimensiones.$\;$El desplazamiento, la velocidad y aceleración se describen mediante las ecuaciones (2.8),(2.9) y (2.10)
2. El movimiento en dos dimensiones es la superposición de dos movimientos rectilíneos independientes, un caso particular es el tiro parabólico el cual se describe mediante las ecuaciones:(2.18), (2.19)y (2.20). Note que el tiro parabólico se realiza en un plano paralelo a la dirección de la aceleración gravitacional$\;\vec{g}$, usualmente caracterizamos este plano como plano $X, Y $, donde $Y$ es la dirección vertical
3. El movimiento circular es un caso particular de movimiento en dos dimensiones en el cual (a diferencia del movimiento rectilíneo)tenemos dos aceleraciones $a_{rad}$ y $a_{tan}$ dadas por las ecuaciones(2.24)
Pregunta
¿Se puede pensar que un satélite en órbita terrestre es un tiro parabólico en el cual el objeto (el satélite)lanzado nunca cae a tierra?

La dinámica es una sección de la física que estudia el movimiento de los cuerpos teniendo presente la causa que lo produce, es decir, la relación que existe entre el movimiento y las fuerzas que lo provocan.
En esta unidad se estudian dos conceptos importantes de la física, la fuerza y la masa.
Los principios de la dinámica fueron establecidos por Isaac Newton (1642-1727) y se conocen como leyes de movimiento de Newton.
La primera ley dice que, si la fuerza neta que actúa sobre un cuerpo es cero, su movimiento no cambia, es decir, el cuerpo permanece en reposo o se mueve con velocidad constante en línea recta.
La segunda ley relaciona la fuerza con la aceleración cuando la fuerza neta es distinta de cero.
La tercera ley conocida como principio de acción – reacción relaciona las fuerzas que interactúan entre dos cuerpos.
Newton dedujo sus tres leyes de varios experimentos realizados por otros científicos, entre ellos está Galileo Galilei.
Las leyes de Newton son fundamentales y además la base de la mecánica clásica o mecánica Newtoniana, que describe la relación entre el movimiento de los objetos en nuestro mundo cotidiano y las fuerzas que actúan sobre ellos.
Las condiciones cuando la mecánica clásica no se aplica son para objetos muy pequeños (tamaños atómicos) y objetos que se mueven cerca de la velocidad de la luz.
La fuerza es una magnitud vectorial, que al actuar sobre un cuerpo o partícula puede cambiar su estado de movimiento o también puede modificar su forma. También se entiende la fuerza como un nombre de determinadas interacciones tales como la interacción gravitacional, la electromagnética, la nuclear etc...
En esta línea de pensamiento podemos nombrar diferentes tipos de fuerza que implican contacto o acción a distancia. Así por ejemplo la fuerza de contacto incluye la fuerza normal, la fuerza de fricción y la fuerza de tensión a lo largo de un cable o una cuerda.
Las fuerzas de largo alcance o de acción a distancia actúan entre cuerpos que están separados por un espacio vacío, así por ejemplo la fuerza gravitacional que ejerce el sol sobre los planetas para mantenerlos orbitando a su alrededor, la fuerza entre dos imanes es otro ejemplo de fuerzas de acción a distancia.
La Tierra atrae cualquier tipo de objeto que se deje caer cerca de su superficie y además la fuerza de atracción gravitacional que ejerce la Tierra sobre un cuerpo se llama peso del cuerpo.
Para caracterizar una fuerza vectorial $\vec{F}$, se debe indicar la dirección en la cual actúa y su magnitud. En el sistema SI la unidad que acompaña la magnitud de la fuerza es el newton, que se abrevia con la letra 𝑁.
$1𝑁 = 1𝑘𝑔 \times \frac{m}{s^2}$
Un instrumento común para medir fuerza o para calcular el peso de un objeto es el dinamómetro, inventado por Isaac Newton y se basa en el estiramiento de un resorte que sigue la ley de elasticidad de Hook en el rango de medición.
$\textbf{Ejemplos de fuerzas de contacto y de acción a distancia}$
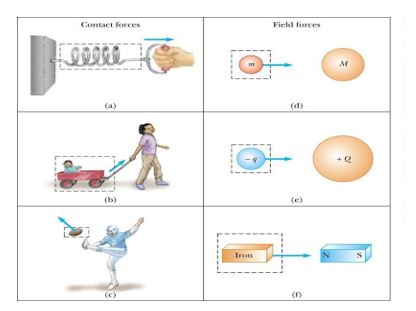
Suma de Fuerzas: Como la fuerza es una cantidad vectorial, las operaciones que se realizan con ellas siguen las mismas reglas de los vectores estudiados en el primer módulo. El efecto de varias fuerzas actuando sobre un punto de un cuerpo es el mismo que el de una sola fuerza igual a la suma vectorial de todas las fuerzas, esto se conoce como superposición de fuerzas.
Primera ley: Los experimentos muestran que, si no hay fuerza neta actuando sobre un cuerpo, este permanece en reposo, o se mueve con velocidad constante en línea recta.
Si sobre un objeto actúan dos fuerzas de igual magnitud, pero con direcciones opuestas, su suma vectorial es cero, en este caso una fuerza es el negativo de la otra, ósea que:
$$\vec{F_2}=-\vec{F_1}$$
De modo que:
$$ \sum{\vec{F}} = \vec{F_1} + \vec{F_2} = \vec{F_1}+(-\vec{F_1}) = 0 $$
Para un cuerpo que está en equilibrio y sobre él están actuando varias fuerzas cuya resultante o fuerza neta es cero, entonces:
$$\sum{\vec{F}}=0\tag{3.1}$$
Para que la ecuación (3.1) se satisfaga, cada componente de la fuerza neta debe ser cero; por lo tanto, para un cuerpo en equilibrio:
$$ \sum{\vec{F_x}}=0 \qquad \sum{\vec{F_y}}=0\tag{3.2}$$
Segunda ley: Recordemos que la inercia es la tendencia de un objeto para continuar en su estado original, es decir, si el objeto está en reposo quiere permanecer en su estado de reposo y si el objeto está en movimiento quiere permanecer en su estado de movimiento.
Otra cantidad importante que hace parte de la segunda ley de Newton es la masa, la cual es una medida de la resistencia de un objeto a cambios en su estado físico (de reposo o de movimiento),es una cantidad escalar y su unidad en el SI es el kg.
La Segunda ley establece que, si una fuerza externa neta actúa sobre un cuerpo, este se acelera. La dirección de la aceleración es la misma que la de la fuerza neta. El vector fuerza neta es igual a la masa del cuerpo multiplicada por su aceleración.
$$\sum{\vec{F}} = m\vec{a}\tag{3.3}$$
Otra forma alternativa de interpretar la segunda ley es: la aceleración de un objeto es directamente proporcional a la fuerza neta que actúa sobre él e inversamente proporcional a su masa.
$$\vec{a}=\frac{\sum{\vec{F}}}{m}$$
La ecuación (3.3) en forma de componentes se escribe:
$$∑ 𝐹_𝑥 = 𝑚𝑎_𝑥 \quad ∑ 𝐹_𝑦 = 𝑚𝑎_𝑦 \quad ∑ 𝐹_𝑧 = 𝑚𝑎_𝑧 \tag{3.4}$$
La primera y segunda ley de newton son válida solo en marcos de referencia inerciales.
$\textbf{Peso de un cuerpo}$
La fuerza debido a la gravedad es la Fuerza de atracción mutua entre dos objetos y esta fuerza se describe mediante la ley de gravitación universal anunciada por Newton:
Si $𝑚_1 \; y \; 𝑚_2$ son dos masas separadas por una distancia 𝑟 la fuerza de atracción entre ellas viene dada por
$$\vec{F_g}=G\frac{m_1m_2}{r^2}\hat{u_r}\tag{3.5}$$
Donde 𝐺 es la constante de gravitación universal, que se obtiene experimentalmente.
En esta ecuación si $𝑚_1 = 𝑀_𝑇$ = 𝑚𝑎𝑠𝑎 𝑑𝑒 𝑙𝑎 𝑇𝑖𝑒𝑟𝑟𝑎 y $𝑚_2 = 𝑚_0$ es una masa prueba cerca de la superficie de la Tierra, entonces $𝑟 = 𝑅_𝑇$ = 𝑟𝑎𝑑𝑖𝑜 𝑑𝑒 𝑙𝑎 𝑡𝑖𝑒𝑟𝑟𝑎, considerando la Tierra aproximadamente esférica, podemos verificar que:
$$G\frac{M_T}{R_T^2} = 9.8\frac{m}{s^2} = g\tag{3.6}$$
Reemplazando en (3.5) tenemos que $𝐹_𝑔 = 𝑔𝑚_0$ de modo que $𝐹_𝑔$ corresponde al peso 𝑤 de $𝑚_0$, entonces la magnitud del peso de un cuerpo de masa $𝑚_0$ cerca de la superficie de la Tierra es:
$$𝑤 = 𝑚_0𝑔\tag{3.7}$$
En conclusión:
La magnitud de la fuerza gravitatoria que actúa sobre un objeto de masa 𝑚 cerca de la superficie de la Tierra se llama el peso 𝑤 del objeto.
𝑤 = 𝑚𝑔 es un caso especial de la segunda ley de Newton.
𝑔 También se puede calcular de la Ley de la Gravitación Universal. Además podemos concluir que:
1. El peso no es una propiedad inherente de un objeto.
2. La masa es una propiedad inherente
3. El peso depende de la ubicación
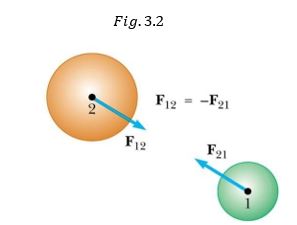
En realidad cualquier fuerza puede ser de acción o de reacción, la fuerza de acción y de reacción actúan sobre objetos diferentes.
Es importante saber con precisión a que fuerza te refieres en algún tipo de situación, en las figuras (3.3) y (3.4) se tienen algunos pares de acción reacción:
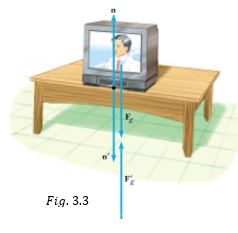
En la figura 3.3 se observan diferentes fuerzas representadas por los vectores: $\vec{n}\; y \; \vec{n’}$. $\vec{n}$ es la fuerza normal, fuerza que la mesa ejerce sobre el TV, y es siempre perpendicular a la superficie. $\vec{n’}$ es la reacción negativa del TV sobre la mesa, es decir, $\vec{n} =-\vec{n’}$.
Los objetos se comportan como partículas y estas se consideran masas concentradas en un punto en el cual se desprecia su extensión espacial.
Por ahora se puede ignorar el movimiento de rotación, también las masas de resortes o cuerdas son insignificantes, (más adelante se tienen en cuenta), sólo consideramos las fuerzas que actúan sobre el objeto y se pueden descuidar las fuerzas de reacción.
Diagrama de cuerpo libre
Se deben identificar todas las fuerzas que actúan sobre el objeto de interés. Elija un sistema adecuado de coordenadas.
Si el diagrama de cuerpo libre es incorrecto, la solución será probablemente incorrecta.
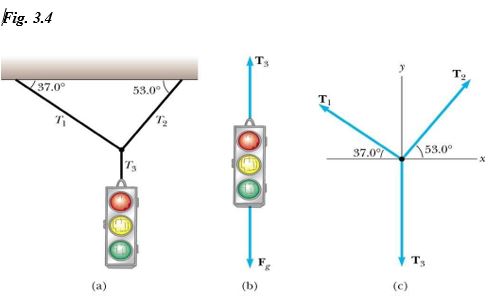
Consideremos que en la figura 3.4.(a) se quiere calcular el valor de las tenciones en las cuerdas. La solución se plantea de la siguiente manera:
1. Se observa que en la figura 3.4.(a) se tiene un sistema en equilibrio que muestra tres cuerdas conectadas con sus respectivos ángulos que sostienen un semáforo de masa 𝑚 además, se etiquetaron las tensiones de las cuerdas de masa despreciable y que corresponden a las incógnitas del problema.
2. En la figura 3.4(b) se dibujan las fuerzas que actúan sobre el semáforo y en la figura
3.4.(c) se dibujan las tensiones que son fuerzas a lo largo de las cuerdas.
3. Planteamiento de las ecuaciones respectivas:
Para la figura 3.4.(b) tenemos: $∑ 𝐹_𝑦 = 0$
$$ 𝑇_3 − 𝐹_𝑔 = 0 \quad 𝑑𝑜𝑛𝑑𝑒 \quad 𝐹_𝑔 = 𝑚𝑔\tag{3.8}$$
Para la figura 3.5.(c) tenemos:
$$∑ 𝐹_𝑥 = 0 ;\qquad ∑ 𝐹_𝑦 = 0$$
$$𝑇_2𝑐𝑜𝑠53^0 − 𝑇_1𝑐𝑜𝑠37^0 = 0\tag{3.9}$$
$$𝑇_2𝑠𝑒𝑛53^0 + 𝑇_1𝑠𝑒𝑛37^0 − 𝑇_3 = 0\tag{3.10}$$
Observe que se tienen tres ecuaciones con tres incógnitas. Lo que sigue a continuación es un problema matemático para dar solución a este ejercicio. (Trate de resolverlo).
En este caso cuando se aplica la segunda ley de Newton hay que tener presente que la fuerza neta que actúa sobre los cuerpos no es cero. Tales cuerpos no están en equilibrio. La fuerza neta es igual a la masa del cuerpo multiplicada por su aceleración.
Para el caso vectorial: $$∑ 𝐹⃗ = 𝑚𝑎⃗\tag{3.11}$$
En sus componentes:
$$∑ 𝐹_𝑥 = 𝑚𝑎_𝑥 ;\quad ∑ 𝐹_𝑦 = 𝑚𝑎_𝑦\tag{3.12}$$
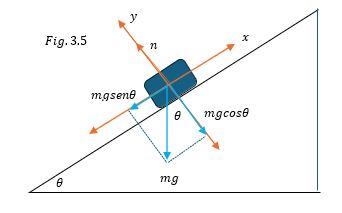
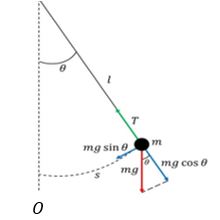
La figura 3.5 es un caso típico de un cuerpo sobre un plano inclinado.
Consideremos que este cuerpo de masa 𝑚 se desliza sin fricción hacia abajo sobre el plano inclinado, donde 𝜃 es el ángulo que hace la horizontal con la inclinación del plano inclinado, y el cuerpo se desliza con aceleración 𝑎 hacia abajo
Podemos escribir las ecuaciones correspondientes para este caso, para ello notamos que en la figura 3.5 se escogió un sistema de referencia y se han dibujado las fuerzas que actúan sobre 𝑚. Se puede ver que el peso 𝑚𝑔 tiene componentes en 𝑥 y en 𝑦, además la normal 𝑛 es perpendicular a la superficie del plano inclinado.
Aplicando la segunda ley de Newton para el caso dinámico tenemos:
$$\sum{F_x} = ma \implies mg\sin\theta = ma\tag{3.13}$$
$$\sum{F_y} = 0 \implies n-mg\cos\theta = 0\tag{3.14}$$
Cuando un objeto está en movimiento sobre una superficie o a través de un medio viscoso, habrá una resistencia al movimiento, esto se debe a las interacciones entre el objeto y su entorno, esta resistencia se llama fuerza de fricción y su valor depende del estado fisico del objeto, es decir, si está en reposo o en movimiento, lo cual se expresa introduciendo los llamados coeficientes de fricción: $\mu_k \; y \; \mu_s$
Consideraciones de la Fuerza de Fricción
La fricción es proporcional a la fuerza normal $\vec{F_𝑛}$.
La fuerza de fricción estática es generalmente mayor que la fuerza de fricción cinética. El coeficiente de fricción ( 𝜇 ) depende de las superficies en contacto.
La dirección de la fuerza de rozamiento es opuesta a la dirección del movimiento. Los coeficientes de fricción son casi independientes del área de contacto
Fricción Estática, $f_s$
La Fricción estática actúa para que el objeto no cambie su estado de quietud. Si la fuerza $\vec{F}$ aplicada al objeto se incrementa, también lo hace $𝑓_𝑠$.
Si la fuerza $\vec{F_𝑛}$ aplicada al objeto disminuye, también disminuye $𝑓_{𝑠}$.El valor máximo de $𝑓_𝑠$ depende de la fuerza normal $\vec{F_𝑛}$, y el factor de proporcionalidad se llama coeficiente de fricción estática $\mu_{𝑠}$.
$𝑓_{𝑠} ≤ \mu_{𝑠}{F_𝑛}$ ; (es la magnitud de la fuerza de fricción estática).
Fricción Cinética,
Actúa cuando un cuerpo se desliza sobre una superficie, su magnitud puede aumentar al aumentar la fuerza normal $\vec{F_𝑛}$ que es aproximadamente proporcional a $𝑓_𝑘$.
La magnitud de $𝑓_𝑘$ se representa mediante la ecuación $𝑓_𝑘 = \mu_{𝑘}{F_𝑛}$, donde $\mu_{𝑘}$ se denomina $\textit{coeficiente de fricción cinética}$.
La fuerza de fricción cinética actúa cuando el objeto está en movimiento.
Las fuerzas de fricción pueden actuar cuando hay o no movimiento relativo. Si no hay movimiento relativo se cumple que $\vec{𝑓𝑠} ≤ \mu_{𝑠}\vec{F_𝑛}$; si hay movimiento relativo se cumple que
$\vec{𝑓_𝑘} = \mu_{𝑘}\vec{F_𝑛}$.
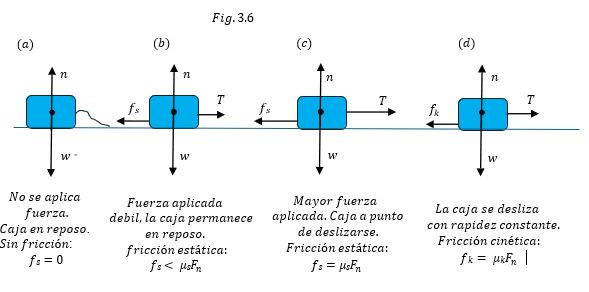
La figura 3.6 es una gráfica que muestra la magnitud de la fuerza de fricción 𝑓 en términos de la tensión 𝑇 aplicada a un objeto de peso 𝑤, la $𝑓_𝑘$ varia conforme se forman y se rompen los enlaces intermoleculares, en la mayoría de los casos, las superficies en contacto se suavizan un poco después de cierto tiempo en movimiento relativo.
Las fuerzas de fricción y la normal siempre son perpendiculares, por lo tanto, las relaciones $\vec{𝑓_𝑘} = \mu_{𝑘}\vec{F_𝑛}$ y $\vec{𝑓_𝑠} ≤ \mu_{𝑠}\vec{F_𝑛}$ no son ecuaciones vectoriales sino relaciones escalares entre las magnitudes de dos fuerzas.
En la figura (3.6.a) se muestra el bloque sin fuerza aplicada y luego situaciones en la cual la tensión en la cuerda se aumenta gradualmente hasta un valor crítico en el que el movimiento del bloque está a punto de iniciar, tan pronto cuando se inicia el desplazamiento (Fig.3.6. d), la fuerza de fricción disminuye.
Cuando consideramos la fricción en planos inclinados, en las ecuaciones se debe sumar la fuerza de fricción en determinada situación, así por ejemplo si el cuerpo de la figura
3.6 se mueve hacia abajo, se debe señalar la fuerza de fricción en dirección contraria al movimiento, entonces la ecuación (3.13) queda así:
$$f_k - mg\sin\theta = -ma\tag{3.15}$$
La ecuación (3.14) no cambia, presenta la misma forma, y recuerde que no hay aceleración en la dirección 𝑦.
Objetos Conectados
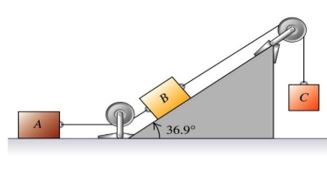
Para objetos conectados como se muestra en la figura 3.7 se aplican las leyes de Newton separadamente para cada objeto, la aceleración de los objetos conectados debe ser la misma y la tensión es la misma para el par de objetos conectados por una polea sin fricción.
Después de escoger un sistema de referencia adecuado, se plantean y se deben resolver las ecuaciones simultáneas que se presenten. Por el momento se desprecia la masa de las cuerdas y la masa de las poleas.
Como ejercicio dibuje todas las fuerzas que actúan sobre cada bloque de la figura 3.7considerando que la fricción entre los bloques y toda la superficie es $𝑓_{𝑘}$. Considere que el bloque $C$ es de masa desconocida $M$ y desciende con velocidad constante.
Los bloques $A$ y $B$ tienen la misma masa 𝑚, y las tensiones en las cuerdas son desconocidas pero diferentes para cada cuerda. Por ultimo aplique la segunda ley de newton en cada bloque y escriba las ecuaciones correspondientes para cada bloque, note que deberá obtener tres ecuaciones las cuales debe resolver simultaneamente

En este capítulo se realizará un resumen de los conceptos de trabajo y energía, pero será importante aprender cuando una fuerza realiza trabajo sobre un objeto, que significa desde la física la energía cinética de un cuerpo y como el trabajo total sobre un cuerpo cambia la energía cinética de este. Al incorporar los conceptos de trabajo y energía aparecerá un principio fundamental, que establece que la energía es una cantidad escalar que puede transformarse de una forma a otra, pero no se crea ni se destruye y se conoce como principio de conservación de la energía.
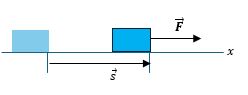
El trabajo es la acción de una fuerza cuando su punto de aplicación se desplaza en la misma dirección de la fuerza.
El trabajo se representa con la letra w y en principio debemos entender cómo se define el trabajo realizado por una fuerza constante. Se debe tener claridad que tipo de fuerza se aplica a un cuerpo y en qué dirección está aplicada para que esta realice trabajo. Por ejemplo, cuando sostenemos un cuerpo con nuestras manos y lo desplazamos horizontalmente cierta distancia, es la fuerza de nuestras manos quien realiza el trabajo. Si soltamos un objeto cerca de la superficie de la Tierra y el objeto cae libremente recorriendo una distancia y, es la fuerza debido a la gravedad quien realiza el trabajo.
A continuación, mostraremos situaciones en las cuales una fuerza constante $\vec{F}$ realiza trabajo sobre un bloque de masa $m$. Si la fuerza tiene la misma dirección del desplazamiento $\vec{s}$ como se muestra en la figura 4.1, la magnitud del trabajo realizado por esta fuerza es:
$$w =Fs\tag{4.1}$$
La unidad de trabajo en el SI es el Joule y se representa con la letra $J$ (en honor al físico inglés James Prescott Joule). Cuando la fuerza aplicada al bloque no tiene la dirección del desplazamiento, sino que hace un ángulo $\theta$ con la horizontal, como se muestra en la figura 4.2, la componente de $\vec{F}$ que realiza trabajo es la que está en la dirección del desplazamiento, es decir, en la dirección horizontal, entonces:
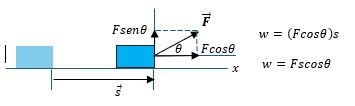
$$w = (F\cos\theta)s$$
$$w = (F\cos\theta)s\tag{4.2}$$
La ecuación (4.2) tiene la muy conocida forma de un producto $\textbf{escalar}$ de dos vectores (los vectores fuerza $\vec{F}$ y desplazamiento $\vec{s})$, por lo tanto, podemos escribir esta ecuación así:
$$w = \vec{F}\cdot\vec{s}\tag{4.3}$$
De acuerdo con las ecuaciones (4.2) o (4.3), el trabajo pude ser positivo, negativo o cero,
dependiendo del ángulo entre $\vec{F}$ y el desplazamiento $\vec{s}$
Cuando varias fuerzas actúan sobre un cuerpo podemos usar las ecuaciones (4.2) o (4.3) para calcular el trabajo total realizado por cada fuerza, de modo que el trabajo total $w_{tot}$ realizado por todas las fuerzas sobre el cuerpo es la suma algebraica de los trabajos realizados por las fuerzas individuales. Otra forma de calcular el $w_{tot}$ es calcular la suma vectorial de todas las fuerzas, encontrando la fuerza neta y usarla en las ecuaciones (4.2) o (4.3).
La Energía Cinética.
Es la que posee un cuerpo en virtud de su movimiento. Mostraremos la relación que hay entre el trabajo total realizado sobre un objeto o partícula y el cambio en la rapidez de $v_1$ a $v_2$ del objeto cuando este experimenta un desplazamiento $s=x_2-x_1$ donde el punto inicial es $x_1$ y el punto final es $x_2$.
Si un objeto de masa $m$ se mueve sobre el eje $X$ debido a la acción de una fuerza constante de magnitud $F$ en la dirección del eje $X$, la aceleración $a_x$ de la partícula es constante y cumple con la segunda ley de Newton. Apliquemos las ecuaciones de la cinemática en línea recta y encontremos la forma que presenta la energía cinética de la partícula:
$$v_2^2=v_1^2+2a_x s \quad\quad a_x= \frac{v_2^2- v_1^2}{2s}$$
multiplicando esta ecuación por $m$ tenemos:
$$ma_x= m \frac{(v_2^2- v_1^2)}{2s}$$ dado que $F= ma_x$
$$Fs= m \frac{v_2^2- v_1^2}{2} =\frac{1}{2}mv_2^2-\frac{1}{2}mv_1^2$$
$$Fs=\frac{1}{2} mv_2^2-\frac{1}{2}mv_1^2\tag{4.4}$$ $Fs$ es el trabajo efectuado por la fuerza neta $F$ y, es igual al trabajo total $w_{tot}$ realizado por todas las fuerzas que actúan sobre la partícula. La cantidad escalar $\frac{1}{2} mv^2$ se llama energía cinética $K$ de la partícula.
$$ K= \frac{1}{2}mv^2\tag{4.5}$$
La energía cinética de una partícula depende de la masa y de la rapidez de la partícula.
La ecuación (4.4) podemos interpretarla en términos de trabajo, de modo que:
$K_2= \frac{1}{2} mv_2^2$ y $K_1= \frac{1}{2}mv_1^2$.
La diferencia de estos dos términos es el cambio en la energía cinética.
$$w_{tot}= K_2- K_1= ∆K\tag{4.6}$$
Este resultado corresponde al teorema de trabajo – energía.
Movimiento Rectilíneo. Debido a que el teorema trabajo -energía es válido aun cuando las fuerzas varíen y la trayectoria de la partícula no sea recta, podemos calcular el trabajo realizado por las fuerzas para casos más generales.
Un ejemplo de una fuerza variable es la que se puede aplicar a un resorte al estirarlo, no obstante, existen otras situaciones en las que una fuerza, que varía, en magnitud, dirección o en ambas, actúa sobre un cuerpo que sigue una trayectoria curva.
Es posible demostrar que el trabajo realizado por una fuerza variable que actúa en la dirección x en un desplazamiento total de $x_1$ a $x_2$ presenta la siguiente forma:
$$w= \int_{x_1}^{x_2}F_xdx\tag{4.7}$$
En una gráfica de fuerza como una función de la posición, el trabajo total realizado por la fuerza está representado por el área bajo la curva de dicha gráfica entre las posiciones inicial y final.
La ecuación (4.7) también expresa que el trabajo $w$ es igual a la fuerza media que actúa a lo largo de todo el desplazamiento, multiplicada por el desplazamiento.
Observe que, si $F_x$ es constante, la ecuación (4.7) se convierte en:
$$w= \int_{x_1}^{x_2}F_xdx= F_x\int_{x_1}^{x_2}dx = F_x (x_2- x_1)\tag{4.8}$$
Empleando estos conceptos al caso de un resorte que se estira una distancia x cuando se le aplica una fuerza $F_x$ vemos que la fuerza aplicada es proporcional al desplazamiento x, entonces:
$$ F_x=kx\tag{4.9}$$donde k es la constante elástica del resorte o constante de fuerza. De acuerdo con la ecuación (4.9) las unidades de $k$ en el SI son: N/m.
Por ser la fuerza directamente proporcional al desplazamiento o alargamiento del resorte, la ecuación (4.9) se conoce como ley de Hooke.
Cuando aplicamos una fuerza $F_x$ en el extremo de un resorte que tiene el otro extremo fijo a una pared, el trabajo realizado por esta fuerza cuando el alargamiento va de cero a un valor máximo X es:
$$w = \int_{0}^{X}F_xdx = \int_{0}^{X}kxdx = \frac{1}{2}kX^2\tag{4.10}$$
En este resultado se considera que el resorte no estaba estirado inicialmente. Cuando el resorte ya está estirado previamente una distancia $x_1$, el trabajo necesario para estirarlo una distancia mayor $x_2$ es:
$$w= \int_{x_1}^{x_2}F_xdx=\int_{x_1}^{x_2}kxdx = \frac{1}{2} kx_2^2- \frac{1}{2}kx_1^2\tag{4.11}$$
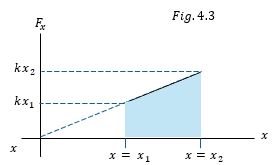
El área sombreada bajo la línea en la figura 4.3 que corresponde a un trapezoide representa el trabajo efectuado sobre el resorte para estirarlo de $x_1$ a $x_2$.
La geometría permite calcular el área bajo la curva en cualquier otro caso y dado por la ecuación (4.11).
Si el resorte tiene espacios entre las espiras cuando no está estirado, se puede comprimir, y la ley de Hook también se cumple para la compresión. En este caso, la fuerza y el desplazamiento tienen direcciones opuestas y el trabajo total sigue siendo el que se encuentra utilizando la ecuación (4.10) o (4.11).
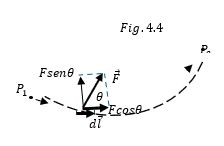
De acuerdo con la figura 4.4 el trabajo total realizado por $\vec{F}$ sobre la partícula al moverse de $P_1$ a $P_2$ en trayectoria curva es:
$$w = \int_{P_1}^{P_2}F\cos\theta{dl}=\int_{P_1}^{P_2}\vec{F}\cdot{\vec{dl}}\tag{4.12}$$
Para una trayectoria curva donde la fuerza varía en magnitud y dirección, la trayectoria se puede dividir en muchos desplazamientos vectoriales infinitesimales $\vec{dl}$, como se muestra en la figura 4.4.
El cálculo permite demostrar que si $\vec{F}$ la es fuerza en cualquier punto de la trayectoria y θ es el ángulo entre $\vec{F}$ y $\vec{dl}$, entonces el trabajo $dw$ realizado sobre la partícula durante el desplazamiento $\vec{dl}$ puede escribirse como $dw=Fcosθdl= \vec{F}\cdot\vec{dl}$ donde $Fcosθ$ es la componente de $\vec{F}$ en la dirección paralela a $\vec{dl}$
Conclusiones: Cuando la fuerza varía en una trayectoria rectilínea el trabajo que realiza está dado por la ecuación 4.7.
Cuando la partícula tiene una trayectoria curva, entonces el trabajo efectuado sobre ella por una fuerza $\vec{F}$ está dado por la ecuación (4.12).
El trabajo al igual que la energía cinética es una cantidad escalar sin dirección en el espacio.
La energía cinética $K$ de una partícula es igual a la cantidad de trabajo necesario para acelerarla desde el reposo hasta una rapidez v.
La potencia se define como la rapidez con que se realiza trabajo y se designa con la letra $P$. La potencia media $P_{med}$ es cantidad de trabajo $∆w$ dividida por un tiempo ∆t.
$$P_{med}= \frac{∆w}{∆t}\tag{4.13}$$
La potencia instantánea es el límite de la potencia media cuando ∆t tiende a cero, es decir,
$$P= \lim_{\Delta{t\to 0}}\frac{∆w}{∆t}=\frac{dw}{dt}\tag{4.14}$$
$$P= \frac{dw}{dt}= \frac{d(\vec{F}\cdot\vec){s}}{dt} = \vec{F}\cdot\vec{v}\tag{4.15}$$
La potencia es una cantidad escalar y su unidad en el SI el vatio o watt, de acuerdo con la ecuación (4.13) o (4.14) vemos que:
$$1watt= (1 Joule)/segundo= J/s$$
$\textbf{La energía potencial}$ es la que posee un cuerpo en virtud de su posición dentro de un campo gravitacional.
Cuando soltamos un cuerpo desde cierta altura h cerca de la superficie de la Tierra, un instante antes de soltarlo, este cuerpo posee una cierta energía potencial gravitacional, inmediatamente después de soltarlo esta energía potencial gravitacional empieza a transformase en energía cinética.
En esta sección veremos como el teorema trabajo – energía da cuenta de esta transformación.
Veremos que, en algunos casos, la suma de las energías cinética y potencial de un sistema es constante durante el movimiento del sistema y se conoce como $\textit{energía mecánica total}$, esto nos conduce a la ley de conservación de la energía.
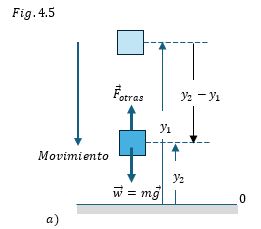
La energía potencial gravitacional es una cantidad asociada con el peso de un cuerpo y con su altura respecto al suelo. Deduciremos la expresión de la energía potencial gravitacional, de un cuerpo de masa m que se mueve verticalmente sobre el eje y, como se muestra en la figura 4.5.
Cuando un cuerpo se mueve verticalmente de una altura inicial $y_1$ a una altura final $y_2$, la fuerza gravitacional $m\vec{g}$ efectúa trabajo y cambia la energía potencial gravitacional.
En la figura 4.5. a) el cuerpo se mueve hacia abajo y cae de una altura $y_1$ sobre el origen a una altura $y_2$. El peso y el desplazamiento tienen la misma dirección, entonces el trabajo efectuado sobre el cuerpo por su peso es positivo.
Observe que en este caso $y_2- y_1\lt 0 $ y la energía potencial gravitacional disminuye, es decir el cambio en la energía potencial gravitacional es negativa. $∆U_{grav}\lt 0$
De la definición de trabajo (Ecuación 4.1) tenemos:
$$W_{grav}=Fs=w(y_1- y_2)$$
$$W_{grav}=mgy_1-mgy_2\tag{4.16}$$
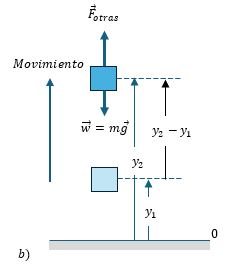
En la figura 4.6.b) el cuerpo se mueve hacia arriba, observe que $y_2- y_1\gt 0$ por lo que el peso realiza trabajo negativo y por lo tanto veremos que la energía potencial gravitacional aumenta, es decir:
$∆U_{grav}\gt 0$
La ecuación (4.16) muestra que el trabajo podemos expresarlo en términos de la cantidad $mgy$ al principio y al final del desplazamiento, este producto es la energía potencial gravitacional, $U_{grav}$:
$$U_{grav}=mgy\tag{4.17}$$
El cambio en la energía potencial gravitacional es:
$∆U_{grav}= U_{grav.2}- U_{grav.1}$ (final menos inicial). Ahora el trabajo realizado por el peso del cuerpo durante un desplazamiento de $y_1 \;a \;y_2$ podemos expresarlo así:
$$ W_{grav}= U_{grav.1}- U_{grav.2}=\\ -(U_{grav.2}- U_{grav.1} )= -∆U_{grav}\tag{4.18}$$
La ecuación (4.18) nos permite concluir que cuando el cuerpo sube respecto al suelo, la energía potencial gravitacional aumenta $(∆U_{grav}\gt 0)$ y el trabajo realizado por la fuerza gravitacional es negativo, si el cuerpo baja la energía potencial gravitacional disminuye $(∆U_{grav}\lt 0)$ y el trabajo realizado por la fuerza gravitacional es positivo.
Conservación de la Energía Mecánica.
Consideremos que en la figura 4.5 solo el peso del cuerpo es la única fuerza que actúa sobre él y por lo tanto solo la fuerza gravitacional es la que realiza trabajo.
Si $v_1$ es la rapidez del cuerpo a la altura $y_1$ y $v_2$ su rapidez a la altura $y_2$, entonces de acuerdo con la ecuación (4.6) tenemos:
$W_{tot}= ∆K= K_2- K_1$.
También
$$W_{tot}= W_{grav}= -∆U_{grav}= -( U_{grav.2}-U_{grav.1} )= U_{grav.1}-U_{grav.2}$$
Igualando estas dos expresiones anteriores nos queda que:
$∆K= - ∆U_{grav}$ o sea que $K_2- K_1= U_{grav.1}-U_{grav.2}$
ordenando y acomodando terminos escribimos:
$$K_1+ U_(grav.1)= K_2+ U_(grav.2)\tag{4.19}$$
$$1/2 mv_1^2+mgy_1= 1/2 mv_2^2+mgy_2\tag{4.20}$$
La ecuación (4.19) o (4.20) es la energía mecánica total del sistema y corresponden a la suma de las energías cinética y potencial que designaremos con la letra $E$.
La energía mecánica total $E$ tiene el mismo valor en todos los puntos del movimiento. Si en el punto 1 la energía total es $E_1$ y en el punto 2 es $E_2$ entonces $E_1=E_2$. Una cantidad que tiene siempre el mismo valor es una cantidad que se conserva, lo que significa que $E$ es constante;
$$E=K+ U_{grav}=constante\tag{4.21}$$
La ecuación (4.21) en este caso equivale a la conservación de la energía mecánica si solo la fuerza de gravedad efectúa trabajo.
Fuerzas distintas de la gravedad que realizan trabajo
Una fuerza típica distinta a la gravedad es la fuerza de fricción, para este caso consideremos que $W_{ff}$ es el trabajo realizado por otras fuerzas, además de la realizada por la gravedad. El trabajo total realizado por todas las fuerzas será:
$W_{tot}=W_{grav}+W_{ff}.$
Como $W_{tot}= ∆K$ tenemos:
$W_{grav}+W_{ff}= ∆K= K_2- K_1$
pero $W_{grav}= U_{grav.1}-U_{grav.2}$
Luego:
$U_{grav.1}-U_{grav.2}+ W_{ff}= K_2- K_1$
Organizando términos:
$$K_1+ U_{grav.1}+ W_{ff}= K_2+ U_{grav.2}\tag{4.22}$$
$$\frac{1}{2} mv_1^2+mgy_1+ W_{ff}= \frac{1}{2}mv_2^2+mgy_2\tag{4.23}$$
Observe que:
$K_1+ U_{grav.1}= E_{TM.inic}$ = Energía Total Mecánica inicial y
$K_2+ U_{grav.2}= E_{TM.final}$ =Energía Total Mecánica final
o sea que
$E_{TM.inic}+ W_{ff}= E_{TM.final} \implies W_{ff}= E_{TM.final}- E_{TM.inic}$
Finalmente: $$ W_{ff}= ∆E_{TM}\tag{4.24}$$
La ecuación (4.24) indica que el trabajo realizado por todas las fuerzas distintas de la fuerza que genera la gravedad es igual al cambio en la energía mecánica total del sistema.
Actividad de simulación-Conservación de la Energía
En la siguiente actividad estudiamos la teoría anterior jugando con la simulación Phet de la Universidad de Colorado: Haga clic en la imagen a continuación y luego haga clic en play de la pantalla inicial, mostrará las cuatro ventanas: Introducción,Medidas, Graficas y Patio de juegos, cada una presenta sus propios parámetros para realizar y estudiar diferentes situaciones
Clic en la ventana de introducción de la simulación
Al hacer clic en esta esta ventana observará una pista parabólica donde se puede deslizar un patinador. podemos observar y estudiar la conservación de la energía para diferentes formas de la pista y en diferentes situaciones, para ello haga clic y arrastre el patinador a cualquier posición sobre la pista. Note que podemos estudiar el movimiento del patinador CON o SIN fricción y variar la masa mediante el uso de las tres barras deslizadoras que están desplegados en la parte superior derecha
Actividad de simulación.
Transmisión y Cambios de la Energía
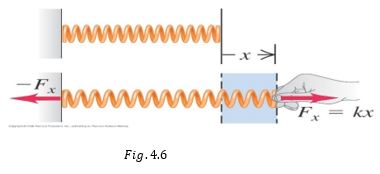
En esta sección vamos a describir el proceso de almacenar energía en un cuerpo deformable, como un resorte o una banda de hule, en términos de una cantidad conocida como energía potencial elástica.
Un cuerpo es elástico si recupera su forma y tamaño original después de deformarse.
Consideremos un resorte ideal, como el que se muestra en figura 4.7, para estirarlo una distancia $x$, debemos aplicar una fuerza $F=kx$, donde $k$ es la constante elástica del resorte, en este estiramiento el resorte almacena cierta energía potencial elástica $U_{el}$ dada por:
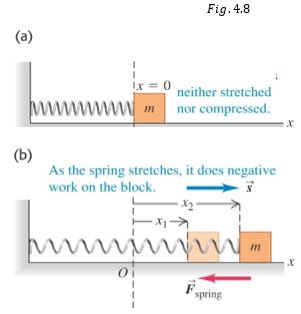
En la figura 4.8 tenemos un resorte ideal con el extremo izquierdo fijo y el extremo derecho sujeto a un bloque de masa m que puede moverse sobre el eje x en una superficie sin fricción
Cuando estiramos el resorte desde un alargamiento previo $x_1$ hasta otro alargamiento distinto $x_2$ como se muestra en la figura 4.8.b), el trabajo que debemos realizar sobre el resorte es positivo e igual a
$$W=\frac{1}{2} kx_2^2-\frac{1}{2}kx_1^2$$
El trabajo efectuado por el resorte al desplazarse de $x_1$ a $x_2$ es negativo y dado por:
$$W_{el}= \frac{1}{2}kx_1^2-\frac{1}{2}kx_2^2$$
Se debe entender que cuando se aplica una fuerza al extremo del resorte esta fuerza realiza trabajo positivo en este caso la fuerza tiene la dirección del desplazamiento, el resorte responde con una fuerza igual pero opuesta al deslazamiento, entonces el trabajo que efectúa el resorte es negativo
En la figura 4.7.b) para expresar el trabajo $W_{el}$ efectuado sobre el bloque por la fuerza elástica en términos del cambio en la energía potencial elástica podemos utilizar la ecuación (4.25):
$$W_{el}= \frac{1}{2}kx_1^2-\frac{1}{2}kx_2^2= U_{el.1}- U_{el.2}= -∆U_{el}\tag{4.26}$$
La ecuación (4.26) se cumple si la energía potencial del sistema es elástica y solo la fuerza elástica realiza trabajo, pero si además de la fuerza elástica tenemos la gravitacional y otras fuerzas, entonces el trabajo total es la suma del trabajo realizado por la fuerza gravitacional más la que realiza la elástica y más las que efectúan otras fuerzas, es decir:
$$W_{Tot}= W_{grav}+ W_{el}+ W_{otras}$$
aplicando el teorema trabajo-energía tenemos que:
$$W_{grav}+ W_{el}+ W_{otras} = K_2- K_1$$
Como $W_{grav}= U_{grav.1}- U_{grav.2}$ y $W_{el}= U_{el.1}- U_{el.2}$ entonces podemos reescribir el teorema trabajo-energía para este caso más general así:
usted puede manejar la longitud de estiramiento, posición de equilibrio y ubicar además un nivel de referencia. Note además una reglilla en el margen derecho de la ventana que puede activar haciendo clic y arrastrándola a cualquier posición.
La frecuencia de oscilación de un resorte viene dada por
$$f= \sqrt\frac{k}{m}$$.
Escoja alguna posición del deslizador y utilizando alguna de las masas conocidas en la parte inferior izquierda colgarla del resorte y estirarlo hasta la posición de equilibrio, en esta posición se debe cumplir (Sin oscilar):
$$Mg=k∆x$$
$$k=\frac{Mg}{∆x}\tag{A1}$$
$M$ es la masa escogida y $∆x$ es la distancia que se estira el resorte a partir de su longitud natural (sin ninguna masa colgando).
Repita el procedimiento con dos o tres masas diferentes y verifique que la ecuación A1 se cumple, es decir, para un resorte determinado la constante elástica $k$ no cambia
2.Clic en la ventana de Oscilación de la simulación.
Este Clic nos despliega esta ventana.
En la parte derecha de la ventana usted puede manejar la longitud de estiramiento, posición de equilibrio y ubicar además un nivel de referencia como en el caso anterior.
Note además un cronometro y una reglilla en el margen derecho de la ventana que puede activar haciendo clic y arrastrándolo a cualquier posición Utilice el procedimiento y la ecuación A1 para encontrar el valor de las masas desconocidas
3. Clic en la ventana de Laboratorio de la simulación
Este Clic nos despliega esta ventana. Desplegamos una ventana parecida a la anterior, pero ahora en la parte derecha de la ventana aparecen tres nuevas opciones: Rastro del periodo, velocidad y aceleración, además de la opción gravedad
I Determine un resorte de constante $k$ cualquiera ( encuentre esta constante usando A1)
II Utilice cualquier masa conocida y estire el resorte 2 cm a partir de su posición de equilibrio, verifique que la energía mecánica total se conserva, es decir
$$ E=K+U$$
Para demostrar esto, encuentre la energía total en los puntos $x =0$, $x = 1cm$ $x = 2cm$ y verifique que el valor para $E$ en esos puntos es el mismo
III Repita el procedimiento anterior para la Luna y luego para el planeta Júpiter
Una fuerza es no conservativa si el proceso de conversión de energía no es reversible y el trabajo realizado por estas fuerzas no puede representarse como una función de la energía potencial. Algunas fuerzas no conservativas como la fricción cinética hacen que la energía mecánica se pierda o se disipe, es decir, la energía total mecánica no se conserva.
Cálculo de la Fuerza a partir de la Energía Potencial.
En algunos apartes de la física encontraremos situaciones donde se tiene la energía potencial como una función de la posición y se necesita determinar la fuerza correspondiente.
En cualquier desplazamiento recordemos que el trabajo W efectuado por una fuerza conservativa es el negativo del cambio ∆U de la energía potencial:
$$W= -∆U$$
En un movimiento rectilíneo para un desplazamiento ∆x, el trabajo efectuado por $F_x (x)$ en este desplazamiento es en general:
$$F_x (x)∆x= -∆U \quad y \quad F_x (x)=- \frac{∆U}{∆x}$$
En el límite cuando $∆x →0$ si la variación de $F_x (x)$ es despreciable el cálculo nos permite escribir la expresión anterior como:
$$F_x (x)= \frac{-dU(x)}{dx}\tag{4.29}$$
La ecuación (4.29) es la fuerza a partir de la energía potencial, en una dimensión. El significado físico de la ecuación (4.29) es que una fuerza conservativa siempre trata de llevar el sistema a una energía potencial menor.
Para el caso de un resorte, la energía potencial elástica es:
$$U(x)= \frac{1}{2}kx^2$$ reemplazando en (4.29) tenemos
$$F_x (x)=\frac{-d}{dx}(\frac{1}{2}kx^2 )= -kx$$
Esta expresión corresponde a la fuerza ejercida por un resorte ideal. De la misma manera para la energía potencial gravitacional, $U(y)=mgy$ $\;$ entonces:
$$F_y= \frac{-dU(y)}{dy}=-\frac{d(mgy)}{dy}= -mg$$
Esta expresión corresponde a la fuerza debida a la gravedad.
En tres dimensiones, las componentes de una fuerza conservativa son las derivadas parciales negativas de la energía potencial $U(x,y,z)$, veamos:
$$F_x= -\frac{∂U}{∂x} ;\quad F_y= -\frac{∂U}{∂y};\quad F_z= -\frac{∂U}{∂x}$$
Vectorialmente:
$$\vec{F} = -(\hat{i}\frac{∂U}{∂x}+\hat{j}\frac{∂U}{∂y} + \hat{k}\frac{∂U}{∂z}\tag{4.30} )$$ Es claro entonces que si conocemos la forma matemática que describe el potencial, es decir, $U(x, y, z)$ podremos conocer la fuerza asociada a este potencial mediante la ecuación (4.30)
Dos conceptos nuevos veremos ahora, el momento lineal e impulso, y una nueva ley de conservación conocida como ley de conservación del momento lineal, en la mecánica newtoniana, esta ley nos permite analizar situaciones donde es muy complicado aplicar las leyes de Newton directamente, entre estas situaciones están las colisiones o choque entre dos cuerpos.
El momento lineal de una partícula se representa con el símbolo $\vec{p}$ y es igual al producto de la masa $m$ de la partícula por la velocidad $\vec{v}$ que esta partícula lleva.
$$p ⃗=mv ⃗\tag{4.31} $$
De la segunda ley de Newton tenemos que:
$$∑\vec{F}=m\vec{a}=m \frac{d\vec{v}}{dt}= \frac{(md\vec{v})}{dt}=\frac{d\vec{p}}{dt}$$
$$∑\vec{F} = \frac{d\vec{p}}{dt}\tag{4.32}$$ La relación (4.32) corresponde a la segunda ley de Newton en término de momento lineal y se lee en la siguiente forma: la fuerza neta que actúa sobre una partícula es igual a la rapidez de cambio del momento lineal de la partícula.
Teorema del impulso y el momento lineal
Para una partícula de masa $m$ con velocidad $v ⃗$ su momento lineal es una cantidad vectorial y su energía cinética es una cantidad escalar, para ver una diferencia física entre estas dos cantidades, definimos una cantidad relacionada con el momento lineal, que se conoce como impulso.
Consideremos una fuerza neta constante $∑\vec{F} ⃗ $ actuando sobre una partícula durante un tiempo $∆t$, el impulso de la fuerza neta, que denotamos como $\vec{J}$, se define como:
$$ \vec{J}= ∑\vec{F} ∆t= ∑\vec{F} (t_2- t_1 )\tag{4.33}$$
Las unidades de impulso en el SI son N∙s=kg∙m⁄s
Como $∑\vec{F}$ es constante, también $\frac{d\vec{p}}{dt}$ es constante.
De la ecuación (4.33) tenemos:
$$\vec{J}= ∑\vec{F} (t_2- t_1 )= ∑\vec{F} t_2- ∑\vec{F} t_1= \vec{p_2}- \vec{p_1}$$
$$\vec{J}= \vec{p_2}- \vec{p_1}\tag{4.34}$$
Este resultado es conocido como teorema del impulso y momento lineal, y establece que el cambio del momento lineal de una partícula durante un intervalo de tiempo es igual al impulso de la fuerza neta que actúa sobre la partícula durante ese intervalo.
El teorema del impulso y momento lineal también se cumple si las fuerzas no son constantes. Podemos integrar la ecuación (4.32) con respecto al tiempo entre los límites $t_1 \; y \; t_2$:
$$∫_{t_1}^{t_2}∑\vec{F}dt= ∫_{t_1}^{t_2}(\frac{d\vec{p}}{dt})dt = ∫_{t_1}^{t_2}d\vec{p}= \vec{p_2}- \vec{p_1}$$
$$\vec{J}= ∫_{t_1}^{t_2}∑\vec{F} dt\tag{4.35}$$
La ecuación (4.35) es la definición general de impulso.
También podemos definir una fuerza neta media $\vec{F}_{med}$ de modo que si aun $∑\vec{F}$ no es constante, el impulso $\vec{J}$ este dado por
$$\vec{J}= \vec{F}_{med} (t_2- t_1 )\tag{4.36}$$
Consideremos dos patinadores que se empujan entre sí mientras patinan en una superficie horizontal sin fricción, además ellos se comportan como partículas, cada partícula ejerce una fuerza sobre la otra, las dos fuerzas son iguales en magnitud y opuestas en dirección, por lo tanto, el impulso que actúa sobre las dos partículas son iguales y opuestos, igualmente los cambios de momento lineal de las dos partículas serán iguales y opuestos.
Vamos a examinar un caso especial de dos partículas que interactúan como un sistema aislado.
En una interacción de dos partículas si $\vec{F}_{2 sobre 1}$ es la fuerza neta sobre la partícula 1 debido a la 2 y $\vec{F}_{1 sobre 2}$ es la fuerza neta sobre la partícula 2 debido a la 1, entonces las tasas de cambio de los momentos lineales de las dos partículas son
$$\vec{F}_{2 sobre 1}= (dp ⃗_1/dt); \quad \vec{F}_{1 sobre 2}= (dp ⃗_2/dt)\tag{4.37} $$
Los cambios en el momento lineal de cada partícula están relacionados entre sí por la tercera ley de Newton, es decir,
$\vec{F}_{2 sobre 1}= -\vec{F}_{1 sobre 2}$
Sumando las expresiones de la ecuación (4.37) tenemos
$$\vec{F}_{2 sobre 1}+ \vec{F}_{1 sobre 2}= \frac{d\vec{p_1}}{dt}+ \frac{d\vec{p_2}}{dt}\\= \frac{d(\vec{p_1}+\vec{p_2})}{dt} =0\tag{4.38}$$
Esto significa que $p ⃗_1+p ⃗_2=0$, luego el momento lineal total $\vec{P}$ del sistema de dos partículas es la suma vectorial de los momentos lineales de las partículas individuales.
Esto es,
$$\vec{P}= p ⃗_1+p ⃗_2\tag{4.39}$$
De modo que
$$\vec{F}_{2 sobre 1}+ \vec{F}_{1 sobre 2}=\frac{d\vec{P}}{dt}=0\tag{4.40}$$
La ecuación (4.40) indica que el momento lineal total del sistema es constante, aunque los momentos individuales de las partículas que constituyen el sistema pueden cambiar. Ahora podemos interpretar de manera sencilla el principio de conservación del momento lineal así: Si la suma vectorial de las fuerzas externas sobre un sistema es cero, el momento lineal total del sistema es constante.
Generalizando, para un sistema con cualquier número de partículas 1, 2, 3, …que sólo interactúan entre sí. El momento lineal total del sistema es
$$ \vec{P}= p ⃗_1+ p ⃗_2+ p ⃗_3+.. = m_1 v ⃗_1+ m_2 v ⃗_2+ m_3 v ⃗_3+..\tag{4.41}$$
Si conocemos los valores iniciales y finales del momento lineal total del sistema podemos afirmar que el momento lineal total del sistema antes de interacción es igual al momento lineal total del sistema después de la interacción.
$$\vec{P}_{Antes}= \vec{P}_{Después}\tag{4.42}$$
En las colisiones de partículas se usa la ley de conservación del momento lineal, para resolver situaciones complejas donde se producen fuerzas impulsivas entre partículas que experimentan contacto durante un breve tiempo. En los choques las fuerzas internas entre las partículas que interactúan son mucho mayor que las externas, como suele suceder en la mayoría de los choques, podemos ignorar las fuerzas externas y tratar las partículas como un sistema aislado. El momento lineal total del sistema tendrá el mismo valor antes y después del choque
El centro de masa de un cuerpo con determinada extensión espacial y compuesto por muchas partículas es un punto muy especial donde se puede suponer que está concentrada toda la masa del cuerpo. Un sistema de partículas puede compararse con una colección de átomos en un recipiente, o un cuerpo extendido y su centro de masa puede describirse como la posición promedio ponderada de la masa del sistema.
Consideremos varias partículas con masas $m_1,m_2,m_3,⋯⋯$ y supongamos que las coordenadas de $m_1$ son $(x_1,y_1 )$, las de $m_2$ son $(x_2,y_2 )$, las de $m_3$ son $(x_3,y_3 )$, y así sucesivamente. El centro de masa del sistema se define como el punto con coordenadas $(x_{cm},y_{cm} )$ dadas por
$$x_{cm}=\frac{m_1 x_1+m_2 x_2+m_3 x_3+⋯⋯ }{m_1+m_2+m_3+⋯⋯} =\frac{∑_i m_i x_i}{∑_im_i } \tag{4.43}$$
$$y_{cm}=\frac{m_1 y_1+m_2 y_2+m_3 y_3+⋯⋯ }{(m_1+m_2+m_3+⋯⋯)}= \frac{∑_i m_i y_i}{∑_im_i } \tag{4.44}$$
Problemas de Aplicación Típicos
1) Choque de asteroides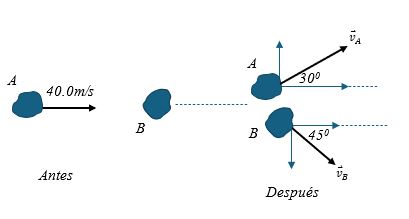
a) Calcular la rapidez de cada asteroide después del choque.
Aplicamos el principio de conservación del momento lineal.
$$\vec{P}_{Antes}= \vec{P}_{Después}$$
Observe que inicialmente el asteroide A se mueve en la dirección del eje $X$, mientras que el asteroide B está en reposo. Después del choque las velocidades tienen componentes en los ejes $X \;y\; Y$. Como las masas de los asteroides son iguales, ⇒
$$M\times{40}\frac{m}{s}\hat{i}=M{(v_A cos30^0 )\hat{i}+(v_A sen30^0 )\hat{j}}\\+ M{(v_B cos45^0 ) \hat{i}-(v_B sen45^0 )\hat{j}}$$
Vemos que inicialmente antes del choque sólo hay una componente del momento lineal en la dirección $\hat{i}$ de modo que la componente en la dirección $\hat{j}$ es cero.
Cancelamos las masas y asociamos los términos en $\hat{i}$ y en $\hat{j}$,
$$40 m/s\hat{j}+0\hat{j}= (v_A cos30^0+ v_B cos45^0 )\hat{i}+ (v_A sen30^0-v_B sen45^0 )\hat{j}$$
Aplicando propiedades de las cantidades vectoriales. (dos vectores son iguales cuando sus magnitudes y direcciones son iguales)
$$40 m/s= v_A cos30^0+ v_B cos45^0\tag{1}$$
$$0 = v_A sen30^0-v_B sen45^0\tag{2}$$
Tenemos un sistema de dos ecuaciones con dos incógnitas. Dado que $sen45^0=cos45^0$, la suma de las ecuaciones (1) +(2) resulta en
$$40 m/s= v_A cos30^0+v_A sen30^0$$
$$ y \qquad v_A=\frac{40 m/s}{cos30^0 +sen30^0 }≅29.3 m/s$$
Reemplazamos en (2) para encontrar $v_B$
$$v_B= \frac{v_A sen30^0}{sen45^0} =\frac{29.3m/s×0.5}{0.7071} =20.7m/s $$
b) ¿Que fracción de la energía cinética original del asteroide A se disipa durante el choque?
Para calcular esta fracción, debemos obtener las energías cinética inicial y final del sistema, es decir,
$$E_{Ki}= \frac{1}{2}m×v_{Ai}^2; \quad E_{KF}=\frac{1}{2} m×v_{AF}^2 +\frac{1}{2} m×v_{BF}^2$$
$$\frac{E_{KF}}{E_{Ki}}= \frac{\frac{1}{2} m×v_{AF}^2 + \frac{1}{2} m×v_{BF}^2}{\frac{1}{2} m×v_{Ai}^2} = \frac{v_{AF}^2+v_{BF}^2}{v_{Ai}^2} =0.804$$
Para el asteroide A tenemos que:
$$\frac{∆E_K}{E_{Ki}}=\frac{E_{KF}-E_{Ki}}{E_{Ki}}= -0.196$$
De modo que el 19.6% de la energía cinética original se disipa durante la colisión.
2)
Se deja caer un objeto de masa $m$ partiendo del reposo, desde una altura $h$. Al golpear el suelo (rígido), este le imparte un impulso, demuestre que este impulso es proporcional a $m\sqrt{h}$.
Solución:
Conocemos que: $v_0=0$ ; y el impulso es $\vec{J}= ∆\vec{p}$; $\;$ $\vec{p}=m\vec{v}$ El movimiento es en una dimensión, entonces al golpear el suelo rígido tenemos:
$$J= p_{fy}-p_{iy}= -mv_{fy}-m\times(+v_{iy} )\tag{1}$$
En la caída libre:
$$v_f^2= v_i^2-2gh=0-2gh ⟹ -v_{fy}= \sqrt{2gh}$$
Si el suelo es rígido ⟹ $v_{fy}= v_{iy}$ ⟹ Reemplazando en (1) tenemos:
$$ j= -m(-\sqrt{2gh}-\sqrt{2gh})⟹j=m2\sqrt{2gh} $$ la cantidad $2\sqrt{2gh}$ es constante. Luego el impulso $j$ es proporcional a $m\sqrt{h}$ es decir: $j ∝ m\sqrt{h}$
3)
Una partícula viaja en la dirección + $X$ con rapidez $v$. Una segunda partícula con la mitad de la masa de la primera viaja en la dirección opuesta, con la misma rapidez y va al encuentro para chocar con la primera partícula. Las dos partículas experimentan un choque totalmente inelástico. Encuentre la velocidad de cada partícula inmediatamente después del choque.
Solución:
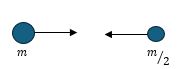
$m \; y \; \frac{m}{2}$ son las masas de cada partícula y $v$ es la rapidez.
Como el choque es totalmente inelástico las partículas quedan pegadas y después del choque las dos partículas tendrán la misma velocidad. El movimiento es en una dimensión, entonces:
$P_{antes}=P_{después}⟹ mv-\frac{1}{2} mv = (m+\frac{1}{2}m) v^⋆$
$\frac{1}{2}mv= \frac{3}{2} mv^⋆ ⟹ v^⋆=\frac{1}{3} v$
Esta es la velocidad de cada partícula inmediatamente después del choque.
4)Una pelota de golf de 0.0450kg, en reposo, adquiere una rapidez de 25.0m/s al ser golpeada por un palo. Si el tiempo de contacto es de 2.00ms, ¿qué fuerza media actúa sobre la pelota? ¿Es significativo el efecto del peso de la pelota durante el tiempo de contacto? ¿Por qué?
Solución:
La fuerza neta media $\vec{F}_{med}$ y el impulso de la fuerza neta o cambio en la cantidad de movimiento (impulso $\vec{J}$) están relacionados por la ecuación:
$$\vec{F}_{med} = \frac{\vec{J}}{t_2-t_1}\tag{1}$$
Donde $\vec{J}= p ⃑_2- p ⃑_1 =mv ⃑_2-mv ⃑_1$ . Considerando que la pelota se mueve en la dirección del eje $X$ entonces
$\vec{J}=m\vec{v}_{2x}-m\vec{v}_{1x} \quad$ reemplazando en (1)
$$(\vec{F}_{med})_x= \frac{(m\vec{v_{2x}}-m\vec{v}_{1x})}{(t_2-t_1 )}$$
La pelota inicialmente está en reposo ⇒ $\vec{v}_{1x}=0$
$$(\vec{F}_{med} )_x= \frac{0.0450kg×25m/s}{2×10^{-3} s}=562.5N$$
Pregunta:
¿Es significativo el efecto del peso de la pelota durante el tiempo de contacto? ¿por qué?
Si comparamos la fuerza ejercida por el palo (562.5N) y el peso de la pelota ($w=mg=0.0450kg×9.8m/s^2=0.441N$) vemos que la fuerza ejercida es mucho mayor que el peso de la pelota, por lo que el efecto del peso de la pelota durante el tiempo de contacto no es significativo
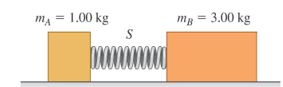
El bloque A de la figura tiene una masa de 1.00kg y el bloque B de 3.00kg. A y B se comprimen de manera forzada, comprimiendo un resorte S entre ellos; luego, el sistema se suelta del reposo en una superficie plana sin fricción. El resorte, de masa despreciable, está suelto y cae a la superficie después de extenderse. El bloque B adquiere una rapidez de 1.20m/s.
a) ¿Qué rapidez final tiene A? b) ¿Cuanta energía potencial se almacenó en el resorte comprimido?
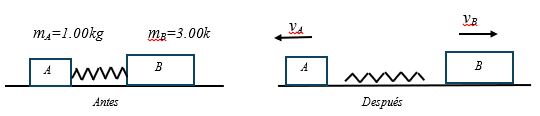
a) Aplicamos principio de conservación del momento lineal, Considerando el movimiento sobre el eje $X$.
Inicialmente los bloques A y B están en reposo comprimiendo el resorte. Cuando el sistema se suelta, el bloque A se mueve hacia la izquierda y el B hacia la derecha, entonces
$P_{Antes}= P_{Después}\\ ⇒ 0= - m_A v_{Ax}+ m_B v_{Bx} ⇒ v_{Ax}=\frac{(m_B v_{Bx})}{m_A} $
$$v_{Ax} = \frac{3kg×1.2m/s}{1kg} =3.6 m/s$$ En dirección contraria a la del bloque B
b) Para encontrar cuanta energía potencial se almacena en el resorte comprimido, aplicamos principio de conservación de la energía.
$E_{Antes}= E_{Después}$ ⇒ La $E_{Antes}$ corresponde a la energía potencial elástica almacenada en el resorte y la $E_{Después}$ es la suma de las energías cinética de cada bloque.
⇒
$$E_{PE}= \frac{1}{2} m_A v_{Ax}^2+\frac{1}{2}m_B v_{Bx}^2 = 6.48J+2.16J = 8.64J$$
Nota: Como ejercicio, de la misma forma puedes resolver el siguiente ejercicio:
Dos masas idénticas de 1.50kg se presionan contra los extremos opuestos de un resorte ligero con constante de fuerza de 175N/m, comprimiendo el resorte 20.0cm a partir de su longitud normal. Calcule la rapidez de cada masa cuando se mueven libremente sobre una mesa horizontal sin fricción. (Respuesta: 1.53m/s para ambas masas)
6)
Un astronauta de 80 kg se separa de su nave espacial. Está a 15 m de la nave y en reposo relativo respecto a la nave. En un esfuerzo por regresar, lanza un objeto de 0.5 kg con una rapidez de 8 m/s en dirección opuesta a la nave. Calcule cuánto tarda el astronauta en regresar a la nave.
Solución:
Consideremos que:$\;$$m_A$ es la masa del astronauta y $v_A$ la rapidez que adquiere el astronauta cuando lanza el objeto, además $m_0$ es la masa del objeto y $v_0$ la rapidez del objeto cuando es lanzado
Entonces:
$$P_{Antes}= P_{Después}$$
$$0= m_A v_A- m_P v_P ⟹ v_A= \frac{m_P}{m_A}×v_P$$
$$v_A = \frac{0.5 kg}{80 kg}×8m/s =0.05m/s$$
$$v_A= \frac{x}{t} ⟹ t = \frac{x}{v_A} =\frac{15 m}{0.05 m/s}= 300 s$$
7)Se comprime un resorte de constante elástica $k$ una distancia $d$ con un bloque de masa $m_1$ y se suelta. La longitud natural del extremo del resorte donde está $m_1$ coincide con el extremo de la mesa y el coeficiente de fricción dinámico entre el bloque y la mesa es $μ$. Justamente en el borde de la mesa de altura $h$ respecto al suelo, se encuentra en reposo otro bloque de masa $m_2$ (como se muestra en la figura).
a) Calcule en términos de $k,d,m_1,μ, \; y \; g$ la velocidad con que el bloque de masa $m_1$ llega al extremo de la mesa.
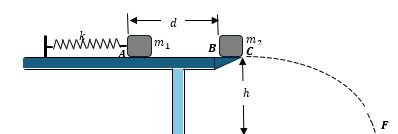
c) Considere ahora que $v_c$ es la velocidad inmediatamente después del choque y determine la magnitud de la velocidad con la cual el sistema $(m_1+ m_2 )$ llega al piso
Solución:
¿Qué es un cuerpo rígido? Un cuerpo rígido es un agregado de muchas partículas en el que la distancia entre cualquier par de ellas permanece constante, es decir, es un cuerpo cuyas dimensiones no cambian en ninguna circunstancia, pero se puede representar como un objeto extendido formado por un gran número de partículas, cada una con su propia velocidad y aceleración
Por esta razón , un cuerpo rígido se puede trasladar, rotar alrededor de algún eje o puede trasladarse y rotar a la vez sin cambiar su forma
En general un cuerpo rígido puede tener tres tipos distintos de movimiento simultáneamente:
1.Traslación a lo largo de una trayectoria cualquiera
2. Rotación mientras se está trasladando, en este caso la rotación puede ser sobre un eje que pase por el cuerpo
3.movimiento de precesión (por ejemplo, un trompo), cuando el eje de rotación a su vez está girando en torno a un eje vertical
Como vemos, el estudio del movimiento de un cuerpo rígido puede ser en general muy complejo y por esta razón se estudia cada movimiento en forma independiente sin embargo podemos afirmar que en general:
El movimiento general de un cuerpo rígido es una combinación de movimientos de traslación y de rotación.
Para hacer una descripción adecuada de su movimiento es conveniente estudiar en forma separada la traslación y la rotación de los cuerpos rígidos. Empezaremos por estudiar el movimiento de traslación y luego su movimiento de rotación producido cuando una fuerza produce un torque sobre el cuerpo
Cuando un cuerpo rígido se desplaza obedece la Segunda Ley de Newton y es suficiente conocer el movimiento del centro de masa, pues la posición de cualquier otro punto permanece invariable respecto a este centro de masa. Para determinar la ecuación de movimiento del centro de masa de un cuerpo rígido comencemos por considerar un sistema de n partículas que van desde la 1 hasta la partícula n-ésima la letra $i$ nos identifica a cualquiera de ellas.
Puede haber fuerzas internas y externas actuando sobre las partículas, las internas no cambian el estado del movimiento del sistema, las externas sí lo hacen;
Las fuerzas internas en el cuerpo rígido son las ejercidas entre las partículas que conforman el sistema, en general son fuerzas de acción y reacción entre ellas, en cambio las fuerzas externas son realizadas por agentes completamente distintos al cuerpo.
Si consideramos al cuerpo rígido compuesto de un gran número de partículas sabemos que para cada una de ellas se cumple la Segunda Ley de Newton'.
$$m_i \vec{a_i} = \vec{F_i}\tag{5.1}$$
si las sumamos obtenemos
$$ ∑_{i=1}^n m_i\vec{a_i}= ∑_{i=1}^n\vec{F_i}$$
Ahora recordemos que para el centro de masa de un sistema de partículas se cumple que
$$ ∑_{i=1}^n m_i\vec{r_i} =M\vec{r_{cm}}$$
donde $r_i$ es la posición de cada partícula y $r_{cm}$ es la posición del centro de masa. Si derivamos dos veces obtendremos que:
$$∑_{i=1}^n m_i\vec{a_i} =M\vec{a}_{cm}$$
Si tenemos en cuenta (5.1)
$$∑_{i=1}^n\vec{F}_i =M\vec{a}_{cm}$$
Es decir $$\vec{F} =Ma ⃗_{cm}\tag{5.2}$$
Esto nos indica que la aceleración del centro de masa (cm). de un cuerpo rígido, es la de un punto cuya masa es igual a la masa del cuerpo y al que se aplican todas las fuerzas externas. Para un movimiento en el plano
$$M(a_x )_{cm}= ∑(F_x)_i\tag{5.2a}$$ $$M(a_y )_{cm}= ∑(F_y)_i\tag{5.2b}$$ Donde :
$$\vec{a}_{cm}=\hat{i}(a_x )_{cm}+\hat{j}(a_y )_{cm}\tag{5.3}$$ Estas son las ecuaciones para el movimiento de traslación de un cuerpo rígido. Observe que cualquier partícula del cuerpo rígido se mueve con la misma velocidad que el centro de masa, ya que hemos definido que en el movimiento de traslación las trayectorias que describen las partículas de un cuerpo rígido son paralelas y que la distancia entre cualquier par de ellas es constante. Cuando estudiamos el movimiento de los cuerpos rígidos es necesario tener en cuenta la rotación del cuerpo en caso de que la tenga, en este caso el cuerpo se traslada y rota a la vez
Torque de una Fuerza.
Cuando se aplica una fuerza en algún punto de un cuerpo rígido, el cuerpo tiende a realizar un movimiento de rotación en torno a algún eje. La propiedad de la fuerza para hacer girar al cuerpo se mide con una magnitud física que llamamos torque o momento de la fuerza. Se prefiere usar el nombre torque y no momento, porque este último se emplea para referirnos al momento lineal, al momento angular o al momento de inercia, que son todas magnitudes físicas diferentes para las cuales se usa el mismo término.
Consideremos como cuerpo rígido a una regla fija CON UN PUNTO de rotación en O (ubicado en un extremo de la regla), como se muestra en la figura 5.1.
La fuerza $\vec{F_1}$ aplicada en el punto $a$ produce una rotación en sentido antihorario alrededor del punto de giro O.
La fuerza $\vec{F_2}$ aplicada en el punto $b$ produce una rotación horaria y con mayor rapidez de rotación que en $a$,
La fuerza $\vec{F_3}$ aplicada en $b$, pero en la dirección de la línea de acción que pasa por O, no produce rotación (ninguna fuerza aplicada en el punto de giro o que pase por el punto de giro produce rotación ).
La fuerza $\vec{F_4}$ que actúa inclinada en el punto b produce una rotación en sentido horario
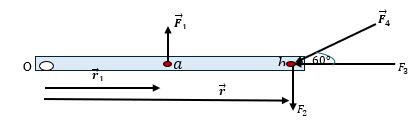
Se define el torque $τ$ de una fuerza $\vec{F}$ que actúa sobre algún punto de un cuerpo rígido, como el producto vectorial entre la posición r de la fuerza aplicada en ese punto y la fuerza $\vec{F}$, por la siguiente expresión:
$$τ ⃗=r ⃗×\vec{F}\tag{5.4}$$
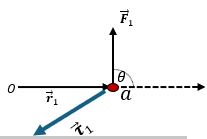
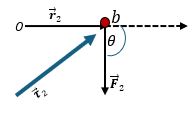
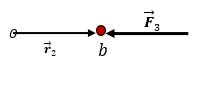
Torque de la fuerza $\vec{F_3}$:
$\vec{τ_3}= \vec{r_3}×\vec{F_3}=(r_3 F_3 Senθ) \hat{u}$
Pero θ= π $\qquad$
$ 👉 τ_3=0$
La línea de acción de la fuerza $F_3$ pasa por el punto de rotación y por lo tanto no produce rotación
Torque de la fuerza $\vec{F_4}$:
Notemos que la fuerza $\vec{F_4}$ esta aplicada en el punto $b$ y la podemos descomponer en sus componentes rectangulares $\vec{F_{4x}}$ y $\vec{F_{4y}}$, La componente$\vec{F_{4x}}$ hace un ángulo π con el vector posición $\vec{r}$:
$$τ ⃗_4= r ⃗ ×\vec{F_4}= r ⃗×(\vec{F_{4x}}+\vec{F_{4y}} )= \vec{r}×\vec{F_{4x}}+ \vec{r}×\vec{F_{4y}}$$
$$\vec{τ_4}= (rF_4 Senπ)(-u ⃗ )+ (rF_{4y} )(-u ⃗ )=0+(rF_4 Sen60°)(-u ⃗ )$$
$$ 👉 τ ⃗_4= -(rF_4 Sen60°)(u ⃗ )$$
El torque total será entonces la suma de todos los torques producidos por cada una de las fuerzas:
$$τ_{total} = τ_1+ τ_2+ τ_3+ τ_4 $$
$ 👉 \vec{τ_{total}}= ( rF_1 )\vec{u}+ (r_2 F_2 )\vec{u}+0+(rF_4 Sen60°)\vec{u}$
Un cuerpo rígido está en equilibrio cuando tanto su aceleración lineal como angular son cero respecto a un marco de referencia inercial, es decir: $$∑F ⃗=0 ⟹a ⃗=0 \tag{5.5}$$ $$∑τ ⃗=0 ⟹α ⃗=0\tag{5.6}$$
Esto significa que un cuerpo en equilibrio puede estar en movimiento, pero si es así, sus velocidades lineal y angular deberán ser constantes.
Decimos que un cuerpo rígido está en equilibrio estático cuando está en reposo en nuestro marco de referencia seleccionado. Aquí, la suma en (5.5) es de todas las fuerzas externas que actúan sobre el cuerpo, y $\vec{a}$ es la aceleración lineal de su centro de masa, por lo tanto, en equilibrio, la aceleración lineal es cero. La ecuación (5.5) es llamada la Primera condición de equilibrio de un cuerpo rígido y expresa el equilibrio traslacional.
De forma análoga la ecuación (5.6), expresa que la aceleración angular $\vec{\alpha}$ de un cuerpo rígido alrededor de un eje de rotación fijo es cero, por lo tanto, en equilibrio
la aceleración rotacional es cero. Esta es llamada la segunda condición de equilibrio
y expresa el equilibrio estático rotacional de un cuerpo rígido
Para poder describir con precisión y coherencia cómo se comportan los cuerpos cuando rotan debemos tener en cuenta que la velocidad angular $\vec{W}$ y la aceleración angular $\vec{\alpha}$ son vectores, la dirección de estos dos vectores se determina según sentido de rotación del eje de giro y de acuerdo con la regla de la mano derecha, además, podemos relacionar las magnitudes angulares anteriores con las lineales velocidad de y aceleración instantánea a través de las siguientes expresiones:
$$\vec{v} =\vec{W}×\vec{R}\tag{5.7a}$$ $$a ⃗ =α ⃗ ×\vec{R}\tag{5.7b}$$ Para un movimiento circular $\vec{W} \quad y \quad \vec{R}$ son perpendiculares, por lo tanto, $\;$ $\vec{v}=(WR)\hat{u_T} \quad y \quad \vec{a} =(αR)\hat{u_T}$
Note que $\;$(ver figura 5.5)
$$v = WR \quad y \quad a = αR\tag{5.7c}$$

Ejemplo de equilibrio de un Cuerpo Rígido
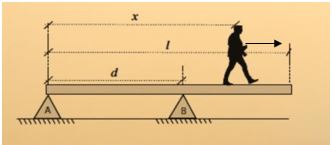
Se tiene una tabla muy delgada de longitud $l$ con un peso $w$ en Kgf reposando sobre los pivotes A y B. Un hombre con peso en Kgf $W$ camina sobre la tabla alejándose del pivote B como se aprecia en la figura 5.6.¿Hasta dónde puede caminar el hombre sin que la tabla gire y se rompa el equilibrio?
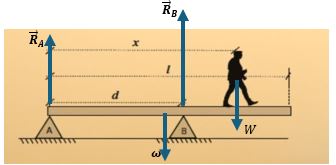
Observemos que el punto de giro para la tabla en esta situación particular es el pivote B. Debemos dibujar las fuerzas que actúan sobre la tabla las cuales son las reacciones $R_A$ en el pivote A, la reacción $R_B$ en el
pivote B, y el peso $ω$ de la tabla el cual suponemos concentrado en el punto medio de la tabla, es decir, a una distancia $l⁄2$ del pivote A , por último, dibujamos el peso $W$ del hombre a una distancia $x$ del pivote A. Suponemos que $x$ es la distancia en la cual se rompe el equilibrio de la tabla y empieza a girar. El punto de giro es el pivote B y dado que la tabla está en equilibrio (no está rotando) escribimos
$$(∑Torques)_{con\; respecto\; a\; B}=0$$
$$τ ⃗_{RA}+τ ⃗_{RB}+τ ⃗_ω+τ ⃗_W= 0$$
$$\vec{R_A} ×\vec{d}+\vec{R_B} ×0+ ω ⃗×(d-l/2)+\vec{W}\times\vec{x}=0\tag{5.8}$$
Note que con respecto al pivote B:
El brazo de la reacción $\vec{R_B}$ es cero y por lo tanto no produce ningún torque
$\vec{R_A}$ rota la tabla en sentido horario (torque positivo)
$\vec{w}$ rota la tabla en sentido antihorario (torque negativo)
$\vec{W}$ rota la tabla en sentido horario (torque positivo)
La Ecuación (5.8) nos queda
$$R_A d+0-ω(d-l/2)+Wx =0 \\ ⟹R_A d-ω(d-l/2)+Wx=0\tag{5.9}$$
La ecuación (5.9) describe la tabla en equilibrio para cualquier posición $x$ del hombre antes de romperse el equilibrio. Cuando se rompe el equilibrio, la tabla gira en el sentido horario, por lo tanto, se levanta y deja de tener contacto con el pivote A en consecuencia la reacción $R_A$ ya no existe y el primer término de (5.9) se anula, $x$ toma ahora el valor que corresponde al rompimiento del equilibrio. Podemos escribir entonces:
$$-ω(d-l/2)+Wx=0 \quad 👉 x= \frac{ω}{W (d-l/2)}\tag{5.10}$$
Actividad de simulación. Equilibrio de Cuerpo Rígido
En la siguiente actividad estudiamos la teoría anterior jugando con la simulación Phet de la Universidad de Colorado: haga clic en el enlace a continuación y abra el hipervínculo, haga clic en play de la pantalla inicial, al hacerlo mostrará ventanas: Introducción, Laboratorio de Equilibrio y Modo de Juego, cada una presenta sus propios parámetros para realizar y estudiar diferentes situaciones lo cual realizamos en las siguientes actividades
Actividades
Clic en la ventana de introducción
Despliega esta ventana. Observe que aparece una tabla sostenida por dos columnas y un trípode y al lado dos masas de 5 kg y una de 10 kg, puede quitar las dos columnas desplazando el botón de abajo a la derecha. En la parte derecha de la pantalla tenemos dos recuadros con diferentes entradas y usos.
Despliegue la regla y ponga una de las dos masas de 5 kg a una distancia de 1.75 ms a la izquierda del trípode y la otra masa de 5kg a una distancia de 1.25ms, luego utilice la masa de 10 kg para equilibrar la tabla. Para trabajar cómodamente no quite las columnas hasta haber ubicado las masas que pretende equilibrar
Utilice la ecuación $∑τ=0$ para encontrar matemáticamente la distancia a la cual debe ubicar la masa de 10kg. Verifique que este resultado es el mismo que encontró con la simulación.
Invierta el orden de trabajo y ahora utilizando posiciones diferentes a las anteriores y calcule primero cual debe ser la distancia necesaria para que la masa de 10kg equilibre las otras dos y luego utilice la simulación para verificar que su resultado es correcto
Clic en la ventana de Laboratorio de equilibrio
Despliega la ventana de abajo con la misma tabla de balanceo y trípode que antes, pero con más pesas para balancear. Básicamente es la misma práctica o simulación, pero con más opciones. Se invita al lector construir varias situaciones de equilibrio
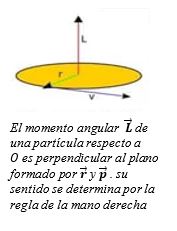
El momento angular de una partícula puntal se define a partir del vector posición $\vec{r}$ de la partícula y su cantidad de movimiento $\vec{p}$ . El momento angular es una magnitud vectorial que utilizamos en física para caracterizar el estado de rotación de los cuerpos.
Observe que no es una magnitud propia del cuerpo, sino que depende del punto de referencia que se escoja. Su significado físico tiene que ver con la rotación:
El momento angular caracteriza el estado de rotación de un punto material, del mismo modo que el momento lineal caracteriza el estado de traslación lineal.
Se define el momento angular de una partícula respecto a un punto O como
$$\vec{L}=r ⃗×p ⃗ \tag{5.11}$$
Donde:
$\vec{L}$ : Momento angular del cuerpo. Su unidad de medida en el Sistema Internacional (S.I.) es el $kg·m^2·s^{-1}$
$\vec{r}$: Vector de posición del cuerpo respecto al punto O
$\vec{p}$ :Cantidad de movimiento del cuerpo. También se le conoce como momento lineal. Es el producto de la masa del cuerpo $m$, con la velocidad $v$ Su unidad de medida en el Sistema Internacional, es el $kg·m·s^{-1}$
En un movimiento circular los vectores $\vec{r} \; y \; \vec{p} $ son perpendiculares entonces:
$$\vec{L}=r ⃗×p ⃗=(rp×sen π⁄2)\hat{u_z} ⟹ \vec{L}=(rmv)\hat{u_z}=(mr^2 w)\hat{u_z}$$
$$👉 I= mr^2\tag{5.12}$$
A la cantidad $I$ se le conoce como momento de inercia de una partícula de masa $m$ Su unidad de medida en el Sistema Internacional (S.I) es el $kg·m^2$
Observe la analogía que hay entre las expresiones:
$$I= mr^2 \quad y \quad p=m·v.$$
Como se puede deducir de las expresiones, el papel que juega el momento inercial I en el momento angular L es análogo al que juega la masa inercial m en el momento lineal p.
En los movimientos rectilíneos, cuanto mayor sea la masa de un cuerpo, más difícil es modificar su momento lineal. En los movimientos circulares, cuanto mayor sea el momento inercial I, más resistencia existe a modificar el estado de rotación (el momento angular)
Consideremos un cuerpo rígido en rotación. Queremos describir la rotación del sólido rígido respecto a su eje de giro o eje de rotación .¿Cómo procederemos? Podemos pensar que todo cuerpo solido rígido está construido de muchas partículas materiales cada una rotando con su propio momento angular $Li$ respecto a dicho eje de rotación . El momento angular del solido rígido será la suma de todos los momentos angulares de cada una de las partículas. A continuación, consideramos como un caso ilustrativo un disco solido rígido que rota con velocidad angular $ω$. El momento angular de cada partícula genérica $i$ viene dado por:
$$\vec{L_i}=\vec{r_i}×\vec{p_i}\tag{5.13}$$
El momento angular para el sólido rígido será entonces
$$\vec{L}=\sum_{i}\vec{L_i}=\sum_{i}\vec{r_i}\times\vec{p_i} \tag{5.14}$$ Teniendo en cuenta que en los movimientos circulares ambos vectores son perpendiculares, podemos escribir:
$$\vec{L_i}=(r_i p_i Sen π⁄2)\hat{u_z} ⟹\vec{L_i}=(r_i p_i )\hat{u_z}=(r_i m_i v_i )\hat{u_z}=(m_i r_i^2 ω_i )\hat{u_z}$$
Note que el término entre paréntesis es similar a la expresión del momento de inercia de una partícula. decimos que $I=∑_im_i i^2$ es el momento de inercia del sólido rígido discreto. A partir de él, podemos definir el momento angular del sólido rígido como
$$\vec{L}= Iω\hat{u_z}\tag{5.15}$$
$\vec{L}$: Momento angular del sólido rígido. Su unidad de medida en el Sistema internacional (S.I.) es l kg·m2·s-1. Nos restringimos al caso de que el eje de referencia sea un eje principal
$I$ : Momento de inercia del sólido. Representa un factor de oposición a los cambios en el estado de rotación del cuerpo. Depende de la masa del sólido y de la distribución de dicha masa con respecto al eje de rotación elegido.
Aunque en general existen infinitos momentos de inercia posibles, tanto como ejes de rotación se puedan elegir, su expresión, para el caso del sólido rígido discreto, es:
$$I=∑_im_i r_i^2$$
Su unidad de medida en el Sistema Internacional (S.I.) es el $kg·m^2$
$\vec{w}$: Velocidad angular del sólido rígido. Es un vector axial (se asigna dirección y sentido por convenio). Su dirección es perpendicular al plano de giro y su sentido viene dado por la regla de la mano derecha. Su unidad de medida en el Sistema Internacional (S.I.) es el radián por segundo ( rad/s )
Para llegar a la expresión (5.15) del momento angular hemos considerado como referencia el eje de giro de un disco. En general, la elección de un eje adecuado tiene importancia para el cálculo del momento angular.
Note además que las expresiones $L=I·ω$ $\;$ y $\;$ $p=m·v$ presentan analogías:
En el momento angular la velocidad angular $ω$ está presente. En el momento lineal la velocidad lineal $v$ está presente
En el momento angular el momento inercial $I$ se opone a los cambios en el estado de rotación del cuerpo. En el momento lineal la masa $m$ se opone a los cambios en el estado de traslación
EJERCICIOS SOBRE CINEMÁTICA DE CUERPO RIGIDO
Problemas de Aplicación Típicos
Nota: Se recomienda leer y entender la teoría de rotación de cuerpos rígidos, intentar resolver cada ejercicio por su propia cuenta, por último, estudiar la solución de cada problema.
1) Una tornamesa gira con aceleración angular constante de 2.25$rad/s^2$. Después de 4s ha girado un ángulo de 60rad. ¿Cuál era su velocidad angular al iniciar el intervalo de 4s?
Solución:
Datos:$\quad$ $∝ =2.25 rad/s^2$;$\quad$ $t=4s$ ; $\quad$ $θ=60 rad$ ;
De la ecuación $θ= θ_0+w_{0z} t+ \frac{1}{2} ∝_z t^2$ vemos que:
Despejando $w_{0z}$ de esta ecuación; con $θ_0 =0$
tenemos:
$w_{0z} t= θ-\frac{1}{2} ∝_z t^2\\ ⇒ w_{0z}=1/t (θ- \frac{1}{2} ∝_z t^2 )= θ/t - \frac{1}{2}∝_z t$
Reemplazando los datos en la ecuación anterior obtenemos
$$w_{0z}=\frac{60 rad}{4 s}- \frac{1}{2}(2.25 rad/s^2 )×4 s\\ = 15 rad/s - 4.5rad/s$$
$$👉 w_0z=10.5 rad/s$$
2) Centrifugador. En un anuncio se asegura que un centrifugador solo ocupa 0.127m de espacio en una mesa de trabajo, pero que puede producir una aceleración radial de 3000g a 5000rev/min. Calcule el radio que debe tener el centrifugador. ¿Es verosímil el anuncio?
Solución.
Datos: Espacio que ocupa el centrifugador 0.127m.
$a_{rad}=3000g=3000×9.8m/s^2 =29400 m/s^2$;
f=5000 rev/min =5000 rev/(60 s) = 500/6 rev/s ; R= ?
$a_{rad} = v^2/R ⇒ 29400 m/s^2 = v^2/R$
como $v=wR \quad y \quad w =2πf$
obtenemos
$29400 m/s^2 =\frac{2πfR)^2}{R}=\frac{4π^2f^2 R^2}{R}$
$$R = \frac{29400 m/s^2}{4π^2f^2}$$
$$👉 R = \frac{(29400 m/s^2)}{4π^2 (500 rev/s)/6)^2} = 1.07m $$
Como se dice que el centrifugador ocupa un espacio de 0.127m y su radio es de 1.07m, el anuncio No es verosímil, ya que no cabría en la mesa de trabajo.
3) Cuatro esferas pequeñas, que pueden considerarse como puntos con masa de 0.200kg cada una, están colocadas en un cuadrado de 0.400m de lado, conectadas por varillas muy ligeras (masa despreciable)
como se muestra en la figura 5.10.
Calcule el momento de inercia del sistema alrededor de un eje que
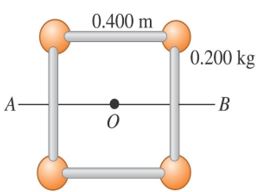
a) que pasa por el centro del cuadrado, perpendicular a su plano (que pasa por o en la figura).
b) Calcular el momento de Inercia I del sistema alrededor de un eje que biseca dos lados opuestos del cuadrado (a lo largo de línea AB en la figura)
c) Calcular el momento de Inercia I del sistema alrededor de un eje que pasa por los centros de las esferas superior izquierda e inferior derecha y por O.
Solución
a) En este caso la distancia que hay de las masas al centro del cuadrado, (lugar donde está el eje de rotación del sistema) es la misma.
Como se trata de un cuadrado de lado 0.4m, entonces la distancia que va de una de las masas al centro es:
$r = \sqrt{(0.2m)^2+(0.2m)^2 } =0.2m×\sqrt{2} $
⟹ Aplicando la ecuación:
$I = m_1 r_1^2+ m_2 r_2^2+ m_3 r_3^2+⋯ = ∑_im_i r_i^2 $
Como las masas son iguales y las distancias también tenemos:
$I =4mr^2 =4×0.2kg×(0.2m×\sqrt{2})^2 =0.064 kgm^2$
$$ 👉 I =0.064 kgm^2$$
b)
En este caso la distancia de las masas a la línea $AB$ es la misma y tiene un valor de 0.2m, por lo tanto:
$I = ∑_im_i r_i^2 = 4mr^2 =4×0.2kg×(0.2m)^2 = 0.032 kgm^2$
$$👉 I = 0.032 kgm^2$$
c)
En este caso tenemos sólo dos masas que rotarían alrededor de la línea diagonal que va de la esfera superior izquierda a la esfera inferior derecha, pasando por O.
Observamos que la distancia que hay de las masas a esta diagonal es: $r=0.2m×√2$ luego:
$$ 👉 I = 0.032 kgm^2$$
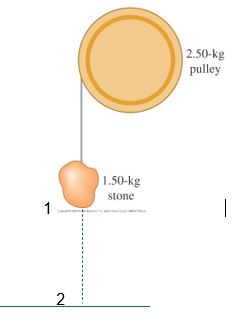
4) Una polea sin fricción tiene la forma de un disco sólido uniforme de masa igual a 2.50 kg y radio de 20.0 cm. Una piedra de 1.50 kg se sujeta a un alambre muy ligero que se enrolla alrededor del borde de la polea como se muestra en la figura, y el sistema se libera del reposo. a) ¿Qué distancia debe descender la piedra para que la polea tenga 4.50J de energía cinética? b) ¿Qué porcentaje de la energía cinética total tiene la polea?
Solución
Consideremos dos instantes: La posición 1 donde el sistema está en reposo y la posición 2 cuando la piedra a recorrido la distancia $y_2=-h$ y la energía cinética rotacional de la polea sea 4.50J. De este modo la posición 1 corresponde a $y_1=0$ (nivel de referencia)
Entre otros datos tenemos:
$M=2.5 kg$ ; masa de la polea
$R =20 cm$ radio de la polea ;
$m=1.5 kg$ masa de la piedra
Para un disco sólido:
$I=\frac{1}{2}MR^2= \frac{1}{2} ×2.5kg ×(0.2m)^2 =0.05kgm^2$
Si $E_{kRP}$ es la energía cinética rotacional de la polea, tenemos:
$$E_{kRP}= \frac{1}{2}I w^2 ⇒ w = \sqrt{\frac{2E_{kRP}}{I}}$$
$$E_{kRP}=\sqrt{\frac{2×4.5J}{0.05 kg m^2}} =13.4rad/s$$
Si $E_{kTS}$ es la energía cinética de traslación de la piedra, tenemos:
$E_{kTS} =\frac{1}{2}mv^2 \quad pero \quad v =wR ⇒$
$E_{kTS} = \frac{1}{2} m(wR)^2 $
$$E_{kTS}=frac{1}{2}×1.5kg\times(13.4 rad/s×0.2m)^2 =5.39J $$
Aplicamos ahora el principio de conservación de la energía en los instantes 1 y 2 es decir la energía en la posición 1 es igual a la energía en la posición 2
$mg(-h) = E_{kTS} + E_{kRP} ⇒ -h = \frac{E_{kTS} + E_{kRP}}{mg} $
$-h = \frac{(5.39J + 4.5J)}{1.5kg×9.8} = 0.673m$
$$ 👉 0.673m \;es \;la \;distancia\; que\; desciende\; la\; piedra.$$
b) Que porcentaje de la energía cinética total tiene la polea?
$E_{KT} = E{_kT}s + E_{kRP} = 5.39J + 4.5J =9.89J$
$E_{kRP}/E_{KT} = 4.5J/9.89J =0.455$
$$👉 Porcentaje \;de \;la \;energía\; cinética: \quad 0.455×100% es decir 45.5%$$
5) El volante de alta velocidad de un motor giraba a 500 rpm cuando se interrumpió la alimentación eléctrica. El volante tiene una masa de 40 kg y un diámetro de 75 cm. El motor no recibe electricidad durante 30 s y, en ese lapso, el volante disminuye su velocidad por la fricción en los cojinetes de su eje, realizando 200 revoluciones completas. a) ¿Con que rapidez está girando el volante cuando se restablece la alimentación eléctrica? b) ¿Cuánto tiempo después de la interrupción eléctrica se habría detenido el volante, si el suministro no se hubiera restablecido, y cuantas revoluciones habría girado el volante en ese tiempo?
Solución
$f=500rpm ⇒ w_0=2πf=2π×500rpm ⇒w_(0 )= 100/6×π rad/s$
$Masa\quad m=40kg, Diametro \quad D=75cm ⇒ r=37.5cm=0.375m $
$t=30s$ es el tiempo en el cual el motor no recibe electricidad. Durante este tiempo realiza 200 revoluciones completas
⇒
$θ=200×2π =400π rad$ (ángulo girado)
De la ecuación:
$θ= \frac{1}{2}(w_0+ w_f )t$ podemos despejar $w_f$, para ello tenemos en cuenta que $θ_0=0$ y, por lo tanto: $ w_f= \frac{20}{t}-w_0$
Reemplazando valores
$$w_f= \frac{2×400π}{30}rad/s - \frac{100}{6}×π \quad rad/s$$
$$👉 w_f=10π\quad rad/s$$
Observe que se ha calculado la velocidad o frecuencia angulares, de modo que como:
$w_f= 2πf ⇒ f= w_f/2π = (10π rad/s)/(2π rad) \\=5 rev/s =5 Hz$
o también:
$$f= 5 rev/s =5 rev/(1/60min)=300 rpm$$
¡Ojo! se debe diferenciar entre la frecuencia $f$ y la frecuencia angular $w$.
b) ¿Cuánto tiempo después de la interrupción eléctrica se habría detenido el volante, si el suministro no se hubiera restablecido, y cuantas revoluciones habría girado el volante en ese tiempo?
Para dar solución a esta parte tengamos en cuenta que:
$1 rev/s =2π rad/s$
y además $w_f=(10π)rad/s \quad y\quad w_0=(100/6)π rad/s$
Realizando una regla de 3 teniendo presente la igualdad anterior encontramos que:
$w_f=10π rad/s = 5 rev/s =5 Hz$
De la misma forma:
$w_0=\frac{100πrad/s}{6}=8.3333 rev/s$
Para calcular el tiempo debemos determinar la aceleración angular $\alpha$. Con $\; t_i=30 s$.
Reemplazando los valores de $w_f\; y \;w_o$ obtenemos para $\alpha$:
$ \alpha = \frac{w_f- w_0}{t_i} = (5 rev/s -8.3333 rev/s)/30s = - 0.1111 rev/s^2$
De modo que el tiempo $t_f$ cuando el volante se detiene ( $w_{f2}=0 $) es:
$$t_f = \frac{w_{f2}-w_0}{\alpha} =\frac{- 8.3333rev/s}{- 0.1111rev/s^2}=75.0072s=75 s$$
$$👉 t_f = 75 s$$
Y finalmente obtenemos las revoluciones (número de vueltas giradas) con la ecuación:
$$θ-θ_0= \frac{(w_{0z}+w_{fz})t_f}{2} $$
Con $\;$ $ θ_0=0 \quad w_{fz}=0 \quad y\quad t_f=75 s$
$$θ= \frac{(8.3333rev/s+0)75 s}{2}$$
$$👉 θ ≅ 312.5 rev$$
6) Un bloque de masa $M$ resbala por un plano inclinado, hacia abajo, mientras que un cilindro macizo rueda sin resbalar hacia abajo por el mismo plano inclinado. Si ambos se sueltan al mismo tiempo desde una altura $h$, demuestre que la velocidad del bloque es mayor que la velocidad del cilindro macizo cuando ellos pasan por la base del plano inclinado.
Solución.
Consideremos que $M$ es la masa del bloque y que
$m$ es masa del cilindro macizo.
Aplicando el principio de conservación de la
energía para el cilindro tenemos:
$$Mgh= \frac{1}{2}Iw^2+ \frac{1}{2} Mv^2 , \quad w= \frac{v}{r}$$
$$Mgh= \frac{1}{2}×\frac{1}{2}Mr^2×\frac{v^2}{r^2} +\frac{1}{2}Mv^2 \\= \frac{1}{4} Mv^2+ \frac{1}{2} Mv^2= \frac{3}{4}Mv^2 $$
$$Mgh= \frac{3}{4}Mv^2$$
la velocidad del cilindro al llegar a la base del plano inclinado es:
$$v_c= \sqrt{\frac{4}{3} gh}\tag{1}$$
Ahora aplicando el principio de conservación de la energía para el bloque:$$mgh=\frac{1}{2}mv_b^2 ⟹ v_b= \sqrt{2gh}\tag{2}$$
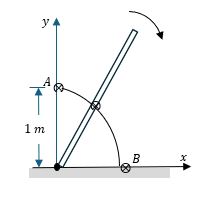
7) Una barra homogénea mide $2m$ de longitud y está inicialmente en posición vertical. Si la barra se cae, tal como se muestra en la figura, ¿con qué velocidad angular golpeará el suelo? Considere que el extremo inferior en contacto con el suelo no se desliza y el símbolo ⨂ representa el centro de masa.
Solución:
Para una barra homogénea o varilla delgada, el momento de inercia respecto a un eje a través de un extremo es:
$$I= \frac{1}{3} Ml^2$$
$E_A= E_B ⟹ E_A=Mgh$
con $h= \frac{l}{2} \quad y \quad E_B= \frac{1}{2} $
$Iw^2$ $\quad$ donde $I= \frac{1}{3}Ml^2 \quad l =2m$
obtenemos:
$Mg \frac{l}{2} =\frac{1}{2}×\frac{1}{3}Ml^2 w^2$
$$ w= \sqrt{\frac{3g}{l}}= \sqrt{\frac{3\times9.8m/s^2}{2m}}=3.83 rad/s$$
$$ 👉 w= 3.83 rad/s$$
Ecuación de movimiento. Consideremos un cuerpo rígido rotando alrededor de un eje principal, las ecuaciones (5.14) y (5.15) son iguales, es decir:
$$Iω\hat{u_z} = ∑_ir ⃗_i ×p ⃗_i $$
Tomando la derivada temporal en ambos lados de esta ecuación obtenemos:
$$\frac{d(Iw)}{dt}\hat{u_z}= \frac{d}{dt}(∑_ir ⃗_i×p ⃗_i )$$
$$ I\frac{d(w)}{dt}\hat{u_z}= ∑_i\frac{d\vec{r_i}}{dt} ×p ⃗_i+∑_ir ⃗_i × \frac{d\vec{p_i}}{dt}$$
El primer término del lado derecho de esta ecuación se anula pues la velocidad de cualquier partícula es paralela a su momento lineal $(v ⃗_i )|| m_i v ⃗_i)$ y el producto vectorial de dos vectores paralelos es cero
$$(Iα)\hat{u_z}= ∑_i(v ⃗_i ) ×p ⃗_i+∑_ir ⃗_i × \vec{F_i}$$
$$(Iα) \hat{u_z}= ∑_ir ⃗_i × \vec{F_i}$$
Utilizando la ecuación (5.1) que nos dice que: $\;$ $τ ⃗=r ⃗×\vec{F_i}$
escribimos finalmente
$$(Iα)\hat{u_z}= ∑_iτ ⃗_i = r ⃗×\vec{F_i} $$
$$(Iα)\hat{u_z}= τ ⃗_{externo}=r ⃗×\vec{F_i}\tag{5.16} $$
El momento angular se conserva cuando el momento de las fuerzas exteriores que actúan sobre el cuerpo es nulo.
Observe que según la ecuación (5.16) existen fundamentalmente dos condiciones bajo las cuales se cumple la conservación del momento angular:
1. La fuerza neta $\vec{F}$ que actúa sobre la partícula es nula
2.La fuerza $\vec{F}$ es paralela a $\vec{r}$. Esto se cumple en el caso de las fuerzas centrales
Algunos ejemplos de conservación del Momento Angular son los sistemas planetarios, estos son sistemas de fuerzas centrales. La Tierra al igual que todos los planetas de nuestro sistema solar experimenta fuerzas atractivas definidas por la ley de gravitación universal y dirigidas hacia el centro de Sol. Su momento angular es constante (ver figura abajo).
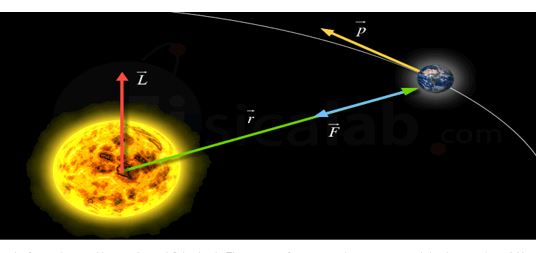
Esto nos garantiza que todos los planetas del sistema solar conservarán su trayectoria orbital a no ser que una fuerza externa intervenga como por ejemplo el choque con un asteroide
Otro ejemplo interesante es el de una patinadora que mientras gira recoge sus brazos. Al recoger sus brazos la distribución de masas respecto al eje varía: toda la masa se concentra más cerca del mismo por lo que el momento de inercia disminuye. En el movimiento de plegar los brazos no son necesarios momentos de fuerza, por lo que el momento angular permanece constante. Observa qué ocurre entonces:
$$ I_1 ω_1= I_2 ω_2$$
Esto significa que, dado que $I_2$ es menor que $I_1$, la velocidad angular $ω_2$ debe ser mayor que $w_1$ .Es decir, cuando el patinador pliega sus brazos, su velocidad angular aumenta.
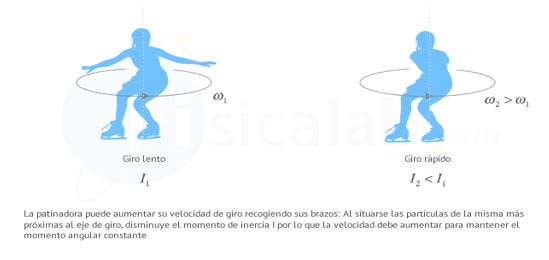

Aplicación de la Conservacion del Momento Angular en la Vida Real.
La patinadora sobre hielo NATALIA KANOUNNIKOV consigue un récord mundial en el número de giros(308 giros en un minuto) gracias a su excelente manejo del momento de inercia $I$. Note como recoge totalmente sus brazos uniéndolos a su cuerpo y junta sus piernas con el fin de disminuir al máximo su momento de inercia y aumentar asi su velocidad angular $w$
Algunos Ejemplos Típicos
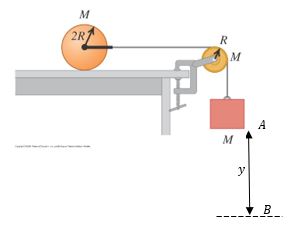
1) Un cilindro sólido uniforme de masa $M$ y radio $2R$ descansa en una mesa horizontal. Se ata una cuerda mediante un yugo a un eje sin fricción que pasa por el centro del cilindro, de modo que este pueda girar sobre el eje. La cuerda pasa por una polea con forma de disco de masa $M$ y radio $R$, que está montada en un eje sin fricción que pasa por su centro. Un bloque de masa $M$ se suspende del extremo libre del hilo (tal como se muestra en la figura). La cuerda no resbala en la polea, y el cilindro rueda sin resbalar sobre la mesa. Si el sistema se libera desde el reposo, determine la magnitud de la aceleración del bloque.
Solución:
En la figura dibujamos una altura y
dos posiciones del bloque de masa $M$, el punto $A$ donde inicia el movimiento y el punto $B$ donde el bloque pasa con determinada aceleración.
Para el cilindro el momento de inercia es:
$I_c= \frac{1}{2} M(2R)^2$
Para la polea el momento de inercia es:
$I_p= \frac{1}{2}MR^2$
Ahora consideremos las posiciones o instantes $A$ y $B$ y usamos las consideraciones de energía:$\;$
$E_A= E_B ⟹ E_A=Mgy$
$$E_B= \frac{1}{2} Mv^2+ \frac{1}{2} I_P w_P^2 + \frac{1}{2} I_C w_C^2 + \frac{1}{2} Mv_{cm}^2$$
La velocidad del centro de masa del cilindro sólido es igual a la velocidad del bloque.
$$v= v_{cm} \quad ; \quad w_P= \frac{v}{R}w_C= \frac{v}{2R}$$ Reemplazando:
$$E_B=\frac{1}{2} Mv^2+\frac{1}{2}×\frac{(MR^2)}{2}×(\frac{v}{R})^2 \\ + \frac{1}{2}×\frac{M}{2}(2R)^2 (\frac{v}{2R})^2 +\frac{1}{2} Mv^2$$
$$E_B= Mv^2+ \frac{1}{4}×Mv^2 + \frac{1}{4}×Mv^2 = \frac{3}{2} Mv^2\\⟹E_B= \frac{3}{2} Mv^2$$
$E_A=Mgy$ $\;$ Para el bloque $\;$ $v^2= v_0^2+2ay =0+ 2ay$
$$⟹ v^2= 2ay$$
$$ Mgy = \frac{3}{2} Mv^2 ⟹ Mgy=\frac{3}{2} M 2ay$$
$$g=3a \quad 👉 a=\frac{1}{3} g$$
2)
Un cilindro de masa $M$ y radio $R$ es obligado a rodar sin resbalar por una superficie horizontal al aplicarle una fuerza $T$ a una distancia $r$ del centro tal como se muestra en la figura.
a)
Calcular el valor de la aceleración del centro de masa en términos de $M,R,r$ y $T$
b) Si el cilindro partió del reposo y $M=3 kg,\quad R=0.6 m, \; r=0.4 m \; y \; T=3N.$ Calcule la energía cinética total del cilindro cuando han trascurrido 3 segundos.
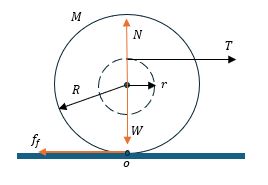
Solución:
a) En la figura se ha dibujado en color rojo las
fuerzas que actúan sobre el cilindro, además de la tensión $T$.
$\;$ $\;$
Para este cilindro tenemos las siguientes ecuaciones de movimiento :
$∑τ_0= I_0 α\quad \quad y \quad ∑F= Ma_{cm}$
⟹
$T(r+R)= I_0 α \quad y \quad T- f_{f}= Ma_{cm} $
Notemos que:
$I_0= I_{cm}+MR^2 ⟹ I_0= \frac{MR^2}{2}+MR^2 = \frac{3}{2} MR^2$
$$T(r+R)= \frac{3}{2} MR^2 α\tag{1}$$ $$N=W\tag{2}$$
$$a_{cm}= αR ⟹ α= \frac{a_{cm}}{R}$$ $\quad$
b)
$$w_{f}=w_{0}+ αt =0+αt ⟹ w_{f}= αt= \frac{a_{cm}}{R}t$$
como $$ a_{cm}= \frac{2T(r+R)}{3MR} \quad y \quad t=3s$$:
Reemplazando en (1) tenemos
$$T(r+R)= (\frac{3}{2} MR^2 ) \frac{a_{cm}}{R}$$
$$👉 a_{cm}= \frac{2T(r+R)}{3MR}$$
$$w_f= \frac{2T(r+R)3}{3MR^2} = \frac{3MR^2}{MR^2}$$
$$E_k= \frac{1}{2}Mv_cm^2+ \frac{1}{2} Iw_f^2 = \frac{1}{2} Mw_f^2 R^2+ \frac{1}{2}Iw_f^2$$
Reemplazando valores en $E_k$ obtenemos:
$$👉E_k=3T^2 \frac{(r+R)^2}{MR^2}=25J$$
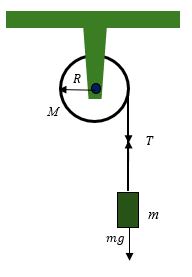
Ecuación de movimiento para $m$:
$$T-mg= -ma\tag{1}$$
Ecuación de movimiento de rotación para el disco:
$$ TR= Iα\tag{2}$$ para un disco: $$I=\frac{1}{2}MR^2; \quad α= \frac{a}{R}$$
De (1) tenemos $T= mg-ma$
Reemplazando en (2)
$$(mg-ma)R=\frac{1}{2}MR^2 \frac{a}{R}$$
$$👉 a=1.126 m/s^2$$
b) Tensión en la cuerda:
$$ T= I \frac{a}{r^2}$$
$$T=0.5 kgm^2×\frac{1.126 m/s^2}{0.04 m^2} = 14.075 N $$
$$👉T ≅ 14.1N$$
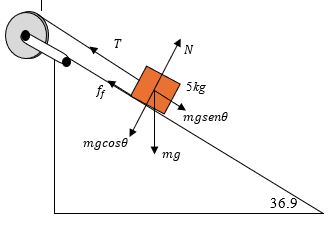
Solución:
a) Se han etiquetado todas las fuerzas
que actúan en el sistema.
Entre los datos tenemos:$m=5kg;\; θ= 36.9^0; \; μ_k=0.25; \; M_V=25 kg$
$r=0.2 m$ (radio del volante)
$I=0.5 kgm^2$ (momento de inercia del volante)
$$f_f= μ_k N= μ_k mgcosθ$$
$$∑F_x=ma ⟹mgsenθ-T-f_f=ma\tag{1}$$
$τ=Tr; \quad τ=Iα; \quad y \quad a=rα;$ $\quad$
$Tr= Iα ⟹ Tr=I \frac{a}{r} ⟹ T= I\frac{a}{r^2}$
Reemplazando en (1) tenemos:
$$mgsenθ - I a/r^2 - μ_k mgcosθ = ma$$
Asociando terminos
$$mgsenθ - μ_k mgcosθ=m+\frac{I}{r^2}a$$
$$a= \frac{mgsenθ - μ_k mgcosθ}{m+\frac{I}{r^2}}$$
5) Un disco plano de madera de $120 kg$, tiene un radio de $2 m$. Inicialmente el disco gira alrededor de un eje vertical, que pasa por su centro, a $3 rad/s$. De repente, una masa de $70 kg$ se posa suavemente en un punto muy cerca al borde del disco.
a) Calcule la velocidad angular del disco después de que la masa de 70 kg se posa muy cerca al borde del disco. (Suponga que la masa de 70 kg puede tratarse como una partícula)
b) Calcule la energía cinética del sistema antes y después de que se posa la masa de 70 kg cerca al borde del disco.
Solución:
a) Aplicamos el principio de conservación del momento angular:
$$L_1= L_2 ⟹ I_1 w_1= I_2 w_2 ⟹ w_2= \frac{I_1}{I_2}w_1$$
donde para un disco:
$$I_1= \frac{1}{2}MR^2= \frac{1}{2} (120kg) (2m)^2=240 kgm^2$$
Aplicamos ahora el teorema de los ejes paralelos para encontrar $I_2$.
$$I_2= I_1+ I_m = 240 kgm^2+mR^2= 240 kgm^2+70kg(2m)^2\\=520kgm^2$$
$I_2= 520kgm^2 ⟹ w_2= \frac{I_1}{I_2}w_1\quad 👉w_2= 1.38rad/s$
(velocidad angular del disco después de que la masa de 70 kg se posa
muy cerca al borde del disco)
b) La energía cinética del sistema antes de que la masa de 70 kg se pose en el borde del disco es:
$$E_{k1}= \frac{1}{2} I_1 w_1^2 = \frac{1}{2} (240kgm^2 )×(3rad/s)^2=1080 J$$
La energía cinética del sistema después de que la masa de $70 kg$ se pose en el borde del disco es:
$$E_{k2}= \frac{1}{2} I_2 w_2^2= \frac{1}{2} (520kgm^2 )×(1.38rad/s)^2 ≅ 495.1 J$$
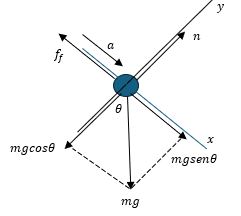
En la figura se ha escogido un sistema de referencia para la esfera que baja por la ladera y además se muestran las fuerzas que actúan sobre la esfera sólida.$\;$Vemos que:
$$∑F_y =0 ⟹ n=mgcosθ;$$
$$∑F_x =ma$$
$$mgsenθ- f_f=ma$$ $$mgsenθ- μ_s mgcosθ=ma$$
$$ g(senθ- μ_s cosθ)=a\tag{1}$$
Observamos que la normal $n$ y el peso $mg$ actúan en el centro de la esfera y por lo tanto no producen torque.
Ahora el torque que hace la fuerza de fricción $f_f$ es:
$$∑τ= τ_f ⟹ τ_f= f_f R= (μ_s mgcosθ)R$$
$$∑τ= Iα; \quad I= \frac{2}{5} mR^2$$
igualando:
$$(μ_s mgcosθ)R = \frac{2}{5} mR^2 α$$
$\;$ Como no hay deslizamiento $α=a/R$
.Reemplazando $α$ en la ecuación anterior y simplificando términos tenemos:
$$ \frac{5}{2} μ_s gcosθ= a\tag{2}$$
igualando las ecuaciones (1) y (2) podemos obtener $μ_s$
$g(senθ- μ_s cosθ)=\frac{5}{2} μ_s gcosθ ⟹ 👉 μ_s= 0.613$
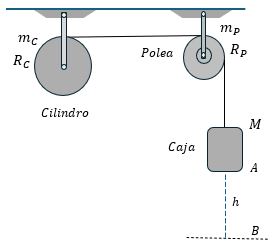
7) En la figura de la derecha, el cilindro sólido y la polea giran sin fricción en torno a ejes horizontales estacionarios que pasan por sus respectivos centros. Se enrolla una cuerda ligera en el cilindro, la cual pasa por una polea y tiene una caja suspendida en su extremo libre. No hay deslizamiento entre la cuerda y la superficie de la polea. Consideremos que el cilindro es uniforme con una masa $m_C$ y radio $R_C$; la polea es un disco uniforme de masa $m_P$ y radio $R_P$ y que la caja tiene una masa $M$. La caja se suelta desde el reposo y desciende mientras la cuerda se desenrolla del cilindro. Calcule (en términos de las cantidades conocidas) la rapidez que tiene la caja cuando ha descendido una distancia $h$.
Solución:
En la figura se agregaron los puntos $A$ y $B$ para aplicar el principio de conservación de la energía entre esos dos puntos
$$E_A= E_B ⟹ Mgh= \frac{1}{2} Mv_M^2+ \frac{1}{2} I_P w_P^2+ \frac{1}{2} I_C w_C^2\tag{1}$$
Consideramos que:
$v_M$ es la rapidez de la caja, $w_P$ es la velocidad angular de la polea, $w_C$ es la velocidad angular del cilindro
$$w_P= \frac{v_M}{R_P} \quad y \quad w_C= \frac{v_M}{R_C}$$
donde $R_P$ es el radio de la polea y $R_C$ es el radio del cilindro.
Reemplazando en (1) tenemos:
$$Mgh= \frac{1}{2} Mv_M^2 + \frac{1}{2} (\frac{1}{2} m_P R_P^2 )\frac{v_M^2}{R_P^2}\\ + \frac{1}{2}(\frac{1}{2}m_C R_C^2 ) \frac{v_M^2}{R_C^2}$$
Simplificando esta expresión obtenemos:
$$Mgh= (\frac{1}{2} M+ \frac{1}{4} m_P+ \frac{1}{4} m_C ) v_M^2$$
Despejando $v_M$
$$👉\quad v_M = \sqrt{\frac{Mgh}{\frac{1}{2} M+ \frac{1}{4} m_P+ \frac{1}{4} m_C}}$$

¿Qué es una oscilación?
Una oscilación es un movimiento periódico alrededor de un punto de equilibrio. Los parámetros característicos que describen una oscilación son los siguientes:
Elongación x. Distancia que en cada instante separa la partícula móvil del centro de oscilación $O$, tomado como origen de las elongaciones es la coordenada de posición de la partícula en un momento dado . Consideramos positivos los valores de esta coordenada a la derecha del pto $O$ y negativos a la izquierda.
Amplitud A : valor máximo de la elongación a partir del punto de equilibrio.
Periodo T : tiempo empleado por la partícula en efectuar una oscilación completa.
Frecuencia f : , número de oscilaciones efectuadas en la unidad de tiempo. La frecuencia es el Inverso del periodo. f = 1/T (Hertz)
Posición de equilibrio O :
es la posición en la cual no actúa ninguna fuerza neta sobre la partícula oscilante.
Algunos Ejemplos de Movimientos Oscilatorios muy comunes son:
Masa pegada a un resorte. Fig. 6.1,
Péndulo Simple.Fig.6.2,
Cualquier rotación alrededor de un eje fijo. Fig6.3,
Una masa $m$ Oscilando sin fricción en un hemisferio de radio $R$. Fig.6.4
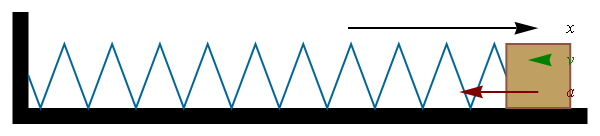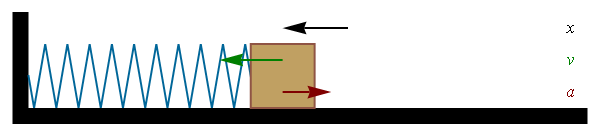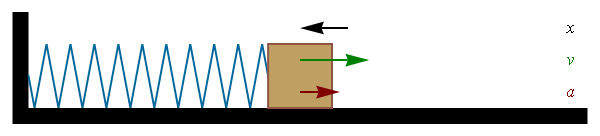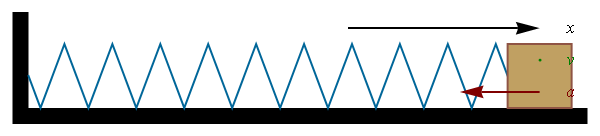
Masa pegada a un resorte
Cualquier masa $m$ unida a un resorte de constante $k$ oscila cuando el resorte es estirado o comprimido a partir de su posición de equilibrio. La posición de equilibrio es aquella posición en la cual el resorte no está comprimido ni estirado.
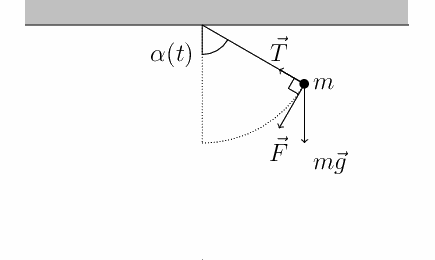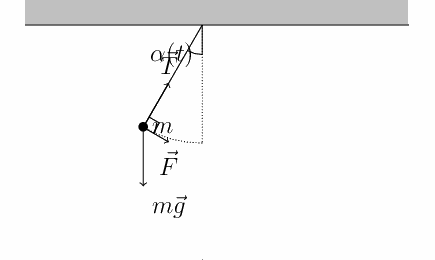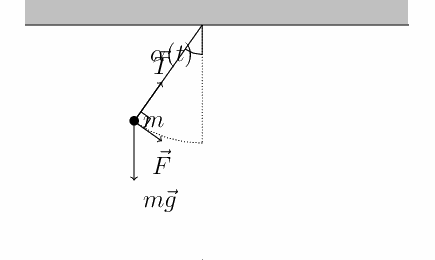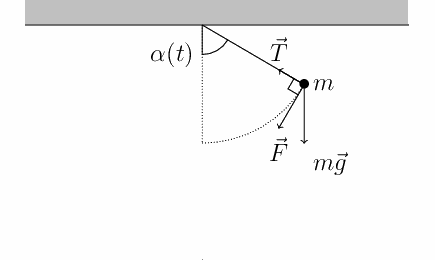
Pendulo Simple
Consiste en un hilo inextensible de masa despreciable, con una masa puntual sujeta en su extremo inferior que oscila libremente en un plano vertical fijo. Para cualquier valor de θ un péndulo es un movimiento oscilatorio normal , pero, para valores pequeños de θ el péndulo se convierte en un péndulo con M.A.S,
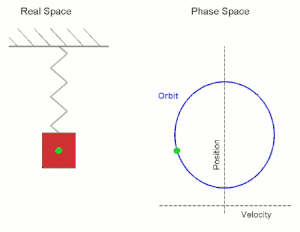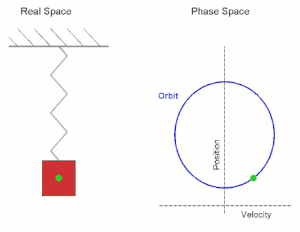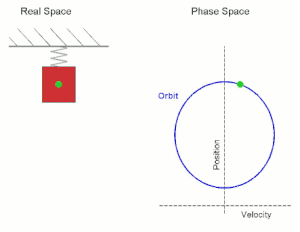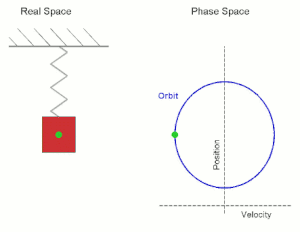
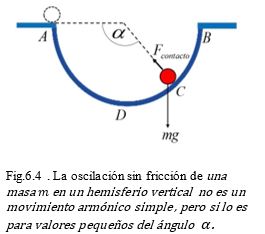


La fórmula anterior simplemente nos indica que la fuerza presente en un movimiento oscilatorio actúa en calidad de fuerza restauradora, y siempre trata de devolver al cuerpo a su posición de equilibrio desde el punto en el que se encuentre. Esto nos permite establecer un criterio dinámico para determinar cuándo una oscilación es armónica simple es el siguiente :
Todo movimiento armónico simple está gobernado por una fuerza del tipo
$$\vec{F}= -k\vec{x}$$
Por lo tanto, cuando analizamos las fuerzas que actúan sobre un cuerpo que oscila y las sumamos, la resultante debe tener la forma (6.1) para que su movimiento sea del tipo M.A.S.
¡¡Atención!! no toda fuerza restauradora produce oscilaciones armónicas simples
Como sabemos la dinámica de cualquier cuerpo en movimiento la describimos en física con la segunda ley de Newton, es decir :
$$\vec{F}=m\vec{a}$$
Para un movimiento de oscilación esta ecuación nos queda :
$$-k\vec{x}=m\vec{a}$$
Para un cuerpo oscilando en la dirección horizontal $X$, podemos escribir en términos del vector unitario $\hat{i}$
$$(-kx)\hat{i}=(ma)\hat{i}$$