ESTRUCTURAS EN
MADERA
Nociones Básicas
John Jairo García Mora
Sonia Jaquelliny Moreno Jiménez
Grupo de investigación GNOMON
Línea Gestión del conocimiento y nuevas tecnologías
aplicadas a la educación
Córdoba (España)
2021
Título de la obra:
Estructuras en madera
Nociones básicas
Autores:
John Jairo García Mora
Sonia Jaquelliny Moreno Jiménez
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Imagen de portada: Dimitris Christou from Pixabay
Imagen de portada en capítulos: Dimitris Christou from Pixabay
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN: 978-84-18834-22-6
LICENCIA
En este libro interactivo se presentan las NOCIONES BÁSICAS acerca de las estructuras de madera, esta conceptualización es presentada por medio de imágenes, vídeos, escenas interactivas y lúdicas que permiten conocer una pequeña parte de este gran campo: la madera. Todas las imágenes presentadas fueron obtenidas de repositorios libres o con licencia Creative Commons y en ellas se dá su respectivo crédito. En lo referente a las escenas interactivas propias y ajenas, estás fueron diseñadas con DescartesJS o en su defecto son ajustes de las plantillas disponibles en el proyecto Descartes.
https://proyectodescartes.org/plantillas/index.htm
.
Las expresiones matemáticas que sirven para efectuar los cálculos de las propiedades descritas son las mismas fórmulas univesales que se pueden encontrar en cualquier texto de mecánica de materiales así como también algunas específicas del tema que nos ocupa.
En su mayoría las imágenes son creaciónes propias de archivos creados con la licencia educativa de Autodesk Inventor, las imagénes con el logo de YouTube como el de la página 19 nos enlazan a videos de la Web que permiten complementar los conceptos, además, las tablas de propiedades que se describen son compendios de normas internacionales y nacionales entre las cuales citamos las siguientes sin ningún orden en particular:
Las anteriores normas y muchas otras existentes dan pautas las construcciones en madera que han evolucionado el sector estructural, históricamente antes de las construcciones de piedra el hombre de la prehistoria se vío obligado a la construcción de estructuras más provisionales y rápidas donde guarecerse de la inclemencias de la naturaleza hasta llegar a construir rascacielos.
No solo los árboles sino las plantas en general desempeñan un papel importante a la hora de producir oxígeno y reducir el dióxido de carbono en la atmósfera, además de controlar las temperaturas en el suelo.
Las fibras de celulosa unidas con lignina constituyen el tronco del árbol y es lo que conoce como madera: el insumo de la industria maderera para ser empleado como material de construcción y de paisajismo.
En algunas regiones son una fuente de energía primaria, los árboles desempeñan también un importante papel en muchas religiones e historias de la creación de los pueblos.
Veamos algunos de esos papeles del árbol en las religiones y las culturas:
Las creencias del cristianismo relatan que el consumo de la fruta del árbol del conocimiento del bien y del mal fue el pecado original, descrito como el significado de obedecer o no las directrices del creador, conocido como la caída del hombre.

San Agustín de Hipona un escritor, teólogo y filosofo enseñó que el árbol debe entenderse como un árbol tanto simbólico como real que es tanto una ciudad real como una figura de la Jerusalén celestial.
Agustín subrayó que los frutos de ese árbol no eran malos en sí mismos, porque todo lo que creó Dios fue bueno.
Fue la indisciplina de Adán y Eva, que había sido anunciado Dios de no comer del árbol (que era desagradable y causó desorden en la creación, por lo que tanto la humanidad heredó el pecado y la culpa del pecado de Adán y Eva.
En la literatura cuneiforme se habla del árbol de la vida y del árbol de la verdad, que están a la puerta del cielo en el arte cristiano occidental Árbol_del_conocimiento_del_bien_y_del_mal , el fruto del árbol se representa como una manzana, que se originó en Asia central. Esta representación pudo haberse originado de un juego de palabras en latín: al comer la malum (manzana), Eva contrajo el mālum (el mal) o simplemente debido a la licencia artística de los pintores religiosos.
Para las comunidades mayas, la ceiba o ya’ax’che es un árbol sagrado que sostiene el cielo con sus ramas y teje el inframundo con sus raíces. Esta creencia se fundamentó en que la ceiba puede crecer hasta 70 metros de altura y alcanzar un diámetro de tres metros, su frondosa copa crece formando diversos “pisos” de ramas y hojas, y sus flores de carnosos pétalos despiden un particular aroma.La ceiba se adhiere al suelo fuertemente por unas raíces potentes que se esparcen aleatoriamente.
La cultura maya fue una civilización que habitó la parte meridional de México, Guatemala, Belice y la parte occidental de Honduras y El Salvador.

Por último y no menos importante, sembraron una quinta ceiba en el centro, la “gran madre ceiba”.
Fueron un conjunto de pueblos que hablaban lenguas con las mismas raíces y fueron bautizados a sí por los romanos.
Los sacerdotes Celtas eran conocidos como druidas que significa “hombre del roble” o “el que aprende del roble” y druidesa: “la que cuida de la sabiduría del roble”.
Los Druidas impartían su conocimiento y creencias en la escuela de la naturaleza, en los bosques al aire libre donde habitaban.

Al no ser una nación única, esos pueblos adoraron varios árboles.:
A pesar de que la Biblia expresa que Adán y Eva al comer del árbol prohibido, cuando vieron su desnudez se taparon con la higuera, los cristianos no lo consideran un árbol sagrado.
Solo en la india aparece la higuera sagrada (Ficus religiosa), también conocida como Akshayavat, la leyenda dice que al amparo de una higuera de la cual se conservan retoños, alcanzó la iluminación el Buda.
Existe un árbol sagrado de gran importancia espiritual para los Hindúes, así como para los Budistas: Thimmamm. se tiene la creencia bajo este árbol habita la triada divina que orienta su fé.

Dicha creencia expresa que en el ábol sagrado sus raíces son Brahma, dios de la creación, el tronco representa a Krishna y las hojas Shiva, dios de la muerte y el renacimiento, ese ábol lo podemos apreiar en al figura 03.
Mientras que todos los demás árboles suelen crecer hacia el cielo, esta ficus religiosa utiliza la tierra como su medio de expansión, lo que se logra cuando sus semillas caen en otros troncos sobre los que sus raíces se expanden para al final matarlos de asfixia.
EL BAOBAB, es el árbol sagrado de la cultura Africana, también conocido como adansonia.

En el continente africano todas y cada una de las especies de baobab son veneradas, queridas, protegidas y cuidadas por los habitantes de las zonas donde crecen porque, tal y como cuenta la leyenda, estamos ante 'el primer árbol creado por Dios'.
Ha sido considerado un símbolo sagrado desde sus inicios, prueba de ello es que solo 'el sabio' puede subirse a él para recoger sus frutos y hojas, desde hace siglos es utilizado como lugar donde se reúnen las comunidades y a su alrededor las tribus africanas toman decisiones importantes. El BAOBAB es símbolo de resistencia, tolerancia, vida comunitaria y longevidad, valorado como manifestación de vitalidad, y dotado de propiedades mágicas”.
La leyenda cuenta que estos árboles eran tan presumidos que el mismo Dios les dio la vuelta para poner las ramas en la tierra y las raíces en la parte superior del tronco, de ahí su forma y disposición tan peculiar que parece que crezca al revés.
Cuando se habla de árboles maderables se hace referencia a plantas de mediano o gran tamaño, los cuales son cultivados con la finalidad de extraer la madera para ser utilizada en determinados productos tales como, la construcción, la elaboración de papel, entre otros productos de gran envergadura para el uso por parte de los seres humanos.
Sin embargo en algunas zonas del planeta entra en juego La deforestación o desforestación, generalmente con el objetivo de destinar el suelo a otra actividad.
Los árboles madereros se clasifican a grandes rasgos, en árboles de maderas blandas, semiduras y duras.En la siguiente escena se muestran los 10 más empleados y una nota que describe a cada uno de ellos.
En la actualidad se conocen más de 100.000 especies maderables, o sea con madera en su tronco y en sus ramas, sin embargo, se calcula que solo 500 de esas especies son comercializables.
Además la mayoría de las maderas que se obtienen de estos árboles se utilizan en otras regiones diferentes y distantes de aquellas de donde son nativos.
Hay que tener en cuneta que de esos árboles comercializables existen algunas especies en peligro de extinción tal lo expresa Alberto Cajal https://www.lifeder.com/plantas-maderables/. : el Abarco, el Cedro, el Caobo, el Canelo y la Palorosa.
En la siguiente escena podemos visualizar algunos de esos árboles maderables y su descripción:
Haz clic sobre la imagen y observa el vídeo del canal de YouTube "Entre barras, gráficos y mapas" sobre los mayores países productores de madera.
AVATAR, ambientada en el año 2154, los acontecimientos que narra se desarrollan en Pandora, una luna del planeta Polifemo habitada por una raza humanoide llamada na'vi, ![]() con la que los humanos se encuentran en conflicto debido a que uno de sus clanes está asentado alrededor de un gigantesco árbol que cubre una inmensa veta de un mineral muy cotizado y que supondría la solución a los problemas energéticos de la Tierra: el unobtainium.
con la que los humanos se encuentran en conflicto debido a que uno de sus clanes está asentado alrededor de un gigantesco árbol que cubre una inmensa veta de un mineral muy cotizado y que supondría la solución a los problemas energéticos de la Tierra: el unobtainium.
El conflicto entre humanos y los nativos del clan Omaticaya surge debido a que están asentados alrededor de ese gigantesco árbol, conocido por ellos como Árbol Madre.
La existencia de unobtainium ha llevado a una empresa privada a crear un proyecto de explotación de recursos minerales y que a pesar de estar creada en un ambiente de ficción el filme no se encuentra alejado de la realidad.
Los árboles son venerados todavía hoy en en medio oriente, entre ellos Iraq, Israel, Líbano y la República Árabe Siria.
Entre los árabes drusos y musulmanes, algunos árboles se consideran sagrados. Tales árboles están a menudo cerca de las tumbas de santos o santas a las que los peregrinos realizan rogativas
Es común la promesa de realizar buenas obras si sus peticiones son escuchadas, hacen ofrendas a los árboles como indicación solemne de su promesa de cumplir sus votos.
"El cristianismo adoptó y transformó las costumbres paganas relacionadas con el culto a los árboles sagrados" https://historia.nationalgeographic.com.es/a/de-donde-viene-arbol-navidad_9997 y aún perdura en la actualidad
En este capítulo se tratará de definir la terminología especializada de la madera y los procesos constructivos que la involucran. Los diccionarios especializados, como cualquier otro diccionario, son obras de consulta que describen el léxico propio de una ciencia o técnica (Martínez de Sousa 2002: 21).
Los diccionarios especializados son obras en las que se recoge el léxico propio de una determinada disciplina científica; por tanto, se trata de recopilaciones de léxico especializado por la temática o términos, unidades que estudia y recopila la disciplina llamada terminología.
La lectura de este capitulo permitirá entender características de las estructuras con madera que poseen nombre propio y de los procesos que caracterizan el trabajo con la madera.

Abuhardillado: se refiere a una planta de un edificio o de una habitación o que tiene el techo en pendiente, como las buhardillas.
Alabeo: deformación que puede experimentar una pieza de madera por la curvatura de sus ejes longitudinal o transversal o de ambos.
Alero: parte del techo que sobresale del muro en voladizo, dicho de otra manera es la parte inferior del tejado que sobresale del plano de los cerramientos verticales ycuya función es proteger a la pared de la lluvia.
Albura, madera de: proveniente de la parte periférica del árbol, constituida por capas de leño en estado de maduración. Por lo general, la atacan fácilmente hongos e insectos.
Alfarje: techo con maderas labradas y entrelazadas artísticamente, dispuesto o no para transitar sobre él.
Apear: sostener provisionalmente con armazones de maderos todo o parte de algún edificio, construcción o terreno.

Aserrado: proceso mediante el cual se corta longitudinalmente una troza, para obtener piezas de madera de sección transversal cuadrada o rectangular, denominadas comúnmente bloques o tablones.
Contracción: reducción de las dimensiones de una pieza de madera causada por la disminución del contenido de humedad por debajo de la zona de saturación de las fibras, que se presenta en los sentidos radial, tangencial y longitudinal.
Aglomerado: es un tablero de partículas fabricado a partir de astillas de madera o astillas de yute y una resina sintética u otro aglutinante adecuado, que se prensa y extruye.
Axial: fuerza paralela al corazón del árbol.
Basa: es la parte inferior de una columna, que tiene como fin servir de punto de apoyo al fuste, ampliando aquel, y está compuesto generalmente por molduras.
Biaxial, flexión: en las columnas que forman parte de un entramado espacial y están solicitadas a flexión simultáneamente respecto a sus dos ejes principales. Las columnas sometidas a carga axial pura no existen.
Bóveda: superficie curvada, que cubre el espacio entre dos muros, pilares o columnas.
Cabeza: parte superior de una sección de madera escuadrada.
Cambium: en un árbol es la capa de celúlas que produce madera nueva, rodean las partes vivas del árbol durante la etapa de crecimiento.
Cantos: superficies menores, perpendiculares a las caras paralelas entre si y al eje longitudinal de una pieza de madera.
Caras: son las superficies mayores paralelas entre si y al eje longitudinal de una pieza de madera.
Carrera: viga horizontal de madera que se apoya sobre los costales de un encofrado, haciendo la función de atado y arriostrado de los mismos.
Cimiento: es el conjunto de elementos estructurales cuya misión es transmitir sus cargas o elementos apoyados en ella al suelo.

Colapso: contracción anormal de la madera ocurrida durante la salida de agua libre (por encima del punto de saturación de la fibra, al comienzo del secado).
Cubierta: se da este nombre a la parte superior y exterior de una vivienda que cumple la función de proteger de las variaciones del tiempo a la construcción y a quienes la habitan.
Chapa: lámina de madera con un espesor no mayor a 6 mm, obtenida por corte plano o desenrollado de un bloque o rollizo, respectivamente. Cualquier la' mina de madera con las mismas características de espesor.
Clavija: trozo cilíndrico o ligeramente cónico de madera, metal u otra materia apropiada, que se encaja en un taladro hecho al efecto en una pieza sólida.
Clavo: es un objeto delgado y alargado con punta filosa hecho de un metal duro (por lo general acero), utilizado para sujetar dos o más elementos independientes de madera.
Contrachapado: también conocido como multilaminado, plywood, triplay o madera terciada, es un tablero elaborado con finas chapas de madera reforzada pegadas con las fibras transversalmente una sobre la otra con resinas sintéticas mediante fuerte presión y calor.
Corte: es la acción de fuerzas que tienden a cortar una sección transversal o longitudinal de la madera.
Crujía: espacio comprendido entre dos muros de carga.
Densidad: peso específico que define la relación entre el peso de la madera y su volumen, ambos medidos con el mismo grado de humedad.
Dintel: pieza horizontal superior de puertas, ventanas y otros huecos, apoyada en sus extremos sobre las jambas y destinada a soportar cargas.
Duramen, madera de: proveniente de la zona central del árbol, constituida por células maduras. Es, por lo general, menos susceptible de ser atacada por hongos e insectos.

Encofrado: medio auxiliar compuesto de molde y apuntalamiento cuya misión es dar forma al hormigón en la obra, vertiéndolo en el interior del molde antes del fraguado. Protege al hormigón hasta que adquiere unas condiciones mínimas de endurecimiento y resistencia. El encofrado debe ser rígido, indeformable y resistente, estable, estanco y sencillo.
Elasticidad: es la habilidad de la madera de retomar su forma original cuando se haya parado la fuerza que lo modifica. Maderas pesadas suele ser más elásticas.
Empalme: los ensambles realizados en la madera para prolongarla en su sentido longitudinal.
Entramado: esqueleto estructural de una edificación. Conjunto de piezas unidas entre sí, sobre las que se fija un elemento de revestimiento.
Escuadría: dos dimensiones de la sección transversal de una pieza de madera que está o va a ser maquinada a escuadra.
Encorvadura: alabeo de los cantos en sentido longitudinal.

Esbeltez: cociente entre la altura del árbol y su diámetro.
Fibra: célula alargada con extremos puntiagudos y casi siempre con paredes gruesas;típica de las maderas latifoliadas.
Flexibilidad: es la capacidad de la madera para cambiar su forma sin dañar su estructura o quebrarse.
Flexión: es la capacidad de la madera para resistir cargas que tienden a flectarla, cuando se aplican en dirección perpendicular a las fibras.
Grano: término que se refiere a la dirección de los elementos celulares axiales con relación al eje del árbol o al canto de una pieza de madera aserrada.
Grieta: separación de los elementos constitutivos de la madera cuyo desarrollo no alcanza a afectar dos caras de una pieza aserrada o dos puntos opuestos de la periferia de una madera rolliza.

Herraje: se definen así a todos aquellos sistemas o soluciones mecánicas que permiten unir o ensamblar dos o más elementos de madera.
Higroscópica: se refiere al contenido de agua que conforma la madera que puede disminuir o aumentar dependeindo de la humedad del ambiente. Sus efectos se reflejan en la contracción o en la hinchazón de la madera.
Hinchamiento: aumento de las dimensiones de una pieza causada por el incremento de su contenido de humedad.
Jácena: es una viga maestra que sostiene otros maderos horizontales.
Jamba: cada una de las dos piezas que, dispuestas verticalmente en los dos lados de una puerta o ventana, sostienen el dintel o el arco de ella.

Junta, de madera: también denominadas acoplamientos es la unión de dos o más maderas por sus caras o cantos.
Lengüeta: espiga prolongada que se labra a lo largo del canto de una tabla o un tablón, generalmente de un tercio de grueso, con objeto de encajarla en una ranura de otra pieza.
Lignina: compuesto orgánico básico de los tejidos leñosos de las plantas, es una sustancia que refuerza las células confiriéndoles resistencia y rigidez.
Maquinado: operación realizada en la madera para reducirla al estado o forma conveniente para su uso, con herramientas apropiadas tales como planeadoras, cepillos y sierras.
MDF: material fabricado mediante un prensado realizado a altas frecuncia y está compuesto por fibras de madera y resinas sintécticas aglutinantes que previenen la humedad y los hongos.
Medianería: cerramiento que linda en toda su superficie o en parte de ella con otros edificios ya construidos, o que puedan construirse legalmente.
Médula: es el núcleo del árbol y al igual que el duramen es un componente muerto que puede tener sección circular, poligonal o estrellada.
Montaje: acción y efecto de armar o ensamblar los elementos y componentes de una construcción.
Muro cortafuego: pared de separación de material resistente al fuego, que divide una construcción a lo ancho y a lo alto para impedir que el fuego se propague de un lado a otro.

Nudo: rama incrustada que marca los anillos de crecimiento del árbol.
Nudo de arista: surge de la arista y no puede trabajar a flexión, si es utilizado en una viga trabajará a compresión.
Nudo axial: es aquél cuyo eje está ubicado en el plano de una cara o sea transversal a la fibra longitudinal haciendo que su resistencia a la flexión no exista.
Nudo de canto: en una viga se debe colocar en la parte superior en el caso de que su tamaño sea inferior a las 3/4 partes de la medida del canto.
Pandeo: es el efecto que una fuerza externa produce al ser aplicada sobre la longitud de una viga y tiende a cortarla por el lugar donde se aplica.
Panel: tablero, de dimensiones y materiales diversos, que puede formar parte de cualquier unidad de la construcción, como muros, pisos y techos.
Partícula: en tableros aglomerados o de partículas, es la porción diminuta bien definida de madera u otra materia orgánica producida mecánicamente para constituir la masa con que se fabrica el tablero.
Pendolón: elemento secundario utilizado para evitar la formación de catenaria en elementos tales como tensores.
Pie de amigo: elemento diagonal localizado en un plano vertical utilizado para reducir la luz efectiva de una viga.
Pie tablar: unidad de medida representada por el volumen de una tabla de un pie de largo (aproximadamente 0,30 m), un pie de ancho (aproximadamente 0,30 m) y una pulgada de espesor (exactamente 0,025 4 m). Un metro cúbico tiene 424 pies tablares.

Pilote: son elementos de madera esbeltos para transmitir las cargas en profundidad de cimentaciones profundas. Según su puesta en obra existen dos tipos, los excavados o perforados
y los hincados, también denominados pilotes de desplazamiento, cuya característica principal es que el pilote se introduce en el terreno mediante percusión o vibración sin hacer excavaciones previas que faciliten su alojamiento, aunque existen casos donde la hinca se facilita con perforaciones de menor diámetro que la del pilote o con la ayuda de lanzas de agua.

Platina: placas de metal que pueden ser fijadas a una estructura de madera pueden ser de acero o de cualquier otro material, planas o troqueladas con forma rectangular, fabricadas en material de hierro (más pesadas, bastas y oxidables, pero más baratas) o en materiales industriales más duraderos y sofisticados, pero más costosos como pudieran ser el aluminio o el acero inoxidable.
Precortado: obtención de piezas o elementos de madera con determinadas características, tales como cortes, y perforaciones que luego serán utilizadas en obra.
Prefabricación: producción en fábrica de partes de la construcción como cerchas, páneles, o inclusive habitaciones y casas completas.
Preservación: tratamiento que consiste en aplicar sustancias capaces de prevenir o contrarrestar la acción de alguno o varios tipos de organismos que destruyen o afectan la integridad de la madera. Generalmente, estos tratamientos son efectivos por lapsos más o menos largos, que dependen de la calidad del tratamiento.
Preservante: sustancia que se aplica para prevenir o contrarrestar por un período, la acción de alguno o varios de los tipos de organismos capaces de destruir o afectar la madera.
Rampa: estructura que funciona como plano inclinado dispuesto para subir y bajar por él.

Revestimiento: Es cubrir superficies de fachadas, paredes o techos con una estética diferente, en la que la madera, por sus particularidades estéticas es la protagonista aportando una textura, tonalidad y veteado diferente en función de cada especie
Riostra: pieza que puesta transversal u oblicuamente asegura la invariabilidad de forma de un armazón.
Secado: proceso natural o artificial, mediante el cual se reduce el contenido de humedad de la madera.
Sección: perfil o figura que resulta de cortar una pieza o cuerpo cualquiera por un plano.
Sección longitudinal: sección que resulta de cortar una madera en sentido paralelo a las fibras.
Sección mínima: son las dimensiones obtenidas después de cortar una pieza de madera en el sentido paralelo a sus fibras y ya descontado lo que las máquinas de corte, planeado y cepillado disminuyen de la sección nominal.
Sección nominal: son las dimensiones establecidas para cortar una pieza de madera en el sentido paralelo a sus fibras de lo cual se obtiene un perfil o figura.
Sección radial: corte longitudinal de un tronco en la dirección perpendicular a los anillos de crecimiento.
Sección tangencial: corte longitudinal de un tronco tangente a los anillos de crecimiento.
Sección transversal: sección que resulta de cortar una madera en sentido perpendicular a las fibras.
Solera: recibe el nombre de durmiente, es una pieza de madera que se coloca horizontal en la parte superior de un muro en el mismo sentido de éste, y sobre el cual se apoya la estructura que soportará la techumbre.

Soportal: espacio cubierto que precede en algunas construcciones a la entrada principal, tembién se conocen como portal, pórtico o porche.
Tirante: elemento interior de un sistema estructural que, para cargas gravitacionales trabaja a tensión.

Tornapunta: se refiere a todo madero colocado oblicuamente para apear a otro que está en posición horizontal. La tornapunta es también la pieza de madera colocada oblicuamente para ligar dos maderos ensamblados manteniéndolos de este modo separados, mientras se presta solidez al conjunto.
Torsión: resistencia que se opone a su deformación, la cual esta fija por uno de sus extremos. La resistencia de la madera a esfuerzos producidos por torsión es del mismo orden que su resistencia a esfuerzo cortante paralelo a las fibras.
Tracción: es la acción a la que se somete un elemento de madera por la aplicación de dos fuerzas que actúan en sentido contrario.
Traslapo: tabla que posee un rebajo a media madera en ambos cantos.
Troza: significa tronco aserrado por los extremos para sacar tablas.

Veteado: también conocido como figura de la madera, es cualquier rasgo o motivo que altere su uniformidad. Son debidas a las variaciones de los elementos estructurales de la madera, tanto en forma como en distribución y composición química.
Viga de madera: grandes piezas de madera aserrada de sección rectangular que incorporan la médula en su interior y en la que la diferencia entre el espesor y la anchura es superior a 25 mm.
Voladizo: en un edificio tradicional de madera se le denomina jetty. En la construcción también se usan a menudo voladizos temporales los que cuando la estructura se completa no actúa como voladizo.
Xilófago: hongo que afecta principalmente a la madera de las coniferas.
La Madera es un material de estado natural, por lo tanto podemos afirmar que es el recurso más antiguo de que dispone el hombre. Este material se ha convertido en una parte esencial de la historia de la humanidad: ha proporcionado combustible, herramientas, alimentos y protección a millones de personas. En este libro se tratará de una de sus aplicaciones: las estructuras constructivas.
Este recurso que hasta ahora parecía difícil de agotar, esta empezando a preocupar el mundo entero por las talas masivas y sin reposición, la madera se clasifica de la siguiente manera:.
$$ Tipo \begin{dcases} Madera \space natural &\begin{dcases} Madera \space dura & \\ Madera \space blanda & \end{dcases} \\ \\ {Madera \space artificial} &\begin{dcases} Aglomerados & \\ Tableros \space de \space fibras:DM & \\ Contrachapados & \end{dcases} \\ \end{dcases}$$Algunas maderas duras y sus características:
Es muy apreciada para construir muebles de calidad.
Es la madera utilizada en la construcción de cajas de cepillo y garlopas.
La gran ventaja que tienen respecto a las maderas duras, es que tienen un periodo de crecimiento mucho más corto (los de hoja perenne), que provoca que su precio sea mucho menor.
Este tipo de madera no tiene una vida tan larga como las duras. Dar forma a las maderas blandas es mucho más sencillo, aunque tiene la desventaja de producir mayor cantidad de astillas, por lo que el acabado es mucho peor.
Además de lo anterior, la carencia de veteado de esta madera le resta atractivo, por lo que casi siempre es necesario pintarla, barnizarla o teñirla.
Veamos algunos ejemplos de maderas blandas y sus características:
A diferencia de otros materiales en estado natural no es posible modificarla como se hace con los metales, su estructura depende de la forma en que crece y no de la manipulación por parte de los seres humanos, como en el caso del hierro y el cobre entre otros.
La forma larga, esbelta, cilíndrica de los árboles crea una estructura interna compuesta de celdas longitudinales.
Conforme crece el árbol, se agregan anillos por afuera de la madera más vieja. Así, el núcleo llamado corazón de la madera tiene propiedades diferentes que la madera alburente o tierna, cerca de la superficie externa.
La especie de la madera también afecta sus propiedades, ya que las diferentes clases de árboles producen madera más dura o más blanda, más fuerte o más débil.
En algunos casos la misma especie presenta la variabilidad a causa de las diferentes condiciones de crecimiento, tales como diferencias en el suelo y la cantidad de sol y lluvia.
La estructura celular de la madera da lugar al grano que es tan evidente cuando se sierra en forma de tablas y maderos. La resistencia de la madera depende de la forma en que se le aplican cargas: perpendicular o paralelamente al grano.
Además, siguiendo el grano, la resistencia es diferente en una dirección radial que en una dirección tangencial con respecto al tronco del árbol original del cual fue obtenido.
Otra variable importante que afecta la resistencia de la madera es el contenido de humedad. Los cambios en la humedad relativa puede variar la cantidad de agua absorbida por las celdas de la madera.
Recordemos que la humedad relativa es la relación entre la presión parcial del vapor de agua y la presión de vapor de equilibrio del agua a una temperatura dada.
La humedad relativa de la madera es un aspecto importante a tener en cuenta para su destino final: depende de la temperatura y la presión del sistema interior o sistema exterior.
.jpg)
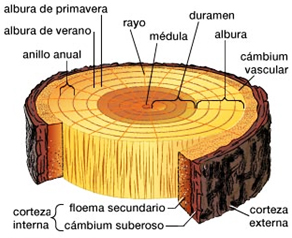
En la figura 1.1 que corresponde al corte transversal de un árbol maduro se pueden destacar claramente las siguientes componentes:
En la figura 1.2 podemos observar el esquema de la estructura interna del tronco:
Existen tres funciones básicas que debe satisfacer la parte maderable de un árbol:
En composición media se compone de un 49% de carbono (C), un 43% de oxígeno (O), un 6% de hidrógeno (H) y el 2% restante de nitrógeno (N) y otros elementos minerales. La combinación de los anteriores elementos da origen a los componentes principales de la madera:
Las funciones de la celulosa son las de servir de aguante a la planta y la de darle una protección vegetal. Es muy resistente a los agentes químicos, insoluble en casi todos los disolventes y además inalterable al aire seco.
El grado de lignificación afecta notablemente a la digestibilidad de la fibra.
La lignina aumenta de manera considerable en la pared celular de la planta con el curso de la maduración, es resistente a la degradación bacteriana, y su contenido en fibra reduce la digestibilidad de los polisacáridos fibrosos.
La madera contiene agua bajo tres formas diferentes:
A medida que disminuye el grado de agua de impregnación aumenta sus resistencias mecánicas, pero algunas propiedades como la tenacidad o la resistencia al choque disminuyen.
Cuando la madera se expone al medio ambiente, se inicia un proceso de secado perdiendo el agua contenida. Inicialmente se pierde el agua líquida o libre, luego el agua higroscópica, es de anotar que el agua de constitución solo se pierde cuando existe la combustión de la madera
En función de la cantidad de agua presente en la madera existen tres estados:
El contenido de humedad en equilibrio de la madera es un estado relacionado con la temperatura del aire y la humedad relativa, en el que el contenido de humedad de la madera permanece constante. El contenido de humedad en equilibrio de la madera viene determinado por la humedad relativa del aire y no por la humedad absoluta.
La humedad relativa del aire es la proporción de cantidad de agua que hay en el aire en relación con la cantidad máxima de agua que puede almacenar el aire a su temperatura actual. La madera secada previamente alcanza su contenido de humedad en equilibrio en dos semanas.
El punto de saturación de la veta de la madera representa la proporción de humedad presente en la madera cuando las paredes celulares están saturadas de agua sin que haya agua libre presente en los lúmenes de las células.
El contenido de humedad de la madera representa la relación entre la masa de agua que contiene y la masa de madera sin agua. (Es decir, si un trozo de madera de 100 kg contiene 50 kg de agua, el porcentaje de humedad es del 100 %). El contenido de humedad de una madera cortada recientemente suele ser del 40-200 %. En un uso normal, el contenido de humedad de la madera oscila entre el 8 % y el 25 % según su peso, dependiendo de la humedad relativa del aire.
En otras palabras, el contenido de humedad de los productos de madera depende de la temperatura y de la humedad relativa del aire (HR), en la siguiente escena podemos visualizar (mueve el botón de color amarillo con el ratón) un contenido de humedad sin aplicar la ecuación 1 que veremos más adelante:
$$HM = Humedad \space de \space la \space madera \space \space HR = humedad \space relativa \space del \space aire$$El contenido de humedad (CH) de la madera es el porcentaje en peso que posee el agua libre más el agua higroscópica con respecto al agua anhidra. Ello se calcula mediante:
$$\tag{2.1} CH \space \% = \frac{Peso \space húmedo - Peso \space anhidro}{Peso \space anhidro} * 100 $$En la madera al igual que en todos los cuerpos existe una relación entre la masa y el volumen, relación denominada densidad del cuerpo. El peso de la madera es igual a la suma del peso del componente sólido con el peso del agua contenida. Es de resaltar que en estado verde la densidad es constante.
Podemos diferenciar cuatro densidades asociadas a una misma madera:
La densidad aparente de la madera varía entre $0.3 – 0.9 \space g/cm^3$ (para una madera completamente seca), claro que ese valor depende de la especie de árbol del que proviene debido a la cantidad de huecos de cada especie y del porcentaje de agua en la madera.
La densidad real de la madera es aproximadamente $1.56 \space g/cm^3$, dependiendo de la especie se obtienen variaciones poco significativas, a mayor densidad, mayor resistencia.
Tabla 1. Densidades de algunas especies maderables
| Especie | Densidad | Especie | Densidad | |
|---|---|---|---|---|
| Algarrobo | $0.76 gr/cm^3$ | Nogal | $0.60-0.81 gr/cm^3$ | |
| Caobo | $0.57 gr/cm^3$ | Pino | $0.32-0.76 gr/cm^3$ | |
| Cedro | $0.42-0.76 gr/cm^3$ | Roble | $0.71 gr/cm^3$ | |
| Eucalipto | $0.45-0.55 gr/cm^3$ | Tormillo | $0.71-0.77 gr/cm^3$ | |
Peso específico $Pe$: se expresa como el cociente entre la densidad de la madera y la densidad del agua, por lo tanto es una cantidad adimensional.
$$\tag{2.2} Pe = \frac{Densidad \space de \space la \space madera \space (g/cm^3)}{Densidad \space del \space agua \space (g/cm^3)}$$ $$\tag{2.3} Densidad \space de \space la \space madera = \frac{Peso \space de \space la \space madera \space (g)}{Volumen \space de \space la \space madera \space (cm^3)} \space \space \space \space \space \space \space \space \space \space \space \space$$Por lo tanto:
$$\tag{2.4} Pe = \frac{Peso \space de \space la \space madera}{Volumen \space de \space la \space madera * Densidad \space del \space agua}$$El $Pe$ más usado es el peso seco volumétrico (PSV) o densidad relativa básica (Drb) que está dado por:
$$\tag{2.5} PSV \space (Drb) = \frac{Po}{Vv * \sigma_{H_2O}}$$Dado que ese numerador no se altera y que el volumen de la madera crece (por hinchamiento) a medida que aumenta el contenido de humedad, en el intervalo entre el estado anhidro y el punto de saturación de las fibras, el peso específico disminuye a medida que aumenta el contenido de humedad hasta llegar a un mínimo en el $Punto \space de \space Saturación \space de \space las \space Fibras (PSF)$, a partir del cual permanece constante.
Como el agua tiene una densidad igual a 1 podemos afirmar de la ecuación 2 que la densidad de la madera dividida por la densidad del agua igualan a su peso específico, en el sistema métrico la densidad y el peso específico poseen el mismo valor pero este último no tiene unidades.
Son cambios ocasionados principalmente por la pérdida o incremento del agua higroscópica en la pared celular, dicho de otra manera se deben a las variaciones del contenido de humedad.
El agua libre de las cavidades celulares no influye en la variación de las dimensiones puesto que dichos cambios se producen cuando el contenido de humedad varía por debajo del punto de saturación de las fibras (PSF).
Estas alteraciones dimensionales resultan de las variaciones de volúmenes debido a los procesos de adsorción y desorción de agua entre el estado anhidro y el PSF, afectando y/o limitando el uso de algunas maderas.
El aumento de volumen (hinchamiento) se debe a la inclusión de moléculas de agua en los espacios intermicelares de la pared celular por debajo del PSF.
Esto ocasiona las aproximaciones de las micelas originando la reducción de las dimensiones de la pieza de madera. Estas variaciones en volumen influyen en los procesos industriales de secado, impregnación y curvado de la madera entre otros, como así también en su uso final.
Los parámetros que permiten evaluar los cambios dimensionales son: la contracción normal máxima en sentido radial ($Cn_{rdmáx}$) y tangencial ($Cn_{tgmáx}$), el coeficiente de contracción radial ($v_{rd}$) y tangencial ($v_{tg}$), el punto de saturación de las fibras (PSF) y el coeficiente de anisotropía ($T/R$). La contracción axial generalmente no es determinada puesto que su valor se considera despreciable en madera normal.
La contracción y la expansión presentan valores diferentes las tres direcciones de la madera:
Estas dos últimas son las causantes del cambio volumétrico
La contracción normal ($Cn$) se define como la reducción de las dimensiones de una pieza de madera causada por la disminución del contenido de humedad a partir del PSF. Del mismo modo, la contracción normal máxima ($Cn_{máx}$) es la producida entre el PSF y el 0% del contenido de humedad.
Ese aplastamiento de los lúmenes celulares es consecuencia de una pérdida brusca de humedad y ese colapso puede eliminarse por procesos de vaporización una vez obtenido un contenido de humedad de 16 a 18% aproximadamente; o evitarse sometiendo la madera a un secado lento durante los primeros estados de dicho proceso y se puede determinar por la ecuación:
$$\tag{2.6} Cn_{máx} \space \% = \frac{Lv - Lo}{Lo} * 100 $$Donde:
$Cn_{máx} = Contracción \space normal \space máxima \space expresada \space en \space \%$
$Lv = longitud \space verde \space expresada \space en \space mm$
$Lo = longitud \space anhidra \space expresada \space en \space mm$
El coeficiente de contracción ($v$) expresa cuanto contrae una madera cuando pierde 1% en su contenido de humedad. Se calcula:
$$\tag{2.7} Cn_{máx} \space \% = \frac{\frac{lh - lo}{lo} *100}{\frac{Mh - Mo}{Mo}* 100} $$Donde:
$ v = Coeficiente \space de \space contracción \space (adimensional) $
$ Lh = longitud \space entre \space clavos \space de \space las \space probetas \space secas \space al \space aire$
$ Lo = longitud \space anhidra \space expresada \space en \space mm$
$ Mh = Masa \space húmeda \space o \space inicial \space en \space g $
$ Mo = Masa \space anhidra \space en \space g $
Debido a su anisotropía, las variaciones dimensionales no serán las mismas en las direcciones axial, radial y tangencial. Estas contracciones o mermas modifican también como es natural su volumen. Para evaluarlas se han definido los coeficientes de contracción: contracción volumétrica total, contracción tangencial y contracción radial.
La diferencia entre la contracción radial y la tangencial es la causa por la que se deforman las maderas durante el proceso de secado; por esa razón, en ebanistería se emplean maderas cuyas contracciones radiales y tangenciales son muy parecidas, siendo más apreciada la madera cuanto menor es la diferencia entre ambas. Según sus coeficientes la madera se clasifica como: muy nerviosa, nerviosa, moderadamente nerviosa y poco nerviosa. Para determinar la contracción se utilizan probetas tal como aparece en la imagen:
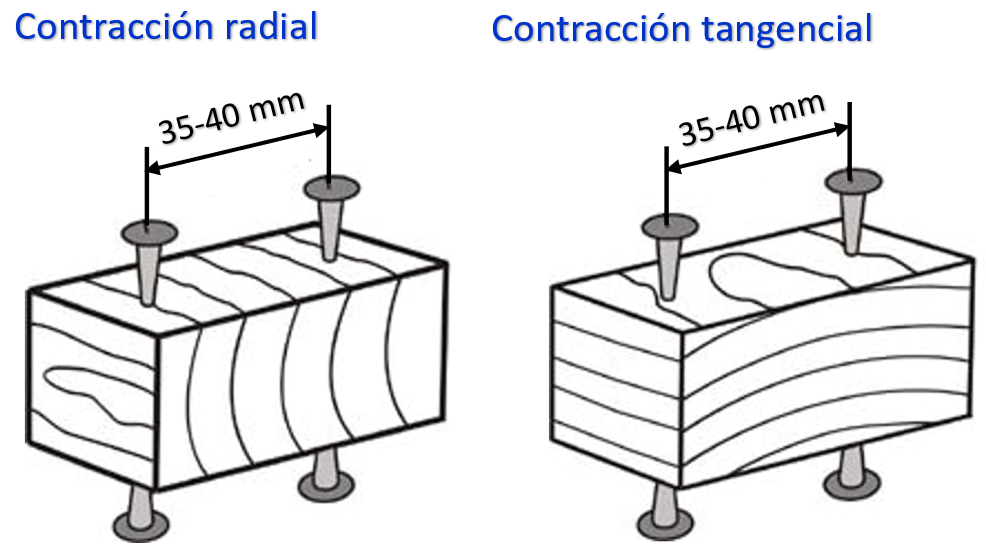
El punto de saturación de fibras ocurre cuando las paredes celulares se encuentran totalmente saturadas, y se ha eliminado toda el agua libre, quedando solamente el agua higroscópica o de imbibición.
En la madera de latifoliadas con porosidad difusa el PSF se encuentra aproximadamente entre 32 y 35 % de humedad. En coníferas y latifoliadas con porosidad anular varía entre 21 y 28 %.
En la práctica con el fin de facilitar los cálculos se generaliza el PSF en 28 a 30 % de humedad sin especificar la especie. Cuando la madera se encuentra por encima del punto de saturación de fibras, no sufre variación dimensional, solo aumento de peso y porcentaje de humedad. Por debajo del punto de saturación de fibras comienza a producirse cambios en las dimensiones de la madera.
Cuando se habla de conductividad térmica de los materiales se hace referencia a la expansión del mismo y la cantidad de calor que emana de ese material y se puede medir: esa conductividad térmica se expresa en $kCal/mh°C$.
La madera es un mal conductor del calor debido a la escasez de electrones libres, coeficiente de conductividad calorífica de la coníferas (pino y abetos) en la dirección perpendicular varía aproximadamente de $ 0,09 \space a \space 0,12 \space kCal / m \space h \space ºC$.
La condutividad térmica de la madera es directamente proporcional al contenido de humedad y a su densidad, depende de la dirección en la cual se mide (longitudinal, radial o tangencial)siendo mayor en la dirección longitudinal
Esta conductividad térmica de la madera se calcula basándose en el principio de transferencia de calor por conducción entre dos placas frías y una caliente central.
Ese estado permanente permite que se calcule la conductividad térmica con la ecuación:
$$\tag{2.8} \lambda = \frac{q*L}{\Delta T*A}$$Donde:
$ \lambda = Es \space la \space condutividad \space térmica \space (W/m K)$
$ q = Rapidez \space del \space flujo \space de \space calor \space a \space través \space del \space espécimen \space (W)$
$ L = Espesor \space de \space la \space muestra \space (m)$
$∆T = Diferencia \space de \space temperaturas \space a \space través \space del \space espécimen $
$A = Área \space de \space la \space sección \space transversal $
Según lo anterior es necesario determinar la rapidez de ese flujo $q$ mediante:
$$\tag{2.9} q = \frac{k*A*\Delta T}{L}$$La capacidad de los cuerpos de absorver las ondas sonoras es directamente proporcional a su densidad y depende de su estructura fibrovascular y la naturaleza elastoplástica. La madera conduce el sonido de mejor manera en sentido longitudinal a la veta.
Una estructura de madera densa refleja el sonido, esta propiedad es de utilidad en instrumentos musicales y salas de conciertos ya que se puede integrar fácilmente en superficies que canalicen las reflexiones de sonido.
En los materiales elásticos la velocidad de propagación de las ondas está dada por la ecuación:
$$\tag{2.10} v = \sqrt {\frac{E}{\rho}}$$Donde:
$ v = Es \space la \space velocidad \space de \space propagación$
$ E = Módulo \space de \space elásticidad \space o \space de \space Young \space expresado \space en \space (N/m^2)$
$ \rho = Densidad \space expresada \space en \space (kg/m^3)$
Tabla 2. Velocidad de propagación del sonido
| Material | Velocidad de propagación $m/seg$ |
|---|---|
| Aire | $340$ |
| Agua | $1435-1640$ |
| Acero | $4700-5000$ |
| Corcho | $40-50$ |
| Concreto | $4000$ |
| Madera | $1000-5000$ |
| Vidrio | $5000-6000$ |
Podemos concluir que el rendimiento insonorizador de la madera no es el ideal pero se puede mejorar con una estructura de madera gruesa, homogénea y con una superficie densa es capaz de amortiguar el sonido de la mejor manera.
En la madera podemos distinguir tres direcciones que se pueden considerar normales(perpendiculares) entre sí: longitudinal, radial y transversal siendo las dos primeras perpendiculares al grano.
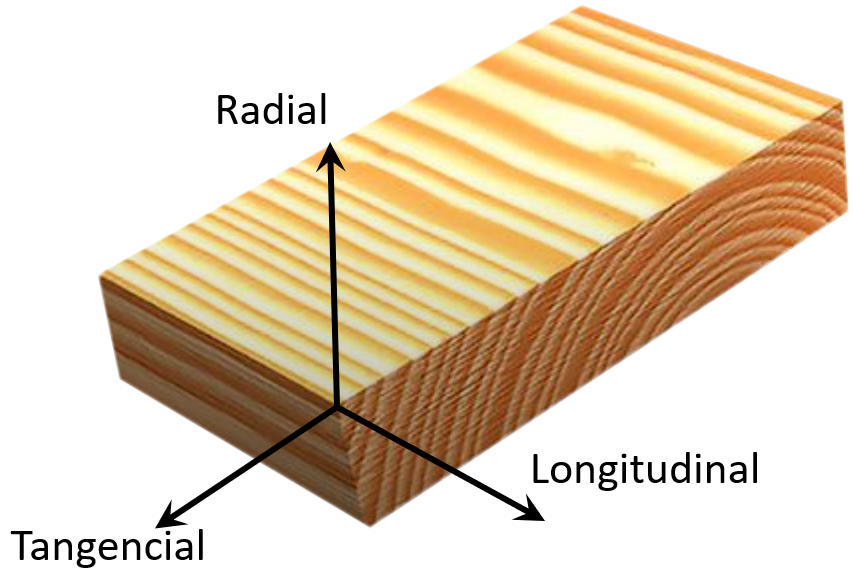
Para los diseños se consideran las siguientes propiedades de resistencia:
La determinación de dichos valores de resistencia debe ser realizado con probetas libres de defectos.
Vamos a recordar los conceptos de lo que es un esfuerzo normal directo que pueden ser a compresión (tiende a comprimir el elemento) o de tensión (tiende a realizar un incremento de la longitud del elemento), el análisis del esfuerzo tiene como fin último garantizar la seguridad de la estructura diseñada.
"Se denomina esfuerzo a la resistencia interna que genera un área unitaria del material al cual se le aplica una carga externa"
Esquema del esfuerzo de compresión:

El esfuerzo se denota por la la letra griega sigma $\sigma$, es común encontrarnos con unidades en el sistema anglosajón cuya unidad de fuerza es la libra, y la unidad de área es la pulgada cuadrada, la unidad de esfuerzo se conoce como $psi$.
En el sistema SI la unidad de fuerza es el $Newton$ y la unidad de superficie es el metro cuadrado, esa unidad de esfuerzo en este sistema se conoce como $pascal$.
$$\tag{2.11} \sigma = \frac{fuerza}{área} = \frac{F}{A}$$La resistencia al compresión se define como Esfuerzo máximo que puede soportar un material sometido a una carga de aplastamiento.
La resistencia a la compresión de un material que falla debido a la rotura de una fractura se puede definir, en límites bastante ajustados, como una propiedad independiente.
Sin embargo, la resistencia a la compresión de los materiales que no se rompen en la compresión se define como la cantidad de esfuerzo necesario para deformar el material una cantidad arbitraria. La resistencia a la compresión se calcula dividiendo la carga máxima por el área transversal original de una probeta en un ensayo de compresión.
Dado que las fibras de la madera se encuentran orientadas con su eje longitudinal como podemos apreciar en la figura 1.4 y que además, coincide con la orientación de las microfibras que constituyen la pared celular, la madera ofrece gran resistencia a los esfuerzos de compresión paralela a esa fibras.
La resistencia a compresión paralela a la fibra es elevada, alcanzando valores característicos en la madera clasificada de $16 a 23 N/mm2$.
En el cálculo de los elementos comprimidos se ha de realizar la comprobación de la inestabilidad de la pieza (pandeo), en el que influye decisivamente el módulo de elasticidad.
El valor relativamente bajo de este módulo reduce en la práctica la resistencia a la compresión en piezas esbeltas. Esta propiedad resulta importante en una gran cantidad de tipos de piezas, como pilares y montantes de muros entramados, entre otros elementos. En la imagen podemos visualizar un piso de cerchas sometido a esfuerzos de compresión:

La resistencia a la compresión de manera que la fuerza ejercida sea paralela a las fibras es aproximadamente un 50% de la resistencia a la tracción.
Esta resistencia se produce cuando las fibras del elemento están sometidas a cargas que generan esfuerzos perpendiculares a su eje y tiene a reducir el tamaño de las separaciones entre dichas fibras.
Cuando la madera es sometida a este tipo de esfuerzo las fallas no se distinguen a simple vista. Al incrementarse la carga de manera paralela a las fibras el elemento se comprime aumentando su densidad a la vez que se incrementa la capacidad para resistir mayores cargas. Esa resistencia se expresa mediante el módulo de rotura (MOR) dado por la expresión:
$$\tag{2.12} MOR \bigg(\frac{kg}{cm^2} \bigg) = \frac{Carga \space aplicada}{área \space contacto} = \frac{F}{A_c}$$Donde:
$ MOR = Módulo \space de \space rotura$
$ k = Carga \space de \space rotura $
$ A = Área \space de \space la \space sección \space transversal $
Se consideran valores altos cuando se obtienen resultado mayores a $75 \frac{kg}{cm^2}$ por lo tanto son maderas ideales para ser sometidas a este tipo de esfuerzo.
La resistencia a tracción o tensión, es el esfuerzo máximo al que está sometida la madera, por dos fuerzas de sentido opuesto que tratan es alargar el material.
Ofrece alta resistencia en dirección paralela a la fibra y depende en gran medida de los defectos que posea la madera estructural empleada.
La resistencia a la tensión en el sentido de la veta oscila entre 10-20 veces mayor que su resistencia en perpendicular a la veta. La resistencia a la tensión también depende de la densidad de la madera, una comparación de la resistencia a la tracción y la resistencia a la compresión de la madera secada indica esta última es aproximadamente, la mitad de su correspondiente resistencia a la tensión.
La resistencia a la cizalladura de la madera es equivalente al 10-15 % de su resistencia a la tensión en el sentido de la veta. La resistencia a la cizalladura se ve debilitada por los nudos, los defectos o las grietas que aparecen en la madera.
Este esfuerzo por corte se presenta cuando el elemento está sometido a flexión y se presenta en dos direcciones: la resistencia paralela a las fibras es de 3-4 veces mayor que la dirección paralela.
El esfuerzo de flexión ocurre en elementos de gran longitud respecto a su sección transversal, la acción de la carga normal a su eje longitudinal provoca una curvatura y allí se producen tres esfuerzos fundamentales:
La combinación de los dos primeros esfuerzos origina en la viga una concavidad en la zona de compresión y convexidad en la zona de tracción. De la Norma Técnica Colombiana NTC 663 que tiene como referencia a la Norma Alemana DIN 52186 presentamos algunas definiciones concernientes a los ensayos de flexión.
Esfuerzo de flexión ($σ f$): cociente del momento de flexión (MF) y el módulo resistente (MR) de la probeta:
$$\tag{2.13} (\sigma f) = \frac{M \space F}{M \space R} $$Resistencia máxima a la flexión (Módulo de rotura, $\sigma f_{máx}$): esfuerzo de flexión máximo soportado por la probeta en el momento de la rotura
Resistencia a la flexión en el límite proporcional: esfuerzo de flexión máximo soportado por la probeta en el momento en que la deformación y el esfuerzo dejan de ser directamente proporcionales.
Módulo de elasticidad (E): relación entre el esfuerzo unitario y la deformación unitaria.
Corte radial: corte longitudinal, perpendicular a los anillos de crecimiento.
Corte tangencial: corte longitudinal, tangente a los anillos de crecimiento.
En la figura 1.7 podemos observar la disposición del ensayo de flexión y la aplicacón correcta de la carga y la dirección incorrecta de hacerlo: para ello es necesario ampliar la imagen
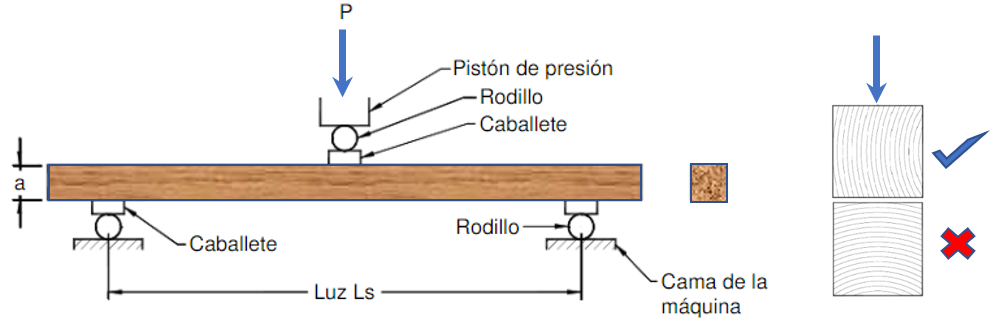
Una madera está sometida a la flexión estática cuando sobre ella ejercen cargas en forma lenta que tienden a curvarla. Las maderas en uso generalmente están solicitadas por cargas o fuerzas que tienden a flexionarlas como puede deducirse de la figura 1.7.
La resistencia a la flexión se calcula mediante la ecuación:
$$\tag{2.14} \sigma_{máx}= \frac{3 \space K \space L}{2 \space a \space e^2}$$Donde:
$ \sigma_{máx} = Resistencia \space máxima \space a \space la \space flexión (kg/cm^2)$
$ k = Carga \space de \space rotura (Newtons)$
$ L = Distancia \space entre \space los \space soportes (cm) $
$a = Ancho \space de \space la \space probeta \space en \space dirección \space radial(cm) $
$a = Altura \space de \space la \space probeta \space en dirección \space tangencial(cm) $
Las características de la madera varían según su contenido de humedad, la duración de la carga y la calidad de la madera (dureza, densidad y defectos entre otros.
Las características mecánicas de la madera pueden ser analizadas a través de las fibras paralelas y las fibras perpendiculares. Normalmente se analizan las fibras en el sentido paralelo, pues la resistencia es mayor que en sentido perpendicular.
En la tabla 3 podemos observar las principales propiedades mecánicas de algunos tipos de madera, recalcando que estas tablas varián acorde con la norma que impera en la región de procedencia:
Tabla 3. Propiedades mecánicas de algunas maderas.
| Madera | Fb | Ft | Fv | Fp | Fc | E | $\rho$ |
|---|---|---|---|---|---|---|---|
| Pino | $116$ | $78$ | $7$ | $26$ | $81$ | $130000$ | $660$ |
| Cedro real | $85$ | $57$ | $5$ | $19$ | $60$ | $8000$ | $481$ |
| Cedro macho | $70$ | $47$ | $4$ | $15$ | $49$ | $6400$ | $615$ |
| Guayabo | $175$ | $117$ | $10$ | $39$ | $122$ | $15500$ | $738$ |
| Laurel hembra | $115$ | $77$ | $7$ | $25$ | $80$ | $9000$ | $561$ |
| Laurel macho | $130$ | $87$ | $8$ | $29$ | $91$ | $150000$ | $565$ |
| Coba | $106$ | $70$ | $6$ | $23$ | $74$ | $8500$ | $500$ |
| Roble | $180$ | $120$ | $10$ | $40$ | $126$ | $150000$ | $745$ |
En la tabla tenemos::
$ Fb = Resistencia \space máxima \space a \space la \space flexión (kg/cm^2)$
$ Ft = Carga \space de \space rotura (Newtons)$
$ Fv = Resistencia \space máxima \space a \space la \space flexión (kg/cm^2)$
$ Fp = Carga \space de \space rotura (Newtons)$
$ Fc = Resistencia \space máxima \space a \space la \space flexión (kg/cm^2)$
$ E = Carga \space de \space rotura (Newtons)$
$ \rho = Carga \space de \space rotura (Newtons)$
Las normas de diseño de estructuras solicitan revisiones periódicas y oportunas, que surgen de nuevas experiencias e investigaciones.
Se considera que un reglamento o norma se vuelve obsoleto después de no más de diez años de su publicación, o inmediatamente después de la ocurrencia de un sismo fuerte, que manifieste un comportamiento poco satisfactorio de las estructuras que fueron diseñadas y construidas con determinadas normas de construcción estructural.
Al diseñar una estructura nos encontramos con dos criterios de diseño y es necesario conocer esas dos perspectivas, dónde están las diferencias entre estos dos criterios de diseño y cuál es digamos el más actual y qué se prefiere al momento de diseñar estructuralmente.
Las investigaciones a lo largo de muchos años se han sintetizado en un procedimiento de diseño práctico y racional, para proporcionar una herramienta de diseño de estructuras con niveles de seguridad, aceptables y económicas dentro de ciertos límites.
El desarrollo de numerosos programas de computadoras para el análisis y diseño de estructuras ha permitido que las reglas de diseño se apliquen de manera versátil, con revisiones rápidas para optimizar el material y evitar cálculos laboriosos.
La perspectiva acerca del método del criterio de diseño en torno a los esfuerzos permisibles se denomina método ASD, básicamente es un criterio donde se diseña un perfil de un miembro estructural seleccionando sus propiedades geométricas y de la sección transversal para garantizar que nunca se sobrepase un esfuerzo máximo en el material esfuerzo máximo, se le denomina esfuerzo permisible y que se ubica de un rango elástico del material.
Si hablasemos de acero normalmente el esfuerzo permisible es un porcentaje del esfuerzo de fluencia, al diseñar una sección un elemento estructural en tensión o en flexión podemos expresar que los cálculos van a oscilar en un rango del 60 por ciento del esfuerzo de fluencia el material.
Ello implica que sólo estamos aprovechando la ventana del rango elástico del material.
Matemáticamente este método se expresa como: $$\tag{2.15} R_a \leq \frac{R_n}{\Omega}$$
Donde:
$ R_{a} = Es \space la \space resistencia \space requerida \space \space determinada \space por \space medio \space del \\ \space \space \space \space \space \space \space \space \space \space \space análisis \space de \space una \space serie \space de \space combinaciones \space de \space carga.$
$ R_{n} = Es \space el \space esfuerzo \space nominal \space de \space los \space materiales, \space los \space cuales \space \\ \space \space \space \space \space \space \space \space \space \space \space son \space estandarizados \space y/o \space comprobados \space en \space base \space a \space \\ \space \space \space \space \space \space \space \space \space \space \space diferentes \space pruebas \space de \space materiales.$
$ \Omega = Es \space el \space factor \space de \space seguridad \space el \space cual \space hace \space que \space los \space materiales \\ \space \space \space \space \space \space \space \space \space trabajen \space dentro \space de \space sus \space estados \space límites $
El método más nuevo y se apoya en los factores de carga y resistencia, utiliza factores de carga que acompañan la carga muerta o las cargas muertas y las cargas vivas. Esos factores de carga están diferenciados ya que afectan a un conjunto de acciones.
Matemáticamente está dado por la expresión: $$\tag{2.16} R_u \leq \Phi \space R_n $$
Donde:
$ R_{u} = Es \space la \space suma \space de \space la \space carga \space segmentada \space o \space cargas \space de \space servicio \\ \space \space \space \space \space \space \space \space \space \space \space cada \space una \space de \space las \space cargas \space multiplicada \space por \space su \space propio \\ \space \space \space \space \space \space \space \space \space \space factor \space de \space servicio.$
$ \Phi = Es \space el \space factor \space de \space resistencia \space dado \space por \space las \space especificaciones \\ \space \space \space \space \space \space \space \space \space para \space cada \space uno \space de \space sus \space estados \space límites $
$ R_{n} = Es \space el \space esfuerzo \space nominal \space de \space los \space materiales, \space los \space cuales \space \\ \space \space \space \space \space \space \space \space \space \space \space son \space estandarizados \space y/o \space comprobados \space en \space base \space a \space \\ \space \space \space \space \space \space \space \space \space \space \space diferentes \space pruebas \space de \space materiales.$
En el otro miembro de la derecha en la ecuación 16, se ubican las resistencias a esos efectos, las resistencias llevan su factor de resistencia y de ahí el nombre de este criterio.
Normalmente los factores de resistencia son menores a 1 en caso de las capacidades y en el caso de los efectos de las acciones son mayores a 1.
Esto significa un criterio mucho más óptimo precisamente porque la afectación se da en función del tipo de efecto, es un factor de resistencia para diseño en un elemento en tensión o en compresión.
Por el método de la resistencia última, también llamado solamente método de la resistencia, se puede estudiar el comportamiento de la estructura en el instante de falla; por tanto, si este instante se hace lo suficientemente mayor que el de su trabajo para las cargas que soporta normalmente, se podrá tener un diseño con factores de seguridad adecuados.
En forma general, este método trata de que los miembros resistan como cargas máximas aquellas que no hagan alcanzar sus estados límites de falla.
Dicho de otra forma, el objetivo principal de este método es proveer una confiabilidad uniforme a la estructura bajo varias consideraciones de carga.
La tabla presentada en la figura 1.8 podemos observar los ajustes de diseño que involucran ambos sistemas o métodos de diseño y que fueron unificados a partir del año 2005.
Uso de la tabla para el cálculo del esfuerzo de comprensión modificado para ambos sistemas:
Tabla 4. Ajustes de valores de diseño de referencia.
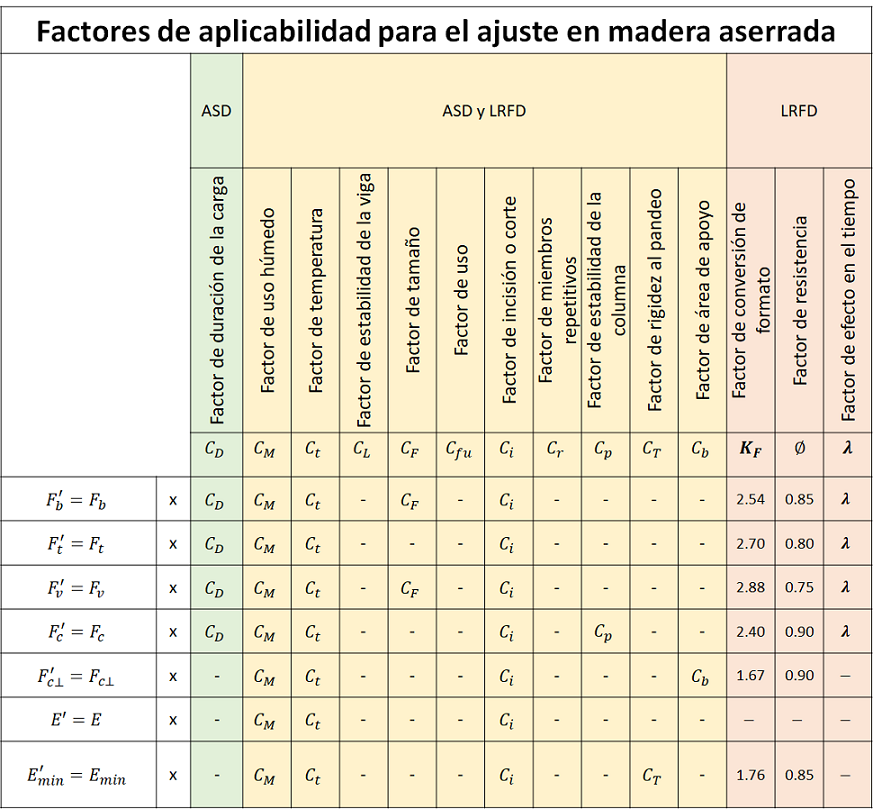
La nomenclatura para esos ajustes es:
$F'_b : Esfuerzo \space de \space flexión \space admisible \space ajustado.$
$F'_t : Esfuerzo \space de \space tensión \space paralelo \space a \space las \space fibras \space ajustado.$
$F'_v : Esfuerzo \space de \space cortante \space admisible \space ajustado.$
$F'_c : Esfuerzo \space de \space compresión \space paralelo \space a \space las \space fibras \space ajustado.$
$F'_{c ⊥} : Esfuerzo \space de \space compresión \space perpendicular \space a \space las \space fibras \\ \space \space \space \space \space \space \space \space \space \space ajustado.$
$E': Módulo \space de \space elasticidad \space ajustado.$
$E'_{min} : Módulo \space de \space elasticidad \space mínimo \space longitudinal \space ajustado.$
Básicamente existen dos procedimientos de clasificación estructural de la madera: procedimiento de clasificación visual y de clasificación mecánica.
La clasificación visual consiste en medir los defectos o singularidades de la pieza de madera y asignar una determinada calidad a la pieza observada en función de la disposición de sus defectos como los nudos, fendas, gemas, acebolladuras y las desviaciones de la fibra.
Es el método más común a nivel internacional.
El problema que se plantea es que cada país tiene su propia norma de clasificación visual, normalmente adaptada a las especies locales, y por lo tanto nos encontraremos distintas nomenclaturas.
La norma de clasificación española es la UNE 56544 y establece 2 calidades: ME-1, ME-2 (hay una tercera que es ME-G para grandes escuadrías). En la tabla podemos ver algunas de las calidades asignadas por las distintas normas de clasificación visual según cada país:
La segunda clasificación se realiza a partir de los módulos de elasticidad y su capacidad de resistencia medida en sus esfuerzos admisibles: de flexión, compresión paralela, compresión perpendicular, cortante y tensión.
Se han clasificado en maderas tipo ES1, ES2, ES3, ES4, ES5, ES6:
En el reglamento Colombiano de construción sismo-resistente se presenta la siguiente descripción al respecto:
Tabla 5. Clasificación de las maderas a partir de los módulos de elasticidad y capacidad de resistencia.
| ESFUERZOS ADMISIBLES (Norma NRS-10) | |||||
|---|---|---|---|---|---|
| Grupo | Flexión | Tensión | Comprensión $||$ | Compresión $\perp$ | Cortante |
| ES1 | $29.5$ | $21.0$ | $23.0$ | $6.0$ | $2.0$ |
| ES2 | $28.5$ | $20.0$ | $22.0$ | $4.3$ | $2.0$ |
| ES3 | $23.0$ | $17.0$ | $19.0$ | $3.0$ | $1.6$ |
| ES4 | $17.0$ | $12.0$ | $15.0$ | $2.8$ | $1.5$ |
| ES5 | $15.0$ | $11.0$ | $13.0$ | $2.0$ | $1.1$ |
| ES6 | $12.5$ | $9.0$ | $10.0$ | $1.5$ | $1.3$ |
Los valores dados en la tabla se expresan en $MP_a$ para maderas con contenido de humedad del 12%. Así, la madera obtenida de las coníferas pertenece al grupo ES6.
El pino es de fibra gruesa, muy resistente a la humedad y a la sequedad. Como existen diferentes variedades de pinos es conveniente probar por medio de ensayos de resistencia las cualidades estructurales que poseen.
Existen otras variedades de especie que más se utilizan en el medio para construcción están la mayoría dentro del grupo ES5 Y ES6.
Especies de madera pesada: Se encuentran principalmente las especies de los grupos ES1 y ES2.
Especies de madera liviana: las cuales son abarcadas por los grupos ES3 y ES4.
Existe otra clasificación según la dureza y densidad de la madera estudiada, esta clasificación corresponde a maderas del grupo Andino (Sudamérica) con las propiedades físico mecánicas:
Tabla 6. Clasificación de las maderas a partir de la dureza y la densidad.
| GRUPOS | |||
|---|---|---|---|
| Propiedades ($kg/cm^2$) | A | B | C |
| E0.05 o Emin | $95'000$ | $75'000$ | $55'000$ |
| Eprom | $130'000$ | $100'000$ | $90'000$ |
| fm | $210$ | $150$ | $100$ |
| fc | $145$ | $110$ | $80$ |
| fc=perp | $40$ | $28$ | $15$ |
| fv | $15$ | $12$ | $8$ |
| ft | $145$ | $105$ | $75$ |
En la tabla tenemos:
$\begin{aligned} E0.05 \space o \space Emin &= \text{Es el Módulo elástico mínimo o con límite }\\ &\quad\text{de exclusión al 5\% (percentil)} \end{aligned}$ $\begin{aligned} Eprom &= \text{Módulo elástico promedio de todas las muestras}\\ &\quad \text{ensayadas} \end{aligned}$ $\begin{aligned} fm &= \text{Resistencia axial producto de efectos de flexión}\\ \end{aligned}$ $\begin{aligned} fc &= \text{Resistencia axial a compresión paralela a la fibras}\\ \end{aligned}$ $\begin{aligned} fc-perm &= \text{Resistencia axial a compresión perpendicular } \\ &\quad \text { a las fibras} \end{aligned}$ $\begin{aligned} fv &= \text{Resistencia a cortante}\\ \end{aligned}$ $\begin{aligned} ft &= \text{Resistencia a tracción paralela a las fibras}\\ \end{aligned}$Ahora hagamos referencia a las maderas artificiales, son derivados de la madera elaborados a partir de láminas o virutas de madera tratadas convenientemente. Esta nomenclatura se debe al preoceso de fabricación:
Las maderas de este tipo son el resultado de la combinación de fibras de madera con resinas termoplásticas de alta resistencia. De esta combinación se ha obtenido un compuesto conocido como madera tecnológica, sintética o composite (WPC o Wood Plastic Composite)

Estos productos se obtienen bajo un exhaustivo proceso de ingeniería en el cual se incide, de forma especial, en el procesado de cada pieza logrando un acabado estético similar a la madera natural pero mejorada con el rendimiento y durabilidad de los polímeros de mayor calidad.
En este sentido las resinas termoplásticas y en concreto el polietileno, es que alcanza los mejores resultados debido a sus inherentes propiedades: bajo grado de expansión, buena resistencia al impacto y baja absorción de líquidos.
Una referencia muy popular son las placas MDF (Medium Density Fiberboard), son construidas con una mezcla de pequeñas partículas de madera (generalmente pinos) y colas especiales, prensadas en condiciones de presión y temperatura controladas. Obteniéndose planchas, de medidas fijas estandarizadas, con características mecánicas y físicas uniformes y bien definidas.
Estas placas MDF, a diferencia del Aglomerado, pueden se mecanizadas obteniendo excelentes terminaciones y por lo general son de color claro y de superficie lisa y uniforme.
En la imagen podemos observar la "columna vertebral" de una construcción con madera prefabricada:

La estabilidad y rigidez de una estructura de madera depende en gran medida de la selección adecuada elección de la madera empleada, así como del correcto diseño de la estructura y una buena ejecución en obra.
Un mecanismo concluyente que influirá en la funcionalidad total de la estructura de madera son las uniones, es decir, aquellos mecanismos que sirven para acoplar los nudos en los que confluyen dos o más elementos de la estructura. Vemos los tipos de uniones en las estructuras de madera.
En este aspecto, las estructuras de madera presentan una ventaja frente a las estructuras metálicas, ya que existe una mayor variedad de uniones que resultan más sencillas de realizar.
Existen diferentes criterios para definir el tipo de unión estructural a emplear, principalmente se dividen en dos grandes grupos, en función del elemento utilizado en la unión: las uniones simples y las uniones mecanizadas.
Las uniones simples en estructuras de madera son aquellas uniones que no requieren elementos externos y se basan en acoplar las piezas de la estructura de madera mediante el mecanizado de estas encajándolas entre sí como un puzle. Hay muchos tipos de uniones tradicionales, pero se pueden dividir en tres grandes grupos:
Los ensambles también llamados acoplamientos, son la unión de dos o mas maderas por sus caras o cantos respectivos, y tienen como resultado final ensanchar la madera para conseguir dimensiones imposibles de obtener una pieza única.
Existen dos grupos muy diferenciados:
Las uniones mecánicas son aquellas donde se emplean elementos denominados herrajes para el acople de diferentes piezas de la estructura que les permiten transmitir esfuerzos.
Inicialmente hagamos referencia a los empalmes:
Se denomina unión o empalme estructural a los entramados que permiten ensamblar diferentes componentes que por su complejidad serián imposibles de construir de una sola pieza.
Con madera las uniones estructurales son hechas de madera maciza y tableros que requieren que puedan conservar una adecuada resistencia mecánica, durante el tiempo y las condiciones de clima en que deban prestar servicio.
Un canto de madera es esa linea que forma la terminación de la superficie de algún elemento de madera.
Según el diccionario de Arquitecturahttps://www.parro.com.ar/definicion-de-canto. canto se denomina a línea que forma la terminación de la superficie de una pieza o elemento. También llamado borde. También puede definirse el canto como cualquiera de las dos superficies longitudinales opuestas más estrechas, en la madera canteada.
Allí también se define el canto útilcomo la profundidad medida desde la capa de compresión hasta el centroide una armadura de tracción.:
Por medio de las uniones de elementos menores se puede lograr mayores longitudes trasponiendo (traslapando) esos elementos sucesivamente, también nos permite lograr mayores espesores o anchos mediante la fijación de elementos paralelos, generalmente cara a cara. Tal como se observa en la escena interactiva anterior.
De igual manera podemos según la definición de junta de canto de la pagína anterior lograr caras más amplias realizando el ajuste entre cantos de los elementos menores.
En la escena de la siguiente pagína veremos las posibilidades de lograr este tipo de ajuste.
Por último, veremos el empalme de un extremo de un elemento largo denominado viga con la cara de otro elemento.
Es de anotar que estos ajustes se fijan mediantes dispositivos que pueden ser igualmente de madera o metalicos, entre los cuales se conocen los calvos, pernos, tirafondos, platinas, zunchos y ángulos metálicos.
De los dispositivos de unión más fáciles de emplear por su bajo costo son los clavos puesto que no requieren procesos o elementos adicionales como los pernos, platinas, zunchos y demás.
Un ensamble se define como el proceso de unir piezas de madera o de otro material por medio de encajes denominados macho y hembra.
Con el tiempo las técnicas de ensamble se van perfeccionando y han multiplicado las aplicaciones de la madera y el trabajo de los carpinteros. En la actualidad se utilizan estructuras y componentes prefabricados o por módulos, en vez de productos en bruto. En la construcción por módulos, se realizan secciones enteras en las fábricas y se colocan más tarde en la obra.
En las siguientes páginas observaremos las uniones estructurales básicas entre componentes de madera, recordando antes que en la vida cotidiana nos encontraremos con uniones apoyadas con elementos de hormigón o metalicos como aparece en la figura.

La unión más antigua se denomina de caja y espiga: el agujero de la caja o mortaja y la lengua de la espiga. La espiga, formada en el extremo de un miembro referido generalmente como un carril, se inserta en un agujero cuadrado o rectangular cortado en el otro miembro correspondiente.
Las estructuras de caja y espiga deben soportar fuerzas originadas por el viento, así como las catastrofes naturales, dando muestras de gran rigidez.
La elección del método de ensamble depende de la calidad de la madera, de las tensiones a las que va a estar sometida y de los gustos del ensamblador. Muchos ensambles requieren ajustes con pocas tolerancias y el uso de cola o pegamento;otras se aseguran con cuñas o con puntas y clavos.
En la siguiente escena se puden visualizar algunos de los ensambles más populares:
El ensamble más sencillo es el que se utiliza para hacer cajas. Las dos piezas de madera se colocan en ángulo recto y se aseguran con clavos, tornillos o cola.
El machihembrado como se le denomina es una de las técnicas más antiguas. Este tipo de junta se realiza actualmente en la serrería, y el carpintero sólo se encarga de acoplar las piezas.
Existen infinidad de tipos de ensambles para asegurar piezas de madera y su función es absorber los esfuerzos de tracción, compresión y flexión a los que son sometidas las piezas de madera que trabajan en el armazón de una cubierta. Los acoples transmiten el esfuerzo uniformemente a través de toda la armazón.
Además de los ensambles mostrados en la escena existen algunos otros entre los que encontramos:
La madera por su naturaleza debe materializar o “cimentar” sus conexiones y sus uniones o empalmes. Pero cuando se utiliza como elemento prefabricado, la madera es dimensionada en las secciones deseadas y luego es conectada o ensamblada con los otros elementos que componen una estructura.
Desde la unión mediante amarras, y empleando sistemas de articulación o de trozos de madera o amarres ya que la madera no puede materializar la conexión de los distintos elementos o miembros de la estructura o del revestimiento.
Las uniones mecánicas en estructuras de madera son el elemento responsable de acoplar las piezas de la estructura y transmitir los esfuerzos entre estas son los denominados herrajes, es decir, objetos metálicos que unen las piezas de madera entre sí. Se clasifican según los siguientes criterios:
Las uniones a tope se refuerzan mediante elementos externos a las maderas que componen la unión y normalmente son visibles al exterior de las piezas unidas.
A pesar de existir cierto nivel de normalización para dichas uniones mecánicas, la necesidad o ingenio del fabricante de la estructura juega un papel importante, en la siguiente escena podemos visualizar algunos ejemplos:
Además de lo anterior encontramos:
Los elementos mecánicos de unión son aquellos que al quedar solicitados a esfuerzos cortantes, admiten desplazamientos relativos entre las piezas conectadas que se originan por las deformaciones por aplastamiento que sufre la madera en la zona de contacto entre la madera y el medio de unión y,adicionalmente, como en el caso de medios cilíndricos, por las deformaciones por flexión de los medios cilíndricos.
Dependiendo de su posición en la unión, los elementos mecanismos pueden quedar solicitados en dirección axial.
En las uniones empernadas es necesario considerar el cizallamiento simple y el doble cizallamiento como podemos apreciar en la figura:
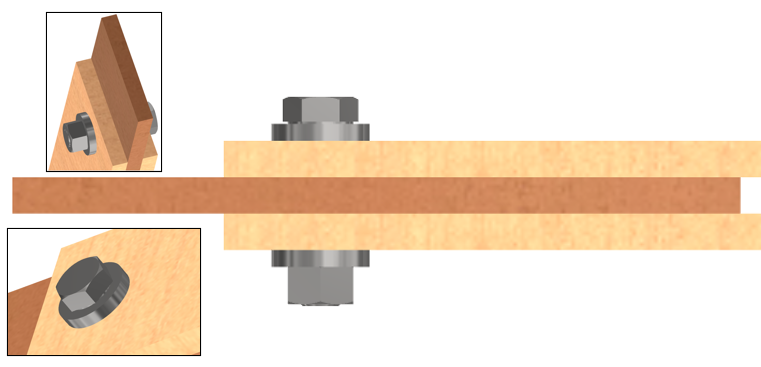
Este método se aplicará a uniones de dos o más elementos de madera, o entre un elemento de madera o pletina metálica. Las uniones empernadas son muy eficientes en grupos estructurales A, B pero también se puede usar en grupo estructural C.
En las estructuras de madera muchas piezas de tamaño menor se unen entre sí para formar componentes más robustos que le den continuidad a los elementos para soportar las cargas a las que están sometidos.
Las uniones permiten obtener elementos de mayores longitudes traslapando piezas de manera sucesiva o también conseguir elementos de mayor espesor uniendo piezas de manera paralela, con estos dos sistemas se tiene la ventaja de que es más facíl su manipulación. Según vimos en el capitulo anterior esas uniones pueden ser de manera perpendicular, paralela, inclinada o con refajo. Los elementos comunes que facilitan estas uniones son conocidos como clavos, pernos, tirafondos, zunchos, platinas y ángulos metálicos lo que facilita los sistemas de entramado.
Es un sistema formado por elementos de sección transversal pequeña pero con la esbeltez necesaria para que cuando se coloquen a distancia corta (de 40 a 60cm normalmente) entre ellos formen un sistema con componentes auto-estables, pero necesitan al resto de los entramados transversales para alcanzar la estabilidad general de la estructura y se clasifican de la siguiente manera: $$ Entramados \begin{dcases} Verticales &\begin{dcases} Abiertos & \\ Cerrados & \end{dcases} \\ Horizontales &\begin{dcases} Ligeros & \\ Pesados & \end{dcases} \\ \end{dcases}$$
La principal aplicación de los entramados de madera son las viviendas unifamiliares de una o dos plantas. Una experiencia interesante es la aplicación de entramados len la construcción de grandes voladizoscomo módulos, terrazas o miradores.
El sistema de entramado de madera admite la prefabricación tanto parcial como total. La principal característica del entramado de madera es su ligereza y sencillez de construcción, lo que no está reñido con la estabilidad y confortabilidad que proporcionan sus construcciones.
Las estructuras de entramado funcionan de forma tridimensional, donde elementos muy livianos soportan cargas elevadas a base de repartirlas y arriostrar adecuadamente los elementos. Este comportamiento unitario presenta ventajas para soportar cargas sismicas y de viento.


En la Web de la Fundación Antonio Font de Bedoya Tipos de entramado de madera se encuentra la siguiente clasificación de los entramados de acuerdo a la posición que ocupan en el edificio, aunque también hablan de una clasificación por su aspecto :
Normalmente sus cimientos se ubican en una primera planta o la parte más baja de la construcción elaborada con piedra o con ladrillo y sus componentes se detallan a continuación:
El soportal pertenece a la primera crujía que antecede al edificio. Éste queda delimitado estructuralmente con un entramado que consta de:
Paralelo al entramado de soportal, va a continuación de éste y es igual al conocido como de fachada.
Este tipo de entramado ee diferencia del entramado de fachada en que no requieren llevar las contracarreras puesto que no se requieren.
Concentran los esfuerzos de los entramados horizontales o forjados de cada crujía, transmitiéndolos al terreno. Son similares a los de cierre frontal, pasando a la fachada si hay soportal y tiene los siguientes componentes:
Similares a los entramados de fachada pero disponen de soportes extremos de una planta en la zona más exterior de los forjados que constituyen el voladizo de la planta situada inmediatamente debajo.
Los entramados de voladizos tienen los siguientes componentes:
Muy usado en los edificios cuyas medianerías, perpendiculares a la calle, se hallen muy próximas.
Los entramados de jácenas y los jabalcones trabajan a compresión y canalizan los esfuerzos del centro del vano o del vuelo a los estribos y los muros, tienen las siguientes funciones:
El sistema de entramado permite que las estructuras funcionen como bloque, pero con cierta flexibilidad a las deformaciones, la hace ser una estructura adecuada frente al sismo siempre que la cimentación permita una cierta independencia de la estructura. Además, las uniones metálicas (clavadas o con herrajes de cuelgue) presentan una cierta ductilidad, que permiten la recuperación de la forma tras el desplazamiento lateral.
En los entramados de madera es fundamental el papel del cerramiento rigidizante de la estructura y la flexibilidad de las uniones del entramado para que la estructura se adapte con facilidad al desplazamiento, con los entramados podemos obtener diferentes componentes para muros, piso, entrepisos y techos entre otros ya que las cargas se reparten a través de cada uno los componentes provocados por el viento.
Haz clic sobre la imagen donde veremos algunos otros conceptos:

Variantes de un sistema de entramado: 1) Entramado plataforma y 2) Entramado global:
Los pisos constituyen la plataforma desde donde se leantan los muros, esa plataforma está comformada por viguetas paralelas y por entablado o tablero con revestimiento.
Los muros con o sin revestimiento están compuestos por pie-derechos paralelos con soleras clavadas en los extremos y se colocan sobre la plataforma desde la cual se levantan y se fijan desde sus soleras inferiores a las viguetas, se conoce como solera de amarre. En los sistemas constructivos de entramados de plataforma, se recomienda que los entramados verticales que conforman los muros posean la altura de un piso.
Sobre estos entramados que rematan en la parte superior en una sobresolera de nivelación, se colocan y apoyan los envigados de entrepiso que conforman los entramados horizontales del sistema, que con los elementos de rigidización más el entablado de piso configuran una plataforma que constituye la superficie de trabajo para el piso siguiente y así sucesivamente.
Esta solución permite considerar el aumento de peso que, por las cargas fijas y móviles, requieran soportar los diafragmas verticales inferiores que se resuelven con un aumento de sección tanto en los pies derechos como en las soleras inferiores, superiores, sobresoleras y en el encuentro con cimientos, las soleras basales.
Para la mejor transmisión de las cargas verticales, deben coincidir en el mismo plano la disposición de los pies derechos con los envigados, o sea, deben ser coplanares.
El sistema de unión fundamental es el clavo industrial de alambrón. La separación de los pies derechos fluctúan entre los 40 a 60 cm. entre ejes, esto es 1’ – 4” a 2’ – 0.
La rigidización ante los empujes horizontales en los elementos verticales o diafragmas fue mediante diagonales de la misma sección que la empleada para los pies derechos y posteriormente se ha resuelto con placas de contrachapados u otros materiales similares
La rigidización de las plataformas se obtiene con un entablado en diagonal sobre los envigados de entrepiso y posteriormente al entablado de piso colocado sobre el diagonal y ortogonal al envigado.
Posteriormente se está resolviendo con placas de contrachapados y sobre ésta se coloca cualquier piso.
Existen diversos tipos de entramados según función son de piso, entrepiso, cielo. Para construir este tipo de es necesario conocer los elementos lo conforman, estos se denominan:
Permiten además realizar un apoyo sólido para los tableros orientados perpendicularmente a la dirección de las vigas.
Debe utilizarse madera seca, proteger los extremos de las piezas de madera y si posee uniones metálicas, estas deben estar protegidas contra la corrosión. Además de lo anterior se debe tener en cuenta la denominada protección hidrófuga entre materiales con diferente capacidad de absorber agua.
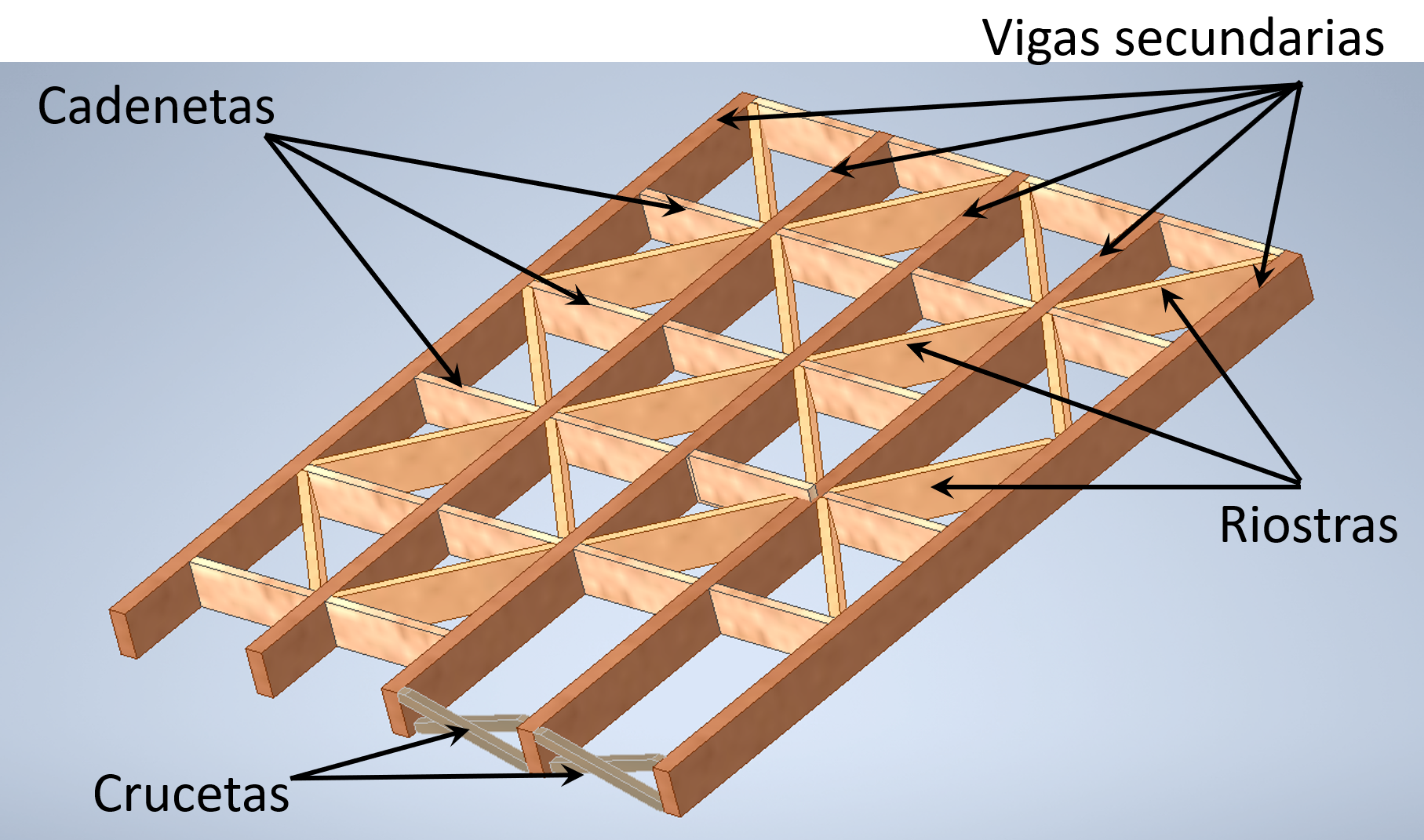
Conocidos como light-frame construction son estructuras formadas por piezas de madera muy esbeltas y delgadas, separadas a escasa distancia y fijadas a marcos cerrados (Conocidos como frames) o formando celosía (principalmente cerchas). Sus componentes son auto-estables, pero necesitan al resto de los entramados transversales para alcanzar la estabilidad general de la estructura.
Los entramados ligeros de madera pueden ser verticales, horizontales e inclinados, estos sistemas admiten la prefabricación tanto parcial como total. La principal característica del entramado ligero de madera es su ligereza y sencillez de construcción, lo que no está reñido con la estabilidad y confortabilidad que proporcionan sus construcciones.
Las estructuras de entramado ligero funcionan de forma tridimensional, donde elementos muy livianos soportan cargas elevadas a base de distribuirlas y arriostrar convenientemente los elementos. Este comportamiento unitario presenta ventajas de cara al sismo y al viento.
Estas estructuras funcionan como bloque, pero con cierta flexibilidad a las deformaciones, la hace ser una estructura adecuada frente al sismo siempre que la cimentación permita una cierta independencia de la estructura. Además, las uniones metálicas (clavadas o con herrajes de cuelgue) presentan una cierta ductilidad, que permiten la recuperación de la forma tras el desplazamiento lateral. Por otro lado, las consecuencias de derrumbe en estas estructuras son menores que la construcción tradicional.
En los entramados ligeros de madera es esencial el papel del cerramiento rigidizante de la estructura y la flexibilidad de las uniones en el entramado, ello con el fin de que la estructura se adapte con facilidad al desplazamiento ocasionado por el viento.

En este tipo de entremado se emplea la madera como elemento estructural puro, ello debido a que la estructura es independiente del cerramiento y los esfuerzos principales actúan en dirección paralela a la fibra.
Admite luces mayores y entramados en altura de hasta 6 plantas, cuando la madera se combina con otros materiales de relleno, tendiendo a formar una estructura mixta con muros de carga y permite aprovechar los espacios abuhardillados, ya que la cubierta deja estancias con más luz.

Más allá de la belleza de la madera vista, las estructuras de madera gozan de una durabilidad inigualable comparación las casas construidas convencionalmente.
Versiones diferentes de entramados pesados o heavy timber:
Cuando una estructura está construida a base de pies derechos y dinteles o arquitrabes se denomina arquitectura adintelada o arquitrabada, es el sistema constructivo más antiguo.
Las primeras muestras de arquitectura adintelada pétrea (Que tiene la dureza, textura u otra característica propia de la piedra) la encontramos en los dólmenes prehistóricos, en los que grandes losas de piedra verticales sostenían otras colocadas horizontalmente sobre ellas. Si la distancia entre las piedras verticales era demasiado amplia para una única losa, se realizaba la denominada falsa bóveda.
Esa falsa bóveda se elabora por el procedimiento de aproximación de hiladas: cada hilada de piedras sobresale con respecto a la inferior; así, dos muros paralelos en su base llegarán a tocarse en su parte alta.

Los arcos y las bóvedas indican un paso más avanzado al sistema adintelado ya que permite obtener este tipo de estructura con materiales diferentes tal como podemos apreciar en la imagen, claro está que empleando la madera como molde:

El sistema constructivo timber frame, o de paredes portantes entramadas, se caracteriza por la realización de paredes portantes con un entramado formado por montantes que luego se rellena con material aislante.
El término timber frame describe típicamente un sistema de paredes y pisos estructurales panelados construidos con postes de madera de sección pequeña , revestidos con productos de tablero , en los que el marco de madera transmite cargas verticales y horizontales a los cimientos.
En este sistema los muros se forman con pies derechos de gruesa escuadría a separaciones muy reducidas. Estructuralmente funciona como muro de carga, donde la madera trabaja en dirección paralela a la fibra. El arriostramiento se consigue mediante barras diagonales denominadas riostras.Las uniones se realizan mediante caja y espiga, y son generalmente de menor complejidad que en el sistema aporticado.
El cerramiento en este sistema se realiza rellenando los espacios dejados por las piezas de madera con materiales cerámicos, tapial y trenzados vegetales revocados con arcilla entre otros.
El conjunto Timber Frame forma una estructura de madera maciza que queda vista desde el interior y, a veces, desde el exterior del edificio. Las maderas y las uniones están a la vista y son parte de la estética del edificio, normalmente se tratan con aceites naturales y ceras o, simplemente se deja sin tratar, en su forma natural; las vigas representan una gran obra de arte estructural. Existen varias vertientes en el modelo Timber Frame que incluso pueden estar presentes en una misma estructura:
Consiste en organizar las vigas en forma de portones, armazones, o secciones de la estructura como los muros. Se colocan unas vigas sobre otras, se nivelan, se aploman y se marcan las intersecciones. Así se pueden incorporar vigas de cualquier tipo, curvadas o torcidas.
Así como el Scribe rule, este sistema también uno de los sistemas más antiguos, consiste en realizar en el piso totalmente nivelado previamente, un dibujo a escala real de la forma del armazón o sección que está fabricando.
El proceso continúa ubicando cada viga sobre el dibujo, apoyándolas en bloques, unas sobre otras. Como en el scribing, se aploman las intersecciones y posiciones de cada viga para marcar cada unión.
Es necesario tener en cuenta las imperfecciones de cada viga, el carpintero copia “scribes” el perfil de cada viga, con o sin imperfecciones, en la cara de la otra viga para realizar uniones exactas y naturales.
Las maderas pueden ser irregulares, sin cepillar y con su propia forma.
Las vigas están organizadas en líneas de vigas comunes, es un sistema de producción, donde se fabrican todas las piezas a la vez, basado en la estandarización de las mismas que se puede utilizar en espacios pequeños y en interiores.
Se asume que, dentro de cada viga irregular hay una viga perfectamente escuadrada y que en toda intersección entre vigas en los puntos donde habrá uniones, se cepillan las vigas para lograr una dimensión estándar, es un ajuste de medidas y cálculos donde el maderero trabaja con sus dimensiones estándares.
Este sistema es una variante de sistema Square rule, las vigas generalmente llegan bien cepilladas a cuatro caras desde los aserraderos y las imperfecciones son mínimas; se analiza cada viga para ver si está a escuadra, repasando y cepillando cada punto de unión a mano para que quede perfectamente a escuadra. No se utiliza la estandarización y no hace falta cepillar todos los encuentros a una dimensión fija y uniforme, como en square rule.
Los muros son construidos con un armazón de madera en el que se emplean materiales de relleno en los intersticios existentes entre los diferentes miembros. Estos rellenos suelen estar constituidos por materiales pesados y con una cierta capacidad resistente, como de ladrillo o adobe, mampostería o rellenos vertidos de piedra que son mezclados normalmente con yeso.
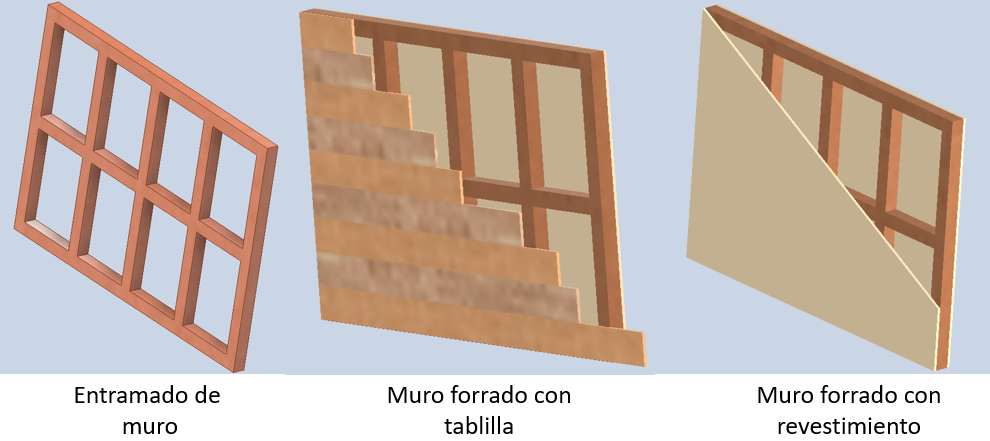
El sistema tiene elementos comunes a los sistemas de adintelado y de entramado. El forjado se levanta con un conjunto de viguetas que se apoyan en las carreras y los estribos, y un entrevigado. Las vigas principales no suelen tener dimensiones normalizadas y las viguetas tradicionalmente tenían escuadrías de mayor anchura.
Pero también pueden obtenerse normalizadas en determinadas gamas dimensionales. En la figura podemos visualizar el esquema de este tipo de sistema:
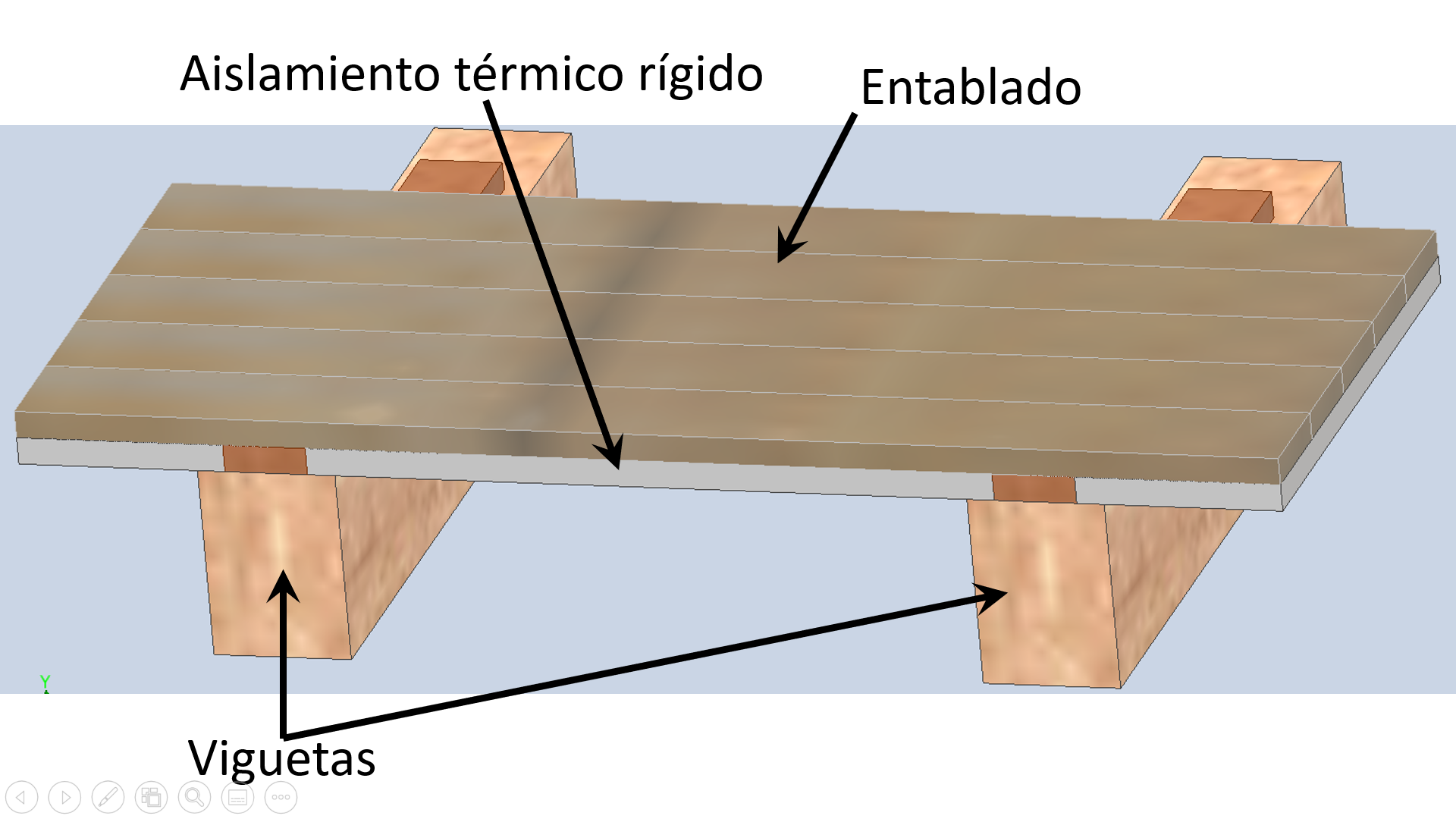
Una estructura de madera utiliza un sistema de clavijas de madera, acero e incluso plástico insertadas en agujeros hechos en la madera o forzados como ocurre con los clavos. En este sistema, todas las partes de la estructura de madera, incluidas las cerchas, los postes y las vigas se entrelazan entre sí.
Cada uno de los componentes descritos debe cumplir ciertas características de resistencia mecánicas que garanticen la seguridad de la estructura, en este capítulo se describen los postes, vigas, cerchas y techos como componentes principales.
En la imagen de Paul Brenan publicada en Pixebay podemos observar la construcción de una estructura sobre una base de hormigón, en ella se emplean todos los elementos descritos:

Una columna es un elemento estructural que trabaja a compresion, cuya longitud es varias veces mayor que su dimension lateral mas pequeiia. Normalmente el termino columna se aplica a elementos verticales pesados y el termino puntal se refiere a elementos mas pequeños sometidos a compresion, y no necesariamente en posicion vertical.
EI tipo de columna de madera que se usa con mayor frecuencia es la columna sólida sencilla, que consiste en una sola pieza de madera de sección transversal cuadrada u oblonga.
Las columnas solidas de seccion transversal circular tambien se consideran columnas solidas simples, pero se usan con menos frecuencia.
Una columna formada con varios miembros es un ensamble de dos o mas miembros cuyos ejes longitudinales son paralelos; se impide que se toquen los elementos mediante unos bloques separadores colocados en los extremos y puntos medios de su longitud.
Otros dos tipos son las columnas compuestas, con sujetadores mecanicos y las columnas laminadas pegadas. Los pies derechos en los marcos ligeros de madera tambien son columnas.
Las columnas de madera a menudo se utilizan como elementos decorativos, pueden ser ser de varios tipos: maciza, ensamblada, compuesta y laminadas unidas con pegamento. De este tipo de columnas la maciza es la más empleada, las demás son formadas por varios elementos. Dependiendo de su relación con otros elementos de la estructura se pueden calsificar como:
Cuando se habla de columnas altas su falla se produce por la denominada inestabilidad elástica más conocida como pandeo, es el tipo de falla estructural que en lugar de aplastar la columna o fragmentarla, la deflexiona o la curva o la pandea. Al hablar de columnas es neceario referirse a la razón de esbeltez, la longitud real de la columna y la fijación de los extremos.
La medida de la esbeltez de una columna se calcula a partir de su longitud, de su sección transversal y sus dimensiones y quizá lo más importante: la manera de ser sujetada en sus extremos, esa medida está dada por la expresión: $$\tag{5.1} SR = \frac{K \space L}{r} = \frac{L_e}{r}$$
Donde:
$ SR = Razón \space de \space esbeltez (Reason \space for \space slenderness).$
$ L = Longitud \space real \space medida \space entre \space los \space puntos \space de \space apoyo \space $
$\space \space \space \space \space \space \space \space o \space también \space la \space restricción \space lateral.$
$ K = Factor \space de \space fijación \space en \space los \space extremos.$
$ L_e = Longitud \space efectiva.$
$ r = Radio \space de \space giro \space mínimo \space de \space la \space sección \space transversal $
$\space \space \space \space \space \space \space \space de \space la \space columna.$
Es la longitud de una columna simple con una carga aplicada en uno de los extremos y la respectiva reacción que se genera en el otro extremo.
Es necesario tener en cuenta que en postes o columnas que sufren cargas de compresión se evita el pandeo mediante recursos de sujeción o restricciones laterales, esta longitud real se considera para cada uno de los segmentos a partir de esa restricción.
El factor de fijación $k$ de los extremos mide el grado al cual cada extremo de la columna está limitado contra rotación:
Las columnas que poseen pasador en uno de sus extemos están imposibilitadas para generar rotación. Es necesario tener en cuenta que si dicha columna posee pasadores en cada uno de sus extremos, al deformarse, adquiere la forma de una curva uniforme entre sus extremos.
Los extremos fijos en ambos extremos impiden la rotación. A medida que la columna tiende a pandearse, la curva de flexión del eje de la columna debe aproximarse al extremo fijo sin inclinación (pendiente igual a cero). Las columnas con extremos fijos son mucho más rígidas y por ello son capaces de soportar cargas mayores antes de pandearse.
Las columnas con extremos libres se caracterizan por pueden girar además de trasladarse.
En texto de "Resistencia de materiales" de Robert L. Mott se describen las siguientes relaciones para establecer la longitud efectiva acorde con las características de sus extremos:
Tabla 7. Longitudes efectivas en columnas.
| Tipo de columna | Longitud efectiva $L_e$ |
|---|---|
| Extemos con pasadores | (1.0) $L$ |
| Extremo con pasador y extremo fijo | (0.8) $L$ |
| Ambos extremos fijos | (0.65) $L$ |
| Un extremo fijo y el otro extremo libre | (2.10) $L$ |
En la tabla se visualizan las posibilidades de posicionamiento de las columnas.
En la siguiente escena podemos observar algunos tipos de anclaje de las columnas de madera a los cimientos que soportan la estructura:
Al momento de relaizar cálculos entran en acción conceptos como:
El radio de giro, $r$, depende del eje con respecto al cual se tiene que calcular. En ingeniería estructural, el radio de giro describe la forma en la cual el área transversal o una distribución de masa se distribuye alrededor de su eje centroidal. En la mayoría de los casos, se debe determinar el eje con respecto al cual el radio de giro es mínimo, debido a que es el eje con respecto al cual la columna se pandearía.
El radio de giro está determinado por la expresión: $$\tag{5.2} r = \sqrt {\frac{I}{A}}$$
Donde:
$ r = Radio \space de \space giro $
$ I = Momento \space de \space inercia \space de \space la \space sección \space de \space uno \space de \space los \space ejes$
$\space \space \space \space \space \space \space \space ejes \space principales.$
$ A = Área \space de \space la \space sección \space transversal.$
El momento de inercia mide la medida en que un objeto resiste la aceleración rotacional respecto de un eje particular, y es el análogo rotacional a la masa.
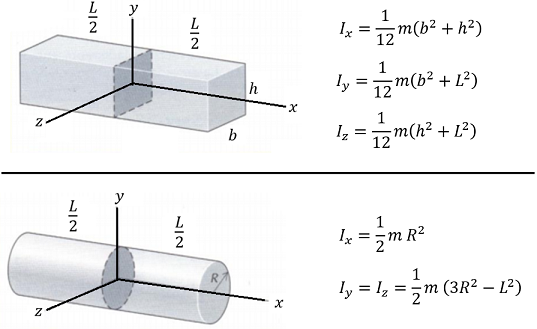
Los momentos de inercia en masa tienen unidades de magnitud ML ([masa] × [longitud] ), normalmente las columnas de madera tienen secciones trasversales circulares, rectangulares o cuadradas.
En la figura podemos apreciar los momentos de inercia de estas columnas:
A continuación un resumen gráfico de los conceptos de pandeo:
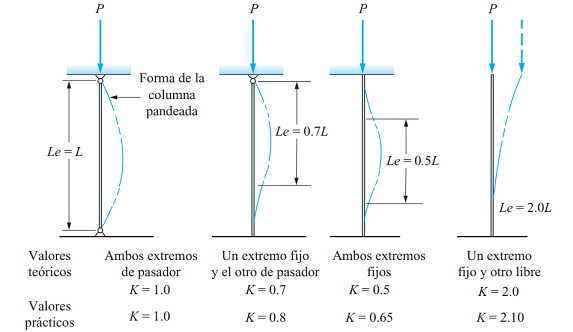
Los resultados de la esbeltez de una columna se refleja en reducción de su capacidad de carga se evalúa en forma independiente al diseño propiamente dicho, mediante la consideración de los momentos generados por las deformaciones transversales de las columnas (momentos de 2do. orden) o mediante procesos aproximados que comprenden la estimación de factores que corrigen a los momentos del análisis estructural (momentos de 1er orden).
Además, adicionalmente se presenta el problema de la flexión biaxial, el cual siempre existe si se consideran momentos de sismo en una dirección y simultáneamente momentos de cargas verticales en la otra. Los efectos de esbeltez en las columnas incrementan a veces significativamente los momentos calculados en el análisis normal elástico de una estructura.
Si una columna presenta un grado de esbeltez tal que, para el nivel de carga axial aplicado, se generen deformaciones transversales que aumenten significativamente la excentricidad considerada en el diseño, deberá evaluarse el momento generado por la nueva excentricidad, denominado como “momento de segundo orden”.
Consideremos una columna perfectamente recta, comprimida axialmente y biarticulada en sus extremos, pandea cuando el esfuerzo axial alcanza el valor dado por la siguiente ecuación, es conocido como la carga crítica de pandeo de Euler: $$\tag{5.3} P_{cr} = \frac{\pi^2 \space E \space A}{\bigg(\frac{L_e}{r}\bigg)^2}$$
Existe una expresión más práctica llamada $\lambda$ o esbeltez mecánica que está dada por la expresión: $$\tag{5.4} \lambda = \frac{K \space L}{r}$$
La norma NSR-10 de Colombia expresa que esa razón de esbeltez esta dada por la expresión: $$\tag{5.5} \lambda = \frac{L_e}{r \space \sqrt{12}}$$
Del cálculo realizado en las dos direcciones principales se ha de utilizar el mayor valor de $\lambda$ según lo mostrado en el siguiente gráfico:
Tabla 8. $\lambda$ Según NSR-10.
| Geometría transversal | $\lambda$ |
|---|---|
| Circular con diámetro $D$ | $\frac{\sqrt{3} \space L_e}{2D}$ |
| Cuadrada con lado $d$ | $\frac{L_e{_{1,2}}}{d}$ |
| Rectangular con $d_1 (ancho)\lt d_2 (altura)$ | $\frac{L_{e_1}}{d_1}, \space \frac{L_{e_2}}{d_2}$ |
| Otras secciones | $\frac{L_e}{r \space \sqrt{12}}$ |
Una columna se considera larga cuando larga cuando la relación de esbeltez efectiva es mayor que la constante de columna dada por la expresión donde $S_y$ es resistencia a la cedencia: $$\tag{5.6} C_c = \sqrt {\frac{2 \space \pi^2 \space E}{S_y}}$$
Esto no solo se realiza para columnas sino para todo elemento estructural y algunos lo expresan como predimensionado y se trata de aplicar un conjunto de técnicas que permiten calcular elementos estructurales de manera sintetizada.
El objetivo de esta sintetización o reducción es el de encontrar unas magnitudes orientativas en cuanto a dimensiones o características del elemento que puedan servir para rectificar un proceso de diseño mediante el cálculo integral del elemento considerado.
En siguiente video del canal de Gustavo Héctor Soloa podemos observar el cálculo de una columna de madera, haz clic en la imagen:

Una viga es un miembro que soporta cargas transversales perpendiculares a su eje largo. Expresado de otra manera se denomina viga a aquellos elementos estructurales que normalmente se colocan en posición horizontal (aunque pueden ser de posición oblicua), que se apoyan sobre los pilares, son elementos destinados a soportar cargas.
El conjunto vigas-pilares forman los pórticos
La madera estructural se clasifica acorde con su tamaño y uso de la siguiente manera:

Las vigas pueden soportar fuerzas concentradas, fuerzas distribuidas y pares a lo largo de su longitud. Hasta este momento no hemos hablado de la forma como se les aplican las fuerzas a los elementos de una estructura en madera. A una viga también se le pueden aplicar fuerzas que están distribuidas sobre varios puntos de ella, o sea,fuerzas distribuidas. Una fuerza distribuida para efectos de cálculo puede ser sustituida por una fuerza concentrada tal como se describirá en el capitulo 5.
Igual que en el caso de una armadura, una viga está estáticamente determinada cuando el número máximo de incógnitas, debido a las reacciones en los apoyos o conexiones, es igual a tres.
En una viga considerada como un miembro que se somete a cargas transversales (cargas perpendiculares a lo largo de su eje), es necesario analizar entre otros:
Una viga de madera puede sufrir deformaciones por los esfuerzos causados por su propio peso, por las denominadas cargas muertas y por las cargas del entorno y normalmente se clasifican como:
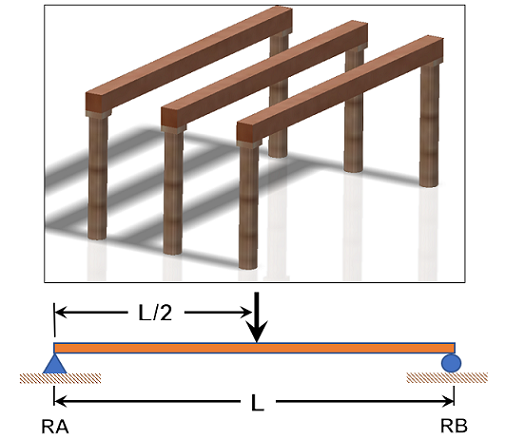
En la figura anterior hemos observado una viga simplemente apoyada y su diagrama de cuerpo libre cuya única carga es su propio peso, es una viga que está soportada por apoyos simples en los extremos y que permiten el libre movimiento de los mismos. También llamada viga simplemente apoyada.
Una viga saliente es aquella que solo tiene un extremo como apoyo. Ese apoyo necesariamente debe estar fijo porque debe servir como apoyo vertical para las cargas aplicadas con un momento de reacción opuesto al momento producido por las cargas.
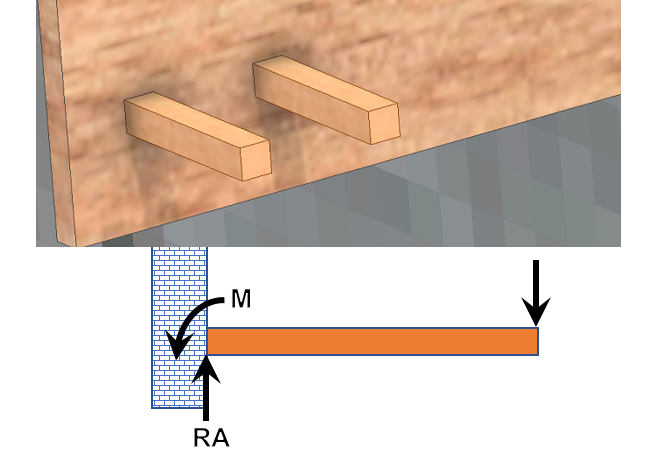
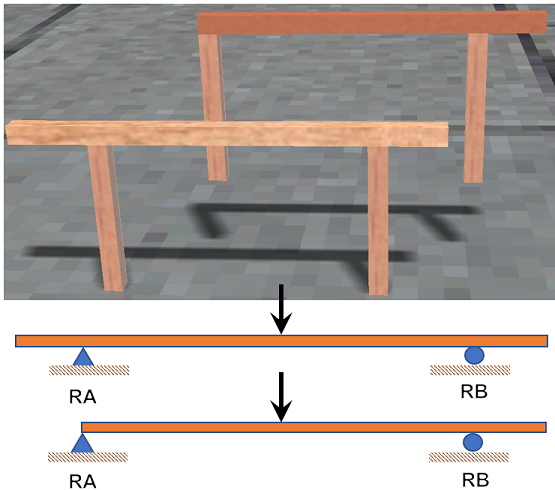
Normalmente en el estudio de la flexión y los esfuerzos se considera la homogeneidad del material, que las secciones son planas y que los esfuerzos y deformaciones son proporcionales a la distancia de la línea neutra (E.N.).
Esto no ocurre cuando el material no es homogéneo.
En las vigas compuestas se recurre a la transformación a una viga homogénea equivalente a la cual se le pueda aplicar los conceptos de la teoría de la flexión donde la deformación y la capacidad de carga no varíen.
Aquí observamos dos tipos de viga de madera laminada verticalmente, fabricada mediante la unión de diversos miembros menores mediante clavos o pernos, formando una viga de mayores dimensiones para emular una viga de acero compuesta por diferentes planchas rematadas o soldadas entre sí.
Las vigas compuestas se conocen con el nombre de viga ensamblada, viga de alma llena.
Las vigas pueden estar apoyadas o conectadas por medio de articulaciones, pasadores o rodillos.
Viga consistente en una tabla de madera laminada que sirve de alma a la que se le han fijado dos alas, también de madera, a lo largo de los cantos superior e inferior. También llamada viga de doble T.

Además de las vigas descritas en la construcción se encuentran:
Ahora que hemos estudiado los conceptos de columna y de vigas, veremos que en conjunto forman una plataforma y como se distribuyen las cargas que producen los esfuerzos en esos elementos, iniciemos de arriba hacia abajo:
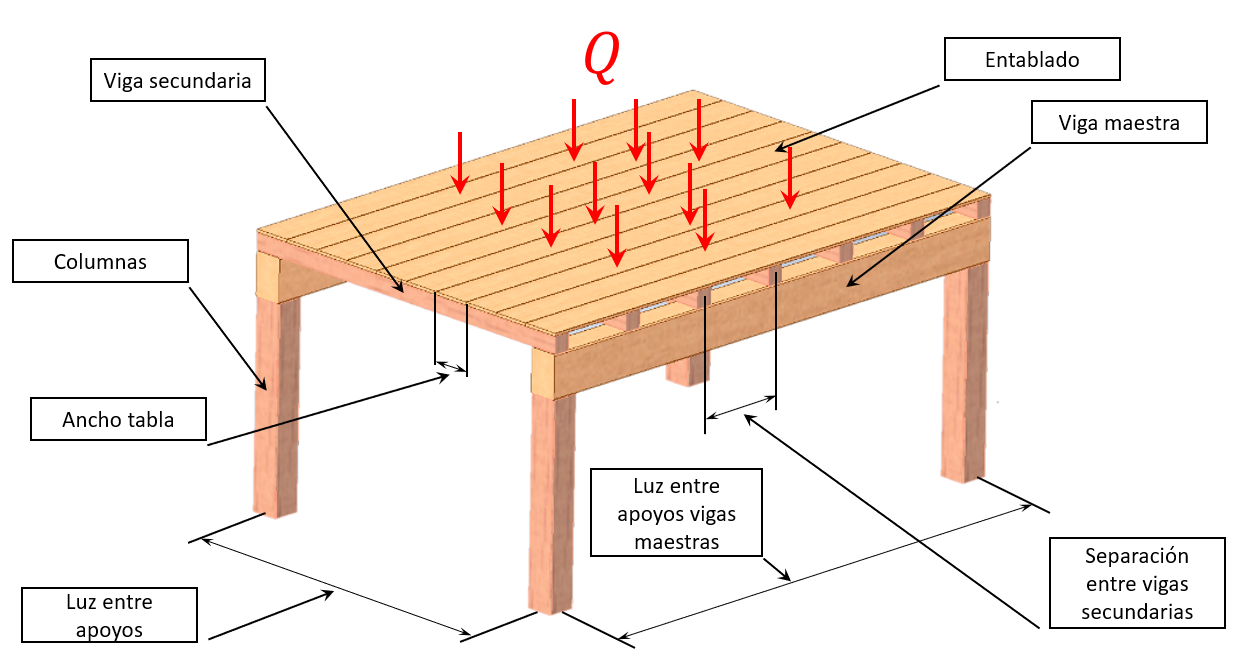
Sobre él se aplican las cargas de uso, ya sean cargas muertas o cargas vivas y para efectos de cálculo se consideran uniformemente distribuidas.
Las tablas se pueden considerar son vigas cuya sección es rectangular, tienen un ancho $b$ y una altura que corresponde al espesor de la tabla $a$.
La carga por metro lineal que toma cada tabla corresponde a la carga por metro cuadrado por el ancho tributario que es en este caso el ancho de la tabla es decir $b$.
Es de resaltar que para verificar la flexión y corte de la tabla se considerará que son elementos están simplemente apoyados en las vigas secundarias. $$\tag{5.7} Q_{tablas} \bigg(\frac{kgf}{m^2} \bigg) = q_{tablas} \bigg(\frac{kgf}{ml} \bigg)\cdot ancho_{tablas}\bigg(\frac{1}{ml} \bigg)$$
En estas se apoya el entablado. El sistema de tablas corresponde a vigas continuas de varios tramos, esto nos lleva a dimensionar o verificar con un momento que resulta crítico si se considera desde el punto de vista de la seguridad, ésta es una consideración ya que se debe tener en cuenta de la madera y su comportamiento viscoelástico
El momento flector está dado por la expresión: $$\tag{5.8} M_{kgf \cdot m} = \frac{q_{tablas(\frac{kgf}{ml})}}{8} \cdot S_{s(m)}^2$$
Donde $S$ es la distancia entre ejes de las vigas secundarias.
El esfuerzo de corte crítico es igua a: $$\tag{5.9} V_{kgf} = \frac{q_{tablas(\frac{kgf}{ml})}}{2} \cdot S_{s(m)}$$
Reciben la distribución de las cargas ejercidas sobre las vigas secundarias. Son vigas horizontales, que permiten sostener vigas secundarias o viguetas. También llamada jácena.
Los pilares son delgadas columnas verticales, que pueden soportar cargas pesadas o servir a los propósitos de visualización. Soportan cargas pesadas sobre ellos y transmiten el peso de las estructuras que están encima hacia otras estructuras que se encuentran debajo a través de la compresión.
Las cerchas de madera son un elemento constructivo que nacen como solución a tres necesidades fundamentales que surgen en el diseño de una cubierta de madera:
En esencia una cercha es una estructura normalmente diseñada para dos vertientes y por lo tanto es de forma triangualar compuesta por barras unidas mediante juntas o nodos, cada cecha que se diseña para que soporte las cargas que actuán sobre un plano.
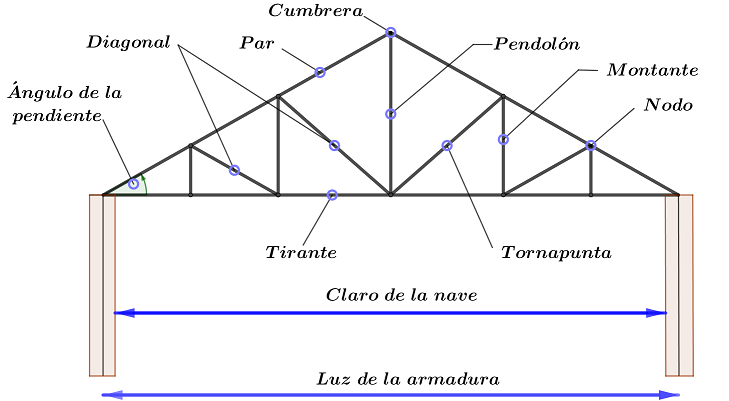
Es el elemento horizontal encargado de soportar y transferir las acargas a los apoyos, une el extremo inferior de los pares o cuerdas superiores impidiendo que se separen.
Existen los tirantes de resorte los que poseen incisiones en los extremos que permiten su rotura fácilmente al retirar los moldes.
Tambien existen los tirante ajustables: son metálicos y están formados por dos componentes trabados que permiten la adaptación a dos hojas situadas a diferente altura.
Una o más piezas inclinadas que junto con el tirante forman las aguas de la armadura.
Aunque en la vista frontal no se visualiza, es un elemento horizontal que une dos o más cerchas por el vértice superior
Elemento vertical que une el punto de la cumbrera con otro punto del tirante o cuerda inferior y cuya misión es evitar el pandeo.
Elementos verticales paralelos al peral y que unen un punto del par con otro punto de la cuerda inferior.
Elemento inclinado que tiene como función unir un punto del par con el tirante.
Distancia entre dos nodos adyacentes de la cuerda.Es una estructura en forma de red de tiras de madera o barras de metal, usada a modo de pantalla en construcciones ornamentales o para la ventilación. También llamada enrejado, enrejillado.
En la siguiente escena se visualizan esquemas de cerchas comunes:
Se denomina cubierta o techo a la superficie entramada inclinada que cierra una edificación por su parte superior, destinada a proteger su interior de los agentes climatológicos.
Es una cubierta cuya función es brindar una adecuada evacuación y al mismo tiempo asegura del agua de lluvia, proporcionando al mismo tiempo un aislamiento térmico acústico al conjunto así obtenido.
Los techos pueden ser permanentes o provisionales, dependiendo de los materiales de lo que estén elaborados.
Para la elaboración de los techos existen desde: paja, sácate, tejamil, palapa, tablas y piedras entre otros hasta materiales de ladrillo,madera, plástico, asbesto, acrílico, lamina y concreto.
Los techos en cuanto a su forma son: planos horizontales, planos inclinados y curvos.
Estos planos inclinados se manufacturan con una gran variedad de materiales, se clasifican de acuerdo con el número y forma de planos inclinados que conforman la edificación:
Se aplican en edificios rectangulares y se forman con un plano inclinado.
Este tipo de techo de madera a dos aguas, si se le mira por el lateral se verá que forma un triángulo.
Las dos vertientes son aplicadas generalmente a estructuras aisladas de planta cuadrada, rectangular o trapezoidal y están formadas por dos planos inclinados que se cortan superiormente en una arista llamada cumbrera.
Entre la cumbrera y la base plana que forman los dos faldones, se puede utilizar o para crear una cámara de ventilación para la vivienda. También se puede utilizar como parte de habitaciones de las casas con techos inclinados.
Normalmente se proyectan más allá de la estructura para conformar el alero que facilita el desague de las aguas pluviales de la planta de conjunto de la edificación.
Son utilizados en construcciones rectangulares y están formadas por cuatro vertientes que se intersectan, dan lugar a aristas salientes que son divisorias de aguas o aristas entrantes, cuando se retienen las aguas de dos vertientes por el encuentro de dos secciones de la estructura formando una L.
Dependiendo de la magnitud de la cubierta puede existir con mayor cantidad de vertientes, en el mosaico con imágenes tomadas de https://free-images.com/ podemos observar cubiertas con diferente número de vertientes:

Los techos se conocen como planos inclinados. Cuando la pendiente es menor de 2:12, se dice que el techo es plano.
Como techos inclinados se conocen todos aquellos que exceden esta relación. Con mucha frecuencia la inclinación de un techo se determina por consideraciones estéticas o bien puede ser que la inclinación del techo este limitada por el tipo de material generalmente por consideraciones económicas. En la siguiente tabla se pueden observar algunos datos con respecto a las inclinaciones de los techos.
Tabla 9. Pendientes en techos.
| Pendientes en techos | ||||||
|---|---|---|---|---|---|---|
| Inclinación | $\frac{1}{8}$ | $\frac{1}{6}$ | $\frac{1}{5}$ | $\frac{1}{4}$ | $\frac{1}{3}$ | $\frac{1}{2}$ |
| Ángulo | $14°\space 3'$ | $18° \space 26'$ | $21° \space 48'$ | $26° \space 34'$ | $33° \space 41'$ | $45° \space 0'$ |
| Pendiente | $0.25$ | $0.33$ | $0.40$ | $0.50$ | $0.66$ | $1.00$ |
Las estructuras de madera como cualquier otro material y elemento constructivo en la mecánica de materiales, deben diseñarse para resistir las fuerzas sísmicas , con las combinaciones de carga para esfuerzos admisibles, y para el diseño de los elementos estructurales.
En el diseño estructural de madera sismo resistente, las fuerzas dependen del sitio de implantación geográfica del proyecto, con las propiedades inherentes al tipo de suelo de emplazamiento y la buena distribución interna de masa y rigidez de los elementos que conforman la estructura de la construcción.
Una estructura de madera debe ser adecuada para soportar todas las cargas a las que pueda estar sometida durante su vida útil, aquí es donde la seguridad juega un papel importante ya que cuando existan deflexiones y vibraciones no se traduzcan en daños visibles. Diseñar estructuras requiere tener en cuenta un factor de seguridad por la incertidumbre existente por las furzas de la naturaleza o cambios repentinos por variación de cargas, entre estas incertidumbres tenemos:
Las cargas estructurales se clasifican acorde a su caráter y su permanencia en el tiempo, las más comunes son:
De acuerdo al uso de la estructura diseñada las cargas muertas pueden incluir los sistemas de ventilación y aire acondicionado, las instalciones eléctricas y sanitarias,los equipos de cocina como lavaplatos y refrigeradoras.
Al calcular la magnitud de las cargas vivas en una estructura en madera es necesario tener en cuenta el uso futuro de la misma ya que pueden estar sujetas a modificaciones por el anexo de nuevos elementos, tal es el caso de la división de una habitación para albergar un nuevo individuo (más carga viva).

Analicemos ahora un poco más las cargas vivas:
Las cargas causadas por impacto ocasionan vibración y ocurren por el desprendimiento de objetos del entorno como árboles y postes de líneas de transmisión de energía eléctrica entre otros lo que ocasionan cargas mayores a las previstas al diseñar la estuctura.
Las cargas de impacto son equivalentes a la diferencia entre la magnitud de las cargas reales y la magnitud de las cargas en el caso de que estas se considerasen cargas muertas, expresado de otra forma son cargas con efectos dinámicos.
En el caso de las cargas estáticas, esos efectos son de corta duración y estarían exentas de cualquier analísís estructural dinámico y suelen calcularse porcentualmente como si las cargas se aplicasen sin brusquedad y de manera gradual.
La carga viva es la carga a la que se somete una estructura además de su propio peso. En otras palabras, es el peso adicional que se coloca en una estructura además del peso de la estructura en sí.
Para este tipo de cargas, la pendiente del mismo afecta la cantidad de carga que puede colocarse sobre el techo realmente. Al incrementarse la pendiente, la magnitud de la carga que puede colocarse sobre el techo, antes de que empice a resbalar disminuye, hay que tenr en cuenta que a medida que se incrementa el área del del techo que contribuye a soportar la carga sobre un elemento de soporte, es menos probable que el área total del techo se encuentre cargada totalmente.
Las cargas vivas máximas en los techos ocurren por operaciones de mantenimiento y no ocupan toada el área del mismo a diferencia de las cargas por nieve o por lluvia que pueden realizar incrementos significativos en la carga viva.
Existen normas que especifican las cargas vivas mínimas para los techos como la Sociedad Estadounidense de Ingenieros Civiles (en inglés American Society of Civil Engineers (ASCE).
De la norma ASCE 7-05 elaborada por la Sociedad Americana de Ingenieros Civiles (ASCE) presentamos los siguientes valores máximos para dos tipos de pendiente de techo:
La pendiente o inclinación de un techo se puede expresar de diferentes maneras. Un método común es expresarla en términos de la relación del peralte al claro.
Por ejemplo, una inclinación de un medio, indica que la armadura tiene como peralte la mitad del claro; un claro de 14.6 m (48 ft) un peralte de 3.6 m (12 ft) se conoce como una inclinación de un cuarto.
La inclinación se puede expresar a partir del ángulo que la cuerda superior hace con la cuerda inferior, por ejemplo 30° o 45° de inclinación.
Para armaduras simétricas, la base es la mitad del claro y frecuentemente, la inclinación se expresa como la relación del peralte a la base, generalmente en metro/metro.
Frecuentemente la inclinación de un techo se determina por estéticas o bien puede ser que la inclinación del techo este limitada por el tipo de material, generalmente por situaciones económicas.
Los techos con inclinaciones fuertes deben resistir mayores cargas de viento y requieren el uso de una mayor cantidad de material para cubrir el techado, mientras que las inclinaciones menos fuertes originan mayores esfuerzos en los miembros de la armadura.
El viento constituye la principal carga viva para cualquier región y normalmente se consideran algunos los siguientes aspectos para su cálculo:

Determinar la carga ejercida por viento sobre una columna delgada de madera de $1.20 m$ de altura y $2 cm$ de díametro, sabiendo que el viento que sopla a $140 \frac{km}{h}$
El viento ejerce una presión extraordinaria sobre los objetos que encuentra a su paso como edificios, árboles y vallas publicitarias entre otros, esa fuerza aumenta con el cuadrado de la velocidad del viento o del objeto.
Esa fuerza está dada por la expresión (fórmula práctica):
$$\tag{6.1} F = A *1.22*V^2 $$Donde:
$F = Resistencia \space al \space avance, \space o \space ejercida \space por \space el \space viento$
$ A = Proyección \space área \space del \space frente \space de \space ataque$
$ V = Velocidad \space del \space viento \space en \space m/s$
El producto $1.22*V^2 = P$ es la presión del viento expresada en $N/m^2$
Calculemos las unidades del problema: $$A = 1.2m*2cm*\frac{m}{100cm}= 0.24m^2$$ $$V = 140 \frac{km}{h}* \frac{1000m}{km}*\frac{h}{3600s}= 38.88 \frac{m}{s}$$ $$P = 1.22 * \Big(38.88 \frac{m}{s}\Big)^2 = 1844.21 \frac{N}{m^2}$$ $$F = 0.24m^2* 1844.21 \frac{N}{m^2} = 442.61 N$$
Este es un cálculo simplificado, en otro contexto se deben tener en cuenta otros aspectos: tabla de la figura 2.8.
En la sección 5.2 establecimos los aspectos que caracterizan los postes o columnas de madera, la National Design Specification for Wood Construction conocida cono DNS nos presenta las siguientes fórmulas para el cálculo básico de columnas:
$$\tag{6.2} P = \Big( {F_c}^*\Big)\Big( C_p\Big) \Big(A \Big)$$
Donde:
${F_c}^* = Valor \space de \space diseño \space admisible \space para \space compresión \space paralela \space a \space \\ \space \space \space \space \space \space \space \space \space \space \space \space la \space veta$
$ A = Área \space de \space la \space sección \space transversal \space de \space la \space columna$
$ V = Velocidad \space del \space viento \space en \space m/s$
Donde:
$K_{cE} = Valor \space constante$
$ E = Módulo \space de \space elasticidad \space de \space la \space madera $
$ L_e = Longitud \space efectiva \space viento \space en \space m/s$
$ d = Ancho \space de \space la \space columna$
"$K_{cE}$ es igual $0.3$ para maderas clasificadas visualmente y, 0.418 para maderas clasificadas en máquina de esfuerzos y para piezas de madera laminada pegada.."
" La longitud efectiva se refiere a la altura de la columna sin arrostramiento, modificada por cualquier factor para condiciones de apoyo."
"El ancho de la columna es la dimensión de la sección transversal en la cual se presenta el pandeo."
Donde:
${F_c}^* = Valor \space del \space esfuerzo$
$ F_{CE} = Esfuerzo \space de \space pandeo \space de \space Euler, \space ecuación \space 6.3 $
$ c = constante$
"c es igual a 0.8 para madera aserrada, 0.85 para columnas circulares y 0.9 para piezas de madera pegadas."
Una columna es un elemento que está sometido a compresión y debe diseñarse bajo el siguiente procedimiento:

Vamos a determinar las características de diseño de una columna bajo la norma NSR-10 para que dure cerca de 10 años y con las siguientes especificaciones:
El diseño estructural de la columna se inicia con la definición de los factores de corrección especificados para el método ASD tal como se específica en la tabla de la figura 2.8:
Como paso inicial se debe definir el esfuerzo admisible para la compresión ($Fc$), el cual dependerá principalmente del tipo de madera con el cual se desea realizar el elemento.
Para ello se selecciona de la tabla de esfuerzos admisibles de NRS-10 que hemos presentado en la página 76.
Para el diseño que nos ocupa tenemos que $ F_c = 22.0 \space MP_a$
A continuación se establece el coeficiente de modificación por duración de la carga ($C_D$), también con valores de la NSR-10:
Tabla 10. Duración de la carga.
| Duración de la carga $C_D$ | ||||||
|---|---|---|---|---|---|---|
| $Duración \;carga$ | $F_b$ | $F_t$ | $F_c\space ||$ | $F_p\space \perp$ | $F_v$ | $Carga\;\;típica$ |
| Permanente | $0.90$ | $0.90$ | $0.90$ | $1.00$ | $0.90$ | $Muerta$ |
| Diez años | $1.00$ | $1.00$ | $1.00$ | $1.00$ | $1.00$ | $Viva \space de\\Ocupación$ |
| Dos meses | $1.15$ | $1.15$ | $1.15$ | $1.00$ | $1.15$ | |
| Siete días | $1.25$ | $1.25$ | $1.25$ | $1.00$ | $1.25$ | $Construcción$ |
| Diez minutos | $1.60$ | $1.60$ | $1.60$ | $1.00$ | $1.60$ | $Viento \space y\\Terremoto$ |
| Impacto | $2.00$ | $2.00$ | $2.00$ | $1.00$ | $2.00$ | $Impacto$ |
Para nuestra columna $C_D = 1.0$
Tabla 11. Coeficiente por contenido de humedad.
| Coeficiente del contenido de humedad $C_m$ | |||
|---|---|---|---|
| $Durante \space la\\construcción$ | $En \space servicio$ | $Esfuerzos \\ admisibles$ | $Módulos \space de \\elasticidad$ |
| $CH \space c > 19\%$ | $CH \space s > 19\%$ | $CH \space > 19\%$ | $CH \space > 19\%$ |
| $*CH \space c> 19\%$ | $*CH \space s \leq 12\%$ | $*CH \space = 12\%$ | $*CH \space = 12\%$ |
| $CH \space c \leq 12\%$ | $CH \space s \leq 12\%$ | $CH \space = 12\%$ | $CH \space = 12\%$ |
| $CH \space c \leq 12\%$ | $CH \space s > 19\%$ | $CH \space > 19\%$ | $CH \space = 12\%$ |
Hay que recalcar que el segundo renglón de la siguiente tabla se utiliza si: a) Espesor de la Madera no excede de 50 mm. b) La carga total de diseño se aplique cuando CH sea menor del 12% y las cargas no originen esfuerzos efectivos mayores a los admisibles en condición verde.
Tabla 12. Coeficiente de afectación para esfuerzos.
| Coeficientes de afectación para esfuerzos $F_i$ y módulos de elasticidad $E_i$ | |||
|---|---|---|---|
| $Esfuerzos$ | $Identificación$ | $CH \space \leq 12 \%$ | $CH \space > \space 19\%$ |
| $Flexión$ | $F_b$ | $1.0$ | $0.75$ |
| $Tensión$ | $F_t$ | $1.0$ | $0.75$ |
| $Compresión \space ||$ | $F_c$ | $1.0$ | $0.70$ |
| $Compresión \space \bot$ | $F_p$ | $1.0$ | $0.80$ |
| $Cortante$ | $F_v$ | $1.0$ | $0.80$ |
| $Módulos \\ elasticidad$ | $E_{0.5}$ | $1.0$ | $0.80$ |
| $E_{0.05}$ | $1.0$ | $0.80$ | |
| $E_{min}$ | $1.0$ | $0.80$ | |
Para una humedad mayor de 19% el factor a emplear será $C_m = 0.75$ para compresión paralela ($F_c$), el cual afectará el esfuerzo admisible y el módulo de elasticidad.
Tomaremos el valor correspondiente a la compresión y verificando en cuál de los rangos de temperatura se encuentra el elemento.
Tabla 13. Variación de las propiedades mecánicas por temperatura.
| Coeficiente de modificación por temperatura $C_t$ | ||||
|---|---|---|---|---|
| $Parámetros \space \\ diseño$ | $Condiciones \space \\ servicio$ | $T ≤ 37.8°C$ | $37.8°C < T ≤ 51.7°C$ | $51.7°C< T ≤ 65°C$ |
| $F_t , E_{0.5} , E_{0.05} , E_{min}$ | $Húmedo/Seco$ | $1.0$ | $0.9$ | $0.9$ |
| $Fb , Fv , Fc , Fc⊥$ | $Seco$ | $1.0$ | $0.8$ | $0.7$ |
| $Húmedo$ | $1.0$ | $0.7$ | $0.5$ | |
En la tabla se observa que este factor también afecta a los módulos de elasticidad promedio ($E_{0.5}$), mínimo ($E_{min}$) y al percentil 5º ($E_{0.05}$).
Nuestros datos nos dicen que $C_t = 1.0$
Este coeficiente se refiere a consideraciones de la forma del elemento, tanto de ancho ($b$), como de alto ($d$) , como de largo (A) , de los elementos rectangulares sometidos a flexión, tensión o compresión paralela. Los valores de $F_b$ , $F_t$ y $F_c$ , se multiplicarán por los valores de las tablas donde se expresan las dos componentes del factor y que está dado por la ecuación: $$\tag{6.6} C_F = (C_d)(C_l)$$
Donde:
$C_d = Valor \space de \space altura$
$C_l = Valor \space de \space longitud \space o \space largo $
Tabla 14. Factor de ajuste $C_d$
| $Factor \space de \space ajuste \space C_d$ | ||||
|---|---|---|---|---|
| $Madera \\ aserrada\\ visualmente \\ seleccionada\\ como \space E.S.$ | (d) mm | $F_b$ | $F_t$ | |
| (b) mm | (b) mm | |||
| 50 -75 | 100 | |||
| 50 a 100 | 1.15 | 1.15 | 1.15 | |
| 127 | 1.10 | 1.10 | 1.10 | |
| 150 | 1.10 | 1.10 | 1.10 | |
| 203 | 1.10 | 1.10 | 1.0 | |
| 254 | 1.00 | 1.00 | 1.00 | |
| 300 | 1.00 | 1.00 | 1.00 | Construcción normal E.N | 50 a 100 | 1.00 | 1.00 | 1.00 |
Según la tabla el valor es $C_d = 1.15$
Tabla 15. Factor de ajuste $C_l$
| $Factor \space de \space ajuste \space C_l$ | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A (m), longitud | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| $C_t$ A tensión, flexión | 1.00 | 0.94 | 0.90 | 0.87 | 0.84 | 0.82 | 0.80 | 0.78 | ||
| $C_{fc}$ Compresión | 1.00 | 0.97 | 0.95 | 0.93 | 0.92 | 0.91 | 0.90 | 0.89 | ||
$C_l = 1.00$
Con los valores de $C_d$ y de $C_l$ podemos aplicar la ecuación $6.6$ $$C_F = 1.15* 1.0 = 1.15$$
Dado que no se especifica incisión alguna en nuestro enunciado no es necesario realizar operación alguna, por lo tanto $C_{in} = 1.00$ ya que la norma específica que los valores de esfuerzos admisibles y módulos de elasticidad, serán multiplicados por el factor de incisión ($C_{in}$) cuando se hagan incisiones en los elementos de madera.
Para incisiones excediendo los límites indicados, el coeficiente ($C_{in}$) se determinará por ensayos, o por cálculo, usando la sección reducida para incisiones. Estos valores se aplicarán para madera aserrada.
Tambien conocido como coeficiente de modificación por acción conjunta. La norma expresa que los esfuerzos admisibles podrán incrementarse en un 15%, cuando exista una acción de conjunto garantizada de tres o más elementos de igual rigidez.
Para elementos de madera de 50 a 100 milímetros de espesor , que se encuentren en contacto o espaciados no más de 61 centímetros, como en el caso de viguetas, pies derechos de entramados, entablados, cuerdas de cercha, viguetas de techo, siempre que estén unidos por pisos o techos u otros elementos.
Como estamos calculando una sola columna, $C_r = C_F = 1.15 $
Determinamos el valor de la longitud efectiva $l_e$, suponiendo que nuestra columna estará impedida para desplazarse en ambos extremos y uno de ellos impedido de rotar, utilizamos la ecuación:
Donde:
$L_e $ = Longitud efectiva en mm.
$K_e $ = Coeficiente de longitud efectiva.
$L_u $= Longitud no soportada lateralmente de la columna en la dirección considerada en mm.
Tabla 16. Coeficientes de longitud efectiva de columna.
| Coeficientes de longitud efectiva de columna $k_e$ | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| $Condición \space de \space los \\ apoyos$ | $k_e1 \\Teórico$ | $k_e2 \\Recomendado$ | ||||||||
| Empotradas en ambos extremos | 0.50 | 0.65 | ||||||||
| Impedido de desplazarse en ambos extremos y uno de ellos impedido de rotar | 0.70 | 0.85 | ||||||||
| Articulado en ambos extremos | 1.00 | 1.00 | ||||||||
| Empotrado en un extremo y el otro impedido de rotar pero libre de desplazamiento | 1.00 | 1.20 | ||||||||
| Empotrado en un extremo y el otro parcialmente libre de rotar y libre de desplazamiento | 1.50 | 1.50 | ||||||||
| Articulado en un extremo y el otro impedido de rotar pero libre de desplazamiento | 2.00 | 2.40 | ||||||||
| Empotrado en un extremo y el otro libre de rotar y libre de desplazamiento | 2.00 | 2.10 | ||||||||
La norma nos amplía la tabla especificada en la página 131. Teniendo en cuenta las condiciones del problema, el valor $l_u = 3m = 3000 mm$
Por lo tanto la longitud efectiva será: $$l_e = 0.85 \cdot 3m = 2.55m = 2550mm $$
Ahora calculemos la relación de esbeltez que habiamos definido en la ecuación $4.1$ $$\lambda = \frac{2550mm}{100mm} = 25.5$$
El valor debe ser $\lambda \leq 50$, excepto durante la construcción que podría ser $\lambda \leq 75$
Determinemos el esfuerzo crítico $F_{CE}$ dado por la expresión: $$\tag{6.8} F_{CE} = \frac{0.822 \cdot E'_{min}}{\lambda^2}$$
Donde:
$F_{CE}$ = Esfuerzo critico de pandeo para elementos en compresión. Expresado en ($MPa$)
$E'_{min}$ = Módulo de elasticidad mínimo modificado, en $MPa$
$\lambda$ = Parámetro de esbeltez
Calculemos $E_{min}$ modificado el cual se utilizará para calcular los coeficientes de estabilidad de vigas ($C_L$) y de columnas ($C_p$ ) $$\tag{6.9} E'_{min} = E_{min} \cdot C_t \cdot C_{in}$$
Para los grupos estructurales se tiene la siguiente tabla expresada en $MPa$:
Tabla 17. Módulos de Elasticidad Longitudinal.
| Módulos de Elasticidad Longitudinal $E_i$ | |||
|---|---|---|---|
| $Grupo$ | $Módulo \space promedio \\ E_{0.5}$ | $Módulo \space 5° \space percentil \\ E_{0.05}$ | $Módulo \space mínimo \\ E_{min}$ |
| ES1 | 18000 | 13250 | 7130 |
| ES2 | 18000 | 13250 | 7130 |
| ES3 | 14000 | 11000 | 5500 |
| ES4 | 12500 | 10000 | 5000 |
| ES5 | 11200 | 8250 | 4435 |
| ES6 | 9000 | 6500 | 3564 |
Por lo tanto: $$ E'_{min} = 7130\space MPa \cdot 1.00 \cdot 1.00 = 7130 \space MPa$$
Nuestro esfuerzo crítico será: $$F_{CE} = \frac{0.822 \cdot 7130 \space MPa}{25.5^2} = 9.01 \space MPa$$
El esfuerzo admisible de compresión paralelo al grano (${F_c}^*)$: $$\tag{6.10} {F_c}^* = F_c \cdot C_D \cdot C_m \cdot C_t \cdot C_F \cdot C_{in} \cdot C_r$$
Por lo tanto tenemos: $${F_c}^* = 22.00 \cdot 1.00 \cdot 0.75 \cdot 1.00 \cdot 1.15 \cdot 1.00 \cdot 1.15 = 21.82 MPa$$
Con los valores obtenidos y la ecuación $6.4$ calculamos el coeficiente de estabilidad de nuestra columna:
Con este valor podemos determinar el esfuerzo de compresión modificado como expresa la ecuación $6.5$ $$F'_c = 22.00 \cdot 1.00 \cdot 0.75 \cdot 1.00 \cdot 1.15 \cdot 1.00 \cdot 1.15 \cdot 0.276 = 6.02 MPa$$
Calculemos la carga admisible que puede soportar la columna: $$\tag{6.11} P_a = F'_c \cdot A_n$$
Donde:
$P_a$ = Fuerza o carga admisible de la columna en N.
$F'_c$ = Esfuerzo admisible modificado a compresión paralela al grano en $MPa$
$A_n$ = Área neta de la columna en $mm^2$ $$ P_a = 6.02 \space MPa \cdot 10000 \space mm^2 = 60200 \space N > 28000 \space N$$
Podemos decir que nuestra columna satisface las condiciones, solo nos queda por verificar el valor del acortamiento de los elementos sometidos a compresión mediante: $$\tag{6.12} \Delta dc = \frac{P \cdot l_u}{An \cdot E'_{0.5}}$$
Donde:
$\Delta dc$ = Acortamiento en el sentido paralelo a las fibras, en $mm$
P = Carga axial actuante en N
$l_u$ = longitud no soportada de la columna en $mm$
$An$ = Área neta de la sección de la columna en $mm^2$
$E'_{0.5}$ = Módulo de elasticidad $E_{0.5}$ modificado paralelo a las fibras en $MPa$
Calculamos el módulo de elasticidad modificado $$\tag{6.13} E'_{0.5} = E_{0.5} \cdot C_m \cdot C_r \cdot C_{in}$$ $$E'_{0.5} = 18000 \space MPa \cdot 0.75 \cdot 1.00 \cdot 1.00 = 13500 \space MPa$$
El acortamiento paralelo a las fibras es: $$ \Delta dc = \frac{28000 \space N \cdot 3000 \space mm}{10000 \space mm^2 \cdot 13500 \space MPa} = 0.62 \space mm$$
El acortamiento debido a la compresión no es signficativo para los 10 años para los que se preve la duranción de la columna.
Los esfuerzos cortantes los producen las fuerzas cortantes que son la suma algebraica de las fuerzas externas en un elemento en cualquiera de los lados que determinan una sección del elemento a considerar y que son perpendiculares a su eje tal como se aprecia en la escena de la próxima página.
Es el esfuerzo resultante de las tensiones paralelas a las fibras a la sección transversal de un elemento prismático. Casos:
El modelo presentado en la escena anterior es un clásico de los libros de mecánica de materiales dónde se calcula el área requerida para soportar un esfuerzo dado por un pegamento.
El esfuerzo cortante simple está determinado por la expresión: $$\tag{6.14} \tau=\frac{F}{A}$$
La hipótesis más simple que puede hacerse respecto a la deformación de una rebanada de una pieza prismática sometida a cortadura es que “las secciones transversales permanecen planas y se mueven paralelas a sí mismas en la dirección del esfuerzo cortante”
Un problema clásico de cortante se presenta en la figura donde nos piden calcular los esfuerzos cortantes en dos piezas con medidas en milímetros:
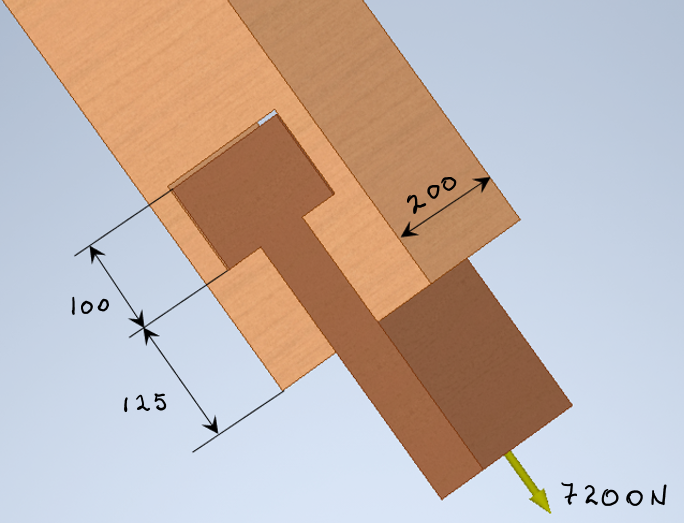
En la madera es necesario considerar los esfuerzos máximos de corte paralelo a las fibras, estos deben ser calculados en secciones a una distancia del apoyo igual a la altura $(d)$, de la viga, excepto en voladizos para los que los esfuerzos máximos serán evaluados en la cara del apoyo.
El máximo esfuerzo cortante paralelo a las fibras $fv $ se determina teniendo en cuenta la distribución no uniforme de estos esfuerzos en la sección, no debiendo ser mayor que el esfuerzo admisible para corte paralelo a las fibras $Fv$ y que se modifica por los valores de la siguiente tabla:
Tabla 18. Coeficientes de corrección $C_c \space de \space E_{0.5}$
| $Coeficientes \space de \space corrección \space C_c \space de \space E_{0.5} $ | ||||
|---|---|---|---|---|
| $l:d$ | $E:G = 15$ | $E:G =16$ | $E:G = 20$ | $E:G = 25$ |
| 7 | 0.760 | |||
| 10 | 0.8741 | 0.8389 | 0.8065 | |
| 12 | 0.9091 | 0.900 | 0.8824 | 0.8571 |
| 14 | 0.9316 | 0.9108 | 0.8909 | |
| 16 | 0.9467 | 0.9302 | 0.9143 | |
| 18 | 0.9547 | 0.950 | 0.9441 | 0.9310 | 20 | 0.9653 | 0.956 | 0.9542 | 0.9434 |
El esfuerzo al corte en la dirección perpendicular a las fibras es mucho mayor, y por lo tanto no requiere de verificación. El esfuerzo cortante origina tensiones tangenciales que actúan sobre las fibras de la madera según diversos modos.
En las piezas sometidas a flexión y a cortante, las tensiones que intervienen son conjuntamente las de cortadura y deslizamiento. Sus valores característicos (por deslizamiento) varían entre 1,7 y 3,0 N/mm^2 en las especies y calidades utilizadas habitualmente en la construcción.
Las tensiones tangenciales por rodadura de fibras sólo se producen en casos muy concretos, como son las uniones encoladas entre el alma y el ala de una vigueta con sección en doble T. El valor de la resistencia por rodadura es del orden del 20 al 30% de la resistencia por deslizamiento.
Es un elemento estructural de gran extensión y grosor que sirve para sostener los techos de las construcciones o asegurar la estructura tal como se definió en la sección $5.4$, ahora veremos como realizar cálculos típicos de columnas.
La viga es un elemento que funciona a flexión, cuya resistencia provoca tensiones de tracción y compresión.
En la siguiente escena podemos visualizar el cálculo del entablado de una plataforma teniendo en cuenta el peso de la estructura misma con diferentes tipos de madera y las cargas muertas o vivas que ha de soportar dicho entablado.
Esta es la imagen de una plataforma con todos sus componentes, en la escena podrás variar el ancho de las tablas, la longitud de las mismas, su cantidad y espesor. A partir de estos datos podras visualizar los cálculos dependiendo de la madera elegida, ello nos brindará herramientas para entender los cálculos que se pueden realizar mediante software:
Cálculos como los realizados en la plataforma anterior y recordando que una plataforma es un entramado horizontal compuesto de vigas principales y secundarias, nos permite determinar las reacciones en las vigas, que es el principio de acción y reacción corresponde a la tercera ley de Newton.
“Todo cuerpo A que ejerce una fuerza sobre un cuerpo B experimenta una fuerza de igual intensidad en la misma dirección pero en sentido opuesto”
Todas las vigas deben estar apoyadas de una manera estable para que se mantengan en equilibrio. Es necesario que todas las cargas y momentos externos deben ser resistidos por uno o más apoyos. Los diferentes tipos de apoyos ofrecen diferentes tipos de reacciones:
Un apoyo simple se caracteriza porque puede resistir únicamente fuerzas que actúan perpendiculares a la viga
Un apoyo fijo es aquel que se mantiene firmemente sujeto, de tal modo que resiste fuerzas en cualquier dirección y que también impide la rotación de la viga en el apoyo
Este tipo de apoyo proporciona un soporte adecuado y al mismo tiempo permite que la viga se flexione libremente. La junta de pasador resistiría cualquier fuerza horizontal.
En el cálculo de vigas de madera es necesario hablar de tres elementos básicos de la mecánica de materiales:
Se dice que un cuerpo rígido se halla en equilibrio cuando la suma de todas las fuerzas externas que actúan sobre él es igual a cero, y la suma de todos los momentos producidos por estas fuerzas, respecto a un punto ubicado dentro o fuera del cuerpo, así como los momentos de par, también es igual a cero. Dicho de otra manera se requiere que la fuerza resultante y el momento resultante actuando sobre el cuerpo sean iguales a cero.
Ecuaciones vectoriales: $$\tag{6.15} \displaystyle\sum \hat{F} = 0 \longrightarrow \displaystyle\sum F_x \hat{i} + \displaystyle\sum F_y \hat{j} + \displaystyle\sum F_z \hat{k} = 0$$ $$\tag{6.16} \displaystyle\sum \hat{M} = 0 \longrightarrow \displaystyle\sum M_x \hat{i} + \displaystyle\sum M_y \hat{j} + \displaystyle\sum M_z \hat{k} = 0$$
Igualmente se dispone de tres ecuaciones escalares de equilibrio y tres ecuaciones escales de momentos que nos han de permitir solucionar las incognitas que surgen en los diagramas de cuerpo libre (DCL). $$\tag{6.17} \displaystyle\sum F_x = 0 \space \space \space \space \space\displaystyle\sum F_y = 0 \space \space \space \space \space \displaystyle\sum F_z = 0 $$
También conocido como flexor, o momento de flexión, se refiere a un momento de fuerza resultante de una distribución de tensiones sobre una sección transversal de un prisma mecánico flexionado o una placa que es perpendicular al eje longitudinal a lo largo del que se produce la flexión.
En el diseño de estructuras es una solicitación típica en vigas y pilares y también en losas ya que todos estos elementos suelen deformarse predominantemente por flexión.
El momento flector puede aparecer cuando se someten estos elementos a la acción de un momento (torque) o también de fuerzas puntuales o distribuidas.
Los signos que determinan los momentos flectores en vigas como positivos o negativos dependen del efecto que dicho momento produce , cuando el efecto del momento produce tensiones en las fibras inferiores de la viga se habla de un momento positivo, mientras que si el momento produce tensiones en las fibras superiores de la viga se hablara que se produjo un momento negativo.
Esos momentos se representan en un diagrama de momento flector el que, para elementos lineales perpendiculares tipo barra, el momento flector se define como una función a lo largo del eje neutro del elemento, donde "x" representa la longitud a lo largo de dicho eje.
Definido de esta manera y en condiciones de equilibrio coincide con la resultante de fuerzas de todas las fuerzas situadas a uno de los dos lados de la sección en equilibrio en la que pretendemos calcular el momento flector.
Debido a que un elemento puede estar sujeto a varias fuerzas, cargas distribuidas y momentos, el diagrama de momento flector varía a lo largo del mismo. Asimismo las cargas estarán completadas en secciones y divididas por tramos de secciones.
En una pieza de plano medio, si se conoce el desplazamiento vertical del eje baricéntrico sobre dicho plano el momento flector puede calcularse a partir de la ecuación de la curva elástica: $$\tag{6.19} M_f(x) = \frac{d}{dx} \Big(EI_f \frac{d}{dx}\Big)$$
Donde:
$y(x)$ = Es el desplazamiento vertical o desplazamiento de la curva elástica.
$E$ = Es el módulo de Young del material de la viga.
$I_{f}$ = Es el segundo momento de área de la sección transversal de la viga.
Existen dos maneras básicas de calcular estos momentos flectores:
Empleado para construir diagramas consiste en realizar cortes imaginarios a lo largo de un elemento y aplicar las ecuaciones del equilibrio. En una viga, se supone un corte imaginario y como la pieza continúa en su lugar, se puede considerar que se encuentra empotrado a la otra parte de la viga, por lo que existen reacciones que impiden el desplazamiento.
En el caso del momento, es posible realizar una suma de momentos en el punto en el que se realizó el "corte".
Se debe contar cada fuerza, carga distribuida y momento hasta donde se realizó el corte. En el método de secciones es necesario realizar un corte por cada factor que cambie la distribución del diagrama de momentos.
Empleando funciones discontinuas se construye una función continua a tramos. Cuando un elemento está sometido a varias fuerzas, cargas y momentos la cantidad de cortes que serían necesarios vuelve al procedimiento tedioso y repetitivo.
Al trabajar de esta manera, la ecuación de momento aumenta un término por cada corte que se realiza debido a la nueva fuerza, carga distribuida o momento que se agrega. El uso de las funciones discontinuas consiste en agregar funciones rampa que se "activen" cuando se llega a cierta posición (donde antes se colocaba el corte).
Estas funciones se definen como: $$\tag{6.20} (x-a)^n = \begin{cases} 0 &\text{si } x \text{\textless} {a} \\ (x-a)^n &\text{si} \space x \geq {a} \end{cases}$$
Son las fuerzas que generan el esfuerzo cortante, de corte, de cizalla o de cortadura, este es un esfuerzo interno que resulta de las tensiones paralelas a la sección transversal de un prisma mecánico como las vigas e incluso como en los postes.
La construcción de los diagramas de Momento flector y fuerza cortante son importantes al realizae cálculos de vigas de cualquier material.
En el siguiente video de veremos la construcción de estos diagramas, ello nos permitirá entender la grafica generada en el problema de aplicación que veremos más adelante.
Del canal de YouTube "Salvador FI Facultad de Ingeniería" veremos los diagramas de Fuerza Cortante y de Momento Flector, para ello haz clic en la imagen:


Vamos a determinar el comportamiento de una viga biapoyada (apoyada en dos muros fijos)de madera del grupo ES3 que tiene una luz entre esos apoyos de $5 m$ y debe soportar una carga de distribuida de $8.50 kN/m$. Determinar las posibles dimensiones de la sección.
En la siguiente escena de Juan Guillermo Rivera Berrío podemos visualizar el comportamiento del cálculo que realizaremos a continuación:
EL primer paso es convertir esa fuerza distribuida de $8.5 \space kN/m$ en una carga puntual ubicada en el centroide de la viga: $$q = 8.5 \space \frac{kN}{m} \cdot 5m = 42.5 \space kN = 42500 \space N$$
Ahora podemos interactuar con la siguiente escena donde debemos insertar los valores de la longitud de la viga y la carga que soporta.
Luego de interactuar con la escena comprobaremos los cálculos realizados:
Cálculo de las racciones. Para ello tomamos momentos con respecto a uno de apoyos,descartando de esa manera una de las incognitas lo que nos permite hallar el valor de una de las fuerzas de reaccion desconocidas: $$\displaystyle\sum M_{R1} \curvearrowleft + = 0$$ $$ -42500 \space N * 2.5m + 5m * R2 = 0$$ $$ R2 = \frac{42500 \space N * 2.5m}{5m} = 21250\space N$$
Ahora calculemos el valor de la reacción en R1:
Para calcular el área de la sección transversal y poder determinar las dimensiones emplearemos además de los valores de inercia presentado en la figura 5.2, las siguientes ecuaciones: $$\tag{6.21} \Large {\sigma_{máx}} = \normalsize {\frac{M_{máx} \cdot c}{I}}$$ $$\tag{6.22} \Large {\tau_{máx}} = \normalsize {\frac{V_{máx} \cdot Q_{máx}}{I \cdot t}}$$
Donde:
$\sigma_{máx}$ = Esfuerzo normal máximo
$M_{máx}$ = Momento flector máximo
$c$ = Distancia desde el eje neutro
$\tau_{máx}$ = Cortante máximo
$V_{máx} $= Esfuerzo cortante máximo
$t$ = Espesor de la viga
Vamos a realizar el cálculo de la sección transversal para una viga cuadrada, primero lo realizaremos por el máximo momento flector y luego por el máximo esfuerzo cortante. El segundo momento de área que se conoce como Momento de inercia ($I$) a calcular tiene como esquema:
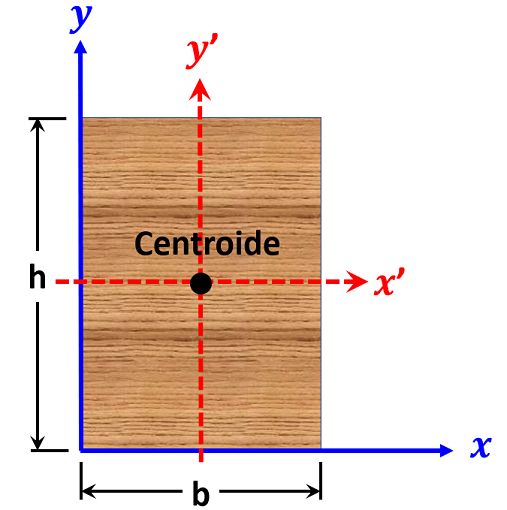
$$\tag{6.23} I_x=\frac{b \cdot h^3}{12} \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space $$
$$\tag{6.24} I_y=\frac{h \cdot b^3}{12} \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space $$
Tomaremos los valores obtenidos en el enunciado y en la escena para los siguientes cálculos: $$I_x = \frac{b \cdot b^3}{12} = \frac{b^4}{12}$$
De la tabla 5: $ \sigma = 28.5 \space MPa; \space \tau = 2.0 \space MPa $ $$28.5 \space MPa = \large {\frac{26562.5 N \cdot m \cdot c}{\frac{b^4}{12}}}$$ $$28500000 \space \frac{N}{m^2} = \large {\frac{26562.5 N \cdot m \cdot {\frac{b}{2}}}{\frac{b^4}{12}}}$$ $$28500000 \space \frac{N}{m^2} = \large {\frac{26562.5 \cdot 6 \space N \cdot m }{b^3}}$$ $$ b^3 = \large {\frac{26562.5 \cdot 6 \space N \cdot m }{28500000 \space \frac{N}{m^2}}}$$
Ello quiere decir que la viga de sección cuadrada tendría lados de $177mm$, ahora realizaremos el cálculo por el esfuerzo cortante admisible: $$ 2.0 \space MPa = {\frac{V_{máx} \cdot Q_{máx}}{I \cdot t}}$$
Aquí se requiere $Q_{máx}$ $$\tag{6.25} Q_{máx} = A \cdot \bar{y}_i = b \cdot \frac{b}{2} \cdot \frac{b}{4} = \frac{b^3}{8}$$
De la ecuación $6.22$ tenemos: $$ 2000000 \space \frac{N}{m^2} = {\frac{21250 \space N \cdot \frac{b^3}{8}}{\frac{b^4}{12} \cdot b}}$$ $$ 2000000 \space \frac{N}{m^2} = {\frac{21250 \space N \cdot 12 \cdot b^3}{b^5 \cdot 8}}$$ $$ 2000000 \space \frac{N}{m^2} = \frac{31875 \space N }{b^2}$$ $$ b^2 = \frac{31875 \space m^2 }{2000000} = 0.0159375 \space m^2 $$ $$\sqrt{b^2} = \sqrt{0.0159375 \space m^2} $$
La sección requerida para que soporte ambos esfuerzos es la viga cuya sección transversal es un cuadrado de lado $177mm$
Para nuestra siguiente aplicación es conveniente observar inicialmente el comportamiento de las denominadas cargas inclinadas en una escena tambien creada por Juan Guillermo Rivera Berrío

Vamos a determinar las medidas de una viga empotrada de sección rectangular donde la altura es igual a $\frac{5 \cdot base}{4}$, tiene una longitud de 3 metros, soporta una carga concentrada de $14 \frac{kN}{m}$ tal como aparece en la figura y debe ser construida con madera del grupo ES3.
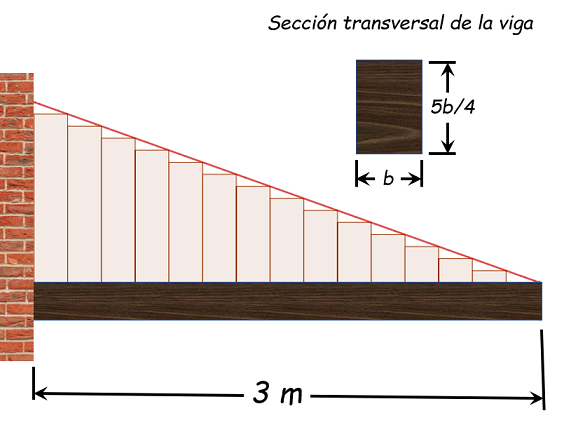
En este tipo de problemas al momento de calcular las reacciones nos encontramos en el empotramiento:
Claro que al no existir fuerzas en la dirección horizontal $F_x = 0$
Hallemos la carga equivalente sabiendo que la figura de carga es un triángulo: $$q = \frac{Fuerza \space concentrada * Longitud}{2} \space \Longrightarrow q = \frac{14\frac{kN}{m} * 3m}{2}$$ $$q = 21 \space kN = 21000\space N$$
La carga debe ubicarse en el centroide del triángulo tal como se especifica en la figura
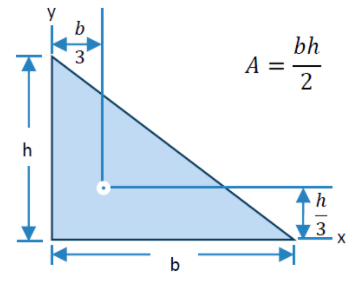
Por lo tanto: $$distancia = 3m * \frac{1}{3} = 1m$$
Esto quiere decir que para calcular la reacción nuestro diagrama de cuerpo libre será:
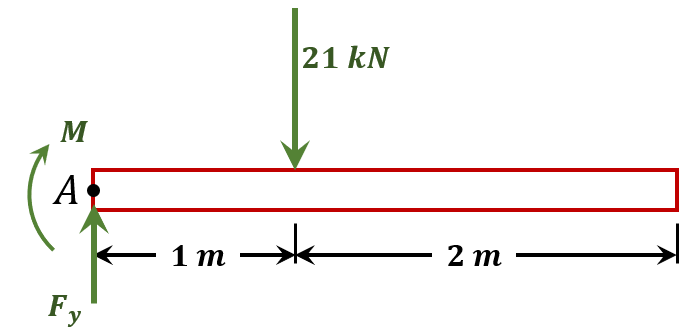
Ahora tomaremos momentos con respecto al punto $A$: $$\displaystyle\sum M_{A} \curvearrowleft + = 0$$ $$ -21000 \space N * 1m + M = 0$$ $$ M = 21000\space N \cdot m$$
El calculo de $F_y$ es: $$\displaystyle\sum F_{y} \uparrow + = 0 \Longrightarrow -21000 \space N + F_y = 0$$ $$ F_y = 21000 \space N $$
Los diagramas de Cortante y momento flector de la viga son:
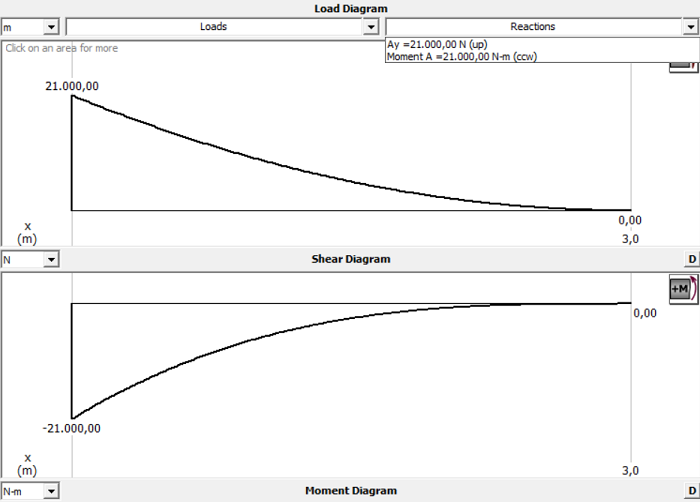
De la ecuación $6.23$ y según los datos del problema calculemos $I_x$: $$I_x=\frac{b \cdot h^3}{12} = \frac{b \cdot \Big( \frac{5}{4} b \Big)^3}{12} =\frac{\frac{125}{64}b^4}{12} = 0.1627 b^4$$
De la tabla 5 para la madera ES3: $ \sigma = 23.0 \space MPa; \space \tau = 1.6 \space MPa $ $$23.0 \space MPa = {\frac{21000 N \cdot m \cdot 0.625b}{0.1627 b^4}}$$ $$23000000 \space \frac{N}{m^2} = {\frac{13125 N \cdot m \cdot {b}}{0.1627 b^4}}$$ $$23000000 \space \frac{N}{m^2} = {\frac{80669.944 \space N \cdot m }{b^3}}$$ $$ b^3 = {\frac{80669.944 \space N \cdot m }{23000000 \space \frac{N}{m^2}}}$$ $$ b^3 = 0.0035m^3 \Longrightarrow \sqrt[3]{b^3} = \sqrt[3]{0.0035 \space m^3}$$ $$b = 0.151m = 151mm = medida \space base$$
La altura de la viga es: $$0.151m * \frac{5}{4} = 0.188m = 188mm$$
Verifiquemos con el cortante máximo: ecuación $6.22$ $$ \Large {\tau_{máx}} = \normalsize {\frac{V_{máx} \cdot Q_{máx}}{I \cdot t}}$$
Para solucionar la ecuación solo nos hace falta $Q_{máx}$
La altura según el cortante es: $$0.125m \cdot 1.25 = 0.156m = 156mm$$
Al comparar ambos diseños observamos que el valor obtenido del diseño por flexión satisface ambos esfuerzos máximos.
Una armadura es una estructura compuesta por un conjunto de elementos estructurales dispuestos generalmente en forma de triángulos unidos entre si tal como aparece en la figura $5.11$ donde aparece la nomenclatura de todos sus componentes. En la figura podemos observar una estructura con triángulos y otras formas geométricas:

En el video del profesor Salvador Centeno podemos tener una idea acerca del método de los nodos para calcular armaduras (Haz clic en la imagen:


En la figura nos encontraremos con un armadura plana donde se especifican las cargas a la que está sometida, debemos especificar los ángulos en cada nodo, determinar la fuerza en el mienbro $DE$ e indicar si está sometido a una fuerza de compresión o una fuerza de tensión. Inicialmente dibujamos el diagrama de cuerpo libre de donde se obtienen las ecuaciones de equilibrio que nos permitirán establecer los parámetros que determinar la armadura.
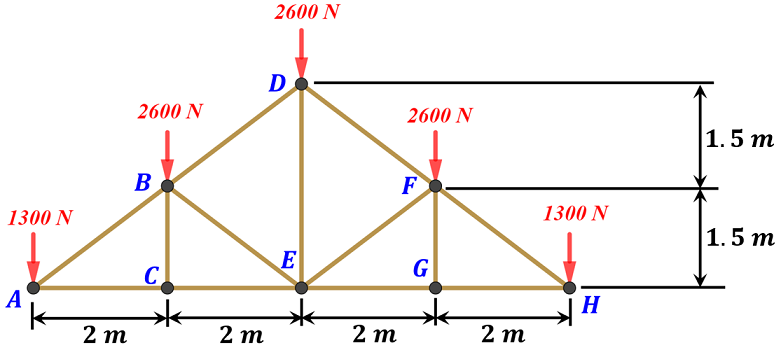
Calculemos la reacción de cada uno de los apoyos y para ello tomaremos momentos con respecto a cualquiera de ellos. $$\displaystyle\sum M_{A} \curvearrowleft + = 0$$ $$ -(2600N)(2m)-(2600N)(4m)-(2600N)(6m)\\-(1300N)(8m)+ R_H(8m) = 0$$ $$ R_H = \frac{41600N \cdot m}{8 \cdot m} = 5200\space N $$
El calculo de $R_A$ es: $$\displaystyle\sum F_{y} \uparrow + = 0$$ $$ -1300N -2600N-2600N-2600N-1300N + 5200N+R_A =0$$ $$ R_A = 5200N $$
Esto es evidente por la simetría de la armadura, esto implica que si vamos a analizar el nodo $A$, sus resultados serán los mismos que se obtienen en el nodo $H$, veamos las fuerzas en el nodo:
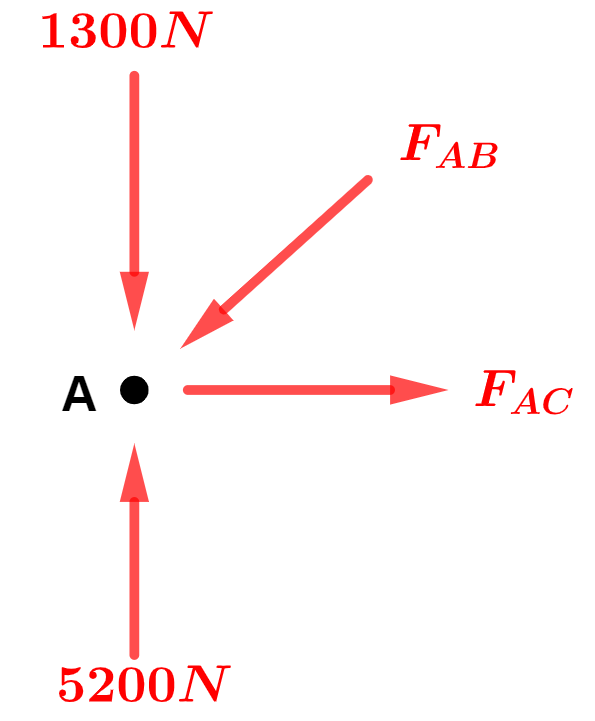
Antes de realizar las sumatorias de las fuerzas horizontales y de las fuerzas verticales es necesario descomponer la fuerza $AB$ en sus componentes rectángulares, para ello necesitamos su ángulo: $$\theta = Tan^{-1} \Big(\frac{1.5m}{2m} \Big) = 36.86°$$ $$\theta = Tan^{-1} \Big(\frac{3}{4} \Big) = 36.86°$$
Con estos valores se obtiene una terna Pitágorica: 5, 4, 3
Por lo tanto tenemos:
$$F_{AB(y)} = Sin \space \theta \cdot F_{AB} = \frac{3}{5}F_{AB} $$ $$F_{AB(x)} = Cos \space \theta \cdot F_{AB} = \frac{4}{5}F_{AB} $$Ya conocido esto: $$\displaystyle\sum F_{y} \uparrow = 0$$ $$ -1300N + 5200N - \frac{3}{5}F_{AB} = 0 $$ $$ F_{AB} = 3900N \frac{5}{3} = 6500N (Compresión)$$
Volvamos a la figura $6.6$ y nos concentramos en el nodo $C$:
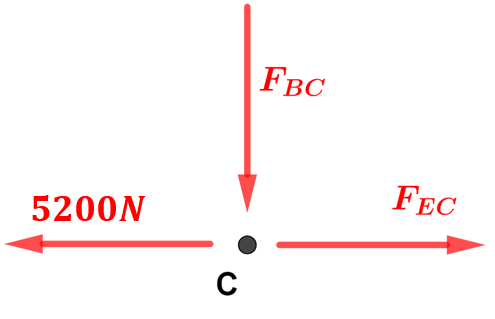
Aquí existe un concepto que se denomina miembros de fuerza cero, que expresa que si existen dos fuerzas a lo largo de elementos longitudinales que tengan la misma línea de acción pero que existe una fuerza perpendicular donde no se tenga ninguna fuerza aplicada podemos concluir que la fuerza a lo largo del elemento $BC$ será igual a cero, este es un elemento de fuerza cero. $$F_{BC} = 0 $$
Luego tenemos: $$\displaystyle\sum F_{x} \rarr + = 0$$ $$ -5200N + F_{EC} = 0 \Longrightarrow F_{EC} = 5200N$$ Pasemos al nodo $B$ donde nos encontraremos cinco fuerzas:
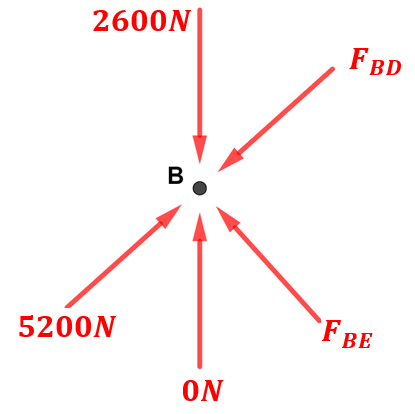 $$\displaystyle\sum F_{x} \rarr + = 0$$
$$ F_{AB}\frac{4}{5}- F_{BE}\frac{4}{5} - F_{BD}\frac{4}{5} = 0 $$
$$\frac{4}{5}\Big[F_{AB} - F_{BE} - F_{BD} \Big] = 0$$
$$\Big[F_{AB} - F_{BE} - F_{BD} \Big] = 0$$
$$5200N - F_{BE} - F_{BD} = 0$$
$$\tag{a}F_{BE} + F_{BD} = 5200N $$
$$\displaystyle\sum F_{x} \rarr + = 0$$
$$ F_{AB}\frac{4}{5}- F_{BE}\frac{4}{5} - F_{BD}\frac{4}{5} = 0 $$
$$\frac{4}{5}\Big[F_{AB} - F_{BE} - F_{BD} \Big] = 0$$
$$\Big[F_{AB} - F_{BE} - F_{BD} \Big] = 0$$
$$5200N - F_{BE} - F_{BD} = 0$$
$$\tag{a}F_{BE} + F_{BD} = 5200N $$
Hemos obtenido una ecuación con dos incógnitas, por tanto para saber su valor se requiere de otra ecuación: $$\displaystyle\sum F_{y} \uparrow = 0$$ $$F_{AB}\frac{3}{5}-2600N + F_{BE}\frac{3}{5} - F_{BD}\frac{3}{5} = 0$$ $$6500N \frac{3}{5}-2600N + F_{BE} \frac{3}{5}- F_{BD}\frac{3}{5} = 0$$ $$3900N -2600N + F_{BE} \frac{3}{5}- F_{BD}\frac{3}{5} = 0$$ $$F_{BE} \frac{3}{5}- F_{BD}\frac{3}{5} = -1300N$$ $$\tag{b}F_{BE} - F_{BD} = \frac{-1300N *5}{3}$$
Solucionando $a$ y $b$ se obtiene: $$F_{BE} = 1516.\bar{6}N \space \space \space y \space \space \space F_{BD} = 3683.\bar{3}N$$
Ahora el nodo $D$ que nos permitirá determinar el valor pedido:
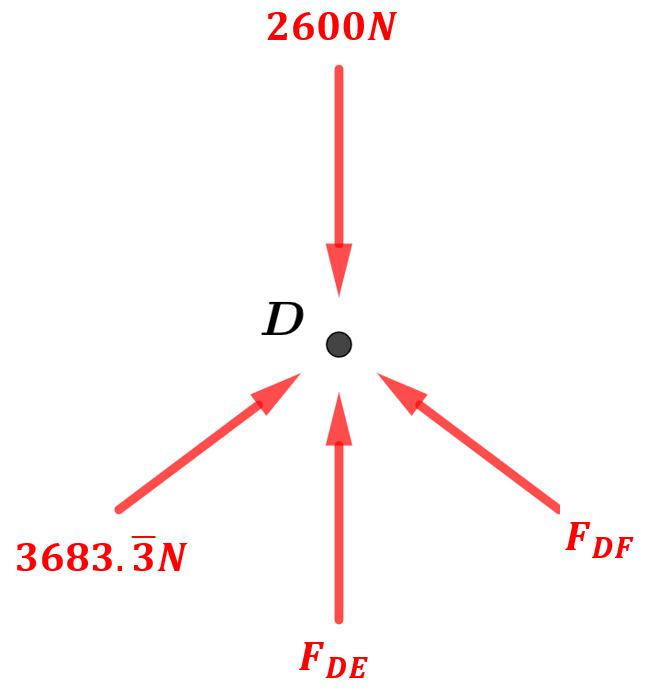
Por simetría podemos afirmar que la fuerza del elemento $DF$ tiene la misma magnitud del la fuerza del elemento $BD$ o sea que $F_{DF} = 3683.\bar{3}N$, entonces solo hallaremos:
$$\displaystyle\sum F_{y} \uparrow = 0$$
$$F_{DE}+F_{BD}\frac{3}{5}+F_{DF}\frac{3}{5} = 2600N$$
$$F_{DE}+3683.\bar{3}N \frac{3}{5}+3683.\bar{3}N \frac{3}{5} = 2600N$$
$$F_{DE} + 22210N + 22210N = 2600N$$
$$F_{DE}= 2600N - 4420N \Longrightarrow F_{DE}= -1820N (Compresión)$$
Este es el resultado pedido en el enunciado del problema, es una solución desde la física estática.
Gestionar el espacio público empleando tácticas a pequeña escala, bajo una lógica experimental en constante movimiento, gradual, y de socialización permanente, es un modelo de intervención de los ciudadanos de grandes y pequeñas ciudades con o sin ayuda de las administraciones locales—esto es urbanismo táctico— y puede llegar a ser un componente de los actos administrativos de planeación y ejecución de proyectos: es de bajo costo, es de ágil implementación y brinda de espacios agradables a las colectividades a las que pretende servir.
El urbanismo táctico es una transformación urbana acompañada de una innovación social, también se puede considerar una ampliación del tradicional enfoque urbanístico con conceptos como el de ‘Urbanismo de Código Abierto’.

Haciendo clic en la imagen observaremos un vídeo de Belafonte en el blog CooltureB podemos tener un acercamiento a la necesidad de la ejecución de proyectos de Urbanismo Táctico.

La madera contribuye en grandes proporciones a la capacidad de autogestión de las ciudades ya que comunica una vivienda y sus servicios básicos con el espacio público y comunitario, siendo sus ciudadanos los que se hagan cargo de la gestión cultural, política, social e infraestructural de espacio próximo, mejorándola cualitativamente para mejorar su calidad de vida y evidenciar el derecho de pertenencia.
La madera contribuye en grandes proporciones a la capacidad de autogestión de las ciudades ya que comunica una vivienda y sus servicios básicos con el espacio público y comunitario, siendo sus ciudadanos los que se hagan cargo de la gestión cultural, política, social e infraestructural de espacio próximo.
La madera contribuye en grandes proporciones a la capacidad de autogestión de las ciudades ya que comunica una vivienda y sus servicios básicos con el espacio público y comunitario, siendo sus ciudadanos los que se hagan cargo de la gestión cultural,  política, social e infraestructural de espacio próximo, mejorándola cualitativamente para mejorar su calidad de vida y evidenciar el derecho de pertenencia.
política, social e infraestructural de espacio próximo, mejorándola cualitativamente para mejorar su calidad de vida y evidenciar el derecho de pertenencia.
Esa autogestión tiene su origen en el desarrollo de sociedad y el crecimiento poblacional, sin medidas y restricciones estimula deterioro al medio ambiente, destrucción de la fauna y flora además de provocar impactos ambientales como la contaminación en términos generales, y el Urbanismo Táctico que ha ido emergiendo en las ciudades y poco a poco se han notado grandes cambios en algunos entornos, Myke Lyndon y Antoni García (2109) expresan que el urbanismo táctico son “acciones a corto plazo y cambio a largo plazo” que se han ido desarrollando en el tiempo.
De igual manera, el urbanismo táctico y su relación con la madera se fundamenta en que esta es uno de sus insumos primordiales en el diseño y cambios de entornos en diferentes lugares de la ciudad que se intervienen con estas iniciativas urbanísticas.
Además de ofrecer beneficios en los territorios y comunidades donde se han implementado el Urbanismo Táctico, este se ha convertido en un actor fundamental de la implementación a pequeña escala en los espacios existentes, caracterizada por proyectos de bajo costo, que por lo general no son permanentes y pueden estar sujetos a cambios de acuerdo con quien lo desarrolle o proponga, a continuación se describen algunos de sus beneficios:
Normalmente los diseños y herramientas necesarias para implementar un proyecto de Urbanismo Táctico suelen ser de bajo costo.
Entre estos elementos de facíl adquisición por la comunidad tenemos los elementos de barrera, conos de tráfico, cilindros, delineador gratuito, separadores de carril, barricadas de control de tráfico, barreras plásticas, bloques de granito, caja de madera, plantas de neumáticos, plantaciones de madera personalizada, plantas de plástico de gran polímero y sembradoras de auto-riego entre otros.
Aunque no todos los proyectos de Urbanismo Táctico son de bajo costo, en la Web podemos observar innumerables ejemplos que a través del tiempo ha generado impactos en el bienestar de la comunidad interviniendo el entorno con el apoyo de elementos de madera.
Veamos algunos ejemplos:
En el Departamento de Antioquia en Colombia, esta obra fue proyectada y construida por el ingeniero colombiano José María Villa entre 1887 y 1895. El Puente de Occidente, es uno de los más lindos he innovadores del país, es un puente colgante que comunica dos localidades una al oriente y otra al occidente del Río Cauca, respectivamente en su momento fue considerado el séptimo puente colgante más importante en todo el mundo, creado con una madera debidamente embalsamada y cuya imagen podemos observar:

En la ciudad de Medellín, una obra que ha intervenido su espacio es el jardín botánico. La historia del Jardín Botánico de Medellín comenzó a finales del siglo XIX, cuando los terrenos que hoy ocupa empezaron a tener vocación recreativa, en lo que entonces era conocido como la casa de baños El Edén. Con una riqueza urbanística y su papel cultural en la ciudad lo ha constituido como un escenario de valor enriquecido con eventos culturales tales como: Fiesta del libro y cultura y feria de flores (Exposición Orquídeas, pájaros y flores).

A nivel internacional hallamos iniciativas que destacan la decoración con madera, los ejemplos reivindicativos más emblemáticos en España quizá hayan sido el Campo de la Cebada (2009) en Madrid y Can Batlló (2011) en Barcelona.
Este fue un espacio hecho por y para los vecinos tras la demolición de una piscina pública que hubiera dejado un solar vacío durante años si no llega a ser por esta iniciativa que lo transformó en un espacio lleno de vida, cultura, deporte y aprendizaje que ha sembrado un fértil sentimiento de ciudadanía.

Son tantas muestras de proyectos de Urbanismo Táctico alrededor del planeta que nos quedariamos cortos en su relación, lo cierto es que con la intervención de los organismos estatales se pueden mostrar grandes obras, en la página "Plataforma Urbana" hemos encontrado un artículo de Constanza Martínez que habla de los 15 parques y plazas públicas que se destacan por su mobiliario urbano.
Esos parques y plazas públicas citadas en el artículo son:
El listado que hemos descrito solo habla de grandes ciudades en su mayoría del viejo continente y que se pueden visualizar AQUÍ, pero surge la pregunta: ¿No existen en Sudamérica?
Todas las intervenciones del Urbanismo Táctico con madera requieren de muchos cuidados puesto que es necesario tener en cuenta el medio ambiente y los microorganismos que pueden afectar la madera.
La madera es el material de construcción más ligero, resistente y fácil de trabajar, pero al mismo tiempo puede sufrir los embates del medio ambiente.
El agua de lluvia que humedece y penetra la superficie de la madera sin protección se debe a que esa agua es absorbida rápidamente por capilaridad por la capa superficial de la madera seguida por la adsorción en las paredes de las células.
El vapor de agua es absorbido directamente por adsorción por las paredes de las células. La diferencia de humedad entre el interior y la capa superficial que tenderá a hinchar provoca un estado de tensiones en la pieza, que si no está equilibrado origina que se arquee o adquiera una combadura.
Una de las principales causas del deterioro superficial de la madera se debe a los cambios rápidos del contenido de humedad en la capa externa.
La humedad es uno de los factores de agresividad del medio ambiente para la madera y determinan diferentes niveles de deterioro tal como podemos observar en la siguiente escena:
El deterioro producido por el medio ambiente.

Otro de los elementos que afectan la madera que podemos emplear en el urbanismo táctico es la radiación solar, es uno de los agentes que más afectan a la madera puesto que las radiaciones ultravioletas del sol como su espectro infrarrojo pueden llegar a estropearla.
La radiación ultravioleta puede actuar sobre la celulosa de la madera, pudiendo ser la responsable de la pérdida del color original. Por tanto, mientras mayor sea la exposición de la madera a la radiación ultravioleta, mayor será su decoloración.
La experiencia de expertos en maderas dice que este deterioro suele centrarse en los primeros 7 años, luego, el nivel de degradación se mantiene.

El efecto que producen los rayos ultravioleta se refleja en un agrisamiento y descamado de la madera, más acentuado en las maderas rojas como la Tectona grandis más conocida como teca, por ejemplo.
De igual manera, el impacto de la radiación ultravioleta puede multiplicarse en el caso de que al mismo tiempo haya exposiciones a la lluvia.
Las zonas al aire libre como pueden ser terrazas y jardines resultan especialmente dañadas por los efectos de la climatología. Los cambios bruscos de temperatura, la lluvia, hielo y el sol producen efectos muy negativos sobre la madera tradicional, la cuartean, pudren, producen un cambio de tonalidad a verde-grisáceo y la agrietan.
Además de los aspectos ambientales que afectan la madera podemos afirmar que el ataque por microorganismos y los insectos es casi inevitable. Con el fin de evitar ese desgaste y como medida preventiva se empezaron a fabricar disolventes, aceites y una gran cantidad de productos químicos que evitasen ese cambio de aspecto en la madera o, al menos, preservarla por un tiempo y luego volver a su aplicación.
Emplear productos químicos para proteger la madera tradicional no es una solución ecológica, encarece el material a medio plazo y requiere de esfuerzos adicionales., una solución fueron los modelos de compuestos termoestables desarrollados donde se acoplaron fibras celulósicas en una matriz polimérica.
Veamos algunos microorganismos e insectos que afectan la madera del mobiliario empleado en ese urbanismo táctico:
Atacan la celulosa de la madera transformáqndola por medio de enzimas inicialmente en celubiosa, luego en hidrógeno, en metano, en anhidrido carbónico y por último en ácidos grasos.
Conocidos como actinobacterias, la mayoría de ellas se encuentran en el suelo, e incluyen algunas de las más típicas formas de vida terrestre, jugando un importante rol en la descomposición de materia orgánica, como la celulosa y quitina.
Crecen en la madera como una red microscópica a través de los agujeros o directamente penetrando la pared celular de la misma y la convierten en su fuente de alimento.
Las hifas (celúlas alargadas que son los cuerpos fructíferos) producen las enzimas que degradan la celulosa, hemicelulosa, o lignina que absorbe el material degradado para terminar el proceso de desintegración.
Constantemente todas las estructuras de madera están dispuestas al ataque de los hongos cuando la humedad y otros requisitos adecuados al crecimiento de los hongos estén presentes.
Existen una serie de factores ambientales que propician la aparición de los hongos:
Esta es, sin lugar a dudas, la variable que determinará si aparecerán y proliferarán hongos en la madera.
Normalmente, los hongos solo se desarrollan cuando la humedad supera el 20% aproximadamente, ello quiere decir que se logra mantener la madera por debajo de este porcentaje de humedad, los hongos no deberían ser un problema.
Existen un amplio abanico de temperaturas entre la cuales los hongos de la madera pueden desarrollarse, aproximadamente entre los 3 y los 50 grados centígrados. Dentro de estas, el intervalo especialmente propicio es el de 30-35 grados.
Entre los hongos más comúnes tenemos:
Son los típicos hongos de humedad, no influyen en las propiedades de resistencia mecánica de la madera, solamente se desarrollan en su superficie y no en el interior; producen proliferaciones algodonosas de micelio (El micelio es el conjunto de hifas que forman la parte vegetativa de un hongo) de diversas tonalidades.
Los mohos crean condiciones para el desarrollo de los hongos pudridores, debido a que les otorgan humedad.
Su presencia se nota cuando aparecen las esporas en forma de espuma blanquecina en la superficie de la madera.
Se denominan así a todos los hongos capaces de producir cambios de coloración en los tejidos de la madera, los cuales se alimentan de los azúcares que se encuentran en el tejido parenquimático, los desechos metabólicos que se dan en el momento del ataque son coloreados y producen una pigmentación azulada-negruzca característica, el crecimiento de estos hongos en la madera es muy rápido, de hasta 1 cm en el espesor en 24 horas.
Atacan las paredes celulares alimentándose de la celulosa o de la lignina, es un ataque destructivo ya que que los elemntos atacado pierden rápidamente sus propiedades fisicomecánicas bajando su densidad y aumentando su temperatura. Existen tres tipos de este hongo:
El hongo de pudrición blanca se alimenta principalmente de lignina, y muy poco de celulosa. El resultado es una madera blanquecina de aspecto fibroso, de ahí que también se conozca como pudrición fibrosa. Es la más habitual y su resultado es muy variable, llegando en casos extremos a perdidas de peso superiores al 95%.
Afecta en mayor medida a especies de maderas frondosas. Estas tienen mayor contenido en lignina, a diferencia que las coníferas, la madera se vuelve fibrosa, toma un color blancuzco y se desmenuza con facilidad.
El elemento químico que degrada este tipo de hongos es la lignina, a través de un proceso de oxidación.
En la pudrición blanca existe una relación lineal entre pérdida de peso y daño en la madera.
Cuando es la madera es atacada por este tipo de hongo se desmenuza y resquebraja en sentido transversal a la fibra y se torna de color pardo-café.
Es un proceso complejo en el cual se da la degradación de la celulosa, a través de que se denomina hidrólisis enzimática.
Al contrario de la pudrición blanca no hay relación directa entre pérdida de peso y daño, ello implica que una pequeña pérdida de peso conlleva a una gran disminución de las propiedades físico mecánicas.
Es causada principalmente por la degradación de los carbohidratos de la madera y producen un reblandecimiento superficial. Los hongos de pudrición blanda atacan la celulosa de las paredes celulares y forman a menudo cavidades microscópicas en la pared celular secundaria.
Entre los insectos que pueden atacar la madera nos encontramos:
Las termitas son insectos sociales, agrupados en clases (reina, rey, obreros, soldados y ninfas), viven en colonias poco numerosas, no requieren suministros especiales de agua, basta con el contenido de humedad de la madera.
Las termitas abren las galerías en la madera ó aprovechan grietas y ranuras; los obreros hacen agujeros pequeños, conectados con el exterior, por donde secretan restos de lignina, haz clic para observar un vídeo de la universidad de Valencia.
