EJERCICIOS DE
TRIGONOMETRÍA
Procesos, métodos y actitudes
José Antonio Salgueiro González
Red Educativa Digital Descartes, España
Profesor de Matemáticas en IES Bajo Guadalquivir
de Lebrija (Sevilla) durante treinta años
Córdoba (España)
2021
Título de la obra:
Ejercicios de Trigonometría.
Procesos, métodos y actitudes.
Autor:
José Antonio Salgueiro González
Diseño del libro: Juan Guillermo Rivera Berrío
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN: 978-84-18834-21-9
LICENCIA
A Rocío.
Toda una vida apoyando mis proyectos.
Al Departamento de Matemáticas del
IES Bajo Guadalquivir de Lebrija y a todos
mis compañeros y compañeras, con quienes tanto
he compartido y aprendido durante treinta años.
A todos mis alumnos y alumnas del
IES Bajo Guadalquivir de Lebrija, que
tanto me enseñaron durante treinta años.
No importa lo lento que vayas mientras no te detengas
Confucio
Inicio con la frase de Confucio, pues el diseño de un libro interactivo es un proceso lento que requiere de mucha paciencia y disciplina. El libro "Ejercicios de Trigonometría", que nos presenta José Antonio Salgueiro González, es una evidencia de este proceso lento, en tanto que el autor dedicó un número significativo de horas para comprender y aplicar algunos elementos mínimos de programación HTML5 (CSS, HTML y JavaScript), además de los comandos $\KaTeX$ necesarios para la escritura de expresiones matemáticas.
Este esfuerzo de aprendizaje y aplicación de lo aprendido, sobre el diseño de libros interactivos, no fue suficiente para el autor, pues los objetos interactivos incorporados en el libro son de su autoría, que dan cuenta de otro proceso previo: el diseño de escenas interactivas con el editor DescartesJS.
Pero, desarrollar las competencias necesarias para el diseño de libros y objetos interactivos, no significa que ya podemos escribir libros, porque hay que dar respuesta a algunas preguntas, entre ellas: ¿qué voy a escribir?, ¿tiene utilidad el libro?, ¿quiénes serán los usuarios de mi libro?, ¿cómo hago atractivo mi libro?, ¿qué objetos interactivos debo usar?
La presente obra da respuesta a estas preguntas. El autor propone un libro para que el usuario "aprenda a pensar y a razonar" en torno a ejercicios de trigonometría, a través de diferentes estrategias, que incluyen ejemplos, ejercicios propuestos, autoevaluación y escenas interactivas.
Juan Guillermo Rivera Berrío
Desde que comenzaron a proliferar los canales de vídeos para aprender matemáticas, cada vez más alumnas y alumnos se han ido haciendo fieles seguidores de aquellos que más les benefician y, además, acostumbran a pedir opinión a sus profesores y profesoras sobre los mismos, a la vez que solicitan recomendaciones adecuadas a sus edades y capacidades. Suelen usarlos como complemento a la enseñanza presencial, bien para reforzar, aclarar o ampliar aspectos tratados en el aula, o incluso por sus inquietudes innatas hacia el conocimiento.
Por otra parte, las consecuencias derivadas de la pandemia han puesto de relevancia la importancia de disponer de recursos educativos abiertos de la mayor calidad posible que permitan, de forma gratuita, atender las necesidades de nuestro alumnado en cualquier modalidad de enseñanza, a la vez que favorecer y facilitar la tarea docente.
Con objeto de atender las dos circunstancias mencionadas surge este libro interactivo, centrado en aprender a pensar y razonar mostrando las estrategias más adecuadas con todas las explicaciones y argumentos detallados.
Se aborda la resolución de ejercicios de la que podríamos denominar "trigonometría algebraica", es decir, fórmulas de adición, ángulos doble y mitad, transformación de sumas y diferencias en producto y ecuaciones trigonométricas, con escasa visualización geométrica y de gran interés en cursos posteriores a la hora de simplificar derivadas, cálculo de primitivas o la obtención de los máximos y mínimos de funciones trigonométricas. Así que, en este libro, no encontrarás lo relativo a la resolución de triángulos, que podría ser objeto de otra obra dedicada a las aplicaciones de la Trigonometría.
Cada capítulo tiene la misma estructura y se compone de introducción, motivación, recopilación de fórmulas a emplear, cuestionario para toma de contacto y familiarización con dichas fórmulas, ejemplos y ejercicios resueltos y completamente explicados, en ocasiones con distintas estrategias para un mismo ejercicio, alternancia con retos interactivos para ir asentando todo lo aprendido, un proyecto de investigación y finalizamos con un elemento clave en el proceso de aprendizaje que permite al alumnado valorar sus logros y reflexionar sobre sus fortalezas y debilidades: la autoevaluación.
Al respecto, presentamos dos modelos de autoevaluación: una para conceptos básicos, de rápida y corta respuesta previa reflexión. Y una segunda, con algo más de complejidad, destinada a la resolución de tradicionales ejercicios relacionados con los conceptos tratados y usando las diferentes estrategias mostradas a lo largo del desarrollo del capítulo. Ambas se acompañan de las correspondientes orientaciones para que el proceso de autoevaluación sea efectivo.
Finalmente, hemos aprovechado la página posterior a la portada de cada capítulo para "introducir el conocimiento histórico, social y cultural de la Trigonometría, que servirá para la comprensión de los conceptos a través de la perspectiva histórica, así como para contrastar las situaciones sociales de otros tiempos y culturas con las realidades actuales", como se recoge en el diseño curricular de la materia.
Lebrija, octubre de 2021
La Trigonometría nace con la observación de los fenómenos astronómicos.Trigonometría. Proyecto ED@D" RED Descartes.
En el conjunto megalítico de Stonehenge (Gran Bretaña), construido entre 2200 y 1600 a.C., la alineación de dos grandes piedras indica el día más largo del año, el solsticio de verano.

El gran círculo de piedras, dividido en 56 partes, podía utilizarse para determinar la posición de la Luna a lo largo del año y también para predecir eclipses.
El primer antecedente escrito de la Trigonometría lo encontramos en el problema 56 del papiro de Rhind, escrito por Ahmés alrededor del 1800 a.C. transcribiendo otro del 5000 a.C., que plantea calcular el "seked" de una pirámide, es decir, el número de palmos en la base que corresponden a un codo de altura.
La palabra Trigonometría procede de las voces griegas tri-gonon-metron, que significa “medida de tres ángulos”. El objetivo prioritario de esta rama de las Matemáticas es el estudio de las medidas de los ángulos y lados de los triángulos.
Una vez superados los conocimientos de Trigonometría elemental, sabemos que es posible extender el cálculo de las razones trigonométricas a los ángulos obtusos y, en general, a cualquier ángulo, sin necesidad de que formen parte de un triángulo. Aprenderemos a manejar con soltura las razones trigonométricas de un ángulo, de su doble y mitad, así como las transformaciones usuales y la resolución de ecuaciones trigonométricas.
Se conocen con este nombre las fórmulas que permiten obtener las razones trigonométricas de una suma o una diferencia de ángulos.
Por ejemplo, supongamos que tenemos dos ángulos expresados en grados sexagesimales, como 60º y 30º, deseando calcular
Obviamente, podemos sorprendernos de la pregunta, ya que
Entonces, ¿para qué necesitamos fórmulas que nos permitan calcular, en este caso, el coseno de una suma de ángulos? Pues bien, imaginemos que vemos a una persona realizar esta operación: $$(3+2)^{2}=3^{2}+2\cdot3\cdot2+2^{2}=9+12+4=25$$
Rápidamente, otra persona podría advertirnos del esfuerzo que se está realizando y sugerirnos que apliquemos la jerarquía de operaciones para proceder de la siguiente forma:
Gracias a la formación matemática adquirida en años anteriores, hemos sido capaces de identificar que la primera persona utiliza una identidad notable y que la segunda puede realizar el cálculo más fácilmente por tratarse de una expresión artimética, pero ¿cómo actuaría la segunda persona si algún valor fuera desconocido? Estaremos de acuerdo en que se vería obligada a desarrollar el cuadrado de una suma. Por ejemplo, si fuera desconocido el primer sumando de la operación anterior, se enfrentaría a:
Algo similar sucede si uno de los dos ángulos es desconocido, es decir, si en vez de 60º y 30º nos encontramos con el ángulo $x$ y el de 30º, debiendo calcular $\cos(x+30º)$.
Esperamos que este sencillo ejemplo donde vemos la importancia de la identidad notable para desarrollar el cuadrado de un binomio suma, sea suficientemente motivador para comprender la necesidad de disponer de una fórmula que nos permita desarrollar el coseno del ángulo suma.
Como esta obra posee un enfoque eminentemente práctico y tiene como objetivo primordial mostrar diversas estrategias en la resolución de ejercicios, no se contempla la demostración de las fórmulas trigonométricas que usaremos, aunque podemos encontrar una demostración de las mismas en los "Apuntes de Trigonometría", iniciando sesión como invitados.
La primera vez que el alumnado de bachillerato se enfrenta al reto de evaluar la expresión $\cos(x+30º)$ suele inclinarse por $\cos x + \cos 30º$ como valor estimado de la misma, presentándose una gran
oportunidad para tratar el tema de conjeturas, contraejemplos y demostraciones en Matemáticas.
En ese momento, el alumnado se encuentra ante una conjetura, derivada de una sospecha o intuición basada en su experiencia matemática, siendo de gran interés abrir un debate para que surja un contraejemplo
que refute la hipótesis y extraer una consecuencia.
Por ejemplo, si tomamos $x=60º$ en nuestra expresión, tendremos para el primer miembro
Mientras que en el segundo miembro obtendremos
En consecuencia, queda demostrado que $cos(x+30º) \not= \cos x + \cos 30º$.
Conviene realizar algunos ejercicios para practicar y afianzar los conceptos tratados.
Utiliza la estrategia del contraejemplo para refutar las siguientes conjeturas:
Para fomentar la realización de investigaciones matemáticas y el espíritu científico, en general, debemos plantearnos preguntas como:
Daremos respuesta a la última pregunta en la siguiente sección.
Se conocen con este nombre las fórmulas que posibilitan el cálculo de las razones trigonométricas directas, seno, coseno y tangente, de una suma de dos ángulos desconocidos.
Llega el momento de usar estas fórmulas para encontrar el verdadero valor de las expresiones trigonométricas que hemos investigado anteriormente. Así que debemos ser capaces de conseguir:
Hubo un tiempo en el que no existían calculadoras científicas ni herramientas de cálculo simbólico, así que había que recurrir al ingenio y a las denominadas tablas trigonométricas, auténticos libros que contenían los valores aproximados de las razones de los ángulos del primer cuadrante. Se aplicaban, para otros casos, las fórmulas de reducción al primer cuadrante y las de adición, que estudiamos en este capítulo.
Cuando trabajamos con valores exactos no podemos dar respuestas con aproximaciones o números decimales, ni tampoco ofrecer el resultado proporcionado por la calculadora científica o simbólica, sino que deberemos aplicar puro razonamiento matemático, en base a nuestros conocimientos, experiencia y creatividad.
Sin calculadora científica ni herramienta de cálculo simbólico, debemos obtener los valores exactos del seno y coseno del ángulo de $75º$.
Posteriormente, comprobaremos con una de las herramientas tecnológicas que nuestro resultado es correcto.
Como no podemos utilizar calculadoras ni herramientas similares, tendremos que recurrir a los ángulos cuyas razones trigonométricas
conocemos, es decir, 30º, 45º, 60º y a los que hacen de frontera entre cada cuadrante, o sea, 0º, 90º, 180º, 270º y 360º.
Pensaremos en expresar 75º como combinación de dos de los ángulos mencionados anteriormente, y parece lógico que lo conseguiremos con la suma de 45º y 30º. Así que aplicaremos las razones trigonométricas del ángulo suma con esos dos valores, obteniendo:
En resumen, la estrategia consiste en expresar el ángulo como suma de otros dos cuyas razones conozcamos y aplicar las fórmulas de adición.
Debemos obtener el valor exacto de $\tg75º$ siguiendo tres procedimientos diferentes:
Con el primer procedimiento deberemos obtener como valor exacto $\tg75º=2+\sqrt{3}$.
Con el segundo procedimiento tendríamos el siguiente desarrollo:
Finalmente, ya sabemos que lo conseguiremos con la suma de 45º y 30º y la fórmula de la tangente del ángulo suma.
Con la realización de este ejercicio, además de adiestrar en el cálculo de valores exactos y afianzar la estrategia mostrada, se fomentan la curiosidad e indagación en matemáticas, además de reconocer los números reales, efectuar operaciones numéricas con eficacia e insitir en que existen diversas estrategias para afrontar un reto, surgiendo preguntas para debatir como:
Obviamente, se nos presenta una buena oportunidad para recordar, repasar y valorar la importancia de conocer y dominar la racionalización de denominadores en un contexto de investigación matemática y no de forma aislada, como suele ser habitual.
Un error frecuente en parte del alumnado es pretender racionalizar elevando al cuadrado los dos términos de la fracción, así que conviene insistir en que únicamente se obtienen fracciones equivalentes al multiplicar o dividir ambos términos por un mismo
valor, es decir, lo que se conoce como amplificar o simplificar la fracción.
A su vez, la eliminación de los números irracionales o radicales del denominador, se logra multiplicando ambos términos de la fracción por la expresión conjugada del denominador. Por ejemplo, la expresión conjugada de $\sqrt{a}+\sqrt{b}$ es $\sqrt{a}-\sqrt{b}$ y la conjugada de $\sqrt{a}-\sqrt{b}$ es $\sqrt{a}+\sqrt{b}$, y suele representarse con una línea horizontal encima. En general:
La mayoría del alumnado conoce la técnica de la racionalización, pero no comprende el sentido de la conjugación, es decir, ¿por qué se eliminan los radicales al multiplicar una expresión por su conjugada?
A estas edades es fundamental analizar, comprender, expresar verbalmente, de forma razonada y con el rigor y precisión adecuados los procesos seguidos. Por ello, insistiremos en que todo es posible gracias a que el producto de una expresión por su conjugada no es más que una identidad notable del tipo suma por diferencia o diferencia de cuadrados.
Por otra parte, nuestro alumnado interioriza y mecaniza la simplificación anterior con la expresión verbal típica de que el cuadrado "se va" con la raíz, pero pocos son capaces de argumentarlo. Por ello, debemos recordar la expresión de un radical como potencia de exponente fraccionario.
De esta forma, podemos justificar y argumentar lo anterior:
$$(\sqrt{a})^{2}=\sqrt{a^{2}}=a^{\frac{2}{2}}=a^{1}=a$$Estamos preparados para abordar, intentando comprender y justificar, cada paso de la racionalización de denominadores:
Así que obtenemos el mismo valor exacto que el proporcionado por la calculadora científica o la herramienta de cálculo simbólico.
Pasamos, pues, al tercer y último procedimiento:
En definitiva, hemos conseguido demostrar que el valor de $\tg 75º$ es único independientemente del procedimiento de cálculo empleado, y ha sido posible gracias a la estrategia o técnica de racionalizar el denominador, que será de gran utilidad cuando llegue el momento de calcular límites de funciones irracionales.
En cualquier momento del desarrollo de una clase de Matemáticas, surgen momentos, oportunidades y ocasiones para proponer retos que motiven a nuestro alumnado a reflexionar, debatir, encontrar líneas de investigación matemática a su alcance, promover su curiosidad y animarlos a indagar, así como a establecer debates abiertos.
Por ejemplo, en la página anterior hemos escrito la siguiente expresión:
con objeto de justificar con argumentos matemáticos la conocida, típica y muy usada frase de "el cuadrado se va con la raíz". En consecuencia, si aceptamos el argumento expuesto, podremos escribir que:
Todo parece sencillo, claro y aceptado hasta que alguien nos presenta las siguientes operaciones:
Se abre un debate de gran interés donde aparecen cuestiones conceptuales de años anteriores que no han sido bien adquiridas, como:
Es de gran importancia que nuestro alumnado vaya detectando y admitiendo que la ampliación de conocimientos facilita enormemente las labores propias del quehacer matemático y del científico, en general.
Tendremos que esperar a conocer los conceptos funcionales básicos para acceder a la explicación matemática formal y saber que, en ese contexto funcional, $\sqrt{a^{2}} \not = a$, sino que $\sqrt{a^{2}}=|a|$, siendo $|a|$ el valor absoluto de $a$. De esta forma:
Otra interesante línea de investigación que se presenta en esta etapa y contexto es la que hace referencia a la racionalización de denominadores con una diferencia o resta de radicales cúbicos, que permite dar respuesta a este reto desde la factorización polinómica, incluso utilizando la regla de Ruffini, mostrando así que la matemática no se debe enseñar en compartimentos estancos.
Se conocen con este nombre las fórmulas que posibilitan el cálculo de las razones trigonométricas directas, seno, coseno y tangente, de una resta o diferencia de dos ángulos desconocidos.
Sabemos que cualquier fórmula matemática puede aplicarse en ambos sentidos de la igualdad, es decir, de izquierda a derecha, como venimos haciendo al desarrollar el seno, coseno o tangente de un ángulo suma, pero también es posible de derecha a izquierda, consiguiendo en este caso contraer y expresar en una sola razón.
$$\begin{aligned} \frac{\sqrt{2}}{2}\cos x + \frac{\sqrt{2}}{2} \text{sen}\space x &= \cos\frac{\pi}{4}\cdot \cos x + \text{sen}\space \frac{\pi}{4}\cdot \text{sen}\space x=\\ & = \cos(\frac{\pi}{4}-x)= \cos(x-\frac{\pi}{4})\\ \end{aligned}$$Sin calculadora científica ni herramienta de cálculo simbólico, debemos obtener los valores exactos de las razones trigonométricas directas de $\displaystyle\frac{\pi}{12} \space rad$.
Aunque el radián es la unidad de medida de ángulos en el Sistema Internacional, parece que nos manejamos mejor en grados sexagesimales, así que, en primer lugar, aplicaremos el factor de conversión:
Utilizaremos la estrategia de expresar el ángulo como diferencia de otros dos cuyas razones conozcamos y aplicaremos las fórmulas de adición para el ángulo diferencia. Pensaremos en expresar 15º como combinación de dos ángulos cuyas razones trigonométricas conozcamos sin calculadora, como 45º y 30º.
Para la tangente podemos aplicar su fórmula de adición o realizar el cociente entre el seno y el coseno, que ya son conocidos. Lo haremos con su fórmula, con objeto de familiarizarnos con ella.
La otra opción, es decir, el cociente entre seno y coseno, también nos obliga a racionalizar para obtener el resultado lo más simplificado posible:
No existe un procedimiento estándar que nos permita simplificar una expresión trigonométrica, al igual que sucede a la hora de simplificar una expresión algebraica o aritmética. No obstante, podemos dar algunas orientaciones que pueden ser de utilidad:
Simplifica al máximo la siguiente expresión trigonométrica:
$$\text{sen}\space b \cdot \cos(a-b) + \cos b \cdot \text{sen}(a-b)$$Si después de dedicar algunos segundos a observar la expresión, no detectamos ninguna peculiaridad o información para afrontar el reto, pasamos directamente a utilizar fórmulas, realizar las operaciones y reducir al máximo, como podemos apreciar en la escena inferior pulsando el botón para conocer la primera estrategia.
Existen diversas estrategias a la hora de resolver una misma situación en el contexto matemático o en la vida misma.
Hemos dejado para el final la que podríamos denominar estrategia directa, que consiste en dedicar unos segundos a la observación de la expresión trigonométrica para intentar encontrar alguna peculiaridad, detectar una estructura o composición conocida, por analogía con una fórmula, con un reto similar al que nos hayamos enfrentado con anterioridad y que nos permita dar una respuesta cómoda y ahorrarnos un esfuerzo superfluo.
En algunas ocasiones, puede aportar información leer las razones trigonométricas de la expresión sin mencionar los ángulos, es decir, "seno, coseno, más coseno, seno" y, dado que los ángulos son iguales y
están en el mismo orden, puede recordarnos al seno del ángulo suma, como mostramos en la siguiente escena:
Explica cómo puedes obtener, sin calculadora, el valor exacto de la siguiente expresión:
$$\displaystyle\frac{\tg\displaystyle\frac{\pi}{9}+\tg\displaystyle\frac{5\pi}{36}}{1-\tg\displaystyle\frac{\pi}{9}\cdot\tg\displaystyle\frac{5\pi}{36}}$$Como debemos hacerlo sin calculadora y vemos que los ángulos presentados no son ninguno de los habituales cuyas razones trigonométricas se conocen, tendremos que buscar una estrategia como las anteriores, es decir, ¿se podrán descomponer en suma o diferencia de algunos de los habituales?
Aplicaremos el factor de conversión para conocer mejor con qué ángulos estamos tratando:
Parece complicado expresar $20º$ y $25º$ como combinación de $30º$, $45º$ o $60º$. Además, tampoco conduce a buen camino relacionarlos con sus complementarios o suplementarios, dado que no podemos usar calculadora.
Si escribimos la expresión en grados sexagesimales y la observamos con calma, incluso leyéndola en voz alta, quizás caigamos en la cuenta de que estamos ante la tangente de un ángulo suma, pero aplicada de derecha a izquierda, como exponemos seguidamente:
Como podemos apreciar con este ejercicio, es muy importante familiarizarnos y conocer bien las fórmulas de adición en ambos sentidos, es decir, de izquierda a derecha o de derecha a izquierda.
A continuación, ofrecemos un nuevo reto para practicar con la fórmula de adición de la tangente.
A la hora de resolver este reto, lo más habitual que podemos encontrarnos es que el alumnado que carece de experiencias previas, sustituya $\tg(a+b)$ por la fórmula de adición correspondiente y se encuentre con un cálculo tedioso y algo complicado. Sin embargo, siempre hay alguna persona que, ante lo que se avecina, descubre otro procedimiento que lo facilite.
A pesar de todo el trabajo que conlleva, recomendamos que se intente, pues siempre supone un adiestramiento en la ejecución técnica de un ejercicio, tan necesario en estas edades.
Pasamos directamente a utilizar fórmulas, realizar las operaciones y reducir al máximo, como puedes apreciar en la escena inferior pulsando el botón para conocer la primera estrategia.
Como ya hemos advertido, la realización del ejercicio con esta estrategia requiere bastantes cálculos y varios niveles entre fracciones, por lo que resulta incómoda la visualización de la escena embebida. Por ello, la escena dispone de un enlace con flecha en la zona superior derecha que permite su ampliación en ventana emergente, facilitando su correcta visualización.
Resulta mucho más adecuado y satisfactorio resolver este ejercicio con la estrategia del cambio de variables, pues se repite el ángulo $a+b$, como se detalla en la escena siguiente.
A veces, la manera en la que enseñamos y aprendemos una fórmula matemática puede limitar la capacidad de abstracción en parte del alumnado. Así ocurre, por ejemplo, cuando ya avanzado el estudio de la Trigonometría elemental planteamos un reto del siguiente estilo:
El alumnado conoce y aplica la fórmula fundamental de la Trigonometría para calcular las razones trigonométricas de un ángulo conocida una de ellas o para simplificar expresiones e identidades trigonométricas, pero puede bloquearse con la expresión anterior. Aunque, obviamente, podemos emplear un cambio de variables, recomendamos insistir en que el significado de la fórmula es "seno cuadrado de un ángulo más coseno cuadrado del mismo ángulo vale uno", aunque escribiremos, como es normal, $\,\text{sen}^{2}\alpha+\text{cos}^{2}\alpha=1$.
¿Cómo podemos ayudar a esta parte del alumnado?
Obviamente, podremos aplicar la estrategia que hemos denominado directa cuando nos enfrentemos a ejercicios con unas características muy concretas, o sea, a los que se conocen familiarmente como "ejercicios preparados", que son de gran utilidad para conseguir la perfecta comprensión y el dominio de las fórmulas.
Inventa una expresión trigonométrica que podamos simplificar con la que hemos denominado estrategia directa, es decir, por aplicación inmediata de una de las fórmulas de adición.
Estamos convencidos de que las mejores creaciones procederán de nuestras alumnas y alumnos. No obstante, a ver qué nos parecen estas propuestas:
Finalizaremos esta sección con una sencilla pregunta: ¿qué estrategia es recomendable para simplificar expresiones trigonométricas?
A la hora de afrontar un reto matemático o en otro ámbito de nuestra vida, es de gran valor conocer distintas estrategias, analizar la situación y adoptar la que sea más conveniente. Por tanto, recomendamos aprender el mayor número posible de estrategias.
En cursos anteriores, hemos aprendido la relación existente entre las razones trigonométricas de ángulos complementarios, suplementarios y, en general, la reducción al primer cuadrante. Recomendamos repasar y conocer bien el uso de esas expresiones. No obstante, las fórmulas de adición también posibilitan este tipo de operaciones. Por ejemplo:
Ahora bien, nos llevaremos una ingrata sorpresa si pretendemos aplicar la fórmula de la tangente del ángulo diferencia para el mismo ejemplo. ¿Por qué? Basta observar que en dicha fórmula intervienen las tangentes de los ángulos $a$ y $b$
$$tg(a-b)=\displaystyle\frac{\tg a - \tg b}{1+\tg a\cdot\tg b}$$
Así que si uno de ellos, $a$ o $b$, es $\displaystyle\frac{\pi}{2}$, su tangente no existe y, en consecuencia, no podemos aplicar la fórmula en este caso, llegando el momento de plantearse algunas cuestiones:
Resolver la situación pasa por expresar la tangente como cociente entre seno y coseno:
La no existencia de la tangente de un ángulo está motivada por la ilicitud de la división entre cero. Por tanto, necesitamos averiguar en qué casos se anula el denominador de la tangente, es decir, el coseno. Como ya sabemos, en el primer giro, el coseno vale cero en 90º y 270º. Usando la unidad de medida de ángulos en el Sistema Internacional:
Si continuamos recorriendo la circunferencia, por periodicidad,
Obtenemos como solución ángulos que son múltiplos impares de $\displaystyle\frac{\pi}{2}$
Ofrecemos una escena interactivaMedir ángulos en radianes. Consolación Ruiz Gil. para practicar y comprender la medida en radianes de ángulos sobre la circunferencia trigonométrica. Recomendamos seguir las instrucciones, representar los ángulos propuestos y, cuando estemos preparados, ponernos a prueba con la autoevaluación.
¿Habíamos intuido que serían infinitos los ángulos que anulan el coseno? ¿Cómo podemos resumirlos todos?
Como todos son múltiplos impares del ángulo mencionado, debemos centrarnos en la sucesión de los números impares: $$1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21,...$$
Se trata de una progresión aritmética de diferencia 2, así que su tér-
mino general vendrá dado por la expresión que recordamos:
Término general de una progresión aritmética de diferencia $d$
$$a_{n}=a_{1}+(n-1)\cdot d$$
En nuestro caso
Ya podemos recoger el conjunto de los infinitos ángulos que anulan el coseno:
En definitiva, las fórmulas de adición que proporcionan $\text{sen}(a\pm b)$ y $\cos(a\pm b)$ son aplicables cualesquiera que sean los valores de los ángulos $a$ y $b$. Sin embargo, las fórmulas para $\tg(a\pm b)$ no pueden emplearse cuando alguno de los ángulos es un múltiplo impar de $\displaystyle\frac{\pi}{2}$. En estos casos, deberá expresarse la tangente como el cociente entre seno y coseno.
Además, las fórmulas para $\tg(a\pm b)$ tampoco se pueden utilizar cuando $\tg a\cdot \tg b = \pm 1$. ¿Por qué? ¿A qué ángulos afecta?
Simplifica al máximo la siguiente expresión trigonométrica: $$\displaystyle\frac{\tg(\displaystyle\frac{\pi}{2}-\alpha)\cdot \sec(\pi-\alpha)\cdot \text{sen}(\displaystyle\frac{3\pi}{2}+\alpha)}{\cot(2\pi-\alpha)}$$
Si optamos por la estrategia de las fórmulas de adición, deberemos actuar con cautela cuando aparecen tangentes o cotangentes con algún ángulo múltiplo impar de $\displaystyle\frac{\pi}{2}$.
Existe un tradicional método gráfico para visualizar en la circunferencia trigonométrica las relaciones entre las razones trigonométricas de ángulos complementarios, suplementarios, ángulos que difieren en $\pi$ y, en general, todos los que se suelen usar en la reducción al primer cuadrante. No obstante, a lo largo de la historia de la enseñanza de las Matemáticas, el profesorado ha necesitado diseñar estrategias didácticas para atender a la diversidad de su alumnado y, a su vez, éste ha ideado reglas nemotécnicas para facilitar su aprendizaje.
En la siguiente estrategia para resolver el mismo ejemplo, veremos unas reglas prácticas, que carecen de rigor pero que agilizan el cálculo o simplificación de expresiones trigonométricas basadas en la reducción al primer cuadrante, y que son fruto de esas reglas nemotécnicas por parte del alumnado y de estrategias didácticas emanadas del profesorado.
Al aplicar las dos primeras reglas, decimos que la razón permanece invariable, es decir, que no cambia de nombre si intervienen los ángulos $\pi \pm \alpha$ o $2\pi \pm \alpha$, queriendo decir con ello que si tenemos un seno, el resultado seguirá siendo seno, o un coseno, permanece como tal. Por ejemplo, $\text{sen}(\pi - \alpha)=\text{sen}\space \alpha$ o $\cos(\pi + \alpha)=-\cos \alpha$.
Sin embargo, cuando intervienen los ángulos $\displaystyle\frac{\pi}{2} \pm \alpha$ o $\displaystyle\frac{3\pi}{2} \pm \alpha$, la razón cambia su nombre de seno a coseno, tangente a cotangente, secante a cosecante, y recíprocamente. Por ejemplo, si tenemos un seno, el resultado cambiará a coseno, y una tangente a cotangente, como ocurre con
Proponemos una autoevaluación para afianzar las reglas.
Otro de los aspectos a tener en cuenta a la hora de aplicar las reglas prácticas es la localización del cuadrante al que pertenece el ángulo, lo que hacemos tomando $\alpha$ en el primer cuadrante y razonarlo mentalmente o con un ejemplo concreto, si fuera necesario.
Con objeto de dejarlo claro antes de aplicar las reglas prácticas, ofrecemos una nueva autoevaluación.
A la hora de aplicar las fórmulas para la reducción al primer cuadrante, ya sabemos identificar las razones trigonométricas que cambian de nombre, las que permanecen invariables y localizar el cuadrante al que pertenece cada uno de los ángulos implicados.
En la página siguiente, proponemos una autoevaluación para consolidar el manejo ágil y seguro de la reducción al primer cuadrante. Para que el aprendizaje sea efectivo, recomendamos aplicar de forma razonada las reglas prácticas antes de emparejar
cada razón trigonométrica con su equivalente.
La autoevaluación se compone de seis test que debemos superar con paciencia y seguridad, pensando en la regla práctica antes de dar la respuesta.
Ha llegado el momento de sacar el máximo rendimiento a las reglas prácticas y lo haremos mostrando un ejemplo y la estrategia de razonamiento, que recomendamos aprender bien y seguir la explicación con la máxima atención.
En una rápida observación detectamos una resta de fracciones en las que aparecen cuatro razones trigonométricas que debemos reducir al primer cuadrante, aplicando las reglas prácticas:
Llamando $E$ a la expresión que vamos a simplificar y sustituyendo los valores de las razones, tendremos:
Recomendamos el uso de las reglas prácticas a la hora de simplificar expresiones trigonométricas en las que aparecen razones para reducir al primer cuadrante, pues con las fórmulas de adición, que es posible, se genera un esfuerzo superfluo.
¿Cómo afrontaremos este reto? Si vamos directamente a la expresión trigonométrica, nos encontramos con el seno del ángulo suma, pero si aplicamos su fórmula de adición, el primer miembro de la igualdad se complica. Por eso, en la siguiente escena descubriremos la estrategia habitual para resolver este ejercicio y que nos servirá de referencia para casos análogos.
Proponemos a continuación una serie de retos en los que veremos algunas aplicaciones de las fórmulas de adición, sobre todo para insistir en que las de reducción al primer cuadrante están limitadas a determinados ángulos: $\frac{\pi}{2}$, $\pi$, $\frac{3\pi}{2}$ y $2\pi$.
En cualquier momento tendremos que hacer uso de los conocimientos básicos de Trigonometría elemental. Así, por ejemplo, ya hemos empleado la fórmula fundamental, y ahora pasamos a recordarla junto a otras dos, necesarias para calcular las razones trigonométricas a partir de una dada.
De la lectura del ejercicio, se desprende que lo más razonable es utilizar la estrategia directa, es decir, aplicar la fórmula para la tangente del ángulo suma, donde uno de ellos es conocido y del otro nos proporcionan el valor de una razón trigonométrica y el cuadrante al que pertenece. Así que, en la siguiente escena presentamos la ejecución técnica del ejercicio acompañada del planteamiento razonado.
En primer lugar, podemos plantearnos afrontar este reto con la estrategia directa, es decir, obtener el valor de $\tg\beta$ aplicando alguna fórmula que nos conduzca al éxito. Para ello, necesitamos saber quién es $\beta$. ¿Podemos conseguir su valor a partir de la relación $\alpha+\beta=\frac{\pi}{4}$?
¿Habrá otra estrategia para resolver este ejercicio? ¿Podremos relacionar la suma de ángulos que aparecen como dato con las fórmulas de adición?
¿Cómo afrontaremos este reto? Debemos demostrar que, en cualquier triángulo, la suma de las tangentes de sus ángulos coincide con el producto de las mismas. ¿Y qué información o dato tenemos? Pues partimos de una relación implícita, ya que los tres ángulos de un triángulo suman un llano, es decir, sabemos que
En la siguiente escena veremos una variación de la estrategia, con el mismo planteamiento razonado y una técnica diferente, con un factor común muy especial y poco frecuente en estas edades.
Finalmente, vamos a resolver este ejercicio con otra estrategia partiendo, como no puede ser de otra manera, de la relación
En las anteriores, hemos despejado $C=\pi-(A+B)$, dejando constancia de que $C$ y $A+B$ son suplementarios. Pues bien, actuaremos de forma similar, pero despejando $A+B=\pi-C$. ¿Cómo afectará este nuevo enfoque a la resolución del ejercicio?
Una identidad trigonométrica es una igualdad entre expresiones con razones trigonométricas que se cumple o verifica para cualquier valor del ángulo. Por ejemplo, la igualdad $\cos x - 1 = 0$ no es una identidad trigonométrica. ¿Por qué?
Podemos comprobar fácilmente que la igualdad se cumple o verifica
para $x=0$, es decir, que al sustituir el ángulo por ese valor obtenemos el segundo miembro de la igualdad. Efectivamente:
$$\cos 0 - 1 = 1 - 1 = 0$$Sin embargo, no se verifica para $x=\displaystyle\frac{\pi}{3}$, ya que al sustituir en la igualdad no obtenemos el segundo miembro:
$$\cos \displaystyle\frac{\pi}{3} - 1 = \cos 60º - 1 = \displaystyle\frac{1}{2} - 1 = -\displaystyle\frac{1}{2} \not = 0$$Como ya sabemos, con un
Recordemos con este ejemplo de cursos anteriores la estrategia a seguir y que, inmediatamente, detallaremos:
Hemos comenzado por el primer miembro de la igualdad, sustituido la tangente por el cociente entre seno y coseno, efectuado las operaciones que aparecen, como potencia y suma de fracciones. Por último, aplicamos la fórmula fundamental de la Trigonometría y sustituimos la inversa del coseno por la secante, llegando al segundo miembro de la igualdad.
En la siguiente escena, resolvemos el ejercicio con la estrategia descrita, concretamente empezando por $A$, es decir, por el primer miembro, y recomendamos no intentarlo empezando desde el segundo miembro sin tener conocimientos para transformar sumas en productos ni sobre las razones trigonométricas del ángulo doble.
En el siguiente ejercicio aplicaremos la estrategia para demostrar una identidad trigonométrica empezando, indistintamente, por el primer miembro o por el segundo, poniendo de manifiesto algunas técnicas que recomendamos aprender.
En las primeras demostraciones de identidades surgen cuestiones sobre orientaciones o indicaciones antes de tomar la decisión de seleccionar el miembro de la identidad por el que empezar. Algunas pueden ser, por ejemplo, elegir la expresión de mayor complejidad en apariencia, pues parece lógico que será más sencillo emplear fórmulas, operar y simplificar para llegar a la más reducida. No obstante, solo la experiencia, basada en la práctica y en el conocimiento de diversas estrategias pueden conducirnos al éxito.
Hemos dejado para el final la estrategia que consideramos más cómoda y que parte del segundo miembro de la identidad, como mostramos en la próxima escena.
La autoevaluación es un elemento clave en el proceso de aprendizaje que permite al alumnado valorar sus logros y reflexionar sobre sus fortalezas y debilidades. Para ello, ofrecemos dos propuestas muy dispares entre sí. La primera es una autoevaluación sobre conceptos básicos, donde únicamente debemos contestar si o no, previa reflexión. Se compone de bloques con cuatro cuestiones y deberemos realizar el mayor número posible de los mismos, hasta conseguir un resultado satisfactorio que nos garantice el dominio básico sobre los aspectos tratados en este primer capítulo.
La segunda está orientada a la resolución de ejercicios relacionados con las fórmulas de adición usando las diferentes estrategias mostradas a lo largo del desarrollo de este primer capítulo.
Para que sea efectiva, debemos seguir las siguientes recomendaciones:
En la antigua Babilonia se introdujo la medida del ángulo en grados. La división de la circunferencia en 360º, probablemente va unida a la del año en 360 días. Así, como el Sol recorre una circunferencia en un año, un grado sería el recorrido en un día.Trigonometría. Proyecto ED@D" RED Descartes.

Con la cultura griega, la Trigonometría experimentó un nuevo y definitivo impulso. Aristarco de Samos (s. III a.C.), famoso por haber propuesto el primer sistema heliocéntrico, halló la distancia al Sol y a la Luna utilizando triángulos. Hiparco de Nicea (s. II a.C.) mejoró las observaciones de Aristarco y es considerado como el “inventor” de la Trigonometría. Ptolomeo, en el siglo II, escribió el “Almagesto”, que influyó a lo largo de toda la Edad Media.
Al igual que las fórmulas de adición, las razones trigonométricas del ángulo doble surgen en una época en la que no existían herramientas tecnológicas como calculadoras científicas, de cálculo simbólico, aplicaciones para dispositivos móviles o cualquier software para ordenador y había que recurrir a las conocidas como tablas trigonométricas. Hoy en día son de gran utilidad a la hora de resolver ecuaciones trigonométricas, para calcular y simplificar derivadas de funciones o en el cálculo integral, por ejemplo.
Dado un ángulo $a$, se llama ángulo doble el ángulo $2a$, y nos planteamos el cálculo de las razones trigonométricas del ángulo doble conociendo las del ángulo simple o sencillo, es decir, $a$.
Podemos encontrar una demostración de las mismas en los "Apuntes de Trigonometría", iniciando sesión como invitados.
Antes de comenzar a conocer estrategias para la resolución de ejercicios en los que interviene el ángulo doble, pasaremos a realizar una sencilla actividad interactiva que tiene por objeto familiarizarnos con las fórmulas que, con más asiduidad, aplicaremos en este capítulo.
Antes de pasar a la ejecución técnica del ejercicio, que es bastante sencillo, debemos comenzar marcando la diferencia entre $\text{sen}\displaystyle\frac{a}{2}$ y $\displaystyle\frac{\text{sen}\space a}{2}$
La expresión y simbología matemáticas deben estar escrita con la mayor claridad posible para evitar confusiones y errores habituales entre algunos alumnos y alumnas. Así, cuando escribimos $\text{sen}\displaystyle\frac{a}{2}$, debemos entender que estamos calculado el seno de la mitad del ángulo, mientras que en la expresión $\displaystyle\frac{\text{sen}\space a}{2}$, calcularemos la mitad del seno del ángulo. Por ejemplo, si trabajamos con el ángulo $a=60º$, tendremos que:
En cuanto a la resolución del ejemplo propuesto, recomendamos aplicar las fórmulas del seno y coseno del ángulo doble leídas de derecha a izquierda:
Haremos un recorrido análogo al seguido en el primer capítulo, así que empezaremos por calcular el valor exacto de las razones trigonométricas del ángulo doble conocida una de las razones del ángulo simple o sencillo.
Conviene observar que nos dan el valor de una razón trigonométrica, pero no se sitúa al ángulo en ningún cuadrante, así que tendremos dos posibles soluciones. Además, consideramos que debemos aplicar una estrategia directa, es decir, utilizar las fórmulas correspondientes a cada razón trigonométrica solicitada.
En primer lugar, mostramos la estrategia directa, es decir, aplicaremos la fórmula correspondiente usando el coseno, que obtenemos de la secante, y el seno a partir de la fórmula fundamental de la Trigonometría.
En la segunda estrategia, nos planteamos si existe la posibilidad de obtener el valor del coseno del ángulo doble sin necesidad de recurrir a la fórmula fundamental de la Trigonometría y hallar, además, el seno. Es decir, ¿podremos resolver el ejercicio únicamente con el dato aportado?
Proponemos a continuación un ejercicio en el que se involucran las fórmulas de adición y las del ángulo doble.
Consideramos que procede abordar este nuevo reto con una estrategia directa, o sea, aplicando la fórmula para la tangente del ángulo suma y, posteriormente, la de la tangente del ángulo doble.
En la siguiente escena, debemos introducir los valores solicitados en los campos de texto activos y PULSAR INTRO, produciéndose una interactividad que permite avanzar siempre que se aporte la respuesta correcta.
Como ya comentamos en el capítulo anterior, no existe un procedimiento estándar que nos permita simplificar una expresión trigonométrica, únicamente la experiencia basada en la práctica. No obstante, recomendamos las siguientes pautas de actuación:
Uno de los errores más habituales al simplificar o trabajar con expresiones trigonométricas racionales o de cociente, es intentar dividir, en este caso, el seno por el coseno, algo que no es posible si algún término de la fracción está constituido por sumandos, como ocurre en el denominador. Por otra parte, el enunciado nos proporciona la solución, pues debemos conseguir una razón trigonométrica directa: seno, coseno o tangente.
En la siguiente escena mostramos una técnica que puede ayudar a un sector del alumnado en muchas ocasiones, consistente en aplicar la fórmula fundamental de la Trigonometría de izquierda a derecha y que nos permite reemplazar el número 1 por $\text{sen}^2\alpha + \cos^2\alpha$.
Antes de conocer la estrategia de resolución que proponemos conviene prevenir, para quien lo necesite, sobre ciertos aspectos que conducen a situaciones erróneas:
Nos dedicaremos ahora a realizar algunas operaciones entre expresiones trigonométricas racionales o de cociente.
En la primera estrategia actuaremos de forma independiente sobre cada fracción para, posteriormente, efectuar la operación indicada, es decir, una división.
En la segunda estrategia, efectuaremos la división de fracciones y simplificaremos la fracción resultante.
En esta ocasión, nos enfrentamos a una diferencia de fracciones y, como estrategia primera, efectuaremos la operación reduciendo a común denominador, lo que nos lleva a obtener el mínimo común múltiplo de los denominadores.
En la segunda estrategia, actuaremos sobre cada fracción de forma independiente para reducirlas y, finalmente, calcularemos la diferencia solicitada.
En el capítulo anterior hemos aportado el concepto de
Entre los procesos, métodos y actitudes en matemáticas, debemos aprender a reflexionar sobre los procesos desarrollados, tomando conciencia de sus estructuras, obteniendo conclusiones, utilizando argumentos lógicos y coherentes, así como practicar estrategias para la generación de investigaciones matemáticas. Por ello, seguidamente, proponemos un proyecto de investigación matemática basado en la resolución errónea del ejemplo planteado, es decir, presentamos una ejecución técnica incorrecta, aunque conduce al resultado esperado, generando así escepticismo, y debemos investigar para encontrar el error cometido, los conceptos o principios matemáticos vulnerados, reflexionar sobre el error como elemento de aprendizaje en matemáticas, las consecuencias que pueden derivarse de un error en un proyecto científico o técnico y elaborar un informe digital, en el formato que estimemos adecuado, con las conclusiones de esta investigación.
Después del proyecto de investigación, en la siguiente escena mostramos una estrategia correcta de resolución para este ejemplo, que no quiere decir que sea la única.
En este ejercicio conjugamos fórmulas de adición con fórmulas del ángulo doble, con la pregunta ¿cómo podremos pasar del ángulo simple o sencillo al ángulo doble o recíprocamente? ¿En qué momento del proceso se producirá ese cambio?
Durante el desarrollo o ejecución técnica del ejercicio, incluimos en la escena una serie de indicaciones en diversos colores con objeto de ayudar al alumnado que lo requiera, y que siempre han sido bien aceptadas por los mismos.
No obstante, debemos insitir en que nunca procederemos a su incorporación en la ejecución técnica del ejercicio.
Seguidamente, mostramos una escena con otra alternativa para la resolución de este mismo ejercicio, aunque es más una variación de la primera estrategia, pues el desarrollo es completamente análogo y cambiamos ciertas operaciones, técnica que conviene conocer.
Uno de los errores más frecuentes presentes en estas identidades con expresiones trigonométricas racionales o de cociente, y que debemos corregir, consiste en cancelar la $\tg \alpha$ del numerador con la $\tg \alpha$ del denominador, con la célebre y común frase de "la tangente, se va con la tangente". Insistimos en que se trata de una acción ilícita cuando algún término de la fracción contiene sumandos, como sucede en este ejercicio con la diferencia de tangentes existente en el denominador.
En la siguiente escena mostramos la estrategia directa, que sería la abordada por la mayor parte del alumnado.
En la próxima escena presentamos una variación de esta estrategia con una extracción de factor común que pocos alumnos y alumnas utilizan, siendo importante ir conociendo esta técnica que puede facilitarnos el cálculo en determinadas circunstancias.
En la tercera y última estrategia, posiblemente la menos ocurrente por falta de experiencia, intervenimos, en primer lugar, sobre la diferencia de tangentes que figura en el denominador del primer miembro de la identidad.
Aunque se trata de un ejercicio con menor dificultad que los anteriores, no por ello deja de tener su interés. Por ejemplo, podemos seguir la recomendación de empezar por el miembro de la igualdad que presente más dimensión, en este caso, el segundo. Pues bien, nos encontramos con una igualdad o producto notable del tipo diferencia de cuadrados. Efectivamente, recordemos que:
Así que, aplicado a nuestra expresión trigonométrica tendremos:
Donde, obviamente, hemos aplicado la fórmula fundamental de la Trigonometría y la fórmula para el coseno del ángulo doble.
Nos planteamos, ahora, la demostración recíproca, es decir, empezando por el primer miembro que, posiblemente, no se nos habría ocurrido, pero que resulta importante conocer este tipo de técnicas y procedimientos en matemáticas.
Como podemos apreciar, la estrategia consiste en utilizar el 1 como elemento neutro del producto para, posteriormente, emplear la técnica, que ya hemos aprendido, de escribir ese 1 con su valor equivalente en la fórmula fundamental de la Trigonometría. Finalmente, efectuamos el producto de suma por diferencia como diferencia de cuadrados y conseguimos nuestro objetivo.
La autoevaluación es un elemento clave en el proceso de aprendizaje que permite al alumnado valorar sus logros y reflexionar sobre sus fortalezas y debilidades. Para ello, ofrecemos dos propuestas muy dispares entre sí. La primera es una autoevaluación sobre conceptos básicos, donde únicamente debemos contestar si o no, previa reflexión. Se compone de tres actividades con cuatro cuestiones cada una, y deberemos realizarla y repetirla hasta conseguir un resultado satisfactorio que nos garantice el dominio básico sobre los aspectos relacionados con las razones trigonométricas del ángulo doble.
La segunda, con algo más de complejidad, está orientada a la resolución de ejercicios relacionados con las razones trigonométricas del ángulo doble, usando las diferentes estrategias mostradas a lo largo del desarrollo de este segundo capítulo, y requiere de un importante esfuerzo, concentración y conocimientos para desarrollar de forma conjunta los procesos, métodos y actitudes transmitidas.
Para que la autoevaluación dedicada a la resolución de ejercicios sea efectiva, debemos seguir las siguientes recomendaciones:
El desarrollo de la Trigonometría debe mucho a la obra de los árabes, quienes transmitieron a Occidente el legado griego. Fueron los primeros en utilizar la tangenteTrigonometría. Proyecto ED@D" RED Descartes.. Hacia el año 833, Al-Kwuarizmi construyó la primera tabla de senos.

En Europa se publica en 1533, el primer tratado de Trigonometría: “De trianguli omnia modi, libri V”. Escrito en 1464 en Köningsberg, por Johann Müller, conocido como el Regiomontano.
Newton utiliza en 1671 las coordenadas polares. La física de los fenómenos ondulatorios, como el producido por una cuerda que vibra, llevó a Euler (1707-1783) al estudio de las funciones trigonométricas.
Se llama ángulo mitad de $\alpha$ el ángulo $\displaystyle\frac{\alpha}{2}$, y nos planteamos como objetivo poder calcular las razones trigonométricas del ángulo mitad conocidas las del ángulo sencillo o simple, para lo que usaremos las siguientes fórmulas.
Podemos encontrar una demostración de las fórmulas para las razones trigonométricas del ángulo mitad en los "Apuntes de Trigonometría", iniciando sesión como invitados.
El doble signo queda determinado cuando se conoce el cuadrante al que pertenece el ángulo $\displaystyle\frac{a}{2}$
Antes de comenzar a conocer estrategias para la resolución de ejercicios en los que interviene el ángulo mitad, pasaremos a realizar una sencilla actividad interactiva que tiene por objeto familiarizarnos con las fórmulas que aplicaremos en este capítulo.
Consideramos la estrategia directa como la idónea para resolver este ejemplo, ya que necesitaremos el coseno para la tangente del ángulo mitad.
A la complejidad de las fórmulas para las razones trigonométricas del ángulo mitad, debidas a los radicales, hay que añadir el doble signo que les preceden y que depende del cuadrante al que pertenezca el ángulo mitad. Ello nos obliga, en primer lugar, a localizar el cuadrante para asignar el signo. Proponemos, a continuación, un ejercicio para mostrar este tratamiento y que resolveremos con la denominada estrategia directa.
En la segunda estrategia de resolución separamos el ángulo en dos sumandos y aplicamos las fórmulas de adición, concretamente la del coseno del ángulo suma, aunque no podremos evadir las del ángulo mitad.
Como primera estrategia mostramos el proceso que suele seguir la mayor parte del alumnado, un proceso basado en usar la fórmula de la tangente del ángulo mitad para obtener el coseno del ángulo simple y, a partir de ahí, la cotangente solicitada pasando por el seno y coseno del ángulo doble.
En la segunda estrategia resolvemos el ejercicio usando la relación entre los ángulos mitad, simple y doble, que nos facilita enormemente la forma de abordar y superar el reto.
Como no podemos usar calculadora ni herramientas tecnológicas, tendremos que expresar el ángulo en función de los denominados ángulos notables, es decir, 30º, 45º y 60º o como combinación entre ellos. Además, en caso de necesidad, puede facilitar la búsqueda de esa relación o combinación aplicar el factor de conversión de radianes a grados sexagesimales.
Es en este contexto del cálculo de valores exactos de razones trigonométricas, utilizando las fórmulas de adición, del ángulo doble o del ángulo mitad, hasta ahora, donde realmente se pueden llegar a comprender la necesidad e importancia de dominar las operaciones entre radicales, y muy especialmente, la racionalización de denominadores.
Proponemos, seguidamente, un ejercicio de características similares y que debemos resolver con la estrategia directa, mostrada en el ejemplo, y con las mismas técnicas.
Recordamos, nuevamente, que no existe un procedimiento estándar que nos permita simplificar una expresión trigonométrica, únicamente la experiencia basada en la práctica. No obstante, recomendamos las siguientes pautas de actuación:
Con un simple reconocimiento, la expresión nos recordará a la fórmula para la tangente del ángulo mitad. ¿Tendrá alguna relación? Parece lógico escribir la secante en función del coseno, su razón inversa con respecto al cociente. En la siguiente escena, mostramos la estrategia directa de resolución y una pequeña ayuda con el cambio de variables, en caso de necesidad.
Emplearemos, en primer lugar, la estrategia directa que, como podemos imaginar, consiste en sustituir la tangente del ángulo mitad por su fórmula correspondiente, realizar las operaciones que aparecen respetando la jerarquía, emplear otras fórmulas y reducir al máximo.
En la segunda estrategia expresaremos la tangente que aparece como cociente entre seno y coseno, realizaremos las operaciones, emplearemos fórmulas y simplificaremos.
En la tercera estrategia, aunque es más una variación de la segunda, comenzaremos con la misma idea y utilizaremos en el denominador la conocida fórmula que relaciona tangente con coseno, es decir:
pero aplicada al ángulo mitad, o sea:
Podemos ver el desarrollo en la escena de la página siguiente.
Ya hemos tratado en capítulos anteriores, tanto en fórmulas de adición como en el ángulo doble, la
En la segunda estrategia también comenzamos a demostrar la identidad por el segundo miembro, aunque veremos una técnica sencilla que nos permitirá expresar con el mismo ángulo las razones trigonométricas que aparecen, facilitando la resolución del ejercicio.
¿Por dónde comenzar a demostrar esta identidad? ¿Por el miembro de mayor dimensión? En ese caso, si decidimos iniciar el proceso por el segundo miembro, que se compone de seno y coseno, ¿cómo llegar a cotangente? ¿Cómo pasar del ángulo sencillo o simple al ángulo mitad? Si nos decantamos o decidimos por el primer miembro, de momento es fácil pasar de cotangente a seno y coseno, que es el objetivo, pero ¿cómo pasar del ángulo mitad al simple?
En la segunda estrategia proporcionamos una técnica poco frecuente en el alumnado de esta edad, pero que conviene ir conociendo para facilitar la resolución de futuros retos.
En Matemáticas, como en cualquier otra ciencia, cuantos más conocimientos y experiencias tengamos, más herramientas o técnicas, así como estrategias, más cómodo puede resultar afrontar un reto. Además, cada descubrimiento realizado supone algo así como un escalón sobre el que apoyarnos para avanzar y llegar a nuevos descubrimientos que, tarde o temprano, van a repercutir en mejoras para la ciencia y, por ende, para la sociedad. Ahora bien, no es posible conseguirlo sin realizar labores de investigación, para lo que se hace necesario invertir en recursos humanos, con buenos equipos multidisciplinares, y en recursos materiales, con buenas instalaciones específicas para cada ámbito.
Por todo ello, proponemos a continuación un nuevo proyecto de investigación para ampliar conocimientos.
Llega el momento de utilizar los descubrimientos realizados en nuestro proyecto de investigación para resolver el ejercicio con la tercera estrategia.
Como estrategia primera empezaremos por el primer miembro de la igualdad, usaremos la fórmula de la tangente para el ángulo mitad, realizaremos las operaciones que aparecen, tendremos que utilizar alguna otra fórmula, simplificar y llegar al segundo miembro.
En la segunda estrategia comenzaremos también por el primer miembro, pero nos apoyaremos en los recientes descubrimientos de nuestro proyecto de investigación.
Como hemos manifestado en capítulos anteriores, la autoevaluación es un elemento clave en el proceso de aprendizaje que permite al alumnado valorar sus logros y reflexionar sobre sus fortalezas y debilidades. Para ello, ofrecemos dos propuestas muy dispares entre sí. La primera es una autoevaluación sobre conceptos básicos, donde únicamente debemos contestar cierto o falso, previa reflexión. Se compone de doce preguntas con el valor añadido de límite temporal, y deberemos realizarla y repetirla hasta conseguir un resultado satisfactorio que nos garantice el dominio básico sobre los aspectos relacionados con las razones trigonométricas del ángulo mitad.
La segunda, con algo más de complejidad, está orientada a la resolución de ejercicios relacionados con las razones trigonométricas del ángulo mitad, usando las diferentes estrategias mostradas a lo largo del desarrollo de este tercer capítulo, y requiere de un importante esfuerzo, concentración y conocimientos para desarrollar de forma conjunta los procesos, métodos y actitudes transmitidas.
Para que la autoevaluación dedicada a la resolución de ejercicios sea efectiva, debemos seguir las siguientes recomendaciones:
Hoy en nuestros días, las utilidades de la Trigonometría abarcan los más diversos campos: de la Topografía a la Acústica, la Óptica y la Electrónica.
Pero, ¿cuándo se utilizó por primera vez el término Trigonometría? ¿Quién lo promovió?
En el año 1595, el matemático, astrónomo y teólogo Bartholomaeus Pitiscus fue el primero en acuñar el término Trigonometría en su libro "Trigonometria: sive de solutione triangulorum tractatus brevis et perspicuus".Trigonometría: la primera vez" ZTFNews.org

Comenzamos el capítulo que mayor potencial ofrece y que produce un gran impacto entre el alumnado, posiblemente por la dificultad innata de las fórmulas, unas expresiones que, combinadas con estrategias y técnicas ya conocidas, nos permitirán simplificar fracciones trigonométricas.
Por ejemplo, supongamos que nos piden simplificar la siguiente fracción trigonométrica:
Pues bien, la respuesta habitual entre el alumnado de esta edad sería:
siendo muy probable que un sector del alumnado proporcionara similar respuesta para la fracción
Por ello, es de suma importancia ir conociendo los fundamentos teóricos que nos permiten emplear expresiones lingüísticas que son familiares en el contexto matemático como "cancelar", "tachar", "simplificar", "se van", etc. Así, para la primera fracción, podremos argumentar o justificar de esta forma:
Son tres los elementos que hacen posible la cancelación, a saber:
Si intentamos hacer lo propio con la segunda fracción, nos encontramos que
y observamos lo siguiente:
¿Y si tuviéramos que simplificar la fracción que mostramos a continuación?
¿Se nos ocurre alguna estrategia para descomponer esta fracción como combinación de otras? ¿Se pueden cancelar las expresiones trigonométricas que se repiten en el numerador y en el denominador? ¿Cuál sería el resultado final? ¿Necesitaremos ampliar conocimientos?
Situaciones análogas se producen cuando nos encontramos ante fracciones trigonométricas que poseen expresiones en el numerador y en el denominador cuyo cociente es un resultado conocido, y nos preguntamos si podemos realizar esas operaciones de forma independiente. Por ejemplo, en la fracción
¿podemos dividir por separado los senos del numerador entre los cosenos del denominador y escribir tangentes? Pues la respuesta es muy sencilla, así como los argumentos que lo justifican:
Vemos que es factible gracias a que el producto de fracciones se realiza "en línea", es decir, multiplicando los numeradores y multiplicando los denominadores, lo que nos permite descomponer la fracción en producto de otras dos fracciones. Pero, ¿qué pasa si alguno de los términos de la fracción se compone de sumandos y no de factores? Por ejemplo:
Sobre factorización para resolver ecuaciones trigonométricas, podemos visitar la página 180.
Aunque el numerador se compone de sumandos, lo hemos logrado descomponiendo la fracción en suma de otras dos con el mismo denominador para, posteriormente, descomponer cada una de ellas en producto de otras dos fracciones, gracias a que sus términos, es decir, numerador y denominador, se componen de factores. Finalmente, nos queda plantearnos qué ocurre si los dos términos de la fracción se componen de sumandos, como en el caso que mostramos a continuación:
En este caso, al igual que en el anterior, no podemos operar los senos del numerador con los cosenos del denominador, pues los sumandos impiden descomponer en producto de fracciones. De ahí la importancia de que ambos términos se compongan de factores. Es exactamente lo mismo que sucede al simplificar fracciones polinómicas, debiendo factorizar el numerador y denominador, por las técnicas conocidas, como factor común, productos notables o regla de Ruffini, para cancelar los factores repetidos en ambos términos.
En este capítulo, aprenderemos a factorizar sumas o diferencias de senos, sumas o diferencias de cosenos e investigaremos la posibilidad de factorizar sumas o diferencias de tangentes, cotangentes, secantes, cosecantes e incluso sumas de razones trigonométricas diferentes. Es lo que se conoce como transformar sumas y diferencias en productos.
Sólo podremos simplificar cuando los dos términos de la fracción estén compuestos por factores, de ahí la importancia de la factorización.
Como acabamos de argumentar con varios ejemplos, necesitamos factorizar los dos términos de una fracción para poder simplificarla y operar de forma independiente entre unos y otros. Y, para ello, se utilizan las conocidas como fórmulas que transforman en producto sumas y diferencias de razones trigonométricas, como las que se aplican para sumas y diferencias de senos.
Antes de tomar contacto con las fórmulas para familiarizarnos con ellas, conviene mencionar la diferencia simbólica de la lingüística, ya que son fórmulas completamente similares. Así, mientras en los primeros miembros tendremos sumas o diferencias de senos con ángulos sencillos o simples, en los segundos nos encontramos con tres factores, uno numérico y otros dos con seno y coseno, pero de ángulos "algo especiales": una vez la mitad de la suma de los ángulos sencillos y otra la mitad de la diferencia de los mismos.
Según el diccionario de la RAE, para indicar el medio o la mitad de algo se utiliza el elemento compositivo semi, por lo que la expresión
lingüística de las fórmulas es la siguiente:
Ya tenemos conocimientos para simplificar una de las fracciones trigonométricas propuestas anteriormente, previa factorización del numerador y denominador con las fórmulas que acabamos de presentar:
No olvidemos que todo ha sido posible gracias a la factorización del numerador y denominador, a la descomposición en producto de fracciones y al elemento neutro del producto.
Llega el momento de conocer las fórmulas que nos permitirán factorizar sumas y diferencias de cosenos.
Para una correcta comunicación matemática, son de suma importancia tanto las expresiones simbólicas como las lingüísticas, que las utilizadas para estas fórmulas son:
Podemos encontrar una demostración de las fórmulas que transforman sumas y diferencias en producto en los "Apuntes de Trigonometría", iniciando sesión como invitados.
Ya podemos simplificar la segunda fracción trigonométrica propuesta anteriormente, pero agilizaremos el cálculo, pues ya conocemos la forma de argumentar y justificar todo lo que lo hace factible. Por supuesto, en primer lugar tenemos que factorizar los dos términos de la fracción.
Antes de comenzar a conocer estrategias para la resolución de ejercicios en los que intervienen las transformaciones trigonométricas, pasaremos a realizar dos sencillas actividades interactivas que tienen por objeto familiarizarnos con las fórmulas que, con más asiduidad, aplicaremos en este capítulo.
En la primera actividad, debemos concentrarnos únicamente en el cálculo mental de la semisuma y semidiferencia de los ángulos que aparecen. Mientras que en la segunda, además deberemos identificar los dos factores algebraicos que faltan en cada ejercicio, seleccionándolos de la zona inferior de la escena. Como allí recalcamos, para que se produzca aprendizaje, es necesario resolverlo mentalmente, con las fórmulas a la vista, incluso podemos escribirlo en otro lugar.
Al igual que ocurre con las fracciones algebraicas, debemos factorizar los dos términos de la fracción para poder dividir razones del numerador entre razones del denominador, gracias a la descomposición en producto de fracciones.
Básicamente, la estrategia mostrada es la habitual en la simplificación de fracciones trigonométricas cuyos términos se componen de sumas de senos o cosenos.
En el siguiente reto nos enfrentamos a una suma de tres senos en el numerador y tres cosenos en el denominador. ¿Cómo lo afrontaremos?¿Qué estrategia será adecuada?
Hemos superado el reto de tres sumandos con una estrategia mixta en la que aplicamos, a los dos primeros, las transformaciones trigonométricas para, seguidamente, sacar factor común. ¿Cómo actuaremos si nos enfrentamos a una fracción trigonométrica cuyos términos están integrados por cuatro sumandos?
Después de la experiencia adquirida con los anteriores retos, parece buena idea factorizar por parejas. ¿Estamos de acuerdo?
La estrategia y técnicas que nos han permitido resolver este reto ha consistido en factorizar por parejas, sacar factor común y volver a utilizar las fórmulas que transforman sumas en producto. No obstante, podemos plantearnos alguna pregunta para analizar la posibilidad de dar respuesta al ejercicio con otras combinaciones entre las parejas de senos en el numerador y las de cosenos en el denominador.
Como ya sabemos, cuando se nos piden valores exactos, no podemos dar respuestas con aproximaciones o números decimales, ni tampoco ofrecer el resultado proporcionado por la calculadora científica o simbólica, así que usaremos las transformaciones trigonométricas y todos los conocimientos adquiridos hasta el momento.
Presentamos una estrategia basada en agrupar dos de los tres términos para aplicar una de las transformaciones trigonométricas y, con el resultado obtenido, reiterar el proceso hasta conseguir el valor exacto solicitado, usando la razón de algún ángulo notable que resulta al aplicar la transformación correspondiente.
Conviene analizar si sería posible abordar este reto pero realizando una agrupación diferente entre sus términos.
Podemos utilizar la estrategia de agrupamiento, es decir, aplicar las transformaciones trigonométricas por parejas, pero siempre es recomendable evaluar cada ángulo por separado por si alguno fuera notable.
Hemos conjugado técnicas como reducción al primer cuadrante, ángulos notables y doble agrupamiento para aplicar transformaciones trigonométricas.
Utilizaremos la estrategia que nos permite factorizar los dos términos de la fracción numérica aplicando las fórmulas que transforman en producto sumas o diferencias de senos y cosenos.
Afrontaremos a continuación un reto similar pero con una fracción trigonométrica de carácter algebraico.
Dada la experiencia adquirida durante el desarrollo del capítulo, sabemos que no es posible dividir razones del numerador entre razones del denominador, pues ambos términos de la fracción se componen de sumandos, siendo necesario proceder a su factorización aplicando las transformaciones trigonométricas.
El nuevo agente acelerador del crecimiento económico son las matemáticas: la ciencia más abstracta no solo ocupa el epicentro de la revolución digital, sino que es el poder invisible que aumenta la productividad en todos los sectores. El primer estudio que mide la “intensidad matemática” de la economía en España, por encargo de la Red Estratégica en Matemáticas (REM), concluye que las matemáticas son ya directamente responsables de “más de un millón de ocupados” -el 6% del empleo total- y de más del 10% del PIB”.
Entre las conclusiones del estudio, se deduce que el crecimiento económico de un país depende de la formación matemática de su población, de la inversión en investigación matemática y de su aplicabilidad en entornos industriales y tecnológicos.
En el ámbito educativo, es recomendable, y así se contempla en los diseños curriculares, fomentar el trabajo colaborativo y plantear retos o proyectos de investigación matemática, e incluso interdisciplinares, con objeto de que el alumnado pueda poner en práctica sus aprendizajes, elaborar un informe con sus conclusiones y darles difusión en entornos apropiados.
Presentamos en esta sección una recopilación de retos que se afrontan con la estrategia de factorización.
En este reto se combinan las estrategias de agrupamiento con las técnicas habituales de factorización, desde las transformaciones trigonométricas al factor común.
Además, se nos presenta una gran oportunidad para mostrar al alumnado el enorme potencial que proporciona a las matemáticas el uso de parámetros. Concretamente, de una función en apariencia, nos encontramos ante una familia de funciones, es decir, infinitas funciones contenidas en una sola fórmula.
Pero aquí no termina todo, pues la simplificación de la fracción nos conduce a un resultado sin parámetro, es decir, la función no depende del parámetro, siendo importante insistir sobre este hecho. Finalmente, conviene que el alumnado aprenda a detectar el momento del proceso de simplificación donde se manifiesta esa independencia paramétrica.
Antes de comenzar un ejercicio, debemos siempre prestar suma atención a su enunciado. Así, en este nuevo reto, conocemos la gama de soluciones posibles, ya que el resultado será $\,n \cdot \text{sen}\, x$, $n \cdot \text{cos}\, x$ o $n \cdot \text{tg}\, x$, siendo $n$ un número par, ya que seno, coseno y tangente son las razones trigonométricas directas. Además, se nos indica la estrategia a seguir, que consiste en transformar en productos las sumas de senos. Por otra parte, la mencionada suma solo consta en el numerador, término de la fracción sobre el que debemos intervenir, obviamente, y usando la estrategia de agrupamiento, pues nos encontramos con más de dos.
Proponemos seguidamente lo que se conoce como reto guiado, es decir, un ejercicio que presenta alguna dificultad fuera de lo habitual y se acompaña de recomendaciones o sugerencias para afrontarlo con éxito. Obviamente, podemos intentarlo sin atender a dichas pautas o resolverlo con nuestras propias y creativas ideas.
Regresamos a un reto planteado en el primer capítulo consistente en demostrar una identidad trigonométrica. En su momento, dimos respuesta empezando por el primer miembro y recomendamos no intentarlo desde el segundo sin tener conocimientos para transformar sumas en productos ni sobre las razones trigonométricas del ángulo doble. Pues bien, ya disponemos de esos conocimientos. Afrontaremos, por tanto, el reto con la que será segunda estrategia
Abordamos un nuevo desafío que podemos superar con relativa comodidad aplicando las transformaciones trigonométricas, incluso posteriormente aplicaremos la fórmula para la tangente del ángulo doble.
La pregunta previa que deberíamos plantearnos es cómo aparecerá el ángulo doble si únicamente encontramos en la identidad ángulos triple y simple.
Nos enfrentamos a un reto algo diferente a los que hemos tratado hasta el momento, ya que sabemos factorizar una suma de cosenos, pero...
Además, el único coseno que aparece viene afectado por un coeficiente. ¿Cómo actuar en este caso? ¿Qué estrategia podemos aplicar?La demostración forma parte del quehacer diario en el mundo de las matemáticas y es, probablemente, su herramienta más potente. Pero, ¿qué tratamiento debemos ofrecer en la etapa del bachillerato?
En el bloque de contenidos correspondientes al primer curso del bachillerato de ciencias del sistema educativo español, se contempla:
En los inicios del primer capítulo de esta obra ya proporcionamos una sencilla
Hablamos de contenidos que deben tratarse de forma transversal y simultánea en cada uno de los bloques, junto a otros procesos básicos e imprescindibles en el quehacer matemático. Una tarea nada fácil para el profesorado, que se enfrenta a extensos temarios y a las condiciones en las que se desarrolla el segundo curso, donde el alumnado debe enfrentarse a la denominada Prueba de Evaluación y Acceso a la Universidad, con unos modelos establecidos que no contemplan preguntas teóricas ni mucho menos demostraciones.
Por curiosidad, hemos decidido compartir la prueba de selectividad a la que tuvo que enfrentarse el autor de esta obra en el año 1979, sin afán de establecer comparativas ni debates al respecto. Eran otros tiempos, ni mejores, ni peores, simplemente diferentes.

En las condiciones expuestas no corresponde tratar demostraciones de teoremas, lemas, corolarios, etc, pero podemos cumplir con una parte importante de lo solicitado usando los denominados ejercicios o retos tipo demostración.
Antes de presentar dos estrategias para afrontar este nuevo reto, conviene familiarizarnos con los detalles básicos en un proceso de demostración, como distinguir bien la información de la conclusión.
En la escena anterior, hemos comentado el significado de las iniciales c.q.d. al final de una demostración, aunque también podemos encontrarnos con q.e.d. Para más información, recomendamos esta entrada en Wikipedia.
La autoevaluación es un elemento clave en el proceso de aprendizaje que permite al alumnado valorar sus logros y reflexionar sobre sus fortalezas y debilidades. Para ello, ofrecemos dos propuestas muy dispares entre sí. La primera es una autoevaluación sobre conceptos básicos, donde únicamente debemos contestar si o no, previa reflexión. Se compone de bloques con cuatro cuestiones y deberemos realizar el mayor número posible de los mismos, hasta conseguir un resultado satisfactorio que nos garantice el dominio básico sobre los aspectos tratados en este capítulo.
Recomendamos tener a mano el formulario de las transformaciones trigonométricas y practicar el cálculo mental, dada la sencillez de las cuestiones.
La segunda, con algo más de complejidad, está orientada a la aplicación de las transformaciones trigonométricas.
Para que la autoevaluación dedicada a la resolución de ejercicios sea efectiva, debemos seguir las siguientes recomendaciones:
No queremos finalizar este pequeño recorrido por la historia de la Trigonometría sin reflexionar sobre lo facilísimo que resulta hoy en día calcular la razón trigonométrica de cualquier ángulo, incluso con gran precisión y cifras decimales. Pero, ¿cómo se calculaban el seno, coseno o tangente de un ángulo antes de la invención de las calculadoras científicas, ordenadores personales o dispositivos móviles?
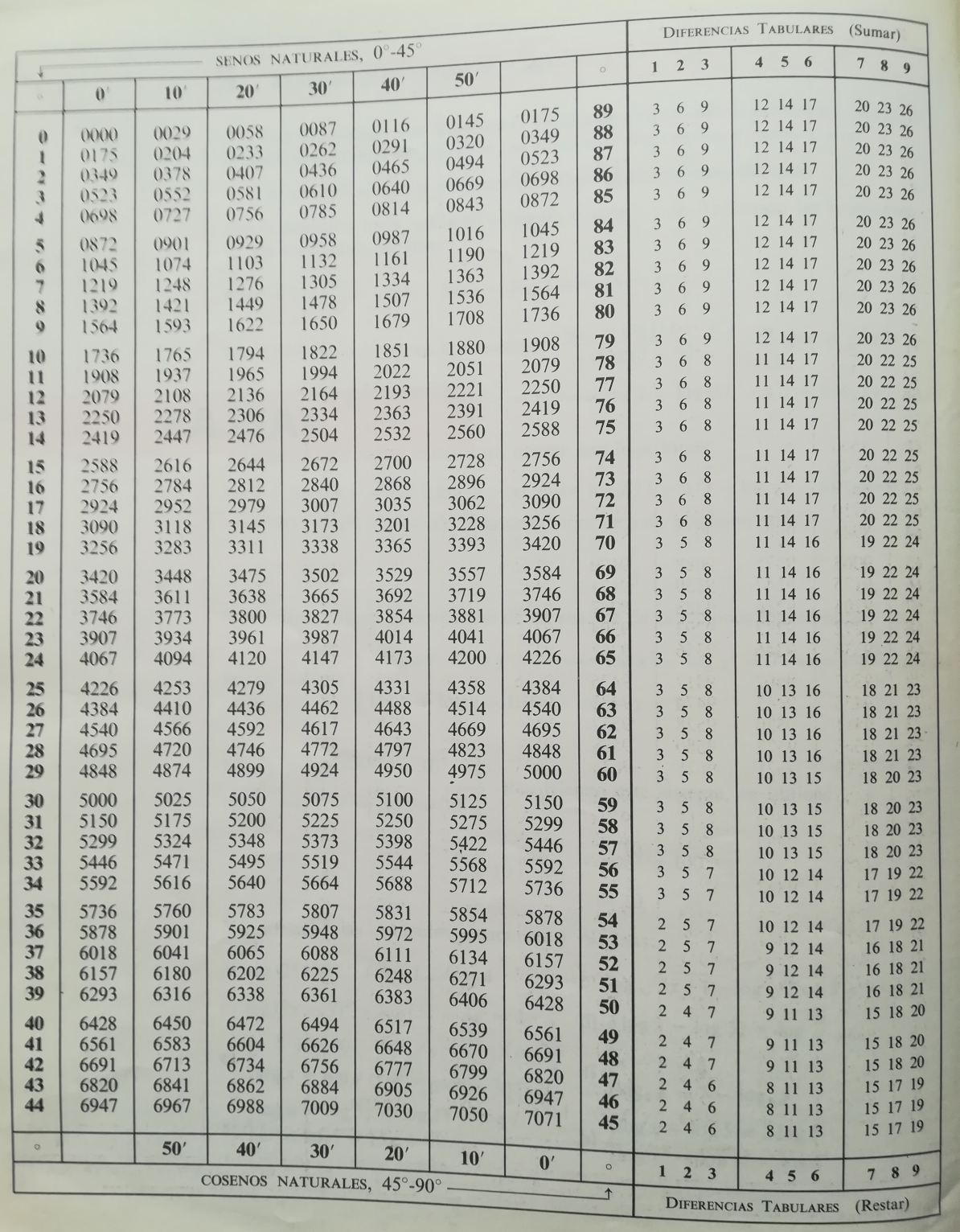
Existían las denominadas tablas trigonométricas, donde se consultaba el valor de una razón, generalmente para ángulos del primer cuadrante, aplicando las fórmulas de reducción para otros casos. Pero, ¿quiénes elaboraban estas tablas? ¿Cómo las construían sin herramientas tecnológicas como las actuales?
Se conocen como ecuaciones trigonométricas aquellas que contienen razones trigonométricas de ángulos desconocidos.
Por ejemplo, en la ecuación trigonométrica
buscamos ángulos que tengan coseno cero. Obviamente, son soluciones de esta ecuación los ángulos
ya que $\cos 90º=0$ y $\cos 270º=0$. Además, son los únicos ángulos en el primer giro, es decir, la primera vuelta a la circunferencia, que tienen coseno cero. Pues bien, reciben el nombre de soluciones particulares de la ecuación. A partir de ahora, aprenderemos a calcular las soluciones particulares de una ecuación trigonométrica, primera etapa para su resolución.
Al resolverlas, tendremos en cuenta que a cada ángulo le corresponde un valor único para cada razón trigonométrica, sin embargo, puede haber varios ángulos con la misma razón, como sucede con el ejemplo anterior, donde $$\cos 90º = \cos 270º$$
En la siguiente escena interactiva aprenderemos a localizar, según cada cuadrante, los ángulos que tienen el mismo coseno, y lo haremos utilizando la circunferencia trigonométrica. Para ello, debemos leer las instrucciones y realizar las actividades propuestas.
Escena interactiva adaptada y reutilizada por el autor.Livro Digital Interativo: Um exemplo em Trigonometria. Eduardo Alejandro Flores Araya.
Reciben este nombre aquellas ecuaciones trigonométricas que permiten despejar el coseno y escribir la ecuación en la forma
donde, obviamente, $a \in [-1,1]$. En primer lugar, buscamos las soluciones particulares, es decir, ángulos $x$ que tengan por coseno $a$ y se encuentren en el primer giro, o sea $x \in [0º,360º)$ o $x \in [0,2\pi)$, según la unidad de medida de ángulo utilizada.
Dada la importancia que tienen la localización y visualización de las soluciones particulares de la ecuación, en la primera estrategia haremos uso de la escena interactiva anterior.
La segunda estrategia está dedicada a calcular las soluciones particulares de una ecuación tipo coseno mediante una calculadora científica compartida en la red de internet, incluyendo en la escena un tutorial para conocer su funcionamiento.
 Ante la diversidad de modelos de calculadoras científicas y la proliferación de aplicaciones para dispositivos móviles o en línea, se hace cada vez más necesario que el alumnado, no solo aprenda a manejar su calculadora científica habitual, sino que conozca la existencia de las calculadoras en la red y seleccione la que considere más adecuada a cada situación.
Recomendamos la calculadora DescartesCalculadora Descartes. Enric Ripoll Mira y María José García Cebrián.
y el libro Calculadoras electrónicas, que ofrece diversos modelos en JavaScript o HTML para usar en dispositivos móviles e integrar en cualquier proyecto de cultura digital.
Ante la diversidad de modelos de calculadoras científicas y la proliferación de aplicaciones para dispositivos móviles o en línea, se hace cada vez más necesario que el alumnado, no solo aprenda a manejar su calculadora científica habitual, sino que conozca la existencia de las calculadoras en la red y seleccione la que considere más adecuada a cada situación.
Recomendamos la calculadora DescartesCalculadora Descartes. Enric Ripoll Mira y María José García Cebrián.
y el libro Calculadoras electrónicas, que ofrece diversos modelos en JavaScript o HTML para usar en dispositivos móviles e integrar en cualquier proyecto de cultura digital.
Como tercera estrategia mostraremos el método más tradicional, consistente en obtener las soluciones particulares de la misma ecuación sin emplear herramientas tecnológicas, algo que únicamente es posible cuando los valores de las razones trigonométricas que aparecen corresponden a las de los denominados ángulos notables y se emplean las fórmulas de reducción al primer cuadrante.
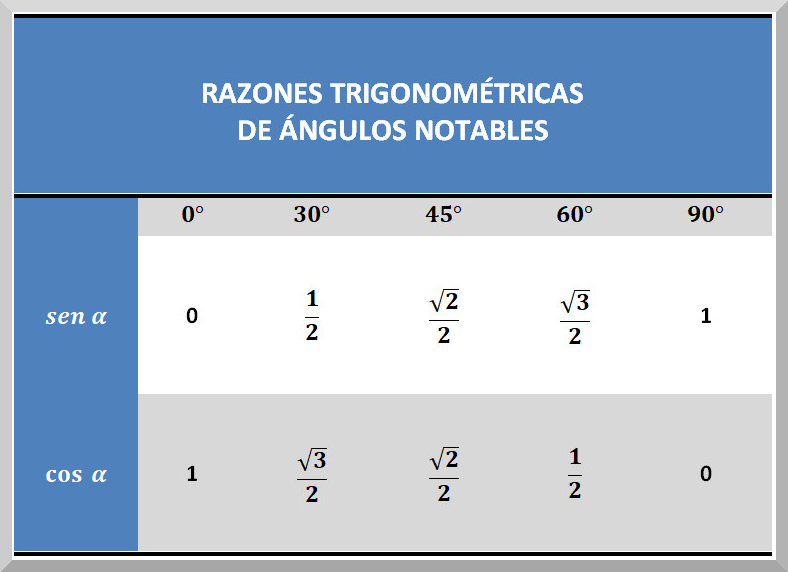
Llega el momento de preguntarnos cómo se resolvían las ecuaciones trigonométricas antes de inventar las calculadoras científicas, los ordenadores personales o el descubrimiento de internet.
En la escena interactiva anteriorLivro Digital Interativo: Um exemplo em Trigonometria. Eduardo Alejandro Flores Araya., adaptada y reutilizada por el autor, hemos aprendido a localizar, según cada cuadrante, los ángulos que tienen el mismo seno, así como los ángulos en los que se anula esta razón trigonométrica y sus valores máximo y mínimo, y lo hemos hecho utilizando la circunferencia trigonométrica. Para conseguir el objetivo, es imprescindible leer las instrucciones y realizar las actividades propuestas.
Reciben este nombre las ecuaciones trigonométricas que permiten despejar el seno y escribir la ecuación en la forma
donde, obviamente, $b \in [-1,1]$. En primer lugar, buscamos las soluciones particulares, es decir, ángulos $x$ que tengan por seno $b$ y se encuentren en el primer giro, lo que significa que $x \in [0º,360º)$ o $x \in [0,2\pi)$, según la unidad de medida de ángulo utilizada.
Dada la similitud entre las dos ecuaciones, que únicamente se diferencian en un signo, procederemos a la resolución simultánea en el primer giro, y lo haremos utilizando la escena interactiva anterior, que nos permite localizar, visualizar y calcular las soluciones particulares.
A la hora de obtener las soluciones particulares de una ecuación trigonométrica tipo seno con una calculadora científica, debemos tener en cuenta que, al pulsar la tecla arco seno, la calculadora nos devolverá un ángulo del intervalo $[-90º,90º]$, así que podemos encontrarnos con un ángulo negativo como respuesta y que no aceptaremos como solución particular, pues las buscamos en el primer giro, es decir, en el intervalo $[0º,360º)$ y, por tanto, de signo positivo.
Esta situación no se nos presenta con la tecla arco coseno, que devuelve como respuesta ángulos del intervalo $[0º,180º]$, por cuestiones del recorrido, unos conceptos funcionales que se estudian en el bloque de Análisis.
En la escena interactiva anteriorLivro Digital Interativo: Um exemplo em Trigonometria. Eduardo Alejandro Flores Araya., adaptada y reutilizada por el autor, hemos aprendido a localizar, según cada cuadrante, los ángulos que tienen la misma tangente, así como los ángulos en los que se anula esta razón trigonométrica. Además, mientras todo ángulo tiene un seno y un coseno, no ocurre así con la tangente, ya que dos ángulos del primer giro no tienen tangente. Tampoco tiene un valor máximo o uno mínimo, como el seno y el coseno, que oscilan entre -1 y 1, sino que, en las proximidades de los dos ángulos en los que no se encuentra definida, la tangente crece o decrece sin tope. Y todo lo hemos hecho utilizando la circunferencia trigonométrica. Ahora bien, para conseguir el objetivo, es imprescindible leer las instrucciones y realizar las actividades propuestas.
Reciben este nombre las ecuaciones trigonométricas que permiten despejar la tangente y escribir la ecuación en la forma
En primer lugar, buscamos las soluciones particulares, es decir, ángulos $x$ que tengan por tangente $c$ y se encuentren en el primer giro, lo que significa que $x \in [0º,360º)$ o $x \in [0,2\pi)$, según la unidad de medida de ángulo utilizada.
Conviene observar que en estas ecuaciones no existe limitación alguna para el término independiente, $c$, pues la tangente puede tomar cualquier valor, no así el seno y el coseno, cuyos valores se encuentran acotados en el intervalo $[-1,1]$.
Dada la similitud entre las dos ecuaciones, que únicamente se diferencian en un signo, procederemos a la resolución simultánea en el primer giro, y lo haremos utilizando la escena interactiva anterior, que nos permite localizar, visualizar y calcular las soluciones particulares.
A la hora de obtener las soluciones particulares de una ecuación trigonométrica tipo tangente con una calculadora científica, debemos tener en cuenta que, al pulsar la tecla arco tangente, la calculadora nos devolverá un ángulo del intervalo $(-90º,90º)$, así que podemos encontrarnos con un ángulo negativo como respuesta y que no aceptaremos como solución particular, pues las buscamos en el primer giro, es decir, en el intervalo $[0º,360º)$ y, por tanto, de signo positivo. Explicamos cómo se razona en estos casos con el tutorial incorporado a la escena siguiente.
Finalizado el estudio de las ecuaciones trigonométricas de tipos seno, coseno y tangente, disponemos ya de los conocimientos mínimos necesarios para afrontar el cálculo de las soluciones particulares de ecuaciones trigonométricas incompletas de segundo grado, que nos abrirá el camino hacia la resolución de ecuaciones trigonométricas.
Mostramos en esta sección estrategias básicas para obtener las soluciones particulares de ecuaciones trigonométricas de segundo grado incompletas, concretamente aquellas que no disponen de término de primer grado.
Además del cálculo de las soluciones particulares, hemos representado en la circunferencia trigonométrica los puntos asociados a cada una de ellas, siendo de gran relevancia la visualización de las mismas y observar la simetría presentada por las soluciones.
Con un tratamiento análogo, mostramos en la escena siguiente un procedimiento para calcular las soluciones particulares de una ecuación trigonométrica de segundo grado incompleta tipo seno.
Esta ecuación trigonométrica tiene, también, cuatro soluciones particulares, una en cada cuadrante, de tal manera que se diferencian en 180º las de los cuadrantes primero y tercero, así como las de los cuadrantes segundo y cuarto. Como la calculadora nos devuelve un ángulo orientado negativamente, que no podemos aceptar, razonamos y mostramos visualmente cómo localizar la correspondiente solución orientada positivamente.
El hecho de que, al representar en la circunferencia trigonométrica, los puntos asociados a las soluciones particulares de una ecuación trigonométrica de segundo grado, presenten la simetría que hemos podido visualizar en los ejemplos anteriores, nos puede facilitar enormemente la obtención de las soluciones de la ecuación. Por ello, proponemos la realización de la siguiente actividad interactiva, traducida y adaptada por el autor sobre la originalLivro Digital Interativo: Um exemplo em Trigonometria. Página 42 Eduardo Alejandro Flores Araya..
Hemos aprendido a calcular las soluciones particulares de una ecuación trigonométrica, así que ya estamos preparados para resolver la ecuación, es decir, calcular todas sus soluciones. ¿Cuántas soluciones tendrá una ecuación trigonométrica? ¿Pueden existir ecuaciones trigonométricas sin solución?
Resulta sumamente sencillo, y así damos respuesta a la última pregunta formulada, poner ejemplos de ecuaciones trigonométricas incompatibles, es decir, que no tienen ninguna solución. Tal es el caso de la ecuación
Obviamente, no existe ángulo alguno cuyo seno valga 2, ya que $-1 \le \text{sen}\, x \le 1$. Por tanto, estamos ante una ecuación incompatible. Pero, ¿qué ocurrirá con las ecuaciones compatibles, es decir, aquellas que tienen alguna solución? Por ejemplo, es evidente que la ecuación
tiene una única solución particular, pues sólo existe un ángulo en el primer giro que tenga por seno 1, y se trata de 90º. Ahora bien, si queremos determinar todas las soluciones de la ecuación, no podemos contentarnos con dar una vuelta a la circunferencia. Así, al recorrer nuevamente la circunferencia trigonométrica, obtendremos otra solución cuando el punto asociado llegue de nuevo al mismo lugar de la primera vuelta, es decir, cuando haya barrido un ángulo de 90º+360º, teniendo entonces dos soluciones. Pero este proceso podemos continuarlo indefinidamente y conseguiríamos un número infinito de soluciones. En consecuencia, cuando una ecuación trigonométrica sea compatible lo será indeterminada, es decir, tendrá infinitas soluciones. Pero, ¿cómo vamos a encontrarlas todas? ¿Cómo las vamos a escribir siendo infinitas?
Daremos respuesta a estas cuestiones en la siguiente escena interactiva.
Llamamos solución general al conjunto formado por las infinitas soluciones de una ecuación trigonométrica. En la escena anterior, hemos utilizado una estrategia didáctica para visualizar, localizar y escribir la solución general de la ecuación trigonométrica $\textbf{\text{sen} \, x = 1}.$ Ahora bien, salvo que se diga lo contrario, debemos expresar la solución general empleando la unidad de medida de ángulos en el Sistema Internacional, es decir, en radianes. Para ello, únicamente debemos convertir a radianes los grados sexagesimales, teniendo en cuenta que la expresión $k \cdot 360º$ se escribe como $k \cdot 2\pi = 2k\pi$.
Así, la solución general de la ecuación trigonométrica $\text{sen}\, x = 1$ viene dada por
A diferencia de los tradicionales métodos algebraicos, sustitución, igualación y reducción, para resolver sistemas de ecuaciones lineales, no existe un método general para resolver las ecuaciones trigonométricas, no obstante daremos algunos procedimientos o estrategias que pueden servir de modelo.
Resolver una ecuación significa encontrar todas sus soluciones, así que debemos obtener la solución general.
Observamos que aparece la misma razón trigonométrica, pero una vez con el ángulo simple y otra con su ángulo doble. Por tanto, es recomendable expresar todas las razones con el mismo ángulo, siendo, en este caso, lo más sencillo aplicar la fórmula del ángulo doble para el seno:
En la escena de la siguiente página mostramos cómo obtener la solución general de la ecuación por factorización.
Nos encontramos con una ecuación similar a la anterior, es decir, aparecen el ángulo simple y su doble, así que, en base a la experiencia adquirida, aplicaremos la fórmula del seno del ángulo doble y expresaremos la ecuación únicamente en función del ángulo simple.
Recomendamos, por "seguridad", utilizar la primera estrategia, pero ofrecemos una segunda en la que aclaramos un error muy frecuente, con objeto de que pueda superarse gradualmente.
Mucha atención con la segunda estrategia, donde intentamos aclarar un error bastante frecuente en la resolución de todo tipo de ecuaciones, no sólo en las trigonométricas.
Si en una ecuación aparecen varias razones trigonométricas, suele dar muy buen resultado expresarlas todas en función de la misma empleando las fórmulas trigonométricas conocidas y realizar un cambio de variables.
Aunque el cambio de variables no es necesario y puede obviarse, recomendamos su uso hasta que se domine la resolución de la ecuación trigonométrica de segundo grado completa.
En la primera estrategia mostramos la reacción más habitual en el alumnado, consistente en expresar todas las razones en función de seno y coseno, sin más que aplicar las fórmulas de la Trigonometría elemental.
Existe otra fórmula elemental a la que se suele recurrir con menor frecuencia y que facilita la resolución de esta misma ecuación, que mostramos como segunda estrategia en la página siguiente.
Al elevar al cuadrado los dos miembros de una ecuación, la igualdad se mantiene o conserva, pero no resulta una ecuación equivalente, es decir, que tenga las mismas soluciones que la ecuación inicial. Suelen aparecer lo que se conocen como soluciones extrañas, es decir, soluciones de la ecuación resultante pero no de la de partida. Para averiguarlo, debemos recurrir a algo tan sencillo como realizar la comprobación.
Recordemos que es exactamente lo que hacemos al resolver ecuaciones irracionales o ecuaciones en las que la incógnita aparece bajo el signo radical. El proceso es aislar una raíz, elevar al cuadrado, resolver la ecuación resultante y, obligatoriamente, realizar la comprobación en la ecuación inicial para eliminar las soluciones extrañas.
Comenzamos con un sencillo ejemplo que ilustre la situación.
En la segunda estrategia, que veremos ya en la página siguiente, mostramos la forma de afrontar este mismo reto expresando todas las razones en función de una sóla, lo que nos llevará a despejar una de ellas en la fórmula fundamental de la Trigonometría y sustituir en la ecuación. ¿Nos libraremos de elevar al cuadrado?
Recomendamos reflexionar sobre este hecho antes de acceder a la respuesta, pues de esta forma aprendemos a razonar, pensar y ¡a verlas venir!
Reciben este nombre aquellas ecuaciones trigonométricas tipos seno, coseno o tangente en las que, en vez de aparecer la razón trigonométrica acompañada del ángulo simple, $x$, nos podemos encontrar con el ángulo doble, $2x$, triple, $3x$, cuádruple, $4x$, etc. Es el caso de la ecuación trigonométrica
Aquí, por ejemplo, no aconsejamos aplicar la fórmula del seno del ángulo doble, pues complicaría enormemente la resolución de la ecuación, sino que debemos aprender a tratarla como ecuación con ángulo múltiplo.
Hay que tener presente que, a la hora de resolver una ecuación trigonométrica, buscamos, en primer lugar, las soluciones particulares,
es decir, ángulos $x$, en el primer giro, que verifiquen la ecuación. Por tanto, $x \in [0º, 360º)$. Sin embargo, $2x \in [0º, 720º)$, así que, el ángulo doble, puede recorrer la circunferencia dos veces, mientras que el simple lo hace una vez.
En la siguiente escena, intentaremos aclarar esta situación empleando una estrategia didáctica de gran valor, consistente en resolver, simultáneamente, las ecuaciones trigonométricas

Recomendamos practicar y asimilar esta estrategia para resolver ecuaciones trigonométricas con ángulos múltiplos. No obstante, por si algún alumno o alumna tuviera dificultades iniciales de comprensión, lo que es bastante normal, presentamos una segunda opción en la página siguiente basada en la estrategia del cambio de variables.
Dedicaremos esta sección a exponer la resolución de ecuaciones trigonométricas algo más complicadas, pues intervienen diversas fórmulas de la Trigonometría y requieren el dominio de los modelos tratados hasta el momento. Por ello, recomendamos no abordar esta categoría sin haber aprendido bien las bases de este capítulo.
En la segunda estrategia resolvemos la ecuación trigonométrica sin usar ángulos múltiplos, aunque sigue siendo primordial la factorización.
Exponemos, seguidamente, una ecuación en la que aparecen razones trigonométricas inversas. ¿Habrá que expresarla en función de una sóla razón? ¿Habrá que elevar al cuadrado? ¿Habrá que realizar un cambio de variables? ¿Se podrá resolver con ángulo múltiplo? ¿Será compatible?
Estamos ante una ecuación trigonométrica racional, pues las razones que aparecen se expresan como fracción, así que debemos poner cuidado en los posibles valores que anulen alguno de los denominadores.
Abordamos, nuevamente, lo que se conoce como un reto guiado, donde los sucesivos apartados que componen el ejercicio no son más que orientaciones para indicarnos o sugerirnos el camino más adecuado a nuestros conocimientos, sin eliminar otras posibilidades. La dificultad del ejercicio está en resolver la ecuación
Recordemos que no es posible dividir razones del numerador entre razones del denominador hasta que hayamos factorizado ambos términos de la fracción, que es lo que nos solicitan en el primer apartado.
En el capítulo anterior hemos dedicado una sección a motivar sobre la importancia de la factorización. Además, conocidas son de cursos anteriores las estrategias de sacar factor común, utilizar identidades notables o aplicar la regla de Ruffini para resolver por factorización una ecuación polinómica. Pues bien, insistimos en este hecho con el reto que planteamos a continuación, pero habrá que factorizar sumas de senos.
La resolución de problemas y los proyectos de investigación constituyen ejes fundamentales en el proceso de enseñanza y aprendizaje de las Matemáticas. La resolución de problemas, proyectos de investigación matemática, la matematización y modelización, las actitudes adecuadas para desarrollar el trabajo científico y la utilización de medios tecnológicos, son considerados como los procesos básicos e imprescindibles en el quehacer matemático.
Así se contempla, entre otros aspectos, en el desarrollo curricular del primer curso de la modalidad de ciencias en bachillerato, por lo que ha llegado el momento, al igual que en los anteriores capítulos, de afrontar un nuevo proyecto de investigación relacionado con las ecuaciones trigonométricas.
Exactamente, vamos a investigar sobre la existencia o no de triángulos isósceles que tengan nula la suma de los cosenos de sus ángulos, por lo que deberemos tratar con mucha concentración lo recogido en la siguiente escena interactiva.
Afrontamos ahora el reto de una ecuación trigonométrica en la que aparecen cuatro razones diferentes, el ángulo simple y el ángulo doble. Además, nos encontramos con una ecuación racional, a consecuencia de las razones trigonométricas que se expresan como cociente, es decir, la cosecante, la tangente y la secante, por lo que debemos estar atentos para evitar "divisiones por cero". Ello nos obliga a realizar la comprobación de las soluciones obtenidas. ¡No lo olvidemos!
En esta ocasión, tenemos una sola razón trigonométrica, el ángulo doble y el ángulo simple, así que, en base a la experiencia adquirida, aconsejamos expresar la ecuación únicamente con el ángulo simple. Además, no podemos olvidar que la tangente es un cociente y nos veremos obligados a realizar la comprobación para determinar qué valores candidatos a solución lo son en verdad.
En la siguiente escena mostramos la que consideramos estrategia más adecuada para la resolución de esta ecuación.
Abordamos un reto con un enunciado algo diferente a lo habitual, con objeto de mostrar que, a veces, tendremos que utilizar alguna solución no particular, siendo de gran importancia comprender cómo se consiguen determinadas soluciones de una ecuación trigonométrica.
Como ya hemos comentado en capítulos precedentes, la autoevaluación es un elemento clave en el proceso de aprendizaje que permite al alumnado valorar sus logros y reflexionar sobre sus fortalezas y debilidades. Para ello, ofrecemos dos propuestas muy dispares entre sí.
La primera es una autoevaluación sobre conceptos básicos, donde únicamente debemos contestar si o no, previa reflexión. Se compone de bloques con tres cuestiones y deberemos realizar el mayor número posible de los mismos, hasta conseguir un resultado satisfactorio que nos garantice el dominio básico sobre los aspectos tratados en este último capítulo, dedicado a la resolución de ecuaciones trigonométricas, que tanto necesitaremos en cursos posteriores a la hora de, por ejemplo, calcular los máximos y mínimos de funciones trigonométricas o, incluso, en otras materias del ámbito científico y técnico.
La segunda autoevaluación, con algo más de complejidad, está orientada a la resolución de ecuaciones trigonométricas aplicando las diversas estrategias abordadas en el capítulo.
Para que esta autoevaluación dedicada a la resolución de ejercicios sea efectiva, debemos seguir las siguientes recomendaciones:
Portada: Vector de Tarjeta de visita creado por macrovector - www.freepik.es
Plantilla de volante-trigonometría vector gratuito
Página 15: Capítulo I.Vector de Fondo creado por pikisuperstar - www.freepik.es
Fondo dibujos animados elementos matemáticas vector gratuito
Páginas 16 y otras: Vector de Abstracto creado por freepik - www.freepik.es
Página 34 y otras: Puertas - Estrategia. Licencia CC0. Dominio público en pxhere.com
Página 69: Capítulo II.Vector de Fondo creado por pikisuperstar - www.freepik.es
Fondo dibujos animados elementos matemáticas vector gratuito
Página 72 y otras: Cuestionario. Licencia CC0. Dominio público en pxhere.com
Página 77 y otras: Escritorio, computadora, móvil. Licencia CC0. Dominio público en pxhere.com
Página 85 y otras: Tablero, inspiración. Licencia CC0. Dominio público en pxhere.com
Página 95: Capítulo III. Vector de Escuela creado por macrovector - www.freepik.es
Página 117: Capítulo IV. Vector de Fondo creado por freepik - www.freepik.es
Fondo isométrico concepto matematicas vector gratuito
Página 137: Audio. Claude Debussy, Arabesco número 1 (Andantino con moto) en Mi mayor, L. 66. Licencia CC BY-NC-SA. Banco de imágenes y sonidos de INTEF.
Página 145: Formación, aprendizaje. Licencia CC0. Dominio público en pxhere.com
Página 151: Capítulo V. Vector de Banner creado por macrovector - www.freepik.es Teacher at school composición isométrica banner vector gratuito