Curvas y
superficies
paramétricas
INTERACTIVO
Curvas y superficies
paramétricas
INTERACTIVO
Juan Guillermo Rivera Berrío
Institución Universitaria Pascual Bravo
Josep Ma Navarro Canut
Red Descartes - España
Fondo Editorial Pascual Bravo
Medellín
Título de la obra
Curvas y superficies paramétricas
Autores:
Juan Guillermo Rivera Berrío
Josep Ma Navarro Canut
2018
Diseño del libro: Juan Guillermo Rivera Berrío
Diseño de cubierta:
Librería turn.js: Emmanuel García
Herramienta de edición: DescartesJS
Fuente: Amaranth
Fondo Editorial Pascual Bravo
Calle 73 73A-226
PBX: (574) 4480520
Apartado 6564
Medellín, Colombia
www.pascualbravo.edu.co
ISBN: 978-958-56858-1-9
Tabla de contenido
1. Curvas paramétricas en el plano11
1.11 Otras curvas especiales46
2. Curvas paramétricas en el espacio55
iii
2.6 Costura en las bolas de tenis72
2.14.4 Nudo del rizo o del marino91
3.1 Superficies cilíndricas y cónicas101
3.2 Cicloides y epicicloides de revolución 106
3.3 hipocicloides de revolución109
3.4 Hipotrocoides de revolución114
3.8 Piriforme de revolución124
iv
3.10 Paraboloides e hiperboloides127
3.10.1 Paraboloide de revolución128
3.10.2 Paraboloide hiperbólico130
3.10.3 Hiperboloide de una hoja133
3.17 Superficies seno y coseno162
3.20 Superficies mínimas o minimales175
3.21 Superficies retorcidas184
3.23 Superficies relacionadas con el plano proyectivo real196
Prefacio
Este libro digital interactivo se ha diseñado con fundamento en la filosofía del Proyecto Descartes: "Trabajando altruistamente por la comunidad educativa de la aldea global", que sólo busca desarrollar contenidos educativos para el provecho de la comunidad académica, esperando únicamente como retribución el uso y difusión de estos contenidos. El contenido del libro, al igual que los objetos interactivos se han diseñado de tal forma que se puedan leer en ordenadores y dispositivos móviles sin necesidad de instalar ningún programa o plugin. El libro se puede descargar para su uso en local sin dependencia con la red, a excepción de algunos vídeos incluidos en el texto. Todos los objetos interactivos se han diseñado con el Editor DescartesJS.
El contenido de este libro tiene como propósito mostrar la gran variedad de curvas y superficies que se pueden obtener con las ecuaciones paramétricas, tanto en espacios 2D como 3D.
7
Los sistemas de ecuaciones paramétricas permiten representar diversas curvas o superficies, a partir de variables cuyos valores se encuentran en un intervalo de números reales. Estas variables, en matemáticas, son llamadas parámetros, por ello, la denominación de ecuaciones paramétricas. Presentamos dos ejemplos que ilustran nuestro propósito en este libro:
El primer ejemplo es una curva paramétrica en el plano
Con clic izquierdo sostenido puedes desplazar la curva, y con el derecho haces zoom sobre ella.
8
El segundo ejemplo es una superficie gaussiana en un espacio 3D.
Con clic izquierdo sostenido puedes rotar la superficie, y con el derecho haces zoom sobre ella.
9
Capítulo i
Curvas paramétricas en el plano
Introducción
Las ecuaciones paramétricas posibilitan una gran variedad de curvas, algunas conocidas, otras extrañas, algunas complejas, otras sorprendentes por su simetría y belleza. Estas curvas se generan cuando las variables x e y se expresan en función de una tercera llamada parámetro. En gráficos 2D se usa el parámetro t y en gráficos 3D los parámetros u y v
Si x e y se dan como funciones de una tercera variable t (llamada parámetro) mediante las ecuaciones x = f(t) e y = g(t) (llamadas ecuaciones paramétricas), entonces cada valor de t determina un punto (x,y) que se puede representar en un sistema de coordenadas. Cuando t varía, el punto (x,y)= (f(t),g(t)) varía y traza una curva C (llamada curva paramétrica).
El estudio de estas curvas demanda más tiempo del que nos proponemos con este libro. Nuestro objetivo es sólo mostrar cómo se representan estas curvas y cuáles son las ecuaciones que las gobiernan.
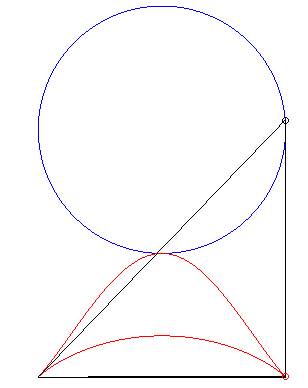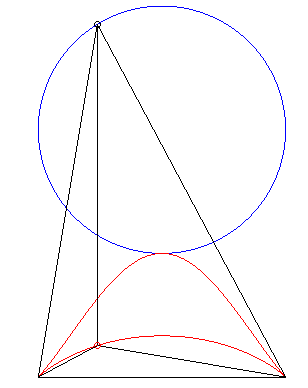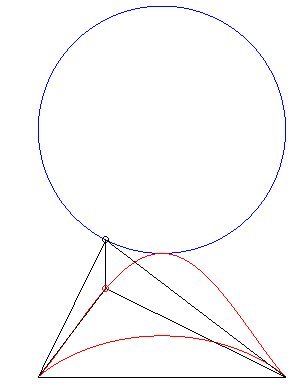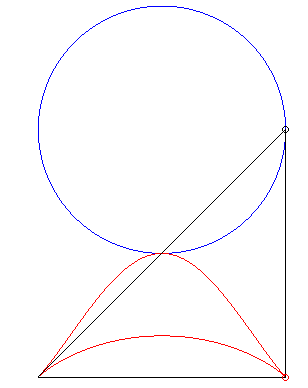
1.1 La cicloide
Este tipo de curva recibió el nombre de "Helena de los geométras"2. Pese a que fue Mersenne, en 1615, quien la define como cicloide, su estudio fue de mucho interés para Galileo, Torricelli, Fermat, Descartes, Huygens y Pascal (Ibid).
Dado su gran interés para estos ilustres matemáticos, vamos a describir su construcción geométrica y, posteriormente, las ecuaciones paramétricas que la definen.
13
Construcción geométrica
De la miscelánea (Ruleta cicloidal), diseñada por Rita Jiménez Igea, Ildefonso Fernández Trujillo y Ángel Cabezudo Bueno, encontramos que,
Una ruleta cicloidal es una curva plana que describe la trayectoria de un punto vinculado a una circunferencia, llamada generatriz, que rueda tangencialmente sin deslizarse sobre otra curva plana llamada directriz. Según sea la curva directriz sobre la que rueda la circunferencia, la ruleta cicloidal recibe nombres diferentes. Se llama cicloide a la ruleta cicloidal que rueda sobre una recta. El punto vinculado a la circunferencia puede ser interior, exterior o estar en la circunferencia; en este último caso se dice que la cicloide es normal.
En la escena interactiva de la página siguiente, al pulsar el botón animar/parar, vemos cómo se genera la cicloide normal. El punto vinculado a la circunferencia es el punto P que inicialmente hace contacto con la recta.
Algunas propiedades geométricas que nos ilustra Jiménez et al., son las siguientes:
- La longitud de la trayectoria recorrida por el punto P en una vuelta es 8r y el área bajo el arco correspondiente es 3πr2, es decir 3 veces el área del círculo, que encierra la circunferencia.
- La cicloide es una función periódica, es decir el punto P toma la misma posición (altura) sobre la trayectoria a intervalos regulares D = 2πr de la variable d, f(d) = f(d + kD). D es el periodo de la cicloide y k es el número de vueltas que da la circunferencia.
Por otra parte, el interés que esta curva ha tenido entre los matemáticos y físicos a lo largo de la historia ha permitido descubrir propiedades "físicas":
14
Ecuaciones paramétricas
Las ecuaciones paramétricas que permiten trazar la cicloide, son:
x = a(t - sen(t))
y = a(1-cos(t))
16
1.2 La trocoide
La trocoide4 es una generalización de la cicloide: es una trayectoria de un punto de una circunferencia que rueda sin deslizamiento sobre una recta fija. Cuando el punto se encuentra en la circunferencia, se trata del caso particular de la cicloide. Moviendo los parámetros a y r en los controles de la escena interactiva, puedes observar que en el caso de que el punto se encuentre en el exterior de la circunferencia (a > r), la trocoide tiene "lazos" y en el caso contrario no los tiene. Esta curva fué estudiada por Durero en 1525 y Rømer en 1674. Su nombre se deriva del griego trokhos: rueda.
17
En la figura de la escena interactiva se ha representado la situación que se produce un poco después de que el círculo ha empezado a rodar. Lo más natural es escoger como parámetro a t en radianes como el ángulo, pues éste corresponde al ángulo de rotación del círculo. La trayectoria que sigue un punto cualquiera (x,y) de la trocoide es el resultado de sumar dos trayectorias: (x,y) = r(t) = h(t) + c(t). El primer término de esta suma es h(t) =(rt, t) , y corresponde al movimiento del centro del círculo con radio r que se mueve hacia la derecha a lo largo de la recta horizontal, comenzando en el punto (0 ,r), es decir, cuando t=0. Por cada momento t, el punto se mueve rt, pues el círculo rueda sobre el eje X sin resbalarse. Por otra parte, el segundo término de la suma será c(t) = (-asen t, -acos t) que corresponde a la trayectoria que sigue un punto que se mueve en una circunferencia con centro en (0, 0) y radio a en el sentido de las manecillas del reloj empezando en el punto (0, -a), es decir, para t=0. Al sumarse estas dos trayectorias, el resultado es que el punto va girando en el sentido de las manecillas del reloj, mientras el centro de la circunferencia se mueve horizontalmente en la recta horizontal y estos dos movimientos combinados van generando la trocoide. De esta manera, las ecuaciones paramétricas de la trocoide son:
x(t) = rt - asen(t) y y(t) = r - acos(t)
18
1.3 Las epicicloides
Hemos visto que las cicloides se generan, por un punto P, al rotar una circunferencia (generatriz) sobre una recta (directriz). Cuando la directriz es otra circunferencia se generan epicicloides, siempre que la circunferencia generatriz rote exteriormente.
Construcción geométrica
Las epicicloides ordinarias son curvas que se generan por un punto P de una circunferencia de radio b al rotar exteriormente y sin deslizamiento sobre otra circunferencia de radio a.
Un caso sencillo de epicicloide es aquel en que la relación de radios n = a/b es un número entero. Dando una sola vuelta completamos la epicicloide y ésta tendrá n cúspides o puntos de retroceso.
Puedes verlo en la escena de la siguiente página, variando el radio a pero condicionando a que b sea un divisor, con lo que n = a/b debe valer 1, 2, 3, 4, etc. Así, con a = 6 y n = 1 tenemos b = 6 y una sola cúspide: la curva se llama cardioide (por su forma de corazón); con a = 6 y n = 2 tenemos que b = 3 y dos cúspides: la curva se llama nefroide (por su forma de riñón); etc. (Jiménez et al).
Pero antes de interactuar con la escena, queremos destacar la importancia de este tipo de curvas por sus propiedades físicas, lo que motivó el interés de grandes pensadores matemáticos y físicos5. Por ejemplo, el diseño de engranajes cicloidales ha estado dado por la combinación de las curvas epicicloidales, la cardioide puede ser usada como leva y, también, es la figura central grande del conjunto de Mandelbrot.
19
En la siguiente escena interactiva, diseñada también por Jiménez et al., puedes variar el valor del radio a y probar para distintos valores de n. Usa el zoom para ajustar el tamaño de la epicicloide adecuadamente dentro de la escena.
20
Ecuaciones paramétricas
Como lo hemos advertido, en este libro no presentamos la deducción de estas ecuaciones, así que sólo las describimos como elemento constitutivo de la escena interactiva que permite analizar la curva, interactuando con sus atributos.
21
Las ecuaciones paramétricas que permiten trazar las epicicloides, son:
x = (r + R)cos(t) - rcos(tR/r + t)
y = (r + R)sen(t) - rsen(tR/r + t)
Usa el pulsador t para generar la epicicloide.
22
1.4 La epitrocoide
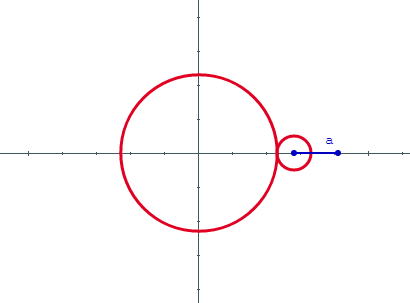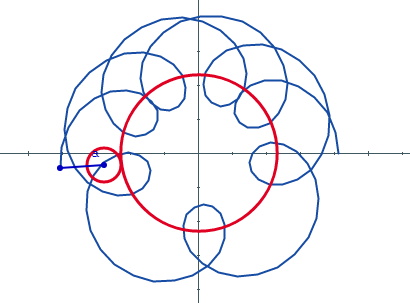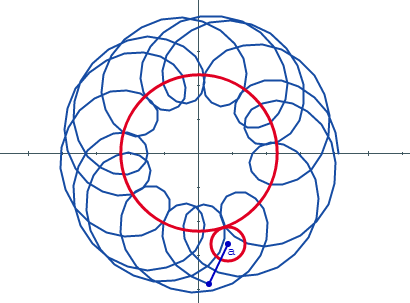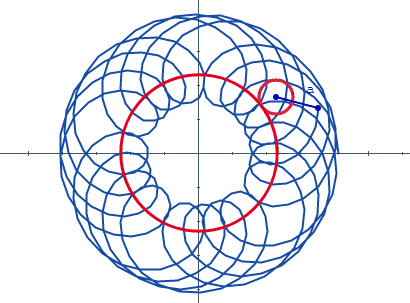
Una epitrocoide es la curva que describe la trayectoria de un punto a una distancia a del centro de una circunferencia que gira sin resbalar o deslizar sobre otra circunferencia de base.
En este caso la circunferencia generatriz tiene un radio r y la circunferencia de base tiene radio R. Si el punto está en la circunferencia del círculo que rueda, la curva generada es una epicicloide; si el punto generador no está en la circunferencia, la curva es una epitrocoide
En la siguiente escena interactiva presiona el pulsador t para generar la curva. Prueba distintos valores de a, r y R. El gif animado de esta página fue diseñado con dicha escena.
23
Las coordenadas del centro Ct son:
Ct = ((R+r)cos(t),( R+r)sen(t))
Consideremos ahora la posición del punto Pt con respecto a Ct. Como Pt está a una distancia a de Ct, y el ángulo está retrasado π rad, tenemos que:
24
PtCt = (acos(φ - π), asen(φ - π)) = (-acos φ,-asen φ)
¿Cuál es la relación entre los ángulos formados entre los segmentos CtPt y el radio r y entre el radio R y el eje X ? Mueve los parámetros para analizar esta relación.
El ángulo φ formado por el segmento CtPt con el radio r horizontal, depende del ángulo t, porque la longitud de los arcos en que las circunferencias han estado en contacto es la misma, por lo que Rt = r(φ - t). Despejando obtenemos que φ = (R+r)t/r. Entonces las coordenadas (x(t), y(t)) del punto Pt son:
x(t) = (R + r)cost - acos((r + R)t/r)
y(t) = (R + r)sent - asen((r+R)t/r).
1.5 El caracol de Pascal
El caracol de Pascal, o Limaçon de Pascal, es un caso especial de epitrocoide. Este nombre corresponde no a una curva, sino a una familia de curvas que se genera cuando R = r, es decir el radio de la cirunferencia de base y el de la circunferencia generatriz, son iguales. Esta curva fue estudiada por Durero en 1525 (bajo el nombre de arachnée) Étienne Pascal y Roberval en 1650. Este último le dió el nombre de Limaçon de Pascal en honor a Étienne Pascal (1588 -1651), magistrado y matemático amateur y padre del matemático, físico y filósofo Blaise Pascal6.
25
La cardioide y la trisectriz son casos especiales de Limaçon, que se generan cuando a es igual o mayor a r respectivamente. En la siguiente escena interactiva, diseñada por Leticia Monserrat Vargas, intenta generar las curvas de la imagen de la derecha.
1.6 Las hipocicloides
De la miscelánea de Monserrat, extraemos: las hipocicloides ordinarias son curvas que se generan por un punto P de una circunferencia de radio b al rotar interiormente y sin deslizamiento sobre otra circunferencia de radio a.
26
Un caso sencillo de hipocicloide es aquel en que la relación de radios n = a/b es un número entero. Dando una sola vuelta completamos la hipocicloide y ésta tendrá n cúspides. Puedes verlo en la siguiente Escena interactiva. Dando valores enteros a n de 3 ,4 ,5, etcétera, se obtienen distintas hipocicloides, algunas con nombres especiales (deltoide, astroide,...) que aluden a su forma y que se cierran con la primera vuelta.
Construcción geométrica
En la siguiente escena interactiva, observa cómo se generan las hipocicloides, a partir de punto P de una circunferencia de radio b que rota interiormente y sin deslizamiento sobre otra circunferencia de radio a.
27
Un caso interesante es cuando el radio de la circunferencia directriz es de tamaño doble del de la circunferencia generatriz que rueda interiormente sobre la primera (En la escena con n=2, por ejemplo: a = 6 y b = 3).
Podemos observar que el punto generatriz, cuando el centro M gira alrededor del centro O, recorre el diámetro de la circunferencia directriz. Esta hipocicloide tiene 2 cúspides y la forma de un segmento de recta: se denomina Recta de La Hire debido a la descripción hecha por el astrónomo, físico y matemático francés Philippe de La Hire (1640-1718).
28
Ecuaciones paramétricas
Las ecuaciones paramétricas que permiten trazar las epicicloides, son:
x = (R - r)cos(t) + rcos(t - tR/r)
y = (R - r)sen(t) + rsen(t - tR/r)
29
Cuando la relación k = R/r no es un número entero, la hipocicloide se cierra en más de una vuelta. En la siguiente imagen, las dos primeras hipocicloides se cierran en cinco vueltas y la tercera en 16.
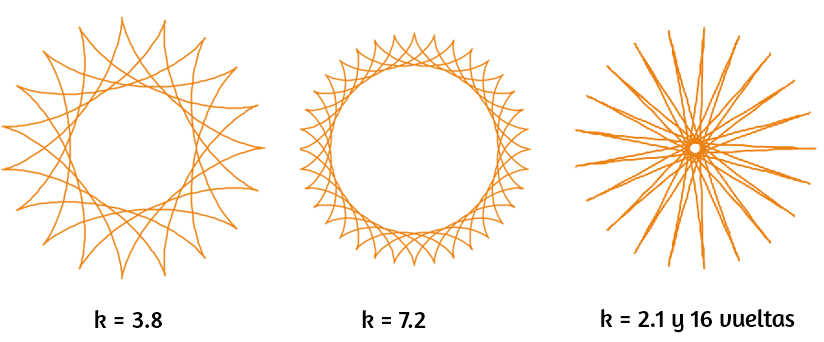
Construye estas hipocicloides en la siguiente escena interactiva y prueba con otros valores de k.
Por ejemplo, para la tercera curva:
- Asigna 5 a b
- Asigna 5*2.1 a a (DescartesJS permite que ingrese operaciones en el cuadro de texto)
- Ingresa 16 vueltas
- Aumenta el zoom a 14
El valor de k inicial en la escena es de 4.2
30
1.7 Las hipotrocoides
Hemos visto que una hipocicloide es la curva que describe la trayectoria de un punto que está a una distancia a del centro de una circunferencia que gira sin resbalar en el interior de otra circunferencia de base, en las que la circunferencia generatriz tiene un radio r y la circunferencia de base tiene radio R.
31
La siguiente escena interactiva, en principio, se ajusta a la definición anterior. Aumenta los valores de t y obtendrás una deltoide, pero ¿Cómo es la curva cuando la relación a/r es un número menor a uno? ¿Cómo es la curva cuando esta relación es mayor a uno?
32
Para dar respuesta a la primera pregunta, cambia el valor de a por 0.5 ¿qué observas? La curva obtenida, se conoce como hipotrocoide recortada. Ahora, cambia el valor de a por 2 y obtendrás una hipotrocoide alargada, en este caso una linda flor de tres pétalos.
Prueba con R = 2r y a diferente de r ¿qué observas? Practica cambiando valores en los hipotrocoides alargados y obtendrás curvas espectaculares.
1.8 Espirales
No haremos una inmersión profunda en las bellas curvas llamadas "espirales"7, pues sólo nos detendremos en tres de ellas y acudiendo a los trabajos sobre este tema que vienen realizando nuestros amigos cartesianos Ildefonso Fernández Trujillo, José Román Galo Sánchez y Ángel Cabezudo Bueno, de los cuales destacamos:
- Espirales generalizadas de Durero
- Sobre el crecimiento cordobés del nautilus pompilius
- El grillo y la espiral logarítmica
- La hormiga y la espiral de Arquímedes
Antes de iniciar con las espirales que hemos seleccionado, te invitamos a observar el siguiente vídeo que da cuenta de la presencia de las espirales en la naturaleza.
33
Ninguna curva ha fascinado al ser humano desde los tiempos más remotos como la espiral. Su presencia en los objetos vivos, tanto animales como vegetales, llamó la atención de nuestros antepasados desde los albores de la humanidad. No existe ninguna cultura que no la haya utilizado como elemento simbólico, mágico u ornamental. El mundo mágico de las espirales es un universo hipnótico, que a veces nos produce sensaciones de vértigo y en otras ocasiones nos transporta a paraísos de calma y placidez, pero que siempre deja en nuestro espíritu la zozobra y la inquietud del infinito (Espirales de Antonio Pérez Sanz).
34
1.8.1 Espiral de Arquímedes
La espiral de Arquímedes, o espiral aritmética, obtiene su nombre del matemático griego Arquímedes (siglo III A.C).
Matemáticamente la espiral de Arquímedes se define como el lugar geométrico de un punto del plano que partiendo del extremo de una semirrecta se mueve uniformemente sobre ella, mientras que la semirrecta gira también uniformemente sobre uno de sus extremos. En palabras del propio Arquímedes:
"Imaginaos una línea que gira con velocidad constante alrededor de un extremo, manteniéndose siempre en un mismo plano, y un punto que se mueve a lo largo de la línea con velocidad lineal constante: ese punto describirá una espiral".
Es decir, es una curva mecánica. Para definirla necesitamos recurrir al movimiento. Es de hecho la primera curva mecánica de la historia. Su ecuación en coordenadas polares es r = aθ donde r es la distancia al origen, a una constante y θ es el ángulo girado (Ibid).
Las aplicaciones de la espiral de Arquímedes son muchas, por ejemplo, se usan en la bombas de compresión o compresores rotativos, los cuales están diseñados con dos espirales de Arquímedes para máquinas de aire acondicionado o los surcos de las primeras grabaciones para gramófonos (disco de vinilo) que forman una espiral de Arquímedes. Hasta en los diagnósticos de enfermedades neurológicas se usa esta espiral, al pedirle a un paciente que la dibuje para cuantificar el temblor humano (https://es.wikipedia.org).
A continuación, presentamos las ecuaciones paramétricas que definen la espiral de Arquímedes.
35
Ecuaciones paramétricas de la espiral de Arquímedes
x = a•t cos t
y = a•t sen t
donde t es el ángulo (mayor que cero) y a es una constante de amplificación. Genera, entonces, la espiral en la siguiente escena interactiva:
36
La hormiga y la espiral de Arquímedes
Finalmente, presentamos la miscelánea diseñada por Ildefonso Fernández Trujillo, José Román Galo Sánchez y Ángel Cabezudo Bueno.
37
1.8.2 Espiral logarítmica
El término espiral logarítmica se debe a Pierre Varignon, aunque otros autores afirman que se debe a Jakob Bernouilli8, quien le dedicó un libro en el que la llamó Spira mirabilis «la espiral maravillosa». Esta espiral también fue estudiada por Descartes, Torricelli y D'Arcy Thompson, que en 1917 le dedicó un capítulo de su tratado On Growth and Form «Sobre crecimiento y forma» (https://es.wikipedia.org). Esta curva maravillosa es la que más se presenta en la naturaleza (galaxias, tornados, girasoles, conchas, ...),
En la naturaleza hay cosas que crecen así, a velocidades constantes, simultáneamente hacia "afuera" y "alrededor" de algo. Es por eso que a la "espiral logarítmica" también se le suele llamar "espiral de crecimiento". Hace millones de años, en la familia de los cefalópodos, había muchas especies de animales con concha en forma de "espiral logaritmica", si observamos la imagen del "Nautilus", cuya concha bisectada, puede apreciarse que está formada por compartimentos separados por tabiques y comunicados por un sifón (http://mariac457.blogspot.com)

38
Ecuaciones paramétricas
La ecuación polar de la espiral logarítmica está dada por la expresión: r = abθ, que equivale a θ =logb(r/a), por ello el nombre de "logarítmica". Por otra parte, las ecuaciones paramétricas, son:
x = a•btcos t
y = a•btsen t
39
El grillo y la espiral logarítmica
Presentamos la miscelánea diseñada por Ildefonso Fernández Trujillo, José Román Galo Sánchez y Ángel Cabezudo Bueno.
40
1.8.3 Espiral hiperbólica
Terminamos este apartado con la espiral hiperbólica, la cual se define por la ecuación polar rθ = a, que es la inversa de la espiral de Arquímedes. Esta curva fue estudiada por Pierre Varignon, Johann Bernoulli y Roger Cotes. Sus ecuaciones paramétricas son:
x = a•cos(t)/t
y = a•sen(t)/t
41
1.9 Figuras de Lissajous
Las figuras de Lissajous fueron descubiertas por el físico francés Jules Antoine Lissajous, quien empleó sonidos de diferentes frecuencias para hacer vibrar un espejo. La luz reflejada en el espejo trazaba una curva cuya forma dependía de la frecuencia del sonido. Estas figuras, entonces, se obtienen de la superposición de dos movimientos armónicos perpendiculares (http://www.euclides.dia.uned.es).
42
En la anterior escena interactiva, diseñada en GeoGebra por Julio Mulero, puedes apreciar la gran diversidad de figuras de Lissajous que puedes obtener.
Ecuaciones paramétricas
En la siguiente escena interactiva, diseñda por José Luis Abreu, puedes observar las ecuaciones paramétricas que definen las figuras de Lissajous. Cambia los valores de los parámetros m y n y trata de obtener las figuras mostradas en la escena de Mulero.
43
1.10 La Superfórmula
La superfórmula es una generalización en coordenadas polares de la superelipse, propuesta por Johan Gielis, quien supuso que la fórmula puede ser usada para describir distintas curvas y cuerpos presentes en la Naturaleza. La fórmula es:
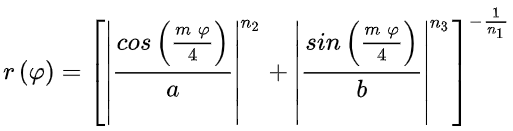
donde r es el radio y φ el ángulo. La fórmula apareció en abril de 2003, en el número 90 de la revista American Journal of Botany, en un artículo del biólogo Johan Gielis. Fue obtenida generalizando la superelipse, creada por el matemático danés Piet Hein9 (https://es.wikipedia.org/).
En la escena interactiva de la página siguiente, hemos definido la función f dada por Gielis, con la cual generamos las siguientes ecuaciones paramétricas:
x = 1f(t)cos(t)
y = 1f(t)sen(t)
44
En la escena interactiva, cambia los valores de los parámetros dados en los diferentes controles (pulsadores), para obtener diferentes figuras. Puedes observar algunos ejemplos obtenidos con la escena, pulsando en el botón "Ver ejemplos".
45
1.11 Otras curvas especiales
Para terminar este capítulo, hemos seleccionado un grupo de curvas especiales, lo que no significa que con ellas agotamos el maravilloso mundo de las curvas... ¡son sólo una muestra!
Curva bicorn
El bicorn o bicorne, conocido también como el sombrero de tres picos (ver imagen en la página siguiente de un sombrero antiguo de la armada británica), hace parte de las curvas cuárticas estudiadas por James Joseph Sylvester en 1864 y por Arthur Cayley en 1867, sus ecuaciones paramétricas son de la forma:
x = a•sen(t)
y = a(cos2t(2+ cos(t))/(3 + sen2t)
46
En esta escena interactiva, puedes construir el bicorne (aumenta el valor del parámetro t):

47
Curva bifolio
Curva estudiada por de Longchamps en 1886 y Brocard en 1887. Se le conoce, también, como doble folio o curva bifoliada. Sus ecuaciones paramétricas son:
x = (a + bt)/(1 + t2)2
y = b(a + bt)/(1 + t2)2
En esta escena interactiva empieza por aumentar el valor del ángulo t, luego interactúa con los parámetros a y b
48
Curva cornoide
Curva geométrica descubierta por el ingeniero y matemático salvadoreño Alberto Sánchez. Las ecuaciones paramétricas de esta curva, son:
x = a•cos(t)cos(2t)
y = a•sen(t)(2 + cos(2t))
En esta escena interactiva empieza por aumentar el valor del ángulo t, luego interactúa con el parámetro a
49
Curva folio cartesiano
Curva estudiada por Descartes y Roberval en 1638 y luego por Huygens en 1672. Otro nombre es la flor de jazmín y sus ecuaciones paramétricas son:
x = 3at/(1 + t3)
y = 3a2t/(1 + t3)
En esta escena interactiva empieza por aumentar el valor del ángulo t, luego interactúa con el parámetro a
50
Curva folio de Durero
Esta curva del alemán Alberto Durero es un caso especial de la rosa, para n = 1/2; por lo tanto, también es un caso especial de epitrocoide.
Las ecuaciones paramétricas de esta curva, son:
x = a(cos(t) + cos(3t))/2
y = a(sen(t) + sen(3t))/2
51
Curva bruja de Agnesi
María Gaetana Agnesi estudió con detalle una curva, que había sido llamada versiera (del latín vertere, que significa virar, girar). Parece ser que el nombre de "bruja" le viene a la curva de una traducción incorrecta al inglés de una palabra italiana parecida, avversiera, que significa "hechicera, bruja" (http://www.iesezequielgonzalez.com).
Las ecuaciones paramétricas de esta curva, son:
x = at
y = a/(1+ t2)
52
Curva gota de agua
Curva estudiada por Wallis en 1685 y Bonnet en 1844 (también se conoce como pera).
Las ecuaciones paramétricas de esta curva, son:
x = a•cos2t
y = a*cos3t•sen(t)
53
Capítulo ii
Curvas paramétricas en el espacio
Introducción
Todas las curvas en el plano, que hemos visto en el capítulo anterior, son posibles de representar en un espacio tridimensional. Por ejemplo, las curvas epicicloides y las hipocicloides que tanto llamaron la atención de personalidades como Durero, Desargues, Roemer, Huygens, Leibniz, Newton, L’Hôpital, Jakob Bernoulli, La Hire, Johann Bernoulli, Daniel Bernoulli y Euler la puedes observar en este interactivo:
57
Pero en dicha escena, sólo llevamos una curva plana al espacio tridimensional. Lo que nos interesa son la curvas tridimensionales, así que... a disfrutar.
2.1 Cicloides esféricas
58
En la escena interactiva de la página anterior, puedes observar que cuando w = 0, encontramos el hipocicloide plana, y cuando w = π (3.14) la epicicloide plana. A excepción de estos dos casos, las curvas se trazan en la esfera común al círculo rodante, de ahí su nombre de cicloide esférico. El cicloide esférico es, por lo tanto, una ruleta de un movimiento de esfera sobre esfera.
Coordenadas paramétricas
x = a((q - cos(w))cos(t) + cos(w)cos(t)cos(qt) + sen(t)sen(qt))/q
y = a((q - cos(w))sen(t) + cos(w)sen(t)cos(qt) - cos(t)sen(qt))/q
z = asen(w)(1 - cos(qt))/q
Como lo habíamos dicho antes, fueron varios ilustres científicos que se ocuparon de estas maravillosas curvas,
Christiaan Huygens (1629 -1695), un matemático holandés que construyó relojes de péndulo. El era, en realidad, un científico de renombre y reputación internacional a quien se recuerda, sobre todo, por el principio que lleva su nombre en la teoría ondulatoria de la luz. Fue maestro de Leibniz y anticipó muchas de las ideas del cálculo infinitesimal. El sabía también que las oscilaciones de un péndulo simple no son estrictamente isócronas (es decir, que tarden lo mismo) sino que dependen del tamaño del columpio. En otras palabras, si un objeto se coloca sobre el lado de un recipiente redondo invertido y se suelta, el tiempo que le toma llegar al punto más bajo será casi (pero no exactamente) independiente de la altura desde la cual se suelte, lo cual restaba exactitud a los relojes. Sucedió que Huygens inventó el reloj de péndulo casi al mismo tiempo que Pascal convocara al concurso de la cicloide, en 1658. Se le ocurrió considerar qué pasaría si se sustituyera el recipiente esférico por uno cuyo sección transversal, en lugar de ser redonda, fuera un arco de cicloide invertida. Se maravilló al encontrar que, para tal recipiente, el objeto llegará al punto más bajo en exactamente el mismo tiempo; sin importar desde qué altura de la superficie interior del recipiente se suelte. Es decir, la partícula exhibe movimiento armónico simple y el periodo es independiente de la altura inicial.
59
En otras palabras, en su péndulo, el periodo de oscilación es independiente de su amplitud. La curva cicloide es, en realidad, una tautócrona: esto es, sobre un arco cicloidal invertido, un objeto deslizará desde cualquier punto a la base, en exactamente el mismo tiempo, sin importar en qué punto comience. Un gran logro de Huygens fue demostrar que la cicloide es la única curva que tiene esta propiedad. De esta propiedad de la cicloide se valió Huygens, en 1673, (en Horologium oscillatorium) para diseñar los péndulos isócronos con un aditamento que fuerza al péndulo a columpiarse en un arco de cicloide. No obstante, el estudio de estos relojes le valió a Huygens descubrir una verdad matemática de capital importancia: la involuta de una cicloide es una cicloide similar, o, inversamente, la evoluta de una cicloide es una cicloide similar. Gracias a estas propiedades Huygens desarrolló una teoría general de evolutas. Su razonamiento va más allá del cálculo diferencial e integral y alcanza dominios nuevos del pensamiento (http://arquimedes.matem.unam.mx/PUEMAC/)

Al interactuar con las curvas cicloides, puedes verificar que es una curva hermosa con propiedades sorprendentes: Sabemos, por ejemplo, que dada la naturaleza del número p, el área de un círculo puede expresarse solamente de manera aproximada, sin embargo, con la ayuda de la cicloide se puede construir un área exactamente igual al área de un círculo dado (Ibid).
60
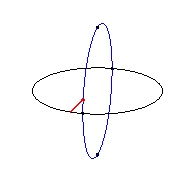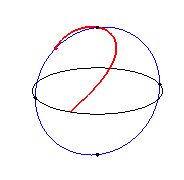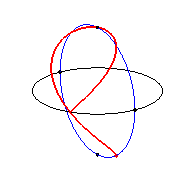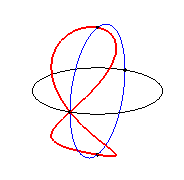
2.2 Curvas de Lissajous 3D
Las figuras 3D de Lissajous son curvas paramétricas, donde cada una de las coordenadas x(t), y(t) y z(t) es una función sinusoidal. Observa e interactúa:
61
Observa en este vídeo, algunas figuras que se pueden obtener:
Ecuaciones paramétricas
x = acos(nt)
y = asen(nt)
z = bcos(mt)
62
2.3 Anillos sinusoidales
Los anillos sinusoidales son los devanados de una sinusoide alrededor de un cilindro (en otras palabras, si un anillo sinusoidal se enrolla en un plano, se obtiene una sinusoide) (https://www.mathcurve.com/courbes3d/l).
63
Ecuaciones paramétricas
Los anillos sinusoidales son una variante de las curvas llamadas "Hélices". En la siguiente escena interactiva, diseñada por Brenda Casandra Vargas Rocha (Instituto de Ciencia e Ingeniería de Materiales, UNAM), puedes observar y cambiar las ecuaciones paramétricas de una hélice.
Te recomendamos explorar la escena en forma ampliada.
64
2.4 Solenoide tórico
Este tipo de curva es un solenoide cuya curva central es un círculo, que se envuelven regularmente alrededor de un toro. También pueden verse como una trayectoria de un punto que tiene un movimiento circular uniforme en un plano que gira uniformemente alrededor de un eje (https://www.mathcurve.com/courbes3d/).
En Física, un solenoide (del griego, «solen», 'tubo', 'conducto', y «eidos», 'en forma de') es cualquier dispositivo físico
capaz de crear un campo magnético sumamente uniforme e intenso en su interior, y muy débil en el exterior. Un ejemplo teórico es el de una bobina de hilo conductor aislado y enrollado helicoidalmente, de longitud indeterminada. En ese caso ideal el campo magnético sería uniforme en su interior y, como consecuencia, afuera sería nulo. En la práctica, una aproximación real a un solenoide es un alambre aislado, de longitud finita, enrollado en forma de hélice (bobina) o un número de espirales con un paso acorde a las necesidades, por el que circula una corriente eléctrica (https://es.wikipedia.org/wiki/Solenoide).
65
En la imagen anterior se pueden observar varias bobinas solenoidales, entre ellas la tórica.
En la siguiente escena interactiva del solenoide tórico, puedes vambiar el número de espiras y los radios, además de mostrar la superficie del toro.
66
Ecuaciones paramétricas
x = (R + rcos(nt))cos(t)
y = (R + rcos(nt))sen(t)
z = rsen(nt)
Los solenoides toroidales también se obtienen por la intersección del conoide de Plücker generalizado10, formando varios solenoides girados. En la siguiente imagen se aprecia, en la escultura de John Robinson llamada "nudo gordiano", un ejemplo de esta intersección (https://www.mathcurve.com/courbes3d/).
67
2.5 Anillos de Borromeo
También conocido como "Nudo de Borromeo". Derivan su nombre de una famosa familia de príncipes italianos del Renacimiento, los Borromeos, quienes los adoptaron como un símbolo heráldico. Están grabados en la piedra de su castillo, en una de las islas borromeas del lago Maggiore (isla bella), en el norte de Italia.
Este entrelazamiento también se encuentra en piedras talladas a partir del siglo IX en adelante en Gotland, una isla del Mar Báltico frente a la costa sureste de Suecia. Se cree que corresponden a leyendas derivadas de mitos nórdicos. Por otro lado, los pueblos del norte de Escandinavia conocen una representación de los anillos Borromeos en forma de triángulos bajo el nombre de "triángulo de Odín", o "nudo de los muertos". El símbolo también estaba grabado en las camas utilizadas durante el funeral en el mar (https://www.mathcurve.com/courbes3d/).
Anillos de Borromeo - versión elipses
En esta versión, las ecuaciones paramétricas de la primera elipse, son:
x = a•cos(t)
y = b•sen(t)
z = 0
68
Para la segunda elipse:
x = 0
y = a•cos(t)
z = b•sen(t)
Ya habrás deducido cómo es la tercera elipse. Esta es la escena interactiva para esta versión de anillos de Borromeo:
69
Anillos de Borromeo - versión círculos
Si observas la imagen, podrás darte cuenta que no son círculos planos, pues es imposible la construcción del nudo con ellos.
En esta versión, las ecuaciones paramétricas del primer círculo, son:
x=a•cos(t) + a1
y = a•sen(t) + b1
z = b•cos(3t)
En las que a1 = a/2 y b1 = 0.866a
Las ecuaciones paramétricas del segundo círculo, son:
x = a•cos(t) + a2
y = a•sen(t) + b2
z = b•cos(3t)
En forma similar para el tercer círculo, donde a2 = -a/2 , b2 = a√3/2, a3 = 0 y b3 = √3
70
Esta es la escena interactiva, para la versión de los círculos, de los curiosos anillos de Borromeo:
Tres anillos entrelazados entre sí, de manera que quedan liberados los otros dos, eliminando uno cualquiera de ellos.
71
2.6 Costura en las bolas de tenis
Las ecuaciones paramétricas usadas en la escena anterior, son:
x = a•cos(t) + b•cos(3t)
y = a•sen(t) - b•sen(3t)
z = c•sen(2t)
donde c = 2√a•b
72
2.7 Curva Clelia
En matemáticas, una curva Clelia es un tipo de curva inscrita en una superficie esférica, parametrizada por las ecuaciones siguientes:
x =Rcos(nt)cos(t)
y = Rcos(nt)sen(t)
z = Rsen(nt)
73
Luigi Guido Grandi denominó así la curva en honor a Clelia Grillo Borromeo
Cuando n = 1, la clelia resultante es una curva de Viviani.

La curva de Viviani o ventana de Viviani es una curva algebraica cerrada, generada a partir de la intersección de una esfera y de un cilindro de radio mitad del de la esfera, y que pasa por el centro de la esfera. John Wallis, Gottfried Leibniz y Johann Bernoulli estudiaron de forma natural el caso simple de ventanas circulares, y tuvieron que estudiar la curva intersección del cilindro y del hemisferio, dando a esta curva el nombre de «ventana de Viviani» (https://es.wikipedia.org/wiki/Curva_de_Viviani).
Fuente de las imágenes animadas: https://www.mathcurve.com/
74
2.8 Rosa cónica
Las rosas cónicas son las curvas en un cono de revolución con la proyección del plano de rosas. Pueden considerarse como "elevaciones" cónicas de rosas (https://www.mathcurve.com/courbes3d.gb/).
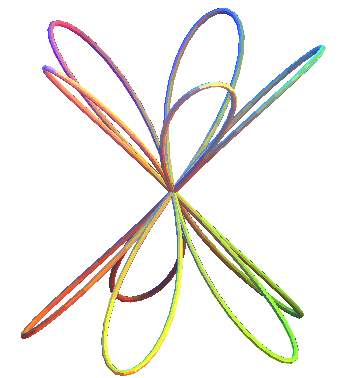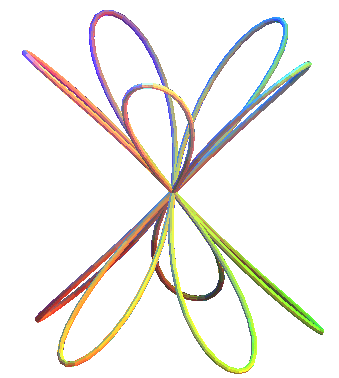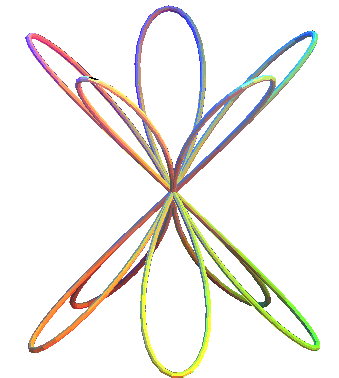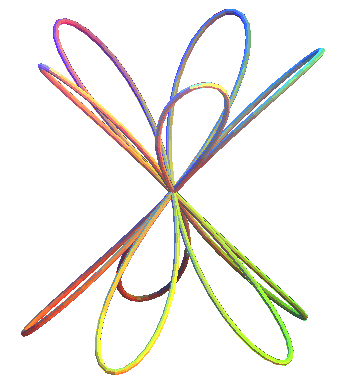
Ecuaciones paramétricas
x = a•cos(nt)cos(t)
y = a•cos(nt)sen(t)
z = b•cos(nt)
En la siguiente escena interactiva cambia los valores de n, para diferentes números de pétalos.
75
¿Qué ocurre cuando n es igual a uno?
2.9 Hélice cónica
Esta curva tiene las siguientes ecuaciones paramétricas:
76
x = t•cos(t)
y = t•sen(t)
z = kt
En la siguiente escena interactiva, observa que al aumentar k el cono se desplaza hacia arriba y si k es menor que cero, se desplaza hacia abajo.
77
2.10 Hélice esférica
Esta curva tiene las siguientes ecuaciones paramétricas:
x = a•cos(mt)cos(t/2)
y = a•sen(mt)cos(t/2)
z = a•sen(t/2)
78
2.11 Nefroide esférico
Esta curva tiene las siguientes ecuaciones paramétricas:
x = 3cos(t)- cos(3t)
y = 3sen(t) - sen(3t)
z = √12cos(t)
79
2.12 Cardioide esférico
Esta curva tiene las siguientes ecuaciones paramétricas:
x = a•cos(mt)cos(t/2)
y = a•sen(mt)cos(t/2)
z = a•sen(t/2)
80
2.13 Sinusoide esférico
Esta curva tiene las siguientes ecuaciones paramétricas:
x = b(1 - c2(cos2(at))1/2cos(t))
y = b(1 - c2(cos2(at))1/2sen(t))
z =b•c•cos(at)
81
2.14 Nudos
Como lo hemos reiterado, el propósito de este libro es de caracter ilustrativo, pues tanto las curvas como las superficies paramétricas gozan de una amplia teoría matemática que no está al alcance de este texto; por ejemplo, una introducción a la teoría de nudos, es esta:
En topología, la teoría de nudos es el estudio de los nudos matemáticos. Aunque está inspirado en nudos que aparecen en la vida cotidiana, como en los cordones de los zapatos y las cuerdas, un nudo matemático difiere en que los extremos se unen para que no se puedan deshacer, el nudo más simple es un anillo. En el lenguaje matemático, un nudo es una incrustación de un círculo en el espacio euclidiano tridimensional R3 (en topología, un círculo no está vinculado al concepto geométrico clásico, sino a todos sus homeomorfismos). Dos nudos matemáticos son equivalentes si uno puede transformarse en el otro a través de una deformación de R3 sobre sí mismo (conocida como isotopía ambiental); estas transformaciones corresponden a manipulaciones de una cadena anudada que no implican cortar la cadena o pasarla a través de sí misma (https://www.revolvy.com/page/Knot-theory).
El interés por los nudos se remontan a tiempos prehistóricos, por su estética y simbolismo espiritual "los nudos aparecen en varias formas de obras de arte chinas que datan de varios siglos antes de Cristo. El nudo interminable aparece en el budismo tibetano, mientras que los anillos de Borromeo han hecho apariciones repetidas en diferentes culturas, representando a menudo la fuerza en la unidad. Los monjes celtas, que crearon el Libro de Kells, prodigaron páginas enteras con intrincados nudos celtas" (Ibid).
Ya habíamos ilustrado los anillos de Borromeo; sin embargo, en la siguiente escena interactiva los volvemos a mostrar, diseñados a partir de superficies paramétricas, como un abrebocas al próximo capítulo.
82
Dada la complejidad matemática o, si se prefiere, topológica, de los nudos, sólo presentamos una pequeña muestra con sus respectivas ecuaciones paramétricas.
83
2.14.1 Nudo de trébol
El nudo de trébol se puede definir como la curva obtenida de las siguientes ecuaciones paramétricas:
x = sen(t) + 2sen(2t)
y = cos(t) - 2cos(2t)
z = -sen(3t)
84
Habíamos visto un solenoide toroidal con el nombre de "nudo gordiano", pues ocurre que el nudo de trébol también es un nudo gordiano muy popular en piezas de joyería; obviamente, ambos nudos son muy diferentes, lo que merece la siguiente explicación:

Según cuenta la leyenda, mientras Alejandro Magno (356 – 323 a.c.), rey de Macedonia y de los griegos, se encontraba conquistando el Imperio Persa, llegó a Gordion, capital del reino de Frigia, que formaba parte del Imperio Persa. El nombre de la capital se debía a su rey Gordio (padre del rey Midas, el que transformaba en oro todo lo que tocaba). Parece ser que en el templo de Zeus, situado en la acrópolis de Gordion, se encontraba un carro que estaba atado a un yugo mediante un complicadísimo nudo. Según las creencias de Frigia, un antiguo oráculo estableció que aquel que consiguiese deshacer el nudo se convertiría en el Rey de Frigia, y se le abrirían las puertas de toda Asia.
Alejandro Magno se vio atraído por la leyenda e intentó beneficiarse de las creencias locales desatando el nudo gordiano, sin embargo, este era muy intrincado y se le resistía. Por este motivo, el general mecedonio tomó una solución radical, sacó su espada y con ella cortó el nudo. Se cuenta que esa noche hubo una gran tormenta de rayos, lo que se interpretó como que el propio dios Zeus estaba de acuerdo con aquella solución, y Alejandro afirmó que "¡Es lo mismo cortarlo que desatarlo!". Por cierto, en once años Alejandro Magno conquistó todo el oriente… su imperio se extendió desde Grecia y Egipto hasta el valle del rio Indo (https://culturacientifica.com).
85
Resulta, entonces, que a los matemáticos se les ocurrió asignar un "número gordiano" a ciertos nudos, el cual es el mínimo número de cruces que hay que cambiar en un nudo para deshacerlo, para obtener el nudo trivial.
Más concretamente, dado un nudo N, se dice que el número gordiano de N es n, y se denota u(N) = n (la u viene del inglés unknotting number, que es otro de los nombres que recibe), si existe un diagrama D del nudo N tal que si se cambian n cruces del mismo, el nuevo diagrama obtenido es equivalente al trivial, y no existe ningún otro diagrama D' del nudo N tal que con menos cambios que n se obtenga un diagrama equivalente al trivial. Este es un invariante, es decir, para cualesquiera dos nudos equivalentes N1 y N2, su número gordiano es el mismo, u(N1) = u(N2) (ibid).
Para nuestro nudo de trébol, el número gordiano es igual a 1, puesto que si se cambia uno de los cruces se obtiene el no-nudo o nudo trivial o, mejor aún, la circunferencia.
Existen otros nudos con números gordianos como aquellos con un número mínimo de cruces igual a 5 como el de la siguiente imagen, que se conoce con los nombres de nudo de cinco lóbulos, nudo pentagrama o nudo sello de Salomón, el cual tiene un número gordiano igual a 2.

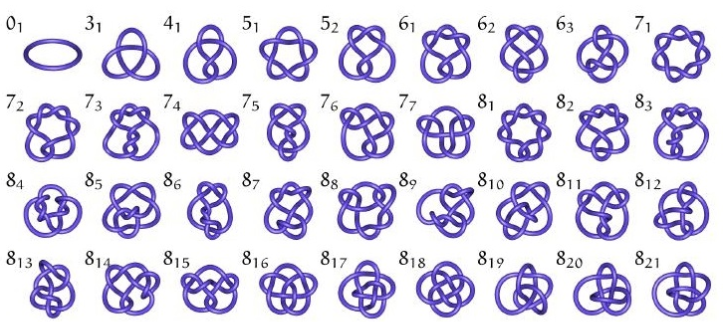
86
Existen varias clasificaciones de este tipo de nudos que no vamos a detallar; sin embargo, "en la actualidad están clasificados todos los nudos primos hasta un mínimo número de cruces igual a 16, para lo cual Jim Hoste, Jeff Weeks, y Morwen Thistlethwaite realizaron búsquedas por ordenador mediante algoritmos diseñados por ellos mismos" (Ibid), de los cuales mostramos algunos en la siguiente imagen:
2.14.2 Nudos de toro
En la teoría de nudos, un nudo de toro es un tipo especial de nudo que se encuentra en la superficie de un toro en R3. Cada nudo de toro se especifica por un par de números enteros coprimos p y q. Un nudo de toro es trivial si y sólo si p o q es igual a 1 o −1. El ejemplo más simple no trivial es el nudo de trébol. Las ecuaciones paramétricas son:
87
x = r•cos(p•t)
y = r•sen(p•t)
z = −sen(q•t)
r = cos(q•t) + 2 y 0 < t < 2π
En la siguiente escena interactiva puedes generar diferentes nudos de toro, entre ellos el trébol.
88
En la siguiente imagen puedes observar seis nudos de toro que, excepto el cuarto y el sexto, se pueden obtener con la escena interactiva anterior (imagen tomada de http://katlas.math.toronto.edu).

2.14.3 Nudo del ocho
Este nudo, también llamado nudo de Saboya, presenta un diagrama de cuatro cruces. Aparece en el escudo de armas de la Casa de Saboya.

89
El nudo en ocho o del ocho11 es emplado por los marinos para rematar la punta de un cabo, evitando que se deshaga. "Tiene una gran ventaja sobre el medio nudo, y es que, aunque sufra tensión, se aflojará con facilidad. Su apariencia entrelazada ha sido vista como un símbolo de afectos cruzados. En heráldica tiene el significado de amor leal, mostrándose en diferentes escudos, y es de aquí de donde provienen sus diferentes nombres" (https://es.wikipedia.org).
Las ecuaciones paramétricas para el nudo del ocho, son las siguientes:
x =10(cos(t) + cos(3t)) + cos(2t) + cos(4t)
y = 6sen(t) + 10sen(3t)
z = 4sen(3t)•sen(5t/2) + 4sen(4t) - 2sen(6t)
En la siguiente escena interactiva puedes observar este nudo. Rota la imagen para que puedas ver los detalles de los cruces del nudo. Haz clic den el botón para que observes el nudo del doble ocho12.
90
2.14.4 Nudo del rizo o del marino
El nudo del rizo o nudo cuadrado se usa para asegurar una cuerda alrededor de un objeto. A veces también se le conoce como un nudo de Hércules.
91
"El nudo se forma atando un nudo de mano izquierda y luego un nudo de mano derecha, o viceversa. Un mnemotécnico común para este procedimiento es "de derecha a izquierda; de izquierda a derecha", que a menudo se agrega con el sufijo que rima "... hace un nudo ordenado y apretado". Dos sobresaltos consecutivos de la misma mano harán un nudo de abuelita. Los extremos de trabajo del nudo de arrecife deben emerger tanto en la parte superior como en la inferior, de lo contrario se produce un nudo de ladrón" (https://www.revolvy.com).

Este se confunde fácilmente con el nudo de la abuelita, que es un nudo muy pobre (Ibid).

Para este último nudo, las ecuaciones paramétricas son:
x = -22cos(t) - 128sen(t) - 44cos(3t) - 78sen(3t)
y = -10cos(2t) - 27sen(2t) + 38cos(4t) + 46sen(4t)
z = 70cos(3t) - 40sen(3t)
92
2.14.5 Nudo simple
Terminamos este capítulo con el nudo más simple, el que normalmente realizamos en las actividades cotidianas.
El nudo simple es uno de los nudos fundamentales y forma la base de muchos otros nudos. El nudo simple es muy seguro, al punto de atarlo fuertemente. Debería utilizarse si se intenta que el nudo sea permanente (https://es.wikipedia.org).
93
Obviamente el nudo simple es el de trébol pero, para este último nudo no uniremos sus extremos.

Las ecuaciones paramétricas son las siguientes:
x = 3sen(t) + t
y = cos(2t)
z = sen(2.5(t - 0.5))
En la siguiente escena interactiva, aumenta el valor de t para construir varios nudos simples con una sonla cuerda. Tambien puedes rotarlo y ampliarlo para observar los detalles del nudo.
94
Capítulo iii
Superficies paramétricas
Introducción
En este capítulo presentamos superficies en el espacio generadas mediante un conjunto de ecuaciones paramétricas o mediante una función vectorial. Recuerda que para las curvas usamos un solo parámetro t. En el caso de las superficies, son dos los parámetros, que llamaremos u y v. Si bien nuestra pretensión es despertar la curiosidad sobre algunos aspectos geométricos y topológicos a partir de la visualización de un conjunto de superficies más o menos complejas y curiosas, evitando los aspectos matemáticos más formales, consideramos pertinente describir la definición matemática de una superficie paramétrica.
Sean x,y y z funciones de u y v, continuas en un dominio D del plano uv. Al conjunto de puntos (x, y, z) dado por
r(u,v) = x(u,v)i + y(u,v)j + z(u,v)k
se le llama una superficie paramétrica. Por otra parte, a las ecuaciones
x = x(u,v), y = y(u,v) y z = z(u,v)
se denominan ecuaciones paramétricas.
Si S es una superficie paramétrica dada por la función vectorial r, entonces S es trazada por el vector posición r(u,v) a medida que el punto (u,v) se mueve por el dominio D. En la siguiente escena interactiva, puedes desplazar el vector posición que genera la superficie paramétrica que conocemos con el nombre de cilindro; sin embargo, en sentido estricto, se trata de una superficie cilíndrica. En la escena, hemos dispuesto el vector de posición, de tal forma que se desplace sobre una de las tantas curvas características del cilindro, en este caso la hélice cilíndrica.
99
A propósito del cilindro, nuestro primer apartado lo dedicamos a las superficies paramétricas: cilindro y cono.
100
3.1 Superficies cilíndricas y cónicas
3.1.1 Superficie cilíndrica
Esta superficie se puede obtener al rotar un rectángulo sobre el eje que pasa por uno de sus lados, es decir, una superficie de revolución; no obstante, fiel a nuestros propósitos, mostramos cómo se genera la superficie cilíndrica a partir de sus ecuaciones paramétricas, que en este caso son:
x = r•cos(u)
y = r•sen(u)
z = h•v
Si conoces algo de matemáticas, ya habrás identificado las ecuaciones paramétricas de la circunferencia en las dos primeras ecuaciones y, en la dirección z, la altura del cilindro. En una forma sencilla, podríamos decir que:
en el espacio tridimensional R3 dotado del sistema de coordenadas (x,y,z). Dada una recta l y una curva plana C, una superficie cilíndrica en este espacio es una superficie generada por una familia de rectas paralelas a l y que tienen un punto en C (https://matematicas.uniandes.edu.co).
Observa, en la siguiente página, una escena interactiva en la cual puedes cambiar los parámetros r y h, que corresponden al radio y a la altura, respectivamente, de la superficie cilíndrica:
101
Volviendo a las dos primeras ecuaciones paramétricas y cambiándolas por:
x = r1•cos(u)
y = r1•sen(u)
z = h•v
obtendríamos una superficies de cilindros elípticos, con los cuales puedes interactuar en la siguientes escena:
102
3.1.2 Superficie cónica
Esta superficie se puede obtener al rotar un triángulo rectángulo sobre el eje que pasa por uno de sus catetos. Pero aquí vamos a ver cómo se genera una superficie cónica a partir de ecuaciones paramétricas. En el caso de la superficie que nos ocupa (cono circular recto), las ecuaciones usadas son:
103
x = r•v•cos(u)
y = r•v•sen(u)
z = c•v
con u variando en el intervalo [0,1] y v variando en el intervalo [0, 2pi]. En la siguiente escena se muestra un cono recto (superficie cónica, ya que no tiene base). Podemos modificar el radio y la altura correspondientes al cono generado.
104
Si en las dos primeras ecuaciones anteriores, tal como lo vimos para la superficie cilíndrica, hacemos diferentes los valores de r, es decir: x = r1•v•cos(u) e y = r2•v•sen(u), obtenemos conos de base elíptica, tal como se muestra en la siguiente escena. En ese caso el cono se generaría por el recorrido de un segmento de longitud variable con un extremo apoyado sobre una elipse y el otro extremo situado sobre la mediatríz del eje mayor de dicha elipse y fijo. ¿Qué relación tienen los parámetros r1 y r2 con la elipse de base?
105
3.2 Cicloides y epicicloides de revolución
Son muchas las superficies paramétricas que se pueden generar a partir de una curva plana. En este apartado retomamos las cicloides y las epicicloides como primera muestra de este universo de superficies.
Cicloides de revolución
Creemos que vale la pena continuar con la historia de esta curva:
Los historiadores de las matemáticas han propuesto varios candidatos como descubridores de la cicloide. El matemático Paul Tannery citó un trabajo del filósofo sirio Jámblico como evidencia de que la curva era probablemente conocida en la antigüedad. Por su parte, en 1679 el matemático inglés John Wallis atribuyó el descubrimiento a Nicolás de Cusa, pero los eruditos posteriores indicaron que o bien Wallis estaba equivocado o bien las pruebas utilizadas por Wallis habían desaparecido. El nombre de Galileo Galilei fue presentado al final del siglo XIX y al menos un autor da el crédito a Marin Mersenne (monje, antiguo amigo de Descartes). A partir de la obra de Moritz Cantor y de Siegmund Günther, los estudiosos dan ahora prioridad al matemático francés Charles de Bovelles basándose en su descripción de la cicloide en su Introductio in geometriam, publicado en 1503.
Galileo acuñó el término cicloide y fue el primero en hacer un estudio riguroso de la curva. Según su discípulo Evangelista Torricelli, en 1599 Galileo intentó la cuadratura de la cicloide (construcción de un cuadrado con un área igual al área bajo la cicloide) con un enfoque inusualmente empírico que involucraba el trazado tanto del círculo generador como de la cicloide resultante sobre una hoja de metal, para luego cortarlos y pesarlos. Descubrió que la relación era de aproximadamente 3:1, pero de forma incorrecta concluyó que la relación era una fracción irracional, lo que hacía imposible la cuadratura. Alrededor de 1628, Gilles Persone de Roberval probablemente supo del problema de la cuadratura por Mersenne y lo resolvió en 1634 mediante el uso del teorema de Cavalieri. Sin embargo, este trabajo no fue publicado hasta 1693 (en su Traité des Indivisibles) (https://es.wikipedia.org)
106
Las ecuaciones paramétricas para la cicloide de revolución, son las siguientes:
x = a(u - sen(u))cos(v)/2
y = a(u - sen(u))sen(v)/2
z = a(1 - cos(u))/2
¡Observa! e ¡Interactúa!
107
En la escena interactiva anterior, hemos diseñado la cicloide y dos curvas epicicloides, las cuales generan tres superficies de revolución. Observa el vídeo:
Pudiste notar que con b = 0, obtenemos la curva generatriz de la superficie de revolución. Ahora, te presentamos las ecuaciones paramétricas de las dos epicicloides de revolución de la escena interactiva.
108
La nefroide de revolución
x = a•cos(u)(3cos(v) - cos(3v))
y = a•sen(u)(3cos(v) -cos (3v))
z = a•(3sen(v) - sen(3v))
La cardioide de revolución
x = -2a•cos(u)(1 + cos(u))cos(v)
y = 2a•cos(u)(1 + cos(u))sen(v)
z = 2a•sen(u)(1 + cos(u))
3.3 hipocicloides de revolución
Superficies obtenidas por revolución de curvas hipocicloides.
Astroide de revolución
Superficie obtenida por revolución de una curva astroide. Su parametrización es la siguiente:
x = k•cos3(v)cos(u)
y = k•cos3(v)sen(u)
z = k•sen3(v)
En la siguiente escena interactiva, genera la astroide de revolución, aumentando el valor de b.
109
Utiliza la vista transparente para que observes tanto la curva como la superficie de revolución.
110
Las curvas tipo hipocicloide, incluyendo la astroide, fueron descubiertas por Roemer (1674) en su búsqueda de la forma óptima para los engranajes. Fue estudiada por Johann Bernoulli. La doble generación fue advertida en primer lugar por Daniel Bernoulli en 1725. El nombre de astroide apareció por vez primera en 1838, en un libro publicado en Viena; antes fue conocida con distintos nombres como cubocicloide, paraciclo, curva tetracúspide.
Hipocicloides de revolución (Eje OX)
Superficie obtenida por revolución de una curva hipocicloide alrededor del eje X. Su parametrización es la siguiente:
x = (a-b)cos(v) + b•cos(((a-b)/b)•v)
y = ((a-b)sen(v) - b•sen(((a-b)/b)v))cos(u)
z = ((a-b)sen(v) - b•sen(((a-b)/b)v))sen(u)
En la siguiente escena interactiva, genera varias hipocicloides de revolución aumentando, inicialmente, el valor de t hasta 0.5. Si usas a=3 y b=1, obtendrás el deltoide de revolución, generada por la curva deltoide que fue concebida por Euler en 1745 en conexión con el estudio de las curvas cáusticas. Fue también investigada por Steiner en 1856 y a veces se le denomina hipocicloide de Steiner.

111
Utiliza la vista transparente para que observes tanto la curva como la superficie de revolución.
112
En la siguiente escena interactiva, presentamos la hipocicloide de revolución, generado por una curva hipocicloide rotando alrededor del eje Z.
Utiliza la vista transparente para que observes tanto la curva como la superficie de revolución.
113
3.4 Hipotrocoides de revolución
Superficie obtenida por revolución de una curva hipotrocoide. Su parametrización es la siguiente:
x = ((a-b)cos(u) + h•cos(((a-b)/b)•u))cos(v)
y = ((a-b)cos(u) + h•cos(((a-b)/b)u))sen(v)
z = (a-b)sen(u) - h•sen(((a-b)/b)u)

Las dos imagenes animadas anteriores, fueron tomadas de http://xtsunxet.usc.es/cordero
En la siguiente escena interactiva, presentamos la hipotricoide de revolución, generado por una curva hipotrocoide rotando alrededor del eje Z.
Usa los pulsadores para obtener diferentes superficies asombrosas; por ejemplo, con a=6 y b=0.5 y h=1 obtienes una forma de fuente, o con a=6, b=0.5, h=0 obtienes una esfera.
114
Como lo hemos dicho, es posible generar una superficie esférica en este escena interactiva; sin embargo, veamos cómo obtenerla a partir de la circunferencia o, al menos, con la mita de ella.
115
3.5 Superficies esféricas
Esfera
Recordemos que la esfera es el cuerpo geométrico de los puntos del espacio que equidistan de uno fijo que es el centro de la esfera. Pero también podemos considerar a la esfera como el cuerpo de revolución generado por una circunferencia al girar sobre uno de sus diámetros. Las ecuaciones paramétricas de una esfera centrada en el origen de coordenadas (0,0,0) son:
x = r•cos(U)sen(V)
y = r•sen(U)sen(V)
z = r•cos(V)
En las que r es el radio de la superficie esférica, U = a•2πu y V = π•v (el parámetro a permite rotar media circunferencia, generando la superficie).
En la siguiente escena interactiva, desarrolla la superficie esférica. Observa que en la revolución se pueden obtener casquetes esféricos.

116
Esfera de Viviani
A continuación presentamos una superficie esférica, generada con la curva de Viviani.
117
En realidad, a Viviani se le conoce por su famoso problema llamado "la bóveda de Viviani".
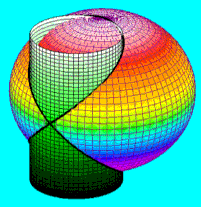
Vincenzo Viviani (1622-1703), discípulo de Torricelli y Galileo, planteó en 1692 el siguiente problema: "¿Cómo cortar, de una bóveda semiesférica, cuatro ventanas de tal manera que la superficie que quede sea cuadrable?" Desde entonces se le conoce como el problema florentino o la bóveda de Viviani.
118
En resolverlo se interesaron Wallis, Leibniz, L´Hospital y Johann Bernoulli, de la que llegó a dar cinco soluciones. Aquí se emplearon por primera vez los nuevos métodos del cálculo diferencial e integral para calcular el área de una superficie. En la imagen se muestra la solución que dio el mismo Viviani, donde se corta la esfera por un cilindro cuyo diámetro en la base está sobre el radio de la esfera. Se comprueba que si a es el radio de la esfera, la parte de superficie esférica que cae dentro del cilindro es (π/2 - 1)a2, luego si colocamos cuatro cilindros tangentes el área de la bóveda será S = 2(π - 2)a2. Luego el resto es 4πa2 - S = 4a2. Esta solución de Viviani ha sido también el típico ejemplo que han usado desde siempre los textos de cálculo integral para este tipo de problemas https://www.uam.es.
Elipsoide o esferoide
De forma general una elipsoide o esferoide es una superficie generada a partir de transformaciones afines de una esfera, es decir, modificando su diámetro en una, dos o las tres direcciones del espacio (es una cuádrica con centro de simetría). Un caso particular es cuando dos de esas direcciones sufren la misma transformación y, entonces, podemos considerar al elipsoide como una superficie de revolución generada por la rotación de una elipse alrededor de uno de sus ejes. Las ecuaciones paramétricas, con el centro de simetria del elipsoide en el origen de coordenadas (0,0,0), son:
119
x = a•cos(v)cos(u)
y = b•cos(v)sen(u)
z = c•sen(v)
En la siguiente escena interactiva, aumenta lentamente los valores de t, para que observes la generación del elipsoide al rotar la elipse.
120
3.6 Elipsoide tetraédrico
La superficie que se muestra en la siguiente escena interactiva, resulta muy interesante por su forma. Podemos imaginarla como un tetraedro con cuatro aristas elípticas y dos rectas.
121
Pero, son muchas las superficies extrañas, curiosas e, incluso, artísticas que podemos crear en el universo matemático; por ejemplo, en la siguiente escena se muestra una curiosa superficie de revolución que recuerda a una especie de vasija (sin su base). Las ecuaciones paramétricas, publicadas por José Luis Abreu León (UNAM) y Marta Oliveró Serrat, son:
x = largo•(0.5v - v3)cos(u); y = ancho•(0.5v - v3)sen(u);
z = alto•(2v - 1)
122
3.7 Ocho de revolución
Esta superficie se obtinenes al rotar la curva Ocho, también llamada lemniscata12 de Gerono o lemniscata de Huygens, o curva en forma de ocho, que es una curva algebraica plana de grado cuatro y género cero. La curva Ocho (polar) es un caso especial de una curva lissajous (https://www.flickr.com/).
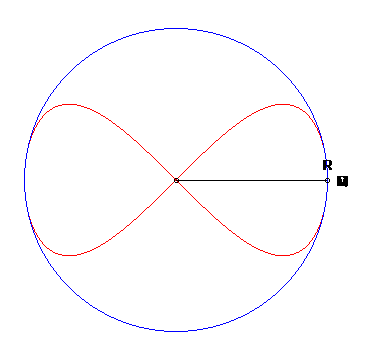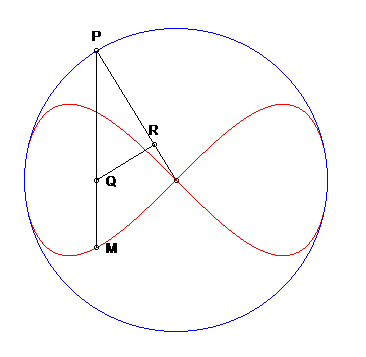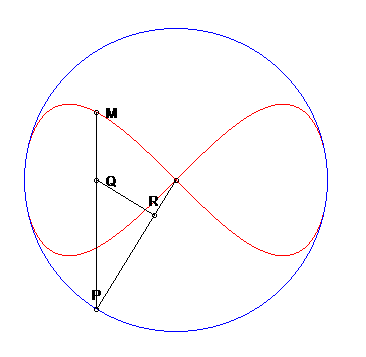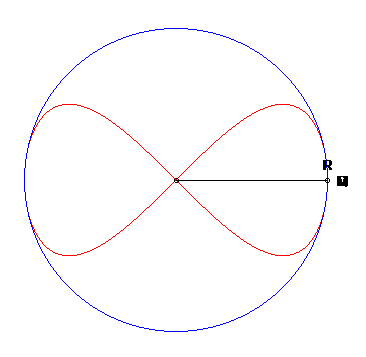
Imagen tomada de https://www.mathcurve.com/
123
La superficie del ocho, obtenida por revolución de una curva en ocho, tiene ecuaciones paramétricas tal como se muestra en la siguiente escena interactiva:
3.8 Piriforme de revolución
En la siguiente escena interactiva se muestra la superficie de revolución engendrada a partir de curva piriforme (en forma de pera) con el eje de simetría sobre el eje OZ, rotando sobre dicho eje. Las ecuaciones paramétricas que definen a esa superficie son:
124
x = x = a(1 + sen(u))
y = (b(1 + sen(u))cos(u)cos(v)
z=(b(1 + sen(u))cos(u)sen(v)
Una superficie similar es la llamada gota de agua o gota de lágrima, que veremos a continuación.
125
3.9 Gota de agua
En la siguiente escena se muestran dos superficies de revolución que son muy parecidas a la piriforme. La primera superficie fue denominada lágrima por Paul Bourke y partió de una curva 2D muy similar a la piriforme, buscando un modelo aproximado de gota de agua. Posteriormente el arquitecto Peter Taylor Ermst desarrolló el proyecto que presentó al concurso para lo que debería ser el acceso al "World Trade Center Memorial", a partir de una modificación de la curva de Bourke que realizó Rolfe A. Leary y que se materializó en una pequeña pieza de vidrio.

Esa segunda superficie también se muestra en la escena. Las ecuaciones paramétricas que definen a esa superficie son:
x = k(1 - cos(v))sen(v)cos(u)
y = k(1 - cos(v))sen(v)sen(u)
z = cos(v)
126
3.10 Paraboloides e hiperboloides
En los apartados anteriores hemos visto superficies que pueden considerarse generadas por la rotación de curvas cerradas (circunferencia, elipse, piriforme, ...) alrededor de uno de sus ejes de simetría. En este apartado veremos varias superficies generadas a partir de la rotación de curvas cónicas abiertas, como son la parábola y la hipérbola.
127
3.10.1 Paraboloide de revolución
Cuando hacemos girar una parábola alrededor de su directriz obtenemos una superficie abierta denominada paraboloide de revolución. Sus ecuaciones paramétricas son:
x = a•u•cos(b•2pi•v)
y = a•u•sen(b•2pi•v)
z=x2 + y2
128
Ejemplos de paraboloides de revolución son los hornos solares y las antenas parabólicas para captar las señales de televisión vía satélite. Pero, veamos un paraboloide de base elíptica.
Paraboloide elíptico
129
3.10.2 Paraboloide hiperbólico
También conocido como silla de montar por su conformación geométrica. En la siguiente escena interactiva, puedes observar cinco edificaciones cuyo diseño es un paraboloide hipérbolico13.
130
Las ecuaciones paramétricas del Paraboloide Hiperbólico son:
x = 2u - 1
y = v - 1
z = x2 - y2
131
Silla de mono
Las construcciones de paraboloides hiperbólicos se diseminaron por todo el mundo gracias a la obra de Félix Candela; sin embargo, no se conocen obras diseñadas o ejecutadas con la forma de las sillas de mono para monos de una o más colas.
132
3.10.3 Hiperboloide de una hoja
Cuando hacemos girar una hipérbola alrededor de su eje imaginario obtenemos una superficie abierta denominada hiperboloide de revolución. Hay muchos ejemplos de superficies reales que son hiperboloides de una hoja o parabólicos: la torre del puerto de Köbe en Japón (ver imagen), las torres de refrigeración de centrales nucleares, la catedral de Brasilia diseñada por Óscar Niemeyer, la torre de televisión de Cantón (República Popular China) o la torre de control dl aeropuerto de Barcelona. Las primeras estructuras hiperboloides fueron creadas por el ingeniero ruso Vladimir Shukhov (1853-1939) quien la usa por primera vez para la torre de sustentación de un depósito de agua en una exposición panrusa en Nizhni Nóvgorod (1896), aunque Antoni Gaudí ya había usado algunas, integradas en sus obras, como por ejemplo en la bóveda del Palacio Güell (1888).

133
Las ecuaciones paramétricas del hiperboloide de una hoja, son:
x = r•cos(u) - f•sen(u)
y = r•sen(u) + f•cos(u)
z = b•(2v - 1)cos(&pi/6)
134
Hiperboloide de dos hojas
El hiperboloide de dos hojas se obtiene como una superficie de revolución al rotar una hipérbola alrededor de su eje real.
135
3.11 Helicoides
El helicoide circular, o simplemente helicoide, es la superficie minimal de la hélice circular14. Por muchos años, el helicoide seguía siendo el único ejemplo que se conocía de una superficie minimal encajada completa en la topología finita con curvatura infinita. Sin embargo, en 1992 un segundo ejemplo fue descubierto, conocido como la superficie minimal de Hoffman que consiste en un helicoide con un agujero (http://www.dim.uchile.cl).
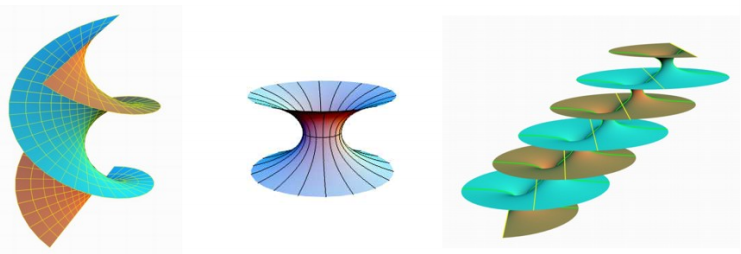
Superficies minimales foliadas por rectas y circunferencias (aparte del plano): helicoide, catenoide y superficie minimal de Riemann (Rodríguez Pérez).
136
Helicoide recto
Un helicoide recto (o cilíndrico) es una superficie minimal reglada generada por un segmento rectilíneo que se desplaza sobre una curva hélice, girando sobre el eje de dicha curva. Los tornillos sinfín de muchos mecanismos, las escaleras de caracol típicas, la pasta italiana denominada "fusilli" y los tornillos de filo cuadrado son sólo algunos ejemplos de helicoides rectos. Las ecuaciones paramétricas que definen a un helicoide recto son:
x = a•v•cos(b•u)
y = a•v•sen(b•v)
z = r•b•u

Los fusilli son un tipo de pasta que se origina al sur de Italia (https://lorenzovinci.it).
137
En la siguiente escena interactiva, puedes observar las características del helicoide.
Helicoide parabólico
De forma natural podemos extender las ecuaciones paramétricas de un helicoide recto a un helicoide parabólico, tan solo hay que modificar un par de parámetros:
138
x = d•a•v•cos(b•u)
y = c•a•v•sen(b•u)
z = r•b•u
Helicoide desarrollable
Es un tipo especial de helicoide generada por las tangentes a una hélice circular o cilíndrica.
139
La parte inferior de las escaleras de acceso al museo del Louvre por la "Pirámide", corresponden a una porción de un helicoide desarrollable. Las ecuaciones paramétricas correspondientes son:
x = a(cos(u) - v•sen(u))
y = a(sen(u) + v•cos(u))
z = b(u + v)
140
Helicoide sobre círculo
La superficie que se muestra a continuación recuerda más a un tubo que a un helicoide, pero su desarrollo es el de una helicoide. Este tipo de superficie se puede encontrar en algunas columnas en iglesias, columnas monumentales, objetos decorativos,... (vease la página de Robert Ferréol).
141
Muelle
Todos hemos visto muelles en algún momento y, quizás, hemos visto algún serpentín15.

Diferentes tipo de muelles a compresión, torsión o tracción (https://www.pspring.com).
142
Las ecuaciones paramétricas que definen al muelle son:
x = (1 - r•cos(v))cos(k•u)
y = (1 - r•cos(v))sen(k•u)
z = r(sen(v) + periodo(k/1.6•u/π)
143
3.12 Cinta de Möbius
Si tomamos una tira de papel larga y algo estrecha, la retorcemos (medio giro) y unimos sus extremos obtenemos una superficie muy peculiar y sencilla: la cinta o banda de Möbius. Esa superficie se caracteriza por tener una sola cara y una sola arista (o borde) y ser no orientable. Si tomamos una de esas cintas hecha con papel, la apoyamos sobre una esquina de una mesa, tomamos un bolígrafo y vamos tirando de la cinta, veremos que el trazo del bolígrafo se encuentra con su inicio, sin que hayamos levantado y dado la vuelta a la cinta. Otra curiosidad de esa superficie es que, si hacemos una incisión en medio y la cortamos longitudinalmente, obtendremos una cinta de Möbius de longitud doble que la original y al repetir la operación obtenemos, ¡sorpresa!, dos cintas de Möbius entrelazadas. ¡Probadlo!.
La banda de Möbius es una superficie que, por sus sorprendentes propiedades, ha sido y es utilizada en campos tan dispares como la Matemática, el Arte, la Ingeniería, la Magia, la Ciencia, la Arquitectura, la Música, el Diseño, la Literatura, etc., ya sea de manera explícita o simplemente como una metáfora. Simboliza la naturaleza cíclica de muchos procesos, la eternidad, el infinito… presente ya en la iconografía alquimista como la serpiente mordiendo su cola – el ouroboros (Macho Stadler).
Estadio Lansdowne Road de Dublín (Macho Stadler).
144
Aplicaciones de la cinta de Möbius
Macho Stadler nos ilustra una gran infinidad de aplicaciones de esta banda mágica, descubierta de forma independiente por los matemáticos alemanes August Ferdinand Möbius y Johann Benedict Listing en 1858, algunas de estas aplicaciones son:
En 1923, Lee De Forest obtuvo una patente norteamericana para una película de Möbius que grababa el sonido en ambas caras. Richard L. Davis obtuvo en 1964 la patente norteamericana de una banda de Möbius con resistencia no reactiva. En 1963, James W. Jacobs patentó un filtro auto limpiante destinado a máquinas de limpieza en seco que, por tener forma de banda de Möbius, facilitaba el lavado por ambas caras, quedando la suciedad depositada en el filtro, al ir éste dando vueltas. En algunos aeropuertos ya hay bandas de Möbius para las cintas que transportan los equipajes o la carga: el aprovechamiento es doble, igual que el rendimiento, y el desgaste se reduce a la mitad. Investigadores japoneses de la Hokkaido Univertsity (S. Tanda, T. Tsuneta, Y. Okajima, K. Inagaki, K. Yamaya and N. Hatakenaka, Nature, 2002, 417, 397–398) han demostrado que los cristales – conjuntos ordenados de átomos, iones o moléculas – pueden crecer en forma de bandas, incluso añadiéndoles algún giro. La proteina antiviral Kalata, sustancia extraída de la planta Oldenlandia se enrolla siguiendo una banda de Möbius. Existen numerosas aplicaciones y patentes que involucran a la banda de Möbius, y cada vez más estudios científicos descubren diferentes objetos con topología de Möbius.

145
Las ecuaciones paramétricas que definen a la cinta de Möbius, son:
x = (a + v•r•sen(u/2))cos(u)
y = (a + V•r•sen(u/2))sen(u)
z = v•r•cos(u/2)
146
Superficie de Möbius
Es una superficie que no hay que confundir con la cinta del mismo nombre, aunque ambas están relacionadas. De hecho, modificando un determinado parámetro en las ecuaciones paramétricas de esa superficie obtendremos una cinta de Möbius (de ahí su nombre). La superficie de Möbius es una superficie reglada no desarrollable y no orientable además de ser un caso especial de rotoide debido a su construcción. En la siguiente escena se representa dicha superficie. Si al parámetro a le damos valor 10 y al parámetro k1 un valor de 1 ¿qué vemos en la escena? (se han elegido esos dos valores para que se vea mejor la superficie obtenida).
147
3.13 Botella de Klein
Aunque realmente la botella de Klein16 es una superficie de dimensión 4, se suele conocer por su inmersión en el espacio euclídeo tridimensional en la que aparece una auto-inserción. Topológicamente la botella de Klein es una superficie no orientable, de una sola cara y sin borde. En realidad ese objeto no puede ser contenido en un espacio de tres dimensiones, por lo tanto no se puede construir un objeto físico real con dicha forma.
Explora la siguiente botella, rotándola con clic izquierdo sostenido.
148
En la siguiente escena interactiva, el parámetro a nos permite modificar el diámetro máximo tangencial de la botella de Klein. Para conseguir la representación que se muestra, se necesitan dos juegos de ecuaciones paramétricas, una para la base de la botella y otra para el resto de la superficie.
Dada la complejidad de la superficie, la mostramos inicialmente en el modo de color "alambre", que permite una mejor visualización de la botella.
149
3.14 El toro o toroide
Un toro es un cuerpo geométrico generado al trasladar una circunferencia de radio r perpendicularmente sobre una trayectoria circular de radio R que pasa por su centro. Es un caso particular de los denominados toroides, en los que la trayectoria que sigue la circunferencia es una elipse. Físicamente podemos construir un toro o toroide doblando un tubo cilíndrico y uniendo sus extremos.
Las ecuaciones paramétricas que nos definen a un toro o superficie toroidal (también denominada rosquilla matemática) son:
x = (R + r•cos(θ))cos(φ)
y = (R + r•cos(θ))sen(φ)
z = r•sen(θ)
en las que las variables angulares toman valores en el intervalo [0, 2π].
Sí damos el mismo valor a R y r, el toro pierde su "agujero" (en inglés "horn torus"). Si damos a r valores mayores que R obtenemos una superficie similar a una esfera algo aplastada por sus polos, con una doble cavidad interior (en inglés "spindle torus"). Usando la siguiente escena interactiva se puede comprobar.
Ejemplos de toros son: las rosquillas o "donuts", las cámaras de aire de las ruedas de vehículos, algunos modelos de flotadores, tubos fluorescentes circulares, cámaras de algunos reactores nucleares (por ejemplo los tipo "tokamak"),...
En topología un toro es una superficie equivalente a una taza de café ya que mediante determinadas transformaciones contínuas (es decir sin realizar ningún tipo de "corte" o incisión), podemos pasar de una superficie a la otra. Pero eso es otro cantar.
150
En la siguiente escena interactiva, modificando los valores de los parámetros a y b, podremos "abrir" la superficie toroidal tanto tangencial como longitudinalmente. También podemos modificar r y R.
151
Supertoros
Si en las ecuaciones paramétricas anteriores elevamos a unos determinados exponentes los senos y cosenos, se obtienen una familia de superficies basadas en los toros:
x = (R + r•cos(θ)n1)cos(φ)n2
y = (R + r•cos(θ)n1)sen(φ)n2
z = r•sen(θ)n2
En la siguiente escena se pueden comprobar diferentes combinaciones de valores para los exponentes de seno y coseno.
152
En los trabajos realizados por Paul Bourke (en algunas usando ecuaciones atribuidas a Roger Bagula) se muestran otras superficies que, por su forma geométrica, tienen relación con el toro y a las que Paul Bourque denomina: toro elíptico, toro lapa, toro pajarita y el hexatoro triaxial. En la siguiente escena podemos ver esas superficies, así como las ecuaciones paramétricas que las definen, usando el selector denominado "superficie".
153
La superficie que se muestra a continuación, es el denominado toro senoidal de primera especie (nombre dado por el profesor Robert Ferréol), es otra representación de la botella de Klein con valores de los parámetros mostrados inicialmente. Pero esta superficie es generada por la rotación de una elipse variable alrededor de un eje, la elipse situada en un plano perpendicular al eje, un eje de la elipse se mantiene constante y el otro varía senoidalmente. Si modificamos el valor del parámetro k con valores mayores a 0,5, veremos como se transforma apareciendo diversos "valles" y "lóbulos".
154
En la siguiente escena se muestra un toro senoidal de 2ª especie. Las ecuaciones paramétricas que lo definen son:
x = (R + r•cos(v))cos(k•u)
y = (R + r•cos(v)cos(k•u))sen(u)
z = r•sen(v)cos(k•u)
cuando el parámetro k es igual a 0,5 tenemos el denominado toro "pinzado". Para valores mayores de k se van formando diferentes "lóbulos".
155
3.15 Superformas
Un biólogo belga ha descubierto una 'superformula' que representa una vasta constelación de formas muy diferentes: triángulos, pentágonos, estrellas, espirales, pétalos ... Cuando vio en esta pantalla de computadora este enjambre de geometrías elementales y complejas pensó que había cometido algunos errores en el programa, pero estaba bien, se le informó, habló con muchos matemáticos: su fórmula es completamente nueva, ¡nadie la había descubierto antes! El artículo de Johan Gielis ha sido publicado en el número 90 (2003) del American Journal of Botany. En el hermoso sitio del astrofísico Paul Bourke se encuentra (entre infinitas curvas hermosas) una página dedicada a la superformula y sus criaturas! (http://users.quipo.it/)
El matemático Johan Gielis, de la Universidad de Antwerpen (Bélgica), tomando como base la ecuación de la denominada superelipse, desarrolló una fórmula (superfórmula) con la que se pueda representar formas naturales bidimensionales, alrededor del año 2000. A partir de ese trabajo el profesor Paul Bourke la extendió al espacio tridimensional para crear lo que denominó "superformas".
Una ecuación polar que define las formas 2D (adaptación de la superfórmula) es:

A partir de la ecuación anterior, usando coordenadas esféricas, obtenemos la siguiente parametrización para las superformas 3D:
156
x = r(φ)•cos(φ)•r(θ)•cos(θ)
y = r(φ)•sen(φ)•r(θ)•cos(θ)
z = r(θ)•sen(θ)
siendo los límites de los valores angulares: -π/2 ≤ φ ≤ π/2 y -π ≤ θ ≤ π
En la siguiente escena se generan esas superformas. Modificando los parámetros que aparecen (a, b, m, n1, n2 y n3) se verán diferentes cuerpos, algunos de los cuales resultan muy curiosos e interesantes.
157
Algunas combinaciones que te sorprenderán: con n1=n2=n3=1, varía m en 3, 4, 5, 6, 7...; con n1=25, n2=n3=10, varía en 3, 4, 5, 6, 7... La siguiente imagen interactiva corresponde a valores n1=n2=n3=1 y m=20, explórala rotándola con clic izquierdo sostenido.
En la superforma anterior las superficies están generadas en base a una esfera topológica, pero se pueden generar en base a otros cuerpos. En la siguiente escena se pueden ver superformas en base a un toro o toroide. Se aplican las siguientes ecuaciones paramétricas, en las que "r" corresponde a la función definida anteriormente. Obsérvese que la coordenada z no varía, pero sí lo hacen x e y.
x = cos(φ)•(r(φ)•r(θ)•cos(θ))
y = sen(φ)•(r(φ)•r(θ)•cos(θ))
z = r(θ)•sen(θ)
158
Los parámetros k1 y k2 nos permiten abrir cada superficie y de esa forma podremos ver detalles interiores. El parámetro k1 corta a la superficie tangencialmente, mientras que el parámetro k2 la corta longitudinalmente.
159
3.16 Armónicos esféricos
Vamos a ver, a continuación, un conjunto de superficies muy curiosas. Jugad con la escena aquí presentada y divertíos obteniendo superficies inimaginadas. A pesar de su nombre los armónios esféricos aquí presentados solamente guardan una remota relación con determinadas soluciones relativas a ecuaciones de onda. No deben confundirse con ningún conjunto de soluciones ortogonales de la ecuación de Laplace. Su definición en coordenadas paramétricas cartesianas depende de un conjunto de ocho parámetros, cuyos valores serán enteros positivos o cero si deseamos que las superficies representadas sean cerradas, y las correspondientes variables angulares. En la siguiente escena se pueden modificar dichos parámetros y obtener, así, diferentes superficies correspondientes a los denominados armónicos esféricos.
Las ecuaciones paramétricas usadas son:
x= r(U,V)•cos(V)•sen(U)
y = y 0 r(U,V)•cos(U)
z = r(u,V)•sen(V)•sen(U)
donde
r(U,V) = sen(n0•U)n1 + cos(n2•U)n3 + sen(n4•V)n5 + cos(n6•V)n7
función obtenida a partir de la definición de dichos armónicos en su forma polar:
r = sen(n0•φ)n1 + cos(n2•φ)n3 + sen(n4•θ)n5 + cos(n6•θ)n7
160
Si damos el valor 0 (cero) a los ocho parámetros obtenemos un cuerpo de sobras conocido ¿Cuál?. Si se coge bolígrafo y papel y realizamos esa sustitución en las ecuaciones cartesianas de los armónicos esféricos veremos que corresponden a ecuaciones paramétricas que nos definen una esfera. En realidad si uno prueba un poco verá que hay tres parámetros que no se necesita que tengan valor 0 (cero), ¿cuáles son esos parámetros?
161
Los armónicos esféricos nos ofrecen una gran variedad de formas curiosas e interesantes. Si las observamos en el modelo alambre o transparente se verá cómo su interior no siempre está totalmente hueco. Id probando combinaciones de valores de los diferentes parámetros y a buen seguro que lográis obtener imágenes más que llamativas, como la que se muestra en la siguiente imagen interactiva.
3.17 Superficies seno y coseno
Superficie seno
Se presenta una curiosa superficie que fue bautizada como superficie seno por Gray en 1997. Esta superficie presenta los mismos tipos de simetría que un cubo. Por otra parte se puede considerar como la unión de un conjunto de elipses variables.
162
Las ecuaciones paramétricas que definen a dicha superficie son:
x = a•sen(u)
y = a•sen(v)
z = a•sen(u + v)
163
Superficie coseno
Si en las ecuaciones anteriores sustituimos el seno por el coseno, se define una nueva superficie a la que podríamos llamar superficie coseno, por simetría con la anterior.
x = a•cos(u)
y = a•cos(v)
z = a•cos(u + v)
164
Esta última superficie corresponde a la parte teraédrica de una superficie mucho más compleja: la superficie de Cayley17.
3.18 Trompetas y embudos
Algunas curvas como parábolas o hiperbolas en un intervalo dado, al rotarlas con respecto a un eje, producen una superficie similar a una trompeta, tal como lo muestra la siguiente imagen interactiva (usa el pulsador para observar la curva generatriz):
165
Trompeta de Gabriel o de Torricelli
La trompeta de Gabriel18 es la superficie de revolución obtenida al girar una hipérbole equilátera alrededor de una de sus asíntotas. Esta superficie presenta una paradoja realmente sorprendente: si queremos llenar el tubo formado por esta superficie (que tiene una longitud infinita), será suficiente como una cantidad finita de líquido, pero si queremos pintarlo, ¡se necesitará una cantidad infinita de pintura!

Fuente: http://www.servidoresdelaluz.com.
Esta superficie apocalíptica fue estudiada en 1641 por Roberval y por Torricelli. Sus ecuaciones paramétricas son:
166
x = r1•u•cos(v)
y = r2•u•sin(v)
z = r1/u
En la siguiente escena interactiva, reduce el valor del parámetro t a cero y observarás la hipérbola generatriz de la trompeta.
167
Embudo
Esta superficie se puede generar con las siguientes ecuaciones paramétricas:
x = a•u•cos(v)
y = b•u•sin(v)
z = c•ln(u)
168
Superficie de la torre a presión constante
La torre de presión constante es la superficie de revolución obtenida al girar una curva logarítmica alrededor de su asíntota. Su nombre proviene del hecho de que, al estar esta superficie llena de un material homogéneo, la presión ejercida en cualquier sección horizontal por la parte superior es constante. Sus ecuaciones paramétricas son:
x = r1•e-r2•u•cos(v) y = r1•e-r2•u•sen(v) z = r1•u
169
3.19 Pseudoesferas
Las pseudoesferas son superficies de revolución generadas por la rotación de una curva tractriz alrededor de su asíntota. Una curva tractriz se genera cuando un objeto arrastra a otro, de manera que su distancia de separación se mantiene constante. El nombre de "pseudoesfera" se puso por determinadas analogías con la esfera. Una de ellas tiene que ver con el concepto de curvatura de Gauss (número real que mide la curvatura intrínseca en cada punto regular de una superficie). La esfera y la pseudoesfera tienen curvatura constante e igual en valor absoluto aunque de signos opuestos, positiva para la esfera y negativa para la pseudoesfera. Un cilindro, por ejemplo, tiene curvatura gaussiana nula. Así mismo, aunque la pseudoesfera en realidad es una figura no acotada, su área es finita e igual al área de una esfera con su mismo radio y el volumen encerrado por esa superficie también es finito e igual al de la semiesfera del mismo radio (el radio de la pseudoesfera es la distancia desde el punto "vértice" de la curva tractriz que la genera, hasta la asíntota de dicha generatriz). Quien le puso el citado nombre fue Eugenio Beltrami (1835-1900), matemático italiano que desarrolló notables trabajos, tanto en geometría diferencial como en física matemática.
Pseudoesfera
En la siguiente escena se muestra una pseudoesfera. El parámetro a varía su "radio" y el parámetro t nos permite abrir la pseudoesfera longitudinalmente. Las ecuaciones paramétricas empleadas son:
x = a•cos(2πb•u)sen(v)
y = a•sen(2πb•u)sen(v)
z = -(cos(v) + log(tan(v/2)))
170
Si se da el valor cero al parámetro t, se puede ver la tractriz generatriz.
Breather
La superficie que se muestra a continuación, cuyo nombre no tiene una traducción clara del término en inglés, tiene una fuerte relación con la pseudoesfera. Los "breathers" son soluciones a determinados sistemas no lineales (generalmente
171
descritos mediante ecuaciones en derivadas parciales), como por ejemplo es el caso de la ecuación no lineal de Schrödinger. Asociado a este tipo de ondas también están los denominados solitones, que son ondas solitarias que se propagan sin deformación en medios no lineales. Los "breathers" pueden constituir un mecanismo de transferencia de energía en medios contínuos. Pero estamos entrando en un terreno muy complejo y complicado que se aleja totalmente de los propósitos de este libro.
172
Superficie de Dini
La superficie de Dini es la superficie generada por la rotación de una tractriz sobre una helicoide alrededor de la asíntota de dicha tractriz. Su propiedad principal es la de ser una superficie de curvatura total constante, como la pseudosfera (también generada por la rotación de una tractriz alrededor de su asíntota). Debido a esa relación con la pseudoesfera es por lo que esa superficie se incluye en este apartado.
173
Superficie de Kuen
La superficie de Kuen es una superficie de curvatura total negativa y constante. Esa superficie se obtiene de la pseudoesfera aplicando la denominada transformación de Bianchi.
174
3.20 Superficies mínimas o minimales
¿Qué relación pueden tener la arquitectura tensional (en España denominada "textil"), la tensión superficial de un líquido, las pompas de jabon y la denominada geometría diferencial? A primera vista parece que ninguno, pero si uno investiga un poco verá que sí hay una relación: las denominadas superficies minimales o mínimas. El estudio de estas superficies tomó un fuerte impulso en la segunda mitad del siglo XIX. En esa época Joseph A. F. Plateau (1801-1883), físico belga que vivió sus últimos cuarenta años de vida totalmente ciego, llevó a cabo una gran cantidad de experimentos con pelicula de jabón y bastidores de diferentes formas y quedó planteado el que hoy se conoce como el problema de Plateau. De una forma muy simplificada el problema consistía en demostrar, matemáticamente, que para cada curva cerrada del espacio real tridimensional existe una superficie de área mínima cuyo contorno o frontera es, exactamente, esa curva.
Por otro lado, la tensión superficial del agua es la responsable de que determinados cuerpos u objetos, a pesar de que sean más densos que ella, floten debido a una película que se forma y que tiende a una área mínima (por eso podemos ver un clip flotando en el agua o al insecto denominado zapatero (Gerris Lacustris), sosteniéndose en la superficie de un una charca con el único apoyo de sus finísimas patitas). Finalmente, se cita a Frei Otto (1925-2015), arquitecto e ingeniero alemán que, entre otras obras, diseñó el estadio olímpico de Munich y que estudiaba la forma de conseguir determinadas estructuras, lo más ligeras posibles, que permitieran la reducción del material a emplear (membranas tensadas por cables), que dio lugar a la denominada arquitectura tensional o textil. Aquí solamente se muestran seis de esas superficies minimales o mínimas, aunque ya se ha visto una en páginas anteriores: la helicoide.
175
Catenoide
¿Qué hace una curva como esta en un lugar como ese? La catenoide es la superficie generada por la rotación de una catenaria alrededor de un eje coplanario, perpendicular a su eje de simetría y que no la corte pero, además, es una superficie minimal o mínima. Por eso se muestra en este apartado. Las pompas de jabón toman, precisamente, esa forma, así como cualquier superficie líquida sometida a tensión superficial.

La figura de esta imagen, construida por la membrana de jabón y agua, es conocida como un catenoide (http://bubbles-burbujas.blogspot.com).
Las ecuaciones paramétricas de la catenoide son:
x = a•cosh(u)cos(v)
y = a•cosh(u)sen(v)
z = a•u
176
con u variando en el intervalo [0, 2π] y v variando en el intervalo [0, 1]. Hay que tener en cuenta que la coordenada z, tal como se representa la superficie, debe tomar valores en el intervalo [-a•u, a•u].
De helicoide a catenoide y viceversa
En la siguiente escena interactiva, modificando el valor del parámetro a, se ve como una helicoide se transforma en una catenoide y viceversa.
177
Ambas superficies recordemos que son minimas o minimales
Superficie de Enneper
Puede definirse, geométricamente, como la envolvente de los planos mediadores de dos puntos situados en dos parábolas homofocales (es decir, parábolas cuyos planos son perpendiculares y en la que el vértice de una pasa por el foco de la otra). Las ecuaciones paramétricas usadas para representar la superficie de Enneper son:
178
x = u - u3/3 + u•v3
y = u2 - v2
z = v -v3/3 + v•u2
Las variables u y v toman valores en el intervalo [-a, a], siendo a un parámetro que podemos modificar en la escena.
179
Superficie de Catalan
El matemático belga Eugène Charles Catalan (1814 -1894) descubrió esa superficie periódica mínimal en el espacio tridimensional en 1855. Las ecuaciones paramétricas correspondientes son:
x = u•sen(u)cos(v)
y = 4sen(u/2)senh(v/2)
z = 1 - cos(u)cosh(v)
En este caso u toma valores en el intervalo [0, 3pi] y v en el intervalo [-2, 2].
180
Superficie de Henneberg
Superficie minimal no orientable llamada así en honor de Lebrecht Henneberg (1850 - 1933), matemático alemán. Las ecuaciones paramétricas usadas para representar esa superficie en la escena siguiente son:
x = 2u•senh(u)cos(v)-(2/3)senh(3u)cos(3v)
y = 2cosh(2u)cos(2v)
z = 2u•senh(u)sen(v) + (2/3)senh(3u)sen(3v)
Los intervalos u y v son [-π/2, π/2] para u y [-1, 1] para v.
181
Superficie de Scherk
Superficie minimal doblemente periódica , llamada así por Heinrich Ferdinand Scherk (1798-1885), matemático alemán que la estudió en 1834. Téngase en cuenta que la superficie de Scherk, en realidad, está formada por un sinfín de superficies como la que se muestra en la escena. Las ecuaciones paramétricas, con el intervalo de variación de u y v es [0, 3.1], son:
182
Superficie minimal de Verril
Por su curioso aspecto se muestra esta superficie minimal, descrita en la página de Paul Bourke y cuya matematización se atribuye a Roger Bagula. Sus ecuaciones paramétricas son:
x = 2u•cos(v) + 2cos(v)/u - 2u2cos(3v)/3
y = 6usen(v) - 2sen(v)/u - 2u3sen(3v)/3
z = 4ln(u)
Los intervalos de u y v son [0,5 , 1] para u y [0, 2π] para v.
183
3.21 Superficies retorcidas
En este apartado se muestran diferentes superficies cuyo aspecto recuerda a elementos que han sido deformados por la aplicación de fuerzas de torsión.
Esfera retorcida
Las ecuaciones paramétricas de esta curiosa superfcie son:
x = a•cos(v)cos(u)
y = a•sen(v)cos(u)
z = b•v + a•sen(u)
184
A continuación, presentamos otras superficies "retorcidas" con sus nombres, cuyas ecuaciones paramétricas puedes consultar en la red.
185
186
3.22 Conoides
El conoide es una superficie reglada alabeada con un plano director y dos directrices, una rectilínea y otra curva. Si la directriz curva es un círculo se tiene el conoide circular, si es una elipse tenemos el conoide elíptico, etcétera. Si la recta directriz es paralela al plano de la directriz curva y perpendicular al plano director la superficie engendrada se denomina conoide recto, en caso de que no lo sea se denomina oblicuo (Néstor Martín Gulias).
Conoide recto
Superficie reglada generada por una familia de líneas rectas que se intersectan perpendicularmente a una línea recta fija, llamada eje del conoide recto. Usando un sistema de coordenadas cartesiano en el espacio tridimensional, si tomamos el eje z como el eje de un conoide recto, entonces el conoide puede representarse mediante las ecuaciones paramétricas:
x = v•cos(u)
y = v•sen(u)
z = h(u)
donde h (u) es una función.
En la siguiente escena interactiva, hemos usado h(u)=h•sen(u), además, hemos puesto dos factores a y b a las ecuaciones para x e y respectivamente. Cambia estos valores para observar el comportamiento del conoide.
187
Borde cónico de Wallis
Es una superficie reglada dada por las siguientes ecuaciones paramétricas:
x = v•cos(u)
y = v•sen(u)
z = c2√a2 - b2cos2(u)
188
donde a, b y c son constantes. El borde cónico de Wallis19 es también una especie de conoide recto.
189
Conoide senoidal
Las superficies conoidales están presentes en la naturaleza (en las hojas y en las flores, por ejemplo). Quizá por la belleza de estas formas fue que el maestro Gaudí se inspiró para algunas de sus obras arquitectónicas usando, entre tantas superficies, la conoide senoidal o sinusoidal20.
190
Las ecuaciones paramétricas del conoide sinoidal son:
x = u•cos(v)
y = u•sen(v)
z=k•U•cos(n•v)
Realizando la siguiente variación: z = k•cos(n•v), obtenemos el Conoide de Plücker21:
191
Paraguas de Whitney
Este conoide recto se construye tomando un eje, por ejemplo el eje Z, de coordenadas, y considerando una parábola contenida en un plano paralelo al eje Z, pero que no pase por el origen. Entonces, la unión de las rectas que cortan perpendicularmente al eje y que intersecan a la parábola, es justamente un paraguas de Whitney. Las ecuaciones paramétricas son:
x = u•v
y = u
z = v2
Interactúa con el paraguas en la siguiente escena interactiva:
192
Paraguas de Cartan
Superficie estudiada por los matemáticos franceses Henri Cartan y Hassler Whitney en 1957. Las ecuaciones paramétricas son:
x = u•cos(v)
y = u•sen(v)
z = u•cos3(v)
Interactúa con el paraguas en la siguiente escena interactiva:
193
Berlingot (bolsita)
Esta superficie fue estudiada por Cundy y Rollett en 195122, a partir de las siguientes ecuaciones:
x = k•a(1 + u)cos(v)
y = k•a(1 - u)sen(v)
z = a•u
Se trata de una superficie cuártica, con dos líneas dobles. Dadas dos líneas rectas ortogonales no intersecantes (D1) y (D2), (H1H2) su perpendicular común, O la mitad de [H1H2] y (C) un círculo del centro O con el plano paralelo a (D1) y (D2), el berlingot es la superficie regulada no desarrollable generada por las líneas rectas que se encuentran (D1), (D2) y (C); Es por tanto una superficie conoidal (https://www.mathcurve.com)
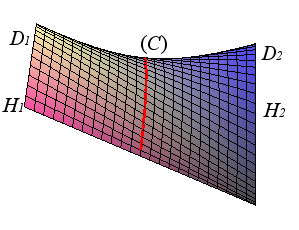
194
En la siguiente escena interactiva, puedes usar los controles así: i. los controles a y k amplían o reducen la superficie, ii) el control t permite generar la superficie completa (t > 0.5) y iii) el control desplaza permite desplazar verticalmente el berlingot.
195
3.23 Superficies relacionadas con el plano proyectivo real
Aunque la denominada geometría proyectiva tiene sus orígenes en la antigua Grecia y empieza a tomar cuerpo en los trabajos del arquitecto y matemático italiano del Renacimiento Leon Battista Alberti (fue el primero en escribir un tratado sistemático sobre arte en 1436, en el que describe por primera vez las leyes de la perspectiva desde un punto de vista científico), es en el siglo XVII con los trabajos de Desargues, que enuncia un teorema básico en dicha geometría, así como las aportaciones de Pascal, que se considera el inicio como disciplina matemática. Aunque una de sus épocas de oro es en el siglo XIX cuando toma un importante empuje con Gaspard Monge y Poncelet, al recuperarse los trabajos sobre geometría pura. En esta geometría es fundamental el concepto de plano proyectivo. El plano proyectivo viene a ser el plano afín usual más una recta llamada recta de infinito, que contiene los denominados puntos de infinito (el concepto de punto de infinito lo introduce Johannes Kepler en 1604, en sus trabajos sobre óptica, para dotar a la parábola de un segundo foco). Si pensamos en el concepto intuitivo que tenemos de rectas y puntos, un plano proyectivo se puede definir por un conjunto de cuatro axiomas de incidencia entre puntos y rectas:
- Dos puntos determinan una única recta
- En cada recta hay al menos tres puntos
- Existen tres puntos no alineados
- Dos rectas cualesquiera se cortan en un punto.
Si nos fijamos en el tercer axioma, lo que en nuestro plano afín habitual son rectas paralelas en el plano proyectivo son rectas que se "cortan" en un punto de infinito. Sin entrar a abordar cuestiones de topología, resulta que si se intenta realizar una "inmersión" del plano proyectivo en el espacio afín ordinario, necesariamente
196
se producen lo que se denominan autoinserciones y aparecen unos puntos especiales llamados puntos singulares.
Se puede encontrar información muy interesante en http://www.mat.ucm.es/, donde se recogen textos e imágenes de una exposición que tuvo lugar durante el mes de noviembre de 1999 en la Facultad de Matemáticas de la Universidad Complutense de Madrid (UCM), dedicada a la historia de la Geometría Proyectiva. Las superficies que se muestran en esta página son "inmersiones" en el espacio tridimensional real del plano proyectivo. Se muestran: la superficie romana de Steiner, la superficie "crosscap" o bonete cruzado y la superficie de Boy.
Superficie romana de Steiner
Jacob Steiner, matemático suizo, encontró una manera de hacer inmersiones del plano proyectivo en el espacio afín ordinario, y los modelos que obtuvo se denominan hoy superficies de Steiner. Una de ellas es la Superficie Romana, denominada así porqué Steiner descubrió algunas propiedades geométricas de la superficie que había construido en una visita a Roma que realizó en 1844. Las ecuaciones paramétricas usadas son:
x = (n2/2)sen(2u)•cos2(v)
y = (n2/2)sen(u)sen(2v)
z = (n2/2)cos(u)sen(2v)
En la siguiente escena interactiva rota la superficie para que observes las características gráficas de la romana de Steiner.
197
Supreficie "Crosscap" (Bonete cruzado)
Es otra de las superficies obtenidas por Steiner y, por tanto, otra inmersión del plano proyectivo en el espacio afín ordinario. En este caso las ecuaciones paramétricas correspondientes son:
198
x = R•sen(2u)cos(v)
y = R•sen(2u)sen(v)
z = R•cos(2u) + sen2(u)cos2(v)
donde u y v toman valores en el intervalo [0, π].
199
Superficie de Boy
Esta superficie es otra inmersión del plano proyectivo real en el espacio afín ordinario, estudiada por el matemático aleman Werner Boy en 1901. Se usa la parametrización de Morin-Apéry (1987) con una pequeña modificación que se verá observando las paramétricas usadas en la última escena de este apartado:
x = √2•cos2v•cos(2u) + cos(u)sen(2v)2 - √2•sen(3u)sen(2v)
y = √2•cos2v•sen(2u) - sen(u)sen(2v)2 - √2•sen(3u)sen(2v)
z = 3cos2(v)2 - √2•sen(3u)sen(2v)
donde u toma valores en el intervalo [0, π/2] y v toma valores en el intervalo [0, π].

Superficie Boy en el programa MathMod.
200
Superficie Boy en DescartesJS:
De superficie romana de Steiner a superficie Boy
Para acabar este apartado, mostramos visualmente como una superficie romana se convierte en una superficie de Boy y viceversa. Para ello basta con ir modificando los valores del parámetro que aparece en la escena (alfa) entre 0 y 1. La parametrización usada es la auténtica parametrización de Morin-Apéry para la superficie de Boy.
201
Viendo estas ecuaciones paramétricas se verá que, en la escena anterior, se ha asignado el valor 1 al parámetro alfa (y por eso no aparece en las ecuaciones mostradas antes).
x = √2•cos2v•cos(2u) + cos(u)sen(2v)2 - α√2•sen(3u)sen(2v)
y = √2•cos2v•sen(2u) - sen(u)sen(2v)2 - α√2•sen(3u)sen(2v)
z = 3cos2(v)2 - α√2•sen(3u)sen(2v)
202
3.24 Caracolas y cuernos
En matemáticas, una superficie de concha marina es una superficie formada por un círculo que gira en espiral hacia arriba del eje z mientras disminuye su propio radio y distancia desde el eje z. No todas las superficies de conchas describen las conchas reales que se encuentran en la naturaleza (https://en.wikipedia.org).
Caracola
Este primer modelo lo hemos obtenido con estas ecuaciones paramétricas:
x = a(1 - v/(2π))cos(n•v)(1 + cos(u)) + c•cos(n•v)
y = a(1 - v/(2π))sen(n•v)(1 + cos(u)) + c•sen(n•v)
z = b•v/(2•π) + a(1 - v/(2π))sen(u)
203
Los parámetros a, b, c y n, los puedes explorar interactuando con la superficie que presentamos a continuación:
Existen varios modelos de caracoles, conchas o cuernos, que han propuestos diferentes autores, entre ellos, David M. Raup y Chris Illert
Las conchas de caracol tienen una característica muy importante: giran logarítmicamente. Esta característica fue notada por los filósofos griegos y expuesta en profundidad en 1917 por D’Arcy Thompson en su libro seminal On Growth and Form. En un sentido muy burdo,
204
estos primeros tomos proporcionan los primeros pasos para representar realmente la totalidad de la forma de una concha con números. En la década de 1960, Raup ideó un modelo con cuatro parámetros que iban mucho más allá de un simple dibujo de líneas en un solo plano (Raup 1961, Raup 1962, Raup 1966) (http://www.deepseanews.com/).
Cuerno
Esta curiosa superficie se puede obtener con la ecuaciones:
x = (2 + u•cos(v))sen(2π•u)
y = (2 + ucos(v))cos(2π•u) + 2u
z = u•sen(v)
205
Otras caracolas
Como lo habíamos dicho antes, existen varios modelos, de los cuales presentamos dos. El primero corresponde a las siguientes ecuaciones paramétricas:
x = 1.2v(sen2(u)sen(v))
y = 1.2v(sen2(u)cos(v))
z = 1.2vsen(u)cos(u)
206
Una segunda caracola la obtenemos con estas ecuaciones:
x = 2(1 - eu/6π)cos(u)cos2(v/2)
y = = 2(1 - eu/6π)sen(u)cos2(v/2)
z = 1 - eu/3π - sen(v) + eu/6πsen(v)
207
3.25 Superficies curiosas
Para terminar este capítulo, dejamos una pequeña colección de superficies que, por su forma, te sorprendrán. Incluimos el nombre dado a la superficie que, en la mayoría de los casos, hace honor a la figura persentada, tanto que no habría necesidad de nombrarlas. También, incluimos las ecuaciones paramétricas que permitieron el desarrollo de estas superficies.
208
La manzana, inicialmente, es una superficie de revolución definida por Kepler, que consiste en más de la mitad de un arco circular girado alrededor de un eje que pasa a través de los puntos finales del arco. Para nuestra escena el arco no es circular sino elípitico, pruébalo haciendo t=0. Ahora observa la siguiente superificie curiosa.
Obviamente, ya habrás deducido que es sinusoidal... haz t=0 para comprobarlo.
Observa la siguiente curiosidad.
209
Algo sencillo que se puede lograr con la curva generatriz, pero veamos algo un poco más complejo.
Se trata de una superficie generada por una ecuación séxtica... he ahí la complejidad, pero en la fórmula no en la superficie obtenida.
210
Esta superficie fue lograda por Taubin (1993-1994). Nordstrand y Kuska, en 2004, crearon esa misma superfície con una ligera variación. Algunos autores la han llamado la "superficie del amor", por ello hemos usado el rojo ¡pasión!
Ahora, observa otra superficie curiosa... muy curiosa.
211
Esta vez no es tan fácil observar la correspondencia entre el nombre y la superficie, pero con una buena observación se comprenderá el nombre dado.
Otros nombres de superficies corresponden a formas poco conocidas como el Tornillo de Steinbach, que presentamos a continuación.
212
Esta superficie contiene una línea recta sobre la cual se desarrolla, puede estar relacionada con una clase de superficies con forma de espiral.
213
Se trata de na superficie mínimal encontrada por Roman Maeder, que presentamos a continuación.
En la página siguiente, presentamos dos superficies que no dan equívocos con el nombre asignado.
214
215
216
La estereoesfera
El nombre de esta curiosa superficie tiene un origen técnico;
Una estereosfera es la proyección de una cuadrícula plana sobre una esfera con las líneas de proyección atravesando el polo superior de la esfera. En la siguiente imagen hay una luz de fuente puntual en el polo norte de la estereosfera (la luz está representada por el punto amarillo). Esta luz luego hace una proyección estereográfica de la esfera de nuevo sobre el plano produciendo la cuadrícula presente en el plano de tierra (http://elfnor.com/).

Ignoramos si entendiste la explicación técnica, pero en la siguiente escena interactiva puedes observar lo curiosa y hermosa que es esta superficie.
217
219
Terminamos este capítulo con una bonita estrella de mar.
Obviamente, se nos escapan muchas más superficies curiosas, pero lo dejamos para que consultes nuestro listado final de referencias, es decir, lo dejamos a tu curiosidad.
220
221
Referencias
Estas son las referencias consultadas, según el orden de aparición en el libro:
Curvas paramétricas en el plano
- http://revistasuma.es/IMG/pdf/30/103-111.pdf
- https://jucarmarsa.blogia.com/2009/020201-la-cicloide.php
- http://proyectodescartes.org/miscelanea/materiales_didacticos/ruletas_cicloidales-JS/index.html
- https://es.wikipedia.org/wiki/Caracol_de_Pascal
- https://definicion.de/espiral/
- http://www.ite.educacion.es/formacion/enred/web_espiral/
- https://es.wikipedia.org/wiki/Espiral_de_Arquímedes
- https://es.wikipedia.org/wiki/Espiral_logarítmica
- http://mariac457.blogspot.com/2011/09/la-espiral-logaritmica.html
- http://www.euclides.dia.uned.es/simulab-pfp/Ejs33/Simulations/lissajous_es_Figuras_de_Lissajous.html
- https://es.wikipedia.org/wiki/Superf%C3%B3rmula
- https://en.wikipedia.org/wiki/Superellipse
- http://www.iesezequielgonzalez.com/matematicas/brujagne.htm
Curvas paramétricas en el espacio
- http://arquimedes.matem.unam.mx/PUEMAC/PUEMAC_2008/rincon/curvas/html/cuadciclo.html
- https://www.mathcurve.com/courbes3d/couronnesinusoidale/couronnesinusoidale.shtml
- https://www.mathcurve.com/courbes3d/solenoidtoric/solenoidtoric.shtml
222
- https://es.wikipedia.org/wiki/Solenoide
- https://www.mathcurve.com/courbes3d/solenoidtoric/solenoidtoric.shtml
- https://formaprogramada.wordpress.com/2014/01/05/conoide-de-plucker/
- http://unesdoc.unesco.org/images/0006/000640/064092so.pdf
- https://www.mathcurve.com/courbes3d/borromee/borromee.shtml
- https://es.wikipedia.org/wiki/Curva_de_Viviani
- https://www.mathcurve.com/courbes3d/viviani/viviani.shtml
- https://www.mathcurve.com/courbes3d.gb/rosaceconique/rosaceconique.shtml
- https://www.revolvy.com/page/Knot-theory
- https://culturacientifica.com/2017/12/27/del-nudo-gordiano-al-nudo-los-enamorados-territorio-matematico/
- http://katlas.math.toronto.edu/wiki/36_Torus_Knots
- https://es.wikipedia.org/wiki/Nudo_de_ocho
- https://culturacientifica.com/2017/12/13/la-artista-anni-albers-the-walking-dead-la-teoria-nudos/
- http://retovertical.blogspot.com/2011/10/el-ocho-doble-nudo-de-encordamiento.html
- https://es.wikipedia.org/wiki/Nudo_simple
- https://es.wikipedia.org/wiki/Nudo_simple
Superficies paramétricas
- https://matematicas.uniandes.edu.co/~jarteaga/coord-calvec/material/cap1-superficies.pdf
- https://es.wikipedia.org/wiki/Cicloide
- http://xtsunxet.usc.es/cordero/revolucion/revolucion.htm
- https://www.uam.es/personal_pdi/ciencias/barcelo/fcmatematicas/problemasfamosos.html
- https://www.mathcurve.com/courbes2d/gerono/gerono.shtml
223
- http://matecuriosos.blogspot.com/p/la-belleza-de-las-curvas.html
- http://paulbourke.net/geometry/teardrop/
- https://www.ecured.cu/Paraboloide_hiperbólico
- http://www.dim.uchile.cl/~simetria/matematico/nodo321.html
- http://wpd.ugr.es/~geometry/seminar/files/talks/20050208MRodr%C3%ADguez.pdf
- https://lorenzovinci.it/magazine/recipe/i-fusilli-ricette-come-farli-in-casa-sughi-e-abbinamenti/
- http://www.mathcurve.com/surfaces/helicoidcercle/helicoidcercle.shtml
- https://www.pspring.com/products/ext-tor-comp-springs/
- https://www.acxesspring.com/espanol/resortes-y-muelles.html
- http://www.ehu.eus/~mtwmastm/IngenieriaArquitectura.pdf
- https://es.wikipedia.org/wiki/Botella_de_Klein
- http://users.quipo.it/base5/analisi/superforma.htm
- https://www.revolvy.com/page/Cayley-surface?
- https://es.wikipedia.org/wiki/Cuerno_de_Gabriel
- http://superficies-regladas-alabeadas.blogspot.com/
- https://wikivisually.com/wiki/Wallis%27s_conical_edge
- http://textos.pucp.edu.pe/pdf/413.pdf
- https://www.mathcurve.com/surfaces/berlingot/berlingot.shtml
- https://ia801606.us.archive.org/28/items/MathematicalModels-/HMartynCundy_APRollett-mathematicalModels-oxfordClarendonPress1961.pdf
- http://www.mat.ucm.es/~jesusr/expogp/expogp.html#topplan
- https://en.wikipedia.org/wiki/Seashell_surface
- http://www.deepseanews.com/2015/07/digital-seashells-and-david-raup/
- http://elfnor.com/parametric-surfaces-in-blender.html





