Título
Livro Digital Interativo: Um exemplo em Trigonometria.

Eduardo Alejandro Flores Araya

Desenho do livro: Juan Guillermo Rivera Berrío
Livraria turn.js: Emmanuel García
Código JavaScript para o livro: Joel Espinosa Longi, IMATE, UNAM.

Desenho e construção dos Interativos: Eduardo Alejandro Flores Araya
Desenho da capa: Eduardo Alejandro Flores Araya

Ferramenta de edição: DescartesJS

Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org https://proyectodescartes.org

Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm

ISBN: 978-84-18834-13-4

  by-nc-sa/4.0/es       by-nc-sa/4.0/pt_BR

Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
Todos los objetos interactivos y los contenidos de esta obra colectiva están protegidos por la Ley de Propiedad Intelectual.

Este obra está licenciado com uma Licença Creative Commons Atribuição-NãoComercial-CompartilhaIgual 4.0 Internacional.

IV.- Círculo trigonométrico39

1. Arcos no círculo trigonométrico40

2. Relações trigonométricas no círculo43

3. Redução das relações trigonométrica ao primeiro quadrante46

V.- Identidades trigonométricas49

1. Identidades fundamentais50

2. Lei dos senos52

3. Lei dos cossenos54

4. Completar triângulos usando a lei dos senos e cossenos56

5. Razões trigonométricas de soma e diferença de ângulos58

6. Razões trigonométricas do arco duplo e arco metade60

VI.- Equações trigonométricas63

1. Identificar uma equação trigonométrica64

2. Resolvendo equações trigonométricas66

3. Identificar inequações trigonométricas68

4. Resolvendo inequações trigonométricas69

VII.- As funções trigonométricas71

1. Funções trigonométricas72

1.1. Função seno73

1.2. Função cosseno76

1.3. Senoides79

1.4. Função tangente84

1.5. Função cossecante88

1.6. Função secante91

1.7. Função cotangente94

iv

Para ver as instruções do livro,

clique no ícone

no canto superior direito

vi

Comentários

O mundo está passando por uma evolução digital na educação, a tecnologia passou a fazer parte do cotidiano do ser humano e o mesmo passou a aprender por meio da TDIC (Tecnologias Digitais de Informação e Comunicação). A informação evoluiu por meio da internet, no início era texto, passou a utilizar imagens, evoluiu com o som e hoje pessoas do mundo todo disponibilizam vídeos.
As novas gerações são consideradas nativas digitais. Em meio a este contexto, o ensino da matemática tem evoluído e passou a utilizar diversos recursos tecnológicos.
O professor Eduardo Alejandro Flores Araya mergulhou no processo de aprendizagem digital ao disponibilizar um livro totalmente interativo e lúdico. Este livro utiliza recursos de texto, imagem, som e vídeo para entregar ao estudante o melhor da trigonometria. Dividido em 9 capítulos, este livro fantástico aborda a teoria e a prática de forma digital. Aproveite ao máximo este conteúdo, bons estudos!

Renan Osório Rios, Professor do Ifes Campus Colatina.
Graduado em Sistemas de Informação, Doutor em Educação.

viii

Para ver as instruções do livro,

clique no ícone

no canto superior direito

x

1. Medição de Ângulos.

O estudo dos ângulos é fundamental para compreender conceitos ligados à geometria e à trigonometria, entre outros ramos da Ciência. O estudo dos ângulos é um dos responsáveis pelos avanços que possuímos atualmente em várias áreas, como a navegação e a astronomia. Um exemplo notável é o astrolábio náutico (inventado pelo grego Hiparco) usado para medir ângulos.
Nos séculos V e VI, os navegadores construíram esse instrumento para medir a elevação das estrelas e do sol com o intuito de localizar suas embarcações. Mais tarde, o astrolábio deu origem ao sextante, mais simplificado, mas que cumpria a mesma função. ²

Numa calculadora científica podemos ver que existem três “modos” de unidades de ângulos (Deg, Rad e Gra). ‘Deg’ representa os graus (Sistema Sexagesimal), ‘Rad’ representa os radianos (sistema Radial) e ‘Gra’ representa os Grados (Sistema Centesimal). Muitos de nós conhecemos bem os graus e suas divisões, alguns compreendemos e utilizamos os radianos, mas muito poucas pessoas conhecem os grados e seu uso. Neste Módulo estudaremos os três sistemas para compreendermos melhor de onde vêm e suas funcionalidades.

Antes de continuarmos precisamos definir o conceito de quadrante, veja a cena na página seguinte.

2

Coordenadas retangulares de um ponto.

4

2. Sistema Sexagesimal.

Um pouco de historia³ 
O grau é originário da Babilônia. Para estabelecerem o grau, os babilônios dividiram o círculo em 360 partes iguais, pois acreditavam que essa era a quantidade de dias referente ao período de um ano, e porque seu sistema de numeração era de base sessenta ou sexagesimal. Outra herança dos babilônios é a divisão das horas em minutos e os minutos em segundos.

6

3. Sistema Centesimal (Sistema Francês)

No Sistema Centesimal a unidade de medida é o grado (^g) também chamado gon.

Um gon (1^g) equivale a de uma circunferência, ou seja, 1^g corresponde a uma das 400 partes em que a circunferência foi dividida. A circunferência fica dividida em quatro quadrantes com 100^g cada um. Neste sistema o ângulo reto mede 100^g.

As equivalências com relação ao sistema Sexagesimal são:

... 0º = 0^g .. . . . . . . . . . . . . . . 45° = 50^g. . . . . . . . . . . . . 90° = 100^g

180° = 200^g . . . . . . . . . . . . .270° = 300^g . . . . . . . . . . .360° = 400^g

Um pouco de historia⁴ 
O termo grado tem origem no termo francês grade e foi proposto para uso em conjunto com o sistema métrico. Foram feitas tentativas para a introdução generalizada do grado como unidade de ângulo plano, mas a unidade foi adoptada apenas por alguns países e em áreas especializadas, como a topografia e a artilharia. A artilharia francesa usa o grado há décadas. Uma vantagem do grado como unidade é tornar o ângulo reto fácil de somar e subtrair na aritmética mental. Outra vantagem, decorre da definição original do metro, de 1889, que estabelecia que 1 metro é o comprimento equivalente a décima milionésima parte de um quarto do meridiano terrestre. Portanto, 1 grado, quando medido sobre um círculo máximo terrestre, equivale a aproximadamente 100 km sobre a superfície da Terra, pelo que 1 centigrado do arco terrestre equivale a 1 km

8

4. Sistema Radial.

No Sistema Radial a unidade é o radiano (rad, mas neste livro usaremos também ( ^r )). A ideia era utilizar o raio da circunferência como unidade de medição de ângulo, então um radiano ( 1^r ou 1 rad) corresponde a um ângulo formado por um arco de tamanho igual ao raio, determinado numa circunferência.
A circunferência, completa uma volta em 360°, como vimos anteriormente, e o arco da volta completa mede 2π radianos (se multiplicamos 2π pelo raio (r) obtêm-se o perímetro de dita circunferência 2π• r). Dessa forma podemos deduzir que a metade da circunferência mede π radianos. Geralmente as medidas de ângulos em radianos se escrevem como frações de π, por exemplo, 30° equivale a rad.

As equivalências dos ângulos notáveis entre o sistema Sexagesimal e o Radial são:

Um pouco de historia⁵ 
O termo radiano (radian) aparece impresso pela primeira vez no dia 5 de junho de 1873, em exames de James Thonson na faculdade de Queens, nos Estados Unidos. Em 1871, Thomas Muir da Universidade de Andrew, também nos Estados Unidos, já tinha hesitado entre rad, radial e radian (radiano). Em 1874, Muir adotou radian depois de uma consulta a Thonson. Os termos acima descritos provavelmente são inspirados pela palavra radius (raio). A proposta de radiano, como nos é apresentada hoje, é a de usar o raio como unidade de medida comum para o arco e meia corda.

10

12

6.Reduzir ângulos à Primeira Volta.

Já vimos que a circunferência completa corresponde a 360° ou 2rad. Quando temos ângulos maiores que 360° ou 2 rad, descontamos as voltas completas na circunferência e obtemos um ângulo entre 0 e 360° ou entre 0 e 2 π rad. Para isso dividimos o ângulo por 360 e o resto da divisão será o correspondente na primeira volta (menor determinação positiva do arco). Veja os exemplos na seguinte cena interativa.

Quando o arco está dado em fração de radianos, basta fazer o mesmo processo, só que com o denominador da fração, como mostra a seguinte cena.

14

1. Definições.

O triângulo retângulo tem um ângulo reto (90°), o lado oposto a ele se chama hipotenusa e os lados que formam o ângulo reto recebem o nome de catetos.

Na seguinte cena interativa podemos ver algumas definições.

(Cena do Proyecto Descartes, traduzida por nós)⁶.

18

3. Teorema de Pitágoras.

O teorema de Pitágoras é uma das relações métricas mais importantes no triângulo retângulo.

Um pouco de história⁷ 
O Teorema de Pitágoras é um dos teoremas mais conhecidos, importantes e utilizados na matemática. Ele é imprescindível na resolução de problemas da geometria analítica, geometria plana, geometria espacial e trigonometria. Pitágoras de Samos, (570 a.C. - 495 a.C.) foi um filósofo e matemático grego, que fundou a Escola Pitagórica. Também chamada de Sociedade Pitagórica, incluía estudos de Matemática, Astronomia e Música. Acredita-se que a primeira demonstração do teorema tenha sido feita pelos integrantes dessa escola, os chamados Pitagóricos, por isso o nome dado a esse teorema.

20

4. Aplicações do Teorema de Pitágoras.

Duas das aplicações do Teorema de Pitágoras são o cálculo da diagonal de um quadrado e da altura do triângulo equilátero. Estes resultados são muito utilizados, por isso é recomendável ter sempre presente e poder realizá-los com muita rapidez.

Na seguinte cena interativa temos os cálculos dos valores da diagonal do quadrado e a altura do triângulo equilátero.

22

1. Calcular as razões trigonométricas num triângulo retângulo

As relações trigonométricas são razões entre as medidas dos lados de um triângulo retângulo.

São elas: seno⁸, cosseno, tangente, secante, cossecante e cotangente.

Elas dependem somente da medida do ângulo α, e não do tamanho do triângulo.

26

2. Utilizar as razões trigonométricas para completar triângulos.

Completar um triângulo retângulo é determinar todos seus elementos principais, ou seja, calcular seus ângulos agudos e seus lados. Para obtermos todos esses elementos necessitamos de dois deles, sendo um deles, pelo menos, um dos seus lados, ou algum segmento ligado ao triângulo (lado, mediana, mediatriz, etc).

Agora pratiquemos um pouco.

28

4. Calcular todas as razões trigonométricas a partir de uma delas.

Na seguinte cena interativa temos exemplos e exercícios de como calcular o cosseno e a tangente, sabendo o valor do seno.

Na seguinte cena interativa temos exemplos e exercícios de como calcular o seno e a tangente, sabendo o valor do cosseno.

30

Calcular o cosseno e a tangente quando temos o seno em fração.

32

6. Expressões Trigonométricas e Simplificação.

'Expressão numérica': "Uma expressão numérica é uma sequência de números que aparecem associados por operações que devem ser efetuadas obedecendo-se a seguinte ordem:".⁹

1. Potenciações e radiciações (se houver);
2. Multiplicações e divisões (se houver).
3. Adições e subtrações.

Se procurarmos no Google por 'Expressões algébricas' Teremos como primeiro resultado a seguinte definição: "São expressões matemáticas que apresentam números, letras e operações. As expressões desse tipo são usadas com frequência em fórmulas e equações. As letras que aparecem em uma expressão algébrica são chamadas de variáveis e representam um valor desconhecido".¹⁰

Então, poderíamos dizer que uma Expressão Trigonométrica é uma expressão matemática que contém números, letras, operações e relações trigonométricas. Uma expressão pode ser uma equação, uma identidade ou representar um número.

34

7. Aplicações

36

1. Arcos no Círculo Trigonométrico.
Arcos.¹¹

40

Arcos simétricos¹²
São aqueles que possuem mesma abscissa ou mesma ordenada (do sistema de coordenadas), ou seja, são diametralmente opostos.
Assim, qualquer arco do círculo trigonométrico possui um simétrico nos outros quadrantes. Esses 4 arcos simétricos serão representados pelos vértices de um retângulo e, seus valores, são determinados a partir dos arcos de 0, 180°, 360° e seus arcos côngruos.

42

Cosseno.

44

3. Redução das relações Trigonométrica ao Primeiro Quadrante.

Quando estamos trabalhando com Trigonometria e nos deparamos com um ângulo que não se encontra no primeiro quadrante, sempre podemos reduzi-lo de forma a encontrar o ângulo correspondente a esse que esteja justamente no 1° quadrante. Isso é possível graças à simetria presente no ciclo trigonométrico. Mas precisamos nos atentar para o que ocorre com os sinais das funções trigonométricas em cada quadrante. Vejamos a seguir algumas formas de trabalhar a mudança de quadrante no ciclo trigonométrico.¹³

46

1. Identidades Fundamentais.

Identidade. Refere-se a uma igualdade que permanece sempre verdadeira, independente do valor das variáveis que estejam envolvidas.
A principal identidade trigonométrica diz.

Para todo x pertencente aos reais se verifica a relação
sen²(x) + cos² (x) = 1    de fato.

Na seguinte cena interativa temos a demonstração da identidade fundamental. Notemos que esta construção não se aplica para ângulos múltiplos de 90º, porque não há triângulo. Mas basta saber que se seno de um múltiplo de 90º é 1 então o cosseno é zero, ou vice-versa, portanto a relação se verifica.

50

2. Lei dos Senos.

52

3. Lei dos Cossenos.¹⁵

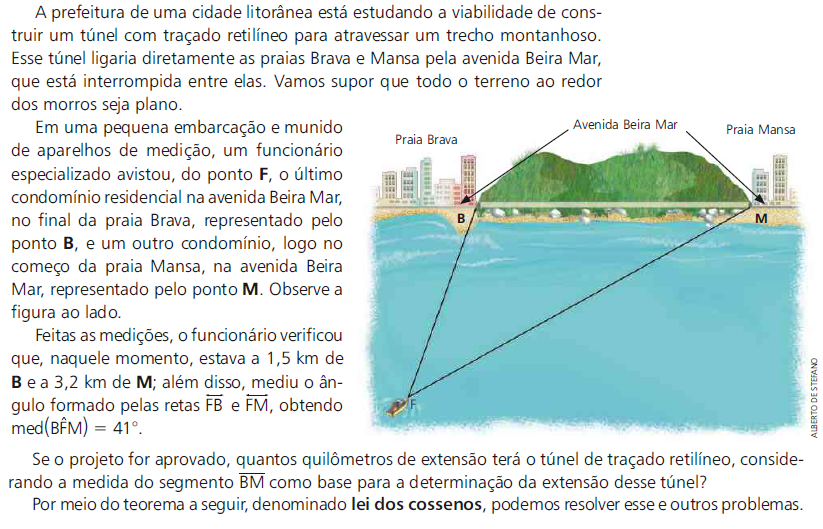
54

4. Completar triângulos usando lei dos senos e cossenos.

Aplicações de completar triângulos utilizando as leis dos senos e dos cossenos.

56

5. Razões Trigonométricas de Soma e Diferença de Ângulos.

58

6. Razões Trigonométricas do Arco Duplo e Arco Metade.

Desde a Antiguidade, vários matemáticos elaboraram tabelas de cordas. Essas tabelas forneciam o comprimento de cada corda de uma circunferência (em geral com raio 60) em função do ângulo central de 0º a 180º. No século II, Claudio Ptolomeu (90-168), astrônomo grego que viveu em Alexandria (Egito), publicou uma obra chamada Almagesto (que significa O grande tratado) sobre Astronomia. O primeiro dos 15 livros dessa obra é dedicado à natureza do Universo e à teoria trigonométrica; é por ele que sabemos o que se conhecia de trigonometria naquela época. O Almagesto foi escrito em grego, mas foi logo traduzido para várias línguas, sendo um dos textos científicos mais influentes de todos os tempos. Os hindus começaram a calcular as razões entre lados de um triângulo retângulo por volta do século VIII; utilizar essas razões mostrou-se mais eficiente do que consultar as tabelas de cordas.¹⁷

60

1. Identificar uma Equação Trigonométrica.

64

2. Resolvendo Equações Trigonométricas.

66

3. Identificar uma Inequação Trigonométrica.

Inequações trigonométricas são desigualdades que possuem pelo menos uma razão trigonométrica envolvendo um ângulo desconhecido. Dessa maneira, a solução de uma inequação trigonométrica é um conjunto de ângulos, geralmente apresentados na forma de arco, em radianos. Para encontrar essa solução, é necessário usar alguns conhecimentos básicos a respeito de ciclo trigonométrico, que serão discutidos a seguir.²⁰

68

1. Funções Trigonométricas no Círculo.

As funções trigonométricas são funções angulares, importantes no estudo dos triângulos e na modelagem de fenômenos periódicos. Podem ser definidas como razões entre dois lados de um triângulo retângulo em função de um ângulo, ou, de forma mais geral, como razões de coordenadas de pontos no círculo unitário. Na análise matemática, estas funções recebem definições ainda mais gerais, na forma de séries infinitas ou como soluções para certas equações diferenciais. Neste último caso, as funções trigonométricas estão definidas não só para ângulos reais como também para ângulos complexos.
Existem seis funções trigonométricas básicas em uso, cada uma com a sua abreviatura notacional padrão conforme tabela abaixo. As inversas destas funções são chamadas de função de arco ou funções trigonométricas inversas. A nomenclatura é feita através do prefixo "arco-", ou seja, arco seno, arco cosseno, etc. Matematicamente, são designadas por "arcfunção", isto é, arcsen, arccos, etc.; a notação usando-se −1 como na notação da função inversa não é recomendada, pois causa confusão com o inverso multiplicativo, como em sen^-1 e cos^-1. O resultado da função inversa é o ângulo que corresponde ao parâmetro da função. Por exemplo:¹⁷

72

A função seno é uma função ímpar, ou seja, ∀ x ∈ ℜ, sen(−x) = −sen(x).

Para fazermos o gráfico do seno utilizaremos a seguinte tabela.

74

1.2 Função Cossenos.

A função cosseno é uma função par, ou seja, ∀ x ∈ ℜ, cos(−x) = cos(x).

Para fazermos o gráfico do cosseno, utilizaremos a seguinte tabela.

76

78

Aqui termos uma cena interativa onde podemos ver e modificar todos os parâmetros na função seno.

80

Nesta cena interativa podemos ingressar a função desejada e visualizar o gráfico.

82

1.4 Função Tangente.

84

86

1.5 Função Cossecante.

88

90

92

1.7 Função Cotangente.

94

96

1. Definição.

100

2. Arco Seno²⁴.

102

3. Arco Cosseno²⁵.

104

4. Arco Tangente²⁶.

106

108

1. Introdução.

O objetivo deste capítulo é mostrar a versatilidade do programa (pois não é muito conhecido no Brasil) e que não é utilizado somente para o ensino da matemática, se não que em quase todas as áreas e níveis da educação. Para isso mostramos 4 aplicações que não são de trigonometria, algumas de estas aplicações não foram traduzidas completamente, pois acreditamos que não era necessário, para o objetivo que é somente mostrá-las.
Acreditamos que o uso de Projeto Descartes pode ser uma boa opção na educação à distância e na melhora da qualidade na utilização das TIC nos processos educativos.

Primeiramente colocamos uma das poucas aplicações da trigonometria em 3D que é a propagação das ondas eletromagnéticas e com deslocamento horizontal de 90º entre o campo magnético e e o campo elétrico.

Os outros três exemplos não foram criados por mim, foram tomados das aplicações já criadas em espanhol e que se encontram no portal dos administradores do projeto https://proyectodescartes.org/.

O primeiro desses três é uma aplicação de química, o modelo atômico de Rutherford.

O seguinte uma aplicação explicando a multiplicação de matrizes.

Por último, a divisão do cubo em três pirâmides.

112

3. Modelo Atômico de Rutherford.

Cena Interativa do Projeto Descartes²⁸. (Tradução nossa)

114

5. Divisão do cubo em três pirâmides.

Cena Interativa do Projeto Descartes³⁰.

116

• BEZERRA, Juliana. Pitágoras. TodaMatéria, 2019. Disponível em:
  < https://www.todamateria.com.br/pitagoras >. Acesso em 8 de julho, 2019.


• BIANCHINI, Edwaldo; PACCOLA, Herval. Matemática 1. São Paulo: Editora Moderna, [2010?]. 434 p.


• DIAS, Diogo Lopes. O que é modelo de Rutherford?; Brasil Escola. Disponível em: < https://brasilescola.uol.com.br/o-que-e/quimica/o-que-e-modelo-rutherford.htm >. Acesso em 23 de maio de 2020.


• DUARTE, Daniel. Ângulos; InfoEscola, [2016?]. Disponível em: < https://www.infoescola.com/matematica/angulos/ >. Acesso em: 17 janeiro, 2020.


• E–CÁLCULO, USP. . História da Trigonometria; [S.I][2009?]. Disponível em: < http://ecalculo.if.usp.br/historia/historia_trigonometria.htm >. Acesso em 16 janeiro, 2020.


• ENEMEX. Arcos simétricos. [S.I][2018?]. Disponível em:
  < http://enemex-matematica.com.br/estudos/geometria/trigonometria/aula-3-simetria >. Acesso em 3 de outubro, 2019.


• GALO, José R. Partición de un cubo en tres pirámides cuadradas iguales. Proyecto Descartes [2018?]. Disponível em: <
  https://proyectodescartes.org/miscelanea/materiales_didacticos/Cubo3PiramidesCuadradas-JS/index.html >. Acesso em 2 de junho, 2020.


• GARCÍA, María José Cebrian. Los números complejos.Universidad Pascual Bravo. Medellín, 2017. Disponível em: <
  https://proyectodescartes.org/descartescms/matematicas/icartisilibri/item/3173-los-numeros-complejos>. Acesso em 6 de junho, 2019.

118

• LIMA, Elon Lages. Teorema de Pitágoras. RPM-08. Rio de Janeiro 1986. Disponível em: <
  < http://www.rpm.org.br/cdrpm/8/3.htm >. Acesso em: 23 de novembro, 2019.


• PRADO, Julio. Trigonometria. Adaptación a DescartesJS: Juan G. Rivera B. e José R. Galo S. (2016). Tradução de Eduardo Alejandro F. Araya. Disponível em: <
  < https://proyectodescartes.org/descartescms/matematicas/item/2039-trigonometria >. Acesso em: 20 de novembro, 2019.


• QUINTANEIRO, W. ;GIRALDO, V. ; PINTO, M. De onde vem a unidade radiano e por que seu uso é necessário?. [2010?]. Disponível em: < https://www.academia.edu/1630196/DE_ONDE_VEM_A_UNIDADE_RADIANO_E_POR_QUE_ SEU_USO_É_NECESSÁRIO >. Acesso em: 22 de janeiro, 2020.


• RAMOS, Danielle de Miranda. Funções trigonométricas do arco duplo. Brasil Escola. Disponível em: < https://brasilescola.uol.com.br/matematica/funcoes-trigonometricas-arco-duplo.htm>. Acesso em: 6 de outubro, 2019.


• RECIO, Joaquín Miñarro. " Estructura del átomo y enlaces químicos. Proyecto Edad, 2017. Disponível em: < https://proyectodescartes.org/descartescms/fisica-y-quimica/item/2815-estructura-del-atomo-y-enlaces-quimicos>. Acesso em: 23 de maio de 2020.


• RIBEIRO, Amanda G. Redução ao primeiro quadrante no ciclo trigonométrico, Brasil Escola. Disponível em: < https://brasilescola.uol.com.br/matematica/reducao-ao-primeiro-quadrante-no-ciclo-trigonometrico.htm>. Acesso em: 5 de outubro, 2019.


• RIVERA, Juan G. B. ; ESPINOSA, Joel L. ; RADILLO, Alejandro D. Capacitación DescartesJS Nivel I, iCartesiLibri. Medellin, 2018. Disponível em: < https://proyectodescartes.org/descartescms/matematicas/icartisilibri/item/3316-descartes-js-nivel-i>. Acesso em: 1 de junho, 2019.

120