John Jairo García Mora
Sonia Jaquelliny Moreno Jiménez
Margarita Emilia Patiño Jaramillo
Grupo de investigación GNOMON
Córdoba (España)
2024
Título de la obra:
Modelos Matemáticos para el Aprendizaje Adaptativo: Un enfoque integral
Autores:
John Jairo García Mora
Sonia Jaquelliny Moreno Jiménez
Margarita Emilia Patiño Jaramillo
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Portada: Imagen de Moondance en Pixabay
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN: 978-84-18834-90-5

Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
Este libro surge de un proyecto para la adaptación de los contenidos básicos para estudiantes de ingeniería, dichos contenidos son herramientas que permiten a un estudiante desempeñarse con suficiencia en su entorno laboral.
Partimos del concepto de aprendizaje adaptativo que tiene sus raíces en la teoría del constructivismo y en la psicología cognitiva. El constructivismo sostiene que el aprendizaje es un proceso activo en el que los individuos construyen su conocimiento a través de la interacción con el entorno y la construcción de significados, el aprendizaje adaptativo hace referencia a la utilización de tecnologías y metodologías para personalizar el proceso de aprendizaje según las necesidades y preferencias individuales de los estudiantes.
El término "aprendizaje adaptativo" comenzó a utilizarse más ampliamente en el campo de la tecnología educativa a partir de la década de 1970. Durante este tiempo, con el surgimiento de las computadoras personales y las tecnologías digitales, se exploraron nuevas posibilidades para personalizar y adaptar el proceso de aprendizaje utilizando tecnología.
Uno de los hitos importantes en el desarrollo del aprendizaje adaptativo fue el trabajo pionero de Benjamín Bloom en la década de 1980 quién propuso un enfoque denominado "mastery learning" (aprendizaje basado en la maestría) que se centraba en permitir que los estudiantes avanzaran a su propio ritmo y dominaran un tema antes de pasar al siguiente.
Esta idea de Bloom sentó las bases para la adaptación individualizada en el proceso de aprendizaje.
Con el tiempo, el desarrollo de algoritmos y tecnologías de inteligencia artificial ha permitido avanzar aún más en el aprendizaje adaptativo. Los algoritmos pueden analizar datos y patrones de comportamiento del estudiante para personalizar la experiencia de aprendizaje, ofreciendo recomendaciones y recursos adaptados a las necesidades y preferencias individuales.
El concepto de aprendizaje adaptativo se originó en la convergencia de ideas provenientes del constructivismo, la psicología cognitiva y el avance de la tecnología educativa en la segunda mitad del siglo XX.
Esta metodología, tiene su origen hacia los años 50, asociada a la teoría de Skinner, cuando hizo referencia al aprendizaje programado, quien diseñó la máquina que pretendía que el estudiante aprendiera nuevos conceptos y los interiorizara efectivamente, en lugar de potencializar la memorización, así que, orientaba entonces el aprendizaje reforzando los nuevos conceptos respondiendo preguntas, y si, al responder la pregunta el estudiante lo hacía de manera correcta se le daba “una retroalimentación o refuerzo positivo” tal como lo relacionan Ricardo (2020)
El libro consta de cinco capítulos: en el primero de ellos hacemos referencia a la epistemología del concepto de aprendizaje adaptativo, los estilos que lo caracterizan y los tipos de este tipo de aprendizaje y sus tendencias.
Un segundo capítulo trata los modelos matemáticos como enfoque del aprendizaje adaptativo, no como herramienta para diseñar estrategias para el aprendizaje adaptativo de los estudiantes. Además, se describen diferentes tipos de aprendiz.
El tercer capítulo trata de los modelos matemáticos como estrategia del aprendizaje adaptativo en el aula a partir de la abstracción y la representación formal y su origen filosófico de la ciencia, como procesar las interpretaciones del conocimiento para ser adaptado y como inferir el conocimiento a partir de hechos establecidos.
El penúltimo capítulo describe cuatro modelos matemáticos necesarios para adaptación básica de conceptos en ingeniería: el modelo de optimización, el modelo fundamentado en ecuaciones diferenciales de primer orden, el modelo de análisis vectorial y cálculo de varias variables y el modelo que trata la matematización de la incertidumbre.
El capítulo cinco trata sobre la integración de contenidos del tipo STEM + H en el aula, sus fundamentos, la identificación de las habilidades y competencias necesarias que deben desarrollar los estudiantes de ingeniería.
Lo descrito hasta este momento será ilustrado mediante escenas interactivas propias de los autores o ajustadas del subproyecto Plantillas del Proyecto Descartes, con videos interactivos propios o con licencias Creative Commons y por último, el lector encontrará las referencias bibliográficas y los créditos a los autores de las imágenes utilizados a lo largo del libro.
El concepto de aprendizaje adaptativo tiene sus raíces en la teoría del constructivismo y en la psicología cognitiva. En el constructivismo, según lo describen Zambrano et al
Uno de los hitos importantes en el desarrollo del aprendizaje adaptativo fue el trabajo pionero de Benjamín Bloom en la década de 1980. Bloom propuso un enfoque denominado "mastery learning" (aprendizaje basado en la maestría) que se centraba en permitir que los estudiantes avanzaran a su propio ritmo y dominaran un tema antes de pasar al siguiente. Esta idea sentó las bases para la adaptación individualizada en el proceso de aprendizaje.
Con el tiempo, el desarrollo de algoritmos y tecnologías de inteligencia artificial ha permitido avanzar aún más en el aprendizaje adaptativo. Los algoritmos pueden analizar datos y patrones de comportamiento del estudiante para personalizar la experiencia de aprendizaje, ofreciendo recomendaciones y recursos adaptados a las necesidades y preferencias individuales.
Según lo anterior podemos expresar que el concepto de aprendizaje adaptativo se originó en la convergencia de ideas provenientes del constructivismo, la psicología cognitiva y el avance de la tecnología educativa en la segunda mitad del siglo XX.
El título del libro incluye una disyunción reflejada en dos enfoques ligeramente diferentes en la implementación del aprendizaje adaptativo, la principal diferencia radica en la amplitud y el papel de los modelos matemáticos en el proceso de aprendizaje adaptativo. En el primer caso, los modelos son la base sobre la cual se construye y opera todo el sistema adaptativo, mientras que, en el segundo caso, los modelos son herramientas utilizadas para mejorar el aprendizaje adaptativo.
Desarrollar las habilidades cognitivas a la vez que se adquiere conocimiento es un enfoque efectivo para promover un aprendizaje más profundo y duradero y el aprendizaje adaptativo es un excelente marco para aplicar algunas de las siguientes estrategias para lograrlo:
En lugar de simplemente memorizar información, aplicar el conocimiento hace referencia a fomentar la ejecución dinámica del conocimiento en situaciones prácticas como lo expresa Inzunza-Mejía
Se refiere a la aplicación práctica de conocimientos teóricos y habilidades adquiridas para abordar situaciones complejas en la vida personal, profesional o académica.
Promueve la capacidad de los estudiantes para analizar, evaluar y cuestionar la información. En el aprendizaje adaptativo el estudiante debe adquirir la capacidad para examinar los procesos de aprendizaje desde diferentes perspectivas, encuentra evidencia relevante y que generen conclusiones basadas en el razonamiento lógico..
Es una actividad que le proporciona a los estudiantes problemas auténticos y desafiantes.
Esos problemas deben ser auténticos y desafiantes, que requieran el uso de habilidades cognitivas, como el pensamiento analítico, la creatividad y la toma de decisiones.
Expresado en otras palabras es animar a los estudiantes a explorar diferentes enfoques, probar soluciones alternativas y reflexionar sobre sus estrategias.
Ayuda a los estudiantes a reflexionar sobre su propio proceso de pensamiento y aprendizaje. Este proceso metacognitivo le exige al estudiante que se autoevalúe, que identifique fortalezas y áreas de mejora, el establecimiento de metas y la utilización de estrategias de autorregulación como mencionan Jiménez et al
El aprendizaje en grupo y la colaboración permiten a los estudiantes compartir ideas, discutir conceptos y resolver problemas juntos. Esto fomenta habilidades cognitivas como la comunicación efectiva, el pensamiento crítico y la resolución de conflictos.
Esa integración ocurre cuando se utilizan herramientas y recursos tecnológicos que tiene como fin el fomentar el pensamiento crítico y la resolución de problemas.
Esas herramientas normalmente incluyen simulaciones interactivas, entornos de aprendizaje en línea y herramientas de visualización de datos.
La retroalimentación regular y específica sobre el rendimiento de los estudiantes, destaca en el proceso de aprendizaje adaptativo tanto el conocimiento adquirido como las habilidades cognitivas demostradas, les ayuda a los estudiantes a comprender cómo pueden mejorar su pensamiento y aprendizaje.
Es necesario tener presente que el desarrollo de habilidades cognitivas requiere tiempo, práctica y oportunidades continuas para aplicar el conocimiento en contextos relevantes. Al combinar el enfoque en el conocimiento con el desarrollo de habilidades cognitivas, se prepara a los estudiantes para un aprendizaje más completo y transferible.
Existen varios enfoques y estilos de aprendizaje adaptativo que se utilizan en la educación, aunque antes de hablar de ellos es necesario hacer hincapié en que existen dos tipos: el aprendizaje adaptivo involuntario y el aprendizaje adaptativo voluntario.
El primero de ellos se da a través de la experiencia en la vida, mientras que el aprendizaje adaptativo voluntario se da mediante el proceso de enseñanza-aprendizaje realizado por medio de la educación, ellos surgen algunos estilos de aprendizaje adaptativo:
Este enfoque utiliza reglas predefinidas para adaptar el contenido y las actividades de aprendizaje según el rendimiento del estudiante. Las reglas en palabras de Quintanar-Casillas y Hernández-López
Este enfoque del aprendizaje adaptativo permite ajustar el contenido y la presentación del material de aprendizaje de acuerdo con las características y el progreso de cada estudiante de manera individualizada.
Utiliza una evaluación constante para recopilar datos sobre el desempeño del estudiante y ajustar las reglas de adaptación en tiempo real.
Proporciona retroalimentación instantánea a los estudiantes, lo que les permite corregir errores y mejorar su aprendizaje de manera oportuna.
Permite a los estudiantes avanzar a su propio ritmo, brindando oportunidades para la revisión y el repaso de conceptos, así como para el avance a nuevos materiales.
Realiza un seguimiento detallado del progreso de cada estudiante, lo que permite identificar áreas de fortaleza y debilidad, y ofrecer intervenciones específicas según sea necesario.
Al adaptarse a las necesidades individuales de cada estudiante, este enfoque mejora la efectividad del aprendizaje al proporcionar contenido relevante y desafíos adecuados.
Al personalizar la experiencia de aprendizaje, se fomenta una mayor retención y comprensión de los conceptos, ya que los estudiantes pueden trabajar en áreas que les resultan más difíciles.
Al permitir a los estudiantes avanzar a su propio ritmo y ofrecer retroalimentación inmediata, se fomenta la motivación intrínseca y el compromiso con el aprendizaje.
Este enfoque ayuda a cerrar la brecha de conocimiento entre los estudiantes, ya que se adaptará a las necesidades individuales de aquellos que requieren apoyo adicional.
Al permitir a los estudiantes avanzar más rápidamente en los conceptos que ya dominan, se optimiza el tiempo de aprendizaje al enfocarse en áreas que requieren más atención.
Veamos un ejemplo de este enfoque en las ciencias básicas, más concretamente en el aprendizaje de las matemáticas, mediante un diseño se presenta una serie de problemas de matemáticos y, con base en las respuestas del estudiante, se adapta la dificultad y el tipo de problemas que se te presentarán a continuación. El programa tiene reglas predefinidas para adaptarse al rendimiento del estudiante, veamos algunas de ellas:
Basándose en estas reglas, el programa evalúa las respuestas a los problemas y determina el nivel de dificultad adecuado para el siguiente conjunto de problemas.
Si el estudiante demuestra un alto rendimiento, el programa deberá presentar problemas más desafiantes para mantener tu interés y promover un aprendizaje más profundo.
Si por el contrario se presentan dificultades, el programa adaptará el contenido para proporcionar ejercicios más básicos que ayuden a reforzar los conceptos necesarios.
El aprendizaje basado en reglas es solo uno de los enfoques utilizados en el aprendizaje adaptativo. Proporciona una manera sistemática de adaptar el contenido y las actividades en función de los resultados del estudiante, asegurando que se le brinde un nivel apropiado de desafío y apoyo para su aprendizaje.
Este estilo de aprendizaje adaptativo se basa en la evaluación continua del conocimiento del estudiante, utiliza tecnologías, algoritmos y modelos para analizar y comprender el nivel de dominio que el estudiante tiene sobre un determinado tema y, en base a eso, personaliza el contenido y las actividades de aprendizaje.
El aprendizaje adaptativo con enfoque fundamentado en el conocimiento personaliza la experiencia de aprendizaje de cada estudiante, teniendo en cuenta su nivel de conocimiento, habilidades, necesidades y preferencias individuales. En otras palabras hacemos referencia a la diversidad del aprendizaje. Este enfoque reconoce que los estudiantes son únicos y que pueden tener diferentes estilos de aprendizaje, capacidades cognitivas, antecedentes culturales y circunstancias personales y se caracteriza por:
El aprendizaje adaptativo con enfoque fundamentado en el conocimiento adapta el contenido, la secuencia y la metodología de enseñanza de acuerdo con las necesidades individuales de cada estudiante. Esto permite que los estudiantes avancen a su propio ritmo y se centren en las áreas que requieren más atención.
Los sistemas de aprendizaje adaptativo proporcionan retroalimentación inmediata a los estudiantes sobre su progreso y desempeño, esto les permite identificar rápidamente sus fortalezas y debilidades, y ajustar su enfoque de estudio en consecuencia.
Los sistemas de aprendizaje adaptativo suelen estar disponibles en línea, lo que brinda a los estudiantes la flexibilidad de acceder a los materiales de aprendizaje en cualquier momento y lugar. Esto facilita el aprendizaje a distancia y el acceso a la educación para personas con limitaciones geográficas o físicas.
El enfoque fundamentado en el conocimiento utiliza modelos y algoritmos sofisticados para comprender el nivel de conocimiento de cada estudiante y adaptar el contenido de acuerdo con sus necesidades específicas. Esto permite una educación verdaderamente individualizada, donde cada estudiante recibe la atención y los recursos que se ajustan a su nivel de habilidad y estilo de aprendizaje.
Al adaptar el contenido y las actividades de aprendizaje según el nivel de conocimiento de cada estudiante, el aprendizaje adaptativo con enfoque fundamentado en el conocimiento puede ayudar a optimizar el tiempo dedicado al estudio. Los estudiantes pueden enfocarse en áreas que necesitan mejorar, lo que les permite avanzar más rápidamente en su aprendizaje.
Además de beneficiar a los estudiantes, el aprendizaje adaptativo proporciona a los educadores información detallada sobre el progreso de cada estudiante. Esto les permite identificar patrones, evaluar el rendimiento individual y realizar ajustes en la enseñanza para satisfacer mejor las necesidades de los estudiantes.
El aprendizaje adaptativo con enfoque fundamentado en el conocimiento tiene varios beneficios cognitivos para los estudiantes que contribuyen a un proceso de aprendizaje más efectivo y significativo para los estudiantes:
La personalización del aprendizaje adaptativo permite que los estudiantes se involucren de manera más activa en su propio proceso de aprendizaje. Al tener la capacidad de avanzar a su propio ritmo y abordar áreas de interés o desafío personal, los estudiantes se sienten más motivados y comprometidos con su aprendizaje.
Al adaptar el contenido y las actividades de aprendizaje según el nivel de conocimiento y las necesidades individuales de cada estudiante, el enfoque fundamentado en el conocimiento promueve un aprendizaje más significativo. Los estudiantes pueden construir sobre sus conocimientos previos y establecer conexiones más sólidas entre los conceptos nuevos y existentes.
Al recibir retroalimentación inmediata y adaptada a su nivel de conocimiento, los estudiantes pueden abordar rápidamente las áreas en las que tienen dificultades y reforzar su comprensión. Esto contribuye a una mayor retención de conocimientos a largo plazo, ya que se les brinda la oportunidad de practicar y aplicar repetidamente los conceptos que aún no dominan.
El enfoque adaptativo fomenta la reflexión y la autorreflexión en los estudiantes. Al monitorear su propio progreso, identificar sus fortalezas y debilidades, y tomar decisiones sobre su propio aprendizaje, los estudiantes desarrollan habilidades metacognitivas.
Estas habilidades les permiten ser más conscientes de su proceso de aprendizaje, regular su propio aprendizaje y planificar estratégicamente su estudio. Promover el desarrollo de estas habilidades es enseñar a los estudiantes a reflexionar sobre sus procesos de aprendizaje, establecer metas claras, utilizar estrategias de estudio efectivas y ajustar su enfoque según las circunstancias.
Al enfrentar desafíos adaptados a su nivel de conocimiento, los estudiantes tienen la oportunidad de desarrollar habilidades de resolución de problemas y pensamiento crítico.
A medida que los estudiantes avanzan en su aprendizaje y se enfrentan a tareas más complejas, se les anima a analizar, sintetizar y evaluar información de manera más profunda y creativa.
En el contexto de las matemáticas básicas, el aprendizaje adaptativo basado en el conocimiento se puede aplicar para personalizar la enseñanza y el contenido en función del nivel de competencia matemática del estudiante. Veamos un ejemplo para ilustrar cómo funcionaría:
Tomando como punto de partida un programa de aprendizaje adaptativo de matemáticas básicas. Al comenzar, se le presenta al estudiante una serie de problemas o preguntas para evaluar su conocimiento en áreas como aritmética, geometría o fracciones.
Según las respuestas a estas preguntas, el programa evalúa su nivel de competencia en cada área y adapta el contenido en consecuencia.
Por ejemplo, si las respuestas indican que ya se tiene un buen dominio de las operaciones básicas de suma y resta, el programa puede omitir las lecciones introductorias sobre estos conceptos y pasar directamente a problemas más desafiantes que involucren multiplicación o división.
En caso de que las respuestas muestren dificultades en ciertos temas, el programa adaptaría el contenido para proporcionar explicaciones y ejercicios adicionales en esas áreas específicas. Por ejemplo, si se tienen dificultades con fracciones, el programa podría ofrecer ejercicios de práctica y recursos interactivos diseñados para ayudar a comprender mejor este concepto.
A medida que se progresa y se demuestra un mayor dominio en un área determinada, el programa ajustará el nivel de dificultad y profundidad del contenido.
Por ejemplo, si se muestra un dominio sólido en geometría básica, el programa puede comenzar a presentar problemas más complejos que involucren áreas y volúmenes.
A manera de conclusión, el aprendizaje adaptativo basado en el conocimiento en matemáticas básicas se centra en evaluar y adaptar el contenido en función del nivel de competencia matemática del estudiante.
Al personalizar las lecciones y los ejercicios de acuerdo con el conocimiento previo del estudiante, se busca proporcionar un aprendizaje más efectivo y eficiente, enfocándose en las áreas donde se requiere mayor apoyo y desafiando al estudiante en áreas en las que ya muestra dominio.
Este estilo de aprendizaje adaptativo tiene en cuenta el contexto del estudiante, como su ubicación geográfica, el dispositivo que está utilizando o el momento en que está accediendo al material de aprendizaje.
Es un estilo de aprendizaje que adapta el contenido y la presentación para que se ajusten mejor al contexto del estudiante, el objetivo es proporcionar una experiencia de aprendizaje más relevante y efectiva al considerar las circunstancias específicas del estudiante.
Este es un enfoque educativo del aprendizaje adaptativo que considera el contexto en el que ocurre el aprendizaje, teniendo en cuenta factores como los mencionados por Torres et al :
El enfoque fundamentado en el contexto reconoce la influencia del entorno y las experiencias de los estudiantes en su proceso de aprendizaje. Se tienen en cuenta elementos como la cultura, el lenguaje, las características socioeconómicas y las experiencias previas para adaptar la enseñanza de manera relevante.
El enfoque se centra en hacer que el aprendizaje sea relevante y aplicable al contexto de los estudiantes. Se busca establecer conexiones significativas entre los contenidos de aprendizaje y las situaciones de la vida real, lo que facilita la comprensión y retención del conocimiento.
Se fomenta el aprendizaje situado, donde los estudiantes están inmersos en situaciones reales o simuladas que reflejan el contexto en el que se aplicará el conocimiento. Esto promueve una comprensión más profunda y facilita la transferencia de conocimiento a situaciones del mundo real.
Este aprendizaje también conocido como aprendizaje contextualizado o aprendizaje basado en situaciones, es una teoría pedagógica que sostiene que el aprendizaje es más efectivo cuando se coloca en un contexto relevante y significativo. se enfoca en la idea de que el conocimiento y las habilidades se adquieren y comprenden mejor cuando se aplican y se enseñan en situaciones o entornos que se asemejan a los lugares donde serán utilizados o cuando tienen una aplicación práctica clara en la vida cotidiana.
Con respecto a los beneficios cognitivos que adquieren los estudiantes cuando su trabajo de aprendizaje está soportado en el contexto en el cual se desenvuelve tenemos:
Al hacer que el aprendizaje sea relevante y aplicable al contexto de los estudiantes, se promueve una mayor motivación y compromiso. Los estudiantes perciben que el aprendizaje tiene sentido y valor en su vida diaria, lo que fomenta una actitud más positiva hacia el aprendizaje.
Al conectar los contenidos de aprendizaje con el contexto de los estudiantes, se facilita una comprensión más profunda. Los estudiantes pueden relacionar nuevos conceptos con situaciones familiares, lo que les permite construir conexiones significativas y una comprensión más sólida.
El aprendizaje adaptativo con enfoque fundamentado en el contexto facilita la transferencia de conocimiento a situaciones del mundo real.
Al estar expuestos a situaciones auténticas o contextualizadas, los estudiantes pueden aplicar y transferir su conocimiento a problemas y desafíos del mundo real.
Al abordar el aprendizaje desde una perspectiva contextual, se enfatiza el desarrollo de habilidades prácticas relevantes para la vida y el trabajo. Los estudiantes adquieren habilidades que pueden aplicar directamente en su entorno, lo que aumenta su capacidad para resolver problemas y enfrentar desafíos del mundo real.
Al considerar el contexto cultural y las experiencias individuales de los estudiantes, se fomenta la conciencia cultural y la apreciación de la diversidad. Los estudiantes tienen la oportunidad de explorar y comprender diferentes perspectivas, lo que promueve la empatía y el respeto por las diferencias.
Supongamos que está utilizando una plataforma de aprendizaje adaptativo de idiomas en línea. El sistema tiene en cuenta tu ubicación geográfica para adaptar la experiencia de aprendizaje. Si el estudiante se encuentra en un país de habla inglesa, el programa podría ofrecerle actividades y ejercicios de práctica que se centren en situaciones cotidianas y vocabulario relevante para esa cultura y contexto específico.
Además del contexto geográfico, el aprendizaje adaptativo basado en el contexto también considera el dispositivo utilizado. Por ejemplo, si estás accediendo a la plataforma desde un teléfono móvil, el programa puede presentar el contenido de manera más compacta y adaptada a la pantalla más pequeña, con ejercicios interactivos que se pueden completar fácilmente en dispositivos móviles.
Otro aspecto del contexto es el entorno físico. Si la plataforma detecta que el estudiante se encuentra en un lugar ruidoso, el programa puede proporcionar actividades que se centren más en la comprensión oral y la práctica auditiva, utilizando auriculares para facilitar la concentración y minimizar las distracciones.
Además, el momento en el que el estudiante accede al material de aprendizaje también se considera en el aprendizaje adaptativo basado en el contexto. Por ejemplo, si se accede por la noche, el programa puede ofrecer actividades de revisión o práctica más relajadas y enfocadas en la consolidación del conocimiento, mientras que, si se accede por la mañana, puede proporcionar desafíos más estimulantes para activar la mente y promover la atención y el enfoque.
Podemos expresar entonces que el aprendizaje adaptativo basado en el contexto utiliza información sobre la ubicación geográfica, el dispositivo utilizado, el entorno físico y el momento de acceso al material de aprendizaje para personalizar la experiencia de aprendizaje.
Cuando se consideran los anteriores factores contextuales, se busca proporcionar una experiencia de aprendizaje más relevante y efectiva, teniendo en cuenta las circunstancias específicas del estudiante como las detallan González et al
Este enfoque se centra en las preferencias individuales del estudiante, como su estilo de aprendizaje preferido, sus intereses y sus objetivos de aprendizaje. Utiliza esta información para adaptar el contenido y los recursos de aprendizaje para que sean más relevantes, atractivo y efectivos para el para el estudiante.
El aprendizaje adaptativo con este enfoque se basa en tener en cuenta las preferencias individuales de los estudiantes, como su estilo de aprendizaje, intereses, ritmo de aprendizaje y modalidades de presentación preferidas.
En el marco de este enfoque existe una adaptación del contenido de aprendizaje y la metodología de enseñanza para satisfacer las preferencias individuales de los estudiantes. Esto implica ofrecer diferentes formas de presentar la información, actividades interactivas, opciones de exploración y elección de temas relacionados con los intereses de los estudiantes.
Este enfoque se caracteriza por brindar opciones y flexibilidad a los estudiantes. Se les permite elegir el orden de estudio, las actividades que prefieren realizar y las formas en que desean interactuar con el contenido de aprendizaje.
El aprendizaje adaptativo con enfoque fundamentado en las preferencias ofrece beneficios cognitivos como mayor motivación y compromiso.
Además de motivación y compromiso brinda otros beneficios que contribuyen a un proceso de aprendizaje más efectivo y satisfactorio para los estudiantes, veamos:
Al tener en cuenta el estilo de aprendizaje preferido de los estudiantes, se optimiza la forma en que reciben y procesan la información, esto puede conducir a una mejor retención y comprensión, ya que los estudiantes están más receptivos a la información presentada en la forma en que les resulta más efectiva.
Al brindar opciones y flexibilidad, el enfoque fomenta el aprendizaje autodirigido. Los estudiantes tienen la oportunidad de tomar decisiones sobre su propio proceso de aprendizaje, lo que promueve habilidades de toma de decisiones y autorregulación.
Al tener la capacidad de elegir y adaptar su experiencia de aprendizaje, los estudiantes desarrollan habilidades metacognitivas. Aprenden a evaluar sus preferencias, identificar lo que funciona mejor para ellos y tomar decisiones informadas sobre su propio proceso de aprendizaje.
Al adaptar el contenido y la metodología a las preferencias individuales, se brinda a los estudiantes la oportunidad de aprender de acuerdo con su propio estilo y ritmo.
Lo anterior implica que se puede conducir a una mejor adaptación a los estilos de aprendizaje individuales y a una mayor eficacia en el proceso de aprendizaje.
Si utilizamos una aplicación de aprendizaje adaptativo de matemáticas básicas que se basa en tus preferencias de aprendizaje, se inicia con la presentación de algunas opciones o preguntas sobre cómo le gustaría a un estudiante abordar las lecciones y actividades.
Estas opciones deben permitir una selección de preferencias como:
El estudiante, a medida que continúa utilizando la aplicación, el programa también puede adaptarse a las preferencias en función de sus interacciones y respuestas. Si el usuario demuestra un mayor compromiso y rendimiento en ciertos tipos de actividades o formatos de contenido, el programa puede ajustarse para ofrecer más oportunidades en esas áreas específicas.
Este enfoque utiliza modelos matemáticos y algoritmos para adaptar el proceso o experiencia de aprendizaje. Dichos modelos se construyen a partir de datos recopilados sobre el estudiante, como respuestas a preguntas y actividades, y se utilizan para predecir y adaptar las experiencias de aprendizaje futuras.
En el marco de este enfoque se utilizan modelos matemáticos y algoritmos para adaptar el proceso o experiencia de aprendizaje. Esos modelos se construyen a partir de datos recopilados sobre el estudiante, como respuestas a preguntas y actividades, y se utilizan como lo postula Gaviria
Este enfoque se fundamenta en modelos cognitivos que representan el conocimiento y las habilidades de los estudiantes.
Los modelos cognitivos se emplean para adaptar la experiencia de aprendizaje a cada estudiante de manera individualizada. Esto implica ajustar el nivel de dificultad, la secuencia de los contenidos y las estrategias de enseñanza para satisfacer las necesidades específicas de cada estudiante.
Los modelos cognitivos en el marco de este enfoque permiten proporcionar retroalimentación continua y personalizada a los estudiantes. Esa retroalimentación personalizada implica identificar errores y áreas problemáticas específicas, ofrecer sugerencias y recomendaciones, y guiar a los estudiantes en su proceso de aprendizaje.
Los modelos que se utilizan para el aprendizaje adaptativo ofrecen beneficios cognitivos que contribuyen a un aprendizaje más efectivo, significativo y autónomo para los estudiantes.
El aprendizaje adaptativo con enfoque fundamentado en modelos permite la individualización y personalización de la experiencia de aprendizaje.
Ello significa que, al adaptar el contenido y las actividades a las necesidades y nivel de conocimiento de cada estudiante, se fomenta un aprendizaje más efectivo y significativo.
Al basarse en modelos cognitivos, este enfoque se centra en construir un conocimiento sólido y estructurado. Los modelos permiten identificar lagunas en el conocimiento de los estudiantes y proporcionarles oportunidades para reforzar y ampliar su comprensión.
Al recibir retroalimentación continua y adaptada a su nivel de conocimiento, los estudiantes desarrollan habilidades de autorregulación. Aprenden a evaluar su propio progreso, ajustar su enfoque de aprendizaje y tomar decisiones informadas sobre sus estrategias de estudio.
El enfoque basado en modelos fomenta el desarrollo de habilidades metacognitivas, ya que los estudiantes reflexionan sobre su propio proceso de aprendizaje, monitorean su progreso y toman conciencia de sus propias fortalezas y debilidades.
La adaptación individualizada y la retroalimentación personalizada proporcionadas por los modelos cognitivos pueden aumentar la motivación y el compromiso de los estudiantes.
Al abordar desafíos adaptados a su nivel y recibir retroalimentación positiva, los estudiantes se sienten más involucrados y motivados en su proceso de aprendizaje.
En el próximo capítulo se detallan con mayor profundidad las características y beneficios del aprendizaje adaptativo enfocado en modelos.
El aprendizaje adaptativo enfocado en modelos matemáticos se basa en la utilización de algoritmos y modelos matemáticos para adaptar el proceso de aprendizaje según las características y necesidades individuales del estudiante. Estos modelos se construyen a partir de datos recopilados sobre el estudiante y se utilizan para predecir y adaptar las experiencias de aprendizaje futuras.
Cuando utilizamos un diseño adaptativo para matemáticas básicas, estamos utilizando un modelo matemático para adaptar la experiencia de aprendizaje. independiente del programa diseñado para tal efecto, este debe recopilar datos sobre las respuestas a preguntas y actividades, así como información sobre el tiempo que tarda en responder, los errores comunes que comete y los temas en los que el estudiante suele tener dificultades.
El modelo matemático utiliza estos datos para analizar los patrones de comportamiento y crear un perfil de aprendizaje personalizado. Por ejemplo, el modelo puede identificar que se tiene un buen rendimiento en operaciones de suma y resta, pero tiene dificultades con los productos notables y las factorizaciones.
En base a este perfil, el programa adaptará el contenido y las actividades para abordar las necesidades específicas del estudiante. Por ejemplo, podría ofrecer ejercicios adicionales y explicaciones detalladas sobre fracciones, así como retroalimentación específica cuando se cometen errores en este tema.
También podría proporcionar recursos interactivos, como manipulativos virtuales, una ayuda para visualizar y comprender mejor los conceptos de fracciones.
Una interactividad de este tipo es la diseñada por Óscar Escamilla González y Deyanira Monroy Zariñán, la podemos visualizar en la siguiente escena:
A medida que se continúa utilizando el programa, el modelo matemático seguirá recopilando datos sobre las respuestas y comportamiento del estudiante. Utilizando estos datos actualizados, el programa podrá ajustar aún más el contenido y las actividades en función del progreso.
Por ejemplo, si se detecta una mejora significativa en el manejo de las fracciones, el programa podría introducir problemas más desafiantes que involucren operaciones más complejas con fracciones en forma de expresiones racionales que involucren el álgebra.
Resumiendo lo descrito hasta el momento podemos expresar que el aprendizaje adaptativo enfocado en modelos utiliza algoritmos y modelos matemáticos para analizar los datos del estudiante y personalizar el proceso de aprendizaje.
Al utilizar estos modelos, el programa puede adaptar el contenido, las actividades y los recursos de manera precisa y personalizada, brindando una experiencia de aprendizaje que se ajuste a las necesidades del estudiante y le permita avanzar de manera efectiva en las matemáticas básicas.
Un modelo cognitivo es una simulación utilizada como herramienta en la educación y en la psicología para comprender cómo las personas procesan la información, adquieren conocimientos y resuelven problemas.
Estos modelos ayudan a capturar el nivel de conocimiento actual de un individuo, identificar sus fortalezas y debilidades, y permiten adaptar el contenido y las actividades de aprendizaje, describe cómo las percepciones de las personas o los pensamientos espontáneos sobre las situaciones problema influyen en sus reacciones emocionales o en su conducta. Un modelo cognitivo en el aprendizaje adaptativo es la herramienta que permite adaptar el contenido y las actividades de aprendizaje de la siguiente manera:
Dicha apreciación del estado actual del conocimiento se logra mediante la administración de pruebas o cuestionarios que evalúan el nivel de comprensión de conceptos, habilidades y habilidades cognitivas relacionadas con un tema específico.
Los modelos cognitivos pueden analizar los resultados los procesos evaluativos del conocimiento, un modelo cognitivo puede identificar las áreas en las que un estudiante tiene un conocimiento sólido (aquél que se basa en hechos y pruebas concretas y que ha sido verificado por expertos en el campo) y que permanece en memoria a largo plazo del estudiante(fortalezas) y las áreas en las que necesita mejorar (debilidades).
Con base en la evaluación del conocimiento actual y la identificación de fortalezas y debilidades, los modelos cognitivos pueden recomendar contenido y actividades de aprendizaje específicas personalizadas.
Esa personalización implica incluir la selección de materiales de lectura, videos-lección, ejercicios prácticos y tareas que se adapten al nivel de conocimiento y las necesidades de aprendizaje de cada estudiante que adquirido cierto nivel de comprensión de conceptos, las habilidades motoras y las habilidades cognitivas requeridas.Aunque muchos autores dudan de la validez de los estilos de aprendizaje, los modelos cognitivos tenerlos en cuenta al momento de recomendar estrategias y enfoques de enseñanza.
Algunos estudiantes pueden aprender mejor a través de la visualización, mientras que otros pueden preferir la lectura o la interacción práctica.
La recopilación de datos sobre el rendimiento en diversas actividades de aprendizaje y la comparación de los resultados con los objetivos de aprendizaje previamente establecidos permite ajustar continuamente las estrategias de enseñanza para garantizar que los estudiantes estén avanzando de manera efectiva.
Un modelo cognitivo también puede utilizarse para rastrear el progreso de los estudiantes a lo largo del tiempo.
El modelo cognitivo debe brindar una retroalimentación específica y detallada, resaltando áreas de mejora y proporcionando sugerencias concretas para el desarrollo del conocimiento y las habilidades.
Considerando que el aprendizaje adaptativo centrado en modelos normalmente hace uso de algoritmos y datos en tiempo real para tomar decisiones de adaptación para satisfacer necesidades específicas de aprendizaje, se infiere que admite una personalización continua y dinámica del proceso de aprendizaje.
Lo anterior se refleja en ajustar:
Cuando el modelo detecta un avance exitoso del estudiante y que al mismo tiempo demuestra comprensión acerca de un nivel de dificultad determinado, el sistema puede aumentar gradualmente la dificultad al presentar contenido más desafiante o problemas más complejos.
Si por el contrario las acciones del estudiante constantemente muestran un avance lento, el sistema puede disminuir la dificultad, proporcionando ejercicios más simples o material de apoyo para fortalecer las bases.
En el marco del aprendizaje adaptativo enfocado en modelos, el diseño del sistema debe poseer los algoritmos necesarios satisfacer la capacidad para adaptar el orden en que se presentan los temas o conceptos.
Esos algoritmos deben captar si un estudiante ya tiene conocimientos sólidos en un área particular, si la respuesta es positiva, el sistema puede permitirle saltar ese contenido y avanzar a temas más avanzados.
En contraste, si un estudiante no demuestra poseer la comprensión requerida en un área específica, el sistema puede presentar primero los conceptos fundamentales antes de avanzar a temas más avanzados.
Esta adaptación se refiere las estrategias para presentar la información de un tema específico y cómo se guía el aprendizaje del mismo.
Es el algoritmo que elige los diferentes métodos de instrucción, como videos-lección, lecturas, ejercicios interactivos, retroalimentación inmediata o incluso la adaptación de los estilos de enseñanza, como un enfoque más visual o auditivo, según las preferencias y necesidades del estudiante que satisfacen su estilo de aprendizaje.
El ajuste de los anteriores aspectos se refleja en una personalización de la experiencia de aprendizaje para cada estudiante, lo que les permite avanzar a su propio ritmo y abordar sus áreas de fortaleza y debilidad de manera eficaz.
Esto tiene el potencial de mejorar significativamente la retención de información y la comprensión, ya que se adapta al nivel de competencia y al estilo de aprendizaje de cada individuo realizado en tiempo real, lo que puede resultar en un aprendizaje más efectivo y eficiente.
El feedback es una herramienta valiosa para el aprendizaje, la mejora y el desarrollo en una amplia gama de situaciones y contextos, como pudimos observar en el video de la Escuela Europea:
El feedback o Retroalimentación es español es una parte fundamental en la educación, en el trabajo y en muchas otras áreas de la vida, ya que contribuye al aprendizaje, el crecimiento y la mejora continua, en el aprendizaje adaptativo enfocado en modelo se caracteriza por:
El feedback implica la comunicación de información, ya sea de forma verbal o escrita, de manera que el estudiante pueda comprender claramente la retroalimentación proporcionada por el sistema.
Esta retroalimentación puede surgir a partir de una respuesta positiva del estudiante reforzando su comprensión conceptos más avanzados, o a partir de una respuesta deficiente del estudiante para que comprenda lo básico del tema en cuestión.
La retroalimentación suele ser más efectiva cuando se proporciona de manera oportuna, es decir, tan pronto como sea posible después de que se haya observado o realizado el comportamiento o la acción que se está evaluando y que le permita al estudiante comprender conceptos más avanzados.
Una retroalimentación es más útil cuando se proporciona de manera específica y con detalles concretos, le permite al estudiante comprender qué hizo bien o mal y cómo puede mejorar.
Un detalle concreto se proporciona a partir de un ejemplo específico, de una descripción de una acción, de la medición de un resultado, de la descripción del impacto generado o de una comparación.
No podemos especificar las cualidades de un estudiante para que pueda participar exitosamente en sistema de aprendizaje adaptativo enfocado en modelos, pero si debe poseer algunas de las que citamos en el video donde hemos realizado una descripción de ellas
A medida que avanza la popularidad de la inteligencia artificial se hace necesario un ciudadano global, Figueroa y Leyton
El modelo NETS-S fue desarrollado por la International Society for Technology in Education (ISTE) para guiar la integración efectiva de la tecnología en la educación.
NETS-S establece estándares y competencias que los estudiantes deben alcanzar en relación con la tecnología y su uso en el aprendizaje. Proporciona pautas sobre cómo los estudiantes deben utilizar las tecnologías digitales y cómo desarrollar habilidades esenciales para el siglo XXI.
Veamos algunos aspectos que le permitirán a un diseñador instruccional establecer los parámetros que con fundamento en las clasificaciones de los aprendices del modelo NETS-S y la manera de relacionarlos con el aprendizaje adaptativo enfocado en modelos:
Según lo expresan Polanco_Padrón et al
Son primordiales las opciones de respuesta que permiten evaluar el nivel de habilidad de los estudiantes para utilizar el pensamiento computacional en la comprensión y uso de modelos cognitivos en el aprendizaje adaptativo.
Veamos algunas cualidades ideales para ese pensador computacional:
El nivel de habilidad para utilizar el pensamiento computacional, incluyendo la resolución de problemas, la lógica, el diseño algorítmico y la abstracción, necesarios para comprender y utilizar modelos cognitivos en el aprendizaje adaptativo
Los niveles que a continuación se describen permiten evaluar el nivel de habilidad de los estudiantes para utilizar el pensamiento computacional en la comprensión y uso de modelos cognitivos en el aprendizaje adaptativo, permitiendo como lo expresa Motoa
Identificar desde un modelo cognitivo el nivel de conocimiento actual, las fortalezas y debilidades, y ajustando el contenido y las actividades en función de esos modelos.
Las posibilidades de identificación que justifican este aspecto permiten evaluar el nivel de conocimiento y comprensión de los estudiantes sobre cómo se utilizan los modelos cognitivos en la adaptación de la experiencia de aprendizaje, he aquí esas posibilidades:
Se requiere profundizar en los conceptos para facilitar la comprensión de lo que se requiere ajustar en el aprendizaje.
Capacidad de aplicar habilidades tecnológicas que incluyen el uso de herramientas y software educativos, la navegación por la Web y la programación, para utilizar y aprovechar al máximo los modelos cognitivos.
Hace referencia al nivel de confianza y habilidades tecnológicas de los estudiantes para aplicar y aprovechar los modelos cognitivos en el aprendizaje adaptativo, Alvarracín et Al
Esas situaciones básicas tienen relación con características de los denominados estilos de aprendizaje.
¿Cuál es el sentimiento al asumir la responsabilidad del propio aprendizaje cuando se establecen metas personales y tomar decisiones informadas utilizando modelos cognitivos y adaptación en el aprendizaje?
El aprendiz empoderado asume y percibe de una manera particular su capacidad para apropiarse de la responsabilidad de su propio aprendizaje, establecer metas personales y tomar lo que Ballbé
Hablar de empoderamiento es hacer referencia a sinónimos que cualifican al ser humano como competente, facultado, capacitado o acreditado entre otros, veamos ocho pasos que nos presenta Daniel Colombo para lograrlo:
Esos niveles de responsabilidad pueden ser descritos de la siguiente manera:
Las anteriores características hablan sobre la capacidad para describir cómo utilizar la retroalimentación proporcionada por los modelos cognitivos y el aprendizaje adaptativo para evaluar el progreso y ajustar las estrategias de aprendizaje, enfatizan la capacidad de utilizar modelos cognitivos y aprendizaje adaptativo para evaluar y mejorar el proceso de aprendizaje.
Los siguientes aspectos permiten evaluar el nivel de comprensión y habilidad de los estudiantes para utilizar la retroalimentación proporcionada por los modelos cognitivos y el aprendizaje adaptativo.
Al igual que las caracterizaciones anteriores, los siguientes aspectos permiten evaluar el nivel de disposición y motivación de los estudiantes para colaborar y comunicarse efectivamente con otros estudiantes en entornos adaptativos basados en modelos cognitivos y aprendizaje adaptativo.
En palabras de Ramos "el conocimiento construido por el estudiante no es una reproducción del conocimiento elaborado por la disciplina, sino que es una reconstrucción personal que responde, entre otros factores, al contexto social y cultural en el que está inmerso."
Pero ¿qué es el conocimiento?, veamos un video de la UMNG al respecto:
Quién construye conocimiento puede explicar cómo los modelos cognitivos se utilizan para representar el conocimiento y las habilidades de los estudiantes en el aprendizaje adaptativo.
Además, también adquiere la experiencia en la manera de adaptarlos al contenido y a las actividades de aprendizaje en función de esos modelos.
Con los siguientes niveles podemos evaluar el nivel de comprensión y habilidad de los estudiantes para explicar cómo se utilizan los modelos cognitivos en el aprendizaje adaptativo y cómo se adapta el contenido y las actividades de aprendizaje en función de esos modelos.
También se describe la forma de adaptar el contenido y las actividades de aprendizaje de manera efectiva y personalizada en función de esos modelos.
¿Cómo construir activamente el propio conocimiento a partir de modelos cognitivos para, identificar fortalezas y debilidades y, al mismo tiempo seleccionar las actividades de aprendizaje que ayudarán a ampliar la comprensión del aprendiz? En la siguiente escena puedes identificar los niveles que permiten realizar la evaluación descrita:
Con la anterior escena de caracterización es posible evaluar el nivel de utilización y efectividad de los estudiantes al utilizar los modelos cognitivos y el aprendizaje adaptativo para construir activamente su propio conocimiento, identificar fortalezas y debilidades, y seleccionar actividades de aprendizaje adecuadas.
La descripción de la manera de aplicar el conocimiento y las habilidades adquiridas a través de los modelos cognitivos en contextos del mundo real, y cómo emplearlos para resolver problemas y tomar decisiones informadas.
Los niveles que describiremos a continuación son una guía para evaluar el estado de aplicación y efectividad de los estudiantes al utilizar el conocimiento y las habilidades adquiridas a través de los modelos cognitivos en contextos del mundo real y para resolver problemas.
En este rol, el aprendiz asume un compromiso ético en el uso de la información digital y de las TIC, incluyendo el respeto por los derechos de autor, la propiedad intelectual y la referencia adecuada de las fuentes.
Además, promueve y practica el uso seguro (proteger la información de accesos no autorizados), legal (implica el cumplimiento de las leyes de protección de datos personales) y responsable de la información (tomar decisiones éticas y conscientes en relación con la información, implica no difundir información falsa y respetar la privacidad de las personas) y de las Tecnologías de la Información y Comunicación (TIC).
Otra característica del aprendiz jugando este papel está en que demuestra la responsabilidad personal para el aprendizaje a lo largo de la vida utilizando esas TIC.

Esa responsabilidad lo hace competente para hacer críticas constructivas, juzgando y haciendo aportaciones a los trabajos TIC desarrollados colaborativamente e incluso ejercer un liderazgo para la ciudadanía digital dentro de un grupo
Lozano y Fernández (2019)
Vamos inicialmente a mirar las condiciones que le permiten a un diseñador instruccional evaluar el nivel de competencia digital y ética de los estudiantes como ciudadanos digitales.
Que estrategia o procedimiento se realiza para aplicar la capacidad de buscar, evaluar y utilizar críticamente información en línea para tomar decisiones informadas, resolver problemas y participar activamente como ciudadano digital
Al evaluar la aplicación y efectividad de los estudiantes al utilizar su capacidad para buscar, evaluar y utilizar críticamente la información obtenida en línea para tomar decisiones informadas, resolver problemas y participar activamente como ciudadanos digitales.
Implica respetar los derechos y la privacidad de otros usuarios, evitar la difusión de información falsa o perjudicial, y participar en debates y actividades en línea de manera constructiva.
Para ello debemos tener en cuenta los siguientes niveles:
Facilidad para describir la manera de utilizar las herramientas y recursos en línea para participar de manera activa en la sociedad, colaborar con otros, promover la diversidad y la inclusión, y contribuir al bienestar digital de la comunidad.
Los siguientes niveles permiten programar la evaluación del estado de aplicación y efectividad de los estudiantes al utilizar herramientas y recursos en línea para participar activamente en la sociedad, colaborar con otros.
Esa colaboración implica promover la diversidad y la inclusión, y contribuir al bienestar digital de la comunidad.
Un estudiante o aprendiz se denomina diseñador innovador cuando el pensamiento creativo, la resolución de problemas hacen parte del diseño iterativo propio y la mejora permanente juegan un papel importante en colaboración y comunicación en el proceso de diseño.
De qué manera se utilizan los modelos cognitivos y el aprendizaje adaptativo para fomentar el pensamiento creativo y resolver problemas de manera innovadora en el proceso de diseño.
Como en los niveles que hemos descrito hasta ahora para todas las categorías de aprendiz, aquí visualizaremos las opciones.
Con respecto al pensamiento creativo, de Carvaho et Al (2021) haciendo alusión a Cropley sostienen que:
"... el pensamiento creativo es una dimensión compleja del comportamiento humano, en la que se involucran varias facetas de la persona, desde procesos básicos, como la percepción, hasta procesos más complejos, como los de organización mental y tratamiento de la información, además de otras variables personales como la motivación, la apertura a la experiencia y la emoción".Veamos ahora los niveles en los que podemos categorizar desde tres puntos de vista a ese aprendiz diseñador innovador: al fomento del pensamiento creativo, a la retroalimentación recibida y a la comunicación utilizando tecnología.
Estas alternativas nos permiten evaluar el nivel de aplicación y efectividad de los estudiantes al utilizar los modelos cognitivos y el aprendizaje adaptativo para fomentar su pensamiento creativo y resolver problemas de manera innovadora en el proceso de diseño.
Veamos ahora como se aplica el enfoque fundamentado en modelos para iterar y mejorar continuamente un diseño, basándose en la retroalimentación proporcionada por los modelos cognitivos y el aprendizaje adaptativo
Las siguientes descripciones de los niveles en esta categoría permiten evaluar el nivel de aplicación y efectividad de los estudiantes al utilizar el enfoque fundamentado en modelos para iterar y mejorar continuamente sus diseños:
Analicemos a continuación la capacidad para describir la manera de involucrarse en la colaboración y la comunicación efectiva con otros estudiantes y profesionales del diseño, utilizando herramientas tecnológicas y aprovechando las oportunidades de aprendizaje en red.
Aquí se describen las posibilidades que permiten evaluar el nivel de participación y efectividad de los estudiantes en la colaboración y la comunicación efectiva con otros estudiantes y profesionales del diseño.
En este apartado hablaremos del aprendiz y sus habilidades de comunicación digital, del uso estratégico de los recursos multimediales y del diseño que esas habilidades requieren y la narrativa inmersa en ellas.
Al respecto de esa narrativa digital, Choez
Es decir, los que posibilitan la interacción de los argumentos de una forma dinámica e interactiva.
La manera de utilizar las herramientas y tecnologías digitales para comunicar las ideas de manera creativa, efectiva y significativa, considerando el público objetivo y los objetivos de comunicación
Al diseñar un programa de aprendizaje adaptativo enfocado en modelos, esos niveles nos permiten evaluar el grado de aplicación y efectividad de los estudiantes al utilizar las herramientas y tecnologías digitales para comunicar sus ideas de manera creativa, efectiva y significativa, considerando el público objetivo y los objetivos de comunicación que se pretende lograr.
La descripción de la forma cómo seleccionar y utilizar recursos multimedia, como imágenes, videos, sonidos y presentaciones, para enriquecer la comunicación y transmitir mensajes de manera impactante.
La Hipermedia según lo expresan Aparicio et Al
Al diseñar un entorno adaptativo enfocado en modelos dirigido (aunque no exclusivamente) al aprendiz que se puede catalogar como creador creativo, podemos encontrarnos con las situaciones descritas en el interactivo de la página anterior.
Cómo aplicar el enfoque fundamentado en modelos para diseñar narrativas digitales atractivas y convincentes, que involucren a tu audiencia y transmitan tus ideas de manera clara y coherente.
Con las siguientes descripciones podemos realizar una evaluación acerca del nivel de aplicación y efectividad de los estudiantes al utilizar el enfoque fundamentado en modelos para diseñar narrativas digitales atractivas y convincentes, que involucren a su audiencia y transmitan sus ideas de manera clara y coherente.
Teniendo en cuenta que la competencia intercultural y la comunicación global son habilidades fundamentales en un mundo cada vez más interconectado, el aprendiz como comunicador global es una necesidad tanto para él como para que esa interconexión sea más efectiva.
En una aldea global gobernada por la tecnología donde las fronteras geográficas se desdibujan, la capacidad de entender y respetar las diferencias culturales se convierte en un activo invaluable. La conciencia y adaptabilidad cultural son esenciales para navegar con éxito en contextos internacionales, ya que permiten a las personas interpretar los diversos matices culturales.

Además de lo descrito, la participación del aprendiz en redes y comunidades globales amplía las perspectivas y fomenta la colaboración entre individuos de diferentes orígenes puesto que las redes permiten compartir conocimientos, ideas y experiencias en un espacio donde la diversidad es apreciada y valorada, promoviendo así un diálogo intercultural más enriquecedor y constructivo.
La forma de emplear las herramientas y tecnologías digitales para comunicación y colaboración de manera efectiva con personas de diferentes culturas y contextos globales, considerando las diferencias culturales y lingüísticas.
Las condiciones a tener en cuenta al diseñar pensado en ese comunicador global tenemos:
Cuando se utilizan las herramientas y tecnologías digitales para comunicarse y colaborar de manera efectiva con personas de diferentes culturas y contextos globales a nivel de experto.
Ello considerando las diferencias culturales y lingüísticas que llevan a generar interacciones fluidas con las que se facilita la adaptación adecuada a cualquier contexto.
La descripción de la manera de adaptar la comunicación y los mensajes que la hacen posible por ser comprensibles y apropiados para contextos culturales diversos, pero, considerando las normas y las sensibilidades culturales de los destinatarios.
La descripción aquí requerida da pautas al diseñador instruccional para evaluar el nivel de aplicación y efectividad de los estudiantes al adaptar su comunicación y sus mensajes para ser comprensibles y apropiados en diferentes contextos culturales, considerando las normas y sensibilidades culturales de los destinatarios.

Un mensaje se considera comprensible y apropiado para diferentes contextos culturales cuando es elaborado teniendo en cuenta una serie de factores. En primer lugar, conocer y comprender las normas culturales específicas de cada grupo o comunidad con la que se interactúa.
Ese primer aspecto incluye características como el lenguaje, las costumbres, las tradiciones, la religión y las creencias.
En segundo lugar, es necesario tener en cuenta que cada cultura tiene su propia forma única de comunicarse, ello implica respetar estas diferencias comunicativas.
Veamos en la siguiente escena la caracterización de la comunicación para el aprendiz como comunicador global:
Por último, hablemos del nivel de participación y efectividad de los estudiantes en el uso de redes y comunidades virtuales globales para intercambiar ideas, obtener diferentes perspectivas y colaborar con personas de todo el mundo utilizando tecnologías de comunicación y colaboración en línea.
Cómo involucrarse en redes y comunidades virtuales globales para intercambiar ideas, obtener diferentes perspectivas y colaborar con personas de todo el mundo, utilizando tecnologías de comunicación y colaboración en línea.
El término "inteligencia artificial" fue acuñado por John McCarthy, un científico de la computación estadounidense, en el año 1956. McCarthy es considerado uno de los pioneros y líderes en el campo de la inteligencia artificial. Durante una conferencia en Dartmouth College, McCarthy propuso el término "inteligencia artificial" para referirse a la capacidad de las máquinas de imitar o simular la inteligencia humana.
Desde entonces, el término "inteligencia artificial" ha sido ampliamente utilizado para describir el campo de estudio y desarrollo de sistemas y tecnologías que exhiben características asociadas con la inteligencia humana, como el aprendizaje, el razonamiento, la percepción y la toma de decisiones.
A lo largo de los años, la inteligencia artificial ha experimentado avances significativos y se ha convertido en un campo de investigación multidisciplinario que abarca áreas como el aprendizaje automático, la visión por computadora, el procesamiento del lenguaje natural y la robótica, entre otros.
Ahora que conocemos las características del aprendizaje adaptativo enfocado en modelos establecer conexión entre los estilos de ese aprendizaje adaptativo y la inteligencia artificial para repensar como lo expresan Ocaña-Fernández et Al
Veamos en el siguiente video un resumen de lo que ha sido el desarrollo de la inteligencia artificial el siglo XX, desde los primeros intentos hasta llegar al controvertido ChatGPT:
Con respecto a la aplicación de la AI en la educación, Sánchez y Lama (2007)
Ello permitiría adaptarlos a la evolución de los recursos que cada día surgirián de esa inteligencia artificial y la actualización de contenidos y actividades de aprendizaje enfocados a la AI.
Hablamos de lo integral cuando de aprendizaje adaptativo se trata, de igual manera podemos afirmar que la implementación exitosa de la inteligencia artificial en la educación requiere un enfoque integral y colaborativo que involucre a todos los actores del proceso: educadores, desarrolladores de tecnología y diseñadores instruccionales.

La integración de la inteligencia artificial (IA) en la educación puede ser beneficiosa para mejorar la enseñanza y el aprendizaje, veamos algunas técnicas y estrategias ideales para utilizar la IA en la educación:
La IA puede personalizar el contenido y las actividades para garantizar un aprendizaje efectivo, puesto que emplea sistemas de aprendizaje adaptativo que se ajusten automáticamente al nivel de competencia de cada estudiante.
Un sistema de recomendación se define como un diseño tipo software que facilita la identificación de la información que le interesa a un usuario para su aprendizaje, sugieren contenido educativo personalizado a los estudiantes. La IA puede analizar el progreso y las preferencias de cada estudiante para ofrecer recomendaciones adaptadas a sus necesidades y habilidades.
Son sistemas que pueden responder preguntas, explicar conceptos y ofrecer retroalimentación en tiempo real. Los tutores virtuales basados en IA se desarrollan para que puedan proporcionar ayuda individualizada a los estudiantes.
Se implementan herramientas de analítica de datos impulsadas por IA para recopilar, analizar y utilizar datos sobre el rendimiento de los estudiantes. Esta implementación en el proceso de aprendizaje permite identificar áreas de mejora y ajustar los enfoques de enseñanza.
Facilita automatizar tareas administrativas, entre otras la gestión de horarios, el seguimiento de la asistencia y la administración de recursos, lo que permite a los educadores centrarse más en la enseñanza.
Implementar la IA en experiencias de realidad virtual (RV) y la realidad aumentada (RA) facilitan crear entornos de aprendizaje inmersivos, ayudan a los estudiantes a comprender conceptos complejos de manera más efectiva.
La RV y la RA se complementan con representaciones digitales (simulaciones) de situaciones o procesos del mundo real para comprender conceptos abstractos o practicar habilidades en un entorno seguro.
La AI permite desarrollar chatbots educativos que puedan responder preguntas comunes y proporcionar información útil a los estudiantes las 24 horas del día. Esto puede mejorar la accesibilidad al contenido educativo. Veamos una historia sobre el surgimiento de los chatbots en un podcast de Alex Hurtado
Este tipo de evaluación, utilizando IA para la evaluación automatizada de exámenes y tareas puede agilizar el proceso de calificación y proporcionar retroalimentación inmediata a los estudiantes.
Otro de los beneficios de la AI en la educación es el fomento de la colaboración entre educadores y sistemas basados en IA.
Se refiere a que la IA puede ayudar a los maestros a identificar áreas donde se necesita intervención humana y a personalizar la enseñanza.
Un aspecto que debe ser considera prioritariamente al utilizar AI en la educación es asegurarse de que cualquier implementación de IA en la educación respete la privacidad de los estudiantes y cumpla con estándares éticos, la transparencia y la responsabilidad son fundamentales.
No se puede dejar de la lado la formación a los educadores para que comprendan cómo utilizar la IA en el aula de manera efectiva. Esto incluye la comprensión de las herramientas disponibles y cómo interpretar los datos que generan.
Es necesario realizar una evaluación continua de la efectividad de las soluciones basadas en IA y ajustar las estrategias de enseñanza en función de los resultados y las necesidades cambiantes de los estudiantes a medida que se edentren en los procesos donde la AI aparece involucrada.
Un modelo matemático es una representación simplificada de un sistema o fenómeno del mundo real utilizando conceptos y ecuaciones matemáticas. Los modelos matemáticos son herramientas poderosas en el aula de matemáticas, ya que ayudan a los estudiantes a comprender y aplicar conceptos matemáticos en situaciones prácticas y a desarrollar habilidades de resolución de problemas.
Con el desarrollo avanzado de los sistemas informáticos surgen las simulaciones de esos sistemas mencionados, vamos una de esas simulaciones:
Simulaciones como la anterior de PhET involucran a los estudiantes mediante un ambiente intuitivo en donde el modelo matemático que la representa se consolida puesto que permite aprender explorando y descubriendo.
Un modelo matemático como herramienta en el aula de matemáticas debe poseer entre otras las siguientes características:
Los modelos matemáticos simplifican situaciones del mundo real a través de abstracciones. Esto implica identificar las variables y relaciones clave y omitir detalles irrelevantes para centrarse en lo esencial.
Hay que pensar que existen diferentes tipos de razonamiento abstracto y cuyas características dependen de diversas disciplinas y contextos.
Cada tipo de razonamiento abstracto requiere habilidades específicas y puede ser útil en diferentes situaciones de resolución de problemas y toma de decisiones.
La abstracción en el contexto del aprendizaje adaptativo se refiere a la capacidad de resumir o generalizar información específica para identificar patrones o conceptos más amplios.
Esta capacidad permite a los sistemas de aprendizaje adaptativo comprender mejor las necesidades y habilidades de los estudiantes, lo que a su vez les permite personalizar la experiencia de aprendizaje de manera más efectiva.
Un modelo matemático como herramienta de aula permite analizar las respuestas incorrectas de un estudiante en una serie de ejercicios matemáticos, ello le facilita descubrir los errores consistentes debido a la abstracción que le indica la identificación de un patrón de errores en lugar de solo observar respuestas incorrectas.
Gamboa et Al
Los modelos matemáticos se expresan mediante ecuaciones, fórmulas, gráficos u otras representaciones formales. Esto permite a los estudiantes trabajar con precisión y claridad.
En el ámbito de la lógica y el análisis racional, la representación formal se refiere a la utilización de sistemas lógicos y simbólicos para expresar y manipular conocimiento. Feregrino et al
Esos sistemas permiten representar información de manera estructurada y precisa, lo que facilita el análisis y la toma de decisiones.
Los modelos matemáticos son una estructuración del conocimiento que es organizado con el propósito de que un estudiante pueda apropiarse de los elementos de la esencia de un problema particular:
Se refiere a la acción de trabajar con información o datos de naturaleza no numérica o no cuantitativa para comprender, analizar, organizar o presentar de manera efectiva dicho conocimiento. El conocimiento cualitativo se fundamenta en características descriptivas, observaciones subjetivas y narrativas.
Se origina en el análisis del contenido del problema del modelo: Consiste en examinar y categorizar mentalmente el contenido del saber previo originado por documentos, diálogos, textos u otras fuentes cualitativas para identificar patrones que permitan la solución de problemas similares.
Estructurar el conocimiento inmerso en un modelo matemático en el aula para todo estudiante varía según su estilo de aprendizaje, preferencias personales y el campo del saber que esté estudiando. Sin embargo, hay algunas estrategias generales que pueden ser útiles para una representación formal que le permita organizar y retener información de manera efectiva:
La estructuración del conocimiento desde los modelos matemáticos nace de una representación simplificada de un problema particular o de sus variantes utilizando símbolos y el lenguaje matemático que les da significado. Esos modelos le permiten al estudiante comprender y predecir el resultado del comportamiento de sistemas físicos, sistemas naturales e incluso sistemas sociales.
Pasos para estructurar el conocimiento desde un modelo matemático como herramienta de aula:
Así estemos hablando de los modelos matemáticos como herramienta debemos hablar de una no tan sutil diferencia entre el significado del complejo como número y el significado complejo del número en una situación de aprendizaje:
Los números complejos son una de las herramienta de trabajo del álgebra, se representa por $ \Complex $ e indica que es la suma de un número real $ ( a ) $ y un número imaginario múltiplo real $ ( b ) $ de la unidad imaginaria, que se indica con la letra $ ( i ) $ tal como aparece a continuación:
$$\Complex = a ± bi$$El número complejo se ha convertido en la herramienta de las matemáticas puras y aplicadas como variable compleja, ecuaciones diferenciales y en campos específicos del saber aplicado tal como la aerodinámica, la hidrodinámica y electromagnetismo como componentes de la física.
El número complejo usado en modelos matemáticos, es lo ideal para abordar situaciones en las que los números reales no son suficientes para describir completamente el fenómeno que se describe porque su resultado ese contiene ese múltiplo real del imaginario.
Entre los modelos matemáticos donde se usan tenemos:
El pensamiento complejo se refiere a una habilidad innata que permite a las personas comprender, interpretar y enfrentar situaciones que presentan múltiples dimensiones, factores y desafíos
El significado complejo del número al interior de un modelo matemático ocurre cuando se recurre a varias fuentes al mismo tiempo y compara argumentos, busca conexiones y entrelaza una comprensión multifacética de los temas en cuestión.
Para este significado complejo del número al interior de un modelo matemático es necesario adentrarnos la teoría del significado funcional de los números, es una perspectiva en la filosofía de las matemáticas que se centra en la función que desempeñan los números en la cotidianidad y en la comprensión del contexto.
Es de anotar que existe una diferencia entre diversas teorías de la matemática, algunas se centran en cuestiones más abstractas o formales, esta teoría se enfoca en el papel práctico y funcional que desempeñan los números en nuestra vida cotidiana y en la descripción de fenómenos del mundo real.
Ese significado funcional del número como teoría es el resultado de complementar varias teorías, veamos:
La palabra "pragmático" se refiere a las acciones o resultados relacionados con la práctica, con la utilidad o con la efectividad de las matemáticas tal como lo relacionan Montaluisa-Vivas et al
En un sentido más amplio de la filosofía, puede describir a una persona o un enfoque que se centra en la aplicación práctica de las matemáticas o que prioriza lo que es útil y funcional.
Lo anterior quiere decir que, en el contexto de la filosofía, la verdad y el significado de las ideas se determinan por su utilidad práctica y su efectividad en lo cotidiano.
Es dejar de lado sin que sean eliminados, los conceptos abstractos o teorías que pueden carecer de aplicabilidad, el pragmatismo se enfoca en lo que funciona en la práctica y en cómo las ideas y creencias pueden tener un impacto positivo en la vida de las personas.
Se les atribuye la fundación de la filosofía del Pragmatismo a los estadounidenses John Dewey, Sanders Peirce y William James quienes destacan la importancia de las matemáticas como una herramienta útil para la resolución de problemas prácticos.
En el campo de la filosofía de las ciencias empíricas, de la cual hace parte la filosofía de la ciencia matemática se han planteado preguntas sobre la función de los números en la representación y la medición de fenómenos naturales, expresan Fayos y Escalada
La filosofía de la ciencia es un campo de estudio distinto y en constante desarrollo que aborda preguntas fundamentales sobre la naturaleza de la ciencia, el método científico y la relación entre la teoría y la evidencia empírica. La historia de la filosofía de la ciencia en su desarrollo ha tenido componentes como:
Aunque los filósofos de la antigua Grecia no se centraron específicamente en la ciencia en el sentido que hoy conocemos, sentaron las bases para la reflexión filosófica sobre la naturaleza y el conocimiento. Tales de Mileto, Parménides y Heráclito entre otros, plantearon preguntas relacionadas con la naturaleza del mundo y el conocimiento.
Hay que reconocer que esos pensamientos filosóficos no aparecen en ninguna obra escrita, fueron el legado de otros pensadores y filósofos posteriores, quienes recogieron sus enseñanzas.
Filósofos como el escolástico Santo Tomás de Aquino incorporaron ideas aristotélicas en su obra, estableciendo una relación entre la filosofía y la teología. Si bien la filosofía medieval se centró en gran medida en la religión, sentó las bases para la discusión sobre la relación entre la fe y la razón, que es relevante para la filosofía de la ciencia.
Según lo expresa Sanguineti
De igual manera Torrijos-Castrillejo
En el mundo islámico, el médico y filosofo Abu Ali al-Husayn ibn Abd Allah ibn Sina conocido como Avicena se encuentran algunos conceptos filosóficos como aporte a la ciencia:
Para Avicena, el conocimiento intuitivo (al-ʿilm al-ḥadschí) es el conocimiento adquirido a través de la percepción y la intuición, mientras que el conocimiento demostrativo (al-ʿilm al-burhānī) es el conocimiento adquirido mediante razonamiento lógico y pruebas. Esta distinción influyó en la epistemología posterior y la metodología científica.

Tomando como punto de partida la anterior distinción, Abu Ali al-Husayn ibn Abd Allah ibn Sina argumentó que la ciencia se fundamenta en la evidencia empírica y el razonamiento lógico, por lo tanto, la necesidad de la observación con fines de percibir, la prueba o experimentación y el pensamiento lógico son los contenidos fundamentales al momento de adquirir el conocimiento.
No existe mucha variación en lo concerniente a la teoría del conocimiento dado por Avicena con respecto a lo que entendemos hoy día por el término, en palabras de Talavera
La teoría del filosófo se fundamentó en la percepción y el conocimiento, argumentando que el conocimiento comienza con la percepción sensorial y se desarrolla a través del proceso de abstracción y generalización, la que no debe confundirse con la reducción de combinar áreas de conocimiento sin el adecuado manejo epistemológico en la relación interdisciplinaria.
Otro de los aspectos en los cuales Avicena intento hacer en el conocimiento de la época fue defender una armonía entre la filosofía y la ciencia, él creía que la filosofía y la ciencia no eran incompatibles, sino que se complementaban mutuamente en la búsqueda del conocimiento.
Al respecto, Rodas et al
Dado que el pensamiento complejo contribuye a una comprensión más profunda y equilibrada del contexto, la historia nos cuenta que en esta época las artes y alguna aproximación a la ciencia en general estuvieron vinculadas al pensamiento complejo al promover la interdisciplinariedad, la observación detallada, el pensamiento sistémico, la exploración de problemas abstractos y la creatividad en la resolución de problemas.
Durante el Renacimiento, se promovió la idea de que el conocimiento no debía estar fragmentado, sino que las diversas disciplinas debían relacionarse entre sí.
Lo anterior fomentó un enfoque más integral y complejo para comprender el mundo y se crearon las bases de la ciencia moderna ya que se desarrollaron algunas características:
El pensamiento sistémico se distingue del enfoque más tradicional, ya que no busca aislar cada variable de una situación o fenómeno para su estudio independiente. En lugar de esto, su objetivo es comprender lo que se va a estudiar como un conjunto en el que las partes se influyen mutuamente. Por lo tanto, se enfoca en comprenderlo como un todo interconectado.
El Renacimiento también contribuyó al desarrollo del pensamiento sistémico, que implica ver los sistemas en su conjunto y comprender cómo las partes interactúan entre sí. En la actualidad, este tipo de pensamiento es esencial especialmente en los modelos matemáticos donde se estudian sistemas complejos y sus interacciones.
En palabras de Calvo
Es importante destacar que los estudios interdisciplinarios no deben llevar a la generalización de las disciplinas ni a la simple combinación de áreas de conocimiento sin una gestión epistemológica adecuada en las relaciones interdisciplinarias.
En el renacimiento según lo expresa Gribbin,
Durante el Renacimiento, los científicos y artistas comenzaron a observar la naturaleza y el mundo que los rodeaba con más atención. Este enfoque en la observación detallada de patrones y fenómenos naturales llevó a una comprensión más profunda de la complejidad de la realidad. Durante este período de la historia, las matemáticas, en particular la geometría, se convirtieron en una herramienta esencial para describir y analizar estos patrones y fenómenos.
Se destaca en este período el modelo matemático desarrollado por el matemático François Viète a quién se considera el padre del Álgebra Moderna por haber sido el primero en representar los parámetros de una ecuación mediante letras, siendo un destacado precursor de la utilización del álgebra en la codificación y decodificación de mensajes, conocida criptografía, lo que le facilitó descifrar los mensajes cifrados de la Corona Española.
Surgieron la teoría de números avanzada, la teoría de grupos y de ecuaciones,
Durante este período, los matemáticos comenzaron a explorar problemas más abstractos y teóricos que requerían un pensamiento más complejo y abstracto, surgieron la teoría de números avanzada, la teoría de grupos y la teoría de ecuaciones, estas teorías desarrolladas durante el renacimiento involucraron un pensamiento matemático más complejo y abstracto.
Expresan López et al
Ese pensamiento sistémico es la habilidad para considerar múltiples factores y planificar en consecuencia es una manifestación del pensamiento complejo y origen se encuentra en la evolución de nuestra especie. Cuando hacemos referencia al pensamiento complejo tenemos que aludir a Edgar Morin quién el prologo de su obra "Introducción al pensamiento complejo" expresaba:
"Legítimamente, le pedimos al pensamiento que disipe las brumas y oscuridades, que ponga orden y claridad en lo real, que revele las leyes que lo gobiernan, El término complejidad no puede más que expresar nuestra turbación, nuestra confusión, nuestra incapacidad para definir de manera simple, para nombrar de una manera clara, para poner en orden nuestras ideas" . A pesar de que en el renacimiento se alimentaron algunas características de la ciencia moderna, estamos de acuerdo con las palabras de Koyré
Con respecto a los modelos matemáticos que caracterizaron la Revolución Científica del siglo XVII, la historia nos relata que proporcionaron un lenguaje preciso para describir y comprender la ciencia, dicho de otra forma, fueron una herramienta analítica para explicar los fenómenos naturales con el apoyo matemático.
Este mecanismo analítico marcó un cambio significativo en la forma en que se abordaba la ciencia y sentó las bases para el desarrollo continuo de la física y las matemáticas durante esa revolución y fue el fundamento para encarar la ciencia posterior.
La revolución científica se inicia finalizando el renacimiento y se prolonga hasta comienzos de la denominada La Ilustración en el siglo 18.
La revolución científica alcanzó un notable impulso gracias a los avances de las matemáticas y de la astronomía, ayudó a derrumbar que las diversas creencias y supersticiones basadas en la religión, la institución más poderosa en la edad media.
Cuando hablamos de la teoría heliocéntrica hacemos referencia a que el Sol está en el centro del sistema solar y que los planetas, incluida la Tierra, orbitan alrededor de él, tiene sus raíces en la antigua Grecia, aunque su formulación más completa y convincente se atribuye principalmente a Nicolás Copérnico en el siglo XVI.
En el Renacimiento, Copérnico publicó su obra "De revolutionibus orbium coelestium" (Sobre las revoluciones de las esferas celestes) y más tarde con el trabajo de Galileo Galilei, de Johannes Kepler y Tycho Brahe, fue donde que la teoría heliocéntrica tomó fuerza.

Esto hace referencia a la aplicación sistemática de una serie de operaciones sobre las diferentes maneras en que las personas comprenden, explican y dan sentido a la información y al conocimiento que adquieren.
Estas interpretaciones pueden variar según diversos factores, como la cultura, la experiencia personal, la educación y las creencias individuales. Existen diversas formas para que el conocimiento se manifieste en los seres humanos y cada una se diferencia de la otra:
El conocimiento se manifiesta desde los paradigmas que guían la forma en que se conciben y se investigan los fenómenos naturales los cuales a su vez están influenciadas por los paradigmas dominantes en una determinada disciplina.
En las aulas aún hoy tienen relevancia muchos de los paradigmas del conocimiento de la antigüedad como en lo Mitológico/Religioso que prorcionaban explicaciones sobre el origen del mundo, la naturaleza y los fenómenos naturales que a menudo incluían dioses, héroes y eventos sobrenaturales como en las matemáticas de la antigua Grecia y en civilizaciones como la babilónica y la egipcia, en la escena de la siguiente página veremos algunos paradigmas relevantes:
El mundo globalizado que hoy nos agobia es el resultado del conocimiento inferido a partir de hechos establecidos mediante observaciones y experimentos rigurosos, lo que permite construir teorías y modelos que explican fenómenos naturales, este libro sería un volumen muy extenso si se nombrasen todos ellos. Veamos algunos relevantes en el campo matemático y vigentes hoy día:
A partir de la observación de la caída de objetos y el movimiento de los planetas, Newton en su libro Philosophiae Naturalis Principia Mathematica de 1687 estableció esta ley que describe la atracción entre dos objetos con masa y cómo varía en función de la distancia entre ellos, formalmente se enuncia que “La fuerza con que se atraen dos objetos es proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que los separa.”
"Sin embargo, hoy en día sabemos que, a partir de cierta cantidad de masa, esta ley pierde su validez (en caso de objetos supermasivos), y se hace necesario trabajar con la Ley de Relatividad General formulada en 1915 por Albert Einstein" según se enuncia en la Enciclopedia online
En la física clásica, las leyes del movimiento de Newton se expresan en forma de ecuaciones matemáticas que describen cómo los objetos se mueven bajo la influencia de fuerzas.

Estas leyes establecen la base para el cálculo de trayectorias, velocidades y aceleraciones de objetos en el espacio.
La mecánica newtoniana o mecánica vectorial es una formulación específica de la mecánica clásica que estudia el movimiento de partículas y sólidos en un espacio euclídeo tridimensional. Los cuerpos tienen velocidad inicial básica de la misma se hace en sistemas de referencia inerciales donde las ecuaciones básicas del movimiento, entre ellas el principio fundamental de la dinámica (segundo principio de Newton) relaciona la masa y la aceleración de un móvil con una magnitud vectorial, la fuerza.
En disciplinas como la biología, la economía y la sociología, se utilizan métodos probabilísticos y estadísticos para analizar datos experimentales y muestras de poblaciones. A partir de hechos establecidos mediante observaciones, se pueden inferir modelos matemáticos que describen la distribución y variabilidad de los fenómenos estudiados.
En una aplicación real dónde el cambio climático es influyente hay interés en entender la distribución de especies de árboles en un bosque, se realizan observaciones detalladas sobre la cantidad de cada especie en diferentes áreas.
Para entender el fenómeno se registran factores como el tipo de suelo, la altitud, la luz solar y la disponibilidad de agua.
A partir de estas observaciones, identifican patrones: algunas especies prefieren suelos húmedos, mientras que otras se encuentran en áreas más secas o a diferentes altitudes.
Utilizando estos datos, desarrollan un modelo matemático que relaciona variables ambientales con la probabilidad de encontrar una especie en una ubicación específica. Este modelo permite predecir cambios en la distribución de especies debido al cambio climático o la deforestación, y también ayuda a identificar áreas prioritarias para la conservación de la diversidad en el bosque.
En el video de IAC Astrofísica veremos esa teoría:
La teoría de la relatividad de Einstein pertenece al campo de la física moderna, expresa mediante ecuaciones tensoriales que describen cómo la gravedad afecta al espacio y al tiempo.
Estas ecuaciones proporcionan predicciones matemáticas precisas sobre fenómenos como la curvatura del espacio-tiempo y la formación de agujeros negros.
En sistemas dinámicos complejos, como el clima o la economía, se pueden inferir patrones matemáticos a partir de hechos establecidos mediante la observación de comportamientos aparentemente caóticos.
La teoría del caos estudia cómo pequeñas variaciones en las condiciones iniciales de un sistema pueden llevar a resultados completamente diferentes a largo plazo, y se expresa mediante ecuaciones no lineales.
La teoría del caos surgió de la intersección de diversas disciplinas científicas, como la física, las matemáticas y la meteorología, a través del estudio de sistemas dinámicos complejos y su comportamiento impredecible, aunque tiene raíces en diversas disciplinas, su desarrollo moderno se puede atribuir a varios hitos importantes.
Henri Poincaré investigó sistemas dinámicos como el problema de los tres cuerpos en la mecánica celeste. Descubrió fenómenos como la sensibilidad a las condiciones iniciales, sentando las bases para la comprensión del caos.
En la década de 1960, investigadores como Mitchell Feigenbaum exploraron la teoría de bifurcaciones en sistemas dinámicos no lineales, descubriendo patrones repetitivos en el comportamiento caótico.
Edward Lorenz realizó simulaciones meteorológicas con ecuaciones simplificadas y descubrió que pequeñas variaciones en las condiciones iniciales podían llevar a resultados completamente diferentes. Este descubrimiento se conoció como el "efecto mariposa".
Durante esta conferencia, se discutieron los conceptos de estabilidad y transición en sistemas complejos. Robert May presentó un trabajo sobre la dinámica de sistemas de ecuaciones no lineales simples, mostrando que podían exhibir comportamiento caótico.
A partir de estos trabajos y otros, se desarrolló la teoría del caos como una forma de comprender y modelar sistemas dinámicos complejos y no lineales, que exhiben comportamiento sensible a las condiciones iniciales y son inherentemente impredecibles a largo plazo.
La anterior clasificación es un resumen de la consulta realizada a la AI de ChatGPT
Esta representación de principios matemáticos significa traducir conceptos abstractos en formas visuales o simbólicas para comprender y analizar mejor fenómenos naturales, situaciones cotidianas o problemas específicos, es en este punto donde el software de geometría dinámica, las simulaciones y los lenguajes de programación (Java Script y Phyton entre otros) muestran su aporte a la interactividad que facilita la adaptabilidad de los procesos de enseñanza y aprendizaje. Representar un principio implica expresarlo mediante fórmulas matemáticas y gráficos.
El interactivo 3.3 de la página anterior utilizado como recurso del aprendizaje adaptativo permite comprender mediante su aplicación los conceptos medibles y expresados mediante ecuaciones:
Mediante dicha simulación se permiten como objetivos aquellos que facilitan adquirir competencias, entre otros tenemos: la identificación de situaciones en que las fuerzas están equilibradas o desequilibradas, determinar la fuerza neta que actúa sobre objeto como resultado de la suma de fuerzas, predecir el movimiento de un objeto cuando la fuerza neta que se le aplica es igual a cero y además, predicir la dirección de un movimiento dada una combinación de fuerzas.
En las matemáticas existen principios generales básicos entre los que nos encontramos:
En las matemáticas existen principios generales básicos entre los que nos encontramos:
Los modelos matemáticos son una herramienta esencial en la práctica de la ingeniería moderna, ya que nos permiten comprender, describir y predecir el comportamiento de sistemas altamente complejos e interconectados.
El proceso de construcción y aplicación de modelos matemáticos requiere una serie de habilidades y competencias, que incluyen la abstracción, la formulación de ecuaciones y sistemas, la solución de problemas y la validación e interpretación de resultados.
Debido a lo anteriormente expuesto, una exploración de los fundamentos de los modelos matemáticos y su aplicación en el contexto de la ingeniería, a través de ejemplos concretos y detallados que ilustren su potencial y alcance.
Según lo descrito en capítulos anteriores, es fundamental en ingeniería entender que un modelo matemático es una representación simplificada y abstracta de un fenómeno o sistema del mundo real, elaborado mediante la formulación de relaciones y ecuaciones matemáticas entre variables y parámetros que describen las propiedades y el comportamiento del sistema.
Los modelos matemáticos en ingeniería pueden ser de diversos tipos, desde modelos algebraicos y geométricos hasta modelos de ecuaciones diferenciales y sistemas dinámicos. La elección del tipo de modelo y las técnicas de solución dependerán de la naturaleza del problema.
Dominar y la aplicar de manera efectiva de modelos matemáticos en ingeniería es uno de los mayores retos y oportunidades en la educación y la práctica profesional en nuestros tiempos.
En este escenario, solo aquellos profesionales que sean capaces de asimilar y aplicar estas herramientas de manera creativa, eficiente y versátil podrán marcar la diferencia y liderar proyectos y soluciones de ingeniería que realmente contribuyan a la construcción de un mundo mejor y más sustentable para las generaciones futuras.
Un modelo matemático en el contexto de la ingeniería incluye variables, parámetros, ecuaciones y soluciones; Estos elementos juegan un papel crucial en la construcción, comprensión y aplicación de los modelos matemáticos para describir y resolver problemas de la vida real.
Son las cantidades que varían o pueden llevar diferentes valores en el modelo. En la ingeniería civil y en la ingeniería mecánica, por ejemplo, las variables pueden ser las longitudes, los ancho, las alturas, la distribución de cargas y la resistencia de los materiales entre otras.
Las variables son fundamentales para definir las características y propiedades del problema y, en consecuencia, del modelo matemático.
Son constantes que no cambian en el modelo y tienen un valor específico. En los ejemplos del apartado anterior, los parámetros podrían ser las propiedades de los materiales utilizados, como la densidad, el módulo de elasticidad y la resistencia a la tracción.
Los parámetros ayudan a precisar y acotar el modelo, al establecer el marco dentro del cual las variables pueden fluctuar.
Las ecuaciones son las relaciones matemáticas que vinculan las variables y los parámetros en el modelo.
Estas relaciones pueden ser formuladas a partir de leyes físicas, como las leyes de Newton en mecánica o las ecuaciones de continuidad y conservación en fluidos, o mediante supuestos y aproximaciones basadas en la experiencia, el conocimiento o la intuición.
Solucionar un modelo matemático implica resolver las ecuaciones o relaciones matemáticas que componen el modelo. Esto se hace para obtener valores específicos, predecir comportamientos futuros o tomar decisiones informadas.
El comportamiento de un fenómeno o sistema utilizando lenguaje matemático se apoya en los métodos numéricos y algoritmos para encontrar las soluciones.
La ingeniería en sus diversas áreas requiere una variedad de modelos matemáticos que permiten comprender, analizar y resolver problemas. Veamos los modelos básicos que un ingeniero debe aplicar en sus diseños:
La investigación operativa es uno de los campos de la matemática en cuyas bases funciona la optimización, que consiste en maximizar o minimizar una función real eligiendo sistemáticamente determinados valores pertenecientes a la función y recalculado dicha función.
La optimización matemática o programación matemática es la que puede definirse como la selección del mejor elemento (con respecto a algún criterio) de un conjunto de elementos disponibles es un procedimiento útil en matemáticas, estadística, economía, ciencias empíricas y ciencia de la computación y la optimización entre otras.
El cálculo diferencial estudia cómo computar la función que describe el cambio de otra función de variables continuas (operación de orden superior llamada "derivada"), dada $f : A \space \rightarrow \space B$.
Se busca un elemento $x_0$ que cumpla una de las siguientes opciones:
$Minimización$
$$\tag{1} x_0 \in A \space | \space f(x_0) \leq f(x) \space \forall \space x \in \space A $$$Maximización$
$$\tag{2} x_0 \in A \space | \space f(x_0) \geq f(x) \space \forall \space x \in \space A $$Para optimizar una función debemos tener en cuenta las siguientes definiciones cuando una función $f$ está definida en un intervalo $I$:
$$\tag{3} f(x)\nearrow \space \in I \space \Rightarrow \space f(x_1) < f(x_2) $$O sea que $f(x)$ es creciente siempre que $\space \space x_1 \wedge x_2 \in I \wedge x_1 < x_2$
O sea que $f(x)$ es decreciente siempre que $\space \space x_1 \wedge x_2 \in I \wedge x_1 < x_2$
O sea que $f(x)$ es constante siempre que $\space \space x_1 \space = \space x_2 \space \in \space I \space \forall \space x$
Si además de que la función esté definida en el intervalo $I$ y $c$ un número en $I$, entonces:
En palabras de Hoffmann (1988)
La derivada representa:
El cálculo dedica gran esfuerzo a determinar el comportamiento de la función.
Si $f$ está definida en un intervalo $I$ y además contiene un punto $c$ podemos definir los extremos de dicha función:
Si $f$ es continua en un intervalo cerrado $[a, b]$, entonces $f$ posee un $máximo$ y también un $mínimo$ en ese intervalo.
Si $f$ está definida en $c$, se dice que $c$ es un número crítico de $f$ si $f´(c) = 0$ pero también si $f´$ no está definida en $c$. Ello indica que los extremos relativos solo curren en números críticos.
Sea $c$ un número crítico de una $f$ continua en un intervalo abierto $I$ que contiene a $c$. Si $f$ es derivable en el intervalo, excepto tal vez en el valor de $c$, entonces $f(c)$ se caracteriza de la siguiente forma:
Sea $c$ un número crítico de una $f$ continua en un intervalo abierto $I$ que contiene a $c$. Si $f$ es derivable en el intervalo, excepto tal vez en el valor de $c$, entonces $f(c)$ se caracteriza de la siguiente forma:
Es en este punto donde entran en juego los denominados puntos de inflexión donde la gráfica pasa de ser cóncava hacia a ser cóncava hacia abajo o viceversa.
Veamos un recurso acerca de la optimización diseñado por María de Lourdes Velasco Arregui con Descartes
Muchos fenómenos en ingeniería se modelan utilizando ecuaciones diferenciales, ya que describen cómo cambian las variables con respecto al tiempo u otras variables independientes.
Son ecuaciones que poseen derivadas, en proyectos de ingeniería se hace necesario resolver este tipo de ecuaciones para predecir el comportamiento de sistemas dinámicos como circuitos eléctricos, sistemas mecánicos, y fenómenos de transferencia de calor y masa.
Expresan Zill y Wright (2011)
En situaciones en las que el sistema experimenta cambios a lo largo del tiempo, ya sea aumentando o disminuyendo a una tasa específica, siendo esta tasa de cambio una derivada, el modelo matemático del sistema puede manifestarse como una ecuación diferencial.
Si la ecuación contiene derivadas respecto a una sola variable independiente entonces se dice que es una ecuación diferencial ordinaria (E. D. O.).
$$\tag{9} \frac{dy}{dx}-10y = 4 \space \space \space \space \space \space \space \space \space \space 3ydy - (x+4)dx = 0$$ $$\tag{10} \frac{d^2y}{dx^2} - 2\bigg(\frac{dy}{dx}\bigg)^3 + 5y = 0$$Si contiene las derivadas parciales respecto a dos o más variables independientes se llama ecuación en derivadas parciales (E. D. P.).
$$\tag{11} x\frac{∂u}{∂x} + y\frac{∂u}{∂y} = u$$ $$\tag{12} \frac{{∂}^3u}{{∂}x^3} + 4\frac{∂u}{∂t} = \frac{{∂}^2u}{{∂}t^2} $$Se llama orden de la ecuación diferencial al orden de la derivada o derivada parcial más alta que aparece en la ecuación.
En las ecuaciones que aparecen en el numeral (9) son ecuaciones de orden 1, en la ecuación del numeral (10) es de orden 3. Ya en el numeral 11 aparece una E.D.P. de orden 1 y en el numeral(12) nos encontramos una E.D.P. de orden 3.
Una ecuación diferencial (de orden $n$) está expresada en forma implícita cuando tiene la forma
$$\tag{13} F(x, y, y′, . . . , y(n) ) = 0$$Siendo $F$ una función $F: Ω ⊂ R^{n+2} → R$ con $Ω$ un subconjunto (generalmente abierto) de $R^{n+2}$. Dicha ecuación está expresada en forma explícita cuando tiene la forma:
$$\tag{14} y^{n} = f(x, y, y′, . . . , y^{n−1})$$con $f: D \subset R^{n+1} → R$ una función definida en un subconjunto $D$ (generalmente abierto) de $R^{n+1}$
Una ecuación diferencial es lineal si tiene la forma de $(15)$ y se llama lineal homogénea si, además, $g(x) = 0$.
$$\tag{15} a_n(x)\frac{d^{n}y}{dx^{n}}+ a_{n−1}(x)\frac{d^{n−1}y}{dx^{n−1}}+ · · · +\\ a_1(x)\frac{dy}{dx} + a_0(x)y = g(x);$$Decimos que una función $y = ϕ(x)$ definida en un intervalo $I$ (es decir, $ϕ: I ⊂ R → R$) es solución de una ecuación diferencial en el intervalo si, sustituida en dicha ecuación, la reduce a una identidad.
Una E. D. se dice resoluble (o integrable) por cuadraturas si su solución es expresable mediante integrales.
Una ecuación diferencial separable es aquella que puede ser reescrita con todas las ocurrencias de la variable dependiente multiplicando la derivada y todas las ocurrencias de la variable independiente en el otro lado de la ecuación.
Se dice que una ecuación diferencial separable de primer orden es cualquier ecuación $\frac{dy}{dx} = F(x, y)$ que puede escribirse en la forma:
$$\tag{16} \frac{dy}{dx} = g(x)f(y)$$La estrategia más común para resolver este tipo de ecuaciones es separar las variables y luego integrar ambos lados de la ecuación con respecto a sus variables correspondientes.
Esta integración conduce a una solución general que puede incluir una constante arbitraria ya que cuando se integra ambos lados de la ecuación, se pueden incluir constantes de integración en cada lado. Sin embargo, debido a la independencia de estas constantes, se puede agrupar todas en una sola constante de integración en la solución final.
El proceso para resolver ecuaciones diferenciales de variables separadas implica generalmente los siguientes pasos:
Cuando una E.D. de variables separables de orden 1 puede estar sujeta a una condición lateral prescrita del tipo $y(x_0) = y_0$ se denomina problema con valor inicial (PVI), se busca al menos una solución de la ecuación diferencial en el intervalo $I$ que contiene a $x_0$ tal que la curva de la solución pase por el punto ($x_0, y_0$). Estos dos valores son los que permiten encontrar el valor de la constante $C$ al integrar las variables separables.
La ecuación $(15)$ que hace referencia a la ecuación diferencial lineal indica que tanto la variable independiente como su derivada son de primer grado.
Dicho de otra forma indica que la potencia de cada término que implica a la variable dependiente es igual a 1 y que cada coeficiente depende a lo máximo de una solo varaible independiente o sea:
$$a_1(x) \frac{dy}{dx} + x_0(x)y = g(x)$$El proceso para resolver ecuaciones diferenciales lineales implica generalmente los siguientes pasos:
Hasta aquí hemos descrito lo básico de las ecuaciones diferenciales que le permiten a los procesos de ingeniería describir cómo cambian las variables con respecto a sí mismas o a otras variables, y son fundamentales en la modelización de una amplia gama de fenómenos en ciencia, ingeniería y otras áreas.
Entre muchos procesos, las ecuaciones diferenciales permiten modelar cómo cambia el tamaño de una población a lo largo del tiempo en función de factores como la tasa de natalidad, la mortalidad y la interacción con el entorno, otro proceso consiste en describir el comportamiento de corriente y voltaje en circuitos eléctricos complejos.
Además de los ejemplos anteriores, una ecuación diferencial permite predecir el movimiento de objetos en función de fuerzas aplicadas, como en el movimiento de un péndulo o un sistema de resortes, estudiar cómo se mueven los fluidos en respuesta a fuerzas externas, como en el flujo de agua en un río o la dinámica atmosférica y modelar la velocidad de reacción en función de la concentración de reactivos y otros factores entre muchas otras aplaicaciones.
Este modelo, es un campo que permite organizar y analizar campos vectoriales, como campos de velocidades en fluidos, campos gravitatorios alrededor de cuerpos celestes o campos electromagnéticos además, el diseño y análisis de estructuras, el procesamiento de señales y la simulación de sistemas físicos.
Expresan Grossman y Flores
... el estudio de vectores comenzó esencialmente con el trabajo del gran matemático irlandés sir William Hamilton (1805-1865). Su deseo de encontrar una forma de representar un cierto tipo de objetos en el plano y el espacio lo llevó a descubrir lo que él llamó cuaterniones. Esta noción condujo al desarrollo de lo que ahora se conoce como vectores.
Un vector de $n$ componentes se define como un conjunto ordenado de $n$ números escritos como renglón o como columna:
$$\tag{20} \begin{bmatrix} x_1 & x_2 & x_3 & x_n \end{bmatrix} = Vector \space fila \\ \space \space \space \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_n \end{bmatrix} = Vector \space columna $$Hace referencia a estructuras matemáticas fundamentales en álgebra lineal. Formalmente, un espacio vectorial es un conjunto V, sobre un campo F (generalmente los números reales o los números complejos), junto con dos operaciones, la suma vectorial y la multiplicación por un escalar, que satisfacen ciertas propiedades:
En la ingeniería, un espacio vectorial es el análisis de fuerzas en una estructura como el de una grúa que levanta contenedores en un puerto. Las fuerzas aplicadas por los cables de la grúa para levantar esos objetos pesados forman un espacio vectorial.
Los vectores que representan estas fuerzas tienen propiedades como la cerradura bajo la suma (la suma de dos fuerzas aplicadas ofrece como resultado otra fuerza aplicada), la existencia de un vector cero (la fuerza nula), y la distributividad de la multiplicación por escalares (si se multiplica una fuerza por un escalar, se obtiene otra fuerza).
Las funciones vectoriales son fundamentales en diversas áreas, como física, ingeniería, informática gráfica, y ciencias de la computación, se utilizan para modelar y analizar fenómenos que implican cantidades vectoriales, como posición, velocidad, aceleración, fuerza, entre otros.
Son funciones cuyo dominio es un conjunto de números reales (o un intervalo de números reales) y cuyo codominio es un conjunto de vectores. Es decir, a cada valor de la variable independiente se le asigna un vector en el espacio.
Por ejemplo, en física, por ejemplo, una partícula que se mueve en el espacio puede describirse utilizando una función vectorial, es decir que su posición estaría dada por las coordenadas $x(t)$, $y(t)$ y $z(t)$ donde $t$ representa el tiempo. La posición de la partícula en cualquier momento estaría representada por:
Permiten analizar cómo cambian las funciones vectoriales con respecto a cada una de sus variables independientes, se utilizan para entender y calcular el gradiente, la divergencia y el rotacional de campos vectoriales.
En matemáticas, la derivada parcial de una función de varias variables es la derivada con respecto a cada una de esas variables manteniendo las otras como constantes. Las derivadas parciales son usadas en cálculo vectorial y geometría diferencial, se denotan como:
$$\tag{22} \frac{\partial f}{\partial x}, \frac{\partial }{\partial x}f, D_1 f, \partial_x f, f'_x, f_x $$Las derivadas parciales permiten entender cómo cambian los campos vectoriales en diferentes direcciones y proporcionan herramientas para analizar propiedades importantes de estos campos, como la variación de densidad de flujo, la rotación y la tasa de cambio máxima de una función escalar.
En el cálculo vectorial, las integrales múltiples permiten calcular magnitudes que están distribuidas en regiones del espacio tridimensional, como masa, densidad, flujo de un campo vectorial, entre otras. Se utilizan para calcular:
La integral doble de una función positiva de dos variables representa el volumen de la región entre la superficie definida por la función y el plano que contiene el dominio de la función.
Este tipo de integrales permiten calcular el área de una región en el plano XY o calcular el volumen de un sólido en el espacio tridimensional. Estas integrales son esenciales en el cálculo de centroides, momentos de inercia, y en la evaluación de flujos de campos vectoriales a través de superficies bidimensionales.
Según Leithol
Se utilizan para calcular volúmenes de regiones tridimensionales en el espacio, como sólidos o regiones delimitadas por superficies. Además, las integrales triples son fundamentales para calcular masas, centros de masa, momentos de inercia, y para evaluar flujos de campos vectoriales a través de sólidos tridimensionales.
El tipo más simple de región en el espacio tridimensional ($R^3$) es un paralelepído rectangular acotado por seis ($6$) planos:
$$\tag{24} x=a_1,\space x=a_2,\space y=b_1,\space y=b_2,\space z=c_1,\space z=c_2$$en donde:
$$ a_1 \space< \space a_2 \space; \space \space b_1\space < \space b_2 \space; \space \space c_1 \space< \space c_2 $$Por lo tanto, el volumen estaría dado por:
$$\tag{25} \begin{equation} V = \int _{a_1}^{a_2} \int _{b_1}^{b_2} \int _{c_1}^{c_2} f(x,y,z) \cdot dz \cdot dy \cdot dx \end{equation} $$Son integrales empleadas para calcular longitudes de curvas en el espacio y áreas de superficies en el espacio tridimensional, respectivamente. Son fundamentales en el cálculo de trabajo realizado por campos vectoriales a lo largo de trayectorias curvas y en la evaluación de flujos de campos vectoriales a través de superficies.
El gradiente de una función escalar $f$ de varias variables es un campo vectorial que apunta en la dirección de la máxima tasa de cambio de $f$ y cuya magnitud es la tasa de cambio máxima. Se calcula tomando las derivadas parciales de $f$ con respecto a cada una de sus variables.
El gradiente se denota comúnmente por $\nabla f$.
La divergencia de un campo vectorial $F$ mide la variación de densidad de flujo en un punto dado. Se calcula mediante el producto escalar del gradiente y el campo vectorial $F$, es decir, $\nabla \cdot F$. Esta operación implica tomar las derivadas parciales de cada componente del campo vectorial.
En campo vectorial $F$, el rotacional de mide la tendencia de rotación o "giro" de dicho campo alrededor de un punto. Se calcula mediante el operador rotacional, denotado por $\nabla$ x $F$, es un operador que involucra una combinación de derivadas parciales cruzadas de las componentes del campo vectorial.
Según hemos observado, el Modelo de Análisis Vectorial y Cálculo Multivariable para el aprendizaje adaptativo en ingeniería implica combinar una comprensión conceptual sólida, visualización efectiva, aplicaciones prácticas, resolución de problemas, recursos educativos adaptativos y feedback continuo para promover un aprendizaje significativo y eficaz.
El paradigma de la probabilidad y la estadística surge históricamente de diversas contribuciones y desarrollos a lo largo del tiempo. Los fundamentos de la probabilidad, como rama de las matemáticas que estudia los fenómenos aleatorios y estocásticos se remontan al menos al siglo XVII con trabajos de matemáticos como Blaise Pascal y Pierre de Fermat, quienes abordaron problemas relacionados con los juegos de azar. Sin embargo, el enfoque moderno de la teoría de la probabilidad comenzó a tomar forma en el siglo XVIII con los trabajos de matemáticos como Jacob Bernoulli y Thomas Bayes.
Por otro lado, el desarrollo de la estadística como disciplina formal se aceleró en el siglo XIX con el trabajo pionero de estadísticos como Sir Francis Galton, Adolphe Quetelet y Sir Ronald Fisher, quienes sentaron las bases para la teoría estadística moderna, incluyendo conceptos como la distribución normal, la regresión y la inferencia estadística.
Como modelo matematico, la estadística se distribuye básicamente como aparece en la imagen:
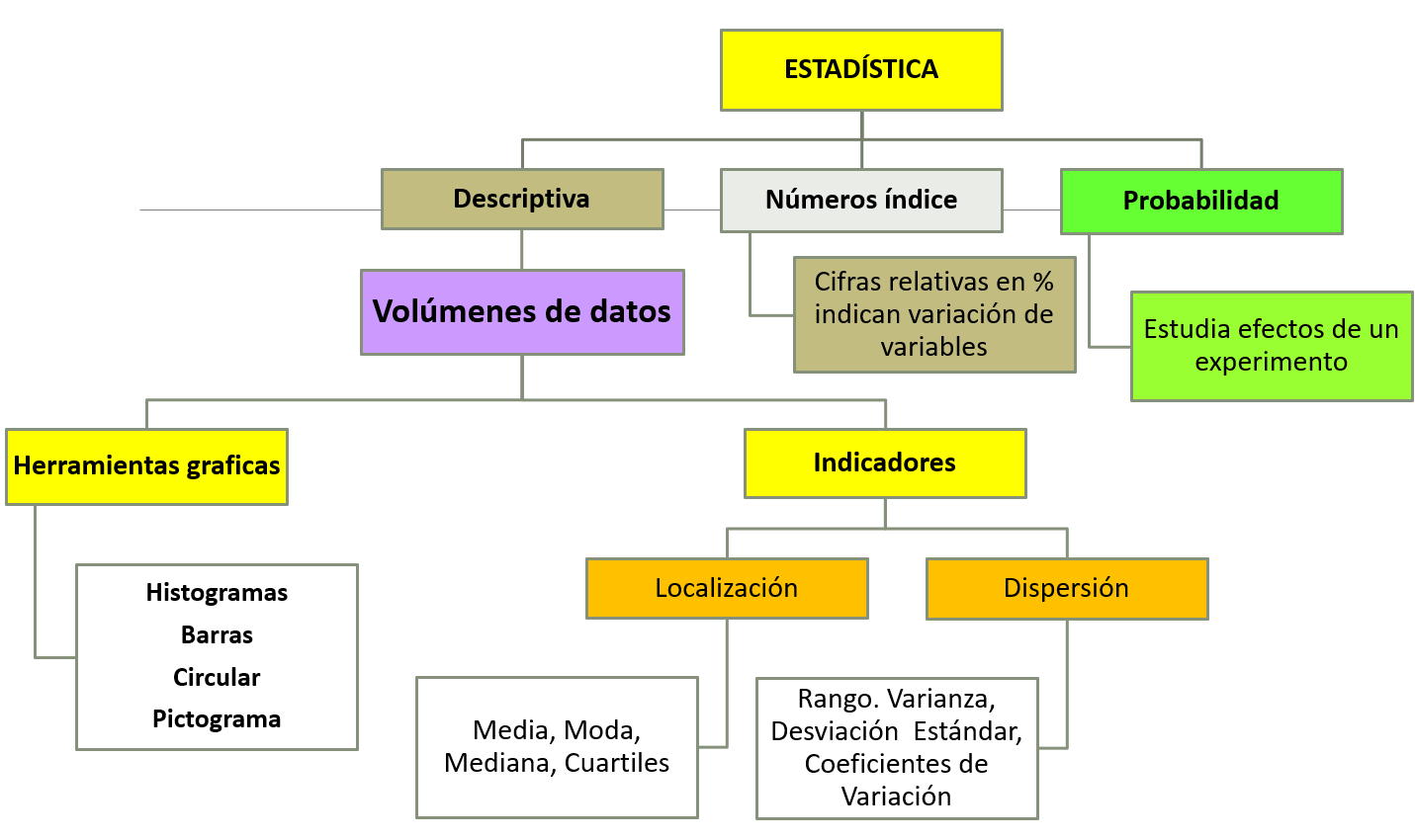
La probabilidad es la matematización de la incertidumbre y, al igual que los modelos descritos hasta el momento se sustentan con ecuaciones y la manipulación de los datos tiene como punto de partida las técnicas de conteo:
El principio fundamental de conteo se soporta en:
Si una tarea o acción puede realizarse de 𝑚 formas diferentes, y otra tarea o acción puede realizarse de 𝑛 formas diferentes, pero de modo que no es posible realizarlas simultáneamente, entonces, tendremos $𝑚+𝑛$ formas diferentes de realizar una de ellas.
Si un procedimiento o actividad puede descomponerse en las etapas primera y segunda, y existen m resultados posibles para la primera etapa y si, para cada uno de estos resultados, existen 𝑛 resultados posibles para la segunda etapa, entonces el procedimiento total puede realizarse, en el orden dado, de $𝑚· 𝑛$ formas.
Un modelo probabilístico es la descripción matemática de un fenómeno aleatorio y sus elementos son:
La probabilidad de un suceso es un número, comprendido entre 0 y 1, que indica las posibilidades que tiene de verificarse cuando se realiza un experimento aleatorio.
𝑆𝑖 𝑡𝑜𝑑𝑜𝑠 𝑙𝑜𝑠 𝑟𝑒𝑠𝑢𝑙𝑡𝑎𝑑𝑜𝑠 𝑑𝑒 𝑢𝑛 𝑒𝑠𝑝𝑎𝑐𝑖𝑜 𝑚𝑢𝑒𝑠𝑡𝑟𝑎𝑙 𝑠𝑜𝑛 𝑖𝑔𝑢𝑎𝑙𝑚𝑒𝑛𝑡𝑒 𝑝𝑟𝑜𝑏𝑎𝑏𝑙𝑒𝑠, 𝑦 𝑢𝑛 𝑛ú𝑚𝑒𝑟𝑜 𝒂 𝑑𝑒 𝑒𝑙𝑙𝑜𝑠 𝑠𝑜𝑛 𝑓𝑎𝑣𝑜𝑟𝑎𝑏𝑙𝑒𝑠 𝑎𝑙 𝑒𝑣𝑒𝑛𝑡𝑜 𝐸, 𝑦 𝑙𝑜𝑠 𝑟𝑒𝑠𝑡𝑎𝑛𝑡𝑒𝑠 𝒃 𝑠𝑜𝑛 𝑑𝑒𝑠𝑓𝑎𝑣𝑜𝑟𝑎𝑏𝑙𝑒𝑠 𝑎 𝐸, 𝑒𝑛𝑡𝑜𝑛𝑐𝑒𝑠 𝑙𝑎𝑠 𝑝𝑜𝑠𝑖𝑏𝑖𝑙𝑖𝑑𝑎𝑑𝑒𝑠 𝑎 𝑓𝑎𝑣𝑜𝑟 𝑑𝑒 𝐸 𝑠𝑜𝑛 𝑑𝑒 𝒂 a 𝒃 𝑦 𝑙𝑎𝑠 𝑝𝑜𝑠𝑖𝑏𝑖𝑙𝑖𝑑𝑎𝑑𝑒𝑠 𝑒𝑛 𝑐𝑜𝑛𝑡𝑟𝑎 𝑑𝑒 𝐸 𝑠𝑜𝑛 𝒃 a 𝒂
Sea $E$ un evento en el espacio muestral $S$. Esto es, $E$ es un subconjunto de $S$, entonces:
$$\tag{26} 0 \leq {P(E)} \leq 1 \newline {P(\phi)}=0 \newline {P(S)} = 1$$Expresados de otra forma podemos decir que:
Para todo evento $A$ se tiene que $P(A)\geq 0$
Si $A$ y $B$ son dos eventos disjuntos (En matemáticas, dos conjuntos son disjuntos si no tienen elementos en común, es decir, si su intersección es el conjunto vacío) necesariamente se cumple que $P(A \cup B) = P(A) + P(B)$
En cualquier situación probabilística, la certeza total equivale a una probabilidad de 1, mientras que la imposibilidad total equivale a una probabilidad de 0. Por lo tanto, todos los eventos posibles deben tener una probabilidad asignada entre 0 y 1, inclusive: $P(\Omega) = 1$
En la figura podemos observar un diagrama de Venn donde se alojan los experimentos aleatorios dentro del espacio muestral que deben cumplir los axiomas que se detallaron.
Un evento o suceso seguro al que se denomina $E$ que está formado por todos los posibles resultados (es el espacio muestral) da origen a la probabilidad teórica conocida como regla de Laplace:
Empíricamente dicha probabilidad se expresa como:
$$\tag{28} P(E) = \frac{N^° \space de \space veces \space que \space tuvo \space lugar \space el \space evento \space E}{N^° \space de \space veces \space que \space se \space realizó \space el \space experimento}$$En la realización de un determinado experimento, dos eventos cualesquiera no pueden ocurrir al mismo tiempo, se denominan mutuamente excluyentes.
Si $A$ y $B$ son dos eventos cualesquiera la suma de las probabilidades es:
$$\tag{29} P(A \cup B) = P(A) + p(B) - p(A \cap B)$$La probabilidad del evento $B$, calculada bajo la suposición de que el evento $A$ ya ha ocurrido, se denomina probabilidad condicional de $B$ y se denota como $P(B|A)$.
Ahora, dos eventos $A$ y $B$ son independientes si el conocimiento de la incidencia de uno de ellos no tiene efecto en en la probabilidad de la ocurrencia del otro o sea $P(B|A) = P(B)$.
Si $A$ y $B$ son dos eventos cualesquiera:
$$\tag{30} P(A \cap B) = P(A)\cdot P(B|A)$$Si $A$ y $B$ son dos eventos independientes:
$$\tag{31} P(A \cap B) = P(A)\cdot P(B)$$Las anteriores expresiones son herramientas fundamentales por su capacidad para modelar y analizar el comportamiento aleatorio y la incertidumbre en una variedad de sistemas y procesos entre los que podemos citar:
La estadística descriptiva y la teoría de probabilidad son utilizadas para analizar la variabilidad en los procesos de fabricación y para establecer límites de control que ayuden a mantener la calidad del producto. Según Ishikawa "practicar el control de calidad es desarrollar, diseñar, manufacturar y mantener un producto de calidad que sea el más económico, el más útil y siempre satisfactorio para el consumidor"
La estadística experimental se utiliza para planificar y analizar experimentos con el fin de identificar los factores que afectan un proceso o sistema, y optimizar su rendimiento, se hace necesario tener en cuenta según lo expresan Melo et al
La experimentación es una herramienta poderosa para probar teorías, generar conocimiento nuevo y proporcionar evidencia empírica para respaldar o refutar afirmaciones científicas. Es fundamental para el avance de la ciencia y la tecnología en muchas áreas del conocimiento.
La experimentación generalmente sigue un proceso sistemático que incluye los siguientes pasos:
Se establece una proposición o suposición sobre la relación entre variables que se va a investigar y el posible resultado que se puede obtener.
La estructura se soporta definiendo las variables independientes (las que se manipulan), las variables dependientes (las que se miden como resultado) y cualquier variable de control que se mantenga constante, así como datos irrelevantes en el experimento.
Se elige el grupo de sujetos, muestras o unidades experimentales que participarán en el estudio, representando la población de interés y que posean características similares dentro de un contexto.
Se lleva a cabo la intervención planificada sobre las variables independientes según el diseño experimental.
Se registran y recopilan los datos relevantes de las variables dependientes antes, durante y después de la manipulación de las variables independientes.
Se aplican técnicas estadísticas y de análisis para examinar los datos recopilados y determinar si hay efectos significativos de las variables independientes sobre las variables dependientes.
Se interpretan los resultados del análisis de datos en términos de la hipótesis planteada, evaluando si se confirma o se rechaza dependiendo de la magnitud del error que respalda dicha decisión.
Se informan los hallazgos del experimento a través de informes, artículos científicos, presentaciones u otros medios de comunicación académica. Para los ingenieros, la experimentación es un método de investigación que implica la manipulación deliberada de variables en un entorno controlado para observar y medir los efectos producidos por dicha manipulación.
La teoría de la fiabilidad utiliza métodos probabilísticos para evaluar la confiabilidad de sistemas y componentes, lo que ayuda en la toma de decisiones sobre mantenimiento preventivo y predictivo.
Es una estrategia de gestión de activos que implica la realización de actividades de mantenimiento planificadas de manera regular con el objetivo de prevenir fallos, reducir el riesgo de averías y prolongar la vida útil de los equipos, máquinas o sistemas.
Ello implica que en lugar de esperar a que ocurra una falla o un problema, el mantenimiento preventivo se lleva a cabo de forma proactiva según un programa establecido, que puede basarse en el tiempo transcurrido, el uso del equipo o ciertos indicadores de desgaste.
Estas actividades pueden incluir inspecciones regulares, lubricación, ajustes, limpieza, calibración y reemplazo de componentes según sea necesario, acciones que se traducen en:
Según IBM este tipo de mantenimiento se define como:
"El mantenimiento predictivo (PdM) se fundamenta en la monitorización basada en las condiciones para optimizar el rendimiento y la vida útil de los equipos mediante la evaluación continua de su estado en tiempo real. Al recopilar datos de sensores y aplicar herramientas y procesos analíticos avanzados como el aprendizaje automático (ML), el mantenimiento predictivo puede identificar, detectar y abordar los problemas a medida que ocurren, así como predecir el posible estado futuro del equipo y, por lo tanto, reducir el riesgo. La clave es proporcionar la información correcta en el momento adecuado a las personas adecuadas"
La estadística y la probabilidad se utilizan para modelar sistemas complejos y simular su comportamiento bajo diferentes condiciones. Esto es fundamental en áreas como la ingeniería de sistemas, la ingeniería de software y la ingeniería de procesos.
Recordemos que un modelo es un conjunto de ecuaciones que representa procesos, variables y relaciones entre las variables que describen un fenómeno del mundo que nos rodea y se caracteriza porque:
El aprendizaje adaptativo es una metodología de enseñanza que se adapta al ritmo de aprendizaje y a las necesidades individuales de cada estudiante, haciendo uso de las tecnologías, permitiendo la educación mixta, presencial y en línea; orientada a analizar los aciertos académicos y los errores de los estudiantes, así que el aprendizaje es adaptado a tiempo real y permite conocer justamente donde el estudiante requiere tener ayuda y apoyo, permitiendo al profesor conocer las fortalezas y debilidades de cada uno de sus estudiantes tal como lo relacionan Rubiales(2021)
El aprendizaje adaptativo con enfoque STEM+H representa un nuevo paradigma educativo que busca fusionar saberes de disciplinas como ciencia, tecnología, ingeniería y matemáticas con las humanidades, con dicha fusión se buscar formar individuos y profesionales con una visión más amplia y holística con habilidades en diversos campos.
Esta integración no solo aborda los retos multidisciplinarios del mundo actual, sino que también fomenta una educación más humanista y ética en una sociedad cada vez más globalizada y digitalizada. La implementación del enfoque STEM+H nos conduce hacia un nuevo panorama educativo en el siglo XXI, donde el conocimiento técnico se combina armónicamente con la reflexión, la creatividad y el sentido humanitario.
El aprendizaje adaptativo como metodología presenta bastantes beneficios a los estudiantes e igualmente a los profesores, destacamos en la figura adaptada de "Compartir Palabra Maestra" , los beneficios que relaciona Morillo (2016)
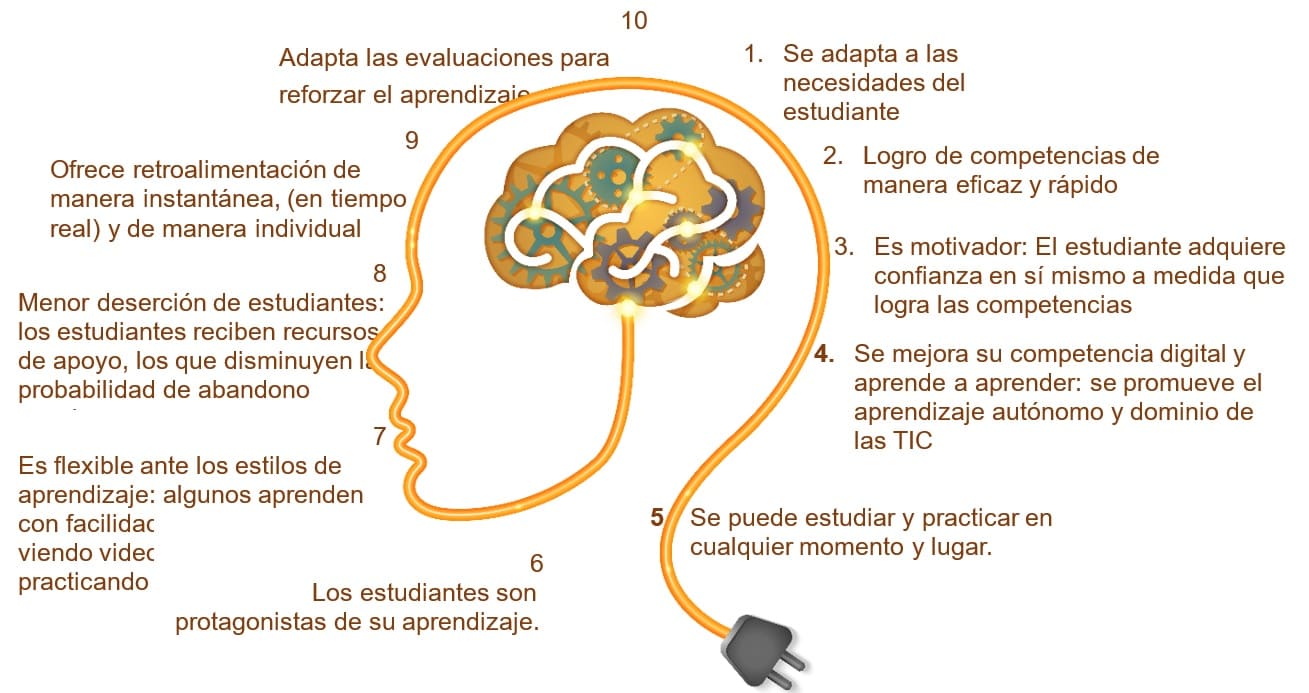
El aprendizaje adaptativo se adapta al ritmo y estilo de aprendizaje de cada estudiante, lo que puede mejorar la comprensión y e interiorización del material en estudio.
Los estudiantes pueden sentirse más motivados y comprometidos con su propio aprendizaje estando frente a esta metodología del aprendizaje adaptativo, ya que pueden sentir progreso académico, y tener posibilidad de recibir retroalimentación inmediata como describe UNIR (2021)
El aprendizaje adaptativo puede ser más eficiente que los métodos de enseñanza tradicionales, le permite a los estudiantes avanzar rápidamente en áreas en las que ya tienen competencia, y lo enfoca en áreas donde necesitan más apoyo, puesto que las actividades y los contenidos y los estilos de aprendizaje son adaptados automáticamente a sus necesidades, lo que influye directamente en obtener mayor participación y aprobación, manifestándose directamente en disminuir la deserción estudiantil tal como lo describe Pearson (2022)
El software de aprendizaje adaptativo puede identificar rápidamente cuando un estudiante presenta algún inconveniente con un tema o concepto en particular, lo que permite a los maestros intervenir lo más rápido posible para brindar su apoyo (Linkous, 2020)
Una retroalimentación personalizada para cada estudiante, lo que puede ayudarlos a entender sus errores y a mejorar en el tema que se trate e incluso en un área específica (Trends, 2019)
La definición y fundamentos del enfoque STEM+H se basa en la inclusión de disciplinas de ciencias, tecnología, ingeniería y matemáticas (STEM, por sus siglas en inglés) junto con las de humanidades (H), creando una interconexión educativa que aborda diferentes dimensiones del pensamiento humano como sus objetivos principales y crucial en la educación del siglo XXI.Esta combinación tiene como objetivo no solo mejorar la comprensión y aplicación de los conocimientos de ciencias y tecnología, sino también enriquecer el aprendizaje con habilidades y conocimientos adquiridos en las disciplinas de humanidades.
En primer lugar, es necesario abordar la definición de STEM y humanidades de forma individual para poder luego comprender cómo su combinación es fundamental en el enfoque STEM+H. STEM es un acrónimo que engloba las disciplinas de ciencias, tecnología, ingeniería y matemáticas, y hace hincapié en la integración y aplicación de estas disciplinas en actividades y proyectos de aprendizaje.
Por otro lado, las humanidades incluyen disciplinas como la literatura, filosofía, historia, arte y lenguas, las cuales dota a los estudiantes con habilidades críticas y analíticas y les enseña a cuestionar, reflexionar y comprender el mundo a su alrededor.
El enfoque STEM+H es fundamental en la educación contemporánea para preparar a los estudiantes para los desafíos del siglo XXI, ya que fomenta la aplicación de conocimientos y habilidades en situaciones reales y promueve la colaboración, el pensamiento crítico, la capacidad de innovación y solución de problemas y la toma de decisiones ética e informada.
Este enfoque plantea la necesidad de ir más allá de la enseñanza compartimentada entre disciplinas e integrar conceptos, metodologías y habilidades de ambas áreas para acercar a los estudiantes a una educación más completa y holística.
Son principios enfocados a garantizar que se alcance un equilibrio adecuado y complementario entre las habilidades y conocimientos técnicos requeridos en las disciplinas STEM y las habilidades analíticas y reflexivas impartidas por las humanidades. La escena de la página siguiente ilustra estos principios clave.
Ciertamente, la adaptación y adopción de estos principios clave para la enseñanza STEM+H no es una tarea sencilla. Requiere una profunda transformación en el paradigma educativo y una constante actualización y capacitación por parte de los docentes.
No obstante, al llevar a cabo esta integración, la educación STEM+H se convierte, más allá de un modelo meramente técnico y utilitario, en una verdadera herramienta de preparación para los desafíos actuales y futuros en nuestra sociedad globalizada tal como lo describen Bernate y Guativa (2020)
Con estos principios en mente, podemos profundizar en la identificación de las habilidades y competencias esenciales que los estudiantes deben adquirir a través de la educación STEM+H adaptativa. Este tema permitirá completar el panorama de cómo este enfoque conduce a la formación de individuos y profesionales capaces de enfrentar un mundo complejo y en constante cambio con creatividad, empatía y responsabilidad.
La educación STEM+H adaptativa se caracteriza por integrar de manera dinámica y personalizada conocimientos técnicos, científicos y humanísticos en la enseñanza. Para lograr una formación integral en estas disciplinas y enfrentar los desafíos y oportunidades del mundo actual, es fundamental identificar y desarrollar habilidades y competencias esenciales en los estudiantes. En este apartado, exploraremos algunas de estas habilidades y competencias, presentando ejemplos concretos y situaciones en las que se manifiestan en el contexto educativo STEM+H adaptativo.
Uno de los aspectos clave en la adquisición de habilidades y competencias en STEM+H es el pensamiento crítico y analítico como se describe lo veremos en el video de "Educación para la vida". Los estudiantes deben ser capaces de comprender y utilizar conceptos científicos, matemáticos y tecnológicos para analizar problemas y proponer soluciones creativas.
Por ejemplo, al enfrentar un problema de contaminación ambiental, un estudiante con sólidas habilidades analíticas podría identificar las variables intervinientes y las posibles relaciones entre ellas, reflexionar sobre el impacto a corto y largo plazo en la comunidad y proponer estrategias innovadoras para mitigar este problema.
Otra habilidad esencial en la educación STEM+H adaptativa es la comunicación y colaboración.
En la era digital, la competencia en el uso de tecnologías de la información y comunicación (TIC) también es crucial en la educación STEM+H adaptativa. Los estudiantes deben aprender a utilizar de manera responsable y crítica diversas herramientas y recursos digitales para buscar información, analizar y procesar datos, comunicarse con otros y realizar trabajos académicos y profesionales.
Además de lo anterior, deben estar preparados para adaptarse a nuevas tecnologías y plataformas emergentes en el campo de la educación digital.
La capacidad de aprendizaje autónomo y autorregulación también es fundamental en un enfoque adaptativo STEM+H. La personalización del aprendizaje implica que cada estudiante tenga la responsabilidad de establecer objetivos, realizar un seguimiento de su propio progreso y ser consciente de sus fortalezas y debilidades. Por ejemplo, un estudiante que tiene dificultades en matemáticas puede reconocer su necesidad de dedicar más tiempo a esta área o buscar apoyo adicional, al mismo tiempo que mantiene un buen rendimiento en otras áreas, como la historia o las ciencias sociales.
La creatividad y la innovación son habilidades esenciales para enfrentar problemas y desafíos del mundo actual, que exigen soluciones nuevas y originales. Los estudiantes en STEM+H adaptativo deben ser capaces de explorar diferentes puntos de vista, imaginar escenarios alternativos y proponer soluciones disruptivas e innovadoras.
Un ejemplo de ello ocurre si en un proyecto de diseño de una ciudad sostenible, los alumnos podrían pensar en cómo integrar fuentes de energía renovables, sistemas de transporte público eficientes y espacios verdes con la participación activa de los ciudadanos.
Por último, la ética y la responsabilidad social también son competencias fundamentales en la educación STEM+H adaptativa. Al abordar problemas complejos y de relevancia global, los estudiantes deben aprender a reflexionar sobre las implicaciones éticas y sociales de sus acciones e ideas, y tomar decisiones que contribuyan al bienestar de la comunidad y el medio ambiente.
Podemos visualizar la posibilidad de que, al investigar sobre la extracción y uso de recursos naturales, los estudiantes deben considerar aspectos como la equidad en el acceso a estos recursos y los impactos ambientales de su explotación.
En conclusión, la identificación y desarrollo de habilidades y competencias esenciales en la educación STEM+H adaptativa es crucial para formar estudiantes y profesionales capaces de enfrentar un mundo complejo y en constante cambio con creatividad, empatía y responsabilidad.
La interacción y complementariedad entre estos elementos en cada alumno permitirá un aprendizaje profundo y significativo, y trascenderá en sus vidas más allá del ámbito académico, convirtiéndolos en ciudadanos activos y comprometidos en la construcción de un mundo mejor y más sostenible.
Al pasar a la siguiente sección, discutiremos cómo se dará la interdisciplinariedad y trabajo colaborativo en la enseñanza STEM+H adaptativa, y cómo estos elementos se interconectan con las habilidades y competencias discutidas para generar aprendizajes profundos y transformadores.
La interdisciplinariedad y el trabajo colaborativo son características fundamentales del enfoque STEM+H adaptativo, ya que permiten abordar problemas y desafíos complejos desde una perspectiva más amplia y enriquecedora.
En este apartado, exploraremos cómo estos conceptos se interrelacionan en la enseñanza, presentando ejemplos concretos y reflexiones teóricas que demuestren la importancia de la integración disciplinaria y la colaboración en la educación adaptativa.
La interdisciplinariedad se refiere a la combinación y conexión de diferentes campos de conocimiento en el proceso de aprendizaje.
En el enfoque STEM+H adaptativo, esto significa que no solo se busca enseñar conceptos y habilidades de ciencias, tecnología, ingeniería, matemáticas y humanidades de manera separada, sino también integrar y conectar estos conocimientos en un marco comprensivo que permita a los estudiantes explorar problemas y temáticas desde diversas perspectivas.
Este tipo de enfoque interdisciplinario no solo fomenta la convergencia de distintas disciplinas, sino también el trabajo colaborativo entre los estudiantes y docentes. Como mencionamos anteriormente, estudiantes de diferentes campos de estudio deben colaborar en un mismo proyecto, lo que implica saber comunicarse, escuchar y aprender de los demás, así como aportar sus propios conocimientos y puntos de vista.
El trabajo colaborativo en la enseñanza STEM+H adaptativa va más allá de la simple agrupación de estudiantes en equipos, ya que este tipo de aprendizaje implica la co-construcción de conocimientos y la asunción de responsabilidades compartidas. Así, en lugar de depender únicamente de las explicaciones y directrices del docente, los alumnos se convierten en agentes activos en su proceso de aprendizaje, aportando ideas y soluciones a problemas a través del diálogo y la colaboración.
Para lograr una enseñanza efectiva basada en la interdisciplinariedad y el trabajo colaborativo en STEM+H adaptativo, es fundamental tener en cuenta ciertos aspectos pedagógicos y metodológicos:
Inicialmente el docente debe estar preparado para guiar y facilitar el trabajo en equipo y la discusión interdisciplinaria
Lo anterior implica no solo tener un sólido conocimiento en su propio campo, sino también mantenerse actualizados en otros campos relacionados.
Además, se necesita una constante retroalimentación para que los estudiantes puedan evaluar sus propias contribuciones y estrategias de colaboración, y ajusten sus habilidades y actitudes en función de las necesidades del proyecto y del grupo.
Una experiencia concreta que ilustra la efectividad de la interdisciplinariedad y el trabajo colaborativo en la enseñanza STEM+H adaptativa es la realización de proyectos en los que se aborda el diseño y construcción de prototipos de dispositivos o sistemas tecnológicos.
En estos proyectos, la colaboración entre estudiantes de distintas disciplinas, como ingeniería electrónica, programación, diseño industrial y ciencias sociales, resulta en soluciones más innovadoras y contextualizadas, haciendo posible el desarrollo de productos o servicios tecnológicos que respondan efectivamente a las necesidades y demandas de la sociedad.
Equilibrando lo teórico con lo práctico, la educación adaptativa STEM+H confirma el argumento central: la suma de todos los elementos disciplinarios es mayor que sus partes individuales.
Al comprender y aplicar efectivamente el enfoque interdisciplinario y colaborativo en la enseñanza adaptativa, los educadores y estudiantes pueden transformar la educación STEM+H en una experiencia de aprendizaje profunda y significativa, contribuyendo al desarrollo de habilidades y competencias esenciales para enfrentar los desafíos sociales y ambientales que nos plantea el siglo XXI.
La articulación entre estos conceptos y las habilidades y competencias discutidas en la sección anterior representa un camino prometedor para la formación de ciudadanos y profesionales ingeniosos y reflexivos, capaces de co-crear un mundo más sostenible y equitativo.
El diseño curricular y la implementación de metodologías activas en la integración de contenidos adaptativos STEM+H representan un reto y una oportunidad para transformar la enseñanza y el aprendizaje en nuestras escuelas y universidades. Pero ¿qué son las metodologías activas? Veamos el siguiente video de Sprouts Español acerca del tema:
Para abordar este desafío, es necesario un profundo entendimiento de los principios, teorías y prácticas pedagógicas que respaldan una educación STEM+H adaptativa.
Además de lo anterior, se requiere poseer también la capacidad de innovar y adaptar estas ideas al contexto específico en el que se enseña y aprende.
En el diseño curricular, uno de los aspectos clave es el entendimiento de que los alumnos tienen diferentes estilos de aprendizaje, ritmos, conocimientos previos y habilidades. Por lo tanto, es necesario estar dispuesto a ajustar los contenidos y métodos de enseñanza para satisfacer estas necesidades individuales, lo que se logra a través de un proceso constante de reflexión, revisión y adaptación.
Es importante también considerar en el diseño curricular la integración de tecnologías educativas y plataformas digitales que faciliten la adaptación y personalización de los contenidos. Sin embargo, es fundamental que la adopción de estas herramientas no sea una simple sustitución de los recursos y métodos tradicionales, sino que se utilice de manera estratégica y planificada para potenciar y transformar la enseñanza de STEM+H.
Una práctica común del profesor de matemáticas es incorporar el uso de software de geometría dinámica en sus clases, permitiendo a los alumnos explorar y manipular objetos geométricos de manera interactiva y adaptada a su nivel de habilidad y comprensión.
De esta manera, cuando se recurre a dicho tipo de software se promueve un aprendizaje más activo, visual y lúdico, que ayuda a los estudiantes a construir comprensiones más profundas y duraderas de los conceptos matemáticos.
En conclusión, el diseño curricular y la implementación de metodologías activas para la integración de contenidos adaptativos STEM+H representan un desafío y una oportunidad para repensar y transformar la educación de nuestros alumnos en el siglo XXI.
Al adoptar un enfoque interdisciplinario, flexible y centrado en las necesidades y capacidades individuales de los estudiantes, se allana el camino hacia una enseñanza más integral, inclusiva y transformadora, en la que se cultivan habilidades y competencias esenciales para enfrentar un mundo complejo y en constante cambio.
La enseñanza integradora de STEM+H se basa en la idea de que el conocimiento y las habilidades adquiridas en ciencias, tecnología, ingeniería, matemáticas y humanidades no deben ser vistas como entidades separadas y aisladas, sino como elementos interconectados esenciales para abordar desafíos y problemas complejos en el mundo actual.
Dentro de este enfoque, las metodologías activas desempeñan un papel crucial en la promoción de un aprendizaje significativo e interdisciplinario, al colocar al estudiante en el centro del proceso educativo y facilitar la construcción de conocimientos y la adquisición de habilidades en un contexto colaborativo y contextualizado.
A continuación, se presentan algunos enfoques y metodologías activas que han demostrado ser particularmente efectivos en la enseñanza integradora de STEM+H:
Esta metodología permite a los estudiantes abordar problemas y desafíos del mundo real a través de proyectos interdisciplinarios y colaborativos que integran conocimientos y habilidades en STEM+H.
Veamos una posibilidad: un proyecto que involucre la construcción de un vehículo alimentado por energía solar requeriría conocimientos de física, matemáticas, ingeniería y tecnología, así como habilidades para analizar el impacto medioambiental y social, y comunicar efectivamente sus ideas y propuestas. La experiencia de trabajar en un proyecto real fomenta la responsabilidad, la autonomía y la creatividad, al mismo tiempo que permite a los estudiantes contextualizar y aplicar sus aprendizajes de manera significativa y personalizada.
Similar al ABP, este enfoque se centra en la resolución de problemas del mundo real, pero con un mayor énfasis en el proceso de investigación y la adquisición de habilidades de pensamiento crítico y analítico.
Como aplicación de la estrategia, los estudiantes podrían ser desafiados a analizar y proponer soluciones a una crisis de escasez de agua en una región específica, utilizando conocimientos de ciencias naturales, matemáticas y estudios sociales, así como habilidades para analizar datos, evaluar evidencias y comunicar sus hallazgos y propuestas persuasivamente.
Este enfoque promueve la interacción y el trabajo en equipo entre los estudiantes, fomentando la responsabilidad individual y la colaboración en el logro de objetivos comunes. Al trabajar juntos en tareas y proyectos que requieren habilidades y conocimientos en STEM+H, los estudiantes aprenden a valorar las perspectivas, experiencias y conocimientos de sus compañeros, y a desarrollar habilidades interpersonales y comunicativas clave para el éxito en el ámbito profesional y personal.
Mediante esta estrategia, los estudiantes adquieren conocimientos previos de manera autónoma, utilizando recursos en línea como videos, lecturas o podcasts, antes de participar en actividades prácticas y colaborativas en el aula que les permiten aplicar y consolidar sus aprendizajes.
El aprendizaje invertido en STEM+H puede facilitar la personalización y adaptabilidad del aprendizaje, al permitir a los estudiantes progresar a su propio ritmo y nivel de habilidad y a los docentes a enfocarse en la resolución de problemas y el trabajo colaborativo durante el tiempo en clase.
Este enfoque se centra en la creatividad y la innovación como elementos fundamentales para resolver problemas e identificar oportunidades en STEM+H. A través de un proceso estructurado pero flexible, los estudiantes aprenden a comprender las necesidades y expectativas de los usuarios, generar ideas y prototipos, y evaluar y mejorar sus propuestas en función de la retroalimentación y la iteración.
El pensamiento de diseño fomenta una mentalidad de crecimiento, adaptabilidad y empatía, habilidades esenciales para enfrentar los desafíos y cambios del siglo XXI.
Al adoptar una perspectiva interdisciplinaria y centrada en el aprendizaje activo, es posible crear ambientes educativos en los que los estudiantes se sientan motivados, comprometidos e inspirados para explorar y transformar el mundo a través de sus habilidades y conocimientos en ciencia, tecnología, ingeniería, matemáticas y humanidades.
Por supuesto, estos enfoques y metodologías activas no son mutuamente excluyentes y pueden combinarse para enriquecer y diversificar la enseñanza STEM+H adaptativa.
En última instancia, la clave para un enseñanza integradora de STEM+H exitosa radica en la capacidad de los docentes y educadores para diseñar, implementar y adaptar sus enfoques y metodologías a las necesidades, intereses y potencialidades de cada estudiante en su diversidad y singularidad, construyendo así puentes y conexiones entre las disciplinas y las experiencias de aprendizaje que permiten a los alumnos ver y comprender la complejidad y la interdependencia del mundo que les rodea y al que pueden contribuir en formas significativas y creativas.
El proceso de diseño e implementación de currículos adaptativos en STEM+H es un elemento fundamental para fomentar la enseñanza interdisciplinaria, personalizada y dinámica, potenciando el aprendizaje y el desarrollo de habilidades y competencias esenciales en el siglo XXI. Sin embargo, como todo proceso complejo y multifacético, el diseño e implementación de currículos adaptativos en STEM+H enfrenta desafíos y etapas que requieren de una adecuada planificación, seguimiento y evaluación. A continuación, se describen algunos pasos clave y ejemplos prácticos en este ámbito.
Antes de diseñar un currículo adaptativo en STEM+H, es fundamental llevar a cabo un diagnóstico y análisis de las necesidades y características del contexto educativo en el que se implementará.
Esto implica, por ejemplo, identificar las habilidades y competencias previas de los estudiantes, los recursos y capacidades disponibles, las políticas educativas y los estándares de nivel, así como conocer los intereses y expectativas de la comunidad educativa involucrada.
Un ejemplo práctico sería realizar encuestas, entrevistas y observaciones en el aula para detectar los estilos y niveles de aprendizaje de los estudiantes, así como sus preferencias, inquietudes y dificultades en las diferentes áreas STEM+H. Con estos datos, se puede elaborar un perfil de alumno adaptativo que servirá de base para la planificación e implementación del currículo y las estrategias de enseñanza.
En función de las necesidades y contextos identificados, se deben establecer objetivos y competencias claros, medibles y alcanzables en términos del aprendizaje adaptativo en STEM+H.
Estos objetivos y competencias deben contemplar tanto aspectos disciplinarios específicos (como el dominio de conceptos y habilidades en ciencias, tecnología, ingeniería, matemáticas y humanidades) como aspectos transversales e interdisciplinarios (como el pensamiento crítico, la creatividad, la comunicación y la colaboración).
A manera de ejemplo observemos el siguiente objetivo con el cual se trataría de cumplir lo anterior:
"Desarrollar habilidades para resolver problemas complejos y realistas en el contexto de la sostenibilidad ambiental, a través de la aplicación e integración de conocimientos y competencias en ciencias, matemáticas, tecnología, ingeniería y humanidades".
La consecución de este objetivo requeriría del diseño de experiencias de aprendizaje y evaluación que impliquen la colaboración e interacción entre las diferentes disciplinas STEM+H.
Con base en los objetivos y competencias definidos, se deben diseñar e integrar estrategias y metodologías activas y adaptativas que permitan a los alumnos apropiarse y aplicar los contenidos STEM+H de acuerdo a sus estilos, intereses y niveles de aprendizaje. Esto implica, por ejemplo, la implementación de proyectos interdisciplinarios, el uso de plataformas digitales adaptativas, o la incorporación de la evaluación formativa y personalizada en el aula.
Un ejemplo práctico podría ser la implementación de un proyecto de aprendizaje basado en proyectos (ABP) que involucre el diseño y construcción de una solución tecnológica para reducir el consumo de energía en un hogar.
El proyecto implicaría aplicar conocimientos de física, matemáticas, ingeniería, tecnología y estudios sociales.
Para adaptar este proyecto a las necesidades y capacidades de los estudiantes, se podría ofrecer diferentes niveles de complejidad y opciones de trabajo individual o colaborativo, según sus preferencias e intereses.
Una vez diseñado el currículo y las estrategias adaptativas en STEM+H, se procede a su implementación en el aula, en un proceso de enseñanza y aprendizaje dinámico, flexible y diferenciado. Es esencial establecer mecanismos de seguimiento y retroalimentación, tanto a nivel de los estudiantes como de los docentes, que permitan detectar y ajustar a tiempo cualquier dificultad o desafío que surja en la implementación del currículo adaptativo.
Una aplicación concreta: se podría monitorear el desempeño y progreso de los estudiantes en un proyecto de diseño y programación de videojuegos educativos, utilizando una plataforma digital adaptativa que proporcione datos e indicadores de aprendizaje, y ajustar las actividades y recursos según las necesidades observadas.
Asimismo, se podría llevar a cabo reuniones periódicas entre docentes para compartir experiencias, preocupaciones y buenas prácticas en la enseñanza adaptativa de STEM+H.
Finalmente, es fundamental realizar una evaluación integral y sistemática del impacto y la efectividad del currículo adaptativo en STEM+H, tanto a nivel de los aprendizajes y competencias desarrolladas por los estudiantes, como de los procesos de enseñanza, la formación docente y la gestión educativa.
Esta evaluación debería proporcionar retroalimentación válida, confiable y útil para la mejora continua y la actualización del currículo adaptativo, en función de los cambios y desafíos del contexto educativo y social.
Queda claro que el proceso de diseño e implementación de currículos adaptativos en STEM+H es un desafío constante, que exige la capacidad de adaptarse y aprender de las experiencias y situaciones que se presente en el aula. Solo así, será posible ayudar a los estudiantes a encontrar su camino y desarrollar sus potencialidades en el apasionante y cambiante mundo de la educación STEM+H adaptativa.
Este proceso es fundamental para abordar con éxito las problemáticas y retos que presenta la enseñanza interdisciplinaria en un mundo cada vez más complejo y tecnológico. Lograr esto será crucial para enfrentar los retos y cambios futuros en la enseñanza adaptativa STEM+H.
La integración de la interdisciplinariedad y la adaptabilidad en proyectos educativos STEM+H (Ciencias, Tecnología, Ingeniería, Matemáticas y Humanidades) se encuentra en el corazón de una educación efectiva y significativa que aborde las necesidades y desafíos del siglo XXI.
En un mundo cada vez más interconectado y cambiante, los estudiantes deben aprender a enfrentar y resolver problemas complejos y globales, utilizando y combinando conocimientos y habilidades de diversas disciplinas y enfoques.
Si consideremos la problemática del cambio climático y sus múltiples repercusiones a nivel ambiental, social, económico y político. Para abordar esta cuestión de manera efectiva, es necesario un enfoque integrador y adaptativo que permita a los estudiantes comprender las relaciones y dinámicas entre, por ejemplo, la física atmosférica, la biología de los ecosistemas, la tecnología de energías renovables, la economía del carbono y las políticas públicas de mitigación y adaptación, así como las perspectivas y valores culturales y éticos en torno a la sostenibilidad y la justicia ambiental.
En este contexto, la implementación de proyectos educativos STEM+H que promuevan la interdisciplinariedad y la adaptabilidad es clave para fomentar el aprendizaje y el desarrollo de habilidades y competencias esenciales en los estudiantes. A continuación, se presentan algunas estrategias y ejemplos concretos de este enfoque integrador y adaptativo en STEM+H.
Un proyecto educativo STEM+H adaptativo podría, por ejemplo, invitar a los estudiantes a investigar y proponer soluciones para reducir las emisiones de gases de efecto invernadero en su escuela o comunidad. Para ello, los alumnos deberán utilizar conocimientos de química y física para analizar las fuentes y mecanismos de emisión, aplicar conceptos de matemáticas y tecnología para medir y modelar el impacto potencial de distintas acciones, y emplear herramientas de ingeniería y diseño para desarrollar e implementar soluciones viables y sostenibles. Además, deberán considerar aspectos sociales, culturales y políticos que puedan influir en la efectividad y aceptabilidad de las propuestas, así como reflexionar crítica y éticamente sobre las implicaciones y responsabilidades de sus decisiones y acciones en un contexto global.
Un proyecto educativo STEM+H adaptativo debe ser flexible y personalizable para adaptarse a las necesidades, intereses y habilidades de cada estudiante. Por ejemplo, en un proyecto sobre el diseño y construcción de robots para limpiar y monitorear la calidad de un río contaminado, es importante ofrecer diferentes niveles de complejidad y opciones de trabajo colaborativo o individual, según las preferencias e intereses de los estudiantes.
Además, se deben ofrecer oportunidades para que los alumnos exploren y desarrollen habilidades creativas y expresivas, como el diseño y presentación de sus prototipos y resultados a través de imágenes, vídeos o narrativas, incorporando elementos de arte y comunicación visual y verbal.
La incorporación de plataformas y herramientas digitales en los proyectos educativos STEM+H puede facilitar la adaptabilidad y personalización del aprendizaje, así como potenciar la colaboración y la comunicación entre los estudiantes y docentes. Por ejemplo, una plataforma de aprendizaje en línea podría ofrecer tutoriales específicos y desafíos adaptativos para cada alumno en función de su nivel y estilo de aprendizaje, así como proporcionar retroalimentación y seguimiento personalizados a lo largo del desarrollo del proyecto.
Asimismo, herramientas digitales como simuladores o software de modelado y visualización podrían enriquecer la exploración y comprensión de fenómenos y conceptos STEM+H de manera integrada e interactiva.
Veamos un recurso simulador de PhET para explicar la llamada ley de Faraday, fundamental para determinar y controlar la dirección en la que se desplaza el flujo eléctrico de un circuito:
Aunque la ley de Faraday es un concepto fundamental en la física y las ciencias de la ingeniería, también puede ser una herramienta valiosa para explorar temas humanísticos más amplios, como la historia, la filosofía, el arte y la ética, es decir contribuye con una adaptabilidad del tipo STEAM + H:
Explorar la historia detrás del descubrimiento de la ley de Faraday, incluyendo el contexto social, económico y político en el que vivía Faraday, nos proporciona una visión más amplia de cómo se desarrollaron las ideas científicas y cómo interactúan con la sociedad en general.
Reflexionar sobre el proceso mediante el cual Faraday llegó a sus conclusiones y cómo estas fueron aceptadas por la comunidad científica en su tiempo puede ser una excelente oportunidad para discutir temas de epistemología y filosofía de la ciencia.
Las innovaciones tecnológicas basadas en los principios de la ley de Faraday, como los motores eléctricos y los generadores, han tenido un impacto profundo en la sociedad y la cultura. Explorar cómo la electricidad ha influido en el arte, la literatura y la música puede ser una forma interesante de conectar la ley de Faraday con las humanidades.
Considerar las implicaciones éticas y sociales de la tecnología derivada de la ley de Faraday, como la generación de energía eléctrica y su impacto en el medio ambiente, puede ser una forma de integrar perspectivas humanísticas en el estudio de la ciencia y la tecnología.
La evaluación de proyectos adaptativos en STEM+H debe ser formativa y reflexiva, con el objetivo de valorar tanto el proceso de aprendizaje y construcción de conocimientos como los resultados obtenidos. En este sentido, se debe fomentar la autoevaluación y la metacognición por parte de los estudiantes, así como la retroalimentación y el apoyo por parte de los docentes y compañeros a lo largo de todo el proceso.
La evaluación debe ser integral y considerar múltiples dimensiones e indicadores de desempeño en las distintas áreas de STEM+H, además de incluir aspectos relacionados con habilidades transversales como el pensamiento crítico, la creatividad, la comunicación y la colaboración.
En definitiva, la integración de la interdisciplinariedad y la adaptabilidad en proyectos educativos STEM+H es un desafío y una oportunidad clave para una formación integral, personalizada y dinámica en el siglo XXI.
Frente a los problemas y paradojas de nuestro mundo hiperconectado, es fundamental que los estudiantes aprendan a navegar y transformar sus realidades cotidianas y globales con sabiduría, empatía y responsabilidad, utilizando y combinando los recursos y metodologías de las ciencias, la tecnología, la ingeniería, las matemáticas y las humanidades de manera flexible, creativa y significativa.
Este enfoque integrador y adaptativo no solo permitirá a los estudiantes enfrentar los retos actuales y futuros con mayor competencia, sino también impulsar y ampliar sus horizontes de comprensión y acción en un mundo en constante cambio y evolución.
Al fin y al cabo, el propósito fundamental de la educación STEM+H adaptativa es formar ciudadanos activos, reflexivos y comprometidos que sean capaces de desafiar y reimaginar los límites y conexiones de sus conocimientos y habilidades, para buscar y construir soluciones innovadoras y justas a los dilemas y oportunidades de nuestra época y más allá.
NO podemos ignorar que la investigación educativa desempeña un papel clave en el impulso de la adaptación e integración de contenidos STEM+H.
Uno de los aspectos fundamentales en los procesos de adaptación e integración de contenidos STEM+H es la construcción de un marco teórico conceptual que fundamente y oriente dichos procesos a partir de investigaciones previas en el campo educativo. Dicho marco debe considerar no solo la convergencia y relación entre las disciplinas STEM+H, sino también la adaptabilidad y personalización, la interdisciplinariedad y el trabajo colaborativo, así como la incorporación de tecnologías educativas y enfoques pedagógicos innovadores.
Este tipo de investigaciones puede realizarse a través de metodologías cualitativas y cuantitativas, como estudios de caso, encuestas, análisis de registros, entre otros, permitiendo una comprensión más completa y contextualizada de los fenómenos educativos involucrados en la adaptación e integración de contenidos STEM+H.
Asimismo, la investigación educativa debe ocuparse de la identificación y medición de habilidades y competencias que son esenciales en el enfoque adaptativo STEM+H. Es necesario determinar no solo cuáles de estas habilidades son claves en la educación y formación de estudiantes y docentes, sino también cómo evaluar y fomentar su desarrollo a lo largo del proceso educativo.
Iconos. Imagen de dawnydawny en Pixabay
Capitulo I. Imagen de Sunrise Pohtam en Pixabay
Capitulo II. Imagen de Gürkan Özsoy en Pixabay
Página 58-59. Imagen creada con DALL-E3 de Bing
Página 63. Imagen de Karolina Grabowska en Pixabay
Página 66.Imagen de Stafford GREEN en Pixabay
Página 68-69. Imagen creada con DALL-E3 de Bing
Página 74-75. Imagen creada con DALL-E3 de Bing
Página 76. Imágenes del interactivo creadas con DALL-E3 de Bing
Página 78. Imagen de Gino Crescoli en Pixabay
Página 80. Imagen de Alana Jordan en Pixabay
Página 81. Caracterización de la comunicación
Página 81. Continuación
Página 85. Imagen de Faisal Mehmood en Pixabay
Capitulo III. Imagen de Brigitte Werner en Pixabay
Página 103. Imagen creada con DALL-E3 de Bing
Página 104. Imagen de 16374644 en Pixabay
Página 106-107. Imagen creada con DALL-E3 de Bing
Página 108. Imágenes del interactivo
Página 111. Imagen creada con DALL-E3 de Bing
Página 113. Imágenes del Interactivo
Página 115. Imagen de NASA-Imagery en Pixabay
Capitulo IV. Imagen de u_0sfi6af9w2 en Pixabay
Página 122. Imagen de hskotamraju en Pixabay
Página 124-125. Imagen de Sergey en Pixabay
Página 132. Imagen de Wolfgang Stemme en Pixabay
Página 148- Imagen de NoName_13 en Pixabay
Capitulo V. Imagen de Faisal Mehmood en Pixabay
Página 160-161. Imagen de Wolfgang Stemme en Pixabay
Página 166. Imágenes del interactivo.
Página 170-171. Imagen de RAEng_Publications en Pixabay
Página 180-181. Imagen de Imagen de Dirk Wouters en Pixabay
Capitulo Referencias y créditos. Imagen de Michael Brandl en Pixabay