Tabla de contenido

INTRODUCCIÓN

El editor consiste en un programa ejecutable (DescartesJS.exe en Windows, DescartesJS.app en Mac OS o DescartesJS.bin en el sistema operativo Linux), el instalador puede descargarse desde: https://descartes.matem.unam.mx/, que se encuentra en constante mantenimiento incluyendo nuevas mejoras, de tal forma que es siempre una buena práctica reinstalarlo con cierta frecuencia. El programa del editor es una interfaz gráfica para el usuario mediante la cual podrá guardar archivos html con diversos tipos de interactivos. En la Figura 1.1 se muestra la ventana inicial del editor, el cual se puede buscar dentro de los programas en el ordenador, una vez que se haya instalado.

Editor de configuraciones

Puedes explorar el menú del editor o consultar la información presentada en la documentación de Radillo et al, sobre la cual no nos detendremos en este apartado, en tanto que a medida que avancemos podrás comprender mejor algunas opciones presentadas en el menú del editor.

El editor de configuraciones es una nueva ventana desde donde se realiza la programación del recurso interactivo y se muestra al oprimir el botón con forma de engranaje, que se encuentra en el extremo derecho de la ventana principal del Editor (la Figura 1.2 muestra la ubicación de dicho botón), o presionado las teclas CTRL + E.

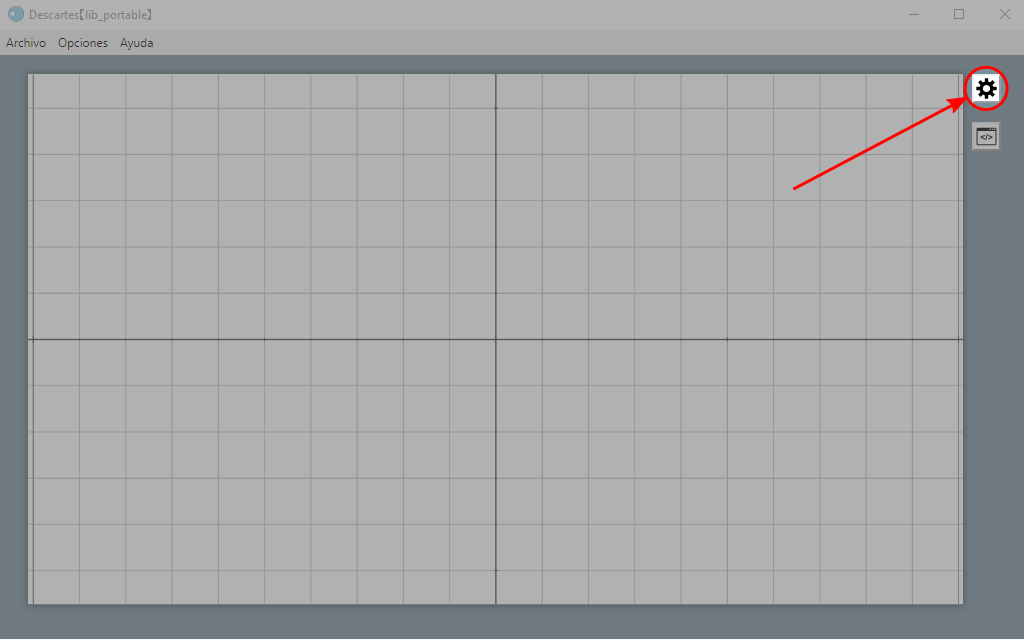
El botón inferior con los corchetes muestra una pantalla en la que se puede editar directamente el código de la escena, que no usaremos en este curso. En la Figura 1.3 se muestra la ventana del editor de configuraciones. Como se observa, contiene en su parte superior un menú de selectores esenciales para su uso.

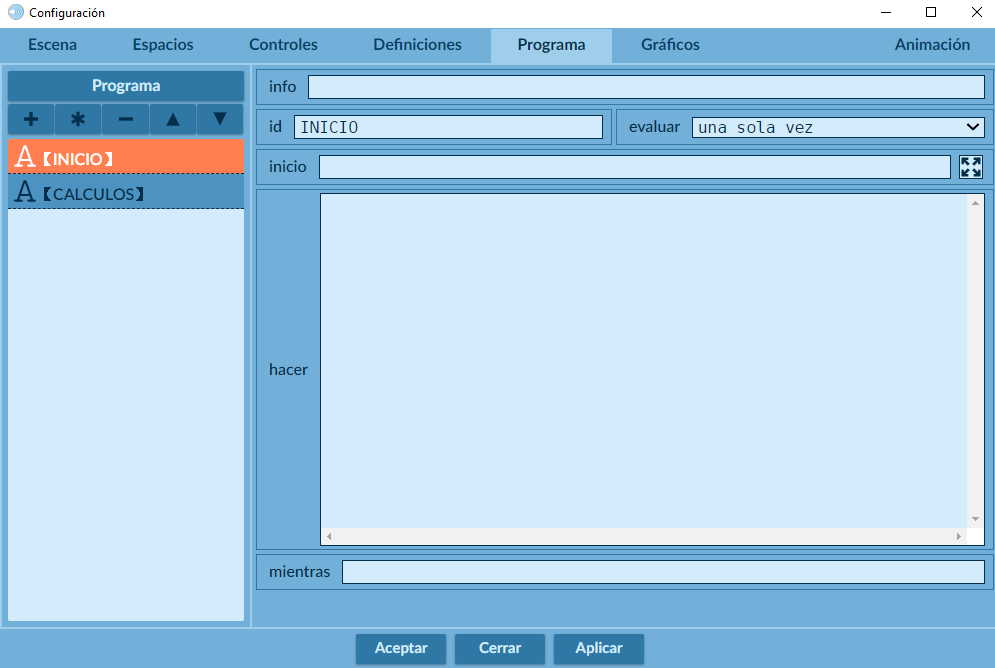
Selectores

El contenido principal del editor de configuraciones consiste en siete selectores para editar diferentes partes del interactivo, que aumenta a ocho cuando se crea un espacio 3D. La comprensión de cada uno de ellos se hará a medida que avances en los siguientes capítulos; no obstante, de Radillo et al, transcribimos:

El selector Escena permite hacer cambios de la interfaz general de la escena con el usuario.

El selector Espacios se usa para añadir, duplicar, eliminar o editar las propiedades de los espacios existentes en un interactivo. Los espacios son áreas en las que se presenta material gráfico al usuario.

El selector Controles permite añadir, duplicar, eliminar o editar las propiedades de los controles que se encuentran en el interactivo. Dichos controles son aquellos elementos con los que el usuario puede interactuar directamente.

El selector Definiciones permite añadir, duplicar, eliminar o editar las propiedades de los elementos que componen la programación del interactivo. Esta parte contiene elementos dentro de los cuales se encuentra el código fuente dentro de un interactivo.

El selector Programa contiene los algoritmos y eventos. Al igual que las definiciones, éstos contienen parte del código que permite el funcionamiento del interactivo. En particular, se refiere a la preparación inicial del interactivo para que esté listo para usarse, pero también a instrucciones que se repiten siempre o dadas ciertas condiciones.

El selector Gráficos permite añadir, duplicar, eliminar o editar las propiedades de los gráficos mostrados en los espacios 2D.

El selector Gráficos 3D permite añadir, duplicar, eliminar o editar las propiedades de los gráficos mostrados en los espacios 3D.

El selector Animación permite editar las instrucciones y condiciones de una animación en caso de haberla.

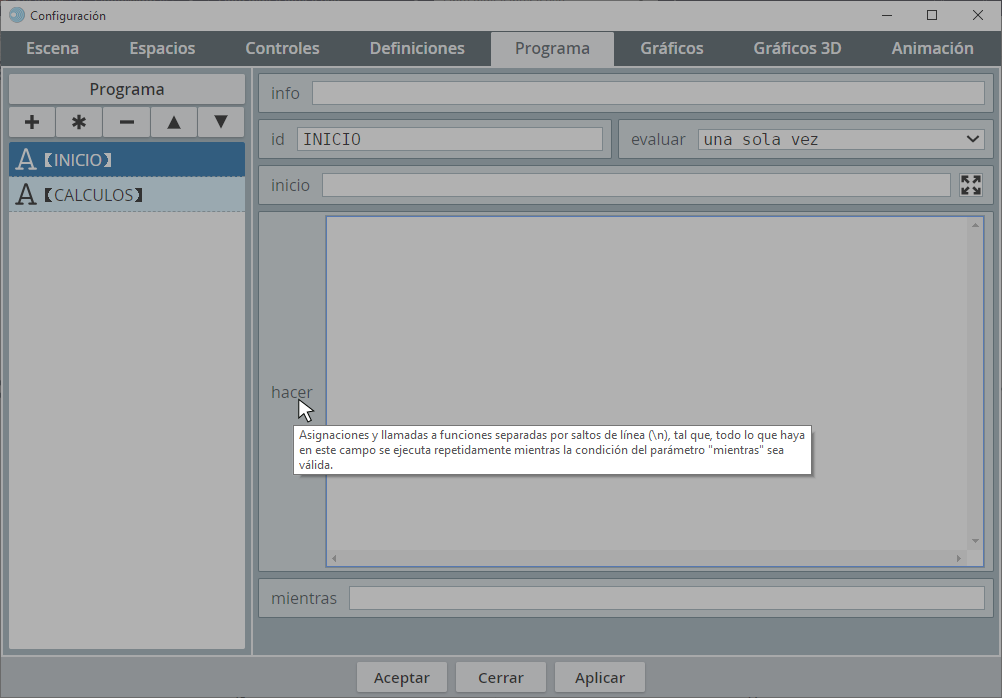
Todos estos selectores los abordaremos con más detalle en los siguientes capítulos. Cabe mencionar que hay disponible una explicación o información emergente (tipo tooltips) para los diferentes elementos dentro de los selectores. Por ejemplo, el parámetro hacer mostrará su tooltip si se posa el ratón sobre el texto hacer y se deja ahí un breve momento, Figura 1.4. La información aparece como un panel pequeño con la información más importante respecto al parámetro que se esté consultando. La información emergente desaparece al momento de quitar el ratón. Aunque la mayoría de los elementos de los selectores cuentan ya con información emergente, cabe mencionar que hay algunos que todavía no están disponibles.

Actividad del capítulo

Al terminar este capítulo, habrás diseñado el siguiente objeto interactivo:

En el espacio bidimensional de la esquina superior izquierda, puedes mover el plano cartesiano con clic sostenido. Sobre el espacio tridimensional, puedes rotar el objeto con clic izquierdo sostenido, o cambiar su tamaño con clic derecho sostenido. En el espacio de la parte inferior, se muestra un vídeo de YouTube que puedes reproducir. El objeto interactivo no tiene ninguna intencionalidad didáctica, es sólo un ejemplo demostrativo de las propiedades de los espacios cartesianos.

Espacios cartesianos

Son tres los espacios que podemos usar con DescartesJS: $ℝ^2$ o bidimensional, $ℝ^3$ o tridimensional y los de tipo HTMLIframe que permiten incorporar cualquier tipo de página web.

Cuando ejecutas el Editor de DescartesJS, por defecto, siempre se muestra un espacio cartesiano bidimensional. Este espacio se identifica (en el selector Espacios) normalmente como E1. En la Figura 2.1 se pueden observar los controles para este espacio (debes activar el selector Espacios).

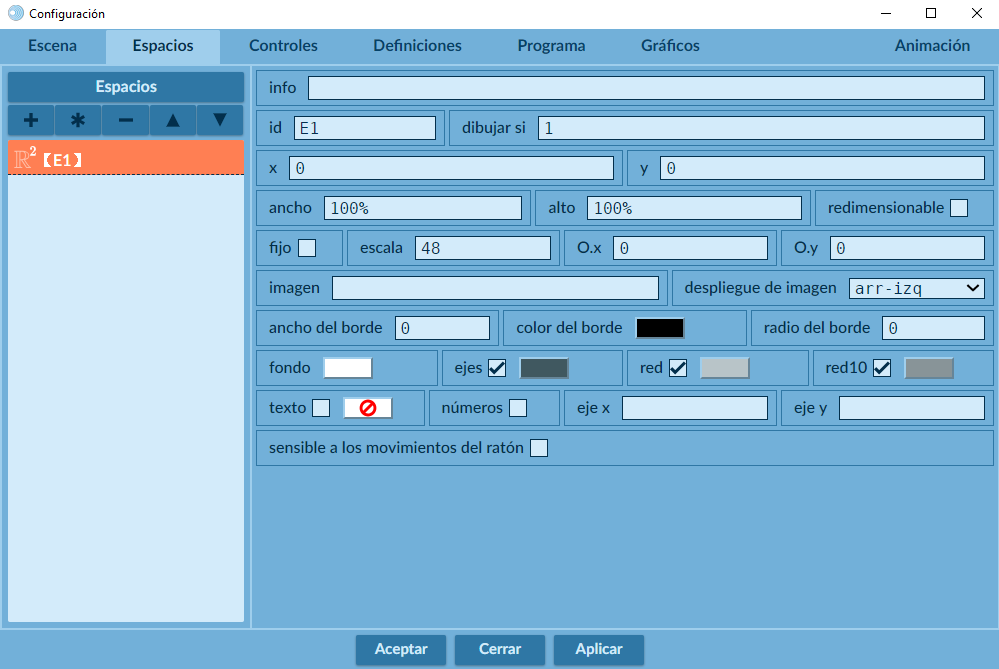
Las propiedades de un espacio bidimensional, las puedes consultar en el siguiente texto:

Diseñando nuestros primeros espacios

Iniciamos nuestra primera actividad, diseñando espacios cartesianos bidimensionales.

Inicialmente, reconfiguramos el espacio de trabajo para que quede con un fondo blanco. Luego insertamos un espacio $ℝ^2$ (bidimensional) en la esquina superior izquierda, cuyo tamaño es el 25% del área de trabajo. El procedimiento lo puedes observar en el siguiente vídeo.

Resumiendo el vídeo, observamos que cambiamos las dimensiones de la escena (selector Escena) o, si se prefiere, espacio de trabajo, a $800\times 600$ pixeles. El tamaño de la escena depende de su contenido, que irás cambiando a medida que produzcas nuevo material digital interactivo.

Posteriormente, desactivamos en el espacio de trabajo (selector Espacios) las casillas ejes, red y red10, además de fijar el espacio, todo ello con el propósito de dejar un espacio de trabajo limpio. Finalmente, creamos un espacio nuevo (haciendo clic en el botón +), al cual sólo le cambiamos el tamaño (ancho y alto) al 50%, es decir, con un área del 25% del espacio de trabajo. Obteniendo, hasta ahora, la siguiente escena:

Los dos espacios restantes (tridimensional y el tipo HTMLIFrame), los insertamos tal como se muestra a continuación:

Observa que el espacio $ℝ^3$ es, también, del 25% del tamaño de la escena, mientras que el HTMLIFrame es del 50%. A diferencia del primer espacio insertado, estos dos los ubicamos en posiciones diferentes; por ejemplo, el espacio tipo $ℝ^3$ lo ubicamos en una abscisa (x) a partir de la mitad de la escena, mientras que el HTMLIFrame en una ordenada (y) a partir de la mitad de la escena.

Es importante, para la posición de objetos, tener en cuenta que los valores de $x$ aumentan hacia la derecha y los de $y$ hacia abajo, teniendo el origen $(0,0)$ en la esquina superior izquierda del espacio de trabajo. Lo anterior no significa que los puntos geométricos del espacio $ℝ^2$ se comporten igual, éstos se rigen por las coordenadas tradicionales de un plano cartesiano.

Contenido de los espacios

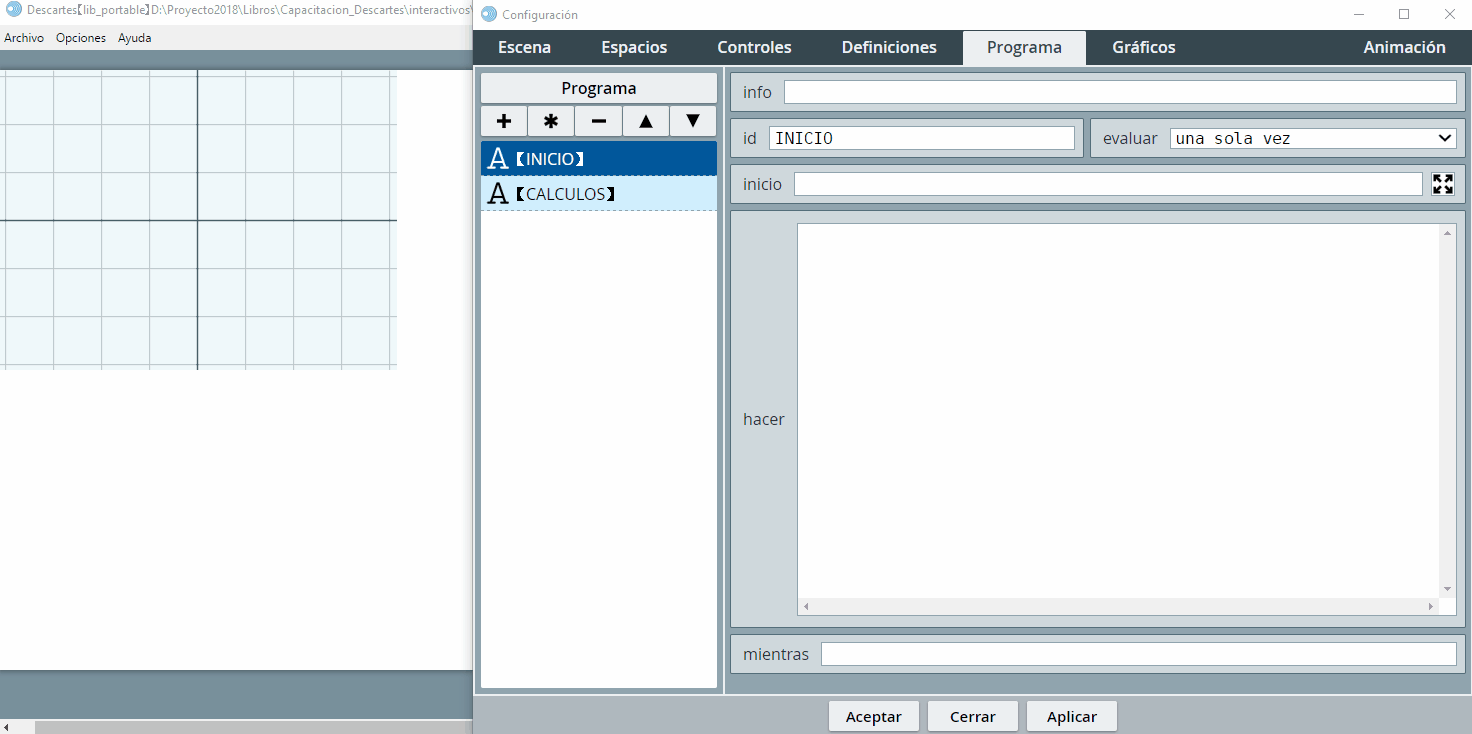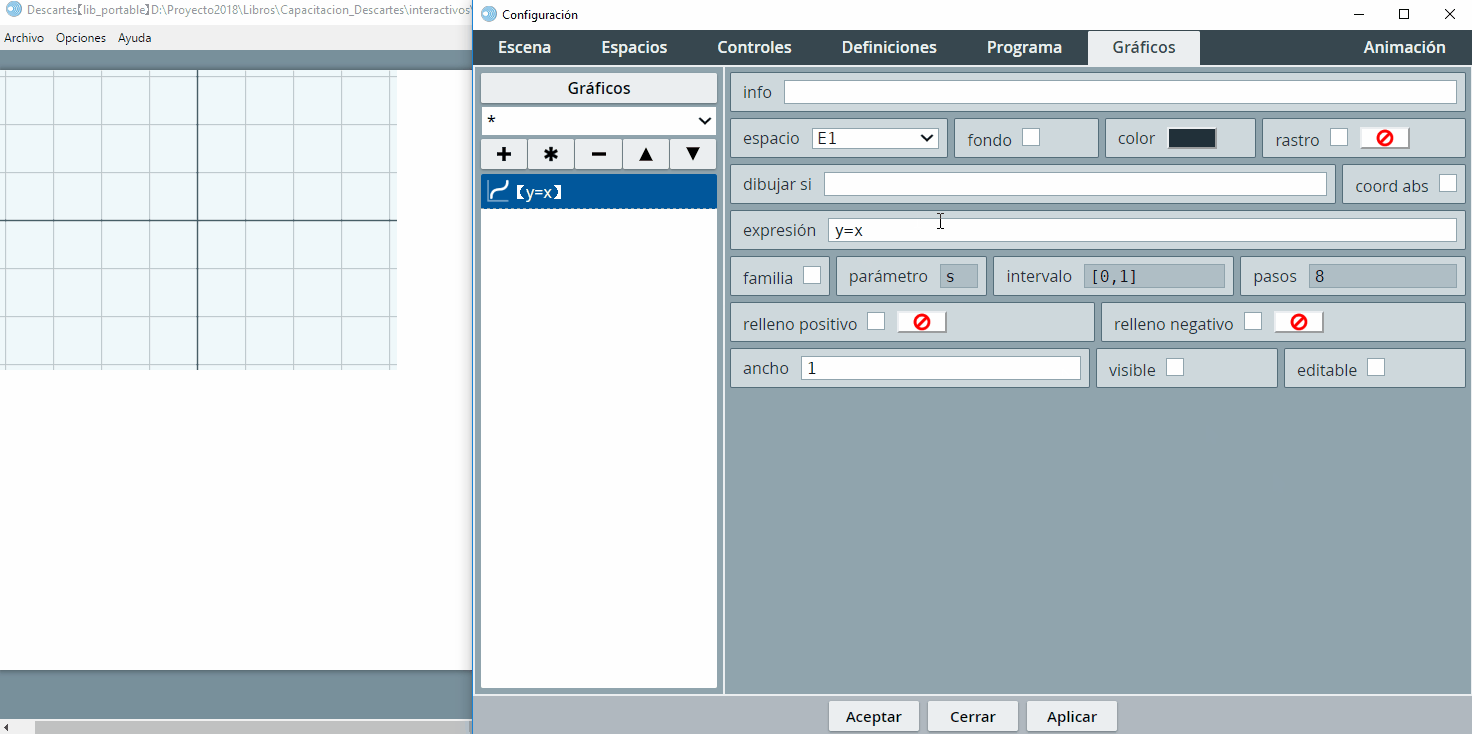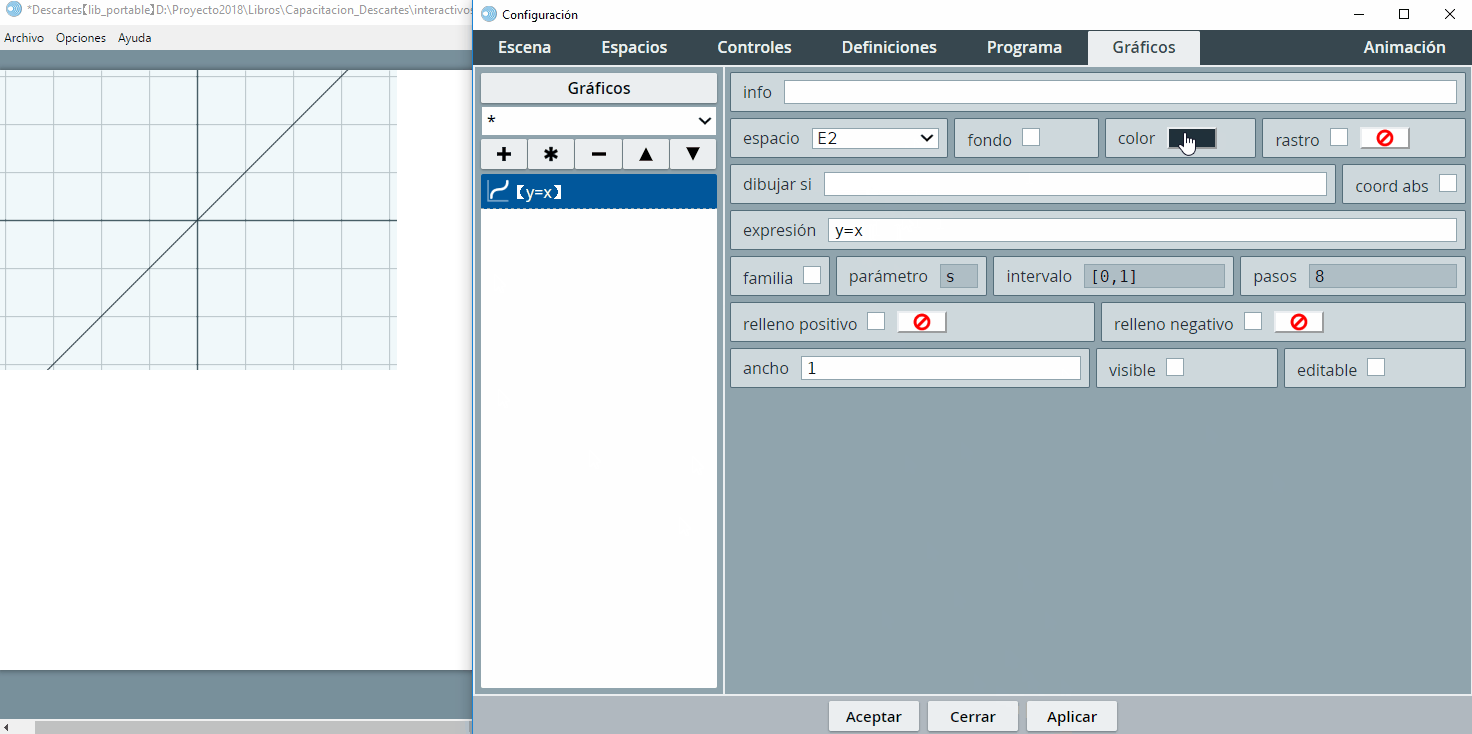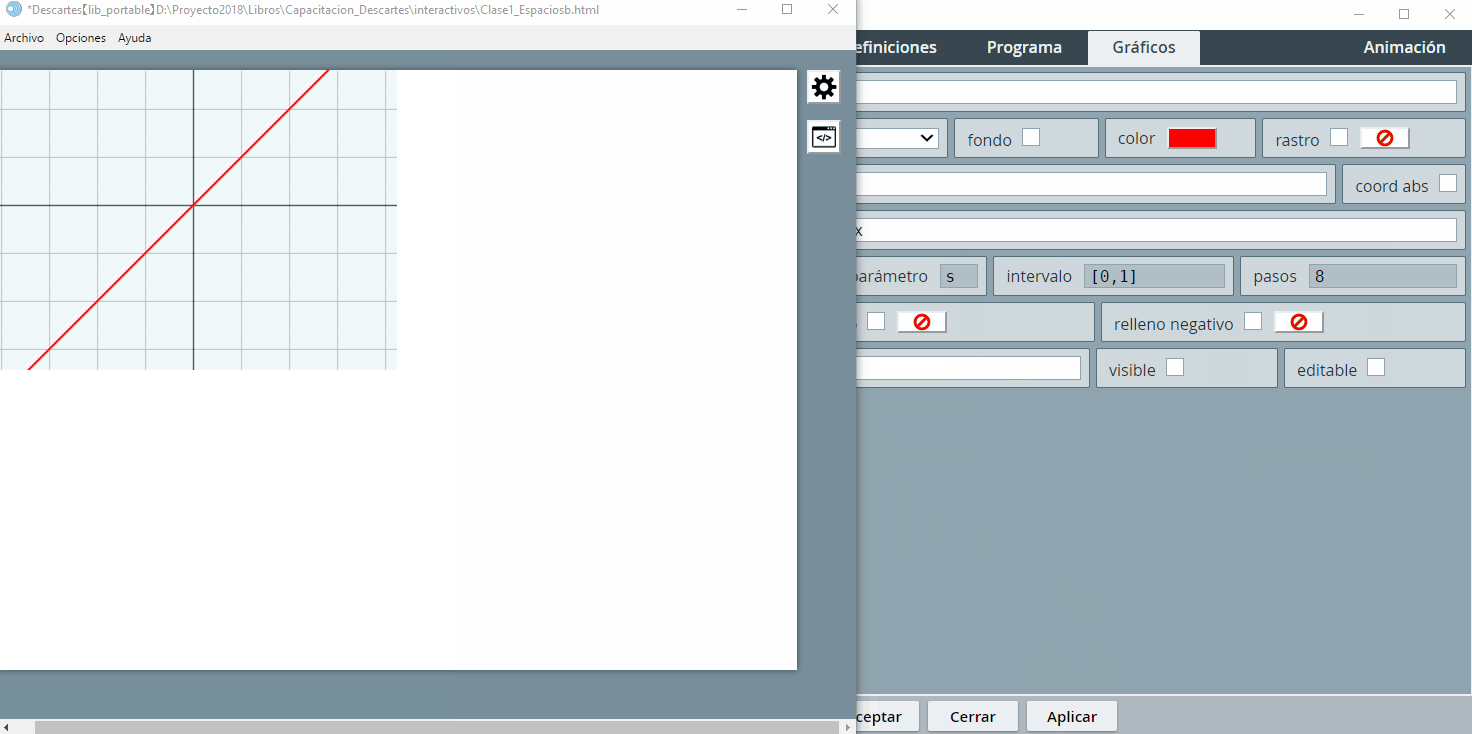
En los espacios bidimensionales es posible incluir contenidos de tipo gráfico (funciones, ecuaciones, objetos geométricos), controles, imágenes. Y, como ocurre en nuestra primera actividad, podemos incluir varios espacios. Para nuestro ejemplo, hemos dibujado una función lineal ($y=x$), procedimiento que se muestra en la siguiente imagen animada:

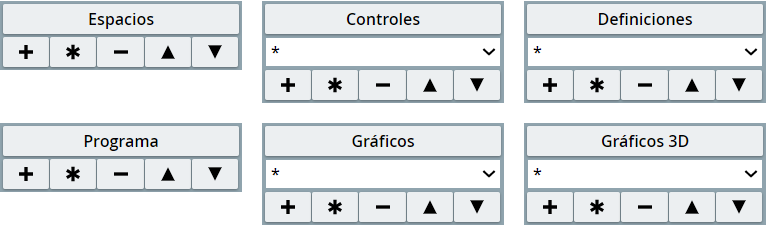
Este panel permite crear nuevos elementos, seleccionar los elementos a editar, duplicar elementos, eliminarlos o alterar el orden de los mismos, dependiendo de selector en el que nos encontremos. A continuación, explicamos el uso de este panel, para el selector Gráficos.

• Este botón gris claro, con la palabra Gráficos dentro, abre una ventana de edición de texto, donde puedes realizar la edición manual de todos los gráficos que hayas creado en un interactivo. Por ahora, no verás su utilidad; sin embargo, cuando tengas una escena con un gran número de gráficos te darás cuenta de lo importante de esta opción de edición. Por ejemplo, en la animación anterior habrás notado que el gráfico $y = x$ se dibujó en el espacio de trabajo E1, lo que obligó a cambiar el espacio de destino a E2. Cuando tenemos un gran número de gráficos es más fácil hacer este tipo de cambios, desde la ventana de edición de texto.

• Este botón abre una ventana que permite, a través de un menú, agregar un gráfico.



• Este botón permite duplicar el gráfico previamente seleccionado.
• Este botón permite eliminar el gráfico previamente seleccionado.
• Estos botones permiten cambiar el orden en que aparecen los gráficos.

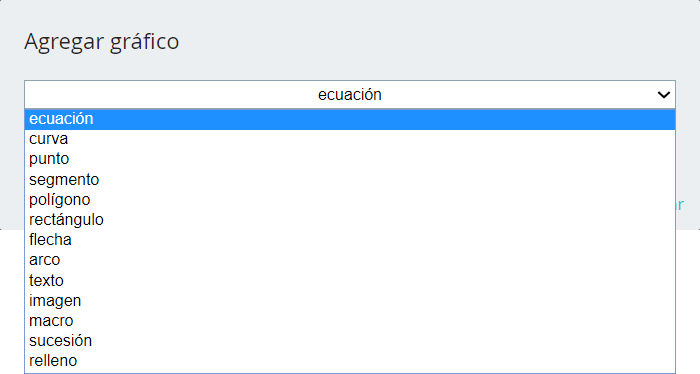
Retornando a nuestra actividad, el contenido del espacio E2 es la función lineal $y=x$, la cual agregamos con el botón +. Adicionalmente, cambiamos el ancho de la línea de $1$ a $2$ y el color de la línea.

Si haces una exploración a los diferentes selectores, notarás que es frecuente la aparición de botones que permiten el cambio de color de un texto, un control o un gráfico.

Observa, a continuación, una escena interactiva que te permite realizar combinaciones de color. La escena corresponde a una versión anterior de DescartesJS, pero tiene la misma funcionalidad de la versión actualVéase en el artículo Colores CSS del primer número de la Revista Digital Red Descartes el apartado "Colores en Descartes JS" (página 6)..

En esta primera práctica, el color amarillo, en formato hexadecimal, sería ffff00. Pero, si observas bien, notarás que es posible incluir transparencia al color seleccionado que, para la escena anterior no está activada. Veamos, en la siguiente escena, cómo se puede usar la transparencia.

El editor DescartesJS se encuentra en permanente revisión y actualización, en procura de incorporar nuevas herramientas y mejorar las existentes, por esto siempre es buena idea descargar e instalar la versión más actual, y disfrutar de las novedades de cada versión.

Una de las mejoras es la edición de los textos contenidos en las cajas de texto, por ejemplo, en la escena de la página siguiente, hemos simulado el editor de configuraciones, para el contenido de nuestro espacio bidimensional. Lo hemos hecho de tal forma que puedas cambiar la ecuación cuadrática $y=x^2$. DescartesJS permite incluir diversas ecuaciones matemáticas, incluidas las paramétricas, sin embargo, para la escena interactiva, sólo podrás cambiar la ecuación por otra de la forma y = [expresión en x]. Veamos algunos ejemplos con los cuales puedes practicar (recuerda hacer clic en el botón Aplicar para ver los cambios):

• Ecuación cúbica, $y = x^3$, que debes escribir de la siguiente manera: y=x^3
• Ecuación cuadrática, $y = 0.5x^2 - 3x + 1$ que debes escribir así: y=0.5*x^2-3*x+1
• Función sinusoidal, $y = sen(4x)$, que debes escribir así: y=sen(4*x)
• Función racional, $y = \sqrt{4 - x^2}$, que debes escribir así: y=sqrt(4-x^2)

En el apartado en el que trabajemos los textos enriquecidos, notarás las mejoras significativas, que facilitan la escritura de textos simples y los de tipo científico.

En otro capítulo profundizaremos sobre las funciones que soporta el editor DescartesJS.

Recuerda hacer clic en el botón Aplicar para ver los cambios.

Espacios tridimensionales

La mayoría de los controles de estos espacios son iguales a los de espacios bidimensionales, con algunas excepciones, a saber:

• despliegue: al usar tres dimensiones, los objetos colocados en el espacio pueden estar unos frente a otros. Para determinar cuáles quedan frente a cuáles hay 2 métodos distintos:
• orden: pinta los objetos de atrás hacia adelante. Involucra menos cálculos y es el más rápido, pero suele fallar para objetos muy grandes.
• pintor: dibuja las partes de los objetos de atrás hacia adelante, dibujando primero los objetos que son tapados por otros. Involucra más cálculos y es más lento, pero es más preciso que el método orden.
• cortar: es un checkbox que por defecto se encuentra inactivo. Es útil cuando diversos objetos tridimensionales se intersectan entre sí, pues permite un correcto despliegue de los objetos. Si los objetos desplegados no se cortan, no es necesario marcar esta opción.

Los espacios 3D se manipulan pulsando y arrastrando. De esta forma se producen giros para poder visualizar los objetos desde diferentes perspectivas. Si se pulsa el botón derecho del ratón y se arrastra hacia arriba mientras éste está pulsado, se realizará un acercamiento. Si el arrastre es hacia abajo, se realizará un alejamiento.

Puedes practicar añadiendo un gráfico en el selector Gráficos 3D pero, para nuestra actividad, es suficiente con seleccionar el gráfico superficie.

En la siguiente escena interactiva hemos incluido un menú con varios de los gráficos de este selector. Prueba con algunos de ellos y, en algunos casos, notarás que aparecen cuadros de texto para los parámetros Nu y Nv, que puedes aumentar de valor para una mejor resolución del gráfico, sin embargo no exageres porque puedes bloquear la escena, usa valores entre $20$ y $30$.

Habrás notado, al cambiar los valores de Nu y Nv, que algunos gráfico 3D se construyen como una malla compuesta de varias superficies; por ejemplo, el cilindro se dibuja con siete rectángulos (Nu = 7) que, obviamente, poco se parece a un cilindro; por ello, al aumentar el valor de Nu (80, por ejemplo), la resolución obtenida es mucho mejor.

Por su parte, la esfera se construye con triángulos, trapecios y rectángulos, en la que los campos Nu y Nv, respectivamente, definen el número de paralelos y de meridianos. Utilizar valores de $80\times 80$ ($6400$ superficies) para Nu×Nv, el gráfico se verá más parecido a una esfera, pero al exagerar el valor de estos parámetros puede resultar en un interactivo de lenta actualización; puedes hacerlo con una resolución de $30\times 30$, que da como resultado una esfera de apariencia aceptable.

Espacios HTMLIFrame

En este espacio podemos incorporar una página web con formato html. Este tipo de espacio contiene un campo archivo que los demás no tienen. En él se ingresá la dirección web o local a un archivo html que se desea abrir en dicho espacio que, para nuestra actividad, es https://www.youtube.com/embed/vd5VahGPWus, la cual es una dirección a un vídeo de YouTube, donde la expresión vd5VahGPWus es el código asignado por YouTube para identificar el vídeo.

Hasta aquí terminamos la actividad propuesta en este capítulo. Una vez tengas tu escena interactiva, debes guardarla en una carpeta (podrías llamarla actividades). El nombre de la escena es actividad1. DescartesJS le agrega la extensión html en caso de no escribirla explícitamente, lo que significa que la escena guardada puede abrirse desde tu navegador.

Al final del capítulo tendrás una tarea propuesta, que puedes llamarla name.html, donde name es tu nombre; por ejemplo: cocampo, que es la abreviatura de Carlos Ocampo.

Aplicaciones

Puzles

La posibilidad de añadir espacios sobre un área de trabajo, nos ha permitido diseñar un puzle giratorioEste puzle es tomado del Proyecto Plantillas, que describimos en la sesión 1 de este curso., cuyas imágenes son descargadas de flickr; lo interesante es que se logra la disposición de las fichas del puzle gracias a la incorporación de 24 espacios 2D (uno por cada ficha).

Evaluación formativa

Una segunda aplicación es una lupa (E1) que se desplaza sobre un mapa (E0). Esta aplicación, a su vez, la hemos utilizado para una actividad evaluativa, que puedes consultar en https://reddescartes.org/documentacion/?s=lupa

Comunicación DescartesJS - GeoGebra

Otra aplicación muy útil es el uso de dos espacios reservados para dos herramientas de autor que, para nuestro ejemplo, se trata de DescartesJS y GeoGebra. Pero, no se trata de poner dos escenas de cada herramienta, sino ponerlas a "comunicarse".

Comprueba esta interacción en los siguientes ejemplos:

Aprendiendo GeoGebra con DescartesJS

Construcciones de GeoGebra explicadas con DescartesJS

Tarea 1

Para terminar este apartado, te proponemos el siguiente ejercicio:

Diseñar una escena con dos espacios.

El primero debe ser un espacio 2D o 3D, cuyo contenido es un gráfico cualquiera. El segundo es un espacio HTMLIframe que debe contener un vídeo o una página web cuyo contenido hace referencia al gráfico del primer espacio. En la siguiente escena verás un ejemplo.

El ejemplo consta de un espacio 3D con el gráfico de un toroide (se ha cambiado el color del fondo a blanco) y un espacio HTMLIframe correspondiente a una entrada de Wikipedia que contiene información sobre este gráfico.

¡Recuerda que puedes mover el espacio y por consiguiente el toroide, con clic izquierdo sostenido!

¡Hasta la próxima sesión!