CÁLCULO DIFERENCIAL
Modulo I
INTERACTIVO

Carlos Alberto Rojas Hincapié
Red Educativa Digital Descartes, Colombia
1ª edición – 2022
Medellín
Colombia
Título de la obra:
CÁLCULO DIFERENCIAL
Módulo I
Autores:
CARLOS ALBERTO ROJAS HINCAPIÉ
1ª edición – 2022
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Red Educativa Digital Descartes
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN Obra completa: 978-84-18834-30-1
ISBN Módulo I: 978-84-18834-31-8
LICENCIA
 Sonido de fondo en videos. Música por e-soundtrax.
Sonido de fondo en videos. Música por e-soundtrax.
Tabla de contenido
Prefacio
Estudiar Cálculo implica directamente estudiar funciones. El cálculo diferencial nos proporciona métodos para el estudio y análisis de funciones, las cuales constituyen una herramienta eficaz para resolver y comprender desde el punto de vista gráfico y analítico los fenómenos de la naturaleza, de los procesos físicos, el desarrollo de los avatares de la economía, los continuos avances en la ingeniería y la biología, entre otros, donde se nos exige el conocimiento de la modelación matemática. En está unidad se estudiará, no solo la definición de función real, sino también algunas clases de funciones con el análisis de su respectivo dominio, como tema de gran interés en el estudio de funciones, además se proponen situaciones problema que van dirigidos a la modelación de funciones.
Funciones
Concepto de función
Una función, en matemáticas, es el término usado para indicar la relación o correspondencia entre dos o más cantidades.
Puede decirse que una función $f$ es una relación entre un conjunto dado $x$ (el dominio) y otro conjunto de elementos $y$(el codominio) de forma que, a cada elemento $x$ del dominio le corresponde un único elemento del codominio $f(x)$ Se denota por:
$$f : x \longrightarrow \; y$$
Las funciones se pueden representar por medio de diagrama sagital, gráfica en el plano o por fórmula matemática.
Cuando las funciones están escritas como fórmulas, a $x$ se le llama variable independiente, a $y$ variable dependiente porque este valor depende del valor que se elija para la $x$.
La forma en que $y$ varía está determinada por la regla con la que se ha definido la función. Observa la siguiente imagen, no representan funciones, ¿porque?
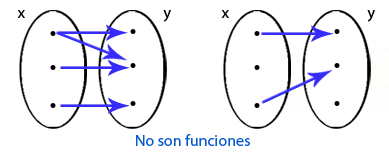
La escritura de las expresiones matemáticas nos permite identificar si hablamos o no de una función.
Notación y evaluación de una función
Es cuando se usa la expresión $f$ como nombre de la función. Este tipo de expresiones tiene la ventaja de permitir identificar la variable dependiente $f(x)$ como informando al mismo tiempo que la variable independiente es $x$
Ecuación explícita: es cuando en la ecuación que actúa como regla de correspondencia, se tiene despejada la variable dependiente $y$ en términos de la variable independiente $x$.
Por ejemplo – la función $\begin{aligned} y &= 3x^2 + 5x - 4 \end{aligned}$ es una ecuación explicita, dado que, es la regla de correspondencia y permite calcular directamente para cualquier valor x del dominio, su imagen correspondiente y en la imagen.
Ecuación implícita: se caracteriza porque en la expresión que actúa como regla de correspondencia, la variable dependiente $y$ no se encuentra despejada.
Por ejemplo – $\begin{aligned} y^2 + 3x^2 + 5xy - 4 &= 0 \end{aligned}$ , no tiene una forma sencilla de despejar la $y$, por lo que deja de ser una expresión funcional.
Veamos una expresión en forma implícita que puede llevarse a forma explícita, en otras palabras, que es posible despejar la variable $y$:
- Forma implícita: $\qquad - 2x - 4y + xy - 3 = 0$
- Forma explícita $\qquad y = f(x) \quad$ donde, $\quad y = { {2x+3} \over x-4} $
Criterio de la recta vertical
Si conocemos una gráfica, podemos determinar si ella corresponde a una función o no usando el criterio de la recta vertical.
Si al trazar alguna recta vertical corta la gráfica de una ecuación más de una vez, entonces la gráfica no es la gráfica de una función.
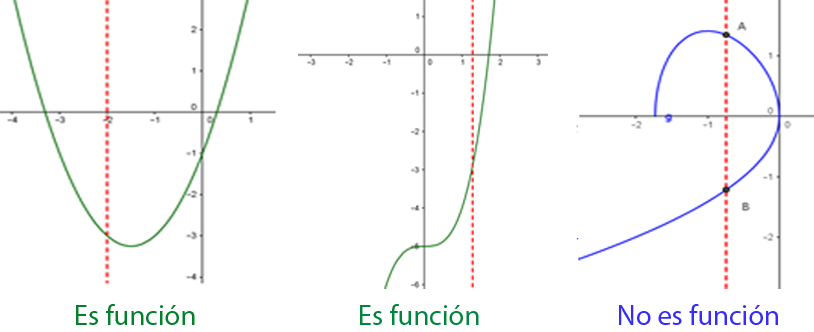
Ejercicio.
Determinar si la gráfica que se muestra es una función o no, oprime para verificar en los botones SI o NO
Escena de Alberto Bravo Garcia. Tomada de: Cálculo Diferencial, iCartesiLibri.
 GeoGebra. Utiliza el software para graficar y verificar.
GeoGebra. Utiliza el software para graficar y verificar.
Clic aquí.
Grafique otras ecuaciones y la recta vertical $x=a$ y verifique si la ecuación es o no una función.
Para utilizar el software de GeoGebra, escriba la expresión a graficar en la barra de entrada, por ejemplo $\quad y=x^2 + 4$ se escribe:
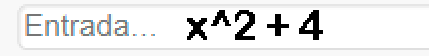
Evaluación de una función
Para evaluar una función, se toma el valor dado de la variable independiente x y se sustituye ese valor por x en la expresión.
Por ejemplo, si la función a evaluar es: $$\begin{aligned} y = { {2x^2+4} \over x-4} \end{aligned}$$
Cuando la variable independiente es x = 2 la expresión queda asi:
 Ejercicio.Escena de Alberto Bravo Garcia. Tomada de: Cálculo Diferencial, iCartesiLibri.
Ejercicio.Escena de Alberto Bravo Garcia. Tomada de: Cálculo Diferencial, iCartesiLibri.
Evaluar una función, oprime los números del lado izquierdo y observa su resultado.
Intersecciones con los ejes
 La intersección con los ejes hace referencia a las coordenadas $(x,0)$ y $(0,y)$ es decir, son los puntos en que la gráfica corta (hace intersección con)
el eje $x$ o con el eje $y$.
La intersección con los ejes hace referencia a las coordenadas $(x,0)$ y $(0,y)$ es decir, son los puntos en que la gráfica corta (hace intersección con)
el eje $x$ o con el eje $y$.
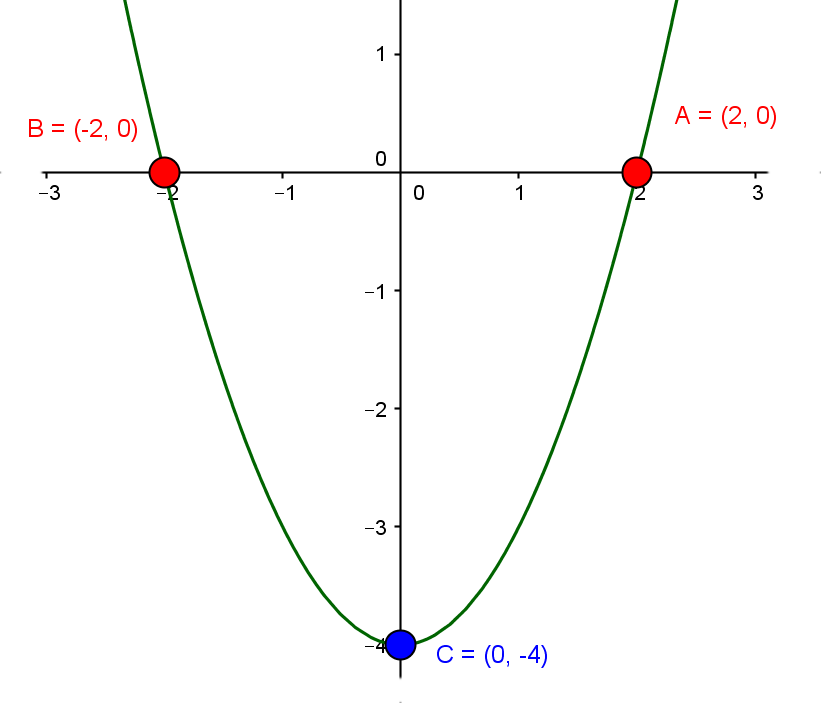
Por ejemplo, la gráfica de la función (ver imagen) $$y=x^2 - 4$$
Vemos que los corte con el eje $x$ son dos, $(2,0)$ y $(-2,0)$ y tiene un corte con el eje $y$ $(0,-4)$
- Para encontrar el corte con el eje y, se hace $x =0$ y se encuentra $y$, obteniendo la coordenada $(0,y)$
- Para encontrar el corte con el eje x, se hace $y =0$ y se encuentra $x$, obteniendo la coordenada $(x,0)$
Es posible que la gráfica no tenga intersección con los ejes (no corta los ejes), o que presente varias de ellas.
Cuando no es posible utilizar el método analítico para determinar las intersecciones con los ejes, se recurre al método gráfico, buscando los puntos donde la gráfica toca los ejes, observa la gráfica.
A las intersecciones con el eje $x$, se le denominan ceros de la función.
Para hallar los ceros de la función, casi siempre se recurre a métodos de factorización, como se muestra en el ejercicio siguiente.
 Ejercicio.
Ejercicio.
Ceros de la de la función (intersecciones en el eje $x$).
Encontrar los ceros de la función (si los hay), señala el método de solución, resuelve la expresión y oprime el botón Verificar.
En el caso de factorización, haz clic sobre el coeficiente o signo para cambiar su valor.
Después de ver el análisis de la función en el ejercicio anterior, ¿Cuál será la intersección con el eje y, como puedo encontrarla?
 GeoGebra. Utiliza el software para graficar y verificar.
GeoGebra. Utiliza el software para graficar y verificar.
Clic aquí.
Grafique las ecuaciones y observe las intersecciones para cada función.
Clases de funciones
Las funciones se clasificación en:
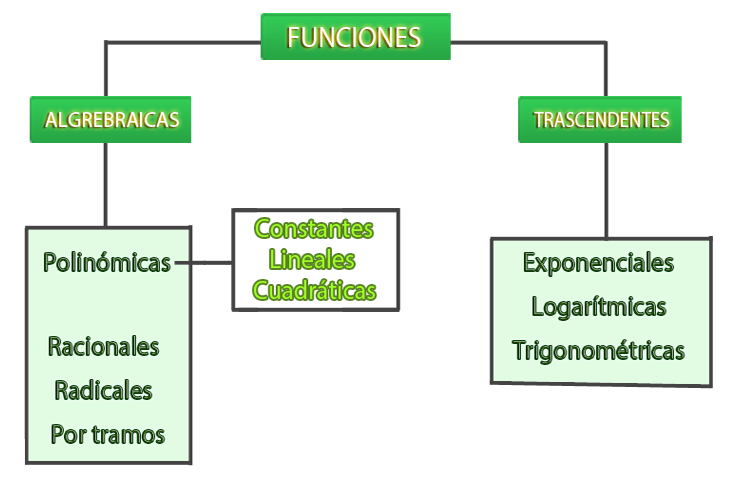 Funciones algebraicas, se obtienen, a partir de operaciones algebraicas y las funciones trascendentes, son las funciones exponenciales, logarítmicas, trigonométricas y las inversas.
Funciones algebraicas, se obtienen, a partir de operaciones algebraicas y las funciones trascendentes, son las funciones exponenciales, logarítmicas, trigonométricas y las inversas.
 Exploración. Observa algunos tipos de funciones, haz clic sobre el botón otra función y observa.
Exploración. Observa algunos tipos de funciones, haz clic sobre el botón otra función y observa.
Función Polinómica
Características principales de las funciones polinomiales.
- Grado: es el mayor exponente de la función polinomial ($\begin{aligned} x^n \end{aligned}$).
- Coeficiente principal: es el coeficiente de la variable con mayor grado en el polinomio ($\begin{aligned} a_n \end{aligned}$).
- Término constante: es el término del polinomio que no tiene variable ($\begin{aligned} a_0 \end{aligned}$).
Identifica en la siguiente gráfica los términos del polinomio.
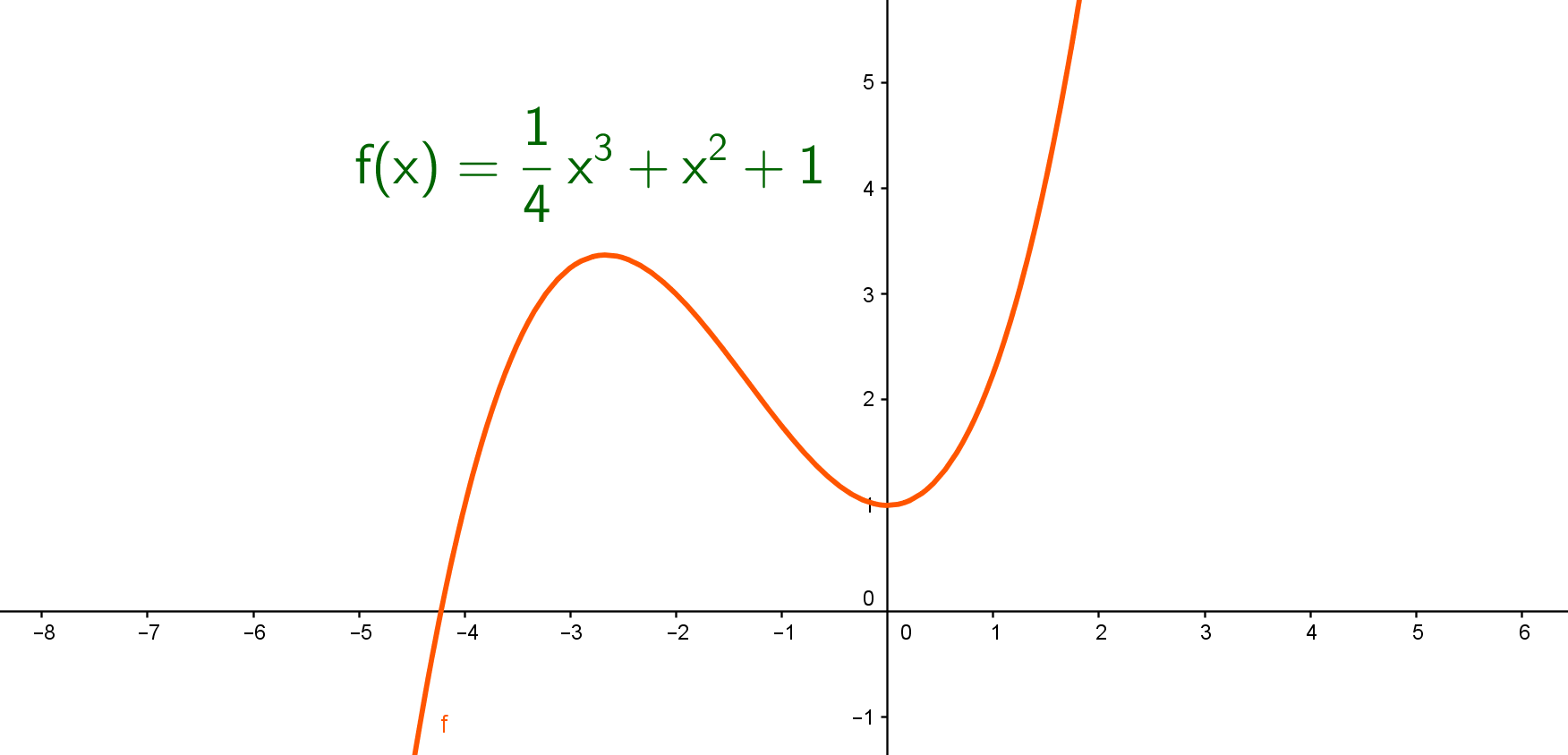
Las funciones polinomiales se denominan como lineales si el grado es uno, cuadráticas si el grado es dos, cúbica si el grado es tres, y así sucesivamente. Observemos algunas de ellas.
La Función Constante. $f(x) = b$
Una función $f$ es constante si la variable dependiente toma el mismo valor $b$ para cualquier valor de $x$.
 Exploración. Observa la siguiente escena interactiva de la función constante, cambia los valores de $b$.
Exploración. Observa la siguiente escena interactiva de la función constante, cambia los valores de $b$.
La Función Lineal. $f(x) = mx + b$
La función lineal es una función de primer grado, donde $m$ se conoce como la pendiente (grado de inclinación de la línea recta) y $b$ es el intercepto con el eje $y$ (el punto de corte $(0, b))$.
Una de las formas de hallar la pendiente $m$ de una recta es tomar dos puntos sobre dicha recta, entonces sean los puntos $\begin{aligned} P_1 (x_1, y_1) \end{aligned}$ y $\begin{aligned} P_2 (x_2, y_2) \end{aligned}$ donde la pendiente está dada por la expresión:
$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$
 Ejercicio.Escena de Zinnya del Villar modificada por el autor
Ejercicio.Escena de Zinnya del Villar modificada por el autor
Desplaza el punto rojo o azul, observa el resultado de la pendiente según los puntos.
Observa en la gráfica y piensa, que sucede cuando la pendiente es $m > 0$ o $m < 0$ o $m = 0$ (cero)
Si se tienen dos puntos que pertenecen a una recta se puede hallar la ecuación de la recta que pasa por estos puntos aplicando el método conocido como punto- pendiente
Donde, con la pendiente y uno de los puntos se aplica la expresión: $$ y - y_1 = m (x - x_1)$$
 Ejercicio.Escena de Zinnya del Villar.
Ejercicio.Escena de Zinnya del Villar.
Hallar la ecuación de la recta dados dos puntos:
La ecuación lineal puede también tener la siguiente forma: $$ Ax + By + C = 0$$ que se conoce como forma general de la ecuación de una recta, donde despejando $y$ obtendríamos una expresión equivalente a $$ y = \frac{-A}{B}x + \frac{-C}{B} $$ donde la pendiente es $ m = \frac{-A}{B}$ y el intercepto con el eje $y$ es $b = \frac{-C}{B} $
Se puede presentar en la ecuación de la forma general que:
- Si $A = 0$, la recta será una recta horizontal con $m=0$, generando una función constante.
- Si $B = 0$, la recta será una recta vertical y la pendiente no está definida.
 Ejercicio.
Ejercicio.
Función lineal en forma general. Escribe el valor de la pendiente y para verificar pulsa la tecla "enter <┘"
Rectas paralelas y perpendiculares
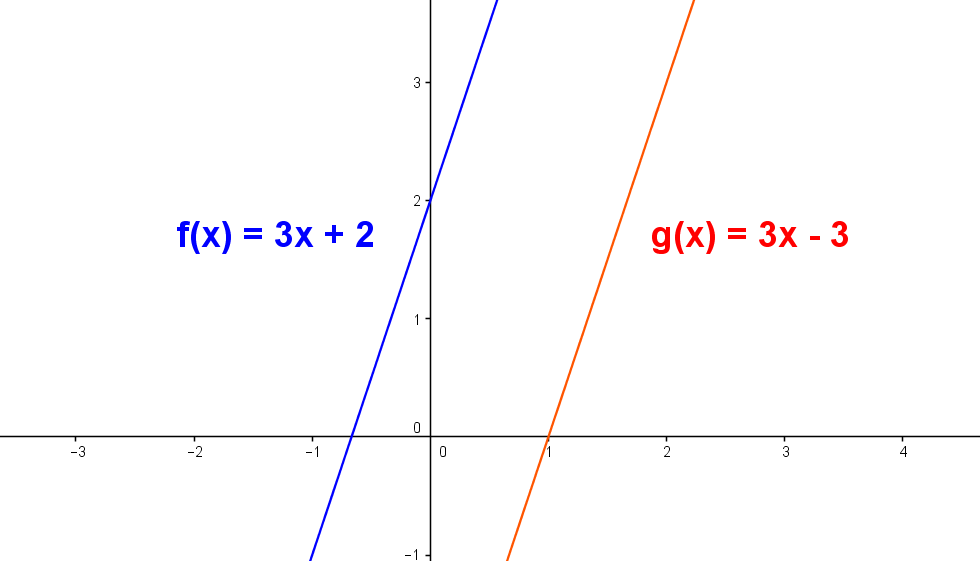
Dos rectas en el plano son paralelas si sus pendientes son iguales. $ m_1 = m_2 $.
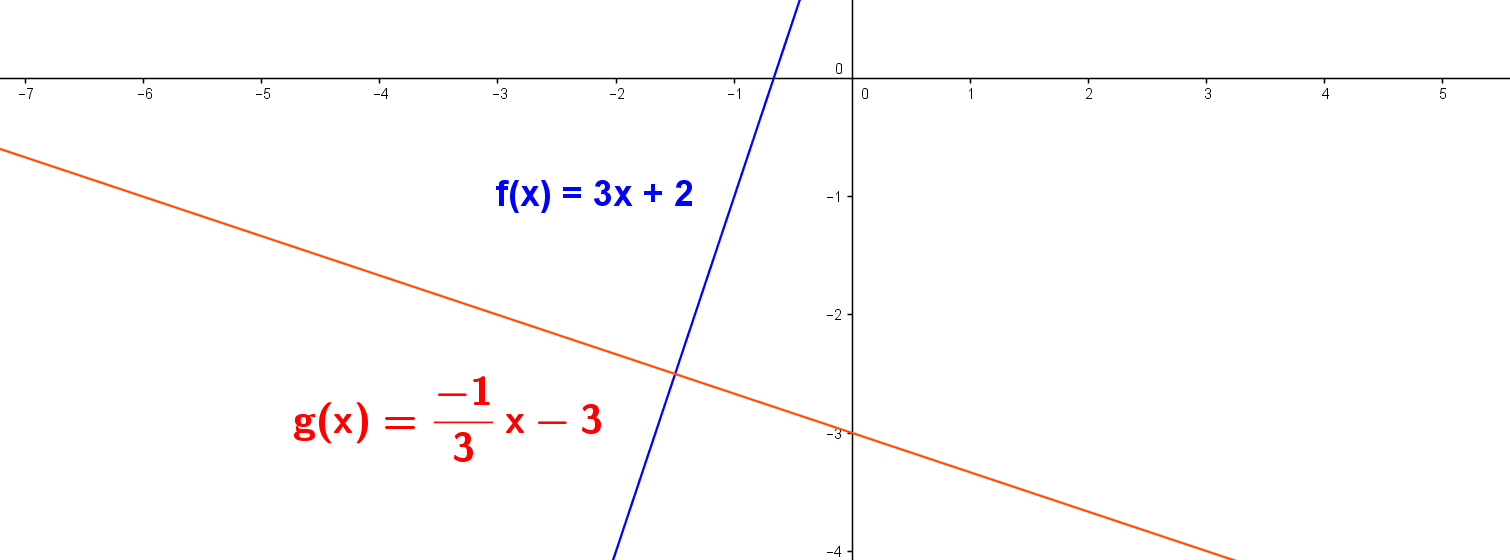
Dos rectas en el plano son perpendiculares si sus pendientes $ m_1 $ y $ m_2 $ son tales que cumplen que: $ m_1 . m_2 = (-1) $.
En la gráfica anterior se tiene que la pendiente de la recta uno es $ m_1 = 3 $. y la pendiente de la recta dos es $ m_2= \frac{-1}{3} $. por tanto $ m_1 . m_2 = \frac{-1}{3} . 3 = \frac{-3}{3} = (-1) $, con lo cual se verifica que la rectas son perpendiculares.
 Simulación lineal.
Simulación lineal.
Situación problema.
Una práctica en un laboratorio de Física Mecánica consistió en colocar un carrito sobre una pista recta, este se pone en marcha con velocidad constante y se mide la posición $s(t)$ del carrito con respecto al inicio de la pista en centímetros ($cm$) con un tiempo $t$ en segundos ($seg$).
Completa la tabla con varios puntos $(t, s(t))$, por ejemplo, el tiempo se muestra $t= 5seg \space 2 décimas = 2,5$ y distancia 13 $cm$, entonces el punto será $(t, s(t))=(2.5, 13)$La Función Cuadrática. $f(x) = ax^2 + bx + c$
La función cuadrática es una función de segundo grado y representa la gráfica de una parábola.
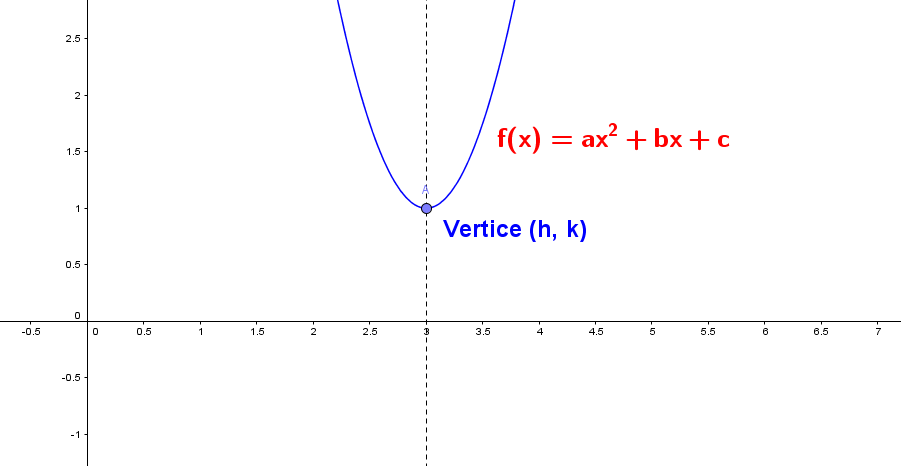
Un caso particular de la función cuadrática cuando se tiene que el valor de:
$a = 1$, $b = c = 0$ se obtiene la expresión $f(x) = x^2$, es una parábola con vertice en el origen $(0, 0)$
La función cuadrática también se puede expresar como: $$f(x) = a(x - h)^2 +k$$ Se conoce como la forma estándar de la función cuadrática donde $(h, k)$ representa el vértice de la parábola.
¿Porque la función cuadrática con vértice $(h, k)$ solo tiene concavidad hacia arriba o hacia abajo?
Elementos de la función cuadrática. Modifique los valores de a, b y c, observe algunos datos de la función cuadrática y su gráfica.
Valor máximo o mínimo de la función cuadrática.
- Si $a > 0$, entonces existe un valor mínimo en el vértice $(h, k)$, la parábola tiene abertura hacia arriba.
- Si $a < 0$, entonces existe un valor máximo en el vértice $(h, k)$, la parábola tiene abertura hacia abajo.
 Simulación cuadrática.
Simulación cuadrática.
Situación problema. Autor: Carlos Mario Restrepo Restrepo.
En una práctica de laboratorio, se va a calcular la altura máxima que alcanza una pelota lanzada verticalmente a una velocidad determinada y el tiempo que demora en alcanzar esa altura, ¿cómo se debe lanzar una pelota, para que alcance la máxima distancia horizontal?, Observa la trayectoria curva que describe la pelota.
Ingresa la velocidad y oprime el botón ver animación, observa la trayectoria que describe la pelota. Toma los datos de la gráfica para calcular altura máxima $Y(t)$ que alcanza y el tiempo $t$ que demora en alcanzar dicha altura.
Función Racional
La función racional es el cociente de dos funciones, $f(x)$ y $g(x)$, pueden ser polinomiales, radicales, entre otras y tiene la forma: $$ y = \frac{f(x)}{g(x)}$$
 GeoGebra.
Escena interactiva, modifica los controles y observa el cambio de la función $f(x)$.
GeoGebra.
Escena interactiva, modifica los controles y observa el cambio de la función $f(x)$.
Ejemplos de funciones racionales:
$y = \frac{5x+3}{x^2 - 3}$, $f(x) = \frac{x^2+9}{5x^2 - 3x+8}$, $y = \frac{-2}{x^3 - 6x^2-3}$
Función Radical
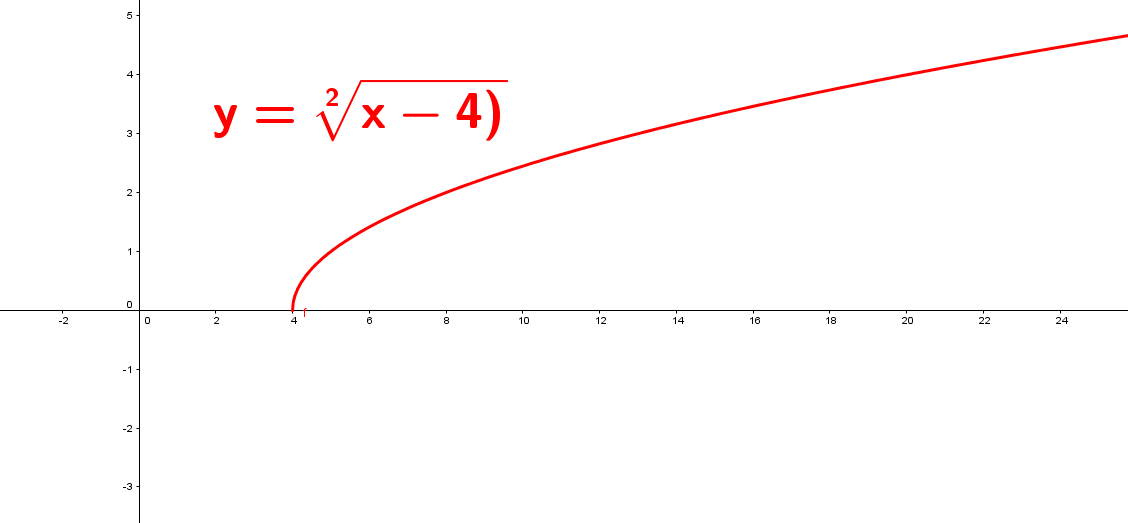
Si f es una función radical está tiene la forma: $$ f(x) = \sqrt[n]{g(x)}$$
donde $g(x)$ es una función polinomial, racional, entre otras.
n se conoce como el índice de la función radical, donde $n \ge 2$ e indica para que valores reales existe, el cual se analizara en una sección más adelante.
Ejemplos de funciones radicales:
$y = \sqrt[3]{x^3-2}$, $y = \sqrt[5]{2x^3-4}$, $y = \sqrt[3]{\frac{-2}{x^3 - 6x^2-3}}$,
Función por tramos
La función definida por tramos o por partes, está formada por varias funciones $g(x)$, $h(x)$... en un determinado intervalo para la variable independiente $x$, son de cualquier tipo. La función se expresa como: $$f(x) = \begin{cases} g(x) &\text{si } x \le a \\ h(x) &\text{si } x \ge b \end{cases}$$
 GeoGebra.
Escena interactiva, modifica el control y observa el cambio de la función $f(x)$.
GeoGebra.
Escena interactiva, modifica el control y observa el cambio de la función $f(x)$.
Dominio y rango de funciones
Es el conjunto $X$ de todos los números reales para los cuales la función $f$ existe o está definida.
Algunos autores nos dan la siguiente definición:
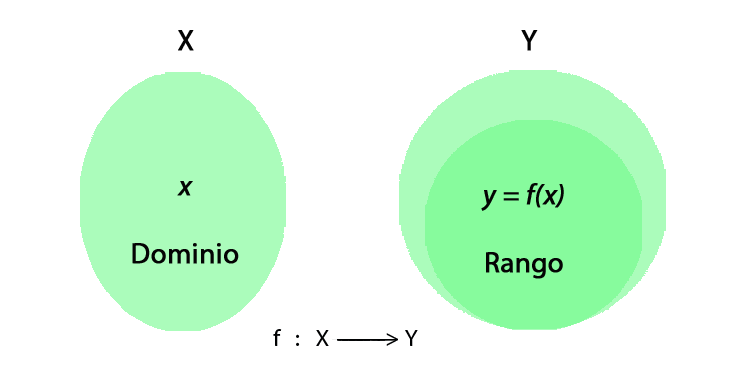
También llamado recorrido o imagen, es el conjunto de todos los valores que cumplen $y=f(x)$, o sea el valor de la función
f en el número x. Son las
imágenes de los elementos que pertenecen al dominio.¿Cómo hallar el dominio de una función?
Para hallar el dominio de una función debe analizarse la forma en la cual está presentada la función.
Si la función está dada de manera gráfica, para hallar el dominio es necesario determinar, desde la gráfica, cuales valores de x tienen asignada una imagen en y,
esto se puede lograr trazando una línea paralela al eje y, si está línea corta una vez la gráfica de la función el valor de x tiene asignada una imagen y por tanto
pertenece al dominio de la función.
 GeoGebra. Para ver la animación Escena de Elkin Alberto Castrillón con licencia CC by-nc-sa oprime el botón
GeoGebra. Para ver la animación Escena de Elkin Alberto Castrillón con licencia CC by-nc-sa oprime el botón  .
Observa el dominio y rango de la función $f(x)$.
.
Observa el dominio y rango de la función $f(x)$.
4x = 104, pertenece al domino dado que tiene un valor de $y=0$.
$x = -3$, no pertenece al domino, no tiene un valor de $y$ asignado.
$x = 3,5$, no pertenece al domino, no tiene un valor de $y$ asignado.
Si se sigue este procedimiento con todos los valores de $x$ se podrá determinar que el dominio de la función $f$ está compuesto por todos los valores de $x$ tales que $x \in (-\infty, -4] \cup (-3, \infty)$.
Consideremos los siguientes casos de funciones para hallar el dominio y rango.
Si $f$ es una función polinómica, polinomio de grado $n$ de la forma: $$\begin{aligned} f(x) &= a_nx^n + a_{n-1}x^{n-1} + ... + a_2x^2 + a_1x + a_0 \end{aligned}$$ entonces el dominio serán todos lo números reales dado que la regla mediante la cual se define la función puede asignarle una imagen a cualquier número real, $R$.
Por ejemplo - si tenemos la función $ f(x) = 3x^4 + 5x^2 - 2x -5$ y asignamos a $x$valores reales, siempre vamos a tener una imagen real.
$ f(0) = 3(0)^4 + 5(0)^2 - 2(0)-5 = -5$
$ f(-2) = 3(-2)^4 + 5(-2)^2 - 2(-2)-5 = 59$
$ f(\frac{1}{3}) = 3(\frac{1}{3})^4 + 5(\frac{1}{3})^2 - 2(\frac{1}{3})-5 = -\frac{125}{27}$
 Exploración. Gráficas de funciones polinómicas. Escena de Juan Guillermo Rivera adaptada por el autor.
Exploración. Gráficas de funciones polinómicas. Escena de Juan Guillermo Rivera adaptada por el autor.
Mueve el punto verde y verifica que todos los puntos están en el dominio de la función
Si $f$ es una función racional de la forma: $$ y = \frac{f(x)}{g(x)}$$
donde $f(x)$ y $g(x)$ son funciones polinomiales, entonces el dominio estará dado por todos aquellos valores de $x$ (números reales) tales que el denominador
de la fracción sea diferente de cero, por tanto
$g(x) \equiv\not 0$.
Ejemplo. Sea la función $ y = \frac{3x - 2}{2x -2}$ entonces el valor de $x = 1$ no pertenece al dominio de la función, dado que $ y = \frac{3(1) - 2}{2(1) -2} = \frac{1}{0} $ y la división por cero no está definida (no se le puede asignar una imagen al valor de uno); ahora como no hay otro valor real que haga que el denominador sea cero, se puede concluir que el dominio de la función $f(x)$ son todos los números reales diferentes de 1. Simbólicamente se podría escribir así: $$dom f = \{ x\in R | x \equiv\not 1 \} = R - \{ 1 \}$$
Se lee: “el dominio de $f$ son los $x$ que pertenecen a los reales tales que $x$ sea diferente de uno”
 Ejemplo. Como hallar el dominio de una función racional cuyo denominador se descompone en factores.
Ejemplo. Como hallar el dominio de una función racional cuyo denominador se descompone en factores.
 Exploración. Como hallar el dominio de una función racional.Escena de Valentina Muñoz Porras. Tomada de: Cálculo Diferencial, iCartesiLibri.
Exploración. Como hallar el dominio de una función racional.Escena de Valentina Muñoz Porras. Tomada de: Cálculo Diferencial, iCartesiLibri.
Haz clic en el botón Continuar, observar el paso a paso para encontrar el dominio de una función racional.
Si $f$ es una función radical de la forma: $$ f(x) = \sqrt[n]{x}$$
Si la función se define mediante una expresión algebraica que contiene radicales pares (raíz par), entonces el dominio estará dado por todos los valores de $x$ (números reales) tales que el argumento de la raíz (radicando) sea mayor igual que cero, esto por el hecho de que no es posible determinar un número real que elevado a potencia par de negativo. Simbólicamente se podría escribir así: $$dom f = \{ x\in R | x \ge 0 \} $$
Ejemplo 1. Dominio de la función $ f(x) = \sqrt[2]{3x - 6}$
Se debe garantizar que el argumento de la raíz siempre sea mayor igual que cero y despejando a $x$ se tiene que:
$ 3x - 6 \ge 0$
$3x \ge \ 6$
$x \ge \frac{6}{3}=2$
$x \ge 2$
Por lo tanto, encontramos que el dominio es el conjunto de todos los números reales tales que $x$ sea mayor que 2. Simbólicamente se puede escribir: $$dom f = \{ x\in R | x \ge 2 \} $$
Se puede presentar una combinación de restricciones cuando se combinan funciones
Ejemplo 2. Encontremos el dominio de una función combinada $$ f(x) = \frac{\sqrt{x + 1}}{2x - 4}$$
Como se ve la función está definida mediante una regla algebraica compuesta por una fracción y una raíz cuadrada, en este caso se combinan dos restricciones, por lo cual, se analizará por separado.
- Sea la función $g(x) = \frac{1}{2x - 4}$ donde el dominio de $g(x)$ son todos los $x$ tales que $ x \equiv\not 2$
- Sea la función $h(x)= \sqrt{x + 1}$ donde el dominio de $h(x)$ son todos los $x$ tales que $x \ge -1 $
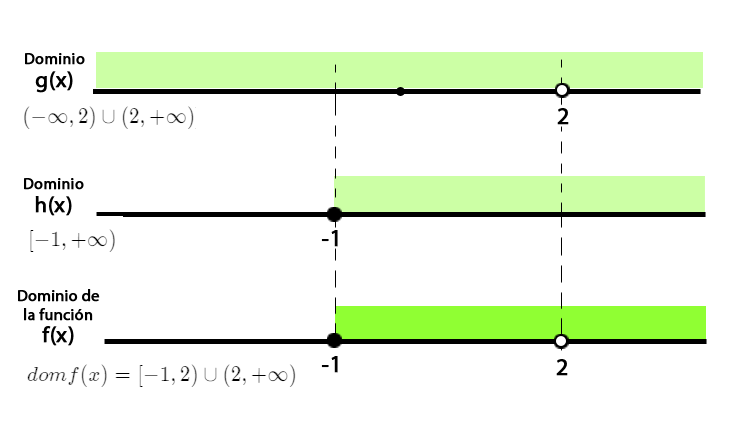
Por lo tanto, el dominio de $f(x)$ será la intersección del dominio de las funciones $g(x)$ y $h(x)$ , esto es, $$ [(-\infty, 2)\cup (2, +\infty)] \cap [-1, +\infty)$$ $$ dom f(x) = [-1, 2)\cup (2, +\infty)$$
El dominio de $f(x)$ son todos los valores de $x$ tales que $x$ este entre $-1$ y $2$ unido a $2$ y $+\infty$, se debe excluir el dos dado que sólo pertenece al dominio de $h(x)$ y no al de $g(x)$,
Observemos de manera gráfica el esquema de la forma de hallar el dominio de $f(x)$
Ejemplo 3. Encontremos el dominio de la función $ f(x) = \frac{1}{\sqrt {x^2 - 9}}$
Por tener una fracción combinada con una raíz par es necesario garantizar que su denominador sea diferente de cero,
$ x^2 -9 > 0$
$ (x - 3)(x + 3) > 0$
Para que el producto de dos cantidades sea positivo, es necesario que ambas cantidades sean al mismo tiempo positivo, o ambas negativas.
- Para que se cumpla que el factor $ (x - 3) > 0$ se deben tener todos los valores de $x$ tales que: $ x > 3$
- Para que se cumpla que el factor $ (x - 3) > 0$ se deben tener todos los valores de $x$ tales que: $x < -3$
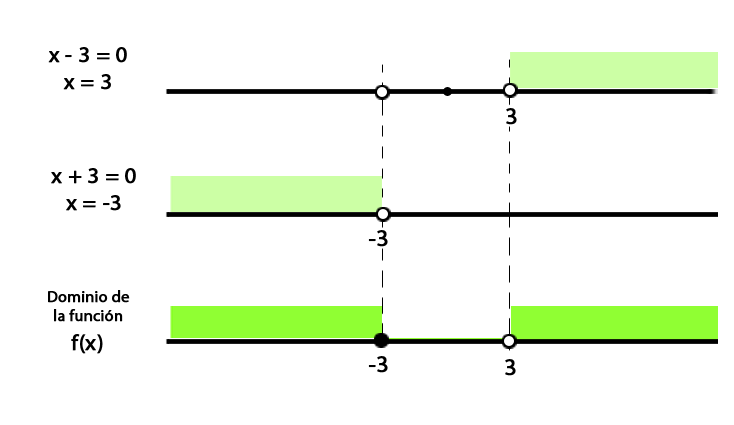
Por lo tanto el dominio es: $\qquad dom f(x) = (-\infty, -3)\cup (3, +\infty)$
En la siguiente gráfica se ve de manera esquemática la forma de hallar el dominio de $f(x)$
 Ejemplo. Como hallar el dominio de una función radical con indice par cuyo radicando es una función racional.
Ejemplo. Como hallar el dominio de una función radical con indice par cuyo radicando es una función racional.
Si $f(x)$ es una función raíz de índice impar (n= 3, 5, 7,...), $ f(x) = \sqrt[n]{x}$, el dominio son todos los números reales donde la cantidad subradical esté definida.
Si $f(x)$ es una función por partes o tramos (ver), es decir, definida por varias funciónes, el dominio es la unión de los intervalos donde fue definida cada función. La función por partes puede tener tantas partes como se requieran, por ejemplo $$f(x) = \begin{cases} {2x+3} &\text{si } 0 \ge x \\ {x^2+1} &\text{si } x > 3 \end{cases}$$
$$dom f(x) = (-\infty, 0]\cup (3, +\infty)$$¿Cómo hallar el rango de una función?
Para determinar el rango de una función $f(x)$ se deben hallar todos los valores de $y$ que son imágenes de un valor de $x$.
Un procedimiento para hacer esto en una gráfica, consiste en trazar líneas paralelas al eje $x$ y si esa línea corta la gráfica de la función entonces ese valor de $y$ pertenece al rango de dicha función.
 Exploración. Rango de una función.Escena de Juan Guillermo Rivera adaptada por el autor.
Exploración. Rango de una función.Escena de Juan Guillermo Rivera adaptada por el autor.
Observa la escena interactiva, selecciona la función y arrastra el punto verde y verifica el rango de las funciones polinómicas.
Para determinar el rango de una función $f(x)$ de forma analítica, se recurre a despeja la variable independiente $x$ en función de la variable dependiente $y$ (si es posible), y se realiza el mismo procedimiento que se utiliza para hallar el dominio de una función.
 GeoGebra. Para ver la animación Escena de Elkin Alberto Castrillón con licencia CC by-nc-sa oprime el botón
GeoGebra. Para ver la animación Escena de Elkin Alberto Castrillón con licencia CC by-nc-sa oprime el botón  .
Observa el dominio y rango de la función $f(x)$.
.
Observa el dominio y rango de la función $f(x)$.
Por lo general el rango de una función se halla utilizando la gráfica de la función, ya que en ocasiones despejar la variable independiente, $x=f(y)$, no es posible.
 Preguntas. Selección múltiple con única respuesta.
Preguntas. Selección múltiple con única respuesta.
Haz click sobre la respuesta correcta.
Encontrar el dominio y rango de la siguiente gráfica y responder:
Aritmética de funciones
Las funciones se pueden operar entre sí, de tal manera que:
Para hallar el dominio de las funciones anteriores, se halla la intersección de los dominios de las funciones $f$ y $g$.
Ejemplo.
Sean las funciones $f(x) = 3x^2- 3x -1$ y $g(x)= 5x -3$
- Sumar
$(f+g)(x) = f(x) + g(x) = 3x^2- 3x -1 + 5x -3$
$(f+g)(x) = 3x^2 +2x -1$.
El dominio son todos los reales, dado que son polinomios todas las funciones.
- Restar
$(f-g)(x) = f(x) - g(x) = 3x^2- 3x -1 -(5x -3)$
$(f-g)(x) = 3x^2 -8x +2$.
El dominio son todos los reales, dado que son polinomios todas las funciones.
- Multiplicar
$(f*g)(x) = f(x) * g(x) = (3x^2-3x -1)*(5x -3)$
$(f*g)(x) = 15x^3-24x^2 +4x +3$.
El dominio son todos los reales, dado que son polinomios todas las funciones.
- Dividir
$(f\div g)(x) = \frac{f(x)}{g(x)} = \frac{3x^2-3x -1}{5x -3}$
El dominio de la función son todos los reales excepto cuando $g(x)=0$, por tanto cuando $ x = \frac{3}{5}$,
Para hallar el dominio de está función, se halla la intersección de los dominios de las funciones $f$ y $g$, siempre que $g(x)\equiv\not 0$ (esto significa que hay que excluir el valor de $x$ que haga que el denominador sea cero)
$$dom f = \{ x\in R | x \equiv\not \frac{3}{5} \} $$Función compuesta
Una función compuesta se denota como $(f\circ g)(x) = f(g(x))$
El símbolo $(f\circ g)$ se lee "$f$ compuesta $g$".
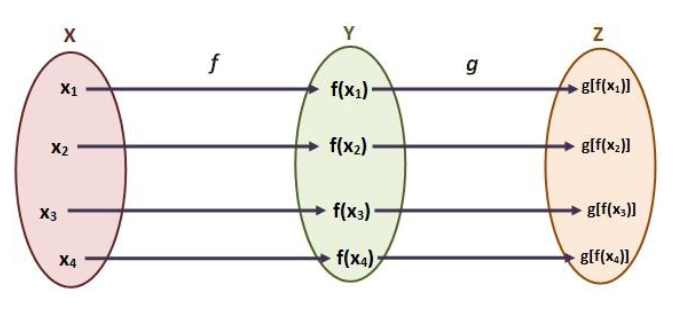
Ejemplo - Sean las funciones $f(x) = x^2 -1$ y $g(x) = \frac{x+1}{x-4}$
Con las funciones $f(x)$ y $g(x)$ , se tiene que, la expresión de la función compuesta $(f\circ g)(x)=f(g(x))$ será:
Encontremos $(f\circ g)$ y su respectivo dominio:
$(f\circ g)(x) = f(g(x)) = (\frac{x+1}{x-4})^2 +1$
Por tanto, el dominio de la función $(f\circ g)$ es: $$ dom_(f\circ g) = \{ x\in R | x \equiv\not 4\}$$
 Preguntas. Selección múltiple con única respuesta.
Preguntas. Selección múltiple con única respuesta.
Haz click sobre la respuesta correcta.
 ¡Recuerda!
¡Recuerda!
Dadas dos funciones, podemos combinarlas de tal manera que las salidas de una función se conviertan en las entradas de otra. Está acción define una función compuesta.
¿Identificas el procedimiento?
No, entonces para ver el procedimiento haz click en:
Ver explicación
Transformaciones de funciones
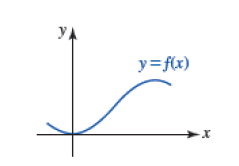 Para la gráfica de una función $y = f(x)$, podemos obtener nuevas funciones a partir de diferentes transformaciones como son: desplazamientos, reflexiones, estiramientos y compresiones.
Para la gráfica de una función $y = f(x)$, podemos obtener nuevas funciones a partir de diferentes transformaciones como son: desplazamientos, reflexiones, estiramientos y compresiones.
Suponga que $y = f(x)$ es una función, $c$ una constante positiva, entonces las transformaciones de la gráfica de la función pueden ser:
Desplazamientos
- Desplazamiento vertical
$y = f(x) + c$ : hacia arriba c unidades.
$y = f(x) - c$ : hacia abajo c unidades.

Por ejemplo, sea la función $y =x^2$, entonces $y =x^2 + 3$ sufre un desplazamiento vertical hacia arriba 3 unidades.
- Desplazamiento horizontal
$y = f(x + c)$ : hacia la izquierda c unidades.
$y = f(x - c)$ : hacia la derecha c unidades.

 Exploración. Observa los desplazamientos que puede sufrir la función, mueve los controles vertical o horizontal.
Exploración. Observa los desplazamientos que puede sufrir la función, mueve los controles vertical o horizontal.
Reflexiones
$y = -f(x)$ : la función $f(x)$ se refleja en el eje $x$.
$y = f(-x)$ : la función $f(x)$ se refleja en el eje $y$.
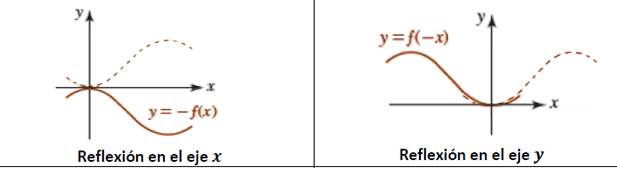
 Exploración. En la siguiente escena interactiva, selecciona la función y observa e identifica el tipo de reflexión.
Exploración. En la siguiente escena interactiva, selecciona la función y observa e identifica el tipo de reflexión.
Estiramientos y compresiones
- Estiramiento y compresión vertical
$y = c.f(x)$ : la función $f(x)$ estirada vertical si $(c>1)$ .
$y = c.f(x)$ : la función $f(x)$ comprimida vertical si $(0>c>1)$.
- Estiramiento y compresión horizontal
$y = f(c.x)$ : la función $f(x)$ estirada horizontal si $(0>c>1)$ .
$y = f(c.x)$ : la función $f(x)$ comprimida horizontal si $(c>1)$.
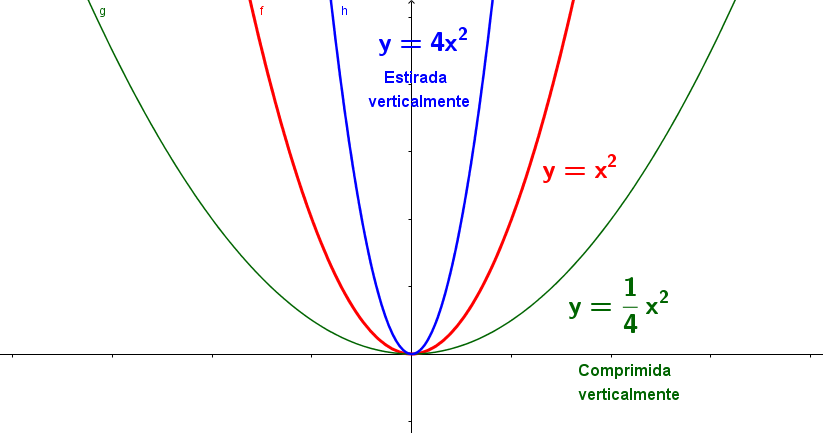
Se debe tener presente que si $c>1$ el factor $c$ es una constante positiva y si $0>c>1$ el factor es una fracción constante positiva $\frac{1}{c}$.
 Descarga:
Transformaciones de una función. Resumen gráficas de funciones iniciales y las transformaciones.
Descarga:
Transformaciones de una función. Resumen gráficas de funciones iniciales y las transformaciones.
Simetría de la gráfica de una función
La gráfica de una función $f(x)$ con dominio $X$ es simétrica con respecto a:
- Eje y, si se cumple que $f(x) = f(-x)$ para todo $x$ en $X$. En este caso, se dice que la función $f$ es par.
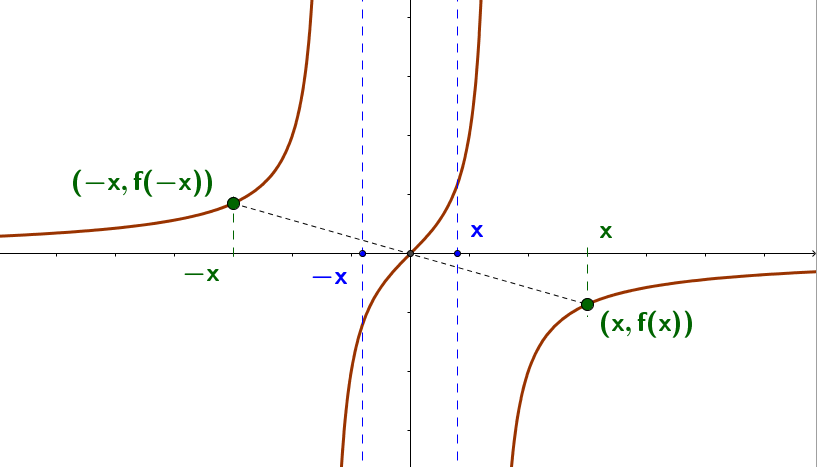
- Origen, si se cumple que $f(x) = -f(-x)$ para todo $x$ en $X$. En este caso, se dice que la función $f$ es impar.
Por ejemplo, sea la función $f(x)= \frac{x}{2-x^2}$, analicemos si la función es par o impar remplazando la variable $x$ por la variable $-x$
$f(-x) = \frac{(-x)}{2-(-x)^2}= \frac{-x}{2-x^2}=-\frac{x}{2-x^2} = -f(x)$ por tanta es una función impar ya que $f(x) = -f(-x)$. Entonces es simétrica al origen. Observemos la siguiente gráfica:
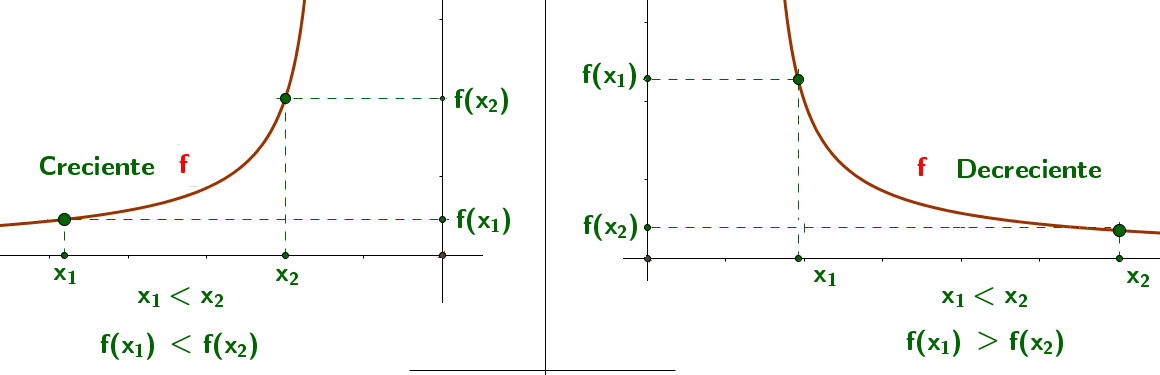
Función creciente y decreciente
Algunas funciones crecen y/o decrecen a medida que avanzan a lo largo del eje x. Estas variaciones ocurren en los valores que toma la función; es decir, en el cambio de las ordenadas.
En términos formales, una función $f(x)$ en un intervalo es:
Creciente
Decreciente
Observa la función cuando es creciente, constante y decreciente:
Gráfica de función $f(x)$ cuando es creciente o decreciente.
 Práctica lo aprendido.
Práctica lo aprendido.
Mide lo que has aprendido, comprueba tus conocimientos respondiendo las siguientes preguntas.
Funciones trascendentes
Las funciones trascendentes, son aquellas que no son funciones algebraicas, como son : las funciones trigonométricas, logarítmicas, exponenciales.
Funciones trigonométricas
 Exploración. Gráfica de las funciones trascendentes, selecciona una función y observa su gráfica.
Exploración. Gráfica de las funciones trascendentes, selecciona una función y observa su gráfica.
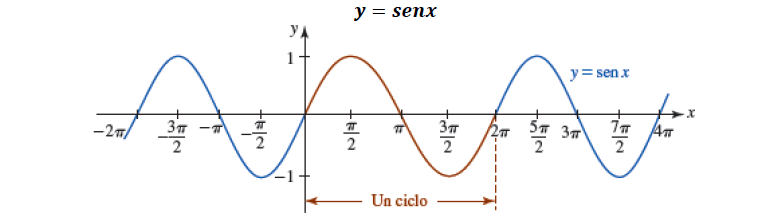
Observemos las siguientes gráficas de la función $Sen(x)$ y $Cos(x)$ donde se tienen algunas propiedades, como son: periodo, dominio, rango, simetría.
Función periódica, de periodo $2 \pi$, es decir $sen(x)=sen(x + 2\pi)$
Dominio: $(-\infty, +\infty) \quad$ Rango: $[-1, 1 ]$
Función impar: simétrica con respecto al origen.
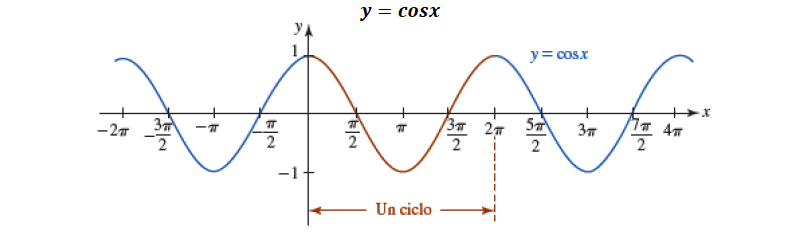
Función periódica, de periodo $2 \pi$, es decir $sen(x)=sen(x + 2\pi)$
Dominio: $(-\infty, +\infty) \quad$ Rango: $[-1, 1 ]$
Función impar: simétrica con respecto al eje $y$.
Transformaciones de funciones trigonométricas
Sean $A>0$, $B>0$, C y D constantes reales $$ y = D + A.Sen( Bx + C)$$ $$ y = D + A.Cos( Bx + C)$$
Donde
D: Desplazamiento vertical
A: Estiramiento, compresión, reflexión vertical
B: Estiramiento, compresión horizontal al cambiar el periodo
C: Desplazamiento horizontal
Algunas observaciones:
El número $|A|$, se denomina amplitud. Para las funciones $y= Sen(x)$ y $y=Cos(x)$ , la amplitud es $|A|=1$ .
El periodo para las funciones básicas $y= Sen(x)$ y $y=Cos(x)$ y está dado por $\frac{2\pi}{B}, B > 0$. .
La porción de la gráfica para las funciones básicas y sobre el intervalo $[0, \frac{2\pi}{B}]$ , se denomina un ciclo.
Ejemplo.
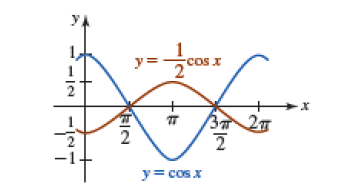
Analiza la siguiente función, a partir de la gráfica de $\quad y=Cos(x)$,
Construya la gráfica de $\quad y=-\frac{1}{2}Cos(x)= - 0.5Cos(x) $
Solución. La gráfica de $y=-\frac{1}{2}Cos(x)$, es la gráfica de $y=Cos(x)$ comprimida verticalmente por un factor de 2.
El signo menos, indica que la gráfica de se refleja luego con respecto al eje $x$. Dado que $A=-\frac{1}{2}$, se tiene que la amplitud es $|A|$.
 Ejercicio. Con ayuda del interactivo, gráfica la función
Ejercicio. Con ayuda del interactivo, gráfica la función
$y=Sen(x)$ y construya la gráfica de $y=1+2Sen(x)$
Observa las transformaciones de una función trigonométrica.
Función Inversa
Una función inversa, que se denota $ f^{-1}(x)$, es una función que parte del rango y llega al dominio. Para hallar la función inversa se procede de la siguiente manera:
Paso 1. Probar que la función es uno a uno. (Si la función no es uno a uno en todo su dominio se puede restringir el intervalo para que sea). Paso 2. Despejar la variable $x$ en términos de la variable $y$. Paso 3. Sustituir la variable $y$ por la variable $x$ y viceversa.Se cumple con la función $f$ y la función inversa de $f$ que:
Ejemplo. Se tiene la siguiente función $\displaystyle f(x) = \frac{2x - 5}{3 + 5x}$, encontrar la función inversa de $f$
$$y = \frac{2x - 5}{3 + 5x}$$ $$y.(3 + 5x) = 2x - 5$$ $$3y + 5xy = 2x - 5$$ $$ 5xy - 2x = - 5 - 3y$$ $$ x.(5y - 2) = - 5 - 3y$$Por lo tanto la función inversa de $f$ es $$x = \frac{- 5 - 3y}{5y - 2} \qquad donde \qquad f^{-1} = \frac{- 5 - 3x}{5x - 2}$$
¡Comprueba!
Se tiene que si el punto $(a, b)$ pertenece a la función $f$ entonces el punto $(b, a)$ pertenece a la función inversa de $f$ . Esto implica que la gráfica de la función $f$ y la gráfica de su inversa $f^{-1}$ se reflejan con respecto a la gráfica de la función $y=x$, por lo tanto, son simétricas.
 Exploración. Comprobemos que la función $f$ y su inversa son simétricas respecto a la recta $y=x$.
Exploración. Comprobemos que la función $f$ y su inversa son simétricas respecto a la recta $y=x$.
 Preguntas. Selección múltiple con única respuesta.
Preguntas. Selección múltiple con única respuesta.
Haz click sobre la respuesta correcta.
 Preguntas. Selección múltiple con única respuesta.
Preguntas. Selección múltiple con única respuesta.
Haz click sobre la respuesta correcta.
Función Exponencial
Sea $b>0$ y $b \equiv\not 1$, entonces una función exponencial $y=f(x)$ es una función de la forma: $$ f(x)= b ^x$$
Se presentan dos tipos de graficas dependiendo de la base $b$:
Si $b>1$, por ejemplo, sea la función $f(x) = 2^x$ su gráfica será:
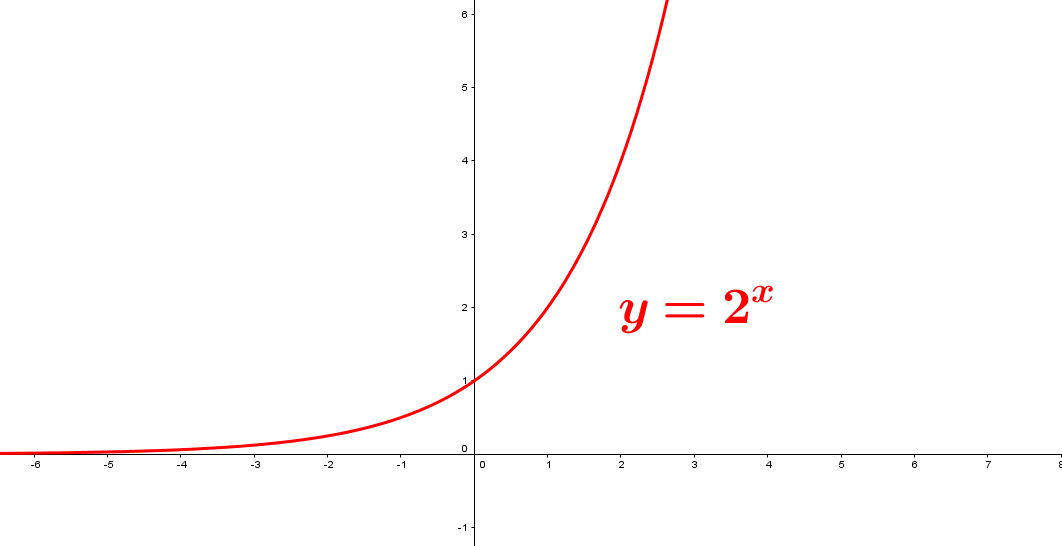
- La base es positiva entonces todos los valores de $f(x)$ son positivos para todo número real.
- Los valores de $f(x)$ tienden a $0$ cuando $x$ decrece, es decir, tiene una asíntota horizontal en $y=0$. No corta el eje $x$.
- Se intercepta en el eje $y$ en el punto (0,1).
- Función es creciente en el intervalo $(-\infty, +\infty)$.
Sea $0 < b < 1$ considere la función $f(x)= (\frac{1}{3})^x$ representada por la gráfica.
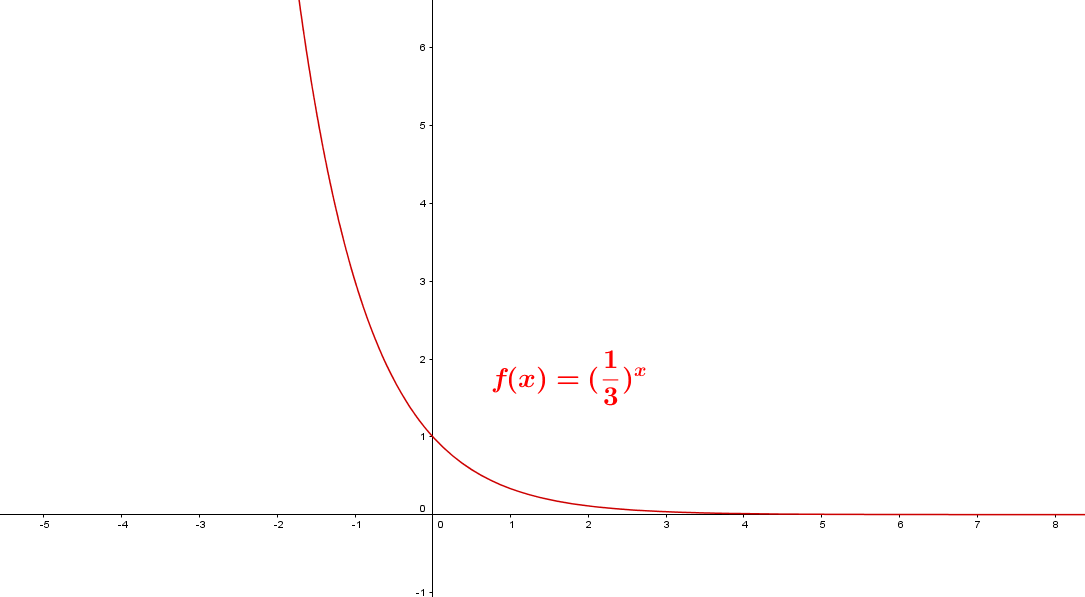
De la gráfica se tiene que:
- La base es una fracción entre cero y uno.
- Los valores de $f(x)$ tienden a $0$ cuando $x$ crece, es decir, tiene una asíntota horizontal en $y=0$. No corta el eje $x$.
- Se intercepta en el eje $y$ en el punto (0,1).
- Función es decreciente en el intervalo $(-\infty, +\infty)$.
Por ejemplo - Considere una base $x$ y un exponente, el cual es un número racional $ \frac{1}{5}$, luego la función exponencial sería: $ \quad y=x^\frac{1}{5} = \sqrt[5]{x} $
Recordemos las propiedades de la potenciación con la siguiente escena interactiva:
Propiedades de las funciones exponenciales- Dominio: conjunto de números reales, $ dom(f)=(-\infty, +\infty)$ .
- Rango: reales positivos, $ ran(f)=(0, +\infty)$.
- Intersección: la gráfica no tiene intersección en eje $x$ , se intercepta en el eje $y$ en el punto (0,1).
- La función $f$ es creciente en $(-\infty, +\infty)$ para $ b > 1$ y decreciente en $(-\infty, +\infty)$ para $0 < b < 1$ .
- El eje $x$, es una asíntota horizontal para la gráfica de $f$.
- La función es uno a uno.
Situación problema. Observa la siguiente escena interactiva, con la solución de situaciones problema de funciones transcendentes.
 Solución problema 1.
Solución problema 1. Como evaluamos la función, supongamos que t = 2, $$ f(2)=\frac {300}{1+ 150e^{-100t}} = \frac {300}{1+ 150e^{-100(2)}}$$ $$= \frac {300}{1+ 150e^{-200}} = 300$$ $$f(2) = 300$$
Función Logarítmica
La función logarítmica es la inversa de la función exponencial.
El logaritmo de $x$ en base $b$, se denota por:
$y= log_b (x)\quad$ si y solo si $\quad x= b^y$
Con $b>0$ y $b \equiv\not 1$ y $x$ un número real.
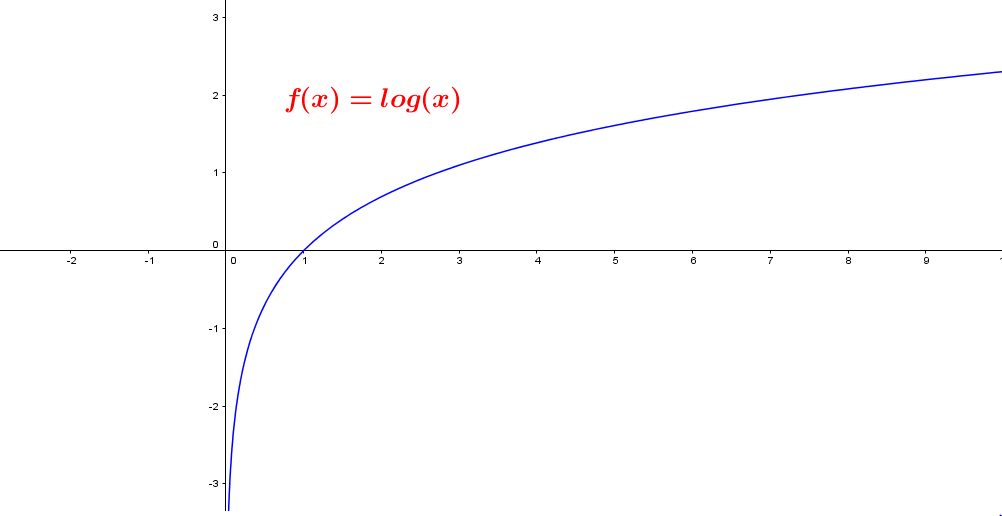
Algunas precisiones:
- Si $b = 10$, se tiene que:
$log_{10} (x) = log (x)$ y se lee: logaritmo en base 10 de $x$. - Si $b = e$, se tiene que:
$log_e (x) = ln(x)$ y se lee: logaritmo natural de $x$.
Propiedades de los logaritmos.
Sea $m$ y $n$ números positivos, entonces:
- $log_b{(m.n)} = log_b{(m)} + log_b{(n)}$.
- $log_b{\frac{m}{n}} = log_b{(m)} - log_b{(n)}$.
- $log_b{(m^n)} = nlog_b{(m)}$.
- $log_b\sqrt[n]{m} = {\frac{1}{m}}. log_b(m)$.
- $log_b{b}= 1$
- $log_b{b^x}= x$.
- $log_b{1}= 0$
- $log_m{n}= \frac{ln(m)}{ln(n)}$
Ejemplo.
Aplique propiedades para simplificar la siguiente expresión:
$$log_4{(2)} + log_4{(32)}=$$
Solución.
$$log_4{(2)} + log_4{(32)} = log_4{(2.32)} = log_4 {(64)} $$ $$log_4{(4^3)} = 3. log_4{(4)} = 3.(1) = 3$$ ¡Recuerda!
¡Recuerda!  Preguntas. Selección múltiple con única respuesta.
Preguntas. Selección múltiple con única respuesta.
Haz click sobre la respuesta correcta.
Ejemplo.
Encontrar utilizando propiedades el valor de $x$.
Solución. $$ln{(2)} + ln{(4x-1)} = ln{(2x+10)} \\ ln{(2.(4x-1))}= ln{(2x+10)} \\ 8x - 2 = 2x + 10 \\ 6x = 12$$ $$x = 2$$
 Preguntas. Selección múltiple con única respuesta.
Preguntas. Selección múltiple con única respuesta.
Haz click sobre la respuesta correcta.
 Ejemplo. Hallar el dominio de una función logarítmica.
Ejemplo. Hallar el dominio de una función logarítmica.
 Actividades complementarias
Actividades complementarias
Con el objetivo de complementar lo aprendido en la sección y desarrollar competencias, realiza las siguientes actividades propuestas.
 Refuerza lo aprendido.
Refuerza lo aprendido.
Analiza los siguientes ejercicios resueltos Tomado de: Cálculo Diferencial mediado por TIC y videos. (2016). Pag. 64
y practica.
 Práctica lo aprendido.
Práctica lo aprendido.
Practica lo apendido en esta sección. Tomado de: Cálculo Diferencial mediado por TIC y videos. (2016). Pag. 64
Límites de una función
Definición no formal de límite
Suponga que $L$ denota un número finito. El concepto de $f(x)$ que tiende a $L$ a medida que $x$ tiende a un número $a$ puede definirse informalmente de la siguiente manera:
Notación $$\lim_{x \to a}{f(x)}= L$$ Se lee: "el Límite de $f(x)$ cuando $x$ tiende $a$ es igual a $L$", o de otra manera “ cuando $x$ se acerca $a$ es igual a $L$”.
Limites laterales, son límites que tienden por la derecha o izquierda:
- ${x \to a^-}$
Se lee: "$x$ tiende $a$ por la izquierda" o de otra manera “$x$ se acerca $a$ por valores ligeramente menores que $a$”. - ${x \to a^+}$
Se lee: "$x$ tiende $a$ por la derecha" o de otra manera “$x$ se acerca $a$ por valores ligeramente mayores que $a$”.
Existencia del límite
Consideremos las siguientes funciones en la escena interactiva y analiza el límite de cada función. Mueva el punto y observe el límite.
“La existencia de un límite de una función $f$ cuando $x$ tiende a $“a”$ (desde un lado o desde ambos lados) no depende de si $f$ está definida en $a$, sino sólo de si está definida para $x$ cerca del número $a$.” D. Zill.
Consideremos la función $y= \frac{x^2-9}{x-3}$ que no está definida en $x=3$.

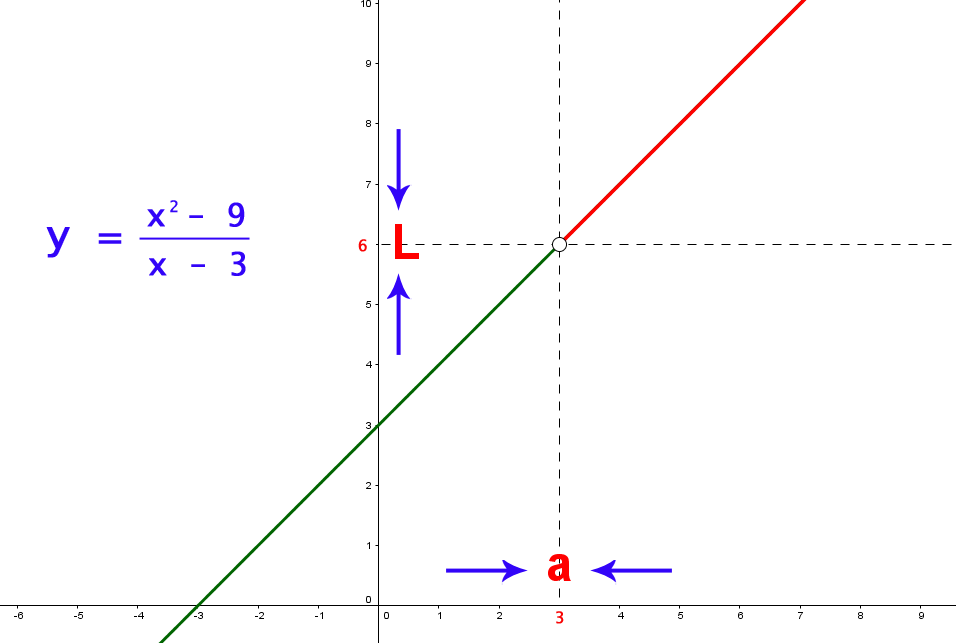
Evaluando los limites laterales, coinciden con los valores en la tabla:
$$\lim_{x \to 3^-}{f(x)}= 6$$
$$\lim_{x \to 3^+}{f(x)} = 6$$
 Ejercicio.Escena de José R. Galo Sánchez y Mª José García Cebrian adaptadas por el autor.
Ejercicio.Escena de José R. Galo Sánchez y Mª José García Cebrian adaptadas por el autor.
Use las gráficas para analizar los límites laterales, ingrese el valor de todos los límites propuestos y pulsa la tecla "enter <┘", verifique sus respuestas.
Si hay errores, modifique los resultados y pulsa la tecla "enter <┘".
Propiedades de los límites
Supongamos $f$ y $g$ funciones y $l_1$ y $l_2$ números reales, entonces las propiedades de los límites son:
Cálculo de límites
Sustitución directa de un límite
Si $f$ es un función y $a$ está definida en el dominio de la función $f$, entonces $$\lim_{x \to a}{f(x)}= f(a)$$
Se evalúa la función en el punto $x$ dado y se simplifican las expresiones resultantes, al valuar la función el símbolo de límite desaparece
Ejemplo 1 $$\lim_{x \to 0}{x^2+3x-2}= $$
Evaluando el límite se tiene que $(0)^2 + 3(0) - 2 = -2$, luego el límite existe cuando $x = 0$, se acerca a $-2$.
Ejemplo 2 $$\lim_{x \to -3} \frac{3x-2}{x-5}= $$ $$= \frac{3(-3)-2}{(-3)-5}=\frac{-11}{-8} $$ por lo tanto $$\lim_{x \to -3} \frac{3x-2}{x-5}=\frac{11}{8} $$
Las funciones con la propiedad de sustitución directa se denominan continuas en $x=a$.
No obstante, no todos los límites pueden ser evaluados por sustitución directa, ya que puede suceder que no podemos hallar el límite al sustituir $x=a$ porque $f(a)$ no está definida en la función.
Ejemplos Escena de Carlos Hernandéz Garciadiego. Límites de funciones, elige el tipo de función y oprime los botones numéricos para seguir pasos a paso la solución.
Límites con indeterminación $\frac{0}{0}$
Son límites que al evaluarse presentan la forma $\frac{0}{0}$, por lo cual se busca eliminar esa indeterminación con algún procesos matemático.
Como primer paso para resolver cualquier límite es sustituir el valor de la variable $x$ por el número al que tienda y ver si se obtiene un valor por sustitución directa, pero si obtenemos un valor de $\frac{0}{0}$, procedemos así:
Descomponemos en factores los polinomios del numerador y del denominador, simplificando los factores comunes.
 Ejemplo.
Ejemplo.
Hallar el siguiente límite $$\lim_{x \to -3} \frac{x^2-9}{x+3}$$
Primero se evalúa el límite por sustitución directa: $$\lim_{x \to -3} \frac{x^2-9}{x+3}= \frac{3^2-9}{-3-3}=\frac{0}{0} $$ factorizando se tiene que:$$ \lim_{x \to -3} \frac{(x-3)\cancel{(x+3)}}{\cancel{(x+3)}}=\lim_{x \to -3} {(x-3)} = (-3-3) = -6 $$
$$\lim_{x \to -3} \frac{x^2-9}{x+3}= -6 $$
En ocasiones, los límites con indeterminación tienen raíces y en estos casos se dificulta factorizar los polinomios para eliminar factores del numerador y del denominador.
Para esta situación, se utiliza multiplicar el numerador y el denominador por el conjugado del binomio donde esté la raíz.
$\sqrt{a}-\sqrt{b}$, donde su conjugada es: $\sqrt{a}+\sqrt{b}$, de está forma obtenemos que: $$(\sqrt{a}-\sqrt{b}).(\sqrt{a}+\sqrt{b}) = (\sqrt{a})^2-(\sqrt{b})^2=a-b$$
Ejemplo.
Resolver el siguiente límite:
$$\lim_{x \to 4} \frac{\sqrt{x}-2}{x-4}$$
Primero se evalúa el límite por sustitución directa: $$\lim_{x \to 4} \frac{\sqrt{x}-2}{x-4}= \frac{\sqrt{4}-2}{4-4}= \frac{0}{0} $$ La simplificación de una expresión que contiene radicales, se resuelve en este caso multiplicando y dividiendo toda la función por la conjugada del numerador, o sea por $({\sqrt{x}+2})$
$$\lim_{x \to 4} \frac{(\sqrt{x}-2)(\sqrt{x}+2)}{(x-4)(\sqrt{x}+2)}= \lim_{x \to 4} \frac{(\sqrt{x})^2-(2)^2}{(x-4)(\sqrt{x}+2)}= $$
$$=\lim_{x \to 4} \frac{\cancel{(x-4)}}{\cancel{(x-4)}(\sqrt{x}+2)}= \frac{1}{\sqrt{4}+2} = \frac{1}{2+2} = \frac{1}{4} $$
Para este caso, realizamos las operaciones matemáticas que se presenten para llegar a una simplificación de una expresión equivalente.
Ejemplo.
Resolver el siguiente límite: $$\lim_{x \to 0} \frac{1 + \frac{4}{x}}{1 - \frac{2}{x}}$$
Primero se evalúa el límite por sustitución directa: $$\lim_{x \to 0} \frac{1 + \frac{4}{x}}{1 - \frac{2}{x}}= \frac{1 + \frac{4}{0}}{1 - \frac{2}{0}} $$
Para eliminar la indeterminación en este caso, resolvemos la expresión racional y simplificamos los resultados.
$$\lim_{x \to 0} \frac{1 + \frac{4}{x}}{1 - \frac{2}{x}}= \lim_{x \to 0} \frac{\frac{x+4}{x}}{\frac{x-2}{x}} = \lim_{x \to 0} \frac{\cancel{x}.(x+4)}{\cancel{x}.(x-2)} $$
$$\lim_{x \to 0} \frac{x+4}{x-2} = \frac{0+4}{0-2} = \frac{4}{-2} = -2 $$
$$\lim_{x \to 0} \frac{1 + \frac{4}{x}}{1 - \frac{2}{x}}= -2$$Se debe tener presente en la solución del límite de una función lo siguiente:
Límite es único
Si $lim_{x \to a} f(x)$ existe, entonces es único.
Límite que no existe
Si $f(x)\equiv\not 0$ y $g(x) = 0$ cuando ${x \to a}$ entonces $\lim_{x \to a} \frac{f(x)}{g(x)}$ no existe.
Observa la siguiente escena interactivaEscena de Carlos Hernandéz Garciadiego. con ejemplos de la solución de límites de diferentes funciones. Sigue pasos a paso la solución.
 Ejemplo. Límites indeterminados.
Ejemplo. Límites indeterminados.
 Preguntas. Selección múltiple con única respuesta.
Preguntas. Selección múltiple con única respuesta.
Haz click sobre la respuesta correcta.
Límites trigonométricos
Para los límites trigonométricos, resulta útil aplicar los límites:
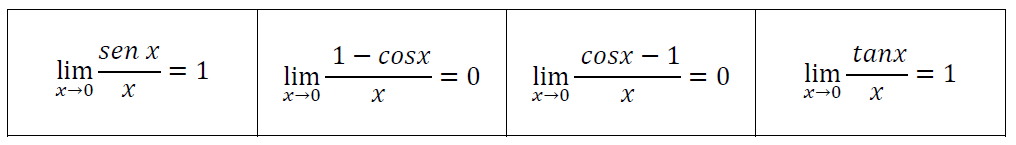
 Ejemplo 1. Evaluar el siguiente límite $$\lim_{x \to 0} \frac{Sen(x)}{4x} = $$
Ejemplo 1. Evaluar el siguiente límite $$\lim_{x \to 0} \frac{Sen(x)}{4x} = $$
$$\lim_{x \to 0} \frac{Sen(x)}{4x} = \lim_{x \to 0} \frac{1}{4} \frac{Sen(x)}{x} = \frac{1}{4} \lim_{x \to 0} \frac{Sen(x)}{x} = \frac{1}{4} (1) = \frac{1}{4} $$ por lo tanto $$\lim_{x \to 0} \frac{Sen(x)}{4x} = \frac{1}{4} $$
 Ejemplo 2. Evaluar el siguiente límite $$\lim_{x \to 0} \frac{Sen(3x)}{2x} = $$
Ejemplo 2. Evaluar el siguiente límite $$\lim_{x \to 0} \frac{Sen(3x)}{2x} = $$
$$\lim_{x \to 0} \frac{Sen(3x)}{2x} = \lim_{x \to 0} \frac{1}{2} \frac{Sen(3x)}{x} = \frac{1}{2} \lim_{x \to 0} \frac{3}{3}\frac{Sen(3x)}{x} = $$ $$\frac{1}{2}.(3) \lim_{x \to 0} \frac{Sen(3x)}{3x} = \frac{3}{2}.(1) = \frac{3}{2} $$
 Ejemplo 3. Evaluar el siguiente límite $$\lim_{x \to 0} \frac{x-x Cos(x)}{3x^2} = $$
Ejemplo 3. Evaluar el siguiente límite $$\lim_{x \to 0} \frac{x-x Cos(x)}{3x^2} = $$
$$\lim_{x \to 0} \frac{x-x Cos(x)}{3x^2} = \lim_{x \to 0} (x).(\frac{1}{3}).\frac{1-Cos(x)}{x^2} = $$ $$ (\frac{1}{3}) \lim_{x \to 0} \cancel{x}.\frac{1-Cos(x)}{x\cancel{^2}} = (\frac{1}{3}) \lim_{x \to 0} \frac{1-Cos(x)}{x} = (\frac{1}{3}).(0) = 0 $$ por lo tanto $$\lim_{x \to 0} \frac{x-x Cos(x)}{3x^2} = 0$$
 Ejercicio.Escena de Carlos Hernandéz Garciadiego adaptada por el autor.
Escribe en el recuadro la solución, puedes utilizar 2 decimales o fracción $\frac{a}{b}$.
Verifica pulsando la tecla "enter <┘", para continuar debes tener correcto el ejercicio.
Ejercicio.Escena de Carlos Hernandéz Garciadiego adaptada por el autor.
Escribe en el recuadro la solución, puedes utilizar 2 decimales o fracción $\frac{a}{b}$.
Verifica pulsando la tecla "enter <┘", para continuar debes tener correcto el ejercicio.
 Ejemplo. Límites trigonométricos.
Ejemplo. Límites trigonométricos.
 Preguntas. Selección múltiple con única respuesta.
Preguntas. Selección múltiple con única respuesta.
Haz click sobre la respuesta correcta.
Se pueden presentar otros límites de sustitución directa o que se puedan utilizar identidades o en algunos casos resulta útil utilizar sustituciones para eliminar las indeterminaciones, como:
 Ejemplo 1.
Ejemplo 1.
Sustitución directa. (Utiliza la calculadora para verificar).
 Ejemplo 2.
Ejemplo 2.
Utilicemos una identidad trigonométrica. $$\lim_{x \to \frac{\pi}{2}} \frac{Cos(x)}{Cot(x)} $$
$$\lim_{x \to \frac{\pi}{2}} \frac{Cos(x)}{Cot(x)} = \lim_{x \to \frac{\pi}{2}} \frac{Cos(\frac{\pi}{2})}{Cot(\frac{\pi}{2})} = \frac{0}{0} $$
entonces, utilizamos la identidad para sustituir $cot(x)$,
$$\lim_{x \to \frac{\pi}{2}} \frac{Cos(x)}{Cot(x)} = \lim_{x \to \frac{\pi}{2}} \frac {Cos(x)}{\frac{Cos(x)}{Sen(x)} } = \lim_{x \to \frac{\pi}{2}} \frac{Sen(x)}{1} = \frac{Sen(\frac{\pi}{2})}{1} = \frac{1}{1} = 1 $$
$$\lim_{x \to \frac{\pi}{2}} \frac{Cos(x)}{Cot(x)}=1 $$
En algunos casos resulta útil aplicar sustituciones, para eliminar las indeterminaciones en el cálculo de un límite trigonométrico.
 Ejemplo.
Ejemplo.
Limite por sustitución con cambio de variable.
Sea $y = \frac{\pi}{2}-x$, donde si ${x \to \frac{\pi}{2}}$ entonces se tiene que ${y \to 0}$. por tanto
$$\lim_{x \to \frac{\pi}{2}} \frac{\frac{\pi}{2}-x}{Cos(x)} = \lim_{y \to 0} \frac{y}{Cos(\frac{\pi}{2}-y)}= (identidad) $$ $$= \lim_{y \to 0} \frac{y}{\cancel{Cos(\frac{\pi}{2})cos(y)} + \cancel{sen(\frac{\pi}{2})}sen(y)} $$ donde tenemos que $Cos(\frac{\pi}{2}) = 0$ y $Sen(\frac{\pi}{2}) = 1$, entonces, $$ = \lim_{y \to 0} \frac{y}{Sen(y)} = \lim_{y \to 0} (\frac{sen(y)}{y})^{-1} = $$ $$= (\cancel{\lim_{y \to 0} (\frac{sen(y)}{y})})^{-1} = 1^{-1} = 1$$ por lo tanto $$\lim_{x \to \frac{\pi}{2}} \frac{\frac{\pi}{2}-x}{Cos(x)} = 1 $$ Ejemplo. Límites con cambio de variable.
Ejemplo. Límites con cambio de variable.
 Preguntas. Selección múltiple con única respuesta.
Preguntas. Selección múltiple con única respuesta.
Haz click sobre la respuesta correcta.
Límites Infinitos
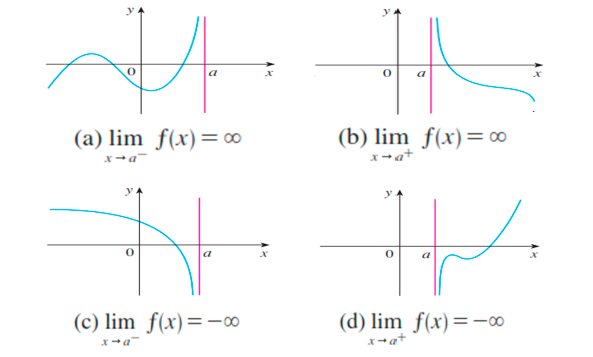
El límite de una función no existe siempre que a medida que ${x \to a}$, $f(x)$ crece o decrece sin límite. Esto es. $$\lim_{x \to a} f(x) = \infty$$ $$\lim_{x \to a} f(x) = -\infty$$
Definiciones de límites infinitos laterales que se presentan:
 ¡Recuerda!
¡Recuerda!
"${x \to a^-}$" significa que consideramos sólo valores de $x < a$, y "${x \to a^+}$" significa que consideramos sólo valores de $x >a$.
Límites al Infinitos
Indican a qué valor se aproxima la función, cuando ${x \to +\infty}$ o ${x \to -\infty}$. En este caso, diremos que:
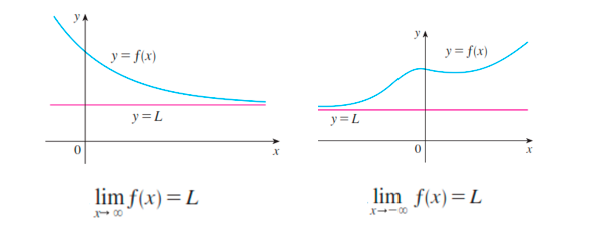
En ambos casos, el limite existe y es igual a $L$
Analicemos el siguiente límite: $\quad \displaystyle \lim_{x \to \infty} \frac{1}{x}$
Si $x$ toma valores cada vez más grandes, $\frac{1}{x}$ es más pequeña.
Por ejemplo: $\frac{1}{10}= 0,1$, $\frac{1}{100}= 0,01$, $\frac{1}{10000}= 0,0001$

Por tanto, al tomar $x$ lo suficientemente grande, podemos hacer que $\frac{1}{x}$ sea tan cercana a $0$ como queramos, por tanto, se tiene que:
$$\lim_{x \to \infty} \frac{1}{x} = 0$$Igual razonamiento cuando $x$ es grande negativa, $\frac{1}{x}$ es cercana a cero.
Por tanto, obtenemos la siguiente regla para calcular límites que tienden a $\pm \infty$
Evaluar límites en el infinito de una función racional.
Se debe dividir numerador y denominador por la potencia más grande de $x$
que se encuentre en el numerador o denominador de la función racional,
 ¡Recuerda!
¡Recuerda!
Veamos los siguientes ejemplos y análisis:
 Ejemplo1. Evaluar el siguiente límite: $$\lim_{x \to \infty} \frac{3x^2-2x+2}{6x^2-x+3}$$
Ejemplo1. Evaluar el siguiente límite: $$\lim_{x \to \infty} \frac{3x^2-2x+2}{6x^2-x+3}$$
Dividimos por la mayor potencia de $x$, en este caso $x^2$ $$\lim_{x \to \infty} \frac{\frac{3x^2-2x+2}{x^2}}{\frac{6x^2-x+3}{x^2}} = \lim_{x \to \infty} \frac{\frac{3x^2}{x^2}-\frac{2x}{x^2}+\frac{2}{x^2}}{\frac{6x^2}{x^2}-\frac{x}{x^2}+\frac{3}{x^2}} =$$ simplificamos cada termino que sea posible $$= \lim_{x \to \infty} \frac{\frac{3\cancel{x^2}}{\cancel{x^2}}-\frac{2\cancel{x}}{x\cancel{^2}}+\frac{2}{x^2}}{\frac{6\cancel{x^2}}{\cancel{x^2}}-\frac{\cancel{x}}{x\cancel{^2}}+\frac{3}{x^2}} = \lim_{x \to \infty} \frac{\frac{3}{1}-\frac{2}{x}+\frac{2}{x^2}}{\frac{6}{1}-\frac{1}{x}+\frac{3}{x^2}} = $$ por tanto,
Aplicando las propiedades de los límites y distribuyendo en toda la expresión tenemos que: $$\lim_{x \to \infty} \frac{3-\frac{2}{x}+\frac{2}{x^2}}{6-\frac{1}{x}+\frac{3}{x^2}} = \frac{\lim_{x \to \infty} 3- \lim_{x \to \infty} \frac{2}{x}+ \lim_{x \to \infty} \frac{2}{x^2}}{\lim_{x \to \infty} 6 - \lim_{x \to \infty} \frac{1}{x} + \lim_{x \to \infty} \frac{3}{x^2}}$$ Aplicando la regla $\lim_{x \to \infty} \frac{1}{x^n} = 0$, obtenemos, $$\frac{3 - 0 + 0}{6 - 0 + 0} = \frac{3}{6} = \frac{1}{2}$$
 Ejercicio.Escena de Juan Guillermo Rivera adaptada por el autor.
Escribe en los recuadros la solución en fracción $\frac{a}{b}$, para verificar pulsa la tecla "enter <┘"
Ejercicio.Escena de Juan Guillermo Rivera adaptada por el autor.
Escribe en los recuadros la solución en fracción $\frac{a}{b}$, para verificar pulsa la tecla "enter <┘"
 Ejemplo2. $\quad \displaystyle \lim_{x \to \infty} \frac{x^3 + x}{2 - x}$
Ejemplo2. $\quad \displaystyle \lim_{x \to \infty} \frac{x^3 + x}{2 - x}$
Dividimos por la mayor potencia de $x$, en este caso $x^3$ $$\lim_{x \to \infty} \frac{\frac{x^3-x}{x^3}}{\frac{2-x}{x^3}} = \lim_{x \to \infty} \frac{\frac{x^3}{x^3}-\frac{x}{x^3}}{\frac{2}{x^3}+\frac{x}{x^3}} = \lim_{x \to \infty} \frac{\cancel{\frac{x^3}{x^3}}-\frac{\cancel{x}}{x\cancel{^3}}}{\frac{2}{x^3}+\frac{\cancel{x}}{x\cancel{^3}}} = \lim_{x \to \infty} \frac{1-\frac{1}{x^2}}{\frac{2}{x^3}+\frac{1}{x^2}}$$
Aplicando las propiedades y distribuyendo tenemos que: $$\frac{\lim_{x \to \infty} 1- \lim_{x \to \infty} \frac{1}{x}}{\lim_{x \to \infty} \frac{2}{x^3} + \lim_{x \to \infty} \frac{1}{x^2}} = \frac{1 - 0}{0 + 0} = \frac{1}{0} = \infty$$ por tanto el límite no existe.
 Ejemplo3. $\quad \displaystyle \lim_{x \to \infty} \frac{3 + 2x}{2 - 2x^2}$
Ejemplo3. $\quad \displaystyle \lim_{x \to \infty} \frac{3 + 2x}{2 - 2x^2}$
Dividimos por la mayor potencia de $x$, en este caso $x^2$ $$\lim_{x \to \infty} \frac{\frac{3+2x}{x^2}}{\frac{2-2x^2}{x^2}} = \lim_{x \to \infty} \frac{\frac{3}{x^2}+\frac{2x}{x^2}}{\frac{2}{x^2}-\frac{2x^2}{x^2}} = \lim_{x \to \infty} \frac{\frac{3}{x^2}+\frac{2}{x}}{\frac{2}{x^2} - 2}$$
Aplicando las propiedades de los límites y distribuyendo en toda la expresión tenemos que: $$\frac{\lim_{x \to \infty} \frac{3}{x^2} + \lim_{x \to \infty} \frac{2}{x}}{\lim_{x \to \infty} \frac{2}{x^2} - \lim_{x \to \infty} 2} = \frac{0 + 0}{0 - 2} = \frac{0}{2} = 0$$ por tanto el límite existe y es igual a cero.
 Ejercicio.Escena de Juan Guillermo Rivera adaptada por el autor.
Observa el límite y selecciona la respuesta correcta para verificar la solución.
Ejercicio.Escena de Juan Guillermo Rivera adaptada por el autor.
Observa el límite y selecciona la respuesta correcta para verificar la solución.
¿Qué se puede deducir al solucionar limites donde $x \to \pm\infty$ de una función racional si la máxima potencia se encuentra en el numerador?
¿Qué se puede deducir al solucionar limites donde $x \to \pm\infty$ de una función racional si la máxima potencia se encuentra en el denominador?
 ¡Conclusión!
¡Conclusión!
Para hallar el límite al infinito de una función racional de la forma $y= \frac{f(x)}{g(x)}$ (cociente entre dos polinomios), se compara el grado de $f(x)$ y $g(x)$.
Sean $m$ y $n$ el grado de los polinomios $f(x)$ y $g(x)$ respectivamente, entonces:
- Si $m < n$, entonces $\lim_{x \to \infty}f(x) = 0$
- Si $m > n$, entonces $\lim_{x \to \infty}f(x) = \pm \infty$
- Si $m = n$, entonces $\lim_{x \to \infty}f(x) = \frac{a_m}{b_n}$
 Ejemplo4. Veamos cuando la función es radical
$$\lim_{x \to \infty} \frac{x}{\sqrt{x^2}}$$
Ejemplo4. Veamos cuando la función es radical
$$\lim_{x \to \infty} \frac{x}{\sqrt{x^2}}$$
Dividimos por la mayor potencia de $x$, en este caso sería $x$ $$\lim_{x \to \infty} \frac{x}{\sqrt{x^2}}=\lim_{x \to \infty} \frac{\frac{x}{x}}{\sqrt{\frac{x^2}{x^2}}}=\frac{1}{1}=1$$
Este valor corresponde a una asíntota $y=1$, las cuales se estudiarán a continuación.
 Ejemplo. Límites que tienden al infinito.
Ejemplo. Límites que tienden al infinito.
 Preguntas. Selección múltiple con única respuesta.
Preguntas. Selección múltiple con única respuesta.
Haz click sobre la respuesta correcta.
Estudio de las asíntotas
Cuando la gráfica de una función se acerca a una recta, donde $x$ o $y$ tienden a infinito, dicha recta se llama asíntota de la función, y se clasifican en: verticales, horizontales y/o oblicuas. No todas las funciones tienen rectas asíntotas.
1. Asíntota vertical.
Se dice que $x=a$ es una asíntota vertical si cualquiera de las afirmaciones siguientes se cumple:
| $$ \lim_{x \to a^-}f(x) = -\infty$$ | $$ \lim_{x \to a^+}f(x) = -\infty$$ | $$ \lim_{x \to a}f(x) = -\infty$$ |
|---|---|---|
| $$ \lim_{x \to a^-}f(x) = \infty$$ | $$ \lim_{x \to a^+}f(x) = \infty$$ | $$ \lim_{x \to a}f(x) = \infty$$ |
Gráfica de una asíntota vertical en $x=a$.
2. Asíntota horizontal.
Hasta el momento hemos analizado el límite de una función $f(x)$ cuando "$x \to a$" un número real $L$. Sin embargo, también es posible analizar el comportamiento de una función $f(x)$, cuando $x$ toma valores cada vez más grandes, sean éstos positivos o negativos; es decir cuando ${x \to +\infty}$ o cuando ${x \to -\infty}$.
La recta $y=b$ es una asíntota horizontal de $f(x)$, si se cumple que: $$ \lim_{x \to \pm\infty}f(x) = b$$
Gráfica de una asíntota horizontal en $y=b$.
 ¡Recuerda!
¡Recuerda!Las indeterminaciones pueden presentarse de la forma :
$$\frac{\infty}{\infty} \qquad \infty - \infty \qquad \frac{0}{0} \qquad 0^\infty \qquad 0^0 \qquad \infty ^0 \qquad 1^\infty$$
Ejemplo 1 - Asíntotas de funciones racionales.
Veamos la función $y=\frac{1+2x}{2+x}$, que asíntotas tiene:
Asíntota vertical: $x=-2$, ya que $2+x =0 \to x=-2$ y límite $$\lim_{x \to -2}\frac{1+2x}{2+x}=\infty$$
Asíntota horizontal: $y=2$ ya que el límite cuando $x \to \infty$ es: $$\lim_{x \to \infty}\frac{1+2x}{2+x}=2$$
 GeoGebra.
Observa la escena interactiva, modifica los controles y genera las asintotas de la función $f(x)$.
GeoGebra.
Observa la escena interactiva, modifica los controles y genera las asintotas de la función $f(x)$.
3. Asíntota oblicua.
Cuando la función $f(x)$ es el cociente de dos polinomios, y el grado del numerador supera en uno al del denominador, entonces la curva $y=f(x)$ tiene una asíntota oblicua cuya ecuación es la función lineal $y=mx+b$ $(m \equiv\not 0)$, donde: $$m=\lim_{x \to \infty}\frac{f(x)}{x} \qquad b= \lim_{x \to \infty}(f(x)- m(x))$$
Gráfica de una asíntota oblicua en $y=mx+b$.
Nota:
Ejemplo 2 - Asíntotas de una función.
Veamos la función $y=\frac{x^2}{x +1}$, que asíntotas tiene:
Ya que $x+1 =0 \to x=-1$ y límite de la función cuando $x \to -1$ $$\lim_{x \to -1}\frac{x^2}{x+1}= \frac{1}{0}=\infty$$
Ya que el límite cuando $x \to \infty$ es: $$\lim_{x \to \infty}\frac{x^2}{x+1}=\lim_{x \to \infty}\frac{\frac{x^2}{x^2}}{\frac{x}{x^2}+\frac{1}{x^2}}=\frac{1}{0}=\lim_{x \to \infty}\frac{1}{\frac{1}{x}+\frac{1}{x^2}}=\frac{1}{0}=\infty$$
Como no tiene asíntota horizontal, podemos analizar la oblicua:
Encontremos la recta $y=mx+b$, donde $$m=\lim_{x \to \infty}\frac{f(x)}{x}= \lim_{x \to \infty}\frac{\frac{x^2}{x+1}}{x}=\lim_{x \to \infty}\frac{x^2}{x^2+x}=1$$ $$b= \lim_{x \to \infty}(f(x)- m(x))=\lim_{x \to \infty}(\frac{x^2}{x+1}- x)=\lim_{x \to \infty}\frac{-x}{x+1}=-1$$
Observa la gráfica de la función $f(x)$ con sus asíntotas.
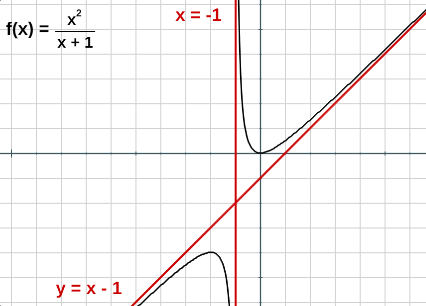
En conclusión, Las asíntotas son rectas a las cuales la función se va aproximando indefinidamente, cuando por lo menos una de las variables $x$ o $y$ tienden al infinito. Realiza el análisis de las siguientes funciones, respondiendo a las siguientes preguntas:
 Preguntas. Selección múltiple con única respuesta.
Preguntas. Selección múltiple con única respuesta.
Haz click sobre la respuesta correcta.
Continuidad de una función
Una función $f$ es continua en un punto $x=a$, si cumplen las siguientes condiciones:
- $f(a)$ exista, que este definida.
- $\displaystyle \lim_{x \to a} f(x)$ exista
- $\displaystyle \lim_{x \to a} f(x)= f(a)$
Si alguna de las condiciones no se cumple, entonces se dice que $f$ es discontinua en el punto $x=a$.
Ejemplo. Verificar si $f(x) = \begin{cases} x^2+1 &\text{si } x\le -1 \\ 2x &\text{si } x>-1\end{cases} $ es continua.
- $f(a)=f(-1)= (-1)^2+1 = 2$, entonces $f(-1)=2\space$ Existe.
- Analizamos los limites laterales:
Por izquierda, $\displaystyle \lim_{x \to a^-} f(x)=\lim_{x \to -1^-} x^2+1=(-1)^2+1=2$
Por derecha, $\displaystyle \lim_{x \to a^+} f(x)=\lim_{x \to -1^+} 2x=2(-1)=-2$
Luego, como los límites laterales son diferentes, el $\displaystyle \lim_{x \to -1} f(x)$ no existe, por tanto, $f(x)$ es discontinua en $x=-1$.
Ejemplos.
Observa algunos ejemplos que ilustran la no continuidad en una gráfica de una función $f$ en un punto $x=a$. Para ver más ejemplos, oprime el botón Otro ejemplo.
Las discontinuidades se pueden clasificar como de salto, infinitas, removibles, de punto final o mixtas.
Casos que se pueden presentar en la discontinuidad:
Discontinuidad removible.
Caso 1.
Si se tiene que $f(a)$ no está definida, pero se cumple que el $\displaystyle\lim_{x \to a} f(x)$ existe, se dice que las discontinuidades son removibles o puntuales, para remover está discontinuidad basta con redefinir la función para $x=a$, por ejemplo:
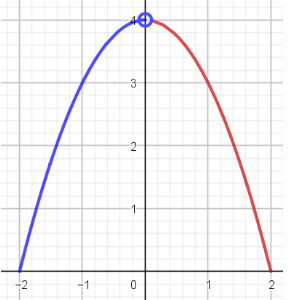
La función cuya gráfica se presenta no es continua en el punto $x=0$ debido a que en ese punto la imagen para $x=0$ no está definida, pero el límite si existe, ya que: $$\lim_{x \to 0^-} f(x)=\lim_{x \to 0^+} f(x)=4$$
Caso 2.
Si se tiene que $f(a)$ está definida y que el $\displaystyle \lim_{x \to a} f(x)$ existe, pero no se cumple la tercera condición, que $\displaystyle \lim_{x \to a} f(x)= f(a)$, se dice que la función tiene discontinuidad removible, por ejemplo:
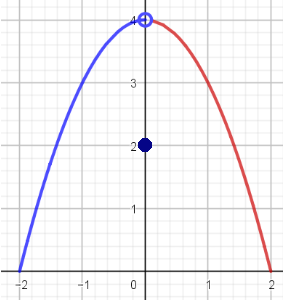
La función cuya gráfica se presenta no es continua en el punto $x=0$ debido a que en ese punto la imagen para $x=0$ está definida, $$f(0)=2$$ y el límite existe, ya que: $$\lim_{x \to 0^-} f(x)=\lim_{x \to 0^+} f(x)=4$$
pero no se cumple que $$\lim_{x \to 0} f(x)= f(0)$$
Discontinuidad no removible.
Caso 3.
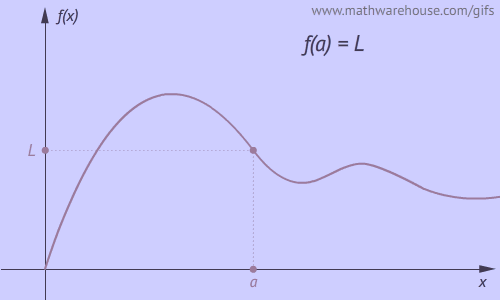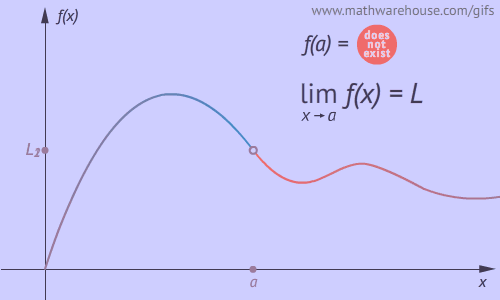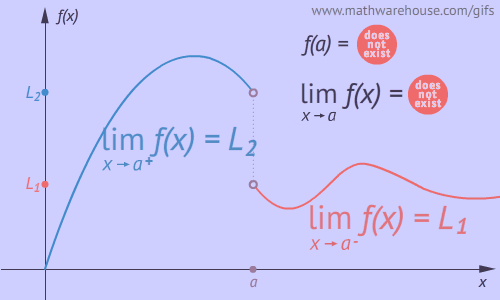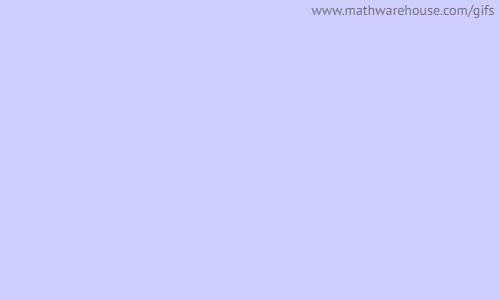
Si se tiene que no se cumple la condición 2, que: $$\lim_{x \to a} f(x) \space no \space existe$$ se dice que la discontinuidad en NO removible, porque la gráfica de la función presenta un salto, por ejemplo:
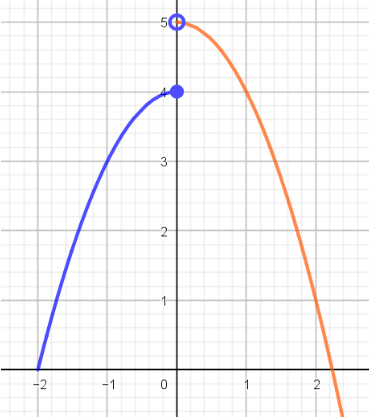
La función cuya gráfica se presenta no es continua en el punto $x=0$ debido a que en ese punto la imagen para $x=0$ está definida, $$f(0)=4$$ pero el límite no existe, ya que: $$\lim_{x \to 0^-} f(x) \space \cancel{=} \lim_{x \to 0^+} f(x)$$
En la gráfica de la función $f$, analiza la continuidad en cada punto.
Continuidad de una función compuesta.
Si $g$ es continua en un punto $x=a$ y $f$ es continua en $g(a)$, entonces la función compuesta $(f\circ g)(x) = f(g(x))$ es continua en $x=a$.
Teorema. Límite de una función compuesta.
Si $\displaystyle \lim_{x \to a} g(x)=L$ y $f$ es continua en $L$, entonces: $$\lim_{x \to a} f(g(x))= f(\lim_{x \to a} g(x))= f(L)$$
Ejemplo. Determinar el valor de $c$ y $k$ para que la función sea continua si $f(x) = \begin{cases} x &\text{si } x\le 1 \\ cx+k &\text{si } 4 >x>1 \\ -2x &\text{si } 4\le x \end{cases}$
Analizando cuando $x=1$, se tiene que:
$f(a)=f(1)=1$.
- hallamos el $\displaystyle \lim_{x \to 1} f(x)$ con los Límites laterales:
Por izquierda, $\displaystyle \lim_{x \to a^-} f(x)=\lim_{x \to 1^-}x =1$
Por derecha, $\displaystyle \lim_{x \to a^+}f(x)=\lim_{x \to 1^+}cx+k =c(1)+k=c+k$
Como $\displaystyle \lim_{x \to 1^-} f(x)=\lim_{x \to 1^+}f(x)$ entonces $\quad c+k=1 \quad (1)$
Analizando cuando $x=4$, se tiene que:
$f(a)=f(4)=-2(4)=-8$
- hallamos el $\displaystyle \lim_{x \to 4} f(x)$ con los Límites laterales:
Por izquierda, $\displaystyle \lim_{x \to a^-}f(x)=\lim_{x \to 4^-}cx+k =c(4)+k=4c+k$
Por derecha, $\displaystyle \lim_{x \to a^+} f(x)=\lim_{x \to 4^+}x =-2(4)=-8$
Como $\displaystyle \lim_{x \to 4^-} f(x)=\lim_{x \to 4^+}f(x)$ entonces $\quad 4c+k=-8 \quad (2)$
Resolviendo el sistema de ecuaciones obtenido
$\qquad (1) \quad c+k=1 $
$\qquad (2)\quad 4c+k=-8 $
Se tiene que: $\quad c=-3$, $\quad K=4$. $\quad$
Comprobar que la función $f(x)$ es continua en un intervalo $[1,4]$.
 Ejercicio.Escena de José R. Galo Sánchez y Mª José García Cebrian adaptadas por el autor.
Ejercicio.Escena de José R. Galo Sánchez y Mª José García Cebrian adaptadas por el autor.
Calcular el valor de $k$ para que la función sea continua en el punto propuesto $x=a$. Ingresar el valor para $k$ y pulsa la tecla "enter <┘", oprime el botón Comprobar para verificar.
Teorema. Continuidad de una suma, un producto y un cociente.
Si las funciones $f$ y $g$ son continuas en un punto $x=a$, entonces la suma $f+g$, el producto $f.g$ y el cociente $\frac{f}{g}$; siempre que $g(a)\cancel{=} 0 $ son continuos en $x=a$
Derivada de una función
Concepto de derivada
La derivada de una función es la pendiente de la recta tangente a la función en un punto, es el cambio instantáneo de la función en ese punto.
Definición.
La derivada de una función $f(x)$ respecto de $x$ está dada por el límite:
$$f'(x)=\lim_{h \to 0} \frac{f(x+h)-f(x)}{h}$$
Al cálculo de este límite se denomina derivación, y se dice que $f(x)$ es derivable en $c$ si existe $f'(c)$, es decir, si el límite existe.
 ¡Notación!
¡Notación!La derivada de la función $y=f(x)$ se escribe como: $$y'=f'(x)=\frac{dy}{dx}$$
La notación $\frac{dy}{dx}$ puede considerarse como “la razón de cambio de $y$ respecto a $x$.”
Ejemplo. Usar la definición de la derivada para calcular la derivada de la función $y=5x^2+3x-1$ en cualquier punto de su dominio. $$f(x)=5x^2+3x-1$$ $$f(x+h)=5(x+h)^2+3(x+h)-1$$
Aplicando la definición de la derivada, se tiene que: $$\lim_{h \to 0} \frac{5(x+h)^2+3(x+h)-1-(5x^2+3x-1)}{h}$$ $$\lim_{h \to 0} \frac{\cancel{5x^2}+10xh+5h^2+\cancel{3x}+3h -\cancel{1} -\cancel{5x^2} -\cancel{3x}+\cancel{1}}{h}$$ $$\lim_{h \to 0} \frac{10xh+5h^2+3h}{h} = \lim_{h \to 0} \frac{\cancel{h}(10x+5h+3)}{\cancel{h}}$$
Evaluando el límite, se tiene que: $$\lim_{h \to 0}(10x+\cancel{5h}+3)= 10x+3$$
Por tanto, la derivada de la función $f$ es: $\qquad y'=10x+3$
Para hallar el valor de la derivada en un punto basta con evaluar la derivada en ese punto.
Ejemplo. Determinar la pendiente de la recta tangente a la gráfica de la función $f(x)=5x^2+3x-1$ en el punto $x=-2$
La derivada de la función $f(x)$ es: $\qquad y'=10x+3$.
La derivada en un punto $x=c$, corresponde a la pendiente de la recta tangente en el punto, se denota como: $$m=f'(c)=\frac{dy}{dx} \Big|_{x=c}$$ $$m=f'(-2)=\frac{dy}{dx} \Big|_{x=-2}=10(-2)+3=-17$$
Definición de derivada puntual.
Para hallar la derivada de una función $f$ en un punto $x=c$ dado, se puede utilizar también la definición que se muestra a continuación: $$y'(c)=\lim_{x \to c} \frac{f(x)-f(c)}{x-c}$$
 Así, la derivada de una función es la pendiente de una recta tangente a una curva en un punto dado o una razón de cambio instantánea.
Así, la derivada de una función es la pendiente de una recta tangente a una curva en un punto dado o una razón de cambio instantánea. Otras formas de definir la derivada son: $$y' = \lim_{{\triangle}x \to 0} \frac{f(x+{\triangle}x)-f(x)}{{\triangle}x}=\lim_{{\triangle}x \to 0} \frac{{\triangle}y}{{\triangle}x}=\frac{dy}{dx}$$
Funciones diferenciables.
Una función es diferenciable en un número $c$ en un intervalo $(a,b)$ si y solo si $f_+'(c)=f_-'(c)$
Esto es, si el valor del límite mediante el cual está definida la derivada es igual a ambos lados del número en el cual se está evaluando.
Una función no es diferenciable en un número $x=a$ si.
- La función es discontinua en el número $x=a$.
- La gráfica de $f$ tiene un pico en $x=a$.
- La gráfica de $f$ en $x=a$ tiene una recta tangente vertical.
 "Diferenciabilidad implica continuidad".
"Diferenciabilidad implica continuidad".Una función $f$ diferenciable en $x=a$ es continua en $x=a$.
Nota: Continuidad no implica diferenciabilidad.
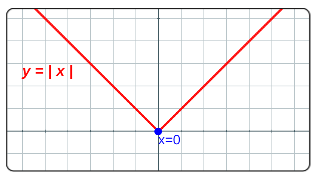
Por ejemplo, la función $f(x)=|x|$, es continua en $x=0$, pero no es diferenciable en $x=0$
Derivada como pendiente de una recta tangente a una curva en un punto x=c
 GeoGebra. La pendiente de la recta tangente a una función $y=f(x)$ en el punto $(c,f(c))$ está dada por $m_{tg}=f'(c)$
como se ilustra en la escena, desplace el punto $P$ o $Q$.
GeoGebra. La pendiente de la recta tangente a una función $y=f(x)$ en el punto $(c,f(c))$ está dada por $m_{tg}=f'(c)$
como se ilustra en la escena, desplace el punto $P$ o $Q$.
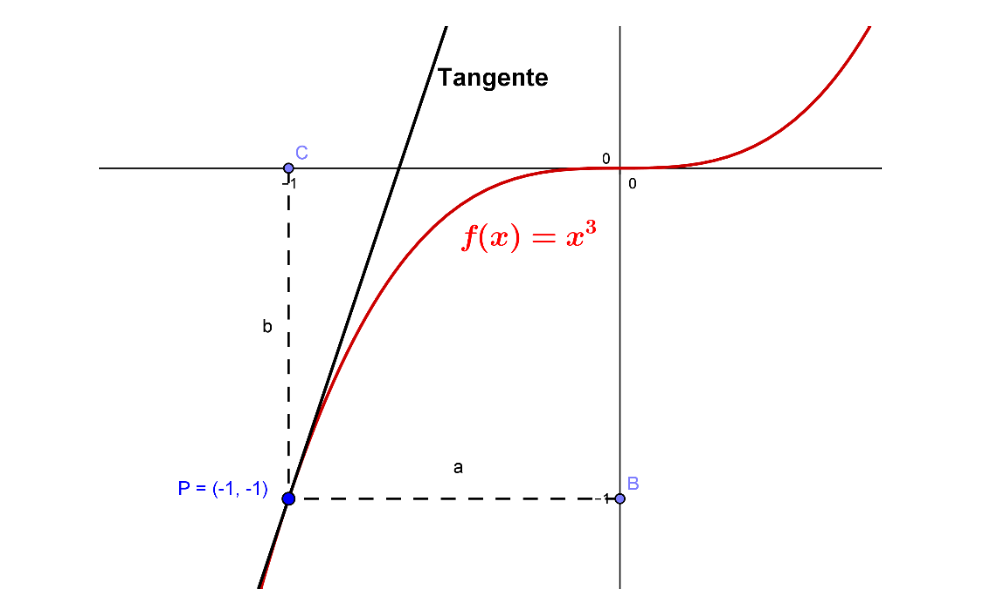
Ejemplo 1. ¿Cuál es la ecuación de la recta tangente a la curva $y=x^3$ en el punto $P(-1,-1)$?
Encontremos la ecuación de la recta en el punto dado, con la ecuación punto-pendiente, donde remplazando el punto $P(-1,-1)$, se tiene que: $$y+1=m_{tg}(x+1)$$
Esta es la ecuación de la recta tangente a la curva $y=x^3$ en el punto $P(-1,-1)$, ahora solo debemos encontrar el valor de la pendiente $m_{tg}$ que está dada por la derivada de la curva evaluada en $x=-1$, $$m_{tg}=f'(-1)$$
Utilizando la definición de derivada para $f'(x)$ se obtiene: $$f'(x)=\lim_{h \to 0} \frac{f(x+h)-f(x)}{h}=\lim_{h \to 0} \frac{(x+h)^3-x^3}{h}$$ $$f'(x)=\lim_{h \to 0} \frac{x^3+3x^2h+3xh^2+h^3-x^3}{h}=\lim_{h \to 0} \frac{h(3x^2+3xh+h^2)}{h}$$ $$f'(x)=3x^2$$
Por lo tanto, la pendiente cuando $x=-1$ es: $$m_{tg}=f'(-1)=3(-1)^2=m_{tg}=3$$
Entonces, la ecuación de la recta tangente a la curva $y=x^3$ en el punto $P(-1,-1)$ es: $\qquad \quad y= 3x+2$
Ejemplo 2. Encuentre los puntos sobre la gráfica de la función
$f(x)=-\frac{4}{3}+4x-1$ donde la recta tangente es horizontal.
Encontramos la derivada de la función $f(x)$, luego igualamos la derivada a cero, o sea, $f'(x)=0$, entonces
$f'(x)=-4x^2+4 =0$ por tanto, $-4x^2+4 =0$, donde $x= \pm 1$
por tanto, se obtienen los puntos: $\qquad p_1(1,0)$ y $p_2(-1,0)$
 Exploración. Utiliza la graficadora de GeoGebra para verificar las gráficas de las funciones $y=f(x)$ y las rectas tangentes en un punto $P(x,y)$.
Exploración. Utiliza la graficadora de GeoGebra para verificar las gráficas de las funciones $y=f(x)$ y las rectas tangentes en un punto $P(x,y)$.
 ¡Recuerda! $\quad$ Tangentes horizontales.
¡Recuerda! $\quad$ Tangentes horizontales.
Si $y=f(x)$ es continua en un número $a$ y $f'(a)=0$ entonces la recta tangente en $(a, f(a))$ es horizontal.
Velocidades
Si una función escribe el cambio de posición en el tiempo de un móvil entonces la derivada se podrá interpretar como la velocidad del móvil esto es, el cambio instantáneo de la posición del móvil en el tiempo.
En general, suponga que un objeto se mueve a lo largo de una recta de acuerdo a una ecuación de movimiento $s=f(t)$, donde $s$ es el desplazamiento (distancia dirigida) del objeto desde el origen en el tiempo $t$. La función $f$ que describe el movimiento se denomina función de posición del objeto. En el intervalo de $t=a$ a $t=a+h$ el cambio en posición es $f(a+h)-f(a)$.
La velocidad promedio en este intervalo es: $$velocidad \space promedio \space = \frac{desplazamiento}{tiempo}=\frac{f(a+h)-f(a)}{h}$$
Calculando las velocidades promedio en intervalos cada vez más pequeños, o sea, cuando $h$ se aproxime a $0$, definimos la velocidad o velocidad instantánea como: $$v'(a)=\lim_{h \to 0} \frac{f(a+h)-f(a)}{h}$$
Esto significa que la velocidad en el tiempo $t=a$ es igual a la pendiente de la recta tangente en el punto $P$.
Ejemplo. Sea $f(t)=5t+3$ la posición de un móvil en el tiempo $t$, dada en metros, determinar su velocidad en cualquier instante.
La velocidad está definida como el cambio de posición en un intervalo de tiempo $\triangle t$ esto es $v=\frac{d}{t}$ (la velocidad es la distancia entre el tiempo).
Si la distancia recorrida por el móvil en un cierto intervalo de tiempo $\triangle t$ es $\triangle y$ entonces la velocidad del móvil es $\frac{\triangle y}{\triangle x}$ ahora si se requiere la velocidad instantánea del móvil entonces ${\triangle t \to 0}$ para calcular la velocidad cuando esto ocurra será necesario hallar: $$\lim_{\triangle t \to 0} \frac{\triangle y}{\triangle x}$$ que es precisamente la definición de la derivada de $f(t)$; por lo tanto la velocidad del móvil será $f'(t)$, entonces $$\lim_{h \to 0} \frac{f(t+h)-f(t)}{h}=\lim_{h \to 0} \frac{5(t+h)+3-5t-3}{h}= $$ $$v'(t)=5 \space m/s$$
El cálculo de derivadas se ha realizado por medio del cálculo de un límite, que a veces resulta un poco tedioso, en la siguiente sección se van a trabajar algunas reglas que facilitan el cálculo de estas derivadas.
 Descarga:
Tabla de Derivadas básicas.
Descarga:
Tabla de Derivadas básicas.
Reglas de derivación
Reglas que facilitan el cálculo de las derivadas de $y=f(x)$.
Reglas básicas
Tabla de derivadas de funciones básicas.
Funciones | Derivada |
|---|---|
| Función potencia. Sea $n$ un número real, $\quad y=x^n$ | $\space y'=n.x^{n-1}$ |
| Función constante. Si $f(x)$ es la función constante, $\quad y=C$ | $\space y'=0$ |
| Constante por una función. Sea $C$ una constante, $\quad y=Cx^{n}$ | $\space y'=C.n.x^{n-1}$ |
| Suma y resta de funciones . Sean las funciónes $f$ y $g$, $\quad y=f(x) \pm g(x)$ | $\space y'=f'(x) \pm g'(x)$ |
| Producto de funciones . Sean las funciónes $f$ y $g$, $\quad y=f(x).g(x)$ | $\space y'=f'(x).g(x)+f(x).g'(x)$ |
| División de funciones . Sean las funciónes $f$ y $g$, $\quad \displaystyle y=\frac{f(x)}{g(x)}$ | $\displaystyle \space y'=\frac{f'(x).g(x)-f(x).g'(x)}{(g(x))^2}$ |
Derivada de funciones trigonométricas.
Funciones | Derivada |
|---|---|
| $\quad y=Sen(x)$ | $\space y'=Cos(x)$ |
| $\quad y=Cos(x)$ | $\space y'=-Sen(x)$ |
| $\quad y=Tan(x)$ | $\space y'=Sec^2(x)$ |
| $\quad y=Cot(x)$ | $\space y'=-Csc^2(x)$ |
| $\quad y=Sec(x)$ | $\space y'=Sec(x)Tan(x)$ |
| $\quad y=Csc(x)$ | $\space y'=-Csc(x)Cot(x)$ |
¿Por qué? $\quad y'=-Csc^2(x) \space$ es la derivada de $\space y=Cot(x)$
Se tiene la siguiente relación trigonométrica: $$y=Cot(x)=\frac{cos(x)}{sen(x)}$$ Entonces, aplicando la regla de divisón de funciones, tenemos: $$ y'= \frac{-sen(x).sen(x) - cos(x).cos(x)}{(sen(x))^2} \\ y'=\frac{-[sen^2(x) + cos^2(x)]}{sen^2(x)} $$ donde se tiene la identidad: $\quad sen^2(x) + cos^2(x)=1$, por tanto, $$y'=\frac{-1}{sen^2(x)}$$ $$y'=-Csc^2(x)$$
Derivada de orden superior $\quad \displaystyle y'= \frac{dy}{dx}$, $\quad \displaystyle y''= \frac{d^2y}{dx^2}\space$...$\space \displaystyle y^n= \frac{d^ny}{dx^n}$
Derivadas de orden superior. |
|---|
|
Sea $f$ una función diferenciable en $𝑥$, entonces |
Derivada de función exponencial.
Funciones | Derivada |
|---|---|
| $\quad y=e^x$ | $\space y'=e^x$ |
| Sea $b$ un número real, $\quad y=b^x$ | $\space y'=b^x.(Ln (b))$ |
Ejemplo.
Calcular la derivada de la función $\quad \displaystyle y=5^x$
Aplicando la derivada de función exponencial, se tiene que: $$y'=5^x.(Ln(5))$$
Derivada de función logarítmica.
Funciones | Derivada |
|---|---|
| $\quad y=Ln|x|$ | $\space \displaystyle y'=\frac{1}{x}$ |
| Sea $b$ un número real, $\quad y=Log_b(x)$ | $\space \displaystyle y'=\frac{1}{x(Ln(b))}$ |
Ejemplo.
Calcular la segunda derivada $\displaystyle\frac{d^2y}{dx^2}$ de la función dada.
$$y=Log_3(x)$$
Aplicando la derivada de función logarítmica, se tiene que: $$\frac{dy}{dx}=\frac{1}{x.Ln(3)}$$
Ahora aplicamos de nuevo la derivada a la expresión hallada $\displaystyle\frac{dy}{dx}$ para encontrar la segunda derivada, donde se tiene la constante: $$\frac{1}{Ln(3)}$$ Entonces solo aplicamos la derivada a la expresión siguiente: $$\frac{dy}{dx}=\frac{1}{x}$$ $$\frac{dy}{dx}=x^{-1}$$
por tanto, aplicando regla de la potencia, las segunda derivada es: $$\frac{d^2y}{dx^2}=\frac{1}{Ln(3)}.\frac{(-1)}{x^2}$$ $$\frac{d^2y}{dx^2}=-\frac{1}{Ln(3)x^2}$$
 ¡Recuerda!
$$Ln(x)=Log_e(x)$$
¡Recuerda!
$$Ln(x)=Log_e(x)$$
Si comparamos está expresión con $y=Log_b(x)$, se tiene que $b=e$.
Ejemplos de la derivada de una función $f(x)$ aplicando reglas básicas.
Ejemplo.
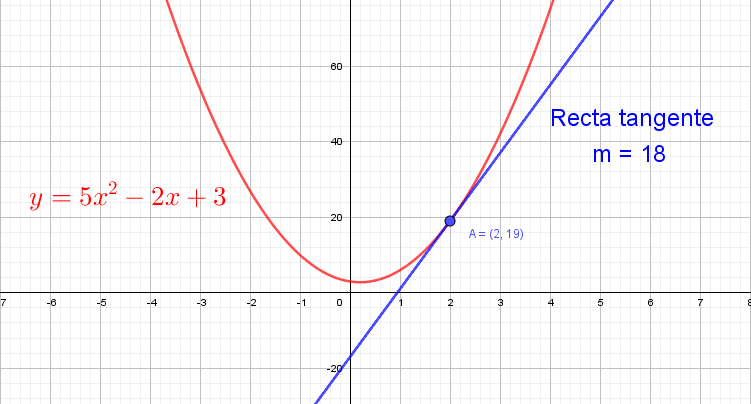
Encuentre el punto sobre la gráfica de $f(𝑥) = 5𝑥^2− 2𝑥 + 3$ donde la pendiente de la recta tangente es $18$.
Se halla primero la derivad de $f(x)$: $$f'(x) = 10x-2$$
Luego, como $m=f'(x)=18$, entonces, despejando $x$, se tiene que: $$\begin{aligned} 10x-2 &=18 \\ x &= 2 \end{aligned}$$
Ahora evaluando en la función $f(x)$ para encontrar $y$, entonces,
$$y=f(2)=5(2)^2− 2(2) + 3 = 19$$
por tanto, el punto es: $\qquad (2, f(2)) = (2,19)$.
 Ejercicio.
Ejercicio.
Resuelva el problema de la recta tangente planteado y oprima el botón solución para verificar su respuesta.
Observe la gráfica de la solución, oprima el botón Ver gráfica, para realizar otro ejercicio oprima el botón Ejercicio.
Amplia la gráfica, con clic derecho sostenido sobre la gráfica o con los controles.
Regla de la cadena.
Si la función $f$ es diferenciable en $u=g(x)$ y la función $g$ es diferenciable en $x$, entonces, se tiene que la composición de las funciones $y=(f\circ g)(x)=f(g(x))$ es diferenciable en $x$ y $$y' = f(g(x))=f'(g(x)).g'(x)$$ De otra manera, $$\frac{dy}{dx}=\frac{dy}{du}.\frac{du}{dx}$$
Ejemplo 1.
Calcular la derivada de la función dada.
$$y=Tan(5x^3)$$
Se puede ver que la función $y$ está conformada por dos funciones una de ellas es $f(x)=Tan(x)$ y la otra que es $g(x)=5x^3$
Es una función compuesta, de tal manera que se debe derivar usando la regla de la cadena. $$y' = f(g(x))=f'(g(x)).g'(x) \\ f'(x)= Sec^2(x) \\ g'(x)=15x^2$$ por tanto, $$y' = f'(g(x)).g'(x)=Sec^2(x).5x^2$$ $$y'=5x^2Sec^2(x)$$
Ejemplo 2.
Calcular la derivada de la función dada.
$$g(x)=\sqrt{sen(x^3-2x)}$$
La función $g(x)$ está conformada por tres funciones, $g_1(x)=\sqrt{x}$, $g_2(x)=Sen(x)$ y $g_3(x)=x^3-2x$
Usando la regla de la cadena, se tiene que: $$y' = f(g(h(x)))=g_1'(g_2(g_3(x))).g_2'(x).g_3'(x) \\ g_1'(x)= \frac{1}{2. \sqrt{sen(x^3-2x)}} \\ g'_2(x)=Cos(x^3-2x) \\ g'_3(x)=3x^2-2$$ por tanto, $$g'(x)= \frac{(3x^2-2) Cos(x^3-2x)}{2 \sqrt{sen(x^3-2x)}}$$
 Preguntas. Selecciona verdadero o falso.
Preguntas. Selecciona verdadero o falso.
Haz click sobre la respuesta correcta.
Derivadas de una función aplicando regla de la cadena:
 Ejercicio. Adaptación de una escena de Miguel Ángel Cabezon Ochoa con licencia CC by-nc-sa
Ejercicio. Adaptación de una escena de Miguel Ángel Cabezon Ochoa con licencia CC by-nc-sa
Selecciona una función y encuentra la derivada de la función que se plantea, oprima el botón solución para verificar la respuesta.
Para realizar otro ejercicio oprima el botón ejercicio o otra función.
Derivada implícita.
Es común que, en variadas ocasiones no se pueda obtener la forma explícita $y=f(x)$ a partir de la ecuación $f(x,y)=0$ para diferenciarla normalmente.
Aun así, se puede hallar $\frac{dy}{dx}$ por diferenciación implícita.
 ¡Recuerda!
¡Recuerda!
Forma explícita $\quad y=f(x)$
Si una función se expresa en la forma $y=f(x)$, es decir, la variable dependiente $y$ está expresada explícitamente en términos de $x$ en el lado izquierdo, se dice que la función
está dada en forma explícita.
Forma implícita $\quad f(x,y)=0$
Son expresiones de la forma $f(x,y)=0$, en donde la función $y$ no está explícitamente en términos de la variable independiente $x$.
¿Cómo se halla la derivada implícita $\frac{dy}{dx}$ de una función definida implícitamente por $f(x,y)=0$?
Si fuera posible escribir $y$ explícitamente a partir de $f(x,y)=0$, o sea, despejar $y$ en términos de $x$, es posible que sea sencillo hallar $\frac{dy}{dx}$ con las reglas básicas de diferenciación.
La cuestión es que, no siempre es posible obtener una forma explícita $y=f(x)$, aunque fuera posible despejar $y$ explícitamente, puede suceder que la derivada sea más complicada o dispendiosa.
Ejemplo. Sea la función $\qquad 3x^3y^3+5=2y^3+7x$
Si despejamos la variable $y$ tendríamos: $$3x^3y^3-2y^3=7x-5 \\ y^3(3x^3-2)=7x-5$$ $$y =\sqrt[3]{\frac{7x-5}{3x^3-2}}$$
Con esta forma explícita, calcular $\frac{dy}{dx}$ sería dispendioso e implicaría utilizar la regla de la cadena y la derivada para un cociente.
Una alternativa, es aplicar la regla de la cadena a la forma implícita $f(x,y)=0$ para determinar $\frac{dy}{dx}$ sin tener que despejar $y$, está técnica alternativa, se conoce como derivación implícita.
 Directrices para diferenciación implícita.Definición tomada de: Cálculo: Transcendentes tempranas. D. Zill. 4Ed.
Directrices para diferenciación implícita.Definición tomada de: Cálculo: Transcendentes tempranas. D. Zill. 4Ed.
- Al diferenciar con respecto a $x$ ambos miembros de la ecuación, use las reglas de diferenciación y considere a $y$ como una función diferenciable de $x$. Para potencias del símbolo $y$, multiplique por $\frac{dy}{dx}$ .
- Agrupe todos los términos donde aparece $\frac{dy}{dx}$ en el lado izquierdo de la ecuación diferenciada. Mueva todos los otros términos al lado derecho de la ecuación.
- Factorice $\frac{dy}{dx}$ en todos los términos donde aparezca este término. Luego, despeje $\frac{dy}{dx}$.
Ejemplo 1.
Calcular la derivada implícita de la función dada.
$$x^3+y^3=6xy$$
Está expresión resulta más complicada expresarla explícitamente, por tal motivo derivamos cada término de la siguiente forma:
$(1)$. Derivar la forma implícita $x^3+y^3=6xy$ con respecto a $x$ aplicando reglas de derivación, cuando se derive $y$ se multiplica por $\frac{dy}{dx}$: $$3x^2+3y^2.\bigg(\frac{dy}{dx}\bigg)=6(1)y+6x(1).\bigg(\frac{dy}{dx}\bigg)$$ $\hspace{3.8cm}\color{green}\uparrow\underline{\color{green}\hspace{1.0cm}{\quad\frac{dy}{dx}}\hspace{1.3cm}}\hspace{0.0cm}\uparrow\\$
$(2)$. Pasamos todos los términos que contengan el factor $\frac{dy}{dx}$ al lado izquierdo, los demás al lado derecho: $$3y^2\bigg(\frac{dy}{dx}\bigg)-6x\bigg(\frac{dy}{dx}\bigg)=6y-3x^2$$
$(3)$. Se factoriza y se despeja $\frac{dy}{dx}$: $$\bigg(\frac{dy}{dx}\bigg)3(y^2-2x)=3(2y-x^2)$$ $$\frac{dy}{dx}=\frac{2y-x^2}{y^2-2x}$$
Ejemplo 2. Calcular la derivada de la función $Cos(x+y) + y = 0$
Se deriva respectoa a $x$, entonces la derivada $\frac{dy}{dx}$ es: $$-sen(x+y)(1+\frac{dy}{dx}) + \frac{dy}{dx} = 0$$ $$-sen(x+y)-sen(x+y)\frac{dy}{dx} + \frac{dy}{dx} = 0 \\ \frac{dy}{dx}(1-sen(x+y))=sen(x+y)$$ $$\frac{dy}{dx}=\frac{sen(x+y)}{1-sen(x+y)}$$
 Ejemplo. Encontrar la derivada implícita de una ecuación.
Ejemplo. Encontrar la derivada implícita de una ecuación.
 Ejercicio.Escena de Juan Guillermo Rivera adaptada por el autor.
Ejercicio.Escena de Juan Guillermo Rivera adaptada por el autor.
Encuentra la derivada implícita de la función que se plantea, oprima el botón solución para verificar la respuesta.
Para realizar otro ejercicio oprima el botón Otro ejercicio .
¿Será posible encontrar la recta tangente a la curva dada en un punto $( x , y )$? A continuación responderemos a está pregunta.
Ejemplo.
Encuentre la ecuación de la recta tangente al círculo $x^2+y^2=25$ en el punto $P(3,4)$.
$$\frac{d}{dx}(x^2+y^2)=\frac{d}{dx}(25) \\ 2x+2y.\bigg(\frac{dy}{dx}\bigg)=0\\ 2y.\bigg(\frac{dy}{dx}\bigg)=-2x$$
$$\frac{dy}{dx}=-\frac{x}{y}$$
La pendiente de la recta en el punto $P(3,4)$, $\quad m=\frac{dy}{dx} \bigg|_{(3,4)}=-\frac{3}{4}$
Utilizando la ecuación punto-pendiente, se tiene: $$y-4=-\frac{3}{4}(x-3)\\ y=-\frac{3}{4}x +\frac{9}{4}+4$$
Por tanto, la ecuación de la recta tangente al círculo $x^2+y^2=25$ en el punto $P(3,4)$ es: $$y=-\frac{3}{4}x +\frac{25}{4}$$
 GeoGebra. Utiliza el software para graficar y verificar.
GeoGebra. Utiliza el software para graficar y verificar.
Clic aquí.
Grafique la curva, el punto $P(x,y)$ y la ecuación de la recta tangente en el punto dado.
 Preguntas. Selección múltiple con única respuesta.
Preguntas. Selección múltiple con única respuesta.
Haz click sobre la respuesta correcta.
 Demos online. Utiliza el software para graficar y verificar.
Demos online. Utiliza el software para graficar y verificar.
Clic Aqui.
Grafique la curva, el punto $P(x,y)$ y la ecuación de la recta tangente en el punto dado.
Aplicaciones de la derivada
La derivada tiene una gran variedad de aplicaciones además de encontrar la pendiente de la tangente a una curva en un punto. Se puede usar la derivada para estudiar aplicaciones físicas, razones de cambio relacionadas, tasas de variación, valores máximos y mínimos de una función, concavidad y convexidad, entre otras.
Movimiento rectilíneo
Es el movimiento de una partícula en línea recta, sea vertical o horizontal, entonces la función de la posición donde $t$ representa el tiempo y $s(t)$ la distancia a partir de un punto de referencia $s=0$, está dada por: $$s=s(t)$$
Definiciones.
Función Velocidad: Si $s(t)$ es una función posición de un objeto en movimiento rectilíneo, entonces su función velocidad $v(t)$ en el instante $t$ es: $$v(t)=\frac{ds}{dt}$$ La rapidez del objeto en el instante $t$ es $|v(t)|$.
Función Aceleración: Si $v(t)$ es la función posición de un objeto en movimiento rectilíneo, entonces su función velocidad $v(t)$ en el instante $t$ es: $$v(t)=\frac{dv}{dt}=\frac{d^2s}{dt^2}$$
Un objeto desacelera cuando su rapidez $|v(t)|$ es decreciente y acelera cuando su rapidez es creciente.
En otras palabras, un objeto en movimiento rectilíneo:
- Acelera cuando su velocidad y aceleración tienen el mismo signo algebraico.
- Desacelera cuando su velocidad y aceleración tienen signos algebraicos opuestos.
Ejemplo. Una partícula se mueve sobre una recta horizontal según la función posición $s(t)=t^3-\frac92t^2-7t$ con $t \ge 0$, donde $s$ se mide en $cm$ y $t$ en $seg.$ responder:
- ¿Cuál es la posición de la partícula a los $0$ y $1$ segundos?
Al evaluar $s(t)$ cuando $t=0$ y $t=1$, obtenemos $$s(0)=(0)^3-\frac92(0)^2-7(0)=0 \\ s(1)=(1)^3-\frac92(1)^2-7()=1-\frac92-7=-\frac{21}{2}$$ Por tanto $s(0)=0$ y $s(1)=-\frac{21}{2}$, donde $s(1)<0$, significa que la partícula es a la izquierda del punto de referencia $s=0$.
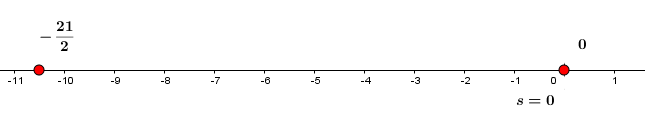
Posición de una partícula en varios instantes de tiempo.
- ¿Cuándo la partícula alcanza una velocidad de $5 \frac{m}{s}$?
Hallamos $v(t)=s'(t)$, entonces $$\frac{dv}{dt}=3t^2-9t-7$$ Como $\displaystyle \frac{dv}{dt}=5 \frac{m}{s}$, igualamos y despejando $t$, se tiene $$3t^2-9t-7=5 \\ 3t^2-9t-12=0 \\ 3(t^2-3t-4)=0 \\ 3(t-4)(t+1)=0$$ por tanto, $t=4$ y $t=-1$ este tiempo negativo se descarta.
R. El Objeto alcanza una $v(t)=5 \space m / s$ transcurridos $4 \space seg$.
- ¿Cuándo la partícula tiene una aceleración cero?
Hallamos $a(t)=s''(t)=v(t)$, entonces $$\frac{da}{dt}=6t-9$$ Como $\displaystyle \frac{da}{dt}=0$, igualamos y despejando $t$, se tiene $$6t-9=0 \\ t=\frac96=\frac32$$
R. El Objeto tiene una $a(t)=0$ cuando ha transcurrido $1,5 \space seg$.
 Ejercicio.
Ejercicio.
Movimiento de una partícula.
Encontrar la función $v(t)$ y la función $a(t)$, según la función posición plateada en el problema, oprima el botón solución para verificar las respuestas.
Para realizar otro ejercicio oprima el botón otro ejercicio.
 ¡Recuerda!
¡Recuerda!
La velocidad media de un cuerpo en movimiento sobre un intervalo de tiempo $$v(t) = \frac{cambio\space en \space posición}{cambio\space en \space tiempo}=\frac{s(t+\triangle t)-s(t)}{\triangle t}$$
La posición $s(t)$, se mide en $cm$, $m$, $km$,...
La velocidad $v(t)$, se mide en $cm/s$, $m/s$, $km/h$,...
La aceleración $a(t)$, se mide en $cm/s^2$, $m/s^2$, $km/h^2$,...
En el sistema ingles se utilizan unidades de medida como: $pie(ft)$, $millas(mi)$, $pulgadas(in)$, entre otras.
 Preguntas. Selecciona verdadero o falso.
Preguntas. Selecciona verdadero o falso.
Haz click sobre la respuesta correcta.
Razones de cambio
La razón de cambio es la proporción en la que una variable cambia con respecto a otra, de manera más explícita es como en el tiempo unas componentes cambian a medida que el tiempo transcurre.
La derivada $\frac{dy}{dx}$ de una función $y=f(x)$ es una razón de cambio instantánea con respecto a la variable $x$. Si la función representa posición o distancia entonces la razón de cambio con respecto al tiempo se interpreta como velocidad, $v(t)=\frac{ds}{dt}$.
En conclusión, podemos expresar que, si dos cantidades están relacionadas entre sí, entonces cuando una de ellas cambia con el tiempo, la otra también cambiará. Por lo tanto, sus razones de cambio (con respecto al tiempo) están relacionadas entre sí. Por lo tanto, a está situaciones se les llama razones de cambio relacionadas.
 Pasos para enfrertar una situación problema.
Pasos para enfrertar una situación problema.
- Lea atentamente el problema varias veces, elabore un esquema o dibujo de la situación, si es posible.
- Asignar una notación, letras o símbolos a todas las cantidades que sean funciones que cambian con el tiempo.
- Expresar la información que nos dan y la información requerida en términos de derivadas con respecto al tiempo.
- Escribir una ecuación o una función que relacione todas las variables de la situación.
- Derivar la ecuación encontrada respecto al tiempo $t$ (derivada implícita), y sustituya la información dada en la ecuación resultante, despeje la cantidad desconocida.
Ejemplo 1.
Se infla una bomba plástica en forma de esfera a una velocidad de 8 pulgadas cúbicas por minuto. ¿Cuál será la velocidad con que cambia el radio cuando dicho
radio es de 3 pulgadas?
 Solución.
Solución.
(1). Observa la gráfica de la situación.
(2). Denotamos el radio de la esfera como $R=3 \space pul$.
(3). Ahora, en el instante $t$, el volumen $V$ de una esfera en función del radio que cambia en relación al tiempo, está dado por $\displaystyle \frac{dV}{dt}= 8 \frac{pul^3}{min}$.
Para la situación, nos piden encontrar la velocidad con que cambia el radio, por tanto, es hallar $\displaystyle \frac{dR}{dt}=?$
(4). La ecuación que expresa el volumen es: $\quad \displaystyle V=\frac43 \pi R^3$
(5). Derivamos el volumen respecto al tiempo: $\space \displaystyle\frac{dV}{dt}=\frac43 \pi (3R^2)\frac{dR}{dt}$
Despejando y remplazando tenemos que: $$\frac{dR}{dt}=\frac{\frac{dV}{dt}}{4R^2 \pi}=\frac{8 \frac{pul^3}{min}}{4(3 \space pul)^2 \pi} = 0,07\frac{pul}{min}$$ R.El radio crece cada vez más lentamente, a razón de $0,07$ pulgadas por minuto.
Ejemplo 2. Dos barcos salen simultáneamente de un puerto; uno viaja hacia el este a una velocidad de $40 km/h$ y el otro hacia el sur a una velocidad de $30 km/h$, después de $2$ horas de haber partido del mismo puerto.
Si consideramos que $z(t)$ es la distancia que separa a los barcos en cierto instante $t$, entonces lo que se desea es calcular la rapidez (razón de cambio) con que cambia la distancia $z(t)$ al paso del tiempo.
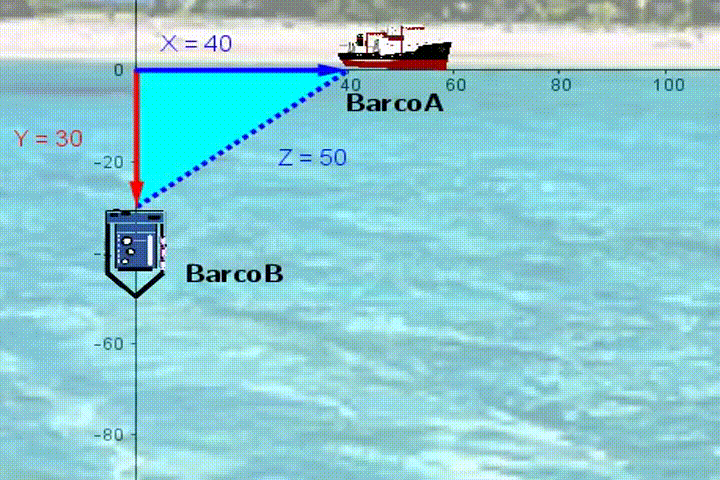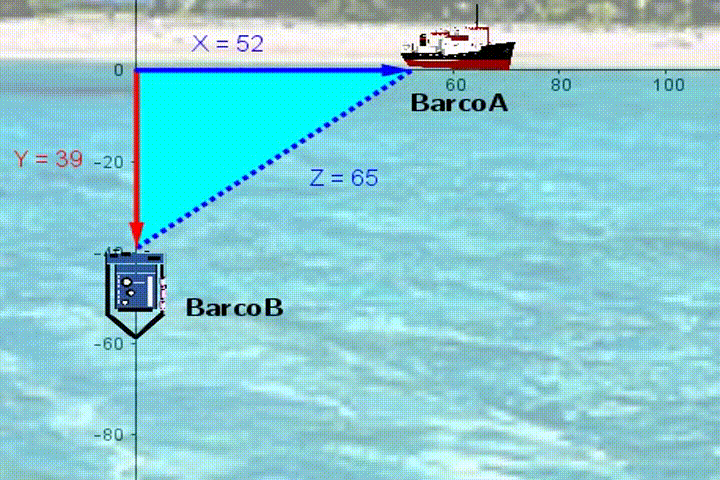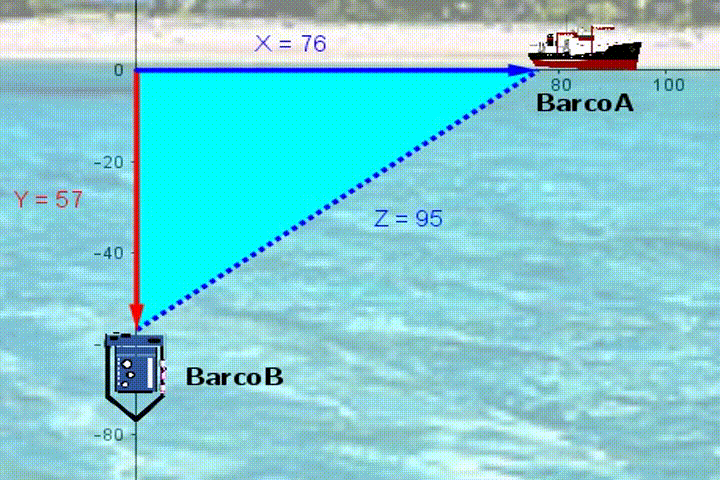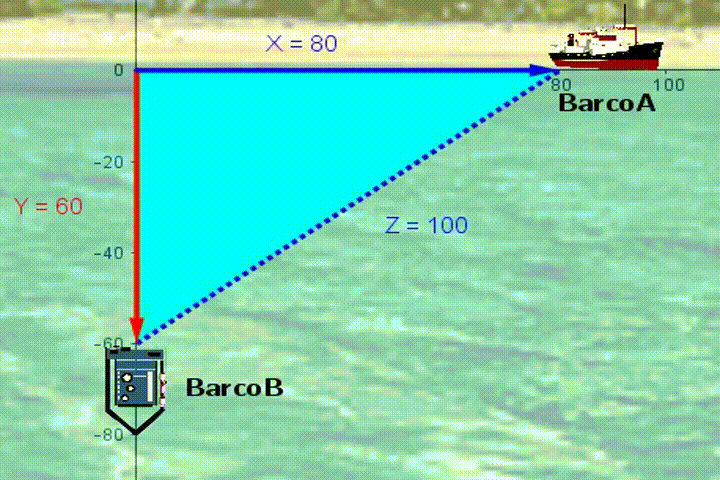
Solución. Encontremos la derivada $\displaystyle z'(t)=\frac{dz}{dt}$ (Rapidez), después de transcurridas $2$ horas del punto de partida, entonces, se tiene:
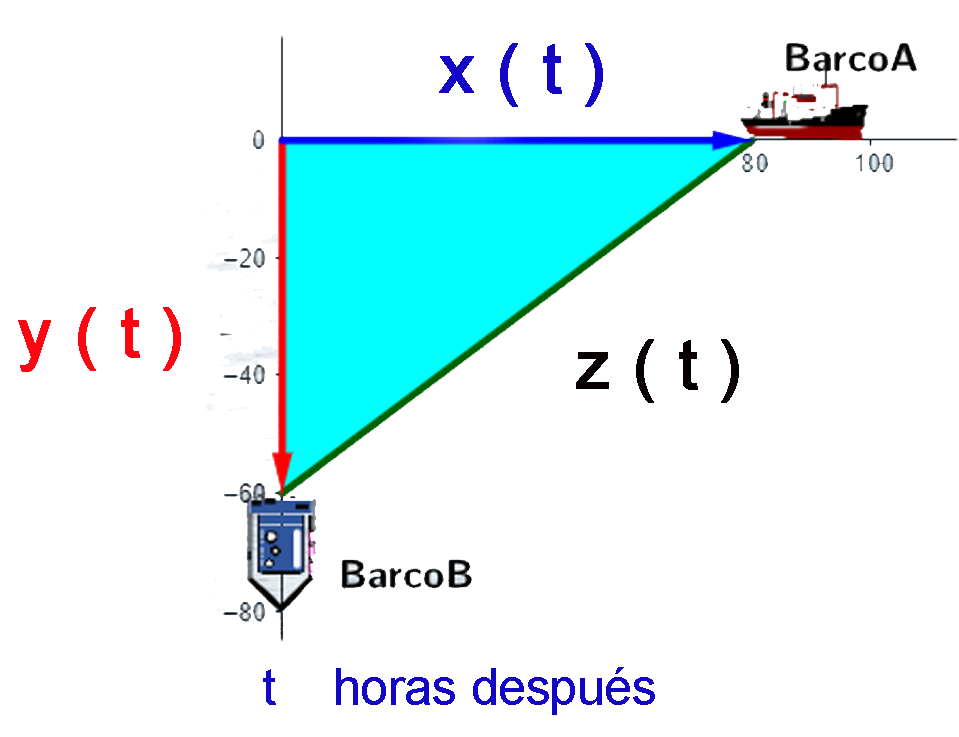
Barco A:
$\quad x(t)$ distancia en $t$ horas, $\quad x(t)=40\frac{km}{\cancel{h}}.t\space \cancel{h}= 40t \space km$
Barco B:
$\quad y(t)$ distancia en $t$ horas, $\quad y(t)=30\frac{km}{\cancel{h}}.t\space \cancel{h}= 30t \space km$
Para la distancia $z(t)$, se satisface el teorema de Pitágoras: $$[z(t)]^2=[x(t)]^2+[y(t)]^2=(40t)^2+(30t)^2=2500t^2 \\ z(t)=50t \space km$$
R. Para cualquier instante $t>0$, los barcos se están separando a una velocidad constante de $\quad \quad z'(t)=\frac{dz}{dt}= 50 \space \frac{km}{h}$
 GeoGebra. Para ver la animaciónEscena de Castrillón, Elkin y Rojas, Carlos con licencia CC by-nc-sa oprime el botón
GeoGebra. Para ver la animaciónEscena de Castrillón, Elkin y Rojas, Carlos con licencia CC by-nc-sa oprime el botón  .
.
Situación similar sucede con la siguiente escena de dos ciclistas que parten de un mismo punto con velocidad constante.
 GeoGebra. Para ver la animaciónAdaptación de una escena de Elkin Castrillón con licencia CC by-nc-sa oprime el botón
GeoGebra. Para ver la animaciónAdaptación de una escena de Elkin Castrillón con licencia CC by-nc-sa oprime el botón  .
.
En este tipo de problemas, podemos ver que la distancia de separación depende del tiempo transcurrido. Este concepto se extiende igualmente a otros campos del saber como por ejemplo el de las finanzas, si tienes ahorrado un dinero en un banco, los intereses que recibes sobre este dinero dependen del tiempo que los dejes depositado en él. En este sentido estas componentes se constituyen en cantidades variables que pueden ser expresadas como funciones dependientes del tiempo.
 Ejercicio.
Ejercicio.
Ingresa condiciones diferentes y realiza el análisis.
Dos autos viajan hacia una intersección de dos carreteras, uno de los cuales se dirige hacia el Este a razón de $70 Km/h$ y el otro hacia el Norte a razón de $55 Km/h$.
 GeoGebra. Analiza la situación planteada y encuentra los resultados, cambia las condiciones dadas.
GeoGebra. Analiza la situación planteada y encuentra los resultados, cambia las condiciones dadas.
¿A qué rapidez se acercan en el instante en que el primer automóvil se encuentra a $65 km$ y el segundo a $32 km$ de la intersección?
Se deriva la expresión respecto al tiempo: $\quad z^2=x^2+y^2 \space$ por tanto, $$\frac{dz}{dt}=\frac{1}{z}(x\frac{dx}{dt}+y\frac{dy}{dt})$$
Ejemplo. Un helicóptero vuela a una velocidad de $30\frac{km}{h}$ horizontalmente acercándose a la torre de control del aeropuerto. El helicóptero vuela a una altura de $8\space km$.
¿A que velocidad se acerca el helicóptero a la torre de control cuando su distancia está a $20\space km$?
Representamos $\quad \displaystyle v=\frac{dz}{dt}\quad $ como la velocidad a encontrar.
Dado el triángulo rectángulo que se forma, se cumple el teorema de Pitágoras, donde podemos encontrar $x$: $$z^2=x^2+y^2 \\ x^2=20^2-8^2$$ $$ x= 18.33\space km$$ Ahora, derivamos respecto al tiempo $t$: $\qquad z^2=x^2+8^2$ $$2z\frac{dz}{dt}=2x\frac{dx}{dt}$$
Por consecuencia, $\qquad \displaystyle \frac{dz}{dt}=\frac{x}{z}\frac{dx}{dt}$
Remplazando en la ecuación obtenida, se tiene: $$\frac{dz}{dt}=\frac{18.33\space \cancel{km}}{20\space \cancel{km}}(30\frac{km}{h})=27,49 \frac{km}{h}$$
R. Para cualquier instante $t>0$, el helicóptero se acerca a una velocidad constante de $\quad \quad v=\frac{dz}{dt}= 27,49 \space \frac{km}{h}$
A continuación, se presenta una escena interactiva, para manipular y comprender mejor la situación problema plateada.
 Ejercicio.
Ejercicio.
Ingresa condiciones diferentes y analiza la situación.
 GeoGebra. Para ver la animación
GeoGebra. Para ver la animación
Observa y analiza la situación planteada.
 Ejercicio.
Ejercicio.
Ingresa condiciones diferentes y analiza la situación.
 GeoGebra. Analiza la situación planteada y encuentra los resultados, cambia las condiciones dadas. Adaptación de una escena de Juan Guillermo Arango con licencia CC by-nc-sa
GeoGebra. Analiza la situación planteada y encuentra los resultados, cambia las condiciones dadas. Adaptación de una escena de Juan Guillermo Arango con licencia CC by-nc-sa
 Ejercicio.
Ejercicio.
Ingresa condiciones diferentes y analiza la situación.
 GeoGebra. Analiza la situación planteada y encuentra los resultados, cambia las condiciones dadas.
GeoGebra. Analiza la situación planteada y encuentra los resultados, cambia las condiciones dadas.
Utiliza semejanza de triángulos como ayuda para obtener una relación entre el radio y la altura.
Regla de L'Hopital
La regla de L'Hôpital es un proceso que nos permite resolver algunas indeterminaciones que se dan en el cálculo de límites mediante el uso de las derivadas.
 ¡Recuerda!
¡Recuerda!Las indeterminaciones pueden presentarse de la forma :
$$\frac{\infty}{\infty} \qquad \infty - \infty \qquad \frac{0}{0} \qquad 0^\infty \qquad 0^0 \qquad \infty ^0 \qquad 1^\infty$$
Para hallar el límite introducimos el siguiente teorema:
TeoremaDefinición tomada de: Cálculo: Transcendentes tempranas. D. Zill. 4Ed.
Suponga que $f$ y $g$ son diferenciables sobre un intervalo abierto que contiene al número $a$, excepto posiblemente en $a$ mismo, y que $g'(x) =\not 0$ para toda $x$ en el intervalo salvo posiblemente en $a$.
Si $\displaystyle \lim_{x \to a}{\frac{f(x)}{g(x)}}= \frac00 \quad$ o $\quad \displaystyle \lim_{x \to a}{\frac{f(x)}{g(x)}}= \frac{\infty}{\infty}\quad$ y $\quad\displaystyle \lim_{x \to a}{\frac{f'(x)}{g'(x)}}=L$
entonces $$ \lim_{x \to a}{\frac{f(x)}{g(x)}}=\lim_{x \to a}{\frac{f'(x)}{g'(x)}}=L$$ La regla de L'Hopital puede ser utilizada de manera reiterada hasta que al final resolvamos la indeterminación original.
Ejemplo 1. Resolver el siguiente límite: $$\lim_{x \to 4} \frac{\sqrt{x}-2}{x-4}$$
Primero se evalúa el límite por sustitución directa: $$\lim_{x \to 4} \frac{\sqrt{x}-2}{x-4}= \frac{\sqrt{4}-2}{4-4}= \frac{0}{0} $$ Entonces, aplicando el teorema de la Regla de L'hopital, se tiene que:
$$ \lim_{x \to a}{\frac{f(x)}{g(x)}}=\lim_{x \to a}{\frac{f'(x)}{g'(x)}}$$$$\lim_{x \to 4} \frac{\sqrt{x}-2}{x-4}= \lim_{x \to 4} \frac{\frac{1}{2\sqrt{x}}-(0)}{(1)-(0)}=\frac{1}{2\sqrt{x}} = \frac{1}{2\sqrt{4}} = \frac{1}{4} $$
Ejemplo 2. Resolver el siguiente límite: $$\lim_{x \to \frac{\pi}{2}} \frac{\frac{\pi}{2}-x}{Cos(x)} $$
Primero se evalúa el límite por sustitución directa: $$\lim_{x \to \frac{\pi}{2}} \frac{\frac{\pi}{2}-x}{Cos(x)} = \frac{\frac{\pi}{2}-\frac{\pi}{2}}{Cos(\frac{\pi}{2})} = \frac{0}{0}$$ Entonces, aplicando el teorema de la Regla de L'hopital, se tiene que:
$$\lim_{x \to \frac{\pi}{2}} \frac{\frac{\pi}{2}-x}{Cos(x)} =\lim_{x \to \frac{\pi}{2}} \frac{(0)-1}{- Sen(x)} = \frac{(0)-1}{- Sen(\frac{\pi}{2})}= \frac{-1}{-1}=1 $$ Ejercicio.
Ejercicio.
Resolver los límites utilizando el teorema de la regla de L'hopital, para verificar la respuesta obtenida, oprima el botón solución. Para realizar otro ejercicio oprima el botón otro ejercicio
 ¡Recuerda!
¡Recuerda!
La regla de L'Hopital puede ser utilizada de manera reiterada hasta que al final resolvamos la indeterminación original.
Gráfico de funciones
Para representar una función $y=f(x)$, se estudia el significado de la primera y la segunda derivada, a partir de estos criterios se determina de una manera más o menos acertada la gráfica.
Se puede seguirse el siguiente esquema para representar gráficamente una función:
- Dominio de la función.
Determinar el dominio de $f(x)$, el conjunto de valores para los cuales $x$ está definida (Pag.32).
Esto permite el estudio de posibles discontinuidades y de las regiones: intervalos en los que $f(x)$ es positiva o negativa; para su determinación deben conocerse los puntos de corte de la función con el eje $x$.
- Intersecciones con los ejes.
Hallar los puntos donde la gráfica corta los ejes $x$ y $y$ (Pag.16).

- Para hallar las intersecciones en $x$, si hay, en la gráfica de una función, haga $y = 0$ en la ecuación y resuelva para $x$, $f(x)=0$.
- Para hallar las intersecciones en $y$, si hay, en la gráfica de una función, haga $x=0$ en la ecuación y resuelva para $y$.
- Simetrías.
Para estudiar la simetría debemos de estudiar cual es la imagen de $–x$ (Pag.52). El estudio de las simetrías no es imprescindible, aunque facilita el trazado de la curva.
- Si $f(-x) = f(x)$, entonces la función es par y simétrica respecto al eje de ordenadas $y$.
Simetría con respecto al eje $y$. - Si $f(-x) = –f(x)$, entonces la función es impar y simétrica respecto al origen $O$ o la recta $y=x$.
Simetría con respecto al eje $y$. - Si $f(-x) = f(x)$, entonces la función es par y simétrica respecto al eje de ordenadas $y$.
- Análisis de las asíntotas.
Puede ser verticales, horizontales y oblicuas (Pag.100):
- Verticales: Son rectas de la forma $x=a$. Las asíntotas verticales sólo pueden darse en puntos en los que la función no esté definida, donde se cumple que: $$\lim_{x \to a}f(x) = \pm\infty$$
- Horizontales: Son rectas de la forma $y=b$, donde se cumple que: $$\lim_{x \to \pm\infty}f(x) = b$$
- Oblicuas: Son rectas de la forma $y=mx +b$, donde $m$ pendiente y $b$ intercepto con el eje $y$, y se obtienen mediante: $$m=\lim_{x \to \pm\infty}{\frac{f(x)}{x}} \qquad y \qquad b=\lim_{x \to \pm\infty} (f(x)-mx) $$
- Puntos críticos.
Hallar los puntos donde la recta tangente a la gráfica es horizontal, vertical (picos) o no existe.
Si $f(x)$ está definida en el valor $x=c$, se dirá que $c$ es un número crítico de $f(x)$ si $f'(c)=0$; ó si $f'(c)$ no está definida.
Los valores críticos son posibles puntos de máximo, o de mínima, o de “pico”
 Teorema. Prueba de la primera derivada
Teorema. Prueba de la primera derivada
Sea f continua sobre $[a, b]$ y diferenciable sobre $(a, b)$ excepto tal vez en el número crítico $c$.
- Si $f'(x)$ cambia de positiva a negativa en $c$, entonces $f(c)$ es un máximo relativo.
- Si $f'(x)$ cambia de negativa a positiva en $c$, entonces $f(c)$ es un mínimo relativo.
- Si $f'(x)$ tiene el mismo signo algebraico a cada lado de $c$, entonces $f(c)$ no es un extremo.
En conclusión, del teorema, pueden resumirse en una frase:
"Una función $f$ tiene un extremo relativo en un número crítico $c$ donde $f'(x)$ cambia de signo".
Máximos. El punto $c$ es un máximo relativo cuando la función es creciente a su izquierda y decreciente a su derecha.
Por tanto: $c$ es un máximo si: $f´(a^-) >0$ , $f´(a)=0$ , $f´(a^+) <0$
Mínimos. El punto $c$ es un mínimo relativo cuando la función es decreciente a su izquierda y creciente a su derecha.
Por tanto: $c$ es un mínimo si: $f´(a^+) <0$ , $f´(a)=0$ , $f´(a^-) >0$
En un máximo o mínimo, la recta tangente a la curva es horizontal: su pendiente es igual a $0$
- Análisis de crecimiento y decrecimiento.
Determinar el conjunto de valores $x$ para los cuales $f'(x)$ es positiva o negativa.
Tomar sobre el eje $x$ los puntos críticos y aquellos en los que la función no está definida. Esos puntos dividen al eje $x$ en varios intervalos.
Estudiar el signo de la primera derivada en cada intervalo, deducir si la función es:
- Creciente, si $f'(x)>0$ (positiva).
- Decreciente, si $f'(x)<0$ (negativa).
Podemos deducir (de lo anterior) dónde se dan los puntos máximos y los mínimos, si es el caso.Intervalo 1 Intervalo 2 Intervalo 3... $$f'(x)$$ Se realiza el análisis tomando un punto de cada intervalo y ver si $f´(x)$ es positiva o negativa.
Ejemplo. Puntos críticos, análisis del crecimiento y decrecimiento.
Sea la función racional $\displaystyle f(x)=\frac{x^2-3}{x^2+1}$
Tenemos que la derivada aplicando la regla del cociente se obtiene: $$ f'(x)=\frac{8x}{(x^2+1)^2}$$
Se hallan los puntos críticos, donde $f´(x) = 0$, por tanto, se tiene cuando $x=0$. En consecuencia, $0$ es un único punto crítico.
Crecimiento y decrecimiento, se tiene:
| Intervalos | ||
|---|---|---|
$f'(x)<0$ Decreciente | $f'(x)>0$ Creciente |
Aplicando la prueba de la primera derivada, se tiene $f(0) = -3$ es un mínimo relativo
- Puntos de inflexión.
Los puntos en los que la curva cambia de concavidades (cóncava a convexa, o al revés), se llaman puntos de inflexión; en esos puntos, la tangente corta la curva.
Se cumple que:
Si $x = a$ es un punto de inflexión de $f (x)$ ⇒ $f´´(a) = 0$.Por tanto, se determinan los valores de $x$ para los cuales $f´´(x) = 0$.
Si $(c, f(c))$ es un punto de inflexión para la gráfica de una función $f$, entonces $f´´(x) = 0$ ó $f´´(x)$. no existe. - Concavidades.
La concavidad es una característica de la gráfica de una función, relacionada con su forma. Una gráfica que tiene forma cóncava, es porque al trazarla forma una cavidad o hueco.
 Teorema. Prueba para concavidades
Teorema. Prueba para concavidades
Sea $f$ una función para la cual $f''(x)$ existe sobre $(a, b)$.
- Si $f''(x)>0$ para toda $x$ en $(a, b)$, entonces la gráfica de $f$ es cóncava hacia arriba sobre $(a, b)$.
- Si $f''(x)<0$ para toda $x$ en $(a, b)$, entonces la gráfica de $f$ es cóncava hacia abajo sobre $(a, b)$.
Una curva puede presentar concavidad hacia arriba, hacia abajo o ambas. En este último caso se dice que tiene doble concavidad.
Se debe determinar el conjunto de valores $x$ para los cuales $f''(x)$ es positiva o negativa, para esto se estudia el signo de la segunda derivada en cada intervalo, deducir si la función es:
- Cóncava hacia arriba, si $f''(x)>0$ (positiva).
- Cóncava hacia abajo, si $f''(x)<0$ (negativa).
| Intervalo 1 | Intervalo 2 | Intervalo 3... | |
|---|---|---|---|
| $$f''(x)$$ |
Se realiza el análisis tomando un punto de cada intervalo y ver si $f´'(x)$ es positiva o negativa.
Ejemplo. Punto de inflexión y concavidades.
Sea la función $\displaystyle f(x)=x^5$, entonces se tiene que:
- La primera derivada es:
$f'(x)= 5x^4$ ⇒ $x=0$, es un punto crítico. - La segunda derivada es:
$f''(x)= 20x^3$ ⇒ $x=0$, es un punto de inflexión.
Por tanto, el punto $f(0)=0$ presenta un cambio de concavidad.
Análisis de las concavidades con la prueba de la segunda derivada:
| Intervalos | ||
|---|---|---|
$f''(x)<0$ Cóncava hacia abajo | $f''(x)>0$ Cóncava hacia arriba |
- Trazo de la gráfica.Adaptación de una escena de Elkin Castrillón con licencia CC by-nc-sa
Por último, se emplea toda la información obtenida en los pasos anteriores para realizar el trazo de la gráfica de la función.
 Exploración.
Exploración.
A continuación, por medio de un ejemplo, se plantea el procedimiento general para representar funciones gráficamente.

Oprima el botón de los conceptos estudiados, observa su procedimiento y su utilidad en el trazado de gráficas.
Optimización
En la vida diaria son innumerables los problemas donde se debe realizar optimización.
Los problemas llamados de optimización, desde el punto de vista matemático se reducen a problemas de determinación de máximos (beneficios) y mínimos absolutos (costos) de funciones de una variable real en determinados intervalos.
 Como plantear un problema de optimización.
Como plantear un problema de optimización.
- Comprender el problema.
El primer paso es leer cuidadosamente el problema hasta que se entienda con claridad. - Dibujar un diagrama.
Es útil trazar un diagrama e identificar en él los datos dados y pedidos. - Introduzca símbolos.
Asignar símbolos (letras) a las cantidad que ha de ser maximizada o minimizada y símbolos para cantidades desconocidas. - Expresar la incógnita.
Exprese la incógnita a maximizar o minimizar en términos de los símbolos del punto anterior, m = f(x). - Use la información dada para hallar relaciones (en forma de ecuaciones), Si usa más de una variable, reduzca a una sola función la incógnita.
- Encuentre el dominio de esta función, hallar el valor máximo o mínimo absoluto de la función ($f'(x)=0$).
 ¡Recuerda!
¡Recuerda!
Existirán relaciones entre variables que se han elegido que permitirán reducir el problema a una única variable (en algunos casos, nos tocara relacionar dos o más expresiones analíticas para dejar una sola expresión analítica en términos de una sola variable incógnita).
Un problema de optimización vendrá dado, generalmente, en términos de enunciado.
Se dice que está planteado cuando se sabe exactamente qué función hay que hacer máxima o mínima;
quedará resuelto cuando se halle y analice la solución. Para ello, se sigue el proceso anterior.
Una vez lograda la expresión analítica de la función buscada se debe derivar la función e igualar está derivada a cero para de esta forma, encontrar los valores de la variable a optimizar donde la función tiene puntos críticos, correspondientes a puntos de máxima o mínima y que este dentro del intervalo de variación de la variable elegida. $$f'(x)=0$$
 ¡Recuerda!
¡Recuerda!
Un punto crítico de una función es entonces un punto del dominio donde siendo continua la función, su derivada es nula o no existe (punto singular).
Ejemplo 1. Maximizar.
Se quiere construir una caja, sin tapa, partiendo de una lámina rectangular de $4 cm$ de largo por $6 cm$ de ancho. Para ello se recortará un cuadradito en cada esquina y se doblará.
¿Cuál debe ser el lado del cuadradito cortado para que el volumen de la caja resultante sea máximo?
 Dibujo o diagrama.
Dibujo o diagrama.
La caja es un prisma rectangular, cuyo volumen es área de la base por la altura (x).
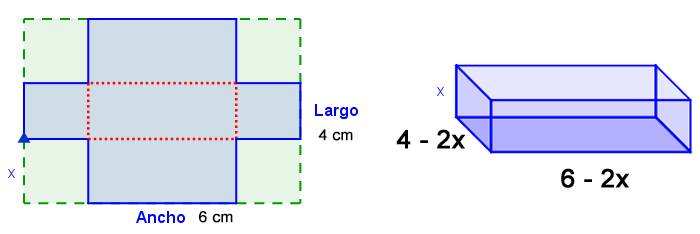
Si se corta un cuadradito de lado $x$ (altura), el volumen de la caja obtenida será:
$$V(x)=(6 - 2x )(4 -2x )x \\ V(x)=24x-8x^2-12x^2+24x $$ $$V(x)=4x^3-20x^2+24x $$
Una vez lograda la expresión analítica de la función buscada se debe derivar la función e igualar está derivada a cero.
Los puntos máximos o mínimos se encuentran, si existen, entre las soluciones de: $$V'(x)=0$$ $$V(x)=4x^3-20x^2+24x $$ $$V'(x)=12x^2-40x+24 $$
Encontrando las soluciones de $V'(x)=0$, obtenemos: $$4(3x^2-10x+6)=0 \\ 3x^2-10x+6=0$$ donde $$b^2-4ac= (-10)^2-4(3)(6)= 100-72=28$$ por tanto, $$x=\frac{-(-10)\pm \sqrt{28}}{2(3)}$$ $$x_1 \approx 2,55$$ $$x_2 \approx 0,79$$
Veamos para qué valor se obtiene el máximo, utilicemos la 2° derivada y evaluamos las soluciones encontradas: $$V''(x)=24x-40$$
 Teorema. Prueba de la segunda derivada
Teorema. Prueba de la segunda derivada
Sea $f$ una función para la cual $f''$ existe sobre el intervalo $(a, b)$ que contiene al número crítico $c$.
- Si $f''(x)>0$, entonces $f(c)$ es un mínimo relativo.
- Si $f''(x)<0$, entonces $f(c)$ es un máximo relativo.
- Si $f''(x)=0$, entonces la prueba falla y $f(c)$ puede ser o no un extremo relativo. En este caso se usa la prueba de la primera derivada.
$$V''(2,55)=24(2,55)-40 = 21.2>0$$ $$V''(0,79)=24(0,79)-40 = 21.04<0$$
Por lo tanto, la solución buscada es $x \approx 0,79$, este es el lado del cuadradito cortado para que el volumen de la caja resultante sea máximo.
El volumen máximo correspondiente $V$ lo calculamos remplazando el valor de $x \approx 0,79$ en la función de volumen: $$V(x)=(6 - 2x )(4 -2x )x$$ $$V(x)=(6 - 2(0.79) )(4 -2(0.79) )(0.79)$$ $$V(x)\approx 8,45 \space cm^3$$
 Ejercicio.Adaptación de una escena de Elkin Castrillón con licencia CC by-nc-sa
Ejercicio.Adaptación de una escena de Elkin Castrillón con licencia CC by-nc-sa
Modifica condiciones diferentes y analiza la situación.
 GeoGebra. Analiza la situación planteada y encuentra los resultados, cambia las condiciones dadas.
GeoGebra. Analiza la situación planteada y encuentra los resultados, cambia las condiciones dadas.
Se quiere construir una caja, con tapa, partiendo de una lámina.
 GeoGebra. Observa la situación cuando la caja tiene tapa, cambia las condiciones dadas, modifica los controles.
GeoGebra. Observa la situación cuando la caja tiene tapa, cambia las condiciones dadas, modifica los controles.
 ¡Recuerda!
Se dice que está planteado cuando se sabe exactamente qué función hay que hacer máxima o mínima;
quedará resuelto cuando se halle y analice la solución.
¡Recuerda!
Se dice que está planteado cuando se sabe exactamente qué función hay que hacer máxima o mínima;
quedará resuelto cuando se halle y analice la solución. Ejemplo 2. Minimizar.
Se desea construir, una zona de parada de buses a un borde de la via. Tendrá forma rectangular y estará enmallada por los tres lados que no linda con la vía.
Si su área es de 7200 m². ¿Qué dimensiones debe tener para que el coste de la malla sea mínimo?
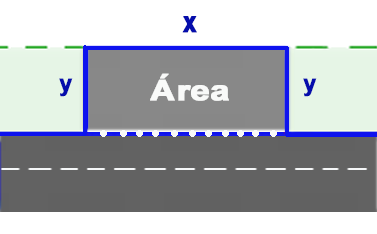 Dibujo o diagrama.
Dibujo o diagrama.
Representación gráfica, Área de forma rectangular, cuya área es base (x) por altura (y).
El objetivo es minimizar. Esto se deduce de la lectura del enunciado, donde hay que hacer el mínimo costo para el enmallado.
Para que el costo sea mínimo, la longitud (L) de la malla debe ser mínimo. por tanto, $$L=x + 2y$$
La función depende de varias variables; $x$ y $y$. Hay que determinar cuál de ellas depende de la otra y buscar en el enunciado la relación que liga esas variables; está relación siempre es una igualdad.
Como se tiene que el área de la zona es de $7200 \space m^2$, entonces se tiene que: $$A=x.y$$
La optimización se encuentran entre los puntos críticos de la función, que son las soluciones de $f '(x)=0$ . Para que sea máximo hay que verificar que $f ´( x ) <0$ ; y para que sea mínimo, que $f ´( x ) >0$.
Para este caso hay que buscar un punto que cumpla: $L ´( x ) = 0$ y $L´( x) >0$.
Donde, $\quad L´( x )= 1-\frac{14400}{x^2} \quad$ igualando a cero, se tiene: $$1-\frac{14400}{x^2}=0 \quad ⇒ \quad x^2 =14400 $$ $$x = ± 120$$
La solución $x = –120$ hay que descartarla por no ser del dominio de la función.
Ahora, encontremos la segunda derivada, y analizamos si $L´( x) >0$: $$ L´'( x )= \frac{28800}{x^3} $$ donde, evaluando cuando $x = –120$, se tiene: $$ L´'( 120 )= \frac{28800}{(120)^3}>0 $$
Por lo tanto, las dimensiones de la forma rectangular para que los costos de la malla sean mínimos, son: $$x = 120m, \quad y=60m$$

