S'apliquen les identitats notables: diferència de quadrats=suma per diferència
(2x3+x+3/2)2–(x3+5x–3/2)2 =(3x3+6x)·(x3–4x+3)
|
El primer factor (3 x3+6x) es descompon traient el factor comú 3x,
(3x3+6x)=3x·(x2+2); x2+2 és primer, ja que l'equació de segon grau x2+2 =0 no té arrels reals.
|
En el factor (x3–4x+3) es busquen les seves arrels racionals
Veiem que 1 és arrel 1 0 -4 3 1) 1 1 –3 ________________ 1 1 -3 0 |
(x3–4x+3)=(x–1)·(x2+x–3)
Per descompondre x2+x–3 es resol l'equació de segon grau
x2+x–3=0, que té com a solucions 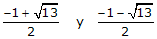
|