
Cuatro imágenes del mismo cuásar rodean una galaxia: un
típico espejismo topológico.
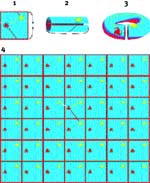
Un universo sumamente simple de dos
dimensiones ilustra cómo un observador situado en la galaxia A
(roja) puede ver imágenes múltiples de la galaxia B (amarilla). Este
modelo de universo, llamado “tore”, está construido a partir de un
cuadrado cuyos bordes opuestos se han pegado. La luz de la galaxia B
puede llegar a la galaxia A siguiendo varios trayectos, de
modo que el observador, en la galaxia A, ve las imágenes de la
galaxia B procedentes de varias direcciones. Aunque el espacio
del tore sea limitado, un ser que vive en él tiene la ilusión de ver
un espacio, si no infinito (en la práctica, hay horizontes que
limitan la vista), al menos más grande de lo que es en la realidad.
Este espacio ficticio tiene el aspecto de una red construida a
partir de una célula fundamental, que repite indefinidamente
cada uno de los objetos de la célula. |
En vez de ser plano e infinito, el universo podría estar
replegado en sí mismo y nuestra percepción distorsionada por rayos
luminosos que se multiplican. Como en un
espejismo.
¿cuál es
la forma del universo? El problema es más complejo de lo que parece.
Si bien el espacio inmediato, el que nos rodea, está correctamente
descrito en la geometría euclidiana1, el
espacio microscópico (en muy pequeña escala) y el espacio
cosmológico (en muy gran escala) son totalmente distintos. Según las
leyes de la mecánica cuántica, el espacio microscópico es tan
caótico y fluctuante como la espuma en la superficie del mar.
Asimismo, el espacio cosmológico es curvo.
¿Qué entendemos por
espacio curvo? La cosmología moderna se basa en gran medida en la
teoría de la relatividad general formulada por Albert Einstein a
comienzos del siglo XX. Según sus ecuaciones, todo espacio está
deformado —curvado— por la distribución de la materia en su
interior. Esta curvatura se manifiesta a través de una de las
fuerzas más esenciales del universo: la gravedad.
Si estudiamos
la forma del espacio en una escala suficientemente alta (superior a
1025 metros), sabemos que está globalmente curvado por una
distribución casi uniforme de la materia (conjuntos de galaxias).
Por consiguiente, su curvatura misma es uniforme, o sea, constante
de un punto a otro del espacio. Además, el universo posee una
dinámica global: teóricamente puede estar en expansión o en
contracción. En la actualidad, las observaciones indican que está en
expansión.
Los modelos de curvatura espacial constante, fruto de
la teoría de la relatividad, fueron descubiertos por Alexandre
Friedmann y Georges Lemaître en el decenio de 1920. En el modelo más
simple, un espacio de curvatura positiva (denominado de tipo
esférico) se dilata inicialmente a partir del Big Bang, alcanza un
radio máximo y luego se contrae para acabar en un big-crunch.
También podría ser que el espacio sea de curvatura nula (llamado de
tipo euclidiano) o negativa (de tipo hiperbólico, es decir, en forma
de silla de montar). En ambos casos el universo está en expansión
perpetua, pero el índice de expansión disminuye con el correr del
tiempo.
De hecho, ciertas observaciones recientes sugieren que el
espacio cósmico se aproxima al euclidiano, o sea es plano y conforme
a nuestra percepción. Pero indican también que está en expansión
acelerada. El “motor” de esta expansión obedece a otra ley: la
“constante cosmológica”, que puede interpretarse como la energía del
vacío.
Quedan por resolver algunas cuestiones cruciales.
¿Disponemos de una descripción satisfactoria de la forma del espacio
en gran escala con la cosmología relativista? A primera vista se
podría creer que sí, pero la respuesta es negativa. Incluso la
cuestión de la finitud o la infinitud del espacio no está claramente
zanjada. En efecto, así como un universo esférico es forzosamente
finito, un universo euclidiano o de curvatura negativa es
compatible, en cambio, con espacios finitos o infinitos.
A estas
alturas necesitamos un nuevo enfoque para progresar: el de la
topología, que trata de ciertas formas invariables de los espacios.
Un espacio euclidiano no es tan sencillo como parece. Una superficie
sin curvatura, por ejemplo, no es necesariamente plana. Basta cortar
una tira en una superficie plana y pegar sus extremos para obtener
un cilindro. Pero éste presenta una diferencia fundamental con algo
plano: está acabado en una dirección Este tipo de propiedad
corresponde a la topología y no a la curvatura. Al recortar una
superficie plana y pegarla, no hemos cambiado su forma local, su
curvatura, pero hemos cambiado radicalmente su forma global, su
topología.
En un espacio plano o monoconexo (en la jerga de la
topología), dos puntos cualesquiera están unidos por una sola
geodésica —el equivalente de la recta—, mientras que en un espacio
multiconexo, una infinidad de geodésicas unen dos puntos (ver
diagrama). Esta propiedad confiere a los espacios multiconexos un
interés excepcional en cosmología.
Una enorme ilusión óptica
En
efecto, los rayos luminosos siguen las geodésicas del
espacio-tiempo. Cuando observamos una galaxia lejana, creemos ver un
ejemplar único en una dirección y una distancia determinadas. Ahora
bien, si el espacio cósmico es multiconexo, ello significa que los
rayos luminosos se multiplican y crean así imágenes múltiples de la
galaxia observada. Como toda nuestra percepción del espacio procede
del análisis de esas trayectorias, si vivimos en un espacio
multiconexo estamos sumidos en una enorme ilusión óptica que hace
que el universo nos parezca más grande de lo que es. Galaxias
lejanas, que creemos originales, son en realidad imágenes múltiples
de una sola galaxia.
Un espacio arrugado es, pues, un espacio
multiconexo de volumen limitado, de menor tamaño que el universo
observado (radio aparente: unos 15.000 millones de años-luz). Los
espacios arrugados crean un espejismo topológico que multiplica las
imágenes de las fuentes luminosas. Los astrónomos conocen muy bien
los espejismos gravitacionales: cerca de un cuerpo masivo, situado
en la línea de mira de un objeto más lejano, la curvatura del
espacio multiplica los trayectos de los rayos luminosos procedentes
del segundo plano. Percibimos así imágenes fantasmas agrupadas en la
dirección del cuerpo intermedio llamado “lentilla”. Este tipo de
espejismo se debe a la curvatura local del espacio en torno a la
lentilla.
En el caso del espejismo topológico, no es un cuerpo en
particular el que deforma el espacio, es el propio espacio el que
cumple la función de la lentilla. Por consiguiente, las imágenes
fantasmas se esparcen en todas direcciones y en todas las etapas del
pasado. Este espejismo global nos permitiría ver los objetos no sólo
en todas sus orientaciones posibles, sino también en todas las fases
de su evolución.
Si el espacio está arrugado, lo es sutilmente y
en muy gran escala, pues si no, habríamos identificado ya imágenes
fantasmas de nuestra propia galaxia o de otras estructuras muy
conocidas. Sin embargo, no es así.
¿Cómo detectar entonces la
topología del universo? Recientemente se han elaborado dos métodos
de análisis estadístico. Uno, la cristalografía cósmica, trata de
descubrir ciertas repeticiones en la distribución de los objetos
lejanos. El otro estudia la distribución de las fluctuaciones de
temperatura de la radiación fósil —un vestigio enfriado de Big
Bang—, lo que permitiría, si el espacio está arrugado, poner al
descubierto determinadas correlaciones.
Los proyectos
experimentales de cristalografía cósmica y de detección de esas
correlaciones están en curso. Por el momento, las observaciones no
bastan para sacar conclusiones sobre la topología global del
espacio. Pero los años venideros abren perspectivas fascinantes de
sondeos profundos que localizarán numerosos conjuntos lejanos de
galaxias y de cuásares, y mediciones de la radiación fósil, gracias
a los satélites Map y Planck. Tal vez podamos entonces atribuir una
forma al espacio. |
