
 |
FUNCIONES: Funciones elementales: Dependencia lineal. |
| Análisis. | |
| Funciones elementales. | |
|
En los apartados anteriores hemos visto que si una función puede expresarse en términos matemáticos nos permite obtener mucha información de ella con facilidad. Así pues, vamos a estudiar en este apartado y en los siguientes algunas de las funciones matemáticas más sencillas. Vamos a estudiarlas de forma abstracta, pero también vamos a ver ejemplos de cómo se aplican en situaciones concretas. De hecho, las funciones que vamos a estudiar en estos apartados son aquéllas con las que con más frecuencia nos vamos a encontrar. |
|
| 1. Funciones constantes. | |
|
Las
funciones constantes son las más simples de todas las funciones. Su
expresión analítica es y=K, o f(x)=K, siendo K un número real
cualquiera. Esto significa que sea cual sea el valor de x la función
siempre toma el valor K. y = f(x) = K |
|
|
En la imagen adjunta puedes ver el aspecto que tiene cualquier función constante. Sin más que variar K puedes obtener distintas funciones constantes. Contesta a las preguntas que se te plantean al margen, referentes a las propiedades de las funciones. | |
|
|
1.- Determina el dominio y el recorrido de cualquier función constante. |
|
2.- Estudia sus intervalos de monotonía y sus extremos relativos. | |
|
3.- Estudia sus posibles simetrías. ¿Son funciones pares, impares o ninguna de ambas cosas? | |
|
4.- ¿Son funciones acotadas? Si la respuesta es afirmativa, ¿superior, inferiormente o ambas cosas a la vez? Determina sus extremos absolutos (si los tiene). | |
| 2. Funciones polinómicas de primer grado. Dependencia lineal. | |
|
La expresión analítica de estas funciones es un polinomio de primer grado, es decir, una expresión del tipo.
y = ax + bsiendo a y b dos números reales cualesquiera con a distinto de cero. (Observa que si a=0 se trataría de la función constante y = b). | |
|
Cuando una función es de este tipo se dice que la y depende linealmente de la x. El motivo es que la gráfica de esta función es siempre una línea recta como puedes comprobar en la imagen adjunta. Sin más que variar a y b obtendrás distintas funciones lineales. Contesta a las preguntas que se te plantean al margen referentes a sus propiedades. | |
|
|
1.- Modifica los valores de a y de b e intenta encontrar un significado gráfico para cada uno de ellos. ¿Qué puede decirse de dos funciones lineales con el mismo valor de a, pero distinto valor de b? ¿Qué puede decirse de dos funciones lineales con el mismo valor de b, pero distinto valor de a? ¿Qué tiene de especial una función lineal en la que b=0? |
|
2.- Determina el dominio y el recorrido de cualquier función lineal. | |
|
3.- Estudia sus intervalos de monotonía y sus extremos relativos. ¿Qué pasa si a es negativo? | |
|
4.- Estudia sus posibles simetrías. ¿Son funciones pares, impares o ninguna de ambas cosas? | |
| 5.- ¿Son funciones acotadas? Si la respuesta es afirmativa, ¿superior, inferiormente o ambas cosas a la vez? Determina sus extremos absolutos (si los tiene). | |
|
El coeficiente a de las funciones lineales se denomina pendiente de la recta, pues es una medida de la inclinación de la misma. Por su parte, el coeficiente b se denomina ordenada en el origen puesto que es el valor que toma la función cuando x es igual a cero. | |
|
Este tipo de funciones aparecen siempre que la variación (o incremento) de la varible dependiente sea proporcional a la variación (o incremento) de la variable independiente. La siguiente imagen te aclarará lo que acabamos de decir: | |
|
|
1.- Los segmentos rojos de la imagen adjunta representan las variaciones (o incrementos) de las variables x e y. Pulsa el botón Inicio. Observa cuánto vale el cociente entre ambas. ¿Con quién coincide ese cociente? Modifica el parámetro incr, sin modificar ni a ni b. Este parámetro hace que obtengamos distintos incrementos de la variable x que a su vez se transforman en distintos incrementos de la variable y. Como puedes observar, los valores de var(x) y var(y) van cambiando, sin embargo, su cociente permanece constante e igual ¿a quién? |
|
2.- Repite la práctica con otros valores de a y de b. ¿Sigue siendo cierta la respuesta que has dado a la cuestión anterior? | |
| 3.- Como ves, el cociente entre la variación de la variable dependiente y la variación de la variable independiente es siempre constante e igual a la pendiente de la recta. En otras palabras, la pendiente, además de medir la inclinación de la recta, mide también la proporción entre ambas variaciones. Observa que si cambias el valor de a, cambia la constante de proporcionalidad, en cambio si alteras el valor de b la constante de proporcionalidad es la misma. ¿Podrías dar una interpretación de este hecho? | |
|
Es conocido el hecho de que por dos puntos distintos de un plano pasa una recta y sólo una. Esto permite que si estoy estudiando una función cuya dependencia sé que es lineal y conozco sólo dos valores de la misma pueda representarla gráficamente con facilidad. Pero además, lo dicho antes me permite encontrar con facilidad su expresión analítica. En efecto, supongamos que la recta que pretendemos dibujar pasa por los puntos P(x1,y1) y Q(x2,y2). Se supone que estos puntos pertenecen a la gráfica de una función lineal y=f(x)=ax+b. Esto significa que f(x1)=y1 y que f(x2)=y2. Según lo que hemos dicho en el párrafo anterior el cociente entre la variación de la y y la variación de la x tiene que ser igual a la pendiente de la recta, es decir: 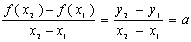 Si ahora consideramos otro punto desconocido de la recta X(x,y), se cumple que y=f(x), pero la variación de y con respecto a la variación de x tiene que seguir siendo la misma, es decir: 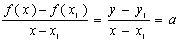 Igualando ambas expresiones obtenemos la expresión implícita de la recta buscada: 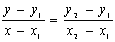 | |
|
Vamos a hacer algunos ejercicios para asentar todo esto. Se trata de calcular las ecuaciones de las rectas que pasan por dos puntos que se te dan al margen. Además hay que dibujarlas. En la gráfica tienes ya resuelto el primero de los ejemplos. Haz lo mismo con los demás. Intenta obtener después las ecuaciones en la forma y=ax+b. | |
|
|
1.- Halla la recta que pasa por los puntos P(2,3) y Q(1,5) |
|
2.- Lo mismo con P(-5,-3) y Q(3,1) | |
|
3.- Lo mismo con P(-4,3) y Q(5,-2) | |
|
4.- Lo mismo con P(-3,0) y Q(0,5) | |
|
5.- Hazlo ahora con la pareja de puntos que quieras. | |
| EJERCICIO. | |||
|
Vamos a terminar este apartado con una aplicación práctica. Se trata de un problema monetario: Tenemos una cantidad x en euros y queremos cambiarlos a dólares americanos. En el banco A por cada euro me dan 0.92 dólares, pero me cobran una comisión fija de 5 euros por la operación. Por su parte, en el banco B me dan 0.80 dólares por cada euro, pero no me cobran comisión. Halla las expresiones que relacionan en cada caso la cantidad "y" de dólares con la cantidad "x" de euros. Representa ambas en la gráfica siguiente y determina en qué banco es más ventajoso el cambio en función de la cantidad que se quiere cambiar. | |||
|
|
| ||
| José Luis Alonso Borrego Adaptación a DescartesJS: Joan Carles Fiol Colomar |
||
 |
||
| ProyectoDescartes.org Año 2015 | ||

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.