INTRODUCCIÓN
| No agotamos con estas propiedades todas las que tiene la cicloide, solo pretendemos con esta breve referencia, extraida de Wikipedia, complementar el material que aquí nos ocupa y poner de relieve el interés que esta curva ha tenido entre los matemáticos y físicos a lo largo de la historia y animar al lector a que se documente con mas detalles por los distintos medios que tiene a su alcance. | ||
| "En
1696 el matemático Johann Bernoulli anunció a la
comunidad matemática la solución al problema de la braquistócrona
(curva que sigue el descenso más rápido cuando existe
gravedad y que es objeto de estudio en el cálculo de
variaciones), mostrando que la solución era una cicloide.
Leibniz, Newton, Jakob Bernoulli y Guillaume
de l'Hôpital, encontraron la solución del problema
enunciado por Bernoulli. La cicloide se
emplea para resolver el problema de la tautócrona (descubierto
por Christian Huygens), en el que si se desprecia el
rozamiento y si se invirtiese una cicloide dejando
caer un objeto por la misma, por ejemplo una bola, esta
llegará a la parte más baja de la curva en un intervalo de
tiempo que no depende del punto de partida." "Fueron muchos los esfuerzos realizados en el siglo XVII para tratar de comprender esta curva y sus propiedades, tanto geométricas como físicas, que posteriormente han permitido desarrollar un gran número de aplicaciones industriales." |
PROPIEDADES FÍSICAS
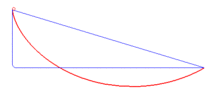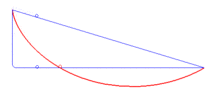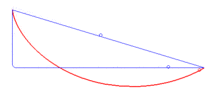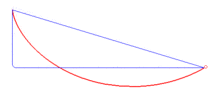
| Curva
braquistócrona "La
cicloide es una curva braquistócrona en el
sentido de Roberval, es decir, que representa la
curva en la que debe deslizarse sin fricción y sin
velocidad inicial un punto material pesado, colocado en un
campo gravitatorio uniforme, de manera que su tiempo de
recorrido es el mínimo de entre todas las curvas que unen
dos puntos fijos dados. En otras palabras, es la curva de
descenso más rápida para conectar dos puntos dados."
|
 |
|||
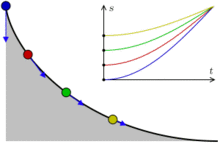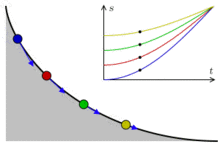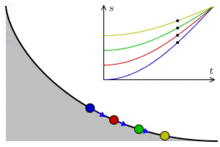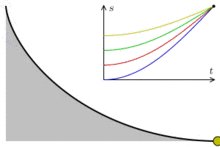
| Curva tautócrona "El
semiarco de una cicloide es también una curva tautócrona,
es decir, una curva tal que cualquier punto material
dejado caer sin velocidad inicial en la curva llega a un
punto dado (el que tiene la menor altura de la cicloide)
al mismo tiempo independientemente del punto de partida."
"En la
imagen de la derecha, las flechas azules representan la
aceleración. En el gráfico, t es el tiempo y s
la longitud de arco a lo largo de la curva."
|
 |
|||