INDICACIONES: Curvas EPICICLOIDE/HIPOCICLOIDE

INTRODUCCIÓN

Las distintas posiciones que adopta un punto determinado de una circunferencia generatriz de centro M y radio b que rueda, sin deslizar, sobre otra circunferencia directriz de centro O y radio a dibuja una curva plana. Si la circunferencia que rueda lo hace exteriormente a la circunferencia directriz, la curva que se genera es una epicicloide y si rueda interiormente la curva es una hipocicloide.

 OBJETIVOS

  • Dar a conocer las curvas EPICICLOIDE e HIPOCICLOIDE cuyo punto vinculado pertenece a la circunferencia generatriz. Tomaremos el punto que inicialmente está en contacto con la recta directriz.
  • Interaccionar con la escena traves de los controles para observar las distintas formas de curvas dependiendo de los distintos valores que pueden tomar los radios a y b de ambas circunferencias.

INSTRUCCIONES

Se pueden modificar los parámetros de la escena y observar como cambian las figuras, esto se hace a través de los siguientes controles:
  • Radio a de la circunferencia directriz: puede variar desde 2 a 8 u.d.l (unidades de longitud)
  • Radio b de la circunferencia generatriz: puede variar desde 0.5 u.d.l hasta el valor actual de a
  • Ángulo ang que describe el centro  M de la circunferencia generatriz alrededor del centro O de la circunferencia directriz. Este ángulo viene dado en radianes y varía de 0 rad a 2π rad ≅ 6.28 rad, es decir una vuelta completa.
  • Cambio de escala zum: el zum inicial es 20 puntos por u.d.l. pero podrá variar entre 6 y 100. Para los mismos radios a y b las imagenes de la escena se podrán ver más grandes o más pequeñas, aumentando o disminuyendo el zum.
  • Inicio: Restablece las condiciones iniciales de la escena.
  • animar/parar: al pulsar por primera vez este control de botón, se incrementa automáticamente y de manera uniforme el valor del ángulo ang en 0.01 rad con lo que el punto vinculado a la circunferencia generatriz va dibujando la curva correspondiente. Al pulsar de nuevo el control se detiene el incremento del ángulo y el dibujo queda en suspenso.
PRIMERAS OBSERVACIONES
  1. La curva se puede dibujar pulsando sucesivamente el control ang para incrementar cada vez en 0.01 rad el ángulo o dejar que la curva se dibuje sola después de pulsar el control animar/parar
  2. Comprobar el aspecto de la curva epicicloide o hipocicloide cuando el centro M realiza una vuelta completa para distintos valores de los radios a y b
  3. Cuando a es un múltiplo de b o sea a = n·b (n entero) la curva se cierra en una vuelta completa de M con formas y nombres especiales. Generar estas curvas, dando valores correspondientes a los radios a y b:
    Epicicloides 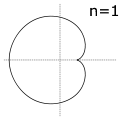epicicloide 1
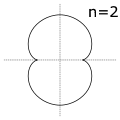
    		 epicicloide 2
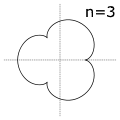
    		 epicicloide 3
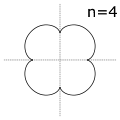
    		 epicicloide 4
    Hipocicloides hipocicloide 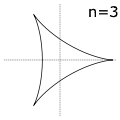3
    		 hipocicloide 4
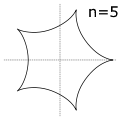
    		 hipocicloide 5
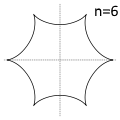
    		 hipocicloide 6

  4. Cuando a no es múltiplo de b, la curva no se cierra en una vuelta completa del punto M. Probar algunos casos en ambas escenas como a=3 y b=2 (n=1.5), a=4 y b=2.5 (n=1.6), a=4 y b=3 (n=1.333...). Nos podemos preguntar aquí si la curva se podrá cerrar en más de una vuelta. Este caso se analiza en los apartados siguientes.