INTRODUCCIÓN
Albrecht Dürer (Alberto Durero) en su libro "De la medida" (1532) nos lego múltiples construcciones geométricas de amplia aplicación práctica en la arquitectura y en la artesanía. De hecho muestra y describe esas construcciones, pero no las analiza desde el punto de vista matemático, es un artista y como tal se centra en la herramienta y no en el porqué de la misma. En la página 24 de ese libro podemos observar una espiral que es, quizás, la primera manifestación o precedente de la conocida espiral logarítmica (posteriormente analizada formalmente por Descartes y Jacob Bernoulli). No es una espiral logarítmica, pero se puede aproximar por ella o viceversa, es decir, utilizar esta construcción para abordar un dibujo aproximado de una espiral logarítmica.
Durero, describe su trazado y refleja una representación de la misma realizada a mano alzada y que es la mostrada a continuación.
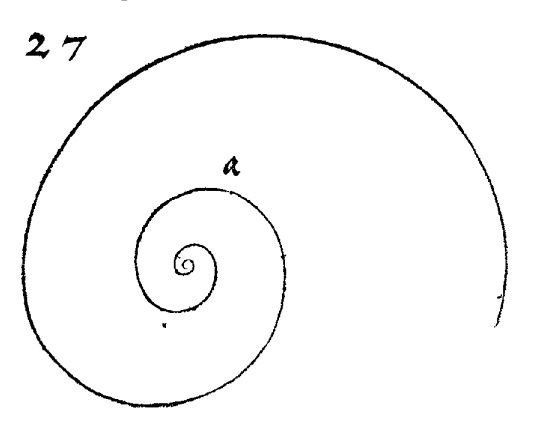
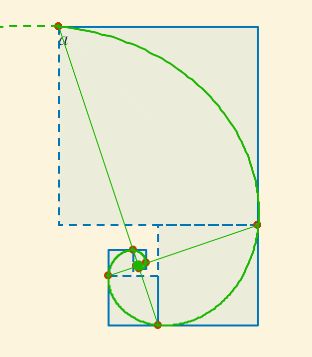
Imagen de la espiral descrita y trazada por Durero en el libro "De la Medida".Como veremos, realmente Durero lo que describe es una pseudoespiral, dado que es una concatenación de arcos de circunferencia, y no propiamente una curva que refleje de manera uniforme propiedades similares en todo su trazado. Pero independientemente de ello, actualmente, si preguntamos por la "espiral de Durero" lo usual es encontrar una construcción basada en un rectángulo áureo al que se concatenan cuadrados (el cuadrado es el gnomon de un rectángulo áureo, es decir, que al añadirle un cuadrado obtenemos otro rectángulo áureo semejante) en los que se trazan arcos de circunferencia formando dicha espiral, que es lo mostrado en la siguiente imagen.
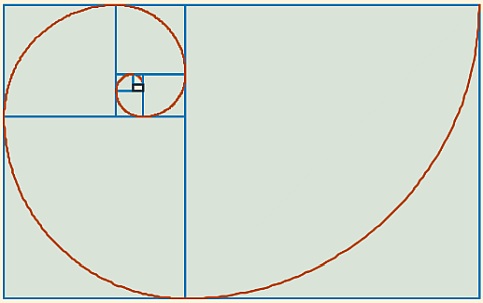
Imagen de la espiral de Durero según se muestra, usualmente, en la actualidad.
En esta miscelánea seguiremos las instrucciones originales dadas por Durero, en concreto consideraremos la descripción realizada en la edición de Jeanne Peiffer, en el año 2000, con traducción de Jesús Espino. Pero no nos quedaremos en la mera reproducción de esas indicaciones (de por sí, como veremos, no muy precisas por lo que requieren reinterpretación) sino que analizaremos las mismas, obtendremos propiedades y llegaremos a comprender por qué se presenta la pseudoespiral Durero asociada con el rectángulo áureo. En definitiva el qué, el cómo y el porqué de la matemática que relaciona a las dos imágenes anteriores.
Durero traza su espiral siguiendo un sentido dextrógiro, según el movimiento de las agujas del reloj o sentido negativo de medición de ángulos. En nuestro caso, procederemos a dibujar en sentido levógiro, contrario al movimiento de las agujas del reloj o sentido positivo de medición de ángulos. Un caso u otro son equivalentes por simetría.
Con esta miscelánea no cerramos nuestra crítica de la pseudoespiral de Durero, veremos que hay otras facetas que plantear y analizar y, por tanto, serán objeto de otro trabajo posterior.
OBJETIVOS
- Conocer las directrices dadas por Durero para el trazado de una espiral próxima a la denominada espiral logarítmica.
- Abordar, paso a paso, la representación gráfica de la pseudoespiral de Durero representada en su libro "De la medida".
- Detectar que las indicaciones dadas por Durero para su costrucción son imprecisas y quedan abiertas a interpretaciones de sus lectores.
- Tomar decisiones que eviten las imprecisiones de Durero, fijando parámetros, y procediendo con ellas a concretar la respectiva construcción.
- Comprobar que Durero realmente realiza dos construcciones diferentes en su espiral según nos desplacemos "hacia dentro" o "hacia fuera" de esa curva.
- Ver que ambas pseudoespirales "hacia dentro" y "hacia fuera" se aproximan por espirales logarítmicas o son aproximadoras de éstas.
- Analizar cuándo las espirales logarítmicas aproximadoras "hacia dentro" y "hacia fuera" son coincidentes.
- Deducir qué ha de cumplirse para que los cuadrados que intervienen en la construcción no se solapen.
- Concluir qué condición ha de cumplirse para que esos cuadrados recubran el plano y determinen una pseudoespiral de Durero aproximadora de una única espiral logarítmica y cómo surge su relación con el rectángulo áureo.
- Dejar para un trabajo posterior el análisis de la construcción considerando otros parámetros como que el paso angular no sea de $\frac{\pi}{2}$ radianes.
INSTRUCCIONES
Inicialmente la escena es meramente descriptiva y, por ello, sólo cuenta con un control ubicado en la esquina inferior derecha que permite avanzar o retroceder en los 11 pasos secuenciales que contiene (númerados de 0 a 10). De ellos, hasta el tercero, nos limitamos a abordar el proceso que describe Durero, si bien, con comentarios a su imprecisión y consecuentemente con la necesaria toma de decisiones. A partir del cuarto paso abordamos nuestro análisis personal.
En esta zona inferior además hay otros dos botones adicionales. Uno, representado con una "i" que al pulsarlo le da acceso a estas instrucciones y documentación; y otro con el símbolo "©" que le permite ver la autoría y licencia.
En todos los pasos desde el primero al noveno, podrá distinguir dos zonas o espacios. Uno superior donde se refleja la parte gráfica, en la que puede interactuar, y una inferior donde podrá consultar la descripción literaria que detalla lo representado en la parte gráfica y algunos posibles comentarios. En el décimo paso, en la parte descriptiva, si ubica su ratón en las palabras "rectángulo áureo" podrá ver una forma de construir un rectágulo áureo.
Salvo en la página de portada, en todas se cuenta con una barra lateral auxiliar que incluye controles tipo botón cuya funcionalidad respectiva es la siguiente:
- Pulsadores para cambio de escala, incrementar (lupa +) o decrementar (lupa -), es decir, zum hacia dentro o zum hacia fuera.
- Botón para centrar la imagen en polo teórico de la espiral.
- Mostrar u ocultar (icono sin tachar o tachado) la pseudoespiral de Durero.
Mostrar u ocultar (icono sin tachar o tachado) los puntos extremos de los arcos de la pseudoespiral de Durero.- Mostrar u ocultar (icono sin tachar o tachado) los cuadrados que intervienen en la construcción de los arcos de la pseudoespiral de Durero.
- Mostrar u ocultar (icono sin tachar o tachado) la poligonal de los centros de las circunferencias que se usan en la construcción de la pseudoespiral de Durero.
- Mostrar u ocultar (icono sin tachar o tachado) las espirales logarítmicas que aproximan respectivamente a la pseudoespiral de Durero hacia dentro y a la hacia fuera.
- Mostrar u ocultar (icono sin tachar o tachado) los segmentos que unen puntos alternos de los puntos extremos de los arcos de la pseudoespiral hacia dentro y hacia fuera.
Según el contexto o paso en el que se encuentre, algunos controles puede estar deshabilitados para el usuario.
Adicionalmente se tienen otros controles numéricos que permiten modificar, en algunos momentos, su valor:
- arco n.º: permite ir dibujando/borrando cada uno de los arcos de la circunferencia que determina la construcción.
- amplitud arco: ángulo en radianes que cubre el trazado del arco de la circunferencia (en esta escena esa amplitud está siempre fija a $\frac{\pi}{2} \simeq 1,5708$). Éste es uno de los parámetros no fijados por Durero.
- factor reductor: cantidad decimal que indica el porcentaje de reducción del radio, según indica Durero en su construcción hacia dentro. Este porcentaje lo fija en el $50\% = 0,5$, pero obviamente puede considerarse como un parámetro en la construcción y así lo consideraremos en algunos pasos en esta escena.
- factor amplificador: cantidad decimal que indica el porcentaje de incremento del radio, según indica Durero en su construcción hacia fuera. Este porcentaje lo fija en el $150\% = 1,5$, pero obviamente también puede considerarse como otro parámetro en la construcción y también así lo consideraremos en esta escena en determinadas situaciones.
DESCRIPCIÓN MATEMÁTICA, PASO A PASO
Procedemos a describir cada paso de la escena interactiva.
- Paso 0.
En este paso, a la izquierda se muestra una imagen de Durero y a la derecha la descripción completa que él realiza sobre la construcción de una espiral muy especial que teóricamente cambia continuamente de forma, de manera uniforme, aunque realmente por su descripción no sea así. Se refleja el dibujo original realizado por Durero. Ésta espiral se verá que es un antecedente de la espiral logarítmica. También se detalla la fuente de la traducción que hemos usado.
- Paso 1.
Iniciamos la ejecución de las instrucciones de Durero, abordando la espiral "hacia dentro".
- En la parte inferior descriptiva, leemos a la izquierda lo que nos indica este autor y a la derecha hacemos un comentario relativo a lo que no nos indica, en este caso cuál es la amplitud del arco a trazar —esta indeterminación nos lleva a poder construir infinitas espirales diferentes, una por cada amplitud considerada—, aquí optaremos por considerar que la amplitud es $\frac{\pi}{2}$ radianes, dibujando por tanto cuadrantes de circunferencia —realizamos esta elección porque es la que actualmente se considera cuando se habla de esta pseudoespiral, pero en otro trabajo optaremos por que sea un parámetro en la construcción—.
- En la zona gráfica usando el factor reductor 0,5, se puede construir progresivamente la espiral "hacia dentro" usando el parámetro "arco n.º", y usando las herramientas laterales se puede ver la sucesión de cuadrados auxilares, centros, etc.
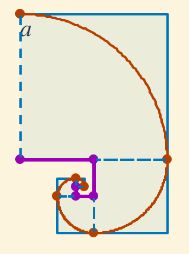
Fig. 1 La pseudoespiral "hacia dentro", poligonal de los centros y sucesión de cuadrados.- Formulación matemática
Considerando que el centro del arco de la circunferencia inicial es $C_0 (0, 0)$, que el radio inicial es $r$ (sin ser restrictivos, podría considerarse $r=1$ ya que sólo supone un cambio de escala) y que la amplitud de los arcos a trazar es $\alpha = \frac{\pi}{2}$, entonces al reducir el radio por un factor $f$ tendríamos que para $n \ge 0$ el radio del arco $n$-ésimo será $r^n=r·g^n$ con $g=1-f$ y el arco que recorre abarcaría el intervalo $-n \, \frac{\pi}{2} \le \theta \le (1-n) \, \frac{\pi}{2}$.
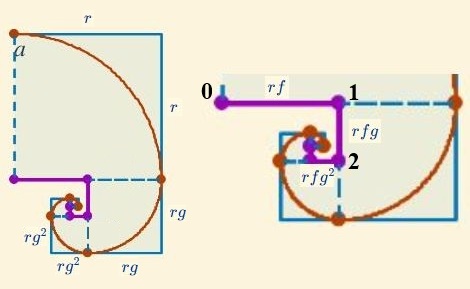
Fig. 2. A la izq. Longitud de los radios en la construcción "hacia dentro" y a la dcha. longitud de los segmentos de la poligonal de los centros.
Adicionalmente, los segmentos de la poligonal de centros (los numeraremos de fuera hacia dentro, según el orden constructivo) miden $\{r \, f, r \, f \, g, r \, f \, g^2,...\} $, es decir, la distancia entre dos centros consecutivos es $d({\color{#9b00b6} C_{i-1}},{\color{#9b00b6} C_i}) = r \, f \, g^{i-1}$, donde $\color{#9b00b6} C_k$ es el centro del arco $k$-ésimo. Y, por tanto, podemos obtener la coordenadas de dichos centros. que vendría dadas para $k \ge 1$ por:
$$\color{#9b00b6} \small \begin{cases} C_{2k} ( r \, f (1 - g^2 + g^4- \dotsb + (-g^2)^{k-1}, - r \, f \, g (1 - g^2 + g^4- \dotsb + (-g^2)^{k-1} ))\\ C_{2k+1} ( r \, f (1 - g^2 + g^4- \dotsb + (-g^2)^{k}, - r \, f \, g (1 - g^2 + g^4- \dotsb + (-g^2)^{k-1} )) \end{cases} $$ siendo $\color{#9b00b6} C_0(0,0)$ y $\color{#9b00b6} C_1(r \, f, 0)$.
O bien, efectuando en cada coordenada la suma de los términos de una progresión geométrica de razón $-g$ tendríamos: $$\color{#9b00b6} \begin{cases} C_{2k} ( r \, f \large \frac{1 - (-g^2)^k}{1+g^2}, \normalsize -r \, f \, g \large \frac{1 - (-g^2)^k}{1+g^2})\\ C_{2k+1} ( r \, f \large \frac{1 - (-g^2)^{k+1}}{1+g^2}, \normalsize -r \, f \, g \large \frac{1 - (-g^2)^k}{1+g^2}) \end{cases} \tag{1}$$
Consecuentemente, bajo los supuestos anteriores, la pseudoespiral "hacia dentro" de Durero en el paso $n$-ésimo, con $n \ge 0$ viene dada por: $$ \color{#b63f00} \begin{cases} x=C_{n_x} + r·g^n cos (\theta)\\ y=C_{n_y} + r·g^n sen (\theta) \end{cases} \tag{2} $$ con $-n \, \frac{\pi}{2} \le \theta \le (1-n) \, \frac{\pi}{2}$.
Si bien lo hemos expresado de manera general para cualquier reducción $f$, en el caso particular expresado por Durero tenemos que $f=0,5$ y $g=1-0,5=0,5$.
- Paso 2.
- En la parte inferior, al igual que el paso anterior, se refleja el detalle constructivo de la espiral "hacia fuera", donde de nuevo queda imprecisa la amplitud del arco y además indica "cada vez que doy una vuelta", o sea que la amplitud se interpretaría como $2 \pi$ radianes, pero tomaremos como antes una amplitud $\alpha=\frac{\pi}{2}$. El factor amplificador sería 1,5, por tanto distinto al de la espiral "hacia dentro" (no se entiende esta diferente elección, y sólo podemos sugerir cierta interpretación errónea al asociar disminuir la mitad, que significa en sentido inverso duplicar, con incrementar la mitad, ¡los porcentajes y lo difíciles que pueden llegar a ser cuando llega la hora de interpretarlos! ¿verdad?).
- En la zona gráfica usando el factor amplificador 1,5, se construye progresivamente la espiral "hacia fuera" usando el parámetro "arco n.º", disponiendo también de las herramientas auxiliares.
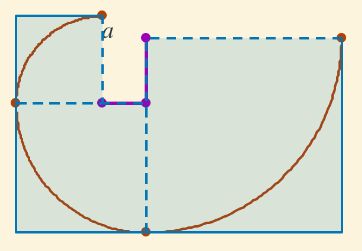
Fig. 3 La pseudoespiral "hacia fuera", poligonal de los centros y sucesión de cuadrados.- Formulación matemática
Considerando también en este caso "hacia fuera" que el centro del arco de la circunferencia inicial es $\color{#9b00b6} D_0 (0, 0)$, que el radio inicial es $r$ (de nuevo sin ser restrictivos, podría considerarse $r=1$ ya que sólo supone un cambio de escala) y que la amplitud de los arcos a trazar es $\alpha = \frac{\pi}{2}$, entonces al aumentar el radio un porcentaje $h$, el factor amplificador sería $m=1+h$ y tendríamos que para $n \ge 1$ el radio del arco $n$-ésimo será $r^n=r·m^n$ y el arco que recorre abarcaría el intervalo $n \, \frac{\pi}{2} \le \theta \le (n+1) \, \frac{\pi}{2}$.Adicionalmente, los segmentos de la poligonal de centros (los numeraremos de dentro hacia fuera, según el orden constructivo) miden $\{r \, h, r \, h \, m, r \, h \, m^2,...\} $, es decir, la distancia entre dos centros consecutivos es $d({\color{#9b00b6}D_{i-1}},{\color{#9b00b6}D_i}) = r \, h \, m^{i-1}$, donde $\color{#9b00b6} D_k$ es el centro del arco $k$-ésimo. Y, por tanto, podemos obtener la coordenadas de dichos centros que vendrían dadas para $k \ge 1$ por:
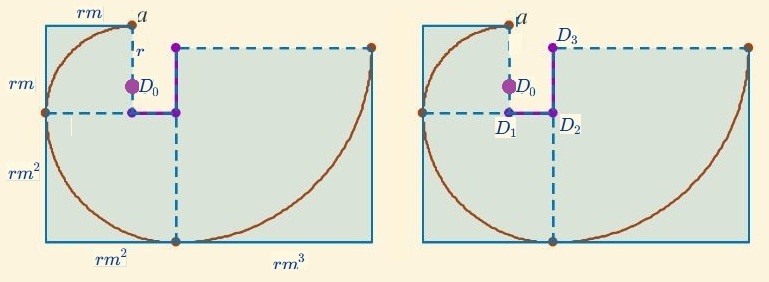
Fig. 4. A la izq. Longitud de los radios en la construcción "hacia fuera" y a la dcha. longitud de los segmentos de la poligonal de los centros.$$\color{#9b00b6} \small \begin{cases} D_{2k} ( r \, h \, m (1 - m^2 + m^4- \dotsb + (-m^2)^{k-1}), - r \, h (1 - m^2 + m^4- \dotsb + (-m^2)^{k-1} ))\\ D_{2k+1} ( r \, h \, m (1 - m^2 + m^4- \dotsb + (-m^2)^{k-1}), - r \, h (1 - m^2 + ,m^4- \dotsb + (-m^2)^{k} )) \end{cases} $$
siendo $\color{#9b00b6} C_0 \equiv D_0$, $\color{#9b00b6} D_0(0,0)$ y $\color{#9b00b6} D_1(0, -r \, h)$. O bien, efectuando en cada coordenada la suma de los términos de una progresión geométrica de razón $-g$ tendríamos: $$ \color{#9b00b6} \begin{cases} D_{2k} ( r \, h \, m \large \frac{1 - (-m^2)^k}{1+m^2}, \normalsize -r \, h \large \frac{1 - (-m^2)^k}{1+m^2})\\ D_{2k+1} ( r \, h \, m \large \frac{1 - (-m^2)^k}{1+m^2}, \normalsize -r \, h \large \frac{1 - (-m^2)^{k+1}}{1+m^2}) \end{cases} \tag{3} $$
Consecuentemente, bajo los supuestos anteriores, la pseudoespiral "hacia fuera" de Durero en el paso $n$-ésimo, con $n \ge 1$ viene dada por: $$\color{#b63f00} \begin{cases} x=D_{n_x} + r·m^n cos (\theta)\\ y=D_{n_y} + r·m^n sen (\theta) \end{cases} \tag{4} $$ siendo $n \, \frac{\pi}{2} \le \theta \le (n+1) \, \frac{\pi}{2}$.
Si bien lo hemos expresado de manera general para cualquier aumento $h$, en el caso particular expresado por Durero tenemos que $h=0,5$ y $m=1+0,5=1,5$.
- Paso 3.
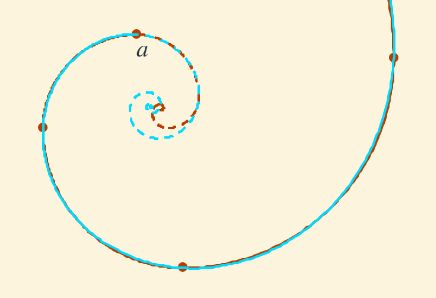
- En la parte inferior, se refleja el comentario final que realiza Durero, marcando un cambio continuo de esta curva de contracción hacia dentro y dilatación hacia fuera. Y en la parte gráfica se muestra la espiral "hacia dentro" y "hacia fuera" concatenadas.
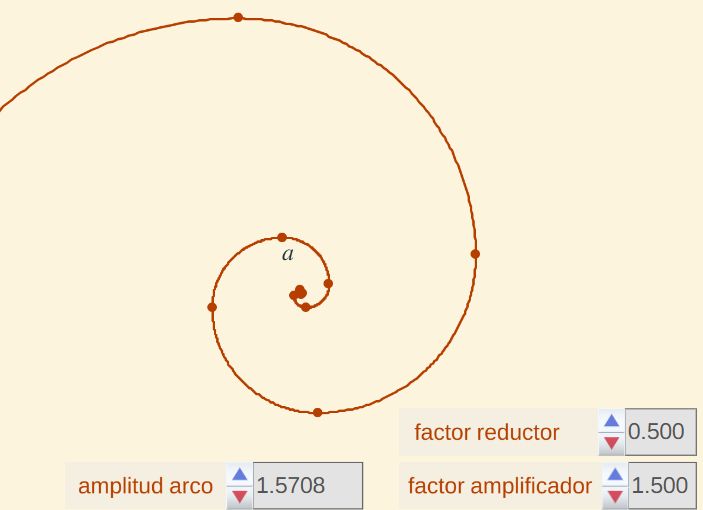
Fig. 5. La pseudoespiral de Durero.- Formulación matemática
En este caso, para expresar la pseudoespiral completa de Durero basta considerar la unión o concatenación de (2) y (4).
- Paso 4.
- En este paso iniciamos nuestro análisis personal de esta pseudoespiral y como se refleja en la imagen se verifica que por todos los extremos de los arcos de la pseudoespiral "hacia dentro" de Durero pasa la espiral logarítmica $\large \color{#1bb600} \rho = r · 0,54874... · 2^{\frac{2}{\pi} \theta}$ con polo en el punto $\color{#1bb600} (0,4·r, -0,2·r)$.
Por tanto, la pseudoespiral "hacia dentro" se aproxima a una espiral logarítmica o viceversa.
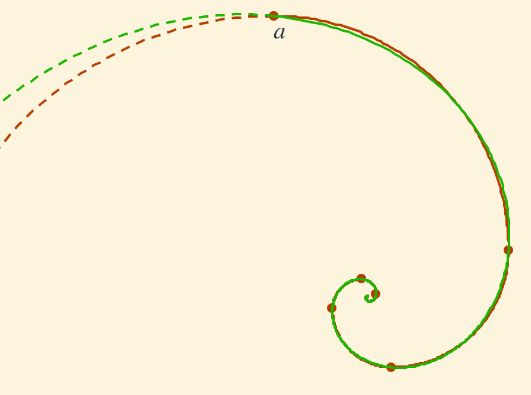
Fig. 6. La pseudoespiral "hacia dentro" de Durero (línea continua), pseudoespiral "hacia fuera" de Durero (línea discontinua) y espiral logarítmica aproximadora de la pseudoespiral "hacia dentro" (línea continua y discontinua).
- Esta espiral logarítmica no aproxima a la pseudoespiral "hacia fuera". En la imagen anterior puede observarse la espiral logarítmica citada en la línea discontinua de color verde y en la discontinua de color marrón a la pseudoespiral "hacia fuera" y cómo divergen ambas.
- Formulación matemática
Si consideramos la espiral logarítmica $$\color{#1bb600} \rho = a \, b^{\theta} \tag{5}$$ siendo $(\rho, \theta)$ sus coordenadas polares, entonces su crecimiento cuadrantal (cada $\large \frac{\pi}{2}$ radianes) sería $\Large \frac{\rho_{\theta+\frac{\pi}{2}}}{\rho_{\theta}} = \normalsize b^{\frac{\pi}{2}}$.
Por otra parte, según realizamos la construcción de la pseudoespiral "hacia dentro", resulta que si el factor reductor en cada paso ($\frac{\pi}{2}$ radianes) es $g$, entonces el factor amplificador (lectura inversa de la construcción) vendría dado por $\frac{1}{g}$ en cada cuadrante, es decir, que su factor de crecimiento cuadrantal es $\large \frac{1}{g}$.
Por tanto, la espiral logarítmica que tiene el mismo crecimiento cuadrantal que la "hacia dentro" de Durero sería aquella en la que $\large b^{\frac{\pi}{2}} = \frac{1}{g}$, es decir, cuando $$\large b=(\frac{1}{g})^{\frac{2}{\pi}}. \tag{6}$$ En la situación indicada por Durero para la pseudoespiral "hacia dentro" tenemos que $g=0,5$ y por tanto sería $$\large b=2^{\frac{2}{\pi}}. \tag{7}$$ Pero (5) no está determinada unívocamente, necesitaremos calcular el coeficiente $\color{#1bb600} a$, que es un factor de escala que es equivalente a realizar un giro, y también cuál sería la ubicación de su polo, sus coordenadas.
Para determinar el polo, podemos considerar la sucesión de centros (1) y ver si converge a un punto y qué punto sería. Dado que $|g| \lt 1$, entonces $$\lim_{k \to{+}\infty}{(-g^2)}^k =0$$ y, por tanto esos puntos convergen al punto $$\color{#1bb600} P(r \, \frac{1-g}{1+g^2}, r \, \frac{g(g-1)}{1+g^2}). \tag{8}$$ Y, para el caso particular de la construcción "hacia dentro" de Durero, dado que $f=0,5$ y $g=0,5$, entonces el polo sería el punto $P (r \, \frac{0,5}{1,25},-r \, \frac{0,25}{1,25})$, es decir $\color{#1bb600} P (0,4 \, r, -0,2 \, r)$.
Finalmente, una vez conocido el polo $P$, para determinar el coeficiente $\color{#1bb600} a$ en (5), podemos hallar el ángulo $\gamma$ que forma la dirección del eje polar $\theta =0$ con la semirrecta determinada por el polo $P$ y $A(0,r)$, es decir, determinar $\gamma = \measuredangle(\overrightarrow{PA}, \overrightarrow{i})$ siendo $\overrightarrow{i}$ el vector director del eje de abscisas en sentido positivo del mismo. $$ \begin{aligned} \gamma &= arccos (\frac{\overrightarrow{PA}·\overrightarrow{i}}{|\overrightarrow{PA}| \, |\overrightarrow{i}|})\\ &= arccos(\frac{-P_x}{\sqrt{P_x^2+(r-P_y)^2}})\\ &=arcos(\frac{-f}{\sqrt{f^2+(1+g^2+ f \, g)^2}} \tag{9}) \end{aligned} $$
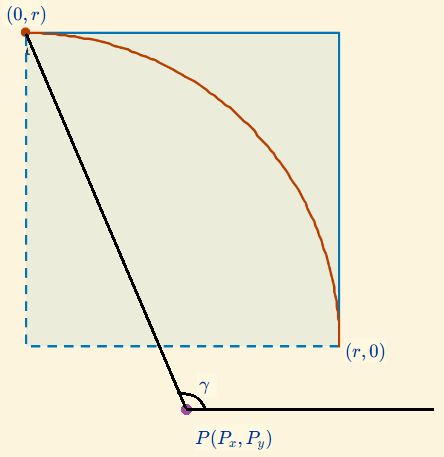
Fig. 7. Determinación del coeficiente $\color{#1bb600} a$ en la espiral logarítmica aproximadora de la pseudoespiral "hacia dentro" de Durero.
Determinado este ángulo, impongamos que la espiral (5) pase por el punto $A(0, r)$ cuando el ángulo polar sea $\gamma$, y para ello escribamos su ecuación cartesiana $$\color{#1bb600} \begin{cases} x= P_x + a \, b^\theta cos(\theta) \\ y= P_y + a \, b^\theta sen(\theta) \end{cases} \tag{10} $$ y, entonces, ha de ser $$\color{#1bb600} \begin{cases} 0= P_x + a \, b^\gamma cos(\gamma) \\ r= P_y + a \, b^\gamma sen(\gamma) \end{cases} \tag{11} $$ de donde obtenemos que $\color{#1bb600} P_x^2+(r-P_y)^2=a^2\, b^{2 \gamma}$, y consecuentemente $$\color{#1bb600} a = \frac{\sqrt{P_x^2+(r-P_y)^2}}{b^\gamma} = r \frac{\sqrt{f^2+(1+g^2+ f \, g)^2}}{(1+g^2) \, b^\gamma}. \tag{12}$$ En el caso particular de la espiral "hacia dentro", $\color{#1bb600} a = r·0,54874...$, obteniéndose la espiral aproximadora indicada al inicio de este paso.
Los puntos extremos de los arcos de la espiral "hacia fuera" no pueden pertenecer a la espiral aproximadora anterior ya que el factor de crecimiento cuadrantal en este caso sería $1,5^{\frac{2}{\pi}}$, como veremos a continuación, diferiendo del factor de crecimiento cuadrantal $2^{\frac{2}{\pi}}$ antes determinado.
No obstante, nos queda por verificar que los puntos extremos $\color{#b63f00} P_n$ de los arcos de la pseudoespiral "hacia dentro" verifican la ecuación de la espiral obtenida, lo que nos obliga a determinar las coordenadas de esos puntos y ver que cumplen dicha ecuación, o bien que el crecimiento cuadrantal, en este caso dado por el cociente de las distancias del polo $\color{#1bb600} P$ a un punto $\color{#b63f00} P_n$, $d( {\color{#1bb600} P}, {\color{#b63f00} P_n})$, y al posterior $\color{#b63f00} P_{n+1}$ es $\frac{1}{g}$, es decir que $$\frac{d( {\color{#1bb600} P}, {\color{#b63f00} P_n})}{d( {\color{#1bb600} P}, {\color{#b63f00} P_{n+1}})}= \frac{1}{g}. \tag{13}$$ Para determinar las coordenadas de $\color{#b63f00} P_n$, fijándonos en la imagen izquierda de la figura 2, obtenemos que para $\color{#b63f00} k \ge 1$
$$\color{#b63f00} \tiny \begin{cases} P_{2k} ( r \, [1 - g - (g^2 - g^3) + (g^4 - g^5) - \dotsb + (-1)^{k-1}(g^{2k-2}- g^{2k-1})], r [ -g + (g^2+g^3)-(g^4+g^5) + \dotsb + (-1)^{k}(g^{2k-2}- g^{2k-1})])\\ P_{2k+1} ( r \, [1-(g+g^2)+(g^3+g^4)- \dotsb + (-1)^{k}(g^{2k-1}+ g^{2k})], r \, [-(g-g^2)+(g^3-g^4)- \dotsb + (-1)^{k}(g^{2k-1}- g^{2k})]) \end{cases} $$ siendo $\color{#b63f00} P_0(0,r)$ y $\color{#b63f00} P_1(r , 0)$.
Y simplificando las sumas que aparecen en dichas coordenadas tenemos que $$\color{#b63f00} \small \begin{cases} P_{2k} ( r \, (1-g) \large \frac{1-(-g^2)^k}{1+g^2}, \normalsize r [1-(1+g) \large \frac{1-(-g^2)^k}{1+g^2} ])\\ P_{2k+1} ( \normalsize r [1-g(1+g) \large \frac{1-(-g^2)^k}{1+g^2} ], \normalsize r \, (g^2-g) \large \frac{1-(-g^2)^k}{1+g^2} ) \tag{14} \end{cases} $$ Subsucesiones y sucesión que convergen al polo $\color{#1bb600} P$ hallado también en (8).
Consecuentemente se obtiene que $$d( \color{#1bb600} P, {\color{#b63f00} P_n})= \frac{\sqrt{2}}{\sqrt{1+g^2}} g^k \tag{15}$$ y, por tanto, que se cumple la relación (13) indicada.
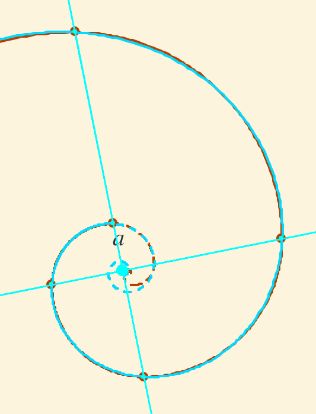
También, otra alternativa para demostrar que estos puntos $\color{#b63f00} P_n$ están en una espiral es ver que el crecimiento cuadrantal es constante —lo realizado antes en (15)— y viendo que la intersección de las rectas que unen cada dos puntos alternos conducen todas a un mismo punto, el cual es el polo de la espiral. Y, efectivamente, se puede comprobar que $\forall k$,: $$\large r_{P_{2k}P_{2k+2}} \cap r_{P_{2k+1}P_{2k+3}} \equiv \normalsize \color{#1bb600} P \tag{16}$$ Esto último puede observarse activando en la barra lateral de herramientas el botóny es lo observado en la siguiente figura, la 8.
Fig. 8. Rectas que pasan por puntos alternos de los extremos de los arcos de la pseudoespiral de Durero e intersección de las mismas.- Paso 5.
- En este quinto paso mostramos cómo la espiral logarítmica $\large \color{#00daff} \rho = r · 0,74549 · 1,5^{\frac{2}{\pi} \theta}$ con polo en $\color{#00daff} (0,230...·r, -0,153...·r)$ pasa por todos los extremos de los arcos de la pseudoespiral de Durero "hacia fuera" .
Por tanto, la pseudoespiral "hacia fuera" se aproxima a una espiral logarítmica o viceversa.
Fig. 9. La pseudoespiral "hacia fuera" de Durero (línea continua), pseudoespiral "hacia dentro" de Durero (línea discontinua) y espiral logarítmica aproximadora de la pseudoespiral "hacia fuera" (línea continua y discontinua).
- Esta espiral logarítmica no aproxima a la pseudoespiral "hacia dentro". En la imagen anterior puede observarse la espiral logarítmica citada en la línea discontinua de color turquesa y en la discontinua de color marrón a la pseudoespiral "hacia dentro" y cómo ambas son muy diferentes.
- Formulación matemática
De manera análoga al paso anterior determinaremos una espiral logarítmica $$\color{#00daff} \rho = c \, d^{\theta} \tag{17}$$ que aproxime a la pseudoespiral "hacia fuera". En este caso, el factor de crecimiento cuadrantal de esta pseudoespiral es $m=1+h$, luego la base de la espiral buscada ha de ser $$\large d=m^{\frac{2}{\pi}}. \tag{18}$$
En la situación indicada por Durero para la pseudoespiral "hacia fuera" tenemos que $m=1,5$ y por tanto sería $$\large d=1,5^{\frac{2}{\pi}} \tag{19}$$ Pero para que (16) quede determinada de manera unívoca, necesitaremos calcular el coeficiente $\color{#00daff} c$ y también las coordenadas de su polo.
Para determinar el polo, podremos considerar la sucesión de centros (3), pero teniendo encuenta que serían los centros de esta espiral que reprodujeran el crecimiento hacia dentro, es decir, $\color{#9b00b6} D_{-1}, D_{-2} D_{-3},..., D_{-n}$ y ver si convergen a un punto y qué punto sería éste. Las coordenadas de esos puntos son: $$ \color{#9b00b6} \begin{cases} D_{-2k} ( r \, h \, m \large \frac{1 - (-m^2)^{-k}}{1+m^2}, \normalsize -r \, h \large \frac{1 - (-m^2)^{-k}}{1+m^2})\\ D_{-2k+1} ( r \, h \, m \large \frac{1 - (-m^2)^{-k}}{1+m^2}, \normalsize -r \, h \large \frac{1 - (-m^2)^{-k+1}}{1+m^2}) \end{cases} \tag{20} $$ es decir, $$ \color{#9b00b6} \begin{cases} D_{-2k} ( r \, h \, m \large \frac{1 - (-\frac{1}{m^2})^{k}}{1+m^2}, \normalsize -r \, h \large \frac{1 - (-\frac{1}{m^2})^{k}}{1+m^2})\\ D_{-2k+1} ( r \, h \, m \large \frac{1 - (-\frac{1}{m^2})^{k}}{1+m^2}, \normalsize -r \, h \large \frac{1 - (-\frac{1}{m^2})^{k+1}}{1+m^2}) \end{cases} \tag{21} $$ Dado que $|\frac{1}{m}| \lt 1$, entonces $$\lim_{k \to{+}\infty}{(-\frac{1}{m^2})}^k =0$$ y, por tanto esos puntos convergen al punto $$\color{#00daff} Q(r \, h \, m \, \frac{1}{1+m^2}, -r \, h \, \frac{1}{1+m^2}). \tag{22}$$ Y, para el caso particular de la construcción "hacia fuera" de Durero, dado que $h=0,5$ y $m=1,5$, entonces el polo sería el punto $Q (r \, \frac{0,5·1,5}{1+1,5^2},-r \, \frac{0,5}{1+1,5^2})$, es decir $\color{#00daff} Q (0,230...·r, -0,153...·r)$.
Conocido el polo $\color{#00daff} Q$, de manera análoga al paso anterior, para calcular el coeficiente $\color{#00daff} c$ en (17) determinamos el ángulo $\delta$ que forma la dirección del eje polar $\theta =0$ con la semirrecta determinada por el polo $Q$ y $A(0,r)$, es decir, $\delta = \measuredangle(\overrightarrow{QA}, \overrightarrow{i})$ siendo $\overrightarrow{i}$ el vector director del eje de abscisas en sentido positivo del mismo. $$ \begin{aligned} \delta &= arccos ({\frac{\overrightarrow{QA}·\overrightarrow{i}}{|\overrightarrow{QA}| \, |\overrightarrow{i}|}}) \\ &= arccos ({\frac{-Q_x}{\sqrt{Q_x^2+(r-Q_y)^2}}}) \\ &=arcos ({\frac{-h \, m}{\sqrt{h^2 \, m^2+(1+m^2+ h)^2}} }) \tag{23} \end{aligned} $$
Determinado este ángulo, imponiendo que la espiral (17) pase por el punto $A(0, r)$ cuando el ángulo polar sea $\delta$, y para ello escribamos su ecuación cartesiana $$\color{#00daff} \begin{cases} x= Q_x + c \, d^\theta cos(\theta) \\ y= Q_y + c \, d^\theta sen(\theta) \end{cases} \tag{24} $$ y, entonces, ha de ser $$\color{#00daff} \begin{cases} 0= Q_x + c \, d^\delta cos(\gamma) \\ r= Q_y + c \, d^\delta sen(\gamma) \end{cases} \tag{25} $$ de donde obtenemos que $\color{#00daff} Q_x^2+(r-Q_y)^2=c^2\, d^{2 \delta}$, y consecuentemente $$\color{#00daff} c = \frac{\sqrt{Q_x^2+(r-Q_y)^2}}{d^\delta} = r \frac{\sqrt{h^2 \, m^2+(1+m^2+ h)^2}}{(1+m^2) \, d^\delta}. \tag{26}$$ En el caso particular de la espiral "hacia fuera", $\color{#00daff} c = r·0,74549...$, obteniéndose la espiral aproximadora indicada al inicio de este paso.
Análogamente al paso cuarto, Los puntos extremos de los arcos de la espiral "hacia dentro" no pueden pertenecer a la espiral aproximadora anterior ya que el factor de crecimiento cuadrantal en este caso era $2^{\frac{2}{\pi}}$, y difiere del factor de crecimiento cuadrantal $1,5^{\frac{2}{\pi}}$ determinado en este caso.
No obstante, también de manera análoga al paso 4, nos quedaría por verificar que los puntos extremos $\color{#b63f00} Q_n$ de los arcos de la pseudoespiral "hacia fuera" verifican la ecuación de la espiral obtenida, lo que nos obliga a determinar las coordenadas de esos puntos y ver que cumplen dicha ecuación, o bien que el crecimiento cuadrantal, en este caso dado por el cociente de las distancias del polo $\color{#00daff} Q$ a un punto $\color{#b63f00} Q_n$, $d( {\color{#00daff} Q}, {\color{#b63f00} Q_n})$, y al anterior $\color{#b63f00} Q_{n-1}$ es $m$, es decir que $$\frac{d( {\color{#00daff} Q}, {\color{#b63f00} Q_n})}{d( {\color{#00daff} Q}, {\color{#b63f00} Q_{n-1}})}= m. \tag{27}$$ Para determinar las coordenadas de $\color{#b63f00} Q_n$, podríamos apoyarnos en la imagen izquierda de la figura 2 y realizar el mismo planteamiento realizado en el paso 4, o considerar los puntos $\color{#b63f00} P_n$ de (14) con $g = \frac{1}{m}$ y $k \in \mathbb{Z}^-$. Así pues, sería redundante reproducir esa demostración.
Análogamente la intersección de las rectas que unen cada dos puntos alternos conducen todas a un mismo punto, el cual es el polo de la espiral. Es decir, se verifica que $\forall k$,: $$\large r_{Q_{2k}Q_{2k+2}} \cap r_{Q_{2k+1}Q_{2k+3}} = \normalsize \color{#00daff} Q \tag{28}$$ Que puede observarse activando en la barra lateral de herramientas el botóny hemos reflejado en la siguiente figura
Fig. 10. Rectas que pasan por puntos alternos de los extremos de los arcos y espiral logarítmica aproximadora de la pseudoespiral "hacia fuera" (línea continua y discontinua).- Paso 6.
- Si en la pseudoespiral de Durero $f$ es el factor reductor y $m$ el factor amplificador entonces para que las espirales logarítmicas que aproximan respectivamente a las pseudoespirales de Durero "hacia dentro" y "hacia fuera" coincidan ha de verificarse que $$m (1-f) =1 \tag{29}$$.
- Puesto que, según la descripción de Durero, $f = 0,5$ y $m =1,5$ tenemos que $m (1-f) =1,5 ·0,5 = 0,75 \neq 1$ y, entonces, ambas espirales logarítmicas aproximadoras no coinciden.

Fig. 11. espiral logarítmica aproximadora de la pseudoespiral "hacia dentro" y espiral logarítmica aproximadora de la pseudoespiral "hacia fuera" .- Si $f=0,5$ para que ambas espirales aproximadoras coincidan ha de ser $m=\frac{1}{0,5}=2$. Y si $m=1,5$, entonces coincidirán si $1-f = \large \frac{1}{1,5}=\frac{2}{3}$, es decir, cuando $f= \large \frac{1}{3}$. En la escena, puede variar el valor de estos factores y comprobar lo indicado en este apartado.
- Formulación matemática
En las condiciones indicadas, para que las espirales (5) y (17) coincidan han de ser que $b = d$ y por (6) y (18) tiene que ser $\frac{1}{g} = m$ que conduce a la condición (29) antes citada. Cuando se da esa igualdad, entonces los coeficientes $a$ y $c$ son iguales puesto que ambas espirales pasan por el mismo punto $A (0,r)$ y ambas tienen el mismo polo ya que cuando se cumple (29), entonces los centros $C_k$ y $D_k$ tienen las mismas coordenadas (ver (1) y (3) y sustituir $g=\frac{1}{m}$ y $f=1-\frac{1}{m}$) y, por tanto, convergen al mismo punto, el polo común de ambas.
- Paso 7.
- Si $f$ es el factor reductor y consideramos que $g = 1-f$, entonces para que los cuadrados que intervienen en la construcción "hacia dentro" de Durero no se solapen ha de verificarse que se cumpla la desigualdad $g^2 + g -1 \lt 0$, es decir, que $g \lt \large \frac{-1+\sqrt{5}}{2} = \small \Phi^{-1} =0,618...$, equivalemte a que $f \gt 1 - \Phi^{-1} =0,3819...$, siendo $\Phi = 1,6180...$ el número áureo.
- En la siguiente imagen $f =0,310 \lt 1 - \Phi^{-1}$ y, consecuentemente, dichos cuadrados se solapan. Puede cambiar el valor de $f$ y comprobar lo que aquí se indica.
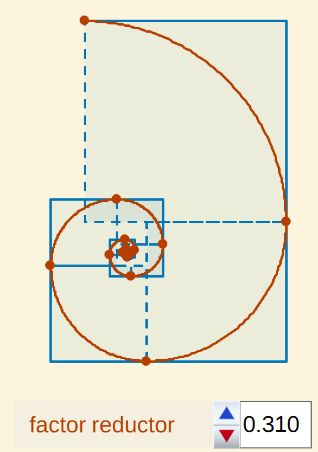
Fig. 12. Sucesión de cuadrados en la construcción de la pseudoespiral de Durero "hacia dentro".- Formulación matemática
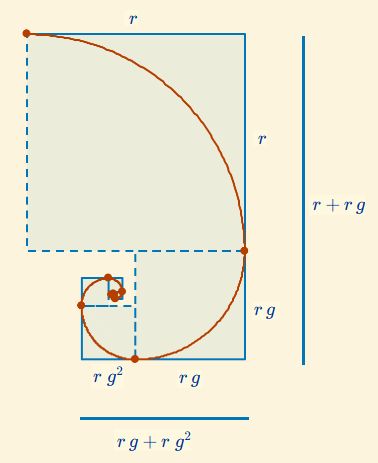
Fig. 13. Proporciones en la construcción de la pseudoespiral de Durero "hacia dentro".
Si observamos las proporciones que acontecen en la Fig. 13, podemos concluir que para que la sucesión de cuadrados de la construcción "hacia dentro" no se solapen ha de cumplirse que $$r \gt r \, g + r \, g^2$$, es decir, $$g^2+g-1 \lt 0 \tag{30}$$ y, por tanto, ha de ser $$g \lt \Phi^{-1}, f \gt 1-\Phi^{-1}. \tag{31}$$
- Paso 8.
- Si $m$ es el factor amplificador, entonces para que los cuadrados que intervienen en la construcción "hacia fuera" de Durero no se solapen ha de verificarse que se cumpla la desigualdad $m^2 + m -1 \gt 0$, es decir, que $m \gt \large \frac{1+\sqrt{5}}{2} = \small \Phi =1,618...$, siendo $\Phi = 1,6180...$ el número áureo.
- En la siguiente imagen $m =1,720 \gt \Phi$ y, consecuentemente, dichos cuadrados no se solapan. Puede cambiar el valor de $m$ y comprobar lo que aquí se indica.
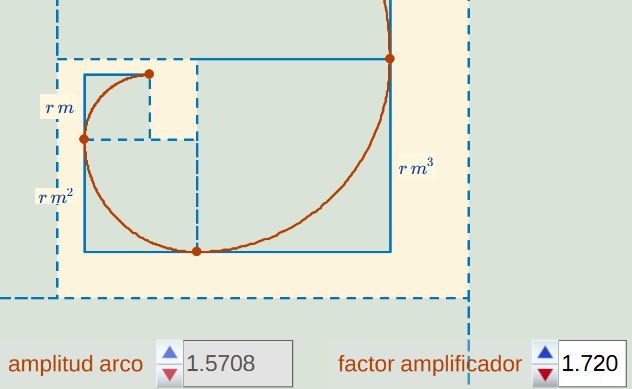
Fig. 14. Sucesión de cuadrados en la construcción de la pseudoespiral de Durero "hacia fuera" y proporciones que acontecen.- Formulación matemática
En este caso para que la sucesión de cuadrados de la construcción "hacia fuera" no se solapen ha de verificarse que que $$r \, m + r \, m^2 \lt r \, m^3,$$ es decir, $$m^2-m+1 \gt 0 \tag{32}$$ y, por tanto, ha de ser $$m \gt \Phi. \tag{33}$$
- Paso 9.
- Si el factor amplificador $m = \Phi$ y el factor reductor es $f = 1 - \Phi^{-1}$, entonces los cuadrados que intervienen en la construcción de Durero (tanto "hacia dentro", como "hacia fuera") recubren el plano sin solapamiento (se intersecan en las aristas que tienen área nula) y ambas pseudoespirales se aproximan por la espiral logarítmica áurea $\rho = r · 0,692... · \Phi^{\frac{2}{\pi} \theta}$ con polo en $(0,276... \, r, -0,170... \, r)$.
En la escena interactiva puede cambiar el valor de ambos factores y comprobar lo que aquí se indica.
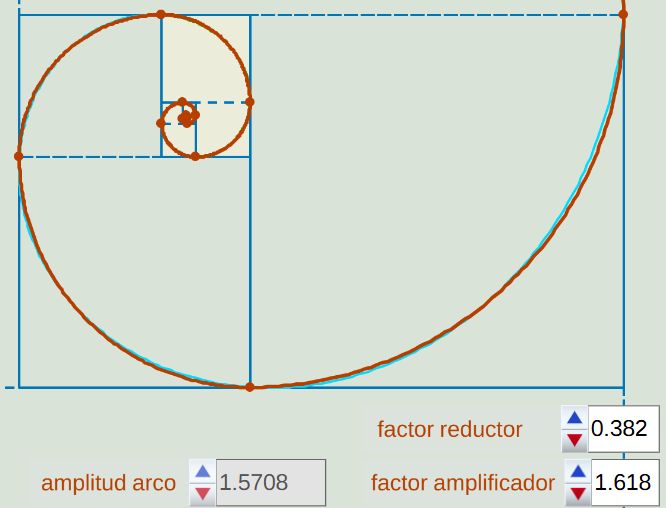
Fig. 15. Sucesión de cuadrados en la construcción de la pseudoespiral de Durero "hacias dentro" y "hacia fuera" para $f = 1 - \Phi^{-1}$ y $m = \Phi$.
- En esta construcción se obtiene una sucesión de rectangulos semejantes que son áureos, es decir, su proporción es el número áureo $\Phi$.
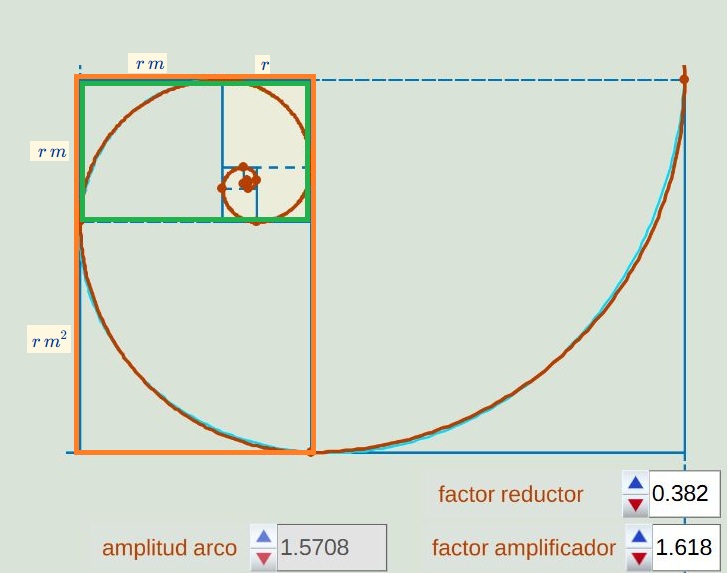
Fig. 16. Sucesión de rectángulos áureos semejantes.- Si observa bien (amplie la imagen en la escena interactiva), podrá comprobar que la espiral logarítmica áurea aproxima a la pseudoespiral de Durero, pero no coincide con ella.
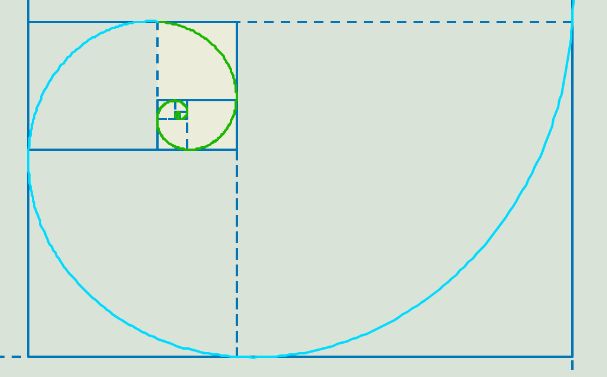
Fig. 17. La espiral logarítmica áurea interseca a la construcción de Durero en los puntos extremos de los arcos, pero no coinciden.- Formulación matemática
Este resultado es consecuencia de lo obtenido en el paso séptimo y octavo, basta ver (31) y (33). Para este caso particular se cumple que $m (1-f)=1$ que es la condición (29) y consecuentemente la espiral aproximadora "hacia dentro" y "hacia fuera" coinciden, la base de esta espiral logarítmica, por (6), es $b=\Phi^{\frac{2}{\pi}}$, las coordenadas del polo se obtienen de (8) y el coeficiente de (12).
Adicionalmente, en la Fig. 17 podemos observar la sucesión de rectángulos que se obtiene en esta construcción en la que $m=\Phi$.La proporción del rectángulo de color verde es $\large \frac{r+r \, m}{r \, m}=\frac{1}{m}+\small m = \large \frac{1}{\Phi}+\small \Phi= \Phi$ (la última igualdad es una propiedad del número áureo), por tanto es un rectángulo áureo.
La proporción del rectángulo de color naranja es $\large \frac{r \, m+r \, m^2}{r +r \, m}= \small m= \Phi$, es decir, es también áureo. Pero de partida, este rectángulo naranja se sabe que es áureo porque al rectángulo áureo verde se le ha concatenado un cuadrado y dado que el gnomon de cualquier rectángulo áureo es el cuadrado construido sobre uno de sus lados, obtenemos un nuevo rectángulo áureo. Así pues, al ir concatenando cuadrados vamos obteniendo una sucesión de rectángulos áureos.
Por otro lado, la pseudoespiral de Durero es una concatenación de arcos de circunferencia, luego mantiene su curvatura dentro de cada arco, sin embargo la curvatura de una espiral logarítmica cambia en cada punto, por tanto no puede coincicidir la pseudoespiral con la espiral.
- Paso 10.
- Si partimos de un rectángulo áureo, al concatenarle un cuadrado se obtiene otro rectángulo áureo (el gnomon de un rectángulo áureo es un cuadrado). Si sobre ese gnomon cuadrado se dibuja un cuarto de circunferencia y reiteramos la construcción, entonces se obtiene la pseudoespiral denominada "espiral de Durero".
Puede cambiar el valor del parámetro "arco n.º" para ir construyendo dicha espiral.
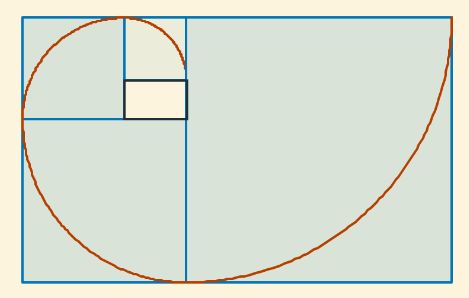
Fig. 18. Construcción de la pseudoespiral de Durero a partir de un rectángulo áureo.
- Actualmente la espiral de Durero se presenta de esta forma, la cual, como hemos comprobado, difiere de la descripción original de este reconocido artista y aquí hemos establecido un hilo conductor que justifica el porqué de esta elección tan, tan particular.
- Puesto que la construcción parte de dibujar un rectángulo áureo, si en la parte descriptiva inferior posiciona el ratón en "rectángulo áureo" podrá ver las indicaciones para construir un rectángulo áureo con regla y compás.
- Formulación matemática
La construcción señalada en este paso coincide con la construcción de la pseudoespiral de Durero en el caso en el que las sucesiones de cuadrados "hacia dentro" y "hacia fuera", ambas, no se solapen y este caso es cuando $m=\Phi$, que hemos analizado en el paso noveno.
BIBLIOGRAFÍA
Dürer, Albrecht, and Christian Wechel (1532) Albertus Durerus Nurembergensis pictor huius [a]etatis celeberrimus, versus è Germanica lingua in Latinam, ... adeò exacte quatuor his suarum Institutionum geometricarum libris, lineas, superficies & solida corpora tractauit .... Lutetiae : apud Christianum Wechelum. Consulta en línea (fuente: Biblioteca digital hispánica, Biblioteca nacional de España.
Durero, A. (2000) De la medida.Bogotá: Universidad Jorge Tadeo Lozano. Edición de Jeanne Peiffer y traducción de Jesús Espino. Consulta en línea.
Cardona Suárez, C.A. (2006) La Geometría de Alberto Durero. Madrid, Ediciones Akal, S. A. Consulta en línea.