| ¿Dónde acaba el juego y dónde
empieza la matemática seria? (...) Para muchos que la ven desde
fuera, la matemática, mortalmente aburrida, no tiene nada que
ver con el juego. En cambio para la mayoría de los matemáticos,
la matemática nunca deja de ser totalmente un juego, aunque,
además, pueda ser muchas otras cosas. MIGUEL DE GUZMÁN (matemático español 1936-2004) creía que los juegos podían ser una herramienta muy efectiva para enseñar y aprender matemáticas, y que los juegos matemáticos podían ayudar a desarrollar habilidades importantes, como el razonamiento lógico y la resolución de problemas. |
Los pentominós o pentaminós son figuras
geométricas compuestas por cinco cuadrados del mismo tamaño unidos por
sus lados. Son por tanto unas curiosas formas de polígonos que recubren,
por ejemplo, cinco cuadros o escaques interconectados de un tablero de
ajedrez. Así al menos fueron presentados por Solomon Wolf Golomb en
1954 al mundo matemático, como subformas de un concepto más
general llamado poliominó. Debido a sus propiedades y características,
tienen diversas aplicaciones en matemáticas, geometría, diseño, y
juegos, entre otras áreas.
Son doce las posibles formas que adoptan los pentominós:
Estas formas se pueden recordar por su
parecido con otras tantas letras T U V W X Y Z (las
7 últimas del abecedario) y las mayúsculas que componen la palabra F
I L i P i N o
En
algunos casos el parecido es muy grande, T, U, Z,
L, I, P, en otros la forma del pentominó
tiene cierta semejanza con la letra, Y, F, N
y en otros tenemos que hacer un pequeño movimiento a la figura para
lograrlo, V, W, X
Los pentominós obtenidos a partir de
otros por reflexión o volteado (simetría axial) o por rotación no
cuentan como un pentominó diferente.
Obsérvese
que los pentominós van a poder recubrir 5 cuadros interconectados de un
tablero bien rotando o bien volteando horizontalmente la forma original
del pentominó. Las formas que necesitan voltearse para generar la
correspondiente forma simétrica axial son Y, F, L, P y N. En cualquier
caso basta con hacer una rotación de 90º, 180º, 270º a la forma
original o a la volteada.
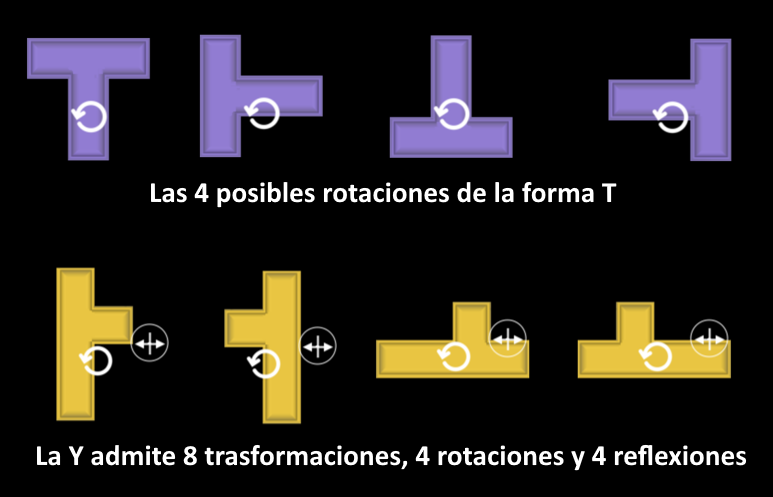
| Las formas que se pueden encajar en 5 cuadros interconectados de un tablero usando la forma original o realizando una rotación con ella son T, U, V, W, X, I; la I admite sólo una rotación de 90º y la X no precisa rotación. |  |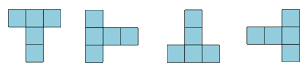
| Las formas Y, Z, F, L P y N se pueden
trasformar por rotación de la original o de la volteada
horizontalmente. Por ejemplo, la L, N, Y, P y F admite 8 orientaciones, 4 por rotación y 4 por simetría axial. |
 |
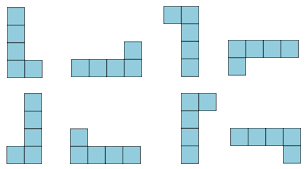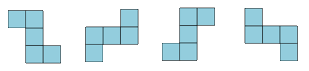
| La
Z puede orientarse de 4 formas, 2 por rotación y 2 por simetría
axial. |
 |
Los
pentominós han sido utilizados para resolver una gran variedad de
problemas en diferentes áreas, desde la matemática y la geometría hasta
la programación y la robótica. A continuación, se presentan algunos
ejemplos de los diferentes problemas que se han propuesto para resolver
con pentominós:
En
general, los pentominós son una herramienta versátil que se ha utilizado
en una amplia variedad de problemas matemáticos y de ingeniería. Su
naturaleza geométrica y su simplicidad hacen que sean un objeto de
estudio interesante para el desarrollo cognitivo y el aprendizaje en
general.
Se ha demostrado que trabajar con pentominós puede mejorar la habilidad espacial, la creatividad, el pensamiento lógico y la resolución de problemas en personas de todas las edades. Al manipular y combinar estas piezas, se estimula la percepción espacial y se promueve el desarrollo de habilidades de razonamiento y visualización.
Además,
los pentominós pueden ser una herramienta útil en la educación
matemática, ya que permiten a los estudiantes explorar conceptos como la
simetría, los patrones, las relaciones entre formas y las propiedades
geométricas. También pueden ser utilizados para enseñar habilidades de
pensamiento crítico y estrategias de resolución de problemas, lo que
puede ser beneficioso en una amplia gama de disciplinas académicas y
profesionales.
En resumen, el uso de los pentominós
puede tener un impacto positivo en el desempeño intelectual al mejorar
habilidades espaciales, creatividad, pensamiento lógico y resolución de
problemas. Además, los pentominós pueden ser una herramienta educativa
útil para enseñar habilidades matemáticas y estrategias de pensamiento
crítico.
A lo largo
de los años, muchos autores han publicado investigaciones y trabajos
sobre pentominós y su uso en el desarrollo cognitivo. A continuación, se
presentan algunos de los autores más destacados en este campo:
Solomon Golomb: Golomb es considerado uno
de los padres fundadores del campo de los pentominós. En su libro de
1965 "Polyominoes: A Guide to Puzzles and Problems in Tiling", Golomb
exploró la teoría y la matemática detrás de estas piezas geométricas.
Martin Gardner: Gardner, un popular
escritor de rompecabezas y divulgador científico, también ha escrito
sobre pentominós en sus libros y artículos. En particular, su artículo
"The Remarkable Puzzling Career of Martin Gardner" describe el papel que
los pentominós jugaron en su trabajo.
Richard K. Guy: Guy es un matemático
británico conocido por su trabajo en teoría de juegos y teoría de
números. En su libro "Unsolved Problems in Number Theory", Guy presentó
algunos problemas relacionados con pentominós y sus variantes.
Stewart T. Coffin: Coffin es un diseñador
de rompecabezas y juegos conocido por su trabajo con pentominós. En
particular, ha diseñado varios rompecabezas que utilizan estas piezas,
incluyendo el "Pentominoes Puzzle".
Piet Hein: Hein
fue un poeta, inventor y diseñador danés que también realizó
contribuciones importantes en matemáticas. En general, las
contribuciones de Piet Hein a las matemáticas se centran en la
intersección entre las matemáticas, el diseño y la creatividad, y han
tenido un impacto significativo en la teoría matemática y la cultura
popular.
Publicó un
libro llamado "Pentominoes and Puzzles" en el que presentó una gran
cantidad de problemas y juegos relacionados con los pentominós. En el
libro, Hein exploró diferentes configuraciones y patrones de pentominós
y desarrolló una gran cantidad de juegos y acertijos que involucraban
estas piezas.
Una de las contribuciones más notables de Hein en este campo fue la
creación de un pentominó con una simetría única, que se conoce como el
pentominó Plus. Este pentominó se puede utilizar para crear patrones y
diseños interesantes y desafiantes.
En resumen, las contribuciones de Piet Hein al estudio de los problemas
con pentominós son significativas y han tenido un impacto en el campo de
la teoría de juegos y los acertijos matemáticos.
Estos
autores, que solo representan una pequeña muestra, han contribuido
significativamente al campo de los pentominós mediante la exploración de
sus propiedades matemáticas, su uso en rompecabezas y juegos, y su
aplicación en el desarrollo cognitivo. En conjunto, sus trabajos han
ayudado a establecer los pentominós como una herramienta útil para el
aprendizaje y la exploración matemática, así como para el desarrollo de
habilidades cognitivas clave.
Los pentominós pueden
representarse dibujándolos en una escena de DescartesJS. Después se podrán
desplazar, rotar o voltear para acoplarlos en cinco cuadrados
interconectados de un tablero. Todo esto es lo que se necesita
para abordar cualquier reto que se proponga como problema a
resolver con estas singulares piezas planas.
|
 |
 |
| Por
ello se puede trabajar con los pentominós simulando cualquier
juego de los existentes en el mercado comercial con piezas físicas
hechas básicamente en madera. |
 |
 |
Estas son las opciones del menú de la
escena, con las que podremos gestionar los retos que se proponen es este
trabajo.
Inicio: Permite reiniciar la escena volviendo a las condiciones iniciales.
Problemas:
Proporciona un listado de todos los problemas que proponen en este
trabajo. A cada problema se puede acceder seleccionándolo en dicho
listado.
Los diferentes problemas se organizan en las siguientes categorías:
|
|
||||||||||||||||||||||||||||||||||||||||||
Observar que no
se muestran los casos equivalentes asociados a las formas
simétricas respecto de los dos ejes horizontal y vertical que se
cortan en el centro del tablero. Por ejemplo la figura 2 de la
primera fila (1 solución) sería similar si los 4 cuadrados negros
se disponen a lo largo de la diagonal secundaria; la forma 6 de la
primera fila (5027 soluciones) sería equivalente a otros 3 casos
que se corresponden con el bloque en las restantes tres esquinas
del tablero, etc.
▲
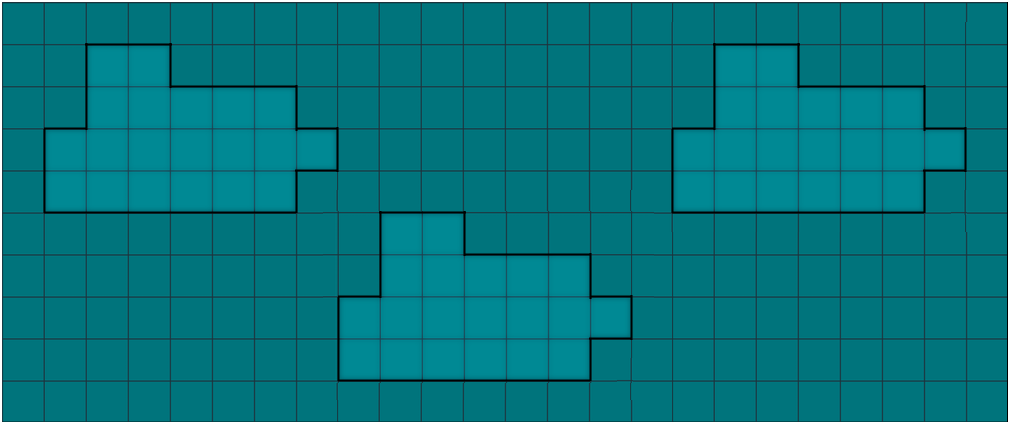
 Este problema
es equivalente al de distribuir 12 pentominós en dos rectángulos
de 6x5 pues resuelto el anterior de 5x6 bastaría realizar un giro
de 90º a los tableros para obtener los correspondientes a
6x5.
 Estas dos
últimas distribuciones están relacionadas con el problema
consistente en evitar líneas de fractura en una construcción de
albañilería. Una vez distribuidos los 12 pentominós en dos
rectángulos de dimensión 5x6 o en dos rectángulos de 5x5 y de 5x7
se ha conseguido construir un rectángulo 5x12 con una línea de
fractura vertical precisamente en el lado de unión de los dos
rectángulos. Una línea de fractura en una construcción de
albañilería supone una debilidad estructural en la obra por donde
puede producirse una falla. Este problema es más frecuente cuando
se utilizan ladrillos que pueden se asimilados a dominós
(poliominós de dos cuadrados).
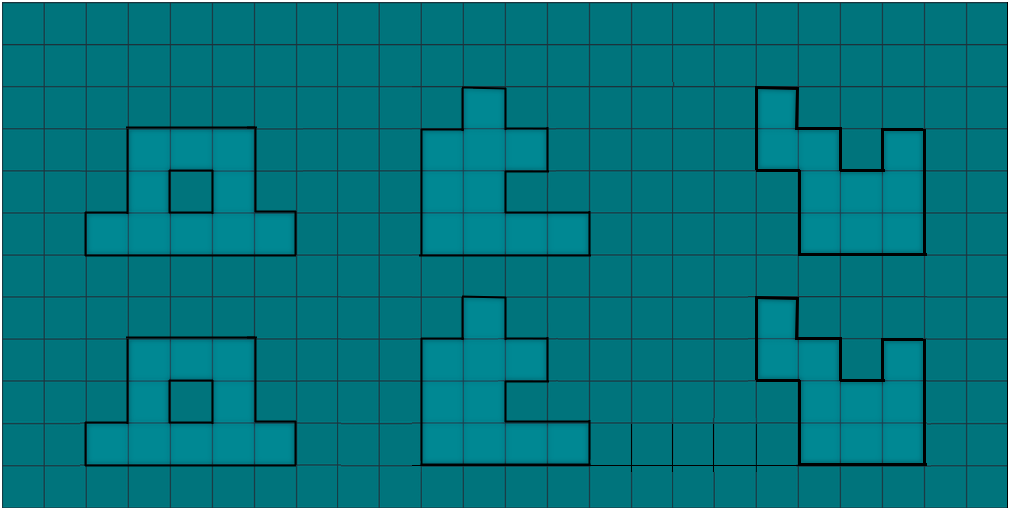
Este problema
que hemos llamado "Animalia" consiste en llenar con los 12
pentominós las formas cuyo contorno nos recuerda a diferentes
animales, 8 en total: camello, canguro, cocodrilo, mariposa,
pingüino, reno, gallo y gato.
Este tablero
está pensado para que el usuario pueda dibujar sus propias
plantillas donde encajar algunas o todas las piezas del
pentominó.
Para habilitar
la opción de dibujar tenemos el control representado por un
rotulador
 , y para dejar de dibujar  .
Dejar de dibujar puede resultar práctico si queremos mover los
pentominós y evitar que por descuido se pueda dibujar puntos no
deseados.Para dibujar,
basta ir haciendo clic izquierdo sobre los nudos de la cuadrícula
e iremos viendo aparecer los sucesivos segmentos que configuran el
contorno de la plantilla. Hay que volver al primer punto para
cerrar la poligonal trazada y dar por terminado el dibujo.
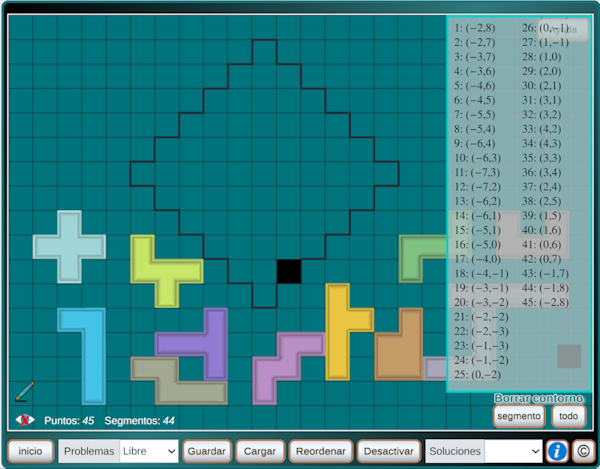 Admite 50
puntos y 49 segmentos como máximo. La poligonal en este caso queda
abierta y no se puede seguir dibujando si el punto 50 no coincide
con el primer punto
También, es
posible poner hasta 12 bloques negros
en el interior de la plantilla para descartar algunas posiciones a
los pentominós; basta arrastrarlos con el puntero.Se dispone de
dos controles uno para borrar el último segmento dibujado y otro
para borrar todos los segmentos de una vez. También se puede ver
 /ocultar
el listado de las coordenadas de los puntos dibujados.Plantillas
En el siguiente
enlace puede obtener una serie de plantillas para dibujar, con las que se
puede practicar el encaje de los pentominós. Otras plantillas
pueden ser creadas por el lector interesado y guardadas en el
fichero .txt de parámetros para posterior uso.
▲ |
Guardar: Esta opción del menú permite guardar los
parámetros actuales de un determinado problema. Se trata de memorizar el
estado de cualquier momento en la resolución de un problema. Guarda, en
una carpeta local, los datos en un archivo de
texto
cuyo nombre es de libre elección a los efectos de poder
memorizarlo para su posterior recuperación y poder consular y
actualizar. Hemos pensado que el nombre de la carpeta local sea
"memoria" pero este nombre es opcional.
Cargar:
Permite recuperar para la escena los parámetros guardados en un archivo
de texto.
Reordenar:
Al seleccionar cualquier problema del menú se disponen de forma
aleatoria las 12 piezas del pentominó en la mitad inferior de la escena.
La opción de reordenar permite volver a obtener otra disposición
aleatoria de las 12 formas.
Desactivar:
En algún momento la última pieza que ha sido seleccionada ha
quedado activada mostrando las imágenes de los controles que nos
permite rotarla  o voltearla  , con
esta opción la pieza queda desactivada y no presenta estos
símbolos. |
 |
 |
Proporciona
un listado con las mismas opciones que en el de Problemas,
excepto la solución al problema Libre (que se puede consular en
el apartado Plantillas)
Permite consultar una posible solución relacionada con un
determinado problema. Para poder ver dicha solución hay que tener
seleccionada la opción del problema correspondiente. En este
supuesto se muestra la imagen durante unos 10 segundos de una
posible solución correspondiente al problema en que se está
trabajando. Un temporizador indica la cuenta atrás: 3, 2, 1.
|
En la figura adjunta se puede ver como se muestra una solución, de las 16 soluciones posibles, al problema de distribución de los 12 pentominós en dos rectángulos de 5x6. |
 |
▲ |
Este apartado está dirigido a los
docentes que necesiten utilizar materiales de enseñanza en sus clases de
matemáticas.
Los pentominós son un material
que está aconsejado para construir y consolidar el conocimiento
matemático para
1. Introducir el principio de conservación de la cantidad y no de la forma.
 |
En
éste ejemplo se ha tomado como unidad de superficie un cuadrado de
la cuadrícula y se ha dibujado tres figuras con igual área
pero distinta forma. Cada figura se puede construir con dos
pentominós diferentes, Z-N, X-L y W-V. Dibujar diferentes figuras con el mismo área tomando el mismo número de pentominós. |
 |
Dada una unidad de superficie,
por ejemplo el cuadrado de la cuadrícula, y dibujada una forma,
por ejemplo la letra L de un pentominó de área 5
unidades es posible dibujar otra de la misma forma L de
tamaño doble, para ello basta duplicar las dimensiones. Como la
L tiene dimensión 4x2 dibujaremos una letra L
de dimensión (2x4)x(2x2) = 8x4 esta nueva forma tiene un área de
4x5=20 unidades ¡El área de cuadriplica?
¿Cuál el área de otra forma L
de tamaño triple de la forma L del pentominó de 5
unidades?
¿Cuál es la nueva dimensión de
la L?
|
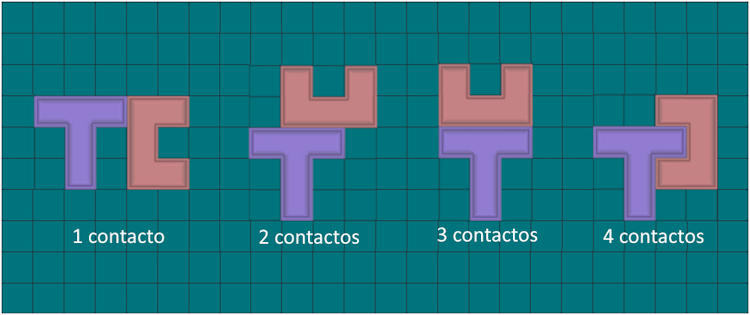
| Una estrategia
para determinar los posibles perímetros es analizar en cuantos
segmentos de longitud 1 pueden hacen contacto la T y la U.
Es inmediato obtener que los posibles contactos son 1, 2, 3 o 4.
Obtener una composición T-U para cada uno de estos
contactos. Después será fácil calcular el perímetro para cada
caso. Probar la misma estrategia para componer diferentes formas con otro par de pentominós y determinar el perímetro máximo y mínimo. |
 |
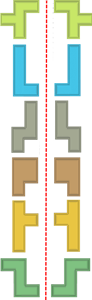
2. Introducir el concepto de simetría en el plano
 |
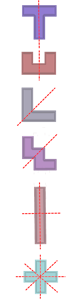Sobre el tablero cuadriculado, donde estamos trabajando con los pentominós, se pueden girar 90º cada vez que se pulsa el control de giro, hasta completar una vuelta completa, manteniendo la misma forma y acomodándose a la cuadrícula. Con DescartesJS el centro de giro es el centro del rectángulo donde encaja la forma, en cada giro el centro de los sucesivos rectángulos cambia debido a un efecto "imán" programado que obliga a encajar el rectángulo en la cuadrícula.  |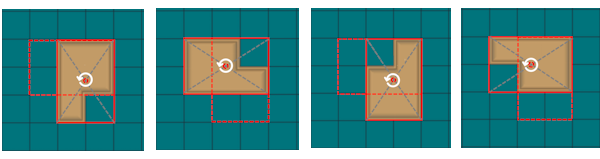
 |
3. Región mínima donde pueden alojarse cualquiera de los doce pentominós
Un problema interesante es este que consiste en determinar la región mínima de un tablero cuadriculado, p.e el de ajedrez, en el que tomándolos de uno en uno podrían alojarse los doce pentominós.
Se puede verificar empíricamente que la región mínima tiene nueve cuadrados. Sólo existen dos formas posibles de esta región mínima.
 |
 |
Utilícese el tablero libre, en el menú Problemas, para dibujar en dos instancias diferentes la región mínima que se muestra en la imagen anterior probando alojar los doce pentominós.
Obsérvese que no es posible encontrar una región con menos de nueve cuadrados en la que puedan encajar los doce pentominós. Si fuera posible, solamente las formas I-V-X no podrían ocupar menos de ocho cuadrados, como se muestra en la siguiente imagen
 |
 |
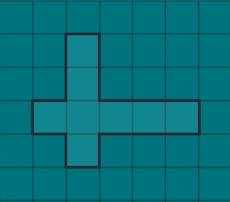