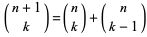INTRODUCCIÓN

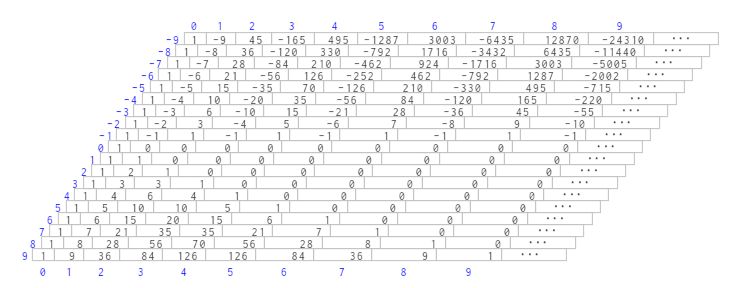
El paralelogramo de Newton se obtiene al extender el triángulo de Pascal mediante la introducción de números combinatorios (coeficientes binomiales) con índice superior un número entero.

Si a esos coeficientes binomiales se le aplican congruencias numéricas, por ejemplo todos los números congruentes con 0 módulo 2, y se le asigna un color a todos lo que cumplen esa condición, entonces acontecen curiosas regularidades que reflejan atractivas formas geométricas de tipo fractal:

Estos resultados, obviamente, engloban a las congruencias en el Triángulo de Pascal.

OBJETIVOS

Conocer las regularidades geométricas que acontecen en el paralelogramo de Newton al considerar congruencias numéricas.

INSTRUCCIONES

Al iniciar la escena, en la parte central, se muestra el que hemos denominado paralelogramo de Newton representando los coeficientes binomiales de índice superior entre -19 y 19 y de índice inferior desde 0 a 39 y, en él, se colorea en naranja aquellos que son congruentes con 0 módulo 2 y en blanco los congruentes con 1 módulo 2. En el lateral izquierdo del paralelogramo, en azul, se muestra el índice superior y en los lados superior e inferior, también en azul, los índices inferiores.

Hay que indicar que a medida que aumenta el número de filas y columnas la representación de este paralelogramo numérico entraña cierta dificultad para su visualización global. No obstante, en la escena se puede modificar la escala para que cada coeficiente pueda, en caso extremo, corresponderse con un píxel. Paralelamente, ese incremento en el número de coeficientes representado conlleva un aumento sustancial en las necesidades de cálculo. Por ello, por defecto, la representación se ha limitado a un máximo de 400 filas y 400 columnas (obviamente dichas limitaciones pueden modificarse editando la escena).
El cálculo de estas congruencias no necesitan la determinación previa de los coeficientes binomiales sino la traslación de las propiedades recursivas existentes entre estos coeficientes:

Ello permite salvar las limitaciones que entraña el cálculo de estos números enteros que superan rápidamente el número designado como MAX_SAFE_INTEGER y que en javascript es 2⁵³-1 (superior a 9 mil billones). Por tanto Así pues, no se introduce ninguna limitación adicional a las previamente indicadas.

En la parte superior de la escena pueden observarse diferentes controles cuya funcionalidad es la siguiente:

• Selector de inclinación: Es una barra de desplazamiento con la que puede modificarse la inclinación del paralelogramo y representarlo, si se desea, como un rectángulo.
• Escala: Permite modificar la escala a la que se representa el paralelogramo de Newton.
• Selección paralelogramo o triángulo: mediante este menú puede seleccionarse la representación del paralelogramo de Newton o el triángulo de Pascal.
• Filas: Número de filas correspondientes a cada familia de coeficientes binomiales a representar, tanto de índice superior positivo como negativo. Por ejemplo, para 10 filas se representan las congruencias correspondiente a los números combinatorios de índice superior desde -9 a 9. Cada fila queda etiquetada con su respectivo índice superior. En la escena el rango se ha restringido desde -199 a 199.
• Columnas: Número de columnas correspondientes a cada familia de coeficientes binomiales a representar. Por ejemplo, para 10 columnas se representan los números combinatorios de índice inferior desde 0 a 9. En la escena el rango se ha restringido a un máximo de 400 columnas.
• Divisor y resto: En la gráfica se reflejará con fondo color naranja todos los coeficientes binomiales que sean congruentes con el resto indicado y con módulo el del divisor seleccionado. Por defecto se asigna el valor de 2 al divisor y 0 al resto, pero pueden cambiarse. Mediante esta coloración pueden observarse pautas geométricas de cómo se distribuyen estos coeficientes, lo cual es el objetivo de esta miscelánea.