Espiral logarítmica cordobesa.

MORFOLOGÍA Y CRECIMIENTO GNOMÓNICO CORDOBÉS DEL NAUTILUS I

Al ser la espiral logarítmica geométrica de razón

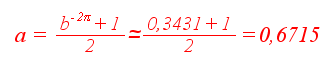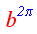
se dice que ese valor es su factor de crecimiento. Por tanto, el factor de crecimiento del Nautilus pompilius sería

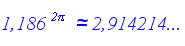
Thompson en su libro On Growth an Form p. 770 le asigna un factor de crecimiento medido empíricamente por Mosley de 3,00 (para más detalles consultar el documento enlazado en la página de indicaciones). 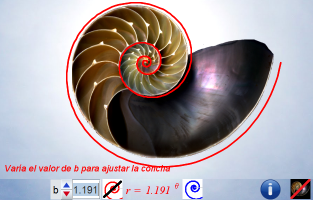Ese factor de crecimiento se correspondería con la espiral logarítmica de base b=1,191 y en la escena anterior puede verificarse cómo esa espiral no se ajusta adecuadamente a la concha del Nautilus, según reflejamos en las imágenes siguientes. Nosotros abogamos y defendemos el factor de crecimiento de 2,914214... correspondiente a la espiral logarítmica cordobesa.


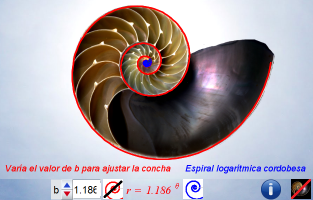Factor de crecimiento 3,00	Factor de crecimiento cordobés 2,914214...

Es lógico intuir que cualquier punto ubicado en el interior de la concha habrá surgido como consecuencia de un crecimiento análogo al de la concha, si bien afectado por un factor de escala, es decir, todo punto pertenecerá a una espiral logarítmica de ecuación:

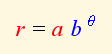
Ello se puede observar en la escena sin más que cambiar el valor de a, obteniéndose que 0.34<a<1. En particular podemos comprobar que los puntos del sifúnculo están ubicados en una espiral de este tipo. ¿Cómo podemos obtener teóricamente esos valores?

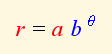
Al crecer el Nautilus una vuelta podemos ver cómo lo que era el exterior de la concha pasa a ser el interior. Si hacemos una distinción en todo instante de lo que es la capa interior (en la imagen dibujada en color rojo) de la exterior (en la imagen en color azul)

podemos asimilar que la concha está compuesta por dos capas digamos coincidentes o más bien que se solapan, pero que se diferencian en una vuelta, es decir, se corresponden con las espirales de ecuaciones:

o bien

lo cual puede interpretarse como que la velocidad o razón de crecimiento entre la capa interior y exterior es de 0,3431... a 1, o bien que la capa exterior crece 2,914214... veces más rápido que la interior (en definitiva el factor de crecimiento).

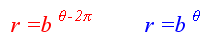
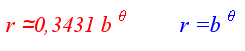
Consecuentemente la sección del Nautilus es una región del plano de ecuación:

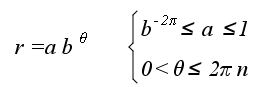
donde b es 1,185580... correspondiente a la espiral logarítmica cordobesa y n el números de ciclos o verticilos que en este caso contabilizamos tres menos un octavo (para conocer como se cuentan estos puede consultarse este enlace: whorl). Siendo precisos podemos señalar que la región anterior se corresponde con la teleoconcha o concha generada al crecer, mientras que la protoconcha, que es la correspondiente a la fase larvaria, se ajustaría teóricamente con los valores

El planteamiento anterior puede ser asimilado al realizado por Ghyca, M. en su libro "Estética de las Proporciones en la Naturaleza y en las artes. Barcelona: Poseidón (1983). ISBN 84-85083-06-7" en el que asimila la espiral logarítmica a la sección meridiana del volumen de un cono flexible que se enrolla según lo representado en la siguiente imagen (tomada de la página 136 de dicho libro):

Para profundizar en estos aspectos puede consultarse el cap XI (pp 798-803) del libro citado de Thompson On Growth an Form.

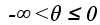
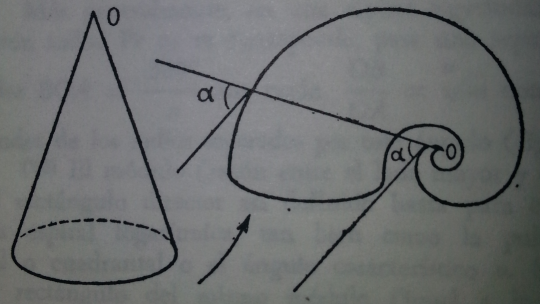
¿Cuál de las espirales anteriores ajusta el sifúnculo?

Utilizando la escena puede observarse que el sifúnculo se corresponde con una espiral que toma valores en el intervalo de extremos a=0,65 y a=0,7, que es el que se usa en la escena para distinguirlo. El valor teórico que nosotros le asignamos sería considerando la espiral media entre la interior y la exterior --lo cual concuerda con el hecho de que debería corresponderse con el eje del cono indicado en la imagen anterior. Así pues la espiral del sifúnculo es aquella en la que:

Con el ajuste realizado el crecimiento gnomónico del Nautilus puede aproximarse discretamente con un paso 2pi/16, de manera análoga a como se realizó en el paso anterior, pero considerando esa aproximación en cada una de las dos zonas que delimita el sifúnculo. Puede observarse cómo mejora el modelo al abordar esta simulación.