De lo analizado anteriormente, tenemos que para cada pareja de valores $\alpha$ y $m$ se obtiene una pseudoespiral de Durero y por los puntos extremos de los arcos de ella pasa una espiral logarítmica $$\large \rho = r \, a \, (m^{\frac{1}{\alpha}})^\theta$$. De esta expresión se deduce que:

• Fijado un valor de $m$, la amplitud del arco $\alpha$ y el factor de crecimiento radial de la espiral logarítmica, cuyo valor es $(m^{\frac{1}{\alpha}})^{2 \pi}$, son inversamente proporcionales.

  
  
  Relación entre $\alpha$ y el factor de crecimiento radial de la espiral logarítmica $(m^{\frac{1}{\alpha}})^{2 \pi}$ para un factor $m$ fijo.

• Fijado un valor de $\alpha$, el factor amplificador de la pseudoespiral $m$ y el factor de crecimiento radial de la espiral logarítmica, cuyo valor es $(m^{\frac{1}{\alpha}})^{2 \pi}$, son directamente proporcionales.

  
  
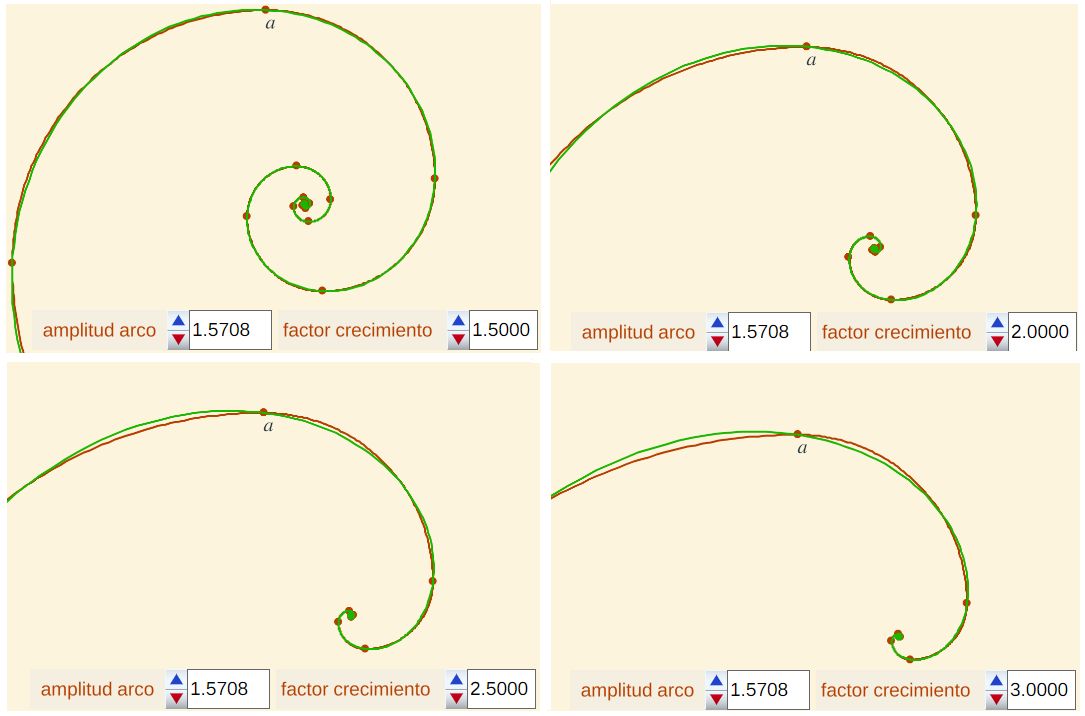
  Relación entre $m$ y el factor de crecimiento radial de la espiral logarítmica $(m^{\frac{1}{\alpha}})^{2 \pi}$ para un ángulo $\alpha$ fijo.