Paso 5. Demostración matemática.
Lo probado anteriormente en el paso 4 podemos aplicarlo analogamente a los centros ${\color{#9b00b6}C_{k}}$, los cuales también son puntos de una espiral con igual polo ${\color{#1bb600}P}$, según hemos visto antes, de igual base $m^{\frac{1}{\alpha}}$, pero con diferente coeficiente (lo que equivale a un giro de la misma o bien se puede interpretar como un ángulo de retardo).
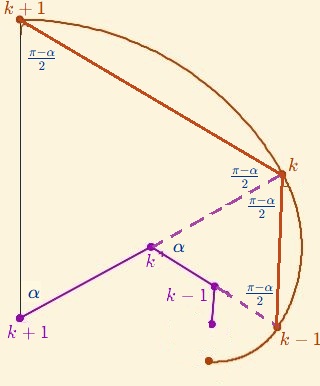
Fig. 5.1. Ángulos de los segmentos de la poligonal formada por los extremos de los arcos $P_k$ y los centros de los mismos $C_k$
En la Fig. 5.1 se observa que $ {\color{#9b00b6}\widehat{C_{k-1} C_k C_{k+1}}} = \pi - \alpha $ y también se verifica que $\dfrac{|\color{#9b00b6}{\overrightarrow{ C_k C_{k+1}}}|}{|{\color{#9b00b6}\overrightarrow{ C_{k-1} C_k }}|} = m$, luego aplicando el Lema citado, los puntos ${\color{#9b00b6}C_{k}}$ están en una espiral del tipo (27) (el mismo tipo que (15)). Para hallar $c$ en esa expresión impongamos que ha de pasar por ${\color{#9b00b6}C_{0}(0,0)}$ y para ello hallemos el ángulo $\gamma_c$ que forma $\overrightarrow{{\color{#1bb600}P}{\color{#9b00b6}C_0}}$ con el eje polar $\theta=0$
$$
\begin{aligned}
\gamma_{\color{#9b00b6}C_0} &= arccos (\frac{\overrightarrow{{\color{#1bb600}P}{\color{#9b00b6}C_0}}·\overrightarrow{i}}{|\overrightarrow{{\color{#1bb600}P}{\color{#9b00b6}C_0}}| \, |\overrightarrow{i}|})\\
&= arccos(\frac{-A}{\sqrt{A^2+B^2}})\\ \tag{29}
\end{aligned}
$$
y
$$\begin{aligned}
\rho_{\color{#9b00b6}C_0}
&=\text{distancia}({\color{#1bb600}P},{\color{#9b00b6}C_0})\\
&=r \sqrt{A^2+B^2}.
\\ \tag{30}
\end{aligned}
$$
Por tanto, se ha de cumplir que
$$
r \sqrt{A^2+B^2} = d \, (m^{\frac{1}{\alpha}})^{\gamma_{\color{#9b00b6}C_0}} \tag{31}
$$
de donde obtenemos que
$$
d = r \sqrt{A^2+B^2} \, (m^{\frac{1}{\alpha}})^{-\gamma_{\color{#9b00b6}C_0}} \tag{32}
$$
y, consecuentemente la espiral logarítmica sigue la expresión (15) antes indicada con
$$
{\color{#9b00b6} a_c} = \sqrt{A^2+B^2} \, (m^{\frac{1}{\alpha}})^{-\gamma_{\color{#9b00b6}C_0}}. \tag{33}
$$
Y, análogamente a lo que acontece en en la espiral de los extremos de los arcos, en esta espiral de centros los ángulos que determinan a dichos puntos ${\color{#9b00b6}C_k}$ en la espiral logarítmica (15) son $\theta=\gamma_{\color{#9b00b6}C_0}+ {\color{#9b00b6} k} \, \alpha$, con $\gamma$ dado por (27).
Nota: En el cálculo de $\gamma_{\color{#9b00b6}C_0}$, si el valor de la ordenada del polo es positiva, es decir $B \gt 0$ (el punto ${\color{#1bb600}P}$ tiene una ordenada mayor se ubica "por encima" del punto ${\color{#9b00b6}C_0 (0,0)}$) y consecuentemente el ángulo que forma es cóncavo, así pues hay que considerar el valor opuesto al aportado por (29) $- \,arccos(\frac{-A}{\sqrt{A^2+B^2}})$, o bien $2 \pi- arccos(\frac{-A}{\sqrt{A^2+B^2}})$.

