Como primer paso, supuesto que los puntos $ {\color{#b63f00} { P}_{k}}$ son puntos de una espiral logarítmica, determinemos cuál tendría que ser el polo $\color{#1bb600} P$ de la citada espiral y este punto vendría dado por: $$ \lim_{k \to{-}\infty}{\color{#b63f00} { P}_{k}} = \color{#1bb600} P \tag{17}$$
Su determinación es sencilla ya que al ser $m \gt 1$, entonces $ \lim_{k \to{-}\infty} {m^k}=0$ y, consecuentemente, por (12) se obtiene que las coordenadas de dicho polo $\color{#1bb600} P$ son las indicadas en (16).
Adicionalmente, por (1), se verifica también que el polo es el límite de los centros de los arcos de circunferencia que intervienen en la construcción de Durero, es decir, $$ \lim_{k \to{-}\infty}{\color{#9b00b6}C_{k}} = \color{#1bb600} P \tag{18}$$ Lo anterior está representado gráficamente en la Fig. 4.1.

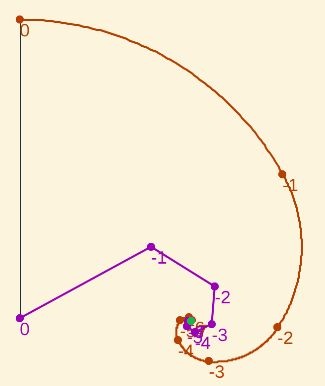
Fig. 4.1. Convergencia de los extremos de los arcos y centros de los mismos al polo de la espiral.

Para verificar que los $ {\color{#b63f00} { P}_{k}}$ son puntos de una espiral logarítmica basta aplicar el lema citado, el cual se cumple en nuestro caso ya que de (6),tenemos que $$ \begin{aligned} {\color{#b63f00} |\overrightarrow{O P_{k}} -\overrightarrow{O P_{k-1}}}| &= r \, m^k \, |\overrightarrow{u}_{k} - \overrightarrow{u}_{k-1}| \\ &= r \, m^k \, 2 |sen \frac{\alpha}{2}| , \\ \end{aligned} \tag{19} $$ es decir, se verifica la primera hipótesis del Lema: $\dfrac{|\color{#b63f00}{\overrightarrow{ P_k P_{k+1}}}|}{|{\color{#b63f00}\overrightarrow{ P_{k-1} P_k }}|} = m$ y según puede observarse y deducirse en la Fig. 4.2, se cumple la segunda hipótesis ${\color{#b63f00}\widehat{P_{k-1} P_k P_{k+1}}} = \pi - \alpha$, pues el triángulo $\color{#b63f00} P_k P_{k+1} \color{#9b00b6} C_{k+1} $ es isósceles $\forall k$, con ángulo desigual $\alpha$, al ser $| {\color{#9b00b6} C_{k+1}} {\color{#b63f00} P_k}| $ y $| {\color{#9b00b6} C_{k+1}} {\color{#b63f00} P_{k+1}}| $ los radios del arco $\color{#b63f00} P_k P_{k+1}$.

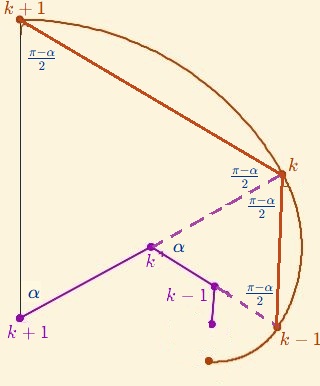
Fig. 4.2. Ángulos de los segmentos de la poligonal formada por los extremos de los arcos $P_k$ y los centros de los mismos $C_k$.

Así pues, por el lema anterior los puntos $ {\color{#b63f00} { P}_{k}}$ son puntos de una espiral $\large \rho= d \, (m^{\frac{1}{\alpha}})^\theta$ con polo el punto $\color{#1bb600} P$ expresado en (16) y para determinar el valor del coeficiente $d$ basta imponer que dicha espiral pase por el punto $ {\color{#b63f00} { P}_{0} (0,r)}$ y ello conlleva la necesidad de conocer las coordenadas polares de este punto, es decir, concretar el valor del radio polar $\rho_{\color{#b63f00} P_0} =\text{distancia}({\color{#1bb600}P},{\color{#b63f00} P_0})$ y el argumento del mismo $\theta_{\color{#b63f00} P_0}$ denotado como $\gamma$ en la Fig.4.3.

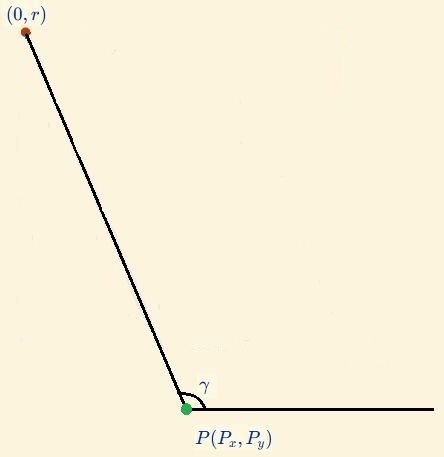
Fig. 4.3. Determinación del coeficiente $\color{#1bb600} a$ en la espiral logarítmica que contiene a los $P_k$.

$\gamma$ es el ángulo que forma la dirección del eje polar $\theta =0$ con la semirrecta determinada por el polo ${\color{#1bb600}P}$ y ${\color{#b63f00}P_0(0,r)}$, es decir, $\gamma = \measuredangle(\overrightarrow{{\color{#1bb600}P}{\color{#b63f00}P_0}}, \overrightarrow{i})$ siendo $\overrightarrow{i}$ el vector director del eje de abscisas en sentido positivo del mismo. Para simplificar la escritura de estos cálculos consideremos las coordenadas del polo escritas como ${\color{#1bb600}P(r\, A, r \, B)}$ (ver (16)) y entonces: $$ \begin{aligned} \gamma &= arccos (\frac{\overrightarrow{{\color{#1bb600}P}{\color{#b63f00}P_0}}·\overrightarrow{i}}{|\overrightarrow{{\color{#1bb600}P}{\color{#b63f00}P_0}}| \, |\overrightarrow{i}|})\\ &= arccos(\frac{-A}{\sqrt{A^2+(1-B)^2}})\\ \tag{20} \end{aligned} $$ y $$\begin{aligned} \rho_{\color{#b63f00} P_0} &=\text{distancia}({\color{#1bb600}P},{\color{#b63f00} P_0})\\ &=r \sqrt{A^2+(1-B)^2}. \\ \tag{21} \end{aligned} $$ Por tanto, se ha de cumplir que $$ r \sqrt{A^2+(1-B)^2} = d \, (m^{\frac{1}{\alpha}})^\gamma \tag{22} $$ de donde obtenemos que $$ d = r \sqrt{A^2+(1-B)^2} \, (m^{\frac{1}{\alpha}})^{-\gamma} \tag{23} $$ y, consecuentemente la espiral logarítmica sigue la expresión (15) antes indicada con $$ {\color{#1bb600} a_p} = \sqrt{A^2+(1-B)^2} \, (m^{\frac{1}{\alpha}})^{-\gamma}. \tag{24} $$
Finalmente, veamos que el ángulo que forman los radios vectores de los puntos ${\color{#b63f00}P_k}$ en la espiral logarítmica, es decir respecto al polo ${\color{#1bb600}P}$ son múltiplos de $\alpha$, es decir, ${\color{#b63f00}k} \, \alpha$. En la figura 10 podemos observar que dado que se cumple la proporcionalidad entre los segmentos $\color{#b63f00} \overline{P_kP_{k+1}}$ $ \forall{k}$, según hemos visto antes, y que estos son puntos de una espiral logarítmica, entonces los radios vectores $\overrightarrow{{\color{#1bb600}P}{\color{#b63f00}P_k}}$ son también proporcionales y por ende los triángulos ${\color{#b63f00}P_k}{\color{#1bb600}P}{\color{#b63f00}P_{k+1}}$ son semejantes, consecuentemente los ángulos homólogos son iguales. En la Fig. 4.4 observamos que el ángulo $${\color{#b63f00}\widehat{P_{k-1} P_k P_{k+1}}} = \pi - \alpha = \delta + \epsilon \tag{25}$$ y en el triángulo ${\color{#b63f00}{P_{k-1}} {\color{#1bb600}P} {\color{#b63f00}P_{k+1}}}$ tenemos que $$\beta+\delta+\epsilon=\pi \tag{26}$$ obteniendo que $\beta = \alpha$.

Por tanto los ángulos que determinan a dichos puntos ${\color{#b63f00}P_k}$ en la espiral logarítmica (15) son $\theta=\gamma+ {\color{#b63f00} k} \, \alpha$, con $\gamma$ dado por (20).

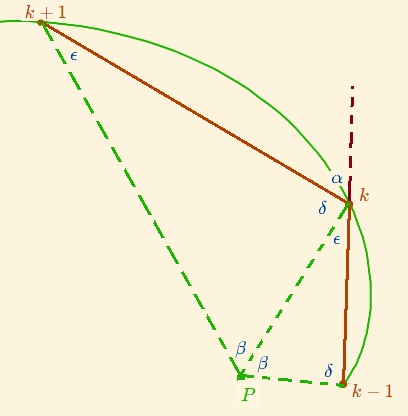
Fig. 4.4. Determinación del angulo $\beta$ en la pseudoespiral de Durero respecto al polo $\color{#1bb600} P$ de la espiral logarítmica. Se concluye que $\beta$ es igual a $\alpha$ que es lo afirmado anteriormente.