FICHAS DE TRABAJO PARA EL
ALUMNO DEL LIBRO ELECTRÓNICO
Autora: Rita Jiménez
Igea. Año 2017
MEDIDA DE ÁNGULOS
Los ángulos se miden en grados sexagesimales y en radianes.
Utiliza la escena de la página 9 del libro para completar los siguientes ejercicios.
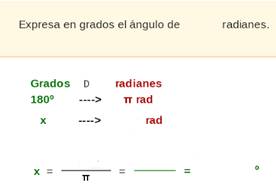
PASAR
de GRADOS a RADIANES






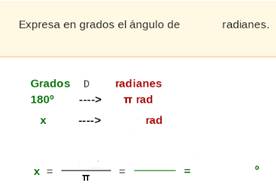
PASAR
DE RADIANES a GRADOS




RECUERDA
FUNCIONES TRIGONOMÉTRICAS
1.- Representación gráfica de y = senx
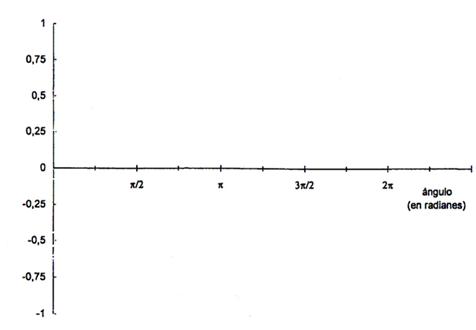
a) Completar la siguiente tabla b) Representar gráficamente
|
|
Ángulo en grados |
x (rad) |
y =senx |
|
|
|
0º |
0 |
0 |
|
|
|
30º |
p/6 |
0.5 |
|
|
|
45º |
p/4 |
0.70 |
|
|
|
60º |
p/3 |
0.86 |
|
|
|
90º |
p/2 |
1 |
|
|
|
120º |
2p/3 |
0.86 |
|
|
|
135º |
3p/4 |
0.70 |
|
|
|
150º |
5p/6 |
0.5 |
|
|
|
180º |
p |
0 |
|
|
|
210º |
7p/6 |
-0.5 |
|
|
|
225º |
5p/4 |
-0.70 |
|
|
|
240º |
4p/3 |
-0.86 |
|
|
|
270º |
3p/2 |
-1 |
|
|
|
300º |
5p/3 |
-0.86 |
|
|
|
315º |
7p/4 |
-0.70 |
|
|
|
330º |
11p/6 |
-0.5 |
|
|
|
360º |
2p |
0 |
2.- Observa que la gráfica anterior solo se ha construido para ángulos entre 0º y 360º es decir de la 1ª vuelta ¿qué gráfico se obtiene si lo extendemos a todos los ángulos?
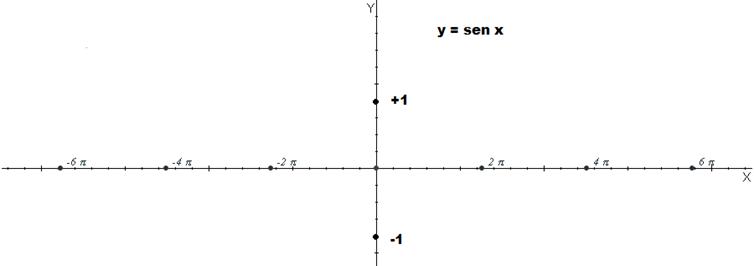
2.- Representación gráfica de y = cos x
|
|
Ángulo en grados |
x (rad) |
y =cosx |
|
|
|
0º |
0 |
1 |
|
|
|
30º |
p/6 |
|
|
|
|
45º |
p/4 |
|
|
|
|
60º |
p/3 |
|
|
|
|
90º |
p/2 |
0 |
|
|
|
120º |
2p/3 |
|
|
|
|
135º |
3p/4 |
|
|
|
|
150º |
5p/6 |
|
|
|
|
180º |
p |
-1 |
|
|
|
210º |
7p/6 |
|
|
|
|
225º |
5p/4 |
|
|
|
|
240º |
4p/3 |
|
|
|
|
270º |
3p/2 |
0 |
|
|
|
300º |
5p/3 |
|
|
|
|
315º |
7p/4 |
|
|
|
|
330º |
11p/6 |
|
|
|
|
360º |
2p |
1 |
2.- Observa que la gráfica anterior solo se ha construido para ángulos entre 0º y 360º es decir de la 1ª vuelta
¿Qué gráfico se obtiene si lo extendemos a todos los
ángulos? y= cosx
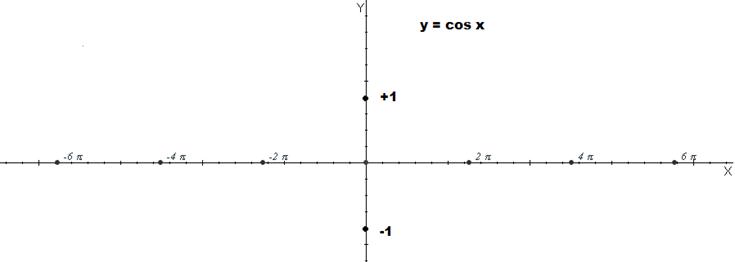
3.- Representación gráfica de y = tg x
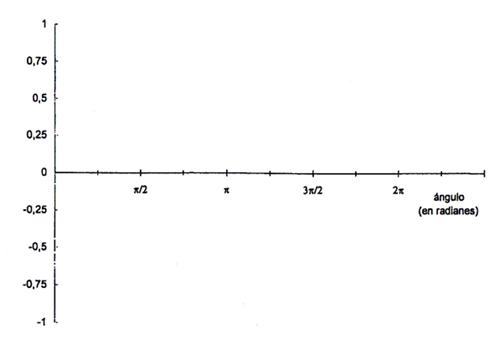
1 a ) Completar la siguiente tabla b) Representar gráficamente
|
|
Ángulo en grados |
x (rad) |
y = tg x |
|
|
|
0º |
0 |
0 |
|
|
|
30º |
p/6 |
|
|
|
|
45º |
p/4 |
|
|
|
|
60º |
p/3 |
|
|
|
|
90º |
p/2 |
No existe |
|
|
|
120º |
2p/3 |
|
|
|
|
135º |
3p/4 |
|
|
|
|
150º |
5p/6 |
|
|
|
|
180º |
p |
0 |
|
|
|
210º |
7p/6 |
|
|
|
|
225º |
5p/4 |
|
|
|
|
240º |
4p/3 |
|
|
|
|
270º |
3p/2 |
No existe |
|
|
|
300º |
5p/3 |
|
|
|
|
315º |
7p/4 |
|
|
|
|
330º |
11p/6 |
|
|
|
|
360º |
2p |
0 |
2.- Observa que la gráfica anterior solo se ha construido para ángulos entre 0º y 360º es decir de la 1ª vuelta ¿qué gráfico se obtiene si lo extendemos a todos los ángulos?
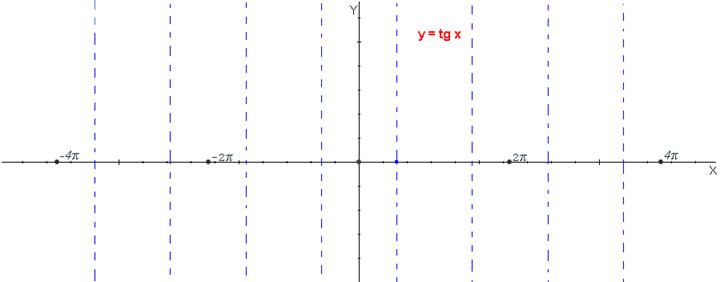
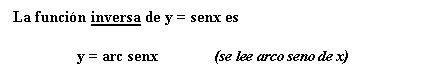
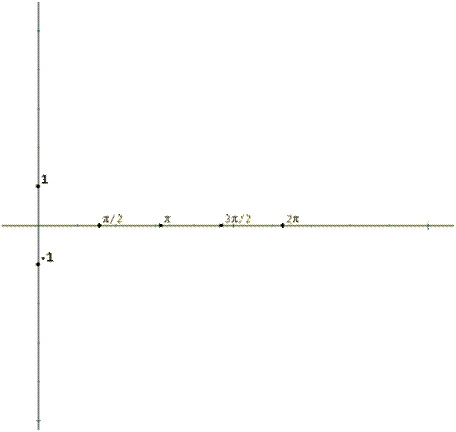
1.-a) Completar la siguiente tabla b)
Representar gráficamente con todos los
ángulos
(simplemente debes dar la
vuelta a la tabla de y = sen x)
![]()
|
|
x (es el seno) |
y (
ángulo en
radianes) |
|
|
|
|
0 |
0 |
0º |
|
|
|
0’5 |
p/6 |
30º |
|
|
|
0’7 |
p/4 |
45º |
|
|
|
0’86 |
p/3 |
60º |
|
|
|
1 |
p/2 |
90º |
|
|
|
0’86 |
2p/3 |
120º |
|
|
|
0’7 |
3p/4 |
135º |
|
|
|
0’5 |
5p/6 |
150º |
|
|
|
0 |
p |
180º |
|
|
|
-0’5 |
7p/6 |
210º |
|
|
|
-0’7 |
5p/4 |
225º |
|
|
|
-0’86 |
4p/3 |
240º |
|
|
|
-1 |
3p/2 |
270º |
|
|
|
-0’86 |
5p/3 |
300º |
|
|
|
-0’7 |
7p/4 |
315º |
|
|
|
-0’5 |
11p/6 |
330º |
|
|
|
0 |
2p |
360º |
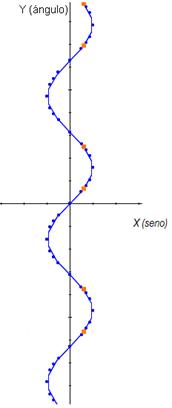
2.- a) ¿El dibujo anterior
corresponde a una función? ¿Por qué?
b) ¿Qué condición debemos imponer para que sea función?
c) Dibuja la gráfica de la función y =arc sen x Señala el dominio y el recorrido
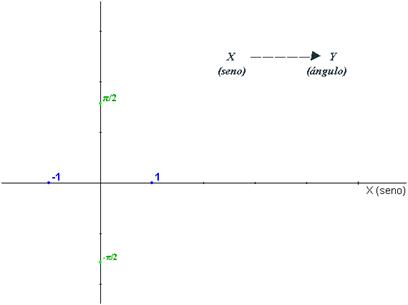
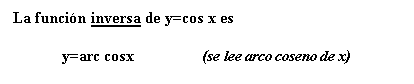
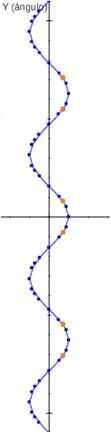
1.-a) Completar la siguiente tabla b) Representar gráficamente con todos los ángulos
(simplemente debes dar la
vuelta a la tabla de y = cos x)
![]()
|
|
x (es el coseno) |
y (
ángulo en
radianes) |
|
|
|
|
1 |
0 |
0º |
|
|
|
0’86 |
p/6 |
30º |
|
|
|
0’7 |
p/4 |
45º |
|
|
|
0’5 |
p/3 |
60º |
|
|
|
0 |
p/2 |
90º |
|
|
|
-0’5 |
2p/3 |
120º |
|
|
|
-0’7 |
3p/4 |
135º |
|
|
|
-0’86 |
5p/6 |
150º |
|
|
|
-1 |
p |
180º |
|
|
|
-0’86 |
7p/6 |
210º |
|
|
|
-0’7 |
5p/4 |
225º |
|
|
|
-0’5 |
4p/3 |
240º |
|
|
|
0 |
3p/2 |
270º |
|
|
|
0’5 |
5p/3 |
300º |
|
|
|
0’7 |
7p/4 |
315º |
|
|
|
0’86 |
11p/6 |
330º |
|
|
|
1 |
2p |
360º |
2.-a) ¿El dibujo anterior corresponde a una
función? ¿Por qué?
b)¿Qué
condición debemos imponer para que sea función?
b)
Dibuja la gráfica de la función y =arc cosx Señala el dominio y el
recorrido
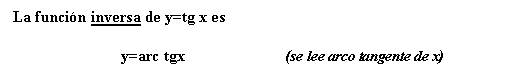
1.-a) Completar la siguiente tabla b)
Representar gráficamente con todos los
ángulos
(simplemente debes dar la
vuelta a la tabla de y = tg x)
|
|
x (es la tangente) |
y (ángulo en
radianes) |
|
|
|
|
0 |
0 |
0º |
|
|
|
0’57 |
p/6 |
30º |
|
|
|
1 |
p/4 |
45º |
|
|
|
1’73 |
p/3 |
60º |
|
|
|
no existe |
p/2 |
90º |
|
|
|
-1’73 |
2p/3 |
120º |
|
|
|
-1 |
3p/4 |
135º |
|
|
|
-0’57 |
5p/6 |
150º |
|
|
|
0 |
p |
180º |
|
|
|
0’57 |
7p/6 |
210º |
|
|
|
1 |
5p/4 |
225º |
|
|
|
1’73 |
4p/3 |
240º |
|
|
|
no existe |
3p/2 |
270º |
|
|
|
-1’73 |
5p/3 |
300º |
|
|
|
-1 |
7p/4 |
315º |
|
|
|
-0’57 |
11p/6 |
330º |
|
|
|
0 |
2p |
360º |
2.-a) El dibujo anterior corresponde a una función?
¿Por qué?
b)¿Qué
condición debemos imponer para que sea función?
c)
Dibuja la gráfica de la función y =arc tgx Señala el dominio y el recorrido
PROPIEDADES DE LAS FUNCIONES
TRIGONOMÉTRICAS
Observa la gráfica siguiente que corresponde a la función y= sen
x en el intervalo [0,2p]
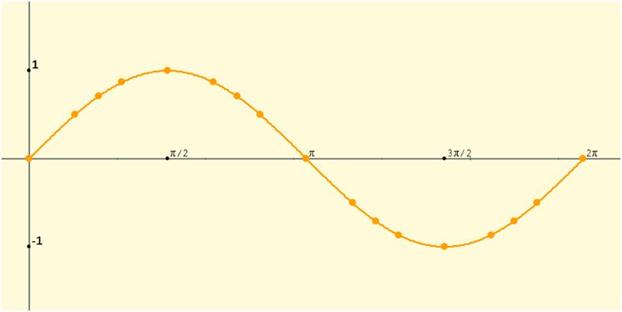
Completa el siguiente cuadro con sus propiedades:
![Cuadro de texto: Propiedades de la función y= sen x en el intervalo [0,2p]
Dominio =
Puntos de corte con el eje de ordenadas:
Puntos de corte con el eje de abscisas:
Intervalos de crecimiento:
Intervalos de decrecimiento:
Máximos/mínimos relativos:
Intervalos de concavidad:
Intervalos de convexidad:
Puntos de inflexión:
Asíntotas verticales:
Puntos de discontinuidad:](fichastrabajolibro1_archivos/image039.gif)
Observa la gráfica siguiente que corresponde a la función y= cos
x en el intervalo [0,2p]
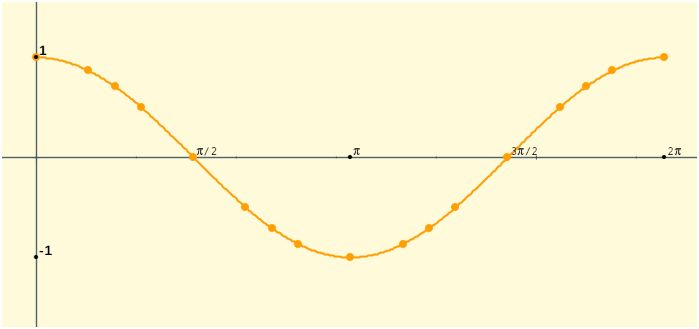
Completa el siguiente cuadro con sus propiedades:
![Cuadro de texto: Propiedades de la función y= cos x en el intervalo [0,2p]
Dominio =
Puntos de corte con el eje de ordenadas:
Puntos de corte con el eje de abscisas:
Intervalos de crecimiento:
Intervalos de decrecimiento:
Máximos/mínimos relativos:
Intervalos de concavidad:
Intervalos de convexidad:
Puntos de inflexión:
Asíntotas verticales:
Puntos de discontinuidad:](fichastrabajolibro1_archivos/image041.gif)
Observa la gráfica siguiente que corresponde a la función y= tg
x en el intervalo [0,2p]
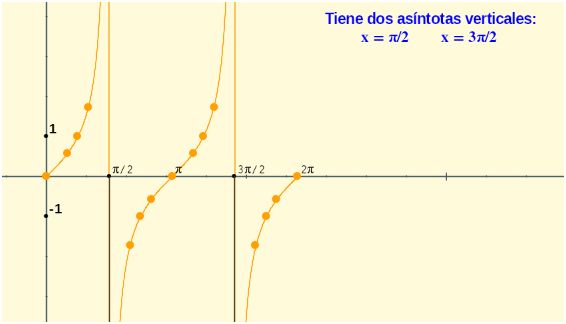
Completa el siguiente cuadro con sus propiedades:
![Cuadro de texto: Propiedades de la función y= tg x en el intervalo [0,2p]
Dominio =
Puntos de corte con el eje de ordenadas:
Puntos de corte con el eje de abscisas:
Intervalos de crecimiento:
Intervalos de decrecimiento:
Máximos/mínimos relativos:
Intervalos de concavidad:
Intervalos de convexidad:
Puntos de inflexión:
Asíntotas verticales:
Puntos de discontinuidad:](fichastrabajolibro1_archivos/image043.gif)
CONSTRUCCIÓN DE FUNCIONES TRIGONOMÉTRICAS
POR TRASLACIÓN Y DILATACIÓN
En la escena de la página 32 del libro debes seguir las instrucciones que
se dan a continuación
Al hacer clic en PULSAR PARA COMENZAR te aparece el menú Ver
transformadas de.
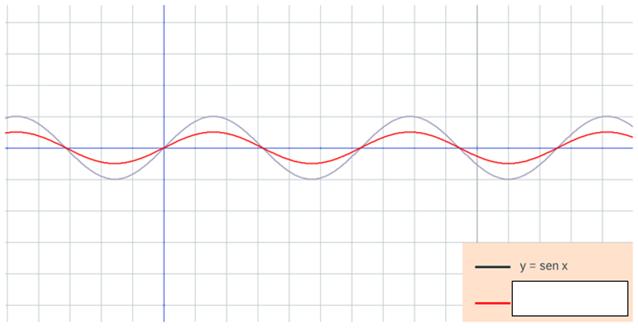
Debes seleccionar la función y = sen x
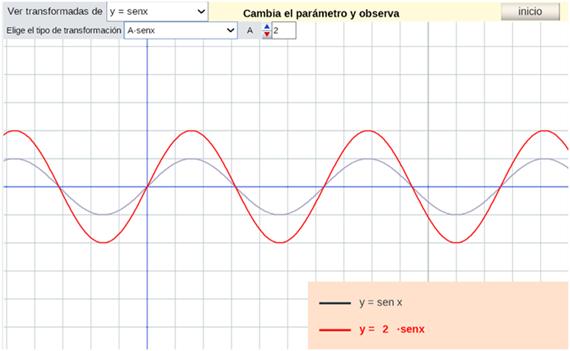
Una vez hayas seleccionado lo anterior tienes en pantalla la función y =
sen x en gris y la función
y = 2senx en otro color. Modifica
el valor de A y observa los cambios que se producen en la función
de color. De esta forma podrás averiguar
qué efecto produce en la gráfica multiplicar por un número.
Repite lo anterior con todas las posibilidades del menú
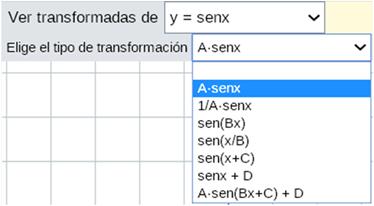
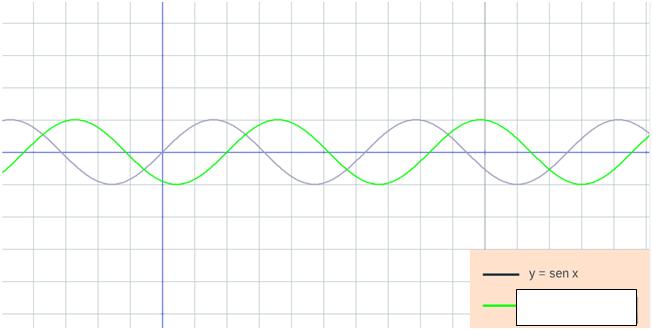
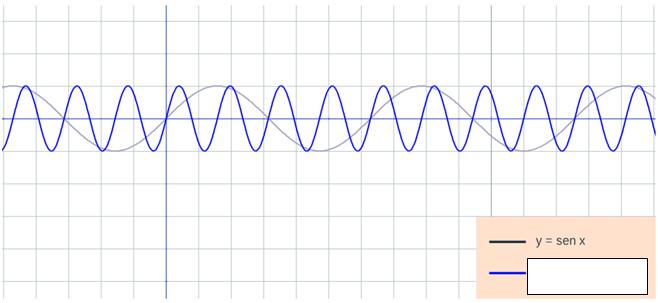
Completa el siguiente recuadro resumen siguiendo el ejemplo:
|
Transformación |
Efecto que se
produce en la gráfica |
|
y = 2 senx y = 3 senx |
|
|
y =1/2 senx y =1/3 senx |
|
|
y = sen(2x) y = sen(3x) |
|
|
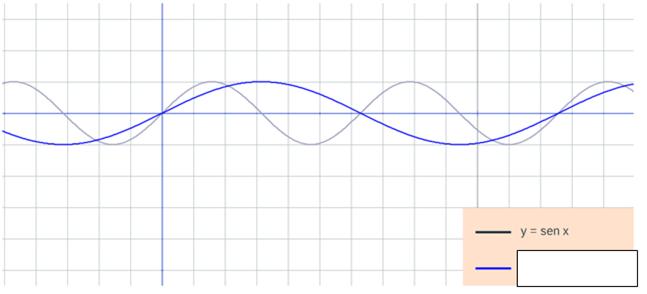
y = sen (x/2) y = sen (x/3) |
|
|
y = sen(x+2) y = sen(x+3) |
|
|
y = sen(x-2) y = sen(x-3) |
|
|
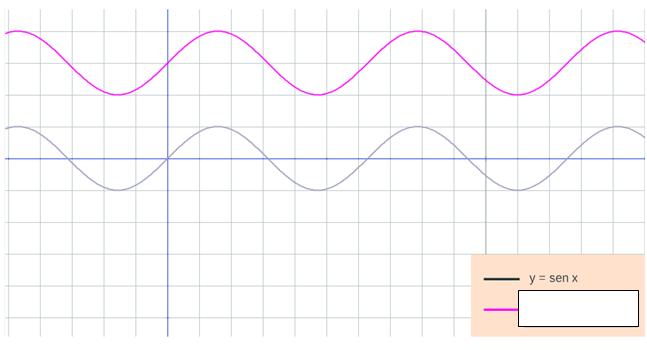
y = senx + 2 y = senx + 3 |
La función y = senx sube hacia arriba 2 unidades La función y = senx sube hacia arriba 3 unidades |
|
y = senx – 2 y = senx - 3 |
|
Cambia de función eligiendo y = cos x
en el menú

Repite lo anterior con la función y = cos x y completa el siguiente
recuadro resumen:
|
Transformación |
Efecto que se
produce en la gráfica |
|
y = 4 cosx y = 5 cosx |
|
|
y =1/4 cosx y =1/5 cosx |
|
|
y = cos (4x) y = cos (5x) |
|
|
y = cos (x/4) y = cos (x/5) |
|
|
y = cos (x+4) y = cos (x+5) |
|
|
y = cos (x-4) y = cos (x-5) |
|
|
y = cos x + 4 y = cos x + 5 |
La función y = cosx sube hacia arriba 4 unidades La función y = cosx sube hacia arriba 5 unidades |
|
y = cos x – 4 y = cos x - 5 |
|
PARA PRACTICAR
Haz ejercicios con la escena de la página 33 del libro y escribe la expresión algebraica de las siguientes
funciones transformadas de la función y = sen x en el recuadro