ESTUDIO Y APLICACIONES
DE LAS FUNCIONES TRIGONOMÉTRICAS
Y SUS INVERSAS

INTERACTIVO
ESTUDIO Y APLICACIONES DE LAS
FUNCIONES TRIGONOMÉTRICAS
Y SUS INVERSAS
INTERACTIVO
Rita Jiménez Igea
RED EDUCATIVA DIGITAL DESCARTES, España

Fondo Editorial Pascual Bravo
Medellín
Título de la obra
Estudio y aplicaciones de las funciones trigonométricas y sus inversas
Rita Jiménez Igea
Primera edición: 2017
Diseño del libro: Juan Guillermo Rivera Berrío
Diseño de cubierta: Diana María Velásquez García
Librería turn.js: Emmanuel García
Herramienta de edición: DescartesJS
Fuente: Amaranth
Fondo Editorial Pascual Bravo
Calle 73 73A-226
PBX: (574) 4480520
Apartado 6564
Medellín, Colombia
www.pascualbravo.edu.co
ISBN: 978-958-58510-8-5

Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual. Todos los objetos interactivos y los contenidos de esta obra colectiva están protegidos por la Ley de Propiedad Intelectual.
Tabla de contenido
La función y = sen x en el intervalo [0, 2π]12
La función y = sen x en todo R13
La función y = cos x en el intervalo [0, 2π]14
La función y = cox x en todo R15
La función y = tg x en el intervalo [0, 2π]16
La función y = tg x en todo R17
Propiedades de las funciones trigonométricas27
Transformaciones de las funciones trigonométricas30
Las funciones trigonométricas a nuestro alrededor36
Funciones trigonométricas en arquitectura38
Funciones trigonométricas en la naturaleza40
Funciones trigonométricas en Física42
La música de las funciones trigonométricas46
iii
Introducción
En este libro electrónico abordamos la construcción y el estudio de las funciones trigonométricas
y sus inversas. En un principio las funciones circulares surgen como razones trigonométricas para
caracterizar ángulos pero multitud de fenómenos naturales se describen mediante las funciones "seno" y "coseno", de
ahí su importancia.
La construcción de las inversas suele plantear dificultades a los alumnos dado que las funciones trigonométricas no
son funciones inyectivas. Tratamos este problema haciendo que el alumno visualice la
situación y comprenda la necesidad de imponer ciertas restricciones.
La relación matemáticas-ciencia, matemáticas–vida real permanece, muchas veces, oculta en la escuela.
Las explicaciones se dan de forma tan abstracta que el alumno no percibe la utilidad y la relación de las Matemáticas con otras asignaturas o con
el entorno más cercano. Ello lo aleja irremediablemente de la materia.
En la primera parte del libro mostramos las funciones desvinculadas de cualquier fenómeno físico.
En la segunda tratamos, por un lado, que el alumno conozca y reconozca la variedad de situaciones en las que las funciones
trigonométricas aparecen y compruebe que el tema impartido está presente en su entorno de una forma que no
podía ni imaginar.
Por otro,tratamos de establecer la conexión existente en este tema entre las asignaturas de Matemáticas y Física.
La realidad es que los temarios de ambas materias discurren, la mayor parte del tiempo, por caminos paralelos e independientes cuando
deberían secuenciarse de forma conjunta para conseguir que determinados conceptos matemáticos se impartieran antes de ser necesarios en Física.
En la última parte del libro nos encontramos con la página del profesor y el cuaderno con las fichas de trabajo del alumno para utilizar en
clase.
5
parte i
Medida de ángulos
Medida de ángulos
 Euclides define un ángulo como la inclinación entre dos líneas que se encuentran una a otra en un plano
y no están en línea recta. A lo largo de la historia han aparecido otras definiciones.
Euclides define un ángulo como la inclinación entre dos líneas que se encuentran una a otra en un plano
y no están en línea recta. A lo largo de la historia han aparecido otras definiciones.
Se utilizan varias unidades para medir los ángulos, la más utilizada es la sexagesimal, también es utilizada sobre todo por los topógrafos la centesimal y por los matemáticos el radián.1
RECUERDA:
Los ángulos pueden medirse en grados sexagesimales y en radianes
La conversión de una unidad a otra se consigue con una sencilla regla de tres, teniendo en cuenta la relación:
180º-----> π rad
En la escena interactiva de la página siguiente2, podrás realizar ejercicios para repasar
8
parte II
Representación de funciones trigonométricas y de sus inversas
La función y = sen x en el intervalo [0, 2π]
En la escena adjunta partiendo de una tabla de valores para ángulos menores de 360º obtendremos la gráfica de función y = senx en ese intervalo.
Basta con pulsar el botón Dibujar
12
La función y = sen x en todo R
¿Qué sucede con los valores del seno tras dar una vuelta completa a la circunferencia? Los valores vuelven a repetirse. Veamos cómo queda la gráfica.
En la escena dibuja la función en la 1ª y 2ª vueltas en sentido positivo. Repite para ángulos negativos. Modifica el zoom (hasta 30) para poder visualizar lo representado
Se obtiene la gráfica de la función y = sen x hasta el número de vueltas que se decida.
Observa que es una función PERIÓDICA y puedes visualizar su periodo.
¿La función es simétrica ? En caso afirmativo indica de qué tipo.
13
La función y = cos x en el intervalo [0, 2π]
En esta escena partiendo de una tabla de valores para ángulos menores de 360º obtendremos la gráfica la función y = cos x en ese intervalo.
Para ello debes pulsar el botón Dibujar.
14
La función y = cos x en todo R
¿Qué sucede con los valores del coseno tras dar una vuelta completa a la circunferencia? También en este caso vuelven a repetirse. Veamos la gráfica.
Como en el caso anterior dibuja la función en la 1ª y 2ª vueltas (en positivo y negativo) y deja el zoom en 30.
Se obtiene la gráfica de la función y = cos x hasta el número de vueltas que se decida.
También es una función PERIÓDICA. ¿Cuál es su periodo?
¿La función es simétrica? En caso afirmativo indica de qué tipo.
15
La función y = tg x en el intervalo [0, 2π]
Nuevamente partimos de una tabla de valores para ángulos menores de 360º para obtener la gráfica, en este caso, de la función y = tg x. Pulsa en Dibujar.
Observa que hay puntos para los que la función no está definida. ¿Cuáles son?
La función NO ES CONTINUA en esos puntos.
16
La función y = tg x en todo R
Tras dar vueltas en la circunferencia los valores de la tangente también se repiten. Para ver la gráfica dibuja la función en la 1ª y 2ª vueltas (en positivo y negativo) y cambia el zoom a 30.
Obtendrás la gráfica de la función y = tg x hasta el número de vueltas que decidas.
Es PERIÓDICA pero ¿cuál es el periodo?
Observa los puntos de discontinuidad.
¿La función es simétrica? En caso afirmativo indica de qué tipo.
17
La función y = arc sen x
|
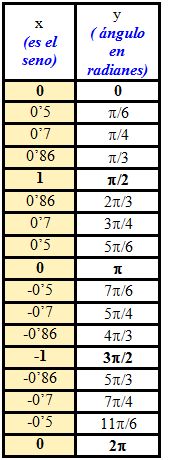
Observa la tabla de la izquierda. ¿Te resulta familiar? Efectivamente, es la tabla que resulta al invertir la de la función y = sen x en el intervalo [0, 2π] Es decir, hemos intercambiado x con y. Así, en este caso: x es el seno y es el ángulo (medido en radianes) Se nos plantean varias preguntas:
La tabla adjunta es una pequeña parte de los valores que toma la función y = sen x. Si invertimos la tabla completa de la función y = sen x con todos los posibles valores para el ángulo ¿qué gráfica obtendremos? El objetivo de la escena de la página siguiente es contestar a estas preguntas. Pulsa el botón Avanzar y sigue las indicaciones |
18
La función y = arc sen x
Hacemos un zoom en la zona que nos interesa de la escena anterior para visualizar mejor la función.
Pulsa el botón y =arc sen x.
¿Cuál es el dominio de la función?
¿Cuál es su recorrido?
20
La función y = arc cos x

|
En esta ocasión te presentamos otra tabla que esperamos te resulte familiar.
Efectivamente,es la tabla que se obtiene al invertir la de la función y = cos x en el intervalo [0, 2π] Así, en este caso: x es el coseno
y es el ángulo (medido en radianes) Vamos a plantearnos las mismas preguntas:
Como antes la tabla adjunta es una pequeña parte de los valores que toma la función y = cos x. Si invertimos la tabla completa de la función y = cos x con todos los posibles valores para el ángulo ¿qué gráfica obtendremos? El objetivo de la escena de la página siguiente es contestar a estas preguntas. Pulsa en Avanzar y sigue las indicaciones |
21
La función y = arc cos x
Hacemos un zoom en la zona que nos interesa de la escena anterior para visualizar mejor la función.
Pulsa el botón y =arc cos x.
¿Cuál es el dominio de la función?
¿Cuál es su recorrido?
23
La función y = arc tg x

|
En esta ocasión tenemos la tabla que resulta al invertir la de la función y = tg x para ángulos positivos menores que 360º. Ahora : x es la tangente y es el ángulo (medido en radianes) Nuevamente debemos responder a las mismas preguntas:
Después de trabajar con la escena de la página siguiente estarás en condiciones de contestarlas. Como siempre Pulsa en Avanzar. |
24
La función y = arc tg x
Hacemos un zoom en la zona que nos interesa de la escena anterior para visualizar mejor la función.
Pulsa el botón y =arc tg x.
¿Cuál es el dominio de la función?
¿Cuál es su recorrido?
26
Propiedades de las funciones trigonométricas
Observa la gráfica de la función y = sen x en el intervalo [0, 2π]
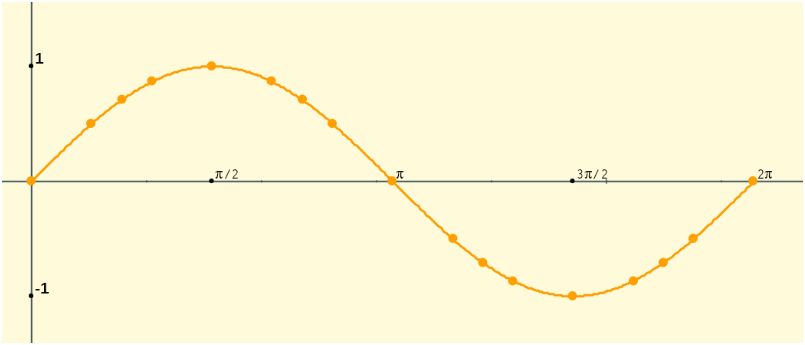
Señala sus propiedades:
| 1) Dom f(x) = 2) Ptos de corte con el eje de ordenadas: Ptos de corte con eje de abscisas: 3) Intervalos de crecimiento: Intervalos de decrecimiento: Máximos relativos: Mínimos relativos: |
4) Intervalos de concavidad: Intervalos de convexidad: Puntos de inflexión: 5) Asíntotas verticales: Puntos de discontinuidad: |
27
Observa la gráfica de la función y = cos x en el intervalo [0, 2π]
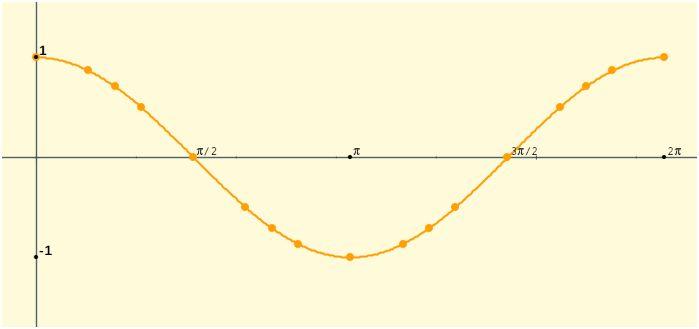
Señala sus propiedades:
| 1) Dom f(x) = 2) Ptos de corte con el eje de ordenadas: Ptos de corte con eje de abscisas: 3) Intervalos de crecimiento: Intervalos de decrecimiento: Máximos relativos: Mínimos relativos: |
4) Intervalos de concavidad: Intervalos de convexidad: Puntos de inflexión: 5) Asíntotas verticales: Puntos de discontinuidad: |
28
Observa la gráfica de la función y = tg x en el intervalo [0, 2π]

Señala sus propiedades:
| 1) Dom f(x) = 2) Ptos de corte con el eje de ordenadas: Ptos de corte con eje de abscisas: 3) Intervalos de crecimiento: Intervalos de decrecimiento: Máximos relativos: Mínimos relativos: |
4) Intervalos de concavidad: Intervalos de convexidad: Puntos de inflexión: 5) Asíntotas verticales: Puntos de discontinuidad: |
29
Transformaciones de las funciones trigonométricas
Ya conocemos la gráfica de la función y = sen x y haciendo algunas transformaciones podemos construir
otras muchas funciones trigonométricas.
Si k es un número positivo podemos encontrar distintas transformaciones que clasificamos en dos tipos:
Dilataciones
- y = k·sen x la función y = sen x se dilata verticalmente k veces
- y = 1/k·sen x la función y = sen x se comprime verticalmente k veces
- y = sen(kx) la función y = sen x se dilata horizontalmente k veces
- y = sen(x/k) la función y = sen x se comprime horizontalmente k veces
Traslaciones
- y = sen x + k la función y = sen x se traslada k unidades hacia arriba
- y = sen x - k la función y = sen x se traslada k unidades hacia abajo
- y = sen ( x + k) la función y = sen x se traslada k unidades hacia la izquierda
- y = sen ( x - k) la función y = sen x se traslada k unidades hacia la derecha
De forma análoga podemos conseguir las transformaciones de la función y = cos x
30
En las siguientes escenas podemos visualizar lo que hemos expuesto anteriormente.
Para ello debemos
- elegir la función básica
- elegir el tipo de transformación
- cambiar el valor de los parámetros
la escena nos irá modificando la función original, debemos observar la gráfica de la función transformada y comparar. La escena mantiene en gris la función básica y dibuja a color la transformada por lo que resultará más fácil obtener conclusiones sobre el cambio producido.
31
Transformaciones de las funciones trigonométricas
Observa los cambios que se producen en la función y = sen x y en la función y = cos x. Basta con que selecciones una u otra función.
32
Para practicar
Vamos a comprobar que has aprendido lo que te acabamos de explicar. Elige una de las funciones básicas. Observa la función coloreada que se muestra en pantalla,indica el tipo de transformación que se ha aplicado y su expresión algebraica.
33
parte III
Las funciones trigonométricas a nuestro alrededor
Funciones trigonométricas a nuestro alrededor
Encontramos funciones trigonométricas con facilidad a nuestro alrededor aunque no seamos consciente de ello. Hay más ejemplos de los que podemos imaginar. Te mostramos algunos en el vídeo siguiente:
Haz clic para ampliar el vídeo
36
Muchos movimientos oscilatorios pueden matematizarse mediante funciones trigonométricas
(la altura de un punto en un movimiento circular u oscilante, la longitud de un resorte elástico etc..)
Por otra parte, ocurre que existen vibraciones o perturbaciones que se producen en un lugar y se propagan a través del espacio produciendo
las denominadas ondas. Se trasmite la vibración y la energía asociada pero no la materia. Es el caso de la luz
y del sonido. Ello permite que podamos oir la radio, ver la TV, hablar por teléfono aunque el foco emisor esté a muchos Kms de distancia.
En medicina también hallamos ejemplos de tratamientos que utilizan ondas (los rayos X, ecografías, litotricias ).
Otros ejemplos los encontramos en los actuales sistemas de detección de objetos en tierra, mar y aire (radares terrestres y aéreos, sonar).
En todos esos casos las ondas se propagan siguiendo funciones trigonométricas.
Como ves están presentes en muchos fenómenos de nuestro entorno más próximo.
Y si te fijas bien encontrarás funciones sinusoidales en arquitectura e incluso en la naturaleza
Sigue leyendo...
37
Funciones trigonométricas en arquitectura
Hay materiales básicos que con forma sinusoidal se utilizan con frecuencia en la construcción. Unos son conocidos como las chapas sinusoidales o acanaladas (tejados de uralita) y otros lo son menos, como las vigas alveolares sinusoidales.
Te los mostramos:


Podrás encontrar más información visitando estas páginas webs:
http://insumasur.com/chapas/chapas-conformadas/chapas-sinusoidales
http://www.tectonica-online.com/productos/1742/sinusoidales_alveolos_acero_vigas_angelina/
38
Utilizando ondas y formas sinusoidales en la construcción se obtienen edificios muy singularses, de gran belleza e impacto visual como se puede apreciar en el siguiente video que hemos preparado:
Haz clic para ampliar el vídeo
Para tener más información sobre estos edificios (nombres, lugares en que se encuentran etc) ve a la página 52 de este libro
39
Funciones trigonométricas en la naturaleza
Algunos animales por su anatomía se mueven formando ondas dibujando así, auténticas funciones trigonométricas. A continuación puedes ver algunos ejemplos:
Las serpientes
 https://es.wikipedia.org/wiki/Pseudonaja_textilis
https://es.wikipedia.org/wiki/Pseudonaja_textilis
|
 http://www.fondosanimales.com/fondos-de-pantalla-de-serpientes
http://www.fondosanimales.com/fondos-de-pantalla-de-serpientes
|
40
La anguila de cinta es un tipo de anguila morena. Todos nacen como machos, pero conforme van madurando desarrollan órganos femeninos.

Observa su movimiento en el siguiente video:
:41
Funciones trigonométricas en Física
La aparición de funciones trigonométricas en Física es muy frecuente. Muchos fenómenos son periódicos y pueden representarse con una funcion trigonométrica. Este vídeo te va a explicar de forma amena algunas de esas situaciones:
42
La pregunta que cabe plantearse ahora es si todos esos fenómenos producen ondas iguales y la respuesta es no.
En el cuadro que te facilitamos a continuación podrás observar que cada fenómeno tiene una longitud de onda, frecuencia y energía
propias lo que te permite compararlos
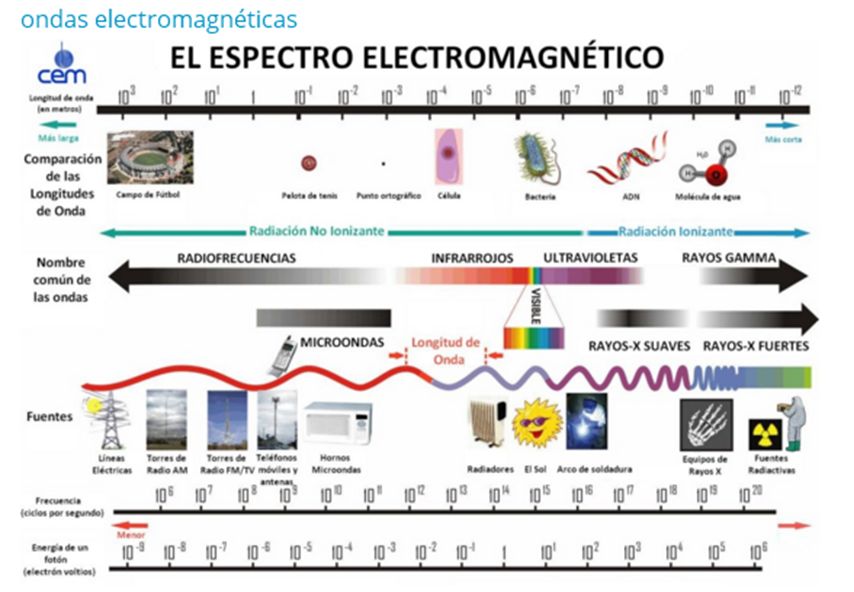
Fuente: www.electromagneticos.es
43
Visualizando el sonido
Daniel Palacios es el artista creador de la instalación Waves: ¿Cómo se mueve el sonido?
Un largo trozo de cuerda genera ondas tridimensionales flotando en el espacio por la propia física de
su movimiento: la cuerda que crea las ondas visuales, crea simultáneamente el sonido al cortar el aire,
conformando un único elemento.

¿Cómo funciona?
La cuerda se mantiene en constante movimiento mediante la rotación de los puntos de anclaje de esta.
En función de la presencia de público, las frecuencias de giro en cada extremo son variadas, lo cual
provoca unas visibles y audibles, alteraciones en la onda.
Cuando no se detecta presencia alguna, la instalación entra en modo ‘reposo’, desconectando los motores
que generan las ondas en la cuerda y creándose por tanto una línea entre ambos módulos.
44
La vibración producida en la cuerda es amplificada al cortar esta con el aire a gran velocidad,
dando como resultado la ambientación sonora en función de la actividad de la pieza (los movimientos del
público).Cuanto más inmóviles estemos frente a la pieza más armónicas serán las ondas y los sonidos;
generando unos gráficos más irregulares, a la vez que sonidos más fuertes y abruptos, cuanto más
se mueva el público.
Te lo mostramos en el siguiente vídeo
Más información en la página web http://danielpalacios.info/es/waves
45
La música de las funciones trigonométricas
Oscillate es una animación de Daniel Sierra, un viaje audiovisual a través de las propiedades emergentes de superposición de ondas sinusoidales:
El autor presenta su trabajo de esta manera:1
The concept of universal building blocks that can be assembled to form complex structures is something I find very exciting and alluring. Sound follows this concept in that any sound, for example a snare drum or a human voice, can be deconstructed as the summation of varying sine waves; hence making sine waves the building blocks of sound so to speak. This concept, which comes from the Fourier Series (named after Joseph Fourier) was the inspiration for my thesis, “Oscillate”.
46
parte IV
Material complementario
Página del profesor
El objetivo de este libro electrónico es estudiar las funciones trigonométricas, sus inversas y tomar conciencia de la cantidad de fenómenos que se pueden matematizar con ellas. Como conceptos previos el alumno debe conocer las razones trigonométricas, la circunferencia goniométrica y los conceptos de función, función inversa, dominio y recorrido.
Medida de ángulos.Iniciamos el libro con un repaso del concepto de radián. Se propone una escena para recordar cómo pasar un ángulo en forma sexagesimal a radianes y viceversa. El alumno debe saber que, al trabajar con funciones trigonométricas, la unidad de medida de ángulos utilizada es el radián.
Funciones trigonométricas básicas. Comenzamos con la función y = sen x que dibujamos a partir de una tabla en [0,2π].
Los alumnos están más familiaridos con la forma sexagesimal por ello se ha añadido a la tabla otra columna con los ángulos en esa forma. Eso facilita
su trabajo cuando deben colocar los puntos en los ejes. En el resto de los casos mantenemos el criterio.
Generalizamos a cualquier ángulo,obtenemos la gráfica la función y = sen x en todo R y visualizamos periodo y simetría.
Análogamente estudiaremos por separado las funciones y = cos x e y = tg x.
Funciones inversas de las trigonométricas. Partiendo de una tabla invertida de la función y = sen x con ángulos de la 1ª vuelta se llega a la función y = arc sen x.
Debemos insistir en que es necesario acotar el recorrido para cumplir la definición de función.
Procediendo de forma análoga se llega a las funciones y = arc cos x y = arc tg x.
50
Propiedades de las funciones trigonométricas básicas. El alumno debe indicar dominio, puntos destacados (cortes con ejes, máximos y minimos relativos, puntos de inflexión) monotonía y curvatura de cada una de las funciones trigonométricas básicas en el intervalo [0,2π]. Así descubre ciertas características que son inherentes a cada una ellas. En las soluciones facilitadas no se han considerado como máximos ni mínimos relativos los extremos del intervalo.
Transformaciones de las funciones trigonométricas. Una vez conocidas las funciones básicas se pasa a estudiarlas de forma general: y = Asen(Bx+C)+D.
Inicialmente se propone al alumnos que haga de uno en uno los cambios de parámetro para visualizar el efecto producido de forma independiente.
En una fase posterior se hacen todos simultáneamente.
Finalmente, el alumno, debe aplicar lo aprendido, dando la ecuación de las gráficas que aparecen en pantalla.
Las funciones trigonométricas a nuestro alrededor. En las siguientes páginas se muestra la abundancia de fenómenos que se pueden parametrizar con funciones trigonométricas en campos tan diversos como la arquitectura, la biología y la física.
El cuaderno de trabajo del alumno. Es un libro de actividades de 17 páginas. Sigue la estructura del libro para que el alumno registre los ejercicios que va realizando. Puede descargarse y modificarse para adecuarlo a las características de cada grupo.
51
Cuaderno de trabajo del alumno
En esta página se facilita un cuaderno de trabajo para el alumno.
Puedes visualizarlo a continuación.
Haz clic para ampliar el cuaderno
52
El cuaderno de trabajo del alumno tiene 17 páginas, viene en dos versiones (Word y pdf) y es imprimible.
La primera permite a cada profesor hacer las modificaciones que estime oportunas para adecuarlas al ritmo y circunstancias de su clase.
Para descargar el cuaderno de trabajo


53
Anexo
A continuación se facilitan los nombres, ciudades o lugares donde se encuentran los edificios del vídeo de la página del libro y las páginas webs donde puede obtenerse más información:
Edificio de estructura sinusoidal del Centro de investigación Neurospin en Saclay (sur de París)
http://www.constructalia.com/espanol/galeria_de_proyectos/francia/
Centro Paul Klee
http://tecnne.com/arquitectura/refrendar-la-topografia/
Ysios es una bodega diseñada por Santiago Calatrava, convertida en parte del paisaje de Laguardia (Álava), a los pies de la Sierra de Cantabria.
http://terroaristas.com/2012/10/20/ysios-y-santiago-calatrava/
Alcoa Corporate Center de Pittsburg
http://www.worldarchitecturemap.org/buildings/alcoa-corporate-center
https://cl.pinterest.com/pin/515310382343267529/
54
La sede de la Jefatura de Gobierno en Buenos Aires (Argentina). Diseñada por el despacho del arquitecto británico Norman Foster.
http://proyectodigital.com/buenos-aires-estrena-sede-del-gobierno-de-la-ciudad-de-fosterpartners
Sobre el Parque "Güell" de Barcelona
http://traveltu.ru/evropa/ispaniya/park-guelya-v-barselone.html
http://lasombradegaudi.blogspot.com.es/2012/10/un-paseo-diferente-por-el-park-guell.html
https://audiovista.wordpress.com/2010/07/06/el-parque-guell/
55
